第六章 自相关 答案
计量经济学课后答案第六章 自相关

第六章课后答案6.1(1)收入—消费模型为Se = (2.5043) (0.0075)t = (-3.7650) (125.3411)R2 = 0.9978,F = 15710.39,d f = 34,DW = 0.5234(2)对样本量为36、一个解释变量的模型、5%显著水平,查DW统计表可知,d L=1.411,d U= 1.525,模型中DW<d L,显然消费模型中有自相关。
(3)采用广义差分法查5%显著水平的DW统计表可知d L = 1.402,d U = 1.519,模型中DW= 2.0972>d U,说明广义差分模型中已无自相关。
同时,判定系数R2、t、F统计量均达到理想水平。
由差分方程式可以得出:所以最终的消费模型为:6.2(1)给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
给定n=16, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中不存在自相关。
(2)自相关可能由于模型6.1的误设,因为它排除了趋势的平方项。
(3)虚假自相关是由于模型的误设造成的,因此就要求对可能的函数形式有先验知识。
真正的自相关是可以通过广义差分法等方法来修正。
6.3(1)收入—消费模型为(2)DW=0.575,取,查DW上下界,说明误差项存在正自相关。
(3)采用广义差分法使用普通最小二乘法估计的估计值,得DW=1.830,已知,模型中因此,在广义差分模型中已无自相关。
由差分方程式可以得出:因此,修正后的回归模型应为6.4(1)回归结果如下:(2)模型检验:从回归结果可以看出,参数均显著,模型拟和较好。
异方差的检验:通过white检验可以得知模型不存在异方差。
DW检验:给定n=25, ,在的显著水平下,查DW统计表可知,。
模型中,所以可以判断模型中存在正自相关。
(3)采用广义差分法修正模型中存在的自相关问题:给定n=24,,在的显著水平下,查DW统计表可知,。
计量经济学 第六章 自相关

计量经济学
第六章
自相关
6
一阶自相关系数
自相关系数 的定义与普通相关系的公式形式相同
n
utut-1
t=2
n
n
ut2
u2 t 1
t2
t2
的取值范围为 -1 1
(6.1)
式(6.1)中 ut-1是 ut 滞后一期的随机误差项。 因此,将式(6.1)计算的自相关系数 称为一阶 自相关系数。
模型中
ut
是
-1
ut
滞后一期的值,因此称为一阶。
此式中的 也称为一阶自相关系数。
18
如果式中的随机误差项 vt 不是经典误差项,即
其中包含有 ut 的成份,如包含有 ut2 则需将 vt
显含在回归模型中,其为
ut = 1ut-1 + 2ut-2 + vt
其中,1 为一阶自相关系数,2为二阶自相关系
另外回归模型中的解释变量在不同时期通常是
正相关的,对于
Xt和
X
t
来说
j
Xt Xt+j 是大于0的。
33
因此,普通最小二乘法的方差 Var(ˆ2) = 2 Σxt2
通常会低估 ˆ2 的真实方差。当 较大和 Xt 有
较强的正自相关时,普通最小二乘估计量的方 差会有很大偏差,这会夸大估计量的估计精度, 即得到较小的标准误。 因此在有自相关时,普通最小二乘估计 ˆ2 的标 准误就不可靠了。
许多农产品的供给呈现为 蛛网现象,供给对价格的 反应要滞后一段时间,因 为供给需要经过一定的时
间才能实现。如果时期 t
的价格 Pt 低于上一期的 价格 Pt-1 ,农民就会减少 时期 t 1 的生产量。如
第六章 自相关 思考题

第六章 自相关 思考题6.1 如何使用 DW 统计量来进行自相关检验 ? 该检验方法的前提条件和局限性有哪些 ?6.2 当回归模型中的随机误差项为 AR(1) 自相关时 , 为什么仍用OLS 法会低估的ˆjβ标准误差 ? 6.3 判断以下陈述的真伪,并给出合理的解释。
1) 当回归模型随机误差项有自相关时 , 普通最小二乘估计量是有偏误的和非有效的。
2)DW 检验假定随机误差项i u 的方差是同方差。
3) 用一阶差分法消除自相关是假定自相关系数ρ为-1。
4)当回归模型随机误差项有自相关时 , 普通最小二乘估计的预测值的方差和标准误差不再是有效的。
6.4 对于四个解释变量的回归模型011223344t t t t t t Y X X X X u βββββ=+++++如果样本量 n=50, 当 DW 统计量为以下数值时 , 请判断模型中的自相关状况。
1)DW=1.05 2)DW=1.40 3)DW=2.50 4)DW=3.97 6.5 如何判别回归模型中的虚假自相关 ? 6.6 在回归模型12t t t Y X u ββ=++中 ,t u 无自相关。
如果我们错误地判定模型中有一阶自相关 , 即1t t t u u v ρ-=+, 并使用了广义差分模型1121(1)()t t t t t Y Y X X v βρβρ---=-+-+ 将会产生什么问题 ? 练习题 6.1 表 6.6 给出了美国 1960~1995 年 36 年个人实际可支配收入 X 和个人实际消费支出Y 的数据。
1) 用普通最小二乘法估计收入-消费模型 ;12t t t Y X u ββ=++表 6.6 美国个人实际可支配收入和个人实际消费支出 ( 单位 :1010 美元 )资料来源:Economic Report of the Prsident 注 : 数据为 1992 年价格2) 检验收入 -消费模型的自相关状况 (5% 显著水平 ): 3) 用适当的方法消除模型中存在的问题。
六章自相关

Econometrics 2005
18
6.3 自相关的检验
6.3.1 图解法
时间序列图(Time Sequence plot):将残差对时间描点。 如图(a)所示,扰动项的估计值呈循环形,并不频繁 地改变符号,而是相继若干个正的以后跟着几个负的。 表明存在正自相关。
t
t
Econometrics 2005
小于临界值,表示存在序列相关。
Econometrics 2005
28
6.4 自相关的补救1: ( 已知)广义差分法
以双变量回归模型和AR(1)为例。
Yutt
1 2 X t ut1 t
ut
Yt 1 2 X t ut
(1)
Yt1 1 2 X t1 ut1
( 2)
(1) (2) :
Yt Yt1 b0 (1 ) b1( X t X t1) t
差分形式
Yt b0 (1 ) Yt1 b1X t b1X t1 t
a0 b0 (1 )
a1 b1
Yt a0 Yt1 a1 X t a2 X t1 t
a2 b1
往也是正的。于是在不同的样本点之间,随机误差项出现了相关
性,这就产生了序列相关性。
Econometrics 2005
16
再如,以绝对收入假设为理论假设、以时间序列数据
作样本建立居民总消费函数模型:
Ct 0 1 I t t
t=1,2,…,n
消费习惯没有包括在解释变量中,其对消费量的影响被
包含在随机误差项中。如果该项影响构成随机误差项的
类似一阶自相关的定义, 若rs Cov(ut ,uts ) 0, s 2 则称为是高阶自相关。
Econometrics 2005
《计量经济学》第六章精选题及答案

第六章自相关二、问答题1、那些原因可以造成自相关;2、存在自相关时,参数的OLS估计具有哪些性质;3、如何检验是否存在自相关;4、当存在自相关时,如何利用广义差分法进行参数估计;5、当存在自相关时,如何利用广义最小平方估计法进行参数估计;6、异方差与自相关有什么异同;三、计算题1、证明:当样本个数较大时,)d。
≈-1(2ρα2、通过D-W检验,判断下列模型中是否存在自相关,显著性水平%5=(1)样本大小:20;解释变量个数(包括常数项):2;d=0.73;(2)样本大小:35;解释变量个数(包括常数项):3;d=3.56;(3)样本大小:50;解释变量个数(包括常数项):3;d=1.87;(4)样本大小:80;解释变量个数(包括常数项):6;d=1.62;(5)样本大小:100;解释变量个数(包括常数项):5;d=2.41;3、假定存在下表所示的时间序列数据:请回答下列问题:(1)利用表中数据估计模型:t t t x y εββ++=10;(2)利用D-W 检验是否存在自相关?如果存在请用d 值计算估计自相关系数ρ;(3)利用广义差分法重新估计模型:'''1011(1)()t t tt t y y x x ρβρβρε---=-+-+。
第三部分 参考答案二、问答题1、那些原因可以造成自相关?答:造成自相关的原因大致包括以下六个方面:(1)经济变量的变化具有一定的倾向性。
在实际的经济现象中,许多经济变量的现值依赖于他的前期值。
也就是说,许多经济时间序列都有一个明显的相依性特点,这种现象称作经济变量所具有的惯性。
(2)缺乏应有变量的设定偏差。
(3)不正确的函数形式的设定错误。
(4)蛛网现象和滞后效应。
(5)随机误差项的特征。
(6)数据拟合方法造成的影响。
2、存在自相关时,参数的OLS 估计具有哪些性质?答:当存在自相关,即I D ≠ΩΩ=,)(2σε时,OLS 估计的性质有:(1)βˆ是观察值Y 和X 的线性函数;(2)βˆ是β的无偏估计;(3)βˆ的协方差矩阵为112)()()ˆ(--'Ω''=X X X X X X D σβ;(4)βˆ不是β的最小方差线性无偏估计;(5)如果nX X n Ω'∞→lim存在,那么βˆ是β的一致估计;(6)2σ 不是2σ的无偏估计;(7)2σ不是2σ的一致估计。
计量经济学练习题答案(第六章)
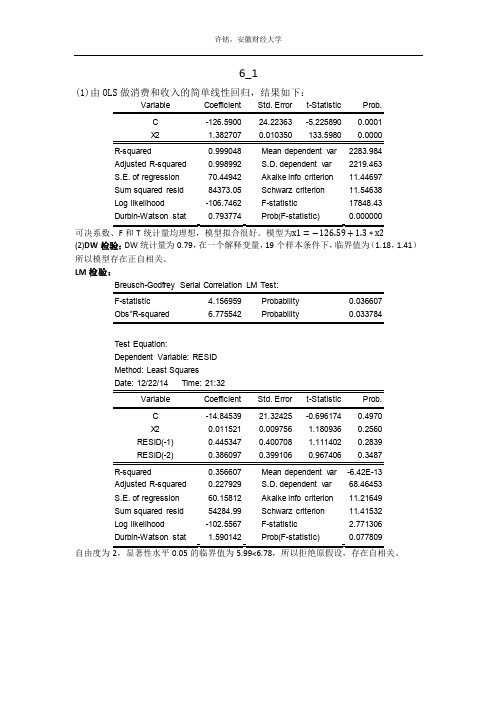
6_1(1)由OLS做消费和收入的简单线性回归,结果如下:Variable Coefficient Std. Error t-Statistic Prob.C -126.5900 24.22363 -5.225890 0.0001R-squared 0.999048 Mean dependent var 2283.984Adjusted R-squared 0.998992 S.D. dependent var 2219.463S.E. of regression 70.44942 Akaike info criterion 11.44697Sum squared resid 84373.05 Schwarz criterion 11.54638Log likelihood -106.7462 F-statistic 17848.43Durbin-Watson stat 0.793774 Prob(F-statistic) 0.000000可决系数、F和T统计量均理想,模型拟合很好。
模型为x1=−126.59+1.3∗x2(2)DW检验:DW统计量为0.79,在一个解释变量,19个样本条件下,临界值为(1.18,1.41)所以模型存在正自相关。
LM检验:F-statistic 4.156959 Probability 0.036607Test Equation:Dependent Variable: RESIDMethod: Least SquaresDate: 12/22/14 Time: 21:32C -14.84539 21.32425 -0.696174 0.4970X2 0.011521 0.009756 1.180936 0.2560RESID(-1) 0.445347 0.400708 1.111402 0.2839RESID(-2) 0.386097 0.399106 0.967406 0.3487R-squared 0.356607 Mean dependent var -6.42E-13Adjusted R-squared 0.227929 S.D. dependent var 68.46453S.E. of regression 60.15812 Akaike info criterion 11.21649Sum squared resid 54284.99 Schwarz criterion 11.41532Log likelihood -102.5567 F-statistic 2.771306Durbin-Watson stat 1.590142 Prob(F-statistic) 0.077809自由度为自相关分析:解释变量和被解释变量有显著二阶自相关。
北理随机信号分析第六章作业及答案

1、某雷达接收机系统如下图所示:
X(t) 线性窄带系统 Y(t) 线性包络检波器 Z(t)
X(t) 为白噪声,现测得 Z(t) 的均值为 m ,求:① Z(t) 的一维概率密度;② Z(t) 的平均功率。 2、对于零均值、方差为 σ2 的窄带平稳高斯过程:
2 K X (τ) = σX exp{−βτ2 } , β ≥ 0 ,将其通过下图所示系统,则
(1) (2)
试求输出 Y(t) 的均值、方差和自相关函数 试求输出 Y(t) 的一维概率密度函数 f Y (y ; t)
X(t)
d(i) / dt
X(t)( i) 2 NhomakorabeaY(t) = X2 (t)
Z(t) = B(t) cos[ω0 t + Φ (t)] = X(t) cos ω0 t − Y(t)sin ω0 t
证明:包络任意时刻状态 B+ 满足:
E{B+ } =
π π⎞ ⎛ σ , D{B+ } = ⎜ 2 − ⎟ σ2 2 2⎠ ⎝
3、现已知某均方可微高斯平稳随机过程 X(t) ,其均值为 α ,并且 α ≠ 0 ;其协方差函数为
计量经济学第六章课后作业.doc
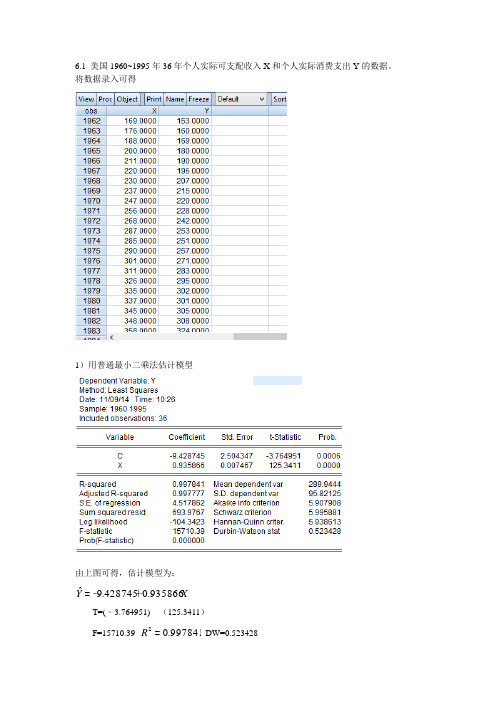
6.1 美国1960~1995年36年个人实际可支配收入X 和个人实际消费支出Y 的数据。
将数据录入可得1)用普通最小二乘法估计模型由上图可得,估计模型为:X Y 935866.0428745.9ˆ+﹣=T=(﹣3.764951) (125.3411)F=15710.39 997841.02=R DW=0.5234282)检验自相关问题-------DW 检验根据DW=0.523428<411.1=L d ,可知此回归模型中误差项1μ,2μ......n μ间存在正相关关系。
3)用适当的方法消除模型中的问题----------广义差分法 首先得到t e 和1-t e 的回归结果。
如下图所示:由上图回归结果可知,回归方程为1721594.0ˆ﹣t t e e =故721594.0ρˆ=,对原模型进行广义差分,得到广义差分方差为 t t t t t X X Y Y υβ721594.01β1211)+-()+-(---= 对广义差分方程进行回归,。
可得以下回归结果:可得回归方程为:••=t t X Y 948215.0858791.3ˆ+﹣Se= (1.868548) (0.018453)t= (﹣2.065129) (51.38528)987656.02=R F=2640.445 DW=2.082177通过查表可知DW=1.255999>1.195,故可以判断不存在自相关关系。
画出t e 和1-t e 的散点图由图形可知,随机误差项之间不存在相关性。
6.3北京市连续19年城镇居民家庭人均收入与人均支出的数据1)为了消除价格变动因素对城镇居民人均收入和人均支出的影响,不宜直接采用现价的人均纯收入和现价的人均消费支出的数据,而需要采用经消费价格指数进行调整后的基期的可比价格计的人均纯收入和人居消费支出的数据作回归分析。
根据表中的数据,使用普通最小二乘法估计消费模型得:根据上图分析结果可知:21690488.093004.79ˆX X += Se= (12.39919) (0.012877) t= (6.446390) (53.62068)994122.02=R 178.2875=F 574663.0=DW该方程的可决系数较高,回归系数显著,对于样本容量为19、一个解释变量的模型、1%的显著性水平,查DW 统计表可得,928.0=L d ,132.1=U d ,模型中DW<928.0=L d ,显然模型中存在自相关。
统计学第六章课后题及答案解析

第六章一、单项选择题1.下面的函数关系是( )A现代化水平与劳动生产率 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D亩产量与施肥量2.相关系数r的取值范围( )A -∞< r <+∞B -1≤r≤+1C -1< r < +1D 0≤r≤+13.年劳动生产率x(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度高,则计算出的相关系数应接近于( )A +1B -1C 0.5D 15.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( )A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建立线性回归方程ŷ=a+bx。
经计算,方程为ŷ=200—0.8x,该方程参数的计算( )A a值是明显不对的B b值是明显不对的C a值和b值都是不对的D a值和b值都是正确的7.在线性相关的条件下,自变量的均方差为2,因变量均方差为5,而相关系数为0.8时,则其回归系数为:( )A 8B 0.32C 2D 12.58.进行相关分析,要求相关的两个变量( )A都是随机的 B都不是随机的C一个是随机的,一个不是随机的 D随机或不随机都可以9.下列关系中,属于正相关关系的有( )A合理限度内,施肥量和平均单产量之间的关系B产品产量与单位产品成本之间的关系C商品的流通费用与销售利润之间的关系D流通费用率与商品销售量之间的关系10.相关分析是研究( )A变量之间的数量关系 B变量之间的变动关系C变量之间的相互关系的密切程度 D变量之间的因果关系11.在回归直线y c=a+bx,b<0,则x与y之间的相关系数 ( )A r=0B r=lC 0< r<1D -1<r <012.当相关系数r=0时,表明( )A现象之间完全无关 B相关程度较小C现象之间完全相关 D无直线相关关系13.下列现象的相关密切程度最高的是( )A某商店的职工人数与商品销售额之间的相关系数0.87B流通费用水平与利润率之间的相关系数为-0.94C商品销售额与利润率之间的相关系数为0.51D商品销售额与流通费用水平的相关系数为-0.8114.估计标准误差是反映( )A平均数代表性的指标 B相关关系的指标C回归直线方程的代表性指标 D序时平均数代表性指标二、多项选择题1.下列哪些现象之间的关系为相关关系( )A家庭收入与消费支出关系 B圆的面积与它的半径关系C广告支出与商品销售额关系D商品价格一定,商品销售与额商品销售量关系2.相关系数表明两个变量之间的( )A因果关系 C变异程度 D相关方向 E相关的密切程度3.对于一元线性回归分析来说( )A两变量之间必须明确哪个是自变量,哪个是因变量B回归方程是据以利用自变量的给定值来估计和预测因变量的平均可能值C可能存在着y依x和x依y的两个回归方程D回归系数只有正号4.可用来判断现象线性相关方向的指标有( )A相关系数 B回归系数 C回归方程参数a D估计标准误5.单位成本(元)依产量(千件)变化的回归方程为y c=78- 2x,这表示( ) A产量为1000件时,单位成本76元B产量为1000件时,单位成本78元C产量每增加1000件时,单位成本下降2元D产量每增加1000件时,单位成本下降78元6.估计标准误的作用是表明( )A样本的变异程度 B回归方程的代表性C估计值与实际值的平均误差 D样本指标的代表性7.销售额与流通费用率,在一定条件下,存在相关关系,这种相关关系属于( ) A完全相关 B单相关 C负相关 D复相关8.在直线相关和回归分析中( )A据同一资料,相关系数只能计算一个B据同一资料,相关系数可以计算两个C据同一资料,回归方程只能配合一个D据同一资料,回归方程随自变量与因变量的确定不同,可能配合两个9.相关系数r的数值( )A可为正值 B可为负值 C可大于1 D可等于-110.从变量之间相互关系的表现形式看,相关关系可分为( )A正相关 B负相关 C直线相关 D曲线相关11.确定直线回归方程必须满足的条件是( )A现象间确实存在数量上的相互依存关系B相关系数r必须等于1C y与x必须同方向变化D现象间存在着较密切的直线相关关系12.当两个现象完全相关时,下列统计指标值可能为( )A r=1B r=0C r=-1D S y=013.在直线回归分析中,确定直线回归方程的两个变量必须是( )A一个自变量,一个因变量 B均为随机变量C对等关系 D一个是随机变量,一个是可控制变量14.配合直线回归方程是为了( )A确定两个变量之间的变动关系 B用因变量推算自变量C用自变量推算因变量 D两个变量都是随机的15.在直线回归方程中( )A在两个变量中须确定自变量和因变量 B一个回归方程只能作一种推算C要求自变量是给定的,而因变量是随机的。
概率论与数理统计第六章课后习题及参考答案

概率论与数理统计第六章课后习题及参考答案1.已知总体X ~),(2σμN ,其中2σ已知,而μ未知,设1X ,2X ,3X 是取自总体X 的样本.试问下面哪些是统计量?(1)321X X X ++;(2)μ31-X ;(3)222σ+X ;(4)21σμ++X ;(5)},,max{321X X X ;(6)σ221++X X ;(7)∑=3122i i X σ;(8)2μ-X .解:(1)(3)(4)(5)(6)(7)是,(2)(8)不是.2.求下列各组样本值的平均值和样本差.(1)18,20,19,22,20,21,19,19,20,21;(2)54,67,68,78,70,66,67,70.解:(1)9.19)21201919212022192018(101101101=+++++++++==∑=i i x x ;43.1)(9110122=-=∑=i i x x s .(2)5.67)7067667078686754(1018181=+++++++==∑=i i x x ;018.292)(718122=-=∑=i i x x s .3.(1)设总体X ~)1,0(N ,则2X ~)1(2χ.(2)设随机变量F ~),(21n n F ,则F1~),(12n n F .(3)设总体X ~),(2σμN ,则X ~),(2n N σμ,22)1(S n σ-~)1(2-n χ,nS X /μ-~)1(-n t .(4)设总体X ~)10(2χ,Y ~)15(2χ,且X 与Y 相互独立,则=+)(Y X E 25,=+)(Y X D 50.4.设随机变量X 与Y 都服从标准正态分布,则(C )A .Y X +服从正态分布B .22Y X +服从2χ分布C .2X 与2Y 均服从2χ分布D .22YX 服从F 分布5.在总体X ~)3.6,52(2N 中随机抽取一容量为36的样本,求样本平均值X 落在8.50到8.53之间的概率.解:因为X ~)3.6,52(2N ,即52=μ,223.6=σ,因为36=n ,22205.1363.6==n σ,所以X ~)05.1,52(2N .由此可得)8.538.50(≤≤X P 05.1528.50()05.1528.53(-Φ--Φ=8302.0)1429.1()7143.1(=-Φ-Φ=.6.设总体X ~)1,0(N ,1X ,2X ,…,10X 为总体的一个样本,求:(1))99.15(1012>∑=i i X P ;(2)写出1X ,2X ,…,10X 的联合概率密度函数;(3)写出X 的概率密度.解:(1)由题可知∑==1012i i X X ~)10(2χ,查2χ分布表有99.15)10(210.0=χ,可得10.0=α,即10.0)99.15(1012=>∑=i i X P .(2)1X ,2X ,…,10X 相互独立,则联合概率密度函数为}exp{321}21exp{21),,,(1012510121021∑∏==-=-=i i i i x x x x x f ππ .(3)X Y =~)1.0,0(N ,所以有2251.02)0(e 5e1.021)(y y y f -⋅--==ππ.7.设总体X ~)1,0(N ,1X ,2X ,…,5X 为总体的一个样本.确定常数c ,使25242321)(XX X X X c Y +++=~)3(t .解:因为i X ~)1,0(N ,5,,2,1 =i ,所以21X X +~)2,0(N ,)(2121X X +~)1,0(N ,252423X X X ++~)3(2χ,因为25242321252423212632XX X X X X X X X X +++=+++~)3(t ,所以有23=c .8.设1X ,2X ,3X ,4X 是来自正态总体)4,0(N 的样本.已知243221)43()2(X X b X X a Y -+-=为服从自由度为2的2χ分布,求a ,b 的值.解:由题可知i X ~)4,0(N ,4,3,2,1=i ,故有0)2(21=-X X E ,20)2(21=-X X D ,所以212X X -~)20,0(N .同理4343X X -~)100,0(N .而20)2(221X X -~)1(2χ,100)43(221X X -~)1(2χ,故有100)43(20)2(243221X X X X -+-~)2(2χ,比较可知201=a ,1001=b .9.设总体X ~)3.0,(2μN ,1X ,2X ,…,n X 为总体的一个样本,X 是样本均值,问样本容量n 至少应取多大,才能使95.0)1.0(≥<-μX P .解:易知X ~)3.0,(2nN μ,由题意有95.013(2/3.01.0/3.0()1.0(≥-Φ=<-=<-nnnX P X P μμ,即应有975.0)3(≥Φn,查正态分布表知975.0)96.1(=Φ,所以取96.13≥n,即5744.34≥n ,取35=n .10.设总体X ~)16,(μN ,1X ,2X ,…,10X 为总体的一个样本,2S 为样本方差,已知1.0)(2=>αS P ,求α的值.解:由抽样分布定理知22)1(σS n -~)1(2-n χ,因为10=n ,故有2249S ~)9(2χ,得1.0)169169()(22=>=>ααS P S P ,查2χ分布表得684.14)9(21.0=χ,即684.14169=α,解得105.26=α.11.设(1X ,2X ,…,1+n X )为来自总体X ~),(2σμN 的一个样本,记∑==n i i n X n X 11,∑=--=n i in X X n S 122(11,求证:nn n S X X n n T -⋅+=+11~)1(-n t .证:由题可知n X ~),(2nN σμ,n n X X -+1~)11(,0(2σn N +,标准化得σnX X nn 111+-+~)1,0(N .又因为∑=-=-ni inX XS n 1222)(1)1(σσ~)1(2-n χ,从而有nn nnn S XX n n n S n n X X -+=--+-++122111)1(11σσ~)1(-n t ,即nnn S X X n n T -⋅+=+11~)1(-n t .。
汽车理论第六章答案

−W
当W=2时
⎛n⎞ 1 u ⎜ ⎟ = Gq (n0 )n0 2 2 Gq ( f ) = Gq (n0 )⎜ ⎟ u f ⎝ n0 ⎠
2
2 Gq ( f ) = (2πf ) Gq ( f ) = 4π 2Gq (n0 )n0 u 速度功率谱密度 &
2 加速度功率谱密度 Gq& ( f ) = (2πf ) Gq ( f ) = 16π 4Gq (n0 )n0 uf 2 & 4
§6-3 汽车振动系统的简化,单 质量系统的振动
一、汽车振动系统的简化 1.四轮汽车简化的立体模型
汽车的悬挂质量为:m2(车身、车架等) 汽车的非悬挂质量:m1(车轮、车轴) 汽车共7个自由度:
车身垂直、俯仰、侧倾3个自由度 车轮4个垂直自由度
6-3 单质量系统的振动
一、汽车振动系统的简化
1.四轮汽车简化 的立体模型
⎡ W 2 ( f )G ( f )df ⎤ aw= ∫ a ⎢ 0 .5 ⎥ ⎣ ⎦
80
1 2
3)当同时考虑椅面xs、ys、zs,这三个轴向振动时
,三个轴向的总加权加速度均方根值按下式计算
av= (1.4a xw ) + (1.4a yw ) + a
2 2
[
2 zw
]
1 2
6-1 人体对振动的反应和平顺性的评价
1.基本的评价方法 用基本的评价方法来评价时,先计算各轴向加权 加速度均方根值。具体有两种计算方法: 1)对记录的加速度时间历程a(t),通过相应频率 加权函数w(f)的滤波网络得到加权加速度时间历程 aw(t),按下式计算加权加速度均方根值
⎡1 T 2 ⎤ aw= ⎢ ∫ aw (t )dt ⎥ ⎣T 0 ⎦
自相关试题及答案

自相关试题及答案一、选择题1. 自相关函数是描述什么特性的统计量?A. 随机变量的分布特性B. 随机过程的统计特性C. 随机变量的独立性D. 随机过程的独立性答案:B2. 自相关函数的计算公式是什么?A. R(τ) = E[X(t)X(t+τ)]B. R(τ) = E[X(t) - μ][X(t+τ) - μ]C. R(τ) = E[X(t)X(t-τ)]D. R(τ) = E[X(t) + μ][X(t+τ) + μ]答案:B3. 自相关函数的值在什么范围内?A. -∞ 到+∞B. 0 到+∞C. -1 到 1D. 0 到 1答案:B二、简答题1. 什么是自相关函数,它在信号处理中有什么应用?答:自相关函数是一种描述信号或随机过程在不同时间点上值之间相关程度的统计量。
在信号处理中,自相关函数用于分析信号的周期性,检测信号中的重复模式,以及估计信号的功率谱。
2. 请简述自相关函数和互相关函数的区别。
答:自相关函数是描述同一信号在不同时间点上的值之间的相关性,而互相关函数是描述两个不同信号在不同时间点上的值之间的相关性。
自相关函数通常用于分析单个信号的特性,而互相关函数用于分析两个信号之间的相似性或时延。
三、计算题1. 给定一个离散时间信号 x[n] = {1, 2, 3, 4, 3, 2},请计算其自相关函数 R(0) 和 R(1)。
解:根据自相关函数的定义R(τ) = E[x[n]x[n-τ]],计算得:R(0) = (1*1 + 2*2 + 3*3 + 4*4 + 3*3 + 2*2) / 6 = 40 / 6 =20/3R(1) = (1*2 + 2*3 + 3*4 + 4*3 + 3*2 + 2*1) / 6 = 38 / 6 ≈ 6.33332. 如果一个随机过程 X(t) 的自相关函数为R(τ) = e^(-|τ|),请说明该过程的性质。
解:该自相关函数表明,随着时间延迟τ 的增加,随机过程 X(t) 的值之间的相关性指数级衰减。
计量经济学题库第6章自相关

第6章 自相关习 题一、单项选择题 1.设为随机误差项,则一阶线性自相关是指( )2.已知样本回归模型残差的一阶自相关系数接近于1,则DW 统计量近似等于( )A. 0B. 1C. 2D. 43.在序列自相关的情况下,参数估计值仍是无偏的,其原因是( )A. 无多重共线性假定成立B. 同方差假定成立C. 零均值假定成立D. 解释变量与随机误差项不相关假定成立4.应用DW 检验方法时应满足该方法的假定条件,下列不是其假定条件的为( )A. 解释变量为非随机的B. 被解释变量为非随机的C. 线性回归模型中不能含有滞后内生变量D. 随机误差项服从一阶自回归 5.广义差分法是( )的一个特例A. 加权最小二乘法B. 广义最小二乘法C. 普通最小二乘法D. 两阶段最小二乘法6.在下列引起序列自相关的原因中,不正确的是( )A. 经济变量具有惯性作用B. 经济行为的滞后性C. 设定偏误D. 解释变量之间的共线性 7.已知模型的形式为,在用实际数据对模型的参数进行估计的时候,测得DW 统计量为0.6453,则广义差分变量是( )A . t u 1211221.cov(,)0()...t s t t t t t t tt t t A u u t s B u u C u u u D u u ρερρερε----≠≠=+=++=+011t t t Y X u ββ=++11110.6453,0.6453tt t t Y Y X X ----B .C .D .8.在修正序列自相关的方法中,能修正高阶自相关的方法是( )A. 利用DW 统计量值求出B. Cochrane-Orcutt 法C. Durbin 两步法D. 移动平均法9.在DW 检验中,当d 统计量为2时,表明( )A. 存在完全的正自相关B. 存在完全的负自相关C. 不存在自相关D. 不能判定 10.在给定的显著性水平之下,若DW 统计量的下和上临界值分别为dL 和du,则当dL<DW<du 时,可认为随机误差项( )A. 存在一阶正自相关B. 存在一阶负相关C. 不存在序列相关D. 存在序列相关与否不能断定 11. 在序列自相关的情况下,参数估计值的方差不能正确估计的原因是( )12.在DW 检验中,当d 统计量为0时,表明( )A.存在完全的正自相关B.存在完全的负自相关C.不存在自相关D.不能判定 13.在DW 检验中,存在正自相关的区域是( )A. 4-﹤﹤4B. 0﹤﹤C. ﹤﹤4-D. ﹤﹤,4-﹤﹤4-14.如果回归模型违背了无自相关假定,最小二乘估计量是( )A .无偏的,有效的 B. 有偏的,非有效的 C .无偏的,非有效的 D. 有偏的,有效的 15.广义差分法是对( )用最小二乘法估计其参数。
第06章 自相关(讲稿)

第6章自相关1. 自相关定义1)非自相关由第2节知回归模型的假定条件之一是,Cov(u i,u j )=E(u i u j) =0, (i, j∈T, i ≠ j),(1.1)即误差项u t的取值在时间上是相互无关的。
称误差项u t非自相关。
2)自相关如果Cov (u i ,u j ) ≠ 0, (i ≠ j)则称误差项u t存在自相关。
自相关又称序列相关。
原指一随机变量在时间上与其滞后项之间的相关。
这里主要是指回归模型中随机误差项u t 与其滞后项的相关关系。
自相关也是相关关系的一种。
2.自相关类型1)自相关按滞后阶数可分为两类。
(1)一阶自回归形式当误差项u t只与其滞后一期值有关时,即u t = f (u t - 1),称u t具有一阶自回归形式。
(2) 高阶自回归形式当误差项u t的本期值不仅与其前一期值有关,而且与其前若干期的值都有关系时,即u t = f (u t – 1, u t – 2 , … ), 则称u t 具有高阶自回归形式。
2)按函数形式分为线性自相关和非线性自相关 (1)线性自相关 f 为线性函数形式 (2)非线性自相关 f 为非线性函数形式 3.一阶线性自相关通常假定误差项的自相关是线性的。
因计量经济模型中自相关的最常见形式是一阶自回归形式,所以下面重点讨论误差项的线性一阶自回归形式,即 u t =1a u t -1 + v t (1.2)其中1a 是自回归系数,v t 是随机误差项。
v t 满足通常假设E(v t ) = 0, t = 1, 2 …, T, Var(v t ) = σv 2, t = 1, 2 …, T,Cov(v i , v j ) = 0, i ≠ j, i, j = 1, 2 …, T, Cov(u t-1, v t ) = 0, t = 1, 2 …, T,依据普通最小二乘法公式,模型(1.2)中 1 的估计公式是,1ˆa= ∑∑=-=-Tt t Tt t tuuu 22121 (1ˆβ=∑∑---2)())((x x x x y y t t t ) (1.3)其中T 是样本容量。
北方民族大学计量期末习题第六章 自相关

一、单项选择题1.在给定的显著性水平之下,若DW 统计量的下和上临界值分别为dL 和dU,则当L U d d d <<时,可认为随机误差项( )A.存在一阶正自相关B.存在一阶负相关C.不存在序列相关D.存在序列相关与否不能断定2.在序列自相关的情况下,参数估计值的方差不能正确估计的原因是( )A22() i E u σ≠ B ()0() i j E u u i j ≠≠ C ()0 i i E x u ≠ D ()0 i E u ≠ 3.在检验异方差的方法中,不正确的是( )A. Goldfeld-Quandt 方法B. X-Y 散点图检验法C. White 检验法D. DW 检验法4.在DW 检验中,当d 统计量为0时,表明( )A.存在完全的正自相关B.存在完全的负自相关C.不存在自相关D.不能判定5.在下列产生序列自相关的原因中,不正确的是( )A.经济变量的惯性作用B.经济行为的滞后作用C.设定偏误D.解释变量的共线性6.加权最小二乘法是( )的一个特例A.广义差分法B.普通最小二乘法C.广义最小二乘法D.两阶段最小二乘法8.设为随机误差项,则一阶线性自相关是指( )A cov(,)0()t s u u t s ≠≠B 1t t t u u ρε-=+C 1122t t t t u u u ρρε--=++ D21t t t u u ρε-=+ 9.在自相关情况下,常用的估计方法( )A .普通最小二乘法 B. 广义差分法 C .工具变量法 D. 加权最小二乘法10.在DW 检验中,不能判定的区域是( )A 0,44l l d d d d <<-<<B 4u u d d d <<-C ,44l u u l d d d d d d <<-<<-D 上述都不对11.用于检验序列相关的DW 统计量的取值范围是( )。
A.0≤DW ≤1B.-1≤DW ≤1C.-2≤DW ≤2D.0≤DW ≤412.已知DW 统计量的值接近于2,则样本回归模型残差的一阶自相关系数ρˆ近似等于( )。
(完整版)概率论第六章答案

习题6-11. 若总体(2,9)X N :, 从总体X 中抽出样本X 1, X 2, 问3X 1-2X 2服从什么分布?解 3X 1-2X 2~N(2, 117).2. 设X 1, X 2, …, X n 是取自参数为p 的两点分布的总体X 的样本, 问X 1, X 2, …, X n 的联合分布是什么?解 因为总体X 的分布律为P {X =k }= p k (1-p )1-k , k =0,1,…,所以样本X 1, X 2, …, X n 的联合分布为11221111111{,}(1)(1)(1)(1).n nnniii i x x x x x x n n X n X P X x X x p p p p p p p p ==----==⋅-⋅-⋅⋅-∑∑=⋅-…,=…习题6-21. 选择题(1) 下面关于统计量的说法不正确的是( ).(A) 统计量与总体同分布. (B) 统计量是随机变量. (C) 统计量是样本的函数. (D) 统计量不含未知参数.解 选(A).(2) 已知X 1,X 2,…,X n 是来自总体2(,)X N μσ:的样本, 则下列关系中正确的是( ).(A) ().E X n μ= (B) 2().D X σ=(C)22().E S σ= (D) 22().E B σ=解 选(C).(3) 设随机变量X 与Y 都服从标准正态分布, 则( ).(A) X +Y 服从正态分布.(B) X 2+Y 2服从2χ分布.(C)X 2和Y 2都服从2χ分布. (D)22X Y服从F 分布.解因为随机变量X 与Y 都服从标准正态分布, 但X 与Y 不一定相互独立,所以(A),(B),(D)都不对, 故选(C).2. 设X 1,X 2,…,X n 是来自总体X 的样本, 总体X 的均值μ已知,方差σ2未知. 在样本函数1nii X=∑,1nii Xμσ=-∑,1nii XSμ=-∑, n μ(21X +22X +…+2n X )中, 哪些不是统计量?解1nii Xμσ=-∑不是统计量.3. 设总体X 服从正态分布21(,)N μσ, 总体Y 服从正态分布22(,)N μσ,112,,,n X X X L 和 212,,,n Y Y Y L 分别是来自总体X 和Y 的简单随机样本, 求12221112()()2.n n i j i j X X Y Y E n n ==-+-+-⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦∑∑解 因为 122111[()]1ni i E X X n σ=-=-∑, 222121[()]1n j j E Y Y n σ=-=-∑ 习题6-31.填空题 (1) 设总体~(2,25)XN ,12100,,,X X X L 是从该总体中抽取的容量为n 的样本, 则()E X = ; ()D X = ; 统计量~X .解 因为总体~(2,25)X N , 而12100,,,X X X L 是从该总体中抽出的简单随机样本, 由正态分布的性质知, 样本均值也服从正态分布, 又因为1001111(()22100)nii i E E X nX =====∑∑,而1002111125(()251001)1004ni i i D D X nX ======∑∑. 所以1~(2,)4N X .(2) 设总体X 服从正态分布2(,)N μσ,12,,,n X X X L 是来自X 的简单随机样本, 则统计量服从 分布;服从 分布;222=12(1)()nii n SXX σσ--=∑服从 分布;212()nii Xμσ=-∑服从 分布.解 由抽样分布定理知,2~(,)X N nσμ. 再由正态分布的标准化公式,服从标准正态分布.由抽样分布定理知,服从自由度为n -1的t 分布.由抽样分布定理知,22(1)n S σ-服从自由度为n -1的2χ分布.由题设, 2~(,),1,2,,i X N i μσ=L 所以~(0,1),1,2,.i X N i μσ-=L再由2χ分布的定义知, 212()nii Xμσ=-∑服从自由度为n 的2χ分布.(3) 设12,,,n X X X L,1,,n n m X X ++L 是来自正态总体2(0,)N σ的容量为n +m 的样本, 则统计量2121ni i n mi i n m X n X =+=+∑∑服从的分布是 .解 因为2121nii n mii n m Xn X=+=+∑∑=2121nii n mii n XnXm=+=+∑∑, 而2212~()nii Xn χσ=∑,2212~()n mii n Xm χσ+=+∑.由F 分布的定义, 得到2121~(,)ni i n mi i n m X F n m n X =+=+∑∑.2. 选择题(1) 设随机变量21~()(1),X t n n Y X >=, 则下列关系中正确的是( ).(A) 2~()Y n χ. (B) 2~(1)Y n χ-. (C) ~(,1)Y F n . (D) ~(1,)Y F n解 由题设知,X =, 其中2~(0,1),~()U N V n χ, 于是21Y X ==221UV V n n U =,这里22~(1)Uχ, 根据F 分布的定义知21~(,1).Y F n X=故应选(C).(2) 设z α,2αχ(n ),()t n α,12(,)F n n α分别是标准正态分布N (0,1)、2χ(n )分布、t 分布和F 分布的上α分位点, 在下列结论中错误的是( ).(A)1z z αα-=-. (B) 2αχ(n )=1-21αχ-(n ).(C) 1()()t n t n αα-=-. (D) 121211(,)(,)F n n F n n αα-=.解 应选(B).3. 在总体2(52,6.3)N 中随机抽取一个容量为36的样本, 求样本均值X落在50.8到53.8 之间的概率.解 因为2~(,)X N n σμ,所以26.3~(52,)36X N .于是, 标准化随机变量52~(0,1)6.3X N -.因此(50.852)6(52)6(53.852)6{50.853.8}{}6.3 6.36.3X P X P -⨯-⨯-⨯=≤≤剟10.87.2()()0.82936.36.3ΦΦ-=-=.4. 已知1210,,,X X X L 是来自正态总体2(0,)X N σ:的样本, 求概率{<2.82}P X S .解 由定理1知,2229(0,1),(9),XS N χσσ::因此(9)XXt S=:, 所以 { 2.82}{2.82}1{ 2.82}10.010.99.X XP XS P P S S<=<=->=-=。
自相关性习题集与答案解析

自相关性一、名词解释1 序列相关性2 虚假序列相关3 差分法4 广义差分法5 自回归模型6 广义最小二乘法7 DW 检验 8 科克伦-奥克特跌代法 9 Durbin 两步法10 相关系数二、单项选择题1、如果模型y t =b 0+b 1x t +u t 存在序列相关,则()(x t , u t )=0 (u t , u s )=0(t ≠s) C. cov(x t , u t )≠0 D. cov(u t , u s ) ≠0(t ≠s)2、DW 检验的零假设是(ρ为随机误差项的一阶相关系数)A 、DW =0B 、ρ=0C 、DW =1D 、ρ=13、下列哪个序列相关可用DW 检验(v t 为具有零均值,常数方差且不存在序列相关的随机变量)A .u t =ρu t -1+v tB .u t =ρu t -1+ρ2u t -2+…+v tC .u t =ρv tD .u t =ρv t +ρ2 v t-1 +…4、DW 的取值范围是()A 、-1≤DW ≤0B 、-1≤DW ≤1C 、-2≤DW ≤2D 、0≤DW ≤45、当DW =4时,说明()A 、不存在序列相关B 、不能判断是否存在一阶自相关C 、存在完全的正的一阶自相关D 、存在完全的负的一阶自相关6、根据20个观测值估计的结果,一元线性回归模型的DW =。
在样本容量n=20,解释变量k=1,显著性水平为时,查得dl=1,du=,则可以决断()A 、不存在一阶自相关B 、存在正的一阶自相关C 、存在负的一阶自D 、无法确定7、当模型存在序列相关现象时,适宜的参数估计方法是()A 、加权最小二乘法B 、间接最小二乘法C 、广义差分法D 、工具变量法8、对于原模型y t =b 0+b 1x t +u t ,广义差分模型是指()0t 1t t t 01t t t t-101t t-1t t-1b B. y =b x uC. y =b +b x uD. y y =b (1-)+b (x x )(u u )ρρρρ++++--+- 9、采用一阶差分模型一阶线性自相关问题适用于下列哪种情况()A 、ρ≈0B 、ρ≈1C 、-1<ρ<0D 、0<ρ<110、假定某企业的生产决策是由模型S t =b 0+b 1P t +u t 描述的(其中S t 为产量,P t 为价格),又知:如果该企业在t-1期生产过剩,经营人员会削减t 期的产量。
计量经济学第六章部分课后题(庞皓(第三版))

计量经济学第六章作业思考题:6.1 如何使用DW统计量来进行自相关检验?该检验方法的前提条件和局限性有哪些?答:(1)DW 检验是J.Durbin(杜宾)和G.S.Watson(沃特森)于1951年提出的一种适用于样本容量大于等于15的检验自相关的方法,许多计量经济学和统计学计算机软件都可以计算出DW 值。
给定显著水平α,依据样本容量n和解释变量个数k’(不包括常数项),查D.W.分布表可得临界值(d统计量的上界d U和下界d L),当0<DW<d L时,表明存在一阶正自相关,而且正自相关的程度随DW向0的靠近而增强。
当d L<DW<d U时,表明为不能确定是否存在自相关。
当d U<DW<4-d U时,表明不存在一阶自相关。
当4-d U<DW<4-d L时,表明不能确定是否存在自相关。
当4-d L<DW<4时,表明存在一阶负自相关,而且负自相关的程度随DW向4的靠近而增强。
(2)DW检验的前提条件:<1>解释变量是非随机的(因此与随机扰动项不相关);<2>随机扰动项是一阶自回归形式,即u t=ρu t-1 +v t (v t满足古典假定);<3>线性模型的解释变量中不包含滞后的被解释变量,如不应出现下列形式:Y t =β1 +β2 X t +β 3 Y t-1 +u t;<4>截距项不为零,即只适用于有常数项的回归模型;<5>数据序列无缺失项,样本比较大。
(3)DW检验的局限性:<1>DW检验有两个不能确定的区域,一旦DW值落在这两个区域,就无法判断。
这时,只有增大样本容量或选取其他方法;<2>DW统计量的上、下界表要求n≥15, 这是因为样本如果再小,利用残差就很难对自相关的存在性做出比较正确的诊断;<3> DW检验不适应随机误差项具有高阶序列相关的检验;<4> DW检验有运用的前提条件,只有符合这些条件DW检验才是有效的。
自相关试题及答案

自相关试题及答案一、选择题1. 自相关函数是衡量时间序列中各个时刻的观测值之间的相关性,其定义为:A. 同一时间序列不同时刻观测值的协方差B. 同一时间序列不同时刻观测值的方差C. 同一时间序列不同时刻观测值的均值D. 同一时间序列不同时刻观测值的标准差答案:A2. 在自相关分析中,滞后1的自相关系数表示:A. 同一时间序列中相邻两个观测值之间的相关性B. 同一时间序列中相隔一个观测值的两个观测值之间的相关性C. 同一时间序列中相隔两个观测值的两个观测值之间的相关性D. 同一时间序列中相隔三个观测值的两个观测值之间的相关性答案:B3. 以下哪个选项不是自相关函数的性质:A. 自相关函数是对称的B. 自相关函数的值域在[-1, 1]之间C. 自相关函数的滞后0总是等于1D. 自相关函数的值随着滞后的增加而增加答案:D4. 自相关图(ACF图)是用于观察时间序列数据中自相关系数随滞后变化的图形,以下哪个选项不是自相关图的特点:A. 自相关图可以显示自相关系数的大小B. 自相关图可以显示自相关系数的显著性C. 自相关图可以显示时间序列的周期性D. 自相关图可以显示时间序列的方差答案:D5. 以下哪个选项是自相关系数的显著性检验方法:A. t检验B. F检验C. 卡方检验D. 曼-惠特尼U检验答案:A二、填空题1. 自相关系数的取值范围是________。
答案:[-1, 1]2. 如果一个时间序列是白噪声序列,那么它的自相关系数在滞后1及以上的值应该接近________。
答案:03. 自相关系数的平方和可以用来估计时间序列的________。
答案:信息量4. 在时间序列分析中,如果自相关系数在某个滞后显著不为0,这可能表明时间序列存在________。
答案:自相关性5. 滞后k的自相关系数记为________。
答案:ρ_k三、简答题1. 简述自相关函数的定义及其在时间序列分析中的作用。
答案:自相关函数是衡量同一时间序列中不同时刻观测值之间相关性的统计量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章 自相关一、判断题1.模型中的解释变量含有滞后被解释变量的时候可以使用DW 检验法检验自相关。
(F ) 2.可以作残差对某个解释变量的散点图来大概判断是否存在自相关。
(F ) 3.存在序列相关时,使用标准公式估计的随机扰动项的方差不再具有无偏性。
(T ) 4.杜宾—瓦尔森检验能够检验出任何形式的自相关。
( F ) 5.不存在负的自相关关系。
(F ) 6.LM 检验与DW 检验结果不一致是很有可能的。
(T ) 7. 存在序列相关时,有可能会高估或者低估随机扰动项的真实方差,但通常会低估。
(T )二、单项选择题1.如果模型t t 10t u x y ++=ββ存在序列相关,则( D )。
A. ()0x u Cov t t =,B. ()()s t 0u u Cov s t ≠=,C. ()0x u Cov t t ≠,D. ()()s t 0u u Cov s t ≠≠,2.DW 检验的零假设是(ρ为随机误差项的一阶相关系数)( B )。
A .DW =0B .0=ρC .DW =1D .1=ρ3.下列哪个序列相关可用DW 检验(t v 为具有零均值,常数方差且不存在序列相关的随机变量)( A )。
A . t 1t t v u u +=-ρB .t 2t 21t t v u u u +++=-- ρρC .t t v u ρ= ++=-1t 2t t v v u ρρ4.DW 的取值范围是( D )。
A .-1≤DW≤0B .-1≤DW≤1C .-2≤DW≤2D .0≤DW≤45.当DW =4时,说明( D )。
A .不存在序列相关B .不能判断是否存在自相关C .存在完全的正的自相关D .存在完全的负的自相关6.根据20个观测值估计的结果,一元线性回归模型的DW =2.3。
在样本容量n=20,解释变量k=1,显著性水平为0.05时,查得d L =1,d U =1.41,则可以决断( A )。
A .不存在自相关B .存在正的自相关C .存在负的自相关D .无法确定7.当模型存在序列相关现象时,适宜的参数估计方法是( C )。
A .加权最小二乘法B .间接最小二乘法C .广义差分法D .工具变量法8.对于原模型t t 10t u x y ++=ββ,广义差分模型是指( D )。
A .()()()()t t t t 1t 0t t x f u x f x x f 1x f y ++=ββ B .t t 1t u x y ∆+∆=∆βC .t t 10t u x y ∆+∆+=∆ββD .()()()1t t 1t t 101t t u u x x 1y y ----+-+-=-ρρβρβρ9.假定某企业的生产决策是由模型t t 10t u P S ++=ββ描述的(其中t S 为产量,t P 为价格),又知:如果该企业在t -1期生产过剩,经营人员会削减t 期的产量。
由此决断上述模型存在( B )。
A .异方差问题B .序列相关问题C .多重共线性问题D .随机解释变量问题10.根据一个n=30的样本估计t 01t tˆˆy =+x +e ββ后计算得DW =1.4,已知在5%的置信度下,d L =1.35,d U =1.49,则认为原模型( D )。
A .存在正的自相关B .存在负的自相关C .不存在自相关D .无法判断是否存在自相关11. 对于模型t 01t tˆˆy =+x +e ββ,以ρ表示t e 与1t e -之间的线性相关关系,则下列明显错误的是( B )。
A .40DW 80.,.==ρB .40DW 80.,.-=-=ρC .2DW 0==,ρD .0DW 1==,ρ12.在回归模型满足DW 检验的前提条件下,当统计量等于2时,表明( C )A. 存在完全的正自相关B. 存在完全的负自相关C. 不存在自相关D. 不能判定13.用矩阵形式表示的广义最小二乘参数估计量为,此估计量为( D )。
A.有偏、有效的估计量B.有偏、无效的估计量C.无偏、无效的估计量D.无偏、有效的估计量14.采用广义最小二乘法关键的一步是得到随机误差项的方差—协方差矩阵Ω,这就需要对原模型Y X U β=+ 首先采用( C )以求得随机误差项的近似估计量,从而构成矩阵Ω的估计量。
A.一阶差分法B.广义差分法C.普通最小二乘法 B.加权最小二乘法三、多项选择题1.DW 检验不适用下列情况的序列相关检验( ABC )。
A .高阶线性自回归形式的序列相关B .一阶非线性自回归的序列相关C .移动平均形式的序列相关D .正的一阶线性自回归形式的序列相关E .负的一阶线性自回归形式的序列相关2.以dl 表示统计量DW 的下方临界值,du 表示统计量DW 的上方临界值,则DW 检验的不确定区域是( BC )。
A .du≤DW≤4-duB .4-du≤DW≤4-dlC .dl≤DW≤duD .4-dl≤DW≤4E .0≤DW≤dl3.DW 检验不适用于下列情况下的自相关检验( ABCD )。
A .模型包含有随机解释变量B .样本容量太小d Y X X X 1'11')(ˆ---ΩΩ=βC .自相关形式不是一阶自回归形式D .含有滞后的被解释变量E .包含有虚拟变量的模型4.针对存在序列相关现象的模型估计,下述哪些方法可能是适用的( BCD )。
A .加权最小二乘法B .科克兰(Cochrane )—奥卡特(Orcutt )迭代法C .广义差分法D .Durbin 两步法5.如果模型t t 10t u x y ++=ββ存在自相关,普通最小二乘估计仍具备( AB )。
A .线性B .无偏性C .有效性D .真实性6.DW 检验不能用于下列哪些现象的检验( ABCD )。
A .递增型异方差的检验B .t 2t 21t t v u u u ++=--ρρ形式的序列相关检验C .t j 10i u x b b x ++=形式的多重共线性检验D .t1t 2t 10t e y x y +++=-βββˆˆˆ的自相关检验 7.在下列引起序列自相关的原因中,正确的有( ABC )A .经济变量具有惯性作用B .经济行为的滞后性C .设定偏误D .解释变量之间的共线性四、简答题1.简述DW 检验的局限性。
答:DW 检验存在三个主要的局限性:(1)有假定前提条件:解释变量非随机;模型包括截距项;解释变量中不包含滞后的被解释变量;残差扰动项的自相关形式为一阶线性自回归形式;无缺损数据。
(2)要求有足够样本量,一般要求n≥15。
(3)有不确定区域。
2.序列相关性的后果。
答:(1)参数的OLS 估计式仍然是无偏的,但用OLS 估计的参数的方差不再具有最小方差;(2)使用标准公式计算出的方差通常会严重低估真实的方差;(3)模型的显著性检验失效;(4)区间估计和预测区间的精度降低。
3.简述序列相关性的几种检验方法。
答:(1)图示法;(2)D -W 检验;(3)LM 检验法。
4.自相关性产生的原因有那些?答:(1)经济变量本身的惯性作用;(2)经济行为本身的滞后性;(3)设定偏倚;(4)数据的加工引起自相关;(5))扰动项自身特性引起自相关。
5.DW 值与一阶自相关系数的关系是什么? 答:2DW 1p -≈ˆ或者()p 12DW ˆ-≈ 五、计算题1.根据某地1961—1999年共39年的总产出Y 、劳动投入L 和资本投入K 的年度数据,运用普通最小二乘法估计得出了下列回归方程:(0.237) (0.083) (0.048),DW=0.858上式下面括号中的数字为相应估计量的标准误差。
在5%的显著性水平之下,由DW 检验临界值表,得d L =1.38,d u =1.60。
问: (1) 题中所估计的回归方程的经济含义; (2) 该回归方程的估计中存在什么问题?应如何改进?答:(1) 题中所估计的回归方程的经济含义:当其他解释变量保持不变时,劳动投入每增加1%,平均而言总产出将增加1.451%;当其他解释变量保持不变时,资本投入每增加1%,平均而言总产出将增加0.384%。
换言之,该回归方程是一个对数线性模型,可还原为指数的形式为:3841.0451.1938.3Y K L -=∧,是一个C -D 函数,1.451为劳动产出弹性,0.3841为资本产出弹性。
因为1.451+0.3841〉1,所以该生产函数存在规模经济。
(2) 因为DW=0.858, d L =1.38,即0.858<1.38,故存在正自相关。
可利用广义差分法消除自相关的影响。
2.根据我国1978——2000年的财政收入Y 和国内生产总值X 的统计资料,可建立如下的计量经济模型: X 119806477556Y ⨯+=..t=(2.5199) (22.7229) 2R =0.9609,E S .=731.2086,F =516.3338,W D .=0.3474请回答以下问题:(1) 何谓计量经济模型的自相关性?(2) 试检验该模型是否存在自相关,为什么?(3) 自相关会给建立的计量经济模型产生哪些影响?(临界值24.1=L d ,43.1=U d )答:(1)对于t kt k t t t u x b x b x b b y +++++=...22110,如果随机扰动项的各期值之间存在着相关关系,即)...,2,1,(0)(),cov(k s t u u E u u s t s t =≠=,称随机误差项之间存在自相关性。
(2)存在,因为W D .=0.3474,24.1=L d ,即L d W D <.,故存在正自相关。
(3)①参数的OLS 估计量仍然具有无偏性;②参数的OLS 估计式的方差不再是最小的;③用标准公式估计出的方差通常会严重低估真实的方差;④显著性检验失效;⑤区间预测精度下降,区间估计变得无意义。
3.以某地区22年的年度数据估计了如下工业就业回归方程321X 620X 250X 510893Y ln .ln .ln ..+-+-=(-0.56) (2.3) (-1.7) (5.8)20.996R = 147.1=DW式中,Y 为总就业量;X 1为总收入;X 2为平均月工资率;X 3为地方政府的总支出。
(1)试证明:自相关的DW 检验是无定论的。
(2)逐步描述如何使用LM 检验。
答:(1)查表得临界值05.1=L d ,66.1=U d 。
147.1=DW 正位于1.05和1.66之间,恰是D -W 检验的无判定区域,所以自相关的DW 检验是无定论的。
(2)对于模型t kt k t t t u x b x b x b b y +++++=...22110,设自相关的形式为t p t p t t t v u u u u ++++=---ρρρ (2211)假设0...210====p H ρρρ:,LM 检验检验过程如下:首先,利用OLS 法估计模型,得到残差序列t e ;其次,将t e 关于残差的滞后值进行回归,并计算出辅助回归模型的判定系数2R ;最后,对于显著水平α,若2nR 大于临界值)(2p αχ,则拒绝原假设,即存在自相关性。
