网络计划技术时间参数求解作业
工程网络计划有关时间参数的计算典型例题
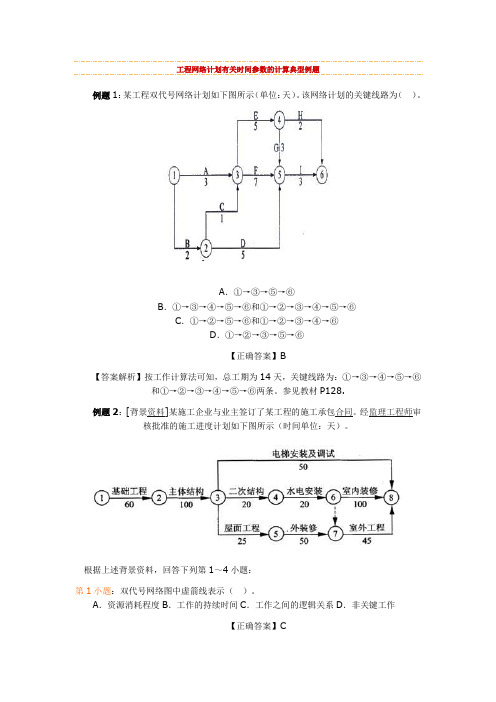
工程网络计划有关时间参数的计算典型例题例题1:某工程双代号网络计划如下图所示(单位:天)。
该网络计划的关键线路为()。
A.①→③→⑤→⑥B.①→③→④→⑤→⑥和①→②→③→④→⑤→⑥C.①→②→⑤→⑥和①→②→③→④→⑥D.①→②→③→⑤→⑥【正确答案】B【答案解析】按工作计算法可知,总工期为14天,关键线路为:①→③→④→⑤→⑥和①→②→③→④→⑤→⑥两条。
参见教材P128.例题2:[背景资料]某施工企业与业主签订了某工程的施工承包合同。
经监理工程师审核批准的施工进度计划如下图所示(时间单位:天)。
根据上述背景资料,回答下列第1~4小题:第1小题:双代号网络图中虚箭线表示()。
A.资源消耗程度B.工作的持续时间C.工作之间的逻辑关系D.非关键工作【正确答案】C【答案解析】在双代号网络图中,为了正确地表达图中工作之间的逻辑关系,往往需要用虚箭线。
虚线是实际工作中并不存在的一项虚设工作,故它们既不占用时间,也不消耗资源。
在双代号网络图中,任意一条实箭线都要占用时间、消耗资源。
参见教材P116.第2小题:监理工程师审核批准的施工进度计划工期是()天。
A.210B.245C.280D.300【正确答案】D【答案解析】本题实质就是计算该网络计划的工期。
计算得到的最早开始时间、最早完成时间、最迟开始时间、最迟完成时间、总时差和自由时差。
由图可知计划工期是300天。
由于该网络计划图较简单,也可以分别计算四条线路的持续时间,关键线路的长就是计划工期。
参见教材P127.工期泛指完成任务所需要的时间,一般有以下3种;(1)计算工期,根据网络计划时间参数计算出来的工期,用T c表示;(2)要求工期,任务委托人所要求的工期,用T r表示;(3)计划工期,根据要求工期和计算工期所确定的作为实施目标的工期,用T p表示。
网络计划的计划工期T p应按下列情况分别确定:当已规定了要求工期T r时,T p≤T r;当未规定要求工期时,可令计划工期等于计算工期,T p=T r。
203-习题作业-习题作业及参考答案——网络计划技术

习题作业:1.网络计划技术如何分类?2.双代号网络计划如何绘图,时间参数如何计算以及关键工作和关键线路如何确定?3.双代号时标网络计划如何编制?4.单代号网络计划如何绘图,时间参数如何计算以及关键工作和关键线路如何确定?5.单代号搭接网络计划如何绘图,时间参数如何计算以及关键工作和关键线路如何确定?习题作业参考答案:1.网络计划技术如何分类?答:网络计划技术可以从不同的角度进行分类。
(1) 按工作之间逻辑关系和持续时间的确定程度分类,分为肯定型网络计划和非肯定型网络计划;(2) 按节点和箭线所表示的含义分类,分为双代号网络计、单代号搭接网络计划、事件节点网络计划;(3) 按目标分类,分为单目标网络计划和多目标网络计划;(4) 按层次分类,分为分级网络计划、总网络计划、局部网络计划;(5) 按表达方式分类,分为时标网络计划和非时标网络计划。
2.双代号网络计划如何绘图,时间参数如何计算以及关键工作和关键线路如何确定?答:(1) 网络图必须正确地表达整个工程或任务的工艺流程和各工作开展的先后顺序及它们之间相互依赖、相互制约的逻辑关系。
因此,绘制网络图时必须遵循一定的基本规则和要求。
1) 双代号网络图必须正确表达已定的逻辑关系。
2) 双代号网络图中,严禁出现循环回路。
3) 双代号网络图中,在节点之间严禁出现带双向箭头或无箭头的连线。
4) 双代号网络图中,严禁出现没有箭头节点或没有箭尾节点的箭线。
5) 当双代号网络图的某些节点有多条外向箭线或多条内向箭线时,为使图形简洁,可使用母线法绘制。
6) 绘制网络图时,箭线不宜交叉。
7)双代号网络图中应只有一个起点节点和一个终点节点 (多目标网络计划除外),而其他所有节点均应是中间节点。
8) 双代号网络图应条理清楚,布局合理。
(2) 双代号网络计划时间参数的计算。
按工作计算法在网络图上计算六个工作时间参数,必须在清楚计算顺序和计算步骤的基础上,列出必要的公式,以加深对时间参数计算的理解。
网络时间参数计算
2020/5/14
四.关键线路的确定方法: 1.分析线路进行确定; 2.通过计算时间参数进行确定; 3.破圈法:
关键线路走最长的线路,逢圈保留最长线路。 例如以下两例:
2020年5月14日星期四
建筑施工组织与管理
10
2020年5月14日星期四
建筑施工组织与管理
3
2-4工序:LS2-4=[ LS4-7,LS5-9]min-5=[8,11]min-5=3;
2-3工序:LS2-3=5-3=2;
2-6工序:LS2-6=9-4=5;
1-2工序:LS1-2=[ LS2-3,LS2-4,LS2-6]min-2
=[2,3,5]min-2=0
1.4.2.3网络计划时间参数:
六个参数:
最早可能开始时间(ES)、最早可能结束时间(EF)、 最迟必须开始时间(LS)、最迟必须结束时间(LF)、 工序时差(TF)、自由时差(FF)。
方法:1.分析计算法;2.图上计算法;3.表上计算法
4.计算机计算法。
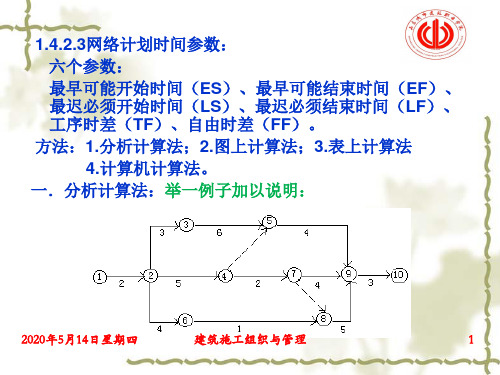
一.分析计算法:举一例子加以说明:
2020年5月14日星期四
通过以上原理可以得到: ESjk=[ESji+tij]max=[ EFij]max。
3.计算最迟必须开始时间(LS): 逆算:LSij=T-[∑tjk]max-tij=[LSjk]min- tij 9-10工序:LS9-10=18-3=15; 5-9工序:LS5-9=15-4=11; 7-9工序:LS7-9=15-4=11; 8-9工序;LS8-9=15-5=10; 4-7工序:LS4-7=[ LS7-9,LS8-9]min-2=[11,10]min-2=8; 6-8工序:LS6-8=10-1=9; 3-5工序:LS3-5=11-6=5;
网络计划时间参数计算

网络计划时间参数计算网络计划是一种项目管理工具,可以帮助团队有效规划和管理项目进度。
在网络计划中,时间参数的计算是至关重要的一部分。
下面将介绍一些计算网络计划时间参数的方法和技巧。
首先是活动的持续时间计算。
活动的持续时间是完成该活动所需的时间。
在计算持续时间时,可以参考历史数据、专家意见和类似项目的经验。
还可以根据该活动所需的资源数量、人力、物资等来计算持续时间。
定期对活动持续时间进行更新和调整,以确保计划与实际相符。
其次是关键路径的确定。
关键路径是项目中最长的路径,它决定了整个项目的最短完成时间。
确定关键路径的方法是绘制网络图,计算每个活动的最早开始时间(EST)和最晚开始时间(LST),以及最早完成时间(EFT)和最晚完成时间(LFT)。
通过计算活动的总浮动时间,可以确定哪些活动位于关键路径上,从而确定整个项目的关键路径。
接下来是总浮动时间和自由浮动时间的计算。
总浮动时间是活动可以延迟的最长时间,而不会影响到整个项目的完成时间。
计算总浮动时间的公式为:总浮动时间 = LST – EST 或 LFT – EFT自由浮动时间是活动可以延迟的时间,而不会影响到后续活动的开始时间。
计算自由浮动时间的公式为:自由浮动时间 = ES(后继活动)– EF(当前活动)–持续时间(当前活动)最后是加速项目进度的方法。
如果项目进度比计划滞后,可以考虑采用加速方法来弥补时间差。
加速方法包括调整资源分配,增加人力,缩短持续时间等。
其中,缩短持续时间需要谨慎处理,因为如果过度缩短持续时间会增加风险和成本。
通过以上方法和技巧,团队可以更好地计算和管理网络计划时间参数,确保项目进度的稳定和高效。
工期控制1(双代号网络绘制与时间参数计算)

网络计划技术的应用步骤概述
进行网络计划方案的优化:
找出关键路径,也就初步确定了完成整 个计划任务所需要的工期。这个总工期, 是否符合合同或计划规定的时间要求,是 否与计划期的劳动力、物资供应、成本费 用等计划指标相适应,需要进一步综合平 衡,通过优化,择取最优方案。然后正式 绘制网络图,编制各种进度表,以及工程 预算等各种计划文件。
同一项任务,用上述两种方法画出的网络图是相同的。 一般习惯于按反工艺顺序安排计划的企业,如机器制造企 业,采用逆推较方便,而建筑安装等企业,则大多采用顺 推法。按照各项作业之间的关系绘制网络图后,要进行结 点的编号。
网络计划技术的应用步骤概述
计算网络时间,确定关键路线:
根据网络图和各项活动的作业时间,就 可以计算出全部网络时间和时差,并确定 关键线路。具体计算网络时间并不太难, 但比较烦琐。在实际工作中影响计划的因 素很多,要耗费很多的人力和时间。因此, 只有采用电子计算机才能对计划进行局部 或全部调整,这也是为推广应用网络计划 技术提出了新内容和新要求。
起始工作:没有紧前 工作的工作。
紧后工作:本工作完成之后 才能开始的工作。
紧前工作:在完成本工作 之前必须完成的工作。
工作间 的关系
结束工作:没有紧后 工作的工作。
平行工作:可以和本工作 同时开始同时结束的工作。
后续工作:本工作结束节点之后至终点 节点之前各条线路上的所有工作。
先行工作:自起点节点至本工作开始 节点之前各条线路上的所有工作。
网络计划技术即是一种科学的计划方法, 又是一种有效的生产管理方法。
基本原理
基本模型
首先应用网络图来表示 一项计划(或工程)中各项 工作的开展顺序及其相互 之间的关系;通过对网络 图进行时间参数的计算, 找出计划中的关键工作和 关键线路;通过不断改进 网络计划,寻求最优方案, 保证合理地利用人力、物 力和财力,以最小的消耗
监理工程师网络计划技术第三节网络计划时间参数的计算

网络计划技术第三节网络计划时间参数的计算上一、网络计划时间参数的概念序号参数名称知识要点表示方法双单1.持续时间指一项工作从开始到完成的时间Di-jDi2.工期计算工期根据网络计划时间参数计算而得到的工期Tc3.要求工期是任务委托人所提出的指令性工期Tr4.计划工期指根据要求工期和计算工期所确定的作为实施目标的工期Tp5.最早开始时间指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻ESi-jESi6.最早完成时间指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻EFi-jEFi7.最迟完成时间在不影响整个任务按期完成的前提下本工作必须完成的最迟时刻LFi-jLFi8.最迟开始时间在不影响整个任务按期完成的前提下,工作必须开始的最迟时刻LSi-jLSi9.总时差在不影响总工期的前提下,本工作可以利用的机动时间TFi-jTFi10.自由时差在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间FFi-jFFi11.节点的最早时间在双代号网络计划中,以该节点为开始节点的各项工作的最早开始时间ETi12.节点的最迟时间在双代号网络计划中,以该节点为完成节点的各项工作的最迟完成时间LTj13.时间间隔指本工作的最早完成时间与其紧后工作最早开始时间之间可能存在的差值LAGi-j二、双代号网络计划时间参数的计算双代号网络计划的时间参数既可以按工作计算,也可以按节点计算.(一)按工作计算法所谓按工作计算法,就是以网络计划中的工作为对象,直接计算各项工作的时间参数。
这些时间参数包括:工作的最早开始时间和最早完成时间、工作的最迟开始时间和最迟完成时间、工作的总时差和自由时差。
此外,还应计算网络计划的计算工期。
为了简化计算,网络计划时间参数中的开始时间和完成时间都应以时间单位的终了时刻为标准。
如第3天开始即是指第3天终了(下班)时刻开始,实际上是第4天上班时刻才开始;第5天完成即是指第5天终了(下班)时刻完成。
二、网络计划时间参数的计算

二、网络计划时间参数的计算二、网络计划时间参数的计算网络中的时间参数工作持续时间在双代号网络计划中,工作i—j的持续时间用Di—j表示;在单代号网络计划中,工作i的持续时间用Di表示。
工期1)计算工期,用Tc表示。
2)要求工期是任务委托人所提出的指令性工期,用Tr表示。
3)计划工期,用Tp表示。
当已规定了要求工期时,计划工期不应超过要求工期,即:Tp≤Tr当未规定要求工期时,可令计划工期等于计算工期,即:Tp=Tc工作的六个时间参数最早开始时间ES 最早完成时间EF最迟开始时间LS, 最迟完成时间LF工作的总时差是指在不影响总工期的前提下,本工作可以利用的机动时间。
工作的总时差用TF表示。
工作的自由时差是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
自由时差用FF表示。
从总时差和自由时差的定义可知,对于同一项工作而言,自由时差不会超过总时差。
当工作的总时差为零时,其自由时差必然为零。
在网络计划的执行过程中,工作的自由时差是该工作可以自由使用的时间。
但是,如果利用某项工作的总时差,则有可能使该工作后续工作的总时差减小。
节点时间节点最早时间是指在双代号网络计划中,以该节点为开始节点的各项工作的最早开始时间。
节点i的最早时间用ETi表示。
节点最迟时间是指在双代号网络计划中,以该节点为完成节点的各项工作的最迟完成时间。
节点j的最迟时间用LTj表示。
相邻两项工作之间的时间间隔相邻两项工作之间的时间间隔是指本工作的最早完成时间与其紧后工作最早开始时间之间可能存在的差值。
工作i与工作j之间的时间间隔用LAGi,j表示。
双代号网络计划参数计算(工作计算法)(1)计算工作的最早开始时间和最早完成时间。
1)以网络计划起点节点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零。
2)EFi—j=ESi—j+Di—j3)ESi—j=Max{EFh—i}=Max{ESh—i+Dh—i}4)Tc=Max{EFi—n}=Max{ESi—n+Di—n} (2)确定网络计划的计划工期。
网络计划的时间参数计算

第四节
网络计划的时间参数计算
计算网络计划的时间参数,是确定机动时间和关键线 路的基础,是确定计划工期的依据,又是进行计划调 整与优化的前提。可按工序、节点计算。 一、双代号网络计划时间参数计算 (一)工序时间参数计算 以工序为对象计算:最早开始时间-最早完成时间 最迟开始时间-最迟完成时间 工序总时差、自由时差 网络计划时间参数计算的基础:工序作业持续时间 方法:手工计算法(表上计算法、图上计算法),电算 法。
tij
EFij
ESjk
tjk
ESij
LSij
LFij
2、表上计算法
88
(1)
工序 编号
(2)
持续 时间
(3)
最早 开始
(4)
最早 完成
(5)
最迟 开始
(6)
最迟 完成
(7)
总时 差
(8)
自由 时差
(9)
关键 工序
(10)
1
2 3 4
1-2
2-3 2-4 3-5
2
3 2 0
0
2 2 5
2
5 4 5
1、图上计算法 1)工序的最早开始时间(ESij) 也叫最早开始时间,是指一个工序在具备了一定工作 条件和资源条件后可以开始工作的最早时间。在工作 程序上,它要等紧前工序完成以后方能开始。 起点节点--终点节点 紧前工序--本工序 加法过程
与起点节点联系的工作(工序):最早开始时间为零
网络计划-单代号网络图详解例题

❖【解】(1)计算最早开始时间和最早完成时间
网络计划-单代号网络图详解例题
❖(2)计算相邻两项工作之间的时间间隔LAGij
网络计划-单代号网络图详解例题
❖(3)计算工作的总时差TFi 已知计划工期等于计算工期:Tp=Tc=15,故终点节点⑥节 点的总时差为零,即:
B
C
D
E
F
紧前 工作
-
-
-
A、B
B C、D、E
网络计划-单代号网络图详解例题
工作 A
B
C
D
E
F
紧前 工作
-
-
-
A、B
B C、D、E
A
D 3
B
E
F
1
2
4
5
C
网络计划-单代号网络图详解例题
作业
作业7:根据表中逻辑关系,绘制双代号网络图。
工作 A
B
C
D
E
F
紧前 工作
-
A
A
A B、C、D D
网络计划-单代号网络图详解例题
D(6) 5 F(4)
00
11
1
2
3
A(1)
B(3) 4 4 C(1)
4 5 10
15 15
7
8
14 14 H(1)
网络计划-单E代(号2网)络图详6解61例2题 G(2) TP=TC=15天
工作 A B C D E F G H
紧前 工作
-
A
B
B
B C、D C、E F、G
时间 1 3 1 6 2 4 2 1
00000 110
1 A(1)
网络计划时间参数计算

网络计划时间参数计算在项目管理中,网络计划是一种用于规划和控制项目进度的方法。
在网络计划中,时间参数的计算是非常重要的,它直接影响着项目的进度和完成时间。
本文将介绍网络计划时间参数的计算方法,帮助读者更好地理解和应用网络计划。
首先,我们需要了解网络计划中的几个重要概念,最早开始时间(ES)、最晚开始时间(LS)、最早完成时间(EF)、最晚完成时间(LF)以及浮动时间。
最早开始时间是指活动可以开始的最早时间,最晚开始时间是指活动必须开始的最晚时间,最早完成时间是指活动可以完成的最早时间,最晚完成时间是指活动必须完成的最晚时间,浮动时间是指活动可以延迟的时间,而不影响整个项目的进度。
其次,我们需要了解如何计算这些时间参数。
在网络计划中,通常使用关键路径法来计算时间参数。
关键路径是指项目中不能延误的活动序列,它决定了整个项目的完成时间。
计算最早开始时间和最早完成时间的方法是通过逆推法,从起点开始,依次计算每个活动的最早开始时间和最早完成时间;计算最晚开始时间和最晚完成时间的方法是通过正推法,从终点开始,依次计算每个活动的最晚开始时间和最晚完成时间。
最后,通过计算最早开始时间和最晚开始时间的差值,可以得到活动的总浮动时间。
在实际应用中,网络计划时间参数的计算可以通过项目管理软件来完成。
这些软件通常提供了直观、快捷的方式来绘制网络计划图,并自动计算时间参数。
但是,作为项目管理人员,我们也需要了解手工计算的方法,以便更好地理解和分析项目进度。
总之,网络计划时间参数的计算是项目管理中的重要内容,它直接关系到项目的进度和完成时间。
通过本文的介绍,相信读者对网络计划时间参数的计算有了更深入的了解,希望能够在实际项目管理中加以应用,提高项目的进度控制能力。
网络图时间参数计算例题

(二)工作的最早完成时间EFi-j
--各紧前工作全部完成后,本工作可能完成 的最早时刻。
3
6
14
6
3 14
7 18
B(3)
D(8)
G(4)
0
6
6
6
11 11
18
3
1
2
5 11
6
20
9
10
A(3)
E(5)
I(2)
6
C(3)
6
3
6
4 10 F(4)
11 11
8
11
H(2)
6
13
二、工作计算法
(二)工作的最早完成时间EFi-j
10
I(2)
H(2)
8
11 16 5 13 18 5
二、工作计算法
(六)自由时差FFi-j
FFi-j=ESj-k-EFi-j
三、节点计算法
三、节点计算法
ETi LTi
i
ETj LTj
j
3
7
B(3)
D(8)
G(4)
1
2
A(3)
C(3)
5
6
E(5)
4
8
F(4)
9
10
I(2)
H(2)
三、节点计算法
E(5)
I(2)
C(3)
69
69
6 12
4 10 16
36
F(4)
11 16 11 16
8
11 16
H(2)
69
13 18
二、工作计算法
(四)工作最迟开始时间LSi-j
LSi-j=LFi-j-Di-j
11.2 网络计划图的时间参数计算

例1的ES,EF计算值在表11-3的③,④列中。 表11-3
工作 i-j ① A(1-2) B(2-7) C(2-3) D(2-4) E(2-5) E’(4-5)
工作 i-j F(3-7) G(4-6) H(5-7) K(6-7) L(7-8)
持续时间 Di-j ② 60 45 10 20 40 0(虚工作)
最早完工时间 = 最早开始时间 + 活动持续时间 tEF(i, j) = tES (i, j) + D(i, j)
tES (i, j) = maxk tEF (k, i)
tEF(i, j) = tES (i, j) + D (i, j)
tES + D(i, j) = tEF tLF tEF tES tLF
时间参数的关系可以用下图11-6表示工作的关系 状态。
最早开始 最迟开始 EF i-j 工作 A LFi-j 工作 A 的紧后工作 B ES j-k LSi-k EF j-k LFj-k
TF i-j=LFi-j-EF i-j ES i-j 工作持续时间 D i
i-j
工作a的总时差
工作 A
LSi-j 工作A的总时差 工作a的自由时差 FF i-j=ES j-k-EF i-j
tLF (i, j) = mink tLS (j, k) tLS (i, j) = tLF (i, j) - D(i, j)
tES
tLS + D (i, j) = tLF
tES tLS
tES
tLS
在表11-4中进行。计算从下到上地进行,从工作 (7-8)开始,令表11-4的⑤列最后一行 LF7-8=EF7-8=170.
1 a 2m 2m b a 4m b D(i , j) ( ) 2 3 3 6 1 a 4m 2 2 D [( ) ( ) ] ( ) 2 6 3 6 3 6
二级建造师双代号网络计划时间参数计算详解

二级建造师双代号网络计划时间参数计算详解双代号网络计划的时间参数主要包括工作活动的最早开始时间(ES)、最早完成时间(EF)、最晚开始时间(LS)、最晚完成时间(LF)和工作活动的总时差(TF)。
首先,我们需要明确几个概念。
在网络计划中,每个工作活动都有一个最早开始时间(ES),它是该工作活动前面所有前置工作的最早完成时间。
最早完成时间(EF)等于最早开始时间(ES)加上该工作活动的持续时间(D)。
最晚完成时间(LF)是工作活动的后继工作的最晚开始时间减去持续时间(D)。
最晚开始时间(LS)等于最晚完成时间(LF)减去持续时间(D)。
工作活动的总时差(TF)等于最晚开始时间(LS)减去最早开始时间(ES)。
具体的计算步骤如下:1. 绘制网络图,标识出所有的工作活动和它们之间的依赖关系。
网络图分为两个部分,一个是前置关系图,表示工作活动的先后顺序;另一个是持续时间图,表示工作活动的持续时间。
2. 确定项目的开始节点和结束节点。
开始节点没有前置工作,所以它的最早开始时间(ES)和最早完成时间(EF)都为0。
3. 从开始节点开始,按照前置关系图的先后顺序,依次计算每个工作活动的最早开始时间(ES)和最早完成时间(EF)。
对于每个工作活动来说,它的最早开始时间(ES)等于前置工作的最早完成时间(EF),最早完成时间(EF)等于最早开始时间(ES)加上该工作活动的持续时间(D)。
4. 从结束节点开始,按照前置关系图的逆序,依次计算每个工作活动的最晚开始时间(LS)和最晚完成时间(LF)。
对于每个工作活动来说,它的最晚完成时间(LF)等于后继工作的最晚开始时间(LS)减去持续时间(D),最晚开始时间(LS)等于最晚完成时间(LF)减去持续时间(D)。
5. 计算每个工作活动的总时差(TF)。
工作活动的总时差(TF)等于最晚开始时间(LS)减去最早开始时间(ES)。
通过以上的计算步骤,我们就可以得到双代号网络计划的时间参数。
管理学之网络计划技术

工期优化
网络优化一般包括 工期费用优化
工期资源优化
(一)网络计划调整与优化内容
一项好的计划,必须在保证项目质量和工期的 前提下,不仅能使项目总的费用支出及资源使用 不超出规定的范围,并尽可能节约,而且在项目 的各个阶段,都能使实际进度、费用资源得到有 效的保障和控制。
所以网络计划的调整和优化在项目管理中十分重 要,但又是一项十分复杂的工作。一般来说,网 络计划的调整与优化工作包括时间分析、费用分 析和资源分析三方面的工作。
式中赶工时间是指谋活动的作业时间从正常状 态慢慢加以缩短,知道无法再缩短为止的时间, 该时间所需的费用为赶工时间。
例3、某项工程共有七项活动,其作业时间、费 用及费用变化率如表所示,该计划的简介费用 为每天10 000元,求直接费用之和最低的工期
时间费用优化表
活动 紧后 作业时间 费用(千元) 代号 活动 正常 赶工 正常 赶工
它是指该项作业最迟在什么时间结束,其大
小等于代表该项作业的箭线的箭头结点的最迟结 束时间。
即:T ijLF=TLj
4)作它业是的指最该迟项开作始业时最间迟(T应ij在LS)什么时间开始,其
大小等于代表该项作业的箭线的箭头结点的最迟 结束时间减去该项作业本身的作业时间。
计算公式为:T ijLS=TLj-Tij
2.结点时间参数的计算 1)结点最早开始时间(TiE) 其计算公式为:TjE=max{TiE+Tij}
2.结点时间参数的计算 1)结点最早开始时间(TiE) 计算公式为:TJE=max{TiE+Tij} 一般假定起始节点最早开始时间为零,其余节点最 早可能开始的时间按下式计算:
ET(j)={ET(i ) +t(i,,j )}
网络计划时间参数计算的介绍

总时差的特性:
(1)凡是总时差为最小的工作就是关键工作;由关键 工作连接构成的线路为关键线路;关键线路上各 工作时间之和即为总工期。如图4—47所示,工作 1—3、3—4、4—6为关键作,线路1—3—4—6为关 键线路。
(2)当网络计划的计划工期等于计算工期时,凡是 时差大于零的工作为非关键工作,凡是具有非关 短工作的线路即为非关短线路。非关短线路与关 键线路相交时的相关节点把非关键线路划分成若 干个非关键线路段,各段有各段的总时差,相互 没有关系。
成的时间,用D表示。主要计算方法有: (1)参照以往实践经验估算; (2)经过试验推算; (3)有标准可查,按定额计算。
2.工期
二、双代号网络计划时间参数的计算
5
11
11
0
5
11
0
1
1
10
14
5 1
11 11
16 4
3
工作的最早时间计算时应特别注意以下三点:一是计算程序, 即从起点节点开始顺着箭线方向,按节点次序逐项工作计算; 二是要弄清该工作的紧前工作是哪几项,以便准确计算;三 是同一节点的所有外向工作最早开始时间相同。
(3)总时差的使用具有双重性,它既可以被该工 作使用,但又属于某非关键线路所共有。当某 项工作使用了全部或部分总时差时,则将引起 通过该工作的线路上所有工作总时差重新分配。
例如图4—47中,非关键线路段3—5—6中,TF35=3天, TF5-6 =2天,如果工作3—5使用了3天
机动时间,则工作5—6就没有总时差可利用; 反之若工作5—6使用了2天机动时间,则工作 3—5就只有1天时差可以利用了。
13
16
13
5
11
16
2
5
网络计划图的时间参数计算

专题七 网络计划技术
Network Planning Technique
7.1 网络计划概述 7.2 网络计划图及其绘制 7.3 网络计划图的时间参数计算 7.4 网络计划的调整与优化
统筹方法/OR
7.3 网络计划图的时间参数计算
➢工序工期的确定
工序工期是指完成工序作业所需要的时间,用 tij 表示.确定方法有:
C 4
5
F 3
78
统筹方法/OR
➢工序的时间参数计算
⑴ 工序的最早开始时间tES(i, j) (Earliest Starting Time)
指所有紧前工序最早结束时间.
tES (i, j) = tE (i)
0
1
A 2
00
2 B 3
2
2
D 5
22
2 C 4
5
3
E 4
57
7 G 44 77
7
5
F 3
24 B2 3
22
2
D 5
0
22
24 C2 4
57
3
E 4
2
57
77
11 11
4
G 4
0
77
6
H 2
0
11 11
7 13 13
78
5
F 3
1
78
统筹方法/OR
②单时差 r(i,j ) :在不影响紧后工序最早开始时间前提下,工序
完工期有多少机动时间.
r (i, j ) = t E ( j ) − [t E (i) + tij ]
⚫乐观时间 (a):在非常顺利情况下,完成工序所需的最少时间估计;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7
18
18
7
0
√(4,5)ຫໍສະໝຸດ 121218
18
6
(4,6)
12
19
23
16
4
(5,6)
18
23
23
18
0
√
(6,7)
23
26
26
23
0
√
(7,8)
26
32
37
31
5
(7,9)
26
28
28
26
0
√
(8,10)
32
32
37
37
5
(9,10)
28
37
37
28
0
√
关键线路:A----B----D----E----G----H----J
关键线路时间:37周
TL(5 )=TL(6 )-te(5,6 ) =18
TL(4)=min =min =16
TL(3)=min =min =7
TL(2 )=TL(3 )-te(2,3 ) =5
TL(1 )=TL(2 )-te(1,2 ) =0
根据作业时间参数计算公式
1作业最早开始时间
TES(i,j)=TE(i )
2作业最早结束时间
TEF(i,j)=TE(i )+t(i,j)
3作业最迟结束时间
TLF(i,j)=TL(j)
4作业最迟开始时间
TLS(i,j)=TL(j )-t(i,j)
通过参数计算得到活动时间参数表
活动
TES
TEF
TLF
TLS
R(i,j)
关键活动
(1,2)
0
5
5
0
0
√
(2,3)
5
7
7
5
0
√
(3,4)
7
12
16
11
4
TE(1 )=0
TE(2 )=TE(1 )+te(1,2 )=5
TE(3 )=TE(2 )+te(2,3 )=7
TE(4 )=TE(3 )+te(3,4 )=12
TE(5 )=max max =18
TE(6 )=max max =23
TE(7 )=TE(6 )+te(6,7 )=26
TE(8 )=TE(7 )+te(7,8 )=32
TE(9 )=TE(7 )+te(7,9 )=28
TE(10 )=max max =37
事项的最迟结束时间:
TL(10 )=37
TL(9 )=TL(10 )-te(9,10 ) =28
TL(8 )=TL(10 )-te(8,10 ) =37
TL(7)=min =min =26
TL(6 )=TL(7 )-te(6,7 ) =23
网络计划技术作业
例题:某机械厂开发新产品有多项工作需要完成,试绘出网络图,并计算各项时间。
1
市场调查
A
-----
5
2
新产品开发决策
B
A
2
3
筹集资金
C
B
5
4
设计
D
B
11
5
采购设备
E
C,D
5
6
厂房改建
F
C
7
7
设备安装
G
E,F
3
8
试生产
H
G
2
9
建立营销网络
I
G
6
10
生产并投放市场
J
H
9
事项的最早开始时间:
