思维特训(九) 密度
特训09 相似三角形的基本模型-2021-2022学年九年级数学上学期重难题型思维特训(北师大版)
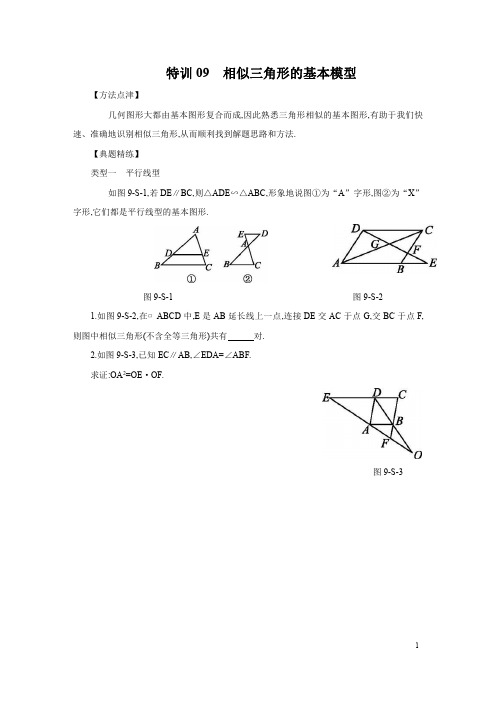
特训09相似三角形的基本模型【方法点津】几何图形大都由基本图形复合而成,因此熟悉三角形相似的基本图形,有助于我们快速、准确地识别相似三角形,从而顺利找到解题思路和方法.【典题精练】类型一平行线型如图9-S-1,若DE∥BC,则△ADE∽△ABC,形象地说图①为“A”字形,图②为“X”字形,它们都是平行线型的基本图形.图9-S-1图9-S-21.如图9-S-2,在▱ABCD中,E是AB延长线上一点,连接DE交AC于点G,交BC于点F,则图中相似三角形(不含全等三角形)共有对.2.如图9-S-3,已知EC∥AB,∠EDA=∠ABF.求证:OA2=OE·OF.图9-S-3常见的有如下三种情形:如图9-S-4①,已知∠1=∠B,则结合公共角∠A得△ADE∽△ABC.如图②,已知∠1=∠B,则结合公共角∠A得△ADE∽△ACB.如图③,已知∠B=∠D,则结合对顶角∠1=∠2得△ADE∽△ABC.图9-S-43.如图9-S-5,在△ABC中,点D,E分别在边AB,AC上,且∠ABE=∠ACD,BE,CD相交于点G.(1)求证:△AED∽△ABC;(2)如果BE平分∠ABC,求证:DE=CE.图9-S-54.如图9-S-6①,在△ABC中,∠ACB=90°,AD平分∠CAB交BC于点E,过点D作BD⊥AD,垂足为D.(1)若AE=2BD,求证:CA=CB;(2)在(1)的条件下,过点C作CF⊥AE,垂足为F,如图②,直接写出图中所有与△BDE相似的三角形.图9-S-6将图9-S-4②中的DE向下平移使点C与点E重合,则得图9-S-7①,有△ACD∽△ABC,称之为“母子”型的基本图形.特别地,令∠ACB=90°,CD为斜边上的高(如图②),则有△ACD ∽△ABC∽△CBD.图9-S-7图9-S-85.如图9-S-8,在△ABC中,P为AB上一点,要使△ACP∽△ABC,还需具备的一个条件是_____.6.如图9-S-9,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,E是AC的中点,DE的延长线与BC 的延长线交于点F.求证:(1)△FDC∽△FBD;(2)AC·BF=BC·DF.图9-S-9将图9-S-10中的△ADE绕点A旋转一定角度,得到△ABC,称之为旋转型的基本图形.图9-S-107.如图9-S-11,△ABC和△CEF均为等腰直角三角形,点E在△ABC内,∠CAE+∠CBE=90°,连接BF.(1)求证:△CAE∽△CBF;(2)若BE=1,AE=2,求CE的长.图9-S-118.如图9-S-12,设D为锐角三角形ABC内一点,∠ADB=∠ACB+90°.(1)求证:∠CAD+∠CBD=90°;(2)如图②,过点B作BE⊥BD,BE=BD,连接EC,若AC·BD=AD·BC,求证:△ACD∽△BCE.图9-S-12类型五一线三等角型(1)三等角型相似三角形是以等腰三角形或等边三角形为背景的.图9-S-13(2)三直角型相似三角形是以正方形或矩形为背景的.图9-S-149.如图9-S-15,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B,C重合),满足∠DEF=∠B,且点D,F分别在边AB,AC上.(1)求证:△BDE∽△CEF;(2)当点E移动到BC的中点时,求证:FE平分∠DFC.图9-S-1510.在△ABC中,AB=AC,点D,E,F分别在BC,AB,AC上,∠EDF=∠B.(1)如图9-S-16①,求证:DE·CD=DF·BE.(2)若D为BC的中点,如图②,连接EF.①求证:ED平分∠BEF;②若四边形AEDF为菱形,求∠BAC的度数及AE AB的值.图9-S-1611.(1)如图9-S-17①,已知AB⊥l,DE⊥l,垂足分别为B,E,C是l上一点,且∠ACD=90°.求证:△ABC∽△CED;(2)如图9-S-17②,在四边形ABCD中,已知∠ABC=90°,AB=3,BC=4,CD=10,AD=55,求BD 的长.图9-S-17特训09相似三角形的基本模型1.5【解析】本题图中有两组平行线,故存在平行线型的基本图形,把它们一一分离出来,如图①~④.又由于△ADE∽△BFE∽△CFD,故共有5对相似三角形.2.证明:∵EC∥AB,∴OA OE=OB OD,∠EDA=∠DAB.∵∠EDA=∠ABF,∴∠DAB=∠ABF.∴AD∥BC.∴∠OBF=∠ODA,∠OFB=∠OAD.∴△OBF∽△ODA.∴OB OD=OF OA.∴OA OE=OF OA.∴OA2=OE·OF.3.证明:(1)∵∠ABE=∠ACD,且∠A是公共角,∴△ABE∽△ACD.∴AE AD=AB AC,即AE AB=AD AC.又∵∠A是公共角,∴△AED∽△ABC.(2)∵∠ABE=∠ACD,∠BGD=∠CGE,∴△BGD∽△CGE.∴DG EG=BG CG,即DG BG=EG CG.又∵∠DGE=∠BGC,∴△DGE∽△BGC.∴∠GDE=∠GBC.∵BE平分∠ABC,∴∠GBC=∠ABE.∵∠ABE=∠ACD,∴∠GDE=∠ACD.∴DE=CE.4.解:(1)证明:如图,延长AC,BD交于点F.∵AD⊥BD,∴∠ADB=∠ADF=90°.∵AD平分∠CAB,∴∠DAB=∠DAF.又∵AD=AD,∴△ADB≌△ADF.∴BD=FD.∵AE=2BD,∴AE=BF.∵∠ACE=∠BDE=90°,∠AEC=∠BED,∴∠CAE=∠CBF.又∵∠ACE=∠BCF=90°,AE=BF,∴△ACE≌△BCF.∴CA=CB.(2)∵CF⊥AD,BD⊥AD,∴∠CFE=∠D=90°.又∵∠BED=∠CEF,∴△BDE∽△CFE.∵∠ACE=90°,CF⊥AE,∴△CFE∽△ACE∽△AFC∽△BDE.∵∠ACE=∠ADB=90°,∠CAE=∠DAB,∴△ACE∽△ADB.∴△ADB∽△BDE.∴图中与△BDE相似的三角形有△CFE,△ACE,△AFC,△ADB.5.答案不唯一,如∠PCA=∠B【解析】本题为开放题,答案不唯一.注意到△APC与△ACB属于“母子”型基本图形,而∠A为公共角,故还需具备的一个条件是∠PCA=∠B或∠APC=∠ACB或AC2=AP·AB即AC AP=AB AC.6.证明:(1)∵CD⊥AB,∴∠ADC=90°.又∵E是AC的中点,∴DE=EC.∴∠EDC=∠ECD.∵∠ACB=90°,∠BDC=90°,∴∠ECD+∠DCB=90°,∠DCB+∠B=90°.∴∠ECD=∠B.∴∠FDC=∠B.又∵∠F=∠F,∴△FDC∽△FBD.(2)∵△FDC∽△FBD,∴DF BF=DC BD.∵∠BDC=∠BCA=90°,∠B=∠B,∴△CBD∽△ABC.∴BD BC=DC AC,即DC BD=AC BC.∴DF BF=AC BC.∴AC·BF=BC·DF.7.解:(1)证明:∵△ABC和△CEF均为等腰直角三角形,∴AC BC=CE CF=2,∠ACB=∠ECF=45°.∴∠ACE=∠BCF.∴△CAE∽△CBF.(2)∵△CAE∽△CBF,∴∠CAE=∠CBF,AE BF=AC BC=2.又∵AE=2,∴BF=2.∵∠CAE+∠CBE=90°,∴∠CBF+∠CBE=90°.∴∠EBF=90°.∴EF2=BE2+BF2=12+(2)2=3.∴EF=3.∵CE2=2EF2=6,∴CE=6.8.证明:(1)如图,延长CD交AB于点E.∵∠ADE=∠CAD+∠ACD,∠BDE=∠CBD+∠BCD,∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB.又∵∠ADB=∠ACB+90°,∴∠CAD+∠CBD=90°.(2)∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,∴∠CAD=∠CBE.∵AC·BD=AD·BC,BD=BE,∴AC BC=AD BE.∴△ACD∽△BCE.9.证明:(1)∵AB=AC,∴∠B=∠C.∵∠BDE=180°-∠B-∠DEB,∠CEF=180°-∠DEF-∠DEB,∠DEF=∠B,∴∠BDE=∠CEF.∴△BDE∽△CEF.(2)∵△BDE∽△CEF,∴BE CF=DE EF.∵E是BC的中点,∴BE=CE.∴CE CF=DE EF,即DE CE=EF CF.又∵∠DEF=∠B=∠C,∴△DEF∽△ECF.∴∠DFE=∠EFC.∴FE平分∠DFC.10.解:(1)证明:∵在△ABC中,AB=AC,∴∠B=∠C.∵∠B+∠BDE+∠DEB=180°,∠BDE+∠EDF+∠FDC=180°,∠EDF=∠B.∴∠FDC=∠DEB.∴△BDE∽△CFD.∴DE DF=BE CD,即DE·CD=DF·BE.(2)①证明:同(1)可证△BDE∽△CFD,∴BE CD=DE DF.∵D为BC的中点,∴BD=CD.∴BE BD=DE DF,即BE DE=BD DF.又∵∠B=∠EDF,∴△BDE∽△DFE.∴∠BED=∠DEF.∴ED平分∠BEF.②∵四边形AEDF为菱形,∴∠AEF=∠DEF,AE=AF=DE.又∵∠BED=∠DEF,∴∠AEF=∠BED=∠DEF=60°.又∵AE=AF,∴∠BAC=60°.又∵AB=AC,∴△ABC是等边三角形.∴∠B=60°.∴△BED是等边三角形.∴BE=DE.又∵AE=DE,∴AE=12AB.∴AE AB=12.11.解:(1)证明:∵AB⊥l,DE⊥l,∴∠ABC=∠CED=90°,∠ACB+∠BAC=90°.∵∠ACD=90°,∴∠ACB+∠ECD=90°.∴∠BAC=∠ECD.∴△ABC∽△CED.(2)如图,连接AC.∵∠ABC=90°,AB=3,BC=4,∴AC=AB2+BC2=5.又∵AD=55,CD=10,∴AC2+CD2=AD2.∴∠ACD=90°.过点D作DE⊥BC交其延长线于点E.由(1)得此时△ABC∽△CED,∴CE AB=DE BC=CD AC=2.∴CE=6,DE=8.在Rt△BDE中,BD=BE2+DE2=(4+6)2+82=241.。
小学一年级数学思维提升特训题+答案

思维训练题1、A、B、 C 三名运动员在一次运动会上都得了奖。
他们各自参加的项目是篮球、排球和足球。
现在我们知道:(1)A 的身材比排球运动员高;(2)足球运动员比 C 和篮球运动员都矮。
请你想一想:A 是( )运动员,B 是( )运动员,C 是( )运动员。
2、爸爸买了 3 个皮球,两个红的,一个黄的。
哥哥和妹妹都想要。
爸爸叫他们背对着背坐着,爸爸给哥哥塞了个红的,给妹妹塞了个黄的,把剩下的一个球藏在自己背后。
爸爸让他们猜他手里的球是什么颜色的,谁猜对了,就把球给谁。
那么,谁一定能猜对呢 ? ( )。
3、小菲、小南、小阳三个小朋友,分别戴着红、黄、蓝三顶帽子,排着队儿向前走,谁也不回头。
小南能看见一顶红帽子和一顶黄帽子,小菲只能看到一顶黄帽子,而小阳一顶帽子也看不到。
你知道走在第一个的是谁 ?谁又走在第二个 ?最后一个又是谁呢 ?他们又各自戴着什么颜色的帽子呢 ? ( )走在第一个,戴着( )帽子;( )走在第二个,戴着( )帽子;( )走在最后,戴着( )帽子;4、黑兔、灰兔和白兔三只兔子在赛跑。
黑免说:“我跑得不是最快的,但比白兔快。
”请你说说,谁跑得最快 ?谁跑得最慢 ? ( )跑得最快,( )跑得最慢。
5、三个小朋友比大小。
根据下面三句话,请你猜一猜,谁最大 ?谁最小?(1) 芳芳比阳阳大 3 岁;(2) 燕燕比芳芳小 1 岁;(3) 燕燕比阳阳大 2 岁。
( )最大,( )最小。
6、根据下面三句话,猜一猜三位老师年纪的大小。
(1) 王老师说:“我比李老师小。
”(2) 张老师说:“我比王老师大。
”(3) 李老师说:“我比张老师小。
”年纪最大的是( ),最小的是( )。
7、光明幼儿园有三个班。
根据下面三句括,请你猜一措,哪一班人数最少 ?哪一班人数最多 ?(1) 中班比小班少;(2) 中班比大班少;(3) 大班比小班多。
( )人数最少,( )人数最多。
8、三个同学比身高。
甲说:我比乙高;乙说:我比丙矮;丙:说我比甲高。
思维特训(一) “填幻方”问题-文档资料

思维特训(一)“填幻方”问题方法点津·一、杨辉法中国南宋时期杰出的数学家杨辉在《续古摘奇算法》中介绍了一种排三阶幻方的编写方法,如图1-S-1.九子斜排,上下对易,左右相更,四维挺出.图1-S-1也就是将1~9九个自然数依次斜排为三行三列(如图①),再把上下两个数(1和9)对换,左右两个数(7和3)对换(如图②),最后将四角上的数向四个角挺出,就得到三级幻方(如图③).注意:“九子斜排”的时候,要么都按照从下向上的顺序依次填写,要么都按照从上向下的顺序依次填写,如果打乱顺序,结果可能就错了.二、口诀法一填首行正中央,依次斜上莫要忘,上出下填右出左,若是重了填下方.具体解释如下:如图1-S-2,“一填首行正中央”,指的是1~9这九个数按照从小到大的顺序,第一个数要填在第一行的正中间一个方格中;“依次斜上莫要忘”,指的是后面一个数字填在前一个数的右上方;“上出下填右出左”,指的是如果向上超出幻方,就填在这一列的最下方,如果向右超出幻方,就填在这一行的最左边一个方格中;“若是重了填下方”,若是发现要填的方格已经有数字了,那么就填在前一个数字的正下方.对于数字“7”它正好位于行和列的交叉位置,我们当作重复对待,填在前一个数字“6”的正下方.这种方法适合三阶、五阶、七阶等所有奇数阶幻方.图1-S-2典题精练·1.我国古代的“河图”是由3×3的方格构成的,每个方格内均有数目(个数为1~9)不同的点图,每一行、每一列以及每一条对角线上的三个点图的点数之和均相等.如图1-S-3给出了“河图”的部分点图,请你推算出P处所对应的点图是()图1-S-3图1-S-42.在3×3的方格上做填字游戏,要求每行、每列及每条对角线上的三个方格中的数字和都等于S,填在图中三格中的数字如图1-S-5所示,若要填成,则S=________.图1-S-53.教材在七年级数学(上册)的第21页介绍了填幻方,这部分内容就是传说中的“龟背图”,也就是“九宫图”.如图1-S-6,根据所给的“九宫图”请你找找规律,利用发现的规律将3,5,-7,1,7,-3,9,-5,-1这九个数字分别填入图中的九个方格中,使得横、竖、斜对角的三个数字和相等.图1-S-64.将5,7,9,11,13,15,17,19,21填入如图1-S-7所示的小方格中,使之成为一个3×3的幻方,即各行、各列以及各对角线上3个数的和都相等.图1-S-75.试将-2,-1,0,1,2,3,4,5,6填入如图1-S-8所示的3×3的方格中,使得每行、每列及每条对角线上的三个数之和相等.图1-S-86.将-15,-12,-9,-6,-3,0,3,6,9填入如图1-S-9所示的3×3方格中,使大方格的横、竖、斜对角的3个数字之和都相等.图1-S-97.图1-S-10是一个3×3的幻方,每行的三个数、每列的三个数、每斜对角上的三个数相加的和均相等.如何把9个连续整数迅速填入一个3×3方格中,使每行、每列、每斜对角上的三个数相加的和均相等,是我们祖先早就在研究的问题.古代的“洛书”、汉朝徐岳的“九宫算”就揭示出祖先们得到的神奇填写方法.图①是把-4,-3,-2,-1,0,1,2,3,4填入一个3×3方格中,使每行、每列、每斜对角上的三个数相加的和均相等的一种方法.(1)请观察图①中数字的填写规律,将下列各数组中的9个数分别填入图②③④所示的3×3方格中,使得每行的三个数、每列的三个数、每斜对角上的三个数相加的和均相等.第一组:6,5,4,3,2,1,0,-1,-2;第二组:9,8,7,6,5,4,3,2,1;第三组:-8,-6,-4,-2,0,2,4,6,8.图1-S-10(2)拓展探究:在图1-S-11所示的9个空格中,填入5个2和4个-2,使得每行、每列、每斜对角上的三个数的乘积都是8.图1-S-11(3)拓展探究:将25,24,23,22,21,20,19,18,17,16,15,14,13,12,11,10,9,8,7,6,5,4,3,2,1这25个数分别填入图1-S-12所示的25个空格中,使得每行、每列、每斜对角上的五个数相加的和均相等.图1-S-12详解详析1.C2.30[解析] 如图,因为每行、每列及每条对角线上的三个方格中的数字和都等于S,所以x +10+y=8+y+13,所以x=11.所以b+11+a=8+10+a,所以b=7,所以S=b+10+13=30.3.解:填法不唯一,如图:4.解:填法不唯一,如图:5.解:填法不唯一,根据杨辉法填图如下:故答案如下:6.解:填法不唯一,填图如下:7.解:(1)如图所示(填法不唯一):(2)填法不唯一,填写如图所示:(3)填写如图所示(填法不唯一):。
思维特训(九) 抛物线背景下线段和(差)的最值问题

思维特训(九) 抛物线背景下线段和(差)的最值问题类型一二次函数中的“饮马问题”基本原理:两点之间,线段最短.解题思路:利用抛物线自身的轴对称性找到抛物线上某点关于对称轴的对称点,实现化“折”为“直”,再结合函数的相关知识解决.1.如图9-1,抛物线y=ax2+bx+c 经过A(-1,0),B(3,0),C(0,3)三点,直线l 是抛物线的对称轴.(1)求抛物线的解析式;(2)设P 是直线l 上的一个动点,当PA+PC 最小时,求点P 的坐标.图9-12.如图9-2,抛物线y=ax2+bx+3 经过A(1,0),B(4,0)两点.(1)求抛物线的解析式.(2)在抛物线的对称轴上是否存在点P,使得四边形PAOC 的周长最小?若存在,求出四边形PAOC 周长的最小值;若不存在,请说明理由.图9-23.如图9-3,已知抛物线y=ax2+bx+c 经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l 与x 轴交于点H.(1)求该抛物线的解析式;(2)PQ 是该抛物线对称轴l 上的动线段,且PQ=1,求PC+QB 的最小值.图9-3类型二二次函数中线段差的最大值问题基本原理:三角形任何两边之差小于第三边.解题思路:先根据原理确定线段差的最值问题时的图形,再根据已知条件进行求解.4.如图9-4,抛物线y=x2+bx+c 过点A(3,0),B(1,0),交y 轴于点C,P 是该抛物线上一动点,点P 从点C 沿抛物线向点A 运动(点P 不与点A,C 重合),过点P 作PD∥y 轴交直线AC 于点D.(1)求抛物线的解析式.(2)当D 在线段AC 上运动时,求点P 在运动的过程中线段PD 长度的最大值.(3)在抛物线的对称轴上是否存在点M,使|MA-MC|的值最大?若存在,请求出点M 的坐标;若不存在,请说明理由.图9-45.2016·眉ft已知:如图9-5,在平面直角坐标系xOy 中,A,B,C 分别为坐标轴上的三个点,且OA=1,OB=3,OC=4,(1)求经过A,B,C 三点的抛物线的解析式.(2)在平面直角坐标系xOy 中是否存在一点P,使得以点A,B,C,P 为顶点的四边形为菱形?若存在,请求出点P 的坐标;若不存在,请说明理由.(3)若M 为该抛物线上一动点,在(2)的条件下,请求出当|PM-AM|取最大值时点M 的坐标,并直接写出|PM-AM|的最大值.图9-56.已知:如图9-6,在平面直角坐标系xOy 中,直线y 3+6 与x 轴、y 轴的交点=-4x分别为A,B,将∠OBA 对折,使点O 的对应点H 落在直线AB 上,折痕交x 轴于点C.(1)直接写出点C 的坐标,并求经过A,B,C 三点的抛物线的解析式.(2)若(1)中抛物线的顶点为D,在直线BC 上是否存在点P,使得四边形ODAP 为平行四边形?若存在,求出点P 的坐标;若不存在,说明理由.(3)若把(1)中的抛物线向左平移3.5 个单位长度,则图象与x 轴交于G,N(点G 在点N 的左侧)两点,交y 轴于点E,则在此抛物线的对称轴上是否存在一点Q,使点Q 到E,N 两点的距离之差最大?若存在,请求出点Q 的坐标;若不存在,请说明理由.图9-63 典题讲评与答案详析 1.解:(1)∵抛物线 y =ax 2+bx +c 经过 C (0,3),∴c =3.∵抛物线 y =ax 2+bx +3 经过 A (-1,0),B (3,0),⎧0=a -b +3, ∴⎨ ⎧a =-1, 解得⎨⎩0=9a +3b +3, ⎩b =2,∴抛物线的解析式为 y =-x 2+2x +3. (2)∵y=-x 2+2x +3=-(x -1)2+4,∴对称轴为直线 x =1.∵A ,B 是抛物线与 x 轴的交点,∴点 A ,B 关于直线 l 对称,∴PA +PC 最小时,点 P 就是直线 BC 与直线 l 的交点(如图).∵B (3,0),C (0,3),∴直线 BC 的解析式为 y =-x +3.∵点 P 在直线 l 上,∴点 P 可设为(1,m ).将(1,m )代入 y =-x +3,可得 m =2,∴P (1,2).2.解:(1)由已知,得⎧a +b +3=0, ⎧a =4, ⎨ 解得⎨ 15 ⎩16a +4b +3=0, ⎩b =- 4 . ∴抛物线的解析式为 y 3 2 15+3.=4x - 4 x(2)∵A ,B 关于对称轴对称,如图,连接 BC ,∴BC 与对称轴的交点即为所求的点 P ,此时 PA +PC =BC ,∴四边形 PAOC 的周长的最小值为 OC +OA +BC .∵A (1,0),B (4,0),C (0,3), ∴OA =1,OC =3,BC = OB 2+OC 2=5,∴OC +OA +BC =3+1+5=9,∴在抛物线的对称轴上存在点 P ,使得四边形 PAOC 的周长最小,四边形 PAOC 周长的最小值为 9.3. 解:(1)∵抛物线 y =ax 2+bx +c 经过 C (0,3),∴c =3.∵抛物线 y =ax 2+bx +3 经过 A (-3,0),B (1,0),⎧0=a +b +3, ∴⎨ ⎧a =-1, ∴⎨⎩0=9a -3b +3, ⎩b =-2,∴抛物线的解析式为 y =-x 2-2x +3.(2)过点 C 作直线 l 的对称点 E ,过点 E 作 EG ⊥AB 于点 G ,过点 Q 作 QF ∥PE ,交 EG 于点 F ,连接 FB ,如图,则有 PC =PE ,EF ∥PQ .∵EF ∥PQ ,QF ∥PE ,∴四边形 EFQP 是平行四边形,∴EF =PQ =1,PE =FQ ,∴PC =FQ ,∴PC +QB =FQ +QB ,根据两点之间线段最短可得 FQ +QB (即 PC +QB )的最小值为 FB .∵抛物线 y =-x 2-2x +3 的对称轴为直线 x =-1,C (0,3),∴点 E 的坐标为(-2,3), ∴点 F 的坐标为(-2,2).在 Rt △FGB 中,FG =2,GB =1-(-2)=3,根据勾股定理可得 FB = FG 2+GB 2= 13.∴PC +QB 的最小值为 13.4.解:(1)∵抛物线 y =x 2+bx +c 过点 A (3,0), B (1,0), ⎧9+3b +c =0, ⎧b =-4, ∴⎨ ⎩1+b +c =0, 解得⎨ ⎩c =3, ∴抛物线的解析式为 y =x 2-4x +3. (2)令 x =0,则 y =3,∴点 C (0,3), 则直线 AC 的解析式为 y =-x +3. 设点 P (x ,x 2-4x +3).∵PD ∥y 轴, ∴D (x ,-x +3), ∴PD =(-x +3)-(x 2-4x +3)=-x 2+3x =-(x 3 2 9 .∵a =-1<0,∴当 x 3 -2) +4(0<x <3) PD 的长度有最大值9=2时,线段 4.(3)∵抛物线的对称轴垂直平分 AB ,∴MA =MB .由三角形的三边关系,可知|MB -MC |<BC ,∴当 M ,B ,C 三点共线时,|MB -MC |的值最大,为 BC 的长度. 设直线 BC 的解析式为 y =kx +m (k ≠0),⎧k +m =0, ⎧k =-3, 则⎨ ⎩m =3, 解得⎨⎩m =3,∴直线 BC 的解析式为 y =-3x +3.∵抛物线 y =x 2-4x +3 的对称轴为直线 x =2,∴当 x =2 时,y =-3×2+3=-3,∴M (2,-3),即抛物线的对称轴上存在点 M (2,-3),使|MA -MC |的值最大.5.解:(1)设抛物线的解析式为 y =ax 2+bx +c .3 ⎧ =-4, , ⎨ 由题意易知 A (1,0),B (0,3),C (-4,0),⎧a +b +c =0, ∴⎨c =3, ⎩16a -4b +c =0,⎧a 3 解得⎨b9 ⎩=-4, c =3, ∴经过 A ,B ,C 三点的抛物线的解析式为 y =-3 2 9 +3.(2)存在.∵OB =3,OC =4,OA =1,∴BC =AC =5,AB = 10. 如图,当 BP 綊 AC 时,四边形 ACBP 为菱形,∴BP =AC =5,且点 P 到 x 轴的距离等于 OB ,∴点 P 的坐标为(5,3).4x -4x当点 P 在第二、三象限时,以点 A ,B ,C ,P 为顶点的四边形只能是平行四边形,不 是菱形,∴当点 P 的坐标为(5,3)时,以点 A ,B ,C ,P 为顶点的四边形为菱形.(3)设直线 PA 的解析式为 y =kx +m (k ≠0).∵点 A (1,0),P (5,3)在直线 PA 上,⎧k = , ⎧5k +m =3,4 ∴⎨ ⎩k +m =0, 解得⎨ ⎩m =-3 4 ∴直线 PA 的解析式为 y 3 3=4x -4.当点 M 与点 P ,A 不在同一直线上时,根据三角形的三边关系,知|PM -AM |<PA , 当点 M 与点 P ,A 在同一直线上时,|PM -AM |=PA ,∴当点 M 与点 P ,A 在同一直线上时,|PM -AM |的值最大,即 M 为直线 PA 与抛物线的交点. 3 3 y = x - , 解方程组 4 4 3 9 ⎩y =-4x 2-4x +3, ⎧x 1=1,⎧⎪x 2=-5, 得⎨ ⎨ 9 ⎩y 1=0,⎪⎩y 2=-2, ∴点 M 的坐标为(1,0)或(-59 时,|PM -AM |的值最大.此时|PM -AM |的最大值 为 5.6.解:(1)如图①,连接 CH .,-2)由轴对称的性质,得 CH ⊥AB ,BH =BO ,CH =CO ,∴在 Rt △CHA 中,由勾股定理,得4 AC 2=CH 2+AH 2. ∵直线 y 3 +6 与 x 轴、y 轴的交点分别为 A ,B , =-4x ∴当 x =0 时,y =6,当 y =0 时,x =8, ∴B (0,6),A (8,0), ∴BO =6,OA =8, 在 Rt △AOB 中,由勾股定理,得 AB =10. 设 C (p ,0),则 OC =p , ∴CH =p ,AH =4,AC =8-p , ∴(8-p )2=p 2+42,解得 p =3,∴C (3,0). 设抛物线的解析式为 y =ax 2+bx +c . ⎧a 1 ⎧6=c , =4, 由题意,得⎨64a +8b +c =0,解得⎨b 11 ⎩0=9a +3b +c , =- , ⎩c =6, ∴抛物线的解析式为 y 1 2 11x +6. =4x - 41 2 11 1⎛x 11⎫ (2)不存在.理由:如图②,设抛物线对称轴交 x 轴于点 F .∵y =4x - 4 x +6=4⎝ - 2 ⎭ 2 25 -16, ∴ 11 25 25 D ( 2 ,-16),∴DF =16. 设直线 BC 的解析式为 y =kx +b ′,则有 ⎧6=b ′, ⎨ ⎧k =-2, 解得⎨ ⎩0=3k +b ′, ⎩b ′=6, ∴直线 BC 的解析式为 y =-2x +6. 设存在点 P 使四边形 ODAP 是平行四边形,P (m ,n ). 过点 P 作 PM ⊥OA 于点 M , 则∠PMO =∠AFD =90°,PO =DA ,PO ∥DA , ∴∠POM =∠DAF ,∴△OPM ≌△ADF , ∴PM =DF =n 25 25 2m +6, =16,∴16=- ∴m 71 =32, 但 OM =AF =8 11 5 71 - 2 =2≠32, ∴点 P 不在直线 BC 上,即直线 BC 上不存在满足条件的点 P . (3)由题意得,平移后的抛物线的解析式为 y 1 -2)225 为直线 x =2.=4(x -16,∴平移后抛物线的对称轴1 9∴⎨9当x=0 时,y=-16;当y=0 时,01(x-2)225=41 9解得x1=-,x2=.-16,2 2∵点G 在点N 的左侧,∴G(19 9-2,0),E(0,-16),N(2,0).如图③,连接EG,直线EG 交直线x=2 于点Q,则此时点Q 到E,N的距离之差最大.设直线EG 的解析式为y=k0x+b0,则⎧0=-2k0+b0,⎧k0=-8,⎨9 解得⎨9⎩b0=-16,⎩b0=-16,∴直线EG 的解析式为y=-9 9⎧y 9 9 8x-16,⎧x=2,⎪=-8x-16,⎪解得⎨ 45⎪⎩x=2,∴Q(2 45 .⎪⎩y=-16,,-16)。
七年级数学(上)思维特训(9):整式加减中的“无关”问题(含答案)

思维特训(九)整式加减中的“无关”问题方法点津·一般来说,整式的值与整式所含字母的取值是有关的,当字母取唯一数值时,得到的整式的值也是唯一的,但当整式不含这个字母时,整式的值便与这个字母的取值无关.典题精练·类型一同一字母取不同数值时,整式的值不变此种情况说明整式的值与此字母的取值无关,即整式化简后的结果中这个字母的系数为0.1.一天,数学老师布置了一道数学题:已知x=2018,求整式(x3-6x2-7x+8)-(-x2-3x+2x3-3)+(x3+5x2+4x-1)的值,小明观察后提出:“已知x=2018是多余的.”你认为小明的说法有道理吗?请说明理由.2.课堂上李老师给出了一道整式求值的题目,李老师把要求的整式(7a3-6a3b+3a2b)-(-3a3-6a3b+3a2b+10a3-3)写在黑板上,让王红同学给出一组a,b的值,老师自己说答案,当王红说完:“a=65,b=-2005”后,李老师不假思索,立刻就说出答案为3.同学们莫名其妙,觉得不可思议,但李老师用坚定的口吻说:“这个答案准确无误”.你能说出其中的道理吗?3.已知x2+ax-2y+7-(bx2-2x+9y-1)的值与x的取值无关,求a+b的值.4.已知2x2+ax-y+6-bx2+3x-5y-1的值与字母x的取值无关,且A=4a2-ab+4b2,B=3a2-ab+3b2,求3A-[2(3A-2B)-3(4A-3B)]的值.类型二 同一字母取值互为相反数时,整式的值不变此种情况说明整式化简后的结果要么不含有这个字母,要么只含这个字母的偶次方项或绝对值项.5.小强与小亮在同时计算这样一道题:当a =-3时,求整式7a 2-[5a -(4a -1)+4a 2]-(2a 2-a +1)的值.小亮正确求得结果为7,而小强在计算时,错把a =-3看成了a =3,但他计算的结果也正确,你能说明为什么吗?6.有这样一道计算题:求3x 2y +[2x 2y -(5x 2y 2-2y 2)]-5(x 2y +y 2-x 2y 2)的值,其中x =12,y =-1.小明同学把“x =12”错看成“x =-12”,但计算结果仍正确;小华同学把“y =-1”错看成“y =1”,计算结果也是正确的,你知道其中的道理吗?请加以说明.详解详析1.解:小明的说法有道理.理由如下:原式=x3-6x2-7x+8+x2+3x-2x3+3+x3+5x2+4x-1=(1-2+1)x3+(-6+1+5)x2+(-7+3+4)x+(8+3-1)=10.由此可知整式的值与x的取值无关,所以小明的说法有道理.2.解:原式=7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+3=3.整式的结果与a,b的取值无关,恒为3.3.解:原式=(1-b)x2+(a+2)x-11y+8,因为整式的值与x的取值无关,所以1-b=0,a+2=0,解得a=-2,b=1,则a+b=-2+1=-1.4.解:2x2+ax-y+6-bx2+3x-5y-1=(2-b)x2+(a+3)x-6y+5,由结果与x的取值无关,得到2-b=0,a+3=0,解得a=-3,b=2,则原式=3A-6A+4B+12A-9B=9A-5B=9(4a2-ab+4b2)-5(3a2-ab+3b2)=36a2-9ab+36b2-15a2+5ab-15b2=21a2-4ab+21b2=189+24+84=297.5.解:原式=7a2-5a+4a-1-4a2-2a2+a-1=a2-2,当a=3和a=-3时,整式的结果都为9-2=7,故小亮正确求得结果为7,而小强在计算时,错把a=-3看成了a=3,但计算的结果也正确.6.解:原式=3x2y+2x2y-5x2y2+2y2-5x2y-5y2+5x2y2=-3y2,整式化简后的结果不含x,所以整式的值与x的取值无关.当y=±1时,y2=1,原式=-3.。
【思维特训案例-讲练合卷】四年级数学上册思维特训案例第9集《应用题综合》(附试题+答案解析)

四年级数学上册《应用题综合(一)》思维特训案例班级:姓名:效果:例1.一人看见山上有一群羊,他自言自语道:“我如果有这些羊,再加上这些羊,然后加上这些羊的一半.又加上这些羊一半的一半,最后再加上我家里的那一只,一共有100只羊。
”山上的羊群共有()只。
例2.2011年3月11日,日本发生里氏9级大地震.在3月15日,日本本州岛东海岸附近海发生5级地震,已知里氏地震级数每升2级,地震释放能量扩大到原来的1000倍,那么3月11日的大地震释放能量是3月1 5日东海岸地震的()倍.例3.上午黑猩猩推着两筐桃子去集市卖,大筐有400个,小筐有240个,到了中午,两筐都卖了相等个数的桃子,剩下桃子的数量大筐恰好是小筐的5倍,上午共卖出了()个桃子。
例4.一张试卷共有21道题,答对一道得8分,答错一道扣6分.小明答完了所有的题目,却得了零分,他答对()道题.例5.已知7个红球和5个白球共重43克,5个红球和7个白球共重47克,那么4个红球和8个白球共重()克。
例6.甲、乙、丙三条公路,甲公路的长度是乙公路的3倍,乙公路的长度比丙公路的2倍少25千米,甲公路的长度比丙公路长240千米,甲公路长()千米,乙公路长()千米,丙公路长()千米,例7.某班43名同学围成一圈.由班长起从1开始连续报数,谁报到100,谁就表演一个节目;然后再由这个同学起从1开始连续报数,结果第一个演节目的是小明,第二个演节目的是小强.那么小明和小强之间有()名同学.例8.几个小朋友在一起做游戏,选一个小朋友做队长,男孩做队长时,队员中女孩比男孩多一倍;女孩做队长时,队员中男孩和女孩一样多.男孩有()人,女孩有()人.例9.柯南家2008年一年用电10200千瓦时,上半年的月平均用电比下半年的月平均用电少100千瓦时.柯南家下半年月平均用电为()千瓦时.例10.某校男老师的平均年龄是27岁,女老师的平均年龄是32岁,全体老师的平均年龄是30岁.如果男老师比女老师少13名,那么该校共有()名老师.例11.喜羊羊等一群小羊割了一堆青草准备过冬吃.他们算了一下,平均每只小羊割了45千克.如果除了他们自己外,再分给慢羊羊村长一份,那么每只小羊可分得36千克.回到村里,懒羊羊走来,也要分一份,这样一来,每只小羊就只能分得()千克草了.例12.某汽车厂同时建成两条生产线.第一条生产线第一个月生产了1000辆汽车,以后每个月比前一个月多生产100辆;第二条生产线第一个月也生产了1000辆汽车,以后每半个月比前半个月多生产50辆.那么,该厂生产20000辆汽车需()个月.例13.某校学生总人数比四年级人数的6倍少78人,并且除了四年级外其他各年级的学生人数总和力2222人,那么该校共有学生()人.例14.如下图所示,有海、陆、空三个兵种组成的仪仗队,每兵种队伍有400人,都平均分成8竖行并排前进,海军前后两排间隔1米,陆军前后两排间隔2米,空军前后两排间隔3米,各兵种队伍之间相隔5米,三兵种士兵每分钟都走90米,仪仗队通过检阅台需4分钟.那么检阅台总长为()米.8竖行例15.某商场有一些糖果,其中水果糖每千克5.6元,奶糖每千克7.2元,巧克力每千克8.8元.奶糖比水果糖少3千克,比巧克力多2千克,这些糖果平均价格每千克7元.那么,巧克力有()千克.例16. 宁宁、蕾蕾和凡凡三人合租一辆轿车从学校回家(见下图).他们约定:共同乘坐的部分所产生的车费由乘坐者平均分摊;单独乘坐的部分所产生的车费,由乘坐者单独承担,结果,三人承担的车费分别为10元、25元、85元.宁宁家距离学校12公里,凡凡家距离学校()公里。
中考物理专题《 质量与密度计算题》特训提升培优原卷

专题02 质量与密度计算题专题特训学生(提升培优)二、计算题31.(2021·江苏徐州·八年级期中)细心的小明发现寒冷的冬天在室外的盛水缸常常被裂,如图所示,是什么原因呢?请你帮他做个计算:一个容积为0.18m3的水缸盛满水,则缸中(g取10N/kg)(1)水的重力是多少N?(2)水全部结冰后,冰的体积是多少m3?( 浮=0.9×103kg/m3)32.(2021·江苏泰州中学附属初中八年级月考)小明利用天平和烧杯测量某种液体的密度,得到的数据如表所示。
(1)根据数据绘出图像,并指出图线与m轴交点的物理意义。
(2)液体的密度是多大?33.(2021·江苏泰州中学附属初中八年级月考)有个体积为0.5 dm3的铁球,其质量为1.58 kg,问:(1)它是实心的还是空心的?(ρ铁=7.9×103 kg/m3)(2)若它是空心的,空心部分的体积是多大?34.(2021·吴江市高级中学八年级月考)酒的度数表示每100毫升酒液中所含酒精量的毫升数,若现有60度和30度的酒液若干,酒液中的微量元素忽略不计,不考虑酒液混合后体积减少。
求:(1)60度酒液的密度。
(2)如果用这两种酒液进行勾兑,获得42度、1000mL的酒液,那么需要这两种酒液各多少毫升。
(已知ρ酒精=0.8×103kg/m3,ρ水=1.0×103kg/m3,不考虑酒液混合后体积减小)(3)我国法律规定:当驾驶员每100mL血液中的酒精含量大于或者等于20mg,小于80mg的驾驶行为,就属于饮酒驾驶;当驾驶员每100mL血液中的酒精含量大于或者等于80mg的驾驶行为,就属于醉酒驾驶。
一个质量为60kg的人体血液总量约为4000mL,则一个60kg的人只要喝了多少毫升的40度白酒就会达到饮酒驾驶的标准?(酒精的密度为0.8×103kg/m3,设人饮酒后酒精全部进入血液,且血液总体积不变)35.(2021·江苏苏州·八年级期中)小聪家最近装修房子,买来一车体积为35m的沙子堆m=的桶,用这只在家门口,为了帮助爸爸估测这堆沙子的质量,他找来一只质量11kgm=;再用这只桶平平地装满一桶沙子,测得桶装满一桶水,测得水和桶的总质量27kgm=。
思维特训(二) 四冲程内燃机

思维特训(二) 四冲程内燃机|典|例|分|析|四冲程内燃机中的计算例 2021·内江汽车的发动机工作时,吸入汽缸的汽油和空气的比例,决定了汽车的动力性能和经济性能。
某汽车四冲程汽油发动机的汽缸总排量为2 L (发动机每个工作循环吸入或排出的流体体积称为汽缸排量),发动机工作时,吸入汽缸的是由汽油和空气所形成的混合物,混合物的密度ρ=1.44 kg /m 3,汽油和空气的质量比为1∶15,汽油的热值q =4.5×107 J /kg 。
假如发动机曲轴在1 min 内转动3×103转,发动机的效率为40%,那么,在这种情况下:(1)汽车在1 min 内做的有用功是多少?(2)汽车在平直的公路上匀速行驶时受到的阻力为f =3×103 N ,汽车行驶的速度是多少?[答案] (1)发动机转速为3×103 r /min ,那么每分钟完成的工作循环数为1500个,其中吸气冲程1500个,吸入的混合气的体积为1500×2 L ,根据空气和汽油的质量比为15∶1可知,汽油的质量占这些混合气体质量的116。
每分钟吸入汽油的质量:m =116ρV =116×1.44 kg /m 3×1500×2×10-3 m 3=0.27 kg ; 这些汽油完全燃烧放出的热量:Q 放=qm =4.5×107 J /kg ×0.27 kg =1.215×107 J ;汽车在1 min 内做的有用功:W =Q 放η=1.215×107 J ×40%=4.86×106 J 。
(2)汽车在1 min 内做的有用功的功率:P =W t =4.86×106 J 60 s=8.1×104 W 。
因为汽车匀速行驶,所以汽车受到的阻力与牵引力是一对平衡力,大小相等,即F =f =3×103 N ,根据P =Fv 可得,汽车行驶的速度:v=PF=8.1×104W3×103N=27 m/s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
思维特训(九) 密度|典|例|分|析|混合密度的计算例题 2019·呼和浩特王慧同学利用所学知识,测量一件用合金制成的实心构件中铝所占比例。
她首先用天平测出构件质量为374 g ,用量杯测出构件的体积是100 cm 3。
已知合金由铝与钢两种材料合成,且铝的密度为2.7×103 kg /m 3,钢的密度为7.9×103 kg /m 3。
如果构件的体积等于原来两种金属体积之和,求:(1)这种合金的平均密度。
(2)这种合金中铝的质量占总质量的百分比。
[答案] (1)这种合金的平均密度:ρ=m V =374 g 100 cm3=3.74 g /cm 3=3.74×103 kg /m 3。
(2)设铝的质量为m 铝,钢的质量为m 钢,则m 铝+m 钢=374 g ①;构件的体积等于原来两种金属体积之和,则m 铝ρ铝+m 钢ρ钢=100 cm 3,即m 铝2.7 g /cm 3+m 钢7.9 g /cm 3=100 cm 3②。
联立①①式,解得m 铝=216 g 。
则这种合金中铝的质量占总质量的百分比为216 g 374 g×100%≈57.8%。
|思|维|集|训|1.有两个质量相等的球,其体积之比V 1∶V 2=1∶5,密度之比ρ1∶ρ2=4①1,其中一个球是空心的,已知实心球的体积为 V ,则空心球的空心部分的体积为( )A .2VB .VC .0.2VD .0.25V2.阿基米德采用排水法解决了王冠掺假问题,现有一个金和银做成的王冠,用排水法测量出其体积为56.9 cm 3,若与王冠质量相同的纯金块和纯银块的体积分别为52.5 cm 3和96.5 cm 3,则王冠中银的质量和金的质量之比为( )A .1∶8B .1①9C .1∶10D .1∶113.(多选)现有密度分别为ρ1、ρ2(ρ1<ρ2)的两种液体,质量均为m 0,某工厂要用它们按体积比1①1的比例配制一种混合液(设混合前后总体积不变),且使所得混合液的质量最大,则( )A .这种混合液的密度为2ρ1ρ2ρ1+ρ2B .这种混合液的密度为ρ1+ρ22C .按要求配制后,剩下的那部分液体的质量为⎝ ⎛⎭⎪⎫1-ρ1ρ2m 0 D .按要求配制后,剩下的那部分液体的质量为⎝⎛⎭⎪⎫1-ρ2ρ1m 0 4.如图9-TX -1所示,A 、B 两个高度相等、底面积不同的薄壁圆柱形容器中,分别盛有质量相等的甲、乙两种液体。
若在两容器中分别再倒入原液体至倒满,则( )A .倒入的质量m 甲一定小于m 乙B .倒入的质量m 甲可能等于m 乙C .倒入的质量m 甲可能大于m 乙D .倒入的体积V 甲一定等于V 乙图9-TX -15.如图9-TX -2所示,甲、乙为两个实心均匀正方体,它们的质量相等。
若在两个正方体的上部,沿水平方向分别截去相同高度的部分,并将截去部分叠放在对方剩余部分上,此时它们的质量分别为m 甲′和m 乙′,下列判断正确的是( )图9-TX -2A .m 甲′可能小于m 乙′B .m 甲′一定小于m 乙′C .m 甲′可能大于m 乙′D .m 甲′一定大于m 乙′6.如图9-TX -3所示,一个实心圆球分为内外两层。
内层由甲物质组成,外层由乙物质组成,且内层半径是外层半径的13,内层质量是外层质量的12。
那么,甲、乙两种物质的密度之比是________。
(球的体积V =4πR 33) 图9-TX -37.2019·乌鲁木齐2019年5月5日,凝聚着国人梦想的国产大飞机C 919首飞成功。
C 919为了减重,使用了大量新型合金材料。
飞机某合金部件由甲、乙两种金属构成,已知甲、乙按质量比2①1混合后的密度与甲、乙按体积比3①4混合后的密度相等,则甲、乙的密度之比为________。
若该合金部件比传统上全部使用金属甲时质量减少了50%,则该合金部件中甲、乙的质量之比为________。
8.为了保护环境,治理水土流失,学校的环保小组测定了山洪冲刷地面时洪水中的平均含沙量(即每立方米的洪水中所含泥沙的质量)。
治理环境之前,他们共采集了40 dm 3的水样,称得其总质量为40.56 kg ,已知干燥的泥沙的密度为2.4×103 kg /m 3,试求洪水中的平均含沙量。
9.某校“STS ”活动小组前往酒厂考察,同学们了解到白酒是发酵后的粮食里的酒精,从酒糟中蒸煮汽化出来注入储酒罐中的,罐里的白酒度数很高,一般不宜饮用,需要与适量水勾兑(混合)后才能出售。
有关行业规定:白酒的“度数”是指气温在20 ℃时,100 mL 酒中所含酒精的毫升数。
试回答:该厂生产的每瓶装“500 mL 45度”的白酒,质量是多少?是否恰好为一斤酒(一斤等于500 g )?这种酒的密度是多少?(ρ酒精=0.8×103 kg /m 3)详解详析1.B [解析] 球的实心部分的体积之比V 1实V 2实=mρ1m ρ2=ρ2ρ1=14,而球的体积之比为1①5,且只有一个球是空心的,所以球2是空心的,球1是实心的,即V V 2实=14,且V V 2实+V 空=15,解得空心部分的体积为V 空=V 。
2.B [解析] 王冠的质量:m =m 金+m 银;设王冠中含金和银的体积分别为V 金、V 银,则V 金+V 银=56.9 cm 3,即m 金ρ金+m 银ρ银=56.9 cm 3。
根据题意得:ρ金=m 金+m 银52.5 cm 3,ρ银=m 金+m 银96.5 cm 3,故可以得出:m 金 m 金+m 银52.5 cm 3+m 银m 金+m 银96.5 cm 3=56.9 cm 3,解得:m 银:m 金=1∶9。
3.BC [解析] 我们设混合液中两种液体的体积均为V ,则混合液体的体积为2V ,两种液体的质量分别为m 1=ρ1V ,m 2=ρ2V ,则混合液体的质量为m =m 1+m 2=ρ1V +ρ2V ,所以混合液体的密度为ρ=ρ1V +ρ2V 2V =ρ1+ρ22,故A 错误、B 正确。
因为ρ1<ρ2,按体积比1①1的比例配制的溶液中混合液的最大质量:m =m 1+m 0=ρ1V +m 0=ρ1m 0ρ2+m 0=(1+ρ1ρ2)m 0,则剩下的那部分液体的质量为2m 0-(1+ρ1ρ2)m 0=(1-ρ1ρ2)m 0,故C 正确、D 错误。
4.A [解析] 图中甲液面高于乙液面,而甲、乙两种液体的质量相等,可以理解为倒入相同质量的甲、乙两种液体,A 容器中的液面升高得快一些,故假设再倒入质量相等的甲、乙两种液体,A 容器恰好装满,而B 容器则还未装满,仍需再加一部分液体,故装满时倒入的甲液体的质量一定小于乙液体的质量,A 项正确,B 、C 项错误;由图可知,甲液体的体积较大,密度应较小,又倒入的甲液体的质量小于乙液体的质量,由公式V =m ρ可知,在m 、ρ大小均不相等,且又“同小”的条件下,不能确定体积的大小关系,故D 项是错误的。
5.D [解析] 根据题设条件可知,甲、乙两个正方体的质量是相等的,若截去相同的高度,则甲截去的质量比例较小,乙截去的质量比例较大,故甲截去的质量小于乙截去的质量,将截去部分叠放在对方剩余部分上后,则甲的质量一定大于乙的质量。
6.13∶1 [解析] 假设实心圆球的半径为R ,则内层半径为R 3,内层的体积为481πR 3,外层的体积为V 外=43πR 3-481πR 3=10481πR 3;设内层的质量为m ,故ρ内=81m 4πR 3,ρ外=81m 52πR 3,所以ρ内:ρ外=13①1。
7.8∶3 2①3 [解析] 甲、乙按质量比2①1混合时,m 甲=2m 乙,由密度公式可得混合后密度ρ=m 甲+m 乙V 甲+V 乙=2m 乙+m 乙2m 乙ρ甲+m 乙ρ乙=3ρ甲ρ乙ρ甲+2ρ乙。
甲、乙按体积比3∶4混合时,V 甲=34V 乙,由密度公式可得混合后密度ρ′=m 甲′+m 乙′V 甲′+V 乙′=ρ甲·34V 乙+ρ乙V 乙34V 乙+V 乙=37ρ甲+47ρ乙。
混合后的密度相等,所以3ρ甲ρ乙ρ甲+2ρ乙=37ρ甲+47ρ乙,解得:ρ甲ρ乙=83或ρ甲ρ乙=11(不合题意,舍去)。
该合金部件比传统上全部使用金属甲时质量减少了50%,即m 合=12M 甲,使用合金和传统上使用甲制作该部件的体积应相等,所以ρ合=12ρ甲,由密度公式有:m 甲″+m 乙″m 甲″ρ甲+m 乙″38ρ甲=12ρ甲,解得:m 甲″m 乙″=23。
8.设所取水样总体积为V ,依题意可知,V 是水的体积V 水与水中泥沙体积V 泥之和;水样总质量m 同样是水的质量与水中泥沙质量之和,即:⎩⎨⎧V 水+V 泥=V ρ水V 水+ρ泥V 泥=m 水样中泥沙体积:V 泥=m -ρ水V ρ泥-ρ水=40.56 kg -1.0×103 kg/m 3×40×10-3 m 32.4×103 kg/m 3-1.0×103 kg/m 3=4×10-4 m 3。
水样中泥沙的总质量:m ′=ρ泥V 泥=2.4×103 kg/m 3×4×10-4 m 3=0.96 kg ,水样共40 dm 3,即40×10-3 m 3,因此洪水中的平均含沙量为m ′V =0.96 kg 40×10-3 m 3=24 kg/m 3。
9.由题知,“45度”指气温在20 ℃时,100 mL 酒中所含酒精的体积为45 mL ,则所含水的体积为55 mL 。
故500 mL 酒中所含酒精的体积:V 酒精=5×45 mL =225 mL =225 cm 3,酒精的质量:m 酒精=ρ酒精V 酒精=0.8 g/cm 3×225 cm 3=180 g ;所含水的体积:V 水=500 mL -225 mL =275 mL =275 cm 3,水的质量:m 水=ρ水V 水=1 g/cm 3×275 cm 3=275 g ;白酒的质量:m =m 酒精+m 水=180 g +275 g =455 g 。
因为455 g <500 g ,故每瓶酒质量小于一斤。
白酒的体积:V =500 mL =500 cm 3,这种白酒的密度:ρ=m V =455 g 500 cm 3=0.91 g/cm 3。
