梁的内力图
梁的内力图—剪力图和弯矩图(23)

6kN
1
1
A 2mΒιβλιοθήκη 6kN m2 q 2kN m 3 4
5
B
2
34
5
C
3m
3m
FQ1 6kN M1 6 2 12kNm FQ2 6 13 7kN M 2 6 2 12kNm
FA 13kN
问题:最大内力的数
FB 5kN
FQ3 6 13 23 1kN
变化的(有的大、有的小)。
一、 梁的内力图—剪力图和弯矩图
1 、剪力方程和弯矩方程
由前面的知识可知:梁的剪力和弯矩是随截面位置
变化而变化的,如果将x轴建立在梁的轴线上,原点取 在梁左端,向右为正向, 坐标x表示截面位置,则FQ和M
就随x的变化而变化,V和M就是x的函数,这个函数式就 叫剪力方程和弯矩方程。
南充职业技术学院土木工程系建筑力学多媒体课件
任课 陈德先 教师
授课 12造价与建 班级 筑
授课 时间
2013/
学 时
4
课 剪力图和弯矩图 题
课型 新授课
教学 方法
讲练结合法
教学 熟练列出剪力方程和弯矩方程、并绘制剪力图和弯矩图; 目的 利用载荷集度、剪力和弯矩间的微分关系绘制剪力图和弯
矩图.
教学 剪力图和弯矩图;剪力、弯矩和荷载集度的微分关系及其 重点 应用.
l,求梁剪力、弯矩方程的微分,并画剪力、弯矩图。
q
解 :1.建立剪力、弯矩方程
A x
B
l
FQ x
ql ql 2/2
FQ (x) qx M (x) qx x qx2
22
2.对剪力、弯矩方程取微分
dM (x) dx
梁弯矩图梁内力图(剪力图和弯矩图)

注:表中的K为轴向力变形影响的修正系数。
(1)无拉杆双铰拱
1)在竖向荷载作用下的轴向力变形修正系数
式中 Ic——拱顶截面惯性矩;
Ac——拱顶截面面积;
A——拱上任意点截面面积。
当为矩形等宽度实腹式变截面拱时,公式I=Ic/cosθ所代表的截面惯性矩变化规律相当于下列的截面面积变化公式:
简单载荷梁力图(剪力图与弯矩图)
梁的简图
剪力Fs图
弯矩M图
1
2
3
4
5
6
7
8
9
10
ቤተ መጻሕፍቲ ባይዱ注:外伸梁 = 悬臂梁 + 端部作用集中力偶的简支梁
表2 各种载荷下剪力图与弯矩图的特征
某一段梁上的外力情况
剪力图的特征
弯矩图的特征
无载荷
水平直线
斜直线
集中力
突变
转折
集中力偶
无变化
突变
均布载荷
斜直线
抛物线
零点
极值
表3 各种约束类型对应的边界条件
2)三跨等跨梁的力和挠度系数 表2-12
注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql; 。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F; 。
3)四跨等跨连续梁力和挠度系数 表2-13
注:同三跨等跨连续梁。
4)五跨等跨连续梁力和挠度系数 表2-14
注:同三跨等跨连续梁。
注:1.在均布荷载作用下:M=表中系数×ql2;V=表中系数×ql; 。
2.在集中荷载作用下:M=表中系数×Fl;V=表中系数×F; 。
[例1] 已知二跨等跨梁l=5m,均布荷载q=11.76kN/m,每跨各有一集中荷载F=29.4kN,求中间支座的最大弯矩和剪力。
第6章-梁的内力PPT课件

(3)计算截面C稍右处的剪力FsR、弯矩MCR。
M C
MCR
A
l/2
FA
Fy 0
FsR
ql FsRFA2 0
MCF0
解之得:
FsR
ql 4
M CR MFA2 lq 2 l4 l0
精选PPT课M件CR 0
14
建筑力学
❖ 计算剪力和弯矩的规律
(1) 梁内任一截面上的剪力,其大小等于该截面左侧(或右侧) 梁上所有外力的代数和;梁内任一截面的弯矩,其大小等 于该截面左侧(或右侧)梁上所有外力对于该截面形心之矩的
★ 由平衡方程 F得y ,0
F s x F s x d s x F q x d 0 x
dFsx qx
dx
(9-1)
几何意义:剪力图上某点处的切线斜率等于该点处荷载
集度的大小。
精选PPT课件
23
建筑力学
★ 由平衡方程 MC 得,0
M x dx M M x F sx d q x x d d 2 x 0 x
(3)列出各段的剪力方程和弯矩方程:各段列剪力方程和弯矩方程时, 所取的坐标原点与坐标轴x的正向可视计算方便而定,不必一 致。
(4) 画剪力图和弯矩图:先根据剪力方程(或弯矩方程)判断剪力图(或 弯矩图)的形状,确定其控制截面,再根据剪力方程(或弯矩方 程)计算其相应截面的剪力值(或弯矩值),然后描点并画出整个 全梁的剪力图(或弯矩图)
解之得: Fs 4kN 精选PPTM 课件144 kNm
12
[例]
简支梁受均布荷载q和集中力偶M=ql2/4的作用,如图所示。求截面C 的剪力和弯矩。
M
q
梁的内力分析

FQ 3 为负剪力, M 3 为正弯矩。
在计算梁的剪力和弯矩时,可以通过下面的结论直接计算: (1)某截面上的剪力等于该截面左侧(或右侧)梁段上所 有横向外力的代数和。(左上右下剪力为正;反之则为负) 以该截面左侧杆段上的外力进行计算时,则向上的外力产生 正剪力,反之为负。以该截面右侧杆段的外力计算时,则 向下的外力产生正剪力,反之为负。 (2)某截面上的弯矩等于该截面左侧(或右侧)所有外力对该 截面之矩的代数和。(左顺右逆弯矩为正;反之则为负) 以左侧的外力进行计算时,则绕截面顺转的外力产生正弯矩, 反之为负。以右侧的外力计算时,绕截面逆转的外力产生 正弯矩,反之为负。
F
Q1
、 M 1 为正值,表示该截面上剪力和弯矩与所设方向一致,故为正剪力,正弯矩。
例 7- 1
(3)求 2-2 截面的内力。用截面法把梁从 2-2 截面处切成两段,取左段为研究对象,受 力如图 7-6c。图中剪力和弯矩都假设为正。由平衡方程得 ∑Fy=0,
FA - F Q 2 =0, F Q 2 = FA =2 kN
FQ1 FA 2kN M1 FA 2 2 2 4kN m
图
FQ2=FA-F=2-3=-1kN
M 2 FA 2 2 2 4kN m
(3)求3-3和4-4截面的剪力和弯矩,取右侧计算。
FQ 3 FB 1kN
M3 FB 4 m 1 4 2 2kN m
MA 0
MB ql ql 2 l 0 2 2 ql l q l ql 2 M C ( )2 2 2 2 2 8
当x =l 时
当x=l/2时,
时将三点用一光滑曲线连成一抛物线即得梁的弯矩图,见图7-9c。
梁的内力图课程设计

梁的内力图课程设计一、课程目标知识目标:1. 学生能够理解梁内力的基本概念,掌握梁受力分析的方法。
2. 学生能够识别并绘制不同工况下的梁内力图,包括弯矩图、剪力图和轴力图。
3. 学生能够运用力学原理,解释梁内力与外力之间的关系。
技能目标:1. 学生能够运用几何法或解析法进行梁内力图的绘制。
2. 学生能够运用计算机软件辅助分析梁的内力,并进行简单的结构优化。
3. 学生能够通过实际案例,分析并解决工程中的梁内力问题。
情感态度价值观目标:1. 学生能够培养对力学学科的浓厚兴趣,增强探究精神和创新意识。
2. 学生能够认识到力学知识在实际工程中的应用价值,培养工程意识和责任感。
3. 学生能够通过团队合作,培养沟通协调能力和解决问题的能力。
课程性质:本课程属于高中物理力学部分,以理论教学和实践操作相结合的方式进行。
学生特点:高中年级的学生已具备一定的物理基础和空间想象力,对实际问题具有较强的探究欲望。
教学要求:结合学生特点,注重理论与实践相结合,提高学生的动手操作能力和实际问题解决能力。
通过课程学习,使学生能够将理论知识运用到实际工程中,培养学生的创新意识和实践能力。
教学过程中,关注学生的个体差异,激发学生的学习兴趣,提高教学效果。
将课程目标分解为具体的学习成果,为后续教学设计和评估提供依据。
二、教学内容1. 梁的基本概念:介绍梁的定义、分类及受力特点,结合课本第三章第一节内容。
2. 梁的受力分析:讲解梁在外力作用下的弯矩、剪力和轴力的产生,运用课本第三章第二节的方法进行分析。
3. 梁内力图的绘制:a. 几何法:介绍利用几何法绘制梁内力图的方法,结合课本第三章第三节的案例。
b. 解析法:讲解运用解析法绘制梁内力图的过程,参考课本第三章第四节的内容。
4. 计算机软件辅助分析:引入相关软件(如CAD等),帮助学生更直观地观察和分析梁内力图,结合课本第三章第五节。
5. 实际案例解析:分析典型工程案例,使学生了解梁内力在实际工程中的应用,结合课本第三章第六节。
梁的内力图课程设计

梁的内力图课程设计一、教学目标本节课的教学目标是使学生掌握梁的内力图的基本概念、绘制方法和应用。
通过本节课的学习,学生应能够:1.理解梁的内力图的概念,知道梁的内力图的作用。
2.掌握梁的内力图的绘制方法,能够独立完成简单梁的内力图的绘制。
3.能够应用内力图进行梁的受力分析,解决实际问题。
二、教学内容本节课的教学内容主要包括以下几个部分:1.梁的内力图的基本概念:介绍梁的内力图的定义、作用及其与梁的受力状态的关系。
2.梁的内力图的绘制方法:讲解梁的内力图的绘制原理,引导学生掌握绘制方法,并通过示例进行演示。
3.梁的内力图的应用:结合实际问题,让学生学会运用内力图进行梁的受力分析,解决问题。
三、教学方法为了实现本节课的教学目标,我们将采用以下几种教学方法:1.讲授法:通过讲解梁的内力图的基本概念、绘制方法和应用,使学生掌握相关知识。
2.案例分析法:通过分析实际案例,让学生学会运用内力图解决实际问题。
3.实验法:安排一定的实验课时,让学生在实验中观察、分析梁的内力图的绘制和应用,提高学生的实践能力。
四、教学资源为了保证本节课的教学效果,我们将准备以下教学资源:1.教材:选用权威、实用的教材,为学生提供系统的学习资料。
2.参考书:提供相关参考书籍,丰富学生的知识体系。
3.多媒体资料:制作精美的PPT,生动展示梁的内力图的绘制和应用。
4.实验设备:准备充足的实验设备,确保每位学生都能参与到实验中来,提高实践能力。
以上就是本节课的教学设计,希望通过以上设计,能够帮助学生更好地理解和掌握梁的内力图相关知识,提高学生的实践能力。
五、教学评估为了全面、客观地评估学生的学习成果,本节课的评估方式将包括以下几个方面:1.平时表现:通过观察学生在课堂上的参与程度、提问回答等情况,评估学生的学习态度和理解程度。
2.作业:布置适量的作业,要求学生独立完成,通过作业的完成质量评估学生的掌握程度。
3.考试:安排一次期中考试,测试学生对梁的内力图知识的掌握情况,包括理论知识和应用能力。
梁 弯矩图 梁 内力图 (剪力图与弯矩图)

简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
实用文档2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
梁弯矩图梁内力图(剪力图与弯矩图)
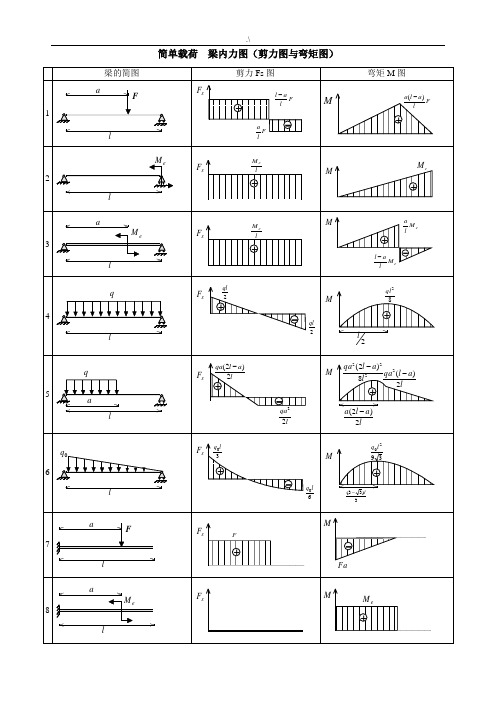
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
.\2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
4.4.3静定梁的内力方程及内力图

4.4.3
梁的内力方程及 内力图
剪力图和弯矩图
剪力方程和弯矩方程
• 若以横坐标x表示横截面在梁轴线上的 位置,则各横截面上的剪力和弯矩皆可表示 为坐标x的函数,即 • Q=Q(x) • M=M(x) • 以上两函数表达了剪力和弯矩沿梁轴线 的变化规律,分别称为梁的剪力方程和弯矩 方程。
பைடு நூலகம் x=0,MA=0
x=l/2,MC=ql2/8 x=l,MB=0 弯矩图如图9.15(c)所示。 从所作的内力图可知,最大剪力发生在梁端,其值为|Qmax|=ql/2,最 大弯矩发生在剪力为零的跨截面,其值为|Mmax|=ql2/8。
【例 9.6】简支梁受集中力P作用如图9.16(a)所示,试画出梁的剪力图和弯矩 图。 【解】(1) 求支座反力 以整梁为研究对象,由平衡方程求支座反力。 ∑mB(F)= 0,-RAl+Pb=0 RA=Pb/l ∑Fy=0,RA+RB-P=0 RB=Pa/l (2) 列剪力方程和弯矩方程 梁在C截面处有集中力P作用,AC段和CB段所受的外力不同,其剪力方 程和弯矩方程也不相同,需分段列出。取梁左端A为坐标原点
剪力图和弯矩图
为了形象地表示剪力和弯矩沿梁轴的变化规律, 把剪力方程和弯矩方程用其图像表示,称为剪力图 和弯矩图。 剪力图和弯矩图的画法与轴力图、扭矩图很相 似,用平行于梁轴的横坐标x表示梁横截面的位置, 用垂直于梁轴的纵坐标表示相应截面的剪力和弯矩。
在土建工程中,习惯上将正剪力画在x轴上方, 负剪力画在x轴的下方;正弯矩画在x轴下方,负弯 矩画在x轴的上方,即把弯矩图画在梁受拉的一侧。
梁的内力 剪力弯矩方程 剪力弯矩图

(3)若某截面处FS=0
dF S dx
q(x)
dM dx
FS
d M dx
2
2
q(x)
则该截面上M取极值:当q>0, M取到极小值 当q<0, M取到极大值 (4)集中力F作用处,FS突变,跳跃值为F,M有尖点; q>0 q<0
集中力偶M作用处,M突变,跳跃值为M, FS不受影响。 F M
例题
例 题 2
2qa
A
§9 变形体静力学概述 及一般杆件内力分析
qa2 q
B C
解: 1.求约束力
FB q 2 a a 2 qa 3 a qa 2a 7 2 qa ( )
2
D
a
3 2 qa
FB a
a
a 2
FD
F D 4 qa
7 2
qa
1 2
qa ( )
D
FD
FD
F Ax 1 2 2 ( kN )( )
A
FAx
FAy
2m
F Ay 5 3 2 kN ( )
例题
例 题 4
5kN B
§9 变形体静力学概述 及一般杆件内力分析
4kN· m C
2.作内力图 D 3kN 轴力图: AB段 F N 2 kN
1m
1m
(F S )
1 qa
2
2.作内力图
1 2 qa
M
7 2
1 4 qa
2
B
2 qa
2
2qa (M)
qa
8
第四章 梁的内力

q=2kN/m MC B
M C ( F ) 0
l ql 2 M C FB 4.5kN m 2 8
l/4 FSC
FSC
l/2
FB
图4.11
三、用直接法求剪力、弯矩 F=5kN
直接法:梁任一横
截面上的剪力在数 值上等于该截面一
(a)
q=2kN/m
F=5kN
A C l/4 FA l/4
F
A
B
x
例题:作悬臂梁的剪
x
l FS
x
力图和弯矩图。
解:建立坐标系,将坐 标原点取在梁的左端, 写出梁的剪力方程和弯 矩方程 :
FS图
F
FS (x) F
x
(0 x l) (0 x l)
M(x) Fx
M
M图
x 0时,M(0) 0 x l时, M(l) Fl
FRA
A
x
q
FRB
例题:作如图简支梁
的剪力图和弯矩图。
解:先求两个支反力
FRA FRB ql 2
B
l
FRA
A
q
M(x) FS (x)
建立坐标系,梁的剪力
x
方程和弯矩方程为:
ql FS (x) FRA qx qx (0 x l) 2 x qlx qx 2 M(x) FRA x qx (0 x l) 2 2 2
FRA
A
x
q
FRB
由弯矩方程得弯矩图为一 条二次抛物线。
B
l
x 0,
M 0
ql 2
x =l ,
解:1、求截面C的剪力和弯矩
梁的内力图剪力图和弯矩图(共16张PPT)

V Rqx qlqx 作3、此依梁方的程剪x作力剪图力和图弯和矩A弯图矩。图
(0<x<l)
2、判断各段V、M图形状:
快速绘制剪力图和弯矩图
突变大小等于集中荷载的大小。
弯矩图出现转折,转折方向与
3、依方程作剪力图和弯矩图
Vmax= 1 ql 2
Mmax 1 ql 2 8
例2 简支梁受集中荷载作用,如图示,
斜率的大小等于对应梁段上剪力的大小。V>0时向右下方斜斜,
V<0时向右上方倾斜,V=0时为水平线。
在均布荷载作用的梁段上:剪力图为斜直线,斜率等于荷载 集度,q<0〔 〕向右下方倾斜,反之,向右上方倾斜。 弯矩图为二次抛物线,q<0,向下凸起;q>0〔 〕向上凸。 遇到集中荷载:剪力图突变,突变方向与集中荷载方向相同, 突变大小等于集中荷载的大小。弯矩图出现转折,转折方向与 集中力的方向相反。 遇到集中力偶:剪力图不变,弯矩图突变,突变方向由力偶的
弯矩图为二次抛物线,q<0,向下凸起;
V>0时向右下方斜斜,
v
而变化的,如果将x轴建立在梁的轴线上,原点建立在梁
q>0〔 〕向上凸。
q>0〔 〕向上凸。
v 1、可以检查剪力图和弯矩图是否正确。
集度,q<0〔 〕向右下方倾斜,反之,向右上方倾斜。
作此梁的剪力图和弯矩图。
作此梁的剪力图和弯矩图。
〔4〕逐段绘制出V和M图即梁的V和M图
极值弯矩:集中力作用截面、集中力偶截面或弯矩为零的截面。
v
利用上述规律:
1、可以检查剪力图和弯矩图是否正确。
2、可以快速的绘制剪力图和弯矩图,步骤如下:
〔1〕将梁正确分段 〔2〕根据各段梁上的荷载情况,判断剪力图和弯矩图的 形状
14-梁的内力及梁的内力图

B FB CB段(x > a)时 M2(x) FS2(x) FB
AC段(x < a)时 M1(x) FA
x
FS1(x)
Fb (0 < x < a ) FS1 ( x ) = l
Fb M 1 (x ) = x (0 ≤ x ≤ a ) l
Fa (a < x < l ) FS2 ( x ) = − FB = − l Fa (l − x ) M 2 ( x ) = FB (l − x) = l (a ≤ x ≤ l )
M M 2 ( x ) = FB (l − x ) = − (l − x ) l
(0 ≤ x < a )
(a < x ≤ l )
第九章 梁的内力
(3)作剪力图和弯矩图 M a A C l FS图
bM l
b
B
M FS1 ( x ) = l M FS2 ( x ) = l
M M 1 (x ) = x l
FS1 = − F
M1 + F × a = 0
M 1 = − Fa
1 FS1 截面2—2 F C22 M2 FA 2 F
S2
∑F
y
=0
− FS2 + FA − F = 0
FS 2 = FA − F = 2 F
∑M
o2
=0
M2 + F ×a = 0
M 2 = − Fa
第九章 梁的内力
y F 1A2 1 2 FA a
工程力学
第九章 梁的内力
第九章 梁的内力
§9-1 弯曲变形
梁 ——以弯曲为主要变形的杆件。
第九章 梁的内力
最基本最常见的弯曲问题 ——对称弯曲
简 支梁的内力包络图和绝对最大弯矩

注意 : FR为梁上实有荷载的合力。在安排FR与Fcr的位 置时,可能会有来到或离开梁上的荷载,需要
a
b
F左 Fcr F右
a
b
30 30 20 10 10
10
10
Байду номын сангаас
30 30 20 10 10
10
10
验算其他荷载均不满足判别式,故轮2作用力是使 梁跨中截面C产生最大弯矩的临界荷载Fcr。 2)求梁的绝对最大弯矩。
FR =30 kN+30 kN+20 kN+10 kN+10 kN=100 kN FR ·x=10kN×2 m+20kN×4m+
当简支梁受一组移动集中荷载作用时,例如图
9.18(a)、(b)所示
A
B
5.625 6.375 9.6 0 1.2 2.4 3.6 4.86.0 7.28.4 10.8 12
12m
(a)
215
F2=82kN F3=82kN
366
F1=82kN 3.5m 1.5m 3.5m F4=82kN
465
559 574 578
1 2 34 5
(a) A
2m 2m 2m 2m
C
x'=5.2m B
10 (b)
10m
10m
5
图9.20
MC的影响线 (单位:m)
将轮2作用力置于影响线的顶点[图9.20(c)],
梁弯矩图梁内力图
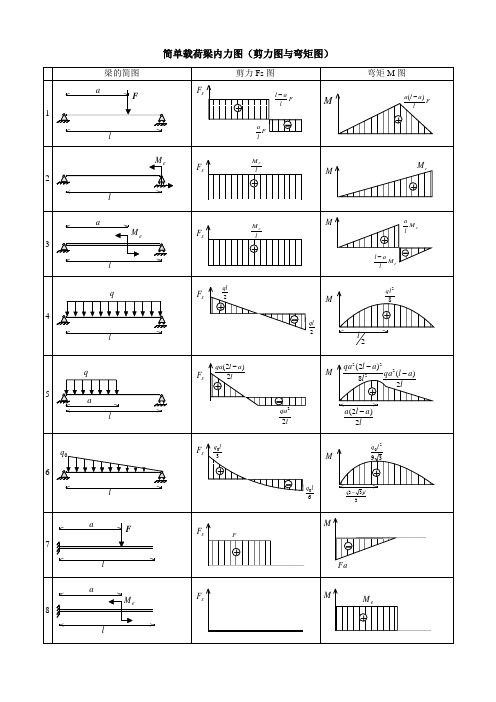
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
作图示梁的内力图:
梁:由支座支承,承受的外力以横向力和剪力为主,以弯曲为主要变形的构件称为梁。
1、从功能上分,有结构梁,如基础地梁、框架梁等;与柱、承重墙等竖向构件共同构成空间结构体系,有构造梁,如圈梁、过梁、连系梁等,起到抗裂、抗震、稳定等构造性作用。
2、梁按照结构工程属性可分为:框架梁、剪力墙支承的框架梁、内框架梁、梁、砌体墙梁、砌体过梁、剪力墙连梁、剪力墙暗梁、剪力墙边框梁。
3、从施工工艺分,有现浇梁、预制梁等。
地梁
4、从材料上分,工程中常用的有型钢梁、钢筋混凝土梁、木梁、钢包砼梁等。
5、梁依据截面形式,可分为:矩形截面梁、T形截面梁、十字形截面梁、工字形截面梁、匚形截面梁、囗形截面梁、不规则截面梁。
6、从受力状态分,可分为静定梁和超静定梁。
静定梁是指几何不变,且无多余约束的梁。
超静定梁是指几何不变,且有多余约束的梁。
7、梁按照其在房屋的不同部位,可分为:屋面梁、楼面梁、地下框架梁、基础梁。
所以梁很复杂。
部分梁定义:
1.地梁(DL):地梁也叫基础梁、地基梁,简单地说就是基础上的梁。
一般用于框架结构和框-剪结构中,框架柱落在地梁或地梁的交叉处。
其主要作用是支撑上部结构,并将上部结构的荷载转递到地基上。
2.框架梁(KL):框架梁是指两端与框架柱相连的梁,或者两端与剪力墙相连但跨高比不小于5的梁。
框架梁可以分为:
a、屋面框架梁(WKL):屋面框架梁指的是框架结构屋面最高处的框架梁;
b、楼层框架梁(KL):楼层框架梁指的是各楼面的框架梁;
c、地下框架梁(DKL):地下框架梁指设置在基础顶面以上且低于建筑标高正负零(室内地面)以下并以框架柱为支座,不受地基反力作用,或者地基反力仅仅是地下梁及其覆土的自重产生,不是由上部荷载的作用所产生,这样的地下梁,称为地下框架梁。
3.圈梁(QL):圈梁是沿建筑物外墙四周及部分内横墙设置的连续封闭的梁。
其目的是为了增强建筑的整体刚度及墙身的稳定性。
在房屋的基础上部的连续的钢筋混凝土梁叫基础圈梁,也叫地圈梁;而在墙体上部,紧挨楼板的钢筋混凝土梁叫上圈梁。
在砌体结构中,圈梁有钢筋砖圈梁和钢筋混凝土圈梁两种。
4.连梁(LL):在剪力墙结构和框架—剪力墙结构中 ,连接墙肢与墙肢 ,连梁是指两端与剪力墙相连且跨高比小于5的梁。
连梁一般具有跨度小、截面大,与连梁相连的墙体刚度又很大等特点。
一般在风荷载和地震荷载的作用下,连梁的内力往往很大。
5.暗梁(AL):完全隐藏在板类构件或者混凝土墙类构件中,钢筋设置方式与单梁和框架梁类构件非常近似。
暗梁总是配合板或者墙类构件共同工作。
板中的暗梁可以提高板的抗弯能力,因而仍然具备梁的通用受力特征。
混凝土墙中的暗梁作用比较复杂,已不属于简单的受弯构件,它一方面强化墙体与顶板的节点构造,另一方面为横向受力的墙体提供边缘约束。
强化墙体与顶板的刚性连接。
6.边框梁(BKL):框架梁伸入剪力墙区域就变成边框梁。
7.框支梁(KZL):因为建筑功能要求,下部大空间,上部部分竖向构件不能直接连续贯通落地,而通过水平转换结构与下部竖向构件连接。
当布置的转换梁支撑上部的剪力墙的时候,转换梁叫框支梁,支撑框支梁的柱子就叫做框支柱。
8.悬挑梁(XL):不是两端都有支撑的,一端埋在或者浇筑在支撑物上,另一端伸出挑出支撑物的梁。
一般为钢筋混凝土材质。
9.井式梁(JSL):井式梁就是不分主次,高度相当的梁,同位相交,呈井字型。
这种一般用在楼板是正方形或者长宽比小于1.5的矩形楼板,大厅比较多见,梁间距3m左右,由同一平面内相互正交或斜交的梁所组成的结构构件。
又称交叉梁或格形梁。
10.次梁:在主梁的上部,主要起传递荷载的作用。
11.拉梁:是指独立基础,在基础之间设置的梁。
12.过梁(GL):当墙体上开设门窗洞口时,为了支撑洞口上部砌体所传来的各种荷载,并将这些荷载传给窗间墙,常在门窗洞口上设置横梁,该梁称为过梁。
13.悬臂梁:梁的一端为不产生轴向、垂直位移和转动的固定支座,另一端为自由端(可以产生平行于轴向和垂直于轴向的力)。
14.平台梁:指通常在楼梯段与平台相连处设置的梁,以支承上下楼梯和平台板传来的荷载。
15.冠梁(GL): 设置在基坑周边支护(围护)结构(多为桩和墙)顶部的钢筋混凝土连续梁,其作用其一是把所有的桩基连到一起(如钻孔灌注桩,旋挖桩等),防止基坑(竖井)顶部边缘产生坍塌,其二是通过牛腿承担钢支撑(或钢筋混凝土支撑)的水平挤靠力和竖向剪力。
