材料力学专题一梁的内力和内力图
材料力学专题一梁的内力和内力图

专题一 梁的内力和内力图例1求图1(a)所示梁截面 A 、C 的剪力和弯矩。
解:1)求反力kN 5=A F ,kN 4=B F2)求A 左截面的内力,如图(a)所示。
0=∑i Y , 0=+左SA p F F ,kN 3-=左SA F0=∑O M ,02=+⨯左A p M F , m kN 6⋅-=左A M3)求A 右截面的内力,如图(b)所示。
0=∑i Y ,0=+--A SA p F F F 左,kN 2=左SA F0=∑O M ,02=+⨯右A p M F , m kN 6⋅-=右A M4)求C 左截面的内力,如图(c)所示。
0=∑i Y ,02=-⨯--左SC P A F q F F ,0=左SC F0=∑O M ,01224=+⨯⨯+⨯-⨯左C A p M q F F ,=左C M m kN 4⋅-=5)求C 右截面的内力,如图(d)所示。
0=∑i Y ,02=-⨯--右SC P A F q F F ,0235=--=右SC F 0=∑O M ,012241=++⨯⨯+⨯-⨯右C A p M M q F F ,=右C M m kN 6⋅-=【小结】①求指定截面上的内力时,既可取梁的左段为脱离体,也可取右段为脱离体,两者计算结果一致。
一般取外力比较简单的一段进行分析。
②在解题时,通常假设截面上把内力为正,若最后计算结果是正,则表示假设的内力方向(转向)与实际是相同的,否则是相反的。
③该题也可以不画受力图,不写平衡方程而由前面的结论直接求得结果。
图1(a)(b)(c)(d) (e)例2试计算图2所示各梁指定截面(标有细线者)的剪力与弯矩。
解:(a)取A +截面左段研究,, 0SA A F F M ++==取C 截面左段研究,, 2SC C Fl F F M == 取B -截面左段研究, , SB BF F M Fl ==(b) 求A 、B 处约束反力如图(d)所示,l M F F e B A /==取A +截面左段研究,, e SA A A e M F F M M l++=-=-=取C 截面左段研究,, 22e e SC A A e A M Ml F F M M F l +=-=-=-⨯=取B 截面右段研究,, 0e SB B B MF F M l=-=-=(c) 求A 、B 处约束反力 取A +截面右段研究,233, 22248SA A l ql l l ql F q M q ++=⨯==-⨯⨯=-取C -截面右段研究,2, 22248SC C l ql l l ql F q M q --=⨯==-⨯⨯=-取C +截面右段研究,2, 22248SC C l ql l l ql F q M q ++=⨯==-⨯⨯=-取B -截面右段研究,0, 0SB B F M --==图2 (b) (a) qB (c) B图(d)例3试写出图3所示梁的内力方程,并画出剪力图和弯矩图。
第6章-梁的内力PPT课件

(3)计算截面C稍右处的剪力FsR、弯矩MCR。
M C
MCR
A
l/2
FA
Fy 0
FsR
ql FsRFA2 0
MCF0
解之得:
FsR
ql 4
M CR MFA2 lq 2 l4 l0
精选PPT课M件CR 0
14
建筑力学
❖ 计算剪力和弯矩的规律
(1) 梁内任一截面上的剪力,其大小等于该截面左侧(或右侧) 梁上所有外力的代数和;梁内任一截面的弯矩,其大小等 于该截面左侧(或右侧)梁上所有外力对于该截面形心之矩的
★ 由平衡方程 F得y ,0
F s x F s x d s x F q x d 0 x
dFsx qx
dx
(9-1)
几何意义:剪力图上某点处的切线斜率等于该点处荷载
集度的大小。
精选PPT课件
23
建筑力学
★ 由平衡方程 MC 得,0
M x dx M M x F sx d q x x d d 2 x 0 x
(3)列出各段的剪力方程和弯矩方程:各段列剪力方程和弯矩方程时, 所取的坐标原点与坐标轴x的正向可视计算方便而定,不必一 致。
(4) 画剪力图和弯矩图:先根据剪力方程(或弯矩方程)判断剪力图(或 弯矩图)的形状,确定其控制截面,再根据剪力方程(或弯矩方 程)计算其相应截面的剪力值(或弯矩值),然后描点并画出整个 全梁的剪力图(或弯矩图)
解之得: Fs 4kN 精选PPTM 课件144 kNm
12
[例]
简支梁受均布荷载q和集中力偶M=ql2/4的作用,如图所示。求截面C 的剪力和弯矩。
M
q
材料力学 内力与内力图.

5
RA
74
qa
RB 4 qa
(2)求剪力与弯矩
FQ1 RA 5qa / 4 M 2 M1 RA a 5qa2 / 5
FQ3 FQ2 RA qa qa/ 4
M 3 2aRA qa a 3qa2 / 2
FQ4 qa RB
3qa 4
,
M4
5qa 2 4
图
(3) 弯矩的数值标在受拉边,轴力、
刚 架
剪力画在里侧和外侧均可,但需 标出正负号;
内 力
(4) 注意节点处的平衡关系。
图
例:绘刚架内力图
解:一)求支反力:
MA 0:
8kN
1m D
2m C
E
q=1kN/m 4m 3m
RB
81 811 3
5kN
X 0:
4q RAx 1 0 RAx 3k N
静定梁的基本形式1求支反力211面上的内力梁的剪力与弯矩剪力弯矩剪力f的符号规定弯矩m的符号规定左上右下为正上压下拉上凹下凸为正例61求梁112233和44截面上的剪力和弯矩
弯曲内力
§6-1对称弯曲的概念及梁的计算简图
一. 弯曲的概念
1.工程实例 桥梁,屋梁,车轴都 是最常见梁的例子。 2.定义
当作用在杆件上的载荷和 支反力都垂直于杆件轴线 时,杆件的轴线因变形由 直线变成了曲线,此变形 称为弯曲变形。
N3 RAy 3k N Q( x3 ) RAx qx3
8kN
DN13m
2m C
M (x3 ) EQ( x3X)2
q=1kN/m 4Xm3 3m
(3) 1x3 3 x3
M
( x2
)
RAx x3
1 2
第六章 梁的内力图--剪力图和弯矩图

一、列剪力方程、弯矩方程,作梁的剪力图、弯矩图 梁内各截面上的剪力和弯矩一般都随截面的位置而变 化,以横坐标 x表示梁横截面的位置,反映梁的剪力、弯 矩值随 x值变化的方程分别就是剪力方程 Q(X) 和弯矩方程 M(X)。
根据剪力方程和弯矩方程可分别绘制剪力图和弯矩图, 其画法与轴力图相似。 用平行于梁轴的坐标 x表示横截面的位置,垂直于梁 第 六 轴的纵坐标表示相应截面的剪力或弯矩。一般习惯把正剪 章 建 直 力画在 X 轴的上方,负剪力画在 X 轴下方;而把弯矩图画在 筑 梁 力 弯 梁受拉的一侧。 学 曲
第 六 章 直 梁 弯 曲
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
第 六 章 直 梁 弯 曲
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
第 六 章 直 梁 弯 曲
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
第 六 章 直 梁 弯 曲
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
二、在集中力偶作用下梁的内力图: 例6-6简支梁AB在C截面处作用有集中力偶m(如图),试画出梁 的剪力图和弯矩图
绝对值等于该集中力偶的力偶矩。
第 六 章 直 梁 弯 曲
建 筑 特点:在集中力偶作用处V图无变化,M图发生突变,突变的力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
建 筑 力 学
第三 节 梁的内力图—剪力图和弯矩图(1)
在集中力作用下梁的内力图的特点: 在梁上只有集中力作用时,集中力把梁分为若干段 无荷载作用区。 在无荷载作用区:V图是与x轴平行的直线;M图是 斜直线。 在集中力作用处:V图发生突变,突变的绝对值等 于该集中力;M图发生转折。
建筑力学 材料力学 梁的内力

x
②写出内力方程 Q( x ) YO P
M ( x) YO x M O P( x L)
x
③根据方程画内力图。
q
解:①写出内力方程
L Q(x) ○ x – qL
qL2 2
Q( x ) qx
1 M ( x ) qx2 2
②根据方程画内力图
⊕ M(x) x
x
Q(x)
2
106 .30 1.855rad
3.14 1 0.01 7800 9.8 [3.14 0.52 1 0.52(1.855 sin106.3)] 1000 9.8 2
9 (kN/m)
q — 均布力
§4–3 一、弯曲内力:
举例
梁的内力及其求法
目
录
§4–1 工程中的弯曲问题 §4–2 梁的荷载和支座反力 §4–3 梁的内及其求法 §4–4 内力图 — 剪力图和弯矩图
§4–5 弯矩、剪力、荷载集度间的关系
§4–1 工程中的弯曲问题 一、弯曲的概念
1. 弯曲: 杆受垂直于轴线的外力或外力偶矩矢的作用时,轴 线变成了曲线,这种变形称为弯曲。 2. 梁:以弯曲变形为主的 构件通常称为梁。
mB (Fi ) 0 , 1 2 qLx2 M 2 q( x2 a) 0 2
图(a) B M2 x2 Q2
1 M 2 q( x2 a)2 qLx2 2
图(c)
§4–4 内力图 — 剪力图和弯矩图
一、 内力方程:内力与截面位置坐标(x)间的函数关系式。
Q Q( x ) M M (x)
Q Q 图 特 征
水平直线
Q Q
斜直线
Q
梁的内力图2-2-3-1

注:最后利用规律3、4、5校核 规律3 规律
例: 画出 V图和 M 图。 图和 解:1、求反力 由∑MA= 0,FB= 148 kN. , ∑MB= 0,FA= 72 kN. , 2、判断各段V、M图形状 判断各段V 分段 q V M AC q=0 水平线 斜直线 CB q=c<0 < 下斜直线 下凸曲线 下凸曲线 BD q=c<0 < 下斜直线 下凸曲线 下凸曲线 A FA
0
画剪力图和弯矩图时,一定要将梁正确分段, 画剪力图和弯矩图时,一定要将梁正确分段, 分段建立方程, 分段建立方程,依方程而作图。
0 x x
M
二 、列方程法画内力图(基本方法) 列方程法画内力图(基本方法) 列方程法画内力图 例:简支梁受均布荷载作用,如图示, 简支梁受均布荷载作用,如图示, 作此梁的剪力图和弯矩图。 作此梁的剪力图和弯矩图。 解:1 、求支座反力 (利用结构对称 利用结构对称 性简化计算; 性简化计算;悬臂结构可不求反力)
2
、剪力图和弯矩图
以梁横截面沿梁轴线的位置为横坐标, 以梁横截面沿梁轴线的位置为横坐标,以垂直 于梁轴线方向的剪力或弯矩为纵坐标, 于梁轴线方向的剪力或弯矩为纵坐标,分别绘 制表示V(x) M(x)的图象 V(x)和 的图象。 制表示V(x)和M(x)的图象。这种图象分别称为 剪力图和弯矩图,简称V图和M 剪力图和弯矩图,简称V图和M图。 绘图时一般规定正号的剪力画在x轴的上侧, 绘图时一般规定正号的剪力画在x轴的上侧, 负号的剪力画在x轴的下侧;正弯矩画在x 负号的剪力画在x轴的下侧;正弯矩画在x轴下 负弯矩画在x轴上侧,即把弯矩画在梁受 侧,负弯矩画在x轴上侧,即把弯矩画在梁受 拉的一侧。 拉的一侧。 V
A FA V
(kN)
1
梁 弯矩图 梁 内力图 (剪力图与弯矩图)

简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5标准标准标准标准标准标准标准注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
实用文档2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
梁弯矩图梁内力图(剪力图与弯矩图)
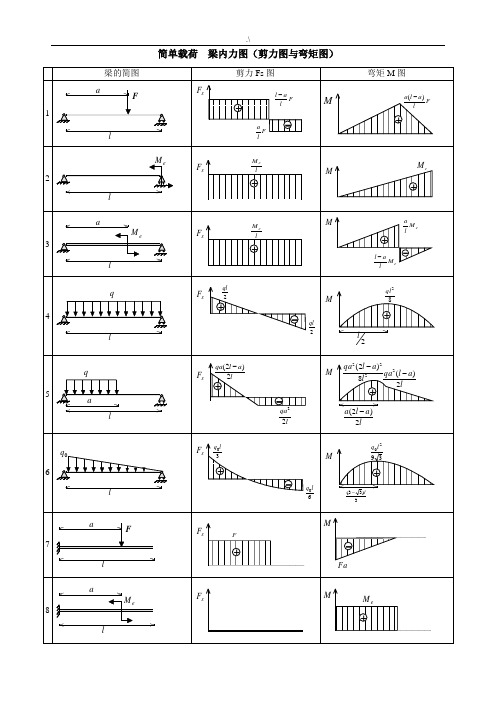
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:maxy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
.\2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
建筑力学 第4章内力和内力图

建筑力学
内力和内力图
38
§4-3 扭矩和扭矩图
A l
B
建筑力学
内力和内力图
39
如上图所示,杆件在横向平面内的外力偶作 用下发生扭转变形。其侧面上原有的直线ab变为 螺旋线ab′, 诸横截面绕杆的轴线相对转动,例 如B截面相对于A截面转过一角度∠bO'b′。 为了分析横截面上的内力,取m--m截面。
建筑力学
内力和内力图
1
第 4 章 内力和内力图
§4-1 平面桁架的内力 §4-2 轴力和轴力图 §4-3 扭矩和扭矩图 §4-4 剪力和弯矩·剪力图和弯矩图
建筑力学
内力和内力图
2
外力:物体或系统所承受的其它物体对它的作用力 (包括约束力)。 内力:物体或系统内部,因外力作用而产生的各物 体之间或各部分之间的相互作用力。 内力必然成对存在,它们是大小相等、指向 相反的力,或大小相等、转向相反的力偶。 为了求得物体内部各部分之间的相互作用 力,需将物体假想地截开,取其一部分来研究; 对于系统,也须截取某一部分来研究。
内力和内力图
19
2. 截面法
例题 4-2
F A a a C FC E FE a D a B
如图平面桁架,已 知铅垂力FC = 4 kN,水 平力FE = 2 kN。求FE, CE,CD杆内力。
建筑力学
内力和内力图
20
例题 4-2
解: 先取整体为研究对象,受力如图所示。由平衡方程
FAy A FAx
F a a
建筑力学
内力和内力图
33
例题 4-3
3 30 kN A 2 20 kN 1 1 20kN D 20kN D 20kN 30 kN B 20 kN C D B 2 FN2
内力与内力图

常见载荷作用下剪力图和弯矩图的特点
若一段梁上无载荷(即q=0),则剪力图为水平直线,弯 矩图为倾斜直线。剪力为正时,弯矩图为向右上方倾斜的 直线,剪力为负时则弯矩图向右下方倾斜,剪力为零时弯 矩图成为水平直线。 若一段梁上作用着均布载荷,则剪力图为斜直线,弯矩图 为二次抛物线。若均布力方向向下,则剪力图为向右下方 倾斜的直线,弯矩图为开口向下的抛物线,抛物线的顶点 的剪力等于零的截面。 在集中力作用的截面上,剪力图有突变,变化值等于该集 中力的大小,弯矩图上由出现折角。 在集中力偶作用的截面上,剪力图无变化,弯矩图上有突 变,变化值等于该集中力偶的力偶矩的大小。
2
ql
五 弯矩、剪力与载荷集度间的关系
在例3中,将弯矩方程对x求一阶导数,得
dM qx F Q dx
将剪力方程对x求一阶导数,得
dF Q dx
q
也就是说,弯矩方程对x的一阶导数等于剪力方程;剪力方程对x的一阶导数 等于载荷集度。这一关系并非只存在于该问题中,而是普遍成立的一个规律。 根据导数的几何意义,以上关系表明:弯矩图上某点的切线的斜率,等于对 应截面上的剪力;剪力图上某点切线的斜率等于对应截面上的载荷集度。根 据这一规律,还可得到常见载荷下剪力图和弯矩图的特点。
例4
例4 外伸梁受力如图所示,试画出其剪力图和弯矩图。
解:(1)根据梁的平衡条件求出梁的支座反力。
FA
qa 4
FB
3qa 4
例1 杆件受力如图所示,求指定截面上的轴力并画出轴力图。
• • • • • • • • • • • • • • 解:(1)用截面法求内力。 沿截面1-1截开,由左侧一段的平衡,有 FN1+10=0 所以 FN1=-10(kN) 沿截面2-2截开,由左侧一段的平衡,有 FN2-40+10=0 所以 FN2=40-10=30(kN) 沿截面3-3截开,由右侧一段的平衡,有 -FN3+20=0 所以 FN3=20( kN ) (2)根据计算结果作出轴力图。 (3)讨论:由以上计算过程可以看出,将 平衡方程中的外力都移至等号右端,则有 FN=ΣFie 也就是说,横截面上的轴力,等于其左侧 (或右侧)一段杆上所有外力的代数和。掌 握这一关系,有利于快速计算轴力并画出轴 力图。
材料力学-内力与内力图

结论 直梁某横截面上的弯矩等于该截面一端(左或右端)
全部力偶矩及全部作用力(包括支反力)对该截面矩的代数和。
MI m(F, q, Me ) (左顺右逆取+号,反之取负号)
26
例3 求承受均布荷载作用的简支梁的内力方程,并画出相应 的剪力图和弯矩图。 1 [ 解] (1)先求支反力 RA R qL [解] B A B y 2 (2)求梁的内力方程 q M 1 x FSS qL qx 剪力 2 x FS S 所有力对截面形心的力矩平衡 L qL / 2 m0 1 2 1 qx 2 qLx M ( x) 0 2 2 1 弯矩 M ( x) qx( L x) 2 结论 直梁某横截面上的弯矩等于该截面一端(左或右端) 全部力偶矩及全部作用力(包括支反力)对该截面矩的代数和。
准确理解杆件内力的定义和符号规定。 能利用截面法建立内力方程,能迅速求出指定 截面的内力。 深入理解梁中弯矩、剪力和分布荷载之间的微 分关系,并能利用这些关系熟练地画出梁的剪力弯 矩图;能正确画出刚架、曲杆的内力图。
4
2.1 内力 ( internal forces ) 定义 和符号规定 定义和符号规定
0,
M
z z
0
T T ( x), M yy M yy( x), M zz M zz( x).
由内力方程作出杆件的内力图
(a x b) —作内力图的列方程法
14
2.2 内力方程及内力图
用截面法求内力方程 方法和步骤 -“截面法”
“切” 、(“留 ”)、“代”、“平”
1) 在必要和可能的条件下,先求出所有约束的反力。 2) 在要求内力的截面位置,用一假想截面将杆件切开。 (留下 一部分作为研究对象,舍去另一部分) 下一部分作为研究对象,舍去另一部分 3) 舍去部 分对留下部分的作用代之以相应的力 ( 即为要求的 舍去部分对留下部分的作用 (即为要求的 内力 ) 。将这种内力作用的方向按假设为正内力方向(即 设 内力) 正法)画在截面上。 4) 留下部分的所有内力、外力(包括约束反力)按照理论 力学的符号规定建立力或力矩的平衡方程式。 5) 求解方程即可得内力。若所得内力为负值,表明实际内 力方向与设想方向相反。 15
14-梁的内力及梁的内力图

B FB CB段(x > a)时 M2(x) FS2(x) FB
AC段(x < a)时 M1(x) FA
x
FS1(x)
Fb (0 < x < a ) FS1 ( x ) = l
Fb M 1 (x ) = x (0 ≤ x ≤ a ) l
Fa (a < x < l ) FS2 ( x ) = − FB = − l Fa (l − x ) M 2 ( x ) = FB (l − x) = l (a ≤ x ≤ l )
M M 2 ( x ) = FB (l − x ) = − (l − x ) l
(0 ≤ x < a )
(a < x ≤ l )
第九章 梁的内力
(3)作剪力图和弯矩图 M a A C l FS图
bM l
b
B
M FS1 ( x ) = l M FS2 ( x ) = l
M M 1 (x ) = x l
FS1 = − F
M1 + F × a = 0
M 1 = − Fa
1 FS1 截面2—2 F C22 M2 FA 2 F
S2
∑F
y
=0
− FS2 + FA − F = 0
FS 2 = FA − F = 2 F
∑M
o2
=0
M2 + F ×a = 0
M 2 = − Fa
第九章 梁的内力
y F 1A2 1 2 FA a
工程力学
第九章 梁的内力
第九章 梁的内力
§9-1 弯曲变形
梁 ——以弯曲为主要变形的杆件。
第九章 梁的内力
最基本最常见的弯曲问题 ——对称弯曲
材料力学教材--内力与内力图

F1 1 kN F2 3 kN
例 最大剪力。
L 10 m d 1 m
求图示结构中梁的最大弯矩和
梁中弯矩图呈如图形状,故弯
RA RB
矩极大值出现在 C 截面或 D 截面。
设 C 截面到 A 端距离为 , 可得 A 端支反力
L L d 1 RA F1 F2 37 4 L L 10 1 M C RA 37 4 2 故有 C 截面弯矩 10
C
YB 14 kN
m
F
0
X C 5 kN
X 0
X B 11 kN
例
画出结构的剪力和弯矩图。
F=5 2 kN/m XXF F
画剪力图
4m 4m
2 kN/m
E XE=8 YF=10 YF Y X XA =11 YEE=4CC=5 C XB B=11 B X =5
YA=4
4m 4m助 学 习 资 料
重 点 与 难 点
◆ 应透彻理解内力符号规定与外力的区别,尤其应熟练掌握轴力和
弯矩的正负规定。 ◆ 截面法是建立内力方程的最基本的方法,应熟练掌握。注意先将 未知内力设正,建立方程时,内力和外力在一起按理论力学的规则进 入方程。因此建立内力方程过程中事实上用了两套符号规定。 ◆ 但是在求某个指定截面的内力时,尽量用更简便的方法,不必通 过建立内力方程求解。 ◆ 计算梁横截面的内力时,应特别注意外力的方向与其引起的内力 符号的关系,以保证内力的正负号正确。 ◆ 正确地计算支座反力是绘制内力图的关键,应确保无误。利用平 衡方程求出支反力后,应进行校核。
例
画出结构的内力图。
A
P1 在 BC 段引起剪力和弯矩。
z
L
梁弯矩图梁内力图
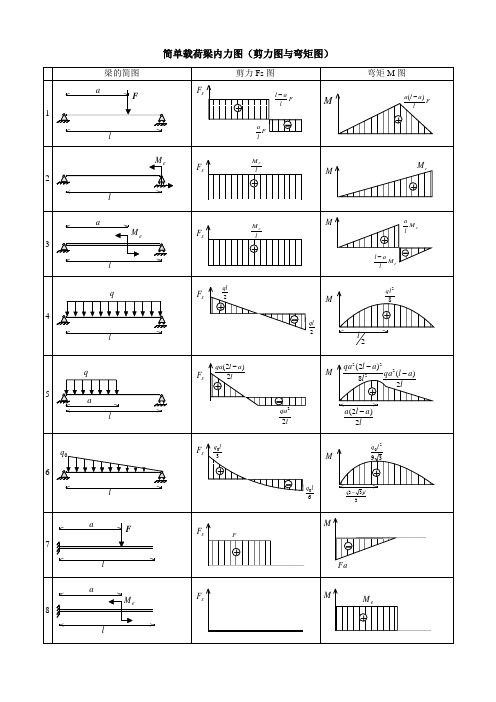
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
梁-弯矩图-梁-内力图--(剪力图与弯矩图)
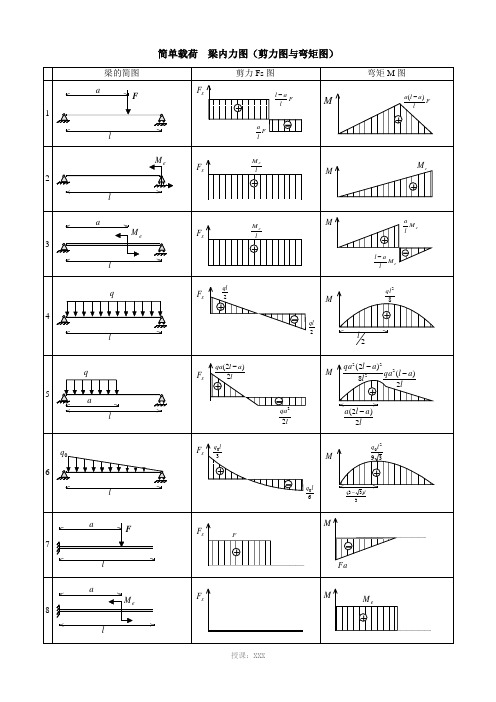
简单载荷梁内力图(剪力图与弯矩图)表2 各种载荷下剪力图与弯矩图的特征表3 各种约束类型对应的边界条件注:力边界条件即剪力图、弯矩图在该约束处的特征。
常用截面几何与力学特征表表2-5授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX授课:XXX注:1.I 称为截面对主轴(形心轴)的截面惯性矩(mm 4)。
基本计算公式如下:⎰•=AdA yI 22.W 称为截面抵抗矩(mm 3),它表示截面抵抗弯曲变形能力的大小,基本计算公式如下:m axy I W =3.i 称截面回转半径(mm ),其基本计算公式如下:AIi =4.上列各式中,A 为截面面积(mm 2),y 为截面边缘到主轴(形心轴)的距离(mm ),I 为对主轴(形心轴)的惯性矩。
5.上列各项几何及力学特征,主要用于验算构件截面的承载力和刚度。
2.单跨梁的内力及变形表(表2-6~表2-10)(1)简支梁的反力、剪力、弯矩、挠度表2-6(2)悬臂梁的反力、剪力、弯矩和挠度表2-7(3)一端简支另一端固定梁的反力、剪力、弯矩和挠度表2-8(4)两端固定梁的反力、剪力、弯矩和挠度表2-9(5)外伸梁的反力、剪力、弯矩和挠度表2-103.等截面连续梁的内力及变形表(1)等跨连续梁的弯矩、剪力及挠度系数表(表2-11~表2-14)1)二跨等跨梁的内力和挠度系数表2-11注:1.在均布荷载作用下:M =表中系数×ql 2;V =表中系数×ql ;EIw 100ql 表中系数4⨯=。
2.在集中荷载作用下:M =表中系数×Fl ;V =表中系数×F ;EIw 100Fl 表中系数3⨯=。
[例1] 已知二跨等跨梁l =5m ,均布荷载q =11.76kN/m ,每跨各有一集中荷载F =29.4kN ,求中间支座的最大弯矩和剪力。
[解] M B 支=(-0.125×11.76×52)+(-0.188×29.4×5)=(-36.75)+(-27.64)=-64.39kN ·m V B 左=(-0.625×11.76×5)+(-0.688×29.4)=(-36.75)+(-20.23)=-56.98kN[例2] 已知三跨等跨梁l =6m ,均布荷载q =11.76kN/m ,求边跨最大跨中弯矩。
2018年材料力学专题一梁的内力和内力图

材料力学专题一梁的内力和内力图专题一梁的内力和内力图例1求图1(a)所示梁截面 A、C的剪力和弯矩。
解:1)求反力FA=5kN,FB=4kN2)求A左截面的内力,如图(a)所示。
∑Yi=0, Fp+FSA左=0,FSA左=-3kN∑MO=0,Fp⨯2+MA左=0, MA左=-6kN⋅m3)求A右截面的内力,如图(b)所示。
∑Yi=0,-Fp-FSA左+FA=0,FSA左=2kN∑MO=0,Fp⨯2+MA右=0, MA右=-6kN⋅m4)求C左截面的内力,如图(c)所示。
∑Yi=0,FA-FP-q⨯2-FSC左=0,FSC左=0∑MO=0,Fp⨯4-FA⨯2+q⨯2⨯1+MC左=0,MC左==-4kN⋅m5)求C右截面的内力,如图(d)所示。
∑Yi=0,FA-FP-q⨯2-FSC右=0,FSC右=5-3-2=0∑MO=0,Fp⨯4-FA⨯2+q⨯2⨯1+M1+MC右=0,MC右==-6kN⋅m(a)(b)(c)(d) (e)图1【小结】①求指定截面上的内力时,既可取梁的左段为脱离体,也可取右段为脱离体,两者计算结果一致。
一般取外力比较简单的一段进行分析。
②在解题时,通常假设截面上把内力为正,若最后计算结果是正,则表示假设的内力方向(转向)与实际是相同的,否则是相反的。
③该题也可以不画受力图,不写平衡方程而由前面的结论直接求得结果。
例2试计算图2所示各梁指定截面(标有细线者)的剪力与弯矩。
(b) (a)qB图2 图(d) (c)解:(a)取A+截面左段研究,FSA+=F, MA+=0取C截面左段研究,FSC=F, MC=取B-截面左段研究, FSB=F, MB =Fl(b) 求A、B处约束反力如图(d)所示,FA=FB=Me/l取A+截面左段研究,FSA+=-FA=-Me, MA+=Mel取C截面左段研究,MlMFSC=-FA=-e, MA+=Me-FA⨯=el22M取B截面右段研究,FSB=-FB=-e, MB=0l(c) 求A、B处约束反力取A截面右段研究,FSA++BFl 2lqll3l3ql2=q⨯=, MA+=-q⨯⨯=-222482取C-截面右段研究,FSC-=q⨯l=ql, MC-=-q⨯l⨯l=-ql22248lqlllql2取C截面右段研究,FSC+=q⨯=, MC+=-q⨯⨯=-22248-取B截面右段研究,FSB-=0, MB-=0+例3试写出图3所示梁的内力方程,并画出剪力图和弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
如有你有帮助,请购买下载,谢谢!
专题一 梁的内力和内力图
例1求图1(a)所示梁截面 A 、C 的剪力和弯矩。
解:1)求反力
kN 5=A F ,kN 4=B F
2)求A 左截面的内力,如图(a)所示。
0=∑i Y , 0=+左SA p F F ,kN 3-=左SA F
0=∑O M ,02=+⨯左A p M F , m kN 6⋅-=左A M
3)求A 右截面的内力,如图(b)所示。
0=∑i Y ,0=+--A SA p F F F 左,kN 2=左SA F
0=∑O M ,02=+⨯右A p M F , m kN 6⋅-=右A M
4)求C 左截面的内力,如图(c)所示。
0=∑i Y ,02=-⨯--左SC P A F q F F ,0=左SC F
0=∑O M ,01224=+⨯⨯+⨯-⨯左C A p M q F F ,=左C M m kN 4⋅-=
5)求C 右截面的内力,如图(d)所示。
0=∑i Y ,02=-⨯--右SC P A F q F F ,0235=--=右SC F 0=∑O M ,012241=++⨯⨯+⨯-⨯右C A p M M q F F ,=右C M m kN 6⋅-=
【小结】①求指定截面上的内力时,既可取梁的左段为脱离体,也可取右段为脱离体,两者计算结果一致。
一般取外力比较简单的一段进行分析。
②在解题时,通常假设截面上把内力为正,若最后计算结果是正,则表示假设的内力方向(转向)与实际是相同的,否则是相反的。
③该题也可以不画受力图,不写平衡方程而由前面的结论直接求得结果。
例2试计算图2所示各梁指定截面(标有细线者)的剪力与弯矩。
解:, A F M +==, 2C Fl
M = 取B -SB B M Fl =
(b) 求A 、B 处约束反力
如图(d)所示,l M F F /==
, e A M F M l =-取B 截面右段研究,, 0e
SB B B M F F M l
=-=-= (c) 求A 、B 处约束反力
取A +
截面右段研究,2
33, 22248
SA A l ql l l ql F q M q +
+=⨯==-⨯⨯=-
图1 (d) 图2 (b) (a) q B (c) B
图(d)
如有你有帮助,请购买下载,谢谢!
(a) (b) (c)
图4
取C -截面右段研究,2, 22248
SC C l ql l l ql F q M q --
=⨯==-⨯⨯=-
取C +
截面右段研究,2
, 22248
SC C l ql l l ql F q M q +
+=⨯==-⨯⨯=-
取B -截面右段研究,0, 0SB B F M --==
例3试写出图3所示梁的内力方程,并画出剪力图和弯矩图。
解:(a ) 求支反力
0=∑C M : 0310126=⨯--⋅Ay F , kN 7=Ay F
0=∑Y : 010=-+By Ay F F , kN 3=By F 列内力方程,
⎩⎨
⎧<<-<<=63
kN 330 kN 7)(S x x x F , ⎩⎨⎧≤≤≤≤⋅-⋅-=63 30 m kN )6(3m kN 127)(x x x x x M 作剪力图和弯矩图。
(b ) 求支反力
0=∑B M :02212=⋅+-⋅l
ql ql l F Ay , F Ay =0 0=∑Y :0=-⋅-+ql l q F F By Ay ,ql F By 2=
列内力方程
作剪力图和弯矩图。
例4利用内力方程作图4(a)所示 简支梁的剪力图和弯矩图。
解:AC 段有:x x q 5)(=
25.210)(x x F S -=,
(0<x <2) 36
510)(x x x M -=,
(0≤x ≤2)
其剪力图和弯矩图如图(b)(c)所示。
由于结构是对称的,荷载也是对称的,
BC 段与AC 段的F S 图是反对称的,M 图 是对称的,据此特点可方便地作出AC 段
的剪力图和弯矩图。
例5试用剪力、弯矩与荷载集度之间的微分关系判断图5所示各梁的内力图形态,画出剪力图和弯矩图。
解:(a ) 根据微分关系:()()x F x
x M S d d = 和 ()()q x x M x x F ==22S d d d d AC 段:q 为常数,且0<q ,F S 图从左到右为向下的斜直线,M 图为向上凸的抛物线。
CB 段:q 为常数,且0>q ,F S 图从左到右为向上的斜直线,M 图为向下凹的抛物线。
在C 截面处,F S 图连续,M 图光滑。
(b)
图3
(a)
如有你有帮助,请购买下载,谢谢!
求得几处特殊截面的内力值后即可作出梁的剪力图与弯矩图。
(b ) 求支反力
0=∑A M : ()022
1322
=⋅⋅-+⋅a q qa a F By
, 3qa F By = 0=∑Y : 02=⋅-+a q F F By Ay , 35qa
F Ay = 判断内力图形态并作内力图
AC 段:q 为常数,且q <0,F S 图从左到右为向下的斜直线,M 图为向上凸的抛物线,在
距A 端a 3
5
截面处,M 取极大值。
CB 段:0=q ,F S 图为水平直线,且F S <0,M 图从左到右为向下的斜直线。
在C 截面处,F S 图连续,M 图光滑。
求得几处特殊截面的内力值后即可作出梁的剪力图与弯矩图。
(c) 求支反力
0=∑A M :()022132=⋅-⋅⋅-⋅a qa a q a F By , qa F By = 0=∑Y : 02=-⋅-+qa a q F F By Ay , qa F Ay 2= 判断内力图形态并作内力图
AC 段:q 为常数,且0<q ,F S 图从左到右为向下的斜直线,M 图为向上凸的抛物线。
C
截面处,有集中力F 作用,F S 图突变,M 图不光滑。
CD 段:q 为常数,且0<q ,F S 图从左到右为向下的斜直线,M 图为向上凸的抛物线。
DB 段:0=q ,Q F 图为水平直线,且F S <0; M 图从左到右为向下的斜直线。
(d)求支反力
0=∑B M : 0462
1
862=⨯⨯--⋅Ay
F ,kN 33.9=Ay F 0=∑Y : 046=⨯-+By Ay F F , kN 67.14=By F 判断内力图形态,作内力图
F S 图:AD 段,0=q ,为水平直线;
DB 段,0<q ,从左到右为向下的斜直线。
M 图:AC 段,0=q ,且F S >0,从左到右为向上的斜直线; C 截面处,有集中力偶e M 作用,有突变;
CD 段,0=q ,且F S >0,从左到右为向上的斜直线,且ab c b //'; DB 段,0<q ,为向上凸的抛物线,且c b '与ce 在c 点相切;
在距D 端m 9
22
截面处,F S =0,M 取极大值17.93kN •m 。
例6试用叠加法画出图6所示梁的弯矩图。
解:(a)
(b)
(a)
(b) (c)
图5 (d)。
