数据插值、函数逼近问题的计算机求解.ppt
合集下载
插值法(共7张PPT)
( x 1 , y 1 ), ( x 2 , y 2 ), , ( x n , y n ), 有
n
[ y k ( x k )] 2
k 1
n
[ y k ( a 0 a 1 x k )] 2 k 1
f (a 0,a1)
可见 , f ( a 0 , a 1 )的极大值点
即为所待定的常数
(a 0,a1)
由a0,a1) 0 a0
f (a0,a1) 0 a1
2
n
(yk
a0
a1xk )
0
k 1
n
2 ( y k a 0 a 1 x k ) x k 0
k 1
na
0
n
xk
a1
n
yk
k 1
k 1
n k 1
x
k
a
0
n x k 2 a 1 k 1
g(x) f(x)
xx
0
1
x
x
2
第一页,共7页。
x
x
3
4
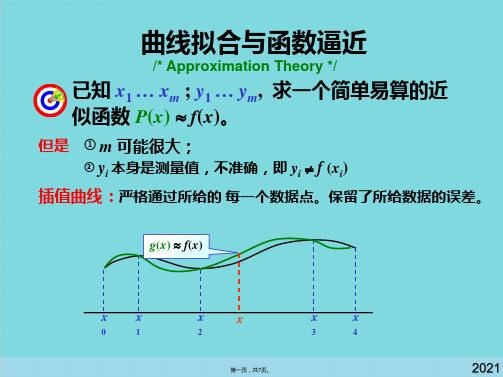
拟合曲线:从数据中找出的趋势性、规律性曲线。消除了数据 的 局部波动。
y
(xi , yi) , i = 1, 2, …, m
x
这时不是取 P(xi) = yi , 而要使 P(xi) yi 总体上尽可能小。
常见做法:
太复杂
➢ 使 m 1im a|P x(xi)yi |最小 /* mini(max()) problem? */
m
m
2
aj
y x
j i
k
=
xk
ii
j0
i1
i 1
m
m
记 bk xik , ck yi xik
插值逼近 样条函数解读 PPT

20 输出u, v
分段插值函数
I1 ( x)
I ( x)
I 2 ( x)
I
n
(
x)
x (x0 , x1)
x (x1, x2 ) ...... x (xn1, xn )
其中I j
x xj x j1 x j
y j1
x x j1 x j x j1
zi1
hi 1 3
zi
yi hi
1 1
yi hi 1
(9)
利用Si' (ti )=Si' -1(ti ),得到
hi zi1 2(hi hi1)zi
hi
zi1
6 hi
(
yi1
yi
)
6 hi 1
(
yi
yi1)
(10)
其中i 1,2,...n -(1 内节点).
zi 1 6hi
(
x
ti
)3
C(
x
ti
)
D(ti
1
x)
(6)
这里,C 和D是积分常数
由插值条件 Si (ti ) yi 以及 Si (ti 1) yi 1 可以确定C和 D
Si (x)
zi 6hi
(ti
1
x)3
zi 1 6hi
(x
ti )3
(
yi 1 hi
x=linspace(0,2.25,10); y=sqrt(x); xx=linspace(0,2.25,100);yy = spline(x,y,xx);
课件:插值与逼近

f(x2) f[x1,x2]
f(x3) f[x2,x3]
¦
¦
f(xn) f[xn-1,xn]
f [x0,x1,x2] f[x1,x2,x3]
¦
f[xn-2,xn-1,xn]
f[x0,x1,x2,…,xn]
• 差商的性质
1. 差商关于所含节点是对称的,即与节点位置无关.
2. f[x0,x1,…,xn]=
• 逼近的度量方式的要求 :插值,一致逼近,平方逼近(要求必 须提得合理否则无解或许多解),
• 如何构造逼近函数P(x).
• 逼近的效果.
插值的概念
• 插值是由离散数据来构造一个函数的近似函数 的重要方法, 插值要求近似函数与被近似函数 在一些点处取相同的函数值,甚至导数值.
• 已知函数y=f(x)在[a, b]中n+1个互异点x0, x1, …, xn上的函数值分别为f(x0), f(x1), …, f(xn) ,构造 一个简单的函数P(x),满足条件
f [x0 , x1
, xk ] f [x0, x1
, xk2 , xk ] f [x0, x1, xk xk1
, xk1]
称为函数f(x)在点x0,x2,…,xk处的k阶差商.
• 差商表
xi
x0 x1 x2 x3 ¦ xn
f(xi) 一阶差商 二阶差商 … n阶差商
f(x0)
f(x1) f[x0,x1]
而Ln(x)=Pn(x), Lagrange插值问题的解存在且唯一.
称li(x) (i=1,2,…n)为Lagrange插值基函数.称(3.1.2)为
Lagrange插值多项式.
• 记pn+1(x)=(x-x0)(x-x1) …(x-xn)
教学课件:第三章-插值与逼近

最佳一致逼近在数值分析、计算数学等领域有广泛应用,如多项式插值、样条插值 等算法都是基于最佳一致逼近的思想。
最佳平方逼近
最佳平方逼近是指在平方误差意义下, 函数空间中最佳逼近原函数的逼近元 所在的函数类。
最佳平方逼近在数值分析、计算数学 等领域有广泛应用,如多项式插值、 样条插值等算法都是基于最佳平方逼 近的思想。
图像处理
在图像处理中,插值用于 放大缩小图像,而逼近则 用于图像的平滑和锐化。
物理学模拟
在物理模拟中,插值用于 确定未知点的物理量,而 逼近则用于简化复杂的物 理过程。
02 插值方法
线性插值
总结词
线性插值是最简单的插值方法,通过连接两个已知点的直线来估计中间点的值。
详细描述
线性插值基于两点之间的直线关系,通过已知的x和y坐标计算出中间点的值。 它适用于数据点分布较为均匀的情况,但在数据点分布不均或存在弯曲趋势时, 线性插值的误差较大。
随着科学技术的不断发展,插值与逼近的应用领域也 在不断扩大。未来,插值与逼近将会在人工智能、大 数据分析、机器学习等领域发挥更加重要的作用。
随着教育技术的发展,未来插值与逼近的教学将会更 加注重实践和应用。学生可以通过更多的实践项目和 案例分析,深入理解和掌握插值与逼近的概念和方法 ,提高解决实际问题的能力。
06 总结与展望
总结
• 插值与逼近是数学中重要的概念,广泛应用于实际问题的解决。通过学习插值 与逼近,学生可以更好地理解数学在解决实际问题中的应用,提高数学素养和 解决问题的能力。
• 本章主要介绍了线性插值、多项式插值、样条插值和最小二乘法等插值方法, 以及代数逼近、多项式逼近和样条逼近等逼近方法。这些方法在数值分析、计 算物理、计算机图形学等领域有着广泛的应用。
最佳平方逼近
最佳平方逼近是指在平方误差意义下, 函数空间中最佳逼近原函数的逼近元 所在的函数类。
最佳平方逼近在数值分析、计算数学 等领域有广泛应用,如多项式插值、 样条插值等算法都是基于最佳平方逼 近的思想。
图像处理
在图像处理中,插值用于 放大缩小图像,而逼近则 用于图像的平滑和锐化。
物理学模拟
在物理模拟中,插值用于 确定未知点的物理量,而 逼近则用于简化复杂的物 理过程。
02 插值方法
线性插值
总结词
线性插值是最简单的插值方法,通过连接两个已知点的直线来估计中间点的值。
详细描述
线性插值基于两点之间的直线关系,通过已知的x和y坐标计算出中间点的值。 它适用于数据点分布较为均匀的情况,但在数据点分布不均或存在弯曲趋势时, 线性插值的误差较大。
随着科学技术的不断发展,插值与逼近的应用领域也 在不断扩大。未来,插值与逼近将会在人工智能、大 数据分析、机器学习等领域发挥更加重要的作用。
随着教育技术的发展,未来插值与逼近的教学将会更 加注重实践和应用。学生可以通过更多的实践项目和 案例分析,深入理解和掌握插值与逼近的概念和方法 ,提高解决实际问题的能力。
06 总结与展望
总结
• 插值与逼近是数学中重要的概念,广泛应用于实际问题的解决。通过学习插值 与逼近,学生可以更好地理解数学在解决实际问题中的应用,提高数学素养和 解决问题的能力。
• 本章主要介绍了线性插值、多项式插值、样条插值和最小二乘法等插值方法, 以及代数逼近、多项式逼近和样条逼近等逼近方法。这些方法在数值分析、计 算物理、计算机图形学等领域有着广泛的应用。
计算方法PPT课件第五章 插值与拟合

因此
li (x)
(x x0 )(x x1 ) (xi x0 )(xi x1 )
(x ( xi
xi1 )(x xi1 ) ( x xi1 )( xi xi1 ) ( xi
xn ) xn
)
n x x j . j0 xi x j ji
5.2.2 拉格朗日插值多项式
设用试验或观测方法得到函数 的如下函数y 值f表(x)
xi x0 , x1, , xn
yi y 0 , y1 , , y n
(5.11)
其中:yi f (xi )(i 0,1,..., n).我们用插值基函数li (x)(i 0, 1,..., n)的线性组合来构造满足式(5.11)的插值多项式,令
2020年1月26日星期日
主讲 韩光朋
17
(2) 将x 2.5代入,得L2 (2.5) 1.2625,因此
f (2.5) L2 (2.5) 1.2625.
(3)
f
(x)
ln(1
x), 求出f
''' ( x)
2 (1 x)3
,
从而max f ''' ( x) 1 .
1 x3
Rn (x)
f (n1) ( )
(n 1)!
n1
(
x)
,
(5.6)
其中: (a,b)且依赖于x,而x [a,b].
证明(见P111)略
2020年1月26日星期日
主讲 韩光朋
9
在实际插值问题中,由 于一般不知道,且实
际插值中f (x)一般较复杂或者未知, 因此用余项公 式(5.6)求误差是较困难的, 只能对其进行估计。 若
《函数的数值逼近》PPT课件

(1)满足插值条件的P ( x) 是否存在唯一? (2)若满足插值条件的P(x) 存在,如何构造P(x)? (3)如何估计用P (x)近似替代 f ( x) 产生的误差?
精选课件ppt
7
2、插值多项式的存在唯一性
定理 若插值结点 x0,x1,…, xn是(n+1)个互异点,则满足插值条件 P(xk)= yk (k = 0,1,…,n)
精选课件ppt
10
§2 代数多项式插值
一、线性插值与抛物线插值
1. 线性插值(n =1)
设已知区间[ xk , xk+1]端点处的函数值yk= f (xk),yk+1 = f (xk+1),
求线性插值多项式L 1(x ) ,使其满足
L1 ( xk ) yk
L1
(
xk
1
)
yk 1
x 0 xk
y = L1(x)
P(x) = a0 + a1 x + ⋯ + an xn
则称P( x)为n 次插值多项式. 相应的插值法称为多项式插 值法(代数插值法)。
x
y = f (x) •
(xi, yi)
y = P(x) 曲线 P ( x)
近似 f ( x)
0 a=x0 x1 x2 x3
xn=b y
精选课件ppt
6
研究问题:
构造法:
先求 插值基函数l k-1(x), l k (x), l k+1(x) (二次函数), 满足:
lk1(xk1)1, lk1(xk)lk1(xk1)0;
lk(xk)1,
lk(xk1)lk(xk1)0;
(4)
lk1(xk1)1, lk1(xk1)lk1(xk)0,
精选课件ppt
7
2、插值多项式的存在唯一性
定理 若插值结点 x0,x1,…, xn是(n+1)个互异点,则满足插值条件 P(xk)= yk (k = 0,1,…,n)
精选课件ppt
10
§2 代数多项式插值
一、线性插值与抛物线插值
1. 线性插值(n =1)
设已知区间[ xk , xk+1]端点处的函数值yk= f (xk),yk+1 = f (xk+1),
求线性插值多项式L 1(x ) ,使其满足
L1 ( xk ) yk
L1
(
xk
1
)
yk 1
x 0 xk
y = L1(x)
P(x) = a0 + a1 x + ⋯ + an xn
则称P( x)为n 次插值多项式. 相应的插值法称为多项式插 值法(代数插值法)。
x
y = f (x) •
(xi, yi)
y = P(x) 曲线 P ( x)
近似 f ( x)
0 a=x0 x1 x2 x3
xn=b y
精选课件ppt
6
研究问题:
构造法:
先求 插值基函数l k-1(x), l k (x), l k+1(x) (二次函数), 满足:
lk1(xk1)1, lk1(xk)lk1(xk1)0;
lk(xk)1,
lk(xk1)lk(xk1)0;
(4)
lk1(xk1)1, lk1(xk1)lk1(xk)0,
计算方法第二章ppt

当方程组的系数矩阵为非奇异 矩阵(即满秩矩阵)时,高斯 消元法可求得唯一解。
列主元高斯消元法
列主元高斯消元法的 基本思想
在高斯消元法的基础上,每次选取列 中绝对值最大的元素作为主元进行消 元,以避免出现小主元导致的误差放 大问题。
列主元高斯消元法的 步骤
首先选取第一列中绝对值最大的元素 作为主元,通过行交换将其移到第一 行第一列位置,然后进行高斯消元。 在后续的消元过程中,每次均选取当 前列中绝对值最大的元素作为主元进 行消元。
100%
数值解法
通过计算机求解常微分方程的近 似解的方法,主要包括欧拉方法 和龙格-库塔方法等。
80%
离散化与步长
将连续的时间或空间域离散化, 取离散点上的函数值作为近似解 ,步长是相邻离散点间的距离。
欧拉方法
显式欧拉法
一种简单的数值解法,通过前 一步的函数值及其导数来推算 下一步的函数值。
隐式欧拉法
通过求解一个非线性方程来得 到下一步的函数值,具有较高 的精度和稳定性。
改进欧拉法
结合显式欧拉法和隐式欧拉法 的优点,提高算法的精度和效 率。
龙格-库塔方法
龙格-库塔法基本思想
自适应步长龙格-库塔法
通过多步计算并利用泰勒级数展开式, 得到更高精度的近似解。
根据误差估计自动调整步长,实现精 度和计算效率的动态平衡。
标准四阶龙格-库塔法
一种常用的高精度数值解法,具有局 部截断误差为$O(h^5)$的优点。
常微分方程数值解法误差分析
局部截断误差
数值解法在单步计算中所产生的误差,可以通过泰勒级数展开式进行估计。
全局误差
数值解法在整个计算过程中所产生的累积误差,与算法稳定性、步长选择等因素有关。
数值分析方法【ch01】插值与逼近 培训教学课件

二、多项式插值
0 5 Hermite插值
二、多项式插值
0 5 Hermite插值
二、多项式插值
0 5 Hermite插值
03
三、径向基函数插值
0 1 概述
三、径向基函数插值
0 1 概述
Hale Waihona Puke 三、径向基函数插值0 1 概述
三、径向基函数插值
0 2 再生核空间
三、径向基函数插值
0 2 再生核空间
二、多项式插值
0 4 分片线性插值
则Lagrange插值与Newton 插值失效,表现为: 当n增大时,在区间[-5,5]两端附近误差迅速增大(见 图1-2).
图1-2显示了当n=10时Lagrange插值与Newton 插值的效果,明显可以看出,在区间的两端附近插值 曲线出现振荡.
二、多项式插值
解:使用最小二乘方法可以求解.上 面的超定方程组,从而得到
四、最佳逼近
0 2 最佳一致逼近
常用的范数如下:
四、最佳逼近
0 2 最佳一致逼近
四、最佳逼近
0 2 最佳一致逼近
四、最佳逼近
0 3 最佳平方逼近
四、最佳逼近
0 3 最佳平方逼近
四、最佳逼近
0 4 正交多项式
四、最佳逼近
0 4 正交多项式
二、多项式插值
0 2 Lagrange插值
图1-1给出了7次Lagrange插值曲线,该曲线较好地通过了给定的样本数 据(图中的○表示样本数据,曲线为插值曲线).
二、多项式插值
0 3 Newton插值
当我们需要扩充试探空间的时候,之前所有的基函数都没有被保留,这非 常不利于大规模数值计算.克服这一缺陷的有效方法之一是Newton插值.选择 如下形式的试探空间
数值分析课件 第四章 多项式插值与函数逼近1

n
j =0 j ≠i
′ ω n+1 ( xi ) = ∏ ( xi − x j ) l i ( x ) =
j=0 j≠i
n
ω n +1 ( x ) ′ ( x − x i )ω n +1 ( x i )
( x − x0 )( x − x1)L( x − xi−1)( x − xi+1)L( x − xn ) li ( x) = ( xi − x0 )( xi − x1)L( xi − xi−1)( xi −系数矩阵是Vandermonde矩阵 矩阵 方程组的系数矩阵是
1 1 M 1
x0 x L x x1 x L x = ∏ ( xi − xj ) ≠ 0 M M M 0≤ j <i ≤n 2 n xn xn L xn
2 0 2 1
n 0 n 1
方程组存在唯一解,因此满足插值条件(*) 方程组存在唯一解,因此满足插值条件(*) 的不超过n次的插值多项式是唯一存在的 次的插值多项式是唯一存在 的不超过 次的插值多项式是唯一存在的.
§1
插值问题
/* Interpolation Problem */
(插值的定义) Def 4.1.1 插值的定义)
n
已知定义于区间 [a , b] 上的实值函数 f ( x )在 n+1 互异节点 + 个互异节点
{ xi }i = 0 ⊂ [a , b] 处的函数值 { f ( xi )}i = 0 ,若函数集合 Φ 中的函
( n+1)
( x) ≤ Mn+1 , x∈(a,b) ∈
M n +1 n 作为误差估计上限。 将 ∏ | x − xi |作为误差估计上限。 ( n + 1)! i = 0
j =0 j ≠i
′ ω n+1 ( xi ) = ∏ ( xi − x j ) l i ( x ) =
j=0 j≠i
n
ω n +1 ( x ) ′ ( x − x i )ω n +1 ( x i )
( x − x0 )( x − x1)L( x − xi−1)( x − xi+1)L( x − xn ) li ( x) = ( xi − x0 )( xi − x1)L( xi − xi−1)( xi −系数矩阵是Vandermonde矩阵 矩阵 方程组的系数矩阵是
1 1 M 1
x0 x L x x1 x L x = ∏ ( xi − xj ) ≠ 0 M M M 0≤ j <i ≤n 2 n xn xn L xn
2 0 2 1
n 0 n 1
方程组存在唯一解,因此满足插值条件(*) 方程组存在唯一解,因此满足插值条件(*) 的不超过n次的插值多项式是唯一存在的 次的插值多项式是唯一存在 的不超过 次的插值多项式是唯一存在的.
§1
插值问题
/* Interpolation Problem */
(插值的定义) Def 4.1.1 插值的定义)
n
已知定义于区间 [a , b] 上的实值函数 f ( x )在 n+1 互异节点 + 个互异节点
{ xi }i = 0 ⊂ [a , b] 处的函数值 { f ( xi )}i = 0 ,若函数集合 Φ 中的函
( n+1)
( x) ≤ Mn+1 , x∈(a,b) ∈
M n +1 n 作为误差估计上限。 将 ∏ | x − xi |作为误差估计上限。 ( n + 1)! i = 0
【全版】数值分析课件第四章多项式插值与函数逼近2推荐PPT

全导数的hermite插值多项式的几何意义如n1时hermite插值多项式二全导数的hermite插值多项式的存在唯一性和余项满足前述插值条件的不超过2n1次的插值多因此多项式有n1个二重零点设被插值函数在区间ab上有2n1阶连续导关于互异节点的满足前述插值条件的不超过2n1次的插值多项式则对成立证明方法同完全类似应用hermite插值计算的近似值
1(13x)(x1)2(x2)2 4
1(x)[12(x1)(1 101 12)][((x 1 0 0))((1x22))]2
x2(x2)2
2(x)[12(x2)(2 10211)][((x2 00))((2x11))]2
1(73x)x2(x1)2 4
0(x)(x0 )l0 2(x)1 4x (x 1 )2(x2 )2
如n=1时Hermite插值多项式 H 3 (为x )
H3(x)f(x0)12xx00xx1xx0xx112f(x1)12xx11xx0xx1xx002 f(x0)(xx0)xx0xx112f(x1)(xx1)xx1xx002
全导数的Hermite插值多项式的几何意义
H9(x) f(x)
x0
x1
满足如下的2n+2个条件
H 2n1(xi)f(xi) H 2 n1(xi)f(xi)
i0,1,2, ,n
称上述问题为全导数的Hermite插值问题
一、全导数的Hermite插值多项式的构造
思想 类似于Lagrange插值多项式的构造方法,即通过构 造一组插值基函数来表示Hermite插值多项式。
并推导其插值余项(已知 f ( x具) 有4阶连续导数)。
解:首先构造满足插值条件 H 3 (x i)f(x i)的i多 项0 ,式1 ,2
1(13x)(x1)2(x2)2 4
1(x)[12(x1)(1 101 12)][((x 1 0 0))((1x22))]2
x2(x2)2
2(x)[12(x2)(2 10211)][((x2 00))((2x11))]2
1(73x)x2(x1)2 4
0(x)(x0 )l0 2(x)1 4x (x 1 )2(x2 )2
如n=1时Hermite插值多项式 H 3 (为x )
H3(x)f(x0)12xx00xx1xx0xx112f(x1)12xx11xx0xx1xx002 f(x0)(xx0)xx0xx112f(x1)(xx1)xx1xx002
全导数的Hermite插值多项式的几何意义
H9(x) f(x)
x0
x1
满足如下的2n+2个条件
H 2n1(xi)f(xi) H 2 n1(xi)f(xi)
i0,1,2, ,n
称上述问题为全导数的Hermite插值问题
一、全导数的Hermite插值多项式的构造
思想 类似于Lagrange插值多项式的构造方法,即通过构 造一组插值基函数来表示Hermite插值多项式。
并推导其插值余项(已知 f ( x具) 有4阶连续导数)。
解:首先构造满足插值条件 H 3 (x i)f(x i)的i多 项0 ,式1 ,2
数据插值、函数逼近问题的计算机求解101页PPT

第8章 数据插值、函数逼近问题
的计算机求解
薛定宇、陈阳泉著《高等应用数学问题的 MATLAB求解》,清华大学出版社2019
CAI课件开发:刘莹莹、薛定宇
2019/9/30
高等应用数学问题的 MATLAB 求解
1
主要内容
插值与数据拟合 样条插值与数值微积分 由已知数据拟合数学模型 信号分析与数字信号处理基础
样条插值的结果与理论之间的比较:
2019/9/30
高等应用数学问题的 MATLAB 求解
13
【例8-5】
2019/9/30
高等应用数学问题的 MATLAB 求解
14
8.1.3 二维网格数据的插值问题
2019/9/30
高等应用数学问题的 MATLAB 求解
15
【例8-6】
2019/9/30
高等应用数学问题的 MATLAB 求解
2019/9/30
高等应用数学问题的 MATLAB 求解
47
8.3.2 给定函数的连分式展开及基 于连分式的有理近似
连分式的一般形式
2019/9/30
高等应用数学问题的 MATLAB 求解
48
Cauer II 型连分式
2019/9/30
高等应用数学问题的 MATLAB 求解
49
调用Maple的连分式展开函数
94
2019/9/30
高等应用数学问题的 MATLAB 求解
95
2019/9/30
高等应用数学问题的 MATLAB 求解
96
2019/9/30
高等应用数学问题的 MATLAB 求解
97
由已知样本点去计算其他点函数值的方法
称为数据插值,本章介绍了一维数据插值 的方法及 MATLAB 求解,介绍了曲线平滑 处理与基于样本数据的定积分计算还介绍
的计算机求解
薛定宇、陈阳泉著《高等应用数学问题的 MATLAB求解》,清华大学出版社2019
CAI课件开发:刘莹莹、薛定宇
2019/9/30
高等应用数学问题的 MATLAB 求解
1
主要内容
插值与数据拟合 样条插值与数值微积分 由已知数据拟合数学模型 信号分析与数字信号处理基础
样条插值的结果与理论之间的比较:
2019/9/30
高等应用数学问题的 MATLAB 求解
13
【例8-5】
2019/9/30
高等应用数学问题的 MATLAB 求解
14
8.1.3 二维网格数据的插值问题
2019/9/30
高等应用数学问题的 MATLAB 求解
15
【例8-6】
2019/9/30
高等应用数学问题的 MATLAB 求解
2019/9/30
高等应用数学问题的 MATLAB 求解
47
8.3.2 给定函数的连分式展开及基 于连分式的有理近似
连分式的一般形式
2019/9/30
高等应用数学问题的 MATLAB 求解
48
Cauer II 型连分式
2019/9/30
高等应用数学问题的 MATLAB 求解
49
调用Maple的连分式展开函数
94
2019/9/30
高等应用数学问题的 MATLAB 求解
95
2019/9/30
高等应用数学问题的 MATLAB 求解
96
2019/9/30
高等应用数学问题的 MATLAB 求解
97
由已知样本点去计算其他点函数值的方法
称为数据插值,本章介绍了一维数据插值 的方法及 MATLAB 求解,介绍了曲线平滑 处理与基于样本数据的定积分计算还介绍
数据插值、函数逼近问题的计算机求解PPT105页

日·法拉兹
42、只有在人群中间,才能认识自 己。——德国
数据插值、函数逼近问题的计算机求解
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
42、只有在人群中间,才能认识自 己。——德国
数据插值、函数逼近问题的计算机求解
1、合法而稳定的权力在使用得当时很 少遇到 抵抗。 ——塞 ·约翰 逊 2、权力会使人渐渐失去温厚善良的美 德。— —伯克
3、最大限度地行使权力总是令人反感 ;权力 不易确 定之处 始终存 在着危 险。— —塞·约翰逊 4、权力会奴化一切。——塔西佗
5、虽然权力是一头固执的熊,可是金 子可以 拉着它 的鼻子 走。— —莎士 比
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
37
【例8-14】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
38
【例8-15】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
39
8.2.2.2 基于样条插值的数值积分运算
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
2021/2/28
东北大学信息学院
21
【例8-8】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
22
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
23
8.1.5 高维插值问题
三维的网格数据:
维网格数据的生成:
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
24
【例8-9】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
25
8.2 样条插值与数值微积分
样条插值的 MATLAB 表示 基于样条插值的数值微积分运算
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
26
8.2.1 样条插值的MATLAB表示
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
32
【例8-12】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
33
8.2.1.2 B 样条函数及其MATLAB表示
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
34
【例8-13】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
35
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
36
8.2.2 基于样条插值的数值微积分运算
8.2.2.1 基于样条插值的数值微分运算
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
比较梯形法和插值法:
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
12
已知 5 个不均匀分布的样本点:
样条插值的结果与理论之间的比较:
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
13
【例8-5】
高等应用数学问题的 MATLAB 求解
Байду номын сангаас2021/2/28
40
【例8-16】考虑
中较稀疏的样本点,用
样条积分的方式求出定积分及积分函数
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
41
8.3
由已知数据拟合数学模型
多项式拟合 连分式拟合 有理式拟合
近似
函数线性组合的曲线拟合方法 最小二乘曲线拟合
高等应用数学问题的 MATLAB 求解
8.2.1.1 三次样条函数及其MATLAB表示
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
27
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
28
【例8-10】
已知其中的 150 个数
据点,求此稀疏数据的三次样条插值结果
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
29
【例8-11】 点,用三次样条插值的方法对这些数据进行拟合
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
30
分段多项式拟合结果
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
31
处理多个自变量的网格数据三次样条插值类:
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
2
8.1 插值与数据拟合
一维数据的插值问题 已知样本点的定积分计算 二维网格数据的插值问题 二维一般分布数据的插值问题 高维插值问题
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
3
8.1.1 一维数据的插值问题
8.1.1.1 一维插值问题的求解
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
4
【例8-1】已知的数据点来自函数
根据生成的数据进行插值处理,得出较平滑的曲线 直接生成数据。
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
5
高等应用数学问题的 MATLAB 求解
东北大学信息学院
14
8.1.3 二维网格数据的插值问题
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
15
【例8-6】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
16
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
17
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
9
【例8-3】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
10
8.1.2 已知样本点的定积分计算
编写函数:
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
11
【例8-4】 求解
第8章 数据插值、函数逼近问题
的计算机求解
薛定宇、陈阳泉著《高等应用数学问题的 MATLAB求解》,清华大学出版社2004
CAI课件开发:刘莹莹、薛定宇
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
1
主要内容
插值与数据拟合 样条插值与数值微积分 由已知数据拟合数学模型 信号分析与数字信号处理基础
2021/2/28
东北大学信息学院
6
【例8-2】编写一段程序,允许利用插值方法手工绘
制一条光滑的曲线
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
7
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
8
8.1.1.2 Lagrange 插值算法及应用
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
18
8.1.4 二维一般分布数据的插值问题
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
19
【例8-7】
高等应用数学问题的 MATLAB 求解
2021/2/28
东北大学信息学院
20
高等应用数学问题的 MATLAB 求解
