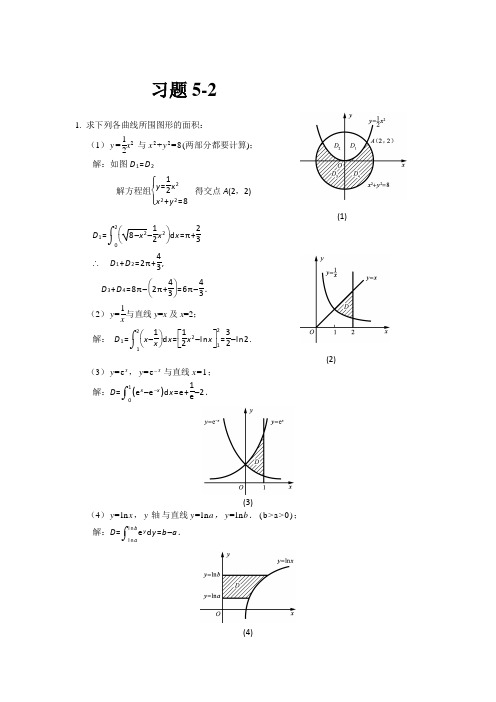
高数习题第十一章习题黄立宏第4版

合集下载

高等数学下册黄立宏黄云清答案详解

习题九答案1. 求函数u =xy 2+z 3-xyz 在点（1，1,2）处沿方向角为πππ,,343αβγ===的方向导数。

解：(1,1,2)(1,1,2)(1,1,2)cos cos cos u u u uy l x z αβγ∂∂∂∂=++∂∂∂∂22(1,1,2)(1,1,2)(1,1,2)πππcos cos cos 5.(2)()(3)343xy xz y yz z xy =++=---2. 求函数u =xyz 在点（5,1,2）处沿从点A （5,1,2）到B （9，4，14）的方向导数。

解：{4,3,12},13.AB AB ==AB 的方向余弦为4312cos ,cos ,cos 131313αβγ=== (5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)2105u yz x u xz y u xyz∂==∂∂==∂∂==∂ 故4312982105.13131313u l ∂=⨯+⨯+⨯=∂ 3. 求函数22221x y z a b ⎛⎫=-+ ⎪⎝⎭在点处沿曲线22221x y a b +=在这点的内法线方向的方向导数。

解：设x 轴正向到椭圆内法线方向l 的转角为φ，它是第三象限的角，因为2222220,x y b x y y a b a y''+==-所以在点处切线斜率为2.b y a a '==-法线斜率为cos a bϕ=.于是tan sin ϕϕ==∵2222,,z z x y x a y b∂∂=-=-∂∂∴2222z la b ⎛∂=--=∂⎝ 4.研究下列函数的极值： (1)z =x 3+y 3－3(x 2+y 2); (2)z =e 2x (x +y 2+2y ); (3)z =(6x －x 2)(4y －y 2); (4)z =(x 2+y 2)22()ex y -+;(5)z =xy (a －x －y ),a ≠0.解：（1）解方程组22360360x yz x x z y y ⎧=-=⎪⎨=-=⎪⎩ 得驻点为（0,0）,(0,2),(2,0),(2,2).z xx =6x －6, z xy =0, z yy =6y －6在点（0，0）处，A =－6，B =0，C =-6，B 2－AC =－36<0，且A <0,所以函数有极大值z (0,0)=0. 在点（0，2）处，A =－6，B =0，C =6，B 2－AC =36>0，所以(0,2)点不是极值点. 在点（2，0）处，A =6，B =0，C =－6，B 2－AC =36>0，所以(2,0)点不是极值点.在点（2，2）处，A =6，B =0，C =6，B 2－AC =－36<0，且A >0,所以函数有极小值z (2,2)=-8.(2)解方程组222e (2241)02e (1)0x x xy z x y y z y ⎧=+++=⎪⎨=+=⎪⎩ 得驻点为1,12⎛⎫-⎪⎝⎭. 22224e (21)4e (1)2e x xx x xy xyy z x y y z y z =+++=+=在点1,12⎛⎫-⎪⎝⎭处,A =2e,B =0,C =2e,B 2-AC =-4e 2<0,又A >0,所以函数有极小值e 1,122z ⎛⎫=-- ⎪⎝⎭.(3) 解方程组22(62)(4)0(6)(42)0x y z x y y z x x y ⎧=--=⎪⎨=--=⎪⎩ 得驻点为（3,2）,(0,0),(0,4),(6,0),(6,4).Z xx =－2(4y -y 2), Z xy =4(3－x )(2－y ) Z yy =－2(6x －x 2)在点（3，2）处，A =－8，B =0，C =－18，B 2－AC =－8×18<0,且A <0，所以函数有极大值z (3,2)=36.在点（0，0）处，A =0，B =24，C =0，B 2－AC >0，所以(0,0)点不是极值点. 在点（0，4）处，A =0，B =-24，C =0，B 2－AC >0，所以(0,4)不是极值点.在点（6，0）处，A =0，B =-24，C =0，B 2－AC >0，所以(6,0)不是极值点. 在点（6，4）处，A =0，B =24，C =0，B 2－AC >0，所以(6,4)不是极值点.(4)解方程组2222()22()222e(1)02e(1)0x y x y x x y y x y -+-+⎧--=⎪⎨--=⎪⎩得驻点P 0(0,0),及P (x 0,y 0),其中x 02+y 02=1，在点P 0处有z =0，而当（x ,y ）≠(0,0)时，恒有z >0，故函数z 在点P 0处取得极小值z =0.再讨论函数z =u e -u由d e (1)d u z u u-=-，令d 0d zu =得u =1, 当u >1时，d 0d z u <；当u <1时，d 0d zu>,由此可知，在满足x 02+y 02=1的点（x 0,y 0）的邻域内，不论是x 2+y 2>1或x 2+y 2<1,均有2222()1()e e xy z x y -+-=+≤.故函数z 在点（x 0,y 0）取得极大值z =e -1(5)解方程组(2)0(2)0x yz y a x y z x a y x =--=⎧⎨=--=⎪⎩得驻点为 12(0,0),,33a a P P ⎛⎫⎪⎝⎭z xx =-2y , z xy =a -2x -2y , z yy =-2x .故z 的黑塞矩阵为 222222ya x y H a x y x ---⎡⎤=⎢⎥---⎣⎦于是 122033(),().0233aa a H P H P a aa ⎡⎤--⎢⎥⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦ 易知H （P 1）不定，故P 1不是z 的极值点，H （P 2）当a <0时正定，故此时P 2是z 的极小值点，且3,2733aa a z ⎛⎫= ⎪⎝⎭,H （P 2）当a >0时负定，故此时P 2是z 的极大值点，且3,2733aa a z ⎛⎫= ⎪⎝⎭.5. 设2x 2+2y 2+z 2+8xz -z +8=0，确定函数z =z (x ,y )，研究其极值。

高数习题第五章习题黄立宏第4版

（1）ຫໍສະໝຸດ 函数；（2）计算不定积分 .
解：由题设，两边关于求导数，有，由此得
6.已知某容器内表面形状是由曲线段，（单位：m）绕轴旋转一周所成.
（1）求该容器的容积；
（2）如果容器装满水，问将水全部提升到高出容器顶面1m处时，需做功多少？
解：（1）容器的容积
（2）利用微元法可得将水全部提升到高出容器顶面1m处所做的功为
（2
．
（3）
=4.
(4)
(5)
(6)
2.设星形线的参数方程为x=acos3t，y=asin3t，a>0求
（3）星形线所围面积；
（4）绕x轴旋转所得旋转体的体积；
（5）星形线的全长．
解：(1)
．
(2)
(3)xt′=3acos2tsint
yt′=3asin2tcost
xt′2+yt′2=9a2sin2tcos2t，利用曲线的对称性，
．
3.求对数螺线r=eaθ相应θ=0到θ=φ的一段弧长．
解：
．
4.求半径为R，高为h的球冠的表面积．
解：
=2Rh．
5.求曲线段y=x3(0x1)绕x轴旋转一周所得旋转曲面的面积．
解：
．
习题
1.把长为10m，宽为6m，高为5m的储水池内盛满的水全部抽出，需做多少功？
解：如图19，区间[x，x+dx]上的一个薄层水，有微体积dV=10·6·dx
3.(1)求曲线与坐标轴所围成图形的面积；
(2)曲线与坐标轴围成的图形是否存在有限面积？请说明理由.
4.记为介于曲线与轴之间的无界图形，求的面积及绕轴旋转一周所得旋转体的体积.
解：的面积为 .

高等数学课后习题及参考答案(第十一章)

高等数学课后习题与参考答案〔第十一章〕习题11-11.写出下列级数的前五项:<1>∑∞=++1211n nn;解 51514141313121211111112222212⋅⋅⋅+++++++++++++++=++∑∞=n n n . 解 3762651045311112⋅⋅⋅+++++=++∑∞=n n n .<2>∑∞=⋅⋅⋅⋅-⋅⋅⋅⋅12 42)12( 31n n n ; 解 10864297531864275316425314231212 42)12( 311⋅⋅⋅+⋅⋅⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅+=⋅⋅⋅⋅-⋅⋅⋅⋅∑∞=n n n . 解 3840945384105481583212 42)12( 311⋅⋅⋅+++++=⋅⋅⋅⋅-⋅⋅⋅⋅∑∞=n n n .<3>∑∞=--115)1(n n n ; 解 51515151515)1(543211⋅⋅⋅-+-+-=-∑∞=-n n n . 解 3125162511251251515)1(11⋅⋅⋅-+-+-=-∑∞=-n n n . <4>∑∞=1!n n nn.解 5!54!43!32!21!1!543211⋅⋅⋅+++++=∑∞=n n n n. 解3125120256242764211!1⋅⋅⋅+++++=∑∞=n n n n . 2.写出下列级数的一般项:<1> 7151311⋅⋅⋅++++; 解一般项为121-=n u n . <2> 5645342312⋅⋅⋅-+-+-; 解一般项为nn u n n 1)1(1+-=-. <3> 86426424222⋅⋅⋅+⋅⋅⋅+⋅⋅+⋅+x x x x x ; 解一般项为!22n x u n n =.<4> 97535432⋅⋅⋅+-+-a a a a . 解一般项为12)1(11+-=+-n a u n n n . 3.根据级数收敛与发散的定义判定下列级数的收敛性:<1>∑∞=-+1)1(n n n ;解因为)1( )34()23()12(n n s n -++⋅⋅⋅+-+-+-=)()11(∞→∞→-+=n n ,所以级数发散.<2> )12)(12(1 751531311⋅⋅⋅++-+⋅⋅⋅+⋅+⋅+⋅n n ; 解因为)12)(12(1 751531311+-+⋅⋅⋅+⋅+⋅+⋅=n n s n)121121(21 )7151(21)5131(21)3111(21+--+⋅⋅⋅+-+-+-=n n )121121 715151313111(21+--+⋅⋅⋅+-+-+-=n n )(21)1211(21∞→→+-=n n , 所以级数收敛.<3> 6sin 63sin 62sin 6sin ⋅⋅⋅+⋅⋅⋅+++ππππn . 解 6sin 63sin 62sin 6sin ππππn s n ⋅⋅⋅+++= )6sin 12sin 2 62sin 12sin 26sin 12sin 2(12sin 21πππππππn +⋅⋅⋅++= )]1212cos 1212(cos )125cos 123(cos )123cos 12[(cos 12sin 21πππππππ+--+⋅⋅⋅+-+-=n n )1212cos 12(cos 12sin 21πππ+-=n . 因为π1212cos lim +∞→n n 不存在,所以n n s ∞→lim 不存在,因而该级数发散. 4.判定下列级数的收敛性: <1> 98)1( 9898983322⋅⋅⋅+-+⋅⋅⋅+-+-n n n ; 解这是一个等比级数,公比为98-=q ,于是198||<=q ,所以此级数收敛. <2> 31 916131⋅⋅⋅++⋅⋅⋅+++n; 解此级数是发散的,这是因为如此级数收敛,则级数) 31 916131(311⋅⋅⋅++⋅⋅⋅+++==∑∞=n n n 也收敛,矛盾.<3> 31 3131313⋅⋅⋅++⋅⋅⋅+++n ; 解因为级数的一般项)(013311∞→≠→==-n u n n n ,所以由级数收敛的必要条件可知,此级数发散.<4> 232323233322⋅⋅⋅++⋅⋅⋅+++n n ; 解这是一个等比级数,公比123>=q ,所以此级数发散. <5> )3121( )3121()3121()3121(3322⋅⋅⋅+++⋅⋅⋅++++++nn . 解因为∑∞=121n n 和∑∞=131n n 都是收敛的等比级数,所以级数 )3121( )3121()3121()3121()3121(33221⋅⋅⋅+++⋅⋅⋅++++++=+∑∞=n n n n n 是收敛的.习题11-21.用比较审敛法或极限形式的比较审敛法判定下列级数的收敛性:<1> )12(1 51311⋅⋅⋅+-+⋅⋅⋅+++n ; 解因为211121lim =-∞→nn n ,而级数∑∞=11n n发散,故所给级数发散. <2> 11 313121211222⋅⋅⋅++++⋅⋅⋅+++++++n n ; 解因为n n n n n n u n 111122=++>++=,而级数∑∞=11n n发散, 故所给级数发散.<3> )4)(1(1 631521⋅⋅⋅++++⋅⋅⋅+⋅+⋅n n ; 解因为145lim 1)4)(1(1lim 222=++=++∞→∞→n n n nn n n n ,而级数∑∞=121n n 收敛, 故所给级数收敛.<4> 2sin 2sin 2sin 2sin 32⋅⋅⋅++⋅⋅⋅+++n ππππ;解因为πππππ==∞→∞→nn n n n n 22sin lim 212sin lim ,而级数∑∞=121n n 收敛, 故所给级数收敛.<5>∑∞=>+1)0(11n n a a . 解因为 ⎪⎩⎪⎨⎧>=<<==+=+∞→∞→11 1 2110 0 1lim 111lim a a a l a a a a n n n n n n ,而当a >1时级数∑∞=11n n a 收敛,当0<a ≤1时级数∑∞=11n n a 发散, 所以级数∑∞=+111n n a 当a >1时收敛,当0<a ≤1时发散. 2.用比值审敛法判定下列级数的收敛性:<1>23 2332232133322⋅⋅⋅+⋅+⋅⋅⋅+⋅+⋅+⋅nn n ; 解级数的一般项为n n n n u 23⋅=.因为 123123lim 322)1(3lim lim 111>=+⋅=⋅⋅⋅+=∞→++∞→+∞→n n n n u u n n n n n n n n n , 所以级数发散.<2>∑∞=123n n n ; 解因为131)1(31lim 33)1(lim lim 22121<=+⋅=⋅+=∞→+∞→+∞→nn n n u u n n n n n n n , 所以级数收敛.<3>∑∞=⋅1!2n n n n n ;解因为12)1(lim 2!2)1()!1(2lim lim 111<=+=⋅⋅++⋅=∞→++∞→+∞→e n n n n n n u u n n n n n n n n n n , 所以级数收敛.<3>∑∞=+112tann n n π. 解因为121221lim 2tan 2tan )1(lim lim 12121<=⋅+=+=++∞→++∞→+∞→n n n n n n n n n n n n n u u ππππ, 所以级数收敛.3.用根值审敛法判定下列级数的收敛性:<1>∑∞=+1)12(n n n n ; 解因为12112lim lim<=+=∞→∞→n n u n n n n ,所以级数收敛. <2>∑∞=+1)]1[ln(1n n n ; 解因为10)1ln(1lim lim<=+=∞→∞→n u n n n n ,所以级数收敛. <3>∑∞=--112)13(n n n n ; 解因为n n n n n n n n n n n u 1212)13(1lim)13(lim lim -∞→-∞→∞→-=-= 131)311(31lim 321212<⋅=-⋅=--∞→en n n n , 所以级数收敛.<4>∑∞=1)(n n na b ,其中a n →a <n →∞>,a n ,b ,a 均为正数.解因为a b a b u nn nn n ==∞→∞→lim lim , 所以当b <a 时级数收敛,当b >a 时级数发散.4.判定下列级数的收敛性:<1> )43( )43(3)43(24332⋅⋅⋅++⋅⋅⋅+++n n ; 解这里n n n u )43(=,因为 143431lim )43()43)(1(lim lim 11<=⋅+=+=∞→+∞→+∞→n n n n u u n nn n n n n , 所以级数收敛.<2>!!33!22!114444⋅⋅⋅++⋅⋅⋅+++n n ; 解这里!4n n u n =,因为 10)1(1lim !)!1()1(lim lim 3441<=+⋅=⋅++=∞→∞→+∞→n n nn n n n u u n n n n n , 所以级数收敛.<3>∑∞=++1)2(1n n n n ; 解因为121lim 1)2(1lim =++=++∞→∞→n n nn n n n n ,而级数∑∞=11n n发散, 故所给级数发散.<4>∑∞=13sin2n nn π; 解因为1323232lim 3sin 23sin 2lim 1111<=⋅⋅=++∞→++∞→n n n n n n n n n n ππππ, 所以级数收敛.<5> 1 232⋅⋅⋅+++⋅⋅⋅++nn ; 解因为011lim lim ≠=+=∞→∞→n n u n n n , 所以级数发散.<6>)0 ,0( 1 211>>⋅⋅⋅+++⋅⋅⋅++++b a bna b a b a . 解因为n a b na u n 111⋅>+=,而级数∑∞=11n n发散, 故所给级数发散.5.判定下列级数是否收敛？如果是收敛的,是绝对收敛还是条件收敛？<1> 4131211⋅⋅⋅+-+-; 解这是一个交错级数∑∑∞=-∞=--=-11111)1()1(n n n n n n u ,其中n u n 1=. 因为显然u n ≥u n +1,并且0lim =∞→n n u ,所以此级数是收敛的. 又因为∑∑∞=∞=-=-1111|)1(|n n n n nu 是p <1的p 级数,是发散的,所以原级数是条件收敛的.<2>∑∞=---1113)1(n n n n ; 解∑∑∞=-∞=--=-111113|3)1(|n n n n n n n . 因为131331lim 1<=+-∞→n n n n n ,所以级数∑∞=-113n n n 是收敛的, 从而原级数收敛,并且绝对收敛.<3> 2131213121312131432⋅⋅⋅+⋅-⋅+⋅-⋅;解这是交错级数∑∞=-⋅-112131)1(n n n ,并且∑∑∞=∞=-⋅=⋅-1112131|2131)1(|n n n n n . 因为级数∑∞=⋅12131n n 是收敛的,所以原级数也收敛,并且绝对收敛. <4> 5ln 14ln 13ln 12ln 1⋅⋅⋅+-+-; 解这是交错级数∑∑∞=-∞=-+-=-1111)1ln()1()1(n n n n n n u ,其中)1ln(1+=n u n . 因为u n ≥u n +1,并且0lim =∞→n n u ,所以此级数是收敛的. 又因为11)1ln(1+≥+n n ,而级数∑∞=+111n n 发散, 故级数∑∑∞=∞=-+=-111)1ln(1|)1(|n n n n n u 发散,从而原级数是条件收敛的. <5>∑∞=+-11!2)1(2n n n n . 解级数的一般项为!2)1(21n u n n n +-=. 因为∞=⋅⋅⋅⋅⋅-⋅-⋅===∞→∞→∞→∞→122232 22122lim !)2(lim !2lim ||lim 2n n n n n n n n n n n n n n n n n n u , 所以级数发散.习题11-31. 求下列幂级数的收敛域:<1>x +2x 2+3x 3+⋅⋅⋅+nx n +⋅⋅⋅;解 11lim ||lim 1=+=∞→+∞→nn a a n n n n , 故收敛半径为R =1. 因为当x =1时, 幂级数成为∑∞=1n n , 是发散的;当x =-1时, 幂级数成为∑∞=-1)1(n n n , 也是发散的,所以收敛域为<-1,1>.<2> )1( 21222⋅⋅⋅+-+⋅⋅⋅++-nx x x n n ; 解 1)1(lim 1)1(1lim ||lim 22221=+=+=∞→∞→+∞→n n n n a a n n n n n , 故收敛半径为R =1. 因为当x =1时, 幂级数成为∑∞=-221)1(n n n , 是收敛的; 当x =-1时, 幂级数成为∑∞=+1211n n , 也是收敛的, 所以收敛域为[-1,1].<3> )2( 42 64242232⋅⋅⋅+⋅⋅⋅⋅+⋅⋅⋅+⋅⋅+⋅+n x x x x n ; 解 0)1(21lim )!1(2!2lim ||lim 11=+=⋅+⋅⋅=∞→+∞→+∞→n n n a a n n n n n n n , 故收敛半径为R =+∞, 收敛域为<-∞,+∞>. <4> 33332313322⋅⋅⋅+⋅+⋅⋅⋅+⋅+⋅+⋅n n n x x x x ; 解 31131lim 3)1(3lim ||lim 11=+⋅=⋅+⋅=∞→+∞→+∞→n n n n a a n n n n n n n , 故收敛半径为R =3. 因为当x =3时, 幂级数成为∑∞=11n n , 是发散的; 当x =-3时, 幂级数成为∑∞=-11)1(n n n , 也是收敛的, 所以收敛域为[-3,3>. <5> 12 102522223322⋅⋅⋅+++⋅⋅⋅+++n n x n x x x ;解 21)1(1lim 2211)1(2lim ||lim 222211=+++=+⋅++=∞→+∞→+∞→n n n n a a n n n n n n n , 故收敛半径为21=R . 因为当21=x 时, 幂级数成为∑∞=+1211n n , 是收敛的; 当x =-1时, 幂级数成为∑∞=+-1211)1(n n n , 也是收敛的, 所以收敛域为]21 ,21[-. <6>∑∞=++-11212)1(n n n n x ; 解这里级数的一般项为12)1(12+-=+n x u n nn . 因为212321|1232|lim ||lim x x n n x u u n n n n n n =+⋅+=++∞→+∞→, 由比值审敛法, 当x 2<1, 即|x |<1时, 幂级数绝对收敛; 当x 2>1, 即|x |>1时, 幂级数发散, 故收敛半径为R =1.因为当x =1时, 幂级数成为∑∞=+-1121)1(n n n , 是收敛的; 当x =-1时, 幂级数成为∑∞=++-11121)1(n n n , 也是收敛的, 所以收敛域为[-1, 1].<7>∑∞=--122212n n n x n ; 解这里级数的一般项为22212--=n nn x n u . 因为22212121|)12(22)12(|lim ||lim x x n x n u u n n n n n n n n =-⋅+=-+∞→+∞→, 由比值审敛法, 当1212<x , 即2||<x 时, 幂级数绝对收敛; 当1212>x , 即2||>x 时, 幂级数发散, 故收敛半径为2=R . 因为当2±=x 时, 幂级数成为∑∞=-1212n n , 是发散的, 所以收敛域为)2 ,2(-.<8>∑∞=-1)5(n nn x . 解 11lim ||lim 1=+=∞→+∞→n n a a n n n n , 故收敛半径为R =1, 即当-1<x -5<1时级数收敛, 当|x -5|>1时级数发散.因为当x -5=-1, 即x =4时, 幂级数成为∑∞=-1)1(n nn , 是收敛的; 当x -5=1, 即x =6时, 幂级数成为∑∞=11n n, 是发散的, 所以收敛域为[4, 6>. 2. 利用逐项求导或逐项积分, 求下列级数的和函数:<1>∑∞=-11n n nx ;解设和函数为S <x >, 即∑∞=-=11)(n n nx x S , 则][][])([)(1010110'='='=∑⎰⎰∑⎰∞=-∞=-n xn x n n x dx nx dx nxdx x S x S)11( )1(1]111[][21<<--='--='=∑∞=x x x x n n . <2>∑∞=++11414n n n x ; 解设和函数为S <x >, 即∑∞=++=11414)(n n n x x S , 则dx x dx n x dx x S S x S x n n x n n x ⎰∑⎰∑⎰∞=∞=+='+='+=01401140]14[)()0()( ⎰⎰-⋅++⋅+-=--=x x dx x x dx x02204)112111211()111( )11( arctan 2111ln 41<<--+-+=x x x x x .提示: 由)0()()(0S x S dx x S x -='⎰得⎰'+=xdx x S S x S 0)()0()(. <3>⋅⋅⋅+-+⋅⋅⋅+++- 12 531253n x x x x n . 解设和函数为S <x >, 即⋅⋅⋅+-+⋅⋅⋅+++=-=-∞=-∑ 12 5312)(1253112n x x x x n x x S n n n , 则 ⎰∑⎰∑⎰∞=-∞=-='-='+=x n n x n n x dx x dx n x dx x S S x S 012201120]12[)()0()( )11( 11ln 211102<<--+=-=⎰x x x dx xx . 提示: 由)0()()(0S x S dx x S x -='⎰得⎰'+=xdx x S S x S 0)()0()(.习题11-41. 求函数f <x >=cos x 的泰勒级数, 并验证它在整个数轴上收敛于这函数.解 )2cos()()(π⋅+=n x x f n <n =1,2,⋅⋅⋅>, )2cos()(00)(π⋅+=n x x f n <n =1,2,⋅⋅⋅>, 从而得f <x >在x 0处的泰勒公式)(!2)cos())(2cos(cos )(200000⋅⋅⋅+-++-++=x x x x x x x x f ππ )( )(!)2cos(00x R x x n n x n n +-++π. 因为)!1(|||)()!1(]21)(cos[||)(|101000+-≤-+++-+=++n x x x x n n x x x x R n n n πθ<0≤θ≤1>, 而级数∑∞∞→++-n n n x x )!1(||10总是收敛的, 故0)!1(||lim 10=+-+∞→n x x n n , 从而0|)(|lim =∞→x R n n . 因此 )(!2)cos())(2cos(cos )(200000⋅⋅⋅+-++-++=x x x x x x x x f ππ⋅⋅⋅+-++ )(!)2cos(00n x x n n x π,x ∈<-∞,+∞>.2. 将下列函数展开成x 的幂级数, 并求展开式成立的区间: <1>2sh x x e e x --=; 解因为∑∞==0!n n xn x e ,x ∈<-∞,+∞>,所以 ∑∞=--=0!)1(n n nx n x e ,x ∈<-∞,+∞>, 故 ∑∑∑∑∞=-∞=∞=∞=-=--=--=012000)!12(!])1(1[21]!)1(![21sh n n n n n n n n n n n x n x n x n x x ,x ∈<-∞,+∞>. <2>ln<a +x ><a >0>;解因为)1ln(ln )1(ln )ln(a x a a x a x a ++=+=+,∑∞=++-=+011)1()1ln(n n nn x x <-1<x ≤1>, 所以 ∑∑∞=++∞=++-+=+-+=+01101)1()1(ln )(11)1(ln )ln(n n n n n n n a n x a a x n a x a <-a <x ≤a >. <3>a x ;解因为∑∞==0!n n x n x e ,x ∈<-∞,+∞>, 所以 ∑∑∞=∞=====00ln !)(ln !)ln (n n n n n x a x x x n a n a x e ea ,x ∈<-∞,+∞>, <4>sin 2x ; 解因为x x 2cos 2121sin 2-=,∑∞=-=02)!2()1(cos n n nn x x ,x ∈<-∞,+∞>, 所以 ∑∑∞=-∞=⋅-=--=1212022)!2(2)1()!2()2()1(2121sin n n n n n n n n x n x x x ∈<-∞,+∞>. <5><1+x >ln<1+x >;解因为∑∞=++-=+011)1()1ln(n n nn x x <-1<x ≤1>, 所以 ∑∞=++-+=++011)1()1()1ln()1(n n nn x x x x ∑∑∞=+∞=++-++-=02011)1(1)1(n n n n n nn x n x ∑∑∞=++∞=+-++-+=11111)1(1)1(n n n n n n n x n x x 111])1(1)1([+∞=+∑-++-+=n n n n x n n x 111)1()1(+∞=-∑+-+=n n n x n n x <-1<x ≤1>. <6>21x x +. 解因为∑∞=--+=+122/12!)!2(!)!12()1(1)1(1n n n x n n x <-1≤x ≤1>, 所以 ∑∑∞=+∞=+⋅-+=--+=+11221122)2()!()!2(2)1(!)!2(!)!12()1(1n n n n n n x n n x x n n x xx <-1≤x ≤1>. 3. 将下列函数展开成<x -1>的幂级数, 并求展开式成立的区间: <1>3x ;解因为)11( !)1( )1( !2)1(1)1(2<<-⋅⋅⋅++-⋅⋅⋅-+⋅⋅⋅+-++=+x x n n m m m x m m mx x n m . 所以 233)]1(1[-+=x x )1(!)123( )123(23 )1(!2)123(23)1(2312⋅⋅⋅+-+-⋅⋅⋅-+⋅⋅⋅+--+-+=n x n n x x)111(<-<-x ,即 )1(!2)25( )3()1(13 )1(!2213)1(231223⋅⋅⋅+-⋅-⋅⋅⋅-⋅-⋅⋅+⋅⋅⋅+-⋅⋅+-+=n n x n n x x x )20(<<x .上术级数当x =0和x =2时都是收敛的, 所以展开式成立的区间是[0,2].<2>lg x .解 ∑∞=-≤-<---=-+==11)111( )1()1(10ln 1)]1(1ln[10ln 110ln ln lg n n n x nx x x x , 即 ∑∞=-≤<--=11)20( )1()1(10ln 1lg n n n x nx x . 4. 将函数f <x >=cos x 展开成)3(π+x 的幂级数. 解 3sin )3sin(3cos )3cos(]3)3cos[(cos ππππππ+++=-+=x x x x )3sin(23)3cos(21ππ+++=x x ∑∑∞=+∞=++-++-=01202)3()!12()1(23)3()!2()1(21n n n n n n x n x n ππ )( ])3()!12(3)3()!2(1[)1(211202+∞<<-∞++++-=+∞=∑x x n x n n n n n ππ. 5.将函数xx f 1)(=展开成<x -3>的幂级数. 解 ∑=<-<---=-+=-+=n n n n x x x x x 0)1331( )33()1(313311313311, 即 ∑=<<--=n n n n x x x 0)60( )33()1(311. 6.将函数231)(2++=x x x f 展开成<x +4>的幂级数. 解 2111231)(2+-+=++=x x x x x f ,而 ∑∞=<++-=+--=++-=+0)1|34(| )34(31341131)4(3111n n x x x x x , 即 )17( 3)4(1101-<<-+-=+∑∞=+x x x n n n ; ∑∞=<++-=+--=++-=+0)1|24(| )24(21241121)4(2121n n x x x x x , 即 )26( 2)4(2101-<<-+-=+∑∞=+x x x n n n . 因此 ∑∑∞=∞=+++++-=++=001122)4(3)4(231)(n n n n n n x x x x x f )26( )4)(3121(011-<<-+-=∑∞=++x x n n n n . 习题11-51. 利用函数的幂级数展开式求下列各数的近似值:<1>ln3<误差不超过0.0001>; 解)11( ) 121 5131(211ln 1253<<-⋅⋅⋅+-+⋅⋅⋅+++=-+-x x n x x x x x n , ) 21121 2151213121(2211211ln 3ln 1253⋅⋅⋅+⋅-+⋅⋅⋅+⋅+⋅+=-+=-n n . 又 ] 2)32(12)12(1[2||3212⋅⋅⋅+⋅++⋅-=+-n n n n n r ] 2)52(2)12(2)32(2)12(1[2)12(25212321212⋅⋅⋅+⋅+⋅++⋅+⋅+++=+++++n n n n n n n n n n 2242122)12(31) 21211(2)12(2-+-=⋅⋅⋅++++<n n n n , 故 00012.021131||85≈⋅⋅<r ,00003.021331||105≈⋅⋅<r . 因而取n =6, 此时1.0986 )21111219121712151213121(23ln 119753≈⋅+⋅+⋅+⋅+⋅+=. <2>e <误差不超过0.001>;解 )( !1 !2112+∞<<-∞⋅⋅⋅+⋅⋅⋅+++=x x n x x e n x , 21!1 21!212112⋅⋅⋅+⋅⋅⋅⋅+⋅++=nn e . 由于 21)!2(121)!1(121⋅⋅⋅+⋅++⋅+=++n n n n n r 21)1()2(121111[2!12⋅⋅⋅+⋅+⋅++⋅++⋅=n n n n n 22!3141112!1-⋅⋅=-⋅⋅<n n n n , 故 0003.02!53134≈⋅⋅=r . 因此取n =4得648.121!4121!3121!21211432≈⋅+⋅+⋅++≈e . <3>9522<误差不超过0.00001>; 解)11( !)1( )1( !2)1(1)1(2<<-⋅⋅⋅++-⋅⋅⋅-+⋅⋅⋅+-++=+x x n n m m m x m m mx x n m , 9/199)2101(2522+= ] )210(!33178)210(!298210911[23922929⋅⋅⋅-⋅⋅⋅+⋅⋅-⋅+=. 由于002170.0210919≈⋅,000019.0)210(!298292≈⋅⋅, 故00430.2)000019.0002170.01(25229≈-+=.<4>cos 2︒<误差不超过0.0001>.解 )( )!2()1( !4!21cos 242+∞<<-∞⋅⋅⋅+-+⋅⋅⋅-+-=x n x x x x n n , )90(!61 )90(!41)90(!21190cos 2cos 642⋅⋅⋅+⋅-⋅+⋅-==︒ππππ.由于42106)90(!21-⨯≈⋅π,8410)90(!41-≈⋅π, 故 9994.00006.01 )90(!2112cos 2=-≈⋅⋅-≈︒π.2.利用被积函数的幂级数展开式求下列定积分的近似值:<1>⎰+5.00411dx x <误差不超过0.0001>; 解⎰⎰⋅⋅⋅+-+⋅⋅⋅+-+-=+5.00412845.004] )1( 1[11dx x x x x dx x n n 5.001395|) 1319151(⋅⋅⋅+-+-=x x x x 2113121912151211395⋅⋅⋅+⋅-⋅+⋅-. 因为00625.021515≈⋅,00028.021919≈⋅,000009.02113113≈⋅, 所以4940.0219121512111955.004≈⋅+⋅-≈+⎰dx x . <2>⎰5.00arctan dx xx <误差不超过0.0001>. 解)11( 121)1( 5131arctan 1253<<-⋅⋅⋅++-+⋅⋅⋅-+-=+x x n x x x x n n, dx x n x x dx x x n n ] 121)1( 51311[arctan 5.002425.00⎰⎰⋅⋅⋅++-+⋅⋅⋅-+-= 5.00753|) 49125191(⋅⋅⋅+-+-=x x x x 2149121251219121753⋅⋅⋅+⋅-⋅+⋅-=. 因为0139.021913≈⋅,0013.0212515≈⋅,0002.0214917≈⋅, 所以487.021*********arctan 535.00≈⋅+⋅-=⎰dx x x . 3.将函数e x cos x 展开成x 的幂级数. 解)(21cos ix ix e e x -+=, ][21)(21cos )1()1(i x i x ix ix x x e e e e e x e -+-+=+⋅=∑∑∑∞=∞=∞=-++=-++=000!)1()1(21!)1(!)1([21n n n n n n n n n n x n i i x n i x n i . 因为421πi e i =+,421πi e i -=-, 所以4cos 2)4cos 2(2][2)1()1(122442ππππn n e e i i n n n i n i n n n +-==+=-++. 因此)( !4cos 2cos 02+∞<<-∞=∑∞=x x n n x e n n n x π.习题11-7 1.下列周期函数f <x >的周期为2π,试将f <x >展开成傅里叶级数,如果f <x >在[-π,π>上的表达式为:<1>f <x >=3x 2+1<-π≤x <π>;解因为)1(2)13(1)(1220+=+==⎰⎰--πππππππdx x dx x f a , ⎰-=ππππdx n x f a n cos )(1 2212)1(cos )13(1n dx n x n -=+=⎰-ππππ <n =1,2,⋅⋅⋅>, ⎰-=ππππdx n x f b n sin )(1 0sin )13(12=+=⎰-ππππdx n x <n =1,2,⋅⋅⋅>, 所以f <x >的傅里叶级数展开式为)( cos )1(121)(122+∞<<-∞-++=∑∞=x nx n x f n n π.<2>f <x >=e 2x <-π≤x <π>;解因为πππππππππ21)(12220----===⎰⎰e e dx e dx x f a x ,⎰-=ππππdx n x f a ncos )(1πππππππ)4()()1(2cos 12222+--==--⎰n e e dx n e n x<n =1,2,⋅⋅⋅>, ⎰-=ππππdx n x f b n sin )(1πππππππ)4()()1(sin 12222+---==--⎰n e e n dx n e n x<n =1,2,⋅⋅⋅>, 所以f <x >的傅里叶级数展开式为∑∞=--+-+-=1222)sin cos 2(4)1(41[)(n n nx n nx n e e x f πππ<x ≠<2n +1>π,n =0,±1,±2,⋅⋅⋅>.<3>⎩⎨⎧<≤<≤-=ππx ax x bx x f 0 0)(<a ,b 为常数,且a >b >0>.解因为)(211000b a axdx bxdx a -=+=⎰⎰-πππππ, ]cos 1cos 100⎰⎰+=-ππππnxdx ax nxdx bx a nn n a b )1(1[2---=π<n =1,2,⋅⋅⋅>,⎰⎰+=-ππππ00sin 1sin 1nxdx ax nxdx bx b nnb a n +-=+1)1(<n =1,2,⋅⋅⋅>, 所以f <x >的傅里叶级数展开式为∑∞=-+-+---+-=112}sin )()1(cos )]()1(1[{)(4)(n n n nx n b a nx n a b b a x f ππ <x ≠<2n +1>π,n =0,±1,±2,⋅⋅⋅>.2.将下列函数f <x >展开成傅里叶级数:<1>3sin2)(x x f =<-π≤x ≤π>; 解将f <x >拓广为周期函数F <x >, 则F <x >在<-π,π>中连续, 在x =±π间断, 且)()]()([21πππ-≠-+-+-f F F ,)()]()([21πππf F F ≠++-, 故F <x >的傅里叶级数在<-π,π>中收敛于f <x >, 而在x =±π处F <x >的傅里叶级数不收敛于f <x >. 计算傅氏系数如下: 因为3sin2x <-π<x <π>是奇函数, 所以a n=0<n =0,1,2,⋅⋅⋅>,⎰⎰+--==ππππ00])31cos()31[cos(2sin 3sin 22dx x n x n nxdx x b n19318)1(21-⋅-=+n nn π<n =1,2,⋅⋅⋅>, 所以∑∞=+--=12119sin )1(318)(n n n nx n x f π<-π<x <π>.<2>⎩⎨⎧≤≤<≤-=ππx x e x f x 0 10)(.解将f <x >拓广为周期函数F <x >, 则F <x >在<-π,π>中连续, 在x =±π间断, 且)()]()([21πππ-≠-+-+-f F F ,)()]()([21πππf F F ≠++-,故F <x >的傅里叶级数在<-π,π>中收敛于f <x >, 而在x =±π处F <x >的傅里叶级数不收敛于f <x >. 计算傅氏系数如下:ππππππ---+=+=⎰⎰e dx dx e a x 1][1000, )1()1(1]cos cos [1200n e nxdx nxdx e a n xn +--=+=--⎰⎰πππππ<n =1,2,⋅⋅⋅>,]sin sin [100⎰⎰+=-πππnxdx nxdx e b xn})1(11])1(1[{12n n e n n n --++---=-ππ<n =1,2,⋅⋅⋅>, 所以πππ21)(--+=e x f∑∞=----++-+-++--+122}]sin )1(11)1([cos 1)1(1{1n n n n nx n n ne n nx n e πππ <-π<x <π>.3.设周期函数f <x >的周期为2π,证明f <x >的傅里叶系数为⎰=ππ20cos )(1nxdx x f a n <n =0, 1, 2,⋅⋅⋅>,⎰=ππ20sin )(1nxdx x f b n <n =1, 2,⋅⋅⋅>.证明我们知道, 若f <x >是以l 为周期的连续函数, 则⎰+la adx x f )(的值与a 无关, 且⎰⎰=+lla adx x f dx x f 0)()(,因为f <x >,cos nx ,sin nx 均为以2π为周期的函数, 所以f <x >cos nx ,f <x >sin nx 均为以2π为周期的函数, 从而⎰⎰+---==πππππππ2cos )(1cos )(1nxdx x f nxdx x f a n⎰=ππ20cos )(1nxdx x f <n =1, 2,⋅⋅⋅>.同理 ⎰=ππ20sin )(1nxdx x f b n <n =1, 2,⋅⋅⋅>.4.将函数2cos )(xx f =<-π≤x ≤π>展开成傅里叶级数: 解因为2cos )(x x f =为偶函数, 故b n =0<n =1, 2,⋅⋅⋅>, 而⎰⎰==-πππππ0cos 2cos 2cos 2cos 1nxdx x nxdx x a n⎰+--=ππ0])21cos()21[cos(1dx x n x n 1414)1(21-⋅-=+n n π<n =1, 2,⋅⋅⋅>. 由于2cos )(x x f =在[-π,π]上连续, 所以 ∑∞=+--+=121cos 141)1(422cos n n nx n x ππ<-π≤x ≤π>. 5.设f <x >的周期为2π的周期函数, 它在[-π,π>上的表达式这⎪⎪⎩⎪⎪⎨⎧<≤<≤--<≤--=ππππππππx x x x x f 2 222 2 2)(,将f <x >展开成傅里叶级数.解因为f <x >为奇函数, 故a n =0<n =0,1,2,⋅⋅⋅>, 而]sin 2sin [2sin )(22200⎰⎰⎰+==πππππππnxdx nxdx x nxdx x f b n2sin 2)1(2ππn n n n +--=<n =1,2,⋅⋅⋅>,又f <x >的间断点为x =<2n +1>π,n =0,±1,±2,⋅⋅⋅, 所以nx n n n x f n n sin ]2sin 2)1([)(121∑∞=++-=ππ< x ≠<2n +1>π,n =0,±1,±2,⋅⋅⋅>.6. 将函数2)(x x f -=π<0≤x ≤π>展开成正弦级数.解作奇延拓得F <x >:⎪⎩⎪⎨⎧<<---=≤<=0)(0 00 )()(x x f x x x f x F ππ,再周期延拓F <x >到<-∞,+∞>, 则当x ∈<0,π]时F <x >=f <x >,)0(20)0(f F =≠=π.因为a n =0<n =0,1,2,⋅⋅⋅>, 而nnxdx x b n 1sin 220=-=⎰πππ <n =1,2,⋅⋅⋅>, 故 nx nx f n sin 1)(1∑∞==<0<x ≤π>,级数在x =0处收敛于0.7.将函数f <x >=2x 2<0≤x ≤π>分另别展开成正弦级数和余弦级数. 解对f <x >作奇延拓,则a n =0<n =0, 1, 2,⋅⋅⋅>,而]2)2()1[(4sin 2232302n n n nxdx x b n n ---==⎰ππππ<n =1, 2,⋅⋅⋅>,故正弦级数为nx n n n x f n n sin ]2)2()1[(4)(1323∑∞=---=ππ<0≤x <π>, 级数在x =0处收敛于0.对f <x >作偶延拓,则b n =0<n =1, 2,⋅⋅⋅>,而20203422πππ==⎰dx x a , 2028)1(cos 22nnxdx x a n n -==⎰ππ <n =1, 2,⋅⋅⋅>, 故余弦级数为nx nx f n n cos )1(832)(122∑∞=-+=π<0≤x ≤π>.8.设周期函数f <x >的周期为2π, 证明<1>如果f <x -π>=-f <x >, 则f <x >的傅里叶系数a 0=0,a 2k =0,b 2k =0<k =1,2,⋅⋅⋅>; 解因为020200)(1)(1)(1a dt t f dx t f dx x f a xt -=-=-=⎰⎰⎰+=-πππππππππ令,所以a 0=0. 因为dx t k t f kxdx x f a xt k )(2cos )(12cos )(1202ππππππππ--=⎰⎰+=-令k a ktdt t f 2202cos )(1-=-=⎰ππ,所以a 2k =0.同理b 2k =0<k =1,2,⋅⋅⋅>.<2>如果f <x -π>=f <x >, 则f <x >的傅里叶系数a 2k +1=0,b 2k +1=0<k =1,2,⋅⋅⋅>. 解因为)12cos()(112⎰-++=πππxdx k x f a kdx t k t f xt ))(12cos()(1 20πππππ-+-⎰+=令1220)12cos()(1+-=+-=⎰k a tdt k t f ππ,所以a 2k +1=0<k =1,2,⋅⋅⋅>. 同理b 2k +1=0<k =1,2,⋅⋅⋅>.习题11-81. 将下列各周期函数展开成傅里叶级数<下面给出函数在一个周期内的表达式>: <1>)2121(1)(2<≤--=x x x f ;解因为f <x >=1-x 2为偶函数, 所以b n =0<n =1,2,⋅⋅⋅>, 而611)1(4)1(2/12210221020=-=-=⎰⎰dx x dx x a ,⎰-=21022/1cos )1(2/12dx x n x a n π2212102)1(2cos )1(4ππn xdx n x n +-=-=⎰<n =1,2,⋅⋅⋅>,由于f <x >在<-∞,+∞>内连续, 所以∑∞=+-+=12122cos )1(11211)(n n x n n x f ππ,x ∈<-∞,+∞>.<2>⎪⎪⎩⎪⎪⎨⎧<≤-<≤<≤-=121 1210 101 )(x x x x x f ;解 21)(1212100111-=-+==⎰⎰⎰⎰--dx dx xdx dx x f a n ,⎰⎰⎰⎰-+==--1212100111cos cos cos cos )(xdx n xdx n xdx n x xdx n x f a n ππππ2sin 2])1(1[122πππn n n n +--= <n =1,2,⋅⋅⋅>,dx x n xdx n xdx n x xdx n x f b n ⎰⎰⎰⎰-+==--121210111sin sin sin sin )(πππππππn n n 12cos 2+-= <n =1,2,⋅⋅⋅>.而在<-∞,+∞>上f <x >的间断点为x =2k ,212+k ,k =0,±1,±2,⋅⋅⋅,故 }sin 2cos 21cos ]2sin 2)1(1{[41)(122x n n n x n n n n x f n nπππππππ-++--+-=∑∞= <x ≠2k ,212+≠k x ,k =0,±1,±2,⋅⋅⋅>.<3>⎩⎨⎧<≤<≤-+=30 1 03 12)(x x x x f .解 1])12([31)(313003330-=++==⎰⎰⎰--dx dx x dx x f a ,]3cos 3cos )12([313cos )(31300333⎰⎰⎰--++==dx x n dx x n x dx x n x f a n πππ])1(1[622n n --=π<n =1,2,⋅⋅⋅ >, ]3sin 3sin )12([313sin )(31300333⎰⎰⎰--++==dx x n dx x n x dx x n x f b n πππn n )1(6-=π<n =1,2,⋅⋅⋅ >, 而在<-∞,+∞>上,f <x >的间断点为 x =3<2k +1>,k =0,±1,±2,⋅⋅⋅,故 }3sin 6)1(3cos])1(1[6{21)(1122∑∞=+-+--+-=n n n x n n x n n x f ππππ,<x ≠3<2k +1>,k =0,±1,±2,⋅⋅⋅>.2. 将下列函数分别展开成正弦级数和余弦级数:<1>⎪⎩⎪⎨⎧≤≤-<≤=lx x l l x x x f 2l20 )(; 解正弦级数:对f <x >进行奇延拓, 则函数的傅氏系数为 a 0=0<n =0,1,2,⋅⋅⋅>,2sin 4]sin )(sin [22221210ππππn n l dx l x n x l dx l x n x l b l n =-+=⎰⎰<n =1,2,⋅⋅⋅ >故 ∑∞==122sin 2sin14)(n l x n n nl x f πππ,x ∈[0,l ].余弦级数:对f <x >进行偶延拓, 则函数的傅氏系数为2])([2212100l dx x l xdx l a l=-+=⎰⎰,⎰⎰-+=l n dx l x n x l dx l x n x l a 21210]cos )(cos [2ππ ])1(12cos 2[222n n n l ---=ππ <n =1, 2,⋅⋅⋅ > b n =0<n =1, 2,⋅⋅⋅ >,故lx n n n l l x f n n πππcos ])1(12cos2[124)(122∑∞=---+=,x ∈[0,l ].<2>f <x >=x 2<0≤x ≤2>.解正弦级数:对f <x >进行奇延拓, 则函数的傅氏系数为 a 0=0<n =0, 1, 2,⋅⋅⋅>,]1)1[()(168)1(2sin 2231202--+-==+⎰n n n n n dx x n x b πππ,故 2sin }]1)1[()(168)1{()(131x n n n x f n n n πππ∑∞=+--+-=2sin }]1)1[(2)1({81231x n n n n n n πππ∑∞=+--+-=,x ∈[0,2>. 余弦级数:对f <x >进行偶延拓, 则函数的傅氏系数为38222020==⎰dx x a2202)(16)1(2cos 22ππn dx x n x a n n -==⎰<n =1, 2,⋅⋅⋅>, b n =0<n =1, 2,⋅⋅⋅>,故 2cos )(16)1(34)(12x n n x f n n ππ∑∞=-+=2cos )1(1634122x n n n n ππ∑∞=-+=,x ∈[0,2].总习题十一 1.填空: <1>对级数∑∞=1n n u ,0lim =∞→n n u 是它收敛的________条件,不是它收敛的________条件; 解必要; 充分.<2>部分和数列{s n }有界是正项级数∑∞=1n n u 收敛的________条件; 解充分必要. <3>若级数∑∞=1n n u 绝对收敛,则级数∑∞=1n n u 必定________;若级数∑∞=1n n u 条件收敛,则级数∑∞=1||n n u 必定________. 解收敛; 发散.2.判定下列级数的收敛性: <1>∑∞=11n n nn ; 解因为11lim 11lim ==∞→∞→n n nn nnn n ,而调和级数∑∞=11n n发散,故由比较审敛法知,级数发散. <2>∑∞=1222)!(n nn ;解因为∞==⋅++=∞→∞→+∞→222221lim )!(2)1(2])!1[(lim lim n n n n n u u n n n n n , 故由比值审敛法知,级数发散.<3> ∑∞=1223cos n n n n π; 解因为n n n n n 223cos 2<π,12121lim 2lim <==∞→∞→n n n n n n n所以由根值审敛法,级数∑∞=12n n n 收敛;由比较审敛法,级数∑∞=1223cos n nn n π收敛. <4>∑∞=110ln 1n n;解因为∞==∞→∞→nn n u n n n 10ln lim 1lim, 而调和级数∑∞=11n n发散, 故由比较审敛法知, 原级数发散. 提示:∞===⋅⋅⋅==⋅=∞→∞→∞→∞→∞→xx x x x x x x x x x x x x 11lim !101ln lim !101 ln lim 1011ln 101limln lim9910<5>∑∞=1n s nna <a >0,s >0>. 解因为a n a n a s n n ns n n ==∞→∞→)(lim lim , 故由根值审敛法知, 当a <1时级数收敛, 当a >1时级数发散.当a =1时, 原级数成为∑∞=11n s n, 这是p =s 的p -级数, 当s >1时级数收敛, 当s ≤1时级数发散. 3.设正项级数∑∞=1n n u 和∑∞=1n n v 都收敛,证明级数∑∞=+12)(n n n v u 与收敛. 证明因为∑∞=1n n u 和∑∞=1n n v 都收敛, 所以0lim =∞→n n u ,0lim =∞→n n v . 又因为0)2(lim 2lim 2=+=+∞→∞→n n n nn n n n v u u v u u ,0lim lim 2==∞→∞→n n n n n v v v , 所以级数∑∞=+12)2(n n n n v u u 和级数∑∞=12n n v 都收敛, 从而级数 ∑∑∞=∞=+=++12122)(])2[(n n n n n n n n v u v v u u也是收敛的.4.设级数∑∞=1n n u 收敛,且1lim =∞→n n n u v ,问级数∑∞=1n n v 是否也收敛？试说明理由. 解级数∑∞=1n n v 不一定收敛. 当∑∞=1n n u 和∑∞=1n n v 均为正项级数时, 级数∑∞=1n n v 收敛, 否则未必. 例如级数∑∞=-11)1(n n 收敛, 但级数∑∞=+-1]11)1[(n n n 发散, 并且有 11)1(11)1(lim =-+-∞→nn n n .5.讨论下列级数的绝对收敛性与条件收敛性:<1>∑∞=-11)1(n p n n ; 解∑∑∞=∞==-111|1)1(|n p n p n n n 是p 级数.故当p >1时级数∑∞=11n p n 是收敛的,当p ≤1时级数∑∞=11n p n 发散.因此当p >1时级数∑∞=-11)1(n p n n 绝对收敛. 当0<p ≤1时,级数∑∞=-11)1(n p n n 是交错级数,且满足莱布尼茨定理的条件,因而收敛,这时是条件收敛的. 当p ≤0时,由于01)1(lim ≠-∞→p nn n ,所以级数∑∞=-11)1(n p n n 发散. 综上所述,级数∑∞=-11)1(n p n n 当p >1时绝对收敛,当0<p ≤1时条件收敛,当p ≤0时发散. <2>∑∞=+++-1111sin )1(n n n n ππ; 解因为1111|1sin )1(|+++≤+-n n n n πππ,而级数∑∞=+111n n π收敛,故由比较审敛法知级数|1sin )1(|111∑∞=+++-n n n n ππ收敛,从而原级数绝对收敛. <3> ∑∞=+-11ln )1(n n n n ; 解因为1ln )11ln(lim 1ln lim 1|1ln )1(|lim ==+=+=+-∞→∞→∞→e n n n n nn n n n n n n ,而级数∑∞=11n n发散,故由比较审敛法知级数|1ln )1(|1∑∞=+-n n n n 发散,即原级数不是绝对收敛的. 另一方面,级数∑∞=+-11ln )1(n n n n 是交错级数,且满足莱布尼茨定理的条件,所以该级数收敛,从而原级数条件收敛.<4>∑∞=++-11)!1()1(n n nn n . 解令1)!1()1(++-=n n n n n u .因为 11)11(112lim )1(12lim )!1()1()!2(lim ||||lim 121<=+⋅++=+⋅++=+⋅++∞→∞→++∞→+∞→enn n n n n n n n n n u u n n n n n n n n n n , 故由比值审敛法知级数|)!1()1(|11∑∞=++-n n n n n 收敛,从而原级数绝对收敛. 6.求下列级限: <1>∑=∞→+n k k k n k n 12)11(311lim ; 解显然∑=+=nk k k n k s 12)11(31是级数∑∞=+12)11(31n n n n 的前n 项部分和. 因为13)11(31lim )11(31lim 2<=+=+∞→∞→e n n n n n n n n , 所以由根值审敛法, 级数∑∞=+12)11(31n nn n 收敛, 从而部分和数列{s n }收敛.因此01lim )11(311lim 12=⋅=+∞→=∞→∑n n n k k k n s n k n . <2>])2( 842[lim 312719131n n n ⋅⋅⋅⋅⋅∞→. 解n n nn 3 27392313127191312)2( 842+⋅⋅⋅+++=⋅⋅⋅⋅⋅.显然n n n s 3 2739231+⋅⋅⋅+++=是级数∑∞=13n n n 的前n 项部分和. 设∑∞=-=11)(n n nx x S ,则210)1(1]111[][])([)(x x x dx x S x S n n x -='--='='=∑⎰∞=. 因为43)311(131)31(31)31(3132111=-⋅===∑∑∞=-∞=S n n n n n n , 所以43lim =∞→n n s , 从而 4331271913122lim ])2( 842[lim ==⋅⋅⋅⋅⋅∞→∞→nn s n n n .7.求下列幂级数的收敛域:<1>∑∞=+153n n n n x n ; 解 51)53(5)53(31lim 53153lim ||lim 111=++⋅+=+⋅++=∞→++∞→+∞→n n n n n n n n n n n n n n n a a , 所以收敛半径为51=R . 因为当51=x 时, 幂级数成为]1)53[(11+∑∞=n n n , 是发散的; 当51-=x 时, 幂级数成为]1)53[()1(1+-∑∞=n n n n , 是收敛的, 所以幂级数的收敛域为)51,51[-. <2>∑∞=+12)11(n n n x n ; 解 n n n x n u 2)11(+=, 因为||||)11(lim ||lim x e x nu n n n n n =+=∞→∞→, 由根值审敛法, 当e |x |<1, 即ex e 11<<-时, 幂级数收敛; 当e |x |>1,时幂级数发散. 当e x 1-=时, 幂级数成为∑∞=+1)1()11(2n n n e n ;。

高等数学方明亮版第十一章答案

高等数学方明亮版第十一章
习题 11-1
1．判断下列方程是几阶微分方程？
（1）；（2）；
（3）；（4）．
解微分方程中所出现的未知函数的导数（或微分）的最高阶数，叫做微分方程的阶．所以有，
（1）一阶微分方程；（2）一阶微分方程；
（3）三阶微分方程；（4）三阶微分方程．
2．指出下列各题中的函数是否为所给微分方程的解：
，
故有．
设子弹穿过木板的时间为秒，则
，
又已知时，米/秒，于是
，
从而，
，
为此有
，
所以
（秒），
故子弹穿过木板运动持续了（秒）．
4．求下列齐次方程的通解或特解：
（1）；（2）；
（3）；（4）；
（5），；（6），．
解（1）原方程变形，得
，
令，即，有，则原方程可进一步化为
，
分离变量，得
．
（4）显然，原方程是一个齐次方程，又注意到方程的左端可以看成是以为变量的函数，故令，即，有，则原方程可化为
，
整理并分离变量，得
，
两端积分，得
，
即
．
将代入上式并整理，得原方程的通解为
．
（5）原方程可化为
．
令，有，则原方程可进一步化为
，
即
，
两端积分，得
，
将代入上式，得
，
代入初始条件，得
（1），；
（2），；
（3），；
（4），．
解（1）将代入所给微分方程的左边，得左边，而右边＝2 左边，所以是的解．
（2）将，代入所给微分方程的左边，得左边右边，所以是所给微分方程的解．

高中数学必修第四册第十一章综合测试01含答案解析

加油！有志者事竟成答卷时应注意事项１、拿到试卷，要认真仔细的先填好自己的考生信息。

２、拿到试卷不要提笔就写，先大致的浏览一遍，有多少大题，每个大题里有几个小题，有什么题型，哪些容易，哪些难，做到心里有底；３、审题，每个题目都要多读几遍，不仅要读大题，还要读小题，不放过每一个字，遇到暂时弄不懂题意的题目，手指点读，多读几遍题目，就能理解题意了；容易混乱的地方也应该多读几遍，比如从小到大，从左到右这样的题；４、每个题目做完了以后，把自己的手从试卷上完全移开，好好的看看有没有被自己的手臂挡住而遗漏的题；试卷第１页和第２页上下衔接的地方一定要注意，仔细看看有没有遗漏的小题；５、中途遇到真的解决不了的难题，注意安排好时间，先把后面会做的做完，再来重新读题，结合平时课堂上所学的知识，解答难题；一定要镇定，不能因此慌了手脚，影响下面的答题；６、卷面要清洁，字迹要清工整，非常重要；７、做完的试卷要检查，这样可以发现刚才可能留下的错误或是可以检查是否有漏题，检查的时候，用手指点读题目，不要管自己的答案，重新分析题意，所有计算题重新计算，判断题重新判断，填空题重新填空，之后把检查的结果与先前做的结果进行对比分析。

亲爱的朋友，你们好!经过两个月的学习，你们一定有不小的收获吧，用你的自信和智慧，认真答题，相信你一定会闯关成功。

相信你是最棒的！第十一章综合测试基础练习一、单选题1.如图，四棱锥P ABCD −，AC BD O =，M 是PC 的中点，直线AM 交平面PBD 于点N ，则下列结论正确的是（）A.O ，N ，P ，M 四点不共面B.O ，N ，M ，D 四点共面C.O ，N ，M 三点共线D.P ，N ，D 三点共线2.如图，直三棱柱111ABC A B C −中，1AA AB AC BC ===，则异面直线1AB 和1BC 所成角的余弦值为（）A.12−B.12C.14−D.143.如图，在四面体ABCD 中，截面PQMN 是正方形，则在下列命题中，错误的为（）A.AC BD ⊥B.AC ∥截面PQMNC.AC BD =D.异面直线PM 与BD 所成的角为45︒4.设E ，F 分别是正方体ABCD—A 1B 1C 1D 1的棱DC 上两点，且2AB =，1EF =，给出下列四个命题：①三棱锥11D B EF −的体积为定值； ②异面直线11D B 与EF 所成的角为45︒； ③11D B ⊥平面1B EF ；④直线11D B 与平面1D EF 所成的角为60︒。

高等数学下册黄立宏廖基定著复旦大学出版社...

（1）（2）
课后
I = ∫∫
D
4 + xy dσ , D = {( x, y ) | 0 ≤ x ≤ 2, 0 ≤ y ≤ 2}
2 2
答
∫∫
ln( x + y )dσ < ∫∫ [ln( x + y )]2 dσ
案
ln( x + y ) < [ln( x + y )]2
网
ww w.
图 10-2 ; ;
1
3
3− y
0
f ( x, y )dx = ∫ dx ∫x
0
2
( x 2 + y 2 )dxdy
1 4 π 3 dθ = a ∫ 2 cos 4 θ dθ = πa 4 0 2 32 .
图 10-11
kh da
3− x
x ≤ y ≤ 3 − x; 2
f ( x, y )dy
w.
图 10-10
co
m
1 ⎡ 1 1 ⎤ 1 1 88 = ∫ ⎢ x 2 y + y 3 ⎥ dx = ∫ ( x 2 + − x 4 − x 6 )dx = . −1 −1 3 ⎦ x2 3 3 105 ⎣
f ( x, y )dy
x 0 ≤ x ≤ π, − sin ≤ y ≤ sin x. 2 (4) 相应二重积分的积分区域 D 为：如图 10-9 所示.
图 10-9
D 亦可看成由 D1 与 D2 两部分之和，其中
w.
.
co
m
D1： −1 ≤ y ≤ 0, D2： 0 ≤ y ≤ 1,
π sin x
f ( x, y )dx + ∫ dy ∫

高等数学上(修订版)黄立宏(复旦出版社)__习题四答案详解

1. 利用定义计算下列定积分：（1）d ();bax x a b <⎰解：将区间[a , b ]n 等分，分点为(), 1,2,,1;i i b a x a i n n-=+=- 记每个小区间1[,]i i x x -长度为,i b ax n-∆=取, 1,2,,,i i x i n ξ==则得和式211()2(1)()[()]()2nni i i i i b a b a n n f x a b a a b a n n n ξ==--+∆=+-⋅=-+∑∑ 由定积分定义得22122()(1) d lim ()lim[()]21().2nbi i an i b a n n x x f x a b a n b a λξ→→∞=-+=∆=-+=-∑⎰(2)1e d .x x ⎰解：将区间[0, 1] n 等分，分点为 (1,2,,1),i i x i n n ==- 记每个小区间长度1,i x n∆=取 (1,2,,),i i x i n ξ== 则和式111()innni i i i f x enξ==∆=∑∑ 12101111111e d lim e lim (e e e )1e (1e )1e (e 1)limlim 1e e 11e (e 1)1lim e 1.1i nn xn n n n n n i n n n nn n n n n x n n n nn n n →∞→∞=→∞→∞→∞==+++--==---==-∑⎰2. 用定积分的几何意义求下列积分值:1(1)2 d x x ⎰；解:由几何意义可知,该定积分的值等于由x 轴、直线x =1、y =2x 所围成的三角形的面积，故原式=1.(2)(0)x R >⎰.解：由几何意义可知，该定积分的值等于以原点为圆心，半径为R 的圆在第一象限内的面积，故原式=21π4R . 3. 证明下列不等式：2e 22e(1)e e ln d 2(e e)x x -≤≤-⎰；证明：当2e e x ≤≤时，2ln e ln ln e ,x ≤≤即1ln e.x ≤≤ 由积分的保序性知：222e e e e eed ln d 2d x x x x ≤≤⎰⎰⎰即 2e 22ee e ln d 2(e e).x x -≤≤-⎰(2) 211e d e.x x ≤≤⎰证明：当0 1.x ≤≤时，21e e,x ≤≤由积分的保序性知：2111d ed ed x x x x ≤≤⎰⎰⎰即211e d e.x x ≤≤⎰4. 证明：（1） 12lim0;nn x →∞=⎰证明：当12x ≤≤时，0,n n x ≤≤ 于是11120110d (),12n n x x n +≤≤=⋅+⎰⎰ 而111lim()0,12n n n +→∞⋅=+由夹逼准则知：12lim 0.nn x →∞=⎰(2) π4limsin d 0.n n x x →∞=⎰证明：由中值定理得π440ππsin d sin (0)sin ,44n n x x ξξ=⋅-=⎰其中π0,4ξ≤≤故π4πlim sin d lim sin 0 ( 0sin 1).4n n n n x x ξξ→∞→∞==≤<⎰5.计算下列定积分：3(1);x ⎰解：原式43238233x ==-.221(2)d x x x --⎰;解：原式01222211()d ()d ()d x x x x x x x x x -=-+-+-⎰⎰⎰1232233210111111132233251511.6666x x x x x x -⎛⎫⎛⎫⎛⎫=++--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=++= π(3)()d f x x ⎰,其中π,0,2()πsin ,π;2x x f x x x ⎧≤≤⎪⎪=⎨⎪<≤⎪⎩ 解：原式πππ2π222π0π221πd sin d cos 1.28x x x x xx=+=-=+⎰⎰ 222(4)max{1,}d ;x x -⎰解：原式121122233211212011d d d 2.333x x x x x x x -----=++=++=⎰⎰⎰(5).x解：原式πππ242π04d (cos sin )d (sin cos )d sin cos x x x x x x x x x ==-+--⎰⎰⎰ππ24π04(sin cos )(cos sin )1).x x x x =++--=6. 计算下列导数：2d (1)d x t x ⎰解：原式2=32d (2)d x x x ⎰解：原式32200d d d d x x x x =-=⎰⎰ 7. 求由参数式2020sin d cos d t tx u uy u u⎧=⎪⎨⎪=⎩⎰⎰所确定的函数y 对x 的导数d d y x . 解：222d d cos d cot .d d sin d yy t t t x x tt=== 8. 求由方程e d cos d 0yxtt t t +=⎰⎰所确定的隐函数()y y x =的导数.解：方程两边对x 求导，有e cos 0y y x '⋅+=又 e 1sin yx =- 故 c o s s i n 1xy x '=-.9. 利用定积分概念求下列极限：111(1)lim 122n n n n →+∞⎛⎫+++ ⎪++⎝⎭解：原式110011111lim d ln 2.ln(1)121111n x x n n xnn n →+∞⎛⎫+++ ⎪=⋅===++++ ⎪+⎝⎭⎰21(2)limn n →+∞解：原式13200122lim ..33n x x n →+∞====+⎰ 10. 求下列极限：203ln(12)d (1)lim;xx t tx →+⎰解：原式21222300ln(12)22lim limln(12).333x x x x x x →→+==+=2220020e d (2)lim .e d x t x x tt t t→⎡⎤⎣⎦⎰⎰ 解：原式2222222002e d e e d 1lim2lim2lim2.12e e xxt xt xxx x x t tx x x →→→⋅====+⎰⎰11. a , b , c 取何实数值才能使201limsin x bx t c x ax →=-⎰ 成立. 解：因为0x →时，sin 0x ax -→而该极限又存在，故b =0.用洛必达法则，有220000,1,lim lim 2cos cos lim 2, 1.sin x x x a x x x x a x a a x→→→≠⎧⎪==⎨--=-=⎪-⎩ 所以 1,0,2a b c ===- 或 1,0,0a b c ≠==.12. 利用基本积分公式及性质求下列积分：2(1)5)d x x -;解：原式51732222210d 5d 73x x x x x x c =-=-+⎰⎰.(2)3e d x x x ⎰；解：原式=(3e)(3e)d .ln(3e)xxx c =+⎰23(3)d ;1x x⎛ +⎝⎰ 解：原式=321d 23arctan 2arcsin .1x x x x c x -=-++⎰22(4)d ;1x x x +⎰解：原式=22211d d d arcsin .11x xx x x x c x x+-=-=-+++⎰⎰⎰ 2(5)sin d 2x x ⎰;解：原式=1cos 1d sin .222x x x x c -=-+⎰21(6);1x x ⎛- ⎝⎰解：原式=357144444d d 4.7x x x x x x c ---=++⎰⎰2d (7);x x⎰解：原式=21d x x c x-=-+⎰.(8);x ⎰解：原式=35222d 5x x x c =+⎰.(9)解：原式=25322d 3x x x c --=-+⎰.2(10)(32)d ;x x x -+⎰解：原式=32132.32x x x c -++ 422331(11)d ;1x x x x +++⎰解：原式=23213d d arctan .1x x x x x c x +=+++⎰⎰ 3(12)d 2e x x x ⎛⎫+ ⎪⎝⎭⎰;解：原式=2e 3ln .xx c ++(13)e d ;1x xx-⎛ ⎝⎰解：原式=e d e .xx x x c-=-⎰2352(14)d ;3x xxx ⋅-⋅⎰解：原式=5222d 5d 2233ln 3x xx x x c ⎛⎫⎛⎫-=-⋅+ ⎪ ⎪⎝⎭⎝⎭⎰⎰. (15)sec (sec tan )d x x x x -⎰；解：原式=2sec d sec tan d tan sec x x x x x x x c -=-+⎰⎰.1(16)d 1cos 2x x+⎰;解：原式=22111d sec d tan 2cos 22x x x x c x ==+⎰⎰.cos 2(17)d cos sin xx x x-⎰;解：原式=(cos sin )d sin cos .x x x x x c +=-+⎰22cos 2(18)d cos sin xx x x⎰.解：原式=2211d d cot tan .sin cos x x x x c xx -=--+⎰⎰ 13. 一平面曲线过点（1，0），且曲线上任一点（x , y ）处的切线斜率为2x －2，求该曲线方程.解：依题意知：22y x '=- 两边积分，有22y x x c =-+又x =1时，y =0代入上式得c =1，故所求曲线方程为221y x x =-+. 14. （略）.15. 利用换元法求下列积分：2(1)cos()d x x x ⎰;解：原式=22211cos d sin .22x x x c =+⎰(2)x ;解：原式=12333(sin cos )d(sin cos )(sin cos ).2x x x x x x c ---=-+⎰21x -解：原式=1d 112x c =+-+⎰.c =+ 3(4)cos d x x ⎰;解：原式=231(1sin )dsin sin sin .3x x x x c -=-+⎰(5)cos cos d 2xx x ⎰；解：原式=1133d sin sin .cos cos 232222x x x x c x ⎛⎫=+++ ⎪⎝⎭⎰ (6)sin 2cos3d x x x ⎰;解：原式=111(sin 5sin )d cos cos5.2210x x x x x c -=-+⎰2arccos (7)xx ;解：原式=2arccos 2arccos 1110d(2arccos )10.22ln10x xx c -=-⋅+⎰ 21ln (8)d (ln )xx x x +⎰; 解：原式=21(ln )d(ln ).ln x x x x c x x-=-+⎰(9)x ;解：原式=22arctan.c =+⎰ln tan (10)d cos sin xx x x⎰;解：原式=21ln tan d(ln tan )(ln tan ).2x x x c =+⎰5(11)e d x x -⎰;解：原式=51e5xc --+.12x -解：原式=1ln .122c x -+-(13)t;解：原式=2sin .c =-⎰102(14)tan sec d x x x ⎰;解：原式=10111tan d(tan )tan .10x x x c =+⎰2d (15)ln xx x⎰;解：原式=21(ln )d(ln ).ln x x c x--=+⎰(16)tan x ⎰;解：原式=ln .c =-+⎰d (17)sin cos xx x⎰;解：原式=2d d tan ln .tan tan cos tan x xc x x x x==+⎰⎰ 2(18)e d x x x -⎰;解：原式=22211e d()e .22x x x c ----=-+⎰ 10(19)(4)d x x +⎰;解：原式=111(4)11x c ++.(20)解：原式=123311(23)d(23)(23)32x x x c ----=--+⎰.(21)x ;解：原式=12222d 1112(94)d(94)arcsin .2823x x x x c -⎛⎫ ⎪+--=+⎰(22)x ; 解：原式=122222d 1()d()2x x a a x a x -⎛⎫ ⎪=--⎰⎰arcsin .xa c a=⋅- d (23)e ex xx-+⎰; 解：原式=2d(e )arctane .1(e )x xx c =++⎰ ln (24)d xx x⎰; 解：原式=21ln d(ln )(ln ).2x x x c =+⎰23(25)sin cos d x x x ⎰;解：原式=223511sin (1sin )d(sin )sin sin .35x x x x x c -=-+⎰(26);解：原式32tan 444sec cos 1sin d d d(sin )tan sin sin x tt t tt t t t t t =-==⎰⎰⎰令311,3sin sin c t t=-++又cos t t ==故上式23(2.3x c x-=+(27)100d ln |1|ln(1.1tt t t c c t =-++=+++(28) ;x 解：原式3sec 223tan d 3(sec 1)d 3tan 3x tt t t t t t c ==-=-+⎰⎰令,又3tan arccos ,t t x === 故上式33arccosc x+. (29);解：原式2tan 3sec d cos d sin sec x ttt t t t c t ===+⎰⎰令,又sec t =所以sin t =,故上式c =+.(30)解：原式sin cos d sin cos x ttt t t =+⎰令① sin d sin cos tt t t +⎰②① + ② = t + c 1② － ① = ln |sin t +cos t | + c 2 故cos 1d ln sin cos sin cos 2211arcsin ln .22t t t ct t t t x c x =++++=++⎰16. 用分部积分法求下列不定积分：2(1)sin d x x x ⎰;解：原式=222d cos cos 2cos d cos 2d sin x x x x x x x x x x x -=-+⋅=-+⎰⎰⎰1012cos 2sin 2cos .x x x x x c =-+++ (2)e d x x x -⎰;解：原式=dee e d e e .xx x x x x x x x c ------=-+=--+⎰⎰(3)ln d x x x ⎰;解：原式=222211111ln d ln d ln 22224x x x x x x x x x c ⋅=-=-+⎰⎰. 2(4)arctan d x x x ⎰;解：原式=3332111arctan d arctan d 3331x x x x x x x=-+⎰⎰ 322111arctan ln(1).366x x x x c =-+++ (5)arccos d x x ⎰;解：原式=arccos arccos x x x x x c +=.2(6)tan d x x x ⎰;解：原式=22211(sec 1)d d tan tan tan d 22x x x x x x x x x x x -=-=--⎰⎰⎰ 21tan ln .cos 2x x x c x =+-+(7)e cos d x x x -⎰;解：ecos d e d sin e sin e sin d xx x x x x x x x x ----==⋅+⎰⎰⎰e sin e d cos e sin e cos e cos d x x x x x x x x x x x -----=-=--⎰⎰∴原式=1e (sin cos ).2xx x c --+ (8)sin cos d x x x x ⎰;解：原式=1111sin 2d d cos 2cos 2cos 2d 2444x x x x x x x x x =-=-+⎰⎰⎰ 11cos 2sin 248x x x c =-++.32(ln )(9)d x x x ⎰;102解：原式=332111(ln )d (ln )3(ln )d x x x x x x ⎛⎫⎛⎫-=--⎪ ⎪⎝⎭⎝⎭⎰⎰32131(ln )(ln )6ln d x x x x x x ⎛⎫=--- ⎪⎝⎭⎰321366(ln )(ln )ln .x x x c x x x x =----+(10)x ⎰.解：原式tan 23sec d .x a ta t t =⎰又32sec d sec (tan 1)d tan d(sec )sec d t t t t t t t t t =+=+⎰⎰⎰⎰ 3tan sec sec d ln sec tan t t t t t t =⋅-++⎰所以 311sec d tan sec ln sec tan 22t t t t c t t '=+++⎰ 故11ln .22x c x =+17. 求下列不定积分：221(1)d (1)(1)x x x x ++-⎰; 解：原式=2111111d ln ln 1122122(1)(1)(1)x c x x x x x x ⎛⎫ ⎪-=++++-++ ⎪+++-⎝⎭⎰ 211ln .112c x x =++-+ 33d (2)1xx +⎰; 解：原式=22211112d ln ln d 1122111x x x x x x x x x x x -+⎛⎫=-+++-+⎪-++-+⎝⎭⎰⎰c =. 5438(3)d x x x x x+--⎰; 解：原式=2843d 111x x x x x x ⎛⎫+++-- ⎪+-⎝⎭⎰10332118ln 4ln 3ln .1132x x x c x x x =+++--++- 26(4)d 1x x x +⎰;解：原式=33321d()1arctan .31()3x x c x =++⎰ sin (5)d 1sin xx x +⎰;解：原式=222sin 1d tan d (sec 1)d sec tan .cos cos x x x x x x x x x c x x-=--=-++⎰⎰⎰ cot (6)d sin cos 1xx x x ++⎰;解：原式22tan 222222212d 1111111d d d 22(1)22211111x t t t t t t t t t t t t t t t t t t =-⋅-++==-+⎛⎫-++⎪+++⎝⎭⎰⎰⎰⎰令1111ln ln tan .tan 222222x x t c c t =-+=-+(7)x ;解：原式=2.c =+(8)x ;解：原式=2d 2ln 2d 1x x x x x x ⎛=+-+⎝⎰⎰ 又2x2221d 44d 11t t t t t t =+--⎰⎰142ln1t t c c t -''=++=+故原式=1)x c -+.18. 求下列不定积分，并用求导方法验证其结果正确否：104d (1)1e xx+⎰; 解：原式=e d 11de ln(1e ).e (1e )e 1e x x xx x x xx x c ⎛⎫==-++- ⎪++⎝⎭⎰⎰ 验证：e 1(ln(1e ))1.1e 1ex xx xx c '-++=-=++ 所以，结论成立.(2)ln(x x +⎰;解：原式=ln(ln(.x x x x x c -=+验证：ln(ln(x x x x c '⎡⎤=+++-⎣⎦ln(x =+所以，结论成立.2(3)ln(1)d x x +⎰;解：原式=2222ln(1)2d ln(1)22arctan 1x x x x x x x x c x+-=+-+++⎰. 验证：2222222ln(1)2ln(1).ln(1)22arctan 11x x x x x x x x c x x'=++⋅-+=+⎡⎤+-++⎣⎦++ 所以，结论正确.(4)x ;解：原式=9212)arcsin (.232x x x c ++=++验证：921arcsin (232x x '+⎡++⎢⎣211(2)32x =+== 所以，结论正确.(5)sin(ln )d x x ⎰;105解：1sin(ln )d sin(ln )cos(ln )d x x x x x x x x=-⋅⋅⎰⎰ sin(ln )cos(ln )sin(ln )d x x x x x x =--⎰所以，原式=().sin(ln )cos(ln )2xc x x +- 验证： ()sin(ln )cos(ln )2x c x x '⎡⎤+-⎢⎥⎣⎦()111sin(ln )cos(ln )cos(ln )sin(ln )22sin(ln ).x x x x x x x x ⎛⎫=+-⋅+⋅ ⎪⎝⎭= 故结论成立.2e (6)d (e 1)xx x x +⎰; 解：原式=1e 1d d d e 1e 1e 11e e 1x x x x xx x x x x x --⎛⎫-=-+=-+ ⎪+++++⎝⎭⎰⎰⎰ ln(1e ).e 1x xxc --=-+++ 验证：22(e 1)e e e ln(1e )(e 1)1e (e 1)e 1x xx x xx x x x x x x c ---'-++--⎡⎤=-=-++⎢⎥++++⎣⎦. 故结论成立.23/2ln (7)d (1)xx x +⎰; 解：原式=1ln d d ln(.x x x c x =-=++⎰验证：ln(x c '⎤-+⎥⎦2223/223/2(1ln )(1)ln ln .(1)(1)x x x x x x x =++-==++所以，结论成立.sin (8)d 1cos x x x x++⎰;106解：原式=2d cos d d tan ln(1cos )1cos 22cos 2x x xx x x x x -=-++⎰⎰⎰tan tan d ln(1cos )22tan ln(1cos )ln(1cos )2tan 2x xx x x xx x x c x x c=--+=++-++=+⎰验证：2221sin sin (tan)tan sec 22221cos 2cos 2cos 22x x x x x x xx c x x x x +'+=+⋅=+=+ 所以，原式成立.(9)()d xf x x ''⎰;解：原式=d ()()()d ()().x f x xf x f x x xf x f x c ''''=-=-+⎰⎰验证：[]()()()().()()f x xf x f x xf x xf x f x c ''''''''=+-=-+ 故结论成立.(10)sin d n x x ⎰ (n >1，且为正整数).解：1sin d sind cos nn n I x x x x -==-⎰⎰1221212cos sin (1)cos sin d cos sin (1)sin d (1)sin d cos sin (1)(1)n n n n n n n nx x n x x xx x n x x n x x x x n I n I ------=-+-=-+---=-+---⎰⎰⎰ 故 1211cos sin .n n n n I x x I n n---=-+ 验证： 1211cos sin sin d n n n x x x x n n --'-⎡⎤-+⎢⎥⎣⎦⎰22222111sin cos (1)sin cos sin 111sin (1sin )sin sin sin .n n n n n n n n x x n x x x n n n n n x x x xn n n x -----=-⋅-⋅+--=--+= 故结论成立.19. 求不定积分max(1,)d x x ⎰.107解： ,1max(1,)1,11,1x x x x x x -<-⎧⎪=-≤≤⎨⎪>⎩故原式=212231,12,111,12x c x x c x x c x ⎧-+<-⎪⎪+-≤≤⎨⎪⎪+>⎩又由函数的连续性，可知：213111,1,2c c c c c c =+=+= 所以 221,121max(1,)d ,11211,12x c x x x c x x x c x ⎧-+<-⎪⎪⎪=++-≤≤⎨⎪⎪++>⎪⎩⎰20. 计算下列积分：4(1)x ⎰;333211221313d .36222t t t t ⎛⎫⎛⎫==++ ⎪ ⎪⎝⎭⎝⎭2e 1(2)⎰;解：原式=221e211).(1ln )d(1ln )x x -=++=⎰1(3);解：原式=211112⎛⎫+ ⎪-== π40sin (4)d 1sin xx x+⎰;108解：原式=πππ244422000sin(1sin )sin d d tan d cos cos x xx x x x xx -=-⎰⎰⎰π40π1 2.tan 4cos x x x ⎛⎫==+-+ ⎪⎝⎭ ln3ln 2d (5)e e x xx--⎰;解：原式=ln 3ln 32ln 2ln 2de 113e 1ln ln .(e )1222e 1x x x x -==-+⎰(6)x ⎰;解：原式=πππ2π02d cos d cos d cos x x x x x x x ==⎰⎰ππ2π02xx==(7)x ⎰;解：原式=π33π222π02d sin d sin sin d sin x x x x x x =-⎰⎰⎰ππ55222π02422.sin sin 555x x =-=231(8)ln d x x x ⎰;解：原式=22243411111151ln d d 4ln 2.ln 44164x x x x x x =-=-⎰⎰π220(9)e cos d x x x ⎰;解：ππππ222222220e cos d e dsin e sin 2e sin d xx xx x x x xx x ==⋅-⎰⎰⎰πππ2π2π22220e 2e d cos e 2e cos 4e cos d xxx x xx x =+=+-⎰⎰所以，原式=π1(e 2)5-.109120ln(1)(10)d (2)x x x +-⎰;解：原式=111000111ln(1)ln(1)dd 2212x x x x x x x ++=-⋅--+-⎰⎰ 101100111ln 2d 321111ln 2ln 2ln(2)ln(1)333x x x x x ⎛⎫=-+ ⎪-+⎝⎭=+-=-+⎰322d (11)2xx x +-⎰; 解：原式=3322111111d ln ln 2ln 5.333122x x x x x -⎛⎫==-- ⎪-++⎝⎭⎰21(12)x ⎰; 解：原式11611d 6d (1)t 1t t t t t ⎫=-⎪++⎝⎭()67ln 26ln ln ln(1)1t t ==--+ππ3π(13)sin d 3x x ⎛⎫+ ⎪⎝⎭⎰;解：原式ππ3πcos 03x ⎛⎫=-=+ ⎪⎝⎭ 212(14)e d t t t -⎰;解：原式=221212200ed e 12t t t --⎛⎫-=-=-- ⎪⎝⎭⎰π22π6(15)cos d u u ⎰.解：原式=ππ22ππ661π11(1cos 2)d sin 226824u u u u ⎛⎫+==-+ ⎪⎝⎭⎰21. 计算下列积分（n 为正整数）：110（1）1;n x ⎰解：令sin x t =,d cos d x t t =, 当x =0时t =0，当x =1时t=π2, ππ12200sin cos d sin d cos n n n tx t t t t t==⎰⎰⎰由第四章第五节例8知11331π, 24221342,253n n n n n n x n n n n n --⎧⋅⋅⋅⋅⋅⎪⎪-=⎨--⎪⋅⋅⋅⋅⎪-⎩⎰为偶数, 为奇数. (2)π240tan d .n x x ⎰解：πππ2(1)22(1)22(1)4440π2(1)411tan tan d tansec d tan d 1tan d tan 21n n n n n n n I x x x x x x x xx x I I n ------==-=-=--⎰⎰⎰⎰由递推公式 1121n n I I n -+=- 可得 111(1)(1)[(1)].43521n nn I n π--=---+-+- 22. 证明下列等式：232001(1)()d ()d 2aa x f x x xf x x =⎰⎰ (a 为正常数)；证明：左222222000111()d()()d ()d 222a a a x t x f x x tf t t xf x x ====⎰⎰⎰ 令右所以，等式成立.(2)若()[,]f x c a b ∈，则ππ220(sin )d (cos )d f x x f x x =⎰⎰.证明：左πππ0222π02(cos )(d )(cos )d (cos )d x tf t t f t t f x x =--==⎰⎰⎰令.所以，等式成立.23. 利用被积函数奇偶性计算下列积分值（其中a 为正常数）(1)sin d ;||aa x x x -⎰111解：因sin ||xx 为[－a , a ]上的奇函数，故s i n d 0.||aa xx x -=⎰(2)ln(aax x -⎰;解：因为ln(ln(x x -=-+即被积函数为奇函数，所以原式=0.12212sin tan (3)d ln(1)3cos3x x x x x -⎡⎤+-⎢⎥+⎣⎦⎰;解：因为2sin tan 3cos3x xx+为奇函数，故原式=111222111222d 0ln(1)d ln(1)1xx x x x x x---++-=--⎰⎰()121231ln 3ln 2 1.ln 3ln 2ln(1)22x x -==----+-π242π23(4)sin d sin ln 3x x x x x -+⎛⎫+ ⎪-⎝⎭⎰.解：因为3ln3xx+-是奇函数，故原式=ππ6622π02531π5sin d 2sin d 2π642216x x x x -==⋅⋅⋅⋅=⎰⎰24. 利用习题22(2)证明：ππ2200sin cos πd d sin cos sin cos 4x x x x x x x x ==++⎰⎰,并由此计算a⎰(a 为正常数)证明：由习题22(2)可知ππ2200sin cos d d sin cos sin cos x xx x x x x x=++⎰⎰又πππ222000sin cos πd d d .sin cos sin cos 2x x x x x x x x x +==++⎰⎰⎰112故等式成立.a⎰πsin 20cos πd .sin cos 4x a tx t t t ==+⎰令25. 已知201(2),(2)0,()d 12f f f x x '===⎰, 求120(2)d x f x x ''⎰.解：原式=11122000111d (2)2(2)d (2)222x f x xf x x x f x ''='-⎰⎰11100012001111(2)d (2)0(2)d (2)22221111(2)(2)d(2)1()d 1402444f x f x f x x xf x f f x x f t t '=-=-+=-+=-+=-+⨯=⎰⎰⎰⎰26. 用定义判断下列广义积分的敛散性，若收敛，则求其值：22π11(1)sin d x x x+∞⎰; 解：原式=22ππ1111lim sin d lim cos lim cos 1.bbb b b x b x x →+∞→+∞→+∞⎛⎫-=== ⎪⎝⎭⎰2d (2);22xx x +∞-∞++⎰解：原式=02200d(1)d(1)arctan(1)arctan(1)(1)1(1)1x x x x x x +∞+∞-∞-∞+++=+++++++⎰⎰πππππ.4242⎛⎫=-+-=- ⎪⎝⎭ 0(3)e d n x x x +∞-⎰(n 为正整数)解：原式=10e d deen x n xn xn x x x x +∞+∞+∞----+-=-⎰⎰100e d !e d !n x x n x x n x n +∞+∞---=+===⎰⎰(4)(0)aa >⎰;解：原式=00000πlim lim arcsin lim arcsin .12a a xa a εεεεεε+++--→→→⎛⎫===- ⎪⎝⎭⎰e1(5)⎰;113解：原式=()e e 011πlim arcsin(ln )lim lim arcsin .ln(e )2x εεεεεε+++--→→→===-⎰1(6)⎰解：原式=110+⎰21212211121202lim 2lim πππlim arcsin lim 2222π.424εεεεεε++-→→→→=⎛⎫=+=⋅+=- ⎪⎝⎭⎰⎰27. 讨论下列广义积分的敛散性：2d (1)(ln )kxx x +∞⎰;解：原式=2122112,1ln(ln )1d(ln ),1(ln )1(ln )1(ln 2),1(ln )11k kkk k x x k x k x k x k k +∞+∞-+∞-+∞-⎧=∞=⎪⎪⎪=∞<=⎨-⎪⎪=>⎪--⎩⎰ 故该广义积分当1k >时收敛；1k ≤时发散.d (2)()()bkaxb a b x >-⎰. 解：原式=1100011lim ()()1,1lim ()d()1lim 1ln()b kk b a k a b a k b x b a k k b x b x k k b x εεεεεε+++-----→→-→⎧>⎧⎪⎪=-⎨--⎪-<---=⎪⎨-⎩⎪⎪-=-⎩⎰ 发散,发散, 综上所述，当k <1时，该广义积分收敛，否则发散.28. 已知0sin πd 2x x x +∞=⎰，求： 0sin cos (1)d ;x x x x+∞⎰解：(1)原式=001sin(2)1sin πd(2)d .2224x t x t x t +∞+∞==⎰⎰22sin (2) d .xx x +∞⎰114解：222002200200020000sin 1cos 2d d 21cos 2d d 22111d cos 2d 2211111d cos 2dcos2222111sin 2cos 2d2222ππ0.22xx x xx x x x x x x x x x xx x x x x xx x xx x x +∞+∞+∞+∞+∞+∞+∞+∞+∞+∞+∞-==-=+=+⋅-⎡⎤=-+⋅+⎢⎥⎣⎦=+=⎰⎰⎰⎰⎰⎰⎰⎰⎰29. 已知()d 1p x x +∞-∞=⎰,其中1,()0,1,x p x x <=≥⎩求c .解：1111()d 0d 0d p x x x x x x +∞-+∞-∞-∞--=⋅++⋅=⎰⎰⎰⎰⎰11001arcsin arcsin π1x x c x c xc --=+=⋅+⋅==⎰⎰所以1πc =. 30. 证明：无穷积分敛散性的比较判别法的极限形式，即节第六节定理2. 证明：如果|()|lim0()x f x g x ρ→+∞=≠，那么对于ε(使0ρε->),存在x 0，当0x x ≥时|()|0()f xg x ρερε<-<<+ 即 ()()|()|()()g x f x g x ρερε-<<+ 成立，显然()d ag x x +∞⎰与|()|d af x x +∞⎰同进收敛或发散.如果0ρ=，则有|()|()f x g x ε<, 显然()d ag x x +∞⎰收敛, 则|()|d af x x +∞⎰亦收敛.如果ρ=+∞，则有|()|()()f x g x ρε>-，显然()d ag x x +∞⎰发散，则|()|d af x x +∞⎰亦发散.*31. 计算下列广义积分的柯西主值：(1) V.P.x +∞-∞⎰;115解：原式=0lim AA x x -→+∞⎡⎤+⎢⎥⎣⎦⎰⎰lim lim 0.11A A A →+∞→+∞⎤=⎦==+212d (2) V.P.ln xx x⎰; 解：原式=121211001212d d lim lim ln ln ln ln ln ln x x x x x x x x εεεεεε++--+→→+⎡⎤⎡⎤⎢⎥+=+⎢⎥⎢⎥⎣⎦⎣⎦⎰⎰01lim ln ln(1)ln ln ln 2ln ln(1)0.ln 2εεε+→⎡⎤=--+-+=⎢⎥⎣⎦2d (3) V.P.32xx x +∞-+⎰; 解：x =1, x =2是奇点. 故原式1222201200d d d lim323232b n b x x x x x x x x x εηεηε++--++→→→+∞⎡⎤=++⎢⎥-+-+-+⎣⎦⎰⎰⎰ 120000120222lim ln lim ln lim ln 111bb x x x x x x εηεεηεηη++++--→→→++→∞→⎡-⎤⎡-⎤⎡-⎤=++⎢⎥⎢⎥⎢⎥---⎣⎦⎣⎦⎣⎦ 0000112lim ln ln 2lim ln ln lim ln ln 1111ln 2ln .2b b b εεηηεηεηεηεη++++→→→→∞→⎡⎤⎡⎤+--⎡⎤=-+-+-⎢⎥⎢⎥⎢⎥--+⎣⎦⎣⎦⎣⎦=-=30d (4) V.P.1xx-⎰. 解：原式=1313010001d d lim lim ln ln 1111xx x xx x εεεεεε++--+→→+⎡⎤⎡⎤=--+--⎢⎥⎢⎥--⎣⎦⎢⎥⎣⎦⎰⎰ []0lim ln 2ln ln 2ln εεε+→==---+.。

高数习题第一二章习题黄立宏第4版

习题1-11. 下列函数是否相等,为什么?222(1)()();(2)sin (31),sin (31);1(3)(),() 1.1f xg x y x u t x x f x g x x x ===+=+-==+- 解: (1)相等.因为两函数的定义域相同,都是实数集R ;x =知两函数的对应法则也相同;所以两函数相等.(2)相等.因为两函数的定义域相同,都是实数集R ,由已知函数关系式显然可得两函数的对应法则也相同,所以两函数相等.(3)不相等.因为函数()f x 的定义域是{,1}x x x ∈≠R ,而函数()g x 的定义域是实数集R ,两函数的定义域不同,所以两函数不相等. 2. 求下列函数的定义域211(1)arctan ;(2);lg(1)(3); (4)arccos(2sin ).1y y x x xy y x x ==-==-解: (1)要使函数有意义,必须400x x -≥⎧⎨≠⎩即 40x x ≤⎧⎨≠⎩所以函数的定义域是(,0)(0,4]-∞.(2)要使函数有意义,必须30lg(1)010x x x +≥⎧⎪-≠⎨⎪->⎩即 301x x x ≥-⎧⎪≠⎨⎪<⎩所以函数的定义域是[-3,0)∪(0,1).(3)要使函数有意义,必须210x -≠ 即 1x ≠±所以函数的定义域是(,1)(1,1)(1,)-∞--+∞.(4)要使函数有意义,必须12sin 1x -≤≤ 即 11sin 22x -≤≤即ππ2π2π66k x k -+≤≤+或5π7π2π2π66k x k +≤≤+,(k 为整数). 也即ππππ66k x k -+≤≤+ (k 为整数).3. 设1()1x f x x -=+,求1(0),(),().f f x f x-解: 10(0)110f -==+,1()1(),1()1x x f x x x --+-==+--1111().111x x f x x x--==++ 4. 设1,10()1,02x f x x x -≤<⎧=⎨+≤≤⎩,求(1)f x -.解: 1,1101,01(1).(1)1,012,13x x f x x x x x -≤-<≤<⎧⎧-==⎨⎨-+≤-≤≤≤⎩⎩5. 设()2,()ln xf xg x x x ==,求(()),(()),(())f g x g f x f f x 和(())g g x . 解: ()ln (())22,g x x x f g x ==(())()ln ()2ln 2(ln 2)2,x x x g f x f x f x x ==⋅=⋅()2(())22,(())()ln ()ln ln(ln ).xf x f f xg g x g x g x x x x x ====6. 求下列函数的反函数及其定义域:2531(1); (2)ln(2)1;1(3)3; (4)1cos ,[0,π].x xy y x xy y x x +-==+++==+∈ 解: (1)由11xy x-=+解得11y x y -=+,所以函数11x y x -=+的反函数为1(1)1xy x x-=≠-+. (2)由ln(2)1y x =++得1e 2y x -=-,所以,函数ln(2)1y x =++的反函数为1e2()x y x -=-∈ R .(3)由253x y +=解得31(log 5)2x y =- 所以,函数253x y +=的反函数为31(log 5)(0)2y x x =-> .(4)由31cos y x =+得cos x =又[0,π]x ∈,故x =又由1cos 1x -≤≤得301cos 2x ≤+≤,即02y ≤≤,故可得反函数的定义域为[0,2],所以,函数31cos ,[0,π]y x x =+∈的反函数为3arccos 1(02)y x x =-≤≤ .7. 判断下列函数在定义域内的有界性及单调性:2(1); (2)ln 1xy y x x x ==++ 解: (1)函数的定义域为(-∞,+∞), 当0x ≤时,有201x x ≤+,当0x >时,有21122x x x x ≤=+, 故(,),x ∀∈-∞+∞有12y ≤.即函数21xy x =+有上界. 又因为函数21xy x =+为奇函数,所以函数的图形关于原点对称,由对称性及函数有上界知,函数必有下界,因而函数21xy x =+有界. 又由1212121222221212()(1)11(1)(1)x x x x x x y y x x x x ---=-=++++知,当12x x >且121x x <时,12y y >,而当12x x >且121x x >时,12y y <. 故函数21xy x=+在定义域内不单调. (2)函数的定义域为(0,+∞),10,0M x ∀>∃>且12;e 0M x M x >∃>>,使2ln x M >.取012max{,}x x x =,则有0012ln ln 2x x x x M M +>+>>, 所以函数ln y x x =+在定义域内是无界的. 又当120x x <<时,有12120,ln ln 0x x x x -<-<故1211221212(ln )(ln )()(ln ln )0y y x x x x x x x x -=+-+=-+-<. 即当120x x <<时,恒有12y y <,所以函数ln y x x =+在(0,)+∞内单调递增.8. 已知水渠的横断面为等腰梯形,斜角ϕ=40°,如图所示.当过水断面ABCD 的面积为定值S 0时,求湿周L (L =AB +BC +CD )与水深h 之间的函数关系式,并指明其定义域.图1-1解:011()(2cot )(cot )22S h AD BC h h BC BC h BC h ϕϕ=+=++=+从而 0cot SBC h hϕ=-.000()22cot sin sin 2cos 2cos 40sin sin 40L AB BC CD AB CD S h hBC h hS S h h h hϕϕϕϕϕ=++==+=+---=+=+由00,cot 0S h BC h hϕ>=->得定义域为.9. 下列函数是由哪些基本初等函数复合而成的?5122412(1)(1);(2)sin (12);1(3)(110);(4).1arcsin 2xy x y x y y x-=+=+=+=+解: (1)124(1)y x =+是由124,1y u u x ==+复合而成.(2)2sin (12)y x =+是由2,sin ,12y u u v v x ===+复合而成. (3)512(110)x y -=+是由152,1,10,w y u u v v w x ==+==-复合而成.(4)11arcsin 2y x=+是由1,1,arcsin ,2y u u v v w w x -==+==复合而成.习题1-21. 写出下列数列的通项公式,并观察其变化趋势:1234579(1)0,,,,,; (2)1,0,3,0,5,0,7,0,; (3)3,,,,.3456357----解: 1(1),1n n x n -=+当n →∞时,1n x →.1(2)cos π2n n x n -=,当n 无限增大时,有三种变化趋势:趋向于+∞,趋向于0,趋向于-∞.21(3)(1)21n n n x n +=--,当n 无限增大时,变化趁势有两种,分别趋于1,-1.2. 对下列数列求lim n n a x →∞=,并对给定的ε确定正整数()N ε,使对所有()n N ε>,有n x a ε-<:1π(1)sin ,0.001; (2)0.0001.2n n n x x n εε====解: (1)lim 0n n a x →∞==,0ε∀>,要使11π0sin2n n x n n ε-=<<,只须1n ε>.取1N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,必有0n x ε-<.当0.001ε=时,110000.001N ⎡⎤==⎢⎥⎣⎦或大于1000的整数. (2)lim 0n n a x →∞==,0ε∀>,要使0n x ε-==<=<1ε>即21n ε>即可.取21N ε⎡⎤=⎢⎥⎣⎦,则当n N >时,有0n x ε-<. 当0.0001ε=时, 821100.0001N ⎡⎤==⎢⎥⎣⎦或大于108的整数. 3. 根据数列极限的定义，证明:21313(1)lim0;(2)lim ;212(3)1;(4)lim 0.999 1.n n n n n n n n →∞→∞→∞→∞-==+== 个证: (1)0ε∀>,要使22110n n ε=<-,只要n >.取N =,则当n>N 时,恒有210nε<-.故21lim 0n n →∞=. (2) 0ε∀>,要使555313,2(21)4212n n n n n ε-=<<<-++只要5n ε>,取5N ε⎡⎤=⎢⎥⎣⎦,则当n>N 时,恒有313212n n ε-<-+.故313lim212n n n →∞-=+. (3) 0ε∀>,要使2221a n ε=<<-,只要n >,取n =,则当n>N 时,1ε<-,从而lim 1n →∞=. (4)因为对于所有的正整数n ,有10.99991n <-个,故0ε∀>,不防设1ε<,要使1,0.999110n n ε=<-个只要ln ,ln10n ε->取ln ,ln10N ε-⎡⎤=⎢⎥⎣⎦则当n N >时,恒有,0.9991n ε<-个故lim 0.9991n n →∞=个.4. 若lim n n x a →∞=,证明lim n n x a →∞=,并举反例说明反之不一定成立.证:lim 0n n x →∞=,由极限的定义知,0,0N ε∀>∃>,当n N >时,恒有n x a ε-<.而 n n x x a a ε-<-<0,0N ε∴∀>∃>,当n N >时,恒有n x a ε-<,由极限的定义知lim .n n x a →∞=但这个结论的逆不成立.如(1),lim 1,nn n n x x →∞=-=但lim n n x →∞不存在.5. 利用收敛准则证明下列数列有极限,并求其极限值:1111(1)1,2,; (2)1,1,1,2,.1nn n nx x x n x x n x ++=====+=+证: (1)122x =<,不妨设2k x <,则12k x +<=.故对所有正整数n 有2n x<,即数列{}n x 有上界.又1n n n x x x+-==0>,又由2n x <从而10n n x x +->即1n n x x +>, 即数列{}n x 是单调递增的.由极限的单调有界准则知,数列{}n x 有极限. 设lim n n x a →∞=,则a =,于是22a a =,2,0a a ==(不合题意,舍去),lim 2n n x →∞∴=.(2) 因为110x =>,且111nn nx x x +=++, 所以02n x <<, 即数列有界又 111111111(1)(1)nn n n n n n n n n x x x x x x x xx x --+---⎛⎫⎛⎫++-=-= ⎪ ⎪++++⎝⎭⎝⎭由110,10n n x x -+>+>知1n n x x +-与1n n x x --同号，从而可推得1n n x x +-与21x x -同号，而 1221131,1,022x x x x ==+=-> 故10n n x x +->, 即1n n x x +>所以数列{}n x 单调递增，由单调有界准则知，{}n x 的极限存在. 设lim n n x a →∞=, 则11a a a=++，解得1122a a +-==(不合题意，舍去). 所以1lim 2n n x →∞+=习题1-31. 选择题（1）设1,1()0,1x f x x ≠⎧=⎨=⎩，则0lim ()x f x →=（） A.不存在 B.∞ C.0 D.1（2）设()f x x =，则1lim ()x f x →=（） A.1- B.1 C.0 D.不存在（3）0(0)f x +与0(0)f x -都存在是函数()f x 在点0x x =处有极限的一个（）A.必要条件B.充分条件C.充要条件D.无关条件（4）函数()f x 在点0x x =处有定义，是当0x x →时()f x 有极限的（）A.必要条件B.充分条件C.充分必要条件D.无关条件（5）设1()1x f x x -=-，则1lim ()x f x →=（）A.0B.1-C.1D.不存在 2.证明01lim arctanx x→不存在. 3. 用函数极限定义证明：22222102sin 314(1)lim 0; (2)lim 3; (3)lim 4; 42141(4)lim 2; (5)lim sin 0.21x x x x x x x x xx x x x x x →+∞→∞→-→→---===-++-==+证：(1)0ε∀>,要使1sin sin 0x xx x xε=≤<-, 只须1x ε>,取1X ε>，则当x X >时，必有sin 0xxε<-, 故sin lim0x xx→+∞=.(2)0ε∀>,要使22221313313||44x x x x ε-=<<-++,只须x >取X =X x >时，必有223134x x ε-<-+, 故2231lim 34x x x →∞-=+. (3) 0ε∀>,要使24(4)22x x x ε-=<--++, 只要取δε=，则当02x δ<<+时，必有24(4)2x x ε-<--+,故224lim42x x x →--=-+.(4) 0ε∀>,要使21142221221x x x x ε-==<+-++,只须122x ε<+，取2εδ=，则当102x δ<<+时，必有214221x x ε-<-+故21214lim 221x x x →--=+.(5) 0ε∀>,要使11sin0sin x x x x xε=≤<-, 只要取δε=，则当00x δ<<-时，必有1sin0x xε<-, 故01lim sin0x x x→=. 习题1-41. 选择题：（1）设α和β分别是同一变化过程中的无穷小量与无穷大量，则αβ+是同一变化过程中的（）A.无穷小量B.有界变量C.常量D.无穷大量（2）“当0x x →时，()f x A -是一个无穷小量”是“函数()f x 在点0x x =处以A 为极限”的（）A.必要而不充分条件B.充分而不必要的条件C.充分必要条件D.无关条件（3）当0x →时，11cos x x是（） A.无穷小量 B.无穷大量 C.无界变量 D.有界变量 2.求下列极限：（1）201lim cos x x x →；（2）arctan lim x xx→∞.习题1-51.若对某极限过程，()lim f x 与()lim g x 均不存在，问()()()lim f x g x ±是否一定不存在？举例说明.2.若对某极限过程，()lim f x 存在，()lim g x 不存在，问()()()lim f x g x ±，()()()lim f x g x ⋅是否存在？为什么？3. 求下列极限：2222313242233112131(1)lim ;(2)lim ;1211(3)lim ;(4)lim ;3121131(5)lim ;(6)lim ;111(7)lim 1x x x x x x x x x x x x x x x x x x x x x x x x →→∞→→∞→∞→→→--+---+-++-⎛⎫- ⎪---⎝⎭- ()()33212(8)lim .23x x x x x →∞+--+-解：()()2232233lim 33933(1)lim 1lim 9151x x x x x x x →→→---===+++. 22223334224241111(2)limlim .1121221111lim (3)lim lim 0.3131311lim 1x x x x x x x x x x x xx x x x x x x x x x x x →∞→∞→∞→∞→∞→∞--==----⎛⎫-- ⎪-⎝⎭===-+⎛⎫-+-+ ⎪⎝⎭(4)(5) (6) (7) (8)习题1-61. 选择题：（1）当n →∞时，1sinn n是一个（） A.无穷小量 B.无穷大量 C.无界变量 D.有界变量（2）若x a →时，有0()()f x g x ≤≤，则lim ()0x ag x →=是()f x 在x a →过程中为无穷小量的（）A.必要条件B.充分条件C.充要条件D.无关条件 2. 利用夹逼定理求下列数列的极限:1(1)(2)lim[(1)],01;(3);(4)lim(123).n k k n n nn nn n n k →∞→∞+-<<++其中为给定的正常数解: (1)11111n n<+<+ 而1lim10,lim(1)1n n n→∞→∞=+=故 1n =. 1111(2)0(1)(1)1(1)1k k k kk k n n n n n n n -⎡⎤⎡⎤<+-=<=+-+-⎢⎥⎢⎥⎣⎦⎣⎦而lim 00n →∞=,当1k <时,11lim0kn n -→∞=lim[(1)]0k k n n n →∞∴+-=.(3)记12max{,,,}m a a a a =则有n<<即 1na m a <<⋅而1lim , lim ,nn n a a m a a →∞→∞=⋅=故n a =即 12lim max{,,,}m n a a a =.(4)111(3)(123)(33)n nn n nn n<++<⋅即 113(123)3n nn nn+<++<而 1lim33,lim33n nn n +→∞→∞==故 1lim(123)3nn nn →∞++=.3.求下列极限:(1)0sin 2lim;sin 5x xx → (2) 0lim cot ;x x x →(3)0arctan lim;x x x → (4) 201lim 1;xx x →⎛⎫+ ⎪⎝⎭(5)213lim ;2x x x x +→∞+⎛⎫ ⎪-⎝⎭(6) ()2cot 2lim 13tan ;xx x →+习题1-71. 当1x →时，无穷小量1x -与221(1)1,(2)(1)2x x --是否同阶？是否等价？解：211111(1)limlim 112x x x x x →→-==-+ ∴当1x →时，1x -是与21x -同阶的无穷小.2111(1)12(2)lim lim 112x x x xx →→-+==-∴当1x →时，1x -是与21(1)2x -等价的无穷小.2. 当0x →时，22x x -与23x x -相比，哪个是高阶无穷小量？解：232200limlim 022x x x x x x x x x→→--==-- ∴当0x →时，23x x -是比22x x -高阶的无穷小量.3.利用等价无穷小量，求下列极限：(1)0sin lim;sin x mxnx → 0(2)lim cot ;x x x →01cos 2(3)lim ;sin x xx x→- (4) tan sin 601lim 1x x x e e →--. 解：(1)因为当0x →时，sin ~,sin ~,mx mx nx nx所以00sin limlim .sin x x mx mx mnx nx n→→==00002000limcos cos (2)lim cot lim cos lim 1.sin sin sin lim1cos 22sin sin (3)lim lim 2lim 2.sin sin x x x x x x x x x x x x x x x xx x xx x x x x x x x→→→→→→→→=⋅===-=== (4)习题1-81. 研究下列函数的连续性，并画出图形：2,1,,01,(1)()(2)()1,1;2,12;x x x x f x f x x x x≤⎧≤≤⎧==⎨⎨>-<<⎩⎩ 解：(1)由初等函数的连续性知，()f x 在（0，1），（1，2）内连续，又21111lim ()lim(2)1,lim ()lim 1x x x x f x x f x x ++--→→→→=-=== 1lim ()1,x f x →∴= 而(1)1f =，()f x ∴在1x =处连续，又，由2lim ()lim 0(0)x x f x x f ++→→===，知()f x 在0x =处右连续，综上所述，函数()f x 在[0，2)内连续. 函数图形如下：图1-2(2) 由初等函数的连续性知()f x 在(,1),(1,1),(1,)-∞--+∞内连续，又由1111lim ()lim 11,lim ()lim 1,x x x x f x f x x --++→-→-→-→-====-知1lim ()x f x -→-不存在，于是()f x 在1x =-处不连续.又由1111lim ()lim 1,lim ()lim11,x x x x f x x f x --++→→→→==== 及(1)1f =知1lim ()(1)x f x f →=，从而()f x 在x =1处连续，综上所述，函数()f x 在(,1)-∞-及(1,)-+∞内连续，在1x =-处间断.函数图形如下：图1-32. 下列函数在指定点处间断，说明它们属于哪一类间断点，如果是可去间断点，则补充或改变函数的定义，使它连续：221(1),1,2;32π(2),π,π,0,1,2,.tan 2x y x x x x x y x k x k k x -===-+===+=±±解：22111(1)(1)(1)lim lim 232(1)(2)x x x x x x x x x →→--+==--+-- 2221lim 32x x x x →-=∞-+ 1x ∴=是函数的可去间断点.因为函数在x =1处无定义，若补充定义(1)2f =-，则函数在x =1处连续；x =2是无穷间断点.π0π2(2)lim1,lim 0tan tan x x k x x x x →→+==当0k ≠时，πlimtan x k xx →=∞.π0,π,0,1,2,2x x k k ∴==+=±±为可去间断点，分别补充定义f (0)=1,π(π)02f k +=，可使函数在x =0,及ππ2x k =+处连续.(0,1,2,k =±±);π,0,1,2,x k k k =≠=±±为无穷间断点3. 当x =0时，下列函数无定义，试定义(0)f 的值，使其在x =0处连续:tan2(1)()(2)().xf x f xx ==解：0003(1)lim ()2x x x f x →→→=== ∴补充定义3(0),2f =可使函数在x =0处连续. 000tan 22(2)lim ()lim lim 2.x x x x xf x x x→→→=== ∴补充定义(0)2,f =可使函数在x =0处连续. 4. 怎样选取a , b 的值，使f (x )在(－∞,+∞)上连续？π1,,e ,0,2(1)()(2)()π,0;sin ,.2xax x x f x f x a x x x b x ⎧+<⎪⎧<⎪==⎨⎨+≥⎩⎪+≥⎪⎩解：(1)()f x 在(,0),(0,)-∞+∞上显然连续，而0lim ()lim(),x x f x a x a ++→→=+= 0lim ()lim e 1,xx x f x --→→== 且(0)f a =, ∴当(0)(0)(0)f f f -+==，即1a =时，()f x 在0x =处连续，所以，当1a =时，()f x 在(,)-∞+∞上连续.(2)()f x 在ππ(,),(,)22-∞+∞内显然连续.而ππ22ππ22lim ()lim (sin )1,πlim ()lim (1)1,2π()1,2x x x x f x x b b f x ax a f b ++--→→→→=+=+=+=+=+ ∴当π112b a +=+，即π2b a =时，()f x 在π2x =处连续，因而()f x 在(,)-∞+∞上连续.5. 试证：方程21xx ⋅=至少有一个小于1的正根.证：令()21xf x x =⋅-，则()f x 在[0,1]上连续，且(0)10,(1)10f f =-<=>,由零点定理，(0,1)ξ∃∈使()0f ξ=即210ξξ⋅-=即方程21xx ⋅=有一个小于1的正根. 6. 利用取对数的方法求下列幂指函数的极限：()11002(1)lim ;(2)lim ;e 3111(3)lim ;(4)lim .sin cos 1x x xxxxx x x xx x a b c x x x x →→→∞→∞⎛⎫+++ ⎪⎝⎭⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭(5) ()23lim cos 2.x x x →解：(1)令1(e )xxy x =+，则1ln ln(e )x y x x=+于是：()0000ln e ln 111e lim ln lim ln lim ln e lim 1e e x x x x x x x x x x x y x x x x →→→→⎛⎫++ ⎪⎛⎫⎝⎭===++ ⎪⎝⎭e 0001e 1lim 1lim lim ln 1ln 11e e e e 11ln e 2x xxx x x x x x x x x x →→→⎡⎤⎛⎫⎛⎫==+⋅+⋅++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦=+⋅= 即()lim ln 2x y →= 即20lim e x y →= 即()120lim e e x x x x →=+. (2)令13xxxxa b c y ⎛⎫++= ⎪⎝⎭，则1ln ln3x x x a b c y x ++= 于是00333303300001lim(ln )lim ln 313lim ln 1333lim lim ln 1331111lim ln lim 13x x x x x x xxx x x xx x a b c x x x a b c x xxxxxxa b c x x x x x x x x x x a b c y x a b c x a b c a b c x a b c a b c x x x →→++-++-→++-→→→→++=⎡⎤⎛⎫++-=⎢⎥+ ⎪⎢⎥⎝⎭⎣⎦++-⎛⎫++-=⋅+ ⎪⎝⎭⎛⎫---++=⋅++ ⎪+⎝⎭33331(ln ln ln )ln e ln 3x x x a b c a b c ++-⎡⎤⎛⎫-⎢⎥ ⎪⎢⎥⎝⎭⎣⎦=++⋅=即0lim(ln )ln x y →= 即()lim ln x y →=故0lim x y →=即1lim 3x x xxx a b c →⎛⎫++=⎪⎝⎭(3)令11sin cos xy x x ⎛⎫=+ ⎪⎝⎭，则11ln ln sin cos y x x x ⎛⎫=+ ⎪⎝⎭ 于是11sin cos 1111sin cos 1111sin cos 111lim ln lim ln 1sin cos 11111lim ln 1sin cos 1sin cos 111sin 1cos lim ln lim 11xx x x x x x xx x y x x x x x x x x x x x x ⎛⎫+- ⎪⎝⎭+-→∞→∞+-→∞→∞⎧⎫⎪⎪⎡⎤⎛⎫=⎨⎬++- ⎪⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭⎡⎤⎛⎫⎛⎫=⋅++-+- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎛⎫- ⎪=-⋅ ⎪ ⎪⎝⎭111sin cos 1111sin cos 1x x x x x +-→∞⎧⎫⎪⎪⎡⎤⎛⎫⎨⎬++- ⎪⎢⎥⎝⎭⎪⎪⎣⎦⎩⎭2111sin 2ln e (10)ln e 1limlim 11x x x x x x →∞→∞⎛⎫⎛⎫ ⎪⎪⎝⎭=⋅=-⋅= ⎪- ⎪ ⎪⎝⎭ 即limln 1x y →∞= 从而()lim ln 1x y →∞= 故lim e x y →∞= 即 11lim e sin cos xx x x →∞⎛⎫=+ ⎪⎝⎭.(4)令211xy x ⎛⎫=+ ⎪⎝⎭，则21ln ln 1y x x ⎛⎫=+ ⎪⎝⎭于是：22221222211lim(ln )lim ln lim ln 111111lim ln lim lim ln 110ln e 0x x x x x x x x x x y x x x x x x x x →∞→∞→∞→∞→∞→∞⎡⎤⎛⎫⎛⎫==+⎢⎥ ⎪+ ⎪⎝⎭⎝⎭⎣⎦⎛⎫⎛⎫==⋅++ ⎪ ⎪⎝⎭⎝⎭=⋅= 即 ()lim lim(ln )0,ln 0x x y y →∞→∞== lim 1x y →∞∴= 即21lim 11xx x →∞⎛⎫=+ ⎪⎝⎭.习题一1. 填空题（1）已知当0x →时，1与2x 是等价无穷小，则常数a = -2 .（2）()ln 1lim1cos x x x x→+=- 2 .（3）3332lim 3x x x x →∞⎛⎫+=⎪-⎝⎭5e . （4）若函数22,4,()20,4x c x f x cx x ⎧-<=⎨+≥⎩在(),-∞+∞上连续，则常数c 的值为 -2 .（5）已知0x =是函数2x e ay x+=的第一类间断点，则常数a 的值为 -1 .2. 选择题（1）设函数f x ()在∞∞(-,+)内单调有界，{}n x 为数列，下列命题正确的是（ B ）.A.若{}n x 收敛，则(){}n f x 收敛B.若{}n x 单调，则(){}n f x 收敛 C.若(){}n f x 收敛，则{}n x 收敛 D.若(){}n f x 单调，则{}n x 收敛（2）当0x +→B ）.A. 1-B. 1xC. 1D. 1-（3）极限2lim ()()xx x x a x b →∞⎡⎤=⎢⎥-+⎣⎦（ C ），这里,a b 为常数. A. 1 B. e C. a b e - D. b ae -（4）设函数1112,0,()22,0,x xe xf x e x ⎧+⎪≠⎪=⎨+⎪⎪=⎩则0x =是函数()f x 的（ B ）.A.可去间断点B.跳跃间断点C.无穷间断点D.连续点（5）设*n N ∈，则函数21()lim1nn xf x x →∞+=+（ D ）.A. 存在间断点1x =B. 存在间断点1x =-C. 存在间断点0x =D. 不存在间断点3. 求函数⎧≠⎪=⎨⎪=⎩1sin ,0,0,x y xx 的定义域与值域.4. 判断下列函数的奇偶性:22(1)()(2)e e sin .x x f x y x -=+=-+解: (1)()()f x f x -==()f x ∴=.(2)222222()e e sin()e e sin (e e sin )()x x x x x x f x x x x f x ----=-+-=-+=--+=-∴函数22e e sin x x y x -=-+是奇函数.5. 设()f x 定义在(-∞,+∞)上,证明:(1) ()()f x f x +-为偶函数; (2)()()f x f x --为奇函数. 证: (1)设()()()F x f x f x =+-,则(,)x ∀∈-∞+∞, 有()()()()F x f x f x F x -=-+= 故()()f x f x +-为偶函数.(2)设()()(),G x f x f x =--则(,)x ∀∈-∞+∞,有()()()[()()]()G x f x f x f x f x G x -=---=---=- 故()()f x f x --为奇函数.6. 某厂生产某种产品,年销售量为106件,每批生产需要准备费103元,而每件的年库存费为0.05元,如果销售是均匀的,求准备费与库存费之和的总费用与年销售批数之间的函数(销售均匀是指商品库存数为批量的一半). 解: 设年销售批数为x , 则准备费为103x ;又每批有产品610x 件,库存数为6102x 件,库存费为6100.052x ⨯元. 设总费用为,则63100.05102y x x⨯=+.7. 邮局规定国内的平信,每20g 付邮资0.80元,不足20 g 按20 g 计算,信件重量不得超过2kg,试确定邮资y 与重量x 的关系. 解: 当x 能被20整除,即[]2020x x =时,邮资0.802025x x y =⨯=; 当x 不能被20整除时,即[]2020x x ≠时,由题意知邮资0.80120x y ⎡⎤=⨯+⎢⎥⎣⎦.综上所述有,02000;2520200.80,02000.1202020x xx x y x x x x ⎧⎡⎤<≤=⎪⎢⎥⎪⎣⎦=⎨⎡⎤⎡⎤⎪⨯<≤≠+⎢⎥⎢⎥⎪⎣⎦⎣⎦⎩且且其中20x ⎡⎤⎢⎥⎣⎦,120x ⎡⎤+⎢⎥⎣⎦分别表示不超过20x ,120x +的最大整数. 8. 证明:11(1)arcsin h ln(h ln ,1121xx x x x x+=+=-<<-证: (1)由e e sinh 2x x y x --==得2e 2e 10x xy --=解方程2e2e 10xx y --=得e x y =因为e 0x >,所以e x y =ln(x y =+所以sinh y x =的反函数是arcsin h ln(().y x x x ==-∞<<+∞(2)由e e tanh e e x x x xy x ---==+得21e 1xy y +=-,得1112ln ,ln 121y y x x y y ++==--;又由101yy+>-得11y -<<, 所以函数tanh y x =的反函数为11arctan h ln (11).21xy x x x+==-<<-9.设数列{}n x 满足10x π<<，()1sin 1,2,n n x x n +==.证明lim nn x →∞存在，并求该极限.解：当1n =时，10x π<<，1sin n n x x += 则有1sin 1n n x x +=≤所以，数列{}n x 有界.令函数()sin f x x x =-，其中(0,)x π∈ 则 ()cos 10f x x '=-≤ ()(0)f x f ≤sin x x ≤1sin n n n x x x +=≤所以数列{}n x 单调递减根据单调收敛定理知：数列{}n x 极限存在令lim n n x A →∞=在1sin n n x x +=两边去极限得sin A A = 所以 0A = 故lim 0n n x →∞=10.设函数()f x =1()()x f x ϕ=，1()(())n n x f x ϕϕ-=，2,3,n =试计算极限()n n x .解：由题设()()21()x x f x ϕϕ====，依此类推，一般地，有()n xϕ=()1,0,,0,0,0,1,0.0,0n n n x xx x x x x x >⎧⎧≠⎪⎪====⎨⎨⎪⎪-<=⎩⎩=11. 求下列极限：221(1)lim(1)(1)(1)(1);)(1)nx n x x x x x x →∞→+++<-122222(1)lim(1)(1)(1)(1)(1)(1)(1)(1)lim 111lim .11nnn x x x x x x x x x x x x x x x+→∞→∞→∞+++<-+++=--==--111211211(1)(1)(2)lim (1))(1))(1)11.234!n n x n n n n x n n n n x n x x x x x x x x n n -→--→-→--=++++=++++==⨯⨯⨯⨯12.利用等价无穷小量，计算下列极限：0arctan 3(1)lim;(2)lim 2sin ;2n n x n x xx →→∞()22102320020041arctan (3)lim ;(4)lim ;arcsin(12)sin arcsin 2tan sin cos cos (5)lim ;(6)lim ,;sin 1cos 4(8)lim 2sin x x x x x x x x x x x x x x x x x x x αβαβ→→→→→→----- 为常数()222200;tan ln cos ln(sin e )(9)lim ,0;(10)lim .ln cos ln(e )2x x x x x x ax x xa b b bx x x→→++-≠+- 为常数,解：(1)因为当0x →时，arctan3~3,x x 所以00arctan 33limlim 3x x x xx x →→==.sin sin 22(2)lim 2sin lim lim .222n nn n n n n n nx x x x x x x x →∞→∞→∞=⋅== (3)因为当12x →时，arcsin(12)~12x x --,所以22111122224141(21)(21)lim lim lim lim(21) 2.arcsin(12)1212x x x x x x x x x x x x →→→→---+===-+=---- (4)因为当0x →时，22arctan ~,sin~,arcsin ~,22x xx x x x 所以 2200arctan lim lim 2sin arcsin 22x x x x xx x x →→==⋅.(5)因为当0x →时，2331sin ~,1cos ~,sin ~2x x x x x x -,所以 233300001tan sin sin (1cos )2lim lim lim sin sin cos cos 11lim .2cos 2x x x x x x x x x x x x xx x x →→→→⋅--==⋅== (6)因为当0x →时，sin~,sin~2222x x x x αβαβαβαβ++--，所以220020222sin sin cos cos 22lim lim 222lim 1().2x x x x xx x x x x xxαβαβαβαβαββα→→→+---=+--⋅⋅==- (7)因为当0x →时，~)~,x x --所以00 1.x x x →→→==-=-(8)因为当0x →时，sin ~,sin 2~2,x x x x 所以2222200222200201cos 42sin 2lim lim 2sin tan sin (2sec )2(2)8lim lim (2sec )2sec 84.lim(2sec )x x x x x x xx x x x x x x x x x x xx x →→→→→-=++⋅==++==+ (9)因为ln cos ln[1(cos 1)],ln cos ln[1(cos 1)],ax ax bx bx =+-=+- 而当0x →时，cos 10,cos 10ax bx -→-→故 ln[1(cos 1)]~cos 1,ln[1(cos 1)]~cos 1,ax ax bx bx +--+-- 又当x →0进，2222111cos ~,1cos ~,22ax a x bx b x --所以22220000221ln cos cos 11cos 2lim lim lim lim .1ln cos cos 11cos 2x x x x a xax ax ax a bx bx bx b b x→→→→--====-- (10)因为当0x →时，222sin 0,0e exx x x →→ 故 222222sin sin ln ~,ln ~,11e ee e x x xx x xx x ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭ 所以22222222200022222000020sin ln 1ln(sin e )ln(sin e )ln e e lim lim lim ln(e )2ln(e )ln e ln 1e sin sin sin e lim lim e lim e lim e e 1 1.x x x x x x x x x x x x x x x x x x x x x x x x x x x xx x x x x →→→→→→→⎛⎫+ ⎪+-+-⎝⎭==+-+-⎛⎫+ ⎪⎝⎭⎛⎫⎛⎫==⋅=⋅ ⎪ ⎪⎝⎭⎝⎭=⋅= 13.设n N *∈，研究下列函数的连续性，并画出图形：221(1)()lim ;(2)()lim .1x x nx x nn n n n x f x f x x n n x --→∞→∞--==++(1)∵当x <0时，221()lim lim 1,1x x x xx x n n n n n f x n n n --→∞→∞--===-++ 当x =0时，00()lim 0,n n n f x n n →∞-==+ 当x >0时，2222111()limlim lim 1111x xxx x xx n n n xn n n n f x n n n n --→∞→∞→∞---====+++1,0,()lim0,0,1,0.x xx xn x n n f x x n n x --→∞-<⎧-⎪∴===⎨+⎪>⎩由初等函数的连续性知()f x 在(,0),(0,)-∞+∞内连续，又由 0lim ()lim11,lim ()lim(1)1x x x x f x f x ++--→→→→===-=-知0lim ()x f x →不存在，从而()f x 在0x =处间断.综上所述，函数()f x 在(,0),(0,)-∞+∞内连续，在0x =处间断.图形如下：图1-4(2)当|x |=1时，221()lim0,1nnn x f x x x →∞-==+ 当|x |<1时，221()lim,1nnn x f x x x x →∞-==+ 当|x |>1时，2222111()limlim 111nnn nn n x x f x x x x x x →∞→∞⎛⎫- ⎪-⎝⎭==⋅=-+⎛⎫+ ⎪⎝⎭即 ,1,()0,1,, 1.x x f x x x x <⎧⎪==⎨⎪->⎩由初等函数的连续性知()f x 在(－∞,－1),(－1,1),(1,+∞)内均连续，又由1111lim ()lim ()1,lim ()lim 1x x x x f x x f x x --++→-→-→-→-=-===-知1lim ()x f x →-不存在，从而()f x 在1x =-处不连续.又由 1111lim ()lim()1,lim ()lim 1x x x x f x x f x x ++--→→→→=-=-== 知1lim ()x f x →不存在，从而()f x 在1x =处不连续.综上所述，()f x 在(－∞,－1),(－1,1),(1,+∞)内连续，在1x =±处间断. 图形如下：图1-514. 下列函数在指定点处间断，说明它们属于哪一类间断点?21(1)cos,0;y x x == 1,1,(2) 1.3,1,x x y x x x -≤⎧==⎨->⎩解：(1)∵当0x →时，21cosx 呈振荡无极限， ∴x =0是函数的振荡间断点.(第二类间断点). (2)∵11lim lim(1)0x x y x --→→=-= ∴x =1是函数的跳跃间断点.(第一类间断点.)15. 当x =0时，下列函数无定义，试定义(0)f 的值，使其在x =0处连续:11(1)()sin sin ;(2)()(1).x f x x f x x x==+解：01(1)limsin sin0x x x→= ∴补充定义(0)0,f =可使函数在x =0处连续.10(2)lim ()lim(1)e xx x f x x →→=+=∴补充定义(0)e,f =可使函数在x =0处连续16. 试证：方程sin x a x b =+至少有一个不超过a b +的正根，其中0,0a b >>. 证：令()sin f x x a x b =--，则()f x 在[0,]a b +上连续，且 (0)0,()(1sin )0f b f a b a x =-<+=-≥, 若()0f a b +=，则a b +就是方程sin x a x b =+的根. 若()0f a b +>，则由零点定理得.(0,)a b ξ∃∈+,使()0f ξ=即sin 0a b ξξ--=即sin a b ξξ=+，即ξ是方程sin x a x b =+的根，综上所述，方程sin x a x b =+至少有一个不超过a b +的正根.17. 设a 为正常数，()f x 在[0,2]a 上连续，且(0)(2)f f a =,证明：方程()()f x f x a =+在[0，a ]内至少有一根.证：令()()()F x f x f x a =-+,由()f x 在[0,2]a 上连续知，()F x 在[0,]a 上连续，且(0)(0)(),()()(2)()(0)F f f a F a f a f a f a f =-=-=-若(0)()(2),f f a f a ==则0,x x a ==都是方程()()f x f x a =+的根，若(0)()f f a ≠，则(0)()0F F a <，由零点定理知，至少(0,)a ξ∃∈,使()0F ξ=, 即()()f f a ξξ=+，即ξ是方程()()f x f x a =+的根，综上所述，方程()()f x f x a =+在[0,]a 内至少有一根.18. 设()f x 在[0,1]上连续，且0()1f x ≤≤，证明：至少存在一点[0,1]ξ∈，使()f ξξ=. 证：令()()F x f x x =-,则()F x 在[0,1]上连续，且(0)(0)0,(1)(1)10,F f F f =≥=-≤ 若(0)0f =，则0,ξ=若(1)1f =,则1ξ=,若(0)0,(1)1f f ><,则(0)(1)0F F ⋅<,由零点定理，至少存在一点(0,1)ξ∈,使()0F ξ=即()f ξξ=.综上所述，至少存在一点[0,1]ξ∈，使()f ξξ=. 19. 若()f x 在[,]a b 上连续，12n a x x x b <<<<<,证明:在1[,]n x x 中必有ξ，使12()()()()n f x f x f x f nξ+++=.证: 由题设知()f x 在1[,]n x x 上连续，则()f x 在1[,]n x x 上有最大值M 和最小值m ，于是12()()()n f x f x f x m M n+++≤≤,由介值定理知，必有1[,]n x x ξ∈，使12()()()()n f x f x f x f nξ+++=.。

线性代数答案第四版(高等教育出版社)

(1) 1 2 3 4;
(2) 4 1 3 2;
(3) 3 4 2 1;
(4) 2 4 1 3;
(5) 1 3 · · · (2n − 1) 2 4 · · · (2n);
(6) 1 3 · · · (2n − 1) (2n) (2nห้องสมุดไป่ตู้− 2) · · · 2.
解
(1) 逆序数为 0.
(2) 逆序数为 4: 4 1, 4 3, 4 2, 3 2.
(4)
x
y x+y
y x + y x = x(x + y)y + yx(x + y) + (x + y)yx − y3 − (x + y)3 − x3
x+y x
y
= 3xy(x + y) − y3 − 3x2y − 3y2x − x3 − y3 − x3 = −2(x3 + y3).
2 . 按自然数从小到大为标准次序, 求下列各排列的逆序数:
70
第一章行列式
课后的习题值得我们仔细研读. 本章建议重点看以下习题: 5.(2), (5); 7; 8.(2). (这几个题号建立有超级链接.) 若您发现有好的解法, 请不吝告知.
1 . 利用对角线法则计算下列三阶行列式:
201 (1) 1 −4 −1 ;
−1 8 3
abc (2) b c a ;
1
2
第一章行列式
(3) 逆序数为 5: 3 2, 3 1, 4 2, 4 1, 2 1.
(4) 逆序数为 3: 2 1, 4 1, 4 3.
(5)
逆序数为
n(n−1) 2
:
3 2...........................................................................1 个 5 2, 5 4 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 2 个 7 2, 7 4, 7 6 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3 个 .................................................................................. (2n − 1) 2, (2n − 1) 4, (2n − 1) 6, . . . , (2n − 1) (2n − 2). . . . . . . . . . . . . .(n − 1) 个

高等数学黄立宏

第六章3．判定下列级数的敛散性： (1) ()11n n n ∞=+-∑；(2)()()11111661111165451n n +++++⋅⋅⋅-+ ；(3) ()23133222213333n n n--+-++- ；(4)311115555n+++++ ；解：(1) ()()()3212111n S n n n =+++-+--=+-从而lim n n S →∞=+∞，故级数发散． (2) 1111111115661111165451111551n S n n n ⎛⎫=-+-+-++- ⎪-+⎝⎭⎛⎫=- ⎪+⎝⎭从而1lim 5n n S →∞=，故原级数收敛，其和为15．(3)此级数为23q =-的等比级数，且|q |<1，故级数收敛．(4)∵15n nU =，而lim 10n n U →∞=≠，故级数发散．5．用比较审敛法判别下列级数的敛散性． (1)()()111465735n n ++++⋅⋅++ ；(2)22212131112131n n+++++++++++(3)1πsin3nn ∞=∑；(4) 3112n n∞=+∑；(5)()1101nn a a∞=>+∑；(6) ()1121n n ∞=-∑．解：(1)∵ ()()21135n U nn n =<++而211n n∞=∑收敛，由比较审敛法知1n n U ∞=∑收敛．(2)∵221111n n n U nn nn++=≥=++而11n n∞=∑发散，由比较审敛法知，原级数发散．(3)∵ππsin sin33limlim ππ1π33nnn n n n →∞→∞=⋅=而1π3nn ∞=∑收敛，故1πsin3nn ∞=∑也收敛．(4)∵33321112n U nnn =<=+而3121n n ∞=∑收敛，故3112n n∞=+∑收敛．(5)当a >1时，111n nnU aa =<+，而11nn a∞=∑收敛，故111nn a∞=+∑也收敛．当a =1时，11lim lim022n n n U →∞→∞==≠，级数发散．当0<a <1时，1lim lim101n nn n U a→∞→∞==≠+，级数发散．综上所述，当a >1时，原级数收敛，当0<a ≤1时，原级数发散． (6)由021limln 2xx x→-=知121limln 211n x n→∞-=<而11n n∞=∑发散，由比较审敛法知()1121nn ∞=-∑发散6．用比值判别法判别下列级数的敛散性：(1) 213nn n ∞=∑；(2)1!31nn n ∞=+∑；(3)232333331222322n nn +++++⋅⋅⋅⋅ ；(4) 12!nnn n n∞=⋅∑解：(1) 23n nn U =，()2112311limlim 133nn n n n nU n U n ++→∞→∞+=⋅=<，由比值审敛法知，级数收敛． (2) ()()111!311limlim 31!31lim 131nn n n n nnn n U n U n n ++→∞→∞+→∞++=⋅++=⋅++=+∞所以原级数发散． (3) ()()11132limlim2313lim 21312n nn n nn n nn U n U n nn +++→∞→∞→∞⋅=⋅⋅+=+=>所以原级数发散． (4) ()()1112!1limlim2!1lim 21122lim1e11n nn n nn n nnn nn U nn U n n n n n +++→∞→∞→∞→∞⋅+=⋅⋅+⎛⎫= ⎪+⎝⎭==<⎛⎫+ ⎪⎝⎭故原级数收敛．7．用根值判别法判别下列级数的敛散性：(1) 1531nn n n ∞=⎛⎫⎪+⎝⎭∑；(2) ()[]11ln 1nn n ∞=+∑；(3) 21131n n n n -∞=⎛⎫⎪-⎝⎭∑；(4) 1nn n b a ∞=⎛⎫⎪⎝⎭∑，其中a n →a （n →∞），a n ，b ，a 均为正数．解：(1)55lim lim1313n n n n n U n →∞→∞==>+，故原级数发散． (2) ()1lim lim01ln 1n n n n U n →∞→∞==<+，故原级数收敛． (3)121lim lim 1931nn n n n nU n -→∞→∞⎛⎫==< ⎪-⎝⎭，故原级数收敛． (4) limlim nnn n n nb b b a a a →∞→∞⎛⎫== ⎪⎝⎭，当b <a 时，ba<1，原级数收敛；当b >a 时，ba>1，原级数发散；当b =a 时，ba=1，无法判定其敛散性．8．判定下列级数是否收敛？若收敛，是绝对收敛还是条件收敛？ (1)1111234-+-+ ；(2)()()1111ln 1n n n ∞-=-+∑；(3) 2341111111153535353⋅-⋅+⋅-⋅+；(4)()21121!nn n n ∞-=-∑；(5)()()1111n n R nαα∞-=∈-∑；(6) ()11111123nn n n ∞=⎛⎫-++++⎪⎝⎭∑ ．解：(1)()111n n U n-=-，级数1n n U ∞=∑是交错级数，且满足111nn >+，1lim0n n→∞=，由莱布尼茨判别法级数收敛，又11121n n n U n ∞∞===∑∑是P <1的P 级数，所以1n n U ∞=∑发散，故原级数条件收敛． (2)()()111ln 1n n U n -=-+，()()1111ln 1n n n ∞---+∑为交错级数，且()()11ln ln 12n n >++，()1lim0ln 1n n →∞=+，由莱布尼茨判别法知原级数收敛，但由于()11ln 11n U n n =≥++所以，1n n U ∞=∑发散，所以原级数条件收敛．(3)()11153n n nU -=-⋅民，显然1111115353n nnn n n U ∞∞∞=====⋅∑∑∑，而113nn ∞=∑是收敛的等比级数，故1n n U ∞=∑收敛，所以原级数绝对收敛．(4)因为2112limlim1n n n n nU U n ++→∞→∞==+∞+．故可得1n n U U +>，得lim 0n n U →∞≠，∴lim 0n n U →∞≠，原级数发散．(5)当α>1时，由级数11n nα∞=∑收敛得原级数绝对收敛．当0<α≤1时，交错级数()1111n n nα∞-=-∑满足条件：()111nn αα>+；1limn nα→∞=，由莱布尼茨判别法知级数收敛，但这时()111111n n n nnαα∞∞-===-∑∑发散，所以原级数条件收敛．当α≤0时，lim 0n n U →∞≠，所以原级数发散．(6)由于11111123nn n ⎛⎫⋅>++++⎪⎝⎭而11n n∞=∑发散，由此较审敛法知级数()11111123nn n n ∞=⎛⎫-⋅++++⎪⎝⎭∑发散．记1111123n U nn ⎛⎫=⋅++++⎪⎝⎭ ，则()()()()()()1222111111123111111112311111111231110n n U U n n n n n n n n n n n n n n +⎛⎫⎛⎫-=-++++- ⎪ ⎪+⎝⎭⎝⎭+⎛⎫=-++++ ⎪⎝⎭++⎛⎫⎛⎫-=++++ ⎪ ⎪⎝⎭+++⎝⎭>即1n n U U +> 又01111lim lim12311d n n n nU n n xnx→∞→∞⎛⎫=++++ ⎪⎝⎭=⎰由0111limd lim 01t t t t x tx→+∞→+∞==⎰知lim 0n n U →∞=，由莱布尼茨判别法，原级数()11111123nn n n ∞=⎛⎫-⋅++++ ⎪⎝⎭∑ 收敛，而且是条件收敛．13．求下列幂级数的收敛半径及收敛域： (1)x +2x 2+3x 3+…+nx n+…；(2)1!nn x n n ∞=⎛⎫⎪⎝⎭∑；(3)21121n n xn -∞=-∑；(4)()2112nn x n n∞=-⋅∑；解：(1)因为11limlim1n n n na n a nρ+→∞→∞+===，所以收敛半径11R ρ==收敛区间为(-1,1)，而当x =±1时，级数变为()11nn n ∞=-∑，由l i m(1)0nx nn →-≠知级数1(1)n n n ∞=-∑发散，所以级数的收敛域为(-1,1)． (2)因为()()1111!11limlimlim lim e1!11nnnn n n n n n na nn n a n n n n ρ-+-+→∞→∞→∞→∞⎡⎤+⎛⎫⎛⎫==⋅===+ ⎪⎢⎥ ⎪+⎝⎭+⎝⎭⎣⎦所以收敛半径1e R ρ==，收敛区间为(-e,e)．当x =e 时，级数变为1e nnn n n∞=∑；应用洛必达法则求得()1e e1lim 2x x x x →-+=-，故有111lim 12n n n a n a +→∞⎛⎫-=-<⎪⎝⎭由拉阿伯判别法知，级数发散；易知x =-e 时，级数也发散，故收敛域为(-e,e)．(3)级数缺少偶次幂项．根据比值审敛法求收敛半径．211212221limlim2121lim 21n n n n n nn U xn U n xn xn x++-→∞→∞→∞-=⋅+-=⋅+=所以当x 2<1即|x |<1时，级数收敛，x 2>1即|x |>1时，级数发散，故收敛半径R =1．当x =1时，级数变为1121n n ∞=-∑，当x =-1时，级数变为1121n n ∞=--∑，由1121lim 012n n n→∞-=>知，1121n n ∞=-∑发散，从而1121n n ∞=--∑也发散，故原级数的收敛域为(-1,1)．(4)令t =x -1，则级数变为212nn tn n∞=⋅∑，因为()()2122limlim1211n n n na n na n n ρ+→∞→∞⋅===⋅++所以收敛半径为R =1．收敛区间为 -1<x -1<1 即0<x <2. 当t =1时，级数3112n n∞=∑收敛，当t =-1时，级数()31112nn n∞=-⋅∑为交错级数，由莱布尼茨判别法知其收敛．所以，原级数收敛域为 0≤x ≤2，即[0,2]14．利用幂级数的性质，求下列级数的和函数：(1)21n n nx∞+=∑；(2) 2221n n xn +∞=+∑；解：(1)由()321limn n n xn xnx++→∞+=知，当|x |=<1时，原级数收敛，而当|x |=1时，21n n nx∞+=∑的通项不趋于0，从而发散，故级数的收敛域为(-1,1)．记 ()23111n n n n S nxxnx x ∞∞+-====∑∑易知11n n nx∞-=∑的收敛域为(-1,1)，记()111n n S nxx ∞-==∑则()1011xnn x S x x x∞===-∑⎰于是()()12111xS x xx '⎛⎫==⎪-⎝⎭-，所以()()()3211xS x x x =<-(2)由2422221lim23n n n xn xn x++→∞+=⋅+知，原级数当|x |<1时收敛，而当|x |=1时，原级数发散，故原级数的收敛域为(-1,1)，记()222102121n n n n xxS x x n n ++∞∞====++∑∑，易知级数21021n n xn +∞=+∑收敛域为(-1,1)，记()211021n n xS x n +∞==+∑，则()21211nn S x x x∞='==-∑，故()1011d ln 21xx S x x x +'=-⎰ 即()()1111ln021x S S x x+-=-，()100S =，所以()()()11ln 121x x S xS x x x x+==<-15．将下列函数展开成x 的幂级数，并求展开式成立的区间：(1)f (x ) = ln(2+x )； (2)f (x ) = cos 2x ； (3)f (x )=(1+x )ln(1+x )； (4)()221xf x x=+；(5)()23x f x x=+；(6)()()1e e 2x x f x -=-；解：(1)()()ln ln 2ln 2ln 11222x x f x x ⎛⎫⎛⎫===++++ ⎪ ⎪⎝⎭⎝⎭由于()()ln 111nnn xx n ∞==+-+∑，(-1<x ≤1)故()()11ln 11221n nn n xx n +∞+=⎛⎫=+- ⎪⎝⎭+∑，(-2≤x ≤2)因此()()()11ln ln 22121n nn n xx n +∞+==++-+∑，(-2≤x ≤2)(2)()21cos 2cos 2xf x x +==由()()20cos 1!2nnn xx n ∞==-∑，(-∞<x <+∞)得()()()()()22042cos 211!!22nn nnnn n xx x n n ∞∞==⋅==--∑∑所以()()22011()cos cos 222114122!2nnnn f x x x xn ∞===+⋅=+-∑，(-∞<x <+∞)(3)f (x ) = (1+x )ln(1+x )由()()()10ln 111n nn xx n +∞==+-+∑，(-1≤x ≤1)所以()()()()()()()()()()()()()112111111111111111111111111111n nn n n nnn n n n nn n n nn n n n n n xf x x n xxn n xxx n n n n x xn n x xn n +∞=++∞∞==++∞∞+==+∞+=-∞+==+-+=+--++=++--+++--=+⋅+-=++∑∑∑∑∑∑∑(-1≤x ≤1)(4)()2222111xf x x xx==⋅++由于()()()2211!!2111!!21nnn n xn x∞=-=+-+∑(-1≤x ≤1)故()()()()221!!2111!!2nnn n xf x x n ∞=⎛⎫-+=- ⎪⎝⎭∑()()()()2211!!211!!2nn n n x xn ∞+=-=+-∑(-1≤x ≤1)(5)()()()()2202111313133133nn n n nn n x f x xxx xx∞=+∞+==⋅+⎛⎫=⋅- ⎪⎝⎭=-<∑∑(6)由0e !nx n xn ∞==∑，x ∈(-∞,+∞)得()01e!nnxn xn ∞-=⋅-=∑，x ∈(-∞,+∞)所以()()()()()()000211e e 2112!!1112!,!21x x n n n n n nnn n n f x x x n n xn xx n -∞∞==∞=+∞==-⎛⎫-=- ⎪⎝⎭=⋅⎡⎤--⎣⎦=∈-∞+∞+∑∑∑∑第七章14. 三个力F 1=(1,2,3), F 2=(-2,3,-4), F 3=(3,-4,5)同时作用于一点. 求合力R的大小和方向余弦.解：R =（1-2+3，2+3-4，3-4+5）=（2，1，4）222||21421=++=R 214cos , cos , cos .212121αβγ===15. 求出向量a = i +j +k , b =2i -3j +5k 和c =-2i -j +2k 的模，并分别用单位向量,,a b c e e e 来表达向量a , b , c .解：222||1113=++=a222||2(3)538=+-+=b222||(2)(1)23=-+-+=c20. 已知a , b 的夹角2π3ϕ=，且3,4==b a ，计算：(1) a ·b ; (2) (3a -2b )·(a + 2b ). 解：（1）a ·b =2π1cos ||||cos3434632ϕ⋅⋅=⨯⨯=-⨯⨯=-a b(2) (32)(2)3624-⋅+=⋅+⋅-⋅-⋅a b a b a a a b b a b b2223||44||334(6)41661.=+⋅-=⨯+⨯--⨯=-a a b b21. 已知a =(4,-2, 4), b =(6,-3, 2),计算：（1）a ·b ; (2) (2a -3b )·(a + b )；（3）2||-a b 解：（1）46(2)(3)4238⋅=⨯+-⨯-+⨯=a b (2) (23)()2233-⋅+=⋅+⋅-⋅-⋅a b a b a a a b a b b b222222222||3||2[4(2)4]383[6(3)2]23638349113=-⋅-=⨯+-+--+-+=⨯--⨯=-a a b b (3) 222||()()2||2||-=-⋅-=⋅-⋅+⋅=-⋅+a b a b a b a a a b b b a a b b36238499=-⨯+=3, 38, 3. a b c ===a e b e c e25. 已知a =3i +2j -k , b =i -j +2k ,求： (1) a ×b ; (2) 2a ×7b ; (3) 7b ×2a ; (4) a ×a . 解：（1） 211332375122111--⨯=++=----a b i j k i j k(2) 2714()429870⨯=⨯=--a b a b i j k(3) 7214()14()429870⨯=⨯=-⨯=-++b a b a a b i j k (4) 0⨯=a a .26. 已知向量a 和b 互相垂直，且||3, ||4==a b .计算： (1) |(a ＋b )×(a －b )|； (2) |(3a ＋b )×(a －2b )|.（1）|()()|||2()|+⨯-=⨯-⨯+⨯-⨯=-⨯a b a b a a a b b a b b a bπ2||||sin242=⋅⋅=a b(2) |(3)(2)||362||7()|+⨯-=⨯-⨯+⨯-⨯=⨯a b a b a a a b b a b b b aπ734sin842=⨯⨯⨯=37. 求过点(4,1,-2)且与平面3x -2y +6z =11平行的平面方程. 解：所求平面与平面3x -2y +6z =11平行故n ={3,-2,6}，又过点(4,1,-2)故所求平面方程为：3(x -4)-2(y -1)+6(z +2)=0 即3x -2y +6z +2=0.38. 求过点M 0(1,7,-3)，且与连接坐标原点到点M 0的线段OM 0垂直的平面方程.解：所求平面的法向量可取为0{1,7,3}OM ==-n故平面方程为：x -1+7(y -7)-3(z +3)=0 即x +7y -3z -59=039. 设平面过点(1,2,-1)，而在x 轴和z 轴上的截距都等于在y 轴上的截距的两倍，求此平面方程.解：设平面在y 轴上的截距为b 则平面方程可定为122x y z bb b++=又(1,2,-1)在平面上，则有121122bbb-++=得b =2.故所求平面方程为1424xy z ++=40. 求过(1,1,-1), (-2,-2,2)和（1，-1，2）三点的平面方程. 解：由平面的三点式方程知1112121213131310x x y y z z x x y y z z x x y y z z ------=--- 代入三已知点，有1112121210111121x y z --+----+=---+化简得x -3y -2z =0即为所求平面方程. 47. 求下列直线与平面的交点： (1) 11126x y z -+==-, 2x +3y +z -1=0;(2)213232x y z +--==, x +2y -2z +6=0.解：（1）直线参数方程为1126x t y t z t =+⎧⎪=--⎨⎪=⎩代入平面方程得t =1 故交点为（2，-3，6）.（2）直线参数方程为221332x t y t z t =-+⎧⎪=+⎨⎪=+⎩代入平面方程解得t =0. 故交点为（-2，1，3）.49. 求满足下列各组条件的直线方程：（1）经过点（2，-3，4），且与平面3x -y +2z -4=0垂直；（2）过点（0，2，4），且与两平面x +2z =1和y -3z =2平行；（3）过点（-1，2，1），且与直线31213x y z --==-平行.解：（1）可取直线的方向向量为 s ={3，-1，2}故过点（2，-3，4）的直线方程为234312x y z -+-==-（2）所求直线平行两已知平面，且两平面的法向量n 1与n 2不平行，故所求直线平行于两平面的交线，于是直线方向向量12102{2,3,1}013=⨯==--ij ks n n 故过点（0，2，4）的直线方程为24231x y z --==-（3）所求直线与已知直线平行，故其方向向量可取为 s ={2，-1，3}故过点（-1，2，1）的直线方程为121213x y z +--==-.50. 试定出下列各题中直线与平面间的位置关系：（1）34273x y z ++==--和4x -2y -2z =3;（2）327x y z ==-和3x -2y +7z =8;（3）223314x y z -+-==-和x +y +z =3.解：平行而不包含. 因为直线的方向向量为s ={-2，-7，3} 平面的法向量n ={4，-2，-2}，所以(2)4(7)(2)3(2)0⋅=-⨯+-⨯-+⨯-=s n于是直线与平面平行.又因为直线上的点M 0（-3，-4，0）代入平面方程有4(3)2(4)2043⨯--⨯--⨯=-≠.故直线不在平面上.(2) 因直线方向向量s 等于平面的法向量，故直线垂直于平面.(3) 直线在平面上，因为3111(4)10⨯+⨯+-⨯=,而直线上的点（2，-2，3）在平面上.51. 求过点（1，-2，1），且垂直于直线23030x y z x y z -+-=⎧⎨+-+=⎩的平面方程.解：直线的方向向量为12123111-=++-ijki j k , 取平面法向量为{1，2，3}，故所求平面方程为1(1)2(2)3(1)0x y z ⨯-+++-=即x +2y +3z =0. 52. 求过点（1，-2，3）和两平面2x -3y +z =3, x +3y +2z +1=0的交线的平面方程. 解：设过两平面的交线的平面束方程为233(321)0x y z x y z λ-+-++++= 其中λ为待定常数，又因为所求平面过点（1，-2，3）故213(2)33(13(2)231)0λ⨯-⨯-+-++⨯-+⨯+= 解得λ=-4.故所求平面方程为2x +15y +7z +7=0第八章5. 求下列各极限：2210ln(e )(1)lim;yx y x x y→→++22001(2)lim;x y x y→→+0024(3)lim;x y xy xy→→-+00(4)lim;11x y xyxy →→+-00sin (5)lim;x y xy x→→222222001cos()(6)lim.()ex yx y x y x y +→→-++解：(1)原式=22ln(1e )ln 2.10+=+(2)原式=+∞. (3)原式=00441lim.4(24)x y xy xy xy →→--=-++(4)原式=00(11)lim2.11x y xy xy xy →→++=+-(5)原式=00sin lim100.x y xy y xy→→⋅=⨯=(6)原式=22222222222()0001()2limlim0.()e2ex yx y x x y y x y x y x y ++→→→→++==+8. 求下列函数的偏导数： (1)z = x 2y +2x y; (2)s =22u v uv+;(3)z = x ln 22x y +; (4)z = lntan x y;(5)z = (1+xy )y ; (6)u = z xy ;(7)u = arctan(x -y )z; (8)yz u x =.解：(1)223122,.z z x xy x xyyy∂∂=+=-∂∂(2)u v s vu=+2211,.s v s u uvuvvu∂∂=-=-+∂∂(3)22222222222111ln 2ln(),22z xx y x x x y xx yx yx y∂=++⋅⋅⋅=++∂+++222222112.2z xy x y yx yx yx y∂=⋅⋅⋅=∂+++(4)21122seccsc ,tanz x x x xy y y yy∂=⋅⋅=∂222122sec()csc.tanz x x x x x yyyyyy∂=⋅⋅-=-∂(5)两边取对数得ln ln(1)z y xy =+ 故[]221(1)(1)(1).ln(1)1yyy x z yxy xy y xy y xy x xy-∂'=+⋅=+⋅=++∂+[]ln(1)(1)(1)ln(1)1ln(1)(1).1y y y y x zxy yxy xy y xy xy y xy xy xy xy ∂⎡⎤'++=+⋅=++⎢⎥+∂⎣⎦⎡⎤++=+⎢⎥+⎣⎦(6)1ln ln xyxyxy u u u z zy z zx xy zx yz-∂∂∂=⋅⋅=⋅⋅=⋅∂∂∂(7)11221()().1[()]1()z z z zu z x y z x y x x y x y --∂-=⋅-=∂+-+-112222()(1)().1[()]1()()ln()()ln().1[()]1()z z z zzzzzu z x y z x y y x y x y u x y x y x y x y zx y x y --∂-⋅--==-∂+-+-∂----==∂+-+-(8)1.yz u y x xz-∂=∂2211ln ln .ln ln .y yzzyyz z u x x x x y zzuy y x x x x z z z ∂=⋅=∂∂⎛⎫=⋅=-- ⎪∂⎝⎭13.求下列函数的二阶偏导数： (1)z = x 4+ y 4-4x 2y 2; (2)z = arctan y x;(3)z = y x; (4)z = 2ex y+.解：(1)2322224812816z z z x xy x y xy xxx y∂∂∂=-=-=-∂∂∂∂，，由x ,y 的对称性知22222128.16.z z y x xy yy x∂∂=-=-∂∂∂(2)222211z y y xx y x y x ∂⎛⎫=⋅=-- ⎪∂+⎝⎭⎛⎫+ ⎪⎝⎭，2222222222222222222222222222222222222222()022,()()11,12,()()2,()()2.()()z x y y xxy x x y x y z x yxx yy x z xy yx y z x y y yy xx y x y x y z x y x x y xy xx y x y ∂+⋅-⋅=-=∂++∂=⋅=∂+⎛⎫+ ⎪⎝⎭∂=-∂+∂+-⋅-=-=∂∂++∂+-⋅-=-=∂∂++(3)222ln ,ln ,xx z z y y y y xx∂∂==∂∂21222112111,(1),1ln (1ln ),ln (1ln ).x x xx x x x x z z xyx x yyyz y xyy yx y x y yz y x y y yx y y x-------∂∂==-∂∂∂=⋅+=+∂∂∂=+⋅⋅=+∂∂(4)22e2,e,x yx yz z x xy++∂∂=⋅=∂∂222222222e 22e 22e(21),e,2e ,2e.x yx yx yx yx yx yz x x x x zz zx x yx yy x++++++∂=⋅⋅+⋅=+∂∂∂∂===∂∂∂∂∂15.设z = x ln ( x y )，求32z x y∂∂∂及32z x y∂∂∂.解：ln()1ln(),z y x xy xy xxy∂=⋅+=+∂232223221,0,11,.z y z xxy x x y z xz x yxyyx yy∂∂===∂∂∂∂∂===-∂∂∂∂16.求下列函数的全微分： (1)22e xyz +=; (2)22y z x y=+;(3)zyu x =;(4)yz u x =.解：(1)∵2222e2,e2x yx yz z x y xy++∂∂=⋅=⋅∂∂∴222222d 2e d 2ed 2e(d d )x yx yx yz x x y y x x y y +++=+=+(2)∵22223/22212()2zx xy y x y x x y x y∂⎛⎫-=⋅⋅=- ⎪+∂+⎝⎭+ 2222222223/2()y x y y x yz xyx yx y +-⋅+∂==∂++∴ 223/2d (d d ).()x z y x x y x y =--+(3)∵11,ln zzz y yz u u y xxx zyxy--∂∂==⋅⋅∂∂2ln ln yzu x xy yz∂=⋅⋅⋅∂∴211d d ln d ln ln d .zzzy yz yzu y x x xx zy y x xy y z --=+⋅+⋅⋅⋅(4)∵1y zu y x xz-∂=∂1ln yz u x x yz∂=⋅⋅∂ln yz uy x x z z 2∂⎛⎫=⋅⋅- ⎪∂⎝⎭ ∴121d d ln d ln d .y yyzzz y y u xx x x y x x z zz z -⎛⎫=+⋅⋅+⋅⋅- ⎪⎝⎭22. 求下列复合函数的偏导数或全导数：(1)22,cos ,sin ,z x y xy x u v y u v =-==求z u ∂∂,z v ∂∂； (2)z ＝arc tanx y, x ＝u ＋v ,y ＝u －v , 求z u∂∂,z v∂∂；(3)ln(e e )x y u =+, y ＝x 3, 求d d u x;(4) u ＝x 2＋y 2＋z 2, x ＝e cos t t , y ＝e sin t t , z ＝e t , 求d d u t.解：（1）222(2)cos (2)sin 3sin cos (cos sin )z z x z y xy y v x xy v ux u y u u v v v v ∂∂∂∂∂=⋅+⋅=-⋅+-∂∂∂∂∂=-223333(2)sin (2)cos 2sin cos (sin cos )(sin cos ).z z x z y xy y u v x xy u v vx v y v u v v v v u v v ∂∂∂∂∂=⋅+⋅=--⋅+-⋅∂∂∂∂∂=-+++(2)222222211111x z z x z y y x v y ux u y uyx y u v x x y y ∂∂∂∂∂--⎛⎫-=⋅+⋅=⋅+⋅== ⎪∂∂∂∂∂++⎝⎭⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭2222222111(1)11.x z z x z y y vx v y vyx x y y y x u x yu v-∂∂∂∂∂⎛⎫=⋅+⋅=⋅+⋅⋅- ⎪∂∂∂∂∂⎝⎭⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭+==++ (3)33222d d d 11e 3e e 3e e e 3.d d d e e e e e ee exyxxx y x y x y x y xxu u x u y x x x x x x y x ∂∂++=⋅+⋅=⋅+⋅⋅==∂∂++++(4)d d d d d d d d u u x u y u ztx t y t z t∂∂∂=⋅+⋅+⋅∂∂∂ 22(e cos e sin )2(e sin e cos )2e 4ettttttx t t y t t z =-+++⋅=.第九章1. 求下曲线在给定点的切线和法平面方程： (1)x =a sin 2t ,y =b sin t cos t ,z =c cos 2t ,点π4t =;(2)x 2+y 2+z 2=6,x +y +z =0,点M 0(1,-2,1);(3)y 2=2mx ,z 2=m -x ,点M 0(x 0,y 0,z 0).解：2sin cos ,cos 2,2cos sin x a t t y b t z c t t '''===- 曲线在点π4t =的切向量为{}πππ,,,0,444T x y z a c ⎧⎫⎛⎫⎛⎫⎛⎫'''==-⎨⎬ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎩⎭ 当π4t =时， ,,222a b c x y z ===切线方程为2220a b c x y z a c ---==-.法平面方程为0()0.222a b c a c x y z ⎛⎫⎛⎫⎛⎫++-=--- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭即 22022acax cz --+=.（2）联立方程组22260x y z x y z ⎧++=⎨++=⎩它确定了函数y =y (x ),z =z (x )，方程组两边对x 求导，得d d 2220d d d d 10d d y z x y z x xy z x x ⎧+⋅+⋅=⎪⎪⎨⎪++=⎪⎩解得d d ,,d d y z x z x y xy zxy z--==--在点M 0（1，-2，1）处，d d 0,1d d M M y z xx==-所以切向量为{1，0，-1}.故切线方程为12111x y z -+-==-法平面方程为1(x -1)+0(y +2)-1(z -1)=0即x -z =0.(3)将方程y 2=2mx ,z 2=m -x 两边分别对x 求导，得d d 22,21d d y z ym zxx==-于是d d 1,d d 2y m z xyxz==-曲线在点（x 0,y 0,z 0）处的切向量为0011,,2my z ⎧⎫-⎨⎬⎩⎭,故切线方程为00,112x x y y z z m y z ---==-法平面方程为00001()()()02m x x y y z z y z -+---=5. 求下列曲面在给定点的切平面和法线方程：(1)z = x 2+y 2,点M 0(1,2,5); (2)z = arctan y x,点M 0(1,1,π4);解：（1）02, 4.22y xm m m m z z yx ====故曲面在点M 0(1,2,5)的切平面方程为z -5=2(x -1)+4(y -2).即 2x +4y -z =5. 法线方程为125241x y z ---==-（2）0222211,.22yxm m m m y x z z x yx y-==-==++故曲面在点M 0(1,1,π4)的切平面方程为z -π4=-12(x -1)+12(y -1).法线方程为π11411122z x y ---==--. 8. 求函数u =xy 2+z 3-xyz 在点（1，1,2）处沿方向角为πππ,,343αβγ===的方向导数。

高数习题第章习七题黄立宏第4版

11.通过点作垂直于两平面和的平面.
解：设所求平面方程为Ax+By+Cz+D=0
其法向量n={A,B,C}
n1={1,-1,1},n2={2,1,1}
又（1，－1，1）在所求平面上，故A－B+C+D=0，得D=0
故所求平面方程为
即2x-y-3z=0
12.求平行于平面，且垂直于向量的单位向量.
解：设此向量的起点A的坐标A(x,y,z)，则
解得x=-2,y=3,z=0
故A的坐标为A(-2, 3, 0).
6.一向量的起点是，终点是，试求:
(1) 在各坐标轴上的投影；(2) 的模；
(3) 的方向余弦；(4) 方向的单位向量.
解：（1）
(2)
(3)
.
(4) .
7.三个力同时作用于一点，求合力的大小和方向余弦.
a+b={2,4,-2}
a-b={-6,10,14}
又(a+b)·(a-b)= 2×(-6)+4×10+(-2)×14=0
故(a+b) (a-b).
7.一平行四边形以向量和为邻边，求其对角线夹角的正弦.
解：
与平行的单位向量
.
8.已知三点，点分别是的中点，证明:
证明：中点M，N，P的坐标分别为
解：由平面的三点式方程知
代入三已知点，有
化简得x-3y-2z=0即为所求平面方程.
5.指出下列各平面的特殊位置，并画出其图形：
(1) ；(2) ；
(3) ；(4) ；
(5) .
解：(1)y=0表示xOz坐标面（如图2）
(2) 3x-1=0表示垂直于x轴的平面.(如图3)

高等数学(本科)第十一章课后习题解答

习题11.11.回答下列问题.(1)何谓级数∑∞=1n n u 的前n 项部分和？何谓级数∑∞=1n n u 的收敛和发散？何谓收敛级数的和？【答】（1）∑∞=1n n u 的前n 项部分和是指(),...2,11==∑=n u S nk k n ；（2）∑∞=1n n u 收敛是指s S n n =∞→lim 存在，这时并称s 为∑∞=1n n u 的和；∑∞=1n nu发散是指n n S ∞→lim 不存在.(2)当公比q 取何值时，等比级数∑∞=-11n n aq 收敛？当公比q 取何值时，等比级数∑∞=-11n n aq发散？写出收敛时的和数.【答】（1）当1<q 时，∑∞=-11n n aq 收敛，且其和数为qas -=1；（2）当1≥q 时，∑∞=-11n n aq 发散.(3) 级数∑∞=1n n u 收敛的必要条件是什么？它是否也是充分条件.请举例说明.【答】（1）∑∞=1n n u 收敛的必要条件是0lim =∞→n n u ；（2）0lim =∞→n n u 不是∑∞=1n n u 收敛的充分条件.比如，01lim =∞→n n ，但∑∞=11n n发散.2.若级数()()()......2211+++++++n n b a b a b a 收敛，去掉括号之后的级数级数......2211+++++++n n b a b a b a 是否还收敛？它说明了什么？【答】未必，比如()()() (1111111)+-++-+=-∑∞=-n n .3.把下列级数写成级数”“∑的形式.(1) ...5ln 5ln 5ln 32+++ ；【解】∑∞==+++1325ln ...5ln 5ln 5ln n n ；(2) (8)141211-+-+- ；【解】()11211...8141211-∞=∑-=-+-+-n n n ；(3) ...001.0001.0001.03+++ ；【解】()nn 113001.0...001.0001.0001.0∑∞==+++；(4)...751531311+⨯+⨯+⨯. 【解】()()∑∞=+-=+⨯+⨯+⨯112121...751531311n n n . 4.根据级数收敛与发散的定义，判别下列级数的敛、散性.(1) (8)1614121++++；【解】nn 1.21...816141211∑∞==++++发散.(2)∑∞=⎪⎭⎫⎝⎛-2211ln n n；【解】记()()n n n n n n n n u n 1ln 1ln 11ln11ln 22++-=+-=⎪⎭⎫ ⎝⎛-=,...)2(=n 则 1432...+++++=n n u u u u S⎪⎭⎫ ⎝⎛++-++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛+=n n n n 1ln 1ln ...45ln 43ln 34ln 32ln 23ln 21lnn n n n n n 1ln1ln 1ln ...43ln 34ln 32ln 23ln 21ln ++⎪⎭⎫ ⎝⎛-+-++⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛++= ,...)2,1(11ln 21ln =⎪⎭⎫⎝⎛++=n n因为 21ln lim =∞→n n S ，所以∑∞=⎪⎭⎫⎝⎛-2211ln n n 收敛. (3) ∑∞=⎪⎪⎭⎫ ⎝⎛+14122ln n nn n ；【解】因∑∞=122ln n n n ∑∞=⎪⎭⎫⎝⎛=122ln n n及∑∞=141n n nn ⎪⎭⎫ ⎝⎛=∑∞=141均收敛，故∑∞=⎪⎪⎭⎫ ⎝⎛+14122ln n n n n 收敛. (4) (1)31...2191131+++++++n n ；【解】因为 (3)1...9131++++n 收敛，但 (1)...211++++n 发散，故原级数发散.(5) (4)33221+++ ；【解】级数的通项为 ,...)2,1(1=+=n n nu n ，因为01lim ≠=∞→n n u ，故...433221+++发散.(6) ...cos ...3cos 2cos cos +++++nππππ ；【解】级数的通项为 ,...)2,1(cos ==n nu n π，因为010cos lim ≠==∞→n n u ，故...cos ...3cos 2cos cos +++++nππππ发散.(7) nn n n ∑∞=⎪⎭⎫⎝⎛-12ln ；【解】级数的通项为 ,...)2,1(2ln =⎪⎭⎫⎝⎛-=n n n u nn ，因为02ln 21ln lim lim 222≠-==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=---∞→∞→en u n n n n ，故nn n n ∑∞=⎪⎭⎫⎝⎛-12ln 发散.(8) (9)898983322+-+-.【解】...9898983322+-+-nn ∑∞=⎪⎭⎫⎝⎛-=198是等比级数，且公比98-的绝对值小于1，故...9898983322+-+-收敛.5.已知级数∑∞=1n n u 的部分和3n S n =，当2≥n 时，求n u .【解】(),...)2(13312331=+-=--=-=-n n n n n S S u n n n .6.若级数∑∞=1n n u 收敛，记∑==ni i n u S 1，则（B ）A. 0lim =∞→n n S ； B. n n S ∞→lim 存在；C. n n S ∞→lim 可能不存在； D. {}n S 是单调数列.7.若级数∑∞=1n n u 收敛，则下列级数中收敛的是（A ）A. ∑∞=110n n u； B.()∑∞=+110n nu；C. ∑∞=110n nu ； D.()∑∞=-110n nu.8.设501=∑∞=n n u ，1001=∑∞=n n v ，则()∑∞=+132n n n v u （D ）A. 发散；B. 收敛，和为100；C. 收敛，和为50；D. 收敛，和为400. . 9.下列条件中，使级数()∑∞=+1n n n v u 一定发散的是（A ）A.∑∞=1n nu发散且∑∞=1n n v 收敛； B.∑∞=1n nu发散；C.∑∞=1n nv发散； D.∑∞=1n nu和∑∞=1n n v 都发散.10.设级数()∑∞=-11n n u 收敛，求n n u ∞→lim .【解】因为()∑∞=-11n n u 收敛，故根据级数收敛的必要条件知()01lim =-∞→n n u ，所以 =∞→n n u lim ()[]=--∞→n n u 11lim ()1011l i m1=-=--∞→n n u .11.将下列循环小数表示为分数 (1) ∙3.0 ；【解】...003.003.03.03.0+++=∙是公比为1.0=q 的等比级数，故311.013.03.0=-=∙. (2) ∙∙370.0.【解】...0000073.000073.0073.0370.0+++=∙∙是公比为01.0=q 的等比级数，故.9907301.01073.0370.0=-=∙∙12.设级数∑∞=1n n u 满足条件：（1）0lim =∞→n n u ；（2）()∑∞=-+1212n n n u u 收敛，证明级数∑∞=1n n u 收敛.【解】记∑∞=1n n u 的前n 次部分和数列为{}n S .又记()∑∞=-+1212n n n u u 的前n 次部分和数列为{}n σ.则有(),...2,12==n S n n σ.因为已知()∑∞=-+1212n n n u u ，故根据级数收敛的定义知 =∞→n n σl i ms S n n =∞→2lim ①存在；又已知0lim =∞→n n u ，故0lim 12=+∞→n n u ，从而=+∞→12lim n n S ()s s S u n n n =+=++∞→0lim 212②也存在.综合①、②式知s S n n =∞→lim 存在，所以级数∑∞=1n n u 收敛.13.小球从1米高处自由落下，每次弹起的高度均为前一次高度的一半，问小球会在自由下落约多少秒后停止运动？【解】小球为自由落体运动，即212s gt =。

(人教版B版)高中数学必修第四册第十一章综合测试试卷02及答案

第十一章综合测试一、选择题1.已知两个平面相互垂直，下列命题①一个平面内已知直线必垂直于另一个平面内的任意一条直线②一个平面内已知直线必垂直于另一个平面内的无数条直线③一个平面内任意一条直线必垂直于另一个平面④过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面其中正确命题个数是（）A.1B.2C.3D.42.我国古代数学名著《九章算术》中“开立圆术”曰：置积尺数，以十六乘之，九而一，所得开立方除之，即立圆径，“开立圆术”相当于给出了已知球的体积V，求其直径d的一个近似公式d»，人们还用p»L判断，下列近似公式中最精确的一个是（）过一些类似的近似公式，根据 3.14159A.d»B.d»C.d»D.d»∥的充要条件是（）3.设a，b为两个平面，则a bA.a内有无数条直线与b平行B.a内有两条相交直线与b平行C.a，b平行于同一条直线D.a，b垂直于同一平面4.如图，在直角梯形SABC中，90^交SC于点D，以AD为折痕把ABC BCS°Ð=Ð=，过点A作AD SC-的的体积最大时，则下列命题中正确的个数是（）△折起，当几何体S ABCDSAD①AC SB^②AB∥平面SCD③SA与平面SBD所成的角等于SC与平面SBD所成的角④AB与SC所成的角等于DC与SA所成的角A.4B.3C.2D.15.（多选题）设l为直线，a，b是两个不同的平面，下列命题中错误的是（）A .若l a ∥，l b ∥，则a b∥B .若l a ^，l b ^，则a b ∥C .若l a ^，l b ∥，则a b ∥D .若a b ^，l a ∥，则l b^6.（多选题）如图正方体ABCD —A 1B 1C 1D 1的棱长为a ，以下结论正确的是（）A .异面直线A 1D 与AB 1所成的角为60°B .直线A 1D 与BC 1垂直C .直线A 1D 与BD 1平行D .三棱锥A —A 1CD 的体积为316a 二、填空题7.一个正方体内接于一个球（即正方体的8个顶点都在球面上），过球心作一截面，则截面的图形可能是________.8.现有橡皮泥制作的底面半径为5、高为4的圆锥和底面半径为2，高为8的圆柱各一个，若将它们重新制作成总体积与高均保持不变，但底面半径相同的新的圆锥和圆柱各一个，则新的底面半径为________.9.在正方体ABCD —A'B'C'D'中，过对角线BD'的一个平面交AA'于点E ，交CC'于点F ，则：①四边形BFD'E 一定是平行四边形；②四边形BFD'E 有可能是正方形；③四边形BFD'E 在底面ABCD 内的投影一定是正方形；④平面BFD'E 有可能垂直于平面BB'D .以上结论正确的为________.（写出所有正确结论的编号）10.如图所示，以等腰直角三角形ABC 斜边BC 上的高AD 为折痕，使ABD △和ACD △折成互相垂直的两个平面，则：（1）BD与CD的关系为________；（2）BACÐ=________.三、解答题11.如图，直四棱柱ABCD—A1B1C1D1的底面是菱形，14AA=，2AB=，60BADÐ=°，E，M，N分别是BC，BB1，A1D的中点.（1）证明：MN∥平面C1DE；（2）求点C到平面C1DE的距离.12.如图，在三棱锥P—ABC中，90ACBÐ=°，PA^底面ABC.（1）求证：平面PAC^平面PBC；（2）若AC BC PA==，M是PB的中点，求AM与平面PBC所成角的正切值.第十一章综合测试答案解析一、1.【答案】B【解析】由题意，对于①，当两个平面垂直时，一个平面内的不垂直于交线的直线不垂直于另一个平面内的任意一条直线，故①错误；对于②，设平面m a b =I 平面，n a Ì，l b Ì，Q 平面a ^平面b ，\当l m ^时，必有l a ^，而n a Ì，l n \^，而在平面b 内与l 平行的直线有无数条，这些直线均与n 垂直，故一个平面内的已知直线必垂直于另一个平面内的无数条直线，即②正确；对于③，当两个平面垂直时，一个平面内的任一条直线不垂直于另一个平面，故③错误；对于④，当两个平面垂直时，过一个平面内任意一点作交线的垂线，则此垂线必垂直于另一个平面，这是面面垂直的性质定理，故④正确；故选：B 。

高等数学(下册)第十一章

第二节第二类曲线积分
•性质
(1) Pdx Qdy Pdx Qdy Pdx Qdy
L
L1
L2
(L L1 L2 )
(2)L k(Pdx Qdy) k L Pdx Qdy
(3) P(x, y)dx Q(x, y)dy P(x, y)dx Q(x, y)dy
注 :定积分、二重积分、三重积分的积分域
方程不能代入到被积函数中.而曲线、曲面
的积分，积分域方程可代入到被积函数中.
例求 xyds : (1)OAB;(2)OB : y x; L
(3)OMB : y x2.
解 (1) xyds xyds 1 ydy 1
OA
AB
0
记作
L P(x, y)dx Q(x, y)dy
L
M ykk B
Mxkk1
A
x
第二节第二类曲线积分
定义设 L 为xOy 平面内从 A 到B 的一条有向光滑弧, 在L 上定义了一个向量函数
若对 L 的任意分割和在局部弧段上任意取点,
n
极限
lim
0
P(k
k 记1 作
, k )xk Q(k
ab P[x, (x)] Q[x, (x)] (x)dx
x (t) 对空间光滑曲线弧 : y (t) t : ,类似有
z (t)

P
[
(t),
(t)
,

(t)]
(t
)
(t)
(t )
第二节第二类曲线积分
例求L xydx ydy,
2π a2 k 2 (3a2 4π 2k 2 ) 3

(人教版B版2019课标)高中数学必修第四册第十一章综合测试(含答案)

第十一章综合测试一、单项选择题（本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.如图，O A B '''△是水平放置的OAB △的直观图，6AO ''=，2B O ''=，则OAB △的面积是（）A .6B .3C .6D .12 2.一个球的内接正方体的表面积为54，则球的表面积为（） A .27πB .18πC .9πD .54π3.已知m ，n 表示两条不同直线，α表示平面，下列说法中正确的是（） A .若m α⊥，n α⊂，则m n ⊥ B .若m α∥，n α∥，则m n ∥ C .若m α⊥，m n ⊥，则n α∥ D .若m α∥，m n ⊥，则n α⊥4.已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为（）A .B .12πC .D .10π5.BC 是Rt ABC △的斜边，PA ⊥平面ABC ，PD BC ⊥于D 点，则图中共有直角三角形的个数是（）A .8个B .7个C .6个D .5个6.在正方体1111ABCD A B C D －中，点O 是四边形ABCD 的中心，关于直线1A O ，下列说法正确的是（） A .11AO D C ∥B .1A O ∥平面11B CDC .1AO BC ⊥D .1AO ⊥平面11AB D 7.已知长方体1111ABCD A B C D －中，1B C 、1C D 与底面ABCD 所成的角分别为60︒和45︒，则异面直线1B C 和1C D 所成角的余弦值为（）A B .14C D 8.已知平面α∥平面β，P 是α、β外一点，过点P 的直线m 与α、β分别交于点A 、C ，过点P 的直线n 与α、β分别交于点B 、D ，且6PA =，9AC =，8PD =，则BD 的长为（）A .16B .24或245C .14D .20二、多项选择题（本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得3分，有选错的得0分.）9.如图，在正四棱锥S －ABCD 中，E ，M ，N 分别是BC ，CD ，SC 的中点，动点P 在线段MN 上运动时，下列四个结论中恒成立的为（）A .EP AC ⊥B .EP BD ∥C .EP ∥平面SBDD .EP ⊥平面SAC10.如图，点P 在正方体1111ABCD A B C D －的面对角线1BC 上运动，则下列四个结论正确的是（）A .三棱锥1A D PC －的体积不变B .1A P ∥平面ACD 1C .1DP BC ⊥D .平面1PDB ⊥平面1ACD11.如图，在四棱柱1111ABCD A B C D －中，1AA ⊥平面ABCD ，AB CD ∥，90DCB ∠=︒，12AB AD AA DC ===，Q 为棱1CC 上一动点，过直线AQ 的平面分别与棱1BB ，1DD 交于点P ，R ，则下列结论正确的是（）A .对于任意的点Q ，都有AP QR ∥B .对于任意的点Q ，四边APQR 不可能为平行四边形C .存在点Q ，使得ARP △为等腰直角三角形D .存在点Q ，使得直线BC ∥平面APQR12.如图，矩形ABCD 中，2AB AD =，E 边AB 的中点，将ADE △沿直线DE 翻折成1A DE △（1A ∉平面ABCD ），若M 为线段1A C 的中点，则在ADE △翻折过程中，下列结论正确的是（）A .11:1:3VA A DE VA BCDE =－－B .存在某个位置，使1DE AC ⊥ C .总有BM ∥平面1A DED .线段BM 的长为定值三、填空题（本题共4小题，每小题5分，共20分.）13.设O 为平行四边形ABCD 对角线的交点，P 为平面AC 外一点，且有PA PC =，PB PD =，则PO 与平面ABCD 的关系是________.14.（多空题）如图，正方体1111ABCD A B C D －的棱长为1，E 、F 分别为线段1AA 、1B C 上的点，则直线1B C 到平面1DED 的距离为________，三棱锥1D EDF －的体积为________.15.如图，在四棱锥S －ABCD 中，底面ABCD 为平行四边形，E 是SA 上一点，当点E 满足条件：________时，SC ∥平面EBD .16.如图，四面体P －ABC 中，PA PB =平面PAB ⊥平面ABC ，90ABC ∠=︒，8AC =，6BC =，则PC =________.四、解答题（本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.）17.如图所示，在四边形ABCD 中，90DAB ∠=︒，135ADC ∠=︒，5AB =，2CD =，2AD =，求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.18.如图，长方体1111ABCD A B C D －的底面ABCD 是正方形，点E 在棱1AA 上，1BE EC ⊥. （1）证明：BE ⊥平面11EB C ；（2）若1AE A E =，3AB =，求四棱锥11E BB C C －的体积.19.如图所示，在四棱锥C －ABED 中，四边形ABED 是正方形，点G ，F 分别是线段EC ，BD 的中点.（1）求证：GF ∥平面ABC ；（2）线段BC 上是否存在一点H ，使得平面GFH ∥平面ACD ，若存在，请找求出点H 并证明；若不存在，请说明理由.20.如图，直四棱柱1111ABCD A B C D －的底面是菱形，14AA =，2AB =，60BAD ∠=︒，E ，M ，N 分别是BC ，1BB ，1A D 的中点. （1）证明：MN ∥平面1C DE ；（2）求点C 到平面1C DE 的距离.21.如图，在三棱锥P －ABC 中，E ，F 分别为AC ，BC 的中点.（1）求证：EF ∥平面PAB ；（2）若平面PAC ⊥平面ABC ，且PA PC =，90ABC ∠=︒，求证：平面PEF ⊥平面PBC .22.如图，已知1AA ⊥平面ABC ，11BB AA ∥，3AB AC ==，BC =，1AA =1BB =E 和F 分别为BC 和1A C 的中点.（1）求证：EF ∥平面11A B BA ；（2）求证：平面1AEA 平面1BCB ；（3）求直线11A B 与平面1BCB 所成角的大小.第十一章综合测试答案解析一、 1.【答案】D【解析】OAB △是直角三角形，其两条直角边分别是4和6，则其面积是12。

人教B版高中数学必修第四册课后习题第十一章 11.1.5 旋转体

11.1.5 旋转体A级必备知识基础练1.一个等边圆柱(底面直径等于高)的轴截面的面积是2S,则它的一个底面的面积是( )A.πS2B.πS4C.SD.πS2.(多选题)(广东华南高一阶段练习)以钝角三角形的某条边所在的直线为轴,其他两边旋转一周所得到的几何体可以是( )A.两个圆锥拼接而成的组合体B.一个圆台C.一个圆锥D.一个大圆锥挖去一个同底的小圆锥3.在长方形ABCD中挖掉半圆O,得到如图所示的图形,则将该图形绕着AB 所在的直线旋转一周后得到的几何体为( )A.一个长方体内部挖去一个球B.一个长方体内部挖去半个球C.一个圆柱体内部挖去一个球D.一个圆柱体内部挖去半个球4.设长方体的长、宽、高分别为2a,a,a,其顶点都在一个球面上,则该球的表面积为( )A.3πa2B.6πa2C.12πa2D.24πa25.用长为4、宽为2的矩形做侧面围成一个高为2的圆柱,此圆柱的轴截面面积为( )A.8B.8πC.4πD.2π6.我国古代数学名著《数学九章》中有云:“今有木长二丈四尺,围之五尺.葛生其下,缠木两周,上与木齐,问葛长几何?”其意思为“圆木长2丈4尺,圆周为5尺,葛藤从圆木的底部开始向上生长,绕圆木两周,刚好顶部与圆木平齐,问葛藤最少长多少尺?”(注:1丈等于10尺)( )A.29尺B.24尺C.26尺D.30尺7.下列说法正确的是.(填序号)①连接圆柱上、下底面圆周上两点的线段是圆柱的母线;②以直角梯形的一腰所在直线为轴旋转所得的旋转体是圆台;③圆柱、圆锥、圆台都有两个底面;④圆锥的侧面展开图为扇形,这个扇形所在圆的半径等于圆锥的母线长.8.图中平面图形从下往上依次由等腰梯形、矩形、半圆、圆、等腰三角形拼接形成,若将它绕直线l旋转形成一个组合体,下面说法不正确的是.(填序号)①该组合体可以分割成圆台、圆柱、圆锥和两个球;②该组合体中的圆锥和球只有一个公共点;③该组合体中的球和半球只有一个公共点.9.一个圆锥的轴截面为边长为a的正三角形,则其表面积为.10.已知H是球O的直径AB上一点,AH∶HB=1∶2,AB⊥平面α,H为垂足,α截球O所得截面的面积为π,求球O的半径.B级关键能力提升练11.如果圆锥的侧面展开图是半圆,那么这个圆锥的轴截面对应的等腰三角形的底角是( )A.30°B.45°C.60°D.90°12.一个四面体各棱长都为√2,四个顶点在同一球面上,则此球的表面积为( )A.3πB.4πC.3√3πD.6π13.已知一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( )A.1+2π2πB.1+4π4πC.1+2ππD.1+4π2π14.(多选题)一个正方体内接于一个球,过球心作一截面,如图所示,则截面图形可能是( )15.一个圆台上、下底面的半径分别为3 cm和8 cm,若两底面圆心的连线长为 12 cm,则这个圆台的母线长为 cm,表面积为cm2. 16.如图所示的几何体是从一个圆柱中挖去一个以圆柱的上底面为底面,下底面圆心为顶点的圆锥而得到的.现用一个平面去截这个几何体,若这个平面垂直于圆柱底面所在的平面,那么截面图形可能是图中的.(填序号)17.定义如图所示的几何体为斜截圆柱(由不平行圆柱底面的平面截圆柱得到),已知斜截圆柱底面的直径为40 cm,母线长最短为50 cm、最长为80 cm,则斜截圆柱侧面展开图的面积S= cm2.18.已知球的两个平行截面的面积分别为5π和8π,且两截面位于球心的同侧,且距离等于1,求这个球的半径.C级学科素养创新练19.如图,已知在直角三角形ABC中,AC⊥BC,BC=2,tan∠ABC=2√2.(1)若以直线AC为轴,直角三角形ABC旋转一周,试说明所得几何体的结构特征并求所得几何体的表面积.(2)一只蚂蚁在问题(1)形成的几何体上从点B绕着几何体的侧面爬行一周回到点B,求蚂蚁爬行的最短距离.11.1.5 旋转体1.A 设底面半径为r,则4r 2=2S,故底面面积=πr 2=π·S2=πS 2.故选A.2.AD 以钝角三角形的最长边所在的直线为轴,旋转一周所得到的几何体是两个同底圆锥拼接而成的组合体,故A 正确;以钝角三角形的较短边所在的直线为轴,旋转一周所得到的几何体都是一个大圆锥挖去一个同底的小圆锥,故D 正确. 故选AD. 3.C4.B 长方体的长,宽,高分别为2a,a,a,其顶点都在一个球面上,长方体的对角线就是外接球的直径,所以球的直径长为√(2a )2+a 2+a 2=√6a,所以球的半径为√62a,所以球的表面积是4π(√62a)2=6πa 2,故选B.5.B 易知2πr=4,则2r=4π,所以轴截面面积=4π×2=8π.故选B.6.C 由题意,圆柱的侧面展开图是矩形,一条边(即木棍的高)长24尺,另一条边长5×2=10尺,因此葛藤长√242+102=26尺,故选C.7.④ 根据圆柱母线的定义,①错误;以直角梯形垂直于上、下底的腰为轴旋转得到的旋转体是圆台,以另一腰为轴旋转所得的旋转体不是圆台,故②错误;圆锥只有一个底面,故③错误;根据圆锥母线的定义,④正确.8.① 该组合体可以分割成圆锥、球、半球、圆柱、圆台,故①错,②③正确.9.34πa 2 由题知,圆锥的底面半径r=a2,母线长l=a,则其表面积为S 表=πr(r+l)=π·a 2·(a 2+a)=34πa 2.10.解如图,设球O 的半径为R,则由AH ∶HB=1∶2得HA=13·2R=23R,所以OH=R3.因为截面面积为π=π·(HM)2,所以HM=1. 在Rt △HMO 中,OM 2=OH 2+HM 2, 所以R 2=19R 2+HM 2=19R 2+1,所以R=3√24,即球O 的半径为3√24.11.C 设圆锥的底面半径是r,母线长是l.如图所示,2πr=πl, 所以2r=l,所以rl=12.所以轴截面对应的等腰三角形的底角为60°.故选C.12.A 把正四面体扩展为正方体,二者有相同的外接球,扩展后正方体的棱长为1,所以正方体体对角线的长度就是外接球的直径,体对角线长为√12+12+12=√3,所以球的半径为√32,所以球的表面积为4πR2=4π×(√32)2=3π,故选A.13.A 设圆柱的底面半径为r,高为h,则由题设知h=2πr,∴S 全=2πr 2+2πr·h=2πr 2(1+2π).又S 侧=h 2=4π2r 2,∴S 全S 侧=1+2π2π.故选A.14.ABC 当截面平行于正方体的一个侧面时得C,当截面过正方体的体对角线时得B,当截面不平行于任何侧面也不过对角线时得A,但无论如何都不能截出D.15.13 216π 如图,过点A 作AC ⊥OB,交OB 于点C.在Rt △ABC 中,AC=12cm,BC=8-3=5cm,所以AB=√122+52=13(cm). 表面积为S=π(32+82+3×13+8×13)=216π(cm 2).16.①③ 在与圆柱底面垂直的截面中,随着截面位置的变化,截面图形也会发生变化.当截面经过圆柱的轴时,所截得的图形是图①.当截面不经过圆柱的轴时,截得的图形是图③.而图②④是不会出现的.17.2 600π 把斜截圆柱补成底面半径20cm,高130cm 的圆柱,则侧面展开可得斜截圆柱侧面展开圆面积S=12(50+80)×40π=2600π(cm 2). 18.解如图,设这两个截面的半径分别为r 1,r 2,球心到截面的距离分别为d 1,d 2,球半径为R.则πr 12=5π,πr 22=8π,∴r 12=5,r 22=8.∵R 2=r 12+d 12=r 22+d 22,∴d 12−d 22=8-5=3,即(d 1-d 2)(d 1+d 2)=3.又d 1-d 2=1,∴d 1+d 2=3,解得{d 1=2,d 2=1.∴R=√r 12+d 12=√5+4=3.19.解(1)在直角三角形ABC中,由BC=2,tan∠ABC=2√2,即tan∠ABC=ACBC=2√2,得AC=4√2.若三角形ABC以直线AC为轴旋转一周,形成的几何体为以BC=2为半径,高AC=4√2的圆锥,则AB=√22+(4√2)2=6,其表面积为S=π×22+π×2×6=16π.(2)由问题(1)的圆锥,要使蚂蚁爬行的距离最短,则沿过点B的母线把圆锥侧面展开为平面图形,如图所示,所求最短距离就是点B到点B1的距离,∠BAB1=2π×26=2π3,在△ABB1中,由余弦定理得BB1=√62+62-2×6×6×cos2π3=6√3.。

人教B版高中数学必修第四册课后习题第十一章 11.1.3 多面体与棱柱 11.1.4 棱锥与棱台

11.1.3 多面体与棱柱11.1.4 棱锥与棱台A级必备知识基础练1.下列四种说法:①底面是矩形的平行六面体是长方体;②棱长相等的直四棱柱是正方体;③有两条侧棱垂直于底面一边的平行六面体是直平行六面体;④侧面对角线相等的平行六面体是直平行六面体.其中,正确的个数是( )A.1B.2C.3D.42.下列说法正确的是( )A.有两个面平行,其余各面都是四边形的几何体是棱柱B.有两个面平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行的几何体是棱柱C.若棱柱被一平面所截,则分成的两部分一定是棱柱D.有两个面平行,其余各面都是平行四边形的几何体是棱柱3.如图,已知正三棱柱ABC-A1B1C1的底面边长为1 cm,高为5 cm,一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为( )A.12 cmB.13 cmC.√61 cmD.15 cm4.在正方体ABCD-A1B1C1D1中,三棱锥D1-AB1C的表面积与正方体的表面积的比为( )A.1∶1B.1∶√2C.1∶√3D.1∶25.在正方体ABCD-A1B1C1D1中,M,N,Q分别为棱AB,B1B,C1D1的中点,过点M,N,Q作该正方体的截面,则所得截面的形状是( )A.三角形B.四边形C.五边形D.六边形6.一个正四棱台,其上、下底面均为正方形,边长分别为8 cm 和18 cm,侧棱长为13 cm,则其表面积为.7.若A={四棱柱},B={平行六面体},C={直平行六面体},D={正方体},E={正四棱柱},F={长方体},则它们之间的包含关系为.8.已知正四棱锥V-ABCD的底面面积为16,侧棱长为4,则这个棱锥的斜高为,高为.9.如图,M是棱长为2 cm 的正方体ABCD-A1B1C1D1的棱CC1的中点,沿正方体表面从点A到点M的最短路程是cm.10.若一正四棱台的上底面、下底面边长分别为2,4,其表面积为80,求该四棱台的高.B级关键能力提升练11.某同学制作了一个对面图案均相同的正方体礼品盒,如图所示,则这个正方体礼品盒的表面展开图应该为(对面是相同的图案)( )12.(北京高一阶段练习)一个正方体的六个面上分别有字母A,B,C,D,E,F,如下图所示是此正方体的两种不同放置,则与D面相对的面上的字母是( )图①图②A.BB.EC.FD.E或F13.鲁班锁(也称孔明锁、难人木、六子联方)起源于中国古代建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙.鲁班锁类玩具比较多,形状和内部的构造各不相同,一般都是易拆难装.如图①,这是一种常见的鲁班锁玩具,图②是该鲁班锁玩具的直观图,每条棱的长均为2,则该鲁班锁的表面积为( )A.8(6+6√2+√3)B.6(8+8√2+√3)C.8(6+6√3+√2)D.6(8+8√3+√2)14.在五棱柱中,不同在任何侧面且不同在任何底面的两顶点的连线称为它的对角线,那么一个五棱柱的对角线共有条.15.已知棱长为a,各面均为等边三角形的四面体S-ABC,则其表面积为.C级学科素养创新练16.在一个长方体的容器中,里面装有少量水,现在将容器绕着某底部的一条棱倾斜,在倾斜的过程中:(1)水面的形状不断变化,可能是矩形,也可能变成不是矩形的平行四边形,对吗?(2)水的形状不断变化,可能是棱柱,也可能变为棱台或棱锥,对吗?(3)如果倾斜时,不是绕着底部的一条棱,而是绕着其底部的一个顶点,上面的第(1)题和第(2)题对不对?11.1.3 多面体与棱柱11.1.4 棱锥与棱台1.A ①不正确,除底面是矩形外还应满足侧棱与底面垂直才是长方体;②不正确,当底面是菱形时就不是正方体;③不正确,两条侧棱垂直于底面一边不一定垂直于底面,故不一定是直平行六面体;④正确,对角线相等的平行四边形是矩形,由此可以推测此时的平行六面体是直平行六面体.故选A.2.B 对于A,如图①所示的几何体中有两个面平行,其余各面都是四边形,该几何体不是棱柱,故A不正确;对于B,由棱柱的定义可知正确;对于C,分成的两部分不一定是棱柱,故C不正确;对于D,如图②所示的几何体中有两个面平行,其余各面都是平行四边形,该几何体不是棱柱.图①图②3.C 将正三棱柱ABC-A1B1C1沿侧棱展开,再拼接一次,其侧面展开图如图所示,在展开图中,最短距离是六个矩形对角线的连线的长度,也即为三棱柱的侧面上所求距离的最小值.由已知求得矩形的长等于6×1=6cm,宽等于5cm,由勾股定理d=√62+52=√61cm.4.C 设正方体的棱长为a,则三棱锥D1-AB1C的棱长均为√2a,∴S D1-AB1C =4×12×(√2a)2×sin60°=2√3a2,S正方体=6a2,S D1-AB1CS正方体=2√3a26a2=1∶√3.故选C.5.D 如图所示,E,F,H分别为棱AD,DD1,B1C1的中点,M,N,Q确定平面α,NH ∥MQ且N∈α,故NH⊂α,Q∈α,H∈α,故QH⊂α.同理可得FQ⊂α,EF⊂α,EM⊂α,故截面为六边形.故选D.6.1 012 cm2由已知可得正四棱台侧面梯形的高为h=√132-(18-82)2=12(cm),所以S侧=4×12×(8+18)×12=624(cm2),S上底=8×8=64(cm2),S下底=18×18=324(cm2),则正四棱台的表面积为S=624+64+324=1012(cm2).7.D⫋E⫋F⫋C⫋B⫋A8.2√32√2如图所示,由题意知,正四棱锥底面边长为4,又侧棱长为4,所以侧面为等边三角形,取G为CD的中点,在等边三角形VCD中,VG=√32VC=2√3,点V在平面ABCD 的投影为正方形ABCD的中心O,在Rt△BCD中,DB=√BC2+DC2=4√2.则DO=12DB=2√2,所以在Rt△VOD中,VO=√VD2-DO2=2√2.9.√13由题意,若以BC为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为2cm,3cm,故两点之间的距离是√13cm.若以BB1为轴展开,则A,M两点连成的线段所在的直角三角形的两直角边的长度分别为1,4,故两点之间的距离是√17cm.故沿正方体表面从点A到点M的最短路程是√13cm.10.解设该正四棱台的斜高为h',高为h,由题意得,22+42+4×(2+4)ℎ'2=80,解得h'=5.∴h=√ℎ'2-(2-1)2=√25-1=2√6.∴该四棱台的高为2√6.11.A 根据正方体礼品盒的表面展开图的对面是相同的图案可知,展开图同图案不能相邻,B,C,D中都有相同的图案相邻,故选A.12.A 根据两个不同放置的图形,明显可知C的对面不是A,B,D,E,故C的对面是F,则与D相对的面为E或B,若E面与D面相对,则A面与B面相对,这时与图②放置矛盾,故与D面相对的是B面.故选A.13.A 由题图可知,该鲁班锁玩具可以看成是一个棱长为2+2√2的正方体截去了8个正三棱锥所余下来的几何体,且被截去的正三棱锥的底面边长为2,侧棱长为√2,则该几何体的表面积为S=6×[(2+2√2)2-4×12×√2×√2]+8×12×2×√3=8(6+6√2+√3).故选A.14.10 在上底面选一个顶点,同时在下底选一个顶点,且这两个顶点不在同一侧面上,这样上底面每个顶点对应两条对角线,所以共有10条.第11页共11页 15.√3a 2 由于四面体S-ABC 的四个面是全等的等边三角形,所以四面体的表面积等于其中任何一个面的面积的4倍.所以S △SBC =12a 2sin60°=√34a 2. 因此,四面体S-ABC 的表面积S=4×√34a 2=√3a 2.16.解(1)不对.水面的形状就是用一个与棱(倾斜时固定不动的棱)平行的平面截长方体时截面的形状,因而可以是矩形,但不可能是其他非矩形的平行四边形.(2)不对.水的形状就是用与棱(将长方体倾斜时固定不动的棱)平行的平面将长方体截去一部分后,剩余部分的几何体,此几何体是棱柱,水比较少量,是三棱柱,水多时,可能是四棱柱或五棱柱,但不可能是棱台或棱锥.(3)①不对.只有一条棱着地水面才是矩形;②不对.只有一条棱着地水才是棱柱.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题11-21.设L 为xOy 面内直线x a =上的一段，证明：(,)d 0LP x y x =⎰,其中(),P x y 在L 上连续.证：设L 是直线x =a 上由(a ,b 1)到(a ,b 2)这一段，则 L ：12x ab t b y t =⎧≤≤⎨=⎩，始点参数为t =b 1，终点参数为t =b 2故 ()()()221d ,d d 0d 0d b b L b b a P x y x P a,t t P a,t t t ⎛⎫=⋅=⋅= ⎪⎝⎭⎰⎰⎰2.设L 为xOy 面内x 轴上从点(,0)a 到点(,0)b 的一段直线，证明：(,)d (,0)d bLaP x y x P x x =⎰⎰,其中(),P x y 在L 上连续.证：L ：0x xa xb y =⎧≤≤⎨=⎩，起点参数为x =a ，终点参数为x =b ．故()(),d ,0d bLaP x y x P x x =⎰⎰3.计算下列对坐标的曲线积分: （1）22()d Lxy x -⎰,其中L 是抛物线2y x =上从点(0,0)到点(2,4)的一段弧；（2）d Lxy x ⎰，其中L 为圆周()222x a y a -+=(0)a >及x 轴所围成的在第一象限内的区域的整个边界（按逆时针方向绕行）；（3）d d Ly x x y +⎰,其中L 为圆周cos ,sin x R t y R t ==上对应t 从0到π2的一段弧；（4）22()d ()d Lx y x x y y x y+--+⎰,其中L 为圆周222x y a +=（按逆时针方向绕行）；（5）2d d d x x z y y z +-⎰Γ,其中Γ为曲线,,x k y acos z asin θθθ===上对应θ从0到π的一段弧；（6） 322d 3d ()d x x zy y xy z ++-⎰Γ,其中Γ是从点3,2,1（）到点0,0,0（）的一段直线；（7）d d d x y y z -+⎰Γ,其中Γ为有向闭折线ABCA ，这里AB C 、、依次为点1,0,0（）、010（，，）、(001)，，；（8）22(2)d (2)d Lx xy x y xy y -+-⎰,其中L 是抛物线2y x =上从点(1,1)-到点(1,1)的一段弧.解：(1)L ：y =x 2，x 从0变到2，()()22222435001156d d 3515L x y x x x x x x ⎡⎤-=-=-=-⎢⎥⎣⎦⎰⎰ (2)如图11-1所示，L =L 1+L 2．其中L 1的参数方程为图11-1cos 0πsin x a a tt y a t =+⎧≤≤⎨=⎩L 2的方程为y =0(0≤x ≤2a ) 故()()()()()12π20π320ππ32203d d d 1+cost sin cos d 0d sin 1cos d sin d sin dsin π2LL L axy x xy x xy xa a t a a t t x a t t ta t t t ta =+'=⋅++=-+=-+=-⎰⎰⎰⎰⎰⎰⎰⎰(3)()π20π220π220d d sin sin cos cos d cos 2d 1sin 220Ly x x y R t R t R tR t t Rt tR t +=-+⎡⎤⎣⎦=⎡⎤=⎢⎥⎣⎦=⎰⎰⎰(4)圆周的参数方程为：x =a cos t ，y =a sin t ，t :0→2π．故()()()()()()222π202π220d d 1cos sin sin cos sin cos d 1d 2πLx y x x y yx ya t a t a t a t a t a t t a a t a +--+=+---⎡⎤⎣⎦=-=-⎰⎰⎰(5)()()()2π220π3220π3320332d d d sin sin cos cos d d 131ππ3x x z y y zk k a a a a k a k a k a Γθθθθθθθθθθ+-=⋅+⋅--=-⎡⎤=-⎢⎥⎣⎦=-⎰⎰⎰(6)直线Γ的参数方程是32=⎧⎪=⎨⎪=⎩x t y t z t t 从1→0．故()()322322103141d 3d d 27334292d 87d 1874874x x zy y x y z t t t t t tt tt Γ++-⎡⎤=⋅+⋅⋅+-⋅⎣⎦==⋅=-⎰⎰⎰(7)AB BC CA Γ=++(如图11-2所示)图11-21:0y x AB z =-⎧⎨=⎩，x 从0→1()01d d d 112AB x y y z dx -+=--=-⎡⎤⎣⎦⎰⎰． 0:1x BC y z =⎧⎨=-⎩，z 从0→1()()()1010120d d d 112d 12232BC x y y z z dz z zz z -+=--+-⎡⎤⎣⎦=-⎡⎤=-⎢⎥⎣⎦=⎰⎰⎰0:1y CA z x =⎧⎨=-⎩，x 从0→1[]1d d d 1001CAx y y z dx -+=-+=⎰⎰．故()()d d d d d d 312122LABBCCAx y y zx y y z-+=++-+=-++=⎰⎰⎰⎰(8)()()()()()221224211235412d 2d 222d 224d 1415L x xy x y xy yx x x x x x x xxx x x x---+-⎡⎤=-⋅+-⋅⋅⎣⎦=-+-=-⎰⎰⎰4. 计算()d ()d Lx y x y x y ++-⎰,其中L 分别是：（1）抛物线2y x =上从点(1,1)到点(4,2)的一段弧；（2）从点(1,1)到点(4,2)的直线段；（3）先沿直线从点(1,1)到点(1,2)，然后再沿直线到点(4,2)的折线；（4）曲线2221,1x t t y t =++=+上从点(1,1)到点(4,2)的一段弧. 解：(1)L ：2x y y y ⎧=⎨=⎩，y ：1→2，故()()()()()2221232124321d d 21d 2d 111232343L x y x y x yy y y y y yy y y yy y y ++-⎡⎤=+⋅+-⋅⎣⎦=++⎡⎤=++⎢⎥⎣⎦=⎰⎰⎰ (2)从(1,1)到(4,2)的直线段方程为x =3y -2，y ：1→2 故()()()()()2121221d d 32332d 104d 5411L x y x y x yy y y y y y yy y ++-=-+⋅+-+⎡⎤⎣⎦=-⎡⎤=-⎣⎦=⎰⎰⎰ (3)设从点(1,1) 到点(1,2)的线段为L 1，从点(1,2)到(4,2)的线段为L 2，则L =L 1+L 2．且 L 1：1x y y=⎧⎨=⎩，y ：1→2；L 2：2x x y =⎧⎨=⎩，x ：1→4；故()()()()()12122211d d 101d 1d 212L x y x y x yy y y y y y y ++-=+⋅+-⎡⎤⎣⎦⎡⎤=-=-⎢⎥⎣⎦=⎰⎰⎰()()()()()()24144211d d 220d 12d 22272L x y x y x yx x x x x x ++-=++-⋅⎡⎤⎣⎦⎡⎤=+=+⎢⎥⎣⎦=⎰⎰⎰从而()()()()()12d d d d 1271422LL L x y x y x yx y x y x y++-=+++-=+=⎰⎰⎰(4)易得起点(1,1)对应的参数t 1=0，终点(4,2)对应的参数t 2=1，故()()()()()()122132014320d d 32412d 10592d 10592432323L x y x y x y t t t tt t tt t t tt t t t ++-⎡⎤=++++--⋅⎣⎦=+++⎡⎤=+++⎢⎥⎣⎦=⎰⎰⎰5. 设质点受力作用，力的反方向指向原点，大小与质点离原点的距离成正比.若质点由(,0)a 沿椭圆移动到0,Bb （）,求力所做的功. 解：依题意知 F =kxi +kyj ，且L ：cos sin x a t y a t=⎧⎨=⎩，t ：0→π2()()()()π2022π20π222022d d cos sin sin cos d sin 2d 2cos 2222LW kx x ky yka t t kb t b t t k b a t tk b a t k b a =+=-+⋅⎡⎤⎣⎦-=--⎡⎤=⎢⎥⎣⎦-=⎰⎰⎰(其中k 为比例系数)6. 计算对坐标的曲线积分：（1）d xyz z ⎰Γ,Γ为2221x y z ++=与z y =相交的圆，方向按曲线依次经过第Ⅰ、Ⅱ、Ⅶ、Ⅷ卦限；（2）222222(-)d ()d ()d y z x z x y x y z +-+-⎰Γ,Γ为2221x y z ++=在第Ⅰ卦限部分的边界曲线，方向按曲线依次经过xOy 平面部分，yOz 平面部分和zOx 平面部分. 方向按曲线依次经过xOy 平面部分，yOz 平面部分和zOx 平面部分．解:(1)Γ：2221x y z y z ⎧++=⎨=⎩ 即2221x z y z ⎧+=⎨=⎩其参数方程为：cos x ty tz t =⎧⎪⎪⎪=⎨⎪⎪=⎪⎩ t ：0→2π 故：2π2π222π22π222d cos sin sin cos d2sin cos d2sin2d21cos4d22πxyz z t t t t tt t tt tttΓ=⋅⋅⋅==-==⎰⎰⎰⎰⎰(2)如图11-3所示．图11-3Γ=Γ1+Γ2+Γ3．Γ1：cossinx ty tz=⎧⎪=⎨⎪=⎩t：0→π2，故()()()()()1222222π222π332π32d d dsin sin cos cos dsin cos d2sin d24233y z x z x y x y zt t t t tt t tt tΓ-+-+-⎡⎤=--⋅⎣⎦=-+=-=-⋅=-⎰⎰⎰⎰又根据轮换对称性知()()()()()()1222222222222d d d3d d d4334y z x z x y x y zy z x z x y x y zΓΓ-+-+-=-+-+-⎛⎫=⨯- ⎪⎝⎭=-⎰⎰习题11-31. 应用格林公式计算下列积分：（1）(24)d (356)d Lx y x x y y -+++-⎰,其中L 为三顶点分别为()()0,0,3,0和(32)，的三角形正向边界；（2）222(cos 2sin e )d (sin 2e )d x x Lx y x xy x y x x x y y +-+-⎰,其中L 为正向星形线222333x y a +=0a >（）；（3）3222(2cos )d (12sin 3)d Lxy y x x y x x y y -+-+⎰,其中L 为抛物线22πx y =上由点0,0（）到点π,12⎛⎫⎪⎝⎭的一段弧；（4）22()d (sin )d Lxy x x y y --+⎰,其中L 是圆周22y x x =-上由点0,0（）到()1,1的一段弧；（5）(e sin )d (e cos )d x x Ly my x y m y -+-⎰，其中m 为常数，L 为由点(),0a 到0,0（）经过圆22x y ax +=上半部分的路线（a 为正数）.图11-4解：(1)L 所围区域D 如图11-4所示，P =2x -y +4，Q =3x +5y -6，3Qx∂=∂，1P y ∂=-∂，由格林公式得 ()()d d 24356d d 4d d 4d d 1432212LD DDx yx y x y Q P x y x y x yx y+-++-∂∂⎛⎫-= ⎪∂∂⎝⎭===⨯⨯⨯=⎰⎰⎰⎰⎰⎰⎰(2)P =x 2y cos x +2xy sin x -y 2e x ，Q =x 2sin x -2y e x ，则2cos 2sin 2e x Px x x x y y∂=+-∂，2cos 2sin 2e x Qx x x x y x∂=+-∂．从而P Qy x∂∂=∂∂，由格林公式得．()()222d dcos2sin e sin2ed d++--∂∂⎛⎫-= ⎪∂∂⎝⎭=⎰⎰⎰x xLDx yx y x xy x y x x yQ Px yx y(3)如图11-5所示，记OA，AB，BO围成的区域为D．（其中BO=-L）图11-5P=2xy3-y2cos x，Q=1-2y sin x+3x2y2262cosPxy y xy∂=-∂，262cosQxy y xx∂=-∂由格林公式有：d d d d0L OA AB DQ PP x Q y x yx y-++∂∂⎛⎫-+==⎪∂∂⎝⎭⎰⎰⎰故π2122001222d d d dd d d dππd d12sin3243d12π4π4++=+=+++⎛⎫=+-+⋅⋅⎪⎝⎭⎛⎫=-+⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰L OA ABOA ABP x Q y P x Q yP x Q y P x Q yO x yy yyy y(4)L、AB、BO及D如图11-6所示．图11-6由格林公式有d d d d++∂∂⎛⎫-+=- ⎪∂∂⎝⎭⎰⎰⎰L AB BO DQ PP x Q y x yx y而P=x2-y，Q=-(x+sin2y)．1∂=-∂Py ，1∂=-∂Q x，即，0∂∂-=∂∂Q P x y 于是()d d d d 0+++++=+=⎰⎰⎰⎰LABBOL AB BOP x Q y P x Q y从而()()()()()()()22222211220011300d d d d sin d d d d sin sin d d 1sin 131sin 232471sin 264LLBA OB P x Q y x yx y x y x y x yx y x y x y x y y x x y x y y +=--+=-+--+-+=-++⎡⎤⎡⎤=+-+⎢⎥⎢⎥⎣⎦⎣⎦=-+⎰⎰⎰⎰⎰⎰(5)L ，OA 如图11-7所示．图11-7P =e x sin y -my ， Q =e x cos y -m ， e cos x P y m y ∂=-∂，e cos x Q y x ∂=∂ 由格林公式得：22d d d d d d d d 1π22π8L OA D DDQ P P x Q y x y x y m x ym x ya m m a +∂∂⎛⎫-+= ⎪∂∂⎝⎭==⎛⎫=⋅⋅ ⎪⎝⎭=⎰⎰⎰⎰⎰⎰⎰ 于是：()()[]220202πd d d d 8πd 0e sin 00e cos08π0d 8π8+=-+=-+⋅⋅-⋅⋅-=-=⎰⎰⎰⎰L OA a x x a m a P x Q y P x Q y m a xm m m a xm a2. 设a 为正常数，利用曲线积分，求下列曲线所围成的图形的面积：（1）星形线 33cos ,sin ;x a t y a t == （2）双纽线 22cos2;r a θ= （3）圆 22x y ax ++=解：(1) ()()()()()2π3202π2π242222002π202π202π202d sin 3cos d sin 33sin cos d sin 2sin d 43d 1cos 41cos 2163d 1cos 2cos 4cos 2cos 416312π+d cos 2cos 61623π8LA y x a t a t tt a t t t a t t t a t t t a tt t t t a t t t a =-=-⋅-==⋅=--=--+⎡⎤=+⎢⎥⎣⎦=⎰⎰⎰⎰⎰⎰⎰(2)利用极坐标与直角坐标的关系x =r cos θ，y =r sin θ得 cos cos 2x a θ=sin cos 2y a θ=从而x d y -y d x =a 2cos2θd θ．于是面积为：[]π24π4π24π4212d d 2cos 2d sin 22LA x y y x a a a θθθ--=⋅-===⎰⎰(3)圆x 2+y 2=2ax 的参数方程为 cos 02πsin x a a y a θθθ=+⎧≤≤⎨=⎩故()()[]()2π022π021d d 21d a+acos sin 2d 1cos 2πcos sin L A x y y xa a a a a θθθθθθθ=-=-=+=⋅-⎰⎰⎰ 3. 证明下列曲线积分与路径无关，并计算积分值：（1）(1,1)(0,0)()(d d )x y x y --⎰；（2）(3,4)2322(1,2)(6)d (63)d xy y x x y xy y -+-⎰；（3）(1,2)2(1,1)d d y x x yx +⎰沿在右半平面的路径；（4）(6,8)(1,0)⎰.证：(1)P =x -y ，Q =y -x ．显然P ，Q 在xOy 面内有连续偏导数，且1P Q y x∂∂==-∂∂，故积分与路径无关．取L 为从(0,0)到(1,1)的直线段，则L 的方程为：y =x ，x ：0→1．于是()()()()11,100,00d 0d d x x y x y ==--⎰⎰(2) P =6xy 2-y 3，Q =6x 2y -3xy 2．显然P ，Q 在xOy 面内有连续偏导数，且2123Pxy y y∂=-∂，2123Qxy y x∂=-∂，有P Q y x ∂∂=∂∂，所以积分与路径无关．取L 为从(1,2)→(1,4)→(3,4)的折线，则()()()()()()[]3,423221,2432214323212d d 663d d 63966434864236x y xyy x y xy y x y y x y y x x +--=+--=+⎡⎤--⎣⎦=⎰⎰⎰(3)2y P x =，1Q x =-，P ，Q 在右半平面内有连续偏导数，且21P y x ∂=∂，21Q x x ∂=∂，在右半平面内恒有P Qy x∂∂=∂∂，故在右半平面内积分与路径无关．取L 为从(1,1)到(1,2)的直线段，则()()()21,2211,1d d d 11x y x x y y -==--⎰⎰(4) P =，Q ，且P Qy x∂∂==∂∂分在不含原点的区域内与路径无关，取L 为从(1,0)→(6,0)→(6,8)的折线，则()()686,811,0801529x y =+⎡=+⎣=⎰⎰⎰4．验证下列()(),d ,d P x y x Q x y y +在整个xOy 平面内是某一函数(),u x y 的全微分，并求这样的一个函数(),u x y :（1）()()2d 2d x y x x y y +++；（2）22d d xy x x y +;（3）223238d 812e d yx y xy x x x y y y ++++（）（）；（4）222cos cos d 2sin sin d x y y x x y x x y y ++-（）（）. 解：证：(1)P =x +2y ，Q =2x +y ．2P Q y x ∂∂==∂∂，所以(x +2y )d x +(2x +y )d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分． ()()()()()(),0,0022022d d ,22d d 2222222x y xy yu x y x y x y x y x x yx y x y xy x y xy =+++=++⎡⎤=++⎢⎥⎣⎦=++⎰⎰⎰(2)P =2xy ,Q =x 2, 2P Qx y x∂∂==∂∂，故2xy d x +x 2d y 是某个定义在整个xOy 面内的函数u (x ,y )的全微分．()()(),20,02022d d ,0d d x y xy u xy x x y x y x x yx y=+=+=⎰⎰⎰(3)P =3x 2y +8xy 2，Q =x 3+8x 2y +12y e y ，2316∂∂=+=∂∂P Qx xy y x，故(3x 2y +8xy 2)d x +(x 3+8x 2y +12y e y )d y 是某个定义在整个xOy 面内函数u (x ,y )的全微分， ()()()()()(),22320,03200322d ,38812e 0d d 812e 412e 12e 12x y y xyyy y u x x y x y x y x x y y x y x x y y x y x y y =++++=+++=++-+⎰⎰⎰(4)P =2x cos y +y 2cos x ，Q =2y sin x -x 2sin y ，2sin 2cos P x y y x y ∂=-+∂，2cos 2sin Qy x x y x∂=-∂，有P Qy x∂∂=∂∂，故(2x cos y +y 2cos x )d x +(2y sin x -x 2sin y )d y 是某一个定义在整个xOy 面内的函数u (x ,y )的全微分，()()()()()(),220,020022d d ,2cos cos 2sin sin 2d d 2sin sin sin cos x y xyu x y x y x y y x y x x y x x yy x x y y x x y=++-=+-=+⎰⎰⎰5.证明：22xdx ydyx y ++在整个xOy 平面内除y 轴的负半轴及原点外的开区域G 内是某个二元函数的全微分，并求出这样的一个二元函数。