找规律填图形
第1讲 找规律画图形

第1讲找规律画图形
我们在认识图形、数图形、按规律填数的基础上来学习按规律填图。
对于一组按一定的变化规律排列起来的图形,我们通过对图形大小、图形的颜色,图形的排列及图形所处的位置等方面的仔细观察,找出其中变化规律,并正确地画出所要填的图。
【例题】找规律在空格处填图形。
【思路点拨】:仔细观察所给的第一、三行,可以发现,每行的第二个图形平移到第一个图形中就变成了第三个图形。
因此可以推断,第二行空格处应填图形“×”。
【解法】:空格处应填图形“×”。
1.请你根据前面几幅的规律接着画。
练习与思考
训练目标
例题与方法
2.摆一摆,画一画,一个横线上画一个图形。
(1)☆○☆○☆○☆
(2)◆◆◆◇◆◆◆◇◆
(3)▲△▲△△▲△△△
3.根据前面几幅图的规律,接着画。
4.后面2个方框里应该怎么画?请你试一试。
○○○○○○○○○○○○○○○
△△△△△△
5. 下面的4组图形中,哪一组的排列规律与其它3组不同?在()里打“√”。
()
()
()
()。
找规律填图形、数(含答案)

找规律填图形、数
(一)
1
、从方框中选择一个合适的填入虚线框内。
(1)
(3)
① ② ③ ④
(3)
①
② ③ ④
2、请根据规律画上合适的图形。
3、选一选,哪个图形填在“?”处比较合适。
①
② ③ ④ ⑤
(1
A B C D
(二)
一、根据规律画或写,哪一行的规律与其他三行不同?
(1
二、把左右卡片中规律相同的行用线连起来。
三、按规律填下去
找规律填图形、数(红色为答案)
(一)
1
、从方框中选择一个合适的填入虚线框内。
(1)②
(2)④
① ② ③ ④
(3)④
①
② ③
④
2、请根据规律画上合适的图形。
(隐形线三角形)
第二行圆形,第三行菱形
3A (1
① ② ③ ④ ⑤
A
D
(二)
一、根据规律画或写,哪一行的规律与其他三行不同?
(1
二、把左右卡片中规律相同的行用线连起来。
-2 +1
-3 +4
+5 -2
+1 -3
+4 +5
三、按规律填下去。
三上 第9讲 找规律填图形

【随堂练习】 1.你能按对称轴画出另一半吗?
【随堂练习】 2.分别画出以横线和竖线为对称轴的两个图形。
【复习】
【随堂练习】 1.下面哪些是平移?在□里画“√”;哪些是旋转?在□里画“○”。
滑轮 □ 石头 □ 车轮□ 汽车□ 2.下列图形中,( )是①通过旋转后得到的。
□
□
①
A.
B.
C.
【小窍门】判定图形是平移或旋转,要抓住运动的方向是否是直线,不是直 线,一定不是平移。要注意平移和旋转都不改变图形的形状和大小。
)
(
)
4.在下列图形中,不是轴对称图形的是(
)。
A
B
C
D
E
F
5.找一找下面哪些字是轴对称图形,圈出来。
正 天 大 小 春 画 四 坐
再想想,写几个我们学过的轴对称的汉字。
□□□□□□□□
6.下面的图形分别是从哪张对折后的纸上剪下来的?连一连。
【小窍门】有些图形的两部分折叠后能完全重合,这样的图形就是 轴对称图形。判断是否是轴对称图形,要看图形沿某一条直线折叠, 两部分能否重合。
第13讲 平移、对称和旋 转
【复习】
【例题精选】 例 1 如图,每一个三角形都是等边三角形,图中共有( 5 )个等边 三角形。其中有( 2 ) 个是由阴影部分三角形平移得到的。
【小窍门】 要找图形的形状一样,方向也要一样,因为方向不一样的要旋 转才能得到。
【随堂练习】 1.把图中通过平移得到的图形用同一种颜色填充。
【综合练习】 1.下列图形哪个不是由①通过旋转得到的( )。
①
A.
B.
C.
D.
E.
F.
2.在水里看到的猫的图像正确的是(
奥数-01找规律填图形+答案

练习一
找规律画图。
1、
2、
3、
【例 2】 找规律填图。
解析:相邻图形之间是空心与实心的变化,从形状看,以三角形、五角星、正 方形和圆 4 个图形为一组,所以填 和●。 练习二
找规律在框内填图。 1、
2、
3、A 和 B 重叠后得到右边的四个图形,根据变化规律,画出第 4 个图。
5
【例 3】 找规律填图。 解析:先看台灯底座的颜色,每一
【例 6】 根据前面几幅图的规律,接着画。 解析:前两幅图重叠后得到第三幅图。
练习六
根据前面几幅图的规律,接着画图。
1、
2、
3、
4、
5、
6、
4
【例 1】 要使下面的图形按一定的规律排列,那么应在三个空白处填上怎样的图 形?请你画一画。
解析:这里既有形状的变化,又有大 小的变化,每行都有大、小正方形、圆和 三角形,根据这一规律,画上所缺的图形。
二、方向的变化
观察下图,在空白处填出适当的图形。
三、形状变化
在下图中寻找变化规律,在图 的空白处填上合适的图形。
四、位置变化
仔细观察下图,并按照它的变 化规律,在空白处填上适当的图。
五、循环变化
黑棋子和白棋子排成一行,如图所示,问:第 99 个棋子是什么颜色?这 99 个棋 子中,有多少个白棋子?
1
观察右图,按照变 化规律在“?”处画图。
【例 4】 观察下图,并按照变化规律在右边空白处填上合适的图形
解析:既有位置的变化,又有方向的变化。 练习四
观察图,按照变化规律在空白处填上合适的图形。 1、
3
2、
【例 5】 按照下图的排列规律,第 23 个图形是什么小动物?
找规律填图形、数(含答案)

找规律填图形、数
(一)
1
、从方框中选择一个合适的填入虚线框内。
(1)
(3)
① ② ③ ④
(3)
①
② ③ ④
2、请根据规律画上合适的图形。
3、选一选,哪个图形填在“?”处比较合适。
①
② ③ ④ ⑤
(1
A B C D
(二)
一、根据规律画或写,哪一行的规律与其他三行不同?
(1
二、把左右卡片中规律相同的行用线连起来。
三、按规律填下去
找规律填图形、数(红色为答案)
(一)
1
、从方框中选择一个合适的填入虚线框内。
(1)②
(2)④
① ② ③ ④
(3)④
①
② ③
④
2、请根据规律画上合适的图形。
(隐形线三角形)
第二行圆形,第三行菱形
3A (1
① ② ③ ④ ⑤
A
D
(二)
一、根据规律画或写,哪一行的规律与其他三行不同?
(1
二、把左右卡片中规律相同的行用线连起来。
-2 +1
-3 +4
+5 -2
+1 -3
+4 +5
三、按规律填下去。
二年级找规律填图

二年级找规律填图(总5页) -CAL-FENGHAI.-(YICAI)-Company One1
-CAL-本页仅作为文档封面,使用请直接删除
创智教育内部讲义二年级找规律填图
姓名
例1、根据前面几幅图的规律,接下去该怎么画?
试一试:在空白处填上合适的图形.
(1)
(2)
例2、根据前面几幅图的规律,接着画。
试一试:根据前面三幅图的规律,接着画。
例3、观察前几幅图的变化规律,再接着画。
试一试:仔细观察下图,根据规律,接着画。
例4、观察下图的变化,想一想第四幅图应是画上怎样的图形。
试一试:按顺序仔细观察下图,画一画第三幅图。
例5、仔细观察下图的变化,按规律把图填在横线上。
▲▲▲▲○○▲▲▲▲○▲▲○○▲▲▲▲○○
试一试:找规律填图。
○○○●●○○○●●○○○●●
二年级找规律填图练习题
姓名家长签名
1.接着画,我能行!
2.看一看,填一填。
3.下面应画什么图形呢?
4、“”处应填什么图形?
要认真
哟!!
5、接下去该怎么画?
6、仔细观察下图,想一想第三幅图应怎么填?
7、仔细观察下图,回答下面问题。
8、认真观察下图,找找变化规律,画出第三组图。
第一组第二组第三组
9、根据前面几幅图的规律,接着画。
(1)
(2)
10、观察下图的变化规律,在空白处填上适当的图形.
11、下图的变化很多,请你认真仔细地观察,画出第四幅图的答案.
12、依照下面图中所给图形的变化规律,在空格中填图.。
二年级上册第2讲--找规律填图

重叠后长度=重叠前总长度-重叠部分长度
第2讲 找规律填图
你能发现这里面哪些图形存在规律吗?
下一个小孩应该是女孩还是男孩呢?
练一练:你能继续往下画吗?
练一练:你能猜出来下一个是什么图形吗?
• 根据前面几幅图的规律接着画
○○ △前面几幅图的规律接着画
找规律填图是把图形按一定的规律 排列起来,从图形的多少、大小、形 状、位置、方向等方面多角度认真观 察,找出变化规律,得出正确答案。
1.观察下面图的变化,想一想第四幅图应画 上怎样的图形?
□
△
○
□
☆
○
○
☆
☆
△
△
□
2.根据前面几幅图的变化规律,接着画。
△△ ○○○○○○ △△△△ ○○○○○
△△△△△△
○○○○
3.画出被盖部分的白珠和黑珠
●○○○○
○●●●●●●○○○●●●● ○○
□□□□□ ☆ □□□□ ☆☆ □□□ ☆☆☆
• 在空格里画出适当的图形
• 观察下面 图的变化, 想一想第 四幅图应 画上怎样 的图形?
□ ○ ☆
△ ☆ ○
○ ☆
□ △
△
□
P7能力检测2(2) P7综合应用1(3) P7能力检测2(1)
●
○○○○ ○○○○
●●
○○○ ○○○
●●●
○○ ○○
根据前面几幅图的规律接着画
△ ▲▲ △ ▲▲▲
△
▲▲▲▲
△
▲▲▲▲▲
根据前面几幅图的规律接着画
△△ ○○○○○○ △△△△ ○○○○○
△△△△△△
○○○○
△△△△ △△△△
○○○
●○○○ ○●●●●●●○○○●●●● ○○
找规律--图形
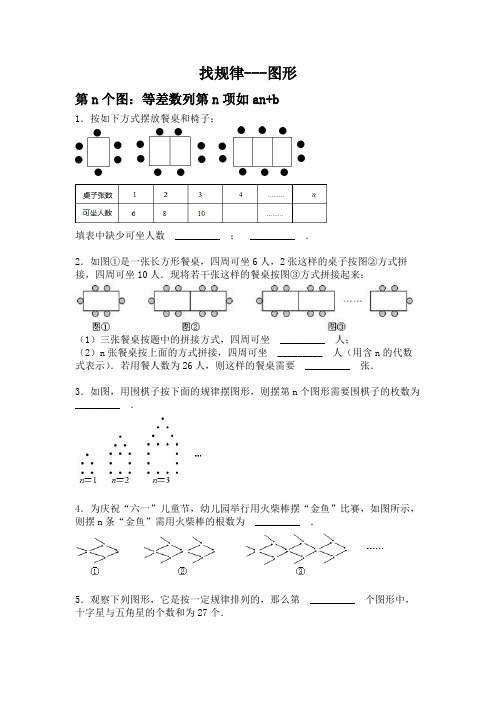
找规律---图形第n个图:等差数列第n项如an+b1.按如下方式摆放餐桌和椅子:填表中缺少可坐人数_________ ;_________ .2.如图①是一张长方形餐桌,四周可坐6人,2张这样的桌子按图②方式拼接,四周可坐10人.现将若干张这样的餐桌按图③方式拼接起来:(1)三张餐桌按题中的拼接方式,四周可坐_________ 人;(2)n张餐桌按上面的方式拼接,四周可坐_________ 人(用含n的代数式表示).若用餐人数为26人,则这样的餐桌需要_________ 张.3.如图,用围棋子按下面的规律摆图形,则摆第n个图形需要围棋子的枚数为_________ .4.为庆祝“六一”儿童节,幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,则摆n条“金鱼”需用火柴棒的根数为_________ .5.观察下列图形,它是按一定规律排列的,那么第_________ 个图形中,十字星与五角星的个数和为27个.6.如图所示是由火柴棒按一定规律拼出的一系列图形:依照此规律,第7个图形中火柴棒的根数是_________ .7.用火柴棒按如图所示的方式搭图形,按照这样的规律搭下去,填写下表:图形编号(1)(2)(3)…n火柴根数从左到右依次为_________ _________ _________ _________ .8.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6 图形中的棋子(2)照这样的方式摆下去,写出摆第n个图形棋子的枚数;(用含n的代数式表示)(3)如果某一图形共有99枚棋子,你知道它是第几个图形吗?9.如图所示,第1个图案是由黑白两种颜色的正六边形地面砖组成,第2个,第3个图案可以看作是第1个图案经过平移而得,那么设第n个图案中有白色地面砖m块,则m与n的函数关系式是_________ .10.下列图案是晋商大院窗格的一部分.其中,“o”代表窗纸上所贴的剪纸.探索并回答下列问题:(1)第6个图案中所贴剪纸“o”的个数是_________ ;(2)第n个图案中所贴剪纸“o”的个数是_________ ;(3)是否存在一个图案,其上所贴剪纸“o”的个数为2012个?若存在,指出是第几个;若不存在,请说明理由.11.用同样大小的黑色棋子按如图所示的规律摆放:(1)分别写出第6、7两个图形各有多少颗黑色棋子?(2)写出第n个图形黑色棋子的颗数?(3)是否存在某个图形有2012颗黑色棋子?若存在,求出是第几个图形;若不存在,请说明理由.12.如图,给出四个点阵,s表示每个点阵中点的个数,按照图形中的点的个数变化规律,(1)猜想第n个点阵中的点的个数s= _________ .(2)若已知点阵中点的个数为37,问这个点阵是第几个?13.用棋子摆出下列一组图形:(1)填写下表:图形编号 1 2 3 4 5 6图中棋子数 5 8 11 14 17 20 (2)照这样的方式摆下去,写出摆第n个图形所需棋子的枚数;(3)其中某一图形可能共有2011枚棋子吗?若不可能,请说明理由;若可能,请你求出是第几个图形.14.如图,是用相同的等腰梯形拼成的等腰梯形图案.第(1)个图案只有1个等腰梯形,其两腰之和为4,上下底之和为3,周长为7;第(2)个图案由3个等腰梯形拼成,其周长为13;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为_________ .(用正整数n表示)15.观察下列由等腰梯形组成的图形和所给表中数据的规律后填空:梯形的个数1 2 3 4 5 …图形的周长5 8 11 14 17 …当梯形个数为2007个时,这时图形的周长为_________16.下列各图均是用有一定规律的点组成的图案,用S表示第n个图案中点的总数,则S= _________ (用含n的式子表示).17.用火柴棍象如图这样搭图形,搭第n个图形需要_________ 根火柴棍.18.观察图中的棋子:(1)按照这样的规律摆下去,第4个图形中的棋子个数是多少?(2)用含n的代数式表示第n个图形的棋子个数;(3)求第20个图形需棋子多少个?19.图1是一个正方形,分别连接这个正方形的对边中点,得到图2;分别连接图2中右下角的小正方形对边中点,得到图3;再分别连接图3中右下角的小正方形对边中点,得到图4;按此方法继续下去,第n个图的所有正方形个数是_________ 个.20.如下图是用棋子摆成的“上”字:如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第④、第⑤个“上”字分别需用_________ 和_________ 枚棋子;(2)第n个“上”字需用_________ 枚棋子;(3)七(3)班有50名同学,把每一位同学当做一枚棋子,能否让这50枚“棋子”按照以上规律恰好站成一个“上”字?若能,请计算最下一“横”的学生数;若不能,请说明理由.21.如图是用棋子摆成的“H”字.(1)摆成第一个“H”字需要_________ 个棋子;摆第x个“H”字需要的棋子数可用含x的代数式表示为_________ ;(2)问第几个“H”字棋子数量正好是2012个棋子?22.如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,(1)第5个“广”字中的棋子个数是_________ .(2)第n个“广”字需要多少枚棋子?23.如图是用棋子成的“T ”字图案.从图案中可以出,第一个“T ”字图案需要5枚棋子,第二个“T ”字图案需要8枚棋子,第三个“T ”图案需要11枚棋子.(1)照此规律,摆成第八个图案需要几枚棋子?(2)摆成第n 个图案需要几枚棋子?(3)摆成第2010个图案需要几枚棋子?24.观察表中三角形个数的变化规律:图形横截线 条 数0 1 2 … n三角形 个 数6 ? ? … ?若三角形的横截线有0条,则三角形的个数是6;若三角形的横截线有n 条,则三角形的个数是 _________ (用含n 的代数式表示).25.观察下列图案:它们是按照一定规律排列的,依照此规律,第6个图案中共有 _________ 个三角形.26.如图,各图表示若干盆花组成的形如三角形的图案,每条边(包括两个顶点)有n (n >1)盆花,每个图案中花盆的总数为S .问:①当每条边有2盆花时,花盆的总数S 是多少?②当每条边有3盆花时,花盆的总数S 是多少?③当每条边有4盆花时,花盆的总数S 是多少?④当每条边有10盆花时,花盆的总数S 是多少?⑤按此规律推断,当每条边有n 盆花时,花盆的总数S 是多少?27.如图是用五角星摆成的三角形图案,每条边上有n(n>1)个点(即五角星),每个图案的总点数(即五角星总数)用S表示.(1)观察图案,当n=6时,S= _________ ;(2)分析上面的一些特例,你能得出怎样的规律?(用n表示S)(3)当n=2008时,求S.28.下列各图是由若干花盆组成的形如正方形的图案,每条边(包括两个顶点)有n(n>1)个花盆,每个图案花盆总数是S.(1)按要求填表:n 2 3 4 5 …S 4 8 12 …(2)写出当n=10时,S= _________ .(3)写出S与n的关系式:S= _________ .(4)用42个花盆能摆出类似的图案吗?第n个图:等差数列第n项如an29.以下各图分别由一些边长为1的小正方形组成,请填写图2、图3中的周长,并以此推断出图10的周长为_________ .30.用水平线和竖直线将平面分成若干个边长为1的小正方形格子,小正方形的顶点,叫格点.观察图中每一个正方形(实线)四条边上的格点的个数,请回答下列问题:(1)由里向外第1个正方形(实线)四条边上的格点个数共有_________个;由里向外第2个正方形(实线)四条边上的格点个数共有_________ 个;由里向外第3个正方形(实线)四条边上的格点个数共有_________ 个;(2)由里向外第10个正方形(实线)四条边上的格点个数共有_______个;(3)由里向外第n个正方形(实线)四条边上的格点个数共有________个.第n个图形:数列求和31.如图,在线段AB上,画1个点,可得3条线段;画2个不同点,可得6条线段;画3个不同点,可得10条线段;…照此规律,画10个不同点,可得线段_________ 条.32.下列表格是一张对同一线段上的个数变化及线段总条数的探究统计.线段上点的个数线段的总条数11+2=31+2+3=6……(1)请你完成探究,并把探究结果填在相应的表格里;(2)若在同一线段上有10个点,则线段的总条数为_________ ;若在同一线段上有n个点,则有_________ 条线段(用含n 的式子表示)(3)若你所在的班级有60名学生,20年后参加同学聚会,见面时每两个同学之间握一次手,共握手_________ 次.33.下列各图形中的小正方形是按照一定规律排列的,根据图形所揭示的规律我们可以发现:第1个图形有1个小正方形,第2个图形有3个小正方形,第3个图形有6个小正方形,第4个图形有10个小正方形…,按照这样的规律,则第10个图形有_________ 个小正方形.34.淮北市为创建文明城市,各种颜色的菊花摆成如下三角形的图案,每条边(包括两个顶点)上有n(n>1)盆花,每个图案花盆的总数为S,当n=2时,S=3;n=3时,S=6;n=4时,S=10.(1)当n=6时,S= _________ ;n=100时,S= _________ .(2)你能得出怎样的规律?用n表示S.35.下列图形都是由相同大小的单位正方形构成,依照图中规律,第六个图形中有_________ 个单位正方形.36.如图,用正方体石墩垒石梯,下图分别表示垒到一、二、三阶梯时的情况.那么照这样垒下去,请你观察规律,并完成下列问题.(1)填出下表中未填的两个空格:阶梯级数一级二级三级四级石墩块数 3 9(2)当垒到第n级阶梯时,共用正方体石墩多少块(用含n的代数式表示)?并求当n=100时,共用正方体石墩多少块?37.如图,用相同的火柴棒拼三角形,依此拼图规律,第7个图形中共有_________ 根火柴棒.38.如图,下面是一些小正方形组成的图案,第4个图案有_________ 个小正方形组成;第n个图案有_________ 个小正方形组成.39.如图,两条直线相交只有1个交点,三条直线相交最多有3个交点,四条直线相交最多有6个交点,五条直线相交最多有10个交点,六条直线相交最多有_________ 个交点,二十条直线相交最多有_________ 个交点.40.如图,一块圆形烙饼切一刀可以切成2块,若切两刀最多可以切成4块,切三刀最多可以切成7块…通过观察、计算填下表(其中S表示切n刀最多可以切成的块数)后,可探究一圆形烙饼切n刀最多能切成_________ 块(结果用n的代数式表示).n 0 1 2 3 4 5 …nS 1 2 4 7第n个图形:通过乘积找规律41.图中的每个图形都是由若干个棋子围成的正方形图案,图案的每条边(包括两个顶点)上都有n(n≥2)个棋子,每个图案的棋子总数为s,按图的排列规律推断,s与n之间的关系可用式子_________ 表示.42.找规律:观察下面的星阵图和相应的等式,探究其中的规律.(1)在④、⑤和⑥后面的横线上分别写出相应的等式:①1=12②1+3=22③1+3+5=32④_________ ;⑤_________ ;⑥_________ ;(2)通过猜想,写出第n个星阵图相对应的等式.43.如图,用同样规格黑白两色的正方形瓷砖铺设矩形地面,请观察图形并解答有关问题:(1)在第n个图中共有_________ 块黑瓷砖,_________ 块白瓷砖;(2)是否存在黑瓷砖与白瓷砖块数相等的情形?你能通过计算说明吗?44.如图所示,用同样规格正方形瓷砖铺设矩形地面,请观察下图:按此规律,第n个图形,每一横行有_________ 块瓷砖,每一竖列有_________ 块瓷砖(用含n的代数式表示)按此规律,铺设了一矩形地面,共用瓷砖506块,请问这一矩形的每一横行有多少块瓷砖,每一竖列有多少瓷砖?45.如图,由若干盆花摆成图案,每个点表示一盆花,几何图形的每条边上(包括两个顶点)都摆有n(n≥3)盆花,每个图案中花盆总数为S,按照图中的规律可以推断S与n(n≥3)的关系是_________ .第n个图形:周期图形46.现有黑色三角形“”和白色三角形“”共有2011个,按照一定的规律排列如下:则黑色三角形有_________ 个.47.假设有足够多的黑白围棋子,按照一定的规律排成一行:○●●○○●○●●○○●○●●○○●○●●○○●…请问第2011个棋子是黑的还是白的?答:_________ .48.观察图中四个顶点的数字规律:(1)数字“30”在_________ 个正方形的_________ ;(2)请你用含有n(n≥1的整数)的式子表示正方形四个顶点的数字规律;(3)数字“2011”应标在什么位置.第n个图形:与前一个图联系紧密49.如图,依次连接一个边长为1的正方形各边的中点,得到第二个正方形,再依次连接第二个正方形各边的中点,得到第三个正方形,按此方法继续下去,则第二个正方形的面积是_________ ;第六个正方形的面积是_________ .50.有一张厚度为0.05毫米的纸,将它对折1次后,厚度为2×0.05毫米.(1)对折3次后,厚度为多少毫米?(2)对折n次后,厚度为多少毫米?(3)对折n次后,可以得到多少条折痕?51.下面是按照一定规律画出的一系列“树枝”经观察,图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出4个“树枝”,图(4)比图(3)多出8个“树枝”,按此规律:图(5)比图(4)多出_________ 个树枝;图(6)比图(5)多出_________ 个树枝;图(8)比图(7)多出_________ 个树枝;…图(n+1)比图(n)多出_________ 个树枝.52.将一张正方形纸片剪成四个大小一样的小正方形,然后将其中的一个正方形再剪成四个小正方形,如此循环下去,如图所示:(1)完成下表:所剪次数n 1 2 3 4 5正方形个数Sn 4(2)剪n次共有Sn 个正方形,请用含n的代数式表示Sn= _________ ;(3)若原正方形的边长为1,则第n次所剪得的正方形边长是_________ (用含n的代数式表示).53.图(1)是一个黑色的正三角形,顺次连接三边中点,得到如图(2)所示的第2个图形(它的中间为一个白色的正三角形);在图(2)的每个黑色的正三角形中分别重复上述的作法,得到如图(3)所示的第3个图形.如此继续作下去,则在得到的第5个图形中,白色的正三角形的个数是_________ .54.如图是由数字组成的三角形,除最顶端的1以外,以下出现的数字都按一定的规律排列.根据它的规律,则最下排数字中x的值是_________ ,y的值是_________ .参考答案:1.结合图形和表格,不难发现:1张桌子座6人,多一张桌子多2人.4张桌子可以座10+2=12.即n张桌子时,共座6+2(n﹣1)=2n+4.2.(1)结合图形,发现:每个图中,两端都是坐2人,剩下的两边则是每一张桌子是4人.则三张餐桌按题中的拼接方式,四周可坐3×4+2=14(人);(2)n张餐桌按上面的方式拼接,四周可坐(4n+2)人;若用餐人数为26人,则4n+2=26,解得n=6.故答案为:14;(4n+2),63.依题意得:(1)摆第1个“小屋子”需要5个点;摆第2个“小屋子”需要11个点;摆第3个“小屋子”需要17个点.当n=n时,需要的点数为(6n﹣1)个.故答案为6n﹣14.由图形可知:第一个金鱼需用火柴棒的根数为:2+6=8;第二个金鱼需用火柴棒的根数为:2+2×6=14;第三个金鱼需用火柴棒的根数为:2+3×6=20;…;第n个金鱼需用火柴棒的根数为:2+n×6=2+6n.故答案为2+6n5.∵第1个图形中,十字星与五角星的个数和为3×2=6,第2个图形中,十字星与五角星的个数和为3×3=9,第3个图形中,十字星与五角星的个数和为3×4=12,…而27=3×9,∴第8个图形中,十字星与五角星的个数和=3×9=27.故答案为:86.根据已知图形可以发现:第2个图形中,火柴棒的根数是7;第3个图形中,火柴棒的根数是10;第4个图形中,火柴棒的根数是13;∵每增加一个正方形火柴棒数增加3,∴第n个图形中应有的火柴棒数为:4+3(n﹣1)=3n+1.当n=7时,4+3(n﹣1)=4+3×6=22,故答案为:227.如表格所示:图形编号(1)(2)(3)…n火柴根数7 12 17 …5n+28.(1)如图所示:1 2 3 4 5 6图形编号6 9 12 15 18 21图形中的棋子(2)依题意可得当摆到第n个图形时棋子的枚数应为:6+3(n﹣1)=6+3n﹣3=3n+3;(3)由上题可知此时3n+3=99,∴n=32.答:第32个图形共有99枚棋子9.首先发现:第一个图案中,有白色的是6个,后边是依次多4个.所以第n个图案中,是6+4(n﹣1)=4n+2.∴m与n的函数关系式是m=4n+2.故答案为:4n+2.10.二个图案为2×3+2=8个窗花;第三个图案为3×3+2=11个窗花;…从而可以探究:第n个图案所贴窗花数为(3n+2)个.(1)20(2)3n+2(3)存在,令3n+2=2012,则3n=2010 n=670 因此是第670个11.第一个图需棋子6,第二个图需棋子9,第三个图需棋子12,第四个图需棋子15,第五个图需棋子18,…第n个图需棋子3(n+1)枚.(1)当n=6时,3×(6+1)=21;当n=7时,3×(7+1)=24;(2)第n个图需棋子3(n+1)枚.(3)设第n个图形有2012颗黑色棋子,根据(1)得3(n+1)=2012解得n= ,所以不存在某个图形有2012颗黑色棋子12.(1)由点阵图形可得它们的点的个数分别为:1,5,9,13,…,并得出以下规律:第一个点数:1=1+4×(1﹣1)第二个点数:5=1+4×(2﹣1)第三个点数:9=1+4×(3﹣1)第四个点数:13=1+4×(4﹣1)…因此可得:第n个点数:1+4×(n﹣1)=4n﹣3.故答案为:4n﹣3;(2)设这个点阵是x个,根据(1)得:1+4×(x﹣1)=37解得:x=10.答:这个点阵是10个13.(1)观察图形,得出枚数分别是,5,8,11,…,每个比前一个多3个,所以图形编号为5,6的棋字子数分别为17,20.故答案为:17和20.(2)由(1)得,图中棋子数是首项为5,公差为3的等差数列,所以摆第n个图形所需棋子的枚数为:5+3(n﹣1)=3n+2.(3)不可能由3n+2=2010,解得:n=669 ,∵n为整数,∴n=669 不合题意故其中某一图形不可能共有2011枚棋子14.根据题意得:第(1)个图案只有1个等腰梯形,周长为3×1+4=7;第(2)个图案由3个等腰梯形拼成,其周长为3×3+4=13;第(3)个图案由5个等腰梯形拼成,其周长为3×5+4=19;…第(n)个图案由(2n﹣1)个等腰梯形拼成,其周长为3(2n﹣1)+4=6n+1;故答案为:6n+115.依题意可求出梯形个数与图形周长的关系为3n+2=周长,当梯形个数为2007个时,这时图形的周长为3×2007+2=6023.故答案为:6023.16.观察发现:第1个图形有S=9×1+1=10个点,第2个图形有S=9×2+1=19个点,第3个图形有S=9×3+1=28个点,…第n个图形有S=9n+1个点.故答案为:9n+117.结合图形,发现:搭第n个三角形,需要3+2(n﹣1)=2n+1(根).故答案为2n+118.(1)第4个图形中的棋子个数是13;(2)第n个图形的棋子个数是3n+1;(3)当n=20时,3n+1=3×20+1=61∴第20个图形需棋子61个19. 图1中,是1个正方形;图2中,是1+4=5个正方形;图3中,是1+4×2=9个正方形;依此类推,第n个图的所有正方形个数是1+4(n﹣1)=4n﹣3.20.(1)第①个图形中有6个棋子;第②个图形中有6+4=10个棋子;第③个图形中有6+2×4=14个棋子;∴第⑤个图形中有6+3×4=18个棋子;第⑥个图形中有6+4×4=22个棋子.故答案为18、22;(3分)(2)第n个图形中有6+(n﹣1)×4=4n+2.故答案为4n+2.(3分)(3)4n+2=50,解得n=12.最下一横人数为2n+1=25.(4分)21.(1)摆成第一个“H”字需要7个棋子,第二个“H”字需要棋子12个;第三个“H”字需要棋子17个;…第x个图中,有7+5(x﹣1)=5x+2(个).(2)当5x+2=2012时,解得:x=402,故第402个“H”字棋子数量正好是2012个棋子22.由题目得:第1个“广”字中的棋子个数是7;第2个“广”字中的棋子个数是7+(2﹣1)×2=9;第3个“广”字中的棋子个数是7+(3﹣1)×2=11;第4个“广”字中的棋子个数是7+(4﹣1)×2=13;发现第5个“广”字中的棋子个数是7+(5﹣1)×2=15…进一步发现规律:第n个“广”字中的棋子个数是7+(n﹣1)×2=2n+5.故答案为:1523.(1)首先观察图形,得到前面三个图形的具体个数,不难发现:在5的基础上依次多3枚.即第n个图案需要5+3(n﹣1)=3n+2.那么当n=8时,则有26枚;故摆成第八个图案需要26枚棋子.(2)因为第①个图案有5枚棋子,第②个图案有(5+3×1)枚棋子,第③个图案有(5+3×2)枚棋子,依此规律可得第n个图案需5+3×(n﹣1)=5+3n﹣3=(3n+2)枚棋子.(3)3×2010+2=6032(枚)即第2010个图案需6032枚棋子24.当横截线有n条时,在6个的基础上多了n个6,即三角形的个数共有6+6n=6(n+1)个.故应填6(n+1)或6n+625.∵第1个图案中有2×2+2×1=6个三角形;第2个图案中有2×3+2×2=10个三角形;第3个图案中有2×4+2×3=14个三角形;…∴第6个图案中有2×7+2×6=26个三角形.故答案为2626.依题意得:①n=2,S=3=3×2﹣3.②n=3,S=6=3×3﹣3.③n=4,S=9=3×4﹣3④n=10,S=27=3×10﹣3.…⑤按此规律推断,当每条边有n盆花时,S=3n﹣327.(1)S=15(2)∵n=2时,S=3×(2﹣1)=3;n=3时,S=3×(3﹣1)=6;n=4时,S=3×(4﹣1)=9;…∴S=3×(n﹣1)=3n﹣3.(3)当n=2008时,S=3×2008﹣3=6021.28.由图可知,每个图形为边长是n的正方形,因此四条边的花盆数为4n,再减去重复的四个角的花盆数,即S=4n﹣4;(1)将n=5代入S=4n﹣4,得S=16;(2)将n=10入S=4n﹣4,得S=36;(3)S=4n﹣4;(4)将S=42代入S=4n﹣4得,4n﹣4=42解得n=11.5所以用42个花盆不能摆出类似的图案29. ∵小正方形的边长是1,∴图1的周长是:1×4=4,图2的周长是:2×4=8,图3的周长是3×4=12,…第n个图的周长是4n,∴图10的周长是10×4=40;故答案为:8,12,4030. 第1个正方形四条边上的格点共有4个第2个正方形四条边上的格点个数共有(4+4×1)个第3个正方形四条边上的格点个数共有(4+4×2)个…第10个正方形四条边上的格点个数共有(4+4×9)=40个第n个正方形四条边上的格点个数共有[4+4×(n﹣1)]=4n个31.∵画1个点,可得3条线段,2+1=3;画2个点,可得6条线段,3+2+1=6;画3个点,可得10条线段,4+3+2+1=10;…;画n个点,则可得(1+2+3+…+n+n+1)= 条线段.所以画10个点,可得 =66条线段;32.(1)5个点时,线段的条数:1+2+3+4=10,6个点时,线段的条数:1+2+3+4+5=15;(2)10个点时,线段的条数:1+2+3+4+5+6+7+8+9=45,n个点时,线段的条数:1+2+3+…+(n﹣1)=;(3)60人握手次数==1770.故答案为:(2)45,;(3)1770.33.∵第一个有1个小正方形,第二个有1+2个,第三个有1+2+3个,第四个有1+2+3+4,第五个有1+2+3+4+5,∴则第10个图形有1+2+3+4+5+6+7+8+9+10=55个.故答案为:5534. (1)由分析得:当n=6时,s=1+2+3+4+5+6=21;当n=100时,s=1+2+3+…+99+100=5050;(2)用n表示S得:S=35.根据题意分析可得:第1个图案中正方形的个数2个,第2个图案中正方形的个数比第1个图案中正方形的个数多4个,第3个图案中正方形的个数比第2个图案中正方形的个数多6个…,依照图中规律,第六个图形中有2+4+6+8+10+12=42个单位正方形36.(1)第一级台阶中正方体石墩的块数为:=3;第一级台阶中正方体石墩的块数为:=9;第一级台阶中正方体石墩的块数为:;…依此类推,可以发现:第几级台阶中正方体石墩的块数为:3与几的乘积乘以几加1,然后除以2.一级二级三级四级阶梯级数石墩块3 9 18 30数(2)按照(1)中总结的规律可得:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,∴当n=100时,共用正方体石墩15150块.答:当垒到第n级阶梯时,共用正方体石墩块;当n=100时,共用正方体石墩15150块37.图形从上到下可以分成几行,第n行中,斜放的火柴有2n根,下面横放的有n根,因而图形中有n排三角形时,火柴的根数是:斜放的是2+4+…+2n=2(1+2+…+n)横放的是:1+2+3+…+n,则每排放n根时总计有火柴数是:3(1+2+…+n)= 把n=7代入就可以求出.故第7个图形中共有 =84根火柴棒38.观察图形知:第一个图形有1=12个小正方形;第二个图形有1+3=4=22个小正方形;第三个图形有1+3+5=9=32个小正方形;…第n个图形共有1+2+3+…+(2n﹣1)=n2个小正方形,当n=4时,有n2=42=16个小正方形.故答案为:16,n239.6条直线两两相交,最多有 n(n﹣1)= ×6×5=15,20条直线两两相交,最多有 n(n﹣1)= ×20×19=190.故答案为:15,190.40.n=1时,S=1+1=2,n=2时,S=1+1+2=4,n=3时,S=1+1+2+3=7,n=4时,S=1+1+2+3+4=11,…所以当切n刀时,S=1+1+2+3+4+…+n=1+n(n+1)=n2+n+1.故答案为n2+n+141.观察图形发现:当n=2时,s=4,当n=3时,s=9,当n=4时,s=16,当n=5时,s=25,…当n=n时,s=n2,故答案为:s=n242.等号左边是从1开始,连续奇数相加,等号右边是奇数个数也就是n的平方.(1)①1+3+5+7=42;②1+3+5+7+9=52;③1+3+5+7+9+11=62.(2)1+3+5+…+(2n﹣1)=n2(n≥1的正整数)43.(1)在第n个图形中,需用黑瓷砖4n+6块,白瓷砖n(n+1)块;(2)根据题意得n(n+1)=4n+6,n2﹣3n﹣6=0,此时没有整数解,所以不存在.故答案为:4n+6;n(n+1)44.由图形我们不难看出横行砖数量为n+3,竖行砖数量为n+2,总数量为n2+5n+6;若用瓷砖506块,可以求n2+5n+6=506;所以答案为:(1)n+3,n+2;(2)每一行有23块,每一列有22块45.n=3时,S=6=3×3﹣3=3,n=4时,S=12=4×4﹣4,n=5时,S=20=5×5﹣5,…,依此类推,边数为n数,S=n•n﹣n=n(n﹣1).故答案为:n(n﹣1).46.因为2011÷6=335…1.余下的1个根据顺序应是黑色三角形,所以共有1+335×3=1006.故答案为:100647.从所给的图中可以看出,每六个棋子为一个循环,∵2011÷6=335…1,∴第2011个棋子是白的.故答案为:白48.(1)由图可知,每个正方形标4个数字,∵30÷4=7…2,∴数字30在第8个正方形的第2个位置,即右上角;故答案为:8,右上角;(2)左下角是4的倍数,按照逆时针顺序依次减1,即正方形左下角顶点数字:4n,正方形左上角顶点数字:4n﹣1,正方形右上角顶点数字:4n﹣2,正方形右下角顶点数字:4n﹣3;(3)2011÷4=502…3,所以,数字“2011”应标第503个正方形的左上角顶点处49.∵正方形的边长是1,所以它的斜边长是:=,所以第二个正方形的面积是:×=,第三个正方形的面积为=()2,以此类推,第n个正方形的面积为()n﹣1,所以第六个正方形的面积是()6﹣1=;故答案为:,.50.由题意可知:第一次对折后,纸的厚度为2×0.05;可以得到折痕为1条;第二次对折后,纸的厚度为2×2×0.05=22×0.05;可以得到折痕为3=22﹣1条;第三次对折后,纸的厚度为2×2×2×0.05=23×0.05;可以得到折痕为7=23﹣1条;…;第n次对折后,纸的厚度为2×2×2×2×…×2×0.05=2n×0.05.可以得到折痕为2n﹣1条.故:(1)对折3次后,厚度为0.4毫米;(2)对折n次后,厚度为2n×0.05毫米;(3)对折n次后,可以得到2n﹣1条折痕51.(1)图(5)比图(4)多出25﹣1=16个;(2)图(6)比图(5)多出26﹣1=32个;(3)图(8)比图(7)多出28﹣1=128个;(4)图(n+1)比图(n)多出2n个.52. (1)依题意得:所剪次数n 1 2 3 4 54 7 10 13 16正方形个数Sn=3n+1.(2)可知剪n次时,Sn(3)n=1时,边长=;n=2时,边长=;n=3时,边长=;…;剪n次时,边长=.53.设白三角形x个,黑三角形y个,则:n=1时,x=0,y=1;n=2时,x=0+1=1,y=3;n=3时,x=3+1=4,y=9;n=4时,x=4+9=13,y=27;当n=5时,x=13+27=40,所以白的正三角形个数为:40,故答案为:4054.根据图形可以发现,第七排的第一个数和第二数与第八排的第二个数相等,而第八排的第二个数就是x,所以x=61.另外,由图形可知,x右边的数是2×61=122,y左边的数是2×61+56=178,所以y=178+46=224。
小学一年级数学思维训练找规律填空

精心整理
精心整理
一年级数学思维训练4找规律填空
1、找规律画图
例1仔细观察,寻找规律,在问号处填上合适的图形。
例2想一想,接着怎么画?
例3从下列四个选项中选出与其他三个图不同的一个图形.
例4有一堵墙上的砖坏了一部分,现在请你仔细观察排列规律,猜一猜要补上多少块同样的砖,才能把墙补好?
2
例5例6例7例 12、45(1)(2)(3)678、9、仔细观察,寻找规律,在方框中填上合适的图形。
10、按规律填上第五个数组中的数.
{1,5,10},{2.10,20},{3,15,30},{4,20,40},{_____,_____,_____}
提高练习
1.找出下面数列的排列规律,并填空。
(1)1,2,5,10,(),26,37;
精心整理
精心整理
(2)1,7,13, (),25,31;
(3)1,50,2,45,3,40,(),(),5,30;
2.在括号里填上适当的数。
(1)(2,6);(5,10),(8,),(,18),(14,22);
(2)(1,25);(2,36);(4,49);(8,);(,81);
3.找出下面数列的规律,并填空。
1,3,7,15,31,(),127,255,511;
4.5.从5是这6.从7.从8. 9.
1011、。
第1讲:找规律,填图形_教师版_

.观察1-6,并按照变化规律在“?”处填上合适的图形.
分析首先,图中(1)与(4)成对,(2)与(5)成对,所以(3)与(6)也应成对.(5)的左图是(2)的左图颠倒过来,(4)的左图也是(1)的左图颠倒过来,所以(3)的左图也应当是(6)的左图颠倒过来.(4)的右图是(1)的左图的右半部分,(5)的右图是(2)的左图的右半部分,所以(6)的右图也应当是(3)的左图的右半部分.
解(3)、(6)处的图形分别如图1-7.
观察图1-8,按照变化规律住“?”处填图.
.观察图1-9,并按照变化规律在“?”处填上合适的图形.
分析首先,在(1)、(2)、(3)各图中都只有三角形、长方形、圆、正方形这四种图形,所以(4)中的图形也是三角形、长方形、圆、正方形四种其次,从第二幅图开始,每一幅图都是由前一幅图逆时针方向旋转90 而得到的,所以,(3)再逆时针旋转90 就得到(4).
.仔细观察图1-3,并按照它的变化规律,在“?”处填上适当的图.
分析首先,我们从图形的形状上看,每一行有三个图,分别是三角形、圆与正方形,所以在“?”处应当填人一个三角形.其次,从涂色的变化看,每一行都有一个图打上条形纹,一个图全被涂上,一个图没涂,所以,在“?”处的图形应当全被涂上.
解在“?”处应当填入的图形如图1-4.
分析与解从第一个图形起,每四个图形一组,按顺序 重复出现,由于23=4×5+3,重复出现5次后,第六组的第三个图形即第23个图形,是
黑棋子与白棋子排成一列,如图1-13所示。问:第99个棋子是什么颜色?这99个棋子中,有多少个白棋子?
一般地,观察图形变化的规律,应从以下几点考虑:
(1)时数:
学员姓名:辅导科目:数学学科教师:
一年级数学找规律图形

1. 摆一摆,填一填。
4
3
先观察图形列规 律,可以帮助我们 检查填的对不对。
2. 做动作,猜规律。
四、布置作业
作业:第86页“做一做”第2题。 第89页练习二十,第1题、第2题。 第90页练习二十,第10题。
找规律
找规律(1)
你有什么发现?
图中的人和物都是 按规律排列的。
小旗的规律是按1面 、 1面 为一组重复排列。
仔小细旗观的察规小律旗是的1面排列、, 你1面发现,了又什1么面规律、? 1面 ……
再 是的来!看看它美们都丽是的重 小 复花 排吧 列!的。
我像发彩现旗小、花小的 花排 、列 灯规 笼律 、是 小: 朋友 灯1这朵笼样和,、小几1朋个朵友为的一为排组一列重组复出现的 也重规有复律类排叫似列做的。重规复律排吗列?的规律。
找规律,填数。
(1) 23 2
先观察碗的 排列规律。
3
2
3
2
3
碗的排列规律是按 重复排列。
我发现,也可以直接观察数字的 规律,是以2和3为一组重复排列 的,所以3的后面分别填2和3。
找规律,填数。
(2)
1
3
后面该填哪 你能试两一个试数吗呢??
1
3
1
3
小鸡的排列规律是按 重复排列。
直接看数字就是1、 3为一组重复出现。
1、涂一涂,说一说
尽情发挥你们的 创造力吧!
3. 按自己喜欢的规律涂色。
我用的是今天学习的 重复排列规律,我涂 得漂亮吗?
谁真还漂愿亮意!展再示看一看下我 自创己造的的作规品律?吧,你 能看懂吗?
4. 猜一猜,后面是什么?
?
看到你们越来越
会思考,真替你 该们怎高样兴想!呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
这三个图形都由上、下两个部分组成,上半部分是空白部分,下半部分是阴影部分。
三、练一练
1、仔细观察下面的三个图形,然后在方框中选择一个合适的图形填在空白处。
2、仔细观察下面的图形,并按其变化规律在“”处画上合适的图形。
找规律填图形
华顿国际学校三年级上思维课教案
教师:魏帼巾、李雪梅
课题:找规律填图形课时:1总课时:1
教学目标:
1、找规律,是解决数学问题的一种重要手段,而发现规律既需要敏锐的观察力,又需要一定的逻辑推理能力。
2、通过观察它们在某一方面的特征,找到它们的变化规律,并根据找到的规律来推断结果。
3、从图形的个数、形状、性质入手,逐步探求规律,培养学生细心观察,归纳推理能力。
3、根据左边的图形的关系,画出右边图形的另一半。
四、总结:
你有什么收获?
学生自主观察,分析题意
学生自主尝试完成,全班交流
学生在练习本上独立完成,再全班交流
作业设计:
完成练习
板书设计:
找规律填图形
数量、颜色、形状、位置、方向、大小
简单化
排列规律
教后反思
答案:每行圆形的个数依次减少,个数分别为5、4、3、2、1;二每行正方形的个数却是依次增加,个数分别为1、2、
、4、5。显然,第三行应该有3个正方形。
二、初出茅庐
下面哪个图形和其他几个不一样?请你找出来,并打上勾。
思路点拨:
1、对于一组几何图形,要仔细观察这组图形中大部分图形所
共有的特征,如排列方式、图形位置等。这样就能找出规律并把不符合规律的图形从中找出来。
2、第一组图形都是连接各边中点组成的复合图形,但在组成图形的边数上有些不同。第二组图形主要是构图上的差异,大部分的小图形都在大图形的内部边上。
3、第三组图形中构成组合图形的两个基本图形在位置上大多是下面的图形盖住上面的图形。第四组图形都是由三个基本部分组成,仔细观察可以发现第二、三、五个图形是由第一个图形在一个平面内旋转得到的。
教学重难点:
根据图形在某一方面的特征,找到它们的变化规律,并根据找到的规律来推断结果。
教法、学法设计:观察法、总结法
教学准备:
教师方面的准备:课件
学生方面的准备:练习本
教学过程:
教师活动
学生活动
一、拜师学艺
观察图,并按照图形的变化规律,在空白处填上适当的图形。
“”处应填什么图形。思路点拨:图中分别由若干个圆形和正方形排列而成,应该从图形的数量上来寻找排列规律。
