巴特沃兹低通滤波8极点
巴特沃斯滤波原理

巴特沃斯滤波原理
在信号处理领域中,巴特沃斯滤波原理是一种常用的滤波方法,它能够在频域中改变信号的频率特性,从而实现信号的滤波处理。
巴特沃斯滤波器是一种用于滤波的频域滤波器,其设计基于巴特沃斯滤波原理。
巴特沃斯滤波原理的核心思想是通过设计一个特定的频率响应函数来滤波信号。
这个频率响应函数通常采用巴特沃斯极点的形式,巴特沃斯极点是一种在频域中具有特定频率和幅度特性的点。
通过合理选择巴特沃斯极点的分布和数量,可以设计出符合要求的滤波器。
巴特沃斯滤波器通常分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
其中,低通滤波器可以通过滤除高频成分来平滑信号,高通滤波器则可以去除低频成分以突出信号中的高频信息。
带通滤波器和带阻滤波器则可以选择特定的频段进行滤波处理。
在设计巴特沃斯滤波器时,一般需要确定一些参数,如截止频率、阶数等。
截止频率决定了滤波器的频率特性,阶数则反映了滤波器的复杂程度。
通过调节这些参数,可以实现对不同频率信号的滤波效果。
值得注意的是,巴特沃斯滤波器在实际应用中可能存在一些问题,如频率失真、幅度失真等。
这些问题的出现可能是由于滤波器设计不当或阶数选择不当导致的。
因此,在使用巴特沃斯滤波器时需要仔细选择滤波器类型和参数,以达到最佳的滤波效果。
总的来说,巴特沃斯滤波原理是一种重要的信号处理方法,能够有效地滤波信号并提取出感兴趣的信息。
通过合理设计滤波器的频率响应函数,可以实现对不同频率信号的精准处理,为信号处理领域提供了重要的工具和方法。
1。
matlab巴特沃斯低通滤波函数

matlab巴特沃斯低通滤波函数
MATLAB中的巴特沃斯低通滤波函数用于设计和应用巴特沃斯低通滤波器。
巴特沃斯滤波器是一种常见的数字滤波器类型,可以对信号进行频率域的滤波处理。
巴特沃斯低通滤波器的特点是在通带内具有最平坦的幅度响应,并且有一个明确的截止频率。
它可以将高于截止频率的信号分量抑制或删除,而保留低于截止频率的信号分量。
巴特沃斯低通滤波器的作用是滤除高于截止频率的噪声或不需要的信号分量,以提取出所需的信号内容。
它常用于信号处理、图像处理、音频处理等领域,如用于去除图像中的高频噪声,平滑时间序列数据等。
在MATLAB中,设计巴特沃斯低通滤波器的函数是butter。
该函数可以根据指定的阶数、截止频率和滤波器类型来设计滤波器,并返回巴特沃斯低通滤波器的系数。
你可以使用这些系数来应用滤波器到信号上,使用filter函数实现滤波操作。
关于八阶巴特沃斯低通滤波器的设计

关于⼋阶巴特沃斯低通滤波器的设计⽬录1、课程设计⽬的 (1)2、课程设计内容和要求 (1)2.1、设计内容 (1)2.2、设计要求 (1)3、设计⽅案及实验情况 (1)3.1、设计思路 (1)3.2、电路及滤波原理 (1)3.3、芯⽚介绍 (3)3.4、⼯作原理及硬件设计 (4)3.5、硬件电路原理图 (9)4、课程设计总结 (11)5、参考⽂献 (11)1、课程设计⽬的(1)掌握电⼦电路的⼀般设计⽅法和设计流程;(2)学习简单电路系统设计,掌握Protel99或其它⼯具软件的使⽤⽅法;(3)学习掌握硬件电路设计的全过程。
2、课程设计内容和要求2.1、设计内容(1)查阅相关资料,完成系统总体⽅案设计;(2)利⽤Multisim软件仿真;(3)利⽤protel99软件画出电路原理图与PCB版图;(4)按照要求撰写设计说明书。
2.2、设计要求滤波技术是信号分析、处理技术的重要分⽀,⽆论是信号的提取、传输,还是信号的处理和交换都离不开滤波技术,它对信号安全可靠和有效灵活地传递是⾄关重要的。
在近代各种电⼦设备和控制系统中,滤波技术应⽤极为⼴泛。
在所有的电⼦系统中,使⽤最多,技术最复杂要算滤波器了。
滤波器的优劣直接决定着产品的优劣。
本课程设计设计⼀个有源滤波器,滤波范围:10Hz-2KHz,⾼通滤波电路采⽤⼆阶⾼通滤波电路,低通部分采⽤⼋阶巴特沃斯滤波电路。
3、设计⽅案及实验情况3.1、设计思路带通滤波器是由低通RC环节和⾼通RC环节组合⽽成的。
要将⾼通的下限截⽌频率设置为⼩于低通的上限截⽌频率。
电路是由有源低通滤波器,有源⾼通滤波器两部分组成的有源带通滤波器。
⾼通滤波电路采⽤截⽌频率为10HZ的压控电压源⼆阶⾼通滤波电路,低通部分采⽤截⽌频率为2K的⼋阶巴特沃斯滤波器。
其中,⼋阶巴特沃斯滤波器是由四个压控电压源⼆阶低通滤波器级联构成。
3.2、电路及滤波原理(1)压控⼆阶电路压控电压源⼆阶滤波电路的特点:运算放⼤器为同相接法,滤波器的输⼊阻抗很⾼,输出阻抗很低,滤波器相当于⼀个电压源。
巴特沃斯低通滤波器

带最小衰减α =30dB,按照以上技术指标设计巴特沃斯低通滤波器。 0.1a s
1a p
1a s
2.4
0242 4.25, 2.4
2.4 10 1 2 f lg 0.0242 lg 0.0242 NN 2 4.25, 55 lgf 2.4 4.25, N N s sp lg 2.4 2.4 2 f p
H( a s)
N c
(s s
k 0
N 1
k
)
7 j 3
• 例如N=3, 通过下式可以计算出6个极点 5 2 4 j j j j s 3 c 3 s 2 c 3 s 0 c 3 s1 c
s 4 c
j2
s 5 c
要求
f i g u r e ; p l o t ( Q , H a s ) ; a x i s ( [ 0 5]);xlabel('f(kHz)'),ylabel('20lg(abs(H_{a}(j{\Omega})))(dB)');
3 0
- 7 0
• • • • •
L=length(Ha); Yt=Xt(1:L).*Ha; figure;plot(Q,abs(Yt));axis([0 60 0 150]); yt=ifft(Yt); figure;plot(Q,yt);
• 模拟低通滤波器的设计指标 • 构造一个逼近设计指标的传输函数Ha(s) • Butterworth(巴特沃斯)低通逼近
模拟低通滤波器的设计指标及逼近方法(续)
• 模拟低通滤波器的设计指标有αp, Ωp,αs和Ωs。 • Ωp;通带截止频率 • Ωs:阻带截止频率
巴特沃斯低通滤波器设计

2
-1
3.443
2
lg
2 2 104 2 1.304 104
H a ( jΩ ) 1 2
o
c
N=2 N =4 N =8
取整后得阶数:4,按其设计的滤波器,通 带实际特性优于给定之指标。
或者利用公式:
N
lg
1
2 s
-1
2021/6/18
2 lg s / c
4
一:求巴特沃斯阶数N 二:求系统函数(可以省略)
滤波器插在负载电RS阻 和内I阻1 之间
Es
V1
LC 无损 网络
I2
RL V0
1'
2'
Z11(s)
2021/6/18
RL
Rs
9
三:归一化电路的实现
由于N阶巴特沃斯滤波器的分母多项式是霍尔为茨多项式,并且 全部传输零点在 用达林顿电路结构实现。
处,因而可以
s=
一 此般 时情 满况 足下,电路是在匹配情况下工H 作a (,s )所以取信源内阻
6
一:求巴特沃斯阶数N 二:求系统函数(可以省略)
设计步骤
三:归一化电路的实现 备注:(1,根据连除法得到;2,直接根据阶次查表得到)
四:实际电路的实现,即去归一化
H a(s)
2021/6/18
7
三:归一化电路的实现
由于N阶巴特沃斯滤波器的分母多项式是霍尔为茨多项式,并且 全部传输零点在 用达林顿电路结构实现。
7 20( s2' )17 /46.4/914 08( s ' ) 6 1 0 .0 9 7 8 ( s ' ) 5 1 4 .5 9 1 8 ( s ' ) 4 1 4 .5 9 1 8 ( s ' ) 3 1 0 .0 9 7 8 ( s ' ) 2 4 .4 9 4 0 ( s ' ) 1
巴特沃斯滤波器设计
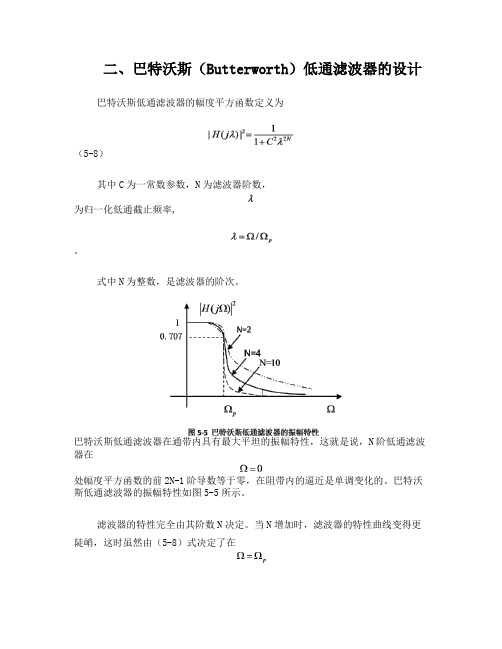
二、巴特沃斯(Butterworth)低通滤波器的设计巴特沃斯低通滤波器的幅度平方函数定义为(5-8)其中C为一常数参数,N为滤波器阶数,为归一化低通截止频率,。
式中N为整数,是滤波器的阶次。
巴特沃斯低通滤波器在通带内具有最大平坦的振幅特性,这就是说,N阶低通滤波器在处幅度平方函数的前2N-1阶导数等于零,在阻带内的逼近是单调变化的。
巴特沃斯低通滤波器的振幅特性如图5-5所示。
滤波器的特性完全由其阶数N决定。
当N增加时,滤波器的特性曲线变得更陡峭,这时虽然由(5-8)式决定了在处的幅度函数总是衰减3dB,但是它们将在通带的更大范围内接近于1,在阻带内更迅速的接近于零,因而振幅特性更接近于理想的矩形频率特性。
滤波器的振幅特性对参数N的依赖关系如图5-5所示。
设归一化巴特沃斯低通滤波器的归一化频率为,归一化传递函数为,其中,则由(5-6)式和(5-8)式得:由于(5-9)所以巴特沃斯滤波器属于全极点滤波器。
1、常用设计巴特沃斯低通滤波器指标:通带截止频率;:通带衰减,单位:dB;:阻带起始频率;:阻带衰减,单位:dB。
说明:(1)衰减在这里以分贝(dB)为单位;即(2)当时为通常意义上的截止频率。
(3)在滤波器设计中常选用归一化的频率,即2、巴特沃斯低通滤波器设计实质根据设计指标要求,,,确定归一化巴特沃斯低通滤波器幅度平方函数中的待定系数C及滤波器的阶数N;然后再根据幅度平方函数确定巴特沃斯低通滤波器的传递函数H(s)。
(1)将实际频率归一化得,,再根据已知的,,幅度平方函数确定C和N。
(2)求C和N由并带入,,,得即因为,所以由两边取对数得:其中这样可以求出C和N。
注意:当时,,即C=1,此时巴特沃斯滤波器只剩下一个参数N。
(3)确定巴特沃斯滤波器的传递函数H(p)。
由于由,解得极点为:将p左半平面的极点赋予即其中为了便于设计,工程上已将当时,各阶巴特沃斯低通滤波器系统函数设计成表格供查阅,该表如表5-1所示。
巴特沃斯低通滤波器

巴特沃斯低通滤波器简介巴特沃斯低通滤波器(Butterworth low-pass filter)是一种常用的模拟滤波器,被广泛应用于信号处理和电子系统中。
它的设计原则是在通带中具有平坦的幅频特性,而在截止频率处具有最大衰减。
这种滤波器的设计目的是能够尽可能滤除高频噪声,而保留低频信号。
巴特沃斯滤波器的特性巴特沃斯低通滤波器具有以下特性:•通带幅度为1:在通带中,滤波器的增益保持不变,也就是幅度为1。
•幅度频率响应的过渡带是由通带到停带的渐变区域,没有任何波纹。
•幅度频率响应在通带之外都有指数衰减。
•巴特沃斯滤波器是最平滑的滤波器之一,没有任何截止角陡峭度。
巴特沃斯滤波器的传递函数巴特沃斯低通滤波器的传递函数由下式给出:H(s) = 1 / (1 + (s / ωc)^2n)^0.5其中,H(s)为滤波器的传递函数,s为复变量,ωc为截止频率,n为滤波器的阶数。
阶数决定了滤波器的过渡带宽度和滤波特性。
巴特沃斯滤波器设计步骤巴特沃斯滤波器的设计步骤如下:1.确定所需滤波器的阶数和截止频率。
2.根据阶数和截止频率选择巴特沃斯滤波器的标准传递函数,可以从经验图表或计算公式中得到。
3.将标准传递函数的复频域变量进行频率缩放,以得到实际的传递函数。
4.将传递函数进行因式分解,得到一系列一阶巴特沃斯滤波器的传递函数。
5.根据一阶传递函数设计电路原型。
6.将一阶电路原型按照阶数进行级联或并联,构成所需的滤波器电路。
巴特沃斯滤波器的优点和缺点巴特沃斯低通滤波器具有以下优点:•平坦的传递特性:在通带中,滤波器的增益保持不变,不会引入频率响应的波纹或衰减。
•平滑的过渡带:巴特沃斯滤波器的过渡带具有指数衰减特性,没有任何波纹或突变。
•简单的设计:巴特沃斯滤波器的设计步骤相对简单,可以通过标准传递函数和电路原型进行设计。
然而,巴特沃斯滤波器也具有一些缺点:•较大的阶数:为了达到较陡的阻带衰减,巴特沃斯滤波器需要较高的阶数,导致电路复杂度增加。
巴特沃斯低通滤波器设计

计算机科学与技术学院数字信号处理课程作业学号:S*********专业:计算机科学与技术学生:董程凤任课教师:丽颖教授2015年12月巴特沃斯低通滤波器设计摘要:本文分析了国外数字滤波器技术的应用现状与发展趋势,介绍了低通滤波器的基本结构和常见的几种低通滤波器的设计比较,重点介绍了巴特沃斯低通滤波器。
首先分析了巴特沃斯低通滤波器的特性,然后用MATLAB的信号处理工具箱提供的函数设计了巴特沃斯低通滤波器,使得巴特沃斯滤波器的设计变得更加简单、快捷、直观。
关键词:低通滤波器,巴特沃斯低通滤波器,MATLAB1.引言在信号处理过程中,所处理的信号往往混有噪音,从接受到的信号中消除或减弱噪音是信号传输和处理中十分重要的问题。
根据有用信号和噪音的不同特性,提取有用信号灯过程成为滤波,实现滤波功能的系统称为滤波器。
在近代电信设备和各类控制系统中,滤波器应用极为广泛,例如,滤波器最早应用于语音处理,除此之外,还应用于图像处理、通信、音视频压缩和生物医学信号处理等领域中。
滤波技术是数字信号分析、处理技术的重要分支。
无论是信号的获取、传输,还是信号的处理和交换都离不开滤波技术,它对信号安全可靠和有效灵活地传输是至关重要的。
根据滤波器的选频作用可以将它分为低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
低通滤波器和高通滤波器是滤波器的两种最基本的形式,其它的滤波器都可以分解为这两种类型的滤波器,例如:低通滤波器与高通滤波器的串联为带通滤波器,低通滤波器与高通滤波器的并联为带阻滤波器。
根据“最佳逼近特性”标准还可以把滤波器分为巴特沃斯滤波器、切比雪夫滤波器和贝塞尔滤波器。
巴特沃斯滤波器是一种具有最大平坦幅度响应的低通滤波器,它广泛应用于通信领域、电测中,目前人们已经成功地将巴特沃斯低通滤波器应用于电动测试中。
2.低通滤波器2.1滤波器的基本概念从输入信号中滤出噪声和干扰以提取有用信息的过程称为滤波,相应的装置称为滤波器。
巴特沃斯低通滤波电路设计

巴特沃斯低通滤波电路设计:
巴特沃斯低通滤波电路的设计主要包括以下几个步骤:
1.确定系统函数的极点:巴特沃斯滤波器的极点位于Z平面的单位圆上,因此可以通
过选取适当的滤波器阶数和电气参数,使得滤波器的极点位于单位圆上。
2.设计传递函数:根据滤波器的性能要求,如通带增益、阻带增益、过渡带宽度等,
设计出传递函数。
巴特沃斯滤波器的传递函数具有固定的形式,可以通过选取电气参数来调整其性能。
3.实现电路结构:将设计好的传递函数转换为实际电路结构。
根据不同的电路形式,
可以选择不同的电路元件和结构,如运算放大器、RC电路等。
4.参数调整:对电路中的元件参数进行适当调整,以保证滤波器的性能符合设计要求。
参数调整是滤波器设计中非常关键的一步,需要通过实验和仿真反复验证和调整。
5.测试和验证:对设计好的滤波器进行测试和验证,包括频率响应、相位响应、群延
迟等性能指标的测试。
如果测试结果不符合设计要求,需要对电路或参数进行调整。
八阶巴特沃斯低通滤波器的设计方法

八阶巴特沃斯低通滤波器的设计方法设计八阶巴特沃斯低通滤波器可以通过以下步骤进行:
1. 确定滤波器的规格:首先确定滤波器的截止频率和通带衰减。
截止频率是指滤波器开始降低信号幅度的频率,通带衰减是指滤波器在通带内允许的最大幅度变化。
2. 计算极点位置:使用巴特沃斯滤波器的公式可以计算出滤波器极点的位置。
对于八阶低通滤波器,共有四对共轭极点。
这些极点会决定滤波器的频率响应。
3. 进行归一化:对于滤波器的极点位置,需要对其进行归一化处理,将其转换为标准低通滤波器的情况。
4. 进行极点频率转换:通过将归一化后的极点位置转换为实际的截止频率,即可得到实际滤波器的极点位置。
5. 构造传递函数:使用极点位置构造滤波器的传递函数,可以表示为巴特沃斯多项式的形式。
6. 计算滤波器系数:通过将传递函数展开并与标准低通滤波器的传递函数进行比较,可以计算滤波器的系数。
7. 实施滤波器:将计算得到的滤波器系数应用于数字滤波器的差分方程中,从而实现滤波器的效果。
需要注意的是,设计巴特沃斯滤波器需要一定的信号处理和滤波器设计知识。
如果不熟悉滤波器设计或数字信号处理的相关概念,建议咨询专业的工程师或使用现成的滤波器设计软件来完成滤波器设计任务。
巴特沃斯(Butterworth)滤波器(1)

巴特沃斯(Butterworth)滤波器(1)
下⾯深⼊浅出讲⼀下Butterworth原理及其代码编写。
1. ⾸先考虑⼀个归⼀化的低通滤波器(截⽌频率是1),其幅度公式如下:
当n->∞时,得到⼀个理想的低通滤波反馈: ω<1时,增益为1;ω>1时,增益为1;ω=1时,增益为0.707。
如下图所⽰:
将s=jω带⼊上式得:
根据以下三个公式
a. ,这⾥取σ=0
b.
c. 拉普拉斯变换在虚轴s=jω上的性质:
可以得到:
因此极点(分母为0的解)为:
根据和得到:
因此可以求得极点在单位圆上:
如果k从0开始的话,上式括号⾥可以写作2k+n+1:
由于我们只对H(s)感兴趣,⽽不考虑H(-s)。
因此低通滤波器的极点全部在负实半平⾯单位圆上:
该滤波器的传递函数为
下⾯是n=1到4阶的极点位置:
例如四阶Butterworth低通滤波器的极点所在⾓度为:
5π/8, 7π/8, 9π/8, 11π/8
极点位置在:
因此传递函数为:
1到10阶的Butterworth多项式因⼦表格如下:
以上我们考虑的是幅度-3分贝时的截⽌频率为1时的情况:
其它截⽌频率可将传递函数中的s替换为:
例如⼆阶截⽌频率为100的传递函数为:。
巴特沃斯低通滤波器公式 巴特沃斯低通滤波器设计原理

巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
关于“巴特沃斯低通滤波器公式巴特沃斯低通滤波器设计原理”的详细说明。
1.巴特沃斯低通滤波器公式
巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:
其中, = 滤波器的阶数= 截止频率= 振幅下降为-3分贝时的频率=通频带边缘频率在通频带边缘的数值。
2.巴特沃斯低通滤波器设计原理
巴特沃斯型低通滤波器在现代设计方法设计的滤波器中,是最为有名的滤波器,由于它设计简单,性能方面又没有明显的缺点,又因它对构成滤波器的元件Q值较低,因而易于制作且达到设计性能,因而得到了广泛应用。
其中,巴特沃斯滤波器的特点是通频带的频率响应曲线最平滑。
滤波器的截止频率的变换是通过先求出待设计滤波器的截止频率与基准滤波器的截止频率的比值M,再用这个M去除滤波器中的所有元件值来实现的,其计算公式如下:M=待设计滤波器的截止频率/基准滤波器的截止频率。
滤波器的特征阻抗的变换是通过先求出待设计滤波器的特征阻抗与基准滤波器的特征阻抗的比值K,再用这个K去乘基准滤波器中的所有电感元件值和用这个K去除基准滤波器中的
所有电容元件值来实现的。
巴特沃斯滤波器原理
二级巴特沃斯低通滤波器目录[隐藏]∙ 1 巴特沃斯滤波器的特性∙ 2 传递函数o 2.1 根据衰减度求滤波器的阶数o 2.2 幅度最平坦的滤波器o 2.3 高频衰减∙ 3 实例∙ 4 规一化的巴特沃斯多项式∙ 5 与其他类型滤波器的比较巴特沃斯滤波器的特性巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
在振幅的对数对角频率的波得图上,从某一边界角频率开始,振幅随着角频率的增加而逐步减少,趋向负无穷大。
一阶巴特沃斯滤波器的衰减率为每倍频6分贝,每十倍频20分贝。
二阶巴特沃斯滤波器的衰减率为每倍频12分贝、三阶巴特沃斯滤波器的衰减率为每倍频18分贝、如此类推。
巴特沃斯滤波器的振幅对角频率单调下降,并且也是唯一的无论阶数,振幅对角频率曲线都保持同样的形状的滤波器。
只不过滤波器阶数越高,在阻频带振幅衰减速度越快。
其他滤波器高阶的振幅对角频率图和低级数的振幅对角频率有不同的形状。
传递函数巴特沃斯低通滤波器可用如下振幅的平方对频率的公式表示:其中, n = 滤波器的阶数ωc =截止频率=振幅下降为-3分贝时的频率ωp = 通频带边缘频率1/(1 + ε2) = |H(ω)|2在通频带边缘的数值.在二维复平面上在s = jω点的数值= |H(ω)|2, 因此通过解析延拓:上述函数的极点等距离地分布在半径为ωc的圆上k = 0, 1, 2, ....., n-1因此,k = 0, 1, 2, ...., n-1n阶巴特沃斯低通滤波器的振幅和频率关系可用如下的公式表示:其中:∙G表示滤波器的放大率,∙H表示转移函数,∙j是虚数单位,∙n表示滤波器的级数,∙ω是信号的角频率,以弧度/秒为单位,∙ωc是振幅下降3分贝时的截止频率。
令截止频率ωc = 1), 将上列公式规定一化成为:根据衰减度求滤波器的阶数令1/A=G n(ω)例:在(ω) = 2 时G n(ω)=0.005A= 200, n=7.6, 取大一号整数,即需要8 阶巴特沃斯滤波器。
基于Pspice的八阶巴特沃斯低通滤波器设计与优化

L PBW :L PBW (vdb (vout) ,3)
图 3 滤波器电路优化结果 优化结果如图 3 所示 ,系统共进行了 6 次迭代 ,调用了 26 次电路模拟程序 。由图 3 的结果可见 ,如果 8 个待调整 的元器件参数分别取为优化设计值 : R1Val = 1. 30165 、R4Val = 12. 9892 、R5Val = 1. 42624k 、 R8Val = 6. 40001 、R9Val = 956. 95 、R12Val = 7. 20543k 、 R13Val = 958. 982 、R14Val = 5. 28602k ,可以使 2 个设计指标 达到 :
山西电子技术 应用实践
2006 年第 3 期
基于 Pspice 的八阶巴特沃斯低通滤波器设计与优化
叶 榆 贺国权
(涪陵师范学院物理学及电子信息工程系 ,重庆 408003)
摘 要 :介绍了低通滤波器的原理 ,采用有源滤波器的快速实用设计方法设计了八阶巴特沃斯低通滤波器 ,并 用 Pspice 进行了电路仿真分析和优化设计 ,仿真结果与实际测试基本吻合 ,对滤波器的设计具有实际指导意义 。
给定截止频率 f c ( Hz ) , 增益 G , 阶数 n 和滤波器类型 后 ,按下面的步骤设计参数 :
第一步 :按表 2[5 ]选择二阶基本节电容 C 值 , f c = 1MHz = 1 ×106 Hz ,故选取 C = 100p F ,由下式计算简化设计参数 K。
K
=
100 f cC
=
1
×106
5) 在 w = 0 处平方幅度响应的各级导数均存在 , 且等 于 0 ;因此| H ( jw ) | 2 在该点上取得最大值 ,且具有最大平坦 特性 。
巴特沃斯滤波过调-概述说明以及解释

巴特沃斯滤波过调-概述说明以及解释1.引言1.1 概述巴特沃斯滤波器是一种常用的数字信号处理方法,其原理是基于巴特沃斯滤波器设计的。
巴特沃斯滤波器是一种理想的滤波器,能够对信号进行频率域的调整,从而实现对信号的频率特性的控制。
然而,在实际应用中,巴特沃斯滤波器的过调问题却是一个不可忽视的挑战。
过调是指巴特沃斯滤波器在滤波过程中对信号的过度调整或失真现象。
这种失真可能导致输出信号频谱发生变化,从而影响对信号的准确处理和分析。
过调问题在实际应用中非常常见,特别是在对信号进行高频或低频滤波时更加突出。
本文旨在通过对巴特沃斯滤波器的原理和过调问题进行分析,探讨过调问题的成因和对应的解决方案,从而提供有效的指导和建议,帮助读者更好地理解和应用巴特沃斯滤波器。
在第二节中,我们将详细介绍巴特沃斯滤波器的原理,包括其基本特性、滤波器的传递函数和其在频率域上的调整能力。
接着,我们将在第三节中深入分析巴特沃斯滤波器的过调问题,探究其形成的原因以及可能的影响。
在最后一节中,我们将总结本文的要点,并提出解决巴特沃斯滤波器过调问题的有效方案。
通过本文的阅读,读者将能够更好地理解巴特沃斯滤波器的原理和应用,并掌握解决过调问题的方法和策略。
无论是从理论研究的角度,还是从实际应用的需求考虑,对巴特沃斯滤波器过调问题的深入认识都具有重要意义。
接下来,让我们一起深入探索巴特沃斯滤波器过调问题的奥秘。
1.2文章结构文章结构部分的内容可以如下编写:1.2 文章结构本篇文章主要分为引言、正文和结论三个部分,具体结构如下:1. 引言引言部分主要对本文的背景和目的进行介绍。
首先,概述了巴特沃斯滤波的基本原理和应用场景。
在介绍了滤波原理后,本文将主要讨论巴特沃斯滤波的一个常见问题——过调问题,并提出解决方案。
最后,明确了本文的目的,即通过对巴特沃斯滤波过调问题的分析和解决方案的探讨,帮助读者更好地理解和应用巴特沃斯滤波技术。
2. 正文正文部分将详细介绍巴特沃斯滤波的原理以及过调问题的分析。
巴特沃兹低通滤波8极点

Rev.0“Circuits from the Lab” from Analog Devices have been designed and built by Analog Devices engineers. Standard engineering practices have been employed in the design and construction of each circuit, and their function and performance have been tested and verified in a lab environment at room temperature. However, you are solely responsible for testing the circuit and determining its suitability and applicability for your use and application. Accordingly, in no event shall Analog Devices be liable for direct, indirect, special, incidental, consequential or One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A. Tel: 781.329.4700 电路笔记CN-0127连接/参考器件利用ADI 公司产品进行电路设计双通道、低功耗、精密、轨到轨输出运算放大器AD8622放心运用这些配套产品迅速完成设计。
欲获得更多信息和技术支持,请拨打4006-100-006或访问ADA4062-2低功耗JFET 输入运算放大器/zh/circuits 。
利用运算放大器AD8622和ADA4062-2构建精密、低噪声、高增益8极点有源低通滤波器电路功能与优势该滤波器提供业界功耗最低的解决方案(使用±15 V 电源时,总静态电流为760 μA ),不仅具有精密和低噪声特性,而且提供高增益。
巴特沃斯数字低通滤波器要点

巴特沃斯数字低通滤波器要点⽬录1.题⽬.......................................................................................... .22.要求 (2)3.设计原理 (2)3.1 数字滤波器基本概念 (2)3.2 数字滤波器⼯作原理 (2)3.3 巴特沃斯滤波器设计原理 (2)3.4脉冲响应不法 (4)3.5实验所⽤MATLAB函数说明 (5)4.设计思路 (6)5、实验内容 (6)5.1实验程序 (6)5.2实验结果分析 (10)6.⼼得体会 (10)7.参考⽂献 (10)⼀、题⽬:巴特沃斯数字低通滤波器⼆、要求:利⽤脉冲响应不变法设计巴特沃斯数字低通滤波器,通带截⽌频率100HZ,采样频率1000HZ ,通带最⼤衰减为0.5HZ ,阻带最⼩衰减为10HZ ,画出幅频、相频相应相应曲线。
并假设⼀个信号x(t)=sin(2*pi*f1*t)+sin(2*pi*f2*t),其中f1=50HZ,f2=200HZ 。
⽤此信号验证滤波器设计的正确性。
三、设计原理1、数字滤波器的基本概念所谓数字滤波器,是指输⼊、输出均为数字信号,通过数值运算处理改变输⼊信号所含频率成分的相对⽐例,或者滤波器除某些频率成分的数字器件或程序,因此,数字滤波的概念和模拟滤波相同,只是的形式和实现滤波⽅法不同。
正因为数字滤波通过数值运算实现滤波,所以数字滤波处理精度⾼、稳定、体积⼩、质量轻、灵活、不存在阻抗匹配问题,可以实验模拟滤波器⽆法实现的特殊滤波功能。
如果要处理的是模拟信号,可通过A\DC 和D\AC,在信号形式上进⾏匹配转换,同样可以使⽤数字滤波器对模拟信号进⾏滤波。
2、数字滤波器的⼯作原理数字滤波器是⼀个离散时间系统,输⼊x(n)是⼀个时间序列,输出y(n)也是⼀个时间序列。
如数字滤波器的系统函数为H(Z),其脉冲响应为h(n),则在时间域内存在下列关系y(n)=x(n) h(n) 在Z 域内,输⼊输出存在下列关系 Y(Z)=H(Z)X(Z)式中,X(Z),Y(Z)分别为输⼊x(n)和输出y(n)的Z 变换。
巴特沃斯低通滤波器查表法

巴特沃斯低通滤波器查表法巴特沃斯低通滤波器是一种常用的信号处理工具,可以用于去除高频噪声,保留信号中的低频成分。
在实际应用中,我们常常需要根据需要的滤波参数来设计滤波器,而巴特沃斯低通滤波器查表法就是一种常用的设计方法。
巴特沃斯低通滤波器查表法的基本原理是根据巴特沃斯低通滤波器的传递函数公式,计算出滤波器的各个参数,然后使用查表法得到具体的滤波器系数。
下面将详细介绍巴特沃斯低通滤波器查表法的步骤和应用。
我们需要确定滤波器的截止频率和阶数。
截止频率是指在滤波器输出信号中,高于该频率的信号将被滤除。
阶数是指滤波器的阶次,阶次越高,滤波器的滤波效果越好。
接下来,根据所需的滤波器截止频率和阶数,查找巴特沃斯低通滤波器设计表。
设计表中记录了不同截止频率和阶数下的滤波器参数。
根据表中给出的参数,我们可以得到滤波器的传递函数。
然后,根据滤波器的传递函数,计算出滤波器的各个参数,包括截止频率、阻带增益、极点和零点等。
这些参数的计算需要一定的数学公式和计算方法,但根据要求,我们在这里不输出公式。
需要注意的是,不同的阶数和截止频率对应不同的参数计算方式。
根据计算得到的滤波器参数,使用查表法得到具体的滤波器系数。
查表法是一种将连续函数近似离散化的方法,通过查表可以得到滤波器的离散表示,方便实际应用。
查表法的具体步骤是,将滤波器的传递函数按照一定的步长进行离散化,然后查表得到离散的滤波器系数。
巴特沃斯低通滤波器查表法的优点是设计简单、计算快捷,适用于实时滤波和嵌入式系统等资源有限的应用场景。
但也需要注意的是,查表法得到的滤波器系数是近似值,滤波器的实际性能可能会受到一定的影响。
因此,在具体应用中需要根据实际需求进行调整和优化。
巴特沃斯低通滤波器查表法是一种常用的滤波器设计方法,通过查表法可以方便地得到滤波器的离散表示。
在实际应用中,我们可以根据需要的滤波参数选择对应的查表结果,从而实现滤波器的设计和实现。
这种方法简单高效,适用于资源有限的系统。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Rev.0“Circuits from the Lab” from Analog Devices have been designed and built by Analog Devices engineers. Standard engineering practices have been employed in the design and construction of each circuit, and their function and performance have been tested and verified in a lab environment at room temperature. However, you are solely responsible for testing the circuit and determining its suitability and applicability for your use and application. Accordingly, in no event shall Analog Devices be liable for direct, indirect, special, incidental, consequential or One Technology Way, P.O. Box 9106, Norwood, MA 02062-9106, U.S.A. Tel: 781.329.4700 电路笔记CN-0127连接/参考器件利用ADI 公司产品进行电路设计双通道、低功耗、精密、轨到轨输出运算放大器AD8622放心运用这些配套产品迅速完成设计。
欲获得更多信息和技术支持,请拨打4006-100-006或访问ADA4062-2低功耗JFET 输入运算放大器/zh/circuits 。
利用运算放大器AD8622和ADA4062-2构建精密、低噪声、高增益8极点有源低通滤波器电路功能与优势该滤波器提供业界功耗最低的解决方案(使用±15 V 电源时,总静态电流为760 μA ),不仅具有精密和低噪声特性,而且提供高增益。
它使用两个双通道运算放大器,而不是一个四通道运算放大器,这也使得PCB 布局更加灵活、简便。
ADA4062-2还提供1.3 mm × 1.6 mm LFCSP 封装(小于SC-70),是业界最小的JFET 输入运算放大器。
因此,设计人员不必担心使用两个双通道放大器比使用一个四通道放大器要占用更多电路板空间的问题。
本电路是一个精密、低噪声、低功耗、8极点有源低通滤波器,其增益为40 dB ,它采用Sallen-Key 拓扑结构,可提供巴特沃兹响应。
本电路不是采用一个四通道运算放大器简单构建,而是精选双通道运算放大器组合来提供更加优化的解决方案。
低噪声(0.2 μV 峰峰值,0.1 Hz 至10 Hz )、低失调电压(典型值10 μV )运算放大器AD8622用于输入和增益级。
相对于其功耗(±15 V 时每个放大器215 μA ),AD8622提供的失调电压和噪声为业界最低。
JFET 输入运算放大器低通滤波器经常用作数据采集系统中的抗混叠滤波器,或者用作噪声滤波器以限制高频噪声。
巴特沃兹滤波器是一种幅度响应极为平坦的滤波器,通带和阻带中均无纹波。
然而,与其它有纹波的响应相比,无纹波是以频率响应的过渡带更宽为代价而实现的,因此,通常需要高阶巴特沃兹滤波器。
ADA4062-2用于最后两级,其功耗同样很低(每个放大器165 μA )。
ADA4062-2的低输入偏置电流允许最后两级使用较大的电阻和较小的电容,从而减小无源器件板的面积。
图1.利用AD8622和ADA4062-2构建的8极点Sallen Key 巴特沃兹低通滤波器,V SY = ±15 V (未显示去耦)CN-0127 电路笔记有源滤波器设计比无源滤波器设计更为复杂,因为前者必须选择拓扑结构和适当的运算放大器。
然而,有源设计可提供信号增益,而且无需实现低频无源滤波器所要求的大电感和电容。
Sallen-Key拓扑结构也称为电压控制电压源(VCVS)结构,其设计简单,电路元件少,在业界广为使用。
所示滤波器的截止频率f C为10 Hz,总增益为100 V/V或40 dB。
使用标准滤波器设计技术,可以将该设计轻松调整到其它频率。
电路描述该8极点低通滤波器具有4个复数共轭极点对,由4个双极点Sallen Key低通滤波器级联而成。
A、B部分配置为增益各为10的双极点低通滤波器,C、D部分则配置为单位增益滤波器。
级联的排列非常重要。
如果需要增益,则应在前面几级产生增益,以便降低输出端的总噪声。
另一个避免运算放大器饱和或削波的极佳原则是按照Q(品质因素)由小到大的顺序排列各级。
表1显示巴特沃兹滤波器各级的Q要求和极点位置。
另外,有关s平面上的极点位置和不同阶滤波器的Q要求,请参考线性电路设计手册第8章(“模拟滤波器”)。
表1:8极点巴特沃兹低通滤波器设计表部分极点QA - 0.9808 ± j 0.1951 0.5098B - 0.8315 ± j 0.5556 0.6013C - 0.5556 ± j 0.8315 0.9000D - 0.1951 ± j 0.9808 2.5628为了降低成本和减小电路板空间,一般使用一个四通道放大器来实现8极点滤波器。
然而,也应当考虑利用两个双通道放大器的方案,因为这会带来其它好处。
使用两个双通道运算放大器时,PCB布局更简单,有时还可以减少电路板层数。
走线可以分散分布,从而降低寄生电容和串扰。
滤波器各级都有不同的增益、带宽、噪声和直流精度要求,因此必须为各级选择适当的放大器。
滤波器第一级应使用低噪声和低失调电压运算放大器,因为来自第一级的噪声和失调电压会被所有四级的噪声增益放大。
AD8622是一款双通道、低功耗、精密运算放大器。
电源电压为±15 V时,0.1 Hz至10 Hz电压噪声为0.2 μV峰峰值,失调电压典型值仅为10 μV。
AD8622具有直流精度和低噪声特性,因而成为滤波器前两级的不错选择。
前两级选择较小的电阻,以降低其对滤波器总噪声的热噪声贡献。
当滤波器总增益集中在前两级时,其余级对运放的噪声要求就不那么重要,可以使用成本和精度较低的运算放大器。
C、D部分选择低功耗放大器ADA4062-2。
它具有JFET差分对输入,输入阻抗较高,偏置电流非常低。
由于后两级的噪声要求降低,而且ADA4062-2的偏置电流非常低,因此可以使用较大的电阻值和较小的电容。
JFET的低输入偏置电流对电路的直流误差贡献极小。
一个双极点低通滤波器的截止频率f C和Q可以通过下式计算:一般来说,为使上述公式具有较高的精度,所选运算放大器的增益带宽积至少应比滤波器的f C、Q和增益的乘积大100倍。
为获得足够的全功率带宽,还需要考虑压摆率。
压摆率的通用计算公式为:对于10 Hz截止频率,AD8622和ADA4062-2均有足够的压摆率,不会发生压摆率限制现象。
选择适当的电阻和电容值也很重要。
较大电阻会导致热噪声增加。
虽然可以使用较小的电容来实现特定的f C,但现在放大器的输入电容可能很大。
该电容至少应比放大器输入电容大100倍。
电阻和电容对于确定性能随工艺容差、时间和温度的变化非常重要。
建议使用1%或更佳容差的电阻以及5%或更佳容差的电容。
还需要旁路电容(图中未显示)。
本例中,每个双通道运放的每个电源引脚上都应有一个10 μF钽电容与一个0.1 μF陶瓷电容并联。
有关正确去耦技术的详细说明,请参考教程MT-101。
电路笔记CN-0127(Continued from first page) "Circuits from the Lab" are intended only for use with Analog Devices products and are the intellectual property of Analog Devices or its licensors. While you may use the "Circuits from the Lab" in the design of your product, no other license is granted by implication or otherwise under any patents or other intellectual property by application or use of the "Circuits from the Lab". Information furnished by Analog Devices is believed to be accurate and reliable. However, "Circuits from the Lab" are supplied "as is" and without warranties of any kind, express, implied, or statutory including, but not limited to, any implied warranty of merchantability, noninfringement or fitness for a particular purpose and no responsibility is assumed by Analog Devices for their use, nor for any infringements of patents or other rights of third parties that may result from their use. Analog Devices reserves the right to change any "Circuits from the Lab" at any time without notice, but is under no obligation to do so. Trademarks and registered trademarks are the property of their respective owners.©2010 Analo 进一步阅读图2显示该低通滤波器的频率响应实测结果,其中: V AN-202 Application Note, An IC Amplifier User’s Guide to Decoupling, Grounding, and Making Things Go Right for a Change . Analog Devices.1为第一级的输出。
