如何证明正多面体只有正四面体 正六面体 正十二面体 和正二十面体
什么是多面体有哪些常见类型

什么是多面体有哪些常见类型在我们的日常生活和数学世界中,多面体是一个常见而又有趣的概念。
那到底什么是多面体呢?简单来说,多面体是由多个平面多边形所围成的立体图形。
多面体的每个平面多边形都被称为多面体的面,两个面的公共边叫做多面体的棱,多条棱的公共顶点叫做多面体的顶点。
多面体有着各种各样的类型,下面我们就来介绍一些常见的多面体。
首先,我们来认识一下棱柱。
棱柱是一个相当常见的多面体类型。
它有两个互相平行且全等的底面,侧面都是平行四边形。
如果棱柱的底面是三角形,那就叫做三棱柱;底面是四边形,那就是四棱柱,以此类推。
比如,我们常见的长方体就是一种四棱柱,它的六个面都是矩形。
接下来是棱锥。
棱锥有一个多边形的底面,其余各面都是有一个公共顶点的三角形。
如果底面是三角形,那就是三棱锥,也叫四面体,因为它有四个面。
如果底面是四边形,那就是四棱锥。
棱锥的顶点到底面的距离叫做棱锥的高。
还有棱台,棱台可以看作是用一个平行于棱锥底面的平面去截棱锥,截面和底面之间的部分就是棱台。
棱台的上下底面是相似的多边形。
再说说正多面体。
正多面体是指各个面都是全等的正多边形,并且各个多面角都是全等的多面角。
正多面体只有五种,分别是正四面体、正六面体(也就是正方体)、正八面体、正十二面体和正二十面体。
正四面体的四个面都是等边三角形,它是最简单也是最对称的正多面体。
正方体大家就更熟悉了,六个面都是正方形,十二条棱长度相等,八个顶点。
正八面体是由八个等边三角形围成的,它有六个顶点。
正十二面体有十二个正五边形的面,二十个顶点。
正二十面体则由二十个等边三角形组成,有十二个顶点。
多面体在我们的生活中有着广泛的应用。
在建筑设计中,许多建筑物的外形都可以看作是由不同的多面体组合而成。
比如,一些现代的体育馆、展览馆,其独特的造型往往包含了各种多面体的元素。
在包装设计中,多面体的结构也经常被运用,以达到节省材料、增加稳定性等目的。
在数学研究中,多面体的性质和相关定理也是一个重要的领域。
正多面体只有5种的又一证法

vt
= 2e ,即
v
=
2e t
.
正多面体每个面由 h 条边围成 ,则 f h =
2e ,即
f
=
2e h
.
把
v
=
2e t
,
f
=
2 e代入
h
(1)
式得
2e t
-
e
+
2e h
=
2
,
∴e
=
2
h
-
2 ht ht
+
2
t
(2)由Biblioteka (2) 得 2 h - ht + 2 t > 0 ,
32
数 学 通 讯 2003 年第 1 期
正多面体只有 5 种的又一证法
周素芬
(集美中学 ,福建 361021)
中图分类号 :O123. 3 文献标识码 :A 文章编号 :0488 - 7395 (2003) 01 - 0032 - 01
瑞士数学家欧拉在 1752 年发现各种正
多面体均有的关系 :
v - e + f = 2
(1)
其中 v , e , f 分别表示凸多面体的顶点数 、棱
数及面数. (1) 式后人称为欧拉公式 , 它在空
间图形及图论中有许多重要应用.
所谓正多面体是指多面体的各个面均是
全等正多边形 , 每个正多面体的各边的长和 顶角的交角均相等. 那么空间有多少种不同 正多面体 ? 本文对此问题给出了一种新的简 便论证方法.
正四面体 正八面体 正六面体
正十二面体 正二十面体 图 1 正多面体
参考文献 :
正多面体证明

正多面体只有正四面体、正六面体、正八面体、正十二面体、正二十面体五种。
证明
顶点数V,面数F,棱数E
设正多面体的每个面是正n边形,每个顶点有m条棱。
棱数E应是面数F与n的积的一半(每两面共用一条棱),即
nF=2E--------------①
同时,E应是顶点数V与m的积的一半,即
mV=2E--------------②
由①、②,得
F=2E/n,V=2E/m,
代入欧拉公式V+F-E=2,
有
2E/m+2E/n-E=2
整理后,得1/m+1/n=1/2+1/E.
由于E是正整数,所以1/E>0。
因此
1/m+1/n>1/2--------------③
说明m,n不能同时大于3,否则③不成立。
另一方面,由于m和n的意义(正多面体一个顶点处的棱数与多边形的边数)知,m≥3且n≥3。
因此m和n至少有一个等于3当m=3时,因为1/n>1/2-1/3=1/6,n又是正整数,所以n只能是3,4,5
同理n=3,m也只能是3,4,5
所以有以下几种情况:
n m类型
33正四面体
43正六面体
34正八面体
53正十二面体
35正二十面体
由于上述5种多面体确实可以用几何方法作出,而不可能有其他种类的正多面体所以正多面体只有5种。
立体几何——正多面体专题

立体几何——正多面体专题
一、引言
立体几何研究了空间中的各种几何形状及其性质。
正多面体是指拥有相等大小的正多边形作为面的多面体。
本文将深入探讨正多面体的定义、分类及特性。
二、定义
正多面体是由相等的正多边形完全围成的几何体。
它们具有以下特点:
- 每个面都是相等的正多边形。
- 每个顶点都相连于相等数量的边。
- 每个边都与相等数量的面相接。
三、分类
根据面的数量,正多面体可以分为以下几类:
1.三个面:三角形棱柱和三角形棱锥。
2.四个面:四面体和正四面体。
3.八个面:八面体和正八面体。
4.二十个面:二十面体和正二十面体。
四、特性
正多面体具有一些独特的特性:
1.对称性:正多面体在各个面和顶点上具有对称性,这使其在空间中呈现出美感。
2.空间效率:正多面体在空间中填充效率高,因此在建筑、工程和科学领域具有广泛的应用。
3.共面性:正多面体的面都可以完全位于同一个平面内。
五、结论
正多面体作为立体几何中的重要概念,不仅具有美学价值,还有着实际应用。
通过了解正多面体的定义、分类及特性,我们可以更好地理解空间中的几何形状,并将其运用到实际场景中。
参考文献:
[1] 张三。
李四。
王五。
空间几何学导论[M]。
北京:科学出版社。
2010.
[2] 陈六。
赵七。
欧几里得几何学基础[M]。
上海:___。
2008.。
正多面体-高中数学知识点讲解
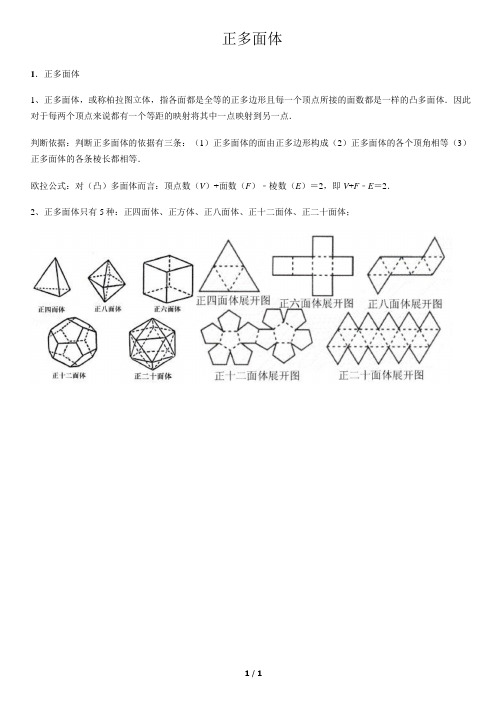
正多面体
1.正多面体
1、正多面体,或称柏拉图立体,指各面都是全等的正多边形且每一个顶点所接的面数都是一样的凸多面体.因此对于每两个顶点来说都有一个等距的映射将其中一点映射到另一点.
判断依据:判断正多面体的依据有三条:(1)正多面体的面由正多边形构成(2)正多面体的各个顶角相等(3)正多面体的各条棱长都相等.
欧拉公式:对(凸)多面体而言:顶点数(V)+面数(F)﹣棱数(E)=2,即V+F﹣E=2.
2、正多面体只有 5 种:正四面体、正方体、正八面体、正十二面体、正二十面体;
1/ 1。
常见正多面体总结-六面体八面体十二面体和二十面体
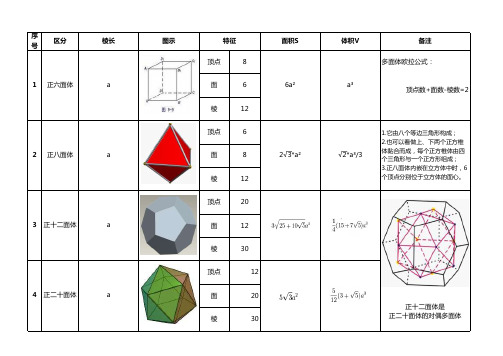
序号
区分
棱长
图示 顶点
特征ቤተ መጻሕፍቲ ባይዱ8 6 12 6 8 12 20 12 30 12 20 30
面积S
体积V
备注 多面体欧拉公式:
1
正六面体
a
面 棱 顶点
6a²
a³
顶点数+面数-棱数=2
2
正八面体
a
面 棱 顶点
2√3*a²
√2*a³/3
1.它由八个等边三角形构成; 2.也可以看做上、下两个正方椎 体黏合而成,每个正方椎体由四 个三角形与一个正方形组成; 3.正八面体内嵌在立方体中时,6 个顶点分别位于立方体的面心。
3
正十二面体
a
面 棱 顶点
4
正二十面体
a
面 棱
正十二面体是 正二十面体的对偶多面体
多面体欧拉定理的发现 (1)2

多面体欧拉定理的发现我们知道,平面多边形由它的边围成,它的顶点数与边数相等,按边数可以对多边形进行分类,同类的多边形具有某些相同的性质。
多面体是由它的面围成立体图形,这些面的交线形成棱,棱与棱相交形成顶点。
在研究多面体的分类等问题中,人们逐步发现它的顶点数,面数和棱数之间有特定的关系。
以下我们将体验这种关系的发现及证明过程。
探索研究问题1:下列共有五个正多面体,分别数出它们的顶点数V、面数F和棱数E,并填表1观察表中填出的数据,请找出顶点数V、面数F及棱数E之间的规律。
教师巡视指导,如正十二面体,先定面数E=12;再定棱数,每个面有5条棱,共有12×5=60条,由于每条棱都是两个面的公共边,所以上面的计算每条棱被算过两次,于是棱数E=60/2=30;最后算顶点数,每个顶点处连有三条棱,所以它共有3V条棱,又因为每条棱连着两个顶点,所以上面的计算每条棱被算过两次,因此实际上只有3V/2条棱,即E=3V/2,所以V=20。
表1中多面体的面数F都随顶点数目V的增大而增大吗?(不一定).请举例说明.(如八面体和立方体的顶点数由6增大到8,而面数由8减小到6).此时棱的数目呢?(棱数都是一样的).所以我们得到:棱的数目也并不随顶点数目的增大而增大.大家从表中还发现了其他的什么规律,请积极观察,勇于发言.(当多面体的棱数增加时,它的顶点与面数的变化也有一定规律).上面的归纳引导去猜想,棱数与顶点数+面数即E与V+F是否有某种关系,请大家按这个方向考察表中的数据,发现并归纳出它们都满足的关系.(积极验证,得出)V+F-E=2以上同学们得到的V+F-E=2这个关系式是由表1中的五种多面体得到,那么这个关系式对于其他的多面体是否也成立吗?请大家尽可能的画出多个其他多面体去验证.(许多同学可能举出前面学过的图形)四棱锥、五棱锥、六棱柱等.(教师应启发学生展开想象,举出更多的例子)一个三棱锥截去含3条棱的一个顶得到的图形、一个立方体截去一个角所得的图形等.好,同学们现在想象,例如:n棱锥在它的n边形面上增加一个“屋顶”或截去含n条棱的一个顶后,刚才的猜想是否成立?能证明吗?所得的多面体的棱数E为3n条,顶点数V为2n个,面数V为2+n 个,因2n +(2+n )-3n =2,故满足V +F -E =2这个关系式.请继续来观察下面的图形,填表2,并验证得出的公式工V +F -E =2_A(学生观察,数它们的顶点数V、面数F、棱数E,并填入表2,可能有些同学出错,教师在巡视时要及时给予指导,帮助学生填完)观察你们的数据,请验证这些图形是否符合前面找出的规律吗?其中哪些图形符合?一起来设想问题1和问题2中的图形.在某个橡皮膜上,当橡皮膜变形后,有的地方伸长、有的地方压缩,但不能破裂或折叠,橡皮膜上的图形的形状也跟着改变,这种图形的变化过程我们称之为连续变形.那么请大家试想这些图形中的哪些在连续变形中最后其表面可变为一个球面?问题1中的(1)~(5)和问题2中的(1)个图形表面经过连续变形能变为一个球面.请同学们继续设想问题2中⑴~⑻在连续变形中,其表面最后将变成什么图形?问题2中第⑻个图形;表面经过连续变形能变为环面像以上那些在连续变形中,表面能变为一个球面的多面体叫简单多面体.请大家判断我们前面所学的图哪些是简单多面体?棱柱、棱锥、正多面体、凸多面体是简单多面体.简单多面体的顶点数V、面数F的和与棱数E之间存在规律V+F -E=2.我们将它叫做欧拉公式,以上3个问题的解决让我们体会到了数学家欧拉发现V+F-E=2的过程.那么如何证明欧拉公式呢?请大家打开课本P65的欧拉公式证明方法中的一种,认真体会它的证明思路和其间用到的数学思想.(学生自学、教师查看,发现问题,收集问题下节课处理)在欧拉公式中,令f(p)=V+F-E。
正多面体证明范文

正多面体证明范文正多面体是指所有的面都是正多边形的立体形状。
在数学中,有五种常见的正多面体,分别是四面体、六面体(或立方体)、八面体、十二面体和二十面体。
下面将分别对这些正多面体进行证明。
首先来证明四面体是正多面体。
四面体由四个三角形组成,每个三角形都是正三角形,因此四面体的每个面都是正多边形。
此外,四面体的每个顶点处有三个面相交,且每个面都能通过相邻两个面沿边构建正角,满足正多面体的性质。
因此,四面体是正多面体。
接下来证明六面体(或立方体)是正多面体。
六面体由六个正方形组成,每个面都是正方形,因此满足正多面体的定义。
此外,六面体的每个顶点处有三个面相交,且每个面都能通过相邻两个面沿边构建正角,满足正多面体的性质。
因此,六面体是正多面体。
再来证明八面体是正多面体。
八面体由八个正三角形组成,每个面都是正三角形,满足正多面体的定义。
此外,八面体的每个顶点处有四个面相交,且每个面都能通过相邻三个面沿边构建正角,满足正多面体的性质。
因此,八面体是正多面体。
继续证明十二面体是正多面体。
十二面体由十二个正五边形组成,每个面都是正五边形,满足正多面体的定义。
此外,十二面体的每个顶点处有五个面相交,且每个面都能通过相邻四个面沿边构建正角,满足正多面体的性质。
因此,十二面体是正多面体。
最后证明二十面体是正多面体。
二十面体由二十个正三角形组成,每个面都是正三角形,满足正多面体的定义。
此外,二十面体的每个顶点处有五个面相交,且每个面都能通过相邻三个面沿边构建正角,满足正多面体的性质。
因此,二十面体是正多面体。
综上所述,四面体、六面体、八面体、十二面体和二十面体都是正多面体。
每个正多面体都有对应的面数、边数和顶点数,可以通过欧拉公式进行验证。
欧拉公式表达为:V+F-E=2,其中V代表顶点数,F代表面数,E代表边数。
对于正多面体,欧拉公式可以写为V+F-E=2、根据每个正多面体的顶点数、面数和边数计算,都能满足欧拉公式。
利用欧拉公式证明正多面体有且仅有5种

利用欧拉公式证明正多面体有且仅有5种正多面体是指所有面都是相等且全等的多面体,其中每个顶点的度数相等。
欧拉公式是描述多面体的顶点、边、面之间的关系的一个数学公式,可以用来推导正多面体的种类。
根据欧拉公式,一个多面体的顶点数(V)、边数(E)和面数(F)满足以下关系式:V-E+F=2首先,假设正多面体有n个面,m个顶点和k个边。
由于每个面都是正多边形,所以每个面的边数为p(p≥3),而每个顶点的度数为q(q≥3)。
由此可以得到以下关系:m = kp/2 (每条边连接两个顶点)n = mp/q (每个面包含p个边)将这些关系代入欧拉公式,得到m-m/q+n=2k-p/q+m/p=2将上述两个式子相加,消去m项,得到k+n-p/q+m/p-m/q=4k+n-(p/q)*(q/p)=4k+n-1=4k+n=5由此,我们得到了正多面体的另一个重要结论:正多面体的边数和面数之和等于5接下来,我们可以考虑不同的情况来讨论正多面体的种类。
情况1:假设正多面体的面数为3,则p/q=1/3,代入k+n=5,得到k=4-n。
根据以上条件,考虑正多面体的可能性。
-当n=3时,k=1,即一个正四面体。
-当n=4时,k=0,但是没有边的多面体是不存在的。
因此,不存在4个面的正多面体。
-当n=5时,k=-1,同样由于没有负数个边的多面体,所以也不存在5个面的正多面体。
结论1:没有三个面的正多面体。
情况2:假设正多面体的面数为4,则p/q=1/2,代入k+n=5,得到k=5-n。
根据以上条件,考虑正多面体的可能性。
-当n=3时,k=2,即一个正六面体。
-当n=4时,k=1,即一个正四面体。
-当n=5时,k=0,即一个正十二面体。
结论2:存在一个4个面的正多面体,即正四面体;存在一个6个面的正多面体,即正六面体;存在一个12个面的正多面体,即正十二面体。
情况3:假设正多面体的面数为5,则p/q=2/5,代入k+n=5,得到k=5-n。
正多面体的有关历史
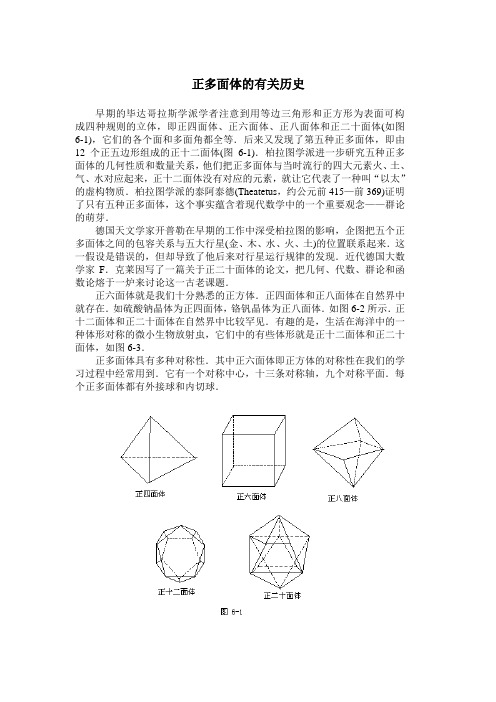
正多面体的有关历史早期的毕达哥拉斯学派学者注意到用等边三角形和正方形为表面可构成四种规则的立体,即正四面体、正六面体、正八面体和正二十面体(如图6-1),它们的各个面和多面角都全等.后来又发现了第五种正多面体,即由12个正五边形组成的正十二面体(图6-1).柏拉图学派进一步研究五种正多面体的几何性质和数量关系,他们把正多面体与当时流行的四大元素火、土、气、水对应起来,正十二面体没有对应的元素,就让它代表了一种叫“以太”的虚构物质.柏拉图学派的泰阿泰德(Theatetus,约公元前415—前369)证明了只有五种正多面体,这个事实蕴含着现代数学中的一个重要观念——群论的萌芽.德国天文学家开普勒在早期的工作中深受柏拉图的影响,企图把五个正多面体之间的包容关系与五大行星(金、木、水、火、土)的位置联系起来.这一假设是错误的,但却导致了他后来对行星运行规律的发现.近代德国大数学家F.克莱因写了一篇关于正二十面体的论文,把几何、代数、群论和函数论熔于一炉来讨论这一古老课题.正六面体就是我们十分熟悉的正方体.正四面体和正八面体在自然界中就存在.如硫酸钠晶体为正四面体,铬钒晶体为正八面体.如图6-2所示.正十二面体和正二十面体在自然界中比较罕见.有趣的是,生活在海洋中的一种体形对称的微小生物放射虫,它们中的有些体形就是正十二面体和正二十面体,如图6-3.正多面体具有多种对称性.其中正六面体即正方体的对称性在我们的学习过程中经常用到.它有一个对称中心,十三条对称轴,九个对称平面.每个正多面体都有外接球和内切球.在我国,最早介绍五种正多面体的是意大利传教士罗雅各(J.Rho,1593—1638),在1631年完成的《测量法义》和《比例规解》两书之中有记载.清初数学家梅文鼎根据罗雅谷书中提供的线索,在《几何补编》中详尽地研究了正多面体的性质,并订正了《比例规解》中关于正二十面体体积计算的错误.。
正多面体的施莱夫利符号

正多面体的施莱夫利符号
正多面体的施莱夫利符号(Schläfli symbol)用于描述和表示不同种类的正多面体的拓扑结构。
它由一组数字构成,每个数字表示每个顶点周围的边的数量。
以下是一些常见正多面体的施莱夫利符号:
1.正四面体(tetrahedron):{3, 3},每个顶点周围有3条边。
2.正六面体(hexahedron 或cube):{4, 3},每个顶点周围有
4条边。
3.正八面体(octahedron):{3, 4},每个顶点周围有3条边。
4.正十二面体(dodecahedron):{5, 3},每个顶点周围有5
条边。
5.正二十面体(icosahedron):{3, 5},每个顶点周围有3条
边。
施莱夫利符号通过明确和简洁的方式表示了正多面体的拓扑结构,它揭示了每个顶点周围边的数量和种类,对于研究和描述正多面体非常有用。
立体几何同步训练14多面体及欧拉公式

立体几何同步训练14多面体及欧拉公式欧拉公式是在立体几何中一个非常重要的定理,它描述了一个多面体的顶点数、边数和面数之间的关系。
欧拉公式的形式可以用如下的式子表示:V-E+F=2其中,V代表多面体的顶点数,E代表多面体的边数,F代表多面体的面数。
多面体是指一个由平面多边形所围成的立体体积,根据多边形的数量和形状不同,可以得到不同的多面体,例如正多面体、凸多面体和凹多面体等。
首先,我们来讨论一些常见的多面体。
1.正多面体:所有的面都是相等的正多边形,且每个顶点都相等,例如正方体、正八面体和正二十面体等。
所有的正多面体都具有着完全相同的顶点、边和面的数量。
2.非正多面体:所有的面不都是相等的正多边形,例如长方体、八面体和十二面体等。
相比于正多面体,非正多面体的顶点、边和面的数量可以有所不同。
3.凸多面体:多面体内部的所有点都位于多面体表面的同一侧。
一个常见的例子是立方体,它是一个边相等、面相等且角相等的凸多面体。
4.凹多面体:多面体内部的一些点位于多面体表面的两侧。
一个常见的例子是镂空的球。
根据欧拉公式,我们可以通过任意两个量确定多面体的第三个量。
假设我们知道多面体的顶点数和面数,我们就可以通过欧拉公式计算出边数。
同样地,如果我们知道多面体的边数和面数,我们也可以计算出顶点数。
例如,我们考虑一个正四面体。
它有4个面,因此F=4、每个面都是一个等边三角形,有3条边,所以E=3x4/2=6、通过欧拉公式,我们可以计算出这个正四面体有多少个顶点:V-6+4=2,因此V=4同样地,我们可以计算其他正多面体的顶点数、边数和面数。
欧拉公式在立体几何中有着广泛的应用。
它不仅可以用来计算多面体的未知量,还能帮助我们理解多面体的结构和性质。
在数学研究和实际应用中,欧拉公式发挥着重要的作用,例如在蛋白质结构的研究中,欧拉公式可以用来计算蛋白质的拓扑特性。
总结起来,欧拉公式是立体几何中的一个重要定理,它描述了多面体的顶点数、边数和面数之间的关系。
多面体的几何算法

正多面体:各个面是全等的正多边形并且各个多面角也是全等的多面角的多面体。
正多面体只有五种,即正四面体、正六面体、正八面体、正十二面体和正二十面体。
五种正多面体又称为柏拉图氏体。
以下均以a表示棱长。
一、正四面体:由四个全等的正三角形所组成的几何体。
它有四个面、四个 顶点、六条棱。
每个二面角均为70°32′。
有四个三面角, 每个三面角的面角均为60°。
a=
Area=0
V=0
二、正六面体:又称“正方体”、“立方体”、“六等面体”或“直角方体 ”。
指由六个全等的正方形组成的几何体。
它有六个面、八 个顶点、十二条棱。
每一棱上的二面角均为90°。
有八个三 面角,每个三面角的面角都是90°。
a=
Area=0
V=0面对角线长0体对角线长0
内切球V=0
外切球V=0
正 多 面 体 类 形 体 几 何 计 算
三、正八面体:由八个全等的正三角形组成的几何体。
它有八个面、六个顶 点及十二条棱。
每个二面角约为109°28′。
有六个四面角 ,每个四面角的面角均为60°。
a=Area=0V=
四、正十二面体:又名“十二等面体”。
由十二个全等的正五边形组成的几
a=Area=0V=。
(word完整版)用欧拉公式证明只有五种正多面体
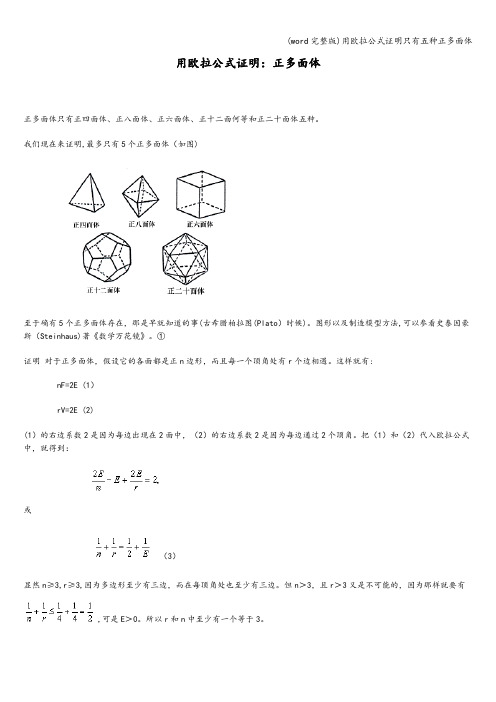
用欧拉公式证明:正多面体
正多面体只有正四面体、正八面体、正六面体、正十二面何等和正二十面体五种。
我们现在来证明,最多只有5个正多面体(如图)
至于确有5个正多面体存在,那是早就知道的事(古希腊柏拉图(Plato)时候)。
图形以及制造模型方法,可以参看史泰因豪斯(Steinhaus)著《数学万花镜》。
①
证明对于正多面体,假设它的各面都是正n边形,而且每一个顶角处有r个边相遇。
这样就有:
nF=2E (1)
rV=2E (2)
(1)的右边系数2是因为每边出现在2面中,(2)的右边系数2是因为每边通过2个顶角。
把(1)和(2)代入欧拉公式中,就得到:
或
(3)
显然n≥3,r≥3,因为多边形至少有三边,而在每顶角处也至少有三边。
但n>3,且r>3又是不可能的,因为那样就要有 ,可是E>0。
所以r和n中至少有一个等于3。
设n=3,那末,因此r=3,4,5,由是E=6,12,30,而F=4,8,20,这就给出了正四面体,正八面体和正二十面体。
设r=3,那末,因此n=3,4,5,由是E=6,12,30,而F=4,6,12,这就给出了正四面体,正六面体(即立方体)和正十二面体.。
相同表面积的四面体,六面体,正十二面体

相同表面积的四面体,六面体,正十二面体相同表面积的四面体、六面体、正十二面体1. 介绍在几何学中,三维几何图形是研究的重要对象之一。
在这种图形中,四面体、六面体和正十二面体是三种常见的多面体,它们都有着不同的特点和性质。
但如果它们具有相同的表面积,将会呈现怎样的形态和关系呢?本文将从深度和广度的角度对这一问题展开探讨和分析,希望能够为读者带来新的思考和启发。
2. 相同表面积的四面体、六面体、正十二面体的形态我们来探讨一下具有相同表面积的四面体、六面体和正十二面体的形态。
一般情况下,这三者的形态并不相同,因为它们的面数、边数和顶点数都存在差异。
四面体是一个四面体,有四个面;六面体是一个六面体,有六个面;而正十二面体则是一个具有十二个相等面的几何体。
但如果它们的表面积相同,意味着它们的具体形态会出现怎样的变化呢?3. 相同表面积的意义要探讨相同表面积的四面体、六面体、正十二面体的形态,首先我们需要明确相同表面积的含义。
在数学中,表面积是用来描述一个几何体外部覆盖的总面积的概念。
对于不同形状的多面体来说,它们的表面积计算方法各不相同,因此如何确保它们的表面积相同是一个需要深入研究和推演的问题。
4. 对于相同表面积的研究有研究表明,相同表面积的四面体、六面体和正十二面体的形态并不相同。
在这一研究中,先通过数值计算得出它们的表面积,并且进行了详细的对比分析。
结果显示,尽管这三种多面体的形态各不相同,但在满足表面积相同的条件下,它们的体积和其他性质产生了一些有趣的关联和规律。
这一研究为我们拓展了对几何图形的认识,也为相关领域的研究提供了新的思路和方法。
5. 个人观点和理解在我看来,相同表面积的四面体、六面体和正十二面体的研究具有重要的意义。
通过深入研究和分析,我们可以更好地理解不同几何体之间的关系和性质,也可以为相关领域的研究提供新的思路和方法。
未来,我希望能够深入探讨这一问题,挖掘出更多的规律和特点,为数学和几何学的发展贡献自己的一份力量。
正六面体和正四面体的认识说课稿

正六面体和正四面体的认识说课稿正六面体和正四面体的认识简介本说课稿将介绍正六面体和正四面体,这是几何学中常见的多面体。
正六面体和正四面体都具有特殊的形状和性质,有助于学生理解和掌握几何知识。
目标通过本课,学生将能够:了解正六面体和正四面体的定义;能够分辨正六面体和正四面体;理解正六面体和正四面体的性质和特征。
教学内容本课将涵盖以下内容:1.正六面体的认识:定义:由六个相等的正方形面组成的多面体。
特征:各个面均为正方形,相邻面相互平行且边长相等。
实例:骰子是一个常见的正六面体。
2.正四面体的认识:定义:由四个相等的三角形面组成的多面体。
特征:三个侧面均为等边三角形,底面为等腰三角形。
实例:矩形金字塔是一个常见的正四面体。
3.区分正六面体和正四面体:形状:正六面体具有六个面,而正四面体具有四个面。
面的类型:正六面体的面为正方形,正四面体的面为三角形。
性质:正六面体的每个面都是正方形,而正四面体的侧面是等边三角形。
教学方法为了帮助学生更好地理解正六面体和正四面体,我将采用以下教学方法:1.图像呈现:使用图片或模型展示正六面体和正四面体的形状和特征。
2.比较对比:通过比较正六面体和正四面体的面的数量、类型和性质,帮助学生区分它们。
3.互动练:组织学生进行小组活动或讨论,让他们彼此交流关于正六面体和正四面体的认识和理解。
教学评估教学评估是了解学生研究情况的重要手段,在本课中,我将采用以下评估方式:1.视觉确定:通过观察学生对正六面体和正四面体的描述和比较,评估他们对这两个形状的理解程度。
2.口头回答:提问学生关于正六面体和正四面体的问题,评估他们对相关概念的掌握程度。
教学扩展为了进一步拓展学生的研究,我建议以下扩展活动:1.进一步研究:要求学生进一步了解其他多面体的定义和属性,比如正八面体、正十二面体等。
2.建模实践:让学生使用纸张或其他材料制作正六面体和正四面体的模型,并进行展示和分享。
结束语通过本课的学习,学生将对正六面体和正四面体有更清晰的认识,并能够区分它们的不同特征和性质。
欧拉多面体公式

多面体欧拉公式的历史、成立进程和方式古希腊的毕达哥拉斯学派和柏拉图学派,他们发觉了五种正多面体:正四面体、正六面体、正八面体、正十二面体、正二十面体。
欧几里得在《几何本来》中曾试图证明只有这五种正多面体,但没有成功。
在很长的历史时期里,那个问题没有解决。
后来,人们慢慢熟悉到,依托角度、长度、面积等几何量的测量或计算,那个问题难以解决,而从多面体的极点数、棱数和面数的关系入手,有可能取得成功。
1639年,笛卡儿考察了五种正多面体极点数(V)、棱数(E)和面数(F)的关系,采纳不完全归纳法,猜想到:极点数与面数之和减去棱数,是一个不变量2,也确实是:V+F-E=2。
后来,他又用一些简单的多面体来验证自己的猜想,可是没有给出严格的证明,也没有发表。
1751年,欧拉给出了这一性质的一个证明。
后人称它为多面体欧拉公式。
欧拉之因此对这一性质感爱好,是要用它来做多面体的分类。
[1]但欧拉没有考虑到持续变换下的不变性。
欧拉问题的提出:任意一个三角形的内角和为180度,与三角形的形状无关,进而取得任一个凸n 边形的内角和为π)2(-n ,说明凸多边形的内角和由边数完全决定,而与形状无关。
那么,推行到空间,关于由假设干个多边形围成的凸多面体,是不是也有某种类似的简单性质呢?欧拉就如此由类比提出了问题。
欧拉证明如下:一个多面体有几种角呢?每条棱处有一个由两个面组成的二面角;每一个极点处,有一个由相交于那个极点的各个面所围成的角,叫立体角(它的大小等于以立体角极点为球心的单位球面被那个立体角的各个面所截出的球面多边形的面积的大小);每一个面多边形的每一个内角,叫多面体的一个面角。
欧拉第一考察多面体的所有二面角之和(记为∑δ)及所有立体角之和(记为∑ω),看它们是不是有某种简单的性质。
欧拉从最简单的多面体—四面体开始考察。
四面体由四个三角形围成(图1),为了便于计算,欧拉考察了两种退化的情形。
(1)四面体退化成一个三角形和它内部一点与三个极点所连成的线段(图2)。
正n面体体积公式

正n面体体积公式
正n面体是指具有n个相等的正多边形作为各个面的多面体。
其体积公式可以根据不同的情况而不同。
下面是一些常见正n面体的体积公式:
1. 正四面体(四面体):
体积公式:V = (a^3 * √2) / 12
其中,a代表四面体的边长。
2. 正六面体(立方体):
体积公式:V = a^3
其中,a代表立方体的边长。
3. 正八面体:
体积公式:V = (a^3 * √2) / 3
其中,a代表正八面体的边长。
4. 正十二面体:
体积公式:V = (16 * a^3 * √2) / 9
其中,a代表正十二面体的边长。
5. 正二十面体:
体积公式:V = (15 + 7 * √5) * a^3 / 4
其中,a代表正二十面体的边长。
对于其他正n面体,其体积公式可能会更加复杂,具体公式可以通过几何推导得出。
需要注意的是,这些公式都是基于对称的正多面体,且边长单位一致。
