均匀无耗传输线的工作状态
合集下载
电磁场课件--第二章无耗均匀传输线的工作状态
Z
2 0
X
2 L
e
j
x
e j 2x
Z
2 0
X
2 L
e
j x
U d j
Z
2 0
X
2 L
IL
sind
x
Id
1 Z0
Z
2 0
X
2 L
IL
cosd
x
Zin d jZ0 tgd x
传输线终端接纯电抗负载时，沿线电压、 电流幅值分布与终端开路或短路时不同之 处，只是线终端处不是电压、电流的波腹 或波节。这一点其实可以这样来理解：终 端开路或短路的传输线，其输入阻抗均为 纯电抗，那么现在传输线接纯电抗负载， 就相当于在线终端处接入一段终端开路或 短路的传输线。也就是说以纯电抗为负载 的传输线，就相当于负载端延长一段长度 的开路或短路线。
• 在实测时把这种专用的测量线替代一段实际系统 的传输线接入，可在系统输入端接入信号源作模 拟测试，必要时也可以进行在线测试。对于不同 型号的同轴线或金属波导，必须配用相符合的测 量线。
测量原理和步骤
• 测电压驻波比 测量电压波腹电压和波节电压，为使测试
结果准确可靠，波腹值和波节值尽可能由 多个波腹、波节值取平均而定。 • 测电压反射系数
m in
行波
d 0
S 1
驻波
d ej S
行驻波
0 d 1 1 S
纯阻负载驻波比的计算
d RL Z0
RL Z0
d Z0 RL
Z0 RL
S
1 1
d d
RL Z0
S
1 1
d d
Z0 RL
驻波比与反射系数
• 电压驻波比与电压反射系数都是表征传输 线工作状态的参量，驻波比与反射系数模 值之间存在一一对应的关系。
传输线基本理论2_工作状态
的终端短路同轴线， 例：填充空气、Zc = 50 、长度为 0.1m 的终端短路同轴线， 填充空气、 求其输入阻抗。 当频率分别为 0.75GHz 、1.5GHz 、4GHz 时，求其输入阻抗。
传输线的绝对长度 l = 传输线的电长度 le＝ 工作频率对应的波导波长 λ g 2π l e λ g = 2π l e βl= l = leλg λg 解： le Z in = jZ c tan(β l ) = jZ c tan(2π l e ) f (GHz) λg (m)
三、输入阻抗: 输入阻抗
Γ (z ) = 0 ,
1 + Γ (z ) Z in (z ) = Z c ⋅ = Zc 1 − Γ (z )
传输线上，任意点的输入阻抗均等于特性阻抗。 传输线上，任意点的输入阻抗均等于特性阻抗。
四、优点
行波状态是理想的工作状态，能量被负载完全 行波状态是理想的工作状态， 接收。但实际工作中， 接收。但实际工作中，不可能达到理想的行波状 总是或多或少存在反射。 态，总是或多或少存在反射。 在天线、微波器件、微波电路的设计中， 在天线、微波器件、微波电路的设计中，如何 采取各种措施，使负载尽量匹配、尽量减少反射， 采取各种措施，使负载尽量匹配、尽量减少反射， 是很重要的一项工作内容。 是很重要的一项工作内容。
λg
6 2π λ g − j2 λg 6 2π 3
= -e Γ 6
λg
− j2β
= -e
= -e
−j
例： 欲用特性阻抗为 欲用特性阻抗为50 、终端短路的传输线来得到
值为 j25 的电抗，则该段传输线最短应为多长。 的电抗，则该段传输线最短应为多长。
Z c = 50 Ω
0.75 1.5 4
第1.3节 无耗传输线的状态分析
传输线上反射波的大小，可用反射系数的模、 传输线上反射波的大小，可用反射系数的模、驻波比 和行波系数三个参量来描述。 和行波系数三个参量来描述。 反射系数模的变化范围为 驻波比的变化范围为 行波系数的变化范围为
,,
0≤ Γ ≤1
1≤ ρ ≤ ∞
0≤ K ≤1
传输线工作参数 反射系数
Γ(z' )
输入阻抗 Zin (z)
ρ
1+ | Γl | ρ= 1− | Γl |
ρ=
(R1 + Z0 )2 + xl2 + (R1 − Z0 )2 + xl2 (R1 + Z0 )2 + xl2 − (R1 − Z0 )2 + xl2
| U(z) |max ρ= | U(z) |min
例题： 例题： 在一均匀无耗传输线上传输频率为3GHz的信号，已知其 特性阻抗 Z 0 = 100Ω ，终端接 Z l = 75 + j100Ω 的负载， 试求： 1)传输线上的驻波系数； 1) 2)离开终端10cm处的反射系数； 3)离开终端2.5cm处的输入阻抗；
解： 1)终端反射系数： 终端反射系数：
Z l − Z 0 75 + j100 − 100 − 1 + j 4 9 + j 32 Γl = = = = = 0.51e j74.3 Z l + Z 0 75 + j100 + 100 7 + j 4 65
故，传输线上的驻波系数： 传输线上的驻波系数：
纯驻波状态下传输线上的电压和电流： 纯驻波状态下传输线上的电压和电流：
U ( z ) = U + + U − = j2 A1 sin βz 2A I ( z ) = I + + I − = 1 cos βz Z0 传输线上任意一点z处的输入阻抗为 处的输入阻抗为： 传输线上任意一点 处的输入阻抗为：
第四节均匀无耗传输线的工作状态
Ui (z) A1
UiL Ui
Ii (z)
U iL Z0
Ui Z0
二、驻波状态(全反射情况)
当终端短路(ZL=0)、开路(ZL=∞)或接纯电抗负载 (ZL=±jXL)时，︱(z)︱=︱L︱=1，终端全反射，沿 线入、反射波叠加形成驻波分布。负载与传输线完全
失配。驻波状态下，︱︱=1，r=∞，K=0。
z
Xin(z)
z长度短路线 的等效电路
0 =0(短路) 串联谐振
0~l/4 >0(感性) 电 感
l/4 =±∞(开路) 并联谐振
l/4 ~ <0(容性) 电 容
l/2
l/2 =0 (短路) 串联谐振
沿线每经过l/4，阻抗性质变化一次；每经过
l/2，阻抗重复原有值。
2. 终端开路(ZL=∞)
L 1 e j0 IL 0 ，U L UiL (1 L ) 2UiL ,
1）沿线电压、电流分布
以上关系代入式(2-4e)得
UI((zz))UjUZ2
cos z
2 sin
0
2Ui2 cos
z j2Ii2 sin
z
z
UiL IiLZ0
电压、电流瞬时表达式为：
u( z, t )
2 U i 2
cos
z
cos(
t
2)
i( z, t )
2
Ii 2
sin
z cos(
z
得
(2 4e)
U (z) j2UiLsin z I(z) 2IiL cos z
设UiL Ui e j 2， 则电压、电流瞬时表达式为：
u( z, t )
2 U i
sin
lec04 传输线工作状态分析
三 均匀无耗传输线工作状态 2)终端负载开路 终端负载开路 负载阻抗Zl=∞ ；终端电流：Il=0 此时，线上任意位置的电压和电流复振幅表示式为： U(z)=Ulcosβz U I(z)= j l sinβz Zc 输入阻抗为： Z in ( z ) = − jZ c ctgβ z 反射系数为： Γ(z)=e -j2βz 驻波系数为：s→∞
三 均匀无耗传输线工作状态
2. 纯驻波状态 纯驻波状态
纯驻波状态就是全反射状态, 也即终端反射系数|Γl|=1。 在此状态下, 由式（1.3-23），负载阻抗必须满足
Zl − Zc = Γl = 1 Zl + Zc
由于无耗传输线的特性阻抗Zc为实数, 因此要满足上式 负载阻 要满足上式, 要满足上式 抗必须为短路（ 抗必须为短路（Zl=0）、开路（Zl→∞）或纯电抗（Zl=±jXl） ） 开路（ ）或纯电抗（ 三种情况之一。在上述三种情况下, 传输线上入射波在终端将 三种情况之一 全部被反射, 沿线入射波和反射波叠加都形成纯驻波分布, 唯一 的差异在于驻波的分布位置不同。
λ X ( 1) lsl= arctan Zc 2π
三 均匀无耗传输线工作状态
同理可得, 当终端负载为Zl=-jX1的纯电容时, 可用长度小于 λ/4的开路线loc来代替（或用长度为大于λ/4小于λ/2的短路线来 代替）,由式Zin(z)=-jZcctgβz有：
λ X1 loc = arcctg ( ) 2π Zc
(
2
)
根据上述分析结果，开路线电压、电流复振幅、输入 阻抗分布图如下：
三 均匀无耗传输线工作状态
无耗终端开路线的驻波特性
三 均匀无耗传输线工作状态
分析： 分析 ： 终端开路时传输线上的电压和电流也呈 纯驻波分布, 因此也只能存储能量而不能传输能量。 在 z=nλ/2 (n=0,1,2, …) 处 为 电 压 波 腹 点 , 而 在 z=(2n+1)λ/4(n=0, 1, 2, …)处为电压波节点。 实际上终 端开口的传输线并不是开路传输线, 因为在开口处会 , 有辐射, 所以理想的终端开路线是在终端开口处接上 λ/4短路线来实现的。前页的图给出了终端开路时的 驻波分布特性。O′位置为终端开路处, OO′为λ/4短路 线。
无耗传输线的状态分析
第一章 均匀传输线理论之•状态分析
(3) 终端接纯电抗 in= ±jX 终端接纯电抗 电抗Z
当均匀无耗传输线端接纯电抗 负载时，可以将纯电抗 纯电抗Z 当均匀无耗传输线端接纯电抗Zin= ±jX 负载时，可以将纯电抗 in= ±jX 纯电抗 负载用一段短路线或开路线来等效，因而对这种情况的分析与（ ）（ ）（2） 负载用一段短路线或开路线来等效，因而对这种情况的分析与（1）（ ） 的情况类似。 的情况类似。
Z L + jZ 0tg (β z ) Z in ( z ) = Z 0 = jZ 0 tan β z Z 0 + jZ L tg (β z )
U ( z ) = U i + U r = A1e jβz - A1e -jβz = j2 A1 sin βz 纯驻波状态下传输 线上的电压和电流： 线上的电压和电流： 2A I ( z ) = I i + I r = 1 cos βz Z0
传输线上电压电 流瞬时表达式为： 流瞬时表达式为： 传输线上任意一点z处的输入阻抗为： 传输线上任意一点 处的输入阻抗为： 处的输入阻抗为
u ( z , t ) = 2 A1 cos(ωt + φ0 + π ) sin β z 2 i( z, t ) = 2 A1 Z0 cos(ωt + φ0 ) cos β z
第一章 均匀传输线理论之•状态分析
1.3 无耗传输线的状态分析
本节要点
行波 纯驻波 行驻波状态 传输线的等效
微波工程基础
1
第一章 均匀传输线理论之•状态分析
对于无耗传输线， 对于无耗传输线 ， 负载阻抗不同则波的 反射也不同；反射波不同则合成波不同； 反射也不同 ；反射波不同则合成波不同 ； 合成波的不同意味着传输线有不同的工 作状态。归纳起来， 作状态。 归纳起来 ，无耗传输线有三种 不同的工作状态： 不同的工作状态： Γ(z ) Γ (0 ) 行波状态； 行波状态； Z (z ) Z 纯驻波状态； 纯驻波状态； Z 行驻波状态。 行驻波状态。
微波技术基础1.4 均匀无耗传输线的工作状态
I (z)
Il
cos z
j Ul Zc
sin
z
U (z) jIlZc sin z
I (z) Il cos z
(1-36) (1-37)
§1.4 均匀无耗传输线的工作状态
1. 终端短路
也可以写成入射波和反射波之和：
U(z)
jIl Zc sin z
IlZc 2
(e jz
e jz )
U (z) U (z) U (0)(e jz e jz )
3 /4 / 2 /4
开路线特性
z
z
|U (z) | | I(z) | Z in ( z )
开路线的特性
§1.4 均匀无耗传输线的工作状态
2. 终端开路
结论
• 对于开路线可以认为，从终端算起，把短路线截去λ/4 。
• 因此，在短路线中的电压和电流沿线分布、瞬时状态等规律， 也适合于开路线。
• 根据(1.3-43)，开路线的输入阻抗为
§1.4 均匀无耗传输线的工作状态
1.4.1 行波状态
结论
（1）电压、电流瞬时值同相； （2）传输线上电压、电流幅值不变； （3）电压、电流随时间做简谐振荡(如图),
把信号源的能量不断地传向负载，并被负载所吸收.
u(z,t)
z
t1 o
t2
终端匹配时线上电压分布
|U(z)|
电流分布图类似， 只是幅度不一样.
1.4.1 行波状态
若令 U (0) U ，(0) e ju0 I (0) I (0) e ji0
因为
U (0) I (0)
Zc
所以
i0 u0 0
则电压和电流瞬时值可表示：
u(z,t) Re[U (z)e j t ] U (0) cos(t 0 z) (1-69)
讲5无耗线的工作状态分析
传输线终端的入射波将被全反射， 传输线终端的入射波将被全反射，沿线入射波与反射 波叠加形成驻波分布。入射功率一点也没有被负载吸收， 波叠加形成驻波分布。入射功率一点也没有被负载吸收， 负载与传输线完全失配。 负载与传输线完全失配。
ρ =∞
Κ =0
+
−
Zg
i u
Il Ul
~ Eg
z’
Zl
z’
1 短路状态
z' =
z' =
mλ g
2 ( 2m + 1)λ g
4
电压波节点， 电压波节点，电流波腹点 电压波腹点， 电压波腹点，电流波节点
m = 0.1,2L
Zg
i u
Il Ul
+
−
~ E g
Zl
z’
z’
λg
3λg 4
λg
2
λg
4
Z ( z ' ) = jZ 0 tan βz '
(2) 传输线阻抗沿线周期变化，周期为 g/2。 传输线阻抗沿线周期变化，周期为λ 。
jβ z '
(1.4-1)有错 有错
z’
z’
u ( z ) = U 0 e − jβ z
u ( z , t ) =| U 0 | cos(ωt − β z + ϕ1 ) i ( z , t ) =| I 0 | cos(ωt − β z + ϕ1 ) u ( z ' , t ) =| U l | cos(ωt − β z '+ϕ1 ' ) i ( z ' , t ) =| I l | cos(ωt − β z '+ϕ1 ' )
无耗传输线的状态分析
电长度： 意义：改变频率 和改变长度等效
传输线的等效 (equivalent)
一段短路与开路传输线的输入阻抗分别为
一段长度
的短路线等效为一个电感，若等效电感
的感抗为Xl，则传输线的长度为
一段长度
的开路线等效为一个电容，若等效电容
的容抗为Xc，则传输线的长度为
(3) 终端接纯电抗Zin= ±jX
在，0相<当z<于/4一内个，纯相电当容于Z一in=个–纯jX电；感Zin=jX；在/4<z</2内 从终端起每隔/4阻抗性质就变换一次，这种特性称为阻
抗变换性。
(2) 终端开路(open circuit)
相当于此处开路
终端短路
U
I
U
z
串联谐振
并联谐振
例：长度为10cm终端短路传输线的输入阻抗
当反射波较大时，波腹电场要比行波电场要大得多，容 易发生击穿，这限制了传输线能最大传输的功率，因此 要采取措施进行负载阻抗匹配。
设终端负载为ZL= RL+jXL ，其终端反射系数为：
线上各点电压电流时谐表达式：
设A1=A1ej0，则传输线上电压、电流的模值为：
显然，当负载确定时，线上电压、电流随z而变化， 在一些点电压取极大值，电流取极小，称为电压波腹点， 在另一些点电压取极小值，电流取极大，称为电压波节点。
电压波腹点Г(z)为正实数，阻抗为纯电阻 电压波节点Г(z)为负实数，阻抗为纯电阻 波腹点、波节点阻抗的乘积等于特性阻抗的平方！
终端短路的传输线或终端开路的传输线不仅可 以等效为电容或电感，而且还可以等效为谐振元 件。谐振器与分立元件电路一样也有Q值和工作 频带宽度。
3. 行驻波(traveling-standing wave)状态
传输线的等效 (equivalent)
一段短路与开路传输线的输入阻抗分别为
一段长度
的短路线等效为一个电感，若等效电感
的感抗为Xl，则传输线的长度为
一段长度
的开路线等效为一个电容，若等效电容
的容抗为Xc，则传输线的长度为
(3) 终端接纯电抗Zin= ±jX
在，0相<当z<于/4一内个，纯相电当容于Z一in=个–纯jX电；感Zin=jX；在/4<z</2内 从终端起每隔/4阻抗性质就变换一次，这种特性称为阻
抗变换性。
(2) 终端开路(open circuit)
相当于此处开路
终端短路
U
I
U
z
串联谐振
并联谐振
例：长度为10cm终端短路传输线的输入阻抗
当反射波较大时，波腹电场要比行波电场要大得多，容 易发生击穿，这限制了传输线能最大传输的功率，因此 要采取措施进行负载阻抗匹配。
设终端负载为ZL= RL+jXL ，其终端反射系数为：
线上各点电压电流时谐表达式：
设A1=A1ej0，则传输线上电压、电流的模值为：
显然，当负载确定时，线上电压、电流随z而变化， 在一些点电压取极大值，电流取极小，称为电压波腹点， 在另一些点电压取极小值，电流取极大，称为电压波节点。
电压波腹点Г(z)为正实数，阻抗为纯电阻 电压波节点Г(z)为负实数，阻抗为纯电阻 波腹点、波节点阻抗的乘积等于特性阻抗的平方！
终端短路的传输线或终端开路的传输线不仅可 以等效为电容或电感，而且还可以等效为谐振元 件。谐振器与分立元件电路一样也有Q值和工作 频带宽度。
3. 行驻波(traveling-standing wave)状态
《电磁场与微波技术》补充练习题1(1)
2《电磁场与微波技术》补充练习一、填空：1、波速随频率变化的现象称为波的色散，色散波的群速度表达式=z ν⎪⎭⎫⎝⎛-x c λ21。
2、测得一微波传输线的反射系数的模21=Γ，则行波系数K=1/3；若特性阻抗Z 0=75Ω，则波节点的输入阻抗R in (波节)=25欧。
3、微波传输线是一种分布参数电路，其线上的电压和电流沿线的分布规律可由传输线方程来描述。
4、同轴线传输的主模是TEM 模，微带线传输的主模是准TEM 模。
5、矩形波导尺寸a = 2cm, b = 1.1cm.若在此波导中只传输TE 10模，则其中电磁波的工作波长范围为2.2<λ<4。
6、微波传输线按其传输的电磁波波型，大致可划分为TEM 波传输线，TE 、TM 传输线和表面波传输线。
7、长线和短线的区别在于：前者为分布（长线）参数电路，后者为集中参数电路。
8、均匀无耗传输线工作状态分三种：(1)行波(2)驻波(3)行驻波。
10、从传输线方程看，传输线上任一点处的电压或电流等于该处相应的入射波和反射波的叠加。
11、当负载为纯电阻L R ，且0Z R L 时，第一个电压波腹点在终端，当负载为感性阻抗时，第一个电压波腹点距终端的距离在0<z 0<4λ范围内。
12、导波系统中的电磁波纵向场分量的有无，一般分为三种波型(或模)：TEM 波；TE 波；TM 波。
13、导波系统中传输电磁波的等相位面沿着轴向移动的速度，通常称为相速；传输信号的电磁波是多种频率成份构成一个“波群”进行传播，其速度通常称为群速。
14、波速随着频率变化的现象称为波的色散，色散波的相速大于无限媒质中的光速，而群速小于无限媒质中的光速。
15、矩形波导传输的主模是TE 10模；同轴线传输的主模是TEM 模。
16、线性媒质的本构关系为→→=E D ε，→→=H B μ；17、媒质为均匀媒质时，媒质的ε、μ、υ与空间坐标无关。
18、媒质的ε、μ、σ与电磁场的幅度无关时，此媒质为线性媒质；19、若媒质的ε、μ、σ与电磁场的方向无关时，则称此媒质为各向同性媒质； 20、若媒质的ε、μ、σ与电磁场的频率无关 时，则称此媒质为非色散媒质。
第1.4节 传输线的传输功率、效率与损耗
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
3.功率容量 功率容量(power capacity) 功率容量
功率容量：传输线上容许传输的最大功率。 功率容量：传输线上容许传输的最大功率。 当传输线的结构和介质材料选定后，功率容量由额定电 当传输线的结构和介质材料选定后， 和额定电流I 决定。 压UM和额定电流 M决定。 设传输线的驻波比为 ρ ，则功率容量可表示为
结论
1 − Γl
2 ρ
(1)回波损耗和插入损耗虽然都与反射信号即反射系数 回波损耗和插入损耗虽然都与反射信号即反射系数 有关，但回波损耗取决于反射信号本身的损耗， Γ 越 有关，但回波损耗取决于反射信号本身的损耗，|Γl|越 越小； 大，则|Lr|越小； 越小 (2)插入损耗 i则表示反射信号引起的负载功率的减小， 插入损耗L 则表示反射信号引起的负载功率的减小， 插入损耗 |Γl|越大，则| Li |也越大。 越大， 也越大。 Γ 越大 也越大
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
Z l − Z 0 (40 − Z 0 ) 2 + 30 2 Γl = = 2 2 Z l + Z 0 (40 + Z 0 ) + 30
将上式对Z0求导, 并令其为零, 经整理可得
1 2
402+302-Z02=0
回波损耗取决于反射信号本身的损耗，|Γl|越大，则|Γr|越小； 插入损耗|Li|则表示反射信号引起的负载功率的减小，|Γl|越大，则|Li|也越大。
图 1- 9 | Lr|、 |Li|随反射系数的变化曲线
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗 [例 1-4]现有同轴型三路功率分配器，如图1-10所示，设该功分器在 2.5GHz-5.5GHz频率范围内其输入端的输入驻波比均小于等于1.5，插入损耗 为，设输入功率被平均地分配到各个输出端口，试计算（1）输入端的回波 损耗（用分贝表示）；（2）每个输出端口得到输出功率与输入端总输入功 率的比值（用百分比表示）。 解（1）由于驻波比为1.5，因而反射系数的大小为
第一章 均匀传输线理论之•传输功率、效率与损耗
3.功率容量 功率容量(power capacity) 功率容量
功率容量：传输线上容许传输的最大功率。 功率容量：传输线上容许传输的最大功率。 当传输线的结构和介质材料选定后，功率容量由额定电 当传输线的结构和介质材料选定后， 和额定电流I 决定。 压UM和额定电流 M决定。 设传输线的驻波比为 ρ ，则功率容量可表示为
结论
1 − Γl
2 ρ
(1)回波损耗和插入损耗虽然都与反射信号即反射系数 回波损耗和插入损耗虽然都与反射信号即反射系数 有关，但回波损耗取决于反射信号本身的损耗， Γ 越 有关，但回波损耗取决于反射信号本身的损耗，|Γl|越 越小； 大，则|Lr|越小； 越小 (2)插入损耗 i则表示反射信号引起的负载功率的减小， 插入损耗L 则表示反射信号引起的负载功率的减小， 插入损耗 |Γl|越大，则| Li |也越大。 越大， 也越大。 Γ 越大 也越大
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
Z l − Z 0 (40 − Z 0 ) 2 + 30 2 Γl = = 2 2 Z l + Z 0 (40 + Z 0 ) + 30
将上式对Z0求导, 并令其为零, 经整理可得
1 2
402+302-Z02=0
回波损耗取决于反射信号本身的损耗，|Γl|越大，则|Γr|越小； 插入损耗|Li|则表示反射信号引起的负载功率的减小，|Γl|越大，则|Li|也越大。
图 1- 9 | Lr|、 |Li|随反射系数的变化曲线
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗 [例 1-4]现有同轴型三路功率分配器，如图1-10所示，设该功分器在 2.5GHz-5.5GHz频率范围内其输入端的输入驻波比均小于等于1.5，插入损耗 为，设输入功率被平均地分配到各个输出端口，试计算（1）输入端的回波 损耗（用分贝表示）；（2）每个输出端口得到输出功率与输入端总输入功 率的比值（用百分比表示）。 解（1）由于驻波比为1.5，因而反射系数的大小为
微波技术基础1.4 均匀无耗传输线的工作状态
3. 终端接纯电抗性负载
传输特性（参见图1-12和图1-13)： • 把一段短路线或开路线接在原来传输线的终端（即 ±jXι 的位置），从而构成了一个包含该线段在内 的、终端短路或开路的传输线。
• 画出新构成的短路或开路线的电压和电流幅值，以 及输入阻抗的分布图。
• 抹掉所接短路或开路线，剩下的便是传输线终端接 有纯电抗负载时的图形。 纯驻波
u(z,t) Re[U (z)e j t ] 2U (0) cos z cos(t 0)
i(
z,
t
)
Re[I
(
z)e
j
t
]
2
I
(0)
sin
z
cos(t
0
2
)
2. 终端开路
§1.4 均匀无耗传输线的工作状态
将瞬时值形式也写成入射波和反射波的叠加：
u(z,t) u (z,t) u(z,t)
为了更清楚了解纯驻波形成，将U(z)和I(z)写成入射波和反射 波叠加的形式：
U (z) Ul (e j z e j z ) U (z) U (z) 2
U (0)(e j z e j z ) 2U (0) cos z
(1-85)
I (z) Ul (e j z e j z ) I (z) I (z) 2Zc
Ul 2
cos(t
0
z)
Ul 2
cos(t 0 z)
2 I (0) Zc cosz cos(t 0 )
i(z,t) i (z,t) i(z,t)
Ul 2Zc
cos(t
0
z)
Ul 2Zc
cos(t
0
z)
2
U
(0) Zc
传输特性（参见图1-12和图1-13)： • 把一段短路线或开路线接在原来传输线的终端（即 ±jXι 的位置），从而构成了一个包含该线段在内 的、终端短路或开路的传输线。
• 画出新构成的短路或开路线的电压和电流幅值，以 及输入阻抗的分布图。
• 抹掉所接短路或开路线，剩下的便是传输线终端接 有纯电抗负载时的图形。 纯驻波
u(z,t) Re[U (z)e j t ] 2U (0) cos z cos(t 0)
i(
z,
t
)
Re[I
(
z)e
j
t
]
2
I
(0)
sin
z
cos(t
0
2
)
2. 终端开路
§1.4 均匀无耗传输线的工作状态
将瞬时值形式也写成入射波和反射波的叠加：
u(z,t) u (z,t) u(z,t)
为了更清楚了解纯驻波形成，将U(z)和I(z)写成入射波和反射 波叠加的形式：
U (z) Ul (e j z e j z ) U (z) U (z) 2
U (0)(e j z e j z ) 2U (0) cos z
(1-85)
I (z) Ul (e j z e j z ) I (z) I (z) 2Zc
Ul 2
cos(t
0
z)
Ul 2
cos(t 0 z)
2 I (0) Zc cosz cos(t 0 )
i(z,t) i (z,t) i(z,t)
Ul 2Zc
cos(t
0
z)
Ul 2Zc
cos(t
0
z)
2
U
(0) Zc
传输线的工作状态
U max = Ui 2 (1 + Γ 2 ) I min = I i 2 (1 − Γ2 )
行驻波状态
(2)当 (2)当 2 β z '−φ2 = (2n + 1)π
(n = 0,1,2,L)
φLλ λ + (2n + 1) 时，即 z ' = 4π 4
在线上这些点处，电压振幅为最小值(波节) 在线上这些点处，电压振幅为最小值(波节)， 电流振幅为最大值(波腹) 电流振幅为最大值(波腹)，即
Z0 ZL=Z0 z
U 1m )= e Z 0
j (φ1 − β z )
ω ∼ U &1
Z in (z ) = Z 0
行波状态(无反射情况) 行波状态(无反射情况)
沿线电压、 沿线电压、电流和阻抗分布
Γ2 Z0
ZL=Z0
(1) 线上电压和电流的振幅 ω ∼ 恒定不变
(2) 电压行波与电流行波同相，沿 电压行波与电流行波同相， 传 播 方 向 按 线 性 关 系 -βz 不 断 滞 后 . 线上的输入阻抗处处相等， (3) 线上的输入阻抗处处相等，且 均等于特性阻抗 Z in (z ) = Z 0 举例: 举例:
行驻波状态(部分反射情况) 三、行驻波状态(部分反射情况)
当均匀无耗传输线终端接一般复阻抗 Z L = R L + jX L
沿线电压、 1. 沿线电压、电流分布
& & U ( z ′) = Ui ( z ′)(1 + Γ( z ′)) & Ui ( z ′) & I ( z ′) = (1 − Γ( z ′)) Z0
1.条件: 1.条件: 条件
(1)半无限长均匀无耗传输线 (1)半无限长均匀无耗传输线 ∼ Z0
微波技术基础期末试题与答案(一)
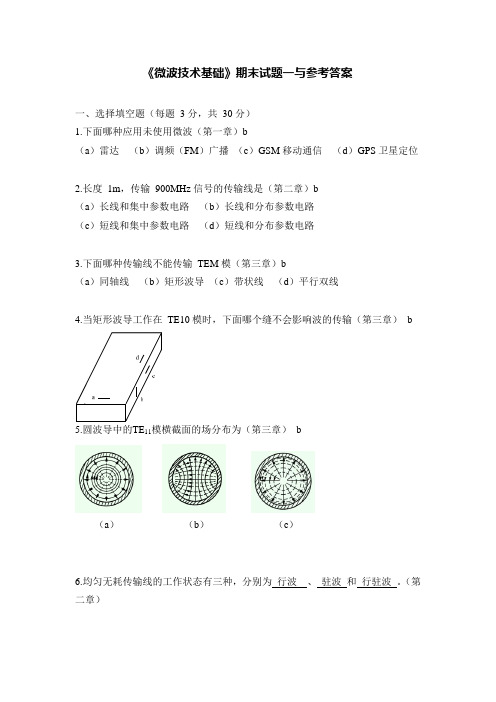
《微波技术基础》期末试题一与参考答案一、选择填空题（每题 3 分，共30 分）1.下面哪种应用未使用微波（第一章）b（a）雷达（b）调频（FM）广播（c）GSM 移动通信（d）GPS 卫星定位2.长度1m，传输900MHz 信号的传输线是（第二章）b（a）长线和集中参数电路（b）长线和分布参数电路（c）短线和集中参数电路（d）短线和分布参数电路3.下面哪种传输线不能传输TEM 模（第三章）b（a）同轴线（b）矩形波导（c）带状线（d）平行双线4.当矩形波导工作在TE10 模时，下面哪个缝不会影响波的传输（第三章）b5.圆波导中的TE11模横截面的场分布为（第三章）b（a）（b）（c）6.均匀无耗传输线的工作状态有三种，分别为行波、驻波和行驻波。
（第二章）Z L 0L 7.耦合微带线中奇模激励的对称面是 电 壁，偶模激励的对称面是 磁 壁。
（第三章）8.表征微波网络的主要工作参量有阻抗参量、 导纳 参量、 传输 参量、散射参量和 转移参量。
9.衰减器有吸收衰减器、 截止衰减器和 极化衰减器三种。
10.微波谐振器基本参量有 谐振波长 、 固有品质因数 和等效电导衰减器三种。
二、传输线理论工作状态（7 分）（第二章）在特性阻抗Z 0=200Ω的传输线上，测得电压驻波比ρ=2，终端为电压波节点，传输线上电压最大值 U max =10V ，求终端反射系数、负载阻抗和负载上消耗的功率。
解： Γ = ρ -1 = 12ρ +1 3由于终端为电压波节点，因此Γ =- 123由Γ =Z L - Z 0= - 12+ Z 3 可得，Z L =100Ω 负载吸收功率为P 2Z 0 ρ三、Smith 圆图（10 分）（第二章）已知传输线特性阻抗Z 0=75Ω，负载阻抗Z L =75+j100Ω，工作频率为 900MHz ，线长l =0.1m ，试用Smith 圆图求距负载最近的电压波腹点与负载的距离和传输线的输入阻抗Z 0Z L解：由工作频率为900 MHz，可得λ=1 m 3而线长为l=0.3λ1.计算归一化负载阻抗ZL=ZLZ= 1+j1.33在阻抗圆图上找到 A 点。
2-4无耗传输线工作状态解析
2 j Z 02 X L e 2 j Z 02 X L e
x x x
e j(2 )
其中φx是阻抗Z0 + jXL的辐角。由上式可知电压反 射系数的模│Γ│=1，这就是说终端接纯电抗负载的 传输线也呈驻波状态。
的情况，传输线将呈现一种极端工作状态。由于终端没有吸
收功率的电阻元件，传输线将会产生全反射而形成驻波。
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
7
（1）终端开路。ZL=∞，电压反射系数在负载点处为
(Z Z0 ) (0) L 1 (Z L Z0 )
2U (0) U L i I L 0
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 4
1.行波状态(匹配状态、无反射状态)（2/3）
• 传输线与其终端负载匹配时，线上任一位置处的输入阻抗：
(d ) (d ) U U Z in (d ) i Z0 Z L I (d ) I i (d )
即Zin(d)与位置d无关， 恒等于负载ZL或传输线 的波阻抗Z0，
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 10
（2）终端短路。ZL=0，终端处（短路点处）电压反
射系数为
(Z L Z 0 ) ( 0) 1 (Z L Z 0 )
0 U L (0) 2U i I L Z0
终端短路的传输线终端处为电压波节电流波腹。电流、电 压沿线分布的表达式为
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 8
终端开路传输线沿线电压、电流幅值及输入阻抗的分布：
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
9
x x x
e j(2 )
其中φx是阻抗Z0 + jXL的辐角。由上式可知电压反 射系数的模│Γ│=1，这就是说终端接纯电抗负载的 传输线也呈驻波状态。
的情况，传输线将呈现一种极端工作状态。由于终端没有吸
收功率的电阻元件，传输线将会产生全反射而形成驻波。
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
7
（1）终端开路。ZL=∞，电压反射系数在负载点处为
(Z Z0 ) (0) L 1 (Z L Z0 )
2U (0) U L i I L 0
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 4
1.行波状态(匹配状态、无反射状态)（2/3）
• 传输线与其终端负载匹配时，线上任一位置处的输入阻抗：
(d ) (d ) U U Z in (d ) i Z0 Z L I (d ) I i (d )
即Zin(d)与位置d无关， 恒等于负载ZL或传输线 的波阻抗Z0，
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 10
（2）终端短路。ZL=0，终端处（短路点处）电压反
射系数为
(Z L Z 0 ) ( 0) 1 (Z L Z 0 )
0 U L (0) 2U i I L Z0
终端短路的传输线终端处为电压波节电流波腹。电流、电 压沿线分布的表达式为
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 8
终端开路传输线沿线电压、电流幅值及输入阻抗的分布：
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
9
第节传输线的传输功率效率和损耗
Lr
(
z)
10
lg
Pin Pr
10 lg
l
1 e2 4z
20 lg l
2(8.686z)
(dB)
对于无耗线 Lr (z) 20 lg l (dB)
若负载匹配，则Lr，表达无反射波功率。
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
插入损耗(insertion loss):入射波功率与传播功率之比
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
总之，回波损耗和插入损耗虽然都与反射信号即反射系数有关；
回波损耗取决于反射信号本身旳损耗，|Γl|越大，则|Γr|越小； 插入损耗|Li|则表达反射信号引起旳负载功率旳减小，|Γl|越大，则|Li|也越大。
图 1- 9 | Lr|、 |Li|随反射系数旳变化曲线
1.4 传播线旳传播功率、效率与损耗
本节要点
传播功率 传播效率 损耗 功率容量
《微波技术率、效率与损耗
1. 传播功率(transmission power)与效率
设均匀传播线特征阻抗为实数且传播常数 j ；
则沿线电压、电流旳体现式为：
U (z) A1 eze jz le jzez
所以有
Pin Pr 3Pout Pi
可见，输入功分器旳功率分可分为反射功率，输出功率 和损耗功率三部分。
《微波技术与天线》
第一章 均匀传输线理论之•传输功率、效率与损耗
Decibels (dB)作为单位
功率值常用分贝来表达，这需要选择一种功率单位 作为参照，常用旳参照单位有1mW和1W。
假如用1mW作参照，分贝表达为：
P(dBm) 10 lg P(mW)
2-4无耗传输线工作状态
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 10
（2）终端短路。ZL=0，终端处（短路点处）电压反
射系数为
(Z L Z 0 ) ( 0) 1 (Z L Z 0 )
0 U L (0) 2U i I L Z0
终端短路的传输线终端处为电压波节电流波腹。电流、电 压沿线分布的表达式为
电磁场、微波技术 与天线
许 明 妍
北教6-108 myxu@
本节主要内容
均匀无耗传输线工作状态
行波、驻波、行驻波
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
2
均匀无耗传输线的工作状态
传输线的工作状态是指沿线电压、电流以及阻抗 的分布规律。
接有负载阻抗ZL的传输线在正弦时变信源激励下，
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 16
在行驻波状态下，电压幅值沿传输线的分布规律。用电压反射
(d ) 的模值为： 系数Γ(d)表示，传输线上任一点处电压 U
(d ) U ( d ) 1 ( d ) U i ( d ) 1 ( d ) e j U i (d ) 1 (d ) cos 2 (d ) sin 2 U i (d ) 1 (d ) 2 2 (d ) cos U i
5. 终端短路的传输线其输入阻抗为纯电抗。
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 13
（3）终端负载为纯电抗。ZL = jXL，此时终端处的
电压反射系数为
( jX L Z 0 ) ( Z 0 jX L ) (0) ( jX L Z 0 ) ( Z 0 jX L )
的情况，传输线将呈现一种极端工作状态。由于终端没有吸
（2）终端短路。ZL=0，终端处（短路点处）电压反
射系数为
(Z L Z 0 ) ( 0) 1 (Z L Z 0 )
0 U L (0) 2U i I L Z0
终端短路的传输线终端处为电压波节电流波腹。电流、电 压沿线分布的表达式为
电磁场、微波技术 与天线
许 明 妍
北教6-108 myxu@
本节主要内容
均匀无耗传输线工作状态
行波、驻波、行驻波
电磁场、微波技术与天线
2-4 均匀无耗传输线工作状态
2
均匀无耗传输线的工作状态
传输线的工作状态是指沿线电压、电流以及阻抗 的分布规律。
接有负载阻抗ZL的传输线在正弦时变信源激励下，
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 16
在行驻波状态下，电压幅值沿传输线的分布规律。用电压反射
(d ) 的模值为： 系数Γ(d)表示，传输线上任一点处电压 U
(d ) U ( d ) 1 ( d ) U i ( d ) 1 ( d ) e j U i (d ) 1 (d ) cos 2 (d ) sin 2 U i (d ) 1 (d ) 2 2 (d ) cos U i
5. 终端短路的传输线其输入阻抗为纯电抗。
电磁场、微波技术与天线 2-4 均匀无耗传输线工作状态 13
（3）终端负载为纯电抗。ZL = jXL，此时终端处的
电压反射系数为
( jX L Z 0 ) ( Z 0 jX L ) (0) ( jX L Z 0 ) ( Z 0 jX L )
的情况，传输线将呈现一种极端工作状态。由于终端没有吸
无耗均匀传输线的工作状态分析
阻抗 。均匀无耗 传输线上 的 电压 、电流及 阻抗分布
可 以表 示为 ：
收稿 日期 ：２ ０ －３０ ０ ６０ －４
无反射 的条
件 为Ｚ＝ ｏ ，Ｚ 。即传 输线 上只 有入 射 的行波 ，而 无反 射波 。因此 ，传输线上 的 电压 、电流及阻抗 的分布
为：
作者简介：朱磊 （９ ２ ） １８ － ，女，黑龙江牡丹江人。助教。主要研究方 向为微波技术、天线技术 、电磁场与电磁波技术 。
图 １ 微波 传输 系统
Ｆｉ． １ Ｍ ｉｒ ｗａ ｅｔａ ｍ ｉｓｏ ｙ ｔｍ ｇ ｃ ｏ ｖ ｎｓ ｓ ｉ ｎ ｓ ｓｅ ｒ
下面 根据 上述 表达 式详 细 的分析 ３种 工作状 态。 １１ 行 波工作 状 态 ． 根据终端 反射系数 Ｚ－Ｚ可知 ， 。
，
图 １是 传 输 线 的 示 意 图 ，其 始 端 接 信 号 源 （ ， ） ｏ ，Ｚ为传输 线 的特 性 阻抗 ，的 电压 、 电流及 阻抗 分布为 ：
其 中， 为始端 电压 ， 为始端 电流 。 由以上表达式 可知 ， 终端 匹配的传输 线上任意
一
ｚ＝ Ｕｃｓ（一 ） ）２ ｔ ｆ／ ｚ ｏｌ
， ｒ ’ ｒ
（Ｏ １）
处 的电压 、电流 可用始端 电压、电流表 示 ，从无
无 耗 均 匀传 输 线 的 工作 状 态 分 析
朱 磊 ，董 亮 ，孙道礼
（ ．齐齐哈 尔大学 通信 与电子工程 学院，黑龙江 齐齐哈 尔 １１０ ） １ ６ ０ ６
摘 要 ：传输线上终端接不 同的负载时 ，具有不同的工作状态 ，分析这些工作状态下的特性对微波电路 的分析
和 设 计 极 为 有 用 。当 传 输线 上 的损 耗 较 小 被 忽 略 时 ，可 看 作 无 耗 均 匀 传 输 线 。 本文 对 无 耗 均 匀传 输 线 的 ３种 工 作 状 态 、９种终 端 负 载 进 行 了 详 细 的 分 析 ，并 根 据 分 析 结 果 使 用 ＭＡ Ｌ Ｔ ＡＢ 实现 了无 耗 均 匀 传 输线 工 作状 态 的模 拟仿真 。 关键 词 ：均 匀 传 输 线 ： 工 作状 态 ：仿 真 中 图分 类 号 ： Ｔ ９ １ Ｎ １ 文 献标 识 码 ：Ａ
可 以表 示为 ：
收稿 日期 ：２ ０ －３０ ０ ６０ －４
无反射 的条
件 为Ｚ＝ ｏ ，Ｚ 。即传 输线 上只 有入 射 的行波 ，而 无反 射波 。因此 ，传输线上 的 电压 、电流及阻抗 的分布
为：
作者简介：朱磊 （９ ２ ） １８ － ，女，黑龙江牡丹江人。助教。主要研究方 向为微波技术、天线技术 、电磁场与电磁波技术 。
图 １ 微波 传输 系统
Ｆｉ． １ Ｍ ｉｒ ｗａ ｅｔａ ｍ ｉｓｏ ｙ ｔｍ ｇ ｃ ｏ ｖ ｎｓ ｓ ｉ ｎ ｓ ｓｅ ｒ
下面 根据 上述 表达 式详 细 的分析 ３种 工作状 态。 １１ 行 波工作 状 态 ． 根据终端 反射系数 Ｚ－Ｚ可知 ， 。
，
图 １是 传 输 线 的 示 意 图 ，其 始 端 接 信 号 源 （ ， ） ｏ ，Ｚ为传输 线 的特 性 阻抗 ，的 电压 、 电流及 阻抗 分布为 ：
其 中， 为始端 电压 ， 为始端 电流 。 由以上表达式 可知 ， 终端 匹配的传输 线上任意
一
ｚ＝ Ｕｃｓ（一 ） ）２ ｔ ｆ／ ｚ ｏｌ
， ｒ ’ ｒ
（Ｏ １）
处 的电压 、电流 可用始端 电压、电流表 示 ，从无
无 耗 均 匀传 输 线 的 工作 状 态 分 析
朱 磊 ，董 亮 ，孙道礼
（ ．齐齐哈 尔大学 通信 与电子工程 学院，黑龙江 齐齐哈 尔 １１０ ） １ ６ ０ ６
摘 要 ：传输线上终端接不 同的负载时 ，具有不同的工作状态 ，分析这些工作状态下的特性对微波电路 的分析
和 设 计 极 为 有 用 。当 传 输线 上 的损 耗 较 小 被 忽 略 时 ，可 看 作 无 耗 均 匀 传 输 线 。 本文 对 无 耗 均 匀传 输 线 的 ３种 工 作 状 态 、９种终 端 负 载 进 行 了 详 细 的 分 析 ，并 根 据 分 析 结 果 使 用 ＭＡ Ｌ Ｔ ＡＢ 实现 了无 耗 均 匀 传 输线 工 作状 态 的模 拟仿真 。 关键 词 ：均 匀 传 输 线 ： 工 作状 态 ：仿 真 中 图分 类 号 ： Ｔ ９ １ Ｎ １ 文 献标 识 码 ：Ａ
1.3均匀无耗传输线三种状态分析
L
ZL ZL
Z0 Z0
R Z0 R Z0
jX jX
R2 Z02 X 2 (R Z0)2 X 2
j
(R
2Z0 X Z0)2
X2
u jv L e jL
式中终端反射系数的模和相角分别为:
L
( (
R R
Z0 Z0
)2 )2
X X
2 2
;
L
tan1
R2
2Z0 X Z02
X
I (z) Ii
z
Ui1 e j z Z0
（2）电压、电流的瞬时值表达式为：
u(z, t) Ui1 cos(t z 1)
i(z,t)
U i1 Z0
cos(t z 1)
（3）沿线各点的阻抗为：
Zin
(z)
U (z) I (z)
Ui (z) Ii (z)
Z0
（4）沿线各点的输入阻抗、反射系数、驻波比为：
I (z) Ii2 (z) 1 (z) Ii2e j z 1 L e j(L 2 z)
上式取模得:
U (z) Ui2 1 L e j2 zL I (z) Ii2 1 L e j2 zL
由此可知：
(1)沿线电压电流呈非正弦周期分布；
(2)当 2 z L 2n 即
z
4
L
n
Zin Z0, z 0, 1
（5）负载吸收的功率为：
PL
1 2
Re U
z
I
z
*
1 2
Re
U
i1e
j
z
U
* i1
Z0
e jz
1 2
Ui1 2 Z0
Pi
无耗传输线状态
oc Zin (d ) jZ0ctg d
sc Zin (d ) jZ0 tg d
Z (d ) Z (d ) Z
oc in sc in
2 0
对于一定长度d的传输线，通过开路和短路的测量， 可以得到如下参数：
oc sc Z 0 Z in (d ) Z in (d )
2.3 1
可见：电压电流同相，振幅不变，各点阻抗为Z
驻波：（全反射） 条件：ZL=0/（短路、开路）ZL=jXL（纯电抗） 特性： Z L Z0 （a）短路时：
GL
V (d ) V (d ) V (d ) VL e j d e j d j 2VL sin d 2VL I (d ) cos d 2 I L cos d Z0
2.4 均匀无耗传输线的状态 共有三种状态：行波、驻波、行驻波 1. 行波状态（无反射）－匹配 条件：ZL=Z0 ＝> G＝0 r=1, K=1
V0 I 0 Z 0 j z j z V ( z) e V0 e 2 V I Z j z 0 0 0 j z I ( z) e I0 e 2Z 0
oc in
XL XL leo ctg arcctg Z 2 Z 0 0 1
1
三、行驻波状态(部分反射情况)
ZL RL jX L
条件：当均匀无耗传输线终端接一般复阻抗，产生部分 反射，在线上形成行驻波 。
R jX L Z 0 R Z 0 jX L R Z 0 GL 2 2 R jX L Z 0 R Z0 X L
1 Z (d ) arctg d Z (d )
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
I(z)
Ii (z)
A1 Z0
e j
z
Zin ( z)
U(z) I(z)
Z0
电压、电流瞬时值表达式为(设 A1 A1 e j 0 )：
u(z,t) ui (z,t) A1 cos( t z 0)
i( z, t )
ii (z,t)
A1 Z0
cos( t
z
0)
(2 15a)
由此可得行波工作状态的特点(如图2-13所示)：
UiL Z0
Ui Z0
二、驻波状态(全反射情况)
当终端短路(ZL=0)、开路(ZL=∞)或接纯电抗负载 (ZL=±jXL)时，︱(z)︱=︱L︱=1，终端全反射，沿 线入、反射波叠加形成驻波分布。负载与传输线完全
失配。驻波状态下，︱︱=1，r=∞，K=0。
(1) 终端短路(ZL=0)
L
ZL ZL
)、电流波腹点(
I max
2 Ii2
)。
2）开路线的输入阻抗
Zin(z) Z0
ZL Z0
jZ0 tg jZL tg
z z
jZ0 ctg
z
j Xin(z) (2 17c)
亦为纯电抗。f 固定时，Zin(z)按余切规律变化，T= /2。
由输入阻抗的等效观点出发， 可将任意长度的
一段开路线等效为相应的等效电路。
z 0 0~l/4 l/4 l/4 ~l/2 l/2
Xin(z) =±∞(开路) <0(容性) =0(短路) >0(感性) =±∞(开路)
z长度开路线的等效电路 并联谐振 电容 串联谐振 电感 并联谐振
沿线每经过l/4，阻抗性质变化一次；每经过
l/2，阻抗重复原有值。
3）短路线与开路线比较 各对应量的相位相差 /2(即l/4)。
z
z
设UiL Ui e j 2， 则电压、电流瞬时表达式为：
u( z, t )
2Ui sin
z
cos(
t
2
2
)
i(z,t) 2 Ii cos z cos( t 2 )
短路时的驻波状态分布规律：
①沿线电压、电流均为驻
波分布。
②电压、电流之间在位置
或时间上，相位都相差/2。
③在z=n·(l/2) (n=0,1, …)
① 沿线电压、电流均为驻波分布。
② 电压、电流之间在位置或时间上，相位都相差/2。
③ 在z=n·(l/2) (n=0,1,2, …)处ຫໍສະໝຸດ ( 含终端 ) 为电压波腹点(
) 、电流波节点(
)。
④ 在Uz=max(2n+2U1)i·2 (l/4)
I 0
(n=0,1,2, …)m处in 为电压波
节点( U 0 min
对相同长度的 均匀无耗长线，有：
Z0
Z sc(z) Z oc(z)
in
in
Z
sc
in
(
z
)
jZ0
tg
z
Z
oc
in
(
z
)
jZ0
ctg
z
3. 终端接纯电抗负载 ( ZL=±jX (X>0))
L
ZL ZL
Z0 Z0
jX Z0 jX Z0
(X
2
Z 2) 2 0 X2 Z2
(2) 负载全反射的驻波状态
(3) 负载部分反射的行驻波状态
一、行波状态(无反射情况)
当ZL=Z0 时,L=(ZL－ Z0)/(ZL＋ Z0)=0； 或传输 线为无限长时，无反射，只有入射行波。
取z 轴原点在波源、指向负载，则行波状态下， 线上电压、电流复数表达式为
U(z)
Ui (z)
A1e
j
z
(1)︱︱=0，r=1，K=1，沿线只有入射行波而
无反射波；入射波的能量全部被负载吸收，传输效率
最高。 故称 ZL=Z0 时，负载与传输线匹配。
(2) Zin(z)=Z0 ，为 纯阻。
(3)电压和电流始终 同相。
(4)沿线电压、电流 的振幅恒定不变，
Ui (z) A1
UiL Ui
Ii (z)
U(z) I(z)
U2 cos z j U2 sin
Z0
2Ui2 cos
z j2Ii2 sin
z
z
UiL IiLZ0
电压、电流瞬时表达式为：
u( z, t )
2Ui2
cos
z
cos(
t
2
)
i( z, t )
2
Ii 2
sin
z cos(
t
2
)
2
开路时的驻波状态分布规律：
(2 17b)
Z0 Z0
输入阻抗
Zin ( z)
Z0
ZL Z0
jZ0 jZL
tg tg
z z
Z
in
(
z
)
Z0
1 1
( (
z) z)
ZL
Z0
1 L 1 L
第四节 均匀无耗传输线的工作状态
传输线的工作状态是指沿线电压、电流及阻抗 的分布规律。均匀无耗传输线的工作状态分为三种：
(1) 负载无反射的行波状态
处 ( 含终端 ) 为电压波节点
( U 0 ) 、电流波腹点
min
(
I max
2 Ii2
)。
(2 16b)
④在z=(2n+1)·(l/4) (n=0,1, …)处为电压波腹点
(
U max
2UiL
)、电流波节点( I 0 min
)。
2）短路线的输入阻抗
Zin ( z)
Z0
ZL Z0
jZ0 jZL
传输=入射+反射
U(z) ULie jz ULre jz
U( z)[1 ( z)] U(z) ULie jz ULre jz i
I(z) ILie jz ILre jz
Ii (z)[1 (z)]
反射系数
(z) L e j2 z
(z) Zin(z) Z0 Zin(z) Z0
L
ZL ZL
Z0 Z0
1 e j
UL 0 UiL UrL IiLZ0
IL IiL (1 L ) 2IiL
1）沿线电压、电流分布
以上关系式代入式(2-4e)
U(z)
UL
cos
z
IL
jZ0
sin
z
I(z) UL
j
sin
Z0
z
IL cos
z
得
(2 4e)
UI((zz))2jI2iLUcioL ssin
tg tg
z z
jZ0 tg z
j Xin(z) (2 16c)
为纯电抗。f 固定时，Zin(z)按正切规律变化，T= /2。 由输入阻抗的等效观点出发， 可将任意长度的一段
短路线等效为相应的等效电路。
z
Xin(z)
z长度短路线 的等效电路
0 =0(短路) 串联谐振
0~l/4 >0(感性) 电 感
l/4 =±∞(开路) 并联谐振
l/4 ~ <0(容性) 电 容
l/2
l/2 =0 (短路) 串联谐振
沿线每经过l/4，阻抗性质变化一次；每经过
l/2，阻抗重复原有值。
2. 终端开路(ZL=∞)
L 1 e j0
IL 0 ，UL UiL (1 L ) 2UiL ,
1）沿线电压、电流分布
以上关系代入式(2-4e)得