描述正弦量的三要素
正弦量的三要素和有效值

如Im 、Um。
首页
2.角频率、周期、频率 正弦量在单位时间内所经历的电角度,称为角频率,用ω 表示,单位是弧度/秒,即
t
正弦量完成一次周期变化所需要的时间,称为周期,用T 表示,单位是秒。
正弦量在1秒钟内完成周期性变化的次数,称为频率,用 f 表示,单位是赫兹。
选零点为计时起点,则初相ψ =0,如图3-7所示是不同初相时
几种正弦电流的解析式和波形图。
首页
i
Im
i Im sint
0
t
a)
i i Im sin(t π 6)
i
i Im sin(t π 2)
0
t
b)
i i Im sin(t π 6)
0
t
0
t
π/6
π/6
首页
例3-3 两个同频率正弦电流的波形如图3-6所示,试写出 它们的解析式,并计算二者之间的相位差。
解 解析式
i/A 10 i1
i1
10 s in(314t
π )A 4
8
i2
i2
8 s in(314t Nhomakorabeaπ )A 4
0
4
4
0.02s
相位差
ωt/rad
i1
i2
π 4
(
c)
d)
图3-3 初相不同的几种正弦电流的波形图 a)初相为0; b)初相为π/2; c)初相为π/6; d)初相为-π/6
首页
注意:正弦量的初相、相位以及解析式都与参考方向有 关。改变参考方向,就是将正弦量的初相加上或减去π。
3-1正弦量的表示方法

已知: i = 141.4 sin( 314t +
u = 311.1sin(314t −
π
6
) A
π
3 求: i 、u 的相量表达式及相量图。
) V
i = 141.4 sin( 314t +
u = 311.1sin(314t −
解:
π
π
6
3
) A
) V
I
141.4 j 30 j 30 I= e = 100e = 100∠ 30 A 2
u = 5 2 sin(ω t − 126 ⋅ 9 )
b. 复数的四则运算
已知:
jθ 1 A1 = a1 + jb1 = A1e
jθ 2 A2 = a 2 + jb2 = Ae
±A = ( a ± a ) + j( b ± b ) 加减:A 1 2 1 2 1 2
乘除:
⋅A = A ⋅ A e j ( θ 1 +θ 2 ) A 1 2 1 2
Im = 2
同理
Um U= 2
Em E= 2
•相位和初相位
i
i = 2 I sin (ω t + ϕ )
ωt
ϕ
相位(相位角): ωt + ϕ
单位:弧度( rad)、度( )
初相位: t = 0 时的相位,即 ϕ
相位差 两个同频率正弦量间的相位差(初相差)
i1
ϕ2
i2
ϕ1
ωt
i1 = I m 1 sin(ω t + ϕ 1 )
30 60
311.1 − j 60 U= e = 220∠ − 60 V 2 相位哪一个超前? 哪一个滞后?
正弦量的三要素及相量表示法基尔霍夫

正弦电流电路导论
内容提要
1.正弦量的相量表示法; 2.两类约束的相量形式; 3.正弦电流电路的分析计算; 4.正弦电流电路的功率。
5.1 正弦量电压和电流的基本概念
一 时变的电压和电流 ◆ 时变电压和电流:随时间变动的电压和电流。
第五章
正弦电流电路
u(t )
◆瞬时值:时变电压和电流在任一时刻的数值,用 和 i (t ) 表示。
2π u2 =100 2sin(100t )V 3
3
0
6
I1
解:
π I1 =50 A 6 π U1 =100 V 3 2π U 2 =100- V 3
2 3
U 2
相量图
第三章 正弦电流电路
四 用相量求正弦量的和与差
i1 (t ) 70.7 2 sin(ωt 45 )A i2 (t ) 42.4 2 sin(ωt 30 )A
③角频率ω:每秒变化的弧度。单位:弧度/秒(rad/s)
第五章 正弦电流电路
三者间的关系:
1 f T
2 2 f T
* 电网频率(工频):我国:50Hz;美国和日本:60Hz * 无线通信频率: 30 kHz ~ 30GMHz ◆ 相位和初相位 ①相位:正弦波的 (ωt ψ ) 。 ②初相位 :t =0 时的相位。 ③规定:初相位的绝对值不超过π。
第五章 正弦电流电路
三 用相量表示正弦量
相量:表示正弦量的复数称为相量。
相量表示法:用模值等于正弦量的最大值(或有效值)、
辐角等于正弦量的初相的复数对应地表示相应的正弦量。
即:相量 Im (或 I )
j
模用最大值表示时,为最 I ψ 大值相量,即 I m m
正弦量的瞬时值、幅值和有效值(精)

正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u U m sin(t u ) i I m sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值(或最大值); ω为角频率; φu, φi分别
为电压和电流的初相角, 如图所示。
注意: 交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
u ~
i
R
+ U _
I
R
பைடு நூலகம்
通入正弦交流电,T时 间内,电流热效应:
T
通入直流电,T时间内, 电流热效应:
Q = I2 RT
Q
2 i Rdt 0
则有: 同理:
I
Im 2
U U m 2
E
Em 2
1.瞬时值、最大值、有效值
i I m sin t
母u, i, e 表示 。 母带下标m表示, 如:Im, 有效值。以大写字母I、U、
瞬时值 : 描述正弦量在任一瞬间的值 ,以小写字 最大值 :瞬时值中的最大数值,也称幅值 ,以大写字 Um, Em. 有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
7 正弦量与相量

C B
ϕb ϕb ϕa + ϕb A
C=A/B
+j
A
B
B jA A
-jB
+1 O C
+1
ϕ a- ϕ b
O 旋转因子示意 +1
O 复数的乘法
复数的除法
7.4 正弦量的相量表示法
一、正弦稳态电路的特点
1、角频率不变性:在线性电路中,如 角频率不变性:在线性电路中, 果电路的所有激励都是同频率的正弦量, 果电路的所有激励都是同频率的正弦量, 激励都是同频率的正弦量 则电路中各支路的稳态响应也为同频率 稳态响应也为 则电路中各支路的稳态响应也为同频率 的正弦量。 ( P208) 的正弦量。 2、计算的复杂性:在列写VCR、KCL、 计算的复杂性:在列写VCR、KCL、 KVL方程的时候会遇到微分、积分和 KVL方程的时候会遇到微分、积分和和 方程的时候会遇到微分 差化积的问题 的问题。 差化积的问题。
二、复数的四则运算
1、加减运算 1)定量运算 1)定量运算------用代数形式计算 定量运算------用代数形式计算
F1 ± F2 = (a1 + jb1 ) ± (a2 + jb2 ) = (a1 ± a2 ) + j (b1 ± b2 )
法则:实部加减,虚部加减。 法则:实部加减,虚部加减。
7 正弦量与相量
重点
1、正弦量的三要素 2、复数的几种表示形式的转换及计算 3、 KCL、KVL 、VCR的相量表示 KCL、 VCR的相量表示
难点
相量图的绘制
本章作业
P217 7.1 7.2 7.5 7.7 7.10 7.12
03 电工电子技术 拓展阅读:正弦量的三要素

正弦量的三要素 大小和方向都随时间按一定规律周期性变化的电压或电流,称为交变电压或电流,简称交流电,或交流量。
交流电压或电流在任一时刻的数值称为它们的瞬时值,用小写字母u 或i 表示。
一、正弦量的三要素交流量中应用最广泛的是正弦交流量,它们的量值是时间的正弦函数,简称正弦量。
正弦量的特征表现在变化的快慢、大小和初始值三个方面,而它们分别由频率(或周期)、幅值(或有效值)和初相位来确定。
所以称频率、有效值和初相位为正弦量的三要素。
1、周期和频率:以正弦电压为例,解析式为:)sin(u m t U u ψω+=波形图为:正弦量变化一个循环所需要的时间(秒)称为周期T ,它的SI 主单位是秒(s)。
每秒时间内变化的循环数称为频率f 。
频率的SI 主单位是S -1,常称为赫[兹],以符号Hz 表示。
在无线电工程中,还常用千赫(kHz)、兆赫(MHz)和吉赫(GHz)等十进倍数单位。
频率是周期的倒数,即:Tf 1= (式3-1) 我国和大多数国家都采用50Hz 作为工业标准频率,称为工频。
有些国家(如美国、日本等)工频采用60Hz 。
无线电用的频率较高,广播频段大约是几百千赫到几十兆赫,电视广播频段则在几十到几百兆赫范围之内。
正弦量变化的快慢除用周期和频率表示外,还可用正弦量对应的角度随时间变化的速率来表示,称为角频率,用符号ω来代表。
因为在一个周期内正弦量对应的角度变化了2π弧度,所以角频率为:f T ππω22== (式3-2)由此可见:ω与f 成正比。
角频率表示了每秒变化的弧度数,它的SI 主单位为弧度每秒(rad/s)。
2、幅值和有效值: 图3-1瞬时值:(1)瞬时值的概念及表示方法:正弦量某时刻的值称为瞬时值。
用小写字母表示。
如:i 、u 、e 分别表示电流、电压和电动势的瞬时值。
)sin(u m t U u ψω+=)sin(i m t I i ψω+=)sin(e m t E e ψω+=(2)瞬时值的正、负:象分析直流电路一样,在分析交流电路时也应选择一个参考方向,如果交流电压或电流某时刻的实际方向与参考方向一致,则其瞬时值为正,反之,为负。
正弦量的三要素

设一交变电流i通过电阻R,在一个周期内该电阻消耗的 电能是:
W~ = ∫ i Rdt = R∫ i dt
2 2 0 0
T
T
i
R
如果有一个直流电流I通过同一电阻R,在同一时间T内 所消耗的电能为:
W = I RT
2
I
R
在一个周期时间内,W~=W—, 于是
R∫ i dt = I RT
2 2 0
T
1 T 2 I= ∫0 i dt T
最大值(幅值) 最大值(幅值):在一个周期里 最大的瞬时值叫最大值, 最大的瞬时值叫最大值,它是交 流电的振幅,通常用大写字母并 流电的振幅, 加注下标m表示。 加注下标m表示。如Im、Um及Em。 可见, 可见,最大值实际上就是最大的 瞬时值,也是与时间有关的量。 瞬时值,也是与时间有关的量。
Im
ω
= 2πf
Um
ψu
e = Em sin( ωt +ψe )V
Em
ψe
相位差:两个同频率的正弦交流电在相位上的差值 定义位相位差,用φ表示。
ui = (ωt +ψu ) (ωt +ψi ) =ψu ψi
同频率的两个正弦交流电的相位差等于它们的 初相之差。 i, u i, u
ψi ψu
0
t
ψu 0
Im i t4 t
t3 0 t1 t2
.
每秒时间内重复变化的周期数称 T 为频率,用字母 表示,它的单位是赫 为频率 用字母 f 表示 它的单位是赫 简称赫,周期和频率互为倒数 兹(Hz),简称赫 周期和频率互为倒数 简称赫 周期和频率互为倒数, 1 2π 即有 f = ωT = 2π ω = = 2πf T T 的交流电(称为工频交流电),其角 例如频率 f =50Hz的交流电 称为工频交流电 其角 的交流电 称为工频交流电 频率和周期分别为: 频率和周期分别为 ω=2π f=314 rad/s T=0.02s
正弦量的三要素及相量表示法基尔霍夫

三 相位差
第五章
正弦电流电路
相位差 :两个同频率正弦量间的相位之差,即初相位 之差。
i
u
如:
u
t
i
u U m sin t u
i I m sin t i 则相位差为:
t u t i u i
第五章 正弦电流电路 两个正弦量的相位关系
上述相量图是根据平行四边形法则进行加、减获得的。实际上, 可采用三角形法则作图。如下图所示。
I1
0
I2
I I1 I 2
0
I2
I1
I I1 I 2
两相量相加
两相量相减
第五章 正弦电流电路
5.4基尔霍夫定律的相量形式
一 基尔霍夫电流定律(KCL) 瞬时值形式:
i 0
0 相量形式(同频率的正弦量) : I
◆周期量:每个值在经过相等的时间间隔后循环出现的 时变电压和电流。 ◆交流量:一个循环内波形面积平均值为零的周期量。
u i i
O
t
时变电压
O
t
周期量
O
t
交流量
第五章 正弦电流电路 二 正弦量的三要素
正弦量:按正弦规 律变化的交流量。 设正弦电流
Im
i
O
T
2
t
i I m sin(ωt ψ )
二 基尔霍夫电压定律(KVL)
瞬时值形式:
u 0
相量形式(同频率的正弦量) : U 0
第五章 正弦电流电路 二 旋转矢量与正弦量 设正弦量: i I m sin(ωt ψ )
j B ω t1
0
i
Im
正弦量的瞬时值、幅值和有效值(精)

瞬时值 : 描述正弦量在任一瞬间的值 ,以小写字
母u, i, e 表示 。
最大值 :瞬时值中的最大数值,也称幅值 ,以大写字 母带下标m表示, 如:Im, Um, Em.
有效值 : 与交流热效应相等的直流定义为交流电的 E表示 。
注意:
有效值。以大写字母I、U、
电路基础
正弦量的瞬时值、幅值和有效值
3.2 正弦量的三要素
u Um sin(t u ) i Im sin(t i )
其中u、i分别为电压和电流的瞬时值; Um、Im分别为 电压和电流的幅值(或最大值); ω为角频率; φu, φi分别 为电有效值
交流电压、电流表测量数据为有效值 交流设备名牌标注的电压、电流均为有效值
~u i R
+
U IR _
通入正弦交流电,T时
间内,电流热效应:
T
Q i2Rdt
0
则有:
I Im 2
同理:
U
Um 2
通入直流电,T时间内, 电流热效应:
Q = I2 RT
E Em 2
知识回顾 Knowledge Review
电路分析基础简答题

1、对于无源一端口网络,如何用等效阻抗Z 或等效导纳Y 计算复功率S 以及有功功率P 和无功功率Q ? 答:设无源一端口网络的等效阻抗Z 、等效导纳Y 分别为,Z R jX Y G jB =+=+,则2、为什么将RLC 串联电路的串联谐振称为电压谐振?答:因为当RLC 串联电路发生串联谐振时,0000Q ,Q ,0L S C S L C U j U U j U U U ==-→+=,故将串联谐振称为电压谐振。
(因为Im[所以又称并联谐振为电流谐振) 3、对称Δ联接三相负载的线电流和相电流之间有什么关系?答:对于对称Δ联接三相负载,设其线电流为A B C I I I '''、、,相电流为A B B C C A I I I ''''''、、。
它们之间的关系为330,330,330A A B B B C C C A I I I I I I '''''''''=∠-=∠-=∠-。
4、简述非正弦周期电流()i t 的傅里叶级数展开式和其有效值I 的计算公式。
答: 20131()cos(),km k k i t I I k t I ωψ∞==++==∑ 5、对于对称的无源、松弛二端口网络,其Y 参数存在什么关系?答:对于对称的无源、松弛二端口网络,其Y 参数存在12211122,Y Y Y Y == 的关系。
6、对耦合电感元件,标记同名端有何意义? 答:对耦合电感元件,根据标记的同名端和电感电流参考方向,就能确定耦合电感元件上互感电压的方向以及性能方程中正负号。
7、复频域(s 域)的网络函数是如何定义的,他有几种不同的形式?答:线性时不变电路在单一电源激励下,其零状态响应象函数R (s )与激励象函数E(s)之比为电路的网络函数H(s),即H(s)= ( )网络函数有驱动点阻抗,驱动点导纳,转移阻抗,转移导纳,转移电压比,转移电流比。
正弦量的三要素

i
t
如果 u i 180o
称电压与电流反相。
例1:已知:i(t)=100sin(6280t-/4)mA (1)说明它的Im,I,,f,T, (2)画出波形图。 解:(1) I m 100mA I 100 /
2 70.7mA
6280rad / s 6280 f 1000 Hz 2 2 3.14Fra bibliotek 45
o
i 2 30
o
i1 i 2 o o o 12 45 (30 ) 75
2. 正弦量的计时起点 ——初相位与相位差
对于已知的正弦量:
相位:称(ωt+ψi) 为正弦交流电流的相位角,简称相位。 在不同的时刻正弦量的相位也不同,交流电流的大小 和方向也不同。 初相位:称t = 0时的相位角ψ i为初相角,简称初相位。 初相位用来确定交流电初始瞬时状态。 i i O o i I m sin(t 90 ) i I m sin(t 90 )
Im 2 0.707 I m
0.707U m
T 1 T dt cos( 2t 2 )dt 0 2 2
I
同理
U
Um 2
Em E 0.707 Em 2
正弦交流电的有效值等于 它的最大值除以 2 , 而与 其频率及初相无关。 有效值与最大值之间的 2 关系不适用于其他非正 弦交流量
Im
i ( t )
i
t
t3
0
t1 t2
.
t4 t
i (t )
T
t
有效值:若有一交流电流 i 通过电阻R,在一个周期时 间内消耗的电能,与直流电流I在同样时间内通过同一 电阻所消耗的电能相等,则该直流电流I的数值称为该 交流电流 i 的有效值。 在工程中,正弦电压与电流的计量不是瞬时值也 不是幅值,而是有效值。
《正弦量的基本概念》课件

contents
目录
• 正弦量及其表示方法 • 正弦量的运算 • 正弦量的线性性质 • 正弦量的初值与相位角 • 正弦量在交流电中的应用
பைடு நூலகம் 01
正弦量及其表示方法
正弦量的定义
总结词
正弦量是随时间按正弦规律变化 的量,是交流电的基本特征。
详细描述
正弦量是随时间变化且符合正弦 函数规律的物理量,如交流电的 电压、电流等。它们具有周期性 、波动性和相位差等特性。
正弦交流电的表示方法
正弦交流电的三要素
幅值、角频率和相位。幅值表示交流 电的最大值,角频率表示交流电变化 的快慢,相位表示交流电与时间的关 系。
正弦交流电的波形图
正弦交流电的相量图
相量图是一种用复数表示正弦交流电 的方法,可以方便地表示出正弦交流 电的相位和幅度。
正弦交流电的波形图可以直观地表示 出其随时间变化的规律。
03
正弦量的线性性质
线性性质的定义
线性性质
正弦量在经过加、减、数乘运算后,其波形 沿时间轴平移或拉伸,但不改变其形状。
数学表达式
若 $y_1(t) = A_1 sin(omega_1 t + varphi_1)$ 和 $y_2(t) = A_2 sin(omega_2 t + varphi_2)$,则 $y(t) = A_1 y_1(t) + A_2 y_2(t)$ 或 $y(t) = k y_1(t)$,其中 $k$ 是常数。
实例分析
在交流电路中,多个电压和电流源产 生的正弦量可以通过线性性质进行叠 加,得到总电压和总电流,方便计算 电路的性能指标。
04
正弦量的初值与相位角
正弦量的基本概念正弦量的相量表示法电容元件
3.旋转因子及旋转相量
相量与ejwt相乘是一个随时间变化的函数,它随时
间的推移而旋转,且旋转速度为ω。我们把相量乘
以ejwt再乘以常数 2 称为旋转相量,旋转相量在虚 轴上的投影Imsin(ωt+φi)为正旋量的瞬时值。 Imsinφi为i(t)的初始值,如图3-2-1(b)所示。
所以也可以用正弦相量来表示正旋量。
0
2T
I
Im 2
0.707Im
U
Um 2
0.707Um
Um 220 2 311V
例 3-4 一个正弦电流的初相角为60°,在T/4 时 电流的值为5A,试求该电流的有效值。
解 该正弦电流的解析式为
it I m sin wt 60 A
代入已知量有:5
Im
sin wT 4
60 A
5
Im
sin
2
3
A
则有:I
=
m
5
sin5
/ 6
5 1
10A
2
I I m 7.07A 2
3.2 正弦量的相量表示法
复数及四则运算
1.复数 在数学中常用A=a+bi表示复数。其中a为实部, b为虚部,
i 1 称为虚单位。在电工技术中, 为区别于电流的符
号, 虚单位常用j表示。 +j
3
A
O
确定φ角正负的零点均指离计时起点最近的那个零点
i i1=Imsint
i i2=Imsin(t+ 2)
i i3=Imsin(t+ 6)
i
i4=Imsin(t-
6)
0
t 0
t 0
t 0
t
2
6
6
正弦量的相量表示

(3)正弦量的相量表示
分析正弦稳态的有效方法是相量法 (Phasor method),相量法的基础是用相 量(向量)或复数来表示正弦量的振 幅和初相。注意:其频率不变。
j 相量图
Fm sin
Fm
+1
称为:f (t)的振幅相量 0 Fm cos
相量图的另一个好处是可平行四边形法则。
可得电流的表达式为
电路与模拟电子技术
j a2
复数A的 复平面表 示
a +
0
a1 1
(2)复数运算
A=a1+ja2= aej , B1=b1+jb2=bejφ
则: A+B =a1+b1 +j(a2+b2 ) A×B= abej(+φ)
[例3-2] 已知A=4+j3,B=10∠-60°。试求:A+B,A-B, A·B。
解:A=4+j3 =5∠36.9°, B=10∠-60°=5-j8.66 则 A+B=4+j3+5-j8.66=9-j5.66; A-B=4+j3-(5-j8.66)=-1+j11.66
参考相量:上图中假设为零相位的相量。
例 4 已 知 电 流 i1(t)=5cos(314t+60)A , i2(t)=-10sin(314t+60)A 。 写 出 它 们 的 相 量,画出相量图,并求i(t)=i1(t)+ i2(t) 。 解:
相量图如图所示。
从相量图容易看 出各正弦电压电 流的相位关系: i2(t)超前于 i1(t) 90°。
电路与模拟电子技术
幅值(最大值),又称峰值,用带下标m的大写字母表示,如

三要素:图中对应的正弦电压的瞬时值表达式为,式中幅值、角频率和初相位构成描述正弦量的三个基本要素,称为三要素。
I,反映了正弦量变化幅值(最大值):又称峰值,用带下标m的大写字母表示,如、m的幅度大小,幅值越大,说明正弦量变化的幅度越大。
周期:图中,正弦量变化一次所需的时间称为周期T。
频率:图中,正弦量在单位时间内变化的次数称为频率f,单位为赫[兹] 。
频率与周期的关系是。
角频率:角频率是正弦量在单位时间内变化的角度,有时也称为电角速度,单位是弧度/秒(rad/s)。
角频率反映了正弦量变化的快慢,与周期、频率的关系是。
相位:在正弦电压的瞬时值表达式中,称为正弦量的相位。
初相位:在正弦电压的瞬时值表达式中,称为正弦量的相位,时的相位为,称为初相位(初相),它决定了正弦量在计时起点()的大小,其单位是"弧度"(rad)。
初相位与计时起点有关,如图所示。
起点取在A处,电压的初相位;计时起点取在 B 处,电压的初相位。
初相位可以是一个任意数,但习惯上常取初相位的绝对值小于。
有效值:交流电流通过电阻在一个周期内产生的热量如与某一直流电流I 通过同一电阻在相同时间内所产生的热量相等时,则称此直流电流I 的数值是该交流电流的有效值。
有效值与幅值的关系是。
相位差:两个同频率正弦量的相位之差,称为相位差,用表示。
设则两者相位差可见,相位差等于初相位之差。
相位差与计时起点无关,因而,常用相位差描述正弦量之间的相位关系。
正弦量的相位关系:根据相位差的大小,相位关系有四种,即超前、滞后、同相和反相。
超前:如图a所示,相位差,即,则电压比电流先到达正的最大值或零值,就称电压超前电流角。
滞后:如图a所示,相位差,即,则电流比电压先到达正的最大值或零值,就称电流滞后电压角。
同相:如图b所示,相位差,即,则二者同时到达最大值、零值,就称二者同相。
反相:如图c所示,相位差,即二者变化趋势相反,就称二者反相。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
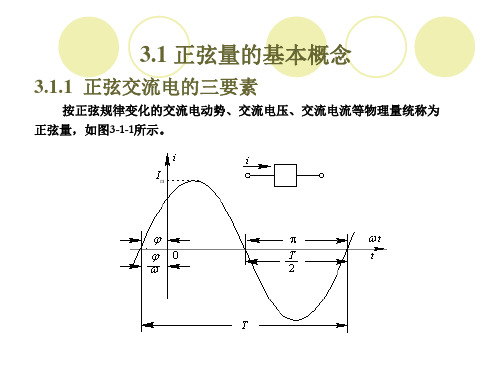
描述正弦量的三要素
描述正弦量的数学表达式:i=Imsin(ωt+φ)
下面是正弦量的波形图
(1)频率f、周期Τ和角频率ω:表示正弦量变化的快慢。
①周期
表示正弦量变化一次所需的时间,规定用字母T来表示,单位是秒(s)。
②频率
表示正弦量在单位时间内重复变化的次数,规定用字母f来表示,单位是赫兹(Hz)。
③角频率
交流电量在一个周期T内变化的角度是2л个弧度,将交流电在1秒内变化的弧度数称为交流电的角频率,用ω来表示,单位是弧度/秒(rad/s)。
三者关系为
我国及世界上许多国家工业电网所采用的交流电频率是50Hz,这种频率的交流电又称为工频交流电。
当频率很高时,可用千赫(kHz)或兆赫(MHz)作单位。
换算关系是 1MHz=103kHz=106Hz
无线电广播信号中波段的频率从535kHz到1605kHz,电视广播和手机通讯信号的频率高达几十到几千兆赫兹。
(2)有效值和幅值:表示正弦量的大小。
瞬时值:任意时刻交流量的大小,有正值、负值。
幅值或最大值:瞬时值中的最大正值。
有效值是根据交流电流和直流电流具有相等的热效应来定义的。
有效值:在交流电变化的一个周期内,交流电流在电阻R上产生的热量相当于多大数值的直流电流在该电阻上所产生的热量,此直流电流的数值就是该交流电流的有效值。
i=Imsin(ωt+φ)
→
同理:,。
注意:交流仪表测得的电压、电流的数值是有效值。
区别各量的表达方式:
瞬时值:用表示。
幅值或最大值:用,,表示。
有效值:用U,E,I表示。
注意:交流电的有效值和最大值都有实用意义。
当考虑能量转化时要用有效值;当考虑用电器的绝缘性能时要用最大值。
(3)相位和初相位
①相位角或相位:任意瞬间的电角度ωt+φ。
反映了正弦量在t 时刻所处的状态,当相位角随时间连续的变化时,正弦量的瞬时值也随之作连续的变化。
②初相角或初相位:t=0时的相位,用符号φ来表示。
它反映了正弦量在初始时刻所处的状态。
初相角在波形图形中的计算方法是:
变化起点:正弦量的瞬时值由负变正过程中,与横坐标相交的点。
变化起点在纵坐标的左面,则φ为正,在右边为负。
在下图中,,。
初相角与计时起点有关,不同的计时起点,对应于不同的初相角。
同一电路中有许多相关的正弦量时,只能取一个共同的计时起点,从而确定各自的初相位。
取值范围:
③相位差:描述两个同频率的正弦交流电在任何瞬时的相位之差。
相位差等于初相位之差,不随计时起点而变。
同相:,表示u与i同相。
反相:,表示u与i反向。
超前:表示u超前于i。
滞后:表示u滞后于i。
在同一个周期内,一个正弦量比另一个正弦量早些或晚些到达最大值,前者被称为超前,后者被称为滞后。
如果两个同频率的正弦量同时达到最大值,则这两个正弦量称为同相。
如果两个同频率正弦量同时达到零值,但当一个达到正的最大值时,另一个达到负的最大值,则这两个正弦量的相位互差180°,称为反相。
注意:超前和滞后的概念是相对的。
相位差可以通过观察波形来确定,方法是:在波形图中确定同一个周期内两个波形的最大值之间的角度差,即为两者的相位差。
在波形图中,先到达最大值的为超前,后到达最大值的为滞后。
