一维无限深势阱的能量

量子力学2.6一维无限深势阱

2008.5
Quantum Mechanics
a、偶宇称态由于这里内外解
(
2 (x)
x)和 '(
~ cos kx
x)在 | x | a
| x | a 2
处是连续的，
2
更方便的方法是取 ' 连续或 (ln )' 连续。
因此在x
a 处，有 2
ln(cos
kx)
' x a
2
ln(
ex
)
' x
a
，得
2
k tan ka
2
（5）
在x a 处，结果同上。 2
2008.5
Quantum Mechanics
令则(5)式化为
ka， a
2
2
tan
（6）
（7）
由
2m(V0
E)
,
k
2mE
有
2mV0 2k 2
再利用(6)式,有
2
2
mV0 a 2 2 2
2008.5
(8)
2008.5
Quantum Mechanics
写出分区定态方程在阱外(经典禁介区)
d2 dx 2
1
2m 2
(V0
E ) 1
0
(1)
令
方程(1)变为
其解为
2m(V0 E)
(2)
1'' 21 0
1 ~ ex
都是方程的解？
2008.5
Quantum Mechanics
考虑到束缚态边界条件：| x | 时 0，有
2008.5
Quantum Mechanics

一维无限深势阱的能量

一维无限深方势阱的能量班级：姓名：学号：一维无限深方势阱的能量一、引言：222220202()d E x d m dx d U x E x d ψ⎧-ψ=ψ<<⎪⎪⎨⎪-ψ+=ψ≥⎪ （1）（2）9/10m-020406080100120140160文案编辑词条B 添加义项?文案，原指放书的桌子，后来指在桌子上写字的人。

现在指的是公司或企业中从事文字工作的职位，就是以文字来表现已经制定的创意策略。

文案它不同于设计师用画面或其他手段的表现手法，它是一个与广告创意先后相继的表现的过程、发展的过程、深化的过程，多存在于广告公司，企业宣传，新闻策划等。

基本信息中文名称文案外文名称Copy目录1发展历程2主要工作3分类构成4基本要求5工作范围6文案写法7实际应用折叠编辑本段发展历程汉字"文案"(wén àn)是指古代官衙中掌管档案、负责起草文书的幕友,亦指官署中的公文、书信等;在现代，文案的称呼主要用在商业领域，其意义与中国古代所说的文案是有区别的。

在中国古代，文案亦作" 文按"。

公文案卷。

《北堂书钞》卷六八引《汉杂事》:"先是公府掾多不视事，但以文案为务。

"《晋书·桓温传》:"机务不可停废，常行文按宜为限日。

" 唐戴叔伦《答崔载华》诗:"文案日成堆，愁眉拽不开。

"《资治通鉴·晋孝武帝太元十四年》:"诸曹皆得良吏以掌文按。

"《花月痕》第五一回:" 荷生觉得自己是替他掌文案。

"旧时衙门里草拟文牍、掌管档案的幕僚，其地位比一般属吏高。

《老残游记》第四回:"像你老这样抚台央出文案老爷来请进去谈谈，这面子有多大!"夏衍《秋瑾传》序幕:"将这阮财富带回衙门去，要文案给他补一份状子。

"文案音译文案英文:copywriter、copy、copywriting文案拼音:wén àn现代文案的概念:文案来源于广告行业，是"广告文案"的简称，由copy writer翻译而来。

一维无限深势阱

n*dx
=
a −a
A sin ⎢⎣⎡
nπ 2a
(x
+
a)⎥⎦⎤dx
= aA2 = 1
A= 1 a
ψn =
1 a
sin
⎡ ⎢⎣
nπ 2a
(
x
+
a)⎥⎦⎤
ψ
n
( x, t )
=
ψ
− i Et
ne h
=
1 a
sin
⎡ ⎢⎣
nπ 2a
(x
+
a)⎥⎦⎤
⋅
−i
eh
Et
En
=
n2π 2h 2 8μA2
ΔEn
=
En +1
§2.6 一维无限深势阱（1）序
一维运动相互作用用势函数 U 表示
势场
⎧散射场 ⎩⎨束缚态
势垒
方形势阱
⎧方形势阱 ⎪⎪谐振子势阱 ⎪⎨δ 阱 ⎪⎩周期阱
一维无限深势阱，图 2.1 所示
Fig 2.1 一维无限深势阱
（2）一维无限深势阱在一维空间中运动的粒子，粒子在一定区域内（x=-a 到 x=a）为零，而在此区域外，势能为无
a −a
⎢⎣⎡cos
n
+ n′ 2a
(
x
+
a)
−
cos
n
− n′ 2a
(
x
+
a)⎥⎦⎤
dx
=0
——此即为波函数的正交条件。
8．波函数可视为两波波函数的迭加
ψ = c e + c e i h
(
nπh 2a
−
Ent
)
−

19.8一维无限深势阱

( x 0, x a)
2 nπ sin x , (0 x a) a a
19.8 一维无限深势阱
概率密度
2 2 nπ ( x) sin x a a
2
能量
h En n 2 8ma
2
2
讨论：
19.8 一维无限深势阱
(1) 粒子能量量子化能量
2 h En n 2 2 8ma
Ep
o
a
a
x

2
dx dx 1
* 0

nπ xdx 1 a
2 A a
19.8 一维无限深势阱
2 nπ ( x) sin x , (0 x a ) a a
波动方程波函数
0,
d 2 8 π 2 mE 0 2 2 dx h
( x)
nπ k , n 1, 2, 3, a
8π mE k h2
2
o
a
x
量子数
2 2
h En 2 8ma
19.8 一维无限深势阱
( x) A sin kx
nπ k , n 1, 2, 3, a nπ ( x) A sin x a
归一化条件
2 a 2 A sin 0
2 nπ sin x a a
概率密度
2 2 nπ ( x) sin ( x) a a
2
例如,当 n =1时,粒子在 x = a /2处出现的概率最大
19.8 一维无限深势阱
(3) 波函数为驻波形式,阱壁处为波节,波腹的个数与量子数 n 相等
( x ) A sin
n4
n
nπ x a

一维无限深势阱

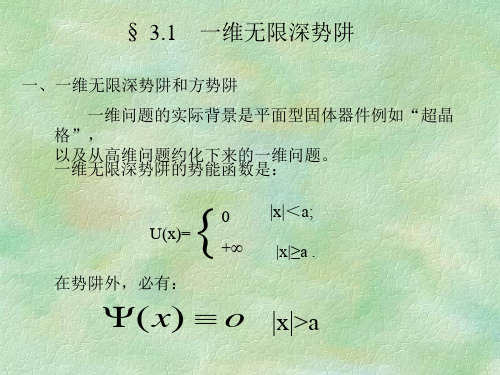
A e ikx B e ikx , ( x ) F e k3 x G e k3 x , C e ikx ,
2 2
x0 0 xa xa
(k k3 ) sh k3a B 2 , 2 A (k k3 ) shk3a 2ikk3chk3a
1 x x 1 x x shx (e e ), chx (e e ). 2 2
ik1 x
2
x0 0 xa xa
2 Beik x B e ik x
ik1 x 3 Ce C e (C 0) ik1 x
这里 k1 因子
ikx e 波数为K的平面波，则是向左运动的平面波。在I、II两
x 0,
2mE ，k 2 2m( E V0 ) 。考虑到时间 ikx iEt / i t ，因此代表向右运动的 e e
2
1 2
所以几率密度与 (1
2
/a )
2

1 2
成比例。
一、方势垒
1.方势垒是：
§3.3势垒贯穿 U(x)
U0
x 0 or 0, U ( x) U 0 0 0 x a
xa
0 a x
其特点是： (1)对于势阱，波函数在无穷远处趋于零，能谱是分立的。但对于势垒，波函数在无穷远处不为零。下面将看到，粒子能量可取任意值。 (2)按照经典力学观点，若E<U0 ,则粒子不能进入势垒,在x=0处全被弹回；若 E> U0, 则粒子将穿过势垒运动。但从量子力学的观点，由于粒子的波动性，此问题将与波透过一层介质相似，总有一部分波穿过势垒，而有一部分波被反射回去。因此，讨论的重点是反射和透射系数。

一维无限深方势阱中的能量本征态

一维无限深方势阱中的能量本征态1. 引言在量子力学中，一维无限深方势阱是一个经典的问题。

研究一维无限深方势阱中的能量本征态，可以帮助我们更好地理解量子力学中的基本概念和原理。

通过对这一问题的深入探讨，我们可以揭示能量本征态的性质、数学描述以及物理意义，从而为我们理解更为复杂系统的量子行为奠定基础。

2. 能量本征态的概念能量本征态是指在某一势场中，系统的波函数满足薛定谔方程，并且具有确定的能量值。

在一维无限深方势阱中，系统的势能在有限区间内为无穷大，而在无限远处为零。

在区间内，粒子的动能足够克服势能，所以能量本征态中的波函数不为零，在无穷远处趋于零。

3. 数学描述对于一维无限深方势阱，我们可以通过薛定谔方程来描述能量本征态。

薛定谔方程可以写作：\[ -\frac{\hbar^2}{2m} \frac{d^2 \psi(x)}{dx^2} = E\psi(x) \] 其中 \( E \) 为能量本征值，\( \psi(x) \) 为能量本征态的波函数，\( m \) 为粒子的质量，\( \hbar \) 为约化普朗克常数。

在一维无限深方势阱中，我们可以通过求解该薛定谔方程得到能量本征态的波函数形式和能量值。

4. 能量本征态的求解与性质通过求解一维无限深方势阱中的薛定谔方程，我们可以得到一系列的能量本征态。

这些能量本征态之间呈现离散的能级，且能级间隔相等。

这一性质恰好符合了量子力学中的能量量子化条件，从而验证了能量本征态的物理意义。

5. 主题文字的再次提及通过以上对能量本征态的深入讨论，我们可以看到，一维无限深方势阱中的能量本征态不仅是一个重要的量子力学问题，更是我们理解量子力学基本原理的重要工具之一。

能量本征态的性质和数学描述为我们提供了在量子力学中理解和描述复杂系统的基础。

6. 总结与回顾通过本文对一维无限深方势阱中的能量本征态的全面评估，我们不仅了解了能量本征态的基本概念和数学表达，更深入地理解了能量本征态的物理意义。

一维定态问题无限深方势阱

(1) 粒子的位置 r
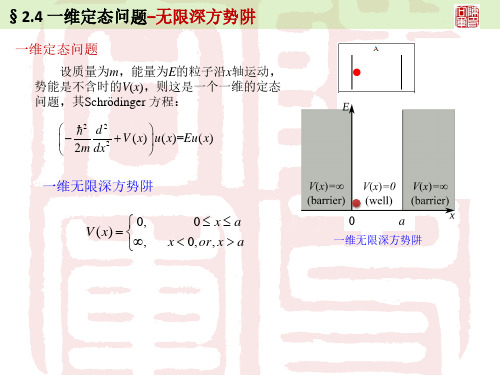
例如：一维无限深方势阱
粒子的位置是不确定的，取值在[0, a]之间。但粒子的概率分布是确定的，是
u(x)
2
=
2 sin2 nπ a a 0
x, ,
0≤ x≤a x < 0,or, x > a
n = 1, 2,3,
所以，可以得到粒子位置的平均值 (假设粒子处在基态 n =1 态)：
Spherical coordinates
(r,θ ,ϕ )
x = r sinθ cosϕ y = r sinθ sinϕ z = r cosθ
r = x2 + y2 + z2
θ = arccos
z
x2 + y2 + z2
ϕ = arctan y
x
§2.5 力学量的平均值、算符表示—算符表示
角动量算符 Lˆ= r × pˆ 在球坐标系中的三个分量为
§2.5 力学量的平均值、算符表示—平均值
粒子在外场 V(r)中运动，体系的
定态薛定谔方程：
−
2
2m
∇2
+
V
(r)
u (r)=Eu (r)
求解该方程，可以得到体系的波函数和能量E。
例如：粒子束缚在一维无限深方势阱中
波函数能量
u(x)
=
2 sin nπ x , a a,
0
En
=
π2 2
则V(r, t)的平均值为：
∫ ∫ +∞
= V (r,t) = V (r,t)ρ (r,t)dτ
+∞
ψ
*
(r
,
t
)V
(r

一维无限深势阱粒子能量的可能测量值和相应的几率

一维无限深势阱粒子能量的可能测量值和相应的几率一维无限深势阱粒子能量的可能测量值和相应的几率在量子力学中，一维无限深势阱是一个经典的模型系统，用于研究粒子在受限空间内的性质和行为。

其中，粒子的能量是一个非常重要的物理量，其可能的测量值和相应的几率分布是量子力学中的基本课题之一。

在本文中，我们将深入探讨一维无限深势阱粒子能量的可能测量值和相应的几率，并从简到繁地进行全面评估，帮助读者更深入地理解这一主题。

1. 一维无限深势阱的基本概念在一维无限深势阱中，粒子被限制在一个无限深的势阱内运动，即在势阱内能量为负无穷，在势阱外能量为正无穷。

这样的势阱能够构建一个简单而理想化的量子力学模型，便于对粒子的性质进行研究。

2. 粒子在一维无限深势阱中的波函数和能量本征态根据量子力学的基本原理，粒子在一维无限深势阱中的波函数可以用薛定谔方程进行描述。

解出薛定谔方程后，可以得到粒子的能量本征态和对应的波函数表达式，这些能量本征态对应着粒子可能的能量。

3. 能量的可能测量值和相应的几率分布在量子力学中，能量的测量值是一个物理量的可能取值，其对应的几率分布描述了在测量中可能得到某个值的概率。

对于粒子在一维无限深势阱中的能量，我们可以通过对波函数进行归一化处理，得到能量的可能测量值和相应的几率分布。

这些可能的测量值和几率分布将帮助我们理解粒子在势阱内的能量分布规律。

4. 总结与回顾通过对一维无限深势阱粒子能量的可能测量值和相应的几率进行全面评估，我们可以更深入地理解量子力学中的基本概念和原理。

这也有助于我们在实际研究或应用中更灵活地处理粒子能量的测量和分布问题。

个人观点和理解：量子力学中的一维无限深势阱模型是一个简单而重要的系统，通过对其粒子能量的可能测量值和相应的几率进行深入研究，我们可以更好地理解量子世界中的奇妙规律。

对于我而言，通过撰写本文并深入思考这一主题，我对量子力学中的能量测量和分布问题有了更全面的认识，并且能够更好地应用于我的研究和工作中。

一维无限量子深势阱能量

一维无限量子深势阱能量学院：理学院专业：应用物理学一班姓名：黄凯学号：10510111一、摘要本文主要从推导出量子阱一维空间中粒子的能量公式入手，介绍量子阱的基本理论，通过建立理想模型，利用一些基础知识从理论上推导出一维无限深势阱中势能与阱宽的关系，从而绘出能量与量子阱宽度的关系曲线。

更直观的了解了势能随阱宽变化的变化趋势。

关键词：量子阱模型势能二、引言量子阱是由两种不同的半导体材料相间排列形成宽度为d 的两个无限高势垒壁的具有明显量子限制效应的电子或空穴的势阱。

最基本特征是，由于量子阱宽度(只有当阱宽尺度足够小时才能形成量子阱)的限制，导致载流子波函数在一维方向上的局域化。

并在一维势力场作用下运动着，这个抽象出来的计算模型，称为一维无限深方形势阱，本文将建立理想模型，通过理论推导结合计算机模拟绘出E —a 曲线，更直观的了解了势能与阱宽的关系。

三、理论公式推导设想在一维空间中运动的粒子是最简单的量子力学体系，这一体系施加给粒子的势能如下：∞ )(x v ∞0)(=x u 0)(=x u由定态薛定谔方程式Eu vu u mh =+∇-222，粒子在势阱内的方程为：xd0)(8)(2222=+x u hmEdx x u d π （1）式中：m 为粒子的质量，E 为粒子的总能量。

若令228hmE k π= （2）则粒子在势阱内的方程可改写为：0)()(222=+x u k dxx u d （3）（3）式的通解为kx B kx A x u cos sin )(+=。

式中，A,B 为两个积分常数，可根据波函数的边界条件求出。

据边界条件，0=x 时，0)0(=u ，由上式可知B=0，于是：kx A x u sin )(= （4）又根据边界条件0=x 时，0)0(=u ,式（4）可写为：0sin )(==kd A d u一般来说，A 不能为零（否则)(x u 为零解，无意义），故必有0sin =kd ，即πn kd = 或d n k π= 1=n ，2, 3，…；将上式与（2）比较，可得在一维势阱中运动的粒子的能量值为：2228mdh n E = 即22222mdnE π=式中，n 是量子数，表明粒子的能量只能取不连续的离散的值。

一维无限深方势阱的力公式及在费米气体中的应用

一维无限深方势阱的力公式及在费米气体中的应用
一维无限深方势阱是一个理想的物理模型，它可以帮助我们理解量子力学的基本概念。

在这个模型中，粒子被限制在一个无限深的平方势能盒子中运动，它们的能量和波函数是离散的，具有不同的量子态。

对于一维无限深方势阱，我们可以推导出力公式。

根据量子力学的基本原理，粒子在势阱中运动时，受到的力是由势能的梯度决定的。

在一维无限深方势阱中，粒子受到的力是一个恒定的值，它的大小等于势阱两侧之间的势能差。

因此，力公式可以表示为： F = -dE/dx
其中，F是受力大小，E是能量，x是位置。

这个公式告诉我们，粒子受到的力和它的能量密切相关，而且在势阱两侧之间的能量差越大，受到的力就越大。

在费米气体中，一维无限深方势阱的力公式可以应用于描述粒子之间的相互作用。

费米气体是由费米子组成的系统，如电子、质子、中子等。

在这种气体中，费米子具有反对称的波函数，遵循泡利不相容原理，因此它们不能占据同一量子态。

这种排斥力可以通过一维无限深方势阱的力公式来描述，它可以帮助我们理解费米气体的行为和性质。

总之，一维无限深方势阱的力公式可以帮助我们理解量子力学的基本概念，而在费米气体中的应用则可以帮助我们理解费米子之间的相互作用和排斥力。

一粒子在一维无限深势阱中运动,求粒子的能级和波函数

一粒子在一维无限深势阱中运动,求粒子的能级和波函数一维无限深势阱是量子力学中常用的模型之一，它能够帮助我们理解粒子在一维空间中的运动以及对应的能级和波函数。

首先，我们来看一下什么是一维无限深势阱。

这是一个理想化的模型，由两堵非常高的无限高势垒所夹，其中粒子的运动只能在这一段距离内进行，并且在势垒外是无法找到粒子的。

这种模型可以用来描述电子在原子中的运动，或者光子在光导纤维中的传播。

在量子力学中，波函数是描述粒子性质的数学函数。

对于一维无限深势阱模型，波函数可以通过解薛定谔方程获得。

薛定谔方程可以用来描述波函数随时间的演化，它是量子力学的基本方程之一。

对于一维无限深势阱，薛定谔方程可以简化为亥姆霍兹方程的形式。

亥姆霍兹方程是一个常微分方程，它的解由定态波函数给出。

定态波函数允许我们计算粒子在一维无限深势阱中的能量和波函数。

解一维无限深势阱的亥姆霍兹方程，我们可以得到一系列能量的解，这些能量称为能级，用n来表示。

每个能级都对应着一个定态波函数，这些波函数描述了粒子在势阱内的运动方式。

对于一维无限深势阱，能级的表达式为En = (n^2 *h^2)/(8*m*L^2)，其中n为能级的序数，h为普朗克常数，m为粒子的质量，L为势阱的宽度。

对应于每个能级，还有一个对应的波函数。

波函数用Ψ(x)来表示，描述了在不同位置概率密度的分布。

在一维无限深势阱中，波函数能够取到零点以外的任意位置。

波函数的形式为Ψn(x) = sqrt(2/L) * sin(n * π * x / L)，其中x为位置，L为势阱的宽度，n为能级的序数。

通过求解亥姆霍兹方程，我们可以得到多个能级和对应的波函数，它们描述了粒子在一维无限深势阱中的运动和性质。

这些能级和波函数不仅在理论计算中起到了重要作用，而且在实验中也得到了验证。

总之，一维无限深势阱模型是量子力学中研究粒子运动和性质的重要工具。

通过解亥姆霍兹方程，我们可以得到一系列能级和对应的波函数，这些能级和波函数描述了粒子在势阱中的行为。

一维无限深势阱中的能级公式(一)

一维无限深势阱中的能级公式(一)一维无限深势阱中的能级公式一维无限深势阱简介•一维无限深势阱是指在一维空间中的一个势能函数，其势能在有限范围内为无穷大，而在这个范围外为零。

•这个模型常用于量子力学研究中，用于描述束缚电子在限定区域内的能级结构。

能级公式的推导•根据经典力学的思想，势能为零区域内的粒子应该是运动不受限制的，因此在这个区域内的能量取任意值，可以看作连续的。

•而在势能无穷大的区域外，粒子无法存在，因此能量必须是有限的。

•具体推导过程如下：一维薛定谔方程•在量子力学中，波函数满足薛定谔方程。

•对于一维无限深势阱，薛定谔方程可以表示为:d2ψdx2+2mℏ2(E−V(x))ψ=0•其中，ψ为波函数，x为位置坐标，m为质量，E为能量，V(x)为势能函数。

薛定谔方程的解•由于势能函数V(x)为零，因此在势阱内，薛定谔方程可以简化为:d2ψdx2+2mEℏ2ψ=0•这是一个二阶常微分方程，其解可以表示为：ψ(x)=Asin(kx)+Bcos(kx)•其中，A和B为常数，k为波数，可以表示为：k=√2mE ℏ2波函数的边界条件•在势阱内，波函数必须满足边界条件，在势能函数为无穷大的区域外，波函数必须趋于零。

•因此，当x=0时，ψ(0)=0；当x=L时，ψ(L)=0。

边界条件的限制•根据边界条件，可以得到以下关系式：Asin(k⋅0)+Bcos(k⋅0)=0Asin(kL)+Bcos(kL)=0•上述两个方程同时成立时，波函数满足边界条件。

求解能级•根据上述边界条件，可以解得k n L=nπ，其中n为正整数。

•将k n代入波数的公式中，可得能量的公式：E n=ℏ2k n22m=n2π2ℏ22mL2能级公式的解释与例子•以上推导得到的能级公式表明，在一维无限深势阱中，粒子的能量只能取离散的值，且与n的平方成正比。

–n越大，能级越高。

•这也意味着在一维无限深势阱中，粒子存在着多个能级，且能级之间的能量差是固定的。

一维势阱中粒子的能量

一维势阱中粒子的能量
在一维无限深势阱中，粒子的能量可以用下列公式表示：
E = n²ħ²/(2mV²) + V(x)
其中，E表示粒子的能量，n为量子数，ħ为普朗克常数除以2π，m为粒子质量，V(x)为势函数。

当粒子处于势阱中时，其能量被分为两部分：一部分是由于粒子的动量和高度所引起的能量，另一部分是由于势函数所引起的能量。

由于势函数是无限深的，因此粒子只能处于某些特定的能量状态，这些能量状态被称为量子数n的状态。

量子数n的取值范围是从0开始，当n=0时，对应的能量为E₀=0，当n=1时，对应的能量为E₀=ħ²/(2mV²)，当n=2时，对应的能量为E₀=2ħ²/(2mV²)，以此类推。

可以看出，量子数n越大，对应的能量也越大，这是因为在势阱中，粒子的高度越高，势能也越大，因此需要更高的能量才能克服势垒，跃迁到更高的能级上。

需要注意的是，上述公式仅适用于无限深势阱，对于其他类型的势阱，粒子的能量公式会有所不同。

一维无限深方势阱中势阱中粒子的能级公式推导

一维无限深方势阱中势阱中粒子的能级公式推导一维无限深方势阱是量子力学教学中常见的模型之一。

在这个模型中，粒子被限制在一个长度为L的势阱中运动，势阱的势能在阱内为零，而在阱外则无限大。

研究一维无限深方势阱中粒子的能级公式推导，可以帮助我们更深入地理解量子力学中的基本概念和数学工具。

下面我将按照深度和广度的要求，从简单的物理概念和数学原理开始，逐步推导一维无限深方势阱中粒子的能级公式，并带有个人的观点和理解。

一、基本概念和数学工具1.1 势阱势阱是一种常见的量子力学模型，它可以用来描述粒子在受限空间中的运动。

在一维无限深方势阱中，势能在阱内为零，而在阱外为无限大，这意味着粒子在阱内具有确定的能量，而在阱外无法存在。

1.2 薛定谔方程薛定谔方程是描述量子力学中粒子运动的基本方程。

对于一维无限深方势阱而言，薛定谔方程可以简化为一维定态薛定谔方程：\[ -\frac{\hbar^2}{2m}\frac{d^2\psi(x)}{dx^2} = E\psi(x) \]其中，ψ(x)是粒子的波函数，m是粒子的质量，E是粒子的能量，ħ是普朗克常数。

二、能级公式的推导2.1 边界条件在一维无限深方势阱中，粒子受到势阱两侧的限制，因此波函数在势阱边界处为零。

这意味着在x=0和x=L处，波函数满足边界条件：\[ \psi(0) = 0 \]\[ \psi(L) = 0 \]2.2 波函数的解根据边界条件，我们可以求解一维定态薛定谔方程得到波函数的解。

波函数的解具有以下形式：\[ \psi_n(x) = \sqrt{\frac{2}{L}}\sin(\frac{n\pi x}{L}) \]其中，n为能级量子数。

2.3 能级公式将波函数的解代入一维定态薛定谔方程中，可以得到粒子的能级公式：\[ E_n = \frac{n^2\pi^2\hbar^2}{2mL^2} \]其中，En为粒子的能量，n为能级量子数。

三、个人观点和理解在推导一维无限深方势阱中粒子的能级公式过程中，我们利用了量子力学基本的数学工具和物理概念，如薛定谔方程、波函数和边界条件。

一维无限深势阱粒子能量的平均值

一维无限深势阱粒子能量的平均值下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。

文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢！本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注！Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!一维无限深势阱是量子力学中经典的问题之一，它可以用来描述一个粒子在一个无限宽度的势阱中的运动情况。

量子力学基本概念之一维无限深势阱

一维无限深势阱的实际模型
• • • • • • • • • 自由电子在一块金属中的运动相当于在势阱中的运动。在阱内，由于势能为零，粒子受到的总的力为零，其运动是自由的。在边界上 x=0或x=a处，由于势能突然增加到非常大，粒子受到非常大指向阱内的力。因此，粒子的位置不可能到达0<x<a 的范围以外。图像如右图所示。
量力学基本概念之
一维无限深势阱
史英娜 103797
一维无限深势阱的定义
• • • • • • • • • 粒子在一种简单外力场中做一维运动，其势能函数为U(X)=0 （0<x<a)； U(x)=∞ (x≥a或x≤0)。由于其函数图形像阱，且势能在一定区域为0，而在此区域外势能为无穷大，所以这种势能分布叫做一维无限深势阱，图像如右图所示。
一维无限深势阱的波函数和概率密度
波函数
概率密度
一维无限深势阱总结
• 一维无限深势阱是一种理想模型。 • 一维无限深势阱是自由电子的实际模型的极端化和简化。 • 图形表示为
极限
一维无限深势阱中粒子运动的波函数为 Ψ (x)=√(2/a)·sin(nπx/a) (0<x<a)
thank you!

一维无限深势阱中粒子的能级

一维无限深势阱中粒子的能级
一维无限深势阱中粒子的能级：
1、定义：一维无限深势阱中粒子的能级是物理学涉及的一个重要概念，指的是势
阱中粒子被限制在有限的空间内，力量为无穷大的情形，因此粒子的运动能力只能像一个有限单元阱中的粒子一样静止。

2、能量阶：一维无限深势阱中粒子的能级分为几个阶段，分别是最低能量阶、次
低能量阶，以及更高能量阶。

阶根据粒子的运动状态可以分成三类：常规状态，即粒子在最低能量阶的状态；次轨道状态，即粒子在次低能量阶的状态；第三状态，即粒子在更高能量阶的状态。

3、能量关系：一维无限深势阱中粒子能量等级关系按照能级阶梯式由低到高，比
如最低能量阶为0；次低能量阶为1；更高能量阶则会随着势阱深度增加、产生无
穷多个能量阶。

4、可变规律：一维无限深势阱中粒子的包络规律是其能量随势阱深度的变化可以
表示为一次函数。

势阱深度越深，粒子的能量的越大，其能量曲线越接近抛物线。

5、局域性：无论是费米子陷阱系统还是一维无限深势阱系统，都存在局域性特性，也就是当粒子分子数量发生变化时，其能量等级也会发生变化，比如势阱深度一定时，一个粒子的能量和两个粒子的能量是不同的。

6、可以控制的方式：为了获得更高的精度，人们可以通过控制势阱深度，来改变
一维无限深势阱中粒子的能级，以获得最佳的实验效果。

例如，研究者可以改变势阱的深度，使粒子的能量阶达到自己所期望的精确值，从而达到更好的实验精度。

一维有限深方势阱能量本征值的推导过程

一维有限深方势阱能量本征值的推导过程好吧，今天我们来聊聊一维有限深方势阱的能量本征值，听起来有点高深，但别担心，我会尽量让它变得简单有趣。

想象一下你在一个很大的游乐场，四周围着高高的围墙，只有一个小门能进出。

这就是我们的势阱，里面的小子可以尽情玩耍，但出不去，真是像被困在了“笼子”里。

好啦，势阱的高度就是这围墙的高度，势阱的深度就是游乐场的“深度”。

这个“深度”可不是说人掉进去就会淹死，而是说在这个区域内，粒子能量的状态会发生变化。

像我们的小子，如果他的能量低于围墙的高度，那他就只能在这个游乐场里转悠。

想象一下，你有个小朋友，他拼命想往外跑，可是墙太高了，根本出不去。

他只能在里面玩各种游戏。

那么这个游乐场里有多少个不同的游戏呢？这就要说到能量本征值了。

每一个能量状态都对应着一个游戏，越高的能量对应着越刺激的游戏。

粒子在这个势阱里，就像个小孩子，能量越高，玩得越欢。

能量低的时候，玩得不开心，越过围墙根本不可能。

简单来说，能量本征值就是粒子在这个势阱里“玩”的规则和限制。

说到这里，咱们就得动手算一算了，别担心，这个算式并不复杂。

想象你在算一个简单的数学题。

我们用一个数学模型来描述这个势阱，叫做薛定谔方程。

听起来像个高深的名词，但其实就是一个公式，让你知道在这个“游乐场”里，粒子的行为如何。

我们把这个势阱的边界设定为某个值，这样粒子就只能在这个范围内活动。

计算的过程有点像拼图，边边角角都得对上。

你能得到一些特定的能量值，嘿，这就是本征值，像是每个游戏的入场券。

哇，终于到了关键时刻。

算出来的结果像是一个个数字的密码，每个数字背后都有一个小故事。

比如，第一个能量本征值就像你在游乐场里第一个能玩的游戏，简单但充满乐趣；第二个能量本征值就像升级了，难度加大，但挑战更刺激。

你会发现，随着能量的增加，粒子能“玩”的游戏越来越多，仿佛整个游乐场的乐趣都被打开了。

但别以为这就完事了，咱们还得考虑势阱的深度。

越深的势阱，粒子“玩”的方式也会不同。

求一维无限深势阱(势箱)中粒子的坐标和动量在能量表

P402 1. 求一维无限深势阱（势箱）中粒子的坐标和动量在能量表象中的矩阵元。解：在一维无限深势阱中，能量的本征值为 E n 本征函数
ψn = 2 nπx sin( ) ， n = 1,2,3..... a a Gij = i G j = n 2π 2 h 2 2ma 2
由算符 G 在 T 表象中的分量形式
n
PDF 文件使用 "pdfFactory" 试用版本创建
证明： ∵ A 为厄米矩阵， ∴ A + ∵ e iA = ∑ i
n n
=A (−i ) n n + (−i ) n n (A ) = ∑ A = e −iA n! n ! n
e iA 为么正矩阵
n!
An ，
这就是线性谐振子的零点能。
6.从动量算符在动量表象中的矩阵元出发，求坐标表象中的动量算符。解：动量算符在动量表象中的矩阵元为
p = p′ p p′′ = p ′δ ( p ′ − p′′ )
变换到坐标表象中，
x p x′ = ∫ x p ′ p′ p p′′ p ′′ x′ d p′dp′′
= ∫ x p′ p ′δ ( p′ − p′′) p′′ x′ d p ′dp ′′
即为坐标表象的动量算符。
7.从角动量的对易关系ξ5.4.6 （6.1）式出发，证明ξ5.4.6 （6.4 式 [ J + , J − ] = 2hJ z ， [ J z , J + ] = hJ + ， [ J z , J − ] = −hJ − 以及
[J 2 , J x ] = [J 2 , J y ] = [J 2 , J z ] = [J 2 , J ± ] = 0 。
ˆ 的矩阵表示 ∴在 A 表象中， A