进位制
1.3.2 进位制(共31张PPT)

4.把 98(5)转化为九进制数为 解析:98(5)=9×51+8×50=53,
.
故 98(5)=58(9). 答案:58
5.127(8)化为六进制数的最高位数字是 解析:∵127(8)=1×82+2×8+7=87,
.
∴127(8)=223(6). 答案:2
应用示例 例 1 把二进制数 110011(2)化为十进制数. 解:110011(2)=1×25+1×24+0×23+0×22+1×21+1×20=1×32+1×1 6+1×2+1=51. 点评:先把二进制数写成不同位上数字与 2 的幂的乘积之和的 形式,再按照十进制的运算规则计算出结果.
题型二
k 进制数化为十进制数
【例题 2】将下列各数化成十进制数. (1)11001000(2); (2)310(8). 分析:解答本题可按其他进制转化为十进制的方法,先写成不同 位上的数乘以基数的幂的形式,再相加求和. 解:(1)11001000(2)=1×27+1×26+0×25+0×24+1×23+0×22+0×21+ 0×20=200; (2)310(8)=3×82+1×81+0×80=200.
程序框图如图所示.
程序: INPUT “a,k,n=”;a,k,n b=0 i=1 t=a MOD 10 DO b=b+t������k (i-1) a=a\10 t=a MOD 10 i=i+1 LOOP UNTIL i>n PRINT b END
^
(3)十进制数 a 化为非十进制的 k 进制数 b 的算法是除 k 取余 法. 算法步骤: 第一步,给定十进制正整数 a 和转化后的数的基数 k. 第二步,求出 a 除以 k 所得的商 q,余数 r. 第三步,将得到的余数依次从右到左排列. 第四步,若 q≠0,则 a=q,返回第二步;否则,输出全部余数 r 排列得 到的 k 进制数.
进位制

进位制是人们为了计数和运算方便而约定的记数系统。 进位制是人们为了计数和运算方便而约定的记数系统。 比如:
满二进一,就是二进制; 满十进一,就是十进制; 满二进一,就是二进制; 满十进一,就是十进制; 满十二进一,就是十二进制; 满六十进一,就是六十进制 满十二进一,就是十二进制; 满六十进一,
基数: 基数:
所以, 所以,89=324(5)
)、非十进制之间的转换 (4)、非十进制之间的转换
借助十进制来转化 你能将1234 转化为八进制吗? 你能将1234(5)转化为八进制吗?
1234(5) =1×5 +2×5 +3×5 +4×5 =194
3 2 1 0
8 8
194 24 8 3 0
余数 2 0 3
∴ 1234(5) = 194 = 302 (8)
89=2×44+1 × 89=2×44+1 × 44=2×22+0 =2×(2×22+0)+1 × × × 22=2×11+0 =2×(2×(2×11+0)+0)+1 × × × × 11=2×5+1 =2×(2×(2×(2×5+1)+0)+0)+1 × × × × × 5= 2×2+1 × =2×(2×(2×(2×(2×2+1)+1)+0)+0)+1 × × × × × 所以89=2×(2×(2×(2×(2 ×2+1)+1)+0)+0)+1 所以 × × × × =2×(2×(2×(2×(22+1)+1)+0)+0)+1 × × × × =2×(2×(2×(23+2+1)+0)+0)+1=2×(2×(24+22+2+0)+0)+1 × × × × × =2×(25+23+22+0+0)+1=26+24+23+0+0+20 × 89=1×26+0×25+1×24+1×23+0×22+0×21+1×20 × × × × × × × 所以: 所以:89=1011001(2) ) 除2取余法
进位制 课件

类型 一 k进制数转化为十进制数
【典型例题】
1.把七进制数123化成十进制数为
.
2.下列各数85(9),301(5),
1000(4)中最小的数是
.
【解题探究】1.七进制数从右边数第二位的数字若是 k(k=0,1,2,3,4,5,6),其在十进制中表示的数是多少? 2.相同进制中,位数越多的数越大对吗?不同进制中的数如何比 较大小? 探究提示:1.表示的数是7k. 2.对,相同进制中,位数越多的数越大,不同进制中的数需化为同 进制中的数比较大小,通常都化为十进制数.
【互动探究】把题2中的四进制数化为十二进制数. 【解题指南】结合题2的解法,转化为十进制数458,然后再化 为十二进制数. 【解析】由本题2的解答知13022(4)=458, 再把十进数458化为十二进制数. 458=322(12), 故13022(4)=322(12).
【解析】1.选C.因为 所以15=1111(2),故C正确.
2.先把四进制数13022化为十进制数. 13022(4)=1×44+3×43+0×42+2×4+2×40 =256+192+0+8+2 =458. 再把十进制数458化为六进制数. 458=2042(6). 故13022(4)=2042(6).
除k取余法
判断:(正确的打“√”,错误的打“×”) (1)七进制的基数是7,用0,1,2,3,4,5,6六个数字表示.( ) (2)任何进位制中都要用到数字0.( ) (3)不同进位制中,十进制的数比二进制的数大.( )
提示:(1)正确.由几进制的基数就是几知(1)正确. (2)正确.0在进位制中都是要用到的数. (3)错误.不同进位制中的数,要化为同一进位制下的数才能比 较大小. 答案:(1)√ (2)√ (3)×
进位制 课件

进位制的概念
【问题导思】 十进制使用 0~9 十个数字,那么二进制使用哪些数字? 六进制呢? 【提示】 二进制使用 0~1 两个数字,六进制使用 0~ 5 六个数字.
进位制是人们为了 计数和运算方便 而约定的记数系 统,“满几进一”就是几进制,几进制的基数就是 几 .
进位制之间的相互转化
例如:230 451(k)=2×k5+3×k4+0×k3+4×k2+5×k+ 1.
十进制转化为k进制 (1)将 194 化成八进制数; (2)将 48 化成二进制数. 【思路探究】 除 k 取余→倒序写出→标明基数 【自主解答】 (1)
∴194 化为八进制数为 302(8).
(2) ∴48 化为二进制数为 110 000(2).
1.将十进制化成 k 进制的方法:用除 k 取余法,用 k 连 续去除十进制数所得的商,直到商为零为止,然后将各步所 得的余数倒序写出,即为相应的 k 进制数.
2.为了区分不同的进位制,常在数的右下角标明基数.十 进制数一般不标注基数.
不同进位制之间的转化 将七进制数 235(7)转化为八进制数. 【思路探究】 七进制→十进制→八进制 【自主解答】 235(7)=2×72+3×71+5×70=124, 利用除 8 取余法(如图所示).
∴124=174(8), ∴235(7)转化为八进制为 174(8).
1.本题在书写八进制数 174(8)时,常因漏掉右下标(8)而 致误.
2.对于非十进制数之间的互化,常以“十进制数”为中 间桥梁,用除 k 取余法实现转化.
【问题导思】 二进制数 110 011(2)化为十进制数是多少? 【提示】 110 011(2)=1×25+1×24+0×23+0×22+ 1×21+1×20=51.
数字进位制

数字进位制一、十进制(Decimal System)十进制是我们日常生活中最常用的进位制。
它由0-9这10个数字组成。
每一位的权值都是10的幂次方,从右往左依次为10^0、10^1、10^2...以此类推。
在十进制中,数字的数值大小由高位到低位依次递增,方便人们理解和计算。
二、二进制(Binary System)二进制是计算机系统中最基础的进位制。
它只由0和1这两个数字组成。
每一位的权值都是2的幂次方,从右往左依次为2^0、2^1、2^2...以此类推。
二进制中的数值大小由高位到低位递增,与十进制不同的是,每一位只能是0或1,所以运算更加简单高效。
三、八进制(Octal System)八进制是一种较为少见的进位制,它由0-7这8个数字组成。
每一位的权值都是8的幂次方,从右往左依次为8^0、8^1、8^2...以此类推。
八进制在计算机领域中用得较少,但在Unix系统中经常使用,例如文件权限的表示就是用八进制。
四、十六进制(Hexadecimal System)十六进制是计算机系统中常见的进位制之一。
它由0-9和A-F这16个数字组成,其中A-F分别表示10-15。
每一位的权值都是16的幂次方,从右往左依次为16^0、16^1、16^2...以此类推。
十六进制在计算机领域中广泛应用,例如表示颜色、内存地址等。
五、三进制(Ternary System)三进制是一种基于3的进位制。
它由0-2这3个数字组成。
每一位的权值都是3的幂次方,从右往左依次为3^0、3^1、3^2...以此类推。
三进制在现实生活中较少使用,但在某些领域如电子工程中有一定应用,例如存储器中的三值逻辑。
六、五进制(Quinary System)五进制是一种基于5的进位制。
它由0-4这5个数字组成。
每一位的权值都是5的幂次方,从右往左依次为5^0、5^1、5^2...以此类推。
五进制在现实生活中较少使用,但在某些领域如音乐理论中有一定应用,例如五线谱的音符表示就是用五进制。
进位制

a=rnrn-1„r1r0(2)
思考 你会把三进制数10221(3)化为二进制数吗? 解:第一步:先把三进制数化为十进制数: 10221(3)=1×34+0×33+2×32+2×31+1×30 =81+18+6+1=106.
第二步:再把十进制数化为二进制数: 106=1101010(2).
∴10221(3)=106=1101010(2).
思考:那么二进制数与十进制数之间是如 何转化的呢?
例1:把二进制数110011(2)化为十进制数.
分析:先把二进制数写成不同位上数字与2的 幂的乘积之和的形式,再按照十进制数的运算规 则计算出结果. 解:110011(2) =1×25+1×24+0×23+0×22+1×21+1×20 =1×32+1×16+1×2+1=51. [引申]你会把三进制数10221(3)化为十进制数吗? 解:10221(3)=1×34+0×33+2×32+2×31 +1×30 =81+18+6+1=106.
如十进制可使用的数字有0 ~ 9十个数字,基数是10; 二进制可使用的数字有0和1,基数是2; 十六进制可使用的数字或符号有0 ~ 9等10个数字以 及A ~ F等6个字母(规定字母A ~ F对应10~15),十六进制的 基数是16.
注意:为了区分不同的进位制,常在数字的 右下脚标明基数. 如111001(2)表示二进制数,34(5)表示5进制数. 十进制数一般不标注基数.
意思是:(1)第一个数字an不能等于0; (2)每一个数字an,an-1,…,a1,a0都须小于k.
进位制

例如: 例如:
十进制
2398(10) )
表示的是: 个一千 个一千; 个一百 个一百; 个十 个十; 个一组成的数字 个一组成的数字。 表示的是:2个一千;3个一百;9个十;8个一组成的数字。 也可以用一个式子来表示: 也可以用一个式子来表示:
与十进制的计数类似, 与十进制的计数类似,其他的进位制也是可以按照上面 的方法计数。 的方法计数。 例: 可以表示为: 可以表示为: 八进制 425(8) )
例:(1)平时的计算,是满十进一的,我们称十进制 平时的计算,是满十进一的, (2)计算机里面,是满二进一的,我们称二进制 计算机里面,是满二进一的, 一年有十二个月,每过十二个月就叫一年, (3)一年有十二个月,每过十二个月就叫一年, 是满十二进一的。 是满十二进一的。 我们称是十二进制 一天有二十四个小时, (4)一天有二十四个小时,每过二十四个小时就 叫一天。即满二十四进一。 叫一天。即满二十四进一。称二十四进制
( D )
D。111111(2) 。 )
答:将四个答案全部转化为十进制的数字
A:77 :
B:78 :
C:64 :
D:63 :
本节课我们主要学习了关于进 位制的一些知识 1:进位制的定义。 :进位制的定义。 2:进位制的基数,表示,判断,计数,互化。 :进位制的基数,表示,判断,计数,互化。
),(3) 一:P48 A组。3(1),( )要求写出计算式子 组 ( ),( 二:思考:P40 思考: 探究。 探究。
(1) 111001(2) ; ) ) (2) ) 421(5) ) (3) 12012(3) ; ) ) (4) 3276(8) ) )
答:
(1) ) (2) ) (3) ) (4) )
数的进位制

数的进位制预备知识:进位制的基本概念及p 进制化为10进制。
1...我们已知道10进制的记数原理。
如一个10进制数1999=910991101023+⨯+⨯+⨯。
一般地,a b c d e =ed c b a +⨯+⨯+⨯+⨯10101010234(其中a,b,c,d,e 均是0—9的数码,且a 0≠)也就是说每个数都可以按.......10..的方幂形式展开.......10进制数有以下特点:(1)“10”是这种进位制的基数,逢....10..进一..。
(2)表示一个数需要用0,1,2…9 这10个不同的数码。
(3)数码处在不同的位置(数位)表示的意义不同,如在1999中左边第一个9代表900,而左边第二个9代表90。
说每个数都可以按10的方幂形式展开。
2.按照10进制数的特点,我们可以推广到p 进制数。
设p 是不为1的正整数,我们可以选p 为基数,确定p 进制数。
要求(1) 逢p 进一(2) 在p 进制中有0,1,2…(p-1)共p 个数码。
(3) 每个数都能按p 的方幂展开。
如p=5时就是5进制数,在5进制中5为基数,逢5进一,只使用0,1,2,3,4共5个数码。
每个数都能按5的方幂展开,5进制a 记为(a )5 ,例(12345)5=453215523+⨯+⨯+⨯ 一. 把一个p 进制数转化为10进制数。
一般的一个p 进制数N=(a a a a n 321)p 转化为10进制数,只要 把N 按p 的降幂形式展开即可,然后安通常的十进制数相加就得到所求的十进制数。
即(a a a a n 321)p =a p a p a n n n +⨯+⨯--2211 例1将)7215(12化为10进制。
例2在哪个进制中,10进制数52记为34?例3如果在某个进位制中4466=⨯,那么在这个进位制中76是10进制中的哪个数?。
进位制

二,概念介绍
进位制:进位制是人们为了计数和运算方便而约定的 计数系统。 比如:满二进一,就是二进制;满十进一,就是十进 制;满十六进一,就是十六进制。 基数: “满几进一”就是几进制,几进制的基数就是几 例如:满二进一,就是二进制,二进制的基数就是二
三,探究新知
哪位同学能描述一下十进制的有关内容呢?(从下面 几个方面描述)
• 89=2*44+1 44=2*22+0 22=2*11+0 11=2*5+1 5=2*2+1
2
44
2 22 2 11 2 5 2 2 21 0
1
0 0
1 1
0
1
练习:一组同学把89转化为4进制的数 二组同学把89转化为5进制的数
三组同学把89转化为6进制的数制数的算法,称为除K取余法
获胜组的奖励是: 将你的算法用程序框图表示出来,并把它设计为程序 ,明天上课展示给大家。 我们在使用计算机的时,我们输入的一般是10进制的 数,计算机把它们要转化为2进制的数,然后再进行 运算,那么怎样把10进制的数化为2进制的数呢?
k进制 转化为十进制
例1、把89化为二进制数.
2 89
余数
一,知识背景
我们平时在数数的时候,19后面是20,29后面是 30,等等,也就是说,当数数时候,每当个位数满十, 十位数上就进一位,由1变成2,由2变成3,等等,其 他各位数上都是如此。在此过程中,我们已经用到了进 位制中的十进制。 我们常见的数字都是十进制的,传说,这与古人曾经以手 指计数有关,比如十两等于一斤,十厘米等于一分米等 但是并不是生活中的每一种数字都是十进制的,同学们, 你们能不能举一些生活中其它进位制的例子,同时说一 说他们的应用呢?
进位制概念及应用

进位制概念及应用一、数的进制1.十进制:我们常用的进制为十进制,特点是“逢十进一”。
在实际生活中,除了十进制计数法外,还有其他的大于1的自然数进位制。
比如二进制,八进制,十六进制等。
2.二进制:在计算机中,所采用的计数法是二进制,即“逢二进一”。
因此,二进制中只用两个数字0和1。
二进制的计数单位分别是1、21、22、23、……,二进制数也可以写做展开式的形式,例如100110在二进制中表示为:(100110)2=1×25+0×24+0×23+1×22+1×21+0×20。
二进制的运算法则:“满二进一”、“借一当二”,乘法口诀是:零零得零,一零得零,零一得零,一一得一。
注意:对于任意非零自然数n ,我们有n 0=1。
3.k 进制:一般地,对于k 进位制,每个数是由0,1,2,L ,1k -()共k 个数码组成,且“逢k 进一”.1k k >()进位制计数单位是0k ,1k ,2k ,L .如二进位制的计数单位是02,12,22,L ,八进位制的计数单位是08,18,28,L .4.k 进位制数可以写成不同计数单位的数之和的形式1110110n n n n k n n a a a a a k a ka k a ---=⨯+⨯++⨯+L L () 十进制表示形式:1010101010n n n n N a a a --=+++L ;二进制表示形式:1010222n n n n N a a a --=+++L ;为了区别各进位制中的数,在给出数的右下方写上k ,表示是k 进位制的数如:8352(),21010(),123145(),分别表示八进位制,二进位制,十二进位制中的数.5.k 进制的四则混合运算和十进制一样先乘除,后加减;同级运算,先左后右;有括号时先计算括号内的。
二、进制间的转换:一般地,十进制整数化为k 进制数的方法是:除以k 取余数,一直除到被除数小于k 为止,余数由下到上按从左到右顺序排列即为k 进制数.反过来,k 进制数化为十进制数的一般方法是:首先将k 进制数按k 的次幂形式展开,然后按十进制数相加即可得结果.如右图所示:1. 将下面的数转化为十进制的数:()21111 ()21010010 ()54301 ()1608B巩固:请将十进制数90转化成二进制、七进制和十六进制。
1.3.3-进位制

30241(5)=5450(7)
三、教材 P45 第3题
※对自己说,你有什么收获? ※对同学说,你有什么提示? ※对老师说,你有什么疑惑?
2021年3月21日 1次
必做题:《学海导航》 P31-P32 A组所有题目 必做题:《学海导航》 P32 B组
【课后作业】课本P50 《总复习》
89=44×2+1, 44=22×2+0, 22=11×2+0, 11=5×2+1, 5=2×2+1, 2=1×2+0, 1=0×2+1,
89=44×2+1, 44=22×2+0,
11=5×2+1, 89=44×2+1,
5=2×2+1,
=(22×2+0)×2+1
=((11×2+0)×2+0)×2+1
思考3:将除k取余法的算法步骤用程序框图如何表示?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
a=q q=0? 否
是 输出全部余数r排 列得到的k进制数
结束
思考4:该程序框图对应的程序如何表述?
开始
输入a,k
求a除以k的商q
求a除以k的余数r
把所得的余数依次从右到左排列
否则,输出全部余数r排列得到的二进制数.
思考2:利用除k取余法,将十进制数a化为k进制数 的算法步骤如何设计?
第一步,输入十进制数a和基数k的值. 第二步,求出a除以k所得的商q,余数r. 第三步,把所得的余数依次从右到左排列. 第四步,若q≠0,则a=q,返回第二步;
否则,输出全部余数r排列得到的k进制数.
进位制与计算

进位制与计算在数学和计算机科学中,进位制是一种基数系统,用于计数和表示数字。
常见的进位制有十进制、二进制、八进制和十六进制。
每种进位制都有其特定的表示方法和计算规则。
一、十进制十进制是最常用的进位制,使用了0-9这10个数字。
它的计算规则是每个数字的位权是10的幂次方,从右往左逐位相加。
例如,数字123的计算方法如下:1 × 10^2 + 2 × 10^1 +3 × 10^0 = 100 + 20 + 3 = 123二、二进制二进制是计算机系统中最基本的进位制,只使用了0和1这两个数字。
它的计算规则与十进制类似,只是每个数字的位权是2的幂次方。
例如,数字101的计算方法如下:1 × 2^2 + 0 × 2^1 + 1 × 2^0 = 4 + 0 + 1 = 5在计算机中,二进制广泛用于表示和存储数据。
由于计算机内部使用的是二进制,将数据转化为二进制可以更便于计算和处理。
三、八进制八进制使用了0-7这8个数字。
它的计算规则与十进制和二进制类似,每个数字的位权是8的幂次方。
例如,数字47的计算方法如下:4 × 8^1 + 7 × 8^0 = 32 + 7 = 39在计算机领域,八进制不如二进制广泛使用,但在某些特定场景下仍然起到重要作用。
四、十六进制十六进制使用了0-9和A-F这16个数字,其中A-F分别代表10-15。
它的计算规则与其他进位制相同,每个数字的位权是16的幂次方。
例如,数字3A的计算方法如下:3 × 16^1 + 10 × 16^0 = 48 + 10 = 58十六进制在计算机领域中被广泛使用,特别是在表示存储地址和颜色等方面。
总结:进位制是一种基数系统,用于计数和表示数字。
十进制、二进制、八进制和十六进制是常见的进位制。
每种进位制都有其特定的表示方法和计算规则。
十进制是最常用的,二进制是计算机系统中最基本的。
进位制PPT教学课件

PPT教学课件
谢谢观看
Thank You For Watching
14
湖南省长沙市一中卫星远程学校
思考2:上述化十进制数为二进制数的 算法叫做除2取余法,转化过程有些复 杂,观察下面的算式你有什么发现吗?
2 89
2 44 2 22 2 11 25 22 21 0
余数 1 0 0 1 1
0 1
思考3:上述方法也可以推广为把十进 制数化为k进制数的算法,称为除k取 余法,那么十进制数191化为五进制数 是什么数?
5 191
余数
5 38
1
57
3
51
2
191=1231(5)
0
1
理论迁移
例2 将十进制数458分别转化为四进制 数和六进制数.
4 458 4 114 4 28
47 41
0
余数
2 2 0 3 1
6 458 6 76 6 12
62 0
余数
2 4 0 2
458=13022(4)=2042(6)
例3 将五进制数30241(5)转化为七进制数.
10303(4)=1×44+3×42+3×40=307. 1234(5)=1×53+2×52+3×51+4×50=194.
知识探究(三):除k取余法
思考1:二进制数101101(2)化为十进制 数是什么数?十进制数89化为二进制 数是什么数?
101101(2)=25+23+22+1=45.
89=2×(2×(2×(2×(2×2+1)+1)+0)+0)+1 =1×26+0×25+1×24+1×23+0×22+0×21 +1×20=1011001(2).
上课:进位制
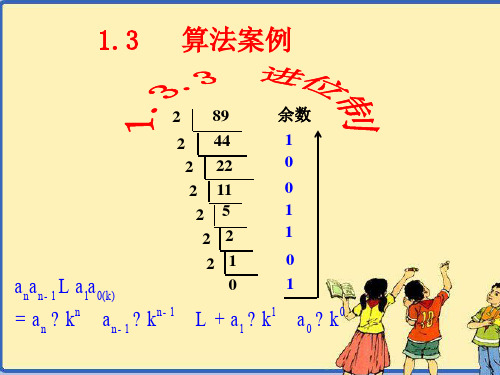
89 =1×26+0×25+1×24+1×23 +0×22+0×21+1×20 =1011001(2)
即把余数按从下向上的顺序 书写即可得到把十进制数89
化为二进制数
上述方法也可以推广为把十进制数化为k进 制数的方法,称为除k取余法,那么十进制数 191化为五进制数是什么数?
5 5 5 5 191 余数 1
【解析】先把五进制数3241化为十进制数后,
再化为七进制数
30241(5)=3×54+2×52+4×5+1=1946.
7 7 7 7
1946 278
39
余数 0 5 4 5
课外探究
5
0
30241(5)=5450(7)
思考题:
用程序框图如何表示除k取余法?
开始
输入a,k 求a除以k的商q 求a除以k的余数r 把所得的余数依次从右到得到的k进制数
1.3
2
算法案例
89 44 2 2 22 2 11 2 5 2 2 2 1 0 余数 1 0 0 1 1 0 1
1
an an - 1 L a1a 0(k ) = an ? k
n
an - 1 ? k
n- 1
L + a1 ? k
a0 k
0
人们为了计数和运算方便,约定了各种 进位制,这些进位制是什么概念,它们与十 进制之间是怎样转化的?
一、进位制的概念
进位制是为了计数和运算方便而约定的记数系统, 如逢十进一,就是十进制;每七天为一周,就是七进制; 每十二个月为一年,就是十二进制,每六十秒为一分钟, 每六十分钟为一个小时,就是六十进制;等等.一般地, “满k进一”就是k进制,其中k称为k进制的基数.那么k是 一个什么范围内的数? 思考1:十进制使用0~9十个数字,那么二进制、五进制、 七进制分别使用哪些数字? 答案:二进制使用0,1两个数字; 五进制使用0~4五个数字;
数的进位知识点

数的进位知识点进位是数学中非常基础的概念,它涉及到整数的表示和运算。
在日常生活和各个学科都会涉及到进位的概念,尤其在计算机科学和金融领域中更为重要。
本文将介绍数的进位的相关知识点,包括进位制、进位运算和进位的应用。
一、进位制进位制是一种计数的方法,根据不同的进位基数,可以分为十进制、二进制、八进制和十六进制等。
具体如下:1. 十进制:十进制是我们常用的计数方式,以0-9的十个数字为基础。
每当个位到达9时,就需要进位到十位,十位到达9时就需要进位到百位,以此类推。
2. 二进制:二进制是计算机中最常用的进位制,只包含0和1两个数字。
每当个位到达1时,就需要进位到十位,十位到达1时就需要进位到百位,以此类推。
3. 八进制:八进制以0-7的八个数字为基础。
每当个位到达7时,就需要进位到十位,十位到达7时就需要进位到百位,以此类推。
4. 十六进制:十六进制以0-9和A-F的共十六个数字表示。
其中A代表10,B代表11,依此类推。
每当个位到达F时,就需要进位到十位,十位到达F时就需要进位到百位,以此类推。
进位制的转换非常常见,可以通过多种方法进行计算和转换。
例如,将十进制转换为二进制可以使用除以2取余法,将十进制转换为八进制可以使用除以8取余法,将十进制转换为十六进制可以使用除以16取余法。
二、进位运算进位运算是指在进行数学运算中,当某一位的结果超过了进位制的基数时,需要把多余的进位向高位进行传递的过程。
进位运算的常见形式包括加法进位和乘法进位。
1. 加法进位:在两个数相加的过程中,当某一位的结果超过了进位制的基数时,就会产生进位。
例如,对于十进制数相加时,当个位相加的结果大于10时,就会产生进位,将个位的进位加到十位上。
2. 乘法进位:在两个数相乘的过程中,当某一位的结果超过了进位制的基数时,也会产生进位。
例如,对于十进制数相乘时,当个位相乘的结果大于10时,就会产生进位,将个位的进位加到十位上。
进位运算在数学计算过程中非常常见,可以通过列竖式的方法进行演算和解决。
进位制

二进制:
在电子计算机中,数是以二进制的形式表示的。二 进制数每个数位只可能取两个不同的数码,0和1。
二进制数与十进制数的转换:
(1)二进制数化为十进制数:
例1 把二进制数110011(2)化为十进制数.
110011 1 25 1 24 0 23 0 22 1 21 1 20 (2)
A)
an an1 a1a0( k ) (0 an k ,0 an1 ,, a1 , a0 k ).
751 7 16 5 16 116 1873 (16) (10)
2 1 0
110011 1 25 1 24 0 23 0 22 1 21 1 20 (2) =51
——进位制
一、进位制
进位制是人们为了计数和运算方便而约定的计数 系统。
比如:
满二进一,就是二进制; 满十进一,就是十进制; 满十二进一,就是十二进制; 满六十进一,就是六十进制
基数: “满几进一”就是几进制,几进制的基数就是几.
十进制: 我们最常用最熟悉的就是十进制数,它 的数值部分是十个不同的数字符号0,1,2, 3,4,5,6,7,8,9来表示的。
探究:P34
若an an 1 a1a0( k ) 表示一个k 进制数,请你把它写成各位 上数字与k的幂的乘积之和的形式。
an an 1 a1a0( k ) an k an 1 k
n n 1
a1 k a0 k
1
0 (10)
其它进制数化成十进制数公式
n
n 1
a1 k a0 k
1
0 (10)
2、十进制数化成k进制数
除k取余法
1.3.3进位制

练习:下列写法正确的是: (A ) A、751 (16) B、751 (7) C、095 (12) D、901 (2)
三、二进制与十进制的转换
1、二进制数转化为十进制数
例1:将二进制数110011(2)化成十进制数。
K进制数转化成十进制数的方法:
先将k进制数写成各位上数字与 k的幂的乘积之和的形式,再按照 十进制数的运算规则计算出结果
算法案例 ——进位制
一、进位制
1、什么是进位制?
进位制是人们为了计数和运算方便而约定的记数系统。 约定满二进一,就是二进制;满十进一,就是十进制, 等等,也就是说“满几进一”就是几进制,几进制的基 数就是几。
进位制是一种记数方式,用有限的数字在不同的 位置表示不同的数值。若基数为k,即可称k进位制, 简称k进制。
练习:将下面的数转化成十进制数
1012(4) 24(12)
练习: 把下列各数转化为十进制: (1)1031(4)= (2) 235(7)= (3) 213(4)= (4) 131(5)= ; ; ; ;
十进制化K进制
例1:把十进制数89化为二进制数. 根据二进制“满二进一”的原则,可以用2连续去 除89或所得商,然后取余数. 余数 89 2 1 2 44 0 2 22 0 2 11 上述化十进 1 2 5 制数为二进制数 1 2 2 的算法叫做除2 0 2 1 取余法. 1 0
最常见的进位制是什么?除此之外还有哪些常 见的进位制?请举例说明.
• 最常见的进位制应该是我们数学中的十进制,比如一般的 数值计算,但是并不是生活中的每一种数字都是十进制的. • 电子计算机用的是二进制。 实际上,十进制数只是计数法中的一种,但它不是唯 一记数法。除了十进制数,生产生活中还会遇到非十进制 的记数制。如时间:一周七天,它是七进制;一年十二个 月,它是十二进制;60秒为1分,60分为1小时,它是六 十进制的。
进位制的计算方法

进位制的计算方法进位制是一种数学计数系统,常见的进位制包括二进制、八进制、十进制和十六进制。
在日常生活和计算机领域中,我们经常会接触到各种进位制。
本文将介绍各种进位制的计算方法,帮助读者更好地理解和运用进位制。
首先,我们来谈谈十进制计算方法。
十进制是我们最常用的计数系统,也是最容易理解的一种进位制。
在十进制计算中,我们使用0到9这十个数字来表示任意一个数。
例如,1234就是一个十进制数,它表示了一千两百三十四这个数量。
在十进制计算中,我们采用逢十进一的规则,即当某一位的数达到10时,就向高一位进位,这就是十进制的进位规则。
接下来,我们来看看二进制的计算方法。
二进制是计算机中最常用的进位制,它只使用0和1两个数字来表示任意一个数。
在二进制计算中,我们同样采用逢二进一的规则,当某一位的数达到2时,就向高一位进位。
例如,二进制数1011表示了十进制的11,其中12^3 + 02^2 + 12^1 + 12^0 = 11。
因此,理解二进制的进位规则对于理解计算机内部的运算方式非常重要。
其次,我们来介绍八进制的计算方法。
八进制使用0到7这八个数字来表示任意一个数。
在八进制计算中,同样采用逢八进一的规则,当某一位的数达到8时,就向高一位进位。
八进制在计算机领域中并不常用,但了解其计算方法有助于我们对进位制有一个更全面的认识。
最后,我们来讨论十六进制的计算方法。
十六进制使用0到9和A到F这十六个数字来表示任意一个数。
在十六进制计算中,同样采用逢十六进一的规则,当某一位的数达到16时,就向高一位进位。
十六进制在计算机领域中应用广泛,特别是在表示内存地址和颜色数值时,常常会使用十六进制表示法。
总结一下,不同进位制的计算方法都遵循着逢X进一的规则,其中X表示该进位制的基数。
了解各种进位制的计算方法有助于我们更好地理解计算机内部的运算方式,同时也方便我们在日常生活中处理各种进位制的数据。
希望本文对读者有所帮助,谢谢阅读!。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
进位制
我们平常熟悉的十进制:
(2012)10=2×103+0×102+1×101+2
其他进制转化为十进制:
(a…bcde)n=a×n k-1+……+b×n3+c×n2+d×n+e
十进制转化为其他进制:
例1.A,B是两个自然数,如果A进位制数47和B进位制数74相等,那么A+B的最小可能值是多少?
[答疑编号0518330101]
【解答】由已知:4A+7=7B+4,即4A=7B-3,可见B除以4余1。
又B进制中有7出现,说明B>7,因此B的最小值是9,相应的计算出A=15。
所以A+B最小值是9+15=24。
例2.一个十进制的两位数A,它的十位数字为5,另一个R进制数为B,它的各位数字与A分别相等,而且B在十进制中恰好是A的3倍,那么数A 和B在十进制中各是多少?
[答疑编号0518330102]
【解答】设A 在十进制中表示是(),
由已知:5×R+m=3×(50+m),即5×R=150+2×m,
1
可见m是5的倍数,因此m=0或5。
相应的计算出R=30或32。
所以A和B分别是50、150,或者55,165。
例3.一个自然数的六进制表示与九进制表示均为三位数,并且它们各位数字的排列顺序恰好相反,那么此自然数用十进制表示法写出是多少?
[答疑编号0518330103]
【解答】设自然数在六进制中表示是(),则在九进制中表示是()。
则36a+6b+c=81c+9b+a,35a=3b+80c,通过对等式的观察,可以发现b是5的倍数。
又由于b是在六进制中的数,所以,b是0或5。
(1)若b=0, 则上式变为35a=80c,即7a=16c,a需要是16的倍数,a又小于6。
所以,a=0。
但是a在首位,a又不能等于0。
所以,这样的数字不存在。
(2)若b=5, 则上式变为7a=3+16c,a=5,c=2。
所以,这个六进制数是(552)6化为十进制是5×62+5×6+2=212。
例4.如果某个自然数可以写成2的两个不同次幂(包括零次幂)的和,我们就称这样的数为“双子数”,比如9=+,36=+,它们都是双子数。
现有一个双子数是1040。
(1)把1040写成2的两个不同次幂(包括零次幂)的和。
这样的写
2
法唯一吗?
(2)比1040小的双子数共有多少个?
[答疑编号0518330104]
【解答】
(1)1040=1024+16=+,写法是唯一的。
(2)若某个双子数可以表示成的样子(k>m),
而且小于1040,则k<10或者k=10,m<4。
当k<10:则m也小于10,也就是k、m在0到9之间取值,
且不相同,利用排列组合,有=45种。
当k=10:m<4:m=0、1、2或3,4种情况。
因此共有45+4=49个。
例5.一副双色牌中,红、黑两种颜色各有10张,分别写着1、2、4、8、16、……、512.小梁从中任意抽取一些牌,计算抽出的牌面上所有数的和.
(1)若算出的和为183,那么小梁最多可能抽取了多少张牌?
(2)小梁有多少种抽取牌的方法,使得算出的和为23?
[答疑编号0518330105]
【解答】
(1)183=27+25+24+22+21+20,其中 26、22、21、20是恰有一个颜
3
色选择,
25、24、23是两种颜色都可以选择的。
所以,最多可能抽取10张。
(2)23=0+23=1+22=2+21=……=23+0。
所以,总共有24种。
例6.有些正整数可以表示成496的不同约数之和,例如36符合条件,因为36可以表示成1+4+31;而62本身就是496的约数,那么认为62
也符合条件.
(1)请把104写成496的不同约数之和;
(2)不能写成496的不同约数之和的最小正整数是多少?
[答疑编号0518330106]
【解答】(1) 496=31×16,所以,104=62+31+8+2+1
(2)496=31×16,因此496的约数有1,2,4,8,16,1×31,2×31,4×31,8×31,16×31。
其所有约数的和为:
1+2+4+8+16+1×31+2×31+4×31+8×31+16×31=31+
31×31=992。
对于小于992的任何一个正整数,都可以表示成n=31×k+r,其中
0≤k,r≤31,
将k和r分别用二进制表示,可知31×k可以表示成1×31,2×31,4×31,8×31,16×31中若干个数之和,r可以表示成1,2,4,8,16中若干个数之和。
4
因此n=31×k+r一定可以表示成496的若干个互不相同的约数之和。
又993比496的所有约数之和还要大,因此它不能写成496的不同约数之和,
故所求最小正整数就是993。
例7.用a、b、c、d、e分别代表五进制中五个互不相同的数字,如果(ade)5、(adc)5、(aab)5是由小到大排列的连续正整数,那么(cde)
5所表示的整数写成十进制的表示是多少?
[答疑编号0518330107]
【解答】通过分析,得到c=4,d=1,e=3。
(413)5=4×52+1×5
+3=108。
例8.三个两位数恰构成公差为6的等差数列,而在五进制的表示中,
这三个数的数字和是依次减少的.那么符合这样要求的等差数列有多少
个?
[答疑编号0518330108]
【解答】将6化成五进制数,就是11.因为这3个数的数字和是依次减
少的,这就是说要找到1个五进制数,它加上1个11后有进位,再加1个
11后还有进位.
,说明每一个两位数化成五进制数后最多只有3位.那么进
5
位只可能在个位和十位.
由此我们可以找到两种符合要求的数:a24、a43.在这两种数中,a都有3种选择0、1、2.所以一共有6个符合要求的等差数列.
6。
