Matlab画函数图像
Matlab绘制图像

第一种方法 在Workspace中绘制
绘图基本线型和颜色
符号 y m c r g b w k 颜色 黄色 紫红 青色 红色 绿色 蓝色 白色 黑色 符号 . 。 x + * : -. -线型 点 圆圈 x 标记 加号 星号 实线 点线 点划线 虚线
绘图命令
绘图命令plot 主要是在数值计算中绘制函数图像。 绘制反函数图像非常容易。
绘图命令plot
调用格式1:plot(x,y)
1. 首先定义自变量X的取值向量(横坐标) 2. 再定义函数Y的取值向量(纵坐标) 3. 用plot(x,y)命令给出平面曲线图。 在绘图参数中可以给出绘制图形的线型和颜 色的参数。例:plot(x,y,’r*’) 就是用红色的 ****线型绘图。
技巧
x=0:0.1:2*pi; y1=sin(x); y2=exp(-x); plot(x,y1,'--*',x,y2,':o'); xlabel('t=0 to 2\pi'); ylabel('value of sin(t) and e^{-x}') title('Function sin(t) and e^{-x}'); legend('sin(t)','e^{-x}') 后期的制作
ቤተ መጻሕፍቲ ባይዱ
绘出下面函数及其反函数的图像
1 1 y (x ) 2 x (1 x )
程序如下: x=1:0.001:5; %定义横坐标 y=1/2*(x+1./x); %定义纵坐标 plot(x,y,'r',y,x,'b') %红色画f(x) 蓝色画f(y).
第三章 利用MATLAB绘制函数图形

四、特殊平面图形的绘制
五、三维曲线图形
plot3
如果输入自变量是三个大小相同的矩阵 x、y、z,那么 plot3 会
依序画出每个行矢量在三维空间所对应的曲线
格式:plot3(x1,y1,z1,S1, x2,y2,z2,S2,…) 说明:一次和绘制多条曲线
ezplot3
空间曲线的简易绘图命令
polar(theta,rho,'--r')
% 进行极坐标绘图
用ezpolar作图,输入: ezpolar('5*(1-sin(theta)')
四、特殊平面图形的绘制
hist指令
绘制统计直方图,对大量的资料,显示资料的分布情况和统计特性 格式:hist(Y, n) %n是一个标量,表明使用n个箱子. 将资料依大小分成数堆,将每堆的个数画出 例12:>> x=randn(500,1); %产生500个正态分布随机数 hist(x,25) %将数据绘制成25个直方
>> x= 0:0.1:4*pi; subplot(2, 2, 1); plot(x, sin(x)); subplot(2, 2, 2); plot(x, cos(x)); subplot(2, 2, 3); plot(x, exp(-x/3)); subplot(2, 2, 4); plot(x, x.^2);
注:还可直接输入 ezplot3('x','x*sin(x)*cos(x)','x*cos(x)*cos(x)',[0,20]).
举例—三维绘图
例15:同时绘制两条空间曲线. >> t = linspace(0, 10*pi, 501); plot3(t.*sin(t), t.*cos(t), t, t.*sin(t), t.*cos(t), -t); % 同时画两条曲线
matlab绘图(一维、二维、三维)
Matlab 二维作图
数学实验
基本形式(续)
plot(y): 绘制向量 y 中元素的线性图 以下标为横坐标,元素值为纵坐标,等价于:
x=[1:length(y)];plot(x,y);
例:>> y=[0,0.48,0.84,1,0.91,6.14];
>> plot(y); >> figure(2); plot([1:length(y)], y)
数学实验
图形的其他属性
标题 title(’text’)
例:
数学实验
可以指定文本的属性 title('text', 'Property1', value1, ' Property2', value2, ...)
Property: linewidth, markersize, fontsize, fontweight, fontname, …
Matlab 二维作图
数学实验
基本形式
plot(x,y)
✓ x, y 都是向量,则以 x 中元素为横坐标, y 中元素为 纵坐标作平面曲线。此时 x, y 必须具有相同长度。 ✓ x, y 都是矩阵,则将 x 的列和 y 中相应的列相组合, 绘制多条平面曲线。此时 x, y 必须具有相同的大小。 ✓ x 是向量, y 是矩阵,若 x 的长度与 y 的行数相等, 则将 x 与 y 中的各列相对应,绘制多条平面曲线;否 则,若 x 的长度与 y 的列数相等,则将 x 与 y 中的各 行相对应,绘制多条平面曲线。此时 x 的长度必须等 于 y 的行数或列数。
数学实验
空间曲面作图举例
例:绘制边界面屏蔽 meshz
Matlab绘图

第二章绘图要画一个函数的图像,先是选取一堆x,求出相对应的y值,然后按照数值描点,接着用光滑的曲线把点连接起来。
和数学课讲的一样,在matlab中,我们画图也分为三步1. 建立一个x的点集;2. 根据函数关系式算出每个x对应y的点集;3. 将这些点用平滑的曲线连接起来。
例如要画y=sinx在[0,10]区间内的图像,首先我们要确定出x的区间>>x = [0:0.1:10];命令的意思是,产生一个数集,它从0开始,每次加0.1,一直加到10为止注意,命令后面的分号记得加上,否则matlab会把x的元素都打印出来,下面就是不加分号的后果:有了x的数集后,我们再根据函数关系式y=sinx得出y的点集>>y = sin(x);同样的,别忘了把分号加上抑制程序输出y的具体值,以及sin(x)的括号别忘了加到这里,我们已经把x和y确定下来,接下来只需用plot(x,y)命令即可绘制出图像>>plot(x,y)当然,如果你不定义y,而直接用一下嵌套命令也是可以的>>plot(x,sin(x))我们将x的增量变大一点,改为0到10,每次增幅为1,即>>x = [0:1:10];然后我们输入>>plot(x,y)我们会得到错误信息:原因是之前我们定义的y是由之前的x决定的,当x改变后,y依然没有改变,为了解决这个问题,我们要把y重新定义一遍,即命令要完整再输入一遍>>x = [0:1:10];>>y = sin(x);>>plot(x,y)然后程序会绘制出和我们预期相同的图像没错,我们将看到不光滑的曲线,这告诉我们,当使用plot(x,y)画图的时候x的增加幅度尽可能小一些,画出的图像才精确(跟数学里点越多图像越精确原理一样的)为了美化图像(有时是为了更清楚的辨析图像),我们经常要为图像加上网格,为坐标轴命名,改变曲线的颜色、形状这些命令2.1 加上网格我们使用grid on 命令我们这样书写:>>x=[0:0.1:10];y=sin(x);>>plot(x,y),grid on这样就画出了带网格的图像当然,也可以先画出没有网格的图像,再把窗口切回matlab命令输入窗口,输入grid on,这样图像就会加上网格,即>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>grid on2.2 为坐标轴命名为x坐标轴命名的命令是xlabel(),显然,y的就应该是ylabel()比如这里,我想让x命名为x,y命名为sinx,则如下输入:>>x=[0:0.1:10];y=sin(x);>>plot(x,y),xlabel(‘x’),ylabel(‘sinx’)注意,坐标轴的名字要用引号括起来,表示字符串当然也可以画图后再标坐标轴,即:>>x=[0:0.1:10];y=sin(x);>>plot(x,y)>>xlabel(‘x’)>>ylabel(‘sinx’)然后我们就可以看到坐标轴带命名的图像:2.3 绘制多条曲线绘制多条曲线有两种情况,一种是在同一个坐标面内画多条曲线,另一种是在一个面内画多个独立的曲线我们先讲第一种,假设我们要在一个坐标面内画sinx,cosx,tanx的图像先定义x,y>>x=[0:0.1:10]>>y1=sin(x);>>y2=cos(x);>>y3=tan(x);接着画图>>plot(x,y1)这时候函数绘制出了sinx的图像接着我们继续画>>plot(x,y2)我们会发现程序会把之前的sinx图像抹掉,然后绘制cosx的图像为了让他们同时存在,我们使用hold on命令,即画完一个图后,hold on,继续画当我们再加上tanx后会得到这个图像这是因为函数显示区间设置的原因,后面讲2.4 更改图像显示区间从楼上我们已经在一个图中画出了sinx、cosx、tanx的图像,但是我们知道tanx的值域是负无穷到正无穷,而sin,cos的值域是-1到1,这导致了我们基本上看不到sin,cos的图像,为了解决这个问题,我们只需用axis命令即可,命令格式为axis([xmin xmax ymin ymax])即括号内跟一个区间,四个数字分别是x的起点,x的终点,y的起点,y的终点。
matlab--函数图形绘制实验报告1

实验报告课程名称: 数学实验学院名称: 数学与统计学院班级:姓名:学号:2012-2013 学年第学期数学与统计学院制(二)参数方程作图例2: 画出星形线{ 及旋轮线{ 的图形解: 输入以下命令:%星形线作图t=linspace(0,2*pi,5000);x=2*(cos(t)).^3;y=2*(sin(t)).^3;plot(x,y),grid;结果:%旋轮线作图t=linspace(0,4*pi,5000); x=2*(t-sin(t));y=2*(1-cos(t));plot(x,y),axis equal; axis(0,8*pi,0,5);grid;结果:(三)极坐标方程图形例3:画出四叶玫瑰线的图形。
知其极坐标方程: ρ=acos(2 )。
解: 取a=5做图。
在命令窗口输入下命令theta=linspace(0,2*pi);r=2*cos(2*theta);polar(theta,r)结果:(四)空间曲面(线)的绘制例4: 绘制双曲抛物面z= 。
解:将其化为参数方程:{ , 编写m文件运行以下命令r=linspace(-4,4,30);s=r;[u,v]=meshgrid(r,s);x=u;y=v;z=(u.^2-v.^2)./4;surf(x,y,z);bix on;结果:(五)空间曲线在坐标平面上的投影曲面和投影柱面例5: 画出螺旋线{ , 在xOz面上的正投影曲线的图形。
解:化为参数方程{ , 运行下列程序t=linspace(-2*pi,2*pi);x=10*cos(t);z=2*t;h=plot(x,z);grid;xlabel('x');ylabel('z');set(h,'linewidth',2);结果:(一)实验分析:(二)在本次实验中我们初步了解了matlab。
(三)学会了一些简单绘图。
(四)在编制中我们要很明确“点乘的重要性”。
Matlab3 画图

\leftritharrow ↔
3.7 二维作图的附加类型
附加的二维作图类型 函数 描述 bar(x,y) 创建一个水平的条形图,x代表第 一个X轴的取值,y代表对应于Y的 取值 barh(x,y) 创建一个竖直的条形图 pie(x) 创建一个饼状图,x代表占总数的 pie(x,explode) 百分数
柱状图
• 在一系列数值中范围被平均划分,并确定某一个范围中数值 的个数,并把这个数目通过函数画出图来。 • 格式:hist (y)、hist(y, nbins)、hist(y, x) • 例:y = randn(10000,1); hist(y,15) • 例:y = randi(10,[10000,1]); hist(y,1:10) • 重做练习6 n=10^5; a=vpa('pi',n); a=char(a); a(2)=[]; b=arrayfun(@str2num,a); figure; hist(b,0:9); count2=hist(b,0:9)
n=10^5; a=vpa('pi',n); % pi,sqrt(2),exp(1).... a=char(a); % 将符号转化成字符串 count=zeros(1,10); % 预分配内存
format 结果 string %d 把值作为整数来处理 %e %f %g \n 用科学记数法来显示数据 用于浮点数格式显示这个数 用科学记数格式,或浮点数格式,根据那 个短,并显示之 转到新的一行
用legend来制作 图例
• 基本形式: legend('string1','string2',...,pos) • 其中string1,string2等等是轨迹标签名,而pos是 一个整数,用来指定图例的位置。 x=0:pi/100:2*pi; y1=sin(2*x); y2=2*cos(2*x); plot(x,y1,'k-',x,y2,'b--'); title(' Plot of f(x)=sin(2x) and its derivative'); legend('f(x)','d/dx f(x)');
MATLAB画函数图像

MATLAB画函数图像CWW的博客 2019-04-19 15:56:34 43732 收藏 95展开MATLAB绘制图时设置坐标轴的一些常用函数命令Justin_YWX 2019-08-13 17:53:06 1048 收藏 1展开利用MATLAB作图时,一些常用的函数命令:、figure()----创建新图窗;subplot(121)-----创建子图,12表示创建的子图为1行2列排列,1表示其中第一幅子图;xlim,ylim----横纵坐标的范围;xlabel,ylabel-----横纵坐标的名称;xticks,yticks-----横纵坐标刻度;xticklabels,yticklabels-----横纵坐标刻度名;title ---- 有子图时,为子图标题;无子图时,为总标题;suptitle ------ 有子图时,设置总标题。
1 画图基础(1)一元一次函数1.x=0:0.1:1;2.y=x;3.plot(x,y); %图像见下图1图1图2(2)一元多次函数1. x=0:0.1:1;2.y=x.^2;3.plot(x,y); % 图像见图22 分段函数图像1.x=0:0.1:2;2.y=x.*(x>=0&x<=1)+(-(x-1).^2+1).*(x>1&x<=2);3.plot(x,y); %图像见图34.%组合函数y=y1.*(x定义域)+y2.*(x定义域)图3图43 其他小技巧(1)多条曲线画在同一个图像里tip:使用hold on 函数1.t=[0:0.01:1];2.q1=120-180*t.^2+120*t.^3;3.q2=120-600*t.^3+900*t.^4-360*t.^5;4.plot(t,q1);hold on;5.plot(t,q2);6.%图形见图4(2)改变图像中线的颜色和线条形式(针对plot函数)1.t=[0:0.01:1];2.q1=120-180*t.^2+120*t.^3;3.q2=120-600*t.^3+900*t.^4-360*t.^5;4.plot(t,q1,'r');hold on;5.plot(t,q2,'b');6.%见图5图5通过在plot()函数括号里面增加特性来改变图线,常见的颜色和类型如图6图6(3)增加图例tip:利用l egend 函数1.t=[0:0.01:1];2.q1=120-180*t.^2+120*t.^3;3.q2=120-600*t.^3+900*t.^4-360*t.^5;4.plot(t,q1,'r'); hold on;5.plot(t,q2,'b');6.legend('a)函数图像','b)函数图像') %要按函数的顺序来添加7.%见图7。
Matlab绘制函数图像函数示例汇总

matlab中最基本的函数plot()的用法之杨若古兰创作标签: matlab plot 指令5.1 二维平面图形5.1.1 基本图形函数plot 是绘制二维图形的最基本函数,它是针对向量或矩阵的列来绘制曲线的.也就是说,使用plot 函数之前,必须首先定义好曲线上每一点的x 及y 坐标,经常使用格式为:(1)plot(x) 当x 为一贯量时,以x 元素的值为纵坐标,x 的序号为横坐标值绘制曲线.当x 为一实矩阵时,则以其序号为横坐标,按列绘制每列元素值绝对于其序号的曲线,当x 为m× n 矩阵时,就由n 条曲线.(2)plot(x,y) 以x 元素为横坐标值,y 元素为纵坐标值绘制曲线.(3)plot(x,y1,x,y2,…) 以公共的x 元素为横坐标值,以y1,y2,… 元素为纵坐标值绘制多条曲线.例5.1.1 画出一条正弦曲线和一条余弦曲线.>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,x,y2)图5.1.1 函数plot 绘制的正弦曲线在绘制曲线图形时,经常采取多种色彩或线型来区分分歧的数据组,MATLAB 软件专门提供了这方面的参数选项(见表5.1.1),我们只需在每个坐标后加上相干字符串,就可实现它们的功能.- 2 -表5.1.1 绘图参数表色彩字符色彩线型字符线型格式标识表记标帜符号数据点方式标识表记标帜符号数据点方式y 黄- 实线. 点< 小于号m 紫:点线o 圆s 正方形c 青-. 点划线x 叉号d 菱形r 红- - 虚线+ 加号h 六角星g 绿* 星号p 五角星b 蓝v 向下三角形w 白^ 向上三角形k 黑> 大于号例如,在上例中输入>> plot(x,y1,'r+-',x,y2,'k*:')图5.1.2 使用分歧标识表记标帜的plot 函数绘制的正弦曲线5.1.2 图形润色MATLAB 软件为用户提供了一些特殊的图形函数,用于润色曾经绘制好的图形.函数含义grid on (/off) 给当前图形标识表记标帜添加(取消)收集xlable(‘string’) 标识表记标帜横坐标ylabel(‘string’) 标识表记标帜纵坐标title(‘string’) 给图形添加题目text(x,y,’string’) 在图形的任意地位添加说明性文本信息gtext(‘string’) 利用鼠标添加说明性文本信息axis([xmin xmax ymin ymax]) 设置坐标轴的最小最大值- 3 -例5.1.2 给例5.1.1 的图形中加入收集和标识表记标帜.(见图5.1.3 和5.1.4)>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot(x,y1,x,y2)>> grid on>> xlabel('independent variable X')>> ylabel('Dependent Variable Y1 & Y2')>> title('Sine and Cosine Curve')>> text(1.5,0.3,'cos(x)')>> gtext('sin(x)')>> axis([0 2*pi -0.9 0.9])图5.1.3 使用了图形润色的plot 函数绘制的正弦曲线5.1.3 图形的比较显示在普通默认的情况下,MATLAB 每次使用plot 函数进行图形绘制,将从头发生一个图形窗口.但有时但愿后续的图形能够和前面所绘制的图形进行比较.普通来说有两种方法一是采取hold on(/off)命令,将新发生的图形曲线叠加到已有的图形上;二是采取subplot(m,n,k)函数,将图形窗口分隔成n m× 个子图,并选择第k 个子图作为当前图形,然后在同一个视图窗口中画出多个小图形.例5.1.3 在同一窗口中绘制线段.(见图5.1.5)>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> y3=x;>> y4=log(x);>> plot(x,y1,x,y2)>> hold on>> plot(x,y3)>> plot(x,y4)>> hold off例5.1.4 在多个窗口中绘制图形.(见图5.1.6)>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> y3=exp(x);>> y4=log(x);>> subplot(2,2,1);>> plot(x,y1);>> subplot(2,2,2);>> plot(x,y2);>> subplot(2,2,3);>> plot(x,y3);>> subplot(2,2,4);>> plot(x,y4);[说明] (1)子窗口的序号按行由上往下,按列从左向右编号.(2)如果不必指令clf 清除,当前图形将被绘制在子图形窗口中.图5.1.4 设置坐标轴最大最小值的正弦曲线- 5 -- 6 -5.2 三维立体图形5.2.1 三维曲线图与二维图形绝对应,MATLAB 提供了plot3 函数,可以在三维空间中绘制三维曲线,它的格式类似于plot,不过多了z 方向的数据.plot3 的调用格式为:plot3(x1,y1,z1,x2,y2,z2,...)其中x1,y1,z1,x2,y2,z2,…等分别为维数不异的向量,分别存储着曲线的三个坐标值,该函数的使用方式和plot 类似,也能够采取多种的色彩或线型(见表5.1.1)来区分分歧的数据组,只需在每组变量后面加上相干字符串即可实现该功能.例5.2.1 绘制方程x=ty=sin(t)z=cos(t)在t=[0,2*pi]上的空间方程.(见图5.2.1)>> clf>> x=0:pi/10:2*pi;>> y1=sin(x);>> y2=cos(x);>> plot3(y1,y2,x,'m:p')>> grid on>> xlabel('Dependent Variable Y1')>> ylabel('Dependent Variable Y2')>> zlabel('Independent Variable X')>> title('Sine and Cosine Curve')图5.2.1 函数plot 绘制的三维曲线图- 7 -5.2.2 三维曲面图如果要画一个三维的曲面,可以使用mesh(X,Y,Z)或surf(X,Y,Z)函数来实现.mesh 函数为数据点绘制网格线,图形中的每一个已知点和其附近的点用直线连接.surf函数和mesh 的用法类似,但它可以画出着色概况图,图形中的每一个已知点与其相邻点以平面连接.为方便测试立体绘图,MATLAB 提供了一个peaks 函数,它可以发生一个的高斯分布矩阵,其生成方程是N N ×z=3*(1-x).^2.*exp(-(x.^2)-(y+1).^2)-10*(x/5-x.^3-y.^5).*exp(-x.^2-y.^2)-1/3*exp(-(x+1).^2-y.^2)对应的图形是一个凹凸有致的曲面,包含了三个局部极大点及三个局部极小点.上面使用peaks 函数来比较一下mesh 和surf 的区别.例5.2.2 分别用mesh 函数和surf 函数绘制高斯矩阵的曲面. >> z=peaks(40);>> mesh(z);>> surf(z);图5.2.2 mesh 函数绘制的三维曲面图- 8 -图5.2.3 surf 函数绘制的着色概况图在曲面绘图中,另一个经常使用的函数是meshgrid 函数,其普通援用格式是:[X, Y]=meshgrid (x, y)其中x 和y 是向量,通过meshgrid 函数就可将x 和y 指定的区域转换成为矩阵X 和Y.如许我们在绘图时就可以先用meshgrid 函数发生在x-y 平面上的二维的网格数据,再以一组z 轴的数据对应到这个二维的网格,即可画出三维的曲面.例5.2.3 绘制方程sin((x^2+y^2)^(1/2))z = ---------------------(x^2+y^2)^(1/2)在x∈[-7.5,7.5];y∈[-7.5,7.5] 的图形.>> x=-7.5:0.5:7.5;y=x;>> [X,Y]=meshgrid(x,y);>> R=sqrt(X.^2+Y.^2)+eps;>> Z=sin(R)./R;>> surf(X,Y,Z)>> xlabel('X 轴方向')>> ylabel('Y 轴方向')>> zlabel('Z 轴方向')例 5.2.4 绘制由方程构成的立体图.(见图5.2.5)z=xe-(x^2+y^2)>> clear>> x=-2:0.1:2;y=x;>> [X,Y]=meshgrid(x,y);>> Z=X.*exp(-X.^2-Y.^2);- 9 ->> surf(X,Y,Z)- 10 -5.2.3 观察点MTALAB 答应用户设置观察点,其指令是:view(azimuth,elevation)其中方位角azimuth 是观察点和坐标原点连线在x-y 平面的投影和y 轴负方向的夹角,仰角elevation 是观察点与坐标原点的连线和x-y 平面的夹角.对于这两个角度,三维图形的默认值分别是-37.5 和30,二维图形的默认值是0 和90.例5.2.5 从分歧的角度观察高斯矩阵的曲面.>> z=peaks(40);>> subplot(2,2,1);>> mesh(z);>> subplot(2,2,2);>> mesh(z);>> view(-37.5,-30);>> subplot(2,2,3);>> mesh(z);>> view(180,0);>> subplot(2,2,4);>> mesh(z);>> view(0,90);图5.2.6 对应分歧观察点的三维曲面图5.3 其他图形函数除了plot 绘图函数之外,在有些场合对绘制的曲线会有一些特殊请求,这就要其他函数来实现,经常使用的几种函数如下(见表5.3.1)- 11 -表5.3.1 其他图形函数表函数含义loglog 使用对数坐标系绘图semilogx 横坐标为对数坐标轴,纵坐标为线性坐标轴semilogy 横坐标为线性坐标轴,纵坐标为对数坐标轴polar 绘制极坐标图fill 绘制实心图bar 绘制直方图pie 绘制饼图area 绘制面积图quiver 绘制向量场图stairs 绘制阶梯图sterm 绘制火柴杆图>> x=0:pi/10:2*pi;>> y1=sin(x);>> subplot(2,2,1);>> plot(x,y1);>> subplot(2,2,2);>> bar(x,y1);>> subplot(2,2,3);>> fill(x,y1,'g');>> subplot(2,2,4);>> stairs(x,y1,'k');图5.3.1 其他图形函数- 12 -5.3.1 直方图函数bar(x)可以绘制直方图,这对统计或者数据收集非常直观实用.它共有四种方式:bar,bar3,barh 和bar3h,其中bar 和bar3 分别用来绘制二维和三维竖直方图,barh 和bar3h 分别用来绘制二维和三维水平直方图,调用格式是:bar(x,y) 其中x 必须单调递增或递减,y 为n m× 矩阵,可视化结果为m 组,每组n 个垂直柱,也就是把y 的行画在一路,同一列的数据用不异的色彩暗示;bar(x,y,width) (或bar(y,width))指定每个直方条的宽度,如width>1,则直方条会堆叠,默认值为width=0.8;bar(…,’grouped’) 使同一组直方条紧紧靠在一路;bar(…,’stack’) 把同一组数据描述在一个直方条上.>> y=[5 3 2 9;4 7 2 7;1 5 7 3];>> subplot(2,2,1),bar(y)>> x=[5 9 11];>> subplot(2,2,2),bar3(x,y)>> subplot(2,2,3),bar(x,y,'grouped')>> subplot(2,2,4),bar(rand(2,3),.75,'stack')图5.3.2 直方图5.3.2 面积图函数area 用来绘制面积图,面积图在plot 的基础上填充x 轴和曲线之间的面积,该图用于检查某个数在该列所无数的总和中所占的比例.>> x=-3:3;>> y=[3 2 5;6 1 8;7 4 9;6 3 7;8 2 9;4 2 9;3 1 7];>> area(x,y)- 13 -图5.3.3 面积图5.3.3 饼图函数pie 用来绘制饼图,它可以抽象地暗示出向量中各元素所占比例.其调用格式是:pie(x) x 中的元素通过x/sum(x)进行归一化,以确定饼图中的份额;pie(x,explode) 向量explode 和x 元素数不异,用来指出须要分开的饼片,explode 中不为零的部分会被分开.图5.3.4 饼图- 14 -例5.3.4 设某班的某课程的考试成绩如下:90 分以上有32 人,81 至90 有58 人,71至80 分有27 人,60 至70 分为21 人,60 分以下有16 人,画出饼图.(见图5.3.4)>> x=[32 58 27 21 16];>> explode0=[1 0 0 0 0];>> subplot(1,2,1)>> pie(x,explode0)>> explode1=[0 0 0 0 1];>> subplot(1,2,2)>> pie(x,explode1)5.3.4 分歧坐标系中的绘图Semilogx,semilogy,loglo,polar(theta,rho)的使用方法和plot 完整类似,分歧的只是绘制到分歧的图形坐标上.函数semilogx 绘制x 轴为对数标度的图形,在半对数坐标系中绘图;函数semilogy 绘制y 轴为对数标度的图形;函数loglog 绘制两个轴都为对数间隔的图形;函数polar(theta,rho)绘制极坐标图形,其中theta 为相角,rho 为其对应的半径.例5.3.5 绘制ρ=acos(3θ),a=2 的图形.(见图5.3.5)>> theta=-pi:pi/80:pi;>> polar(theta,2*cos(3*theta))图5.3.5 极坐标图5.4 符号表达式绘图MATLAB 软件提供了将表达式进行图形显示的功能.完成此功能需调用fplot 函数和ezplot 函数.- 15 -函数fplot 用来绘制数学函数,其调用格式为: fplot(fun,lims)其中fun 就是所要绘制的函数,可所以定义函数的M 文件名,也能够是以x 为变量的可计算字符串.例如’diric(x,10)’或’[sin(x),cos(x)]’,对于向量x 的每个元素,函数fun(x)必须返回一个行向量.如果fun 返回[f1(x),f2(x),f3(x)],输入[x1;x2],就会返回矩阵f1(x1) f2(x1) f3(x1)f1(x2) f2(x2) f3(x2)lims=[XMIN XMAX YMIN YMAX]限制了x,y 轴上的绘图空间.>> subplot(2,2,1),fplot('humps',[0 1])>> subplot(2,2,2),fplot('abs(exp(-j*x*(0:9))*ones(10,1))',[0 2*pi]) >> subplot(2,2,3),fplot('[tan(x),sin(x),cos(x)]',2*pi*[-1 1 -1 1])>> subplot(2,2,4),fplot('sin(1./x)',[0.01 0.1],1e-3)图5.4.1 fplot 函数绘制表达式图形ezplot 函数是简捷绘图指令之一,它无需数据筹办,直接画出函数图形,基本调用格式为ezplot(f)其中f 是字符串或代表数学函数的符号表达式,只要一个符号变量,可所以x,缺省情况下x 轴的绘图区域为] 2 , 2 [ π π ? ,但我们可以用ezplot(f,xmin,xmax)或ezplot(f,[xmin,xmax])来指定x 的范围. >> y='x^2';>> subplot(1,2,1)- 16 ->> ezplot(y)>> subplot(1,2,2)>> y='sin(x)';>> ezplot(y,[-pi,pi])图5.4.2 ezplot 函数绘制表达式图形5.5 plot 函数MATLAB 对数据是按列存储和计算的,应用plot(x)时,当x 为一个向量时,以其元素为纵坐标,其序号为横坐标值绘制曲线.当x 为实矩阵时,则以其序号为横坐标,按列绘制每列元素绝对于序号的曲线,当x 为n m× 矩阵时,就有n 条曲线.如果x,y 是同维向量,plot(x,y)指令以x 元素为横坐标值,y 元素为纵坐标值绘制曲线.如x 是向量,y 是有一维与x 元素数量相等的矩阵,则以x 为共同横坐标,按列绘制y 每列元素值,曲线数为y 的另一维的元素数.如果x,y 是同维矩阵,则以x,y 对应列元素为、纵坐标分别绘制曲线,数目等于矩阵的列数.>> x=[3 5 10 8];>> subplot(2,2,1)>> plot(x)>> x=[3 5 10 8;7 2 9 4;2 7 2 7]';>> subplot(2,2,2)>> plot(x)>> x=[3 5 6 8];>> y=[1 5 10 4];- 17 ->> subplot(2,2,3)>> plot(x,y)>> x=[1 3 5 7;2 4 6 8]';>> y=[6 2 5 10;3 5 2 6]';>> subplot(2,2,4)>> plot(x,y,'k:*')5.6 交互式图形指令ginput 是一个比较特殊的图形指令,用作获取图上数据,例如指令>>[x,y]=ginput(6) % 从图形上拔取6 个点.此时,ginput 指令将把当前图形调入前台,同时光标变成十字叉,挪动光标,使交叉点落在目标点上,单击鼠标,即可获得该点数据.>> fplot('humps',[0 1])>> ginput(6)x =- 18 -y =。
Matlab符号函数的作图

通常工程中用到的符号函数都是以表达是形式体现的,这样有利于计算。
但是,如果有时需要直观地表示符号函数的物理意义,就需要用图形来实现。
1、ezplot函数:画符号函数图形ezplot(f):对于显式函数f=f(x),在默认的范围[-pi<x<pi]上画函数f(x);对于隐函数f=f(x,y),在默认的平面区域[-pi<x<pi,-pi<y<pi]上画函数f(x,y)的图像。
ezplot(f,[min,max]):在指定的范围[min<x<max]内画函数表达式f=f(x)。
若没有图形窗口存在,则该函数先生成标题为Figure N o.1的新窗口,再在该窗口中操作;若已经有图形窗口存在,这在标号最该的图形窗口中进行操作。
ezplot(f,[xmin xmax],fing):在指定标号为fign的窗口中、指定范围[xmin xmax]内画函数f=f(x)的图形。
ezplot(f,[xmin,xmax,ymin,ymax]):在平面矩形区域[xmin<x<xmax, ymin<y<ymax]上画出f(x,y)=0的图像。
ezplot(x,y):在默认范围0<t<2pi内画出参数形式函数x=x(t)与y =y(t)的图形。
ezplot(x,y,[tmin,tmax)]:在指定范围[tmin<t<tmax]内画参数形式函数x=x(t)与y=y(t)的图形。
ezplot(…,figure):在由参量文件figure句柄指定的图形窗口中画函数图形。
例如:画下面的隐函数>> syms x y>> ezplot(2*x^4-y^9)2、ezplot3:三维曲线图ezplot3(x,y,z):在默认的范围0<t<2pi内画参数形式的曲线x=x(t), y=y(t),z=z(t)图像。
ezplot3(x,y,z,[tmin,tmax]):在默认的范围tmin<t<tmax内画参数形式的曲线x=x(t),y=y(t),z=z(t)图像。
matlab简介(解常微分方程绘制函数图像)

MATLAB简介MATLAB是矩阵实验室(Matrix Labora tory)的简称,是美国Mat hWork s公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境。
一、基本功能MATLAB是由美国m a thwo rks公司发布的主要面对科学计算、可视化以及交互式程序设计的高科技计算环境。
它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言(如C、Fortra n)的编辑模式,代表了当今国际科学计算软件的先进水平。
MATLAB和Math ematica、Maple并称为三大数学软件。
它在数学类科技应用软件中在数值计算方面首屈一指。
MA TLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATL AB来解算问题要比用C,FORTRA N等语言完成相同的事情简捷得多,并且MATL AB也吸收了像Map le等软件的优点,使MATLA B成为一个强大的数学软件。
在新的版本中也加入了对C,FORTRA N,C++,JAVA的支持。
可以直接调用,用户也可以将自己编写的实用程序导入到MAT LAB函数库中方便自己以后调用,此外许多的M A TLAB爱好者都编写了一些经典的程序,用户可以直接进行下载就可以用。
matlab 函数作图

03 函数作图1 平面图形(1)竖直条形图调用格式为:bar(x,y)(2)用描点法绘制函数y f ( x) 随x 从a 到b 间的图形.调用格式为:x=a:h:b ;y=f(x) ;plot(x,y)(3)在同一坐标系下绘制多个函数图形.调用格式为:x=a:h:b ;plot(x,y1,x,y2,…)(4)绘制函数y=f(x)随x 从a 到b 间的图形.调用格式为:explo t(‘f(x)’, [a,b])(5)x 从xa 到xb和y 从ya到yb间隐函数 f ( x, y) 0 的图形.调用格式为:ezplo t(‘x’,’y’,[xa, x b , y a , y b ])(6)绘制t 从ta 到tb间参数方程x x(t ),y y(t )的函数图形.调用格式为:ezplo t(‘x’,’y’,[ta, t b ])(7)在一坐标系下可以绘制一个或多个显函数图形,对变化剧烈的函数,用此命令来进行较精确的绘画.调用格式为:fplot(’fun(x)’,[a,b])fplo t (‘[f1(x),f2(x),…]’,[a,b])其中fun(x)可以是自定义函数,[f1(x),f2(x),…]是函数组.(8)绘制散点图.调用格式为:scatter(x,y)2 空间图形(1)空间曲线.调用格式为:plot3(x,y,z)(2)产生一个以向量x 为行,向量y 为列的矩阵.调用格式为:meshgrid(x,y)(3)空间曲面.调用格式为:surf(x,y,z)(4)网格曲面.调用格式为:mesh(x,y,z)例 1 一次考试成绩0~10 分有0 人,10~20 分有0 人,20~30 分1 人,30~40 分有1 人,50~60 分有2 人,60~70 分有18 人,70~80 分有20 人,80~90 分有9 人,90~100 分有6 人.绘出成绩分析竖直条形图.【matlab 命令】>> x=0:10:90;>> y=[0,0,1,1,0,2,18,20,9,6];>> bar(x,y)【输出结果】20002图1例1输出图像例 2 绘制显函数图形.x(1)设 y 1x 3 2x , y2000 cos2sin x请分别作出这两个函数在区间 x[20,40] 的图像,然后将它们的图像在一个平面直角坐标系中,并判断方程 y 1x 3 2 x 1500cos x2sin x 有几个实数解.(2)在 x[0,4] 上画出分段函数方法一:【matlab 命令】>> x=-20:0.1:40;>> y1=x.^3-35*x.^2+100*x+1500; >> y2=2000*(cos(x/2)-sin(x)); >> figure(1)>> plot(x,y1,'b-'); >> figure(2) >> plot(x,y2,'k');f ( x )32 x 2x 20 x 2 x 2的图像>> figure(3)>> plot(x,y1,'b-',x,y2,'k')【输出结果】图2例2(1)函数y1图3 例 2(1)函数 y 2 输出图像图4例 2(1)函数 y 1 和 y 2 输出图像 从图中知:有 7 个交点,也就是有 7 个实数根.说明:绘制图形着色时,g 表示绿色,r 表示红色,b 表示蓝色,k 表示黑色.方法二:【matlab 命令2】%自定义函数M文件fx1 function y1=fx1(x)y1=x^3-35*x.^2+100*x+1500%自定义函数M文件fx2 function y2=fx2(x)y2=2000*(cos(x/2)-sin(x));Matlab命令窗口输入以下命令: >> figure(1)>> fplot('fx1(x)',[-20,40]); >> figure(2)>> fplot('fx2(x)',[-20,40]); >> figure(3)>> fplot('[fx1(x) , fx2(x)] ', [-20,40]); 【输出结果2】结果同上.【matlab 命令3】>> x=0:0.01:2;>> y=(2*x-x.^2).^(1/3);>> plot(x,y,'k','linewidth',2)>> hold on>> x=2:0.01:4;>> y=x-2;>> plot(x,y,'k','linewidth',2)【输出结果3】图5例2(2)函数f(x)的输出图像例3绘制隐函数和参数方程所确定函数的图形.(1)在x [3,3] 上画隐函数x 2 2 9 的图像.(2)在t [0,2] 上画参数方程x cos3 t ,y sin 3 t 的图像.【matlab 命令1】>> ezplot('x^2+y^2-9',[-3,3])>> axis equal【输出结果1】图6例3(1)输出图像说明:axis on 显示坐标轴,axis off 取消坐标轴,grid on 表示加网格线,grid off 表示不加网格线,clf 清楚图形窗口中的图形.也可以通过编辑图像的方法改变或增加设置,比如在图形窗口中,菜单栏Tools中鼠标选中Edit-Plot,可改变图像的颜色.【matlab 命令2】>> ezplot('cos(t)^3','sin(t)^3',[0,2*pi])【输出结果2】图7例3(2)输出图像例4将图4,5,6,7在同一个图形窗口表现出来.【matlab 命令】clfsubplot(2,2,1)x=-20:0.1:40;y1=x.^3-35*x.^2+100*x+1500;y2=2000*(cos(x/2)-sin(x));plot(x,y1,'b-',x,y2,'k');subplot(2,2,2)x=0:0.01:2;y=(2*x-x.^2).^(1/3);plot(x,y) holdon x=2:0.01:4;y=x-2;plot(x,y)subplot(2,2,3)ezplot('x^2+y^2-9',[-3,3])axis equal subplot(2,2,4)ezplot('cos(t)^3','sin(t)^3',[0,2*pi])【输出结果】图8 例4输出图像例5已知平面内8个散点的坐标(1,15,2,20(3,27(4,36(5,49,(6,65(7,87(8,117,在直角坐标系中绘制点图.【matlab 命令】 clf x=1:8; y=[15.3,20.5,27.4,36.6,49.1,65.6,87.8,117.6]; scatter(x,y,'ko') 【输出结果】图9例6 在区间[0,10] 上画出参数曲线x sin t, y cos t, z t .【matlab 命令】clft=0:pi/50:10*pi;plot3(sin(t),cos(t),t)【输出结果】图10例7画函数Z ( X Y) 2 的图形.【matlab 命令】clfx=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=(X+Y).^2;surf(X,Y,Z)shading flat【输出结果】图11例8画出马鞍曲面Z X 2 Y2 在不同视角的网格图.【matlab 命令】clfx=-3:0.1:3; y=1:0.1:5;[X,Y]=meshgrid(x,y);Z=X.^2-Y.^2;mesh(X,Y,Z)【输出结果】图123 习题1.某城市一年12个月的日平均气温(单位: 0C )分别为:-10,-6,5,10,20,25,30,24,22,19,10,6,试画出条形图. 2.作出函数 f ( x )cos(e x ) e x / 2) 在区间 x [4,4] 的图形3.作隐函数 sin( xy ) 0 在 [6,6] 内的图形.cos x 2 x 2 4.已知分段函数 y x x 1 ,作出 15 x 15 的函数图形. 2 sin( x 1) 1x 15.在同一直角坐标系中,作出函数 y5 的图形和函数 x 3 的图形.6.已知sin( x 2 2 )7.绘制空间图形:(墨西哥帽子).x 2 2。
Matlab画函数图像
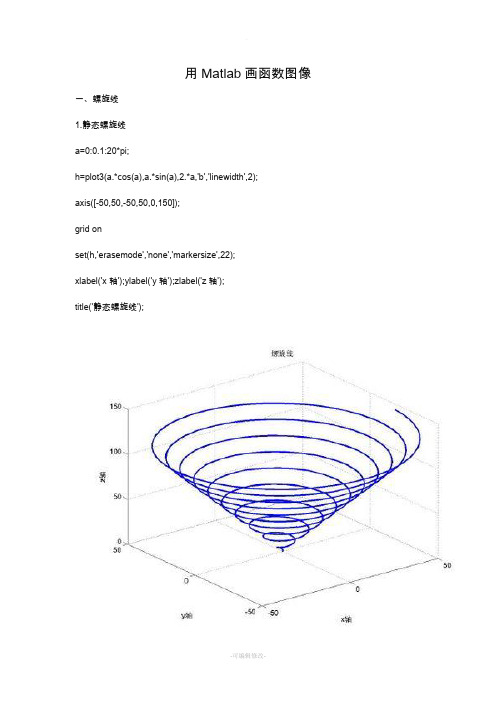
用Matlab画函数图像一、螺旋线1.静态螺旋线a=0:0.1:20*pi;h=plot3(a.*cos(a),a.*sin(a),2.*a,'b','linewidth',2);axis([-50,50,-50,50,0,150]);grid onset(h,'erasemode','none','markersize',22);xlabel('x轴');ylabel('y轴');zlabel('z轴');title('静态螺旋线');2.动态螺旋线t=0:0.1:10*pi;i=1;h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none'); grid onaxis([-2 2 -2 2 0 35])for i=2:length(t)set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));drawnowpause(0.01)endtitle('动态螺旋线');(图略)3.圆柱螺旋线t=0:0.1:10*pi;x=r.*cos(t);y=r.*sin(t);z=t;plot3(x,y,z,'h','linewidth',2);grid onaxis('square')xlabel('x轴');ylabel('y轴');zlabel('z轴'); title('圆柱螺旋线')二、旋转抛物面b=0:0.2:2*pi;[X,Y]=meshgrid(-6:0.1:6);Z=(X.^2+Y.^2)./4;meshc(X,Y,Z);axis('square')xlabel('x轴');ylabel('y轴');zlabel('z轴');title('旋转抛物面')或直接用:ezsurfc('(X.^2+Y.^2)./4')三、椭圆柱面load clownezsurf('(2*cos(u))','4*sin(u)','v',[0,2*pi,0,2*pi]) view(-105,40)%视角处理shading interp%灯光处理colormap(map)%颜色处理grid on%添加网格线axis equal%使x,y轴比例一致xlabel('x轴');ylabel('y轴');zlabel('z轴');%添加坐标轴说明title('椭圆柱面')%添加标题四、椭圆抛物面b=0:0.2:2*pi;[X,Y]=meshgrid(-6:0.1:6);Z=X.^2./9+Y.^2./4;meshc(X,Y,Z);axis('square')xlabel('x轴');ylabel('y轴');zlabel('z轴');title('椭圆抛物面')或直接用:ezsurfc('X.^2./9+Y.^2./4')五、'双叶双曲面ezsurf('8*tan(u)*cos(v)','8.*tan(u)*sin(v)','2.*sec(u)',[-pi./2,3*pi./2,0,2*pi]) axis equalgrid onaxis squarexlabel('x轴');ylabel('y轴');zlabel('z轴');。
matlab在同一个坐标系绘制几个函数的图像

matlab画复数函数图象和黎曼面

用matlab画复数函数图像探究及体会黄清华学号1207020025(物理一班)戴刘江学号1207020013(物理一班)摘要:本文主要写了小组自学用matlab画黎曼面的一些体会,并给出了数学物理方法课本上固定a值的黎曼面,同时给出了一些常见黎曼面的程序画法.一:复数函数图像了解:在老师讲多值函数这一节的时候,以w=z^1/2的给我们讲了多值函数的相关性质,并且给出了其黎曼面,其优美的黎曼面图像深深的迷住了我们,于是,我们打算探究用matlab画出一些黎曼面的想法。
经过了一定时间的自学与探究,我们终于学得了一些复数函数画法的了解,并且成功的画出了一部分复数函数图像。
二:学习经历;在学习复数函数画法的时候,主要以w=z^3为例,程序如下:z=cplxgrid(40);view(-37。
5,30);w=z。
^3;%复数函数subplot(1,1,1);cplxmap(z,w);colorbartitle(‘w=z^3’)将此程序带入matlab里,得到如下图像:当然,在书写这个程序的时候,也经历了很多的错误,在一步步的修改之后才完成的,在此基础上,我们做了w=z。
^(1/2),和书上作业给出的复数函数图像,只需要修改的部分只有上面的复数函数和题目做修改就可以。
相关修改如下:(1)w=z.^3;%复数函数……..title(‘根号z‘)输入matlab后得到的图像:’(2)学习书上22面当a取得1时候的四个小题的复数图像:W=ln(z)的函数图像,类似与一个漩涡状:W=ln(z-1)的图像,类似一条鱼三:黎曼面的画法在复数函数图像里面,matlab有一类专门的李曼面画法,其母程序如下;z=cplxgrid(45);view(—37.5,30);cplxroot(3);title(‘3叶的面')可以得到图像如下:当我们改变cplxroot(x)中x的值时,就会得到不同数量叶面的黎曼面图像:当x的值取得小数的时候,图像叶面会有缺省,如:当x=1时,应该只有一个叶面,图像是:四:体会经过这次学习,我们成功的画出了一些复数函数的图像,给我们今后的学习带来了乐趣,让我们更有兴趣去学习好数学物理方法这门课。
用matlab画出余弦函数的傅里叶变换图像

⽤matlab画出余弦函数的傅⾥叶变换图像⽤matlab画出δ函数和余弦函数的傅⾥叶变换⼀、由狄拉克函数的定义:它在原点以外的所有点函数值为0,只在原点为⽆穷:并且满⾜约束条件代码可写为:x=-100:1:100; %将x取区间[-100,100],最⼩单位为1,y=(x==0); %只有x=0的时候,y才为“1”plot(x,y);syms t v;xlabel('t'),ylabel('δ(t)'),title('狄拉克函数');%标注x,y轴⼆.Cos(100πt)函数的傅⾥叶变换:利⽤matlab⾥⾯的快速傅⾥叶变换(fft)。
画出的只有正半轴的频率图像代码:fs=10000;%采样频率N=100; %采样点数n=0:N-1;t=n/fs;g=cos(1000*pi*t);%给定信号figure(1);subplot(211);plot(g);%绘出信号的时域波形xlabel('时间/t');ylabel('幅值');title('信号的时域波形');grid on;y=fft(g,N);%进⾏fft变换m=abs(y(1:N/2))*2*pi/N;%求信号的真实幅值f=n*fs/N; %进⾏对应的频率转换subplot(212);stem(f(1:N/2),m(1:N/2));%绘出频谱图xlabel('频率/Hz');ylabel('幅值');title('信号频谱图');grid on;——许振远。
MATLAB如何画分段函数的图像
MATLAB如何画分段函数的图像通常要⽤MATLAB画分段函数图像的话,总要分段去画⾮常⿇烦,还需要hold on,现在教你⼀种简单化分段函数的⽅法,让你⼀下⼦知道这个⽅法的魅⼒!数学软件Matlab R2019b for Linux 64位中⽂最新正式版(附安装⽅法+镜像)类型:编程其它⼤⼩:126MB语⾔:简体中⽂时间:2019-10-01查看详情Matlab R2018b Win64位中⽂特别版(附许可⽂件+安装密钥+激活⽅法)类型:编程其它⼤⼩:12.0GB语⾔:简体中⽂时间:2018-09-19查看详情步骤如下:第⼀步⽐如我们要画这样⼀个分段函数图像“-4<x<4;y=3*x;4<=x<12;y=20;12<=x<18;y=-5x+2;”,如下图所⽰:第⼆步我们先⽤matlab表达出来,y=(3*x).*(x>=-4&x<4) + 20*(x>=4&x<12)+(-5*x+2).*(x>12&x<=18),如下图所⽰:第三步输⼊x=-4:0.1:18,这个x的范围也是分段函数x的条件范围,如下图所⽰:第四步m脚本输⼊“x=-4:0.1:18y=(3*x).*(x>=-4&x<4) + 20*(x>=4&x<12)+(-5*x+2).*(x>12&x<=18)plot(x,y)”代码,如下图所⽰:第五步运⾏脚本,可以看到已经画出了分段函数图像,主要是先⽤matlab表⽰出分段函数,然后使⽤plot画图就可以,如下图所⽰:相关阅读:。
matlab画图函数plot使用方法

matlab画图函数plot使用方法plot函数可以接一些参数,来改变所画图像的属性(颜色,图像元素等)。
下面是一些属性的说明b blue(蓝色). point(点)- solid(实线)g green(绿色)o circle(圆圈): dotted(点线)r red(红色)x x-mark(叉号)-. dashdot (点画线)c cyan(墨绿色)+ plus(加号)-- dashed(虚线)m magenta(紫红色)* star(星号)(none) no liney yellow(黄色)s square(正方形)k black(黑色)d diamond(菱形)v triangle (down)^ triangle (up)< triangle (left)> triangle (right)p pentagramh hexagramExamplex = -pi:pi/10:pi;y = tan(sin(x)) - sin(tan(x));plot(x,y,'--rs','LineWidth',2,...'MarkerEdgeColor','k',...'MarkerFaceColor','g',...'MarkerSize',10)xlabel('x');ylabel('y');·用Matlab画图时,有时候需要对各种图标进行标注,例如,用“+”代表A 的运动情况,“*”代表B的运动情况。
legend函数的基本用法是LEGEND(string1,string2,string3, ...)分别将字符串1、字符串2、字符串3……标注到图中,每个字符串对应的图标为画图时的图标。
例如:plot(x,sin(x),'.b',x,cos(x),'+r')legend('sin','cos')这样可以把"."标识为'sin',把"+"标识为"cos"还可以用LEGEND(...,'Location',LOC) 来指定图例标识框的位置这些是Matlab help文件。
在Matlab软件包中画多个函数的图形
在Matlab软件包中画多个函数的图形在Matlab软件包中将多个函数图像画在一起,可以使用fplot命令。
(1)多个函数的图形画在一起第一步写一个M—文件opt_fplot_1,必须存放在Matlab文件夹的work文件夹中。
function y=f(x)y(:,1)=sin(x(:));y(:,2)=cos(x(:));y(:,3)=(x(:)).^2;即,定义了一个矩阵函数Y,其第一列是sin(x),第二列是cos(x),第三列是2x。
x(:)定义了自变量x是一个向量。
第二步写另外一个M—文件opt_fplot_2,调用刚刚存盘的opt_fplot_1。
fplot(@opt_fplot_1,[0,2*pi])存盘,按F5键执行,得到图形1如下:0123456如果需要图形与函数对应,可以在图形界面依次点击Insert →Legend,得到图形2:图形2中,蓝色曲线对应data1,即,蓝色曲线是第一个函数sin(x);绿色曲线对应data2,即,绿色曲线是第二个函数cos(x);红色曲线对应data3,即,红色曲线是第三个函数2x。
(2)在图形中增加格子线在第二个M—文件opt_fplot_2中增加一条命令即可:fplot(@opt_fplot_1,[0,2*pi])grid on执行后得到图形3:(3)在图形中标记曲线与格子线交点的坐标在图形3界面点击这个键然后点击图形中需要坐标的点如果还需要其他点的坐标,按住CTRL 键,点击需要坐标的点,画面如下:选择第三项:“Creat New Datatip ”选项,然后,再一次点击相应的点,即可。
这个点的坐标来啦。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
title('旋转单叶双曲面')
十三、圆柱面
subplot(1,2,1)
ezsurf('(2*cos(u))','2*sin(u)','v',[0,2*pi,0,2*pi])
grid on
shading interp
axis equal
title('双叶双曲面')
六、双曲柱面
load clown
ezsurf('2*sec(u)','2*tan(u)','v',[-pi/2,pi/2,-3*pi,3*pi])
hold on %在原来的图上继续作图
ezsurf('2*sec(u)','2*tan(u)','v',[pi/2,3*pi/2,-3*pi,3*pi])
四、椭圆抛物面
b=0:0.2:2*pi;
[X,Y]=meshgrid(-6:0.1:6);
Z=X.^2./9+Y.^2./4;
meshc(X,Y,Z);
axis('square')
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('椭圆抛物面')
或直接用:ezsurfc('X.^2./9+Y.^2./4')
Z=X.^2./8-Y.^2./6;
meshc(X,Y,Z);
view(85,20)
axis('square')
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('双曲抛物面')
或直接用:ezsurfc('X.^2./8-Y.^2./6')
八、抛物柱面
[X,Y]=meshgrid(-7:0.1:7);
ezsurfc('(5*cos(u))*sin(v)','(3*sin(u))*sin(v)','4*cos(v)',[0,2*pi,0,2*pi])
axis equal
grid on
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('椭球')
十一、单叶双曲面
Z=Y.^2./8;
h=mesh(Z);
rotate(h,[1 0 1],180) %旋转处理
%axis([-8,8,-8,8,-2,6]);
axis('square')
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('抛物柱面')
或直接用:ezsurfc('Y.^2./8')
九、环面
ezmesh('(5+2*cos(u))*cos(v)','(5+2*cos(u))*sin(v)','2*sin(u)',[0,2*pi,0,2*pi])
axis equal
grid on
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('环面')ing interp %灯光处理
colormap(map) %颜色处理
grid on %添加网格线
axis equal %使x,y轴比例一致
xlabel('x轴');ylabel('y轴');zlabel('z轴'); %添加坐标轴说明
title('椭圆柱面') %添加标题
五、'双叶双曲面
ezsurf('8*tan(u)*cos(v)','8.*tan(u)*sin(v)','2.*sec(u)',[-pi./2,3*pi./2,0,2*pi])
axis equal
grid on
axis square
xlabel('x轴');ylabel('y轴');zlabel('z轴');
z=t;
plot3(x,y,z,'h','linewidth',2);
grid on
axis('square')
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('圆柱螺旋线')
二、旋转抛物面
b=0:0.2:2*pi;
[X,Y]=meshgrid(-6:0.1:6);
colormap(map)
shading interp
view(-15,30)
axis equal
grid on
axis equal
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('双曲柱面')
七、双曲抛物面(马鞍面)
[X,Y]=meshgrid(-7:0.1:7);
用Matlab画函数图像
一、螺旋线
1.静态螺旋线
a=0:0.1:20*pi;
h=plot3(a.*cos(a),a.*sin(a),2.*a,'b','linewidth',2);
axis([-50,50,-50,50,0,150]);
grid on
set(h,'erasemode','none','markersize',22);
ezsurf('4*sec(u)*cos(v)','2.*sec(u)*sin(v)','3.*tan(u)',[-pi./2,pi./2,0,2*pi])
axis equal
grid on
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('单叶双曲面')
十二、旋转单叶双曲面
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('静态螺旋线');
2.动态螺旋线
t=0:0.1:10*pi;
i=1;
h=plot3(sin(t(i)),cos(t(i)),t(i),'*','erasemode','none');
grid on
axis([-2 2 -2 2 0 35])
colormap(); %hot/cool/copper/gray/hsv/spring/summer/winter...
colormap(hsv)
colormap(hot)
colormap(gray)
colormap(cool)
colormap(copper)
下面做了旋转("view([ ])")、灯光(“shading interp”)、透明(“alpha()”)处理:
for i=2:length(t)
set(h,'xdata',sin(t(i)),'ydata',cos(t(i)),'zdata',t(i));
drawnow
pause(0.01)
end
title('动态螺旋线');
(图略)
3.圆柱螺旋线
t=0:0.1:10*pi;
x=r.*cos(t);
y=r.*sin(t);
Z=(X.^2+Y.^2)./4;
meshc(X,Y,Z);
axis('square')
xlabel('x轴');ylabel('y轴');zlabel('z轴');
title('旋转抛物面')
或直接用:ezsurfc('(X.^2+Y.^2)./4')
三、椭圆柱面
load clown
ezsurf('(2*cos(u))','4*sin(u)','v',[0,2*pi,0,2*pi])
load clown
ezsurf('8*sec(u)*cos(v)','8.*sec(u)*sin(v)','2.*tan(u)',[-pi./2,pi./2,0,2*pi])
colormap(map)
view(-175,30)
%alpha(.2) %透明处理
axis equal
grid on
axis square
xlabel('x轴');ylabel('y轴');zlabel('z轴');
