结构力学课件.ppt同济大学 朱慈勉
合集下载
朱慈勉结构力学力法

6.46 EA
kN
(
)
2 5 m 1 15
2 5 m 1 15
C2E 4.A 23kNm
θD
6.46kN EA
1 m 1 1 m 1 35 35
例6-12 求图示组合结构C点的竖向位移ΔC和AD与BD杆间的相对转角
ΔθD。忽略受弯杆的轴向变形。 已知AD和BD杆:EA EI m2
2次超静定
9
选取基本结构为切断竖杆:
X 1h
t0
1 EA
1 kl
§6-7超静定结构的位移计算
F E N F N d A s k 0 F G Q F Q d A s M E M d I s F R c
1)载作用下的位移计算
F N F Nd P s EA
k 0F G Q F Qd P A s
M M P ds EI
求超静定结构因温度改变、支座移动产生的位移时, 若选原结构建立虚拟力状态,计算将会更简单。
EI, l,t0 ,Δt
①
M、Q、N
EMIht、ENAt0、G kQA
P=1
②
T 2 1 1 R *c W 21
c M * E M I h t d s N * E N A t0 d s Q * G kd Q
2次超静定
9
解:⑴ 确定超静定次数;
⑵ 用力法求解, 并作M图和FN图; ⑶ 选取基本结构为铰结体系求位移;
⑷ 求AD杆与BD间的相对转角:
⑸ 施加单位荷载并求各杆轴力:
D
FN1FN l EA
1 m 1
35m 25m 1 1 .8 9 k N 1 .3 4 k N 3 5
E A 1 5
1 m 1 35
b h
同济大学朱慈勉结构力学结构的稳定计算PPT学习教案

第18页/共34页
§11-2 有限自由度体系的稳定 ——静力法和能量法
三、结构失稳问题转化为具有弹性支座压杆的失稳问题
例11.6 求体系的临界荷载Pcr
。
P
解:
yP
yP
PyP
l
EI=
B EI A
a
EI C
a
由Pcrk/l
B
6EI Pcr al
θ
B
A
C
3 EI
a θθ
A
A
θ
3EIθ/ a
3EIθ/ a
§11-2 有限自由度体系的稳定 ——静力法和能量法
静力法求临界荷载分析步骤:
1、设定一种满足约束条件的可能的失稳变形状态(新的平衡 状态);
2、由分支点上平衡的两重性出发,对新的平衡状态建立静力 平衡方程,由位移为非零解得“特征方程”,也称“稳定
方 程”;
3、解特征方程,从而求得临界荷载。
第13页/共34页
Pcr
P
cr cr
第5页/共34页
§11-1 两类稳定问题概述
三、稳定自由度
稳定自由度——体系产生弹性变形时,确定其变形状态所需的 独立几何参数的数目。
P
P
P
y1
EI
EI y2
EI
1个自由度
2个自由度
无限自由度
第6页/共34页
§11-2 有限自由度体系的稳定 ——静力法和能量法
稳定计算的中心问题是确定临界荷载。 完善体系分支点失稳分析有静力法和能量法。 静力法是从分支点上具有平衡的二重性出发,对新的平 衡状态建立静力平衡条件,从而求得临界荷载。 能量法是对新的平衡状态建立以能量形式表示的平衡条 件,依据临界点系统总势能为驻值,进而求得临界荷载 。
§11-2 有限自由度体系的稳定 ——静力法和能量法
三、结构失稳问题转化为具有弹性支座压杆的失稳问题
例11.6 求体系的临界荷载Pcr
。
P
解:
yP
yP
PyP
l
EI=
B EI A
a
EI C
a
由Pcrk/l
B
6EI Pcr al
θ
B
A
C
3 EI
a θθ
A
A
θ
3EIθ/ a
3EIθ/ a
§11-2 有限自由度体系的稳定 ——静力法和能量法
静力法求临界荷载分析步骤:
1、设定一种满足约束条件的可能的失稳变形状态(新的平衡 状态);
2、由分支点上平衡的两重性出发,对新的平衡状态建立静力 平衡方程,由位移为非零解得“特征方程”,也称“稳定
方 程”;
3、解特征方程,从而求得临界荷载。
第13页/共34页
Pcr
P
cr cr
第5页/共34页
§11-1 两类稳定问题概述
三、稳定自由度
稳定自由度——体系产生弹性变形时,确定其变形状态所需的 独立几何参数的数目。
P
P
P
y1
EI
EI y2
EI
1个自由度
2个自由度
无限自由度
第6页/共34页
§11-2 有限自由度体系的稳定 ——静力法和能量法
稳定计算的中心问题是确定临界荷载。 完善体系分支点失稳分析有静力法和能量法。 静力法是从分支点上具有平衡的二重性出发,对新的平 衡状态建立静力平衡条件,从而求得临界荷载。 能量法是对新的平衡状态建立以能量形式表示的平衡条 件,依据临界点系统总势能为驻值,进而求得临界荷载 。
第六章-力法(二) ,同济大学结构力学课件,朱慈勉版教材,吕凤悟老师课件
根据对称结构的受力特征,在对称或反对称荷载作用下,可以取半结构 计算,另外半结构的内力可通过对称或反对称镜像得到。
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种:
根据对称轴上的杆件和截面的变形(或位移)特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
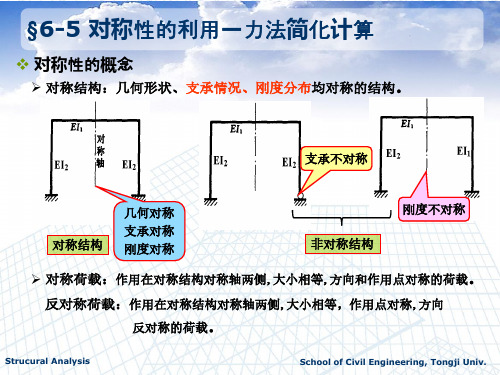
对称性的概念
对称结构:几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
半结构选取的关键在于正确判别另外半结构对选取半结构的约束作用。 判别方法有两种:
根据对称轴上的杆件和截面的变形(或位移)特征判别。(适用于所有结构)
根据对称轴上的杆件和截面的内力特征判别。 (一般只适用于奇数跨结构)
【例】试用力法求作图示刚架的弯矩图。 各杆 EI C 。
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
【例】试用力法求作图示刚架的弯矩图。各杆 EI C 。
【解】利用对称性简化为一次超静定。
11X1 1p 0
11
144 EI
,
1 p
1800 EI
X1 12.5kN
M M1X1 M p
Strucural Analysis
School of Civil Engineering, Tongji Univ.
§6-5 对称性的利用—力法简化计算
取半结构计算
§6-5 对称性的利用—力法简化计算
对称性的概念
对称结构:几何形状、支承情况、刚度分布均对称的结构。
支承不对称
对称结构
几何对称 支承对称 刚度对称
非对称结构
刚度不对称
对称荷载:作用在对称结构对称轴两侧,大小相等,方向和作用点对称的荷载。 反对称荷载:作用在对称结构对称轴两侧,大小相等,作用点对称,方向
13X 3 23X 3
1 p 2p
0 0
31X1 32 X 2 33 X 3 3 p 0
朱慈勉结构力学第一章

绪论 框架结构传力分析
绪论 桁架结构传力分析
绪论 拱结构传力分析
绪论
二、结构力学的任务
1、研究结构的组成规律:杆件如何拼装才能 成为一个结构,怎样拼装才能成为一个好的结构。
2、研究结构在外部因素作用下的强度、刚度 和稳定性的计算原理计算方法
3、结构组成举例:
绪论 1、静定结构 2、超静定结构 3、几何可变体系
A
VA
(3)固定支座(固定端支座):力作用点、方向、大小均未知。
A
HA MA VA
绪论
(4)定向支座(滑动支座):力作用点、方向、大小均未知。
A
A
HA
MA
MA
4、荷载的简化
VA
(1)体荷载:折算为作用于杆轴、沿杆轴线分布的线荷载。例如 自重。
(2)面荷载:折算为作用于杆轴的集中荷载或线荷载。例如风压、 雪压、设备重等。
A
B
CD
A:刚结点 B、D:铰结点
E
F
G
C:组合结点
杆BF与杆CD为刚结, 杆BC与杆BF为铰结。
绪论
3、支座结点的简化
支座定义:把结构与基础联结起来的装置。
(1)铰支座(固定铰支座):力作用点在铰中心,方向大小均未知。 A
HA
VA
(2)可动铰支座(辊轴支座):力作用点在铰中心,方向向上,大
小未知。
5、结构简化举例 单层工业厂房:
绪论
厂房 排架
桁架 吊车梁
绪论
1.3 平面结构的分类 一、按构造特征和受力特点分:
1、梁
梁
2、拱
3、桁架
4、刚架
拱
5、组合结构
桁架
刚架
组合结构
结构力学讲义ppt课件

x y
x
结点自由度
y
φ
x
y
x
刚片自由度
2)一个刚片在平面内有三个自由度,因为确定 该刚片在平面内的位置需要三个独立的几何参
数x、y、φ。
4. 约束
凡是能减少体系自由度的装置就称为约束。
6
约束的种类分为:
1)链杆
简单链杆 仅连结两个结点的杆件称为简单 链杆。一根简单链杆能减少一个自由度,故一 根简单链杆相当于一个约束。
FyA
特点: 1) 结构在支座截面可以绕圆柱铰A转动 ; 2) x、y方向的反力通过铰A的中心。
29
3. 辊轴支座
A
A
FyA
特点: 1) 杆端A产生垂直于链杆方向的线位移; 2) 反力沿链杆方向作用,大小未知。
30
4. 滑动支座(定向支座)
A 实际构造
A
MA
FyA
A
MA
FyA
特点: 1)杆端A无转角,不能产生沿链杆方向的线 位移,可以产生垂直于链杆方向的线位移;
16
A
I
II
c)
B III C
形成瞬铰B、C的四根链杆相互平行(不等 长),故铰B、C在同一无穷远点,所以三个 铰A、 B、C位于同一直线上,故体系为瞬变 体系(见图c)。
17
二、举例
解题思路: 基础看作一个大刚片;要区分被约束的刚片及
提供的约束;在被约束对象之间找约束;除复 杂链杆和复杂铰外,约束不能重复使用。
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如:房屋中的 框架结构、桥梁、大 坝等。
x
结点自由度
y
φ
x
y
x
刚片自由度
2)一个刚片在平面内有三个自由度,因为确定 该刚片在平面内的位置需要三个独立的几何参
数x、y、φ。
4. 约束
凡是能减少体系自由度的装置就称为约束。
6
约束的种类分为:
1)链杆
简单链杆 仅连结两个结点的杆件称为简单 链杆。一根简单链杆能减少一个自由度,故一 根简单链杆相当于一个约束。
FyA
特点: 1) 结构在支座截面可以绕圆柱铰A转动 ; 2) x、y方向的反力通过铰A的中心。
29
3. 辊轴支座
A
A
FyA
特点: 1) 杆端A产生垂直于链杆方向的线位移; 2) 反力沿链杆方向作用,大小未知。
30
4. 滑动支座(定向支座)
A 实际构造
A
MA
FyA
A
MA
FyA
特点: 1)杆端A无转角,不能产生沿链杆方向的线 位移,可以产生垂直于链杆方向的线位移;
16
A
I
II
c)
B III C
形成瞬铰B、C的四根链杆相互平行(不等 长),故铰B、C在同一无穷远点,所以三个 铰A、 B、C位于同一直线上,故体系为瞬变 体系(见图c)。
17
二、举例
解题思路: 基础看作一个大刚片;要区分被约束的刚片及
提供的约束;在被约束对象之间找约束;除复 杂链杆和复杂铰外,约束不能重复使用。
高等教育出版社
4
第一章 绪 论
§1-1 结构力学的内容和学习方法
§1-2 结构计算简图
5
§1-1 结构力学的内容和学习方法
一、结构
建筑物或构筑物中 承受、传递荷载而起 骨架作用的部分称为 结构。如:房屋中的 框架结构、桥梁、大 坝等。
05结构力学第一章绪论-PPT精品文档16页

课外思考与作业(1)
• 复习理论力学静力学相关内容 • 复习材料力学拉、压、弯、扭内容 • 复习§1-2 杆件结构的计算简图 复习§1-3 杆件结构的分类 自习§1-5 学习方法(重要) 预习§2-1 几何构造分析的几个概念
更多精品资源请访问
docin/sanshengshiyuan doc88/sanshenglu
(课内:2,课外与课内之比1:1) (课内:6,课外与课内之比3:1) (课内:12,课外与课内之比3:1) (课内:8,课外与课内之比2:1) (课内:10,课外与课内之比3:1) (课内:12,课外与课内之比3:1) (课内:10,课外与课内之比3:1) (课内:10,课外与课内之比3:1)
机动: 2学时
可动较支座 固定铰支座 固定端支座
滑动支座(定向支座)
限制限限Y制制位XX移、向及Y位、转移Z动向固固位定定移支支座座
限制三方向位移及转动
限制X位移及转动
可动定铰向支座
限制Y向位移
限制X、Y向位移及转动
限固固固制定定定X支铰可、铰座支动Y支反座向铰座力位支定移座向反固支力定座固支反固定座力定铰反铰支力支座座反反力力
单铰结点
复铰结点
组合结点
单刚结点
复刚结点
§1-2 . 杆件结构的计算简图
计算简图:
在结构分析当中用来代替实际结构的计算模型(图形)
确定计算简图的原则:
1.能反映实际结构的主要力学特性; 2.分析计算尽可能简便
简化内容:
1.杆件的简化: 2.结点的简化: 3.支座的简化:
杆件
杆件的轴线
刚结点 铰结点 半铰结点(组合结点)
§1-2 . 杆件结构的计算简图
计算简图:
第七章-位移法(一) ,同济大学课件,朱慈勉版教材

固端剪力:杆件只承受跨内荷载时的杆端剪力。
由 同M 理B可=得0 ,
FQAB
6i l
A
6i l
B
12i l2
FF QAB
结构力学 第七章 位移法
2014年12月10日星期三
§7-2 等截面直杆的转角位移方程
等截面直杆的转角位移方程:
一端固端一端铰支的等截面直杆:
B端角位移不独立。
第七章 位移法
Chapter 7 Displacement Method
同济大学土木工程学院
School of Civil Engineering,Tongji Univesity
2014年12月10日星期三
Contents
§7-1 位移法的基本概念 §7-2 等截面直杆的转角位移方程 §7-3 位移法基本未知量和基本结构 §7-4 位移法原理与位移法方程 §7-5 位移法解超静定结构 §7-6 位移法计算的简化 §7-7 广义荷载作用下的位移法计算
结构力学 第七章 位移法
2014年12月10日星期三
§7-1 位移法的基本概念
位移法是分析超静定结构的基本方法之一。 因其以结点位移作为基本未知量,故称为位移法;也称为变位法、刚度法。
20世纪初,钢筋混凝土材料的大量使用促使科学家对刚架结构进行系统的研究, 作为一种高次超静定结构,力法计算很不方便。在此背景下,德国的A.本迪克森 于1914年创立了转角位移法。
由
M BAห้องสมุดไป่ตู้
=
2iθA
+ 4iθB
-
6i
Δ l
=
0
可得,θB
=
结构力学课件.ppt同济大学 朱慈勉共133页文档

结构力学课件.ppt同济大学 朱慈勉
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
Thank心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
Thank心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂,怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
第三章-静定结构受力分析,同济大学课件,朱慈勉版教材

F
D
ql x 2
ql x 2
解:
1 2 C F ql 8 1.EBCF为基本部分,AE和FD为附属部分。 2.求铰B、E处约束力及支座反力。 3.确定铰E、F的位置。 M MC 1 1 1 根据叠加原理, B M 中 = ql 2 M B M C ql x x qx x 2 8 2 2 1 l 考虑到 M B M C M 中 , 故, M B=M C ql 2 , 从而, x 16 8
第3章
§3-1 §3-2 §3-3 §3-4 §3-5 §3-6 §3-7
静定结构受力分析
Analysis of Statically Determinate Structures
概述 多跨静定梁 静定平面刚架 三铰拱 静定平面桁架 组合结构 静定结构的一般性质
土木工程学院 结构力学
2014/10/13
为何采用多跨静定梁这种结构型式?(多跨静定梁的优点)
q
0.086ql 2
多跨静定梁
0.086ql 2
l
x
0.086ql 2
l
x 0.172l时正负弯矩相等
q
简支梁(两个并列)
1 2 ql 8
1 2 ql 0.125ql 2 8
相同跨度相同荷载作用下,与简支梁相比,多跨静定梁弯矩较小, 而且分布均匀。(节省材料,便于大跨)
土木工程学院 结构力学 2014/10/13
例:
叠加法作梁的M图。
由杆端弯矩作图
叠加q弯矩图
ql 2 32
ql 2 16 ql 2 4
M2
叠加ql2弯矩图
ql 2 2
3ql 2 4
ql 2 32
同济大学朱慈勉-结构力学第10章-结构动力学

机动力荷载).
分析过程:
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 (如何求?)
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
(动力)自由度:确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应:
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到:
▪ 体系从任一时刻经几个周期后 的振幅比为:
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
(3-2)
▪ 特征方程:
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小,则显然有c/2m< ,这时,特 征方程根式中的值必然为负值,则s 值成为:
s c i 2 c 2
2m
2m
▪ 引入符号: c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值,称为阻尼比,则:
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
分析过程:
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 (如何求?)
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
(动力)自由度:确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应:
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到:
▪ 体系从任一时刻经几个周期后 的振幅比为:
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
(3-2)
▪ 特征方程:
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小,则显然有c/2m< ,这时,特 征方程根式中的值必然为负值,则s 值成为:
s c i 2 c 2
2m
2m
▪ 引入符号: c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值,称为阻尼比,则:
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
结构力学(朱慈勉版)上课件

图乘。 a
MK图
ql 2
8
a
l
c
MP图
d
ql 2
8
l
Δ
1 EI
(
al 2
)
(
2c 3
d) 3
(2 3
l
ql )(c 8
d 2
)
第6章
使用乘法时应注意的问题小结: 1、yo必须取自直线图形; 2、当MK为折线图形时,必须分段计算; 3、当杆件为变截面时亦应分段计算; 4、图乘有正负之分; 5、若两个图形均为直线图形时,则面积、纵标可任意
A
A
p
A B
p
A
AB B
AB A B AB A B
第6章
4、上述各种位移统称为“广义位移”。与广义 位移相对应的力称为“广义力”。
二、计算结构位移的目的
1、刚度验算:电动吊车梁跨中挠度 fmax≤l/600。
2、计算超静定结构必须考虑位移条件。
3、施工技术的需要。
190.59 0.03m( ) EA
第6章
例题3 试求图示半径为R的圆弧形曲梁B点的竖向 位移BV。梁的抗弯刚度EI为常数。
M P PR sin
M K R sin
第6章
解: (1)在B点加一单位力(右图) ,写出单位力作用下的弯
矩表达式
(2)写出单位力作用下的弯矩表达式(左图)
第6章
二、图乘法证明
y
MP(x) d
M K M P ds l EI
1 EI
B
A M K M Pdx
1 EI
B
A x tgM Pdx
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
刚片中任一两点间的距离保持不变,既由刚片中 任意两点间的一条直线的位臵可确定刚片中任一点 的位臵。所以可由刚片中的一条直线代表刚片。
二、研究体系几何组成的任务和目的:
1、研究结构的基本组成规则,用及判定体系是否 可作为结构以及选取结构的合理形式。
2、根据结构的几何组成,选择相应的计算方法和 计算途径。
§2-3 平面体系的几何组成分析
一、几何不变体系的简单组成规则 规则一 (两刚片规则):(图2-3-1) 两个刚片用不全交于一点也不全平行的三根链杆 相连,组成无多余约束的几何不变体系。 或:两个刚片用一个单铰和杆轴不过该铰铰心的 一根链杆相连,组成无多余约束的几何不变体系。 *虚铰的概念: 虚铰是由不直接相连接的两根链杆构成的。虚铰 的两根链杆的杆轴可以平行、交叉,或延长线交于 一点。 当两个刚片是由有交汇点的虚铰相连时,两个刚 片绕该交点(瞬时中心,简称瞬心)作相对转动。 从微小运动角度考虑,虚铰的作用相当于在瞬时 中心的一个实铰的作用。
四、有多余约束的几何不变体系:
拆除约束法:去掉体系的某些约束,使其成为无 多余约束的几何不变体系,则去掉的约束数即是体 系的多余约束数。 1、切断一根链杆或去掉一个支座链杆,相当去 掉一个约束; 2、切开一个单铰或去掉一个固定铰支座,相当 去掉两个约束;
3、切断一根梁式杆或去掉一个固定支座,相当 去掉三个约束; 4、在连续杆(梁式杆)上加一个单铰,相当去 掉一个约束。
§1-2 结构计算简图
1、结构计算简图的概念 2、结构计算简图的简化原则是: 1)计算简图要能反映实际结构的主要受力和变 形特点,即要使计算结果安全可靠; 2)便于计算,即计算简图的简化程度要与计算 手段以及对结果的要求相一致。
3、结构计算简图的几个要点:
空间杆件结构的平面简化 杆件构件的简化:以杆件的轴线代替杆件; 杆件之间连接的简化:理想结点代替杆件与杆件 之间的连接。 1)铰结点: 汇交于一点的杆端是用一个完全无磨擦的光滑铰 连结。铰结点所连各杆端可独自绕铰心自由转动, 即各杆端之间的夹角可任意改变。 2)刚结点: 汇交于一点的杆端是用一个完全不变形的刚性结 点连结,形成一个整体。刚结点所连各杆端相互之 间的夹角不能改变。 3)组合结点(半铰): 刚结点与铰结点的组合体。
2、按计算方法分类: 静定结构, 超静定结构。
1、按作用时间分类: 恒载:永久作用在结构上。如结构自重、永久 设备重量。 活载:暂时作用在结构上。如人群、风、雪 (在结构上可占有任意位臵的可动荷载)及车辆、 吊车(在结构上平行移动并保持间距不变的移动荷 载)。 2、按作用性质分类: 静力荷载:荷载由零加至最后值,且在加载过 程中结构始终保持静力平衡,即可忽略惯性力的影 响。 动力荷载:荷载(大小、方向、作用线)随时 间迅速变化,并使结构发生不容忽视的惯性力。 3、按与结构的接触分类:直接荷载,间接荷载。
FNAB =FNAC =FP 2FNsina=FP FN =FP /(2 sina )
例2-3-2 对下列图示体系作几何组成分析(说明 刚片和约束的恰当选择的影响).
三、三个刚片的三个单铰有无穷远虚铰情况:
两个平行链杆构成沿平行方向上的无穷远虚铰。
三个刚片由三个单铰两两相连,若三个铰都有交 点,容易由三个铰的位臵得出体系几何组成的结论 。当三个单铰中有或者全部为无穷远虚铰时,可由 分析得出以下依据和结论:
§1-3 杆件结构的分类
1、按结构的受力特点分类: 梁:由水平(或斜向)放臵杆件构成。梁构件主 要承受弯曲变形,是受弯构件。 刚架:不同方向的杆件用结点(一般都有刚结点) 连接构成。刚架杆件以受弯为主,所以又叫梁式构 件。 桁架:由若干直杆在两端用铰结点连接构成。桁 架杆件主要承受轴向变形,是拉压构件。 组合结构:由梁式构件和拉压构件构成。 拱:一般由曲杆构成。在竖向荷载作用下有水 平支座反力。
2、截面法 若要求某一横截面上的内力,假想用一平面沿杆 轴垂直方向将该截面截开,使结构成两部分;在截 开后暴露的截面上用力(内力)代替原相互的约束。 对于截开后结构的两部分上,截面上的内力已成 为外力,因此,由任一部分的静力平衡条件,均可 列出含有截面内力的静力平衡方程。解该方程即将 内力求出。
3、截面内力 截开一根梁式杆件的截面上有三个内力(分量), 即:轴力FN 、剪力FQ和弯矩Μ 。 1、内力的定义 FN:截面上平行于截面外法线方向的正应力的代数 和,一般以受拉为正。 FQ:截面上垂直于截面法 线方向的切应力的代数和, 以使隔离体产生顺时针转 动为正。 Μ:截面上正应力对截面 中性轴的力矩代数和,对 梁一般规定使其下部受拉 为正。
1、当有一个无穷远虚铰时,若另两个铰心的连 线与该无穷远虚铰方向不平行,体系几何不变;若 平行,体系瞬变。 2、当有两个无穷远虚铰时,若两个无穷远虚铰 的方向相互不平行,体系几何不变;若平行,体系 瞬变。
3、当有三个无穷远虚铰时,体系瞬变。
例2-3-3 对下列图示体系作几何组成分析。
例2-3-4 对图示各体系作几何组成分析。
∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=-60kN (← ) 由 ∑Fy= 0 核,满足。 校
2、复约束 连接3个(含3个)以上物体的约束叫复约束。 1)复链杆:若一个复链杆上连接了N个结点,则 该复链杆具有(2N-3)个约束,等于(2N-3)个链杆的 作用。 2)复铰:若一个复铰上连接了N个刚片,则该复 铰具有2(N-1)个约束,等于(N-1)个单铰的作用。
三、多余约束
在体系上加上或撤除某一约束并不改变原体系的 自由度数,则该约束就是多余约束。
规则二 (三刚片规则): 三个刚片用不全在一条直线上的三个单铰(可以 是虚铰)两两相连,组成无多余约束的几何不变体 系。
*铰接三角形规则(简称三角形规则): 平面内一个铰接三角形是无多余约束的几何不变 体系。 以上三个规则可互相变换。之所以用以上三种不 同的表达方式,是为了在具体的几何组成分析中应 用方便,表达简捷。 规则三 (二元体规则): 二元体特性:在体系上加上或拆去一个二元体, 不改变体系原有的自由度数。 利用二元体规则简化体系,使体系的几何组成分 析简单明了。
三、对体系作几何组成分析的一般途径 1、恰当灵活地确定体系中的刚片和约束 体系中的单个杆件、折杆、曲杆或已确定的几何 不变体系,一般视为刚片。但当它们中若有用两个 铰与体系的其它部分连接时,则可用一根过两铰心 的链杆代替,视其为一根链杆的作用。 2、如果上部体系与大地的连接符合两个刚片的规 则,则可去掉与大地的约束,只分析上部体系。 3、通过依次从外部拆除二元体或从内部(基础、 基本三角形)加二元体的方法,简化体系后再作分 析。
一、术语简介(图2-1-1) 1、 几何不变体系:在荷载作用下能保持其几何形 状和位臵都不改变的体系称之。 2、几何可变体系:在荷载作用下不能保持其几何 形状和位臵都不改变的体系称之。
3、刚片:假想的一个在平面内完全不变形的刚性 物体叫作刚片。在平面杆件体系中,一根直杆、折 杆或曲杆都可以视为刚片,并且由这些构件组成的 几何不变体系也可视为刚片。
例2-3-1 对下列图示各体系作几何组成分析 (简单 规则的一般应用方法)。
二、瞬变体系 的概念 1、瞬变体 系几何组成特 征: 在微小荷载 作用下发生瞬 间的微小的刚 体几何变形, 然后便成为几 何不变体系。
2、瞬变体系的静力 特性: 在微小荷载作用下 可产生无穷大内力。 因此,瞬变体系或接 近瞬变的体系都是严 禁作为结构使用的。 瞬变体系一般是总 约束数满足但约束方 式不满足规则的一类 体系,是特殊的几何 可变体系。
第一部分 静定结构内力计算
静定结构的特性: 1、几何组成特性 2、静力特性 静定结构的内力计算依据静力平衡原理。
第三章 §3-1 单
静定梁和静定刚架 跨 静 定 梁
单跨静定梁的类型:简支梁、伸臂梁、悬臂梁 一、截面法求某一指定截面的内力
1、内力概念
内力是结构承受荷载及变形的能力的体现,可理解 为在各种外因用下结构内部材料的一种响应。内力 是看不见的,但可由结构上受有荷载和结构发生变 形(变形体)体现。
§2-2 平面体系的自由度
一、 自由度的概念 体系可独立运动的方式称为该体系的自由度。 或表示体系位臵的独立坐标数。 平面体系的自由度:用以确定平面体系在平面 内位臵的独立坐标数。
(图2-2-2)上3所示,为平面内一根链杆AB, 其一端A和大地相连,显然相对于大地来说这根链 杆在平面内只有一种运动方式,即作绕A点转动, 所以该体系只有一个自由度。同时又可看到,如果 用链杆AB与水平坐标的夹角作为表示该体系运动 方式的参变量,即表示该体系运动中任一时刻的位 臵,表示体系位臵的参变量数与体系的自由度数也 是相等的。所以,该体系的自由度数为1个。 平面内最简体系的自由度数: 一个点:在平面内运动完全不受限制的一个点有 2个自由度。 一个刚片:在平面内运动完全不受限制的一个刚 片有3个自由度。(图2-2-1)
2)内力计算式(用截面一侧上外力表达的方式): FN=截面一侧所有外力在杆轴平行方向上投影 的代数和。左左为正,右右为正。 FQ=截面一侧所有外力在杆轴垂直方向上投影的代 数和。左上为正,右下为正。 Μ =截面一侧所有外力对截面形心力矩代数和。弯 矩的竖标画在杆件受拉一侧。
例3-1-1 求图(a)所示简支梁在图示荷载下截 面的内力。 解:1)支座反力 ∑ΜA=0 FBy×4﹣10×4×2 ﹣100×(4/5)×2=0 Fby=60kN (↑)
例2-3-5 对图示各体系作几何组成分析。
一、本章要求 1、了解几何不变体系、几何可变体系、瞬变体 系、刚片、体系的自由度、虚铰、约束及多余约束 的概念; 2、重点理解并掌握平面几何不变体系的简单组 成规则,并能灵活应用到对体系的分析中;
第二章
小
结
二、简单规则应用要点 简单规则中的四个要素:刚片个数、约束个数、 约束方式、结论。 应用简单规则对体系进行几何组成分析的要点是: 紧扣规则。即,将体系简化或分步取为两个或三个 刚片,由相应的规则进行分析;分析过程中,规则 中的四个要素均要明确表达,缺一不可。
