同济大学结构力学
合集下载
同济大学结构力学
目前，加拿大多伦多电视塔高554米，但这一高度算上了天线。台北101大楼高508米，但屋顶高度仅 480米。此外，东京的胜美达通讯大楼即将动工，设计高度610米。迪拜塔2008年9月1日已达688米， 设计高度700米，传言812米，科威特打算建造1001米的标志性建筑。
金茂大厦421m
西尔斯大厦 442m
同济大学结构力学
学习方法 1、采用课堂讲课和自学教材相结合的方法，以讲课为主，有部分内容给大家自学，目的是培养大家自学的能 力。在自学过程中，不能理解的内容，大家可以相互讨论，当然也可将看不懂的问题和我一起探讨。 2、希望同学们应以讲课内容为主，作简单笔记，在学习理论、概念的同时，一定要作相当数量的习题，通过 手算的方法和技巧来掌握力学的概念以及分析和计算的方法。
几何特征：其横截面上两个方向的尺寸远小于长度。 典型形式：梁、刚架、拱和珩架。 （b）板壳结构——也称薄壁结构。 几何特征：其厚度远小于其余两个方向上的尺度。 典型形式：房屋建筑中的楼板、壳体屋盖及飞机和轮船的外 壳等。 （c）实体结构——也称三维连续体结构。 几何特征：结构的长、宽、高三个方向的尺寸大小相仿。 典型形式：重力式挡土墙、水工建筑中的重力坝等。
人类建筑师总想将摩天大楼越盖越高，美国有527米高的芝加哥西尔斯大厦，加拿大有553米高的多 伦多CN电视塔，阿联酋迪拜市正在建造一座高达807米的世界最高楼。然而这些摩天大楼和日本大成 建筑公司蓝图中的“X-Seed 4000”摩天巨塔相比，却全都是“小巫见大巫”。
美国“高层建筑及城市居住委员会”设定了4个衡量标准：最高一层地板的高度、最高一层屋顶的高度、 大厦尖顶的高度及大厦最高点的高度。
吉隆坡的双子塔452m
台北市的101大楼508m
芝加哥“螺旋之尖”摩天大楼的建设方案获得了政府批 准，“螺旋之尖”摩天大楼全高610米，建成后将是全 美最高的大楼，它也将是世界各大城市里高楼建筑的一 个典范。
金茂大厦421m
西尔斯大厦 442m
同济大学结构力学
学习方法 1、采用课堂讲课和自学教材相结合的方法，以讲课为主，有部分内容给大家自学，目的是培养大家自学的能 力。在自学过程中，不能理解的内容，大家可以相互讨论，当然也可将看不懂的问题和我一起探讨。 2、希望同学们应以讲课内容为主，作简单笔记，在学习理论、概念的同时，一定要作相当数量的习题，通过 手算的方法和技巧来掌握力学的概念以及分析和计算的方法。
几何特征：其横截面上两个方向的尺寸远小于长度。 典型形式：梁、刚架、拱和珩架。 （b）板壳结构——也称薄壁结构。 几何特征：其厚度远小于其余两个方向上的尺度。 典型形式：房屋建筑中的楼板、壳体屋盖及飞机和轮船的外 壳等。 （c）实体结构——也称三维连续体结构。 几何特征：结构的长、宽、高三个方向的尺寸大小相仿。 典型形式：重力式挡土墙、水工建筑中的重力坝等。
人类建筑师总想将摩天大楼越盖越高，美国有527米高的芝加哥西尔斯大厦，加拿大有553米高的多 伦多CN电视塔，阿联酋迪拜市正在建造一座高达807米的世界最高楼。然而这些摩天大楼和日本大成 建筑公司蓝图中的“X-Seed 4000”摩天巨塔相比，却全都是“小巫见大巫”。
美国“高层建筑及城市居住委员会”设定了4个衡量标准：最高一层地板的高度、最高一层屋顶的高度、 大厦尖顶的高度及大厦最高点的高度。
吉隆坡的双子塔452m
台北市的101大楼508m
芝加哥“螺旋之尖”摩天大楼的建设方案获得了政府批 准，“螺旋之尖”摩天大楼全高610米，建成后将是全 美最高的大楼，它也将是世界各大城市里高楼建筑的一 个典范。
同济大学结构力学课程第一章
实验
结构动力计算
结构稳定计算**
结构极限荷载**
第一章 绪论
1～1 结构力学的研究对象和基本任务 1.工程结构的概念
指建筑物、构筑物和其它工程对象中支承和传递荷载而起骨架作用 的部分。 2.工程结构的受力特性和承载能力与结构的几何特征有着密切的联系。 3.结构分类： 按照几何特征分： （a）杆系结构——由若干个杆件相互联接组成的结构。
环球金融中心的多个“第一”
■ 屋顶高度世界第一：492米，超过 了目前屋顶高度世界第一的台北101大 楼（480米）。 ■ 人可达到高度世界第一：474米， 大楼100层的观光天阁是世界上人能到 达的最高观景平台。
■ 世界最高中餐厅：416米，设在93 层的中餐厅，将成为全球最高中餐厅。
■ 世界最高游泳池：366米，设在85 层的游泳池，将夺得“世界最高游泳 池”称号。
•1～2 结构的计算简图
一、结构计算简图
1. 概念：在计算中把实际结构中的一些次要因素加以忽略，
但又反映出实际结构主要受力特征的经过简化的结构图形。
2. 计算简图的选择原则：
（1）存本去末原则：保留主要因素，略去次要因素，使 计算简图能反应出施加架构的主要受力特征。 （2）计算简便原则：根据需要和可能，并从实际出发， 力求使计算简图便于计算。 （3）据不同的要求与具体情况，对同一实际结构可选择 不同的计算简图。
斜拉桥
拱桥
1999年1月4日，我国重庆市綦江县 彩虹桥发生垮塌，造成：
40人死亡； 14人受伤； 直接经济损失631万元。
垮塌前的彩虹桥
垮塌后的彩虹桥
简单力学问题－ 大部队过桥时不能齐步走
高等力学问题－ 冲击载荷的概念： 人跑步时脚上的力量有多大？ 损伤累积与结构寿命 与跑步的次数有关
结构动力计算
结构稳定计算**
结构极限荷载**
第一章 绪论
1～1 结构力学的研究对象和基本任务 1.工程结构的概念
指建筑物、构筑物和其它工程对象中支承和传递荷载而起骨架作用 的部分。 2.工程结构的受力特性和承载能力与结构的几何特征有着密切的联系。 3.结构分类： 按照几何特征分： （a）杆系结构——由若干个杆件相互联接组成的结构。
环球金融中心的多个“第一”
■ 屋顶高度世界第一：492米，超过 了目前屋顶高度世界第一的台北101大 楼（480米）。 ■ 人可达到高度世界第一：474米， 大楼100层的观光天阁是世界上人能到 达的最高观景平台。
■ 世界最高中餐厅：416米，设在93 层的中餐厅，将成为全球最高中餐厅。
■ 世界最高游泳池：366米，设在85 层的游泳池，将夺得“世界最高游泳 池”称号。
•1～2 结构的计算简图
一、结构计算简图
1. 概念：在计算中把实际结构中的一些次要因素加以忽略，
但又反映出实际结构主要受力特征的经过简化的结构图形。
2. 计算简图的选择原则：
（1）存本去末原则：保留主要因素，略去次要因素，使 计算简图能反应出施加架构的主要受力特征。 （2）计算简便原则：根据需要和可能，并从实际出发， 力求使计算简图便于计算。 （3）据不同的要求与具体情况，对同一实际结构可选择 不同的计算简图。
斜拉桥
拱桥
1999年1月4日，我国重庆市綦江县 彩虹桥发生垮塌，造成：
40人死亡； 14人受伤； 直接经济损失631万元。
垮塌前的彩虹桥
垮塌后的彩虹桥
简单力学问题－ 大部队过桥时不能齐步走
高等力学问题－ 冲击载荷的概念： 人跑步时脚上的力量有多大？ 损伤累积与结构寿命 与跑步的次数有关
同济大学推荐结构力学习题集 含答案
《结构力学》习题集 （上册）
第一章 平面体系的几何组成分析
一、判断题：
1、在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变 体系。 2、图中链杆 1 和 2 的交点 O 可视为虚铰。
1
O
2
二、分析题：对下列平面体系进行几何组成分析。
3、
4、
C
B
D
C
B
D
A
5、
A
6、
A
B
A
B
C
D
E
7、
5
1
2
3
25、
26、
27、
28、
—— 3 ——
29、
《结构力学》习题集 （上册）
30、
31、
32、
33、
A
B
C
F D
E
三、在下列体系中添加支承链杆，使之成为无多余约束的几何不变体系。
34、
35、
第二章 静定结构内力计算
—— 4 ——
《结构力学》习题集 （上册）
一、判断题：
1、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。
P
44、
ql
l
a
q
l
l
l
45、
46、
—— 9 ——
ql 2 l
《结构力学》习题集 （上册）
ql
3m
3m 10kN
3m
3m
47、
20kN 4× 2m=8m
48、
2m 2m
m C
EB 4m
D
2m A
4m
2m
49、
16kN . m
50、
第一章 平面体系的几何组成分析
一、判断题：
1、在任意荷载下，仅用静力平衡方程即可确定全部反力和内力的体系是几何不变 体系。 2、图中链杆 1 和 2 的交点 O 可视为虚铰。
1
O
2
二、分析题：对下列平面体系进行几何组成分析。
3、
4、
C
B
D
C
B
D
A
5、
A
6、
A
B
A
B
C
D
E
7、
5
1
2
3
25、
26、
27、
28、
—— 3 ——
29、
《结构力学》习题集 （上册）
30、
31、
32、
33、
A
B
C
F D
E
三、在下列体系中添加支承链杆，使之成为无多余约束的几何不变体系。
34、
35、
第二章 静定结构内力计算
—— 4 ——
《结构力学》习题集 （上册）
一、判断题：
1、静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。
P
44、
ql
l
a
q
l
l
l
45、
46、
—— 9 ——
ql 2 l
《结构力学》习题集 （上册）
ql
3m
3m 10kN
3m
3m
47、
20kN 4× 2m=8m
48、
2m 2m
m C
EB 4m
D
2m A
4m
2m
49、
16kN . m
50、
同济大学朱慈勉 结构力学第11章_结构的稳定计算
§11-2 有限自由度体系的稳定 ——静力法和能量法
P
即 : P 3klP k l 0
2 2 2
A 1.618
1
2.618kl 3 5 特征值: P kl 2 0.382kl
B C
k
Pcr 0.382kl ---临界荷载
y1 1 ---失稳形式 y2 1.618
P A
EI
y1
k k
y2
ky1
l
B
EI
ky2
l
C
(2lk P ) y1 kly2 0 整理得 ：(kl P ) y Py 0 1 2
为使y1、y2 不同时为零，令：
HB’
P
A’ B’
VB’
ky1 ky2
2kl P kl 0 ----稳定方程 kl P P
y
y(l ) l
y(l ) tanl
经试算： (l )min 4.493
2 Pcr min EI 4.493 2 EI ( ) EI 20.19 2 l l
2
3 2
5 2
l
§11-3 无限自由度体系的稳定——静力法
例11.8 求体系的临界荷载Pcr 。 P P
第十一两类稳定问题概述 §11-2 有限自由度体系的稳定 ——静力法和能量法
§11-3 无限自由度体系的稳定 ——静力法 §11-4 无限自由度体系的稳定 ——能量法
§11-1 概述
强度验算 薄壁结构 刚度验算 结构设计 高强材料结构 稳定验算——某些时候是必须的 （如钢结构） 主要受压的结构等 强度验算与刚度验算是在结构静力平衡的状态下、采用未变形的 结构的计算简图来分析的； 而稳定验算是在结构产生大变形后的几何形状和位置上进行计算 的，其方法已经属于几何非线性范畴，叠加原理不再适用。
同济大学结构力学第五章-3(图乘法)
FP
解：作荷载内力图和单位荷载内力图
FPl/2 FPl/2 FPl/2 FP FPl/4
MP 图
EI 2EI
M 图
FPl/4
在
M
图求面积， 图取竖标， 图求面积，在 MP图取竖标，有：
ωyc
1 l FPl 1 3l FPl Ay = ∑ = × ×l × ×l × × EI EI 2 2 2EI 2 4 FPl 3 = ( ↓) 16EI
2
B
l 1 1 l 3ql 1 l ql 3 l × × + × × × × ) Cy = ( × EI 2 8 2 2 3 2 8 4 2 1 ql 4 3ql 4 5ql 4 = ( + ( ↓) )= EI 64 128 128EI ?
解法一、 解法一、
ql 2 2
A
q
ql 2 8
. 已知 EI 为常数，求刚架 、D两点 距离的改变 CD 。
解：作荷载内力图和单位荷载内力图
p117
2
yc = h
1 2 ql 2 = × × ×l ×h CD = ∑ EI EI 3 8 qhl 3 = (→←) 12EI
ωyc
为常数，求刚架A点的竖向位 例 3. 已知 EI 为常数，求刚架 点的竖向位 并绘出刚架的变形曲线。 移 Ay ，并绘出刚架的变形曲线。
b c 取 负 值
(4) 阶梯形截面杆
ωj yj Mi MK ω1 y1 ω2 y2 ω3 y3 dx = + + =∑ ∫ EI E1I1 E2I2 E3I3 Ej I j
四、应用举例 为常数， 例 1. 设 EI 为常数，求 Cy 和 θB 。
l
2
l
同济大学-结构力学课件
• 加里莱·伽利略 （Galileo·Galilei 1564—
1642年）是意大利伟大的物理学家、力 学家、天文学家。他推翻了当时最权威 的 亚里斯多德 的学说， 1582年，他先 后发明了“摆锤摆动等时性定律、落体 定律、惯性定律”。伽利略的成就被公 认为——近代科学的起源。
牛顿（1642-1727年、英国）使力学 成为一门较完整与系统的学科。
2008年5月底，上海新的“第一高”方案确定——580米的 “上海中心”，被设计成盘旋上升的龙形。
截止到2009年1月23日， 迪拜塔封顶，高达818米。
在“迪拜塔”之前，纽 约帝国大厦(381米)、中国 上海金茂大厦(420.5米)、 美国芝加哥希尔斯大厦 (442.3米)、马来西亚双子 星塔(451.9米)、中国台北 101大楼(508米)都曾是享誉 世界的著名高楼。
■ 世界最高酒店：设在大楼79至93层 的柏悦酒店，将成为世界最高酒店。
■ 燃气输送至93层416米的高度，生 活用水最高处在434米的97层观光天 桥上，而消防用水则通过4节系统送至 楼顶，均创下了新高。
被誉为“江苏省 第一高楼”的南京绿地广场紫峰大厦2008 年6月封顶。该大厦位于南京中心鼓楼广场西北角，总高88 层，主体高度最高达381米、天线顶高450米，因其高度超 过420米的上海金茂大厦，而成为中国第二高楼
• 建筑是在力学基础上发展起来的，古
人根据经验设想来构造结构，直到18 世纪有了系统力学分析后，以受力状
态为依据的结构设计才逐渐代替经验 设想。
建筑历史
• 1、历代建筑的演变 • 穴居 巢居 棚居 房屋（人类生活逐步
稳定和发明工具）
• 2、建筑三要素 • 公元前32-22年间，古罗马奥古斯都时代的
同济大学 朱慈勉版 结构力学 课后答案(下)
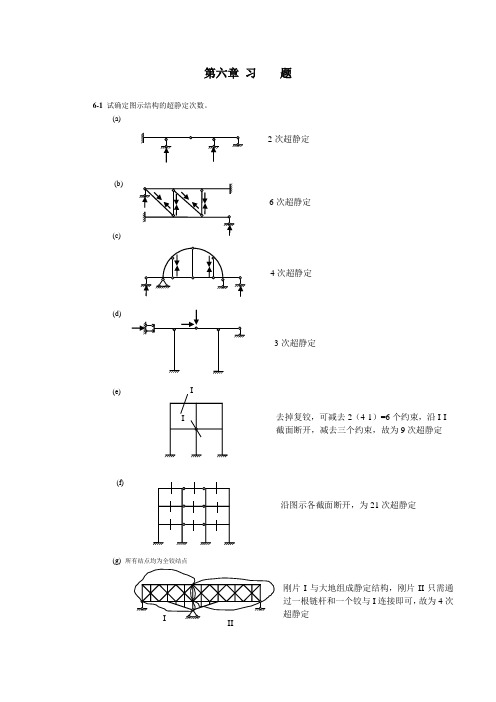
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰，可减去2（4-1）=6个约束，沿I-I 截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定刚片I 与大地组成静定结构，刚片II 只需通过一根链杆和一个铰与I 连接即可，故为4次超静定(h)6-2 试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？ 6-3 试用力法计算图示超静定梁，并绘出M 、F Q 图。
(a) 解：上图=l1M p M01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误，为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解：基本结构为：l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构，并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解：基本结构为：1Mp M01111=∆+p X δ p M X M M +=11(b)解：基本结构为：4a 2a4a4a3m6m 6m810810计算1M，由对称性知，可考虑半结构。
同济大学 结构力学课后习题及答案解析(完整版)
R=2m
4m
A O
M ( ) 1 (R sin )2 1 2 R(1 cos ) 2
M ( ) 1
B
1 EI
2 1 [1 (R sin )2 1 2 R(1 cos )]Rd 02
= (8-3 ) -1.42 (逆时针)
EI
EI
(d) A q
R EI=常数
O
B
5-7 试用图乘法计算图示梁和刚架的位移：（a） ΔyC ；（b） ΔyD ；（c） ΔxC ；（d） ΔxE ；（e） D ；（f） ΔyE 。 (a)
5-5 已知桁架各杆的 EA 相同，求 AB、BC 两杆之间的相对转角 ΔB 。 5-6 试用积分法计算图示结构的位移：（a） ΔyB ；（b） ΔyC ；（c） B ；（d） ΔxB 。
(a)
q2 q1
A
EI
B
l
以B点为原点，向左为正方向建立坐标。
q( x)
q2
l
q1
x
q1
M
p(x)
1 2
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架，并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构，求出链杆轴力并绘出 M 图。
2
30kN 2m
(a)
a 1.5m
l
A
kθ=
12EI l
2 3
2 3
6 1 20 62 8
3 2
1 6180 3 2
同济大学结构力学第三章-8(桁架)
因为
FN=±M0/r ±
其中：M0为同样跨度的简支梁相应位置的弯矩， 其中： 为同样跨度的简支梁相应位置的弯矩， 其中 为弦杆内力对矩心的力臂。 r 为弦杆内力对矩心的力臂。
平行弦杆的竖杆内力及斜杆的竖向 分力等于简支梁相应位置的剪力， 简支梁相应位置的剪力， 简支梁相应位置的剪力 由中间向两端递增。 由中间向两端递增。
I
12 G E 4m
M图(kN . m)
B 2m 4m
C -6
D 4m 2m 2m
I
3 kN
一般情况下应先计算链杆的轴力 取隔离体时宜尽量避免截断受弯杆件返Leabharlann 回§3-7 静定结构的一般性质
在线性弹性范围内，静定结构满足平衡 条件的反力和内力解答是唯一的。 非荷载因素不引起静定结构的反力和内 力。 非荷载因素：温度变化、支座位移、材
§3-5 静定组合结构
特点 既有桁架杆， 既有桁架杆，又有弯曲杆 一般有一些关键的联系杆 求解的关键点 选择恰当方法解决关键杆内力计算 选择截面时， 选择截面时，必须注意区分两类杆
组合结构的计算
组合结构——由链杆和受弯杆件混合组成的结构。 由链杆和受弯杆件混合组成的结构。 组合结构 由链杆和受弯杆件混合组成的结构 8 kN A FN图(kN) 5 kN 4 -6 F 6 12
抛物线形弦杆的上弦符合合理 抛物线形弦杆的上弦符合合理 拱轴线，腹杆内力为零。 拱轴线，腹杆内力为零。
三角形桁架的腹杆内力由中间向两 三角形桁架的腹杆内力由中间向两 端递减。 端递减。
小 结
熟练掌握 计算桁架内力的基 本方法： 结点法和截面法 本方法： 采取最简捷 最简捷的途径计算桁架 采取最简捷的途径计算桁架 内力
§3-4 静定平面桁架-续 静定平面桁架-
同济大学朱慈勉-结构力学第10章-结构动力学
机动力荷载).
分析过程：
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 （如何求？）
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
（动力）自由度：确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应：
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到：
▪ 体系从任一时刻经几个周期后 的振幅比为：
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
（3-2）
▪ 特征方程：
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小，则显然有c/2m< ，这时，特 征方程根式中的值必然为负值，则s 值成为：
s c i 2 c 2
2m
2m
▪ 引入符号： c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值，称为阻尼比，则：
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
分析过程：
第1阶段:位移时间历史 y y(x)
第2阶段: 应力、应变及内力 （如何求？）
已知荷载的类型
周期荷载: 简谐荷载
复杂荷载
F
t
F
t
建筑物上的偏心电机
内燃机连杆
任意复杂周期荷载可以用傅里叶级数展开为简谐荷载
非周期荷载:
F
t
F
t
爆破
地震
§10-2 体系振动的自由度
（动力）自由度：确定体系上全部质量位置所需的独立参 数的数目
确定体系阻尼比的一种方法
▪ 阻尼体系动力反应：
y(t) et sin(dt )
▪ 体系的阻尼比可以通过测试体 系运动的衰减规律得到：
▪ 体系从任一时刻经几个周期后 的振幅比为：
y (t)
e tk
e (tk nT )
t
0 tk
t k + nT
e t
T 2/d
y e tk
tk
n T
2nπ d
my cy ky 0
（3-2）
▪ 特征方程：
s c
c
2
2
2m 2m
▪ 如果体系的阻尼比临界阻尼小，则显然有c/2m< ，这时，特 征方程根式中的值必然为负值，则s 值成为：
s c i 2 c 2
2m
2m
▪ 引入符号： c c cc 2m
c 2m
▪ 其中 表示体系阻尼与临界阻尼的比值，称为阻尼比，则：
y3 y2
y1
忽略楼板变形
3个自由度
y1 y2
2个自由度
1个自由度
y1
忽略杆件轴向变形
4个自由度
y1
同济大学 结构力学2～5章习题(填空选择题)
）
[12]图示结构中 AB 杆弯矩为零。 （
）
[13]图示结构
。 （
）
[14]图示结构中 A、B 支座反力均为零。 （
）
[15]图示结构 K 截面弯矩值 MK=Pd,上侧受拉。 （
）
[16]图示结构 支座反力矩值
。 （
）
[17]图示拱的水平推力为 P（以指向内为正） 。
（
）
[18]图示桁架结构杆 1 的轴力
。 （
）
[19]图示桁架结构杆 1 轴力
。
（
）
[20]图示桁架结构杆 1 的轴力
。
（
）
[21]图示结构杆 1 和杆 2 的轴力相同。
（
）
[22]图示结构杆 1 的轴力 N1=－1.414P。
（
）
[23]如图所示多跨静定梁不管 p、q 为何值，其上任一截面的剪力均不为零。(
)
[24]图示桁架 AB 杆的内力为零。(
[29]图示结构支座 A 的反力矩（以右侧受拉为正）是： A.m/4; B.m/2; C.－m/2; D.－m。 [30]图示结构 ABC 柱 B 截面的弯矩（右侧受拉为正）是: A.0; B.4Pd; C.－8Pd; D.8Pd.
[31]图示桁架 C 杆的内力是： A.P; B.－P/2; C.P/2; D.0。
第二章（几何组成分析）习题
一、是非判别
[1]图中链杆 1 和 2 的交点 O 可视为虚铰。 （ ）[2]图示对称体 Nhomakorabea为几何瞬变。
二、选择
[1]图示体系是： A．几何瞬变有多余约束； B．几何不变； C．几何常变； D．几何瞬变无多余约束。
[2]图示体系为： A．几何不变无多余约束； B．几何不变有多余约束； C．几何常变； D．几何瞬变。
同济大学结构力学第四章-(2)
与最大值对应的临界位置就是最不利荷载位置。 • 可以任意布置的均布荷载的最不利位置，是将荷载布满影响线的正号部
分或负号部分，如图4(a)所示。 • 一段可移动的均布荷载的最不利位置按 的条件判断，当影响线为三角
形时，满足下式的荷载位置即最不利荷载位置。
式中各值的意义如图4(b)所示。
P1=P2=P3=P4=P5=90kN（中—活载） P1 P2 P1 P3 P2 P4P3 P5 P4
临界荷载
R1R1
R2R2
的判断条件 P1
P2
P3
P4
Z1右2点))==Z偏上有达R移。一1Zy极R影1，集iy值响i∑中R时2线yR力2，itPa荷cRnr位3α载yy3于i稍必影向变响左号线α、。D2>顶y01
Dy2 y
2
1
α1>0 D x
Dx
Dyi = Dxtgi DZ = RiDyi = Dx Ritgi
Z成为极大值条件：荷载左、右稍移
DZ = Dx Ritgi ≤0
当Δx＞0时(右移) 当Δx＜0时(左移)
Z成为极小值条件：荷载左、右稍移
DZ = Dx Ritgi ≥ 0
当Δx＞0时(右移) 当Δx＜0时(左移)
点击左键，一步步播放。结束播放请点“后退”。
R3R3
P5
P6
α3<0
y
Dy
3
3
Dx
的荷载的合力。向下为正。
1) 当行列荷载移动时,MK按折线规律变化。
影响2线) M顶K点的上极。值b表)将现K行为列尖荷点载P值1自=。P此其向特左点或是P2向=：2右Pa）稍有移一一集点中, M力KP的cr位值于均
减少。
4m
2m x
分或负号部分，如图4(a)所示。 • 一段可移动的均布荷载的最不利位置按 的条件判断，当影响线为三角
形时，满足下式的荷载位置即最不利荷载位置。
式中各值的意义如图4(b)所示。
P1=P2=P3=P4=P5=90kN（中—活载） P1 P2 P1 P3 P2 P4P3 P5 P4
临界荷载
R1R1
R2R2
的判断条件 P1
P2
P3
P4
Z1右2点))==Z偏上有达R移。一1Zy极R影1，集iy值响i∑中R时2线yR力2，itPa荷cRnr位3α载yy3于i稍必影向变响左号线α、。D2>顶y01
Dy2 y
2
1
α1>0 D x
Dx
Dyi = Dxtgi DZ = RiDyi = Dx Ritgi
Z成为极大值条件：荷载左、右稍移
DZ = Dx Ritgi ≤0
当Δx＞0时(右移) 当Δx＜0时(左移)
Z成为极小值条件：荷载左、右稍移
DZ = Dx Ritgi ≥ 0
当Δx＞0时(右移) 当Δx＜0时(左移)
点击左键，一步步播放。结束播放请点“后退”。
R3R3
P5
P6
α3<0
y
Dy
3
3
Dx
的荷载的合力。向下为正。
1) 当行列荷载移动时,MK按折线规律变化。
影响2线) M顶K点的上极。值b表)将现K行为列尖荷点载P值1自=。P此其向特左点或是P2向=：2右Pa）稍有移一一集点中, M力KP的cr位值于均
减少。
4m
2m x
同济大学朱慈勉版结构力学课后答案(下)
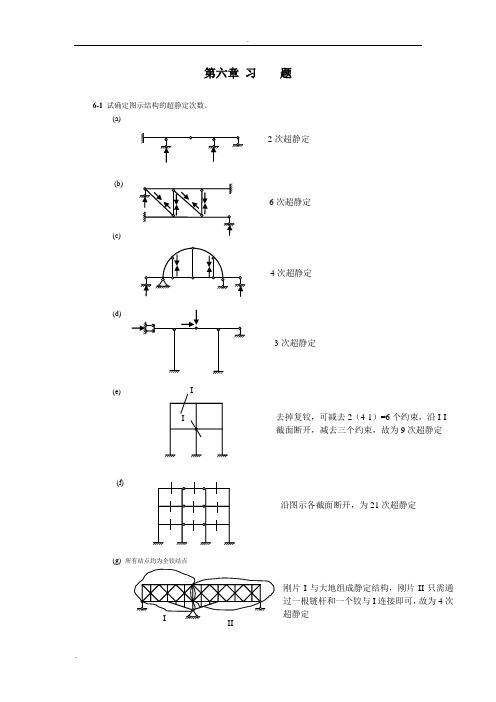
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰，可减去2（4-1）=6个约束，沿I-I 截面断开，减去三个约束，故为9次超静定沿图示各截面断开，为21次超静定刚片I 与大地组成静定结构，刚片II 只需通过一根链杆和一个铰与I 连接即可，故为4次超静定(h)6-2 试回答：结构的超静定次数与力法基本结构的选择是否有关？力法方程有何物理意义？ 6-3 试用力法计算图示超静定梁，并绘出M 、F Q 图。
(a) 解：上图=l1M p M01111=∆+p X δ其中：EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误，为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解：基本结构为：l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构，并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解：基本结构为：1Mp M01111=∆+p X δ p M X M M +=11(b)解：基本结构为：4a 2a4a4a3m6m6m810810计算1M，由对称性知，可考虑半结构。
同济大学结构力学第五章-2(单位荷载法)
设待求的实际广义位移为ΔBX ，与ΔBX对 应的广义力为1。
设仅在广义力1作用下，与之平衡的轴 力、剪力和弯矩分别为FN 、 FQ和M。
实际位移状态
B FP C
虚设的力状态
P=1 B C
Bx ?
A
FN 、 FQ和 M
A
又设与内力FN 、 FQ和M对应的微段实 际变形分别为δε、δγ和δθ。
§5-2 单位荷载法 一、位移计算的一般公式
(General Formula of Displacements)
应用虚功原理计算结构的位移，假设一个 虚拟状态，设置一个单位力1，这就是求 解结构位移的实际协调位移和虚设平衡力 状态间方法——单位荷载法。 下面从虚功方程入手，讨论杆系结构位移 计算的一般公式。
2 E
G
3
取：
h l
1
10
，E G 2.5 ，有：
, ( Ay )Q ~
4
( Ay ) N ~
1 750
1 500
即： Ay
( Ay )Q ( Ay ) M
5ql
(1
1
1
)
8 EI
0.2%
,
750 500 ( Ay ) N 0.13% ( Ay ) M
A
1 d2
d2
AB AC ?
试确定指定广义位移对应的单位广义力。
P=1
A
(e)
B
AB ?
P=1
P=1
C
P=1
(f)
C 左右
=？
试确定指定广义位移对应的单位广义力。
P=1
A
(g)
A ?
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
核电建筑
（实体、坝体结构、 钢筋混凝土结构）
（实体结构、钢筋混凝土结构）
结构力学的学科性质、研究目的和基本任务
• 学科性质：
研究结构的合理形式以及结构在受力状态下内力、变形、动力反应和稳定性等方面的规律性的 学科；是结构工程类专业的一门重要的技术基础课。
• 研究目的：
使结构满足安全性、适用性和经济方面的要求。
•1～2 结构的计算简图
一、结构计算简图 1. 概念：在计算中把实际结构中的一些次要因素加以忽略，但又反映出实际结构主要受力特征的经过简
化的结构图形。 2. 计算简图的选择原则：
（1）存本去末原则：保留主要因素，略去次要因素，使计算简图能反应出施加架构的主要受力特征。 （2）计算简便原则：根据需要和可能，并从实际出发，力求使计算简图便于计算。 （3）据不同的要求与具体情况，对同一实际结构可选择不同的计算简图。
同济大学结构力学
学习方法 1、采用课堂讲课和自学教材相结合的方法，以讲课为主，有部分内容给大家自学，目的是培养大家自学的能 力。在自学过程中，不能理解的内容，大家可以相互讨论，当然也可将看不懂的问题和我一起探讨。 2、希望同学们应以讲课内容为主，作简单笔记，在学习理论、概念的同时，一定要作相当数量的习题，通过 手算的方法和技巧来掌握力学的概念以及分析和计算的方法。
位移法 力矩分配法 结构矩阵分析 实验
结构极限荷载**
第一章 绪论
1～1 结构力学的研究对象和基本任务 1.工程结构的概念
指建筑物、构筑物和其它工程对象中支承和传递荷载而起骨架作用的部分。 2.工程结构的受力特性和承载能力与结构的几何特征有着密切的联系。 3.结构分类：
按照几何特征分： （a）杆系结构——由若干个杆件相互联接组成的结构。
3.在选择计算简图时，对实际结构的情况进行多方面的简化如下：
（1）结构体系的简化
a.平面杆系结构
b.空间杆系结构
（2）杆件的简化
杆件用杆件的轴线表示，杆长用轴线交点间距离表示。
（3）结点的简化
杆件相互连接处称为结点。按结点的计算简图可分为以下两种类型：
a.铰结点（特征：所联结各杆可以绕铰转动，可用一理想光滑铰表示。实例：木屋架的下弦中间 节点。）
飞鸟与空中客车机翼相撞
钢结构接头
振动试 验
振动试 验
高层建筑结构振动中的仿真试验
风洞试验
风洞试验
几何组成分析 结
构
力
静定结构受力分析
学
基 础
结构位移计算
梁 刚架 拱 桁架
组合结构 力法
结 构 力 学
结 构 力 学 专 题
超静定结构受力分析 影响线
计算结构力学
结构动力计算 结构稳定计算**
澳门桥
斜拉桥
拱桥
1999年1月4日，我国重庆市綦江县 彩虹桥发生垮塌，造成：
40人死亡； 14人受伤； 直接经济损失631万元。
垮塌前的彩虹桥
垮塌后的彩虹桥
简单力学问题－ 大部队过桥时不能齐步走
高等力学问题－ 冲击载荷的概念： 人跑步时脚上的力量有多大？ 损伤累积与结构寿命 与跑步的次数有关
人类建筑师总想将摩天大楼越盖越高，美国有527米高的芝加哥西尔斯大厦，加拿大有553米高的多 伦多CN电视塔，阿联酋迪拜市正在建造一座高达807米的世界最高楼。然而这些摩天大楼和日本大成 建筑公司蓝图中的“X-Seed 4000”摩天巨塔相比，却全都是“小巫见大巫”。
美国“高层建筑及城市居住委员会”设定了4个衡量标准：最高一层地板的高度、最高一层屋顶的高度、 大厦尖顶的高度及大厦最高点的高度。
■ 世界最高酒店：设在大楼79至93层的柏悦酒店，将 成为世界最高酒店。
■ 燃气输送至93层416米的高度，生活用水最高处在 434米的97层观光天桥上，而消防用水则通过4节系统 送至楼顶，均创下了新高顶。该大厦位于南 京中心鼓楼广场西北角，总高88层，主体高度最高达381米、天线顶高450米，因其 高度超过420米的上海金茂大厦，而成为中国第二高楼
吉隆坡的双子塔452m
台北市的101大楼508m
芝加哥“螺旋之尖”摩天大楼的建设方案获得了政府批 准，“螺旋之尖”摩天大楼全高610米，建成后将是全 美最高的大楼，它也将是世界各大城市里高楼建筑的一 个典范。
水立方和盘古大观大厦
上海港国际客运中心 上海港国际客运中心 （一滴水）2008年8月5日投入使用
了当时最权威的 亚里斯多德 的学说， 1582年，他先后发明了“摆锤摆动等时性定律、落体定律、惯性 定律”。伽利略的成就被公认为——近代科学的起源。
牛顿（1642-1727年、英国）使力学成为一门较完整与系统的学科。
• 在数学上，牛顿创立了微积分学，制定了二项式定理，发展了关于方程式的大部分理论，引进了字母
2008年8月28日，高达492米共101层的 上海环球金融中心正式宣布落成启用 。上
海环球金融中心是建筑顶面最高和人可到达 最高的建筑，创下了多项世界之最。在85层 建有“世界最高的游泳池”，在79-93层建 “世界最高档次的酒店”，在93层设置“世 界最高的中餐厅”，94层的观光大厅和100 层、距地面474米处建造的“观光天阁”， 是欣赏上海都市全景的最佳观光景点。
2008年5月底，上海新的“第一高”方案确定——580米的“上海中心”，被设计成盘旋上升的龙形。
截止到2009年1月23日，迪拜塔封顶，高达 818米。
在“迪拜塔”之前，纽约帝国大厦(381米)、 中国上海金茂大厦(420.5米)、美国芝加哥希尔 斯大厦(442.3米)、马来西亚双子星塔(451.9米)、 中国台北101大楼(508米)都曾是享誉世界的著名 高楼。
台北101大楼--“最高建筑物”(508米)
国家石油公司双塔大楼（452米）
高层建筑
高耸结构
（杆系结构、框架结构、 钢筋混凝土结构等）
（壳体结构、钢筋混凝土结构、 空间结构等）
大跨结构 （杆系结构、空间网架结构、薄壳结构、钢结构等）
桥梁结构 （杆系结构、悬索结构、钢筋混凝土结构等）
水利建筑
b.刚结点（特征：所联结杆件之间不能在节点处产生相对转动，即刚节点处各杆件之间的夹角在 变形前后保持不变。实例：混凝土多层刚架边柱与横梁结点构造图。）
4.支座的简化 结构与基础相连接的部分称为支座。结构通过支座将荷载传给基础和地基。支座多结构的反作用力称 为支座反力。平面结构的支座形式有以下五种：
人跑步时脚上的力量有多大？ 脚上的力量
12500N
3000N
3500N
6000N 4500N
假设人体重量为750N
高等力学问题－ 损伤累积与结构寿命 与跑步的次数有关
力学研究方法
理论分析方法 －20世纪初，探索新设计、新结构。
实验方法 －具体设计的实验验证
飞机静载试验
战斗机的仿真振动模态分析
几何特征：其横截面上两个方向的尺寸远小于长度。 典型形式：梁、刚架、拱和珩架。 （b）板壳结构——也称薄壁结构。 几何特征：其厚度远小于其余两个方向上的尺度。 典型形式：房屋建筑中的楼板、壳体屋盖及飞机和轮船的外 壳等。 （c）实体结构——也称三维连续体结构。 几何特征：结构的长、宽、高三个方向的尺寸大小相仿。 典型形式：重力式挡土墙、水工建筑中的重力坝等。
环球金融中心的多个“第一”
■ 屋顶高度世界第一：492米，超过了目前屋顶高度 世界第一的台北101大楼（480米）。 ■ 人可达到高度世界第一：474米，大楼100层的观光 天阁是世界上人能到达的最高观景平台。
■ 世界最高中餐厅：416米，设在93层的中餐厅，将 成为全球最高中餐厅。
■ 世界最高游泳池：366米，设在85层的游泳池，将 夺得“世界最高游泳池”称号。
路、桥梁、舰船、兵器等大型工业推动了近代科学技术和社会的进步。
• 20世纪中，一些高科技及其在各工业领域的应用与力学指导密不可分。
1997年环球金融中心开始桩基施工，后 因为亚洲金融风暴的影响，一度停工，至 2003年进行大楼基坑开挖，2005年11月由 中建总公司和上海建工组成的总承包联合体 负责大楼的全面施工开始。
1742年由理论家提出加固方案，在大园顶上加8道铁箍。
• 2、科学时代—由专业班子分工合作主持工程
• 1811 年巴黎麦仓园顶工程第一次建筑和结构专业分开设计。
• 1889年巴黎国际博览会建成机械馆与埃菲尔铁塔第一次完全按力学结构理论设计出来的建筑物，标
志着人类在建筑史上进入科学时代。
• 20世纪以前,在力学知识的积累、应用 和完善的基础上，渐形成和发展起来的蒸汽机、内燃机、铁
目前，加拿大多伦多电视塔高554米，但这一高度算上了天线。台北101大楼高508米，但屋顶高度仅 480米。此外，东京的胜美达通讯大楼即将动工，设计高度610米。迪拜塔2008年9月1日已达688米， 设计高度700米，传言812米，科威特打算建造1001米的标志性建筑。
金茂大厦421m
西尔斯大厦 442m
（1）活动铰支座 a.机动特征：结构可绕铰做自由转动，并允许沿支承面有微量的移动，但限制铰沿垂直于支承面方向的
移动。 b.实 例：桥梁结构中的辊轴支座及摇轴支座的等。 c.计算简图：用一根竖向支座链杆的计算简图代表。 （2）固定铰支座 a.机动特征：结构仍可绕铰转动，但沿水平和竖向的位移受到限制。 b.实 例：钢筋混凝土结构中柱子和基础连接处交叉布筋时。 c.计算简图：用交于一点的两个支座链杆表示。
（3）固定支座 a.机动特征:结构与支座联结处，既不能发生转动，也不能发生水平和竖直的移动。 b.实 例:插入杯型基础较深的混凝土柱的杯口面处。 c.计算简图:如图所示
细石混凝土填实 FxA
杯形基础
A MA
FyA
（4)滑动支座（亦称定向支座） a.机动特征:能限制结构的转动和沿一个方向上的移动，但允许结构在另一方向上有滑动的自由。 b.实 例： c.计算简图：