!完整的结构力学答案-同济大学朱慈勉!
同济大学朱慈勉版结构力学课后答案(下)
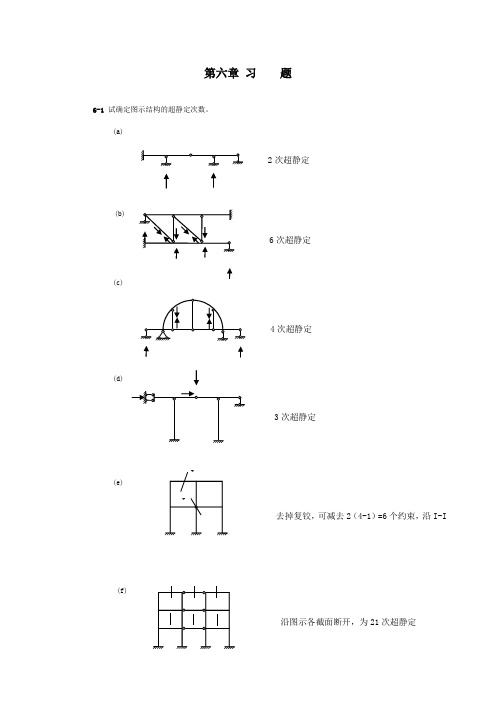
第六章习题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(f)2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 沿图示各截面断开,为21次超静定(g) 所有结点均为全铰结点(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关力法方程有何物理意义 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δ2l 3l 3II刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4题目有错误,为可变体系。
+lF 2 X=1EIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 p Q X Q Q +=11p F 21p 2(b) 解:基本结构为:l1Ml l2l 2l2lEI =常数l 2M 图Q 图F PXXl 2Ml F p 21p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)解:基本结构为:3m6m6m20kN/m1 MpM1111=∆+pXδpMXMM+=11(b)解:基本结构为:计算1M,由对称性知,可考虑半结构。
1M4a2a4a4a6810810X2计算pM:荷载分为对称和反对称。
(完整版)完整的结构力学答案-同济大学朱慈勉
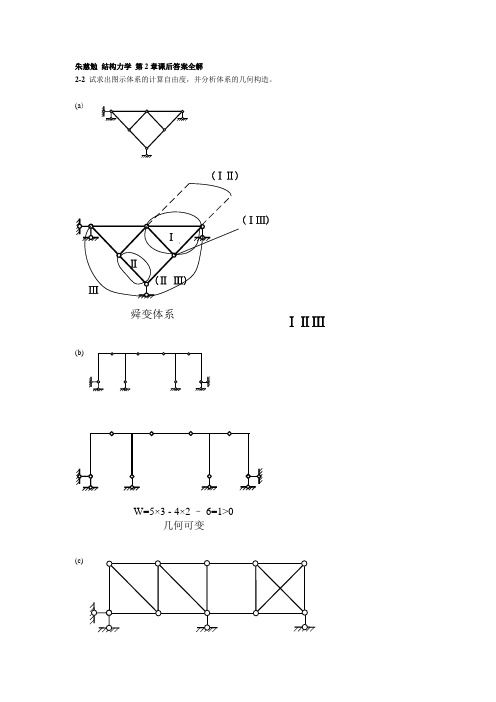
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
同济大学朱慈勉版结构力学课后答案(下)
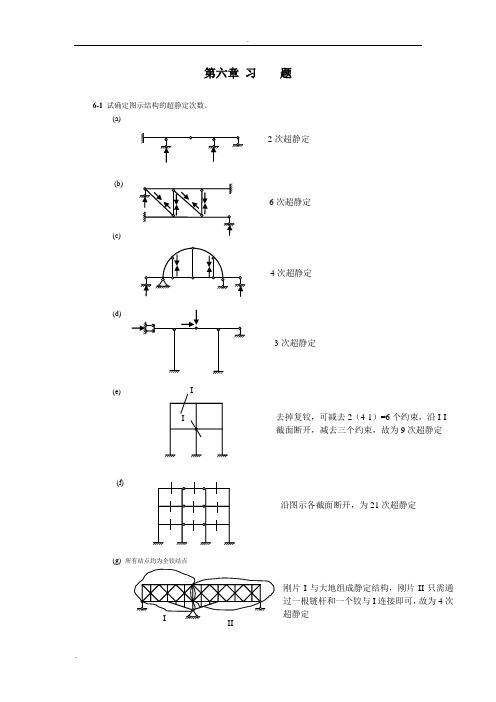
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m6m810810计算1M,由对称性知,可考虑半结构。
结构力学答案(下册).

k 23 ② k33② + k 33③
0 k34 ③
⎥
⎢
⎥ 2EI ⎢6l
⎥= ⎥
l3
⎢⎢0
-6l 18 -3l -6 2l 2 -3l 6l 2 -3l 0 -6 -3l 12
3l l2 0
⎢⎣0 0
k 43③
k 44 ③
⎥ ⎦
⎢0
0 3l l 2 0 4l 2
⎢
⎢0 0 0 0 -6 -3l
⎢⎣0
① 1→2
l
cosα
1
sin α
0
② 3→4 ③ 1→3 ④ 2→4 ⑤ 2→3
⑥ 1→4
l
1
l
0
l
0
2l − 2
2
2l
2 2
0 -1 -1
−2 2
2 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ1 ν 1 µ2 ν 2 µ3 ν 3 µ4 ν 4 T
[ ] F = Fx1 Fy1 0 -Fp Fx3 Fy3 0 0 T
1
⎥ ⎥
k⑥ = k⑤ =
⎢1
EA ⎢ 2
2l
⎢ ⎢-
1
1 2 -1
2 2⎥
⎢2 2
1 1⎥ ⎥
2 2⎦
⎢ ⎢-
1
-1
⎣2 2
4
-1 2
-
1 2
⎤ ⎥ ⎥
-1 2
-
1 2
⎥ ⎥
1
1
⎥ ⎥
2 2⎥
1 1⎥ ⎥
2 2⎦
(4)形成刚度矩阵,刚度方程
1
2
3
4
⎡4+ 2
⎢ ⎢
(参考资料)结构力学答案(下册)

2l 2 -3l
-3l 6
l2
⎥ ⎥
-3l ⎥
⎥
⎢⎣3l l 2 -3l 2l2 ⎥⎦
(4)总刚度矩阵
12
3
4
1
2
3
⎡12 6l -12 6l 0 0
⎢⎢6l 4l 2 -6l 2l 2 0 0
⎢⎡k11① k12 ①
kθ
=
⎢k ⎢
① 21
⎢0
k 22 ① + k 22 ② k32 ②
0
0⎤
⎢-12
2m
解:(1)结构标识 y
②3 ③2
①
1x
单元 局部坐标系( i → j ) 杆长
① 1→2
2
② 2→3
2
cosα
0
3 2
sin α
1
1 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ2 ν 2 θ2 θ3 T
F = [20 0 - 30 0]T
(3)建立单元刚度矩阵(l=2m)
µ2
⎡12 EI
(3)计算单元刚度矩阵
1
2
⎡12 6l -12 6l ⎤
k①
= ⎢⎡k11①
⎢⎣k
① 21
k12 ① k 22 ①
⎤ ⎥ ⎥⎦
=
2EI l3
⎢⎢6l ⎢−12 ⎢
4l 2 -6l
-6l
2l
2
⎥ ⎥
12 -6l ⎥
⎥
⎢⎣6l 2l 2 -6l 4l 2 ⎥⎦
1
2
⎡6 3l -6 3l ⎤
k ② = ⎢⎡k22② ⎢⎣k32②
③
x
1
2
同济大学朱慈勉版结构力学课后答案(下)-精品.pdf
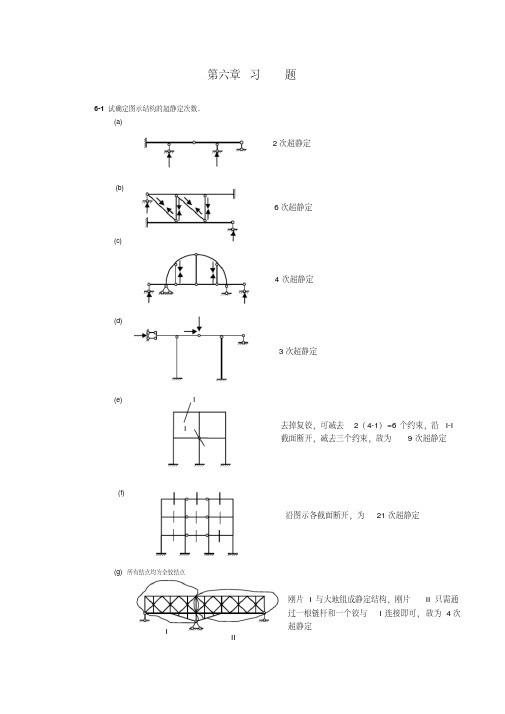
M BF 6 8.69 9 17.39 104.37 KN m
M FE 3 17.39 52.17 KN m M CG 6 8.69 52.14KN m
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 (a)
1、 2 杆的内力。设各杆的 EA 均相同。 (b)
C l
解:取 1/4 结构: q
基本结构为: q
X2 X1
l
1
M1
1
1
1 M2
q2 l
2
ql2
q 2
2
Mp
1 l2
2
l3
11
EI
l 23
3EI
12
1 1 l2 1
l2
EI 2
2 EI
22 1 l 1 1 l 1 1
3l
EI 2
2EI
1p
1 1 l ql 2 l 3
EI 3
2
4
ql 4 8EI
2 p 1 1 l ql 2 1
l
11
1 12
EI 2
EI
1 1 l ql 2
l ql 2
ql 2
1p
EI 3 2
1
8
2
1 8
12EI
11 X 1
1p 0
X1
ql 2
12
M M 1 X1 M p
ql 2 24
ql 2 12
ql 2
ql 2
24
24
ql 2
12 ql 2
12
2
2
ql
ql
M
24
24
结构力学朱慈勉版课后答案【重要】

朱慈勉 结构力学 第2章课后答案全解(b)解:基本结构为:1M2Mp M M()EIEI 1086623323326611=⨯⨯+⨯⨯+⨯⨯=δ EI=常数6m6m6mEDACB20kN/m X1 X120kN/mX2 X2363361 11 118090 15030150()03323326612=⨯⨯-⨯⨯=EI δ ()EIEI 1086623323326622=⨯⨯+⨯⨯+⨯⨯=δEI EI p 27003231806212362081632323180621121=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆EI EI p 5403231806212362081632323180621122=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯-⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆ ⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧=+=+5250540108027001082111X X EI X EIEIX EI m KN M CA ⋅=⨯-⨯-=9035253180 m KN M CB ⋅=⨯+⨯-=12035253180 ()m KN M CD ⋅-=-⨯=3056(c)解:基本结构为: ⊕6m 3m5III 10kN ·m10kN ·mEA =∞C ABD 5I12m10kN ·m10kN ·mX110kN ·m 119 339 10kN ·m10kN ·m 10 101N 1M p M()EI I E EI 5558293299233256633263111=⨯⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯=δ ()EI I E p 1442103109109231025661-=⨯⎥⎦⎤⎢⎣⎡⨯+⨯+⨯⨯+⨯⨯⨯-=∆ 01111=∆+p X δ29.11=⇒Xm KN M AC ⋅=-⨯=61.11029.19m KN M DA ⋅-=-⨯=13.61029.13 m KN M DC ⋅=⨯=87.329.13M题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
同济大学朱慈勉 结构力学 第4章习题答案(1).

同济大学朱慈勉结构力学第 4章习题答案(14-5 试用静力法作图示结构中指定量值的影响线。
(alF P =1M A 、 F Q A 、 M C 、F Q C, 10, 0(( , 1(A QA P C QC P C QC M x F F C M F x a F C M x a a x F x a =-== =≤=--=-=≥坐标原点设在 A处,由静力平衡可知当在点以左时, 当在点以右时, M A 的影响线F Q A 的影响线M C 的影响线的影响线(b1R B 、 M C 、 F Q C/(/,(0(,( ,( ,( cos ,(0 (1,( C QC A x l x l a l x a l a x a M aa x a a x l x a l xx a l F x a x l l αα=-≤≤⎧⨯-≤⎧⎪==⎨⎨⨯>-≥≥⎩⎪⎩⎧-≤≤⎪⎪=⎨⎪-≤≤⎪⎩RB RB RB RA 以为坐标原点,方向如图所示假设 F 向上为正,由静力分析知 F F F F R B 的影响线 M C 的影响线F 2a cos lα(1alα-F Q C 的影响线(cF N CD 、 M E 、 M C 、 F Q C R 3355 041(7 05121232(5,(05532,(5753,(030,(373311,(03 ,(03544371,(37 ,(37 544B NCD NCD NCDENCDCNCDRQCNCDM F x F xF x xMF xx xMxF x x xFF x x x=⨯⨯-⨯-=→=- ⎧⨯⨯--≤≤⎪⎪=⎨⎪⨯⨯≤≤⎪⎩-≤≤⎧=⎨≤≤⎩⎧⎧-≤≤-≤≤⎪⎪⎪⎪==⎨⎨⎪⎪≤≤-≤≤⎪⎪⎩⎩∑由知,3NCDF 的影响线 EM 的影响线CM 的影响线341RQCF 的影响线(d5mM C 、 F Q C 111 , ,848 RB C QC Dx x x F M F---===以点为坐标原点,向右为正1494189 8CM 的影响线 QCF 的影响线(e1,(0 0,(0, 0,(7 1,(70,(05 ,(05 , 1,(57 4,(57LR QAQA QC C x a x a F F a x a a x a x a x a x a F M a x a a a x a -≤≤≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩≤≤-≤≤⎧⎧==⎨⎨≤≤≤≤⎩⎩2a 4a F Q A 、 F Q A 、 F Q C 、 M CL R(fF R A 、 F Q B 、 M E 、 F Q F1,(02 ,(02 , 220,(25 0,(25,(02 ,(0 423,(2, ,(242220,(25 5,(45 22RA QB E QF x xx a x a F F a aa x a a x a x xx a x a a x xM a a x a F ax a aa x a x a x a a ⎧⎧-≤≤-≤≤⎪⎪==⎨⎨⎪⎪≤≤≤≤⎩⎩⎧⎧≤≤≤≤⎪⎪⎪⎪⎪⎪=-≤≤=-≤≤⎨⎨⎪⎪≤≤⎪⎪-≤≤⎪⎪⎩⎩11RA F 的影响线QB F 的影响线a/21/21/21/2E M 的影响线QF F 的影响线4-6 试用机动法作图示结构中指定量值的影响线。
同济大学朱慈勉结构力学课后习题答案

更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
同济大学 朱慈勉版 结构力学 课后答案(下)
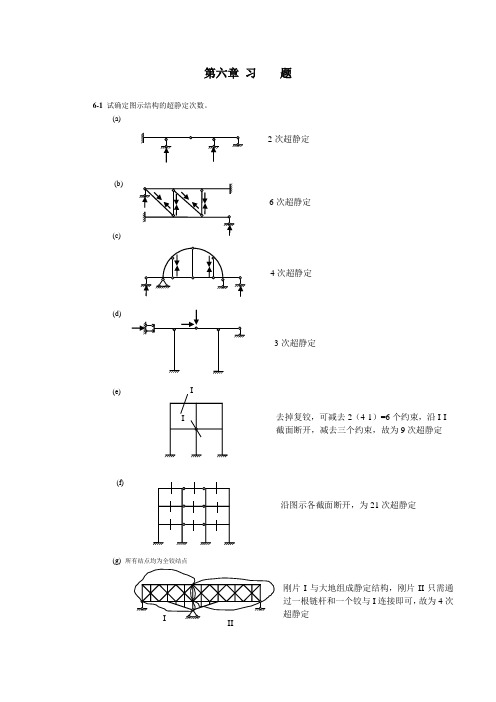
第六章 习 题6-1 试确定图示结构的超静定次数。
(a)(b)(c)(d)(e)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I 截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l 3 题目有错误,为可变体系。
+ lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Ml l 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m 6m810810计算1M,由对称性知,可考虑半结构。
(完整版)!完整的结构力学答案-同济大学朱慈勉!

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)几何不变2-4 试分析图示体系的几何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)几何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)二元杆有一个多余约束的几何不变体ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)无多余约束内部几何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体(h)ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a M4P F Q34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m42020M Q10/326/3410(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。
新版朱慈勉_结构力学_第4章课后习题(全)-新版.pdf

(b)
以 A 为坐标原点,向右为
当0
x
a 时,
分析 F 以右部分,
x/a
F
B
G
E Fp=1
F
B
G
x 轴正方向。弯矩
MF
0
F RA
1
GCD 为附属部分,可不考虑
x ()
a
ME F NE
x x a
当a
x
M E =(2a-x),F
3 a 时,去掉
AF,GCD
NE
1
M 以右侧受拉为正 附属部分结构
, 分析中间部分
18. 405.
2 1010
x (0x75).
A=1186
1
x
x
1
(153x).2
(75.
x
44 12)015.x2 27x.
742. 5(75.x
12)
2 52 102 5
1 18x153.x
09x. 1147.5(12x153).
[
] 45.(12x153).
25 5
当75.x1时2d,A03x. 27.0 x9。此A=时29.-7801.15-7.425=4.725 dx
Fy
0
F N2
3x 16 d
x 4d
F N2 5 2
x 2
4d 5x
16 d
F N1
5 4
2
F RB
0
5
2
F RA
5
F N1 F N1
5x 16 d
5x
5
16 d
2
F N1
F N2
35 16
F N3
1
15
结构力学朱慈勉习题答案

结构力学朱慈勉习题答案结构力学朱慈勉习题答案结构力学是工程学中非常重要的一门学科,它研究物体在外力作用下的变形和破坏行为。
学习结构力学,需要通过大量的习题来加深对理论的理解和应用能力的培养。
本文将为大家提供一些结构力学朱慈勉习题的答案,希望能够对大家的学习有所帮助。
1. 问题描述:一根长为L,截面积为A的均匀杆件,两端分别固定在两个支座上。
当杆件受到均匀分布的荷载q时,求支座反力。
解答:根据结构力学的基本原理,杆件在平衡状态下,支座反力的合力等于荷载的合力。
因此,我们可以通过计算荷载的合力来求得支座反力。
荷载的合力可以通过荷载的大小乘以荷载的作用长度得到。
在这个问题中,荷载的大小为q,作用长度为L。
所以荷载的合力为F = qL。
由于杆件在平衡状态下,支座反力的合力等于荷载的合力,所以支座反力的大小为F = qL。
2. 问题描述:一根长为L,截面积为A的均匀杆件,两端分别固定在两个支座上。
当杆件受到一点荷载P时,求支座反力。
解答:与上一个问题类似,我们可以通过计算荷载的合力来求得支座反力。
由于荷载是作用在一点上的,所以荷载的合力等于荷载的大小P。
因此,支座反力的大小为F = P。
3. 问题描述:一根长为L,截面积为A的均匀杆件,两端分别固定在两个支座上。
当杆件受到均匀分布的荷载q时,求杆件的弯矩分布。
解答:在这个问题中,我们需要求解杆件的弯矩分布。
弯矩是指杆件在外力作用下产生的曲率效应。
根据结构力学的基本原理,杆件的弯矩可以通过荷载和杆件的几何形状来计算。
在这个问题中,杆件受到均匀分布的荷载q,所以杆件上的任意一点的荷载大小为q。
杆件的截面积为A,所以杆件上的任意一点的弯矩大小为M = qL/2。
由此可见,在这个问题中,杆件的弯矩分布是线性的,即弯矩随着位置的增加而线性增加。
4. 问题描述:一根长为L,截面积为A的均匀杆件,两端分别固定在两个支座上。
当杆件受到均匀分布的荷载q时,求杆件的挠度分布。
!完整的结构力学答案-同济大学朱慈勉!

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aaaa a2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m 3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m 6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
《结构力学》 朱慈勉

混凝土结构理论作业(受弯部分)混凝土结构设计原理(第四版)第一部分简答题P69 思考题——3.2 3.4 3.6 第二部分计算题P70 习题——3.1,3.2,3.4 在3.1 题目的基础上,增加如下4 问,题目间互相独立(1)其他条件不变,若a). 将f c 提高10%,重新计算所需的A s1 ; b). 将f y 提高10%,重新计算所需的A s2 ; c). 将b 提高10%,重新计算所需的A s3 ; d). 将h 提高10%,重新计算所需的A s4 ; 对比A s1 、A s2 、A s3 、A s4 与A s (原计算面积)的关系,说明哪个因素影响最大,为什么?(2)其他条件不变,若在此梁的拉区配置3φ18,请问此梁的极限受弯承载力M 为多少?(3)若已知压区配置了2φ16 的钢筋,重新计算所需要的钢筋面积A s5 ,并与A s (原计算面积)进行对比。
(4)若此题截面变成如下图情况,重新计算所需要的钢筋面积A s6 ,并与原计算面积A s 进行对比。
550 1 0 0 5 0 0 第三部分证明题或公式推导题(后两题选作,建议学有余力的同学完成,可增加对课本知识的理解)(1)推导ξ b 与ρ b 或称ρ max 之间的关系(即推导书本中P49 的公式3-19),并计算C25 及C30 混凝土情况下HPB235、HRB335、HRB400 钢筋的ρ max 数值。
(2)推导超筋梁的钢筋应力σ s 与相对受压区高度ξ 之间的关系。
(假设平截面假定仍然成立,用几何关系和物理关系,利用σ s =E s ε s 及ε s 与ε cu ,x,h 0 之间的关系进行推导)(3)A、B 二梁其他参数完全相同,唯有配筋量不同,其中A 梁为超筋梁,B 梁为适筋梁。
证明:A 梁的极限抗弯承载力M uA 大于B 梁的极限抗弯承载力M uB 。
结构力学章答案
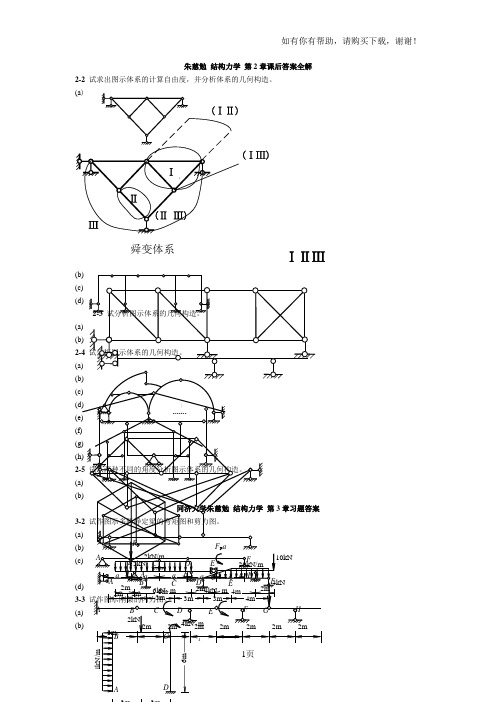
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b) (c) (d)2-3 试分析图示体系的几何构造。
(a) (b)2-4 试分析图示体系的几何构造。
(a) (b) (c) (d) (e) (f) (g) (h)2-5 试从两种不同的角度分析图示体系的几何构造。
(a) (b)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a) (b) (c) (d) 3-3 试作图示刚架的内力图。
(a) (b) AB C a aa a a F P aD E F F P2m 6m 2m 4m 2m A B C D 10kN 2kN/m 3m 2m 2m A B C E F 15kN 3m 3m 4m 20kN/mD 3m 2m 2m 2m2m 2m 2m AB C D E F G H 6kN·m 4kN ·m 4kN 2m4kN ·m2kNC B(c)(d)(e) (f) 3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a) (b) (c) (d)(e) (f)3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
3-6 试作图示刚架的弯矩和剪力图。
(a) (b)5.75111MQ4.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩:对点求矩:2 2.93.754.252.1(c)6m 10kN3m3m40kN ·m A B CD 3m 3m 2kN/m6kN 6m 4kN A B C D 2kN 6m2m2m 2kN 4kN ·m A C B DE 4m4mA B C4m 1k N /mD4m4kNA B C2m 3m 4m2kN/m lBC EFx DAq llx8016016016010060401680/38030MQ8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/316/38/34/343543520354/3MQ88414233:41614284()4:441426()38(),03DA B B B B A A M A V V C H H H V =⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a )ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(Ⅱ Ⅲ)舜变体系`ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)2-3 试分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(Ⅱ Ⅲ)几何不变W=3×3 - 2×2 – 4=1>0可变体系ⅠⅡⅢ(ⅠⅡ)(ⅠⅢ)(ⅡⅢ)几何不变2-4 试分析图示体系的几何构造。
(a)(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)ⅠⅡⅢ几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系ⅢⅠⅡ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)几何不变(d)(ⅠⅡ)ⅢⅠⅡ(ⅡⅢ)(ⅠⅢ)二元杆有一个多余约束的几何不变体ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)ⅠⅡⅢ(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)无多余约束内部几何不变ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体(h)ⅠⅡⅢ(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)二元体多余约束W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)(ⅠⅢ)几何不变同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)4P F a2P F a 2P F a M4P F Q34P F 2P F(b)ABCaa aaaF P a DEFF P2m6m2m4m2mABCD10kN2kN/m42020M Q10/326/3410(c)21018018040M1560704040Q(d)3m2m2mA B CEF15kN 3m3m4m20kN/mD 3m2m2m2mA2m 2m2mABCD E FG H 6kN ·m4kN ·m 4kN2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ1820(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D3030301101010QM 210(c)664275MQ(d)3m3m2kN/m6kN6m4kNAB CD2kN6m2m 2m2kN4kN ·m ACBDE444444/32MQN(e)44814``(f)4m 4mABC4m1k N /mD 4m4kNA B C2m3m4m2kN/m222220 0.815M QN3-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)F P(d)M(e)(f)F PF P3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件,确定E、F两铰的位置。
lB CE FxDAql lxB C EFDA28ql M2221()222116121618c B C BC C q ql M l x x qx xM M M M ql ql x ql x l=-+===∴=∴=∴=中F D()2ql x -3-6 试作图示刚架的弯矩和剪力图。
(a)909045135405MQ2B 209(4.53)645()0.5209459405,135()453135,0.5209900.520990F F E E CF CD BA R R M R M M M ⨯⨯-=⨯∴=↑=⨯⨯-⨯==↑=⨯==⨯⨯==⨯⨯=对点求矩5.75111MQ4.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩:对点求矩:2 2.93.754.252.1(c)8016016016010060401680/38030MQ8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/316/38/34/343543520354/3MQ88414233:41614284()4:441426()38(),03DA B B B B A A M A V V C H H H V =⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)2FaF2Fa2Fa F F F2F----+2Fa2Fa2FaMQ02(),020322222(),2()4(),0C B p E B F BP H P F H P F P D P D M V F M H V MF a a H F a V aH F V F H F V =→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑(f)88利用对称性进一步简化BH BV IH IV 88:4(),4()4(),4(),42810B B I I A H KN V KN H KN V KN M N m=→=↓=-←=-↑=⨯=•可知88888844444444-+---+++(g)qa 2aaaaaa aA B CG HFJDE I qq22qa 232qa 2qa22qa 2qa 232qa 232qa 22qa 2qaqa2qa1.5qa1.5qa22221.5()21.50 1.5()0,, 1.5C C A A D GF GH H qa qa H a H qa qa a H a H qa H M qa M qa +=⨯→=→⨯+⨯=→=-←===对点求矩:对F 点求矩:同济大学朱慈勉结构力学第5章习题答案5-1 试回答:用单位荷载法计算结构位移时有何前提条件?单位荷载法是否可用于超静定结构的位移计算?aAF P F PBCa a a aD ENCD NCE NBE NAD NBC NAC DEF F0, F F2 F F FA B P P P PR R F F F F=========-由对称性分析知道1-22-2211212121222-22N NP122(2)2F F1()2 6.832222()P PPcx PF a F al F aF aEA EA EA EA EA⨯⨯-⨯-⨯-⨯-⨯∆==⨯+⨯+=↓∑5-4已知桁架各杆截面相同,横截面面积A=30cm2,E=20.6×106N/cm2,F P=98.1kN。
试求C点竖向位移yCΔ。
k5PF -5PF -5PF -5PF -54P F 54P F 54PF2PF 2PF 25544P P P P F F F F ===NAD NAE NEC NEF 由节点法知:对A 节点 F =-5F 对E 节点 F Fk1 115(122516()()24)4 11.46 ()N NP yc P P P F F l F F F EA EA cm =∆==⨯⨯⨯+⨯⨯+⨯-⨯⨯=↓∑NAD NAE 由节点法知:5对A 节点 F =-F 25-5525-5 已知桁架各杆的EA 相同,求AB 、BC 两杆之间的相对转角B Δθ。
8kN42424242-42-4244884444-4-4-8-8-12-12杆的内力计算如图所示施加单位力在静定结构上。
其受力如图142142141414-28141424-其余未标明的为零力杆11(1242)N NP BF F l EA EAθ∆==-∑5-6 试用积分法计算图示结构的位移:(a )yB Δ;(b )yC Δ;(c )B θ;(d )xB Δ。
211232113421yc 1004142B ()1()26()111 ()()()26111 =()30120p llp q q q x x q l q qM x q x x lM x x q q M x M x dx q x x dx EI EI l q l q l EI -=+-=+=-∴∆=⨯=++⎰⎰以点为原点,向左为正方向建立坐标。
显然,(b)22q l 254q l PM l74l M2224113153251315127()()324244342243416yc ql q l l ql l ql l l l l l ql EI EI ∆=⨯⨯+⨯⨯+⨯⨯+⨯⨯+⨯⨯=↓ABq 2q 1 lEI l3l4ABCql EI=常数22201()(sin )12(1cos )2()1111[(sin )12(1cos )]2(8-3)-1.42=()EI EIB M R R M R R Rd EI πϕϕϕϕθϕϕϕπ=⨯-⨯-==⨯⨯-⨯-=⎰逆时针(d)ϕθqds qRd θ=20()sin()(1cos )M qRd R qR ϕϕθϕθϕ=⨯-=-⎰2240()sin 111()()(1cos )sin ()2xBM R M M ds qR R Rd qR EI EI EIπϕϕϕϕϕϕϕ=∆==-=←⎰⎰5-7 试用图乘法计算图示梁和刚架的位移:(a )yC Δ;(b )yD Δ;(c )xC Δ;(d )xE Δ;(e )D θ;(f )yE Δ。
(a)OAB1kN/m2kNR =2m4m BORAqEI=常数3212121A x 以为原点,向右为正方向建立坐标26yc 0()51(0x 3)2()13 (3x 6)2181()()()M x x x x M x x M x M x dx EI EI =-⎧≤≤⎪⎪=⎨⎪-≤≤⎪⎩∆=⨯=↓⎰(b)6m2m2m2kN/m 6kN AB C D E1m EI=常数A0.5163PM M611211(23)623662384311(32162(3)(6))62225+612()62yD EI EI EI EI EI∆=⨯⨯-⨯⨯⨯⨯⨯⨯+⨯⨯⨯+⨯⨯+-+⨯-⨯⨯⨯=↓(c)2kN 2kN 2EI6mA DC B EI EI 2k N /m3m3m3m2323611183036PM642M23(21822182230423018423042366436630)6261226918 +(2366)63()638xc EI EI EI EI ∆=⨯⨯+⨯⨯+⨯⨯+⨯+⨯+⨯⨯+⨯⨯+⨯+⨯⨯⨯⨯⨯+⨯⨯⨯⨯=→(e)EIA BC EIEIDk4kN2kN/m6mk6.56.513.542261216MP M181211110(1231)(2121)2612141111311(1016)(226)(416)13.5326232486227=()316PD PM Mds F FEI k EI EIEI EI EI kEI kθ=+=⨯⨯⨯+⨯⨯-⨯⨯⨯-⨯⨯-⨯⨯⨯⨯+⨯⨯-+∑⎰顺时针5-9 图示结构材料的线膨胀系数为α,各杆横截面均为矩形,截面高度为h。
