24)线面垂直的性质定理
线面定理性质

线面、面面平行和垂直的定理性质
一、线面平行
1、判定定理:平面外一条直线与平面内一条直线平行,那么这条直线与这个平面平行。
符合表示:
2、性质定理:如果一条直线与平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行。
符号表示:
二、面面平行
1、判定定理:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面平行。
符号表示:
变形:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行。
2、性质定理:如果两个平面平行同时与第三个平面相交,那它们的交线平行。
符号表示:
(更加实用的性质:一个平面内的任一直线平行另一平面)
三、线面垂直
1、判定定理:如果一条直线与一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
符号表示:
(经常考到这种逻辑)在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。
符号表示:
三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。
2、性质定理:垂直同一平面的两条直线互相平行。
(更加实用的性质是:一个平面的垂线垂直于该平面内任一直线。
)
变形:垂直于同一条直线的两个平面平行
四、面面垂直
1、判定定理:经过一个平面的垂线的平面与该平面垂直。
(如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直)
其他:两个平面相交,如果它们所成的二面角是直角,则这两个平面互相垂直。
2、性质定理:已知两个平面垂直,在一个平面内垂直于交线的直线垂直于另一个平面。
线线垂直、线面垂直、面面垂直的判定和性质

空间中的垂直关系1.线面垂直直线与平面垂直的判定定理:如果 ,那么这条直线垂直于这个平面。
推理模式:直线与平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线 。
2.面面垂直两个平面垂直的定义:相交成 的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直⇒面面垂直)如果 ,那么这两个平面互相垂直。
推理模式:两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的 的直线垂直于另一个平面。
一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面就是判定定理,而从后面推出前面就是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,下面举例说明.例题:1.如图,AB 就是圆O 的直径,C 就是圆周上一点,PA ⊥平面ABC.(1)求证:平面PAC ⊥平面PBC;(2)若D 也就是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.2、如图,棱柱111ABC A B C -的侧面11BCC B 就是菱形,11B C A B ⊥证明:平面1AB C ⊥平面11A BC3、如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 就是棱CC 1的中点 (Ⅰ)求异面直线A 1M 与C 1D 1所成的角的正切值;(Ⅱ)证明:平面ABM ⊥平面A 1B 1M 14、如图,AB 就是圆O的直径,C就是圆周上一点,PA ⊥平面ABC .若AE ⊥PC ,E为垂足,F就是PB 上任意一点,求证:平面AEF ⊥平面PBC .5、如图,直三棱柱ABC —A 1B 1C 1 中,AC =BC =1,∠ACB =90°,AA 1 =2,D 就是A 1B 1 中点.(1)求证C 1D ⊥平面A 1B ;(2)当点F 在BB 1 上什么位置时,会使得AB 1 ⊥平面C 1DF ?并证明您的结论6、S 就是△ABC 所在平面外一点,SA ⊥平面ABC,平面SAB⊥平面SBC,求证AB ⊥BC 、7、在四棱锥中,底面ABCD 就是正方形,侧面VAD 就是正三角形,平面VAD ⊥底面ABCD证明:AB ⊥平面VAD8、如图,平行四边形ABCD 中,60DAB ︒∠=,2,4AB AD ==,将CBD ∆沿BD 折起到EBD ∆的位置,使平面EDB ⊥平面ABD 、求证:AB DE ⊥VDC B A SAB9、如图,在四棱锥ABCD P -中,平面PAD ⊥平面ABCD,AB=AD,∠BAD=60°,E 、F 分别就是AP 、AD 的中点求证:(1)直线EF ‖平面PCD;(2)平面BEF ⊥平面PAD10、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,AB AS BC AB =⊥,、过A 作SB AF ⊥,垂足为F ,点G E ,分别就是棱SC SA ,的中点。
24)线面垂直的性质定理

两个平面垂直,则一个平面内垂直于交线 的直线与另一个平面垂直。
β a
符号语言:
l
α A
al 作用: 面面垂直线面垂直
l a a
何时用:已知面面垂直时. 关键:在一个平面内作(找)出垂直于交线的直线.
© 2006 NENU 济南九中高三数学备课组
直线与平面垂直的性质2:
如果两条平行直线中的一条垂直于一个 平面,那么另一条也垂直于这个平面.
a / /b 符号语言: a
图形语言:
b
a b
O
© 2006 NENU
济南九中高三数学备课组
直线与平面垂直的性质3:
如果两条直线同时垂直于一个平面, 那么这两条直线平行.
a 符号语言: b
线线垂直
线面垂直
关键:线不在多,在于相交
二、新知探究
如图,长方体ABCD—A1B1C1D1中,棱 AA1,BB1,CC1,DD1 所在直线与底面ABCD的 位置关系如何?它们彼此之间具有什么 位置关系? C1
D1
B1 C B
A1
D
A
无忧PPT整理发布
3 线面垂直的性质定理:
垂直于同一平面的两直线互相平行.
图形语言:
a // b
a b
O
简述为:线面垂直 线线平行
© 2006 NENU 济南九中高三数学备课组
温故知新
面面垂直的判定方法: 1、定义法: 找二面角的平面角 2、判定定理: 要证两平面垂直,只要在其中一个平面 内找到另一个平面的一条垂线。
说明该平面角是直角。
(线面垂直面面垂直)
© 2006 NENU 济南九中高三数学备课组
线面垂直面面垂直的判定定理和性质定理

线面垂直面面垂直的判定定理和性质定理
线面垂直面面垂直的判定定理是指两个射线有一定的关系即垂直面是垂直的,其中一个起点在另一个终点上。
简单来说就是两线垂直于一个面,则这两条线的垂直的面也是垂直的。
由线面垂直面面垂直的判定定理可以得出线面垂直面面垂直的性质定理,这是建立在线面垂直面面的判断定理的基础之上的定理。
线面垂直面面垂直的性质定理:若两个射线分别与两个平面成垂直,则它们两个平面所成的平面也是垂直的。
该定理也可以用图形来表示,如下图所示:
从图中可以看出,射线AB和CD都是垂直于两个平面m、n,其中AB与m,CD与n成垂直。
而平面m和n又组成一个新平面mn,根据线面垂直面面垂直的性质定理可以知道AB与mn也是垂直的,同样CD也与mn是垂直的。
线面垂直面面垂直的定理主要应用在几何中,它可以用来证明两个平面的面积计算方法是正确的,也可以用来证明两个球面的夹角是垂直的。
同时,它同样可以应用在工程技术中,例如对于地面上的建筑物,我们可以用它来判断其是否与地面垂直。
由此可以看出,线面垂直面面垂直的判定定理和性质定理对于各类几何计算和工程技术应用具有十分重要的意义。
它能有效地帮助人们判断两面之间是否是垂直的关系,从而实现各种几何计算和工程技术应用。
线面垂直的性质定理

b
α
a
b ∥α
无忧PPT整理发布
性质定理: a ⊥α , b ⊥α
1.类比探究:
①交换“平行”与“垂直” a ⊥α , b ∥α a⊥ b ②交换“直线”与“平面” a ⊥α , β ∥α a ⊥β
a ∥b
变式探究
a
b
α
b
α
a
2.逆向探究:
交换“条件”与“结论” ①a ⊥α , a ⊥ b
a ∥b
变式探究
2.逆向探究:
交换“条件”与“结论” ①a ⊥α , b ∥α
a⊥ b
无忧PPT整理发布
性质定理: a ⊥α , b ⊥α
1.类比探究:
①交换“平行”与“垂直” a ⊥α , b ∥α a⊥ b ②交换“直线”与“平面” a ⊥α , β ∥α a ⊥β
a ∥b
变式探究
a
b
α
2.逆向探究:
①交换“平行”与“垂直” a ⊥α , b ∥α a⊥ b ②交换“直线”与“平面” a ⊥α , β ∥α a ⊥β
a ∥b
变式探究
a
b
c
无忧PPT整理发布
2.逆向探究:
①
α 交换“条件”与“结论” β
性质定理: a ⊥α , b ⊥α
1.类比探究:
①交换“平行”与“垂直” a ⊥α , b ∥α a⊥ b ②交换“直线”与“平面” a ⊥α , β ∥α a ⊥β
1.类比探究:
①交换“平行”与“垂直” a ⊥α , b ∥α a⊥ b ②交换“直线”与“平面”
a ∥b
变式探究
b
l
a
线面垂直性质

符号语言:a b
a // b
ab
图形语言:
O
简述为:线面垂直 线线平行
已知:直线l∥平面a 则有:直线l上各点到平面a的距离相等。
直线和平面的距离:
b A lB
如果一条直线和一个平面平
行,这条直线上任意一点到
这个平面的距离,叫做这条
A’
B’
直线和这个平面的距离.
例:如图,P是△ABC所在平面外的一 点,PA⊥PB , PB⊥PC , PC⊥PA , H是 △ABC的垂心 , 求证:PH⊥平面ABC
线面垂直的性质
复习
直线与平面垂直的判定定理:
如果一条直线和一个平面内的两条相交直线 都垂直,那么这条直线垂直于这个平面
符号表示:
m ,n
l
m nP
l
l m,l n
P
mn
简记为:线线垂直
线面垂直
直线与平面垂直的性质1:
如果一条直线垂直于一个平面,那么这 条直线垂直于面上任意直线.(定义)
符号语言:a b
a
b
ab
图形语言:
O
简述为:线面垂直 线线垂直
直线与平面垂直的性质2:
推论1
如果两条平行直线中的一条垂直于一个 平面,那么另一条也垂直于这个平面.
符号语言:a / /b
a
b a b
图形语言: O
直线与平面垂直的性质3:
推论2
如果两条直线同时垂直于一个平面,
那么这两条直线直
C EH D
B
线线垂直
练习
12.如图,在三棱锥V ABC中,VA VC, AB BC 求证VB AC
V
.D
C
A
考点24 空间几何中的垂直(解析版)

考点24 空间几何中的垂直知识理解一.直线与平面垂直(1)直线和平面垂直的定义:直线l与平面α内的任意一条直线都垂直,就说直线l与平面α互相垂直(2)直线与平面垂直的判定定理及性质定理:二.平面与平面垂直的判定定理与性质定理三.证明线线垂直的思路平行四边形:正方形、菱形、矩形图形三角形:等腰(等边)三角形--取中点正余弦定理边关系或边长勾股逆定理线面垂直的定义面面垂直的性质⎧⎧⎪⎪⎨⎪⎩⎪⎪⎧⎪⎪⎨⎨⎪⎩⎪⎪⎪⎪⎩ 考向一 线面垂直【例1】3.(2021·江西吉安市·高三期末节选)如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形,//AD BC ,90ADC ∠=︒,22AD DC BC ===,PAD △为正三角形,Q 为AD 的中点,求证:AD ⊥平面PBQ【答案】证明见解析【解析】∵PAD △为正三角形,Q 为AD 的中点,∴PQ AD ⊥.∵//AD BC ,2AD DC BC ==,Q 为AD 的中点.∴四边形BCDQ 为平行四边形,∴//BQ CD . 又90ADC ∠=︒,∴90AQB ∠=︒,即BQ AD ⊥.又PQBQ Q =,∴AD ⊥平面PBQ.考向分析【举一反三】1.(2021·河南信阳市节选)如图所示,四棱锥S ABCD -中,//AB CD ,AD DC ⊥,2224CD AD AB SD ====,SD ⊥平面ABCD ,求证:BC ⊥平面SBD【答案】证明见解析【解析】证明://,,2AB CD AD DC AB AD ⊥==,BD BC ∴==又4CD =,222CD BD BC ∴=+,故BC BD ⊥, 又SD ⊥平面,ABCD BC ⊂平面ABCD ,BC SD ∴⊥, 又SD BD D =,BC ∴⊥平面SBD .2.(2021·江西赣州市节选)如图,已知三棱柱111ABC A B C -的所有棱长均为2,13B BA π∠=,证明:1B C ⊥平面1ABC【答案】证明见解析【解析】证明:如图取AB 中点D ,连接1,B D CD .因为四边形11BCC B 为菱形,所以11B C BC ⊥ 又因为三棱柱的所有棱长均为2,13B BA π∠=,所以ABC 和1ABB △是等边三角形,所以1,B D AB CD AB ⊥⊥因为1,B D CD ⊂平面11,B CD B D CD D ⋂=,所以AB ⊥平面1B CD 所以1B C AB ⊥,而1BC AB B ,所以1B C ⊥平面1ABC3.(2020·山东德州市节选)如图,四棱锥P ABCD -中,四边形ABCD 是边长为2的正方形,PAD ∆为等边三角形,,E F 分别为PC 和BD 的中点,且EF CD ⊥,证明:CD ⊥平面PAD【答案】证明见解析【解析】如图所示,连接AC ,由ABCD 是边长为2的正方形, 因为F 是BD 的中点,可得AC 的中点,在PAC △中,因为,E F 分别是,PC AC 的中点,可得//EF PA , 又因为EF CD ⊥,所以PA CD ⊥,又由AD CD ⊥,且ADAP A =,所以CD ⊥平面PAD .考向二 面面垂直【例2】(2021·河南高三期末节选)如图,直四棱柱1111ABCD A B C D -的底面ABCD 为平行四边形,3AD =,5AB =,3cos 5BAD ∠=,1BD DD =,E 是1CC 的中点,求证:平面DBE ⊥平面1ADD【答案】证明见解析【解析】由题意可得2222cos 16BD AD AB AB AD BAD =+-⨯∠=, 所以222AD BD AB +=,因此AD BD ⊥. 在直四棱柱1111ABCD A B C D -中,1DD ⊥平面ABCD ,BD ⊂平面ABCD ,所以1.DD BD ⊥又因为1ADDD D =,1,AD DD ⊂平面1ADD ,所以BD ⊥平面1ADD ,因为BD ⊂平面DBE ,所以平面DBE ⊥平面1ADD . 【举一反三】1.(2021·河南焦作市节选)如图所示,在四棱锥РABCD -中,底面ABCD 是菱形,PA ⊥平面,ABCD 点Q 为线段PC 的中点,求证:平面BDQ ⊥平面PAC【答案】证明见解析【解析】因为四边形ABCD 是菱形,所以,AC BD ⊥ 因为PA ⊥平面,ABCD BD ⊂平面,ABCD 所以,BD PA ⊥ 又因为,PA AC A ⋂=所以BD ⊥平面,PAC 因为BD ⊂平面,BDQ 所以平面BDQ ⊥平面PAC .2.(2021·山东青岛市·高三期末节选)如图,在直角梯形ABED 中,//BE AD ,DE AD ⊥,BC AD ⊥,4AB =,BE =将矩形BEDC 沿BC 翻折,使得平面ABC ⊥平面BCDE ,若BC BE =,证明:平面ABD ⊥平面ACE【答案】证明见解析【解析】证明:连接BD ,因BC BE =所以BD CE ⊥ 因为平面ABC ⊥平面BCDE ,平面ABC 平面BCDE BC =,AC BC ⊥所以AC ⊥平面BCDE因为BD ⊂平面BCDE ,所以AC BD ⊥ 因为ACCE C =,所以BD ⊥平面ACE因为BD ⊂平面ABD ,所以平面ABD ⊥平面ACE3.(2021·安徽马鞍山市节选)如图,BE ,CD 为圆柱的母线,ABC 是底面圆的内接正三角形,M 为BC 的中点,证明:平面AEM ⊥平面BCDE【答案】证明见详解【解析】根据题意可得,AM BC ⊥. 又BE 为圆柱的母线,BE ∴⊥平面ABC .BE AM ∴⊥,BC BE B =,AM ∴⊥平面BCDE .又AM ⊂平面AEM ,∴平面AEM ⊥平面BCDE .考向三 线线垂直【例3】(2021·江西宜春市·高安中学节选)如图,四棱锥P ABCD -的底面ABCD 是边长为2的菱形,60BAD ∠=,已知2,PB PD PA ===,E 为PA 的中点,求证PC BD ⊥【答案】证明见解析【解析】,AC BD 交点为O ,连接PO ,ABCD 是边长为2的菱形,,AC BD O ∴⊥是,AC BD 的中点,,PD O B BD P P =∴⊥,又PO ⊂平面POC ,AC ⊂平面POC ,POAC O =,BD ∴⊥平面POC ,PC ⊂平面POC ,.C BD P ∴⊥【举一反三】1.(2021·江苏南通市·高三期末节选)如图,在四棱锥A BCDE -中,//BC DE ,22BC DE ==,BC CD ⊥,F 为AB 的中点,BC EF ⊥,求证:AC BC ⊥【答案】证明见解析【解析】取AC 中点M ,连接FM ,DM ,,F M 分别为AB ,AC 中点,12FMBC ∴, 1,2DEBC FM DE ∴, ∴四边形DEFM 是平行四边形,//DM EF ∴,,EF BC DM BC ⊥∴⊥,,,CD DM CD DM ⊥⊂平面ACD ,CD DM D ⋂=,BC ∴⊥平面CDM ,AC ⊂平面CDM ,BC AC ∴⊥;2.(2020·山东德州市节选)如图,已知四棱锥P ABCD -中,底面ABCD 为菱形,60,ABC PA ∠=︒⊥平面,,ABCD E F 分别为,BC PA 的中点.(1)求证:AE PD ⊥; (2)求证://EF 平面PCD .【答案】(1)证明见解析;(2)证明见解析.【解析】证明:(1)连AC ,60ABC ∠=,底面ABCD 为菱形,ABC ∴是等边三角形, BE EC =,AE BC ∴⊥,又//BC AD ,AE AD ∴⊥,又PA ⊥面,ABCD AE ⊂面ABCD ,PA AE ∴⊥, PA AD A ⋂=,AE ∴⊥面,PAD PD ⊂面PAD ,AE PD ∴⊥.()2取PD 的中点M ,连,FM MC ,PF FA =,所以11//,22FM AD FM AD =, 又11//,22EC AD EC AD =, //,FM EC FM EC ∴=, ∴四边形FECM 是平行四边形,//EF MC ∴,又EF ⊄面,PCD MC ⊂面PCD ,//EF ∴面PCD .3.(2021·山东枣庄市节选)如图,四棱锥P ABCD -的侧面PAD △是正三角形,底面ABCD 是直角梯形,90BAD ADC ∠=∠=,22AD AB CD ===,M 为BC 的中点,求证:PM AD ⊥【答案】(1)证明见解析;(2)7. 【解析】证明:取AD 中点N ,连PN ,NM , 因为PAD △是正三角形,所以PNAD .又M 是BC 中点,所以//NM AB .因为90BAD ∠=,即AB AD ⊥.所以NM AD ⊥,因为NM PN N ⋂=,NM 、PN ⊂平而PMN , 所以AD ⊥平面PMN ,PM ⊂平面PMN ,所以AD PM ⊥.1.(2021·山东泰安市·高三期末节选)如图,在四棱锥P ABCD -中,底面ABCD 是菱形,60BAD ∠=︒,PB PD =,F 为PC 上一点,过AF 作与BD 平行的平面AEFG ,分别交PD ,PB 于点E ,G ,证明:EG ⊥平面PAC【答案】证明见解析【解析】证明:连接BD ,交AC 于点O ,连接PO . ∵//BD 平面AEFG ,平面PBD平面AEFG EG =,BD ⊂平面PBD ,∴//EG BD .∵底面ABCD 是菱形,∴AC BD ⊥,且O 为AC ,BD 中点,强化练习又PB PD =,∴PO BD ⊥,又AC PO O =,,AC PO ⊂平面PAC ,∴BD ⊥平面PAC ,∴EG ⊥平面PAC .2.(2021·浙江金华市·高三期末节选)在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PA PB AB ====,)证明:PC ⊥平面ABC【答案】证明见解析;【解析】证明:取AB 中点D ,连接PD ,DC∵PA PB =,AC BC =,则AB PD ⊥,AB DC ⊥, 而PD DC D ⋂=,∴AB ⊥平面PDC , 因为PC ⊂平面PDC ,故AB PC ⊥.在ABC 中,AB ==,故222AB AC BC =+,∴BC AC ⊥.又∵平面PAC ⊥平面ABC ,且交线为AC ,BC ⊂平面ABC , ∴BC ⊥平面PAC ,因为PC ⊂平面PAC ,故BC PC ⊥. 因为AB BC B ⋂=,∴PC ⊥平面ABC .3.(2021·河南焦作市节选)如图,四棱锥P ABCD -的底面为正方形,PA ⊥底面ABCD ,E ,F ,H 分别为AB ,PC ,BC 的中点,求证:DE ⊥平面PAH【答案】证明见解析【解析】因为PA ⊥底面ABCD ,DE ⊂底面ABCD ,所以PA DE ⊥,因为E ,H 分别为正方形ABCD 的边AB ,BC 的中点,,,AB DA BH AE HBA EAD ,所以Rt ABH Rt DAE ≌△△,所以BAH ADE ∠=∠,由90AED ADE ∠+∠= 所以90BAH AED ∠+∠=,所以DE AH ⊥, 因为PA ⊂平面PAH ,AH ⊂平面PAH ,PA AH A ⋂=,所以DE ⊥平面PAH .4.(2021·浙江温州市节选)如图,已知三棱锥P ABC -﹐PC AB ⊥,ABC 是边长为形,PB =60PBC ∠=,点F 为线段AP 的中点,证明:PC ⊥平面ABC【答案】证明见解析【解析】在PBC 中,PB =BC =60PBC ∠=,由余弦定理可得2222cos 36PC PB BC PB BC PBC =+-⋅∠=,222PC BC PB ∴+=,PC BC ∴⊥,PC AB ⊥,AB BC B ⋂=,PC ∴⊥平面ABC ;5.(2021·陕西咸阳市·高三一模节选)如图,在三棱锥P ABC -中,平面PAC ⊥平面ABC ,PC AC ⊥,BC AC ⊥,2AC PC ==,4CB =,M 是PA 的中点,求证:PA ⊥平面MBC【答案】证明见解析【解析】平面PAC ⊥平面ABC ,平面PAC 平面ABC =AC ,BC ⊂平面ABC ,BC AC ⊥,∴BC ⊥平面PAC , ∵PA ⊂平面PAC , ∴BC PA ⊥,∵AC PC =,M 是PA 的中点, ∴CM PA ⊥, ∵CMBC C =,,CM BC ⊂平面MBC ,∴PA ⊥平面MBC .6.(2021·浙江金华市节选)如图,在四棱锥P ABCD -中,底面ABCD 为矩形,PD AB ==,平面PCD ⊥平面ABCD ,若E 为PC 的中点,求证:DE ⊥平面PBC【答案】证明见解析【解析】因为平面PCD ⊥平面ABCD ,且平面PCD平面ABCD CD =,底面ABCD 为矩形,所以BC CD ⊥,又CD ⊂平面PDC ,所以BC ⊥平面PDC ,又DE ⊂平面PDC ,所以BC DE ⊥;因为PD AB DC ==,所以PDC △为等腰三角形,E 为PC 的中点,所以DE CP ⊥,因为CPBC C =,,BC CP ⊂面PBC ,所以DE ⊥面PBC7.(2021·西安市铁一中学节选)如图,在底面为菱形的四棱锥P ABCD -中,60,1,ABC PA AC PB PD ︒∠=====,点E 在PD 上,且2PEED=,求证:PA ⊥平面ABCD【答案】证明见详解【解析】因为底面ABCD 是菱形,60ABC ︒∠=, 所以1AB AC AD ===,在PAB △中,1,PA PB ==由222PA AB PB +=,可得PA AB ⊥.同理,PA AD ⊥,又AB AD A ⋂=所以PA ⊥平面ABCD .8.(2021·河南高三期末节选)如图,直四棱柱1111ABCD A B C D -的底面ABCD 为平行四边形,133,5,cos ,,5AD AB BAD BD DD E ==∠==是1CC 的中点,求证:平面DBE ⊥平面1ADD【答案】证明见解析【解析】由题意可得2222cos 16BD AD AB AB AD BAD =+-⨯∠=, 所以222AD BD AB +=,因此AD BD ⊥,在直四棱柱1111ABCD A B C D -中,1DD ⊥平面ABCD ,所以1DD BD ⊥, 又因为1ADDD D =,所以BD ⊥平面1ADD ,因为BD ⊂平面DBE ,所以平面DBE ⊥平面1ADD .9.(2021·江苏南通市节选)如图,四面体ABCD 中,O 是BD 的中点,点G 、E 分别在线段AO 和BC 上,2BE EC =,2AG GO =,2CA CB CD BD ====,AB AD ==(1)求证://GE 平面ACD ; (2)求证:平面ABD ⊥平面BCD . 【答案】(1)证明见解析;(2)证明见解析.【解析】证明:(1)连接BG 并延长,交AD 于M ,连接MC ,在ABD △中,O 为BD 中点,G 在AO 上,2AG GO =, ∴G 为ABD △的重心∴21BG GM =, 又21BE EC =∴BG BEGM EC=∴//GE MC , ∵GE ⊄平面ACD ,AC ⊂平面ACD , ∴//GE 平面ACD ;(2)在ABD △中,O 为BD 中点,2BD =,AB AD ==∴AO BD ⊥∴1AO ==,在BCD △中,2BC CD BD ===,O 为BD 中点,连接OC ,则OC =又2CA =,∴222OA OC CA +=,∴AO OC ⊥ 由AO OC ⊥,AO BD ⊥,OC BD O =,,OC BD ⊂平面BCD ,得AO ⊥平面BCD , 又AO ⊂平面ABD , ∴平面ABD ⊥平面BCD .10.(2021·山西吕梁市·高三一模节选)如图,四棱锥S ABCD -中,//AB CD ,BC CD ⊥,侧面SCD为等边三角形, 4AB BC ==,2CD =,SB =BC SD ⊥【答案】证明见解析【解析】由已知4BC =,2SC =,SB =222SB BC SC =+,所以90BCS ∠=︒,所以BC CS ⊥,又,BC CD CDCS C ⊥=,所以BC ⊥平面SCD ,又SD ⊂平面SCD ,所以BC SD ⊥.11.(2021·云南高三期末)如图所示,在正方体ABCD A B C D ''''-中,点M 为线段B D ''的中点.(1)求证:DD AC '⊥; (2)求证://BM平面ACD '.【答案】(1)证明见解析;(2)证明见解析. 【解析】(1)在正方体ABCD A B C D ''''-中, ∵DD AD '⊥,DD CD '⊥,且CDAD D =,∴DD '⊥平面ACD ,AC ⊂平面ACD . ∴DD AC '⊥(2)如图所示,连接BD ,交AC 于N ,连接D N '.由题设得:BN MD '=,//BN MD ', ∴四边形BMD N '为平行四边形. ∴//BM ND '.又∵ND '⊂平面ACD ',BM ⊄平面ACD ', ∴//BM平面ACD '.12.(2021·江西景德镇市节选)如图,已知四棱锥S ABCD -,其中//AD BC ,AB AD ⊥,45BCD ∠=,22BC AD ==,侧面SBC ⊥底面ABCD ,E 是SB 上一点,且ECD 是等边三角形,求证:CE ⊥平面SAB【答案】证明见解析 【解析】//AD BC ,AB AD ⊥,AB BC ∴⊥,侧面SBC ⊥底面ABCD ,侧面SBC底面ABCD BC =,AB平面ABCD ,AB ∴⊥平面SBC ,CE ⊂平面SBC ,CE AB ∴⊥,如下图所示,取BC 的中点F ,连接DF 、EF ,2BC AD =,且F 为BC 的中点,则AD BF =,//BC AD ,则//AD BF ,所以,四边形ABFD 为平行四边形,则//DF AB , DF ⊥∴平面SBC ,EF 、BC ⊂平面SBC ,DF EF ∴⊥,DF BC ⊥,ECD 为等边三角形,则EF CF BF ===,所以,FBE BEF ∠=∠,FCE CEF ∠=∠,由2FBE BEF FCE CEF BEC π∠+∠+∠+∠=∠=,2BEC π∴∠=,即CE SB ⊥,SB AB B =,因此,CE ⊥平面SAB ;13.(2021·江西景德镇市·景德镇一中)如图,在三棱柱111ABC A B C -中,平面11A ACC ⊥平面ABC ,2,AB BC == 30ACB ∠=,13AA =,11BC A C ,E 为AC 的中点.(1)求证:1//AB 平面1C EB ; (2)求证:1A C ⊥平面1C EB .【答案】(1)证明见解析;(2)证明见解析. 【解析】(1)如下图所示,连接1AB 、1B C ,设11B CBC F =,连接EF ,在三棱柱111ABC A B C -中,四边形11BB C C 为平行四边形, 因为11B CBC F =,在点F 为1B C 的中点,又因为点E 为AC 的中点,1//EF AB ∴,1AB ⊄平面1C EB ,EF ⊂平面1C EB ,所以,1//AB 平面1C EB ;(2)AB BC =,E 为AC 的中点,BE AC ∴⊥,因为平面11A ACC ⊥平面ABC ,平面11A ACC ⋂平面ABC AC =,BE ⊂平面ABC ,BE ∴⊥平面11A ACC ,1A C ⊂平面11A ACC ,1A C BE ∴⊥, 11BC AC ⊥,1BE BC B =,1A C ∴⊥平面1C EB .14.(2021·陕西咸阳市)在三棱锥A BCD -中,E 、F 分别为AD 、DC 的中点,且BA BD =,平面ABD ⊥平面ADC .(1)证明://EF 平面ABC ;(2)证明:BE CD ⊥.【答案】(1)证明见解析;(2)证明见解析.【解析】(1)在ADC 中,E 、F 分别是AD 、DC 的中点,//EF AC ∴.EF ⊄平面ABC ,AC ⊂平面ABC ,//EF ∴平面ABC ;(2)在ABD △中,BA BD =,E 为AD 的中点,BE AD ∴⊥, 又平面ABD ⊥平面ADC ,平面ABD ⋂平面ADC AD =,BE ⊂平面ABD ,BE ∴⊥平面ADC .CD ⊂平面ADC ,BE CD ∴⊥.15.(2021·全国)已知四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,PAB △为等边三角形,底面ABCD 为直角梯形,90DAB ∠=︒且2AB CD =,点M 为PB 的中点,求证:PB DM ⊥.【答案】证明见解析.【解析】因为PAB △为等边三角形,M 为PB 的中点,所以AM PB ⊥,因为平面PAB ⊥平面ABCD ,平面PAB ⋂平面ABCD AB =,DA AB ⊥,DA ⊂平面ABCD , 所以DA ⊥平面PAB ,因为PB ⊂平面PAB ,所以DA PB ⊥,因为DA AM A ⋂=,所以PB ⊥平面ADM ,因为DM ⊂平面ADM ,所以PB DM ⊥.16.(2020·全国)如图,矩形ABCD 所在平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)若P 点是线段AM 的中点,求证://MC 平面PBD .【答案】(1)证明见解析;(2)证明见解析.【解析】证明:(1)因为矩形ABCD 所在平面与半圆弦CD 所在平面垂直,面ABCD 面CDM CD =,AD DC ⊥,AD ⊂面ABCD ,所以AD ⊥半圆弦CD 所在平面,且CM ⊂半圆弦CD 所在平面,所以CM AD ⊥;又M 是CD 上异于C ,D 的点,所以CM DM ⊥;又DM AD D =,所以CM ⊥平面AMD ;又CM ⊂平面CMB ,所以平面AMD ⊥平面BMC ;(2)由P 是AM 的中点,连接BD 交AC 于点O ,连接OP ,如图所示:由中位线定理得//MC OP ;又MC ⊂/平面BDP ,OP ⊂平面BDP ,所以//MC 平面PBD .17.(2021·全国高三专题练习)如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.证明:平面AMD ⊥平面BMC .【答案】证明见解析【解析】由题设知,平面CMD ⊥平面ABCD ,交线为CD .因为BC ⊥CD ,BC ⊂平面ABCD ,所以BC ⊥平面CMD ,故BC ⊥DM .因为M 为CD 上异于C ,D 的点,且DC 为直径,所以DM ⊥CM .又BC CM =C ,所以DM ⊥平面BMC .而DM ⊂平面AMD ,故平面AMD ⊥平面BMC .18.(2020·全国高三专题练习)已知四棱锥P ABCD -中,平面PAB ⊥平面ABCD ,PAB △为等边三角形,底面ABCD 为直角梯形,90DAB ∠=︒且2AB CD =,点M 为PB 的中点,求证:DM PB .【答案】证明见解析.【解析】证明:∵PAB ∆为等边三角形,M 为PB 的中点,∴AM PB ⊥, 又∵平面PAB ⊥平面ABCD ,且平面PAB 平面ABCD AB =, DA AB ⊥,DA ⊂平面ABCD ,∴DA ⊥平面PAB ,又PB ⊂平面PAB ,∴DA PB ⊥,∵DA AM A ⋂=,∴PB ⊥平面ADM ,又DM ⊂平面ADM ,∴PB DM ⊥.19.(2020·江苏苏州市·高三三模)如图,在三棱柱111A B C ABC -中,AB AC =,D 为BC 中点,平面ABC ⊥平面11BCC B ,11BC B D ⊥.(1)求证:1//A C 平面1AB D ;(2)求证:11AB BC ⊥.【答案】(1)证明见解析(2)证明见解析【解析】证明:(1)连结1A B 交1AB 于点O ,连结OD .因为111A B C ABC -是三棱柱,所以11ABB A 是平行四边形,所以O 为1A B 中点. 有因为D 为BC 中点,所以1OD AC . 又1AC ⊄平面1AB D ,OD ⊂平面1AB D ,所以1A C 平面1AB D . (2)因为AB AC =,D 为BC 中点,所以AD BC ⊥.又因为平面ABC ⊥平面11BCC B ,平面ABC 平面11BCC B BC =,AD ⊂平面ABC , 所以AD ⊥平面11BCC B . 因为1BC ⊂平面11BCC B ,所以1AD BC ⊥. 又因为11BC B D ⊥,1AD B D D ⋂=,AD ⊂平面1AB D ,1B D ⊂平面1AB D , 所以1BC ⊥平面1AB D . 因为1AB ⊂平面1AB D ,所以11AB BC ⊥.。
高中数学必修二4.线面垂直的性质及判定

αO A B CαOAB授课内容 线面垂直的判定及性质教学内容知识梳理1 、线面垂直定义:如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面互相垂直其中直线叫做平面的垂线,平面叫做直线的垂面交点叫做垂足直线与平面垂直简称线面垂直,记作:a ⊥α2、直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面3 直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那麽这两条直线平行4、斜线,垂线,射影⑴垂线 自一点向平面引垂线,垂足叫这点在这个平面上的射影. 这个点和垂足间的线段叫做这点到这个平面的垂线段.⑵斜线 一条直线和一个平面相交,但不和这个平面垂直,这条直线叫做这个平面的斜线斜线和平面的交点叫斜足;斜线上一点与斜足间的线段叫这点到这个平面的斜线段⑶射影 过斜线上斜足外的一点向平面引垂线,过垂足和斜足的直线叫做斜线在这个平面内的射影垂足和斜足间线段叫这点到这个平面的斜线段在这个平面内的射影直线与平面平行,直线在平面由射影是一条直线直线与平面垂直射影是点斜线任一点在平面内的射影一定在斜线的射影上5.直线和平面所成角(1)定义:平面的一条斜线和它在平面上的射影所成的锐角叫做这条斜线和这个平面所成的角一直线垂直于平面,所成的角是直角一直线平行于平面或在平面内,所成角为0︒角。
直线和平面所成角范围: [0,2π](2)定理:斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角【同步练习】1、下列命题中正确的个数是( )①如果直线l 与平面α内的无数条直线垂直,则α⊥l ; ②如果直线l 与平面α内的一条直线垂直,则α⊥l ;③如果直线l 不垂直于α,则α内也没有与l 垂直的直线; ④如果直线l 不垂直于α,则α内也有无数条直线与l 垂直。
A 、0 B 、1 C 、2 D 、32、若直线l ⊥平面α,直线α⊂m ,则( )A 、m l ⊥B 、l 可能和m 平行C 、l 和m 相交D 、l 和m 不相交3、直线a ⊥直线b ,b ⊥平面β,则a 与β的关系是( ) A 、β⊥a B 、a ∥β C 、β⊂a D 、β⊂a 或a ∥β4、给出下列四个命题:①若直线垂直于平面内的两条直线,则这条直线垂直于这个平面;②若直线与平面内的任意一条直线都垂直,则这条直线垂直于这个平面;③互相平行的两条直线,在同一个平面内的射影必然是互相平行的两条直线; ④过点P 有且仅有一条直线与异面直线l ,m 都垂直。
线面垂直性质定理内容

线面垂直性质定理内容《线面垂直性质定理》指的是一种几何学定理,它认为在任意空间中,两个平行的直线的投影到任意一个平面上仍然是垂直的。
这一定理有着悠久的历史,可以追溯到古希腊的学者、欧拉等,它被认为是几何学中最重要的定理之一,是西方数学发展史上的里程碑式的贡献。
线面垂直性质定理可以用来证明许多几何形态之间的关系。
比如,如果有一条直线l1和一个平面s1,那么根据定理,它们的投影是垂直的,即l1的投影到s1上的一条线是垂直的。
又如,如果有两个平行的直线l1和l2,和两个平面s1,s2,那么根据定理,它们的投影也是垂直的。
也就是说,l1的投影到s1上的直线与l2的投影到s2上的直线是垂直的。
定理的证明可以从多角形的几何形态入手,如三角形和四边形等。
如果我们有一个三角形ABC,它有三条边AB,BC,CA,和斜边AC。
由于ABC三角形的三边都是垂直的,所以ABC三角形的斜边AC也是垂直的。
同样,如果有一个四边形ABCD,它有四条边AB,BC,CD,AD,和斜边BD,由于ABCD四边形的四边都是垂直的,所以它的斜边BD也是垂直的,从而可以解释线面垂直性质定理的真实性。
线面垂直性质定理同样可以作为许多几何问题的理论基础。
比如,由于空间中的任意两个垂直平面,它们的投影到同一个平面上也是垂直的,这就可以用来解释一组平行截面的平行性。
同样,如果有一组垂直截面,其投影到同一个平面上也是垂直的,这就可以用来解释一组垂直截面的垂直性。
此外,在空间几何中,有时需要求取两条平行线的距离,这时可以利用线面垂直性质定理的推论,即任意一条平行线的投影到任意一个平面上仍然是垂直的,可以求出两条平行线之间的距离。
线面垂直性质定理是一条用来证明垂直线和垂直面之间关系的重要定理,也是数学发展史上不可缺少的一个里程碑,它也可以用来解决许多几何问题,如求取两条平行线之间的距离等。
希望本文能够对大家对几何学中线面垂直性质定理的理解有所帮助,并能够为你们提供一些问题的解决方案。
数学线面垂直的知识点总结归纳

数学线面垂直的知识点总结归纳数学是一座高山,哪怕是高考数学这样的小山丘,也让无数学子望其背而心戚戚,更有人混淆知识点。
下面是小编为大家整理的关于数学线面垂直的知识点,希望对您有所帮助!数学直线与平面平行、垂直知识点直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直,线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.推论:如果两条直线同垂直于一个平面,那么这两条直线平行.注:①垂直于同一平面的两个平面平行.(×)(可能相交,垂直于同一条直线的两个平面平行)②垂直于同一直线的两个平面平行.(√)(一条直线垂直于平行的一个平面,必垂直于另一个平面)③垂直于同一平面的两条直线平行.(√)5. ⑴垂线段和斜线段长定理:从平面外一点向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.注:垂线在平面的射影为一个点. [一条直线在平面内的射影是一条直线.(×)]⑵射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上高中数学线面垂直知识点1)直线垂直于平面内两条非平行的线,则直线垂直于该平面2)直线的两条不平行的垂线与平面平行,则直线垂直于该平面3)有A、B两个面都与C平面垂直,则A、B两个面的交线也垂直于C平面4)直线垂直于与A平面平行的B平面,则直线垂直于A平面5)直线任意点在平面上的投影都重合,则直线垂直于该平面6)直线上任意点到平面的距离,都等于这一点到线面交点的距离,则直线垂直于该平面线面垂直性质定理1:如果一条直线垂直于一个平面,那么该直线垂直于平面内的所有直线。
2:经过空间内一点,有且只有一条直线垂直已知平面。
线线垂直、线面垂直、面面垂直的判定和性质

空间中的垂直关系1.线面垂直直线与平面垂直的判定定理:如果 ,那么这条直线垂直于这个平面。
推理模式:直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线 。
2.面面垂直两个平面垂直的定义:相交成 的两个平面叫做互相垂直的平面。
两平面垂直的判定定理:(线面垂直⇒面面垂直)如果 ,那么这两个平面互相垂直。
推理模式:两平面垂直的性质定理:(面面垂直⇒线面垂直)若两个平面互相垂直,那么在一个平面内垂直于它们的 的直线垂直于另一个平面。
一般来说,线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为:线线垂直−−−→←−−−判定性质线面垂直−−−→←−−−判定性质面面垂直.这三者之间的关系非常密切,可以互相转化,从前面推出后面是判定定理,而从后面推出前面是性质定理.同学们应当学会灵活应用这些定理证明问题.在空间图形中,高一级的垂直关系中蕴含着低一级的垂直关系,下面举例说明.例题:1.如图,AB 是圆O 的直径,C 是圆周上一点,PA ⊥平面ABC .(1)求证:平面PAC ⊥平面PBC ;(2)若D 也是圆周上一点,且与C 分居直径AB 的两侧,试写出图中所有互相垂直的各对平面.2、如图,棱柱111ABC A B C -的侧面11BCC B 是菱形,11B C A B ⊥证明:平面1AB C ⊥平面11A BC3、如图所示,在长方体1111ABCD A B C D -中,AB=AD=1,AA 1=2,M 是棱CC 1的中点(Ⅰ)求异面直线A 1M 和C 1D 1所成的角的正切值;(Ⅱ)证明:平面ABM ⊥平面A 1B 1M 14、如图,AB是圆O的直径,C是圆周上一点,PA 平面ABC.若AE⊥PC,E为垂足,F是PB上任意一点,求证:平面AEF⊥平面PBC.5、如图,直三棱柱ABC—A1B1C1中,AC=BC=1,∠ACB=90°,AA1=2,D是A1B1中点.(1)求证C1D⊥平面A1B;(2)当点F在BB1上什么位置时,会使得AB1⊥平面C1DF并证明你的结论6、S是△ABC所在平面外一点,SA⊥平面ABC,平面SAB⊥平面SBC,求证AB⊥BC.B7、在四棱锥中,底面ABCD是正方形,侧面VAD是正三角形,平面VAD⊥底面ABCD证明:AB⊥平面VAD8、如图,平行四边形ABCD中,60DAB︒∠=,2,4AB AD==,将CBD∆沿BD折起到EBD∆的位置,使平面EDB⊥平面ABD.求证:AB DE⊥9、如图,在四棱锥ABCDP-中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E、F分别是AP、AD的中点求证:(1)直线EF‖平面PCD;(2)平面BEF⊥平面PADVD CBA10、如图,在三棱锥ABC S -中,平面⊥SAB 平面SBC ,AB AS BC AB =⊥,.过A 作SB AF ⊥,垂足为F ,点G E ,分别是棱SC SA ,的中点。
线面垂直判定与性质

•知识点1•直线和平面垂直定义如果一条直线和一个平面内的任何一条直线都垂直,就说这条直线和这个平面垂直 •2. 线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面 判定定理:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面 判定定理: ______ . 性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行 .3. 三垂线定理和它的逆定理.三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它和这条斜 线垂直. 逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在该平 面上的射影垂直. •题型示例【例1】 如图所示,已知点 S 是平面ABC 外一点,/ ABC=90 ° , SA 丄平面 ABC ,点A 在直线SB 和SC 上的 射影分别为点 E 、F ,求证:EF 丄SC.【解前点津】 用分析法寻找解决问题的途径,假设 EF 丄SC 成立,结合 AF 丄SC 可推证SC 丄平面AEF ,这样 SC ± AE ,结合AE 丄SB ,可推证 AE 丄平面SBC ,因此证明 AE 丄平面SBC 是解决本题的关键环节.由题设SA 丄平面ABC , / ABC=90。
,可以推证 BC 丄AE ,结合 AE 丄SB 完成AE 丄平 面SBC 的证明.【规范解答】【解后归纳】 题设中条件多,图形复杂,结合题设理清图形中基本元素之间的位置关系是解线面垂直例1题图决问题的关键•【例2】已知:M A N=AB,PQ丄M于Q , P0丄N于O, 0R丄M于R,求证:QR丄AB.【解前点津】由求证想判定,欲证线线垂直,方法有(1) a // b,a丄c= b丄c;(2)a丄a ,b~ a = a丄b;(3)三垂线定理及其逆定理.由已知想性质,知线面垂直,可推出线线垂直或线线平行【解后归纳】处于非常规位置图形上的三垂线定理或逆定理的应用问题,要抓住“一个面”“四条线” •所谓“一个面”:就是要确定一个垂面,三条垂线共处于垂面之上所谓“四条线”:就是垂线、斜线、射影以及平面内的第四条线,这四条线中垂线是关键的一条线,牵一发而动全身,应用时一般可按下面程序进行操作:确定垂面、抓准斜线、作出垂线、连结射影,寻第四条线.【例3】已知如图⑴所示,矩形纸片AA' A' !A I,B、C、B i、C i分别为AA' ,A i A'的三等分点,将矩形纸片沿BB i,CC i折成如图⑵形状(正三棱柱),若面对角线AB i丄BC i,求证:A i C丄AB i.例3题图解(i)【解前点津】题设主要条件是AB i丄BC,而结论是AB i丄A i C,题设,题断有对答性,可在2 / i0ABB i A i上作文章,只要取A I B I中点D i,就把异面直线AB i与BC i垂直关系转换到ABB J A I同一平面内AB i与BD i 垂直关系,这里要感谢三垂线逆定理•自然想到题断AB i与A i C垂直用同法(对称原理)转换到同一平面,取AB 中点D即可,只要证得A i D垂直于AB i,事实上DBD i A i,为平行四边形,解题路子清楚了•【解后归纳】证线线垂直主要途径是:(i)三垂线正逆定理,(2)线面,线线垂直互相转化• 利用三垂线正逆定理完成线线归面工作,在平面内完成作解任务证线线垂直,线面垂直,常常利用线面垂直,线线垂直作为桥梁过渡过来,这种转化思想有普遍意义,利用割补法把几何图形规范化便于应用定义定理和公式,也是不容忽视的常用方法【例4】空间三条线段AB,BC,CD,AB丄BC,BC丄CD,已知AB=3,BC=4,CD=6,则AD的取值范围是____________ •【解前点津】如图,在直角梯形ABCD i中,CD i=6,AD i的长是AD的最小值,其中AH丄CD i,AH=BC=4,HD i=3,••• AD i=5;在直角△ AHD 2中,CD2=6,AD2是AD的最大值为.HD;AH 2= ;(6 3)242 = 97例4题图a//b =b_Ma _M b_ M =allha_M③ a:b Mal/M④a_b "丄M.D.①②④B.DM丄平面PEFC.PM丄平面A. DP丄平面PEF4. 设a、b是异面直线,下列命题正确的是(A. 过不在a、b上的一点P 一定可以作一条直线和B. 过不在a、b上的一点P 一定可以作一个平面和C. 过a 一定可以作一个平面与b垂直D. 过a 一定可以作一个平面与b平行5. 如果直线l,m与平面a ,3,丫满足:1= 3门Y ,l II DEF D. PF 丄平面DEF)a、b都相交a、b都垂直A. a丄丫且I丄m6.AB是圆的直径,的距离为(),m:- a和m l 丫,那么必有()C是圆周上一点,PC垂直于圆所在平面,若BC=1,AC=2,PC=1,贝U P到ABA.1B.2 2.5C.-53.5D.-5【解后归纳】本题出题形式新颖、灵活性大,很多学生对此类题感到无从入手,其实冷静分析, 找出隐藏的条件很容易得出结论••对应训练分阶提升一、基础夯实1•设M表示平面,a、b表示直线,给出下列四个命题:其中正确的命题是()A. ①②B.①②③C.②③④2. 下列命题中正确的是()A. 若一条直线垂直于一个平面内的两条直线,则这条直线垂直于这个平面B. 若一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面C. 若一条直线平行于一个平面,则垂直于这个平面的直线必定垂直于这条直线D. 若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必垂直于这个平面3. 如图所示,在正方形ABCD中,E、F分别是AB、BC的中点.现在沿DE、DF及EF把厶ADE、△ CDF和厶BEF折起,使A、B、C三点重合,重合后的点记为P.那么,在四面体P —DEF中,必第3题图7. 有三个命题:①垂直于同一个平面的两条直线平行;£ B E个平面与a垂直; ②过平面a的一条斜线I有且仅有-二、思维激活11.如图AB 是斜边,三个顶点在平面 a 的同侧,它们在a 内的射 B ' C '是正三角形,且 AA '= 3cm, BB '= 5cm, CC '= 4cm ,ZV71:\1 \ i*广\ // *BC第12题图12. 如图所示,在直四棱柱A i B i C i D i — B i D i (注:填上你认为正确的一种条件即可 13. 如图所示,在三棱锥 V — ABC 中,当三条侧棱 VA 、VB 、VC 之间满足条件 VC 丄AB.(注:填上你认为正确的一种条件即可)ABCD 满足条件 ,不必考虑所有可能的情形) 时,有A i C时,有③ 异面直线a 、b 不垂直,那么过a 的任一个平面与 b 都不垂直其中正确命题的个数为 ()A.0B.1C.2D.38. d 是异面直线a 、b 的公垂线,平面 a 、 3满足a 丄a, b 丄B ,则下面正确的结论是 ( )A. a 与3必相交且交线m // d 或m 与d 重合B. a 与3必相交且交线 m // d 但m 与d 不重合C. a 与3必相交且交线 m 与d 一定不平行D. a 与3不一定相交9. 设I 、m 为直线,a 为平面,且I 丄a ,给出下列命题①若m l a ,贝U m// I ;②若m 丄I ,贝U m // a ;③若m // a ,贝U m ± I ;④若m // I ,贝U m ± a , 其中真命题的序号是 ()A.①②③B.①②④C.②③④D.①③④10. 已知直线I 丄平面a ,直线m 平面3,给出下列四个命题:①若a // 3,贝y I 丄m ;②若a 丄3,则I // m ;③若I // m ,则a 丄3 ;④若I 丄m ,则a // 3 . 其中正确的命题是 ( )A.③与④B.①与③C.②与④D.①与②三、能力提高14. 如图所示,三棱锥V-ABC 中,AH 丄侧面VBC,且 H 是厶VBC 的垂心,BE 是VC 边上的高. (1) 求证:VC 丄AB;(2) 若二面角E — AB — C 的大小为30° ,求VC 与平面ABC 所成角的大小.15. 如图所示,PA丄矩形ABCD所在平面,M、N分别是AB、PC的中点.(1) 求证:MN //平面FAD.(2) 求证:MN丄CD.⑶若/ PDA = 45 °,求证:MN丄平面FCD.16. 如图所示,在四棱锥P—ABCD中,底面ABCD是平行四边形,/ BAD = 60 ° , AB = 4, AD=2,侧棱PB = J5 , PD = ,3 .(1)求证:BD丄平面PAD.(2)若PD与底面ABCD成60°的角,试求二面角P —BC—A的大小.17. 已知直三棱柱ABC-A1B1C1 中,/ ACB=90 °,/BAC=30° ,BC=1 , AA j= .. 6 , M 是CC1 的中点, 求证:AB」A1M .A M B第15题图第16题图18. 如图所示,正方体 ABCD — A ' B ' C ' D '的棱长为a , M 是AD 的中点,N 是BD '上一点, 且 D ' N : NB = 1 : 2, MC 与 BD 交于 P.(1) 求证:NP 丄平面 ABCD.(2) 求平面PNC 与平面CC ' D ' D 所成的角 (3) 求点C 到平面D ' MB 的距离.第18题图第4课线面垂直习题解答1. A 两平行中有一条与平面垂直,则另一条也与该平面垂直,垂直于同一平面的两直线平行 .2. C 由线面垂直的性质定理可知.3. A 折后 DP 丄 PE,DP 丄 PF , PE 丄 PF.4. D 过a 上任一点作直线 b '// b,则a , b '确定的平面与直线 b 平行.5. A映世总,m 丄 丫且m U a ,则必有a 丄丫,又因为1= 3 n Y 则有I U 丫,而m 丄丫贝U I 丄m,故选A. 22—AC BC 26. DP 作 PD 丄 AB 于 D ,连 CD ,贝U CD 丄 AB , AB=、AC BC - 5 , CDAB f7. D 由定理及性质知三个命题均正确 .8. A 显然a 与3不平行•9. D 垂直于同一平面的两直线平行,两条平行线中一条与平面垂直,则另一条也与该平面垂直 10. B Ta// 3 , I 丄 a ,• I 丄 m 11.3cm 2设正三角A ' B ' C '的边长为a.22 2 2 2 2 2 ,…AC =a +1,BC =a +1,AB =a +4,A B••• PD= , PC 2 CD 2i5.证明: 又 AC 2+BC 2=AB 2,「・ a 2=2.=H 3232S ^A B ,C 一a cm .4212. 在直四棱柱A i B i C i D i —ABCD 中当底面四边形ABCD 满足条件AC 丄BD (或任何能推导出这个条件 的其它条件,例如 ABCD 是正方形,菱形等)时,有A I C 丄B i D i (注:填上你认为正确的一种条件即可 不必考虑所有可能的情形).点评:本题为探索性题目,由此题开辟了填空题有探索性题的新题型,此题实质考查了三垂线 定理但答案不惟一,要求思维应灵活13. VC 丄 VA , VC 丄AB.由 VC 丄VA , VC 丄AB 知 VC 丄平面 VAB. 14. (i)证明:•/ HVBC 的垂心,••• VC 丄BE,又AH 丄平面VBC,••• BE 为斜线 AB 在平面 VBC 上的射影,• AB 丄VC. (2)解:由(i)知 VC 丄 AB,VC 丄 BE,• VC 丄平面 ABE,在平面 ABE 上,作ED 丄AB,又AB 丄VC, • AB 丄面 DEC.• AB 丄CD, •••/ EDC 为二面角 E —AB — C 的平面角, •••/ EDC=30 ° ,••• AB 丄平面 VCD, •VC 在底面 ABC 上的射影为 CD .•••/ VCD 为VC 与底面 ABC 所成角,又VC 丄AB,VC 丄BE, • VC 丄面 ABE, • VC 丄DE, :丄 CED=90 °,故/ ECD=60 ° ,• VC 与面ABC 所成角为60° .(1)如图所示,取 PD 的中点E ,连结AE , EN ,1 1则有 EN // CD // AB // AM , EN = - CD = - AB = AM ,故 AMNE 为平行四边形 2 2 • MN // AE.•/ AE 平面 PAD , MN 平面 PAD , • MN //平面 PAD. (2) •/ PA 丄平面 ABCD , • PA 丄 AB.又AD 丄AB , • AB 丄平面 PAD. • AB 丄AE ,即卩AB 丄MN. 又 CD // AB , • MN 丄 CD.(3) •/ PA 丄平面 ABCD , • PA 丄 AD. 又/ PDA = 45° , E 为PD 的中点. • AE 丄 PD ,即 MN 丄 PD.又 MN 丄 CD , • MN 丄平面PCD.16.如图(1)证:由已知 AB = 4 , AD =2, / BAD = 60° ,2 2 21第15题图解故BD = AD +AB -2AD • ABcos60°= 4+16-2 X 2X 4 X - = 12.2tan Z PFE =PEEF22、3.317.连结AC1,ACMC1CC1■-6C1A1又AB2= AD2+BD2,•••△ABD是直角三角形,/ ADB = 90°,即AD 丄BD.在厶PDB 中,PD = 3 , PB= ..15 , BD = .. 12 ,•PB2= PD2+BD2,故得PD 丄BD.又PD n AD = D,•BD丄平面FAD.⑵由BD丄平面FAD, BD 平面ABCD.•平面PAD丄平面ABCD .作PE丄AD于E,又PE平面PAD,•PE丄平面ABCD,•/ PDE是PD与底面ABCD所成的角.•/ PDE = 60°,「. PE = PDsin60°=汉也=?2 2 '作EF丄BC于F,连PF,贝U PF丄BF ,•Z PFE是二面角P—BC—A的平面角.又EF = BD = ,12,在Rt△ PEF 中,J3 故二面角P —BC—A的大小为arctan——4•Rt △ACC [S Rt △MC1A1,•Z AC Q= Z MA1C1,•Z A1MC1 + Z AC1C= Z A1MC 计Z MA1C1=90 °.•A1M丄AC1,又ABC-A1B1C1为直三棱柱,•CC1 丄B1C1,又BQ」A1C1,「・B1C1 丄平面AC1M.由三垂线定理知AB1丄A1M.点评:要证AB1I A1M,因B1C1丄平面AC1,由三垂线定理可转化成证AC1 JA1M,而AC1I A1M 一定会成立.18.(1)证明:在正方形ABCD中,•/△ MPD CPB, 且MD =】BC2 ,• DP : PB= MD : BC = 1 : 2.又已知D' N : NB= 1 : 2,由平行截割定理的逆定理得NP // DD ',又DD '丄平面ABCD ,••• NP 丄平面 ABCD.(2) •/ NP // DD '// CC• NP 、CC '在同一平面内,CC '为平面NPC 与平面CC ' D ' D 所成二面角的棱• 又由CC '丄平面 ABCD ,得CC '丄CD , CC '丄CM ,•••/ MCD 为该二面角的平面角•在Rt △ MCD 中可知/ MCD = arctan 1,即为所求二面角的大小 .2a 2 .c⑶由已知棱长为a 可得,等腰△ MBC 面积S i = 2 ,等腰△ MBD '面积$2=4 a 2 ,设所求距离为 h ,即为三棱锥C —D ' MB 的高.•••三棱锥D '— BCM 体积为1S 1 D^=丄&人,3 3S 1 a■. 6--h a. S 2 3。
2.3.3 线面垂直的性质定理

C
P
在Rt△POE中, OE
2 tanPEO 2
1 2 2 ,PO 2
∴ 2 ∴所求的二面角P-AB-C 的正切值为 2
E
O
5.锐二面角α l β中,AB α,AB 2, A l ,AB与l成45 角, 与β成30 角,则二面角 α l β的大小为_____ 45 ___.
1.如图所示,ABCD—A1B1C1D1 为长方体,且底
面ABCD为正方形.求证:截面ACB1⊥平面 BDD1B1.
解:∵四边形ABCD是正方形,∴AC⊥BD.
∵BB1⊥底面ABCD,∴AC⊥B1B.
又BD∩BB1=B,故AC⊥平面BDD1B1,
又AC⊂平面ACB1,
∴截面ACB1⊥平面BDD1B1.
又∵BD⊂平面BDF,∴AF⊥BD.
4.如图,P 是边长为 2 2的正方形 ABCD 外 一点,PA⊥AB,PA⊥BC,且 PC=5,
2 13 . 则二面角 PBDA 的余弦值为________ 13
解析:连 PO,易知 PA⊥面 ABCD,BD⊥AC, ∴BD⊥面 POA,即∠POA 即为二面角 PBDA 的平面角. ∵正方形边长为 2 2,∴AC=4,∴AO=2. 在 Rt△PAC 中,PA2=PC2-AC2=52-42=32, ∴PA=3. ∴PO2=PA2+AO2=32+22=13. 2 2 13 ∴cos∠POA= = 13 . 13
解
(方法一)
B
C A O l
D
∠OAC =120 AO=BD=1, AC=2
CO 2 AC 2 AO 2 2 AO AC COS120 7
四边形ABDO为矩形, DO=AB=3
(精选)面面垂直性质定理

(精选)面面垂直性质定理
1、如果两个平面相互垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。
2、如果两个平面相互垂直,那么经过第一个平面内的一点作垂直于第二个平面的直线在第一个平面内。
3、如果两个相交平面都垂直于第三个平面,那么它们的交线垂直于第三个平面。
4、如果两个平面互相垂直,那么一个平面的垂线与另一个平面平行。
判定定理:
直线与平面垂直的判定定理(线面垂直定理):一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直。
推论1:如果在两条平行直线中,有一条直线垂直于一个平面,那么另一条直线也垂直于这个平面。
推论2:如果两条直线垂直于同一个平面,那么这两条直线平行。
线面垂直的判定与性质

线面垂直●知识点1.直线和平面垂直定义如果一条直线和一个平面内的任何一条直线都垂直,就说这条直线和这个平面垂直.2.线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面.判定定理:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面.判定定理:一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面.性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.3.三垂线定理和它的逆定理.三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它和这条斜线垂直.逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在该平面上的射影垂直.●题型示例【例1】如图所示,已知点S是平面ABC外一点,∠ABC=90°,SA⊥平面ABC,点A在直线SB和SC上的射影分别为点E、F,求证:EF⊥SC.【解前点津】用分析法寻找解决问题的途径,假设EF⊥SC成立,结合AF⊥SC可推证SC⊥平面AEF,这样SC⊥AE,结合AE⊥SB,可推证AE⊥平面SBC,因此证明AE⊥平面SBC是解决本题的关键环节.由题设SA⊥平面ABC,∠ABC=90°,可以推证BC⊥AE,结合AE⊥SB完成AE⊥平面SBC的证明.【规范解答】【解后归纳】题设中条件多,图形复杂,结合题设理清图形中基本元素之间的位置关系是解决问题的关键.【例2】已知:M∩N=AB,PQ⊥M于Q,PO⊥N于O,OR⊥M于R,求证:QR⊥AB.【解前点津】由求证想判定,欲证线线垂直,方法有(1)a∥b,a⊥c⇒b⊥c;(2)a⊥α,b⊂α⇒a ⊥b;(3)三垂线定理及其逆定理.由已知想性质,知线面垂直,可推出线线垂直或线线平行.【解后归纳】处于非常规位置图形上的三垂线定理或逆定理的应用问题,要抓住“一个面”、“四条线”.所谓“一个面”:就是要确定一个垂面,三条垂线共处于垂面之上.所谓“四条线”:就是垂线、斜线、射影以及平面内的第四条线,这四条线中垂线是关键的一条线,牵一发而动全身,应用时一般可按下面程序进行操作:确定垂面、抓准斜线、作出垂线、连结射影,寻第四条线.【例3】已知如图(1)所示,矩形纸片AA′A′1A1,B、C、B1、C1分别为AA′,A1A′的三等分点,将矩形纸片沿BB1,CC1折成如图(2)形状(正三棱柱),若面对角线AB1⊥BC1,求证:A1C⊥AB1.【解前点津】题设主要条件是AB1⊥BC,而结论是AB1⊥A1C,题设,题断有对答性,可在ABB1A1上作文章,只要取A1B1中点D1,就把异面直线AB1与BC1垂直关系转换到ABB1A1同一平面内AB1与BD1垂直关系,这里要感谢三垂线逆定理.自然想到题断AB1与A1C垂直用同法(对称原理)转换到同一平面,取AB中点D即可,只要证得A1D垂直于AB1,事实上DBD1A1,为平行四边形,解题路子清楚了.【解后归纳】证线线垂直主要途径是:(1)三垂线正逆定理,(2)线面,线线垂直互相转化.利用三垂线正逆定理完成线线归面工作,在平面内完成作解任务.证线线垂直,线面垂直,常常利用线面垂直,线线垂直作为桥梁过渡过来,这种转化思想有普遍意义,利用割补法把几何图形规范化便于应用定义定理和公式,也是不容忽视的常用方法.【例4】 空间三条线段AB ,BC ,CD ,AB ⊥BC ,BC ⊥CD ,已知AB =3,BC =4,CD =6,则AD 的取值范围是 .【解前点津】 如图,在直角梯形ABCD 1中,CD 1=6,AD 1的长是AD 的最小值,其中AH ⊥CD 1,AH =BC =4,HD 1=3,∴AD 1=5;在直角△AHD 2中,CD 2=6,AD 2是AD 的最大值为974)36(22222=++=+AH HD【解后归纳】 本题出题形式新颖、灵活性大,很多学生对此类题感到无从入手,其实冷静分析,找出隐藏的条件很容易得出结论.●对应训练 分阶提升 一、基础夯实1.设M 表示平面,a 、b 表示直线,给出下列四个命题: ①M b M a b a ⊥⇒⎭⎬⎫⊥// ②b a M b M a //⇒⎭⎬⎫⊥⊥ ③⇒⎭⎬⎫⊥⊥b a M a b ∥M ④⇒⎭⎬⎫⊥b a M a //b ⊥M . 其中正确的命题是 ( )A.①②B.①②③C.②③④D.①②④ 2.下列命题中正确的是 ( )例4题图A.若一条直线垂直于一个平面内的两条直线,则这条直线垂直于这个平面B.若一条直线垂直于一个平面内的无数条直线,则这条直线垂直于这个平面C.若一条直线平行于一个平面,则垂直于这个平面的直线必定垂直于这条直线D.若一条直线垂直于一个平面,则垂直于这条直线的另一条直线必垂直于这个平面3.如图所示,在正方形ABCD 中,E 、F 分别是AB 、BC 的中点.现在沿DE 、DF 及EF 把△ADE 、△CDF 和△BEF 折起,使A 、B 、C 三点重合,重合后的点记为P .那么,在四面体P —DEF 中,必有 ( )A.DP ⊥平面PEFB.DM ⊥平面PEFC.PM ⊥平面DEFD.PF ⊥平面DEF 4.设a 、b 是异面直线,下列命题正确的是 ( )A.过不在a 、b 上的一点P 一定可以作一条直线和a 、b 都相交B.过不在a 、b 上的一点P 一定可以作一个平面和a 、b 都垂直C.过a 一定可以作一个平面与b 垂直D.过a 一定可以作一个平面与b 平行5.如果直线l ,m 与平面α,β,γ满足:l =β∩γ,l ∥α,m α和m ⊥γ,那么必有 ( ) A.α⊥γ且l ⊥m B.α⊥γ且m ∥β C.m ∥β且l ⊥m D.α∥β且α⊥γ6.AB 是圆的直径,C 是圆周上一点,PC 垂直于圆所在平面,若BC =1,AC =2,PC =1,则P到第3题图AB的距离为( )A.1B.2C.552 D.5537.有三个命题:①垂直于同一个平面的两条直线平行;②过平面α的一条斜线l有且仅有一个平面与α垂直;③异面直线a、b不垂直,那么过a的任一个平面与b都不垂直其中正确命题的个数为( )A.0B.1C.2D.38.d是异面直线a、b的公垂线,平面α、β满足a⊥α,b⊥β,则下面正确的结论是( )A.α与β必相交且交线m∥d或m与d重合B.α与β必相交且交线m∥d但m与d不重合C.α与β必相交且交线m与d一定不平行D.α与β不一定相交9.设l、m为直线,α为平面,且l⊥α,给出下列命题①若m⊥α,则m∥l;②若m⊥l,则m∥α;③若m∥α,则m⊥l;④若m∥l,则m⊥α,其中真命题...的序号是( )A.①②③B.①②④C.②③④D.①③④10.已知直线l⊥平面α,直线m平面β,给出下列四个命题:①若α∥β,则l⊥m;②若α⊥β,则l∥m;③若l∥m,则α⊥β;④若l⊥m,则α∥β.其中正确的命题是( )A.③与④B.①与③C.②与④D.①与②二、思维激活11.如图所示,△ABC 是直角三角形,AB 是斜边,三个顶点在平面α的同侧,它们在α内的射影分别为A ′,B ′,C ′,如果△A ′B ′C ′是正三角形,且AA ′=3cm ,BB ′=5cm ,CC ′=4cm ,则△A ′B ′C ′的面积是 .12.如图所示,在直四棱柱A 1B 1C 1D 1—ABCD 中,当底面四边形ABCD 满足条件 时,有A 1C ⊥B 1D 1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形)13.如图所示,在三棱锥V —ABC 中,当三条侧棱VA 、VB 、VC 之间满足条件 时,有VC ⊥AB .(注:填上你认为正确的一种条件即可)三、能力提高14.如图所示,三棱锥V -ABC 中,AH ⊥侧面VBC ,且H 是△VBC 的垂心,BE 是VC 边上的高. (1)求证:VC ⊥AB ;(2)若二面角E —AB —C 的大小为30°,求VC 与平面ABC 所成角的大小.第11题图第12题图第13题图15.如图所示,PA⊥矩形ABCD所在平面,M、N分别是AB、PC的中点.(1)求证:MN∥平面PAD.(2)求证:MN⊥CD.(3)若∠PDA=45°,求证:MN⊥平面PCD.16.如图所示,在四棱锥P—ABCD中,底面ABCD是平行四边形,∠BAD=60°,AB=4,AD=2,侧棱PB=15,PD=3.(1)求证:BD⊥平面PAD.(2)若PD与底面ABCD成60°的角,试求二面角P—BC—A的大小.第15题图第16题图17.已知直三棱柱ABC-A1B1C1中,∠ACB=90°,∠BAC=30°,BC=1,AA1=6,M是CC1的中点,求证:AB1⊥A1M.18.如图所示,正方体ABCD—A′B′C′D′的棱长为a,M是AD的中点,N是BD′上一点,且D′N∶NB=1∶2,MC与BD交于P.(1)求证:NP⊥平面ABCD.(2)求平面PNC与平面CC′D′D所成的角.(3)求点C到平面D′MB的距离.第18题图第4课线面垂直习题解答1.A 两平行中有一条与平面垂直,则另一条也与该平面垂直,垂直于同一平面的两直线平行.2.C 由线面垂直的性质定理可知.3.A 折后DP ⊥PE ,DP ⊥PF ,PE ⊥PF .4.D 过a 上任一点作直线b ′∥b ,则a ,b ′确定的平面与直线b 平行.5.A依题意,m ⊥γ且m ⊂α,则必有α⊥γ,又因为l =β∩γ则有l ⊂γ,而m ⊥γ则l ⊥m ,故选A. 6.D 过P 作PD ⊥AB 于D ,连CD ,则CD ⊥AB ,AB =522=+BC AC ,52=⋅=AB BC AC CD , ∴PD =55354122=+=+CD PC . 7.D 由定理及性质知三个命题均正确.8.A 显然α与β不平行.9.D 垂直于同一平面的两直线平行,两条平行线中一条与平面垂直,则另一条也与该平面垂直.10.B ∵α∥β,l ⊥α,∴l ⊥m 11.23cm 2 设正三角A ′B ′C ′的边长为a . ∴AC 2=a 2+1,BC 2=a 2+1,AB 2=a 2+4,又AC 2+BC 2=AB 2,∴a 2=2.S △A ′B ′C ′=23432=⋅a cm 2. 12.在直四棱柱A 1B 1C 1D 1—ABCD 中当底面四边形ABCD 满足条件AC ⊥BD (或任何能推导出这个条件的其它条件,例如ABCD 是正方形,菱形等)时,有A 1C ⊥B 1D 1(注:填上你认为正确的一种条件即可,不必考虑所有可能的情形).点评:本题为探索性题目,由此题开辟了填空题有探索性题的新题型,此题实质考查了三垂线定理但答案不惟一,要求思维应灵活.13.VC ⊥VA ,VC ⊥AB . 由VC ⊥VA ,VC ⊥AB 知VC ⊥平面VAB .14.(1)证明:∵H 为△VBC 的垂心,∴VC ⊥BE ,又AH ⊥平面VBC ,∴BE 为斜线AB 在平面VBC 上的射影,∴AB ⊥VC .(2)解:由(1)知VC ⊥AB ,VC ⊥BE ,∴VC ⊥平面ABE ,在平面ABE 上,作ED ⊥AB ,又AB ⊥VC ,∴AB ⊥面DEC .∴AB ⊥CD ,∴∠EDC 为二面角E —AB —C 的平面角,∴∠EDC =30°,∵AB ⊥平面VCD ,∴VC 在底面ABC 上的射影为CD .∴∠VCD 为VC 与底面ABC 所成角,又VC ⊥AB ,VC ⊥BE ,∴VC ⊥面ABE ,∴VC ⊥DE ,∴∠CED =90°,故∠ECD=60°,∴VC 与面ABC 所成角为60°.15.证明:(1)如图所示,取PD 的中点E ,连结AE ,EN ,则有EN ∥CD ∥AB ∥AM ,EN =21CD =21AB =AM ,故AMNE 为平行四边形. ∴MN ∥AE .∵AE 平面PAD ,MN 平面PAD ,∴MN ∥平面PAD .(2)∵PA⊥平面ABCD,∴PA⊥AB.又AD⊥AB,∴AB⊥平面PAD.∴AB⊥AE,即AB⊥MN.又CD∥AB,∴MN⊥CD.(3)∵PA⊥平面ABCD,∴PA⊥AD.又∠PDA=45°,E为PD的中点.∴AE⊥PD,即MN⊥PD.又MN⊥CD,∴MN⊥平面PCD.16.如图(1)证:由已知AB=4,AD=2,∠BAD=60°,1=12.故BD2=AD2+AB2-2AD·AB cos60°=4+16-2×2×4×2又AB2=AD2+BD2,∴△ABD是直角三角形,∠ADB=90°,即AD⊥BD.在△PDB中,PD=3,PB=15,BD=12,第16题图解∴PB2=PD2+BD2,故得PD⊥BD.又PD∩AD=D,∴BD⊥平面PAD.(2)由BD⊥平面PAD,BD平面ABCD.∴平面PAD⊥平面ABCD.作PE⊥AD于E,又PE平面PAD,∴PE⊥平面ABCD,∴∠PDE是PD与底面ABCD所成的角.∴∠PDE =60°,∴PE =PD sin60°=23233=⨯. 作EF ⊥BC 于F ,连PF ,则PF ⊥BF ,∴∠PFE 是二面角P —BC —A 的平面角.又EF =BD =12,在Rt △PEF 中, tan ∠PFE =433223==EF PE . 故二面角P —BC —A 的大小为arctan43. 17.连结AC 1,∵11112263A C CC MC AC ===. ∴Rt △ACC 1∽Rt △MC 1A 1,∴∠AC 1C =∠MA 1C 1,∴∠A 1MC 1+∠AC 1C =∠A 1MC 1+∠MA 1C 1=90°.∴A 1M ⊥AC 1,又ABC -A 1B 1C 1为直三棱柱,∴CC 1⊥B 1C 1,又B 1C 1⊥A 1C 1,∴B 1C 1⊥平面AC 1M .由三垂线定理知AB 1⊥A 1M .点评:要证AB 1⊥A 1M ,因B 1C 1⊥平面AC 1,由三垂线定理可转化成证AC 1⊥A 1M ,而AC 1⊥A 1M 一定会成立.18.(1)证明:在正方形ABCD 中,∵△MPD ∽△CPB ,且MD =21BC , ∴DP ∶PB =MD ∶BC =1∶2.又已知D ′N ∶NB =1∶2,由平行截割定理的逆定理得NP ∥DD ′,又DD ′⊥平面ABCD ,∴NP ⊥平面ABCD .(2)∵NP ∥DD ′∥CC ′,∴NP 、CC ′在同一平面内,CC ′为平面NPC 与平面CC ′D ′D 所成二面角的棱. 又由CC ′⊥平面ABCD ,得CC ′⊥CD ,CC ′⊥CM ,∴∠MCD 为该二面角的平面角.在Rt △MCD 中可知∠MCD =arctan 21,即为所求二面角的大小. (3)由已知棱长为a 可得,等腰△MBC 面积S 1=22a ,等腰△MBD ′面积S 2=246a ,设所求距离为h ,即为三棱锥C —D ′MB 的高.∵三棱锥D ′—BCM 体积为h S D D S 213131='⋅, ∴.3621a S a S h =⋅=。
线面垂直的性质定理

线面垂直的性质定理【学习目标】1. 理解线面垂直的性质定理,并能用定理进行简单的证明;2. 通过性质定理的探究和应用,进一步提高空间想象能力和逻辑推理能力;3. 经历定理的探究过程,从中体验、树立相互转化思想。
【学习重点】线面垂直性质定理及应用定理进行简单证明【学习难点】直线与平面垂直的性质定理的应用【课前预习案】一、课本助读1.复习:线面垂直的定义: ; 反过来,如果一条直线与一个平面垂直,则这条直线与这个平面内任意一条直线垂直。
2.空间两条直线的垂直关系有几种情况?3.如图,已知直线a ⊥平面α,直线b ⊥平面α.①试讨论直线a 与b 的位置关系:_______________________________ ②将讨论结果可用文字语言表述为: ______________________________.二、预习问题设置1.我们知道,“在平面内,如果两条直线同垂直于另一条直线,那么这两条直线平行”。
这空间中这个结论还成立吗?(2)在平面中,有且只有一条直线与已知直线垂直,那么,在空间中,(1)过一点有几条直线与已知平面垂直?(2)过一点有几个平面与已知直线垂直?三、预习自测在空间,判断下列命题知否正确.①平行于同一条直线的两条直线互相平行;( )②垂直于同一条直线的两条直线互相平行;( )③平行于同一个平面的两条直线互相平行;( )④垂直于同—个平面的两条直线互相平行.( )【课堂探究案】1.证明线面垂直的性质定理。
2.如图,在正方体1111D C B A ABCD -中,点,E F 分别在1,A D AC 上,且1EF A D ⊥,EF AC ⊥.求证:1//BD EF3.(1)2题中“正方体1111D C B A ABCD -”换为“长方体1111D C B A ABCD -”,结论1//BD EF 还成立吗?(2)2题中去掉点E ,点F ,线段D A 1,若AC 与BD 的交点O ,1DD 的中点为G ,证明:⊥GO 平面1ACB 。
面面垂直的判定及性质
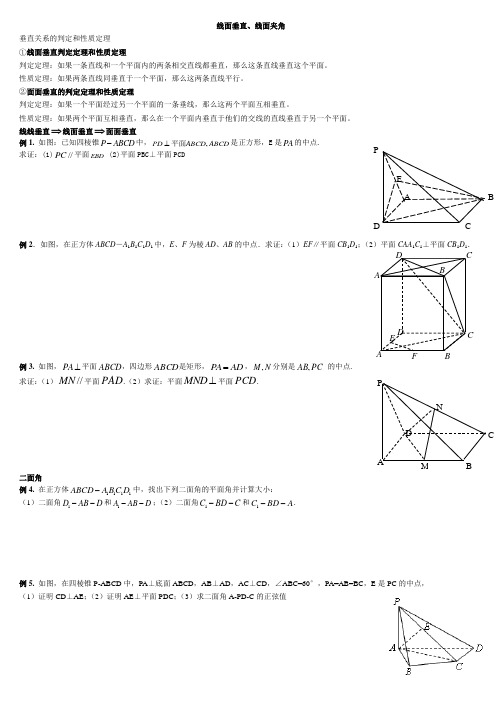
ED C BA PABCDABC DE F 线面垂直、线面夹角垂直关系的判定和性质定理 ①线面垂直判定定理和性质定理判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直这个平面。
性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。
②面面垂直的判定定理和性质定理判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。
性质定理:如果两个平面互相垂直,那么在一个平面内垂直于他们的交线的直线垂直于另一个平面。
线线垂直⇒线面垂直⇒面面垂直例1. 如图:已知四棱锥P ABCD -中,,PD ABCD ABCD ⊥平面是正方形,E 是PA 的中点. 求证:(1)//PC 平面EBD (2)平面PBC ⊥平面PCD例2.如图,在正方体ABCD -A 1B 1C 1D 1中,E 、F 为棱AD 、AB 的中点.求证:(1)EF ∥平面CB 1D 1;(2)平面CAA 1C 1⊥平面CB 1D 1.例3. 如图,⊥PA 平面ABCD ,四边形ABCD 是矩形,PA AD =,,M N 分别是PC AB , 的中点. 求证:(1)//MN 平面PAD .(2)求证:平面⊥MND 平面PCD . 二面角例4. 在正方体1111ABCD A B C D -中,找出下列二面角的平面角并计算大小: (1)二面角1D AB D --和1A AB D --;(2)二面角1C BD C --和1C BD A --.例5. 如图,在四棱锥P-ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC=60°,PA=AB=BC ,E 是PC 的中点, (1)证明CD ⊥AE ;(2)证明AE ⊥平面PDC ;(3)求二面角A-PD-C 的正弦值 DNCBMAP新课标高考真题例6. (2011.18.)如图,四棱锥P ABCD -中,底面ABCD 为平行四边形,60DAB ∠=︒,2AB AD =,PD ⊥底面ABCD .(I )证明:PA BD ⊥; (II )设PD=AD=1,求棱锥D-PBC 的高.例7. (2012全国)如图,三棱柱ABC -A 1B 1C 1中,侧棱垂直底面,∠ACB=90°,AC=BC=12AA 1,D 是棱AA 1的中点(1)证明:平面BDC 1⊥平面BDC ;(2)平面BDC 1分此棱柱为两部分,求这两部分体积的比。
线面垂直的判定及性质

线面垂直、线面夹角1.线面垂直:如果一条直线和一个平面内的任何一条直线都垂直,就说这条直线和这个平面垂直.2.线面垂直判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面. 推论:如果两条平行线中的一条垂直于一个平面,那么另一条也垂直于同一平面. 推论:一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面. 性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.3.三垂线定理:在平面内的一条直线,如果和这个平面的一条斜线的射影垂直,那么它和这条斜线垂直.逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线在该平面上的射影垂直.4.线面角:平面的一条斜线和它在平面内的射影所成的锐角,叫做这条直线和这个平面所成的角;求线面角:“一作,二证,三计算”。
①平面的平行线与平面所成的角:规定为0。
②平面的垂线与平面所成的角:规定为90。
线线垂直⇒线面垂直 (线面垂直⇒线线垂直) 例1.如图:AB 是⊙O 的直径,PA 垂直于⊙O 所在的平面,C 是圆周上不同于B A ,的任意一点,求证: PAC BC 平面⊥例 2. 三棱柱111ABC A B C -的侧棱1A A 垂直于底面ABC ,12A A =,1AC CB ==,90BCA ︒∠=,M 、N 分别是AB 、1A A 的中点.(1)求BN 的长;(2)求证:1A B CM ⊥.例3. 如图,在四棱锥P -ABCD 中,PA ⊥底面ABCD ,AB ⊥AD ,AC ⊥CD ,∠ABC =60°,PA =AB =BC ,E 是PC 的中点(1)求证:CD ⊥AE ;(2)求证:PD ⊥面ABE. 线面角例4. 在长方体ABCD ﹣A 1B 1C 1D 1中,AB=BC=2,AA 1=1,则AC 1与平面A 1B 1C 1D 1所成角的正弦值为 .例5. 如图,在棱长为2的正方体ABCD ﹣A 1B 1C 1D 1中,E 是BC 1的中点,则直线DE 与平面ABCD 所成角的正切值为 _________ .例6. 在正三棱柱ABC ﹣A 1B 1C 1中,侧棱长为,底面三角形的边长为1,则BC 1与侧面ACC 1A 1所成的角是 ________例7.a 是平面α的斜线,b α⊂,a 与b 成3π角,b 与a 在α内的射影成4π角,则a 与α所成角的大小为 。
线面垂直的性质定理

直线与平面垂直的性质教学设计课标要求:以立体几何的概念、公理、定理为起点,通过直观感知、操作确认,归纳出直线与平面垂直的性质定理,并加以证明。
学情分析:在学习本节课的内容之前,方才学习了直线与平面垂直的概念和判定定理,在学完判定定理以后紧接着的例1当中咱们利用判定定理证明了线线平行的性质定理,即若是两条平行直线中的一条垂直于一个平面,那么另一条也垂直于同一个平面,用符号语言表示为假设 a节的作用和地位:本节课是人教版必修 2 第二章直线与平面垂直的第三课时。
空间中直线与平面之间的位置关系中,垂直是一种超级重要的位置关系,它不仅应用较多,而且是空间问题平面化的典范。
空间中直线与平面垂直的性质定理不仅是由线面关系转化为线线关系,而且将垂直关系转化为平行关系,因此直线与平面垂直的性质定理在立体几何中有着重要的地位和作用。
2.本节要紧内容:直线与平面垂直的性质定理的证明及转化思想的渗透。
教学目标:1.知识与技术:把握直线与平面垂直的性质定理,了解线面关系与线线关系,垂直关系与平行关系之间的转化和反证法的应用。
2.过程与方法:在观察长方体模型的基础上进行操作确认,获得对性质定理正确性的认识,进一步推导出定理的证明过程。
3.情感态度与价值观:通过“直观感知、操作确认,推理证明”,提高空间想象的能力和逻辑推理能力。
教学重点:直线与平面垂直的性质定理的证明及转化思想的渗透。
教学难点:直线与平面垂直的性质定理的证明教学理念:高中学生思维活跃,参与意识、自主探讨能力较强,整节课要紧以学生自主探讨为主,教师只起一个组织,引导的作用。
从而增强空间想象能力,养成质疑思辩、创新的精神。
教学方式:探讨讨论法教学用具:长方体模型,量角器,直角三角板,多媒体教学设计:一.创设情境,揭露课题问题:(实物式引入):(1)两根旗杆垂直于地面,给咱们以旗杆平行的形象(2)让学生双手各持一支笔直立与桌面,通过操作确认两支笔平行。
数学来源于生活,把这些问题抽象归纳取得一个新的问题:若a⊥α,b⊥α,那a和 b 会有如何的位置关系呢?让学生自由发言,教师不急于下结论,而是继续引导学生:欲知结论如何,让咱们一路来观看、探讨。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
无忧PPT整理发布
随堂测试
1.判断下列命题是否正确: 正确的是:①④ ①平行于同一条直线的两条直线互相平行; ②垂直于同一条直线的两条直线互相平行; ③平行于同一个平面的两条直线互相平行; ④垂直于同一个平面的两条直线互相平行.
2.若a,b表示直线, 表示平面,下列命题 正确的是 (3)(4) 。
(1)a , a b, 则b // (3)a // , b , 则b a (2)a // , a b, 则b (4)a , b , 则b a
课堂练习:
1、判断下列命题是否正确;
(1)垂直于同一条直线的两个平面互相平行;(
(2)垂直于同一个平面的两条直线互相平行;(
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α ,
a ∥b
变式探究
a
α
β
2.逆向探究:
交换“条件”与“结论” ①a ⊥α , a ⊥ b β ∥α ② a ⊥α ,
b // 或b
a ∥b
变式探究
a
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α , α β
a ∥b
变式探究
a
b
c
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α ,
图形语言:
a // b
a b
O
简述为:线面垂直 线线平行
© 2006 NENU 济南九中高三数学备课组
三、理论迁移 例 1: 如图,已知 l , CA 于点A,CB 于点B, a , a AB, 求证: a // l .
β B l
A a
无忧PPT整理发布
D1 A1 O D N C M B 无忧PPT整理发布 C1
B1
A
性质定理: a ⊥α ,bቤተ መጻሕፍቲ ባይዱ⊥α
1.类比探究:
①交换“平行”与“垂直”
a ∥b
变式探究
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a ⊥α ,b ⊥α ? a ∥ b
a ∥b
变式探究
无忧PPT整理发布
否定结论b’
a b
α
正确推理
o
导出矛盾
肯定结论
© 2006 NENU 济南九中高三数学备课组
线面垂直的性质定理:
垂直于同一个平面的两条直线平行 反证法 已知:a⊥α, b⊥α, 求证:a // b
证明: 假设 a与b不平行. 记直线b和α的交点为o, 则可过o作 b’∥a. ∵a⊥α , ∴b’⊥α. ∴过点o的两条直线 b和 b’都垂直平面α , 这不可能! ∴a∥b .
一、知识回顾 如果直线和这个平面内的任意一条 直线都垂直,则称这条直线和这个平面垂 直.
1. 直线和平面垂直的定义?
注 :若 l , b 则l b.
α
l
b
A
2.直线与平面垂直的判定定理 一条直线与一个平面内的两条相交直线都 垂直,则该直线与此平面垂直。 图形表示 符号表示 m ,n a mnO a m a m, a n O n
线线垂直
线面垂直
关键:线不在多,相交则行
二、新知探究
如图,长方体ABCD—A1B1C1D1中,棱 AA1,BB1,CC1,DD1 所在直线与底面ABCD的 位置关系如何?它们彼此之间具有什么 位置关系? C1
D1
B1 C B
A1
D
A
无忧PPT整理发布
3 线面垂直的性质定理:
垂直于同一平面的两直线互相平行.
a⊥ b
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α ,
a ∥b
变式探究
a
b
α
2.逆向探究:
交换“条件”与“结论” ①a ⊥α , a ⊥ b
b
α
a
b ∥α
无忧PPT整理发布
C
α
无忧PPT整理发布
三、理论迁移
例2 如图,已知 PA 矩形ABCD所在平面,M、N分别 是AB、PC的中点求证: (1) MN CD; P E N A M B D
PDA 45 (2)若 ,求证:MN 面PCD
C
无忧PPT整理发布
典型例题
练习. 如图所示,在正方体ABCD-A1B1C1D1中, M是AB上一点,N是A1C的中点,MN⊥平面 A1DC 求证: (1) MN∥AD1 (2) M是AB的中点.
线线关系 平行关系 平面问题
a ∥b
变式探究
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” a⊥b a ⊥α ,b ∥α β β
a ∥b
变式探究
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α , α β
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面”
a ∥b
变式探究
b
l
a
α
无忧PPT整理发布
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面”
否定结论b’
a b
α
正确推理
o
导出矛盾
肯定结论
© 2006 NENU 济南九中高三数学备课组
直线与平面垂直的性质1:
如果一条直线垂直于一个平面,那么这 条直线垂直于面上任意直线.(定义)
a 符号语言: b
图形语言:
ab
a b
α
简述为:线面垂直 线线垂直
© 2006 NENU 济南九中高三数学备课组
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α ,
a ∥b
变式探究
a
b
α
b
α
a
2.逆向探究:
交换“条件”与“结论” ①a ⊥α , a ⊥ b
②
b ∥α 或 b
无忧PPT整理发布
图形语言:
a b
α
符号语言:
a ,b a // b
无忧PPT整理发布
线面垂直的性质定理:
垂直于同一个平面的两条直线平行 反证法 已知:a⊥α, b⊥α, 求证:a // b
证明: 假设 a与b不平行. 记直线b和α的交点为o, 则可过o作 b’∥a. ∵a⊥α , ∴b’⊥α. ∴过点o的两条直线 b和 b’都垂直平面α , 这不可能! ∴a∥b .
a ∥b
变式探究
a
b
c
无忧PPT整理发布
2.逆向探究:
①
α 交换“条件”与“结论” β
性质定理: a ⊥α ,b ⊥α
1.类比探究:
①交换“平行”与“垂直” a⊥ b a ⊥α ,b ∥α ②交换“直线”与“平面” β ∥α a ⊥β a ⊥α ,
a ∥b
变式探究
2.逆向探究:
交换“条件”与“结论” ①a ⊥α ,b ∥α
直线与平面垂直的性质2:
如果两条平行直线中的一条垂直于一个 平面,那么另一条也垂直于这个平面.
a / /b 符号语言: a
图形语言:
b
a b
O
© 2006 NENU
济南九中高三数学备课组
直线与平面垂直的性质3:
如果两条直线同时垂直于一个平面, 那么这两条直线平行.
a 符号语言: b
(3)一条直线在平面内,另一条直线与这个平面垂 直,则这两条直线互相垂直。( ) 2、已知直线a、b和平面α,且a⊥b,a⊥α,则b与α的 位置关系 ____________ b // 或b
√
√ √
)
)
小 结
1.知识方法
①线面垂直的性质定理及其应用 ③类比探究,逆向探究
2.数学思想
线面关系 转化 垂直关系 空间问题
