利用勾股定理解决折叠问题及答案

合集下载

勾股定理中的常考问题(6种类型48道)—2024学年八年级数学上册(解析版)

勾股定理中的常考问题6种类型48道【类型一用勾股定理解决折叠问题】1．如图，将长方形ABCD沿着AE折叠，点D落在BC边上的点F处，已知AB=8，BC=10，则EC的长为（）A．4B．3C．5D．2【答案】B【分析】长方形ABCD沿着AE折叠，得AD=AF=BC=10，EF=ED，根据勾股定理得BF=6，则CF=4，设EC=x，ED=8−x，根据勾股定理得EF2=EC2+CF2，即可解得EC的长．【详解】解：∵四边形ABCD是长方形，∴AD=BC=10，DC=AB=8，∵长方形ABCD沿着AE折叠，∴AD=AF=BC=10，EF=ED，∴BF=√AF2−AB2=√100−64=6，CF=BC−BF=4，设EC=x，ED=8−x，∴EF2=EC2+CF2，即(8−x)2=x2+42，解得x=3，所以EC=3，故选：B．【点睛】本题主要考查了图形折叠以及勾股定理等知识内容，掌握图形折叠的性质是解题的关键．2．如图，有一块直角三角形纸片，∠C=90°，AC=4，BC=3，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则BD的长为（）【答案】C【分析】利用勾股定理求得AB=5，由折叠的性质可得AB=AE=5，DB=DE，求得CE=1，设DB=DE=x，则CD=3−x，根据勾股定理可得12+(3−x)2=x2，进而求解即可．【详解】解：∵∠C=90°，AC=4，BC=3，∴AB=√32+42=5，由折叠的性质得，AB=AE=5，DB=DE，∴CE=1，设DB=DE=x，则CD=3−x，在Rt△CED中，12+(3−x)2=x2，，解得x=53故选：C．【点睛】本题考查勾股定理、折叠的性质，熟练掌握勾股定理是解题的关键．【答案】B【分析】根据图形翻折变换的性质可知，AE=BE，设AE=x，则BE=x，CE=8−x，再Rt△BCE中利用勾股定理即可求出CE的长度．【详解】解：∵△ADE翻折后与△BDE完全重合，∴AE=BE，设AE=x，则BE=x，CE=8−x，∵在Rt△BCE中，CE2=BE2−BC2，即(8−x)2=x2−62，解得，x=7，4．∴CE=74故选：B【点睛】本题考查了图形的翻折变换，解题中应注意折叠是一种对称变换，属于轴对称，根据轴对称的性质，折叠前后图形的形状和大小不变．4．如图，在Rt△ABC中，∠ABC=90°，AB=3，AC=5，AD为∠BAC的平分线，将△DAC沿AD向上翻折得到△DAE，使点E在射线AB上，则DE的长为（）【答案】B【分析】根据勾股定理求得BC，进而根据折叠的性质可得AE=AC，可得BE=2，设DE=x，表示出BD,DE，进而在Rt△BDE【详解】解：∵在Rt△ABC中，∠ABC=90°，AB=3，AC=5，∴BC=√AC2−AB2=√52−32=4，∵将△DAC沿AD向上翻折得到△DAE，使点E在射线AB上，∴AE=AC，设DE=x，则DC=DE=x,BD=BC−CD=4−x，BE=AE−AB=5−3=2，在Rt△BDE中，BD2+BE2=DE2，即(4−x)2+22=x2，解得：x=52，即DE的长为52故选：B．【点睛】本题考查了勾股定理与折叠问题，熟练掌握勾股定理是解题的关键．5．如图，矩形纸片ABCD的边AB长为4，将这张纸片沿EF折叠，使点C与点A重合，已知折痕EF长为2√5，则BC长为（）A．4.8B．6.4C．8D．10【答案】C【分析】过点F作FG⊥BC于点G，则四边形ABGF是矩形，从而FG=AB=4，在Rt△EFG中，利用勾股定理求得EG=√EF2−FG2=√(2√5)2−42=2．设BE=x，则BG=BE+EG=x+2．由∠AFE=∠CEF=∠AEF 得到AE=AF=BG=x+2，从而在Rt△ABE中，有AB2+BE2=AE2，代入即可解得x的值，从而得到BE，CE的长，即可得到BC．【详解】过点F作FG⊥BC于点G∵在矩形ABCD中，∠DAB=∠B=90°∴四边形ABGF是矩形∴FG=AB=4∴在Rt△EFG中，EG=√EF2−FG2=√(2√5)2−42=2设BE=x，则BG=BE+EG=x+2∵在矩形ABCD中，BC∥AD∴∠AFE=∠CEF由折叠得∠CEF=∠AEF∴AE=AF∵在矩形ABGF中，AF=BG=x+2∴AE=AF=x+2∵在Rt△ABE中，AB2+BE2=AE2∴42+x2=(x+2)2解得x=3即BE=3，AE=5∴由折叠可得CE=AE=5∴BC=BE+EC=3+5=8故选：C【点睛】本题考查矩形的性质，勾股定理的应用，利用勾股定理构造方程是解决折叠问题的常用方法．A．7B．136【答案】B【分析】根据题意可得AD=AB=2，∠B=∠ADB，CE=DE，∠C=∠CDE，可得∠ADE=90°，继而设AE=x，则CE=DE=3−x，根据勾股定理即可求解．【详解】解：∵沿过点A的直线将纸片折叠，使点B落在边BC上的点D处，∴AD=AB=2，∠B=∠ADB，∵折叠纸片，使点C与点D重合，∴CE=DE，∠C=∠CDE，∵∠BAC=90°，∴∠B+∠C=90°，∴∠ADB+∠CDE=90°，∴AD2+DE2=AE2，设AE=x，则CE=DE=3−x，∴22+(3−x)2=x2，，解得x=136即AE=13，6故选：B【点睛】本题考查了折叠的性质，勾股定理，掌握折叠的性质以及勾股定理是解题的关键．7．如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边BC沿CE翻折，点B落在点F处，连接CF交AB于点D，则FD的最大值为（）【答案】D【分析】根据将边BC沿CE翻折，点B落在点F处，可得FD=CF−CD=4−CD，即知当CD最小时，FD最大，此时CD⊥AB，用面积法求出CD，即可得到答案．【详解】解：如图：∵将边BC沿CE翻折，点B落在点F处，∴CF=BC=4，∴FD=CF−CD=4−CD，当CD最小时，FD最大，此时CD⊥AB，∵∠ACB=90°，AC=3，BC=4，∴AB=√AC2+BC2=√32+42=5，∵2S△ABC=AC⋅BC=AB⋅CD，∴CD=AC⋅BCAB =3×45=125，∴FD=CF−CD=4−125=85，故选：D．【点睛】本题考查直角三角形中的翻折问题，涉及勾股定理及应用，解题的关键是掌握翻折的性质．A．73B．154【答案】B【分析】先求出BD=2，由折叠的性质可得DN=CN，则BN=8−DN，利用勾股定理建立方程DN2= (8−DN)2+4，解方程即可得到答案．【详解】解：∵D是AB中点，AB=4，∴AD=BD=2，∵将Rt△ABC折叠，使点C与AB的中点D重合，∴DN=CN，∴BN=BC−CN=8−DN，在Rt△DBN中，由勾股定理得DN2=BN2+DB2，∴DN2=(8−DN)2+4，∴DN=17，4，∴BN=BC−CN=154故选：B．【点睛】本题主要考查了勾股定理与折叠问题，正确理解题意利用方程的思想求解是解题的关键．【类型二杯中吸管问题】9．如图，有一个透明的直圆柱状的玻璃杯，现测得内径为5cm，高为12cm，今有一支15cm的吸管任意斜放于杯中，若不考虑吸管的粗细，则吸管露出杯口外的长度最少为（）A．1cm B．2cm C．3cm D．不能确定【答案】B【分析】吸管露出杯口外的长度最少，即在杯内最长，可用勾股定理解答．【详解】解∶∵CD=5cm,AD=12cm，∴AC=√CD2+AD2=√52+122，露出杯口外的长度为=15−13=2(cm)．故答案为：B．【点睛】本题考查勾股定理的应用，所述问题是一个生活中常见的问题，与勾股定理巧妙结合，可培养同学们解决实际问题的能力．10．如图，一支笔放到圆柱形笔筒中，笔筒内部底面直径是9cm，内壁高12cm．若这支笔长18cm，则这支笔在笔筒外面部分的长度是()A．6cm B．5cm C．3cm D．2cm【分析】根据勾股定理求得AC的长，进而即可求解．【详解】解：根据题意可得图形：AB=12cm，BC=9cm，在Rt△ABC中：AC=√AB2+BC2=√122+92=15(cm)，所以18−15=3(cm)．则这只铅笔在笔筒外面部分长度为3cm．故选：C．【点睛】本题考查了勾股定理，熟练掌握勾股定理是解题的关键．11．如图，一支笔放到圆柱形笔筒中，笔筒内部底面直径是9cm，内壁高12cm．若这支笔长18cm，则这支笔在笔筒外面部分的长度是（）A．6cm B．5cm C．4cm D．3cm【答案】D【分析】首先根据题意画出图形，利用勾股定理计算出AC的长度．然后求其差．【详解】解：根据题意可得：AB BC=9cm，在Rt△ABC中∶AC=√AB2+BC2=√122+92=15(cm)，所以18−15=3(cm),则这只铅笔在笔筒外面部分长度为3cm．故选：D．【点睛】此题主要考查了勾股定理的应用，正确得出笔筒内铅笔的最短长度是解决问题的关键．12．将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度ℎcm，则ℎ的取值范围是（）A．ℎ≤17cm B．ℎ≥16cm C．5cm<ℎ≤16cm D．7cm<ℎ≤16cm【分析】根据勾股定理及直径为最大直角边时即可得到最小值，当筷子垂直于底面时即可得到最大值即可得到答案；【详解】解：由题意可得，当筷子垂直于底面时ℎ的值最大，ℎmax=24−8=16cm，当直径为直角边时ℎ的值最小，根据勾股定理可得，ℎmin=24−√82+152=7cm，∴7cm<ℎ≤16cm，故选D．【点睛】本题考查勾股定理的运用，解题的关键是找到最大与最小距离的情况．13．将一根24cm的筷子，置于底面直径为15cm，高8cm的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度ℎcm，则ℎ的取值范围是（）A．ℎ≤17cm B．ℎ≥16cm C．5cm<ℎ≤16cm D．7cm≤ℎ≤16cm【答案】D【分析】如图，当筷子的底端在A点时，筷子露在杯子外面的长度最短；当筷子的底端在D点时，筷子露在杯子外面的长度最长．然后分别利用已知条件根据勾股定理即可求出的取值范围．【详解】解：如图1所示，当筷子的底端在D点时，筷子露在杯子外面的长度最长，=24−8=16cm，∴ℎ最大如图2所示，当筷子的底端在A点时，筷子露在杯子外面的长度最短，在Rt△ABD中，AD=15cm，BD=8cm，∴AB=√AD2+BD2=17cm，=24−17=7cm，∴此时ℎ最小∴的取值范围是7cm≤h≤16cm．故选：D．【点睛】本题主要考查了勾股定理的应用，明确题意，准确构造直角三角形是解题的关键．A．5B．7C．12D．13【答案】A【分析】根据勾股定理求出h的最短距离，进而可得出结论．【详解】解：如图，当吸管、底面直径、杯子的高恰好构成直角三角形时，h最短，此时AB=√92+122=15（cm），故ℎ＝20−15＝5（cm）；最短故选：A．【点睛】本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．15．如图，某同学在做物理实验时，将一支细玻璃棒斜放入了一只盛满水的烧杯中，已知烧杯高8cm，玻璃棒被水淹没部分长10cm，这只烧杯的直径约是（）A．9cm B．8cm C．7cm D．6cm【答案】D可．【详解】解：由题意，可得这只烧杯的直径是：√102−82=6（cm）．故选：D．【点睛】本题考查了勾股定理的应用，能够将实际问题转化为数学问题是解题的关键．16．如图，一根长18cm的牙刷置于底面直径为5cm、高为12cm的圆柱形水杯中，牙刷露在杯子外面的长度为h cm，则h的取值范围是（）A．4＜h＜5B．5＜h＜6C．5≤h≤6D．4≤h≤5【答案】C【分析】根据题意，求出牙刷在杯子外面长度最小与最大情况即可得出取值范围．【详解】解：根据题意，当牙刷与杯底垂直时，ℎ最大，如图所示：故ℎ最大=18−12=6cm；∵当牙刷与杯底圆直径、杯高构成直角三角形时，ℎ最小，如图所示：在RtΔABC中，∠ACB=90°，AC=5cm，BC=12cm，则AB=√BC2+AC2=√52+122=13cm，∵牙刷长为18cm，即AD=18cm，∴ℎ最小=AD−AB=18−13=5cm，∴h的取值范围是5≤h≤6，故选：C．【点睛】本题考查勾股定理解实际应用题，读懂题意，根据牙刷的放置方式明确牙刷在杯子外面长度最小与最大情况是解决问题的关键．【类型三楼梯铺地毯问题】17．如图在一个高为3米，长为5米的楼梯表面铺地毯，则地毯至少需要（）．A．3米B．4米C．5米D．7米【答案】D【分析】当地毯铺满楼梯时的长度是楼梯的水平宽度与垂直高度的和，根据勾股定理求得水平宽度，即可求得地毯的长度．【详解】解：由勾股定理得：楼梯的水平宽度=√52−32=4（米），∵地毯铺满楼梯的长度应该是楼梯的水平宽度与垂直高度的和，∴地毯的长度至少是3+4=7（米）．故选：D．【点睛】此题考查了生活中的平移现象以及勾股定理，属于基础题，利用勾股定理求出水平边的长度是解答本题的关键．18．如图，在高为5m，坡面长为13m的楼梯表面铺地毯，地毯的长度至少需要（）【分析】当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和，根据勾股定理求得水平宽度，然后求得地毯的长度即可．【详解】解：由勾股定理得：楼梯的水平宽度=√132−52=12m，∵地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和，∴地毯的长度至少是12+5=17(m)．故选B．【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理是解答本题的关键．19．如图是楼梯的示意图，楼梯的宽为5米，AC=5米，AB=13米，若在楼梯上铺设防滑材料，则所需防滑材料的面积至少为（）A．65m2B．85m2C．90m2D．150m2【答案】B【分析】勾股定理求出BC，平移的性质推出防滑毯的长为AC+BC，利用面积公式进行求解即可．【详解】解：由图可知：∠C=90°，∵AC=5米，AB=13米，∴BC=√AB2−AC2=12米，由平移的性质可得：水平的防滑毯的长度=BC=12（米），铅直的防滑毯的长度=AC=5（米），∴至少需防滑毯的长为：AC+BC=17（米），∵防滑毯宽为5米∴至少需防滑毯的面积为：17×5=85（平方米）．故选：B．【点睛】本题考查勾股定理．解题的关键是利用平移，将防滑毯的长转化为两条直角边的边长之和．A．13cm B．14cm C．15cm D．16cm【答案】A【分析】根据勾股定理即可得出结论．【详解】如图，由题意得AC=1×5=5(cm)，BC=2×6=12(cm)，故AB=√122+52=13(cm)．故选：A．【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键．21．如图所示：某商场有一段楼梯，高BC＝6m，斜边AC是10米，如果在楼梯上铺上地毯，那么需要地毯的长度是（）A．8m B．10m C．14m D．24m【答案】C【分析】先根据直角三角形的性质求出AB的长，再根据楼梯高为BC的高＝6m，楼梯的宽的和即为AB的长，再把AB、BC的长相加即可．【详解】∵△ABC是直角三角形，BC＝6m，AC＝10m∴AB＝√AC2−BC2＝√102−62＝8（m），∴如果在楼梯上铺地毯，那么至少需要地毯为AB+BC＝8+6＝14（米）．故选C【点睛】本题考查的是勾股定理的应用，解答此题的关键是找出楼梯的高和宽与直角三角形两直角边的等量关系.22．某酒店打算在一段楼梯面上铺上宽为2米的地毯，台阶的侧面如图所示，如果这种地毯每平方米售价为80元，则购买这种地毯至少需要（）A．2560元B．2620元C．2720元D．2840元【答案】C【分析】根据题意，结合图形，先把楼梯的横竖向上向左平移，构成一个矩形，再求得其面积，则购买地毯的钱数可求．【详解】利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为√132−52=12米、5米，∴地毯的长度为12+5=17米，地毯的面积为17×2=34平方米，∴购买这种地毯至少需要80×34=2720元．故选C.【点睛】本题考查的知识点是勾股定理的应用，生活中的平移现象，解题关键是要注意利用平移的知识，把要求的所有线段平移到一条直线上进行计算．23．如图所示：是一段楼梯，高BC是3m，斜边AC是5m，如果在楼梯上铺地毯，那么至少需要地毯（）A．5m B．6m C．7m D．8m【答案】C【详解】楼梯竖面高度之和等于AB的长．由于AB=√AC2−BC2=√52−32=4，所以至少需要地毯长4＋3＝7（m）．故选C24．如图，是一段楼梯，高BC是1.5m，斜边AC是2.5m，如果在楼梯上铺地毯，那么至少需要地毯（）A．2.5m B．3m C．3.5m D．4m【答案】C【分析】当地毯铺满楼梯时其长度的和应该是楼梯的水平宽度与垂直高度的和，根据勾股定理求得AB，然后求得地毯的长度即可．【详解】解：由勾股定理得：AB=√2.52−1.52=2因为地毯铺满楼梯是其长度的和应该是楼梯的水平宽度与垂直高度的和所以地毯的长度至少是1.5+2=3.5（m）故选C．【点睛】本题考查了图形平移性质和勾股定理，解决本题的关键是要熟练掌握勾股定理.【类型四最短路径问题】25．如图，透明圆柱的底面半径为6厘米，高为12厘米，蚂蚁在圆柱侧面爬行．从圆柱的内侧点A爬到圆柱的外侧点B处吃食物，那么它爬行最短路程是厘米．(π≈3)【答案】30【分析】把圆柱的侧面展开，根据勾股定理即可得到结论．【详解】解：∵透明圆柱的底面半径为6厘米，∴透明圆柱的底面周长为2×6π=厘米≈36厘米，作点A关于直线EF的对称点A′，连接A′B，则A′B的长度即为它爬行最短路程，×36=18厘米，∴A′A=2AE=24厘米，AB=12∴A′B=√AB2+A′A2=√182+242=30(cm)，故答案为：30．【点睛】本题考查平面展开-最短路径问题，解题的关键是计算出圆柱展开后所得长方形的长和宽的值，然后用勾股定理进行计算．【答案】10【分析】将圆柱侧面展开，由图形可知蚂蚁在圆柱侧面爬行，从点A爬到点B的最短路程即为AB的长，再由勾股定理求出．【详解】解：根据圆柱侧面展开图，cm，高为8cm，∵圆柱的底面半径为6π∴底面圆的周长为2×6×π=12cm，π×12=6cm，∴BC=8cm，AC=12由图形可知蚂蚁在圆柱侧面爬行，从点A爬到点B的最短路程即为AB的长，AB=√AC2+BC2=10cm，故答案为：10．【点睛】本题考查了平面展开最短路线问题，勾股定理，将立体图形转化成平面图形求解是解题的关键．27．如图有一个棱长为9cm的正方体，一只蜜蜂要沿正方体的表面从顶点A爬到C点（C点在一条棱上，距离顶点B 3cm处），需爬行的最短路程是cm．【答案】15【分析】首先把正方体展开，然后连接AC，利用勾股定理计算求解即可．【详解】解：如图，连接AC，由勾股定理得，AC=√92+(9+3)2=15，故答案为：15．【点睛】本题考查了正方体的展开图、勾股定理的应用，解题的关键在于明确爬行的最短路线．28．如图，桌上有一个圆柱形玻璃杯（无盖），高6厘米，底面周长16厘米，在杯口内壁离杯口1.5厘米的A处有一滴蜜糖，在玻璃杯的内壁，A的相对方向有一小虫P，小虫离杯底的垂直距离为1.5厘米，小虫爬到蜜糖处的最短距离是厘米．【答案】10【分析】将杯子侧面展开，作A关于杯口的对称点A′，根据两点之间线段最短可知A′P的长度即为所求，再结合勾股定理求解即可．【详解】解：如图所示：将杯子侧面展开，作A关于杯口的对称点A′，连接PA′，最短距离为PA′的长度，)2+(6−1.5+1.5)2=10(厘米)，PA′=√PE2+EA′2=√(162最短路程为PA ′=10厘米．故答案为：10．【点睛】本题考查了平面展开−最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．【答案】20【分析】先把圆柱的侧面展开，连接AS ，利用勾股定理即可求得AS 的长．【详解】解：如图，∵在圆柱的截面ABCD 中，AB =24π，BC =32，∴AB =12×24π×π=12，BS =12BC =16， ∴AS =√AB 2+BS 2=20，故答案为：20．【点睛】本题考查平面展开图−最短路径问题，根据题意画出圆柱的侧面展开图，利用勾股定理求解是解题的关键．30．如图，圆柱形玻璃杯的杯高为9cm ，底面周长为16cm ，在杯内壁离杯底4cm 的点A 处有一滴蜂蜜，此时，一只蚂蚁正好在杯外壁上，它在离杯上沿1cm ，且与蜂蜜相对的点B 处，则蚂蚁从外壁B 处到内壁A 处所走的最短路程为 cm ．（杯壁厚度不计）【答案】10【分析】如图（见解析），将玻璃杯侧面展开，作B关于EF的对称点B′，根据两点之间线段最短可知AB′的长度即为所求，利用勾股定理求解即可得．【详解】解：如图，将玻璃杯侧面展开，作B关于EF的对称点B′，作B′D⊥AE，交AE延长线于点D，连接AB′，BB′=1cm,AE=9−4=5(cm)，由题意得：DE=12∴AD=AE+DE=6cm，∵底面周长为16cm，×16=8(cm)，∴B′D=12∴AB′=√AD2+B′D2=10cm，由两点之间线段最短可知，蚂蚁从外壁B处到内壁A处所走的最短路程为AB′=10cm，故答案为：10．【点睛】本题考查了平面展开——最短路径问题，将图形展开，利用轴对称的性质和勾股定理进行计算是解题的关键．同时也考查了同学们的创造性思维能力．31．如图所示，ABCD是长方形地面，长AB=20m，宽AD=10m．中间竖有一堵砖墙高MN=2m．一只蚂蚱从A点爬到C点，它必须翻过中间那堵墙，则它要走的路程s取值范围是．【答案】s≥26m【分析】连接AC，利用勾股定理求出AC的长，再把中间的墙平面展开，使原来的长方形长度增加而宽度不变，求出新长方形的对角线长即可得到范围．【详解】解：如图所示，将图展开，图形长度增加4m，原图长度增加4m，则AB=20+4=24m，连接AC，∵四边形ABCD是长方形，AB=24m，宽AD=10m，∴AC=√AB2+BC2=√242+102=26m，∴蚂蚱从A点爬到C点，它要走的路程s≥26m．故答案为：s≥26m．【点睛】本题考查的是平面展开最短路线问题及勾股定理，根据题意画出图形是解答此题的关键．【答案】5【分析】要求彩带的长，需将圆柱的侧面展开，进而根据“两点之间线段最短”得出结果，在求线段长时，借助于勾股定理．【详解】解：将圆柱表面切开展开呈长方形，则彩灯带长为2个长方形的对角线长，∵圆柱高3米，底面周长2米，∴AC2=22+1.52=6.25，∴AC=2.5，∴每根柱子所用彩灯带的最短长度为5m．故答案为5．【点睛】本题考查了平面展开−最短路线问题，勾股定理的应用．圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，高等于圆柱的高，本题就是把圆柱的侧面展开成矩形，“化曲面为平面”，用勾股定理解决．【类型五旗杆高度问题】【答案】6m【分析】设AD=x，在△ABC中，利用勾股定理列出方程，解之即可．【详解】解：∵BF=2m，∴CE=2m，∵DE=1m，∴CD=CE−DE=1m，设AD=x，则AB=x，AC=AD−CD=x−1，由题意可得：BC⊥AE，在△ABC中，AC2+BC2=AB2，即(x−1)2+32=x2，解得：x=5，即AD=5，∴旗杆AE的高度为：AD+DE=5+1=6m．【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理的相关知识并在直角三角形中正确运用是解题的关键．34．荡秋千是深受人们喜爱的娱乐项目，如图，小丽发现，秋千静止时踏板离地面的垂直高度DE=0.5m，将它往前推送至点B，测得秋千的踏板离地面的垂直高度BF=1.1m，此时水平距离BC=EF=1.8m，秋千的绳索始终拉的很直，求绳索AD的长度．【答案】3m【分析】设绳索AD的长度为xm=(x−0.6)m，在Rt△ABC中，由勾股定理得出方程，解方程即可．【详解】解：设秋千的绳索AD长为xm，则AB为xm，∵四边形BCEF是矩形，∴BF=CE=1.1m，∵DE=0.5m，∴CD=0.6m则AC为(x−0.6)m在Rt△ABC中，由勾股定理得：AC2+BC2=AB2，即：(x−0.6)2+1.82=x2解得：x=3∴绳索AD的长度为3m．【点睛】本题考查了勾股定理的应用，由勾股定理得出方程是解题的关键．35．如图，数学兴趣小组要测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图1），聪明的小红发现：先测出垂到地面的绳子长，再将绳子拉直（如图2），测出绳子末端C到旗杆底部B的距离n，利用所学知识就能求出旗杆的长，若m=1米，n=5米，求旗杆AB的长．【答案】12米【分析】设旗杆的高为x米，在Rt△ABC中，推出x2+52=(x+1)2，可得x=12，由此解决问题.【详解】解：设AB=x米，因为∠ABC=90°，所以在Rt△ABC中，根据勾股定理，得：x2+52=(x+1)2，解之，得：x=12，所以，AB的长为12米，答：旗杆AB的长为12米．【点睛】本题考查直角三角形、勾股定理等知识，解题的关键是理解题意，学会构建方程.【答案】风筝的高度CE为61.68米．【分析】利用勾股定理求出CD的长，再加上DE的长度，即可求出CE的高度．【详解】解：在Rt△CDB中，由勾股定理，得CD=√CB2−BD2=√652−252=60(米)．∴CE=CD+DE=60+1.68=61.68(米)．答：风筝的高度CE为61.68米．【点睛】本题考查了勾股定理的应用，熟悉勾股定理，能从实际问题中抽象出勾股定理是解题的关键．37．看着冉冉升起的五星红旗，你们是否想过旗杆到底有多高呢？某数学兴趣小组为了测量旗杆高度，进行以下操作：如图1，先将升旗的绳子拉到旗杆底端，发现绳子末端刚好接触到地面；如图2，再将绳子末端拉到距离旗杆8m处，发现绳子末端距离地面2m．请根据以上测量情况，计算旗杆的高度．【答案】17米【分析】根据题意画出示意图，设旗杆高度为xm，可得AC=AD=x m，AB=(x−2)m，BC=8m，在Rt△ABC中利用勾股定理可求出x．【详解】解：如图所示设旗杆高度为x m，则AC=AD=x m，AB=(x−2)m，BC=8m，在Rt△ABC中，AB2+BC2=AC2(x−2)2+82=x2解得：x=17，答：旗杆的高度为17m．【点睛】本题考查了勾股定理的应用，解题的关键是构造直角三角形．38．同学们想利用升旗的绳子、卷尺，测算学校旗杆的高度．爱动脑的小华设计了这样一个方案：如图，将升旗的绳子拉直刚好触底，此时测得绳子末端C到旗杆AB的底端B的距离为1米，然后将绳子末端拉直到距离旗杆5米的点E处，此时测得绳子末端E距离地面的高度DE为1米．请你根据小华的测量方案和测量数据，求出学校旗杆的高度．【答案】12.5米【分析】过点E作EF⊥AB，垂足为F，在Rt△ABC和Rt△AEF中，根据勾股定理得出AC2=AB2+BC2，AE2= AF2+EF2，根据AC=AE，得出AB2+12=(AB−1)2+52，求出AB的长即可．【详解】解：过点E作EF⊥AB，垂足为F，如图所示：由题意可知：四边形BDEF是长方形，△ABC和△AEF是直角三角形，∴DE=BF=1，BD=EF=5，BC=1，在Rt△ABC和Rt△AEF中，根据勾股定理可得：AC2=AB2+BC2，AE2=AF2+EF2，即AC2=AB2+12，AE2=(AB−1)2+52，又∵AC=AE，∴AB2+12=(AB−1)2+52，解得：AB=12.5．答：学校旗杆的高度为12.5米．【点睛】本题主要考查了勾股定理的应用，解题的关键是根据勾股定理列出关于AB方程AB2+12= (AB−1)2+52．39．学过《勾股定理》后，某班兴趣小组来到操场上测量旗杆AB的高度，得到如下信息：①测得从旗杆顶端垂直挂下来的升旗用的绳子比旗杆长1米（如图1）；②当将绳子拉直时，测得此时拉绳子的手到地面的距离CD为1米，到旗杆的距离CE为6米（如图2）．根据以上信息，求旗杆AB的高度．【答案】9米【分析】设AB=x，则AC=x+1，AE=x−1，再根据勾股定理可列出关于x的等式，解出x即得出答案．【详解】解：设AB=x依题意可知：在Rt△ACE中，∠AEC=90°，AC=x+1，AE=x−1，CE=6，根据勾股定理得：AC2=AE2+CE2，即：(x+1)2=(x−1)2+62，解得：x=9答：旗杆AB的高度是9米．【点睛】本题考查勾股定理的实际应用．结合题意，利用勾股定理列出含未知数的等式是解题关键．40．如图，学校要测量旗杆的高度，同学们发现系在旗杆顶端的绳子垂到地面并多出一段（如图1），同学们首先测量了多出的这段绳子长度为1米，再将绳子拉直（如图2），测出绳子末端C到旗杆底部B的距离为5米，求旗杆的高度．【答案】12米【分析】因为旗杆、绳子、地面正好构成直角三角形，设旗杆的高度为x米，则绳子的长度为（x+1）米，根据勾股定理即可求得旗杆的高度．【详解】解：设旗杆的高度AB为x米，则绳子AC的长度为(x+1)米，在Rt△ABC中，根据勾股定理可得：x2+52=(x+1)2，解得，x=12，答：旗杆的高度为12米．【点睛】本题考查了勾股定理的应用，熟知勾股定理是解题关键．【类型六航海问题】【答案】30海里/小时【分析】先根据题意结合方位角的描述求出∠ABC=90°以及AB、BC的长，再利用勾股定理求出AC的长即可得到答案．【详解】解：如图所示，由题意得，∠HAB=90°−60°=30°，∠MBC=90°−∠EBC=60°，∵AH∥BM，∴∠ABM=∠BAH=30°，∴∠ABC=∠ABM+∠MBC=90°，∵巡逻艇沿直线追赶，半小时后在点C处追上走私船，∴BC=18×0.5=9海里，在Rt△ABC中，∠ABC=90°，AB=12海里，BC=9海里，∴AC=√AB2+BC2=15海里，∴我军巡逻艇的航行速度是15=30海里/小时，0.5答：我军巡逻艇的航行速度是30海里/小时．【点睛】本题主要考查了勾股定理的实际应用，正确理解题意在Rt△ABC中利用勾股定理求出AC的长是解题的关键．(1)求点A与点B之间的距离；(2)若在点C处有一灯塔，灯塔的信号有效覆盖半径为处有一艘轮船准备沿直线向点多能收到多少次信号？（信号传播的时间忽略不计）【答案】(1)AB=1000海里(2)最多能收到14次信号【分析】（1）由题意易得∠ACB是直角，由勾股定理即可求得点A与点B之间的距离；（2）过点C作CH⊥AB交AB于点H，在AB上取点M，N，使得CN＝CM＝500海里，分别求得NH、MH的长，可求得此时轮船过MN时的时间，从而可求得最多能收到的信号次数；【详解】（1）由题意，得：∠NCA＝54°，∠SCB＝36°；。

第3讲利用勾股定理解决折叠问题(解析版)

2020-2021学年人教版八年级下册第17章《勾股定理》同步练习【第3讲：利用勾股定理解决折叠问题】一、选择题：1．如图，将矩形ABCD沿EF折叠，使顶点C恰好落在AB边的中点C′上．若AB＝6，BC＝9，则BF 的长为（）A．4B．C．4.5D．5【答案】A【分析】先求出BC′，再由图形折叠特性知，C′F＝CF＝BC﹣BF＝9﹣BF，在Rt△C′BF中，运用勾股定理BF2+BC′2＝C′F2求解．【详解】解：∵点C′是AB边的中点，AB＝6，∴BC′＝3，由图形折叠特性知，C′F＝CF＝BC﹣BF＝9﹣BF，在Rt△C′BF中，BF2+BC′2＝C′F2，∴BF2+9＝（9﹣BF）2，解得，BF＝4，故选：A．【点睛】本题考查了折叠问题及勾股定理的应用，综合能力要求较高．同时也考查了列方程求解的能力．解题的关键是找出线段的关系．2．已知，如图，长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为()A．6cm2B．8 cm2C．10 cm2D．12 cm2【答案】A【分析】首先根据翻折的性质得到ED＝BE，用AE表示出ED，BE的长度，然后在Rt△ABE中利用勾股定理求出AE的长度，进而求出AE的长度，就可以利用面积公式求得△ABE的面积了．【详解】解：∵将此长方形折叠，使点B与点D重合，∴BE=ED．∵AD=9cm=AE+DE=AE+BE．∴BE=9﹣AE，根据勾股定理可知：AB2+AE2=BE2．∴32+AE2=(9﹣AE)2．解得：AE=4cm．∴△ABE的面积为：12×3×4=6(cm2)．故选：A．【点睛】此题主要考查了图形的翻折变换和学生的空间想象能力，解题过程中应注意折叠后哪些线段是重合的，相等的，如果想象不出哪些线段相等，可以动手折叠一下即可．3．如图，ΔABC中，∠C=90°，AC=6，BC=8，D，E分别在AC，BC上，且DE//AB.将ΔABC沿DE折叠，使C点落在斜边AB上的F点处，则AF的长是（）A．3.6B．4C．4.8D．6.4【答案】A【解析】【分析】连接CF ，根据勾股定理求得AB 长，由三角形ABC 的面积可得CF 长，勾股定理可得AF 长.【详解】解：如图，连接CF ，根据题意，得CF ⊥DE .因为DE//AB ，所以CF ⊥AB .因为∠C =90°，AC =6，BC =8，所以AB =10，所以S ΔABC =12AC ⋅BC =12AB ⋅CF ，所以CF =4.8.所以AF 2=AC 2−CF 2=62−4.82=3.62，所以AF =3.6. 故选A.【点睛】本题主要考查了勾股定理，同时涉及了折叠的性质及三角形的面积，在应用勾股定理求线段长时，可通过添加辅助线构造直角三角形求解.4．如图，有一张直角三角形纸片ABC ，两条直角边5AC =，10BC =，将ABC ∆折叠，使点A 和点B 重合，折痕为DE ，则CD 的长为（）A ．1.8B ．2.5C ．3D ．3.75【答案】D【解析】【分析】设CD=x ，则BD=AD=10-x ．在Rt △ACD 中运用勾股定理列方程，就可以求出CD 的长．【详解】解：设CD=x ，则BD=AD=10-x ．∵在Rt△ACD中，（10-x）2=x2+52，100+x2-20x=x2+25，∴20x=75，解得：x=3.75，∴CD=3.75.故选：D.【点睛】本题主要考查了折叠问题和勾股定理的综合运用．解题时，我们常常设要求的线段长为x，然后根据折叠和轴对称的性质，用含x的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．5．如图是一张直角三角形的纸片，两直角边AC＝6 cm、BC＝8 cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（）A．4 cm B．5 cm C．6 cm D．10 cm【答案】B【解析】∵直角边AC＝6 cm、BC＝8 cm ∴根据勾股定理可知：BA=√62+82=10∵A,B关于DE对称，∴BE=10÷2=56．如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点，沿过点E的直线折叠，使点B与点A重合，折痕现交于点F，已知EF=32，则BC的长是（）A B．C．3D．【答案】B【解析】【分析】折叠的性质主要有：1.重叠部分全等；2.折痕是对称轴,对称点的连线被对称轴垂直平分. 由折叠的性质可知45B EAF ∠=∠=︒,所以可求出∠AFB=90°，再直角三角形的性质可知12EF AB =,所以AB AC =,的长可求，再利用勾股定理即可求出BC 的长．【详解】解：E B A 沿过点的直线折叠，使点与点重合， B EAF 45∠∠∴==︒，AFB 90∠∴=︒，E AB AFB 90∠=︒点为中点，且， 1EF AB 2∴=， 3EF 2=， 3AB 2EF 232∴==⨯=， ΔRtABC 在中，AB ＝AC ，AB 3，=BC ∴===故选B.【点睛】本题考查了折叠的性质、等腰直角三角形的判断和性质以及勾股定理的运用，求出∠AFB=90°是解题的关键．7．如图，Rt △ABC 中，∠ACB=90°，AC=3，BC=4，将边AC 沿CE 翻折，使点A 落在AB 上的点D 处；再将边BC 沿CF 翻折，使点B 落在CD 的延长线上的点B′处，两条折痕与斜边AB 分别交于点E 、F ，则线段B′F 的长为（）A ．35B ．45C ．23D 【答案】B【分析】首先根据折叠可得CD=AC=3，BC=4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ，然后求得△BCF 是等腰直角三角形，进而求得∠B /GD=90°，CE -EF=125，ED=AE=95，从而求得B /D=1，DF=35，在Rt △B /DF 中，由勾股定理即可求得B /F 的长．【详解】解：根据首先根据折叠可得CD=AC=3，B /C=B4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ， ∴BD=4-3=1，∠DCE+∠B /CF=∠ACE+∠BCF ，∴∠ACB=90°，∴∠ECF=45°，∴△ECF 是等腰直角三角形，∴EF=CE ，∠EFC=45°，∴∠BFC=∠B /FC=135°，∴∠B /FD=90°，∵S △ABC =12AC×BC=12AB×CE ， ∴AC×BC=AB×CE ，∵根据勾股定理求得AB=5，∴CE=125，∴EF=125，=95∴DE=EF -ED=35，∴B /=45 故选：B ．【点睛】此题主要考查了翻折变换，等腰三角形的判定和性质，勾股定理的应用等，根据折叠的性质求得相等的角是解本题的关键．8．如图，在三角形纸片ABC 中，∠ACB ＝90°，BC ＝3，AB ＝5，在AC 上取一E ，以BE 为折痕，使AB 的一部分与BC 重合，A 与BC 延长线上的点D 重合，则CE 的长度为（）A ．1B ．32C ．2D ．52【答案】B【解析】试题分析：由Rt △ABC 中，BC=3,AB=5,利用勾股定理，可求得AC 的长，由折叠的性质，可得CD 的长，然后设DE=x ，由勾股定理，即可列方程求得结果．∵Rt △ABC 中，BC=3,AB=5,∴由折叠的性质可得：AB=BD=5，AE=DE ，∴CD=BD -BC=2，设DE=x ，则AE=x ，∴CE=AC -AE=4-x ，∵在Rt △CDE 中，DE 2=CD 2+BCE 2，∴x 2=22+（4-x ）2，解得：， ∴．故选B ．考点：此题主要考查了图形的翻折变换，勾股定理点评：解题过程中应注意折叠后哪些线段是重合的，相等的，如果想象不出哪些线段相等，可以动手折叠一下即可．二、填空题9．如图，在Rt ABC △中，90A ∠=︒，12AB =，5AC =，点E 在AB 上，将CAE 沿CE 折叠，使点A 落在斜边BC 上的点A '处，则AE 的长为____．【答案】103【分析】先利用勾股定理求出BC,再根据折叠的性质可得5CA CA '==，AE A E '=，90CA E CAE '∠=∠=︒,设AE x =，最后利用勾股定理列出方程即可求出AE 的长．【详解】解:由勾股定理，得13BC ==．由折叠可知5CA CA '==，AE A E '=，90CA E CAE '∠=∠=︒．设AE x =，则A E x '=，12BE x =-，1358BA '=-=．在Rt EA B '中，()222128x x -=+，解得103x =，即AE 的长为103故答案为: 103．【点睛】此题考查的是勾股定理和折叠问题,掌握利用勾股定理解直角三角形和折叠的性质是解决此题的关键． 10．如图，在Rt ABC △中，90B ∠=︒，3cm AB =，5cm AC =，将ABC 折叠，使点C 与点A 重合，得折痕DE ，则ABE △的周长等于____cm ．【答案】7【分析】根据勾股定理，可得BC 的长，根据翻折的性质，可得AE 与CE 的关系，根据三角形的周长公式，可得答案．【详解】在Rt ABC △中，90B ∠=︒，3cm AB =，5cm AC =，由勾股定理，得4cm BC ==，由翻折的性质，得CE AE =，ABE △的周长为AB BE AE AB BE CE ++=++=7（cm ）．【点睛】本题考查翻折的性质、勾股定理，利用翻折的性质得出CE 与AE 的关系是解题关键．11．如图，将矩形纸片ABCD 的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形EFGH ，若3cm EH =，4cm EF =，则边AD 的长是_______cm ．【答案】5【解析】【分析】先求出△EFH 是直角三角形，再根据勾股定理求出FH=5，再利用全等三角形的性质解答即可．【详解】设斜线上两个点分别为P 、Q ，则P 点是A 点对折过去的，∴∠EPH 为直角,△AEH ≌△PEH ，∴∠HEA=∠PEH ，同理∠PEF=∠BEF ，这四个角互补，∴∠PEH+∠PEF=90∘，∴四边形EFGH是矩形，∴△DHG≌△BFE，△HEF是直角三角形，∴BF=DH=PF，∵AH=HP，∴AD=HF，∵EH=3cm，EF=4cm，∴FH=5cm，∴FH=AD=5cm，故答案为：5.【点睛】此题考查翻折变换（折叠问题），勾股定理，全等三角形的性质，解题关键在于求出FH=5.12．如图，在长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点D与点B重合，折痕为EF，则ΔABE的面积为________cm2.【答案】6【解析】【分析】由折叠的性质可知AE与BE间的关系，根据勾股定理求出AE长可得面积.【详解】解：由题意可知BE=ED.因为AD=AE+DE=AE+BE=9cm，所以BE=(9−AE)cm.在RtΔABE中，根据勾股定理可知，AB2+AE2=BE2，所以32+AE2=(9−AE)2，所以AE=4cm，所以RtΔABE的面积为1 2×AB×AE=12×3×4=6（cm2）.故答案为：6【点睛】本题考查了勾股定理，由折叠性质得出直角边与斜边的关系是解题的关键.13．如图已知长方形ABCD中AB=8cm，BC=10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则CE的长为___________.【答案】3cm【解析】【分析】要求CE的长，应先设CE的长为x，由将△ADE折叠使点D恰好落在BC边上的点F可得Rt△ADE≌Rt△AFE，所以AF=10cm，EF=DE=8-x；在Rt△ABF中由勾股定理得：AB2+BF2=AF2，已知AB、AF的长可求出BF 的长，又CF=BC-BF=10-BF，在Rt△ECF中由勾股定理可得：EF2=CE2+CF2，即：（8-x）2=x2+（10-BF）2，将求出的BF的值代入该方程求出x的值，即求出了CE的长．【详解】∵四边形ABCD是矩形，∴AD=BC=10cm，CD=AB=8cm，根据题意得：Rt△ADE≌Rt△AFE，∴∠AFE=90°，AF=10cm，EF=DE，设CE=xcm,则DE=EF=CD−CE=(8−x)cm，在Rt△ABF中由勾股定理得：AB2+BF2=AF2，即82+BF2=102，∴BF=6cm，∴CF=BC−BF=10−6=4(cm)，在Rt△ECF中,由勾股定理可得：EF2=CE2+CF2，即(8−x)2=x2+42，∴64−16x+x2=x2+16，∴x=3(cm)，即CE=3cm.故答案为：3cm.【点睛】本题考查翻折变换（折叠问题），解题的关键是掌握折叠的性质和勾股定理.14．如图，有一块直角三角形纸片，两直角边AC=6cm ，BC=8cm ，现直角边沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 的长为________．【答案】3cm【分析】先根据勾股定理求出AB 的长,设CD ＝xcm ,则()28BD x =-cm,再由图形翻折变换的性质可知AE ＝AC ＝6cm,DE ＝CD ＝xcm,进而可得出BE 的长,在t BDE R ∆中利用勾股定理即可求出x 的值,进而得出CD 的长.【详解】 ABC ∆是直角三角形,AC ＝6cm,BC ＝8cm,10AB ∴==cm,AED ∆是ACD ∆翻折而成,6cm AE AC ∴==,设DE ＝CD ＝xcm, 90AED ∠=︒,1064cm BE AB AE ∴=-=-=,在t BDE R ∆中, 222BD DE BE =+,即()22284x x -=+,解得x ＝3.故CD 的长为3cm.【点睛】本题考查的是翻折变换及勾股定理,解答此类题目时常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x 的代数式表示其它线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.15．如图，在Rt △ABC 中，∠C ＝90°，AC ＝8，BC ＝6，按图中所示方法将△BCD 沿BD 折叠，使点C 落在边AB 上的点C ′处，则折痕BD 的长为__________．【答案】【详解】由折叠得BC′=BC=6；DC′=DC，∠BC′D=∠C＝90°∵∠C=90°，AC=8，BC=6∴AB=10∴AC′=AB－BC′=10－6=4设DC=x则DC′=DC=x，则AD=AC－DC=8－x在Rt△A C′D中，（C′D）2＋（AC′）2=（AD）2∴x 2＋42=（8－x）2∴x=3∴DC=3∴==故答案为16．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝_______．【答案】1.5【解析】在Rt△ABC中，5AC，∵将△ABC折叠得△AB′E，∴AB′＝AB，B′E＝BE，∴B′C＝5－3＝2．设B′E＝BE＝x，则CE＝4－x．在Rt△B′CE中，CE2＝B′E2＋B′C2，∴（4－x）2＝x2＋22．解之得32x=．17．如图，在Rt△ABC中，∠C=90°，AC=6，∠A=60°，点F在边AC上，并且CF=2，点E为边BC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是_________．【答案】．【解析】【分析】延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．运用勾股定理求解.【详解】解:如图，延长FP交AB于M，当FP⊥AB时，点P到AB的距离最小．∵AC=6，CF=2，∴AF=AC-CF=4，∵∠A=60°，∠AMF=90°，∴∠AFM=30°，∴AM=12AF=2，∴，∵FP=FC=2，∴PM=MF-2，∴点P到边AB距离的最小值是2．故答案为-2．【点睛】本题考查了翻折变换，涉及到的知识点有直角三角形两锐角互余、勾股定理等，解题的关键是确定出点P 的位置.18．如图，在Rt△ABC中，∠B=90°，沿AD折叠，使点B落在斜边AC上，若AB=3，BC=4，BD=．【答案】3 2【解析】如图，点E是沿AD折叠，点B的对应点，连接ED，∴∠AED=∠B=90°，AE=AB=3，∵在Rt△ABC中，∠B=90°，AB=3，BC=4，∴5==．∴EC=AC﹣AE=5﹣3=2．设BD=ED=x，则CD=BC﹣BD=4﹣x，在Rt△CDE中，CD2=EC2+ED2，即：（4﹣x）2=x2+4，解得：x=32．∴BD=32三、解答题19．如图，一张长8cm，宽6cm的矩形纸片，将它沿某直线折叠使得A、C重合，求折痕EF的长．【答案】EF 的长为152【分析】联结CF ，根据翻折的图形全等得到AF=CF ，再根据勾股定理计算即可；【详解】联结CF ，∵翻折的图形全等，∴AF=CF ，设AF=x ，则DF=8-x ，2226(8)x x +-=，254x =， ∵OC=5， ∴OF=154，可证OE=OF ， ∴EF=152．【点睛】本题主要考查了勾股定理的折叠问题，准确计算是解题的关键．20．如图，在ABC 中，90BAC ∠=︒，点D 为BC 边中点，E ，F 分别在AB ，AC 上，且ED FD ⊥，连接EF ．判断BE ，EF ，FC 之间的数量关系，并证明你的结论．【答案】222BE FC EF +=．证明见解析.【分析】将EDF 沿着DF 翻折得到GDF ，连接CG ,由翻折可知FDE FDG ≌，从而得出：DE DG =，EF GF =，90EDF GDF ∠=∠=︒，再利用SAS 证出BDE CDG ≌，从而得出BE CG =，B DCG ∠=∠，最后利用勾股定理和等量代换即可证出结论．【详解】222BE FC EF +=．证明如下：如图，将EDF 沿着DF 翻折得到GDF ，连接CG ．由翻折可知FDE FDG ≌，∴DE DG =，EF GF =，90EDF GDF ∠=∠=︒，∴E ，D ，G 三点共线．∵D 为BC 边中点，∴BD CD =．在△BDE 和△CDG 中BD CD EDB GDC DE DG =⎧⎪∠=∠⎨⎪=⎩∴BDE CDG ≌，∴BE CG =，B DCG ∠=∠．又∵90BAC ∠=︒，∴90B ACB ∠+∠=︒，∴90DCG ACB ∠+∠=︒，即90FCG ∠=︒．在Rt FCG 中，∵222CG FC GF +=，∴222BE FC EF +=．【点睛】此题考查的是全等三角形的判定及性质、勾股定理和折叠问题，掌握全等三角形的判定及性质、利用勾股定理解直角三角形和折叠的性质是解决此题的关键．21．如图所示，已知在ABC 中，22.5B ∠=︒，折叠ABC 使A ，B 两点重合，折痕交BC 于点D ，交AB 于点F，BD =AE BC ⊥于点E ，求AE 的长．【答案】6AE =．【分析】根据折叠的性质可知:AD BD == 22.5BAD B ∠=∠=︒,再根据三角形外角的性质可得45ADE ∠=︒,从而得出AE=DE,最后利用勾股定理即可求出AE ．【详解】解:由折叠的性质可知:AD BD == 22.5BAD B ∠=∠=︒．又∵ADE B BAD ∠=∠+∠，∴45ADE ∠=︒．∵AE BC ⊥，∴△ADE 为等腰直角三角形,AE=DE由勾股定理，得222AE DE AD +=，∴(222AE =，∴6AE =．【点睛】此题考查的是勾股定理和折叠问题,掌握利用勾股定理解直角三角形和折叠的性质是解决此题的关键． 22．如图，将矩形ABCD 沿AE 折叠，使点D 落在BC 边的点F 处，已知AB =DC =8，AD =BC =10．求EC 的长．【答案】3.【解析】【分析】设EC 的长为x ，则DE =8−x ，再利用勾股定理求出BF 的值，得出FC =BC −BF =10−6=4，再根据勾股定理即可解答.设EC的长为x，则DE=8−x．∵ΔADE折叠后的图形是ΔAFE，∴AD=AF，DE=EF．∵AD=BC=10，∴AF=10．∵四边形ABCD是矩形，∴∠B=∠C=90°．在RtΔABF中，BF=√AF2−AB2=6，∴FC=BC−BF=10−6=4．在RtΔEFC中，FC2+EC2=EF2，∴42+x2=(8−x)2，解得x=3，∴EC的长为3．【点睛】此题考查矩形的性质，折叠的性质，勾股定理，解题关键在于求出FC的值.23．把长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，如图，已知AB=8，BC=10，求EC的长．【答案】EC的长度为3．【解析】试题分析：由长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，可得AF=AD=10，DE=EF，然后设EC=x，则DE=EF=CD﹣EC=8﹣x，首先在Rt△ABF中，利用勾股定理求得BF的长，继而可求得CF的长，然后在Rt △CEF中，由勾股定理即可求得方程：x2+42=（8﹣x）2，解此方程即可求得答案．解：∵四边形ABCD是长方形，∴∠B=∠C=90°，AD=BC=10，CD=AB=8，∵△ADE折叠后得到△AFE，∴AF=AD=10，DE=EF，设EC=x，则DE=EF=CD﹣EC=8﹣x，∵在Rt△ABF中，AB2+BF2=AF2，∴82+BF2=102，∴CF=BC﹣BF=10﹣6=4，∵在Rt△EFC中，EC2+CF2=EF2，∴x2+42=（8﹣x）2，解得：x=3，即EC的长度为3．考点：翻折变换（折叠问题）；勾股定理．24．将一矩形纸片OABC放在平面直角坐标系中，O为原点，点A在x轴上，点C在y轴上，OA=10，OC=8，如图在OC边上取一点D，将△BCD沿BD折叠，使点C恰好落在OA边上，记作E点；（1）求点E的坐标及折痕DB的长；（2）在x轴上取两点M、N（点M在点N的左侧），且MN=4.5，求使四边形BDMN的周长最短的点M、点N的坐标．【答案】（1）E（4，0）；（2）M（1.5，0）；N（6，0）；【解析】分析：(1)、根据矩形的性质得到BC=OA=10，AB=OC=8，再根据折叠的性质得到BC=BE=10，DC=DE，易得AE=6，则OE=10-6=4，即可得到E点坐标；在Rt△ODE中，设DE=x，则OD=OC-DC=OC-DE=8-x，利用勾股定理可计算出x，再在Rt△BDE中，利用勾股定理计算出BD；(2)、以D、M、N为顶点作平行四边形DMND′，作出点B关于x轴对称点B′，则易得到B′的坐标，D′的坐标，然后利用待定系数法求出直线D′B′的解析式，令y=0，得-2x+12=0，确定N点坐标，也即可得到M点坐标．详解：(1)、∵四边形OABC为矩形，∴BC=OA=10，AB=OC=8，∵△BCD沿BD折叠，使点C恰好落在OA边E点上，∴BC=BE=10，DC=DE，在Rt△ABE中，BE=10，AB=8，∴AE=6，∴OE=10-6=4，∴E点坐标为（4，0）；在Rt△ODE中，设DE=x，则OD=OC-DC=OC-DE=8-x，∴x2=42+（8-x）2，解得x=5，在Rt△BDE中，=(2)、以D、M、N为顶点作平行四边形DMND′，作出点B关于x轴对称点B′，如图，∴B′的坐标为（10，-8），DD′=MN=4.5，∴D′的坐标为（4.5，3），设直线D′B′的解析式为y=kx+b，把B′（10，-8），D′（4.5，3）代入得，10k+b=-8，4.5k+b=3，解得k=-2，b=12，∴直线D′B′的解析式为y=-2x+12，令y=0，得-2x+12=0，解得x=6，∴M（1.5，0）；N（6，0）．点睛：本题考查了折叠的性质：折叠前后两图形全等，即对应线段相等，对应角相等．也考查了矩形的性质和勾股定理以及待定系数法，综合性非常强．理解翻折图形的性质是解决这个问题的关键．。

勾股定理折叠问题

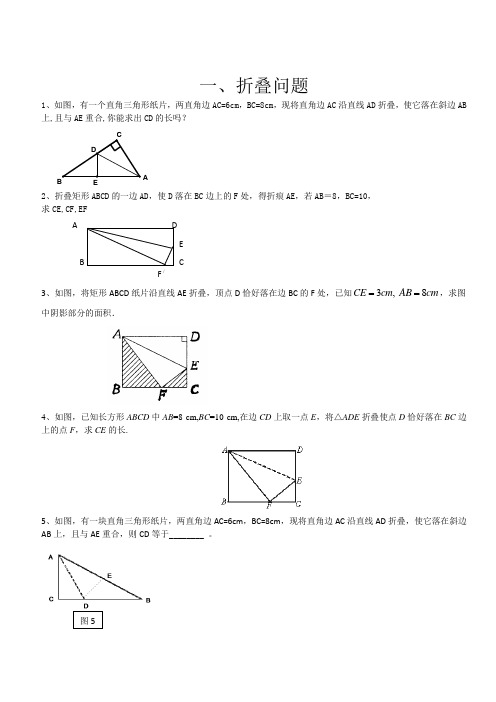
CB ADE一、折叠问题1、如图，有一个直角三角形纸片，两直角边AC=6cm ，BC=8cm ，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上,且与AE 重合,你能求出CD 的长吗？2、折叠矩形ABCD 的一边AD ，使D 落在BC 边上的F 处，得折痕AE ，若AB ＝8，BC=10，求CE,CF,EF3、如图，将矩形ABCD 纸片沿直线AE 折叠，顶点D 恰好落在边BC 的F 处，已知3,CE cm =8AB cm =，求图中阴影部分的面积．4、如图，已知长方形ABCD 中AB =8 cm,BC =10 cm,在边CD 上取一点E ，将△ADE 折叠使点D 恰好落在BC 边上的点F ，求CE 的长.5、如图，有一块直角三角形纸片，两直角边AC=6cm ，BC=8cm ，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 等于________ 。

A CD F ／E图56、将矩形ABCD（A B﹤AD）沿对角线BD折叠，使点C落在C′处，BC′交AD于E，AD=8㎝，AB=4㎝，求三角形BED的面积。

7、如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD=8，AB=4，则DE的长为8、如图，折叠矩形纸片ABCD，先折出折痕（对角线）BD，再折叠使AD边与BD重合，得折痕DG，若AB=4，BC=3，求AG的长。

9、P为正方形ABCD内一点，将△ABP绕B顺时针旋转90°到△CBE的位置，若BP＝a.求：以PE为边长的正方形的面积.二、生活应用D ˊABCD A ˊ B ˊC ˊ1、将穿好彩旗的旗杆垂直插在操场上，旗杆从旗顶到地面的高度为320cm ，在无风的天气里，彩旗自然下垂，如右图. 求彩旗下垂时最低处离地面的最小高度h .彩旗完全展平时的尺寸如左图的长方形（单位：cm ）.2、八（2）班数学课外活动小组的同学测量学校旗杆的高度时，发现升旗的绳子垂到地面要多1米，当他们把绳子的下端拉开5米后，发现下端刚好接触地面。

利用勾股定理解决折叠问题及答案

小专题(二) 利用勾股定理解决折叠与展开问题类型1 利用勾股定理解决平面图形的折叠问题 1．如图，有一张直角三角形纸片，两直角边AC ＝5 cm ，BC ＝10 cm ，将△ABC 折叠，使点B 与点A 重合，折痕为DE ，则CD 的长为( )A.252 cmB.152 cmC.254 cm D.154cm2．如图所示，有一块直角三角形纸片，∠C ＝90°，AC ＝4 cm ，BC ＝3 cm ，将斜边AB 翻折，使点B 落在直角边AC 的延长线上的点E 处，折痕为AD ，则CE 的长为( )A ．1 cmB ．1.5 cmC ．2 cmD ．3 cm3．(青岛中考)如图，将长方形ABCD 沿EF 折叠，使顶点C 恰好落在AB 边的中点C ′上，若AB ＝6，BC ＝9，则BF 的长为( )A ．4B ．3 2C ．4.5D ．54．如图，长方形纸片ABCD 中，已知AD ＝8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF ＝3，则AB 的长为( )A ．3B ．4C ．5D ．65．(铜仁中考)如图，在长方形ABCD 中，BC ＝6，CD ＝3，将△BCD 沿对角线BD 翻折，点C 落在点C ′处，BC ′交AD 于点E ，则线段DE 的长为( )A ．3 B.154 C ．5 D.1526．如图，在长方形ABCD中，AB＝4，AD＝6，E是AB边的中点，F是线段BC上的动点，将△EBF沿EF所在直线折叠得到△EB′F，连接B′D，则B′D的最小值是( )A．210－2B．6C．213－2D．47．如图所示，在△ABC中，∠B＝90°，AB＝3，AC＝5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE 的周长为________．8．如图，在Rt△ABC中，∠C＝90°，BC＝6 cm，AC＝8 cm，按图中所示方法将△BCD沿BD折叠，使点C落在AB 边的C′点，那么△ADC′的面积是________．9．如图，已知Rt△ABC中，∠C＝90°，AC＝6，BC＝8，将它的锐角A翻折，使得点A落在BC边的中点D处，折痕交AC边于点E，交AB边于点F，则DE的值为________．10．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则EB′＝________．11．为了向建国六十六周年献礼，某校各班都在开展丰富多彩的庆祝活动，八年级(1)班开展了手工制作竞赛，每个同学都在规定时间内完成一件手工作品．陈莉同学在制作手工作品的第一、二个步骤是：①先裁下了一张长BC＝20 cm，宽AB＝16 cm的长方形纸片ABCD，②将纸片沿着直线AE折叠，点D恰好落在BC边上的F处，请你根据①②步骤解答下列问题：计算EC，FC的长．类型2 利用勾股定理解决立体图形的展开问题1．如图，一圆柱体的底面周长为24 cm，高AB为5 cm，BC是直径，一只蚂蚁从点A出发沿着圆柱体的表面爬行到点C的最短路程是( )A．6 cm B．12 cmC．13 cm D．16 cm2．如图，圆柱形玻璃杯，高为12 cm，底面周长为18 cm，在杯内离杯底4 cm的点C处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿4 cm与蜂蜜相对的点A处，则蚂蚁到达蜂蜜的最短距离为________cm.3．如图，在一个长为2 m，宽为1 m的长方形草地上，放着一根长方体的木块，它的棱和场地宽AD平行且棱长大于AD，木块从正面看是边长为0.2 m的正方形，一只蚂蚁从点A处到达C处需要走的最短路程是________m(精确到0.01 m)．4．一位同学要用彩带装饰一个长方体礼盒．长方体高6 cm，底面是边长为4 cm的正方形，从顶点A到顶点C′如何贴彩带用的彩带最短？最短长度是多少？5．如图，一个长方体形状的木柜放在墙角处(与墙面和地面均没有缝隙)，有一只蚂蚁从柜角A处沿着木柜表面爬(1)请你画出蚂蚁能够最快到达目的地的可能路径；(2)当AB＝4，BC＝4，CC1＝5时，求蚂蚁爬过的最短路径的长．参考答案类型11．D 2.A 3.A 4.D 5.B 6.A 7.7 8.6 cm29.13310．1.511.因为△ADE与△AFE关于AE对称，所以△ADE≌△AFE.所以DE＝FE，AD＝AF.因为BC＝20 cm，AB＝16 cm，所以CD＝16 cm，AD＝AF＝20 cm.在Rt△ABF中，由勾股定理，得BF＝12 cm.所以CF＝20－12＝8(cm)．因为四边形ABCD是长方形，所以∠C＝90°.设CE＝x，则DE＝EF＝16－x，在Rt△CEF中，由勾股定理，得(16－x)2＝64＋x2.解得：x＝6.所以EC＝6 cm.答：EC＝6 cm，CF＝8 cm.类型21．C 2.15 3.2.604．把长方体的面DCC′D′沿棱C′D′展开至面ABCD上，如图．构成矩形ABC′D′，则A到C′的最短距离为AC′的长度，连接AC′交DC于O，易证△AOD≌△C′OC.∴OD＝OC.即O为DC的中点，由勾股定理，得AC′2＝AD′2＋D′C′2＝82＋62＝100，∴AC′＝10 cm.即从顶点A沿直线到DC中点O，再沿直线到顶点C′，贴的彩带最短，最短长度为10 cm.5．(1)如图，木柜的表面展开图是两个矩形ABC′1D1和ACC1A1.蚂蚁能够最快到达目的地的可能路径有如图所示的AC′1和AC1两种．(2)蚂蚁沿着木柜表面经线段A1B1到C′1，爬过的路径的长l1＝42＋（4＋5）2＝97.蚂蚁沿着木柜表面经线段BB1到C1，爬过的路径的长l2＝（4＋4）2＋52＝89.∵l1>l2，∴最短路径的长是89.。

人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案)

人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案）类型一利用勾股定理解决三角形的折叠问题1．如图 △ABC 中 ∠ACB ＝90° AC ＝8 BC ＝6 将△ADE 沿DE 翻折使点A 与点B 重合则CE 的长为．思路引领：设CE ＝x 则AE ＝BE ＝8﹣x 在Rt △BCE 中由勾股定理可得62+x 2＝（8﹣x ）2 即可解得答案．解：设CE ＝x 则AE ＝BE ＝8﹣x在Rt △BCE 中 BC 2+CE 2＝BE 2∴62+x 2＝（8﹣x ）2解得x =74故答案为：74．总结提升：本题考查直角三角形中的折叠问题解题的关键是掌握折叠的性质熟练应用勾股定理列方程解决问题．2．（2021秋•介休市期中）如图所示有一块直角三角形纸片 ∠C ＝90° AC ＝8cm BC ＝6cm 将斜边AB 翻折使点B 落在直角边AC 的延长线上的点E 处折痕为AD 则CE 的长为 cm ．思路引领：根据勾股定理可将斜边AB 的长求出根据折叠的性质知 AE ＝AB 已知AC 的长可将CE 的长求出．解：在Rt △ABC 中∵∠C＝90°AC＝8cm BC＝6cm∴AB=√AC2+BC2=10cm根据折叠的性质可知：AE＝AB＝10cm∵AC＝8cm∴CE＝AE﹣AC＝2cm即CE的长为2cm故答案为：2．总结提升：此题考查翻折问题将图形进行折叠后两个图形全等是解决折叠问题的突破口．3．（2020秋•金台区校级期末）如图在△ABC中∠ACB＝90°点E F在边AB上将边AC沿CE翻折使点A落在AB上的点D处再将边BC沿CF翻折使点B落在CD的延长线上的点B′处（1）求∠ECF的度数；（2）若CE＝4 B′F＝1 求线段BC的长和△ABC的面积．思路引领：（1）由折叠可得∠ACE＝∠DCE=12∠ACD∠BCF＝∠B'CF=12∠BCB' 再根据∠ACB＝90°即可得出∠ECF＝45°；（2）在Rt△BCE中根据勾股定理可得BC=√41设AE＝x则AB＝x+5 根据勾股定理可得AE2+CE2＝AB2﹣BC2即x2+42＝（x+5）2﹣41 求得x=165得出AE的长和AB的长再由三角形面积公式即可得出S△ABC．解：（1）由折叠可得∠ACE＝∠DCE=12∠ACD∠BCF＝∠B'CF=12∠BCB'又∵∠ACB＝90°∴∠ACD+∠BCB'＝90°∴∠ECD+∠FCD=12×90°＝45°即∠ECF＝45°；（2）由折叠可得：∠DEC＝∠AEC＝90°BF＝B'F＝1 ∴∠EFC＝45°＝∠ECF∴CE＝EF＝4∴BE＝4+1＝5在Rt△BCE中由勾股定理得：BC=√BE2+CE2=√52+42=√41设AE＝x则AB＝x+5∵Rt△ACE中AC2＝AE2+CE2Rt△ABC中AC2＝AB2﹣BC2∴AE2+CE2＝AB2﹣BC2即x2+42＝（x+5）2﹣41解得：x=16 5∴AE=165AB＝AE+BE=165+5=415∴S△ABC=12AB×CE=12×415×4=825．总结提升：本题主要考查了折叠变换的性质、勾股定理、三角形面积等知识；熟练掌握折叠变换的性质由勾股定理得出方程是解题的关键．4．（2022秋•安岳县期末）如图在△ABC中∠C＝90°把△ABC沿直线DE折叠使△ADE与△BDE 重合．（1）若∠A＝34°则∠CBD的度数为；（2）当AB＝m（m＞0）△ABC的面积为2m+4时△BCD的周长为（用含m的代数式表示）；（3）若AC＝8 BC＝6 求AD的长．思路引领：（1）根据折叠可得∠1＝∠A＝34°根据三角形内角和定理可以计算出∠ABC＝56°进而得到∠CBD＝22°；（2）根据三角形ACB的面积可得12AC•BC＝2m+4 进而得到AC•BC＝4m+8 再在Rt△CAB中CA2+CB2＝BA2再把左边配成完全平方可得CA+CB的长进而得到△BCD的周长；（3）根据折叠可得AD＝DB设CD＝x则AD＝BD＝8﹣x再在Rt△CDB中利用勾股定理可得x2+62＝（8﹣x）2再解方程可得x的值进而得到AD的长．解：（1）∵把△ABC 沿直线DE 折叠使△ADE 与△BDE 重合∴∠ABD ＝∠A ＝34°∵∠C ＝90°∴∠ABC ＝180°﹣90°﹣34°＝56°∴∠CBD ＝56°﹣34°＝22°故答案为：22°；（2）∵△ABC 的面积为2m +4∴12AC •BC ＝2m +4 ∴AC •BC ＝4m +8∵在Rt △CAB 中 CA 2+CB 2＝BA 2 AB ＝m∴CA 2+CB 2+2AC •BC ＝BA 2+2AC •BC∴（CA +BC ）2＝m 2+8m +16＝（m +4）2∴CA +CB ＝m +4∵AD ＝DB∴CD +DB +BC ＝m +4．即△BCD 的周长为m +4故答案为：m +4；（3）∵把△ABC 沿直线DE 折叠使△ADE 与△BDE 重合∴AD ＝DB设CD ＝x 则AD ＝BD ＝8﹣x在Rt △CDB 中 CD 2+CB 2＝BD 2x 2+62＝（8﹣x ）2解得：x =74AD ＝8−74=254．总结提升：此题主要考查了图形的翻折变换以及勾股定理完全平方公式关键是掌握勾股定理以及折叠后哪些是对应角和对应线段．5．（2021秋•章丘区期中）（1）如图① Rt △ABC 的斜边AC 比直角边AB 长2cm 另一直角边BC 长为6cm 求AC 的长．（2）拓展：如图②在图①的△ABC的边AB上取一点D连接CD将△ABC沿CD翻折使点B的对称点E落在边AC上．①AE的长．②求DE的长．思路引领：（1）在Rt△ABC中由勾股定理可求AB的长即可求解；（2）①由折叠的性质可得∠DEC＝∠DBC＝90°DE＝DB EC＝BC＝6cm于是得到答案；②在Rt△ADE中由勾股定理可求DE的长．解：（1）设AB＝xcm则AC＝（x+2）cm∵AC2＝AB2+BC2∴（x+2）2＝x2+62解得x＝8∴AB＝8cm∴AC＝8+2＝10（cm）；（2）①由折叠的性质可得∠DEC＝∠DBC＝90°DE＝DB EC＝BC＝6cm∴∠AED＝90°AE＝AC﹣EC＝4（cm）；②设DE＝DB＝ycm则AD＝AB﹣BD＝（8﹣y）cm在Rt△ADE中AD2＝AE2+DE2∴（8﹣y）2＝42+y2解得：y＝3∴DE＝3（cm）．总结提升：本题考查了翻折变换折叠的性质勾股定理利用勾股定理列出方程是本题的关键．类型二利用勾股定理解决长方形的折叠问题6．（2022•纳溪区模拟）如图在矩形ABCD中AB＝5 AD＝3 点E为BC上一点把△CDE沿DE翻折点C 恰好落在AB 边上的F 处则CE 的长为．思路引领：利用勾股定理得出AF 的长度再利用折叠的性质在△BEF 中求解BE 的长即可得出CE 的长度．解：在矩形ABCD 中 AB ＝5 AD ＝3 由折叠的性质可得：DF ＝DC ＝AB ＝5∴AF =√DF 2−AD 2=√52−32=4∴BF ＝AB ﹣AF ＝5﹣4＝1设CE ＝x 则：EF ＝CE ＝x BE ＝BC ﹣CE ＝3﹣x在Rt △BEF 中由勾股定理可得：12+（3﹣x ）2＝x 2解得：x =53∴CE =53故答案为：53．总结提升：本题考查了折叠的性质、矩形的性质和勾股定理等知识点解题的关键是利用AF 求出BF 的长度．7．（2021•郯城县校级模拟）如图在长方形ABCD 中 AB ＝3cm AD ＝9cm 将此长方形折叠使点D 与点B 重合折痕为EF 则△ABE 的面积为（）cm 2．A ．12B ．10C ．6D ．15思路引领：由长方形的性质得BAE ＝90° 再由折叠的性质得BE ＝ED 然后在Rt △ABE 中由勾股定理得32+AE2＝（9﹣AE）2解得AE＝4（cm）即可求解．解：∵四边形ABCD是长方形∴∠BAE＝90°∵将此长方形折叠使点B与点D重合∴BE＝ED∵AD＝9＝AE+DE＝AE+BE∴BE＝9﹣AE在Rt△ABE中由勾股定理得：AB2+AE2＝BE2∴32+AE2＝（9﹣AE）2解得：AE＝4（cm）∴S△ABE=12AB•AE=12×3×4＝6（cm2）故选：C．总结提升：本题考查了翻折变换的性质、矩形的性质以及勾股定理等知识；熟练掌握翻折变换的性质和矩形的性质由勾股定理得出方程是解题的关键．8．（2020春•余干县校级期末）如图把长方形纸片ABCD沿EF折叠使点B落在边AD上的点B'处点A落在点A'处．（1）试说明B'E＝BF；（2）设AE＝a AB＝b BF＝c试猜想a b c之间的关系并说明理由．思路引领：（1）根据折叠的性质、平行的性质及等角对等边即可说明；（2）根据折叠的性质将AE、AB、BF都转化到直角三角形△A'B'E中由勾股定理可得a b c之间的关系．（1）证明：由折叠的性质得：B'F＝BF∠B'FE＝∠BFE在长方形纸片ABCD中AD∥BC∴∠B'EF＝∠BFE∴∠B'FE＝∠B'EF∴B'F＝B'E∴B'E＝BF．（2）解：a b c之间的关系是a2+b2＝c2．理由如下：由（1）知B'E＝BF＝c由折叠的性质得：∠A'＝∠A＝90°A'E＝AE＝a A'B'＝AB＝b．在△A'B'E中∵∠A'＝90°∴A'E2+A'B'2＝B'E2∴a2+b2＝c2．总结提升：本题考查了翻折变换的性质、矩形的性质、等腰三角形的判定、勾股定理等知识；灵活利用折叠的性质进行线段间的转化是解题的关键．9．（2020秋•罗湖区校级期末）如图把一张长方形纸片ABCD折叠起来使其对角顶点A与C重合D 与G重合若长方形的长BC为8 宽AB为4 求：（1）DE的长；（2）求阴影部分△GED的面积．思路引领：（1）设DE＝EG＝x则AE＝8﹣x在Rt△AEG中根据AG2+EG2＝AE2构建方程即可解决问题；（2）过G点作GM⊥AD于M根据三角形面积不变性AG×GE＝AE×GM求出GM的长根据三角形面积公式计算即可．解：（1）设DE＝EG＝x则AE＝8﹣x在Rt△AEG中AG2+EG2＝AE2∴16+x2＝（8﹣x）2解得x＝3∴DE＝3．（2）过G 点作GM ⊥AD 于M则12•AG ×GE =12•AE ×GM AG ＝AB ＝4 AE ＝CF ＝5 GE ＝DE ＝3 ∴GM =125∴S △GED =12GM ×DE =185．总结提升：本题主要考查了折叠的性质、勾股定理以及三角形面积不变性灵活运用折叠的性质、勾股定理等几何知识点来分析、判断、推理是解题的关键．类型三利用勾股定理解决正方形的折叠问题10．（2019•黔东南州一模）如图将边长为6cm 的正方形纸片ABCD 折叠使点D 落在AB 边中点E 处点C 落在点Q 处折痕为FH 则线段AF 的长为（）A ．32B ．3C ．94D ．154思路引领：由正方形的性质和折叠的性质可得EF ＝DE AB ＝AD ＝6cm ∠A ＝90° 由勾股定理可求AF 的长．解：∵将边长为6cm 的正方形纸片ABCD 折叠使点D 落在AB 边中点E 处∴EF ＝DE AB ＝AD ＝6cm ∠A ＝90°∵点E 是AB 的中点∴AE ＝BE ＝3cm在Rt △AEF 中 EF 2＝AF 2+AE 2∴（6﹣AF ）2＝AF 2+9∴AF=9 4故选：C．总结提升：本题考查了翻折变换正方形的性质勾股定理利用勾股定理求线段的长度是本题的关键．11．如图将边长为8cm的正方形纸片ABCD折叠使点D落在BC边的中点E处点A落在点F处折痕为MN则线段CN的长是（）A．3cm B．4cm C．5cm D．6cm思路引领：由折叠的性质可得DN＝NE由中点的性质可得EC＝4cm结合正方形的性质可得∠BCD＝90°；设CN的长度为xcm则EN＝DN＝（8﹣x）cm接下来在直角△CEN中运用勾股定理就可以求出CN的长度．解：∵四边形MNEF是由四边形ADMN折叠而成的∴DN＝NE．∵E是BC的中点且BC＝8cm∴EC＝4cm．∵四边形ABCD是正方形∴∠BCD＝90°．设CN的长度为xcm则EN＝DN＝（8﹣x）cm由勾股定理NC2+EC2＝NE2得x2+42＝（8﹣x）2解得x＝3．故选：A．总结提升：本题考查翻折变换的问题折叠问题其实质是轴对称对应线段相等对应角相等找到相应的直角三角形利用勾股定理求解是解决本题的关键．第二部分专题提优训练1．（2022秋•慈溪市校级期中）在Rt△ABC中∠B＝90°AB＝4 BC＝8 D、E分别是边AC、BC上的点将△ABC沿着DE进行翻折点A和点C重合则EC＝．思路引领：设EC ＝x 在Rt △ABE 中由勾股定理得42+（8﹣x ）2＝x 2 即可解得答案．解：设EC ＝x 则BE ＝8﹣x∵将△ABC 沿着DE 进行翻折点A 和点C 重合∴AE ＝EC ＝x在Rt △ABE 中 AB 2+BE 2＝AE 242+（8﹣x ）2＝x 2解得x ＝5∴EC ＝5故答案为：5．总结提升：本题考查直角三角形中的翻折问题解题的关键是掌握翻折的性质能应用勾股定理列方程解决问题．2．（2021秋•靖江市期中）如图在Rt △ABC 中 ∠C ＝90° D 是AB 的中点 AD ＝5 BC ＝8 E 是直线BC 上一动点把△BDE 沿直线ED 翻折后点B 落在点F 处当FD ⊥BC 时线段BE 的长为．思路引领：分点F 在BC 下方点F 在BC 上方两种情况讨论由勾股定理可BC ＝4 由平行线分线段成比例可得BD AD =BP BC =DP AC =12 求出FP 由勾股定理可求BE 的长．解：若点F 在BC 下方时 DF 与BC 交于点P 如图1所示：∵D 是AB 的中点∴BD ＝AD ＝5∴AB ＝2AD ＝10∵∠C ＝90° BC ＝8∴AC =√AB 2−BC 2=√102−82=6∵点D 是AB 的中点∵FD ⊥BC ∠C ＝90°∴FD ∥AC∴BD AD =BP BC =DP AC =12 ∴BP ＝PC =12BC ＝4 DP =12AC ＝3∵△BDE 沿直线ED 翻折∴FD ＝BD ＝5 FE ＝BE∴FP ＝FD ﹣DP ＝5﹣3＝2在Rt △FPE 中 EF 2＝FP 2+PE 2∴BE 2＝22+（4﹣BE ）2解得：BE =52；若点F 在BC 上方时 FD 的延长线交BC 于点P 如图2所示：FP ＝DP +FD ＝3+5＝8在Rt △EFP 中 EF 2＝FP 2+EP 2∴BE 2＝64+（BE ﹣4）2解得：BE ＝10故答案为：52或10．总结提升：此题考查了折叠的性质、平行线的性质、直角三角形的性质以及勾股定理等知识熟练掌握翻折变换的性质是解题的关键．3．如图在Rt △ABC 中 AC ＝6 BC ＝8 D 为BC 上一点将Rt △ABC 沿AD 折磨点C 恰好落在AB 边上的E 点求BD 的长．思路引领：由勾股定理求出AB＝10 由折叠的性质得出CD＝DE∠C＝∠AED＝90°AE＝AC＝6 得出BE＝AB﹣AE＝4 ∠BED＝90°设CD＝ED＝x则BD＝8﹣x在Rt△BDE中由勾股定理得出方程解方程即可．解：∵Rt△ABC中AC＝6 BC＝8∴AB=√62+82=10由折叠的性质得：CD＝DE∠C＝∠AED＝90°AE＝AC＝6∴BE＝AB﹣AE＝4 ∠BED＝90°设CD＝ED＝x则BD＝8﹣x在Rt△BDE中由勾股定理得：x2+42＝（8﹣x）2解得：x＝3∴BD＝8﹣3＝5．总结提升：本题考查了翻折变换的性质、勾股定理等知识；熟练掌握翻折变换的性质由勾股定理得出方程是解题的关键．4．（2018秋•襄汾县校级月考）如图在Rt△ABC中∠C＝90°AC＝8 BC＝6 按图中所示方法将△BCD沿BD折叠使点C落在边AB上的点C'处求AD的长及四边形BCDC′的面积．思路引领：利用勾股定理列式求出AB根据翻折变换的性质可得BC′＝BC C′D＝CD然后求出AC′设AD＝x表示出C′D、AC′然后利用勾股定理列方程求解即可求出AD；然后根据三角形的面积公式计算即可求出四边形BCDC′的面积．解：∵∠C＝90°AC＝8 BC＝6∴AB=√AC2+BC2=10由翻折变换的性质得BC′＝BC＝6 C′D＝CD∴AC′＝AB﹣BC′＝10﹣6＝4设CD＝x则C′D＝x AD＝8﹣x在Rt△AC′D中由勾股定理得AC′2+C′D2＝AD2即42+x2＝（8﹣x）2解得x＝3即CD＝3∴AD＝8﹣x＝5；由折叠可知：S△BCD＝S△BC′D∴四边形BCDC′的面积＝2S△BCD＝2×12×CD•BC＝3×6＝18．总结提升：本题考查了翻折变换的性质勾股定理此类题目熟记性质并利用勾股定理列出方程是解题的关键．5．（2021春•厦门期中）在矩形ABCD中AB＝3 BC＝4 E是AB上一个定点点F是BC上一个动点把矩形ABCD沿直线EF折叠点B的对应点B′落在矩形内部．若DB′的最小值为3 则AE＝53．思路引领：连接DE则DB′+EB′≥DE由EB′＝EB为定值故当D E B′三点共线时DB′最小利用勾股定理建立方程即可求解．解：如图1 连接DE由折叠性质可得：EB′＝EB∵DB′+EB′≥DE∴DB′≥DE﹣EB′＝DE﹣EB∵点E为定点∴EB为定值∴当D E B′三点共线时DB′最小且最小值为3∴DB′＝3如图2∵四边形ABCD 为矩形∴∠A ＝90° AD ＝BC ＝4设AE ＝x 则：EB ′＝EB ＝AB ﹣AE ＝3﹣x∴ED ＝EB ′+DB ′＝3﹣x +3＝6﹣x在Rt △AED 中由勾股定理可得：x 2+42＝（6﹣x ）2解得：x =53∴AE =53故答案为：53．总结提升：本题考查折叠的性质、矩形的性质、勾股定理等知识点解题的关键是运用方程思想．6．（2021秋•城阳区校级月考）把一张矩形纸片（矩形ABCD ）按如图方式折叠使顶点B 和点D 重合折痕为EF ．若AB ＝3cm BC ＝5cm 则重叠部分△DEF 的面积是（）cm 2．A ．2B ．3.4C ．4D ．5.1思路引领：由矩形的性质得AD ＝BC ＝5cm CD ＝AB ＝3cm ∠A ＝90° 再由折叠的性质得A 'D ＝AB ＝3cm ∠A '＝∠A ＝90° AE '＝AE 设AE ＝xcm 则A ′E ＝xcm DE ＝（5﹣x ）cm 然后在Rt △A 'DE 中由勾股定理得出方程解方程进而得出DE 的长即可解决问题．解：∵四边形ABCD 是矩形 AB ＝3cm BC ＝5cm∴AD＝BC＝5cm CD＝AB＝3cm∠A＝90°由折叠的性质得：A'D＝AB＝3cm∠A'＝∠A＝90°AE'＝AE 设AE＝xcm则A′E＝xcm DE＝（5﹣x）cm在Rt△A'DE中由勾股定理得：A′E2+A′D2＝ED2即x2+32＝（5﹣x）2解得：x＝1.6∴DE＝5﹣1.6＝3.4（cm）∴△DEF的面积=12DE•CD=12×3.4×3＝5.1（cm2）故选：D．总结提升：此题考查了翻折变换的性质、矩形的性质、勾股定理以及三角形面积等知识熟练掌握翻折变换的性质和矩形的性质由勾股定理得出方程是解题的关键．7．（2017秋•金牛区校级月考）如图在矩形ABCD中E是AD的中点将△ABE沿BE折叠后得到△GBE 延长BG交CD于点F结果发现F点恰好是DC的中点若BC＝2√6则AB的长为？思路引领：连接EF由折叠性质得AE＝EG∠A＝∠EGB＝90°BG＝AB则∠EGF＝90°易证EG＝DE由矩形的性质得AB＝CD∠C＝∠D＝90°推出∠EGF＝∠D＝90°由HL证得Rt△EGF≌Rt△EDF得出FG＝FD求得CF＝DF＝FG=12CD=12AB BF＝BG+FG=32AB由勾股定理得出BC2+CF2＝BF2即可得出结果．解：连接EF如图所示：由折叠性质得：AE＝EG∠A＝∠EGB＝90°BG＝AB ∴∠EGF＝90°∵点E是AD的中点∴AE＝DE∴EG＝DE∵四边形ABCD是矩形∴AB＝CD∠C＝∠D＝90°∴∠EGF ＝∠D ＝90°在Rt △EGF 与Rt △EDF 中 {EG =ED EF =EF∴Rt △EGF ≌Rt △EDF （HL ）∴FG ＝FD∵F 点恰好是DC 的中点∴CF ＝DF ＝FG =12CD =12AB∴BF ＝BG +FG ＝AB +12AB =32AB在Rt △BCF 中 BC 2+CF 2＝BF 2即：（2√6）2+（12AB ）2＝（32AB ）2 解得：AB ＝2√3．总结提升：本题考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识熟练掌握折叠的性质证明三角形全等是解题的关键．8．（2018春•新抚区校级期中）如图在矩形ABCD 中已知AD ＝10 AB ＝8 将矩形ABCD 沿直线AE 折叠顶点D 恰好落在BC 边上的F 处求CE 的长．思路引领：先根据矩形的性质得AD ＝BC ＝10 AB ＝CD ＝8 再根据折叠的性质得AF ＝AD ＝10 EF ＝DE 在Rt △ABF 中利用勾股定理计算出BF ＝6 则CF ＝BC ﹣BF ＝4 设CE ＝x 则DE ＝EF ＝8﹣x 然后在Rt △ECF 中根据勾股定理得到x 2+42＝（8﹣x ）2 再解方程即可得到CE 的长．解：∵四边形ABCD 为矩形∴AD ＝BC ＝10 AB ＝CD ＝8∵矩形ABCD 沿直线AE 折叠顶点D 恰好落在BC 边上的F 处∴AF＝AD＝10 EF＝DE在Rt△ABF中∵BF=√AF2−AB2=6∴CF＝BC﹣BF＝10﹣6＝4设CE＝x则DE＝EF＝8﹣x在Rt△ECF中∵CE2+FC2＝EF2∴x2+42＝（8﹣x）2解得x＝3即CE＝3．总结提升：本题考查了折叠的性质：折叠是一种对称变换它属于轴对称折叠前后图形的形状和大小不变位置变化对应边和对应角相等．也考查了矩形的性质和勾股定理．9．（2018秋•通川区校级期中）将一张边长为2的正方形纸片ABCD对折设折痕为EF（如图（1））；再沿过点D的折痕将∠A翻折使得点A落在线段EF上的点H处（如图（2））折痕交AE于点G则EG 的长度是（）A．8﹣4√3B．4√3−6C．4﹣2√3D．2√3−3思路引领：由于正方形纸片ABCD的边长为2 所以将正方形ABCD对折后AF＝DF＝1 由折叠的性质得出AD＝DH＝2 AG＝GH在Rt△DFH中利用勾股定理可求出HF的长进而求出EH的长再设EG＝x在Rt△EGH中利用勾股定理即可求解．解：∵正方形纸片ABCD的边长为2∴将正方形ABCD对折后AE＝DF＝1∵△GDH是△GDA沿直线DG翻折而成∴AD＝DH＝2 AG＝GH在Rt△DFH中HF=√HD2−DF2=√22−12=√3∴EH＝2−√3在Rt△EGH中设EG＝x则GH＝AG＝1﹣x∴GH2＝EH2+EG2即（1﹣x）2＝（2−√3）2+x2解得x＝2√3−3．∴EG＝2√3−3．故选：D．总结提升：本题考查了正方形的性质折叠的性质勾股定理关键是学会用方程的思想方法解题．10．（2020秋•新都区校级月考）如图AD是△ABC的中线∠ADC＝45°把△ADC沿着直线AD对折点C落在点E的位置．如果BC＝6 那么以线段BE为边长的正方形的面积为（）A．6B．72C．12D．18思路引领：由题意易得BD＝CD＝DE＝3 再求出∠BDE＝90°然后根据勾股定理求出BE最后由正方形的面积进行求解即可．解：∵D是BC中点BC＝6∴BD＝CD＝3由折叠的性质得：CD＝DE＝3 ∠ADC＝∠ADE＝45°即∠CDE＝90°∴BD＝DE＝3 ∠BDE＝90°在Rt△BDE中由勾股定理得：BE=√BD2+DE2=√32+32=3√2∴以BE为边的正方形面积为：（3√2）2＝18故选：D．总结提升：本题考查了折叠的性质、勾股定理、正方形的面积计算等知识熟练掌握勾股定理及折叠的性质是解题的关键．。

勾股定理中的折叠问题(分类整理版)

勾股定理中的折叠问题
1、如图，在Rt△ABC中，AB=9，BC=6，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，求
线段BN的长．
2、在一张直角三角形纸片中,两条直角边BC等于6,AC等于8,将三角形ABC按如图所示的方式折叠,使点A 和点B重合,折痕为DE,求CD的长
3、如图所示，在△ABC中，AB=20，AC=12，BC=16，把△ABC折叠，使AB落在直线AC上，求重叠部分（阴影部分）
的面积．
变式：如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使AC恰好落在
斜边AB上，且点C与点E重合，求CD的长。

4、如图所示,折叠长方形的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10CM,求DE的长
5、在长方形ABCD中,AB=6,BC=8,将长方形ABCD沿CE折叠后,点D恰好在对角线AC上的点F处、求EF的长。

6、如图，矩形纸片ABCD的边AB=10cm，BC=6cm，E为BC上一点，将矩形纸片沿AE折叠，点B恰好落
在CD边上的点G处，求BE的长.
7、如图，在长方形ABCD中，将△ABC沿AC对折至△AEC位置，CE与AD交于点F．
（1）试说明：AF=FC；
（2）如果AB=3，BC=4，求AF的长．。

8.C专题勾股定理与折叠问题

专题勾股定理与折叠问题【方法归纳】扣住折叠前后的对应线段、对应角相等，将有关线段转化到直角三角形中用勾股定理来解决.一、折叠直角三角形1.如图，在△ABC 中，∠A ＝90°，点D 为AB 上一点，沿CD 折叠△ABC ，点A 恰好落在边BC 上的A ′处，AB ＝4，AC ＝3，求BD 的长.A BCD A'【解答】由题意得AD ＝A ′D 、AC ＝A ′C ，设AD ＝x ，则BD ＝4－x ,在Rt △A ′BD 中，22＋x 2＝(4－x )2,x ＝32.BD ＝52.二、折叠长方形2.如图，长方形ABCD 中，AB ＝4，BC ＝5，F 为CD 上一点，将长方形沿折痕AF 折叠，点D 恰好落在BC 上的点E 处，求CF 的长.【解答】BE ＝3.设CF ＝x ，DF ＝EF ＝4－x ,CE ＝2, 22＋x 2＝(4－x )2,x ＝32.3. 如图，长方形ABCD 中，AD ＝8cm ，AB ＝4cm ，沿EF 折叠，使点D 与点B 重合，使点C 与点C′重合.(1)求DE 的长; (2)求折痕EF 的长.【解答】(1)由题意得DE ＝EB ，设DE ＝EB ＝x ,则AE ＝8－x .在Rt △AEB 中， x 2＝42＋(8－x )2,x ＝5.(2)作EM ⊥BC 于M ，证∠DEF ＝∠BEF ＝∠BFE ，∴BE ＝BF ＝5，MF ＝2.∴EF ＝EM 2＋MF 2＝2 5.4. 如图，长方形ABCD 中，AB ＝6，AD ＝8，沿BD 折叠使点A 到A ′处，DA ′交BC 于点F .(1)求证：FB ＝FD ；(2) 求证：CA ′∥BD ；(3) 求△DBF 的面积.【解答】(1)∠DBF ＝∠ADB ＝∠DBF ，∴FB ＝FD .(2)A ′D ＝AD ＝BC ，FA ′＝FC ，∠DBF ＝∠BDF ＝∠FCA ′＝∠FA ′C ，(3)设FB ＝FD ＝x ,x 2＝(8－x )2＋62,x ＝254,∴S △BFD ＝12×254×6＝754.三、折叠正方形5.如图，长方形ABCD 中，点E 在边CD 上，将△ADE 沿AE 对折至△AFE ，延长EF 交边BC 于点G ，G 为BC 的中点，连接AG 、CF .(1)求证：AG ∥CF ；(2)求DE CE 的值.【解答】(1)连接BF ，∴BG ＝FG ＝CG .∴CF ⊥BF .∵BG ＝FG ，AB ＝AF ，∴AG 垂直平分BF .∴AG ∥CF .(2)设DE ＝EF ＝x ，BG ＝FG ＝y ,则CE ＝2y －x ，CG ＝y ,在△CEG 中，（x ＋y ）2＝（2y －x ）2＋y 2,3x＝2y ,∴DE CE ＝12。

专题利用勾股定理解决折叠问题(三大题型)(原卷版)

（苏科版）八年级上册数学《第3章勾股定理》专题利用勾股定理解决折叠问题【例题1】（2021•西城区校级模拟）如图，Rt △ABC 中，AB ＝18，BC ＝12，∠B ＝90°，将△ABC 折叠，使点A 与BC 的中点D 重合，折痕为MN ，则线段BN 的长为（）A ．8B ．6C ．4D ．10【变式1-1】（2023•滕州市校级开学）如图，有一张三角形纸片Rt△ABC，两直角边AC＝4，BC＝8，将△ABC折叠，使点B与A重合，折痕为FE，则AE的长为（）A．3B．4C．5D．8【变式1-2】（2022秋•鼓楼区校级期末）如图，在△ABC中，∠C＝90°，AB的垂直平分线交AB、AC 于点D、E，若AC＝8，BD＝5，则CE的长度是．【变式1-3】如图所示，有一块直角三角形纸片，∠C＝90°，AC＝8cm，BC＝6cm，将斜边AB翻折，使点B落在直角边AC的延长线上的点E处，折痕为AD，则CE的长为（）A．1cm B．2cm C．3cm D．4cm【变式1-4】（2021•鞍山一模）如图的三角形纸片中，AB＝8，BC＝6，AC＝5，沿过点B的直线折叠这个三角形，使点C落在AB边上的点E处，折痕为BD，则△AED的周长是（）A．7B．8C．11D．14【变式1-5】（2022秋•高邮市期末）如图，在△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，点D、E 分别在AC、BC边上．现将△DCE沿DE翻折，使点C落在点H处．连接AH，则AH长度的最小值为（）A．0B．2C．4D．6【变式1-6】（2022秋•秦淮区校级月考）如图，将三角形纸片ABC沿AD折叠，使点C落在BD边上的点E处．若BC＝12，BE＝2，则AB2﹣AC2的值为（）A．20B．22C．24D．26【变式1-7】（2022•天津模拟）如图，Rt△ABC中，AB＝8，BC＝6，∠B＝90°，M，N分别是边AC，AB上的两个动点．将△ABC沿直线MN折叠，使得点A的对应点D落在BC边的三等分点处，则线段BN的长为（）A ．3B ．53C ．3或53D ．3或154【变式1-8】（2023•从化区一模）如图，在Rt △ABC 中，∠C ＝90°，AC ＝6，BC ＝8，点F 在AC 上，并且CF ＝2，点E 为BC 上的动点（点E 不与点C 重合），将△CEF 沿直线EF 翻折，使点C 落在点P处，PE 的长为83，则边EF 的长为（）A ．83B ．3C ．103D ．4【变式1-9】（2022春•鲤城区校级期中）如图，矩形纸片ABCD ，AB ＝4，BC ＝3，点P 在BC 边上．将△CDP 沿DP 折叠，点C 落在点E 处．PE 、DE 分别交AB 于点O 、F ，且OP ＝OF ．则AF 的长为（）A ．2B ．85C ．175D ．135【变式1-10】如图，在△ABC 中，D 为BC 中点，连接AD ，把△ABD 沿着AD 折叠得到△AED ，连接EC ，若DE ＝5，EC ＝6，AB ＝AD 的长是（）A．4B．5C．6D．7【变式1-11】直角三角形纸片的两直角边长分别为6，8，现将△ABC如图折叠，使点A与点B重合，则折痕DE的长是（）A．252B．152C．254D．154【变式1-12】如图，三角形纸片ABC中，∠ACB＝90°，AC＝8，BC＝6，折叠△ABC使点A与点B重合，DE为折痕，求DE的长．【例题2】（2023春•新市区期中）如图，将长方形纸片ABCD 折叠，使边DC 落在对角线AC 上，折痕为CE ，且D 点落在对角线D ′处．若AB ＝3，AD ＝4，则ED 的长为（）A ．1B ．43C ．32D ．3【变式2-1】（2023春•越秀区校级期中）如图，在矩形ABCD 中，AB ＝5，AD ＝3，点E 为BC 上一点，把△CDE 沿DE 翻折，C 恰好落在AB 边上的F 处，则CE 的长是（）A ．53B ．32C ．43D ．2【变式2-2】（2022秋•锦江区期末）如图，长方形ABCD 中，AB ＝5，AD ＝25，将此长方形折叠，使点D 与点B 重合，折痕为EF ，则BE 的长为（）A ．12B ．8C ．10D ．13【变式2-3】（2022秋•胶州市校级月考）如图，矩形ABCD中，AB＝16，BC＝8，将矩形沿AC折叠，点D落在点D'处，则重叠部分△AFC的面积为（）A．12B．20C．16D．40【变式2-4】（2022•斗门区一模）如图所示，矩形纸片ABCD中，AB＝4cm，BC＝8cm，现将其沿EF 对折，使得点C与点A重合，则AF的长为．【变式2-5】（2022秋•历城区期末）如图，已知长方形纸片ABCD，点E在边AB上，且BE＝4，BC＝6，将△CBE沿直线CE翻折，使点B落在点G，延长EG交CD于点F，则线段FG的长为．【变式2-6】（2023•泰山区校级一模）如图，矩形ABCD中，AD＝12，AB＝8，E是AB上一点，且EB＝3，F是BC上一动点，若将△EBF沿EF对折后，点B落在点P处，则点P到点D的最短距离为（）A．10B．9.8C．D．【变式2-7】如图，矩形纸片ABCD，AB＝8，BC＝12，点M在BC边上，且CM＝4，将矩形纸片折叠使点D落在点M处，折痕为EF，则AE的长为．【变式2-8】（2023春•武汉期末）如图，点E是矩形ABCD的边BC上的中点，将△ABE折叠得到△AFE，点F在矩形内部，AF的延长线交CD于点G，若AD＝12，CG＝4，则AB的长为（）A．7B．8C．9D．10【变式2-9】（2022秋•梅县区校级期末）如图是一张矩形纸片ABCD，点E，G分别在边BC，AB上，把△DCE沿直线DE折叠，使点C落在对角线BD上的点F处；把△DAG沿直线DG折叠，使点A落在线段DF上的点H处，HF＝1，BF＝8，则矩形ABCD的面积为（）A．420B．360C．D．【变式2-10】（2022秋•城阳区校级月考）把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB＝3cm，BC＝5cm，则重叠部分△DEF的面积是（）cm2．A．2B．3.4C．4D．5.1【变式2-11】（2022秋•宝安区期末）如图，在长方形ABCD中，AB＝6，BC＝8，点E为AB上一点，将△BCE沿CE翻折至△FCE，延长CF交AB于点O，交DA的延长线于点G，且EF＝AG，则BE的长为．【变式2-12】（2023春•东莞市校级月考）如图，矩形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B落在点F处，折痕为AE，且BE＝3．（1）求CF的长；（2）求AB的长．【例题3】（2022春•永嘉县校级期末）如图，将边长为8cm正方形纸片ABCD折叠，使点D落在BC 边的中点E处，点A落在点F处，折痕为MN，则线段CN的长是（）A．6cm B．5cm C．4cm D．3cm【变式3-1】如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在AB边中点E处，点C落在点Q 处，折痕为FH，则线段AF的长是（）A．3cm B．4cm C．5cm D．6cm【变式3-2】（2022春•桂林期末）如图，正方形ABCD的边长为4，将正方形折叠，使顶点D落在BC 边上的点E处，折痕为GH，若BE：EC＝3：1，则线段CH的长是（）A．3B．158C．1D．2【变式3-3】（2022春•荔城区校级月考）如图，在边长为7的正方形ABCD 中，E 为BC 边上一点，F 为AD 边上一点，连接AE 、EF ，将△ABE 沿EF 折叠，使点A 恰好落在CD 边上的A ′处，若A ′D ＝2，则B ′E 的长度为（）A ．2714B ．137C ．2514D ．2【变式3-4】（2023•南京一模）如图，在正方形ABCD 中，E 是CD 边上一点，将△ADE 沿AE 翻折至△AD ′E ，延长ED ′交BC 于点F ．若AB ＝15，DE ＝10，则BF 的长是．【变式3-5】（2022春•社旗县期末）如图，点E 和点F 分别在正方形纸片ABCD 的边CD 和AD 上，连接AE ，BF ，沿BF 所在直线折叠该纸片，点A 恰好落在线段AE 上点G 处．若正方形纸片边长12，DE ＝5，则GE 的长为（）A ．4913B ．5013C ．4D ．3【变式3-6】（2022春•长清区期末）如图1，将正方形纸片ABCD 对折，使AB 与CD 重合，折痕为EF 如图2，展开后再折叠一次，使点C 与点E 重合，折痕为GH ，点B 的对应点为点M ，EM 交AB 于N ，AD ＝4，则CH 的长为（）A ．52B ．65C ．34D ．54【变式3-7】（2022秋•和平区期末）如图，已知正方形ABCD 面积为2，将正方形ABCD 沿直线EF 折叠，则图中阴影部分的周长为（）A B ．2C ．8D ．【变式3-8】将正方形ABCD 折叠，使顶点A 与CD 边上的点M 重合，折痕交AD 于E ，交BC 于F ，边AB 折叠后与BC 边交于点G （如图）．如果DM ：MC ＝3：2，则DE ：DM ：EM ＝（）A ．7：24：25B ．3：4：5C ．5：12：13D ．8：15：17【变式3-9】如图，正方形ABCD中，CD＝6，点E在边CD上，且CD＝3DE．将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF．（1）求证：△ABG≌△AFG；（2）求GC的长；（3）求△FGC的面积．。

勾股定理在折叠问题中的应用(习题及答案).

勾股定理在折叠问题中的应用（习题）例题示范例1：如图，在Rt △ABC 中，∠B =90°，AB =3，BC =4，将△ABC 沿过点A 的直线折叠，使点B 恰好落在AC 边上的点B ′处，若折痕交BC 于点E ，则B′E 的长为_________．思路分析:在Rt △ABC 中，∠B =90°，AB =3，BC =4由勾股定理，得AC =5找折痕，转移，表达设B′E =x ，由折叠，得BE =B′E =x ，AB′=AB =3∴CE =4-x ，B′C =2利用勾股定理列方程在Rt △EB′C 中，由勾股定理，得x 2+22=(4-x )2解得x =32巩固练习1.如图，直角三角形纸片OAB，∠AOB=90°，OA=1，OB=2，折叠该纸片，使点B与点A重合，若折痕交OB于点C，交AB于点D，则OC的长为_________．2.如图，折叠长方形ABCD的一边AD，使点D落在BC边上的点F处，若AB=4cm，BC=5cm，则EF的长为________．3.如图，在长方形纸片ABCD中，AD=8，折叠纸片使点B落在线段AC上的点F处，折痕交BC于点E，若EF=3，则AB 的长为_________．4.如图是一张直角三角形纸片，两直角边AC=6cm，BC=8cm，现将△ABC折叠，使点B与点A重合，若折痕交BC于点D，交AB于点E，则CD=________，DE=_________．5.如图，将正方形纸片ABCD沿MN折叠，使点D落在边AB上，对应点为D′，点C落在C′处．若AB=6，AD′=2，则DM=________，CN=_________．6.如图，长方形ABCD中，AB=8，BC=4，将长方形沿AC折叠，点D落在点D′处，则重叠部分△AFC的面积为_________．7.如图，把长方形纸片ABCD折叠，使点C与点A重合，折痕为EF．若BC=8，AB=4，则AE=________，EF=_________．8.如图，将长方形ABCD折叠，使点A与点C重合，折痕分别交AD，BC于点E，F，若AB=3，AD=4，则DE的长为______．9.如图，在Rt△ABC中，∠C=90°，AC=4，BC=3，若点D在线段BC上，将△ABC沿AD折叠，使点C的对应点C′恰好落在AB边上，则BD的长为_________．10.如图，长方形ABCD中，AB=12，AD=5，点E是CD边上一点，连接AE，把∠D沿AE折叠，使点D落在点D′处．当△CD′E为直角三角形时，DE的长为____________．思考小结1.请回顾轴对称（折叠）的思考层次（1）全等变换：对应边_______、对应角_______．（2）对称轴性质：①对应点所连线段_____________________；②对称轴上的点_______________________．（3）组合搭配：长方形背景下的折叠常出现______三角形．（4）作图：关注_______和________，有时需要依据不变特征分析转化，补全图形．①当对称轴已知时，直接作_____________找对应点；②当对应点已知时，作__________________________，找对称轴（折痕）；③当对称轴过定点时，常作_____找对应点．【参考答案】例题示范1.32巩固练习1.342.5cm23.64.7cm4，15cm 45.103，4 36.107.5，258.789.5310.103或5思考小结1.（1）相等，相等.（2）①被对称轴垂直平分；②到对应点的距离相等.（3）等腰（4）对称轴、对应点①点的对称点②对应点所连线段的垂直平分线③弧。

小专题2 利用勾股定理解决折叠问题

A．1 B．2 C．3 D．4
2．如图，有一张直角三角形纸片，两直角边 AC＝5
cm，BC＝10 cm，将△ABC 折叠，使点 B 与点 A 重
合，折痕为 DE，则 CD 的长为( D )
25 A. 2 cm
25 C. 4 cm
15 B. 2 cm
15 D. 4 cm
3．如图，在长方形纸片 ABCD 中，AB＝8 B 落在点 E 处，AE 交
DC 于点 F.若 AF＝245 cm，则 AD 的长为( C )
A．4 cm
B．5 cm
C．6 cm
D．7 cm
4．(铜仁中考)如图，在长方形 ABCD 中，BC＝6，
CD＝3，将△BCD 沿对角线 BD 翻折，点 C 落在点
C′处，BC′交 AD 于点 E，则线段 DE 的长为( B )
【解答】因为 A1 是 BC 的中点，所以 A1B＝12BC＝4. 因为△ABC 是等腰直角三角形，且∠B＝90°，所以 AB＝BC＝8. 由翻折的性质可知 AE＝A1E，设 AE＝A1E＝x，则 BE＝8－x. 在 Rt△A1BE 中，由勾股定理，得 A1E2＝A1B2＋BE2，即 x2＝42＋(8－x)2. 解得 x＝5. 所以线段 AE 的长为 5.
解决折叠问题的关键是抓住对称性．勾股定理的数学表达式是一个含有平方关系的等式，求线段长时，可利用勾股定理直接计算，也可设未知数，由勾股定理列出方程，运用方程思想分析和解决问题．
1．如图，长方形 ABCD 的边 AD 沿 AE 折叠，使点 D 落在 BC 上的点 F 处，已知 AB＝6，△ABF 的面积是 24，则 FC 等于( B )
A．3
15 B. 4
C．5
15 D. 2

初二数学下册：勾股定理处理折叠的三种模型

初二数学下册：勾股定理处理折叠的三种模型01模型一：折叠构造直角三角形折叠构造直角三角形是比较常见的一种模型，将直角三角形沿着某条线段进行折叠，可以得到另外一个直角三角形，然后设未知数，表示出这个三角形的三边长，利用勾股定理列出方程，求出未知数的值。

例题1：如图，有一块直角三角形纸片，两直角边AC=6cm，BC=8cm，现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，求CD的长．分析：先通过勾股定理求出线段AB的长度，将直角边AC沿直线AD 对折，使它落在斜边AB上，得到AE=AC=6。

求线段CD的长度，可设CD=x，那么DE=CD=x，再表示出线段DB的长度，求出线段BE，利用勾股定理得到关于x的方程。

解：∵两直角边AC=6cm，BC=8cm，在Rt△ABC中，由勾股定理可知AB=10，现将直角边AC沿直线AD对折，使它落在斜边AB上，且与AE重合，则CD=DE，AE=AC=6，∴BE=10-6=4，设DE=CD=x，BD=8-x，在Rt△BDE中，根据勾股定理得：BD^2=DE^2+BE^2，即（8-x）^2=x^2+4^2，解得x=3．即CD的长为3cm．02模型二：折叠构造全等三角形例题2：如图，在平面直角坐标系中，四边形OABC是矩形，点A的坐标为（4，0），点C的坐标为（0，2），把矩形OABC沿OB折叠，点C落在点D处，DB交OA于点E．（1）求证：OE=BE；（2）求△OEB的面积.分析：（1）通过折叠可知：OC=OD，∠D=∠OCB=90°，由于四边形OABC为矩形可得：OC=AB，∠BAO=90°，那么∠D=∠BAO=90°，再加上对顶角∠BEA、∠OED相等，通过“AAS”判定两个三角形全等；（2）可设OE=BE=x，然后表示出线段AE的长度为4-x，在直角三角形ABE中，通过勾股定理得到关于x的方程，求出x的值，然后利用三角形的面积公式求出三角形OEB的面积。

勾股定理解析折叠问题含详细的答案

利用勾股定理解决折叠问题
解题步骤
1、标已知，标问题，明确目标在哪个直角三角形中，设适当的未知数x； 2、利用折叠，找全等。 3、将已知边和未知边（用含x的代数式表示）转化到同一直角三角形中表示出来。 4、利用勾股定理，列出方程，解方程，得解。
三角形中的折叠
例1：一张直角三角形的纸片，如图1所示折叠，使两个锐角的顶点A、B重合。若 ∠B=30°，AC= ，3 求DC的长。 B
C′
求能角重得平叠到分等部线腰分与三△平角B行形E线D的组面合积时,。 A E
D
B
C
在矩形的折叠问题中，求线段长时，常设未知数，找
到相应的直角三角形，用勾股定理建立方程，利用方
程思想解决问题。
探究三如图,矩形纸片ABCD中， AB=6cm,
把矩形ABCD折叠，使点C恰好落在AB边的中点F处，折痕为DE，则AD的长为多少？
（3）在折叠问题中，若直接解决较困难时，可将图形还原，可让问题变得简单明了。有时还可采用动手操作，通过折叠观察得出问题的答案。
谢谢大家！
课后作业
1、如图，矩形ABCD沿AE折叠，使D点落在
BC边上的F点处，如果∠BAF=60°，那么
∠DAE等于
y
AD
B
E
O
C
x
2、如图，将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.在OA上取一点E，将△EOC沿EC折叠，使O落在AB边上的D点，求E点的坐标。
动手折一折
折叠过程就是轴对称变
成用面一积张减直半角的三矩角形形吗形换? 痕,状说折两的痕明边纸就理的片是图由对,形。你称全能轴等，折。折叠
若用一张任意三角形形状的纸片,你还能折叠成面积减半的矩形吗?

(完整版)利用勾股定理解决折叠问题及答案

《勾股定理》典型例题折叠问题

《勾股定理》典型例题折叠问题1、如图，有一张直角三角形纸片，两直角边A Ｃ＝６,ＢＣ＝8，将△AB Ｃ折叠，使点B 与点A 重合,折痕为DE,则CD 等于( ）A. 425B. 322C. 47D ． 352、如图所示,已知△A ＢＣ中,∠C=9０°,ＡB 的垂直平分线交ＢC •于Ｍ,交AB 于N,若AC ＝4，MB=2M Ｃ,求ＡB 的长．3、折叠矩形AB ＣD 的一边ＡＤ,点D 落在BC 边上的点F 处,已知A Ｂ=8ＣＭ,BC=1０C Ｍ,求C Ｆ和EC 。

4、如图，在长方形ＡBCD 中，DC=5,在DC 边上存在一点E,沿直线A Ｅ把△ＡBC 折叠，使点D 恰好在BC 边上，设此点为F ，若△ABF 的面积为30,求折叠的△AE Ｄ的面积B CEDDCBAF E5、如图,矩形纸片ABCD 的长AD ＝9㎝，宽ＡＢ＝3㎝,将其折叠，使点Ｄ与点Ｂ重合，那么折叠后DE 的长是多少?6、如图,在长方形ＡB ＣＤ中,将∆ABC 沿AC 对折至∆ＡEC 位置，C Ｅ与AD 交于点F 。

（1）试说明：AF=FC ；（2)如果ＡＢ=3,B Ｃ=４,求A Ｆ的长7、如图2所示,将长方形ABCD 沿直线A Ｅ折叠,顶点Ｄ正好落在B Ｃ边上Ｆ点处,已知CE=3cm ，AB ＝8ｃｍ,则图中阴影部分面积为_______．8、如图２-3，把矩形ABＣD沿直线BD向上折叠,使点Ｃ落在C′的位置上,已知ＡB=•3,BC=7,重合部分△EＢＤ的面积为___＿＿_＿_.9、如图５,将正方形AＢCD折叠,使顶点A与ＣD边上的点M重合，折痕交ＡD于Ｅ,交BC于Ｆ，边AＢ折叠后与BC边交于点Ｇ。

如果Ｍ为CD边的中点,求证:DE：DM：EM=3:４:５。

１0、如图2-5,长方形ＡBＣＤ中，ＡB=3,BC＝4,若将该矩形折叠，使C点与A点重合，•则折叠后痕迹ＥＦ的长为（ )A．3．74 B．３.75 C．3.7６ D．３.7７2-511、如图1-３-11，有一块塑料矩形模板ABCＤ，长为10cｍ,宽为4cｍ，将你手中足够大的直角三角板ＰHＦ的直角顶点Ｐ落在AD边上(不与A、D重合）,在AD上适当移动三角板顶点P：①能否使你的三角板两直角边分别通过点B与点Ｃ？若能，请你求出这时ＡP 的长；若不能，请说明理由.②再次移动三角板位置,使三角板顶点P在AＤ上移动,直角边ＰH 始终通过点B,另一直角边PＦ与DC的延长线交于点Q,与BC交于点E，能否使CE＝２cm?若能，请你求出这时AP 的长;若不能,请你说明理由．１2、如图所示，△ABC是等腰直角三角形,AB＝AC，D是斜边ＢC的中点，E、Ｆ分别是AB、AC边上的点,且DE⊥DF，若BE=12，CF=５．求线段ＥＦ的长。

培优专题11 勾股定理与折叠问题

＝ CF ＝ CE ＝ AE .
（2）设 AE ＝ a ， ED ＝ b ， DC ＝ c .请写出一个 a ， b ， c 三者之间的数量关系式.
◉答案解：（2） a ， b ， c 三者之间的数量关系式为 a2＝ b2＋ c2.理
由：由（1）得 CE ＝ AE . 因为四边形 ABCD 是长方形，所以∠ D ＝
A. 1cm
A ）
B. 1.5cm
C. 2cm
D. 3cm
第1题图
2. （烟台莱州期中）如图，Rt△ ABC 中， AB ＝9， BC ＝6，∠ B ＝90°，将△
ABC 折叠，使 A 点与 BC 的中点 D 重合，折痕为 MN ，则线段 BN 的长为 4
第2题图
.
⁠
3. 如图，在边长为6的正方形 ABCD 中， E 是边 CD 的中点，将△ ADE 沿 AE 对折至
90°.因为 AE ＝ a ， ED ＝ b ， DC ＝ c ，所以 CE ＝ AE ＝ a .在Rt△
DCE 中， CE2＝ ED2＋ DC2，所以 a ， b ， c 三者之间的数量关系式
为 a2＝ b2＋ c2.
FG ＝ x ，则 GC ＝6－ x .因为 E 为 CD 的中点，所以 CE ＝ DE ＝ EF
＝3，所以 EG ＝3＋ x .在Rt△ CEG 中，32＋（6－ x ）2＝（3＋ x ）2，
解得 x ＝2，所以 BG 的长为2.
类型二：巧用折叠求图形面积
4. （威海文登区期中）如图，在四边形 ABCD 中，∠ A ＝90°， AB ＝4cm， AD ＝
第三章勾股定理
培优专题 11 ：勾股定理与折叠问题
类型一：巧用折叠求线段长

利用勾股定理解决折叠问题及答案

勾股定理中的常考问题(6种类型48道)—2024学年八年级数学上册(解析版)

第3讲 利用勾股定理解决折叠问题(解析版)

勾股定理折叠问题

利用勾股定理解决折叠问题及答案

人教版八年级数学下册《利用勾股定理解决折叠问题的技巧》练习题(附带答案)

勾股定理中的折叠问题(分类整理版)

8.C专题 勾股定理与折叠问题

专题 利用勾股定理解决折叠问题(三大题型)(原卷版)

勾股定理在折叠问题中的应用(习题及答案).

小专题2 利用勾股定理解决折叠问题

初二数学下册：勾股定理处理折叠的三种模型

勾股定理解析折叠问题含详细的答案

(完整版)利用勾股定理解决折叠问题及答案

《勾股定理》典型例题折叠问题

培优专题11 勾股定理与折叠问题

第3讲利用勾股定理解决折叠问题(解析版)

8.C专题勾股定理与折叠问题

专题利用勾股定理解决折叠问题(三大题型)(原卷版)