第一学期医用高等数学期末试卷

合集下载

医药高等数学试卷及答案

中医学院 20-20学年第一学期《医药高等数学》课程期末考试卷命题教师: 试卷编号: 审核人:适用专业考试班级考生姓名学号班级一、单项选择题:本大题共 8小题,每小题 3分,共 24分。

在每题给出的四个选项中,只有一项是符合题目要求的,把正确选项填在括号内。

1、 =+-+-++∞→113 2(3 2(lim n n nn n (。

A 、31 B 、 32C 、 1D 、和 n 取值有关 2、当1→x 时, ( 是 x -1的高阶无穷小。

A 、 231(x - B 、xx+-11 C 、 1(2x - D 、 1-x 3、⎪⎩⎪⎨⎧=≠=0, 9,0, sin (x x x Ax x f 在 x =0处连续,则 A =( 。

A 、 0B 、 -6C 、 -9D 、 94、 0=x 是函数 xxx f sin (=的( 。

A 、不是间断点B 、无穷间断点C 、跳跃间断点D 、可去间断点 5、若函数4(3(2(1( (----=x x x x x f ,则方程 0 (' =x f 的实根个数( 。

A 、 1 B 、 2 C 、 3 D 、 4 6、下列等式中正确的是( 。

A 、 d ⎰= ( (x f dx x fB 、 d ⎰=dx x f dx x f ( (C 、⎰=dx x f dx x f dx d ( ( D 、⎰+=c x f dx x f dxd( (7、满足 0 , (0 , (00' 00' ==y x f y x f y x 且的点 , (00y x 一定是( 。

A 、驻点B 、极值点C 、最大值点D 、最小值点8、σσd y x I d y x I DD221][ln( , ln(⎰⎰⎰⎰+=+=, 其中 D 是矩形闭区域53≤≤x ,10≤≤y ,则 1I 与 2I 之间的关系( 。

A 、21I I ≤B 、21I I ≥C 、 21I I =D 、无法比较二、填空题:本大题共 7小题,每小题 2分,共 14分。

高等数学期末试卷及答案

高数试卷（一）（上册）一、单项选择题（每题4分，共20分，把选择题答案填在括号里）1．当0x →时，()sin f x x ax =-与2()ln(1)g x x bx =-是等价无穷小，则（）．A.11, 6a b ==B.11, 6a b =-= C.11, 6a b ==- D.11, 6a b =-=-2．函数2()sin πx x f x x-=的可去间断点的个数为（）．A.1B.2C.3D.无穷多个3．曲线321x y x =-的渐近线有（）．A.1条B.2条C.3条D.4条 4．下面等式正确的是（）．A. d ()()f x f x '⎡⎤'=⎣⎦⎰B.()d()d ()f x x f x =⎰C.d ()d ()d f x x f x C x =+⎰ D.d ()d ()d ba f x x f x x=⎰ 5．已知广义积分2d 1xkx+∞+⎰收敛1（0k >），则k =（）．A.π22π2 D.2π4二、填空题（每题4分，共20分）6．222111lim π2ππn n n n n n →∞⎛⎫+++= ⎪+++⎝⎭． 7．设函数)(x y y =由方程y x xy+=2所确定，则d x y== ．8．设⎩⎨⎧-=-=),1e (,π)(3tf y t f x 其中f 可导且(0)0f '≠，则0d d t y x == ． 9．不定积分6d (1)xx x =+⎰． 10．定积分π322π2(sin cos )d x x x -+=⎰ ．三、计算题（每题7分，共28分）11．求极限0x →．12．曲线y =的切线与x 轴和y 轴围成一个图形，记切点的横坐标为a ，试求切线方程和这个图形的面积S ．当切点沿曲线趋于无穷远时，该面积的变化趋势如何？13．求不定积分⎰．14．已知21()e d xt f x t -=⎰，求10()d f x x ⎰．四、证明题（本题6分）15．设)(x f 在[0,1]上连续，在(0,1)内可导，且1233()d (0)f x x f =⎰，求证：在(0,1)内存在一点ξ使()0f ξ'=．五、讨论题（每小题8分，共16分）16．已知⎪⎩⎪⎨⎧≤+>+=.0),ln(,0,1sin )(2x x a x bx x x x f 试讨论（1）a 、b 取何值时，)(x f 在0=x 点连续；（2）a 、b 取何值时，)(x f 在0=x 点可导，并求)0(f '．17．讨论函数0()(4)d xF x t t t =-⎰在[1,5]-上的增减性、极值和凹凸区间及拐点．六、应用题（本题10分）18．设2y x =定义在[0,1]上，t 为[0,1]上任意一点，试问t 为何值时，参考答案一、1．C ；2．B ；3．C ；4．A ；5．D ．二、6．1；7． x d )12(ln -；8．3；9．61ln ln(1)6x x C -++；10．2π．三、11．解因为当0→x 时，x x x x 232sin 31~1sin 1-+， x x 2~1e 2-， 22~tan x x ，所以，2222001sin 13lim lim (e 1)tan 2x x x x xxx x →→=-⋅ 2221sin 1sin 1666x x x x ⎛⎫=⋅=⋅= ⎪⎝⎭． 12．解由题设可知切点的横坐标为0>a，代入曲线方程y =可求的切点坐标为a ⎛⎝，因为312212y x x --''⎛⎫'===-= ⎪⎝⎭，所以，曲线在该点的切线斜率x ak y ='==，切线方程为)y x a =-，即230x a +-=．分别令0y =和0,x =得切线在x 轴和y 轴上的截距分别为3, X a Y ==，切线与x 轴和y 轴围成一个图形为直角三角形AOB ∆，（如图所示）其面积为a a a XY S 492332121=⋅⋅==.因为+∞==+∞→+∞→a S a a 49limlim ，049lim lim 00==++→→a S a a ，故当切点沿曲线趋于x 轴正方向无穷远时，面积S 趋于无穷大；当切点沿曲线趋于y 轴正方向无穷远时，面积S 趋于零．13．解设sin x t =，ππ,22t ⎡⎤∈-⎢⎥⎣⎦，则原式1cos d sin cos tI t t t==+⎰，若设2sin d sin cos tI t t t=+⎰，则121cos sin d cos sin t tI I t t C t t++==++⎰，122cos sin d ln sin cos cos sin t tI I t t t C t t--==+++⎰，故()11ln cos sint 2I t t C =+++(1arcsin ln 2x x C =+++． 14．解由题设可得2()e x f x -'=，(1)0f =，则111201()d ()()d 0e d 0x f x x xf x xf x x x x -'=-=-⎰⎰⎰ 122101111e d()(e 1)1222e x x --⎛⎫=-=-=- ⎪⎝⎭⎰．四、15．证明由积分中值定理知12323()d (), ,13f x x f ⎡⎤=∈⎢⎥⎣⎦⎰ηη，即()(0)f f η=．于是)(x f 在[0,]η上满足罗尔定理的条件，知存在(0,)(0,1)ξη∈⊂，使()0f ξ'=.五、16．解（1）因00lim ()lim ln()ln ,x x f x a x a --→→=+= 2001lim ()lim sin 0,x x f x x bx x +-→→⎛⎫=+= ⎪⎝⎭(0)ln ,f a =要使函数)(x f 在0=x 点连续必须使函数在该点左、右极限相等且等于该点的函数值即ln 0, 1a a ==．故当1, a b =为任意实数时，函数)(x f 在0=x 点连续．（2）由于连续是可导的必要条件，所以要使)(x f 在0=x 点可导，必须首先令1a =，此时函数变为⎪⎩⎪⎨⎧≤+>+=.0),ln(,0,1sin )(2x x a x bx xx x f 又因为0()(0)ln(1)0(0)lim lim0---→→-+-'==-x x f x f x f x x1lim ln(1)ln e 1,-→=+==xx x 2001sin 01(0)lim lim sin ,0x x x bx x f x b b x x +++→→+-⎛⎫'==+= ⎪-⎝⎭要使)0(f '存在必须使其在该点左、右导数存在并相等即(0)(0)(0)11f f f b -+'''===⇒=．所以当1a =且1b =时，)(x f 在0=x 点可导，此时(0)1f '=．17．解（1）0()(4)d (4)xF x t t t x x '⎡⎤'=-=-⎢⎥⎣⎦⎰，令()0F x '=，得驻点120, 4x x ==．（2）()24F x x ''=-，令()0F x ''=，得 32x =．（3）列表：（4(1,0)-(0,2)单减且上凸；在区间上(2,4)单减且上凹；在区间(4,5)上单增且上凹．在0x =处取得极大值0，在4x =处取得极小值332-；)316,2(-. 五、18．解如图所示，阴影1S 部分的面积为222331012()d 033t t S t x x t x x t =-=-=⎰，阴影2S 部分的面积为122323221121()d 333t S x t x x t x t t t =-=-=-+⎰，故)10(3134)(2321≤≤+-=+=t t t S S t S ，从而2d 42d S t t t =-，令d 0d S t =，得驻点1210, 2t t ==．分别求出1112(0), , (1),3243S S S ⎛⎫=== ⎪⎝⎭比较可知，当12t =时，1S 与2S 之和最小．检测题（二）（上册）一、单项选择题（每题4分，共20分，把选择题答案填在括号里）1．函数y =ln u x =能构成复合关系的区间是（）．A.1,e e⎡⎤⎢⎥⎣⎦B.(0,)∞C.1,e⎡⎫+∞⎪⎢⎣⎭D.(0,e) 2．设1010()ln , (), ()e xf x xg x xh x ===则当x 充分大时有（）A.()()()g x f x h x <<B.()()()h x g x f x <<C.()()()f x g x h x <<D.()()()g x h x f x <<3．设函数(),()f x g x 具有二阶导数，且()0g x ''<．若0()g x a =是()g x 的极值，则[()]f g x 在0x 取得极大值的一个充分条件是（）．A.()0f a '<B.()0f a '>C.()0f a ''<D.()0f a ''> 4．下面等式正确的是（）． A.21arctan d C 1x x x=++⎰； B.arcsin C x =+； C.1ln d x x C x=+⎰； D.d()d ()d baf x x f x x =⎰．5．已知广义积分11d kx x ⎰收敛2（0k >），则k =（）． A.32； B.1； C.2； D.12．二、填空题（每题4分，共20分）6．若011lim e 1x x a x x →⎡⎤⎛⎫--= ⎪⎢⎥⎝⎭⎣⎦，则a = ． 7．设2()()lim1()x af x f a x a →-=--，则()f x 在x a =取得极值．8．若曲线321y x ax bx =+++有拐点(1,0)-则b = ． 9．定积分π32π2(sin cos )d x x x -+=⎰ ． 10．不定积分22d (1)(4)x xx x =++⎰．三、计算题（每题8分，共32分）11．求极限20ln(1)lim sin x x x x x→+-． 12．已知 ⎩⎨⎧+==),1ln(,arctan 2t y t x 求22d 1d y t x =．13．设可导函数()y y x =由方程2200e d sin d x yxt t x t t --=⎰⎰确定，求d 0d yx x =．14．分别用第一换元法（凑微分法）和第二换元法求不定积分．四、讨论题（12分）15．设函数⎪⎩⎪⎨⎧>+=<+=,0,1e ,0,,0,1)(2x x x x x x f x αα试讨论α的值在什么范围内，函数满足（1）在0x =点有极限；（2）在0x =点连续；（3）在0x =点可导．五、应用题（本题10分）16．设位于曲线)y x t =≤≤下方，x 轴上方的区域为G ，求（1）G 绕x 轴旋转一周所得空间区域的体积()V t ；（2）当t 为何值时，该旋转体的体积()V t 最大？最大体积是多少？六、证明题（6分）17．设)(x f 在[0,)+∞上连续，在(0,)+∞内可导，如果存在两个正数12k k 、满足1212(0)()d 0k k k k f f x x +-=⎰，证明：存在ξ0>使()0f ξ'=．检测题（二）参考答案一、1．A ；2．C ；3．B ；4．B ；5．D ．二、6．2；7．大；8．3；9．34；10．2211ln 64x C x +++．三、11．解因为当0→x 时，22~)1ln(x x x x ⋅+，所以，222000ln(1)3lim lim lim sin sin 1cos x x x x x x x x x x x x x→→→+⋅==--- 061limsin 6x x x →==． 12．解因为2d 2, d 1y t t t =+2d 1d 1x t t=+，所以 22d d d 212 d d d 11y y t t t t x x t t +===+， 2222d d d 2d d 2(1)d d d 11y y t x t x x t t⎛⎫⎪⎝⎭===++， 22211d 2(1)4d t t y t x ===+=． 13．解由题设可知2200e d sin d x yxt t x t t --=⎰⎰，方程两边同时求导得2()220e(1)sin d sin xx y y t t x x --'-=+⎰，把0x =代入上述等式得1y '=，故d 10d yx x ==．14．解法1 凑微分法2C===．解法2 第二类换元积分法==设11sin22x t-=π2t⎛⎫<<⎪⎝⎭，则原式1cos d d2t t t==⎰arcsin(21)t C x C=+=-+．解法3 第二类换元积分法x=⎰，令2πsin02x t t⎛⎫=<<⎪⎝⎭，则d2sin cos dx t t t=，所以原式112sin cos d2dsin cost t t tt t=⋅⋅=⎰⎰2t C C=+=．四、解（1）因为00lim()lim(1)1,x xf x x--→→=+=00lim()lim(e1)1,xx xf x x++→→=+=α可见α是任意实数时，函数在0x=点左、右极限都相等．（2）又因为2(0)f=α，要使函数)(xf在0=x点连续必须使函数在该点极限值等于该点的函数值，即21,1a==±α．故当1±=α时，函数)(xf在0=x点连续.（3）由于连续是可导的必要条件，所以要使)(xf在0=x点可导，必须首先令21=α，此时函数变为⎪⎩⎪⎨⎧>+=<+=,0,1e ,0,1,0,1)(x x x x x x f x α0()(0)(1)1(0)lim lim 10x x f x f x f x x---→→-+-'===-， 00(e 1)1(0)lim lim e ,x x x x x f x+++→→+-'===ααα 要使)0(f '存在必须使其在该点左、右导数存在并相等，即(0)(0)(0) 1 1f f f -+'''====⇒=αα．所以当1=α时，)(x f 在0=x 点可导，此时(0)1f '=．五、16．解（1）222e ee 11()πd πd πd ln (1ln )1ln ttt x V t y x x x x x x ===++⎰⎰⎰ []e ππarctan(ln )πarctan(ln )4t x t ⎛⎫==- ⎪⎝⎭．（2）因为2π()0 (e)(1ln )V t t t t '=>>+，这说明()V t 在[e,)+∞上单调递增，所以当t →+∞时，()V t 取得最大值，其最大值为[]2max e πππ()πlim arctan(ln )π244tt V t x →+∞⎛⎫==-= ⎪⎝⎭．六、17．证明由积分中值定理知[]1212112()d (), ,k k k f x x k f k k k +=∈+⎰ηη，代入题设等式得()(0)f f η=．于是)(x f 在[0,]η上满足罗尔定理的条件，知存在112(0,)[,](0,)k k k ∈⊂+⊂+∞ξη，使()0f ξ'=．。

医学高数期末考试试题

医学高数期末考试试题### 医学高数期末考试试题#### 一、选择题（每题2分，共20分）1. 以下哪项不是微积分的基本定理？A. 牛顿-莱布尼茨公式B. 泰勒级数展开C. 定积分的性质D. 不定积分的计算2. 函数 \( f(x) = x^2 + 3x - 2 \) 在区间 \( [1, 3] \) 上的最大值是：A. 2B. 4C. 6D. 83. 以下哪个选项是 \( e^x \) 的泰勒级数展开式？A. \( 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \ldots \)B. \( 1 - x + \frac{x^2}{2!} - \frac{x^3}{3!} + \ldots \)C. \( 1 + x - \frac{x^2}{2!} + \frac{x^3}{3!} - \ldots \)D. \( 1 + x + \frac{x^2}{2} + \frac{x^3}{3} + \ldots \)4. 已知 \( \lim_{x \to 0} \frac{\sin x}{x} = 1 \)，求\( \lim_{x \to 0} \frac{\sin 2x}{x} \) 的值是：A. 0B. 1C. 2D. 45. 方程 \( y'' - 2y' + y = 0 \) 的通解是：A. \( y = e^{t} \)B. \( y = e^{t} + e^{2t} \)C. \( y = e^{t} + e^{-t} \)D. \( y = e^{t} + e^{2t} + e^{-t} \)#### 二、填空题（每题2分，共20分）6. 若 \( f(x) = \ln(x) \)，则 \( f'(x) = ________ \)。

7. 函数 \( g(x) = x^3 - 6x^2 + 11x - 6 \) 的导数 \( g'(x) \) 是 ________。

2019学年第一学期医用高等数学期末试卷

题号
一
二
三
总分
得分
得分
评卷人
复查人
一、单项选择题（把下列各题的答案填在表格内，每题3分，共计36分）
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
得分
评卷人
复查人
二、填空（每题3分，共计36分）
1、2、3、
4、5、6、
7、8、9、
10、11、12、
得分
评卷人
复查人
三、解答题（每题7分，共计28分）
1、
2、
11、 0.
12、 .
三、解答题（每题7分，共计28分）
1、设函数是由方程所确定，求的值.
2、求定积分 .
3、求由抛物线及直线所围成的图像的面积(要求作图).
4、求解一阶线性微分方程在初始条件下的特解.
贵州医科大学神奇民族医药学院
2016级临床医学《医用高等数学》期末考试答题纸
学院/系专业班学号姓名
2019学年第一学期医用高等数学期末试卷
(2019临床、口腔、麻醉、影像、检验、食卫)
学院/系专业ห้องสมุดไป่ตู้学号姓名
注意：1）本科目为闭卷考试，答题纸在试题单后面，请将答题纸轻轻撕下，注意答题纸的完整性。
2）请将试题答在答题纸上，答在试题册上无效。
3）交卷时，请将答题纸与试题单分开。
4）试题册及答题卡上都要将姓名、专业、学号等填写清楚。
A.2B. C.1D.0
6、已知 ,则 (D).
A. B.
C. D.
7、函数的单调递增区间是 (C).
A． B．

医用高等数学试题

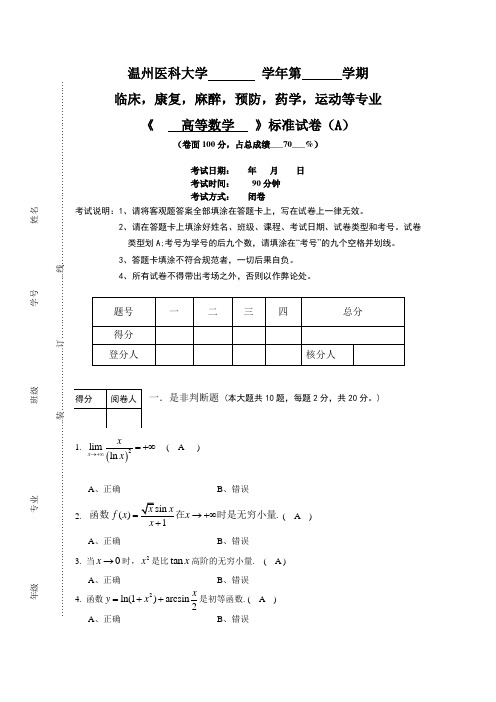
5. 无限个无穷小的和仍然是无穷小（ B ） A 、正确 B 、错误6. 0,sin5~ln(15)x x x →+当时 ( A ) A 、正确 B 、错误()217.ln(1)ln(1)t dt t '+=+⎰ （ B ）A 、正确B 、错误 8.01ln 0xdx ≥⎰( A )A 、正确B 、错误 9. arctan lim0x xx→∞= （ A ）A 、正确B 、错误10.11≤ ( A )A 、正确B 、错误二．单项选择题 (本大题共20题，每题3分，共60分)11. ()f x 在0x 处可微是()f x 在0x 可积的 ( A ).A. 充分条件B. 充要条件C. 必要条件D. 前三者都不是12. 已知函数 1cos 0,()10,xx f x x x x -⎧>⎪=⎨⎪+≤⎩ ，则0lim ()x f x →= ( D ). A. 1 B. 0 C. 2 D. 不存在13．设2221()31x x f x x x ⎧≤⎪=⎨⎪>⎩，则()f x 在1x =处（ B ）A ．左、右导数都存在B ．左导数存在但右导数不存在C ．右导数存在但左导数不存在D ．左、右导数都不存在13011333314.lim(1)().....xx x D A e B e C eD e→---=15. 当x →+∞时，下列函数为无穷小量的是（ D ）. A. 1xe-B.()3100ln x x -C.D.2311001x x x -++.16. 以下各式中能使用洛必达法则计算的是（ A ）. A. 20sin limln(1)x x x x x →-+ B. 2arctan lim tan 3x xx π→C. sin lim x x x x →∞+D. cos lim x x x →∞ ()()317.()3,()1,3A. B. C. D.f x x x f x A =--设则函数在区间上是　先增后减　先减后增　增函数减函数18. 2cos ()3x f x -=，则()df x = ( C ).A. 2cos sin 23ln 3xx dx -- B. 2cos1sin 23ln 3xx dx -- C. 2cos sin 23ln 3x x dx - D. 2cos 1sin 23ln 3x x dx -19.已知)(x f 在0=x 的某个邻域内连续，且0)0(=f ，2cos 1)(lim 0=-→xx f x ，则在点0=x 处)(x f （ D ）A.不可导；B.可导，且0)0('≠f ；C.取得极大值；D.取得极小值。

《高等数学》(第一学期)期末试题

《高等数学》（第一学期）期末试题一、选择题（每小题4分，共24分）1、f(x)＝|x|在x ＝０处（）A 连续且可导B 不连续不可导C 连续但不可导D 可导但不连续 2、下列命题中，不正确的是A /()()f x dx f x ⎡⎤=⎣⎦⎰ B /()()f x dx f x c =+⎰ C /()0ba f x dx ⎡⎤=⎢⎥⎣⎦⎰ D ()()f x dx F x c =+⎰，其中/()()F x f x = 3、如果直线(0)y ax a =>是21y x =+的切线，则a = （）A 0B 2C －2D ±24、0sin 3sin 2limx xx→= （）A 23B 32C 0D 不存在 5、已知/(4)3f =，则0(42)(4)limh f h f h→+-= （）A 3 B23C 6D 9 6、下列方程中是微分方程的是（）A 2350y x -+= B /43y x =+C 21y x =-D cos 0xdx =⎰二、填空题（每小题3分，共33分）7、1(1)lim x x x→∞+= 。

8、2221332lim n n n n n →∞+-=++ 。

9、若224y x x =+-，则在点（1，－1）处的切线方程为。

10、若生产某种产品x 件的成本函数为2()0.15200C x x x =++，则边际成本函数为。

11、某种汽车刹车后运动规律为319.20.4s t t =-，假设汽车作直线运动，则汽车在t = 4s 时的速度为，加速度为。

12、y = 。

13、若sin 2x y e =，那么dy = . 14、微分方程22()24x y y x e '+=的阶数为。

15、微分方程0xy y '+=的通解为。

16、221x dx x=+⎰ 。

17、120(1)x dx -=⎰ 。

三、解答题：（18—22小题每小题7分，23小题8分，共43分） 18、求函数32391y x x x =--+单调区间与极值19、求32321y x x x =-+-的凹凸区间与拐点20、求320sin cos x x dx π⎰.21、求sin x e xdx ⎰.22、求方程30xy y '+=满足初始条件1|2x y ==的特解.23、求由1y x=，y x =，2x =，0y =围成的图形面积.。

高等数学1期末试卷(5套)

试卷（一）一、1、下列等式中成立的是（ B ）.(A) e n nn =⎪⎭⎫⎝⎛+∞→21lim (B) e n n n =⎪⎭⎫ ⎝⎛++∞→211lim (C) e n nn =⎪⎭⎫ ⎝⎛+∞→211lim (D) e n nn =⎪⎭⎫⎝⎛+∞→211lim2、函数()x f 在点0x 处连续是在该点处可导的（）.(A) 必要但不充分条件 (B) 充分但不必要条件 (C)充分必要条件 (D) 既非充分也非必要条件 3、设函数()x f 可导，并且下列极限均存在，则下列等式不成立的是（）.(A) ()()()00limf x f x f x '=-→ (B) ()()()0000lim x f x x x f x f x '=∆∆--→∆(C) ()()()a f h a f h a f h '=-+→2lim(D) ()()()00002lim x f xx x f x x f x '=∆∆--∆+→∆ 4、若(),00='x f 则点0x x =是函数()x f 的（）.(A) 极大值点 (B) .最大值点 (C) 极小值点 (D) 驻点5、曲线12+=x x y 的铅直渐近线是（）.（A ）y =1 （B ）y =0 （C ）1-=x （D ）x =0 6、设xe-是)(x f 的一个原函数，则⎰=dx x xf )(（）.（A ）c x e x+--)1( （B ）c x e x++-)1( （C ）c x e x+--)1( （D ） c x e x++--)1( 二、1、当0x →时，(1cos )x -与2sin2xa 是等价无穷小，则常数a 应等于______ _. 2、若82lim =⎪⎭⎫⎝⎛-+∞→xx b x b x ，则=b .3、函数123++=x x y 的拐点是 .4、函数()x y y =是由方程y x y +=tan 给出，则='y ______________________.5、双曲线1xy =在点()1,1处的曲率为 .6、已知)(x f 在),(∞+-∞上连续，且2)0(=f ，且设2sin ()()x xF x f t dt =⎰，则(0)F '= .三、 1、求极限()xx x x x sin tan cos 1lim20-→ .2、设曲线的方程为33190x y (x )cos(y ),π++++=求此曲线在1x =-处的切线方程.3、求不定积分⎰++322x x xdx.4、求不定积分dx x x ⎰+31. 5、求定积分dx x x ⎰22cos π.6、求定积分⎰--+11242dx xx .四、1、求抛物线12+=x y 与直线1-=x y 所围成的图形. 2、设()f x ''连续，()1f π=，()()0sin 3f x f x xdx π''+=⎡⎤⎣⎦⎰，求()0f .试卷（二）一、1、=+→xx x 2)31(lim ．2、当=k 时，⎪⎩⎪⎨⎧>+≤=00e)(2x kx x x f x 在0=x 处连续．3、设x x y ln +=,则=dydx． 4、曲线x e y x -=在点)1,0(处的切线方程是．5、设两辆汽车从静止开始沿直线路径前进，下图中给出的两条曲线)(1t a a =和)(2t a a =分别是两车的速度曲线．那么位于这两条曲线和直线T t = )0(>T 之间的图形的面积A 所表示的物理意义是．二、1、若函数xx x f =)(，则=→)(lim 0x f x （）．A 、0B 、1-C 、1D 、不存在 2、下列变量中，是无穷小量的为（）.A 、 x 1ln（当+→0x ） B 、x ln （当1→x ） C 、x cos （当0→x ） D 、 422--x x （当2→x ） 3、满足关系式0)(='x f 的x 是函数)(x f y =的（）.A 、极大值点B 、极小值点C 、驻点D 、间断点 4、下列函数)(x f 在]1,1[-上适合罗尔中值定理条件的是（）.A 、32)(x x f =B 、x x x f 2)(=C 、32)(+=x x fD 、x x f sin )(= 5、下列无穷积分收敛的是（）.A 、⎰∞+ 0sin xdx B 、dx x ⎰∞+ 01C 、dx e x ⎰∞+- 0 2D 、dx x⎰∞+ 0 1三、1、求极限 xx x 2sin 24lim-+→ . 2、求极限 2cos 2cos 0lim x dte xx t x ⎰-→.3、设)1ln(25x x e y +++=，求y '.4、设)(x y f =由已知⎩⎨⎧=+=ty t x arctan )1ln(2，求22dx y d . 5、求不定积分dx xx x ⎰+)sin (ln 2.6、设⎪⎩⎪⎨⎧≥<+=-0011)(2x xe x x x f x ，求⎰-20d )1(x x f .四、1、设函数21)(xxx f +=，分别求其单调区间、极值、凹凸性与拐点. 2、设)(x f 在闭区间],[b a 上连续，在开区间),(b a 内可导)0(>a .试证在),(b a 内至少存在一点ξ满足：)(][)]()([2012201220122011ξξf a b a f b f '-=-.试卷（三）一、1．设)sin (cos )(x x x x f +=，则在0=x 处有（）.(A)2)0(='f (B) 1)0(='f (C) 0)0(='f (D) )(x f 不可导 2．设333)(,11)(x x xxx ⋅-=+-=βα，则当1→x 时（）. (A) )(x α与)(x β是同阶无穷小，但不是等价无穷小； (B) )(x α与)(x β是等价无穷小； (C) )(x α是比)(x β高阶的无穷小； (D) )(x β是比)(x α高阶的无穷小.3．函数2)4(121++=x xy 的图形（）. (A) 只有水平渐近线； (B) 有一条水平渐近线和一条铅直渐近线； (C) 只有铅直渐近线； (D) 无渐近线.4．设函数nn x xx f 211lim)(++=∞→，则下列结论正确的为（）.(A) 不存在间断点； (B) 存在间断点1=x ； (C) 存在间断点0=x ； (D) 存在间断点1-=x .5．设函数)(x f 是连续函数，且⎰+=1)(2)(dt t f x x f ，则)(x f = ( ).(A) 22x (B)222+x (C) 1-x (D) 2+x 6.广义积分)0( >⎰∞+a xdxap 当（）时收敛. (A) 1>p (B) 1<p (C) 1≥p (D) 1≤p二、1．=+→xx x sin 20)31(lim .2．曲线⎩⎨⎧=+=321ty t x 在t=2处的切线方程为 . 3．方程0162=-++x xy e y 确定隐函数)(x y y =，则)0(y '= .4．⎰--+2121 2211arcsin dx xx x = .5．已知x x cos 是)(x f 的一个原函数，则dx xxx f ⎰cos )(= . 6.=⎰→22 0sin lim2xtdt e xt x .三、1．（6分）已知tt t x x f ⎪⎪⎭⎫⎝⎛+=+∞→2sin 1lim )(，求)(x f '. 2．（6分）求不定积分dx xx⎰++cos 1sin 1. 3．（8分）设函数⎩⎨⎧≤<-≤=-1010)(2x x x xe x f x ，，，求dx x f ⎰-1 3 )(. 4．（8分）已知2)3(lim 2=++-∞→c bx ax x x ，求常数b a ,.5.（8分）求由曲线)1(2,4,22≥===x x y x y xy 所围图形的面积.6.（8分）由方程)ln(arctan22y x x y +=确定隐函数)(x f y =，求0=y dx dy . 7.（8分）设函数)(x f 在[0,1]上连续且单调递减，证明：对任意的],1,0[∈q ⎰⎰≥qdx x f q dx x f 01)()(.试卷（四）一、1.方程23cos2x y y y e x '''--=的特解形式为（）（A ）cos 2xaxe x ；（B ）cos 2sin 2xxaxe x bxe x +；（C ）cos 2sin 2xxae x be x +；（D ）22cos 2sin 2xxax e x bx e x +.2. 设a 不是π的整数倍，极限ax a x a x -→⎪⎭⎫⎝⎛1sin sin lim 的值是（）.（A ） 1 （B ）e （C ）a e cot （D ）ae tan3. 函数⎪⎩⎪⎨⎧=≠-+=0 ,0 ,1sin )(2x a x xe x xf ax 在0=x 处连续，则=a （）. （A ）1 （B ） 0 （C ）e （D ）1-4. 设2()()lim1()x af x f a x a →-=--，则在x a =处有（）（A ）()f x 的导数存在，且()0f a '≠；（B ）()f x 取得极大值；（C ）()f x 取得极小值；（D ）()f x 取得最大值.5. 设函数)(x f 在点0=x 的某个邻域内连续，且0)0(=f ，2cos 1)(lim0=-→xx f x ，则点0=x （）.（A ）是)(x f 的极大值点（B ）是)(x f 的极小值点(C)不是)(x f 的驻点（D ）是)(x f 的驻点但不是极值点二、1. 设tan 21, 0sin 2(), 0xx e x x f x ae x ⎧->⎪⎪=⎨⎪⎪≤⎩在0x =连续，则a =____________.2. 极限xaa x x ln )ln(lim0-+→（0>a ）的值是 .3. 设()(1)(2)(99)f x x x x x =---L ，则(0)f '=____________.4. 曲线21x xe y =的铅直渐近线是 . 5. 函数)4ln(x x y -=的单调递增区间为 .三、1. 计算极限412921612lim 2332-+-+-→x x x x x x . 2. 求不定积分10arctan d x x x ⎰. 3. 求定积分⎰+41)1(x x dx . 4. 求函数122+=x xy 的极值与拐点.5. 求微分方程52d 2(1)d 1y y x x x -=++的通解. 6. 设1>a ，函数a a x x a x a x y +++=，求dxdy . 四、证明题（本题8分）证明：当02x <<时，有24ln 240x x x x --+>.试卷（五）一、 1. 下列各式正确的是（）.(A)1)11(lim 0=++→x x x (B) e x x x =++→)11(lim 0(C) e x x x -=-∞→)11(lim (D)e xxx =+-∞→)11(lim 2. 设()f x 可导，()()(1sin )F x f x x =+，若欲使()0F x x =在可导，则必有（）.（A ）(0)0f '=（B ）(0)0f = （C ）(0)(0)0f f '+=（D ）(0)(0)0f f '-=3.为，则又设已知　)()20( d )()(21 110 )(12x F x t t f x F x x x x f x ⎰≤≤=⎩⎨⎧≤≤<≤=（）.⎪⎩⎪⎨⎧≤≤<≤21 10 31)(3x x x x A ⎪⎩⎪⎨⎧≤≤<≤-21 10 3131)(3x x x x B ⎪⎩⎪⎨⎧≤≤-<≤21 110 31)(3x x x x C ⎪⎩⎪⎨⎧≤≤-<≤-21 1103131)(3x x x x D 4.当0→x 时，与x ex cos 22-等价的无穷小是（）.（A ）2x . （B ）223x . （C ）22x . （D ）225x . 5.x e y y y x2cos 52=+'-''的一个特解应具有形式（）.（A ）x Ae x2cos （B ）)2sin 2cos (x B x A e x+（C ）)2sin 2cos (x B x A xe x+ （D ）)2sin 2cos (2x B x A e x x+ 二、1. 已知2sin ()d x f x x e C =+⎰,则()f x =____________.2.设函数22, 1()ln(1), 1a x x f x x x x ⎧+>-=⎨++≤-⎩在1x =-处连续，则a = . 3. 设),tan ln(sec x x y +=则='y .4. 设()f x 是连续函数，则dt t f a x x xaa x ⎰-→ )(lim= .5. 已知⎰+=C x dx x f arcsin )(，则=-⎰dx x f x )(12. 6. 由0 , 0)( , , =≥===y x f y b x a x 所围曲边梯形绕x 轴旋转而成的旋转体的体积公式为：V = . 则（应用你给的公式计算）由],[,)(22R R x x R x f y -∈-==与x 轴所围成的图形绕x 轴旋转而成的立体的体积=V . 三、1. (6分) 1.求函数22(,)(2)ln f x y x y y y =++的极值.2. (6分)设arctany x= 求dx dy .3.（6分）求微分方程满足初始条件的特解1,sin ==+=πx y xx x y dx dy . 4. (6分) 设由方程2cos()1x y e xy e +-=-确定y 是x 的函数，求d .0d yx x =5. (7分) 求函数22(,)(2)ln f x y x y y y =++的极值. 6 若函数)(x f 在]1,0[上连续，证明：=⎰π)(sin dx x xf ⎰)(sin 2ππdx x f ，并计算dx xxx ⎰+π2cos 1sin . 8. 过原点(0,0)O 作曲线ln y x =的切线，该切线与曲线ln y x =及x 轴围成一平面图形，求此平面图形的面积.《高等数学》试卷6（下）一.选择题（3分⨯10）1.点1M ()1,3,2到点()4,7,22M 的距离=21M M （）.A.3B.4C.5D.62.向量j i b k j i a+=++-=2,2，则有（）.A.a ∥bB.a ⊥bC.3,π=b aD.4,π=b a3. 设有直线1158:121x y z L --+==-和26:23x y L y z -=⎧⎨+=⎩，则1L 与2L 的夹角为（）（A ）6π；（B ）4π；（C ）3π；（D ）2π. 4.两个向量a 与b垂直的充要条件是（）.A.0=⋅b aB.0 =⨯b aC.0 =-b aD.0 =+b a5.函数xy y x z 333-+=的极小值是（）. A.2 B.2- C.1 D.1-6.设y x z sin =，则⎪⎭⎫ ⎝⎛∂∂4,1πyz ＝（）.A.22 B.22- C.2 D.2- 7. 级数1(1)(1cos ) (0)nn n αα∞=-->∑是（）（A ）发散；（B ）条件收敛；（C ）绝对收敛；（D ）敛散性与α有关.8.幂级数∑∞=1n n n x 的收敛域为（）.A.[]1,1- B ()1,1- C.[)1,1- D.(]1,1-9.幂级数nn x ∑∞=⎪⎭⎫⎝⎛02在收敛域内的和函数是（）.A.x -11 B.x -22 C.x -12 D.x -21 二.填空题（4分⨯5）1.一平面过点()3,0,0A 且垂直于直线AB ，其中点()1,1,2-B ，则此平面方程为______________________.2.函数()xy z sin =的全微分是______________________________.3.设13323+--=xy xy y x z ，则=∂∂∂yx z2_____________________________.4. 设L 为取正向的圆周：221x y +=，则曲线积分2(22)d (4)d Lxy y x xx y -+-=⎰Ñ____________.5. .级数1(2)nn x n ∞=-∑的收敛区间为____________.三.计算题（5分⨯6）1.设v e z usin =，而y x v xy u +==,，求.,yz x z ∂∂∂∂ 2.已知隐函数()y x z z ,=由方程05242222=-+-+-z x z y x 确定，求.,yz x z ∂∂∂∂ 3.计算σd y x D⎰⎰+22sin ，其中22224:ππ≤+≤y x D . 4.．计算1d d yxy x x⎰.试卷6参考答案一.选择题 CBCAD ACCBD 二.填空题1.0622=+--z y x .2.()()xdy ydx xy +cos .3.19622--y y x .4.()n n n n x ∑∞=+-0121. 5.()x e x C Cy 221-+= .三.计算题 1.()()[]y x y x y e x z xy +++=∂∂cos sin ，()()[]y x y x x e y z xy +++=∂∂cos sin . 2.12,12+=∂∂+-=∂∂z y y z z x x z . 3.⎰⎰=⋅πππρρρϕ202sin d d 26π-. 4.3316R . 5.x x e e y 23-=. 四.应用题1.长、宽、高均为m 32时，用料最省.2..312x y =《高数》试卷7（下）一.选择题（3分⨯10）1.点()1,3,41M ，()2,1,72M 的距离=21M M （）. A.12 B.13 C.14 D.152.设两平面方程分别为0122=++-z y x 和05=++-y x ，则两平面的夹角为（）. A.6π B.4π C.3π D.2π 3.点()1,2,1--P 到平面0522=--+z y x 的距离为（）. A.3 B.4 C.5 D.6 4.若几何级数∑∞=0n nar是收敛的，则（）.A.1≤rB. 1≥rC.1<rD.1≤r8.幂级数()nn xn ∑∞=+01的收敛域为（）.A.[]1,1-B.[)1,1-C.(]1,1-D. ()1,1- 9.级数∑∞=14sin n n na是（）. A.条件收敛 B.绝对收敛 C.发散 D.不能确定10. ．考虑二元函数(,)f x y 的下列四条性质：（1）(,)f x y 在点00(,)x y 连续；（2）(,),(,)x y f x y f x y 在点00(,)x y 连续（3）(,)f x y 在点00(,)x y 可微分；（4）0000(,),(,)x y f x y f x y 存在. 若用“P Q ⇒”表示有性质P 推出性质Q ，则有（）（A ）(2)(3)(1)⇒⇒；（B ）(3)(2)(1)⇒⇒ （C ）(3)(4)(1)⇒⇒；（D ）(3)(1)(4)⇒⇒ 二.填空题（4分⨯5）1. 级数1(3)nn x n ∞=-∑的收敛区间为____________.2.函数xye z =的全微分为___________________________.3.曲面2242y x z -=在点()4,1,2处的切平面方程为_____________________________________.4.211x +的麦克劳林级数是______________________. 三.计算题（5分⨯6）1.设k j b k j i a32,2+=-+=，求.b a ⨯2.设22uv v u z -=，而y x v y x u sin ,cos ==，求.,y z x z ∂∂∂∂ 3.已知隐函数()y x z z ,=由233=+xyz x 确定，求.,yz x z ∂∂∂∂ 4. 设∑是锥面1)z z =≤≤下侧，计算y z 2d d 3(1)d d xd d y z x z x y ∑++-⎰⎰四.应用题（10分⨯2）试用二重积分计算由x y x y 2,==和4=x 所围图形的面积.试卷7参考答案一.选择题 CBABA CCDBA. 二.填空题1.211212+=-=-z y x .2.()xdy ydx e xy +.3.488=--z y x .4.()∑∞=-021n n n x . 5.3x y =. 三.计算题1.k j i238+-.2.()()()y y x y y y y x yz y y y y x x z 3333223cos sin cos sin cos sin ,sin cos cos sin +++-=∂∂-=∂∂ .3.22,z xy xz y z z xy yz x z +-=∂∂+-=∂∂. 4. ⎪⎭⎫ ⎝⎛-3223323πa . 5.xx e C e C y --+=221. 四.应用题 1.316. 2. 00221x t v gt x ++-=.《高等数学》试卷3（下）一、选择题（本题共10小题，每题3分，共30分） 1、二阶行列式 2 -3 的值为（）4 5A 、10B 、20C 、24D 、222、设a=i+2j-k,b=2j+3k ，则a 与b 的向量积为（） A 、i-j+2k B 、8i-j+2k C 、8i-3j+2k D 、8i-3i+k3、点P （-1、-2、1）到平面x+2y-2z-5=0的距离为（） A 、2 B 、3 C 、4 D 、54、函数z=xsiny 在点（1，4π）处的两个偏导数分别为（） A 、,22 ,22 B 、,2222- C 、22- 22- D 、22- ,225、设x 2+y 2+z 2=2Rx ，则yzx z ∂∂∂∂,分别为（） A 、z y z R x --, B 、z y z R x ---, C 、zyz R x ,-- D 、zyz R x ,- 6、设圆心在原点，半径为R ，面密度为22y x +=μ的薄板的质量为（）（面积A=2R π） A 、R 2A B 、2R 2A C 、3R 2A D 、A R 221 7、级数∑∞=-1)1(n nnn x 的收敛半径为（）A 、2B 、21C 、1D 、3 8、cosx 的麦克劳林级数为（）A 、∑∞=-0)1(n n)!2(2n x n B 、∑∞=-1)1(n n )!2(2n x n C 、∑∞=-0)1(n n )!2(2n x n D 、∑∞=-0)1(n n)!12(12--n x n9、微分方程(y``)4+(y`)5+y`+2=0的阶数是（）A 、一阶B 、二阶C 、三阶D 、四阶 10、微分方程y``+3y`+2y=0的特征根为（） A 、-2，-1 B 、2，1 C 、-2，1 D 、1，-2 二、填空题（本题共5小题，每题4分，共20分） 1、直线L 1：x=y=z 与直线L 2：的夹角为z y x =-+=-1321___________。

大一高等数学期末考试试卷及复习资料详解

大一高等数学期末考试试卷及复习资料详解大一高等数学期末考试试卷（一）一、选择题（共12分）1.（3分）若/3= 2XXV0,为连续函数,则d的值为（）.a+ x,x>0（A）I （B） 2 （C）3 （D）-I2.（3分）已知厂⑶=2,则Ii y "7⑶的值为（）.λ→0 2hOOl （B） 3 （C）-I （D）I23.（3分）定积分∫>Λ∕1-COS23Xdx的值为（）•■⑷ 0 （B）-2 （C）I （D） 24.（3分）若/⑴在“勺处不连续,则/3在该点处（）・（A）必不可导（B）—定可导（C）可能可导（D）必无极限二、填空题（共12分）1.（3分）平面上过点（0,1）,且在任意一点（Λ∙,y）处的切线斜率为3疋的曲线方程为_________________________ .2.（ 3 分）∫ ι（x2+x4 Sin XyIX = _______ 1-3.（3 分）IilnX2 Sin丄= ・.r→υX4.（3分）y = 2√ -3√的极大值为________________ —2 （6分）设尸冕,求*JT + 1三、计算题（共42分）1.（6 分）求Iim史S.∙*→υ Sin 3x^3.（6分）求不定积分JXIn（I+十）厶.x .v<ι4.（6 分）求J /（X-1）JΛ∖其中/（x）= < l + cosχ,e' +l,x> 1.5.（6分）设函数y = f（x）由方程JO e,M + ［cos∕d∕ = 0所确定,求dy.6.（ 6 分）设 f f{x）dx = Sin + C,求j + 3）dx.7.（6 分）求极限IinJI÷-Γn→30k 2/7 7四、解答题（共28分）1.（7 分）设,Γ（lnx） = l+x,且/（0） = 1,求32.（7分）求由曲线y = cosx［-^-<x<^及X轴所围成图形绕着X轴旋I 2 2）转一周所得旋转体的体积.3.（7分）求曲线y = x3-3√÷24x-19在拐点处的切线方程•4.（7分）求函数y = x + √∏7在［-5,1］上的最小值和最大值.五、证明题（6分）设厂（X）在区间［“］上连续,证明i a f^dx = ¥ ［/（“） + f（b）］+1 ［（X - a）（x - b）fj）dx.（二）一、填空题（每小题3分，共18分）1.设函数/（χ）= 2χ2~1 ,则"1是心）的第_________ 类间断点.X -3x + 23.=∙v→∞V X)4・曲线 V 在点(扣)处的切线方程为・5 .函数J = 2X 3-3X 2在［-1,4］上的最大值 _________________ ,最小值 __________ .二、单项选择题(每小题4分，共20分)1.数列&”｝有界是它收敛的( )•(A)必要但非充分条件； (C)充分必要条件； 2.下列各式正确的是((B)充分但非必要条件; (D)无关条件.)・(A) je-χdx=e"x+C i(B) J In X(IX = _ + C ; (C)JI 2∕x=2hl (l 2x)+C ；(D) f —5—JX = Inlllx+ C ・' ,J XInX3-设/(x)在RM 上，广(x)>O 且厂(x)>0,则曲线y = f(x)在［“问上•6.∣∙arctanx J l +x 2(IX(小沿X轴正向上升且为凹(B)沿兀轴正向下降且为凹的；的；(D)沿X轴正向下降且为凸(C)沿兀轴正向上升且为凸的；的.则/(x)在兀=0处的导? :( )•4. 设/(*)=XInX ’⑷等于1;（C）等于O ；（D）不存在•5.已知Ihn/（x）= 2,以下结论正确的是（）•G）函数在工=1处有定义且/（1）=2 ; （B）函数在；V = I处的某去心邻域内有定义；（C）函数在2 1处的左侧某邻域内有定义；（D）函数在21处的右侧某邻域内有定义.三、计算（每小题6分，共36分）1.求极限:HlnX2 sinx→0X2.已知y = ln（l + χ2）,求几3.求函数J = >0）的导数.5.J X COS XdX ・丄 16.方程y x =X y确定函数y = f（x）f求八四、（H）分）已知/为/（X）的一个原函数，求∫x2∕（x}∕x.五、（6分）求曲线,=壮7的拐点及凹凸区间.六、（10 分）设J广（√∑）/X = X（e、' +1）+C ,求/（X）・（三）填空题（本题共5小题，每小题4分，共20分）・±J_(1)⅛(COSX)r = ________ 石________ .(2)曲线A = Xlnx上及直线X-y + l= °平行的切线方程为y =x-∖(3 )已知f f(e x) = xe~x,且/(D = O ,则大一高等数学期末考试试卷及复习资料详解/(X)= _________ /Cv)= 2(In X)________ .X 211(4)曲线V =3777的斜渐近线方程为 _______ V= 3Λ^9,二、选择题(本题共5小题，每小题4分，共20分)・(1)下列积分结果正确的是(D )(2)函数/W 在［恥］内有定义，其导数广⑴的图形如图1-1所示, 则(D ) •(A)刁宀都是极值点.⑻ g ，/3))，(£，/(£))都是拐点.(C) F 是极值点.，U 是拐点. (D) WJy))是拐点，勺是极值点.(3) 函数y = qe v ÷C 2e-÷A -e'满足的一个微分方程是(D ).(A) /-y-2>∙ = 3xe t . (B) /-y-2y = 3e v . (C) / + y-2y = 3Λ∙e c .(D) / + y~2y = 3e r .lim∕(⅞)-∕(⅞~z0 (4) 设/W 在％处可导，则I h 为(A ) •⑷ 广仇). (B) -f ,M.(C) O. (D)不存在.(5)下列等式中正确的结果是((A) (J* /(x)"∙χ)'Z=/W-(C) 町 /(χ)"χ]=/W -) 微分方程= (V+1)-的通解为三、计算J (本共4小题，每小题6分，共24分).y =3 _5 "3 O(或令 √Γ+χ = r)四、解答题（本题共4小题，共29分）•1. （本题6分）解微分方程r-5∕÷6j = xe -.解：特征方程r 2-5r + 6 = 0 ------------- 1分特征解斤=2,r 2 =3. ------------ 1分 3x大一高等数学期末考试试卷及复习资料详解恤（丄—丄）1∙求极限j X-I In —X 11. xlnx-x+1Iim (—— _ ——)IIm ---------In XIUn I XTl x-1 I---- + In xh ∖x Iim x →,X -1 + xln1.1 + In X 1 IUn -------- =— j 1 + In X +1 2Λ = In Sin t2.方程尸COSWSinf 确定V 为X 的函数,dy y ,(f)-=-一 =∕sm∕, 解 JX 十⑴求dx 及Jx 2 .（3分） (6分)arctan JX3. 4.计算不定积分J石(1+『. arctanA∕√7—— (i + χ)=21 arctan √7t∕ arctan y ∕x ——解 Hatan 仇=2 J √x(l + x)=(arctan2+C ——「一 dx4.计算定积分如+曲.'3χ(l -VTTX) 0解分）oT7⅛7_ V dx = 一J(：(I-、/i+x)〃X（6分）LL i∖l4/1 «\ ? r V 八2.(本题7分)一个横放着的圆柱形水桶(如图4-1),桶内盛有半桶水，设桶的底半径为R ,水的比重为乙计算桶的一端面上所受的压力.解：建立坐标系如图3.(本题8分)设/B在S】上有连续的导数，f(u) = f(b) = θ9且∫O∕2(X)JΛ =1^试求∫>∕ω∕解:J：Xf(X)f∖x)dx = £ Xf(X)df(x) 2 分= -∫n^^W ------------ 2 分=IV 2(Λ-)⅛-|£72(X)厶一一2 分4.(本题8分)过坐标原点作曲线＞, = h^的切线，该切线及曲线y =lnx及X轴围成平面图形D.⑴(3) 求D的面积A;⑵(4) 求D绕直线X = e旋转一周所得旋转体的体积V.解:(1)设切点的横坐标为"，则曲线y = In Λ在点(⅞Jn ⅞)处的切线方程y = Inx0 + —(X-X0).氐__I分由该切线过原点知山心-1 = 0,从而心=匕所以该切线的方程为1y = -X.平面图形D的面积1V = -X(2)切线"及X轴及直线Xe所围成的三角形绕直线Xe旋转V I = -7te1所得的圆锥体积为,3 2分曲线尸IZ及X轴及直线所围成的图形绕直线Xe旋转所得的旋转体体积为V2=(oπ(e-e>)2dy9】分因此所求旋转体的体积为V=V l-V2=-^2-e y)2dy = -(5e2-∖2e + 3).五、证明题(本题共1小题，共7分)•1.证明对于任意的实数Y , eJl + x.e x = l + x + —Λ2≥l + x2解法二设fM = e x-x~^则/(0) = 0.因为f f M = e x-∖. 1 分当Xno时，f,M≥o.f(χ)单调增加，/(χ)≥∕(θ)=o.当x≤0时，∕,ω≤0.∕(Λ∙)单调增加，/(X)≥/(0) =0. 所以对于任意的实数X, ∕3≥°∙即e'≥l + I 解法三：由微分中值定理得，R -1 = “ -60 =^(X-O) = ^Xt 其中§位于0 到X 之一1分2分A = V -ey)dy = ~e~^∙解法一:2分2分1分2分间。

医用高等数学试题

医用高等数学试题1. 建模与微分方程某医院整理了一组病人的实验数据，发现他们在被注射某种药物后，体内药物浓度的变化可以用以下微分方程描述：\[ \frac{{dC}}{{dt}} = -kC \]其中，\( C \) 表示病人体内的药物浓度，\( t \) 表示时间，\( k \) 为常数。

请回答以下问题：a) 请解释该微分方程中各个参数的物理含义，并说明其单位。

b) 利用该微分方程及已知条件，求解出药物浓度 \( C \) 与时间 \( t \) 的关系式。

c) 若某位病人的初始药物浓度为 100 mg/L，且经过 2 小时后浓度下降至 50 mg/L，请计算该药物的半衰期。

2. 曲线拟合与概率某药物在人体内的分布情况可以用以下方程描述：\[ C(t) = \frac{{A \cdot e^{-k_1 \cdot t}}}{{1 + k_2 \cdot t}} \]其中，\( C(t) \) 为药物浓度，\( t \) 为时间，而 \( A \)，\( k_1 \)，\( k_2 \) 均为常数。

某研究小组通过实验得到了一组药物浓度的数据，并希望通过曲线拟合来估计未知的参数值。

请回答以下问题：a) 解释方程中各个参数的物理含义，并说明其单位。

b) 利用已有的实验数据，通过最小二乘法拟合曲线，求解未知参数的数值，并给出拟合的曲线方程。

c) 对于拟合得到的曲线方程，若药物浓度 \( C(t) \) 达到峰值后开始下降，在什么条件下浓度可以收敛到接近零的稳定值？3. 概率与统计某医院对一种特定疾病的诊断准确率进行了研究。

根据数据统计，一个人真正患有该疾病的概率为 0.05，而经过医院的诊断，诊断结果显示该人患有该疾病的概率为 0.98。

进一步，研究还发现该医院通过这种诊断方法错误地将一些没有该疾病的人诊断为患有该疾病，错误率为 0.03。

请回答以下问题：a) 若一个人在该医院被诊断患有该疾病，那么他真正患有该疾病的概率是多少？b) 若一个人在该医院被诊断不患有该疾病，那么他实际上可能患有该疾病的概率是多少？c) 利用统计学相关知识，你认为在这种情况下，该医院的诊断方法的可靠性如何评价？有何改进的建议？4. 误差分析与可行性研究某医疗设备用于测量患者体内某种物质的浓度，设备测得的浓度值与实际浓度存在误差。

《医用高等数学》药学期终试卷B

徐州医学院2006-2007学年第一学期 2006级药学专业《医用高等数学》期终考试试卷（2006年12月19日）一、选择：（共8题，每题3分，总分共24分）1．下列极限运算正确的是：( )A ．e X Xx =+∞→1)1(lim B ．1sin lim =∞→x xx C ．11sin lim 0=⋅→x x x D ．110)1(lim -→=-e x x x2．若()x f 在0x 点满足：()()()()02 0100=''='x f x f 则0x x = 点一定是 ( )A ．驻点B ．极值点C ．拐点D ．不能确定 3．函数xex y 2-⋅=的凹区间为： ( )A ．（1，+∞）B ．（－∞，+∞）C ．（－1，＋∞）D ．（-∞，0） 4．若f(x)的一个原函数为-sinx，则⎰dx x f)('( )A ．cosx ＋cB ．—cosx ＋cC ．sinx ＋cD ．—sinx ＋c5．22a x ＋122=by ()0≥y 绕x 轴旋转所得的旋转体的体积V ：（）A ．b a 234π B ．234ab π C ．b a 232π D ．232ab π6．设212131313232321c c b b a c c b b a c c b b a D +-=，则下面四个等式中正确的是( )A ．c c b b a a 321321321c b a D = B ．321321321c c b b a - a - c b a D =C ．c - c c b - b a a 321321321b a D = D ．321321321c - c b - b a a c b a D -=7．微分方程02=++'y xyy 的通解为( )A ．xxeC y 2= B ．x x C y 12-+= C ．C x y +-=2lnD ．xx Ce y 12-= 8．下列微分方程中阶数最高的是：（）A ．()()2223=-+u u u B ．()()0100"2050'100=-+y y y C ．02'=-y yD ．0"2'3=+-y y y y y二、填空题：（共6题，每题3分，总分18分）9．积分dx xα11⎰是收敛的（α恒正），则α的取值范围_____________ 10．函数f(x)=(x-1)5+4（x+1）的拐点是______________________ 11．z=arctg(x 2+y)在(1，0)处的全微分，dz=______________ 12．dxdy＋ytgx=secx 满足y(0)=1的特解：______________ 13．微分方程y "+06'=-y y ,则方程的通解为____________________ 14．y=π224x -在[-2,2]上的平均值为：_________________三、解答题：15．设⎪⎪⎩⎪⎪⎨⎧<+=>=)0(1cos )0()0()(x b x x x a x xtgxx f ，问：a 、b 为何值时，f(x)在x=0连续。

关于医学用高等数学期末复习题

医学类高等数学期末复习题一、选择题:1.⎪⎩⎪⎨⎧=-为偶数当为奇数当n n n x n ,10,17，则。

（A ）;0lim =∞→n n x （B ）;10lim 7-∞→=n n x （C ）;,10,,0lim 7⎩⎨⎧=-∞→为偶数为奇数n n x n n (D) 不存在n n x ∞→lim 。

2. 下列数列n x 中，收敛的是。

（A ）n n x nn 1)1(--=；（B ）1+=n n x n ；（C ）2sin πn x n =；（D ）n n n x )1(--=。

3. 1→x 时与无穷小x -1等价的是。

(A)()3121x -； (B) ()x -121 ； (C) ()2121x - ； (D) x -1。

4．下列极限中，值为1的是。

(A) xxx sin 2lim π∞→； (B) xxx sin 2limπ→； (C) xxx sin 2lim 2ππ→； (D) xxx sin 2limππ→。

5. 连续的在是00)()()(limx x x f x f x f x x ==→ 。

（A ）必要条件而非充分条件； (B) 充分条件而非必要条件； (C) 充分必要条件； (D) 无关条件。

6. xx x f x 1sin sin )(0⋅==是的。

(A) 可去间断点； (B) 跳跃间断点； (C) 振荡间断点； (D) 无穷间断点。

7. ⎪⎩⎪⎨⎧≥<--=1 ,21 ,11)(2x x x x x x f ，的是则)(1x f x = 。

(A) 连续点； (B) 可去间断点； (C) 跳跃间断点； (D) 无穷间断点。

8.的是则)(0 ,0 ,1cos ,0 ,0,0 ,sin )(x f x x x x x x x xx x f =⎪⎪⎩⎪⎪⎨⎧>=<+= 。

(A) 连续点； (B) 可去间断点； (C) 跳跃间断点； (D) 振荡间断点。

医学大一期末数学试卷

一、选择题（每题5分，共25分）1. 下列函数中，在其定义域内连续的是（）A. f(x) = |x| - 1B. f(x) = x^2 / (x - 1)C. f(x) = 1 / (x - 2)D. f(x) = √(x + 1)2. 已知函数f(x) = x^3 - 3x，则f'(1)的值为（）A. 2B. 0C. -2D. -33. 在下列数列中，收敛于0的是（）A. a_n = (1/2)^nB. a_n = (-1)^nC. a_n = nD. a_n = n^24. 已知一个正方体的边长为a，其表面积为S，则S与a的关系为（）A. S ∝ aB. S ∝ a^2C. S ∝ a^3D. S ∝ a^45. 设向量a = (2, 3)，向量b = (1, -2)，则向量a与向量b的点积为（）A. 7B. -7C. 1D. -1二、填空题（每题5分，共25分）6. 函数f(x) = e^x在x = 0处的导数为__________。

7. 数列{a_n}的前n项和为S_n，若a_1 = 1，a_2 = 2，且a_n = a_{n-1} +a_{n-2}，则S_5 = ________。

8. 设矩阵A = [[1, 2], [3, 4]]，则A的行列式|A| = ________。

9. 向量v = (1, 2, 3)，其模长为__________。

10. 圆的方程为x^2 + y^2 - 4x - 6y + 9 = 0，则圆心坐标为__________。

三、解答题（每题20分，共80分）11. （20分）求函数f(x) = x^3 - 6x^2 + 9x + 1的极值。

12. （20分）已知数列{a_n}的通项公式为a_n = 3^n - 2^n，求该数列的前n项和S_n。

13. （20分）设矩阵A = [[1, 2], [3, 4]]，求矩阵A的逆矩阵A^(-1)。

14. （20分）已知平面直角坐标系中，点P(2, 3)在直线y = 2x + 1上，求点P 到直线y = 2x + 1的距离。

(完整版)大一高等数学期末考试试卷及答案详解

大一高等数学期末考试一试卷一、选择题（共12 分）1.（ 3 分）若 f ( x)2e x , x 0,为连续函数 , 则a的值为 ().a x, x0(A)1 (B)2 (C)3 (D)-12.（ 3 分）已知f(3) 2, 则lim f (3 h) f (3) 的值为（）.h02h(A)1 (B)3 (C)-1(D)1 23.（ 3 分）定积分212xdx 的值为（）.cos2(A)0 (B)-2 (C)1(D)24.（3分）若f (x)在x x0处不连续,则 f ( x) 在该点处().(A)必不行导 (B) 必定可导 (C) 可能可导 (D) 必无极限二、填空题（共 12 分）1．（3 分）平面上过点(0,1) ，且在任意一点 ( x, y) 处的切线斜率为 3x2的曲线方程为.2.（ 31x4 sin x) dx.分）( x213.（ 3分） lim x2 sin1=.x0x4.（ 3分） y2x33x2的极大值为.三、计算题（共42 分）1.（ 6x ln(15x).分）求 limsin 3x2x02.（6 分）设ye xx2, 求 y .13.（ 6分）求不定积分x ln(1 x2 )dx.x 4.（ 63f ( x 1)dx, 此中f (x) 1, x 1,分）求cosxe x1,x 1.5. （ 6 分）设函数 yy x f ( x) 由方程e t dtcostdt 0 所确立 , 求 dy.6. （ 6 分）设 f ( x)dxsin x 2 C, 求 f (2 x 3)dx.3 n7. （ 6 分）求极限 lim 1 .2nn四、解答题（共 28 分）1. （ 7 分）设 f (ln x) 1 x, 且 f (0)1, 求 f ( x). 2. （ 7 分）求由曲线 ycos x2x与 x 轴所围成图形绕着 x 轴旋转一周2所得旋转体的体积 .3. （ 7 分）求曲线 y x 3 3x 2 24x 19 在拐点处的切线方程 .4. （ 7 分）求函数 yx1 x 在 [ 5,1] 上的最小值和最大值 .五、证明题 (6 分)设 f ( x) 在区间 [ a, b] 上连续 , 证明b b a1 bf (x)dx[ f (a) f (b)]( x a)( x b) f ( x) dx.a22 a标准答案一、 1 B;2C; 3D; 4 A.二、 1y x31;22 ;3 0;40.3三、 1解原式limx5x 5 分x 03x 251 分32 解Q ln y lne x x ln( x 2 1),2 分x 2 12y e x[12x] 4 分x 21 2x 2 13 解原式1ln(1 x 2 ) d (1 x 2 )3 分21[(12)ln(12 (12) 12xdx]2xx )xx 22 分1[(1 x 2 )ln(1 x 2 )x 2 ] C1 分24解令 x1 t, 则2 分320 f ( x)dx1 f (t )dt1t2 t11 costdt1 (e 1)dt0 [ e tt ]12e 2 e 15两边求导得 eyy cosx 0,cosxQ ye ycosxsin x 1dycosx dxsin x 16 解f (2 x 3) dx1 f (2 x2 1sin(2 x 3)2 C21 分1 分1 分 1 分2 分1 分1 分2 分3)d(2 x 2)2 分4 分32 n 37 解原式 = lim3 24 分1n2n3= e22 分四、 1 解令 ln xt, 则 xe t ,f (t) 1 e t ,3 分f (t )(1 e t )dt = t e tC.2 分Q f (0)1, C 0,2 分f (x) xe x .1 分2 解V x2 23 分cos xdx222cos 2 xdx2 分2.2 分23 解 y3x 2 6x 24, y6x 6,1 分令 y 0, 得 x 1.1 分当x 1时 , y0; 当 1 x时 , y0,2 分(1,3) 为拐点 ,1 分该点处的切线为 y 3 21(x 1).2 分4 解 y 11x2 1 x 1, 2 分2 12 1 x令 y0, 得 x3 . 1 分4y( 5)56,2.55,y3 5, y(1) 1,2 分44最小值为 y(5)56, 最大值为 y35 . 2 分44五、证明ba)( x b) f(x) ba)( x b) df ( x)1 分(x( xaabb[( x a)( x b) f (x)] aaf ( x)[2 x ( a b)dx1分ba [2 x (a b)df ( x)1分[2 x (a b)] f ( x)(b a)[ f ( a) f (b)]移项即得所证 .b ba2 a f ( x)dx1分b2 a f ( x)dx,1分1分。

大学一年级医用高数期末考试题与答案

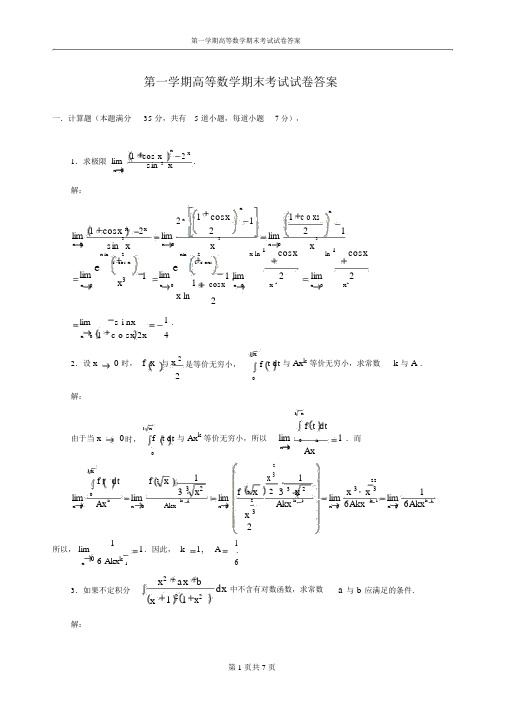
第一学期高等数学期末考试试卷答案第一学期高等数学期末考试试卷答案一．计算题（本题满分35 分，共有 5 道小题，每道小题7 分），1 cos x x2x1．求极限 lim．sin 3xx 0解：1 cosxx1 c o xs x2 x111 cosx x2x22limlimlimsin 3 xx 3x 3x 0x 0x 0x ln 1 cosxln 1 cosxx ln2xln21 cos x1 c oxslimex31 lime11 lim2lim2x 0x 0cosxx 0x3x 0x2x ln2lim1 s i nx 1 ．x 0 c o sx 2x4与 x 23x2．设 x0 时， f x 是等价无穷小，f t dt 与 Ax k 等价无穷小，求常数k 与 A ．2 0解：3x3xf t dt由于当 x0 时，f t dt 与 Ax k 等价无穷小，所以limk 1 ．而x 0 Ax3x21x3 1f t dtf3x22f3x2 3 3 x 2x 3 x 31lim 0lim3 3 x 2limlim limAxkk 12Akxk 1 6Akx k 1 6Akxk 1 x 0xAkxx 0x 0 x 0 x 32所以， lim11．因此， k1,A1．x6 Akx k 163．如果不定积分x 2 ax bdx 中不含有对数函数，求常数a 与b 应满足的条件．x1 2 1 x 2解：x2ax b化为部分分式，有将2x2x11x2ax b A B2Cx D ，2x 1x 1 1 x 2x 1 1 x2因此不定积分x2ax bdx 中不含有对数函数的充分必要条件是上式中的待定系数x 1 21 x2A C0．即x2 ax b B D B 1 x 2 D x 1 2 x 1 2 1x2x 1 2 1 x2x 1 2．1 x 2所以，有 x2ax b B 1x 2 D x 1 2B D x22Dx B D ．比较上式两端的系数，有1B D ,a2D,b B D ．所以，得b1．525．计算定积分min 1,x2dx ．解：m i n1,x2x2x21 1x211x12x1x2 x22x ．3 1x351252213所以， min1,x2dx1dx 2 x dx x 2 dx．00128 5．设曲线C的极坐标方程为r a sin 3，求曲线 C 的全长．3解：曲线 r a sin3一周的定义域为03，即 03．因此曲线 C 的全长为3322333s r r d26a2422 a ．a s i n s i n c o s d a s i n d00333032二．（本题满分 45 分，共有 5 道小题，每道小题9 分），6．求出函数 fxlimsin x的所有间断点，并指出这些间断点的类型．2 nn1 2 x解：sin x 1 x1 21sin xxf xlim2 2．n1 2n1 12 x2x21x2因此 x 11 与 x 21 是函数 fx 的间断点．22l i m f xl i m0 0， limf xlim sin x1 ，因此 x1是函数 f x 的第一类可x1 x1 x1 x 122222去型间断点．lim f xlim s i n x1 ， lim f xlim 0 0 ，因此 x1 是函数 f x 的第一类可去型x111x122xx22 2间断点．7．设是函数 fx arcsinx 在区间 0, b 上使用 Lagrange （拉格朗日）中值定理中的 “中值 ”，求极限 lim．b 0b解：f xa r c sixn 在区间 0,b 上应用 Lagrange 中值定理，知存在 0, b ，使得arcsinb arcsin01 ．b 01 2b2所以，2 1 ．因此，arcsinbb 22122arcsinbblimlima r c sib nb 2lim2b b 2 a rc s bin2t 22t 22l i m 2si n ts i n tl i m 22l i m4b 0bt 0t s i nt t 0tlim 2tsin 2t2 2 cos2t11 c o s2t12s i n2t 14t 3lim12t 2l i mt 2l i m3tt 06 t6 t 02t所以， limb1 ． b 031 x18．设 f xe y 2 ydy ，求f x dx ．0 0 解：11 1f x dxxfxxf x dx1 x在方程 f xe y 2ydy 中，令 x 1 ，得11f 1e y 2ydye y 2 y dy 0 ．1 xx 2再在方程 f xe y2ydy 两端对 x 求导，得 f xe 1，111因此，f x dxxfx1xf x dxxf x dx 0111 1 x 2dx e xex 2xedx ee21x 21e 1 ．29．研究方程 e x a x 2a 0 在区间,内实根的个数．解：设函数 f x ax 2 e x 1， f x 2axe xax 2e xax 2 x e x ．令 f x0，得函数 f x 的驻点 x 10, x 22 ．由于 a0 ，所以lim f xlim ax 2e xxxlim f xlim ax2e xxx1 ，1 a limx 21 a lim2x1 a lim2xxx 1 1 ．xexexe因此，得函数 f x 的性态x,000,222,f x00f x14ae 211⑴若 4ae210，即 a e2f x2x1在,0、0,2、2,内时，函数ax e4各有一个零点，即方程e x a x2在,内有 3 个实根．⑵若 4ae210，即 a e2x2x1在,0、0,内各有一个零时，函数 f ax e4点，即方程 e x a x2在,内有 2 个实根．⑶若 4ae210 ，即 a e2时，函数f x ax2e x1在, 0 有一个零点，即方程4e x a x 2在,内有 1 个实根．10．设函数 f x 可导，且满足f x x f x 1 ， f 00 ．试求函数 f x 的极值．解：在方程 f x x f x 1 中令 t x ，得 f t t f t 1 ，即f x x f x 1 ．f x xf x x中消去 f x，得在方程组xf x f x xf x x x 2．1x2积分，注意 f00，得x t t2．即f x f 001t 2dtx21ln 1f xt t 2 dtxx 2arctanx．1t2由 f xx x 2 得函数 f x 的驻点 x 1 0, x 21．而 f x1 2x x2 ．所以，1 x 21 x2 2f 01 0 ， f11 0 ．21所以， f0 0 是函数 f x 极小值； f11是函数 f x 极大值．ln 22 4三．应用题与证明题（本题满分20 分，共有 2 道小题，每道小题 10 分），11．求曲线y x 的一条切线，使得该曲线与切线 l 及直线 x 0 和 x 2 所围成的图形绕 x 轴旋转的旋转体的体积为最小．解：1 设切点坐标为 t, t ，由 y，可知曲线 yx 在 t,t 处的切线方程为2 tyt1 ，或 y1 x t ．x t2 t2 t因此所求旋转体的体积为 2V1 28 2x tx dx4 2t2 t4 3t所以，dV8 2 0 ．得驻点 t 2 ，舍去 t2 ．由于 dt 43t 233d 2V160 ，因而函数 V 在 t2处达到极小值，而且也是最小值．因此所求切dt 22 4 3t 2 t 3233线方程为 y3 1．x2412．设函数 fx 在闭区间0， 1 上连续，在开区间0， 1 内可导，且2e f xarctan xdx1， f 10 ．2证明：至少存在一点0， 1 ，使得 f1．12 arctan解：因为 f x 在闭区间0, 1 上连续，所以由积分中值定理，知存在2 0,，使得2e f x arctan xdx 2 e f arctan．02由于 e f x arctan xdx 1，所以，2e f arctan1．再由 f 10 ，得022e f arctan e f 1arctan 1．4作函数 g x e f x arctan x ，则函数在区间, 1 0, 1 上连续，在区间, 1 内可导．所以由Rolle 中值定理，存在,10, 1 ，使得 g0 ．而g x e f xe f x2．f x a r c t ax nx1所以存在,10, 1，使得e f f a r c t a n ef2 0．1由于 e f0 ，所以 f arctan120，即 f11．12 arctan。

医用高等数学高数试卷

《高等数学》试卷 (1)一．是非判断题 (本大题共10题，每题2分，共20分。

)1.函数sinln(x y e =是初等函数. ( A )A 、正确B 、错误2. ()ln 0.f x x x +=→函数当时是无穷小量( B ) A 、正确 B 、错误3. 当0x →时，21x e -和sin x 是同阶无穷小量。

( A ) A 、正确 B 、错误4. 01sin()12lim2x x x →-=- ( A ) A 、正确 B 、错误25.(cos )2cos .()x x B '=A 、正确B 、错误 6. 22()()()2xx xx x ex e e '''== ( B )A 、正确B 、错误7.()()f x dx f x C '⋅=+⎰ （ A ） A 、正确 B 、错误8.110〈⎰⎰( A )A 、正确B 、错误9.220cos 1sin 4xdx x ππ=+⎰（ A ）A 、正确B 、错误10. 若是f (x)连续函数，则由曲线y=f (x)和直线x=a 、x=b （a <b ）及x 轴所围成的曲边梯形面积为 S =|()b af x ⎰dx | ( B )A 、正确B 、错误二．单项选择题 (本大题共20题，每题3分，共60分) 11. ()f x 在0x 处左、右极限存在是()f x 在0x 处连续的 (B )A 、充分条件B 、必要条件C 、充要条件D 、前三者都不是12. 已知函数f (x) = ln 11x x x x >⎧⎨-≤⎩ ，则10lim ()x f x →-=（ A ）A. -1;B. 0;C. 1;D. 不存在13．已知21lim232x ax bx x →∞++=-，则a ，b 的值是 ( C ) A 、0，1 B 、1，0 C 、0，6 D 、1，112012214.lim(1)().;.1;.;..xx x A A e B C e D e →+=15. 当x →0时，下列函数为无穷小量的是（ D ） A.xe; B.xe-; C.2x-+ 1; D.1sec sinxx+.16. 以下各式中能直接使用洛必达法则计算的是（ D ）A 、sin lim 3x x x →∞ B、0x → C 、1cos lim x x x →∞- D 、01cos lim 2x xx→-17.ln ()..(,1);.01).(0,);.1)y x x D A B C D =--∞+∞+∞函数的单调递增区间是(,;(,.18. ()sin f x x =，则(())f f x '=（ C ）A 、sin(sin )xB 、sin(cos )xC 、cos(sin )xD 、cos(cos )x 19. 函数y = f (x)的微分可以表示为（ B ）A. y ;B. dy;C.y x ∆∆; D. 0lim x yx →∆∆.20. 设()f x 可导，且2()xy f e =，则()dy D =A 、2()xf e dx '; B 、22()xxf e e dx '; C 、222()xxf e e '; D 、以上都不对.332222222221.10,,().330;.330;.3310;.3310.x y y y x A A x y y y B x y y C x y y D x y '++='''++=++='++=++=设为求将方程两边对求导得223.ln(1),1,().1.;.2.3;.2y x x dy A A dx B dx C dx D =+==函数则当时有;dx.233324.,11.2;.3.1;.(1)33x C A x B x C x D x ++在以下各式中的一个原函数是().25.()()u x dv x =⎰（ B ）A. ()()()()u x v x v x du x +⎰； B. ()()()()u x v x v x du x -⎰；C. ()()()()u x v x u x dv x +⎰；D. ()()()()u x v x u x dv x -⎰26. 函数()f x 在区间[,]a b 上连续是()f x 在区间[,]a b 上可积的（ B ） A 、必要条件 B 、充分条件 C 、充要条件 D 、既不是充分条件又不是必要条件0327.().23;.3;.. 1.x dx A A B C D =-⎰.2;28.cos ()x dx C π=⎰A 、0B 、1C 、2D 、π29. 51421cos 21x xdx x x -=--⎰( D ) A 、-1 B 、1 C 、-2 D 、030. 如图所示，阴影部分的面积是（ C ）A. [()()]b a f x g x dx +⎰;B. [()()]b a f x g x dx -⎰;C. [()()]b a f x g x dx -+⎰;D.[()()]b af xg x dx --⎰（这个题每套卷子基本都有，所以后面几套的30题删了）三．多项选择题(本大题共3题，每题4分，共12分。