梯形常用辅助线的做法
梯形辅助线的常见作法

例谈梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
[例1]如图1,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。
图1析解:过点B作BM//AD交CD于点M,则梯形ABCD转化为△BCM和平行四边形ABMD。
在△BCM中,BM=AD=4,CM=CD-DM=CD-AB=8-3=5,所以BC的取值范围是:5-4<BC<5+4,即1<BC<9。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
[例2]如图2,在梯形ABCD中,AD//BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是A BC的中点,连接EF,求EF的长。
图2析解:过点E分别作AB、CD的平行线,BC于点G、H,可得∠EGH+∠EHG=∠B+∠C=90°则△EGH是直角三角形因为E、F分别是AD、BC的中点,容易证F是GH的中点所以)CHBGBC(21GH21EF--==3、平移对角线:过梯形的一个顶点作对线的平行线,将已知条件转化到一个三角形中[例3]如图3,在等腰梯形ABCD中,AD//B AD=3,BC=7,BD=25,求证:AC⊥BD。
图3析解:过点C作BD的平行线交AD的延长于点E,易得四边形BCED是平行四边形,DE=BC,CE=BD=25,所以AE=AD+DE=AD+BC+7=10。
在等腰梯形ABCD 中,AC=BD=25,所以在△ACE中,22222AE 100)25()25(CE AC ==+=+,从而AC⊥CE ,于是AC ⊥BD 。
[例4]如图4,在梯形ABCD 中,AD//BC ,AC=15cm ,BD=20cm ,高DH=12cm ,求梯形ABCD 的面积。
全等梯形问题中常见的8种辅助线的作法(有答案解析)

全等梯形问题中常见的8种辅助线的作法(有答案解析)梯形是一种四边形,其中两条边是平行而另外两条边不平行。
在解决全等梯形问题时,我们可以使用一些辅助线的方法来简化问题并找到解答。
以下是常见的8种辅助线的作法,每种方法都附有答案解析。
1. 垂直辅助线法:垂直辅助线法是最基本的辅助线作法之一,它通过引入垂直辅助线来将梯形划分为上下两个小三角形或小梯形,并利用全等三角形的性质来解题。
2. 高度辅助线法:高度辅助线法通过引入高度辅助线来找到梯形的高,并利用相似三角形的性质来解题。
3. 中位线辅助线法:中位线辅助线法通过引入中位线辅助线来将梯形划分为两个全等的平行四边形,并利用平行四边形的性质来解题。
4. 对角线辅助线法:对角线辅助线法通过引入对角线辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
5. 平行边辅助线法:平行边辅助线法通过引入平行边辅助线来将梯形划分为两个全等的梯形,并利用梯形的性质来解题。
6. 外接圆辅助线法:外接圆辅助线法通过引入外接圆辅助线来找到梯形的外接圆,并利用外接圆的性质来解题。
7. 中心对称辅助线法:中心对称辅助线法通过引入中心对称辅助线来将梯形划分为两个全等的三角形,并利用全等三角形的性质来解题。
8. 连接线辅助线法:连接线辅助线法通过引入连接线辅助线来划分梯形并利用形成的图形的性质来解题。
这些辅助线的作法可以帮助我们在解决全等梯形问题时更简单而有条理地进行推导和解答。
通过灵活运用这些方法,我们可以提高解决问题的效率和准确性。
请注意:本文档中的答案解析仅供参考,具体解答的正确性应根据实际情况进行确认。
最新梯形常见辅助线作法(教师版)

梯形常见辅助线作法11、平移法2(1)梯形内平移一腰(过一顶点做腰的平行线)3[例1]如图,在等腰梯形ABCD中,AD∥BC,AB=CD,∠C=60°,AD=15cm,4BC=49cm,求CD的长.5解:过D作DE∥AB交BC于E,则四边形ABED为平行四边形.6∴AD=BE=15cm,AB=DE.7∴EC=BC-BE=BC-AD=49-15=34cm.8又∵AB=CD,∴ DE=CD.9又∵∠C=60°,10∴△CDE是等边三角形,11即CD=EC=34cm.12(2)梯形外平移一腰(过一顶点做腰的平行线)13[例2]如图,在梯形ABCD中,AB∥CD,四边形ACED是平行四边形,延长DC交BE于F. 求14证:EF=FB15证明:过点B作BG∥AD,交DC的延长线于G16∴四边形ABGD是平行四边形∴AD=BG17∵ACED中,AD∥CE AD=CE18∴CE∥BG且CE=BG ∴∠CEF=∠GBF 19又∵∠CFE=∠GFB20∴△ECF≌△BGF( ASA)21∴EF=FB22 AD CEFB点评:过梯形上底或下底的一个端点作另一腰的平行线,可将梯形转化为一个平行四边形23和三角形。
24(3)梯形内平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到25同一个三角形中。
26[例3]如图,已知:梯形ABCD中,AD∥BC,27∠C+∠B=90°,M,N分别是AD,BC的中点.28求证:MN=1() 2BC AD29证明:过点E分别作AB、CD的平行线,交BC于点G、H ,30则四边形ABGE,EDCH为平行四边形∴AE=BG,ED=HC31∵AB∥EG ∴∠B=∠EGF32又∵DC∥EH ∴∠C=∠EHF33则∠EGH+∠EHG=∠B+∠C=90°,△EGH是直角三角形34∵E、F分别是AD、BC的中点∴AE=ED,BF=CF ∴GF=FH 35则有EF=12GH=12(BC-BG-HC)=12(BC-AD)36(4)平移对角线(过一顶点做对角线的平行线)37[例4]求证:对角线相等的梯形是等腰梯形38已知:在梯形ABCD中,AD∥BC,对角线39求证:AB=DC40证明:过点D作DE∥AC交BC的延长线于点E 41B B则四边形ACED 是平行四边形 ∴AC=DE42 ∵DE=AC=DB ∴∠DBC=∠E ∠ACB=∠E ∴∠DBC=∠ACB 43 又∵BD=CA BC=CB ∴△ABC ≌△DCB(SAS) 44 ∴AB=DC45 点评:过梯形的一个顶点作对角线的平行线,将对角线的有关条件转化到一个三角形中。
梯形常中的辅助线
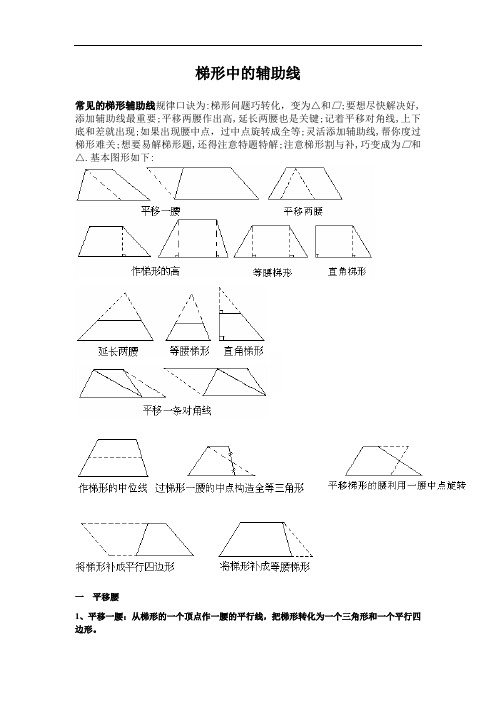
梯形中的辅助线常见的梯形辅助线规律口诀为:梯形问题巧转化,变为△和□;要想尽快解决好,添加辅助线最重要;平移两腰作出高,延长两腰也是关键;记着平移对角线,上下底和差就出现;如果出现腰中点,过中点旋转成全等;灵活添加辅助线,帮你度过梯形难关;想要易解梯形题,还得注意特题特解;注意梯形割与补,巧变成为□和△.基本图形如下:一平移腰1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
例1:梯形两底长分别为14cm 和24cm ,下底与腰的夹角分别是60°和30°,求较短腰长。
DBCA解析:如图,在梯形ABCD 中,AD//BC ,AD=14cm ,BC=24cm ,∠B=60°,∠C=30°。
过点A 作AE//DC 交BC 于E ,得到平行四边形AECD 和△ABE ,故AE=DC ,AD=EC ,∠C=∠AEB=30°。
这样,梯形的两腰,两底之差,下底与腰的两个夹角都集中于Rt △ABE 中,于是得到较短腰巩固练习:如图1,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
析解:过点B 作BM//AD 交CD 于点M ,则梯形ABCD 转化为△BCM 和平行四边形ABMD 。
在△BCM 中,BM=AD=4,CM=CD -DM=CD -AB=8-3=5,所以BC 的取值范围是:5-4<BC<5+4,即1<BC<9。
2.平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
例2:如图,梯形ABCD 中,AD//BC ,E 、F 分别是AD 、BC 的中点,且EF ⊥BC 。
求证:∠B=∠C 。
CFEADB分析:过点E 作EM//AB ,EN//DC ,分别交BC 于点M 、N 。
梯形两腰、下底与腰的两个夹角集中于△EMN 中,由E 、F 分别是AD 、BC 的中点轻易得到,又由EF ⊥BC ,得EM=EN ,故∠EMN=∠ENM ,所以∠B=∠C 。
梯形中添加辅助线的六种常用技巧

梯形中添加辅助线的六种常用技巧Prepared on 22 November 2020梯形中添加辅助线的六种常用技巧浙江唐伟锋梯形是不同于平行四边形的一类特殊四边形,解决梯形问题的基本思路是通过添加辅助线,将梯形进行割补、拼接转化为三角形、平行四边形问题进行解决。
一般而言,梯形中添加辅助线的常用技巧主要有以下几种——一、平移一腰从梯形的一个顶点作一腰的平行线,将梯形转化为平行四边形和三角形,从而利用平行四边形的性质,将分散的条件集中到三角形中去,使问题顺利得解。
例1、如图①,梯形ABCD中AD∥BC,AD=2cm,BC=7cm,AB=4cm,求CD的取值范围。
解:过点D作DE∥AB交BC于E,∵AD∥BC,DE∥AB∴四边形ABED是平行四边形(两组对边分别平行的四边形是平行四边形)∴DE=AB=4cm,BE=AD=2cm∴EC=BC-BE=7-2=5cm在△DEC中,EC-DE<CD<EC+DE(三角形两边之和大于第三边,两边之差小于第三边)∴1cm<CD<9cm。
二、延长两腰将梯形的两腰延长,使之交于一点,把梯形转化为大、小两个三角形,从而利用特殊三角形的有关性质解决梯形问题。
例2、如图②,已知梯形ABCD中,AD∥BC,∠B=∠C,求证:梯形ABCD是等腰梯形。
证明:延长BA、CD,使它们交于E点,∵AD∥BC∴∠EAD=∠B,∠EDA=∠C(两直线平行,同位角相等)又∵B=∠C∴∠EAD=∠EDA∴EA=ED,EB=EC(等角对等边)∴AB=DC∴梯形ABCD是等腰梯形(两腰相等的梯形是等腰梯形)。
三、平移对角线从梯形上底的一个顶点向梯形外作一对角线的平行线,与下底延长线相交构成平行四边形和一特殊三角形(直角三角形、等腰三角形等)。
例3、如图③,已知梯形ABCD中,AD=1.5cm,B C=3.5cm,对角线AC⊥BD,且BD=3cm,AC=4cm,求梯形ABCD的面积。
解:过点D作DE∥AC交BC延长线于E∵AD∥BC,DE∥AC∴四边形ACED是平行四边形(两组对边分别平行的四边形是平行四边形)∴CE=AD=1.5cm,DE=AC=4cm∵AC ⊥BD∴DE ⊥BD∴S 梯形ABCD =111()()222AD BC h CE BC h BE h +⨯=+⨯=⨯(h 为梯形的高) 211346cm 22BD DE =⨯=⨯⨯= 。
梯形中常用添加辅助线的方法

梯形中常用添加辅助线的方法1.作高:过梯形的顶点作底边上的高线,把梯形问题转化为矩形或直角三角形来解决;例1、已知等腰梯形的上底长为5cm,腰长为7 cm,下底角为600,求这个梯形的周长和面积。
练习:在梯形ABCD中,AB=CD,AD∥BC。
求证:AC2=AB2+BC·AD。
2.平移腰:通过平移梯形的一腰或两腰,使梯形问题转化为平行四边形或三角形来解决;例2、在梯形ABCD中,AD∥BC,∠B+∠C=900,E、F分别是AD和BC边上的中点,求证:EF=(BC-AD)/2。
练习:在梯形ABCD中,AD∥BC,∠B=800,∠C=500,求证:AB=BC-AD。
3.延长两腰:延长梯形的两腰相交于一点,使梯形问题转化为三角形来解决;例3、等腰梯形ABCD,AD∥BC,∠B=600,AD=15,AB=45,求BC的长。
练习:梯形ABCD中,AD∥BC,∠B=∠C。
求证:AB=CD。
4.平移对角线:平移其中的一条对角线,使梯形问题转化为直角三角形来解决,此法适合于已知对角线互相垂直的问题;例4、等腰梯形ABCD中,AB∥CD,AD=BC,且AC⊥BD,CH是高,求证:AB+CD=2CH。
练习:在梯形ABCD中,AD∥BC,AB=CD,对角线AC、BD互相垂直,GD⊥BC于G,EF是中位线。
求证:EF=DG。
5.连对角线:连结对角线,将梯形问题转化为平行四边形或三角形来解决;例5、梯形ABCD中,AD=BC,AB∥CD,延长AB到E,使BE=DC,连结AC、CE,求证:AC=CE。
6.取腰的中点:有一腰的中点时,往往取另一腰的中点构成梯形的中位线;例6、梯形ABCD中,AD∥BC,AB=AD+BC,M为CD的中点。
求证:AM、BM平∠分DAB、∠CBA。
7.连结上底与一腰中点并延长与下底的延长线相交,借助于得到的三角形解决梯形问题;例7、梯形ABCD中,AB∥CD,E是腰AD的中点,且AB+CD=BC。
梯形辅助线的常见作法

梯形辅助线的常见作法文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]例谈梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
[例1]如图1,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。
图1析解:过点B作BM//AD交CD于点M,则梯形ABCD转化为△BCM和平行四边形ABMD。
在△BCM中,BM=AD=4,CM=CD-DM=CD-AB=8-3=5,所以BC的取值范围是:5-4<BC<5+4,即1<BC<9。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
[例2]如图2,在梯形ABCD中,AD//BC,∠B+∠C=90°,AD=1,BC=3,E、F 分别是AD、BC的中点,连接EF,求EF的长。
图2析解:过点E分别作AB、CD的平行线,交BC于点G、H,可得∠EGH+∠EHG=∠B+∠C=90°则△EGH是直角三角形因为E、F分别是AD、BC的中点,容易证得F是GH的中点所以)CHBGBC(21GH21EF--==1)13(21)ADBC(21)]DEAE(BC[21)DEAEBC(21=-=-=+-=--=3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。
[例3]如图3,在等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
图3析解:过点C 作BD 的平行线交AD 的延长线于点E ,易得四边形BCED 是平行四边形,则DE=BC ,CE=BD=25,所以AE=AD +DE=AD +BC=3+7=10。
梯形辅助线的常见作法

例谈梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
[例1]如图1,梯形ABCD 的上底AB=3,下底CD=8,腰AD=4,求另一腰BC 的取值范围。
图1析解:过点B 作BM//AD 交CD 于点M ,则梯形ABCD 转化为△BCM 和平行四边形ABMD 。
在△BCM 中,BM=AD=4,CM=CD -DM=CD -AB=8-3=5,所以BC 的取值范围是:5-4<BC<5+4,即1<BC<9。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
[例2]如图2,在梯形ABCD 中,AD//BC ,∠B +∠C=90°,AD=1,BC=3,E 、F 分别是AD 、BC 的中点,连接EF ,求EF 的长。
图2析解:过点E 分别作AB 、CD 的平行线,交BC 于点G 、H ,可得∠EGH +∠EHG=∠B +∠C=90° 则△EGH 是直角三角形因为E 、F 分别是AD 、BC 的中点,容易证得F 是GH 的中点所以)CH BG BC (21GH 21EF --==3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。
[例3]如图3,在等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
图3析解:过点C 作BD 的平行线交AD 的延长线于E ,易得四边形BCED 是平行四边形,则DE=BCE=BD=25,所以AE=AD +DE=AD +BC=3+7=10。
等腰梯形ABCD 中,AC=BD=25,所以在△ACE 中22222AE 100)25()25(CE AC ==+=+,从而ACE ,于是AC ⊥BD 。
梯形辅助线的常见作法[1](古柏教学)
](https://img.taocdn.com/s3/m/18ce01b628ea81c758f578ab.png)
例谈梯形中的常用辅助线在解(证)有关梯形的问题时,常常要添作辅助线,把梯形问题转化为三角形或平行四边形问题。
本文举例谈谈梯形中的常用辅助线,以帮助同学们更好地理解和运用。
一、平移1、平移一腰:从梯形的一个顶点作一腰的平行线,把梯形转化为一个三角形和一个平行四边形。
[例1]如图1,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。
图1析解:过点B作BM//AD交CD于点M,则梯形ABCD转化为△BCM和平行四边形ABMD。
在△BCM中,BM=AD=4,CM=CD-DM=CD-AB=8-3=5,所以BC的取值范围是:5-4<BC<5+4,即1<BC<9。
2、平移两腰:利用梯形中的某个特殊点,过此点作两腰的平行线,把两腰转化到同一个三角形中。
[例2]如图2,在梯形ABCD中,AD//BC,∠B+∠C=90°,AD=1,BC=3,E、F分别是AD、BC的中点,连接EF,求EF的长。
图2析解:过点E分别作AB、CD的平行线,交BC于点G、H,可得∠EGH+∠EHG=∠B+∠C=90°则△EGH是直角三角形因为E、F分别是AD、BC的中点,容易证得F是GH的中点所以)CHBGBC(21GH21EF--==1)13(21)ADBC(21)]DEAE(BC[21)DEAEBC(21=-=-=+-=--=3、平移对角线:过梯形的一个顶点作对角线的平行线,将已知条件转化到一个三角形中。
[例3]如图3,在等腰梯形ABCD中,AD//BC,AD=3,BC=7,BD=25,求证:AC⊥BD。
图3析解:过点C作BD的平行线交AD的延长线于点E,易得四边形BCED是平行四边形,则DE=BC,CE=BD=25,所以AE=AD+DE=AD+BC=3+7=10。
在等腰梯形ABCD中,AC=BD=25,所以在△ACE中,22222AE100)25()25(CEAC==+=+,从而AC⊥CE,于是AC⊥BD。
初中数学梯形中常见辅助线的作法

初中数学梯形中常见辅助线的作法
梯形是一种特殊的四边形,它是平行四边形和三角形的“综合”。接下来店铺为你整理了初中数学梯形中常见辅助线的作法,一起来看看吧。
初中数学梯形中常见辅助线的作法:平移对角线
初中数学梯形中常见辅助线的作法:平移一腰或两腰
初中数学梯形中常见辅助线的作法:延长两腰
初中数学梯形中常见辅助线的作法 将本文的Word文档下载到电脑,方便收藏和打印 推荐度: 点击下载文档文档为doc格式
最新-八年级数学下册梯形辅助线的六种做法人教新课标版精品
B
C
AB=AD=2,∠ A=60°, BC=4,求 CD的长.
12、 已知:如图,在梯形 ABCD 中, ∠A+∠D=90°, M、 N 是 BC, AD 的中点。求证: MN=1 ( AD BC ) 。 2
B
N
三、从小底的两端向大底引垂线。
A
M
13、 如图,在梯形 ABCD 中,AD ∥ BC ,AB AC , B 45 ,AD 求 DC 的长.
如图,在梯形 ABCD中, AD∥BC, AB CD .若 AC⊥BD,
AD+B=C10 3 , 且 ABC 60 , 求 CD的长.
B
A
D
7、 已知在梯形 ABCD中, AD∥ BC,若两底 AD、BC的长分别为 2、8,两 B 条对角线 BD=6, AC=8, 求梯形的面积。
8、 已知:如图,在梯形 ABCD中, AD∥ BC,AC=D。B 求证: AB=D。C
梯形辅助线的做法
一、平移一条对角线。
1、 如图,在梯形 ABCD中, AD∥ BC, AB=CD, AC⊥ BD, AD= 6,
BC= 8, 则梯形的高为
。
A
D
2、 如图,在梯形 ABCD中, AD∥ BC, AC⊥BD, AC=8,
DB=6,则此梯形的高为
。
B
C
3、 如图,在梯形 ABCD中,AD∥ BC,AB= CD,对角线 AC⊥ BD,BD=6,则梯形的高为
2 ,BC 4 2 ,
A
C D
D
B
14、 如图,梯形 ABCD 中, AD ∥ BC ,∠ B 45 ,∠ D 120 ,CD 4 3cm ,求 AB A
的长.
B
梯形常见辅助线

梯形中常见的几种辅助线作法一、跟腰相关的辅助线(1)在梯形内部平移一腰例1(如图1)已知在梯形ABCD中,AD//BC,BA=DC。
求证:B= C(2)梯形内平移两腰例3(如图3)在梯形ABCD中,AD∥BC,AD﹤BC,E、F分别为AD、BC的中点,且EF⊥BC,试说明∠B=∠C(3)延长两腰例4(如图4)在梯形ABCD中,∠B=∠C,AD∥BC。
求证:梯形ABCD是等腰梯形。
练习、如图,在梯形ABCD中,AD∥BC,∠C=90°,E为CD的中点,EF∥AB交于点F。
(1)求证:BF=AD+CF。
(2)当AD=1,BC=7,且BE平分∠ABC时,求EF的长。
二、作梯形的高,梯形转化成矩形与直角三角形例1:如图,在梯形ABCD中,AD∥BC,AB=DC=AD=5,BC=11;求梯形ABCD的面积.例2:已知:梯形ABCD中,∠ABC=90°,∠C=45°,BE⊥CD,AD=1,CD= 22,求:BE练习、如图,直角梯形ABCD中,AD∥BC,∠A=90°,AB=AD=6,DE⊥DC交AB于E,DF平分∠EDC交BC于F,连结EF.(1)证明:EF=CF;(2)当AE:AD=13时,求EF的长.FEDCBA三、利用中点(1)连接梯形一顶点及一腰的中点。
例1:在梯形ABCD中,AD∥BC, E、F分别为AB、CD的中点,求证:EF=(AD+BC)(2)过一腰的中点作另一腰的平行线。
例2::在梯形ABCD中,AD∥BC, E为CD的中点,求证:S=(3)作中位线例3:在梯形ABCD中,AB∥CD,M为AD的中点,AB+CD=BC求证:BM⊥CM练习、如图1所示,在直角梯形ABCD中,AD∥BC,AB⊥BC,∠DCB=75º,以CD为一边的等边△DCE的另一顶点E在腰AB上.(1)求∠AED的度数;(2)求证:AB=BC;(3)如图2所示,若F为线段CD上一点,∠FBC=30º.求DFFC的值.四、平移对角线,将梯形转化成:平行四边形、三角形.A 、把上下底之和,两对角线转移到同一个三角形BDE 中B 、△ABD 与△CDE 面积相等 S 梯形ABCD =S △BDEC 、 BD ⊥AC 推出BD ⊥DE 得到直角三角形BDE例1:如图所示,在梯形ABCD 中,上底AD =1cm ,对角线BD ⊥AC ,且BD =3cm ,AC =4cm. 求下底BC 以及梯形的高。
怎样梯形中的辅助线

难点突破:怎样做梯形中的辅助线梯形是一种特殊的四边形,它是平行四边形和三角形知识的综合,通过适当地添加辅助线,把梯形转化为三角形、平行四边形的组合图形,再运用三角形、平行四边形的知识去解决梯形的有关问题。
下面列举数例,以说明梯形中常见辅助线的作法.一、平移一腰法例1如图1,梯形ABCD中,AB∥CD,以AC、AD为边作ACED.DC 的延长线交BE于F.求证:EF=FB.简析:在梯形ABFD中,过C作CG∥BF交AB于G,由GBFC得CG=FB,再证△EDF≌△CAG,得EF=CG=FB.例 2如图2,梯形ABCD中,AB//CD,︒,80D。
C=∠︒=∠50求证:ABCD=。
AD-图2证明:过点A作AE//BC交DC于E,所以︒C∠50AED==∠因为︒D=∠80所以︒∠50DAE=所以DAE∠=AED∠所以DEAD=易证ECAB=,所以AB=AD-CD二、平移对角线法过梯形上底的一个端点作某一条对角线的平行线,构造平行四边形和三角形,从而引出证题思路。
如:例 3. 如图2,梯形ABCD 中,AB//CD ,中位线EF=7cm ,对角线︒=∠⊥30BDC ,BD AC ,求梯形的高。
图2证明:过点B 作BG//AC 交DC 的延长线于G 。
因为BD AC ⊥,所以CGAB ,BD BG=⊥。
因为︒=∠30BDC所以)CD AB (21GD 21BG+==因为EF 2CD AB =+, 所以7EF BG ==因为︒=∠=∠30G BH BDC , 所以5.3BG 21GH ==, 所以=-=225.37BH237即梯形的高为cm237。
例 4. 如图2,等腰梯形ABCD 中,AD ∥BC ,AB=CD ,AC ⊥BD 于O 点.若中位线长为m ,求梯形ABCD 的面积S .三、延长双腰法延长两腰相交于一点,可构造两个三角形,利用这两个三角形的有关条件和性质进行证明,也是常用的方法之一。
如:例5. 如图5,已知梯形ABCD 中,AB//CD ,︒=∠+∠90B A ,M 、N 分别是AB 、CD 的中点。
梯形中添加辅助线的六种常用技巧

梯形中添加辅助线的六种常用技巧在几何学中,梯形是一种具有两条平行边的四边形。
为了解决梯形问题,往往需要在梯形中添加辅助线。
下面介绍六种常用的技巧。
1.连接两个对角线:首先,连接梯形的两个非平行边的中点,形成一条对角线。
然后,连接梯形的两个对角线中点,即可形成两个等腰三角形。
这样,可以通过等腰三角形性质来得到有关角度和边长的信息。
2.连接平行边的中点:将梯形的两条平行边的中点相连,可以形成一条平行于两条平行边的线段。
这条线段将梯形分成两个平行四边形,从而可以根据平行四边形的性质来解决问题。
3.连接一条平行边的中点和另一条边的中点:将梯形的一条平行边的中点和与之相对的边的中点连接,可以形成一条平行于梯形的底边的中线。
这样,可以通过中线分割线段的性质来得到有关线段和平行边的信息。
4.连接底边的中点和非平行边的中点:将梯形的底边的中点和非平行边的中点连接,可以形成一条平行于两条平行边的线段。
这样,可以根据平行四边形的性质来推导出梯形内部各部分的关系。
5.连接两个顶点和底边上的中点:将梯形的两个顶点和底边上的中点相连,可以得到两个等腰三角形。
利用等腰三角形的性质,可以推导出梯形的各个部分的角度和边长关系。
6.连接梯形的顶点和对角线交点:将梯形的两个顶点和另一条对角线的交点相连,可以形成一个三角形。
根据三角形的性质,可以得到角度和边长的关系,进而解决梯形问题。
这些添加辅助线的技巧可以帮助我们更好地理解和解决梯形问题。
通过巧妙地添加辅助线,可以将原来复杂的问题转化为简单的几何形状,从而更容易得到解答。
在解决梯形问题时,我们可以根据具体情况选择适合的添加辅助线的技巧,以便更加高效地解决问题。
梯形作辅助线做法及应用

F
G
B
E
C
H
2、当AC =BD时,∆BED又是什么三角形? 、 时 又是什么三角形
A 构造旋转变换
D O
( 五 ) 其 他 方
B
证明哪个定理是应用了这个方法
?? 梯形ABCD面积与哪个图形面积相等 面积与哪个图形面积相等? 梯形 面积与哪个图形面积相等
构造中位线
C
E
返
回
梯形辅助线做法应用
应 用
例题:
1、如图,梯形ABCD 中, AB∥CD, ∠D=70 ° , ∠ C=40 ° ∥
梯形中常用辅助线
作
法
一、梯形中常用辅助线
数学思想
梯形转化为三角形和平行四边形或 特殊平行四边形等
二 梯形中常用作辅助线
方 法
梯形中常用作辅助线
方法
(一) 平移腰 (二) 作 高 (三) 补为三角形 (四)平移对角线 (五)其他方法
梯形中常用作辅助线
平移腰
(一) 平移腰 一
A D A D
B
C
B
54º
36º
E
20
C
3、如图,梯形ABCD 中, AD∥BC, ∠B=60 °, ∠ C=45 ° ∥
AB= 2 3 , AD=2,则梯形周长=
A 2 D
2 3
B 60°
3
3 2
45 °
C
3
E` E
3
布置作业:
1、求证:对角线垂直的等腰梯形的高等于它的中位线 2、课本:196页17题、199页5题
例2:已知,梯形ABCD中,AD∥BC,E是腰AB的中点,
DE ⊥CE, 求证: AD+BC=CD。 A 证明:(一)延长DE交CB延长线于F D ∵在梯形ABCD中AD//B ,∠A= ∠ ABF E ∴ AE=BE,∠A= ∠ ABF,∠ AED= ∠ BEF ∴ ∆ADE≌∆BFE F B C ∴ DE=FE,AD=BF
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形常用辅助线的做法常见的梯形辅助线基本图形如下:1.平移梯形一腰或两腰,把梯形的腰、两底角等转移到一个三角形中,同时还得到平行四边形.【例1】已知:如图,在梯形ABCD中,.求证:.分析:平移一腰BC到DE,将题中已知条件转化在同一等腰三角形中解决,即AB=2CD.证明:过D作 ,交AB于E.∵ AB平行于CD,且 ,∴四边形是菱形.∴又∴为等边三角形.∴又 ,∴∴.【例2】如图,在梯形ABCD 中,AD∥BC , E、F 分别是AD 、BC 的中点,若.AD = 7 ,BC = 15 ,求EF .分析:由条件 ,我们通过平移AB 、DC ;构造直角三角形MEN ,使EF 恰好是△MEN 的中线.解:过E 作EM∥AB ,EN ∥DC ,分别交BC 于M 、N ,∵ , ∴∴是直角三角形,∵ , ,∴ .∵、分别是、的中点,∴为的中点,∴ .变式:如图1,梯形ABCD的上底AB=3,下底CD=8,腰AD=4,求另一腰BC的取值范围。
图1析解:过点B作BM//AD交CD于点M,则梯形ABCD转化为△BCM和平行四边形ABMD。
在△BCM中,BM=AD=4,CM=CD-DM=CD-AB=8-3=5,所以BC的取值范围是:5-4<BC<5+4,即1<BC<9。
2.延长梯形的两腰,使它们交于一点,可得到两个相似三角形或等腰三角形、直角三角形等进一步解决问题.【例3】.如图,在梯形中, , ,梯形的面积与梯形的面积相等.求证: .分析:条件是两个梯形的面积相等,而结论是三线段长的平方关系,如果延长两腰交于一点,就可得到三个相似的三角形,再利用相似三角形的面积比与相似比的关系变形就可得出结论.证明:延长、使它们相交于点,∵ ,∴∴.同理,∵故得∴变式1:如图5,在梯形ABCD中,AD//BC,∠B=50°,∠C=80°,AD=2,BC=5,求CD 的长。
图5析解:延长BA、CD交于点E。
在△BCE中,∠B=50°,∠C=80°。
所以∠E=50°,从而BC=EC=5同理可得AD=ED=2所以CD=EC-ED=5-2=3变式2:如图所示,四边形ABCD中,AD不平行于BC,AC=BD,AD=BC. 判断四边形ABCD 的形状,并证明你的结论.变式3:(延长两腰)如图,在梯形中,,,、为、的中点。
3.从梯形上底的两端向下底引垂线作高,可以得到一个矩形和两个直角三角形.然后利用构造的直角三角形和矩形解决问题.例4.如图,在梯形中,.求证:.分析:过上底向下底作两高,构造Rt△,然后利用两三角形全等解决问题.证明:分别过D、C、作AB的垂线,垂足分别为E、F.∵ ,∴ .又 ,∴≌ .∴变式:如图7,在直角梯形ABCD中,AB//DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF//AB,交AD于点E,求证:四边形ABFE是等腰梯形。
图7析证:过点D作DG⊥AB于点G,则易知四边形DGBC是矩形,所以DC=BG。
因为AB=2DC,所以AG=GB。
从而DA=DB,于是∠DAB=∠DBA。
又EF//AB,所以四边形ABFE是等腰梯形。
如图8,在梯形ABCD中,AD为上底,AB>CD,求证:BD>AC。
图8析证:作AE⊥BC于E,作DF⊥BC于F,则易知AE=DF。
在Rt△ABE和Rt△DCF中,因为AB>CD,AE=DF。
所以由勾股定理得BE>CF。
即BF>CE。
在Rt△BDF和Rt△CAE中由勾股定理得BD>AC4.平移对角线一般是过上底的一个端点作一条对角线的平行线,与另一底的延长线相交,得到一个平行四边形和三角形,把梯形问题转化为平行四边形和三角形问题解决.【例5】.如图,等腰梯形中, , ,且 ,是高,是中位线,求证:.分析:由梯形中位线性质得 ,欲证 ,只要证.过点作 ,交的延长线于 ,就可以把、和移到三角形中,再证明等式成立就简单多了.证明:过点作交的延长线于点 ,则四边形是平行四边形.∴ ,∵四边形是等腰梯形,∴ ,∴又∵ ,∴ ,∴ ,∴ .∵ ,∴又∵ ,∴ .【例6】.已知:如图,在梯形中, .求证:梯形 是等腰梯形. 证明:过D 作,交BA 延长线于E.则四边形 是平行四边形.∴.∴又 ,∴于是,可得∴∴梯形ABCD 是等腰梯形.变式1:如图3,在等腰梯形ABCD 中,AD//BC ,AD=3,BC=7,BD=25,求证:AC ⊥BD 。
图3析解:过点C 作BD 的平行线交AD 的延长线于点E ,易得四边形BCED 是平行四边形,则DE=BC ,CE=BD=25,所以AE=AD +DE=AD +BC=3+7=10。
在等腰梯形ABCD 中,AC=BD=25,所以在△ACE 中,22222AE 100)25()25(CE AC ==+=+,从而AC ⊥CE ,于是AC ⊥BD 。
变式2:(平移对角线)已知梯形ABCD 的面积是32,两底与高的和为16,如果其中一条对角线与两底垂直,则另一条对角线长为_____________变式3:如图4,在梯形ABCD 中,AD//BC ,AC=15cm ,BD=20cm ,高DH=12cm ,求梯形ABCD 的面积。
图4析解:过点D 作DE//AC ,交BC 的延长线于点E ,则四边形ACED 是平行四边形,即DCE ACD ABD S S S ∆∆∆==。
所以DBE ABCD S S ∆=梯形由勾股定理得2222DH AC DH DE EH -=-=9121522=-=(cm )161220DH BD BH 2222=-=-=(cm )所以)cm (15012)169(21DH BE 21S 2DBE =⨯+⨯=⋅=∆,即梯形ABCD 的面积是150cm 2。
5.遇到梯形一腰中点的问题可以作出梯形的中位线,中位线与上、下底都平行,且三线段有数量关系. 或利用“等积变形”,连结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形解决问题.【例7】.已知:如图4,在梯形中, 是 的中点,且.求证:.证明:取 的中点F,连结FE.则∵ ,∴.∴.【例8】.已知:梯形 ABCD 中AD BC,E 为AB 中点,且AD +BC=DC , 求证:DE⊥EC,DE 平分∠ADC,CE 平分∠BCD.证法1:取DC 中点F,连结EF,E 为AD 中点,则EF 为梯形的中位线∴EF∥AD∥BC EF=(AD +BC) ∴∠1=∠5,∠3=∠6 ∵DC=AD+BC∴EF=DC=DF=CF ∴∠1=∠2,∠3=∠4 ∴∠2=∠5,∠4=∠6∴∠1+∠3+∠2+∠4=180° ∴∠1+∠3=90°∴DE⊥C,DE 平分ADC,CE 平分∠CD证法2:延长CE 与DA 延长线交于一点F,过程略. 证法3:在DC 上截取DF=AD,连结AF 、BF 、EF 解决.变式1:如图9,在梯形ABCD 中,AB//DC ,O 是BC 的中点,∠AOD=90°,求证:AB +CD=AD 。
图9析证:取AD 的中点E ,连接OE ,则易知OE 是梯形ABCD 的中位线,从而OE=21(AB +CD )①在△AOD 中,∠AOD=90°,AE=DE 所以AD 21OE② 由①、②得AB +CD=AD 。
变式2:在梯形ABCD 中,AD ∥BC , ∠BAD=900,E 是DC 上的中点,连接AE 和BE ,求∠AEB=2∠CBE 。
解、分析:分别延长AE 与BC ,并交于F 点,从而等到△ADE 与△FCE 是全等的,在利用“直角三角形斜边上的中线等于斜边的一半就可以求出结论”。
解:分别延长AE 与BC ,并交于F 点∵∠BAD=900且AD ∥BC∴∠FBA=1800-∠BAD=900又∵AD ∥BC∴∠DAE=∠F(两直线平行内错角相等) ∠AED=∠FEC (对顶角相等)DE=EC (E 点是CD 的中点) ∴△ADE ≌△FCE (AAS ) ∴ AE=FE在△ABF 中∠FBA=900且AE=FE∴ BE=FE (直角三角形斜边上的中线等于斜边的一半) ∴ 在△FEB 中 ∠EBF=∠FEB ∠AEB=∠EBF+ ∠FEB=2∠CBE6.已知梯形两条对角线的中点,连接梯形一顶点与一条对角线中点,并延长与底边相交,使问题转化为三角形中位线。
[例10]如图10,在梯形ABCD 中,AD//BC ,E 、F 分别是BD 、AC 的中点,求证:(1)EF//AD ;(2))AD BC (21EF -=。
图10析证:连接DF ,并延长交BC 于点G ,易证△AFD ≌△CFG 则AD=CG ,DF=GF由于DE=BE ,所以EF 是△BDG 的中位线 从而EF//BG ,且BG 21EF =因为AD//BG ,AD BC CG BC BG -=-= 所以EF//AD ,EF )AD BC (21-=7.当遇到以上的梯形辅助线添加后不能解决问题时,可以特题特解,结合具体问题中的具体条件,寻求特殊的方法解决问题.比如可将对角线绕中点旋转 、利用一腰中点旋转、将梯形补成平行四边形或三角形问题.【例9】.已知:如图5,在梯形ABCD 中,M 、N 分别是BD 、AC 的中点.求证:.证明:连结并延长 ,交于E.则 .∴又N是AC的中点,∴ ,故取一腰的中点,连结顶点和这个中点并延长与对边的延长线相交,可得两个全等三角形.【例10】.如图,梯形中, ,、分别平分和 ,为中点,求证:.分析:要证明 ,可以利用为中点,延长与的延长线交于 ,,得到,再证明即可.证明:延长、交于点 F,显然.∴ , .又∵ ,, ,∴ ,∴∴是线段的垂直平分线.∴ ,∴ .评注:添加辅助线后,沟通了、与的联系,由线段垂直平分线性质得出 ,从而问题获得解决.利用一腰中点旋转【例11】.已知:如图,在梯形中,是CD的中点.求证:.证明:延长AE、BC相交于点F.易证.∴ ,∵ ,∴即 .∴BE是等腰底边上的高.∴ .说明:在图5中,相当于由绕点E旋转得到;在图6中,是由绕点E旋转得到.【例12】.如图,梯形中, ,为腰的中点,求证:.分析:与梯形ABCD的面积关系不明显,如果利用梯形助特点把它补成如图7的平行四边形,它们之间的关系就清晰了.梯形补成平行四边形,各种关系明显、直观,解题思路清晰.证明:延长 ,使 ,延长 ,使;则 ,则四边形是平行四边形.为的中点,连结 ,与交于点 .连结、 ,则.∵ ,是中点,∴为中点且是中点.∴四边形是平行四边形,∴ ,∴【模拟试题】1. 若等腰梯形的锐角是60°,它的两底分别为11cm,35cm,则它的腰长为__________cm.2. 如图所示,已知等腰梯形ABCD中,AD∥BC,∠B=60°,AD=2,BC=8,则此等腰梯形的周长为()A. 19B. 20C. 21D. 223. 如图所示,AB∥CD,AE⊥DC,AE=12,BD=20,AC=15,则梯形ABCD的面积为()A. 130B. 140C. 150D. 1604. 如图所示,在等腰梯形ABCD中,已知AD∥BC,对角线AC与BD互相垂直,且AD=30,BC=70,求BD的长.5. 如图所示,已知等腰梯形的锐角等于60°,它的两底分别为15cm和49cm,求它的腰长.6. 如图所示,已知等腰梯形ABCD中,AD∥BC,AC⊥BD,AD+BC=10,DE⊥BC于E,求DE的长.7. 如图所示,梯形ABCD中,AB∥CD,∠D=2∠B,AD+DC=8,求AB的长.8. 如图所示,梯形ABCD中,AD∥BC,(1)若E是AB的中点,且AD+BC=CD,则DE与BCAD EE C'A BCDPCE 有何位置关系?(2)E 是∠ADC 与∠BCD 的角平分线的交点,则DE 与CE 有何位置关系?【课后演练】1(本小题满分5分)已知:如图,梯形ABCD 中,AD ∥BC ,AB=DC ,∠BAD 、∠CDA 的平分线AE 、DF 分别交直线BC 于点E 、F .求证: CE=BF .2.如图,在梯形ABCD 中,AD BC ∥,9038BD CD BDC AD BC =∠===,°,,.求AB 的长. 3.如图6,在梯形ABCD 中,AD BC ∥,90A ∠=︒,︒=∠45C ,DE=EC ,AB=4,AD=2,求BE 的长.4.如图,在平面直角坐标系中,A (23,0),B (23,2).把矩形OABC 逆时针旋转30︒得到矩形111OA B C . (1)求1B 点的坐标;(2)求过点(2,0)且平分矩形111OA B C 面积的直线l 方程;(3)设(2)中直线l 交y 轴于点P ,直接写出1PC O ∆与11PB A ∆的面积和的值及1POA ∆与11PB C ∆的面积差的值.5. 如图,矩形纸片ABCD 中,BC=4,AB=3,点P 是BC 边上的动点(点P 不与点B 、C 重合).现将△PCD 沿PD 翻折,得到△PC ’D ;作∠BPC ’的角平分线,交AB 于点E .设BP= x,BE= y,则下列图象中,能表示y 与x 的函数关系的图象大致是6.已知:如图,梯形ABCD 中,DC ∥AB ,AD =BC ,对角线AC 、BD 交于点O ,∠COD =60°,若CD =3,AB =8,求梯形ABCD 的高.7.已知如图,直角梯形ABCD 中,AD ∥BC ,AB ⊥BC ,AD=2,BC=DC=5,点P 在BC 上移动,则当PA+PD 取最小值时,△APD 中边AP 上的高为 . 8 如图,在矩形ABCD 中,AB=2,BC=1,动点P 从点B 出发,沿路线B C D →→作匀速运动,那么△ABP 的面积S 与点P 运动的路程x 之间的函数图象大致是备用图 12题图D C PB AxyO9.如图,在四边形ABCD 中,AC 平分∠BAD ,10CD B C ==,21AB =,9AD =.求AC 的长.10如图,直线1l :1y x =+与直线2l :y mx n =+相交于点), 1(b P . (1)求b 的值;(2)不解关于y x ,的方程组 请你直接写出它的解;(3)直线3l :y nx m =+是否也经过点P ?请说明理由.11.已知:关于x 的一元二次方程01)2()1(2=--+-x m x m (m 为实数) 若方程有两个不相等的实数根,求m 的取值范围;12.已知:如图,直线323+-=x y 与x 轴、y 轴分别交于点A 和点B ,D 是y 轴上的一点,若将△DAB 沿直线DA 折叠,点B 恰好落在x 轴正半轴上的点C 处,求直线CD 的解析式.14.如图,在梯形ABCD 中,AD //BC ,BD ⊥DC ,∠C =60°,AD=4,BC=6,求AB 的长.15.已知:如图,在梯形ABCD 中,AD ∥BC ,∠B=45°,∠BAC=105°,AD =CD .求BC 的长.16.已知:将函数33y x =的图象向上平移2个单位,得到一个新的函数的图像. (1)求这个新的函数的解析式;(2)若平移前后的这两个函数图象分别与y 轴交于O 、A 两点,与直线3x =-交于C 、B 两点.试判断以A 、B 、C 、O 四点为顶点的四边形形状,并说明理由;17 如图,在梯形CD AB 中,AB ∥DC ,DC A DB ∠平分,过点A 30B DC =∠°,3AD =求CD 的长.O3 1 1 3 S x A .O11 3 Sx O3 Sx 3O1 1 3 SxB .C .D .2 OxyP10题A BCD x yO D A BC。
