含有绝对值式子化简(与数轴结合)
初中数学《绝对值化简》讲义及练习

内容 基本要求略高要求较高要求绝对值 借助数轴理解绝对值的意义,会求实数的绝对值会利用绝对值的知识解决简单的化简问题绝对值的几何意义:一个数a 的绝对值就是数轴上表示数a 的点与原点的距离.数a 的绝对值记作a . 绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0. 注意:①取绝对值也是一种运算,运算符号是“”,求一个数的绝对值,就是根据性质去掉绝对值符号. ②绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.③绝对值具有非负性,取绝对值的结果总是正数或0.④任何一个有理数都是由两部分组成:符号和它的绝对值,如:5-符号是负号,绝对值是5. 求字母a 的绝对值:①(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩ ②(0)(0)a a a a a ≥⎧=⎨-<⎩ ③(0)(0)a a a a a >⎧=⎨-≤⎩利用绝对值比较两个负有理数的大小:两个负数,绝对值大的反而小.绝对值非负性:如果若干个非负数的和为0,那么这若干个非负数都必为0.例如:若0a b c ++=,则0a =,0b =,0c =绝对值的其它重要性质:(1)任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即a a ≥,且a a ≥-; (2)若a b =,则a b =或a b =-;(3)ab a b =⋅;a ab b=(0)b ≠; (4)222||||a a a ==;(5)a b a b a b -≤+≤+,对于a b a b +≤+,等号当且仅当a 、b 同号或a 、b 中至少有一个0时,等号成立; 对于a b a b -≤+,等号当且仅当a 、b 异号或a 、b 中至少有一个0时,等号成立.板块一:绝对值代数意义及化简【例1】 (2级)⑴ 下列各组判断中,正确的是 ( )中考要求例题精讲绝 对 值 化 简A .若a b =,则一定有a b =B .若a b >,则一定有a b > C. 若a b >,则一定有a b > D .若a b =,则一定有()22a b =-⑵ 如果2a >2b ,则 ( ) A .a b > B .a >b C .a b < D a <b⑶ 下列式子中正确的是 ( ) A .a a >- B .a a <- C .a a ≤- D .a a ≥-⑷ 对于1m -,下列结论正确的是 ( ) A .1||m m -≥ B .1||m m -≤ C .1||1m m --≥ D .1||1m m --≤ ⑸ (2002年江苏省竞赛题)若220x x -+-=,求x 的取值范围.【解析】 ⑴ 选择D .⑵ 选择B .⑶ 我们可以分类讨论,也可以用特殊值法代入检验,对于绝对值的题目我们一般需要代正数、负数、0,3种数帮助找到准确答案.易得答案为D .⑷ 我们可以用特殊值法代入检验,正数、负数、0,3种数帮助找到准确答案C . ⑸ ()22x x -=--,所以20x -≤,即2x ≤.【巩固】 (2级)绝对值等于5的整数有 个,绝对值小于5的整数有 个 【解析】 2;9个【巩固】 (2级)绝对值小于31⋅的整数有哪些?它们的和为多少? 【解析】 绝对值小于31⋅的整数有0,1±,2±,3±,和为0.【巩固】 (2级)有理数a 与b 满足a b >,则下面哪个答案正确 ( ) A .a b > B .a b = C .a b < D .无法确定 【解析】 选择D .【例2】 (2级)已知:⑴52a b ==,,且a b <;⑵()2120a b ++-=,分别求a b ,的值 【解析】 因为55a a ==±,因为22b b ==±,又因为a b <,所以22a b =-=±,即52a b =-=,或52a b =-=-,⑵由非负性可知12a b =-=,【例3】 (2级)已知2332x x -=-,求x 的取值范围【解析】 因为23x -的绝对值等于它的相反数,所以230x -≤,即32x ≤【巩固】 (4级)若a b >且a b <,则下列说法正确的是( )A .a 一定是正数B .a 一定是负数C .b 一定是正数D .b 一定是负数 【解析】 由分析可知a b ,中的较小数b 一定是负数,故选D【例4】 (6级)(2010人大附中练习题)求出所有满足条件1a b ab -+=的非负整数对()a b ,【解析】 根据题意a b -和ab 两个代数式的值只能在0与1中取,用逐一列举的方法,求得满足条件的非负整数对有三对()()()011011,,,,,【巩固】 (6级)(2005年江苏省数学文化节基础闯关试题)非零整数m n ,满足50m n +-=,所有这样的整数组()m n ,共有 【解析】 16【例5】 (4级)(人大附单元测试)如果有理数a 、b 、c 在数轴上的位置如图所示,求11a b b a c c +------的值.【解析】 先判断每个绝对值符号内部的正负,而后化简原式()(1)()(1)a b b a c c =-++-+---112a b b a c c =--+-+--+=-【巩固】 (6级)已知00x z xy y z x <<>>>,,,那么x z y z x y +++--= 【解析】 由00xy x z ><<,可得0y z <<,又因为y z x >>,所以y x z <<,原式0x z y z x y =+---+=【例6】 (10级)(第4届希望杯2试)abcde 是一个五位自然数,其中a 、b 、c 、d 、e 为阿拉伯数码,且a b c d <<<,则a b b c c d d e -+-+-+-的最大值是 . 【解析】 当a b c d e <<<≤时,a b b c c d d e e a -+-+-+-=-,当9e =,1a =时取得最大值8;当a b c d <<<,且a e >时,2a b b c c d d e d a e -+-+-+-=--,当9d =,1a =,0e =时取得最大值17.所以a b b c c d d e -+-+-+-的最大值是17.【例7】 (8级)(河南省竞赛试题)已知2020y x b x x b =-+-+--,其中02020b b x <<,≤≤,那么y的最小值为【解析】 ()()20202040y x b x x b x b x b x =-+--+---=--++=-⎡⎤⎡⎤⎣⎦⎣⎦,当20x =,y 的最小值为20【巩固】 (10级)(华罗庚金杯赛前培训题)a 、b 、c 分别是一个三位数的百、十、个位上的数字,且a b c ≤≤,则a b b c c a -+-+-可能取得的最大值是多少?【解析】 由a b c ≤≤,得2()a b b c c a b a c b c a c a -+-+-=-+-+-=-,要想结果尽可能大,取9c =,1a =即可,最大值为16.【例8】 (8级)(希望杯邀请赛试题)设a b c ,,为整数,且1a b c a -+-=,求c a a b b c -+-+-的值 【解析】 因为a b c ,,为整数,且1a b c a -+-=故a b -与c a -一个为0,一个为1,从而()()1b c b a a c -=-+-=,原式2=【巩固】 (6级)(北京市迎春杯竞赛试题)已知123a b c ===,,,且a b c >>,那么a b c +-= 【解析】 2或0【例9】 (6级)(1)(第10届希望杯2试)已知1999x =,则2245942237x x x x x -+-++++= .(2)(第12届希望杯2试)满足2()()a b b a a b ab -+--=(0ab ≠)有理数a 、b ,一定不满足的关系是( )A . 0ab <B . 0ab >C . 0a b +>D . 0a b +< (3)(第7届希望杯2试)已知有理数a 、b 的和a b +及差a b -在数轴上如图所示,化简227a b a b +---.a-ba+b【解析】 (1)容易判断出,当1999x =时,24590x x -+>,2220x x ++>,所以 224594223710819982x x x x x x -+-++++=-+=-这道题目体现了一种重要的“先估算+后化简+再代入求值”的思想.(2)为研究问题首先要先将题干中条件的绝对值符号通过讨论去掉, 若a b ≥时,222()()()()0a b b a a b a b a b ab -+--=---=≠, 若a b <时,2222()()()()2()a b b a a b a b b a a b ab -+--=-+-=-=,从平方的非负性我们知道0ab ≥,且0ab ≠,所以0ab >,则答案A 一定不满足. (3)由图可知01a b <-<,1a b +<-,两式相加可得:20a <,0a <进而可判断出0b <,此时20a b +<,70b -<, 所以227a b a b +---(2)2()(7)7a b a b =-+--+-=-.【巩固】 (8级)(第9届希望杯1试)若1998m =-,则22119992299920m m m m +--+++= .【解析】211999(11)999199819879990m m m m +-=+-=⨯->, 222999(22)999199819769990m m m m ++=+-=⨯+>,故22(11999)(22999)2020000m m m m +--+++=.【补充】(8级)若0.239x =-,求131********x x x x x x -+-++-------的值.【解析】 法1:∵0.239x =-,则原式(1)(3)(1997)(2)(1996)x x x x x x =-------+++++- 135199721996x x x x x x x =-+-+-+--+++-++-1(32)(54)(19971996)=+-+-++- 111999=+++=法2:由x a b <≤,可得x b x a b a ---=-,则原式(1)(32)(19971996)x x x x x x =--+---++---111999=+++=点评:解法二的这种思维方法叫做构造法.这种方法对于显示题目中的关系,简化解题步骤有着重 要作用.【例10】 (10级)设2020A x b x x b =-+----,其中020b x <≤≤,试证明A 必有最小值 【解析】 因为020b x <≤≤,所以0200200x b x x b ----<≥,≤,,进而可以得到: 2220A x b x x x =--=--≥≥,所以A 的最小值为20-【例11】 (8级)若24513a a a +-+-的值是一个定值,求a 的取值范围.【解析】 要想使24513a a a +-+-的值是一个定值,就必须使得450a -≥,且130a -≤,原式245(13)3a a a =+---=,即1435a ≤≤时,原式的值永远为3.【巩固】 (8级)若1232008x x x x -+-+-++-的值为常数,试求x 的取值范围. 【解析】 要使式子的值为常数,x 得相消完,当10041005x ≤≤时,满足题意.【例12】 (2级)数,a b 在数轴上对应的点如右图所示,试化简a b b a b a a ++-+--【解析】 ()()()2a b b a b a a a b b a b a b ++-+--=-++-+--=.【巩固】 (2级)实数a b c ,,在数轴上的对应点如图,化简a c b a b a c +--++-【解析】 由题意可知:0000a c b a b a c <->+<-<,,,,所以原式2c a =-【巩固】 (2级)若a b <-且0ab>,化简a b a b ab -+++.【解析】 若a b <-且0ab>,0,0a b <<,0,0a b ab +<>2a b a b ab a b a b ab ab a -+++=-+--+=-【例13】 (8级)(北大附中2005-2006学年度第一学期期中考试)设,,a b c 为非零实数,且0a a +=,ab ab =,0c c -=.化简b a b c b a c -+--+-.【解析】 0a a +=,a a =-,0a ≤;ab ab =,0ab ≥;0c c -=,c c =,0c ≥所以可以得到0a <,0b <,0c >;()()()b a b c b a c b a b c b a c b -+--+-=-++----=.【例14】 (6级)如果010m <<并且10m x ≤≤,化简1010x m x x m -+-+--.【解析】 1010101020x m x x m x m x m x x -+-+--=-+-++-=-.【巩固】 (2级)化简:⑴3x -; ⑵12x x +++【解析】 ⑴原式()()3333x x x x ⎧-<⎪=⎨-⎪⎩≥;⑵原式()()()232121231x x x x x --<-⎧⎪=-<-⎨⎪+-⎩≤≥【巩固】 (6级)若a b <,求15b a a b -+---的值. 【解析】 15154b a a b b a a b -+---=-++--=-.【巩固】 (8级)(第7届希望杯2试)若0a <,0ab <,那么15b a a b -+---等于 .【解析】 0a <,0ab <,可得:0b >,所以0b a ->,0a b -<,15154b a a b b a a b -+---=-++--=-.【巩固】 (2级)已知15x <≤,化简15x x -+-【解析】 因为15x <≤,所以1050x x --<≤,,原式154x x =-+-=【例15】 (8级)已知3x <-,化简321x +-+.【解析】 当3x <-时,3213213333x x x x x x +-+=+++=++=--=-=-.【巩固】 (8级)(第16届希望杯培训试题)已知112x x ++-=,化简421x -+-. 【解析】 由112x x ++-=的几何意义,我们容易判断出11x -≤≤.所以421x -+-421434311x x x x x =-+-=--=-+=+=+.【例16】 (8级)若0x <,化简23x x x x---.【解析】 223333x x x x xx x xx x----===----+.【巩固】 (8级)(四中)已知a a =-,0b <,化简22442(2)24323a b a b a b b a +--+++--. 【解析】 ∵a a =-,∴0a ≤,又∵0b <,∴240a b +<,∴24(24)2(2)a b a b a b +=-+=-+,∴22242(2)2(2)(2)2a ba b a b a b a b+-+-==+++又∵20a b +<,∴4442(2)2a b a b a b-=-=+-++ 又∵230a -<,∴2222143(23)242424323b a a b a b a b b a -=-=-==++-++++-- ∴原式24132222a b a b a b a b=-++=++++ 点评:详细的过程要先判断被绝对值的式子x ,再去绝对值的符号.、【例17】 (8级)(第14届希望杯邀请赛试题)已知a b c d ,,,是有理数,916a b c d --≤,≤,且25a b c d --+=,求b a d c ---的值【解析】 因916a b c d --≤,≤,故91625a b c d -+-+=≤,又因为 ()()2525a b c d a b d c a b d c =--+=-+--+-≤≤,所以916a b c d -=-=,,故原式7=-板块二:关于a a的探讨应用【例18】 (6级)已知a 是非零有理数,求2323a a a a a a++的值.【解析】 若0a >,那么23231113a a a a a a ++=++=;若0a <,那么23231111a a a a a a++=-+-=-.【例19】 (10级)(2006年第二届“华罗庚杯”香港中学竞赛试题)已知a b c abc x abcabc=+++,且a b c ,,都不等于0,求x 的所有可能值 【解析】 4或0或4-【巩固】 (10级)(北京市迎春杯竞赛试题)已知a b c ,,是非零整数,且0a b c ++=,求a b c abca b c abc+++的值【解析】 因为a b c ,,是非零有理数,且0a b c ++=,所以a b c ,,中必有一正二负,不妨设000a b c ><<,,,则原式()()11110a b c abca b c abc=+++=+-+-+=--【巩固】 (2级)若0a >,则_____aa =;若0a <,则_____a a=. 【解析】 1;1-.重要结论一定要记得.【巩固】 (6级)当3m ≠-时,化简33m m ++【解析】 3m ≠-,30m +≠,当3m >-,即30m +>时,33m m +=+,所以313m m +=+; 当3m <-,即30m +<时,3(3)m m +=-+,所以313m m +=-+.【例20】 (8级)(2009年全国初中数学竞赛黄冈市选拔赛试题)若01a <<,21b -<<-,则1212a b a ba b a b-++-+-++的值是( ) A .0 B .1- C .3- D .4-【解析】 ⑴ C .特殊值法:取0.5a =, 1.5b =-代入计算即可.【巩固】 (2级)下列可能正确的是( )A .1a b a b +=B .2a b ca b c++=C .3c d a b a b c d +++= D .4a b c d a b c d a b c d abcd+++++++= 【解析】 选D .排除法比较好或特殊值法1,1,1,1-.【巩固】 (6级)如果20a b +=,则12a ab b-+-等于( ) A .2 B .3 C .4 D .5【解析】 B【例21】 (8级)如果000a b c a b c a b c +->-+>-++>,,,则200220022002a b c a b c ⎛⎫⎛⎫⎛⎫-+ ⎪⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭的值等于( )A .1B .1-C .0D .3【解析】 易知200220022002111a b c a b c ⎛⎫⎛⎫⎛⎫=== ⎪⎪ ⎪ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭,,,所以原式1=,故选择A【例22】 (8级)已知0abc ≠,求ab ac bcab ac bc++的值. 【解析】 ∵0abc ≠,∴a 、b 、c 三个数都不为零.若a 、b 、c 三个数都是正数,则ab 、ac 、bc 也都是正数,故原式值为3. 若a 、b 、c 中两正、一负,则ab 、ac 、bc 中一正、两负,故原式值为1-. 若a 、b 、c 中一正、两负,则ab 、ac 、bc 中一正、两负,故原式值为1-. 若 a 、b 、c 中三负,则ab 、ac 、bc 中三正,故原式值为3.【巩固】 (6级)若a ,b ,c 均不为零,求a b ca b c ++.【解析】 若a ,b ,c ,全为正数,则原式3=;若a ,b ,c ,两正一负,则原式1=;若a ,b ,c ,一正两负,则原式1=-;若a ,b ,c ,全为负数,则原式3=-.【例23】 (6级)(第13届希望杯1试)如果20a b +=,求12a ab b-+-的值. 【解析】 由20a b +=得2b a =-,进而有1222a a a a b a a a ===⋅--⋅,122a a ab a a==-⋅- 若0a >,则111212322a a b b -+-=-+--=, 若0a <,则111212322a ab b -+-=--+-=.【巩固】 (6级)若a ,b ,c 均不为零,且0a b c ++=,求a b cabc++. 【解析】 根据条件可得a ,b ,c 有1个负数或2个负数,所以所求式子的值为1或1-【例24】 (8级)a ,b ,c 为非零有理数,且0a b c ++=,则a b b c c aa b b c c a ++的值等于多少? 【解析】 由0a b c ++=可知a ,b ,c 里存在两正一负或者一正两负;a b b c c a b c aa b c a b b c c a a b b c c a++=⋅+⋅+⋅ 若两正一负,那么1111b c aa b c a b b c c a⋅+⋅+⋅=--=-; 若一正两负,那么1111b c aa b c a b b c c a ⋅+⋅+⋅=--=-. 综上所得1a b b c c a a bb cc a++=-.【巩固】 (10级)(海口市竞赛题)三个数a ,b ,c 的积为负数,和为正数,且ab ac bc a b c x a b c ab ac bc=+++++, 求321ax bx cx +++的值.【解析】 a ,b ,c 中必为一负两正,不妨设0a <,则0,0b c >>; 1111110ab ac bca b c x a b c ab ac bc=+++++=-++--+=,所以原式=1.【巩固】 (8级)(第13届希望杯培训试题)如果0a b c +->,0a b c -+>,0a b c -++>,求200220032004()()()a b ca b c-+的值. 【解析】 由0a b c +->,0a b c -+>,0a b c -++>,两两相加可得:0a >,0b >,0c >,所以原式结果为1.若将此题变形为:非零有理数a 、b 、c ,求1b =等于多少?从总体出发:2008()1aa =,所以原式1111=-+=.【例25】 (8级)(“祖冲之杯”初中数学邀请赛试题)设实数a ,b ,c 满足0a b c ++=,及0abc >,若||||||a b c x a b c =++,111111()()()y a b c b c a c a b =+++++,那么代数式23x y xy ++的值为______. 【解析】 由0a b c ++=及0abc >,知实数a ,b ,c 中必有两个负数,一个正数,从而有1x =-.又111111()()()y a b c b c a c a b =+++++=3a b c a b c---++=-,则231692x y xy ++=--+=.【例26】 (8级)有理数a b c ,,均不为零,且0a b c ++=,设a b c x b ca ca b=+++++,则代数式20042007x x -+的值为多少? 【解析】 由0a b c ++=易知a b c ,,中必有一正两负或两正一负,不妨设000a b c ><<,,或000a b c <>>,,所以1a b c x a b a c a b =--=+++或者1a b c x b c a c a b=-++=-+++,所以1x =,所以原式2004=【巩固】 (8级)有理数a b c ,,均不为零,且0a b c ++=,设a b c x b ca ca b=+++++,则代数式19992000x x -+的值为多少?【解析】 由0a b c ++=易知a b c ,,中必有一正两负或两正一负,不妨设000a b c ><<,,或000a b c <>>,,所以1a b c x a b a c a b =--=+++或者1a b cx b c a c a b=-++=-+++,所以当1x =时,原式1902= 当1x =-时,原式2098=【巩固】 (8级)已知a 、b 、c 互不相等,求()()()()()()()()()()()()a b b c b c c a c a a b a b b c b c c a c a a b ------++------的值.【解析】 由题意可得()()()0a b b c c a ---≠且()()()0a b b c c a -+-+-=,把a b -,b c -,c a -当成整体分类讨论:① 两正一负,原式值为1-;② 两负一正,原式值为1-.【例27】 (8级)(第18届希望杯2试)若有理数m 、n 、p 满足1m n p m n p ++=,求23mnp mnp 的值. 【解析】 由1m n p m n p++=可得:有理数m 、n 、p 中两正一负,所以0mnp <,所以1mnpmnp=-, 222333mnp mnp mnp mnp =⋅=-.【巩固】 (6级)已知有理数a b c ,,满足1a b c a b c ++=,则abcabc=( ) A .1 B .1- C .0 D .不能确定【解析】 提示:其中两个字母为正数,一个为负数,即0abc <【巩固】 (8级)有理数a ,b ,c ,d 满足1abcd abcd =-,求a b c da b c d+++的值.【解析】由1abcd abcd=-知0abcd <,所以a ,b ,c ,d 里含有1个负数或3个负数:若含有1个负数,则2a b c d a b c d+++=;若含有3个负数,则2a b c d a b c d +++=-.【例28】 (6级)已知0ab ≠,求a bab+的值 【解析】 ⑴若a b ,异号,则0a ba b += ⑵若a b ,都是正数,则2a ba b+= ⑶若a b ,都是负数,则2a bab+=-【巩固】 (6级)已知0ab ≠,求a b a b--的值.【解析】 分类讨论:当0a >,0b >时,110a b a b --=-=. 当0a >,0b <时,1(1)2a b a b --=--=. 当0a <,0b >时,112a b ab--=--=-.当0a <,0b <时,1(1)0a b ab--=---=.综上所述,a b a b --的值为2-,0,2.【例29】 (6级)若a b c ,,均为非零的有理数,求a b ca b c++的值 【解析】 ⑴当a b c ,,都是正数时,原式3a b ca b c=++= ⑵当a b c ,,都是负数时,原式3=- ⑶当a b c ,,有两个正数一个负数时,原式1=- ⑷当a b c ,,有两个负数一个正数时,原式1=-【巩固】 (6级)(第16届希望杯培训试题)若0abc <,求a b ca b c+-的值. 【解析】 由0abc <可得,a 、b 、c 中有3个负数或1个负数,当a 、b 、c 中有3个负数时,原式11(1)1=----=-;当a 、b 中有1个是负数时,原式1111=-+-=-; 当c 是负数时,原式11(1)3=+--=.板块三:零点分段讨论法(中考高端,可选讲)【例30】 (4级)(2005年云南省中考试题)阅读下列材料并解决相关问题:我们知道()()()0000x x x x x x >⎧⎪==⎨⎪-<⎩,现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式12x x ++-时,可令10x +=和20x -=,分别求得12x x =-=,(称12-,分别为1x +与2x -的零点值),在有理数范围内,零点值1x =-和2x =可将全体有理数分成不重复且不易遗漏的如下3中情况:·⑴当1x <-时,原式()()1221x x x =-+--=-+ ⑵当12x -<≤时,原式()123x x =+--= ⑶当2x ≥时,原式1221x x x =++-=-综上讨论,原式()()()211312212x x x x x -+<-⎧⎪=-<⎨⎪-⎩≤≥通过阅读上面的文字,请你解决下列的问题: ⑴分别求出2x +和4x -的零点值 ⑵化简代数式24x x ++-【解析】 ⑴分别令20x +=和40x -=,分别求得2x =-和4x =,所以2x +和4x -的零点值分别为2x =-和4x =⑵当2x <-时,原式()()242422x x x x x =-+--=---+=-+;当24x -<≤时,原式 ()246x x =+--=;当4x ≥时,原式2422x x x =++-=-所以综上讨论,原式()()()222624224x x x x x -+<-⎧⎪=-<⎨⎪-⎩≤≥【例31】 (6级)求12m m m +-+-的值.【解析】 先找零点,0m =,10m -=,20m -=,解得0m =,1,2.依这三个零点将数轴分为四段:0m <,01m ≤<,12m ≤<,2m ≥. 当0m <时,原式()()1233m m m m =-----=-+;当01m ≤<时,原式()()123m m m m =----=-+; 当12m ≤<时,原式()()121m m m m =+---=+; 当2m ≥时,原式()()1233m m m m +-+-=-.【例32】 (4级)化简:212x x ---【解析】 由题意可知:零点为102x x ==,当12x <时,原式1x =--当122x <≤时,原式33x =- 当2x ≥时,原式1x =+【巩固】 (4级)(2005年淮安市中考题)化简523x x ++-. 【解析】 先找零点.50x +=,5x =- ; 32302x x -==,,零点可以将数轴分成三段. 当32x ≥,50x +>,230x -≥,52332x x x ++-=+;当352x -<≤,50x +≥,230x -<,5238x x x ++-=-; 当5x <-,50x +<,230x -<,52332x x x ++-=--.【巩固】 (6级)(北京市中考模拟题)化简:121x x --++.【解析】 先找零点.10x -=,1x =.10x +=,1x =-.120x --=,12x -=,12x -=或12x -=-,可得3x =或者1x =-;综上所得零点有1,-1,3 ,依次零点可以将数轴分成四段.⑴ 3x ≥,10x ->,120x --≥,10x +>,12122x x x --++=-; ⑵ 13x <≤,10x -≥,120x --<,10x +>,1214x x --++=; ⑶ 11x -<≤,10x -<,120x --<,10x +≥,12122x x x --++=+; ⑷ 1x <-,10x -<,120x --<,10x +<,12122x x x --++=--.【例33】 (6级)(选讲)(北京市中考题)已知2x ≤,求32x x --+的最大值与最小值. 【解析】 法1:根据几何意义可以得到,当2x ≤-时,取最大值为5;当2x =时,取最小值为3-.法2:找到零点3、2-,结合2x ≤可以分为以下两段进行分析:当22x -≤≤时,323212x x x x x --+=---=-,有最值3-和5; 当2x <-时,32325x x x x --+=-++=;综上可得最小值为3-,最大值为5.【巩固】 (8级)(第10届希望杯2试)已知04a ≤≤,那么23a a -+-的最大值等于 . 【解析】 (法1):我们可以利用零点,将a 的范围分为3段,分类讨论(先将此分类讨论的方法,而后讲几何意义的方法,让学生体会几何方法的优越性)(1)当02a ≤≤时,2352a a a -+-=-,当0a =时达到最大值5; (2)当23a <≤时,231a a -+-=(3)当34a <≤时,2325a a a -+-=-,当4a =时,达到最大值3 综合可知,在04a ≤≤上,23a a -+-的最大值为5(法2):我们可以利用零点,将a 的范围分为3段,利用绝对值得几何意义分类讨论,很 容易发现答案:当0a =时达到最大值5.【巩固】 (6级)如果122y x x x =+-+-,且12x -≤≤,求y 的最大值和最小值 【解析】 当10x -<≤时,有12223y x x x x =+-+-=+,所以13y <≤;当02x ≤≤时,有12232y x x x x =+-+-=-,所以13y -≤≤ 综上所述,y 的最大值为3,最小值为1-【巩固】 (6级)(2001年大同市中考题)已知759x -≤≤,求x 取何值时13x x --+的最大值与最小值. 【解析】 法1:13x x --+表示x 到点1和3-的距离差,画出数轴我们会发现当,79x =时两者的距离差最小为329-,即()min 32139x x --+=-;当53x -≤≤-时,两者的距离差最大为4,即max (13)4x x --+=.法2:分类讨论:先找零点,根据范围分段,当53x -≤<-时,134x x --+=;当739x -≤≤时,1322x x x --+=--,当79x =有最小值329-;当3x =-有最大值4.综上所得,当53x --≤≤时,最大值为4;当79x =时,最小值为329-.练习 1. (2级)若ab ab <,则下列结论正确的是 ( ) A. 00a b <<, B. 00a b ><, C. 00a b <>, D. 0ab < 【解析】 答案BC 不完善,选择D .练习 2. (2级)(人大附期中考试)如果有理数a 、b 、c 在数轴上的位置如图所示,求a b a c b c++--+的值.【解析】 原式()()()0a b a c b c =-++-++=练习 3. (6级)已知0,0,x z xy y z x <<>>>,求x z y z x y +++--的值. 【解析】 由0,0x z xy <<>可得:0y z <<,又y z x >>,可得:y x z <<; 原式0x z y z x y =+---+=.练习 4. (8级)(第13届希望杯培训试题)若200122002x =,则|||1||2||3||4||5|x x x x x x +-+-+-+-+-= . 【解析】 因为200122002x =,所以23x <<,原式(1)(2)(3)(4)(5)9x x x x x x =+-+-------=.练习 5. (6级)(2006年七台河市中考题)设2020y x b x x b =-+-+--,其中020,20b b x <<≤≤,求y 的最小值.【解析】 2020(20)(20)40y x b x x b x b x x b x =-+-+--=------=-,则20x =时,y 有最小值为20.练习 6. (4级)若0a <,化简a a --.课后练习【解析】 22a a a a a a --=+==-.练习 7. (6级)若0a <,试化简233a a a a--.【解析】2323553443a a a a a a a a a a-+===-----.练习 8. (6级)若245134x x x +-+-+的值恒为常数,则x 应满足怎样的条件?此常数的值为多少? 【解析】 要使245134x x x +-+-+的值恒为常数,那么须使450x ->,130x -<,即1435x <<,原式2451342453147x x x x x x =+-+-+=+-+-+=.练习 9. (8级)(第6届希望杯2试)a 、b 、c 的大小关系如图所示,求a b b c c a ab aca b b c c a ab ac-----++----的值.【解析】 从图中可知a b c <<且0a <,0b <,0c >,所以0a b -<,0b c -<,0c a ->,0ab >,0ac <, 所以0ab ac ->,原式(1)(1)112=---++=.练习 10. (8级)若0a b c ++=,0abc >,则b c c a a ba b c+++++= . ∵0a b c ++=,0abc >,∴a 、b 、c 中一正二负,∴1b c c a a b a b ca b c a b c+++---++=++=. 练习 11. (6级)求15y x x =--+的最大值和最小值.【解析】 法1:根据几何意义可以得答案;法2:找到零点5-,1,可以分为以下三段进行讨论: 当5x ≤-时,15156y x x x x =--+=-++=;当51x -<<时,151524y x x x x x =--+=---=--; 当1x ≥时,15156y x x x x =--+=---=-; 综上所得最小值为6-,最大值为6.练习 12. (6级)(第2届希望杯2试)如果12x <<,求代数式2121x x xx x x ---+--的值.【解析】 当12x <<时,0x >,10x ->,20x -<,原式21111121x x xx x x--=++=-++=--.。
绝对值的化简问题(汇编)

绝对值的化简问题【知识梳理】绝对值的几何意义:一个数a 的绝对值就是数轴上表示数a 的点与原点的距离.数a 的绝对值记作a .绝对值的代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0. 注意:①取绝对值也是一种运算,运算符号是“”,求一个数的绝对值,就是根据性质去掉绝对值符号.②绝对值的性质:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.③绝对值具有非负性,取绝对值的结果总是正数或0.④任何一个有理数都是由两部分组成:符号和它的绝对值,如:5-符号是负号,绝对值是5.求字母a 的绝对值: ①(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩ ②(0)(0)a a a a a ≥⎧=⎨-<⎩ ③(0)(0)a a a a a >⎧=⎨-≤⎩ 利用绝对值比较两个负有理数的大小:两个负数,绝对值大的反而小.绝对值非负性:如果若干个非负数的和为0,那么这若干个非负数都必为0. 例如:若0a b c ++=,则0a =,0b =,0c =绝对值的其它重要性质:(1)任何一个数的绝对值都不小于这个数,也不小于这个数的相反数,即a a ≥,且a a ≥-;(2)若a b =,则a b =或a b =-;(3)ab a b =⋅;a a b b=(0)b ≠; (4)222||||a a a ==;(5)a b a b a b -≤+≤+,对于a b a b +≤+,等号当且仅当a 、b 同号或a 、b 中至少有一个0时,等号成立; 对于a b a b -≤+,等号当且仅当a 、b 异号或a 、b 中至少有一个0时,等号成立. 绝对值几何意义当x a =时,0x a -=,此时a 是x a -的零点值.零点分段讨论的一般步骤:找零点、分区间、定符号、去绝对值符号.即先令各绝对值式子为零,求得若干个绝对值为零的点,在数轴上把这些点标出来,这些点把数轴分成若干部分,再在各部分内化简求值. a 的几何意义:在数轴上,表示这个数的点离开原点的距离.a b -的几何意义:在数轴上,表示数a 、b 对应数轴上两点间的距离.【例1】 m n -的几何意义是数轴上表示m 的点与表示n 的点之间的距离.x 的几何意义是数轴上表示 的点与 之间的距离;x 0-(>,=,<);【例2】 21-的几何意义是数轴上表示2的点与表示1的点之间的距离;则21-= ;【例3】 3x -的几何意义是数轴上表示 的点与表示 的点之间的距离,若31x -=,则x = .【例4】 2x +的几何意义是数轴上表示 的点与表示 的点之间的距离,若22x +=,则x = .【例5】如果有理数a、b、c在数轴上的位置如图所示,求a b a c b c++--+的值. 【例6】如果有理数a、b、c在数轴上的位置如图所示,求11a b b a c c+------的值.【例7】已知00x z xy y z x,,,那么x z y z x y+++--=<<>>>++-+--【例8】数a b,在数轴上对应的点如右图所示,试化简a b b a b a a【例9】 实数a b c ,,在数轴上的对应点如图,化简a c b a b a c +--++-【例10】 若a b <-且0ab >,化简a b a b ab -+++.【例11】【例12】 若a b <,求15b a a b -+---的值.【例13】 a 、b 、c 的大小关系如图所示,求a b b c c a ab ac a b b c c a ab ac-----++----的值.。
专题突破:绝对值化简问题专项探究(3大题型)(解析版)—24-25学年七年级数学上册单元(浙教版)

专题突破:绝对值化简问题专项探究绝对值化简常见问题方法总结1、根据绝对值的性质化简(1)牢记绝对值的性质:⎪⎩⎪⎨⎧-==)a(a a )a(a a 0000<)(>或⎩⎨⎧≤-≥=)a(a )a(a a 00(2)在”“=的组合中,当“=”左边的部分未知时,求“| |”内部的数,需要分类讨论;当“=”右边的部分未知时,求“=”右边的值,结果只有一个。
(3)绝对值的非负性应用:当“| |+| |=0”时,则“| |”内部的式子整体=02、已知范围的绝对值化简基本步骤第1步:判断绝对值内部式子的正负;第2步:把绝对值改为小括号;第3步:去括号;第4步:化简合并。
3、绝对值化简与最值问题对应规律(1)当x=a 时,|x-a|的最小值=0;(2)当a ≤x ≤b 时,|x-a|+|x-b|的最小值=|a-b|;(3)若a <b <c ,当x=b 时,|x-a|+|x-b|+|x-c|最小值=c-a;题型一 根据绝对值的性质化简【例1】.(2024春•肇源县期中)若|a |+a =0,则a 是( )A .零B .负数C .负数或零D .非负数【分析】根据绝对值的性质解答即可.【解答】解:若|a |+a =0,则a 是负数或零,故选:C .【变式1-1】.(2024•碑林区校级模拟)如果,那么x =( )A .B .或2C .D .2【分析】根据绝对值的意义求解即可.【解答】解:∵∴.故选:C .【变式1-2】.(2023秋•|m |=|n |,那么m ,n 的关系( )A .相等B .互为相反数C .都是0D .互为相反数或相等【分析】利用绝对值的代数意义化简即可得到m 与n 的关系.【解答】解:∵|m |=|n |,∴m =n 或m =﹣n ,即互为相反数或相等,故选:D .【变式1-3】.(2023秋•渑池县期末)若|a +2|+|b ﹣7|=0,则a +b 的值为( )A .﹣1B .1C .5D .﹣5【分析】根据非负数的性质分别求出a 、b ,计算即可.【解答】解:∵|a +2|+|b ﹣7|=0,∴|a +2|=0,|b ﹣7|=0,∴a+2=0,b﹣7=0,解得,a=﹣2,b=7,则a+b=5,故选:C.【变式1-4】.(2023秋•东莞市月考)若|x﹣1|+|2﹣y|=0,求2x﹣y的值.【分析】根据非负数的性质得出x﹣1=0,2﹣y=0,即可求出x、y的值,从而求出2x﹣y的值.【解答】解:∵|x﹣1|+|2﹣y|=0,又∵|x﹣1|≥0,|2﹣y|≥0,∴x﹣1=0,2﹣y=0,∴x=1,y=2,∴2x﹣y=2×1﹣2=0.【变式1-5】.(2023•南皮县校级一模)若ab≠0,那么+的取值不可能是( )A.﹣2B.0C.1D.2【分析】由ab≠0,可得:①a>0,b>0,②a<0,b<0,③a>0,b<0,④a<0,b>0;分别计算即可.【解答】解:∵ab≠0,∴有四种情况:①a>0,b>0,a<0,b<0,③a>0,b<0,④a<0,b>0;①当a>0,b>0时,+=1+1=2;②当a<0,b<0时,+=﹣1﹣1=﹣2;③当a>0,b<0时,+=1﹣1=0;④当a<0,b>0时,+=﹣1+1=0;综上所述,+的值为:±2或0.故选:C.题型二已知范围的绝对值化简【例2】.(2023•成都模拟)化简|π﹣4|+|3﹣π|= .【分析】因为π≈3.414,所以π﹣4<0,3﹣π<0,然后根据绝对值定义即可化简|π﹣4|+|3﹣π|.【解答】解:∵π≈3.414,∴π﹣4<0,3﹣π<0,∴|π﹣4|+|3﹣π|=4﹣π+π﹣3=1.故答案为1.【变式2-1】.(2024春•松江区期中)如果a>3,化简:|1﹣a|﹣|a﹣3|= .【分析】根据绝对值的性质进行解题即可.【解答】解:∵a>3,∴|1﹣a|﹣|a﹣3|=a﹣1﹣(a﹣3)=a﹣1﹣a+3=2.故答案为:2.【变式2-2】.(2024春•海门区校级月考)已知|m|=﹣m,化简|m﹣1|﹣|m﹣2|所得的结果为( )A.2m﹣3B.﹣1C.1D.2m﹣1【分析】由|m|=﹣m,得到m≤0,判断出m﹣1 与m﹣2的正负,然后利用绝对值的性质化简,去括号,合并,即可得到结果.【解答】解:∵|m|=﹣m,∴m≤0,∴m﹣1<0,m﹣2<0,∴|m﹣1|﹣|m﹣2|=﹣(m﹣1)+(m﹣2)=1﹣m+m﹣2=﹣1.故选:B.【变式2-3】.(2022秋•市北区校级期末)当|a|=5,|b|=7,且|a+b|=a+b,则a﹣b的值为( )A.﹣12B.﹣2或﹣12C.2D.﹣2【分析】先根据绝对值的性质,判断出a、b的大致取值,然后根据a+b>0,进一步确定a、b的值,再代入求解即可.【解答】解:∵|a|=5,|b|=7,∴a=±5,b=±7∵|a+b|=a+b,∴a+b≥0,∴a=±5.b=7,当a=5,b=7时,a﹣b=﹣2;当a=﹣5,b=7时,a﹣b=﹣12;故a﹣b的值为﹣2或﹣12.故选:B.【变式2-4】.(2023秋•文登区期末)如图所示,则|﹣3﹣a|﹣|b+1|等于( )A.4+a﹣b B.2+a﹣b C.﹣4﹣a﹣b D.﹣2﹣a+b【分析】先根据数轴判断﹣3﹣a和b+1的正负,再去掉绝对值符号,合并同类项即可.【解答】解:由数轴可知,﹣1<a<0,b>1,∴﹣3<﹣3﹣a<﹣2,b+1>0,∴|﹣3﹣a|﹣|b+1|=(3+a)﹣(b+1)=3+a﹣b﹣1=2+a﹣b.故选:B.【变式2-5】.(2023秋•青羊区校级期末)已知数a,b,c在数轴上的位置如图所示,且|c|>|b|>|a|,化简|a+b|﹣|c﹣b|+|a﹣c|= .【分析】由数轴得c<a<0,b>0,|b|>|a|,进一步判断出a+b>0,c﹣b<0,a﹣c>0,再根据绝对值的意义化简即可.【解答】解:由数轴得c<a<0,b>0,|b|>|a|,∴a+b>0,c﹣b<0,a﹣c>0,∴|a+b|﹣|c﹣b|+|a﹣c|=(a+b)﹣(b﹣c)+(a﹣c)=a+b﹣b+c+a﹣c=2a,故答案为:2a.【变式2-6】.(2023秋•思明区校级期末)如图,化简|a﹣1|= .【分析】判断出a﹣1的取值,再根据绝对值性质计算即可.【解答】解:由题得a<1,∴a﹣1<0,∴|a﹣1|=1﹣a,故答案为:1﹣a.【变式2-7】.(2023秋•余干县期末)有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c 0,a+b 0,c﹣a 0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.【分析】(1)根据数轴判断出a、b、c的正负情况,然后分别判断即可;(2)去掉绝对值号,然后合并同类项即可.【解答】解:(1)由图可知,a<0,b>0,c>0且|b|<|a|<|c|,所以,b﹣c<0,a+b<0,c﹣a>0;故答案为:<,<,>;(2)|b﹣c|+|a+b|﹣|c﹣a|=(c﹣b)+(﹣a﹣b)﹣(c﹣a)=c﹣b﹣a﹣b﹣c+a=﹣2b.题型三绝对值化简与最值问题【例3】.(2022秋•泗阳县期中)式子|x﹣2|+1的最小值是( )A.0B.1C.2D.3【分析】当绝对值有最小值时,式子有最小值,进而得出答案.【解答】解:当绝对值最小时,式子有最小值,即|x﹣2|=0时,式子最小值为0+1=1.故选:B.【变式3-1】.(2023秋•邵阳县校级月考)当a= 时,5﹣|a﹣1|的值最大,最大值为 .【分析】分a<1、a=1和a>1三种情况讨论求出5﹣|a﹣1|≤5,问题随之得解.【解答】解:当a<1时,a﹣1<0,即5﹣|a﹣1|=5﹣(1﹣a)=4+a,∵a<1,∴5﹣|a﹣1|=4+a<5;当a=1时,a﹣1=0,即5﹣|a﹣1|=5;当a>1时,a﹣1>0,即5﹣|a﹣1|=5﹣(a﹣1)=6﹣a,∵a>1,∴﹣a<﹣1,∴5﹣|a﹣1|=6﹣a<5;综上:5﹣|a﹣1|≤5,当且仅当a=1时,5﹣|a﹣1|有最大值,最大值为5,解法二:∵|a﹣1|≥0,∴5﹣|a﹣1|≤5,∴当a=1时,5﹣|a﹣1|的值最大,最大值为5.故答案为:1,5.【变式3-2】.(2023秋•西安校级月考)当x满足 条件时,|x﹣2|+|x+3|有最小值,这个最小值是 .【分析】根据绝对值的性质以及题意即可求出答案.【解答】解:由题意可知:当﹣3≤x≤2时,|x﹣2|+|x+3|有最小值,这个最小值是5.故答案为:﹣3≤x≤2,5.【变式3-3】.(2023春•沙坪坝区校级月考)已知m是有理数,则|m﹣2|+|m﹣4|+|m﹣6|+|m﹣8|的最小值是 .【分析】根据绝对值最小的数是0,分别令四个绝对值为0,从而求得m的四个值,分别将这四个值代入代数式求值,比较得不难求得其最小值.【解答】解:∵绝对值最小的数是0,∴分别当|m﹣2|,|m﹣4|,|m﹣6|,|m﹣8|等于0时,有最小值.∴m的值分别为2,4,6,8.∵①当m=2时,原式=|2﹣2|+|2﹣4|+|2﹣6|+|2﹣8|=12;②当m=4时,原式=|4﹣2|+|4﹣4|+|4﹣6|+|4﹣8|=8;③当m=6时,原式=|6﹣2|+|6﹣4|+|6﹣6|+|6﹣8|=8;④当m=8时,原式=|8﹣2|+|8﹣4|+|8﹣6|+|8﹣8|=12;∴|m﹣2|+|m﹣4|+|m﹣6|+|m﹣8|的最小值是8.故答案为:8.【变式3-4】.(2023秋•新罗区期中)我们已经学习了一个数a的绝对值可分为两种情况:.请用你所学的知识解决下面的问题:(1)若|a﹣3|=5,求a的值;(2)若数轴上表示数a的点位于﹣3与0之间(含端点),化简|a﹣2|﹣|a|;(3)当a= 时,|a﹣5|+|a﹣1|+|a+3|取到最小值,最小值是 .【分析】(1)根据绝对值可得:a﹣3=±5,即可解答;(2)根据已知范围,化简绝对值,再合并即可;(3)分四种情况讨论,即可解答.【解答】解:(1)∵|a﹣3|=5,∴a﹣3=±5,解得:a=8或a=﹣2;(2)∵数轴上表示数a的点位于﹣3与0之间(含端点),∴﹣3≤a≤0,∴|a﹣2|﹣|a|=﹣(a﹣2)+a=﹣a+2+a=2;(3)当a≥5时,原式=a﹣5+a﹣1+a+3=3a﹣3,此时的最小值为3×5﹣3=12;当1≤a<5时,原式=﹣a+5+a﹣1+a+3=a+7,此时的最小值为1+7=8;当﹣3<a≤1时,原式=﹣a+5﹣a+1+a+3=9﹣a,此时的最小值为9﹣1=8;当a≤﹣3时,原式=﹣a+5﹣a+1﹣a﹣3=﹣3a+3,这时的最小值为﹣3×(﹣3)+3=12;综上所述当a=1时,式子的最小值为8,故答案为:1,8.【变式3-5】.(2023秋•芙蓉区校级月考)同学们都知道,|5﹣(﹣2)|表示5与﹣2的差的绝对值,实际上也可理解为5与﹣2两数在数轴上所对应的两点之间的距离,试探索:(1)|5﹣(﹣2)|= ;(2)x是所有符合|x+5|+|x﹣2|=7成立条件的整数,则x= ;(3)由以上探索猜想,对于任何有理数x,|x﹣3|+|x﹣6|的最小值为 ;(4)当x为整数时,|x﹣1|+|x﹣2|+|x﹣3|的最小值为 ;(5)求|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣1997|的最小值.【分析】(1)利用题干中的绝对值的几何意义解答即可;(2)利用题干中的绝对值的几何意义解答即可;【解答】解:(1)|5﹣(﹣2)|=|5+2|=7.故答案为:7;(2)∵|x+5|+|x﹣2|=7表示的是在数轴上x所对应的点到﹣5,2两点之间的距离之和等于7,又∵x为整数,∴x=﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2.故答案为:﹣5,﹣4,﹣3,﹣2,﹣1,0,1,2;(3)|x﹣3|+|x﹣6|表示的是在数轴上x所对应的点到3,6两点之间的距离之和,当3≤x≤6时,|x﹣3|+|x﹣6|∴|x﹣3|+|x﹣6|的最小值为3.故答案为:3;(4)|x﹣1|+|x﹣2|+|x﹣3|表示的是在数轴上x所对应的点到1,2,3三点之间的距离之和,∵x为整数,|x﹣1|+|x﹣2|+|x﹣3|取得最小值,∴x=2时,|x﹣1|+|x﹣2|+|x﹣3|的最小值为2.故答案为:2;(5)由(4)的结论可知:当x=999时,|x﹣1|+|x﹣2|+|x﹣3|+…+|x﹣1997|取得最小值,最小值为2×(1+2+...+998)=997002.。
专题七:结合数轴化简绝对值

结合数轴化简绝对值数轴右边的点比左边的点大,有理数大减小一定是为正绝对值化简三步走:1、判断正负2、去绝对值3、去括号化简1、数a在数轴上的位置如图所示,则|a-2|=______.2、有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c0,a+b0,c﹣a0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.3、若用A、B、C分别表示有理数a,b,c,O为原点,如图所示:化简2c+|a+b|+|c﹣b|﹣|c﹣a|.4、已知a,b,c的位置如图,化简:|a-b|+|b-c|+|c-a|=______________结合数轴化简绝对值解析1、数a在数轴上的位置如图所示,则|a-2|=______.解:由图可知,a>0,所以,a﹣2>0;故答案为:a﹣2;2、有理数a、b、c在数轴上的位置如图:(1)判断正负,用“>”或“<”填空:b﹣c0,a+b0,c﹣a0.(2)化简:|b﹣c|+|a+b|﹣|c﹣a|.解:(1)由图可知,a<0,b>0,c>0且|b|<|a|<|c|,所以,b﹣c<0,a+b<0,c﹣a>0;故答案为:<,<,>;(2)|b﹣c|+|a+b|﹣|c﹣a|=(c﹣b)+(﹣a﹣b)﹣(c﹣a)=c﹣b﹣a﹣b﹣c+a=﹣2b.3、若用A、B、C分别表示有理数a,b,c,O为原点,如图所示:化简2c+|a+b|+|c﹣b|﹣|c﹣a|.解:由数轴上点的位置得:a<c<0<b,|a|>|b|,∴a+b<0,c﹣b<0,c﹣a>0,则2c+|a+b|+|c﹣b|﹣|c﹣a|=2c﹣a﹣b﹣c+b﹣c+a=0.4、已知a,b,c的位置如图,化简:|a-b|+|b-c|+|c-a|=______________解:由数轴上点的位置得:a<c<0<b,∴a﹣b<0,b﹣c>0,c﹣a>0,则|a-b|+|b-c|+|c-a|==﹣(a﹣b)+b﹣c + c﹣a=2b﹣2a.。
关于绝对值的几种题型及解题技巧

关于绝对值的几种题型及解题技巧 所谓绝对值就是只有单纯的数值而没有负号。
即0≥a 。
但是,绝对值里面的数值可以是正数也可以是负数。
怎么理解呢?绝对值符号就相当于一扇门,我们在家里面的时候可以穿衣服也可以不穿衣服,但是,出门的时候一定要穿上衣服。
所以,0≥a ,而a 则有两种可能:o a 和0 a 。
如:5=a ,则5=a 和5-=a 。
合并写成:5±=a 。
于是我们得到这样一个性质:a很多同学无法理解,为什么0 a 时,开出来的时候一定要添加一个“负号”呢?a -。
因为此时0 a ,也就是说a 是一个负数,负数乘以符号就是正号了。
如2)2(=--。
因此,当判断绝对值里面的数是一个负数的时候,一定要在这个式子的前面添加一个负号。
例如:0 b a -,则)(b a b a --=-。
绝对值的题解始终围绕绝对值的性质来展开的。
我就绝对值的几种题型进行详细讲解,希望能对你们有所帮助。
绝对值的性质:(1) 绝对值的非负性,可以用下式表示:|a|≥0,这是绝对值非常重要的性质;a (a >0)(2) |a|= 0 (a=0) (代数意义)a 0 a 0 0=a a - 0 a-a (a <0)(3) 若|a|=a ,则a ≥0;若|a|=-a ,则a ≤0;(4) 任何一个数的绝对值都不小于这个数,也不小于这个数的相反数, 即|a|≥a ,且|a|≥-a ;(5) 若|a|=|b|,则a=b 或a=-b ;(几何意义)(6) |ab|=|a|·|b|;|b a |=||||b a (b ≠0);(7) |a|2=|a 2|=a 2;(8) |a+b|≤|a|+|b| |a-b|≥||a|-|b|| |a|+|b|≥|a+b| |a|+|b|≥|a-b|一:比较大小典型题型:【1】已知a 、b 为有理数,且0 a ,0 b ,b a ,则 ( )A :a b b a -- ;B :a b a b -- ;C :a b b a --;D :a a b b --这类题型的关键是画出数轴,然后将点按照题目的条件进行标记。
绝对值的性质与几何意义、数轴上动点问题(6种常考题型(解析版)

绝对值的性质与几何意义、数轴上动点问题(6种常考题型)题型一利用绝对值的性质化简题型二绝对值非负性的应用题型三利用绝对值的性质求最值题型四绝对值几何意义题型五数轴上两点之间的距离题型六数轴上动点问题一.利用绝对值的性质化简(共15小题)1.已知表示有理数a ,b 的点在数轴上的位置如图所示,则a b a b +的值是()2.若0ab ≠,那么a ab b +的取值不可能是()A .2-B .0C .1D .2【答案】C【分析】本题考查了绝对值的意义,由0ab ≠,可得:①0a >,0b >,②0a <,0b <,③0a >,0b <,④0a <,0b >;分别计算即可,采用分类讨论的思想是解此题的关键.【详解】解:∵0ab ≠,,3.已知有理数a ,b 在数轴上的位置如图所示,则化简1a b a +--的结果为()4.0a <,则化简a a a a a a ++-的结果为()5.三个有理数a ,b ,c 在数轴上表示的位置如图所示,则化简a b c b a +--+的结果是()A .22a b+B .22a b c +-C .c -D .2b c--【答案】C 【分析】本题考查了整式的加减和去绝对值,根据数轴分别判断0a b +<,0c b ->的正负,然后去掉绝对值即可,解题的关键是结合数轴判断绝对值符号里面代数式的正负.6.有理数a ,b ,c ,d 使||1abcd abcd =-,则a b c d a b c d +++的最大值是.7.已知数a b c 、、位置如图所示,化简a b a c --+=.的结果是.【答案】32a b c-+【分析】本题考查的是整式的加减,熟知整式的加减实质上就是合并同类项是解答此题的关键.先根据各点在数轴上的位置判断出a 、b 、c 的符号及大小,再去绝对值符号,合并同类项即可.【详解】解: 由图可知,0b a c <<<,||a c >,0a b ∴->,0a c +<,∴原式()22232a b a c a b a c a b c =-++=-++=-+.故答案为:32a b c -+.9.若12x <<,求代数式21x x x ---+=.10.若0a >,a=;若0a <,||a =;①若0||||a b a b +=,则||ab ab=-;②若0abc <,则||||||a b c a b c ++=.1111||||||a b c a b c ++=-++=,当a 、b 、c 中有三个负数时,1113||||||a b c a b c ++=---=-,故答案为:1或3-.11.有理数0a >,0b >,0c <,且a c b <<.(1)在数轴上将a ,b ,c 三个数在数轴上表示出来如图所示;(2)化简:2b c a b a c +--+-.【答案】(1)见详解(2)3a【分析】(1)根据所给的范围确定数在数轴上的位置即可;(2)由题意可知0b c +>,0a b -<,0a c ->,再化简即可.本题考查实数与数轴,熟练掌握数轴上点的特征,绝对值的意义是解题的关键.【详解】(1)解:依题意,有理数0a >,0b >,0c <,且a c b<<∴如图所示:(2)解:0a > ,0b >,0c <,且a c b <<,0b c ∴+>,0a b -<,0a c ->,|||||2|b c a b a c ∴+--+-()(2)b c b a a c =+--+-2b c b a a c=+-++-3=a .12.已知有理数a b c d 、、、在数轴上对应的点的位置如图所示,化简:a c b d c b++---【答案】2a c d--+【分析】此题综合考查了数轴、绝对值的有关内容,熟练掌握以上知识是解题的关键.先观察数轴,得到0a b c d <<<<,从而得到0a c +<,0b d -<,0c b ->,然后根据绝对值的性质进行化简即可.【详解】解:由数轴可知,0a b c d <<<<,∴0a c +<,0b d -<,0c b ->,∴2a c b d c b a c b d c b a c d++---=---+-+=--+13.a ,b 在数轴上的位置如图,化简b a a a b --++.b ,.【答案】21b -【分析】本题考查数轴、绝对值,解答本题的关键是明确题意,利用数形结合的思想解答.根据数轴可以判断a 、b 、c 的正负和绝对值的大小,从而可以化简题目中的式子.【详解】解:根据数轴,得10,0,0a c b a b c +<->++<,|1|(1),||,||()a a c b c b a b c a b c ∴+=-+-=-++=-++,|1|||||a cb a bc ∴+---++(1)()()a cb a bc =-+--+++1a c b a b c=---++++21b =-.15.有理数a ,b ,c 在数轴上的位置如图所示.(1)用“>”“<”或“=”填空:a b +______0,c a -______0,2b +______0.(2)化简:22a b c a b ++--+.二.绝对值非负性的应用(共11小题)1.如果21(2)0a b ++-=,则a b +的值为()2.若()23a +与1b -互为相反数,则().3,1a b =-=-3.若320x y -++=,则x y +的值是().4.如果有理数x 、y 满足10x x y -++=,那么xy 的值是()5.若()22430||a b ++--=,则b =;a =.【答案】32【分析】根据有理数的非负性解答即可.本题考查了有理数的非负性,熟练掌握性质是解题的关键.【详解】解:∵()22430||a b ++--=,∴20,30a b +=-=-,解得:3,2b a ==.故答案为:3,2.6.已知x 是非负数,且非负数中最小的数是0.(1)已知210a b -+-=,则a b +的值是_________;(2)当a =________时,12a -+有最小值,最小值是______.故答案为:1,2.2y =8.已知,b 是有理数,且满足,求与b 的值.【答案】1a =,2b =【分析】本题考查了绝对值非负的性质.当它们相加和为0时,必须满足其中的每一项都等于0.根据非负数的性质列出方程求出未知数的值.【详解】解:|1||2|0a b -+-= ,10a ∴-=,20b -=,1a ∴=,2b =,故答案为:1a =,2b =.9.已知230x y -++=.(1)求x y +的值.x y -的值.,求、的值.11.若201503b a --+=,求a ,b 的值.【答案】3a =,2015b =根据绝对值的性质去绝对值是解题的关键.三.利用绝对值的性质求最值(共9小题)1.设n 个有理数12,,,n x x x ⋅⋅⋅满足1(1,2,,)i x i n <= ,且12x x +++ 1219n n x x x x =++++ ,则n 的最小值是()2.如果x 为有理数,式子20232x -+存在最大值,这个最大值是()的最小值是()A .0B .1C .2D .3【答案】C【分析】根据绝对值的非负性即可求解.【详解】解:∵a 是有理数∴1a -可为正数、负数、零由绝对值的非负性可知:|1|0a -≥∴2|12|a -+≥即:|1|2a -+的最小值是2故选:C【点睛】本题考查绝对值的非负性.熟记相关结论即可.4.(1)若6m -有最小值,则当m =时,取最小值,最小值为.(2)若260m n -+-=,则m =,n =.(3)5m -有最(填“大”或“小”)值,这个最(大)小值是.5.已知a 为有理数,则24a -+的最小值为.【答案】4【分析】本题考查了绝对值的非负性,解题的关键是掌握正数的绝对值是它本身,负数的绝对值是它的相反数,6.如果x 为有理数,式子20213x --存在最大值,那么这个式子有最值是,此x =a ,b ,c 满足()220240a b c ++-=,则(1)c 的值为.(2)数轴上任意一点P ,点P 对应的数为x ,若存在x 使x a x b x c -+-+-的值最小,则x 的值为.8.阅读材料:x 的几何意义是数轴上数x 的对应点与原点之间的距离,即0x x =-,也可以说x 表示数轴上数x 与数0对应点之间的距离.这个结论可以推广为12x x -表示数轴上数1x 与数2x 对应点之间的距离,根据材料的说法,试求:(1)34x +=;(2)若x 为有理数,代数式32x -+有没有最大值?如果有,求出这个最大值及此时x 的值是多少?如果没有,请说明理由;(3)若x 为有理数,则13x x -+-有最______值(填“大”或“小”),其值为________.点A B ,在数轴上分别表示有理数a b ,,A B ,两点之间的距离表示为AB .当A B ,两点中有一点在原点时,不妨设点A 在原点,如图①所示,AB OB b a b ===-;当A B ,两点都不在原点时,a .如图②所示,点A B ,都在原点的右边,AB OB OA b a b a a b =-=-=-=-;b .如图③所示,点A B ,都在原点的左边,()AB OB OA b a b a a b =-=-=---=-;c .如图④所示,点A B ,在原点的两边,()AB OA OB a b a b a b =+=+=+-=-.综上,数轴上A B ,两点之间的距离AB a b =-.回答下列问题:(1)数轴上表示2和5的两点之间的距离是,数轴上表示2-和5-的两点之间的距离是,数轴上表示1和3-的两点之间的距离是;(2)数轴上表示x 和1-的两点A 和之间的距离是,如果2AB =,那么x 为;(3)当47x y ++-取最小值时,x =,y =.四.绝对值几何意义(共6小题)1.在解决数学实际问题时,常常用到数形结合思想,比如:1x +的几何意义是数轴上表示数x 的点与表示数1-的点的距离,2x -的几何意义是数轴上表示数x 的点与表示数2的点的距离.当12x x ++-取得最小值时,x 的取值范围是()A .12x ≤≤B .1x ≤-或2x ≥ 2.在解决数学实际问题时,常常用到数形结合思想,比如:1x +的几何意义是数轴上表示数x 的点与表示数1-的点的距离,2x -的几何意义是数轴上表示数x 的点与表示数2的点的距离.当12x x ++-取得最小值时,x 的取对x 的值进行分类讨论,进而得出代数式的值.以1-和2为界点,将数轴分成三部分,对x 的值进行分类讨论,然后根据绝对值的意义去绝对值符号,分别求出代数式的值进行比较即可.【详解】解:如图,当1x <-时,10x +<,20x -<,|1||2|x x ++-(1)(2)x x =-+--12x x =---+213x =-+>;当2x >时,10x +>,20x ->,|1||2|x x ++-(1)(2)x x =++-12x x =++-213x =->;当12x -≤≤时,10x +≥,20x -≤,|1||2|x x ++-(1)(2)x x =+--123x x =+-+=;综上所述,当12x -≤≤时,|1||2|x x ++-取得最小值,所以当|1||2|x x ++-取得最小值时,x 的取值范围是12x -≤≤.故答案为:12x -≤≤.3.阅读理解:对于有理数a 、b ,a 的几何意义为:数轴上表示数a 的点到原点的距离;|a -b |的几何意义为:数轴上表示数a 的点与表示数b 的点之间的距离.如:2x -的几何意义即数轴表示数x 的点与表示数2的点之间的距离,请根据你的理解解答下列问题:(1)根据2x +的几何意义,若23x +=,那么x 的值是.(2)画数轴分析23x x +++的几何意义,并求出23x x +++的最小值是.(3)11232023x x x x x x +++-+-+-+⋯+-的最小值是多少?的点之间的距离,当23x -≤≤-时,23x x +++的最小值是为根据绝对值的几何意义,我们知道53-表示5、3在数轴上对应的两点间的距离;535(3)+=--,所以53+表示5、3-在数轴上对应的两点之间的距离;550=-,所以5表示5在数轴上对应的点到原点的距离.一般地,点A 、B 在数轴上分别表示有理数a 、b ,那么A 、B 两点之间的距离可以表示为AB a b =-.回答下列问题:(1)数轴上表示6与9-的两点之间的距离是_________;数轴上表示x 与2的两点之间的距离是_______.(2)若33x -=,则x =_______.(3)满足235x x ++-=的整数x 有_______个.经过有理数运算的学习,我们知道53-可以表示5与3之差的绝对值,同时也可以理解为5与3两个数在数轴上所对应的两点之间的距离,我们可以把这称之为绝对值的几何意义.同理,()52--可以表示5与2-之差的绝对值,也可以表示5与2-两个数在数轴上所对应的两点之间的距离.试探究:(1)5x -表示数轴上有理数x 所对应的点到________所对应的点之间的距离;2x +表示数轴上有理数x 所对应的点到________所对应的点之间的距离.若25x +=,则x =________.(2)利用绝对值的几何意义,请找出所有符合条件的整数x ,使得257x x ++-=.这样的整数x 有________________.(写出所有的整数x )(3)利用绝对值的几何意义,求出123x x x -+++-的最小值,并说明理由.(1)直接写出数轴上点B 表示的数;(2)53-表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如3x -的几何意义是数轴上表示有理数x 的点与表示有理数3的点之间的距离,试探索:①若82x -=,则x =(直接写出);②118x x ++-的最小值为(直接写出);(3)请直接写出所有满足37329a a ++-=的整数a 的值.故答案为:,,0.五.数轴上两点之间的距离(共15小题)1.已A B 、两点在数轴上表示的数分别是3-和6-,若在数轴上找一点C ,使得A 和C 之间的距离是4,使得B D 、之的距离是1,则C D 、之间的距离不可能是()A .0B .6C .2D .4【答案】D【分析】本题考查了数轴,画出数轴,然后根据两种情况确定出点C D 、的位置,再根据数轴上的两点间的距离求出C 的可能值,据此即可求解,掌握数形结合思想和分类讨论思想是解题的关键.【详解】解:如图,C D 、间的距离可能是0268、、、,∴C D 、之间的距离不可能是4,故选:D .2.如图,一条数轴上有点A 、B 、C ,其中点A 、B 表示的数分别是14-,10,现以点C 为折点,将数轴向右对折,若点A 落在射线C 上且到点B 的距离为6,则C 点表示的数是()A .1B .3-C .1或5-D .1或4-【答案】C 【分析】本题考查了数轴,分类讨论思想是解题的关键.先根据两点间的距离公式求出点A 落在对应点表示的数,在利用中点公式求出C 点表示的数.【详解】设A '是点A 的对应点,由题意可知点C 是A 和A '的中点当点A 在B 的右侧,6BA '=,A '表示的数为10616+=,那么C 表示的数为:(1416)21-+÷=,当点A 在B 的左侧,6BA '=,A '表示的数为1064-=,那么C 表示的数为:(144)25-+÷=-,故选:C .3.如图,已知A ,(B B 在A 的左侧)是数轴上的两点,点A 对应的数为12,且18AB =,动点P 从点A 出发,以每秒2个单位长度的速度沿数轴向左运动,在点P 的运动过程中,M ,N 始终为AP ,BP 的中点,设运动时间为(0)t t >秒,则下列结论中正确的有()①B 对应的数是6-;②点P 到达点B 时,9t =;③2BP =时,6t =;④在点P 的运动过程中,线段MN 的长度会发生变化.A .1个B .2个C .3个D .4个【答案】B 【分析】本题考查了数轴上两点距离.利用数轴,分类讨论即可求解.【详解】解: 已知A ,(B B 在A 的左侧)是数轴上的两点,点A 对应的数为12,且18AB =,B ∴对应的数为:12186-=-;故①是正确的;1829÷= ,故②是正确的;当2BP =时,16AP =,1628t =÷=,故③是错误的;在点P 的运动过程中,9MN =,故④是错误的;故选:B .4.在数轴上,点A ,B 在原点O 的两侧,分别表示数a ,2,将点A 向右平移2个单位长度,得到点C .若点C 到A 、B 两个点的距离相等,则a 的值为()A .0B .1-C .2-D .1【答案】C【分析】此题考查了数轴上点的移动,由题意得点A 表示数为a ,点B 表示数为2,点C 表示数为2a +,熟知数轴A .1-B .0C .1D .2【答案】C 【分析】根据已知图形可写出墨水盖住的整数,相加即可;【详解】由图可知,被墨水盖住的整数为:3-,2-,1,2,3,相加为()321231-+-+++=;故选C .【点睛】本题主要考查了有理数的加法运算,准确表示出盖住的整数是解题的关键.6.数轴上表示整数的点称为整点.某数轴的单位长度是1厘米,若在这个数轴上随意画出一条长为2013厘米的线段AB ,则线段AB 盖住的整点的个数是()个,且在数轴上的位置如图所示.已知343a b =-,则代数式5c d -的值是.【答案】12-【分析】根据题意,则2b a =+,3c a =+,7d a =+,结合343a b =-,列式解答即可.本题考查了数轴的意义,有理数的计算,熟练掌握有理数加减运算是解题的关键.【详解】解:仔细观察图形,由数轴可知:a b c d <<<.∵每相邻两点之间的距离是1个单位长,∴2b a =+,3c a =+,7d a =+.∵343a b =-,∴()3423a a =+-,∴5a =-,∴3532c a =+=-+=-,7572d a =+=-+=,∴521012c d -=--=-.故答案为:12-.8.如图,在数轴上,点A 表示的数是10,点B 表示的数为50,点P 是数轴上的动点.点P 沿数轴的负方向运动,在运动过程中,当点P 到点A 的距离与点P 到点B 的距离比是2:3时,点P 表示的数是.现将该刻度尺沿数轴向右平移3个单位,则刻度尺上6.1cm 对应数轴上的数为.平移动,移动后的正方形记为A B C D '''',点、、A B C 、D 的对应点分别为A B C D ''''、、、,点E 是线段AA '的中点,当BEC '△面积为9时,点A '表示的数为.【分析】本题考查了数轴上的动点问题,三角形的面积,解题的关键是根据正方形平移后正确地表示出各线段的长∵113922BEC S BE D A BE '''=⋅=⨯=V ,∴6BE =,∴369AE AB BE =+=+=,∵点E 是线段AA '的中点,∴18AA '=,∵点A 表示的数为4-,∴点A '表示的数为41814-+=;②当正方形ABCD 沿数轴向左移动时,如图,S V Q 6,BE ∴=∴633AE BE AB =-=-=,∵点E 是线段AA '的中点,∴6AA '=,∵点A 表示的数为4-,∴点A '表示的数为4610--=-.综上,数轴上点A '表示的数是14或10-;故答案为:14或10-.11.如图,A ,B ,C 为数轴上的点,4AC =,点B 为AC 的中点,点P 最小值为.【答案】6【分析】根据题意得出2AB BC ==,然后分情况讨论,作出相应图形求解即可.【详解】解:∵4AC =,点B 为AC 的中点,∴2AB BC ==,当点P 位于点A 左侧时,如图所示,()22410PA PB PC PA PA AB PA AC PA ++=++++=+;当点P 与点A 重合时,如图所示,202810PA PB PC ++=++=;当点P 位于点A 与点B 之间时,如图所示:()22226PA PB PC PB BC PB ++=++=+;当点P 与点B 重合时,如图所示,220226PA PB PC ++=++⨯=;当点P 位于点B 与点C 之间时,如图所示:22246PA PB PC AB PB PB PC ++=+++=+=;当点P 与点C 重合时,如图所示,2426PA PB PC ++=+=;当点P 位于点C 右侧时,如图所示,2264PA PB PC AC PC BC PC PC PC ++=++++=+;综上可得:2PA PB PC ++的最小值为6,故答案为:6.【点睛】本题主要考查数轴上两点之间的距离及分类讨论思想,理解题意,进行分类讨论是解题关键.12.如图所示,观察数轴,请回答:(1)点C 与点D 的距离为,点B 与点D 的距离为;(2)点B 与点E 的距离为,点A 与点C 的距离为;发现:在数轴上,如果点M 与点N 分别表示数m ,n ,则他们13.同学们都知道,()73--表示7与3-之差的绝对值,实际上也可理解为数轴上分别表示7与3-的两点之间的距离.试探索:(1)()73--=________;(2)找出所有符合条件的整数x ,使得415x x ++-=;(3)对于任何有理数x ,36x x -+-是否有最小值?若有,请求出最小值;若没有,请说明理由;(4)若169x x ++-=时,求x 的值.+=--=-,617112∴x的值为2-或7.14.已知在纸面上有一数轴(如图),折叠纸面.(1)若1表示的点与1-表示的点重合,则2-表示的点与数表示的点重合;(2)若1-表示的点与3表示的点重合,回答以下问题:①5表示的点与数表示的点重合;②若数轴上A、B两点之间的距离为2023(A在B的左侧),且A、B两点经折叠后重合,求A、B两点表示的数是多少?的和是m.(1)若B为原点.则A点对应的数是__________;点C对应的数是__________,m=__________.CO=.求m.(2)若原点O在图中数轴上点C的右边,且6【答案】(1)2--,1,1(2)22-A B C所对应的数是解题关键.【分析】本题主要考查了数轴的知识,根据题意确定点、、A B C所对应的数,即可获得答案;(1)根据题意,确定点、、A B C所对应的数,即可获得答案.(2)根据题意,确定点、、【详解】(1)解:根据题意,2BC=,AB=,1若B为原点,即点B对应的数为0,则点A 对应的数为2-,点C 对应的数为1,∴2011=-++=-m .故答案为:2-,1,1-;(2)解:根据题意,原点O 在图中数轴上点C 的右边,且6CO =,则点C 对应的数为6-,点B 对应的数为7-,点A 对应的数为9-,∴()()67922m =-+-+-=-.六.数轴上动点问题(共12小题)1.正方形ABCD 在数轴上的位置如图所示,点D 、A 对应的数分别为1-和0,若正方形ABCD 绕着顶点顺时针方向在数轴上连续翻转,翻转1次后,点B 所对应的数为1;则翻转2019次后,数轴上数2019所对应的点是()三次向右跳3个单位长度,第四次向左跳4个单位长度…以此规律跳下去,当它跳第100次落下时,落点处距离原点()个单位长度.A .0B .100C .50D .-50【答案】C【分析】数轴上点的移动规律是“左减右加”.依据规律计算即可.【详解】解:0+1﹣2+3﹣4+5﹣6+…+99﹣100=﹣50,所以落点处离0的距离是50个单位.故答案为:C .【点睛】主要考查了数轴,要注意数轴上点的移动规律是“左减右加”.把数和点对应起来,也就是把“数”和“形”结合起来,二者互相补充,相辅相成,把很多复杂的问题转化为简单的问题,在学习中要注意培养数形结合的数学思想.3.如图,在数轴上点A 、B 表示的数分别为﹣2、4,若点M 从A 点出发以每秒5个单位长度的速度沿数轴向右匀速运动,点N 从B 点出发以每秒4个单位长度的速度沿数轴匀速运动,设点M 、N 同时出发,运动时间为t 秒,经过秒后,M 、N 两点间的距离为8个单位长度.【答案】14或149【分析】已知运动时间为t 秒,根据题意建立含有t 的一元一次方程,解出t 的值即可.【详解】解:已知运动时间为t 秒,根据题意M 、N 两点间的距离为8个单位长度,分析N 点的两种移动方向分别建立一元一次方程可得:当N 向左运动,则有25448t t -+-+=,解得t =149,当N 向右运动,则有25448t t -+--=,解得t =14.故答案为14或149.【点睛】本题主要考查线段的动点和数轴问题,根据题意分情况列出含有t 的一元一次方程是解决本题的关键.4.如图,动点A ,B ,C 分别从数轴-30,10,18的位置沿数轴正方向运动,速度分别为2个单位长度/秒,4个单位长度/秒,8个单位长度/秒,线段OA 的中点为P ,线段OB 的中点为M ,线段OC 的中点为N ,若k PM MN ⋅-为常数,则k 为.【答案】2【分析】运动t 秒后,点P 在数轴上表示的数为-15+t ,点M 在数轴上表示的数是5+2t ,点N 在数轴上表示的数是9+4t ,分别表示出PM =20+t ,MN =2t +4,再代入k PM MN ⋅-,根据k PM MN ⋅-为常数,得到关于k 的方程,解方程即可.【详解】解:根据题意得,点P 在数轴上表示的数为-3022t +=-15+t ,点M 在数轴上表示的数是1042t +=5+2t ,点N 在数轴上表示的数是1882t +=9+4t ,则PM =20+t ,MN =2t +4,(20)(24)(2)204k PM MN k t t k t k ∴⋅-=+-+=-+- k PM MN ⋅-为常数,2=0k ∴-2k ∴=故答案为:2.【点睛】本题考查一元一次方程的应用、数轴上点的位置关系,根据k PM MN ⋅-为常数列方程是解题关键.5.定义:若A ,B ,C 为数轴上三点,若点C 到点A 的距离是点C 到点B 的距离2倍,我们就称点C 是【A ,B 】的美好点.例如:如图1,点A 表示的数为1-,点B 表示的数为2.表示1的点C 到点A 的距离是2,到点B 的距离是1,那么点C 是【A ,B 】的美好点;又如,表示0的点D 到点A 的距离是1,到点B 的距离是2,那么点D 就不是【A ,B 】的美好点,但点D 是【B ,A 】的美好点.如图2,M ,N 为数轴上两点,点M 所表示的数为7-,点N 所表示的数为2(1)点E ,F ,G 表示的数分别是3-,6.5,11,其中是【M ,N 】美好点的是_;写出【N ,M 】美好点H 所表示的数是_.(2)现有一只电子蚂蚁P 从点N 开始出发,以2个单位每秒的速度向左运动.当t 为何值时,P ,M 和N 中恰有一个点为其余两点的美好点?【答案】(1)G ;4-或16-(2)1.5,2.25,3,6.75,9,13.5【分析】本题考查数轴上的动点问题、数轴上两点之间的距离、点是【M ,N 】的美好点的定义等知识,解题的关键是理解题意,灵活运用所学知识解决问题.(1)根据美好点的定义,结合图2,直观考察点E ,F ,G 到点M ,N 的距离,只有点G 符合条件.结合图2,根据美好点的定义,在数轴上寻找到点N 的距离是到点M 的距离2倍的点,在点的移动过程中注意到两个点的距离的变化.(2)根据美好点的定义,P ,M 和N 中恰有一个点为其余两点的美好点分8种情况,须区分各种情况分别确定P 点的位置,进而可确定t 的值.【详解】(1)解:根据美好点的定义,18GM =,9GN =,2GM GN =,只有点G 符合条件,故答案是:G .结合图2,根据美好点的定义,在数轴上寻找到点N 的距离是到点M 的距离2倍的点,点N 的右侧不存在满足条件的点,点M 和N 之间靠近点M 一侧应该有满足条件的点,进而可以确定4-符合条件.点M 的左侧距离点M 的距离等于点M 和点N 的距离的点符合条件,进而可得符合条件的点是16-.故答案为:4-或16-;(2)解:根据美好点的定义,P ,M 和N 中恰有一个点为其余两点的美好点分8种情况,第一情况:当P 为【M ,N 】的美好点,点P 在M ,N 之间,如图1,当2MP PN =时,3PN =,点P 对应的数为231-=-,因此 1.5t =秒;第二种情况,当P 为【N ,M 】的美好点,点P 在M ,N 之间,如图2,当2PM PN =时,6NP =,点P 对应的数为264-=-,因此3t =秒;第三种情况,P 为【N ,M 】的美好点,点P 在M 左侧,如图3,当2PN MN =时,18NP =,点P 对应的数为21816-=-,因此9t =秒;第四种情况,M 为【P ,N 】的美好点,点P 在M 左侧,如图4,当2MP MN =时,27NP =,点P 对应的数为22725-=-,因此13.5t =秒;第五种情况,M 为【N ,P 】的美好点,点P 在M 左侧,如图5,当2MN MP =时,13.5NP =,点P 对应的数为213.511.5-=-,因此 6.75t =秒;第六种情况,M 为【N ,P 】的美好点,点P 在M ,N 左侧,如图6,当2MN MP =时, 4.5NP =,因此 2.25t =秒;第七种情况,N 为【P ,M 】的美好点,点P 在M 左侧,当2PN MN =时,18NP =,因此9t =秒,第八种情况,N 为【M ,P 】的美好点,点P 在M 右侧,当2MN PN =时, 4.5NP =,因此 2.25t =秒,综上所述,t 的值为:1.5,2.25,3,6.75,9,13.5.6.若A 、B 、C 为数轴上三点,若点C 到A 的距离是点C 到B 的距离2倍,我们就称点C 是【A ,B 】的好点.例如,如图1,点A 表示的数为1-,点B 表示的数为2.表示1的点C 到点A 的距离是2,到点B 的距离是1,那么点C 是【A ,B 】的好点;又如,表示0的点D 到点A 的距离是1,到点B 的距离是2,那么点D 就不是【A ,B 】的好点,但点D 是【B ,A 】的好点.知识运用:如图2,M 、N 为数轴上两点,点M 所表示的数为2-,点N 所表示的数为4.(1)数所表示的点是【M ,N 】的好点;(2)如图3,A 、B 为数轴上两点,点A 所表示的数为20-,点B 所表示的数为40.现有一只电子蚂蚁P 从点B 出发,以2个单位每秒的速度向左运动,到达点A停止.当t为何值时,P、A和B中恰有一个点为其余两点的好点?【答案】(1)2或10t=秒或20秒或15秒(2)10【分析】本题考查了数轴上两点之间的距离、数轴上的动点问题:(1)根据数轴求出两点距离,再根据新定义的概念求出结果,注意有两种情况;(2)分情况讨论,根据好点的定义可求出结果;正确理解新定义是解题的关键.【详解】(1)解:设点H是【M,N】的好点,∴=,2HM HN当H在M、N之间时,HM HN MN∴+==--=,4(2)6∴+=,HN HN26∴=,2HN∴表示的数为422H-=,当H在N右边时,设H表示的数为h,h h∴--=-,(2)2(4)∴=,10h故答案为:2或10;(2)解:当P是【A,B】好点时,即2=,PA PB\-=´,t t60222t∴=;10当P是【B,A】好点时,即2=,PB PA∴=-,t t22(602)t∴=;20当B是【A,P】好点时,即2BA BP=,\=´,6022tt∴=,15当A是【B,P】好点时,即2=,AB AP∴=-,602(602)tt∴=;15t=秒或20秒或15秒时,P、A和B中恰有一个点为其余两点的好点.综上所述,当10、两点表示的数是互为相反数;7.如图,数轴上的单位长度为1,A B(1)点A表示的数是______,点B表示的数______.(2)数轴上一个动点P先向左移动2个单位长度,再向右移动5个单位到达点M,若点M表示的数是1,则点P所表示的数是______.(3)在数轴上,点O为坐标原点,若点A、点B分别以2个单位长度/秒和0.5个单位长度/秒的速度向右运动,当两点t>.同时运动时,设运动时间为t秒()0①点A 表示的数为______;点B 表示的数为______.(用含t 的式子表示)②当t 为何值时,点A 、点B 、点O 三点之间恰好有一个点到其他两个点的距离相等?(1)则点A 对应的数是,点B 对应的数是;(2)动点P 、Q 分别同时从A 、C 出发,分别以每秒8个单位和4个单位的速度沿数轴正方向运动.M 在线段AP 上,且AM MP =,N 在线段CQ 上,且14CN CQ =,设运动时间为()0t t >.①求点M、N对应的数(用含t的式子表示)②猜想的长度是否与t的大小有关?如果有关请你写出用t表示的代数式;如果无关请你求出的长度.如图1,在数轴上A点所示的数为a,B点表示的数为b,则点A到点B的距离记为AB,线段AB的长可以用右边=-.的数减去左边的数表示,即AB b a请用上面的知识解答下面的问题:如图2,一个点从数轴上的原点开始,先向左移动2cm到达A点,再向左移动3cm到达B点,然后向右移动9cm到达C点,用1个单位长度表示1cm.(1)请你在数轴上表示出A,B,C三点的位置:(2)点C到点A的距离CA=______cm;若数轴上有一点D,且5AD=,则点D表示的数为_________;x,则移动后的点表示的数为_____;(用代数式表示)(3)若将点A向右移动cm(4)若点B以每秒2cm的速度向左移动,同时A.C点分别以每秒1cm、4cm的速度向右移动,设移动时间为t秒,-的值是否会随着t的变化而改变?请说明理由.试探索:AC AB-,C表示4,图见解析;【答案】(1)A表示2-,B表示5CA=--=+=(cm);(2)4(2)426设D表示的数为a,度向终点C移动,设移动时间为t秒.若用PA,PB,PC分别表示点P与点A、点B、点C的距离,试回答以下问题.(1)当点P运动10秒时,PA=______,PB=______,PC=______;(2)当点P运动了t秒时,请用含t的代数式表示P到点A、点B、点C的距离:PA=______,PB=______,PC=______;(3)经过几秒后,点P到点A、点C的距离相等?此时点P表示的数是多少?(4)当点P运动到B点时,点Q从A点出发,以每秒3个单位长度的速度向C点运动,Q点到达C点后,再立即以同样速度返回,运动到终点A.在点Q开始运动后,P、Q两点之间的距离能否为4个单位长度?如果能,请直接写出点P表示的数;如果不能,请说明理由.当Q 点未到达点,此时3AQ x =,BP x =,则Q 则()10243PQ x x =-+--+此时(343AQ AC QC =-=-则Q 点表示的数为2468-+-两个长方形ABCD 和EFGH 的宽都是3个单位长度,长方形ABCD 的长AD 是6个单位长度,长方形EFGH 的长EH 是10个单位长度,其中点A 、D 、E 、H 在数轴上(如图),点E 在数轴上表示的数是5,且E 、D 两点之间的距离为14,原点记为0.(1)求数轴上点H 、A 所表示的数?(2)若长方形ABCD 以4个单位长度/秒的速度向右匀速运动,同时长方形EFGH 以3个单位长度/秒的速度向左匀速运动,数轴上有M 、N 两点,其中点M 在A 、D 两点之间,且12AM AD =,其中点N 在E 、H 两点之间,且15EN EH =,设运动时间为x 秒.①经过x 秒后,M 点表示的数是,N 点表示的数是(用含x 的式子表示,结果需化简).②求MN (用含x 的式子表示,结果需化简).(3)若长方形ABCD 以2个单位长度/秒的速度向右匀速运动,长方形EFGH 固定不动,设长方形ABCD 运动的时间为()0t t >秒,两个长方形重叠部分的面积为S ,当12S =时,求此时t 的值.。
绝对值大全(零点分段法、化简、最值)..

绝对值⼤全(零点分段法、化简、最值)..绝对值⼤全(零点分段法、化简、最值)⼀、去绝对值符号的⼏种常⽤⽅法解含绝对值不等式的基本思路是去掉绝对值符号,使不等式变为不含绝对值符号的⼀般不等式,⽽后,其解法与⼀般不等式的解法相同。
因此掌握去掉绝对值符号的⽅法和途径是解题关键。
1利⽤定义法去掉绝对值符号根据实数含绝对值的意义,即|x |=(0)(0)x x x x ≥??-(0)c x c c c -<<>≤?;|x |>c (0)0(0)(0)x c x c c x c x R c <->>??≠=∈或2利⽤不等式的性质去掉绝对值符号利⽤不等式的性质转化|x |c (c >0)来解,如|ax b +|>c (c >0)可为ax b +>c 或ax b +<-c ;|ax b +|对于含绝对值的双向不等式应化为不等式组求解,也可利⽤结论―a ≤|x |≤b ?a ≤x ≤b 或-b ≤x ≤-a ‖来求解,这是种典型的转化与化归的数学思想⽅法。
3利⽤平⽅法去掉绝对值符号对于两边都含有―单项‖绝对值的不等式,利⽤|x |2=2x 可在两边脱去绝对值符号来解,这样解题要⽐按绝对值定义去讨论脱去绝对值符号解题更为简捷,解题时还要注意不等式两边变量与参变量的取值范围,如果没有明确不等式两边均为⾮负数,需要进⾏分类讨论,只有不等式两边均为⾮负数(式)时,才可以直接⽤两边平⽅去掉绝对值,尤其是解含参数不等式时更必须注意这⼀点。
4利⽤零点分段法去掉绝对值符号所谓零点分段法,是指:若数1x ,2x ,……,n x 分别使含有|x -1x |,|x -2x |,……,|x -n x |的代数式中相应绝对值为零,称1x ,2x ,……,n x 为相应绝对值的零点,零点1x ,2x ,……,n x 将数轴分为m +1段,利⽤绝对值的意义化去绝对值符号,得到代数式在各段上的简化式,从⽽化为不含绝对值符号的⼀般不等式来解,即令每项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集。
语法知识—有理数的基础测试题附答案解析

一、填空题1.数轴上,如果点A 表示–78,点B 表示–67,那么离原点较近的点是__________.(填A 或B )2.如图,点A 、点B 在数轴上表示的数分别是-4和4.若在数轴上存在一点P 到A 的距离是点P 到B 的距离的3倍,则点P 所表示的数是 ______.3.有理数a 、b 、c 在数轴如图所示,且a 与b 互为相反数,则|b+c|-|a-c|= ______.4.如图,将直径为1个单位长度的圆从原点处沿着数轴无滑动的逆时针滚动一周,使圆上的点A 从原点运动至数轴上的点B ,则点B 表示的数是_______.5.﹣(﹣82)=_____;﹣(+3.73)=_____;﹣(﹣27)=_____.6.12的相反数是_____;_____的相反数是﹣234;﹣23的绝对值是_____.7.已知|x|=3,y 2=16,xy <0,则x ﹣y=_____.8.数轴上点A 距原点3个单位,将点A 向左移动7个单位,再向右移动2个单位到达B 点,则点B 所表示的数是_____. 9.比较大小:_____.(填“<”或“>”).10.如果(2m ﹣6)x |m|﹣2=m 2是关于x 的一元一次方程,那么m 的值是_____. 11.若21(2)03x y -++=,则y =________; 12.已知m ,n 满足关系式(m ﹣6)2+|n+2|=0,则2m ﹣3n 的值为_____.二、解答题13.在湖北抗洪抢险中,解放军战士的冲锋舟加满油沿东西方向的河流抢救灾民,早晨从A 地出发,晚上到达B 地,约定向东为正方向,当天的航行路程记录如下(单位:千米):+14,﹣9,+8,﹣7,+13,﹣6,+12,﹣5. (1)请你帮忙确定B 地相对于A 地的方位? (2)救灾过程中,冲锋舟离出发点A 最远处有多远?(3)若冲锋舟每千米耗油0.5升,油箱容量为28升,求冲锋舟当天救灾过程中至少还需补充多少升油?14.(1)画出数轴,并在数轴上画出表示下列各数的点:﹣4.5,﹣2,3,0,4; (2)用“<”号将(1)中各数连接起来;(3)直接填空:数轴上表示3和表示1的两点之间的距离是_____,数轴上A 点表示的数为4,B 点表示的数为﹣2,则A 、B 之间的距离是_____. 15.阅读下列材料:我们知道x 的几何意义是在数轴上数x 对应的点与原点的距离,即x =0x -,也就是说,x 表示在数轴上数x 与数0对应的点之间的距离;这个结论可以推广为12x x -表示在数轴上数1x 与数2x 对应的点之间的距离;例1.解方程|x |=2.因为在数轴上到原点的距离为2的点对应的数为2±,所以方程|x |=2的解为2x =±.例2.解不等式|x -1|>2.在数轴上找出|x -1|=2的解(如图),因为在数轴上到1对应的点的距离等于2的点对应的数为-1或3,所以方程|x -1|=2的解为x =-1或x =3,因此不等式|x -1|>2的解集为x <-1或x >3.例3.解方程|x -1|+|x +2|=5.由绝对值的几何意义知,该方程就是求在数轴上到1和-2对应的点的距离之和等于5的点对应的x 的值.因为在数轴上1和-2对应的点的距离为3(如图),满足方程的x 对应的点在1的右边或-2的左边.若x 对应的点在1的右边,可得x =2;若x 对应的点在-2的左边,可得x =-3,因此方程|x -1|+|x +2|=5的解是x =2或x =-3.参考阅读材料,解答下列问题: (1)方程|x +3|=4的解为 ; (2)解不等式:|x -3|≥5; (3)解不等式:|x -3|+|x +4|≥9 16.比较下列各组数的大小: (1)56-和67-;(2)1()5--和16--.17.有理数a ,b ,c 在数轴上的位置如图所示,且|a|=|b|. (1)求a+b 与ab的值; (2)化简|c ﹣a|+|c ﹣b|+|a+b|.18.慈善篮球赛,每个队员的得分以20分为标准,超过的部分记为正,不足的部分记为负,已知5位主力队员得分情况分别是(单位:分):4,2,3,﹣7,﹣1. (1)这5位主力队员中,最低得分是多少分?(2)若主力队员每得1分赞助商就额外捐款2000元,那么本次慈善篮球赛赞助商共额外捐款多少元?19.已知a ,b 互为相反数,|m |=3,求34a bm +-的值. 三、1320.已知点P 的坐标为(a ,b )(a >0),点Q 的坐标为(c ,3),且|a ﹣c|+7b -=0,将线段PQ 向右平移a 个单位长度,其扫过的面积为20,那么a+b+c 的值为( ) A .12 B .15 C .17 D .20 21.数轴上与数2-所对应的点相距4个单位长度的点表示的数是( )A .2B .4C .6-D .6-或222.若|x-2y|+2-y =0,则(-xy) 2的值为( )A .64B .-64C .16D .-1623.﹣2018的绝对值是( ) A .±2018B .﹣2018C .﹣12018D .201824.实数a ,b 在数轴上的位置如图所示,以下说法正确的是( )A .|b |<|a |B .a +b=0C .b <aD .ab >025.已知点P(x ,y)的坐标满足|x|=3y ,且xy <0,则点P 的坐标是( ) A .()3,2-B .()3,2-C .()3,4-D .()3,4-【参考答案】***试卷处理标记,请不要删除一、填空题1.B 【分析】讨论谁离原点较近即比较两个数的绝对值的大小【详解】∵|﹣|==|﹣|==∴点B 离原点较近故答案为B 【点睛】理解绝对值的意义会正确计算一个数的绝对值 解析:B 【分析】讨论谁离原点较近,即比较两个数的绝对值的大小. 【详解】∵|﹣78|=78=4956,|﹣67|=67=4856,∴点B 离原点较近.故答案为B . 【点睛】理解绝对值的意义,会正确计算一个数的绝对值.2.2或8【分析】根据题意得到方程再对P 点的值进行分段讨论即可得解【详解】设P 所表示的数为x 由题意可得|x-(-4)|=3|x-4|当x≤-4时方程可化为-4-x=-3x+12∴x=8(舍);当-4<x解析:2或8【分析】根据题意得到方程,再对P点的值进行分段讨论,即可得解.【详解】设P所表示的数为x,由题意可得|x-(-4)|=3|x-4|.当x≤-4时,方程可化为-4-x=-3x+12,∴x=8(舍);当-4<x≤4时,方程可化为x+4=-3x+12,∴x=2;当x>4时,方程可化为x+4=3x-12,∴x=8.故答案为2或8.【点睛】本题主要考查数轴与绝对值结合,关键在于取零点再分区间化简绝对值方程.3.0【解析】由数轴上的点以及已知可得:b<0<a<c|b|=|a|<|c|a+b=0∴b+c>0a-c<0∴|b+c|-|a-c|=(b+c)--(a-c)=b+c+a-c=0故答案为0【点睛】本题考解析:0【解析】由数轴上的点以及已知可得:b<0<a<c,|b|=|a|<|c|,a+b=0,∴b+c>0,a-c<0,∴|b+c|-|a-c|=(b+c)-[-(a-c)]=b+c+a-c=0,故答案为0.【点睛】本题考查了绝对值、数轴、相反数等,解题的关键是要注意借助数轴用几何方法化简含有绝对值的式子.4.-π【解析】【分析】因为圆从原点沿数轴向左滚动一周可知OA=π再根据数轴的特点即可解答【详解】解:∵直径为1个单位长度的圆从原点沿数轴向左滚动一周∴OA之间的距离为圆的周长=πA点在原点的左边∴A点解析:-π【解析】【分析】因为圆从原点沿数轴向左滚动一周,可知OA=π,再根据数轴的特点即可解答.【详解】解:∵直径为1个单位长度的圆从原点沿数轴向左滚动一周,∴OA之间的距离为圆的周长=π,A点在原点的左边.∴A点对应的数是-π.∴点B表示的数是-π故答案为-π.【点睛】此题考查了数轴,关键是熟悉数轴的特点及圆的周长公式.5.﹣373【解析】分析:根据一个数的相反数就是在这个数前面添上-号求解即可详解::-(-82)=82;-(+373)=-373;-(-)=故答案为:82-373点睛:本题考查了相反数的意义一个数的相反解析:﹣3.732 7【解析】分析: 根据一个数的相反数就是在这个数前面添上“-”号,求解即可.详解::-(-82)=82;-(+3.73)=-3.73;-(-27)=27,故答案为:82,-3.73,2 7 .点睛: 本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号:一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.不要把相反数的意义与倒数的意义混淆.6.﹣122【解析】分析:相反数的定义:只有符号不同的两个数互为相反数0的相反数是0;绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0详解:12的相反数是-12;-解析:﹣1223423.【解析】分析: 相反数的定义:只有符号不同的两个数互为相反数,0的相反数是0;绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.详解:12的相反数是-12;-234的相反数是234;|-23|=23.点睛: 主要考查相反数,绝对值的概念及性质.7.±7【解析】分析:本题是绝对值平方根和有理数减法的综合试题同时本题还渗透了分类讨论的数学思想详解:因为|x|=3所以x=±3因为y2=16所以y=±4又因为xy<0所以xy异号当x=3时y=-4所以解析:±7【解析】分析:本题是绝对值、平方根和有理数减法的综合试题,同时本题还渗透了分类讨论的数学思想.详解:因为|x|=3,所以x=±3.因为y2=16,所以y=±4.又因为xy<0,所以x、y异号,当x=3时,y=-4,所以x-y=7;当x=-3时,y=4,所以x-y=-7.故答案为:±7.点睛:本题是一道综合试题,本题中有分类的数学思想,求解时要注意分类讨论.8.﹣2或﹣8【解析】分析:根据题意可以求得点A 表示的数从而可以得到点B 表示的数本题得以解决详解:由题意可得点A 表示的数是3或-3∴当A 为3时点B 表示的数为:3-7+2=-2当A 为-3时点B 表示的数为:解析:﹣2或﹣8【解析】分析:根据题意可以求得点A 表示的数,从而可以得到点B 表示的数,本题得以解决.详解:由题意可得, 点A 表示的数是3或-3,∴当A 为3时,点B 表示的数为:3-7+2=-2, 当A 为-3时,点B 表示的数为:-3-7+2=-8, 故答案为:-2或-8.点睛:本题考查数轴,解答本题的关键是明确数轴的特点,利用数轴的知识解答.9.<【解析】分析:作差比较大小详解:-58--47=-356<0故-58<-47点睛:比较大小的方法:(1)作差比较法:a-b>0⟹a>b;a-b<0⇒a<b(ab 可以是数也可以是一个式子)(2)作商解析:< 【解析】分析:作差比较大小. 详解:,故.点睛:比较大小的方法: (1)作差比较法:;(可以是数,也可以是一个式子)(2)作商比较法:若a >0,b >0,且,则a >b ;若a <0,b <0,且,则a <b .10.﹣3【解析】由题意得:|m|﹣2=1且2m ﹣6≠0解得:m=﹣3故答案为﹣3解析:﹣3 【解析】由题意得:|m |﹣2=1,且2m ﹣6≠0, 解得:m=﹣3, 故答案为﹣3.11.【解析】∵∴x-2=0=0∴x=0y=-故答案是:- 解析:13-【解析】 ∵()21203x y -++=,∴x-2=0,13y =0,∴x=0,y=-1 3 ,故答案是:-1 3 .12.【解析】解:∵(m﹣6)2+|n+2|=0∴m=6n=﹣22m﹣3n=2×6﹣3×(﹣2)=18故答案为:18点睛:本题主要考查了偶次方的性质以及绝对值的性质正确把握相关定义是解题的关键解析:【解析】解:∵(m﹣6)2+|n+2|=0,∴m=6,n=﹣2,2m﹣3n=2×6﹣3×(﹣2)=18.故答案为:18.点睛:本题主要考查了偶次方的性质以及绝对值的性质,正确把握相关定义是解题的关键.二、解答题13.(1)B地在A地的东边20千米;(2)最远处离出发点25千米;(3)还需补充的油量为9升.【分析】(1)把题目中所给数值相加,若结果为正数则B地在A地的东方,若结果为负数,则B 地在A地的西方;(2)分别计算出各点离出发点的距离,取数值较大的点即可;(3)先求出这一天走的总路程,再计算出一共所需油量,减去油箱容量即可求出途中还需补充的油量.【详解】(1)∵14-9+8-7+13-6+12-5=20,∴B地在A地的东边20千米.(2)∵路程记录中各点离出发点的距离分别为14千米,14-9=5(千米),14-9+8=13(千米),14-9+8-7=6(千米),14-9+8-7+13=19(千米),14-9+8-7+13-6=13(千米),14-9+8-7+13-6+12=25(千米),14-9+8-7+13-6+12-5=20(千米).∴最远处离出发点25千米.(3)这一天走的总路程为14+|-9|+8+|-7|+13+|-6|+12+|-5|=74(千米),耗油74×0.5=37(升),37-28=9(升),故还需补充的油量为9升.本题考查的是正数与负数的定义,解答此题的关键是熟知用正负数表示两种具有相反意义的量,注意所走总路程一定是绝对值的和.14.(1)见解析(2)-4.5<-2<0<3<4;(3)2,6.【解析】分析:(1)利用数轴确定表示各数的点的位置即可;(2)根据在数轴上表示的两个有理数,右边的数总比左边的数大用“<”号将各数连接即可;(3)结合数轴可直接得到答案.详解:(1)如图:;(2)-4.5<-2<0<3<4;(3)数轴上表示3和表示1的两点之间的距离是2,数轴上A点表示的数为4,B点表示的数为-2,则A、B之间的距离是6,故答案为2;6.点睛:此题主要考查了数轴,关键是正确确定表示各数的点的位置.15.(1)x=1或x=-7(2)x≤-2或x≥8(3)x≥4或x≤-5【解析】分析:(1)利用在数轴上到-3对应的点的距离等于4的点对应的数为1或-7求解即可;(2)先求出|x-3|=5的解,再求|x-3|≥5的解集即可;(3)先在数轴上找出|x-3|+|x+4|=9的解,即可得出不等式|x-3|+|x+4|≥9的解集.详解:(1)∵在数轴上到-3对应的点的距离等于4的点对应的数为1或-7,∴方程|x+3|=4的解为x=1或x=-7.(2)在数轴上找出|x-3|=5的解.∵在数轴上到3对应的点的距离等于5的点对应的数为-2或8,∴方程|x-3|=5的解为x=-2或x=8,∴不等式|x-3|≥5的解集为x≤-2或x≥8.(3)在数轴上找出|x-3|+|x+4|=9的解.由绝对值的几何意义知,该方程就是求在数轴上到3和-4对应的点的距离之和等于9的点对应的x的值.∵在数轴上3和-4对应的点的距离为7,∴满足方程的x对应的点在3的右边或-4的左边.若x对应的点在3的右边,可得x=4;若x对应的点在-4的左边,可得x=-5,∴方程|x-3|+|x+4|=9的解是x=4或x=-5,∴不等式|x-3|+|x+4|≥9的解集为x≥4或x≤-5.点睛:本题主要考查了绝对值及不等式的知识,解题的关键是理解|x1-x2|表示在数轴上数x1与数x2对应的点之间的距离.16.(1)>;(2)>分析: (1)根据两个负数,绝对值大的其值反而小进行比较即可; (2)根据正数大于一切负数可得答案. 详解: (1)∵﹣56=﹣3542,﹣67=﹣3642,∴﹣56>﹣67; (2)∵(﹣15)=15,﹣|﹣16|=﹣16, ∴﹣(﹣15)>﹣|﹣16|. 点睛: 此题主要考查了有理数的比较大小,关键是掌握法则比较:正数都大于0,负数都小于0,正数大于一切负数.两个负数比较大小,绝对值大的反而小. 17.(1)0;-1;(2)b-a . 【分析】根据有理数a ,b ,c 在数轴上的位置来求值与化简. 【详解】解:(1)根据|a|=|b|,结合数轴得:a 与b 互为相反数, 即a+b=0,ba=﹣1; (2)根据数轴上点的位置得:a <0<c <b ,且a+b=0, ∴c ﹣a >0,c ﹣b <0, 则|c ﹣a|+|c ﹣b|+|a+b| =c ﹣a+b ﹣c+0 =b ﹣a .18.(1)13;(2)202000元.【解析】试题分析:(1)首先比较出4,2,3,-7,-1的大小关系,判断出-7最小,然后用20加上-7,即可求出这5位主力队员中,最低得分是多少分.(2)用5位主力队员一共得到的分数乘主力队员每得1分赞助商就额外捐款的钱数,求出本次慈善篮球赛赞助商共额外捐款多少元即可. 试题解析:解:(1)-7<-1<2<3<4, 20+(-7)=13(分).答:这5位主力队员中,最低得分是13分; (2)4+2+3+(-7)+(-1)=1, (20×5+1)×2000 =101×2000 =202000(元)答:本次慈善篮球赛赞助商共额外捐款202000元.点睛:此题主要考查了正数、负数的含义和应用,以及有理数大小比较的方法,要熟练掌握.19.±9.【解析】试题分析:根据相反数和绝对值的性质得出a+b=0、m=2或-2,再分情况分别代入计算即可.试题解析:解:根据题意知a+b=0、m=3或m=﹣3,当m=3时,原式=04﹣3×3=0﹣9=﹣9;当m=﹣3时,原式=04﹣3×(﹣3)=0+9=9.点睛:本题主要考查代数式求值,解题的关键是根据相反数和绝对值的性质得到a+b=0、m=3或m=﹣3.三、1320.C解析:C【分析】由非负数的性质得到a=c,b=7,P(a,7),故有PQ∥y轴,PQ=7-3=4,由于其扫过的图形是矩形可求得a,代入即可求得结论.【详解】∵且|a-c|+,∴a=c,b=7,∴P(a,7),PQ∥y轴,∴PQ=7-3=4,∴将线段PQ向右平移a个单位长度,其扫过的图形是边长为a和4的矩形,∴4a=20,∴a=5,∴c=5,∴a+b+c=5+7+5=17,故选C.【点睛】本题主要考查了非负数的性质,坐标的平移,矩形的性质,能根据点的坐标判断出PQ∥y 轴,进而求得PQ是解题的关键.21.D解析:D【分析】根据题意得出两种情况:当点在表示−2的点的左边时,当点在表示−2的点的右边时,列出算式求出即可.【详解】分为两种情况:①当点在表示−2的点的左边时,数为−2−4=−6;②当点在表示−2的点的右边时,数为−2+4=2;故选D.【点睛】本题考查了数轴的应用,注意符合条件的有两种情况,不要漏数.22.A解析:A【解析】分析:先根据非负数的性质列出方程组,求出x、y的值,然后将x、y代入(-xy)2中求解即可.详解:由题意,得:2020x yy-=⎧⎨-=⎩,解得42 xy=⎧⎨=⎩;∴(-xy)2=(-4×2)2=64.故选:A.点睛:此题主要考查了非负数的性质,初中阶段有三种类型的非负数:绝对值、偶次方、二次根式(算术平方根).当它们相加和为0时,必须满足其中的每一项都等于0. 23.D解析:D【解析】分析:根据绝对值的定义解答即可,数轴上,表示一个数a的点到原点的距离叫做这个数的绝对值.详解:﹣2018的绝对值是2018,即20182018-=.故选D.点睛:本题考查了绝对值的定义,熟练掌握绝对值的定义是解答本题的关键,正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0.24.A解析:A【解析】解:由数轴可知:﹣2<a<﹣1,0<b<1,|b|<|a|,a+b<0,b>a,ab<0,正确的是A选项.故选A.25.D解析:D【解析】试题解析:∵|x|=3,∴x=3或-3,y=4,∵xy<0,∴x=-3,y=4,∴点P的坐标为(-3,4),故选D.考点:点的坐标.。
人教版七年级数学数轴和绝对值化简

人教版七年级数学数轴和绝对值化简
1.实数a,b,c在数轴上的位置如图所示,化简||||||||
-+-+-.
c a b a
2.如图,数轴上的两点A,B分别表示有理数a,b,
(1)(用“>”或“=”或“<”填空):a b
-0;
+0,b a
(2)化简:||||
+--.
a b b a
3.有理数a、b、c在数轴上的位置如图:
(1)判断正负,用“>”或“<”填空:b c
+0,c a
-0,a b
-0.(2)化简:||||||
b c a b c a
-++--.
4.若用点A ,B ,C 分别表示有理数a ,b ,c ,它们在数轴上的位置如图所示.
(1)比较a ,b ,c 的大小(用“<”连接)
(2)请在横线上填上>,<或:a b =+ 0,b c - 0;
(3)化简:2||||||c a b c b c a +++---.
5.已知a 、b 、c 在数轴上对应的点如图所示,
(1)化简:2||||||||b c b c a c a b --++---;
(2)若2(4)c +与|10|a c ++互为相反数,且||b a c =-,求(1)中式子的值.
6.同学们都知道,|4(2)|--表示4与2-的差的绝对值,实际上也可理解为4与2-两数在数轴上所对应的两点之间的距离;同理|3|x -也可理解为x 与3两数在数轴上所对应的两点之间的距离.试探索:
(1)求|4(2)|--= ;
(2)若|2|5x -=,则x = ;
(3)请你找出所有符合条件的整数x ,使得|1||2|3x x -++=.。
根据数轴去绝对值

(2)化简:|b|+|a+c|-|a|;
练习巩固
1、如图,a,b在数轴上的位置如图所示.
(1)请用“>”、“<”判断下列代数式的大小,a0,c﹣a0,b+c0;
(2)试化简:|a|+|c﹣a|﹣|b+c|。
2、有理数a,b、c在数轴Leabharlann 的位置如图:根据数轴去绝对值
一、基础知识
1、绝对值的性质2、绝对值的几何意义
2、根据数轴去绝对值方法:
先根据数轴判断绝对值里面式子的正负,再根据绝对值的代数意义依次化简。
3、如何判断绝对值里面式子的正负:
① 如果绝对值里面的两数是相加的,利用加法法则,判断正负性;
② 如果绝对值里面的两数是相减的,那么左边的数减去右边的数,差为负;右边的数减去左边的数,差为正
(1)判断正负,用“>”或“<”填空:b-c0,a+b0,c-a0。
(2)化简:|b-c|+|a+b|-|c-a|。
3、有理数a<0、b>0、c>0,且|b|<|a|<|c|,
(1)在数轴上将a、b、c三个数填在相应的括号中。
(2)(用“>”或“=”或“<”填空):2a﹣b0,b﹣c0,c﹣a0。
(3)化简:|2a﹣b|+|b﹣c|﹣|c﹣a|。
(1)一察:第一步观察数轴,确定数轴上的数的符号(是正是负)以及离原点的远近(绝对值的大小);
(2)二判:第二步判断绝对值内式子的符号(是正是负);
(3)三去号:第三步根据绝对值的性质去绝对值(注意:绝对值内的式子要看作一个整体);
(4)合并化简别忘掉:最后一步去括号,合并化简要记好。
例3、已知三个有理数a,b,c在数轴上的对应点如图所示,且满足|b|=|c|。
(完整版)利用数轴化简绝对值

利用数轴化简绝对值 1. 如果有理数a 、b 、c 在数轴上的位置如图所示,求a b a c b c ++--+的值. b -1 c 0 a 12.数a b ,在数轴上对应的点如右图所示,试化简a b b a b a a ++-+--b0a3.实数a b c ,,在数轴上的对应点如图,化简a c b a b a c +--++-0cb a课堂检测:1.实数a 、b 、c 在数轴上的位置如图所示,则代数式 的值等于( ).(A ) (B ) (C ) (D )2.已知有理数c b a ,,在数轴上的对应点的位置如图所示:那么求a c c b b a -+---的值a c x0 b3.有理数c b a ,,在数轴上对应的点(如下图),图中O 为原点,化简a c b b a b a --+++-。
4.a 、b 、c 的大小关系如图所示,求a b b c c a ab ac a b b c c a ab ac-----++----的值. c 10b a5.若用A 、B 、C 、D 分别表示有理数a 、b 、c ,0为原点。
如图所示,已知a<c<0,b>0。
化简下列各式:(1)||||||a c b a c a -+---;(2)||||||a b c b a c -+---+-+;(3)2||||||c a b c b c a +++---a c x0 b已知数轴上两点A、B对应的数分别为—1,3,点P为数轴上一动点,其对应的数为x. (1)若点P到点A、点B的距离相等,求点P对应的数;(2)数轴上是否存在点P,使点P到点A、点B的距离之和为5?若存在,请求出x的值。
若不存在,请说明理由?(3)当点P以每分钟一个单位长度的速度从O点向左运动时,点A以每分钟5个单位长度向左运动,点B一每分钟20个单位长度向左运动,问它们同时出发,几分钟后P点到点A、点B的距离相等?如图,已知A、B分别为数轴上两点,A点对应的数为—20,B点对应的数为100。
七年级数学上册专题提分精练数轴和绝对值的化简结合(解析版)

专题10 数轴和绝对值的化简结合1.已知实数m 在数轴上的位置如图所示,则化简|2||1|m m +--的结果为( )A .21m +B .21m --C .3-D .3【答案】A【解析】【分析】根据数轴,判断m 是负数,且|m |<1,从而判定m -1<0,m +2>0,化简即可.【详解】∵, ∴m <0,且|m |<1,∴m -1<0,m +2>0,∴|2||1|21=21m m m m m +--=+-++,故选A .【点睛】本题考查了数轴的意义,绝对值的化简,正确获取数轴信息,熟练化简绝对值是解题的关键. 2.已知a ,b 两数在数轴上的位置如图所示,则化简代数式12b a a b -----的结果是( )A .1B .2a ﹣3C .-1D .2b ﹣1 【答案】C【解析】【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,即可得到结果.【详解】解:由数轴可知b <−1,1<a <2,∴b -a <0,1-a <0,b -2<0, 则()()()1212121b a a b a b a b a b a b -----=-----=--+-+=-.故选:C .【点睛】此题考查了整式的加减,数轴,以及绝对值,判断出绝对值里边式子的正负是解本题的关键. 3.实数a ,b ,c ,在数轴上的位置如图所示,化简:a b c a b c ---+-的结果是( )A .0B .aC .bD .c【答案】A【解析】【分析】根据数轴上点的位置可知000a b c a b c -<->-<,,,由此求解即可.【详解】 解:由题意得:0a b c a b c <<<>>,, ∴000a b c a b c -<->-<,, ∴a b c a b c ---+-()=b a c a c b ---+-b ac a c b =--++-0=,故选A .【点睛】本题主要考查了根据数轴上点的位置化简绝对值,正确得出000a b c a b c -<->-<,,是解题的关键.4.有理数a ,b ,c 在数轴上的位置如图所示,则a c ++c b --b a +=( )A .-2bB .0C .2D .2c -2b【答案】B【解析】【分析】先由数轴确定a 、b 、c 的符号,进而确定每个绝对值里面的代数式的符号,然后根据绝对值的性质化简绝对值,再进行整式的加减运算即得答案.【详解】解:由图示得:a <0,b <0,c >0,a c >,则a +c <0,c -b >0,b +a <0,所以()()()0a c c b b a a c c b a b a c c b a b ++--+=-++---+=--+-++=⎡⎤⎣⎦故选:B .【点睛】本题考查了绝对值的化简和整式的加减运算,解题的关键是根据加减法则确定代数式的符号并正确的进行绝对值的化简.5.有理数a 、b 、c 在数轴上位置如图,则a c a b b c --++-的值为( ).A .2aB .222a b c +-C .0D .2c -【答案】A【解析】【分析】根据数轴,确定每个数的属性,每个代数式的属性,后化简即可.【详解】根据数轴上点的位置得:0b c a <<<,且a b <,则0a c ->,0a b +<,0b c -<, 则2a c a b b c a c a b b c a --++-=-++-+=.故选A .【点睛】本题考查了数轴和有理数的大小比较与绝对值的化简,掌握获取数轴信息,熟练化简是解题的关键.6.如图,数轴上的三点A ,B ,C 分别表示有理数a ,b ,c ,则化简|a -b |-|c -a |+|b -c |的结果是( )A .2a -2cB .0C .2a -2bD .2b -2c 【答案】B【解析】【分析】根据数轴,得到信息为a <b <0<c ,化简绝对值即可.【详解】∵a <b <0<c ,∴a -b <0,b -c <0,c -a >0,∴|a -b |-|c -a |+|b -c |=b -a -c +a +c -b=0,故选B .本题考查了数轴,有理数的大小比较,绝对值的化简,正确读取数轴信息,准确进行绝对值的化简是解题的关键.7.已知a 、b 、c 的大致位置如图所示:化简a c b c a b ++---的结果是( )A .222a c b +-B .0C .22c b -D .2c 【答案】D【解析】【分析】根据数轴判断出a ,b ,c 的符号,求得a +c 、b -c 、a -b 的符号,然后化简求解即可.【详解】解:由数轴可得:0b a c <<<,0a c +>∴0b c -<,0a b ->, ∴()()()2a c b c a b a c b c a b a c b c a b c ++---=+----=+-+-+=故选:D【点睛】此题考查了数轴以及绝对值,涉及了去括号法则以及合并同类项法则,熟练掌握运算法则是解本题的关键.8.有理数a ,b 在数轴上对应的位置如图所示,那么代数式11a b a b a b a b -++--+的值是( )A .-1B .1C .3D .-3【答案】D【解析】【分析】先根据数轴求出-1<a <0,0<b <1,|a |<|b |,再去掉绝对值,然后根据分式的性质计算即可.【详解】解:根据数轴可知:-1<a <0,0<b <1,|a |<|b |, ∴原式11a b a b a b a b --+=+--+ 111=---3=-.故选:D .本题考查了代数式的化简、数轴和去绝对值的计算,解题的关键是注意去掉绝对值后,要保证得数是非负数.9.有理数a 在数轴上的对应点的位置如图所示,化简2a a --的结果是______.【答案】2-【解析】【分析】由题意可得a >2,利用绝对值化简可求解.【详解】解:由题意可得:a >2,222,a a a a --=--=-∴故答案为:2-【点睛】本题考查绝对值的化简,利用数轴比较数的大小从而正确化简计算是解题关键. 10.已知:数a ,b ,c 在数轴上的对应点如图所示,化简|b ﹣a |+|b ﹣c |=_____.【答案】a c -##-c +a【解析】【分析】由数轴可知a ,b ,c 的大小关系,进而可知绝对内代数式的正负性,进而可得到答案.【详解】解:由数轴可知0a b c >>>∴0,0b a b c --<>∴原式=()b a b c a c --+-=-故答案为:a c -.【点睛】本题考查化简绝对值,熟练掌握相关知识是解题的关键.11.在数轴上,表示实数a 、b 的点的位置如图所示,化简:a b b a -+-= ___________【答案】2a【分析】a 、b 在原点的两侧,a 为正数,b 为负数,且b -a <0,由此根据绝对值的意义和有理数的加减法计算方法化简即可.【详解】解:由实数a 、b 在数轴上的位置可知,b <0<a ,b -a <0,∴|a |-|b |+|b −a |=a -(-b )−(b −a )=a +b −b +a=2a故答案为:2a .【点睛】此题考查整式的加减,绝对值的意义,以及有理数的加减法计算方法,解题的关键是读懂数轴,得到a ,b ,b -a 的符号.12.已知,数a 、b 、c 的大小关系如图所示:化简||||2||3||a c b a a c b c +----+-=____.【答案】222a b c -+【解析】【分析】【详解】由数轴可得:b <0,0<a <c ,∴(a +c )>0,(b -a )<0,(a -c )<0,(b -c )<0,∴||||2||3||a c b a a c b c +----+-=a +c -(a -b )-2(c -a )+3(c -b )=a +c -a +b -2c +2a +3c -3b =2a -2b +2c ,故答案为:2a -2b +2c .【点睛】本题考查了化简绝对值及整式的加减;根据数轴判断子式的正负是解题的关键. 13.有理数a ,b ,c 在数轴上表示的点如图所示,则化简22b c a b c a +----=______.【答案】4a -b【解析】根据数轴可以判断a、b、c的正负和它们的绝对值的大小,从而可以化简题目中的式子.【详解】解:由数轴可得,a<b<c,|b|<|c|<|a|,∴|b+c|﹣2|a﹣b|﹣|c﹣2a|=b+c﹣2(b﹣a)﹣(c﹣2a)=b+c﹣2b+2a﹣c+2a=4a-b.【点睛】本题考查数轴、绝对值,解答本题的关键是明确题意,利用数形结合的思想解答.14.已知有理数a,b在数轴上的位置如图,化简:|2﹣3b|﹣2|2+b|+|a+2|﹣|3b﹣2a|的结果为_____.【答案】8+2b﹣a.【解析】【分析】根据有理数a,b在数轴上的位置可判断绝对值内部各代数式的正负,进而对绝对值进行化简计算即可.【详解】解:根据有理数a,b在数轴上的位置可知:2﹣3b>0,2+b<0,a+2>0,3b﹣2a<0,∴|2﹣3b|﹣2|2+b|+|a+2|﹣|3b﹣2a|=2﹣3b+2(2+b)+a+2+(3b﹣2a)=2﹣3b+4+2b+a+2+3b﹣2a=8+2b﹣a,故答案为:8+2b﹣a.【点睛】本题考查整式的加减,根据点在数轴的位置判断式子的正负,有理数的加法运算和有理数的减法运算,化简绝对值.解题关键是能根据有理数a,b在数轴上的位置,结合有理数的加法运算和有理数的减法运算判断绝对值内各式子的符号,据此化简绝对值.15.已知x、y两数在数轴上表示如图.化简:|2x-3y|-|y|+|x|.【答案】3x﹣2y【解析】【分析】由y<0<x,得到2x-3y>0,然后利用绝对值的代数意义将所求式子化简,合并后即可得到结果.【详解】解:由数轴可得y<0<x,|y|<|x|,∴2x-3y>0,∴|2x-3y|-|y|+|x|=2x-3y+y+x=3x-2y.【点睛】此题考查了数轴以及有理数比较大小,涉及到的知识有:绝对值的代数意义,去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.16.已知A,B,C三点在数轴上如图所示,它们表示的数分别是a,b,c.且|a|<|b|.(1)填空:abc0,a+b0(填“>”“<”或“=”).(2)化简:|a﹣b|﹣2|a+b|+|b﹣c|.【答案】(1)<,>;(2)﹣3a﹣2b+c【解析】【分析】(1)根据数轴上点的位置可知a <0,b>0,c>0,|c|>|b|>|a|,由此求解即可;(2)根据绝对值的含义和求法,化简|a﹣b|﹣2|a+b|+|b﹣c|即可.(1)根据数轴上A、B、C三点的位置,可知a<0<b<c,且|c|>|b|>|a|,∴abc<0,a+b>0,故答案为:<,>;(2)由题意可知,a﹣b<0,a+b>0,b﹣c<0,∴|a﹣b|﹣2|a+b|+|b﹣c|=b﹣a﹣2(a+b)+c﹣b=b﹣a﹣2a﹣2b+c﹣b=﹣3a﹣2b+c此题主要考查了有理数大小比较的方法,绝对值的含义和求法整式的加减,要熟练掌握以上知识点,同时要明确∶当数轴方向朝右时,右边的数总比左边的数大是解题的关键. 17.已知有理数,,a b c 在数轴上的位置如下图所示,化简:22a c c b b a ++--+【答案】a c +【解析】【分析】由数轴上各数的位置可得a <b <0<c ,|c |<|b |<|a |,再根据加减法运算法则得出a +c 、c -b 、b +a 的符号,再化简绝对值,然后去括号合并同类项即可求解.【详解】解:由数轴知:a <b <0<c ,|c |<|b |<|a |,∴a +c <0,c -b >0,b +a <0, ∴22a c c b b a ++--+=-(a +c )+2(c -b )+2(b +a )=2222a c c b b a --+-++=a c +.【点睛】本题考查数轴、绝对值、式子的符号是解答的关键.18.解答下列各题(1)有8筐白菜,以每筐25千克为标准重量,超过的千克数记作正数,不足的千克数记作负数,称后的记录如下:1.5,﹣3,2,﹣0.5,1,﹣1.5,﹣2,﹣2.5.回答下列问题:①与标准重量比较,8筐白菜总计超过多少千克或不足多少千克?②若白菜每千克售价2.6元,则出售这8筐白菜可卖多少元?(2)有理数a 、b 、c 在数轴上的位置如图所示.①用“>”或“<”填空:a +b _____0,c ﹣b______0;②|a +b |=_______,|c |=______,|c ﹣b |=_______;③化简:|a +b |-|c |+|c ﹣b |.【答案】(1)①总计不足5千克;②出售这8筐白菜可卖507元(2)①>,<;②a b +,c -,b c -;③2+a b【分析】(1)①根据有理数加法列式计算,即可求出结果;②先计算这8筐白菜的总重量,再根据单价乘以数量等于总价,即可解答.(2)①先根据数轴先比较出各数的大小,则可得出a b +和c b -与0的关系;②利用①的结果,结合绝对值的非负性,分别去绝对值即可;③利用②的结果,先去绝对值,再合并同类项,即可得出结果.(1)(1)解:①∵()()()()()1.5320.51 1.52 2.5+-++-++-+-+-=()4.59.5+-=5-,∴总计不足5千克;②∵这8筐白菜的总重量=()2585195⨯+-=(千克),∴出售这8筐白菜可卖2.6195507⨯=(元),答:出售8筐白菜可卖507元.(2)解:①由数轴可得:101c a b <-<<<<,∴0a b +>,0c b -<,故答案为:>,<;②∵0a b +>, ∴a b a b ++=,∵0c <, ∴c c -=,∵0c b -<, ∴cb bc =-﹣, 故答案为:a b +,c -,b c - ③a b c c b +-+-=()()()a b c b c +--+-=a b c b c +++-=2+a b .【点睛】本题考查了正数和负数、有理数的加法运算的简单应用,以及与数轴有关的计算,去绝对值和整式运算等知识,理清题中的正数和负数的意义和掌握绝对值的非负性是解答本题的关键.19.已知有理数a 、b 、c 在数轴上的位置如图所示,且a b =(1)求a b +和a b的值 (2)化简:2a a b c a c b b -+--+---【答案】(1)0a b +=;1a b=-;(2)3b . 【解析】【分析】 (1)根据a b =且a 、b 位于原点两侧,得到a 、b 互为相反数,然后进行求解即可; (2)先分别判定绝对值内的数的大小,再去绝对值,再合并同类项即可求解.【详解】(1)∵a b =且a 、b 位于原点两侧∴a 、b 互为相反数∴0a b +=,1a b=- (2)如图可得:c <b <0<a 且||||a b =∴a >0,a=-b 即a+b=0,c -a <0,-b <0,-2b >0因此|||||||||2|a a b c a c b b -+--+---=0()()(2)a a c b c b ---+---=2a a c b c b -++-+=3b【点睛】本题考查了根据数轴取绝对值进行计算的问题,其中根据去掉绝对值是解答本题的关键. 20.已知 a ,b ,c 在数轴上的位置如图所示,则化简|a -b|-|2c+b|+|a+c|.【答案】c .【解析】【分析】根据数轴得出c <b <0<a ,|a|<|c|,所以a -b >0,2c+b <0,a+ c <0,据此去掉绝对值符号,再合并同类项即可;解:∵从数轴可知:c <b <0<a ,|a|<|c|,∴a -b >0,2c+b <0,a+ c <0,∴|a -b|-|2c+b|+|a+c|=a -b -(-2c - b )+(-a -c )= a -b+2c+b -a -c=c ;答案是:c.【点睛】本题考查了数轴和绝对值、合并同类项等知识点,能正确去掉绝对值符号是解此题的关键.21.有理数a 、b 在数轴上的对应点位置如图所示,化简121a b a b ++-++-.【答案】222a b --+【解析】【分析】结合数轴,确定a+1,2-b ,a+b -1的符号是正或负,再结合绝对值的非负性,去掉绝对值符号,最后去括号合并同类项即可完成.【详解】根据数轴,10,20,0a b a b +<->+<121a b a b ++-++-(1)(2)[(1)]a b a b =-++-+-+-121a b a b =--+---+222a b =--+【点睛】本题考查数轴以及绝对值的化简,难度较大,属于易错题,熟练掌握绝对值的非负性以及有理数加减法的运算法则是解题关键.22.已知a 、b 、c 在数轴上位置如图所示:(1)判断正负,用“>”或“<”填空:b -a 0; c -b 0; a +c 0;(2)化简:2b a c b a c ----+【答案】(1)>;<;<;(2)a+3c【解析】(1)先根据数轴判断a 、b 、c 的符号及大小,再根据有理数的加减法,可得答案;(2)由(1)中的判断,再根据绝对值的性质,可化简去掉绝对值,合并同类项,可得答案.【详解】解:(1)由数轴可知c <a <0<b,∴b -a >0; c -b <0; a +c <0;(2)∵b -a >0; c -b <0; a +c <0 ∴2b a c b a c ----+=b -a -(b -c)-2(-a -c)=b -a -b+c+2a+2c=a+3c【点睛】本题考查了绝对值的性质及数轴的有关知识,利用数轴判断出a 、b 、c 的符号及大小关系,再用绝对值的性质化简是解题关键.23.已知,,a b c ,数在数轴上的位置如图所示:(1)化简:a b bc ca abc a b bc ca abc++++; (2)若b a c >>,化简:c a b c b a a c -+--+++.【答案】(1)-3;(2)3a c --【解析】【分析】(1)先判断a 、b 、c 的符号,进而判断相关积的符号,脱去绝对值计算即可;(2)根据条件判断出每一个绝对值内的式子的符号,在根据绝对值的性质脱去绝对值计算即可求解.【详解】解:()1由图中数轴可得0b a c <<<,0,0,0bc ca abc ∴<<> 原式111113a b bc ca abc a b bc ca abc----=++++=----+=-; ()2又b a c >>0,0,0,0c a b c b a a c ∴->+<-<+<∴原式()()()c a b c b a a c =--++--+c a b c b a a c =---+---3a c =--.【点睛】本题考查了绝对值的化简,整式的加减等知识,根据数轴提供的信息判断出绝对值内的符号是解题关键.24.已知a 、b 、c 在数轴上的位置如图所示,(1)用“>”或“<”填空:c b +_________0,ac_________0,abc_________0,ab c +____________0.(2)求代数式a ab abc a ab abc++的值. 【答案】(1) <;<;>;>;(2)1.【解析】【分析】(1)利用有理数的加法和乘法判断式子的符号,即可得到;(2)先去绝对值,然后合并即可.【详解】由数轴可知:b a 0c <<<,b c >(1)0c b +<,0ac <,0abc >,0ab c +>故答案为<,<,>,>;(2)ab 1111a abc a ab abc a ab abc a ab abc++=-++=-++=; 故答案为1-.【点睛】本题考查了有理数的大小比较,有理数的乘除法,有理数的大小比较比较有理数的大小可以利用数轴,它们从左到有的顺序,即从大到小的顺序(在数轴上表示的两个有理数,右边的数总比左边的数大);也可以利用数的性质比较异号两数及0的大小,利用绝对值比较两个负数的大小.也考查了绝对值.。
七年级数学绝对值数形结合(含答案)

绝对值数形结合【1、数轴与实际问题】例1 5个城市的国际标准时间(单位:时)在数轴上表示如下,那么北京时间2006年6月17日上午9时应是( )A 、伦敦时间2006年6月17日凌晨1时B 、纽约时间2006年6月17日晚上22时C 、多伦多时间2006年6月16日晚上20时D 、首尔时间2006年6月17日上午8时解:观察数轴很容易看出各城市与北京...的时差例2在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所。
已知青少年宫在学校东300米处,商场在学校西200米处,医院在学校东500米处。
将马路近似地看成一条直线,以学校为原点,以正东方向为正方向,用1个单位长度表示100米。
① 在数轴上表示出四家公共场所的位置。
② 计算青少年宫与商场之间的距离。
解:(1)(2)青少年宫与商场相距:3-(-2)=5 个单位长度 所以:青少年宫与商场之间的距离=5×100=500(米) 练习1、如图,数轴上的点P 、O 、Q 、R 、S 表示某城市一条大街上的五个公交车站点,有一辆公交车距P 站点3km ,距Q 站点0.7km ,则这辆公交车的位置在( ) A 、R 站点与S 站点之间 B 、P 站点与O 站点之间 C 、O 站点与Q 站点之间 D 、Q 站点与R 站点之间解:判断公交车在P 点右侧,距离P :(-1.3)+3=1.7(km),即在原点O 右侧1.7处,位于Q 、R 间城市名称 时差 北京时间 当地时间纽约 -5-8=-13 17日上午9时 9-13=-4,24-4=20,17日晚上20时 多伦多 -4-8=-12 17日上午9时 9-12=-3,24-3=21,17日晚上21时伦敦 0-8=-8 17日上午9时 9-8=1,16日凌晨1时 首尔9-8=+117日上午9时9+1=10,16日上午10时国际标准时间(时)98-5-4首尔北京伦敦多伦多纽约x商场医院青少年宫学校而公交车距Q 站点0.7km ,距离Q :0.7+1=1.7(km),验证了,这辆公交车的位置在Q 、R 间2、如图,在一条数轴上有依次排列的5台机床在工作,现要设置一个零件供应站P ,使这5台机床到供应站P 的距离总和最小,点P 建在哪?最小值为多少?解: (此题是实际问题,涉及绝对值表示距离,后面会有更深入的理解) 此题揭示了,问题过于复杂时,要“以退为进”,回到问题 的起点,找出规律。
绝对值化简与数轴结合类压轴题
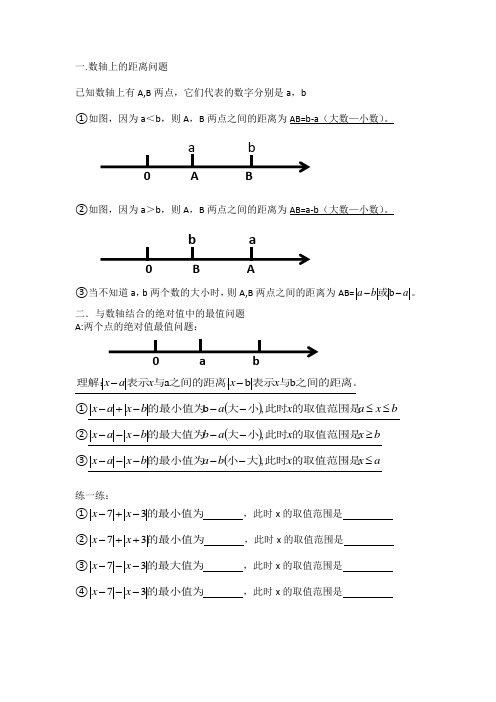
一. 数轴上的距离问题已知数轴上有A,B 两点,它们代表的数字分别是a ,b①如图,因为a <b ,则A ,B 两点之间的距离为AB=b-a (大数—小数)。
②如图,因为a >b ,则A ,B 两点之间的距离为AB=a-b (大数—小数)。
③当不知道a ,b 两个数的大小时,则A,B 两点之间的距离为AB=a b a --b 或。
二.与数轴结合的绝对值中的最值问题A:两个点的绝对值最值问题:之间的距离。
与表示之间的距离,与表示理解:b b a x x x a x -- ①()b x a x a b x a x ≤≤---+-的取值范围是此时小大的最小值为,b ②()b x x a b b x a x ≥-----的取值范围是此时小大的最大值为, ③()a x x b a b x a x ≤-----的取值范围是此时大小的最小值为,练一练: ①的最小值为37-+-x x ,此时x 的取值范围是 ②的最小值为37++-x x ,此时x 的取值范围是 ③的最大值为37---x x ,此时x 的取值范围是 ④的最小值为37---x x ,此时x 的取值范围是B :三个点的绝对值最值问题处取得。
c x = 练一练:()处取得。
最小值在的最小值为=-+-+-x x x x ,345 ()处取得。
最小值在的最小值为=++-+-x x x x ,345C.多个点的最值问题:结论1:当点的各数为奇数个时,最小值在最中间的那个点取得。
如上图:求e x d x c x b x a x -+-+-+-+-的最小值,最小值在c x =处取得,将c x =带入上式即可求得最小值。
练一练:求54321-+-+-+-+-x x x x x 最小值。
结论2:当点的各数为偶数个时,最小值在最中间的那一段的数值中取得。
如上图:求d x c x b x a x -+-+-+-的最小值,最小值在c x ≤≤b 处取得,将x 范围内的任意一个数值带入上式即可求得最小值。
绝对值的化简

“绝对值的化简”例题解析无论是从绝对值的几何定义,还是绝对值的代数定义,都揭示了绝对值的一个重要性质——非负性,也就是说任何一个有理数的绝对值都是非负数,即:无论a取任意有理数都有。
下面关于绝对值的化简题作一探讨。
一、含有一个绝对值符号的化简题1.已知未知数的取值或取值范围进行化简。
如,当时化简(根据绝对值的意义直接化简)解:原式。
2.没有告诉未知数的取值或取值范围进行化简。
如,化简(必须进行讨论)我们把使绝对值符号内的代数式为0的未知数的值叫做界值,显然绝对值符号内代数式是,使的未知数的值是5,所以我们把5叫做此题的界值,确定了界值后,我们就把它分成三种情况进行讨论。
(1)当时,则是一个正数,则它的绝对值应是它本身,所以原式。
(2)当时,则,而0的绝对值为0,所以原式或。
(3)当时,则,是一个负数,而负数的绝对值应是它的相反数,所以原式。
又如,化简此题虽含有一个绝对值符号,但绝对值符号内出现了两个未知数,在这种情况下,我们把含有两个未知数的式子看作一个整体,即把2x +y看作一个整体未知数,找出界值,使的整体未知数的值是,我们把6叫做此题的界值,这样又可分三种情况进行讨论。
(1)当时,(2)当时(3)当时二、含有两个绝对值符号的化简题1.已知未知数的取值或取值范围,进行化简也应根据绝对值的意义直接化简。
如:当时,化简解:原式2.没有告诉未知数的取值或取值范围进行化简也必须进行讨论如:化简的界值为-3,的界值为所以对此类化简题,我们仍从三个方面进行讨论。
解:(1)当时(界值为较大界值,讨论的第(1)种情况为大于大的界值)原式(2)当时,(第(2)种情况为小于小的界值)原式(3)当时(第(3)种情况大于小界值小于大界值)原式又如,化简此题含有两个绝对值符号,且每个绝对值符号内含有两个未知数,且未知数对应项系数相等或成比例,在这种情况下,我们把含有未知数较小的那个式子看作一个整体即把看作一个整体分别求出每个绝对值符号内的界值,仍从三个方面进行讨论。
(必考题)七年级数学上册第一单元《有理数》-填空题专项(含答案解析)

一、填空题1.定义一种正整数的“H运算”:①当它是奇数时,则该数乘3加13;②当它是偶数时,则取该数的一半,一直取到结果为奇数停止.如:数3经过1次“H运算”的结果是22,经过2次“H运算”的结果为11,经过3次“H运算”的结果为46,那么数28经过2020次“H运算”得到的结果是_________.16【分析】从28开始分别按照偶数和奇数的计算法则依次计算直到出现循环即可得解【详解】解:第1次:;第2次:;第3次:;第4次:;第5次:;第6次:;第7次:等于第5次所以从第5次开始奇数次等于1偶解析:16【分析】从28开始,分别按照偶数和奇数的计算法则依次计算,直到出现循环即可得解.【详解】⨯⨯=;解:第1次:280.50.57⨯+=;第2次:371334⨯=;第3次:340.517⨯+=;第4次:3171364⨯⨯⨯⨯⨯⨯=;第5次:640.50.50.50.50.50.51⨯+=;第6次:311316⨯⨯⨯⨯=,等于第5次.第7次:160.50.50.50.51所以从第5次开始,奇数次等于1,偶数次等于16.因为2020是偶数,所以数28经过2020次“H运算”得到的结果是16.故答案为16.【点睛】本题考查了有理数的乘法,发现循环规律,是解题的关键.2.某班同学用一张长为1.8×103mm,宽为1.65×103mm的大彩色纸板制作一些边长为3×102mm的正方形小纸板写标题(不能拼接).则一张这样的大纸板最多能制作符合上述要求的正方形小纸板___________张.30【分析】分别用大彩纸的长宽除以小正方形的边长再取商的整数部相乘即可【详解】解:∵18×103÷(3×102)=6165×103÷(3×102)=55∵纸板张数为整数∴18×103÷(3×102)解析:30【分析】分别用大彩纸的长、宽除以小正方形的边长,再取商的整数部相乘即可.【详解】解:∵1.8×103÷(3×102)=6.1,65×103÷(3×102)=5.5,∵纸板张数为整数,∴1.8×103÷(3×102)=6.1≈6,65×103÷(3×102)=5.5≈5,∴最多能制作5×6=30(张).故答案为30.【点睛】本题考查了有理数的计算,正确应用正方形的边长是解答本题的关键.3.计算:(-0.25)-134⎛⎫-⎪⎝⎭+2.75-172⎛⎫+⎪⎝⎭=___.-175【分析】根据减法法则将减法全部转化为加法同时把分数化成小数然后利用加法的交换结合律进行计算【详解】解:原式=-025+325+275-75=(-025-75)+(325+275)=-775+解析:-1.75【分析】根据减法法则将减法全部转化为加法,同时把分数化成小数,然后利用加法的交换结合律进行计算.【详解】解:原式=-0.25+3.25+2.75-7.5=(-0.25-7.5)+( 3.25+2.75)=-7.75+6=-1.75.故答案为:-1.75.【点睛】本题考查了有理数加减混合运算,一般思路是先把加减法统一为加法,然后利用加法的运算律进行计算.4.如果数轴上原点右边 8 厘米处的点表示的有理数是 32,那么数轴上原点左边 12 厘米处的点表示的有理数是__________.﹣48【分析】数轴上原点右边8厘米处的点表示的有理数是32即单位长度是cm即1cm表示4个单位长度数轴左边12厘米处的点表示的数一定是负数再根据1cm表示4个单位长度即可求得这个数的绝对值【详解】数解析:﹣48【分析】数轴上原点右边 8厘米处的点表示的有理数是 32,即单位长度是14cm,即 1cm表示 4个单位长度,数轴左边12厘米处的点表示的数一定是负数,再根据 1cm表示 4个单位长度,即可求得这个数的绝对值.【详解】数轴左边 12 厘米处的点表示的有理数是﹣48.故答案为﹣48.【点睛】本题主要考查了在数轴上表示数.借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小既直观又简捷.5.给下面的计算过程标明运算依据:(+16)+(-22)+(+34)+(-78)=(+16)+(+34)+(-22)+(-78)①=[(+16)+(+34)]+[(-22)+(-78)]②=(+50)+(-100)③=-50.④①______________;②______________;③______________;④______________.①加法互换律;②加法结合律;③有理数的加法法则;④有理数的加法法则【分析】根据有理数加法法则相关运算律:交换律:a+b=b+a ;结合律(a+b )+c=a+(b+c )依此即可求解【详解】第①步交换了加解析:①加法互换律;②加法结合律;③有理数的加法法则;④有理数的加法法则【分析】根据有理数加法法则,相关运算律:交换律:a+b=b+a ;结合律(a+b )+c=a+(b+c ).依此即可求解.【详解】第①步,交换了加数的位置;第②步,将符号相同的两个数结合在一起;第③步,利用了有理数加法法则;第④步,同样应用了有理数的加法法则.故答案为加法交换律;加法结合律;有理数加法法则;有理数加法法则.【点睛】考查了有理数的加法,关键是熟练掌握计算法则,灵活运用运算律简便计算.6.绝对值小于100的所有整数的积是______.0【分析】先找出绝对值小于100的所有整数再求它们的乘积【详解】:绝对值小于100的所有整数为:0±1±2±3…±100因为在因数中有0所以其积为0故答案为0【点睛】本题考查了绝对值的性质要求掌握绝解析:0【分析】先找出绝对值小于100的所有整数,再求它们的乘积.【详解】:绝对值小于100的所有整数为:0,±1,±2,±3,…,±100,因为在因数中有0所以其积为0.故答案为0.【点睛】本题考查了绝对值的性质,要求掌握绝对值的性质及其定义,并能熟练运用到实际当中.绝对值规律总结:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.7.A ,B ,C 三地的海拔高度分别是50-米,70-米,20米,则最高点比最低点高______米.90【分析】先根据有理数的大小比较法则得出最高点和最低点再列出运算式子计算有理数的减法即可得【详解】因为所以最高点的海拔高度为20米最低点的海拔高度米则(米)即最高点比最低点高90米故答案为:90【解析:90【分析】先根据有理数的大小比较法则得出最高点和最低点,再列出运算式子,计算有理数的减法即可得.【详解】>->-,因为205070-米,所以最高点的海拔高度为20米,最低点的海拔高度70--=+=(米),则20(70)207090即最高点比最低点高90米,故答案为:90.【点睛】本题考查了有理数的大小比较法则、有理数减法的实际应用,依据题意,正确列出运算式子是解题关键.8.如果点A表示+3,将A向左移动7个单位长度,再向右移动3个单位长度,则终点表示的数是__________.-1【分析】根据向右为正向左为负根据正负数的意义列式计算即可【详解】根据题意得终点表示的数为:3-7+3=-1故答案为-1【点睛】本题考查了数轴正负数在实际问题中的应用在本题中向左向右具有相反意义可解析:-1【分析】根据向右为正,向左为负,根据正负数的意义列式计算即可.【详解】根据题意得,终点表示的数为:3-7+3=-1.故答案为-1.【点睛】本题考查了数轴,正负数在实际问题中的应用,在本题中向左、向右具有相反意义,可以用正负数来表示,从而列出算式求解.9.下面是七年级一班在学校举行的足球赛中的成绩,现规定赢球为“正”,输球为“负”,打平为“0”,请按照示例填空:例:若上半场输了2个球,下半场输了1个球,则全场输了3个球,也就是(-2)+(-1)=-3;(1)若上半场赢了3个球,下半场输了2个球,则全场赢了____个球,也就是____;(2)若上半场输了3个球,下半场赢了2个球,则全场输了___个球,也就是_____;(3)若上半场赢了3个球,下半场打平,则全场赢了___个球,也就是____.3+(-2)=11(-3)+2=-133+0=3【分析】根据定义赢球记为正输球记为负打平记为0先用有理数表示出输赢情况然后根据有理数的加减运算求解【详解】(1)上半场赢了3个为3下半场输了2个记为(解析:3+(-2)=1 1 (-3)+2=-1 3 3+0=3【分析】根据定义,赢球记为“正”,输球记为“负”,打平记为“0”,先用有理数表示出输赢情况,然后根据有理数的加减运算求解.【详解】(1)上半场赢了3个,为3,下半场输了2个,记为(-2),也就是:3+(-2)=1;(2)上半场输了3个,为(-3),下半场赢了2个,记为2,也就是:(-3)+2=-1;(3)上半场赢了3个,为3,下半场打平,记为0,也就是:3+0=3.【点睛】本题考查用正负数表示相反意义的量,并求解有理数的加法,解题关键是用正负数正确表示出输赢球的数量关系.10.若m﹣1的相反数是3,那么﹣m=__.2【分析】根据只有符号不同的两个数互为相反数可得关于m的方程根据解方程可得m的值再根据在一个数的前面加上负号就是这个数的相反数可得答案【详解】解:由m-1的相反数是3得m-1=-3解得m=-2-m=解析:2【分析】根据只有符号不同的两个数互为相反数,可得关于m的方程,根据解方程,可得m的值,再根据在一个数的前面加上负号就是这个数的相反数,可得答案.【详解】解:由m-1的相反数是3,得m-1=-3,解得m=-2.-m=+2.故选:A.【点睛】本题考查了相反数的意义,一个数的相反数就是在这个数前面添上“-”号;一个正数的相反数是负数,一个负数的相反数是正数,0的相反数是0.11.气温由﹣20℃下降50℃后是__℃.-70【分析】先将-20-50转化为-20+(-50)再由有理数的加法运算法则进行计算【详解】解:零上的温度用正数来表示零下的温度用负数来表示再根据有理数的减法的运算法则(减去一个数等于加上这个数的解析:-70【分析】先将-20-50转化为-20+(-50),再由有理数的加法运算法则进行计算.【详解】解:零上的温度用正数来表示,零下的温度用负数来表示,再根据有理数的减法的运算法则(减去一个数等于加上这个数的相反数),将有理数的减法化为有理数的加法来进行计算.∵-20-50=-20+(-50)=-70∴答案为:-70.【点睛】本题考查了有理数的减法的运算法则(减去一个数等于加上这个数的相反数),有理数的加法运算法则之一:(同号两数相加,和的正负号取任何一个加数的正负号,和的绝对值取两个加数的绝对值的和),熟记并灵活运用这两个运算法则是解本题的关键. 12.阅读理解:根据乘方的意义,可得:22×23=(2×2)×(2×2×2)=25.请你试一试,完成以下题目:(1)a 3•a 4=(a•a•a )•(a•a•a•a )=__;(2)归纳、概括:a m •a n =__;(3)如果x m =4,x n =9,运用以上的结论,计算:x m+n =__.a7am+n36【分析】(1)根据题意乘方的意义7个a 相乘可以写成a7即可解决;(2)根据题意总结规律可以知道是几个相同的数相乘指数相加即可解决;(3)运用以上的结论可以知道:xm+n =xm•xn 即解析:a 7 a m+n 36【分析】(1)根据题意,乘方的意义,7个a 相乘可以写成a 7即可解决;(2)根据题意,总结规律,可以知道是几个相同的数相乘,指数相加即可解决; (3)运用以上的结论,可以知道:x m+n =x m •x n ,即可解决问题.【详解】解:(1)根据材料规律可得a 3•a 4=(a•a•a )•(a•a•a•a )=a 7;(2)归纳、概括:a m •a n =m n a a a a ⎛⎫⎛⎫ ⎪⎪ ⎪⎪⎝⎭⎝⎭=a m+n ; (3)如果x m =4,x n =9,运用以上的结论,计算:x m+n =x m •x n =4×9=36.故答案为:a 7,a m+n ,36.【点睛】 本题主要考查了有理数的乘方的认识,能够读懂乘方的意义并且能够仿照例题写出答案是解决本题的关键.13.有理数a ,b ,c 在数轴上的位置如图所示:填空:+a b ________0,1b -_______0,a c -_______0,1c -_______0.<<<>【分析】数轴上右边表示的数总大于左边表示的数左边的数为负数右边的数为正数;根据有理数减法法则进行判断即可【详解】由题图可知所以故答案为:<<<>【点睛】考核知识点:有理数减法掌握有理数减法法解析:< < < >【分析】数轴上右边表示的数总大于左边表示的数.左边的数为负数,右边的数为正数;根据有理数减法法则进行判断即可.【详解】由题图可知01b a c <<<<,所以0,10,0,10a b b a c c +<-<-<->故答案为:<,<,<,>【点睛】考核知识点:有理数减法.掌握有理数减法法则是关键.14.绝对值小于4.5的所有负整数的积为______.24【分析】找出绝对值小于45的所有负整数求出之积即可【详解】解:绝对值小于45的所有负整数为:-4-3-2-1∴积为:故答案为:24【点睛】此题考查了有理数的乘法以及绝对值熟练掌握运算法则是解本题解析:24【分析】找出绝对值小于4.5的所有负整数,求出之积即可.【详解】解:绝对值小于4.5的所有负整数为:-4,-3,-2,-1,∴积为:4(3)(2)(1)24-⨯-⨯-⨯-=,故答案为:24.【点睛】此题考查了有理数的乘法,以及绝对值,熟练掌握运算法则是解本题的关键.15.计算:(1)(2)(3)(4)(2019)(2020)++-+++-++++-=_____.【分析】第1个数与第2个数相结合第3个数与第4个数相结合……第2019个数与第2020个数相结合进行计算即可【详解】原式故答案为:【点睛】本题考查了加法的结合律根据加数的特点将从第一个开始的每相邻两解析:1010-【分析】第1个数与第2个数相结合,第3个数与第4个数相结合,……,第2019个数与第2020个数相结合进行计算即可.【详解】原式(12)(34)(20192020)11111010=-+-++-=-----=-. 故答案为:1010-.【点睛】本题考查了加法的结合律,根据加数的特点,将从第一个开始的每相邻两个数结合是解决此题的关键.16.在有理数3.14,3,﹣12 ,0,+0.003,﹣313,﹣104,6005中,负分数的个数为x ,正整数的个数为y ,则x+y 的值等于__.4【解析】负分数为:﹣﹣3共2个;正整数为:36005共2个则x+y=2+2=4故答案为4【点睛】本题主要考查了有理数的分类熟记有理数的分类是解决此题的关键解析:4【解析】 负分数为:﹣12 ,﹣313,共2个;正整数为: 3, 6005共2个, 则x+y=2+2=4,故答案为4. 【点睛】本题主要考查了有理数的分类,熟记有理数的分类是解决此题的关键. 17.下列说法正确的是________.(填序号)①若||a b =,则一定有a b =±;②若a ,b 互为相反数,则1b a=-;③几个有理数相乘,若负因数有偶数个,那么他们的积为正数;④两数相加,其和小于每一个加数,那么这两个加数必是两个负数;⑤0除以任何数都为0.④【分析】利用绝对值的代数意义有理数的加法倒数的定义及有理数的乘法法则判断即可【详解】①若则故或当b<0时无解故①错误;②时ab 互为相反数但是对于等式不成立故②不正确;③几个有理数相乘如果负因数有偶解析:④【分析】利用绝对值的代数意义,有理数的加法,倒数的定义及有理数的乘法法则判断即可.【详解】①若||a b =,则0b ,故a b =或=-a b ,当b<0时,无解,故①错误;②0a b 时,a ,b 互为相反数,但是对于等式1b a=-不成立,故②不正确; ③几个有理数相乘,如果负因数有偶数个,但其中有因数0,那么它们的积为0,故③不正确;④两个正数相加,此时和大于每一个加数;一正数一负数相加,此时和大于负数;一个数和0相加,等于这个数;只有两个负数相加,其和小于每一个加数,故④正确; ⑤0除以0没有意义,故⑤不正确.综上,正确的有④.故答案为:④.【点睛】本题考查了绝对值、相反数、有理数的加法、有理数的除法等基础知识点,这都是必须掌握的基础知识点.18.一个班有45个人,其中45是_____数;大门约高1.90 m ,其中1.90是_____数.准确近似【分析】根据准确数和近似数的定义对数据进行判断【详解】一个班有45个人其中45是准确数;大门约高190m 其中190是近似数故答案为:准确;近似【点睛】本题考查了近似数近似数与精确数的接近程度解析:准确近似【分析】根据准确数和近似数的定义对数据进行判断.【详解】一个班有45个人,其中45是准确数;大门约高1.90 m,其中1.90是近似数.故答案为:准确;近似.【点睛】本题考查了近似数.近似数与精确数的接近程度,可以用精确度表示.一般有,精确到哪一位.19.填空:(1)____的平方等于9;(2)(-2)3=____;(3)-14+1=____;(4)23×212⎛⎫⎪⎝⎭=____.3或-3-802【分析】根据乘方的法则计算即可【详解】解:(1)32=9(-3)2=9所以3或-3的平方等于9;(2)(-2)3=-2×2×2=-8;(3)-14+1=-1+1=0;(4)23×=8解析:3或-3 -8 0 2【分析】根据乘方的法则计算即可.【详解】解:(1)32=9,(-3)2=9,所以3或-3的平方等于9;(2)(-2)3=-2×2×2=-8;(3)-14+1=-1+1=0;(4)23×212⎛⎫⎪⎝⎭=8×14=2.故答案为:3或-3;-8;0;2.【点睛】本题考查了有理数乘方运算,熟记法则和乘方的意义是解决此题的关键.20.已知一个数的绝对值为5,另一个数的绝对值为3,且两数之积为负,则两数之差为____.±8【分析】首先根据绝对值的性质得出两数进而分析得出答案【详解】设|a|=5|b|=3则a=±5b=±3∵ab<0∴当a=5时b=-3∴5-(-3)=8;当a=-5时b=3∴-5-3=-8故答案为:解析:±8【分析】首先根据绝对值的性质得出两数,进而分析得出答案.【详解】设|a|=5,|b|=3,则a=±5,b=±3,∵ab<0,∴当a=5时,b=-3,∴5-(-3)=8;当a=-5时,b=3,∴-5-3=-8.故答案为:±8.【点睛】本题主要考查了绝对值的性质以及有理数的混合运算,熟练掌握绝对值的性质是解题关键.21.在括号中填写题中每步的计算依据,并将空白处补充完整:(-4)×8×(-2.5)×(-125)=-4×8×2.5×125=-4×2.5×8×125______=-(4×2.5)×(8×125)______=____×____=____.乘法交换律乘法结合律-101000-10000【分析】分别利用有理数乘法法则以及乘法分配律和乘法结合律求出即可【详解】(-4)×8×(-25)×(-125)=-4×8×25×125=-4×25×8×解析:乘法交换律乘法结合律 -10 1000 -10000【分析】分别利用有理数乘法法则以及乘法分配律和乘法结合律求出即可.【详解】(-4)×8×(-2.5)×(-125)=-4×8×2.5×125=-4×2.5×8×125(乘法交换律)=-(4×2.5)×(8×125)(乘法结合律)=-10×1000=-10000.故答案为:乘法交换律,乘法结合律,-10,1000,-10000.【点睛】本题主要考查了有理数的乘法运算和乘法运算律,正确掌握运算法则和乘法运算律是解题的关键.22.我国“杂交水稻之父”袁隆平主持研究的某种超级杂交稻平均亩产820千克,某地今年计划栽种这种超级杂交稻30万亩,预计今年这种超级杂交稻的产量_____千克(用科学记数法表示)46×108【分析】本题已知的是亩产量和亩数要求总产量就要利用三者之间的关系式先计算总产量通过简单的计算后用科学计数法表示:总产量=亩产量×总亩数(注意:单位换算)即可得出答案【详解】解:依题意得:解析:46×108【分析】本题已知的是亩产量和亩数,要求总产量,就要利用三者之间的关系式先计算总产量.通过简单的计算后用科学计数法表示:总产量=亩产量×总亩数(注意:单位换算)即可得出答案.【详解】解:依题意得:820×300000=246000000=2.46×108.故答案为:2.46×108.【点睛】此题主要考查科学记数法的表示方法.科学记数法的表示形式为10na⨯的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.23.运用加法运算律填空:212+1(3)3-+612+2(8)3-=1(22+____)+[ ____+2(8)3-].【分析】根据互为相反数的两数的两数之和为0以及同分母的分数相加的原则进行计算即可【详解】解:2++6+=)++故答案为:;【点睛】本题考查了有理数的加法掌握加法法则和运算律是解题的关键解析:1621(3)3-【分析】根据互为相反数的两数的两数之和为0以及同分母的分数相加的原则进行计算即可.【详解】解:212+1(3)3-+612+2(8)3-=1(22+162)+[1(3)3-+2(8)3-].故答案为:162;1(3)3-.【点睛】本题考查了有理数的加法,掌握加法法则和运算律是解题的关键.24.计算1-2×(32+12)的结果是 _____.-18【分析】先算乘方再算括号然后算乘法最后算加减即可【详解】解:1-2×(3+)=1-2×(9+)=1-2×=1-19=-18故答案为-18【点睛】本题考查了含乘方的有理数四则混合运算掌握相关运算解析:-18【分析】先算乘方、再算括号、然后算乘法、最后算加减即可.【详解】解:1-2×(32+12)=1-2×(9+12)=1-2×19 2=1-19=-18.故答案为-18.【点睛】本题考查了含乘方的有理数四则混合运算,掌握相关运算法则是解答本题的关键.25.截至格林尼治标准时间2020年6月7日10时,全球累计报告新冠肺炎确诊病例达7000000例;其中累计死亡病例超过40万例,数据7000000科学记数法表示为_____.7×106【分析】根据科学记数法形式:a×10n其中1≤a<10n为正整数即可求解【详解】解:7000000科学记数法表示为:7×106故答案为:7×106【点睛】本题考查科学记数法解决本题的关键是解析:7×106【分析】根据科学记数法形式:a×10n,其中1≤a<10,n为正整数,即可求解.【详解】解:7000000科学记数法表示为:7×106.故答案为:7×106.【点睛】本题考查科学记数法,解决本题的关键是把一个大于10的数记成a×10n的形式,其中a是整数数位只有一位的数,n是正整数,这种记数法叫做科学记数法.[科学记数法形式:a×10n,其中1≤a<10,n为正整数.26.在|﹣3|、﹣32、﹣(﹣3)2、﹣(3﹣π)、﹣|0|中,负数的个数为_____.2个【分析】分别计算出题目中所给的每一个数即可作出判定【详解】∵|﹣3|=3﹣32=﹣9﹣(﹣3)2=﹣9﹣(3﹣π)=π﹣3﹣|0|=0∴﹣32﹣(﹣3)2是负数故答案为2个【点睛】此题考查的知识解析:2个【分析】分别计算出题目中所给的每一个数,即可作出判定.【详解】∵|﹣3|=3,﹣32=﹣9,﹣(﹣3)2=﹣9,﹣(3﹣π)=π﹣3,﹣|0|=0,∴﹣32、﹣(﹣3)2是负数.故答案为2个.【点睛】此题考查的知识点是正数和负数,关键是理解负数的概念,而且要把这些数化为最后结果才能得出正确答案.这就又要理解平方、绝对值,正负号的变化等知识点.27.绝对值小于2018的所有整数之和为________.0【分析】根据绝对小于2018可得许多互为相反数的数根据互为相反数的和等于可得答案【详解】解:绝对值小于2018的所有整数的和:(-2017)+(-2016)+(-2015)+…+0+1+2+…+2解析:0【分析】根据绝对小于2018,可得许多互为相反数的数,根据互为相反数的和等于,可得答案.【详解】解:绝对值小于2018的所有整数的和:(-2017)+(-2016)+(-2015)+…+0+1+2+…+2017=0,故答案为0.【点睛】本题考查了有理数的加法,先根据绝对值小于2018写出各数,再根据有理数的加法,得出答案.28.已知四个互不相等的整数a,b,c,d满足abcd=77,则a+b+c+d=___________.【解析】77=7×11=1×1×7×11=-1×1×(-7)×11=-1×1×7×(-11)由题意知abcd的取值为-11-711或-117-11从而a+b+c+d=±4故答案为±4解析:4±【解析】77=7×11=1×1×7×11= -1×1×(-7)×11= -1×1×7×(-11),由题意知,a、b、c、d的取值为-1,1,-7,11或-1,1,7,-11,从而a+b+c+d=±4,故答案为±4.29.3-的平方的相反数的倒数是___________.【分析】根据倒数相反数平方的概念可知【详解】−3的平方是99的相反数是-9-9的倒数是故答案为【点睛】此题考查倒数相反数平方的概念及性质解题关键在于掌握各性质定义解析:1 9 -【分析】根据倒数,相反数,平方的概念可知.【详解】−3的平方是9,9的相反数是-9,-9的倒数是1 9 -故答案为1 9 -.【点睛】此题考查倒数,相反数,平方的概念及性质.解题关键在于掌握各性质定义.30.计算:5213(15.5)65772⎛⎫⎛⎫⎛⎫-+++-+-=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭__________.0【分析】将同分母的分数分别相加再计算加法即可【详解】原式故答案为:0【点睛】此题考查有理数的加法计算法则掌握有理数加法的运算律:交换律和结合律是解题的关键解析:0【分析】将同分母的分数分别相加,再计算加法即可.【详解】原式5213615.5510100772⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫=-+-++-=-+= ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故答案为:0.【点睛】此题考查有理数的加法计算法则,掌握有理数加法的运算律:交换律和结合律是解题的关键.。
绝对值的性质及化简(教案)

1.理论介绍:首先,我们要了解绝对值的基本概念。绝对值是一个数在数轴上与原点的距离,它是非负的。绝对值在数学运算中非常重要,它可以帮助我们简化问题,避免考虑正负号。
2.案例分析:接下来,我们来看一个具体的案例。这个案例将展示如何运用绝对值的性质来化简表达式,以及它如何帮助我们解决实际问题。
3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“绝对值在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
2.丰富教学手段,除了数轴演示,还可以利用多媒体、实物等教学资源,增强学生对绝对值的感知。
3.注重培养学生的逻辑思维能力,通过问题驱动,引导学生自主发现和总结绝对值的性质。
4.在课堂练习环节,增加一些综合性的题目,帮助学生巩固所学知识,提高解题能力。
五、教学反思
在本次《绝对值的性质及化简》的教学过程中,我发现学生们对绝对值的概念和性质的理解程度参差不齐。有些同学能够迅速抓住绝对值的本质,但也有一些同学在理解上存在困难。这让我意识到,在今后的教学中,我需要更加关注学生的个体差异,因材施教。
在导入新课环节,通过提问日常生活中的实例,我发现大多数同学能够积极参与,这表明实例导入法对于激发学生的学习兴趣和好奇心是有效的。但在新课讲授环节,我发现在解释绝对值性质时,部分同学显得有些迷茫。为此,我及时调整了教学方法,通过数轴的直观演示,帮助他们更好地理解绝对值的性质。
在总结回顾环节,我发现大部分同学能够掌握绝对值的基本概念和化简方法,但仍有部分同学在应用上存在困难。这说明我在教学中需要更多地关注学生的实际运用能力,通过设置更多具有挑战性的问题,促使他们学以致用。
专题 含有绝对值的式子的化简(解析版)-七年级数学上册

(人教版)七年级上册数学《第二章整式的加减》专题含有绝对值的式子的化简一、选择题(共10小题)1.有理数a、b在如图所示数轴的对应位置上,则|b﹣a|﹣|b|化简后结果为()A.a B.﹣a C.a﹣2b D.b﹣2a【分析】代入化简后的算式,求出算式的值是多少即可.【解答】解:|b﹣a|﹣|b|=a﹣b+b=a,故选:A.【点评】此题主要考查了整式的加减﹣化简求值问题,要熟练掌握,解答此题的关键是要明确:给出整式中字母的值,求整式的值的问题,一般要先化简,再把给定字母的值代入计算,得出整式的值,不能把数值直接代入整式中计算.2.(2022秋•罗湖区校级期末)有理数a,b在数轴上如图所示,则化简|2a|﹣|b|+|2a﹣5|的结果是()A.4a+b﹣5B.4a﹣b﹣5C.b+5D.﹣b﹣5【分析】先结合数轴确定a,b的范围,再运用绝对值知识进行化简.【解答】解:由题意可得,﹣2<b<﹣1<1<a<2,∴|2a|﹣|b|+|2a﹣5|=2a﹣(﹣b)+[﹣(2a﹣5)]=2a+b﹣2a+5=b+5,故选:C.【点评】此题考查了运用数轴表示有理数及绝对值求解的能力,关键是能准确理解并运用以上知识.3.(2022秋•天山区校级期末)已知a,b,c在数轴上位置如图所示,则|a﹣b|﹣|b﹣c|+|c﹣a|可化简为()A.0B.2b﹣2a C.2a﹣2b D.﹣2a【分析】先由数轴确定a,b,c的符号和大小,再分别确定a﹣b,b﹣c,c﹣a的符号,最后化简绝对值并计算求解.【解答】解:由题意得,a<b<0<c且|a|>|b|>|c|,∴a﹣b<0,b﹣c<0,c﹣a>0,∴|a﹣b|﹣|b﹣c|+|c﹣a|=b﹣a+b﹣c+c﹣a=2b﹣2a,故选:B.【点评】此题考查了运用数轴进行绝对值的化简、计算能力,关键是能准确理解并运用以上知识.4.(2022秋•永兴县期末)有理数a,b,c在数轴上的位置如图所示,式子|a|+|b|+|a+b|+|b﹣c|化简为()A.2a+3b﹣c B.3b﹣c C.b+c D.c﹣b【分析】根据正数的绝对值等于它本身,负数的绝对值等于它的相反数可得结果.【解答】解:由数轴得,﹣1<a<0,b>1,c>b,∴a+b>0,b﹣c>0,∴|a|+|b|+|a+b|+|b﹣c|=﹣a+b+a+b﹣b+c=b+c.故选:C.【点评】本题考查了绝对值与数轴,用两种不同的方法即几何方法和代数方法进行求解.通过比较,可以发现借助数轴用几何方法化简含有绝对值的式子,比较有关数的大小有直观、简捷,举重若轻的优势.5.(2022秋•黄埔区期末)已知a、b、c在数轴上位置如图,则|a+b|+|a+c|﹣|b﹣c|=()A.0B.2a+2b C.2b﹣2c D.2a+2c【分析】先根据各点在数轴上的位置判断出其符号,再去绝对值符号,合并同类项即可.【解答】解:由图可知,c<a<0<b,|c|>|b|>|a|,则|a+b|+|a+c|﹣|b﹣c|=a+b﹣a﹣c﹣b+c=0.故选:A.【点评】本题考查的是整式的加减、数轴和绝对值,熟知数轴上右边的数总比左边的大是解答此题的关键.6.已知a、b、c在数轴上位置如图,则|a+b|+|a+c|﹣|c﹣b|=()A.0B.2a+2b C.2b﹣2c D.2a+2c【分析】根据数轴的意义可知:c<a<0<b,结合绝对值的性质化简给出的式子.【解答】解:根据数轴图可知:c<a<0<b,∴a+b>0,a+c<0,c﹣b<0,∴|a+b|+|a+c|﹣|c﹣b|=a+b﹣a﹣c+c﹣b=0.故选:A.【点评】此题考查了数轴、绝对值的有关内容,能够正确判断绝对值内的式子的符号,再根据绝对值的性质正确化简.7.已知有理数a,b在数轴上的位置如图所示,则化简|b+1|﹣|b﹣a|的结果为()A.a﹣2b﹣1B.a+1C.﹣a﹣1D.﹣a+2b+1【分析】先根据数轴判断a、b的大小,再判断所求式子中绝对值内部的符号,再化简求值.【解答】解:由数轴可知,﹣1<b<0,1<a<2,∴b+1>0,|b+1|=b+1,b﹣a<0,|b﹣a|=a﹣b,∴原式=b+1﹣(a﹣b)=1+2b﹣a,故选:D.【点评】本题考查绝对值和数轴.关键在于根据数轴判断b+1、b﹣a的符号,进而取绝对值化简求值.8.有理数a、b、c在数轴上位置如图,则|c﹣a|﹣|a+b|﹣|b﹣c|的值为()A.2a﹣2c+2b B.0C.﹣2c D.2a【分析】根据点所处的位置确定绝对值内数据的符号:c﹣a<0,a+b<0,b﹣c<0,即可求解.【解答】解:根据点所处的位置确定绝对值内数据的符号:c﹣a<0,a+b<0,b﹣c<0,原式=﹣(c﹣a)+(a+b)+(b﹣c)=2a﹣2c+2b,故选:A.【点评】此题综合考查了数轴、绝对值的有关内容,用几何方法借助数轴来求解,非常直观,体现了数形结合的优点.9.已知有理数a,b,c在数轴上的位置如图,且|c|>|a|>|b|,则|a+b|﹣2|c﹣b|+|a+c|=()A.c﹣b B.0C.3b﹣3c D.2a+3b﹣c【分析】由有理数a,b,c在数轴上的位置及|c|>|a|>|b|可得:c<b<0<﹣b<a<﹣c,再按照绝对值的化简法则和有理数的加减运算法则计算即可.【解答】解:由有理数a,b,c在数轴上的位置及|c|>|a|>|b|可得:c<b<0<﹣b<a<﹣c,∴|a+b|﹣2|c﹣b|+|a+c|=a+b﹣2(b﹣c)﹣a﹣c=b﹣2b+2c﹣c=c﹣b.故选:A.【点评】本题考查了借助数轴进行的绝对值化简及有理数的加减运算,数形结合并熟练掌握相关运算法则是解题的关键.10.(2022秋•辉县市校级期末)有理数a,b,c在数轴上所对应的点的位置如图所示,试化简|a﹣b|﹣2|b ﹣c|+|a+b|﹣|c+b|的结果是()A.﹣3b+3c B.3b﹣3c C.﹣2a+3b+c D.2a﹣b+3c【分析】根据有理数a,b,c在数轴上所对应的点的位置得出c<b<0<a,|a|<|b|<|c|,然后化简绝对值即可.【解答】解:∵c<b<0<a,|a|<|b|<|c|,∴a﹣b>0,|b﹣c|>0,|a+b|<0,|c+b|<0,∴|a﹣b|﹣2|b﹣c|+|a+b|﹣|c+b|=a﹣b﹣2(b﹣c)+[﹣(a+b)]﹣[﹣(c+b)]=a﹣b﹣2b+2c﹣(a+b)+(c+b)=a﹣b﹣2b+2c﹣a﹣b+c+b=﹣3b+3c,故选:A.【点评】本题主要考查了绝对值的意义,有理数加法、减法运算,合并同类项,解题的关键是根据有理数a,b,c在数轴上所对应的点的位置得出c<b<0<a,|a|<|b|<|c|.二、填空题(共10小题)11.(2022秋•莱阳市期末)已知数a,b,c在数轴上的位置如图所示,化简|a﹣b|+|a+b+c|﹣|c﹣b|=.【分析】由数轴上右边的数总比左边的数大,且离原点的距离大小即为绝对值的大小,判断出a+b与c ﹣b的正负,利用绝对值的代数意义化简所求式子,合并同类项即可得到结果.【解答】解:由数轴上点的位置可得:c<b<0<a,且|a|<|b|,∴a﹣b>0,c﹣b<0,a+b+c<0,则|a﹣b|+|a+b+c|﹣|c﹣b|=a﹣b﹣a﹣b﹣c+c﹣b=﹣3b.故答案为:﹣3b【点评】此题考查了整式的加减运算,涉及的知识有:去括号法则,以及合并同类项法则,熟练掌握法则是解本题的关键.12.(2022秋•温江区校级期中)有理数a,b,c数轴上的位置如图所示,请化简:|﹣c+b|+|a﹣c|﹣|b+a|=.【分析】结合数轴判断﹣c+b<0,a﹣c>0,b+a<0,再根据绝对值的性质“正数和零的绝对值是本身,负数的绝对值是相反数”可将原式化简,即得答案.【解答】解:由数轴可知:﹣c+b<0,a﹣c>0,b+a<0,∴原式=﹣(﹣c+b)+(a﹣c)+(b+a)=c﹣b+a﹣c+b+a=2a,故答案为:2a.【点评】本题考查了数轴,绝对值,关键是根据绝对值的性质“正数和零的绝对值是本身,负数的绝对值是相反数”将原式化简.13.有理数a、b、c在数轴上的位置如图,则|a+c|+|c﹣b|﹣|a+b|=.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.【解答】解:根据数轴得:a<b<0<c,且|a|>|b|>|c|,∴a+c<0,c﹣b>0,a+b<0,则原式=﹣a﹣c+c﹣b+a+b=0.故答案为:0.【点评】此题考查了整式的加减,熟练掌握运算法则是解本题的关键.14.有理数a,b,c在数轴上的对应点如图所示,化简|a﹣b|﹣|a+c|+|b﹣c|=.【分析】根据绝对值的性质,可化简绝对值,根据整式的加减,可得答案.【解答】解:|a﹣b|﹣|a+c|+|b﹣c|=﹣(a﹣b)+(a+c)+(b﹣c)=﹣a+b+a+c+b﹣c=2b.故答案为:2b.【点评】本题考查了数轴,利用绝对值的性质化简是解题关键.15.有理数a,b,c在数轴上的位置如图所示,化简|a+b﹣c|﹣|c﹣b|+2|a+c|=.【分析】根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,去括号合并即可得到结果.【解答】解:由数轴上点的位置得:a<b<0<c,且|b|<|c|<|a|,∴a+b﹣c<0,c﹣b>0,a+c<0,则原式=﹣a﹣b+c﹣c+b﹣2a﹣2c=﹣3a﹣2c,故答案为:﹣3a﹣2c.【点评】此题考查了整式的加减,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.16.a,b,c三个数在数轴上的位置如图所示,化简|a+b|﹣|b﹣c|+|c﹣a|﹣|a﹣b|=.【分析】根据数轴点的位置得出a+b<0,b﹣c<0,c﹣a>0,a﹣b<0,再去掉绝对值符号,合并同类项即可.【解答】解:∵从数轴可知:a<b<0<c,|b|<|c|,∴a+b<0,b﹣c<0,c﹣a>0,a﹣b<0,∴|a+b|﹣|b﹣c|+|c﹣a|﹣|a﹣b|==﹣(a+b)﹣(c﹣b)+(c﹣a)﹣(b﹣a)=﹣a﹣b﹣c+b+c﹣a﹣b+a=﹣a﹣b,故答案为:﹣a﹣b.【点评】本题考查了整式的加减和数轴的应用,解此题的关键是能根据数轴去掉绝对值符号,题目比较好,难度不是很大.17.已知数a、b、c在数轴上的位置如图所示,则|a﹣c|﹣|a+b+c|﹣|b﹣a|=.【分析】先根据a、b、c在数轴上的位置进行绝对值的化简,然后去括号,合并同类项求解.【解答】解:由图可得,c<b<0<a,则原式=a﹣c+(a+b+c)+(b﹣a)=a﹣c+a+b+c+b﹣a=a+2b.故答案为:a+2b.【点评】本题考查了整式的加减,解答本题的关键是掌握去括号法则和合并同类项法则.18.已知有理数a,b,c在数轴上的位置如图所示,化简:|b﹣c|﹣2|b﹣a|+|c+a|=.【分析】根据数轴上右边的数总比左边的数法,判断大小;原式各项利用绝对值的代数意义化简,去括号合并即可得到结果.【解答】解:根据数轴上点的位置得:c<b<0<a,|c|>|a|,∴﹣c>a,∴b﹣c>0,b﹣a<0,a+c<0,∴原式=b﹣c﹣2(a﹣b)+(﹣c﹣a)=b﹣c﹣2a+2b﹣c﹣a=﹣3a+3b﹣2c;故答案为﹣3a+3b﹣2c.【点评】此题考查了整式的加减,绝对值,以及有理数的大小比较,熟练掌握运算法则是解本题的关键.19.表示有理数a,b,c的点在数轴上的位置如图所示,请化简|a+b|﹣2|a﹣c|+|c﹣a+b|=.【分析】根据数轴先判断a、b、c的符号和大小关系,再判断a+b、a﹣c、c﹣a+b的符号,进而去绝对值化简.【解答】解:根据数轴可知,a<b<0<c,故a+b<0,a﹣c<0,c﹣a+b>b﹣a>0,∴原式=﹣(a+b)﹣2(c﹣a)+(c﹣a+b)=﹣a﹣b﹣2c+2a+c﹣a+b=﹣c.故答案为:﹣c.【点评】本题考查了绝对值的的化简.通过数轴判断a、b、c的符号,再判断绝对值中的式子符号,是解题的关键.有的时候还需要注意有理数与原点距离的远近.20.数a,b,c在数轴上的位置如图所示.化简:2|b﹣a|﹣|c﹣b|+|a+b|=.【分析】根据数轴即可将绝对值去掉,然后合并即可.【解答】解:由数轴可知:c<b<a,b﹣a<0,c﹣b<0,a+b>0,则原式=﹣2(b﹣a)+(c﹣b)+(a+b)=﹣2b+2a+c﹣b+a+b=3a﹣2b+c.故答案为:3a﹣2b+c.【点评】本题考查整式化简运算,涉及数轴,绝对值的性质,整式加减运算等知识.三、解答题(共20小题)21.已知有理数a、b、c在数轴上的位置如图所示,化简:|a﹣b|﹣|a+c|﹣|c﹣a|+|a+b+c|+|b﹣c|【分析】由题意可知:a﹣b>0,a+c<0,c﹣a<0,a+b+c<0,b﹣c>0,根据绝对值的性质化简即可.【解答】解:由题意可知:a﹣b>0,a+c<0,c﹣a<0,a+b+c<0,b﹣c>0,原式=a﹣b+a+c+c﹣a﹣a﹣b﹣c+b﹣c=﹣b【点评】本题考查数轴、绝对值等知识,解题的关键是记住绝对值的性质:数a绝对值要由字母a本身的取值来确定:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.22.已知有理数a、b、c在数轴上对应点的位置如图所示.化简:|a﹣b|+|b﹣c|﹣|c﹣a|+|b+c|.【分析】由数轴得出﹣1<c<0<b<1<a,|b|<|c|<|a|,去掉绝对值符号,再合并即可.【解答】解:∵由数轴可知:﹣1<c<0<b<1<a,|b|<|c|<|a|,∴a﹣b>0,b﹣c>0,c﹣a<0,b+c<0,∴原式=a﹣b+b﹣c+c﹣a﹣(b+c)=﹣b﹣c.【点评】本题考查了数轴和绝对值,能正确去掉绝对值符号是解此题的关键.23.有理数a、b、c在数轴上的位置如图所示.化简:3|a﹣b|+|a+b|﹣|c﹣a|+2|b﹣c|﹣|b﹣a+c|.【分析】根据数轴,先确定a、b、c的正负,再判断a﹣b,a+b,c﹣a,b﹣c,b﹣a+c的正负,最后根据绝对值的意义,对代数式化简.【解答】解:由数轴知:a<b<0<c,∴a﹣b<0,a+b<0,c﹣a>0,b﹣c<0,b﹣a+c>0所以3|a﹣b|+|a+b|﹣|c﹣a|+2|b﹣c|﹣|b﹣a+c|=3(b﹣a)﹣(a+b)﹣(c﹣a)+2(c﹣b)﹣(b﹣a+c)=3b﹣3a﹣a﹣b﹣c+a+2c﹣2b﹣b+a﹣c=﹣b﹣2a.【点评】本题考查了数轴上点的特点、有理数的加减法法则及绝对值的化简.根据绝对值的意义化简代数式是关键.注意:大的数﹣小的数>0,小的数﹣大的数<0.24.有理数a,b,c在数轴上的位置如图:试化简:|a﹣b|﹣|c﹣a|+|b﹣c|﹣|c|【分析】根据绝对值的性质化简即可.【解答】解:由题意:a﹣b>0,c﹣a<0,b﹣c>0,c<0,∴|a﹣b|﹣|c﹣a|+|b﹣c|﹣|c|=a﹣b+c﹣a+b﹣c+c=c.【点评】本题考查绝对值的性质、数轴等知识,熟练掌握绝对值的性质是解决问题的关键.25.已知有理数a、b、c在数轴上的位置如图,化简|a|﹣|a+b|+|c﹣a|.【分析】首先判断出a<0,a+b<0,c﹣a>0,再根据绝对值的性质化简即可.【解答】解:观察数轴可知:a<0,a+b<0,c﹣a>0∴原式=﹣a+a+b+c﹣a=b+c﹣a.【点评】本题考查数轴、绝对值的性质等知识,解题的关键是熟练掌握绝对值的性质,记住如果用字母a表示有理数,则数a绝对值要由字母a本身的取值来确定:①当a是正有理数时,a的绝对值是它本身a;②当a是负有理数时,a的绝对值是它的相反数﹣a;③当a是零时,a的绝对值是零.26.已知a,b在数轴上对应的点如图示化简:|a|+|a+b|﹣|a﹣b|﹣|b﹣a|.【分析】首先根据图示,可得a<0,a+b<0,b﹣a>0,a﹣b<0,然后根据整数的加减的运算方法,求出算式的值是多少即可.【解答】解:根据图示,可得a<﹣b<0<b<﹣a;∴a<0,a+b<0,a﹣b<0,b﹣a>0,∴|a|=﹣a,|a+b|=﹣(a+b),|a﹣b|=﹣(a﹣b,|b﹣a|=b﹣a,∴|a|+|a+b|﹣|a﹣b|﹣|b﹣a|=﹣a﹣a﹣b+a﹣b﹣b+a=﹣3b.【点评】此题考查了在数轴上表示数的方法,以及数轴的特征:一般来说,当数轴方向朝右时,右边的数总比左边的数大.还考查了整式的加减运算,解答此类问题的关键是要明确整式的加减的实质就是去括号、合并同类项.一般步骤是:先去括号,然后合并同类项.27.有理数a,b,c在数轴上的位置如图所示,试化简下式:|a﹣c|+|a﹣b|﹣|b﹣c|+|2a|.【分析】根据数轴判断出a、b、c的正负情况以及绝对值的大小,然后根据绝对值的性质去掉绝对值号,再合并同类项即可.【解答】解:由图可知,a<0,b>0,c<0且|c|>|a|>|b|,所以,a﹣b<0,b﹣c>0,a﹣c>0,所以原式=a﹣c+b﹣a﹣b+c﹣2a=﹣2a.【点评】本题考查了数轴,绝对值的性质,准确识图并判断出各数正负情况是解题的关键.28.已知有理数a、b、c在数轴上的对应点如图所示,化简:|b﹣a|﹣|a+c|+2|c﹣b|.【分析】解决此题关键要对a,b,c与0进行比较,进而确定b﹣a,a+c,c﹣b与0的关系,从而很好的去掉绝对值符号.【解答】解:由数轴可知:a>b>0>c,|a|>|c|,则b﹣a<0,a+c>0,c﹣b<0.∴|b﹣a|﹣|a+c|+2|c﹣b|=﹣(b﹣a)﹣(a+c)﹣2(c﹣b)=﹣b+a﹣a﹣c﹣2c+2b=b﹣3c.【点评】在去绝对值符号时要注意:大于0的数值绝对值是它本身,小于零的数值绝对值是它的相反数.29.已知有理数a,b,c在数轴上对应点的位置如图所示,化简|b﹣c|+2|c+a|﹣3|a﹣b|.【分析】先根据各点在数轴上的位置判断出其符号及绝对值的大小,再去绝对值符号,合并同类项即可.【解答】解:由图可知,c<a<0<b,所以,b﹣c>0,c+a<0,a﹣b<0,所以,原式=b﹣c﹣2(c+a)﹣3(b﹣a)=b﹣c﹣2c﹣2a﹣3b+3a=a﹣2b﹣3c.【点评】本题主要考查了数轴和绝对值,理解绝对值的意义是解答此题的关键.30.如图,数a,b,c在数轴上的位置如图.(1)判断符号:a+b0,b﹣c0,a﹣c0;(填“>”、“<”)(2)化简:|b﹣c|﹣|a+b|﹣|a﹣c|.【分析】(1)根据数轴、有理数的加法可判断a+b,b﹣c,a﹣c的符号;(2)根据绝对值和a+b,b﹣c,a﹣c的符号化简式子|b﹣c|﹣|a+b|﹣|a﹣c|即可.【解答】解:(1)由数轴得,a>c>0<b,|b|>a>c,∴a+b<0,b﹣c<0,a﹣c>0;故答案为:<,<,>;(2)∵a+b<0,b﹣c<0,a﹣c>0,∴|b﹣c|﹣|a+b|﹣|a﹣c|=﹣b+c﹣(﹣a﹣b)﹣(a﹣c)=﹣b+c+a+b﹣a+c=2c.【点评】本题考查了数轴,有理数的加减运算法则,绝对值的性质,整式的加减,掌握正数的绝对值等于它本身,负数的绝对值等于它的相反数,0的绝对值是0是解题的关键.31.(2022秋•綦江区期中)有理数a、b、c在数轴上的对应点的位置如图所示:(1)用“>”“<”或“=”填空:a+b0,c﹣a0,b﹣c0;(2)化简:|a+b|﹣|c﹣a|﹣|b|+|b﹣c|.【分析】(1)根据各点在数轴上的位置判断出a,b,c的符号,进而可得出结论;(2)根据(1)中a,b,c的符号去绝对值符号即可.【解答】解:(1)由各点在数轴上的位置可知,a<0<b<c,|a|>b,∴a+b<0,c﹣a>0,b﹣c<0.故答案为:<,>,<.(2)∵由(1)可知,a+b<0,c﹣a>0,b﹣c<0,∴|a+b|﹣|c﹣a|﹣|b|+|b﹣c|=﹣(a+b)﹣(c﹣a)﹣b+(c﹣b)=﹣a﹣b﹣c+a﹣b+c﹣b=﹣3b.【点评】本题考查的是有理数的大小比较,熟知数轴的特点和绝对值的性质是解题关键.32.(2022春•杜尔伯特县期中)有理数a、b、c在数轴上的位置如图所示.(1)用“<”连接:0,a、b、c.(2)化简:|c﹣a|+2|b﹣c|﹣|a+b|【分析】根据有理数a、b、c在数轴上的位置即可得到结论.【解答】解:(1)a<b<0<c;(2)原式=(c﹣a)+2(﹣b+c)﹣(﹣a﹣b),=c﹣a﹣2b+2c+a+b,=3c﹣b.【点评】本题考查了数轴和有理数的大小比较法则,能熟记有理数的大小比较法则是解此题的关键,注意:在数轴上表示的数,右边的数总比左边的数大.33.有理数a、b、c在数轴上的位置如图所示.(1)判断a﹣b0,a﹣c0,b﹣c0;(2)化简|a﹣b|+|a﹣c|﹣|b﹣c|.【分析】(1)由图可得:c<a<0<b,得a﹣c>0,a﹣b<0,b﹣c>0,从而解决此题.(2)由(1)得:a﹣c>0,a﹣b<0,b﹣c>0.根据绝对值的定义,得|a﹣c|=a﹣c,|a﹣b|=b﹣a,|b ﹣c|=b﹣c,从而解决此题.【解答】解:(1)由图可得:c<a<0<b.∴a﹣c>0,a﹣b<0,b﹣c>0.故答案为:<,>,>.(2)由(1)得:a﹣c>0,a﹣b<0,b﹣c>0,∴|a﹣c|=a﹣c,|a﹣b|=b﹣a,|b﹣c|=b﹣c,∴|a﹣b|+|a﹣c|﹣|b﹣c|=b﹣a+a﹣c+c﹣b=0.【点评】本题主要考查数轴,绝对值、整式的加减运算,熟练掌握实数的大小关系、绝对值的定义、整式的加减运算法则是解决本题的关键.34.有理数a,b,c在数轴上的位置如图所示,(1)用“<”连接0,a,b,c;(2)化简代数式:|a﹣b|+|a+b|﹣|c﹣a|+|b﹣c|.【分析】(1)数轴上右边的数总比左边的数大,从而连接即可;(2)根据数轴得出a﹣b>0,a+b<0,c﹣a<0,b﹣c>0,去掉绝对值后合并即可得出答案.【解答】解:(1)结合数轴可得:c<b<0<a;(2)由题意得:a﹣b>0,a+b<0,c﹣a<0,b﹣c>0,故|a﹣b|+|a+b|﹣|c﹣a|+|b﹣c|=a﹣b﹣a﹣b﹣a+c+b﹣c=﹣a﹣b.【点评】本题考查了整式的加减、数轴及绝对值的知识,掌握数轴上右边的数总比左边的数大是解答本题的关键.35.若有理数a、b、c在数轴上测的点A、B、C位置如图所示:(1)判断代数式c﹣b、a+c的符号;(2)化简:|﹣c|﹣|c﹣b|+|a+b|+|b|.【分析】(1)根据有理数的加减法,可得答案;(2)根据绝对值的性质,可化简去掉绝对值,根据合并同类项,可得答案.【解答】解:(1)因为a<b<0<c,|a|>|c|.所以c﹣b>0,a+c<0;(2)因为a<b<0<c,|a|>|c|.所以﹣c<0,c﹣b>0,a+b<0,原式=c﹣(c﹣b)﹣(a+b)﹣b=c﹣c+b﹣a﹣b﹣b=﹣a﹣b.【点评】本题考查了合并同类项,解题的关键是利用绝对值的性质化简绝对值,利用合并同类项得出答案.36.有理数a,b,c在数轴上的位置如图所示,(1)c0;a+c0;b﹣a0(用“>、<、=”填空)(2)试化简:|b﹣a|﹣|a+c|+|c|.【分析】(1)根据在数轴上原点左边的数小于0,得出c<0;a<0<b,再根据有理数的加减法法则判断a+c与b﹣a的符号;(2)先根据绝对值的意义去掉绝对值的符号,再合并同类项即可.【解答】解:(1)由题意,得c<a<0<b,则c<0;a+c<0;b﹣a>0;故答案为<;<;>;(2)原式=b﹣a+a+c﹣c=b.【点评】本题考查了绝对值:若a>0,则|a|=a;若a=0,则|a|=0;若a<0,则|a|=﹣a.也考查了数轴与整式的加减.37.已知a>b>0,且|a|>|b|.(1)在数轴上画出a,b,﹣a,﹣b对应的点的大致位置;(2)化简|﹣a|﹣2|a﹣b|+|a+b|.【分析】(1)根据a,b的大小关系在数轴上画出对应点即可.(2)根据绝对值的性质化简即可.【解答】解:(1)如图所示.(2)∵a>b>0,∴a﹣b>0,a+b>0,∴|﹣a|﹣2|a﹣b|+|a+b|=a﹣2(a﹣b)+(a+b)=a﹣2a+2b+a+b=3b.【点评】本题考查作图﹣复杂作图、数轴、绝对值的性质,熟练掌握数轴和绝对值的性质是解答本题的关键.38.已知a,b,c在数轴上的位置如图所示,且|a|=|c|.(1)比较a,﹣a,b,c,﹣c大小;(2)化简|a+b|﹣|a﹣b|+|b+(﹣c)|+|a+c|.【分析】(1)根据数轴即可比较大小;(2)根据绝对值的性质对整式进行化简求解.【解答】解:(1)由数轴可知:b<c<0<a,∵|a|=|c|,∴a=﹣c>﹣a=c>b.(2)∵a+b<0,a﹣b>0,b﹣c<0,a+c=0,∴原式=﹣(a+b)﹣(a﹣b)﹣(b﹣c)+0=﹣2a﹣b+c.【点评】本题考查数轴,涉及比较大小,整式化简,绝对值的性质.39.有理数a,b,c在数轴上的位置如图所示.(1)用“<”连接:0,a,b,c;(2)化简代数式:3|a﹣b|+|a+b|﹣|c﹣a|+2|b﹣c|.【分析】(1)根据数轴上的数,右边的总大于左边的进行判断即可;(2)根据绝对值的性质去绝对值进行计算.【解答】解:(1)如图可得,a<b<0<c;(2)由(1)得:a﹣b<0,a+b<0,c﹣a>0,b﹣c<0,3|a﹣b|+|a+b|﹣|c﹣a|+2|b﹣c|=﹣3(a﹣b)+[﹣(a+b)]﹣(c﹣a)+2[﹣(b﹣c)]=﹣3a+3b﹣a﹣b﹣c+a﹣2b+2c=﹣3a+c.【点评】本题考查了整式的加减,解题的关键是比较a,b,c的大小以及绝对值的性质.40.(2022秋•锦江区校级期中)知有理数a、b、c在数轴上所对应的点的位单如图所示,原点为O.(1)试化简|a+2b|﹣|a+c|﹣|c﹣2b|;(2)若数轴上有一点所表示的数为x,且|x﹣5|=3,求﹣3x﹣4|1﹣x|的值.【分析】(1)根据数轴上点的位置判断出绝对值里边式子的正负,利用绝对值的代数意义化简,计算即可得到结果;(2)根据|x﹣5|=3,得x=8或x=2,再依次代入所求式子即可解答.【解答】解:(1)根据数轴上点的位置得:a<b<0<c,∴a+2b<0,a+c<0,c﹣2b>0,则原式=﹣a﹣2b+a+c﹣c+2b=0;(2)∵|x﹣5|=3,∴x﹣5=3或x﹣5=﹣3,∴x=8或x=2,当x=8时,﹣3x﹣4|1﹣x|=﹣3×8﹣4|1﹣8|=﹣52,当x=2时,﹣3x﹣4|1﹣x|=﹣3×2﹣4|1﹣2|=﹣10,综上,﹣3x﹣4|1﹣x|的值为﹣10或﹣52.【点评】此题考查了整式的加减,数轴,以及绝对值,熟练掌握运算法则是解本题的关键.。
有理数、数轴动点、绝对值、求值化简问题(解析版)-初中数学

有理数、数轴动点、绝对值、求值化简问题【题型归纳】题型一:正数与负数1.(2024七年级上·浙江)小戴同学的微信钱包账单如图所示, 5.20+表示收入5.20元,下列说法正确的是( )A . 1.00-表示收入1.00元B . 1.00-表示支出1.00元C . 1.00-表示支出 1.00-元D .收支总和为6.20元【答案】B 【分析】根据 5.20+表示收入5.20元,可以得出“收入”用正数表示,从而“支出”就用负数表示,得出答案.【详解】解:∵ 5.20+表示收入5.20元,“收入”用正数表示,∴“支出”就用负数表示,∴ 1.00-表示支出1.00元,故选:B .2.(2024七年级上·江苏·专题练习)在下列选项中,具有相反意义的量是( )A .上升了6米和后退了7米B .卖出10斤米和盈利10元C .收入20元与支出30元D .向东行30米和向北行30米【答案】C【分析】本题考查了对正负数概念的理解,关键明确正负数是表示一对意义相反的量.根据相反意义的量的概念,逐项判断分析即可解题.【详解】解:A.不是一对具有相反意义的量,不符合题意;B.不是一对具有相反意义的量,不符合题意;C.是一对具有相反意义的量,符合题意;D.不是一对具有相反意义的量,不符合题意.故本题选:C .3.(2024七年级上·江苏·专题练习)机床厂工人加工一种直径为30mm 的机器零件,要求误差不大于0.05mm ,质检员现抽取10个进行检测(超出部分记为正,不足部分记为负,单位:mm )得到数据如下:0.050.040.020.070.030.040.010.010.030.06+--+-+--+-,,,,,,,,,.其中不合格的零件有( )A .1个B .2个C .3个D .4个【答案】B 【分析】本题主要考查了正负数的实际应用,首先审清题意,明确“正”和“负”所表示的意义,找到数值大于0.05的零件数即可得到答案.【详解】解:∵要求误差不大于0.05mm ,∴只有0.07+和0.06-误差大于0.05,∴不合格的零件有2个,故选:B .题型二:有理数的分类4.(2024七年级上·全国·专题练习)下列说法正确的是( )A .正整数、负整数、正分数和负分数统称为有理数B .整数和分数统称有理数C .正数和负数统称有理数D .正整数和负整数统称整数5.(2024七年级上·江苏·专题练习)关于4-,227,0.41,116-,0,3.14这六个数,下列说法错误的是( )A .4-,0是整数B .227,0.41,0,3.14是正数C .4-,227,0.41,116-,0,3.14是有理数D .4-,116-是负数6.(23-24七年级上·贵州黔东南·阶段练习)对于有理数,有下列说法:(1)正整数和负整数的总和就是整数;(2)分数包括了正分数和负分数和0;(3)有理数是整数和分数的统称;(4)0是整数;(5)分数包含有限小数、循环小数,其中说法全正确的有( )A .(1)(2)(3)B .(2)(3)(4)C .(3)(4)(5)D .(1)(4)(5)题型三:利用数轴比较有理数大小7.(23-24七年级上·河南郑州·期末)已知a b ,在数轴上的位置如图所示,则下列结论:①0a b <<,②||||a b <,③0a b->,④b a a b -<+,正确的是( )A .②③B .①②C .①③D .①④【答案】C 【分析】本题考查根据点在数轴上的位置比较代数式大小,熟练掌握利用数轴比较数的大小是解决问题的关键.\故①0a b <<正确;a b >,②错误;由8.(23-24七年级上·四川达州·期末)如图,若A 是有理数a 在数轴上对应的点,则关于a ,a -,1的大小关系表示正确的是( )A .1a a <<-B .1a a <-<C .1a a <-<D .1a a -<<9.(2024·广东广州·二模)有理数a ,b 在数轴上的对应点的位置如图所示,把a ,a -,b 按照从小到大的顺序排列,正确的是( )A .a a b<-<B .a b a -<<C .a a b -<<D .b a a<-<【答案】A 【分析】本题考查了数轴与有理数大小的比较,正确理解数轴与有理数大小的比较的方法是解题的关键.在数轴上标出有理数a 的相反数a -所表示的点,再根据“在数轴上表示的两个数,右边的数总比左边的数大”,即可判断答案.【详解】在数轴上标出有理数a 的相反数a -所表示的点,则a ,a -,b 按照从小到大的顺序排列为a a b <-<.故选:A .题型四:数轴的距离问题10.(2024·福建福州·三模)如图是单位长度为1的数轴,点A,B是数轴上的点,若点A表示的数是3-,则点B 表示的数是()A.1-B.0C.1D.2【答案】C【分析】本题考查了数轴,熟练掌握数轴上两点之间的距离公式是解题的关键.根据数轴上两点之间的距离公式计算即可.【详解】解:Q点A表示的数是3-,点B距离点A有4个单位,\点B表示的数是341-+=,故选:C.11.(2024·北京·二模)在数轴上,点A,B在原点O的两侧,分别表示数a,3,将点A向左平移1个单位长度,=,则a的值为()得到点C.若CO BOA.2-B.1-C.1D.212.(23-24七年级上·河南新乡·期末)如图,在数轴上点A在原点右侧,距离原点5个单位长度,表示的数是5,点B距离点A是6个单位长度,则点B表示的数是()A.6B.6或6-C.11或6-D.11或1-【答案】D【分析】本题考查了数轴上两点之间的距离,根据题意可列的式子,进而求解,求解数轴上两点之间的距离是解题的关键.【详解】解:∵点B 距离点A 是6个单位长度,则5611+=,或561-=-,∴点B 表示的数是11或1-,故选:D .题型五:数轴的动点问题13.(23-24九年级下·河北保定·期中)如图,一个点在数轴上从原点开始先向右移动1个单位长度,再向左移动a 个单位长度后,该点所表示的数为3-,则a 的值是( )A .4-B .4C .3-D .3【答案】B【分析】本题以数轴为背景考查了两点之间距离公式、解一元一次方程等知识,根据题意,数形结合,由数轴上两点之间距离的表示方法列式求解即可得到答案,熟记数轴上两点之间距离的表示方法是解决问题的关键.【详解】解:根据题意可知,13a -=-,∴4a =,故选:B .14.(23-24七年级上·湖南衡阳·期末)一个动点P 从数轴上的原点出发,沿数轴的正方向以前进4个单位,后退2个单位的程序运动,已知点P 每秒前进或后退1个单位.设n x 表示第n 秒点P 在数轴上的位置所对应的数,如22x =,44x =,53x =,则2023x 为( )A .673B .674C .675D .676【答案】C 【分析】本题主要考查了数轴上的动点问题,数字类的规律探索,根据题意可知每6秒点P 完成一次前进和一次后退运动,且每6秒内点P 向数轴正方形运动2个单位,再由202363371¸=K 即可得到答案.【详解】解:∵动点P 从数轴上的原点出发,沿数轴的正方向以前进4个单位,后退2个单位的程序运动,∴每6秒点P 完成一次前进和一次后退运动,且每6秒内点P 向数轴正方形运动2个单位,∵202363371¸=K ,∴2023x 为33721675´+=,故选:C .15.(23-24七年级上·江苏苏州·阶段练习)如图,圆的周长为4个单位长度,在该圆的4等分点处分别标上数字0、1、2、3,先让圆周上表示数字0的点与数轴上表示数1-的点重合,再将数轴按逆时针方向环绕在该圆上,则数轴上表示数2124-的点与圆周上表示数字( )的点重合.A .0B .1C .2D .3【答案】B 【分析】本题主要考查数轴,熟练掌握数轴的特点和围绕圆周对应的数之间的关系的相互关系是解题的关键.根据题意发现规律,即可解得答案.【详解】解:依题意,4次为一个周期,依次为0,3,2,1,21244531¸=,故数轴上表示数2124-的点与圆周上表示数字1的点重合.故选B .题型六:绝对值非负数的应用16.(23-24七年级下·山东潍坊·阶段练习)若5x -与7y +互为相反数,则3x y -的值是( )A .22B .8C .8-D .22-17.(23-24七年级上·河南新乡·阶段练习)若230a b -++=,则a b +的值是( )A .0B .1C .1-D .202118.(23-24七年级上·广东韶关·期末)若320x y -++=,则x y +的值是( ).A .5B .1C .2D .0题型七:化简绝对值问题19.(2024七年级上·全国·专题练习)若0ab ¹,那么a ab b +的取值不可能是( )A .2-B .0C .1D .220.(23-24七年级下·海南省直辖县级单位·期末)实数m 、n 在数轴上的位置如图所示,化简||n m n -+的结果为( )A .mB .m -C .2m n -D .2n m-21.(2024七年级上·江苏·专题练习)若a 、b 、c 均为整数,且||||1a b c a -+-=,则||||||a c c b b a -+-+-的值为( )A .1B .2C .3D .4题型八:有理数的综合问题22.(2024七年级上·浙江·专题练习)把下列各数分别填在表示它所属的横线上:① 3.14-;②(9)++;③425-;④0;⑤(7)+-;⑥13.14;⑦2000;⑧80%-.(填写序号)(1)正数:___________;(2)负数:___________;(3)整数:___________;(4)分数___________.【答案】(1)②⑥⑦(2)①③⑤⑧(3)②④⑤⑦(4)①③⑥⑧【分析】本题考查有理数的分类及定义,掌握有理数的分类及相关定义是解题的关键;(1)根据正数定义进行分类即可;(2)根据负数定义进行分类即可;(3)根据整数定义进行分类即可(4)根据分数定义进行分类即可.【详解】(1)正数:②⑥⑦;故答案为:②⑥⑦;(2)负数:①③⑤⑧;故答案为:①③⑤⑧;(3)整数:②④⑤⑦;故答案为:②④⑤⑦;(4)分数:①③⑥⑧.故答案为:①③⑥⑧.23.(23-24七年级上·广东·单元测试)如图,数轴上的三点A 、B 、C 分别表示有理数a ,b ,c .(1)填空:a b -______0,a c +______0,b c -______0.(用<或>或=号填空)(2)化简:a b a c b c ---+-.24.(23-24七年级下·甘肃陇南·阶段练习)阅读材料:点A ,B 在数轴上分别表示有理数a ,b ,A ,B 两点之间的距离可表示为AB a b =-.例如:7与1-两数在数轴上所对应的两点之间的距离表示为()718--=,6x -的几何意义是数轴上表示有理数x 的点与表示6的点之间的距离.这种数形结合的方法,可以用来解决一些问题.如图,已知数轴上两点A 、B 对应的数分别为1-和2,数轴上另有一个点P 对应的数为有理数x .(1)请根据阅读材料填空:点P 、A 之间的距离PA =________(用含x 的式子表示);若该距离为4,则x =________.(2)根据几何意义,解决下列问题:①若点P 在线段AB 上,则12x x ++-=________.②若125x x ++-=,求点P 表示的有理数x .值等知识.熟练掌握在数轴上表示有理数是,数轴上两点之间的距离,绝对值的几何意义,绝对值方程,化简绝对值是解题的关键.【专题训练】一、单选题25.(23-24七年级上·四川南充)在π223.141500.333 2.010********--¼-¼,,,中,非负数的个数( )A .2个B .3个C .4个D .5个【答案】B【分析】本题考查了非负数的定义,解题的关键是掌握非负数的定义.根据“零和正数统称为非负数”,即可求解.【详解】解:非负数有:3.141502.010010001¼,,,共3个,故选:B .26.(2024七年级上·全国·专题练习)下列各对数中,互为相反数的有( )()1-与1+;()2--与()2+-;12æö--ç÷èø与12æö++ç÷èø;()1-+与()1+-;()2-+与()2--A .1对B .2对C .3对D .4对即互为相反数的有3对.故选:C .27.(2024七年级上·山东青岛·专题练习)下列关于零的说法中,正确的是( )A .零是正数B .零是负数C .零既不是正数,也不是负数D .零仅表示没有【答案】C【分析】本题考查了对数的理解与运用,注意:负数都小于零,正数都大于零,零既不是正数也不是负数,整数包括正整数、零、负整数;零不仅表示没有,还表示一个介于负数与正数之间的一个数.依据题意,零大于负数,小于正数,零既不是正数也不是负数,整数包括正整数、零、负整数,从而即可根据以上内容判断求解.【详解】解:A 、零不是正数,说法错误;B 、零不是负数,说法错误;C 、零既不是正数,也不是负数,说法正确;D 、零不仅仅表示没有,不同情形下,零表示的意义不同,说法错误;故选:C .28.(23-24七年级上·安徽合肥·期末)在()5--,0.8-,0,|6|-四个数中,最小的数是( )A .()5--B .0.8-C .0D .|6|-【答案】B【分析】本题考查了有理数比较大小,正数大于0,0大于负数,两个负数其绝对值大的反而小,负数都小于0是解题关键.根据正数大于0,0大于负数,两个负数其绝对值大的反而小,可得答案.【详解】解:()50.80|6|--<-<<-,故最小的数是5-.故选:B29.(2024七年级上·江苏·专题练习)下列说法正确的是( )A .数轴上的一个点可以表示不同的有理数B .数轴上有两个不同的点可以表示同一个有理数C .任何有理数都可以在数轴上找到与它对应的唯一的点D .有的有理数不能在数轴上表示出来【答案】C【分析】本题考查了数轴的应用,根据数轴上的点与有理数的对应关系进行解答.【详解】解:A .数轴上一个点只能表示一个数,不能表示两个不同的数,故选项错误;B .数轴上两个不同的点表示两个不同的数,故选项错误;C .任何一个有理数都可以在数轴上找到和它对应的唯一的一个点,正确;D .所有的有理数都可以用数轴上的点表示,故选项错误.故本题选:C .30.(23-24七年级上·江苏常州·期末)有理数a ,b 在数轴上的对应点的位置如图所示.把a -,b ,0按照从小到大的顺序排列,正确的是( )A .0a b<-<B .0a b -<<C .0b a <<-D .0b a <-<按照从小到大的顺序排列为0a <-31.(2024七年级上·全国·专题练习)下列有关相反数的说法:①符号相反的数叫相反数;②数轴上原点两旁的数是相反数;③()3--的相反数是3-;④a -一定是负数;⑤若两个数之和为0,则这两个数互为相反数; ⑥若两个数互为相反数,则这两个数一定是一个正数一个负数.其中正确的个数有( )A .2个B .3个C .4个D .5个【答案】A【分析】本题考查相反数的定义,依据相反数的定义进行判断即可.【详解】解:①符号相反的两个数不一定互为相反数,如2-与3,故①错误;②数轴上原点两旁的数不一定互为相反数,如2-和3,故②错误;③()33--=,3的相反数是3-,故③正确;④a -不一定是负数,如0a =时,0a -=,故④错误;⑤若两个数之和为0,则这两个数互为相反数,故⑤正确;⑥0的相反数是0,故⑥错误.故选:A .32.(24-25七年级上·全国·随堂练习)如果0a b c ++=且c b a >>.则下列说法中可能成立的是( )A .a 、b 为正数,c 为负数B .a 、c 为正数,b 为负数C .b 、c 为正数,a 为负数D .a 、b 、c 为正数二、填空题33.(24-25七年级上·河南安阳·开学考试)乒乓球被誉为我国的“国球”,在正规比赛中,乒乓球的标准质量为2.7克.0.15克的乒乓球记作0.15+,那么另一个低于标准质量0.03克的乒乓球记作.【答案】0.03-【分析】本题考查正负数的意义.熟练掌握正负数表示意义相反的量,是解题的关键.【详解】解:把一个超出标准质量0.15克的乒乓球记作0.15+,那么另一个低于标准质量0.03克的乒乓球记作0.03-,故答案为:0.03-.34.(2024七年级上·北京·专题练习)把下列各数填入它所属的集合内3-,30%,215-,0, 5.32-(1)整数集合{____________________……};(2)分数集合{____________________……};(3)非负数集合{____________________……}.【答案】(1)3-,035.(24-25七年级上·河南南阳·开学考试)在56-,2-,0.35,2.4,25%,0,6,1-,97,24,100.2这些数中,( )是自然数,()是整数,( )最大,( )最小.36.(24-25七年级上·全国·随堂练习)已知x 是非负数,且非负数中最小的数是0.(1)已知210a b -+-=,则a b +的值是_________;(2)当a =________时,12a -+有最小值,最小值是______.【答案】(1)337.(2024七年级上·浙江·专题练习)已知m 是有理数,则|2||4||6||8|m m m m -+-+-+-的最小值是.三、解答题38.(2024七年级上·江苏·专题练习)在数轴上表示下列各数的相反数,并比较原数的大小.3, 1.5-,132-,4||5-,0,4-比较原数的大小为:1443 1.50325-<-<-<<-<.39.(2024七年级上·全国·专题练习)化简下列各式的符号,并回答问题:(1)()2--;(2)15æö+-ç÷èø;(3)()4éù---ëû(4)()3.5éù--+ëû;(5)(){}5éù----ëû(6)(){}5éù---+ëû问:①当5+前面有2012个负号,化简后结果是多少?②当5-前面有2013个负号,化简后结果是多少?你能总结出什么规律?(3)()44éù---=-ëû;(4)()3.5 3.5éù--+=ëû;(5)(){}55éù----=ëû;(6)(){}55éù---+=-ëû;①当5+前面有2012个负号,化简后结果是5+;②当5-前面有2013个负号,化简后结果5-,总结规律:一个数的前面有奇数个负号,化简的结果等于它的相反数,有偶数个负号,化简的结果等于它本身.40.(2024七年级上·全国·专题练习)阅读理解:数轴上线段的长度可以用线段端点表示的数进行减法运算得到,例如图,线段()101AB ==--;线段220BC ==-;线段()321AC ==--问题:(1)数轴上点M N 、代表的数分别为9-和1,则线段MN =___________;(2)数轴上点E F 、代表的数分别为6-和3-,则线段EF =___________;(2)解:∵点E F 、代表的数分别为6-和3-,∴线段()363EF =---=;故答案为:3;(3)解:由题可得|2|5m -=,则25m -=或25m -=-,解得7m =或3m =-,∴m 值为7或3-.41.(2024七年级上·江苏·专题练习)同学们都知道,()42--表示4与2-的差的绝对值,实际上也可理解为4与2-两数在数轴上所对应的两点之间的距离;同理3x -也可理解为x 与3两数在数轴上所对应的两点之间的距离.试探索:(1)求()42--= ;(2)若25x -=,则x = ;(3)请你找出所有符合条件的整数x ,使得123x x -++=.。
绝对值最值、化简问题以及动点问题

1.(2022·江苏·七年级专题练习)当式子|x +3|+|x ﹣7|取最小值时,相应的x 的取值范围是_____________,最小值是_______.2.(2021·上海同济大学附属存志学校期末)1234x x x x -+-+-+-的最小值为________,此时x 的取值范围是_____________.3.(2022·河南南阳·七年级期末)|x +8|+|x +1|+|x ﹣3|+|x ﹣5|+|x ﹣2|的最小值为__________,此时x 的值为________.4.(2022·江苏江苏·七年级期末)若x 是有理数,则|x ﹣1|+|x ﹣2|+|x ﹣3|+|x ﹣4|+…+|x ﹣1000|的最小值是______.5.|x ﹣1|+|x ﹣2|+|x ﹣3|+…+|x ﹣2019|的最小值为_________.6.(2022·江苏省江阴市第一中学七年级阶段练习)阅读下列内容:数轴上表示数a 的点与原点的距离叫做数a 的绝对值,记作|a|.数轴上表示数a 的点与表示数b 的点的距离记作|a ﹣b|,如|3﹣5|表示数轴上表示数3的点与表示数5的点的距离,|3+5|=|3﹣(﹣5)|表示数轴上表示数3的点与表示数﹣5的点的距离,|a ﹣3|表示数轴上表示数a 的点与表示数3的点的距离.根据以上材料回答下列问题:(1)若|x ﹣1|=|x+1|,则x=,若|x ﹣2|=|x+1|,则x=;(2)若|x ﹣2|+|x+1|=3,则x 的取值范围是;(3)若|x ﹣2|+|x+1|=5,则x 的值是;(4)当x=时,|x-1|+|x+5|+|x-4|的值最小,最小值是________.1.有理数a 、b 、c 在数轴上位置如图,则a c a b b c --++-的值为().A .2aB .222a b c +-C .0D .2c-2.(2022·山东滨州·七年级期末)若有理数a 、b 、c 在数轴上位置如图所示,则化简c a a b b c --++-的结果为_______.3.(2022·河南周口·七年级期末)有理数a ,b 在数轴上对应的位置如图所示,那么代数式11a b a b a b a b -++--+的值是()A .-1B .1C .3D .-34.(2021·长郡集团郡维学校初一月考)如果a a +b b +cc =-1,那么ab ab +bc bc +ac ac +abc abc 的值为()A .2-B .1-C .0D .不确定5.(2022·内蒙古赤峰·七年级期中)x 、y 、z 是有理数且0xyz <,则||||||x y z x y z ++的值是()A .3-B .3或1-C .1D .3-或1数轴上动点相距问题数轴动点问题本学期必考压轴题型,是高分考生必须要攻克的一块内容,对考生的综合素养要求较高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课题:绝对值化简(与数轴结合)
〖学习目标〗通过实数在数轴上的位置,判断数的大小,去绝对值符号 〖重点难点预见〗读懂数轴判断数的大小 〖学习流程〗
一.知识回顾: 回顾数轴表示数的意义 二.自主学习:
如果有理数a 、b 、c 在数轴上的位置如图所示,求a b a c b c ++--+的值.
小结:如何通过数轴判断正负,去掉绝对值符号
三.课堂练习
1.已知有理数a 、b 的和a b +及差a b -在数轴上如图所示,化简227a b a b +---.
a-b
a+b
1
0-1
2.数a b ,在数轴上对应的点如右图所示,试化简a b b a b a a ++-+--
b
a
3.实数a b c ,,在数轴上的对应点如图,化简a c b a b a c +--++-
c
b
a
四.课堂检测:
1.实数a 、b 、c 在数轴上的位置如图所示,则代数式 的值等于( ).
(A )
(B )
(C )
(D )
b -1
c 0 a 1
2已知有理数c b a ,,在数轴上的对应点的位置如图所示:那么求a c c b b a -+---的值
3.有理数c b a ,,在数轴上对应的点(如下图),图中O 为原点,化简
a c
b b a b a --+++-。
4.a 、b 、c 的大小关系如图所示,求
a b b c c a ab ac
a b b c c a ab ac
-----++
----的值. c
1
b
a
五.小结反思:
a
c
x
b
a c
x
b。
