上海2021年九年级数学·一模考试(静安)
244-5 相似三角形(2021上海各区一模和二模作业2021-2022学年九年级数学上沪教版原卷版

24.4-5相似三角形(2021上海各区一模和二模)一、解答题1.(2021·上海九年级一模)已知:如图,在Rt△ABC中,∠ACB=90°,CH△AB,垂足为点H.点D在边BC上,联结AD,交CH于点E,且CE=CD.(1)求证:△ACE∽△ABD;(2)求证:△ACD的面积是△ACE的面积与△ABD的面积的比例中项.2.(2021·上海九年级一模)已知:如图,在梯形ABCD中,//AD BC,对角线BD、AC相交于点E,过点A作//AF DC,交对角线BD于点F.(1)求证:DF DE BD BE=;(2)如果ADB ACD∠=∠,求证:线段CD是线段DF、BE的比例中项.3.(2021·上海九年级一模)已知:如图,在四边形ABCD中,AB AD=,AC、BD相交于点E,AE CE DE BE⋅=⋅(1)求证:ABE ACB ∽;(2)如果2·DA DE DB =,求证:AB EC BC AE ⋅=⋅.4.(2021·上海九年级一模)如图,在ACB △中,点D 、E 分别在边BC 、AC 上,AD AB =,BE CE =,AD 与BE 交于点F ,且AF DF BF EF ⋅=⋅.求证:(1)ADC BEC ∠∠=;(2)AF CD EF AC ⋅=⋅.5.(2021·上海九年级一模)已知:如图,四边形ABCD 是菱形,点M 、N 分别在边BC 、CD 上,联结AM 、AN 交对角线BD 于E 、F 两点,且MAN ABD ∠=∠.(1)求证:2AB BF DE =⋅;(2)若BE DN DE DC=,求证://EF MN .6.(2021·上海九年级一模)某班级的“数学学习小组心得分享课”上,小智跟同学们分享了关于梯形的两个正确的研究结论:①如图1,在梯形ABCD 中,//AD BC ,过对角线交点O 的直线与两底分别交于点M 、N ,则AM CN DM BN =; ②如图2.在梯形ABCD 中,//AD BC ,过两腰延长线交点P 的直线与两底分别交于点K 、L ,则AK BL DK CL=.接着小明也跟同学们分享了关于梯形的一个推断:过梯形对角线交点且平行于底边的直线被梯形两腰所截,截得的线段被梯形对角线的交点平分.(1)经讨论,大家都认为小明所给出的推断是正确的,请你结合图示(见答题卷)写出已知、求证,并给出你的证明:(2)小组还出了一个作图题考同学们:只用直尺将图3中两条平行的线段AB 、CD 同时平分,请保留作图过程痕迹,并说明你作图方法的正确性(可以直接运用小智和小明得到的正确结论).(注意:请务必在试卷的图示中完成作图草稿,在答题卷上直接用2B 铅笔水笔完成作图,不要涂改)7.(2021·上海九年级一模)Rt ABC 中,∠ACB=90°,点D 、E 分别为边AB 、BC 上的点,且CD=CA ,DE△AB . (1)求证:2CA CE CB =⋅.(2)联结AE ,取AE 的中点M ,联结CM 并延长与AB 交于点H .求证:CH△AB .8.(2021·上海九年级一模)已知:如图,在△ABC 中,DE∥BC ,AD 2=AE•AC .求证:(1)△BCD∽△CDE ;(2)22CD AD BC AB=. 9.(2021·上海九年级一模)如图,点O 是菱形ABCD 的对角线BD 上一点,联结AO 并延长,交CD 于点E ,交BC 的延长线于点F .(1)求证:2AB DE BF =⋅;(2)如果1OE =,2EF =,求CF BF的长. 10.(2021·上海九年级一模)已知:如图,D 、E 分别是ABC 的边AB 、AC 上的点,且AED ABC ∠=∠,连接BE 、CD 相交于点F .(1)求证:ABE ACD ∠=∠;(2)如果ED EC =,求证:22DF EF BD EB=. 11.(2021·上海九年级一模)如图,点E 为ABC 边BC 上一点,过点C 作CD BA ⊥,交BA 的延长线于点D ,交EA 的延长线于点F ,且AF CD BC AD ⋅=⋅.(1)求证:AE BC ⊥;(2)如果BE CE =,求证:22BC BD AC =⋅.12.(2021·上海九年级一模)如图,已知在平行四边形ABCD 中,E 是边AD 上一点,联结BE 、CE ,延长BA 、CE 相交于点F ,2CE DE BC =⋅(1)求证:EBC DCE ∠=∠;(2)求证:··BE EF BF AE =.13.(2021·上海九年级一模)如图,在四边形ABCD 中,,B DCB ∠=∠联结AC .点E 在边BC 上,且,CDE CAD DE ∠=∠与AC 交于点,F CE CB AB CD ⋅=⋅.()1求证://AD BC ;()2当AD DE =时,求证:2AF CF CA =⋅.14.(2021·上海九年级一模)如图,在ABC 中,点D 、G 在边AC 上,点E 在边BC 上,DB DC =,//EG AB ,AE 、BD 交于点F ,BF AG =.(1)求证:BFE CGE △△;(2)当AEG C ∠=∠时,求证:2AB AG AC =⋅.15.(2021·上海九年级一模)如图,已知矩形DEFG 的边DE 在ABC 的边BC 上,顶点G ,F 分别在边AB ,AC 上.ABC 的高AH 交GF 于点I .(1)求证:BD EH DH CE ⋅=⋅;(2)设DE n EF =⋅(n 为正实数),求证:11n BC AH EF+=. 16.(2021·上海九年级一模)已知:如图,//AD BC ,ABD C ∠=∠,AE BD ⊥,DF BC ⊥,点E 、F 分别为垂足.(1)求证:AE BD DF BC=; (2)连结EF ,如果ADB BDF ∠=∠,求证:DF DC EF BC ⋅=⋅.17.(2021·上海九年级二模)如图,已知四边形ABCD 是菱形,对角线AC 、BD 相交于点O ,BD = 2AC .过点A 作AE△CD ,垂足为点E ,AE 与BD 相交于点F .过点C 作CG△AC ,与AE 的延长线相交于点G .(1)求证:△ACG≌△DOA ;(2)求证:2DF BD DE AG ⋅=⋅.18.(2021·上海市实验学校九年级二模)如图,在四边形ABCD 中,AC 平分∠BCD ,AC△AB ,E 是BC 的中点,AD△AE .(1)求证:2AC CD BC =⋅(2)过E 做EG△AB ,延长EG 至点F ,使FG=EG ,若∠B=30°,求证:四边形AFEC 是菱形.19.(2021·上海九年级二模)已知:如图,在正方形ABCD 中,联结BD ,E 是边AB 上一点,BF △DE ,垂足为点F,且EF•BD=BE•BF.(1)求证:∠ADE=∠BDE;(2)延长DF与CB的延长线交于点G,求证:BG=BC+AE.20.(2021·上海九年级二模)如图,在△ABCD中,点G是边BC延长线上一点,联结AG分别交BD和CD于点E 和F,联结DG.(1)求证:AE2=EF•EG;(2)如果∠ABD=∠AGD,求证:四边形ABGD是等腰梯形.21.(2021·上海九年级二模)如图,已知四边形ABCD中,AD∥BC,对角线AC、BD相交于点O,AC平分∠BAD,BD平分∠ABC,点E在边BC的延长线上,联结OE,交边CD于点F.(1)求证:四边形ABCD是菱形;(2)如果OE△CD,求证:CE•OF=CF•OE.22.(2021·上海九年级二模)已知:如图,在△ABCD中,点E、F分别在边BC、边BC的延长线上,四边形AEFD是菱形,菱形的对角线AF分别交DE、DC于点P、Q,AF EF BF PF=.求证:(1)四边形ABCD为矩形;(2)BE•DQ=FQ•PE.23.(2021·上海九年级二模)如图,已知在梯形ABCD中,AD//BC,对角线BD平分∠ABC,点G在底边BC上,联结DG交对角线AC于F,∠DGB=∠DAB.(1)求证:四边形ABGD是菱形;(2)联结EG,求证:BG•EG=BC•EF.24.(2021·上海九年级二模)已知:如图,梯形ABCD中,AD∥BC,AB=DC,点E在下底BC上,∠AED=∠B.(1)求证:CE•AD=DE2;(2)求证:22 CE AB AD AE=.25.(2021·上海九年级二模)如图,在△ACB中,∠ABC=90°,点D是斜边AC的中点,四边形CBDE是平行四边形.(1)如图1,延长ED交AB于点F,求证:EF垂直平分AB;(2)如图2,联结BE 、AE ,如果BE 平分∠ABC ,求证:AB =3BC .26.(2021·上海九年级二模)已知:如图,在梯形ABCD 中,//AD BC ,90B ∠=︒,E 是AC 的中点,DE 的延长线交边BC 于点F .(1)求证:四边形AFCD 是平行四边形;(2)如果22AE AD BC =⋅,求证四边形AFCD 是菱形.27.(2021·上海九年级二模)如图,已知在直角梯形ABCD 中,AD ∥BC ,∠ABC =90°,AE △BD ,垂足为E ,联结CE ,作EF △CE ,交边AB 于点F .(1)求证:△AEF ∽△BEC ;(2)若AB =BC ,求证:AF =AD .28.(2021·上海九年级二模)如图,已知,在平行四边形ABCD 中,E 为射线CB 上一点,联结DE 交对角线AC 于点F ,∠ADE =∠BAC .(1)求证:CF •CA =CB •CE ;(2)如果AC =DE ,求证:四边形ABCD 是菱形.29.(2021·上海九年级二模)如图,在梯形ABCD 中,//,AD BC AB CD =,过点A 作AE BC ⊥,垂足为点E ,过点E 作EF CD ⊥,垂足为点F ,联结DE ,且DE 平分ADC ∠.(1)求证:ABE ECF ≌△△;(2)联结BD ,BD 与AE 交于点G ,当2=⋅AB BG BD 时,求证2=⋅EC BE BC .。
【2021年上海市初中一模数学卷】2021年上海市金山区初中毕业生学业模拟考试试卷九年级数学及答案

金山区2020学年第一学期期末质量检测初三数学试卷(满分150分,考试时间100分钟)(2021.1)一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上.】 1.已知二次函数()122−−=x y ,那么该二次函数图像的对称轴是()(A )直线2=x ; (B )直线2−=x ; (C )直线1=x ; (D )直线1−=x .2.下列各点在抛物线22x y =上的是()(A )()2,2;(B )()42,;(C ))(8,2;(D )()16,2.3.在ABC Rt ∆中, 90=∠C ,那么锐角A 的正弦等于( )(A )的邻边锐角的对边锐角A A ;(B )斜边的对边锐角A ;(C )斜边的邻边锐角A ;(D )的对边锐角的邻边锐角A A .4.若α是锐角,()2215sin =+α,那么锐角α等于( )(A ) 15;(B ) 30;(C ) 45;(D ) 60.5.如图,已知点D 、E 分别在ABC ∆的边AB 、AC 上,BC DE //,2=AD ,3=BD ,a BC =,那么ED 等于()(A )a 32; (B )a 32−;(C )a 52; (D )a 52−.6.如图,已知ABC Rt ∆中, 90=∠C ,3=AC ,4=BC ,如果以点C 为圆心的圆与斜边AB 有公共点,那么⊙C 的半径r 的取值范围是( )(A )5120≤≤r ; (B )3512≤≤r ; (C )4512≤≤r ; (D )43≤≤r . 二、填空题:(本大题共12题,每题4分,满分48分) 【请直接将结果填入答题纸的相应位置】第6题图BCAA第5题图7.计算:=⎪⎭⎫⎝⎛−+b a a 232.8.已知()x x x f 32+=,那么()=−2f .9.抛物线22x y −=沿着x 轴正方向看,在y 轴的左侧部分是.(填“上升”或“下降”)10.正十边形的中心角等于度.11.已知⊙1O 和⊙2O 的半径长分别为3和4,若⊙1O 和⊙2O 内切,那么圆心距21O O 的长等于.12.在ABC Rt ∆中, 90=∠C ,15=AB ,54in =A s ,那么=BC .13.在ABC ∆中,5:2:1::=BC AC AB ,那么=B tan .14.已知:如图,ABC ∆的中线AE 与BD 交于点G ,AE DF //交BC 于F ,那么=AGDF.15.如图,在梯形ABCD 中,BC AD //,AD BC 2=,设a AB =,b AD =,那么向量CD 用向量a 、b 表示为.16.如图,已知⊙O 中, 120=∠AOB ,弦18=AB ,那么⊙O 的半径长等于.17.如图,在□ABCD 中,点E 在边BC 上,DE 交对角线AC 于F ,若BE CE 2=,ABC ∆的面积等于15,那么FEC ∆的面积等于 .18.已知在ABC Rt ∆中,90=∠C ,1=BC ,2=AC ,以点C 为直角顶点的DCE Rt ∆的顶点D 在BA 的延长线上,DE 交CA 的延长线于点G ,若21tan =∠CED ,GE CE =,那么BD 的长等于 .第17题图BACDEF第16题图ABOAGDCBEF第14题图第15题图ACB第18题图三、解答题(本大题共7题,满分78分) 19.(本题满分10分)如图,已知在ABC Rt ∆中,90=∠C ,3=AC ,4=BC .求:30tan 4tan cos 1sin tan 2AB A B +−+⋅的值.20.(本题满分10分,每小题满分5分)已知:如图,⊙1O 与⊙2O 外切于点T ,经过点T 的直线与⊙1O 、⊙2O 分别相交于点A 和点B .(1)求证:B O A O 21//;(2)若21=A O ,32=B O ,7=AB ,求AT 的长. 21.(本题满分10分,每小题满分5分)已知抛物线c bx x y ++−=22经过点()1,0A 、()5,1−B .(1)求抛物线的表达式;(2)把表达式化成()k m x y ++−=22的形式,并写出顶点坐标与对称轴.22.(本题满分10分,每小题满分5分)如图,在距某输电铁塔GH (GH 垂直地面)的底部点H 左侧水平距离60米的点B 处有一个山坡,山坡AB 的坡度3:1=i ,山坡坡底点B 到坡顶A 的距离AB 等于40米,在坡顶A 处测得铁塔顶点G 的仰角为 30(铁塔GH 与山坡AB 在同一平面内).(1)求山坡的高度;(2)求铁塔的高度GH .(结果保留根号)23.(本题满分12分,每小题满分6分)已知:如图,四边形ABCD 是菱形,点M 、N 分别在边BC 、CD 上,联结AM 、AN 交对角线BD 于E 、F 两点,且ABD MAN ∠=∠. (1)求证:DE BF AB ⋅=2;(2)若DCDNDE BE =,求证:MN EF //. C第19题图BAT 第20题图BAO 1 O 2G第22题图ABHABF E C第23题图DMN第24题图第25题备用图24.(本题满分12分,每小题满分4分)在平面直角坐标系xoy 中,直线243+−=x y 与直线321−=x y 相交于点A ,抛物线)0(12≠−+=a bx ax y 经过点A .(1)求点A 的坐标;(2)若抛物线12−+=bx ax y 向上平移两个单位后, 经过点()2,1−,求抛物线12−+=bx ax y 的表达式;(3)若抛物线c x b x a y +'+'=2()0<'a 与2+=ax y 对称,且这两条抛物线的顶点分别是点P '与点P ,当S 求抛物线12−+=bx ax y 的表达式.25.(本题满分14分,第(1)分4分,第(2)分6分,第(3)分4分)定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中,O A ∠=∠21. 已知:如图2,AC 是⊙O 的一条弦,点D 在⊙O 上(与A 、C 不重合),联结DC 交射线AO 于点E ,联结OD ,⊙O 的半径为5,43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时,若DOE ∆与AEC ∆相似,求DCA ∠的正切值.(3)当1=OE 时,求点A 与点D 之间的距离(直接写出答案).ABCO第25题图1第25题图2参考答案和评分标准一.选择题: 1.A ; 2.C ; 3.B ; 4.B ; 5.D ; 6.C .二.填空题: 7.b a 24−; 8.2−; 9.上升;10.36;11.1;12.12;13.2; 14.43;15.b a −−;16.36;17.4;18.52+. 19.解:在ABC Rt ∆中, 90=∠C ,3=AC ,4=BC ,由勾股定理得,222BC AC AB +=, ∴5432222=+=+=BC AC AB ;……………………………………(2分)∴43tan ==BC AC B ;54sin ==AB BC A ;54cos ==AB BC B ;34tan ==AC BC A ……(4分)∴原式2334345415443⎪⎪⎭⎫⎝⎛⨯+−+⨯=;……………………(2分)59154=+=.………………(2分) 20.(1)证明:联结21O O ,即21O O 为连心线,又∵⊙1O 与⊙2O 外切于点T ,……(1分) ∴21O O 经过点T ;………………………………………(1分)∵T O B O T O A O 2211,==;∴TB O B TA O A 21,∠=∠∠=∠;……………………(1分) ∵TB O TA O 21∠=∠; ∴B A ∠=∠;……………(1分) ∴B O A O 21//.……………………(1分) (2)∵B O A O 21// ∴BTATBO AO =21;……………………………(2分) ∵21=A O ,32=B O ,7=AB ; ∴AT AT −=732,解得:514=AT .……………(3分) 21.解:(1)由抛物线c bx x y ++−=22经过点()1,0A 、()5,1−B 两点可得:⎩⎨⎧−=++−=521c b c ………………(2分)解得:⎩⎨⎧=−=14c b ;…………………(2分) ∴抛物线的解析式为:1422+−−=x x y .……………………(1分) (2)1422+−−=x x y ()3122++−=x ;……………(3分)∴()3122++−=x y ,顶点坐标为:()3,1−,对称轴为:直线1−=x .……………(1+1分)22.解:(1)过点A 作AD 垂直HB ,交HB 的延长线于点D .……………(1分) 即 90=∠ADB ;由题意得:3:1=i ,60=AB (米);∴31=BD AD ,即AD BD 3=;………(1分) 又∵222BD AD AB +=,即()222340AD AD +=……………(1分)∴20=AD (米).……………(1分)答:山坡的高度为20米.…………………(1分) (2)作BH AE //交GH 于点E .………………(1分) ∵BH AD ⊥,BH GH ⊥;∴GH AD //; 即:四边形ADHE 是平行四边形;由题意可知: 30=∠GAE ,60=BH (米); ∵3203==AD BD (米); ∴30260+==DH AE (米);……………(1分)在AGE R ∆t 中,AEGEGAE =∠tan ; ∴32020+=GE (米).……………(1分) 又∵20==AD EH (米);∴32040+=+=EH GE GH (米);……………(1分)答:铁塔的高度GH 为)(32040+米.……………(1分)23.证明:(1)∵四边形ABCD 是菱形; ∴AD AB =;……………(1分) ∴ADB ABD ∠=∠;……………(1分)∵BAE ABD AED ∠+∠=∠,BAE MAN BAF ∠+∠=∠; 又∵ABD MAN ∠=∠;∴BAF AED ∠=∠;……………(1分) ∴AED ∆∽FAB ∆;……………(1分) ∴ABDEBF AD =,即DE BF AB AD ⋅=⋅;……………(1分) ∴DE BF AB ⋅=2.……………(1分)(2)∵四边形ABCD 是菱形;∴BC AD =,BC AD //;……………(1分) ∴AD BM DE BE =;……………(2分) ∵DC DNDE BE =; ∴DC DN AD BM =,……………(1分)∴DCDN BC BM =;……………(1分) ∴BD MN //,即MN EF //.……………(1分) 24.解:(1)∵直线243+−=x y 与直线321−=x y 相交于点A , ∴⎪⎪⎩⎪⎪⎨⎧−=+−=321243x y x y ,解得:⎩⎨⎧−==14y x ;……………(3分)∴点A 的坐标为()14−,.……………(1分)(2)∵抛物线)0(12≠−+=a bx ax y 经过点A ()14−,,∴11416−=−+b a 即a b 4−=……………(1分)∴142−−=ax ax y ∴平移后的抛物线的表达式是142+−=ax ax y ;……………(1分)∴142+−=−a a ,解得:1=a ………………(1分)∴抛物线12−+=bx ax y 的表达式是:142−−=x x y .……………(1分)(3)∵142−−=ax ax y ()1422−−−=a x a ∴()142−−a P ,……………(1分)∵抛物线()02<'+'+'=a c x b x a y 与142−−=ax ax y ∴()142+'a P ,……………(1分)∵0<'a ,∴0>a ; ∴28+='a P P ; 又∵2=OD ,P P OD S P OP '⋅⋅='∆21;∴()328221=+⨯⨯a ,解得:81=a .………(1分) ∴抛物线12−+=bx ax y 的表达式是121812−−=x x y .………………(1分)25.(1)解:作AC OH ⊥垂足为点H ,OH 过圆心, 由垂径定理得:AC CH AH 21==;……………………………(1分) ∵在OAH R ∆t 中43tan ==∠AH OH OAC ,设x AH x OH 4,3==,……………(1分)∴在OAH R ∆t 中,可得:222OA AH OH =+,由⊙O 的半径为5可得:()()222543=+x x , 解得:1±=x ,(1−=x 舍去)∴4,3==AH OH ,………………………(1分) ∴82==AH AC .………………………(1分) (2)∵AEC DEO ∠=∠,∴当DOE ∆与AEC ∆相似时可得:A DOE ∠=∠或者ACD DOE ∠=∠; 由定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.可知:DOE ACD ∠=∠21, ∴DOEACD ∠≠∠∴当DOE ∆与AEC ∆相似时不存在ACD DOE ∠=∠情况.………………………(1分) ∴当DOE ∆与AEC ∆相似时,A DOE ∠=∠,∴AC OD //,∴AEOEAC OD =;……………(1分) ∵8,5===AC OA OD ,得AE AE −=585,∴1340=AE ;…………………(1分) 作AC EG ⊥垂足为G ,可得: 90=∠=∠AHO AGE ,∴OH GE //,∴AHAGOH EG AO AE ==即4351340AG EG ==,∴1324=EG ,……………(1分) 1332=AG ,137213328=−=CG ,…………(1分)∴在CEG R ∆t 中,3113721324tan ===∠CG EG DCA .…………………………(1分)(3)当1=OE 时,AD 的长是52或1452918.……………………………(2+2分)。
2021年上海市普陀区中考数学一模试卷(有答案)

2021 年上海市普陀区中考数学一模试卷一、选择题:(本大题共6题,每题4分,满分24分)[下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上]1.下列函数中,y关于x的二次函数是() A.y=ax2+bx+c B.y=x(x﹣1)C.D.y=(x﹣1)2﹣x2【分析】根据二次函数的定义,逐一分析四个选项即可得出结论.【解答】解:A、当 a=0 时,y=bx+c 不是二次函数;B、y=x(x﹣1)=x2﹣x 是二次函数;C、y=不是二次函数;D、y=(x﹣1)2﹣x2=﹣2x+1 为一次函数.故选:B.【点评】本题考查了二次函数的定义,牢记二次函数的定义是解题的关键.2.在Rt△ABC中,∠C=90°,AC=2,下列结论中,正确的是()A.AB=2sinA B.AB=2cosA C.BC=2tanA D.BC=2cotA【分析】直接利用锐角三角函数关系分别计算得出答案.【解答】解:∵∠C=90°,AC=2,∴cosA==,故AB=,故选项 A,B 错误;A . tanA= = ,则 BC=2tanA ,故选项 C 正确;则选项 D错误.故选:C .【点评】此题主要考查了锐角三角函数关系,正确将记忆锐角三角函数关系是解题关键. 3. 如图,在△ABC 中,点D 、E 分别在边AB 、AC 的反向延长线上,下面比例式中,不能判断ED ∥BC 的是()B .C .D .【分析】根据平行线分线段成比例定理,对各选项进行逐一判断即可.【解答】解:A .当时,能判断ED ∥BC ; B. 当时,能判断ED ∥BC ; C. 当时,不能判断ED ∥BC ; D. 当时,能判断ED ∥BC ;故选:C .【点评】本题考查的是平行线分线段成比例定理,如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边.4.已知,下列说法中,不正确的是()A.B.与方向相同C.D.【分析】根据平行向量以及模的定义的知识求解即可求得答案,注意掌握排除法在选择题中的应用.【解答】解:A、错误.应该是﹣5=;B、正确.因为,所以与的方向相同;C、正确.因为,所以∥;D、正确.因为,所以||=5||;故选:A.【点评】本题考查了平面向量,注意,平面向量既有大小,又由方向,平行向量,也叫共线向量,是指方向相同或相反的非零向量.零向量和任何向量平行.5.如图,在平行四边形ABCD中,F是边AD上的一点,射线CF和BA的延长线交于点E,如果,那么的值是()A.B.C.D.【分析】根据相似三角形的性质进行解答即可.【解答】解:∵在平行四边形 ABCD 中,∴AE∥CD,∴△EAF∽△CDF,∵,∴,∴,∵AF∥BC,∴△EAF∽△EBC,∴=,故选:D.【点评】此题考查相似三角形的判定和性质,综合运用了平行四边形的性质和相似三角形的性质是解题关键.6.如图,已知AB和CD是⊙O的两条等弦.OM ⊥AB,ON⊥CD,垂足分别为点M、N,BA、DC的延长线交于点P,联结OP.下列四个说法中:①;②OM=ON;③PA=PC;④∠BPO=∠DPO,正确的个数是()A.1 B.2 C.3 D.4【分析】如图连接 OB、OD,只要证明 Rt△OMB≌Rt△OND,Rt△OPM≌Rt△OPN 即可解决问题.【解答】解:如图连接 OB、OD;∵AB=CD,∴=,故①正确∵OM⊥AB,ON⊥CD,∴AM=MB,CN=ND,∴BM=DN,∵OB=OD,∴Rt△OMB≌Rt△OND,∴OM=ON,故②正确,∵OP=OP,∴Rt△OPM≌Rt△OPN,∴PM=PN,∠OPB=∠OPD,故④正确,∵AM=CN,∴PA=PC,故③正确,故选:D.【点评】本题考查垂径定理、圆心角、弧、弦的关系、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线面构造全等三角形解决问题,属于中考常考题型.二.填空题(本大题共 12 题,每题 4 分,满分 48 分)7.如果 =,那么= .【分析】利用比例的性质由=得到=,则可设a=2t,b=3t,然后把a=2t,b=3t代入中进行分式的运算即可.【解答】解:∵=,∴=,设 a=2t,b=3t,∴==.故答案为.【点评】本题考查了比例的性质:常用的性质有:内项之积等于外项之积;合比性质;分比性质;合分比性质;等比性质.8.已知线段a=4厘米,b=9厘米,线段c是线段a和线段b的比例中项,线段c的长度等于6厘米.【分析】根据比例中项的定义,列出比例式即可得出中项,注意线段不能为负.【解答】解:根据比例中项的概念结合比例的基本性质,得:比例中项的平方等于两条线段的乘积.所以c2=4×9,解得c=±6(线段是正数,负值舍去),∴c=6cm,故答案为:6.【点评】本题考查比例线段、比例中项等知识,解题的关键是熟练掌握基本概念,属于中考常考题型.9.化简:=﹣4+7 .【分析】根据屏幕绚丽的加法法则计算即可【解答】解::=﹣4+6=﹣4+7,故答案为;【点评】本题考查平面向量的加减法则,解题的关键是熟练掌握平面向量的加减法则,注意平面向量的加减适合加法交换律以及结合律,适合去括号法则.10.在直角坐标系平面内,抛物线y=3x2+2x在对称轴的左侧部分是下降的(填“上升”或“下降”)【分析】由抛物线解析式可求得其开口方向,再结合二次函数的增减性则可求得答案.【解答】解:∵在 y=3x2+2x 中,a=3>0,∴抛物线开口向上,∴在对称轴左侧部分 y 随 x 的增大而减小,即图象是下降的,故答案为:下降.【点评】本题主要考查二次函数的性质,利用二次函数的解析式求得抛物线的开口方向是解题的关键.11.二次函数y=(x﹣1)2﹣3的图象与y轴的交点坐标是(0,﹣2).【分析】求自变量为0时的函数值即可得到二次函数的图象与y轴的交点坐标.【解答】解:把x=0代入y=(x﹣1)2﹣3得y=1﹣3=﹣2,所以该二次函数的图象与y轴的交点坐标为(0,﹣2),故答案为(0,﹣2).【点评】本题考查了二次函数图象上点的坐标特征,在y轴上的点的横坐标为0.12.将抛物线y=2x2平移,使顶点移动到点P(﹣3,1)的位置,那么平移后所得新抛物线的表达式是y=2(x+3)2+1 .【分析】由于抛物线平移前后二次项系数不变,然后根据顶点式写出新抛物线解析式.【解答】解:抛物线 y=2x2 平移,使顶点移到点 P(﹣3,1)的位置,所得新抛物线的表达式为 y=2(x+3)2+1.故答案为:y=2(x+3)2+1.【点评】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.13.在直角坐标平面内有一点A(3,4),点A与原点O的连线与x轴的正半轴夹角为α,那么角α的余弦值是.【分析】利用锐角三角函数的定义、坐标与图形性质以及勾股定理的知识求解.【解答】解:∵在直角坐标平面内有一点A(3,4),∴OA==5,∴cosα= .故答案为:.【点评】本题考查了解直角三角形、锐角三角函数的定义、坐标与图形性质以及勾股定理的知识,此题比较简单,易于掌握.14.如图,在△ABC中,AB=AC,点D、E分别在边BC、AB上,且∠ADE=∠B,如果DE:AD=2:5,BD=3,那么AC= ,.【分析】根据∠ADE=∠B,∠EAD=∠DAB,得出△AED∽△ABD,利用相似三角形的性质解答即可.【解答】解:∵∠ADE=∠B,∵∠EAD=∠DAB,∴△AED∽△ABD,∴,即,∴AB=,∵AB=AC,∴AC=,故答案为:,【点评】本题考查了相似三角形的判定与性质.关键是要懂得找相似三角形,利用相似三角形的性质求解.15.如图,某水库大坝的横断面是梯形ABCD,坝顶宽AD=6米,坝高是20 米,背水坡 AB的坡角为30°,迎水坡CD的坡度为1:2,那么坝底 BC 的长度等于(46+20)米(结果保留根号)【分析】过梯形上底的两个顶点向下底引垂线AE、DF,得到两个直角三角形和一个矩形,分别解 Rt△ABE、Rt△DCF求得线段BE、CF的长,然后与EF 相加即可求得 BC 的长.【解答】解:如图,作AE⊥BC,DF⊥BC,垂足分别为点E,F,则四边形ADFE 是矩形.由题意得,EF=AD=6 米,AE=DF=20 米,∠B=30°,斜坡 CD 的坡度为 1: 2,在 Rt△ABE 中,∵∠B=30°,∴BE=AE=20米.在Rt△CFD中,∵=,∴CF=2DF=40 米,∴BC=BE+EF+FC=20+6+40=46+20(米).所以坝底BC的长度等于(46+20)米.故答案为(46+20).【点评】此题考查了解直角三角形的应用﹣坡度坡角问题,难度适中,解答本题的关键是构造直角三角形和矩形,注意理解坡度与坡角的定义.16.已知Rt△ABC中,∠C=90°,AC=3,BC=,CD⊥AB,垂足为点D,以点D为圆心作⊙D,使得点A在⊙D外,且点B在⊙D内.设⊙D的半径为r,那么r的取值范围是.【分析】先根据勾股定理求出AB的长,进而得出CD的长,由点与圆的位置关系即可得出结论.【解答】解:∵Rt△ABC中,∠ACB=90,AC=3,BC=,∴AB==4.∵CD⊥AB,∴CD=.∵AD•BD=CD2,设AD=x,BD=4﹣x.解得x=∴点 A 在圆外,点 B 在圆内,r的范围是,故答案为:.【点评】本题考查的是点与圆的位置关系,熟知点与圆的三种位置关系是解答此题的关键.17.如图,点D在△ABC的边BC上,已知点E、点F分别为△ABD和△ADC 的重心,如果BC=12,那么两个三角形重心之间的距离EF的长等于4 .【分析】连接AE并延长交BD于 G,连接AF并延长交CD于 H,根据三角形的重心的概念、相似三角形的性质解答.【解答】解:如图,连接 AE 并延长交 BD 于 G,连接 AF 并延长交 CD 于 H,∵点 E、F 分别是△ABD 和△ACD 的重心,∴DG=BD,DH=CD,AE=2GE,AF=2HF,∵BC=12,∴GH=DG+DH= (BD+CD)= BC= ×12=6,∵AE=2GE,AF=2HF,∠EAF=∠GAH,∴△EAF∽△GAH,∴==,∴EF=4,故答案为:4.【点评】本题考查了三角形重心的概念和性质,三角形的重心是三角形中线的交点,三角形的重心到顶点的距离等于到对边中点的距离的2倍.18.如图,△ABC中,AB=5,AC=6,将△ABC翻折,使得点A落到边BC 上的点A′处,折痕分别交边AB、AC于点E,点F,如果A′F∥AB,那么BE= .【分析】设BE=x,则AE=5﹣x=AF=A'F,CF=6﹣(5﹣x)=1+x,依据△A'CF ∽△BCA,可得=,即=,进而得到BE=.【解答】解:如图,由折叠可得,∠AFE=∠A'FE,∵A'F∥AB,∴∠AEF=∠A'FE,∴∠AEF=∠AFE,∴AE=AF,由折叠可得,AF=A'F,设 BE=x,则 AE=5﹣x=AF=A'F,CF=6﹣(5﹣x)=1+x,∵A'F∥AB,∴△A'CF∽△BCA,∴=,即=,解得x=,∴BE=,故答案为:.【点评】本题主要考查了折叠问题以及相似三角形的判定与性质的运用,折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,对应边和对应角相等.三、解答题(本大题共 7 题,满分 78 分)19.(10分)计算:45°.【分析】直接利用特殊角的三角函数值进而代入化简得出答案.【解答】解:原式=﹣×= ﹣= .【点评】此题主要考查了特殊角的三角函数值,正确记忆相关数据是解题关键. 20.(10分)已知一个二次函数的图象经过A(0,﹣3),B(1,0),C(m,2m+3),D(﹣1,﹣2)四点,求这个函数解析式以及点C的坐标.【分析】设一般式y=ax2+bx+c,把A、B、D点的坐标代入得,然后解法组即可得到抛物线的解析式,再把 C(m,2m+3)代入解析式得到关于 m 的方程,解关于 m 的方程可确定 C 点坐标.【解答】解:设抛物线的解析式为 y=ax2+bx+c,把A(0,﹣3),B(1,0),D(﹣1,﹣2)代入得,解得,∴抛物线的解析式为 y=2x2+x﹣3,把C(m,2m+3)代入得2m2+m﹣3=2m+3,解得m1=﹣,m2=2,∴C点坐标为(﹣,0)或(2,7).【点评】本题考查了待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与 x 轴有两个交点时,可选择设其解析式为交点式来求解.21.(10分)如图,已知⊙O经过△ABC的顶点A、B,交边BC于点D,点A恰为的中点,且BD=8,AC=9,sinC=,求⊙O的半径.【分析】如图,连接OA.交BC于H.首先证明OA⊥BC,在Rt△ACH中,求出AH,设⊙O的半径为r,在Rt△BOH中,根据BH2+OH2=OB2,构建方程即可解决问题;【解答】解:如图,连接 OA.交 BC 于 H.∵点A为的中点,∴OA⊥BD,BH=DH=4,∴∠AHC=∠BHO=90°,∵sinC==,AC=9,∴AH=3,设⊙O 的半径为 r,在 Rt△BOH 中,∵BH2+OH2=OB2,∴42+(r﹣3)2=r2,∴r=,∴⊙O的半径为.【点评】本题考查圆心角、弧、弦的关系、垂径定理、勾股定理、锐角三角函数等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.22.(10分)下面是一位同学的一道作图题:已知线段a、b、c(如图),求作线段x,使a:b=c:x他的作法如下:(1)、以点O为端点画射线OM,ON.(2)、在OM上依次截取OA=a,AB=b.(3)、在ON上截取OC=c.(4)、联结AC,过点B作BD∥AC,交ON于点D.所以:线段CD就是所求的线段x.①试将结论补完整②这位同学作图的依据是平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例③如果OA=4,AB=5,,试用向量表示向量.【分析】①根据作图依据平行线分线段成比例定理求解可得;②根据“平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例”可得;③先证△OAC∽△OBD得= ,即BD= AC,从而知= =﹣=﹣.【解答】解:①根据作图知,线段 CD 就是所求的线段 x,故答案为:CD;②这位同学作图的依据是:平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例;故答案为:平行于三角形一边的直线截其它两边(或两边的延长线),所得对应线段成比例;③∵OA=4、AB=5,且 BD∥AC,∴△OAC∽△OBD,∴=,即=,∴BD=AC,∴= =﹣=﹣.【点评】本题主要考查作图﹣复杂作图,解题的关键是熟练掌握平行线分线段成比例定理及向量的计算.23.(12分)已知:如图,四边形ABCD的对角线AC和BD相交于点E,AD=DC,DC2=DE•DB,求证:(1)△BCE∽△ADE;(2)AB•BC=BD•BE.【分析】(1)由∠DAC=∠DCA,对顶角∠AED=∠BEC,可证△BCE∽△ADE.(2)根据相似三角形判定得出△ADE∽△BDA,进而得出△BCE∽△BDA,利用相似三角形的性质解答即可.【解答】证明:(1)∵AD=DC,∴∠DAC=∠DCA,∵DC2=DE•DB,∴=,∵∠CDE=∠BDC,∴△CDE∽△BDC,∴∠DCE=∠DBC,∴∠DAE=∠EBC,∵∠AED=∠BEC,∴△BCE∽△ADE,(2)∵DC2=DE•DB,AD=DC∴AD2=DE•DB,同法可得△ADE∽△BDA,∴∠DAE=∠ABD=∠EBC,∵△BCE∽△ADE,∴∠ADE=∠BCE,∴△BCE∽△BDA,∴= ,∴AB•BC=BD•BE.【点评】本题考查了相似三角形的判定与性质.关键是要懂得找相似三角形,利用相似三角形的性质求解.24.(12分)如图,已知在平面直角坐标系中,已知抛物线y=ax2+2ax+c(其中a、c为常数,且a<0)与x轴交于点A,它的坐标是(﹣3,0),与y轴交于点B,此抛物线顶点C到x轴的距离为4(1)求抛物线的表达式;(2)求∠CAB的正切值;(3)如果点P是抛物线上的一点,且∠ABP=∠CAO,试直接写出点P的坐标.【分析】(1)先求得抛物线的对称轴方程,然后再求得点 C 的坐标,设抛物线的解析式为y=a(x+1)2+4,将点(﹣3,0)代入求得a的值即可;(2)先求得A、B、C的坐标,然后依据两点间的距离公式可得到BC、AB、AC的长,然后依据勾股定理的逆定理可证明∠ABC=90°,最后,依据锐角三角函数的定义求解即可;(3)记抛物线与x轴的另一个交点为D.先求得D(1,0),然后再证明∠DBO= ∠CAB,从而可证明∠CAO=ABD,故此当点P与点D重合时,∠ABP=∠CAO;当点P在AB的上时.过点P作PE∥AO,过点B作BF∥AO,则PE∥BF.先证明∠EPB=∠CAB,则tan∠EPB=,设BE=t,则PE=3t,P(﹣3t,3+t),将P(﹣3t,3+t)代入抛物线的解析式可求得t的值,从而可得到点P 的坐标.【解答】解:(1)抛物线的对称轴为x=﹣=﹣1.∵a<0,∴抛物线开口向下.又∵抛物线与 x 轴有交点,∴C 在 x 轴的上方,∴抛物线的顶点坐标为(﹣1,4).设抛物线的解析式为 y=a(x+1)2+4,将点(﹣3,0)代入得:4a+4=0,解得:a=﹣1,∴抛物线的解析式为 y=﹣x2﹣2x+3.(2)将x=0代入抛物线的解析式得:y=3,∴B(0,3).∵C(﹣1,4)、B(0,3)、A(﹣3,0),∴BC=,AB=3,AC=2,∴BC2+AB2=AC2,∴∠ABC=90°.∴tan∠CAB= =.(3)如图1所示:记抛物线与x轴的另一个交点为D.∵点 D 与点 A 关于 x=﹣1 对称,∴D(1,0).∴tan∠DBO=.又∵由(2)可知:tan∠CAB=.∴∠DBO=∠CAB.又∵OB=OA=3,∴∠BAO=∠ABO.∴∠CAO=∠ABD.∴当点 P 与点 D 重合时,∠ABP=∠CAO,∴P(1,0).如图2所示:当点P在AB的上时.过点P作PE∥AO,过点B作BF∥AO,则PE∥BF.∵BF∥AO,∴∠BAO=∠FBA.又∵∠CAO=∠ABP,∴∠PBF=∠ CAB.又∵PE∥BF,∴∠EPB=∠PBF,∴∠EPB=∠CAB.∴tan∠EPB=.设BE=t,则PE=3t,P(﹣3t,3+t).将P(﹣3t,3+t)代入抛物线的解析式得:y=﹣x2﹣2x+3得:﹣9t2+6t+3=3+t,解得t=0(舍去)或t=.∴P(﹣,).综上所述,点P的坐标为P(1,0)或P(﹣,).【点评】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数的解析式、勾股定理的逆定理、等腰直角三角形的性质、锐角三角函数的定义,用含 t 的式子表示点 P 的坐标是解题的关键.25.(14分)如图1,∠BAC的余切值为2,AB=2,点D是线段AB上的一动点(点D不与点A、B重合),以点D为顶点的正方形DEFG的另两个顶点E、F都在射线AC上,且点F在点E的右侧,联结BG,并延长BG,交射线EC于点P.(1)点D在运动时,下列的线段和角中,④⑤是始终保持不变的量(填序号);①AF;②FP;③BP;④∠BDG;⑤∠GAC;⑥∠BPA;(2)设正方形的边长为x,线段AP的长为y,求y与x之间的函数关系式,并写出定义域;(3)如果△PFG与△AFG相似,但面积不相等,求此时正方形的边长.【分析】(1)作BM⊥AC于M,交DG于N,如图,利用三角函数的定义得到=2,设BM=t,则AM=2t,利用勾股定理得(2t)2+t2=(2)2,解得t=2,即BM=2,AM=4,设正方形的边长为x,则AE=2x,AF=3x,由于tan∠GAF==,则可判断∠GAF为定值;再利用DG∥AP得到∠BDG=∠BAC,则可判断∠BDG为定值;在Rt△BMP中,利用勾股定理和三角函数可判断PB在变化,∠BPM在变化,PF在变化;(2)易得四边形DEMN为矩形,则NM=DE=x,证明△BDG∽△BAP,利用相似比可得到y与x的关系式;(3)由于∠AFG=∠PFG=90°,△PFG与△AFG相似,且面积不相等,利用相似比得到PF=x,讨论:当点P在点F点右侧时,则AP=x,所以=x,当点P在点F点左侧时,则AP= x,所以=x,然后分别解方程即可得到正方形的边长.【解答】解:(1)作BM⊥AC于M,交DG于N,如图,在Rt△ABM中,∵cot∠BAC==2,设 BM=t,则 AM=2t,∵AM2+BM2=AB2,∴(2t)2+t2=(2)2,解得t=2,∴BM=2,AM=4,设正方形的边长为 x,在Rt△ADE中,∵cot∠DAE==2,∴AE=2x,∴AF=3x,在Rt△GAF中,tan∠GAF===,∴∠GAF 为定值;∵DG∥AP,∴∠BDG=∠BAC,∴∠BDG 为定值;在Rt△BMP中,PB=,而PM在变化,∴PB 在变化,∠BPM 在变化,∴PF 在变化,所以∠BDG 和∠GAC 是始终保持不变的量;故答案为④⑤;(2)易得四边形DEMN为矩形,则NM=DE=x,∵DG∥AP,∴△BDG∽△BAP,∴=,即=,∴y= (1≤x<2)(3)∵∠AFG=∠PFG=90°,△PFG与△AFG相似,且面积不相等,∴=,即=,∴PF=x,当点P在点F点右侧时,AP=x,∴=x,解得x=,当点P在点F点左侧时,AP=AF﹣PF=3x﹣x=x,∴=x,解得x=,综上所述,正方形的边长为或.【点评】本题考查了相似形综合题:熟练掌握锐角三角函数的定义、正方形的性质和相似三角形的判定与性质.。
2021上海初三数学一模试题分类整理(几何综合题)
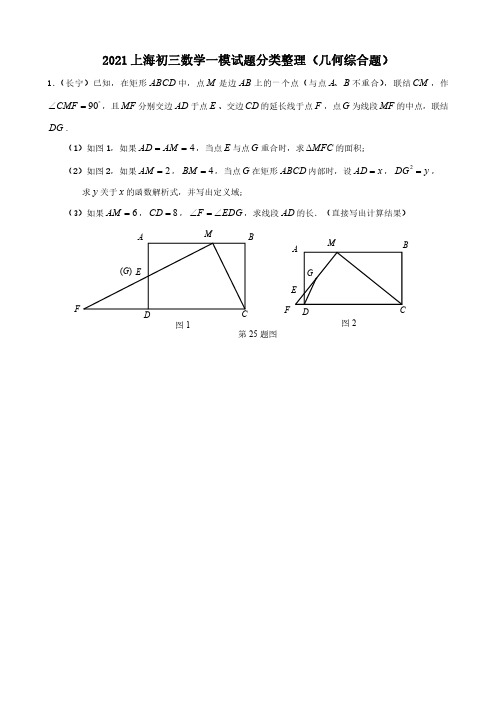
2021上海初三数学一模试题分类整理(几何综合题)1.(长宁)已知,在矩形ABCD 中,点M 是边AB 上的一个点(与点A B 、不重合),联结CM ,作90CMF ︒∠=,且MF 分别交边AD 于点E 、交边CD 的延长线于点F ,点G 为线段MF 的中点,联结DG .(1)如图1,如果4AD AM ==,当点E 与点G 重合时,求MFC ∆的面积;(2)如图2,如果2AM =,4BM =,当点G 在矩形ABCD 内部时,设AD x =,2DG y =,求y 关于x 的函数解析式,并写出定义域;(3)如果6AM =,8CD =,F EDG ∠=∠,求线段AD 的长.(直接写出计算结果)ABCDEF(G )M图1ABCDEFGM图2第25题图2.(杨浦)如图,已知在Rt△ABC 中,∠ACB =90°,AC =BC =4,点D 为边BC 上一动点(与点B 、C 不重合),点E 为边AB 上一点,∠EDB =∠ADC ,过点E 作EF ⊥AD ,垂足为点G ,交射线AC 于点F .(1)如果点D 为边BC 的中点,求∠DAB 的正切值;(2)当点F 在边AC 上时,设CD =x ,CF =y ,求y 关于x 的函数解析式及定义域;(3)联结DF ,如果△CDF 与△AGE 相似,求线段CD 的长.备用图ABC第25题图ABCEDG F3.(徐汇)如图,在ABC Rt ∆中,︒=∠90ACB ,12=AC ,5=BC ,点D 是边AC 上的动点,以CD 为边在ABC ∆外作正方形CDEF ,分别联结AE 、BE ,BE 与AC 交于点G .(1)当BE AE ⊥时,求正方形CDEF 的面积;(2)延长ED 交AB 于点H ,如果BEH ∆和ABG ∆相似,求ABE ∠sin 的值;(3)当AE AG =时,求CD 的长.(备用图)BAC(第25题图)GFED BAC4.(松江)如图,已知在等腰△ABC中,AB=AC=,tan∠ABC=2,BF⊥AC,垂足为F,点D是边AB上一点(不与A,B重合).(1)求边BC的长;(2)如图2,延长DF交BC的延长线于点G,如果CG=4,求线段AD的长;(3)过点D作DE⊥BC,垂足为E,DE交BF于点Q,联结DF,如果△DQF和△ABC相似,求线段BD的长.D·B AFC(图1)DBAFC(图2)G BAFC(备用图)5.(普陀)如图,矩形ABCD 中,1AB =,3BC =,点E 是边BC 上一个动点(不与点B 、C 重合),AE 的垂线AF 交CD 的延长线于点F .点G 在线段EF 上,满足:1:2FG GE =.设BE x =.(1)求证:AD DFAB BE=;(2)当点G 在△ADF 的内部时,用x 的代数式表示ADG ∠的余切;(3)当∠FGD =∠AFE 时,求线段BE 的长.F图14CB A DE G备用图CBAD6.(浦东)四边形ABCD 是菱形,∠B ≤90°,点E 为边BC 上一点,联结AE ,过点E 作EF ⊥AE ,EF 与边CD 交于点F ,且EC =3CF .(1)如图1,当∠B =90°时,求ABE S △与ECF S △的比值;(2)如图2,当点E 是边BC 的中点时,求cos B 的值;(3)如图3,联结AF ,当∠AFE =∠B 且CF =2时,求菱形的边长.(第25题图3)(第25题图2)(第25题图1)7.(闵行)如图,在矩形ABCD 中,2AB =,1AD =,点E 在边AB 上(点E 与端点A 、B 不重合),联结DE ,过点D 作DF ⊥DE ,交BC 的延长线于点F ,联结EF ,与对角线AC 、边CD 分别交于点G 、H .设AE x =,DH y =.(1)求证:△ADE ∽△CDF ,并求EFD ∠的正切值;(2)求y 关于x 的函数解析式,并写出该函数的定义域;(3)联结BG .当△BGE 与△DEH 相似时,求x 的值.(第25题图)B A CF ED GH(备用图)B A CFEDGH8.(静安)已知∠MAN 是锐角,点B 、C 在边AM 上,点D 在边AN 上,∠EBD =∠MAN ,且CE //BD ,sin∠MAN=35,AB =5,AC =9.(1)如图1,当CE 与边AN 相交于点F 时,求证:DF ·CE=BC ·BE ;(2)当点E 在边AN 上时,求AD 的长;(3)当点E 在∠MAN 外部时,设AD =x ,△BCE 的面积为y ,求y 与x 之间的函数解析式,写出定义域.(第25题图)(备用图)(图1)FAB DCE NM9.(嘉定)在矩形ABCD 中,6AB =,8AD =,点E 在CD 边上,1tan 2DAE ∠=.点F 是线段AE 上一点,联结BF ,CF.(1)如图11,如果3tan 4CBF ∠=,求线段AF 的长;(2)如图12,如果12CF BC =,①求证:∠CFE =∠DAE ;②求线段EF 的长.图11图12备用图10.(黄浦)如图10,四边形ABCD 中,AB =AD =4,CB =CD =3,∠ABC =∠ADC =90°,点M 、N 是边AB 、AD 上的动点,且∠MCN =12∠BCD ,CM 、CN 与对角线BD 分别交于点P 、Q .(1)求sin∠MCN 的值;(2)当DN =DC 时,求∠CNM 的度数;(3)试问:在点M 、N 的运动过程中,线段比PQMN的值是否发生变化?如不变,请求出这个值;如变化,请至少给出两个可能的值,并说明点N 相应的位置.P NM DC BAQ(图10)11.(虹口)如图12,在△ABC 中,∠ABC =90°,AB =3,BC =4,过点A 作射线AM //BC ,点D、E 是射线AM 上的两点(点D 不与点A 重合,点E 在点D 右侧),联结BD 、BE 分别交边AC 于点F 、G ,∠DBE =∠C .(1)当AD =1时,求FB 的长;(2)设AD =x ,FG =y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结DG 并延长交边BC 于点H ,如果△DBH 是等腰三角形,请直接写出AD 的长.C FGE D A B 图12C A B 备用图MM12.(奉贤)已知⊙O 的直径AB =4,点P 为弧AB 上一点,联结PA 、PO ,点C 为劣弧AP 上一点(点C 不与点A 、P 重合),联结BC 交PA 、PO 于点D 、E .(1)如图10,当cos∠CBO =87时,求BC 的长;(2)当点C 为劣弧AP 的中点,且△EDP 与△AOP 相似时,求∠ABC 的度数;(3)当AD =2DP ,且△BEO 为直角三角形时,求四边形AOED 的面积.备用图备用图A B图10PA BC D EO A B13.(崇明)如图,Rt△ABC 中,90ACB ∠=︒,6AC =,8BC =.点D 为斜边AB 的中点,ED ⊥AB ,交边BC 于点E .点P 为射线AC 上的动点,点Q 为边BC 上的动点,且运动过程中始终保持PD QD ⊥.(1)求证:△ADP ∽△EDQ ;(2)设AP x =,BQ y =.求y 关于x 的函数解析式,并写出该函数的定义域;(3)联结PQ ,交线段ED 于点F .当△PDF 为等腰三角形时,求线段AP 的长.A D BCPEQ 第25题图A D B C P E Q 第25题备用图F14.(宝山)如图3,已知Rt△ABC 中,∠ACB =90°,AC =BC ,点D、E 在边AB 上,∠DCE =45°,过点A 作AB 的垂线交CE 的延长线于点M ,联结MD.(1)求证:DE BE CE ⋅=2;(2)当AC =3,AD =2BD 时,求DE 的长;(3)过点M 作射线CD 的垂线,垂足为点F .设x BCBD =,y FMD =∠tan ,求y 关于x 的函数关系式,并写出定义域.EM DCAB (图3)15.(青浦)在△ABC 中,∠C=90°,AC =2,BC =23,点D 为边AC 的中点(如图),点P 、Q 分别是射线BC 、BA 上的动点,且BQ =32BP ,联结PQ 、QD 、DP .(1)求证:PQ ⊥AB ;(2)如果点P 在线段BC 上,当△PQD 是直角三角形时,求BP 的长;(3)将△PQD 沿直线QP 翻折,点D 的对应点为点'D ,如果点'D 位于△ABC 内,请直接写出BP 的取值范围.(第25题图)(备用图)A C O 第25题备用图16.(金山)定理:一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中,O A ∠=∠21.已知:如图2,AC 是⊙O 的一条弦,点D 在⊙O 上(与A 、C 不重合),联结DC 交射线AO 于点E ,联结OD ,⊙O 的半径为5,43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时,若DOE ∆与AEC ∆相似,求DCA ∠的正切值.(3)当1=OE 时,求点A 与点D 之间的距离(直接写出答案).AB CO第25题图1第25题图2E D C A O。
【2021年上海市初中一模数学卷】2021年上海市虹口区初中毕业生学业模拟考试试卷九年级数学及答案

虹口区2020学年度第一学期期终学生学习能力诊断测试初三数学 试卷2021.1一、选择题1.在ABC 中,∠C =90°,如果BC =3,AC =4,那么tanA 的值是( )A . 34B . 43C . 35D . 452.如果向量a 和b 是单位向量,那么下列等式中,成立的是( )A .a b =B . a b =C .2a b +=D .0a b −=3.下列函数中,属于二次函数的是( )A . 212y x =−B . y =C . 22y x =−D .()222y x x =−−4.将抛物线23y x =−向右平移2个单位后得到的新抛物线表达式是()A . 21y x =−B . 25y x =−C .()223y x =+−D .()223y x =−−5.如图1,传送带和地面所成斜坡的坡度i =1:2.4,如果它把某物体从地面送到离地面10米高的地方,那么该物体所经过的路程是( )A .10米B .24米C .25米D .26米6.如图2,在Rt ABC 中,∠ACB =90°,D 是边AB 上一点,过D 作DF AB ⊥交边BC 于点E ,交AC 的延长线于点F ,联结AE ,如果1tan 3EAC ∠=,1CBF S =,那么ABC S 的值是( ) A .3B .6C .9D .12二、填空题7.如果:2:3a b =,那么a ab =+____________ 8.计算:()13242a a b −−=____________ 9.如果抛物线2y x a =−经过点(2,0),那么a 的值是____________10.如果抛物线()21y k x =+有最高点,那么k 的取值范围是____________ 11.如果抛物线l 经过点()2,0A −和B (5,0),那么该抛物线的对称轴是直线____________12.沿着x 轴正方向看,抛物线22y x =−在y 轴左侧的部分是____________的(填“上升”或“下降”)13.点P 是线段AB 上的一点,如果2AP BP AB =⋅,那么AP AB的值是____________ 14.已知'''ABC A B C ,顶点A 、B 、C 分别与顶点',','A B C 对应,,''AD A D 分别是BC 、''B C 边 上的中线,如果BC =3,AD =2.4,''2B C =,那么''A D 的长是____________15.如图3,AB //CD ,AD 、BC 相交于点E ,过E 作EF //CD 交BD 于点F ,如果AB =3,CD =6,那么EF的长是____________16.如图4,在梯形ABCD 中,AD //BC ,∠A =90°,∠BDC =90°,AD =4,BC =9,那么BD =____________17.如图5,图中提供了一种求cot 15°的方法,作Rt ABC ,使∠C =90°,∠ABC =30°,再延长CB 到点D ,使BD =BA ,联结AD ,即可得∠D =15°,如果设AC =t ,则可得(2CD t =,那么cot15cot 2CD D AC︒===cot 22.5°的值是____________18.如图6,在Rt ABC 中,∠C =90°,AC =6,BC =8,D 是BC 的中点,点E 在边AB 上,将BDE 沿直线DE 翻折,使得点B 落在同一平面内的点'B 处,线段'B D 交边AB 于点F ,联结'AB ,当'AB F 是直角三角形时,BE 的长为____________三、解答题19.计算:2tan 452sin 60cot 302cos 45︒−︒︒−︒20.已知二次函数的解析式为2122y x x =−. (1)用配方法把该二次函数的解析式化为()2y a x m k =++的形式;(2)选取适当的数据填入下表,并在图7所示的平面直角坐标系xOy 内描点,画出该函数的图像.21.如图8,在ABC 中,点G 是ABC 的重心,联结AG ,联结BG 并延长交边AC 于点D ,过点G 作GE //BC 交边AC 于点E .(1)如果,AB a AC b ==,用,a b 表示向量BG ;(2)当AG BD ⊥,BG =6,∠GAD =45°时,求AE 的长.22.图9-1是一款家用落地式取暖器,如图9-2是其放置在地面上时的侧面示意图,其中矩形ABCD 是取暖器的主体,等腰梯形BEFC 是底座,烘干架连杆GH 可绕边CD 上一点H 旋转,以调节角度,已知CD =50cm ,BC =8cm ,EF =20cm ,DH =12cm ,GH =15cm ,∠CFE =30°,当∠GHD =53°时,求点G 到地面的距离(精确到0.1cm )(参考数据:sin530.80,cos530.60,tan53 1.73︒≈︒≈︒≈≈)23.如图10,在ABC 中,点D 、G 在边AC 上,点E 在边BC 上,DB =DC ,EG //AB ,AE 、BD 交于点F ,BF =AG .(1)求证:BFE CGE ;(2)当∠AEG =∠C 时,求证:2AB AG AC =⋅.24.如图11,在平面直角坐标系xOy 中,已知点()()()1,0,3,0,0,3A B C −,抛物线2y ax bx c =++经过A 、B 两点.(1)当该抛物线经过点C 时,求该抛物线的表达式;(2)在(1)题的条件下,点P 为该抛物线上一点,且位于第三象限,当∠PBC =∠ACB 时,求点P 的坐 标;(3)如果抛物线2y ax bx c =++的顶点D 位于BOC 内,求a 的取值范围.25.如图12,在ABC 中,∠ABC =90°,AB =3,BC =4,过点A 作射线AM //BC ,点D 、E 是射线AM上的两点(点D 不与点A 重合,点E 在点D 右侧),联结BD 、BE 分别交边AC 于点F 、G ,∠DBE =∠C .(1)当AD =1时,求FB 的长;(2)设,AD x FG y ==,求y 关于x 的函数关系式,并写出x 的取值范围;(3)联结DG 并延长交边BC 于点H ,如果DBH 是等腰三角形,请直接写出AD 的长.参考答案一、选择题1.A2. B3. C4. D5. D6.C二、填空题7. 358.22a b +9. 4 10. 1k <− 11. 32x =12.下降 13.1214.1.6 15. 216.61+18.2或4017三、解答题19.原式20.(1)()21222y x =−−(2)x :2,0,2,9,6−y :6,0,2,0,6−;作图略21.(1)2133BG a b=−+(2)22.50.5cm23.(1)证明略(2)证明略24.(1)223y x x =−++ (2)413,39P ⎛⎫−− ⎪⎝⎭(3)102a −<<25.(1(2)()243604520x y x x +=<<+ (3)78。
2021年上海市中考数学考点必杀500题专练13(二次函数压轴题)(30题)(原卷版)

2021中考考点必杀500题专练13(二次函数压轴题)(30道)1.(2021·上海九年级二模)在平面直角坐标系xOy 中,抛物线2y x mx n =-++经过点(5,0)A ,顶点为点B ,对称轴为直线3x =,且对称轴与x 轴交于点C .直线y kx b =+,经过点A ,与线段BC 交于点E . (1)求抛物线2y x mx n =-++的表达式;(2)联结BO 、EO .当BOE △的面积为3时,求直线y kx b =+的表达式;(3)在(2)的条件下,设点D 为y 轴上的一点,联结BD 、AD ,当=BD EO 时,求DAO ∠的余切值.2.(2021·上海虹口区·九年级一模)如图,在平面直角坐标系xOy 中,已知点()1,0A -、()3,0B 、()0,3C ,抛物线2y ax bx c =++经过A 、B 两点.(1)当该抛物线经过点C 时,求该抛物线的表达式;(2)在(1)题的条件下,点P 为该抛物线上一点,且位于第三象限,当PBC ACB ∠=∠时,求点P 的坐标;(3)如果抛物线2y ax bx c =++的顶点D 位于BOC 内,求a 的取值范围.3.(2021·上海金山区·九年级一模)在平面直角坐标系xoy 中,直线324y x =-+与直线132y x =-相交于点A ,抛物线21(0)y ax bx a =+-≠经过点A .(1)求点A 的坐标; (2)若抛物线21y ax bx =+-向上平移两个单位后,经过点()1,2-,求抛物线21y ax bx =+-的表达式; (3)若抛物线2y a x b x c =+'+'()0a '<与21y ax bx =+-关于x 轴对称,且这两条抛物线的顶点分别是点P '与点P ,当3OPP S ∆'=时,求抛物线21y ax bx =+-的表达式.4.(2021·上海徐汇区·九年级一模)已知二次函数224(0)y ax ax a a =-++<的大致图像如图所示,这个函数图像的顶点为点 D .(1)求该函数图像的开口方向、对称轴及点D 的坐标;(2)设该函数图像与y 轴正半轴交于点C ,与x 轴正半轴交于点B ,图像的对称轴与x 轴交于点A ,如果DC BC ⊥,1tan 3DBC ∠=,求该二次函数的解析式; (3) 在(2)的条件下,设点M 在第一象限该函数的图像上,且点M 的横坐标为(1)t t >,如果 ACM ∆的面积是258,求点M 的坐标.5.(2021·上海九年级专题练习)在平面直角坐标系xOy 中,如果抛物线2y ax bx c =++上存在一点A ,使点A 关于坐标原点O 的对称点A '也在这条抛物线上,那么我们把这条抛物线叫做回归抛物线,点A 叫做这条抛物线的回归点.(1)已知点M 在抛物线224y x x =-++上,且点M 的横坐标为2,试判断抛物线224y x x =-++是否为回归抛物线,并说明理由;(2)已知点C 为回归抛物线22y x x c =--+的顶点,如果点C 是这条抛物线的回归点,求这条抛物线的表达式;(3)在(2)的条件下,所求得的抛物线的对称轴与x 轴交于点D .连接CO 并延长,交该抛物线于点E .点F 是射线CD 上一点,如果CFE DEC ∠=∠,求点F 的坐标.6.(2021·上海九年级专题练习)如图,在平面直角坐标系xOy 中,抛物线212y x bx c =-++与x 轴正半轴交于点()4,0A ,与y 轴交于点()0,2B ,点C 在该抛物线上且在第一象限.()1求该抛物线的表达式;()2将该抛物线向下平移m 个单位,使得点C 落在线段AB 上的点D 处,当13AD BD =时,求m 的值; ()3联结BC ,当2CBA BAO ∠=∠时,求点C 的坐标.7.(2021·上海九年级专题练习)在平面直角坐标系xOy 中(如图).已知点()1,2A -,点()1,6B ,点()1,4C .如果抛物线()230y ax bx a =++≠恰好经过这三个点之中的两个点.(1)试推断抛物线23y ax bx =++经过点A 、B 、C 之中的哪两个点?简述理由;(2)求常数a 与b 的值:(3)将抛物线23y ax bx =++先沿与y 轴平行的方向向下平移2个单位长度,再与沿x 轴平行的方向向右平移0t t 个单位长度,如果所得到的新抛物线经过点()1,4C .设这个新抛物线的顶点是D .试探究ABD △的形状.8.(2021·上海九年级专题练习)我们已经知道二次函数()20y ax bx c a =++≠的图像是一条抛物线.研究二次函数的图像与性质,我们主要关注抛物线的对称轴、抛物线的开口方向、抛物线的最高点(或最低点)的坐标、抛物线与坐标轴的交点坐标、抛物线的上升或下降情况(沿x 轴的正方向看).已知一个二次函数()20y ax bx c a =++≠的大致图像如图所示.(1)你可以获得该二次函数的哪些信息?(写出四条信息即可)(2)依据目前的信息,你可以求出这个二次函数的解析式吗?如果可以,请求出这个二次函数的解析式;如果不可以,请补充一个条件,并求出这个二次函数的解析式.9.(2021·上海九年级专题练习)如图,已知对称轴为直线1x =-的抛物线23y ax bx =++与x 轴交于A 、B 两点,与y 轴交于点C ,其中点A 的坐标为()1,0.(1)求点B 的坐标及抛物线的表达式;(2)记抛物线的顶点为P ,对称轴与线段BC 的交点为Q ,将线段PQ 绕点Q ,按顺时针方向旋转120︒,请判断旋转后点P 的对应点P '是否还在抛物线上,并说明理由;(3)在x 轴上是否存在点M ,使MOC △与BCP 相似?若不存在,请说明理由;若存在请直接写出点M 的坐标(不必书写求解过程).10.(2021·上海黄浦区·九年级一模)如图,平面直角坐标系内直线4y x =+与x 轴、y 轴分别交于点A 、B ,点C 是线段OB 的中点.(1)求直线AC 的表达式:(2)若抛物线2y ax bx c =++经过点C ,且其顶点位于线段OA 上(不含端点O 、A ).①用含b 的代数式表示a ,并写出1b的取值范围; ②设该抛物线与直线4y x =+在第一象限内的交点为点D ,试问:DBC △与DAC △能否相似?如果能,请求此时抛物线的表达式:如果不能,请说明由.11.(2021·上海浦东新区·九年级一模)二次函数2y ax bx c =++(0a ≠)的图像经过点A(2,4)、B(5,0)和O(0,0).(1)求二次函数的解析式;(2)联结AO ,过点B 作BC⊥AO 于点C ,与该二次函数图像的对称轴交于点P ,联结AP ,求⊥BAP 的余切值;(3)在(2)的条件下,点M 在经过点A 且与x 轴垂直的直线上,当AMO 与ABP 相似时,求点M 的坐标.12.(2021·上海静安区·九年级一模)如图,在平面直角坐标系xOy 中,直线1(0)2y x m m =-+>与x 轴、y 轴分别交于点A 、B .抛物线24y ax bx =++(a ≠0)经过点A ,且与y 轴相交于点C ,⊥OCA =⊥OAB . (1)求直线AB 的表达式;(2)如果点D 在线段AB 的延长线上,且AD =AC .求经过点D 的抛物线24y ax bx =++的表达式; (3)如果抛物线24y ax bx =++的对称轴与线段AB 、AC 分别相交于点E 、F ,且EF =1,求此抛物线的顶点坐标.13.(2021·上海宝山区·九年级一模)已知抛物线()20y ax bx a =+≠经过 ()4,0A ,()1,3B -两点,抛物线的对称轴与x 轴交于点C ,点 D 与点B 关于抛物线的对称轴对称,联结BC 、BD .(1)求该抛物线的表达式以及对称轴;(2)点E 在线段BC 上,当CED OBD =∠∠时,求点 E 的坐标;(3)点M 在对称轴上,点N 在抛物线上,当以点O 、A 、M 、N 为顶点的四边形是平行四边形时,求这个平行四边形的面积.14.(2021·上海九年级一模)如图,在平面直角坐标系xOy 中,抛物线24y ax bx =+-与x 轴交于点()4,0A -和点()2,0B ,与y 轴交于点C .(1)求该抛物线的表达式及点C 的坐标:(2)如果点D 的坐标为()8,0-,联结AC 、DC ,求ACD ∠的正切值;(3)在(2)的条件下,点P 为抛物线上一点,当OCD CAP ∠=∠时,求点P 的坐标.15.(2021·上海普陀区·九年级一模)在平面直角坐标系xOy 中(如图),已知抛物线21y ax bx =++与y 轴交于点A ,顶点B 的坐标为(2,1)-.(1)直接写出点A 的坐标,并求抛物线的表达式;(2)设点C 在x 轴上,且90CAB ∠=︒,直线AC 与抛物线的另一个交点为点D.①求点C 、D 的坐标;②将抛物线21y ax bx =++沿着射线BD 的方向平移;平移后的抛物线顶点仍在线段BD 上;点A 的对应点为点P .设线段AB 与x 轴的交点为点Q ,如果ADP △与CBQ △相似,求点P 的坐标.16.(2021·上海松江区·九年级一模)如图,在平面直角坐标系xOy 中,抛物线22y ax bx =+-经过点()2,0A 和(1,1)B --与y 轴交于点C .(1)求这个抛物线的表达式;(2)如果点P 是抛物线位于第二象限上一点,PC 交x 轴于点D ,23PD DC =.①求P 点坐标;②点Q 在x 轴上,如果QCA PCB ∠=∠,求点Q 的坐标.17.(2021·上海杨浦区·九年级一模)已知在平面直角坐标系xOy 中,抛物线()24y x m =--+与y 轴交于点B ,与x 轴交于点C 、D (点C 在点D 左侧),顶点A 在第一象限,异于顶点A 的点()1,P n 在该抛物线上.(1)如果点P 与点C 重合,求线段AP 的长;(2)如果抛物线经过原点,点Q 是抛物线上一点,tan 3OPQ ∠=,求点Q 的坐标;(3)如果直线PB 与x 轴的负半轴相交,求m 的取值范围.18.(2021·上海九年级其他模拟)抛物线21y=x +x+m 4的顶点在直线y=x+3上,过点F (-2,2)的直线交该抛物线于点M 、N 两点(点M 在点N 的左边),MA⊥x 轴于点A ,NB⊥x 轴于点B .(1)先通过配方求抛物线的顶点坐标(坐标可用含m 的代数式表示),再求m 的值;(2)设点N 的横坐标为a ,试用含a 的代数式表示点N 的纵坐标,并说明NF =NB ;(3)若射线NM 交x 轴于点P ,且PA×PB =1009,求点M 的坐标.19.(2020·上海浦东新区·九年级三模)在平面直角坐标系xOy 中,已知抛物线2y x bx c =-++与x 轴交于点A (−3,0)和点B ,与y 轴相交于点C (0,3),抛物线的顶点为点D .(1)求抛物线的表达式及顶点D 的坐标;(2)联结AD 、AC 、CD ,求⊥DAC 的正切值;(3)如果点P 是原抛物线上的一点,且⊥PAB =⊥DAC ,将原抛物线向右平移m 个单位(m >0),使平移后新抛物线经过点P ,求平移距离.20.(2020·上海宝山区·九年级二模)如图,在平面直角坐标系xOy中,抛物线y=ax2﹣2ax﹣3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)直接写出点A的坐标,并求直线l的函数表达式(其中k、b用含a的式子表示);(2)点E是直线l上方的抛物线上的动点,若⊥ACE的面积的最大值为54,求a的值;(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,当以点A、D、P、Q为顶点的四边形为矩形时,请直接写出点P的坐标.21.(2020·上海普陀区·九年级二模)在平面直角坐标系xOy中(如图),已知点A在x轴的正半轴上,且与原点的距离为3,抛物线y=ax2﹣4ax+3(a≠0)经过点A,其顶点为C,直线y=1与y轴交于点B,与抛物线交于点D(在其对称轴右侧),联结BC、CD.(1)求抛物线的表达式及点C的坐标;(2)点P是y轴的负半轴上的一点,如果⊥PBC与⊥BCD相似,且相似比不为1,求点P的坐标;(3)将⊥CBD绕着点B逆时针方向旋转,使射线BC经过点A,另一边与抛物线交于点E(点E在对称轴的右侧),求点E的坐标.22.(2020·上海虹口区·九年级二模)如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+3经过点A(﹣1,0)和点B(3,0),该抛物线对称轴上的点P在x轴上方,线段PB绕着点P逆时针旋转90°至PC(点B对应点C),点C恰好落在抛物线上.(1)求抛物线的表达式并写出抛物线的对称轴;(2)求点P的坐标;(3)点Q在抛物线上,联结AC,如果⊥QAC=⊥ABC,求点Q的坐标.23.(2020·上海青浦区·九年级二模)如图,在平面直角坐标系xOy中,二次函数y=ax2﹣4ax+3的图象与x 轴正半轴交于点A、B,与y轴相交于点C,顶点为D,且tan⊥CAO=3.(1)求这个二次函数的解析式;(2)点P是对称轴右侧抛物线上的点,联结CP,交对称轴于点F,当S⊥CDF:S⊥FDP=2:3时,求点P的坐标;(3)在(2)的条件下,将⊥PCD沿直线MN翻折,当点P恰好与点O重合时,折痕MN交x轴于点M,交y轴于点N,求OMON的值.(﹣3,0)和点B(3,2),与y轴相交于点C.(1)求这条抛物线的表达式;(2)点P是抛物线在第一象限内一点,联结AP,如果点C关于直线AP的对称点D恰好落在x轴上,求直线AP的截距;(3)在(2)小题的条件下,如果点E是y轴正半轴上一点,点F是直线AP上一点.当⊥EAO与⊥EAF全等时,求点E的纵坐标.25.(2020·上海奉贤区·)如图,在平面直角坐标系xOy中,抛物线y=x2+bx经过点A(2,0).直线y=1 2x﹣2与x轴交于点B,与y轴交于点C.(1)求这条抛物线的表达式和顶点的坐标;(2)将抛物线y=x2+bx向右平移,使平移后的抛物线经过点B,求平移后抛物线的表达式;(3)将抛物线y=x2+bx向下平移,使平移后的抛物线交y轴于点D,交线段BC于点P、Q,(点P在点Q 右侧),平移后抛物线的顶点为M,如果DP⊥x轴,求⊥MCP的正弦值.的正半轴分别交于A 、B 两点,且OA =OB ,抛物线的顶点为M ,联结AB 、AM .(1)求这条抛物线的表达式和点M 的坐标;(2)求sin⊥BAM 的值;(3)如果Q 是线段OB 上一点,满足⊥MAQ =45°,求点Q 的坐标.27.(2020·上海嘉定区·九年级二模)在平面直角坐标系xOy 中(如图),已知经过点A (﹣3,0)的抛物线y =ax 2+2ax ﹣3与y 轴交于点C ,点B 与点A 关于该抛物线的对称轴对称,D 为该抛物线的顶点. (1)直接写出该抛物线的对称轴以及点B 的坐标、点C 的坐标、点D 的坐标;(2)联结AD 、DC 、CB ,求四边形ABCD 的面积;(3)联结AC .如果点E 在该抛物线上,过点E 作x 轴的垂线,垂足为H ,线段EH 交线段AC 于点F .当EF =2FH 时,求点E 的坐标.28.(2020·上海长宁区·九年级二模)如图,在平面直角坐标系xOy 中,已知抛物线2y x mx n =++经过点()2,2A -,对称轴是直线1x =,顶点为点B ,抛物线与y 轴交于点C .(1)求抛物线的表达式和点B 的坐标;(2)将上述抛物线向下平移1个单位,平移后的抛物线与x 轴正半轴交于点D ,求BCD ∆的面积; (3)如果点P 在原抛物线上,且在对称轴的右侧,联结BP 交线段OA 于点Q ,15BQ PQ =,求点P 的坐标.29.(2020·上海崇明区·九年级二模)已知抛物线24y ax bx =+-经过点(1,0),(4,0)A B -,与y 轴交于点C ,点D 是该抛物线上一点,且在第四象限内,连接AC BC CD BD 、、、.(1)求抛物线的函数解析式,并写出对称轴;(2)当4BCD AOC S S ∆∆=时,求点D 的坐标;(3)在(2)的条件下,如果点E 是x 轴上一点,点F 是抛物线上一点,当以点A D E F 、、、为顶点的四边形是平行四边形时,请直接写出点E 的坐标.30.(2020·上海浦东新区·九年级二模)在平面直角坐标系xOy 中,已知抛物线2y x bx c =-++与x 轴交于点A 和点B (点A 在点B 的左侧),与y 轴交于点(0,3)C ,对称轴是直线1x =.(1)求抛物线的表达式;(2)直线MN 平行于x 轴,与抛物线交于M 、N 两点(点M 在点N 的左侧),且34MN AB =,点C 关于直线MN 的对称点为E ,求线段OE 的长;(3)点P 是该抛物线上一点,且在第一象限内,联结CP 、EP ,EP 交线段BC 于点F ,当:1:2CPF CEF S S =△△时,求点P 的坐标.。
2021年九年级一模数学试题(含解析)

8.D
【分析】
由AB∥CD,利用“两直线平行,内错角相等”可得出∠EHD的度数,利用邻补角互补可求出∠CHG的度数,结合角平分线的定义可求出∠CHM的度数,由AB∥CD,利用“两直线平行,内错角相等”可得出∠GMH=∠CHM=65°,此题得解.
【详解】
【详解】
解: ,
,
又 , ,
,
,
故答案为: .
【点睛】
本题考查了平行四边形的性质,直角三角形斜边上中线的性质;掌握好相关的基础知识是解决本题的关键.
16.
【分析】
连接OC,根据同样只统计得到▱ODCE是矩形,由矩形的性质得到∠ODC=90°.根据勾股定理得到OC=10,根据扇形的面积公式和矩形的面积公式即可得到结论.
二、填空题(共7小题,每小题4分,共28分)
11.分解因式:x2y2-4x2=____.
12.已知一条弧所对的圆周角的度数是 ,则它所对的圆心角的度数是______.
13.已知:一个正数的两个平方根分别是2a﹣2和a﹣4,则a的值是_______.
14.已知a、b满足(a﹣1)2+ =0,则a+b=_____.
解:∵AB∥CD,
∴∠EHD=∠EGB=50°,
∴∠CHG=180°﹣∠EHD=180°﹣50°=130°.
∵HM平分∠CHG,
∴∠CHM=∠GHM= ∠CHG=65°.
∵AB∥CD,
∴∠GMH=∠CHM=65°.
故选D.
【点睛】
本题考查了平行线的性质,牢记“两直线平行,内错角相等”是解题的关键.
9.A
(1)①AB的长为;
②PN的长用含t的代数式表示为;
2020-2021上海静安区教育学院附属学校初三数学上期末一模试题附答案

2020-2021上海静安区教育学院附属学校初三数学上期末一模试题附答案一、选择题1.如图,Rt △ABC 中,∠ABC =90°,AB =8cm ,BC =6cm ,分别以A 、C 为圆心,以2AC 的长为半径作圆,将Rt △ABC 截去两个扇形,则剩余(阴影)部分面积为( )A .(24−254π)cm 2 B .254πcm 2 C .(24−54π)cm 2D .(24−256π)cm 2 2.若⊙O 的半径为5cm ,点A 到圆心O 的距离为4cm ,那么点A 与⊙O 的位置关系是 A .点A 在圆外 B .点A 在圆上 C .点A 在圆内D .不能确定3.设()12,A y -,()21,B y ,()32,C y 是抛物线2(1)y x k =-++上的三点,则1y ,2y ,3y 的大小关系为( )A .123y y y >>B .132y y y >>C .231y y y >>D .312y y y >>4.一个盒子内装有大小、形状相同的四个球,其中红球1个、绿球1个、白球2个,小明摸出一个球不放回,再摸出一个球,则两次都摸到白球的概率是( ) A .12B .14C .16D .1125.关于下列二次函数图象之间的变换,叙述错误的是( ) A .将y =﹣2x 2+1的图象向下平移3个单位得到y =﹣2x 2﹣2的图象 B .将y =﹣2(x ﹣1)2的图象向左平移3个单位得到y =﹣2(x+2)2的图象 C .将y =﹣2x 2的图象沿x 轴翻折得到y =2x 2的图象D .将y =﹣2(x ﹣1)2+1的图象沿y 轴翻折得到y =﹣2(x+1)2﹣1的图象6.如图1,一个扇形纸片的圆心角为90°,半径为4.如图2,将这张扇形纸片折叠,使点A 与点O 恰好重合,折痕为CD ,图中阴影为重合部分,则阴影部分的面积为( )A .4233π- B .8433π- C .8233π- D .843π- 7.若关于x 的一元二次方程()26230a x x --+=有实数根,则整数a 的最大值是( ) A .4B .5C .6D .78.如图,某中学计划靠墙围建一个面积为280m 的矩形花圃(墙长为12m ),围栏总长度为28m ,则与墙垂直的边x 为( )A .4m 或10mB .4mC .10mD .8m9.以394cx ±+=为根的一元二次方程可能是( ) A .230x x c --=B .230x x c +-=C .230-+=x x cD .230++=x x c10.一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是( )A .310B .925C .920D .3511.下列对一元二次方程x 2+x ﹣3=0根的情况的判断,正确的是( ) A .有两个不相等实数根 B .有两个相等实数根 C .有且只有一个实数根 D .没有实数根 12.下列对二次函数y=x 2﹣x 的图象的描述,正确的是( ) A .开口向下 B .对称轴是y 轴C .经过原点D .在对称轴右侧部分是下降的二、填空题13.关于x 的230x ax a --=的一个根是2x =-,则它的另一个根是___.14.如图,⊙O 的半径OD ⊥弦AB 于点C ,连结AO 并延长交⊙O 于点E ,连结EC .若AB =8,CD =2,则EC 的长为_______.15.抛物线y=2(x −3)2+4的顶点坐标是__________________.16.设a 、b 是方程220190x x +-=的两个实数根,则()()11a b --的值为_____. 17.半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于______.18.函数y =x 2﹣4x +3的图象与y 轴交点的坐标为_____.19.如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.已知点A 、B 、C 、D 分别是“果圆”与坐标轴的交点,抛物线的解析式为y=x 2﹣6x ﹣16,AB 为半圆的直径,则这个“果圆”被y 轴截得的线段CD 的长为_____.20.已知扇形的面积为12πcm 2,半径为12cm ,则该扇形的圆心角是_______.三、解答题21.鄂州市化工材料经销公司购进一种化工原料若干千克,价格为每千 克30元.物价部门规定其销售单价不高于每千克60元,不低于每千克30元.经市场调查发现:日销售量y (千克)是销售单价x (元)的一次函数,且当x=60时 ,y=80;x=50时,y=100.在销售过程中,每天还要支付其他费用450元.(1)求出y 与x 的函数关系式,并写出自变量x 的取值范围.(2)求该公司销售该原料日获利w (元)与销售单价x (元)之间的函数关系式. (3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元? 22.小明在解方程2210x x --=时出现了错误,其解答过程如下: 解:221x x -=-(第一步)22111x x -+=-+(第二步)2(1)0x -=(第三步) 121x x ==(第四步)(1)小明解答过程是从第几步开始出错的,写出错误原因. (2)请写出此题正确的解答过程.23.关于x 的一元二次方程x 2﹣2x ﹣(n ﹣1)=0有两个不相等的实数根.(1)求n 的取值范围;(2)若n 为取值范围内的最小整数,求此方程的根.24.某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y (本)与每本纪念册的售价x (元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本. (1)求出y 与x 的函数关系式;(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?(3)设该文具店每周销售这种纪念册所获得的利润为w 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?25.如图,等腰Rt△ABC 中,BA=BC ,∠ABC=90°,点D 在AC 上,将△ABD 绕点B 沿顺时针方向旋转90°后,得到△CBE (1)求∠DCE 的度数;(2)若AB=4,CD=3AD ,求DE 的长.【参考答案】***试卷处理标记,请不要删除一、选择题 1.A 解析:A 【解析】 【分析】利用勾股定理得出AC 的长,再利用图中阴影部分的面积=S △ABC −S 扇形面积求出即可. 【详解】解:在Rt △ABC 中,∠ABC =90°,AB =8cm ,BC =6cm , ∴22228610AC AB BC =+=+=cm ,则2AC=5 cm , ∴S 阴影部分=S △ABC −S 扇形面积=2190525862423604ππ⨯⨯⨯-=-(cm 2),故选:A . 【点睛】本题考查了扇形的面积公式,阴影部分的面积可以看作是Rt △ABC 的面积减去两个扇形的面积.求不规则的图形的面积,可以转化为几个规则图形的面积的和或差来求.2.C解析:C 【解析】 【分析】要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;利用d >r 时,点在圆外;当d=r 时,点在圆上;当d <r 时,点在圆内判断出即可. 【详解】解:∵⊙O 的半径为5cm ,点A 到圆心O 的距离为4cm , ∴d <r ,∴点A 与⊙O 的位置关系是:点A 在圆内, 故选C .3.A解析:A 【解析】 【分析】根据二次函数的性质得到抛物线y =-(x +1)2+k (k 为常数)的开口向下,对称轴为直线x =﹣1,然后根据三个点离对称轴的远近判断函数值的大小. 【详解】解:∵抛物线y =-(x +1)2+k (k 为常数)的开口向下,对称轴为直线x =﹣1,而A (2,y 1)离直线x =﹣1的距离最远,C (﹣2,y 3)点离直线x =1最近,∴123y y y >>. 故选A . 【点睛】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的性质.4.C解析:C 【解析】 【分析】画树状图求出共有12种等可能结果,符合题意得有2种,从而求解. 【详解】 解:画树状图得:∵共有12种等可能的结果,两次都摸到白球的有2种情况,∴两次都摸到白球的概率是:21 126.故答案为C.【点睛】本题考查画树状图求概率,掌握树状图的画法准确求出所有的等可能结果及符合题意的结果是本题的解题关键.5.D解析:D【解析】【分析】根据平移变换只改变图形的位置不改变图形的形状与大小对各选项分析判断后利用排除法求解.【详解】A选项,将y=﹣2x2+1的图象向下平移3个单位得到y=﹣2x2﹣2的图象,故A选项不符合题意;B选项,将y=﹣2(x﹣1)2的图象向左平移3个单位得到y=﹣2(x+2)2的图象,故B选项不符合题意;C选项,将y=﹣2x2的图象沿x轴翻折得到y=2x2的图象,故C选项不符合题意;D选项,将y=﹣2(x﹣1)2+1的图象沿y轴翻折得到y=﹣2(x+1)2+1的图象,故D选项符合题意.故选D.【点睛】本题主要考查了二次函数图象与几何变换,熟练掌握平移变换只改变图形的位置不改变图形的形状与大小的关键.6.C解析:C【解析】【分析】连接OD,根据勾股定理求出CD,根据直角三角形的性质求出∠AOD,根据扇形面积公式、三角形面积公式计算,得到答案.【详解】解:连接OD,在Rt△OCD中,OC=12OD=2,∴∠ODC=30°,CD=2223OD OC+=∴∠COD=60°,∴阴影部分的面积=260418223=23 36023π⨯-⨯⨯π-,故选:C.【点睛】本题考查的是扇形面积计算、勾股定理,掌握扇形面积公式是解题的关键.7.B解析:B【解析】【分析】根据一元二次方程的定义和判别式的意义得到a-6≠0且△=(-2)2-4×(a-6)×3≥0,再求出两不等式的公共部分得到a≤193且a≠6,然后找出此范围内的最大整数即可.【详解】根据题意得a-6≠0且△=(-2)2-4×(a-6)×3≥0,解得a≤193且a≠6,所以整数a的最大值为5.故选B.【点睛】本题考查一元二次方程的定义和跟的判别式,一元二次方程的二次项系数不能为0;当一元二次方程有实数根时,△≥0.8.C解析:C【解析】【分析】设与墙相对的边长为(28-2x)m,根据题意列出方程x(28-2x)=80,求解即可.【详解】设与墙相对的边长为(28-2x)m,则0<28-2x≤12,解得8≤x<14,根据题意列出方程x(28-2x)=80,解得x 1=4,x 2=10 因为8≤x <14∴与墙垂直的边x 为10m 故答案为C. 【点睛】本题考查一元二次方程的应用,根据题意列出方程并求解是解题的关键,注意题中限制条件,选取适合的x 值.9.A解析:A 【解析】 【分析】根据一元二次方程根与系数的关系求解即可. 【详解】设x 1,x 2是一元二次方程的两个根,∵x =∴x 1+x 2=3,x 1∙x 2=-c ,∴该一元二次方程为:21212()0x x x x x x -++=,即230x x c --=故选A. 【点睛】此题主要考查了根据一元二次方程的根与系数的关系列一元二次方程.10.A解析:A 【解析】 【分析】列表或画树状图得出所有等可能的结果,找出两次都为红球的情况数,即可求出所求的概率: 【详解】 列表如下:∴63P 2010==两次红, 故选A.11.A解析:A 【解析】【分析】根据方程的系数结合根的判别式,即可得出△=13>0,进而即可得出方程x 2+x ﹣3=0有两个不相等的实数根. 【详解】∵a=1,b=1,c=﹣3,∴△=b 2﹣4ac=12﹣4×(1)×(﹣3)=13>0, ∴方程x 2+x ﹣3=0有两个不相等的实数根, 故选A .【点睛】本题考查了根的判别式,一元二次方程根的情况与判别式△的关系:(1)△>0⇔方程有两个不相等的实数根;(2)△=0⇔方程有两个相等的实数根;(3)△<0⇔方程没有实数根.12.C解析:C 【解析】【分析】根据抛物线的开口方向、对称轴公式以及二次函数性质逐项进行判断即可得答案. 【详解】A 、∵a=1>0,∴抛物线开口向上,选项A 不正确; B 、∵﹣122b a =,∴抛物线的对称轴为直线x=12,选项B 不正确; C 、当x=0时,y=x 2﹣x=0,∴抛物线经过原点,选项C 正确; D 、∵a >0,抛物线的对称轴为直线x=12, ∴当x >12时,y 随x 值的增大而增大,选项D 不正确, 故选C .【点睛】本题考查了二次函数的性质:二次函数y=ax 2+bx+c (a≠0),对称轴直线x=-2ba,当a >0时,抛物线y=ax 2+bx+c (a≠0)的开口向上,当a <0时,抛物线y=ax 2+bx+c(a≠0)的开口向下,c=0时抛物线经过原点,熟练掌握相关知识是解题的关键.二、填空题13.6【解析】【分析】【详解】解:设方程另一根为x1把x=-2代入方程得(-2)2+2a-3a=0解得a=4∴原方程化为x2-4x-12=0∵x1+(-2)=4∴x 1=6故答案为6点睛:本题考查了一元二解析:6【解析】【分析】【详解】解:设方程另一根为x1,把x=-2代入方程得(-2)2+2a-3a=0,解得a=4,∴原方程化为x2-4x-12=0,∵x1+(-2)=4,∴x1=6.故答案为6.点睛:本题考查了一元二次方程ax2+bx+c=0(a≠0)的根与系数的关系:若方程的两根为x1,x2,则x1+ x2=ba,x1·x2=ca.也考查了一元二次方程的解.14.【解析】【分析】设⊙O半径为r根据勾股定理列方程求出半径r由勾股定理依次求BE和EC的长【详解】连接BE设⊙O半径为r则OA=OD=rOC=r-2∵OD⊥AB∴∠ACO=90°AC=BC=AB=4在解析:213【解析】【分析】设⊙O半径为r,根据勾股定理列方程求出半径r,由勾股定理依次求BE和EC的长.【详解】连接BE,设⊙O半径为r,则OA=OD=r,OC=r-2,∵OD⊥AB,∴∠ACO=90°,AC=BC=12AB=4, 在Rt △ACO 中,由勾股定理得:r 2=42+(r-2)2,r=5,∴AE=2r=10,∵AE 为⊙O 的直径,∴∠ABE=90°,由勾股定理得:BE=6,在Rt △ECB 中,EC ==.故答案是:【点睛】考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形,利用勾股定理求解是解答此题的关键.15.(34)【解析】【分析】根据二次函数配方的图像与性质即可以求出答案【详解】在二次函数的配方形式下x-3是抛物线的对称轴取x=3则y=4因此顶点坐标为(34)【点睛】本题主要考查二次函数的图像与性质解析:(3,4)【解析】【分析】根据二次函数配方的图像与性质,即可以求出答案.【详解】在二次函数的配方形式下,x-3是抛物线的对称轴,取x=3,则y=4,因此,顶点坐标为(3,4).【点睛】本题主要考查二次函数的图像与性质.16.-2017【解析】【分析】根据根与系数的关系可得出将其代入中即可得出结论【详解】∵是方程的两个实数根∴∴故答案为:-2017【点睛】本题考查了根与系数的关系牢记两根之和等于两根之积等于是解题的关键解析:-2017【解析】【分析】根据根与系数的关系可得出1a b +=-,2019ab =-,将其代入()()()111a b ab a b --=-++中即可得出结论.【详解】∵a 、b 是方程220190x x +-=的两个实数根,∴1a b +=-,2019ab =-,∴()()()111a b ab a b --=-++2019112017=-++=-.故答案为:-2017.【点睛】本题考查了根与系数的关系,牢记“两根之和等于b a -,两根之积等于c a”是解题的关键. 17.16﹣4π【解析】【分析】恒星的面积=边长为4的正方形面积-半径为2的圆的面积依此列式计算即可【详解】解:如图2+2=4恒星的面积=4×4-4π=16-4π故答案为16-4π【点睛】本题考查了扇形面解析:16﹣4π【解析】【分析】恒星的面积=边长为4的正方形面积-半径为2的圆的面积,依此列式计算即可.【详解】解:如图.2+2=4,恒星的面积=4×4-4π=16-4π. 故答案为16-4π.【点睛】本题考查了扇形面积的计算,关键是理解恒星的面积=边长为4的正方形面积-半径为2的圆的面积.18.(03)【解析】【分析】令x =0求出y 的值然后写出与y 轴的交点坐标即可【详解】解:x =0时y =3所以图象与y 轴交点的坐标是(03)故答案为(03)【点睛】本题考查了求抛物线与坐标轴交点的坐标掌握二次解析:(0,3).【解析】【分析】令x =0,求出y 的值,然后写出与y 轴的交点坐标即可.【详解】解:x =0时,y =3,所以.图象与y 轴交点的坐标是(0,3).故答案为(0,3).【点睛】本题考查了求抛物线与坐标轴交点的坐标,掌握二次函数与一元二次方程的联系是解答本题的关键.19.20【解析】【分析】抛物线的解析式为y=x2-6x-16可以求出AB=10;在Rt △COM 中可以求出CO=4;则:CD=CO+OD=4+16=20【详解】抛物线的解析式为y=x2-6x-16则D (0解析:20【解析】【分析】抛物线的解析式为y=x 2-6x-16,可以求出AB=10;在Rt △COM 中可以求出CO=4;则:CD=CO+OD=4+16=20.【详解】抛物线的解析式为y=x 2-6x-16,则D (0,-16)令y=0,解得:x=-2或8,函数的对称轴x=-2b a=3,即M (3,0), 则A (-2,0)、B (8,0),则AB=10, 圆的半径为12AB=5, 在Rt △COM 中,OM=5,OM=3,则:CO=4,则:CD=CO+OD=4+16=20.故答案是:20.【点睛】考查的是抛物线与x 轴的交点,涉及到圆的垂径定理.20.30°【解析】设圆心角为n°由题意得:=12π解得:n=30故答案为30° 解析:30°【解析】设圆心角为n°,由题意得:212360n π⨯=12π, 解得:n=30,故答案为30°.三、解答题21.(1)y=-2x+200(30≤x≤60)(2)w=-2(x -65)2 +2000);(3)当销售单价为60元时,该公司日获利最大,为1950元【解析】【分析】(1)设出一次函数解析式,把相应数值代入即可.(2)根据利润计算公式列式即可;(3)进行配方求值即可.【详解】(1)设y=kx+b ,根据题意得806010050k b k b =+⎧⎨=+⎩解得:k 2b 200=-⎧⎨=⎩∴y=-2x+200(30≤x≤60)(2)W=(x -30)(-2x+200)-450=-2x 2+260x -6450=-2(x -65)2 +2000)(3)W =-2(x -65)2 +2000∵30≤x≤60∴x=60时,w 有最大值为1950元∴当销售单价为60元时,该公司日获利最大,为1950元考点:二次函数的应用.22.(1)一,移项没变号(或移项错误或等式性质用错均给分);(2)11x =21x =-【解析】【分析】(1)第一步即发生错误,移项未变号;(2)可将采用配方法解方程即可.【详解】(1)一,移项没变号(或移项错误或等式性质用错)(2)解:221x x -=22111x x -+=+()212x -=即,11x =,21x =【点睛】本题考查了解一元二次方程,熟悉各种解法的特点并灵活选择解法是解题关键.23.(1)n >0;(2)x 1=0,x 2=2.【解析】【分析】(1)根据方程有两个不相等的实数根可知240b ac ∆=-> ,即可求出n 的取值范围; (2)根据题意得出n 的值,将其代入方程,即可求得答案.【详解】(1)根据题意知,[]224(2)41(1)0b ac n ∆=-=--⨯⨯-->解之得:0n >;(2)∵0n > 且n 为取值范围内的最小整数,∴1n =,则方程为220x x -=,即(2)0x x -=,解得120,2x x ==.【点睛】本题主要考查了一元二次方程根的判别式,明确和掌握一元二次方程20(a 0)++=≠ax bx c 的根与24b ac ∆=-的关系(①当>0∆ 时,方程有两个不相等的实数根;②当0∆= 时方程有两个相等的实数根;③当∆<0 时,方程无实数根)是解题关键.24.(1)y=﹣2x+80(20≤x≤28);(2)每本纪念册的销售单价是25元;(3)该纪念册销售单价定为28元时,才能使文具店销售该纪念册所获利润最大,最大利润是192元.【解析】【分析】(1)待定系数法列方程组求一次函数解析式.(2)列一元二次方程求解.(3)总利润=单件利润⨯销售量:w =(x -20)(-2x +80),得到二次函数,先配方,在定义域上求最值.【详解】(1)设y 与x 的函数关系式为y =kx +b .把(22,36)与(24,32)代入,得22362432.k b k b +=⎧⎨+=⎩解得280.k b =-⎧⎨=⎩∴y =-2x +80(20≤x≤28).(2)设当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是x 元,根据题意,得(x -20)y =150,即(x -20)(-2x +80)=150.解得x 1=25,x 2=35(舍去).答:每本纪念册的销售单价是25元.(3)由题意,可得w=(x-20)(-2x+80)=-2(x-30)2+200.∵售价不低于20元且不高于28元,当x<30时,y随x的增大而增大,∴当x=28时,w最大=-2×(28-30)2+200=192(元).答:该纪念册销售单价定为28元时,能使文具店销售该纪念册所获利润最大,最大利润是192元.25.解:(1)90°;(2)【解析】试题分析:(1)首先由等腰直角三角形的性质求得∠BAD、∠BCD的度数,然后由旋转的性质可求得∠BCE的度数,故此可求得∠DCE的度数;(2)由(1)可知△DCE是直角三角形,先由勾股定理求得AC的长,然后依据比例关系可得到CE和DC的长,最后依据勾股定理求解即可.试题解析:(1)∵△ABCD为等腰直角三角形,∴∠BAD=∠BCD=45°.由旋转的性质可知∠BAD=∠BCE=45°.∴∠DCE=∠BCE+∠BCA=45°+45°=90°.(2)∵BA=BC,∠ABC=90°,∴=.∵CD=3AD,∴,.由旋转的性质可知:.∴=考点:旋转的性质.。
2021年中考一模考试《数学卷》含答案解析

数学中考综合模拟检测试题学校________ 班级________ 姓名________ 成绩________一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1.实数4的相反数是( ) A. 14-B. -4C.14D. 42.如图是由4个相同的小正方体组成的一个立体图形,其主视图是( )A. B. C. D.3.2019年1月3日10时26分,“嫦娥四号”探测器飞行约380000千米,实现人类探测器首次在月球背面软着陆.数据380000用科学记数法表示为( ) A. 38×104B. 3.8×104C. 3.8×105D. 0.38×1064.(2018乌鲁木齐)在平面直角坐标系xOy 中,将点()12N --,绕点O 旋转180°,得到的对应点的坐标是( )A. ()12, B. ()12-, C. ()12--, D. ()12-, 5.不等式组12220360x x -<⎧⎨-≤⎩的解集是( )A. 46x -<≤B. 4x ≤-或2x >C. 42x -<≤D. 24x ≤<6.下列图形,既是轴对称图形又是中心对称图形的是( ) A 正三角形B. 正五边形C. 等腰直角三角形D. 矩形7.化简()22x 的结果是( ) A. x 4B. 2x 2C. 4x 2D. 4x8.在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为( ) A.16B.13C.12D.239.如图,将矩形纸片ABCD 沿直线EF 折叠,使点C 落在AD 边的中点C′处,点B 落在点B′处,其中AB=9,BC=6,则FC′的长为( )A.103B. 4C. 4.5D. 510.二次函数2y ax bx c =++的图象如图,且,OA OC =则( )A. 1ac b +=B. 1ab c += C. 1bc a +=D. 以上都不是二、填空题(本题共6小题,每小题3分,共18分)11.如图,EABC ∆边CA 延长线上一点,过点E 作//ED BC .若070BAC ∠=,050CED ∠=,则B ∠=________°.12.如图,∠AOE =∠BOE =15°,EF ∥OB ,EC ⊥OB 于C ,若EC =1,则OF =_____.13.为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况: 捐书(本) 3 4 5 7 10 人数 5710117该班学生平均每人捐书______本.14.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x 两,牛每头y 两,根据题意可列方程组为_____________.15.如图,无人机于空中A 处测得某建筑顶部B 处的仰角为45,测得该建筑底部C 处的俯角为17.若无人机的飞行高度AD 为62m ,则该建筑的高度BC 为__m .(参考数据:sin170.29≈,cos170.96≈,tan170.31≈)16.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是______米.三.解答下列各题(本题共4小题,其中17、18、19题9分、20题12分,共39分)17.计算:1332)182+18.化简: 2212(1)244x x xx x x +--÷--+ 19.如图,EF=BC ,DF=AC ,DA=EB .求证:∠F=∠C .20.某校为了解九年级学生每天参加体育锻炼的时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):306070103011570607590,,,,,,,,,,157040751058060307045,,,,,,,,,对以上数据进行整理分析,得到下列表一和表二:根据以上提供的信息,解答下列问题:()1填空:①a=,b=;②c=,d=;()2如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数.四、解答题(本题共3小题,其中21、22题各9分,23题10分,共28分)21.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为1122m,则小路的宽应为多少?22.如图,函数12y x=的图象与函数kyx=(x>0)的图象相交于点P(4,m).(1)求m,k的值;(2)直线y=3与函数12y x =的图象相交于点A ,与函数k y x=(x >0)的图象相交于点B ,求线段AB 长.23.如图,△ABC 中,AB =AC ,以AC 为直径的⊙O 交BC 于点D ,点E 为AC 延长线上一点,且DE 是⊙O 的切线.(1)求证:∠CDE =12∠BAC ; (2)若AB =3BD ,CE =4,求⊙O 的半径.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图,在平面直角坐标系xOy 中,直线112y x =+与y 轴,x 轴分别相交于点A B 、.点D 是x 轴上动点,点D 从点B 出发向原点O 运动,点E 在点D 右侧,2DE BD =.过点D 作DH AB ⊥于点,H 将DBH △沿直线DH 翻折,得到,DCH 连接CE .设,BD t =DCH 与AOB 重合部分面积为.S 求:(1)求线段BC 的长(用含t 的代数式表示);(2)求S 关于t 的函数解析式,并直接写出自变量t 的取值范围. 25.阅读下面材料,完成()()13-题. 数学课上,老师出示了这样一道题:如图1,在ABC 中,,.BA BC AB kAC ==点F 在AC 上,点E 在BF 上,2BE EF =.点D 在BC 延长线上,连接,180AD AE ACD DAE ∠+∠=、.探究线段AD 与AE 的数量关系并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现CAD ∠与EAB ∠相等.” 小亮:“通过观察和度量,发现FAE ∠与D ∠也相等.”小伟:“通过边角关系构造辅助线,经过进一步推理, 可以得到线段AD 与AE数量关系.”老师:“保留原题条件,延长图1中的,AE 与BC 相交于点H (如图2),若知道DH 与AH 的数量关系,可以求出ABCH的值.”(1)求证:CAD EAB ∠=∠; (2)求ADAE的值(用含k 的式子表示); (3)如图2,若,DH AH =则ABCH的值为 (用含k 的式子表示). 26.已知抛物线2y x bx c =++过点A(m-2,n), B (m+4,n ),C (m ,53n -). (1)b=__________(用含m 的代数式表示); (2)求△ABC 的面积; (3)当1222m x m ≤≤+时,均有6y m -≤≤,求m 的值.答案与解析一、选择题(本题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一个选项是正确的)1.实数4的相反数是()A.14B. -4C.14D. 4【答案】B【解析】【分析】根据相反数的定义即可解答.【详解】∵符号相反,绝对值相等的两个数互为相反数,∴4的相反数是﹣4;故选B.【点睛】本题考查了相反数的定义,熟知只有符号不同的两个数互为相反数是解决问题的关键.2.如图是由4个相同的小正方体组成的一个立体图形,其主视图是()A. B. C. D.【答案】A【解析】【分析】根据三视图的概念即可快速作答.【详解】解:立体图形的主视图,即正前方观察到的平面图,即选项A符合题意;故答案为A.【点睛】本题考查了三视图的概念及正确识别主视图,解题的关键在于良好的空间想象能力.3.2019年1月3日10时26分,“嫦娥四号”探测器飞行约380000千米,实现人类探测器首次在月球背面软着陆.数据380000用科学记数法表示为()A. 38×104B. 3.8×104C. 3.8×105D. 0.38×106【答案】C 【解析】 【分析】对于一个绝对值较大的数,用科学记数法写成10n a ⨯ 的形式,其中110a ≤<,n 是比原整数位数少1的数.【详解】380000=3.8×105. 故选C.【点睛】此题考查了科学记数法的表示方法.科学记数法的表示形式为a ×10n 的形式,其中1≤|a |<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.4.(2018乌鲁木齐)在平面直角坐标系xOy 中,将点()12N --,绕点O 旋转180°,得到的对应点的坐标是( )A. ()12, B. ()12-, C. ()12--, D. ()12-, 【答案】A 【解析】【详解】点N 绕着点O 旋转180°,恰好关于原点对称,点(1,2)N --的中心对称点为(1,2),故选A .5.不等式组12220360x x -<⎧⎨-≤⎩的解集是( )A. 46x -<≤B. 4x ≤-或2x >C. 42x -<≤D. 24x ≤<【答案】C 【解析】 【分析】分别求出每一个不等式的解集,再确定出解集的公共部分即可得解. 【详解】解不等式12220x -<,得:4x >-, 解不等式360x -≤,得:2x ≤, 则不等式组的解集为42x -<≤, 故选C .【点睛】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键. 6.下列图形,既是轴对称图形又是中心对称图形的是( )A. 正三角形B. 正五边形C. 等腰直角三角形D. 矩形【答案】D【解析】【分析】根据轴对称图形与中心对称图形的概念逐一进行分析判断即可得.【详解】A.正三角形是轴对称图形,不是中心对称图形;B.正五边形是轴对称图形,不是中心对称图形;C.等腰直角三角形是轴对称图形,不是中心对称图形;D.矩形是轴对称图形,也是中心对称图形,故选D.【点睛】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后两部分重合.7.化简()22x的结果是()A. x4B. 2x2C. 4x2D. 4x【答案】C【解析】【分析】利用积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘即可.【详解】(2x)²=2²·x²=4x²,故选C.【点睛】本题考查了积的乘方,解题的关键是掌握积的乘方的运算法则.8.在同一副扑克牌中抽取2张“方块”,3张“梅花”,1张“红桃”.将这6张牌背面朝上,从中任意抽取1张,是“红桃”的概率为()A. 16B.13C.12D.23【答案】A【解析】【分析】直接利用概率公式计算可得.【详解】解:从中任意抽取1张,是“红桃”的概率为16,故选A.【点睛】本题主要考查概率公式,随机事件A 的概率P (A )=事件A 可能出现的结果数÷所有可能出现的结果数.9.如图,将矩形纸片ABCD 沿直线EF 折叠,使点C 落在AD 边的中点C′处,点B 落在点B′处,其中AB=9,BC=6,则FC′的长为( )A. 103B. 4C. 4.5D. 5【答案】D【解析】【分析】设FC ′=x ,则FD=9-x ,根据矩形的性质结合BC=6、点C ′为AD 的中点,即可得出C ′D 的长度,在Rt △FC ′D 中,利用勾股定理即可找出关于x 的一元一次方程,解之即可得出结论.【详解】设FC′=x ,则FD=9﹣x ,∵BC=6,四边形ABCD 为矩形,点C′为AD 的中点,∴AD=BC=6,C′D=3,在Rt △FC′D 中,∠D=90°,FC′=x ,FD=9﹣x ,C′D=3,∴FC′2=FD 2+C′D 2,即x 2=(9﹣x )2+32,解得:x=5,故选D .【点睛】本题考查了矩形的性质以及勾股定理,在Rt △FC′D 中,利用勾股定理找出关于FC′的长度的一元二次方程是解题的关键.10.二次函数2y ax bx c =++的图象如图,且,OA OC =则( )A. 1ac b +=B. 1ab c +=C. 1bc a +=D. 以上都不是【答案】A【解析】【分析】 根据题意可知,本题考察二次函数图像与系数的关系,根据图像与坐标轴的交点,运用两边相等求出交点坐标,代入坐标进行求解.【详解】∵OA OC =∴点A 、C 的坐标为(-c ,0),(0,c)∴把点A 的坐标代入2y ax bx c =++得∴2=0ac bc c -+∴()10c ac b -+=∵0c ≠∴10ac b -+=∴1ac b +=故选A【点睛】本题考察二次函数图像与系数关系,解题关键是根据图像得出系数取值范围,再代入点的坐标进行解决. 二、填空题(本题共6小题,每小题3分,共18分)11.如图,E 为ABC ∆边CA 延长线上一点,过点E 作//ED BC .若070BAC ∠=,050CED ∠=,则B ∠=________°.【答案】60【解析】【分析】利用平行线的性质,即可得到∠CED=∠C=50°,再根据三角形内角和定理,即可得到∠B 的度数.【详解】解:∵ED ∥BC ,∴∠CED=∠C=50°,又∵∠BAC=70°,∴△ABC中,∠B=180°-50°-70°=60°,故答案为60.【点睛】本题主要考查了平行线的性质,解题时注意运用两直线平行,内错角相等.12.如图,∠AOE=∠BOE=15°,EF∥OB,EC⊥OB于C,若EC=1,则OF=_____.【答案】2【解析】【分析】作EH⊥OA于H,根据角平分线的性质求出EH,根据直角三角形的性质求出EF,根据等腰三角形的性质解答即可.【详解】作EH⊥OA于H.∵∠AOE=∠BOE=15°,EC⊥OB,EH⊥OA,∴EH=EC=1,∠AOB=30°.∵EF∥OB,∴∠EFH=∠AOB=30°,∠FEO=∠BOE,∴EF=2EH=2,∠FEO=∠FOE,∴OF=EF=2.故答案2.【点睛】本题考查了等腰三角形的判定、角平分线的性质、平行线的性质,掌握角的平分线上的点到角的两边的距离相等是解题的关键.13.为了建设“书香校园”,某校七年级的同学积极捐书,下表统计了七(1)班40名学生的捐书情况:捐书(本) 3 4 5 7 10人数 5 7 10 11 7该班学生平均每人捐书______本.【答案】6【解析】【分析】利用加权平均数公式进行求解即可得. 【详解】该班学生平均每人捐书3547510711107640⨯+⨯+⨯+⨯+⨯=(本), 故答案为6.【点睛】本题考查了加权平均数,熟练掌握加权平均数的计算公式是解题的关键.14.中国清代算书《御制数理精蕴》中有这样一题:“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹x 两,牛每头y 两,根据题意可列方程组为_____________.【答案】46483538x y x y +=⎧⎨+=⎩【解析】【分析】直接利用“马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两”,分别得出方程得出答案.【详解】解:设马每匹x 两,牛每头y 两,根据题意可列方程组为: 46483538x y x y +=⎧⎨+=⎩ 故答案是:46483538x y x y +=⎧⎨+=⎩【点睛】此题主要考查了二元一次方程组的应用,正确得出等式是解题关键.15.如图,无人机于空中A 处测得某建筑顶部B 处的仰角为45,测得该建筑底部C 处的俯角为17.若无人机的飞行高度AD 为62m ,则该建筑的高度BC 为__m .(参考数据:sin170.29≈,cos170.96≈,tan170.31≈)【答案】262【解析】【分析】作AE BC ⊥于E ,根据正切的定义求出AE ,根据等腰直角三角形的性质求出BE ,结合图形计算即可.【详解】作AE BC ⊥于E ,则四边形ADCE 为矩形,62EC AD ∴==,在Rt AEC ∆中,tan EC EAC AE ∠=, 则62200tan 0.31EC AE EAC =≈=∠, 在Rt AEB ∆中,45BAE ∠=,200BE AE ∴==,20032262()BC m ∴=+=,则该建筑的高度BC 为262m ,故答案为262.【点睛】本题考查的是解直角三角形的应用﹣仰角俯角问题,掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键.16.甲、乙两人在直线道路上同起点、同终点、同方向,分别以不同的速度匀速跑步1500米,先到终点的人原地休息,已知甲先出发30秒后,乙才出发,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示,则乙到终点时,甲距终点的距离是______米.【答案】175【解析】试题解析:根据题意得,甲的速度为:75÷30=2.5米/秒,设乙的速度为m 米/秒,则(m -2.5)×(180-30)=75,解得:m =3米/秒,则乙的速度为3米/秒, 乙到终点时所用的时间为:15003=500(秒), 此时甲走的路程是:2.5×(500+30)=1325(米),甲距终点的距离是1500-1325=175(米).【点睛】本题考查了一次函数的应用,读懂题目信息,理解并得到乙先到达终点,然后求出甲、乙两人所用的时间是解题的关键.三.解答下列各题(本题共4小题,其中17、18、19题9分、20题12分,共39分)17.计算:2)+【答案】-1.【解析】【分析】先利用平方差公式简便运算乘法,同时化简二次根式,再合并同类二次根式即可.【详解】解:2)+=3-4+=-1.【点睛】本题考查的是二次根式的混合运算,二次根式的化简,掌握利用平方差公式进行简便运算是解题的关键.18.化简: 2212(1)244x x x x x x +--÷--+ 【答案】3x . 【解析】【分析】先通分,计算括号内的减法,把除法转化为乘法,约分后得到结论. 【详解】解:原式=212(2)122()22(2)2x x x x x x x x x x x x+--+-+--÷=•----323.2x x x x-=•=- 【点睛】本题考查的是分式的化简,考查了分式的加减法,分式的除法,掌握以上运算是解题的关键. 19.如图,EF=BC ,DF=AC ,DA=EB .求证:∠F=∠C .【答案】见解析.【解析】【分析】欲证明∠F =∠C ,只要证明△ABC ≌△DEF(SSS)即可.【详解】证明:DA BE =,DE AB ∴=,在ABC ∆和DEF ∆中,AB DE AC DF BC EF =⎧⎪=⎨⎪=⎩,()ABC DEF SSS ∴∆≅∆,C F ∴∠=∠.【点睛】本题主要考查全等三角形的判定与性质.20.某校为了解九年级学生每天参加体育锻炼的时间,从该校九年级学生中随机抽取20名学生进行调查,得到如下数据(单位:分钟):306070103011570607590,,,,,,,,,,157040751058060307045,,,,,,,,,对以上数据进行整理分析,得到下列表一和表二:根据以上提供的信息,解答下列问题:()1填空:①a=,b=;②c=,d=;()2如果该校现有九年级学生200名,请估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数.【答案】(1)①5,3;②65,70;(2)130人.【解析】【分析】(1)①根据数据统计出a、b;②根据中位数和众数的定义求出c,d即可;(2)先求出样本用样本达到平均水平及以上的学生的概率,然后用九年级学生数×样本达到平均水平及以上的学生的概率即可.【详解】解:()1①经统计:该组数据处于30≤t<60的数据有5个, 处于90≤t<120的数据有3个,∴a=5;b=3故答案为:5;3②将这组数据从小到大排序,位于第10个的数据是60,第11个的数据是70∴中位数为(60+70)÷2=65这组数据中出现次数最多的是70 ∴众数为70 ∴6570,c d==故答案为:65;70.()132********⨯=(人),答:估计该校九年级学生每天参加体育锻炼的时间达到平均水平及以上的学生人数为130人.【点睛】本题考查中位数、众数、平均数、样本估计总体的思想等知识,掌握中位数、众数、平均数等基本知识是解答本题的关键.四、解答题(本题共3小题,其中21、22题各9分,23题10分,共28分)21.改善小区环境,争创文明家园.如图所示,某社区决定在一块长(AD)16m,宽(AB)9m的矩形场地ABCD上修建三条同样宽的小路,其中两条与AB平行,另一条与AD平行,其余部分种草.要使草坪部分的总面积为1122m,则小路的宽应为多少?【答案】小路的宽应为1m .【解析】【分析】设小路的宽应为x 米,那么草坪的总长度和总宽度应该为(16-2x ),(9-x );那么根据题意得出方程,解方程即可.【详解】解:设小路的宽应为x 米,根据题意得:(162)(9)112x x --=,解得:11x =,216x =.∵169>,∴16x =不符合题意,舍去,∴1x =.答:小路的宽应为1米.【点睛】本题考查一元二次方程的应用,弄清“草坪的总长度和总宽度”是解决本题的关键. 22.如图,函数12y x =的图象与函数k y x=(x >0)的图象相交于点P (4,m ). (1)求m ,k 的值;(2)直线y=3与函数12y x =的图象相交于点A ,与函数k y x=(x >0)的图象相交于点B ,求线段AB 长.【答案】(1)m=2,k=8;(2)103.【解析】【分析】(1)将点P(4,m)代入y=x,求出m=2,再将点P(4,2)代入kyx=即可求出k的值;(2) 分别求出A、B两点的坐标,即可得到线段AB的长.【详解】(1)∵函数12y x=的图象过点P(4,m),∴m=2,∴P(4,2),∵函数kyx=(x>0)的图象过点P,∴k=4×2=8;(2)将y=3代入12y x=,得x=6,∴点A(6,3).将y=3代入8yx=,得x=83,∴点B(83,3).∴AB=6﹣83=103.【点睛】本题主要考查了利用待定系数法求函数解析式以及函数图象上点的坐标特征,解题时注意:点在图象上,点的坐标就一定满足函数的解析式.23.如图,△ABC中,AB=AC,以AC为直径的⊙O交BC于点D,点E为AC延长线上一点,且DE是⊙O 的切线.(1)求证:∠CDE=12∠BAC;(2)若AB=3BD,CE=4,求⊙O的半径.【答案】(1)见解析;(2)14.【解析】【分析】(1)根据圆周角定理得出∠ADC=90°,按照等腰三角形的性质和已知的2倍角关系,证明∠ODE为直角即可得到答案;(2)通过证得△CDE∽△DAE,根据相似三角形的性质即可求得.【详解】(1)如图,连接OD,AD,∵AC是直径,∴∠ADC=90°,-∴AD⊥BC,∵AB=AC,∴∠CAD=∠BAD=12∠BAC,∵DE是⊙O的切线;∴OD⊥DE∴∠ODE=90°∴∠ADC=∠ODE∴∠CDE=∠ADO ∵OA=OD,∴∠CAD=∠ADO,∴∠CDE=∠CAD,∠CAD=12∠BAC,∴∠CDE=12∠BAC.(2)解:∵AB=AC,AD⊥BC,∴BD=CD,∵AB=3BD,∴AC=3DC,设DC=x,则AC=3x,∴AD2222,AC DC x-=∵∠CDE=∠CAD,∠DEC=∠AED,∴△CDE∽△DAE,∴CE DC DE DE AD AE∴==,即43422DE DE xx==+∴DE=82,,x=283,∴AC=3x=28,∴⊙O的半径为14.【点睛】本题考查了圆的切线的判定定理、圆周角定理、等腰三角形的性质、三角形相似的判定和性质,解题的关键是作出辅助线构造直角三角形或等腰三角形.五、解答题(本题共3小题,其中24题11分,25、26题各12分,共35分)24.如图,在平面直角坐标系xOy 中,直线112y x =+与y 轴,x 轴分别相交于点A B 、.点D 是x 轴上动点,点D 从点B 出发向原点O 运动,点E 在点D 右侧,2DE BD =.过点D 作DH AB ⊥于点,H 将DBH △沿直线DH 翻折,得到,DCH 连接CE .设,BD t =DCH 与AOB 重合部分面积为.S 求:(1)求线段BC 的长(用含t 的代数式表示);(2)求S 关于t 的函数解析式,并直接写出自变量t 的取值范围.【答案】(1)55t BC =;(2)222420536224825357734288523334t t S t t t t t t ⎧⎛⎫<≤ ⎪⎪⎝⎭⎪⎪⎛⎫=-+-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-+<≤⎪ ⎪⎝⎭⎩ 【解析】【分析】(1)先根据直线112y x =+求得点A 、B 的坐标,利用勾股定理求得AB 的长,进而可求得5555sin ABO cos ABO ∠=∠=,由翻折知DB DC t ==,12BH CH BC ==,最后根据255BH cos ABO BD ∠==求得55t BH =,即可求得BC 的长; (2)分类讨论:当203t <≤时,当2534t <≤时,当524t <≤时,分别画出相应图形,然后利用相似三角形的性质分别表示出对应的底和高,进而可得S 关于t 的函数解析式即可. 【详解】解:()1∵直线112y x =+与y 轴,x 轴分别相交于点A B 、, ∴点()()012,0A B -,,,∴由勾股定理得22125AB =+=∴在直角AOB 中,525,55sin ABO cos ABO ∠=∠=, 由翻折知:DB DC t ==,12BH CH BC ==, 255BH cos ABO BD∠==, 255t BH ∴=, 455t BC ∴=, ()2当203t <≤时, 过点C 做CG BO ⊥于点G ,45CG t ∴=, 55CG sin ABO BC∴∠==, 45GC t ∴=, 14225S t t ∴=⨯⨯ 245t = 当2534t <≤时, 设OA 交CE 于点F ,45CD BD t GC t ===,, ∴由勾股定理得35GD t =,37255GE t t t ∴=-=, 382255GO t t t =--=-, 78 23255OE EG OG t t t ∴=-=-+=-, //OF CG ,EOFCGE ∴, OF OE CG OG∴=, ()4327OF t ∴=-, 12OFE S OE OF =⋅ ()()14323227t t =⋅-⋅- 222(73)t -= , DCE OFE S S S =-∴2622483577t t =-+-, 当524t <≤时, 设CD 交OA 于点P ,//,OP CG,DOP DGC ∴OP OD CG DG∴=, 2OD t =-,()423OP OP t ∴==-,12S OD OP =⋅⋅∴ 2288333t t =-+, ∴综上所述,222420536224825357734288523334t t S t t t t t t ⎧⎛⎫<≤ ⎪⎪⎝⎭⎪⎪⎛⎫=-+-<≤⎨ ⎪⎝⎭⎪⎪⎛⎫-+<≤⎪ ⎪⎝⎭⎩ 【点睛】本题考查了一次函数的图像与性质,解直角三角形、相似三角形的判定及性质,根据点D 的位置画出相应的图形然后运用分类讨论思想以及相似三角形的性质是解决本题的关键.25.阅读下面材料,完成()()13-题.数学课上,老师出示了这样一道题:如图1,在ABC 中,,.BA BC AB kAC ==点F 在AC 上,点E 在BF 上,2BE EF =.点D 在BC 延长线上,连接,180AD AE ACD DAE ∠+∠=、.探究线段AD 与AE 的数量关系并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现CAD ∠与EAB ∠相等.”小亮:“通过观察和度量,发现FAE ∠与D ∠也相等.”小伟:“通过边角关系构造辅助线,经过进一步推理, 可以得到线段AD 与AE 的数量关系.” 老师:“保留原题条件,延长图1中的,AE 与BC 相交于点H (如图2),若知道DH 与AH 的数量关系,可以求出AB CH的值.”(1)求证:CAD EAB ∠=∠;(2)求AD AE的值(用含k 的式子表示); (3)如图2,若,DH AH =则AB CH 的值为 (用含k 的式子表示). 【答案】(1)证明见解析;(2)3AD AE k =;(3)2115AB k CH ++= 【解析】【分析】(1)由BA BC =可知BAC BCA ∠=∠,再通过180ACD DAE ∠+∠=以及平角为180°,可以得到CAD EAB ∠=∠;(2)方法一:过点C 做ACM ABE ∠=∠,交AD 于点M ,通过AEB AMC 可知AC AM CM AB AE BE ==,通过DCM AFE 可知DM CM AE EF =,通过比例关系可推导出AD AE的值;方法二:过点B 做//BN AC 交AE 延长线于点N ,通过AHC DHA 和ACD ABN 相似得到的比例关系即可可推导出AD AE的值; (3)同方法二辅助线,通过证明AHC DHA ,AFE NBE ,然后由对应边成比例即可推导出结论.【详解】()1BA BC =,BAC BCA ∴∠=∠180,ACD DAE ∠+∠=180,ACD ACB ∠+∠=∴∠=∠ADE ACB,∴∠=∠DAE BAC,∴∠=∠DAC BAE,()2方法一:∠=∠,交AD于点M 过点C做ACM ABE∠=∠,DAC BAE∴AEB AMCAC AM CM∴==AB AE BE=AB kAC1∴=AM AEk1=CM BEk=2BE EF2∴=CM FEk∠=∠+∠AEF EAB ABE∠=∠+∠DMC MAC ACM∴∠=∠DMC AEFACB D DAC∠=∠+∠∠=∠+∠DAE DAC FAEDAE ACB∠=∠∴∠=∠D FAE∴DCM AFEDM CM∴=AE EF2∴=DM AEk3∴=+=AD AM DM AEkAD3∴=AE k方法二:BN AC交AE延长线于点,N 过点B做//,∴∠=∠N FAE∠=∠,AFE EBN∴,AFE NBEAE EF∴=NE BE=BE EF2,∴=NE EA2,NA EA∴=3,∠=∠+∠ACB D DAC,DAE DAC FAE∠=∠+∠,DAE ACB∠=∠,∴∠=∠,D FAE,DAC BAE ∴∠=∠ ACD ABN ∴ AC AD AB AN ∴= ,AB kAC = ,AN kAD ∴= 3,AE kAC ∴= 3AD AE k ∴= ()3同方法二辅助线,D CAH ∠=∠ ,AHC DHA ∠=∠ AHC DHA ∴ 2AH HC DH ∴=⋅ 23AH AC DH AD == 23AD AC ∴= AB kAC = 32AD AB k ∴= 3AD AE k =12AE AB ∴= 设2AH a AB BC b ===,13,2DH a AE b ∴== 2NE AE =NE b ∴=EH AH AE EN NH =-=-322NH b a ∴=- 2AH HC DH =⋅43CH a ∴= 53CD a ∴= ∴由方法二相似得53BN ak = ADHNBH ' AD DH NB NH∴= 33253232b a k ak b a ∴=- 222912200b ab a k ∴--=(123a b -∴=(舍),(223ab +=12AB CH +∴= 【点睛】本题考查了相似三角形的判定和性质,正确作出辅助线是解题的关键.26.已知抛物线2y x bx c =++过点A(m-2,n), B (m+4,n ),C (m ,53n -).(1)b=__________(用含m 的代数式表示);(2)求△ABC 的面积;(3)当1222m x m ≤≤+时,均有6y m -≤≤,求m 的值.【答案】(1)b=-2m-2;(2)24;(3)m =. 【解析】【分析】(1)根据A(m-2,n), B (m+4,n )纵坐标一致,结合对称轴即可求解;(2)先用含m 的代数式表示c ,再带入A 点坐标即可求出n=3,最后利用铅锤法即可求出△ABC 的面积; (3)先用只含m 的代数式表示二次函数解析式,再结合带取值范围的二次函数最值求法分类讨论即可.【详解】(1)∵2y x bx c =++过点A(m-2,n), B (m+4,n ), ∴对称轴2422b m m x -++=-= ∴22b m =--(2)∵22b m =--∴2(22)y x m x c =-++把C (m ,53n -)代入2(22)y x m x c =-++ ∴2523c m m n =+-∴225(22)23y x m x m m n =-+++-把A(m-2,n)代入225(22)23y x m x m m n =-+++-得583n n =-∴n=3∴A(m-2,3), B (m+4,3),C (m ,5-)∴AB=6C 点到x 轴的距离为:3﹣(-5)=8,∴S △ABC=12×6×8=24 (3)∵n=3∴22(22)25y x m x m m =-+++-∴2(1)6y x m =---∴当1x m =+时-6y =最小∵6y m -≤≤ ∴由函数增减性知11222m m m ≤+≤+ 即1m ≥-∴当10m -≤<时 由函数增减性知12x m =时,y m =最大 ∴21(1)62m m m =---∴m =±当0m ≥时由函数增减性知22x m =+时,y m =最大∴2(221)6m m m =+---∴1m =(舍)2m =∴12m -+=【点睛】本题考查二次函数综合运用,当参数比较多时可以带入解析式,利用解方程消元法消去多余的参数,在最后一问中对于带取值范围的二次函数最值需要根据对称轴与取值范围的关系确定范围内的最值.。
2021年上海市初中毕业生统一考试(中考)数学试卷及解析
2021年上海市初中毕业生统一考试(中考)数学试卷一.选择题1.(2021•上海)下列实数中,有理数是( )A .12B .13C .14D .152.(2021•上海)下列单项式中,23a b 的同类项是( )A .32a bB .233a bC .2a bD .3ab3.(2021•上海)将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,以下错误的是( )A .开口方向不变B .对称轴不变C .y 随x 的变化情况不变D .与y 轴的交点不变4.(2021•上海)商店准备确定一种包装袋来包装大米,经市场调查后,做出如下统计图,请问选择什么样的包装最合适( )A .2/kg 包B .3/kg 包C .4/kg 包D .5/kg 包5.(2021•上海)如图,在平行四边形ABCD 中,已知AB a =,AD b =,E 为AB 中点,则1(2a b += )A .ECB .CEC .ED D .DE6.(2021•上海)如图,长方形ABCD 中,4AB =,3AD =,圆B 半径为1,圆A 与圆B 内切,则点C 、D 与圆A 的位置关系是( )A.点C在圆A外,点D在圆A内B.点C在圆A外,点D在圆A外C.点C在圆A上,点D在圆A内D.点C在圆A内,点D在圆A外二.填空题7.(2021•上海)计算:72x x÷=.8.(2021•上海)已知6()f xx=,那么(3)f=.9.(2021•上海)已知43x+=,则x=.10.(2021•上海)不等式2120x-<的解集是.11.(2021•上海)70︒的余角是.12.(2021•上海)若一元二次方程2230x x c-+=无解,则c的取值范围为.13.(2021•上海)已知数据1、1、2、3、5、8、13、21、34,从这些数据中选取一个数据,得到偶数的概率为.14.(2021•上海)已知函数y kx=经过二、四象限,且函数不经过(1,1)-,请写出一个符合条件的函数解析式.15.(2021•上海)某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本5元/千克,现以8元卖出,挣得元.16.(2021•上海)如图所示,已知在梯形ABCD中,//AD BC,12ABDBCDSS∆∆=,则BOCBCDSS∆∆=.17.(2021•上海)六个带30度角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 .18.(2021•上海)定义:平面上一点到图形最短距离为d ,如图,2OP =,正方形ABCD 边长为2,O 为正方形中心,当正方形ABCD 绕O 旋转时,则d 的取值范围为 .三.解答题19.(2021•上海)计算:1129|12|28-+--⨯.20.(2021•上海)解方程组:22340x y x y +=⎧⎨-=⎩. 21.(2021•上海)如图,已知ABD ∆中,AC BD ⊥,8BC =,4CD =,4cos 5ABC ∠=,BF 为AD 边上的中线.(1)求AC 的长;(2)求tan FBD ∠的值.22.(2021•上海)现在5G 手机非常流行,某公司第一季度总共生产80万部5G 手机,三个月生产情况如图.(1)求三月份生产了多少部手机?(2)5G 手机速度很快,比4G 下载速度每秒多95MB ,下载一部1000MB 的电影,5G 比4G 要快190秒,求5G 手机的下载速度.24.(2021•上海)已知抛物线2(0)y ax c a =+≠经过点(3,0)P 、(1,4)Q .(1)求抛物线的解析式;(2)若点A 在直线PQ 上,过点A 作AB x ⊥轴于点B ,以AB 为斜边在其左侧作等腰直角三角形ABC . ①当Q 与A 重合时,求C 到抛物线对称轴的距离;②若C 在抛物线上,求C 的坐标.25.(2021•上海)如图,在四边形ABCD 中,//AD BC ,90ABC ∠=︒,AD CD =,O 是对角线AC 的中点,联结BO 并延长交边CD 或边AD 于点E .(1)当点E 在CD 上,①求证:DAC OBC ∆∆∽;②若BE CD ⊥,求AD BC的值; (2)若2DE =,3OE =,求CD 的长.2021年上海市初中毕业生统一考试(中考)数学试卷参考答案与试题解析一.选择题1.(2021•上海)下列实数中,有理数是( )A B C D 【分析】直接利用二次根式的性质分别化简得出答案.【解答】解:=,不是有理数,不合题意;B =12C =,是有理数,符合题意;D = 故选:C .【点评】此题主要考查了二次根式的性质与化简,正确化简二次根式是解题关键.2.(2021•上海)下列单项式中,23a b 的同类项是( )A .32a bB .233a bC .2a bD .3ab【分析】依据同类项的定义:所含字母相同,相同字母的次数相同,据此判断即可.【解答】解:A 、字母a 、b 的次数不相同,不是同类项,故本选项不符合题意;B 、有相同的字母,相同字母的指数相等,是同类项,故本选项符合题意;C 、字母b 的次数不相同,不是同类项,故本选项不符合题意;D 、相同字母a 的次数不相同,不是同类项,故本选项不符合题意;故选:B .【点评】本题主要考查的是同类项的定义,掌握同类项的定义是解题的关键.3.(2021•上海)将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,以下错误的是( )A .开口方向不变B .对称轴不变C .y 随x 的变化情况不变D .与y 轴的交点不变【分析】由于抛物线平移后的形状不变,对称轴不变,a 不变,抛物线的增减性不变.【解答】解:A 、将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,a 不变,开口方向不变,故不符合题意.B 、将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,顶点的横坐标不变,对称轴不变,故不符合题意.C 、将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,抛物线的性质不变,自变量x 不变,则y 随x 的变化情况不变,故不符合题意.D 、将函数2(0)y ax bx c a =++≠的图象向下平移两个单位,与y 轴的交点也向下平移两个单位,故符合题意.故选:D .【点评】本题主要考查了二次函数图象与几何变换,二次函数的性质,注意:抛物线平移后的形状不变,开口方向不变,顶点坐标改变.4.(2021•上海)商店准备确定一种包装袋来包装大米,经市场调查后,做出如下统计图,请问选择什么样的包装最合适( )A .2/kg 包B .3/kg 包C .4/kg 包D .5/kg 包【分析】最合适的包装即顾客购买最多的包装,而顾客购买最多的包装质量即这组数据的众数,取所得范围的组中值即可.【解答】解:由图知这组数据的众数为1.5~2.5kg kg ,取其组中值2kg ,故选:A .【点评】本题主要考查频数(率)分布直方图,解题的关键是根据最合适的包装即顾客购买最多的包装,并根据频数分布直方图得出具体的数据及众数的概念.5.(2021•上海)如图,在平行四边形ABCD 中,已知AB a =,AD b =,E 为AB 中点,则1(2a b += )A.EC B.CE C.ED D.DE 【分析】根据相等向量的几何意义和三角形法则解答.【解答】解:AB a=,∴12a EB=,四边形ABCD是平行四边形,∴BC AD b==,∴12a b EB BC EC+=+=,故选:A.【点评】本题考查平面向量,三角形法则,平行四边形的性质等知识,解题的关键是熟练掌握三角形法则,属于中考常考题型.6.(2021•上海)如图,长方形ABCD中,4AB=,3AD=,圆B半径为1,圆A与圆B内切,则点C、D与圆A的位置关系是()A.点C在圆A外,点D在圆A内B.点C在圆A外,点D在圆A外C.点C在圆A上,点D在圆A内D.点C在圆A内,点D在圆A外【分析】两圆内切,圆心距等于半径之差的绝对值,得圆A的半径等于5,由勾股定理得5AC=,由点与圆的位置关系,可得结论.【解答】解:两圆内切,圆心距等于半径之差的绝对值,设圆A的半径为R,则:1AB R=-,4AB =,圆B 半径为1,5R ∴=,即圆A 的半径等于5,4AB =,3BC AD ==,由勾股定理可知5AC =,5AC R ∴==,3AD R =<,∴点C 在圆上,点D 在圆内,故选:C .【点评】本题考查了点与圆的位置关系、圆与圆的位置关系勾股定理,熟练掌握点与圆的位置关系是关键,还利用了数形结合的思想,通过图形确定圆的位置.二.填空题7.(2021•上海)计算:72x x ÷= 5x .【分析】根据同底数幂的除法法则进行解答即可.【解答】解:72725x x x x -÷==,故答案为:5x .【点评】此题考查了同底数幂的除法,熟练掌握同底数幂相除,底数不变指数相减是解题的关键.8.(2021•上海)已知6()f x x=,那么f =【分析】将x ==【解答】解:由题意将x ==则有:f ==故答案为:【点评】本题考查函数求值问题,只需将自变量的取值代入函数表达式.9.(20213=,则x = 5 .【分析】根据算术平方根的概念:一般地,如果一个正数x 的平方等于a ,即2x a =,那么这个正数x 叫做a 进行解答即可.【解答】解:3=,49x ∴+= 5x ∴=.故答案为:5.【点评】此题考查的是算术平方根的概念,掌握其概念是解决此题关键.10.(2021•上海)不等式2120x -<的解集是 6x < .【分析】不等式移项,把x 系数化为1,即可求出解集.【解答】解:移项,得:212x <,系数化为1,得:6x <,故答案为6x <.【点评】此题考查了解一元一次不等式,熟练掌握不等式的性质是解题的关键.11.(2021•上海)70︒的余角是 20︒ .【分析】根据余角的定义即可求解.【解答】解:根据定义一个角是70︒,则它的余角度数是907020︒-︒=︒,故答案为,20︒.【点评】本题主要考查了余角的概念,掌握互为余角的两个角的和为90度是解决此题关键,12.(2021•上海)若一元二次方程2230x x c -+=无解,则c 的取值范围为 98c > . 【分析】根据根的判别式的意义得到△224(1)0a =-⨯⨯-<,然后求出a 的取值范围. 【解答】解:一元二次方程2230x x c -+=无解,△2(3)420c =--⨯⨯<, 解得98c >, c ∴的取值范围是98c >. 故答案为:98c >. 【点评】本题考查了一元二次方程20(0)ax bx c a ++=≠的根的判别式△24b ac =-:当△0>,方程有两个不相等的实数根;当△0=,方程有两个相等的实数根;当△0<,方程没有实数根.13.(2021•上海)已知数据1、1、2、3、5、8、13、21、34,从这些数据中选取一个数据,得到偶数的概率为 13. 【分析】用偶数的个数除以数的总数即可求得答案. 【解答】解:共有9个数据,其中偶数有3个,∴从这些数据中选取一个数据,得到偶数的概率为3193=,故答案为:13. 【点评】本题主要考查概率公式,解题的关键是掌握随机事件A 的概率P (A )=事件A 可能出现的结果数÷所有可能出现的结果数.14.(2021•上海)已知函数y kx =经过二、四象限,且函数不经过(1,1)-,请写出一个符合条件的函数解析式 2y x =- .【分析】根据正比例函数的性质以及正比例函数图象是点的坐标特征限即可求解.【解答】解:函数y kx =经过二、四象限,0k ∴<.若函数y kx =经过(1,1)-,则1k =-,即1k =-,故函数y kx =经过二、四象限,且函数不经过(1,1)-时,0k <且1k ≠-, ∴函数解析式为2y x =-,故答案为2y x =-.【点评】考查了正比例函数图象上点的坐标特征,熟练掌握正比例函数的性质是解题的关键.15.(2021•上海)某人购进一批苹果到集贸市场零售,已知卖出的苹果数量与售价之间的关系如图所示,成本5元/千克,现以8元卖出,挣得 335k 元.【分析】根据图像求出函数关系式,计算售价为8元时卖出的苹果数量,即可求解.【解答】解:设卖出的苹果数量y 与售价x 之间的函数关系式为y mx n =+,5410m n k m n k +=⎧⎨+=⎩, 解得:357m k n k⎧=-⎪⎨⎪=⎩,375y kx k ∴=-+, 8x =时,3118755y k k k ==-⨯+=, ∴现以8元卖出,挣得1133(85)55k k -⨯=,故答案为:335k.【点评】此题主要考查了函数图象,能够得出卖出的苹果数量y与售价x之间的函数关系式是解题关键.16.(2021•上海)如图所示,已知在梯形ABCD中,//AD BC,12ABDBCDSS∆∆=,则BOCBCDSS∆∆=23.【分析】过D作DM BC⊥于M,过B作BN AD⊥于N,由四边形BMDN是矩形,可得DM BN=,12ADBC=,根据//AD BC,可得12OD ADOB BC==,23OBBD=,即可得到23BOCBCDSS∆∆=.【解答】解:过D作DM BC⊥于M,过B作BN AD⊥于N,如图://AD BC,DM BC⊥,BN AD⊥,∴四边形BMDN是矩形,DM BN=,12ABDBCDSS∆∆=,∴112122AD BNBC DM⋅=⋅,∴12ADBC=,//AD BC,∴12OD ADOB BC==,∴23OBBD=,∴23BOCBCDSS∆∆=,故答案为:23.【点评】本题考查三角形的面积,涉及基本的相似三角形判定与性质,掌握同(等)底三角形面积比等于高之比,同(等)高的三角形面积比等于底之比是解题的关键.17.(2021•上海)六个带30度角的直角三角板拼成一个正六边形,直角三角板的最短边为1,求中间正六边形的面积 332.【分析】利用ABG BCH ∆≅∆得到AG BH =,再根据含30度的直角三角形三边的关系得到2BG AG =,接着证明HG AG =可得结论.【解答】解:如图,ABG BCH ∆≅∆,AG BH ∴=,30ABG ∠=︒,2BG AG ∴=,即2BH HG AG +=,1HG AG ∴==,∴小两个正六边形的面积23336142=⨯⨯=, 故答案为:332.【点评】本题考查了含30度角的直角三角形:在直角三角形中,30︒角所对的直角边等于斜边的一半.也考查了正多边形与圆,解题的关键是求出HG .18.(2021•上海)定义:平面上一点到图形最短距离为d ,如图,2OP =,正方形ABCD 边长为2,O 为正方形中心,当正方形ABCD 绕O 旋转时,则d 的取值范围为 221d .【分析】由题意以及正方形的性质得OP 过正方形ABCD 各边的中点时,d 最大,OP 过正方形ABCD 的顶点时,d 最小,分别求出d 的值即可得出答案.【解答】解:如图:设AB 的中点是E ,OP 过点E 时,点O 与边AB 上所有点的连线中,OE 最小,此时d PE =最大,OP 过顶点A 时,点O 与边AB 上所有点的连线中,OA 最大,此时d PA =最小,如图①:正方形ABCD 边长为2,O 为正方形中心,1AE ∴=,45OAE ∠=︒,OE AB ⊥,1OE ∴=,2OP =,1d PE ∴==;如图②:正方形ABCD 边长为2,O 为正方形中心,1AE ∴=,45OAE ∠=︒,OE AB ⊥,2OA ∴=2OP =,22d PA ∴==;d ∴的取值范围为221d . 故答案为:221d .【点评】本题考查正方形的性质,旋转的性质,根据题意得出d 最大、最小时点P 的位置是解题的关键.三.解答题19.(2021•上海)计算:1129|12-+--【分析】直接利用算术平方根、负整数指数幂、绝对值的性质分别化简得出答案.【解答】解:119122-⨯1912=+182=. 【点评】此题主要考查了实数的混合运算,正确掌握相关运算法则是解题关键.20.(2021•上海)解方程组:22340x y x y +=⎧⎨-=⎩. 【分析】解方程组的中心思想是消元,在本题中,只能用代入消元法解题.【解答】解:22340x y x y +=⎧⎨-=⎩①②, 由①得:3y x =-,把3y x =-代入②,得:224(3)0x x --=,化简得:(2)(6)0x x --=,解得:12x =,26x =.把12x =,26x =依次代入3y x =-得:11y =,23y =-,∴原方程组的解为121226,13x x y y ==⎧⎧⎨⎨==-⎩⎩. 【点评】本题以解高次方程组为背景,旨在考查学生对消元法的灵活应用能力.21.(2021•上海)如图,已知ABD ∆中,AC BD ⊥,8BC =,4CD =,4cos 5ABC ∠=,BF 为AD 边上的中线.(1)求AC 的长;(2)求tan FBD ∠的值.【分析】(1)解锐角三角函数可得解;(2)连接CF ,过F 作BD 的垂线,垂足为E ,根据直角三角形斜边中线等于斜边一半,可得CF FD =,由勾股定理可得213AD =,2EF =,即可求tan FBD ∠.【解答】解:(1)4cos 5BC ABC AB ∠==, 8BC =,10AB ∴=,AC BD ⊥, 在Rt ACB ∆中,由勾股定理得,22221086AC AB BC =-=-=,即AC 的长为6; (2)如图,连接CF ,过F 点作BD 的垂线,垂足E ,BF 为AD 边上的中线,即F 为AD 的中点,12CF AD FD ∴==, 在Rt ACD ∆中,由勾股定理得,222264213AD AC CD =+=+=三角形CFD 为等腰三角形,FE CD ⊥,122CE CD ∴==, 在Rt EFC ∆中,221343EF CF CE =-=-=,33tan 10FE FBD BE BC CE ∴∠===+. 【点评】本题考查解直角三角形,解本题关键根据题意作辅助线,熟练掌握解直角三角函数和勾股定理等基本知识点.22.(2021•上海)现在5G 手机非常流行,某公司第一季度总共生产80万部5G 手机,三个月生产情况如图.(1)求三月份生产了多少部手机?(2)5G 手机速度很快,比4G 下载速度每秒多95MB ,下载一部1000MB 的电影,5G 比4G 要快190秒,求5G 手机的下载速度.【分析】(1)先根据扇形统计图求出三月份所占百分比,即可利用总数乘以三月份所占百分比求解;(2)设5G 手机的下载速度是每秒x MB .则4G 手机的下载速度是每秒(95)x MB -.根据“下载一部1000MB 的电影,5G 比4G 要快190秒”,列方程求解即可. 【解答】解:(1)80(130%25%)36⨯--=(万部),答:三月份生产了36万部手机;(2)设5G 手机的下载速度是每秒x MB .则4G 手机的下载速度是每秒(95)x MB -.1000100019095x x +=-, 解得:1100x =,25x =-(不合题意,舍去),经检验,1100x =是原方程的解,答:5G 手机的下载速度是每秒100MB .【点评】此题主要考查的是如何观察扇形统计图并且从统计图中获取信息,分式方程的应用,理解题意,找出正确的等量关系列出方程是解题的关键.24.(2021•上海)已知抛物线2(0)y ax c a =+≠经过点(3,0)P 、(1,4)Q .(1)求抛物线的解析式;(2)若点A 在直线PQ 上,过点A 作AB x ⊥轴于点B ,以AB 为斜边在其左侧作等腰直角三角形ABC . ①当Q 与A 重合时,求C 到抛物线对称轴的距离;②若C 在抛物线上,求C 的坐标.【分析】(1)(3,0)P 、(1,4)Q 代入2y ax c =+即可得抛物线的解析式为21922y x =-+; (2)①过C 作CH AB ⊥于H ,交y 轴于G ,A 与(1,4)Q 重合时,4AB =,1GH =,由ABC ∆是等腰直角三角形,得122CH AH BH AB ====,C 到抛物线对称轴的距离是1CG =; ②过C 作CH AB ⊥于H ,先求出直线PQ 为26y x =-+,设(,26)A m m -+,则26AB m =-+,3C y m =-+,(3)23C x m m m =--+-=-,将(23,3)C m m --+代入21922y x =-+解得12m =或3m = (与P 重合,舍去),即可求出5(2,)2C -. 【解答】解:(1)(3,0)P 、(1,4)Q 代入2y ax c =+得:094a c a c =+⎧⎨=+⎩,解得1292a c ⎧=-⎪⎪⎨⎪=⎪⎩, ∴抛物线的解析式为:21922y x =-+; (2)①过C 作CH AB ⊥于H ,交y 轴于G ,如图:当A 与(1,4)Q 重合时,4AB =,1GH =,ABC ∆是等腰直角三角形,ACH ∴∆和BCH ∆也是等腰直角三角形,122CH AH BH AB ∴====, 1CG CH GH ∴=-=,而抛物线21922y x =-+的对称轴是y 轴(0)x =, C ∴到抛物线对称轴的距离是1CG =;②过C 作CH AB ⊥于H ,如图:设直线PQ 解析式为y kx b =+,将(3,0)P 、(1,4)Q 代入得:034k b k b =+⎧⎨=+⎩,解得26k b =-⎧⎨=⎩, ∴直线PQ 为26y x =-+,设(,26)A m m -+,则26AB m =-+,132CH AH BH AB m ∴====-+, 3C y m ∴=-+,(3)23C x m m m =--+-=-,将(23,3)C m m --+代入21922y x =-+得: 2193(23)22m m -+=--+, 解得12m =或3m = (与P 重合,舍去), 12m ∴=,232m -=-,532m -+=, 5(2,)2C ∴-. 【点评】本题考查二次函数综合应用,涉及解析式、对称轴、等腰直角三角形、一次函数等知识,解题的关键是用含字母的代数式表示C 的坐标.25.(2021•上海)如图,在四边形ABCD 中,//AD BC ,90ABC ∠=︒,AD CD =,O 是对角线AC 的中点,联结BO 并延长交边CD 或边AD 于点E .(1)当点E 在CD 上,①求证:DAC OBC ∆∆∽;②若BE CD ⊥,求AD BC 的值; (2)若2DE =,3OE =,求CD 的长.【分析】(1)①由等腰三角形的性质得出DAC DCA ∠=∠,由平行线的性质得出DAC ACB ∠=∠,由直角三角形的性质得出OBC OCB ∠=∠,根据相似三角形的判定定理可得出结论;②得出30OCE OCB EBC ∠=∠=∠=︒.过点D 作DH BC ⊥于点H ,设2AD CD m ==,则2BH AD m ==,则可得出答案;(2)①如图3,当点E 在AD 上时,证明四边形ABCE 是矩形.设AD CD x ==,由勾股定理得出方程,解方程即可得出答案;②如图4,当点E 在CD 上时,设AD CD x ==,则2CE x =-,设OB OC m ==,由相似三角形的性质得出2x OC m BC =,证明EOC ECB ∆∆∽,得出比例线段OE EC OC EC EB CB ==,可得出方程3223x OC x m CB -==-+,解方程可得出答案.【解答】(1)①证明:如图1,AD CD =,DAC DCA ∴∠=∠.//AD BC ,DAC ACB ∴∠=∠.BO 是Rt ABC ∆斜边AC 上的中线,OB OC ∴=,OBC OCB ∴∠=∠,DAC DCA ACB OBC ∴∠=∠=∠=∠,DAC OBC∴∆∆∽;②解:如图2,若BE CD⊥,在Rt BCE∆中,OCE OCB EBC∠=∠=∠,30OCE OCB EBC∴∠=∠=∠=︒.过点D作DH BC⊥于点H,设2AD CD m==,则2BH AD m==,在Rt DCH∆中,2DC m=,CH m∴=,3BC BH CH m∴=+=,∴2233 AD mBC m==;(2)①如图3,当点E在AD上时,//AD BC,EAO BCO∴∠=∠,AEO CBO∠=∠,O是AC的中点,OA OC∴=,()AOE COB AAS∴∆≅∆,OB OE∴=,∴四边形ABCE是平行四边形,又90ABC∠=︒,∴四边形ABCE是矩形.设AD CD x ==,2DE =,2AE x ∴=-,3OE =,6AC ∴=,在Rt ACE ∆和Rt DCE ∆中, 222CE AC AE =-,222CE CD DE =-,22226(2)2x x ∴--=-, 解得119x =+,或119x =- (舍去).119CD ∴=+.②如图4,当点E 在CD 上时,设AD CD x ==,则2CE x =-,设OB OC m ==,3OE =,3EB m ∴=+,DAC OBC ∆∆∽,∴DC AC OC BC =, ∴2x OC m BC =, ∴2OC x BC m=. 又EBC OCE ∠=∠,BEC OEC ∠=∠,EOC ECB ∴∆∆∽,∴OE EC OC EC EB CB ==, ∴3223x OC x m CB -==-+, ∴32232x x x m m-==-+, 226x x m -∴=,将226x xm-=代入3223xx m-=-+,整理得,26100x x--=,解得3x=+,或3x=(舍去).3CD∴=综合以上可得CD的长为13+【点评】本题是相似形综合题,考查了等腰三角形的性质,直角三角形的性质,相似三角形的判定与性质,矩形的判定与性质,熟练掌握相似三角形的判定与性质是解题的关键.。
2021年上海市中考数学试卷(2021年初中毕业生学业考试数学试卷附答案解析)

2021年初中毕业生学业考试数学试卷上海中考数学一、选择题(本大题共6题.每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】1.下列实数中,有理数是()A.12B.13C.14D.152.下列单项式中,23a b的同类项是()32A.a b23B.3a b2C.a b3D.ab3.将函数2y a bx c(a0)x的图像向下平移两个单位,以下说法错误的是()A.开口方向不变B.对称轴不变B.y随x的变化情况不变 D.与y轴的交点不变4.商店准备确定一种包装袋来包装大米,经市场调查后,做出如下统计图,请问选择什么样的包装最合适()A.2kg/包B.3kg/包C.4kg/包D.5kg/包5.如图,已知AB a,AD b,E为AB中点,则1a b2=()A.ECB.CEC.EDD.DE6.如图长方形ABCD中,AB=4,AD=3,圆B半径为1,圆A与圆B内切,则点C、D与圆A的位置关系是()A.点C在圆A外,点D在圆A内B.点C在圆A外,点D在圆A外C.点C在圆A上,点D在圆A内D.点C在圆A内,点D在圆A外二、填空题(本大题共12题,每题4分,满分48分)【请将结果直接填入答纸的相应位置上】728.已知6f (x)x ,那么f (3) . 9.已知x 43,则x= .10.不等式2x-12<0的解集是 .11.70°的余角是 °.12. 若一元二次方程22-3x+c=0x 无解,则c 的取值范围为 .13. 已知数据1、1、2、3、5、8、13、21、34,从这些数据中选取一个数据,得到偶数的概率为 .14. 已知函数y kx 的图像经过二、四象限,且不经过(-1,1),请写出一个符合条件的函数解析式 .15. 某人购进一批苹果到集贸市场零售,已经卖出的苹果数量与售价之间的关系如图所示,成本为5元/千克,现以8元/千克卖出,挣得 元.16如图所示,已知在梯形ABCD 中,AD ∥BC ,ABD BCD 1=2S S △△,则BOC BCD=S S △△ . 17.六个带30°角的直角三角板拼成一个正六边形,直角三角板的最短边为1,则中间正六边形的面积为 .18.定义:平面上一点到图形的最短距离为d,如图,OP=2,正方形ABCD 的边长为2,O 为正方形中心,当正方形ABCD绕O 旋转时,d 的取值范围是 .三、解答题(本大题共7题,满分78分)19.计算:112+|12|892---16. 解方程组:22x y 340y x -21.如图,已知在△ABD 中,AC ⊥BD ,BC=8,CD=4,4cos ABC 5,BF 为AD 边上的中线. (1)求AC 的长;(2)求tan ∠FBD 的值.22. 现在5G 手机非常流行,某公司第一季度总共生产80万部5G 手机,三个月的生产情况如下图.(1) 求3月份生产了多少部手机?(2) 5G 手机速度很快,比4G 下载速度每秒多95MB,下载一部1000MB 的电影,5G 比4G 要快190秒,求5G 手机的下载速度.23.已知:在圆O 内,弦AD 与弦BC 相交于点G,AD=CB ,M 、N 分别是CB 和AD 的中点,联结MN 、OG.(1)证明:OG ⊥MN;(2)联结AB 、AM 、BN ,若BN ∥OG ,证明:四边形ABNM 为矩形。
2021年上海市16区中考数学一模考点分类汇编专题01 数与式、方程与不等式(逐题详解版)

2021年上海市16区中考数学一模汇编专题01 数与式、方程与不等式一、单选题1.(2021·上海静安区·九年级一模)如果0a ≠,那么下列计算正确的是( )A .0()0a =-B .0()1a -=-C .01a -=D .01a =--2.(2021·上海静安区·九年级一模)下列多项式中,是完全平方式的为( )A .214x x -+B .21124x x++C .21144x x +-D .21144x x -+ 二、填空题3.(2021·上海长宁区·九年级一模)已知12x y =,那么+-x y x y的值为_______________. 4.(2021·上海静安区·九年级一模)32的相反数是____. 5.(2021·上海松江区·九年级一模)计算sin30cot 60︒⋅︒=____.6.(2021·上海奉贤区·九年级一模)已知点Р是线段AB 上一点,且2BP AP AB =⋅,如果2AP =厘米,那么BP =________________ (厘米).7.(2021·上海浦东新区·九年级一模)如图,ABC 中,AB=10,BC=12,AC=8,点D 是边BC 上一点,且BD :CD=2:1,联结AD ,过AD 中点M 的直线将ABC 分成周长相等的两部分,这条直线分别与边BC 、AC 相交于点E 、F ,那么线段BE 的长为______.8.(20212x -的根为____.9.(2021·上海奉贤区·九年级一模)如图,用一段篱笆靠墙围成一个大长方形花圃(靠墙处不用篱笆),中间用篱笆隔开分成两个小长方形区域,分别种植两种花草,篱笆总长为17米(恰好用完),围成的大长方形花圃的面积为24平方米,设垂直于墙的一段篱筐长为x 米,可列出方程为________________________.10.(2021·上海宝山区·九年级一模)某公司10月份的产值是100万元,如果该公司第四季度每个月产值的增长率相同,都为0)x x >(,12月份的产值为y 万元,那么y 关于x 的函数解析式是______. 三、解答题11.(2021·上海闵行区·九年级一模)计算:24sin 452cos 60cot 30tan 601︒︒︒︒-+-12.(2021·上海静安区·九年级一模)已知线段x 、y 满足2x y x x y y +=-,求x y的值.13.(2021·上海杨浦区·九年级一模)如图,已知在Rt ABC 中,90ACB ∠=︒,4AC BC ==,点D 为边BC 上一动点(与点B 、C 不重合),点E 为边AB 上一点,EDB ADC ∠=∠,过点E 作EF AD ⊥,垂足为点G ,交射线AC 于点F .(1)如果点D 为边BC 的中点,求DAB ∠的正切值;(2)当点F 在边AC 上时,设CD x =,CF y =,求y 关于x 的函数解析式及定义域;(3)联结DF 如果CDF 与AGE 相似,求线段CD 的长.2021年上海市16区中考数学一模汇编专题01 数与式、方程与不等式一、单选题1.(2021·上海静安区·九年级一模)如果0a ≠,那么下列计算正确的是( )A .0()0a =-B .0()1a -=-C .01a -=D .01a =--【答案】D【分析】利用零指数幂的定义分别得出结果即可求解【详解】A 选项0()a =1-,故错误,B 选项0()a =1-,故错误C 选项01a -=-,故错误,D 选项01a -=-,故正确,故选:D【点睛】熟记任何非零次幂的零次幂等于1是解决本题的关键2.(2021·上海静安区·九年级一模)下列多项式中,是完全平方式的为( )A .214x x -+B .21124x x++C .21144x x +-D .21144x x -+ 【答案】A【分析】利用配方法分别转化为完全平方式的形式即可求解.【详解】A 选项214x x -+=212x ⎛⎫- ⎪⎝⎭,故正确,B 选项21124x x++=213416x ⎛⎫++ ⎪⎝⎭,故错误 C 选项21144x x +-=216516256x ⎛⎫+- ⎪⎝⎭,故错误,D 选项21144x x -+=216316256x ⎛⎫-+ ⎪⎝⎭,故错误 故选:A【点睛】本题考查配方法的运用,熟练添加常数项,即一次项系数一半的平方是解决问题的关键,添加之后要注意再减去添加的常数项,进行等价转化.二、填空题3.(2021·上海长宁区·九年级一模)已知12x y =,那么+-x y x y的值为_______________. 【答案】3-【分析】根据已知得到2y x =,代入所求式子中计算即可. 【详解】解:∵12x y =,∴ 2y x =,∴2332x y x x x x y x x x ++===----:故答案为:-3. 【点睛】本题考查了求分式的值,利用已知得到2y x =后再整体代入是解题的关键.4.(2021·上海静安区·九年级一模)32的相反数是____. 【答案】32- 【分析】只有符号不同的两个数叫互为相反数,根据定义解答. 【详解】32的相反数是32-,故答案为:32-. 【点睛】此题考查互为相反数的定义,掌握定义是解题的关键.5.(2021·上海松江区·九年级一模)计算sin30cot 60︒⋅︒=____.【分析】先代入特殊角的三角函数值,然后再进行计算即可.【详解】1sin 30cot 60=236︒⋅︒=⨯,故答案为:6. 【点睛】本题考查了特殊角的三角函数值、实数乘法运算,熟记特殊角的三角函数值是解题关键.6.(2021·上海奉贤区·九年级一模)已知点Р是线段AB 上一点,且2BP AP AB =⋅,如果2AP =厘米,那么BP =________________ (厘米).【答案】1+【分析】设BP x =厘米,得2AB x =+厘米,根据题意得()222x x =⨯+,通过求解方程,即可得到答案. 【详解】设BP x =厘米,根据题意得:2AB AP BP x =+=+厘米∵2BP AP AB =⋅,∴()222x x =⨯+ ,∴1x =±10-,故舍去;∴15x ,即1BP =1+.【点睛】本题考查了一元二次方程、二次根式、线段的知识;解题的关键是熟练掌握一元二次方程、二次根式的性质,从而完成求解.7.(2021·上海浦东新区·九年级一模)如图,ABC 中,AB=10,BC=12,AC=8,点D 是边BC 上一点,且BD :CD=2:1,联结AD ,过AD 中点M 的直线将ABC 分成周长相等的两部分,这条直线分别与边BC 、AC 相交于点E 、F ,那么线段BE 的长为______.【答案】2【分析】如图,过A 作//AN BC 交EF 于N ,设,,BE a AF b == 由三角形的周长关系可得:5,a b +=再证明:,ANM DEM ∽利用相似三角形的性质求解8,AN a =-再证明:,ANF CEF ∽可得:10432,b a ab +-=再解方程组可得答案.【详解】解:如图,过A 作//AN BC 交EF 于N ,设,,BE a AF b ==()1,2AB BE AF AB BC AC ∴++=++ ()1101012815,2a b ∴++=++= 5,a b ∴+=:2:112BD CD BC ==,,84BD CD ∴==,, 8,DE a ∴=- M 为AD 的中点,,AM MD ∴= //AN BC ,,ANM DEM ∴∽ 1AN AM DE DM ∴==, 8,AN a ∴=- //AN BC ,,ANF CEF ∴∽ ,AN AF CE CF ∴= 即:8,848a b a b -=-+- ∴ 10432,b a ab +-= 510432a b b a ab +=⎧∴⎨+-=⎩解得:23a b =⎧⎨=⎩或94a b =⎧⎨=-⎩,经检验:94a b =⎧⎨=-⎩不合题意,舍去, 2.BE ∴= 故答案为:2.【点睛】本题考查的是三角形的相似的判定与性质,二元方程组的解法,一元二次方程的解法,掌握以上知识是解题的关键.8.(20212x =-的根为____.【答案】x 1=【分析】方程两边同时平方,得到一个一元二次方程,解出x 的值,再进行检验即可得出结果.【详解】解:方程两边同时平方得:()2322x x -=-,∴2210x x -+=,即()210x -=,∴x 1=x 2=1,经检验,x=1是原方程的根,故答案为:x=1.【点睛】本题考查了无理方程求解,先平方得到一元二次方程求解再验证根,掌握基本概念和解法是解题的关键.9.(2021·上海奉贤区·九年级一模)如图,用一段篱笆靠墙围成一个大长方形花圃(靠墙处不用篱笆),中间用篱笆隔开分成两个小长方形区域,分别种植两种花草,篱笆总长为17米(恰好用完),围成的大长方形花圃的面积为24平方米,设垂直于墙的一段篱筐长为x 米,可列出方程为________________________.【答案】()17324x x -=【分析】垂直于墙的一段篱筐长为x 米,共有三段垂直于墙的篱笆,所以垂直于墙的篱笆总长度为3x ,又因为篱笆总长为17米(恰好用完),所以大长方形花圃的长为()173x -米,最后根据长方形的面积公式即可求解.【详解】解:由题意可得:()17324x x -=.故答案为:()17324x x -=.【点睛】本题考查了一元二次方程的应用,解题的关键是注意大长方形花圃的宽有三段都是篱笆.10.(2021·上海宝山区·九年级一模)某公司10月份的产值是100万元,如果该公司第四季度每个月产值的增长率相同,都为0)x x >(,12月份的产值为y 万元,那么y 关于x 的函数解析式是______. 【答案】()21001y x =+; 【分析】根据:现有量=原有量×(1+增长率)n,即可列方程求解. 【详解】依题意得:()21001y x =+,故答案为:()21001y x =+【点睛】考查了一元二次方程的应用,可直接套公式:原有量×(1+增长率)n =现有量,n 表示增长的次数. 三、解答题11.(2021·上海闵行区·九年级一模)计算:24sin 452cos 60cot 30tan 601︒︒︒︒-+-【答案】2【分析】分别把特殊角的三角函数值代入,再分别计算,结合分母有理化,合并化简即可解题.【详解】解:原式14122⨯=⨯1= 2=.【点睛】本题考查特殊角的三角函数值,分母有理化等知识,是重要考点,难度较易,掌握相关知识是解题关键.12.(2021·上海静安区·九年级一模)已知线段x 、y 满足2x y x x y y +=-,求x y的值.. 【分析】利用比例性质化比例式化为整式,再移项两边同除以y 2,化为22310x x y y --=,然后解一元二次方程,即可求解.【详解】解:222xy y x xy +=-,2230x xy y --=.∵0y ≠,∴22310x x y y --=,∴x y = ∵x 、y表示线段,∴负值不符合题意,∴x y = 【点睛】本题考查比例的性质、解一元二次方程,利用整体换元的思想方法解方程是解答的关键,注意x 、y 的非负性.13.(2021·上海杨浦区·九年级一模)如图,已知在Rt ABC 中,90ACB ∠=︒,4AC BC ==,点D 为边BC 上一动点(与点B 、C 不重合),点E 为边AB 上一点,EDB ADC ∠=∠,过点E 作EF AD ⊥,垂足为点G ,交射线AC 于点F .(1)如果点D 为边BC 的中点,求DAB ∠的正切值;(2)当点F 在边AC 上时,设CD x =,CF y =,求y 关于x 的函数解析式及定义域;(3)联结DF 如果CDF 与AGE 相似,求线段CD 的长.【答案】(1)1tan 3DAB ∠=;(2)()2402y x x =-+<≤;(3)-4、8-3. 【分析】(1))过点D 作DH AB ⊥于H ,在Rt ACB 中,利用勾股定理解得AD 、AB 的长,再结合等积法,解得DH 、AH 的长即可解题;(2)根据相似三角形对应边成比例的性质,表示()444x EH x -=+, 再证明AFE BDE 由AF AE DB BE =即)4444x y x x --=-+得到与x 的关系; (3)根据相似三角形对应边成比例的性质,结合(2)中y 关于x 的函数解析式联立方程组,继而解得x 、y 的值即可解题.【详解】(1)过点D 作DH AB ⊥于H ,在Rt ACB 中,AD =AB ∴==142ADB S DB AC ∴=⋅=,12ADB S AB DH =⋅,DH ∴=AH ==1tan 3DH DAB AH ∴∠==; (2)过E 作EH ⊥CB 于H∵EDB ADC ∠=∠,90C EHD ∠=∠=︒,∴ACD EHD .∴AC EH CD DH = 即44EH x x EH =--.∴()444x EH x -=+ .∵EH ⊥CB ,90ACB ∠=︒,4AC BC ==,∴)44x EB x -==+ ,AB =∴)44x AE x -=+,∵EF AD ⊥,90C ∠=︒,∴AFG ADC ∠=∠ .∵EDB ADC ∠=∠,∴AFG EDB ∠=∠.∵45FAE B ∠=∠=︒,∴AFE BDE . ∴AF AE DB BE =即)4444x y x x --=-+.整理得,()2402y x x =-+<≤; (3)在Rt △MDB 中,DB=4-x,所以).x - 在Rt △ADM 中,AM=AB 一MB=)(4).22x x -=+ 所以tan ∠DAB=44DM x AM x-=⋅+按照点F 的位置,分两种情况讨论△CDF 与△AGE 相似: ①点F 在线段AC 上,此时y=4-2x.如图,如果∠FDC=∠DAB ,由tan ∠FDC=tan ∠DAB,得44y x x x-=⋅+ 结合y=4-2x ,整理,得x2+8x+16=0.解得-4 或-4 (舍去),如果∠CFD=∠DAB ,由tan ∠CFD=tan ∠DAB ,得4.4x x y x-=+ 结合y=4- -2x,整理,得x 2-16x+16=0.解得8x =-8+②点F 在线段AC的延长线上,此时y=2x-4如图如果∠FDC=∠DAB,由44y xx x-=+结合y=2x-4,整理,得23160.x-=解得或3-(舍去)如果∠CFD=∠DAB,44x xy x-=+与y=2x-4,整理,得238160.x x-+=此方程无解.综上,CD的值为、8-或3.【点睛】本题考查勾股定理、相似三角形的性质,涉及解二元一次方程组等知识,解题关键是根据题意利用相似三角形性质构造方程.。
2021年上海市16区中考数学一模考点分类汇编专题07 相似图形的相关概念(解析版)

2021年上海市16区中考数学一模汇编专题07 相似图形的相关概念一、单选题1.(2021·上海青浦区·九年级一模)如图,已知BD 与CE 相交于点A ,DE BC //,如果2AD =,3AB =,6AC =,那么AE 等于( )A .125B .185C .4D .9【答案】C【分析】根据平行线分线段成比例即可得到结论.【详解】解:∵ED∵BC ,∵AB AC AD AE =,即362AE=,∵AE=4,故选:C . 【点睛】本题考查了平行线分线段成比例的运用,注意:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.2.(2021·上海长宁区·九年级一模)下列命题中,说法正确的是( )A .四条边对应成比例的两个四边形相似B .四个内角对应相等的两个四边形相似C .两边对应成比例且有一个角相等的两个三角形相似D.斜边与一条直角边对应成比例的两个直角三角形相似【答案】D【分析】根据三角形相似和相似多边形的判定解答.【详解】A、四个角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;B、四个内角对应相等,四条边对应成比例的两个四边形相似,原命题是假命题;C、两边对应成比例且其夹角相等的两个三角形相似,原命题是假命题;D、斜边与一条直角边对应成比例的两个直角三角形相似,是真命题;故选:D.【点睛】本题考查了命题与定理的知识,解题的关键是了解三角形相似和相似多边形,难度不大.3.(2021·上海杨浦区·九年级一模)在ABC中,点D、E分别在边AB、AC上,下列条件中,能判定//DE BC 的是()A.AD DEAB BC=B.AD AEDB EC=C.DB AEEC AD=D.AD AEAC AB=【答案】A【分析】根据对应线段成比例,两直线平行,可得出答案.【详解】A、AD DEAB BC=,可证明DE∵BC,故本选项正确;B、AD AEDB EC=,不可证明DE∵BC,故本选项错误;C、DB AEEC AD=,不可证明DE∵BC,故本选项不正确;D、AD AEAC AB=不可证明DE∵BC,故本选项不正确.故选A.【点睛】本题考查了平行线分线段成比例,对应线段成比例,两直线平行.4.(2021·上海浦东新区·九年级一模)A、B两地的实际距离AB=250米,如果画在地图上的距离A B''=5厘米,那么地图上的距离与实际距离的比为()A.1∵500B.1∵5 000C.500∵1D.5 000∵1【答案】B【分析】地图上距离与实际距离的比就是在地图上的距离A B ''与实际距离AB 的比值.【详解】解:∵250米=25000cm ,∵:A B AB ''=5:25000=1:5000.故选:B .【点睛】本题主要考查了比例尺,掌握比例尺的计算方法,注意在求比的过程中,单位要统一. 5.(2021·上海崇明区·九年级一模)已知线段a 、b 、c 、d 的长度满足等式ab cd =,如果某班四位学生分别将该等式改写成了如下四个比例式,那么其中错误的是( )A .a c b d =B .a d c b =C .b d c a =D .b c d a= 【答案】A【分析】根据比例的两内项之积等于两外项之积逐项排查即可.【详解】解:A.由a c b d=可得bc=ad ,故A 选项符合题意; B.由a d c b=可得ab=cd ,故B 选项不符合题意; C.由b d c a=可得ab=cd ,故C 选项不符合题意; D.由b c d a =可得ab=cd ,故D 选项不符合题意.故答案为A . 【点睛】本题主要考查了比例的基本性质,即掌握两内项之积等于两外项之积成为解答本题的关键. 6.(2021·上海闵行区·九年级一模)古希腊艺术家发现当人的头顶至肚脐的长度(上半身的长度)与肚脐至足底的长度(下半身的长度)的比值为“黄金分割数”时,人体的身材是最优美的,一位女士身高为154cm ,她上半身的长度为62cm ,为了使自己的身材显得更为优美,计划选择一双合适的高跟鞋,使自己的下半身长度增加,你认为选择鞋跟高为多少厘米的高跟鞋最佳( )A .4cmB .6cmC .8cmD .10cm【答案】C【分析】根据黄金分割的概念,列出方程直接求解即可.【详解】解:根据题意,设她穿的高跟鞋的高度是x cm ,则620.61815462x =+-, 解得:8.3x ≈,∵我认为选择鞋跟高为8厘米的高跟鞋最佳;故选:C .【点睛】本题主要考查了黄金分割的应用;关键是明确黄金分割所涉及的线段的比.7.(2021·上海奉贤区·九年级一模)下列两个图形一定相似的是( )A .两个菱形B .两个正方形C .两个矩形D .两个梯形【答案】B【分析】对应边成比例,对应角相等的两个四边形相似,根据定义逐一判断各选项即可得到答案.【详解】解:两个菱形满足对应边成比例,但是对应角不一定相等,所以两个菱形不一定相似,故A 不符合题意;两个正方形满足对应边成比例,对应角相等,所以两个正方形一定相似,故B 符合题意;两个矩形满足对应角相等,但是对应边不一定成比例,故C 不符合题意;两个梯形的对应边不一定成比例,对应角也不一定相等,故D 不符题意;故选:.B【点睛】本题考查的是四边形相似的判定,掌握多边形相似的判定是解题的关键. 8.(2021·上海嘉定区·九年级一模)如果实数a ,b ,c ,d 满足a c b d=,下列四个选项中,正确的是( ) A .a b c d b d++= B .a c a b c d =++ C .a c c b d d+=+ D .22a cb d = 【答案】A 【分析】根据比例的性质选出正确选项.【详解】A 选项正确,∵11a c b d+=+,∵a b c d b d ++=; B 选项,当0a b +=或0c d +=时, 不成立;C 选项,当0b d +=时,不成立;D 选项不成立,例如:当1224=时,221224≠;故选:A . 【点睛】本题考查比例的性质,解题的关键是掌握比例的性质.9.(2021·上海松江区·九年级一模)如果两个相似多边形的面积之比为1:4,那么它们的周长之比是( ) A .1:2B .1:4C .1:8D .1:16【答案】A【分析】根据相似多边形周长的比等于相似比,面积的比等于相似比的平方进行解答即可.【详解】解:∵两个相似多边形面积的比为1:4,∵两个相似多边形周长的比等于1:2,∵这两个相似多边形周长的比是1:2.故选:A .【点睛】本题考查的是相似多边形的性质,即相似多边形周长的比等于相似比,面积的比等于相似比的平方.10.(2021·上海青浦区·九年级一模)已知点P 是线段AB 的黄金分割点()AP BP >,若2AB =,则AP 的长为A 1B 1CD .3【答案】A【分析】利用黄金分割点的定义即可求AP 的长度【详解】利用黄金分割点的定义, AP AB = 111.(2021·上海徐汇区·九年级一模)下列说法中,正确的是( )A .两个矩形必相似B .两个含45︒角的等腰三角形必相似C .两个菱形必相似D .两个含30角的直角三角形必相似【答案】D 【分析】根据相似多边形、相似三角形的判定逐项判断即可得.【详解】A 、两个矩形的对应角相等,但对应边不一定成比例,则不一定相似,此项错误;B 、如果一个等腰三角形的顶角是45︒,另一等腰三角形的底角是45︒,则不相似,此项错误;C 、两个菱形的对应边成比例,但四个内角不一定对应相等,则不一定相似,此项错误;D 、两个含30角的直角三角形必相似,此项正确;故选:D .【点睛】本题考查了相似多边形、相似三角形的判定,熟练掌握相似图形的判定方法是解题关键. 12.(2021·上海九年级一模)如图,在ABC 中,点D 在边AB 上,DE BC //,DF AC //,联结BE ,BE 与DF 相交于点G ,则下列结论一定正确的是( )A .AD DE DB BC = B .AE BF AC BC = C .BD BF AD DE = D .DG BF GF FC= 【答案】C【分析】根据相似三角形的判定和平行线分线段成比例进行判断即可.【详解】解:∵DE∵BC ,DF∵AC ,∵四边形DFCE 是平行四边形,∵DE=CF ,DF=CE ,∵DE∵BC ,DF∵AC ,∵∵ADE∵∵ABC ,∵BFD∵∵BAC ,∵AD DE AB BC=,故A 错误;AE AD AC AB BC CF ==,即AE CF AC BC=,故B 错误; ∵DF∵AC ,∵BD BF BF AD CF DE==,故C 正确; ∵DE∵BC ,∵DG DE CF GF BF BF ==,故D 错误,故选:C . 【点睛】本题考查了相似三角形的判定与性质、平行线分线段成比例、平行四边形的判定与性质,熟练掌握相似三角形的性质和平行线分线段成比例是解答的关键.13.(2021·上海浦东新区·九年级一模)如图,在ABC 中,点D 、F 是边AB 上的点,点E 是边AC 上的点,如果∵ACD=∵B ,DE //BC ,EF //CD ,下列结论不成立的是( )A .2AE AF AD =⋅B .2AC AD AB =⋅C .2AF AE AC =⋅D .2AD AF AB =⋅【答案】C【分析】根据相似三角形的判定及性质以及平行线分线段成比例对每个选项逐个证明即可.【详解】解:∵DE //BC ,EF //CD ,∵∵ADE=∵B ,∵ACD=∵AEF ,又∵∵ACD=∵B ,∵∵ADE=∵AEF ,∵∵ADE=∵AEF ,∵A=∵A ,∵AEF∵ADE , ∵AE AD AF AE=,∵2AE AF AD =⋅,故选项A 正确; ∵∵ACD=∵B ,∵A=∵A ,∵ACD∵ABC ,∵AC AD AB AC=,∵2AC AD AB =⋅,故选项B 正确; ∵DE //BC ,∵AE AD AC AB =,∵EF //CD ,∵AE AF AC AD=,∵AF AD AD AB =,∵2AD AF AB =⋅,故选项D 正确;∵EF//CD,∵AE AFAC AD=,∵AF AC AE AD⋅=⋅,故选项C错误,故选:C.【点睛】本题考查了平行线分线段成比例以及相似三角形的判定及性质,熟练掌握相似三角形的判定及性质是解决本题的关键.14.(2021·上海静安区·九年级一模)在∵ABC中,点D、E分别在边BA、CA的延长线上,下列比例式中能判定DE∵BC的为()A.BC ABDE AD=B.AC ABAD AE=C.AC ABCE BD=D.AC BDAB CE=【答案】C【分析】根据平行线分线段成比例定理、平行线的判定定理判断即可.【详解】解:当BC ABDE AD=时,不能判定DE∵BC,A选项错误;AC ABAD AE=时,不能判定DE∵BC,B选项错误;AC ABCE BD=时,DE∵BC,C选项正确;AC BDAB CE=时,不能判定DE∵BC,D选项错误;故选:C.【点睛】本题考查了平行线分线段成比例定理、平行线的判定定理,掌握相关的判定定理是解题的关键.15.(2021·上海长宁区·九年级一模)已知P,Q是线段AB的两个黄金分割点,且AB=10,则PQ长为()A.1)B.C.2) - D.5(3【答案】C【分析】画出图像,根据黄金分割的概念写出对应线段的比值,求出AQ、PB的长度,再根据PQ=AQ+PB-AB即可求出PQ的长度.【详解】解:如图,根据黄金分割点的概念,可知PB AQ AB AB ==∴AQ =PB ,AB =10,∴AQ =PB =11052⨯=,∴PQ =AQ +PB -AB =5510202)+-==. 故选:C .【点睛】本题主要考查黄金分割的概念,熟记黄金分割的概念并根据黄金分割的比值列式是解题关键.二、填空题16.(2021·上海徐汇区·九年级一模)已知点P 在线段AB 上,如果2AP AB BP =⋅,4AB =,那么AP 的长是_____.【答案】2【分析】设AP=x ,则PB=4-x ,根据AP 2=AB•PB 列出方程求解即可,另外,注意舍去负数解.【详解】解:设AP=x ,则PB=4-x ,由题意,x 2=4(4-x ),解得x=2或2-(舍弃)故答案为:2.【点睛】本题考查的是比例线段与黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,他们的比值叫做黄金比.注意方程思想的应用是解题的关键.17.(2021·上海徐汇区·九年级一模)如图,////AB CD EF ,如果2AC =,3CE = , 1.5BD =,那么BF 的长是______.【答案】3.75【分析】直接根据平行线分线段成比例定理即可得出结论.【详解】解:∵直线////AB CD EF ,2AC =,3CE =, 1.5BD =, ∵AC BD AE BE = 22235==+,∵ 1.55=3.752BE ⨯=.故答案为:3.75. 【点睛】本题考查的是平行线分线段成比例定理,熟知三条平行线截两条直线,所得的对应线段成比例是解答此题的关键.18.(2021·上海松江区·九年级一模)如图,已知直线1l ,2l ,3l 分别交直线l 于点A ,B ,C ,交直线l 于点D ,E ,F ,且123////l l l ,4AB =,6AC =,10DF =,则DE =___.【答案】203【分析】根据平行线分线段成比例定理解答即可.【详解】∵123////l l l 4AB =,6AC =,10DF =,∵AB DE AC DF = 即4610DE =, 可得:DE=203,故答案为:203. 【点睛】本题考查了平行线分线段成比例定理的应用,能熟练地运用定理进行计算是解此题的关键. 19.(2021·上海奉贤区·九年级一模)如果4是a 与8的比例中项,那么a 的值为_______________________.【答案】2【分析】根据比例中项的概念:如果a 、b 、c 三个量成连比例,即::a b b c =,b 叫作a 和c 的比例中项,即可求解.【详解】4是a 与8的比例中项,∴:44:8a =,即248a =,∴2a =.故答案为:2.【点睛】本题考查了比例中项的概念,熟练掌握比例中项的概念是解题的关键.20.(2021·上海普陀区·九年级一模)已知52x y =,那么x y x y+=-__________. 【答案】73【分析】由52x y =,设()50x k k =≠,则2y k =,再把,x y 的值代入代数式即可得到答案. 【详解】解: 52x y =,∴ 设()50x k k =≠,则2y k =,52775233x y k k k x y k k k ++∴===--, 故答案为:7.3【点睛】本题考查的是比例的基本性质,掌握设参数法解决比例的问题是解题的关键.21.(2021·上海奉贤区·九年级一模)如果2a =5b (b ≠0),那么a b=_____. 【答案】52【分析】利用比例的基本性质可得答案.【详解】解:∵2a =5b (b ≠0),∵5.2a b = 故答案为:52【点睛】本题考查的是比例的基本性质,掌握基本性质是解题的关键.22.(2021·上海徐汇区·九年级一模)如果:2:3a b =,那么代数式b a a-的值是_____. 【答案】12【分析】根据比例的性质可得23a b =,则代入原代数式计算即可.【详解】由题意:23a b =,∵213223b b b a a b --==,故答案为:12. 【点睛】本题主要考查比例的性质,熟练根据比例的性质变形求解是解题关键.23.(2021·上海长宁区·九年级一模)如图,已知AC ∵EF ∵BD .如果AE :EB =2:3,CF =6.那么CD 的长等于_________.【答案】15【分析】根据平行线分线段成比例定理列出比例式首先求得CF 的长,再求得DC 的长.【详解】解:∵AC ∵EF ∵BD ,CF =6,23AE CF BE DF ==,∵DF=9, ∵CD=DF+CF=9+6=15.故答案是:15.【点睛】本题考查了平行线分线段成比例定理和比例的基本性质,解题的关键是注意数形结合思想的应用. 24.(2021·上海九年级一模)如果34a b =,那么b a b a -=+__________________. 【答案】17【分析】设a=3k ,得到b=4k ,代入b a b a -+化简即可求解. 【详解】解:设a=3k ,∵34a b =,∵b=4k ,∵4314377b a k k k b a k k k --===++.故答案为:17 【点睛】本题主要考查了比例化简求值,理解比例的意义,用含k 的式子分别表示a 、b 是解题关键. 25.(2021·上海黄浦区·九年级一模)已知三角形的三边长为a 、b 、c .满足234a b c ==,如果其周长为36,那么该三角形的最大边长为________.【答案】16 【分析】设234a b c ===k ,根据三角形的周长列出方程即可求出k 的值,从而求出结论. 【详解】解:设234a b c ===k∵a =2k ,b =3k ,c =4k 由题意可知:a +b +c=36∵2k +3k +4k=36解得:k=4∵该三角形的最大边长为4×4=16故答案为:16.【点睛】此题考查的是比例的性质,掌握设参法是解题关键.26.(2021·上海宝山区·九年级一模)已知线段2a =厘米,8c =厘米,那么线段a 和c 的比例中项b 的长度为______厘米.【答案】4【分析】根据线段的比例中项可直接进行列式求解.【详解】解:由题意可得:22816b ac ==⨯=,∵4b =cm ;故答案为4.【点睛】本题主要考查比例中项,熟练掌握比例中项是解题的关键.27.(2021·上海崇明区·九年级一模)已知线段6cm AB =,点C 是AB 的黄金分割点,且AC BC >,那么线段AC 的长为________.【答案】3,列式计算即可.【详解】∵点C 是线段AB 的黄金分割点,AC >BC ,∵AC AB =(3)cm ,故答案为3.【点睛】本题考查的是黄金分割的概念,把一条线段分成两部分,使其中较长的线段为全线段与较短线段叫做黄金比. 28.(2021·上海闵行区·九年级一模)如果23(0)a b b =≠,那么a b=__________. 【答案】32【分析】根据等式的性质解题即可,等式两边同时除以一个不为零的数,等式仍成立 【详解】323(0)2a ab b b =≠∴=故答案为:32. 【点睛】本题考查比例的性质,利用等式的性质解题即可.29.(2021·上海奉贤区·九年级一模)如图,已知点D 在ABC ∆的边BC 上,联结,AD P 为AD 上一点,过点Р分别作AB AC 、的平行线交BC 于点,,E F 如果3BC EF =,那么AP PD=_______________________.【答案】2 【分析】根据平行线分线段成比例性质可得PD DE DF AD BD CD ==,再由等比性质可得13PD AD =,即可得出2AP PD=. 【详解】解:∵PE∵AB ,PF∵AC , ∵PD DE AD BD =,PD DF AD CD =.∵DE DF BD CD=. ∵BC =3EF ,∵13DE DF EF BD CD BC +==+.∵13PD PD AD AP PD ==+.∵2AP PD=.答案:2. 【点睛】本题考查了平行线分线段成比例性质,掌握平行线分线段成比例性质定理及等比性质是解答此题的关键.30.(2021·上海虹口区·九年级一模)如果:3:2a b =,那么a a b=+________. 【答案】35【分析】设a=3k ,然后用k 表示出b ,最后代入a a b+计算即可. 【详解】解:设a=3k∵:3:2a b =∵3:3:2k b =,即3b=6k ,解得b=2k ∵3333255a k k a b k k k ===++.故答案为35. 【点睛】本题主要考查了比例化简求值,设出中间量、分别表示出a 、b 成为解答本题的关键. 31.(2021·上海嘉定区·九年级一模)正方形的边长与其对角线长的比为________.【答案】1【分析】设正方形的边长为1,计算即得结果.【详解】解:设正方形的边长为1,所以正方形的边长与其对角线长的比为1【点睛】此题主要考查对正方形的性质和线段比的定义的理解及运用.难度不大,属于基础题型. 32.(2021·上海杨浦区·九年级一模)已知线段AB 的长为4厘米,点P 是线段AB 的黄金分割点(AP BP <),那么线段AP 的长是______厘米.【答案】6-【分析】根据黄金比值可知AP BP BP AB ==,计算得出结果即可.【详解】解:点P 是线段AB 的黄金分割点(AP BP <),∴12AP BP BP AB ==,可知2BP AB ==(厘米),6AP BP ==-(厘米)故答案为:6-.【点睛】本题考查的是黄金分割比,属于基础题,掌握黄金比值12是解题的关键. 33.(2021·上海青浦区·九年级一模)如图,在ABC 中,点D 是边BC 的中点,直线DF 交边AC 于点F ,交AB 的延长线于点E ,如果::CF CA a b =,那么:BE AE 的值为____.(用含a 、b 的式子表示)【答案】a b a- 【分析】过点B 作BH∵AC 交EF 于点H ,先证明∵BDH∵∵CDF ,得出BH=CF ,再根据BE BH AE AF=得出=BE BH CF AE AF AF=即可得解. 【详解】解:过点B 作BH∵AC 交EF 于点H ,∵BE BH AE AF=,∵C=∵DBH, ∵点D 是边BC 的中点,∵BD=CD ,∵∵BDH=∵CDF ,∵∵BDH∵∵CDF ,∵BH=CF ,∵=BE BH CF AE AF AF =, ∵CF a CA b =,∵CF a AF b a =-,∵BE a AE b a=-,故答案为: a b a -..【点睛】本题考查了全等三角形的判定与性质及平行线分线段成比例定理,解题的关键是正确作出辅助线.34.(2021·上海黄浦区·九年级一模)已知一个矩形的两邻边长之比为1:2.5,一条平行于边的直线将该矩形分为两个小矩形,如果所得两小矩形相似,那么这两个小矩形的相似比为________.【答案】1或0.5或2【分析】根据题意,画出图形,然后分直线l∵AD和直线l∵AB两种情况,然后根据相似图形的性质列出比例式即可分别求出结论.【详解】解:如图所示,矩形ABCD中,AB:AD=1:2.5,∵AD=BC若直线l∵AD,交AB、CD于E、F根据题意和图形可知:矩形AEFD∵矩形BEFC此时这两个小矩形的相似比为AD:BC=1;根据相似图形的性质,两个相似图形中长边必定对应长边,故此时不存在其它情况;若直线l∵AB,交AD、BC于E、F此时存在两种情况:①若矩形ABFE∵矩形DCFE,如下图所示此时这两个小矩形的相似比为AB:DC=1;②若矩形BAEF∵矩形EDCF,如下图所示∵AB AEDE CD=设AB=CD=a,AE=x,则AD=2.5a,DE=2.5a x-∵2.5a xa x a=-解得:x=0.5a或x=2a当x=0.5a时,这两个小矩形的相似比为AE:CD=0.5a:a=0.5;当x=2a时,这两个小矩形的相似比为AE:CD=2a:a=2;综上:这两个小矩形的相似比为1或0.5或2.故答案为:1或0.5或2.【点睛】此题考查的是求相似图形的相似比,掌握相似多边形的性质和分类讨论的数学思想是解题关键.35.(2021·上海浦东新区·九年级一模)如果线段a、b满足52ab=,那么a bb-的值等于______.【答案】3 2【分析】根据1a b a b b -=-,再将52a b =代入计算即可. 【详解】解:∵52a b =,∵1a b a b b -=-512=-32=,故答案为:32. 【点睛】本题考查了比例的性质,将a b b-变形为1-a b 是解决本题的关键. 36.(2021·上海宝山区·九年级一模)如果线段AB 的长为2,点P 是线段AB 的黄金分割点,那么较短的线段AP =______.【答案】3【分析】设较短的线段AP x =,则BP AB AP =-,根据黄金分割点的性质列方程并求解,即可得到答案.【详解】设较短的线段AP x =∵AB 的长为2∵2BP AB AP x =-=- ∵BP AP AB BP= ∵222x x x-=- ∵()222x x -=∵3x =+3-32+>,故舍去∵(22310x -=-=≠∵3x =∵较短的线段3AP =3【点睛】本题考查了黄金分割点、分式方程、一元二次方程、二次根式的知识;解题的关键是熟练掌握黄金分割点、分式方程、一元二次方程、二次根式的性质,从而完成求解. 37.(2021·上海崇明区·九年级一模)已知53x y =,则x y y-=_____. 【答案】23 【分析】由53x y =得到53x y =,代入式子计算即可. 【详解】∵53x y =,∵53x y =,∵x y y -5233y y y -==,故答案为:23.【点睛】此题考查比例的性质,正确进行变形,熟练掌握和灵活运用相关运算法则是解题的关键.38.(2021·上海虹口区·九年级一模)点P 是线段AB 上的一点,如果2AP BP AB =⋅,那么AP AB的值是________.【分析】设AB=1,AP=x ,则BP=1-x ,代入AP 2=BP·AB 求出x 的值,最后代入AP AB即可. 【详解】解:设AB=1,AP=x ,则BP=1-x ,∵AP 2=BP·AB ∵x 2=(1-x )·1,即x 2+x -1=0,解得或(舍)∵21APAB ==. 【点睛】本题考查了成比例线段,设出合适的未知数、根据比例列式求出未知数成为解答本题的关键. 39.(2021·上海嘉定区·九年级一模)已知点P 是线段AB 的一个黄金分割点,且AP >BP ,那么AP :AB 的比值为______.【答案】12【分析】根据黄金分割的定义列即可得答案.【详解】∵点P 是线段AB 的一个黄金分割点,且AP BP >,∵AP :. 【点睛】题考查了黄金分割点的应用,把一条线段分割为两部分,使较大部分与全长的比值等于较小部分;理解黄金分割点的定义是解题的关键.40.(2021·上海宝山区·九年级一模)已知 ()2x 3y y 0=≠,那么x y y+=________. 【答案】52【分析】由已知得出比例式,表示出x ,y ,代入解答即可.【详解】由2x=3y (y≠0),可得:x y =32,所以x y y +=232+=52,故答案为52 【点睛】此题考查了比例的性质,熟练掌握比例的性质是解本题的关键.三、解答题41.(2021·上海浦东新区·九年级一模)如图,已知AD //BE //CF ,它们依次交直线1l 、2l 于点A 、B 、C 和点D 、E 、F ,且AB=6,BC=8.(1)求DE DF的值; (2)当AD=5,CF=19时,求BE 的长.【答案】(1)37;(2)11 【分析】(1)根据AD //BE //CF 可得DE AB DF AC =,由此计算即可; (2)过点A 作AG //DF 交BE 于点H ,交CF 于点G ,得出AD=HE=GF=5,由平行线分线段成比例定理得出比例式求出BH=6,即可得出结果.【详解】解:(1)∵AD //BE //CF ,∵DE AB DF AC =,∵AB=6,BC=8,∵63687DE DF ==+, 故DE DF 的值为37; (2)如图,过点A 作AG //DF 交BE 于点H ,交CF 于点G ,∵AG //DF ,AD //BE //CF ,∵AD=HE=GF=5,∵CF=19,∵CG=CF -GF=14,∵BE //CF ,∵BH AB CG AC =,∵3147BH =,解得BH=6,∵BE=BH+HE=11. 【点睛】本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例;熟练掌握平行线分线段成比例,通过作辅助线运用平行线分线段成比例求出BH 是解决问题的关键.42.(2021·上海静安区·九年级一模)已知线段x 、y 满足2x y x x y y +=-,求x y的值.. 【分析】利用比例性质化比例式化为整式,再移项两边同除以y 2,化为22310x x y y--=,然后解一元二次方程,即可求解.【详解】解:222xy y x xy +=-,2230x xy y --=.∵0y ≠,∵22310x x y y --=,∵x y =.∵x 、y 表示线段,∵负值不符合题意,∵x y =. 【点睛】本题考查比例的性质、解一元二次方程,利用整体换元的思想方法解方程是解答的关键,注意x 、y 的非负性.43.(2021·上海奉贤区·九年级一模)已知:2:3,:3:4a b b c ==,且26a b c +-=,求,,a b c 的值【答案】4a =,6b =,8c =.【分析】根据比的性质,可得a ,b ,c 用k 表示,根据解方程,可得k 的值,即可得答案.【详解】∵:2:3a b =,:3:4b c =,∵设2a k =,3b k =,4c k =,∵()22346k k k ⋅+-=,整理得:36k = ,解得:2k =,∵24a k ==,36b k ==,48c k ==.【点睛】本题考查了比例的性质,利用比例的性质得出2a k =,3b k =,4c k =是解题关键.。
2021-2022学年上海市长宁区九年级上学期期末数学试卷(一模)(含答案解析)

2021-2022学年上海市长宁区九年级上学期期末数学试卷(一模)一、选择题(本大题共6小题,共24.0分)1.如图,在半径为2cm的⊙O中有长为2√3cm的弦AB,则弦AB所对的圆心角的度数为()A. 60°B. 90°C. 120°D. 150°2.下列命题是假命题的是()A. 两条直线被第三条直线所截,内错角相等B. 实数和数轴上的点是一一对应的C. 坐标平面内的点与有序实数对是一一对应的D. 在同一平面内,过一点有且只有一条直线与已知直线垂直3.若向量a⃗与b⃗ 均为单位向量,则下列结论中正确的是()A. a⃗=b⃗B. a⃗=1C. b⃗ =1D. |a⃗|=|b⃗ |4.二次函数y=ax2+bx+c(a≠0)的图象如图所示,c<−1,其对称轴为直线x=−1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,有下列结论:①abc>0;②−3<x2<−2;③4a−2b+c<−1;④a−b>am2+bm(m≠−1);其中,正确的结论个数是()A. 1个B. 2个C. 3个D. 4个5.如图,在矩形ABCD中,将△ADC绕点D逆时针旋转90°得到△FDE,B、F、E三点恰好在同一直线上,AC与BE相交于点G,连接DG.以下结论正确的是()①AC⊥BE;②△BCG∽△GAD;③点F是线段CD的黄金分割点;④CG +√2DG =EG .A. ①②B. ①③C. ①②③D. ①③④ 6. 如图,在△ABC 中,D 、E 分别是AB 、AC 边上的点,点F 在BC 的延长线上,DE//BC ,若∠A =48°,∠1=54°,则下列正确的是( )A. ∠2=48°B. ∠2=54°C. DE BC =AD ABD. DE BC =12二、填空题(本大题共12小题,共48.0分)7.若a 3=b 5=c 7(a ≠0),则a+b+c a = ______ . 8. 已知平行四边形ABCD ,E 是边AB 的中点.设AB ⃗⃗⃗⃗⃗ =a ⃗ ,BC ⃗⃗⃗⃗⃗ =b ⃗ ,那么DE ⃗⃗⃗⃗⃗⃗ =______.(结果用a ⃗ 、b ⃗ 表示).9. 计算:(−1)0+√8×sin45°−23= ______ .10. 已知△ABC∽△DEF ,相似比为2,且△ABC 的面积为4,则△DEF 的面积为______.11. 把抛物线y =12(x −1)2+2向左平移1个单位,在向下平移2个单位,则所得抛物线的解析式为______ .12. 某校数学兴趣小组要测量西山植物园蒲宁之珠的高度.如图,他们在点A 处测得蒲宁之珠最高点C 的仰角为45°,再往蒲宁之珠方向前进至点B 处测得最高点C 的仰角为56°,AB =62m ,根据这个兴趣小组测得的数据,则蒲宁之珠的高度CD 约为______ m.(sin56°≈0.83,tan56°≈1.49,结果保留整数)13. 已知二次函数y =−x 2+2x −2的图象上有两点A(2,y 1),B(3,y 2),则y 1与y 2的大小关系是y 1______y 2(填“<”、“>”或“=”).14. 如图l 1//l 2//l 3,若AB BC =32,DF =10,则DE =______.15. 如图,已知抛物线y =x 2+bx +2与x 轴交于A 、B 两点,顶点为M ,抛物线的对称轴在y 轴的右则,若tan∠BAM =12,则b 的值是______ .16. 在△ABC 中,AB =AC =6cm ,AB 的垂直平分线与AC 相交于E 点,且△BCE 的周长为10cm ,则BC = ______ cm .17. 矩形ABCD 的周长为56,对角线交于点O ,△OAB 比△OBC 周长小4,则AB = ______ .18. 如果点D 、E 分别是△ABC 的AB 、AC 边的中点,那么△ADE 与△ABC 的周长之比是______.三、解答题(本大题共7小题,共78.0分)19. 定义:任何一个一次函数y =px +q ,取出它的一次项系数p 和常数项q ,有序数组[p,q]为其特征数.例如:y =2x +5的特征数是[2,5],同理,[a,b,c]为二次函数y =ax 2+bx +c 的特征数. (1)直接写出二次函数y =x 2−5x 的特征数是:______.(2)若特征数是[2,m +1]的一次函数为正比例函数,求m 的值;(3)以y 轴为对称轴的二次函数抛y =ax 2+bx +c 的图象经过A(2,m)、B(n,1)两点(其中m >0,n <0),连结OA 、OB 、AB ,得到OA ⊥OB ,S △AOB =10,求二次函数y =ax 2+bx +c 的特征数.20. 已知:如图,在平行四边形ABCD 中,E 、F 分别是对角线BD 上的两点,且BE =DF ,AB ⃗⃗⃗⃗⃗ =a ⃗ ,BC ⃗⃗⃗⃗⃗ =b ⃗ ,AF ⃗⃗⃗⃗⃗ =c ⃗ . (1)用向量a ⃗ 、b ⃗ 、c ⃗ 表示下列向量:向量CE⃗⃗⃗⃗⃗ =______,向量BD ⃗⃗⃗⃗⃗⃗ =______,向量DE ⃗⃗⃗⃗⃗⃗ =______; (2)求作:b ⃗ +c ⃗ .21.在平面直角坐标系中,对于点P(a,b),若点P′的坐标为(a+b,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联k点”.(1)点P(−3,4)的“2关联点”P′的坐标是______;(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,9),请直接写出k的值及点P的坐标;(3)如图,点Q的坐标为(0,2),点A在函数y=−8√2(x<0)的图象上运动,且点A是点B的“−√2关联x点”,求线段BQ的最小值.22.如图,某景区的两个景点A、B处于同一水平地面上,一架无人机在空中飞行至点C处时,测得景点A的俯角为45°,景点B的俯角为知75°,已知点C与AB在同铅直平面内,两景点A、B间的距离为100米,求无人机与景点A的距离CA为多少米?(结果保留根号)23.如图1,已知O是锐角∠XAY的边AX上的动点,以点O为圆心、R为半径的圆与射线AY相切于点B,交射线OX于点C,过点C作CD⊥BC,CD交AY于点D.(1)求证:△ABC∽△ACD;.如图2,当点D与点P重合时,求R的值.(2)若P是AY上一点,AP=4,且sinA=3524.如图,在平面直角坐标系中,抛物线y=x2+mx+n与x轴正半轴交于A,B两点(点A在点B左侧),与y轴交于点C.(1)若△OBC是等腰直角三角形,且其腰长为3,求抛物线的解析式;(2)在(1)的条件下,点P为抛物线对称轴上的一点,则PA+PC的最小值为______.25.如图1,我们定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形.(1)如图2,在等边△ABE中,D、C分别是边AE、BE的中点,连接CD,问四边形ABCD是互补等对边四边形吗?请说明理由.∠AEB.(2)如图3,在等腰△ABE中,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=12∠AEB (3)如图4,在非等腰△ABE中,若四边形ABCD是互补等对边四边形,试问∠ABD=∠BAC=12是否仍然成立?若成立,请加以证明;若不成立,请说明理由.参考答案及解析1.答案:C解析:解:如图,作OD⊥AB,由垂径定理知,点D是AB的中点,AD=12AB=√3,∵cosA=ADOA =√32,∴∠A=30°,∴∠AOD=12AOB=60°,∴∠AOB=120°.故选:C.作OD⊥AB于D.根据垂径定理可得AD长,再解直角三角形可得∠AOB.本题利用了垂径定理和正弦的概念求解.2.答案:A解析:解:A、两条平行直线被第三条直线所截,内错角相等,故原命题错误,是假命题,符合题意;B、实数和数轴上的点是一一对应的,正确,是真命题,不符合题意;C、坐标平面内的点与有序实数对是一一对应的,正确,是真命题,不符合题意;D、在同一平面内,过一点有且只有一条直线与已知直线垂直,正确,是真命题,不符合题意,故选:A.利用平行线的性质、实数的性质、两直线的位置关系等知识分别判断后即可确定正确的选项.考查了命题与定理的知识,解题的关键是了解平行线的性质、实数的性质、两直线的位置关系等知识,难度不大.3.答案:D解析:解:由向量的定义可知:∵向量a⃗与b⃗ 均为单位向量,∴可得|a⃗|=1,|b⃗ |=1,即|a⃗|=|b⃗ |.故选D.根据单位向量的定义,因为向量a⃗与b⃗ 均为单位向量,可得出|a⃗|=1,|b⃗ |=1,即|a⃗|=|b⃗ |.此题主要考查了单位向量的定义,以及其性质,此类型题目是本部分基础题目,应注意正确的掌握其性质.4.答案:B解析:解:抛物线开口向上,a>0,对称轴为x=−1,因此a、b同号,b>0,而c<−1,因此abc<0,故①不符合题意;对称轴为x=−1,与x轴的交点为(x1,0)、(x2,0),其中0<x1<1,根据对称性得;−3<x2<−2,因此②符合题意;由对称性可知,当x=0与x=−2时,y的值是相等的,又c<−1,因此4a−2b+c<−1是正确的,故③符合题意;当x=−1时,y最小=a−b+c,当x=m时,y=am2+bm+c,因此a−b+c<am2+bm+c(m≠−1),即;a−b<am2+bm(m≠−1),故④不符合题意;综上所述,正确的结论有2个,故选:B.根据抛物线的开口方向、对称轴、顶点坐标、最大值(小)以及增减性,逐个进行判断,得出答案.考查二次函数的图象和性质,二次函数与一元二次方程的关系,掌握a、b、c的值对抛物线的位置的影响及与坐标轴的交点位置是解决问题的前提.5.答案:D解析:解:∵△FDE是△ADC绕点D逆时针旋转90°得到的,∴△FDE≌△ADC,∴AD=DF,DC=DE,∠DEF=∠DCA,又∵四边形ABCD是矩形,∴∠ADC=90°,∴∠DAC+∠DCA=90°,即∠DAG+DEF=90°,∴∠AGE=90°,即AC⊥BE,故①正确;∵AC⊥BE,∴∠BGC=90°,即△BGC是直角三角形,而△AGD显然不是直角三角形,故②错误;在Rt△FCB和Rt△FDE中,∵∠BFC=∠EFC,∴Rt△FCB∽Rt△FDE,∴ FCDF =BCDE,∵BC=AD=DF,DE=DC,∴FCDF =DFDC,即DF2=FC⋅DC,∴点F是线段CD的黄金分割点,故③正确;在线段EF上取EG′=CG并连接DG′,如图,∵DC=DE,∠DEF=∠DCA,∴∠DEG′=∠DCG,在△DCG和△DEG′中,{DC=DE∠DCG=∠DEG′CG=EG′,∴△DCG≌△DEG′(SAS),∴DG=DG′,∠CDG=∠EDG′,∵∠CDG=∠GDA=90°,∠EDG′+∠GAD=90°,∴∠GDG′=90°,∴△GDG′是等腰直角三角形,∴GG′=√2DG,∵EG′=CG,∴EG=EG′+GG′=CG+√2DG,故④正确;故选:D.由△FDE是△ADC绕点D逆时针旋转90°得到的,得到△FDE≌△ADC,再由矩形的性质得出∠DAC+ DEF=90°从而判断①;由AC⊥BE可得∠BGC=90°,从而判断②;由Rt△FCB∽Rt△FDE及BC=AD=DF,DE=DC,得出FCBC =DFDE可判断③;在线段EF上作EG′=CG,如图所示,连接DG′,通过△DCG≌△DEG′,得出△GDG′是等腰直角三角形,可以判断④.本题主要考查相似三角形的判定和性质以及黄金分割点的性质,全等三角形的判定和性质等综合知识,关键是根据已知比例式确定两个三角形相似.6.答案:C解析:解:∵∠DEC是△ADE的外角,∠A=48°,∠1=54°,∴∠DEC=∠A+∠1=48°+54°=102°,∵DE//BC,∴∠2=∠DEC=102°,故A、B选项错误;∵DE//BC,∴△ADE∽△ABC,∴DEBC =ADAB,故C正确;只有当D、E分别是AB、AC的中点时,DEBD =ADAB=12,故D错误,故选:C.先根据三角形的外角性质求出∠DEC的度数,再根据平行线的性质得出结论即可.本题考查的是相似三角形的判定和性质,平行线的性质及三角形的外角性质,用到的知识点为:两直线平行,内错角相等.7.答案:5解析:解:设a3=b5=c7=x,∴a=3x,b=5x,c=7x,∴a+b+ca =15x3x=5.根据题意,设a3=b5=c7=x,则可得a=3x,b=5x,c=7x,直接代入求得a+b+ca的值.主要考查了比例的性质.根据比例的性质可设其比例值为x ,用x 表示出未知字母的值,代入所求代数式化简即可.8.答案:−b ⃗ +12a ⃗ 解析:解:如图,∵四边形ABCD 是平行四边形,∴AD =BC ,AD//BC∴AD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ =b ⃗ ,∵E 是AB 的中点,∴AE =12AB =12a ⃗ ,∵DE ⃗⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ +AE −,∴DE ⃗⃗⃗⃗⃗⃗ =−b ⃗ +12a ⃗ , 故答案为:−b ⃗ +12a ⃗ . 由三角形法则可知:DE ⃗⃗⃗⃗⃗⃗ =DA ⃗⃗⃗⃗⃗ +AE −,只要求出DA ⃗⃗⃗⃗⃗,AE ⃗⃗⃗⃗⃗ 即可解决问题. 本题考查平面向量,三角形法则,平行四边形的性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型. 9.答案:−5 解析:解:原式=1+2√2×√22−8 =1+2−8=−5.直接利用特殊角的三角函数值、零指数幂的性质、二次根式的性质分别化简得出答案. 此题主要考查了实数运算,正确化简各数是解题关键. 10.答案:1解析:解:设△DEF 的面积为x ,∵△ABC∽△DEF ,相似比为2,△ABC 的面积为4,∴S△ABC:S△DEF=22=4,解得S△DEF=1.故答案为:1.设△DEF的面积为x,再根据相似三角形面积的比等于相似比的平方进行解答即可.本题考查的是相似三角形的性质,即相似三角形周长的比等于相似比,面积的比等于相似比的平方.x211.答案:y=12(x−1)2+2的顶点坐标为(1,2),点(1,2)向左平移1个单位,再向下平移2个解析:解:抛物线y=12x2.单位所得对应点的坐标为(0,0),所以所得抛物线的解析式为y=12x2.故答案为y=12(x−1)2+2的顶点坐标为(1,2),再根据点平移的规律得到点(0,0),然后根据顶先确定抛物线y=12点式写出平移后的抛物线解析式.本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.12.答案:189解析:解:根据题意得:∠CAD=45°,∠CBD=54°,AB=62m,∵在Rt△ACD中,∠ACD=∠CAD=45°,∴AD=CD,∵AD=AB+BD,∴BD=AD−AB=CD−2(m),∵在Rt△BCD中,tan∠CBD=CD,BD∴BD=CD,tan56∘∴AB=AD−BD=CD−CD=62,tan56∘∴CD≈189,(m).答:蒲宁之珠的高度CD约为189,故答案为:189.首先根据题意得:∠CAD=45°,∠CBD=56°,AB=62m,在Rt△ACD中,易求得BD=AD−AB=CD−62;在Rt△BCD中,可得BD=CDtan56∘,即可得AB=AD−BD=CD−CDtan56∘=62,继而求得答案.本题考查了仰角的知识.此题难度适中,注意能借助仰角构造直角三角形并解直角三角形是解此题的关键,注意掌握数形结合思想与方程思想的应用.13.答案:>解析:解:∵二次函数的解析式为y=−x2+2x−2=−(x−1)2−1,∴抛物线的开口向下,对称轴为直线x=1,∴在对称轴的右侧y随x的增大而减小,∵2<3∴y1>y2.故选:>.根据二次函数的性质即可判断y1、y2的大小关系.本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.14.答案:6解析:解:∵l1//l2//l3,ABBC =32,∴ABBC =DEEF=32,∵DF=10,∴DE10−DE =32,解得:DE=6,故答案为:6.根据平行线分线段成比例定理得出比例式,代入即可求出答案.本题考查了平行线分线段成比例定理,能根据平行线分线段成比例定理得出比例式是解此题的关键.15.答案:−3解析:解:过点M作MN⊥x轴于点N,则tan∠BAM=12=MNAN,函数的对称轴为x=−12b,当x=−12b时,y=x2+bx+2=2−b24,则MN=b24−2,令y=x2+bx+2,则xA+xB=−b,xA+xB=2,应该改为:令y=x2+bx+2=0,则xA+xB=−b,xA.xB=2.令y=x2+bx+2,则x A+x B=−b,x A⋅x B=2,则AB=|x A−x B|=√(x A+x B)2−4x A x B=√b2−8=2AN,则AN=12√b2−8,∵AN=2MN,即AN=12√b2−8=2(b24−2),解得b=±3,∵b<0,故b=−3,故答案为−3.函数的对称轴为x=−12b,当x=−12b时,y=x2+bx+2=2−b24,则MN=b24−2,而AB=|x A−x B|=√(x A+x B)2−4x A x B=√b2−8=2AN,由AN=2MN,即可求解.本题考查的是抛物线与x轴的交点,主要考查函数图象上点的坐标特征,要求学生非常熟悉函数与坐标轴的交点、顶点等点坐标的求法,及这些点代表的意义及函数特征.16.答案:4解析:解:∵AB=AC=6cm,DE垂直且平分AB,∴BE=AE.∵△BCE的周长为10cm,BE+CE=AC=AB=6,∴BC=10−6=4(cm).故答案为:4.要求底边BC 的长,现有△BCE 的周长为10cm ,只要求出BE +AE 即可,因为DE 垂直且平分AB ,故BE =AE.可推出AC =BE +EC =AB.易求出BC 的长.本题考查的是线段垂直平分线的性质,熟知线段垂直平分线上任意一点,到线段两端点的距离相等是解答此题的关键.17.答案:12解析:解:∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,OA =OC ,OB =OD ,∵矩形ABCD 的周长为56,∴2AB +2BC =56,∴AB +BC =28①,∵△OAB 比△OBC 周长小4,∴(OC +0B +BC)−(OA +OB +AB)=4,即BC −AB =4②,由①②组成方程组{AB +BC =28BC −AB =4, 解得:BC =16,AB =12,故答案为:12.根据矩形性质求出AB =CD ,AD =BC ,OA =OC ,OB =OD ,根据已知矩形周长得出AB +BC =28,根据△OAB 比△OBC 周长小4求出BC −AB =4,组成方程组,求出方程组的解即可.本题考查了矩形的性质的应用,关键是能根据题意得出方程组,题目比较典型,难度适中. 18.答案:1:2解析:解:∵点D 、E 分别是△ABC 的AB 、AC 边的中点,∴DE 是△ABC 的中位线,∴DE BC =AD AB =AE AC =12,∴l △ADE l △ABC =DE +AD +AE BC +AB +AC =12 故答案为:1:2.根据中位线的定理即可求出答案.本题考查中位线,解题的关键是熟练运用中位线的性质定理,本题属于基础题型.19.答案:(1)[1,−5,0](2)特征数是[2,m+1]的一次函数为y=2x+m+1.∵一次函数y=2x+m+1为正比例函数,∴m+1=0.∴m=−1.(3)∵A(2,m)、B(n,1),作AD⊥x轴于点D,BC⊥x轴于点C.∴CO=−n,BC=1,OD=2,AD=m,∵OA⊥OB,∴∠COB+∠AOD=90°,又∵∠AOD+∠OAD=90°,∴∠COB=∠OAD,又∵∠BCO=∠ADO=90°,∴△CBO∽△DOA,∴CBDO =CODA=BOOA,∴12=BOAO,又∵S△AOB=10,∴12OB⋅OA=10.即BO⋅OA=20,解得:BO=√10,AO=2√10.由勾股定理得:CO=3,AD=6.∵m>0,n<0,∴m=6,n=−3.∴A 坐标为(2,6),B 坐标为(−3,1).设抛物线解析式为:y =ax 2+c ,故{4a +c =69a +c =1, 解得:{a =−1c =10, 故抛物线解析式为:y =−x 2+10,则二次函数y =−x 2+10的特征数为[−1,0,10].解析:解:(1)∵[a,b,c]为二次函数y =ax 2+bx +c 的特征数,∴二次函数y =x 2−5x 的特征数是:[1,−5,0];故答案为:[1,−5,0];(2)见答案(3)见答案(1)根据题意得出二次函数的特征数,进而得出答案;(2)根据题意得出一次函数y =2x +m +1为正比例函数,得出m +1=0,进而得出答案;(3)首先得出△CBO∽△DOA ,即可得出CB DO =CO DA =BOOA ,进而求出BO ,AO 的长,即可得出m ,n 的值,再利用待定系数法求二次函数解析式得出即可.此题主要考查了二次函数综合以及新定义和相似三角形的判定与性质等知识,得出A ,B 点坐标是解题关键.20.答案:(1)−c ⃗ a ⃗ −b ⃗ a⃗ −c ⃗ (2)延长EC 到K ,使得CK =EC ,连接BK ,则向量BK ⃗⃗⃗⃗⃗⃗ 即为所求;解析:解:(1)∵四边形ABCD 是平行四边形,∴AD//BC ,AD =BC ,∴∠ADF =∠CBE ,∵DF =BE ,∴△ADF≌△CBE ,∴∠AFD =∠CEB ,AF =CE ,∴∠AFB =∠CED ,∴AF//CE ,∴CE ⃗⃗⃗⃗⃗ =−EC ⃗⃗⃗⃗⃗ =−AF ⃗⃗⃗⃗⃗ =−c ⃗ ,BD ⃗⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ +CD ⃗⃗⃗⃗⃗ =a ⃗ −b⃗ , DE ⃗⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ +CE ⃗⃗⃗⃗⃗ =a ⃗ −c ⃗ ,故答案为−c ⃗ ,a ⃗ −b ⃗ ,a⃗ −c ⃗ . (2)见答案.(1)根据平面向量的加法法则计算即可;(2)延长EC 到K ,使得CK =EC ,连接BK ,则向量BK⃗⃗⃗⃗⃗⃗ 即为所求; 本题考查平行四边形的性质、三角形法则等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.21.答案:(1)(−1,−2)(2)P′(1,6)、(2,3);(3)∵B 的“−√2关联点”是A ,∴A(a −√2−√2a +b),∵点A 在函数y =−8√2x(x <0)的图象上, ∴(−√2a +b)(a √2)=−8√2, ∴(b −√2a)2=16, ∵b −√2a >0, ∴b −√2a =4, ∴b =√2a +4;∴B 在直线y =√2x +4上.过Q 作y =√2x +4的垂线QB′,垂足为B′,∵Q(0,2),且线段BQ 最短,∴B′即为所求的B 点,由△MB′Q∽△MON 得MQ MN =MB′MO =B′Q ON ,∵ON =2√2,OM =4,∴MN=2√6.又∵MQ=2,∴B′Q=2√33,∴线段BQ的最小值是2√33.解析:解:(1)∵x=−3+42=−1,y=2×(−3)+4=−2,∴P′(−1,−2),故答案为(−1,−2);(2)设P(a,b),则P′(a+bk,ka+b)∴{a+bk=3ka+b=9,∴k=3,∴3a+b=9.∵a、b为正整数∴P′(1,6)、(2,3);(3)见答案(1)根据题中的新定义求出点P(−3,4)的“2关联点”P′的坐标即可;(2)根据题中的新定义求出a与b的关系式即可;(3)根据题意得出A(a−√2−√2a+b),代入y=−8√2x(x<0),求得b=√2a+4,从而求得B在直线y=√2x+4上,过Q作y=√2x+4的垂线QB′,垂足为B′,Q(0,2),且线段BQ最短,B′即为所求的B点,由△MB′Q∽△MON得MQMN =MB′MO=B′QON,由ON=2√2,OM=4,根据勾股定理求得MN=2√6.由MQ=2,求得BQ=2√33.此题属于反比例函数综合题,涉及的知识有:一次函数的交点坐标,坐标与图形性质,弄清题中的新定义是解本题的关键.22.答案:解:过点B作BE⊥AC于点E,如图所示:根据题意得:∠CAB=45°,∠ACB=75°−45°=30°,在Rt△ABE中,sin∠EAB=BEAB ,即sin45°=BE100,∴BE=50√2,∴AE=BE=50√2,在Rt△CBE中,∠ACB=30°,∴BC=2BE=100√2,CE=√3BE=50√6,∴CA=50√2+50√6,答:无人机与景点A的距离CA为(50√2+50√6)米.解析:过点B作BE⊥AC于点E,通过解直角三角形求出AE、CE,即可得出答案.此题考查了解直角三角形−俯角问题、含30°角的直角三角形的性质,通过作辅助线构造直角三角形是解题的关键.23.答案:(1)证明:如图1,连接OB,∵CD⊥BC,∴∠ADC=90°−∠CBD.又∵⊙O切AY于点B,∴OB⊥AB.∴∠OBC=90°−∠CBD.∴∠ADC=∠OBC.又∵在⊙O中,OB=OC=R,∴∠OBC=∠ACB.∴∠ACB=∠ADC.又∵∠A=∠A,∴△ABC∽△ACD.(2)解:如图2,连接OB,∵sinA=35,OB=OC=R,OB⊥AB,∴在Rt△AOB中,AO=OBsinA =R35=53R,AB=√(53R)2+R2=43R.∴AC=53R+R=83R.∵△ABC∽△ACD,∴ACAB =ADAC.∴83R43R=AD83R.∴AD=163R.∵当点D与点P重合时,AD=AP=4,∴163R=4.∴R=34.解析:(1)根据切线的性质得到∠ABO=90°,易证∠ABC=∠ACD,从而根据两个角对应相等得到两个三角形相似;(2)根据(1)中的相似三角形得到对应边的比相等,再结合锐角三角函数的概念,把AD用R表示,根据AD=AP求得R的值.此题考查了切线的性质、等腰三角形的性质、勾股定理、相似三角形的判定与性质以及三角函数的性质等知识.此题难度较大,综合性很强,注意掌握辅助线的作法,注意掌握数形结合思想与方程思想的应用.24.答案:3√2解析:解:(1)如图1,连接BC,∵△OBC是等腰直角三角形,∠BOC=90°,∴OB=OC,∵腰长为3,∴OB=OC=3,∴B(3,0),C(0,3),将点B(3,0),C(0,3)代入抛物线解析式y=x2+mx+n中,得,{9+3m+n=0n=3,∴{m=−4n=3,∴抛物线的解析式为y=x2−4x+3;(2)如图2,由(1)知,抛物线的解析式为y=x2−4x+3=(x−2)2−1,∴抛物线的对称轴直线为x=2,∵点C(0,3),∴点C关于抛物线的对称轴x=2的对称点C′(4,3),连接AC′交抛物线的对称轴于P,此时,PA+PC的值最小,最小值为AC′,针对于抛物线的解析式为y=x2−4x+3,令y=0,则x2−4x+3=0,解得,x=1或x=3,∴A(1,0),∵C′(4,3),∴AC′=√(4−1)2+32=3√2,即:PA+PC的最小值为3√2,故答案为:3√2.(1)先根据等腰直角三角形的腰长求出OB=OC=3,进而求出点B,C坐标,最后用待定系数法即可得出结论;(2)先确定出抛物线的对称轴,进而求出点C′的坐标,找出PA+PC的最小值为AC′,再求出点A坐标,即可得出结论.此题是二次函数综合题,主要考查了等腰直角三角形的性质,待定系数法,对称性,两点间的距离公式,求出点C′的坐标是解本题的关键.25.答案:解:(1)四边形ABCD是互补等对边四边形,理由:如图2,∵△ABE是等边三角形,∴AE=BE,连接AC,BD,∵点D是AE的中点,∴BD⊥AE,∴∠ADB=90°,同理:∠BCA=90°,∴AD=BC,∠ADB+∠BCA=180°∴四边形ABCD 是互补等对边四边形.(2)∵AE =BE ,∴∠EAB =∠EBA ,∵四边形ABCD 是互补等对边四边形,∴AD =BC ,在△ABD 和△BAC 中,{AD =BC∠DAB =∠CBA AB =BA&&,∴△ABD≌△BAC(SAS),∴∠ADB =∠BCA ,又∵∠ADB +∠BCA =180°,∴∠ADB =∠BCA =90°,在△ABE 中,∵∠EAB =∠EBA =180°−∠AEB 2=90°−12∠AEB ,∴∠ABD =90°−∠EAB =90°−(90°−12∠AEB)=12∠AEB ,同理:∠BAC =12∠AEB ,∴∠ABD =∠BAC =12∠AEB ;(3)仍然成立;理由如下:如图4所示:过点A 、B 分别作BD 的延长线与AC 的垂线,垂足分别为G 、F ,∵四边形ABCD 是互补等对边四边形,∴AD =BC ,∠ADB +∠BCA =180°,又∠ADB +∠ADG =180°,∴∠BCA =∠ADC ,又∵AG ⊥BD ,BF ⊥AC ,∴∠AGD =∠BFC =90°,在△AGD 和△BFC 中,{∠AGD =∠BFC ∠BCA =∠ADC AD =BC∴△AGD≌△BFC,∴AG=BF,在△ABG和△BAF中,{AB=BAAG=BF∴△ABG≌△BAF,∴∠ABD=∠BAC,∵∠ADB+∠BCA=180°,∴∠EDB+∠ECA=180°,∴∠AEB+∠DHC=180°,∵∠DHC+∠BHC=180°,∴∠AEB=∠BHC.∵∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,∠AEB.∴∠ABD=∠BAC=12解析:(1)先判断出AE=BE,再判断出∠ADB=90°,即可得出结论.(2)根据等边对等角可得∠EAB=∠EBA,根据四边形ABCD是互补等对边四边形,可得AD=BC,根据SAS可证△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,再根据等腰三角形的性质即可证明;(3)仍然成立;理由如下:如图所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,证明△AGD≌△BFC,得到AG=BF,又AB=BA,所以△ABC≌△BAF,得到∠ABD=∠BAC,根据∠ADB+∠BCA=180°,得到∠EDB+∠ECA=180°,进而得到∠AEB+∠DHC=180°,由∠DHC+∠BHC=180°,所以∠AEB=∠BHC.因为∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,所以∠ABD=∠BAC=1∠AEB.2此题是三角形综合题,主要考查了等边三角形的性质,等腰三角形的性质,全等三角形的判定和性质,理解新定义,判断出△ABD≌△BAC是解本题的关键.。
上海市静安区2021年中考数学一模试卷附答案

中考数学一模试卷一、单选题(共6题;共12分)1.如果,那么下列计算正确的是()A. B. C. D.2.下列多项式中,是完全平方式的为()A. B. C. D.3.将抛物线平移后与抛物线重合,那么平移的方法可以是()A. 向右平移1个单位,再向上平移3个单位B. 向右平移1个单位,再向下平移3个单位C. 向左平移1个单位,再向上平移3个单位D. 向左平移1个单位,再向下平移3个单位4.在△ABC中,点D、E分别在边BA、CA的延长线上,下列比例式中能判定DE∥BC的为()A. B. C. D.5.如果锐角的正切值为,那么下列结论中正确的是()A. B. C. D.6.在Rt△ABC中,∠C=90°,CD是高,如果AB=m,∠A= ,那么CD的长为()A. B. C. D.二、填空题(共12题;共12分)7.的相反数是________.8.函数的定义域为________.9.方程的根为________.10.二次函数图像的开口方向是________.11.抛物线的顶点坐标为________.12.如果一次函数的图像经过第一、二、四象限,那么常数的取值范围为________.13.在二次函数图像的上升部分所对应的自变量x的取值范围是________.14.如图,在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,如果AD=2,AE=3,CE=1,那么BD长为________.15.在△ABC中,点G是重心,∠BGC=90°,BC=8,那么AG的长为________.16.如图,在△ABC中,点D、E分别在边AB、AC上,DE∥BC,如果AB=12,BC=9,AC=6,四边形BCED的周长为21,那么DE的长为________.17.如图,在梯形ABCD中,AD∥BC,BD与AC相交于点O,OB=2OD,设,,那么________.(用向量、的式子表示)18.在Rt△ABC中,∠C=90°,AB=13,(如图),将△ABC绕点C旋转后,点A落在斜边AB上的点A’,点B落在点B’,A’B’与边BC相交于点D,那么的值为________.三、解答题(共7题;共65分)19.计算:.20.已知线段x、y满足求的值.21.如图,点A、B在第一象限的反比例函数图像上,AB的延长线与y轴交于点C,已知点A、B的横坐标分别为6、2,AB= .(1)求∠ACO的余弦值;(2)求这个反比例函数的解析式.22.如图,一处地铁出入口的无障碍通道是转折的斜坡,沿着坡度相同的斜坡BC、CD共走7米可到出入口,出入口点D距离地面的高DA为0.8米,求无障碍通道斜坡的坡度与坡角(角度精确到1',其他近似数取四个有效数字).23.已知:如图,在△ABC中,DE∥BC,AD2=AE•AC.求证:(1)△BCD∽△CDE;(2).24.如图,在平面直角坐标系xOy中,直线与x轴、y轴分别交于点A、B.抛物线(a≠0)经过点A,且与y轴相交于点C,∠OCA=∠OAB.(1)求直线AB的表达式;(2)如果点D在线段AB的延长线上,且AD=AC.求经过点D的抛物线的表达式;(3)如果抛物线的对称轴与线段AB、AC分别相交于点E、F,且EF=1,求此抛物线的顶点坐标.25.已知∠MAN是锐角,点B、C在边AM上,点D在边AN上,∠EBD=∠MAN,且CE∥BD,sin∠MAN= ,AB=5,AC=9.(1)如图1,当CE与边AN相交于点F时,求证:DF·CE=BC·BE;(2)当点E在边AN上时,求AD的长;(3)当点E在∠MAN外部时,设AD=x,△BCE的面积为y,求y与x之间的函数解析式,并写出定义域.答案解析部分一、单选题1.【解析】【解答】A. ,故不符合题意B. ,故不符合题意C. ,故不符合题意D. ,故符合题意故答案为:D【分析】利用零指数幂的定义分别得出结果即可求解2.【解析】【解答】A. = ,故符合题意B. = ,故不符合题意C. = ,故不符合题意D. = ,故不符合题意故答案为:A【分析】利用配方法分别转化为完全平方式的形式即可求解.3.【解析】【解答】抛物线要通过平移得到,需要先向右平移1个单位,再向上平移3个单位,即.故答案为:A.【分析】根据“左加右减,上加下减”的平移原则选出正确选项.4.【解析】【解答】解:当时,不能判定DE∥BC,A选项不符合题意;时,不能判定DE∥BC,B选项不符合题意;时,DE∥BC,C选项符合题意;时,不能判定DE∥BC,D选项不符合题意;故答案为:C.【分析】根据平行线分线段成比例定理、平行线的判定定理判断即可.5.【解析】【解答】∵,,而,∴,故答案为:C.【分析】利用30度角和45度角的正切值与角的正切值比较,即可得到答案.6.【解析】【解答】解:根据题意作图如下:由题意知:AB=m,∠A= ,∴,∴,即,故答案为:B.【分析】此题根据题意作图根据锐角三角函数表示出AC,再表示出CD即可求出结果.二、填空题7.【解析】【解答】的相反数是,故答案为:.【分析】只有符号不同的两个数叫互为相反数,根据定义解答.8.【解析】【解答】解:根据二次根式和分式的性质,,且,解得.故答案是:.【分析】根据二次根式和分式的性质求出该函数的定义域.9.【解析】【解答】解:方程两边同时平方得:,∴,即,∴x1=x2=1,经检验,x=1是原方程的根,故答案为:x=1.【分析】方程两边同时平方,得到一个一元二次方程,解出x的值,再进行检验即可得出结果.10.【解析】【解答】解:∵-3<0,∴二次函数图像的开口方向向下.故答案为:向下【分析】根据a的符号即可做出判断.11.【解析】【解答】抛物线的顶点坐标为(0,-6),故答案为:(0,-6).【分析】根据二次函数的性质解答.12.【解析】【解答】∵一次函数的图像经过第一、二、四象限,∴,解得:1<m<2,故答案为:1<m<2【分析】根据一次函数y=(m-2)x+m-3的图象经过第一、二、四象限,可得函数表达式中一次项系数小于0,常数项大于0,进而得到关于m的不等式组,解不等式组即可得答案取值范围.13.【解析】【解答】∵= ,∴对称轴为直线x=1,∵1>0,图象开口向上,∴当x<1时,y随着x的增大而减小;当x>1时,y随着x的增大而增大,故答案为:x>1.【分析】先将函数解析式化为顶点式形式,根据函数的增减性解答.14.【解析】【解答】AC=AE+CE=3+1=4,∵∠A=∠A,∠AED=∠B,∴△AED∽△ABC,∴,∴,∴AB=6,∴BD=6-2=4,故答案为:4.【分析】根据相似三角形的判定得出△AED∽△ABC,得出比例式,代入求出AB即可.15.【解析】【解答】解:延长AG交BC于D,∵点G是重心,∴点D为BC的中点,且AG=2DG,∵∠BGC=90°,BC=8,∴DG= BC=4,∴AG=2DG=8,故答案为:8.【分析】延长AG交BC于D,根据重心的定义,点D为BC的中点,先由直角三角形斜边上的中线等于斜边的一半求得DG的长,再由重心的性质:三角形的重心到一顶点的距离等于到对边中点距离的2倍进行求解即可.16.【解析】【解答】如图:设DE=x,CE=y∵四边形BCED的周长为21,BC=9,∴BD+DE+CE=21-9=12=AB=BD+AD即AD=DE+CE=x+y∵DE∥BC,∴△ADE∽△ABC∴即即整理得:解得:x=6【分析】先设DE=x,CE=y根据线段数量关系得出AD=DE+CE=x+y,由相似三角形对应线段成比例得到关于x,y的二元一次方程组,解得x即可求解.17.【解析】【解答】∵OB=2OD,∴,∵AD∥BC,∴△AOD∽△COB,∴= ,∴,∵,∴= ,故答案为:.【分析】先证明△AOD∽△COB,推出= ,求出,由三角形法则得出即可根据求出答案.18.【解析】【解答】过作交于点,,,设,,在中,,,,,,,,,由旋转而得,,,,,,,,又,,,.故答案为:.【分析】先过作交于点,根据题意求出和,由面积公式求出,再根据旋转的性质得,,由,则,并求出,利用对顶角相等得,则,最后根据相似三角形性质可得三、解答题19.【解析】【分析】将各三角函数值代入,根据二次根式的混合运算法则计算.20.【解析】【分析】利用比例性质化比例式化为整式,再移项两边同除以y2,化为,然后解一元二次方程,即可求解.21.【解析】【分析】(1)如图,分别过点A、B作AD⊥y轴,BE⊥x轴,可证∠ACO=∠ABH,由点A、B 的横坐标分别为6、2,可得AH=4,再由勾股定理可求得BH,即可求解∠ACO的余弦值;(2)设反比例函数的解析式为,根据点A、B在第一象限的反比例函数图像上,则点A(6,),B(2,),由BH=2可得,求出k值,此题即可得解.22.【解析】【分析】延长DC、AB相交于点E.由题意可知∠CEB=∠CBE,所以CE=CB,即可求出DE长,再利用勾股定理即可求出AE的长度,最后利用坡度计算公式即可求解.23.【解析】【分析】(1)由AD2=AE•AC,易证得△ADC∽△AED,即可得∠ACD=∠ADE,又由DE∥BC,易证得∠ECD=∠B,则可证得△BCD∽△CDE;(2)由△BCD∽△CDE,根据相似三角形的对应边成比例,即可得,又由DE∥BC,可得△ADE∽△ABC,即可得,继而得到结论.24.【解析】【分析】(1)先设OA,OB,通过抛物线可求得OC,结合∠OCA=∠OAB,运用锐角三角形函数定义求解OA,OB即可;(2)过点D作DG⊥x轴,由△DGA≌△AOC推出D的坐标,从而结合A,D坐标运用待定系数法求解即可;(3)设抛物线的对称轴FE与OA交于点H,则可根据平行线分线段成比例列式求解AH和OH,从而求解出抛物线的对称轴,即可求解出抛物线的解析式.25.【解析】【分析】(1)根据CE∥BD,得出∠CEB=∠DBE,∠DBA=∠BCE结合题干证明出△ABD∽△ECB,进而得到,再等量代换即可得到DF·CE=BC·BE.(2)过点B作BH⊥AN,垂足为H.根据条件先证明出△CEB∽△CAE,得到,代入求出CE,再根据求出BD,利用三角函数求出BH,根据勾股定理即可求出AD.(3)过点B作BH⊥AN,垂足为H.BH=4,AH=3,DH= 根据△ECB∽△ABD得到,代入化简为即可求解.。
【2021年上海市初中一模数学卷】2021年上海市青浦区初中毕业生学业模拟考试试卷九年级数学及答案

青浦区2020学年第一学期九年级期终学业质量调研测试数学试卷 Q2021.1(完成时间:100分钟 满分:150分)考生注意:1.本试卷含三个大题,共25题.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效.2.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每小题4分,满分24分)[每题只有一个正确选项,在答题纸相应题号的选项上用2B 铅笔正确填涂] 1.已知线段AB =2,P 是线段AB 的黄金分割点,AP>PB ,那么线段AP 的长度等于()(A)12; (B1; (C; (D)3.2.如图,已知BD 与CE 相交于点A ,DE ∥BC ,如果AD =2,AB =3,AC =6,那么AE 等于( ) (A )125; (B )185; (C )4;(D )9.3.在Rt △ABC 中,∠C =90º,那么cos A 等于( ) (A )BC AB;(B )AC AB;(C )BC AC;(D )AC BC.4.抛物线 的顶点坐标是( )(A )(2,-3);(B )(-2,-3);(C )(2,3);(D )(-2,3).5.已知+=a b c ,2−=a b c ,且0≠c ,下列说法中,不正确的是()(A )||3||=a b ; (B ) a ∥b ; (C )30+=a b ; (D ) a 与b 方向相同.6.如图,在△ABC 中,点D 在边AB 上,DE ∥BC ,DF ∥AC ,联结BE ,BE 与DF 相交于点G ,则下列结论一定正确的是( ) (A )AD DEDB BC=; (B )AE BFAC BC=;(C )BD BFAD DE=;(D )DG BFGF FC=. EDCBA GF E DCBA (第2题图)(第6题图)()223y x =−−−二、填空题:(本大题共12题,每小题4分,满分48分) [请将结果直接填入答题纸的相应位置] 7. 如果 ,那么 ▲ .8. 计算:43(2)−−a a b = ▲ .9. 如果两个相似三角形的周长比为2∶3,那么它们的对应角平分线的比为 ▲.10.将抛物线2y x =−向上平移2个单位,所得抛物线的表达式是 ▲ .11.抛物线223y x =−在y 轴左侧的部分是 ▲ .(填“上升”或“下降”)12.二次函数2+2y x x m =+图像上的最低点的横坐标为 ▲ . 13.在△ABC 中,∠C =90º,如果cot ∠A=2,BC =3,那么AC = ▲.14.小明在楼上点A 处看到楼下点B 处的小丽的俯角是32°,那么点B 处的小丽看点A 处的小明的仰角是 ▲ 度.15.直角三角形的重心到斜边中点的距离为2,那么该直角三角形的斜边长为▲.16.如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长相同,那么∠BAC 的正弦值为 ▲ .17.如图,在△ABC 中,点D 是边BC 的中点,直线DF 交边AC于点F ,交AB 的延长线于点E ,如果CF ∶CA=a ∶b ,那么 BE ∶AE 的值为 ▲ .(用含a 、b 的式子表示)18.如果四边形边上的点,它与对边两个端点的连线将这个四边形分成的三个三角形都相似,我们就把这个点叫做该四边形的“强相似点”.如图①,在四边形ABCD 中,点Q 在边AD 上,如果△QAB 、△QBC 和△QDC 都相似,那么点Q 就是四边形ABCD 的“强相似点”;如图②,在四边形ABCD 中,AD ∥BC ,AB=DC=2,BC=8,∠B=60°,如果点Q 是边AD 上的“强相似点”,那么AQ = ▲ .CBA ABCDEF(第16题图)34=ab−=+b ab aABC DQ(第17题图)A BCD(第18题图①)(第18题图②)三、解答题(本大题共7题,满分78分) [请将解题过程填入答题纸的相应位置] 19.(本题满分10分)计算:()1cot 3012sin 60+cos 60+tan 30︒︒︒︒−−. 20.(本题满分10分, 第(1)小题5分,第(2)小题5分)如图,在△ABC 中,点D 、E 分别在边AB 、AC 上,且AD =2,DB =4,AE =3,EC =6,DE =3.2. (1)求BC 的长;(2)联结DC ,如果DE a =,BA b =,试用a 、b 表示向量CD .21.(本题满分10分, 第(1)小题5分,第(2)小题5分)如图,在平行四边形ABCD 中,BC=8,点E 、F 是对角线BD 上的两点,且BE=EF=FD , AE 的延长线交BC 于点G ,GF 的延长线交AD 于点H . (1)求HD 的长;(2)设△BGE 的面积为a ,求四边形AEFH 的面积.(用含a 的代数式表示)22.(本题满分10分)某条道路上通行车辆限速为40千米/时,在离道路50米的点P 处建一个监测点,道路的AB 段为监测区(如图).在△ABP 中,已知∠P AC= 26.5°,∠PBC = 68.2°.一辆车通过AB 段的时间为9秒,请判断该车是否超速,并说明理由.(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin68.2°≈0.93,cos68.2°≈0.37,tan68.2°≈2.50)23.(本题满分12分,第(1)小题6分,第(2)小题6分)已知:如图,在四边形ABCD 中,AB=AD ,AC 、BD 相交于点E ,AE CE DE BE ⋅=⋅. (1)求证:△ABE ∽△ACB ;(2)如果2DA DE DB =⋅,求证:AB EC BC AE ⋅=⋅.ABCDEFG H AB CDEEDCBA(第20题图)(第21题图)(第23题图)(第22题图)24.(本题满分12分, 其中第(1)小题4分,第(2)小题5分,第(3)小题3分)如图,在平面直角坐标系xOy 中,抛物线24=+−y ax bx 与x 轴交于点A (-4,0)和点B (2,0),与y 轴交于点C .(1)求该抛物线的表达式及点C 的坐标;(2)如果点D 的坐标为(-8,0),联结AC 、DC ,求∠ACD 的正切值;(3)在(2)的条件下,点P 为抛物线上一点,当∠OCD=∠CAP 时,求点P 的坐标.25.(本题满分14分,其中第(1)小题4分,第(2)小题6分,第(3)小题4分)在△ABC 中,∠C= 90°,AC =2,BC=,点D 为边AC 的中点(如图),点P 、Q 分别是射线BC 、BA 上的动点,且BQ=2BP ,联结PQ 、QD 、DP .(1)求证:PQ ⊥AB ;(2)如果点P 在线段BC 上,当△PQD 是直角三角形时,求BP 的长;(3)将△PQD 沿直线QP 翻折,点D 的对应点为点'D ,如果点'D 位于△ABC 内,请直接写出BP 的取值范围.(第24题图)(备用图)DP ABCDQ一、选择题:1.B ;2.C ; 3.B ; 4.A ;5.D ;6.C .二、填空题:7.17;8.6+a b ; 9.2:3; 10.22=−+y x ; 11.下降;12.1−;13.6; 14.32; 15.12; 16.2; 17.−ab a; 18.3 三、解答题:19.解:原式112+22⎛⎫−⨯ ⎪⎝⎭. ································································ (4分)1. ···················································································· (4分). ···············································································································(2分)20.解:(1)∵AD =2,DB =4,AE =3,EC =6,∴12=AD DB ,12=AE EC .∴=AD AEDB EC. ··················································· (2分) ∴DE//BC . ········································································································ (1分) ∴=AD DEAB BC. ······························································································· (1分) 又∵AB =6,DE =3.2, ∴2 3.26=BC.∴BC =9.6. ················································································ (1分) (2)∵DE//BC ,∴=AD DE AB BC .∴13=DE BC . ∴3=BC DE . ······························································································· (1分)青浦区2021 学年第一学期期终学业质量调研九年级数学试卷 参考答案及评分说明∵=DE a ,∴3=BC a . ∴3=−CB a . ··············································· (1分) ∵23=BD BA ,∴23=BD BA . ······································································ (1分) ∵=BA b ;∴23=BD b . ············································································ (1分) ∵=+CD CB BD ,∴233=−+CD a b . ···················································(1分) 21.解:(1)∵四边形ABCD 是平行四边形, ∴AD//BC ,AD =BC .························································································· (1分)∴=AD DE BG BE ,=DH DFBG FB. ······································································ (2分) ∵BE=EF=FD ,AD=BC =8, ∴821=BG , ∴BG =4. ·················································································· (1分) ∴142=DH ,∴DH =2. ·················································································· (1分) (2)∵AD ∥BC ,∴△BEG ∽△DEA ,△HFD ∽△GFB .∴2⎛⎫= ⎪⎝⎭BEG DEAS BE SED ,2⎛⎫= ⎪⎝⎭HFD GFBS DF S FB . ················································· (2分) ∵=BEGSa ,BE =EF ,∴2=BGFSa .∴14=DEAa S,124=HFD S a . ∴=4DEA Sa ,12=HFDS a . ······································································ (2分) ∵=四边形−DEA HFD AEFH S SS,∴17=422四边形−=AEFHS a a a . ··············· (1分)22.解:该车不超速.过点P 作PH ⊥AC ,垂足为点H . ·········································································· (1分) 由题意,得PH =50米.在Rt △AHP 中,∵tan ∠=PH PAC AH ,∴50100tan 26.5=≈︒AH . ················ (3分) 在Rt △BHP 中,∵tan ∠=PH PBH BH ,∴5020tan 68.2=≈︒BH . ·················· (3分) ∵AB =AH -BH ,∴AB =100 -20=80(米). ···························································· (1分) ∵这辆车通过AB 段的时间为9秒,∴这辆车通过AB 段的速度为809米/秒. (1分) ∵809米/秒=32千米/时 < 40千米/时,∴该车不超速. ···································· (1分) 23.证明:(1)∵AE CE DE BE ⋅=⋅,∴=AE DEBE EC. ···························································································· (1分) 又∵∠AED =∠BEC ,∴△AED ∽△BEC . ······················································ (1分) ∴∠ADE =∠BCE . ··························································································· (1分)∵AB =AD ,∴∠ABE =∠ADE . ······································································· (1分) ∴∠ABE =∠BCE . ··························································································· (1分) 又∵∠BAE =∠CAB ,∴△ABE ∽△ACB . ···················································· (1分) (2)∵2DA DE DB =⋅,∴=DE DADA DB. ···························································· (1分) 又∵∠EDA =∠ADB ,∴△EDA ∽△ADB . ··················································· (1分) ∴∠DAE =∠DBA . ·························································································· (1分) ∵∠ABE =∠BCE ,∴∠DAE =∠BCE . ∴AD ∥BC . ····································································································· (1分) ∴=AD AEBC EC. ······························································································ (1分) ∴⋅=⋅AD EC BC AE .∵AB =AD , ∴⋅=⋅AB EC BC AE . ························································· (1分)24.解:(1)将A (-4,0)、B (2,0)代入2+4=−y ax bx ,得164404240.,−−=⎧⎨+−=⎩a b a b 解得:121.,⎧=⎪⎨⎪=⎩a b ····················································· (2分)所以,2142=+−y x x . ············································································ (1分) 当x =0时,4=−y .∴点C 的坐标为(0,-4) ········································· (1分) (2)过点A 作AH ⊥DC ,垂足为点H .∵D (-8,0)、C (0,-4),∴=·································(1分) ∵1122=⋅=⋅ADCSCD AH DA OC , ·································································· (1分)∴44=⨯AH.∴=AH . ······························································· (1分) ∵=,∴5=. ························· (1分) ∴tan ∠ACD=13==AH HC . ····························································· (1分) (2)由题意可知,点P 在第一象限.过点P 作PQ ⊥x 轴,垂足为点Q .∵A (-4,0)、C (0,-4),∴OA =OC .∴∠OAC =∠OCA .∵∠OCD =∠OCA +∠ACD ,∠CAP =∠CAO +∠BAP ,∠OCD =∠CAP ,∴∠ACD =∠BAP .∴tan ∠BAP =tan ∠ACD=13. ·········································· (1分)设PQ =a ,则AQ =3a ,OQ =3a -4.∴P (3a -4,a ). ··························································································· (1分)将P (3a -4,a )代入2142=+−y x x ,得()21343442−+−−=a a a .解得120=9a ,2=0a (舍).∴P (83,209). ········································ (1分)25.解:(1)∵∠C= 90°,AC =2,BC =∴AB 4=. ················································································· (1分)∴2=BC AB .∵BQ =2BP ,∴=BQ BP ∴=BQ BC BP AB. ······························································································· (1分) 又∵∠B =∠B ,∴△BQP ∽△BCA . ······························································ (1分) ∴∠BQP =∠BCA .∵∠C= 90°,∴∠BQP =90°. 即PQ ⊥AB . ····································································································· (1分) (2)(i )当∠PQD =90°时,∵∠PQD < ∠PQA =90°, ∴此种情况不存在. ························································································ (1分) (ii )当∠QPD =90°时,∵∠PQB =∠QPD =90°,∴AB ∥PD ,∴=CP CDBP DA. ∵CD =DA , ∴BP =CP .∵BC =,∴BP . ················································································· (2分) (iii )当∠QDP =90°时,过点Q 作QH ⊥AC ,垂足为点H .设BP =2x ,则BQ x ,PC =2−x ,QA =4.∴AH =22−x ,QH =32−x ,HD =12−x .∵∠QDC =∠CDP +90°,∠QDC =∠DQH +90°, ∴∠CDP =∠DQH .∴tan ∠CDP =tan ∠DQH . ∴=CP HDDC QH.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
23.(本题满分 12 分,其中每小题 6 分) 已知:如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE∥BC, AD2 AE AC .
求证:(1)△BCD∽△CDE;(2)
CD BC
2 2
AD . AB
A
D
E
B
C
(第 23 题图)
第4页共4页
24.(本题满分 12 分,其中每小题 4 分) 如图,在平面直角坐标系 xOy 中,直线 y 1 x m(m 0)与 x 轴、y 轴分别交于点 A、B.抛 2
(B)向右平移 1 个单位,再向下平移 3 个单位;
(C)向左平移 1 个单位,再向上平移 3 个单位;
(D)向左平移 1 个单位,再向下平移 3 个单位.
4.在△ABC 中,点 D、E 分别在边 BA、CA 的延长线上,下列比例式中能判定 DE//BC
的为
(A) BC AB ; (B) AC = AB ; (C) AC = AB ;
物线的顶点坐标. y
C
B
A
O
x
(第 24 题图)
第5页共4页
25.(本题满分 14 分,其中第(1)小题 5 分,第(2)小题 5 分,第(3)小题 4 分) 已知∠MAN 是锐角,点 B、C 在边 AM 上,点 D 在边 AN 上,∠EBD=∠MAN,且 CE//BD,sin
3
∠MAN= ,AB=5,AC=9.
(A) m sin tan ;
(B) m sin cos ;
(C) m cos tan ;
(D) m cos cot .
二、填空题:(本大题共 12 题,每题 4 分,满分 48 分) 7. 3 的相反数是 ▲ . 2 8.函数 f (x) x 1 的定义域为 ▲ . 2x 9.方程 3 2x 2 x 的根为 ▲ .
DE AD
AD AE
CE BD
(D) AC = BD . AB CE
5.如果锐角 的正切值为 3 ,那么下列结论中正确的是 2
(A) 30 ; (B) 60 ; (C) 30 45 ; (D) 45 60 .
6.在 Rt△ABC 中,∠C=90°,CD 是高,如果 AB=m,∠A= , 那么 CD 的长为
21.(本题满分 10 分, 其中每小题 5 分) 如图,点 A、B 在第一象限的反比例函数图像上,AB 的延长线与 y 轴交于点 C,已知点 A、B
的横坐标分别为 6、2,AB= 2 5 . (1)求∠ACO 的余弦值; (2)求这个反比例函数的解析式. y
CB
A
O
x
(第 21 题图)
第3页共4页
第1页共4页
10.二次函数 y 2x 3x2 图像的开口方向是 ▲ . 11.抛物线 y 3x2 6 的顶点坐标为 ▲ . 12.如果一次函数 y (m 2)x m 1 的图像经过第一、二、四象限,那么常数 m 的取值范围为
▲. 13.在二次函数 y x2 2x 3 图像的上升部分所对应的自变量 x 的取值范围是 ▲ . 14.如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,∠AED=∠B, 如果 AD=2,AE=3,CE=1, 那么 BD 长为 ▲ . 15.在△ABC 中,点 G 是重心,∠BGC=90°,BC=8,那么 AG 的长为 ▲ .
A
D
E
D
AA
A D
E
O
B
(第
14
C
题图)
B
(第
16
题图)C
B
(第 17 题图)
CC
B
( 第 18 题
三、解答题:(本大题共 7 题,满分 78 分) 19.(本题满分 10 分)
计算: cot 30 cos 45 . sin 60 tan 45
第2页共4页
20.(本题满分 10 分) 已知线段 x、y 满足 2x y x ,求 x 的值. xy y y
22.(本题满分 10 分) 如图,一处地铁出入口的无障碍通道是转折的斜坡,沿着坡度相同的斜坡 BC、CD 共走 7 米可
到出入口,出入口点 D 距离地面的高 DA 为 0. 8 米,求无障碍通道斜坡的坡度与坡角(角度精确到 1' ,其他近似数取四个有效数字).
D C
A
B
D C
A
B
(第 22 题图)
静安区 2020 分钟 满分:150 分 )
2021.1
一、选择题:(本大题共 6 题,每题 4 分,满分 24 分) 1.如果 a 0 ,那么下列计算正确的是
(A) (a)0=0 ; (B)( a)0= 1 ; (C) a0 1;
(D) -a0= 1 .
16. 如图,在△ABC 中,点 D、E 分别在边 AB、AC 上,DE//BC,如果 AB=12,BC=9,AC=6,四
边形 BCED 的周长为 21,那么 DE 的长为 ▲ .
17.如图,在梯形 ABCD 中,AD//BC,BD 与 AC 相交于点 O,OB=2OD,设 AB a , AD b ,那
么 AO ▲ .(用向量 a 、 b 的式子表示)
18. 在 Rt△ABC 中,∠C=90°,AB=13, tan B 2 (如图),将△ABC 绕点 C 旋转后,点 A 落在斜 3
边 AB 上的点 A’,点 B 落在点 B’,A’B’与边 BC 相交于点 D,那么 CD 的值为 ▲ . A'D
2.下列多项式中,是完全平方式的为
(A) x2 x 1 ; (B) x2 1 x+ 1 ; (C) x2 1 x 1 ; (D) x2 1 x 1 .
4
24
44
44
3.将抛物线 y 2(x 1)2 3 平移后与抛物线 y 2x2 重合,那么平移的方法可以是
(A)向右平移 1 个单位,再向上平移 3 个单位;
物线 y ax2 bx 4 (a≠ 0)经过点 A,且与 y 轴相交于点 C,∠OCA=∠OAB.
(1)求直线 AB 的表达式;
(2)如果点 D 在线段 AB 的延长线上,且 AD=AC.求经过点 D 的抛物线 y ax2 bx 4 的表达
式;
(3)如果抛物线 y ax2 bx 4 的对称轴与线段 AB、AC 分别相交于点 E、F,且 EF=1,求此抛
5
(1)如图 1,当 CE 与边 AN 相交于点 F 时,求证:DF·CE=BC·BE; (2)当点 E 在边 AN 上时,求 AD 的长; (3)当点 E 在∠MAN 外部时,设 AD=x,△BCE 的面积为 y,求 y 与 x 之间的函数解析式,并写出 定义域.
