理论力学答案讲解
理论力学典型例题答案及解析(适用于邓国红版)

联立求解上式,并注意到
JC
1 ml2 12
可得
3g cos j
2l
w
3g l
(sin
j0
sin
j
)
以C点为基点,则A点的加速度为 注: 亦可由加速度合成法求出
aAaCaA tCaA nC
在运动开始时, 到y 轴上,得
w=0,
故
aAnC=0
, 将上式投影
0aCy aA tCsinq
aC yaA tCsinq2 lsinq (4)
知识点:动能定理的运用
分析:对m1与m2进行整体分 析,分别写出初末状态下的动 能,运用动能定理进行求解
解:
系统的初动能T1 0,当转过j角度时有
T2
1 2
Jw2
1 2
m2v2
W12 Mj m2grj sinq fm2grj cosq
由T2 T1 W12求出w,然后对w求导得到
11.15
大小
√
√
?
?
求出滑枕B的加速度
7.15 轮只滚不滑,I点为瞬心
求B点与C点的速度
vA
vB
vC
分析可知:AB杆为瞬时平动,则有
wB
vBvAwO A 2m/s I
wBvB/B I4rad/s
vCwBC I2.8m 3 /s
取A点为基点,对B点作加速度分析 y
an BatBaAan B AatBAaA
vr vo v e
L z2
Jw
M z (mv e mv r )
Jw
m • OM
2 w mv 0 • MA
其中 MA = l cos j r
OM 2 (l r cos j ) 2 (r sin j ) 2
《理论力学》习题三答案讲解

《理论⼒学》习题三答案讲解《理论⼒学》习题三答案⼀、单项选择题(本⼤题共30⼩题,每⼩题2分,共60分)1. 求解质点动⼒学问题时,质点的初始条件是⽤来( C )。
A 、分析⼒的变化规律; B 、建⽴质点运动微分⽅程; C 、确定积分常数; D 、分离积分变量。
2. 在图1所⽰圆锥摆中,球M 的质量为m ,绳长l ,若α⾓保持不变,则⼩球的法向加速度为( C )。
A 、αsin g ;B 、αcos g ;C 、αtan g ;D 、αtan gc 。
3. 已知某点的运动⽅程为2bt a S +=(S 以⽶计,t 以秒计,a 、b 为常数),则点的轨迹为( C )。
A 、是直线;B 、是曲线;C 、不能确定;D 、抛物线。
4. 如图2所⽰距地⾯H 的质点M ,具有⽔平初速度0v ,则该质点落地时的⽔平距离l 与( B )成正⽐。
A 、H ;B 、H ;C 、2H ;D 、3H 。
5. ⼀质量为m 的⼩球和地⾯碰撞,开始瞬时的速度为1v ,碰撞结束瞬时的速度为2v(如图3),若v v v ==21,则碰撞前后质点动量的变化值为( A )。
A 、mv ;B 、mv 2 ;C 、mv 3;D 、 0。
6. ⼀动点作平⾯曲线运动,若其速率不变,则其速度⽮量与加速度⽮量( B )。
A 、平⾏; B 、垂直; C 、夹⾓随时间变化; D 、不能确定。
7. 三棱柱重P ,放在光滑的⽔平⾯上,重Q 的匀质圆柱体静⽌释放后沿斜⾯作纯滚动,则系统在运动过程中( A )。
A 、沿⽔平⽅向动量守恒,机械能守恒;B 、动量守恒,机械能守恒;C 、沿⽔平⽅向动量守恒,机械能不守恒;D 、均不守恒。
图1图2图38. 动点M 沿其轨迹运动时,下列⼏种情况中,正确的应该是( A )。
A 、若始终有a v⊥,则必有v 的⼤⼩等于常量;B 、若始终有a v⊥,则点M 必作匀速圆周运动; C 、若某瞬时有v ∥a ,则点M 的轨迹必为直线;D 、若某瞬时有a 的⼤⼩为零,且点M 作曲线运动,则此时速度必等于零。
理论力学课后题参考答案

1.1 沿水平方向前进的枪弹,通过某一距离s 的时间为t 1,而通过下一等距离s 的时间为2t .试证明枪弹的减速度(假定是常数)为由题可知示意图如题1.1.1图: {{SSt t 题1.1.1图设开始计时的时刻速度为0v ,由题可知枪弹作匀减速运动设减速度大小为a .则有:()()⎪⎪⎩⎪⎪⎨⎧+-+=-=221210211021221t t a t t v s at t v s 由以上两式得 11021at t s v +=再由此式得 ()()2121122t t t t t t s a +-=1.26一弹性绳上端固定,下端悬有m 及m '两质点。
设a 为绳的固有长度,b 为加m 后的伸长,c 为加m '后的伸长。
今将m '任其脱离而下坠,试证质点m 在任一瞬时离上端O 的距离为解 以绳顶端为坐标原点.建立如题1.26.1图所示坐标系.题1.26.1图设绳的弹性系数为k ,则有 kb mg = ① 当 m '脱离下坠前,m 与m '系统平衡.当m '脱离下坠前,m 在拉力T 作用下上升,之后作简运.运动微分方程为 ()ym a y k mg &&=-- ② 联立①② 得 b b a g y b g y +=+&& ③ 0=+y bg y &&齐次方程通解 t b g A t b g A Y sin cos 211+= 非齐次方程③的特解 b a Y +=0 所以③的通解b a t bg A t b g A Y +++=sin cos 211代入初始条件:0=t 时,,c b a y ++=得0,21==A c A ;故有 b a t b g c y ++=cos 即为m 在任一时刻离上端O 的距离.'1.39 一质点受一与距离23次方成反比的引力作用在一直线上运动。
试证此质点自无穷远到达a 时的速率和自a 静止出发到达4a 时的速率相同。
理论力学课后习题答案

理论力学课后习题答案理论力学课后习题答案引言:理论力学是物理学的基础课程之一,对于理解和应用物理学的原理和方法具有重要意义。
在学习理论力学的过程中,课后习题是巩固知识、提高能力的重要途径。
本文将针对理论力学课后习题进行解答,帮助读者更好地理解和掌握这门课程。
第一章:牛顿力学1. 一个物体以初速度v0沿直线运动,加速度为a,求物体的位移与时间的关系。
答:根据牛顿第二定律F=ma,可得物体所受合力F=ma=mv/t,其中m为物体的质量,v为物体的速度,t为时间。
由此可得物体的位移s=vt+1/2at^2。
2. 一个质点在重力作用下自由下落,求它在t时刻的速度和位移。
答:在重力作用下,质点的加速度为g,即a=g。
根据牛顿第二定律F=ma,可得质点所受合力F=mg。
根据牛顿第一定律,质点的速度随时间的变化率为v=g*t,位移随时间的变化率为s=1/2gt^2。
第二章:拉格朗日力学1. 一个质点沿半径为R的圆周运动,求它的动能和势能。
答:质点的动能由动能定理可得,即K=1/2mv^2,其中m为质点的质量,v为质点的速度。
质点的势能由引力势能可得,即U=-GmM/R,其中G为引力常数,M为圆周的质量。
2. 一个质点在势能为U(r)的力场中运动,求它的运动方程。
答:根据拉格朗日方程可得,质点的运动方程为d/dt(dL/dv)-dL/dr=0,其中L=T-U,T为质点的动能,U为质点的势能。
第三章:哈密顿力学1. 一个质点在势能为U(x)的力场中运动,求它的哈密顿量和哈密顿运动方程。
答:质点的哈密顿量由哈密顿定理可得,即H=T+U,其中T为质点的动能,U为质点的势能。
质点的哈密顿运动方程为dp/dt=-dH/dx,其中p为质点的动量。
2. 一个质点在势能为U(x)的力场中运动,求它的哈密顿正则方程。
答:质点的哈密顿正则方程为dx/dt=dH/dp,dp/dt=-dH/dx,其中x为质点的位置,p为质点的动量。
结论:通过对理论力学课后习题的解答,我们可以更深入地理解和应用物理学的原理和方法。
理论力学课后的习题及答案解析...doc
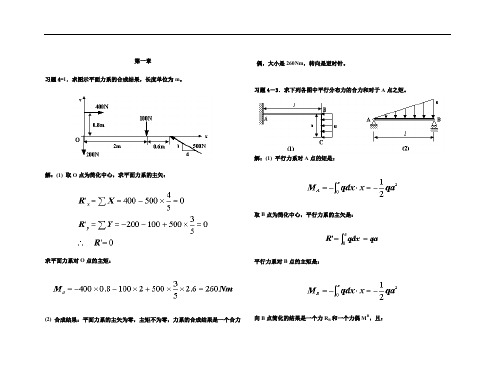
第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学答案完整版(清华大学出版社)1

第一章力和约束 习题解答
1-1 求 图 示 空 间 汇 交 力 系 的 合 力 。 已 知 F1 = 100N , F2 = 200N , F3 = 300N , F4 = 400N ,方向如图示。如果仅改变力 F4 的方向,能否使此力系成为平衡力系?为什么?
解:按合力投影定理计算合力在 x, y, z 轴上的投影: FRx = F1 cosϕ1 + F2 sin γ 2 cosϕ2 − F4 sin2 30o = 111.1 (N); FRy = F2 sin γ 2 sinϕ2 + F3 + F4 sin 30o cos30o
= 601.1 (N); FRz = −F1 sinϕ1 − F2 cosγ 2 sinϕ2 + F4 cos30o
题 1-9(a)图 (b)按三力平衡汇交定理画出整体的受力图,然后依次画出杆 CD、杆 AB、轮 D 的受力图。
题 1-9(b)图
5
(c)折杆 BC 为二力构件,约束力方向一定是沿着 BC 连线。因力偶只能与力偶平衡,所 以,铰链 A 和 B 处的约束力一定互相平行而组成力偶。
题 1-9(c)图 (d)图示结构中,杆 CE 为二力杆,其余杆件的受力按力偶平衡理论确定。
对 x, y, z 轴的力矩和,以及对坐标原点 O 的力矩和。
解:平面 abc 的法向量为 n = 1 i + 1 j + 1 k ,力偶矢为 ab c
M = Mn0 , 其中 i, j,k, n0 依次为 x, y, z, n 方向的单位向
量。力 F 表为 F = Fξ 0
其中ξ 0 为ξ = 1 (a i + b j) − ck 方向的单位向量。
理论力学课后习题解答
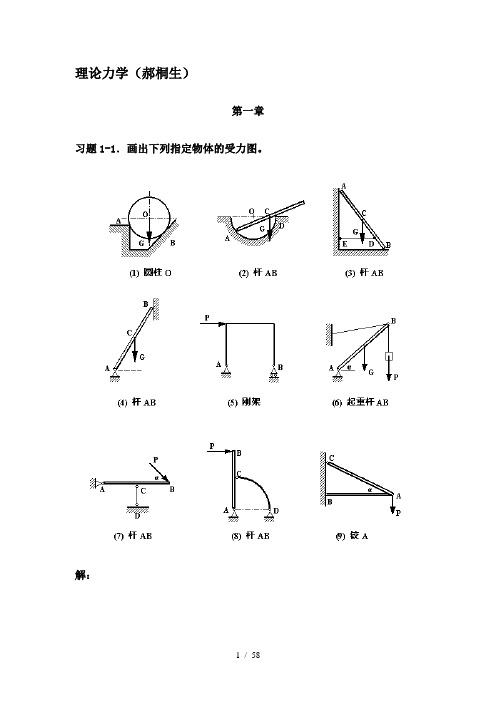
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B 的约束反力。
解:(1) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B 端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向及假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB及水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学课后习题及答案解析

理论力学课后习题及答案解析文稿归稿存档编号:[KKUY-KKIO69-OTM243-OLUI129-G00I-FDQS58-MG129]第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A 点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力RB和一个力偶M B,且:如图所示;将RB向下平移一段距离d,使满足:最后简化为一个力R,大小等于RB。
其几何意义是:R 的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力RA和一个力偶M A,且:如图所示;将RA向右平移一段距离d,使满足:最后简化为一个力R,大小等于RA。
其几何意义是:R 的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学(金尚年-XXX编著)课后习题答案详解

理论力学(金尚年-XXX编著)课后习题答案详解高等教育出版社的《理论力学课后题答案》一书中,第一章包含了以下三个问题的解答:1.2 题目要求写出在铅直平面内的光滑摆线,并分方程。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后证明了质点在平衡位置附近作振动时,振动周期与振幅无关。
1.3 题目要求证明单摆运动的振动周期与摆长无关。
解答中使用了微积分和力学原理,得出了运动微分方程。
最后通过进一步计算,得出了单摆运动的振动周期公式。
1.5 题目要求使用拉格朗日方程计算质点的运动。
解答中使用了拉格朗日方程,并通过进一步计算得出了质点的运动轨迹。
如图,在半径为R时,地球表面的重力加速度可以由万有引力公式求得:g=\frac{GM}{R^2}$$其中M为地球的质量。
根据广义相对论,地球表面的重力加速度还可以表示为:g=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)$$其中c为光速。
当半径增加到R+ΔR时,总质量仍为M,根据XXX展开,可以得到:frac{1}{(R+\Delta R)^2}=\frac{1}{R^2}-\frac{2\DeltaR}{R^3}+\mathcal{O}(\Delta R^2)$$代入上式可得:g'=\frac{GM}{R^2}\left(1-\frac{2GM}{c^2R}\right)\left(1+\frac{2\Delta R}{R}\right)$$ 化简后得:g'=g-\frac{2g\Delta R}{R}$$因此,当半径改变时,表面的重力加速度的变化为:Delta g=-\frac{2g\Delta R}{R}$$2.在平面极坐标系下,设质点的加速度的切向分量和法向分量都是常数,即$a_t=k_1$,$a_n=k_2$(其中$k_1$和$k_2$为常数)。
根据牛顿第二定律,可以得到质点的运动方程:r\ddot{\theta}+2\dot{r}\dot{\theta}=k_2$$ddot{r}-r\dot{\theta}^2=k_1$$其中$r$为极径,$\theta$为极角。
《理论力学》课后习题解答(赫桐生,高教版)
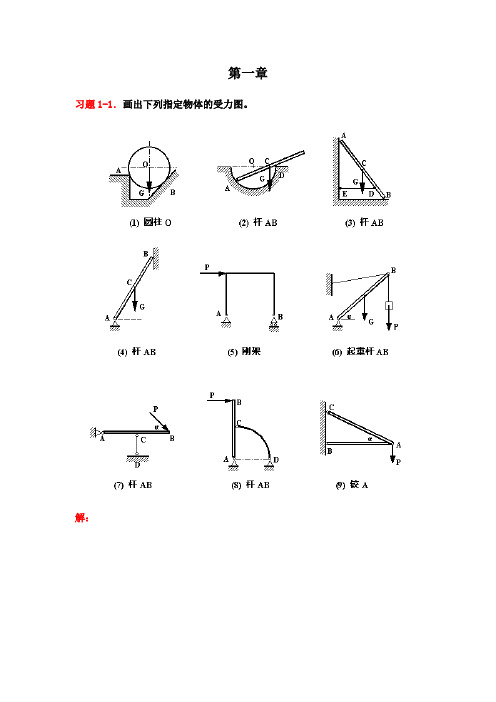
第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
《理论力学》课后习题解答(赫桐生版)
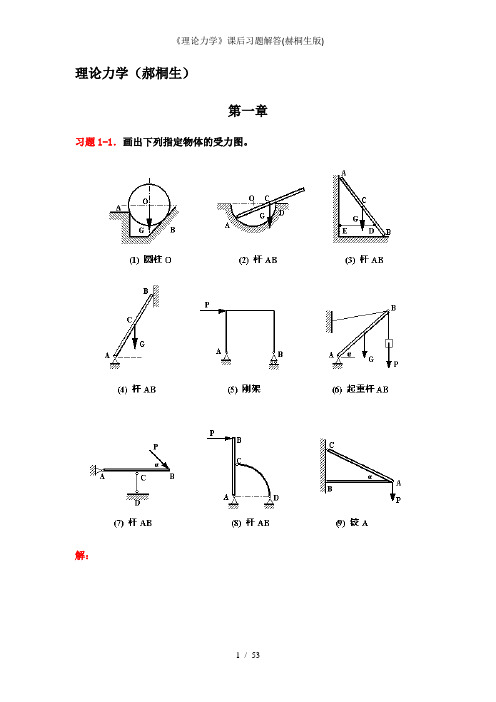
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学课后习题答案

理论力学课后习题答案1. 第一题题目:一个质点从初始点A沿着一条直线运动到达点A,在此过程中质点受到一个恒定的力A的作用。
求解质点从A 到A的位移A和速度A与时间A的关系。
解答:根据牛顿第二定律A=AA,我们可以得到质点在恒定力作用下的运动方程为 $F = m \\frac{dv}{dt}$。
即:$$F = m \\frac{dx}{dt}$$将方程变形可得:$$dx = \\frac{F}{m} dt$$对上式两边同时积分可得:$$\\int_{x_A}^{x_B} dx = \\frac{1}{m} \\int_0^t F dt$$化简后可得:$$x_B - x_A = \\frac{1}{m} \\int_0^t F dt$$即质点从初始点A移动到达点A时的位移A与时间A的关系为:$$x = x_A + \\frac{1}{m} \\int_0^t F dt$$2. 第二题题目:一个滑块在一个光滑的水平轨道上,质量为A,受到一根拉力为A的绳子的作用。
求解滑块的加速度A。
解答:根据牛顿第二定律A=AA,可以得到滑块的加速度A与拉力A的关系为 $a = \\frac{F}{m}$。
3. 第三题题目:一个质点在一个弹簧的作用下振动,弹簧的劲度系数为A,质量为A。
求解质点的振动周期A。
解答:质点在弹簧的作用下振动,其运动方程为 $m\\frac{d^2x}{dt^2} = -kx$,其中A为质点的位移。
对上式进行变形可得:$$\\frac{d^2x}{dt^2} = -\\frac{k}{m}x$$该微分方程的通解为 $x = A \\sin(\\sqrt{\\frac{k}{m}} t + \\phi)$,其中A为振幅,$\\phi$ 为相位角。
振动周期A可以通过求解动能和势能的平衡关系来得到。
在振动过程中,动能 $K = \\frac{1}{2} m v^2$ 和势能 $U =\\frac{1}{2} k x^2$ 之和保持不变。
理论力学课后习题解答

《理论力学》课后习题解答(赫桐生,高教版)(总53页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
理论力学课后习题解答附答案

5.27证取广义坐标
因为
又因为
所以
5.28解 如题5.28.1图
(1)小环的位置可以由角 唯一确定,因此体系的自由度 ,取广义坐标 ,广义速度 。小球的动能:
以 为势能零点,则小环势能
所以拉氏函数
(2)由哈密顿原理
故
所以
又由于
所以
因为 是任意的,所以有被积式为0,即
化简得
5.29解 参考5.23题,设 ,体系的拉氏函数
⑶小球动能
又由
①式得
设小球势能为V,取固定圆球中心O为零势点,则
小球拉氏函数
= ①
根据定义
有
根据正则方程
④
⑤
对式两边求时间得:
故小球球心切向加速度
5.25解根据第二章§2.3的公式有:
①
根据泊松括号的定义:
②
所以
同理可知:
,
由②得:
同理可得:
,
5.26解 由题5.25可知 的表达式
因为
故
同理可求得:
势能:
根据定义式
故
因为
所以 为第一积分.又
故
得 为第二个第一积分.
同理
即
得 为第三个第一积分.
5.23解如题5.23.1图,
由5.6题解得小球的动能
①
根据定义
②
得
③
根据哈密顿函数的定义
代入③式后可求得:
④
由正则方程得:
⑤
⑥
代入⑤得
整理得
5.24如题5.24.1图,
⑴小球的位置可由 确定,故自由度
⑵选广义坐标 ,广义速度 .
①
根据哈密顿原理
故
②
理论力学课后习题解答

《理论力学》课后习题解答(赫桐生,高教版)(总53页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
(完整版)理论力学答案(谢传峰版)
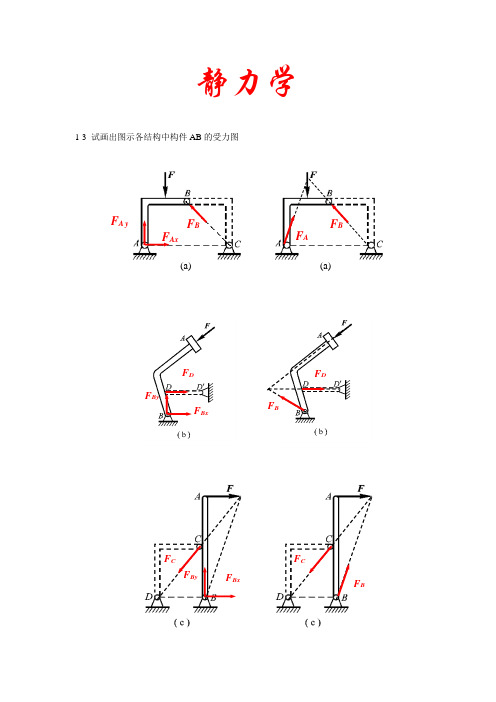
静力学1-3 试画出图示各结构中构件AB 的受力图F AxF A yF B(a)(a)F AF BF BF DF D F BxF ByF BxF CF BF CF By1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a1-5bF AxF A y F DF ByF A F BxF B F AF Ax F A y F DxF Dy WT EF CxF C yWF AxF A yF BxF B yF CxF C yF DxF DyF Bx F ByT EN’F BF DF A N F AF BF D1-8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示: 由共点力系平衡方程,对B 点有:∑=0x F 045cos 02=-BC F F 对C 点有:∑=0x F 030cos 01=-F F BC解以上二个方程可得:22163.1362F F F ==解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点上的力构成封闭的力多边形,如图所示。
对B 点由几何关系可知:0245cos BC F F =对C 点由几何关系可知:0130cos F F BC =解以上两式可得:2163.1F F =F ABF BC F CD 60o F 130o F 2 F BC45o F 2F BC F ABB45oy xF CD C60o F 130o F BC x y450302-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
理论力学第七版答案

8-5 杆OA 长l ,由推杆推动而在图面内绕点O 转动,如图所示。
假定推杆的速度为υ,其弯头高为a 。
试求杆端A 的速度的大小(表示为由推杆至点O 的距离x 的函数)。
题8-5图【知识要点】 点得速度合成定理和刚体的定轴转动。
【解题分析】 动点:曲杆上B ,动系:杆OA绝对运动:直线运动相对运动:直线运动牵连运动:定轴转动【解答】 取OA 杆为动系,曲杆上的点B 为动点v a = v e +v r大小: √ ? ?方向: √ √ √v a = v222222cos :a x vaa x v ax vav v v e e ea +=+=+==ωθη 8-10 平底顶杆凸轮机构如图所示,顶杆AB 可沿导轨上下移动,偏心圆盘绕轴O 转动,轴O 位于顶杆轴线上。
工作时顶杆的平底始终接触凸轮表面。
该凸轮半径为R ,偏心距OC =e ,凸轮绕轴O 转动的角速度为ω,OC 与水平线成夹角ϕ。
求当ϕ=0°时,顶杆的速度。
【知识要点】 点的速度合成定理【解题分析】 动点:点C ,动系:顶杆AB绝对运动:圆周运动相对运动:直线运动牵连运动:平行移动题8-10图【解答】 取轮心C 为动点,由速度合成定理有v a = v e +v r大小: √ ? ?方向: √ √ √解得: v a = v e , v r =0, v e =v a =ωe8-17 图示铰接四边形机构中,O 1A =O 2B =100mm ,又O 1 O 2=AB ,杆O 1A 以等角速度ω=2rad/s 绕O 1轴转动。
杆AB 上有一套筒C ,此筒与杆CD 相铰接。
机构的各部件都在同一铅直面内。
求当ϕ=60°时,杆CD 的速度和加速度。
题8-17图【知识要点】 点的运动速度和加速度合成定理【解题分析】 动点:套筒C,动系:杆AB绝对运动:直线运动相对运动:直线运动牵连运动:平行移动【解答】 取C 点为动点,杆AB 为动系(1)速度 v a =v e + v r , v e = v A =A O 1⋅ω s m v v e a /1.060cos 0=⋅=(2) 加速度 a a = a e +a r ,A O a a n A n e 12⋅==ω20/35.030cos s m a a n e a =⋅=8-20 图示偏心轮摇杆机构中,摇杆O ,A 借助弹簧压在半径为R 的偏心轮C 上。
《理论力学》习题三答案讲解

《理论力学》习题三答案一、单项选择题(本大题共30小题,每小题2分,共60分)1. 求解质点动力学问题时,质点的初始条件是用来( C )。
A 、分析力的变化规律; B 、建立质点运动微分方程; C 、确定积分常数; D 、分离积分变量。
2. 在图1所示圆锥摆中,球M 的质量为m ,绳长l ,若α角保持不变,则小球的法向加速度为( C )。
A 、αsin g ;B 、αcos g ;C 、αtan g ;D 、αtan gc 。
3. 已知某点的运动方程为2bt a S +=(S 以米计,t 以秒计,a 、b 为常数),则点的轨迹为( C )。
A 、是直线;B 、是曲线;C 、不能确定;D 、抛物线。
4. 如图2所示距地面H 的质点M ,具有水平初速度0v ,则该质点落地时的水平距离l 与( B )成正比。
A 、H ;B 、H ;C 、2H ;D 、3H 。
5. 一质量为m 的小球和地面碰撞,开始瞬时的速度为1v ,碰撞结束瞬时的速度为2v(如图3),若v v v ==21,则碰撞前后质点动量的变化值为( A )。
A 、mv ;B 、mv 2 ;C 、mv 3;D 、 0。
6. 一动点作平面曲线运动,若其速率不变,则其速度矢量与加速度矢量( B )。
A 、平行; B 、垂直; C 、夹角随时间变化; D 、不能确定。
7. 三棱柱重P ,放在光滑的水平面上,重Q 的匀质圆柱体静止释放后沿斜面作纯滚动,则系统在运动过程中( A )。
A 、沿水平方向动量守恒,机械能守恒;B 、动量守恒,机械能守恒;C 、沿水平方向动量守恒,机械能不守恒;D 、均不守恒。
图1图2图38. 动点M 沿其轨迹运动时,下列几种情况中,正确的应该是( A )。
A 、若始终有a v⊥,则必有v 的大小等于常量;B 、若始终有a v⊥,则点M 必作匀速圆周运动; C 、若某瞬时有v ∥a ,则点M 的轨迹必为直线;D 、若某瞬时有a 的大小为零,且点M 作曲线运动,则此时速度必等于零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、加减平衡力系公理不但适用于刚体,还适用于变形体。
(×)2、作用于刚体上三个力的作用线汇交于一点,该刚体必处于平衡状态。
(×)3、刚体是真实物体的一种抽象化的力学模型,在自然界中并不存在。
(√)4、凡是受两个力作用的刚体都是二力构件。
(×)5、力是滑移矢量,力沿其作用线滑移不会改变对物体的作用效果。
(×)6、若作用于刚体上的三个力组成平衡力系,那么此三力一定共面,但不一定交于一点。
(√)7、如果所作的受力图是一个显然不平衡的力系,那么受力图一定有错。
(×)8、如果作用在一个刚体上的力系对任何点主矩均不为零,该力系可以等效为一个力偶。
(×)9、作用在一个刚体上的任意两个力平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
(√)10、因为构成力偶的两个力满足F= - F’,所以力偶的合力等于零。
(×)11、用解析法求平面汇交力系的合力时,若选用不同的直角坐标系,则所求得的合力不同。
(×)12、力偶永远不能与一个力等效,共面的一个力与一个力偶总可以合成为一个力。
(√)13、力偶的作用效应用力偶矩来度量。
(√)14、力对于一点的矩不因力沿其作用线移动而改变。
(√)15、只要平面力偶的力偶矩保持不变,可将力偶的力和臂作相应的改变,而不影响其对刚体的效应。
(√)16、当力与轴共面时,力对该轴之矩等于零(√)17、在保持力偶矩不变的情况下,可任意改变力和力偶臂的大小,并可以在作用面内任意搬移(√)18、在任意力系中,若其力多边形自行封闭,则该任意力系的主矢为零。
(√)19、当平面一般力系向某点简化为力偶时,如果向另一点简化,则其结果是一样的。
(×)20、首尾相接构成一封闭力多边形的平面力系是平衡力系。
(×)21、若一平面力系对某点之主矩为零,且主矢亦为零,则该力系为一平衡力系。
(√)22、如果某平面力系由多个力偶和一个力组成,则该力系一定不是平衡力系(√)23、任一力系如果向A、B两点简化的主矩均等于零,则力系的主矢向与AB连线垂直的轴的投影一定为零(√)24、力系的主矢与简化中心的位置有关,而力系的主矩与简化中心的位置无关(√)25、在空间问题中,力对轴之矩是代数量,而力对点之矩是矢量。
(√)26、物体的重心可能不在物体之内。
(√)27、力沿坐标轴分解就是力向坐标轴投影。
(×)28、当力与轴共面时,力对该轴之矩等于零。
(√)29、在空间问题中,力偶对刚体的作用完全由力偶矩矢决定。
(×)30、将一空间力系向某点简化,若所得的主矢和主矩正交,则此力系简化的最后结果为一合力(×)31、在两个相互作用的粗糙表面之间,只要作用的法向反力不为零,两者之间就一定相互作用有摩擦力,且F=fN(×)32、正压力一定等于物体的重力(×)33、只要两物体接触面之间不光滑,并有正压力作用,则接触面处的摩擦力的值一定等于NfF (×)34、只要接触面的全反力与法向反力的夹角不超过摩擦角,则物体与接触面之间就不会发生相对滑动(×)35、在有摩擦的情况下,全约束力与法向约束力之间的夹角称为摩擦角。
(×)36、点作曲线运动时,其加速度的大小等于速度的大小对时间的导数。
(×)37、只要点做曲线运动,则其加速度就一定不等于零(×)38、点做匀速运动时,不论其轨迹如何,点的加速度恒等于零(×)39、用自然法求点的速度、加速度时,需已知点的轨迹和点沿轨迹的运动规律(√)40、点做直线运动时,法向加速度等于零(√)41、在自然坐标系中,如果速度v = 常数,则加速度a = 0。
(×)42、作曲线运动的动点在某瞬时的法向加速度为零,则运动其轨迹在该点的曲率必为零。
(×)43、若与垂直,则v 必为常量(√) 44、若与平行,则点的轨迹必为直线(√) 45、点的<0,τa <0则点作减速运动(×)46、当刚体绕定轴转动时,如ω<0 ,ε<0,则刚体愈转愈快(√) 47、刚体做平动时,其上各点的轨迹均为直线(×) 48、刚体绕定轴转动时,其上各点的轨迹一定是圆(×) 49、刚体作定轴转动时,其转动轴一定在刚体内。
(×) 50、列车沿直线轨道行驶时,车厢和车轮的运动都是平动。
(×) 51、刚体作平动时,刚体上各点的轨迹均为直线。
(×)52、刚体作平动时,其上各点的轨迹可以是直线,可以是平面曲线,也可以是空间曲线。
(√) 53、两个作定轴转动的刚体,若其角加速度始终相等,则其转动方程相同。
(√ ) 54、刚体平动时,若刚体上任一点的运动已知,则其它各点的运动随之确定。
(√)55、在同一瞬时,定轴转动刚体内所有各点的全加速度与该点发法向加速度的夹角均相等(√) 56、动点做合成运动时,它的牵连速度就是动参考系的速度(×) 57、点的合成运动仅指点同时相对两个物体的运动。
(×)58、在复合运动问题中,点的相对加速度是其相对速度对时间的相对导数。
(√)59、动点的速度合成与牵连运动的性质无关,而动点的加速度合成则与牵连运动的性质有关(√) 60、动点速度的方向总是与其运动的方向一致。
(√)61、牵连运动是指动系上在该瞬时与动点重合的点相对于动系的运动。
(×) 62、在复合运动问题中,相对加速度是相对速度对时间的绝对导数。
(×) 63、纯滚动时接触点的滑动摩擦力不做功。
(√)64、在平面运动的刚体上可以找出无数根作平动的直线(√) 65、瞬心如不在做平面运动的刚体上,则该刚体无瞬心(×)66、刚体运动时,若体内任一直线均保持与其最初位置平行,则此刚体做平面运动(×) 67、刚体作平面运动时,平面图形内两点的速度在任意轴上的投影相等。
(×)68、刚体作平面运动时,如果刚体的瞬时角速度不等于零,则刚体的瞬时速度中心一定存在。
(√) 69、若作用于质点上的合力的大小与方向均不随时间改变,则质点的运动轨迹一定为直线(×) 70、质点的速度越大,所受的力也越大(×)71、质点在常力作用下,一定做匀加速度直线运动(×) 72、已知质点的质量和作用于质点的力,质点的运动规律就完全确定。
(×) 73、两自由质点,仅其运动微分方程相同,还不能肯定其运动规律相同。
(√) 74、一个质点的速度越大,该瞬时它所受到的作用力越大(×)。
75、质点系的内力不能改变质点系的动量。
(√)76、质点系的动量等于零,那么质点系每个质点的动量依然必等于零(×)77、如果质点系所受的力对某点(或轴)的矩恒保持不变,这就是质点系的动量矩守恒定律(×) 78、质点系中各质点都处于静止时,质点系的动量为零。
于是可知如果质点系的动量为零,则质点系中各质点必都静止。
(×) 79、设JA 和JB 分别是细长杆对通过A 、B 两端点的一对平行轴的转动惯量,则:JB=JA+md2(×) 80、如果作用于质点系上的外力对某固定点的主矩不为零,那么质点系对过该点的任何轴的动量矩一定不守恒。
(×) 81、质点系的内力不能改变质点系的动量与动量矩(√) 82、质点的速度方向就是质点的动能方向(×)83、由于质点系的内力成对出现,所以内力作功之和恒等于零(×)1、在下述公理、法则、原理中,只适于刚体的有 ③加减平衡力系公理 ④力的可传性原理2、加减平衡力系公理适用于(B)刚体3、图中所示的某汇交力中各力系之间的关系是(C ) F 1+F 2=F 3+F 42、如图所示的平面汇交力系的力多边形表示:(A )力系的合力等于03、力F 在成1200角的Ox 、Oy 轴上的投影为F 21,而沿着Ox 、Oy 轴上的分力的大小为(C ) F1、等边三角板ABC ,边长为b ,今沿其边缘作用三个大小均为F 的力,方向如图所示。
问这三个力向点A 简化的主矢量和主矩的大小等于多少?( B )2、如图所示轮子,在O 点由轴承支座约束,受力和力偶的作用而平衡,下列说法正确的是(B ) 力P 和轴承O 的支座反力组成的力偶与轮子上的力偶相平衡 3、已知刚体某平面内点处作用一个力,同时在该平面内还作 用一个力偶矩为的力偶, 如图所示。
若将此力与力偶简化,其最后的结果是:(B ) 简化为一个合力(作用线不通过点) 1、刚体在五个空间力的作用下处于平衡,若其中有四个作用线汇交于一点, 则第五个力的作用线(A ) 一定通过该汇交点 2、空间汇交力系的独立平衡方程数目为( C ) 3 3、空间力偶矩是 ( D ) 自由矢量。
4、正立方体的顶角上作用着六个大小相等的力,此力系向任一点简化 的结果是( A )主矢等于零,主矩不等于5、已知点的坐标为(5,5,5),如图所示,力在 y 轴上的投影为:(C )6空间力系向三个两两正交的坐标平面投影,得到三个平面一般力系,则其独立的平衡方程数目为(B )6 1、物块A 重W ,它与铅垂面的摩擦角为200,今在物块A 上力F , 且F =W , 力F 与水平线的夹角为600,如图所示。
A 所处的状态为:(C )稳定平衡状态 2、库仑定律N f F ⋅=max 适用于( C )临界平衡状态 3、如图所示若尖劈两侧与槽之间的摩擦角均为,则欲使尖劈被打入后不致自动滑出,角应为多大?( C )4、物块重50N ,在水平向左的推力作用下,靠在铅直墙面上,若如图所示两种情况下,物块与墙面之间的静摩擦因数都是0.3,试问物块是否处于静止状态?( C )(1)运动,(2)静止 1、动点沿半径R=5cm 的圆周运动,其运动方程为s=2t (其中s 以cm 计, t 以s 计),则动点加速度的大小为(C )4/5 cm/s 22、已知动点的速度和切向加速度分别为0,0><v a τ,由此可知(C )点做减速运动3、点在运动过程中,恒有τa =常量,0≠n a ,点做何种运动?(B )点做匀变速曲线运动4、设方程j t y i t x r t f s )()()(+==和表示同一个点的运动,下列四个等式中正确的是(A )dtdr dt ds =; 5、在下列四种说法中,正确的是(C ) 当dtdv与v 同号时,动点做加速运动 1、点作圆周运动,如果知道其法向加速度越来越小,则点的运动速度:(A )越来越小 2、汽车左转弯时,已知车身作定轴转动,汽车右前灯的速度大小为,汽车左前灯的速度大小为,、之间的距离为,则汽车定轴转动的角速度大小为(B )1、水平管以角速度 ω 绕铅垂轴转动,管内有一小球以速度v=r ω沿管运动,r 为小球到 转轴的距离,球的绝对速度是( C )2r ω2、在点的合成运动问题中,当牵连运动为定轴转动时(B )。
