F__学习_陈世民理论力学简明教程(第二版)答案_第六章
(R − r) g [m1 tan ϕ − m1 tan θ − m2 tan ϕ − m2 tan θ ] cos ϕ cos θ
r (R − r) − r
2 2
代入 tan ϕ = 得： tan θ =
=
r R − 2 Rr
2
m1 − m2 tan ϕ m1 + m2
θ = arctan
(m1 − m2 )r (m1 + m2 ) R 2 − 2 Rr
t =0
=
2 6 r 3
皮周长： l = 3d + 2π r = 3 3 4r 2 − h2 + 2π r 依虚功原理： δW = mgδ h + FT δl = mgδ h − 则依： 代入： 得： FT =
δW 3 3h = mg − FT = 0 δh 4r 2 − h 2
h
t =0
3 3h 4r 2 − h 2
2 & 积分得： θ =
&
2m g 2m + m′r
4mgθ (2m + m′ )r
L r
& 当完全释放（ θ = ）时： ω = θ
L θ= r
=
2 mgl r 2m + m′
ks 2 ， s 为绳子的伸长 2
８ ．上题中，如果绳子具有弹性，弹性势能为
证明重物 m 的运动为维持恒定的加速运动上附加一角频率为 ω 的 振动。其中 ω 2 = k
微振动，取近似 sin θ : θ ， 得：
积分： 则： T( = 周期 )
θ = A cos(
m + 2m′g t) + B m + 4m′ l
（Ａ ，Ｂ 为积分常数）
2π m + 2m′g = 2π ω m + 4m′ l
７ ． 一半径为 r 质量为 m′的圆柱形轱辘，其轴线沿水平方向。 轱辘上绕有长为 l 的轻绳，绳的自由端系一质量为 m 的重物。 初始时绳子完全绕在轱辘上，体系静止。尔后重物下落带动轱 辘转动。写出此力学系列化的拉格朗日函数，并求出绳子完全 释放时轱辘转动角速度的大小。 解：如右图，取 θ 为转过的角度， x 为下降的距离。有： x = rθ 。 取Ｏ 为参照点： V = −mgx = −mgrθ
δW = −3mgl sin α + 2 FT l cos α δα
= −3mgl sin α + mgl tan cos α =0
可得：
tan
= 3 tan α
３ ． 用轻质橡皮圈捆扎三个置于光滑水平桌面上的相同球体， 捆扎的高度与还需心的高度相同。将第四个同样的球体置于三 球之上。由虚功原理求出橡皮圈中的张力。已知每个球体的重 量为 P 。 解：如右图所示。取三个桌面上球的球心所在面，及四球心立体 结构可分析得： d = 3 4r 2 − h 2 ; h
５ ． 一半径为 R 的半球形碗内装有两个质量分别为 m1 和 m2 的球 体，它们的半径同为 r （ 2r < R ） 。用虚功原理求出这两个球体 在碗中平衡时它们的连心线与水平线间的夹角 解：如右图所示，以 ｏ 为参照点，取 ∠ O2OO1 = ϕ ， O2O1 与水平线 角为 θ 。则有： hO = −( R − r ) cos(ϕ −θ ), hO = −( R − r ) cos(ϕ + θ )
δW = mgδ h + kxδ x
= −σ gl0 R sin θδθ + k (2π R sin θ − l0 )g 2π R cos θδθ
δW = −σ gl0 R sin θ + 2π 2 R 2 k sin 2θ − 2π kRl0 cos θ = 0 δθ
化简得： sin 2θ −
l0 σ gl cos θ − 2 0 sin θ = 0 πR 2π Rk
ks 2 1 ks 2 2 & ； T = m′ r 2θ + 2 4 2
(
)
1 2 1 ks 2 2 & & &+ ( & = ms m′ + 2m ) r 2θ + mrs θ − + mg ( s + rθ ) 2 4 2 d ∂L ∂L 1 & & & & = ( m′ + 2m ) r 2θ + mrs − mgr = 0 − dt ∂θ & ∂θ 2 可得： d ∂L − ∂L = ms & & & & + mrθ + ks − mg = 0 & dt ∂ s ∂ s
d ∂T ∂T ( )− = Qα & dt ∂q ∂qα α
(a = 1, 2,3,L , s )
在保守力下，取拉氏数 L = T −V 方程为：
d ∂L ∂L ( )− =0 & dt ∂q ∂qα α
若拉氏数中 L 不显含广义坐标 q 即 循环积分： ４ 微振动
p = ∂L = const & ∂q
m′ + 2m ) ( 。求出此种振动的振幅。设初始时绳子 mm′
完全绕在轱辘上，体系静止，尔后释放 解：参数同上题，则可得： x = s + rθ ； V = −mgx + 则： L = T −V
2 1 1 ks 2 2 & & & = m′ r 2θ + m s + rθ + mg ( s + rθ ) − 4 2 2
，则：
∂L =0 ∂q
非线性系统在小角度近似下，对拉氏方程的应用 ５ 哈密顿函数与正则方程 （１ ）哈密顿函数
& H ( p, q, t ) = −L + ∑ pα q α
α =1 s
式中 pα =
∂T ∂L 为广义坐标动量 = & & ∂q ∂q α α
（２ ）正则方程
& q α = ∂H ∂Pα ∂H ∂qα
(a = 1, 2,3,L , s )
& p α =−
∂H ∂L =− ∂t ∂t
&=− 若哈氏函数 H 中不显含广义坐标 q ，则： p
∂H =0 ∂q
即：循环积分
p =
∂T = const & ∂q
s
& 在稳定条件下（Ｈ 中不显含 t ） ， ∑ pα g q α = 2T 则有能量积分：
α =1
4(l 2 − 2r 2 ) 两边平方并代入 * 可解得： l0 = l
l 4 π 4 α 2 l dV π α = mg[ − 0 cos( − ) + r sin α ] = 0 dα 4 4 2
l 2
l 2
π 4
α 2
２ ． 用绳子等距离地在定点 Ｏ 处悬挂两个相同的匀质球， 两球 之上另放置一相同的球体，如图。已知分别悬挂两球的绳长都 是 l 。用虚功原理求出 α 角与 角之间的关系。 解：依受力分析知 FT =
=
π α − 4 2
π l 2 − 2r 2 依余弦定理： sin α = − cos(α + ) = LL * 2 2r 2
知：杆的势能： V = mg ( 0 sin − r cos α ) = mg[ 0 sin( − ) − r cos α ] 因静平衡，应用虚功原理得： 得： 0 cos( − ) = r sin α
mg tan 2
且： δW = −2mgδ (l cos α ) + mgδ (l cos α − 2r cos ) + 2 FT δ (l sin α )
= −2mgl sin αδα − mgl sin αδα + 2mgl sin δ + 2 FT l cos αδα
则：依虚功原理达到平衡时有：
第六章 分析力学
滚滚长江东逝水，浪花淘尽英雄。达朗贝尔， 拉 格朗日，哈密顿等许多前贤相聚于此 冲击波 叱咤风云。 ［ 要点分析与总结］
１ 虚功原理： （平衡时） 理想条件下，力学系的平衡条件是各质 点上的主动力所作的 虚功之和为零：
δW = ∑ Fi •δ ri = 0
i =1 n
力学论剑 ， 其 。微分方程将
= dU
依上亦可得：
pα = ∂U ∂qα ∂U ∂Qα ∂U ∂t
Pα = −
H* −H =
U 为母函数，当 Pα ， Qα ， H 不显含 t 时，
以上条件等于： ∑ ( pα dqα − Pα dQα ) = dU
α =1
s
〈析〉 ： 正则变换妙在不解方程而使问题出解。 得意忘形 到极点了。
［ 解题演示］
６ ． 一轻杆长为 2l ，一端光滑铰链于固定点 Ｏ ， 另一端点及中点 分别焊接有质量为 m′ 和 m 的小球。杆可在铅直平面内绕固定点 摆动。写出此力学 系统的拉格朗日函数，并求出其作微小摆 动时的周期。 解：以 Ｏ 为参照点，取杆与竖直方向夹角为θ 。则有：
V = −mgl cos θ + (−m′ g 2l cos θ ) = −(m + 2m′ ) gl cos θ 1 1 & m + 4m′ 2 & 2 2 & T = J m′ θ + J mθ = l θ2 2 2 2
拉氏函数：
L = T −V =
m + 4m′ 2 & l θ 2 + ( m + 2 m′ ) gl cos θ 2
解拉氏方程：
d ∂L ∂L & & ( & )− = ( m + 4 m′ )l 2θ + ( m + 2 m′ ) gl sin θ = 0 dt ∂θ ∂θ m + 2m′gθ & & θ =− m + 4 m′ l
陈世民理论力学简明教程(第二版)课后答案-精选.pdf
。
解：建立自然坐标系有：
a
d e
dt
2
en
且： d
dt d
2
2k
2kd
ds 2k
dt
ds 2k
ds dt
d
d 2k
dt
积分得： ue 2k （代入 0 u ） 又因为： y 2 2px 在 (p 2 ,p) 点处斜率：
k 1 dy1
d 2px
dx
x
p 2
dx
在 ( p 2 , p) 点处斜率：
p 1
水平线之间的夹角又为 角度时所需时间。
解：依牛顿第二运动定律有： m x mk x , m y mg mk y
积分并代入初始条件： t 0 时： 0x 0 sin , 0 y
解得： x 0 cos e kt , y ( 0 sin
g )e
kt
g
k
k
当再次夹角为 时： y tan
x
0 cos
可解出： t
无滑动地滚动，如图所示，求圆盘边上 M点的深度 υ和加速度 α（用
参量 θ，Ψ表示）。
解：依题知：
Байду номын сангаас
r Rr
r Rr
且 O点处： ek cos( )er sin( )e
则：
rM rO O rOM
(R r)eR rer
[(R r)cos(
) r]er (R r)sin(
)e
rM
rM (
)sin(
)er [(R r)cos(
由 r e t,
t 得： r e t ,
且设： rer r e
则： 得： e
en
r2
2
简明材料力学第二版课后答案
简明材料力学第二版课后答案1. 第一章。
1.1 选择题。
1. A。
2. B。
3. C。
4. D。
5. A。
1.2 填空题。
1. 应力。
2. 变形。
3. 弹性模量。
4. 泊松比。
5. 线弹性。
1.3 简答题。
1. 什么是应力？应力是单位面积上的内力。
2. 什么是应变？应变是材料单位长度上的变形量。
3. 弹性模量的意义是什么？弹性模量是材料在弹性阶段的应力和应变之比，代表了材料的刚度。
4. 什么是泊松比？泊松比是材料在拉伸时横向收缩的比例。
5. 什么是线弹性？线弹性是指材料在应力小于屈服强度时，应力和应变成正比。
2. 第二章。
2.1 选择题。
1. C。
2. A。
3. D。
4. B。
5. C。
2.2 填空题。
1. 弹性极限。
2. 屈服强度。
3. 断裂强度。
4. 韧性。
5. 脆性。
2.3 简答题。
1. 什么是弹性极限？弹性极限是材料在拉伸时，超过该极限会发生塑性变形。
2. 什么是屈服强度？屈服强度是材料在拉伸时开始发生塑性变形的应力值。
3. 断裂强度和韧性有何区别？断裂强度是材料在拉伸时发生断裂的最大应力值，而韧性是材料吸收能量的能力。
4. 什么是脆性？脆性是指材料在受力时发生突然断裂的性质。
3. 第三章。
3.1 计算题。
1. 根据公式σ=F/A，计算出应力值。
2. 利用杨氏模量公式计算材料的弹性模量。
3. 根据泊松比公式计算材料的泊松比值。
3.2 简答题。
1. 什么是拉伸？拉伸是指材料在受力时发生长度增加的现象。
2. 什么是压缩？压缩是指材料在受力时发生长度减小的现象。
3. 什么是剪切？剪切是指材料在受力时发生形状变化但体积不变的现象。
4. 第四章。
4.1 计算题。
1. 根据应变-位移曲线计算出材料的弹性模量。
2. 根据拉伸试验数据计算出材料的屈服强度。
3. 利用断裂强度公式计算出材料的断裂强度值。
4.2 简答题。
1. 什么是应力-应变曲线？应力-应变曲线是材料在受力时应力和应变之间的关系曲线。
2. 什么是屈服点？屈服点是应力-应变曲线上的一个特殊点，表示材料开始发生塑性变形的位置。
陈世民理论力学简明教程(第二版)课后答案
第零章 数学准备一 泰勒展开式 1 二项式的展开()()()()()m23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++！！2 一般函数的展开()()()()()()()()230000000f x f x f x f x f x x-x x-x x-x 123!''''''=++++！！特别:00x =时, ()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++！！3 二元函数的展开(x=y=0处)()()00f f f x y f 0x+y x y ⎛⎫∂∂=++ ⎪∂∂⎝⎭，22222000221f f f x 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭！评注：以上方法多用于近似处理与平衡态处的非线性问题向线>性问题的转化。
在理论力问题的简单处理中，一般只需近似到三阶以内。
二 常微分方程1 一阶非齐次常微分方程： ()()x x y+P y=Q通解：()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰注：()()(),P x dxP x dx Q x e dx ⎰±⎰⎰积分时不带任意常数，()x Q 可为常数。
2 一个特殊二阶微分方程2y A y B =-+ 通解：()02B y=K cos Ax+Aθ+注：0,K θ为由初始条件决定的常量 3 ,4 二阶非齐次常微分方程 ()x y ay by f ++=通解：*y y y =+；y 为对应齐次方程的特解，*y 为非齐次方程的一个特解。
非齐次方程的一个特解 （1） 对应齐次方程0y ay by ++=设x y e λ=得特征方程2a b 0λλ++=。
解出特解为1λ，2λ。
*若12R λλ≠∈则1x 1y e λ=，2x 2y e λ=；12x x 12y c e c e λλ=+*若12R λλ=∈则1x 1y e λ=，1x 2y xe λ=； 1x 12y e (c xc )λ=+*若12i λαβ=±则x 1y e cos x αβ=，x 2y e sin x αβ=；x 12y e (c cos x c sin x)αββ=+（2） "（3） 若()2000x f a x b x c =++为二次多项式*b 0≠时，可设*2y Ax Bx C =++ *b 0≠时，可设*32y Ax Bx Cx D =+++注：以上1c ,2c ,A,B,C,D 均为常数，由初始条件决定。
理论力学第六章习题答案
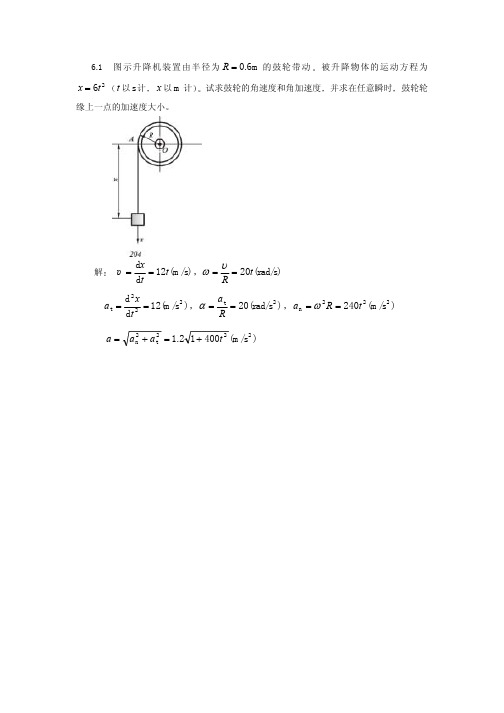
解 y x
a
A 动系圆环
a a = a rn + a en + a k
a ay = −rω 2 − 3rω 2 − 2rω 2 = −6rω 2 a ax = 0
B 动系圆环
a a = a rn + aen + a k
y x b y x
e a ay = −a n ( 2 / 5 ) = − 2 rω 2
o
曲柄长 OA = r
并以匀角速度 ω 绕 O 轴转动
o
装在水平
杆上的滑槽 DE 与水平线成 60 角 杆 BC 的速度
试求当曲柄与水平轴的交角分别为 ϕ = 0
30o 时
解
以 A 为动点
以 BC 杆为动系 有
va = ve + vr
在 ϕ = 0° 时 矢量右如图
υ BC = v e =
3 3 va = ωr 3 3
a a = a an + a at = a e + a rt + a rn + a c
式中各矢量如图 把各矢量分别向 x 方向和 y 方向投影得:
a an cos 60° + a at cos 30° = − a e cos 30° − a r cos 30° + a c cos 60° − a rn cos 60° a at sin 30° − a an sin 60° = − a e sin 30° + a rt sin 30° + a c sin 60° − a rn sin 60°
齿 条 又 带 动 半 径 为 0.1m 的 齿 轮 D 绕 固 定 轴 O1 转 动
ω = 5rad/s
概率论与数理统计(茆诗松)第二版课后第六章习题参考答案
=
1 12n
>
Var⎢⎣⎡
1 2
( X (1)
+
X (n) )⎥⎦⎤
=
2(n
1 + 1)(n
+
2)
，
故
1 2
( X (1)
+
X (n) )
比样本均值
X
更有效．
6．
设
X1,
X2,
X3
服从均匀分布
U
(0,
θ
)，试证
4 3
X (3) 及 4X (1)都是θ
的无偏估计量，哪个更有效？
解：因总体 X 的密度函数与分布函数分别为
且(Y (1), Y (n))的联合密度函数为 p1n ( y(1) , y(n) ) = n(n −1)[FY ( y(n) ) − FY ( y(1) )]n−2 pY ( y(1) ) pY ( y )Ι (n) y(1)<y(n)
=
n(n
− 1)( y(n)
−
y ) Ι n−2
(1)
0< y(1) < y( n) <1
n
∑ 4． 设总体 X ~ N (µ , σ 2)，X1, …, Xn 是来自该总体的一个样本．试确定常数 c 使 c ( X i+1 − X i )2 为σ 2 的无 i=1
偏估计． 解：因 E[(Xi + 1 − Xi )2 ] = Var (Xi + 1 − Xi ) + [E(Xi + 1 − Xi )]2 = Var (Xi + 1) + Var (Xi ) + [E(Xi + 1) − E(Xi )]2 = 2σ 2，
理论力学(陈世民)答案打印稿
第零章 数学准备一 泰勒展开式 1 二项式的展开()()()()()m23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++ ！！2 一般函数的展开 ()()()()()()()()230000000f x f x f x f x f x x-x x-x x-x 123!''''''=++++ ！！特别:00x =时, ()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++ ！！3 二元函数的展开(x=y=0处) ()()00fff x y f 0x+y xy ⎛⎫∂∂=++⎪∂∂⎝⎭，22222000221fffx 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭！ 评注：以上方法多用于近似处理与平衡态处的非线性问题向线性问题的转化。
在理论力问题的简单处理中，一般只需近似到三阶以内。
二 常微分方程1一阶非齐次常微分方程：()()x x y+P y=Q通解：()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰ 注：()()(),P x dxP x dx Q x e dx ⎰±⎰⎰积分时不带任意常数，()x Q 可为常数。
2一个特殊二阶微分方程2y A y B =-+ 通解：()02B y=K cos A x+Aθ+注：0,K θ为由初始条件决定的常量 3二阶非齐次常微分方程()x y ayby f ++= 通解：*y y y =+；y 为对应齐次方程的特解，*y 为非齐次方程的一个特解。
非齐次方程的一个特解 （1） 对应齐次方程0y ayby ++=设x y e λ=得特征方程2a b 0λλ++=。
解出特解为1λ，2λ。
*若12R λλ≠∈则1x 1y e λ=，2x 2y e λ=；12x x 12y c e c e λλ=+*若12R λλ=∈则1x 1y e λ=，1x 2y xe λ=； 1x 12y e (c xc )λ=+*若12i λαβ=±则 x 1y e cos x αβ=， x 2y e sin x αβ=；x12y e(c cos x c sin x )αββ=+（2） 若()2000x f a x b x c =++为二次多项式*b 0≠时，可设*2y Ax Bx C =++ *b 0≠时，可设*32y Ax Bx C x D =+++注：以上1c ,2c ,A,B,C,D 均为常数，由初始条件决定。
物理学专业理论力学简明教程(第二版)-----陈世民答案
【解题演示】1 细杆OL 绕固定点O 以匀角速率ω转动，并推动小环C 在固定的钢丝AB 上滑动，O 点与钢丝间的垂直距离为d ，如图所示。
求小环的速度υ和加速度a。
解：依几何关系知：x d tan θ=又因为：222d d x xi i i cos dωυωθ+===故：22222(d x )x a 2xx i i d d ωυω+=== 2 椭圆规尺AB 的两端点分别沿相互垂直的直线O χ与Oy 滑动，已知B 端以匀速c 运动，如图所示。
求椭圆规尺上M 点的轨道方程、速度及加速度的大小υ与α。
解：依题知：B y (b d)cos θ=+且：B yC (b d)sin θθ=-=-+ 得：C*(b d)sin θθ=+又因M 点位置：M M x bsin ,y dcos θθ==故有：M M M xi |y j b cos i d sin j υθθθθ=+=-代入（*）式得：M bccot dc i j b d b dθυ=-++即：υ=2M M222bc bc a i i (b d)sin (b d)sin θυθθ==-=++1 一半径为r 的圆盘以匀角速率ω沿一直线滚动，如图所示。
求圆盘边上任意一点M 的速度υ 和加速度a（以O 、M 点的连线与铅直线间的夹角θ表示）；并证明加速度矢量总是沿圆盘半径指向圆心。
解：设O 点坐标为（0Rt x ,R ω+）。
则M 点坐标为（0Rt x Rsin ,R R cos ωθθ+++）故：M M M xi y j (R R cos )i R υωωθ=+=+-222M M a R sin i R cos j R (sin i cos j)υωθωθωθθ==--=-+2 一半径为r 的圆盘以匀角深度ω在一半经为R 的固定圆形槽内作无滑动地滚动，如图所示，求圆盘边上M 点的深度υ和加速度α（用参量θ，Ψ表示）。
解：依题知：r rR rR rθωϕ=-=---且O 点处：k r e cos()e sin()e θθϕθϕ=---则：M O O OMR rr r r r (R r)e re [(R r)cos()r]e (R r)sin()e θθϕθϕ'=+=-+=--+---M M r rr r r ()sin()e [(R r)cos()r]e (R r)()cos()e (R r)sin()e r sin()e r [1cos()]e θθθυϕθθϕθϕθϕθθϕθθϕωθϕωθϕ==--+--+----+--=--+--(){}r rr r 2r a r ()cos()e r sin()e r ()sin()e r [1cos()]e r cos()e r sin()e r e r r R r cos()e r sin()e R r θθθθυωϕθθϕωθθϕωϕθθϕωθθϕωϕθϕωϕθϕωθωθϕθϕ==----------=----=---+-⎡⎤⎣⎦-3 已知某质点的运动规律为：y=bt,at θ=,a 和b 都是非零常数。
理论力学(陈世民)答案
第零章 数学准备一 泰勒展开式 1 二项式的展开()()()()()m23m m-1m m-1m-2f x 1x 1mx+x x 23=+=+++ ！！2 一般函数的展开()()()()()()()()230000000f x f x f x f x f x x-x x-x x-x 123!''''''=++++ ！！特别:00x =时, ()()()()()23f 0f 0f 0f x f 0123!x x x ''''''=++++ ！！ 3 二元函数的展开(x=y=0处)()()00f f f x y f 0x+y x y ⎛⎫∂∂=++ ⎪∂∂⎝⎭，22222000221f f f x 2xy+y 2x x y y ⎛⎫∂∂∂++ ⎪ ⎪∂∂∂∂⎝⎭！ 评注：以上方法多用于近似处理与平衡态处的非线性问题向线性问题的转化。
在理论力问题的简单处理中，一般只需近似到三阶以内。
二 常微分方程1一阶非齐次常微分方程： ()()x x y+P y=Q通解：()()()P x dx P x dx y e c Q x e dx -⎛⎫⎰⎰=+ ⎪⎝⎭⎰注：()()(),P x dxP x dx Q x e dx ⎰±⎰⎰积分时不带任意常数，()x Q 可为常数。
2 一个特殊二阶微分方程2yA yB =-+ 通解：()02By=K cos Ax+A θ+注：0,K θ为由初始条件决定的常量 3二阶非齐次常微分方程()x yay by f ++= 通解：*y y y =+；y 为对应齐次方程的特解，*y 为非齐次方程的一个特解。
非齐次方程的一个特解 （1） 对应齐次方程0yay by ++=设x y e λ=得特征方程2a b 0λλ++=。
解出特解为1λ，2λ。
*若12R λλ≠∈则1x 1y e λ=，2x 2y e λ=；12x x 12y c e c e λλ=+ *若12R λλ=∈则1x 1y e λ=，1x 2y xe λ=； 1x 12y e (c xc )λ=+*若12i λαβ=±则 x 1y e cos x αβ=， x 2y e sin x αβ=；x 12y e (c cos x c sin x)αββ=+（2） 若()2000x f a x b x c =++为二次多项式*b 0≠时，可设*2y Ax Bx C =++ *b 0≠时，可设*32y Ax Bx Cx D =+++注：以上1c ,2c ,A,B,C,D 均为常数，由初始条件决定。
陈世民理论力学式
第一章 牛顿力学的基本定律1 质点运动的描述（1） 直线坐标系r xi yj zkr xiyj zk a r xi yj zkυυ=++==++===++r r r rr r r r r &&&&&r r r r r r &&&&&&&&& （2） 平面极坐标系r r 2r r re re r e a (r r )e (r 2r )e θθυθθθθ==+=-++r r r r r &&r r r &&&&&&& （3） 自然坐标系t2t ne v a e e υυυρ==+rrrr r & （4） 柱坐标系2t nz v a e e e e ze ρθυρυρρθ=+=++r r r &rrr r&&&2 牛顿定律惯性定律的矢量表述22d r ma m F dt==rrr（1） 直角坐标系中x y z F mxF my F mz⎧=⎪=⎨⎪=⎩&&&&&&（2） 极挫标系中2r kF m(r r )F m(r 2r )F 0θθθθ⎧=-⎪=+⎨⎪=⎩&&&&&&& （3） 直角坐标系中x y z F mxF my F mz⎧=⎪=⎨⎪=⎩&&&&&&3 质点运动的基本定理几个量的定义：动量 P m υ=rr角动量 L r m r P υ=⨯=⨯rrr rr冲量 21I P P =-r r r力矩 M r F =⨯r r r冲量矩 21t 21t H I I Mdt =-=⎰r r r r 动能 21T m 2υ=（1） 动量定理 dPF dt=r r（2） 动量矩定理 dLM dt=r r（3） 动能定理 d dTF m dt dtυυυ==r r r r g g 4机戒能守恒定理T+V=E1 细杆OL 绕固定点O 以匀角速率ω转动，并推动小环C 在固定的钢丝AB 上滑动，O 点与钢丝间的垂直距离为d ，如图所示。
《物理学简明教程》课后习题及答案
第一章 质点运动学1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t ＋Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ｜r ｜),平均速度为v ,平均速率为v ．(1) 根据上述情况,则必有( )(A) ｜Δr ｜= Δs = Δr(B) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d s ≠ d r(C) ｜Δr ｜≠ Δr ≠ Δs ,当Δt →0 时有｜d r ｜= d r ≠ d s(D) ｜Δr ｜≠ Δs ≠ Δr ,当Δt →0 时有｜d r ｜= d r = d s(2) 根据上述情况,则必有( )(A) ｜v ｜= v ,｜v ｜= v (B) ｜v ｜≠v ,｜v ｜≠ v(C) ｜v ｜= v ,｜v ｜≠ v (D) ｜v ｜≠v ,｜v ｜= v分析与解 (1) 质点在t 至(t ＋Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs ＝PP′, 位移大小｜Δr ｜＝PP ′,而Δr ＝｜r ｜-｜r ｜表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注：在直线运动中有相等的可能)．但当Δt →0 时,点P ′无限趋近P 点,则有｜d r ｜＝d s ,但却不等于d r ．故选(B)．(2) 由于｜Δr ｜≠Δs ,故ts t ΔΔΔΔ≠r ,即｜v ｜≠v ． 但由于｜d r ｜＝d s ,故ts t d d d d =r ,即｜v ｜＝v ．由此可见,应选(C)． 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即 (1)t r d d ； (2)t d d r ； (3)t s d d ； (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x ． 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率．通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量；td d r 表示速度矢量；在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解．故选(D)．1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a ｔ起改变速度大小的作用,而法向分量a n 起改变速度方向的作用．质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的．至于a ｔ是否改变,则要视质点的速率情况而定．质点作匀速率圆周运动时, a ｔ恒为零；质点作匀变速率圆周运动时, a ｔ为一不为零的恒量,当a ｔ改变时,质点则作一般的变速率圆周运动．由此可见,应选(B)．1 -4 质点的运动方程为式中x ,y 的单位为m,t 的单位为ｓ．试求：(1) 初速度的大小和方向；(2) 加速度的大小和方向．分析 由运动方程的分量式可分别求出速度、加速度的分量,再由运动合成算出速度和加速度的大小和方向．解 (1) 速度的分量式为当t ＝0 时, v 0x ＝-10 m·ｓ-1 , v 0y ＝15 m·ｓ-1 ,则初速度大小为设v 0与x 轴的夹角为α,则α＝123°41′(2) 加速度的分量式为2s m 60d d -⋅==ta x x v , 2s m 40d d -⋅-==t a y y v 则加速度的大小为设a 与x 轴的夹角为β,则β＝-33°41′(或326°19′)1 -5 质点沿直线运动,加速度a ＝4 -t2 ,式中a 的单位为m·ｓ-2 ,t 的单位为ｓ．如果当t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1 ,求质点的运动方程．分析 本题属于运动学第二类问题,即已知加速度求速度和运动方程,必须在给定条件下用积分方法解决．由t a d d v =和tx d d =v 可得t a d d =v 和t x d d v =．如a ＝a (t )或v ＝v (t ),则可两边直接积分．如果a 或v 不是时间t 的显函数,则应经过诸如分离变量或变量代换等数学操作后再做积分．解 由分析知,应有得 03314v v +-=t t (1) 由 ⎰⎰=txx t x 0d d 0v 得 00421212x t t t x ++-=v (2) 将t ＝3ｓ时,x ＝9 m,v ＝2 m·ｓ-1代入(1)、(2)得v 0＝-1 m·ｓ-1, x 0＝0.75 m于是可得质点运动方程为1 -6 飞机以100 m·ｓ-1 的速度沿水平直线飞行,在离地面高为100 m 时,驾驶员要把物品空投到前方某一地面目标处,问：(1) 此时目标在飞机正下方位置的前面多远？ (2) 投放物品时,驾驶员看目标的视线和水平线成何角度？(3) 物品投出2.0ｓ后,它的法向加速度和切向加速度各为多少？题 1-13 图分析 物品空投后作平抛运动．忽略空气阻力的条件下,由运动独立性原理知,物品在空中沿水平方向作匀速直线运动,在竖直方向作自由落体运动．到达地面目标时,两方向上运动时间是相同的．因此,分别列出其运动方程,运用时间相等的条件,即可求解．此外,平抛物体在运动过程中只存在竖直向下的重力加速度．为求特定时刻t 时物体的切向加速度和法向加速度,只需求出该时刻它们与重力加速度之间的夹角α或β．由图可知,在特定时刻t ,物体的切向加速度和水平线之间的夹角α,可由此时刻的两速度分量v x 、v y 求出,这样,也就可将重力加速度g 的切向和法向分量求得．解 (1) 取如图所示的坐标,物品下落时在水平和竖直方向的运动方程分别为x ＝v t , y ＝1/2 gt 2飞机水平飞行速度v ＝100 m·s -1 ,飞机离地面的高度y ＝100 m,由上述两式可得目标在飞机正下方前的距离(2) 视线和水平线的夹角为(3) 在任意时刻物品的速度与水平轴的夹角为取自然坐标,物品在抛出2s 时,重力加速度的切向分量与法向分量分别为1 -7 一质点沿半径为R 的圆周按规律2021bt t s -=v 运动,v 0 、b 都是常量．(1) 求t 时刻质点的总加速度；(2) t 为何值时总加速度在数值上等于b ？(3) 当加速度达到b 时,质点已沿圆周运行了多少圈？分析 在自然坐标中,s 表示圆周上从某一点开始的曲线坐标．由给定的运动方程s ＝s (t ),对时间t 求一阶、二阶导数,即是沿曲线运动的速度v 和加速度的切向分量a ｔ,而加速度的法向分量为a n ＝v 2 /R ．这样,总加速度为a ＝a ｔe ｔ＋a n e n ．至于质点在t 时间内通过的路程,即为曲线坐标的改变量Δs ＝s t -s 0．因圆周长为2πR,质点所转过的圈数自然可求得．解 (1) 质点作圆周运动的速率为其加速度的切向分量和法向分量分别为b t s a t -==22d d , Rbt R a n 202)(-==v v 故加速度的大小为其方向与切线之间的夹角为(2) 要使｜a ｜＝b ,由b bt b R R=-+4022)(1v 可得 (3) 从t ＝0 开始到t ＝v 0 /b 时,质点经过的路程为因此质点运行的圈数为1 -8 一升降机以加速度1.22 m·ｓ-2上升,当上升速度为2.44 m·ｓ-1时,有一螺丝自升降机的天花板上松脱,天花板与升降机的底面相距2.74 m ．计算：(1)螺丝从天花板落到底面所需要的时间；(2)螺丝相对升降机外固定柱子的下降距离．分析 在升降机与螺丝之间有相对运动的情况下,一种处理方法是取地面为参考系,分别讨论升降机竖直向上的匀加速度运动和初速不为零的螺丝的自由落体运动,列出这两种运动在同一坐标系中的运动方程y 1 ＝y 1(t )和y 2 ＝y 2(t ),并考虑它们相遇,即位矢相同这一条件,问题即可解；另一种方法是取升降机(或螺丝)为参考系,这时,螺丝(或升降机)相对它作匀加速运动,但是,此加速度应该是相对加速度．升降机厢的高度就是螺丝(或升降机)运动的路程． 解1 (1) 以地面为参考系,取如图所示的坐标系,升降机与螺丝的运动方程分别为 当螺丝落至底面时,有y 1 ＝y 2 ,即(2) 螺丝相对升降机外固定柱子下降的距离为解2 (1)以升降机为参考系,此时,螺丝相对它的加速度大小a ′＝g ＋a ,螺丝落至底面时,有(2) 由于升降机在t 时间内上升的高度为则 m 716.0='-=h h d题 1-8 图1 -9 一无风的下雨天,一列火车以v 1＝20.0 m·ｓ-1 的速度匀速前进,在车内的旅客看见玻璃窗外的雨滴和垂线成75°角下降．求雨滴下落的速度v2 ．(设下降的雨滴作匀速运动)题 1-19 图分析 这是一个相对运动的问题．设雨滴为研究对象,地面为静止参考系Ｓ,火车为动参考系Ｓ′．v 1 为Ｓ′相对Ｓ 的速度,v 2 为雨滴相对Ｓ的速度,利用相对运动速度的关系即可解．解 以地面为参考系,火车相对地面运动的速度为v 1 ,雨滴相对地面竖直下落的速度为v 2 ,旅客看到雨滴下落的速度v 2′为相对速度,它们之间的关系为1'22v v v += (如图所示),于是可得1 -10 如图(a)所示,一汽车在雨中沿直线行驶,其速率为v 1 ,下落雨滴的速度方向偏于竖直方向之前θ 角,速率为v 2′,若车后有一长方形物体,问车速v 1为多大时,此物体正好不会被雨水淋湿？分析 这也是一个相对运动的问题．可视雨点为研究对象,地面为静参考系Ｓ,汽车为动参考系Ｓ′．如图(a)所示,要使物体不被淋湿,在车上观察雨点下落的方向(即雨点相对于汽车的运动速度v 2′的方向)应满足hl αarctan ≥．再由相对速度的矢量关系122v v v -=',即可求出所需车速v 1．题 1-20 图解 由122v v v -='［图(b)］,有 而要使hl αarctan ≥,则 1 -11 用水平力F N 把一个物体压着靠在粗糙的竖直墙面上保持静止．当F N 逐渐增大时,物体所受的静摩擦力F f 的大小( )(A) 不为零,但保持不变(B) 随F N 成正比地增大(C) 开始随F N 增大,达到某一最大值后,就保持不变(D) 无法确定分析与解 与滑动摩擦力不同的是,静摩擦力可在零与最大值μF N 范围内取值．当F N 增加时,静摩擦力可取的最大值成正比增加,但具体大小则取决于被作用物体的运动状态．由题意知,物体一直保持静止状态,故静摩擦力与重力大小相等,方向相反,并保持不变,故选(A)．1 -12 一段路面水平的公路,转弯处轨道半径为R ,汽车轮胎与路面间的摩擦因数为μ,要使汽车不至于发生侧向打滑,汽车在该处的行驶速率( )(A) 不得小于gR μ (B) 必须等于gR μ(C) 不得大于gR μ (D) 还应由汽车的质量m 决定分析与解 由题意知,汽车应在水平面内作匀速率圆周运动,为保证汽车转弯时不侧向打滑,所需向心力只能由路面与轮胎间的静摩擦力提供,能够提供的最大向心力应为μF N ．由此可算得汽车转弯的最大速率应为v ＝μRg ．因此只要汽车转弯时的实际速率不大于此值,均能保证不侧向打滑．应选(C)．1-13 一物体沿固定圆弧形光滑轨道由静止下滑,在下滑过程中,则( )(A) 它的加速度方向永远指向圆心,其速率保持不变(B) 它受到的轨道的作用力的大小不断增加(C) 它受到的合外力大小变化,方向永远指向圆心(D) 它受到的合外力大小不变,其速率不断增加分析与解 由图可知,物体在下滑过程中受到大小和方向不变的重力以及时刻指向圆轨道中心的轨道支持力F N 作用,其合外力方向并非指向圆心,其大小和方向均与物体所在位置有关．重力的切向分量(m g cos θ) 使物体的速率将会不断增加(由机械能守恒亦可判断),则物体作圆周运动的向心力(又称法向力)将不断增大,由轨道法向方向上的动力学方程Rm θmg F N 2sin v =-可判断,随θ 角的不断增大过程,轨道支持力F N 也将不断增大,由此可见应选(B)．*1 -14 图(a)示系统置于以a ＝1/4 g 的加速度上升的升降机内,A 、B 两物体质量相同均为m ,A 所在的桌面是水平的,绳子和定滑轮质量均不计,若忽略滑轮轴上和桌面上的摩擦,并不计空气阻力,则绳中张力为( )(A) 5/8 mg (B) 1/2 mg (C) mg (D) 2mg分析与解 本题可考虑对A 、B 两物体加上惯性力后,以电梯这个非惯性参考系进行求解．此时A 、B 两物体受力情况如图(b)所示,图中a ′为A 、B 两物体相对电梯的加速度,m a 为惯性力．对A 、B 两物体应用牛顿第二定律,可解得F Ｔ ＝5/8 mg ．故选(A)．讨论 对于习题2 -5 这种类型的物理问题,往往从非惯性参考系(本题为电梯)观察到的运动图像较为明确,但由于牛顿定律只适用于惯性参考系,故从非惯性参考系求解力学问题时,必须对物体加上一个虚拟的惯性力．如以地面为惯性参考系求解,则两物体的加速度a A 和a B 均应对地而言,本题中a A 和a B 的大小与方向均不相同．其中a A 应斜向上．对a A 、a B 、a 和a ′之间还要用到相对运动规律,求解过程较繁琐．有兴趣的读者不妨自己尝试一下．1 -15 在如图（a ）所示的轻滑轮上跨有一轻绳，绳的两端连接着质量分别为1 kg 和2 kg 的物体A 和B ，现以50 N 的恒力F 向上提滑轮的轴，不计滑轮质量及滑轮与绳间摩擦，求A 和B 的加速度各为多少？题 1-15 图分析 在上提物体过程中，由于滑轮可以转动，所以A 、B 两物体对地加速度并不相同，故应将A 、B 和滑轮分别隔离后，运用牛顿定律求解，本题中因滑轮质量可以不计，故两边绳子张力相等，且有T 2F F =.解 隔离后，各物体受力如图（b ）所示，有滑轮 02T =-F FA A A A T a m g m F =-B B B B T a m g m F =-联立三式，得 2.15A =a 7.2s m B 2=⋅-a ，2s m -⋅讨论 如由式a m m g m m F )()(B A B A +=+-求解，所得a 是A 、B 两物体构成的质点系的质心加速度，并不是A 、B 两物体的加速度.上式叫质心运动定理. 1 -16 一质量为m 的小球最初位于如图(a)所示的A 点,然后沿半径为r 的光滑圆轨道ADCB 下滑．试求小球到达点C 时的角速度和对圆轨道的作用力．题 1-16 图分析 该题可由牛顿第二定律求解．在取自然坐标的情况下,沿圆弧方向的加速度就是切向加速度a ｔ,与其相对应的外力F ｔ是重力的切向分量mg sin α,而与法向加速度a n 相对应的外力是支持力F N 和重力的法向分量mg cos α．由此,可分别列出切向和法向的动力学方程F ｔ＝m d v /d t 和F n ＝ma n ．由于小球在滑动过程中加速度不是恒定的,因此,需应用积分求解,为使运算简便,可转换积分变量．该题也能应用以小球、圆弧与地球为系统的机械能守恒定律求解小球的速度和角速度,方法比较简便．但它不能直接给出小球与圆弧表面之间的作用力．解 小球在运动过程中受到重力P 和圆轨道对它的支持力F N ．取图(b)所示的自然坐标系,由牛顿定律得tm αmg F t d d sin v =-= (1) Rm m αmg F F N n 2cos v =-= (2) 由tαr t s d d d d ==v ,得v αr t d d =,代入式(1),并根据小球从点A 运动到点C 的始末条件,进行积分,有得 αrg cos 2=v则小球在点C 的角速度为由式(2)得 αmg αmg rm m F N cos 3cos 2=+=v 由此可得小球对圆轨道的作用力为负号表示F ′N 与e n 反向．1 -17 光滑的水平桌面上放置一半径为R 的固定圆环,物体紧贴环的内侧作圆周运动,其摩擦因数为μ,开始时物体的速率为v 0 ,求：(1) t 时刻物体的速率；(2) 当物体速率从v 0减少2/0v 时,物体所经历的时间及经过的路程．题 1-17 图分析 运动学与动力学之间的联系是以加速度为桥梁的,因而,可先分析动力学问题．物体在作圆周运动的过程中,促使其运动状态发生变化的是圆环内侧对物体的支持力F N 和环与物体之间的摩擦力F ｆ ,而摩擦力大小与正压力F N ′成正比,且F N 与F N ′又是作用力与反作用力,这样,就可通过它们把切向和法向两个加速度联系起来了,从而可用运动学的积分关系式求解速率和路程．解(1) 设物体质量为m,取图中所示的自然坐标,按牛顿定律,有＝μF N ,由上述各式可得由分析中可知,摩擦力的大小Fｆ取初始条件t ＝0 时v＝v0 ,并对上式进行积分,有(2) 当物体的速率从v0减少到2/v时,由上式可得所需的时间为物体在这段时间内所经过的路程第二章动量守恒定律和能量守恒定律2 -1对质点系有以下几种说法：(1) 质点组总动量的改变与内力无关；(2) 质点组总动能的改变与内力无关；(3) 质点组机械能的改变与保守内力无关．下列对上述说法判断正确的是()(A) 只有(1)是正确的(B) (1)、(2)是正确的(C) (1)、(3)是正确的(D) (2)、(3)是正确的分析与解在质点组中内力总是成对出现的,它们是作用力与反作用力．由于一对内力的冲量恒为零,故内力不会改变质点组的总动量．但由于相互有作用力的两个质点的位移大小以及位移与力的夹角一般不同,故一对内力所作功之和不一定为零,应作具体分析,如一对弹性内力的功的代数和一般为零,一对摩擦内力的功代数和一般不为零,对于保守内力来说,所作功能使质点组动能与势能相互转换,因此保守内力即使有可能改变质点组的动能,但也不可能改变质点组的机械能．综上所述(1)(3)说法是正确的．故选(C)．2 -2有两个倾角不同、高度相同、质量一样的斜面放在光滑的水平面上,斜面是光滑的,有两个一样的物块分别从这两个斜面的顶点由静止开始滑下,则()(A) 物块到达斜面底端时的动量相等(B) 物块到达斜面底端时动能相等(C) 物块和斜面(以及地球)组成的系统,机械能不守恒(D) 物块和斜面组成的系统水平方向上动量守恒分析与解对题述系统来说,由题意知并无外力和非保守内力作功,故系统机械能守恒．物体在下滑过程中,一方面通过重力作功将势能转化为动能,另一方面通过物体与斜面之间的弹性内力作功将一部分能量转化为斜面的动能,其大小取决其中一个内力所作功．由于斜面倾角不同,故物体沿不同倾角斜面滑至底端时动能大小不等．动量自然也就不等(动量方向也不同)．故(A)(B)(C)三种说法均不正确．至于说法(D)正确,是因为该系统动量虽不守恒(下滑前系统动量为零,下滑后物体与斜面动量的矢量和不可能为零．由此可知,此时向上的地面支持力并不等于物体与斜面向下的重力),但在水平方向上并无外力,故系统在水平方向上分动量守恒．2 -3如图所示,质量分别为m1和m2的物体A和B,置于光滑桌面上,A和B之间连有一轻弹簧．另有质量为m1和m2的物体C和D分别置于物体A与B 之上,且物体A和C、B和D 之间的摩擦因数均不为零．首先用外力沿水平方向相向推压A和B,使弹簧被压缩,然后撤掉外力,则在A和B弹开的过程中,对A、B、C、D 以及弹簧组成的系统,有()(A) 动量守恒,机械能守恒 (B) 动量不守恒,机械能守恒(C) 动量不守恒,机械能不守恒 (D) 动量守恒,机械能不一定守恒分析与解 由题意知,作用在题述系统上的合外力为零,故系统动量守恒,但机械能未必守恒,这取决于在A 、B 弹开过程中C 与A 或D 与B 之间有无相对滑动,如有则必然会因摩擦内力作功,而使一部分机械能转化为热能,故选(D)．2 -4 如图所示,子弹射入放在水平光滑地面上静止的木块后而穿出．以地面为参考系,下列说法中正确的说法是( )(A) 子弹减少的动能转变为木块的动能(B) 子弹-木块系统的机械能守恒(C) 子弹动能的减少等于子弹克服木块阻力所作的功(D) 子弹克服木块阻力所作的功等于这一过程中产生的热分析与解 子弹-木块系统在子弹射入过程中,作用于系统的合外力为零,故系统动量守恒,但机械能并不守恒．这是因为子弹与木块作用的一对内力所作功的代数和不为零(这是因为子弹对地位移大于木块对地位移所致),子弹动能的减少等于子弹克服阻力所作功,子弹减少的动能中,一部分通过其反作用力对木块作正功而转移为木块的动能,另一部分则转化为热能(大小就等于这一对内力所作功的代数和)．综上所述,只有说法(C)的表述是完全正确的． 2 -5 质量为m 的物体,由水平面上点O 以初速为v 0 抛出,v 0与水平面成仰角α．若不计空气阻力,求：(1) 物体从发射点O 到最高点的过程中,重力的冲量；(2) 物体从发射点到落回至同一水平面的过程中,重力的冲量．分析 重力是恒力,因此,求其在一段时间内的冲量时,只需求出时间间隔即可．由抛体运动规律可知,物体到达最高点的时间gαt sin Δ01v ,物体从出发到落回至同一水平面所需的时间是到达最高点时间的两倍．这样,按冲量的定义即可求得结果．另一种解的方法是根据过程的始、末动量,由动量定理求出．解1 物体从出发到达最高点所需的时间为则物体落回地面的时间为于是,在相应的过程中重力的冲量分别为解2 根据动量定理,物体由发射点O 运动到点A 、B 的过程中,重力的冲量分别为2 -6 高空作业时系安全带是非常必要的．假如一质量为51.0 kg 的人,在操作时不慎从高空竖直跌落下来,由于安全带的保护,最终使他被悬挂起来．已知此时人离原处的距离为2.0 m ,安全带弹性缓冲作用时间为0.50 s ．求安全带对人的平均冲力．分析 从人受力的情况来看,可分两个阶段：在开始下落的过程中,只受重力作用,人体可看成是作自由落体运动；在安全带保护的缓冲过程中,则人体同时受重力和安全带冲力的作用,其合力是一变力,且作用时间很短．为求安全带的冲力,可以从缓冲时间内,人体运动状态(动量)的改变来分析,即运用动量定理来讨论．事实上,动量定理也可应用于整个过程．但是,这时必须分清重力和安全带冲力作用的时间是不同的；而在过程的初态和末态,人体的速度均为零．这样,运用动量定理仍可得到相同的结果．解1 以人为研究对象,按分析中的两个阶段进行讨论．在自由落体运动过程中,人跌落至2 m 处时的速度为gh 21=v (1)在缓冲过程中,人受重力和安全带冲力的作用,根据动量定理,有()12Δv v m m t -=+P F (2)由式(1)、(2)可得安全带对人的平均冲力大小为解2 从整个过程来讨论．根据动量定理有2 -7 如图所示,在水平地面上,有一横截面S ＝0.20 m 2 的直角弯管,管中有流速为v ＝3.0 m·ｓ-1 的水通过,求弯管所受力的大小和方向．题 3-12 图分析 对于弯曲部分AB 段内的水而言,由于流速一定,在时间Δt 内,从其一端流入的水量等于从另一端流出的水量．因此,对这部分水来说,在时间Δt 内动量的增量也就是流入与流出水的动量的增量Δp ＝Δm (v B -v A )；此动量的变化是管壁在Δt 时间内对其作用冲量I 的结果．依据动量定理可求得该段水受到管壁的冲力F ；由牛顿第三定律,自然就得到水流对管壁的作用力F′＝-F ．解 在Δt 时间内,从管一端流入(或流出) 水的质量为Δm ＝ρυS Δt ,弯曲部分AB 的水的动量的增量则为Δp ＝Δm (v B -v A ) ＝ρυS Δt (v B -v A )依据动量定理I ＝Δp ,得到管壁对这部分水的平均冲力从而可得水流对管壁作用力的大小为作用力的方向则沿直角平分线指向弯管外侧．2 -8 质量为m′ 的人手里拿着一个质量为m 的物体,此人用与水平面成α角的速率v 0 向前跳去．当他达到最高点时,他将物体以相对于人为u 的水平速率向后抛出．问：由于人抛出物体,他跳跃的距离增加了多少？ (假设人可视为质点)分析 人跳跃距离的增加是由于他在最高点处向后抛出物体所致．在抛物的过程中,人与物之间相互作用力的冲量,使他们各自的动量发生了变化．如果把人与物视为一系统,因水平方向不受外力作用,故外力的冲量为零,系统在该方向上动量守恒．但在应用动量守恒定律时,必须注意系统是相对地面(惯性系)而言的,因此,在处理人与物的速度时,要根据相对运动的关系来确定．至于,人因跳跃而增加的距离,可根据人在水平方向速率的增量Δv 来计算． 解 取如图所示坐标．把人与物视为一系统,当人跳跃到最高点处,在向左抛物的过程中,满足动量守恒,故有式中v 为人抛物后相对地面的水平速率, v -u 为抛出物对地面的水平速率．得人的水平速率的增量为而人从最高点到地面的运动时间为所以,人跳跃后增加的距离2 -9 一质量为0.20 kg 的球,系在长为2.00 m 的细绳上,细绳的另一端系在天花板上．把小球移至使细绳与竖直方向成30°角的位置,然后从静止放开．求：(1) 在绳索从30°角到0°角的过程中,重力和张力所作的功；(2) 物体在最低位置时的动能和速率；(3) 在最低位置时的张力．题 2-9 图分析 (1) 在计算功时,首先应明确是什么力作功．小球摆动过程中同时受到重力和张力作用．重力是保守力,根据小球下落的距离,它的功很易求得；至于张力虽是一变力,但是,它的方向始终与小球运动方向垂直,根据功的矢量式⎰⋅=s d F W ,即能得出结果来．(2) 在计算功的基础上,由动能定理直接能求出动能和速率．(3) 在求最低点的张力时,可根据小球作圆周运动时的向心加速度由重力和张力提供来确定．解 (1) 如图所示,重力对小球所作的功只与始末位置有关,即在小球摆动过程中,张力F Ｔ 的方向总是与运动方向垂直,所以,张力的功(2) 根据动能定理,小球摆动过程中,其动能的增量是由于重力对它作功的结果．初始时动能为零,因而,在最低位置时的动能为小球在最低位置的速率为(3) 当小球在最低位置时,由牛顿定律可得2 -10 一质量为m 的质点,系在细绳的一端,绳的另一端固定在平面上．此质点在粗糙水平面上作半径为r 的圆周运动．设质点的最初速率是v 0 ．当它运动一周时,其速率为v 0 /2．求：(1) 摩擦力作的功；(2) 动摩擦因数；(3) 在静止以前质点运动了多少圈？分析 质点在运动过程中速度的减缓,意味着其动能减少；而减少的这部分动能则消耗在运动中克服摩擦力作功上．由此,可依据动能定理列式解之．解 (1) 摩擦力作功为20202k 0k 832121v v v m m m E E W -=-=-= (1) (2) 由于摩擦力是一恒力,且F ｆ ＝μmg ,故有mg r s F W μπ2180cos o f -== (2)由式(1)、(2)可得动摩擦因数为(3) 由于一周中损失的动能为2083v m ,则在静止前可运行的圈数为 34k 0==W E n 圈 2 -11 如图(a)所示,A 和B 两块板用一轻弹簧连接起来,它们的质量分别为m 1 和m 2 ．问在A 板上需加多大的压力,方可在力停止作用后,恰能使A 在跳起来时B 稍被提起．(设弹簧的劲度系数为k )题 2-11 图分析 运用守恒定律求解是解决力学问题最简捷的途径之一．因为它与过程的细节无关,也常常与特定力的细节无关．“守恒”则意味着在条件满足的前提下,过程中任何时刻守恒量不变．在具体应用时,必须恰当地选取研究对象(系统),注意守恒定律成立的条件．该题可用机械能守恒定律来解决．选取两块板、弹簧和地球为系统,该系统在外界所施压力撤除后(取作状态1),直到B 板刚被提起(取作状态2),在这一过程中,系统不受外力作用,而内力中又只有保守力(重力和弹力)作功,支持力不作功,因此,满足机械能守恒的条件．只需取状态1 和状态2,运用机械能守恒定律列出方程,并结合这两状态下受力的平衡,便可将所需压力求出．解 选取如图(b)所示坐标,取原点O 处为重力势能和弹性势能零点．作各状态下物体的受力图．对A 板而言,当施以外力F 时,根据受力平衡有F 1 ＝P 1 ＋F (1)。