同步奥数培优六年级上 第九讲百分数(百分数应用题)
小学奥数必考知识点:百分数应用题知识点题例详解

《小学奥数必考知识点:百分数应用题知识点题例详解》在小学奥数的学习中,百分数应用题是一个重要的知识点,也是各类考试中经常出现的题型。
掌握百分数应用题的解题方法,不仅能够提高学生的数学思维能力,还能为今后的学习打下坚实的基础。
一、百分数的概念百分数是表示一个数是另一个数的百分之几的数,也叫百分率或百分比。
百分数通常用“%”来表示。
例如,45%表示 45 是 100 的百分之四十五。
二、百分数应用题的类型1. 求一个数是另一个数的百分之几这类问题的关键是找准单位“1”。
一般情况下,“是”“占”“比”后面的量就是单位“1”。
例如:小明有 20 本书,小红有 30 本书,小明的书是小红的百分之几?解:20÷30×100%≈66.7%。
2. 求一个数的百分之几是多少用这个数乘以对应的百分数即可。
例如:一个数是 50,它的 40%是多少?解:50×40% = 20。
3. 已知一个数的百分之几是多少,求这个数这类问题可以用除法或方程来解决。
例如:一个数的 30%是 15,这个数是多少?解法一:15÷30% = 50。
解法二:设这个数为 x,则 30%x = 15,解得 x = 50。
三、典型题例详解1. 折扣问题商店里的商品有时会进行打折销售。
折扣是指商品按原价的百分之几出售。
例如:一件衣服原价 200 元,现在打八折出售,现在的售价是多少?解:八折就是 80%,200×80% = 160(元)。
2. 利润问题利润问题涉及成本、售价和利润三个量。
利润 = 售价 - 成本,利润率 = 利润÷成本×100%。
例如:某商品的成本是 80 元,售价是 100 元,求利润和利润率。
解:利润 = 100 - 80 = 20(元),利润率= 20÷80×100% = 25%。
3. 浓度问题浓度问题主要涉及溶质、溶剂和溶液三个量。
浓度 = 溶质÷溶液×100%。
六年级上册数学百分数应用题讲解

六年级上册数学百分数应用题讲解
百分数在数学中是一个非常重要的概念,它在日常生活和商业活动中也有广泛的应用。
在六年级的数学课程中,学生将开始接触到百分数的应用题,这是理解百分数在实际问题中如何应用的关键一步。
下面是一个关于百分数应用题的示例和讲解:
问题:小明看了一本200页的书,他计划在接下来的10天里每天看15%
的书。
他能在10天内看完这本书吗?
1. 理解题意:首先,我们要明确小明的阅读计划。
他计划每天看书的15%,这意味着如果他连续这样看10天,他会看完整本书的150%(因为10天
的15%加起来就是整本书的150%)。
2. 计算小明每天看的页数:每天小明会看200页的15%,即200 × = 30页。
3. 计算小明10天看的总页数:如果小明每天看30页,那么10天他会看
30 × 10 = 300页。
4. 判断是否能看完:因为300页少于整本书的200页,所以小明能在10
天内看完这本书。
通过这个例子,我们可以看到百分数是如何在解决实际问题中发挥作用的。
在这个问题中,我们用到了百分数的计算(如15%的书是多少页)和逻辑推理(小明是否能按时看完书)。
这些技能在日常生活和商业活动中都非常有用,比如计算投资回报、理解商品折扣等。
因此,理解并掌握百分数的概念和应用是非常重要的。
培优班l六年级奥数百分数应用题精品教案

学生姓名:辅导形式:小班老师:陈波学校:小六【作业检查】检查学生的家庭作业情况,找出作业的错误和了解学生上节课对知识的掌握情况。
【梳理知识】百分数应用题教学目标:1.分析题目确定单位“1”2.准确找到量所对应的率,利用量÷对应率=单位“1”解题3. 教学重点、难点:抓住不变量,统一单位“1”。
教学过程一、知识点概述分数应用题是研究数量之间份数关系的典型应用题,一方面它是在整数应用题上的延续和深化,另一方面,它有其自身的特点和解题规律.在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键.关键:分数应用题经常要涉及到两个或两个以上的量,我们往往把其中的一个量看作是标准量.也称为:单位“1”,进行对比分析。
在几个量中,关键也是要找准单位“1”和对应的百分率,以及对应量三者的关系例如:(1)a是b的几分之几,就把数b看作单位“1”.(2)甲比乙多18,乙比甲少几分之几?方法一:可设乙为单位“1”,则甲为19188+=,因此乙比甲少191889÷=.方法二:可设乙为8份,则甲为9份,因此乙比甲少1 199÷=.2.解应用题必备的公式求分率、百分率问题的公式】比较数÷标准数=比较数的对应分(百分)率;增长数÷标准数=增长率;减少数÷标准数=减少率。
或者是:两数差÷较小数=多几(百)分之几(增);两数差÷较大数=少几(百)分之几(减)。
【增减分(百分)率互求公式】增长率÷(1+增长率)=减少率;减少率÷(1-减少率)=增长率。
比如,乙沙丘比甲丘面积少几分之几?”解这是根据增长率求减少率的应用题。
按公式,可解答为百分之几?”解这是由减少率求增长率的应用题,依据公式,可解答为:【求比较数应用题公式】标准数×分(百分)率=与分率对应的比较数;标准数×增长率=增长数;标准数×减少率=减少数;标准数×(两分率之和)=两个数之和;标准数×(两分率之差)=两个数之差。
六年级上册奥数 百分数的应用

六年级上册奥数百分数的应用1、某校选出一些同学参加作文竞赛,其中男同学比女同学多10人,评选结果有10名男同学获奖,获奖的女同学有30名.参加作文竞赛的女同学人数是________人.2、某班在一次测验中,有26人语文获优,有30人数学获优,其中语数双优的有12人,另外有4人语数成绩均未获优,这个班共有________个学生.3、某班在一次测验中,有26人语文获优,有30人数学获优,其中语数双优的有12人,另外有4人语数成绩均未获优,这个班共有________个学生.4、某班在一次测验中,有26人语文获优,有30人数学获优,其中语数双优的有12人,另外有4人语数成绩均未获优,这个班共有________个学生.5、在100位旅客中,有70人懂英语,65人懂日语,既懂英语又懂日语的有45人,既不懂英语又不懂日语的有________人.6、在100位旅客中,有70人懂英语,65人懂日语,既懂英语又懂日语的有45人,既不懂英语又不懂日语的有________人.7、在某班进行的演讲比赛中,共有5位选手参加,其中3位男生,2位女生,如果2位女生必须连续出场,且男生甲不能排在2位女生之前,那么出场顺序的排法种数为 _______.8、在某班进行的演讲比赛中,共有5位选手参加,其中3位男生,2位女生.如果2位女生必须连续出场,且男生甲不能排在2位女生之前,那么出场顺序的排法种数为 _______.9、在某班进行的演讲比赛中,共有5位选手参加,其中3位男生,2位女生.如果2位女生必须连续出场,且男生甲不能排在2位女生之前,那么出场顺序的排法种数为 _______.10、在某班进行的演讲比赛中,共有5位选手参加,其中3位男生,2位女生.如果2位女生必须连续出场,且男生甲不能排在2位女生之前出场,那么出场顺序的排法种数为 _______.。
小学奥数趣味学习《百分数问题》典型例题及解答

小学奥数趣味学习《百分数问题》典型例题及解答百分数是表示一个数是另一个数的百分之几的数。
百分数是一种特殊的分数。
分数常常可以通分、约分,而百分数则无需;分数既可以表示“率”,也可以表示“量”,而百分数只能表示“率”;分数的分子、分母必须是自然数,而百分数的分子可以是小数;百分数有一个专门的记号“%”。
在实际中和常用到“百分点”这个概念,一个百分点就是1%,两个百分点就是2%。
基础知识:百分数又叫百分率,百分率在工农业生产中应用很广泛,常见的百分率有:增长率=增长数÷原来基数×100%合格率=合格产品数÷产品总数×100%出勤率=实际出勤人数÷应出勤人数×100%出勤率=实际出勤天数÷应出勤天数×100%缺席率=缺席人数÷实有总人数×100%发芽率=发芽种子数÷试验种子总数×100%成活率=成活棵数÷种植总棵数×100%出粉率=面粉重量÷小麦重量×100%出油率=油的重量÷油料重量×100%废品率=废品数量÷全部产品数量×100%命中率=命中次数÷总次数×100%烘干率=烘干后重量÷烘前重量×100%及格率=及格人数÷参加考试人数×100%数量关系:掌握“百分数”、“标准量”“比较量”三者之间的数量关系:百分数=比较量÷标准量标准量=比较量÷百分数解题思路和方法:一般有三种基本类型:(1)求一个数是另一个数的百分之几;(2)已知一个数,求它的百分之几是多少;(3)已知一个数的百分之几是多少,求这个数。
例题1:在植树节里,某校六年级学生在校园内种树8棵,占全校植树数的20%,则该校在植树节里共植树多少棵?解:已知六年级学生的种树棵数以及所种棵数占全校植树数的比值,直接用除法运算即可。
六年级数学《百分数》奥数题

六年级数学《百分数》奥数题
百分数是一种表明一种比例关系的算术表示方法,即百分数表明的是一个数量占另一个数量的比例。
通常在表示比例时,以百分比形式表示,例如:50%表示其中一个数量是另一个数量的一半。
二、用百分数表达的常见情况
1、折扣。
折扣的算法一般用百分比表达,表示实际价格与原价
的比例。
如,折扣50%,则表示只需要付50%的价格即可购买。
2、比例投资。
投资比例时,一般以百分比表示,用于表示投资
者投资公司的比例大小。
如,投资者投资公司的比例为50%,表示投资者拥有该公司50%的股份。
三、百分数的运算
1、百分数的加减法
A:百分数的加减法比较简单,即只需将百分数中的分子加减上去,分母不变,就可以得到新的百分数。
如:50%+20%=70%;50%-20%=30%。
B:百分数的乘除法
A:百分数的乘除法比较复杂,其原理是将百分数中的分子乘除
指定的数,再保持分母不变,求得新的百分数。
如:50%*2=100%;50%/2=25%。
四、今日奥数题
1、小明的投资比例是75%,小张的投资比例是60%,则该公司的投资总额为(。
A:135% B:115% C:95% D:75%
2、如果一个商品折扣了50%,则表示买家可以只需付(的价格即可购买。
六年级数学上册 《百分数》培优提升练习及答案

六年级数学上册《百分数》培优提升练习及答案专项一抓不变量解决问题例1有一堆棋子,其中黑色棋子占总数的45%,如果再放入16颗白色棋子,那么黑色棋子只占总数的25%,那么这堆棋子中有多少颗黑色棋子?分析本题注意到黑色棋子的总量不变,放入16颗白色棋子后,黑色棋子只占总数的25%,说明此时其他的棋子是黑色棋子的(1-25%)÷25%=3倍。
也就是说,放入16颗白色棋子后其他颜色的棋子应是原有棋子总数的45%×3=135%。
但放入16颗白色棋子之前,其他颜色的棋子只占总数的1-45%=55%,所以这堆棋子原有16÷(135%-55%)=20(颗),黑色棋子有2045%=9(颗)。
解答(1-25%)÷25%=3 45%×3=135%1-45%=55% 16÷(135%-55%)=20(颗)20×45%=9(颗)答:黑色棋子有9颗。
反馈练习1.育红小学原有科技书、文艺书若干本,其中科技书占20%。
后又买来科技书150本,这时科技书占50%。
现在这两种书共有多少本?2.甲仓库存粮130吨,乙仓库存粮150吨,两个仓库各运走相同的吨数后,甲仓库剩下的吨数是乙仓库剩下的60%。
求两仓库各运走粮食多少吨?3.甲、乙两仓库共存化肥若干吨,已知乙仓库存放化肥的吨数是甲仓库的50%,如果从甲仓库中运出133吨给乙仓库,这时甲仓库化肥的吨数是乙仓库的60%。
求甲、乙两仓库原来共存放化肥多少吨。
专项二用转化法解决问题例2一家商店在促销活动来临之前,把某件商品加价30%,后来在促销活动期间降价20%出售,结果该商店在原价的基础上多赚了26.4元。
这件商品的原价是多少元?分析该商品价格经历了原价、加价后价格、降价后价格三个阶段,其中,加价后价格是以原价为单位“1”,相当于原价的(1+30%);降价后价格是以加价后价格为单位“1”,相当于加价后价格的80%,即原价的(1+30%)×80%。
北师大版六年级上册数学《百分数的应用》培优专题及答案

北师大版六年级上册数学《百分数的应用》培优专题及答案(共5页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--北师大版六年级上册数学《百分数的应用》培优专题及答案一、单选题1.现在的成本比原来降低了15%,现在的成本是原来的( )。
A. 15%B. 85%C. 115%2.甲乙两数的比是5:4,那么甲数比乙数多()%。
A. 25B. 20C. 125D. 1203.某产品降价前售价是150元,降价后售价是120元,降低了()A. 20%B. 25%C. 80%D. 75 %4.某工地原有大小两堆沙子,共重24吨,在小堆沙子上又加入4吨,从大堆沙子里用去25%后,两堆沙子的重量正好相等,求这两堆沙子原来各是多少吨?正确的解答是()A. 大堆沙重18吨,小堆沙重6吨 B. 大堆沙重16吨,小堆沙重8吨C. 大堆沙重20吨,小堆沙重4吨D. 大堆沙重15吨,小堆沙重9吨二、判断题克糖溶于100克水中,糖占糖水的10%。
6.在100克的水中加入10克的糖,糖占糖水的10%.(判断对错)克糖放入400克水中,糖占糖水的20%。
8.判断对错.红糖质量比白糖质量多10%,就是白糖质量比红糖质量少10%.三、填空题9.一本书,看了全书的5%,还剩________ %没有看.10. 羊城小学进行一次体育考试,合格的有108人,不合格的有12人,这次体育考试的合格率是________.是15的________%;15比12多________%。
12.甲、乙二人合伙卖报纸,甲出资100元,乙出资60元,一共获利80元.他们应该怎样分这80元钱?甲分得________元.乙分得________元.四、解答题13.六(1)班有学生45人,在一次数学期末自测中,优秀率是80%,还有多少人没有达到优秀等次年8月,小红的妈妈将4000元钱存入银行,定期三年,年利率为%,三年到期后,准备用这笔钱购买下面的电脑,钱够吗五、综合题15.某收割机厂2016年生产收割机的情况如下:第一季度生产1000台,第二季度生产1500台,第三季度生产2500台,第四季度生产4000台。
六年级精品奥数资料秋季第九讲:百分数的应用(二)经济问题'

课前热身6+23= 1-23-14= 13×25%= 45÷32=13+13÷13+23= 15×(13+15)= 13÷25% 26-12.65= 11×10111= 5.24-2.4=专题简析市场经济中有许多数学问题:分段经济、利润问题等。
同学们可能都有和父母一起去买东西的经历,都知道商品有定价,但是这个价格是怎样定的呢?这就涉及到商品的成本、利润等听起来有些陌生的名词。
一、核心公式:1、售价=成本+利润=成本×(1+利润率)2、成本=售价÷(1+利润率)3、定价=成本×(1+期望利润率)4、利润=售价-成本 期望利润=定价-成本5、利润率=利润成本×100%=售价−成本成本×100%=(售价成本-1)×100%注:不能死记硬背公式,关键在于理解之后灵活运用。
嘉题一某商店进货的批发价为50元一袋,规定零售价为70元一袋,求商品的利润率是多少?分析与解:利润=售价-成本利润率=利润成本×100%=70-50 =2050×100%=20(元) =40%答:商品的利润率是40%。
随堂练习商店有作业本100本,每本成本为0.5元,按每本0.7元销售,可获利润多少元?利润率是多少?嘉题二红星商店购回一批商品,按20%的利润定价,然后打八折出售,结果亏损400元,这批商品的成本是多少元?分析与解:此题成本不知道,可设成本为x元,然后运用正向思维解题。
定价:x(1+20%)售价:x(1+20%)·0.8利润:亏损400元,即成本-售价=400元嘉题一分析与解:设这批凉鞋共x 双,成本:6.5x 元 利润:20元 售价:(x-200)·8.7 利润=售价-成本20=(x-200)·8.7-6.5x20=8.7x-1740-6.5x 20+1740=8.7x-6.5x1760=2.2x 2.2x=1760 x=800答:这批凉鞋共800双。
六年级数学上册百分数的应用解题公式+例题
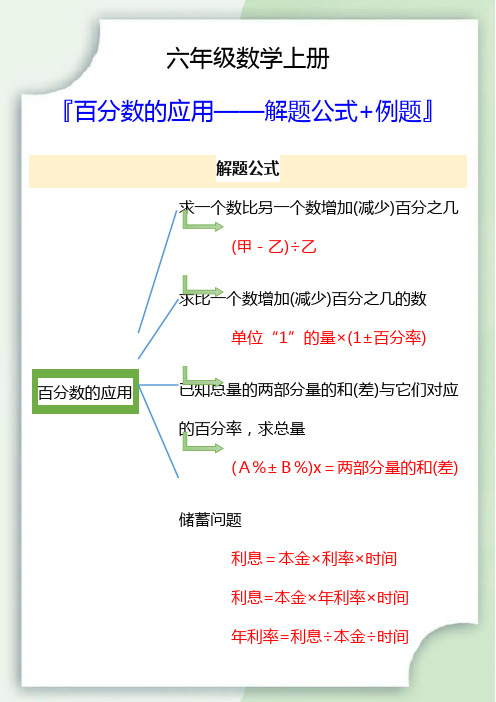
六年级数学上册
『百分数的应用——解题公式+例题』
解题公式
求一个数比另一个数增加(减少)百分之几
(甲-乙)÷乙
求比一个数增加(减少)百分之几的数
单位“1”的量×(1±百分率)
已知总量的两部分量的和(差)与它们对应百分数的应用
的百分率,求总量
(A%±B%)x=两部分量的和(差)
储蓄问题
利息=本金×利率×时间
利息=本金×年利率×时间
年利率=利息÷本金÷时间
题型解析
1.宏华玩具厂计划要做550个布娃娃,实际上做了600个。
实际比计划多做了百分之几?
(600-550)÷550≈9.1%
答:实际比计划多做了9.1%。
六年级数学上册
『百分数的应用——解题公式+例题』
2.新华书店预计售书7000万册,实际售书超出计划的18%。
实际售书多少万册?
7000×(1+18%)=8260(万册)
答:实际售书8260万册。
3.在一次知识竞赛中,小芳答对了总题量的40%,小军答对了总题量的60%,小军答对的题比小芳多6道。
这次知识竞赛中共有多少道题?(用方程解答)
解:设这次知识竞赛中共有x道题。
60%x-40%x=6
x=30
答:这次知识竞赛中共有30道题。
4.张老师在银行存了5000元,定期5年,到期时利息为695元。
银行的年利率是多少?
695÷5÷5000=2.78%
答:银行的年利率是2.78%。
完整版)百分数及其应用(奥数题)

完整版)百分数及其应用(奥数题)基本知识:1、常见的百分率包括达标率、及格率、成活率、发芽率、出勤率等。
求百分率就是求一个数是另一个数的百分之几。
2、求一个数比另一个数多(或少)百分之几。
在实际生活中,人们常用增加了百分之几、减少了百分之几、节约了百分之几等来表示增加或减少的幅度。
求甲比乙多百分之几的公式为(甲-乙)÷乙,求乙比甲少百分之几的公式为(甲-乙)÷甲。
3、求一个数的百分之几是多少,可以用一个数(单位“1”)×百分率来计算。
4、已知一个数的百分之几是多少,可以用部分量÷百分率=一个数(单位“1”)来计算。
5、折扣几折就是十分之几,也就是百分之几十。
6、纳税缴纳的税款叫做应纳税额,应纳税额与各种收入的比率叫做税率,应纳税额=总收入×税率。
7、利率存入银行的钱叫做本金,取款时银行多支付的钱叫做利息,利息与本金的比值叫做利率。
税后利息=利息-利息的应纳税额=利息-利息×5%。
例题1:去年春天,我们学校的同学在小河边先种240棵小树,18棵没有成活,后来补种了160棵,又有7棵没有成活。
这年春天植数的成活率是多少?练1:1、王爷爷在自家的小屋后面种下了150棵小树,过了一段时间发现枯死了10棵,于是又补种了10棵,结果全部成活。
王爷爷去年植树的成活率是多少?2、XXX做了180道口算题,要想使正确率达到98%以上,他至少要做对多少道题?例题2:XXX是一个狂热的“驴友”,每周六都要进行户外活动。
今天又是一个周六,原计划每小时步行6千米。
8小时可以达到目的地。
实际行进中由于天气原因,速度减少了10%,实际用了多长时间到达目的地?练2:1、XXX加工一批零件,计划每小时加工10个,12小时全部完成。
实际每小时多加工20%,实际用了多长时间?2、修一条水渠,每天修500米,5天修了全程的50%,剩下的工作效率提高了20%,剩下这段工程可以提前多少天完工?例题3:一种电脑,每台如果减少定价的10%出售,可盈利225元;如果减少定价的20%出售,就亏本120元。
专题09《百分数—实际应用》六年级数学上册

(2023年秋季班苏教版六上)知识拓展考点培优讲练考察点一:百分数的实际应用1.应纳税额的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率2.利息的计算方法:求应纳税额就是求一个数的百分之几是多少,用乘法计算:应纳税额=营业额×税率3.折扣问题的解法:解决折扣问题,首先看是打几折,打几折就是按原价的百分之几十出售。
现价=原价×折扣考察点二:列方程解应用题1.已知部分数占总数的百分之几和另一部分数,求总数在实际问题中,要找准把哪个数量看做单位“1”,单位“1”未知时,通常设单位“1”为x,先找出题目中的数量关系,再列方程解决问题。
2.已知一个数比另一个数多百分之几,求另一个数在列方程解决倍、差问题时,要注意先找准单位“1”的量,通常情况下设单位“1”的量为x,再根据另一个量与单位“1”的量之间的关系,用含有x的式子表示出另一个量,最后根据它们的和或差列出方程求解。
易错点一:百分率及其应用1.求百分率实质上是求一个数是另一个数的百分之几,只是在计算时要乘100%,把结果化成百分数。
2.及格率、合格率、命中率、出勤率、成活率、出粉率都不能大于100%。
3.“降低了”是指原有数量中减少的部分;“降低到”是指从原有数量中减去一部分后得到的数量。
易错点二:税率利率折扣问题1.任何一种存款,在计算利息时,都要乘存入时间。
2.商品打折后,比原价降低的金额=原价-现价。
3.解决有关百分数的实际问题,在找准单位“1”的同时,还要看清所要求的问题与单位“1”的关系。
【典例精讲】(2022•南开区)1.一件商品八折出售比原来少获利200元,那么原来的售价为()。
A.400元B.600元C.800元D.1000元【变式1-1】(2)第一百货公司2013年的销售额比2012年大约增长了()%。
(3)从2010年到2013年,第()百货公司的销售额增长率较高。
小学六年级奥数_百分数应用题

Research Planning
知识回顾 Knowledge
Review
放映结束 感谢各位的批评指导!
谢 谢!
让我们共同进步
㈠较复杂的百分数应用题
让我们分析一下
首先统一单位“1” 把乙校学生人数看做单位“1”,甲校学生就是40%。
两校总人数用(1+40%)表示。 甲校女生占乙校的40%X30%=12% 乙校女生占乙校的1-42%=58%
㈠较复杂的百分数应用题
解: 40%X30%+(1-42%)=70% 70%÷(1+40%)=50% 答:两校女生总数占两校学生总数的50%
㈠较复杂的百分数应用题
让我们分析一下
首先统一单位“1” 把乙校学生人数看做单位“1”,甲校学生就是40%。
两校总人数用(1+40%)表示。 甲校女生占乙校的40%X30%=12% 乙校女生占乙校的1-42%=58%
㈠较复杂的百分数应用题
㈠较复杂的百分数应用题
① ②
③ ④
⑤
⑥
Thank you !
㈠较复杂的百分数应用题
解: (1+10%)X(1-10%)=99%
答:这个三角形的面积是原来三角形面积的99%
㈠较复杂的百分数应用题
让我们分析一下
㈠较复杂的百分数应用题
解: 答:这堆糖中有奶糖18块。
㈠较复杂的百分数应用题
解:290×4%=11.6(人) 13-11.6=1.4(人) 1.4÷(5%-4%)=140(人) 140×(1+5%)=147(人) (290-140)×(1+4%)=156(人) 答:本年度有男生147人,女生156人。
百分数应用题
六年级上册数学 同步培优奥数 9百分数 商业中的数学

1百分数百分数有两种不同的定义。
(1)分母是100的分数叫做百分数。
这种定义着眼于形式,把百分数作为分数的一种特殊形式。
(2)表示一个数(比较数)是另一个数(标准数)的百分之几的数叫做百分数。
这种定义着眼于应用,用来表示两个数的比。
所以百分数又叫百分比或百分率。
百分数通常不写成分数形式,而采用符号“%”来表示,叫做百分号。
在第二种定义中,出现了比较数、标准数、分率(百分数),这三者的关系如下:比较数÷标准数=分率(百分数),标准数×分率=比较数,比较数÷分率=标准数。
根据比较数、标准数、分率三者的关系,就可以解答许多与百分数有关的应用题。
例1纺织厂的女工占全厂人数的80%,一车间的男工占全厂男工的25%。
问:一车间的男工占全厂人数的百分之几?例2 学校去年春季植树500棵,成活率为85%,去年秋季植树的成活率为90%。
已知去年春季比秋季多死了20棵树,那么去年学校共种活了多少棵树?例3 一次考试共有5道试题。
做对第1,2,3,4,5题的人数分别占参加考试人数的85%,95%,90%,75%,80%。
如果做对三道或三道以上为及格,那么这次考试的及格率至少是多少?例4 育红小学四年级学生比三年级学生多25%,五年级学生比四年级学生少10%,六年级学生比五年级学生多10%。
如果六年级学生比三年级学生多38人,那么三至六年级共有多少名学生?在百分数应用题中有一类叫溶液配比问题。
我们都知道,将糖溶于水就得到了糖水,其中糖叫溶质,水叫溶剂,糖水叫溶液。
如果水的量不变,那么糖加得越多,糖水就越甜,也就是说,糖水甜的程度是由糖(溶质)与糖水(溶液=糖+水)二者重量的比值决定的,这个比值就叫糖水的含糖量或糖含量。
类似地,酒精溶于水中,纯酒精与酒精溶液二者重量的比值就叫酒精含量。
溶质、溶剂、溶液及溶质含量有如下基本关系:溶液重量=溶质重量+溶剂重量,溶质含量=溶质重量÷溶液重量,溶液重量=溶质重量÷溶质含量,溶质重量=溶液重量×溶质含量。
六年级数学上册 《百分数应用题——解决问题》培优提升练习及答案

六年级数学上册《百分数应用题——解决问题》培优提升练习及答案第1关练速度1.填空题。
(1)水果店运进的苹果比橘子多15%。
把运进的()的质量看作单位“1”,运进的苹果是橘子的()(填百分数)。
(2)荔枝原价每千克20元,农博会上降价20%,现价是原价的()%。
(3)200kg的25%是()kg,()比90m多20%,60吨减少10%是()吨。
(4)一堆600kg的石子,运走25%,还剩()kg没有运走。
2.看图列式计算。
(1) 100筐苹果梨比苹果少40%(2)180人五年级六年级?人3.粟子原价每千克20元,农博会上降价20%,农博会上买5千克粟子便宜多少钱?4.某工厂六月份用煤720t,六月份用煤比七月份多用了20%。
七月份用煤多少吨?5.乐吾小学有160人参加校成语大赛,有8人获得一等奖,获得二等奖的占总人数的15%,获得三等奖的人数比获得二等奖的多占总人数的5%。
请提出用百分数解决的问题,并解答。
第2关练准确率6.根据图中信息计算。
文件复制中…剩余16秒已复制163.2M 完成68%(1)完成复制一共需要多少时间?(2)还剩下多少没有复制?7.农机厂今年计划生产农用车2000台,实际上半年就生产了1300台,如果要求今年超产20%,下半年还要再生产多少台农用车?8.一个平行四边形的底是12分米,高是5分米如果它的底增加25%,要使面积不变,高应减少百分之几?9一件商品的进价是4000元。
商场按进价的25%加价后作为定价,然后写上“每满1000元立减100元”,这件商品的售价比进价实际提高了百分之几?10.实验一小的捐款数是实验二小的23,实验小的捐款数比实验三小少20%。
实验一小和实验二小共捐款15000元。
(1)实验一小的捐款数是多少?(2)实验三小的捐款数是多少?第3关练思维11.时装店有一件衣服,第一天按原价出售没人来买;第二天降价10%,仍没有人来买;第三天再降价120元,终于售出。
同步奥数培优六年级上 第九讲百分数(百分数应用题)

第九讲百分数(百分数应用题)【知识概述】百分数表示一个数是另一个数的百分之几,百分数应用题的解题思路与前面学过的分数应用题的解题思路相同。
解答百分数应用题的关键也是找准单位“1”,建立已知数量与分率的对应关系。
例题精学例1一本故事书共100页,芳芳第一天看了总页数的20%,第二天看了总页数的25%,剩下的第三天看完,第三天看了多少页?【思路点拨】根据题意画线段图:把这本故事书的总页数看作单位“1”,第一天看了总页数的20%,也就是看了100页的20%,用100×20%=20(页),同样第二天看了100页的25%,用100×25%=25(页),从100页里去掉两天看的页数,剩下的就是第三天看的页数。
根据“第一天看了总页数的20%,第二天看了总页数的25%”,可以知道还剩1-20%-25%=55%没有看,也就是第三天看了总页数的55%,即100页的55%。
同步精练1.王民看一本80页的文艺书,第一天看了全书的20%,第二天看了全书的25%,还剩多少页没有看?2.为民粮店有一桶油重200千克,第一天售出总数的12.5%,第二天售出总数的20%,第二天比第一天多售出多少千克油?3.某乡要修一条长1800米的环山水渠,第一期工程修了全长的50%,第二期工程修了全长的40%,两期工程一共修了多少米?例2 一筐苹果重60千克,第一次卖出40%,第二次卖出的相当于第一次的80%。
第二次卖出多少千克?【思路点拨】根据“第一次卖出40%”,把苹果的总千克数看作单位“1”,也就是卖出60千克的40%,60×40%=24(千克);再根据“第二次卖出的相当于第一次的80%”,把第一次卖出的千克数看作单位“1”,也就是卖出24千克的80%,24×80%=19.2(千克),第二次卖出19.2千克。
根据“第一次卖出40%,第二次卖出的相当于第一次的80%”,把革果的总千克数看作单位“1”,第一次卖出40%,第二次卖出总千克数40%的80%,也就是40%×80%=32%,第二次卖出总千克数的32%,60×32%=19.2(千克)。
六年级上册百分数应用题奥数

六年级上册百分数应(Ying)用题奥数(1)某商品按照定价的80%出售,仍可获(Huo)得20%的利润,商家定价时期望的利润率是多少?(2)某种商品,每件(Jian)成本是120元,按照获利30%定价,然后按照定价的80%出售,。
每件商品的利润率是多少?(3)一种(Zhong)电脑,如果按定价降低10%出售,仍可盈利200元,如果按定价降低20%出售,那么亏损220元。
这种电脑的进价(Jia)是多少元?(4)一件商品按现价降价10%卖出可(Ke)获利180元,如果降价20%出售,就要亏损240元。
该商品的进价是(Shi)多少?(5)食堂运进一批煤,用去了这批煤的40%,剩下的比用去的多200千克(Ke),食堂原来运进煤多少千克?(6)六(1)班某日有4人请假未到校,班干部统计的出勤率是92%,后来请假的同学中有1人到校。
问这个班最后统计的出勤率是多少?(7)某商场进回一批电视机,按获利20%定价,然后按90%出售,外送50元乘车费的广告,实际每台电视机还可以获利120元的利润。
这批电视机的进价是多少元?(8)甲乙两筐菜共重84千克,从甲筐取出20%放入乙筐,再从乙筐取出2千克放入甲筐,这时两筐的质量正好相等。
求甲乙两筐菜原来各重多少千克?(9)从甲地开往乙地的一辆汽车,到达乙地后返回时,速度减慢了20%,这样来回共用去18小时。
求从乙地返回甲地用了多少小时?(10)一袋面粉,吃(Chi)去后又加进8千克,这时反而(Er)比原来重20%。
原来这袋面粉重多少千克?(11)姐(Jie)妹俩养兔100只,姐姐养的31比妹妹养的10%多(Duo)16只。
求姐,妹各养多少只?(12)育红(Hong)小学六年级举行数学竞赛,参加竞赛的女生比男生多28人。
根据成绩,男生全部获奖,而女生则有25%的人未获奖。
获奖总人数是42人,又知参加竞赛的是全年级学(Xue)生的40%。
六年级学生共有多少人?(13)书店运来一批科技书,第一天(Tian)卖出25%,第二天卖出的是第一天的120%,比第一天多卖35本。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九讲百分数(百分数应用题)
【知识概述】
百分数表示一个数是另一个数的百分之几,百分数应用题的解题思路与前面学过的分数应用题的解题思路相同。
解答百分数应用题的关键也是找准单位“1”,建立已知数量与分率的对应关系。
例题精学
例1一本故事书共100页,芳芳第一天看了总页数的20%,第二天看了总页数的25%,剩下的第三天看完,第三天看了多少页? 【思路点拨】根据题意画线段图:
把这本故事书的总页数看作单位“1”,第一天看了总页数的20%,也就是看了100页的20%,用100×20%=20(页),同样第二天看了100页的25%,用100×25%=25(页),从100页里去掉两天看的页数,剩下的 就是第三天看的页数。
根据“第一天看了总页数的20%,第二天看了总页数的25%”,可以知道还剩1-20%-25%=55%没有看,也就是第三天看了总页数的55%,即100页的55%。
同步精练
1. 王民看一本80页的文艺书,第一天看了全书的20%,第二天看了全书的25%,还剩多少页没有看?
2. 为民粮店有一桶油重200千克,第一天售出总数的12.5%,第二天售出总数的20%,第二天比第一天多售出多少千克油?
100页 第一天看了20% 第二天看了25% 第三天看了?页
3.某乡要修一条长1800米的环山水渠,第一期工程修了全长的50%,第二期工程修了全长的40%,两期工程一共修了多少米?
例2一筐苹果重60千克,第一次卖出40%,第二次卖出的相当于第一次的80%。
第二次卖出多少千克?
【思路点拨】根据“第一次卖出40%”,把苹果的总千克数看作单位“1”,也就是卖出60千克的40%,60×40%=24(千克);再根据“第二次卖出的相当于第一次的80%”,把第一次卖出的千克数看作单位“1”,也就是卖出24千克的80%,24×80%=19.2(千克),第二次卖出19.2千克。
根据“第一次卖出40%,第二次卖出的相当于第一次的80%”,把革果的总千克数看作单位“1”,第一次卖出40%,第二次卖出总千克数40%的80%,也就是40%×80%=32%,第二次卖出总千克数的32%,60×32%=19.2(千克)。
同步精练
1.一种电子产品原售价120元,出售时第一次降价20%,第二次又降了新售价的10%,这种产品现在售价多少元?
2.一根电线长50米,分三天用完。
第一天用了全长的20%,第二天用了余下的25%,第三天用了多少米?
3.工厂11月份运来120吨煤,上旬用去这批煤的25%,中旬用去余下的60%,剩下的在下旬用完,下旬平均每天可用煤多少吨?
例3有一桶油,第一次取出全桶的20%,第二次取出36千克,这时桶里还剩下8千克油,问第一次取出油多少千克?
【思路点拨】根据题意画线段图:
第一次取出?千克还剩下8千克第二次取出36千第一次取出20%
把这桶油的总千克数看作单位“1”,从图上可以看出,第一次用了全桶油的20%以后,还剩36+8=44(千克),44千克所对应的分率是1-20%=80%,先求这桶油的总千克数:44÷80%=55(千克),用总千克数乘20%,求出第一次取出油的千克数。
同步精练
1.工程队修一条路,已经修好全长的60%,距离中点120米。
这条路全长多少米?
2.有一袋米,第一周吃了40%,第二周吃了12千克,还剩6千克。
这袋大米原来有多少千克?
3. 一根电线,剪去全长的5
1后,再接上45米,这时比原来长40%,这根电线剪去多少米?
例4修路队修一条路,已经修的与未修的比是1:3,再修150米,则正好修完全长的50%。
这条路全长多少米?
【思路点拨】根据“已经修的与未修的比是1:3”,可以知道已经修的占总长的
1,也就是25%,根据题意画线段图:
从图上可以看出:150米所对应的分率是50%-25%=25%,求这条路的全长,用150÷25%=600(米)。
同步精练
1. 一辆汽车从甲地开往乙地,已经行的与全程的比是1:4,再行80千米,就正好行了全程的4
3。
甲、乙两地相距多少千米?
2. 李大伯饲养鸡的只数的60%与鹅的只数的
5
4相等。
已知李大伯饲养了120只鸡,那么李大伯饲养了多少只鹅?
3. 师徒两人共同制造840个零件,完成任务时,师傅做的零件的10%相当于徒弟做的零件的25%,徒弟做了多少个零件?
练习卷
一、填空。
1.():5=0.8=( )
20=()%。
2.100千克增加20%后是()千克;()吨减少25%是75吨。
3.()千克比100千克多30%;50克比()克少40%。
4.一个数的20%是100,这个数的一是()。
5.六(1)班今天出勤48人,有2人因病请假,这天的出勤率是()%。
6.服装厂生产的童装与女装的比是2:5,童装是女装的()%。
7.六年级男生人数相当于女生人数的80%,那么,男生人数相当于全年级人数的( )
( )。
8.甲数的5
3等于乙数的75%,已知乙数是80,那么甲数是()。
9.小红从家到学校,用了10分钟,从学校沿原路返回家用了8分钟,速度提高了()%。
二、判断。
1.小王加工101个零件,合格100个,这批零件的合格率是100%。
------------()
2.甲数比乙数多25%,则乙数就比甲数少20%。
------------------------------()
3.男生人数比女生多一,也就是女生人数比男生少20%。
--------------------()
4.女生人数占总人数的65%,男生人数占总人数的35%,女生人数比男生人数多30%。
()
三、选择正确答案的序号填在括号里。
1.男生人数占全年级总人数的62%,女生人数占全年级总人数的()。
A.38%
B.62%
C.不清楚
2.男生人数比女生人数多10%,这里的10%表示()。
A.男生是女生的10%
B.男生比女生多的人数是女生人数的10%
C.男生比女生多的人数是总人数的10%
3.如果甲数的60%等于乙数的一(甲、乙两数不为0),那么()。
A.甲数>乙数
B.甲数<乙数
C.甲数=乙数
D.无法确定
4.一套家具比原价降低了20%,就是说现价相当于原价的()。
A.80%
B.20%
C.120%
5.一条路,已经修了4.5千米,是剩下的45%,这条路长()千米。
A.10
B.14.5
C.4.95
四、解决问题。
1.一条公路已修了720米,剩下的比已修的多20%,这条公路长多少米?
2.修路队修一条路,已经修了4.5千米,还剩下55%没有修,这条路长多少千米?
3. 红山小学今年春季栽松树96棵,比栽的柏树多60%,红山小学今年春季一共栽树多少棵?
4.一批货物运走2.5吨,还剩下5
1,如果运走25%,还剩下多少吨?
5. 一套服装的价格是270元,其中上衣的价格是裤子的125%,上衣与裤子的价格各是多少元?
6. 某煤矿某月上半月完成月计划的8
3,下半月产煤7000吨,本月实际产量超过月计划的25%,这个月实际比计划多产煤多少吨?
7. 两袋化肥的重量相等,甲袋用去45千克,乙袋用去24千克后,余下的化肥甲袋是乙袋的62.5%,两袋化肥原来各有多少千克?
8. 织布厂原有职工250人,其中女工占70%,现在再招收一批女工,那么,女工就占全厂现有职工总数的5
4。
现在全厂有职工多少人?
9.粮店原存一批粮食,运走
5
2后,又运进粮食7.6吨,这时所存粮食恰好是原存粮食的80%。
原存粮食多少吨?。
