讲义直线与圆的位置关系
第2章 2.3.3 直线与圆的位置关系-【新教材】人教B版(2019)高中数学选择性必修一讲义
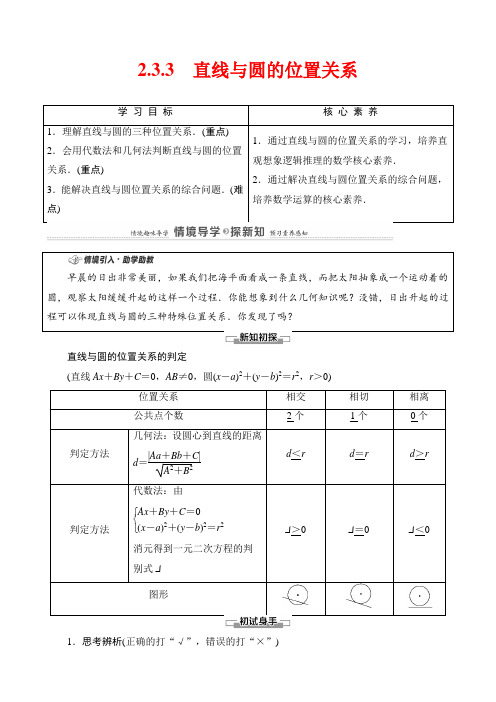
2.3.3直线与圆的位置关系学习目标核心素养1.理解直线与圆的三种位置关系.(重点) 2.会用代数法和几何法判断直线与圆的位置关系.(重点)3.能解决直线与圆位置关系的综合问题.(难点)1.通过直线与圆的位置关系的学习,培养直观想象逻辑推理的数学核心素养.2.通过解决直线与圆位置关系的综合问题,培养数学运算的核心素养.早晨的日出非常美丽,如果我们把海平面看成一条直线,而把太阳抽象成一个运动着的圆,观察太阳缓缓升起的这样一个过程.你能想象到什么几何知识呢?没错,日出升起的过程可以体现直线与圆的三种特殊位置关系.你发现了吗?直线与圆的位置关系的判定(直线Ax+By+C=0,AB≠0,圆(x-a)2+(y-b)2=r2,r>0)位置关系相交相切相离公共点个数2个1个0个判定方法几何法:设圆心到直线的距离d=|Aa+Bb+C|A2+B2d<r d=r d>r判定方法代数法:由⎩⎨⎧Ax+By+C=0(x-a)2+(y-b)2=r2消元得到一元二次方程的判别式ΔΔ>0Δ=0Δ<0图形1.思考辨析(正确的打“√”,错误的打“×”)(1)如果直线与圆组成的方程组有解,则直线与圆相交或相切.( ) (2)若直线与圆只有一个公共点,则直线与圆一定相切. ( )[答案] (1)√ (2)√2.(教材P 110练习A ①改编)直线3x +4y -5=0与圆x 2+y 2=1的位置关系是( ) A .相交 B .相切 C .相离D .无法判断B [圆心(0,0)到直线3x +4y -5=0的距离d =|-5|32+42=1,又圆x 2+y 2=1的半径为1,∴d =r ,故直线与圆相切.]3.直线x +y =1与圆x 2+y 2-2ay =0(a >0)没有公共点,则a 的取值范围是 . 0<a <2-1 [由题意得圆心(0,a )到直线x +y -1=0的距离大于半径a ,即|a -1|2>a ,解得-2-1<a <2-1,又a >0,∴0<a <2-1.]4.直线3x +y -23=0,截圆x 2+y 2=4所得的弦长是 . 2 [圆心到直线3x +y -23=0的距离d =|-23|3+1=3.所以弦长l =2R 2-d 2=24-3=2.]直线与圆位置关系的判定【例1】 只有一个公共点?没有公共点?[思路探究] 可联立方程组,由方程组解的个数判断,也可通过圆心到直线的距离与半径的大小关系进行判断.[解] 法一:由⎩⎨⎧x 2+y 2=2 ①y =x +b ②得2x 2+2bx +b 2-2=0,③方程③的根的判别式Δ=(2b )2-4×2(b 2-2)=-4(b +2)(b -2). (1)当-2<b <2时,Δ>0,直线与圆有两个公共点. (2)当b =2或b =-2时,Δ=0,直线与圆只有一个公共点.(3)当b <-2或b >2时,Δ<0方程组没有实数解,直线与圆没有公共点.法二:圆的半径r =2,圆心O (0,0)到直线y =x +b 的距离为d =|b |2. 当d <r ,即-2<b <2时,圆与直线相交,有两个公共点.当d =r ,|b |=2,即b =2或b =-2时,圆与直线相切,直线与圆只有一个公共点. 当d >r ,|b |>2,即b <-2或b >2时,圆与直线相离,圆与直线无公共点.直线与圆的位置关系的判断方法(1)几何法:由圆心到直线的距离d 与圆的半径r 的大小关系判断. (2)代数法:根据直线方程与圆的方程组成的方程组解的个数来判断.(3)直线系法:若直线恒过定点,可通过判断点与圆的位置关系来判断直线与圆的位置关系,但有一定的局限性,必须是过定点的直线系.[跟进训练]1.已知圆的方程x 2+(y -1)2=2,直线y =x -b ,当b 为何值时,圆与直线有两个公共点,只有一个公共点,无公共点?[解] 法一:由⎩⎨⎧y =x -b ,x 2+(y -1)2=2得2x 2-2(1+b )x +b 2+2b -1=0,① 其判别式Δ=4(1+b )2-8(b 2+2b -1)=-4(b +3)(b -1),当-3<b <1时,Δ>0,方程①有两个不等实根,直线与圆有两个公共点; 当b =-3或1时,Δ=0,方程①有两个相等实根,直线与圆有一个公共点; 当b <-3或b >1时,Δ<0,方程①无实数根,直线与圆无公共点. 法二:圆心(0,1)到直线y =x -b 距离d =|1+b |2,圆半径r =2. 当d <r ,即-3<b <1时,直线与圆相交,有两个公共点; 当d =r ,即b =-3或1时,直线与圆相切,有一个公共点; 当d >r ,即b <-3或b >1时,直线与圆相离,无公共点.直线与圆相切的有关问题【例2】 [思路探究] 利用圆心到切线的距离等于圆的半径求出切线斜率,进而求出切线方程. [解] 因为(4-3)2+(-3-1)2=17>1, 所以点A 在圆外.(1)若所求切线的斜率存在,设切线斜率为k , 则切线方程为y +3=k (x -4).因为圆心C (3,1)到切线的距离等于半径,半径为1, 所以|3k -1-3-4k |k 2+1=1,即|k +4|=k 2+1,所以k 2+8k +16=k 2+1,解得k =-158. 所以切线方程为y +3=-158(x -4), 即15x +8y -36=0. (2)若直线斜率不存在,圆心C (3,1)到直线x =4的距离也为1,这时直线与圆也相切,所以另一条切线方程是x =4. 综上,所求切线方程为15x +8y -36=0或x =4.过一点的圆的切线方程的求法(1)点在圆上时求过圆上一点(x 0,y 0)的圆的切线方程:先求切点与圆心连线的斜率k ,再由垂直关系得切线的斜率为-1k ,由点斜式可得切线方程.如果斜率为零或不存在,则由图形可直接得切线方程x =x 0或y =y 0.(2)点在圆外时①几何法:设切线方程为y -y 0=k (x -x 0).由圆心到直线的距离等于半径,可求得k ,也就得切线方程.②代数法:设切线方程为y -y 0=k (x -x 0),与圆的方程联立,消去y 后得到关于x 的一元二次方程,由Δ=0求出k ,可得切线方程.提醒:切线的斜率不存在的情况,不要漏解.[跟进训练]2.过原点的直线与圆x 2+y 2+4x +3=0相切,若切点在第三象限,求该直线的方程. [解] 圆x 2+y 2+4x +3=0化为标准式(x +2)2+y 2=1,圆心C (-2,0),设过原点的直线方程为y =kx ,即kx -y =0.∵直线与圆相切,∴圆心到直线的距离等于半径. 即|-2k |k 2+1=1,∴3k 2=1, k 2=13,解得k =±33. ∵切点在第三象限,∴k >0, ∴所求直线方程为y =33x .直线截圆所得弦长问题[探究问题]1.已知直线l 与圆相交,如何利用通过求交点坐标的方法求弦长?[提示] 将直线方程与圆的方程联立解出交点坐标,再利用|AB |=(x 2-x 1)2+(y 2-y 1)2求弦长.2.若直线与圆相交、圆的半径为r 、圆心到直线的距离为d ,如何求弦长?[提示] 通过半弦长、弦心距、半径构成的直角三角形,如图所示,求得弦长l =2r 2-d 2.【例3】 直线l 经过点P (5,5)并且与圆C :x 2+y 2=25相交截得的弦长为45,求l 的方程.[思路探究] 设出点斜式方程,利用交点坐标法或利用r 、弦心距及弦长的一半构成直角三角形可求.[解] 据题意知直线l 的斜率存在,设直线l 的方程为y -5=k (x -5),与圆C 相交于A (x 1,y 1),B (x 2,y 2),法一:联立方程组⎩⎨⎧y -5=k (x -5),x 2+y 2=25.消去y ,得(k 2+1)x 2+10k (1-k )x +25k (k -2)=0. 由Δ=[10k (1-k )]2-4(k 2+1)·25k (k -2)>0, 解得k >0.又x 1+x 2=-10k (1-k )k 2+1,x 1x 2=25k (k -2)k 2+1,由斜率公式,得y 1-y 2=k (x 1-x 2).∴|AB |=(x 1-x 2)2+(y 1-y 2)2 =(1+k 2)(x 1-x 2)2 =(1+k 2)[(x 1+x 2)2-4x 1x 2] =(1+k 2)⎣⎢⎡⎦⎥⎤100k 2(1-k )2(k 2+1)2-4·25k (k -2)k 2+1 =45.两边平方,整理得2k 2-5k +2=0,解得k =12或k =2符合题意. 故直线l 的方程为x -2y +5=0或2x -y -5=0.法二:如图所示,|OH |是圆心到直线l 的距离,|OA |是圆的半径,|AH |是弦长|AB |的一半.在Rt △AHO 中,|OA |=5, |AH |=12|AB |=12×45=25, 则|OH |=|OA |2-|AH |2=5. ∴|5(1-k )|k 2+1=5, 解得k =12或k =2.∴直线l 的方程为x -2y +5=0或2x -y -5=0.(变条件)直线l 经过点P (2,-1)且被圆C :x 2+y 2-6x -2y -15=0所截得的弦长最短,求此时直线l 方程.[解] 圆的方程为(x -3)2+(y -1)2=25,圆心C (3,1).因为|CP |=(3-2)2+(1+1)2=5<5,所以点P 在圆内.当CP ⊥l 时,弦长最短.又k CP =1+13-2=2.所以k l =-12,所以直线l 的方程为y +1=-12(x -2),即x +2y =0.直线与圆相交时弦长的两种求法(1)几何法:如图1,直线l 与圆C 交于A ,B 两点,设弦心距为d ,圆的半径为r ,弦长为|AB |,则有⎝ ⎛⎭⎪⎫|AB |22+d 2=r 2,则|AB |=2r 2-d 2.图1 图2(2)代数法:如图2所示,将直线方程与圆的方程联立,设直线与圆的两交点分别是A (x 1,y 1),B (x 2,y 2),则|AB |=(x 1-x 2)2+(y 1-y 2)2=1+k 2|x 1-x 2|=1+1k 2|y 1-y 2|(直线l 的斜率k 存在且不为0).1.如何正确选择判断直线与圆的位置关系的方法(1)若两方程已知或圆心到直线的距离易表达,则用几何法;(2)若方程中含有参数,或圆心到直线的距离的表达式较繁琐,则用代数法. 提醒:能用几何法,尽量不用代数法.(3)已知直线与圆相交求有关参数值时,根据弦心距、半弦长、半径的关系或者这三条线段形成的三角形的性质求解,而弦心距可利用点到直线的距离公式列式,进而求解即可.2.利用代数法判断直线与圆的位置关系时的注意点(1)代入消元过程中消x 还是消y 取决于直线方程的特点,尽量减少分类讨论,如若直线方程为x -ay +1=0,则应将其化为x =ay -1,然后代入消x .(2)利用判别式判断方程是否有根时,应注意二次项系数是否为零,若二次项系数为零,则判别式无意义.1.直线y =x +1与圆x 2+y 2=1的位置关系是( ) A .相切 B .相交但直线不过圆心 C .直线过圆心 D .相离 B [圆心到直线的距离d =112+(-1)2=22<1. 又∵直线y =x +1不过圆心(0,0).∴直线与圆相交但不过圆心.]2.设直线l 过点P (-2,0),且与圆x 2+y 2=1相切,则l 的斜率是( ) A .±1 B .±12 C .±33 D .±3 C [设l :y =k (x +2), 即kx -y +2k =0. 又l 与圆相切,∴|2k |1+k2=1.∴k =±33.] 3.直线x +2y -5+5=0被圆x 2+y 2-2x -4y =0截得的弦长为 .4 [圆的标准方程(x -1)2+(y -2)2=5,圆心(1,2)到直线x +2y -5+5=0的距离d =|1+2×2-5+5|12+22=1,所以弦长为25-1=4.]4.若直线x +y -m =0与圆x 2+y 2=2相离,则m 的取值范围是 . m <-2或m >2 [因为直线x +y -m =0与圆x 2+y 2=2相离,所以|-m |12+12>2,解得m <-2或m >2.]5.过点(-1,-2)的直线l 被圆x 2+y 2-2x -2y +1=0截得的弦长为2,求直线l 的方程.[解] 由题意,直线与圆要相交,斜率必须存在,设为k .设直线l 的方程为y +2=k (x +1).又圆的方程为(x -1)2+(y -1)2=1,圆心为(1,1),半径为1,所以圆心到直线的距离 d =|2k -1-2|1+k 2=12-⎝ ⎛⎭⎪⎫222=22.解得k =1或k =177.所以直线l 的方程为y +2=x +1或y +2=177(x +1),即x -y -1=0或17x -7y +3=0.。
直线与圆的位置关系讲义

九年级数学时间: 学生:第讲直线与圆的位置关系【知识点】1直线和圆的位置关系有三种:, 。
2设r为O O的半径,d为圆心O到直线l的距离, d r, 则直线l与O O相交。
d r,则直线l与O O相切d r,则直线l与O O相离。
3圆的切线的性质:圆的切线垂直于_________________ 的半径。
4圆的切线的判定定理:经过直径的一端,并且____________ 这条直径的直线是圆的切线。
5圆的切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
6.三角形的内切圆:(1)定义:与三角形三边都相切的圆称为三角形的内切圆。
(2)_________________________________ 内切圆的作法;______ .(3)_________________________ 内心的性质:内心是 _______ 的交点,内心到的距离相等,内心与三角形顶点的连线________ 这个内角。
【课前自测】1. (2011?成都)已知O O的面积为9n cm2,若点0到直线I的距离为n cm则直线l与。
O的位置关系是()A、相交B、相切 C 、相离D无法确定2.如图,从O O外一点A引圆的切线AB切点为B,连接AO并延长交圆于点C,连接BC若/ A= 26°,则/ ACB的度数为▲.3.已知O O的半径为5,圆心O到直线AB的距离为2,则O O上有且只有_______________ 到直线AB的距离为3.4.如图,已知AB是O O的一条直径,延长AB至C点,使得AC= 3BQ 个占I 八、、CD与O O相切,切点为D.若CD= d,则线段BC的长度等于5.如图23, PA与O O相切,切点为A, PO交O O于点C,点B是优弧CBA上一点,若 / ABC=32,则/ P的度数为【例题讲解】例1.如图,AB是O O的直径,点D在AB的延长线上,DC切O O于点C,若/ A=25°, 则/ D 等于A. 20°B.30°C.40°D.50°例2已知BD是O O的直径,OAL OB,M是劣弧AB上的一点,过M作O O的切线MP交OA的延长线于点P, MD交OA于点N。
2020版高考数学历史专用讲义:第九章 9.4 直线与圆、圆与圆的位置关系

§9.4 直线与圆、圆与圆的位置关系最新考纲 1.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系.2.能用直线和圆的方程解决一些简单的问题.3.在平面解析几何初步的学习过程中,体会用代数方法处理几何问题的思想.1.判断直线与圆的位置关系常用的两种方法(1)几何法:利用圆心到直线的距离d 和圆的半径r 的大小关系. d <r ⇔相交;d =r ⇔相切;d >r ⇔相离. (2)代数法:――→判别式Δ=b 2-4ac⎩⎪⎨⎪⎧>0⇔相交;=0⇔相切;<0⇔相离.2.圆与圆的位置关系设圆O 1:(x -a 1)2+(y -b 1)2=r 21(r 1>0), 圆O 2:(x -a 2)2+(y -b 2)2=r 22(r 2>0).概念方法微思考1.在求过一定点的圆的切线方程时,应注意什么?提示 应首先判断这点与圆的位置关系,若点在圆上则该点为切点,切线只有一条;若点在圆外,切线应有两条;若点在圆内,切线为零条.2.用两圆的方程组成的方程组有一解或无解时能否准确判定两圆的位置关系?提示 不能,当两圆方程组成的方程组有一解时,两圆有外切和内切两种可能情况,当方程组无解时,两圆有相离和内含两种可能情况.题组一 思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”) (1)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( × )(2)从两圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程.( × )(3)过圆O :x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程是x 0x +y 0y =r 2.( √ )(4)过圆O :x 2+y 2=r 2外一点P (x 0,y 0)作圆的两条切线,切点分别为A ,B ,则O ,P ,A ,B 四点共圆且直线AB 的方程是x 0x +y 0y =r 2.( √ )(5)如果直线与圆组成的方程组有解,则直线与圆相交或相切.( √ ) 题组二 教材改编2.若直线x -y +1=0与圆(x -a )2+y 2=2有公共点,则实数a 的取值范围是( ) A .[-3,-1] B .[-1,3]C .[-3,1]D .(-∞,-3]∪[1,+∞)答案 C解析 由题意可得,圆的圆心为(a,0),半径为2, ∴|a -0+1|12+(-1)2≤2,即|a +1|≤2,解得-3≤a ≤1.3.圆(x +2)2+y 2=4与圆(x -2)2+(y -1)2=9的位置关系为( ) A .内切 B .相交 C .外切 D .相离答案 B解析 两圆圆心分别为(-2,0),(2,1),半径分别为2和3,圆心距d =42+1=17.∵3-2<d <3+2,∴两圆相交.4.圆x 2+y 2-4=0与圆x 2+y 2-4x +4y -12=0的公共弦长为________. 答案 2 2解析 由⎩⎪⎨⎪⎧x 2+y 2-4=0,x 2+y 2-4x +4y -12=0,得两圆公共弦所在直线为x -y +2=0.又圆x 2+y 2=4的圆心到直线x -y +2=0的距离为22= 2.由勾股定理得弦长的一半为4-2=2,所以所求弦长为2 2.题组三易错自纠5.若直线l:x-y+m=0与圆C:x2+y2-4x-2y+1=0恒有公共点,则m的取值范围是() A.[-2,2] B.[-22,22]C.[-2-1,2-1] D.[-22-1,22-1]答案 D解析圆C的标准方程为(x-2)2+(y-1)2=4,圆心为(2,1),半径为2,圆心到直线的距离d=|2-1+m|2,若直线与圆恒有公共点,则|2-1+m|2≤2,解得-22-1≤m≤22-1,故选D.6.(2018·石家庄模拟)设圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|等于()A.4 B.4 2 C.8 D.8 2答案 C解析因为圆C1,C2和两坐标轴相切,且都过点(4,1),所以两圆都在第一象限内,设圆心坐标为(a,a),则|a|=(a-4)2+(a-1)2,解得a=5+22或a=5-22,可取C1(5+22,5+22),C2(5-22,5-22),故|C1C2|=(42)2+(42)2=8,故选C.7.过点A(3,5)作圆O:x2+y2-2x-4y+1=0的切线,则切线的方程为__________.答案5x-12y+45=0或x-3=0解析化圆x2+y2-2x-4y+1=0为标准方程得(x-1)2+(y-2)2=4,其圆心为(1,2),∵|OA|=(3-1)2+(5-2)2=13>2,∴点A(3,5)在圆外.显然,当切线斜率不存在时,直线与圆相切,即切线方程为x-3=0,当切线斜率存在时,可设所求切线方程为y-5=k(x-3),即kx-y+5-3k=0.又圆心为(1,2),半径r=2,而圆心到切线的距离d=|3-2k|k2+1=2,即|3-2k|=2k2+1,∴k=512,故所求切线方程为5x-12y+45=0或x-3=0.题型一 直线与圆的位置关系命题点1 位置关系的判断例1 (2018·贵州黔东南州联考)在△ABC 中,若a sin A +b sin B -c sin C =0,则圆C :x 2+y 2=1与直线l :ax +by +c =0的位置关系是( ) A .相切 B .相交 C .相离 D .不确定答案 A解析 因为a sin A +b sin B -c sin C =0, 所以由正弦定理得a 2+b 2-c 2=0.故圆心C (0,0)到直线l :ax +by +c =0的距离d =|c |a 2+b 2=1=r ,故圆C :x 2+y 2=1与直线l :ax +by +c =0相切,故选A. 命题点2 弦长问题例2 已知直线:12x -5y =3与圆x 2+y 2-6x -8y +16=0相交于A ,B 两点,则|AB |=________. 答案 4 2解析 把圆的方程化成标准方程为(x -3)2+(y -4)2=9,所以圆心坐标为(3,4),半径r =3,所以圆心到直线12x -5y =3的距离d =|12×3-5×4-3|122+(-5)2=1,则|AB |=2r 2-d 2=4 2.命题点3 切线问题例3 已知圆C :(x -1)2+(y +2)2=10,求满足下列条件的圆的切线方程. (1)与直线l 1:x +y -4=0平行; (2)与直线l 2:x -2y +4=0垂直; (3)过切点A (4,-1).解 (1)设切线方程为x +y +b =0, 则|1-2+b |2=10,∴b =1±25, ∴切线方程为x +y +1±25=0.(2)设切线方程为2x +y +m =0, 则|2-2+m |5=10,∴m =±52,∴切线方程为2x +y ±52=0.(3)∵k AC =-2+11-4=13,∴过切点A (4,-1)的切线斜率为-3,∴过切点A (4,-1)的切线方程为y +1=-3(x -4), 即3x +y -11=0.思维升华 (1)判断直线与圆的位置关系的常见方法 ①几何法:利用d 与r 的关系. ②代数法:联立方程之后利用Δ判断.③点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交. 上述方法中最常用的是几何法,点与圆的位置关系法适用于动直线问题.(2)处理直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径构成直角三角形. (3)圆的切线问题的处理要抓住圆心到直线的距离等于半径,从而建立关系解决问题. 跟踪训练1 (1)圆x 2+y 2-2x +4y =0与直线2tx -y -2-2t =0(t ∈R )的位置关系为________. 答案 相交解析 直线2tx -y -2-2t =0恒过点(1,-2), ∵12+(-2)2-2×1+4×(-2)=-5<0, ∴点(1,-2)在圆x 2+y 2-2x +4y =0内,直线2tx -y -2-2t =0与圆x 2+y 2-2x +4y =0相交.(2)过点(3,1)作圆(x -2)2+(y -2)2=4的弦,其中最短弦的长为________. 答案 2 2解析 设P (3,1),圆心C (2,2),则|PC |=2,半径r =2,由题意知最短的弦过P (3,1)且与PC 垂直,所以最短弦长为222-(2)2=2 2.(3)过点P (2,4)引圆(x -1)2+(y -1)2=1的切线,则切线方程为__________________. 答案 x =2或4x -3y +4=0解析 当直线的斜率不存在时,直线方程为x =2,此时,圆心到直线的距离等于半径,直线与圆相切,符合题意;当直线的斜率存在时,设直线方程为y -4=k (x -2),即kx -y +4-2k =0,∵直线与圆相切,∴圆心到直线的距离等于半径,即d =|k -1+4-2k |k 2+(-1)2=|3-k |k 2+1=1,解得k =43,∴所求切线方程为43x -y +4-2×43=0,即4x -3y +4=0.综上,切线方程为x =2或4x -3y +4=0.题型二 圆与圆的位置关系命题点1 位置关系的判断例4 分别求当实数k 为何值时,两圆C 1:x 2+y 2+4x -6y +12=0,C 2:x 2+y 2-2x -14y +k =0相交和相切.解 将两圆的一般方程化为标准方程,得C 1:(x +2)2+(y -3)2=1,C 2:(x -1)2+(y -7)2=50-k , 则圆C 1的圆心为C 1(-2,3),半径r 1=1; 圆C 2的圆心为C 2(1,7),半径r 2=50-k ,k <50.从而|C 1C 2|=(-2-1)2+(3-7)2=5.当|50-k -1|<5<50-k +1,即4<50-k <6,即14<k <34时,两圆相交. 当1+50-k =5,即k =34时,两圆外切;当|50-k -1|=5,即k =14时,两圆内切.所以当k =14或k =34时,两圆相切. 命题点2 公共弦问题例5 已知圆C 1:x 2+y 2-2x -6y -1=0和C 2:x 2+y 2-10x -12y +45=0. (1)求证:圆C 1和圆C 2相交;(2)求圆C 1和圆C 2的公共弦所在直线的方程和公共弦长.(1)证明 由题意得,圆C 1和圆C 2一般方程化为标准方程,得(x -1)2+(y -3)2=11,(x -5)2+(y -6)2=16,则圆C 1的圆心C 1(1,3),半径r 1=11, 圆C 2的圆心C 2(5,6),半径r 2=4,两圆圆心距d =|C 1C 2|=5,r 1+r 2=11+4, |r 1-r 2|=4-11,∴|r 1-r 2|<d <r 1+r 2, ∴圆C 1和C 2相交.(2)解 圆C 1和圆C 2的方程相减,得4x +3y -23=0, ∴两圆的公共弦所在直线的方程为4x +3y -23=0. 圆心C 2(5,6)到直线4x +3y -23=0的距离 d =|20+18-23|16+9=3,故公共弦长为216-9=27.思维升华 (1)判断两圆位置关系的方法常用几何法,即用两圆圆心距与两圆半径和及差的绝对值的大小关系判断,一般不用代数法.重视两圆内切的情况,作图观察. (2)两圆相交时,公共弦所在直线方程的求法两圆的公共弦所在直线的方程可由两圆的方程作差消去x 2,y 2项得到. (3)两圆公共弦长的求法求两圆公共弦长,常选其中一圆,由弦心距d ,半弦长l2,半径r 构成直角三角形,利用勾股定理求解.跟踪训练2 (1)(2016·山东)已知圆M :x 2+y 2-2ay =0(a >0)截直线x +y =0所得线段的长度是22,则圆M 与圆N :(x -1)2+(y -1)2=1的位置关系是( ) A .内切 B .相交 C .外切 D .相离 答案 B解析 ∵圆M :x 2+(y -a )2=a 2(a >0), ∴圆心坐标为M (0,a ),半径r 1为a , 圆心M 到直线x +y =0的距离d =|a |2,由几何知识得⎝⎛⎭⎫|a |22+(2)2=a 2,解得a =2.∴M (0,2),r 1=2.又圆N 的圆心坐标N (1,1),半径r 2=1,∴|MN |=(1-0)2+(1-2)2=2,r 1+r 2=3,r 1-r 2=1.∴r 1-r 2<|MN |<r 1+r 2,∴两圆相交,故选B.(2)圆x 2+y 2+4x -4y -1=0与圆x 2+y 2+2x -13=0相交于P ,Q 两点,则直线PQ 的方程为______________. 答案 x -2y +6=0解析 两个圆的方程两端相减,可得2x -4y +12=0. 即x -2y +6=0.1.若两圆x 2+y 2=m 和x 2+y 2+6x -8y -11=0有公共点,则实数m 的取值范围是( ) A .(-∞,1) B .(121,+∞) C .[1,121] D .(1,121)答案 C解析 x 2+y 2+6x -8y -11=0化成标准方程为 (x +3)2+(y -4)2=36. 圆心距为d =(0+3)2+(0-4)2=5,若两圆有公共点,则|6-m |≤5≤6+m , 所以1≤m ≤121.故选C.2.直线x -3y +3=0与圆(x -1)2+(y -3)2=10相交所得弦长为( ) A.30 B.532 C .4 2 D .3 3答案 A解析 圆(x -1)2+(y -3)2=10的圆心坐标为(1,3),半径r =10,圆心(1,3)到直线x -3y +3=0的距离d =|1-9+3|10=510,故弦|AB |=210-2510=30,故选A.3.已知直线l :x cos α+y sin α=2(α∈R ),圆C :x 2+y 2+2x cos θ+2y sin θ=0(θ∈R ),则直线l 与圆C 的位置关系是( )A .相交B .相切C .相离D .与α,θ有关答案 D解析 圆C :x 2+y 2+2x cos θ+2y sin θ=0(θ∈R ),即(x +cos θ)2+(y +sin θ)2=1(θ∈R ),圆心C 的坐标为(-cos θ,-sin θ),半径为r =1.圆心C 到直线l :x cos α+y sin α=2(α∈R )的距离d =|-cos θcos α-sin θsin α-2|cos 2α+sin 2α=2+cos(θ-α).当cos(θ-α)=-1时,d =r ,直线l 和圆C 相切; 当-1<cos(θ-α)≤1时,d >r ,直线l 和圆C 相离,故选D.4.(2018·福州模拟)过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12C .y =-32D .y =-14答案 B解析 圆(x -1)2+y 2=1的圆心为(1,0),半径为1,以|PC |=(1-1)2+(-2-0)2=2为直径的圆的方程为(x -1)2+(y +1)2=1,将两圆的方程相减得AB 所在直线的方程为2y +1=0,即y =-12.5.若点A (1,0)和点B (4,0)到直线l 的距离依次为1和2,则这样的直线有( ) A .1条 B .2条 C .3条 D .4条 答案 C解析 如图,分别以A ,B 为圆心,1,2为半径作圆.由题意得,直线l 是圆A 的切线,A 到l 的距离为1,直线l 也是圆B 的切线,B 到l 的距离为2,所以直线l 是两圆的公切线,共3条(2条外公切线,1条内公切线).6.(2018·东北三省联考)直线x +2y +m =0(m >0)与⊙O :x 2+y 2=5交于A ,B 两点,若|OA →+OB →|>2|AB →|,则m 的取值范围是( )A .(5,25)B .(25,5)C .(5,5)D .(2,5)答案 B解析 ∵直线x +2y +m =0与⊙O :x 2+y 2=5交于相异两点A ,B ,∴O 点到直线x +2y +m =0的距离d < 5.记OA →+OB →=OD →,则四边形OADB 是菱形,且|OD →|=2d . ∵|OA →+OB →|>2|AB →|,∴2d >2|AB →|, 即d >|AB →|=25-d 2,解得d >2.又d <5,∴2<d <5,即2<|m |5< 5. 又m >0,解得m ∈(25,5).7.(2016·全国Ⅲ)已知直线l :x -3y +6=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D 两点,则|CD |=________. 答案 4解析 设A (x 1,y 1),B (x 2,y 2),由⎩⎪⎨⎪⎧x -3y +6=0,x 2+y 2=12,得y 2-33y +6=0,解得x 1=-3,y 1=3;x 2=0,y 2=23, ∴A (-3,3),B (0,23).过A ,B 作l 的垂线方程分别为 y -3=-3(x +3),y -23=-3x ,令y =0, 则x C =-2,x D =2,∴|CD |=2-(-2)=4.8.过点P (1,3)作圆x 2+y 2=1的两条切线,切点分别为A ,B ,则P A →·PB →=________. 答案 32解析 由题意,得圆心为O (0,0),半径为1.如图所示,∵P (1,3),∴PB ⊥x 轴,|P A |=|PB |= 3.∴△POA 为直角三角形, 其中|OA |=1,|AP |=3,则|OP |=2,∴∠OP A =30°,∴∠APB =60°. ∴P A →·PB →=|P A →||PB →|·cos ∠APB =3×3×cos 60°=32.9.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是________. 答案 43解析 圆C 的标准方程为(x -4)2+y 2=1,圆心为(4,0). 由题意知(4,0)到kx -y -2=0的距离应不大于2, 即|4k -2|k 2+1≤2,整理得3k 2-4k ≤0,解得0≤k ≤43.故k 的最大值是43.10.(2018·成都模拟)已知圆C :(x -3)2+(y -4)2=25,圆C 上的点到直线l :3x +4y +m =0(m <0)的最短距离为1,若点N (a ,b )在直线l 上位于第一象限的部分,则1a +1b 的最小值为____________. 答案7+4355解析 圆C :(x -3)2+(y -4)2=25,圆心坐标(3,4),半径为5,因为圆C 上的点到直线l :3x +4y +m =0(m <0)的最短距离为1,则直线l 与圆C 相离,设圆心到直线的距离为d ,则d -r =1,可得|9+16+m |9+16=6,解得m =-55或m =5(舍去).因为点N (a ,b )在直线l 上位于第一象限的部分, 所以3a +4b =55,a >0,b >0. 则1a +1b =155⎝⎛⎭⎫1a +1b (3a +4b )=155⎝⎛⎭⎫7+4b a +3a b ≥155⎝⎛⎭⎫7+24b a ·3a b =7+4355, 当且仅当a =-55+11033,b =55-5532时取等号.11.已知圆C :x 2+y 2+2x -4y +1=0,O 为坐标原点,动点P 在圆C 外,过P 作圆C 的切线,设切点为M .(1)若点P 运动到(1,3)处,求此时切线l 的方程; (2)求满足条件|PM |=|PO |的点P 的轨迹方程.解 把圆C 的方程化为标准方程为(x +1)2+(y -2)2=4, ∴圆心为C (-1,2),半径r =2.(1)当l 的斜率不存在时,此时l 的方程为x =1, C 到l 的距离d =2=r ,满足条件. 当l 的斜率存在时,设斜率为k , 得l 的方程为y -3=k (x -1), 即kx -y +3-k =0, 则|-k -2+3-k |1+k 2=2,解得k =-34.∴l 的方程为y -3=-34(x -1),即3x +4y -15=0.综上,满足条件的切线l 的方程为x =1或3x +4y -15=0. (2)设P (x ,y ),则|PM |2=|PC |2-|MC |2 =(x +1)2+(y -2)2-4, |PO |2=x 2+y 2,∵|PM |=|PO |, ∴(x +1)2+(y -2)2-4=x 2+y 2, 整理,得2x -4y +1=0,∴点P 的轨迹方程为2x -4y +1=0.12.如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :x 2+y 2-12x -14y +60=0及其上一点A (2,4).(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线x =6上,求圆N 的标准方程; (2)设平行于OA 的直线l 与圆M 相交于B ,C 两点,且BC =OA ,求直线l 的方程; (3)设点T (t,0)满足:存在圆M 上的两点P 和Q ,使得TA →+TP →=TQ →,求实数t 的取值范围. 解 (1)圆M 的方程化为标准形式为(x -6)2+(y -7)2=25,圆心M (6,7),半径r =5, 由题意,设圆N 的方程为(x -6)2+(y -b )2=b 2(b >0). 且(6-6)2+(b -7)2=b +5.解得b =1,∴圆N 的标准方程为(x -6)2+(y -1)2=1. (2)∵k OA =2,∴可设l 的方程为y =2x +m ,即2x -y +m =0.又BC =OA =22+42=2 5.由题意,圆M 的圆心M (6,7)到直线l 的距离为d = 52-⎝⎛⎭⎫BC 22=25-5=2 5.即|2×6-7+m |22+(-1)2=25,解得m =5或m =-15.∴直线l 的方程为y =2x +5或y =2x -15.(3)由TA →+TP →=TQ →,则四边形AQPT 为平行四边形, 又∵P ,Q 为圆M 上的两点,∴PQ ≤2r =10. ∴TA =PQ ≤10,即(t -2)2+42≤10,解得2-221≤t ≤2+221.故所求t 的取值范围为[2-221,2+221].13.(2018·贵阳第一中学月考)已知直线l :(m +2)x +(m -1)y +4-4m =0上总存在点M ,使得过M 点作的圆C :x 2+y 2+2x -4y +3=0的两条切线互相垂直,则实数m 的取值范围是( )A .m ≤1或m ≥2B .2≤m ≤8C .-2≤m ≤10D .m ≤-2或m ≥8答案 C 解析 如图,设切点分别为A ,B .连接AC ,BC ,MC ,由∠AMB =∠MAC =∠MBC =90°及MA =MB 知,四边形MACB 为正方形,故|MC |=2+2=2,若直线l 上总存在点M 使得过点M 的两条切线互相垂直,只需圆心(-1,2)到直线l 的距离d =|-m -2+2m -2+4-4m |(m +2)2+(m -1)2≤2,即m 2-8m-20≤0,∴-2≤m ≤10,故选C.14.若⊙O :x 2+y 2=5与⊙O 1:(x -m )2+y 2=20(m ∈R )相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长是________. 答案 4解析 ⊙O 1与⊙O 在A 处的切线互相垂直,如图,可知两切线分别过另一圆的圆心,∴O 1A ⊥OA .又∵|OA |=5,|O 1A |=25,∴|OO 1|=5. 又A ,B 关于OO 1所在直线对称, ∴AB 长为Rt △OAO 1斜边上的高的2倍, ∴|AB |=2×5×255=4.15.已知圆O :x 2+y 2=9,点P 为直线x +2y -9=0上一动点,过点P 向圆O 引两条切线P A ,PB ,A ,B 为切点,则直线AB 过定点( ) A.⎝⎛⎭⎫49,89 B.⎝⎛⎭⎫29,49 C .(1,2) D .(9,0)答案 C解析 因为P 是直线x +2y -9=0上的任一点,所以设P (9-2m ,m ),因为P A ,PB 为圆x 2+y 2=9的两条切线,切点分别为A ,B ,所以OA ⊥P A ,OB ⊥PB ,则点A ,B 在以OP 为直径的圆(记为圆C )上,即AB 是圆O 和圆C 的公共弦,易知圆C 的方程是⎝⎛⎭⎪⎫x -9-2m 22+⎝⎛⎭⎫y -m 22=(9-2m )2+m24, ① 又x 2+y 2=9, ②②-①得,(2m -9)x -my +9=0,即公共弦AB 所在直线的方程是(2m -9)x -my +9=0,即m (2x -y )+(-9x +9)=0,由⎩⎪⎨⎪⎧2x -y =0,-9x +9=0得x =1,y =2.所以直线AB 恒过定点(1,2),故选C.16.已知抛物线C :y 2=4x 的焦点为F ,过点F 且斜率为1的直线与抛物线C 交于点A ,B ,以线段AB 为直径的圆E 上存在点P ,Q ,使得以PQ 为直径的圆过点D ⎝⎛⎭⎫-32,t ,求实数t 的取值范围.解 由题意可得直线AB 的方程为x =y +1,与y 2=4x 联立消去x ,可得y 2-4y -4=0,显然Δ=16+16>0,设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=4,y 1y 2=-4,设E (x E ,y E ),则y E =y 1+y 22=2,x E =y E +1=3,又|AB |=x 1+x 2+2=y 1+1+y 2+1+2=8,所以圆E 是以(3,2)为圆心,4为半径的圆,所以点D 恒在圆E 外.圆E 上存在点P ,Q ,使得以PQ 为直径的圆过点D ⎝⎛⎭⎫-32,t ,即圆E 上存在点P ,Q ,使得DP ⊥DQ ,设过D 点的两直线分别切圆E 于P ′,Q ′点,要满足题意,则∠P ′DQ ′≥π2,所以|EP ′||DE |=4⎝⎛⎭⎫3+322+()2-t 2≥22,整理得t 2-4t -314≤0,解得2-472≤t ≤2+472,故实数t 的取值范围为⎣⎡⎦⎤2-472,2+472.。
直线与圆、圆与圆的位置关系讲义

直线与圆、圆与圆的位置关系讲义课前双击巩固1.直线与圆的位置关系设圆O 的半径为r (r>0),圆心到直线l 的距离为d ,则直线与圆的位置关系可用下表表示:位置关系 相离 相切 相交图形量化 方程观点 Δ 0 Δ 0 Δ 0 几何观点d r d r d r2.两圆的位置关系设两圆的半径分别为R ,r (R>r ),两圆圆心间的距离为d ,则两圆的位置关系可用下表表示:位置关系 相离 外切 相交 内切 内含图形量的关系常用结论1.求圆的切线方程,常用两种方法(1)代数法:将直线方程代入圆的方程中,消去一个未知数(x 或y),令一元二次方程的判别式等于0,求出相关参数.(2)几何法:将圆的切线方程设为一般式,根据圆心到直线的距离等于半径,求出相关参数.2.直线被圆截得的弦长的求法(1)几何法:运用弦心距d 、半径r 和弦长的一半构成的直角三角形,计算弦长|AB|=2√r 2-d 2.(2)代数法:设直线y=kx+m 与圆x 2+y 2+Dx+Ey+F=0相交于点M,N,将直线方程代入圆的方程中,消去y,得关于x 的一元二次方程,求出x M +x N 和x M ·x N ,则|MN|=√1+k 2·√(x M +x N )2-4x M ·x N.题组一常识题1.[教材改编]直线y=kx+1与圆x2+y2-2x-3=0的位置关系是.2.[教材改编]以点(2,-1)为圆心且与直线x+y=6相切的圆的方程是.3.[教材改编]圆(x+2)2+y2=4与圆(x-2)2+(y-1)2=9的位置关系为.4.[教材改编]直线x-y-5=0被圆x2+y2-4x+4y+6=0所截得的弦的长为.题组二常错题◆索引:忽视分两圆内切与外切两种情形;忽视切线斜率k不存在的情形;求弦所在直线的方程时遗漏一解.5.若圆x2+y2=1与圆(x+4)2+(y-a)2=25相切,则常数a=.6.已知圆C: x2+y2=9,过点P(3,1)作圆C的切线,则切线方程为.且被圆x2+y2=25截得的弦长是8,则该直线的方程7.若直线过点P-3,-32为.课堂考点探究探究点一直线与圆的位置关系1 (1)直线x+ay+1=0与圆x2+(y-1)2=4的位置关系是( )A.相交B.相切C.相离D.不能确定(2)直线x-y+m=0与圆x2+y2-2x-1=0有两个不同交点的一个充分不必要条件是( )A.0<m<1B.-4<m<0C.m<1D.-3<m<1[总结反思]判断直线与圆的位置关系的常用方法:(1)若易求出圆心到直线的距离,则用几何法,利用d与r的关系判断.(2)若方程中含有参数,或圆心到直线的距离的表达式较复杂,则用代数法,联立方程后利用Δ判断,能用几何法求解的,尽量不用代数法.式题 (1)圆2x 2+2y 2=1与直线xsin θ+y -1=0θ∈R ,θ≠π2+kπ,k ∈Z 的位置关系是 (横线内容从“相交、相切、相离、不确定”中选填).(2)过定点P (-2,0)的直线l 与曲线C :(x-2)2+y 2=4(0≤x ≤3)交于不同的两点,则直线l 的斜率的取值范围是 . 探究点二 圆的切线与弦长问题2 (1) 过点(1,1)的直线l 与圆(x-2)2+(y-3)2=9相交于A ,B 两点,当|AB |=4时,直线l 的方程为 .(2) 已知圆的方程是x 2+y 2=1,则经过上一点M √22,√22的切线方程是 .[总结反思] (1)处理直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径构成直角三角形.(2)处理圆的切线问题时,一般通过圆心到直线的距离等于半径建立关系式解决问题.若点M (x 0,y 0)在圆x 2+y 2=r 2上,则过点M 的圆的切线方程为x 0x+y 0y=r 2.式题 (1)已知直线l :x+y-2=0和圆C :x 2+y 2-12x-12y+m=0相切,则实数m 的值为 . (2) 设直线y=kx+1与圆x 2+y 2+2x-my=0相交于A ,B 两点,若点A ,B 关于直线l :x+y=0对称,则|AB |= .(3)已知点M 在直线x+y+a=0上,过点M 引圆O :x 2+y 2=2的切线,若切线长的最小值为 2√2,则实数a 的值为 ( )A. ±2√2B.±3C.±4D. ±2√5探究点三 圆与圆的位置关系3 (1) 已知圆C 1:x 2+y 2=4,圆C 2:x 2+y 2+6x-8y+16=0,则圆C 1和圆C 2的位置关系是 ( )A.相离B.外切C.相交D.内切(2)已知经过点P1,32的两个圆C1,C2都与直线l1:y=12x,l2:y=2x相切,则这两圆的圆心距C1C2等于.[总结反思](1)处理两圆的位置关系时多用圆心距与半径的和或差的关系判断,一般不采用代数法.(2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差得到.式题(1)已知点O(0,0),M(1,0),且圆C:(x-5)2+(y-4)2=r2(r>0)上至少存在一点P,使得|PO|=√2|PM|,则r的最小值是.(2)设P(x1,y1)是圆O1:x2+y2=9上的点,圆O2的圆心为O2(a,b),半径为1,则(a-x1)2+(b-y1)2=1是圆O1与圆O2相切的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件课时作业一、填空题1.将圆x2+y2-2x-4y+1=0平分的直线是________.2.过两圆x2+y2+3x+2y=0及x2+y2+2x+6y-4=0的交点的直线方程是________.3.已知直线l:y=k(x-1)-3与圆x2+y2=1相切,则直线l的倾斜角为________.4.若圆心在x轴上,半径为5的圆C位于y轴左侧,且被直线x+2y=0截得的弦长为4,则圆C的方程是________.5.若过点P(1,3)作圆O:x2+y2=1的两条切线,切点分别为A和B,则弦长|AB|=________.6.过点(1,1)的直线与圆(x-2)2+(y-3)2=9相交于A,B两点,则|AB|的最小值为________.7.已知圆C:x2+y2-4x=0,l是过点P(3,0)的直线,则________.8.在平面直角坐标系xOy中,直线3x+4y-5=0与圆x2+y2=4相交于A、B两点,则弦AB的长等于________.9.设直线l截圆x2+y2-2y=0所得弦AB的中点为(-12,32),则直线l的方程为________;|AB|=________.10.设圆C同时满足三个条件:①过原点;②圆心在直线y=x上;③截y轴所得的弦长为4,则圆C 的方程是________.11.若圆x2+y2=4与圆x2+y2+2ay-6=0(a>0)的公共弦长为23,则a=________.二、解答题12.一个圆与y轴相切,圆心在直线x-3y=0上,且在直线y=x上截得的弦长为27,求此圆的方程.13.已知:圆C:x2+y2-8y+12=0,直线l:ax+y+2a=0.(1)当a为何值时,直线l与圆C相切;(2)当直线l与圆C相交于A、B两点,且AB=22时,求直线l的方程.。
圆与圆有关的位置关系 讲义(教师版)
与圆有关的位置关系1.能根据点到圆心的距离和半径的大小关系确定点与圆的位置关系;2.能根据圆心到直线的距离和半径的大小关系确定直线与圆的位置关系;3.能根据两圆的圆心距与两圆的半径之间的数量关系判定两圆的位置关系.1.点与圆的位置关系的判定;2.直线与圆的位置关系的判定.点与圆的位置关系1.点与圆的位置关系:设⊙O的半径为r,点P到圆心的距离OP = d,则有:点P在圆内⇔d<r点P在圆上⇔d=r点P在圆外⇔d>r【注意】点与圆的位置关系是由点P到圆心的距离d和圆的半径r的数量关系决定的,在运用这一性质时应注意“形”与“数”之间的转化.2.确定圆的条件:不在同一条直线上的三点确定一个圆.【注意】可以让学生通过作图进行归纳总结“不在同一条直线上的三点确定一个圆”,熟练掌握其方法,经过一点或经过两点作圆,因为圆心不能唯一确定,半径也就不能确定.所以作出的圆都有无限多个.“不在同一直线上的三点确定一个圆”,这个“确定”的含义是“有且只有”.3.外接圆与外心:经过三角形的三个顶点可以做一个圆,这个圆叫做三角形的外接圆,外接圆的圆心是三角形三条边垂直平分线的交点,叫做这个三角形的外心,三角形的外心到三角形的三个顶点的距离相等.【注意】要注意的是,锐角三角形的外心在三角形的内部;直角三角形的外心是三角形斜边中点;钝角三角形的外心在三角形的外部,反之成立.例1.矩形ABCD中,AB=8,BC=35,点P在边AB上,且BP=3AP,如果圆P 是以点P为圆心,PD为半径的圆,那么下列判断正确的是()A.点B、C均在圆P外B.点B在圆P外、点C在圆P内C.点B在圆P内、点C在圆P外D.点B、C均在圆P内【答案】解:连接PD、PC,⊙AB=8,点P 在边AB 上,且BP=3AP ,⊙AP=2,BP=6 在Rt APD ∆中,7PD ====,⊙⊙P 的半径r=7, 在Rt BPC ∆中,9PC ===⊙PB=6<r ,PC=9>r⊙点B 在圆P 内、点C 在圆P 外.故选C .【解析】此题主要考查判断点与圆的位置关系.需要比较点到圆心的距离与半径的大小关系,根据BP=3AP 和AB=8求得AP 的长,然后利用勾股定理求得圆P 的半径PD 的长,根据点B 、C 到P 点的距离判断点P 与圆的位置关系即可.练习1.如图,在Rt⊙ABC 中⊙ACB=90°,AC=6,AB=10,CD 是斜边AB 上的中线,以AC 为直径作⊙O ,设线段CD 的中点为P ,则点P 与⊙O 的位置关系是( )A.点P 在⊙O 内B.点P 在⊙O 上C.点P 在⊙O 外D.无法确定 【答案】A【解析】解:⊙AC=6,AB=10,CD 是斜边AB 上的中线, ⊙AD=5,OP=2.5,OC=OA=3, ⊙OP <OA ,⊙点P 在⊙O 内,故选A .练习2.如图,在平面直角坐标系中,⊙O 的半径为1, 点A坐标为12⎛ ⎝⎭,则点A 与⊙O的位置关系是( )ABA.点A 在⊙O 外B.点A 在⊙O 上C.点A 在⊙O 内D.无法判断【答案】解:⊙点A 坐标为12⎛ ⎝⎭,⊙OA = ⊙点A 在⊙O 上,故选B .【解析】本题考查点与圆的三种位置关系:点在圆内,点在圆上,点在圆外.根据点与圆的位置关系比较点到圆心的距离与1的大小关系,然后再确定点在圆上、内、外. 练习3.点P 到⊙O 的圆心O 的距离为d ,⊙O 的半径为r ,d 与r 的值是一元二次方程的两个根,则点P 与⊙O 的位置关系为( )A.点P 在⊙O 内B.点P 在⊙O 外C.点P 在⊙O 上D.点P 不在⊙O 上 【答案】解:解方程2320x x -+=得:x=1或x=2, ⊙d≠r ,⊙点P 不在⊙O 上, 故选D .【解析】本题考查了点与圆的位置关系及用因式分解法解一元二次方程的知识,解题的关键是正确地解方程.解方程求得方程的两个根即可得到d 与r 的值,然后做出判断.点与圆心之间的距离d 和该圆的半径r 有三种不同的大小关系,则点与圆也有三种不同的位置关系,所以在判断点与圆的位置关系时,只需要判断点到圆心的距离与半径的大小即可.例2.如图所示,一圆弧过方格的格点A 、B 、C ,试在方格中建立平面直角坐标系,使点A 的坐标为(-2,4),则该圆弧所在圆的圆心坐标是( )0232=+-xxA.(-1,2)B.(1,-1)C.(-1,1)D.(2,1)【答案】C【解析】解:如图所示,⊙AW=1,WH=3,=⊙BQ=3,QH=1,=⊙AH=BH同理,AD=BD,所以GH为线段AB的垂直平分线,易得EF为线段AC的垂直平分线,H为圆的两条弦的垂直平分线的交点,则BH=AH=HC,H为圆心.则该圆弧所在圆的圆心坐标是(-1,1).故选C.练习1.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,那么这条圆弧所在圆的圆心是()A.点PB.点QC.点RD.点M【答案】B【解析】根据垂径定理的推论,则作弦AB和BC的垂直平分线,交点Q即为圆心.故选B.练习2.如图,小明不慎把家里的圆形玻璃打碎了,其中四块碎片如图所示,为配到与原来大小一样的圆形玻璃,小明带到商店去的一块玻璃碎片应该是()A.第⊙块B.第⊙块C.第⊙块D.第⊙块【答案】B【解析】解:第⊙块出现一段完整的弧,可在这段弧上任做两条弦,作出这两条弦的垂直平分线,就交于圆心,进而可得到半径的长.故选B.三角形外接圆的圆心是三角形三条边垂直平分线的交点,圆上任意两弦的垂直平分线的交点即为该圆的圆心.例3.下列说法中,正确的有()①三点可以确定一个圆;⊙ 三角形的外心是三角形三边中线的交点;⊙ 锐角三角形的外心在三角形外;⊙ 三角形的外心到三角形各顶点的距离相等.A.1个B.2个C.3个D.4个【答案】A【解析】解:⊙不在同一直线上三点才可以作一个圆,⊙⊙错误;⊙三角形的外心是三角形三边垂直平分线的交点,⊙⊙错误;⊙锐角三角形的外心在三角形的内部,⊙⊙错误;⊙三角形的外心是三角形三边垂直平分线的交点,⊙根据垂直平分线性质得出三角形外心到三角形三个顶点的距离相等,⊙⊙正确;故选A.练习1.有如下结论:⊙一个圆只有一个内接三角形;⊙一个三角形只有一个外接圆;⊙直角三角形的外心是它斜边的中点;⊙等边三角形的外心是它角平分线的交点.A.1个B.2个C.3个D.4个【答案】C【解析】解:一个圆有无数个内接三角形,⊙⊙错误;三角形只有一个外接圆,⊙⊙正确;直角三角形斜边的中点到直角三角形三个顶点的距离相等,是直角三角形的外心,⊙⊙正确;等边三角形具有等腰三角形的三线合一的性质,等边三角形的外心是三边垂直平分线的交点,也是三条角平分线的交点,⊙⊙正确;故选C.练习2.正三角形的外接圆的半径和高的比为( )A.1⊙2B.2⊙3C.3⊙4D.1⊙3【答案】B【解析】连接OB,AO,延长AO交BC于D,⊙⊙O是等边三角形ABC的外接圆,⊙AD⊙BC,⊙OBC=12⊙ABC =12×60°=30°,⊙⊙ADB=90°,⊙OBC=30°,⊙12 OD OB⊙AD=OA+OD,⊙AD=OB+12OB =32OB,即OB:AD =2:3.故选B.练习3.已知:如图,⊙O是⊙ABC的外接圆,D为CB延长线上一点,⊙AOC=130°,则⊙ABD 的度数为()A.40°B.50°C.65°D.100°【答案】C【解析】解:在优弧AC上任意找一点E,连接AE、CE,根据圆周角定理得⊙E=65°;⊙四边形ABCE内接于⊙O,⊙⊙ABD=⊙E=65°.故选C不在同一直线上三点才可以作一个圆,在同一直线上三点不能作一个圆,三角形的外心是三角形三边垂直平分线的交点,锐角三角形的外心在三角形的内部.直线与圆的位置关系1.直线与圆的三种位置关系:【注意】判断直线与圆的位置关系时,既可以用直线与圆的公共点个数来判断,也可以用圆心到直线的距离d与r的大小关系来判定.要注意让学生根据不同的条件准确快速地判断直线与圆的位置关系.2.切线的判定方法(1)定义法:和圆有且只有一个公共点的直线是圆的切线.(2)数量法:圆心到直线的距离等于半径的直线是圆的切线(d=r).(3)判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.3.切线的性质定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.例1.已知⊙O 的半径为3cm ,点P 是直线l 上一点,OP 长为5cm ,则直线l 与⊙O 的位置关系为( ) A.相交 B.相切C.相离D.相交、相切、相离都有可能【答案】D【解析】本题知道⊙O 的半径为3cm ,并知道点P 是直线l 上一点,OP 长为5cm ,并没有告诉圆心到直线l 的距离,且根据已知条件无法确定圆心到直线l 的距离的大小,所以此时要根据直线圆的位置关系的三种情况分别探究是否都有可能.通过具体的数值分析,可知直线l 与圆的位置关系三种都有可能,所以选D.练习1.如图,⊙O 的半径OC=5cm ,直线l ⊥OC ,垂足为H ,且l 交⊙O 于点A 、B 两点,AB=8cm ,则l 沿OC 所在的直线向下平移____cm 时与⊙O 相切.【答案】2【解析】本题是一道判断直线与圆相切有关的问题,涉及到垂径定理、勾股定理以及平移等有关知识的应用.要判断直线l 沿OC 的方向平移多少cm 时与⊙O 相切,只要求到CH 的长度即可.因为CH=OC -OH ,所以只要求到OH 就可解决问题. 解:连接OA ,在Rt⊙AOH 中,因为0A=5cm ,AH=4cm , 所以OH=3452222=-=-AH OA cm.所以CH=OC -OH=2cm.即l 沿OC 所在的直线向下平移2cm 时与⊙O 相切.练习2.如图,直线AB 、CD 相交于点O ,⊙AOD=30°,半径为1cm 的⊙P 的圆心在射线OA 上,且与点O 的距离为6cm .如果⊙P 以1cm/s 的速度沿由A 向B 的方向移动,那么( )秒钟后⊙P 与直线CD 相切. A .4B .8C .4或6D .4或8【解析】本题是一道设计比较新颖的题目,要判断几秒种后⊙P与直线CD相切,则需要计算出当P与直线CD相切时,圆心P移动的距离,如图,在移动的过程中,P与直线CD相切有两种情况,如图,当圆心运动到P1、P2的位置时与直线CD相切,只要求到PP1,PP2长度即可.解:当圆心移动到P1、P2的位置时,设P1与直线CD切于E点,则P1E=1,因为⊙POD=30°,所以OP1=2,所以PP1=6-2=4,同样可求PP2=8cm,所以经过4秒或8秒钟后⊙P与直线CD 相切.故选D.练习3.如图,⊙ABC中,AB=6,AC=8,BC=10,D、E分别是AC、AB的中点,则以DE 为直径的圆与BC的位置关系()A.相交B.相切C.相离D.无法确定【答案】A【解析】解:过点A作AM⊙BC于点M,交DE于点N,⊙AM·BC=AC·AB,⊙AM=4.8⊙D、E分别是AC、AB的中点,⊙DE⊙BC,DE=12BC=5⊙AN=MN=12AM,⊙MN=2.4,⊙以DE为直径的圆半径为2.5⊙r=2.5>2.4,⊙以DE为直径的圆与BC的位置关系是:相交.故选A练习4.如图,在平面直角坐标系中,⊙O的半径为1,则直线y=x与⊙O的位置关系是()A.相离B.相切C.相交D.以上三种情况都有可能 【答案】B【解析】解:⊙令x=0,则y=令y=0,则, ⊙A(0,,,0),⊙⊙AOB 是等腰直角三角形, ⊙AB=2,过点O 作OD⊙AB ,则OD=BD=1 ⊙直线y=x与⊙O 相切.故选B判断直线与圆的位置关系时,既可以用直线与圆的公共点个数来判断,也可以用圆心到直线的距离d 与r 的大小关系来判定.例2.如图,在⊙O 中,AB 是直径,AD 是弦,⊙ADE = 60°,⊙C = 30°.判断直线CD是否为⊙O 的切线,并说明理由.【答案】解:连接OD ,如图,⊙⊙ADE=60°,⊙C=30°, ⊙⊙A=⊙ADE -⊙C=60°-30°=30°, 又⊙OD=OA ,⊙⊙ODA=⊙A=30°, ⊙⊙EDO=90°,⊙OD 为⊙O 的半径,⊙CD 是⊙O 的切线【解析】本题考查圆切线的判定方法:若直线与圆有唯一交点,则此直线是圆的切线;若圆心到直线的距离等于圆的半径,则此直线是圆的切线;经过半径的外端与半径垂直的直线是圆的切线.当已知直线过圆上一点,要证明它是圆的切线,则要连接圆心和该点,证明该连线与已知直线垂直即可;当没告诉直线过圆上一点,要证明它是圆的切线,则要过圆心作直线的垂线,证明垂线段等于圆的半径,由题可知直线CD 与圆有公共点,故直接连接OD 证明OD⊙CD 即可.练习1.已知:如图,O 为ABC ∆的外接圆,BC 为O 的直径,作射线BF ,使得BA 平分CBF ∠,过点A 作AD BF ⊥于点D .求证: 直线DA 为⊙O 的切线.【答案】解:连接OA ,⊙BC 为⊙O 的直径,BA 平分⊙CBF ,AD⊙BF ,⊙⊙ADB=⊙BAC=90°,⊙DBA=⊙CBA;⊙⊙OAC=⊙OCA,⊙⊙DAO=⊙DAB+⊙BAO=⊙BAO+⊙OAC=90°,⊙OA为⊙O半径,⊙DA为⊙O的切线.【解析】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.练习2.已知:如图,AB为⊙O的弦,过点O作AB的平行线,交⊙O于点C,直线OC上一点D满足⊙D=⊙ACB.判断直线BD与⊙O的位置关系,并证明你的结论.【答案】直线BD与⊙O相切.证明:如图,连接OB.⊙⊙OCB=⊙CBD+⊙D,⊙1=⊙D,⊙⊙2=⊙CBD,⊙AB⊙OC,⊙⊙2=⊙A,⊙⊙A=⊙CBD.⊙OB=OC,⊙⊙BOC+2⊙3=180°.⊙⊙BOC=2⊙A,⊙⊙A+⊙3=90°.⊙⊙CBD+⊙3=90°.⊙⊙OBD=90°.⊙OB为⊙O半径,⊙直线BD与⊙O相切.【解析】本题考查了切线的判定.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.练习3.如图,D是⊙O的直径CA延长线上一点,点B在⊙O上,且AB=AD=AO,求证:BD是⊙O的切线.【答案】连接BO,⊙AB=AD,⊙⊙D=⊙ABD⊙AB=AO,⊙⊙ABO=⊙AOB又在⊙OBD中,⊙D+⊙DOB+⊙ABO+⊙ABD=180°,⊙⊙OBD=90°,即BD⊙BO⊙OB为⊙O半径,⊙BD是⊙O的切线.练习4.已知:如图,⊙O是⊙ABC的外接圆,AB是⊙O的直径,D是AB延长线上的一点,AE⊙DC,交DC的延长线于点E,且AC平分⊙EAB.(1)求证:DE是⊙O的切线.(2)若⊙ADC=30°,AC=6,求BC的长.【答案】(1)连接OC,则⊙CAO=⊙ACO.⊙AC平分⊙EAB,⊙⊙EAC=⊙CAO.⊙⊙EAC=⊙ACO .⊙AE⊙OC . ⊙⊙DCO=⊙E=90°,即DE⊙OC . ⊙OC 为半径,⊙DE 是⊙O 的切线. (2)⊙⊙ADC=30°,⊙⊙EAD=60°, ⊙⊙BAC=12⊙EAD=30°, ⊙AB 是⊙O 的直径,⊙⊙ACB=90°,⊙BC=【解析】本题考查了切线的判定与性质;证明某一直线是圆的切线时,一般情况下是连接切点与圆心,通过证明该半径垂直于这一直线来判定切线.(1)应用判定定理判定圆的切线时,必须先弄清“题设”中的两个条件:一是经过半径的外端,二是垂直于这条半径,这两者缺一不可;(2)切线的判定定理中,只有证明是切线后,这个交点才能称为切点;(3)证明切线常见题型:⊙已知交点:连半径、证垂直;⊙交点未知:作垂直、证半径.例3.等腰⊙ABC 中,以AC 为直径作⊙O 交BC 于点D ,交AB 于点G ,过点D 作⊙O 的切线交AB 于点E ,交AC 的延长线与点F .求证:EF⊙AB .【答案】解:连接OD ,⊙OC=OD ,⊙⊙ODC=⊙OCD ,又⊙AB=AC,⊙⊙OCD=⊙B,⊙⊙ODC=⊙B,⊙OD⊙AB,⊙ED是⊙O的切线,OD是⊙O的半径,⊙OD⊙EF,⊙AB⊙EF .练习1.如图,⊙O的直径AB=4,C为圆周上一点,AC=2,过点C作⊙O的切线l,过点B 作l的垂线BD,垂足为D,BD与⊙O交于点E.(1)求⊙AEC的度数;(2)求证:四边形OBEC是菱形.【答案】解:(1)在⊙AOC中,AC=2,⊙AO=OC=2,⊙⊙AOC是等边三角形,⊙⊙AOC=60°,⊙⊙AEC=30°;(2)⊙OC⊙l,BD⊙l.⊙OC⊙BD.⊙⊙ABD=⊙AOC=60°.⊙AB为⊙O的直径,⊙⊙AEB=90°,⊙⊙AEB为直角三角形,⊙EAB=30°.⊙⊙EAB=⊙AEC.⊙CE⊙OB,又⊙CO⊙EB,⊙四边形OBEC为平行四边形.又⊙OB=OC=2.⊙四边形OBEC是菱形.归纳切线的性质:(1)切线和圆有唯一公共点(切线的定义);(2)圆心到直线的距离等于圆的半径(判定方法(2)的逆命题);(3)切线垂直于过切点的半径(切线的性质定理);(4)经过圆心垂直于切线的直线必过切点(推论1);(5)经过切点垂直于切线的直线必过圆心(推论2).例4.如图,圆O与正方形ABCD的两边AB、AD相切,且DE与圆O相切于E点.若圆O的半径为5,且AB=11,则DE的长度为()A.5B.6C.√30D.112【答案】B【解析】解:连接OM、ON,⊙四边形ABCD是正方形,⊙AD=AB=11,⊙A=90°,⊙圆O与正方形ABCD的两边AB、AD相切,⊙⊙OMA=⊙ONA=90°=⊙A,⊙OM=ON,⊙四边形ANOM是正方形,⊙AM=OM=5,DE与圆O相切于E点,圆O的半径为5,⊙AM=5,DM=DE,⊙DE=11﹣5=6,故选B.练习1.如图,在Rt⊙AOB中,OA=OB=3,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线PQ的最小值为.【答案】2【解析】解:连接OP、OQ.⊙PQ 是⊙O 的切线,⊙OQ⊙PQ ; 根据勾股定理知PQ 2=OP 2﹣OQ 2, ⊙当PO⊙AB 时,线段PQ 最短, ⊙在Rt⊙AOB 中,OA=OB=3, ⊙AB=OA=6,⊙OP==3, ⊙PQ===2.故答案为:2.练习2.对于平面直角坐标系xOy 中的点P 和⊙C ,给出如下定义:若⊙C 上存在两个点A ,B ,使得⊙APB=60°,则称P 为⊙C 的关联点. 已知点D (21,),E (0,-2),F (32,0) (1)当⊙O 的半径为1时,⊙在点D ,E ,F 中,⊙O 的关联点是__________;⊙过点F 作直线交y 轴正半轴于点G ,使⊙GFO=30°,若直线上的点P (m ,n )是⊙O 的关联点,求m 的取值范围;(2)若线段EF 上的所有点都是某个圆的关联点,求这个圆的半径的取值范围.【答案】(1) ⊙;⊙;(2)21E D 、30≤≤m 1≥r【解析】(1) ⊙;⊙由题意可知,若点要刚好是圆的关联点;需要点到圆的两条切线和之间所夹的角度为; 由图可知,则,连接,则rBC CPBBCPC 22sin ==∠=; ⊙若点为圆C 的关联点;则需点P 到圆心的距离d 满足r d 20≤≤; 由上述证明可知,考虑临界位置的P 点,如图2;点P 到原点的距离212=⨯=OP ;过作轴的垂线,垂足为,; ⊙,⊙; ⊙,⊙; 易得点与点重合,过作轴于点; 易得,⊙;从而若点为圆的关联点,则点必在线段上,⊙;E D 、P C P C PA PB ︒601︒=∠60APB ︒=∠30CPB 图1CBAPBC PO x OH H 3232tan ===∠OG OF OGF ︒=∠60OGF 360sin =︒⋅=OG OH 23sin ==∠OP OH OPH ︒=∠60OPH 1P G 2P x M P ⊥2M ︒=∠302OM P 330cos 2=︒⋅=OP OM P O P 21P P 30≤≤m(2) 若线段上的所有点都是某个圆的关联点,欲使这个圆的半径最小, 则这个圆的圆心应在线段的中点; 考虑临界情况,如图3;即恰好点为圆的关联时,则; ⊙此时;故若线段上的所有点都是某个圆的关联点,这个圆的半径的取值范围为.利用直线与圆相切的性质可以处理一些较综合的问题,其中相切的性质可以为解题提供垂直的条件.圆与圆的位置关系1.圆和圆的位置关系有五种:外离、外切、相交、内切、内含2.设两圆圆心距为d ,两圆半径分别为R ,r (R>r )由圆和圆的位置关系及圆心距d 与R ,r (R>r )之间的关系得: 两圆外离d R r ⇔>+; 两圆外切d R r ⇔=+;EF EFF E 、K2212===EF KN KF 1=r EF r 1≥r两圆相交R r d R r ⇔-<<+;两圆内切d R r ⇔=-;两圆内含0d R r ⇔≤<-3.相交两圆性质定理: 两圆圆心的连线垂直并且平分这两个圆的公共弦.4.相切两圆的性质:如果两圆相切,那么切点一定在连心线上.例1.两圆的半径分别为3和5,圆心距为7,则两圆的位置关系是( )A.内切B.相交C.外切D.外离【答案】B【解析】解:根据题意得R+r=5+3=8,R -r=5-3=2,圆心距=7,⊙2<7<8,⊙两圆相交.故选B .练习1.已知⊙O 1与⊙O 2相交,它们的半径分别是4,7,则圆心距12O O 可能是( )A.2B.3C.6D.12【答案】C【解析】解:两圆半径之差为3,半径之和为11,两圆相交时,圆心距大于两圆半径差,且小于两圆半径和,所以,3<12O O <11.符合条件的数只有C .故选C .练习2.已知⊙O 1与⊙O 2的半径分别是方程2430x x -+=的两根,且两圆的圆心距等于4,则⊙O 1与⊙O 2的位置关系是( )A 、外离B 、外切C 、相交D 、内切【答案】B【解析】解:⊙2430x x -+=,⊙(x -3)(x -1)=0,解得:x=3或x=1,⊙⊙O 1与⊙O 2的半径12,r r 分别是方程2430x x -+=的两实根,⊙124r r +=,⊙⊙O 1与⊙O 2的圆心距d=4,⊙⊙O 1与⊙O 2的位置关系是外切.故选B .练习3.若两个圆相切于A 点,它们的半径分别为10cm 、4cm ,则这两个圆的圆心距为( )A .14cmB .6cmC .14cm 或6cmD .8cm【答案】C 【解析】解:⊙两圆半径分别为10cm 、4cm ,⊙若这两个圆外切,则圆心距为:10+4=14(cm ),若这两个圆内切,则圆心距为:10-4=6(cm ),⊙这两个圆的圆心距为14cm 或6cm .故选C .练习4.定圆O 的半径是4cm ,动圆P 的半径是2cm ,动圆在直线l 上移动,当两圆相切时,OP 的值是( )A.2cm 或6cmB.2cmC.4cmD.6cm【答案】A【解析】解:设定圆O 的半径为R=4cm ,动圆P 的半径为r=2cm ,分两种情况考虑: 当两圆外切时,圆心距OP=R+r=4+2=6cm ;当两圆内切时,圆心距OP=R -r=4-2=2cm ,综上,OP 的值为2cm 或6cm .故选A由圆和圆的位置关系及圆心距d 与R ,r (R>r )之间的关系得:两圆外离d R r ⇔>+; 两圆外切d R r ⇔=+;两圆相交R r d R r ⇔-<<+;两圆内切d R r ⇔=-;两圆内含0d R r ⇔≤<-.例2.已知:如图,⊙O 1与⊙O 2外切于A 点,直线l 与⊙O 1、⊙O 2分别切于B ,C 点,若⊙O 1的半径r 1=2cm ,⊙O 2的半径r 2=3cm .求BC 的长.【答案】解:连接O 1B ,O 2C ,O 1O 2,过点O 1作O 1D⊙O 2C 于D ,⊙直线l 与⊙O 1、⊙O 2分别切于B ,C 点,⊙O 1B⊙BC ,O 2C⊙BC ,⊙四边形O 1BCD 是矩形,⊙CD=O 1B=r 1=2cm ,BC=O 1D ,⊙O 2D=O 2C -CD=3-2=1(cm ),⊙⊙O 1与⊙O 2外切于A 点,在Rt⊙O 2DO 1中,O 2O 1=r 1+r 2=2+3=5(cm ),⊙O 1D=cm ,⊙BC=cm .【解析】此题考查两圆相切的性质、切线的性质、矩形的判定与性质.难度适中,解题的关键是准确作出辅助线,掌握相切两圆的性质.练习1.如图为某机械的截面图,相切的两圆⊙O 1,⊙O 2均与⊙O 的弧AB 相切,且O 1O 2⊙l 1(l 1为水平线),⊙O 1,⊙O 2的半径均为30mm ,弧AB 的最低点到l 1的距离为30mm ,公切线l 2与l 1间的距离为100mm .则⊙O 的半径为( )A.70mmB.80mmC.85mmD.100mm【答案】B【解析】解:如图,设⊙O 的半径为Rmm ,依题意,得CE=100-30=70(mm ),⊙l 2⊙O 1O 2,⊙CD=O 1D=30(mm ),DE=CE -CD=70-30=40(mm ),OD=OE -DE=R -40(mm ),在Rt⊙OO 1D 中,O 1O=R -30(mm ),O 1D=30mm ,由勾股定理,得O 1D 2+OD 2=O 1O 2,即302+(R -40)2 =(R -30)2,解得R=80mm .故选B 练习2.如图,⊙O 1,⊙O 2,⊙O 3两两相切,AB 为⊙O 1,⊙O 2的公切线,AB 为半圆,且分别与三圆各切于一点.若⊙O 1,⊙O 2的半径均为1,则⊙O 3的半径为( )A.1B.121 1 【答案】C 【解析】解:如图,分别作三个圆心到AB 的垂线,垂足分别点E 、D 、F ,⊙O 1与⊙O 2的半径相等且相切于S ,则O 3D 过点S ,且点D 是半圆AB 的圆心,延长DS 交圆D 于点W ,则WD 是半圆AB 的半径.EFO 2O 1是矩形,SDEO 1是正方形,DQ=DW=SD+O 3S+O 3W设圆O 3的半径为R ,由勾股定理得O 3DO 1-1.故选C .两圆相切有两种情况:内切和外切,注意在处理两圆相切问题时需要分类讨论.例3.已知:如图,⊙O 1与⊙O 2相交于A ,B 两点,过A 点的割线分别交两圆于C ,D ,弦CE⊙DB ,连接EB ,试判断EB 与⊙O 2的位置关系,并证明你的结论.【答案】解:过B 作⊙O 2的直径BH ,连接AH ,AB ,⊙BH 是⊙O 2的直径,⊙⊙BAH=90°,⊙CE⊙DB ,⊙⊙ACE=⊙D⊙⊙H=⊙D ,⊙ACE=⊙ABE ,⊙⊙H=⊙ABE⊙⊙H+⊙ABH=90°,⊙⊙ABH+⊙ABE=90°⊙⊙EBH=90°, 又⊙O 2B 为半径,⊙EB 是⊙O 2的切线.【解析】此题考查直线与圆的位置关系,解题的关键是根据题意作出辅助线,再根据在同圆中等弧所对的圆周角相等和三角形的内角和等于180°进行解答.练习1.已知:相交两圆的公共弦的长为6cm ,两圆的半径分别为cm 23,cm 5,求这两个圆的圆心距.【答案】解:当公共弦在圆心的同侧时如图,AB=6cm ,O 1A=5cm ,O 2A=⊙公共弦长为6cm ,⊙AC=3cm ,AC⊙O 1O 2,⊙O 1C=4cm ,O 2C=3cm ,⊙当公共弦在两个圆心之间时,圆心距=4+3=7cm ;当公共弦在圆心的同侧时,圆心距=4-3=1cm .则这两个圆的圆心距是7cm 或1cm .【解析】此题主要考查了相交两圆的性质以及勾股定理.注意此题应考虑两种情况是解题关键.先根据勾股定理,得圆心距的两部分分别是4cm,3cm,然后根据两圆的位置关系确定圆心距.练习2.已知⊙O1和⊙O2相交于A、B两点,过A点作⊙O1的切线交⊙O2于点E,连接EB并延长交⊙O1于点C,直线CA交⊙O2于点D.(1)如图,当点D与点A不重合时,试猜想线段EA=ED是否成立?证明你的结论;(2)当点D与点A重合时,直线AC与⊙O2有怎样的位置关系?此时若BC=2,CE=8,求⊙O1的直径.【答案】解:(1)EA=ED成立.证明:连接AB,在EA延长线上取点F;⊙AE是⊙O1的切线,切点为A,⊙⊙FAC=⊙ABC,⊙⊙FAC=⊙DAE(对顶角),⊙⊙ABC=⊙DAE,而⊙ABC是⊙O2内接四边形ABED的外角,⊙⊙ABC=⊙D,⊙⊙DAE=⊙D,⊙EA=ED;(2)当点D与点A重合时,直线CA与⊙O2只有一个公共点,所以,直线CA与⊙O2相切,直径为4.两圆相交的重点是对相交弦的处理.。
直线与圆的位置关系 讲义
直线与圆的位置关系一、直线和圆的位置关系的定义、性质及判定1、设O ⊙的半径为r ,圆心O 到直线l 的距离为d ,则直线和圆的位置关系如下表:从另一个角度,直线和圆的位置关系还可以如下表示:二、切线的性质及判定1. 切线的性质:定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心. 2. 切线的判定:定义法:和圆只有一个公共点的直线是圆的切线; 距离法:到圆心距离等于半径的直线是圆的切线;定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 3. 切线长和切线长定理:⑴ 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.⑵ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.①切线的判定定理设OA 为⊙O 的半径,过半径外端A 作l ⊥OA ,则O 到l 的距离d=r ,∴l 与⊙O 相切.因此,我们得到:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.注:定理的题设①“经过半径外端”,②“垂直于半径”,两个条件缺一不可.结论是“直线是圆的切线”.举例说明:只满足题设的一个条件不是⊙O 的切线.1)连接半径,证直线与此半径垂直;(2)作垂线,证垂足在圆上②切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径.我们分析:这个定理共有三个条件:一条直线满足:(1)垂直于切线(2)过切点 (3)过圆心三、三角形内切圆1. 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫做圆的外切三角形.2. 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形. 3.直角三角形的内切圆半径与三边关系(1) (2)图(1)中,设a b c ,,分别为ABC ∆中A B C ∠∠∠,,的对边,面积为S _l_ A_ O_ F _ E_ D _ C _ B_ A_ C_ B _ A _ C_ B_ A_c_b _a_c_b_a_ A_l _ T _ A 2M ⎪⎭为切点_ A_l则内切圆半径(1)srp=,其中()12p a b c=++;图(2)中,90C∠=︒,则()12r a b c=+-四、典例分析:切线的性质及判定【例1】如图,AB是O的直径,点D在AB的延长线上,过点D作O的切线,切点为C,若25A=︒∠,则D=∠______.例1 例2【例2】如图,直线AB与O⊙相切于点A,O⊙的半径为2,若30OBA∠=︒,则OB的长为( )A. B.4C. D.2【例3】如图,若O的直径AB与弦AC的夹角为30︒,切线CD与AB的延长线交于点D,且O的半径为2,则CD的长为()A.B.C.2 D.4例3【例4】如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形上底AD、下底BC以及腰AB均相切,切点分别是D C E,,.求证:以AB为直径的圆与CD相切.例4【例5】已知:如图,在ABC∆中,AB AC=,以BC为直径的半圆O与边AB相交于点D,切线DE AC⊥,垂足为点E.求证:(1)ABC∆是等边三角形;(2)13AE CE=.AD_A_O_C_B_O【例6】 如图,ABC ∆中,AB AC =,O 是BC 的中点,以O 为圆心的圆与AB 相切于点D 。
直线与圆、圆与圆的位置关系讲义

直线与圆、圆与圆的位置关系讲义一、知识梳理1.判断直线与圆的位置关系常用的两种方法(1)几何法:利用圆心到直线的距离d 和圆的半径r 的大小关系. d <r ⇔相交;d =r ⇔相切;d >r ⇔相离. (2)代数法:――――→判别式Δ=b 2-4ac⎩⎪⎨⎪⎧>0⇔相交;=0⇔相切;<0⇔相离.2.圆与圆的位置关系设圆O 1:(x -a 1)2+(y -b 1)2=r 21(r 1>0), 圆O 2:(x -a 2)2+(y -b 2)2=r 22(r 2>0).(1)过圆x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程为x 0x +y 0y =r 2.(2)过圆(x -a )2+(y -b )2=r 2上一点P (x 0,y 0)的圆的切线方程为(x 0-a )(x -a )+(y 0-b )(y -b )=r 2. (3)过圆x 2+y 2=r 2外一点M (x 0,y 0)作圆的两条切线,则两切点所在直线方程为x 0x +y 0y =r 2. 2.圆与圆的位置关系的常用结论(1)两圆的位置关系与公切线的条数:①内含:0条;②内切:1条;③相交:2条;④外切:3条;⑤外离:4条.(2)当两圆相交时,两圆方程(x 2,y 2项系数相同)相减便可得公共弦所在直线的方程.二、基础检测题组一:思考辨析1.判断下列结论是否正确(请在括号中打“√”或“×”)(1)如果两个圆的方程组成的方程组只有一组实数解,则两圆外切.( ) (2)如果两圆的圆心距小于两圆的半径之和,则两圆相交.( )(3)从两圆的方程中消掉二次项后得到的二元一次方程是两圆的公共弦所在的直线方程.( ) (4)过圆O :x 2+y 2=r 2上一点P (x 0,y 0)的圆的切线方程是x 0x +y 0y =r 2.( )(5)过圆O:x2+y2=r2外一点P(x0,y0)作圆的两条切线,切点分别为A,B,则O,P,A,B四点共圆且直线AB的方程是x0x+y0y=r2.()(6)如果直线与圆组成的方程组有解,则直线与圆相交或相切.()题组二:教材改编2.若直线x-y+1=0与圆(x-a)2+y2=2有公共点,则实数a的取值范围是()A.[-3,-1]B.[-1,3]C.[-3,1]D.(-∞,-3]∪[1,+∞)3.x2+y2-4=0与圆x2+y2-4x+4y-12=0的公共弦长为________.题组三:易错自纠4.若直线l:x-y+m=0与圆C:x2+y2-4x-2y+1=0恒有公共点,则m的取值范围是() A.[-2,2] B.[-22,22]C.[-2-1,2-1] D.[-22-1,22-1]5.设圆C1,C2都和两坐标轴相切,且都过点(4,1),则两圆心的距离|C1C2|等于()A.4 B.42C.8 D.826.过点A(3,5)作圆O:x2+y2-2x-4y+1=0的切线,则切线的方程为__________.答案5x-12y+45=0或x-3=0三、典型例题题型一:直线与圆的位置关系1.已知点M(a,b)在圆O:x2+y2=1外,则直线ax+by=1与圆O的位置关系是()A.相切B.相交C.相离D.不确定2.圆x2+y2-2x+4y=0与直线2tx-y-2-2t=0(t∈R)的位置关系为()A.相离B.相切C.相交D.以上都有可能思维升华:判断直线与圆的位置关系的常见方法(1)几何法:利用d与r的关系.(2)代数法:联立方程之后利用Δ判断.(3)点与圆的位置关系法:若直线恒过定点且定点在圆内,可判断直线与圆相交.题型二:圆与圆的位置关系典例已知圆C1:(x-a)2+(y+2)2=4与圆C2:(x+b)2+(y+2)2=1外切,则ab的最大值为()A.62 B.32 C.94D.23引申探究:1.若将本典例中的“外切”变为“内切”,求ab的最大值.2.若将本典例条件“外切”变为“相交”,求公共弦所在的直线方程.思维升华:判断圆与圆的位置关系时,一般用几何法,其步骤是 (1)确定两圆的圆心坐标和半径长;(2)利用平面内两点间的距离公式求出圆心距d ,求r 1+r 2,|r 1-r 2|; (3)比较d ,r 1+r 2,|r 1-r 2|的大小,写出结论.跟踪训练:如果圆C :x 2+y 2-2ax -2ay +2a 2-4=0与圆O :x 2+y 2=4总相交,那么实数a 的取值范围是 题型三:直线与圆的综合问题 命题点1:求弦长问题典例已知直线l :mx +y +3m -3=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别做l 的垂线与x 轴交于C ,D 两点,若|AB |=23,则|CD |=________. 命题点2:直线与圆相交求参数范围典例 已知过点A (0,1)且斜率为k 的直线l 与圆C :(x -2)2+(y -3)2=1交于M ,N 两点. (1)求k 的取值范围;(2)若OM →·ON →=12,其中O 为坐标原点,求|MN |. 命题点3:直线与圆相切的问题典例 已知圆C :(x -1)2+(y +2)2=10,求满足下列条件的圆的切线方程. (1)与直线l 1:x +y -4=0平行; (2)与直线l 2:x -2y +4=0垂直; (3)过切点A (4,-1).思维升华:直线与圆综合问题的常见类型及解题策略(1)处理直线与圆的弦长问题时多用几何法,即弦长的一半、弦心距、半径构成直角三角形. (2)圆的切线问题的处理要抓住圆心到直线的距离等于半径,从而建立关系解决问题. 跟踪训练 (1)过点(3,1)作圆(x -2)2+(y -2)2=4的弦,其中最短弦的长为________. (2)过点P (2,4)引圆(x -1)2+(y -1)2=1的切线,则切线方程为__________________. 注意:高考中与圆交汇问题的求解 一、与圆有关的最值问题典例1 (1)已知点A ,B ,C 在圆x 2+y 2=1上运动,且AB ⊥BC .若点P 的坐标为(2,0),则|P A →+PB →+PC →|的最大值为( ) A .6 B .7 C .8D .9(2)过点(2,0)引直线l 与曲线y =1-x 2相交于A ,B 两点,O 为坐标原点,当△AOB 的面积取最大值时,直线l 的斜率等于( ) A.33 B .-33C .±33D .-3二、直线与圆的综合问题典例2 (1)已知直线l :x +ay -1=0(a ∈R )是圆C :x 2+y 2-4x -2y +1=0的对称轴,过点A (-4,a )作圆C 的一条切线,切点为B ,则|AB |等于( ) A .2 B .42 C .6D .210(2)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2x +y -4=0相切,则圆C 面积的最小值为( ) A.45π B.34π C .(6-25)πD.54π 四、反馈练习1.已知圆x 2+y 2+2x -2y +a =0截直线x +y +2=0所得的弦的长度为4,则实数a 的值是( ) A .-2 B .-4 C .-6 D .-82.圆x 2+2x +y 2+4y -3=0上到直线x +y +1=0的距离为2的点共有( ) A .1个 B .2个 C .3个D .4个3.过点P (1,-2)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则AB 所在直线的方程为( ) A .y =-34 B .y =-12C .y =-32D .y =-144.若点A (1,0)和点B (4,0)到直线l 的距离依次为1和2,则这样的直线有( ) A .1条 B .2条 C .3条 D .4条5.已知点P (a ,b )(ab ≠0)是圆x 2+y 2=r 2内的一点,直线m 是以P 为中点的弦所在的直线,直线l 的方程为ax +by =r 2,那么( ) A .m ∥l ,且l 与圆相交 B .m ⊥l ,且l 与圆相切 C .m ∥l ,且l 与圆相离D .m ⊥l ,且l 与圆相离6.已知圆C 的方程为x 2+y 2=1,直线l 的方程为x +y =2,过圆C 上任意一点P 作与l 夹角为45°的直线交l 于点A ,则|P A |的最小值为( ) A.12 B .1 C.2-1D .2-27.已知直线l :x -3y +6=0与圆x 2+y 2=12交于A ,B 两点,过A ,B 分别作l 的垂线与x 轴交于C ,D 两点,则|CD |=________.8.点P 在圆C 1:x 2+y 2-8x -4y +11=0上,点Q 在圆C 2:x 2+y 2+4x +2y +1=0上,则|PQ |的最小值是________.9.过点P (1,3)作圆x 2+y 2=1的两条切线,切点分别为A ,B ,则P A →·PB →=________.10.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是________.11.已知圆C :x 2+y 2+2x -4y +1=0,O 为坐标原点,动点P 在圆C 外,过P 作圆C 的切线,设切点为M .(1)若点P 运动到(1,3)处,求此时切线l 的方程; (2)求满足条件|PM |=|PO |的点P 的轨迹方程.12.已知直线l :4x +3y +10=0,半径为2的圆C 与l 相切,圆心C 在x 轴上且在直线l 的右上方. (1)求圆C 的方程;(2)过点M (1,0)的直线与圆C 交于A ,B 两点(A 在x 轴上方),问在x 轴正半轴上是否存在定点N ,使得x 轴平分∠ANB ?若存在,请求出点N 的坐标;若不存在,请说明理由.13在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4,设圆C 的半径为1,圆心在直线l 上.若圆C 上存在点M ,使|MA |=2|MO |,则圆心C 的横坐标a 的取值范围是14.若⊙O :x 2+y 2=5与⊙O 1:(x -m )2+y 2=20(m ∈R )相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长是________. π|AB |2≥16(2-1)π.故选C.。
2024年新高二数学提升精品讲义直线与圆的位置关系(思维导图+3知识点+8考点+过关检测)(解析版)
2024年新高二数学提升精品讲义直线与圆的位置关系(解析版)模块一思维导图串知识模块二基础知识全梳理(吃透教材)模块三核心考点举一反三模块四小试牛刀过关测1.理解直线与圆的三种基本位置关系:相离、相切、相交,并能准确描述每种关系的特征;2.掌握判断直线与圆位置关系的方法,包括利用圆心到直线的距离与半径的关系进行判断;3.能够运用所学知识解决实际问题,如计算切点坐标、交点坐标等.知识点1直线与圆的位置关系1、直线与圆的三种位置关系(1)直线与圆相交,有两个公共点;(2)直线与圆相切,只有一个公共点;(3)直线与圆相离,没有共同点.2、判断直线与圆位置关系的方法(1)几何法判断直线与圆的位置关系:直线0++=Ax By C 与圆()()222-+-=x a y b r ,圆心到直线的距离22BA C Bb Aa d +++=.>⇔d r 直线与圆相离⇔无交点;=⇔d r 直线与圆相切⇔只有一个交点;<⇔d r 直线与圆相交⇔有两个交点.(2)代数法判断直线与圆的位置关系:联立直线方程与圆的方程,得到⎩⎨⎧=++++=++022F Ey Dx y x C By Ax ,通过解的个数来判断:当0>∆时,直线与圆有2个交点,,直线与圆相交;当0=∆时,直线与圆只有1个交点,直线与圆相切;当0<∆时,直线与圆没有交点,直线与圆相离.知识点2直线与圆相交弦长1、几何法:利用圆的半径r ,圆心到直线的距离d ,弦长l 之间的关系2222⎛⎫=+ ⎪⎝⎭l r d ,整理出弦长公式为:22=-l r d 2、代数法:若直线与圆的交点坐标易求出,求出交点坐标后,直接用两点间距离公式计算弦长.3、弦长公式法:设直线:=+l y kx b 与圆的交点为()11,x y ,()22,x y ,将直线方程代入圆的方程,消元后利用根与系数的关系得到弦长()()222121212114⎡⎤=+-=++-⎣⎦l kx k x x x x 知识点3直线与圆相切1、圆的切线的条数(1)过圆外一点,可以作圆的两条切线;(2)过圆上一点,可以作圆的一条切线;(3)过圆内一点,不能作圆的切线.2、过圆上一点()00,x y 的切线方程法一:先求出切点与圆心的连线斜率k ,若k 不存在,则结合图形可直接写出切线方程0=y y ;若0=k,则结课图形可直接写出切线方程0=x x ;若k 存在且0≠k,则由垂直关系知切线的斜率为1-k,由点斜式写出切线方程.法二:若k 不存在,验证是否成立;若k 存在,设点斜式方程,用圆心到直线的距离等于半径列方程,解出方程即可.3、过圆外一点()00,x y 的圆的切线方程法一:当斜率存在时,设为k ,则切线方程为()00-=-y y k x x ,即000-+-=kx y y kx 由圆心到直线的距离等于半径,即可求出k 的值,进而写出切线方程.法二:当斜率存在时,设为k ,则切线方程为()00-=-y y k x x ,即000-+-=kx y y kx 代入圆的方程,得到一个关于x 的一元二次方程,由0=∆,求得k ,切线方程即可求出.4、与圆的切线相关的结论(1)过圆222+=x y r 上一点()00,P x y 的圆的切线方程为200+=xx yy r .(2)过()()222-+-=x a y b r 上一点()00,P x y 的圆的切线方程为()()()()200--+--=x a x a y b y b r(3)过()()222-+-=x a y b r 外一点()00,P x y 作圆的两条切线,切点分别为A ,B ,则切点弦AB 所在直线方程为:()()()()200--+--=x a x a y b y b r .(4)过圆外一点()00,P x y 引圆()()222-+-=x a y b r 的两条切线,则过圆外一点()00,P x y 的切线长为=d考点一:直线与圆的位置关系判断例1.(23-24高二上·广西南宁·月考)直线240x y ++=与圆22240x y y +--=的位置关系为()A .相交且过圆心B .相交且不过圆心C .相切D .相离【答案】C【解析】圆22240x y y +--=,即()2215x y +-=,其圆心坐标为()0,1,半径为r =,圆心到直线240x y ++=的距离d r ===,直线与圆的位置关系为相切.故选:C【变式1-1】(23-24高二下·安徽芜湖·月考)直线l :20ax y +-=与圆C :()()22121x y -+-=的公共点的个数为()A .0B .1C .2D .1或2【答案】C【解析】由直线:20l ax y +-=,可得直线l 过定点()0,2,又由圆C :()()22121x y -+-=,可得点()0,2在圆C 上,因为直线l 的斜率显然存在,所以公共点的个数为2.故选:C.【变式1-2】(23-24高二上·福建福州·期中)设R m ∈,则直线l :210mx y m +--=与圆225x y +=的位置关系为()A .相离B .相切C .相交或相切D .相交【答案】C【解析】直线l 可化为()210m x y -+-=,由2010x y -=⎧⎨-=⎩可得,21x y =⎧⎨=⎩,所以直线l 恒过点()2,1A .又22215+=,即点A 在圆225x y +=上,所以,过点A 的直线l 与圆相交或相切.故选:C.【变式1-3】(22-23高二上·上海宝山·期中)已知点()00,x y 在圆C :224x y +=外,则直线004x x y y +=与圆C 的位置关系是()A .相交B .相切C .相离D .不确定【答案】A【解析】由点00P x y (,)在圆22:4C x y +=外,可得22004x y +>,求得圆心00C (,)到直线00:4l x x y y +=的距离422d <=,故直线和圆C 相交,故选:A.考点二:根据直线与圆的位置关系求参数例2.(23-24高二下·河南·月考)若直线20x y ++=与圆()()()222:80M x a y a a a -+-=>相切,则圆M 的半径为()A .2B .4C .D .8【答案】C=,解得1a =(负值舍),所以圆M 的半径为故选:C.【变式2-1】(23-24高二下·黑龙江哈尔滨·开学考试)已知直线3y kx =-与圆()2224x y -+=相交,则实数k 的取值范围是()A .5,12⎡⎫+∞⎪⎢⎣⎭B .5,12⎛⎫+∞ ⎪⎝⎭C .5,12∞⎛⎤- ⎥⎝⎦D .5,12⎛⎫-∞ ⎪⎝⎭【答案】B【解析】圆()2224x y -+=的圆心为()2,0,半径2r =,因为直线3y kx =-与圆()2224x y -+=相交,所以圆心()2,0到直线3y kx =-的距离d r <,2<,解得512k >,所以实数k 的取值范围是5,12⎛⎫+∞ ⎪⎝⎭.故选:B.【变式2-2】(23-24高二下·河北衡水·月考)已知圆C :22()1x y m +-=,直线l :()1210m x y m ++++=,则直线l 与圆C 有公共点的必要不充分条件是()A .11m -≤≤B .112m -≤≤C .10m -≤≤D .102m ≤≤【答案】A【解析】由题意可知圆C 的圆心坐标为()0,m ,半径为1.因为直线l 与圆C 有公共点,所以直线l 与圆C 相切或相交,所以圆心()0,C m 到直线l 的距离1d =≤,解得112m -≤≤.其必要不充分条件是把m 的取值范围扩大,所以选项中只有11m -≤≤是112m -≤≤的必要不充分条件.故选:A 【变式2-3】(23-24高二上·河北石家庄·期中)若直线l 过点()0,A a ,斜率为1,圆224x y +=上恰有3个点到l 的距离为1,则a 的值为()A .B .±C .2±D .【答案】D【解析】由题意知,:0l x y a -+=,又圆224x y +=上恰有3个点到l 的距离为1,所以圆心到直线的距离等于半径减去1,则圆心(0,0)到直线l 21=-,解得a =故选:D.考点三:求圆的切线方程例3.(23-24高二上·河北承德·月考)过点()2,3P 引圆222440x y x y +--+=的切线,其方程是()A .2x =B .12590x y -+=C .2x =或3y =D .3x =或2y =【答案】C【解析】根据题意,圆222440x y x y +--+=,即()()22121x y -+-=,其圆心为()1,2,半径1r =;过点()2,3P 引圆222440x y x y +--+=的切线,若切线的斜率不存在,切线的方程为2x =,符合题意;若切线的斜率存在,设其斜率为k ,则有()32y k x -=-,即320kx y k -+-=,1=,解得0k =,此时切线的方程为()302y x -=-,即3y =.综上:切线的方程为2x =和3y =.故选:C .【变式3-1】(22-23高二下·河南安阳·开学考试)已知圆22:42110C x y x y +++-=,过点()2,1作圆C 的切线m ,则m 的方程为()A .2x =B .34100x y +-=C .34100x y +-=或2x =D .34100x y +-=或3420x y --=【答案】C【解析】将圆22:42110C x y x y +++-=化为标准方程()()222116x y +++=,则圆心()2,1C --,4r =,当切线l 的斜率不存在时,切线l 的方程为2x =,当切线l 的斜率存在时,设切线l 的方程为()12y k x -=-,即120kx y k -+-=,由题意知,4=.解得34k =-.此时切线l 的方程为34100x y +-=.综上,切线l 的方程为2x =或34100x y +-=.故选:C.【变式3-2】(23-24高二上·湖南长沙·期中)过点()40,的直线l 与圆2248160x y x y +--+=相切,则直线l 的方程为()A .34120x y +-=或0y =B .34120x y +-=或4x =C .43120x y +-=或0y =D .43120x y +-=或4x =【答案】B【解析】圆2248160x y x y +--+=化为标准方程为22(2)(4)4x y -+-=,得圆心()2,4,半径为2,当直线l 的斜率不存在时,直线4l x =:,此时直线l 与圆2248160x y x y +--+=相切,符合题意;当直线l 的斜率存在时,设直线l 的方程为()4y k x =-,即40kx y k --=,圆心()2,4到直线l 的距离为d =由相切得2d r ==,2=,平方化简得34k =-,求得直线方程为34120x y +-=,综上,直线l 的方程为34120x y +-=或4x =.故选:B【变式3-3】(23-24高二上·天津武清·月考)已知过点()2,3P 的直线与圆()22110x y -+=相切,且与直线10x ay -+=平行,则=a ()A .2B .3-C .12-D .12【答案】B【解析】已知过点()2,3P 的直线与圆()22110x y -+=相切,将点()2,3P 代入圆()22110x y -+=恒成立,则点P 在圆上.即过点()2,3P 的直线与圆()22110x y -+=相切的切线只有一条,令过点()2,3P 的切线的方程为3(2)y k x -=-,即230kx y k --+=,由此切线与10x ay -+=平行,两直线的斜率相等且y 轴截距不等,可得1k a=且123k a -+≠;由圆心到切线的距离等于圆的半径,可得圆的半径22023101k k r k --+==+,13k =-,即3a =-.故选:B .考点四:与切线长有关的问题例4.(23-24高二上·安徽马鞍山·期末)由点(1,4)P -向圆2246120x y x y +--+=引的切线长是()A .3B 5C 10D .5【答案】A【解析】圆2246120x y x y +--+=即圆()()22231x y -+-=的圆心半径分别为()2,3,1r =,点(1,4)P -到圆心()2,3的距离为()()22124310d =--+-所以点(1,4)P -向圆2246120x y x y +--+=1013-=.故选:A.【变式4-1】(23-24高二上·浙江宁波·期末)过点()0,2与圆22410x y x ++-=相切的两条直线的夹角为α,则cos α=()A .14B .154C .154-D .14-【答案】A【解析】因为2202421110++⨯-=>,所以点()0,2在圆外,设圆心为C ,点()0,2为点D ,切点为,A B ,圆22410x y x ++-=化为标准方程得()2225x y ++=,则圆心()2,0C -,半径5r =,在Rt ACD △中,22,5CD AC ==853AD =-=故35cos 2222ADC ADC ∠=∠由圆的切线的性质可得ADC BDC ∠=∠,所以351cos cos cos 2884ADB ADC α=∠=∠=-=.故选:A.【变式4-2】(23-24高二上·四川乐山·期末)已知点(),P x y 是直线23y x =+上一动点,PM 与PN 是圆C :()2211x y -+=的两条切线,M 、N 为切点,则四边形PMCN 的最小面积为()A .4B .25C .2D .1【答案】C【解析】由题意知,圆C :()2211x y -+=的圆心()1,0C ,半径1r =,因为PM 与PN 是圆C :()2211x y -+=的两条切线,所以PM PN =,22221PMPC MC PC =-=-,则21PM PC =-当PC 最小时,PM 也最小,又点(),P x y 是直线23y x =+上一动点,故圆心()1,0C 到直线23y x =+的距离2355d +=PC 的最小值,此时min2PM=,则此时四边形PMCN 的面积S PM MC PM ==也最小,最小值为2S =.故选:C.【变式4-3】(23-24高二上·陕西西安·期中)已知圆O 的半径为2,过圆O 外一点P 作圆O 的两条切线,切点为A ,B ,那么PA PB的最小值为()A .1642-+B .1242-+C .1282-+D .1682-+【答案】C 【解析】如图,设PO d =,则24PA PB d ==-,因为2sin APO d ∠=,所以2228cos 121APB d d ⎛⎫∠=-=- ⎪⎝⎭,所以()2222832411223212212PA PB d d dd ⎛⎫⋅=--=+-≥= ⎪⎝⎭,当且仅当2232d d=,即2424d =>时,等号成立,故PA PB ⋅的最小值为8212,故选:C.考点五:切点弦及其方程应用例5.(23-24高三上·云南曲靖·月考)过点()0,2P 作圆22:430C x x y -++=的两条切线,设切点为A ,B ,则切点弦AB 的长度为()A 14B .142C .144D .147【答案】B【解析】圆22:430C x x y -++=,即()2221x y -+=,易知22PC =C 的半径1r =,所以切线长7PA PB ==.所以四边形PACB 的面积为127172PACB S =⨯=.所以根据等面积法知:172PACB S PC AB ==⨯⨯,所以142AB =.故选:B .【变式5-1】(23-24高二上·河北·期中)过点)3,0M作圆C :()2211x y +-=的两条切线,切点分别为A ,B ,则直线AB 的方程为.30x y -=【解析】由图可知,其中一条切线为x 轴,切点为坐标原点.因为AB CM ⊥,303CM k ==-,则3AB k =所以直线AB 30x y -=.30x y -=.【变式5-2】(22-23高三上·广东·开学考试)过点(2,2)P 作圆224x y +=的两条切线,切点分别为A 、B ,则直线AB 的方程为.【答案】2+-x y 0=【解析】方法1:由题知,圆224x y +=的圆心为()0,0,半径为2r =,所以过点(2,2)P 作圆224x y +=的两条切线,切点分别为()0,2A 、()2,0B ,所以1AB k =-,所以直线AB 的方程为2y x =-+,即20x y +-=;方法2:设()11,A x y ,()22,B x y ,则由2211111142.12x y y y x x ⎧+=⎪-⎨=-⎪-⎩,可得112x y +=,同理可得222x y +=,所以直线AB 的方程为2+-x y 0=.故答案为:20x y +-=【变式5-3】(23-24高二上·江西上饶·期末)P 是直线4x y +=上的一个动点,,A B 是圆224x y +=上的两点,若,PA PB 均与圆O 相切,则弦长AB 的最小值为.【答案】【解析】因为12AB PO OA PA ⋅=⋅,所以AB ==当PO 的长最小时,弦长AB 最小,而PO 的最小值为圆心(即原点)到直线4x y +=的距离,所以min PO =min AB ==故答案为:考点六:直线与圆相交弦问题例6.(23-24高二上·江西上饶·期末)直线30x y -+=被圆22240x y x y ++-=所截得的弦长为()A .2BC.D .10【答案】C【解析】圆22240x y x y ++-=即()()22125x y ++-=,故圆心为()1,2-,显然圆心在直线30x y -+=上,故直线被圆所截得的弦即为圆的直径,长为故选:C .【变式6-1】(23-24高二下·山西运城·开学考试)直线10x y --=将圆()()22238x y -+-=分成两段,这两段圆弧的弧长之比为()A .1:2B .1:3C .1:5D .3:5【答案】A【解析】设直线与圆的两个交点为,A B ,圆心为C ,过点C 作CD AB ⊥交于D ,如图所示设()0πACD αα∠=<<,所以圆心到直线的距离为d CD ===在Rt ACD △中,1cos 2CD AC α===因为0πα<<,所以π3α=,由圆的性质知,2π23ACB α∠==,所以两段圆弧的弧长之比等于两段弧所对圆心角的弧度数之比,等于2π2π:2π1:233⎛⎫-= ⎪⎝⎭.故选:A.【变式6-2】(23-24高二上·山东聊城·期末)写出经过坐标原点,且被圆()()22:124C x y -+-=截得的弦长为l 的一个方程.【答案】0x =或340x y -=(写出一个即可)【解析】由题意,圆心()1,2到直线l 的距离1d ==,当直线l 的斜率不存在时,方程为0x =满足题意;当直线l 的斜率存在时,设直线l 的方程为y kx =,即0kx y -=1=,即()2221k k -=+,解得34k =,此时直线l 的方程为340x y -=.故答案为:0x =或340x y -=(写出一个即可)【变式6-3】(23-24高二上·安徽马鞍山·月考)设圆222210x y x y +---=的圆心为C ,直线l 过(0,3),且与圆C 交于A ,B 两点,若AB =,则l 直线方程为.【答案】0x =或34120x y +-=【解析】圆22(1)(1)3x y -+-=的圆心(1,1)C ,半径r =,圆心(1,1)C 到直线0x =的距离为1,满足||AB ==,直线0x =符合题意;当直线l 的斜率存在时,设直线l 的方程为3y kx =+,即30kx y -+=,圆心(1,1)C 到直线l=34k =-,此时直线l :34120x y +-=,所以直线l 的方程为0x =或34120x y +-=.故答案为:0x =或34120x y +-=考点七:过定点直线的最短弦长例7.(23-24高二下·四川成都·月考)直线()():211850l m x m y m +++--=,被圆22:(2)(1)25C x y -+-=截得最短弦的长为()A .B .C .D 【答案】C【解析】直线()():211850l m x m y m +++--=,即()2850x y m x y +-++-=,由28050x y x y +-=⎧⎨+-=⎩,解得3,2x y ==,设()3,2D ,由于()()223221225-+-=<,所以D 在圆C 内,圆22:(2)(1)25C x y -+-=的圆心为()2,1C ,半径=5r ,如图:当CD AB ⊥时,AB 最短,22112CD +=所以弦长AB 的最小值为()22252223-=故选:C【变式7-1】(22-23高二上·云南临沧·月考)当圆22:450C x x y -+-=截直线:30l x my m -+-=所得的弦长最短时,实数m =()A 2B .1-C .2-D .1【答案】B【解析】由22:450C x y x +--=得22(2)9x y -+=,圆心坐标是()2,0C ,半径是3,直线l :30x my m -+-=过定点()3,1P ,且在圆内,∴当l PC ⊥时,直线l 被圆22450x y x +--=截得的弦长最短,由110132m -⋅=--解得1m =-.故选:B.【变式7-2】(23-24高二下·河北保定·开学考试)已知过点()1,1P a b ++的直线l 与圆22:()()4M x a y b -+-=交于,A B 两点,则AB 的最小值为()A .23B 3C 2D .22【答案】D【解析】因为22(1)(1)4a a b b +-++-<,所以点P 在圆M 内.且圆22:()()4M x a y b -+-=的圆心为(),M a b ,半径为2,则2MP =,当MP l ⊥时,AB 取得最小值,且最小值为24||22MP -=D【变式7-3】(23-24高二上·四川凉山·期末)过点(3,1)的直线与圆22:410C x y x +--=交于A ,B 两点,则当AB 弦长最短时ABC 的面积为()A 6B .22C .23D .26【答案】A【解析】圆22:(2)5C x y -+=的圆心(2,0)C ,半径r =,记(3,1)为点P ,||PC 即点(3,1)P 在圆C 内,则当AB CP ⊥时,弦AB 长最短,此时||AB ===所以ABC 的面积11||||22ABC S AB PC =⋅=⨯= 故选:A 考点八:直线与半圆的相交问题例8.(23-24高二下·上海·月考)已如直线y x m =+和曲线1y =只有一个公共点,则实数m的取值范围.【答案】{|02x m <≤或1m =【解析】因为曲线1y =,所以21,011y x ≤≤-≤,解得01,11y x ≤≤-≤≤,曲线可化为1y -=两边同时平方有,()2211y x -=-,即()2211x y +-=,所以曲线是以()0,1为圆心,1为半径的圆的一部分,而直线y x m =+,所以直线的斜率为1,画图象如下:由于直线与曲线只有一个公共点,当直线过()1,1-时,即11m =-+,解得2m =,当直线过()1,1时,即11m =+,解得0m =,由图象可知02m <≤,1=,解得1m =1m =而m 即为y x m =+在y 轴上的截距,由图象可知1m =,综上:02m <≤或1m =故答案为:{|02x m <≤或1m =.【变式8-1】(23-24高二下·重庆·月考)直线:130l x my m ---=与曲线:2C x =+m 的取值范围是()A .3,44⎛⎤⎥⎝⎦B .13,24⎡⎫⎪⎢⎣⎭C .3,24⎛⎤ ⎥⎝⎦D .30,4⎛⎫ ⎪⎝⎭【答案】B【解析】由题意得,直线:130l x my m ---=过定点(1,3)P -,曲线:2C x =+(2,0)M 为圆心,半径为1的半圆(如图所示),曲线C 的下端点为(2,1)N -.要使直线l 与曲线C 有两个交点,则直线l 应位于直线PN 和切线PQ 之间(可以与PN 重合),此时直线l 的斜率存在,且PQ l PN k k k <≤,即0PN l k k ≥>且圆心(2,0)M 到直线l 的距离小于半径.由1(3)12021PN k m ---==≥>-得12m ≥1<得304m <<,所以1324m ≤<.故选:B.【变式8-2】(23-24高二上·河南许昌·月考)直线y x b =+与曲线y =b 取值范围为()A .(B .(C .⎡⎣D .(【答案】C【解析】由曲线y =()2210x y y +=≥,表示以原点为圆心,半径为1的半圆,当直线y x b =+与半圆y =1=,则b =,此时直线为y x =+;当直线y x b =+过点()0,1时,1b =,此时直线为1y x =+,要使直线y x b =+与曲线21y x =-有两个交点,则b 取值范围为)1,2⎡⎣.故选:C.【变式8-3】(23-24高二上·四川南充·月考)若直线:(1)4l y k x =+-与曲线214x y =--有两个交点,则实数k 的取值范围是()A .3(,)4+∞B .3[,1]4C .[3,)+∞D .(0,3]【答案】C【解析】由已知直线:(1)4l y k x =+-过定点(1,4)P --,曲线214x y =--是以(1,0)M 为圆心,2为半径的圆的左半部分弧 ACB,(1,2)B ,作出它们的图形,如图,直线PB 的斜率为2(4)31(1)PB k --==--,当直线l 斜率不存在时,它与该半圆相切,由图可知,它们有两个交点时,3k ≥,故选:C .一、单选题1.(23-24高二上·天津滨海新·月考)直线l :2y x =+与圆C :()2215x y +-=的位置关系是()A .相交B .相切C .相离D .不确定【答案】A【解析】圆C :()2215x y +-=的圆心(0,1)C ,半径5r =,故圆心到直线的距离220122521(1)d -+==<+-所以直线与圆相交,故选:A2.(23-24高二上·河南焦作·月考)直线10x ky -+=与圆222x y +=的位置关系是()A .相交B .相离C .相交或相切D .相切【答案】A【解析】方法一:直线10x ky -+=恒过定点(1,0)-,而()212-<,所以点(1,0)-在圆222x y +=内,故直线与圆相交.选A.方法二:因为圆心到直线的距离221d r k=<=+,所以直线与圆相交.故选A.方法三:联立直线方程与圆的方程,消去x 并整理,得2210(2)1k y ky +--=,则()222441840k k k ∆=++=+>,所以直线与圆相交.故选A.故选:A.3.(23-24高二上·湖南长沙·期末)直线:2l x y +=,圆22:2220C x y x y +---=.则直线l 被圆C 所截得的弦长为()A .2B .4C .D【答案】B【解析】圆C 的标准方程为()()22114x y -+-=,直线l 过圆心()1,1C ,所以直线l 被圆C 所截得的弦长等于直径长度4.故选:B .4.(23-24高二下·广东茂名·月考)已知圆22:(3)(4)9C x y -+-=,直线()():320l m x m y m +-++=.则直线l 被圆C 截得的弦长的最小值为()A B .C D .【答案】D【解析】直线()()():321320l m x m y m m x y x y +-++=-++-=.恒过定点()2,3P ,圆C 的圆心为()3,4C ,半径为3r =,且()()22233429-+-=<,即P 在圆内,当CP l ⊥时,圆心C 到直线l 的距离最大为d CP ==此时,直线l 被圆C 截得的弦长最小,最小值为=故选:D.5.(22-23高二上·重庆北碚·月考)过点()2,3A 作圆22:1M x y +=的一条切线,切点为B ,则AB =()A .3B .C D【答案】B【解析】因为圆22:1M x y +=,所以圆M 的圆心为(0,0)M ,半径为1r =,因为AB 与圆M 相切,切点为B ,所以AB BM ⊥,则222AB r AM +=,因为AM =,所以AB ==故选:B.6.(23-34高二上·广东珠海·期末)曲线y =与直线()24y k x =-+有两个交点,则实数k 的取值范围是()A .5,112⎛⎤ ⎥⎝⎦B .5,12⎛⎫+∞ ⎪⎝⎭C .3,14⎛⎤⎥⎝⎦D .3,4⎛⎫+∞ ⎪⎝⎭【答案】C【解析】根据题意画出图形,如图所示:由题意可得,曲线y =的图象为以()0,0为圆心,2为半径的半圆,直线l 恒过()2,4A ,由图当直线l 与半圆相切时,圆心到直线l 的距离d r =2=,解得34k =;当直线l 过()2,0B -点时,直线l 的斜率()40122k -==--,则直线l 与半圆有两个不同的交点时,实数k 的取值范围为3,14⎛⎤⎥⎝⎦.故选:C.二、多选题7.(23-24高二上·安徽滁州·期末)若直线20kx y k -+=与圆()()22124x y -+-=有公共点,则实数k 的取值可能是()A .0B .2C .3D .4【答案】AB【解析】直线20kx y k -+=恒过定点()2,0-,圆()()22124x y -+-=的圆心为()1,2,半径为2,显然点()2,0-在圆外,直线与圆有公共点,则圆心到直线的距离2d =≤,解得1205k ≤≤.故选:AB 8.(23-24高二上·福建福州·期末)已知过点(32),的直线l 和圆C :2242110x y x y +---=,则()A .直线l 与圆C 相交B .直线l 被圆C 截得最短弦长为C .直线l 与被圆C 截得的弦长为l 的方程为2y =D .不存在这样的直线l ,使得圆C 上有3个点到直线l 的距离为2【答案】ABD【解析】因为圆C :2242110x y x y +---=,所以圆C 的圆心为()2,1,半径为4.选项A :因为2232432211140+-⨯-⨯-=-<,所以点(32),在圆内,故直线与圆相交,选项A 正确;选项B :设圆心到直线的距离为d ,弦长为m ,则22162m d ⎛⎫+= ⎪⎝⎭,又因为圆心到直线的最长距离()()2232212d =-+-=所以2min max 216214m d =-=B 正确;选项C :直线l 与被圆C 截得的弦长为21516151-=,当直线l 的斜率不存在时,直线方程为3x =,满足题意;当直线l 的斜率存在时,设直线l 的方程为()23y k x -=-,即320kx y k --+=,2213211k k k --+=+,解得0k =,故直线方程为2y =,综上满足题意的直线方程为3x =或2y =,故选项C 不正确;选项D :当直线经过圆心时,圆上到直线的距离为2的点有4个;当直线不经过圆心时,直线将圆分成优弧与劣弧两个部分,由于半径为4,在优弧上一定存在两个点到直线l 的距离为2,那么此时,在劣弧上有且只有一个点到直线的距离为2.2时,此时圆心到直线的距离最大,又因为半径为4,且422->,所以此时劣弧上有两个点到直线的距离为2,所以不存在,所以选项D 正确.故选:ABD.三、填空题9.(23-24高二下·上海静安·期末)圆2225x y +=在点()3,4M -处的切线方程为.【答案】34250x y -+=【解析】由题意可知:圆2225x y +=的圆心为()0,0O ,半径=5r ,因为()223425-+=,可知点()3,4M -在圆上,又因为404303OM k -==---,可知切线方程的斜率34k =,所以切线方程为()3434y x -=+,即34250x y -+=.故答案为:34250x y -+=.10.(21-22高二上·福建宁德·期中)过圆221x y +=外一点(2,1)P -引圆的两条切线,则经过两切点的直线方程是.【答案】210x y --=【解析】设切点分别为()()1122,,,A x y B x y ,因为点,A B 在圆221x y +=上,所以以,A B 为切点的切线方程分别为:11221,1x x y y x x y y +=+=,而点()2,1P -在两条切线上,所以112221,21x y x y -=-=,即点P 满足直线21210x y x y -=⇒--=.故答案为:210x y --=.11.(23-24高二上·福建厦门·期中)已知直线10x my -+=与22:(1)4C x y -+= 交于A ,B 两点,写出满足“ABC 的m 的一个值.,33-中任意一个皆可以,答案不唯一)【解析】22:(1)4C x y -+= 的圆心为()1,0C ,半径2r =,设点C 到直线AB 的距离为d ,由弦长公式得AB =所以12ABC S d =⨯⨯=△,解得1d =或d =由d =1=m =3m =±.四、解答题12.(23-24高二上·北京·期中)求满足下列条件的曲线方程:(1)求过点()A 3,5且与圆22:2410O x y x y +--+=相切的直线方程;(2)求圆心在直线30x y -=上,与x 轴相切,且被直线0x y -=截得的弦长为.【答案】(1)3x =或512450x y -+=;(2)222610x x y y ++++=或222610x x y y -+-+=【解析】(1)据点()A 3,5可设直线方程为()()()()sin 3cos 50t x t y ---=.圆O 的方程可化为()()22124x y -+-=,故点()1,2到所求直线的距离为22=.所以222242sin 3cos 9cos 4sin 12sin cos 45cos 12sin cos t t t t t t t t t =-+=+-=+-,得()cos 5cos 12sin 0t t t -=.这就说明cos 0t =或5tan 12t =,所以所求直线的方程为3x =或512450x y -+=.(2)设所求圆的圆心坐标为(),3P t t ,由于该圆与x 轴相切,故该圆的半径为3t ,所以该圆的方程是()()22239x t y t t -+-=,即222260x tx y ty t -+-+=.而该圆被直线0x y -=截得的弦长为故该圆圆心到直线0x y -=的距离为d ==1t =±.故所求的圆的方程为222610x x y y ++++=或222610x x y y -+-+=.13.(22-23高二上·广东深圳·期末)已知圆22:270C x y y +--=及内部一点0(1,3)P -,过点0P 作倾斜角为α的直线,与圆C 交于A B ,两点.(1)当135α= 时,求弦AB 长;(2)当弦AB 的长度最小时,求直线AB 的方程.【答案】(2)270x y -+=【解析】(1)因为135α= ,则tan1351AB k ==- ,所以直线AB 的方程为3(1)y x -=-+,即20x y +-=,圆C 的标准方程为22270x y y +--=,即22(1)8x y +-=,可得圆C 的圆心(0,1)C ,半径为r =所以圆心(0,1)C 到直线20x y +-=的距离为2d =,可得弦长为AB ===(2)由圆的弦长公式,可得AB =当圆心(0,1)C 到直线AB 的距离d 最大时,此时弦AB 的长度最小,即0CP AB ⊥时,弦AB 的长度最小,因为031210CP k -==---,所以12AB k =,所以AB 的方程为13(1)2y x -=+,即270x y -+=.。
2024年高中数学新高二暑期衔接讲义第12讲直线与圆、圆与圆的位置关系(十大题型)(学生版)

第12讲直线与圆、圆与圆的位置关系【题型归纳目录】题型一:不含参数(含参数)的直线与圆的位置关系题型二:由直线与圆的位置关系求参数、求直线与圆的交点坐标题型三:切线与切线长问题题型四:弦长问题题型五:判断圆与圆的位置关系题型六:由圆的位置关系确定参数题型七:公共弦与切点弦问题题型八:公切线问题题型九:圆中范围与最值问题题型十:圆系问题【知识点梳理】知识点一:直线与圆的位置关系1、直线与圆的位置关系:(1)直线与圆相交,有两个公共点;(2)直线与圆相切,只有一个公共点;(3)直线与圆相离,没有公共点.2、直线与圆的位置关系的判定:(1)代数法:判断直线/与圆。
的方程组成的方程组是否有解.如果有解,直线/与圆。
有公共点.有两组实数解时,直线/与圆C相交;有一组实数解时,直线/与圆C相切;无实数解时,直线/与圆c相离.(2)几何法:由圆C的圆心到直线I的距离日与圆的半径尸的关系判断:当d<r时,直线/与圆。
相交;当d=r时,直线/与圆。
相切;当d>r时,直线/与圆。
相离.知识点诠释:(1)当直线和圆相切时,求切线方程,一般要用到圆心到直线的距离等于半径,记住常见切线方程,可提高解题速度;求切线长,一般要用到切线长、圆的半径、圆外点与圆心连线构成的直角三角形,由勾股定理解得.(2)当直线和圆相交时,有关弦长的问题,要用到弦心距、半径和半弦构成的直角三角形,也是通过勾股定理解得,有时还用到垂径定理.(3)当直线和圆相离时,常讨论圆上的点到直线的距离问题,通常画图,利用数形结合来解决.知识点二:圆的切线方程的求法1、点M在圆上,如图.M法一:利用切线的斜率%与圆心和该点连线的斜率幻肱的乘积等于-1,即k OM•吟=—L.法二:圆心。
到直线/的距离等于半径尸.2、点(Jr。
,%)在圆外,则设切线方程:y-y0=^(x-x0),变成一般式:kx-y+y Q-kx Q=O,因为与圆相切,利用圆心到直线的距离等于半径,解出奴知识点诠释:因为此时点在圆外,所以切线一定有两条,即方程一般是两个根,若方程只有一个根,则还有一条切线的斜率不存在,务必要把这条切线补上.常见圆的切线方程:(1)过圆f+,2二广上一点尸(柘为)的切线方程是x0x+y0y=r2;(2)过圆(x-。
高中 平面解析几何直线与圆、圆与圆的位置关系 知识点+例题

辅导讲义――直线和圆、圆与圆的位置关系圆的切线方程设法:(1)过圆222r y x =+上一点),(00y x P 的圆的切线方程为200r y y x x =+.(2)过圆222)()(r b y a x =-+-上一点),(00y x P 的圆的切线方程为200))(())((r b y b y a x a x =--+--. (3)过圆222r y x =+外一点),(00y x P 作圆的两条切线,则两切点所在直线方程为200r y y x x =+.(4)过圆222)()(r b y a x =-+-外一点),(00y x P 作圆的两条切线,则两切点所在直线方程为200))(())((r b y b y a x a x =--+--.[例]经过点M (2,-1)作圆522=+y x 的切线,则切线方程为_________________. 2x-y-5=0[巩固] 过点P (3,1)作曲线C :0222=-+x y x 的两条切线,切点分别为A ,B ,则直线AB 的方程为____________. 2x+y-3=01.若两圆的半径分别为r 1,r 2,两圆的圆心距为d ,则两圆的位置关系的判断方法如下:位置 关系 外离外切相交内切内含图示d 与r 1,r 2 的关系d >r 1+r 2 d =r 1+r 2 |r 1-r 2|< d < r 1+r 2d =|r 1-r 2|d <|r 1-r 2|两圆的公共点个数0个 1个 2个 1个 0个2.两圆的共切线:(1)当两圆内含时,没有公切线; (2)当两圆内切时有一条公切线; (3)当两圆相交时,有两条外公切线;知识模块4圆与圆的位置关系 精典例题透析知识模块3切线及弦所在直线的方程设法∴切线方程为2x +y ±52=0; ③∵k AC =-2+11-4=13,∴过切点A (4,-1)的切线斜率为-3,∴过切点A (4,-1)的切线方程为y +1=-3(x -4), 即3x +y -11=0.[巩固] (2013·江苏)如图,在平面直角坐标系xOy 中,点A (0,3),直线l :y =2x -4.设圆C 的半径为1,圆心在l 上.(1)若圆心C 也在直线y =x -1上,过点A 作圆C 的切线,求切线的方程; (2)若圆C 上存在点M ,使|MA |=2|MO |,求圆心C 的横坐标a 的取值范围. (1)由题设,圆心C 是直线y =2x -4和y =x -1的交点,解得点C (3,2), 于是切线的斜率必存在.设过A (0,3)的圆C 的切线方程为y =kx +3, 由题意,得|3k +1|k 2+1=1,解得k =0或-34,故所求切线方程为y =3或3x +4y -12=0.(2)因为圆心在直线y =2x -4上,所以圆C 的方程为 (x -a )2+[y -2(a -2)]2=1.设点M (x ,y ),因为|MA |=2|MO |,所以x 2+(y -3)2=2 x 2+y 2,化简得x 2+y 2+2y -3=0,即x 2+(y +1)2=4,所以点M 在以D (0,-1)为圆心,2为半径的圆上.由题意,点M (x ,y )在圆C 上,所以圆C 与圆D 有公共点,则|2-1|≤|CD |≤2+1, 即1≤a 2+(2a -3)2≤3. 由5a 2-12a +8≥0,得a ∈R ; 由5a 2-12a ≤0,得0≤a ≤125. 所以点C 的横坐标a 的取值范围为⎣⎢⎡⎦⎥⎤0,125.题型三:直线与圆相交的问题[例]已知直线kx -y +6=0被圆x 2+y 2=25所截得的弦长为8,求k 的值.设直线kx -y +6=0被圆x 2+y 2=25所截得的弦长为AB ,其中点为C ,则△OCB 为直角三角形.因为圆的半径为|OB |=5,半弦长为|AB |2=|BC |=4,所以圆心到直线kx -y +6=0的距离为3,由点到直线的距离公式得6k 2+1=3,解之得k =±3.[巩固] 求直线x -3y +23=0被圆x 2+y 2=4截得的弦长.如图,设直线x -3y +23=0与圆x 2+y 2=4交于A ,B 两点,弦AB 的中点为M ,则OM ⊥AB (O 为坐标原点),所以OM =|0-0+23|12+(-3)2=3,所以AB =2AM =2OA 2-OM 2=222-(3)2=2.圆x 2+(y -3)2=4的圆心为点(0,3),又因为直线l 与直线x +y +1=0垂直,所以直线l 的斜率k =1.由点斜式得直线l :y -3=x -0,化简得x -y +3=0.3.若圆C 1:x 2+y 2-2ax +a 2-9=0(a ∈R )与圆C 2:x 2+y 2+2by +b 2-1=0 (b ∈R )内切,则ab 的最大值为___________. 圆C 1:x 2+y 2-2ax +a 2-9=0 (a ∈R ).化为:(x -a )2+y 2=9,圆心坐标为(a,0),半径为3.圆C 2:x 2+y 2+2by +b 2-1=0 (b ∈R ),化为x 2+(y +b )2=1,圆心坐标为(0,-b ),半径为1,∵圆C 1:x 2+y 2-2ax +a 2-9=0 (a ∈R )与圆C 2:x 2+y 2+2by +b 2-1=0 (b ∈R )内切,∴a 2+b 2=3-1,即a 2+b 2=4,ab ≤12(a 2+b 2)=2. ∴ab 的最大值为2.4.(2013·山东)过点P (3,1)作圆C :(x -1)2+y 2=1的两条切线,切点分别为A ,B ,则直线AB 的方程为____________.解析 如图所示:由题意知:AB ⊥PC ,k PC =12,∴k AB =-2, ∴直线AB 的方程为y -1=-2(x -1),即2x +y -3=0.5.已知直线y =kx +b 与圆O :x 2+y 2=1相交于A ,B 两点,当b =1+k 2时,OA →·OB →等于___________.设A (x 1,y 1),B (x 2,y 2),将y =kx +b 代入x 2+y 2=1得(1+k 2)x 2+2kbx +b 2-1=0,故x 1+x 2=-2kb 1+k 2,x 1x 2=b 2-11+k 2, 从而·=x 1x 2+y 1y 2=(1+k 2)x 1x 2+kb (x 1+x 2)+b 2=b 2-1-2k 2b 21+k 2+b 2=2b 21+k 2-1=1. 6.若直线y =x +b 与曲线y =3-4x -x 2有公共点,则b 的取值范围是______________.由y =3-4x -x 2,得(x -2)2+(y -3)2=4(1≤y ≤3).∴曲线y =3-4x -x 2是半圆,如图中实线所示.当直线y =x +b 与圆相切时,|2-3+b |2=2.∴b =1±2 2. 由图可知b =1-2 2.∴b 的取值范围是[]1-22,3.7.(2014·上海)已知曲线C :x =-4-y 2,直线l :x =6,若对于点A (m,0),存在C 上的点P 和l 上的Q 使得AP →+AO→=0,则m 的取值范围为________.曲线C :x =-4-y 2,是以原点为圆心,2为半径的圆,并且x P ∈[-2,0],对于点A (m,0),存在C 上的点P 和l 上的Q 使得+=0,(1)求矩形ABCD 的外接圆的方程;(2)已知直线l :(1-2k )x +(1+k )y -5+4k =0(k ∈R ),求证:直线l 与矩形ABCD 的外接圆恒相交,并求出相交的弦长最短时的直线l 的方程.(1)∵l AB :x -3y -6=0且AD ⊥AB ,点(-1,1)在边AD 所在的直线上,∴AD 所在直线的方程是y -1=-3(x +1),即3x +y +2=0.由⎩⎪⎨⎪⎧x -3y -6=0,3x +y +2=0,得A (0,-2). ∴|AP |=4+4=22, ∴矩形ABCD 的外接圆的方程是(x -2)2+y 2=8.(2)直线l 的方程可化为k (-2x +y +4)+x +y -5=0,l 可看作是过直线-2x +y +4=0和x +y -5=0的交点(3,2)的直线系,即l 恒过定点Q (3,2),由(3-2)2+22=5<8知点Q 在圆P 内,∴l 与圆P 恒相交.设l 与圆P 的交点为M ,N ,则|MN |=28-d 2(d 为P 到l 的距离),设PQ 与l 的夹角为θ,则d =|PQ |·sin θ=5sin θ,当θ=90°时,d 最大,|MN |最短.此时l 的斜率为PQ 的斜率的负倒数,即-12, 故l 的方程为y -2=-12(x -3),即x +2y -7=0.11.若直线l :y =kx +1 (k <0)与圆C :x 2+4x +y 2-2y +3=0相切,则直线l 与圆D :(x -2)2+y 2=3的位置关系是_________. 因为圆C 的标准方程为(x +2)2+(y -1)2=2,所以其圆心坐标为(-2,1),半径为2,因为直线l 与圆C 相切.所以|-2k -1+1|k 2+1=2,解得k =±1,因为k <0,所以k =-1,所以直线l 的方程为x +y -1=0.圆心D (2,0)到直线l 的距离d =|2+0-1|2=22<3,所以直线l 与圆D 相交. 12.设曲线C 的方程为(x -2)2+(y +1)2=9,直线l 的方程为x -3y +2=0,则曲线上的点到直线l 的距离为71010的点的个数为____________.B解析 由(x -2)2+(y +1)2=9,得圆心坐标为(2,-1),半径r =3,圆心到直线l 的距离d =|2+3+2|1+(-3)2=710=71010. 能力提升训练要使曲线上的点到直线l 的距离为71010, 此时对应的点在直径上,故有两个点.13.(2013·江西)过点(2,0)引直线l 与曲线y =1-x 2相交于A 、B 两点,O 为坐标原点,当△AOB 的面积取最大值时,直线l 的斜率等于____________.∵S △AOB =12|OA ||OB |sin ∠AOB =12sin ∠AOB ≤12. 当∠AOB =π2时, △AOB 面积最大.此时O 到AB 的距离d =22. 设AB 方程为y =k (x -2)(k <0),即kx -y -2k =0.由d =|2k |k 2+1=22得k =-33. (也可k =-tan ∠OPH =-33). 14.在平面直角坐标系xOy 中,圆C 的方程为x 2+y 2-8x +15=0,若直线y =kx -2上至少存在一点,使得以该点为圆心,1为半径的圆与圆C 有公共点,则k 的最大值是________.圆C 的标准方程为(x -4)2+y 2=1,圆心为(4,0).由题意知(4,0)到kx -y -2=0的距离应不大于2,即|4k -2|k 2+1≤2.整理,得3k 2-4k ≤0.解得0≤k ≤43. 故k 的最大值是43. 15.(2014·重庆)已知直线ax +y -2=0与圆心为C 的圆(x -1)2+(y -a )2=4相交于A ,B 两点,且△ABC 为等边三角形,则实数a =________.圆心C (1,a )到直线ax +y -2=0的距离为|a +a -2|a 2+1.因为△ABC 为等边三角形,所以|AB |=|BC |=2,所以(|a +a -2|a 2+1)2+12=22,解得a =4±15.。
讲义-直线与圆的位置关系

im mmixi、直线和圆的位置关系的定义、性质及判定1、设O O的半径为r,圆心0到直线I的距离为d,则直线和圆的位置关系如下表:公共点个数 2 1 0 圆心到直线的距离d与半径r的关系 d r d r d r切点无公共点名称交占八、、直线名称割线切线无二、切线的性质及判定1. 切线的性质:定理:圆的切线垂直于过切点的半径.推论1:经过圆心且垂直于切线的直线必经过切点.推论2:经过切点且垂直于切线的直线必经过圆心.2. 切线的判定:定义法:和圆只有一个公共点的直线是圆的切线;距离法:到圆心距离等于半径的直线是圆的切线;定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.3. 切线长和切线长定理:⑴ 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长.⑵ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角.①切线的判定定理设OA为O O的半径,过半径外端 A作I丄0A,贝U O到I的距离d=r, ••• I与O O相切.因此,我们得至U:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.注:定理的题设① 经过半径外端”② 垂直于半径”,两个条件缺一不可.结论是直线是圆的切线”•举例说明:只满足题设的一个条件不是O0的切线.②切线的性质定理及其推论切线的性质定理:圆的切线垂直于过切点的半径.OMTTAB三角形内切圆叫做圆的外切三角形 2 直角三角形的内切圆半径与三边关系 3 AA AD __b F OB C C a B_ B图 A B 则内切圆半径cAB 是 BO 'AO(1) 1 2 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形 四、典例分析:切线的性质及判定【例1】如图C 的对边,面积为S的直径,点D 在AB 的延长线上,过点D 作1 )中,设 a b O 的切线,切点为C ,若/ A 251.定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形 E C图(2)中,C 90,则r2 AB③经过切点 1 AM---- 2 M 为切点a ,b, c 分别为 ABC 中 ° - A1) r —,其中p P -a b c2OA 过圆心,OA 过切点A ,则OA AT ②经过圆心,垂直于切线过切点1 AB 过圆心 M 为切点MT垂直于切线过圆心MTAM 过圆心我们分析:这个定理共有三个条件:一条直线满足:(1)垂直于切线(2)过切点 (3)过圆心 定理:①过圆心,过切点 垂直于切线O【例3】【巩固】径为2,则CD 的长为( A . 2 3 B . 4.3C . 2巩固BC AD 于点C ,【例4】巩固则ZD _____例1 例2 巩固【例2】 如图,直线 AB 与O O 相切于点A , O O 的半径为2,若 OBA 30,则0B 的长为()C. 2.3D. 2【巩固】如图,AB 与O O 相切于点B ,线段0A 与弦BC 垂直于点D , AOB 60 , BC 4cm ,则切线AB _________ cm .如图,若 00 的直径AB 与弦AC 的夹角为30,切线CD 与AB 的延长线交于点 D ,且0O 的半AB 2,半圆O 的半径为2,则BC 的长为如图,已知以直角梯形 ABCD 的腰CD 为直径的半圆O 与梯形上底AD 、下底BC 以及腰AB 均相【巩固】如图,已知以直角梯形 ABCD 中,以AB 为直径的圆与CD 相切,求证:以CD 为直径的圆与 AB如图,EB 为半圆O 的直径,点D , C ,E .求证:以 CD 相切.相切.【例5】 【例6】 【例7】 CBOMPCAOBABO如图 C求证 DOC 的值求AD ABO(3) 如图 若OADABO如图 D(2) (1 )AD 平行且交BM 于CCD 是®O 的切线求证:AC 是0O 的切线。
直线与圆的位置关系 - 简单 - 讲义

直线与圆的位置关系知识讲解一、直线与圆的位置关系位置关系有三种:相交、相切、相离 判断直线与圆的位置关系:1)代数法:将直线方程与圆的方程联立成方程组,利用消元法消去一个元后,得到关于另一个元的一元二次方程,求出其∆的值,然后比较判别式∆与0的大小关系, 若0∆<,则直线与圆相离 若0∆=,则直线与圆相切 若0∆>,则直线与圆相交2)几何法:利用圆心到直线的距离d 和圆的半径r 的大小关系:d r <⇔相交,d r =⇔相切,d r >⇔相离.二、计算直线被圆截得的弦长的常用方法1)几何方法:运用弦心距、弦长的一半及半径构成的直角三角形计算.2)代数方法:运用韦达定理及弦长公式A B AB x =-=说明:圆的弦长、弦心距的计算常用几何方法.三、圆与圆的位置关系的判定判定:设2222221111122222:()()(0),:()()(0)C x a y b r r C x a y b r r -+-=>-+-=>,则有: 12121C C r r C >+⇔与2C 外离 12121C C r r C =+⇔与2C 外切 1212121r r C C r r C -<<+⇔与2C 相交 1212121()C C r r r r C =-≠⇔与2C 内切 12121C C r r C <-⇔与2C 内含四、圆的切线方程问题1.求圆切线的方法a)过圆222x y r +=上一点00(,)x y 的切线方程为200x x y y r +=已知圆的方程是222x y r +=,求经过圆上一点00(,)M x y 的切线方程.解:当点M 不在坐标轴上时,设切线的斜率为k ,半径OM 的斜率为1k , ∵圆的切线垂直于过切点的半径,∴11k k =-,又∵010y k x =,∴00x k y =-, ∴经过点M 的切线方程是0000()x y y x x y -=--, 整理得:220000x x y y x y +=+,又∵点00(,)M x y 在圆上,∴22200x y r +=,∴所求的切线方程是200x x y y r +=.注:当点M 在坐标轴上时,可以验证上面的方程同样适用. b)求过圆外一点00(,)x y 的圆的切线方程:几何方法: 设切线方程为00(),y y k x x -=-即000.kx y kx y --+=由圆心到直线的距离等于半径,可求得k ,切线方程即可求出.代数方法:设切线方程为00(),y y k x x -=-即000.kx y kx y --+=代入圆的方程,得到一个关于x 的一元二次方程,由0=求得k ,切线方程即可求出.2.圆的切线方程常见结论a)已知22222222123:,:()(),:0,O x y r O xa yb r O x y D x E y F +=-+-=++++=则以00(,)M x y 为切点的1O 的切线方程200;xx yy r +=2O 的切线方程200()()()(),x a x a y b y b r --+--=3O 切线方程0000()()022D x xE y y xx yyF ++++++=b)已知圆的222x y r +=的切线斜率为k ,则圆的切线方程为y kx =±c)已知切线过圆外一点11(,)P x y ,可设切线方程为11(),y y k x x -=-利用相切条件确定斜率k ,此时必有两条切线,不能漏掉斜率不存在的那一条切线.d)切线段长公式:从圆外一点00(,)P x y 引圆222()()x a y b r -+-=的切线,则P 到切点的切线段长为d ;从圆外一点00(,)P x y 引圆22x y Dx Ey F ++++=的切线,则P 到切点的切线段长为d 五、圆系方程概念:具有某种共同性质的圆的集合,称为圆系.1)同心圆系2220000()(),,x x y y r x y -+-=为常数,r 为参数.2)圆心共线且半径相等圆系22200()(),x x y y r -+-=r 为常数,圆心00(,)x y 在直线0ax by c ++=上移动.3)过两已知圆22(,)0(1,2)i i i i f x y x y D x E y F i =++++==的交点的圆系方程为2222111222()0x y D x E y F x y D x E y F λ+++++++++=即12(,)(,)0(1)f x y f x y λλ+=≠-.当1λ=-时,方程变为121212()()0,D D x E E y F F -+-+-=表示过两圆的交点的直线(当两圆是同心圆时,此直线不存在),当两圆相交时,此直线为公共弦所在直线;当两圆相切时,此直线为两圆的公切线;当两圆相离时,此直线为与两圆连心垂直的直线. 4)过直线与圆交点的圆系方程设直线:0l Ax By C ++=与圆22:0C x y Dx Ey F ++++=相交,则方程22()0x y Dx Ey F Ax By C λ+++++++=表示过直线l 与圆C 的两个交点的圆系方程.典型例题一.选择题(共5小题)1.(2014•浙江)已知圆x2+y2+2x﹣2y+a=0截直线x+y+2=0所得弦的长度为4,则实数a的值是()A.﹣2 B.﹣4 C.﹣6 D.﹣82.(2015•山东)一条光线从点(﹣2,﹣3)射出,经y轴反射后与圆(x+3)2+(y﹣2)2=1相切,则反射光线所在直线的斜率为()A.﹣或﹣B.﹣或﹣C.﹣或﹣D.﹣或﹣3.(2015•广东)平行于直线2x+y+1=0且与圆x2+y2=5相切的直线的方程是()A.2x+y+5=0或2x+y﹣5=0 B.2x+y+=0或2x+y﹣=0C.2x﹣y+5=0或2x﹣y﹣5=0 D.2x﹣y+=0或2x﹣y﹣=0 4.(1993•全国)圆x2+y2=1上的点到直线3x+4y﹣25=0的距离的最小值是()A.6 B.4 C.5 D.15.(2014•湖南)若圆C1:x2+y2=1与圆C2:x2+y2﹣6x﹣8y+m=0外切,则m=()A.21 B.19 C.9 D.﹣11二.填空题(共4小题)6.(2017•山西一模)已知点P在单位圆x2+y2=1上运动,P到直线3x﹣4y﹣10=0与x=3的距离分为d1、d2,则d1+d2的最小值是.7.(2017•江苏模拟)若直线x+y﹣2=0与圆x2+y2=4相交于A,B两点,则弦AB的长度等于.8.过两圆x2+y2=1和x2+y2+2x=0的交点且过点(3,2)的圆的方程为.9.圆的方程为x2+y2﹣6x﹣8y=0,过坐标原点作长度为6的弦,则弦所在的直线方程为.三.解答题(共3小题)10.已知圆M:x2+y2=10和圆N:x2+y2+2x+2y﹣14=0.求过两圆交点且面积最小的圆的方程.11.求面积为10π,且经过两圆x2+y2﹣2x+10y﹣24=0和x2+y2+2x+2y﹣8=0的交点的圆的方程.12.求直线x+y﹣8=0被圆x2+y2﹣4x﹣8y﹣80=0所截得的弦长.。
人教版初中数学同步讲义九年级上册第05讲 直线与圆的位置关系(解析版)

∴直线 y=﹣x 与⊙A 的位置关系是相交,
故选:C.
【即学即练 4】 4.如图,已知 Rt△ABC 中,∠C=90°,AC=3,BC=4,如果以点 C 为圆心的圆与斜边 AB 有公共点,
那么⊙C 的半径 r 的取值范围是( )
A.0≤r≤
B. ≤r≤3
C. ≤r≤4
பைடு நூலகம்
【解答】解:过点 C 作 CD⊥AB 于点 D,
长线于点 E,且 AC 平分∠EAB.求证:DE 是⊙O 的切线.
【解答】证明:连接 0C, ∵OA=OC, ∴∠OAC=∠OCA, ∵AC 平分∠EAB, ∴∠EAC=∠OAC, 则∠OCA=∠EAC, ∴OC∥AE, ∵AE⊥DE, ∴OC⊥DE, ∴DE 是⊙O 的切线.
知识点 02 切线的判定
1. 切线的判定: 经过半径的 外端点 且与这条半径 垂直 的直线叫做圆的切线。
2. 切线的判定的方法: (1)直线与圆有公共点,连半径,证明垂直。 证明垂直的方法:①利用勾股定理证明垂直。 ②利用特殊角或一般角之间的转换证明垂直。 ③利用三角形的全等转换证明垂直。 ④利用平行线转换证明垂直。 (2)直线与圆无公共点:作垂直,证半径。
【即学即练 1】 6.如图,点 C 是⊙O 上一点,点 P 在直径 AB 的延长线上,⊙O 的半径为 3,PB=2,PC=4.求证:PC
2014年中考数学一轮复习讲义:直线与圆的位置关系

2014年中考数学一轮复习讲义:直线与圆的位置关系【考纲要求】1.探索并了解点和圆、直线和圆的位置关系.2.知道三角形的内心和外心.3.了解切线的概念,并掌握切线的判定和性质.【命题趋势】直线与圆位置关系的判定是中考考查的热点,通常出现在选择题中.中考考查的重点是切线的性质和判定,题型多样,常与三角形、四边形、相似、函数等知识结合在一起综合考查.【知识梳理】一、判定一个点P是否在⊙O上:设⊙O的半径为,OP=,则有点P在⊙O 外;点P在⊙O 上;点P在⊙O 内.二、直线和圆的位置关系:设⊙O 半径为R,点O到直线的距离为.(1)直线和⊙O没有公共点直线和圆相离.(2)直线和⊙O有唯一公共点直线和⊙O相切.(3)直线和⊙O有两个公共点直线和⊙O相交.三、切线的判定、性质:(1)切线的判定:①经过半径的外端并且垂直于这条半径的直线是圆的切线.②到圆心的距离等于圆的半径的直线是圆的切线.(2)切线的性质:圆的切线垂直于过切点的半径.(3)切线长:从圆外一点作圆的切线,这一点和切点之间的线段的长度叫做切线长.(4)切线长定理:从圆外一点作圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.题型分类、深度剖析:考点一、点与圆的位置关系【例1】矩形ABCD中,AB=8,BC=35,点P在边AB上,且BP=3AP,如果圆P是以点P为圆心,PD为半径的圆,那么下列判断正确的是( )A .点B ,C 均在圆P 外B .点B 在圆P 外、点C 在圆P 内 C .点B 在圆P 内、点C 在圆P 外D .点B ,C 均在圆P 内解析:画出矩形后求解出DP 的长度即圆的半径,然后求出BP ,CP 的长度与DP 的长度作比较就可以发现答案.在Rt△ADP 中,DP =AD 2+AP 2=7,在Rt△BCP 中,BP =6,PC =BC 2+BP 2=9.∵PC >DP ,BP <DP ,∴点B 在圆P 内,点C 在圆P 外. 答案:C方法总结 解答这类题目的关键是运用数形结合的思想,将点与圆的图形位置关系转化为确定点到圆心的距离与半径之间的数量关系.触类旁通1 若⊙O 的半径为5 cm ,点A 到圆心O 的距离为4 cm ,那么点A 与⊙O 的位置关系是( )A .点A 在圆外B .点A 在圆上C .点A 在圆内D .不能确定 考点二、切线的性质与判定【例2】如图所示,AC 为⊙O 的直径且PA ⊥AC ,BC 是⊙O 的一条弦,直线PB 交直线AC 于点D ,DB DP =DC DO =23.(1)求证:直线PB 是⊙O 的切线; (2)求cos ∠BCA 的值. 分析:(1)连接OB ,OP ,由DB DP =DC DO =23,且∠D =∠D ,根据三角形相似的判定定理得到△BDC ∽△PDO ,可得到BC ∥OP ,易证得△BOP ≌△AOP ,则∠PBO =∠PAO =90°;(2)设PB =a ,则BD =2a ,根据切线长定理得到PA =PB =a ,根据勾股定理得到AD =22a ,又BC ∥OP ,得到DC =2CO ,得到DC =CA =12×22a =2a ,则OA =22a ,利用勾股定理求出OP ,然后根据余弦函数的定义即可求出cos ∠BCA =cos ∠POA 的值.解:(1)证明:连接OB ,OP ,∵DB DP =DC DO =23,且∠D =∠D , ∴△BDC ∽△PDO , ∴∠DBC =∠DPO , ∴BC ∥OP ,∴∠BCO =∠POA ,∠CBO =∠BOP . ∵OB =OC , ∴∠OCB =∠CBO , ∴∠BOP =∠POA . 又∵OB =OA ,OP =OP ,∴△BOP ≌△AOP ,∴∠PBO =∠PAO .又∵PA ⊥AC ,∴∠PAO =90°,∴∠PBO =90°, ∴直线PB 是⊙O 的切线. (2)由(1)知∠BCO =∠POA , 设PB =a ,则BD =2a , 又∵PA =PB =a , ∴AD =DP 2-PA 2=22a . 又∵BC ∥OP ,∴DC =2CO , ∴DC =CA =12AD =12×22a =2a ,∴OA =22a , ∴OP =OA 2+PA 2=⎝ ⎛⎭⎪⎫22a 2+a 2=62a ,∴cos ∠BCA =cos ∠POA =OA OP =33. 方法总结 1.切线的常用判定方法有两种:一是用圆心到直线的距离等于圆的半径来说明直线是圆的切线;二是用经过半径的外端且垂直于这条半径来说明直线是圆的切线.当被说明的直线与圆的公共点没有给出时,用方法一;当圆与直线的公共点已经给出时,常用方法二说明.2.利用切线的性质时,常连接切点和圆心,构造直角.触类旁通2 如图,AD 是⊙O 的弦,AB 经过圆心O ,交⊙O 于点C ,∠DAB =∠B =30°.(1)直线BD 是否与⊙O 相切?为什么? (2)连接CD ,若CD =5,求AB 的长. 考点三、三角形的内切圆【例3】如图,在Rt △ABC 中,∠C =90°,AC =6,BC =8.则△ABC 的内切圆半径r =__________.解析:在Rt △ABC 中,AB =AC 2+BC 2=62+82=10. ∵S △ACB =12AC ·BC =12×6×8=24,∴r =2S a +b +c =486+8+10=2.答案:2方法总结 三角形的内切圆半径r =2Sa +b +c,其中S 是三角形面积,a ,b ,c 是三角形三边长.触类旁通3 如图所示,⊙O 是△ABC 的内切圆,切点分别是D ,E ,F ,已知∠A =100°,∠C =30°,则∠DFE 的度数是( )A .55°B .60°C .65°D .70°。
2020届江苏高考数学(理)总复习讲义: 直线与圆、圆与圆的位置关系

第四节直线与圆、圆与圆的位置关系1.直线与圆的位置关系(半径为r,圆心到直线的距离为d)2.圆与圆的位置关系(两圆半径为r1,r2,d=|O1O2|)[小题体验]1.(2019·徐州调研)已知圆x2+y2=r2与圆x2+y2+6x-8y-11=0相内切,则正数r的值为________.解析:圆x2+y2+6x-8y-11=0的标准方程为(x+3)2+(y-4)2=36,圆心为(-3,4),半径为6,圆x2+y2=r2的圆心为(0,0),半径为r,则圆心距d=||(-3)2+42=5.若两圆内切,则|r-6|=5,得r-6=5或r-6=-5,即r=11或1.答案:1或112.直线l:3x-y-6=0与圆x2+y2-2x-4y=0相交于A,B两点,则AB=________.解析:由x2+y2-2x-4y=0,得(x-1)2+(y-2)2=5,所以该圆的圆心坐标为(1,2),半径r=5,又圆心(1,2)到直线3x -y -6=0的距离为d =|3-2-6|32+(-1)2=102,由⎝⎛⎭⎫AB 22=r 2-d 2,得AB 2=4⎝⎛⎭⎫5-52=10,即AB =10. 答案:103.若直线x -y +1=0与圆(x -a )2+y 2=2有公共点,则实数a 的取值范围为________. 解析:由题意可得,圆的圆心为(a,0),半径为2, 所以|a -0+1|12+(-1)2≤2,即|a +1|≤2,解得-3≤a ≤1.答案:[-3,1]4.若圆x 2+y 2=4与圆x 2+y 2-2mx +m 2-1=0相外切,则实数m =________. 解析:将圆x 2+y 2-2mx +m 2-1=0化成标准方程,得(x -m )2+y 2=1,圆心为(m,0),半径r 1=1,圆x 2+y 2=4的圆心为(0,0),半径r 2=2. 由两圆相外切,得|m |=r 1+r 2=3,解得m =±3. 答案:±31.对于圆的切线问题,尤其是圆外一点引圆的切线,易忽视切线斜率k 不存在的情形. 2.两圆相切问题易忽视分两圆内切与外切两种情形. [小题纠偏]1.过点(2,3)与圆(x -1)2+y 2=1相切的直线的方程为________. 解析:①若切线的斜率存在时,设圆的切线方程为y =k (x -2)+3, 由圆心(1,0)到切线的距离为半径1, 得k =43,所以切线方程为4x -3y +1=0,②若切线的斜率不存在,则切线方程为x =2,也是圆的切线, 所以直线方程为4x -3y +1=0或x =2. 答案:x =2或4x -3y +1=02.若圆x 2+y 2=1与圆(x +4)2+(y -a )2=25相切,则常数a =________. 答案:±25或0考点一 直线与圆的位置关系 (基础送分型考点——自主练透)[题组练透]1.(易错题)(2018·苏北四市调研)直线(a +1)x +(a -1)y +2a =0(a ∈R )与圆x 2+y 2-2x +2y -7=0的位置关系是________.解析:法一:x 2+y 2-2x +2y -7=0化为圆的标准方程为(x -1)2+(y +1)2=9,故圆心坐标为(1,-1),半径r =3,圆心到直线的距离d =|(a +1)-(a -1)+2a |(a +1)2+(a -1)2=|2a +2|2a 2+2.再根据r 2-d 2=9-4a 2+8a +42a 2+2=7a 2-4a +7a 2+1,而7a 2-4a +7=0的判别式Δ=16-196=-180<0,故有r 2>d 2,即d <r ,故直线与圆相交.法二:由(a +1)x +(a -1)y +2a =0(a ∈R )整理得x -y +a (x +y +2)=0,则由⎩⎪⎨⎪⎧x -y =0,x +y +2=0,解得x =-1,y =-1,即直线(a +1)x +(a -1)y +2a =0(a ∈R )过定点(-1,-1),又(-1)2+(-1)2-2×(-1)+2×(-1)-7=-5<0,则点(-1,-1)在圆x 2+y 2-2x +2y -7=0的内部,故直线(a +1)x +(a -1)y +2a =0(a ∈R )与圆x 2+y 2-2x +2y -7=0相交.答案:相交2.(2019·南京学情调研)在平面直角坐标系xOy 中,若直线ax +y -2=0与圆心为C 的圆(x -1)2+(y -a )2=16相交于A ,B 两点,且△ABC 为直角三角形,则实数a 的值是________.解析:因为△ABC 为直角三角形,所以BC =AC =r =4,所以圆心C 到直线AB 的距离为22,从而有|a +a -2|a 2+1=22,解得a =-1. 答案:-13.(2018·苏州高三暑假测试)已知点A (1,0)和点B (0,1),若圆x 2+y 2-4x -2y +t =0上仅有两个不同的点P ,使得△PAB 的面积为12,则实数t 的取值范围是________.解析:由题可得AB =2,若△PAB 的面积为12,则点P 到直线AB 的距离为22,圆x 2+y 2-4x -2y +t =0的标准方程为(x -2)2+(y -1)2=5-t ,圆心到直线AB 的距离为2,所以5-t -22<2<5-t +22,解得12<t <92. 答案:⎝⎛⎭⎫12,92[谨记通法]判断直线与圆的位置关系的两种方法(1)几何法:圆心到直线的距离与圆半径比较大小,即可判断直线与圆的位置关系.这种方法的特点是计算量较小.(2)代数法:将直线方程与圆方程联立方程组,再将二次方程组转化为一元二次方程,该方程解的情况即对应直线与圆的位置关系.这种方法具有一般性,适合于判断直线与圆锥曲线的位置关系,但是计算量较大,能用几何法,尽量不用代数法.考点二 切线、弦长问题 (题点多变型考点——多角探明) [锁定考向]与圆有关的切线及弦长问题,是近年来高考的一个热点,常见的命题角度有: (1)求圆的切线方程(切线长); (2)求弦长;(3)由弦长或切线问题求参数.[题点全练]角度一:求圆的切线方程(切线长)1.已知圆的方程为x 2+y 2=1,则在y 轴上截距为2的切线方程为________________. 解析:在y 轴上截距为2且斜率不存在的直线显然不是切线,故设切线方程为y =kx +2,则|2|k 2+1=1,所以k =±1,故所求切线方程为y =x +2或y =-x + 2. 答案:y =x +2或y =-x + 2 角度二:求弦长2.若a 2+b 2=2c 2(c ≠0),则直线ax +by +c =0被圆x 2+y 2=1所截得的弦长为________. 解析:因为圆心(0,0)到直线ax +by +c =0的距离d =|c |a 2+b2=|c |2|c |=22, 因此根据直角三角形的关系,弦长的一半就等于 1-⎝⎛⎭⎫222=22,所以弦长为 2. 答案: 2角度三:由弦长或切线问题求参数3.(2018·苏州期末)在平面直角坐标系xOy 中,已知过点M (1,1)的直线l 与圆(x +1)2+(y -2)2=5相切,且与直线ax +y -1=0垂直,则实数a =________.解析:因为点M 在圆上,所以切线方程为(1+1)(x +1)+(1-2)(y -2)=5,即2x -y -1=0,所以2a -1=0,即a =12.答案:124.已知圆C :(x -1)2+(y -2)2=2截y 轴所得线段与截直线y =2x +b 所得线段的长度相等,则b =________.解析:记圆C 与y 轴的两个交点分别是A ,B ,由圆心C 到y 轴的距离为1,CA =CB=2可知,圆心C (1,2)到直线2x -y +b =0的距离也等于1才符合题意,于是|2×1-2+b |5=1,解得b =±5.答案:±5[通法在握]1.圆的切线方程的2种求法(1)代数法:设切线方程为y -y 0=k (x -x 0),与圆的方程组成方程组,消元后得到一个一元二次方程,然后令判别式Δ=0进而求得k .(2)几何法:设切线方程为y -y 0=k (x -x 0),利用点到直线的距离公式表示出圆心到切线的距离d ,然后令d =r ,进而求出k .[提醒] 若点M (x 0,y 0)在圆x 2+y 2=r 2上,则过M 点的圆的切线方程为x 0x +y 0y =r 2. 2.弦长的2种求法(1)代数法:将直线和圆的方程联立方程组,消元后得到一个一元二次方程.在判别式Δ>0的前提下,利用根与系数的关系,根据弦长公式求弦长.(2)几何法:若弦心距为d ,圆的半径长为r ,则弦长l =2r 2-d 2.[演练冲关]1.(2019·启东检测)已知点P 是直线y =x 上一个动点,过点P 作圆(x +2)2+(y -2)2=1的切线,切点为T ,则线段PT 长度的最小值为________.解析:圆心C (-2,2),半径r =1,则切线长PT =PC 2-r 2.要使PT 最小,只需PC 最小即可,此时CP 垂直于直线y =x ,则C 到直线x -y =0的距离d =|-2-2|2=42=22,此时PT =(22)2-1=7,故线段PT 长度的最小值为7.答案:72.过原点且与直线6x -3y +1=0平行的直线l 被圆x 2+(y -3)2=7所截得的弦长为________.解析:由题意可得l 的方程为2x -y =0, 因为圆心(0,3)到l 的距离d =33=1, 所以所求弦长l =2R 2-d 2=27-1=2 6. 答案:2 63.已知点A (1,a ),圆x 2+y 2=4.(1)若过点A 的圆的切线只有一条,求a 的值及切线方程;(2)若过点A 且在两坐标轴上截距相等的直线与圆相切,求a 的值及切线方程. 解:(1)由于过点A 的圆的切线只有一条,则点A 在圆上,故12+a 2=4,得a =±3.当a =3,即A (1,3)时,切线的斜率为-33, 故切线方程为y -3=-33(x -1),即x +3y -4=0, 当a =-3,即A (1,-3)时,切线的斜率为33, 故切线的方程为y +3=33(x -1),即x -3y -4=0. 所以a =3时,切线方程为x +3y -4=0,a =-3时,切线方程为x -3y -4=0. (2)设直线方程为x +y =b , 由于直线过点A ,所以1+a =b ,所以直线方程为x +y =1+a ,即x +y -a -1=0. 又直线与圆相切,所以d =|a +1|2=2,所以a =±22-1. 所以切线方程为x +y +22=0或x +y -22=0.考点三 圆与圆的位置关系 (重点保分型考点——师生共研)[典例引领]1.(2019·常州调研)若圆O :x 2+y 2=10与圆M :(x -a )2+y 2=90(a >0)相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是________.解析:由题意得,O (0,0),r 1=10,M (a,0),r 2=310,∴210<|a |<410. ∵OA ⊥MA ,∴在Rt △AOM 中,根据勾股定理,得OM 2=OA 2+MA 2, 即a 2=(10)2+(310)2=100, ∴a =10或a =-10(不合题意,舍去), 则线段AB 的长度为2OA ·MA OM =210×31010=6. 答案:62.(2018·南京、盐城、连云港、徐州二模)已知圆O :x 2+y 2=1,动圆M :(x -a )2+(y -a +4)2=1.若圆M 上存在点P ,过点P 作圆O 的两条切线,切点为A ,B ,使得∠APB =60°,则实数a 的取值范围为________.解析:由题意得圆心M (a ,a -4)在直线x -y -4=0上运动,所以动圆M 是圆心在直线x -y -4=0上,半径为1的圆.又因为圆M 上存在点P ,过点P 作圆O 的两条切线,切点为A ,B ,使∠APB =60°,所以OP =2,即点P 也在x 2+y 2=4上,于是2-1≤a 2+(a -4)2≤2+1,即1≤a 2+(a -4)2≤3,解得2-22≤a ≤2+22,故实数a 的取值范围是⎣⎡⎦⎤2-22,2+22.答案:⎣⎡⎦⎤2-22,2+22 [由题悟法]圆与圆位置关系问题的解题策略(1)处理两圆位置关系多用圆心距与半径和或差的关系判断,一般不采用代数法. (2)若两圆相交,则两圆公共弦所在直线的方程可由两圆的方程作差得到.[即时应用]1.已知圆x 2+y 2=9与圆x 2+y 2-4x +2y -3=0相交于A ,B 两点,则线段AB 的长为________.解析:由题意,两圆的公共弦为2x -y -3=0, ∵圆x 2+y 2=9的圆心坐标为(0,0),半径为3, ∴圆心到直线的距离d =35, ∴线段AB 的长为29-95=1255. 答案:12552.(2019·镇江模拟)若圆C 1:x 2+y 2=1与圆C 2:x 2+y 2-6x -8y +m =0外切,则m =________.解析:圆C 1的圆心为C 1(0,0),半径r 1=1, 因为圆C 2的方程可化为(x -3)2+(y -4)2=25-m , 所以圆C 2的圆心为C 2(3,4),半径r 2=25-m (m <25). 从而C 1C 2=32+42=5. 由两圆外切,得C 1C 2=r 1+r 2, 即1+25-m =5,解得m =9. 答案:9一抓基础,多练小题做到眼疾手快1.(2018·扬州期末)已知直线l :x +3y -2=0与圆C :x 2+y 2=4交于A ,B 两点,则弦AB 的长为________.解析:圆心C (0,0)到直线l 的距离d =|0+3×0-2|1+3=1,所以AB =24-1=23,故弦AB 的长为2 3.答案:2 32.(2019·南京调研)在平面直角坐标系xOy 中,直线x +2y =0与圆(x -3)2+(y -1)2=25相交于A ,B 两点,则线段AB 的长为________.解析:圆(x -3)2+(y -1)2=25的圆心坐标为(3,1),半径为5. ∵圆心(3,1)到直线x +2y =0的距离d =|3+2×1|5=5,∴线段AB 的长为2r 2-d 2=225-5=4 5. 答案:4 53.设圆(x -3)2+(y +5)2=r 2(r >0)上有且仅有两个点到直线4x -3y -2=0的距离等于2,则圆半径r 的取值范围为________.解析:∵圆(x -3)2+(y +5)2=r 2(r >0)的圆心坐标为(3,-5),半径为r , ∴圆心(3,-5)到直线4x -3y -2=0的距离d =|12+15-2|5=5,∵圆(x -3)2+(y +5)2=r 2(r >0)上有且仅有两个点到直线4x -3y -2=0的距离等于2,∴|r -5|<2,解得3<r <7.答案:(3,7)4.(2018·苏锡常镇调研)若直线3x +4y -m =0与圆x 2+y 2+2x -4y +4=0始终有公共点,则实数m 的取值范围是________.解析:圆的标准方程为(x +1)2+(y -2)2=1,故圆心到直线的距离d =|-3+8-m |32+42≤1.即|m -5|≤5,解得0≤m ≤10. 答案:[0,10]5.在平面直角坐标系xOy 中,已知圆C :x 2+y 2-6x +5=0的圆心为C ,点A ,B 在圆C 上,且AB =23,则S △ABC =________.解析:圆C :x 2+y 2-6x +5=0化为标准方程得(x -3)2+y 2=4,圆心为(3,0),半径为2.∵点A ,B 在圆C 上,且AB =23,∴圆心(3,0)到直线AB 的距离为22-(3)2=1, ∴S △ABC =12×23×1= 3.答案: 36.若圆x 2+y 2+mx -14=0与直线y =-1相切,其圆心在y 轴的左侧,则m =________.解析:圆的标准方程为⎝⎛⎭⎫x +m 22+y 2=⎝ ⎛⎭⎪⎫m 2+122,圆心到直线y =-1的距离m 2+12=|0-(-1)|,解得m =±3,因为圆心在y 轴的左侧,所以m = 3.答案: 3二保高考,全练题型做到高考达标1.(2019·苏北四市调研)在平面直角坐标系xOy 中,若点A 到原点的距离为2,到直线 3x +y -2=0的距离为1,则满足条件的点A 的个数为________. 解析:如图,作出直线3x +y -2=0,作出以原点为圆心,以2为半径的圆,∵原点O 到直线3x +y -2=0的距离为1,∴在直线3x +y -2=0的右上方有一点满足到原点的距离为2,到直线3x +y -2=0的距离为1,过原点作直线3x +y -2=0的平行线,交圆于两点,则两交点满足到原点的距离为2,到直线3x +y -2=0的距离为1.故满足条件的点A 共3个. 答案:32.(2018·苏州调研)两圆交于点A (1,3)和B (m,1),两圆的圆心都在直线x -y +c 2=0上,则m +c =________.解析:由题意可知线段AB 的中点⎝⎛⎭⎫m +12,2在直线x -y +c2=0上,代入得m +c =3.答案:33.(2018·南通、扬州、淮安、宿迁、泰州二调)在平面直角坐标系xOy 中,过点P (-2,0)的直线与圆x 2+y 2=1相切于点T ,与圆(x -a )2+(y -3)2=3相交于点R ,S ,且PT =RS ,则正数a 的值为________.解析:因为PT 与圆x 2+y 2=1相切于点T ,所以在Rt △OPT 中,OT =1,OP =2, ∠OTP =π2,从而∠OPT =π6,PT =3,故直线PT 的方程为x ±3y +2=0,因为直线PT 截圆(x -a )2+(y -3)2=3得弦长RS =3,设圆心到直线的距离为d ,则d =|a ±3+2|2,又3=23-d 2,即d =32,即|a ±3+2|=3,解得a =-8或a =-2或a =4,因为a >0,所以a =4.答案:44.(2018·无锡模拟)已知圆C :(x -2)2+y 2=4,线段EF 在直线l :y =x +1上运动,点P 为线段EF 上任意一点,若圆C 上存在两点A ,B ,使得PA ―→·PB ―→≤0,则线段EF 长度的最大值是________.解析:由PA ―→·PB ―→≤0得∠APB ≥90°,从直线上的点向圆上的点连线成角,当且仅当两条线均为切线时,∠APB 才是最大的角,不妨设切线为PM ,PN ,当∠APB ≥90°时, ∠MPN ≥90°,sin ∠MPC =2PC ≥sin 45°=22,所以PC ≤2 2.另当过点P ,C 的直线与直线l :y =x +1垂直时,PC min =322,以C 为圆心,CP =22为半径作圆交直线l 于E ,F 两点,这时的线段长即为线段EF 长度的最大值,所以EF max =2(22)2-⎝⎛⎭⎫3222=14. 答案:145.(2019·镇江调研)若圆O :x 2+y 2=5与圆O 1:(x -m )2+y 2=20(m ∈R )相交于A ,B 两点,且两圆在点A 处的切线互相垂直,则线段AB 的长度是________.解析:如图,因为圆O 1与圆O 在A 处的切线互相垂直,则两切线分别过另一圆的圆心,所以O 1A ⊥OA . 又因为OA =5,O 1A =25,所以OO 1=5.又A ,B 关于OO 1对称,所以AB 为Rt △OAO 1斜边上高的2倍.由12·OA ·O 1A =12OO 1·AC ,得AC =2.所以AB =4.答案:46.(2018·淮阴期末)圆C 1:x 2+y 2+2ax +a 2-4=0和圆C 2:x 2+y 2-2by +b 2-1=0相内切,若a ,b ∈R ,且ab ≠0,则1a 2+4b2的最小值为________.解析:由题意,两圆的标准方程分别为 (x +a )2+y 2=4,x 2+(y -b )2=1, ∴圆心分别为(-a,0),(0,b ),半径分别为2和1. ∵两圆相内切,∴a 2+b 2=1,∴a 2+b 2=1,∴1a 2+4b 2=⎝⎛⎭⎫1a 2+4b 2(a 2+b 2)=5+4a 2b 2+b 2a 2≥5+4=9,当且仅当4a 2b 2=b 2a 2,即a 2=13,b 2=23时等号成立.故1a 2+4b 2的最小值为9. 答案:97.(2018·苏北四市期末)已知A ,B 是圆C 1:x 2+y 2=1上的动点,AB =3,P 是圆C 2:(x -3)2+(y -4)2=1上的动点,则|PA ―→+PB ―→|的取值范围为________.解析:如图,因为A ,B 是圆C 1:x 2+y 2=1上的动点,AB =3,所以线段AB 的中点H 在圆O :x 2+y 2=14上,且|PA ―→+PB ―→|= 2|PH ―→|.因为点P 是圆C 2:(x -3)2+(y -4)2=1上的动点,所以5-32≤|PH ―→|≤5+32,即72≤|PH ―→|≤132,所以7≤2|PH ―→|≤13,从而|PA ―→+PB ―→|的取值范围为[7,13].答案:[7,13]8.(2019·淮安模拟)已知圆O :x 2+y 2=1.若直线y =kx +2上总存在点P ,使得过点P 的圆O 的两条切线互相垂直,则实数k 的最小值为________.解析:圆O 的圆心为O (0,0),半径r =1.设两个切点分别为A ,B ,则由题意可得四边形PAOB 为正方形,故有PO =2r =2,∴圆心O 到直线y =kx +2的距离小于或等于PO =2,即|2|1+k≤2,即1+k ≥2,解得k ≥1, ∴实数k 的最小值为1.答案:19.已知圆C 经过点A (2,-1),和直线x +y =1相切,且圆心在直线y =-2x 上.(1)求圆C 的方程;(2)已知直线l 经过原点,并且被圆C 截得的弦长为2,求直线l 的方程.解:(1)设圆心的坐标为C (a ,-2a ),则(a -2)2+(-2a +1)2=|a -2a -1|2. 化简,得a 2-2a +1=0,解得a =1.所以C (1,-2),半径r =|AC |=(1-2)2+(-2+1)2= 2.所以圆C 的方程为(x -1)2+(y +2)2=2.(2)①当直线l 的斜率不存在时,直线l 的方程为x =0,此时直线l 被圆C 截得的弦长为2,满足条件.②当直线l 的斜率存在时,设直线l 的方程为y =kx , 由题意得|k +2|1+k 2=1,解得k =-34, 所以直线l 的方程为y =-34x . 综上所述,直线l 的方程为x =0或3x +4y =0.10.如图,在平面直角坐标系xOy 中,已知圆C :x 2+y 2-4x =0及点A (-1,0),B (1,2).(1)若直线l ∥AB ,与圆C 相交于M ,N 两点,MN =AB ,求直线l的方程;(2) 在圆C 上是否存在点P ,使得PA 2+PB 2=12?若存在,求点P 的个数;若不存在,请说明理由.解:(1)圆C 的标准方程为(x -2)2+y 2=4,所以圆心C (2,0),半径为2.因为l ∥AB ,A (-1,0),B (1,2),所以直线l 的斜率为2-01-(-1)=1, 设直线l 的方程为x -y +m =0,则圆心C 到直线l 的距离为d =|2+m |2. 因为MN =AB =22+22=22,而CM 2=d 2+⎝⎛⎭⎫MN 22,所以4=(2+m )22+2, 解得m =0或m =-4,故直线l 的方程为x -y =0或x -y -4=0.(2)假设圆C 上存在点P ,设P (x ,y ),则(x -2)2+y 2=4,PA 2+PB 2=(x +1)2+(y -0)2+(x -1)2+(y -2)2=12,即x 2+y 2-2y -3=0,即x 2+(y -1)2=4.因为|2-2|<(2-0)2+(0-1)2<2+2,所以圆(x -2)2+y 2=4与圆x 2+(y -1)2=4相交,所以点P 的个数为2.三上台阶,自主选做志在冲刺名校1.(2019·苏州调研)过曲线y =2|x -a |+x -a 上的点P 向圆O :x 2+y 2=1作两条切线PA ,PB ,切点为A ,B ,且∠APB =60°,若这样的点P 有且只有两个,则实数a 的取值范围是________.解析:根据题意,若经过点P 作圆O :x 2+y 2=1的两条切线,切点为A ,B ,且∠APB =60°,则∠OPA =30°,所以PO =2AO =2,故点P 的轨迹方程为x 2+y 2=4.y =2|x -a |+x -a =⎩⎪⎨⎪⎧3x -3a ,x ≥a ,-x +a ,x <a , 当x ≤a 时,曲线为x +y -a =0,当x ≥a 时,曲线为3x -y -3a =0.故当a <0时,若这样的点P 有且只有两个,必有|3a |1+9<2,即-3a 10<2, 解得a >-2103,即-2103<a <0; 当a =0时,曲线为y =2|x |+x =⎩⎪⎨⎪⎧3x ,x ≥0,-x ,x <0,符合题意;当a >0时,若这样的点P 有且只有两个,必有|a |1+1<2,解得a <22,即0<a <22, 综上,实数a 的取值范围是⎝⎛⎭⎫-2103,22. 答案:⎝⎛⎭⎫-2103,22 2.(2018·苏锡常镇调研)在平面直角坐标系xOy 中,过点M (1,0)的直线l 与圆x 2+y 2=5交于A ,B 两点,其中点A 在第一象限,且BM ―→=2MA ―→,则直线l 的方程为__________.解析:法一:易知直线l 的斜率存在,设l :y =k (x -1).由BM ―→=2MA ―→,可设BM =2t ,MA =t ,如图,过原点O 作OH⊥l 于点H ,则BH =3t 2.设OH =d ,在Rt △OBH 中,d 2+⎝⎛⎭⎫3t 22=r 2=5,在Rt △OMH 中,d 2+⎝⎛⎭⎫t 22=OM 2=1,解得d 2=12. 所以d 2=k 2k 2+1=12,解得k =1或k =-1,因为点A 在第一象限,BM ―→=2MA ―→, 由图知k =1,所以直线l 的方程为y =x -1,即x -y -1=0.法二:设A (x 1,y 1),B (x 2,y 2),所以MA ―→=(x 1-1,y 1),BM ―→=(1-x 2,-y 2).因为BM ―→=2MA ―→,所以⎩⎪⎨⎪⎧ 1-x 2=2(x 1-1),-y 2=2y 1,即⎩⎪⎨⎪⎧ -x 2=2x 1-3,-y 2=2y 1.又x 22+y 22=5,所以(2x 1-3)2+4y 21=5,联立⎩⎪⎨⎪⎧x 21+y 21=5,(2x 1-3)2+4y 21=5,解得x 1=2,代入可得y 1=±1,又点A 在第一象限,故A (2,1),所以直线l 的方程为y =x -1,即x -y -1=0.答案:x -y -1=03.已知圆C 1:(x +1)2+y 2=1和圆C 2:(x -4)2+y 2=4.(1)过点C 1作圆C 2的切线,求该切线方程;(2)过圆心C 1作倾斜角为θ的直线l 交圆C 2于A ,B 两点,且A 为C 1B 的中点,求sin θ;(3)过点P (m,1)引圆C 2的两条割线l 1和l 2.直线l 1和l 2被圆C 2截得的弦的中点分别为M ,N ,试问过点P ,M ,N ,C 2的圆是否过定点(异于点C 2)?若过定点,求出该定点;若不过定点,说明理由.解:(1)显然切线的斜率存在,设切线方程为y =k (x +1), 由题意得|5k |1+k 2=2,解得k =±22121,所以所求直线方程为y =±22121(x +1), 即2x ±21y +2=0.(2)设直线l 的方程为y =k (x +1),则圆心C 2到直线l 的距离d =5k 1+k 2, 设AB 的中点为R ,则AR =4-d 2=12AB =13C 1R =1325-d 2,解得d 2=118. 在Rt △C 1RC 2中,sin θ=C 2R C 1C 2=d 5=2220. (3)依题意,过点P ,M ,N ,C 2的圆即为以PC 2为直径的圆,所以(x -4)(x -m )+(y -1)(y -0)=0,即x 2-(m +4)x +4m +y 2-y =0,整理成关于实数m 的等式(4-x )m +x 2-4x +y 2-y =0恒成立,则⎩⎪⎨⎪⎧ 4-x =0,x 2-4x +y 2-y =0,所以⎩⎪⎨⎪⎧ x =4,y =1或⎩⎪⎨⎪⎧x =4,y =0(舍去). 即存在定点(4,1).命题点一 直线与方程、两条直线的位置关系1.(2017·北京高考)已知x ≥0,y ≥0,且x +y =1,则x 2+y 2的取值范围是________. 解析:依题意,x 2+y 2可视为原点到线段x +y -1=0(x ≥0,y ≥0)上的点的距离的平方,如图所示,故(x 2+y 2)min =⎝ ⎛⎭⎪⎫|-1|22=12,(x 2+y 2)max =|OA |2=|OB |2=1,故x 2+y 2∈⎣⎡⎦⎤12,1.答案:⎣⎡⎦⎤12,12.(2015·山东高考改编)一条光线从点(-2,-3)射出,经y 轴反射后与圆(x +3)2+(y -2)2=1相切,则反射光线所在直线的斜率为________.解析:由已知,得点(-2,-3)关于y 轴的对称点为(2,-3),由入射光线与反射光线的对称性,知反射光线一定过点(2,-3).设反射光线所在直线的斜率为k ,则反射光线所在直线的方程为y +3=k (x -2),即kx -y -2k -3=0.由反射光线与圆相切,则有d =|-3k -2-2k -3|k 2+1=1,解得k =-43或k =-34. 答案:-43或-343.(2016·上海高考)已知平行直线l 1:2x +y -1=0,l 2:2x +y +1=0,则l 1与l 2的距离是________.解析:由两平行线间的距离公式得d =|-1-1|22+12=255. 答案:255 命题点二 圆的方程、直线与圆的位置关系1.(2017·江苏高考)在平面直角坐标系xOy 中,A (-12,0),B (0,6),点P 在圆O :x 2+y 2=50上.若PA ―→·PB ―→≤20,则点P 的横坐标的取值范围是________.解析:设P (x ,y ),则PA ―→·PB ―→=(-12-x ,-y )·(-x,6-y )=x (x +12)+y (y -6)≤20.又x 2+y 2=50,所以2x -y +5≤0,所以点P 在直线2x -y +5=0的上方(包括直线上).又点P 在圆x 2+y 2=50上,由⎩⎪⎨⎪⎧y =2x +5,x 2+y 2=50, 解得x =-5或x =1,结合图象,可得-52≤x ≤1,故点P 的横坐标的取值范围是[-52,1].答案:[-52,1]2.(2018·全国卷Ⅲ改编)直线x +y +2=0分别与x 轴,y 轴交于A ,B 两点,点P 在圆(x -2)2+y 2=2上,则△ABP 面积的取值范围是________.解析:设圆(x -2)2+y 2=2的圆心为C ,半径为r ,点P 到直线x +y +2=0的距离为d , 则圆心C (2,0),r =2,所以圆心C 到直线x +y +2=0的距离为|2+2|2=22, 可得d max =22+r =32,d min =22-r = 2. 由已知条件可得|AB |=22,所以△ABP 面积的最大值为12×|AB |×d max =6, △ABP 面积的最小值为12×|AB |×d min =2. 综上,△ABP 面积的取值范围是[2,6].答案:[2,6]3.(2018·北京高考改编)在平面直角坐标系中,记d 为点P (cos θ,sin θ)到直线x -my -2=0的距离,当θ,m 变化时,d 的最大值为________.解析:由题知点P (cos θ,sin θ)是单位圆x 2+y 2=1上的动点,所以点P 到直线x -my -2=0的距离可转化为单位圆上的点到直线的距离.又直线x -my -2=0恒过点(2,0),所以当m 变化时,圆心(0,0)到直线x -my -2=0的距离21+m 2的最大值为2,所以点P 到直线x -my -2=0的距离的最大值为3,即d 的最大值为3.答案:34.(2018·全国卷Ⅰ)直线y =x +1与圆x 2+y 2+2y -3=0交于A ,B 两点,则|AB |=________.解析:由x 2+y 2+2y -3=0,得x 2+(y +1)2=4.∴圆心C (0,-1),半径r =2.圆心C (0,-1)到直线x -y +1=0的距离d =|1+1|2=2, ∴|AB |=2r 2-d 2=24-2=2 2.答案:2 25.(2017·全国卷Ⅲ)在直角坐标系xOy 中,曲线y =x 2+mx -2与x 轴交于A ,B 两点,点C 的坐标为(0,1),当m 变化时,解答下列问题:(1)能否出现AC ⊥BC 的情况?说明理由;(2)证明过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.解:(1)不能出现AC ⊥BC 的情况,理由如下:设A (x 1,0),B (x 2,0),则x 1,x 2满足x 2+mx -2=0,所以x 1x 2=-2.又C 的坐标为(0,1),故AC 的斜率与BC 的斜率之积为-1x 1·-1x 2=-12, 所以不能出现AC ⊥BC 的情况.(2)证明:由(1)知BC 的中点坐标为⎝⎛⎭⎫x 22,12,可得BC 的中垂线方程为y -12=x 2⎝⎛⎭⎫x -x 22. 由(1)可得x 1+x 2=-m ,所以AB 的中垂线方程为x =-m 2. 联立⎩⎨⎧ x =-m 2,y -12=x 2⎝⎛⎭⎫x -x 22,x 22+mx 2-2=0,可得⎩⎨⎧ x =-m 2,y =-12.所以过A ,B ,C 三点的圆的圆心坐标为⎝⎛⎭⎫-m 2,-12,半径r =m 2+92. 故圆在y 轴上截得的弦长为2r 2-⎝⎛⎭⎫m 22=3,即过A ,B ,C 三点的圆在y 轴上截得的弦长为定值.6.(2016·江苏高考)如图,在平面直角坐标系xOy 中,已知以M 为圆心的圆M :x 2+y 2-12x -14y +60=0及其上一点A (2,4).(1)设圆N 与x 轴相切,与圆M 外切,且圆心N 在直线x =6上,求圆N 的标准方程;(2)设平行于OA 的直线l 与圆M 相交于B ,C 两点,且BC =OA ,求直线l 的方程;(3)设点T (t,0)满足:存在圆M 上的两点P 和Q ,使得TA ―→+TP ―→=T Q ―→,求实数t 的取值范围.解:圆M 的标准方程为(x -6)2+(y -7)2=25,所以圆心M (6,7),半径为5.(1)由圆心N 在直线x =6上,可设N (6,y 0).因为圆N 与x 轴相切,与圆M 外切,所以0<y 0<7,圆N 的半径为y 0,从而7-y 0=5+y 0,解得y 0=1.因此,圆N 的标准方程为(x-6)2+(y -1)2=1.(2)因为直线l ∥OA ,所以直线l 的斜率为4-02-0=2. 设直线l 的方程为y =2x +m ,即2x -y +m =0,则圆心M 到直线l 的距离d =|2×6-7+m |5=|m +5|5. 因为BC =OA =22+42=25,而MC 2=d 2+⎝⎛⎭⎫BC 22,所以25=(m +5)25+5,解得m =5或m =-15. 故直线l 的方程为2x -y +5=0或2x -y -15=0.(3)设P (x 1,y 1),Q (x 2,y 2).因为A (2,4),T (t,0),TA ―→+TP ―→=T Q ―→,所以⎩⎪⎨⎪⎧x 2=x 1+2-t ,y 2=y 1+4.① 因为点Q 在圆M 上,所以(x 2-6)2+(y 2-7)2=25.②将①代入②,得(x 1-t -4)2+(y 1-3)2=25.于是点P (x 1,y 1)既在圆M 上,又在圆[x -(t +4)]2+(y -3)2=25上, 从而圆(x -6)2+(y -7)2=25与圆[x -(t +4)]2+(y -3)2=25有公共点, 所以5-5≤[(t +4)-6]2+(3-7)2≤5+5,解得2-221≤t ≤2+221.因此,实数t 的取值范围是[2-221,2+221 ].。
数学直线与圆的位置关系-讲义

数学课程讲义学科:数学专题:直线与圆的位置关系考点梳理一、直线与圆的位置关系的判定圆的半径为r ,圆心C 到直线l 的距离为d ,则判别直线与圆的位置关系的依据有以下几点:(1)当r d >时,直线l 与圆C 相离;(2)当r d =时,直线l 与圆C 相切;(3)当r d <时,直线l 与圆C 相交.二、关于直线与圆相切(一)切线的求法1. 已知切点求圆的切线方程题一题面:已知圆C 的方程是22(1)4x y +-=,求以P 2)为切点的切线方程.2. 已知圆外一点求圆的切线方程题二题面:求经过点(1、7)与圆x 2 + y 2 = 25相切的切线方程.(二)切线长的求法题三题面:从圆(x-1)2+(y-1)2=1外一点(2,3)P 向这个圆引切线,则切线长为 .三、关于直线与圆相交——弦长问题题四题面:直线250x y -+=与圆228x y +=相交于A 、B 两点,则AB∣∣= .金题精讲题一题面:直线1y x =+与圆221x y +=的位置关系为( )A .相切B .相交但直线不过圆心C .直线过圆心D .相离题二题面:已知直线:40l x y -+=与圆()()22:112C x y -+-=,则C 上各点到l 的距离的最小值为_______.题三题面:在平面直角坐标系xOy 中,已知圆422=+y x 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c 的取值范围是___________题四题面:与直线x y +-20=和曲线221212540x y x y +--+=都相切的半径最小的圆的标准方程是_____课后练习注:此部分为老师根据本讲课程内容为大家精选的课下拓展题目,故不在课堂中讲解,请同学们课下自己练习并对照详解进行自测.题一题面:已知圆心在x的圆O位于y轴左侧,且与直线x+y=0相切,则圆O 的方程是题二题面:直线x+3y-2=0被圆(x-1)2+y2=1所截得的线段的长为( )A.1B.2C.3D.2题三题面:把直线x-2y+λ=0向左平移1个单位,再向下平移2个单位后,所得直线正好与圆x2+y2+2x-4y=0相切,则实数λ的值为()A.3或13B.-3或13C.3或-13D.-3或-13题四题面:若直线mx+ny-3=0与圆x2+y2=3没有公共点,则m、n满足的关系式为____________.讲义参考答案考点梳理题一50y+-=题二答案:4x+3y-25=0 或3x-4y+25=0题三答案:2题四答案:2 3金题精讲题一答案:B题二答案:2题三答案:(-13,13)题四答案:22 (2)(2)2 x y-+-=课后练习题一答案:22(5x y ++=详解:设圆心为(,0)(0)a a <,则r ==,解得5a =-题二答案:C 详解:圆心(1,0),r =1到直线x +3y -2=0的距离d =22)3(1|201|+-+=21. 则21弦长=23 ∴弦长为3.题三答案:A详解:直线x -2y +λ=0按a =(-1,-2)平移后的直线为x -2y +λ-3=0,与圆相切,易得λ=13或3.题四答案:0<m 2+n 2<3详解:将直线方程代入圆方程中“Δ<0”即可.。
中考数学思维方法讲义【第13讲】直线和圆的位置关系(含答案)

状元廊学校数学思维方法讲义之十三年级:九年级第13讲直线和圆的位置关系圆的知识在平面几何中乃至整个初中教学中都占有重要的地位,而直线和圆的位置关系的应用又比较广泛,它是初中几何知识的综合运用,又是在学习了点和圆的位置关系的基础上进行的,在几何证明与计算中,将起到重要的作用,是中考必考查点。
【知识纵横】§Ⅰ直线和圆的位置关系:设圆的半径为r,圆心到直线的距离为d.⑴直线与圆相交⇔d__ ____ r;⑵直线与圆相切⇔d__ ____ r;⑶直线与圆相离⇔d__ ____r。
§Ⅱ圆的切线:1.一个定义:与圆只有一个公共点的直线叫做圆的__ ___;这个公共点叫做__ ___;2.两种判定:⑴若圆心到直线的距离等于半径,则该直线是圆的切线;⑵经过直径的一端,并且垂直于这条直径的直线是圆的切线;3.判定直线和圆的位置,一般考虑如下“三步曲”:一“看”:看看题目中有没有告诉我们直线和圆有几个公共点;二“算”:算算圆心到直线的距离d和圆的半径为r之间的大小关系,然后根据上述关系作出判断;三“证明”:证明直线是否经过直径的一端,并且与该直径的位置关系是否垂直。
4.四条性质:切线有许多重要性质⑴圆心到切线的距离等于圆的_ ____;⑵过切点的半径垂直于_ ____;⑶经过圆心,与切线垂直的直线必经过___ __;⑷经过切点,与切线垂直的直线必经过____ _。
5.弦切角定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角;定理:弦切角等于它所夹的弧所对的圆周角.推论:a)两个弦切角所夹的弧相等,这两个弦切角也相等;b)弦切角的度数等于它所夹弧度数的一半。
【典例精析】考点1: 直线和圆的位置关系【例1】1、如图,已知⊙O是以数轴的原点O为圆心,半径为1的圆,∠=︒,点P在数轴上运动,若过点P且与OA平行的直线与⊙O AOB45=,则x的取值范围是__________.有公共点, 设OP x2、射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心,3为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒).变式一:1、如图,在Rt △ABC 中,∠C =90°,∠A =30°,AB =43D在线段AC 上(不与点A 、C 重合),过点D 作DE ⊥AC 交AB 边于点E . (1)当点D 运动到线段AC 中点时,DE = ;(2)点A 关于点D 的对称点为点F ,以FC 为半径作⊙C ,当DE = 时,⊙C 与直线AB 相切.2、如图,在直角梯形ABCD 中,已知AD ∥BC ,∠C =90°,且AB >AD+ BC ,AB 是⊙O 直径,则直线CD 与⊙O 的位置关系为_____ _.考点2: 圆的切线的性质基本运用【例2】已知直线PD 垂直平分⊙O 的半径OA 于点B ,PD 交⊙O 于点C 、D ,PE 是⊙O 的切线,E 为切点,连结AE ,交CD 于点F . (1)若⊙O 的半径为8,求CD 的长; (2)证明:PE =PF ;(3)若PF =13,sinA =513,求EF 的长.变式二: 如图,⊙O 是△ABC 的外接圆,FH 是⊙O 的切线,切点为F ,FH ∥BC ,连结AF 交BC 于E ,∠ABC 的平分线BD 交AF 于D ,连结BF .(1)证明:AF 平分∠BAC ;(2)证明:BF=FD ;(3)若EF =4,DE =3,求AD 的长.O AD B ED O A B C考点3:切线的判定定理运用【例4】如图,在△ABC中,AB=AC,以AB为直径作半圆⊙O,交BC于点D,连接AD,过点D作DE⊥AC,垂足为点E,交AB的延长线于点F.(1)求证:EF是⊙O的切线;(2)如果⊙O的半径为5,sin∠ADE=45,求BF的长.【例5】如图,在⊙O中,直径AB⊥CD,垂足为E,点M在OC上,AM的延长线交⊙O于点G,交过C的直线于F,∠1=∠2,连结CB与DG交于点N.(1)求证:CF是⊙O的切线;(2)求证:△ACM∽△DCN;(3)若点M是CO的中点,⊙O的半径为4,cos∠BOC=14,求BN的长.12NGEOB M变式三:如图,Rt ABC △中,90ABC ∠=°,以AB 为直径作O ⊙交AC 边于点D ,E 是边BC 的中点,连接DE .(1)求证:直线DE 是O ⊙的切线;(2)连接OC 交DE 于点F ,若OF CF =,求tan ACO ∠的值.【思维拓展】【例6】如图,P A 为⊙O 的切线,A 为切点,直线PO 交⊙O 与点E ,F ,过点A 作PO 的垂线AB 垂足为D ,交⊙O 与点B ,延长BO 与⊙O 交与点C ,连接AC ,BF . (1)求证:PB 与⊙O 相切;(2)试探究线段EF ,OD ,OP 之间的数量关系,并加以证明; (3)若AC =12,tan ∠F =12,求cos ∠ACB 的值.C EBA OF D【例7】已知AB是⊙O的直径,AB=4,点C在线段AB的延长线上运动,点D在⊙O上运动(不与点B重合),连接CD,且CD=OA.(1)当OC=22,求证:CD是⊙O的切线;(2)当OC>22CD所在直线于⊙O相交,设另一交点为E,连接AE.①当D为CE中点时,求△ACE的周长;②连接OD,是否存在四边形AODE为梯形?若存在,请说明梯形个数并求此时AE•ED的值;若不存在,请说明理由.变式四:如图,在边长为2的正方形ABCD中,以点D为圆心、DC为半径作AC,点E在AB上,且与A、B两点均不重合,点M在AD上,且ME=MD,过点E作EF⊥ME,交BC于点F,连接DE、MF.(1)求证:EF是AC所在⊙D的切线;(2)当MA=34时,求MF的长;(3)试探究:△MFE能否是等腰直角三角形?若是,请直接写出MF的长度;若不是,请说明理由.AM【课后测控】1、如图1,60ACB ∠=°,半径为1cm 的O ⊙切BC 于点C ,若将O ⊙在CB 上向右滚动,则当滚动到O ⊙与CA 也相切时,圆心O 移动的水平距离是__________cm .2、如图2,DB 为半圆的直径,A 为BD 延长线上一点,AC 切半圆于点E ,BC ⊥AC 于点C ,交半圆于点F .已知BD =2,设AD =x ,CF =y ,则y 关于x 的函数解析式是 .图1 图2 图33、如图,在Rt △AOB 中,OA =OB =3,⊙O 的半径为1,点P 是AB 边上的动点,过点P 作⊙O 的一条切线PQ (点Q 为切点),则切线PQ 的最小值为 .4、如图,AB 为半圆的直径,C 是半圆弧上一点,正方形DEFG 的一边DG 在直径AB 上,另一边DE 过ΔABC 的内切圆圆心O ,且点E 在半圆弧上。
直线与圆的位置关系讲义

讲义 直线与圆的位置关系一、知识梳理1、直线与圆有相交、相切、相离三种的位置关系,记圆心到直线的距离为d ,圆半径为r ,从几何角度看,相交⇔d r < ;相切⇔d r =;相离d r ⇔>;从代数角度看,联立直线和圆的方程,若有两组解则相交;只有一组解则相切;无解则相离。
2、特别的,如果动直线过圆内一个定点,则动直线与圆必相交。
【2012高考真题重庆理3】任意的实数k ,直线1+=kx y 与圆222=+y x 的位置关系是( )A . 相离 B.相切 C.相交但直线不过圆心 D.相交且直线过圆心【2012高考真题陕西理4】已知圆22:40C x y x +-=,l 过点(3,0)P 的直线,则( )A.l 与C 相交B. l 与C 相切C.l 与C 相离D. 以上三个选项均有可能3、几何性质的运用,尤其是两类直角三角形:相交时,弦心距、半径、半弦组成的直角三角形;相切时, 切点、圆心、圆外的点构成的直角三角形。
二、知识运用 例1、已知直线l :5120x y a ++=,圆C :2220x y x +-=。
(1)若l 与圆C 相切,求a 的值; (2)若l 与圆C 相交,求a 的取值范围;(3)若l 与圆C 相离,求a 的取值范围;(4)若l 被圆C 截得的弦长为1013,求a 的值。
例2、过点(2,4)M 向圆C :22(1)(3)1x y -++=引两条切线,切点分别为,P Q ,求:(1)直线PQ 的方程;(2)切点弦PQ 的长。
例3、圆C 的圆心在直线l 1:x -y -1=0上,圆C 与直线l 2:4x +3y +14=0相切,且截直线l 3:3x +4y +10=0 所得的弦长为6,求圆C 的方程。
例4、已知圆C :()224x y a +-=,点(1,0)A 。
(1)当过点A 的圆C 的切线存在时,求实数a 的取值范围;(2)设,AM AN 是圆C 的两条切线,,M N 为切点,当5MN =时,求MN 所在直线的方程。
直线跟圆的位置关系

高二数学讲义第三讲 直线与圆的位置关系知识小结1.关于直线对称问题:(1)关于l :Ax +By +C =0对称问题:不论点,直线与曲线关于l 对称问题总可以转化为点关于l 对称问题,因为对称是由平分与垂直两部分组成,如求P (x 0 ,y 0)关于l :Ax +By +C =0对称点Q (x 1 ,y 1).有1010x x y y --=-B A (1)与A ·210x x ++B ·210y y ++C =0。
(2)解出x 1 与y 1 ;若求C 1 :曲线f (x ,y )=0(包括直线)关于l :Ax +By +C 1 =0对称的曲线C 2 ,由上面的(1)、(2)中求出x 0 =g 1(x 1 ,y 1)与y 0 =g 2(x 1 ,y 1),然后代入C 1 :f [g 1(x 1 ,y 1),g 2(x 2 ,y 2)]=0,就得到关于l 对称的曲线C 2 方程:f [g 1(x ,y ),g 2(x ,y )]=0。
(3)若l :Ax +By +C =0中的x ,y 项系数|A |=1,|B |=1.就可以用直接代入解之,尤其是选择填空题。
如曲线C 1 :y 2 =4 x -2关于l :x -y -4=0对称的曲线l 2 的方程为:(x -4) 2 =4(y +4)-2.即y 用x -4代,x 用y +4代,这样就比较简单了。
(4)解有关入射光线与反射光线问题就可以用对称问题来解决。
2.点与圆位置关系:P (x 0 ,y 0)和圆C :(x -a ) 2 +(y -b ) 2 =r 2。
①点P 在圆C 外有(x 0 -a ) 2 +(y 0 -b ) 2 >r 2; ②点P 在圆上:(x 0 -a ) 2 +(y 0 -b ) 2 =r 2; ③点P 在圆内:(x 0 -a ) 2 +(y 0 -b ) 2 <r 2 。
3.直线0=++C By Ax 与圆222)()(r b y a x =-+-的位置关系有三种(1)若22BA C Bb Aa d +++=,0<∆⇔⇔>相离r d ;(2)0=∆⇔⇔=相切r d ; (3)0>∆⇔⇔<相交r d 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图形
定义
性质及判定
_r _O
_d
_l
直线与圆没有公共点.
d r 直线 l 与⊙O 相离
_r
_O
_d
_l
直线与圆有唯一公共点,直线叫做 d r 直线 l 与⊙O 相切
圆的切线,唯一公共点叫做切点.
_r
直线与圆有两个公共点,直线叫做
_d _O
_l
d r 直线 l 与⊙O 相交
圆的割线.
从另一个角度,直线和圆的位置关系还可以如下表示:
_O _l
_A
_O
_A
_l
_O _l
_A
证明一直线是圆的切线有两个思路:(1)连接半径,证直线与此半径垂直;(2)作垂线,证垂足在圆上
②切线的性质定理及其推论
切线的性质定理:圆的切线垂直于过切点的半径.
我们分析:这个定理共有三个_A条件:一条直线满足:(1)垂直于切线(2)过切点 (3)过圆心
定理:①过圆心,过切点 垂直于切线
能判定一条直线是否为圆的切线;能 利用直线和圆的位置关系解决简单问 题
能解决与切线有关的 问题
画圆的切线
切线长 了解切线长的概念
会根据切线长知识解决简单问题
一、直线和圆的位置关系的定义、性质及判定
1、设⊙O 的半径为 r ,圆心 O 到直线 l 的距离为 d ,则直线和圆的位置关系如下表:
位置关系 相离 相切 相交
_O
_A
_T
_O
_M
_T
_B
OA 过圆心, OA 过切点 A ,则 OA AT
②经过圆心,垂直于切线 过切点
1 AB过圆心
2
AB
MT
M
为切点
③ 经过切点,垂直于切线 过圆心
1 AM MT 2 M为切点
AM
过圆心
三、三角形内切圆
1. 定义:和三角形各边都相切的圆叫做三角形的内切圆,内切圆的圆心叫做三角形的内心,这个三角形叫 做圆的外切三角形. 2. 多边形内切圆:和多边形的各边都相切的圆叫做多边形的内切圆,这个多边形叫做圆的外切多边形. 3.直角三角形的内切圆半径与三边关系
直线和圆的位置关系
相交
相切
相离
公共点个数 圆心到直线的距离 d 与半径 r 的关系
公共点名称 直线名称
2 d r 交点 割线
1 d r 切点 切线
0 d r
无 无
二、切线的性质及判定
1. 切线的性质: 定理:圆的切线垂直于过切点的半径. 推论 1:经过圆心且垂直于切线的直线必经过切点. 推论2:经过切点且垂直于切线的直线必经过圆心.
M
C
O B
P A
A
【例6】 如图, ABC 中, AB AC , O 是 BC 的中点,以 O 为圆心的圆与 AB 相切于点 D 。
)
A. 4 3 ﻩﻩB. 4
C. 2 3 ﻩD. 2
【巩固】如图, AB 与⊙O 相切于点 B ,线段 OA 与弦 BC 垂直于点 D , AOB 60 , BC 4cm ,则切线 AB cm .
【例3】 如图,若 O 的直径 AB 与弦 AC 的夹角为 30 ,切线 CD 与 AB 的延长线交于点 D ,且 O 的半径为
2. 切线的判定: 定义法:和圆只有一个公共点的直线是圆的切线; 距离法:到圆心距离等于半径的直线是圆的切线; 定理:经过半径的外端并且垂直于这条半径的直线是圆的切线.
3. 切线长和切线长定理: ⑴ 切线长:在经过圆外一点的圆的切线上,这点和切点之间的线段的长,叫做这点到圆的切线
长. ⑵ 切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条 切线的夹角.
2,则 CD 的长为( )
A. 2 3 ﻩB. 4 3
C.2 D.4
D C
E
O
B
A
_C
_A _O
_B _D
例2
巩固
【巩固】如图,EB 为半圆 O 的直径,点 A 在 EB 的延长线上, AD 切半圆 O 于点 D ,BC AD 于点 C ,AB 2 ,
半圆 O 的半径为 2 ,则 BC 的长为_______________.
【例4】 如图,已知以直角梯形 ABCD 的腰 CD 为直径的半圆 O 与梯形上底 AD 、下底 BC 以及腰 AB 均相切,
切点_A 分别是_D
D
,C
,E
.求证:以
AB
为直径的圆与
_A
CD
相_D切.
_O
_O
_B
_C
_B
_C
例4
巩固
【巩固】如图,已知以直角梯形 ABCD 中,以 AB 为直径的圆与 CD 相切,求证:以 CD 为直径的圆与 AB 相
①切线的判定定理 设 OA为⊙O 的半径,过半径外端 A 作 l ⊥OA,则 O 到 l 的距离 d=r,∴ l 与⊙O相切.因此,我 们得到:切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线. 注:定理的题设①“经过半径外端”,②“垂直于半径”,两个条件缺一不可.结论是“直线是圆的切 线”.举例说明:只满足题设的一个条件不是⊙O的切线.
_A
_A
_c
_b
_b
_B
_a
_C _C
_c
_a
_B _B
_A _D
_O
_F
_E _C
(1)
(2)
图(1)中,设 a ,b ,c 分别为 ABC 中 A,B ,C 的对边,面积为 S
则内切圆半径(1) r s ,其中 p 1 a b c ; 图(2)中, C 90,则 r 1 a b c
讲义-直线与圆的位置关系
———————————————————————————————— 作者: ———————————————————————————————— 日期:
板块
A 级要求
考试要求 B 级要求
C 级要求
了解直线与圆的位置关
直线与圆的 位置关系
系;了解切线的概念,理 解切线与过切点的半径 之间关系;会过圆上一点
p
2
2
四、典例分析:切线的性质及判定
【例1】 如图, AB 是 O 的直径,点 D 在 AB 的延长线上,过点 D 作 O 的切线,切点为 C ,若∠A 25,
则∠D ______.
B
O
A
O
D
B
OD
A
C
A
B
C
例1
例2
巩固
【例2】 如图,直线 AB 与⊙O 相切于点 A ,⊙O 的半径为 2 ,若 OBA 30 ,则 OB 的长为(
切.
【例5】 已知:如图,在 ABC 中, AB AC ,以 BC 为直径的半圆 O 与边 AB 相交于点 D ,切线 DE AC ,
_A
垂足为点 E . 求证:(1) ABC 是等边三角形;(2) AE 1 CE . 3
_E
点 M ,直线 OP 交⊙O 于点 A、B ,弦 AC ∥ MP ,求证: MO ∥ BC .
