排队论公式
PPP可用性付费测算公式

PPP可用性付费测算公式PPP(Public-Private Partnership,公私合作)项目的可用性付费测算公式是为了评估项目的可用性,以确定私营合作伙伴应支付的费用。
此公式是通过考虑项目的可用性和相关成本来计算的。
在PPP项目中,可用性是指项目所提供的服务是按照预定要求可供使用的能力。
以下是三种常用的PPP可用性付费测算公式:1. 排队论公式(Queuing Theory Approach)排队论公式是一种广泛应用于PPP项目的可用性测算方法。
它基于排队论原理,通过考虑用户到达时间、服务时间和服务设备效率等因素来计算项目的可用性。
这个公式的形式是:AR=(W-A)/W其中AR是项目的可用性,W是用户的平均等待时间,A是用户的平均使用时间。
这个公式假设用户到达时间服从泊松过程,服务时间服从指数分布。
2. 蒙特卡洛模拟(Monte Carlo Simulation)蒙特卡洛模拟是一种通过随机抽样和统计模拟来估计项目可用性的方法。
它基于大量的随机模拟实验,通过重复执行模拟来计算可用性的概率分布。
在蒙特卡洛模拟中,可以根据项目的具体情况设定各个输入参数(如用户到达时间、服务设备效率等),然后进行多次模拟运算。
最终可以得到可用性的概率分布,并通过统计方法(如均值、标准差等)得到可用性的估计值。
3. 故障树分析(Fault Tree Analysis)故障树分析是一种基于可靠性理论的方法,用于评估系统的可用性和故障风险。
它通过构建系统的故障事件树来分析各种故障可能导致系统失效的概率。
故障树分析基于系统的故障事件关系和概率模型,通过计算概率来估计系统的可用性。
该公式可以表达为:AR=1-P其中AR是项目的可用性,P是系统发生故障事件的概率。
故障树分析需要考虑系统的各种故障事件和其相互关系,并使用概率模型对事件发生的概率进行计算。
这些公式都是根据PPP项目的特点和需求来设计的,可以根据实际情况进行调整和改进。
排队论公式1

系统空闲的概率
系统有n个顾客的概率(顾客损失率)
系统至少有1个顾客的概率
顾客的有效到达率
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
排队论公式一
M/M/1/ /
标准模型
Po = l -
M/G/I/ q
1-Po= P = 7
-p
W n = W s
M/M/1/N/
系统容量有限模型
”=队伍容量+1
1 - p
P°= l- P N + 1
(N + 1)P N* 1
■■:
1=
(1 _
p。
)
L(|
W Q
=
■
入:每小时到达店内人数
卩:每小时可以服务的人数,1/每名客户服务时间的分钟数P:系统忙着的概率,
M/M/1/ q /m
顾客源有限模型
m=^统只有m+1种状态
1
Po =
p m!
zL(ni - i)! p
M/D/1/N/ 严 ------
m!
占=川-vU - P(1)
t q= 3 - (1 -弘)
⑷严-
t- w
tl
排队论公式二
M/M/C/ q /m
多服务台模型
单队,并列C个服务台
C 1
M/ /1/ q /m
(Cp)c p
L[l =C!(l - p
Ls
入:每小时到达店内人数
卩:每小时可以服务的人数,1/每名客户
服务时间的分钟数
P:系统忙着的概率,八命。
排队论公式
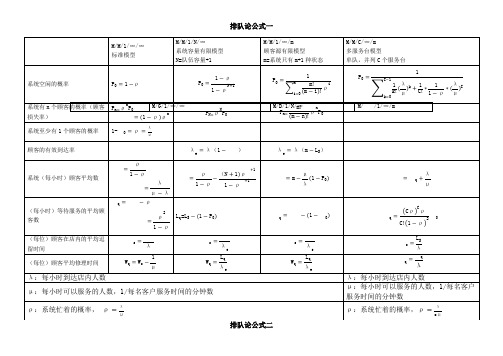
M/D/1/N/∞
M/ /1/∞/m
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
E(v):服务时间v的期望
D(v):方差
ρ:系统忙着的概率,
M/M/1/∞/∞
标准模型
M/M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队,并列C个服务台
系统空闲的概率
ρ
系统有n个顾客的概率(顾客损失率)
系统至少有1个顾客的概率
1-
顾客的有效到达率
系统(每小时)顾客平均数
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
:服务时间v的期望
D(v) :方差
ρ:系统忙着的概率,
((每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
ρ:系统忙着的概率,
ρ:系统忙着的概率,
排队论公式一
排队论公式二
数学排队问题的题型

数学排队问题的题型在我们的日常生活中,排队是一件常见的事情。
你有没有想过,在排队的时候,我们能够利用数学知识帮助我们更加高效地排队呢?今天我们就来讲一讲数学排队问题的题型。
数学排队问题主要涉及到概率论和统计学知识,通常可以分为两种类型:单队列问题和多队列问题。
一、单队列问题单队列问题是指只有一个排队通道的情况。
在这种情况下,我们最想知道的就是队列的平均长度和队列的平均等待时间。
那么如何计算队列的平均长度呢?我们可以用排队论中的公式来计算,它的公式如下:Lq = λWq其中,Lq 表示队列的平均长度,λ 表示单位时间内到达队列的人数,Wq 表示单位时间内在队列中等待的平均时间。
同样地,如何计算队列的平均等待时间呢?我们可以利用排队论中的另一个公式来计算,它的公式如下:Wq = Lq / λ其中,Wq 表示单位时间内在队列中等待的平均时间,Lq 表示队列的平均长度,λ 表示单位时间内到达队列的人数。
二、多队列问题多队列问题是指有多个排队通道的情况。
在这种情况下,我们需要考虑如何将人员分配到不同的队列中,以及如何计算队列的平均长度和队列的平均等待时间。
在多队列问题中,人员的分配可以有多种方法。
最常见的方法是随机分配,即每个人有相同的几率被分配到任何一个队列中。
那么如何计算队列的平均长度呢?我们可以使用排队论中的Kendall’s notation,它由三个参数组成:A/B/C。
其中,A 表示到达队列的时间间隔分布,常见的有常数间隔(M)、泊松分布(P)等;B 表示服务时间的分布,常见的有常数服务时间(M)和指数分布(E)等;C 表示队列的数量,常见的有 FIFO(先进先出)和 LIFO(后进先出)等。
例如,M/M/2 表示到达队列的时间间隔和服务时间都是常数,队列的数量为两个。
那么我们可以利用排队论的公式来计算队列的平均长度和等待时间。
对于多队列问题,计算队列的平均长度和等待时间相对更加复杂,需要更多的排队论知识和模型分析。
排队论-1-2

配件中心的管理员
如果雇佣助手,则 =10人/小时, =15人/小时,
1 1 W 15 10 5
小时,
服务成本 =6 +4=10(元), 时间
期望延迟成本 10 1 5 10 20 时间
雇佣助手后每小时的期望成本为20+10=30元。因此,应 该雇佣该助手,因为平均每小时可以节约50-20=30元的 延迟成本,大于4元/小时的助手工资。
定理3(Little公式)
对于任何存在稳态概率分布的排队系统,下列公式成立:
L W
Lq Wq
Ls Ws
系统中j个顾客的概率
系统中没有顾客的概率 系统中平均顾客的数量 正在排队的平均顾客数量
j (1 )
j
0 1
L
1
系统中正接受服务的人数的期望值为 Ls 。对于一个 M/M/1/GD/∞/∞排队系统,当它达到稳定状态时,
Ls 0 0 1( 1 2 ) 1 0
只有一个服务台, 一名顾客接受服务
1 (1 )
由于一名顾客要么在队列中等待,要么正在接受服务,所 以任何排队系统(不仅仅是M/M/1/GD/ ∞ / ∞排队系统) 都应有, L Ls Lq
期望成本 服务成本 期望延迟成本 = 时间 时间 时间
配件中心的管理员
计算单位时间的服务成本往往很简单。最简单的计算单位 时间延迟成本的方法如下所示:
期望延迟成本 期望延迟成本 顾客数量 = 时间 顾客数量 时间
λ
期望延迟成本 10元 = (机械师在系统中的平 均逗留时间) 顾客数量 人小时
排队论公式

(10.75)
九、顾客源有限(m)的M / M / c模型( Palm模型) (1)系统的稳态概率Ρ n为 1
。
2。
⎡ c −1 ⎛ m ⎞ ⎛ λ ⎞ n m ⎛ m ⎞ k ! ⎛ λ ⎞ k ⎤ Ρ0 = ⎢∑ ⎜ ⎟ ⎜ ⎟ + ∑ ⎜ ⎟ ⎟ ⎥ ;(10.76) k −c ⎜ μ k =0 ⎝ k ⎠ ⎝ μ ⎠ k = c ⎝ k ⎠ c !c ⎝ ⎠ ⎥ ⎢ ⎣ ⎦ n ⎧⎛ m ⎞ ⎛ λ ⎞ 0 ≤ n ≤ c, ⎪⎜ ⎟ ⋅ ⎜ ⎟ Ρ 0, ⎪⎝ n ⎠ ⎝ μ ⎠ (10.77) Ρn = ⎨ n ⎪ ⎛ m ⎞ n! ⎛ λ ⎞ c ≤ n ≤ m. ⎪ ⎜ n ⎟ c !c n −c ⎜ μ ⎟ Ρ 0, ⎝ ⎠ ⎝ ⎠ ⎩ Lq = Ls = Lq + Ws =
λe = Ls − ρ (1 − Ρ N ); μ
(10.64)
3。 顾客的平均逗留时间Ws为 Ws =
λe
Ls
= Ls • λ (1 − Ρ N );
(10.65)
顾客的平均等待时间Wq为 4。 Wq = Ws − 1
μ
= λ (1 − Ρ N ) Ls −
1
μ
;
(10.66)
服务台的利用率为 5。 r= c λ = (1 − Ρ N ) = ρ c (1 − Ρ N ). c cμ (10.67)
N −1 n
⎧ N +1 , ρ = 1, ⎪ ⎪ 2λ Ws = ⎨ (10.29) N +1 ⎪ 1 − Nρ , ρ ≠ 1; N ⎪ ⎩ μ − λ λ (1 − ρ )
4o 顾客在系统中的等待时间分布及平均等待时间Wq , 即 Fq ( w) = 1 − ∑
burke定理

burke定理Burke定理是一种关于任务调度问题的重要定理,它可以帮助我们更好地理解和解决任务调度问题。
本文将从定义、证明、应用等方面全面介绍Burke定理。
一、定义Burke定理是指在一个队列系统中,如果到达率为λ,服务率为μ,那么其平均队列长度L的期望值等于到达率与服务率之比λ/μ乘以平均逗留时间W的期望值,即L=λW。
其中,平均逗留时间W指的是一个顾客在系统中逗留的平均时间。
二、证明下面我们将通过排队论来证明Burke定理。
首先,我们假设队列系统中有一个顾客正在等待服务。
此时,这个顾客需要等待其他所有顾客离开服务才能开始接受服务。
因此,这个顾客在排队中等待的时间就是其他所有顾客逗留时间之和。
而这些逗留时间可以看成是独立同分布的随机变量。
根据排队论的公式可知:L = λW其中L为平均队列长度,λ为到达率,W为平均逗留时间。
接下来我们将证明上述公式成立。
首先考虑到达率λ。
在单位时间内到达系统中的顾客数为λ,因此在一个顾客逗留时间W内,到达系统中的顾客数为λW。
接下来考虑服务率μ。
在单位时间内可以完成的服务数量为μ,因此在一个顾客逗留时间W内,可以完成的服务数量为μW。
由于队列系统中没有阻塞,因此到达率必须等于离开率。
即:λ = μ + λ'其中λ'为进入系统但未被立即服务的顾客到达率。
将上述公式代入L=λW中可得:L = λW = (μ + λ')W将平均逗留时间W表示成等待其他所有顾客离开服务的时间之和可得:W = Wq + 1/μ其中,Wq为平均排队等待时间。
将上述公式代入L=λW中可得:L = λ(Wq + 1/μ) + λ' Wq化简后可得:L = λ Wq + 1/μ这就是Burke定理。
三、应用Burke定理在任务调度问题中有广泛应用。
例如,在计算机网络中,网络节点需要处理大量请求。
如果系统负载过高,就会导致请求排队等待处理,从而影响用户体验。
通过使用Burke定理可以计算出平均排队长度和平均排队等待时间,并根据这些指标来优化任务调度策略,从而提高系统性能。
排队论公式

1排队论公式构成排队模型的三个主要特征指标(1) 相继顾客到达间隔时间的分布;(2) 服务时间的分布;(3) 服务台的个数。
根据这三个特征对排队模型进行分类的Kendall 记号:X/Y/ZX :表示相继到达间隔时间的分布;Y :表示服务时间的分布;Z :并列的服务台的数目。
表示相继到达间隔时间和服务时间的各种分布符号M——负指数分布(M 是Markov 的字头,因为负指数分布具有无记忆性,即Markov 性) D——确定型(deterministic)E k ——k 阶爱尔朗(erlang)分布G—— 一般(general)服务时间的分布Kendall 符号的扩充X/Y/Z/A/B/C其中前三项的意义不变,后三项的意义分别是:A :系统容量限制N ,或称等待空间容量。
B :顾客源数目m 。
分有限与无限两种,∞表示顾客源无限,此时一般∞也可省略不写。
C :服务规则,如先到先服务(FCFS),后到后服务(LCFS),优先权服务(PR)等。
(例如某排队问题为M/M/1/∞/∞/FCFS ,则表示顾客到达间隔时间为负指数分布(即泊松流);服务时间为负指数分布;有1个服务台,系统等待空间容量无限(等待制);顾客源无限,采用先到先服务规则。
)一、M/M/1/∞/∞ 设1λρμ=<, 则: 01P ρ=-;s L λμλ=-,q L ρλμλ=-;1s W μλ=-,q W ρμλ=- 故而:s s L W λ=,q q L W λ=;1s q W W μ=+,s q L L λμ=+ 二、M/M/1/N/∞(系统容量有限) 设λρμ=,则:2 12011,111,11N P P N P ρρρρ+⎧====⎪+⎪=⎨-⎪≠-⎪⎩; 101,12(1),111N s n N n N N L nP N ρρρρρρ+=+⎧=⎪⎪==⎨+⎪-≠--⎪⎩∑; 01(1)(1)Nq n s n L n P L P ==-=--∑;有效到达率0(1)e P λμ=-;ss e L W λ=,1q s W W μ=- 三、M/M/1/∞/m (顾客源有限)001!()!i m i P m m i λμ==⎛⎫ ⎪-⎝⎭∑;0(1)s L m P μλ=--,有效到达率0()(1)e s m L P λλμ=-=- 0(1)q s L L P =--;1=s s e e m L W λλλ=-,1q s W W μ=-四、M/M/c/∞/∞设1c λρμ=<,则: 0101111!!1k c c k P k c λλμρμ-==⎛⎫⎛⎫+⋅⋅ ⎪ ⎪-⎝⎭⎝⎭∑02()!(1)c q c L P c ρρρ=-,s q L L λμ=+; s s L W λ=,q q L W λ=3五、一般服务时间M/G/1T 表示服务时间,当T 服从负指数分布时,1()E T μ=,而在M/G/1模型中,T 的分布是一般的。
排队论公式
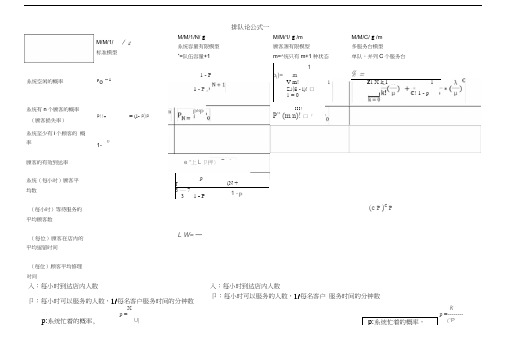
M/M/1/ g /m顾客源有限模型m=^统只有m+1种状态M/M/C/ g /m多服务台模型 单队,并列C 个服务台入:每小时到达店内人数卩:每小时可以服务的人数,1/每名客户 服务时间的分钟数排队论公式一系统空闲的概率 po = 1系统有n 个顾客的概率 (顾客损失率) P 11== (i- P )P系统至少有i 个顾客的 概率 1-()顾客的有效到达率 系统(每小时)顾客平 均数 (每小时)等待服务的 平均顾客数 (每位)顾客在店内的 平均逗留时间 (每位)顾客平均修理 时间 1 - P 1 - Pe =上L 卩押〉P NPpJ(N +3 — 731 - P 1 - PL W= —p ()=1mV m!iZ J (E - i)! 口 1 = 0% =Z 1 X k 11—徨C! 1 - p[]]!P” (m n)! 口 P(c P )C PXkp =p =--------U|p:系统忙着的概率,C Pp:系统忙着的概率,M/M/1// g标准模型M/M/1/N/ g系统容量有限模型”=队伍容量+1入:每小时到达店内人数卩:每小时可以服务的人数,1/每名客户服务时间的分钟数M/G/1/ /系统(每小时)顾客平均数p + k D(v) 耳=P* 2〔1 - P )排队论公式二M/D/1/N/ a M/ /1/ a /m(每小时)等待服务的平均顾客数(每位)顾客在店内的平均逗留时间(k+ 1)P2y p +ik(i^7)f, (k+l)p2q £2k(i - P)(每位)顾客平均修理时间入:每小时到达店内人数卩:每小时可以服务的人数,1/每名客户服务时间的分钟数E(v):服务时间v的期望D(v):方差P:系统忙着的概率, 八迸门瑁讪q qq 丄q n入:每小时到达店内人数卩:每小时可以服务的人数,1/每名客户服务时间的分钟数1J1.(V)-—'U:服务时间V的期望1D(v) 方差P:系统忙着的概率,。
排队论公式
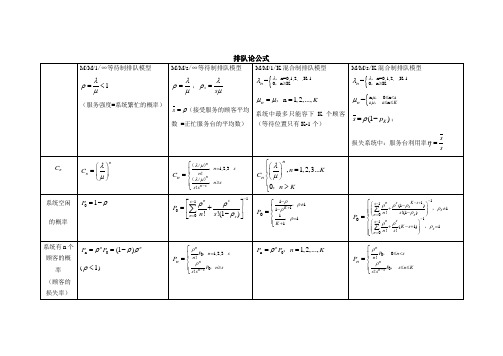
P0 1
s 1 n s P0 n 0 n ! s !(1 s )
1 , 1 K 1 P0 1 1 K 1, 1
Pn n P0,n 1, 2,..., K
s 1 n s (1 s K s 1 ) 1 n! s !(1 ) , s 1 s P0 n 0 1 s 1 n s ( K s 1) , s 1 n 0 n! s !
n P , 0 n s 0 Pn n! n n s P0, s n K s !s
系统有 n 个 顾客的概 率 (顾客的 损失率)
Pn n P0 (1 ) n
( 1)
n P ,n 1,2,3...s 0 Pn n! n n s P0,n s s !s
n 1Βιβλιοθήκη K p0 s s s !(1 s )2 1 s K s 1 (1 s )( K s 1) s K s , Lq p0 s ( K s )( K s 1), 1 s 2s!
数 =正忙服务台的平均数)
n ,n 1, 2,..., K
系统中最多只能容下 K 个顾客 (等待位置只有 K-1 个)
, ,nn=0,1,2,...,K-1 0 K =
n , 0n<s s , sn K
s (1 pK ) ;
损失系统中:服务台利用率
排队论公式
M/M/1/∞等待制排队模型 M/M/s/∞等待制排队模型 M/M/1/K 混合制排队模型 M/M/s/K 混合制排队模型
排队论公式
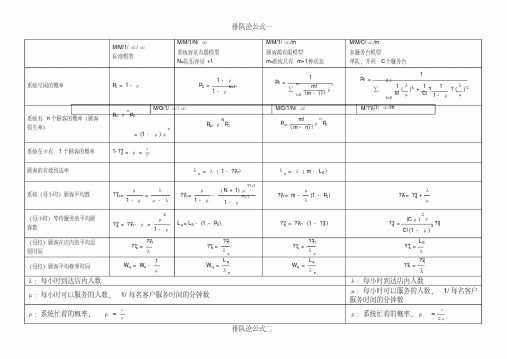
1/ 每名客户
λ
ρ:系统忙着的概率,ρ =
cμ
系统(每小时)顾客平均数
(每小时)等待服务的平均 顾客数 (每位)顾客在店内的平均 逗留时间 (每位)顾客平均修理时间
2
2
ρ + λ D(v)
????= ρ +
2(1 - ρ )
?q? = λ ??q = ????- ρ ????
???? ??s =
λ
e
Lq Wq =
λ
e
μ:每小时可以服务的人数, 1/ 每名客户服务时间的分钟数
λ
e
=
λ( m -
LS)
μ ????= m - (1 - P0 )
λ
??q = ????- (1 - ??0 )
???? ??s =
λ
e
Lq Wq =
λ
e
λ
ρ:系统忙着的概率, ρ = μ
排队论公式二
M/M/C/ ∞ /m 多服务台模型 单队,并列 C个服务台
P0 = ∑
1
C-1
k=0
1 k!
( λ )k μ
+
1 C!
?
1
1 -
ρ
?
λ () μ
C
M/????/1/ ∞ /m
λ ????= ??q +
μ
C
(Cρ ) ρ
??q =
2 ??0
C! (1 - ρ )
LS ??s =
λ
??q ??q =
λ
n
= (1 - ρ ) ρ
1- ??0 =
ρ
排队论公式1

M/M/1/∞/∞标准模型M/M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队,并列C个服务台
系统空闲的概率
ρ
系统有n个顾客的概率
(顾客损失率)
系统至少有1个顾客的
概率
1-
顾客的有效到达率
系统(每小时)顾客平均
数
(每小时)等待服务的平
均顾客数
=
(每位)顾客在店内的平
均逗留时间
(每位)顾客平均修理时
间
λ:每小时到达店内人数λ:每小时到达店内人数
排队论公式一
排队论公式二
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数 ρ:系统忙着的概率,
ρ:系统忙着的概率,
M/G/1/∞/∞
M/D/1/N/∞
M//1/∞/m
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
(每位)顾客在店内的平均
逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数 E(v):服务时间v 的期望 D(v):方差
ρ:系统忙着的概率,
λ:每小时到达店内人数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数
:服务时间v 的期望
D(v)
:方差
ρ:系统忙着的概率,。
队列问题的公式

队列问题的公式通常用于解决一些具有队列特性的数学问题。
下面列举几个常见的队列问题公式:
1.排队论中的M/M/1公式:M/M/1模型表示一个系统有无限个顾客和有限
个服务台,顾客以泊松流到达,服务时间和服务时间是相互独立的,服从
相同的指数分布。
该模型可以用以下公式表示:L = λW,其中L是队列长
度,λ是平均到达率,W是平均服务时间。
2.排队论中的M/M/c公式:M/M/c模型表示一个系统有无限个顾客和c个服
务台,顾客以泊松流到达,服务时间和服务时间是相互独立的,服从相同
的指数分布。
该模型可以用以下公式表示:L = (c / (c - λ)) * λ * W,其中L
是队列长度,λ是平均到达率,W是平均服务时间。
3.优先队列公式:优先队列是一种数据结构,其中元素具有优先级。
最常见
的优先队列公式是查找具有最大优先级的元素的时间复杂度为O(log n),插入新元素的时间复杂度为O(log n),删除具有最大优先级的元素的时间复杂度为O(log n)。
4.循环队列公式:循环队列是一种使用固定大小的数组实现队列的方法,其
中头尾指针可以指向队列的开头和结尾。
循环队列的公式包括:front =
(front + enqueue) % size和rear = (rear + enqueue) % size,其中front是头指针,rear是尾指针,enqueue是入队操作,size是数组大小。
以上是一些常见的队列问题公式,它们可以帮助我们解决一些具有队列特性的数学问题。
(完整版)排队论公式1

M/M/1/∞/∞标准模型M/M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队,并列C个服务台
系统空闲的概率
ρ
系统有n个顾客的概率(顾
客损失率)
系统至少有1个顾客的概率1-
顾客的有效到达率
系统(每小时)顾客平均数
(每小时)等待服务的平均
顾客数
=
(每位)顾客在店内的平均
逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数λ:每小时到达店内人数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数µ:每小时可以服务的人数,1/每名客户服务时间的分钟数
排队论公式一
排队论公式二
ρ:系统忙着的概率,ρ:系统忙着的概率,
M/G/1/∞/∞M/D/1/N/∞M//1/∞/m 系统(每小时)顾客平均数
(每小时)等待服务的平均
顾客数
(每位)顾客在店内的平均
逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数E(v):服务时间v的期望
D(v):方差
ρ:系统忙着的概率,λ:每小时到达店内人数
µ:每小时可以服务的人数,1/每名客户服务时间的分钟数
:服务时间v的期望
D(v):方差
ρ:系统忙着的概率,。
排队论公式

μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
:服务时间v的期望
D(v) :方差
ρ:系统忙着的概率,
M/M/1/∞/∞
标准模型
M/M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队,并列C个服务台
系统空闲的概率
ρ
系统有n个顾客的概率(顾客损失率)
系统至少有1个顾客的概率
1-
顾客的有效到达率
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
=
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
μ:每小时可以服务的人数,1/每名客户服务时间的分
排队论公式一
排队论公式二
M/G/1/∞/∞
M/D/1/N/∞
M/ /1/∞/m
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
E(v):服务时间v的期望
D(v):方差
ρ:系统忙着的概率,
排队论公式

=
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
ρ:系统忙着的概率,
ρ:系统忙着的概率,
排队论公式一
排队论公式二
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
:服务时间v的期望
D(v) :方差
ρ:系统忙着的概率,
M/M/1/∞/∞
标准模型
Mห้องสมุดไป่ตู้M/1/N/∞
系统容量有限模型
N=队伍容量+1
M/M/1/∞/m
顾客源有限模型
m=系统只有m+1种状态
M/M/C/∞/m
多服务台模型
单队,并列C个服务台
系统空闲的概率
ρ
系统有n个顾客的概率(顾客损失率)
系统至少有1个顾客的概率
1-
顾客的有效到达率
系统(每小时)顾客平均数
M/G/1/∞/∞
M/D/1/N/∞
M/ /1/∞/m
系统(每小时)顾客平均数
(每小时)等待服务的平均顾客数
(每位)顾客在店内的平均逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数
μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
E(v):服务时间v的期望
D(v):方差
ρ:系统忙着的概率,
利特尔法则公式

利特尔法则公式利特尔法则(Little's Law)是一个在运营管理和排队论中广泛应用的公式。
咱先来说说这利特尔法则公式到底是啥。
它的表达式是L = λW ,这里的 L 表示系统中的平均库存(或者说平均在制品数量),λ 表示单位时间内的平均顾客到达率,W 表示每个顾客在系统中的平均停留时间。
举个例子哈,比如说咱们去一家很火的小吃店买好吃的。
每天来这家店的顾客数量挺稳定的,平均下来每小时有20 个人来(这就是λ)。
然后呢,每个顾客从进门点餐到拿了东西走人,平均得花 30 分钟(这就是 W )。
那按照利特尔法则,这家店里平均的顾客数量(也就是平均库存 L )就是 20×0.5 = 10 个人。
这法则在咱们生活里用处可大啦!就拿学校来说吧,咱们假设学校图书馆的借书处,平均每小时有 15 个同学来借书还书(λ = 15),而每个同学办理借书还书手续平均需要 12 分钟(W = 0.2 小时),那这个借书处平均就会有 15×0.2 = 3 个同学在等待或者办理手续。
再比如说,一家工厂生产某种产品。
每天开工 8 小时,平均每小时有 5 个订单进来(λ = 5),从原材料投入到成品产出,平均每个产品需要 2 小时(W = 2 ),那这个生产线上正在加工的产品数量,也就是平均库存 L ,就是 5×2 = 10 个。
咱们再把目光放到交通上。
某个十字路口,平均每分钟有 10 辆车要通过(λ = 10),每辆车通过这个路口平均需要 30 秒(W = 0.5 分钟),那这个路口平均就会有 10×0.5 = 5 辆车在等着通过。
利特尔法则不仅能帮我们了解各种系统中的“平均库存”情况,还能帮我们优化系统呢。
比如说,如果我们想减少图书馆借书处的等待人数,要么降低每小时来借书还书的同学数量(这可能不太容易控制),要么想办法缩短每个同学办理手续的时间。
在工厂生产中,如果想降低平均库存,要么减少订单的流入速度,要么加快生产流程,缩短生产时间。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
排队论公式二
M/G/1/∞/∞ 系统(每小时)顾客平均数
M/D/1/N/∞
M/ /1/∞/m
(每小时)等待服务的平均 顾客数
(每位)顾客在店内的平均 逗留时间
(每位)顾客平均修理时间
λ:每小时到达店内人数 μ:每小时可以服务的人数,1/每名客户服务时间的分钟数 E(v):服务时间 v 的期望 D(v):方差
ρ:系统忙着的概率,
λ:每小时到达店内人数 μ:每小时可以服务的人数,1/每名客户服务时间 的分钟数
:服务时间 v 的期望
D(v)
:方差
ρ:系统忙着的概率,
M/M/1/∞/∞ ห้องสมุดไป่ตู้准模型
排队论公式一
M/M/1/N/∞ 系统容量有限模型 N=队伍容量+1
M/M/1/∞/m 顾客源有限模型 m=系统只有 m+1 种状态
M/M/C/∞/m 多服务台模型 单队,并列 C 个服务台
系统空闲的概率
ρ
系统有 n 个顾客的概率 (顾客损失率)
系统至少有 1 个顾客的
概率
1-
顾客的有效到达率
系统(每小时)顾客平 均数
(每小时)等待服务的
平均顾客数
=
(每位)顾客在店内的 平均逗留时间
(每位)顾客平均修理 时间
λ:每小时到达店内人数 μ:每小时可以服务的人数,1/每名客户服务时间的分钟数
ρ:系统忙着的概率,
λ:每小时到达店内人数 μ:每小时可以服务的人数,1/每名客户 服务时间的分钟数
