第八章计算长度
抛物线焦点弦的弦长公式

抛物线焦点弦的弦长公式-CAL-FENGHAI.-(YICAI)-Company One1关于抛物线焦点弦的弦长公式在高中教材第八章中有关于已知倾斜角的焦点弦,求焦点弦的弦长的问题,其中只介绍了开口向右时的焦点弦的长度计算问题:(1)已知:抛物线的方程为px y 22=)0(>p ,过焦点F 的弦AB 交抛物线于A B 两点,且弦AB 的倾斜角为θ,求弦AB 的长。
解:由题意可设直线AB 的方程为)2(p x k y -=)2(πθ≠将其代入抛物线方程整理得:0)84(422222=++-kp k xkx p p ,且θtan =k设A,B 两点的坐标为),(),,(2211y x y x 则:kk xx p p 22212+=+,4221p xx =)(sin )(2212224211||θpAB x x x x k=-+=+当2πθ=时,斜率不存在,1sin =θ,|AB|=2p.即为通径 而如果抛物线的焦点位置发生变化,则以上弦长公式成立吗这只能代表开口向右时的弦长计算公式,其他几种情况不尽相同。
现在我们来探讨这个问题。
(2)已知:抛物线的方程为)0(22>=p py x ,过焦点的弦AB 交抛物线于A,B 两点,直线AB 倾斜角为θ,求弦AB 的长。
解:设A,B 的坐标为),(),,(2211y x y x ,斜率为k )tan (θ=k ,而焦点坐标为)2,0(p ,故AB 的方程为kx py =-2,将其代入抛物线的方程整理得: ,0222=--pxpkx 从而px x x x pk 22121,2-==+,弦长为:)(cos )(2212224211||θpAB x x x x k=-+=+p AB 2||,1cos ,0===θθ,即为通径。
而px y 22-=与(1)的结果一样,py x 22-=与(2)的结果一样,但是(1)与(2)的两种表达式不一样,为了统一这两种不同的表达式,只须作很小的改动即可。
第八章 钢筋混凝土受弯构件变形与裂缝宽度计算汇总

y —裂缝间纵向受拉钢筋应变不均匀系数
f tk y 1.1 0.65 sq te
当y <0.2时,取y =0.2; 当y >1.0时,取y =1.0; 对直接承受重复荷载作
用的构件,取y =1.0。
sq ——按荷载准永久组合计算的钢筋混凝土
构件纵向受拉普通钢筋应力。 对于受弯构件
sq
M M EI M EI EI
截面弯曲刚度EI 就是使截面产生单位曲率所施 加的弯矩值体现了截面抵抗弯曲变形的能力,同时 也反映了截面弯矩与曲率之间的物理关系。 对于弹性均质材料截面,EI为常数,M- 关系 为直线。如下图中的黑线所示。
②钢筋混凝土构件
由于混凝土开裂、弹塑性应力-应变关系和钢筋 屈服等影响,钢筋混凝土适筋梁的M-f 关系不再是直 线,而是随弯矩增大,截面曲率呈曲线变化。如下图 红线所示。
★如果两条裂缝的间距小于2 l,则由于粘结应力传递 长度不够,混凝土拉应力不可能达到ft,因此将不会出 现新的裂缝,裂缝的间距最终将稳定在(l ~ 2 l)之间, 平均间距可取1.5 l。 ★粘接应力传递长度l越短,裂缝分布越密。粘接强度 越高, l越短;钢筋面积相同时小直径钢筋表面积大些, l就短些;低配筋率钢筋, l长些。
8.3.3平均裂缝宽度Wm
c wm s lm clm s (1 )lm s
c (1 ) 0.85 s
s y s y
sk
Es
◆平均裂缝宽度
wm 0.85 y
sk
Es
lm
8.3.4最大裂缝宽度及其验算 实测表明,裂缝宽度具有很大的离散性。取实测 裂缝宽度wt与上述计算的平均裂缝宽度wm的比值 为 s l 。
建筑CAD第八章的计算单选题及答案

建筑CAD第八章的计算单选题及答案(计算单项选择题)注意:选项(abcd)后面数字是一道题对这题的的评分,也就是答案,如果是0,是错误的,.就不要选择。
top/默认广东课程04/第8章、建筑施工图绘制/计算(单选)计算(单选)将长度和角度精度设置为小数点后四位,绘制以下图形,求剖面线区域的面积()。
A. 673522.1316 100B. 673522.1361 0C. 673522.1613 0D. 673522.3161 0计算(单选)将长度和角度精度设置为小数点后四位,绘制以下图形,求剖面线区域的面积()。
A. 105720.0541 100B. 105720.0514 0C. 105720.0415 0D. 105720.0414 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中阴影部分的面积()。
A. 639333.3331 0B. 639333.3332 0C. 639333.3333 100D. 639333.3334 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中蓝色阴影部分的周长()。
A. 12124.8472 100B. 12124.8473 0C. 12124.8474 0D. 12124.8475 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中A.B.C三点所围成的三角形的周长()。
A. 2581.9818 100B. 2581.9819 0C. 2581.9820 0D. 2581.9821 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中房屋整体的周长()。
A. 194.6795 100B. 194.6796 0C. 194.6797 0D. 194.6798 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中红色砖墙的面积()。
A. 301527.4354 0B. 301527.4355 100C. 301527.4356 0D. 301527.4357 0计算(单选)将长度和角度精度设置成小数点后四位,绘制下图,求图中书桌整体面积()。
第八章 轴向拉压杆的强度计算

标准试件:试验段l0称为标距。
试件的尺寸统一的规定:
对于矩形截面试件,记中部原始横截面面积为A0,
短试件: /
=5.65 长试件: /
=11.3
对, 于圆截面试件,设中部直径为d0,则 五倍试件:
十倍试件:
金属材料的压缩试验, 试件一般制成短圆柱体。 为了保证试验过程中试件不 发生失稳,圆柱的高度取为直径的1~3倍。
引入比例系数E,把上式写成
式中E为弹性模量,表示材料抵抗弹性变形的能力,是一个只 与材料有关的物理量,其值可以通过试验测得,量纲与应力量 纲相同。弹性模量E和泊松比ν都是材料的弹性常数。
------轴向拉(压)杆件的变形与EA成反比。
EA称为轴向拉(压)杆的抗拉(压)刚度,表示杆件抵抗 拉伸(压缩)的能力。
材料的力学性质除取决于材料本身的成分和组织结构外, 还与荷载作用状态、温度和加载方式等因素有关。
重点讨论常温、静载条件下金属材料在拉伸或压缩时的力 学性质。
为使不同材料的试验结果能进行对比,对于钢、铁和有色 金属材料,需将试验材料按《金属拉伸试验试样》的规定加工 成标准试件,分为圆截面试件和矩形截面试件。
这种由于杆件形状或截面尺寸突然改变而引起局部区 域的应力急剧增大的现象称为应力集中。
设产生应力集中现象的截面上最大应力为σmax,同一 截面视作均匀分布按净面 积A0计算的名义应力为σ0, 即
则比值
称为应力集中因数,它反映了应力集中的程度,是一个大 于1的因数。
§8–3、轴向拉压杆的变形——胡克定律
§8–1、应力与应变的基本概念
1、应力的概念 应力:指截面上一点处单位面积内的分布内力;
或是指内力在一点处的集度。 平均应力:
M点处的内力集度(总应力):
第八章 屋面及防水工程量计算

按设计图示尺寸以展开 面积计算
按设计图示以长度计算
第 八 章 屋 面 及 防 水 工 程 量
2、屋面防水及其他
变形缝防水做法
第 八 章 屋 面 及 防 水 工 程 量
2、屋面防水及其他
变形缝防水拾接
第 八 章 屋 面 及 防 水 工 程 量
3、墙面防水、防潮
分部 项目 计算规则
1、墙面卷材防水
雨水口
第 八 章 屋 面 及 防 水 工 程 量
第 八 章 屋 面 及 防 水 工 程 量
2、屋面防水及其他
防水卷材
第 八 章 屋 面 及 防 水 工 程 量
2、屋面防水及其他
分部 项目 计算规则
按设计图示尺寸以面积计 算。不扣除房上烟囱、风帽 底座、风道等所占面积 按设计图示尺寸以长度计 算。如设计未标注尺寸,以 檐口至设计室外散水上表面 垂直距离计算
按设计图示尺寸以面 积计算
J.3墙面防水、 防潮
2、墙面涂膜防水 3、墙面砂浆防水(防潮)
4、墙面变形缝
按设计图示以长度计 算
第 八 章 屋 面 及 防 水 工 程 量
4、楼(地)面防水、防潮
分部 项目
1、楼(地)面卷材 防水
计算规则
按设计图示尺寸以面积计算 1.按主墙间净空面积计算,扣 除凸出地面的构筑物、设备基础 等所占面积,不扣除间壁墙及单 2、楼(地)面涂膜 个面积≤0.3m2柱、垛、烟囱和孔 防水 洞所占面积 J.4楼(地)面 防水、防潮 3、楼(地)面砂浆 2.楼(地)面防水反边高度 ≤300mm算作地面防水,反边高度 防水(防潮) >300mm按墙面防水计算 4、楼(地)面变形 按设计图示以长度计算 缝
第 八 章 屋 面 及 防 水 工 程 量
长度计算大班教案

长度计算大班教案一、教学目标1. 知识目标:学生能够正确使用标准度量衡单位对长度进行计算。
2. 能力目标:学生能够灵活运用所学的长度计算方法解决实际生活问题。
3. 情感目标:培养学生的观察力、思考力和团队合作精神。
二、教学重难点1. 教学重点:帮助学生理解并正确使用长度计量单位进行计算。
2. 教学难点:培养学生的应用能力,使其能够运用所学的知识解决实际问题。
三、教学准备1. 教具准备:长度计量工具(尺子、卷尺等)、实物(书本、铅笔等)。
2. 教材准备:相关的课程教材和学案。
四、教学过程步骤一:导入向学生展示一尺子和一张A4纸,提问:“你们知道尺子的长度是多少吗?纸的长度是多少?”引导学生回忆并巩固尺寸和长度的概念。
步骤二:学习1. 学习长度计量单位通过展示和讲解,引导学生认识并记忆长度计量单位的名称和符号。
例如:厘米(cm)、米(m)、千米(km)。
2. 探索长度计量单位的换算关系引导学生进行探究,使用尺子测量教室中各物体的长度,并记录在黑板上。
然后帮助学生发现各物体的长度单位之间的换算关系。
促使他们理解1米(m)= 100厘米(cm),1千米(km)= 1000米(m)。
3. 进行练习组织学生进行练习,包括长度单位间的换算和长度计算的应用题。
步骤三:巩固和拓展1. 游戏:计算比赛将全班分成小组,每组选择一名代表进行长度计算比赛。
根据题目,学生使用所学的长度计算方法进行计算,比赛时间为5分钟。
最后检查答案,确认无误后颁发胜利证书和奖励。
2. 拓展应用引导学生将所学的长度计算方法应用到实际问题中,如测量校园内某条道路的长度或家中某个房间的面积。
五、课堂总结学生通过本节课的学习,掌握了长度计算的方法和技巧,能够准确使用长度计量单位进行计算。
同时,培养了学生的观察力和思考力,提高了他们的团队合作能力。
六、课后作业1. 完成课堂练习题。
2. 自主选择一个实际场景,运用所学的长度计算方法进行测量和计算。
七、教学反思本节课通过导入、学习、巩固和拓展的步骤,有针对性地培养了学生对长度计量单位的理解和计算能力。
第八章 轻型门式刚架钢结构

8.5 门式刚架构件的截面验算
一、截面有效宽度(仅指受压构件) 概念:把在宽度b上分布不均匀的应力图集中到板的 两侧,应力都是fy,即得到有效宽度be=bσcr/fy 影响有效宽度的因素:板件的约束条件、端部作用 应力及其分布。 板件约束的四种类型: ⑴两边支承板件(加劲板件); ⑵一边支承一边卷边(边缘加劲板件) ⑶一边支承、一边自由(未加劲板件) ⑷两边支承且中部有中间加劲肋(中间加劲板件) 各类支承方式板的有效宽度计算(自学)
w 参数 w
hw / t w 37 k 235 / f y
2
当a / hw 1时,k 4 5.34 / a / hw 当a / hw 1时,k 5.34 4 / a / hw 式中
2
a 腹板横向加劲肋的间距,可取a hw 2hw k 腹板在纯剪切荷载作用下的屈曲系数, 当不设中间加劲肋时取为5.34。
荷载效应组合的原则: ⑴屋面均布活荷载不与雪荷载同时考虑,应取两者 中的较大值; ⑵积灰荷载与雪荷载或屋面均布活荷载中的较大值 同时考虑; ⑶施工或检修集中荷载不与屋面材料或檩条自重以 外的其他荷载同时考虑; ⑷多台吊车的组合应符合现行国家荷载规范的规定; ⑸风荷载不与地震作用同时考虑。
二、风荷载
8.2 门式刚架计算简图的确定
门式刚架钢结构的尺寸应符合下列规定 ⑴门式刚架的跨度,应取横向刚架柱轴线间的距离; ⑵门式刚架的高度,应取地坪至柱轴线与斜梁轴线交 点的高度;
⑶柱的轴线可取通过柱下端(小头)中心的竖向直线, 工业建筑边柱的定位轴线宜取外皮,斜梁的轴线可取 通过变截面梁段最小端中心与斜梁上表面平行的轴线。 门式刚架的柱脚多为铰接,通常为平板支座,设一对 或两对地脚螺栓。 当用于工业厂房且有桥式吊车时,宜将柱脚设计为刚 接。 檐口高度,取地坪至房屋外侧檩条上缘的高度; 最大高度,取地坪至屋盖顶部檩条上缘的高度; 房屋的宽度,取房屋侧墙墙梁外皮之间的距离; 房屋的长度,取两端山墙墙梁外皮之间的距离。
建筑给排水-第八章—建筑内部排水管段计算

▪ 在决定室内排水管的管径及坡度之前,首先必须 确定各管段中的排水设计流量。
▪ 以洗涤盆排水量0.33L/s为一个排水当量(1排水当 量=0.33L/s)。将其他卫生器具的排水量与 0.33 L/s的比作为该卫生器具的排水当量 。
▪ 选择排水当量时用下用表8.1。
(二)设计秒流量
概念 排水设计流量应是建筑内部的最大排水瞬时流 量,即设计秒流量,。
(3) 器具通气管
对卫生、安静要求高的建筑物内,生活污水管道宜 设器具通气管。
器具通气管和环形通气管与通气管连接处应高于卫 生器具上边缘0.15m,按不小于0.01的上升坡度与通 气立管连接。
伸顶通气管 与排水立管管径相同或放大一级。
专用通气管、主通气管、器具通气管管径
通气管最小管径
共用通气管管径按下式计算:
(4)最小管径
最小管径 d≥50mm 接大便器 d≥100mm 大便槽排水管 d≥150mm 公共食堂排水支管 d≥75mm, 干管 d≥100mm 多层住宅厨房间的立管d≥75mm 医院污物洗涤盆或污水盆的排水管d≥75mm
2、 横管水力计算方法
qu w v
v
1
2
R3
I
1 2
n
式中:qu——排水设计秒流量,m3/s; w——水流断面积,m2; v——流速,m/s; R——水力半径,m; I——水力坡度,即管道坡度; n——管道粗糙系数。
管径(mm)
75
100
125Leabharlann 2.54.57.0
5.0
9.0 14.0
—
6.0
9.0
1.70 3.80
1.38 2.40
0.92 1.76
0.70 1.36
水力学 第八章课后题答案

8.1 泄水建筑物下游常采用的水面衔接及消能措施有哪几种?它们各自 的水流特征是什么? 答:底流式消能、挑流式消能、面流式消能。 底流式消能:高速流的主流在底部。 挑流式消能:下泄水流余能一部分在空中消散,大部分在水舌落入下游 河道后被消除。 面流式消能:高速流的主流位于表层,避免主流对河床的冲刷,余能通 过水舌扩散,流速分布调整及底部旋滚与主流相互作用而消除。
Frc
q2 ghc3
32.62 9.8 0.993
10.57
Lj 10.8 0.9910.57 1 0.98 87.37
LK 0.7 ~ 0.8 Lj 61.2 ~ 70 m
可取LK 65m
8.7 某电站溢流坝为3孔,每孔宽b为16m;闸墩厚4m; 设计流量Q为6480m3/s;相应的上、下游水位高程
p1 H
7 2.4
2.92
1取H H 0 2.4m E 0 p2 H 0 7 2.4 9.4m
hk
aq 2 3 g
3
1 82 9.8
1.87m
c
E0 hk
9.4 1.87
5.03,
0.95
由公式8.5,试算得:
hc 0.636m hc 4.2m 因hc ht故下游产生远驱式水跃衔接,需要修建消力池。
及河底高程如图所示。今在坝末端设一挑坎,采用 挑流消能。已知:挑坎末端高程为218.5m;挑角θ 为250;反弧半径R为24.5m。试计算挑流射程和冲 刷坑深度,下游河床为Ⅲ类岩基。
解:根据已知数据可得 p1 250.15 180 70.15m H 267.85 250.15 17.7m p1 70.15 3.96 1.33为高坝 H 17.7 ht 210.5 180 30.5m a 218.5 180 38.5m z 267.85 210.5 57.35m S1 267.85 218.5 49.35m p 250.15 218.5 31.65m
《建筑力学》第8章计算题
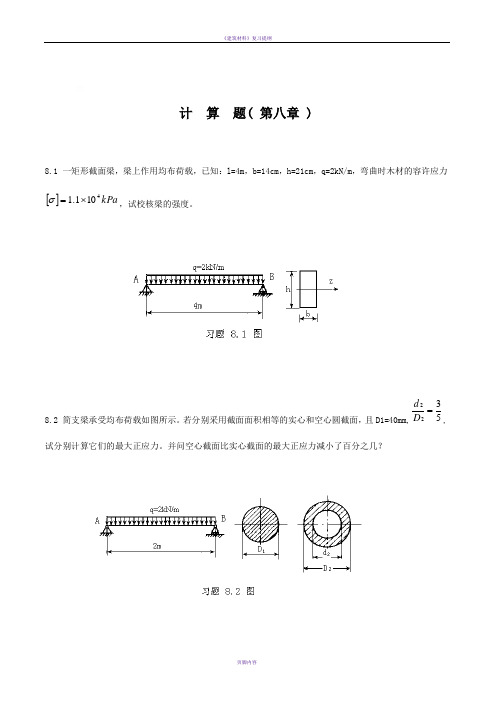
计 算 题( 第八章 )8.1 一矩形截面梁,梁上作用均布荷载,已知:l=4m ,b=14cm ,h=21cm ,q=2kN/m ,弯曲时木材的容许应力[]kPa 4101.1⨯=σ,试校核梁的强度。
8.2 简支梁承受均布荷载如图所示。
若分别采用截面面积相等的实心和空心圆截面,且D1=40mm,5322=D d ,试分别计算它们的最大正应力。
并问空心截面比实心截面的最大正应力减小了百分之几?8.3 图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5kN。
试计算梁内的最大弯曲正应力,及该应力所在截面上K点处的弯曲正应力。
8.4 图示梁,由No-22槽钢制成,弯矩M=80N·m,并位于纵向对称面(即x-y平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
提示:有关槽钢的几何性质可从附录中查得。
8.5 图示变截面梁,自由端承受荷载F作用,梁的尺寸l,b与h均为已知。
试计算梁内的最大弯曲正应力。
8.6 图示截面梁,横截面上剪力FQ=300kN,试计算:(a)图中截面上的最大剪应力和A点的剪应力;(b)图中腹板上的最大剪应力,以及腹板与翼缘交界处的剪应力。
8.7 图示矩形截面木梁,许用应力[σ]=10Mpa。
(1)试根据强度要求确定截面尺寸b。
(2)若在截面A处钻一直径为d=60mm的圆孔(不考虑应力集中),试问是否安全。
8.8 一对称T形截面的外伸梁,梁上作用均布荷载,梁的截面如图所示。
已知:mkNqml/8,5.1==,求梁截面中的的最大拉应力和最大压应力。
8.9 欲从直径为d的圆木中截取一矩形截面梁,试从强度角度求出矩形截面最合理的高h和宽b。
8.10 图示外伸梁,承受荷载F作用。
已知荷载F=20kN,许用应力[σ]=160Mpa,许用剪应力[τ]=90Mpa。
请选择工字钢型号。
8.11一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力的4倍,即[σc]=4[σt]。
第八章(焊缝、螺栓连接)--钢结构习题参考解答

8.4 有一工字形钢梁,采用I50a (Q235钢),承受荷载如图8-83所示。
F=125kN ,因长度不够而用对接坡口焊缝连接。
焊条采用E43型,手工焊,焊缝质量属Ⅱ级,对接焊缝抗拉强度设计值2205/w t f N mm =,抗剪强度设计值2120/w v f N mm =。
验算此焊缝受力时是否安全。
图8-83 习题8.4解:依题意知焊缝截面特性:A=119.25cm 2,Wx =1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ,截面宽度b=158mm ,翼缘厚t=20mm ,腹板厚tw=12.0mm 。
假定忽略腹板与翼缘的圆角,计算得到翼缘与腹板交点处的面积矩S 1=20×158×(250-10)=7.584×105mm 3。
对接焊缝受力:125V F kN ==;2250M F kN m =⨯=⋅ 焊缝应力验算:最大正应力:622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力:33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力:22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。
8.5 图8-84所示的牛腿用角焊缝与柱连接。
钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2f 160/w f N mm =。
T=350kN ,验算焊缝的受力。
图8-84 习题8.5 图8-84-1 焊缝截面计算简图解:(注:焊缝上下翼缘长度114mm 有些问题,应取2130210110l tmm -=-⨯=,黄钜枝06年6月19日)如图8-84-1,截面特性计算如下:2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力:247.52N kN ==;247.52V kN ==; 49.5M V e kN m =⋅=⋅ 应力验算:危险点为a 、b 两点,下面分别验算: 对a 点: 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点:32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。
工程量计算规则1(08清单规范)

A.1土石方工程量计算规则
解:基础土方回填:按清单规范计算规则为 (清单)挖方体积减去设计室外地坪以下埋 没的基础体积(包括基础垫层及其他构筑物)
已知清单开挖土方量为30M3,基础垫层体积为5M3, 室外地坪以下砖基础体积为10M3, 清单量计算如下:V基础回填=30-5-10=15M3
清单量计算如下:
V挖=1×0.75 ×(26.4+3.8)=22.65M3 09定额挖基础土方要考虑工作面及放坡增加的土方量。
计算如下
L外= (3.9+4.5+4.8) ×2=26.4M
L内=4.8- 1.6=3.2M
沟槽宽:1.6M 沟槽深:1.2-0.45=0.75M
V挖=1.6 ×0.75 ×(26.4+3.2)=35.52M3 注开挖深度<1.5m,因此不考虑放坡。
如需按天然密实体积折算时:
A.1土石方工程量计算规则
挖基础土方(010101003)
挖基础土方包括:
➢ 带形基础、独立基础、满堂基础(包括地下室基础) 及设备基础、人工挖孔桩等的挖方。带形基础应按不 同底宽和深度,独立基础和满堂基础应按不同底面积 和深度分别编码列项。 计算规则:
➢ 按设计图示尺寸以基础垫层底面积乘以挖土深 度计算。基础土方、石方开挖深度应按基础垫层底 表面标高至交付施工场地标高确定,无交付施工场 地标高时,应按自然地面标高确定。
室内回填:指室外 地坪和室内地坪之 间的回填
基础回填:指设计室 外地坪以下的回填
A.1土石方工程量计算规则
定额计算规则土方回填图解:
室内回填:指室外 地坪和室内地坪之 间的回填
基础回填:指设计室 外地坪以下的回填
《建筑力学》第8章计算题

《建筑力学》第8章计算题计 算 题( 第八章 )8.1 一矩形截面梁,梁上作用均布荷载,已知:l=4m ,b=14cm ,h=21cm ,q=2kN/m ,弯曲时木材的容许应力[]kPa 4101.1⨯=σ,试校核梁的强度。
8.2 简支梁承受均布荷载如图所示。
若分别采用截面面积相等的实心和空心圆截面,且D1=40mm,5322=D d ,试分别计算它们的最大正应力。
并问空心截面比实心截面的最大正应力减小了百分之几?8.3 图示悬臂梁,横截面为矩形,承受载荷F1与F2作用,且F1=2F2=5kN。
试计算梁内的最大弯曲正应力,及该应力所在截面上K点处的弯曲正应力。
8.4 图示梁,由No-22槽钢制成,弯矩M=80N·m,并位于纵向对称面(即x-y平面)内。
试求梁内的最大弯曲拉应力与最大弯曲压应力。
提示:有关槽钢的几何性质可从附录中查得。
8.5 图示变截面梁,自由端承受荷载F作用,梁的尺寸l,b与h均为已知。
试计算梁内的最大弯曲正应力。
8.6 图示截面梁,横截面上剪力FQ=300kN,试计算:(a)图中截面上的最大剪应力和A点的剪应力;(b)图中腹板上的最大剪应力,以及腹板与翼缘交界处的剪应力。
8.7 图示矩形截面木梁,许用应力[σ]=10Mpa。
(1)试根据强度要求确定截面尺寸b。
(2)若在截面A处钻一直径为d=60mm的圆孔(不考虑应力集中),试问是否安全。
8.8 一对称T形截面的外伸梁,梁上作用均布荷载,梁的截面如图所示。
已知:m,=,求梁截面中的5.1=8l/qkNm的最大拉应力和最大压应力。
8.9 欲从直径为d的圆木中截取一矩形截面梁,试从强度角度求出矩形截面最合理的高h和宽b。
8.10 图示外伸梁,承受荷载F作用。
已知荷载F=20kN,许用应力[σ]=160Mpa,许用剪应力[τ]=90Mpa。
请选择工字钢型号。
8.11一铸铁梁,其截面如图所示,已知许用压应力为许用拉应力的4倍,即[σc]=4[σt]。
第八章计算长度

(7)山形门架柱:
特征:轴向力大; 重力荷载导致柱顶点向 外侧移。 a.拉平法: 倾角小于10° 好 倾角大于20° 差
b.Fraser模型: μ=2+0.45GR (铰接) μ=1+AGR3/2 (嵌固) 斜梁刚度小时误差大。
GR=IclR/IRh
得:
b.摇摆柱的处理:系数1.2→1.0;非摇摆柱不变。
ui PEi P P Sh i
(6)半刚性连接框架柱:
M M Rki 1 Mu
n 1 n
三参数: Rki——原点切线 Mu——连接的极限弯矩 n——曲线的形状参数 Rks--S点割线 Rkd--d点卸载→RKN Rkt--d点切线刚度
2
c.尺解法 梁远端连接的修正: 远端固支时:γ=2/3
远端铰支时:γ=0.5
d.近似计算
1.6 4 K1 K 2 7.5K1 K 2 u K1 K 2 7.5K1 K 2
(4)其它影响因素: a.梁的约束下降:弯矩→屈曲前变形 压力→梁刚度下降 分析表明: 单层框架对称失稳时,梁上分布荷载影响大。 单层框架反对称失稳时,梁上分布荷载影响小。 原因: 失稳模式和屈曲前变 形比较接近; 横梁轴向力的不利影 响在对称失稳时比反 对称更为不利。
应用计算长度解决框架稳定问题,需修正梁的刚度值→
修正的惯性矩
侧移未受阻时: 侧移受阻时:
1 I I 3 dM F 2 1 RkN dM N 1 I 3I 3 dM F 2 1 RkN dM N
第八章 疲劳裂纹扩展寿命计算

m m
当a + RY 1 < ap 当a + RY 1 ≥ ap
由于C p 恒大于零,因此无法反映高载后可能发生的裂纹停滞现象。
Willenborg/Chang模型
2
1 K OL = απ σ ys
2
1 2 ∆ a K = K − Φ K 1 − − K max max OL max,eff Z OL 1 2 ∆ a = K min − Φ K OL 1 − K min, − K max eff Z OL
N
1
f ( ∆K )dN
8.3 不考虑载荷顺序效应时的疲劳裂纹扩展寿命计算
= C (1 − R ) da / dN
= q (m − 1)n
m −1
∆X ⋅ Y ( a )
n
∫
ac
a0
Y
−n
= ∫ ( a ) da 0
Nc
C (1 − R ) ∆X n dN
q
对于由 p 级应力构成的谱块重复作用而构成的块谱而言,若载荷循环数由 0 → N c 对应的谱块(基本周期)数为
q
∑ C (1 − Ri ) ∆X in
Ni 为在第 i 级载荷恒幅作用下裂纹尺寸从 a0 扩展到 ac 所经历的裂纹扩展循环数。
1 λc = p ni ∑ i =1 N i
8.4 高载迟滞模型
高载迟滞现象
延迟迟滞现象
Wheeler模型
da da = Cp dN 迟恒 dN
《长度和时间的测量》教案

《长度和时间的测量》教案第一章:长度测量1.1 目标:让学生了解并掌握长度测量的基本工具和方法。
1.2 内容:1.2.1 长度测量工具:尺子、卷尺、测量带等。
1.2.2 测量方法:直接测量、累加测量、换算测量等。
1.3 教学活动:1.3.1 讲解长度测量工具的使用方法及注意事项。
1.3.2 演示长度测量的实际操作。
1.3.3 学生分组进行长度测量练习,教师巡回指导。
1.4 作业:1.4.1 学生独立完成长度测量练习题。
第二章:时间测量2.1 目标:让学生了解并掌握时间测量的基本工具和方法。
2.2 内容:2.2.1 时间测量工具:秒表、计时器、钟表等。
2.2.2 测量方法:直接测量、累积测量等。
2.3 教学活动:2.3.1 讲解时间测量工具的使用方法及注意事项。
2.3.2 演示时间测量的实际操作。
2.3.3 学生分组进行时间测量练习,教师巡回指导。
2.4 作业:第三章:长度和时间的关系3.1 目标:让学生了解长度和时间的关系,并能够运用其解决实际问题。
3.2 内容:3.2.1 长度和时间的关系:速度、频率等。
3.2.2 实际问题:长度和时间的关系在生活中的应用,如行程、周期等。
3.3 教学活动:3.3.1 讲解长度和时间的关系及其应用。
3.3.2 学生进行长度和时间关系的实际测量,如测量物体运动速度等。
3.3.3 分析测量结果,解决实际问题。
3.4 作业:3.4.1 学生独立完成长度和时间关系练习题。
第四章:长度和时间测量在实际中的应用4.1 目标:让学生了解长度和时间测量在实际中的应用,提高其测量技能。
4.2 内容:4.2.1 实际应用:工程测量、地理测量、生产测量等。
4.2.2 测量技能:精确测量、快速测量等。
4.3 教学活动:4.3.1 讲解长度和时间测量在实际中的应用。
4.3.2 学生进行实际测量操作,如测量教室长度、宽度等。
4.3.3 分析测量结果,提高测量技能。
4.4 作业:第五章:长度和时间测量实验5.1 目标:让学生通过实验,巩固长度和时间测量的知识和技能。
同济大学第八章(焊缝、螺栓连接)--钢结构习题参考解答

8.4 有一工字形钢梁,采用I50a (Q235钢),承受荷载如图8-83所示。
F=125kN ,因长度不够而用对接坡口焊缝连接。
焊条采用E43型,手工焊,焊缝质量属Ⅱ级,对接焊缝抗拉强度设计值2205/w t f N mm =,抗剪强度设计值2120/w v f N mm =。
验算此焊缝受力时是否安全。
图8-83 习题8.4解:依题意知焊缝截面特性:A=119.25cm 2,Wx =1858.9cm 3,Ix=46472cm 4,Sx=1084.1cm 3,截面高度h=50cm ,截面宽度b=158mm ,翼缘厚t=20mm ,腹板厚tw=12.0mm 。
假定忽略腹板与翼缘的圆角,计算得到翼缘与腹板交点处的面积矩S 1=20×158×(250-10)=7.584×105mm 3。
对接焊缝受力:125V F kN ==;2250M F kN m =⨯=⋅ 焊缝应力验算:最大正应力:622325010134.5/205/1858.910w t x M N mm f N mm W σ⨯===<=⨯ 最大剪应力:33224125101084.11024.3/120/464721012w x v x w VS N mm f N mm I t τ⨯⨯⨯===<=⨯⨯ 折算应力:22127.2/205/w zs t N mm f N mm σ=<= 故焊缝满足要求。
8.5 图8-84所示的牛腿用角焊缝与柱连接。
钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2f 160/w f N mm =。
T=350kN ,验算焊缝的受力。
图8-84 习题8.5 图8-84-1 焊缝截面计算简图解:(注:焊缝上下翼缘长度114mm 有些问题,应取2130210110l t mm -=-⨯=,黄钜枝06年6月19日)此注错误,应取消。
罗烈08年10月28日如图8-84-1,截面特性计算如下:2(11425242882)0.75667.2f A h mm =⨯+⨯+⨯⨯= 228820.73225.6w f A h mm =⨯⨯=32741288288[2882114(16)252()4]0.77.913101222f f I h mm =⨯⨯+⨯+⨯+⨯⨯⨯=⨯焊缝受力:247.5N kN =;247.5V kN =; 49.5M V e kN m =⋅=⋅ 应力验算:危险点为a 、b 两点,下面分别验算: 对a 点: 32247.51043.67/5667.2N aN N mm A σ⨯===62749.510160100.09/7.91310M a af My N mm I σ⨯⨯===⨯ 2243.67100.09143.76/195.2/N Mw a a f f N mm f N mm σσβ+=+=<=对b 点:32247.51076.73/3225.6V bw V N mm A τ⨯=== 243.67/N Nb a N mm σσ==62749.51014490.16/7.91310M b bf My N mm I σ⨯⨯===⨯22133.87/160/w f N mm f N mm =<=故焊缝强度满足要求。
计算方法课件第八章常微分方程初值问题的数值解法

整体截断误差与局部截断误差的关系
定理:如果f(x,y)满足李普希兹(Lipschitz)条件
f(x ,y 1 )f(x ,y 2) L y 1y 2
且局部截断误差有界:
|R n|1 2h2M 2
(n1,2, )
则Euler法的整体截断误差n满足估计式:
ne(ba)L 0h 2L M 2(e(ba)L1)
分光滑。初值问题的解析解(理论解)用 y(x表n ) 示, 数值解法的精确解用 y表n 示。
常微分方程数值解法一般分为:
(1)一步法:在计算y n 1 时,只用到x n 1 ,x n和 y,n 即前一步的值。
(2)多步法:计算 y n 1 时,除用到 x n 1 ,x n 和 y n 以外,还要用 x n p 和 y n p (p1 ,2 k;k0) ,即前
其中L为李普希兹常数,b-a为求解区间长度,
M2 mayx(x) 。 axb
证明参见教材。
Remark:该定理表明,整体截断误差比局部截 断误差低一阶。对其它方法,也有类似的结论。
收敛性与稳定性
收敛性定义:如果某一数值方法对于任意固定的
xn=x0+nh,当h0(同时n )时有yn y(xn),
则称该方法收敛。 稳定性定义 定义 用一个数值方法,求解微分方程初值问 题时,对给定的步长h>0,若在计算 y n 时引入 误差 (n 也称扰动),但由此引起计算后面的 ynk(k1,2, )时的误差按绝对值均不增加,则 称这个数值方法是稳定的。
一般的显式rk方法可以写成型钢截面只需少量加工即可用作构件省工省时成本低但型钢截面受型钢种类及型钢号限制难于完全与受力所需的面积相对应用料较多其中为常数选取这些常数的原则是要求第一式的右端在处泰勒展开后按h型钢截面只需少量加工即可用作构件省工省时成本低但型钢截面受型钢种类及型钢号限制难于完全与受力所需的面积相对应用料较多上述公式叫做n级的rungekutta方法其局部截断误差为显然euler法是一级一阶rk方法
材料力学(I)第八章-铆钉连接的计算

r1 r6 (40 mm)2 (40 mm)2 56.6 mm 0.0566 m
19
例题 8-10
r2 r5 (0)2 (60 mm)2 60 mm 0.06 m r3 r4 (40 mm)2 (80 mm)2 89.4 mm 0.0894 m
第 8 章 组合变形及连接部分的计算
§8-6 铆钉连接的计算
1
铆钉连接主要有三种方式: 1.搭接(图a),铆钉受单剪; 2.单盖板对接(图b),铆钉受单剪; 3.双盖板对接(图c),铆钉受双剪。
2
铆钉组承受横向荷载
实际铆钉组中位于 两端的铆钉所传递的力 要比中间的铆钉所传递 的力大。
为了简化计算,假设: (1) 如果作用于连接上的力其作用线通过铆钉组 中所有铆钉横截面的形心,而且各铆钉的材料和直径 均相同,则认为每个铆钉传递相等的力。 (2) 不考虑弯曲的影响。 铆钉连接与螺栓连接的计算方法相同。
(2) 其大小与该连线的长度成正比(将连接板视为刚 体),即 '' '' r1 '' '' r2 '' '' rn F1 Fi , F2 Fi ,, Fn Fi ri ri ri
14
于是由静力关系可导得:
M e Fi''ri F1''r1 F2''r2 Fi''ri Fn''rn
12
II. 作用于连接上的力其作用线不通过铆钉组形心 对于受偏心荷载F的铆钉连接(或螺栓连接) (图a),亦即作用于连接上的力其作用线不通过铆 钉组的形心O时,可如图b所示,简化为通过形心O 的力和力偶矩Me=F· e。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
补充:假定各柱
h
N相同,横梁的约束按线刚度分配。
EI
12
b. μ系数求解 临界条件:
G A 4 G B 2 G A 2G B 2 1 cot 2tg 2 10
GA
A I c h A I B lB
GB
B I c h B I B lB
A、B两点柱与梁线刚度和之比,反映梁柱连接的 柔度。
15
非弹性修正:(切线模量理论)
G A
A A E E ItIB clB hE E t
AIc h AIBlB
GB:同上修正 Et fy E E
实际上,修正与否影响不大。
16
(3)有侧移框架μ系数(多层 框架柱)
a 基本假定:同前(转角同 向、相等)
b 临界条件及μ值:
2
GAGB
36
5.5 杆端约束和杆计算长度
1、计算长度概念 2、平面内计算长度
(1)单层框架柱 (2)多层框架柱 (3)有侧移框架μ系数 (4)其它影响因素 (5)有侧移失稳的层模型 (6)半刚性连接框架柱 (7)山形门架柱 (8)弱支撑框架
3、平面外计算长度
1
1、计算长度概念:
(1)源自轴心压杆(借用):轴压杆件的弹性屈曲分析。 物理意义:把不同支撑情况的轴心压杆等效为一定计算长度的两
2
2、平面内计算长度:(各种类型,源于弹性稳定的临界力)
(1)单层框架柱: a.μ值的计算: 基本假定: 材料弹性; 只有竖向节点荷载; 柱同时达到临界状态; 只考虑相连梁的约束;
无侧移时,横梁反向转角同; 有侧移时,两端转角同; 弯扭屈曲被约束。
3
框架失稳:有侧移和无侧移
柱脚刚性嵌固:
6K1tg
ui l 2
PEi ui2
得:
ui
PEi
1.2
P
Pi
Sh
b.摇摆柱的处理:系数1.2→1.0;非摇摆柱不变。
同理: 代入(1)式:
u3e
h1 h3
P1Ic3 P3 Ic1
u1e
uI1h c1 12uI2h c2 22uI3h c3 32u1 Ieh c1 12P P 1
(P=∑Pi)
令
P
Ic1 u1h1
2uI2hc2 2
2
Ic3 u3h3
2
10
则:
u ie
1 hi
I ci P PP i
Ic Ic P P
两个参数 ρ α
e
7
c.多跨时的情况:
采用式(8.33)、(8.34)或图8.21求得。中柱
K1
(Ib / l) Ic / h
如考虑梁柱之间的相互支援,最不利柱计算长度减小
荷载作用于柱顶,忽略弯矩的影响 8
不考虑相互支援:
P1
2EI
u 1 h1
c1 2
P2
当h1=h2=h3时u:ie
IciP PPi
Ici Pi
Pi
Ici ui2
注:公式的缺陷:未考虑弯曲的P-δ效应相同。 故:对弱柱承受较大荷载时误差大(I2/I1≤4时,误差不大) 设计时应适当放大弱柱截面,减小其它柱截面。
11
(2)多层框架柱:(无侧移)
a.基本假定:同单层框架柱
0
柱脚铰支:
tg 6K1 0
K1
Ibh I cl
表征梁的约束大小
4
b.影响因素: 图中影响μ唯一因
素:柱端约束条件 柱脚(固、铰):下
端转动约束 柱顶(有无侧移):
上端侧向约束 K1值(梁约束):
柱端转动约束
K1
Ibh I cl
5
其它需考虑的因素:
荷载条件影响:
左柱临界荷载提高
6
框架柱刚度影响
2EI
u 2h2
c2 2
考虑相互支援:(实际情况)
P3
2EI
u 3h3
c3 2
P1e
2 E I c1
u1e h1 2
P2e
2EI c2 h3 2
依据总荷载不变原则:( P-△效应不变;弯曲的P-δ效应不
一定不变)
P 1 P 2 P 3 P 1 eP 2 eP 3 e
21
(5)有侧移失稳的层模型:(可解决非刚性梁柱连接情 况)
a.方法:一阶分析→乘以侧移放大系数→二阶内力 (位移)(整体分析得到)
m
1
11.2P Sh
S-侧移刚度
失稳条件:m→∞,即分母=0得:
Pcr
Sh 1.2
22
Picr
Pcr
Pi Pi Sh P P1.2
令
Picr
2EI
原因: 失稳模式和屈曲前变 形比较接近; 横梁轴向力的不利影 响在对称失稳时比反 对称更为不利。
19
b.水平荷载效应: 一阶弹性分析
结论:水平荷载对框架柱计算长度影响不大
20
二阶分析 H作用产生侧移△→附加弯矩 M=P1△ +P2△→框架内力
增大。 P△—荷载的不稳定效应,简称P·△效应。 H在梁中产生轴力,梁约束下降。
即: u I 1 h c 1 12 u I 2 h c 2 22 u I 3 h c 3 32u 1 I e h c 1 12 u 2 I e h c 2 22 u 3 I e h c 3 32 (1)
9
2
∵
P P 1 2 eeIIc c1 2 u u2 1e eh h1 2 u2eh h1 2 P P 12 IIcc 21u1e
6GAGB
cot 0
17
c.尺解法
梁远端连接的修正: 远端固支时:γ=2/3 远端铰支时:γ=0.5
d.近似计算
u 1.64K1K27.5K1K2
K1K27.5K1K2
18
(4)其它影响因素: a.梁的约束下降:弯矩→屈曲前变形 压力→梁刚度下降 分析表明: 单层框架对称失稳时,梁上分布荷载影响大。 单层框架反对称失稳时,梁上分布荷载影响小。
端铰接压杆(有相同临界力) 几何意义:构件弯曲屈曲两反弯点之间的距离。
(2)框架柱稳定计算方法: 方法1:一阶分析求内力→柱当作单独压弯构件计算稳定(考虑杆
件约束→计算长度) 方法2:考虑变形影响的二阶分析。 方法3:考虑P-△(轴力附加弯矩)近似求解内力。 2、3采用几何长度
(3)类型: 平面内计算长度→约束有关;平面外计算长度→支撑有关。
13
尺解法:
14
梁远端连接的修正: 远端固支时:分母→∑(γiIBi/lBi)(γi=2) 远端铰支时:分母→∑(γvIBi/lBi)(γi=1.5)
GA
A I c h A I B lB
GB
B I c h B I B lB
约束刚度:K1=1/GA k2=1/GB
简化公式:
u33 12 .4K K 11 K K 22 10 .2 .6 84 K K 1K 1K 22
