关于分数应用题作线段图分析
分数应用题解题技巧4则

分数应用题解题技巧4则分数应用题是数学中的一大类题目,涉及的概念和计算方法较为抽象,对于很多学生来说是一个难题。
但只要我们掌握了一些基本的解题技巧,这类题目便会迎刃而解。
下面,就为大家介绍四种实用的分数应用题解题技巧。
技巧一:明确题目中的分数表示的是什么很多学生在解分数应用题时,首先就被分数给弄糊涂了。
实际上,我们需要明白,分数只是一个表示比例或者部分的形式。
因此,首要任务就是明确题目中的分数到底表示的是什么。
例如,它可能表示一个整体中的部分,也可能是两个量之间的比例关系。
只有明确了分数的具体意义,我们才能进行下一步的计算。
技巧二:合理转化分数形式在明确了分数的具体意义后,下一步就是进行合理的分数形式转化。
有些分数应用题中,给出的分数形式可能并不适合直接计算,这时就需要我们将其转化为更容易计算的形式。
例如,可以将带分数转化为假分数,或者将复杂的分数化简为更简单的形式。
这样,计算过程就会变得更加简便。
技巧三:利用线段图进行分析对于一些较为复杂的分数应用题,我们可以尝试利用线段图进行分析。
线段图可以直观地表示出各个量之间的关系,使我们更容易理解题目的意思。
通过线段图,我们可以清晰地看出各个部分之间的关系,进而找出解决问题的方法。
技巧四:注意检验答案的合理性在解完分数应用题后,很多学生都忽视了检验答案这一重要步骤。
实际上,检验答案的合理性是非常必要的。
我们可以通过逆运算或者代入原题等方法,检验我们的答案是否正确。
如果答案不合理,那么我们就需要重新审视自己的解题过程,找出错误所在。
以上就是四种实用的分数应用题解题技巧。
当然,要想真正掌握这些技巧,还需要大量的练习和思考。
只有通过不断的实践,我们才能更加熟练地运用这些技巧,解决各种复杂的分数应用题。
希望这些技巧能对大家有所帮助,祝大家在数学学习中取得更大的进步!。
数学课件《画线段图解分数应用题》

课本P18 第5题
单位“1”
杨树: 柳树: 槐树:
杨树的 9
10
柳树的 2
3
画线段图解应用题时,要注意:
1、画两条线段图时,要上下并列画。 2、两条线段图各端点要对齐。 3、线段要按要求平均分。 4、各线段的名称要写清楚。 5、已知条件和问题要显示完整、清楚。 6、量与率的数据,方向相反。 7、要用直尺画大括号。 8、增加的部分画实线,减少的部分画虚线。 9、合理安排书写空间,排版要整洁美观。
画线段图解应用题
1、鸡的孵化期是21天,鸭的孵化期比鸡长 1 ,鸭的孵化 3
期是多少天?
答:鸭的孵化期是28天。
鸡: 鸭:
单位“1”
21天
长
1 3
?天
2、小军的飞机模型在空中飞行了6分钟,小峰的飞机模型 飞行时间比小军的短 1 ,小峰的飞机模型飞行了几分钟?
3
答:小峰的飞机模型飞行了4分钟。
小军: 小峰:
kg放入第二袋,那么两袋面粉同样重,两袋面粉一共重多 少千克?
答:两袋面粉一共重28.5千克。
第一袋: 第二袋:
15kg
3
取出 4 kg
?kg
3
放入 4 kg
课本P16 第7题
430千米/时
磁悬浮列车:
?千米/时
普通列车:
慢 36
43
课本P17 第3题
广州:
北京:
单位“1”
1608小时
1
多2
?小时
2012: 2015:
单位“1”
2000人
1
减Байду номын сангаас 5
?人
5、有两筐苹果,第一筐重30kg,如果从第一筐中取出 1 2
分数应用题线段图画法

“分数应用题线段图画法”之我见
我们知道线段图能帮助学生直观形象地理解题意,分析数量关系;也等于给学生搭建了一个解决实际问题的平台。
分数应用题是小学高年级教学的一个重点也是一个难点。
如果教会学生迅速正确地画出分数应用题的线段图,那么这道题学生就已经会了百分之五十。
怎样使学生尽快掌握线段图的画法呢?本人积三十年教高年级之经验,总结出了行之有效的方法,不妨称为“中点法”。
不管是传统的教材还是新课改后的课本,分数应用题都是先学了分数乘法应用题后再学分数除法应用题。
这两种类型应用题的数量关系可以分成三种:(一)一种量是另一种量的几分之几。
(二)一种量比另一种量多几分之几。
(三)一种量比另一种量少几分之几。
在审题确定单位“1”的量后,首先用线段表示出这个单位“1”的量,分率的分母是几就把单位“1”的量平均分成几份。
怎样才能分的正确呢?当然可以用直尺画,学生要首先计算把单位“1”的量平均分成几份,然后再画,耗时费力,教学实践证实这样太慢。
怎样才能画得又快又对呢?我们知道初学分数应用题时,题中的分率的分母一般都是除0和1以外的不超过10的自然数,如果分率的分母是2就在所画单位“1”的那条线段的中点估计着点个点,这就把单位“1”的量。
画线段图解答分数应用题

用画线段图的方法理解题意,再解答。
1、一种电脑,现价比原价降低了152,正好降低了800元,这种电脑原价多少元?2、某养兔专业户,养的白兔比黑兔多120只,黑兔的只数是白兔的32,这个专业户养白兔多少只?3、甲仓库存粮60吨,乙仓库比甲仓库少52,两个仓库共存粮多少吨?4、普通客车和快车每小时共行132千米,普通客车的速度相当于快车的65,普通客车和快车每小时各行多少千米?5、三个工人一天共做螺钉148个,其中甲做的个数是乙的32,丙做的个数是乙车的54,甲、乙、丙三人各做了多少个螺钉?6、刘师傅第一天做零件80个,第二天比第一天多做了10个,两天共完成了总任务的65,这批零件共有多少个?7、刘星做一批小红花,当做完这批花的83时,再做10朵就完成了一半,刘星应做多少朵?8、张师傅加工一批零件,已经加工了5天,每天加工这批零件的252,已完成了260个,还要加工多少个?9、某车间加工一批零件,已经做好530个,比计划的73多80个,计划加工多少个?10、某商店第一天卖出所有油的51,第二天卖出40千克,第三天卖出所有油的41,三天共卖出124.6千克,这个商店共有油多少千克?11、修一条公路,第一天修了全长的83,第二天修了全长的103,两天修的比全长的一半还多2.8千米,这条公路全长多少千米?某班有学生55人,调出女生人数的61后,这时男女生人数相等,这个班原来有男女生各多少名?初夏早上六点,清亮透明的月儿还躲藏在云朵里,不忍离去,校园内行人稀少,我骑着单车,晃晃悠悠的耷拉着星松的睡眼。
校园内景色如常,照样是绿意盈盈,枝繁叶茂,鸟儿歌唱。
经过西区公园,看那碧绿的草地,飞翔中的亭子,便想起十七那年,在这里寻找春天的日子。
本想就此停车再感受一遍,可惜心中记挂北区的荷塘。
回想起冬日清理完荷塘的枯枝败叶,一片萧条的景色:湖水变成墨绿色,没有鱼儿游动,四处不见了鸟儿的踪影,只有莲藕躺在湖底沉沉睡去。
清洁大叔撑着竹竿,乘一叶扁舟,把一片片黑色腐烂的枯叶残枝挑上船。
利用线段图巧学分数应用题

利用线段图巧学分数应用题作者:陈万福来源:《新课程·上旬》2014年第02期分数应用题是小学阶段教学的一个重、难点,学生理解困难,思路不清晰,大部分学生看见分数应用题就感觉无从入手,从而害怕学习数学,这非常不利于以后数学知识的学习。
在解答分数应用题时,学生的困难往往并不在于如何运算,而是在于如何分析题意,弄清题目的数量关系,列出正确、合理的算式。
那么,我们有什么好的办法让学生能更好地学习分数应用题,激发学生学习数学的兴趣和信心呢?在教学中我用画线段图的方法进行分数应用题的分析和教学,让学生理解和分析题意,学生能够根据线段图直观地解答分数应用题,减轻了学生的学习负担,降低了学习的难度,能更好地激发学生学习数学的信心和兴趣。
那么,利用线段图进行分数应用题的教学该怎样进行呢?一、正确判断单位“1”在分数应用题中,如何判断单位“1”(也就是标准量)是解答分数应用题的首要任务,单位“1”可以看作标准量。
单位“1”不仅可以表示一个计量单位,而且可以表示一个整体。
有很多学生在学习分数应用题时对单位“1”的判断喜欢用找关键词的方法,比如,“是”“像”“比”“相当于”……的方法去判断单位“1”的量,这有其局限性。
要找到单位“1”的量,应从分率入手,抓住一点“谁的几分之几,谁就是单位“1”的量,分析清楚“谁是谁的几分之几”。
分数除法应用题的特点是:单位“1”的量是多少是未知的,就是要求单位“1”。
解题的关键是找出单位“1”的“几分之几正好是多少”这一对应关系,并用已知量除以已知量的对应分率等于单位“1”的量即标准量。
也就是:几分之几相对应的量÷几分之几=单位“1”的量。
根据线段图找准了“量”“率”的对应关系,我们便能轻松地解答分数应用题了。
三、复杂分数应用题中线段图的应用当简单的分数应用题中,根据线段图找准了“量”“率”的对应关系后,在复杂的分数应用题中首先判断单位“1”的量是已知的还是未知的,如果单位“1”的量是未知的,我们要根据“量”“率”的对应关系,首先求出单位“1”的量,再来分析所求的问题,便能轻松地解答分数应用题了。
小六培优专题20-分数应用题(图示法)

图示法解分数应用题一、夯实基础图示法就是用线段图(或其它图形)把题目中的已知条件和问题表示出来,这样可以把抽象的数量关系具体化,往往可以从图中找到解题的突破口。
运用图示法教学应用题,是培养思维能力的有效方法之一。
图示法不仅可以形象地、直观地反映分数应用题中的“对应量和对应分率”间的关系,启发学生的解题思路,帮助学生找到解题的途径,而且通过画图的训练,可以调动学生思维的积极性,提高学生分析问题和解决问题的能力。
二、典型例题例1.一条鱼重的53加上43千克就是这条鱼的重量,这条鱼重多少千克? 分析与解:从题意可以知道,这条鱼的重量是单位“1”,用线段图帮助我们分析数量关系从图上可以看出43千克对应的分率是(1-53)。
鱼的重量:43÷(1-53) = 187(千克)。
答:这条鱼重187千克。
例2.一桶油第一次用去51,第二次比第一次多用去20千克,还剩下22千克。
原来这桶油有多少千克?分析与解:从图中可以清楚地看出:这桶油的千克数×(1-51-51)=20+22 则这桶油的千克数为:(20+22)÷(1-51-51)=70(千克)。
答:原来这桶油有70千克。
例3.缝纫机厂女职工占全厂职工人数的207,比男职工少144人,缝纫机厂共有职工多少人?分析与解:解题的关键是找到与具体数量144人的相对应的分率。
从线段图上可以清楚地看出女职工占207,男职工占1-207=2013,女职工比男职工少占全厂职工人数的2013-207=103,也就是144人与全厂人数的103相对应。
全厂的人数为:144÷(1-207-207)=480(人)答:缝纫机厂共有职工480人。
小升初培优冲刺(图示法解分数应用题)一、熟能生巧1.张亮从甲城到乙城,第一天行了全程的40%,第二天行了全程的920,距乙城还有18千米,甲、乙两城相距多少千米?2.李玲看一本书,第一天看了全书的16,第二天看了18页,这时正好看了全书的一半。
用画线段图解决分数问题

己知一个数比另一个数多(少)几分之几,求另一个数比一个数少(多)几分之几的问题-----运用线段图解决复杂的分数问题教学设计教学内容:己知一个数比另一个数多(少)几分之几,求另一个数比一个数少(多)几分之几的问题教学目标:1.知识与技能:学生自主探究解决“己知一个数比另一个数多(少)几分之几,求另一个数比一个数少(多)几分之几”的应用题;进一步培养学生画线段图的能力,从而提高学生解答这类应用题的熟练程度。
加深对两种应用题的认识,同时培养学生比较、归纳的能力。
2.情感态度与价值观:通过应用所学知识解决生活中的实际问题,对学生进行学习目的性教育,激发学生学习动机和兴趣。
教学重点:通过画线段图分析,正确熟练的解决实际问题。
教学难点:通过画线段图分析,正确熟练的解决实际问题。
教法与学法:自主探究、讨论交流教学准备及手段:课件教学流程:一、复习旧知1.找出单位“1”和比较量并说说两者之间数量关系式。
(1)桃树棵树是杏树棵树的 3/5 ,桃树棵树比杏树少()【单位“1”是(),比较量是()。
数量关系式()】(2)甲数比乙数少 1/3 ,甲数是乙数的()【单位“1”是(),比较量是()。
数量关系式:()】(3)把( )看做单位“1”,用去的占总数的( ),还剩总数的( ),还剩多少千克,列式是( )。
师:请同学们观察后,自己独立思考。
汇报时,让你找到单位“1”的量和比较量,根据关键句能说出基本的数量关系。
2、你还会画线段图解决下面问题吗?(1)小汽车有400辆,大客车比小汽车多 1/4 ,大客车有多少辆?(2)、院子里有鸡40只,鸭比鸡少 1/8 ,鸭有多少只?(3)、为迎接运动会,同学们做了25面黄旗,30面红旗,做的红旗比黄旗多多少面,多几分之几?(4)、一件衣服现在360元,比原价便宜了60元,便宜了几分之几?师:下面我们先来解决问题(1)小汽车有400辆,大客车比小汽车多 1/4,大客车有多少辆?师:第一步,请同学们先找出关键句,确定出单位“1”是谁?生:关键句是大客车比小汽车多 1/4 ,小汽车有400辆是单位“1”的量。
用画线段图的办法巧解分数应用题

2014-01课堂内外分数应用题的教学是小学数学教学中的一个难点。
学生对稍有难度的应用题就找不准对应率,对难度较大的应用题则更无从下手。
但借助线段图学生就能容易理解有关数量与单位“1”的对应关系,故在教学中,应重视画线段图教学。
下面就我解分数应用题的一些探索介绍如下:一、画线段图,找准量率对应关系,提高解题速度例:某工厂10月份用水480吨,比原计划节约了19,10月份原计划用水多少吨?分析:“10月份用水比原计划节约了19”,可以把原计划用水吨数看作单位“1”,先画表示“原计划用水”的线段,才能画出比它少19的“实际用水”的线段。
?吨480吨1-19比原计划节约19原计划用水:实际用水:从图上可以明显看出,480吨相当于原计划用水的(1-19),求原计划用水吨数,列式为:480÷(1-19)由上题可以看出,借助线段图能巧妙地寻找分数应用题中的对应关系,使解题的症结化解,对分析应用题的重点、难点起到了“提领而顿,百毛皆顺”的作用。
在教学中除了引导学生画线段图,从图中找量率列算式外,还必须通过练习,引导学生比较分析分率的加、减与题目的叙述的关系,使学生悟出:提高、增长、重、多、超、盈利、上升、收入等含有“多”的意思,一般“1+?”;节约、减少、下降、轻、短、支出、降低、亏损等含有“少”的意思,一般都用“1-?”找分率的规律,进而提高学生解题列式的速度。
另外还要注意,有些题目的具体数量,用线段表示不容易确定线段的长短的比例,我们就要采用先画分率,再画具体数量的方法来画线段。
如:张静打一份稿件,第一天打了50页,第二天打了40页,还剩58没有打,这份稿件共有多少页?画线段图时50页和40页,不容易画准它们的长度,就要先画还剩的58,再在其余的(1-58)里面画50页和40页就方便多了。
11-58(50+40)页还剩58共有?页二、画线段图,优化解题思路,简化解题步骤,提高解题效率例:某工程队修一条高速公路,前5个月修了20千米,正好修了全长的14,照这样计算,剩下的公路还需几个月?(请用最简单的方法解答)按一般分析计算,往往先求出每月修的距离,然后再用剩下的距离除以每月修的距离,这样分析复杂而且容易出错。
用线段图解答分数应用题

第二次
12千克 还剩下28千克
(28-12)÷(1- 40% - 40%)=
80(千克)
答:这桶油原有80千克。
练习设计:
1 1、李玉看一本书,第一天看了 5 ,第二天
1 5
1 5
比第一天多看7页,这时还有56页没有看,这 本书有多少页?
还剩56页 7页
第二天看的
1 2、一根电线,第一次用去全长的 ,第二次 1 1 5 (56+7)÷ ( =105 (页) 比第一次多用 4.51米,还剩下 10.5 米,问:第一 5 - 5 )
例题1: 1 有一条绳子,第一次剪去全长的 3 ,第 二次剪去3米,这时正好剩下一半,这条绳子 原来是多少米?
1 2 1 剪去全长 3
3米
?米
3÷(
1 2
-
1Байду номын сангаас3
)= 18(米)
例题2: 有一桶汽油,第一次取出40%,第二次取出 的比第一次少12千克,桶里还剩下28千克,这 桶油原有多少千克?
?千克 第一次40%
次用去了多少米?
3 3、食堂有若干袋面粉,用去 5 后,又运进了25
袋,这时的面粉正好是原来袋数的一半,食堂 原有面粉多少袋? 3
用去 5 25袋 是原来的一半( 1 ) 2 1 2
4、有一堆煤运走54吨以后,余下的重量比原 有重量的75%少6吨,这堆煤原有多少吨?
运走54吨
余下的重量 6吨 原来的75%
线段图法解决分数乘法应用题

线段图法解决分数乘法应用题知识回顾解决分数乘法应用题的线段图法一、简便计算复。
38×101=二、根据图中的阴影部分求面积40×38×+(4+)×4×7xxxxxxxx977-55()×()=()()×()=()新课达标一、分数的意义:将一个整体(单位“1”)平均分成若干份,表示其中1份或几份的数。
找出单位“1”,用波浪线划出,并完成数量关系式。
1.鸡的只数是鸭的7/8()×7/8=(49/64)2.已看全书的1/6()×(6/6)=(1/6)3.一件上衣降价2/7()×(5/5)=(10/35)4.男生比女生多1/5()×(6/6-1/5)=(1/6)5.乙数是甲数的1/3()×(3/3-1/3)=(2/3)6.大鸡只数的4/5相当于小鸡的只数。
(5/5-4/5)×(1/1)=(1/5)7.读了一本书的2/7()×(7/7)=(2/7)8.三好学生占全校人数的1/10()×(10/10)=(1/10)9.完成了计划工作量的3/4()×(4/4)=(3/4)10.小军的体重是爸爸体重的3/8.(3/8)×(8/8)=(3/8)11.苹果树的棵数占果树总棵数的2/5()×(5/5-2/5)=(3/5)12.汽车速度相当于飞机速度的1/5()×(5/5-1/5)=(4/5)13.已经修了一条路的1/4()×(4/4)=(1/4)14.黑兔是白兔的3/7(3/7)×(7/7)=(3/7)15.黑兔的3/4相当于白兔(3/4)×(4/4)=(3/4)16.甲数的5/6是乙数(5/6)×(6/6-5/6)=(1/6)17.甲数是乙数的3/4(3/4)×(4/4-3/4)=(1/4)18.苹果树占果园面积的2/5(2/5)×(5/5)=(2/5)19.钢笔的价钱等于书的7/8(7/8)×(8/8)=(7/8)20.甲仓货物的重量相当于乙仓货物的8/9(8/9)×(9/9)=(8/9)21.鹅只数的11/16是鸭的只数(11/16)×(16/16-11/16)=(5/16)22.今年油菜产量比去年增产1/8(1/8)×(8/8+1/8)=(9/64)23.现在每件产品的成本比原来降低了1/9(1/9)×(8/8-1/9)=(7/72)二、线段图像解析75次青少年:婴儿:80分贝次现在?分贝比青少年多三、画线XXX1、画出苹果树棵数的线段图,表示数量关系。
(完整版)看线段图写算式百分数分数应用题六年级数学
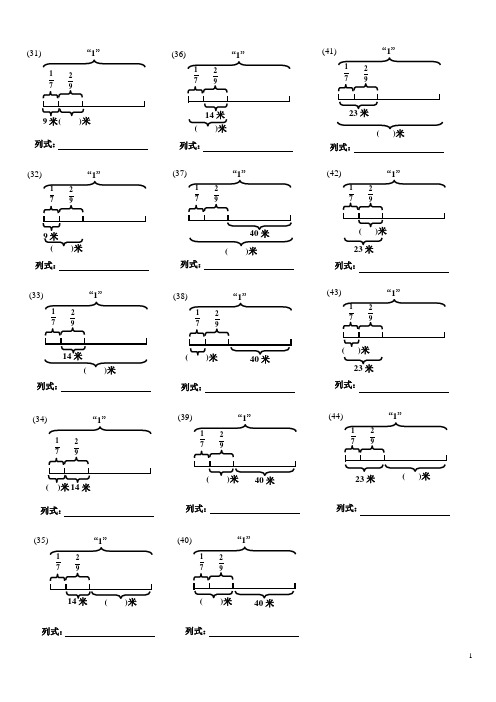
(31)“1”列式: 9米 9271( )米 (32)“1”列式: 9米9271( )米 (34)“1”列式: ( )米 927114米 (33)“1” 列式:( )米927114米(35)“1”列式:( )米 927114米 (36)“1”列式:14米 9271( )米 (37)“1”列式:40米 9271( )米(38)“1”列式: ( )米 927140米(39)“1”列式:( )米 927140米(40)“1”列式:( )米 927140米列式:(41)“1”23米9271( )米列式: (42)“1”23米 9271( )米 列式:(43)“1”23米 9271( )米列式:(44)“1”23米 9271( )米(16) “1”( )吨列式:多25%吨(17)“1”125吨列式:多25% ( )吨(18)吨列式:多25% ( )吨“1”(19) “1”360米列式:少( )米92(20) “1”米列式:少( )米92(23) “1”80米列式:少( )米92(21) “1”360米列式:( )米少92(22) “1”()米列式:少80米92(24) “1”80米列式:( )米少92(20) “1”( )米列式:少280米92(26) “1”()米列式:少280米92(27) “1”280米列式:( )米少92(28) “1”(63)米列式:( )米9271(29) “1”(63)米列式:( )米9271(30) “1”列式:9米9271( )米(1) 52“1”( )米50米列式:(2)52“1”( )米 50列式:(3)52“1”20米( )米列式:(4)52“1”20米 ( )米 列式:(5)52“1”30米( )米列式:(7)53“1”( )米50列式:(6)52“1”30( )米列式:(8)53“1”20米( )米列式:(9)53“1”20米( )米列式:(10)“1”100吨列式:多25%( )吨(11)“1”100吨 列式: 多25%( )吨(12)100吨列式:多25% ( )吨(13)“1”( )吨列式:多25%25吨(14)“1”( )吨列式:多25%25吨(15)25吨列式:多25% ( )吨“1”练 习 题姓名:。
“画线段图”是帮助解答分数应用题

1 3
X
2 3
X
看图写代数式:
1 4
X
5 4
X
看图编题,列方程:
某工厂五月份计划生产一批零件,上半月完成了计划7/12, 下半月比上半月多完成了50个,结果实际比计划多生产 了450个。该工厂五月份的计划生实际
()/()
7/12
多50个
上半月
• 先比较,再解答: • 图书馆有故事书200本,科
技书比故事书的1/4多30本, 科技书多少本?
• 图书馆有故事书200本,故 事书比科技书的1/4多30本, 科技书多少本?
• 小明读一本故事书,上星期已经读了 全书页数的1/4。这个星期又读了30页, 这样已经读的页数是全书的1/3。这本 故事书一共有多少页?
• 小明读一本故事书,上星期已经读的 和没读的比是1:3。这个星期又读了 30页,这样已经读的和没读的比是
1:2。这本故事书一共有多少页?
四、线段图
例1,光明小学六年级毕业生比全校总人数的
还多3O人。新学期一年级新生人学36O人,这样现 在比原全校总人数增加了 。求原来全校学生有多 少人?
看图写代数式:
分数应用题线段图歌
先画单位1,再画对比量。 具体数量标下面,对应分率标上面, 已知写数据,未知写问号,上下对应分辨清!
单位1已知:就用单位1乘以对应的分率,得 到对应的数量; 单位1未知:具体的数量除以对应的分率,得 到单位1。
画段图来分析: 单位“1”
2500m2
已修?m2
还剩下?m2
2
3
5
5
“画线段图”是帮助解答 分数应用题
解题时,根据题的内容画 图,把题的条件、问题在图 上标明,这样有助于我们正 确审题,理解题意,从而正 确解题,提高我们分析和解 决问题的能力。
分数除法应用题的线段图解浅议

分数除法应用题的线段图解浅议
分数除法应用题的线段图解浅议
一、什么是分数除法
所谓的分数除法,就是指把除数和被除数都是分数的情况下的除法。
这个运算是比较复杂的,不像普通的整数除法可以直接用四则运算的
方法进行计算,而是要经历简化步骤和转分母步骤,再进行相应的运
算才能得出结果。
二、分数除法应用题的线段图
分数除法应用题应用线段图是一种简单而有效的方式,通过线段图,
我们可以很直观地把一道分数除法题拆解成两部分,一部分是被除数,另外一部分是除数。
另外,我们可以把每个分数都用一条线段来表示,这样看起来就像是一个真正的线段图。
线段图的关键就是要以最直观的形式来比较被除数和除数的大小,进
而把分数除法题解决掉。
它可以帮助大家快速得出分数除法应用题的
答案,而且还是非常容易的,以上就是关于分数除法应用题的线段图
解浅议。
三、如何应用线段图
首先,我们可以用一条线段来表示被除数,另一条线段来表示除数,
然后比较两条线段的长短。
如果除数比被除数要短,那么答案为商数;如果被除数比除数要短,那么答案为尽数。
最后,我们可以把这个答
案抄写下来作为正确答案。
分数除法应用题的线段图是一种简单而有效的方式,通过这种方式,
我们可以很直观地把一道分数除法题拆解成两部分,从而判断答案为
商数还是尽数,而应用这一方法,则是在最根基上对数字概念进行概
念理解,而不光是死记硬背,以上就是关于分数除法应用题的线段图
解浅议。
分数应用题及线段图的画法

分数应用题及线段图的画法分数应用是数学中重要的一部分,应用于日常生活中。
掌握和掌握正确的使用方法,可以帮助我们准确解决问题,提高我们的学习能力。
线段图是用来表示分数应用的一种图形方法,可以清楚地展示分数的构成关系和相互之间的关系。
本文的主要内容是针对分数的应用题和线段图的画法,将从四个方面进行详细的阐述:(1)基本概念;(2)日常用途;(3)绘制线段图的具体方法;(4)认识线段图的一些特点。
一、基本概念1.什么是分数?分数是一种表示某个细分部分与整体之间关系的数字。
它由一个数字加上分子和分母构成,其中,分子表示细分部分,分母表示整体。
2.什么是线段图?线段图是一种用来表示数据变化关系的图形表示方法。
它由一条水平线段和竖直线段组成,两条线段的交点称为图形的原点。
图形上坐标轴的刻度可以让人直观地看到变化趋势,有助于我们理解统计数据。
二、日常用途分数在日常生活中有着多样的用途,下面列出一些常见的例子: 1.量化描述食物份量:例如,甜点的一份份量可以以1/4(分子表示份量,分母表示整体)的分数表示。
2.量化描述购物支出:例如,买一个新手机需要花费1/3的收入(分子表示花费的金额,分母表示总收入)。
3.表示一天24小时:例如,15个小时可以用15/24的分数表示。
三、绘制线段图的具体方法1.找出要绘制线段图的数据。
2.确定数据的范围,划分横轴和纵轴,并标注横轴和纵轴的坐标轴上刻度值。
3.在横坐标和纵坐标轴上,根据数据的变化情况依次画出线段图上的点,并将点之间连接起来。
4.根据线段图的变化趋势,推断出相关的变化关系,提取出趋势线。
四、认识线段图的一些特点绘制线段图可以让我们直观地观察分数的应用及其变化趋势,从而更好地理解其中的数据和含义。
此外,线段图还具有以下一些特点: 1.线段图可以明确表示出分数的关系,例如1/4=4/16,线段图可以清晰地表示出这种关系。
2.线段图可以表现出随着时间的变化,分数的数量变化趋势,为我们更好地理解数据提供了便利。
怎样利用线段图解决分数应用题?

怎样利⽤线段图解决分数应⽤题?图⽰法是应⽤题常⽤的解题⽅法,合理,巧妙,科学地运⽤各种点,线,图,表来把数量表⽰出来,让抽象的问题形象化,便于我们去观察分析数量之间关系,找到突破⼝,是⼀种有效的解题思考⼯具。
不⼀定是线段图。
我是王⽼师,专注于⼩学数学,很⾼兴为您答疑解惑!分享解题策略,推⼴趣味数学,提供家庭辅导建议,欢迎您的关注。
任何⼀种思考⼯具,都需要经常使⽤,最好系统化,从低年级就要开始导⼊。
实际情况是画⽰意图并没有形成教学体系化,很多学⽣⽆法根据题⽬特点画出恰当的⽰意图。
以下详解,供家长粉丝们参考!⽅块图图⽰建模解题策略王⽼师数学教学主要特⾊是图⽰建模,⽽且具有系统化。
⽅块图⽐线段图更有优势,应⽤更⼴泛,表达的内容更多,也更加整洁。
以下是王⽼师⽅块图体系化教学⽰例。
必须从导⼊到数学教学的⽅⽅⾯⾯,适⽤性越强,使⽤越⼴泛,学⽣使⽤的机会才更多,也更容易掌握。
①数学概念加法和乘法的基础含义,分数、百分数概念理解,⽅块图⽰如下:除数是整数的分数除法,图⽰建模。
②整数应⽤题在王⽼师趣味数学专栏系列中,从⼆年级的两步应⽤题开始就导⼊了⽅块图图⽰建模⽅法教学,并延申⾄倍数关系应⽤题,年龄问题,移多补少问题等等分类应⽤题题型。
③分数应⽤题分数应⽤题是研究数量之间份数关系的典型应⽤题,⼀⽅⾯它是在整数应⽤题上的延续和深化,另⼀⽅⾯,它有其⾃⾝的特点和解题规律。
在解这类问题时,分析中数量之间的关系,准确找出“量”与“率”之间的对应是解题的关键。
图⽰不但适合低年级学⽣,⾼年级复杂分数应⽤题依然需要画图来辅助思考。
以下举例,选⾃我的⼩升初真题巧解专栏。
还有其他如⾏程问题。
可以将⽅块图变为路线图。
结语。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于分数应用题作线段图分析
要注意的几个问题
分数应用题是小学应用题中的重点也是难点,学生在分析应用题的时候往往是由于找不准单位“1”或者无法找到正确的数量关系而束手无策或者错误,正确的线段图能直观的反应出单位“1”和应用题中的数量关系,是解决分数应用题的有效的方法之一,教会学生正确作线段图是我们教学中的很重要的环节,如果学生掌握了有效的作线段图的方法,对正确解决有关分数应用题是十分有帮助的。
那么,如何使学生掌握作线段图的技巧和方法呢,根据我的教学经验,我认为,首先,必须让学生理解分数在应用题中的“意义”。
比如“①一袋大米,吃了4/5,还剩15千克,这袋大米有多少千克?”这里的“4/5”是表示什么意思呢?必须让学生明白:4/5表示把一袋大米平均分成5份,吃了其中的4份。
再比如“②柳树棵数的14/15是杨树,杨树有28棵,柳树有多少棵?”这里的“14/15”表示把柳树的棵数平均分成15份,杨树的棵数占其中的14份。
学生弄清楚分数在应用题中的“意义”了,才能正确地理解下面的作图过程。
下面,重点来说说如何作线段的问题。
作线段要分三步走:
第一步:要弄清作一条线段还是作一条以上的线段的问题。
原来我没仔细研究过这个问题,结果往往作出的线段图不是很科学,学生听了也似懂非懂,有时连我自己也是一头雾水。
后来,我细心琢磨发现,解决这个问题也没那么复杂,其实,只要弄清楚量之间是什么关系即可,这里的“关系”是指:他们是“整体与部分”的关系还是“比较”关系,如果是“整体与部分”的关系,作一条线段即可,在一条线段上分析;如果是“比较”关系,则需要作两条或两条以上的线段。
比如上面的应用题①,属于“整体与部分”的关系,作一条线段即可,在一条线段里表示出“吃了的”、“剩下的”和“一袋大米”的关系;而应用题②则反映的是“杨树棵数”和“柳树棵数”的关系,是一种“比较”关系,则需要作两条线段,一条线段表示柳树的棵数,另一条线段表示杨树的棵数。
需要注意的是,作两条以上的线段,它们的起点要在同一垂线上,即,起点一样。
第二步:线段作多长的问题。
线段要作多长,这跟线段的要分“份数”有关系。
大家知道,“份数”和应用题中分数的分母有关系。
我是这样要求学生的:当“份数”小于或者等于10时,即分母小于或等于10时,每一份的长度为1厘米;如果“份数”在10~20之间,每一份的长度取0.5厘米;如果“份数”在20以上,每一份的长度取0.1厘米,这时提示学生不必把每一份都标出来,以免耽误时间。
以应用题①为例,“一袋大米的重量”画一条长5厘米的线段、平均分成5份即可,而应用题②中柳树的棵数作7.5厘米、平均分成15份即可。
第三步:线段标注的问题。
这是作线段图的重点和难点。
如果标注错误,那么整个分析也就是错误的。
所以正确的标注十分重要。
一条线段,有三种标注:“1”或分数、线段名称及具体数量。
标注“1”或分数:“1”或分数一定要标注在线段相应的上方。
“1”标注在第一条线段上,同时确定第一条线段的名称。
只要弄清楚表示把“谁”平均分成若干份,“谁”就是第一条线段;然后把“分数”标注在线段“1”内或者标注在另一条线段上,表示:是“谁”的几分之几,或者表示:比“谁”多(少)几分之几;
线段的名称标注要分如下情况进行标注:一、如果线段反映的是整体和部分的关系的,即在一条线段分析的,线段名称应该标注在线段的上,以便反映出线段整体与部分间的关系;二、线段反映的是比较关系的,即需要作两条或两条以上的线段进行比较分析的,线段名称一般写在线段的前方,并且用冒号分开;联系两条关系的那部分线段,
则其名称应标注在该线段的上;
具体数量则应标注在线段相应的下方。
作好线段图,并正确标注好。
以刚才的两道题为例,图如下:
第①题图:
第②题图:
接下来就是引导学生观察分析线段图、找数量关系的问题了。
如果学生能正确作出线段图,通过线段图找数量关系是比较容易的,但分析数量关系也有讲究,这个环节把握不好也会出问题。
比如第①题,学生得到如下数量关系:
“一袋大米= 吃了+还剩
4/5 15”
如是,学生得到下面的结果:
“4/5+15=15.8(千克)
答:这袋大米有15.8千克。
”
问题出在哪呢?其实,数量关系没问题,但数据标注错了。
那么,正确的数量关系和数据分析应该是怎样的呢?我是这样做的:
设一袋大米重X千克,则吃了的重量为千克。
于是,上面的关系式写成如下形式:
然后根据数量关系
解:设一袋大米重X千克。
得方程:
解方程即可。
也可以列算式求解,具体如下:
求单位“1”的数量,列式为:
第②题的数量关系及数据分析如下:
求解过程在此就不细述了。
总之,关于分数应用题作线段图分析,让学生学会作图,需要注意如下几点:
第一、理解分数在应用题中的“意义”;
第二、掌握如何作线段图及线段图的标注问题;
第三、根据线段图找出数量关系并能正确分析数量关系;
第四、能根据数量关系解决问题。
以上就是我对分数应用题作线段图分析的一点个人心得,如有不妥之处,欢迎指正。
