含绝对值的不等式知识点
初一数学知识点精讲精练——绝对值不等式

(3)解不等式|x﹣3|>5.
(4)直接写出不等式|x﹣1|+|x+2|<5 的解集:
.
【练习解析】
1. 解:由绝对值的性质得:
7 x 5
7
x
5
,
解得:2≤x≤12. 故绝对值不等式|7﹣x|≤5 的解集为:2≤x≤12.
2. 解:由于零点是 1 和 2,故将数轴分成三段来讨论. ⑴ 当 x≤1 时,原不等式可化为-(x-1)-(x-2)>x+3,即 x<0.故不等式的解集是 x<0. ⑵ 当 1<x≤2 时,原不等式可化为(x-1)-(x-2)>x+3,即 x<-2.故不等式的解集是无解. ⑶ 当 x>2 时,原不等式可化为(x-1)+(x-2)>x+3,即 x>6.故不等式的解集是 x>6. 综上可知,原不等式的解集是 x<0 或 x>6. 3. 解:(1)|x+5|+|2x﹣3|=
③|x﹣3|+|x+2|=8, 当 x<﹣2 时, 3﹣x﹣x﹣2=8, 解得,x=﹣3.5; 当 x=﹣2 时, |﹣2﹣2|+|﹣2+2|=4≠8, ∴x=﹣2 不能使得|x﹣3|+|x+2|=8 成立; 当﹣2<x≤3 时, 3﹣x+x+2=5≠8, 在﹣2<x≤3 时,不能使得|x﹣3|+|x+2|=8 成立; 当 x>3 时, x﹣3+x+2=8, 解得,x=4.5,; 故|x﹣3|+|x+2|=8 的解是 x=﹣3.5 或 x=4.5.
方法一是利用绝对值的几何意义: | x | 表示 x 到原点的距离;
| x | a(a 0) 的解为 x a
含绝对值的不等式知识点

含绝对值的不等式1.绝对值的意义是:⎩⎨⎧<-≥=)0x (x )0x (x x .2.|x |<a (a >0)的解集是{x |-a <x <a }. |x |>a (a >0)的解集是{x |x <-a 或x >a }.【思考导学】1.|ax +b |<b (b >0)转化成-b <ax +b <b 的根据是什么?答:含绝对值的不等式|ax +b |<b 转化-b <ax +b <b 的根据是由绝对值的意义确定.2.解含有绝对值符号的不等式的基本思想是什么?答:解含有绝对值符号的不等式的基本思想是去掉绝对值符号,使不等式变为不含绝对值符号的一般不等式,而后,其解法就与解一般不等式或不等式组相同.【典例剖析】[例1]解不等式2<|2x -5|≤7.解法一:原不等式等价于⎩⎨⎧≤->-7|52|2|52|x x∴⎩⎨⎧≤-≤--<--7|5272522|52x x x 或即⎪⎩⎪⎨⎧≤≤-<>612327x x x 或∴原不等式的解集为{x |-1≤x <23或27<x ≤6}解法二:原不等式的解集是下面两个不等式组解集的并集(Ⅰ)⎩⎨⎧≤-<≥-7522052x x(Ⅱ)⎩⎨⎧≤-<<-7252052x x不等式组(Ⅰ)的解集为{x |27<x ≤6} 不等式组(Ⅱ)的解集是{x |-1≤x <23}∴原不等式的解集是{x |-1≤x <23或27<x ≤6}解法三:原不等式的解集是下面两个不等式解集的并集.(Ⅰ)2<2x -5≤7 (Ⅱ)2<5-2x ≤7不等式(Ⅰ)的解集为{x |27<x ≤6} 不等式(Ⅱ)的解集是{x |-1≤x <23}∴原不等式的解集是{x |-1≤x <23或27<x ≤6}.点评:含绝对值的双向不等式的解法,关键是去绝对值号.其方法一是转化为单向不等式组如解法一,再就是利用绝对值的定义如解法二、解法三. [例2]解关于x 的不等式:(1)|2x +3|-1<a (a ∈R ); (2)|2x +1|>x +1.解:(1)原不等式可化为|2x +3|<a +1 当a +1>0,即a >-1时,由原不等式得-(a +1)<2x +3<a +1-24+a <x <22-a 当a +1≤0,即a ≤-1时,原不等式的解集为∅,综上,当a >-1时,原不等式的解集是{x |-24+a <x <22-a } 当a ≤-1时,原不等式的解集是∅. (2)原不等式可化为下面两个不等式组来解(Ⅰ)⎩⎨⎧+>+≥+112012x x x 或(Ⅱ)⎩⎨⎧+>+-<+1)12(012x x x不等式组(Ⅰ)的解为x >0 不等式组(Ⅱ)的解为x <-32 ∴原不等式的解集为{x |x <-32或x >0} 点评:由于无论x 取何值,关于x 的代数式的绝对值均大于或等于0,即不可能小于0,故|f (x )|<a (a ≤0)的解集为∅.解不等式分情况讨论时,一定要注意是对参数分类还是对变量分类,对参数分类的解集一般不合并,如(1)对变量分类,解集必须合并如(2). 例3]解不等式|x -|2x +1||>1.解:∵由|x -|2x +1||>1等价于(x -|2x +1|)>1或x -|2x +1|<-1(1)由x -|2x +1|>1得|2x +1|<x -1∴⎩⎨⎧-<+-<+⎩⎨⎧-<+≥+1)12(012112012x x x x x x 或即⎪⎩⎪⎨⎧>-<⎪⎩⎪⎨⎧-<≥021221x x x x 或均无解 (2)由x -|2x +1|<-1得|2x +1|>x +1∴⎩⎨⎧+>+≥+112012x x x 或⎩⎨⎧+>+-<+1)12(012x x x 即⎪⎪⎩⎪⎪⎨⎧-<-<⎪⎩⎪⎨⎧>-≥3221021x x x x 或,∴x >0或x <-32 综上讨论,原不等式的解集为{x |x <-32或x >0}.点评:这是含多重绝对值符号的不等式,可以从“外”向“里”,反复应用解答绝对值基本不等式类型的方法,去掉绝对值的符号,逐次化解. 【随堂训练】1.不等式|8-3x |>0的解集是( )A .∅B .RC .{x |x ≠38,x ∈R } D .{38} 答案: C2.下列不等式中,解集为R 的是( )A .|x +2|>1B .|x +2|+1>1C .(x -78)2>- 1D .(x +78)2-1>0 答案: C3.在数轴上与原点距离不大于2的点的坐标的集合是( )A .{x |-2<x <2}B .{x |0<x ≤2}C .{x |-2≤x ≤2}D .{x |x ≥2或x ≤-2} 解析: 所求点的集合即不等式|x |≤2的解集.答案: C4.不等式|1-2x |<3的解集是( )A .{x |x <1}B .{x |-1<x <2}C .{x |x >2}D .{x |x <-1或x >2}解析: 由|1-2x |<3得-3<2x -1<3,∴-1<x <2答案: B5.不等式|x +4|>9的解集是__________.解析: 由原不等式得x +4>9或x +4<-9,∴x >5或x <-13答案: {x |x >5或x <-13}6.当a >0时,关于x 的不等式|b -ax |<a 的解集是________.解析: 由原不等式得|ax -b |<a ,∴-a <ax -b <a∴a b -1<x <ab+1 ∴{x |a b -1<x <ab+1}答案: {x |a b -1<x <ab+1}【强化训练】1.不等式|x +a |<1的解集是( )A .{x |-1+a <x <1+aB .{x |-1-a <x <1-a }C .{x |-1-|a |<x <1-|a |}D .{x |x <-1-|a |或x >1-|a |} 解析: 由|x +a |<1得-1<x +a <1 ∴-1-a <x <1-a 答案: B2.不等式1≤|x -3|≤6的解集是( )A .{x |-3≤x ≤2或4≤x ≤9}B .{x |-3≤x ≤9}C .{x |-1≤x ≤2}D .{x |4≤x ≤9}解析: 不等式等价于⎩⎨⎧≤-≤≥-63103x x 或⎩⎨⎧≤-≤<-63103x x 解得:4≤x ≤9或-3≤x ≤2. 答案: A3.下列不等式中,解集为{x |x <1或x >3}的不等式是( )A .|x -2|>5B .|2x -4|>3C .1-|2x -1|≤21D .1-|2x -1|<21解析: A 中,由|x -2|>5得x -2>5或x-2<-5∴x >7或x <-3同理,B 的解集为{x |x >27或x <-1} C 的解集为{x |x ≤1或x ≥3} D 的解集为{x |x <1或x >3}答案: D4.已知集合A ={x ||x -1|<2},B ={x ||x -1|>1},则A ∩B 等于( )A .{x |-1<x <3}B .{x |x <0或x >3}C .{x |-1<x <0}D .{x |-1<x <0或2<x <3}解析: |x -1|<2的解为-1<x <3,|x -1|>1的解为x <0或x >2.∴A ∩B ={x |-1<x <0或2<x <3}. 答案: D5.已知不等式|x -2|<a (a >0)的解集是{x |-1<x <b },则a +2b = .解析: 不等式|x -2|<a 的解集为{x |2-a <x <2+a }由题意知:{x |2-a <x <2+a }={x |-1<x <b }∴⎩⎨⎧==⇒⎩⎨⎧=+-=-53212c a c a a ∴a +2b =3+2×5=13 答案: 136.不等式|x +2|>x +2的解集是______.解析: ∵当x +2≥0时,|x +2|=x +2,x +2>x +2无解.当x +2<0时,|x +2|=-(x +2)>0>x +2 ∴当x <-2时,|x +2|>x +2 答案: {x |x <-2} 7.解下列不等式:(1)|2-3x |≤2;(2)|3x -2|>2. 解:(1)由原不等式得-2≤2-3x ≤2,各加上-2得-4≤-3x ≤0,各除以-3得34≥x ≥0,解集为{x |0≤x ≤34}. (2)由原不等式得3x -2<-2或3x -2>2,解得x <0或x >34,故解集为{x |x <0或x >34}. 8.解下列不等式:(1)3≤|x -2|<9;(2)|3x -4|>1+2x .解:(1)原不等式等价于不等式组由①得x ≤-1或x ≥5; 由②得-7<x <11,把①、②的解表示在数轴上(如图),∴原不等式的解集为{x |-7<x ≤-1或5≤x <11}.(2)原不等式等价于下面两个不等式组,即原不等式的解集是下面两个不等式组解集的并集:①⎩⎨⎧+>-≥-;2143,043x x x ②⎩⎨⎧+>--<-.21)43(,043x x x由不等式组①解得x >5;由不等式组②解得x <53. ∴原不等式的解集为{x |x <53或x >5}. 9.设A ={x ||2x -1|≤3},B ={x ||x +2|<1},求集合M ,使其同时满足下列三个条件:(1)M ⊆[(A ∪B )∩Z ]; (2)M 中有三个元素; (3)M ∩B ≠∅解:∵A ={x ||2x -1|≤3}={x |-1≤x ≤2}B ={x ||x +2|<1}={x |-3<x <-1} ∴M ⊆[(A ∪B )∩Z ]={x |-1≤x ≤2}∪{x |-3<x <-1}∩Z ={x |-3<x ≤2}∩Z={-2,-1,0,1,2}又∵M ∩B ≠∅,∴-2∈M . 又∵M 中有三个元素∴同时满足三个条件的M 为: {-2,-1,0},{-2,-1,1},{-2,-1,2},{-2,0,1},{-2,0,2},{-2,1,2}.【学后反思】解绝对值不等式,关键在于“转化”.根据绝对值的意义,把绝对值不等式转化为一次不等式(组).|x |<a 与|x |>a (a >0)型的不等式的解法及利用数轴表示其解集.不等式|x |<a (a >0)的解集是{x |-a <x <a }.其解集在数轴上表示为(见图1—7):不等式|x |>a (a >0)的解集是{x |x >a 或x <-a },其解集在数轴上表示为(见图1—8):把不等式|x |<a 与|x |>a (a >0)中的x 替换成ax +b ,就可以得到|ax +b |<b 与|ax +b |>b (b >0)型的不等式的解法.。
高考知识点绝对值不等式
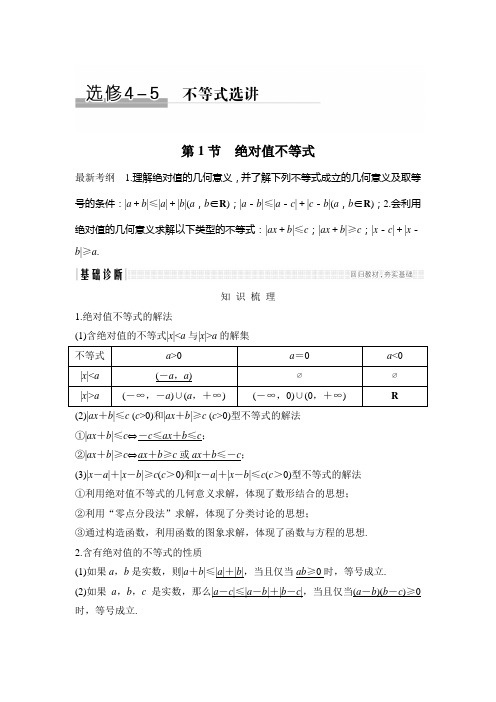
第1节绝对值不等式最新考纲 1.理解绝对值的几何意义,并了解下列不等式成立的几何意义及取等号的条件:|a+b|≤|a|+|b|(a,b∈R);|a-b|≤|a-c|+|c-b|(a,b∈R);2.会利用绝对值的几何意义求解以下类型的不等式:|ax+b|≤c;|ax+b|≥c;|x-c|+|x-b|≥a.知识梳理1.绝对值不等式的解法(1)含绝对值的不等式|x|<a与|x|>a的解集不等式a>0a=0a<0|x|<a (-a,a)∅∅|x|>a (-∞,-a)∪(a,+∞)(-∞,0)∪(0,+∞)R(2)|ax+b|≤c (c>0)和|ax+b|≥c (c>0)型不等式的解法①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c;(3)|x-a|+|x-b|≥c(c>0)和|x-a|+|x-b|≤c(c>0)型不等式的解法①利用绝对值不等式的几何意义求解,体现了数形结合的思想;②利用“零点分段法”求解,体现了分类讨论的思想;③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.2.含有绝对值的不等式的性质(1)如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.(2)如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.诊断自测1.思考辨析(在括号内打“√”或“×”)(1)若|x|>c的解集为R,则c≤0.()(2)不等式|x-1|+|x+2|<2的解集为∅.()(3)对|a+b|≥|a|-|b|当且仅当a>b>0时等号成立.()(4)对|a|-|b|≤|a-b|当且仅当|a|≥|b|时等号成立.()(5)对|a-b|≤|a|+|b|当且仅当ab≤0时等号成立.()答案(1)×(2)√(3)×(4)×(5)√2.不等式|x-1|-|x-5|<2的解集是()A.(-∞,4)B.(-∞,1)C.(1,4)D.(1,5)解析①当x≤1时,原不等式可化为1-x-(5-x)<2,∴-4<2,不等式恒成立,∴x≤1.②当1<x<5时,原不等式可化为x-1-(5-x)<2,∴x<4,∴1<x<4,③当x≥5时,原不等式可化为x-1-(x-5)<2,该不等式不成立.综上,原不等式的解集为(-∞,4).答案 A3.(选修4-5P19习题T9改编)若关于x的不等式|a|≥|x+1|+|x-2|存在实数解,则实数a的取值范围是________.解析由于|x+1|+|x-2|≥|(x+1)-(x-2)|=3,∴|x+1|+|x-2|的最小值为3.要使原不等式有解,只需|a|≥3,则a≥3或a≤-3.答案(-∞,-3]∪[3,+∞)4.若不等式|kx-4|≤2的解集为{x|1≤x≤3},则实数k=________.解析∵|kx-4|≤2,∴-2≤kx-4≤2,∴2≤kx≤6.∵不等式的解集为{x |1≤x ≤3},∴k =2. 答案 25.(2016·江苏卷)设a >0,|x -1|<a 3,|y -2|<a3,求证:|2x +y -4|<a . 证明 因为|x -1|<a 3,|y -2|<a 3, 所以|2x +y -4|=|2(x -1)+(y -2)| ≤2|x -1|+|y -2|<2a 3+a3=a . 故原不等式得证.考点一 绝对值不等式的解法【例1-1】 (2016·全国Ⅰ卷)已知函数f (x )=|x +1|-|2x -3|. (1)在图中画出y =f (x )的图象; (2)求不等式|f (x )|>1的解集.解 (1)f (x )=⎩⎪⎨⎪⎧x -4,x ≤-1,3x -2,-1<x ≤ 32,-x +4,x >32,故y =f (x )的图象如图所示.(2)由f (x )的解析式及图象知,当f (x )=1时,可得x =1或x =3; 当f (x )=-1时,可得x =13或x =5. 故f (x )>1的解集为{x |1<x <3};f (x )<-1的解集为⎩⎨⎧⎭⎬⎫x |x <13,或x >5. 所以|f (x )|>1的解集为⎩⎨⎧⎭⎬⎫x |x <13,或1<x <3,或x >5. 【例1-2】 (2017·全国Ⅰ卷)已知函数f (x )=-x 2+ax +4,g (x )=|x +1|+|x -1|. (1)当a =1时,求不等式f (x )≥g (x )的解集;(2)若不等式f (x )≥g (x )的解集包含[-1,1],求a 的取值范围. 解 (1)当a =1时,f (x )=-x 2+x +4, f (x )≥g (x )⇔x 2-x +|x +1|+|x -1|-4≤0. ①当x >1时,f (x )≥g (x )⇔x 2+x -4≤0, 解之得1<x ≤17-12.②当-1≤x ≤1时,f (x )≥g (x )⇔(x -2)(x +1)≤0, 则-1≤x ≤1.③当x <-1时,f (x )≥g (x )⇔x 2-3x -4≤0,解得-1≤x ≤4, 又x <-1,∴不等式此时的解集为空集.综上所述,f (x )≥g (x )的解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪-1≤x ≤17-12. (2)依题意得:-x 2+ax +4≥2在[-1,1]上恒成立. 则x 2-ax -2≤0在[-1,1]上恒成立.则只需⎩⎨⎧12-a ·1-2≤0,(-1)2-a (-1)-2≤0,解之得-1≤a ≤1.故a 的取值范围是[-1,1].规律方法 1.本题利用分段函数的图形的几何直观性,求解不等式,体现了数形结合的思想.2.解绝对值不等式的关键是去绝对值符号,常用的零点分段法的一般步骤:求零点;划分区间,去绝对值符号;分段解不等式;求各段的并集.此外,还常用绝对值的几何意义,结合数轴直观求解. 【训练1】 已知函数f (x )=|x -2|. (1)求不等式f (x )+x 2-4>0的解集;(2)设g (x )=-|x +7|+3m ,若关于x 的不等式f (x )<g (x )的解集非空,求实数m 的取值范围.解 (1)不等式f (x )+x 2-4>0,即|x -2|>4-x 2. 当x >2时,不等式可化为x 2+x -6>0,解得x >2; 当x <2时,不等式可化为x 2-x -2>0,解得x <-1. 所以原不等式的解集为{x |x >2或x <-1}. (2)依题意,|x -2|<3m -|x +7|解集非空, ∴3m >|x -2|+|x +7|在x ∈R 上有解, 又|x -2|+|x +7|≥|(x -2)-(x +7)|=9, 所以3m >9,解得m >3.故实数m 的取值范围是(3,+∞). 考点二 绝对值不等式性质的应用【例2-1】 设不等式-2<|x -1|-|x +2|<0的解集为M ,a ,b ∈M . (1)证明:⎪⎪⎪⎪⎪⎪13a +16b <14; (2)比较|1-4ab |与2|a -b |的大小,并说明理由.(1)证明设f (x )=|x -1|-|x +2|=⎩⎨⎧3,x ≤-2,-2x -1,-2<x <1,-3,x >1.由-2<-2x -1<0,解得-12<x <12. 因此集合M =⎝ ⎛⎭⎪⎫-12,12,则|a |<12,|b |<12.所以⎪⎪⎪⎪⎪⎪13a +16b ≤13|a |+16|b |<13×12+16×12=14.(2)解 由(1)得a 2<14,b 2<14. 因为|1-4ab |2-4|a -b |2=(1-8ab +16a 2b 2)-4(a 2-2ab +b 2) =16a 2b 2-4a 2-4b 2+1=(4a 2-1)(4b 2-1)>0, 所以|1-4ab |2>4|a -b |2, 故|1-4ab |>2|a -b |.【例2-2】 对于任意的实数a (a ≠0)和b ,不等式|a +b |+|a -b |≥M ·|a |恒成立,记实数M 的最大值是m . (1)求m 的值;(2)(一题多解)解不等式|x -1|+|x -2|≤m . 解 (1)不等式|a +b |+|a -b |≥M ·|a |恒成立,即M ≤|a +b |+|a -b ||a |对于任意的实数a (a ≠0)和b 恒成立,只要左边恒小于或等于右边的最小值.因为|a +b |+|a -b |≥|(a +b )+(a -b )|=2|a |, 当且仅当(a -b )(a +b )≥0时等号成立, 即|a |≥|b |时,|a +b |+|a -b ||a |≥2成立,也就是|a +b |+|a -b ||a |的最小值是2,所以M ≤2.因此m =2.(2)不等式|x -1|+|x -2|≤m ,即|x -1|+|x -2|≤2.法一 由于|x -1|+|x -2|表示数轴上的x 对应点到1和2对应点的距离之和; 而数轴上12和52对应点到1和2对应点的距离之和正好等于2,故|x -1|+|x -2|的解集为⎩⎨⎧⎭⎬⎫x |12≤x ≤52. 法二 ①当x <1时,不等式为-(x -1)-(x -2)≤2, 解得x ≥12,即12≤x <1.②当1≤x ≤2时,不等式为(x -1)-(x -2)≤2, 即1≤x ≤2.③当x >2时,不等式为(x -1)+(x -2)≤2, 解得x ≤52,即2<x ≤52.综上可知,不等式的解集是⎩⎨⎧⎭⎬⎫x |12≤x ≤52.规律方法 1.求含绝对值的函数最值时,常用的方法有三种:(1)利用绝对值的几何意义;(2)利用绝对值三角不等式,即|a |+|b |≥|a ±b |≥|a |-|b |;(3)利用零点分区间法.2.含绝对值不等式的证明中,要注意绝对值三角不等式的灵活应用.【训练2】 对于任意实数a ,b ,已知|a -b |≤1,|2a -1|≤1,且恒有|4a -3b +2|≤m ,求实数m 的取值范围.解 因为|a -b |≤1,|2a -1|≤1, 所以|3a -3b |≤3,⎪⎪⎪⎪⎪⎪a -12≤12,所以|4a -3b +2|=|(3a -3b )+⎝ ⎛⎭⎪⎫a -12+52|≤|3a -3b |+|a -12|+52≤3+12+52=6, 则|4a -3b +2|的最大值为6,所以m ≥|4a -3b +2|max =6,m 的取值范围是[6,+∞). 考点三 绝对值不等式的综合应用【例3】 (2017·全国Ⅲ卷)已知函数f (x )=|x +1|-|x -2|. (1)求不等式f (x )≥1的解集;(2)若不等式f (x )≥x 2-x +m 的解集非空,求m 的取值范围.解(1)f (x )=|x +1|-|x -2|=⎩⎨⎧-3,x ≤-1,2x -1,-1<x <2,3,x ≥2.①当x ≤-1时,f (x )=-3≥1无解; ②当-1<x <2时,2x -1≥1, 解得x ≥1,则1≤x <2;③当x ≥2时,f (x )=3≥1恒成立,∴x ≥2. 综上知f (x )≥1的解集为{x |x ≥1}.(2)不等式f (x )≥x 2-x +m 等价于f (x )-x 2+x ≥m , 得m ≤|x +1|-|x -2|-x 2+x 有解,又|x +1|-|x -2|-x 2+x ≤|x |+1+|x |-2-x 2+|x |=-⎝ ⎛⎭⎪⎫|x |-322+54≤54.当且仅当x =32时,|x +1|-|x -2|-x 2+x =54. 故实数m 的取值范围是⎝ ⎛⎦⎥⎤-∞,54. 规律方法 1.第(1)问分段讨论,求得符合题意的x 取值范围,最后取并集. 2.(1)不等式恒成立问题,解集非空(不能成立)问题,转化为最值问题解决. (2)本题分离参数m ,利用绝对值不等式的性质求解,避免分类讨论,优化了解题过程.【训练3】 (2016·全国Ⅲ卷)已知函数f (x )=|2x -a |+a . (1)当a =2时,求不等式f (x )≤6的解集;(2)设函数g (x )=|2x -1|.当x ∈R 时,f (x )+g (x )≥3,求实数a 的取值范围. 解 (1)当a =2时,f (x )=|2x -2|+2. 解不等式|2x -2|+2≤6得-1≤x ≤3. 因此f (x )≤6的解集为{x |-1≤x ≤3}. (2)当x ∈R 时,f (x )+g (x )=|2x -a |+a +|1-2x |≥|2x -a +1-2x |+a =|1-a |+a ,当x =12时等号成立,所以当x ∈R 时,f (x )+g (x )≥3等价于|1-a |+a ≥3.① 当a ≤1时,①等价于1-a +a ≥3,无解. 当a >1时,①等价于a -1+a ≥3,解得a ≥2. 所以a 的取值范围是[2,+∞).基础巩固题组 (建议用时:50分钟)1.(1)求不等式|x -1|+|x +2|≥5的解集; (2)若关于x 的不等式|ax -2|<3的解集为⎩⎨⎧⎭⎬⎫x |-53<x <13,求a 的值.解 (1)当x <-2时,不等式等价于-(x -1)-(x +2)≥5,解得x ≤-3; 当-2≤x <1时,不等式等价于-(x -1)+(x +2)≥5,即3≥5,无解; 当x ≥1时,不等式等价于x -1+x +2≥5,解得x ≥2. 综上,不等式的解集为{x |x ≤-3或x ≥2}. (2)∵|ax -2|<3,∴-1<ax <5.当a >0时,-1a <x <5a ,-1a =-53,且5a =13无解; 当a =0时,x ∈R ,与已知条件不符; 当a <0时,5a <x <-1a ,5a =-53,且-1a =13,解得a =-3.2.已知函数f (x )=|ax -2|.(1)当a =2时,解不等式f (x )>x +1;(2)若关于x 的不等式f (x )+f (-x )<1m 有实数解,求m 的取值范围.解 (1)当a =2时,不等式为|2x -2|>x +1,当x ≥1时,不等式化为2x -2>x +1,解得x >3.当x <1时,不等式化为2-2x >x +1,解得x <13.综上所述,不等式的解集为⎩⎨⎧⎭⎬⎫x |x >3或x <13. (2)因为f (x )+f (-x )=|ax -2|+|-ax -2| ≥|ax -2-ax -2|=4, 所以f (x )+f (-x )的最小值为4, 又f (x )+f (-x )<1m 有实数解,所以1m >4.则m 的取值范围为⎝ ⎛⎭⎪⎫0,14.3.(2015·全国Ⅰ卷)已知函数f (x )=|x +1|-2|x -a |,a >0. (1)当a =1时,求不等式f (x )>1的解集;(2)若f (x )的图象与x 轴围成的三角形面积大于6,求a 的取值范围. 解 (1)当a =1时,f (x )>1化为|x +1|-2|x -1|-1>0. 当x ≤-1时,不等式化为x -4>0,无解;当-1<x <1时,不等式化为3x -2>0,解得23<x <1; 当x ≥1时,不等式化为-x +2>0,解得1≤x <2. 所以f (x )>1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪⎪23<x <2. (2)由题设可得,f (x )=⎩⎨⎧x -1-2a ,x <-1,3x +1-2a ,-1≤x ≤a ,-x +1+2a ,x >a .所以函数f (x )的图象与x 轴围成的三角形的三个顶点分别为A ⎝ ⎛⎭⎪⎫2a -13,0,B (2a+1,0),C (a ,a +1),△ABC 的面积S =12|AB |·(a +1)=23(a +1)2. 由题设得23(a +1)2>6,故a >2. 所以a 的取值范围为(2,+∞).4.(2018·石家庄三模)在平面直角坐标系中,定义点P (x 1,y 1),Q (x 2,y 2)之间的“直角距离”为L (P ,Q )=|x 1-x 2|+|y 1-y 2|,已知A (x ,1),B (1,2),C (5,2)三点. (1)若L (A ,B )>L (A ,C ),求x 的取值范围;(2)当x ∈R 时,不等式L (A ,B )≤t +L (A ,C )恒成立,求t 的最小值. 解 (1)由定义得|x -1|+1>|x -5|+1, 则|x -1|>|x -5|,两边平方得8x >24,解得x >3. 故x 的取值范围为(3,+∞).(2)当x ∈R 时,不等式|x -1|≤|x -5|+t 恒成立,也就是t ≥|x -1|-|x -5|恒成立, 因为|x -1|-|x -5|≤|(x -1)-(x -5)|=4, 所以t ≥4,t min =4. 故t 的最小值为4.5.设函数f (x )=⎪⎪⎪⎪⎪⎪12x +1+|x |(x ∈R )的最小值为a .(1)求a ;(2)已知两个正数m ,n 满足m 2+n 2=a ,求1m +1n 的最小值.解 (1)f (x )=⎩⎪⎨⎪⎧-32x -1,x <-2,-12x +1,-2≤x ≤0,32x +1,x >0.当x ∈(-∞,0)时,f (x )单调递减;当x ∈[0,+∞)时,f (x )单调递增;∴当x =0时,f (x )的最小值a =1.(2)由(1)知m 2+n 2=1,则m 2+n 2≥2mn ,得1mn ≥2,由于m >0,n >0,则1m +1n ≥21mn ≥22,当且仅当m =n =22时取等号. ∴1m +1n 的最小值为2 2.能力提升题组(建议用时:30分钟)6.已知函数f (x )=|2x -a |+|2x +3|,g (x )=|x -1|+2.(1)解不等式:|g (x )|<5;(2)若对任意的x 1∈R ,都有x 2∈R ,使得f (x 1)=g (x 2)成立,求实数a 的取值范围. 解 (1)由||x -1|+2|<5,得-5<|x -1|+2<5,所以-7<|x -1|<3,解不等式得-2<x <4,所以原不等式的解集是{x |-2<x <4}.(2)因为对任意的x 1∈R ,都有x 2∈R ,使得f (x 1)=g (x 2)成立,所以{y |y =f (x )}⊆{y |y =g (x )},又f (x )=|2x -a |+|2x +3|≥|2x -a -(2x +3)|=|a +3|,g (x )=|x -1|+2≥2, 所以|a +3|≥2,解得a ≥-1或a ≤-5,所以实数a 的取值范围是{a |a ≥-1或a ≤-5}.7.(2018·西安模拟)已知函数f (x )=|x -2|,g (x )=|x +1|-x .(1)解不等式f (x )>g (x );(2)若存在实数x ,使不等式m -g (x )≥f (x )+x (m ∈R )成立,求实数m 的最小值. 解 (1)原不等式f (x )>g (x )化为|x -2|+x >|x +1|,当x <-1时,-(x -2)+x >-(x +1),解得x >-3,即-3<x <-1.当-1≤x ≤2时,-(x -2)+x >x +1,解得x <1,即-1≤x <1.当x >2时,x -2+x >x +1,解得x >3,即x >3.综上所述,不等式f (x )>g (x )的解集为{x |-3<x <1或x >3}.(2)由m -g (x )≥f (x )+x (m ∈R )可得m ≥|x -2|+|x +1|,由题意知m ≥(|x -2|+|x +1|)min ,∵|x -2|+|x +1|≥|x -2-(x +1)|=3,∴m ≥3,故实数m 的最小值是3.8.(2018·郑州模拟)已知不等式|x -m |<|x |的解集为(1,+∞).(1)求实数m 的值;(2)若不等式a -5x <⎪⎪⎪⎪⎪⎪1+1x -⎪⎪⎪⎪⎪⎪1-m x <a +2x对x ∈(0,+∞)恒成立,求实数a 的取值范围.解 (1)由|x -m |<|x |,得|x -m |2<|x |2,即2mx >m 2,又不等式|x -m |<|x |的解集为(1,+∞),则1是方程2mx =m 2的解,解得m =2(m =0舍去).(2)∵m =2,∴不等式a -5x <⎪⎪⎪⎪⎪⎪1+1x -⎪⎪⎪⎪⎪⎪1-m x <a +2x 对x ∈(0,+∞)恒成立等价于不等式a -5<|x +1|-|x -2|<a +2对x ∈(0,+∞)恒成立.设f (x )=|x +1|-|x -2|=⎩⎨⎧2x -1,0<x <2,3,x ≥2,当0<x <2时,f (x )在(0,2)上是增函数,则-1<f (x )<3,当x ≥2时,f (x )=3.因此函数f (x )的值域为(-1,3].从而原不等式等价于⎩⎨⎧a -5≤-1,a +2>3,解得1<a ≤4. 所以实数a 的取值范围是(1,4].。
含有绝对值的不等式以及简单的无理不等式

含有绝对值的不等式以及简单的无理不等式1、绝对值的概念:(),()0,()(),()0.f x f x f x f x f x ≥⎧=⎨-<⎩ 2、绝对值的几何意义:21x x -是指数轴上1x ,2x 两点间的距离. 3、解含有绝对值的不等式解法(1)通法:利用绝对值的定义,去绝对值符号,转化为整式不等式求解(2)常法:结合同解原理进行求解4、含有绝对值的不等式的同解原理(一般不含参数)()()f x g x >同解于()()f x g x >或()()f x g x <-()()f x g x <同解于()()()g x f x g x -<<()()()h x f x g x <<同解于()()()h x f x g x <<或()()()g x f x h x -<<-()()f x g x <同解于22()()f x g x <【注】对含有参数的绝对值不等式,需对参数进行分类..讨论..后才使用同解原理. 【典型例题】例1、解下列不等式(1)32<-x (2)213+<-x x (3)x x ->-213(4)4|23|7x <-≤ (5)2321>-x (6)123x x ->-(7)22x x x x >++ (8)52312≥-++x x (9)121≥++x x 例2、若不等式62<+ax 的解集为()1,2-,则实数a =__________.例3、不等式组:⎪⎩⎪⎨⎧+->+->x x x x x 22330的解集是__________.例4、不等式2430x x -+<的解集为__________.例5、已知{23}A x x a =-<,{B x x =≤10},且A B ⊂≠,求实数a 的取值范围. 例6、若不等式12x x k +-->对x R ∈恒成立,则实数k 的取值范围为__________. 例7、若关于x 的不等式13x x a -++≤有解,则实数a 的取值范围是__________.【典型练习】1、解下列不等式(1)4321x x ->+(2)4|23|7x <-≤(3)xx x x ->-22 (4)x 0)21(>-x (5)x x 3102≤-(6)2560x x -+<2、不等式10832<-+x x 的解集为__________.3、解关于x 的不等式1312++<--x x x .4、若x R ∈,则()()110x x -+>的解集是__________.5、解关于x 的不等式2121x m -<-()m R ∈6、解关于x 的不等式:231x a +->)(R a ∈7、解关于x 的不等式组:2450x x x ⎧≥⎪-⎨⎪->⎩8、求解下列问题(1)对任意实数x ,不等式|1||2|x x a ++-≥恒成立,则实数a 的取值范围是__________.(2)对任意实数x ,不等式|1||3|x x a --+<恒成立,则实数a 的取值范围是__________.(3)关于x 的不等式|4||3|x x a -++<的解集不是空集,则实数a 的取值范围是_______.简单的无理不等式的解法简单无理不等式的同解原理(1()0()()0()()g x f x g x f x g x ≥⎧>⇔>≥⇔⎨>⎩ (2()00()()()()f x f x g x f x g x ≥⎧<⇔≤<⇔⎨<⎩(32()0()()0()[()]f x g x g x f x g x ⎧≥⎪<⇔≥⎨⎪<⎩(42()0()()[()]g x g x f x g x ≥⎧>⇔⎨>⎩或()0()0f xg x ≥⎧⎨<⎩ (5()0()0()0f xg x g x >⎧>⇔⎨>⎩ (6()0()0()0f xg x g x ≥⎧≥⇔⎨≥⎩或()0f x = (7()0()0()0f x g x g x ≥⎧≤⇔⎨≤⎩或()0f x = 【典型例题】例1、解下列无理不等式(10>(2230x +>(3)(20x -例2、不等式1323>--x 的解集是__________.例3、若关于xax >的解集是(0,2),求实数a 的值.【典型练习】1、解下列无理不等式(13x >-(21x ≤+(3)(0x -(4)0x ≥(5)(0x +≤2、若不等式43<-b x 的解集中的整数有且仅有1,2,3,则实数b 的取值范围是__________.3、不等式xx x ||42+-≥0的解集是__________.4、不等式|1|3x +≤的解集为__________.52(0)x a a <+>的解集是__________.6、设0a >2a x >-.7x a +在[1,1]x ∈-时恒成立,则实数a 的取值范围是__________.832ax >+的解集为(4,)b ,则,a b 的值分别为__________.。
含绝对值不等式解法要点归纳

含绝对值不等式解法要点归纳解含绝对值符号的不等式的基本思想是去掉绝对值符号,使不等式变为不含绝对值符号的一般不等式,而后,其解法就与一般不等式相同.因此,掌握去掉绝对值符号的方法和途径是解题关键.一、含有绝对值不等式的几种去掉绝对值符号的常用方法去掉绝对值符号的方法有很多,其中常用的方法有:1.定义法去掉绝对值符号根据实数绝对的意义,即| x | =(0)(0)x xx x≥⎧⎨-<⎩,有:| x |<c⇔(0)(0)c x c ccφ-<<>⎧⎨≤⎩;| x |>c⇔(0)0(0)(0)x c x c cx cx R c<->>⎧⎪≠=⎨⎪∈<⎩或;2.利用不等式的性质去掉绝对值符号利用不等式的性质转化为| x |<c或| x |>c (c>0)来解.不等式|ax+b|>c (c >0)可化为ax+b>c或ax+b<-c,再由此求出原不等式的解集;不等式|ax+b|<c (c>0)可化为-c<ax+b<c,再由此求出原不等式的解集,对于含绝对值的双向不等式应化为不等式组求解,也可利用结论“a≤| x |≤b⇔a≤x≤b或-b≤x≤-a求解.这是一中典型的转化与化归的数学思想方法.3.平方法去掉绝对值符号.对于两边都含有“单项”绝对值的不等式,利用| x |2= x2可在两边脱去绝对值符号求解,这样解题要比按绝对值定义,讨论脱去绝对值符号解题简捷.解题时还要注意不等式两边变量与参变量的取值范围,如果没有明确不等式两边均为非负数,需要分类讨论,只有不等式两边均为非负数,(式)时,才可以直接两边平方,去掉绝对值符号,尤其是解含参数不等式更必须注意的一点.4.零点分段法去掉绝对值符号.所谓“零点分段法”是指:设数x1,x2,x3,…,xn是分别使含有|x-x1|,|x-x2|,|x-x3|,…,|x-xn|的代数式中相应的绝对值为零,称x1,x2,x3,…,xn 为相应绝对值的零点,零点x1,x2,x3,…,xn将数轴分为n+1段,利用绝对值的意义化去绝对值符号,从而得到代数式在各段上的简化式,从而化为不含绝对值的不等式组来解.即令每一项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集.“零点分段法”是解含有多个绝对值符号的不等式的常用手段,这种方法主要体现了化归、分类讨论等数学思想方法,它可以把求解条理化,思路直观.5.数形结合法去掉绝对值符号解绝对值不等式有时要利用数形结合,利用绝对值的几何意义,画出数轴,将绝对值转化为数轴上两点的距离求解.数形结合法形象、直观,可以使复杂问题简单化,此解法适用于| x-a|+| x-b |>m或| x-a|+| x-b |<m (m为正常数)类型的不等式.二、几点注意事项1.根据绝对值定义,将| x |<c或| x |>c (c>0)转化为两个不等式组,这两个不等式组的关系是“或”而不是“且”,因而原不等式的解集是这两个不等式组解的并集,而不是交集.2.| x |<c和| x |>c (c>0)的解集公式要牢记,以后可以直接作为公式使用.但要注意的是,这两个公式是在c>0时导出的,当c≤0时,需要另行讨论,不能使用该公式.3.解不等式问题与集合运算有密切联系,在应用集合有关内容处理绝对值不等式的过程中,要注意在不等式组的解集中,对不等式端点值的取舍情况.再有,因为已学习了集合表示法,所以不等式的解集要用集合形式表示,不要使用不等式的形式.4.解含有绝对值的不等式的关键是把含有绝对值的不等式转化为不含绝对值符号的不等式,然后再求解,但这种转化必须是等价转化,尤其是平方法去掉绝对值符号时,一定要注意两边非负这一条件,否则就会扩大或缩小解集的范围.5.要学会灵活运用分类讨论思想、数形结合思想、等价专化与化归思想方法处理绝对值不等式问题.三、典型例题思路点拨例1 关于x的不等式| kx-1|≤5的解集为{x |-3≤x≤2},求k的值.思路点拨:按绝对值定义直接去掉绝对值符号后,由于k的取值不确定,要以k 的不同取值分类处理.解:原不等式可化为-4≤kx ≤6,当k >0时,-k 4≤x ≤k6,依题意,有 ⎪⎪⎩⎪⎪⎨⎧=-=-.26,34k k ⇒⎪⎩⎪⎨⎧==3,34k k ,此时无解. 当k = 0时,显然不满足题意.当k <0时, k 6≤x ≤-k 4,依题意,有⎪⎪⎩⎪⎪⎨⎧-==-.36,24kk ⇒ k =-2. 例2 解不等式| x -1|<| x +a |.思路点拨:由于两边均为非负数,因此可以两边平方去掉绝对值符号. 解:由于| x -1|≥0,| x +a |>0,所以两边平方有| x -1|2<| x +a |2, 即有x 2-2x +1<x 2+2ax +a 2,整理得:(2a +2)x >1-a 2,当2a +2>0,即a >-1时,不等式的解为x >21(1-a); 当2a +2 = 0,即a =-1时,不等式无解;当2a +2<0,即a <1时,不等式的解为x <21(1-a). 例3 若不等式 | x -4|+| 3-x |<a 的解集为空集,求a 的取值范围. 思路点拨一:此不等式左边含有两个绝对值符号,如何去掉绝对值符号呢?可考虑采用“零点分段”,即令每一项等于零,得到的值作为讨论的分区点,然后再分区间讨论绝对值不等式,最后应求出解集的并集.解一:⑴当a ≤0时,不等式 | x -4|+| 3-x |<a 的解集为空集. ⑵当a >0时,先求不等式 | x -4|+| 3-x |<a 有解时a 的取值范围. 令x -4 = 0,得x = 4,令3-x = 0,得x = 3.①当x ≥4时,原不等式 | x -4|+| 3-x |<a 化为:x -4+x -3<a ,即2x -7<a ,解不等式组⎩⎨⎧<-≥.72,4a x x ⇒ 4≤x <27+a ⇒4<27+a , ∴a >1.②当3<x <4时,原不等式 | x -4|+| 3-x |<a 化为:4-x +x -3<a ,解得a >1.③当x ≤3时,原不等式 | x -4|+| 3-x |<a 化为:4-x +3-x <a ,即7-2x <a ,解不等式组⎩⎨⎧<-≤.27,3a x x ⇒ 27a -<x ≤3⇒,27a -<3, ∴a >1.综合①②③可知,当a >1时,原不等式有解,从而当0<a ≤1时,原不等式解集为空集.由⑴、⑵两种情况可知,不等式 | x -4|+| 3-x |<a 的解集为空集,a 的取值范围是a ≤1.思路点拨二:解法一是按去掉绝对值符号的方法求解,这是处理此类问题的一般方法,但运算量大.若仔细观察不等式左边的结构,联想到绝对值| a +b|≤| a |+| b|,便可把问题简化.解二:∵a >| x -4|+| 3-x |≥| x -4+3-x | = 1,∴当a >1时| x -4|+| 3-x |<a 有解,从而当0<a ≤1时,原不等式解集为空集.例4 对任意实数x ,若不等式| x +1|-| x -2 |>k 恒成立,求 k 的取值范围. 思路点拨一:要使| x +1|-| x -2 |>k 对任意x 恒成立,只要| x +1|-| x -2 |的最小值大于k .因| x +1|的几何意义为数轴上点x 到-1的距离,| x -2 |的几何意义为数轴上点x 到2的距离,| x +1|-| x -2 |的几何意义为数轴上点x 到-1与2的距离的差,其最小值可求.解法一:根据绝对值的几何意义,设数x ,-1,2在 数轴上对应的点分别为P 、A 、B ,原不等式即求| PA|-| PB|>k 成立,因为|AB| = 3,即| x +1|-| x -2 |≥-3,故当k <-3时,原不等式恒成立.思路点拨二:如果把不等式的左边用零点分段的方法改写成分段函数,通过画出其图象,从图象观察k 的取值范围. 解法二:令y = | x +1|-| x -2 |,则 y =⎪⎩⎪⎨⎧≥<<---≤-.2.321,121,3x x x x 要使| x +1|-| x -2 |>k 恒成立,从图象可以看出,只要k <-3即可.故k <-3满足题意思.。
含绝对值的不等式总结

含绝对值不等式一、基础知识1、绝对值的基本性质:⎩⎨⎧<-≥=∈0,0,a a a a a R a 则设()()""001==≥取当且仅当a a ()a a ±≥2 ()a a a ≤≤-3()a b b a a a-=-=-,4 22)5(a a =2、绝对值的运算法则()b a b a b a +≤+≤-1(注意不等式成立的条件) ()b a b a b a+≤-≤-2(注意不等式成立的条件)()b a b a ⋅=⋅3 ()ba ba =43、绝对值不等式的解法()则设R x a∈>,01a x a a x a x <<-⇔<⇔<22a x a x axa x >-<⇔>⇔>或22()()()()()()x g x f x g x g x f <<-⇔<2()()()()()()x g x f x g x f x g x f -<>⇔>或()()()()()()()()()()()0322>-+⇔>⇔>x g x f x g x f x gx fx g x f(4)含有多个绝对值符号的不等式,一般可用零点分段求解。
4、解含绝对值问题的几种常用策略 (1) 定义策略;(2)平方策略;(3)定理策略;(4)等价转化策略;(5)分段讨论策略; (6)数形结合策略 二、题型剖析例1 (1).1122>-x (2)01314<--x (3)解不等式xx ->+215分析:不等式,x a x a x a x a a x a >⇔><-<⇔-<<或(其中0>a )可以推广为任意Ra ∈都成立,且a 为代数式也成立 解:原不等式又化为4361)2(15215-<>--<+->+x x x x x x 或解之得或∴原不等式的解集为}4361{-<>x x x 或点评:可利用)()()()()(),()()()()()(x g x f x g x g x f x g x f x g x f x g x f <<-⇔<-<>⇔>或去掉绝对值符号变式训练:(1)解不等式213+<-x x ()3922+≤-x x解:(2)法一:原不等式⎩⎨⎧+≤-≥-⇔390922x x x ①或⎩⎨⎧+≤-<-390922x x x ② 由①解得433≤≤-=x x 或,由②解得32<≤x ∴原不等式的解集是{}342-=≤≤x x x 或法二:原等式等价于39)3(2+≤-≤+-x x x ⎩⎨⎧≤≤-≥-≤⇔4323x x x 或423≤≤-=⇔x x 或∴原不等式的解集是{}342-=≤≤x x x 或法三:设)33,9221-≥+=-=x x y x y (,由392+=-x x 解得非曲直2,3,4321=-==x x x ,2y y ≤的x 的范围是433≤≤-=x x 或,∴原不等式的解集是{}342-=≤≤x x x 或例2、解不等式52312≥-++x x 。
含绝对值的不等式

{
}
(2) | 2 x + 1 | + | x − 2 |> 4
x > 2 或 2 x + 1 + x − 2 > 4
1 x<− 或 原不等式等价于: 原不等式等价于: 2 解(2) ) − 2 x − 1 − x + 2 > 4
1 − ≤ x ≤ 2 2 2 x + 1 − x + 2 > 4
1 37 37 = −3 x − + ≤ 6 12 12
2
(
)
所以…… 所以
当 a ≠ 0 时, f (a) = 0 , f (−a) = −2a | a |≠ 0, f (x) 是非奇非偶函数
x < a x ≥ a 或 2 (2)x | x − a |≥ 2a ⇔ 2 ) 2 x − ax + 2a ≤ 0 x − ax − 2a 2 ≥ 0 x ≥ a ⇔ x ∈φ 或 ( x − 2a )( x + a ) ≥ 0
2 备用:已知二次函数 备用 已知二次函数 f ( x ) = ax + bx + c (a, b, c ∈ R ) ,
37 当 证明: 若 f (− 1) ≤ 1, f (0) ≤ 3, f (1) ≤ 1 ,证明: x ≤ 1时, f ( x ) ≤ 12 证明: 证明:因为 f (− 1) = a − b + c , f (0) = c , f (1) = a + b + c
含绝对值的不等式
一、基础知识
a (a ≥ 0 ) 1、绝对值的基本性质: 设a ∈ R, 则 a = 、绝对值的基本性质: − a ( a < 0 )
绝对值不等式考点与题型归纳

绝对值不等式考点与题型归纳一、基础知识1.绝对值三角不等式定理1:如果a,b是实数,则|a+b|≤|a|+|b|,当且仅当ab≥0时,等号成立.定理2:如果a,b,c是实数,那么|a-c|≤|a-b|+|b-c|,当且仅当(a-b)(b-c)≥0时,等号成立.↓|a|-|b|≤|a-b|≤|a|+|b|,当且仅当|a|≥|b|且ab≥0时,左边等号成立,当且仅当ab≤0时,右边等号成立.2.绝对值不等式的解法(1)|x|<a与|x|>a型不等式的解法(2)|ax+b|≤c(c>0)和|ax+b|≥c(c>0)型不等式的解法:①|ax+b|≤c⇔-c≤ax+b≤c;②|ax+b|≥c⇔ax+b≥c或ax+b≤-c.|x-a|+|x-b|≥c和|x-a|+|x-b|≤c型不等式的解法及体现数学思想①利用绝对值不等式的几何意义求解,体现了数形结合的思想;②利用“零点分段法”求解,体现了分类讨论的思想;③通过构造函数,利用函数的图象求解,体现了函数与方程的思想.考点一绝对值不等式的解法[典例] (2016·全国卷Ⅰ)已知函数f (x )=|x +1|-|2x -3|.(1)画出y =f (x )的图象; (2)求不等式|f (x )|>1的解集.[解] (1)由题意得f (x )=⎩⎨⎧x -4,x ≤-1,3x -2,-1<x ≤32,-x +4,x >32,故y =f (x )的图象如图所示.(2)由f (x )的函数表达式及图象可知, 当f (x )=1时,可得x =1或x =3;当f (x )=-1时,可得x =13或x =5.故f (x )>1的解集为{x |1<x <3},f (x )<-1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <13或x >5. 所以|f (x )|>1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x <13或1<x <3或x >5.[题组训练]1.解不等式|x +1|+|x -1|≤2. 解:当x <-1时,原不等式可化为-x -1+1-x ≤2, 解得x ≥-1,又因为x <-1,故无解; 当-1≤x ≤1时,原不等式可化为x +1+1-x =2≤2,恒成立; 当x >1时,原不等式可化为x +1+x -1≤2, 解得x ≤1,又因为x >1,故无解;综上,不等式|x +1|+|x -1|≤2的解集为[-1,1]. 2.(2019·沈阳质检)已知函数f (x )=|x -a |+3x ,其中a ∈R . (1)当a =1时,求不等式f (x )≥3x +|2x +1|的解集; (2)若不等式f (x )≤0的解集为{x |x ≤-1},求a 的值. 解:(1)当a =1时,f (x )=|x -1|+3x .法一:由f (x )≥3x +|2x +1|,得|x -1|-|2x +1|≥0, 当x >1时,x -1-(2x +1)≥0,得x ≤-2,无解; 当-12≤x ≤1时,1-x -(2x +1)≥0,得-12≤x ≤0;当x <-12时,1-x -(-2x -1)≥0,得-2≤x <-12.∴不等式的解集为{x |-2≤x ≤0}.法二:由f (x )≥3x +|2x +1|,得|x -1|≥|2x +1|, 两边平方,化简整理得x 2+2x ≤0, 解得-2≤x ≤0,∴不等式的解集为{x |-2≤x ≤0}.(2)由|x -a |+3x ≤0,可得⎩⎪⎨⎪⎧ x ≥a ,4x -a ≤0或⎩⎪⎨⎪⎧x <a ,2x +a ≤0,即⎩⎪⎨⎪⎧ x ≥a ,x ≤a 4或⎩⎪⎨⎪⎧x <a ,x ≤-a 2.当a >0时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤-a 2. 由-a2=-1,得a =2.当a =0时,不等式的解集为{x |x ≤0},不合题意.当a <0时,不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x ≤a 4. 由a4=-1,得a =-4. 综上,a =2或a =-4.考点二 绝对值不等式性质的应用[典例] (2019·湖北五校联考)已知函数f (x )=|2x -1|,x ∈R . (1)解不等式f (x )<|x |+1;(2)若对x ,y ∈R ,有|x -y -1|≤13,|2y +1|≤16,求证:f (x )<1.[解] (1)∵f (x )<|x |+1,∴|2x -1|<|x |+1,即⎩⎪⎨⎪⎧ x ≥12,2x -1<x +1或⎩⎪⎨⎪⎧0<x <12,1-2x <x +1或⎩⎪⎨⎪⎧x ≤0,1-2x <-x +1,得12≤x <2或0<x <12或无解. 故不等式f (x )<|x |+1的解集为{x |0<x <2}.(2)证明:f (x )=|2x -1|=|2(x -y -1)+(2y +1)|≤|2(x -y -1)|+|2y +1|=2|x -y -1|+|2y +1|≤2×13+16=56<1.故不等式f (x )<1得证.[解题技法] 绝对值不等式性质的应用利用不等式|a +b |≤|a |+|b |(a ,b ∈R )和|a -b |≤|a -c |+|c -b |(a ,b ∈R),通过确定适当的a ,b ,利用整体思想或使函数、不等式中不含变量,可以求最值或证明不等式.[题组训练]1.求函数f (x )=|x +2 019|-|x -2 018|的最大值.解:因为f (x )=|x +2 019|-|x -2 018|≤|x +2 019-x +2 018|=4 037, 所以函数f (x )=|x +2 019|-|x -2 018|的最大值为4 037. 2.若x ∈[-1,1],|y |≤16,|z |≤19,求证:|x +2y -3z |≤53.证明:因为x ∈[-1,1],|y |≤16,|z |≤19,所以|x +2y -3z |≤|x |+2|y |+3|z |≤1+2×16+3×19=53,所以|x +2y -3z |≤53成立.考点三 绝对值不等式的综合应用[典例] (2018·合肥质检)已知函数f (x )=|2x -1|. (1)解关于x 的不等式f (x )-f (x +1)≤1;(2)若关于x 的不等式f (x )<m -f (x +1)的解集不是空集,求m 的取值范围. [解] (1)f (x )-f (x +1)≤1⇔|2x -1|-|2x +1|≤1,则⎩⎪⎨⎪⎧ x ≥12,2x -1-2x -1≤1或⎩⎪⎨⎪⎧ -12<x <12,1-2x -2x -1≤1或⎩⎪⎨⎪⎧x ≤-12,1-2x +2x +1≤1, 解得x ≥12或-14≤x <12,即x ≥-14,所以原不等式的解集为⎣⎡⎭⎫-14,+∞. (2)由条件知,不等式|2x -1|+|2x +1|<m 有解, 则m >(|2x -1|+|2x +1|)min 即可.由于|2x -1|+|2x +1|=|1-2x |+|2x +1|≥|1-2x +(2x +1)|=2,当且仅当(1-2x )(2x +1)≥0,即x ∈⎣⎡⎦⎤-12,12时等号成立,故m >2.所以m 的取值范围是(2,+∞). [解题技法] 两招解不等式问题中的含参问题 (1)转化①把存在性问题转化为求最值问题;②不等式的解集为R 是指不等式的恒成立问题;③不等式的解集为∅的对立面也是不等式的恒成立问题,此类问题都可转化为最值问题,即f (x )<a 恒成立⇔a >f (x )max ,f (x )>a 恒成立⇔a <f (x )min .(2)求最值求含绝对值的函数最值时,常用的方法有三种: ①利用绝对值的几何意义;②利用绝对值三角不等式,即|a |+|b |≥|a ±b |≥||a |-|b ||; ③利用零点分区间法. [题组训练]1.(2018·全国卷Ⅱ)设函数f (x )=5-|x +a |-|x -2|. (1)当a =1时,求不等式f (x )≥0的解集; (2)若f (x )≤1,求a 的取值范围.解:(1)当a =1时,f (x )=⎩⎪⎨⎪⎧2x +4,x <-1,2,-1≤x ≤2,-2x +6,x >2.当x <-1时,由2x +4≥0,解得-2≤x <-1, 当-1≤x ≤2时,显然满足题意, 当x >2时,由-2x +6≥0,解得2<x ≤3, 故f (x )≥0的解集为{x |-2≤x ≤3}. (2)f (x )≤1等价于|x +a |+|x -2|≥4.而|x +a |+|x -2|≥|a +2|,且当x =2时等号成立. 故f (x )≤1等价于|a +2|≥4. 由|a +2|≥4可得a ≤-6或a ≥2.所以a 的取值范围是(-∞,-6]∪[2,+∞).2.(2018·广东珠海二中期中)已知函数f (x )=|x +m |+|2x -1|(m ∈R ),若关于x 的不等式f (x )≤|2x +1|的解集为A ,且⎣⎡⎦⎤34,2⊆A ,求实数m 的取值范围.解:∵⎣⎡⎦⎤34,2⊆A ,∴当x ∈⎣⎡⎦⎤34,2时,不等式f (x )≤|2x +1|恒成立, 即|x +m |+|2x -1|≤|2x +1|在x ∈⎣⎡⎦⎤34,2上恒成立, ∴|x +m |+2x -1≤2x +1,即|x +m |≤2在x ∈⎣⎡⎦⎤34,2上恒成立, ∴-2≤x +m ≤2,∴-x -2≤m ≤-x +2在x ∈⎣⎡⎦⎤34,2上恒成立, ∴(-x -2)max ≤m ≤(-x +2)min ,∴-114≤m ≤0,故实数m 的取值范围是⎣⎡⎦⎤-114,0. [课时跟踪检测]1.求不等式|2x -1|+|2x +1|≤6的解集.解:原不等式可化为⎩⎪⎨⎪⎧ x <-12,1-2x -2x -1≤6或⎩⎪⎨⎪⎧-12≤x ≤12,1-2x +2x +1≤6或⎩⎪⎨⎪⎧x >12,2x -1+2x +1≤6. 解得-32≤x ≤32,即原不等式的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪-32≤x ≤32. 2.已知函数f (x )=|x -4|+|x -a |(a ∈R )的最小值为a . (1)求实数a 的值; (2)解不等式f (x )≤5.解:(1)f (x )=|x -4|+|x -a |≥|a -4|=a , 从而解得a =2.(2)由(1)知,f (x )=|x -4|+|x -2|=⎩⎪⎨⎪⎧-2x +6,x ≤2,2,2<x ≤4,2x -6,x >4.故当x ≤2时,由-2x +6≤5,得12≤x ≤2;当2<x ≤4时,显然不等式成立; 当x >4时,由2x -6≤5,得4<x ≤112,故不等式f (x )≤5的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪12≤x ≤112. 3.(2018·全国卷Ⅰ)已知f (x )=|x +1|-|ax -1|. (1)当a =1时,求不等式f (x )>1的解集;(2)若x ∈(0,1)时不等式f (x )>x 成立,求a 的取值范围. 解:(1)当a =1时,f (x )=|x +1|-|x -1|, 即f (x )=⎩⎪⎨⎪⎧-2,x ≤-1,2x ,-1<x <1,2,x ≥1.故不等式f (x )>1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪x >12.(2)当x ∈(0,1)时|x +1|-|ax -1|>x 成立等价于当x ∈(0,1)时|ax -1|<1成立. 若a ≤0,则当x ∈(0,1)时,|ax -1|≥1;若a >0,则|ax -1|<1的解集为⎩⎨⎧⎭⎬⎫x ⎪⎪0<x <2a , 所以2a ≥1,故0<a ≤2.综上,a 的取值范围为(0,2]. 4.设函数f (x )=|3x -1|+ax +3. (1)若a =1,解不等式f (x )≤4;(2)若f (x )有最小值,求实数a 的取值范围. 解:(1)当a =1时,f (x )=|3x -1|+x +3≤4,即|3x -1|≤1-x ,x -1≤3x -1≤1-x ,解得0≤x ≤12,所以f (x )≤4的解集为⎣⎡⎦⎤0,12. (2)因为f (x )=⎩⎨⎧(3+a )x +2,x ≥13,(a -3)x +4,x <13,所以f (x )有最小值的充要条件为⎩⎪⎨⎪⎧a +3≥0,a -3≤0,解得-3≤a ≤3,即实数a 的取值范围是[-3,3].5.(2019·贵阳适应性考试)已知函数f (x )=|x -2|-|x +1|. (1)解不等式f (x )>-x ;(2)若关于x 的不等式f (x )≤a 2-2a 的解集为R ,求实数a 的取值范围. 解:(1)原不等式等价于f (x )+x >0,不等式f (x )+x >0可化为|x -2|+x >|x +1|, 当x <-1时,-(x -2)+x >-(x +1),解得x >-3,即-3<x <-1; 当-1≤x ≤2时,-(x -2)+x >x +1,解得x <1,即-1≤x <1; 当x >2时,x -2+x >x +1,解得x >3,即x >3,综上所述,不等式f (x )+x >0的解集为{x |-3<x <1或x >3}. (2)由不等式f (x )≤a 2-2a 可得|x -2|-|x +1|≤a 2-2a ,∵|x -2|-|x +1|≤|x -2-x -1|=3,当且仅当x ∈(-∞,-1]时等号成立, ∴a 2-2a ≥3,即a 2-2a -3≥0,解得a ≤-1或a ≥3. ∴实数a 的取值范围为(-∞,-1]∪[3,+∞). 6.已知函数f (x )=|x -a |+|x +1|.(1)若a =2,求不等式f (x )>x +2的解集;(2)如果关于x 的不等式f (x )<2的解集不是空集,求实数a 的取值范围. 解:(1)当a =2时,f (x )=⎩⎪⎨⎪⎧-2x +1,x <-1,3,-1≤x <2,2x -1,x ≥2,不等式f (x )>x +2等价于⎩⎪⎨⎪⎧ x <-1,-2x +1>x +2或⎩⎪⎨⎪⎧ -1≤x <2,3>x +2或⎩⎪⎨⎪⎧x ≥2,2x -1>x +2,解得x <1或x >3,故原不等式的解集为{x |x <1或x >3}.(2)∵f (x )=|x -a |+|x +1|≥|(x -a )-(x +1)|=|a +1|,当(x -a )(x +1)≤0时取等号. ∴若关于x 的不等式f (x )<2的解集不是空集,只需|a +1|<2, 解得-3<a <1,即实数a 的取值范围是(-3,1). 7.已知函数f (x )=|2x -a |+a .(1)当a =2时,求不等式f (x )≤6的解集;(2)设函数g (x )=|2x -1|.当x ∈R 时,f (x )+g (x )≥3,求a 的取值范围. 解:(1)当a =2时,f (x )=|2x -2|+2. 解不等式|2x -2|+2≤6,得-1≤x ≤3. 因此f (x )≤6的解集为{x |-1≤x ≤3}.(2)当x ∈R 时,f (x )+g (x )=|2x -a |+a +|1-2x |≥3, 即⎪⎪⎪⎪x -a 2+⎪⎪⎪⎪12-x ≥3-a 2. 又⎝⎛⎭⎫⎪⎪⎪⎪x -a 2+⎪⎪⎪⎪12-x min =⎪⎪⎪⎪12-a 2, 所以⎪⎪⎪⎪12-a 2≥3-a 2,解得a ≥2.所以a 的取值范围是[2,+∞).8.(2018·福州质检)设函数f (x )=|x -1|,x ∈R . (1)求不等式f (x )≤3-f (x -1)的解集;(2)已知关于x 的不等式f (x )≤f (x +1)-|x -a |的解集为M ,若⎝⎛⎭⎫1,32⊆M ,求实数a 的取值范围.解:(1)因为f (x )≤3-f (x -1),所以|x -1|≤3-|x -2|⇔|x -1|+|x -2|≤3⇔⎩⎪⎨⎪⎧x <1,3-2x ≤3或⎩⎨⎧1≤x ≤2,1≤3或⎩⎪⎨⎪⎧x >2,2x -3≤3, 解得0≤x <1或1≤x ≤2或2<x ≤3,所以0≤x ≤3,故不等式f (x )≤3-f (x -1)的解集为[0,3].(2)因为⎝⎛⎭⎫1,32⊆M , 所以当x ∈⎝⎛⎭⎫1,32时,f (x )≤f (x +1)-|x -a |恒成立, 而f (x )≤f (x +1)-|x -a |⇔|x -1|-|x |+|x -a |≤0⇔|x -a |≤|x |-|x -1|,因为x ∈⎝⎛⎭⎫1,32,所以|x -a |≤1,即x -1≤a ≤x +1, 由题意,知x -1≤a ≤x +1对于任意的x ∈⎝⎛⎭⎫1,32恒成立, 所以12≤a ≤2,故实数a 的取值范围为⎣⎡⎦⎤12,2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
含绝对值的不等式x(x 0)x .x(x 0)2.| x |v a(a>0)的解集是{x |—a v x v a}. | x |> a( a>0)的解集是{x | x v—a 或x > a}.【思考导学】1. I ax+ b| v b(b> 0)转化成一b v ax+ b v b的根据是什么答:含绝对值的不等式| ax+ b| v b转化一b v ax+ b v b的根据是由绝对值的意义确定.2. 解含有绝对值符号的不等式的基本思想是什么答:解含有绝对值符号的不等式的基本思想是去掉绝对值符号,使不等式变为不含绝对值符号的一般不等式,而后,其解法就与解一般不等式或不等式组相同.【典例剖析】[例1]解不等式2v| 2x — 5 | w 7.I2x 5I 2解法一:原不等式等价于I I|2x 5| 72x 5|2 或2x 57 2x 5| 73 7原不等式的解集为{x |- K x v 或—v x w 6}2 2解法二:原不等式的解集是下面两个不等式组解集的并集(I)2x252x57(n)2x50252x7不等式组(I )的解集为{x | - v x W 6}2不等式组(n)的解集是{x |- i w x v - }23 7•原不等式的解集是{x |- 1W x v —或—v x w 6}2 2解法三:原不等式的解集是下面两个不等式解集的并集.(I )2 v 2x —5W 7(n )2 v 5—2x w 7不等式(I )的解集为{x | - v x w 6}23不等式(n )的解集是{x |—i w x v23 7•原不等式的解集是{x |— 1 w x v 或—v x w 6}.2 2点评:含绝对值的双向不等式的解法,关键是去绝对值号.其方法一是转化为单向不等式组如解法一,再就是利用绝对值的定义如解法二、解法三. [例2]解关于x的不等式:(1) | 2x + 3 | —i v a(a€ R);1绝对值的意义是:(2) | 2x + 1 |> x+ 1.解:⑴ 原不等式可化为| 2x + 3 |< a+ 1当a+ 1>0,即a>—1时,由原不等式得一(a+ 1) < 2x+ 3<a+ 1a 4 a 2—< x< -2 2当a+ K 0,即a<—1时,原不等式的解集为,综上,当a>—1时,原不等式的解集是{ x | —仝上<x< ±2 }2 2当a w —1时,原不等式的解集是(2)原不等式可化为下面两个不等式组来解2x 1 0 .2x 10(i) 或(n )2x 1 x 1(2x1) x 1不等式组(I )的解为x> 0不等式组(n)的解为x< —23•••原不等式的解集为{ x | 2x< ——或x> 0}3点评:由于无论x取何值,关于x的代数式的绝对值均大于或等于0,即不可能小于0,故| f (x) |< a(aw 0)的解集为解不等式分情况讨论时,一定要注意是对参数分类还是对变量分类,对参数分类的解集一般不合并,如(1)对变量分类,解集必须合并如(2).例3]解不等式| x—|2 x+ 1|| > 1.解:•••由|x—|2x+ 1|| > 1 等价于(x —|2x+ 1|) > 1 或x—|2x+ 1| <—1(1)由x—|2 x+ 1| > 1 得|2 x+ 1| < x—12x 1 0 亠2x 1 0 或2x 1 x 1 (2x 1) x 11 1即2或2均无解x 2 x 0(2)由x—|2 x+ 1| <—1 得|2x+ 1| >x+ 12x 1 0 亠2x 1 0或2x 1 x 1 (2x 1) x 112• x > 0 或x< ——2332综上讨论,原不等式的解集为{x| x<------- 或x> 0}.3点评:这是含多重绝对值符号的不等式,可以从“外”向“里” 方法,去掉绝对值的符号,逐次化解.【随堂训练】1.不等式|8 —3x| > 0的解集是()A. B . R8 8,反复应用解答绝对值基本不等式类型的C. {x| x 半,x € F} D . {3}3 32•下列不等式中,解集为 R 的是()A.| x + 2 |> 1 B X + 2 | + 1 > 1C. (x - 78)2>— 1 D . (x + 78)2 — 1> 0 答案:C 3.在数轴上与原点距离不大于 2的点的坐标的集合是() A. {x |— 2v x v 2}B. {x | 0v x < 2}C. {x |— 2< x w 2}D. {x | x 》2 或 x w — 2}解析:所求点的集合即不等式|x |w 2的解集.答案:C4 •不等式| 1— 2x | v 3的解集是() A. {x | x v 1}B. {x |— 1 v x v 2}C. {x | x >2}D. {x | x v — 1 或 x >2} 解析: 由 | 1 — 2x | v 3 得一3 v 2x — 1 v 3 ,二一1 v x v 2答案: B5.不等式| 解析: x + 4 | > 9的解集是由原不等式得 x + 4> 9或x + 4 v — 9 ,••• x > 5或x v — 13答案: {x | x > 5 或 x v — 13}6 .当a > 0时,关于x 的不等式| b — ax | v a 的解集是 ____________ {x |答案:{x | b — 1v x v - + 1} a a 【强化训练】1.不等式| x + a | v 1的解集是()A. {x | — 1 + a v x v 1+ aB. {x | — 1 — a v x v 1— a}C. {x | — 1 —| a |v x v 1 —| a | }D. {x | x v — 1 —| a |或 x > 1 —| a |}解析: 由 | x + a |v 1 得一1 v x + a v 1答案:B2 .不等式1w| x —3 |w 6的解集是()解析: 由原不等式得 | ax — b |v a , ••— a v ax — b vb —1 v x v — +1A. {x | —3w x w 2 或4w x w 9}B. {x | —3w x w 9}C. {x | —1w x w 2}D. {x | 4w x w 9}解析:x 3 0 x 3 0不等式等价于或1x36 13x6解得:4 w x w 9 或一3w x w 2.答案:A3.卜列不等式中,解集为{ x | x v 1或x >3}的不等式是()A.| x —2 | > 5B.| 2x —4| > 3x1 C. 1—| —- -1 |w22 D. 1—| -- -1 |v122解析:A中,由| x—2 |> 5 得x —2 > 5 或x —2 v —5 x> 7 或x v—3同理,B的解集为{ x | x > 7或x v —1}2C的解集为{ x | x< 1或x> 3}D的解集为{ x | x v 1或x> 3}答案:D4. 已知集合A= {x|| x —1| v 2} , B= {x|| x—1| > 1},贝U A n B等于()A. {x| —1 v x v 3}B. {x| x v 0 或x > 3}C. {x| —1 v x v 0}D. {x| —1 v x v 0 或2v x v 3}解析:| x —1| v 2 的解为一1v x v 3, |x—1| > 1 的解为x v 0 或x > 2.•A n B= {x| —1 v x v 0 或2v x v 3}.答案:D5. ___________________________________________________________________ 已知不等式 | x —2 |v a(a> 0)的解集是{ x |—1 v x v b},贝U a+ 2b= _________________________________ .解析:不等式| x — 2 |v a的解集为{ x | 2 —a v x v 2 + a}由题意知:{x | 2—a v x v 2+ a} = { x | — 1 v x v b}•2 a 1 a 32 a c c 5•- a+ 2b = 3+ 2 x 5 = 13答案:136 .不等式|x + 2| > x + 2的解集是_________ .解析:•••当x+ 2> 0 时,|x + 2| = x + 2, x+ 2>x+ 2 无解.当x+ 2v 0 时,|x+ 2| =—(x+ 2) > 0> x+ 2•••当x v—2 时,| x + 2 |> x+ 2答案: {x | x v —2}7.解下列不等式:(1) |2 —3x| <2; (2)|3 x —2| >2.4 解:⑴由原不等式得—2< 2 —3x< 2,各加上—2得—4W —3x< 0,各除以—3得—》x > 0,解集为{x|03< x< 4}.34 4(2) 由原不等式得3x —2v—2或3x —2>2,解得x v 0或x> ,故解集为{x| x v 0或x> }.3 3&解下列不等式:(1)3 < |x —2| v 9; (2)|3 x—4| > 1 + 2x.解:(1)原不等式等价于不等式组由①得x<—1或x>5;由②得一7v x v 11,把①、②的解表示在数轴上(如图),•原不等式的解集为{x| —7v x w—1或5< x v 11}.(2)原不等式等价于下面两个不等式组,即原不等式的解集是下面两个不等式组解集的并集:① 3x 4 0,② 3x 4 °,3x 4 1 2x; (3x 4) 1 2x.3由不等式组①解得x > 5;由不等式组②解得x v 3.5•••原不等式的解集为{x| x v 3或x > 5}.59.设A={ x | | 2x—1 |< 3}, B={ x | |x+ 2 |v 1},求集合M使其同时满足下列三个条件:(1) M [(A U B n 乙;(2) M中有三个元素;(3) MA B M解:•/ A={ x | | 2x — 1 |< 3} = { x |—K x w 2}B={ x | |x+ 2 | v 1} = { x | —3v x v —1}• M : (A U B) n Z ] = { x |—1 w x w 2} U{ x |—3 v x v—1}A Z={ x |—3 v x w 2}A Z= {—2,—1, °, 1, 2}又••• M A B M ,•—2 € M又••• M中有三个元素•同时满足三个条件的M为:{一2,—1, °}, {—2,—1, 1} , {—2,一1, 2} , {—2, °, 1} , {—2, °, 2}, {—2, 1, 2}.【学后反思】解绝对值不等式,关键在于“转化”.根据绝对值的意义,把绝对值不等式转化为一次不等式(组).| x |v a与| x |> a(a> °)型的不等式的解法及利用数轴表示其解集.不等式| x | v a(a > °)的解集是{ x | —a v x v a}.其解集在数轴上表示为(见图1 —7):不等式| x | > a(a>°)的解集是{ x | x>a或x v —a},其解集在数轴上表示为(见图1 —8):把不等式| x |v a与| x |> a(a> °)中的x替换成ax+ b,就可以得到| ax+ b |v b与| ax+ b |> b( b > °)型的不等式的解法.。
