MS 中高对称设置;磁矩设置分析;密度泛函中GGA、LDA、LSDA的选择
incar中gga参数

incar中gga参数"incar" 是 VASP(Vienna Ab initio Simulation Package)软件中的一个输入文件,用于控制计算的各种参数。
而 "gga" 则代表广义梯度近似(Generalized Gradient Approximation),是一种处理交换-相关能的方法。
在 VASP 的 "incar" 文件中,可以通过设置一些参数来控制 GGA 相关的计算。
下面我将从不同角度来解释 "incar" 中的 "gga" 参数。
首先,"gga" 参数在 "incar" 文件中用于指定交换-相关泛函的类型。
在 VASP 中,可以设置 "gga" 参数为不同的值,如 "PE"(Perdew-Wang 91交换相关泛函)、"RP"(RevPBE交换相关泛函)等,以选择不同的交换-相关泛函来进行计算。
不同的泛函对于材料性质的计算会产生不同的影响,因此合理选择 "gga" 参数是非常重要的。
其次,"gga" 参数还可以影响计算的精度和速度。
不同的交换-相关泛函对计算的精度和收敛性会有所影响,有些泛函可能会导致计算更加耗时,而有些则可能会加快计算速度。
因此,在选择"gga" 参数时,需要权衡计算的精度和速度,以便在保证结果准确的前提下尽量提高计算效率。
此外,"gga" 参数还与磁性材料的计算有关。
对于包含磁性原子的体系,选择合适的 "gga" 参数对于计算磁性性质是至关重要的。
不同的交换-相关泛函对磁性材料的计算结果会产生不同的影响,因此需要根据具体的研究对象来选择合适的 "gga" 参数。
MS4.3磁性体系LDA+U计算设置

MS4.3磁性体系LDA+U计算设置MS 4.3磁性体系LDA +U 计算设置在最新发布的MS 版本中增加了LDA +U 的计算,这是MS 计算性能特别是CASTEP 模块的⼀次巨⼤提⾼,终于解决了已久的d ,f 轨道带隙分裂问题,也不会再被审稿⼈轻视认为是简单DFT 计算结果了。
这⾥讲解⼀下MS.43⾥⾯element 设置⽅⾯的问题,我们选择了Fe3O4体系,该体系是铁磁性的,计算该体系主要涉及到两个参数设置,⼀个是⾃旋设置(SPin parameters ),其次是Fe Hubbard 参数设置。
⾸先介绍需要⽤到的菜单:打开MS 之后看到主菜单,打开如下图所⽰的菜单:(点击此图,可放⼤观看)[ 本帖最后由xbaprs 于 2008-6-23 13:24 编辑 ]附件MS4.3 -1.JPG 、管路敷设技术通过管线敷设技术不仅可以解决吊顶层配置不规范⾼中资料试卷问题,⽽且可保障各类管路习题到位。
在管路敷设过程中,要加强看护关于管路⾼中资料试卷连接管⼝处理⾼中资料试卷弯扁度固定盒位置保护层防腐跨接地线弯曲半径标⾼等,要求技术交底。
管线敷设技术中包含线槽、管架等多项⽅式,为解决⾼中语同时切断习题电源,线缆敷设完毕,要、电⽓课件中调试对全部⾼中资料试卷电⽓设备,在安装过程中以及安装结束后进⾏⾼中资料试卷调整试验;通电检查所有设备⾼中资料试卷相互作⽤与相互关系,根据⽣产⼯艺⾼中资料试卷要求,对电⽓设备进⾏空载与带负荷下⾼中资料试卷调控试验;对设备进⾏调整使其在正常⼯况下与过度⼯作下都可以正常⼯作;对于继电保护进⾏整核对定值,审核与校对图纸,编写复杂设备与装置⾼中资料试卷调试⽅案,编写重要设备⾼中资料试卷试验⽅案以及系统启动⽅案;对整套启动⼚家出具⾼中资料试卷试验报告与相、电⽓设备调试⾼中资料试卷技术电⼒保护装置调试技术,电⼒保护⾼中资料试卷配置技术是指机组在进⾏继电保护⾼中资料试卷总体配置时,需要在最⼤限度内来确保机组⾼中资料试卷安全,并且尽可能地缩⼩故障⾼中资料试卷破坏范围,或者对某些异常⾼中资料试卷⼯况进⾏⾃动处理,尤其要避免错误⾼中资料试卷保护装置动作,并且拒绝动作,来避免不必要⾼中资料试卷突⾏外部电源⾼中资料试卷切除从⽽采⽤由于计算体系位Fe3O4,计算采⽤USPP 完成,Fe 的USPP 价电⼦参数为3d64s2,O 是2s22p4,结构中的磁性主要来⾃于Fe 原⼦磁矩的定向排列,计算中⾃旋参数和Hubbard 参数主要是针对Fe 调整。
LCMS仪器方法优化流程及注意事项

+
++ + - -- + -+ +
+ + -- + +
+
+
溶剂离子簇
+ + +
+
分析离子
ESI实验条件优化
气相离子的产生
表面活性高(具低溶剂化能)的离子将优先转移至雾滴表面,最
终转变为气相离子,故有较高的实验灵敏度—竞争机制:
应采用表面活性低的缓冲剂;
采用低浓度的挥发性的酸、碱及缓冲盐;
分子离子 分子离子是样品分子失去或得到一个电子而形成的M+•。分子离子代表
完整的样品分子,是其所有碎片离子的终极前体(ultimate precursor)。
准分子离子 取决于化合物的性质和质谱离子化方法及条件,可生成质子化或去质 子的分子,即[M+H]+、[M-H]-及加合物离子,如[M+Na]+、[M+Cl]-等,这些均为 偶电子(even electron)离子。 同位素峰 这是由于有丰度的较低的同位素存在而产生的 。
That’s really all there is 有多少
是什么?
和/或
定量信息
质谱峰的强度,色谱峰的峰面积
20
高分辨质谱和元素组成
高分辨质谱——准确质量,元素组成
1000
176 386
100 formulas
882
10
1347 1672
Possible
1
5687
0.1
0.05
0.01
断裂程度
APCI源的探头处于高温,对热不稳定的化合物就足以使其分解. 灵敏度 ESI有利于分析生物大分子及其它分子量大的化合物,而APCI更适合于 分析极性较小的化合物。 APCI源不能生成一系列多电荷离子,ESI可生成一系列多电荷离子 与ESI不同, APCI也是正相液相色谱-质谱的接口
vasp经验总结

加U(LMCO为例)
LDAU=.TRUE. LDAUTYPE=2 #The simplified (rotationally invariant) approach to the LSDA+U
#specifies the l-quantum number for which the on-site LDAUL= -1 2 2 -1 interaction is added (-1=no on-site terms added, 1= p, 2= d, 3= f, Default: LDAUL=2)
bnd000.dat文件的第一列数据是k点距离的绝对值,第二列数据是以 Ferim level为参考的本征值。
简立方的高对称点
能量本征值文件EIGENVAL
第一行,前三个整数无意义,第四个整数,如果是2, 表 示是自旋极化的计算,如果是1, 表示非自旋极化的计算。
60 60 1 1 0.1158924E+02 0.5522500E-09 0.2280000E-08 0.5522500E-09 0.5000000E-15 1.000000000000000E-004 第2至5行的数据含义不大明确,可以不管它。 CAR YFTO 492 32 300 第6行的数据表示:第一个数表示体系总的价电子数目,第二个数 表示的计算能带时总的k点数目,第三个数表示的是计算能带时计 算了多少条能带。 0.3742002E-15 0.1262379E-14 0.3742002E-15 0.1388889E-01 1 -46.511682 第8行的前三个数是k点的坐标,第四个数是相 2 -46.511280 应k点的权重。 3 -46.451176 4 -46.449273 第9行给出的是该k点对应的本征值的序号(即第几 5 -46.199455 条能带),及相应的本征值。 6 -46.197355
高斯软件各半密度泛函方法

高斯软件各半密度泛函方法
高斯软件是一款常用的计算化学软件,其中包括了多种不同的半密度泛函方法来进行量子化学计算。
半密度泛函方法是一种适合用于大分子系统的计算方法,它通过将电子密度分成密度矩阵和密度响应函数两部分来描述电子行为。
在高斯软件中,常用的半密度泛函方法包括:
1. LDA(局域密度近似):这是最简单的半密度泛函方法之一,利用电子密度的局域性质来近似电子-电子相互作用。
2. GGA(广义梯度近似):在LDA的基础上,引入了密度梯
度的信息,以更准确地描述分子中的电子行为。
3. Meta-GGA(元GGA):这是一类对电子密度、密度梯度和动能密度进行更高级近似的方法,从而提供更准确的物理描述。
除了上述常用的半密度泛函方法外,高斯软件还支持许多其他半密度泛函方法,如B3LYP、M06-L、ωB97X-D等。
这些方
法针对不同的应用和分子体系提供了不同的精度和计算效率。
总的来说,高斯软件提供了多种半密度泛函方法来进行量子化学计算,用户可以根据具体的研究需求选择适合的方法。
material studio密度泛函方法

material studio密度泛函方法
密度泛函方法(Density Functional Theory,DFT)是一种计算
凝聚态物理系统的电子结构的方法,可以用于预测分子和固体材料的性质。
在Material Studio软件中,DFT方法使用了一些基本的密度泛
函近似,例如局域密度近似(Local Density Approximation,LDA)和广义梯度近似(Generalized Gradient Approximation,GGA)等。
这些近似方法都是根据密度泛函理论的基本原理
和近似处理方式得到的。
使用密度泛函方法,可以计算材料的电子结构、总能量、电子密度分布、能带结构、原子间力和原子位置等性质。
这些结果可以用于研究材料的性质、反应机理、吸附性能、光学性质等。
在Material Studio中,密度泛函方法通常是由VAMP
(VAMP/VASP)模块来实现的。
用户可以选择不同的泛函和
基组,以及其他计算参数来进行模拟和计算。
同时,Material Studio还提供了一些可视化和后处理工具,以便对计算结果进
行分析和可视化展示。
总而言之,Material Studio中的密度泛函方法是进行凝聚态材
料电子结构计算和预测性质的重要工具,能够提供有关材料性质和行为的重要信息。
MS 4.3磁性体系LDA+U计算设置

MS 4.3磁性体系LDA+U计算设置在最新发布的MS版本中增加了LDA+U的计算,这是MS计算性能特别是CASTEP模块的一次巨大提高,终于解决了已久的d,f轨道带隙分裂问题,也不会再被审稿人轻视认为是简单DFT计算结果了。
这里讲解一下MS.43里面element设置方面的问题,我们选择了Fe3O4体系,该体系是铁磁性的,计算该体系主要涉及到两个参数设置,一个是自旋设置(SPin parameters),其次是Fe Hubbard参数设置。
首先介绍需要用到的菜单:打开MS之后看到主菜单,打开如下图所示的菜单:(点击此图,可放大观看)[本帖最后由 xbaprs 于 2008-6-23 13:24 编辑]附件MS4.3 -1.JPG由于计算体系位Fe3O4,计算采用USPP完成,Fe的USPP价电子参数为3d64s2,O是2s22p4,结构中的磁性主要来自于Fe原子磁矩的定向排列,计算中自旋参数和Hubbard参数主要是针对Fe调整。
再建造好Fe3O4结构之后(注MS结构库中包含此结构),为一个面心立方晶格,一个惯用晶胞包含8个Fe3O4单位,因此整个结构有24个Fe原子,32个O。
计算可以采用FCC结构的初级晶胞结构,也可以采用惯用晶胞。
我们计算采用后者。
打开Modify-electronic configuration菜单,看到Spin和Hubbard U两个子菜单如图:SPin主要是自旋控制参数,由于再铁磁性结构中Fe自旋是高度极化的,因此这个地方设置为High spin state,即3d6结构为4个自旋平行同向电子。
自旋方向不管是Up还是Down当然不会改变Fe原子自旋极化的性质,但会改变总的磁矩(自旋电子数目,这点会再CASTEP计算参数Spin设置中体现出来,可以尝试把部分Fe原子自旋改成High,SPin up,部分为High,Down,然后查看CASTEP计算控制面板的SPin数值)。
报错解决

设置:初始值收敛值结果AMIX =0.0100;BMIX =0.0001 AMIX = 0.01; BMIX = 0.00 计算无误AMIX = 0.1000;BMIX = 0.0010 AMIX = 0.10; BMIX = 0.00 计算无误AMIX =0.20; BMIX = 0.01 AMIX =0.20; BMIX = 0.01 计算无误AMIX=0.2、BMIX=0.001 AMIX=0.2、BMIX=0.001 计算无误AMIX=0.3、BMIX=0.1 AMIX=0.3、BMIX=0.1 计算无误AMIX=0.4 AMIX = 0.40; BMIX = 1.00 静态log: WARNING in EDDRMM: call toZHEGV failed, returncode = 6 3 **,能带一样AMIX=0.02 AMIX = 0.02; BMIX = 1.00 计算无误AMIX=0.1 AMIX = 0.10; BMIX = 1.00 静态log: WARNING in EDDRMM: call toZHEGV failed, returncode = 6 3 **,能带一样AMIX=0.3 AMIX = 0.30; BMIX = 1.00 静态log: WARNING in EDDRMM: call toZHEGV failed, returncode = 6 3 **,能带一样BMIX=0.0001 AMIX = 0.40; BMIX = 0.00 计算无误以上参数设置,得到的能带图都一样,如下图:综上:设置AMIX=0.2(或0.3),BMIX默认(省事,等于1.0),可以保证计算过程无误。
还需进一步调整其他参数,算出正确的能带。
警告:算1QL弛豫、静态、能带时,都有这个提示:ADVICE TO THIS USER RUNNING 'V ASP/V AMP' (HEAR YOUR MASTER'S VOICE ...): You have a (more or less)'small supercell' and for smaller cells it is recommended to use the reciprocal-space projection scheme! The real space optimization is not efficient for small cells and it is also less accurate ... Therefore set LREAL=.FALSE. in the INCAR file对策:对于较小的晶胞(原子数小于20),设置LREAL=.FALSE.,计算结果比较精确。
常用INCAR设置及说明

一、opt(黑色参数为常用,蓝色为不常用)Global Paramemters1. ISTART = 0决定V ASP程序是否在开始时读入波函数,常用的设置有0、1和2。
其中ISTA RT=0代表从头开始计算,不读入波函数文件。
ISTART=1代表读入已有波函数,并继续计算,此时新计算的原胞大小和形状可以和已有波函数中的不同,截断能也可以不同; ISTART=2也代表读入已有波函数,但截断能和原胞都不能改变。
I START有默认设置,如果V ASP程序开始时,没有找到波函数WA VECAR,则IS TART=0,否则为1。
因此通常不需要设置这个参数。
2. ISPIN = 2自旋极化计算开关。
默认值为ISPIN=1,即做非磁性计算; ISPIN=2,做自旋极化计算。
如果做非共线磁结构计算(LNONCOLLINEAR=.TRUE.),则不需要设置ISPI N参数。
3. ICHARG = 2决定V ASP程序是否在开始时读入电荷密度,常用的设置有0、1、2和1.其中I CHARG=0代表从初始的轨道计算电荷密度: ICHARG=1代表读入已有电荷密度文件CHGCAR,并开始新的自洽计算; ICHARG=2代表直接使用原子电荷密度的叠加作为初始密度; ICHARG=11代表读入已有电荷密度,并进行非自洽计算,通常用于电子能带和态密度计算,在此过程中电荷密度保持不变。
在非自洽计算时,特别是在做IDA+U计算时,建议设置LMAXMIX=4(对于d轨道元素)或者6(对于f轨道元素)。
4. LWA VE = .F.5. LCHARG = .F.确定是否输出波函数和电荷密度文件。
6. ENCUT = 500平面波截断能,决定平面波的个数,即基组的大小。
这是一个非常重要的参数,决定了计算的精度。
ENCUT越大,计算精度越高,但计算量会越大。
V ASP可以直接从POTCAR中得到每个元素默认的截断能,并且取最大值作为整个计算ENCUT的默认值。
gc-ms的技术要求

GC-MS技术分析条件的选择主要包括色谱和质谱条件的选择。
在色谱条件中,选择合适的色谱柱类型是关键,常用的色谱柱类型包括填充柱和毛细管柱。
对于极性样品,应选择极性毛细管柱;非极性样品,应选择非极性毛细管柱;对于未知样品,可先试用中等极性毛细管柱,然后再根据需要进行调整。
此外,还要设置汽化温度、载气流量、分流比、温升程序等参数。
在质谱条件中,需要根据样品情况设定电离电压、电子电流、扫描速度和质量范围等参数。
为了保护灯丝和倍增器,还需要设置溶剂去除时间。
此外,GC-MS分析还需要注意进样系统和色谱柱的选择。
进样系统可以根据待测物性质和样品特点进行选择,以实现对复杂样品的高效分离和分析。
色谱柱类型、长度和内径的选择也十分重要,可以影响分离效果、分辨率和灵敏度。
综上所述,GC-MS技术要求涉及到色谱、质谱、进样系统和色谱柱的选择等多个方面。
根据不同的样品特性和分析需求,选择合适的条件和参数是保证分析结果准确性和稳定性的关键。
materialstudio一些基础设置问题

CASTEP的任务1. CASTEP能量任务CASTEP能量任务允许您计算指定系统的总能量,以及它的物理性质。
除了总能量,原子上的力也会在计算结束时报告。
还创建了一个电荷密度文件,允许使用可视化工具直接观察电荷密度的空间分布。
还报告了在计算中使用的monkhorst - pack k点的电子能量,以便在CASTEP分析过程中生成态密度图。
能量任务对于研究可靠的结构信息体系的电子特性是非常有用的。
只要指定了应力特性,它也可以用来计算没有内部自由度的高对称系统的状态方程(即压力体积和/或能量-体积依赖)。
注意:在具有内部自由度的系统中,可以利用几何优化任务得到状态方程。
CASTEP的能量的默认单位是电子伏特(eV)。
1 eV= 0.036749308 Ha =23.0605 kcal/mole =96.4853 kJ/mole2. CASTEP几何优化任务CASTEP几何优化任务允许优化几何结构,以获得一个稳定的结构或多态性。
这是通过执行一个迭代的过程来完成的,在这个过程中,原子的坐标和可能的原胞参数被调整,从而使结构的总能量是最小的。
CASTEP几何优化是基于减小计算力和应力的大小,直到它们变得小于定义的收敛误差。
此外,还可以指定一个外部应力张量,来模拟在张力、压缩、剪切等情况下系统的行为。
在这些情况下,内部应力张量是迭代的,直到它等于施加的外部应力。
几何优化的过程一般会产生一个与实际结构相似的模型结构。
用CASTEP计算的晶格参数的准确性如图1所示(Milman等,2000)。
Figure 1. Experimental vs. CASTEP calculated lattice parameters状态方程的计算应用流体静压法的几何优化可用于确定材料的体积模量,B,压力导数、B ' = dB / dP。
这个过程包括计算状态方程(EOS),它描述了细胞体积对外部流体静压的依赖。
该方法与实际实验非常相似:在几何优化对话框中使用最小化选项键确定外部压力,通过对CASTEP进行几何优化来确定压力的单元体积。
castep中关于磁性的设置

版内有这方面的内容顺磁,意味进行non-spin polarized的计算,也就是ISPIN=1。
铁磁,意味进行spin-polarized的计算,ISPIN=2,而且每个磁性原子的初始磁矩设置为一样的值,也就是磁性原子的MAGMOM设置为一样的值。
对非磁性原子也可以设置成一样的非零值(与磁性原子的一样)或零,最后收敛的结果,非磁性原子的local磁矩很小,快接近0,很小的情况,很可能意味着真的是非磁性原子也会被极化而出现很小的local磁矩。
反铁磁,也意味着要进行spin-polarized的计算,ISPIN=2,这是需采用反铁磁的磁胞来进行计算,意味着此时计算所采用的晶胞不再是铁磁计算时的最小原胞。
比如对铁晶体的铁磁状态,你可以采用bcc的原胞来计算,但是在进行反铁磁的Fe计算,这是你需要采用sc的结构来计算,计算的晶胞中包括两个原子,你要设置一个原子的MAGMOM为正的,另一个原子的MAGMOM设置为负,但是它们的绝对值一样。
因此在进行反铁磁的计算时,应该确定好反铁磁的磁胞,以及磁序,要判断哪种磁序和磁胞是最可能的反铁磁状态,那只能是先做好各种可能的排列组合,然后分别计算这些可能组合的情况,最后比较它们的总能,总能最低的就是可能的磁序。
同样也可以与它们同铁磁或顺磁的进行比较。
了解到该材料究竟是铁磁的、还是顺磁或反铁磁的。
亚铁磁,也意味要进行spin-polarized的计算,ISPIN=2,与反铁磁的计算类似,不同的是原子正负磁矩的绝对值不是样大。
非共线的磁性,那需采用专门的non-collinear的来进行计算,除了要设置ISPIN,MAGMOM的设置还需要指定每个原子在x,y,z方向上的大小。
这种情况会复杂一些。
举个例子来说,对于Mn-Cu(001)c(2x2)这种体系,原胞里面有2个Mn原子,那么你直接让两个Mn原子的MAGMOM的绝对值一样,符号相反就可以了,再加上ISPIN=2。
MS 4.3磁性体系LDA+U计算设置

MS 4.3磁性体系LDA+U计算设置在最新发布的MS版本中增加了LDA+U的计算,这是MS计算性能特别是CASTEP模块的一次巨大提高,终于解决了已久的d,f轨道带隙分裂问题,也不会再被审稿人轻视认为是简单DFT计算结果了。
这里讲解一下MS.43里面element设置方面的问题,我们选择了Fe3O4体系,该体系是铁磁性的,计算该体系主要涉及到两个参数设置,一个是自旋设置(SPin parameters),其次是Fe Hubbard参数设置。
首先介绍需要用到的菜单:打开MS之后看到主菜单,打开如下图所示的菜单:(点击此图,可放大观看)[本帖最后由 xbaprs 于 2008-6-23 13:24 编辑]附件MS4.3 -1.JPG(144.69 KB)2008-6-23 13:23由于计算体系位Fe3O4,计算采用USPP完成,Fe的USPP价电子参数为3d64s2,O是2s22p4,结构中的磁性主要来自于Fe原子磁矩的定向排列,计算中自旋参数和Hubbard参数主要是针对Fe调整。
再建造好Fe3O4结构之后(注MS结构库中包含此结构),为一个面心立方晶格,一个惯用晶胞包含8个Fe3O4单位,因此整个结构有24个Fe原子,32个O。
计算可以采用FCC结构的初级晶胞结构,也可以采用惯用晶胞。
我们计算采用后者。
打开Modify-electronic configuration菜单,看到Spin和Hubbard U两个子菜单如图:SPin主要是自旋控制参数,由于再铁磁性结构中Fe自旋是高度极化的,因此这个地方设置为High spin state,即3d6结构为4个自旋平行同向电子。
自旋方向不管是Up还是Down 当然不会改变Fe原子自旋极化的性质,但会改变总的磁矩(自旋电子数目,这点会再CASTEP 计算参数Spin设置中体现出来,可以尝试把部分Fe原子自旋改成High,SPin up,部分为High,Down,然后查看CASTEP计算控制面板的SPin数值)。
MS 4磁性体系LDA+U计算设置
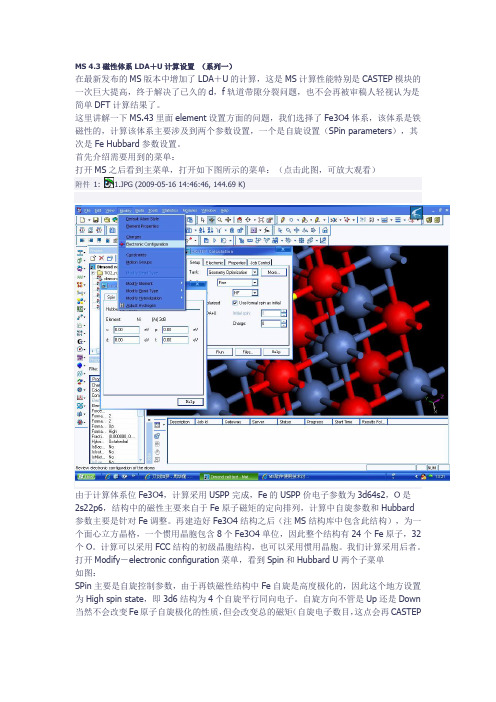
MS 4.3磁性体系LDA+U计算设置(系列一)在最新发布的MS版本中增加了LDA+U的计算,这是MS计算性能特别是CASTEP模块的一次巨大提高,终于解决了已久的d,f轨道带隙分裂问题,也不会再被审稿人轻视认为是简单DFT计算结果了。
这里讲解一下MS.43里面element设置方面的问题,我们选择了Fe3O4体系,该体系是铁磁性的,计算该体系主要涉及到两个参数设置,一个是自旋设置(SPin parameters),其次是Fe Hubbard参数设置。
首先介绍需要用到的菜单:打开MS之后看到主菜单,打开如下图所示的菜单:(点击此图,可放大观看)附件1: 1.JPG (2009-05-16 14:46:46, 144.69 K)由于计算体系位Fe3O4,计算采用USPP完成,Fe的USPP价电子参数为3d64s2,O是2s22p6,结构中的磁性主要来自于Fe原子磁矩的定向排列,计算中自旋参数和Hubbard参数主要是针对Fe调整。
再建造好Fe3O4结构之后(注MS结构库中包含此结构),为一个面心立方晶格,一个惯用晶胞包含8个Fe3O4单位,因此整个结构有24个Fe原子,32个O。
计算可以采用FCC结构的初级晶胞结构,也可以采用惯用晶胞。
我们计算采用后者。
打开Modify-electronic configuration菜单,看到Spin和Hubbard U两个子菜单如图:SPin主要是自旋控制参数,由于再铁磁性结构中Fe自旋是高度极化的,因此这个地方设置为High spin state,即3d6结构为4个自旋平行同向电子。
自旋方向不管是Up还是Down 当然不会改变Fe原子自旋极化的性质,但会改变总的磁矩(自旋电子数目,这点会再CASTEP计算参数Spin设置中体现出来,可以尝试把部分Fe原子自旋改成High,SPin up,部分为High,Down,然后查看CASTEP计算控制面板的SPin数值)。
MassHunter 工作站软件 定性分析气质入门指南

Agilent MassHunter 工作站软件定性分析GC/MS 入门指南声明© Agilent Technologies, Inc. 2012按照美国和国际版权法的规定,未经Agilent Technologies, Inc. 事先同意和书面许可,不得以任何形式或采取任何手段(包括电子存储和检索或翻译成其他语言)复制本手册中的任何内容。
手册部件号G3335-97147版本修订版 A,2012 年 11 月美国印刷Agilent Technologies, Inc.5301 Stevens Creek Blvd.Santa Clara, CA 95051 USA 担保本文档中包含的材料按“现状”提供,若在后续版本中有任何更改,恕不另行通知。
而且,在适用法律允许的最大范围内,Agilent 不对本手册及其所包含的信息做出任何明示或暗示的担保,其中包括但不限于对适销性和对具体用途适用性的暗示的担保。
Agilent 不对因提供、使用或执行本文档或其中所包含的信息而造成的任何错误或任何意外或附带的损失承担责任。
如果Agilent 与用户签有单独的书面协议,且协议中涉及本文档所含材料的担保条款与上述条款发生冲突,则该书面协议中的担保条款具有优先法律效力。
技术许可本文档中所述的硬件和/或软件是依据许可提供的,且只能根据此类许可的条款进行使用或复制。
受限权利声明美国政府受限权利。
授予联邦政府的软件和技术数据权利仅包括通常提供给最终用户的那些权利。
Agilent 根据 FAR12.211(技术数据)和 12.212(计算机软件)和(对于国防部)DFARS 252.227-7015(技术数据-商品)以及 DFARS227.7202-3(商业计算机软件或计算机软件文档中的权利)来提供软件和技术数据方面的此常规商业许可。
安全声明小心小心声明表示存在危险。
它表示在执行某个操作步骤或操作方法时必须加以注意;如果操作不当或没有遵守相应的规程,则可能会导致产品损坏或重要数据丢失。
GC-MS操作规程

GC-MS操作规程开机步骤:打开电脑--打开气体阀门(养成习惯,只开关总阀,分压阀调到0.3-0.5MPa之间)--开质谱--开气相(气相面板上显示开机正常)--双击桌面绿色图标软件GCMSD--开机完成注:MS温度对话框自动弹出后,点应用,点关闭。
头一天开机,第二天测样,保证仪器过夜完全抽真空。
关机步骤:和关机相反,方法--调用方法(off.M)--面板上仪器真空控制--放空--关闭--关闭电脑软件--关闭气相--关闭质谱--关闭气体--关电脑总体步骤:创建方法--创建序列--放置样品--运行序列--数据处理(定性、定量),下面分别对各部分进行详细介绍1、创建方法1.1创建定性方法方法--方法另存为(命名,均以.M为后缀,存储位置使用默认的位置,最好不要更改)--编辑整个方法--确定两次--出现进样口和进样参数,选择进样方式为GC自动进样器,其他默认,这时出现新的对话框:第一步:点击配置模式下的色谱柱,单击编号1,出现编辑已安装GC柱的属性,点击从目录选择,选择实验所需要的色谱柱,完成。
点击前进样器,所有参数默认不更改(进样量1,5个3,一个6);第二步:进样口参数设置,需要更改的有加热器温度、模式、分流比(一般样品浓度越大,分流比越大),从标准方法或者文献中获得具体的参数;第三步:色谱柱参数设置,流速一般都是1;第四步:柱箱参数设置,可以是恒温,也可以是变速(升温速率定后,保持时间自动设定);第五步:辅助加热器(加热温度指的是气相与质谱的接口,一般通过文献定,若无,默认250)完成后点击确定,再次确定,出现单四级杆MS方法编辑器,将采集类型选为扫描模式,此模式下是全扫,定性用。
1.2创建定量方法重复以上步骤,方法另存为的命名方式以SIM.M为后缀,其他所有参数都一样,只是在单四级杆MS方法编辑器对话框下将采集类型更改为SIM模式。
接下来进行SIM时间段对话框的编辑。
若是已知样品,定性离子(1个),定量离子都已知,未测样前就可编辑,若是未知样,必须依据全扫的色谱图和质谱图来确定定性离子个数。
MS常见问题及解答( Materials Studio )

MS常见问题及解答1、问:用MS构造晶体时要先确立空间群,可是那些空间群的代码是啥意思啊,看不懂,我想做的是聚乙烯醇的晶体,嘿嘿,也不知道去哪可以查到它的空间群答:A、要做晶体,首先要查询晶体数据,然后利用晶体数据再建立模型。
晶体数据来源主要是文献,或者一些数据库,比如CCDC。
(你都不知道这个晶体是怎么样的,怎么指定空间群呢?要反过来做事情哦:)B、我不知道你指示的代码是数字代码还是字母代码,数字代码它对应了字母的代码,而字母的代码它含盖了一些群论的知识(晶系,对称操作等),如果要具体了解你的物质或者材料属于那一个群,你可以查阅一下相关的手册,当然你要了解一些基本的群论知识.MS自带了一些材料的晶体结构,你可以查询一下.2、问:各位高手,我用ms中的castep进行运算。
无论cpu是几个核心,它只有一个核心在工作。
这个怎么解决呢?答:请先确认以下几个问题:1,在什么系统下装,是否装了并行版本。
2,计算时设置参数的地方是否选择了并行。
3,程序运算时,并不是时时刻刻都要用到多个CPU3、问:我已经成功地安装了MS3.1的Linux版本,串行的DMol3可以成功运行。
但是运行并行的时候出错。
机器是双Xeon5320(四核)服务器,rsh和rlogin均开启,RHEL4.6系统。
其中hosts.equiv的内容如下:localhostibm-c*****olemachines.LINUX的内容如下:localhost:8现在运行RunDMol3.sh时,脚本停在$MS_INSTALL_ROOT/MPICH/bin/mpirun $nolocal -np $nproc$MS_INSTALL_ROOT/DMol3/bin/dmol3_mpi.exe $rootname$DMOL3_DATA这一处,没法执行这一命令并行运算时,出现以下PIxxxx(x为数字)输出ibm-c*****ole 0 /home/www/MSI/MS3.1/DMol3/bin/dmol3_mpi.exelocalhost 3 /home/www/MSI/MS3.1/DMol3/bin/dmol3_mpi.exe请问这是什么原因?谢谢!答:主要是rsh中到ibm-c*****ole的没有设置把/etc/hosts改为127.0.0.1 localhost.localdomain localhost ibm-c*****ole在后面加个ibm-c*****ole也希望对大家有帮助!4、问:在最后结果的dos图中,会显示不同电子spd的贡献,我想问的是,假设MS考虑的原子Mg的电子组态为2p6 3s2,那么最后的dos结果中的s,p是不是就是2p,跟3s的贡献.比如更高能量的3p是否可能出现在dos中?如果可能的话,在这种情况下,如何区分2p和3p的贡献,谢谢.答:A、取决于你的餍势势里面没有3p电子,DOS怎么会有呢?自然,你的1p1s也不会出现在你的DOS中。
分析参数设定的一般原则

分析参数设定的一般原则问题一、ICP可以测定哪些项目?答:理论上ICP-AES可以测定元素周期表中标有红色外的75个元素,但实际上要根据你的仪器配置和实际样品类型。
比如C,N,Ar,O,H就因为空气和水中存在,或者采用了Ar气而无法测定。
另外因为你的仪器只配置水溶液进样系统而无法测定高盐样品和有机样品。
如果需要测定高盐样品和有机样品及用HF处理的样品需要相应的高盐、有机、耐HF酸进样系统。
问题二、谱线如何选择和优化处理?答:谱线的选择:一般原则:1、对于微量元素的分析,要采用灵敏线,对于高含量元素的分析,要采用次灵敏线;2、UV段尽量选择位置居CID图谱中央的谱线,VIS区的谱线要在同等条件下选择背景低(远离氩线带)的谱线。
3、根据在样品基体及成分的不同,尽量选择无干扰或者干扰小的谱线。
4、选择测定线性好、准确性和稳定性高的谱线。
具体选择:1、选择经过校对过的谱线;2、选择3到5条不同波长的较灵敏的谱线(一般为前3-5条)作为分析用谱线,依次标准化和测定结果;3、一般有2到3个不波长的测定结果接近或者一致,从概率论而言其结果应该更接近真实值。
(因为不同波长出现相同干扰的概率应该很小)。
4、在第2条的基础上,如果有多点标准校准的,选择曲线线性好的谱线结果。
(曲线相关系数高的)。
5、在确保上述情况下,选择谱线强度高(灵敏性高)的谱线。
6、选择谱线干扰小的谱线的结果(从结果的谱线峰形图看:积分位置居中,两边背景低而平)。
如果几根谱线的结果都不一致或者接近,那么我们需要逐个考察其干扰情况,点击结果查看谱线峰形图,确保其积分位置居中,然后调整背景扣除位置和选择。
然后做处理后,查看结果后按上述处理原则做选择和判断。
待方法成熟后,删除不用的方法保存,OK。
如果有已知结果的质量控制样,我们可以尽快选择出正确的谱线:正确的谱线其标准为: A 结果最接近真实值(准确性高);B 测定结果的精密度(稳定性)好;C 谱线的谱峰干扰小;D 谱线的线性关系好;ICP-OES分析参数设定的一般原则一、一般水溶液的分析的条件标准曲线法RF:950-1150wNebulizer:0.15-0.25MPaAUX:0.5 -1.0 L/minPump Rate:50-80r/min选择用带1.5mm管径中心管(一条红圈)、水溶液雾化器、旋流同心雾化室;A、单独分析K、Na等易离解的元素请选择RF 900-1000W,AUX:1.0-1.5 L/min、Pump Rate:50-70r/min Nebulizer 0.15-0.25MPaB、单独分析As Sb Se Cd等难离解的元素请选择RF 1150-1350W,AUX:0.5 L/min、Pump Rate:60-80r/min, Nebulizer: 0.15-0.20MPaC、样品中既有难电离和易电离元素及中间元素可按一般水溶液条件选择。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
体系的哈密顿量 H=T+V+U 可以表示为: 电子-原子核间 原子核的 电子的 总动能 总动能 库仑相互作用
2 2 Ri ˆ H 2M i i 2 2 ri 2me i
2
Zi e2 1 i j 4 0 Ri rj Zi Z j e2
密度泛函交换相关势的选择
能带结构高对称点设置
磁矩数据分析
张恺琪
Hebei Normal University
第一性原理计算时,密度泛函理论中交换相关势的选择
区别
GGA函理论 (DFT)
最早由 Hohenberg、Kohn 和 Sham 提出。对于一个多粒子体系,
E FHK ( r ) d r.
The effective single-particle potential is usually written as: Vs V VH Vxc . V:电子-原子核 库仑相互作用 VH:电子-电 子间库仑斥力 Vxc:所有电子 间交换关联势
U (Ry) 0.19 0.20 0.205 0.2 0.21 0.215
过渡金属的 U 数值和 d 电子排列以及价态有关系,上面的数值是 一个大概的估算数值。
Reference: Physical Review B Vol. 50, Iss. 23, 1994.
高对称点 如何选择,设定?
高对称点
LDA/GGA+U
强关联电子体系:电子间相互作用不可忽略的系统。传统的能带 理论是建立在单电子近似基础上的,忽略了电子之间相互作用, 将电子系统视为相互独立的理想气体,考虑单电子与晶体的周期 结构之间的相互作用,得到了固体的能带结构。然而,在一些物
质 (强关联电子体系) 中,由于电子之间的强相互作用较强,不
High-throughput electronic band structure calculations: Challenges and tool, Computational Materials Science 49 (2010) 299–312
CASTEP 中,高对称点的设置
修改
单击,对 任意对称 点进行更 改,名称 与坐标
DFT 理论中存在的主要问题是交换相关势 Vxc 是未知的,近似 的引入可以很好地解决这个难题。 GGA (generalized gradient approximation) Vxc Vxc n( r ), n( r )
在 LDA 基础上作了一定修 正,认为交换关联能不仅 与小单元体积内的电子密 度相关,并且与邻近单元 的电子密度也相关,引进 了密度梯度的思想。 与 LDA 相比 GGA 结果更 准确,GGA 泛函给出的半 导体带隙值通常比 LDA 更 接近于实验真实值。
1 1 e 1 1 2 i 1 j 1 4 0 ri rj 2 i 1 j 1 4 0 Ri R j
(i j ) (i j )
电子-电子间库 仑相互作用
原子核-原子核 间库仑相互作用
原子核质量 >>电子质量 原子核相对位置是不变的
Born-Oppenheimer Approximation
Hartree-Fock Approximation: It succeeds in mapping a manyelectron problem with U onto a one-electron problem without U. Hohenberg-Kohn 密度泛函理论 基态总能是关于电子密度函数的唯一泛函:
添加对称点
删除对称点
Materials Studio 计算结构磁矩,设置和数据分 析
总磁矩 原子磁矩
总磁矩
计算结果 **.CASTEP文件中
2×Integrated Spin Density A
Spin up 和 Spin down 通道自旋极化 DOS 积分的差值
2×Integrated |Spin Density|B
第一布里渊区 (倒易点阵的维格纳-赛兹原胞 (WS unit cell) ),在计算晶体电子的能 带结构时由 Wigner-Seitz 提出来的一种原胞。它是晶格中比较对称的一种原胞。选
取方法:以某个格点为中心,作其与近邻格点连线的垂直平分面,由这些平分面构成
的单元。
bcc
fcc
四方晶系
六方晶系
计算能带结构时,关于高对称点的选择,可以参考:
LDA (local density approximation) Vxc Vxc n( r )
将材料无限分割成为各个 具有均匀电子密度的小单 元,每个单元对整个交换 关联泛函的贡献等同于相 同体积的均匀电子气的贡 献。 适用于密度变化较小的体 系,但对于电子密度变化 较大的体系,计算误差较 大,不适用。
3d Elements U (Ry) V 0.25 Cr 0.26 Mn 0.28 Fe 0.3 Co 0.31 Ni 0.31 4d Elements Nb Mo Tc Ru Rh Pd 5d Elements Ta W Re Os Ir Pt
U (Ry) 0.19 0.2 0.21 0.22 0.25 0.29
能被忽略。这时就需要引入电子间的相互作用 (加 U) 加以修正。 加 U 主要是针对含 d 电子的过渡金属氧化物,包含非满层 f 轨 道的元素等,高温超导体强关联体系。
1 Ry = 13.6 eV Reference: Vladimir I. Anisimov, Jan Zaanen, and Ole K. Andersen. Band theory and Mott insulators: Hubbard U instead of Stoner I, PRB Vol. 44, Iss. 3 (1991).
自旋极化 DOS 绝对值积分相加
顺磁性
反铁磁 铁磁性
A≈B
A ≈ 0, B=2A A,B 都比较大
原子磁矩
计算结果 **.CASTEP文件中
谢谢!
LSDA (local spin density approximation)
Vxc Vxc n( r ), m( r )
磁性晶体和原子序数 较大的晶体,还应考 虑自旋-轨道耦合
Ref. J. M. D. Coey. Magnetism and Magnetic Materials, 160.
