2022年高考数学总复习:抛物线
高考数学——抛物线-考点复习

【名师点睛】本题主要考查了抛物线的定义,抛物线的标准方程,属于中档题. @#网
典例 2 抛物= 线 y2 2 px( p > 0) 上的动点 Q 到其焦点的距离的最小值为 1,则 p =
1
A.
2
C.2
B.1 D.4
【答案】C
本题选择 C 选项. 【名师点睛】本题主要考查抛物线的定义及其应用,意在考查学生的转化能力和计算求解能力.由题意结合 抛物线的定义确定点的位置,然后求解 p 的值即可.
3
B.
2 9
D.
4
8.曲线 y = 2x2 上两点 A( x1, y1 )、B ( x2 , y2 ) 关于直线 y=
3
A.
2 5
C.
2
B. 2 D. 3
x
+
m 对称,且
x1
⋅
x2
=− 1 2
,则
m
的值为
9.已知抛物线 y2=2px(p>0)的焦点为 F,抛物线上的两个动点 A,B 始终满足∠AFB=60°,过弦 AB 的中点 H 作抛
PF= x + p 或 PF= y + p ,使问题简化.
2
2
3
典例 1 平面内动点 P 到点 F (0, 2) 的距离和到直线 l : y = −2 的距离相等,则动点 P 的轨迹方程为是
_____________.
【答案】 x2 = 8 y
【解析】由题意知,该点轨迹是以 F (0, 2) 为焦点,y = −2 为准线的抛物线,其中 p = 4 ,所以方程为 x2 = 8 y .
则 △OFM 的周长为
A. 4
B. 2 5 +1
C. 5 + 2 或 4
高考数学复习第八单元第47讲抛物线课件理新人教A版5

=
9+25 17
34.故选 C.
课堂考点探究
例2
[2018·山东烟台二模] 已知直线
l1:x=2,l2:3x+5y-30=0,P 为抛物线 y =-8x 上的
2
任一点,则 P 到直线 l1,l2 的距离之和的最小值
为 (
)
A.2
B.2 34
18
C.
17
16
D.
15
34
34
[总结反思] 根据抛物线的定义,将抛物线上
2
则弦 AB 的中点到 y 轴的最短距离为 (
A.3
C.2
B.1
D.4
)
[答案] C
[解析] 抛物线的准线方程为 x=-1,设
A(x1,y1),B(x2,y2),F 为抛物线的焦点,则
|AF|=x1+1,|BF|=x2+1,则弦 AB 的中点
到 y 轴的距离为
1 + 2 1 +1 2 +1
2
是
.
[答案]
1
y=2
[解析] 因为抛物线 x =2py 的准
2
2
线方程是 y=- ,所以抛物线 x =2y
2
1
的准线方程是 y=- .
2
课前双基巩固
3.[教材改编] 抛物线 y=4x 的焦点到准线的距离
2
为
.
[答案]
1
8
[解析] 因为抛物线方程 y=4x 可
2
化为 x
2
1
1
= y=2× ×y,所以
离是 10-1=9.
课前双基巩固
2022年高考数学(文)一轮复习文档:第八章 平面解析几何 第7讲抛物线 Word版含答案
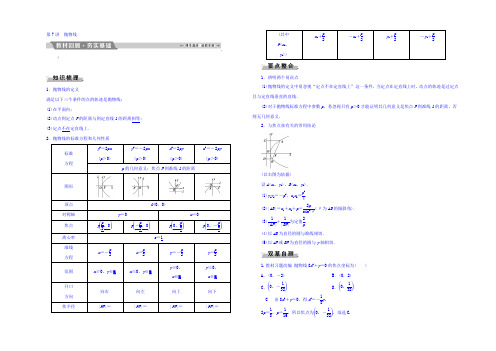
第7讲 抛物线 ,)1.抛物线的定义满足以下三个条件的点的轨迹是抛物线: (1)在平面内;(2)动点到定点F 的距离与到定直线l 的距离相等; (3)定点不在定直线上. 2.抛物线的标准方程和几何性质标准方程y 2=2px(p >0)y 2=-2px(p >0)x 2=2py(p >0)x 2=-2py(p >0)p 的几何意义:焦点F 到准线l 的距离图形顶点 O (0,0)对称轴 y =0x =0焦点 F ⎝ ⎛⎭⎪⎫p 2,0 F ⎝ ⎛⎭⎪⎫-p 2,0 F ⎝⎛⎭⎪⎫0,p 2 F ⎝ ⎛⎭⎪⎫0,-p 2离心率 e =1准线 方程 x =-p2x =p 2y =-p 2y =p 2范围 x ≥0,y ∈Rx ≤0,y ∈Ry ≥0,x ∈Ry ≤0, x ∈R开口方向 向右向左向上 向下 焦半径|PF |=|PF |=|PF |=|PF |=(其中P (x 0, y 0))x 0+p 2-x 0+p2y 0+p 2-y 0+p21.辨明两个易误点(1)抛物线的定义中易忽视“定点不在定直线上”这一条件,当定点在定直线上时,动点的轨迹是过定点且与定直线垂直的直线.(2)对于抛物线标准方程中参数p ,易忽视只有p >0才能证明其几何意义是焦点F 到准线l 的距离,否则无几何意义.2.与焦点弦有关的常用结论(以右图为依据)设A (x 1,y 1),B (x 2,y 2).(1)y 1y 2=-p 2,x 1x 2=p 24.(2)|AB |=x 1+x 2+p =2psin 2θ(θ为AB 的倾斜角).(3)1|AF |+1|BF |为定值2p. (4)以AB 为直径的圆与准线相切. (5)以AF 或BF 为直径的圆与y 轴相切.1.教材习题改编 抛物线8x 2+y =0的焦点坐标为( ) A .(0,-2) B .(0,2) C .⎝⎛⎭⎪⎫0,-132 D .⎝ ⎛⎭⎪⎫0,132C 由8x 2+y =0,得x 2=-18y .2p =18,p =116,所以焦点为⎝⎛⎭⎪⎫0,-132,故选C.2.教材习题改编 以x =1为准线的抛物线的标准方程为( ) A .y 2=2x B .y 2=-2x C .y 2=4xD .y 2=-4xD 由准线x =1知,抛物线方程为y 2=-2px (p >0)且p2=1,p =2,所以方程为y 2=-4x ,故选D.3.M 是抛物线y 2=2px (p >0)位于第一象限的点,F 是抛物线的焦点,若|MF |=52p ,则直线MF 的斜率为( )A .43B .53C .54D .52A 设M (x 0,y 0),由|MF |=52p ,得x 0+p 2=5p2,所以x 0=2p .所以y 20=2px 0=4p 2,取正根得y 0=2p . 即M 的坐标为(2p ,2p ), 又F 的坐标为(p2,0),所以k MF =2p -02p -p 2=43,故选A.4.动圆过点(1,0),且与直线x =-1相切,则动圆的圆心的轨迹方程为________.设动圆的圆心坐标为(x ,y ),则圆心到点(1,0)的距离与到直线x =-1的距离相等,依据抛物线的定义易知动圆的圆心的轨迹方程为y 2=4x .y 2=4x5.教材习题改编 抛物线x 2=2py (p >0)上的点P (m ,2)到焦点F 的距离为3,则该抛物线的方程为________. 依据抛物线定义可知2+p2=3,所以p =2,所以抛物线的方程为x 2=4y .x 2=4y抛物线的定义及其应用(1)若抛物线y 2=2x 上一点M 到它的焦点F 的距离为32,O 为坐标原点,则△MFO 的面积为( )A .22B .24C .12D .14(2)已知抛物线y 2=4x 的焦点是F ,点P 是抛物线上的动点,又有点B (3,2),则|PB |+|PF |的最小值为________.【解析】 (1)由题意知,抛物线准线方程为x =-12.设M (a ,b ),由抛物线的定义可知, 点M 到准线的距离为32,所以a =1,代入抛物线方程y 2=2x , 解得b =±2,所以S △MFO =12×12×2=24.(2)如图,过点B 作BQ 垂直准线于Q ,交抛物线于点P 1,则|P 1Q |=|P 1F |,则有|PB |+|PF |≥|P 1B |+|P 1Q |=|BQ |=4.即|PB |+|PF |的最小值为4. 【答案】 (1)B (2)4若本例(2)中的B 点坐标改为(3,4),试求|PB |+|PF |的最小值.由题意可知点(3,4)在抛物线的外部.由于|PB |+|PF |的最小值即为B ,F 两点间的距离, 所以|PB |+|PF |≥|BF |=42+22=16+4=2 5.即|PB |+|PF |的最小值为2 5.抛物线定义的应用(1)利用抛物线的定义解决此类问题,应机敏地进行抛物线上的点到焦点的距离与到准线距离的等价转化.即“看到准线想到焦点,看到焦点想到准线”.(2)留意机敏运用抛物线上一点P (x ,y )到焦点F 的距离|PF |=|x |+p 2或|PF |=|y |+p2.1.(2021·云南省统一检测)设经过抛物线C 的焦点F 的直线l 与抛物线C 交于A 、B 两点,那么抛物线C 的准线与以AB 为直径的圆的位置关系为( )A .相离B .相切C .相交但不经过圆心D .相交且经过圆心B 设圆心为M ,过点A 、B 、M 作准线l 的垂线,垂足分别为A 1、B 1、M 1, 则|MM 1|=12(|AA 1|+|BB 1|).由抛物线定义可知|BF |=|BB 1|,|AF |=|AA 1|, 所以|AB |=|BB 1|+|AA 1|,|MM 1|=12|AB |,即圆心M 到准线的距离等于圆的半径, 故以AB 为直径的圆与抛物线的准线相切.2.(2021·长春调研)已知直线l 1:4x -3y +6=0和直线l 2:x =-1,则抛物线y 2=4x 上一动点P 到直线l 1和直线l 2的距离之和的最小值是( )A .355B .2C .115D .3B 由题可知l 2:x =-1是抛物线y 2=4x 的准线,设抛物线的焦点F 为(1,0),则动点P 到l 2的距离等于|PF |,则动点P 到直线l 1和直线l 2的距离之和的最小值即为焦点F 到直线l 1:4x -3y +6=0的距离,所以最小值是|4-0+6|5=2.抛物线的标准方程及性质(高频考点)抛物线的标准方程及性质是高考的热点,考查时多以选择题、填空题形式消灭,个别高考题有肯定难度. 高考对抛物线的考查主要有以下三个命题角度: (1)求抛物线方程; (2)由已知求参数p ; (3)抛物线方程的实际应用.(1)(2022·高考全国卷乙)以抛物线C 的顶点为圆心的圆交C 于A 、B 两点,交C 的准线于D 、E两点.已知|AB |=42,|DE |=25,则C 的焦点到准线的距离为( )A .2B .4C .6D .8(2)若抛物线的焦点为直线3x -4y -12=0与坐标轴的交点,则抛物线的标准方程为________.【解析】 (1)由题意,不妨设抛物线方程为y 2=2px (p >0),由|AB |=42,|DE |=25,可取A ⎝ ⎛⎭⎪⎫4p,22,D ⎝ ⎛⎭⎪⎫-p 2,5,设O 为坐标原点,由|OA |=|OD |,得16p 2+8=p 24+5,得p =4,所以选B.(2)对于直线方程3x -4y -12=0,令x =0,得y =-3,令y =0,得x =4,所以抛物线的焦点坐标可能为(0,-3)或(4,0).当焦点坐标为(0,-3)时,设方程为x 2=-2py (p >0),则p2=3,所以p =6,此时抛物线的标准方程为x2=-12y ;当焦点坐标为(4,0)时,设方程为y 2=2px (p >0),则p2=4,所以p =8,此时抛物线的标准方程为y 2=16x . 所以所求抛物线的标准方程为x 2=-12y 或y 2=16x . 【答案】 (1)B (2)x 2=-12y 或y 2=16x(1)求抛物线的标准方程的方法①求抛物线的标准方程常用待定系数法,由于未知数只有p ,所以只需一个条件确定p 值即可. ②由于抛物线方程有四种标准形式,因此求抛物线方程时,需先定位,再定量. (2)确定及应用抛物线性质的技巧①利用抛物线方程确定及应用其焦点、准线等性质时,关键是将抛物线方程化成标准方程.②要结合图形分析,机敏运用平面几何的性质以图助解.角度一 求抛物线方程1.以x 轴为对称轴,原点为顶点的抛物线上的一点P (1,m )到焦点的距离为3,则抛物线的方程是( ) A .y =4x 2B .y =8x 2C .y 2=4xD .y 2=8xD 设抛物线的方程为y 2=2px (p >0),则由抛物线的定义知1+p2=3,即p =4,所以抛物线方程为y2=8x .角度二 由已知求参数p2.(2021·襄阳调研测试)抛物线y 2=2px 的焦点为F ,M 为抛物线上一点,若△OFM 的外接圆与抛物线的准线相切(O 为坐标原点),且外接圆的面积为9π,则p =( )A .2B .4C .6D .8B 由于△OFM 的外接圆与抛物线的准线相切,所以△OFM 的外接圆的圆心到准线的距离等于圆的半径,由于圆面积为9π,所以圆的半径为3,又由于圆心在OF 的垂直平分线上,|OF |=p2,所以p 2+p4=3,所以p =4.角度三 抛物线方程的实际应用3.如图是抛物线形拱桥,当水面在l 时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽为________米.建立坐标系如图所示.则可设抛物线方程为x 2=-2py (p >0).由于点(2,-2)在抛物线上,所以p =1, 即抛物线方程为x 2=-2y . 当y =-3时,x =± 6.所以水位下降1米后,水面宽为26米. 2 6直线与抛物线的位置关系(2022·高考全国卷乙)在直角坐标系xOy 中,直线l :y =t (t ≠0)交y 轴于点M ,交抛物线C :y2=2px (p >0)于点P ,M 关于点P 的对称点为N ,连接ON 并延长交C 于点H .(1)求|OH ||ON |;(2)除H 以外,直线MH 与C 是否有其他公共点?说明理由.【解】 (1)由已知得M (0,t ),P ⎝ ⎛⎭⎪⎫t 22p ,t . 又N 为M 关于点P 的对称点,故N ⎝ ⎛⎭⎪⎫t 2p ,t ,ON 的方程为y =ptx ,代入y 2=2px ,整理得px 2-2t 2x =0, 解得x 1=0,x 2=2t2p.因此H ⎝ ⎛⎭⎪⎫2t 2p ,2t . 所以N 为OH 的中点,即|OH ||ON |=2.(2)直线MH 与C 除H 以外没有其他公共点.理由如下:直线MH 的方程为y -t =p2t x ,即x =2tp(y -t ).代入y 2=2px 得y 2-4ty +4t 2=0,解得y 1=y 2=2t ,即直线MH 与C 只有一个公共点,所以除H 以外直线MH 与C 没有其他公共点.解决直线与抛物线位置关系问题的常用方法(1)直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似,一般要用到根与系数的关系. (2)有关直线与抛物线的弦长问题,要留意直线是否过抛物线的焦点,若过抛物线的焦点,可直接使用公式|AB |=|x 1|+|x 2|+p ,若不过焦点,则必需用一般弦长公式.(3)涉及抛物线的弦长、中点、距离等相关问题时,一般利用根与系数的关系接受“设而不求”“整体代入”等解法.涉及弦的中点、斜率时,一般用“点差法”求解.已知过抛物线y 2=2px (p >0)的焦点,斜率为22的直线交抛物线于A (x 1,y 1),B (x 2,y 2)(x 1<x 2)两点,且|AB |=9.(1)求该抛物线的方程;(2)O 为坐标原点,C 为抛物线上一点,若OC →=OA →+λOB →,求λ的值.(1)由题意得直线AB 的方程为y =22·⎝ ⎛⎭⎪⎫x -p 2,与y 2=2px 联立,消去y 有4x 2-5px +p 2=0,所以x 1+x 2=5p4.由抛物线定义得|AB |=x 1+x 2+p =5p4+p =9,所以p =4,从而该抛物线的方程为y 2=8x . (2)由(1)得4x 2-5px +p 2=0, 即x 2-5x +4=0, 则x 1=1,x 2=4,于是y 1=-22,y 2=42,从而A (1,-22),B (4,42),设C (x 3,y 3), 则OC →=(x 3,y 3)=(1,-22)+λ(4,42) =(4λ+1,42λ-22). 又y 23=8x 3,所以2=8(4λ+1), 整理得(2λ-1)2=4λ+1, 解得λ=0或λ=2.,)——忽视焦点位置而致误已知抛物线的顶点在原点,对称轴为y 轴,它与圆x 2+y 2=9相交,公共弦MN 的长为25,求该抛物线的方程,并写出它的焦点坐标与准线方程.【解】 由题意,设抛物线方程为x 2=2ay (a ≠0). 设公共弦MN 交y 轴于A , 则|MA |=|AN |,且|AN |= 5. 由于|ON |=3,所以|OA |=32-(5)2=2,所以N (5,±2).由于N 点在抛物线上,所以5=2a ·(±2),即2a =±52,故抛物线的方程为x 2=52y 或x 2=-52y .抛物线x 2=52y 的焦点坐标为⎝ ⎛⎭⎪⎫0,58,准线方程为y =-58.抛物线x 2=-52y 的焦点坐标为⎝ ⎛⎭⎪⎫0,-58,准线方程为y =58.(1)解决本题易忽视焦点位置可在y 轴的正半轴也可在负半轴上两种状况,误认为a >0,从而导致漏解.(2)对称轴确定,而开口方向不确定的抛物线方程有如下特点: ①当焦点在x 轴上时,可将抛物线方程设为y 2=ax (a ≠0); ②当焦点在y 轴上时,可将抛物线方程设为x 2=ay (a ≠0).若抛物线y 2=2px 的焦点与椭圆x 29+y 25=1的焦点重合,则抛物线的准线方程为________.由椭圆x 29+y 25=1,得c 2=9-5=4,即c =2,故椭圆的焦点坐标为(±2,0). 即抛物线的焦点坐标为(±2,0).所以当p >0时,抛物线的准线方程为x =-2;当p <0时,抛物线的准线方程为x =2. x =2或x =-2,)1.若抛物线y =4x 2上的一点M 到焦点的距离为1,则点M 的纵坐标是( ) A .1716 B .1516 C .78D .0B M 到准线的距离等于M 到焦点的距离,又准线方程为y =-116,设M (x ,y ),则y +116=1,所以y =1516.2.若抛物线y 2=2x 上一点P 到准线的距离等于它到顶点的距离,则点P 的坐标为( ) A .⎝ ⎛⎭⎪⎫14,±22B .⎝ ⎛⎭⎪⎫14,±1C .⎝ ⎛⎭⎪⎫12,±22D .⎝ ⎛⎭⎪⎫12,±1 A 设抛物线的顶点为O ,焦点为F ,P (x P ,y P ),由抛物线的定义知,点P 到准线的距离即为点P 到焦点的距离,所以|PO |=|PF |,过点P 作PM ⊥OF 于点M (图略),则M 为OF 的中点,所以x P =14,代入y 2=2x ,得y P =±22,所以P ⎝ ⎛⎭⎪⎫14,±22. 3.(2022·高考全国卷甲)设F 为抛物线C :y 2=4x 的焦点,曲线y =kx(k >0)与C 交于点P ,PF ⊥x 轴,则k =( )A .12 B .1C .32D .2D 易知抛物线的焦点为F (1,0),设P (x P ,y P ),由PF ⊥x 轴可得x P =1,代入抛物线方程得y P =2(-2舍去),把P (1,2)代入曲线y =k x(k >0)得k =2.4.设F 为抛物线y 2=2x 的焦点,A 、B 、C 为抛物线上三点,若F 为△ABC 的重心,则|FA →|+|FB →|+|FC →|的值为( )A .1B .2C .3D .4C 依题意,设点A (x 1,y 1),B (x 2,y 2),C (x 3,y 3),又焦点F ⎝ ⎛⎭⎪⎫12,0,x 1+x 2+x 3=3×12=32, 则|FA →|+|FB →|+|FC →|=⎝⎛⎭⎪⎫x 1+12+⎝ ⎛⎭⎪⎫x 2+12+⎝ ⎛⎭⎪⎫x 3+12=(x 1+x 2+x 3)+32=32+32=3.5.直线l 过抛物线y 2=-2px (p >0)的焦点,且与抛物线交于A 、B 两点,若线段AB 的长是8,AB 的中点到y 轴的距离是2,则此抛物线的方程是( )A .y 2=12x B .y 2=-8x C .y 2=6xD .y 2=-4xB 设A (x 1,y 1)、B (x 2,y 2),由抛物线定义可得|x 1|+|x 2|+p =8,又AB 的中点到y 轴的距离为2,即|x 1|+|x 2|=4,所以p =4,所以y 2=-8x .故选B.6.已知抛物线y 2=4x ,圆F :(x -1)2+y 2=1,过点F 作直线l ,自上而下顺次与上述两曲线交于点A ,B ,C ,D (如图所示),则下列关于|AB |·|CD |的值的说法中,正确的是( )A .等于1B .等于4C .最小值是1D .最大值是4A 设直线l :x =ty +1,代入抛物线方程,得y 2-4ty -4=0.设A (x 1,y 1),D (x 2,y 2),依据抛物线的定义知,|AF |=x 1+1,|DF |=x 2+1,故|AB |=x 1,|CD |=x 2,所以|AB |·|CD |=x 1x 2=y 214·y 224=(y 1y 2)216.而y 1y 2=-4,故|AB |·|CD |=1.7.(2021·资阳模拟)顶点在原点,对称轴是y 轴,并且经过点P (-4,-2)的抛物线方程是________. 设抛物线方程为x 2=my ,将点P (-4,-2)代入x 2=my ,得m =-8. 所以抛物线方程是x 2=-8y . x 2=-8y8.(2021·云南省第一次统一检测)已知抛物线C 的方程为y 2=2px (p >0),○· M 的方程为x 2+y 2+8x +12=0,假如抛物线C 的准线与○·M 相切,那么p 的值为________.将○·M 的方程化为标准方程:(x +4)2+y 2=4,圆心坐标为(-4,0),半径r =2,又由于抛物线的准线方程为x =-p2,所以⎪⎪⎪⎪⎪⎪4-p 2=2,p =12或4.12或49.经过抛物线C 的焦点F 作直线l 与抛物线C 交于A ,B 两点,假如A ,B 在抛物线C 的准线上的射影分别为A 1,B 1,那么∠A 1FB 1=________.由抛物线定义可知|BF |=|BB 1|,|AF |=|AA 1|,故∠BFB 1=∠BB 1F ,∠AFA 1=∠AA 1F . 又∠OFB 1=∠BB 1F ,∠OFA 1=∠AA 1F , 故∠BFB 1=∠OFB 1,∠AFA 1=∠OFA 1, 所以∠OFA 1+∠OFB 1=12×π=π2,即∠A 1FB 1=π2.π210.(2021·豫东、豫北十校联考)已知抛物线的顶点在原点,焦点在x 轴的正半轴上,若抛物线的准线与双曲线5x 2-y 2=20的两条渐近线围成的三角形的面积为45,则抛物线方程为________.由双曲线方程5x 2-y 2=20知其渐近线方程为y =±5x ,由题意可设抛物线方程为y 2=2px (p >0),故其准线方程为x =-p 2,设准线与双曲线的两条渐近线的交点为A ,B ,则不妨令A ⎝ ⎛⎭⎪⎫-p2,52p ,B ⎝ ⎛⎭⎪⎫-p 2,-52p ,故S △ABO =12×5p ×p 2=54p 2=45,解得p 2=16,又由于p >0,所以p =4,故抛物线方程为y 2=8x .y 2=8x11.已知抛物线y 2=2px (p >0)的焦点为F ,A 是抛物线上横坐标为4,且位于x 轴上方的点,A 到抛物线准线的距离等于5,过A 作AB 垂直于y 轴,垂足为B ,OB 的中点为M .(1)求抛物线的方程;(2)若过M 作MN ⊥FA ,垂足为N ,求点N 的坐标. (1)抛物线y 2=2px 的准线为x =-p2,于是4+p2=5,所以p =2.所以抛物线方程为y 2=4x .(2)由于点A 的坐标是(4,4), 由题意得B (0,4),M (0,2). 又由于F (1,0),所以k FA =43,由于MN ⊥FA ,所以k MN =-34.所以FA 的方程为y =43(x -1),①MN 的方程为y -2=-34x ,②联立①②,解得x =85,y =45,所以N 的坐标为⎝ ⎛⎭⎪⎫85,45.12.(2021·长春一模)过抛物线y 2=2px (p >0)的焦点F 且倾斜角为120°的直线l 与抛物线在第一、四象限分别交于A ,B 两点,则|AF ||BF |的值等于( ) A .13B .23 C.34 D.43A 记抛物线y 2=2px 的准线为l ′,如图,作AA 1⊥l ′,BB 1⊥l ′,AC ⊥BB 1,垂足分别是A 1,B 1,C ,则有cos ∠ABB 1=|BC ||AB |=|BB 1|-|AA 1||AF |+|BF |=|BF |-|AF ||AF |+|BF |,即cos 60°=|BF |-|AF ||AF |+|BF |=12,由此得|AF ||BF |=13.13.已知抛物线C :y 2=4x 的焦点为F ,直线l 经过点F 且与抛物线C 相交于A 、B 两点. (1)若线段AB 的中点在直线y =2上,求直线l 的方程; (2)若线段|AB |=20,求直线l 的方程.(1)由已知得抛物线的焦点为F (1,0).由于线段AB 的中点在直线y =2上,所以直线l 的斜率存在,设直线l 的斜率为k ,A (x 1,y 1),B (x 2,y 2),AB 的中点M (x 0,y 0),则⎩⎪⎨⎪⎧x 0=x 1+x 22,y 0=y 1+y 22.由⎩⎪⎨⎪⎧y 21=4x 1,y 22=4x 2得(y 1+y 2)(y 1-y 2)=4(x 1-x 2),所以2y 0k =4. 又y 0=2,所以k =1,故直线l 的方程是y =x -1. (2)设直线l 的方程为x =my +1,与抛物线方程联立得⎩⎪⎨⎪⎧x =my +1,y 2=4x ,消元得y 2-4my -4=0,所以y 1+y 2=4m ,y 1y 2=-4,Δ=16(m 2+1)>0. |AB |=m 2+1|y 1-y 2|=m 2+1·(y 1+y 2)2-4y 1y 2 =m 2+1·(4m )2-4×(-4) =4(m 2+1).所以4(m 2+1)=20,解得m =±2, 所以直线l 的方程是x =±2y +1,即x ±2y -1=0.14.已知圆C 过定点F ⎝ ⎛⎭⎪⎫-14,0,且与直线x =14相切,圆心C 的轨迹为E ,曲线E 与直线l :y =k (x +1)(k ∈R )相交于A ,B 两点.(1)求曲线E 的方程;(2)当△OAB 的面积等于10时,求k 的值.(1)由题意,点C 到定点F ⎝ ⎛⎭⎪⎫-14,0和直线x =14的距离相等, 故点C 的轨迹E 的方程为y 2=-x .(2)由方程组⎩⎪⎨⎪⎧y 2=-x ,y =k (x +1),消去x 后,整理得ky 2+y -k =0. 设A (x 1,y 1),B (x 2,y 2),由根与系数的关系有y 1+y 2=-1k,y 1y 2=-1.设直线l 与x 轴交于点N ,则N (-1,0). 所以S △OAB =S △OAN +S △OBN =12|ON ||y 1|+12|ON ||y 2|, =12|ON ||y 1-y 2| =12×1×(y 1+y 2)2-4y 1y 2 =12⎝ ⎛⎭⎪⎫-1k 2+4=10, 解得k =±16.。
2022版新高考数学一轮复习专题限时练习:54 抛物线 (含解析)

2022年新高考数学专题限时练习(五十四) 抛物线建议用时:40分钟一、选择题1.点M (5,3)到抛物线y =ax 2的准线的距离为6,那么抛物线的标准方程是( )A .x 2=112y B .x 2=112y 或x 2=-136y C .x 2=-136yD .x 2=12y 或x 2=-36yD [将y =ax 2化为x 2=1a y .当a >0时,准线y =-14a ,则3+14a =6,∴a =112. 当a <0时,准线y =-14a ,则⎪⎪⎪⎪⎪⎪3+14a =6,∴a =-136.∴抛物线方程为x 2=12y 或x 2=-36y .]2.(2020·泰安模拟)已知抛物线E :y 2=2px (p >0)的焦点为F ,O 为坐标原点,OF 为菱形OBFC 的一条对角线,另一条对角线BC 的长为2,且点B ,C 在抛物线E 上,则p =( )A .1B . 2C .2D .2 2B [由题意,⎝ ⎛⎭⎪⎫p 4,1在抛物线上,代入抛物线方程可得1=p 22,∵p >0,∴p =2,故选B.]3.(2020·北京高考)设抛物线的顶点为O ,焦点为F ,准线为l .P 是抛物线上异于O 的一点,过P 作PQ ⊥l 于Q ,则线段FQ 的垂直平分线( )A .经过点OB .经过点PC.平行于直线OP D.垂直于直线OPB[如图所示:因为线段FQ的垂直平分线上的点到F,Q的距离相等,又点P在抛物线上,根据定义可知,|PQ|=|PF|,所以线段FQ的垂直平分线经过点P.故选B.]4.(多选)(2020·辽宁锦州月考)以下四个命题中,真命题的序号是()①平面内到两定点距离之比等于常数λ(λ≠1)的点的轨迹是圆;②平面内与定点A(-3,0)和B(3,0)的距离之差等于4的点的轨迹方程为x24-y25=1;③点P是抛物线x2=4y上的动点,点P在x轴上的射影是M,点A的坐标是A(1,0),则|P A|+|PM|的最小值是2+1;④已知点P为抛物线y2=4x上一个动点,点Q为圆x2+(y-4)2=1上一个动点,那么点P到点Q的距离与点P到抛物线的准线距离之和的最小值是17-1.A.①B.②C.③D.④AD[对于①,平面内到两定点的距离之比为定值(不等于1)的点的轨迹是圆,这个圆被称为阿波罗尼斯圆,所以①正确;对于②,根据题意,结合双曲线的定义,可知题中点的轨迹是双曲线的一支,所以②错误;对于③,根据题意,结合抛物线的定义,可求得|P A|+|PM|的最小值应为2-1,所以③错误;对于④,根据抛物线的定义,可知抛物线上的点到焦点的距离和到准线的距离是相等的,将其转化为到焦点的距离,结合圆的相关性质可知④是正确的.]5.(多选)(2020·山东胶州一中月考)已知抛物线y2=4x上一点P到准线的距离为d1,到直线l:4x-3y+11=0的距离为d2,则d1+d2的取值可以为()A.3 B.4C. 5 D.10ABD[抛物线上的点P到准线的距离等于到焦点F(1,0)的距离,过焦点F作直线4x-3y+11=0的垂线,则F到直线的距离为d1+d2的最小值,如图所示:所以(d1+d2)min=|4-0+11|42+(-3)2=3,故选ABD.]6.(2020·江西萍乡一模)已知抛物线C:y2=2px(p>0)的焦点为F,准线l:x =-1,点M在抛物线C上,点M在直线l:x=-1上的射影为A,且直线AF的斜率为-3,则△MAF的面积为()A. 3 B.2 3C.4 3 D.8 3C[如图所示,设准线l与x轴交于点N.则|FN|=2.∵直线AF的斜率为-3,∴∠AFN=60°.∴∠MAF=60°,|AF|=4.由抛物线的定义可得|MA|=|MF|,∴△AMF是边长为4的等边三角形.∴S△AMF=34×42=4 3.故选C.]二、填空题7.已知抛物线C:y2=2px(p>0)的焦点为F(2,0),则抛物线C的方程是________;若M是C上一点,FM的延长线交y轴于点N,且M为FN的中点,则|FN|=________.y2=8x6[抛物线C:y2=2px(p>0)的焦点为F(2,0),可得p=4,则抛物线C的方程是y2=8x.由M为FN的中点,得M的横坐标为1,代入抛物线方程得y =±22,则M(1,±22),则点N的坐标为(0,±42),所以|FN|=22+(42)2=6.]8.如图是抛物线形拱桥,当水面在l时,拱顶离水面2米,水面宽4米.水位下降1米后,水面宽________米.26[建立平面直角坐标系如图所示,设抛物线方程为x2=-2py(p>0).由题意可知抛物线过点(2,-2),故4=4p,∴p=1,∴x2=-2y.故当y=-3时,x2=6,即x= 6.所以当水位降1米后,水面宽26米.]9.已知抛物线y2=4x的焦点为F,过点F作一条直线交抛物线于A,B两点.若|AF|=3,则|BF|=________.32[法一:由题意可知F(1,0),设A(x A,y A),B(x B,y B),点A在第一象限,则|AF|=x A+1=3,所以x A=2,y A=22,所以直线AB的斜率为k=222-1=2 2.则直线AB的方程为y=22(x-1),与抛物线方程联立整理得2x 2-5x +2=0,x A +x B =52, 所以x B =12,所以|BF |=12+1=32.法二:由1|AF |+1|BF |=2p 可知1|BF |=1-13=23, ∴|BF |=32.] 三、解答题10.如图,抛物线的顶点在原点,圆(x -2)2+y 2=4的圆心恰是抛物线的焦点.(1)求抛物线的方程;(2)一条直线的斜率等于2,且过抛物线焦点,它依次截抛物线和圆于A ,B ,C ,D 四点,求|AB |+|CD |的值.[解] (1)设抛物线方程为y 2=2px (p >0), ∵圆(x -2)2+y 2=22的圆心恰是抛物线的焦点, ∴p =4.∴抛物线的方程为y 2=8x .(2)依题意直线AB 的方程为y =2x -4, 设A (x 1,y 1),D (x 2,y 2),则⎩⎪⎨⎪⎧y =2x -4,y 2=8x ,得x 2-6x +4=0,∴x 1+x 2=6,|AD |=x 1+x 2+p =6+4=10. |AB |+|CD |=|AD |-|CB |=10-4=6.11.如图,已知点F 为抛物线E :y 2=2px (p >0)的焦点,点A (2,m )在抛物线E 上,且|AF |=3.(1)求抛物线E 的方程;(2)已知点G (-1,0),延长AF 交抛物线E 于点B ,证明:GF 为∠AGB 的平分线.[解] (1)由抛物线定义可得|AF |=2+p2=3,解得p =2.∴抛物线E 的方程为y 2=4x .(2)证明:∵点A (2,m )在抛物线E 上,∴m 2=4×2,解得m =±22,由抛物线的对称性,不妨设A (2,22),由A (2,22),F (1,0),∴直线AF 的方程为y =22(x -1),由⎩⎪⎨⎪⎧y =22(x -1),y 2=4x ,得2x 2-5x +2=0,解得x =2或12,∴B ⎝ ⎛⎭⎪⎫12,-2.又G (-1,0),∴k GA =223,k GB =-223, ∴k GA +k GB =0,∴∠AGF =∠BGF . ∴GF 为∠AGB 的平分线.1.已知P 是抛物线y 2=4x 上的一个动点,Q 是圆(x -3)2+(y -1)2=1上的一个动点,N (1,0)是一个定点,则|PQ |+|PN |的最小值为( )A .3B .4C .5D .2+1A [由抛物线方程y 2=4x ,可得抛物线的焦点F (1,0),又N (1,0),所以N 与F 重合.过圆(x -3)2+(y -1)2=1的圆心M 作抛物线准线的垂线MH ,交圆于Q ,交抛物线于P ,则|PQ |+|PN |的最小值等于|MH |-1=3.]2.(2020·济宁三模)已知抛物线C :y 2=4x 的焦点为F ,过点F 的直线与抛物线C 的两个交点分别为A ,B ,且满足AF→=2FB →,E 为AB 的中点,则点E 到抛物线准线的距离为( )A .114B .94C .52D .54B [由题意得抛物线y 2=4x 的焦点坐标为(1,0),准线方程为x =-1,设 A (x 1,y 1),B (x 2,y 2),∵AF →=2FB →,∴|AF |=2|BF |,∴x 1+1=2(x 2+1), ∴x 1=2x 2+1,∵|y 1|=2|y 2|,∴y 21=4y 22,∴x 1=4x 2,∴x 1=2,x 2=12.∴线段AB 的中点到该抛物线准线的距离为12[(x 1+1)+(x 2+1)]=94.故选B.] 3.已知点A (m,4)(m >0)在抛物线x 2=4y 上,过点A 作倾斜角互补的两条直线l 1和l 2,且l 1,l 2与抛物线的另一个交点分别为B ,C .(1)求证:直线BC 的斜率为定值;(2)若抛物线上存在两点关于BC 对称,求|BC |的取值范围. [解] (1)证明:∵点A (m,4)在抛物线上, ∴16=m 2,∴m =±4, 又m >0,∴m =4. 设B (x 1,y 1),C (x 2,y 2),则k AB +k AC =x 1+44+x 2+44=x 1+x 2+84=0,∴x 1+x 2=-8.∴k BC =y 2-y 1x 2-x 1=x 22-x 214(x 2-x 1)=x 1+x 24=-2,∴直线BC 的斜率为定值-2.(2)设直线BC 的方程为y =-2x +b ,P (x 3,y 3),Q (x 4,y 4)关于直线BC 对称,设PQ 的中点为M (x 0,y 0),则k PQ =y 4-y 3x 4-x 3=x 3+x 44=x 02=12,∴x 0=1.∴M (1,-2+b ). 又点M 在抛物线内部, ∴-2+b >14,即b >94.由⎩⎪⎨⎪⎧y =-2x +b ,x 2=4y ,得x 2+8x -4b =0, ∴x 3+x 4=-8,x 3x 4=-4b . ∴|BC |=1+4|x 3-x 4|=5·(x 3+x 4)2-4x 3x 4 =5×64+16b .又b >94,∴|BC |>10 5.∴|BC |的取值范围为(105,+∞).1.(多选)(2020·黑龙江大庆一中月考)如图,过抛物线y 2=8x 的焦点F ,斜率为k 的直线l 与抛物线交于A ,B 两点,与抛物线准线交于C 点,若B 是AC 的中点,则( )A .k =±2 B .k =±2 2 C .|AB |=9D .|AB |=10BC [如图,设A ,B 在准线上的射影分别为D ,E ,连接AD ,BE ,设AB =BC =m ,直线l 的倾斜角为α,则|BE |=m |cos α|,所以|AD |=|AF |=|AB |-|BF |=|AB |-|BE |=m (1-|cos α|),|cos α|=|AD ||AC |=m (1-|cos α|)2m ,解得|cos α|=13,所以|sin α|=1-⎝ ⎛⎭⎪⎫132=223,故|k |=|tan α|=2 2.由抛物线焦点弦的弦长公式|AB |=2p sin 2α可得|AB |=81-19=9.综上,选BC. 或:由|cos α|=13得tan α=±22,可得直线方程.设A (x A ,y A ),B (x B ,y B ),将直线方程与抛物线方程联立,进而可解得x A +x B =5,于是|AB |=x A +x B +4=9.故选BC.]2.(2020·静安区二模)已知抛物线Γ:y 2=4x 的焦点为F ,若△ABC 的三个顶点都在抛物线Γ上,且F A →+FB→+FC →=0,则称该三角形为“核心三角形”. (1)是否存在“核心三角形”,其中两个顶点的坐标分别为(0,0)和(1,2)?请说明理由;(2)设“核心三角形”ABC 的一边AB 所在直线的斜率为4,求直线AB 的方程;(3)已知△ABC 是“核心三角形”,证明:点A 的横坐标小于2. [解] (1)抛物线Г:y 2=4x 的焦点为F (1,0),由F A →+FB →+FC →=0,得1=x A +x B +x C 3,0=y A +y B +y C3,故第三个顶点的坐标为3(1,0)-(0,0)-(1,2)=(2,-2),但点(2,-2)不满足抛物线的方程,即点(2,-2)不在抛物线上,所以这样的“核心三角形”不存在.(2)设直线AB 的方程为y =4x +t ,与y 2=4x 联立,可得y 2-y +t =0, 设A (x 1,y 1),B (x 2,y 2),C (x 3,y 3), y 1+y 2=1,x 1+x 2=14(y 1+y 2-2t )=14-12t , 由(x 1+x 2+x 3,y 1+y 2+y 3)=(3,0), 可得x 3=12t +114,y 3=-1, 代入方程y 2=4x ,可得11+2t =1, 解得t =-5,所以直线AB 的方程为4x -y -5=0.(3)证明:设直线BC 的方程为x =ny +m ,与y 2=4x 联立,可得y 2-4ny -4m =0,因为直线BC 与抛物线相交,故判别式Δ=16(n 2+m )>0,y 1+y 2=4n , 所以x 1+x 2=n (y 1+y 2)+2m =4n 2+2m , 可得点A 的坐标为(-4n 2-2m +3,-4n ), 又因为A 在抛物线上,故16n2=-16n2-8m+12,可得m=-4n2+3,2,因为m>-n2,所以n2<12故A的横坐标为-4n2-2m+3=-4n2+8n2=4n2<2.。
高考数学复习考点知识与题型专题讲解60---抛物线
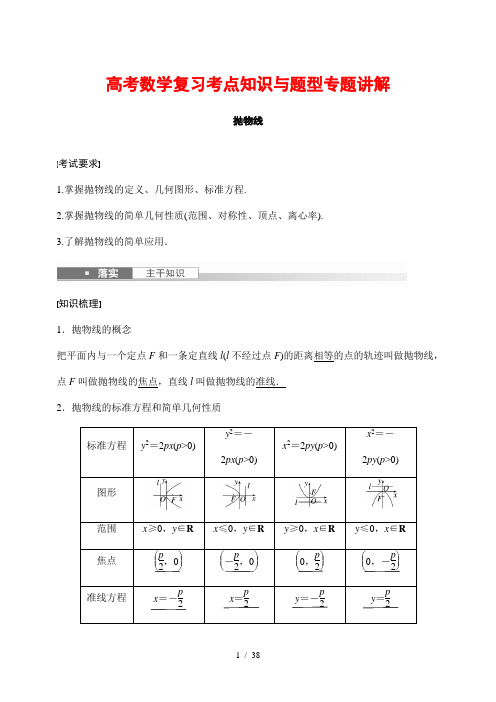
高考数学复习考点知识与题型专题讲解抛物线考试要求1.掌握抛物线的定义、几何图形、标准方程.2.掌握抛物线的简单几何性质(范围、对称性、顶点、离心率).3.了解抛物线的简单应用.知识梳理 1.抛物线的概念把平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线,点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. 2.抛物线的标准方程和简单几何性质标准方程y 2=2px (p >0) y 2=-2px (p >0)x 2=2py (p >0)x 2=-2py (p >0)图形范围 x ≥0,y ∈R x ≤0,y ∈R y ≥0,x ∈R y ≤0,x ∈R 焦点⎝ ⎛⎭⎪⎫p 2,0 ⎝ ⎛⎭⎪⎫-p 2,0 ⎝ ⎛⎭⎪⎫0,p 2 ⎝ ⎛⎭⎪⎫0,-p 2 准线方程x =-p 2x =p 2y =-p 2y =p 2对称轴x轴y轴顶点(0,0)离心率e=1常用结论抛物线焦点弦的几个常用结论设AB是过抛物线y2=2px(p>0)的焦点F的弦,若A(x1,y1),B(x2,y2),则(1)x1x2=p24,y1y2=-p2;(2)若A在第一象限,B在第四象限,则|AF|=p1-cosα,|BF|=p1+cosα,弦长|AB|=x1+x2+p=2psin2α(α为弦AB的倾斜角);(3)1|F A|+1|FB|=2p;(4)以弦AB为直径的圆与准线相切;(5)以AF或BF为直径的圆与y轴相切;(6)过焦点弦的端点的切线互相垂直且交点在准线上;(7)通径:过焦点与对称轴垂直的弦长等于2p.思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)平面内与一个定点F和一条定直线l的距离相等的点的轨迹是抛物线.(×)(2)方程y=4x2表示焦点在x轴上的抛物线,焦点坐标是(1,0).(×)(3)抛物线既是中心对称图形,又是轴对称图形.(×)(4)若直线与抛物线只有一个交点,则直线与抛物线相切.(×) 教材改编题1.抛物线y =2x 2的准线方程为() A .y =-18B .y =-14 C .y =-12D .y =-1 答案A解析由y =2x 2,得x 2=12y ,故抛物线y =2x 2的准线方程为y =-18.2.过抛物线y 2=4x 的焦点的直线l 交抛物线于P (x 1,y 1),Q (x 2,y 2)两点,如果x 1+x 2=6,则|PQ |等于() A .9B .8C .7D .6 答案B解析抛物线y 2=4x 的焦点为F (1,0),准线方程为x =-1.根据题意可得, |PQ |=|PF |+|QF |=x 1+1+x 2+1 =x 1+x 2+2=8.3.已知抛物线C 与双曲线x 2-y 2=1有相同的焦点,且顶点在原点,则抛物线C 的方程是________. 答案y 2=±42x解析由已知可知双曲线的焦点为 (-2,0),(2,0).设抛物线方程为y 2=±2px (p >0),则p2=2, 所以p =22,所以抛物线方程为y 2=±42x .题型一 抛物线的定义和标准方程 命题点1定义及应用例1(1)(2020·全国Ⅰ)已知A 为抛物线C :y 2=2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p 等于() A .2B .3C .6D .9 答案C解析设A (x ,y ),由抛物线的定义知,点A 到准线的距离为12,即x +p2=12. 又因为点A 到y 轴的距离为9,即x =9, 所以9+p2=12,解得p =6.(2)已知A (3,2),点F 为抛物线y 2=2x 的焦点,点P 在抛物线上移动,为使|P A |+|PF |取得最小值,则点P 的坐标为() A .(0,0) B .(2,2) C .(1,2) D.⎝ ⎛⎭⎪⎫12,1答案B解析如图所示,设点P 到准线的距离为d , 准线方程为x =-12, 所以|P A |+|PF |=|P A |+d ≥|AB | =3+12=72,当且仅当点P 为AB 与抛物线的交点时,|P A |+|PF |取得最小值, 此时点P 的坐标为(2,2).思维升华 “看到准线想到焦点,看到焦点想到准线”,许多抛物线问题均可根据定义获得简捷、直观的求解.“由数想形,由形想数,数形结合”是灵活解题的一条捷径.命题点2求标准方程例2(1)设抛物线y 2=2px 的焦点在直线2x +3y -8=0上,则该抛物线的准线方程为() A .x =-4B .x =-3 C .x =-2D .x =-1 答案A解析直线2x +3y -8=0与x 轴的交点为(4,0),∴抛物线y 2=2px 的焦点为(4,0),∴准线方程为x =-4.(2)已知抛物线C:y2=2px(p>0)的焦点为F,准线为l,点A是抛物线C上一点,AD⊥l,交l于D.若|AF|=4,∠DAF=60°,则抛物线C的方程为()A.y2=8x B.y2=4xC.y2=2x D.y2=x答案B解析根据抛物线的定义可得|AD|=|AF|=4,又∠DAF=60°,所以|AD|-p=|AF|cos60°=12|AF|,所以4-p=2,解得p=2,所以抛物线C的方程为y2=4x.教师备选1.已知抛物线y2=4x的焦点为F,M,N是抛物线上两个不同的点.若|MF|+|NF|=5,则线段MN的中点到y轴的距离为()A.3B.32C.5D.52答案B解析由题意知抛物线的准线方程为x=-1,分别过点M,N作准线的垂线,垂足为M′,N′(图略),根据抛物线的定义得|MF|=|MM′|,|NF|=|NN′|,所以|MF |+|NF |=|MM ′|+|NN ′|, 所以线段MN 的中点到准线的距离为12(|MF |+|NF |)=52,所以线段MN 的中点到y 轴的距离为52-1=32.2.(2022·济南模拟)已知抛物线x 2=2py (p >0),过焦点F 的直线与抛物线交于A ,B 两点(点A 在第一象限).若直线AB 的斜率为33,点A 的纵坐标为32,则p 的值为() A.14B.12C .1D .2 答案C解析由题意得,抛物线x 2=2py (p >0)的焦点在y 轴上, 准线方程为y =-p2, 设A (x A ,y A ), 则|AF |=y A +p 2=32+p2, 设直线AB 的倾斜角为α, 则tan α=33,因为α∈[0,π),所以α=π6, 所以|AF |=y A -p 2sin α=32-p2sin α=3-p2sin α=3-p 2×12=3-p , 所以3-p =32+p2,解得p =1.思维升华 求抛物线的标准方程的方法(1)定义法;(2)待定系数法:当焦点位置不确定时,分情况讨论.跟踪训练1(1)设抛物线的顶点为O ,焦点为F ,准线为l ,P 是抛物线上异于O 的一点,过P 作PQ ⊥l 于Q .则线段FQ 的垂直平分线() A .经过点O B .经过点PC .平行于直线OPD .垂直于直线OP 答案B解析连接PF (图略),由题意及抛物线的定义可知|PQ |=|FP |,则△QPF 为等腰三角形,故线段FQ 的垂直平分线经过点P .(2)《九章算术》是我国古代内容极为丰富的数学名著,第九章“勾股”,讲述了“勾股定理”及一些应用,直角三角形的三条边长分别称为“勾”“股”“弦”.设点F 是抛物线y 2=2px (p >0)的焦点,l 是该抛物线的准线,过抛物线上一点A 作准线的垂线,垂足为B ,直线AF 交准线l 于点C ,若Rt △ABC 的“勾”|AB |=3,“股”|CB |=33,则抛物线的方程为 ()A .y 2=2xB .y 2=3xC .y 2=4xD .y 2=6x 答案B解析如图,|AB |=3,|BC |=33, 则|AC |=32+(33)2=6,设直线l 与x 轴交于点H ,由|AB |=|AF |=3,|AC |=6,可知点F 为AC 的中点, 所以|FH |=12|AB |=32, 又|FH |=p ,所以p =32, 所以抛物线的方程为y 2=3x . 题型二 抛物线的几何性质例3(1)(2021·新高考全国Ⅱ)抛物线y 2=2px (p >0)的焦点到直线y =x +1的距离为2,则p 等于()A .1B .2C .22D .4 答案B解析抛物线的焦点坐标为⎝ ⎛⎭⎪⎫p 2,0,其到直线x -y +1=0的距离d =⎪⎪⎪⎪⎪⎪p 2-0+11+1=2,解得p =2(p =-6舍去).(2)已知弦AB 经过抛物线y 2=2px (p >0)的焦点F ,设A (x 1,y 1),B (x 2,y 2),则下列说法中错误的是()A .当AB 与x 轴垂直时,|AB |最小 B.1|AF |+1|BF |=2pC .以弦AB 为直径的圆与直线x =-p2相离 D .y 1y 2=-p 2 答案C解析当AB 与x 轴垂直时,AB 为抛物线的通径,是最短的焦点弦,即|AB |最小,A 正确; 设AB 方程为x =ty +p 2, 由⎩⎨⎧x =ty +p2,y 2=2px ,得y 2-2pty -p 2=0,∴y 1+y 2=2pt ,y 1y 2=-p 2,D 正确;∴x 1+x 2=y 21+y 222p =(y 1+y 2)2-2y 1y 22p=4p 2t 2+2p 22p=2pt 2+p ,x 1x 2=y 21y 224p 2=p 24,∴1|AF |+1|BF |=1x 1+p 2+1x 2+p 2=x 1+x 2+p x 1x 2+p 2(x 1+x 2)+p 24=2pt 2+2p p 2+p 2t 2=2p (t 2+1)p 2(t 2+1)=2p,B 正确; ∵AB 的中点到x =-p 2的距离为12(x 1+x 2+p )=12|AB |,∴以AB 为直径的圆与准线x =-p 2相切,C 错误.教师备选1.抛物线y 2=2px (p >0)准线上的点A 与抛物线上的点B 关于原点O 对称,线段AB 的垂直平分线OM 与抛物线交于点M ,若直线MB 经过点N (4,0),则抛物线的焦点坐标是()A .(4,0)B .(2,0)C .(1,0) D.⎝ ⎛⎭⎪⎫12,0 答案C解析设点B (x 1,y 1),M (x 2,y 2),则点A (-x 1,-y 1),可得-x 1=-p 2,则x 1=p 2,设直线MB 的方程为x =my +4,联立⎩⎪⎨⎪⎧x =my +4,y 2=2px ,可得y 2-2mpy -8p =0, 所以y 1y 2=-8p ,由题意可知,OB →·OM →=x 1x 2+y 1y 2=y 21y 224p 2+y 1y 2 =64p 24p 2-8p =16-8p =0,解得p =2.因此,抛物线的焦点为(1,0).2.(2022·唐山模拟)抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.反之,平行于抛物线对称轴的入射光线经抛物线反射后必过抛物线的焦点.已知抛物线r :y 2=x ,O 为坐标原点,一束平行于x 轴的光线l 1从点P ⎝ ⎛⎭⎪⎫4116,1射入,经过r 上的点A (x 1,y 1)反射后,再经r 上另一点B (x 2,y 2)反射后,沿直线l 2射出,经过点Q ,则下列结论错误的是()A .y 1y 2=-1B .|AB |=2516C .PB 平分∠ABQD .延长AO 交直线x =-14于点C ,则C ,B ,Q 三点共线答案A解析设抛物线的焦点为F ,则F ⎝ ⎛⎭⎪⎫14,0.因为P ⎝ ⎛⎭⎪⎫4116,1,且l 1∥x 轴,故A (1,1),故直线AF :y =1-01-14⎝ ⎛⎭⎪⎫x -14=43x -13.由⎩⎨⎧ y =43x -13,y 2=x ,可得y 2-34y -14=0,故y 1y 2=-14,故A 错误;又y 1=1,故y 2=-14,故B ⎝ ⎛⎭⎪⎫116,-14,故|AB |=1+116+12=2516,故B 正确;直线AO :y =x ,由⎩⎨⎧ y =x ,x =-14,可得C ⎝ ⎛⎭⎪⎫-14,-14,故y C =y 2, 所以C ,B ,Q 三点共线,故D 正确;因为|AP |=4116-1=2516=|AB |,故△APB 为等腰三角形,故∠ABP =∠APB ,而l 1∥l 2,故∠PBQ =∠APB ,即∠ABP =∠PBQ ,故PB 平分∠ABQ ,故C 正确.思维升华 应用抛物线的几何性质解题时,常结合图形思考,通过图形可以直观地看出抛物线的顶点、对称轴、开口方向等几何特征,体现了数形结合思想解题的直观性. 跟踪训练2(1)(2021·新高考全国Ⅰ)已知O 为坐标原点,抛物线C :y 2=2px (p >0)的焦点为F ,P 为C 上一点,PF 与x 轴垂直,Q 为x 轴上一点,且PQ ⊥OP .若|FQ |=6,则C 的准线方程为______________.答案x =-32解析方法一(解直角三角形法)由题易得|OF |=p 2,|PF |=p ,∠OPF =∠PQF ,所以tan ∠OPF =tan ∠PQF ,所以|OF ||PF |=|PF ||FQ |,即p 2p =p 6,解得p =3,所以C 的准线方程为x =-32.方法二(应用射影定理法)由题易得|OF |=p 2,|PF |=p ,|PF |2=|OF |·|FQ |,即p 2=p 2×6,解得p =3或p =0(舍去),所以C 的准线方程为x =-32.(2)直线l 过抛物线C :y 2=2px (p >0)的焦点F (1,0),且与C 交于A ,B 两点,则p =______,1|AF |+1|BF |=________.答案21解析由p 2=1,得p =2.当直线l 的斜率不存在时,l :x =1与y 2=4x联立解得y =±2,此时|AF |=|BF |=2,所以1|AF |+1|BF |=12+12=1;当直线l 的斜率存在时,设l :y =k (x -1),代入抛物线方程,得k 2x 2-2(k 2+2)x +k 2=0, 设A (x 1,y 1),B (x 2,y 2),则x 1x 2=1,1|AF |+1|BF |=|AF |+|BF ||AF ||BF |=x 1+x 2+2(x 1+1)(x 2+1)=x 1+x 2+2x 1x 2+x 1+x 2+1 =x 1+x 2+21+x 1+x 2+1=1. 综上,1|AF |+1|BF |=1.题型三 直线与抛物线例4已知抛物线C :y 2=3x 的焦点为F ,斜率为32的直线l 与C 的交点为A ,B ,与x 轴的交点为P .(1)若|AF |+|BF |=4,求l 的方程;(2)若AP→=3PB →,求|AB |. 解设直线l :y =32x +t ,A (x 1,y 1),B (x 2,y 2).(1)由题设得F ⎝ ⎛⎭⎪⎫34,0, 故|AF |+|BF |=x 1+x 2+32.又|AF |+|BF |=4,所以x 1+x 2=52.由⎩⎨⎧ y =32x +t ,y 2=3x ,可得9x 2+12(t -1)x +4t 2=0,则x 1+x 2=-12(t -1)9.从而-12(t -1)9=52,得t =-78.所以l 的方程为y =32x -78.(2)由AP →=3PB →可得y 1=-3y 2. 由⎩⎨⎧ y =32x +t ,y 2=3x ,可得y 2-2y +2t =0,所以y 1+y 2=2,从而-3y 2+y 2=2,故y 2=-1,y 1=3.代入C 的方程得x 1=3,x 2=13,即A (3,3),B ⎝ ⎛⎭⎪⎫13,-1. 故|AB |=4133.教师备选如图,已知抛物线x 2=y ,点A ⎝ ⎛⎭⎪⎫-12,14,B ⎝ ⎛⎭⎪⎫32,94,抛物线上的点P (x ,y )⎝ ⎛⎭⎪⎫-12<x <32.过点B 作直线AP 的垂线,垂足为Q .(1)求直线AP 斜率的取值范围;(2)求|P A |·|PQ |的最大值.解(1)设直线AP 的斜率为k ,k =x 2-14x +12=x -12,因为-12<x <32,所以直线AP 斜率的取值范围是(-1,1).(2)由(1)得直线AP 的斜率为k ,x =k +12,则直线BQ 的斜率为-1k (k ≠0),设直线AP 的方程为kx -y +12k +14=0,直线BQ 的方程为x +ky -94k -32=0,联立直线AP 与BQ 的方程⎩⎪⎨⎪⎧ kx -y +12k +14=0,x +ky -94k -32=0,解得点Q 的横坐标是x Q =-k 2+4k +32(k 2+1).因为|P A |=1+k 2⎝ ⎛⎭⎪⎫x +12=1+k 2(k +1),|PQ |=1+k 2(x Q -x )=-(k -1)(k +1)2k 2+1,所以|P A |·|PQ |=-(k -1)(k +1)3.令f (k )=-(k -1)(k +1)3,因为f ′(k )=-(4k -2)(k +1)2, 所以f (k )在区间⎝ ⎛⎭⎪⎫-1,12上单调递增,⎝ ⎛⎭⎪⎫12,1上单调递减, 因此当k =12时,|P A |·|PQ |取得最大值2716.当k =0时,|P A |=1,|PQ |=1,|P A |·|PQ |=1,所以|P A |·|PQ |的最大值为2716. 思维升华 (1)求解直线与抛物线问题,一般利用方程法,但涉及抛物线的弦长、中点、距离等问题时,要注意“设而不求”“整体代入”“点差法”以及定义的灵活应用.(2)有关直线与抛物线的弦长问题,要注意直线是否过抛物线的焦点.若过抛物线的焦点(设焦点在x 轴的正半轴上),可直接使用公式|AB |=x 1+x 2+p ,若不过焦点,则可用弦长公式.跟踪训练3设抛物线C :y 2=2px (p >0)的焦点为F ,点A (0,2),O 为坐标原点,过F 的直线l 与C 交于M ,N 两点,当MA ⊥OA 时,|MF |=2.(1)求p 的值;(2)若AM →·AN→=0,求直线l 的方程. 解(1)当MA ⊥OA 时,此时点M 的纵坐标为2,其横坐标x M =2p .因为|MF |=2,根据抛物线的定义,得|MF |=2p +p 2=2,解得p =2.(2)由(1)知,抛物线C 的方程为y 2=4x ,点F 的坐标为(1,0).设直线l :x =ky +1,点M (x 1,y 1),N (x 2,y 2),联立⎩⎪⎨⎪⎧ x =ky +1,y 2=4x ,化简可得y 2-4ky -4=0,则y 1+y 2=4k ,y 1y 2=-4.根据题意AM →=(x 1,y 1-2),AN →=(x 2,y 2-2),且AM →·AN →=0,所以x 1x 2+(y 1-2)(y 2-2)=0.将x 1x 2=y 21y 2216=1,y 1+y 2=4k ,y 1y 2=-4代入化简可得4-2×4k -4+1=0,解得k =18,所以直线l 的方程为x =18y +1,即8x -y -8=0.课时精练1.抛物线x 2=12y 的焦点到准线的距离是()A .2B .1C.12D.14答案D解析抛物线标准方程x 2=2py (p >0)中p 的几何意义为抛物线的焦点到准线的距离,由x 2=12y 得p =14.2.若抛物线y 2=2px (p >0)的焦点到准线的距离为2,过焦点的直线与抛物线交于A ,B 两点,且|AB |=8,则弦AB 的中点到y 轴的距离为()A .2B .3C .4D .6答案B解析因为抛物线y 2=2px (p >0)的焦点到准线的距离为2,所以p =2,抛物线方程为y 2=4x .过焦点的直线与抛物线交于A,B两点,设A(x1,y1),B(x2,y2),由抛物线的定义得,焦点弦|AB|=x1+x2+p,所以8=x1+x2+2,则x1+x2=6,所以AB的中点到y轴的距离为d=x1+x22=62=3.3.(2022·桂林模拟)已知抛物线y=12x2的焦点为F,准线为l,M在l上,线段MF与抛物线交于N点,若|MN|=2|NF|,则|MF|等于()A.2B.3C.2D. 3答案C解析如图,过N作准线的垂线NH,垂足为H,设l与y轴的交点为K.根据抛物线的定义可知|NH|=|NF|,在Rt△NHM中,|MN|=2|NH|,则∠NMH=45°.在Rt△MFK中,∠FMK=45°,所以|MF|=2|FK|.而|FK|=1,所以|MF|= 2.4.中国古代桥梁的建筑艺术,有不少是世界桥梁史上的创举,充分显示了中国劳动人民的非凡智慧.一个抛物线型拱桥,当水面离拱顶2m时,水面宽8m.若水面下降1m,则水面宽度为()A.26mB.46mC.42mD.12m答案B解析由题意,以拱桥顶点为原点,建立平面直角坐标系,设抛物线方程为x2=-2py(p>0),由题意知,抛物线经过点A(-4,-2)和点B(4,-2),代入抛物线方程解得p=4,所以抛物线方程为x2=-8y,水面下降1米,即y=-3,解得x1=26,x2=-26,所以此时水面宽度d=2x1=4 6.5.已知抛物线y 2=2px (p >0)的焦点F 到准线的距离为4,直线l 过点F 且与抛物线交于A (x 1,y 1),B (x 2,y 2)两点,若M (m ,2)是线段AB 的中点,则下列结论不正确的是()A .p =4B .抛物线方程为y 2=16xC .直线l 的方程为y =2x -4D .|AB |=10答案B解析由焦点F 到准线的距离为4,根据抛物线的定义可知p =4,故A 正确;则抛物线方程为y 2=8x ,故B 错误;焦点F (2,0),则y 21=8x 1,y 22=8x 2,若M (m ,2)是线段AB 的中点,则y 1+y 2=4,∴y 21-y 22=8x 1-8x 2,即y 1-y 2x 1-x 2=8y 1+y 2=84=2, ∴直线l 的方程为y =2x -4,故C 正确;又由⎩⎪⎨⎪⎧y 2=8x ,y =2x -4,可得x 2-6x +4=0,∴x 1+x 2=6,∴|AB |=|AF |+|BF |=x 1+x 2+4=10,故D 正确.6.已知A ,B 为抛物线x 2=2py (p >0)上的两个动点,以AB 为直径的圆C 经过抛物线的焦点F ,且面积为2π,若过圆心C 作该抛物线准线l 的垂线CD ,垂足为D ,则|CD |的最大值为()A .2B.2C.22D.12答案A解析根据题意,2π=π⎝ ⎛⎭⎪⎫|AB |22, ∴|AB |=2 2.设|AF |=a ,|BF |=b ,过点A 作AQ ⊥l 于Q ,过点B 作BP ⊥l 于P ,如图,由抛物线定义,得|AF |=|AQ |,|BF |=|BP |,∴在四边形ABPQ 中,2|CD |=|AQ |+|BP |=a +b ,由勾股定理得,8=a 2+b 2,∵|CD |2=⎝ ⎛⎭⎪⎫a +b 22=a 2+b 2+2ab 4=8+2ab 4 =2+ab 2≤2+a 2+b 24=4,∴|CD |≤2(当且仅当a =b 时,等号成立).7.(2021·北京)已知抛物线C :y 2=4x ,焦点为F ,点M 为抛物线C 上的点,且|FM |=6,则M 的横坐标是________,作MN ⊥x 轴于N ,则S △FMN =________.答案54 5解析因为抛物线的方程为y 2=4x ,故p =2且F (1,0),因为|MF |=6,所以x M +p 2=6,解得x M =5,故y M =±25,所以S △FMN =12×(5-1)×25=4 5.8.(2020·新高考全国Ⅰ)斜率为3的直线过抛物线C :y 2=4x 的焦点,且与C 交于A ,B 两点,则|AB |=________.答案163解析如图,由题意得,抛物线的焦点为F (1,0),设直线AB 的方程为y =3(x -1).由⎩⎪⎨⎪⎧y =3(x -1),y 2=4x ,得3x 2-10x +3=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=103,所以|AB |=x 1+x 2+2=163.9.过抛物线C :x 2=2py (p >0)的焦点F 作直线l 与抛物线C 交于A ,B 两点,当点A 的纵坐标为1时,|AF |=2.(1)求抛物线C 的方程;(2)若抛物线C 上存在点M (-2,y 0),使得MA ⊥MB ,求直线l 的方程.解(1)抛物线C :x 2=2py (p >0)的准线方程为y =-p 2,焦点为F ⎝ ⎛⎭⎪⎫0,p 2. ∵当点A 的纵坐标为1时,|AF |=2,∴1+p 2=2,解得p =2,∴抛物线C 的方程为x 2=4y .(2)∵点M (-2,y 0)在抛物线C 上,∴y 0=(-2)24=1.又F (0,1),∴设直线l 的方程为y =kx +1.由⎩⎪⎨⎪⎧y =kx +1,x 2=4y ,得x 2-4kx -4=0.设A (x 1,y 1),B (x 2,y 2),则x 1+x 2=4k ,x 1x 2=-4,MA →=(x 1+2,y 1-1), MB →=(x 2+2,y 2-1). ∵MA ⊥MB ,∴MA →·MB→=0, ∴(x 1+2)(x 2+2)+(y 1-1)(y 2-1)=0,∴-4+8k +4-4k 2=0,解得k =2或k =0.当k =0时,l 过点M (舍去),∴k =2,∴直线l 的方程为y =2x +1.10.已知抛物线E :y 2=2px (p >0),过点P (3,0)的直线l 交抛物线E 于A ,B ,且OA →·OB →=-3(O 为坐标原点).(1)求抛物线E 的方程;(2)求△AOB 面积的最小值.解(1)设直线l 为x =ty +3,代入E :y 2=2px 整理得y 2-2pty -6p =0,设A (x 1,y 1),B (x 2,y 2),所以y 1+y 2=2pt ,y 1y 2=-6p ,所以x 1x 2=(y 1y 2)24p 2=(-6p )24p 2=9,由OA →·OB→=-3, 即x 1x 2+y 1y 2=-3,得9-6p =-3,所以p =2,所以所求抛物线E 的方程为y 2=4x .(2)由(1)得y 1+y 2=4t ,y 1y 2=-12,|AB |=1+t 2(4t )2+48 =41+t 2t 2+3,点O 到直线l 的距离为d =31+t 2,则S △AOB =12|AB |·d=12×31+t 2×41+t 2t 2+3 =6t 2+3≥63,当t =0时,等号成立,故当t =0时,△AOB 面积有最小值6 3.11.设F 为抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若F 为△ABC 的重心,则|F A →|+|FB →|+|FC →|的值为() A .1B .2C .3D .4答案C解析由题意可知,点F 的坐标为⎝ ⎛⎭⎪⎫12,0, 又F 为△ABC 的重心,故x A +x B +x C 3=12, 即x A +x B +x C =32.又由抛物线的定义可知|F A →|+|FB →|+|FC →|=x A +x B +x C +32=32+32=3. 12.某农场为节水推行喷灌技术,喷头装在管柱OA 的顶端A 处,喷出的水流在各个方向上呈抛物线状,如图所示.现要求水流最高点B 离地面4m ,点B 到管柱OA 所在直线的距离为3m ,且水流落在地面上以O 为圆心,以7m 为半径的圆上,则管柱OA 的高度为()A.53mB.74mC.94mD.73m答案B解析以B 为坐标原点建立平面直角坐标系,如图所示,记BM ⊥OC 且垂足为M ,A 在y 轴上的投影为D ,设抛物线方程为x 2=-2py (p >0),由题意可知|AD |=3,|BM |=4,|OC |=7,所以|MC |=|OC |-|AD |=7-3=4,所以C (4,-4),代入抛物线方程可知16=8p ,所以p =2,所以抛物线方程为x 2=-4y ,又因为x A =-3,所以y A =y D =-94,所以|BD |=94,所以|OA |=|DM |=|BM |-|BD |=4-94=74,所以OA 的高度为74m.13.已知抛物线C :y 2=2px (p >0)过点P (1,1),则下列结论不正确的是()A .点P 到抛物线焦点的距离为54B .过点P 作过抛物线焦点的直线交抛物线于点Q ,则△OPQ 的面积为532C .过点P 与抛物线相切的直线方程为x -2y +1=0D .过点P 作两条斜率互为相反数的直线交抛物线于M ,N 两点,则直线MN 的斜率为12答案D解析因为抛物线C :y 2=2px (p >0)过点P (1,1),所以p =12,所以抛物线方程为y 2=x ,焦点坐标为F ⎝ ⎛⎭⎪⎫14,0.对于A ,|PF |=1+14=54,A 正确;对于B ,k PF =43,所以l PF :y =43⎝ ⎛⎭⎪⎫x -14, 与y 2=x 联立得4y 2-3y -1=0,所以y 1+y 2=34,y 1y 2=-14,所以S △OPQ =12|OF |·|y 1-y 2|=12×14×(y 1+y 2)2-4y 1y 2=532,B 正确; 对于C ,依题意斜率存在,设直线方程为y -1=k (x -1),与y 2=x 联立得ky 2-y +1-k =0,Δ=1-4k (1-k )=0,即4k 2-4k +1=0,解得k =12,所以切线方程为x -2y +1=0,C 正确;对于D ,依题意斜率存在,设l PM :y -1=k ′(x -1),与y 2=x 联立得k ′y 2-y +1-k ′=0,所以y M +1=1k ′, 即y M =1k ′-1,则x M =⎝ ⎛⎭⎪⎫1k ′-12, 所以点M ⎝ ⎛⎭⎪⎫⎝ ⎛⎭⎪⎫1k ′-12,1k ′-1, 同理N ⎝ ⎛⎭⎪⎫⎝ ⎛⎭⎪⎫-1k ′-12,-1k ′-1, 所以k MN =1k ′-1-⎝ ⎛⎭⎪⎫-1k ′-1⎝ ⎛⎭⎪⎫1k ′-12-⎝ ⎛⎭⎪⎫-1k ′-12 =2k ′-4k ′=-12,D 错误. 14.已知P 为抛物线C :y =x 2上一动点,直线l :y =2x -4与x 轴,y 轴交于M ,N 两点,点A (2,-4),且AP →=λAM →+μAN →,则λ+μ的最小值为________.答案74解析由题意得M (2,0),N (0,-4),设P (x ,y ),由AP→=λAM →+μAN → 得(x -2,y +4)=λ(0,4)+μ(-2,0).所以x -2=-2μ,y +4=4λ.因此λ+μ=y +44-x -22=x 24-x 2+2=⎝ ⎛⎭⎪⎫x 2-122+74≥74,故λ+μ的最小值为74.15.已知抛物线C :y 2=4x ,其准线与x 轴交于点M ,过其焦点F 的直线与抛物线相交于A ,B 两点,记直线MA ,MB 的斜率分别为k 1,k 2,则1k 21+1k 22的最小值为() A .1B .2C .3D .4答案B解析由题意,可得焦点坐标F (1,0),准线方程为x =-1,可得M (-1,0),设A (x 1,y 1),B (x 2,y 2),直线AB 的方程为x =my +1,联立方程⎩⎪⎨⎪⎧x =my +1,y 2=4x ,可得y 2-4my -4=0,则y 1+y 2=4m ,y 1·y 2=-4,因为1k 1=x 1+1y 1=my 1+1+1y 1=m +2y 1, 1k 2=x 2+1y 2=my 2+1+1y 2=m +2y 2,所以1k 21+1k 22=⎝⎛⎭⎪⎫m +2y 12+⎝ ⎛⎭⎪⎫m +2y 22 =2m 2+4m ⎝ ⎛⎭⎪⎫1y 1+1y 2+4⎝ ⎛⎭⎪⎫1y 21+1y 22 =2m 2+4m ·y 1+y 2y 1·y 2+4·(y 1+y 2)2-2y 1·y 2y 21·y 22 =2m 2+4m ·4m -4+4·16m 2+816=2m 2+2, 所以当且仅当m =0时,1k 21+1k 22取得最小值为2. 16.已知曲线C :y =x 22,D 为直线y =-12上的动点,过D 作C 的两条切线,切点分别为A ,B .(1)证明:直线AB 过定点;(2)若以E ⎝ ⎛⎭⎪⎫0,52为圆心的圆与直线AB 相切,且切点为线段AB 的中点,求四边形ADBE 的面积.(1)证明设D ⎝ ⎛⎭⎪⎫t ,-12,A (x 1,y 1), 则x 21=2y 1.因为y ′=x ,所以切线DA 的斜率为x 1,故y 1+12x 1-t =x 1,整理得2tx 1-2y 1+1=0.设B (x 2,y 2),同理可得2tx 2-2y 2+1=0. 故直线AB 的方程为2tx -2y +1=0.所以直线AB 过定点⎝ ⎛⎭⎪⎫0,12. (2)解由(1)得直线AB 的方程为y =tx +12.由⎩⎪⎨⎪⎧ y =tx +12,y =x 22,可得x 2-2tx -1=0.于是x 1+x 2=2t ,x 1x 2=-1, y 1+y 2=t (x 1+x 2)+1=2t 2+1, |AB |=1+t 2|x 1-x 2| =1+t 2×(x 1+x 2)2-4x 1x 2 =2(t 2+1).设d 1,d 2分别为点D ,E 到直线AB 的距离, 则d 1=t 2+1,d 2=2t 2+1. 因此,四边形ADBE 的面积S =12|AB |(d 1+d 2)=(t 2+3)t 2+1.设M 为线段AB 的中点,则M ⎝ ⎛⎭⎪⎫t ,t 2+12. 因为EM→⊥AB →,而EM →=(t ,t 2-2),AB →与向量(1,t )平行,所以t +(t 2-2)t =0,解得t =0或t =±1.当t =0时,S =3;当t =±1时,S =4 2. 因此,四边形ADBE 的面积为3或4 2.。
抛物线【九大题型】(举一反三)(新高考专用)(解析版)—2025年高考数学一轮复习

抛物线【九大题型】专练【题型1 抛物线的定义及其应用】........................................................................................................................3【题型2 抛物线的标准方程】................................................................................................................................5【题型3 抛物线的焦点坐标及准线方程】............................................................................................................6【题型4 抛物线的轨迹方程】................................................................................................................................7【题型5 抛物线上的点到定点的距离及最值】....................................................................................................9【题型6 抛物线上的点到定点和焦点距离的和、差最值】..............................................................................11【题型7 抛物线的焦半径公式】..........................................................................................................................14【题型8 抛物线的几何性质】..............................................................................................................................16【题型9 抛物线中的三角形(四边形)面积问题】 (18)1、抛物线【知识点1 抛物线及其性质】1.抛物线的定义(1)定义:平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫作抛物线.点F叫作抛物线的焦点,直线l叫作抛物线的准线.(2)集合语言表示设点M(x,y)是抛物线上任意一点,点M到直线l的距离为d,则抛物线就是点的集合P={M||MF|=d}.2.抛物线的标准方程与几何性质(0,0)(0,0)3.抛物线与椭圆、双曲线几何性质的差异抛物线与椭圆、双曲线几何性质的差异:①它们都是轴对称图形,但椭圆和双曲线又是中心对称图形;②顶点个数不同,椭圆有4个顶点,双曲线有2个顶点,抛物线只有1个顶点;③焦点个数不同,椭圆和双曲线各有2个焦点,抛物线只有1个焦点;④离心率取值范围不同,椭圆的离心率范围是0<e<1,双曲线的离心率范围是e>1,抛物线的离心率是e=1;⑤椭圆和双曲线都有两条准线,而抛物线只有一条准线;⑥椭圆是封闭式曲线,双曲线和抛物线都是非封闭式曲线.【知识点2 抛物线标准方程的求解方法】1.抛物线标准方程的求解待定系数法:求抛物线标准方程的常用方法是待定系数法,其关键是判断焦点位置、开口方向,在方程的类型已经确定的前提下,由于标准方程只有一个参数p,只需一个条件就可以确定抛物线的标准方程.【知识点3 抛物线的焦半径公式】1.焦半径公式设抛物线上一点P的坐标为,焦点为F.(1)抛物线:;(2)抛物线:(3)抛物线:;(4)抛物线:.注:在使用焦半径公式时,首先要明确抛物线的标准方程的形式,不同的标准方程对应于不同的焦半径公式.【知识点4 与抛物线有关的最值问题的解题策略】1.与抛物线有关的最值问题的两个转化策略(1)转化策略一:将抛物线上的点到准线的距离转化为该点到焦点的距离,构造出“两点之间线段最短”“三角形两边之和大于第三边”,使问题得以解决.(2)转化策略二:将抛物线上的点到焦点的距离转化为到准线的距离,利用“与直线上所有点的连线中垂线段最短”原理解决.【方法技巧与总结】1.通径:过焦点与对称轴垂直的弦长等于2p.2.抛物线P,也称为抛物线的焦半径.【题型1 抛物线的定义及其应用】【例1】(2024·贵州贵阳·二模)抛物线y2=4x上一点M与焦点间的距离是10,则M到x轴的距离是()A.4B.6C.7D.9【解题思路】借助抛物线定义计算即可得.【解答过程】抛物线y2=4x的准线为x=―1,由抛物线定义可得x M+1=10,故x M=10―1=9,则|y M|===6,即M到x轴的距离为6.故选:B.【变式1-1】(2024·河北·模拟预测)已知点P为平面内一动点,设甲:P的运动轨迹为抛物线,乙:P到平面内一定点的距离与到平面内一定直线的距离相等,则()A.甲是乙的充分条件但不是必要条件B.甲是乙的必要条件但不是充分条件C.甲是乙的充要条件D.甲既不是乙的充分条件也不是乙的必要条件【解题思路】根据已知条件,结合充分条件、必要条件的定义,即可求解.【解答过程】解:当直线经过定点时,点的轨迹是过定点且垂直于该直线的另一条直线,当直线不经过该定点时,点的轨迹为抛物线,故甲是乙的充分条件但不是必要条件.故选:A.【变式1-2】(2024·北京大兴·三模)已知抛物线y2=4x的焦点为F,过F且斜率为―1的直线与直线x=―1交于点A,点M在抛物线上,且满足|MA|=|MF|,则|MF|=()A.1B C.2D.【解题思路】由题意先求出过F且斜率为―1的直线方程,进而可求出点A,接着结合点M在抛物线上且|MA|=|MF|可求出x M,从而根据焦半径公式|MF|=x M+1即可得解.【解答过程】由题意可得F(1,0),故过F且斜率为―1的直线方程为y=―(x―1)=―x+1,令x=―1⇒y=2,则由题A(―1,2),因为|MA|=|MF|,所以MA垂直于直线x=―1,故y M=2,又M 在抛物线上,所以由22=4x M ⇒x M =1,所以|MF |=x M +1=2.故选:C.【变式1-3】(2024·福建莆田·模拟预测)若抛物线C 的焦点到准线的距离为3,且C 的开口朝左,则C 的标准方程为( )A .y 2=―6xB .y 2=6xC .y 2=―3xD .y 2=3x【解题思路】根据开口设抛物线标准方程,利用p 的几何意义即可求出.【解答过程】依题意可设C 的标准方程为y 2=―2px(p >0),因为C 的焦点到准线的距离为3,所以p =3,所以C 的标准方程为y 2=―6x .故选:A.【题型2 抛物线的标准方程】【例2】(2024·山东菏泽·模拟预测)已知点A (a,2)为抛物线x 2=2py (p >0)上一点,且点A 到抛物线的焦点F 的距离为3,则p =( )A .12B .1C .2D .4【解题思路】由题意,根据抛物线的性质,抛物线x 2=2py (p >0),则抛物线焦点为F 0,M (x 1,y 1)为 抛物线上一点,有|MF |=y 1+p 2,可得|AF |=2+p2=3,解得p =2.【解答过程】因为抛物线为x 2=2py (p >0),则其焦点在y 轴正半轴 上,焦点坐标为由于点A (a,2)为抛物线x 2=2py ,(p >0)为上一点,且点A 到抛物线的焦点F 的距离为3, 所以点A 到抛物线的焦点F 的距离为|AF |=2+p2=3,解得p =2,故选:C.【变式2-1】(2024·陕西安康·模拟预测)过点(2,―3),且焦点在y 轴上的抛物线的标准方程是( )A .x 2=―3yB .x 2=―43yC .x 2=―23yD .x 2=―4y【解题思路】利用待定系数法,设出抛物线方程,把点代入求解即可.【解答过程】设抛物线的标准方程为x 2=ay (a ≠0),将点点(2,―3)代入,得22=―3a,解得a=―43,所以抛物线的标准方程是x2=―43y.故选:B.【变式2-2】(2024·新疆·三模)已知抛物线y2=2px(p>0)上任意一点到焦点F的距离比到y轴的距离大1,则抛物线的标准方程为()A.y2=x B.y2=2x C.y2=4x D.y2=8x【解题思路】根据抛物线的定义求解.【解答过程】由题意抛物线y2=2px(p>0)上任意一点到焦点F的距离与它到直线x=―1的距离相,因此―p2=―1,p=2,抛物线方程为y2=4x.故选:C.【变式2-3】(2024·宁夏石嘴山·三模)如图,过抛物线y2=2px(p>0)的焦点F的直线l交抛物线于两点A、B,交其准线于C,AE与准线垂直且垂足为E,若|BC|=2|BF|,|AE|=3,则此抛物线的方程为()A.y2=3x2B.y2=9xC.y2=9x2D.y2=3x【解题思路】过点A,B作准线的垂线,设|BF|=a,得到|AC|=3+3a,结合抛物线的定义,求得a=1,再由BD//FG,列出方程求得p的值,即可求解.【解答过程】如图所示,分别过点B作准线的垂线,垂足为D,设|BF|=a,则|BC|=2|BF|=2a,由抛物线的定义得|BD|=|BF|=a,在直角△BCD中,可得sin∠BCD=|BD||BC|=12,所以∠BCD=30∘,在直角△ACE中,因为|AE|=3,可得|AC|=3+3a,由|AC |=2|AE |,所以3+3a =6,解得a =1,因为BD //FG ,所以1p =2a3a ,解得p =32,所以抛物线方程为y 2=3x .故选:C.【题型3 抛物线的焦点坐标及准线方程】【例3】(2024·内蒙古赤峰·二模)已知抛物线C 的方程为 x =―116y 2, 则此抛物线的焦点坐标为( )A .(-4,0)B .―14,C .(-2,0)D .―12,【解题思路】由抛物线的几何性质求解.【解答过程】依题意得:y 2=―16x ,则此抛物线的焦点坐标为:―4,0,故选:A.【变式3-1】(2024·黑龙江大庆·模拟预测)已知抛物线C:y =6x 2,则C 的准线方程为( )A .y =―32B .y =32C .y =―124D .y =124【解题思路】根据抛物线的准线方程直接得出结果.【解答过程】抛物线C :y =6x 2的标准方程为x 2=16y ,所以其准线方程为y =―124.故选:C.【变式3-2】(2024·河南·三模)抛物线y 2=―28x 的焦点坐标为( )A .(0,―14)B .(0,―7)C .(―14,0)D .(―7,0)【解题思路】根据抛物线的标准方程直接得出结果.【解答过程】∵2p =28,∴p =14,∴抛物线y 2=―28x 的焦点坐标为(―7,0).故选:D.【变式3-3】(2024·福建厦门·模拟预测)若抛物线y 2=mx 的准线经过双曲线x 2―y 2=2的右焦点,则m的值为()A.―4B.4C.―8D.8【解题思路】根据题意,分别求得双曲线的右焦点以及抛物线的准线方程,代入计算,即可得到结果.【解答过程】因为双曲线x2―y2=2的右焦点为(2,0),又抛物线y2=mx的准线方程为x=―m4,则―m4=2,即m=―8.故选:C.【题型4 抛物线的轨迹方程】【例4】(2024·湖南衡阳·三模)已知点F(2,0),动圆P过点F,且与x=―2相切,记动圆圆心P点的轨迹为曲线Γ,则曲线Γ的方程为()A.y2=2x B.y2=4x C.y2=8x D.y2=12x【解题思路】分析题意,利用抛物线的定义判断曲线是抛物线,再求解轨迹方程即可.【解答过程】由题意知,点P到点F的距离和它到直线x=―2的距离相等,所以点P的轨迹是以(2,0)为焦点的抛物线,所以Γ的方程为y2=8x,故C正确.故选:C.【变式4-1】(23-24高二上·北京延庆·期末)到定点F(1,0)的距离比到y轴的距离大1的动点且动点不在x轴的负半轴的轨迹方程是()A.y2=8x B.y2=C.y2=2x D.y2=x【解题思路】根据抛物线的定义即可得解.【解答过程】因为动点到定点F(1,0)的距离比到y轴的距离大1,所以动点到定点F(1,0)的距离等于到x=―1的距离,所以动点的轨迹是以F(1,0)为焦点,x=―1为准线的抛物线,所以动点的轨迹方程是y2=4x.故选:B.【变式4-2】(23-24高二上·重庆·期末)已知点P(x,y)=|x+1|,则点P的轨迹为()A.椭圆B.双曲线C.抛物线D.圆【解题思路】根据已知条件及抛物线的定义即可求解.P(x,y)到点(1,0)的距离;|x+1|表示点P(x,y)到直线x=―1的距离.=|x+1|,所以点P(x,y)到点(1,0)的距离等于点P(x,y)到直线x=―1的距离,所以P的轨迹为抛物线.故选:C.【变式4-3】(23-24高二上·宁夏石嘴山·阶段练习)一个动圆与定圆F:(x+2)2+y2=1相内切,且与定直线l:x=3相切,则此动圆的圆心M的轨迹方程是( )A.y2=8x B.y2=4x C.y2=―4x D.y2=―8x【解题思路】先利用圆与圆的位置关系,直线与圆的位置关系找到动点M的几何条件,再根据抛物线的定义确定动点M的轨迹,最后利用抛物线的标准方程写出轨迹方程.【解答过程】设动圆M的半径为r,依题意:|MF|=r―1,点M到定直线x=2的距离为d=r―1,所以动点M到定点F(―2,0)的距离等于到定直线x=2的距离,即M的轨迹为以F为焦点,x=2所以此动圆的圆心M的轨迹方程是y2=―8x.故选:D.【题型5 抛物线上的点到定点的距离及最值】【例5】(2024·全国·模拟预测)已知A是抛物线C:y2=4x上的点,N(4,0),则|AN|的最小值为()A.2B.C.4D.【解题思路】由抛物线的方程,利用二次函数的性质求最值【解答过程】设,t,则|AN|===≥当且仅当t=±故选:D.【变式5-1】(2024高三·全国·专题练习)已知P是抛物线y2=2x上的点,Q是圆(x―5)2+y2=1上的点,则|PQ |的最小值是( )A .2B .C .D .3【解题思路】将问题转化为求|PC|的最小值,根据两点之间的距离公式,求得|PC|的最小值再减去半径即可.【解答过程】如图,抛物线上点P (x,y )到圆心C (5,0)的距离为|PC |,|CP |≤|CQ |+|PQ |,因此|PQ |≥|CP |―1,当|CP |最小时,|PQ |=|CP |―1最小,而|CP |2=(x ―5)2+y 2=―52+y 2=2―82+9,当y =±|CP |min =3,因此|PQ |的最小值是2.故选:A.【变式5-2】(2024·湖南益阳·三模)已知M 是抛物线y²=4x 上一点,圆C 1:(x ―1)2+(y ―2)2=1关于直线y =x ―1对称的圆为C 2,N 是圆C 2上的一点,则|MN |的最小值为( )A .1B ―1C―1D .37【解题思路】根据对称性求出圆C 2的方程,设y 0,求出|MC 2|的最小值,即可求出|MN |的最小值.【解答过程】圆C 1:(x ―1)2+(y ―2)2=1圆心为C 1(1,2),半径r =1,设C 2(a,b ),=―1―1=0,解得a =3b =0,则C 2(3,0),所以圆C2 :(x ―3)2+y 2=1,设y 0,则|MC 2|==所以当y 20=4,即y 0=±2时,|MC 2|min=所以|MN |的最小值是―1.故选:A.【变式5-3】(2024·黑龙江齐齐哈尔·二模)已知抛物线C:y2=8x的焦点为F,M为C上的动点,N为圆A:x2+ y2+2x+8y+16=0上的动点,设点M到y轴的距离为d,则|MN|+d的最小值为()A.1B C D.2【解题思路】作出图形,过点M作ME垂直于抛物线的准线,垂足为点E,利用抛物线的定义可知d=|MF|―2,分析可知,当且仅当N、M为线段AF分别与圆A、抛物线C的交点时,|MN|+d取最小值,即可得解.【解答过程】根据已知得到F(2,0),圆A:(x+1)2+(y+4)2=1,所以A(―1,―4),圆A的半径为1,抛物线C的准线为l:x=―2,过点M作ME⊥l,垂足为点E,则|ME|=d+2,由抛物线的定义可得d+2=|ME|=|MF|,所以,|MN|+d=|MN|+|MF|―2≥|AM|+|MF|―1―2≥|AF|―1―2=1―2=2.当且仅当N、M为线段AF分别与圆A、抛物线C的交点时,两个等号成立,因此,|MN|+d的最小值为3.故选:D.【题型6 抛物线上的点到定点和焦点距离的和、差最值】【例6】(2024·四川成都·模拟预测)设点A(2,3),动点P在抛物线C:y2=4x上,记P到直线x=―2的距离为d,则|AP|+d的最小值为()A.1B.3C1D【解题思路】根据抛物线的定义,P到焦点F的距离等于P到准线的距离,可得d=|PF|+1,从而转化为求|AP|+|PF|+1的值,当A,P,F三点共线时,d=|PF|+1取得最小值,即可求解.【解答过程】由题意可得,抛物线C的焦点F(1,0),准线方程为x=―1,由抛物线的定义可得d=|PF|+1,所以|AP|+d=|AP|+|PF|+1,因为|AP|+|PF|≥|AF|==所以|AP|+d=|AP|+|PF|+1≥+1.当且仅当A,P,F三点共线时取等号,所以|AP|+d+1.故选:D.【变式6-1】(2024·湖南常德·一模)已知抛物线方程为:y2=16x,焦点为F.圆的方程为(x―5)2+(y―1)2 =1,设P为抛物线上的点,Q|PF|+|PQ|的最小值为()A.6B.7C.8D.9【解题思路】根据抛物线定义将点到焦点的距离转化为点到直线的距离,即|PF|=|PN|,从而得到|PF|+ |PQ|=|PN|+|PQ|,P、Q、N三点共线时和最小;再由Q在圆上,|QN|min=|MN|―r得到最小值.【解答过程】由抛物线方程为y2=16x,得到焦点F(4,0),准线方程为x=―4,过点P做准线的垂线,垂足为N,因为点P在抛物线上,所以|PF|=|PN|,所以|PF|+|PQ|=|PN|+|PQ|,当Q点固定不动时,P、Q、N三点共线,即QN垂直于准线时和最小,又因为Q在圆上运动,由圆的方程为(x―5)2+(y―1)2=1得圆心M(5,1),半径r=1,所以|QN|min=|MN|―r=8,故选:C.【变式6-2】(2024·全国·模拟预测)在直角坐标系xOy中,已知点F(1,0),E(―2,0),M(2,2),动点P满足线段PE的中点在曲线y2=2x+2上,则|PM|+|PF|的最小值为()A.2B.3C.4D.5【解题思路】设P(x,y),由题意求出P的轨迹方程,继而结合抛物线定义将|PM|+|PF|的最小值转化为M 到直线l的距离,即可求得答案.【解答过程】设P(x,y),则PE y2=2x+2,可得y2=4x,故动点P的轨迹是以F为焦点,直线l:x=―1为准线的抛物线,由于22<4×2,故M(2,2)在抛物线y2=4x内部,过点P作PQ⊥l,垂足为Q,则|PM|+|PF|=|PM|+|PQ|,(抛物线的定义),故当且仅当M,P,Q三点共线时,|PM|+|PQ|最小,即|PM|+|PF|最小,最小值为点M到直线l的距离,所以(|PM|+|PF|)min=2―(―1)=3,故选:B.【变式6-3】(2024·陕西西安·一模)设P为抛物线C:y2=4x上的动点,A(2,6)关于P的对称点为B,记P到直线x=―1、x=―4的距离分别d1、d2,则d1+d2+|AB|的最小值为()A B.C+3D.+3【解题思路】根据题意得到d1+d2+|AB|=2d1+3+2|PA|=2(d1+|PA|)+3,再利用抛物线的定义结合三角不等式求解.【解答过程】抛物线C:y2=4x的焦点为F(1,0),准线方程为x=―1,如图,因为d 2=d 1+3,且A (2,6)关于P 的对称点为B ,所以|PA |=|PB |,所以d 1+d 2+|AB |=2d 1+3+2|PA |=2(d 1+|PA |)+3 =2(|PF |+|PA |)+3≥2|AF |+3 ==.当P 在线段AF 与抛物线的交点时,d 1+d 1+|AB |取得最小值,且最小值为.故选:D.【题型7 抛物线的焦半径公式】【例7】(2024·青海西宁·一模)已知F 是抛物线C:x 2=4y 的焦点,点M 在C 上,且M 的纵坐标为3,则|MF |=( )A .B .C .4D .6【解题思路】利用抛物线的标准方程和抛物线的焦半径公式即可求解.【解答过程】由x 2=4y ,得2p =4,解得p =2.所以抛物线C:x 2=4y 的焦点坐标为F (0,1),准线方程为y =―1,又因为M 的纵坐标为3,点M 在C 上,所以|MF |=y M +p2=3+22=4.故选:C.【变式7-1】(2024·河南·模拟预测)已知抛物线C:y 2=2px (p >0)上的点(m,2)到原点的距离为为F ,准线l 与x 轴的交点为M ,过C 上一点P 作PQ ⊥l 于Q ,若∠FPQ =2π3,则|PF |=( )A .13B .12C D .23【解题思路】根据点(m,2)到原点的距离为再设点P 坐标,利用抛物线的定义和等腰三角形的性质列出方程即可求解.【解答过程】因为点(m,2)到原点的距离为所以m 2+22=8,解得m =2,(负值舍),将点(2,2)代入抛物线方程y 2=2px (p >0),得4=4p ,所以p =1,所以C:y 2=2x,F(12,0),l:x =―12.由于抛物线关于x 轴对称,不妨设,因为|PQ|=|PF|=x +12,∠FPQ =2π3,所以△PQF 为等腰三角形,∠PQF =π6,所以|QF|=+12),所以|QF|==+12),解得x =16或x =―12(舍),所以|PF |=16+12=23.故选:D.【变式7-2】(2024·新疆·三模)已知抛物线C :y 2=x 的焦点为F ,在抛物线C 上存在四个点P ,M ,Q ,N ,若弦PQ 与弦MN 的交点恰好为F ,且PQ ⊥MN ,则1|PQ |+1|MN |=( )A B .1C D .2【解题思路】由抛物线的方程可得焦点F 的坐标,应用抛物线焦点弦性质|PF |=p1―cos θ,|QF |=p1+cos θ,|MF |=p1+sin θ,|NF |=p1―sin θ,结合三角的恒等变换的化简可得1|PQ |+1|MN |=12p ,即可求解.【解答过程】由抛物线C:y 2=x 得2p =1,则p =12,F(14,0),不妨设PQ 的倾斜角为θ0<θ<则由|PF |cos θ+p =|PF |,p ―|QF |cos θ=|QF |,得|PF |=p 1―cos θ,|QF |=p1+cos θ,所以|MF |==p1+sin θ,|NF |==p1―sin θ,得|PQ |=|PF |+|QF |=p1―cos θ+p1+cos θ=2psin 2θ,|MN |==2pcos 2θ,所以1|PQ |+1|MN |=12p =1.故选:B.【变式7-3】(2024·北京西城·三模)点F 抛物线y 2=2x 的焦点,A ,B ,C 为抛物线上三点,若FA +FB +FC =0,则|FA |+|FB |+|FC |=( )A .2B .C .3D .【解题思路】设A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),根据抛物线方程求出焦点坐标和准线方程,再由FA +FB +FC =0可得F 为△ABC 的重心,从而可求出x 1+x 2+x 3,再根据抛物线的定义可求得结果.【解答过程】设A(x 1,y 1),B(x 2,y 2),C(x 3,y 3),由y 2=2x ,得p =1,所以F(12,0),准线方程为x =―12,因为FA +FB +FC =0,所以F 为△ABC 的重心,所以x 1+x 2+x 33=12,所以x 1+x 2+x 3=32,所以|FA |+|FB |+|FC |=x 1+12+x 2+12+x 3+12=x 1+x 2+x 3+32=32+32=3,故选:C.【题型8 抛物线的几何性质】【例8】(2024·重庆·模拟预测)A,B 是抛物线y 2=2px(p >0)上的不同两点,点F 是抛物线的焦点,且△OAB 的重心恰为F ,若|AF|=5,则p =( )A .1B .2C .3D .4【解题思路】根据重心可得x 1+x 2=3p 2y 1=―y 2,结合对称性可得x 1=3p4,再根据抛物线的定义运算求解.【解答过程】设A (x 1,y 1),B (x 2,y 2),因为△OAB 的重心恰为F=p2=0,解得x 1+x 2=3p2y 1=―y 2,由y 1=―y 2可知A,B 关于x 轴对称,即x 1=x 2,则x 1+x 2=2x 1=3p2,即x 1=3p 4,又因为|AF |=x 1+p2=5p 4=5,解得p =4.故选:D.【变式8-1】(23-24高二下·福建厦门·期末)等边三角形的一个顶点位于原点,另外两个顶点在抛物线y 2=2x 上,则这个等边三角形的边长为( )A .2B .C .4D.【解题思路】正三角形的另外两个顶点关于x 轴对称,设另外两个顶点坐标分别是A ),B―a),把顶点代入抛物线方程化简即可求解.【解答过程】设正三角形得边长为2a ,由图可知正三角形的另外两个顶点关于x 轴对称,可设另外两个顶点坐标分别是A),B―a ),把顶点代入抛物线方程得a 2=解得a =所以正三角形的边长为故选:D.【变式8-2】(23-24高三下·北京·阶段练习)设抛物线C 的焦点为F ,点E 是C 的准线与C 的对称轴的交点,点P 在C 上,若∠PEF =30°,则sin ∠PFE =( )A B C D 【解题思路】先设P(x 0,y 0),根据图形分别表示出tan ∠ P EF 和sin ∠ P FE 即可得解.【解答过程】由于抛物线的对称性,不妨设抛物线为C:y 2=2px(p >0),则其焦点为F(p2,0),点E 是C 的准线与C 的对称轴的交点,其坐标为E(―p2,0),点P 在C 上,设为P(x 0,y 0),若∠ P EF =30∘,则tan ∠ P EF =|y 0|x 0+p 2=且|PF|=x 0+p 2,则sin ∠ P FE =sin (π―∠ P FE )=|y 0||PF|=故选:B.【变式8-3】(23-24高二下·重庆·阶段练习)已知x 轴上一定点A (a,0)(a >0),和抛物线y 2=2px (p >0)上的一动点M ,若|AM |≥a 恒成立,则实数a 的取值范围为( )A .B .(0,p ]C .D .(0,2p ]【解题思路】设M (x 0,y 0) (x 0≥0),表示出|AM |,依题意可得x 20―(2a ―2p )x 0≥0恒成立,分x 0=0和x 0>0两种情况讨论,当x0>0时x0≥2a―2p恒成立,即可得到2a―2p≤0,从而求出a的取值范围.【解答过程】设M(x0,y0)(x0≥0),则y20=2px0,所以|AM|====因为|AM|≥a恒成立,所以x20―(2a―2p)x0+a2≥a2恒成立,所以x20―(2a―2p)x0≥0恒成立,当x0=0时显然恒成立,当x0>0时x0≥2a―2p恒成立,所以2a―2p≤0,则a≤p,又a>0,所以0<a≤p,即实数a的取值范围为(0,p].故选:B.【题型9 抛物线中的三角形(四边形)面积问题】【例9】(2024·江西新余·二模)已知点Q(2,―2)在抛物线C:y2=2px上,F为抛物线的焦点,则△OQF (O为坐标原点)的面积是()A.12B.1C.2D.4【解题思路】将点Q代入抛物线C的方程,即可求解p,再结合抛物线的公式,即可求解【解答过程】∵点Q(2,―2)在抛物线C:y2=2px上,F为抛物线C的焦点,∴4=4p,解得p=1,故抛物线C的方程为y2=2x,F(12,0),则△OQF的面积S△OQF=12×12×2=12.故选:A.【变式9-1】(23-24高二上·广东广州·期末)已知抛物线C:y2=2px(p>0)的焦点为F,直线l与C相交于A、B两点,与y轴相交于点E.已知|AF|=5,|BF|=3,若△AEF的面积是△BEF面积的2倍,则抛物线C的方程为()A .y 2=2xB .y 2=4xC .y 2=6xD .y 2=8x【解题思路】过A,B 分别作C 的准线的垂线交y 轴于点M,N ,根据抛物线定义可得|AM |=5―p2,|BN |=3―p 2,再由S △AEF S △BEF=|AE ||BE |=|AM ||BN |即可求参数p ,进而可得抛物线方程.【解答过程】如图,过A,B 分别作C 的准线的垂线交y 轴于点M,N ,则AM //BN ,故|AE ||BE |=|AM ||BN |,因为C 的准线为x =―p2,所以|AM |=|AF |―p2=5―p2,|BN |=|BF |―p2=3―p2,所以S △AEFS △BEF=12|EF ||AE |sin ∠AEF 12|EF ||BE |sin ∠BEF =|AE ||BE |=|AM ||BN |=5―p 23―p 2=2,解得p =2,故抛物线C 的方程为y 2=4x .故选:B.【变式9-2】(23-24高二上·广东广州·期末)设F 为抛物线y 2=4x 的焦点,A,B,C 为该抛物线上不同的三点,且FA +FB +FC =0,O 为坐标原点,若△OFA 、△OFB 、△OFC 的面积分别为S 1、S 2、S 3,则S 21+S 22+S 23=( )A .3B .4C .5D .6【解题思路】设点A,B,C 的坐标,再表示出△OFA,△OFB,△OFC 的面积,借助向量等式即可求得答案.【解答过程】设点A,B,C 的坐标分别为(x 1,y 1),(x 2,y 2),(x 3,y 3),而抛物线的焦点F(1,0),|OF|=1,FA =(x 1―1,y 1),FB =(x 2―1,y 2),FC =(x 3―1,y 3),由FA +FB +FC =0,得x 1+x 2+x 3=3,于是S 1=12|y 1|,S 2=12|y 2|,S 3=12|y 3|,所以S 21+S 22+S 23=14(y 21+y 22+y 23)=x 1+x 2+x 3=3.故选:A.【变式9-3】(23-24高二·全国·课后作业)已知抛物线C:y2=8x,点P为抛物线上任意一点,过点P向圆D:x2+y2―4x+3=0作切线,切点分别为A,B,则四边形PADB的面积的最小值为()A.1B.2C D【解题思路】由题意圆的圆心与抛物线的焦点重合,可得连接PD,则S四边形PADB=2S Rt△PAD=|PA|,而|PA|=|PD|最小时,四边形PADB的面积最小,再抛物线的定义转化为点P到抛物线的准线的距离的最小值,结合抛物线的性质可求得结果【解答过程】如图,连接PD,圆D:(x―2)2+y2=1,该圆的圆心与抛物线的焦点重合,半径为1,则S四边形PADB=2S Rt△PAD=|PA|.又|PA|=PADB的面积最小时,|PD|最小.过点P向抛物线的准线x=―2作垂线,垂足为E,则|PD|=|PE|,当点P与坐标原点重合时,|PE|最小,此时|PE|=2.==故S四边形PADBmin故选:C.一、单选题1.(2024·江西·模拟预测)若抛物线x 2=8y 上一点(x 0,y 0)到焦点的距离是该点到x 轴距离的2倍.则y 0=( )A .12B .1C .32D .2【解题思路】根据抛物线的方程,结合抛物线的标准方程,得到抛物线的焦点和准线,利用抛物线的定义,得到抛物线上的点(x 0,y 0)到焦点的距离,根据题意得到关于y 0的方程,求解即可.【解答过程】已知拋物线的方程为x 2=8y ,可得p =4.所以焦点为F (0,2),准线为l :y =―2.抛物线上一点A (x 0,y 0)到焦点F 的距离等于到准线l 的距离,即|AF |=y 0+2,又∵A 到x 轴的距离为y 0,由已知得y 0+2=2y 0,解得y 0=2.故选:D .2.(2024·四川·模拟预测)已知抛物线C:x 2=8y 的焦点为F,P 是抛物线C 上的一点,O 为坐标原点,|OP |=4|PF |=( )A .4B .6C .8D .10【解题思路】求出抛物线焦点和准线方程,设P (m,n )(m ≥0),结合|OP |=n =4,由焦半径公式得到答案.【解答过程】抛物线C:x 2=8y 的焦点为F (0,2),准线方程为y =―2,设P (m,n )(m ≥0)=,解得n =4或n =―12(舍去),则|PF |=n +2=6.故选:B .3.(23-24高二下·甘肃白银·期中)若圆C 与x 轴相切且与圆x 2+y 2=4外切,则圆C 的圆心的轨迹方程为( )A .x 2=4y +4B .x 2=―4y +4C .x 2=4|y |+4D .x 2=4y ―4【解题思路】设圆心坐标为(x,y )=2+|y |,化简整理即可得解.【解答过程】设圆心坐标为(x,y)=2+|y|,化简得x2=4|y|+4,即圆C的圆心的轨迹方程为x2=4|y|+4.故选:C.4.(2024·北京海淀·三模)已知抛物线y2=4x的焦点为F、点M在抛物线上,MN垂直y轴于点N,若|MF|=6,则△MNF的面积为()A.8B.C.D.【解题思路】确定抛物线的焦点和准线,根据|MF|=6得到M.【解答过程】因为抛物线y2=4x的焦点为F(1,0),准线方程为x=―1,所以|MF|=x M+1=6,故x M=5,不妨设M在第一象限,故M×(5―0)×=所以S△MNF=12故选:C.5.(2024·西藏林芝·模拟预测)已知抛物线y2=8x上一点P到准线的距离为d1,到直线l:4x―3y+12=0的距离为d2,则d1+d2的最小值为()A.1B.2C.3D.4【解题思路】点P到直线l:4x―3y+12=0的距离为|PA|,到准线l1:x=―2的距离为|PB|,利用抛物线的定义得|PF|=|PB|,当A,P和F共线时,点P到直线l:4x―3y+12=0和准线l1:x=―2的距离之和的最小,由点到直线的距离公式求得答案.【解答过程】由抛物线y2=8x知,焦点F(2,0),准线方程为l:x=―2,根据题意作图如下;点P到直线l:4x―3y+12=0的距离为|PA|,到准线l1:x=―2的距离为|PB|,由抛物线的定义知:|PB|=|PF|,所以点P到直线l:4x―3y+12=0和准线l1:x=―2的距离之和为|PF|+|PA|,=4,且点F(2,0)到直线l:4x―3y+12=0的距离为d=|8―0+12|5所以d1+d2的最小值为4.故选:D.6.(2024·四川雅安·三模)已知过圆锥曲线的焦点且与焦点所在的对称轴垂直的弦被称为该圆锥曲线的通径,清代数学家明安图在《割圆密率捷法》中,也称圆的直径为通径.已知圆(x―2)2+(y+1)2=4的一条直径与拋物线x2=2py(p>0)的通径恰好构成一个正方形的一组邻边,则p=()B.1C.2D.4A.12【解题思路】根据圆的通径的上端点就是抛物线通径的上右端点,可得抛物线x2=2py(p>0)经过点(2,1),从而可得答案.【解答过程】因为圆(x―2)2+(y+1)2=4的一条直径与抛物线x2=2py(p>0)的通径恰好构成一个正方形的一组邻边,而抛物线x2=2py(p>0)的通径与y轴垂直,所以圆(x―2)2+(y+1)2=4的这条直径与x轴垂直,且圆的直径的上端点就是抛物线通径的右端点,因为圆(x―2)2+(y+1)2=4的圆心为(2,―1),半径为2,所以该圆与x轴垂直的直径的上端点为(2,1),即抛物线x2=2py(p>0)经过点(2,1),则4=2p,即p=2.故选:C.7.(2024·山西运城·三模)已知抛物线C:y 2=4x 的焦点为F ,动点M 在C 上,点B 与点A (1,―2)关于直线l:y =x ―1对称,则|MF ||MB |的最小值为( )AB .12CD .13【解题思路】根据对称性可得B(―1,0),即点B 为C 的准线与x 轴的交点,作MM ′垂直于C 的准线于点M ′,结合抛物线的定义可知|MF ||MB |=|MM ′||MB |= cos θ(∠MBF =θ),结合图象可得当直线MB 与C 相切时,cos θ最小,求出切线的斜率即可得答案.【解答过程】依题意,F(1,0),A(1,―2),设B(m,n)=―1m+12―1,解得m =―1n =0,即B(―1,0),点B 为C 的准线与x 轴的交点,由抛物线的对称性,不妨设点M 位于第一象限,作MM ′垂直于C 的准线于点M ′,设∠MBF =θ,θ∈ (0,π2),由抛物线的定义得|MM ′|=|MF |,于是|MF ||MB |=|MM ′||MB |= cos θ,当直线MB 与C 相切时,θ最大,cos θ最小,|MF||MB|取得最小值,此时直线BM 的斜率为正,设切线MB 的方程为x =my ―1(m >0),由x =my ―1y 2=4x消去x 得y 2―4my +4=0,则Δ=16m 2―16=0,得m =1,直线MB 的斜率为1,倾斜角为π4,于是θmax =π4,(cos θ)min =,所以|MF||MB|的最小值为故选:A.8.(2024·江西九江·二模)已知抛物线C:y 2=2px 过点A (1,2),F 为C 的焦点,点P 为C 上一点,O 为坐标原点,则( )A .C 的准线方程为x =―2B .△AFO 的面积为1C .不存在点P ,使得点P 到C 的焦点的距离为2D .存在点P ,使得△POF 为等边三角形【解题思路】求解抛物线方程,得到准线方程,判断A ;求解三角形的面积判断B ;利用|PF|=2.判断C ;判断P 的位置,推出三角形的形状,判断D .【解答过程】由题意抛物线C:y 2=2px 过点A(1,2),可得p =2,所以抛物线方程为C:y 2=4x ,所以准线方程为x =―1,A 错误;可以计算S △AFO =12×1×2=1,B 正确;当P(1,2)时,点P 到C 的焦点的距离为2,C 错误;△POF 为等边三角形,可知P 的横坐标为:12,当x =12时,纵坐标为:则12×=≠则△POF 为等腰三角形,不是等边三角形,故等边三角形的点P 不存在,所以D 错误.故选:B .二、多选题9.(2024·湖南长沙·二模)已知抛物线C 与抛物线y 2=4x 关于y 轴对称,则下列说法正确的是( )A .抛物线C 的焦点坐标是(―1,0)B .抛物线C 关于y 轴对称C .抛物线C 的准线方程为x =1D .抛物线C 的焦点到准线的距离为4【解题思路】依题意可得抛物线C 的方程为y 2=―4x ,即可得到其焦点坐标与准线方程,再根据抛物线的性。
2022年高考数学一轮复习专题专题41抛物线基础巩固检测题解析版.docx

专题41抛物线基础巩固检测题(解析版)一、单选题1.过抛物线十=4》的焦点F 的直线交抛物线于AB 两点,若F 是线段AB 的中点,则 |AB |=()A. 1B. 2C. 3D. 4【答案】D 【分析】依据题意可知线段AB 为抛物线的通径可得结果. 【详解】由题可知:线段为抛物线的通径 所以|AB| = 4 故选:D2. F 为抛物线y2=2px(p>0)上一点,点尸到抛物线准线和对称轴的距离分别为10和6,则P=()【答案】D 【分析】由抛物线:/=2px(p>0)可得准线/的方程为:x = --|,设点P(x,y),再由点尸到 抛物线准线和对称轴的距离分别为10和6,可得x + ^ = 10, y = ±6,再与抛物线方 2 程y2=2px(p 〉0),联立解方程组,即可求解.【详解】 解:由题意可得:抛物线V=2px(p>0)的准线/的方程为:x =-宣设点P(x, y),又因点P 到抛物线准线和对称轴的距离分别为10和6, 即。
的值分别为18或2.故选:D. 【点睛】B. 4C. 4 或9D. 2或18所以有, 》+农102y = ±6 ,解得<y 2 =2 pxx = l 、或< [p = 18|x = 9[P = 2‘A. 2本题考查了抛物线的标准方程及其性质,考查理解辨析能力及运算求解能力,属于基础题.3.已知抛物线方程为必=4>,则该抛物线的焦点坐标为( )A. (0,-1)B. ^-―C.D. (0,1)【答案】D【分析】根据抛物线方程求出。
=2,即可得抛物线的焦点坐标.【详解】由抛物线方程x2=4y可知2p = 4,所以p = 2,又抛物线的焦点在V轴正半轴上,所以该抛物线的焦点坐标为(0,1).故选:D4.已知抛物线C:x2=2py(p〉0)的焦点在直线x+y-1 = 0上,又经过抛物线C的焦点且倾斜角为60。
的直线交抛物线C于A、8两点,则|仙|=( )A. 12B. 14C. 16D. 18【答案】C【分析】直线x+y-l =。
高考数学 专题13 抛物线解答题解法荟萃(解析版)

专题13 抛物线解答题解法荟萃一.【学习目标】1.掌握抛物线的定义;2.掌握焦点三角形的应用和几何意义;3.掌握抛物线方程的求法;4.掌握直线与抛物线的位置关系;5.熟练掌握定点、定值、最值和范围问题。
二.【知识点】 1.抛物线的定义平面内与一定点F 和一条定直线l 的距离______的点的轨迹叫做抛物线,定点F 叫做抛物线的焦点,直线l 叫做抛物线的准线.2.抛物线的标准方程、图形及几何性质 标准y 2=2px (p >0) y 2=-2px (p >0) x 2=2py (p >0) x 2=-2py (p >0)方程图 形焦点 )0,2(p F 准线x =p 2范围 ① x ≥0,y ∈R ② x ≤0,y ∈R③ x ∈R ,y ≥0 ④ x ∈R ,y ≤0对称轴 ⑤________ ⑥_________ 顶点 O (0,0) O (0,0) 离心率 e =1e =1开口⑦____ ⑧____⑨____ ⑩____3.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点)0,2(pF 的距离|PF |=x 0+p 2.三.【方法总结】1.求抛物线标准方程的实质是求p 值,常用的方法是待定系数法,若开口不定时,可以设抛物线方程为y 2=mx(m≠0)或x 2=ny(n≠0).2.利用抛物线定义可知,抛物线的焦半径与焦点弦有许多特殊的性质,应用起来非常方便.如:已知AB 是抛物线y 2=2px(p>0)的焦点弦,且A(x 1,y 1),B(x 2,y 2),点F 是抛物线的焦点(如图),可以证明:(1)y 1y 2=-p 2,x 1x 2=p 24. (2)|AB|=x 1+x 2+p.(3)1|AF|+1|BF|为定值2p .(4)以AB 为直径的圆与抛物线的准线相切. (5)以AF(或BF)为直径的圆与y 轴相切. (6)∠CFD =90°. 四.【题型方法】(一)抛物线的轨迹方程 (二)定点问题(三)直线与抛物线涉及的面积问题 (四)直线与抛物线中涉及的角的问题 (五)定值问题 (六)范围问题(七)抛物线与向量的综合 (八)最值问题 五.【题型举例】(一)抛物线的轨迹方程例1. 已知曲线()2C:2y x =+上有一点A ,定点()B 2,0,求线段AB 中点P 的轨迹方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第 1 页 共 19 页
2022年高考数学总复习:抛物线
1.抛物线的概念
平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点,直线l 叫做抛物线的准线. 2.抛物线的标准方程与几何性质
标准方程
y 2=2px (p >0)
y 2=-2px (p >0)
x 2=2py (p >0)
x 2=-2py (p >0)
p 的几何意义:焦点F 到准线l 的距离
图形
顶点坐标 O (0,0)
对称轴 x 轴
y 轴
焦点坐标 F ⎝⎛⎭⎫p 2,0
F ⎝⎛⎭
⎫-p
2,0 F ⎝⎛⎭
⎫0,p 2 F ⎝
⎛⎭⎫0,-p
2 离心率 e =1
准线方程 x =-p 2
x =p 2 y =-p
2
y =p 2 范围 x ≥0,y ∈R
x ≤0,y ∈R
y ≥0,x ∈R
y ≤0,x ∈R
开口方向 向右
向左
向上
向下
知识拓展
1.抛物线y 2=2px (p >0)上一点P (x 0,y 0)到焦点F ⎝⎛⎭⎫p 2,0的距离|PF |=x 0+p
2,也称为抛物线的焦半径.
2.y 2=ax (a ≠0)的焦点坐标为⎝⎛⎭⎫a 4,0,准线方程为x =-a
4. 3.设AB 是过抛物线y 2=2px (p >0)焦点F 的弦, 若A (x 1,y 1),B (x 2,y 2),则 (1)x 1x 2=p 2
4
,y 1y 2=-p 2.
(2)弦长|AB |=x 1+x 2+p =2p
sin 2α
(α为弦AB 的倾斜角).。
