matlab 复变函数
matlablaplace反变换 -回复

matlablaplace反变换-回复「matlablaplace反变换」是指使用Matlab软件进行Laplace反变换的过程。
Laplace反变换是一种重要的数学变换,它在解决微分方程和控制系统等问题中具有广泛的应用。
而Matlab作为一种功能强大的数值计算和数据可视化工具,可以方便地进行Laplace反变换计算和结果展示。
本文将以具体步骤回答如何使用Matlab进行Laplace反变换。
首先,我们需要明确Laplace变换的概念和公式。
Laplace变换可以将一个函数或信号在时间域中的表达,转换为在复频域(s域)中的表达。
具体而言,对于一个函数f(t),它的Laplace变换F(s)可表示为:F(s) = ∫[0,∞] e^(-st) * f(t) dt在Matlab中,我们可以使用`laplace`函数来计算Laplace变换。
假设我们有一个函数f(t),我们可以使用如下代码计算其Laplace变换:syms t sf(t) = ... 创建或者定义函数f(t)F(s) = laplace(f(t), t, s)其中,`syms t s`用于定义符号变量,`laplace`函数的输入参数为要进行Laplace变换的函数和变量。
比如,上述代码将函数f(t)的Laplace变换结果保存在F(s)变量中。
计算得到Lapalce变换结果后,我们可以使用`ilaplace`函数进行反变换。
`ilaplace`函数将Laplace变换的结果转换回原函数的形式。
接下来使用如下代码计算Laplace反变换:syms t sF(s) = ... 计算得到Laplace变换结果F(s)f(t) = ilaplace(F(s), s, t)其中,`ilaplace`函数的输入参数为Laplace变换结果和变量,上述代码将变量F(s)的Laplace反变换结果保存在f(t)变量中。
需要注意的是,在使用`laplace`和`ilaplace`函数进行Laplace变换和反变换时,我们需要先在Matlab中定义符号变量,以确保函数和变量的计算和表示可以用于符号计算。
复变函数实验课(一)

湖北民族学院理学院2014年春季学期数学与应用数学专业复变函数实验课(一)计算部分上课教师:汪海玲Matlab中复变函数命令集定义符号变量Syms虚单位z=Sqrt(-1)复数表示z=x+y*i指数表示z=r*exp(i*a)求实部Real(z)求虚部Imag(z)求共轭Conj(z)求模Abs(z)求幅角Angle(z)三角函数z=sin(z)z=cos(z)指数函数z=exp(z)对数函数z=log(z)幂函数z=z^a解方程expr=‘方程式’;Solve(expr)泰劳展开Taylor(e,z)求留数[r,p,k]=residue(p,q)傅立叶变换Fourier(e,z,w)逆傅立叶变换Ifourier(e,w,z)拉普拉斯变换Laplace(e,w,t)逆拉普拉斯变换Ilaplace(e,t,x)一复数的运算1.复数的实部和虚部复数的实部和虚部的提取可由函数real和imag实现。
调用形式real返回复数x的实部(x)(ximag返回复数x的虚部)2.共轭复数复数的共轭可由函数conj实现。
调用形式conj返回复数x的共轭复数(x)3.复数的模和辐角复数的模和辐角的求解由功能函数abs和angle实现。
调用形式abs复数x的模)(xangle复数x的辐角)(x上机操作:课本例题1.2、例题1.4、课后习题(一)1.4.复数的乘除法复数的乘除法运算由“/”和“ ”实现。
5.复数的平方根复灵敏的平方根运算由函数sprt实现。
调用形式)sprt返回复数x的平方根值(x6.复数的幂运算x^,结果返回复数x的n次幂。
复数的幂运算的形式为n上机操作:课本例题1.87.复数的指数和对数运算复数的指数和对数运算分别由函数exp和log实现。
调用形式exp(x返回复数x的以e为底的指数值)log(x返回复数x的以e为底的对数值)上机操作:课本例题2.17、 2.188.复数的三角函数运算复数的三角函数运算函数参见下面的复数三角函数复数三角函数表9.复数方程求根复数方程求根或实方程的复数根求解也由函数solve实现。
实验一计算复变函数极限、微分、积分、留数、泰勒级数展开式

实验一计算复变函数极限、微分、积分、留数、泰勒级数展开式【实验目的】1、熟悉Matlab运行环境,会在窗口操作和运行一些命令2、掌握求复变函数极限、微分、积分、留数以及泰勒级数命令3、熟练在计算机上操作复变函数极限、微分、积分、留数以及泰勒级数命令【实验仪器】一台电脑,要求安装matlab 软件【实验内容】MATLAB实现内容1、MATLAB求复变函数极限2、MATLAB求复变函数微分3、MATLAB求复变函数积分4、MATLAB求复变函数在孤立奇点的留数5、MATLAB求复变函数的泰勒级数展开式【实验步骤】1.打开matlab桌面和命令窗口,方式一,双击桌面快捷方式,方法二,程序里单击matlab图标,方式三,找到matlab文件夹,双击图标2.在matlab命令窗口输入命令3.运行,可以直接回车键,F5键【注意事项】1.命令的输入要细心认真,不能出错2.尤其是分号,逗号等符号的区别3. 注意数学上的运算和matlab中的不同,尤其是括号【实验操作内容】以下的例题都是在命令窗口输入源程序,然后运行,或回车就可以得到结果。
1、MATLAB 求复变函数极限用函数limit 求复变函数极限【Matlab 源程序】syms zf=;limit(f,z,z0) 返回极限结果例 1 求 在 的极限 解 【Matlab 源程序】syms zf=sin(z)/z;limit(f,z,0)ans=1limit(f,z,1+i)ans=1/2*sin(1)*cosh(1)-1/2*i*sin(1)*cosh(1)+1/2*i*cos(1)*sinh(1)+1/2*cos(1)*sinh(12、 MATLAB 求复变函数微分用函数diff 求复变函数极限【Matlab 源程序】zz z f sin )(=i z +=1,0f=();diff(f,z) 返回微分结果解 syms zf=exp(z)/((1+z)*(sin(z)));diff(f)ans =exp(z)/(1+z)/sin(z)-exp(z)/(1+z)^2/sin(z)-exp(z)/(1+z)/sin(z)^2*cos(z)3、 MATLAB 求复变函数积分用函数int 求解非闭合路径的积分.【Matlab 源程序】syms z a bf=int(f,z,a,b) 返回积分结果解 syms zx1=int(cosh(3*z),z,pi/6*i,0)x2=int((z-1)*exp(-z),z,0,i)结果为:例 3 求积分 π60i i 0x1=ch3zdz; x2(1)d z z e z -=-⎰⎰例2 设()()z f z z e z f z'+=求,sin 1)(x2 = -i/exp(i)4、 MATLAB 求复变函数在孤立奇点的留数(1)f(z)=p(z)/q(z);p(z)、q(z)都是按降幂排列的 多项式用函数residue 求f(z)=p(z)/q(z)在孤立奇点的留数【Matlab 源程序】[R,P,K]= residue (B,A) 返回留数,极点说明:向量B 为f(z)的分子系数;向量A 为f(z)的分母系数;向量R 为留数;向量P 为极点位置;向量k 为直接项:例4 求函数 在奇点处的留数. 解 [R,P,K]= residue([1,0,1],[1,1])结果为:R= 2P = -1K = 1 -15、MATLAB 求复变函数的泰勒级数展开式(1)用函数taylor 求f(z)泰勒级数展开式【Matlab 源程序】112++z zf=Taylor(f,z0) 返回f(z)在点z0泰勒级数展开式例5 求函数f=1/(z-b)在点z=a泰勒级数展开式前4项syms z a b;f=1/(z-b);taylor(f,z,a,4)ans =1/(a-b)-1/(a-b)^2*(z-a)+1/(a-b)^3*(z-a)^2-1/(a-b)^4*(z-a)^3(2)求二元函数z=f(x,y)在点(x0,y0)的泰勒级数展开式.【Matlab源程序】syms x y; f=();F=maple(‘mtaylor’,f,‘[x,y]’,m) 返回在(0,0)点处的泰勒级数展开式的前m项.F=maple(‘mtaylor’,f,‘[x=x0,y=y0]’,m) 返回在(x0,y0)点处的泰勒级数展开式的前m项.F=maple(‘mtaylor’,f,‘[x=a]’,m) 返回对单变量在x=a处的泰勒级数展开式的前m项.例6 求函数222==-z f x y x x e---(,)(2)x y xy在原点(0,0),以及(1,a)点处的Taylor展式.【Matlab源程序】syms x y;f=(x^2-2*x)*exp(-x^2-y^2-x*y);maple(‘mtaylor’,f,‘[x,y]’,4)在(0,0)点处的泰勒级数展开式:ans =-2*x+x^2+2*x^3+2*y*x^2+2*y^2*xmaple(‘mtaylor’,f,‘[x=1,y=a]’,2)在(1,a)点处的泰勒级数展开式:ans =-exp(-1-a-a^2)-exp(-1-a-a^2)*(-2-a)*(x-1)-exp(-1-a-a^2)*(-2*a-1)*(y-a)maple(‘mtaylor’,f,‘[x=a]’,2) 在x=a处泰勒级数展开式:ans =(a^2-2*a)*exp(-a^2-y^2-a*y)+((a^2-2*a)*exp(-a^2-y^2-a*y)*(-2*a-y)+(2*a-2)*exp(-a^2-y^2-a*y))*(x-a)。
复变函数的matlab解法探究

科教论坛科技风2020年12月DOC10.19392/kl1671-7341.202034015复变函数的matlab解法探究张春玲魏永亮3冯贵平上海海洋大学海洋科学学院上海201306摘要:结合海洋数学物理理论知识基础,运用matlab编程软件,在学生掌握了理论解法的基础上,利用计算机来实现理论问题的快速自动解法,使学生更好地理解所学的知识,并采用师生互动和同学之间相互讨论的形式,有效地将理论与实际相结合。
关键词:复变函数;matlab;仿真技术;快速求解中图分类号:013海洋数理基础是海洋科学专业的必修课,也是学生们普遍感觉题目难度大,求解繁琐,不易理解的一门专业课⑴。
其中复变函数又是数学理论的一个重要分支,在实际教学过程中,手工解题过程耗时耗力,计算效率低,学生即使能够通过繁琐的计算,得出理论解,也很难直观地理解解的分布及物理意义。
MatGb编程软件具有强大的数值计算能力和卓越的可视化能力,随着信息技术的发展,越来越多地被应用到各个行业⑵&而且,该软件是海洋数据处理的主要工具之一,对于海洋科学专业的学生,学会利用Malb求解海洋数理方程是一个必要的技能"3E#&因此,本文以复变函数论几个典型的例子为例,探究MaGb编程软件在求解海洋数理方程的便利。
1复变函数的Matlab解法1.1求复数的实部、虚部、模、辐角主值、共轭复数女口,利用Matlab求解复数(辔),(槡3+2-的实部、虚部、模、辐角主值、共轭复数。
实验代码如下:a=((3+43i)/(1-23i))S;b=(sqrt(3)+i)S-3);ars=real(a);brs=re a1(b);aim二imaa(a);bini二imaa(b);am二abs(a);bm=abs(b);aang=angla(a);bang=angla(b);ag=co n j(a);b g=conj(b);1.2求解复数方程利用Matlab求解复数方程34+54=0。
实验六、利用MATLAB计算复变函数在孤立奇点处的留数及进行复积分

实验六、利用MATLAB 计算复变函数在孤立奇点处的留数及进行复积分计算一、本实验教学的作用:熟悉MATLAB 基本命令与操作,利用MATLAB 计算复变函数在孤立奇点处的留数;利用MATLAB 计算围线积分。
通过实验具体操作,培养学生综合实践能力。
二、本实验教学目的及学生能力标准:会利用MATLAB 计算复变函数在孤立奇点处的留数;会利用MATLAB 计算围线积分。
三、实验内容:四、相关知识1.在孤立起点处的留数----通过求极限的方法计算留数假设已知奇点α和重数m 则用下面的MATLAB 语句求出相应的留数B=limit(F*(z-α),z, α) 单奇点B=limit(F*(z-α)*m ,z,m -1)/prod(1:m-1),z,α m 重奇点例1 计算z e z z z z f 23)3cos()1(1)(-+-=π在孤立起点处的留数 解 函数)(z f 在0=z 是三重奇点,在1=z 是简单奇点>>syms z>>f=cos(z+pi/3)*exp(-2*z)/z^3*(z-1);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-1),z,1)ans=-1/4-1/2*3^(1/2)1/2*exp(-2)*cos(1)-1/2*3^(1/2)*exp(-2)*sin(1)学生练习1 计算z e z z z z f 23)3sin()1(1)(-+-=π在孤立起点处的留数 提示 函数)(z f 在0=z 是三重奇点,在1=z 是简单奇点>>syms z;>>f=sin(z+pi/3)*exp(-2*z)/z^3*(z-1);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-1),z,1)ans=-1/4*3^(1/2)+1/2-1/2*exp(-2)*sin(1)+1/2*3^(1/2)*exp(-2)*cos(1)例2 计算3542)(zz i z z f ++=在孤立起点处的留数 解 函数)(z f 在0=z 是三重奇点,在i i z 2,2-=是简单奇点>>syms z;>>f= (z+2*i3) /z^5+z^3);>>limit(diff(f*z^3,z,2)/prod(1;2),z,0);>> limit((f*(z-2*i),z,2i)>> limit((f*(z+2*i),z,-2i)ans=i/8-i/8例3 计算函数1)(2-=z e z f z在∞=z 处的留数 解 函数)(z f 在扩充复平面有三个极点:∞-=,1,1z>>syms z>>z1=exp(z)/(z^2-1);>>B1=limit(z1*(z-1),z,1)>>B2=limit(z1*(z+1),z,-1)>>B=B1+B2ansB1=1/2*exp(1)B2=-1/2*exp(-1)B=1/2*exp(1)-1/2*expp(-1)学生练习2 计算函数4sin )(zz z z f +=在0=z 处的留数 提示 函数)(z f 在0=z 是四重奇点>>syms z;>>f= (sin(z)+z)/z^4;>>limit(diff(f*z^4,z,3)/prod(1;3),z,0);ans=-1/6学生练习3 计算下列函数在奇点处的留数:(1) z z z 212-+ (2)14-z z 解 在Matlab 命令窗口键入:>> [r1,p1,k1]=residue([1,1],[1,-2,0])r1 =1.5000-0.5000p1 =2k1 =[ ]>> [r2,p2,k2]=residue([1 0],[1 0 0 0 -1])r2 =0.25000.2500-0.2500 + 0.0000i-0.2500 - 0.0000ip2 =-1.00001.00000.0000 + 1.0000i0.0000 - 1.0000ik2 =[ ]反之:>> [B,A]=residue([0.2500 0.2500 -0.2500 -0.2500],[-1 1 i -i],[])B =0 0 1 0A =1 0 0 0 -12.求积分2.1 非闭合路径的积分非闭合路径的积分,用函数int 求解,方法同微积分部分的积分。
浅谈MATLAB在复变函数教学中的几点应用

浅谈MATLAB在复变函数教学中的几点应用作者:韩英李雁飞汪贤华弓亚鑫舒心来源:《科技资讯》 2014年第32期韩英1 李雁飞2 汪贤华1 弓亚鑫2 舒心2(1.北京石油化工学院数理系;2.北京石油化工学院信息工程学院北京 102617)摘要:复变函数课程的理论比较枯燥。
论文设计了MATLAB软件在复变函数教学中的几个典型案例,将MATLAB引入课堂教学,通过数学实验,让学生感受“看得见”的数学,使得复变函数的理论学习达到事半功倍的效果。
关键词:MATLAB 复变函数泰勒级数洛朗级数中图分类号:O174.55 文献标识码:A 文章编号:1672-3791(2014)11(b)-0121-03“复变函数”课程是通信工程、电子工程、自动化等工科专业必修的专业基础课,该课程理论性强、内容抽象,工科学生普遍感到学习困难。
为了解决这个问题,我们在复变函数的教学中引入MATLAB实践内容,使得复变函数的教学理论与实验相结合,教与学相结合,引导学生利用软件对教学内容进行仿真,激发其学习积极性与主动性,提高其对于复变函数内容的理解。
该文就MATLAB在复变函数中的几点应用加以分析。
通过计算机实现对复变函数主要计算问题的实验,达到传统理论教学无法实现的效果。
1 利用MATLAB进行复变函数的简单运算复数的表示式突出三角表示法和指数表示法,而这两种表示法中辐角的计算公式较复杂,利用MATLAB可以把复数的实部,虚部,共轭复数,辐角,模等利用简单的命令求出。
解:在MATLAB工具窗输入以下矩阵A=[((1+i)*(2-i)^2*(3-i)^3)/((3+4)^4*(2+i)^5) i^i i^(2^1/2) (-8)^(1/3) log(1+i)]A= -0.0016+0.0005i 0.2079+0.0000i 0.0000+1.0000i 1.0000+1.7321i 0.3466+0.7854i>>real(A)-0.0016 0.20791.00000.3466>> imag(A)ans = 0.00051.00001.73210.7854>> angle(A)ans = 2.85781.57081.04721.1552>> abs(A)ans = 0.00170.20791.00002.00000.8585>> conj(A)ans=-0.0016-0.0005i 0.2079+0.0000i 0.0000-1.0000i 1.0000-1.7321i 0.3466-0.7854i用MATLAB可直接计算出复数的四则运算和初等函数的值。
用MATLAB复变实践函数展开及留数

1
当分母出现 s b s c s a1 s
m p n
n 1
an 的情况时,只需先对 s b m 和
s c p 分别展开,之后利用 conv 进行多项式乘积,再与 s n a1 s n1 an 的系数求和
即可。 当 f z 是有理分式的情形时,可以使用 Matlab 中的函数 residue,巧妙的运用该函数,可 以求出有理分式的留数。当 f z 的形式不是有理分式时,求函数在极点 z 0 处的留数方法只 能是先判断极点的重数,然后利用 Matlab 的符号运算功能进行计算。 2. 利用留数计算公式求留数 例3:求出函数 f z
1+z+1/2*z^2+1/6*z^3+1/24*z^4+1/120*z^5 下面的程序画出了指数函数 e z 及其泰勒展式的图形: subplot(1,2,1); z=5*cplxgrid(30); cplxmap(z,exp(z)) title('复变函数 e^z 的图形') subplot(1,2,2); w=1;u=1; for k=1:15 u=u.*z./k; w=w+u; end cplxmap(z,w) title('e^z 泰勒展式的图形')
Matlab在复变函数中应用

Matlab在复变函数中应⽤MATLAB在复变函数中的应⽤复变函数的运算是实变函数运算的⼀种延伸,但由于其⾃⾝的⼀些特殊的性质⽽显得不同,特别是当它引进了“留数”的概念,且在引⼊了Taylor级数展开Laplace 变换和Fourier变换之后⽽使其显得更为重要了。
使⽤MATLAB来进⾏复变函数的各种运算;介绍留数的概念及MAT–LAB的实现;介绍在复变函数中有重要应⽤的Taylor展开(Laurent展开Laplace变换和Fourier变换)。
1 复数和复矩阵的⽣成在MATLAB中,复数单位为)1ji,其值在⼯作空间中都显⽰为=sq rt=(-0+。
.1i00001.1 复数的⽣成复数可由iz+=。
a=语句⽣成,也可简写成biaz*+b另⼀种⽣成复数的语句是)exp(ithetar=,也可简写成)=,*irz*其中theta为复数辐⾓的弧度值,r为复数的模。
1.2 创建复矩阵创建复矩阵的⽅法有两种。
(1)如同⼀般的矩阵⼀样以前⾯介绍的⼏种⽅式输⼊矩阵例如:)]iA**ii=+3[i*-+*,),235336exp(23,exp(9im=;)2,3(rand]5466.07271.05681.02897.07027.05341.08385.03420.03704.03412.03093.06602.0[i i i i ii ++++++注意实、虚矩阵应⼤⼩相同。
2 复数的运算1.复数的实部和虚部复数的实部和虚部的提取可由函数real 和imag 实现。
调⽤形式 )(x real返回复数x 的实部)(x imag返回复数x 的虚部2.共轭复数复数的共轭可由函数conj 实现。
调⽤形式)(x conj返回复数x 的共轭复数3.复数的模和辐⾓复数的模和辐⾓的求解由功能函数abs 和angle 实现。
调⽤形式 )(x abs 复数x 的模)(x angle复数x 的辐⾓例:求下列复数的实部与虚部、共轭复数、模与辐⾓(1)i231+ (2)i i i --131 (3)ii i 2)52)(43(-+(4)i i i +-2184由MATLAB 输⼊如下:]21^48^,2/)52()43(),1/(3/1),23/(1[i i i i i i i i i i a +*--*=--+=.0--i ---50002308.30000i0000i.3.1i500013.0000real%实部)(aans=0.2308 1.5000 –3.5000 1.0000 imag%虚部(a)ans=–0.1538 –2.5000 –13.0000 –3.00000.2308+0.1538i 1.5000+2.5000i–3.5000+13.0000i 1.0000+3.0000i abs%模(a)ans=0.2774 2.9155 13.4629 3.1623angle%辐⾓)(aans=–0.5880 –1.0304 –1.8228 -1.24904.复数的乘除法复数的乘除法运算由“/”和“*”实现。
用matlab计算复变函数的积分

33
可编辑ppt
34
可编辑ppt
4
例3
解析推导
Matlab计算
可编辑ppt
5
例4
解析推导
matlab计算 n为0时 结果为2πi
可编辑ppt
n为其它整数时,结果为零
6
例5
解析推导
Matlab计算
可编辑ppt
7
例6
解析推导 Matlab计算(参数积分)
Matlab计算(留数定理)
可编辑ppt
8
例6
也可用matlab的 residue函数 求留数
21
例10
解析推导结合Matlab求留数(用limit和diff函数,或用residue函数)
Matlab计算(参数积分)
可编辑ppt
22
例11
方法一:用matlab求留数和极点,再通过留数求和计算积分
方法二:用matlab直接积分
在复平面上选取实轴和上半圆弧作为
闭合围道,包围的极点为 i 和 3i, 由于在上半圆弧上的积分为零,因此
当t= -3时做积分
可编辑ppt
26
例13
可编辑ppt
27
例14
可编辑ppt
28
用matlab协助 求留数:
若把它当作更高阶极点对待求留数,结果一样
可编辑ppt
29
用matlab验证这个级数求和,结果一致
可编辑ppt
30
例15
先来计算 这部分积分
可编辑ppt
31
可编辑ppt
32
可编辑ppt
用matlab计算复变函数的积分
张宏浩
可编辑ppt
1
例1
matlab中如何处理复数,matlab中复数的处理函数

matlab中如何处理复数,matlab中复数的处理函数matlab中复数的处理函数MATLAB 中复数的处理函数要说明复数的运算,先从解以下的⼆次⽅程式的复数根谈起上式的根有实部 (-2) 及虚部 (±3),我们就这个复数的表⽰法来说明 MATLAB的复数功能。
MATLAB 是以 i或 j字元来代表虚部,其它的复数相关函数有real, imag, conj, abs, angle等等,详见线上说明 lookfor complex。
如果复数表⽰为 x=a+bi共轭复数 = , 复数⼤⼩ r = , 复数向量的夹⾓ θ= tan -1 (b/a)复数实部 a = r cosθ, 复数虚部 b = r sinθ, 复数指数表⽰法 x=r ei上述各函数对应 MATLAB的复数指令为a=real(x), b=imag(x), =conj(x),r=abs(x), =angle(x), x=r*exp(i*angle(x))以下是⼏个复数表⽰式的例⼦:>> x=1-2*i; % 注意是 2*i 不是 2i>> real(x) % 列出实部ans=1>> imag(x) % 列出虚部ans =-2>> conj(x) % 计算共轭复数ans =1.0000 + 2.0000i>> abs(x) % 计算复数的⼤⼩ans =2.2361>> angle(x) % 计算复数向量的夹⾓(以径度表⽰)ans =-1.1071>> a=1; b=4; c=13;>> x1=(-b+sqrt(b^2-4*a*c))/(2*a) % 以解⼆次⽅程式根的公式计算复数根x1 =-2.0000 + 3.0000i>> x2=(-b-sqrt(b^2-4*a*c))/(2*a)x2 =-2.0000 - 3.0000i>> y=exp(i) % 以复数指数⽅式表⽰⼀个复数y =0.5403 + 0.8415i>> y=exp(i*pi*0.75)y =-0.7071 + 0.7071i和复数有关的图以极座标来表⽰会⽐⼀般的卡⽒座标要合适,polar 指令可以将数据以极座标⽅式加以绘图, 其语法为 polar(theta,r),(theta,r)分别代表极座标上的⾓度及半径值。
Matlab在复变函数与积分变换课堂教学中的应用

Matlab在复变函数与积分变换课堂教学中的应用徐彬【摘要】在复变函数与积分变换的课堂教学中,为了让教学内容更容易被学生接受,提出将Matlab软件引入到课堂教学中.利用Matlab软件在绘图和计算方面的优势,将该课程中抽象且复杂的学习内容用可视化、动态化的形式直观地表现出来,同时简化了计算过程,促进学生对知识的深入理解,提高了学生的学习兴趣,取得了良好的教学效果.【期刊名称】《湖北理工学院学报》【年(卷),期】2016(032)003【总页数】5页(P68-72)【关键词】Matlab软件;复变函数与积分变换;课堂教学【作者】徐彬【作者单位】武昌首义学院基础科学部,湖北武汉430064【正文语种】中文【中图分类】G642.0Matlab软件是数值计算型的数学类科技应用软件,由美国Mathworks公司于20世纪中期推出, Matlab软件有诸多优点:高效的数值计算功能可以使繁杂的数学运算问题得以快速解决;完备的图形处理功能可以实现计算结果或编程的可视化;丰富的应用工具箱提供了大量方便、实用的处理工具;用户界面清晰且操作简单。
若将此软件运用于课堂教学中,势必可以优化教学效果[1]。
笔者长期从事复变函数与积分变换课程的教学工作,在近几年的课堂教学中,将Matlab软件引入到课堂教学中,通过Matlab辅助教学,使学生加深了对知识难点的理解,提高了学生的学习兴趣,开拓了学生的视野。
本文将结合笔者的教学经历,探讨Matlab软件在复变函数与积分变换课堂教学中的应用效果。
复变量的初等函数是实变量初等函数的推广,它们在性质上有许多相似之处,但在教学中应重点强调它们之间的区别,如:指数函数的周期性、对数函数的多值性、正弦余弦函数的无界性。
通过Matlab软件的绘图功能,绘出这些函数的图形,便可直观地观察出函数的变换趋势[2],从而加深学生对该知识点的理解。
复变量的指数函数ez是以2kπi(k=0,±1,±2,…)为周期的周期函数[3],为了让学生更直观地看到复变量的指数函数具有周期性,可以利用Matlab里的“surf”函数,以XOY平面表示自变量所在的平面,以Z轴表示复变函数的实部,以颜色表示复变函数的虚部,画出复变量指数函数的四维表现图[4]。
MATLAB在复变函数与积分变换课程教学中的应用

输人 M , . 语句如下 : A1 B IA
l
互
sr r lz , a() r ( ) ia( ) ; u (e () i g z , a w , g w ) f a m e l m t e 钙 ’; i ( l t 绘 制 图像 如 图 1 。
4 傅 里叶变换及其逆变换
11 1
河南机电高等专科学 校学 报
21年 5 01 期
f l l e( )按 默认 变量进行 L p c 逆 变换 ; =ipa F a c al e a >>f iu e( , , %求 Fu e 逆变换 = f r rF W t oi ) orr i f ip c ( , ,)将 u =l l eFuv aa 的函数变换成 v 的函数。 运行结果 f=ep 一 )’ i( l ) H aid x ( t l n 2, ev i c s ‘ t se 例 7: 函数 f t t s ( + r , 设 ()=e i t 7) 求其 L . .n a () 回原函数。 t返 p c 变换 , le a 并对结果进行 Lp c 逆变换 。 a le a 例 6: 求钟形脉冲函数, t = e2的频谱 函数并 () 4 一2 t 输入 M T A A L B语句如下 : 绘 制频谱 图。
W =z ^ . 3;
图 2 I I: 在映射∞: + 下的像 : 3 j上
在 MA L B语 言 中使 用 f r r TA oi 函数 来 实 现 Fu ue o. tr i 变换 。首先定义符号变量 t e , 描述时域表达式 f直 , 接调用 f rr oi 函数就可求出所需 的时域函数 的 Fu ue o. 例 4: 出圆周 I I= 作 3在映射 ∞= 4 下的 =- tr i 变换式。该函数的调用格式为 e 像。 F f r rf 采用默认的 t = oi () ue 为时域变量 编写相应的 n 文件 y g en为 : l i s .l nh F=fui (, , )用 户 指 定 时 域 变量 U和 频 域 orr fU v e s ms x Y Zt y 变量 v t 一p: . 1 p ; = i O :i 0 使用 iu e 函数来实现 Fu e 逆变换 。它 的使 f rr oi or r i X= cst ; 3 o() 用 格 式 如下 : Y= s () 3 i t; n f iu e( ) = f r rF 按默认变量进行 Fu e 逆变换 oi or r i z=x+i Y; f iu e F U v 将 U的函数变换成 v =f r r , ,) o i( 的函数 W = Z+ 1 /z: . 例 5: 已知 t = s 2u t , () Fu e ) e i t() 求, £ 的 or r n i sb l ( , ,) u po 2 1 1 ; t 变换 , 并对结果进行 Fu e 逆变换。 or r i po() l z; t 输入 M T A 语句如下 : AL B tl( = cs t i 3 s () ie , 3 o()+ i t’; t z n > > s m s tW y
关于MATLAB在复数方面的应用–MATLAB中文论坛

关于MATLAB在复数方面的应用–MATLAB中文论坛最近,看到有不少朋友问MATLAB在复数方面的应用问题,特此发个帖子,给大家分享点资料.matlab在复数中的应用1.复数的生成复数生成语句(其中theta为复数辐角的弧度值,r为复数的模)z=a+b*i,z=a+bi。
z=r*exp(i*theta),z=r*exp(thetai)。
2.创建复矩阵创建复矩阵的方法有两种。
(1)如同一般的矩阵一样以前面介绍的几种方式输入矩阵例如:A=[3+5*i,-2+3i,9*exp(i*6),23*exp(33i)](2)可将实、虚矩阵分开创建,再写成和的形式例如:re=rand(3,2)im=rand(3,2)com=re+i*im注意实、虚矩阵应大小相同。
3.复数的运算real(x)返回复数x的实部imag(x)返回复数x的虚部conj(x)返回复数x的共轭复数angle(x)返回复数x的辐角abs(x)返回复数x的模复数的乘除法运算由“*”和“/”实现。
ex.x=4*exp(pi/3i)y=4*exp(pi/(3i))z=4*exp(pi/3*i)>>x =2.0000 - 3.4641iy =2.0000 - 3.4641iz =2.0000 + 3.4641isprt(x)返回复数x的平方根值x^n返回复数x的n次幂exp(x)返回复数x的以e为底的指数值log(x)返回复数x的以e为底的对数值4.复数三角函数运算sin(x)返回复数x的正弦函数值,asin(x)返回复数x的反正弦值cos(x)返回复数x的余弦函数值,acos(x)返回复数x的反余弦值tan(x)返回复数x的正切函数值,atan(x)回复数x的反正切值cot(x)返回复数x的余切函数值,acot(x)返回复数x的反余切值sec(x)返回复数x的正割函数值,asec(x)返回复数x的反正割值csc(x)返回复数x的余割函数值,acsc(x)返回复数x的反余割值sinh(x)返回复数x的双曲正弦值,coth(x)返回复数x的双曲余切值cosh(x)返回复数x的双曲余弦值,sech(x)返回复数x的双曲正割值tanh(x)返回复数x的双曲正切值,sech(x)返回复数x的双曲余割值5.复数方程求根复数方程求根或实方程的复数根求解由函数solve实现ex.solve('x^3+1=0')或solve('x^3=-1')>>ans =[ -1][ 1/2-1/2*i*3^(1/2)][ 1/2+1/2*i*3^(1/2)]6.留数及其应用[R,P,K]=residue(B,A)s=2*pi*i*sum(R)----找出满足条件的R,求积分值ex1.求f(z)=(z+1)/(z^2-2z)的奇点处的留数[R,P,K]=residue([1,1],[1,-2,0])>>R =1.5000-0.5000P =2K =[]ex2.求积分,f(z)=z/(z^4-1),C为正向圆周abs(z)=2 [R,P,K]=residue([1,0],[1,0,0,0,-1])s=2*pi*i*sum(R)%此处均符合>>R =0.25000.2500-0.2500 + 0.0000i-0.2500 - 0.0000iP =-1.00001.00000.0000 + 1.0000i0.0000 - 1.0000iK =[]s =7.Taylor级数展开taylor(f) 返回函数的五次幂多项式近似taylor(f,n)返回n-1次幂多项式taylor(f,a)返回a点附近的幂多项式近似taylor(r,x)使用独立变量代替函数findsym(f)place变换及其逆变换(1)Laplace变换L=laplace(F)返回以默认独立变量T对符号函数F的Laplace变换。
matlab 复变函数实轴交点 -回复

matlab 复变函数实轴交点-回复Matlab在处理复变函数的求实轴交点问题时,可以通过数值方法、解析方法以及综合方法来实现。
本文将逐步介绍这三种方法,并提供示例代码来说明如何在Matlab中求解复变函数与实轴的交点。
一、数值方法:数值方法是求解实轴交点的一种简单且常用的方法。
它的核心思想是通过迭代计算逼近实轴上的交点。
常用的数值方法包括二分法、牛顿法和割线法等。
首先,把复变函数表示为f(x) = u(x) + iv(x),其中u(x)和v(x)分别是函数f(x)的实部和虚部。
对于实轴上的点x0,如果f(x0)的虚部等于零,那么x0就是f(x)与实轴的交点。
以下是使用二分法求解复变函数与实轴交点的示例代码:matlab定义复变函数f(x)f = @(x) x.^2 - 4;定义实轴区间[a, b]a = 0;b = 2;设置迭代终止条件tolerancetolerance = 1e-6;循环执行二分法求解while abs(b-a) > tolerancec = (a + b) / 2; 计算实轴中点if imag(f(c)) == 0 判断虚部是否为0break;endif sign(imag(f(a))) ~= sign(imag(f(c))) 判断实轴上的交点在左半区间还是右半区间b = c; 更新右半区间elsea = c; 更新左半区间endend输出交点disp(c);这段代码中,我们首先定义了复变函数f(x) = x^2 - 4,并指定了实轴上的区间[a, b]为[0, 2]。
然后通过二分法,不断更新实轴的左右区间来逼近交点的位置,直到实轴上找到一个虚部为0的点为止。
二、解析方法:解析方法是通过复变函数的解析表达式来求解实轴上的交点。
对于一些简单的复变函数,我们可以直接求解其在实轴的交点。
例如,对于f(x) = e^x - 1这个函数来说,在实轴上与f(x)交点的解为x = 0。
matlab复变函数画图形

matlab复变函数画图形第四篇计算机仿真第二十一章计算机仿真在复变函数中的应用基于MATLAB语言的广泛应用,我们介绍的计算机仿真方法主要立足于对MATLAB 语言的仿真介绍,而其它的数学工具软件,MATHEMATIC,MATHCAD,MAPLE,的仿真方法是类似的,本章将重点介绍使用MATLAB进行复数、复变函数的各类基本运算以及定理的验证,并介绍仿真计算留数、积分的方法,以及复变函数中Taylor级数展开,Laplace 变换和Fourier变换,21.1 复数运算和复变函数的图形21.1.1 复数的基本运算1复数的生成复数可由语句z=a+b*i 生成,也可简写成z=a+bi;另一种生成复数的语句是z=r*exp(i*theta),其中theta是复数辐角的弧度值, r 是复数的模( 2复矩阵的生成创建复矩阵有两种方法((1)一般方法例 21.1.1创建复矩阵的一般方法(【解】仿真程序为A=[3+5*I -2+3i i 5-i 9*exp(i*6) 23*exp(33i)]%运行后答案为A =3.0000+5.0000i -2.0000+3.0000i 0+1.0000i5.0000-1.0000i 8.6415-2.5147i -0.3054+22.9980i,说明: %后为注释语句,不需输入)(2)可将实、虚矩阵分开创建,再写成和的形式例 21.1.2 将实、虚部合并构成复矩阵【解】仿真程序为re=rand(3,2);im=rand(3,2);com=re+i*im%运行后答案为 com = 0.9501+0.4565i 0.4860+0.4447i0.2311+0.0185i 0.8913+0.6154i0.6068+0.8214i 0.7621+0.7919i 21.1.2 复数的运算1 复数的实部和虚部复数的实部和虚部的提取可由函数real和 imag 实现(调用形式如下:real(z) 返回复数 z 的实部;imag(z) 返回复数 z 的虚部.2 共轭复数复数的共轭可由函数conj实现(调用形式为:conj(z) 返回复数 z 的共轭复数.3 复数的模与辐角复数的模与辐角的求取由函数 abs 和angle实现(调用形式为:abs(z) 返回复数 z 的模;angle(z) 返回复数 z 的辐角.例 21.1.1求下列复数的实部与虚部、共轭复数、模与辐角(113i(34i)(25i),,,82132i,i4ii,,i1i,2i(1); (2); (3); (4)(【解】 a=[1/(3+2i) 1/i-3i/(1-i) (3+4i)*(2-5i)/2i i^8-4*i^21+i]%a =0.2308 - 0.1538i 1.5000 - 2.5000i -3.5000 -13.0000i 1.0000 -3.0000ireal(a)%ans = 0.2308 1.5000 -3.5000 1.0000(注明:凡ans 及其后面的内容均不需输入,它是前面语句的答案,本句ans 是real(a)的答案)imag(a)%ans = -0.1538 -2.5000 -13.0000 -3.0000conj(a)%ans =0.2308 + 0.1538i 1.5000 + 2.5000i -3.5000 +13.0000i 1.0000 + 3.0000iabs(a)%ans = 0.2774 2.9155 13.4629 3.1623angle(a)%ans =-0.5880 -1.0304 -1.8338 -1.2490 4 复数的乘除法复数的乘除法运算由“*”和“/”实现(5 复数的平方根复数的平方根运算由函数 sqrt 实现(调用形式如下:sqrt(z) 返回复数 z 的平方根值6 复数的幂运算复数的幂运算的形式是 z^n,结果返回复数 z 的 n 次幂( 7 复数的指数和对数运算复数的指数和对数运算分别由函数 exp 和log实现(调用形式如下:exp(z) 返回复数 z 的以 e 为底的指数值;log(z) 返回复数 z 的以 e 为底的对数值. 例21.1.2 求下列式的值(πi2ln(,10)e(1); (2)(【解】log(-10)%ans= 2.3026 + 3.1416iexp(pi/2* i)%ans =0.0000+ 1.0000i 21.1.3 复变函数的图形1.整幂函数的图形2z 例 21.1.6 绘出幂函数的图形.【解】 z=cplxgrid(30);cplxmap(z,z.^2);colorbar('vert');title('z^2')%(如图21.1所示)2z图21.1 复变函数的图形2. 根式函数的图形12z 例 21.1.7 绘出幂函数的图形【解】 z=cplxgrid(30);cplxroot(2);colorbar('vert');title('z^{1/2}' ) %(如图21.2).12z 图21.2 复变函数的图形3. 复变函数中对数函数的图形Lnz例 21.1.3 绘出对数函数的图形.【解】z=cplxgrid(20);w=log(z);for k=0:3w=w+i*2*pi;surf(real(z),imag(z),imag(w),real(w));hold ontitle('Lnz')endLnz 图21.3 对数函数 view(-75,30) %(如图21.3)例 21.1.4 计算机仿真编程实践:nzkn (1,2,,),,,,n,2z,,10k若对应为的根,其中且取整数.试用计算机仿真编程验证下列数学恒等式n1,0,,nk,1()zz,,kmm,1mk(),成立.【解】仿真程序n=round(1000*random('beta',1,1))+1% n=input('please enter n=')su=1;sum=0;for s=1:nN(s)=exp(i*2*s*pi/n);endfor k=1:nfor s=1:nif s~=ksu=1/(N(k)-N(s))*su;endendsum=sum+su;su=1;endsum%仿真验证结果为:n =735 sum =2.2335e-016 -5.1707e-016i其中n的值为随机产生的整数,可见其和的实部和虚部均接近于零。
matlab复变函数求导

matlab复变函数求导Matlab是一种常用的科学计算软件,它提供了丰富的工具箱和函数来进行各种数学计算和数据分析。
在Matlab中,我们可以使用复变函数求导来解决一些复杂的数学问题。
本文将介绍如何使用Matlab 进行复变函数的求导。
复变函数是指输入和输出都是复数的函数。
它可以表示为f(z),其中z是复数。
复变函数的导数也是一个复变函数,表示为f'(z)。
复变函数的求导可以通过求偏导数来实现,即对实部和虚部分别求导。
在Matlab中,我们可以使用syms函数来定义复变函数,并使用diff函数来求导。
首先,我们需要将变量定义为符号变量,以便Matlab能够识别它们是符号而不是数值。
例如,我们可以使用以下代码定义一个复变函数f(z):syms zf = z^2 + 2*z + 1在这个例子中,我们定义了一个复变函数f(z),表示为z的平方加上2乘以z再加上1。
接下来,我们可以使用diff函数来求导,如下所示:df = diff(f, z)这个代码将返回复变函数f(z)的导数df。
在这个例子中,导数df 等于2*z + 2。
我们可以通过将z替换为具体的数值来计算导数的数值结果。
例如,我们可以将z替换为3,然后计算导数的数值结果:df_value = subs(df, z, 3)这个代码将返回导数在z等于3时的数值结果。
除了使用diff函数,Matlab还提供了一些其他函数来处理复变函数的求导问题。
例如,我们可以使用gradient函数来计算复变函数的梯度。
梯度是一个向量,表示函数在每个点的导数。
我们可以使用以下代码来计算复变函数f(z)的梯度:[grad_x, grad_y] = gradient(f, real(z), imag(z))在这个例子中,grad_x和grad_y分别表示复变函数f(z)在实部和虚部方向上的导数。
我们可以将这两个导数合并成一个复变数导数,如下所示:grad = grad_x + 1i * grad_y这个代码将返回复变函数f(z)的导数grad。
Matlab在复变函数中应用

第9章 Matlab在复变函数中的应用从根本上讲,复变函数的运算是实变函数运算的一种延伸,但由于其自身的一些特殊的性质而显得不同,特别是当它引进了“留数”的概念,且在引入了Taylor级数展开,Laplace 变换和Fourier变换之后而使其显得更为重要了。
本章将重点介绍使用Matlab来进行复变函数的各种计算;介绍留数的概念及Matlab的实现;介绍在复变函数中有重要应用的Taylor展开(Laurent展开、Laplace变换和Fourier 变换)。
9.1 复数及其矩阵的生成。
在Matlab中,复数的单位为i和j,即:i = j =19.1.1 复数的生成在Matlab中,产生复数的方法有两种:1.由z = x + y*i产生,可简写成z = x + y i ;2.由z = r*exp (i*theta)产生,可简写成z = r*exp (theta i ),其中r为复数z的模,theta 为复数z辐角的弧度值。
9.1.2 复数矩阵的输入Matlab的矩阵元素允许是复数、复变量和由它们组成的表达式。
复数矩阵的输入方法有两种:1. 与实数矩阵相同的输入方法(见第1章)2. 将实部、虚部矩阵分开输入,再写成和的形式例9-1>> A=[1,3;-2,4]-[5 8;6 -9]*iA =1.0000 - 5.0000i 3.0000 - 8.0000i-2.0000 - 6.0000i 4.0000 + 9.0000i9.2 复数的运算9.2.1 复数的实部与虚部复数的实部和虚部用命令real和imag提取。
格式:real (z) %返回复数z的实部imag (z) %返回复数z的虚部9.2.2 共轭复数复数的共轭复数由命令conj实现。
格式:conj (z) %返回复数z的共轭复数9.2.3 复向量或复矩阵的转置复向量或复矩阵的转置符合两个规则:1. 符合实矩阵转置原则2. 转置后的元素均为共轭复数格式:Z’%Z的共轭转置例9-2>> A=[1,3;-2,4]-[5 8;6 -9]*iA =1.0000 - 5.0000i 3.0000 - 8.0000i-2.0000 - 6.0000i 4.0000 + 9.0000i>> A'ans =1.0000 + 5.0000i -2.0000 + 6.0000i3.0000 + 8.0000i4.0000 - 9.0000i若要得Z的非共轭转置,可用Z .’或conj (Z’)。
MATLAB中关于复数的相关函数
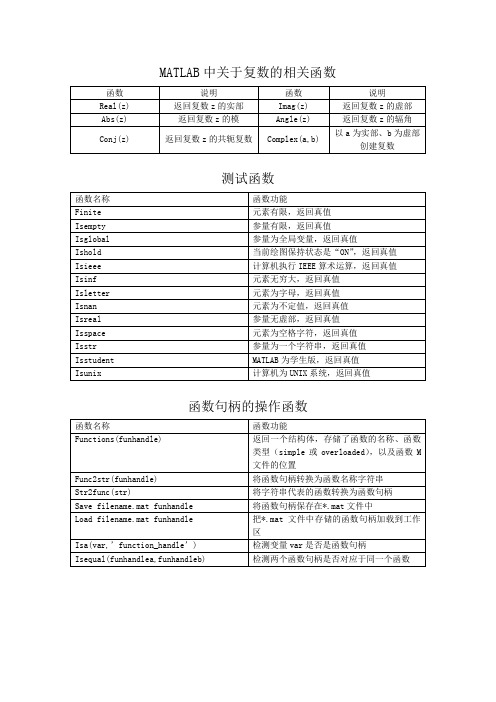
Isstr
参量为一个字符串,返回真值
Isstudent
MATLAB为学生版,返回真值
Isunix
计算机为UNIX系统,返回真值
函数句柄的操作函数
函数名称
函数功能
Functions(funhandle)
返回一个结构体,存储了函数的名称、函数类型(simple或overloaded),以及函数M文件的位置
Isempty
参量有限,返回真值
Isglobal
参量为全局变量,返回真值
Ishold
当前绘图保持状态是“ON”,返回真值
Isieee
计算机执行IEEE算术运算,返回真值
Isinf
元素无穷大,返回真值
Isletter
元素为字母,返回真值
Isnan
元素为不定值,返回真值
Isreal
参量无虚部,返回真值
Isspace
MATLAB中关于复数的相关函数
函数
说明
函数
说明
Real(z)
返回复数z的实部
Imag(z)
返回复数z的虚部
Abs(z)
返回复数z的模
Angle(z)
返回复数z的辐角
Conj(z)
返回复数z的共轭复数
Complex(a,b)
以a为实部、b为虚部创建复数
测试函数
函数名称
函数功能
Finite
元素有限,返回真值
Isa(var,’function_handle’)
检测变量var是否是函数句柄
Isequal(funhandlea,funhandleb)
检测两个函数句柄是否对应于同一个函数
Func2str(funhandle)
matlab中angle函数

matlab中angle函数
Matlab中的angle函数是一种十分实用的代数运算工具。
该函数可以对复数求取相应的角度,并能够指定输出的角度的单位,有助于简化相关任务的繁琐操作。
尤其在求解复变函数的过程中,angle函数的作用更加突出,可大大简化计算复杂度。
Angle函数符合Matlab文档定义的公式:angle(Z) = atan2(imag(Z),real(Z)),它可以根据给定复数Z对应的实部real(Z)与虚部imag(Z),结合atan2函数求取角度,结果可以以角度或者弧度进行输出。
此外,本函数还可以接收矩阵型输入,便于批量处理数据。
由于angle函数的便捷性与全面性,它的应用非常广泛,比如常见的计算机视觉任务,以及解析模型结构和参数估计的优化算法,都可以使用该函数进行支持。
总的来说,angle函数是一款十分强大的计算工具,它可以批量处理复数,从而既可以大大提高计算效率,也能够准确获取所需数据。
因此,angle函数极具价值,值得我们探究学习。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
matlab 复变函数
一、介绍
MATLAB是一个非常强大的数学软件,可以处理各种复杂的数学问题,包括复变函数。
复变函数是一种在复平面上定义的函数,它可以用来
描述许多物理和工程现象。
因此,MATLAB提供了许多功能强大的工
具来处理和分析复变函数。
二、基本概念
1. 复平面
复平面是由实部和虚部组成的平面。
在MATLAB中,可以使用complex(x,y)函数创建一个复数。
其中x表示实部,y表示虚部。
2. 复变函数
复变函数是一个将一个或多个复数映射到另一个复数的函数。
在MATLAB中,可以使用z = f(w)来表示一个复变函数。
3. 解析性
解析性是指一个函数在其定义域内存在导数。
如果一个函数在某个点处存在导数,则称该点为解析点。
4. 共轭
共轭是指将一个复数的虚部取负后得到的结果。
在MATLAB中,可以使用conj(z)来计算一个复数的共轭。
5. 模长
模长是指一个复数到原点距离。
在MATLAB中,可以使用abs(z)来计算一个复数的模长。
三、常用操作
1. 绘制图形
绘制图形是处理和分析复变函数时必不可少的操作之一。
在MATLAB 中,可以使用plot函数来绘制复变函数的图形。
2. 计算导数
计算导数是分析复变函数的重要操作之一。
在MATLAB中,可以使用diff函数来计算复变函数的导数。
3. 计算积分
计算积分也是处理和分析复变函数时必不可少的操作之一。
在MATLAB中,可以使用integral函数来计算复变函数的积分。
4. 计算共轭
计算共轭是处理和分析复变函数时经常需要进行的操作之一。
在MATLAB中,可以使用conj(z)来计算一个复数的共轭。
5. 计算模长
计算模长也是处理和分析复变函数时必不可少的操作之一。
在MATLAB中,可以使用abs(z)来计算一个复数的模长。
四、常用工具箱
1. Symbolic Math Toolbox
Symbolic Math Toolbox是一个用于求解符号数学问题的工具箱。
它
提供了许多功能强大的工具来处理和分析符号表达式。
2. Control System Toolbox
Control System Toolbox是一个用于设计和分析控制系统的工具箱。
它提供了许多功能强大的工具来设计和优化控制系统。
3. Optimization Toolbox
Optimization Toolbox是一个用于求解优化问题的工具箱。
它提供了许多功能强大的工具来求解各种类型的优化问题。
4. Signal Processing Toolbox
Signal Processing Toolbox是一个用于处理信号和图像的工具箱。
它提供了许多功能强大的工具来分析和处理各种类型的信号和图像。
五、示例代码
1. 绘制复平面
function plot_complex_plane()
x = linspace(-2,2,100);
y = linspace(-2,2,100);
[X,Y] = meshgrid(x,y);
Z = complex(X,Y);
scatter(real(Z(:)),imag(Z(:)),'.'); end
2. 计算复变函数的导数
function dz = derivative(z)
syms w
f(w) = z;
df = diff(f,w);
dz = double(df);
end
3. 计算复变函数的积分
function I = integral_f(z)
syms w
f(w) = z;
I = double(int(f,w));
end
4. 计算共轭和模长
function [z_conj,z_abs] = conjugate_and_abs(z) z_conj = conj(z);
z_abs = abs(z);
end。
