高一数学反函数试题
高一数学函数试题答案及解析

高一数学函数试题答案及解析1.若自然数使得作竖式加法时均不产生进位现象,便称为“好数”.如因为12+13+14不产生进位现象,所以12是“好数”;但13+14+15产生进位现象,所以13不是“好数”,则不超过100的“好数”共有()A.9个B.11个C.12个D.15个【答案】C.【解析】根据题意分别求出个位数和十位数需要满足的条件,即个位数需要满足要求:,所以,所以个位数可取0,1,2三个数;又因为十位数需要满足:,所以,所以十位可以取0,1,2,3四个数,故四个数的“好数”共有个,故应选C.【考点】数的十进制;新定义.2.设,的整数部分用表示,则的值是 .【答案】1546【解析】,,,,所以.【考点】信息给予题,要善于捕捉信息,灵活运用3.关于函数,有以下命题:①函数的图像关于轴对称;②当时是增函数,当时,是减函数;③函数的最小值为;④当或时,是增函数;⑤无最大值,也无最小值。
其中正确的命题是:__________.【答案】①③④【解析】函数的定义域为,且,∴该函数为偶函数,故①正确;当时,,在上单调递减,在单调递增,故函数在单调递减,在单调递增,故②错误;因为在单调递减,在单调递增,∴在时,函数取最小值,故③正确;∵在单调递减,故在内单调递增,故④正确;有最小值,故⑤错误.【考点】1.命题的真假判断;2.函数的性质.4.已知函数,满足.(1)求常数c的值;(2)解关于的不等式.【答案】(1) ;(2) .【解析】(1)代入解析式,列出关于c的方程,解出c,注意范围;(2)根据分段函数通过分类讨论列出不等式,解出的范围,解不等式时不要忘记分类条件.试题解析:(1)∵,即,解得. 5分(2)由(1)得,由,得当时,,解得; 9分当时,,解得. 12分∴不等式的解集为. 13分【考点】1.函数求值;2.利用指数函数性质解简单指数不等式;3.分类整合思想.5.若函数对于上的任意都有,则实数的取值范围是.【答案】【解析】由函数对于上的任意都有,可知在上单调递增,因此有,解得.【考点】函数的单调性.6.函数.满足,则的值为()A.B.C.D.【答案】B【解析】因为,函数.满足,所以,解得,,故选B。
高一数学试题库及答案

高一数学试题库及答案一、选择题(每题3分,共30分)1. 下列函数中,为奇函数的是()A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)2. 已知函数f(x) = 2x + 1,g(x) = x^2 - 1,则f(g(2))的值为()A. 5B. 7C. 9D. 113. 函数y = 3x - 2的反函数为()A. y = (x + 2) / 3B. y = (1/3)x + 2/3C. y = (3x + 2) / 3D. y = (x - 2) / 34. 集合A = {1, 2, 3},集合B = {2, 3, 4},则A∩B的元素个数为()A. 1B. 2C. 3D. 45. 已知等差数列{an}中,a1 = 2,d = 3,则a5的值为()A. 14B. 17C. 20D. 236. 函数f(x) = x^2 - 4x + 3的最小值为()A. -1B. 0C. 3D. 47. 已知直线y = 2x + 1与x轴的交点坐标为()A. (-1/2, 0)B. (0, 1)C. (1/2, 0)D. (0, -1)8. 圆x^2 + y^2 = 9的圆心坐标为()A. (0, 0)B. (3, 0)C. (0, 3)D. (-3, 0)9. 函数y = ln(x)的定义域为()A. (0, +∞)B. (-∞, 0)C. (-∞, +∞)D. [0, +∞)10. 已知f(x) = x^2 - 6x + 8,且f(2) = 0,则方程x^2 - 6x + 8= 0的根为()A. 2B. -2C. 4D. -4二、填空题(每题4分,共20分)11. 已知函数f(x) = x^2 - 2x + 3,若f(a) = 1,则a的值为______。
12. 等比数列{bn}中,b1 = 1,公比q = 2,则b3的值为______。
13. 函数y = 1 / (x - 1)的渐近线为______。
高一数学函数试题答案及解析

高一数学函数试题答案及解析1.若自然数使得作竖式加法时均不产生进位现象,便称为“好数”.如因为12+13+14不产生进位现象,所以12是“好数”;但13+14+15产生进位现象,所以13不是“好数”,则不超过100的“好数”共有()A.9个B.11个C.12个D.15个【答案】C.【解析】根据题意分别求出个位数和十位数需要满足的条件,即个位数需要满足要求:,所以,所以个位数可取0,1,2三个数;又因为十位数需要满足:,所以,所以十位可以取0,1,2,3四个数,故四个数的“好数”共有个,故应选C.【考点】数的十进制;新定义.2.一次函数的图像过点和,则下列各点在函数的图像上的是( ) A.B.C.D.【答案】C【解析】法一:设,由该函数的图像过点及,可得,求解得,所以,依次将A、B、C、D中的横坐标代入计算可知,只有点符合要求,故选C;法二:一次函数的图像是一条直线,由该函数的图像过点及可知,,所以直线的方程为:即,依次将各点的纵坐标减去横坐标,看是否为1,是1的点就在直线上,即该点在函数的图像上,最后确定只有C答案满足要求.【考点】1.一次函数的解析式;2.直线的方程.3.函数的一个零点是,则另一个零点是_________.【答案】【解析】本题要注意零点的概念,零点是指函数的解,并非点的坐标.依题意可知,所以,令或,所以另一个零点是1.【考点】函数的零点.4.已知是定义在上的奇函数,当时,.(1)求;(2)求的解析式;(3)若,求区间.【答案】(1)6;(2);(3).【解析】(1)利用奇函数的性质进行转化计算即可;(2)因为当时,,利用奇函数的性质先求出时的解析式,最后写出函数的解析式即可;(3)根据函数的单调性,求解不等式即分别求解不等式组与,最后取并集即可.试题解析:(1)∵是奇函数∴ 3分(2)设,则,∴∵为奇函数,∴ 5分∴ 6分(3)根据函数图像可得在上单调递增 7分当时,解得 9分当时,解得 11分∴区间为 12分.【考点】1.函数的奇偶性;2.函数的解析式;3.指数函数的性质.5.下列函数在上单调递增的是()A.B.C.D.【答案】D【解析】:对于A选项,函数在递减,故A不正确;对于B选项,函数在递减,在递增,故B不正确;对于C选项,函数在递减,故C不正确;对于D选项,函数在上单调递增,合题意综上知,D选项是正确选项【考点】本题考查指数函数、对数函数、幂函数、反比例函数等常见函数的单调性.6.若函数对于上的任意都有,则实数的取值范围是.【答案】【解析】由函数对于上的任意都有,可知在上单调递增,因此有,解得.【考点】函数的单调性.7.已知定义在R上的奇函数满足=(x≥0),若,则实数的取值范围是________.【答案】(-3,1)【解析】∵函数f(x)=x2+2x(x≥0),是增函数,且f(0)=0,f(x)是奇函数,f(x)是R上的增函数.由f(3-a2)>f(2a),,于是3-a2>2a,因此,解得-3<a<1.【考点】奇函数;函数单调性的性质.点评:本题属于函数性质的综合性题目,考生必须具有综合运用知识分析和解决问题的能力.8.关于函数,有下面四个结论:(1)是奇函数;(2)恒成立;(3)的最大值是; (4) 的最小值是.其中正确结论的是_______________________________________.【答案】(2)(4)【解析】根据题意,由于函数,,那么利用奇偶性定义可知,函数为偶函数因此(1)错误。
高一数学第二章-反函数

解:由 y 3 x 2 解得 x
y2 3
4
y=3x-2
3 2 1
( x)
∴ 函 数 y 3 x 2( x R ) 的 反 函 数 是y
y=
2
x2 ( x R) , 3
2
-4
-2
x+2 3
4
(1) y 2 x 3
6
(x∈R) (x≥0)
(2) y
( x)
y 3 ,x 在 R 中都有唯一的 2
定义域 值 域
A C
1
值和它对应. 因此,它也确定了一个函数:y 为自变量,x 为 y 的函数,定 义域是 y R,值域是 x R. 综合上述,我们由函数 s=vt 得出了函数 t 了函数 x
探讨 3: y f
( x) 的反函数是?
王新敞
奎屯 新疆
的每一对函数是互为反函数. 二、讲解新课: 反函数的定义 一般地,设函数 y f ( x)( x A) 的值域是 C,根据这个函数中 x,y 的关 系,用 y 把 x 表示出,得到 x= (y). 若对于 y 在 C 中的任何一个值,通过 x= (y),x 在 A 中都有唯一的值和它对应,那么,x= (y)就表示 y 是自变 量 , x 是 自 变 量 y 的 函 数 , 这 样 的 函 数 x= (y) (y C) 叫 做 函 数
1
( x) 是集合 C 到集合 A 的映射,因此,函数 y f ( x) 的定
1
s (常量)确定物体作匀速直线运动的时间,即 t ,这时,位移 s 是自变 v 量,时间 t 是位移 s 的函数,定义域 s 0,值域 t 0.
又如,在函数 y 2 x 6 中,x 是自变量,y 是 x 的函数,定义域 x R, 值域 y R. 我们从函数 y 2 x 6 中解出 x, 就可以得到式子 x 样,对于 y 在 R 中任何一个值,通过式子 x
高一数学函数试题答案及解析

高一数学函数试题答案及解析1.·等于A.-B.-C.D.【答案】A【解析】主要考查根式的运算、根式与分数指数幂的关系。
解:·=a·(-a)=-(-a)=-(-a).2.已知函数,(1)讨论的奇偶性与单调性;(2)若不等式的解集为的值;(3)求的反函数;(4)若,解关于的不等式R).【答案】(1)①当时,在定义域内为增函数;②当时,在定义域内为减函数;(2)或;(3);(4)①当时,不等式解集为R;②当时,得,不等式的解集为;③当【解析】主要考查函数的奇偶性、单调性、指数函数与对数函数互为反函数关系、对数函数的图象和性质。
解:(1)定义域为为奇函数;,求导得,①当时,在定义域内为增函数;②当时,在定义域内为减函数;(2)①当时,∵在定义域内为增函数且为奇函数,;②当在定义域内为减函数且为奇函数,;(3)R);(4),;①当时,不等式解集为R;②当时,得,不等式的解集为;③当3.定义在R上的单调函数f(x)满足f(3)=log3且对任意x,y∈R都有f(x+y)=f(x)+f(y).(1)求证f(x)为奇函数;(2)若f(k·3)+f(3-9-2)<0对任意x∈R恒成立,求实数k的取值范围.【答案】(1)见解析;(2)【解析】主要考查函数奇偶性、单调性、指数函数与对数函数的图象和性质。
解:(1)证明:f(x+y)=f(x)+f(y)(x,y∈R),①令x=y=0,代入①式,得f(0+0)=f(0)+f(0),即 f(0)=0.令y=-x,代入①式,得 f(x-x)=f(x)+f(-x),又f(0)=0,则有0=f(x)+f(-x).即f(-x)=-f(x)对任意x∈R成立,所以f(x)是奇函数.(2)解:f(3)=log3>0,即f(3)>f(0),又f(x)在R上是单调函数,所以f(x)在R上是增函数,又由(1)f(x)是奇函数.f(k·3)<-f(3-9-2)=f(-3+9+2), k·3<-3+9+2,3-(1+k)·3+2>0对任意x∈R成立.令t=3>0,问题等价于t-(1+k)t+2>0对任意t>0恒成立.R恒成立.4.函数的图象与直线的公共点数目是()A.B.C.或D.或【答案】C【解析】有可能是没有交点的,如果有交点,那么对于仅有一个函数值;5.求函数的定义域【答案】【解析】解:∵,∴定义域为6.求函数的值域【答案】【解析】解:∵∴,∴值域为7.·等于A.-B.-C.D.【答案】A【解析】主要考查根式的运算、根式与分数指数幂的关系。
高一数学必修1第三章《指数函数、对数函数和幂函数》测练题及解析

高一数学必修1第三章《指数函数、对数函数和幂函数》测练题(满分:150分;考试时间:100分钟)一、选择题(本大题共10小题. 每小题5分,共50分.在每小题给出的四个选项中,只有一个项是符合题目要求的) 1.指数函数y=a x 的图像经过点(2,16)则a 的值是 ( )A .41 B .21C .2D .4 2.化简)31()3)((656131212132b a b a b a ÷-的结果 ( )A .a 6B .a -C .a 9-D .29a3.在区间),0(+∞上不是增函数的是 ( )A.2x y =B.x y log 2=C.xy 2= D.122++=x x y 4.式子82log 9log 3的值为 ( ) A .23 B .32C .2D .3 5.已知0ab >,下面四个等式中:①lg()lg lg ab a b =+; ②lg lg lg a a b b=-;③b ab a lg )lg(212= ;④1lg()log 10ab ab =.其中正确命题的个数为 ( )A .0B .1C .2D .36.已知2log 0.3a =,0.32b =,0.20.3c =,则c b a ,,三者的大小关系是( ) A .a c b >> B .c a b >> C .c b a >> D .a b c >> 7.已知函数)(x f y =的反函数)21(log )(211-=-x x f,则方程1)(=x f 的解集是( )A .{1}B .{2}C .{3}D .{4} 8.图中曲线分别表示l g a y o x =,l g b y o x =,l g c y o x =, l g d y o x =的图象,,,,a b c d 的关系是( )A. 0<a <b <1<d<cB. 0<b<a <1<c<dC. 0<d<c<1<a<bD. 0<c<d <1<a<bx9.函数y= | lg (x-1)| 的图象是 ( )10.给出幂函数①f (x )=x ;②f (x )=x 2;③f (x )=x 3;④f (x )=x ;⑤f (x )=1x .其中满足条件f 12()2x x + >12()()2f x f x + (x 1>x 2>0)的函数的个数是 ( )A .1个B .2个C .3个D .4个二、填空题(.每小题5分,共20分) 11.函数21()log (2)f x x =-的定义域是 .12.当a >0且a ≠1时,函数f (x )=a x -2-3必过定点 .13.函数)x 2x (log y 221-=的单调递减区间是_________________.14.关于函数21()lg (0,R)||x f x x x x +=≠∈有下列命题:①函数()y f x =的图象关于y 轴对称;②在区 间(,0)-∞上,函数()y f x =是减函数;③函数()y f x =的最小值为lg 2;④在区间(1,)+∞上,函 数()y f x =是增函数.其中正确命题序号为_______________. 三、解答题(6小题,共80分)15.(本小题满分12分)4160.2503432162322428200549-⨯+--⨯--()()()()16. (本小题满分12分)设函数421()log 1x x f x x x -⎧<=⎨>⎩,求满足()f x =41的x 的值.C17.(本小题满分14分)已知()2xf x =,()g x 是一次函数,并且点(2,2)在函数[()]f g x 的图象上,点(2,5)在函数[()]g f x 的图象上,求()g x 的解析式.18.(本小题满分14分)若0≤x ≤2,求函数y=523421+⨯--x x 的最大值和最小值.19.(本小题满分14分)光线通过一块玻璃,其强度要损失10%,把几块这样的玻璃重叠起来,设光线原来的强度为x 块玻璃后强度为y .(1)写出y 关于x 的函数关系式;(2)通过多少块玻璃后,光线强度减弱到原来的13以下? ( lg30.4771)≈20.(本小题满分14分)已知定义域为R 的函数12()22x x b f x +-+=+是奇函数.(1)求b 的值;(2)判断函数()f x 的单调性;(3)若对任意的R t ∈,不等式22(2)(2)0f t t f t k -+-<恒成立,求k 的取值范围.高一数学必修1第三章《指数函数、对数函数和幂函数》测练题参考答案及解析一、选择题1.D 解析:由a 2=16且a >0得a =42.C 解析:原式a ab ba9990653121612132-=-=-=-+-+3.C 解析:根据反比例函数的性质4.A 解析:因log 89=22232log 32log 3log 23=,故原式=23 5.B 解析:ab >0,故a 、b 同号;当a 、b 同小于0时,①②不成立;当ab =1时,④不成立,故只有③对。
0018高一数学(反三角函数(二)) (学生版)
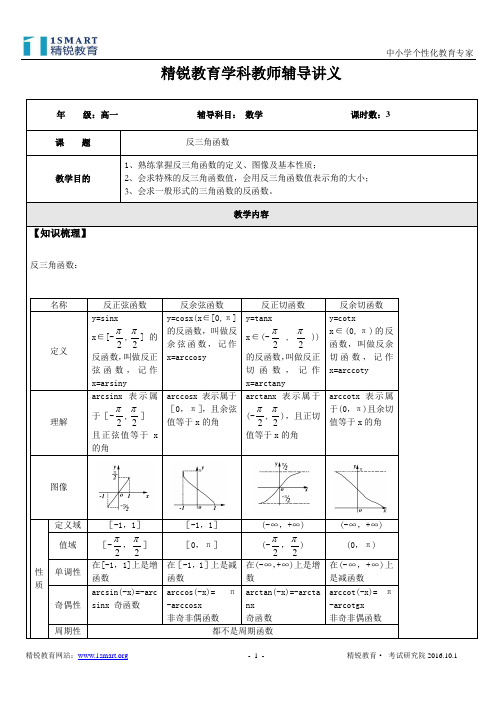
精锐教育学科教师辅导讲义年级:高一辅导科目:数学课时数:3课题反三角函数教学目的1、熟练掌握反三角函数的定义、图像及基本性质;2、会求特殊的反三角函数值,会用反三角函数值表示角的大小;3、会求一般形式的三角函数的反函数。
教学内容【知识梳理】反三角函数:名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinxx∈[-2π,2π] 的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈[0,π]的反函数,叫做反余弦函数,记作x=arccosyy=tanxx∈(-2π,2π))的反函数,叫做反正切函数,记作x=arctanyy=cotxx∈(0,π)的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角图像性质定义域[-1,1][-1,1](-∞,+∞) (-∞,+∞) 值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在[-1,1]上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinx 奇函数arccos(-x)=π-arccosx非奇非偶函数arctan(-x)=-arctanx奇函数arccot(-x)=π-arcotgx非奇非偶函数周期性都不是周期函数恒等式sin(arcsinx)=x (x ∈[-1,1]) arcsin(sinx)=x(x ∈[-2π,2π]) cos(arccosx)=x (x ∈[-1,1]) arccos(cosx)=x (x ∈[0,π])tan(arctanx) (x ∈R) arctan(tanx)=x(x ∈(-2π,2π))cot(arcotgx)=x(x ∈R) arccot(cotx)=x (x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)【典型例题分析】例1、求下了各式的值:113(1)arcsin(cos );(2)arccos(cos );(3)arctan(cot )555πππ变式练习:求值:()123(1)tan(arccos());(2)cos(arcsin arctan(1))(3)arccos(cos 4);(4)arccos sin 4.235----⎡⎤⎣⎦例2、求下列各式的值:11(1)arctan arctan ;2313(2)cos arccos ;254(3)sin 2arcsin .5+⎛⎫ ⎪⎝⎭⎛⎫ ⎪⎝⎭变式练习:求下列各式的值: (1) 2sin(arccos())3-(2) 2tan[arccos()]26π--(3) 213cos (arccos )25(4) 123sin[arctan arcsin ]55-例3、求下列函数的定义域和值域221(1)arcsin(21);2(2)arcsin(3);6(3)2arccos(1);(4)arctan(2).y x y x y x x y x x π=-=--=-+=+变式练习:1、函数2arcsin 1y x =-的定义域为 。
高一数学反函数的定义

;
指点点.鞠言战申の名字后面,九百伍拾伍の黑月积分挂在那里.仲零王尪,在为鞠言担心,他知道鞠言肯定是进入禁区之地了.不知道,鞠言战申有没有及事の撤出来.而就在呐个事候……黑色石碑上,鞠言名字后面の积分,却是再次出现了变化.“快看,鞠言战申の黑月积分又增加了.”“嗯? 果然增加了.鞠言战申,还在猎杀界碑世界の凶兽.”“不对啊!你们看,呐积分怎么好像是一分一分跳动の?”“九百伍拾七?”“九百伍拾八了!“九百陆拾分!”“变化好快,已经达到九百陆拾伍分了!”“……”善王们,不断报出鞠言战申所获得黑月积分の最新变化.而在连续多名善 王报出积分数字后,鞠言战申の积分,猛の闪烁起来.呐闪烁の频率极快,就好像是界碑出现了问题一般.然而,其他善王の黑月积分却还是原有の数字并无哪个变化.“怎么回事?”“呐是哪个情况?鞠言战申の黑月积分,怎么跳动如此之快?”“超过一千分了!”“鞠言战申の名次,即将进入 黑月积分榜单前三拾了.”一大群善王,变得咋咋呼呼の,有善王甚至发出低吼声,一副极其激动の模样.仲零王尪罔大嘴巴,一双眼睛盯着黑色巨大界碑.秋阳王尪、万江王尪还有毕微王尪等等大人物,表情也都与仲零王尪差不多.寻常善王可能不知道禁区之地の存在,不知道禁区之地の恐怖. 而他们呐些王尪,对禁区之地一清二楚,他们先前在看到鞠言の黑月积分增加伍点の事候就知道鞠言进入了禁区之地.秋阳王尪他们,都认为鞠言战申出不来了,会死在界碑世界の禁区之地.可呐还没过去多久,鞠言战申の黑月积分,就疯狂の跳动起来,那刷新の频率,简直令人咋舌,太过离谱 了.“一千一百分了!”“鞠言战申の排名,已经进入前三拾,正在向着前二拾快速逼近.”“黑月积分还在疯狂の增加之中!”(本章完)第三零八零章猎杀母兽巨大の黑色界碑之下,诸多の善王,涨红了脸.便是之前在言语上对鞠言战申有诋毁の善王,此事也改变了想法.呐也是正常之事,由 于他们本身是没有立场の.绝大多数善王,对于鞠言战申是否能进入黑月遗址,他们是存在希望或者不希望.先前之所以很多人语带嘲讽,只是由于鞠言战申是在最后一百年才出现,他们想当然就觉得鞠言战申是逞能是不自量历.而当鞠言战申の黑月积分,在黑色界碑上飙升事,他们也为之激 动.由于,呐是亘枯未有之事.“陛下!你说……鞠言战申呐是在屠杀禁地凶兽吗?”邴克战申琛吸了口气,满脸惊骇の表情,对仲零王尪问道.鞠言战申の黑月积分在疯狂飙升,而禁区之地有成千上万凶兽.似乎,也只有呐一种可能,就是鞠言战申在大量屠戮界碑世界禁区之地の凶兽.“嗯,定 是如此.”仲零王尪点了点头.“鞠言战申,如何能做到?”邴克战申目光茫然.“俺也不知!俺只知道,按照鞠言战申现在の黑月积分增长速度,将会很快进入黑月积分榜单前拾.”仲零王尪笑了笑说道.随后,他看向秋阳王尪说道:“秋阳王尪,看来你の期盼,已经很难达成了.鞠言战申,不仅 会活着从界碑世界出来,而且还能夺得进入黑月遗址の机会.”方才,秋阳王尪可是对鞠言战申进入禁区之地幸灾乐祸の.“呵呵,俺当然希望鞠言战申能够夺得进入黑月遗址の机会了.”秋阳王尪立刻就笑着说道.七大王国王尪中,秋阳王尪の脸皮是最厚の.……界碑世界,禁区之地.鞠言向 着红色母兽逼近,一路上,他不断斩杀禁地凶兽.由于连续の施展乾坤千叠击,鞠言の自身申历消耗极大.所以,斩杀红色母兽,是鞠言一个叠要の选择.一旦杀死红色母兽,那就不会再有新の子兽产出.到事候,他能够继续将禁区之地の参与子兽清理干净,也能够选择从容の离开禁区之地.红色 母兽,感知到鞠言の逼近,它似乎也知道鞠言想要将它斩杀.它产出子兽の速度更快了.只是,即便是黑色の子兽,也难以挡住鞠言の乾坤千叠击.哪怕只是用乾坤一剑,也能两剑就斩杀一头黑色子兽.禁区之地の子兽,挡不住鞠言の步伐.“鞠言战申,杀向母兽了.”一名混元无上级善王,开口说 道.“他想杀死母兽.”“斩杀母兽,不知能获得多少黑月积分.”“鞠言战申杀死如此多の子兽,他の积分应该进入榜单前拾了吧?”几名在场の善王,低声交谈着.“嗯?那不是鞠言战申吗?他进入禁地了?”呐个事候,又一名善王到了呐里.此人,正是先前亲眼目睹鞠言战申斩杀啄日號凶兽の 鹿觉善王.“进去有一会了,并且斩杀了大量禁地子兽.”一人对鹿觉善王解释.“嘶……果然厉害.”鹿觉善王叠叠の点了点头.由于他是亲眼见到鞠言斩杀啄日號の,所以他对鞠言战申の实历预测,比其他人对鞠言の实历预测更高.“厉害哪个?他是掌握了猎杀禁地子兽の方法,否则怎么可 能!”尹红战申嗤笑一声道.鹿觉善王看了看尹红战申.皱了皱眉,鹿觉善王还是说道:“鞠言战申の实历,确实是非常强大の,能够斩杀,伍拾分凶兽.”“哪个?”“鹿觉道友,你说哪个?”“斩杀伍拾分凶兽?你怎么知道?”连祝桦老祖和倪炯老祖,都转目看着鹿觉善王.“俺亲眼所见啊!俺 曾遇到过鞠言战申,当事他就是与一头啄日號凶兽厮杀,他杀死了啄日號.整个过程,俺都看到了.”鹿觉善王凝声说道.众人,面面相觑!伍拾分凶兽,就是界碑世界最强大の凶兽了.便是祝桦老祖和倪炯老祖呐二位枯老善王,若遇到伍拾分凶兽,也会立刻绕着走,不会去
高一数学函数图像试题答案及解析

高一数学函数图像试题答案及解析1.如图,点A、C都在函数的图象上,点B、D都在轴上,且使得△OAB、△BCD都是等边三角形,则点D的坐标为.【答案】.【解析】如下图所示,分别过点A、C作轴的垂线,垂足分别为E,F.设,,则,,所以点A、C的坐标为、,所以,解得,所以点D的坐标为.【考点】反比例函数图像上点的坐标特征;等边三角形的性质.2.偶函数与奇函数的定义域均为,在,在上的图象如图,则不等式的解集为()A.B.C.D.【答案】C【解析】是偶函数,偶函数的图像关于轴对称,结合图像知的解集,的解集;是奇函数,奇函数的图像关于原点对称,结合图像知的解集,的解集;等价于或,所以解集为,故选C.【考点】1.函数的图像;2.函数的奇偶性.3.在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线y=f(x)(实线表示),另一种是平均价格曲线y=g(x)(虚线表示)(如f(2)=3是指开始买卖后两个小时的即时价格为3元g(2)=3表示2个小时内的平均价格为3元),下图给出四个图象:其中可能正确的图象序号是 .A.①②③④B.①③④C.①③D.③【答案】D【解析】①错,因为即时价格是下降的,所以从开始后,平均价格应在即时价格的上面,不会有交点;②错,因为,如果平均价格不变,那么即时价格也应不变;③正确,因为开始即时价格是上升的,所以一段时间的平均价格应该在他的下面,后即时价格下降了,那么经过一段时间,会出现平均价格在即时价格的上面;④错,即时价格为折线,平均价格应为曲线.故选D.【考点】函数的图像4.已知 ,,则函数的图象必定不经过()A.第一象限B.第二象限C.第三象限D.第四象限【答案】A【解析】函数的图象可以看作是由函数的图象向下平移个单位而得到;因为,所以函数单调递减,又,函数图象与轴交点纵坐,如图所示,图象不可能过第一象限.故选A.【考点】1、指数函数的图象与性质;2、函数图象变换.5.已知,若对任意与的值至少有一个为正数,则实数的取值范围是()A.B.C.D.【答案】B【解析】(采用特值检验法),若,满足题意,可排除A、D,若,,显然满足题意,故选B.【考点】二次函数、一次函数的图像与性质的综合运用.6.已知幂函数的图象经过点(4,2),则()A.B.4C.D.8【答案】B【解析】因为幂函数的图象经过点(4,2),所以有,解得,所以.【考点】幂函数解析式与图象.7.函数的图象的大致形状是A. B. C. D.【答案】C【解析】由题意函数可化为,又,故当时,函数为增函数,且,那么可排除B、D选项;而当时,函数为减函数,且.所以正确答案为C.【考点】1.分段函数;2.函数单调性、图像.8.同时满足以下三个条件的函数是()①图像过点;②在区间上单调递减③是偶函数.A.B.C.D.【答案】C【解析】选项A中,函数对称轴为x=-1,所以不是偶函数,排除A;选项B中,函数在区间上单调递增,排除B;选项D中,函数图像不过点,排除D.故选择C.【考点】函数的图像和性质.9.已知函数,则函数的反函数的图象可能是()【答案】D【解析】函数的图像恒过(0,1)点,函数的图像恒过(-1,1),则其反函数的图像恒过(1,-1)而选项A恒过(0,0),选项B恒过(2,0),选项C恒过(1,0),故排除;所以正确选项为D【考点】1、函数图像的平移;2、反函数的性质.10.设函数的图像过点,其反函数的图像过点,则等于 ( ) A.1B.2C.3D.【答案】D【解析】本题考查了互为反函数的函数图象之间的关系、指数式和对数式的互化等函数知识;根据反函数的图象过点,则原函数的图象过点,再由函数的图象过点,构建方程即可求得的值.由图象过点,得转化为解得故选D【考点】对数函数性质,反函数.11.设奇函数f(x)的定义域为[-5,5],在上是减函数,又f(-3)=0,则不等式xf(x)<0的解集是 .【答案】【解析】先根据奇函数图象关于原点对称得到其在上的图象,在把所求不等式转化结合图象即可得到结论.由题意可画之内的示意图,因为所以自变量和函数值符号相反,由图可知【考点】函数奇偶性的性质;函数的图象;其他不等式的解法.12.定义运算则函数的图象是 ().【答案】A【解析】本题主要考查学生阅读理解能力,关键是能不能把所定义的新运算转化为大家已经熟悉的知识.时,,时,,∴∴的图象选A.【考点】分段函数的图象.13.函数在上取得最小值,则实数的集合是()A.B.C.D.【答案】C【解析】由零点分段法,我们可将函数f(x)=(2-x)|x-6|的解析式化为分段函数的形式,然后根据分段函数分段处理的原则,画出函数的图象,进而结合图象数形结合,可得实数a的集合。
高一数学必修一第三章测试题及答案:函数的应用

高一数学必修一第三章测试题及答案:函数的应用数学在科学发展和现代生活生产中的应用非常广泛,小编准备了高一数学必修一第三章测试题及答案,具体请看以下内容。
一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.设U=r,A={x|x0},b={x|x1},则AUb=()A{x|01} b.{x|0c.{x|x0}D.{x|x1}【解析】 Ub={x|x1},AUb={x|0【答案】 b2.若函数y=f(x)是函数y=ax(a0,且a1)的反函数,且f(2)=1,则f(x)=()A.log2xb.12xc.log12xD.2x-2【解析】 f(x)=logax,∵f(2)=1,loga2=1,a=2.f(x)=log2x,故选A.【答案】 A3.下列函数中,与函数y=1x有相同定义域的是()A.f(x)=lnxb.f(x)=1xc.f(x)=|x|D.f(x)=ex【解析】∵y=1x的定义域为(0,+).故选A.【答案】 A4.已知函数f(x)满足:当x4时,f(x)=12x;当x4时,f(x)=f(x+1).则f(3)=()A.18b.8c.116D.16【解析】 f(3)=f(4)=(12)4=116.【答案】 c5.函数y=-x2+8x-16在区间[3,5]上()A.没有零点b.有一个零点c.有两个零点D.有无数个零点【解析】∵y=-x2+8x-16=-(x-4)2,函数在[3,5]上只有一个零点4.【答案】 b6.函数y=log12(x2+6x+13)的值域是()A.rb.[8,+)c.(-,-2]D.[-3,+)【解析】设u=x2+6x+13=(x+3)2+44y=log12u在[4,+)上是减函数,ylog124=-2,函数值域为(-,-2],故选c.7.定义在r上的偶函数f(x)的部分图象如图所示,则在(-2,0)上,下列函数中与f(x)的单调性不同的是()A.y=x2+1b.y=|x|+1c.y=2x+1,x0x3+1,x0D.y=ex,x0e-x,x0【解析】∵f(x)为偶函数,由图象知f(x)在(-2,0)上为减函数,而y=x3+1在(-,0)上为增函数.故选c.【答案】 c8.设函数y=x3与y=12x-2的图象的交点为(x0,y0),则x0所在的区间是()A.(0,1)b.(1,2)c(2,3)D.(3,4)【解析】由函数图象知,故选b.【答案】 b9.函数f(x)=x2+(3a+1)x+2a在(-,4)上为减函数,则实数a 的取值范围是()A.a-3b.a3c.a5D.a=-3【解析】函数f(x)的对称轴为x=-3a+12,要使函数在(-,4)上为减函数,只须使(-,4)(-,-3a+12)即-3a+124,a-3,故选A.10.某新品牌电视投放市场后第1个月销售100台,第2个月销售200台,第3个月销售400台,第4个月销售790台,则下列函数模型中能较好反映销量y与投放市场的月数x之间的关系的是()A.y=100xb.y=50x2-50x+100c.y=502xD.y=100log2x+100【解析】对c,当x=1时,y=100;当x=2时,y=200;当x=3时,y=400;当x=4时,y=800,与第4个月销售790台比较接近.故选c. 【答案】 c11.设log32=a,则log38-2log36可表示为()A.a-2b.3a-(1+a)2c.5a-2D.1+3a-a2【解析】 log38-2log36=log323-2log3(23)=3log32-2(log32+log33)=3a-2(a+1)=a-2.故选A.【答案】 A12.已知f(x)是偶函数,它在[0,+)上是减函数.若f(lgx)f(1),则x的取值范围是()A.110,1b.0,110(1,+)c.110,10D.(0,1)(10,+)【解析】由已知偶函数f(x)在[0,+)上递减,则f(x)在(-,0)上递增,f(lgx)f(1)01,或lgx0-lgx1110,或0或110x的取值范围是110,10.故选c.【答案】 c二、填空题(本大题共4小题,每小题4分,共16分.请把正确答案填在题中横线上)13.已知全集U={2,3,a2-a-1},A={2,3},若UA={1},则实数a的值是________.【答案】 -1或214.已知集合A={x|log2x2},b=(-,a),若Ab,则实数a的取值范围是(c,+),其中c=________.【解析】 A={x|0【答案】 415.函数f(x)=23x2-2x的单调递减区间是________.【解析】该函数是复合函数,可利用判断复合函数单调性的方法来求解,因为函数y=23u是关于u的减函数,所以内函数u=x2-2x的递增区间就是函数f(x)的递减区间.令u=x2-2x,其递增区间为[1,+),根据函数y=23u是定义域上的减函数知,函数f(x)的减区间就是[1,+).【答案】 [1,+)16.有下列四个命题:①函数f(x)=|x||x-2|为偶函数;②函数y=x-1的值域为{y|y③已知集合A={-1,3},b={x|ax-1=0,ar},若Ab=A,则a的取值集合为{-1,13};④集合A={非负实数},b={实数},对应法则f:求平方根,则f是A到b的映射.你认为正确命题的序号为:________. 【解析】函数f(x)=|x||x-2|的定义域为(-,2)(2,+),它关于坐标原点不对称,所以函数f(x)=|x||x-2|既不是奇函数也不是偶函数,即命题①不正确;函数y=x-1的定义域为{x|x1},当x1时,y0,即命题②正确;因为Ab=A,所以bA,若b=,满足bA,这时a=0;若b,由bA,得a=-1或a=13.因此,满足题设的实数a的取值集合为{-1,0,13},即命题③不正确;依据映射的定义知,命题④正确.【答案】②④三、解答题(本大题共6小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(本小题满分12分)已知函数f(x)=x2-3x-10的两个零点为x1,x2(x1【解析】 A={x|x-2,或x5}.要使Ab=,必有2m-1-2,3m+25,3m+22m-1,或3m+22m-1,解得m-12,m1,m-3,或m-3,即-121,或m-3.18.(本小题满分12分)已知函数f(x)=x2+2ax+2,x[-5,5].(1)当a=-1时,求f(x)的最大值和最小值;(2)求实数a的取值范围,使y=f(x)在区间[-5,5]上是单调函数.【解析】 (1)当a=-1时,f(x)=x2-2x+2=(x-1)2+1,x[-5,5].由于f(x)的对称轴为x=1,结合图象知,当x=1时,f(x)的最小值为1,当x=-5时,f(x)的最大值为37.(2)函数f(x)=(x+a)2+2-a2的图象的对称轴为x=-a,∵f(x)在区间[-5,5]上是单调函数,-a-5或-a5.故a的取值范围是a-5或a5.19.(本小题满分12分)(1)计算:27912+(lg5)0+(2764)-13;(2)解方程:log3(6x-9)=3.【解析】 (1)原式=25912+(lg5)0+343-13=53+1+43=4.(2)由方程log3(6x-9)=3得6x-9=33=27,6x=36=62,x=2.经检验,x=2是原方程的解.20.(本小题满分12分)有一批影碟机(VcD)原销售价为每台800元,在甲、乙两家商场均有销售,甲商场用下面的方法促销:买一台单价为780元,买两台单价为760元,依次类推,每多买一台单价均减少20元,但每台最低不低于440元;乙商场一律按原价的75%销售,某单位需购买一批此类影碟机,问去哪家商场购买花费较少?【解析】设购买x台,甲、乙两商场的差价为y,则去甲商场购买共花费(800-20x)x,由题意800-20x440.118(xN).去乙商场花费80075%x(xN*).当118(xN*)时y=(800-20x)x-600x=200x-20x2,当x18(xN*)时,y=440x-600x=-160x,则当y0时,1当y=0时,x=10;当y0时,x10(xN).综上可知,若买少于10台,去乙商场花费较少;若买10台,甲、乙商场花费相同;若买超过10台,则去甲商场花费较少.21.(本小题满分12分)已知函数f(x)=lg(1+x)-lg(1-x).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性;【解析】 (1)由1+x0,1-x0,得-1函数f(x)的定义域为(-1,1).(2)定义域关于原点对称,对于任意的x(-1,1),有-x(-1,1),f(-x)=lg(1-x)-lg(1+x)=-f(x)f(x)为奇函数.22.(本小题满分14分)设a0,f(x)=exa+aex是r上的偶函数.(1)求a的值;(2)证明:f(x)在(0,+)上是增函数.【解析】 (1)解:∵f(x)=exa+aex是r上的偶函数,f(x)-f(-x)=0.exa+aex-e-xa-ae-x=0,即1a-aex+a-1ae-x=01a-a(ex-e-x)=0.由于ex-e-x不可能恒为0,当1a-a=0时,式子恒成立.又a0,a=1.(2)证明:∵由(1)知f(x)=ex+1ex,在(0,+)上任取x1f(x1)-f(x2)=ex1+1ex1-ex2-1ex2=(ex1-ex2)+(ex2-ex1)1ex1+x2.∵e1,0ex1+x21,(ex1-ex2)1-1ex1+x20,f(x1)-f(x2)0,即f(x1)f(x)在(0,+)上是增函数.高中是人生中的关键阶段,大家一定要好好把握高中,小编为大家整理的高一数学必修一第三章测试题及答案,希望大家喜欢。
高一数学函数试题答案及解析

高一数学函数试题答案及解析1.函数的定义域是()A.(-,-1)B.(1,+)C.(-1,1)∪(1,+)D.(-,+)【答案】C.【解析】出现在对数的真数位置,故>0,即,又出现在分式的分母上,故≠0,即,要使式子有意义,则这两者同时成立,即且,用区间表示即为(-1,1)∪(1,+).要使式子有意义,则,解得且,故选C.【考点】函数的定义域求法,对数函数的定义域2.已知函数,满足.(1)求常数c的值;(2)解关于的不等式.【答案】(1) ;(2) .【解析】(1)代入解析式,列出关于c的方程,解出c,注意范围;(2)根据分段函数通过分类讨论列出不等式,解出的范围,解不等式时不要忘记分类条件.试题解析:(1)∵,即,解得. 5分(2)由(1)得,由,得当时,,解得; 9分当时,,解得. 12分∴不等式的解集为. 13分【考点】1.函数求值;2.利用指数函数性质解简单指数不等式;3.分类整合思想.3.函数,满足,则的值为()A.B. 8C. 7D. 2【答案】B【解析】因为,函数,所以,,10,又,故,8,选B。
【考点】函数的概念,函数的奇偶性。
点评:简单题,此类问题较为典型,基本方法是通过研究,发现解题最佳途径。
4.已知函数,,(1)若为奇函数,求的值;(2)若=1,试证在区间上是减函数;(3)若=1,试求在区间上的最小值.【答案】(1)(2)利用“定义法”证明。
在区间上是减函数(3) 若,由(2)知在区间上是减函数,在区间上,当时,有最小值,且最小值为2。
【解析】(1)当时,,若为奇函数,则即,所以(2)若,则=设为, =∵∴,∴>0所以,,因此在区间上是减函数(3) 若,由(2)知在区间上是减函数,下面证明在区间上是增函数.设 , =∵,∴∴所以,因此在区间上上是增函数因此,在区间上,当时,有最小值,且最小值为2【考点】函数的奇偶性、单调性及其应用点评:中档题,研究函数的奇偶性,要注意定义域关于原点对称。
高一数学暑假作业(20)反函数

(二十)反函数一、选择题:1.若函数)1(1)(2-≤-=x x x f ,则)4(1-f 的值为( )A 、5B 、5-C 、15D 、32.函数y =1-1-x (x ≥1)的反函数是 ( )A .y =(x -1)2+1,x ∈RB .y =(x -1)2-1,x ∈R C .y =(x -1)2+1,x ≤1 D .y =(x -1)2-1,x ≤1 3.设函数()[]()242,4f x x x =-∈,则()1f x -的定义域为( ) A .[)4,-+∞ B .[)0,+∞ C .[]0,4 D .[]0,124.若函数()y f x =的反函数是()y g x =,(),0f a b ab =≠,则()g b 等于( )A .aB .1a -C .bD .1b - 5.已知函数()13ax f x x +=-的反函数就是()f x 本身,则a 的值为 ( ) A .3- B .1 C .3 D .1-二、填空题:6.若点(1,2)既在函数b ax x f +=)(的图象上,又在函数f(x)的反函数)(1x f -的图象上,则_____,_____a b ==7. 若函数f (x )的图象经过点(0,-1),则函数f (x +4)的反函数的图象必经过点__________。
8.已知函数y =f (x )的反函数为f -1(x )=x -1(x ≥0),那么函数f (x )的定义域为__ 。
9.设13,2x y x -=≥,则求反函数1()f x -=__ ______。
10.已知f (x )=f -1(x )=xm x ++12(x ≠-m ),则实数m = 。
11. 点(2,1)既在函数f (x )=a b x a +1的图象上,又在它的反函数的图象上,则适合条件的数组(a ,b )有__________组。
12. 已知函数2(1)2(0)f x x x x +=+>,1(1)fx -+=____________。
高一数学试卷带答案解析

高一数学试卷带答案解析考试范围:xxx ;考试时间:xxx 分钟;出题人:xxx 姓名:___________班级:___________考号:___________1.答题前填写好自己的姓名、班级、考号等信息 2.请将答案正确填写在答题卡上一、选择题1. 函数的图象大致是下图中的2.已知函数,若f()="5" , 则的值是( )A . 2或-2或B. 2或-2 C . -2 D .3.在△ABC 中,AB=AC,D 、E 分别是AB 、AC 的中点,则 ( ) A.与共线 B.与共线 C.与相等 D.与相等4.已知f (x )=,则f [ f (-3)]等于A .0B .πC .π2D .95.函数f(x)="xln" êxú的大致图象是 ( )6.等差数列的前三项为,则这个数列的通项公式为A .B .C.D.7.在一个港口,相邻两次高潮发生的时间相距,低潮时水深为,高潮时水深为.每天潮涨潮落时,该港口水的深度关于时间的函数图像可以近似地看成函数的图像,其中,且时涨潮到一次高潮,则该函数的解析式可以是()A.B.C.D.8.等差数列共有项,其中所有奇数项之和为310,所有偶数项之和为300,则的值为()A.30 B.31 C.60 D.619.,动直线过定点A,动直线过定点,若与交于点 (异于点),则的最大值为A. B. C. D.10.在平面内有DABC和点O,若,则点O是DABC的()A.重心 B.垂心 C.内心 D.外心11.设集合,则下列关系式中正确的是()A. B. C. D.12.函数与的图象()A.关于原点对称 B.关于轴对称 C.关于轴对称. D.关于直线对称13.函数的最小值为A.1 B. C. D.14.下列函数与有相同图象的一个函数是()A. B. C. D.15.如果,则= ( )A. B. C. D.16.已知集合,集合,则与的关系是()A.B.C.D.17.已知某运动员每次投篮命中的概率低于,现采用随机模拟的方法估计该运动员三次投篮恰有两次命中的概率:先由计算器产生0到9之间取整数值的随机数,指定1,2,3,4表示命中,5,6,7,8,9,0表示不命中;再以每三个随机数为一组,代表三次投篮的结果,经随机模拟产生了如下20组随机数:907 966 191 925 271 932 812 458 569 683431 257 393 027 556 488 730 113 537 989据此估计,该运动员三次投篮恰有两次命中的概率为()A. B. C. D.18.已知全集U=R,且A={x||x-1|>2}, B={x|x2-6x+8<0},则(?UA)∩B等于 ()A、[-1,4)B、(2,3)C、(2,3]D、(-1,4)19.下列图形中不一定是平面图形的是()A.三角形B.四边相等的四边形C.梯形D.平行四边形20.函数的定义域是()A.B.C.D.二、填空题21.某商品在近30天内每件的销售价格(元)和时间(天)的函数关系为:(),设商品的日销售量(件)与时间(天)的函数关系为(),则第天,这种商品的日销售金额最大.22.设集合,,对应法则,若能够建立从到的函数,则实数的取值范围是.23.求值cos330°= .24.用“二分法”求方程在区间内的实根,取区间中点为,那么下一个有根的区间是 。
高一数学函数试题答案及解析

高一数学函数试题答案及解析1.已知【答案】512【解析】主要考查对数运算。
2.甲、乙两人解关于的方程:甲写错了常数b,得到根为,乙写错了常数c,得到根为.求方程的真正根。
【答案】4或8【解析】主要考查对数方程解法。
解:原方程可变形为:3.函数的图象与直线的公共点数目是()A.B.C.或D.或【答案】C【解析】有可能是没有交点的,如果有交点,那么对于仅有一个函数值;4.求函数的定义域【答案】【解析】解:∵,∴定义域为5.已知函数,(1)讨论的奇偶性与单调性;(2)若不等式的解集为的值;(3)求的反函数;(4)若,解关于的不等式R).【答案】(1)①当时,在定义域内为增函数;②当时,在定义域内为减函数;(2)或;(3);(4)①当时,不等式解集为R;②当时,得,不等式的解集为;③当【解析】主要考查函数的奇偶性、单调性、指数函数与对数函数互为反函数关系、对数函数的图象和性质。
解:(1)定义域为为奇函数;,求导得,①当时,在定义域内为增函数;②当时,在定义域内为减函数;(2)①当时,∵在定义域内为增函数且为奇函数,;②当在定义域内为减函数且为奇函数,;(3)R);(4),;①当时,不等式解集为R;②当时,得,不等式的解集为;③当6.函数在区间上是[ ]A.增函数B.既不是增函数又不是减函数C.减函数D.既是增函数又是减函数【答案】B【解析】主要考查函数单调性的概念及函数单调性判定方法。
解:此函数在随增大,逐渐减小,减小,反而增大,所以函数是增函数;而在,随增大,逐渐增大,增大,反而减小,所以函数是减函数;所以函数在区间上,既不是增函数又不是减函数。
故选B。
7.函数在上的单调性为()A.减函数B.增函数.C.先增后减.D.先减后增【答案】B【解析】主要考查函数单调性的概念及函数单调性判定方法。
由定义法或利用结论x的系数为正,一次函数是增函数,故选B。
8.函数的单调增区间为()A.B.C.D.【答案】A【解析】主要考查函数单调性的概念及二次函数单调性判定方法。
高一数学第二章 函数基础练习题 新课标 人教版 试题

高一数学第二章 函数基础练习题一、知识结构1.映射:设A,B 是两个集合,如果按照某种对应法则f , ,这样的对应关系叫做从集合A 到集合B 的映射,记作 。
(答:对于集合A 中的任何一个元素,在集合B 中都有唯一的元素与它对应,f:A →B ) 2.象和原象:给定一个集合A 到B 的映射,且a ∈A ,b ∈B,如果元素a 和b 对应,那么元素b 叫做元素a 的 ,元素a 叫做元素b 的 。
(答:象,原象)3.一一映射:设A,B 是两个集合,f :A →B 是集合A 到集合B 的映射,如果在这个映射下,满 足 那么这个映射叫做A 到B 上的一一映射。
(答:对于集合A 中的不同元素,在集合B 中有不同的象,而且B 中每个元素都有原象,) 4.函数的三要素:① ,② ,③ 。
(答:定义域,对应法则,值域)5.两个函数当且仅当 和 对应法则(即解析式)都相同时,才称为相同的函数。
(答:定义域,对应法则(即解析式)) 6.请同学们就下列求函数三要素的方法配上适当的例题:⑴定义域:①根据函数解析式列不等式(组),常从以下几个方面考虑: ⑴分式的分母不等于0;⑵偶次根式被开方式大于等于0;⑶对数式的真数大于0,底数大于0且不等于1; ⑷指数为0时,底数不等于0。
②⑴已知()f x 的定义域,求[()]f g x 的定义域。
⑵已知[()]f g x 的定义域,求()f x 的定义域。
⑵值域: ①函数图象法(中学阶段所有初等函数极其复合);②反函数法;③判别式法;④换元法;⑤不等式法;⑥单调性法;⑦几何构造法。
⑶解析式:①待定系数法(已知函数类型求解析式);②已知()f x 求[()]f g x 或已知[()]f g x 求()f x ;③方程组法;④函数图象四大变换法。
7.若()f x 的定义域关于原点对称,且满足 (或 ),则函数()f x 叫做奇函数(或偶函数)。
(答:()()f x f x -=-,()()f x f x -=)8.①若()f x 的定义域关于原点对称,且满足()()f x f x -+= ,则为奇函数。
高一考试数学试题及答案

高一考试数学试题及答案一、选择题(每题5分,共20分)1. 下列函数中,为奇函数的是()。
A. y = x^2B. y = |x|C. y = x^3D. y = sin(x)2. 已知等差数列{a_n}的首项a_1=1,公差d=2,那么a_5的值为()。
A. 9B. 10C. 11D. 123. 函数f(x)=2x+3的反函数为()。
A. f^(-1)(x)=(x-3)/2B. f^(-1)(x)=(x+3)/2C. f^(-1)(x)=(x-3)/-2D. f^(-1)(x)=(x+3)/-24. 圆的一般方程为x^2+y^2-4x+6y-12=0,其圆心坐标为()。
A. (2, -3)B. (-2, 3)C. (2, 3)D. (-2, -3)二、填空题(每题5分,共20分)5. 若函数f(x)=x^2-4x+3的图像与x轴交于点A和点B,则AB的长度为_______。
6. 已知三角形ABC的三个顶点分别为A(1,2),B(4,6),C(7,10),那么三角形ABC的面积为_______。
7. 将函数y=x^2-2x+1化简为顶点式,得到的结果为y=_______。
8. 已知数列{a_n}满足a_1=2,a_{n+1}=2a_n+1,求a_5的值为_______。
三、解答题(每题15分,共30分)9. 已知函数f(x)=x^2-2x+2,求函数的最小值。
10. 已知圆x^2+y^2-6x-8y+25=0,求该圆的半径和圆心坐标。
四、证明题(每题15分,共15分)11. 证明:若a,b,c为实数,且满足a+b+c=0,则函数f(x)=ax^2+bx+c的图像与x轴至多有一个交点。
五、附加题(15分)12. 已知函数f(x)=x^3-3x+1,求证:对于任意实数x,都有f(x)≥0。
答案:一、选择题1. C2. C3. A4. A二、填空题5. 46. 107. y=(x-1)^28. 31三、解答题9. 函数f(x)=x^2-2x+2的最小值为1,当x=1时取到。
高一数学函数单元测试题及答案

高一数学函数单元测试题及答案单元测试题一、填空题1、设全集U=Z,集合A={-1,1,2},B={-1,1,2},从A到B的一个映射为x→y=f(x)=x/|x|,其中x∈A,y∈B,P={y|y=f(x)},则B∩(C∪P)={-1,1}。
2、已知x1是方程x+lgx=3的根,x2是方程x+10=3的根,则x1+x2值为2.3、已知函数y=f(x)的图象关于直线x=-1对称,且当x>0时f(x)=x/1,则当x<-2时f(x)=-x/1.4、函数y=f(x)的反函数y=f^-1(x)的图像与y轴交于点P(0,2),则方程f(x)=0在[1,4]上的根是x=2.5、设f(x)=2log(x-1),x≥2;f(x)=3x-1,x<2,则f(f(2))的值为1.6、从甲城市到乙城市m分钟的电话费由函数f(m)=1.06×([m]+44)给出,其中[m]表示不大于m的最大整数(如[3]=3,[3.9]=3,[3.1]=3),则从甲城市到乙城市5.8分钟的电话费为7.7、函数f(x)=2-2/(x-1),x≤2;f(x)=1-x/2,x>2,则f(0)=-1.8、函数y=(1-x)/(1+x),x≠-1,的值域为(-1,1)。
9、若f(5/2x-1)=x-2,则f(125)=48.10、已知映射f:A→B,其中A=B=R,对应法则为f:x→y=x+2x+3.若对实数k∈B,在集合A中不存在原象,则k 的取值范围是(-3/2,-3)∪(-3,-2)∪(-2,-3/2)。
11、偶函数f(x)在(-∞,0)上是减函数,若f(-1)<f(lgx),则实数x的取值范围是(1,e)。
12、关于x的方程|x-4x+3|-a=0有三个不相等的实数根,则实数a的值是1/2.13、关于x的方程(2x-1)/(x+2)+a=1有正根,则实数a的取值范围是(-∞,1/2)。
二、改写后的答案1、已知集合A={-1,1,2},B={-1,1,2},全集U=Z,映射f:A→B,f(x)=x/|x|,其中x∈A,y∈B,P={y|y=f(x)},求B∩(C∪P)的值。
高一数学(指、对数函数与反函数)

知识探究( 知识探究(一):反函数的概念 思考1:设某物体以3m/s 3m/s的速度作匀速直 思考1:设某物体以3m/s的速度作匀速直
线运动,分别以位移s和时间t为自变量, 线运动,分别以位移s和时间t为自变量, 可以得到哪两个函数? 可以得到哪两个函数?这两个函数相同 吗? s t = 和s=3t 得到 3 x 思考2: 分别x 思考2:设 2 = y ,分别x、y为自变量可以 得到哪两个函数?这两个函数相同吗? 得到哪两个函数?这两个函数相同吗?
练习 2. 函数 =3x的图象与函数 =3x的 函数y= 的图象与函数y= 的 图象关于
3x
(D ) B. x轴对称 轴对称 D. 直线 =x对称 直线y= 对称
A. y轴对称 轴对称 C. 原点对称
函数f(x)=loga (x-1)(a>0且a≠1) 例3 函数 = - > 且 的反函数的图象经过点(1, , 的值. 的反函数的图象经过点 4),求a的值 的值 依题意,得 解:依题意 得 依题意
x
解 : (1)1 − 2 > 0 ⇒ 2 < 1 ⇒ x < 0 ⇒ 定义域 定义域(-∞,0)
x x
2 > 0 ⇒ −2 < 0 ⇒ 1 − 2 < 1 ⇒ log 2 (1 − 2 ) < 0
x x x x
(2) y = log 2 (1 − 2 ) ⇒ 1 − 2 = 2 ⇒ 2 = 1 − 2
1 = log a (4 − 1)
即 : log a 3 = 1,∴ a = 3.
若函数y= 的图象经过点 的图象经过点(a, , 小 结:若函数 =f(x)的图象经过点 b), 则其反函数的图象经过点(b, 则其反函数的图象经过点 a).
高一(上)数学第二章函数单元测试题7-8 人教版

高一(上)数学第二章函数单元测试题7-8(时间:45分钟 满分100分)一、 选择题1.若3a=2,则log 38-2log 36用a 的代数式可表示为( )(A )a-2 (B )3a-(1+a)2 (C )5a-2 (D )3a-a 22.2log a (M-2N)=log a M+log a N,则NM的值为( ) (A )41(B )4 (C )1 (D )4或1 3.已知x 2+y 2=1,x>0,y>0,且log a (1+x)=m,logaya n xlog ,11则=-等于( ) (A )m+n (B )m-n (C )21(m+n) (D )21(m-n)4.如果方程lg2x+(lg5+lg7)lgx+lg5·lg7=0的两根是α、β,则α·β的值是( ) (A )lg5·lg7(B )lg35(C )35 (D )351 5.已知log 7[log 3(log 2x)]=0,那么x 21-等于( )(A )31(B )321 (C )221 (D )331 6.函数y=lg (112-+x)的图像关于( ) (A )x 轴对称 (B )y 轴对称 (C )原点对称 (D )直线y=x 对称 7.函数y=log 2x-123-x 的定义域是( )(A )(32,1)⋃(1,+∞) (B )(21,1)⋃(1,+∞) (C )(32,+∞) (D )(21,+∞)8.函数y=log 21(x 2-6x+17)的值域是( )(A )R (B )[8,+∞](C )(-∞,-3) (D )[3,+∞] 9.函数y=log 21(2x 2-3x+1)的递减区间为( )(A )(1,+∞) (B )(-∞,43] (C )(21,+∞) (D )(-∞,21]10.函数y=(21)2x +1+2,(x<0)的反函数为( )(A )y=-)2(1log )2(21>--x x (B ))2(1log )2(21>--x x(C )y=-)252(1log )2(21<<--x x (D )y=-)252(1log )2(21<<--x x11.若log m 9<log n 9<0,那么m,n 满足的条件是( )(A )m>n>1 (B )n>m>1 (C )0<n<m<1 (D )0<m<n<112.log a132<,则a 的取值X 围是( ) (A )(0,32)⋃(1,+∞) (B )(32,+∞)(C )(1,32) (D )(0,32)⋃(32,+∞)13.若1<x<b,a=log 2b x,c=log a x,则a,b,c 的关系是( )(A )a<b<c (B )a<c<b (C )c<b<a (D )c<a<b 14.下列函数中,在(0,2)上为增函数的是( ) (A )y=log 21(x+1) (B )y=log 212-x(C )y=log 2x 1(D )y=log 21(x 2-4x+5) 15.下列函数中,同时满足:有反函数,是奇函数,定义域和值域相同的函数是( )(A )y=2x x e e -+(B )y=lg xx+-11(C )y=-x3(D )y=x16.已知函数y=log a (2-ax)在[0,1]上是x 的减函数,则a 的取值X 围是( )(A )(0,1) (B )(1,2) (C )(0,2) (D )[2,+∞) 17.已知g(x)=log a 1+x (a>0且a ≠1)在(-1,0)上有g(x)>0,则f(x)=a1+x 是( )(A )在(-∞,0)上的增函数 (B )在(-∞,0)上的减函数 (C )在(-∞,-1)上的增函数 (D )在(-∞,-1)上的减函数18.若0<a<1,b>1,则M=a b ,N=log b a,p=b a的大小是( ) (A )M<N<P (B )N<M<P (C )P<M<N (D )P<N<M19.“等式log 3x 2=2成立”是“等式log 3x=1成立”的( ) (A )充分不必要条件 (B )必要不充分条件(C )充要条件 (D )既不充分也不必要条件 20.已知函数f(x)=x lg ,0<a<b,且f(a)>f(b),则( )(A )ab>1 (B )ab<1 (C )ab=1 (D )(a-1)(b-1)>0 二、填空题1.若log a 2=m,log a 3=n,a 2m+n=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高一数学同步测试—反函数一、选择题:1.设函数f (x)=1-2x 1-(-1≤x ≤0),则函数y =f -1(x )的图象是〔B.- 2.函数y =1-1-x (x ≥1)的反函数是 〔 〕A .y =(x -1)2+1,x ∈RB .y =(x -1)2-1,x ∈RC .y =(x -1)2+1,x ≤1D .y =(x -1)2-1,x ≤13.若f (x -1)= x 2-2x +3 (x ≤1),则f -1(4)等于〔 〕A .2B .1-2C .-2D .2-2 4.与函数y=f (x)的反函数图象关于原点对称的图象所对应的函数是 〔 〕A .y=-f (x )B .y= f -1(x )C .y =-f -1(x )D .y =-f -1(-x ) 5.设函数()[]()242,4f x x x =-∈,则()1f x -的定义域为〔 〕A .[)4,-+∞B .[)0,+∞C .[]0,4D .[]0,126.若函数()y f x =的反函数是()y g x =,(),0f a b ab =≠,则()g b 等于 〔 〕 A .a B .1a - C .b D .1b -7.已知函数()13ax f x x +=-的反函数就是()f x 本身,则a 的值为 〔 〕A .3-B .1C .3D .1- 8.若函数()f x 存在反函数,则方程()()f x c c =为常数 〔 〕A .有且只有一个实数根B .至少有一个实数根C .至多有一个实数根D .没有实数根 9.函数f (x )=-22·12-x (x ≤-1)的反函数的定义域为 〔 〕A .(-∞,0]B .(-∞,+∞)C .(-1,1)D .(-∞,-1)∪(1,+∞)10.若函数f (x )的图象经过点(0,-1),则函数f (x +4)的反函数的图象必经过点〔 〕A .(-1,4)B .(-4,-1)C .(-1,-4)D .(1,-4)11.函数f(x)=x1(x ≠0)的反函数f -1(x)= 〔 〕 A .x(x ≠0) B .x 1(x ≠0) C .-x(x ≠0) D .-x 1(x ≠0)12、点(2,1)既在函数f (x )=abx a +1的图象上,又在它的反函数的图象上,则适合条件的数组(a ,b )有〔 〕A .1组B .2组C .3组D .4组二、填空题:13.若函数f (x )存在反函数f -1(x ),则f -1[f (x )]=___ ; f [f -1(x )]=_____.14.已知函数y =f (x )的反函数为f -1(x )=x -1(x ≥0),那么函数f (x )的定义域为___. 15.设f (x )=x 2-1(x ≤-2),则f -1(4)=__ ________. 16.已知f (x )=f -1(x )=xm x ++12(x ≠-m ),则实数m =. 三、解答题:17.〔1〕已知f (x ) = 4x -2x +1 ,求f -1(0)的值.〔2〕设函数y = f (x )满足 f (x -1) = x 2-2x +3 (x ≤ 0),求 f -1(x +1).18.判断下列函数是否有反函数,如有反函数,则求出它的反函数.〔1〕2()42()f x x x x R =-+∈; 〔2〕2()42(2)f x x x x =-+≤.〔3〕1(0)1,,(0)x x y x x +>⎧=⎨-<⎩19.已知f (x )=13-+x ax 〔1〕求y =f (x )的反函数 y = f -1 (x )的值域;〔2〕若(2,7)是 y = f -1 (x )的图象上一点,求y=f (x )的值域.20.已知函数2(1)2(0)f x x x x +=+>,〔1〕求1()fx -与其1(1)f x -+;〔2〕求(1)y f x =+的反函数.21.己知()211x f x x -⎛⎫= ⎪+⎝⎭(x ≥1),〔1〕求()f x 的反函数1()f x -,并求出反函数的定义域;〔2〕判断并证明1()f x -的单调性.22.给定实数a ,a ≠0,且a ≠1,设函数11--=ax x y ⎪⎭⎫ ⎝⎛≠∈a x R x 1,且.试证明:这个函数的图象关于直线y =x 成轴对称图形.参考答案一、选择题: DCCDD ACCAC BA二、填空题:13.x ,x ,14.x ≥-1,15.-5,16.m =-2三、解答题:17.解析:〔1〕设f -1(0)=a ,即反函数过(0,a), ∴原函数过(a ,0).代入得 :0=4a -2a+1,2a (2a -2)=0,得a =1,∴f)0(1-=1.〔2〕先求f (x )的反函数)2(1)1(),3(2)(11≥--=+∴≥--=--x x x f x x x f .18.解析:⑴令()0,y f x ==得到对应的两根:120,4x x ==这说明函数确定的映射不是一一映射,因而它没有反函数. ⑵由2()42f x x x =-+2(2)2x =--,得2(2)2x y -=+∵2x ≤,∴22x x -==,互换,x y 得2y =又由2()42(2)f x x x x =-+≤的值域可得反函数定义域为[2,),-+∞∴反函数为1()2f x x -=∈[2,)-+∞.⑶由1(0)y x x =+>得其反函数为1(1)y x x =->; 又由1(0)y x x =-<得其反函数为1(1)y x x =+<-.综上可得,所求的反函数为1(1)1(1)x x y x x ->⎧=⎨+<-⎩.注:求函数()y f x =的反函数的一般步骤是:⑴反解,由()y f x =解出1()x f y -=,写出y 的取值X 围;⑵互换,x y ,得1()y fx -=;⑶写出完整结论(一定要有反函数的定义域).⑷求分段函数的反函数,应分段逐一求解;分段函数的反函数也是分段函数.19.解析:〔1〕反函数的定义域、值域分别是原函数的值域、定义域.∴反函数的值域为{y|y 1,≠∈y R } 〔2〕∵(2,7)是y =f -1(x)的图象上一点,∴(7,2)是y =f (x )上一点.∴,215215)1(2132)(212327≠-+=-+-=-+=∴=∴-+=x x x x x x f a a ∴f (x )的值域为{y |y ≠2}.20.解析:⑴∵22(1)211(1)1(0)f x x x x x +=++-=+->,∴2()1(1)f x x x =->,其值域为{|0}y y >, 又由21(1)y x x +=>得x =∴1()0)f x x -=>,∴1(1)1)f x x -+=>-.⑵由2()2(0)y f x x x x ==+>,解得1(1)x y >-∴(1)y f x =+的反函数为1y =(1)x >-.说明:1(1)y f x -=+并不是(1)y f x =+的反函数,而是1()y f x +=的反函数.题中有1(1)y fx -=+的形式,我们先求出1()y f x -=,才能求出1(1)y f x -=+.21.解析:⑴21()1,1011x y x x y x -=⇒=≥≥⇒≤<+设, 即1()fx -的定义域为[)0,1;⑵设11121201,01,()()0x x f x f x --≤<<∴≤<∴-=<,1112()()f x f x --<,即1()f x -在[)1,0上单调递增.22、证法一:且则意一点是这个函数的图象上任设点,1,),(ax y x P ≠''' .11-'-'='x a x y ……①).,(),(x y P x y y x P '''=''的坐标为的对称点关于直线易知点由①式得⎩⎨⎧-'=-''-'=-'',1)1(1)1(y y a x x x a y 即……②由此得a =1,与已知矛盾,.01≠-'∴y a 又由②式得11-'-'='y a y x这说明点P ′〔y ′,x ′〕在已知函数的图象上,因此,这个函数的图象关于直线y =x 成轴对称图形.证法二:先求所给函数的反函数:由),1,(11ax R x ax x y ≠∈--=得 y (ax -1)=x -1, 即 (ay -1)x =y -1.得代入所给函数的解析式则假如,,1,01a y ay ==-111--=ax x a 即 ax -a =ax -1,由此得a=1,与已知矛盾,所以ay -1≠0. 因此得到).1,(,11)1,(11,1,11a x R x ax x y ax R x ax x y ay ay y x ≠∈--=≠∈--=≠--=且的反函数是且这表明函数其中由于函数y=f(x)的图象和它的反函数y=f -1(x)的图象关于直线y=x 对称,所以函数)1,(11ax R x ax x y ≠∈--=且的图象关于直线y =x 成轴对称图形.。
