频响特性
物理实验技术中的光电二极管特性测量与分析

物理实验技术中的光电二极管特性测量与分析光电二极管是一种能够将光能转化为电能的器件,广泛应用在光电传感器、光通信、光电测量和光谱分析等领域。
在物理实验技术中,测量和分析光电二极管的特性对于研究光电效应、了解器件性能以及优化实验设计都具有重要意义。
一、光电二极管原理和基本特性光电二极管的原理是基于光电效应,利用光照射在PN结上产生电子-空穴对,使得PN结两端产生电压。
其关键特性包括响应频率、光电流、暗电流、光电流增益等。
测量这些特性需要合适的实验装置和方法来获取准确的结果。
二、光电二极管特性的测量方法1. 频响特性测量频响特性测量是评估光电二极管对光信号变化的响应速度的重要方法。
常用的实验装置包括函数发生器、光源和示波器。
通过改变函数发生器输入的正弦光信号频率,测量光电二极管输出的电流或电压的变化,从而得到频响特性曲线。
这些曲线反映了光电二极管的截止频率、带宽和相移等信息。
2. 光电流和暗电流测量光电流和暗电流是衡量光电二极管敏感度的重要指标。
光电流指的是光照射下二极管产生的输出电流,可以通过连接电流表或电流放大器进行测量。
而暗电流是指在没有光照射的情况下,二极管自身产生的微弱电流。
暗电流直接影响光电二极管的信噪比和稳定性,需要特殊的实验装置和方法进行测量。
三、光电二极管特性分析测量得到的光电二极管特性数据可以通过分析得到有关器件性能的重要信息。
以下是几个典型的分析方法:1. 截止频率和带宽分析利用频响特性曲线可以确定光电二极管的截止频率和带宽。
截止频率是指光电二极管对信号频率的响应达到3dB衰减的频率,可以通过对频响特性进行插值计算得到。
带宽是指光电二极管在特定条件下能够传输信号的频率范围,可以根据频响特性曲线的满足条件进行判断。
2. 光电流增益分析光电流增益是指光电二极管单位光功率入射时输出电流的增益。
可以通过将测得的光电流与已知的入射光功率相除得到。
光电流增益反映了光电二极管对光信号的放大效果,是评估器件性能的重要指标。
麦克风知识

1、灵敏度:在1KHz的频率下,0.1Pa规定声压从话筒正面0°主轴上输入时,话筒的输出端开路输出电压,单位为10mV/Pa。
灵敏度与输出阻抗有关。
有时以分贝表示,并规定10V/Pa为0dB,因话筒输出一般为毫伏级,所以,其灵敏度的分贝值始终为负值。
2、频响特性:话筒0°主轴上灵敏度随频率而变化的特性。
要求有合适的频响范围,且该范围内的特性曲线要尽量平滑,以改善音质和抑制声反馈。
同样的声压,而频率不同的声音施加在话筒上时的灵敏度就不一样,频响特性通常用通频带范围内的灵敏度相差的分贝数来表示。
通频带范围愈宽,相差的分贝数愈少,表示话筒的频响特性愈好,也就是话筒的频率失真小。
3、指向性:话筒对于不同方向来的声音灵敏度会有所不同,这称为话筒的方向性。
方向性与频率有关,频率越高则指向性越强。
为了保证音质,要求传声器在频响范围内应有比较一致的方向性。
方向性用传声器正面0°方向和背面180°方向上的灵敏度的差值来表示,差值大于15dB 者称为强方向性话筒。
产品说明书上常常给出主要频率的方向极座标响应曲线图案,一般的类型有:单方向性“心形”;双方向性“8字型”;和无方向性“圆形”;以及单指向性“超心型”。
话筒灵敏度的方向性是选择话筒的一项重要因素。
有的话筒是单方向性的,有的则是全方向性的,也有一些是介于二者之间,其方向性是心形的。
a、全方向性全方向性话筒从各个方向拾取声音的性能一致。
当说话者要来回走动时采用此类话筒较为合适,但在环境噪声大的条件下不宜采用。
b、心形指向心形指向话筒的灵敏度在水平方向呈心脏形,正面灵敏度最大侧面稍小,背面最小。
这种话筒在多种扩音系统中都有优秀的表现。
c、单指向性单指向性话筒又称为超心形指向性话筒,它的指向性比心形话筒更尖锐,正面灵敏度极高,其它方向灵敏度急剧衰减,特别适用于高噪音的环境。
4、输出阻抗:从话筒的引线两端看进去的话筒本身的阻抗称为输出阻抗。
信号与系统讲义第四章5系统频率特性及稳定性

06.06.2019
信号与系统
例:图示反馈系统,求系统函数分析稳定性 Q(s)
稳定系统的充要条件: h()d<
06.06.2019
信号与系统
2、根据系统函数零、极点分布判断稳定性
系统稳定的条件
H(s)全部极点在s左半开平面,稳定 H(s)的极点在右半开平面,或虚轴上有二阶以
上高阶极点,不稳定 H(s)虚轴上单极点,不稳定(边界稳定)
06.06.2019
根据幅频特性的不同,可划分成如下几种
06.06.2019
截止频率--下降3dB的频率点
信号与系统
二、由极、零点分布分析频响特性
m
(s z j)
H (s) K
j 1 n
(s pi)
i 1
s沿 虚 轴 移s 动j
m
( j z j )
H ( j) K
j 1 n
信号与系统
1 1 R1C1 R2C2
06.06.2019
信号与系统
小结: (232页)
若函数有一对非常靠近jω轴的极点,则ω 在极点附近,幅频特性出现峰点,相频特性 迅速下降
若函数有一对非常靠近jω轴的零点,则ω 在零点附近,副频特性出现下陷,相频特性 迅速上升
若系统函数的零、极点远离jω轴,则对频 率响应特性曲线的影响较小,只是大小有所 增减。
信号与系统
4.11 线性系统的稳定性
1、稳定系统
有限(界)激励,产生有限(界)输出,稳定系统 有限(界)激励,产生无限(界)输出,为不稳定系统
零极点分布与频响特性
2)在谐振点
0处,Z
j
1 G
;
3)在曲线通带边界频率点(1或2)处,有
Z
j1
1 G
1 2
Z j2
由上式看出,必须满足
1 0 1
2 0 1
解得:1 0 , 2 0
两频率之差,即为通带宽度
B
2
1
2
0
Q
f2
f1
f0 Q
注:1)若网络函数有一对非常靠近jω的极点
p i ji i i
N1 0, 1 90 M 2 20, 2 90
M1e j1 j d
0,d 02 2 0
M1e j1 j 0
所以得: Z
j
1 C
20
0
j
0
1
2C
1
j
1
0
1 G
1
j
1
0
Z j 1
1
G
1
0
2
arctan
0
讨论:1)由上边两式可得高Q值谐振电路的幅频特性和相频特 性曲线;
s
p1 s
p2
其中,p1,2
G 2C
G
2
1
2C LC
令
G,
2C
0
1, LC
d
02 2
p1,2 jd
讨论:1)0为谐振频率;
2) G 0 为衰减因子,越大,表示电路的损耗越大;
2C
2Q
3)Q 0C 称为品质因数,Q愈高,电路的损耗越小;
G
二、随电路损耗α的改变Z(s)的极点位置分布(ω0不变)
1绝对值减小,2增大,1 90减小;
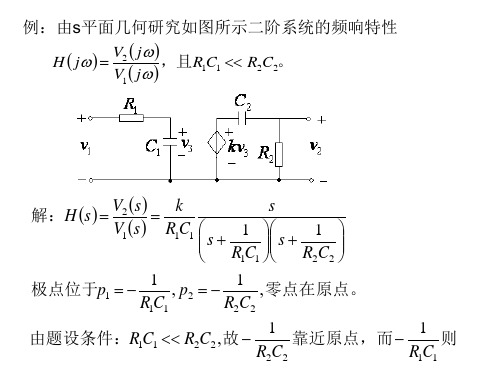
§4-6 系统函数与系统的频响特性

H (s)
k s1
(s 1)(s 2 )
H ( j)
k j1
( j 1)( j 2 )
系统函数的零极图如下:
《Signals & Systems》
《信号与系统》
大连海事大学信息科学技术学院
⑴ 当Ω=0,零点矢量的模等于0,相角
等于π/2,幅频响应|H( jΩ)|=0;极点 矢量的相角均等于零, φ(Ω)= (π/2)。 1
如上两例RC电路,试根据其零极图,粗略的画出其频响曲线。
先看以电容电压为输出的情况。其零极 图如下:
R
ui (t)
C
uo (t)
⑴ 当Ω=0,极点矢量指向原点,其模长 为α,相角等于0;于是 |H( jΩ)|=α/α=1,φ(Ω)=0。
⑵ 当Ω↑,极点矢量模↑,相角↑; |H( jΩ)|↓,φ(Ω)=-arctg(Ω/α)↓。
《信号与系统》
大连海事大学信息科学技术学院
§4-6 系统函数的零极点分布与系统的频率响应
一、H(s)与H(jΩ)
由前所讲,拉氏变换是傅氏变换由实频域Ω至复频域s的推广, 傅氏变换是拉氏变换在s平面虚轴上的特例。即
j
H ( j) H (s) |s j
二、H(s)的零极点分布与H(jΩ)
由于H(s)一般是有理分式,即它可表示为
s
C (s p1)(s p2)
上式中 1 ( 1 )2 4
p1,2 RC
RC 2
LC
1 ( 1 )2 1 2RC 2RC LC
《Signals & Systems》
《信号与系统》
大连海事大学信息科学技术学院
令 1
2RC
1 LC
离散时间系统的频率响应特性

r
p1
O
1 Re z
p2
可见H(z)除一对共轭极点外,
(b)
还在z=0点有一个零点,如图(b)所示。
若把H(z)展成部分分式,得
H zA 1re 1jθz 11re 1 jθz 1
hn
其中
A b1 2jr sinθ
o
n
对H(z)进行逆变换,8-10-3 求图(a)所示二阶离散系统的频率响应。
(教材例8-23)
xn z1 b1
yn
该系统的差分方程为
a1
a2
z 1
y n a 1 y n 1 a 2 y n 2 b 1 x n 1 z1
(a)
系统函数写作 Hz
b1z1
1a1z1a2z2
若a1, a2为实系数,且a12+4a2<0, 则H(z)含有
§8.10 离散时间系统的频率 响应特性
一.一、离散系统频响特性的定义 二.二、频响特性的几何确定法
返回
一.离散系统频响特性的定义
正弦序列作用下系统的稳态响应
xn
Hz
yzs n
x n
A
O θ1 ω
稳定的因果
ω
A sin nω θ 1
离 散 系 统 yzs n
B
O
n
θ2
ω
B sinnω θ 2
例8-10-2
例8-10-3
返回
例8-10-1 已知离散时间系统的框图如图所示,求系
统频率响应特性。
解:系统的差分方程
z1
1
y n 0 . 5 x n 0 . 5 x n 1 xn
1 2
实验三一阶网络频响特性测量,信号与系统,南京理工大学紫金学院实验报告

信号与系统实验报告实验名称:一阶网络频响特性测量姓名:学号:班级:通信时间:2013.6南京理工大学紫金学院电光系一、 实验目的1、 掌握一阶网络的构成方法;2、 掌握一阶网络的系统响应特性;3、 了解一阶网络频响特性图的测量方法;二、实验基本原理系统响应特性是指系统在正弦信号激励下,稳态响应随信号频率变化而变化的特性,称为系统的频率响应特性(frequency response )简称频响特性。
一阶系统是构成复杂系统的基本单元。
学习一阶系统的特点有助于对一般系统特性的了解。
一阶系统的系统函数为H(s),表达式可以写成:γ+⋅=s k s H 1)( k 为一常数 (3-1) 激励信号x(t)为:(3-2)按照系统频响特性的定义可求得该一阶系统的稳态响应为:(3-3)其中⎣⎦00)()(|)(00ϕj j s ej H j H s H Ω=Ω=Ω=,⎣⎦)(00Ω=j H H 。
可见,当改变系统输入信号的频率时,稳态响应的幅度和相位也随之而改变。
因果系统是稳定的要求:0>γ,不失一般性可设τγ1==k 。
该系统的频响特性为:11)(+Ω=Ωτj j H (3-4)从其频响函数中可以看出系统响应呈低通方式,其3dB 带宽点τ1。
系统的频响特性图如下图:0()sin()m x t E t =Ω000()sin()ss m y t E H t ϕ=Ω+θ图1 一阶网络频响特性图一阶低通系统的单位冲击响应与单位阶跃响应如下图:图2 一阶网络单位冲击响应与单位阶跃响应图三、实验内容及结果一阶系统的幅度谱一阶系统相位谱3、用矢量作图法作出该一阶系统的幅度谱和相位谱。
一阶系统的幅度谱一阶系统的相位谱4、作出一阶网络的单位阶跃响应波形,标注在阶跃响应最大值的(1-e-1)倍处的时间t的值,与理论值R1C1是否相符。
四、实验分析1、实验所得一阶网络的频响特性图和用矢量作图法所得的频响特性图有何异同?说明原因。
参数振动系统频响特性研究

动
与
冲
击
第 2 卷第 3 9 期
J OURNAL OF VI BRAT ON AND S I HOCK
参 数 振 动 系 统 频 响 特 性 研 究
王建军 ,韩勤锴 ,李其汉
(. 1 北京航 空航天 大学 能源与动力工程学院 , 北京 10 8 ; . 0 0 3 2 重庆大学 机械传动 国家重点实验室 , 庆 重 4 03 ) 0 00
由于系 统参数 ( 度 、 量 和阻尼 ) 刚 质 的周 期 时变性 , 许 多机 械系 统 的动态特 性 可 以采 用 含周 期 系 数 的二 阶 微 分方 程 ( ) 述 , 些 系 统 在力 学 上 又 被 称 为参 数 组 描 这 振动 系统 。Irhml-j 于 工 程 中 的参 数振 动 问题 进 bai l2 对
也 对 参 数 振 动 的现 象 和 机
参 激振 动响应 是参 数振 动 问题研 究 的 重要 方 面 之
一
振 动系统 强 迫 响 应 频谱 。在 频 域 内分 析 该 响 应 频谱 ,
则可 以定义 得 到参数 振 动 系统 的 频 响 函数 。 以上 是 本 文 的分 析思 路 。 那么 , 本文 的主要 内容是 : 先 在状 态 空 间 内给 出 首 采用 S M 积分表 示 的单 自由度参 数振 动 系统强 迫响 应 T 表 达式 。然 后 , 绍 用 于 响 应 谱 分 解 的 Slet 理 论 介 y sr v e
统 的参 数 识 别 卜 、 障 诊 断 和 状 态 检 测 ¨ ]故
具 有重要 意义 。
等 均
和 F ui 级数展 开 方法 。利用 该理 论并通 过一 定 的代 orr e 数 和积 分运 算 得 到 系 统 响 应 频谱 , 而 定 义适 用 于参 进
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5.1 选择题(每小题可能有一个或几个正确答案,将正确的题号填入( )内)1.若一因果系统的系统函数为01110111)(b s b s b s b a s a s a s a s H n n n n m m m m ++++++=---- ,则有如下结论—————————— ( 2 )(1) 若)2,,1,0(0>=>n n i b i 且 ,则系统稳定。
(2) 若H (s )的所有极点均在左半s 平面,则系统稳定。
(3) 若H (s )的所有极点均在s 平面的单位圆内,则系统稳定。
2.一线性时不变因果系统的系统函数为H (s ),系统稳定的条件是—— (3、4 )(1) H (s )的极点在s 平面的单位圆内; (2) H (s )的极点的模值小于1;(3) H (s )的极点全部在s 平面的左半平面; (4) H (s )为有理多项式。
3.根据图示系统信号流图,可以写出其转移函数H (s )=)()(s X s Y ————( 2 ) X (sY (s )(1)c s a s b +-/1/ (2)as bcs -+(3)⎪⎭⎫ ⎝⎛-ab c s 11 (4)⎪⎭⎫⎝⎛-+a c b s 114.线性系统响应的分解特性满足以下规律————( 2、3 )(1) 若系统的起始状态为零,则系统的自由响应为零; (2) 若系统的起始状态为零,则系统的零输入响应为零; (3) 若系统的零状态响应为零,则强迫响应亦为零; (4) 一般情况下,零状态响应与系统特性无关。
5.系统函数H (s )与激励信号X (s )之间——( 2 )(1)是反比关系; (2)无关系; (3)线性关系; (4)不确定。
6.线性时不变系统输出中的自由响应的形式由——————( 1 )决定(1)系统函数极点的位置; (2)激励信号的形式;(3)系统起始状态; (4)以上均不对。
5.2 是非题(下述结论若正确,则在括号内填入√,若错误则填入×)1.若已知系统函数)1(1)(+=s s s H ,激励信号为)()(2t u e t x t -=,则系统的自由响应中必包含稳态响应分量。
( √ ) 2.强迫响应一定是稳态响应。
( × ) 3.系统函数与激励信号无关 ( √ )5.3 填空题1.已知系统函数1)(2+=s ss H ,起始条件为:0)0(,1)0(='=--y y ,则系统的零输入响应y zi (t )= ( cos ()t u t ⋅ ) 2.已知系统函数11)(+=s s H ,激励信号x (t )=sin t u (t ),则系统的稳态响应为 (45)t - ) 3.根据题图所示系统的信号流图,可以写出其系统函数H (s )=(1221bs cs as ---+-)x (t y (t )4.某线性时不变系统,当起始状态为)0(-y 、激励信号为x (t )的情况下, 系统的零输入响应为21()()2tziy t e u t -=,零状态响应为)()1()(2t u e t y t zs +=-,若起始状变为2)0(-y 、激励信号变为)1(21-t x ,则系统的全响应为(22(1)1()1(1)2t t e u t e u t ---⎡⎤++-⎣⎦)5.已知系统函数H (s )=1)1(12++-+k s k s ,要使系统稳定,试确定k 值的范围( 11k -<< )5.4 已知某系统的系统函数52)()()(++==s s s X s Y s H ,试画出直接型模拟框图或信号流图。
答案:x (t )y (t )5.5 已知系统的微分方程为dtt dx t y dt t dy )()()(=+,求系统函数H (s ),并画出幅频特性与相频特性曲线。
答案: ()1sH s s =+,5.6 已知某系统的系统函数H (s )=2212-++k s s ,1.若使系统稳定,求k 值应满足的条件;2.在系统边界稳定的条件下,画出系统的幅频特性与相频特性曲线。
答案:1. 2k >2.当2k =时,5.7 某一阶线性时不变系统的激励)(t x 与其零状态响应()zs y t 的波形如题图所示tt1.求系统的单位冲激响应h (t );2.写出系统幅频与相频特性表示式,并粗略画出幅频与相频特性曲线。
答案:1. ()()h t u t =2. 1()H j ωω=,02()02πωϕωπω⎧->⎪⎪=⎨⎪<⎪⎩ω90ωω90-180-5.8 电路如题图所示,t =0以前开关位于“1”,电路已进入稳态,t =0时刻开关转至“2”,以流经电阻上的电流作为响应。
1Ωx (t1.求系统函数H (s ),画出零极点分布图,并说明系统是否稳定。
2.画出t ≥0后的s 域模型图(包含等效电源); 3.若激励x (t )=δ(t ),求电流i (t )的零输入响应,零状态响应与全响应,并指出全响应中的暂态响应与稳态响应分量。
答案:1. ()()()1I s sH s X s s ==+由于()H s 的极点-1在左半s 平面,所以系统稳定。
2.X (s R(0)C v -1其中:1(0)10C v V -=3. ()()()t zs i t t e u t δ-=-()10()t zi i t e u t -=-ωσ()()()()11()t zi zs i t i t i t t e u t δ-=+=-()i t 即为暂态响应分量,无稳态响应分量。
5.9 给定系统的微分方程()()2()2()d y t d x ty t x td t d t+=- 1.当激励x (t )为u (t )时,系统全响应y (t )为(5e -2t -1)u (t ),求该系统的起始状态)0(-y (要求用拉氏变换方法求);2.求系统函数H (s ),并画出系统的模拟结构框图或信号流图;3.画出H (s )的零极点图,并粗略画出系统的幅频与相频特性曲线。
答案:1. (0)3y -=2.11()212()()212Y s s s H s X s s s ----===++3.5.10 系统如图所示,x (t )=δ(t ),t ) x1.画出A 点信号y A (t )的波形;y (t)σ ω(ωϕ180ω12.求系统响应y (t );3.粗略画出H 2(s )的零极点图及幅频、相频特性曲线; 4.求整个系统的系统函数H (s ),并根据H (s )写出系统的微分方程。
答案:1. ()()()A y t u t u t T =--2. ()()2()2()()()()t t t T t T y t e e u t ee u t T ------=---- 3.4. 整个系统的系统函数H (s )为:2()1()(1)()32sT Y s H s e X s ss -==-++ 22()()32()()()d y t dy t y t x t x t T dt dt++=--5.11 系统如题图所示(设系统初始无储能),(s )X (s1.求系统函数)()()(s X s Y s H =,并讨论系统的稳定性; 2.粗略画出系统的幅频特性与相频特性曲线; 3.求系统的冲激响应与阶跃响应;4.若激励信号)1()()(--=t u t u t x ,求响应y (t ),并指出暂态响应与稳定响应各分量。
答案:1. ()1()()(1)Y s H s X s s s ==+ 由于()H s 的两极点120,1p p ==-均在左半s 平面,所以系统稳定。
tσ ω(ϕ90-90ω2.3. ()(1)()th t e u t-=-()(1)()t g t t e u t -=-+4. (1)()()(1)(1)()(2)(1)t t y t g t g t t e u t t e u t ---=--=-+--+-其中(1)()(2)(1)t u t t u t ----为稳态响应分量,(1)()(1)t t e u t e u t -----为暂态响应分量。
5.12 如图(a )所示系统,当)()(t t x δ=时,全响应1328()()()39t y t t e u t δ-=-,并已知电容上的起始电压(0)1v V -=1.求系统的零输入响应()zi y t 及)(t h 和)(t g ,并画出波形;t(a )(b )2.粗略画出系统的幅频特性及相频特性曲线;3.若激励信号)1()()(1--=t u t u t x 时,求系统的零状态响应();zs y t 4.若激励信号)(2t x 如图(b )所示,求系统的零状态响应()zs y t 。
答案:1. 132()()3t zi y t e u t -=-)(t h =1322()()39t t e u t δ-- 132()()3t g t e u t -=σ 0 ⨯ j ω ⨯ -1 ωω90-180-2.3. 11(1)3322()()(1)()(1)33t t zs y t g t g t e u t eu t ---=--=-- 4. 1()30022()()()()39t nT zsn n y t h t nT t nT e u t nT δ∞∞--==⎡⎤=-=---⎢⎥⎣⎦∑∑5.13 某系统如题图所示,已知Y (s )=X (s ),X (sY (s )1.求H 1(s ),并画出H 1(s )的结构框图;2.若使H 1(s )是稳定系统的系统函数,求K 值范围;3.当K =1时,写出系统H 1(s )的频响特性H 1(j ω)的表示式,并粗略画出幅频特性与相频特性曲线。
答案:1. 12()s H s s K+=+ 2. 0K >3. 当K =1时,12()1j H j j ωωω+=+5.14 已知系统函数231)(2++=s s s H 1.画出并联形式的结构框图或信号流图;2.画出H (s )的零极点图,粗略画出系统的幅频特性与相频特性曲线。
答案:1.ω90ωωω2.5.15 一线性一阶时不变系统,当激励为x 1(t )=δ(t )时,全响应y 1(t )=δ(t )+e -t u (t ),当激励为x 2(t )=u (t )时,全响应y 2(t )=3e -t u (t )求 1.该系统的系统函数H (s ),画出H (s )的零极点图;2.写出系统幅频与相频特性表达式,并粗略画出幅频特性与相频特性曲线; 3.当激励为x 3(t )=tu (t )时,求系统的全响应y 3(t )并指出其中的暂态与稳态响应分量(三种输入时,系统起始储能相同)。
