切线长定理
切线长定理—知识讲解(基础)

切线长定理一知识讲解(基础)责编:康红梅【学习目标】1. 了解切线长定义;理解三角形的内切圆及内心的定义;2. 掌握切线长定理;利用切线长定理解决相关的计算和证明【要点梳理】要点一、切线长定理1.切线长:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长要点诠释:切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称•切线是直线,而非线段•2 .切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角要点诠释:切线长定理包含两个结论:线段相等和角相等3 •圆外切四边形的性质:圆外切四边形的两组对边之和相等•要点二、三角形的内切圆1.三角形的内切圆:与三角形各边都相切的圆叫做三角形的内切圆•这个三角形叫作圆的外切三角形•2 •三角形的内心:三角形内切圆的圆心是三角形三条角平分线的交点,叫做三角形的内心•三角形的内心是这个三角形的三条角平分线的交点•要点诠释:(1) 任何一个三角形都有且只有一个内切圆,但任意一个圆都有无数个外切三角形;(2) 解决三角形内心的有关问题时,面积法是常用的,即三角形的面积等于周长与内切圆半径乘积的一半,即;:- 1 I':(S 为三角形的面积,P为三角形的周长,r为内切圆的半径).2内心(三角形三角形三条角平分线X(1)到三角形三边距离相等;内切圆的圆的交点(2)OA、OB OC分别平分心)M BAG M ABG M ACB⑶内心在三角形内部.【典型例题】类型一、切线长定理1. (2015秋?湛江校级月考)已知PA PB分别切OO于A B, E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.(1 )若PA=6,求厶PCD的周长.(2)若/ P=50°求/ DOC解:(1)连接OE••• PA PB与圆O相切,••• PA=PB=6同理可得:AC=CE BD=DE△ PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+P;=12(2)T PA PB与圆O相切,•••/ OAP M OBP=90 / P=50°,•••/ AOB=360 - 90°- 90°- 50° =130°,在Rt △ AOC和Rt △ EOC 中,r OA=OEOC=OC,L• Rt△AO Q Rt△EOC( HL),•••/ AOC H COE同理:/ DOE M BOD•••/ COD= M AOB=65 .2【总结升华】本题考查的是切线长定理和全等三角形的判定和性质,掌握切线长定理是解题的关键.2 . (2016秋?江阴市校级期中)如图,AB、AC、BD是O O的切线,P、C、D为切点,如果AB=5 ,AC=3,贝U BD的长为 _________【解析】解: •/ AC 、AP 为O O 的切线, 举一反三: 【变式】已知:如图,OO过点A 作AD _ BF 于点D .求证:DA 为OOAC 、BD 是O O 的切线,贝U AC=AP , BP=BD ,求出BP 的长即可求出 BD 的长.••• AC=AP ,•/ BP 、BD 为O O 的切线,• BP=BD , • BD=PB=AB - AP=5 - 3=2.故答案为:2.【总结升华】本题考查了切线长定理,两次运用切线长定理并利用等式的性质是解题的关键. 为.:ABC 的外接圆,BC 为OO 的直径,作射线 BF ,使得BA 平分三CBF , 的切线.AO = BO2 = . 3 .BA 平分.CBF ,• • 1 =. 2. • Z 3 Z 1 .DB // AO .AD _DB , • £BDA =90 . /.Z DAO =90 .AO 是O O半径,• DA 为O O 的切线. 3.如图,正方形 ABCD 边长为4cm ,以正方形的一边 BC 为直径在正方形 ABCD 内作半圆,过 A 作半圆的切线,与半圆相切于F 点,与DC 相交于E 点,则△ ADE 的面积( )【答案】2.【答案】 连接AO .A.12B.24C.8D.6【答案】D;【解析】••• AE与圆0切于点F,显然根据切线长定理有AF=AB=4cm , EF=EC ,设EF=EC=xcm ,则DE= (4 - x) cm, AE= (4+x) cm ,在三角形ADE中由勾股定理得:2 2 2(4 - x) +4 = (4+x),x=1cm,/• CE=1cm ,.DE=4 -仁3cm ,2--S^\DE=AD ?DE -=2=3 ^4^2=6cm -【总结升华】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF , EF=EC .类型二、三角形的内切圆4. (2015?青江市校级二模)如图,在△ABC中,I是内心,O是AB边上一点,00经过B点且与AI相切于I点.(1)求证:AB=AC(2)若BC=16 00的半径是5,求AI的长.【解题思路】(1)延长AI交BC于D,连结OI,如图,根据内心的性质得/ OBI=Z DBI,则可证明OI// BD 再根据切线的性质得OI 丄AI,贝U BDLAD加上AI平分/ BAC所以△ ABC为等腰三角形,得到AB=AC (2)由OI// BC得到△ AOI sA ABD 得到比例式,再根据勾股定理求得A D JA B2— BD2=贸,于是就可得. 【答案与解析】解:(1)延长AI交BC于D,连结OI,如图,• AI= ?AD= 'XBD 8二11 ~=~••T是厶ABC的内心,••• BI 平分/ ABC 即/ OBI=Z DBI, •/ OB=O|•••/ OBI=Z OIB,•••/ DBI=Z OIB,•01 // BD•/AI为OO的切线,•01 丄AI,•BDLAD•/ AI 平分/ BAC•△ ABC为等腰三角形,•AB=AC(2)T OI // BC•△AOI sA ABD•-y•l i. H i ii,•订:•/.=:,AB』• Ai2"32,【总结升华】本题考查了三角形的内切圆与内心,等腰三角形的判定和性质,相似三角形的判定和性质等,正确的作出辅助线是解题的关键.举一反三:【变式】已知如图,△ ABC中,/ C=90°, BC=4, AC=3求厶ABC的内切圆O O的半径r.【答案】连结OA OB OC•/△ ABC中,/ C=90°, BC=4, AC=3 • AB=5.1111贝U S\AO+S A CO+S^AO(=S^ABC即卩5r+ 4r+ 3r= 3 4 r=12 2 2 2,。
切线长定理—知识讲解

切线长定理—知识讲解【学习目标】1.了解切线长定义,掌握切线长定理;2.了解圆外切四边形定义及性质;3. 利用切线长定理解决相关的计算和证明.【要点梳理】要点一、切线长定理1.切线长:经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长.要点诠释:切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理:从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释:切线长定理包含两个结论:线段相等和角相等.要点二、圆外切四边形的性质1.圆外切四边形四边形的四条边都与同一个圆相切,那这个四边形叫做圆的外切四边形.2.圆外切四边形性质圆外切四边形的两组对边之和相等.【典型例题】类型一、切线长定理1.(2015秋•湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.(1)若PA=6,求△PCD的周长.(2)若∠P=50°求∠DOC.【答案与解析】解:(1)连接OE,∵P A、PB与圆O相切,∴PA=PB=6,同理可得:AC=CE,BD=DE,△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;(2)∵PA PB 与圆O 相切,∴∠OAP=∠OBP=90°∠P=50°,∴∠AOB=360°﹣90°﹣90°﹣50°=130°,在Rt△AOC 和Rt△EOC 中,,∴Rt△AOC≌Rt△EOC(HL ),∴∠AOC=∠COE,同理:∠DOE=∠BOD, ∴∠COD=∠AOB=65°.【总结升华】本题考查的是切线长定理和全等三角形的判定和性质,掌握切线长定理是解题的关键.2. 如图,△ABC 中,∠ACB=90°,以AC 为直径的⊙O 交AB 于D ,E 为BC 中点.求证:DE 是⊙O 切线.【答案与解析】连结OD 、CD ,AC 是直径,∴OA=OC=OD ,∴∠OCD=∠ODC ,∠ADC=90°,∴△CDB 是直角三角形.∵E 是BC 的中点,∴DE=EB=EC ,∴∠ECD=∠EDC ,∠ECD+∠OCD=90°,∴∠EDC+∠ODC=90°,即OD ⊥ED ,∴DE 是⊙O 切线.【总结升华】自然连接OD ,可证OD ⊥DE.举一反三:【变式】已知:如图,⊙O 为ABC ∆的外接圆,BC 为⊙O 的直径,作射线BF ,使得BA 平分CBF ∠,过点A 作AD BF ⊥于点D .求证:DA 为⊙O 的切线. O FDC B A3421O F D CB A【答案】连接AO .∵ AO BO∠=∠.=,∴ 23∵ BA CBF∠平分,∴ 12∠=∠. ∴ 31∠=∠ .∴ DB∥AO.∵ AD DB⊥,∴ 90∠=︒.DAOBDA∠=︒.∴ 90∵ AO是⊙O半径,∴ DA为⊙O的切线.3.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积()A.12B.24C.8D.6【答案】D;【解析】∵AE与圆O切于点F,显然根据切线长定理有AF=AB=4cm,EF=EC,设EF=EC=xcm,则DE=(4﹣x)cm,AE=(4+x)cm,在三角形ADE中由勾股定理得:(4﹣x)2+42=(4+x)2,∴x=1cm,∴CE=1cm,∴DE=4﹣1=3cm,∴S△ADE=AD•DE÷2=3×4÷2=6cm2.【总结升华】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF,EF=EC.类型二、圆外切四边形4.(西青区二模)已知四边形ABCD中,AB∥CD,⊙O为内切圆,E为切点.(Ⅰ)如图1,求∠AOD的度数;(Ⅱ)如图1,若AO=8cm,DO=6cm,求AD、OE的长;(Ⅲ)如图2,若F是AD的中点,在(Ⅱ)中条件下,求FO的长.【答案与解析】解:(Ⅰ)∵⊙O为四边形ABCD的内切圆,∴AD、AB、CD为⊙O的切线,∴OD平分∠ADC,OA平分∠BAD,即∠ODA=∠ADC,∠OAD=∠BAC,∵AB∥CD,∴∠ADC+∠BAC=180°,∴∠ODA+∠OAD=90°,∴∠AOD=90°;(Ⅱ)在Rt△AOD中,∵AO=8cm,DO=6cm,∴AD==10(cm),∵AD切⊙O于E,∴OE⊥AD,∴OE•AD=OD•OA,∴OE==(cm);(Ⅲ)∵F是AD的中点,∴FO=AD=×10=5(cm).【总结升华】本题考查了三角形的内切圆与内心,也考查了切线长定理.举一反三:【变式】在圆外切四边形ABCD中,AB:BC:CD:AD只可能是().A.2:3:4:5B.3:4:6:5C.5:4:1:3D.3:4:2:5【答案】B.。
切线长定理

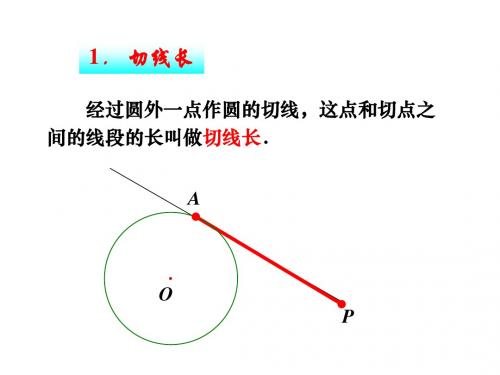
数学探究 经过圆外一点作圆的切线,这点和切点之间的线 段的长叫做切线长。 A
· O ·
B
·
P
切线长和切线的区别和联系: 切线是直线,不可以度量;切线长是指切线上 的一条线段的长,可以度量。
· O ·
B
A
·
P
切线长定理: 从圆外一点可以 引圆的两条切线, 它们的切线长相 等,这一点和圆 心的连线平分两 条切线的夹角。
A O F B E D P
4、如图,在梯形ABCD中,AD//BC, AB⊥BC,以AB为直径的⊙O与DC相切于 E.已知AB=8,边BC比AD大6, 求边AD、BC的长。
A D E O
B
C
数学探究 思考:连结AB,则AB与PO有怎样的位置关系? 为什么? 你还能得出什么结论? A
· O ·E
B
O B C
变式:△ABC中,∠ A=40°,点O是△ABC的内 心,求∠ BOC的度数。
已知:四边形ABCD的边 AB,BC,CD,DA 和圆O分别相切于L,M,N,P。探索圆外 切四边形边的关系。
(1)找出图中所有相等的线段 D N C P AD+BC O M (2)填空:AB+CBD
●
O
2S r . abc
1 S r a b c . 2
B
E
┓
C
1.边长为3、4、5的三角形的内切圆 的半径为——
2. 边长为5、5、6的三角形的内切圆 的半径为—— 3. 已知:△ABC的面积S=4cm,周长 等于 10cm.求内切圆⊙O的半径r.
知识拓展 2.已知:两个同心圆PA、PB是大圆的两条切线, PC、PD是小圆的两条切线,A、B、C、D为 切点。求证:AC=BD A C O· D P B
切线长定理、弦切角定理、切割线定理、相交弦定理

切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段[学习目标]1.切线长概念切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。
(PA长)2.切线长定理对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中,AB、CD为弦,交于P.PA·PB=PC·PD. 连结AC、BD,证:△APC∽△DPB.相交弦定理的推论⊙O中,AB为直径,CD⊥AB于P.PC2=PA·PB.(特殊情况)用相交弦定理.切割线定理⊙O中,PT切⊙O于T,割线PB交⊙O于APT2=PA·PB连结TA、TB,证:△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线,交⊙O于A、CPA·PB=PC·PD过P作PT切⊙O于T,用两次切割线定理(记忆的方法方法)圆幂定理⊙O中,割线PB交⊙O于A,CD为弦P'C·P'D=r2-OP'2PA·PB=OP2-r2r为⊙O的半径延长P'O交⊙O于M,延长OP'交⊙O于N,用相交弦定理证;过P作切线用切割线定理勾股定理证8.圆幂定理:过一定点P向⊙O作任一直线,交⊙O于两点,则自定点P到两交点的两条线段之积为常数||(R为圆半径),因为叫做点对于⊙O的幂,所以将上述定理统称为圆幂定理。
初中数学 什么是切线长定理

初中数学什么是切线长定理
初中数学中,切线长定理是与圆相关的一个重要概念。
下面我将详细介绍切线长定理的定义、性质和相关概念。
1. 切线长定理的定义:
-切线长定理:在一个圆上,一个角的顶点在切点上,另外两个顶点在圆上,这个角的两条边分别与切线相交,那么这两条切线的长度相等。
2. 切线长定理的性质:
-定理性质1:切线长度相等。
如果一个圆上的两条切线与同一个角相交,且角的顶点在切点上,那么这两条切线的长度相等。
3. 切线长定理的相关概念:
-切点:切线与圆相交的点称为切点。
-切线长度:切线的长度即为从切点到圆心的距离。
切线长定理是初中数学中的一个重要概念,它可以帮助我们理解和应用几何知识,解决与切线和圆相关的问题。
在应用切线长定理时,需要注意定理的定义和性质,并运用几何知识进行推理和分析。
例如,如果我们需要判断两条切线的长度是否相等,我们可以先找到这两条切线与同一个角相交,并且角的顶点在切点上。
然后根据切线长定理的性质,我们可以得出这两条切线的长度相等。
希望以上内容能够满足你对切线长定理的了解。
切线长定理及其应用

切线长定理及其应用知识点一 切线长定义及切线长定理1. 切线长定义:过圆外一点作圆的切线,这点和 之间的线段长叫作这点到圆的切线长.注意切线长和切线的区别和联系:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
2. 切线长定理:过圆外一点引圆的两条切线,它们的切线长相等,即PA=PB.推论:(1)△PAB 是等腰三角形;(2)OP 平分△APB ,即△APO=△BPO ;(3)弧AM=弧BM ;(4)在Rt OAP ∆和Rt OBP ∆中,由AB OP ⊥,可通过相似得相关结论;如:222222,,OA OB OE OP AP BP PE PO AE BE OE EP ==⋅==⋅==⋅(5)图中全等的三角形有对,分别是:题型一 切线长定理的直接应用【例1】如图所示,△O 的半径为3cm ,点P 和圆心O 的距离为6cm ,经过点P 的两条切线与△O 切于点E 、F ,求这两条切线的夹角及切线长.【例2】如图,P A 、PB 、DE 分别切△O 于A 、B 、C ,△O 的半径长为6 cm ,PO =10 cm ,求△PDE 的周长.【例3】如图所示,△ABC中,∠C=90°,AC=3,AB=5,D为BC边的中点,以AD上一点O为圆心的⊙O和AB、BC均相切,则⊙O的半径为__________.【过关练习】1.如图所示,PA、PB是△O的切线,A、B为切点,△OAB=30°.(1)求△APB的度数.(2)当OA=3时,求AP的长.2.如图所示,已知PA、PB、DE分别切O于A、B、C三点,△O的半径为5cm,△PED的周长为24cm,△APB=50°.求:(1)PO的长;(2)△EOD的度数.3.如图,在直角梯形ABCD 中,AB ∥CD,AB ⊥BC,以BC 为直径的△O 与AD 相切,点E 为AD 的中点,下列结论正确的个数是( )(1)AB+CD=AD;(2)DCE ABE BCE S S S △△△+=; (3)241BC CD AB =⋅; (4)∠ABE=∠DCE. A.1B.2C.3D.4知识点二 圆外切四边形1、四边形的内切圆定义:四边形的四条边都与圆相切,把这个四边形叫作圆外切四边形,把这个圆叫作圆的内切圆.2、圆外切四边形的性质:圆外切四边形两组对边之和.(如图,即AB +CD =AD +BC ) 题型一 四边形的内切圆计算【例1】已知四边形ABCD 的边AB 、BC 、CD 、DA 与△O 相切于P 、Q 、M 、N ,求证:AB+CD=AD+BC 。
切线长定理

O B
C
P
返回
已知:PA、PB切O于A、B 能推出?……
O、A、P、B四点在同一个圆上吗?
A O B P
返回
已知:PA、PB切O于A、B 能推出?……
C点是△APB的什么心? A H
已知:两圆为同心圆,外圆上一点P 作内圆的两条切线PA、PB交外圆于C,
过A、B的直线交外圆于D、E。
求证:(1)EA=BD (2)
P E A H O
B
PB PD BD DC
D
C
已知:P为O外一点,PA、PB切 O于A、B,OP交AB于M,过M作CD。
求证: MDO=MPC
P
A
D
M
O
A O B P
从圆外一点可以作___条直线与圆相切 你会用尺规作图作出这条切线吗?
给 起 个 名 字 吧 以 后 说 起 来 方 便
PA
从圆外一点可以作___条直线与圆相切 你会用尺规作图作出这条切线吗?
A
O
P
切线长 PA、PB切O于A、B PA=PB APO=BOP
A O B P
切线长定理:从圆外一点引圆的两条切 线,他们的切线长相等,圆心和这一点 的连线平分两条切线的夹角. PA、PB切O于A、B PA=PB APO=BOP
A
PD垂直平分AB
PБайду номын сангаас
D
H
O B C
返回
已知:PA、PB切O于A、B 能推出?……
A
AC=BC;AD=BD.
C
D
H
O B
切线长定理课件

切线长定理的再一个推论
总结词
切线长定理的再一个推论是,若两圆在 同一直线上相切,则它们的切线互相平 行。
VS
详细描述
这个推论是切线长定理的进一步应用。当 两圆在同一直线上相切时,它们的切线不 仅长度相等,而且平行。这个推论在解决 涉及直线和圆的问题时非常有用,特别是 在几何证明和解析几何中。通过掌握这个 推论,学生可以更好地理解几何图形的性 质和关系,提高解决几何问题的能力。
切线长定理的另一个推论
总结词
切线长定理的另一个推论是,若两圆相切于同一点,则该点的切线与两圆心的连线垂直 。
详细描述
这个推论说明了当两圆在同一点相切时,该点的切线与两圆心的连线之间此,该点的切
线与两圆心的连线互相垂直。这个推论在证明几何定理和解决几何问题时非常有用。
切线长定理在数学、物理、工程等领 域有着广泛的应用,通过学习和掌握 这个定理,我们可以更好地理解和应 用相关领域的知识。
通过本次课件的学习,我们深入了解 了切线长定理的证明过程和实际应用 ,掌握了利用切线长定理解决实际问 题的技巧和方法。
展望
随着数学和其他学科的发展,切线长定理的应用范围将会更加广泛,我 们可以通过不断学习和探索,深入了解这个定理的更多应用和推广。
切线长定理的证明方法二
利用三角形的全等定理进行证明。首先,作辅助线连接圆心和切点,将切线分为两段。然后,根据三角形的全等定理,证明三 角形全等,从而得到切线长的平方等于半径的平方和。
切线长定理的证明方法三
利用向量进行证明。首先,根据向量的数量积公式,向量的数 量积等于两向量的模长乘以其夹角的余弦值。然后,利用切线 的性质,切线和半径垂直,从而夹角为90度。结合数量积公式 ,可以证明切线长的平方等于半径的平方和。
切线长定理及其应用

知识点一切线长定义及切线长定理1. _____________________________________________________ 切线长定义:过圆外一点作圆的切线,这点和____________________________________________ 之间的线段长叫作这点到圆的切线长注意切线长和切线的区别和联系:切线是直线,不可以度量;切线长是指切线上的一条线段的长,可以度量。
2. 切线长定理:过圆外一点引圆的两条切线,它们的切线长相等,即PA=PB.推论:(1) △ PAB是等腰三角形;(2) OP 平分△ APB,即△ APO A BPO ;(3) 弧AM=弧BM ;(4)在Rt OAP和Rt OBP中,由AB OP,可通过相似得相关结论;如:OA2 OB2 OE OP, AP2 BP2 PE PO, AE2 BE2 OE EP(5)图中全等的三角形有对,分别是:题型一切线长定理的直接应用【例1】如图所示,AO的半径为3cm,点P和圆心O的距离为6cm,经过点P的两条切线与AO切于点E、F,求这两条切线的夹角及切线长.【例2】如图,FA、PB、DE分别切A0于A、B、C, A O的半径长为6 cm, PO= 10 cm,求APDE的周长.切线长定理及其应用【例3】如图所示,△ ABC中,/ C=90 , AC=3 , AB=5 , D为BC边的中点,以AD上一点0为圆心的O0和AB、BC均相切,则O 0的半径为 ______________ .£4【过关练习】1•如图所示,PA、PB是AO的切线,A、B为切点,△ OAB=30°.( 1)求厶APB的度数.(2)当0A=3时,求AP的长•2•如图所示,已知PA、PB、DE分别切e 0于A、B、C三点,AO的半径为5cm, △ PED的周长为24cm , △ APB=50°求:(1) P0 的长;(2) △ EOD 的度数•3•如图,在直角梯形 ABCD 中,AB // CD,AB 丄BC,以BC 为直径的 △ 与AD 相切,点E 为AD 的中点,下列结论 正确的个数是( )B1 2知识点二圆外切四边形1、四边形的内切圆定义:四边形的四条边都与圆相切,把这个四边形叫作圆外切四边形,把这个圆叫作圆的内切圆2、圆外切四边形的性质:圆外切四边形两组对边之和 __________________ .(如图,即AB+CD=AD+BC )题型一 四边形的内切圆计算【例1】已知四边形 ABCD 的边AB 、BC 、CD 、DA 与AO 相切于P 、Q 、M 、N ,求证:AB+CD=AD+BC 。
切线长定理

8
6
8
达 标 检 测
1、填空:已知⊙O的半径为3cm, 点P和圆心O的距离为6cm,经过点 P有⊙ O的两条切线,则切线长为 ______cm。这两条切线的夹角为 P 60 _____度。 2、证明题:已知:如图,P为⊙ O外 一点,PA、PB 为⊙ O 的切线,A和B 是切点,BC是直径 求证:AC∥OP 证明:连结AB ∵PA、PB分别切⊙O于A、B ∴PA=PB ∴OP⊥AB 又∵BC为⊙O的直径 ∴AC⊥AB ∴AC∥OP ∠OPA=∠OPB P A
已知一条切线时,常有五个性质: 1、切线和圆只有一个公共点; 2、切线和圆心的距离等于圆的半径; 3、切线垂直于过切点的半径; 4、经过圆心垂直于切线的直线必过切点; 5、经过切点垂直于切线的直线必过圆心。
切线长定理
B
。
P
O
A
切线长定理
B
。
P
A
PA、PB分别切⊙O于A、B 、 分别切 分别切⊙ 于 、
PA = PB ∠OPA=∠OPB ∠
如图:PA、PB是⊙O的两条切线,A、B为切点。 B O。 C
思考:由切线长定理 可以得出哪些结论?
P
A
若已知圆的三条切线呢? 设△ABC的BC=a,CA=b,AB=c, 内切圆I和BC、AC、AB分别相切 于点D、E、F
A
x
F . I B E
z
C
y
D
分析:设 AF=x,BD=y,CE=z 分析: AF=x,BD=y, y+z=a x+z=b x+y=c
C
A
A
B
C
O B A C
O
B A
弦切角等于它所夹的弧 所对的圆周角。 所对的圆周角。
切线长定理

B
例题1
已知:如图,PA、PB是⊙O的切线,切点分别是 A、B,Q为弧AB上一点,过Q点作⊙O的切线, 交PA、PB于E、F点,已知PA=12cm,求△PEF ∵EA、EQ是⊙O的切线,切点为A、Q 的周长。
∴EQ=EA,同理可得FQ=FB,PA=PB
A E Q P B F O
∴ PA=PE+AE=PE+EQ=12cm PB=PF+BF=PF+FQ=PA=12cm ∴△PEF的周长为24cm
O
∠AOB+∠APB=180 °
P B
探究2
若连结两切点A、B,AB交OP于点M.你又能得 出什么新的结论?并给出证明. B OP垂直平分AB
O
M
P
A 证明:∵PA,PB是⊙O的切线,点A,B是切点 ∴PA = PB ∠OPA=∠OPB
即△PAB是等腰三角形,PM为顶角的平分线 ∴OP垂直平分AB
(2)连结两切点 (3)连结圆心和圆外一点
巩固练习
已知:P为⊙O外一点,PA、PB为⊙O的 切线,A、B为切点,BC是直径。 求证:AC∥OP A C O
D
P
B
O · P
B
B
思考1:切线与切线长是一回事吗?
切线:是直线,不可以度量。切线长:是线段,可以度量。
A
O · P
B
B
思考2:两条切线长的大小关系如何?
相等
证一证
B
已知PA、PB是⊙O的两条 切线,求证:PA=PB
P O
A 证明:∵PA,PB与⊙O相切,点A,B是切点 ∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
变式:如图所示PA、PB分别切 圆O于A、B,并与圆O的切线分别相交于 C、D,已知PA=7cm, (1)求△PCD的周长. (2) 如果∠P=46°,求∠COD 的度数 A
切线长定理

O P
C
B
P与AOB互补 P BOC
得想 到一 哪想 些: 互根 补据 或图 相形 等你 的还 角可 ?以
练习二
1.如图,PA、PB是⊙O的切线,A、
A P
B为切点,AC是⊙O的直径, ∠BAC=25°,则∠P 的度数是____
C
O
B A O
2.如图,PA、PB分别切⊙O于A、 B,∠P =70°,则∠C= ____
M
y
┑ F C N
x y y x 122
DC 2 FC 2 DF 2
Yx
xy 36
36 y x
解:过点D做DF⊥BC于F ∵AM、BN切⊙O于A、B,且AB为直径 ∴AB⊥AM,AB⊥BN ∴AM∥BN,DF∥AB ∴ABFD是矩形 ∴DF=AB=12,BF=AD=x ∴FC=y-x 又∵ DE切⊙O于E ∴DE=AD=x,CE=CB=y ∴DC=x+y 在直角△DFC中,
2
A x
D x E
P B
2.如图所示,EB、EC是⊙O的两条切线,B、C是 切点,A、D是⊙O上两点,• 如果∠E=46°, ∠DCF=32°,求∠A的度数. B A
O E C D F
综合应用
┍ O ┑ B y
2
如图:⊙O的直径AB=12,AM和BN是 它的两条切线,DE切⊙O于E,交AM 于D,交BN于C,设AD=x,BC=y,求y 与x的函数关系式。
解:∵ △ABC的三边分别与⊙O切于点D、E、F
∴ AE=AF CE=CD BD=BF 设AE=x (cm), 则AF=x (cm) CD=CE=AC﹣AE=13﹣x BD=BF=AB﹣AF=9﹣x 由 BD+CD=BC可得
24.2.2 切线长定理

例题:如图:△ABC的内切圆⊙O与 BC,AC,AB,分别相切于点E、F、 D,且AB=14㎝,BC=19㎝,CA=9 ㎝,求AF,BD,CE,的长。
B E D O C
F
A
反思:在解决有关 圆的切线长的问题 时,往往需要我们 构建基本图形。
A
。OBiblioteka P B(1)分别连结圆心和切点(直角)
(2)连结两切点(等腰三角形)
(3)连结圆心和圆外一点(角平分线)
小结:
(1)切线长定理。 (2)连接圆心和切点是我 们解决切线长定理相关问题 时常用的辅助线。
⌒
P
切线与切线长的区别是什么? 切线是一条直线,不可度量 切线长是一条线段,可以度量
一张三角形的铁皮,如何在它上面截下 一块圆形的用料,并且使圆的面积尽可 能大呢?
A
B C
. 与三角形各边都相切的圆 叫做三 角形的内切圆。内切圆的圆心叫三角形 的 内心 ,它是三角形 三条角平分线 的 交点。
叫做三 角形的外接圆,外接圆的圆心叫三角形 的 外心 ,它是三角形 三边垂直平分线 的 交点。 经过三角形的三个顶点的圆
活动1
O
A
P
. 条件 结论 B PA =PB . PA是⊙O的切线 相等的线段: ∠APO = ∠BPO PB是⊙O的切线. 相等的角: . 切线长定理 从圆外一点引圆的两条 切线,它们的切线长相等,这点和圆心的连 线平分两条切线的夹角.
A
1
O M
2
B 证明:∵PA、PB是⊙O的两条切线,A、B为切点 ∴OA⊥AP,OB⊥BP 又OA=OB,OP=OP, ∴Rt△AOP≌Rt△BOP(HL)∴PA=PB,1=∠2
切线长定理
A
O C
B
6. △ABC的内切圆半径为 r , △ABC的周长为 l ,求△ABC的面积. (提 示:设内心为O,连接OA、OB、OC.) 解:连接OA、OB、OC,则
1 1 S= AB × r + AC × r + 1 BC × rA 2 2 2
= =
1 2 1 2
(AB +AC+BC) × r lr
三角形内切圆的圆心.
(即三角形三条角平分线的交点)
随堂练习
1. 已知⊙O的半径为5cm,点O到直线a的距 离为3cm,则⊙O与直线a的位置关系是________; 相交 直线a与⊙O的公共点个数是_______ 两个 .
2. 已知⊙O的直径是11cm,点O到直线a的距 离是5.5cm,则⊙O与直线a的位置关系是 ______, 直线 a与⊙O的公共点个数是_______.一个 相切
3. 已知⊙O的直径为10cm,点O到直线a的 相离 距离为7cm,则⊙O与直线a的位置关系是 _______; 直线a与⊙O的公共点个数是____ 零 .
4. 直线m上一点A到圆心O的距离等于⊙O的 相切或相交. 半径,则直线m与⊙O的位置关系是____________
5. △ABC中,∠ ABC=50°∠ACB= 75 °,点O是⊙O的内心,求∠ BOC的度数. 解:∵点O是⊙O的内心 ∴∠OBC=1/2∠ABC=25° ∠OCB=1/2∠ACB=37.5° ∴∠BOC=180°-25°-37.5° =117角形的内切圆 与三角形各边都相切的圆. 三角形的内心 三角形内切圆的圆心. (即三角形三条角平分线的交点) O B A
C
定理证明
求证:三角形三条角平分线的交点是内切圆的 圆心. A D F O B E C
7 切线长定理

2.如图,从圆O外一点P引圆O的两条切线PA,PB,切点分别为A,B.如果∠APB= 60°,PA=8,那么弦AB的长是( B )
(A)4
(B)8
(C)4 3 (D)8 3
3.(2019宜兴市二模)如图,PA,PB切☉O于点A,B,PA=10,CD切☉O于点E,交
PA,PB于C,D两点,则△PCD的周长是C (
【导学探究】 1.由切线长定理可得AD=AF,BD= BE
,CF= CE .
(1)证明:法一 因为☉O是△ABC的内切圆,切点为D,E,F, 所以AD=AF,BD=BE,CE=CF. 因为AB=AC, 所以AB-AD=AC-AF,即BD=CF, 所以BE=CE.
法二 连接 OB,OC,OE,
因为☉O 是△ABC 的内切圆, 所以 OB,OC 分别平分 ∠ABC,∠ACB,
,△PAB是 等边 三角形.
33
2.作OC⊥AB于点C,则∠O
解:过点 O 作 OC⊥AB 于点 C,所以 AC= 1 AB,因为 PA,PB 是☉O 的切线,所以 2
PA=PB,OA⊥PA,因为∠P=60°,所以△PAB 是等边三角形,所以∠PAB=60°, 所以∠OAC=90°-∠PAB=30°, 在 Rt△AOC 中,OA=3,
OP 6 2 两条切线的夹角为 60°,切线长为 3 3 cm.
点击进入 训练案
)
(A)10 (B)18 (C)20 (D)22
4.如图,PA,PB分别切☉O于A,B,若∠APB=50°,则∠AOP= 65° .
5.如图所示,已知☉O的半径为3 cm,点P到圆心O的距离为6 cm,经过点P的两 条切线与☉O切于点E,F,求这两条切线的夹角及切线长.
解:如图所示,连接 OE,则 OE⊥PE,由切线长定理可知 PE=PF,易知∠EPF=2∠1, 在 Rt△POE 中,OP=6 cm,OE=3 cm,由勾股定理,得 PE= OP2 OE 2 = 62 32 = 3 3 (cm),sin∠1= OE = 3 = 1 ,所以∠1=30°,所以∠EPF=2∠1=60°,所以这
切线长定理

A
PA = PB
反思:切线长定理为证明线段相等提 供了 新的方法
·A O·
B
切线长定理 过 圆外一点作圆的 两条切线长相等
·P
已知:如图,P为⊙ O外一点,PA、PB为 ⊙ O的切线,A、B为切点,连结PO
求证: PAPB
1、判断
练习
(1)过任意一点总可以作圆的两条切线( )
(2)从圆外一点引圆的两条切线,它们的长相等。
导学卷54页 当堂达标4 课后提高1、2、3题
作业: 课时练55--56页1、4、6--12题
结语
谢谢大家!
。
O
P
(1)分别连结圆心和切点 (2)连结两切点
(3)连结圆心和圆外一点
B
切线长定理为证明 线段相等,角相等,弧 相等,垂直关系提供了 理论依据。必须掌握并 能灵活应用。
例2 如图,已知:在△ABC中,∠B=90°,O是 AB上一点,以O为圆心,OB为半径的圆交AB
于点E,切AC于点D。求证:DE∥OC C
B
PA = PB
。
P
O
A 证明:∵PA,PB与⊙O相切,点A,B是切点
∴OA⊥PA,OB⊥PB 即∠OAP=∠OBP=90°
∵ OA=OB,OP=OP ∴Rt△AOP≌Rt△BOP(HL)
试用文字语言 叙述你所发现 的结论
∴ PA = PB
二、切线长定理 过圆外一点作圆的两条切线 长相等
B
。
P
O
几何语言: PA、PB分别切⊙O于A、B
O
A
B
C
小 结:
1.切线长定理 从圆外一点引圆的两条切线,它们的切 线长相等,圆心和这一点的连线平分两条切线的夹角。
切线长定理

(1)写出图中所有的垂直关系;
(2)如果 PA = 4 cm , PD = 2 cm , 求半径 OA的长. E A P
O
C B
D
2、如图,AC为⊙O的直径,PA、PB分别切 ⊙O于点A、B,OP交⊙O于点M,连结BC。 (1)若OA=3cm, ∠APB=60°,则PA=______. (2)观察OP与BC的位置关系,并给予证明。
A
O
·
B
·
切线长定理 从圆 外一点可以引圆的 两条切线,它们的 P 切线长相等且这一 点和圆心的连线平 分两条切线的夹角。
已知:如图,P为⊙ O外一点,PA、PB为 ⊙ O的切线,A、B为切点,连结PO 则 PA PB, APO BPO
例1 如图,PA、PB、DE分别切⊙O于A、 B、C,DE分别交PA,PB于D、E,已知P 到⊙O的切线长为8CM,求Δ PDE的周长。
A
O P
M B
C
知识回顾 切线长: 从圆外一点引圆的切线,这个点与切点 间的线段的长称为切线长。
切线长定理: 从圆外一点可以引圆的两条切线,它们 的切线长相等。这一点和圆心的连线平分这 两条切线的夹角并且垂直两切点的连线。
思考题 以正方形ABCD的一边BC为直径的半圆上有一 个动点K,过点K作半圆的切线EF,EF分别交 AB、CD于点E、F,试问:四边形AEFD的周长 是否会因K点的变动而变化?为什么? A D E
A P
O C D
(1)图中互相垂直的关系 3 有 对,分别是 OA PA, OB PB, OP AB B
(2)图中的直角三角形有 6 等腰三角形有 2 个,分别是
个,分别是
(3)图中全等三角形
3
对,分别是
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
切线长定理教材分析:本节内容是切线长的概念和切线长定理。
通过本节教学应使学生理解切线长的概念,掌握切线长定理并会运用它解决有关问题。
切线长定理再次体现了圆的轴对称性,它为证明线段相等、角相等、弧相等、垂直关系等提供了理论依据,这个定理经常用到,因此,它是本节的重点。
灵活运用图形语言、文字语言、符号语言三种语言表述切线长定理,学生感觉困难;用切线长定理解决有关问题中,准确应用数学语言进行表述,学生感觉困难;从实际情境中抽象出切线长定理模型解决问题,学生感觉困难;在综合题中迅速找出切线长定理模型, 学生感觉困难;因此,综合应用切线长定理及有关知识解决问题,是本节的难点。
本节内容是在学习了“切线的判定和性质”之后,并进一步了解了“三角形的内切圆”这一内容的基础上进行研究的。
是前面内容的必然延伸,也是后面学习切割线定理等重要内容的基础。
切线长定理的出现,可以让我们对直线与圆位置关系的研究由定性分析深入到定量研究。
再次让我们感触到了圆的轴对称性。
它为我们证明线段相等、角相等、弧相等、垂直关系等提供了理论依据。
通过本节内容的学习,会让学生更客观地认识切线的有关问题。
同时,该定理的学习对我们解决一些实际问题很有指导意义。
因此,本节内容在这部分中具有非常重要的作用,是“直线与圆的位置关系”这部分内容的纽带和桥梁。
同时,它综合运用等腰三角形、直角三角形、全等三角形、相似三角形、四边形等知识解决问题。
切线长定理及其研究方法又是研究两圆相切问题的基础,因此,本节内容在整个初中几何教材体系中,起着承上启下的作用。
学生分析:1、经过前面几节的学习,学生对圆的轴对称性已经有了初步了解,掌握了等腰三角形、直角三角形、全等三角形、相似三角形、四边形等知识,具备了学习本节内容的知识基础。
2、经过前面的学习,学生已经对合情推理和逻辑推理都有了一定的认识,具备了证明线段相等、角相等、弧相等、垂直关系等的基本技能。
3、初三学生已经具备了一定的探索解决问题方法的经验,从心理学的角度分析:他们正处于想成为大人,想得到别人肯定的年龄阶段,因此,他们会不遗余力地提出他们自己的看法并能较有条例地申述自己的理由,这些是很必要的情感准备;但由于特定年龄阶段的关系,他们对问题的分析还不是很全面,用数学语言表述看法,有时还欠准确贴切。
有待于教师不断地加以培养。
设计理念:1、本着“人人都能学好数学”,“人人都学有价值的数学”的理念,我将本节的问题情境设置为两个小朋友玩滚圈游戏,目的是想通过游戏营造一种氛围,在一开始就抓住学生,激发他们解决问题的愿望,让他们体验到:数学源于生活,生活中处处有数学,建立数学模型能解决实际问题;感受到数学探索的乐趣。
2、按照建构主义的理念,本节课试图让学生经历“问题情境——建立模型——求解——解释与应用”的基本过程,体验数学与生活的内在联系,获得方法与经验,发展思维能力,增强应用数学的自信心。
3、本着“数学学习最根本的是数学思想和方法的学习”,“只有亲身经历过,才会是印象最深刻的,哪怕他的探索没有成功,他也会获得很多。
”的理念,本节课在设计时,注重给学生探究的机会,在教师的引导下,让学生自主探索解决问题的途径,通过学生动手实验、观察图形、发现并解决问题培养他们主动获取知识的能力、抽象概括的能力及提出问题的能力。
从而,锻炼学生百折不挠克服困难的精神,增强他们学习数学的内驱力,让他们体会从特殊到一般,从一般到特殊的数学思想方法。
教学目标:知识与技能目标:1、理解切线长的概念,掌握切线长定理并会运用它解决有关问题。
2、通过学生动手实验、观察图形、发现并解决问题培养他们主动获取知识的能力、抽象概括的能力及提出问题的能力。
过程与方法目标:1、经历,领悟从实际问题情境中抽象出数学模型,从而解决实际问题的方法。
2、运用这种方法解决有关实际问题。
情感、态度、价值观目标:1、在切线长定理模型的探索过程中,经历概括、分析、提出问题、克服困难解决问题等阶段,体验成功的喜悦。
2、通过这节课的学习,培养学生热爱生活的积极人生态度,锻炼学生百折不挠克服困难的精神,增强他们学习数学的内驱力,激发学习兴趣。
3、经过本节课的探索,在建立数学模型解决问题的过程中,体会从特殊到一般,从一般到特殊的数学思想方法。
教学准备:1、教师准备:本节教学课件。
2、学生准备:一个圆形硬纸片、一把刻度尺、一副三角板、一个圆规,课本,练习本。
教学过程:一、问题情境:(大屏幕展示动画)小明和小亮在玩滚圈游戏,小亮一不小心把小明的铁圈弄坏了,小明说:“我不用你赔了,但你要用我们近期所学的数学知识,设计出方案测出这个铁圈的直径,以便在做一个和它一样的铁圈。
”小亮用手挠了挠头,有点发愁,聪明的同学们,请你们开动脑筋,帮小亮解决这个问题,好吗?老师相信你们一定能行!赶快动手吧。
[设计目的:通过游戏营造一种氛围,挖掘学生内心乐于助人的潜能,激发他们解决问题的愿望,让他们体验到数学与生活的联系,鼓励他们自己动手,自主探究。
]师:想帮小亮解决这个问题,我们第一步该怎样做?生1:将该问题抽象为数学问题。
师:怎样抽象?抽象出的数学问题又是怎样的?生2:认真阅读,把有关大小、形状、位置等的语言用数学语言翻译出来。
例如,本问题中的铁圈可抽象为一个圆。
这样,抽象出的数学问题是:利用刻度尺、三角板、圆规,运用已学知识,设计一个测量已知圆的直径的方案。
[设计目的:引导学生用数学的眼光看待周围的一切,增强他们数学地解决问题的意识;探索将实际问题抽象为数学问题的方法:关注实际问题中的数量、形状、位置等语言,将其翻译成符号语言、图形语言。
]APBO师:刚才,这两位同学说得很好,下面我们就分小组利用准备的材料,探索设计出这个方案吧!(学生分组活动,教师巡回参与、指导。
)学生们通过探讨提出的方案有:生3:方案(一):如图(1)将铁圈卡在墙角,可用刻度尺测得AP的长度.图(1)理由是: 设铁圈所在的圆的圆心为O,连结OA,OB,由切线的性质得OA⊥AP,OB⊥PB,BADEC又AP ⊥BP,OB=OA,则四边形APBO为正方形.那么,铁圈半径OB=AP,这样就可求出铁圈的直径.图(2)生4:方案(二):如图(2),把三角板顶点A放在铁圈边缘,设三角板一边与铁圈边缘交于点B,另一边交于点C,(若三角板另一边无法达到铁圈边缘, 延长另一边与铁圈边缘交于点C),度量BC长即为直径.二、问题拓展探究:探索问题1师问:方案(一)中由四边形APBO为正方形易得PA=P B,∠BPA如果不是90°,PA=PB还成立吗?做出判断,并说明理由。
请同学们运用任何工具和方法(如:观察、测量、比较、对折、猜想、论证等)研究这个问题。
(分小组研究探索,一个小组确定一个发言人。
)[设计目的:让学生体验数学研究的一种方法:变化其中的特殊条件为一般条件,观察、分析出变中不变的结论,作为规律。
体验从特殊到一般的数学思想方法。
请同学们运用任何工具和方法(如:观察、测量、比较、对折、猜想、论证等)研究这个问题。
目的是想促使学生人人参与,提高参与度。
让他们发现更多的方法,明确逻辑推理是建立在合情推理的基础上的;而合情推理是在观察、对折等实际操作的基础上,加以分析得来的。
]展示探索结果:图(3)生5:第一种证法:如图(3)连结OP,则OP是整个图形的对称轴,沿OP折叠,两侧的部分能够互相重合,可证PA=P B。
教师强调:合情推理也是数学说理的一种方法,运用时语言要简洁明确。
生6:第二种证法:连结OP,OA,OB,由切线的性质得OA⊥AP,OB⊥PB,OB=OA,又∵OP=OP∴Rt△APO≌Rt△BPO∴PA=PB教师给出切线长的定义:在经过圆外一点的切线上,这点和切点之间的线段的长,叫做这点到圆的切线长。
教师强调:切线是直线,切线长是切线上一条线段的长。
问:在图(3)中利用三角形全等你还发现那些特性?请用语言叙述出来。
(叙述时用上切线长这个概念。
)生7:∠OPA=∠OPB,用语言叙述为:在圆外找一点,作圆的两条切线,可得切线长相等,OP平分两切线的夹角。
师:说得好,将OP改换成文字,再简化一下,就更好了。
下面老师板书图(4)定理,请同学们认真体会一下自己的说法与定理叙述间的差距,做好自我教育,提高语言叙述水平。
[设计目的:训练学生的数学表达,体会定理的语言叙述,就是将定理的应用情境及结论用数学语言明确表达。
]教师板书:切线长定理:从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角。
教师强调:(1)此定理用于证明线段相等、角相等、弧相等、垂直关系等(2)此定理有三种表达方式:文字表达(板书的定理)、图形表达(如图4)、符号表达(如下)∵PA、PB切圆O于A点B点∴PA=PB ∠OPA=∠OPB三、理解应用━━巩固练习、变式训练例1、已知:如图PA、PB是圆O的两条切线,A、B 为切点,直线OP交圆于点D、E,交AB于C⑴写出图中所有的垂直关系;⑵写出图中所有的全等三角形;⑶如果PA=4cm,PD=2cm,PABCDOE求半径OA的长(一位同学板演,其他同学在练习本上做。
)[设计目的:本例题较简单,学生能够独立完成,想用它训练学生的规范书写。
]解:⑴OA⊥PA,OB⊥PB,OP⊥AB;图5⑵△OAP≌△OBP,△OCA≌△OCB,△ACP≌△BCP⑶设OA=xcm;在Rt△OAP中,OA=xcm,OP=OD+PD=x+2(cm),P A=4cm,由勾股定理,得PA2+OA2=OP2 即42+x2=(x+2) 2解得,x=3cm所以,OA的长为3cm反馈练习:图61、填空:已知如图4,PA、PB分别与⊙O相切于点A、B,P O与⊙O相交于点D,(1)若PA=12,则PB= ;(2)若∠APB=80º,则∠APO= ,∠AOB=(3)∠APO=30º,OA = 2,则PB=[设计目的:让学生体会一般到特殊的数学思想方法,体会应用切线长定理的关键是读出该定理的应用情境,即定理的前提,得出定理的结论。
初步感受该定理与垂直、三角形全等、解直角三角形的综合应用。
]生8:(1)∵PA、PB分别与⊙O相切于点A、B∴PA=PB=12112生9:(2)∵PA、PB分别与⊙O相切于点A、B 2∴∠OPA=∠OPB= —∠APB =— 80°= 40°OA⊥AP,OB⊥PB∴∠AOP = 50°同理,∠BOP = 50°∴∠AOB = ∠AOP + ∠BOP = 100°师:还有其他方法吗?生10:还可用四边形内角和为360°,得∠AOB = 360°- 90° - 90°- ∠APB= 100°生11:(3)∵PA、PB分别与⊙O相切于点A、B ∴PA = PB,OA⊥AP∵∠APO=30º,OA = 2∴OP = 4,由勾股定理,得3PA = 23PA = PB = 2师:还有其他方法吗?生12:还可用30°角的余弦值来求。
