切线长定理及其应用
切线长定理及应用
A L B （>,<,=) 结论：圆的外切四边形的两组对边和相等。 比较圆的内接四边形的性质：
圆的内接四边形：角的关系
圆的外切四边形：边的关系
练习四 已知：△ABC是⊙O外切三角形，切点
为D，E，F。若BC＝14 cm ，AC＝9cm，AB＝
13cm。求AF，BD，CE。
例1、如图，PA、PB是⊙O的切线，A、B为 切点，∠OAB＝30°． （1）求∠APB的度数； （2）当OA＝3时，求AP的长．
A
O
P
B
随堂训练 如图，AC为⊙O的直径，PA、PB分别切⊙O 于点A、B，OP交⊙O于点M，连结BC。 (1)若OA=3cm, ∠APB=60°，则PA=______.
O
A
B
C
思考：当切点F在弧AB上运动时，问△PED 的周长、∠DOE的度数是否发生变化，请说 明理由。
AD
OF
P
E B
（2）如图，Δ ABC的内切圆分别和BC，AC， AB切于D，E，F；如果 AF=2cm,BD=7cm,CE=4cm,则BC=11cm,
AC= 6cm
AB= 9cm
A
2 F
E 4
2. 边长为5、5、6的三角形的内切圆的半径为——
3. 已知:△ABC的面积S=4cm,周长等于 10cm.求内切圆⊙O的半径r.
例题选讲
例：如图， △ABC的内切圆⊙O与BC、CA、 AB分别相切于点D、E、F，且AB=9cm， BC=14cm，CA=13cm，求AF、BD、CE的长。
x A x F 9﹣x
求证： PA PB, APO BPO
一、判断
切线长定理及其应用
切线长定理及其应用一、基础知识总结1.内切圆和内心定义: 与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心是三角形三条角平分 线的交点,叫做三角形的内心.总结：判断一个多边形是否有内切圆，就是判断能否找到一个点到各边距离都 相等。
2.直角三角形的内切圆半径与三边关系（１）一个基本图形；（２）两个结论：1）四边形OECF 是正方形2）r=(a+b-c)∕2或r=ab ∕(a+b+c)（３）两个方法代数法（方程思想）；面积法3.切线长定义：过圆外一点作圆的切线，该点和切点之间的线段长叫做切线长。
4.切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的交角。
二、典型例题解析【例1】如图△ABC 的内切圆⊙O 与BC 、CA 、AB 分别相交于点D 、E 、F ，且AB=9 cm,BC=14 cm ，CA=13 cm ，求AF 、BD 、CE 的长D E F O CB A 11212902a b c A B C A B C S s r p a b c p C r a b c ∆∠∠∠==++∠=︒=+-设、、分别为中、、的对边，面积为，则内切圆半径（），其中（）；（），则（）【例2】如图，已知⊙O是△ABC的内切圆，切点为D、 E、F，如果AE＝1， CD＝2，BF＝3，且△ABC的面积为6．求内切圆的半径r．【例3】如图，以等腰ABC∆中的腰A B为直径作⊙O，交底边BC于点D．过点D作⊥，垂足为E．D E A C（I）求证：D E为⊙O的切线；（II）若⊙O的半径为5，60∠= ，求D E的长．B A C【例4】如上图等边三角形的面积为S，⊙O是它的外接圆，点P是⌒BC的中点．（1）试判断过C所作的⊙O的切线与直线AB是否相交，并证明你的结论；（2）设直线 CP与AB相交于点D，过点B作BE⊥CD垂足为E，证明BE是⊙O的切线，并求△ BDE的面积．【例5】 已知：在⊙O 中，AB 是直径，AC 是弦，OE ⊥AC 于点E ，过点C 作直线FC ，使 ∠FCA ＝∠AOE ，交AB 的延长线于点D.（1）求证：FD 是⊙O 的切线；（2）设OC 与BE 相交于点G ，若OG ＝2，求⊙O 半径的长；（3）在（2）的条件下，当OE ＝3时，求图中阴影部分的面积.F B DE O A C。
切线长定理及应用
切线长定理及应用切线长定理是解决几何问题中常用的定理之一，它在许多实际应用中发挥着重要的作用。
本文将介绍切线长定理的概念、证明以及一些实际应用。
一、切线长定理的概念切线长定理是指在一个圆上，从圆外一点引出的切线与半径的乘积等于切点到圆心的距离的平方。
换句话说，如果从圆外一点引出一条切线，那么切线与半径的乘积等于切点到圆心的距离的平方。
二、切线长定理的证明为了证明切线长定理，我们可以利用几何推理和一些基本的几何定理。
首先，我们可以通过连接圆心、切点和圆上的一个点，构成一个直角三角形。
然后，利用勾股定理和相似三角形的性质，我们可以得出切线长定理的结论。
三、切线长定理的应用切线长定理在实际应用中有着广泛的应用。
以下是一些常见的应用场景：1. 圆的切线问题：切线长定理可以帮助我们解决与圆相关的问题，例如确定切线的长度、判断两条切线是否相等等。
2. 几何建模：在几何建模中，切线长定理可以用于计算和确定物体表面的切线长度，从而帮助我们进行准确的建模和设计。
3. 光学问题：在光学问题中，切线长定理可以用于计算光线的传播路径和角度，从而帮助我们理解光的行为和性质。
4. 工程测量：在工程测量中，切线长定理可以用于计算和确定测量点与目标物之间的距离和位置关系，从而帮助我们进行精确的测量和定位。
5. 数学建模：在数学建模中，切线长定理可以用于建立数学模型，从而帮助我们解决各种实际问题，例如物体运动的轨迹、曲线的切线方程等。
总结：切线长定理是解决几何问题中常用的定理之一，它在圆的切线问题、几何建模、光学问题、工程测量和数学建模等领域都有着广泛的应用。
通过理解和应用切线长定理，我们可以更好地解决实际问题，提高问题求解的准确性和效率。
切线长定理(共33张PPT)
切线长定理
PA、PB分别切⊙O于A、B
PA = PB
∠OPA=∠OPB
从圆外一点引圆的两条切线，它们的切线长相等。
几何语言:
反思：切线长定理为证明线段相等、角相等提供新的方法
O
P
A
B
试一试
A
P
O
B
若连结两切点A、B，AB交OP于点M.你又能得出什么新的结论?并给出证明.
a＋b－c
2
ab
a＋b＋c
· O
A
B
C
D
E
F
O
A
B
C
D
E
思考：如图，AB是⊙O的直径， AD、DC、BC是切线，点A、E、B 为切点，若BC=9，AD=4，求OE的长.
例题讲解
例1、已知：P为⊙O外一点，PA、PB为⊙O的 切线，A、B为切点，BC是直径。 求证：AC∥OP
P
A
C
B
D
B
A
P
O
C
E
D
（1）写出图中所有的垂直关系
OA⊥PA，OB ⊥PB，AB ⊥OP
（3）写出图中所有相等的线段
（2）写出图中与∠OAC相等的角
∠OAC=∠OBC=∠APC=∠BPC
OA=OB=OD=OE, PA-=PB, AC=BC, AE=BE
已知：如图,PA、PB是⊙O的切线，切点分别是A、B，Q为AB上一点，过Q点作⊙O的切线，交PA、PB于E、F点，已知PA=12CM，求△PEF的周长。
设AD= x , BE= y ,CE＝ r
∵ ⊙O与Rt△ABC的三边都相切
∴AD＝AF,BE＝BF,CE＝CD
切线长定理及应用
切线长定理及应用切线长定理是指在一个圆上，从圆外一点引出两条直线与圆相切，这两条直线的切线长相等。
这是一个非常重要的几何定理，其应用广泛，并被用于解决各种与圆相关的问题。
下面我将详细解释切线长定理及其应用。
首先，我们来证明切线长定理。
考虑一个圆C和直线L1与L2，L1和L2分别与圆C相切于点A和点B。
我们需要证明切线长AP等于切线长BP。
假设圆C的半径为r，圆心为O。
连接OA和OB，与切线AP和BP相交于点C 和点D。
根据切线与半径的性质，我们可以发现∠OAB = ∠OBA = 90度（因为OA和OB分别是切线AP和BP所在直线上的半径）。
因此，三角形OAB是等腰直角三角形，所以OA = OB = r。
另外，我们注意到OC = OD （根据切线与直径的性质），以及O为圆心，所以OC = OD = r。
因此，我们可以得出OC = OD = r，OA = OB = r，根据SSS（边-边-边）准则，三角形OAC和三角形OBD是全等的三角形。
根据全等三角形的定义，对应的角相等，因此∠OCA = ∠ODB。
又因为∠OCA =∠OAB（根据直角三角形性质），所以∠OAB = ∠ODB。
考虑直角三角形AOB和三角形BOC，他们共有角∠OBA和∠OAB。
又根据三角形内角和为180度的性质，我们知道∠OAB + ∠OBA + ∠OBA + ∠OCB = 180度（∠OBA + ∠OBA是两个直角）。
将前面得到的∠OAB = ∠OBA代入，我们可以得到2∠OBA + ∠OCB = 180度。
注意到∠OCB是圆心角，且∠BOA是圆周角，如果我们将∠OCB表示为α，将∠BOA表示为β，根据圆周角和圆心角的关系，我们知道α= 2β。
将α= 2β代入之前的等式，我们得到2∠OBA + 2∠OBA = 180度，化简之后得到4∠OBA = 180度，即∠OBA = 45度。
现在，考虑三角形OAB。
我们可以知道∠OAB = 45度，且OB = OA = r。
切线长定理课件
切线长定理的再一个推论
总结词
切线长定理的再一个推论是，若两圆在 同一直线上相切，则它们的切线互相平 行。
VS
详细描述
这个推论是切线长定理的进一步应用。当 两圆在同一直线上相切时，它们的切线不 仅长度相等，而且平行。这个推论在解决 涉及直线和圆的问题时非常有用，特别是 在几何证明和解析几何中。通过掌握这个 推论，学生可以更好地理解几何图形的性 质和关系，提高解决几何问题的能力。
切线长定理的另一个推论
总结词
切线长定理的另一个推论是，若两圆相切于同一点，则该点的切线与两圆心的连线垂直 。
详细描述
这个推论说明了当两圆在同一点相切时，该点的切线与两圆心的连线之间此，该点的切
线与两圆心的连线互相垂直。这个推论在证明几何定理和解决几何问题时非常有用。
切线长定理在数学、物理、工程等领 域有着广泛的应用，通过学习和掌握 这个定理，我们可以更好地理解和应 用相关领域的知识。
通过本次课件的学习，我们深入了解 了切线长定理的证明过程和实际应用 ，掌握了利用切线长定理解决实际问 题的技巧和方法。
展望
随着数学和其他学科的发展，切线长定理的应用范围将会更加广泛，我 们可以通过不断学习和探索，深入了解这个定理的更多应用和推广。
切线长定理的证明方法二
利用三角形的全等定理进行证明。首先，作辅助线连接圆心和切点，将切线分为两段。然后，根据三角形的全等定理，证明三 角形全等，从而得到切线长的平方等于半径的平方和。
切线长定理的证明方法三
利用向量进行证明。首先，根据向量的数量积公式，向量的数 量积等于两向量的模长乘以其夹角的余弦值。然后，利用切线 的性质，切线和半径垂直，从而夹角为90度。结合数量积公式 ，可以证明切线长的平方等于半径的平方和。
切线长定理及其应用
知识点一切线长定义及切线长定理1. _____________________________________________________ 切线长定义：过圆外一点作圆的切线，这点和____________________________________________ 之间的线段长叫作这点到圆的切线长注意切线长和切线的区别和联系：切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。
2. 切线长定理：过圆外一点引圆的两条切线，它们的切线长相等，即PA=PB.推论:(1) △ PAB是等腰三角形；(2) OP 平分△ APB，即△ APO A BPO ；(3) 弧AM=弧BM ;(4)在Rt OAP和Rt OBP中，由AB OP，可通过相似得相关结论;如：OA2 OB2 OE OP, AP2 BP2 PE PO, AE2 BE2 OE EP(5)图中全等的三角形有对，分别是：题型一切线长定理的直接应用【例1】如图所示，AO的半径为3cm,点P和圆心O的距离为6cm,经过点P的两条切线与AO切于点E、F,求这两条切线的夹角及切线长.【例2】如图，FA、PB、DE分别切A0于A、B、C, A O的半径长为6 cm, PO= 10 cm,求APDE的周长.切线长定理及其应用【例3】如图所示，△ ABC中，/ C=90 , AC=3 , AB=5 , D为BC边的中点，以AD上一点0为圆心的O0和AB、BC均相切，则O 0的半径为 ______________ .£4【过关练习】1•如图所示，PA、PB是AO的切线，A、B为切点，△ OAB=30°.( 1)求厶APB的度数.(2)当0A=3时,求AP的长•2•如图所示，已知PA、PB、DE分别切e 0于A、B、C三点，AO的半径为5cm, △ PED的周长为24cm , △ APB=50°求：(1) P0 的长；(2) △ EOD 的度数•3•如图，在直角梯形 ABCD 中,AB // CD,AB 丄BC,以BC 为直径的 △ 与AD 相切，点E 为AD 的中点，下列结论 正确的个数是( )B1 2知识点二圆外切四边形1、四边形的内切圆定义：四边形的四条边都与圆相切，把这个四边形叫作圆外切四边形，把这个圆叫作圆的内切圆2、圆外切四边形的性质：圆外切四边形两组对边之和 __________________ .（如图，即AB+CD=AD+BC ）题型一 四边形的内切圆计算【例1】已知四边形 ABCD 的边AB 、BC 、CD 、DA 与AO 相切于P 、Q 、M 、N ，求证：AB+CD=AD+BC 。
切线长定理的应用
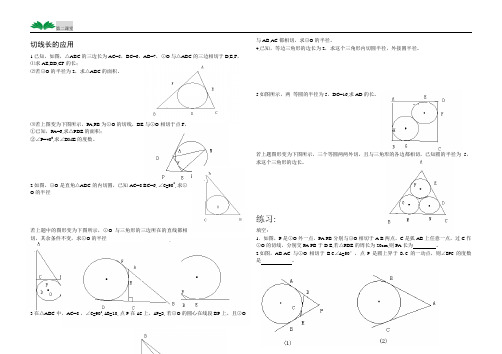
切线长的应用1.已知，如图，△ABC 的三边长为AC=5，BC=6，AB=7，⊙O 与△ABC 的三边相切于D,E,F ， ⑴求AE,BD,CF 的长；⑵若⊙O 的半径为2，求△ABC 的面积。
⑶若上图变为下图所示，PA,PB 为⊙O 的切线，DE 与⊙O 相切于点F ， ①已知，PA=6,求△PDE 的面积； ②∠P=400,求∠DME 的度数。
2.如图，⊙O 是直角△ABC 的内切圆，已知AC=8.BC=6,∠C=900,求⊙O 的半径若上题中的图形变为下图所示，⊙O 与三角形的三边所在的直线都相切，其余条件不变，求⊙O 的半径3.在△ABC 中，AC=8.，∠C=900,AB=10,点P 在AC 上，AP=2,若⊙O 的圆心在线段BP 上，且⊙O与AB,AC 都相切，求⊙O 的半径。
4,已知，等边三角形的边长为2，求这个三角形内切圆半径，外接圆半径。
5.如图所示，两 等圆的半径为5，DC=16,求AD 的长。
若上题图形变为下图所示，三个等圆两两外切，且与三角形的各边都相切，已知圆的半径为5，求这个三角形的边长。
练习:填空：1．如图，P 是⊙O 外一点，PA.PB 分别与⊙O 相切于A.B 两点，C 是弧AB 上任意一点，过C 作⊙O 的切线，分别交PA.PB 于D.E,若△PDE 的周长为20cm,则PA 长为 。
2.如图，AB.AC 与⊙O 相切于B.C ∠A=50°，点P 是圆上异于B.C 的一动点，则∠BPC 的度数是 。
3．如图，若⊙O的直径AB与弦AC的夹角为30°，切线CD与AB的延长线交于点D，且⊙O的半径为2，则CD的长为。
4．如图，PA为⊙O的切线，A为切点，PO交⊙O于B，PA=4,OA=3,则co s∠APO= .5.已知，R t△ABC中，∠C=90°，若AB=5,AC=3,则内切圆半径为，外接圆半径为。
6．边长为6.8.10的三角形的内心与外心的距离为。
第24章圆-《切线长定理》教案
4.实际案例：引入实际生活中与切线长定理相关的例子，如建筑设计、道路规划等。
二、核心素养目标
1.培养学生的几何直观和空间想象能力，通过切线长定理的理解和应用，提升对圆的性质和图形关系的认识；
2.发展学生的逻辑思维和推理能力，通过切线长定理的证明过程，学会运用数学语言和符号进行严谨的ห้องสมุดไป่ตู้证；
(3)提供典型例题，如给定圆的半径和圆外一点，求解切线长度，或给定切线长度和圆外一点，求解圆的半径。
2.教学难点
-几何图形的构建和想象：对于一些空间想象能力较弱的学生，构建切线和圆的关系可能会是一个难点。
-证明过程的逻辑推理：切线长定理的证明涉及到多个几何概念和逻辑推理，学生可能难以理解。
-实际问题的数学建模：将切线长定理应用于解决实际问题时，学生可能不知道如何将现实问题转化为数学模型。
五、教学反思
在本次教学过程中，我发现学生们对切线长定理的概念和应用表现出较大的兴趣。通过引入日常生活中的实例，他们能够更好地理解抽象的几何定理。然而，我也注意到在教学中存在一些需要改进的地方。
首先，学生在理解切线长定理的证明过程中，对相似三角形的运用仍存在困难。在今后的教学中，我应更加注重引导学生逐步推导和解释证明步骤，使他们真正理解几何原理。此外，可以适当增加一些变式题目，让学生在不同情境下运用相似三角形的性质，提高他们的灵活运用能力。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“切线长定理在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
切线长定理内容
切线长定理内容
切线长定理，又称为“切割定理”或“外切线定理”，是平面几何中的一个重要定理，它主要描述圆内接四边形中的一些关系。
具体来说，该定理指出：圆内接四边形的两条对角线相互垂直，当且仅当它们的对边之和相等。
也就是说，如果在一个圆内接四边形中，对角线BD与AC相互垂直，那么有AD+BC=AB+CD。
反之，如果AD+BC=AB+CD，那么对角线BD 与AC相互垂直。
这个定理的证明可以通过使用勾股定理、相似三角形、正弦定理等几何知识进行推导。
根据勾股定理，我们可以得到在半径为r的圆中，切线长度的平方等于切点到圆心的距离的平方减去半径的平方。
然后，应用正弦定理和相似三角形的性质，就可以得到切线长定理了。
切线长定理不仅是几何学中的重要定理，而且在各种实际应用场合中也有着广泛的应用。
例如，它可以用来计算圆内接四边形的对角线长度，或者用于建模和计算机图形学中。
此外，它还有着许多相关的推论和应用，例如垂径定理、欧拉线等等，在数学研究和应用中都有着重要的地位。
第3课时 切线长定理(教案)
第3课时切线长定理教学目标【知识与技能】理解掌握切线长的概念和切线长定理，了解三角形的内切圆和三角形的内心等概念.【过程与方法】利用圆的轴对称性帮助探求切线长的特征.结合求证三角形内面积最大的圆的问题，掌握三角形内切圆和内心的概念.【情感态度】经历观察、实验、猜想、证明等数学活动过程，发展合情推理能力.【教学重点】切线长定理及其应用.【教学难点】内切圆、内心的概念及运用.教学过程一、情境导入，初步认识探究如图，纸上有一⊙O，PA为⊙O的一条切线，沿着直线PO对折，设圆上与点A重合的点为B，回答下列问题：（1）OB是⊙O半径吗？（2）PB是⊙O的切线吗？（3）PA、PB是什么关系？（4）∠APO和∠BPO有何关系？学生动手实验，观察分析，合作交流后，教师抽取几位学生回答问题.分析：OB与OA重合，OA是半径，∴OB也是半径.根据折叠前后的角不变，∴∠PBO=∠PAO=90°（即PB⊥OB），PA=PB，∠POA=∠POB；∠APO=∠BPO.而PB经过半径OB的外端点，∴PB是⊙O的切线.二、思考探究，获取新知1.切线长的定义及性质切线长：经过圆外一点作圆的切线，这点和切点之间的线段的长叫做这点到圆的切线长.我们知道圆的切线是直线，而切线长是一条线段长，不是直线.如右图中，PA、PB是⊙O的两条切线，∴OA⊥PA，OB⊥PB.又OA=OB，OP=OP，∴Rt△AOP≌Rt△BOP，∴PA=PB，∠AOP=∠BOP，∠APO=∠BPO.由此我们得到切线长定理:从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.【教学说明】这个定理要让学生分清题设和结论.题设：过圆外一点作圆的切线.结论：①过圆外的这一点可作该圆的两条切线.②两条切线长相等.③这一点和圆心的连线平分两条切线的夹角.猜想：在上图中连接AB，则OP与AB有怎样的关系？分析：∵PA、PB是⊙O的切线，A、B是切点.∴PA=PB，∠OPA=∠OPB，∴OP⊥AB，且OP平分AB.2.三角形的内切圆思考如图是一张三角形的铁皮，如何在它上面截下一块圆形的用料，并且使圆的面积尽可能大呢？【教学说明】引导学生分析作图的关键，假设圆已经作出，圆心应满足什么条件，怎样根据这些条件确定圆心？圆心确定后，如何确定半径？教师引导，学生要互相讨论来解决这些问题.假设符合条件的圆已作出，那么这个圆与△ABC的三边都相切，这个圆的圆心到△ABC三边的距离都等于半径.又因为我们在角平分线这节中学过，三角形的三条角平分线交于一点，并且这个点到三条边的距离相等.因此，在△ABC 中，作∠B，∠C的角平分线BM和CN，它们相交于点I，则点I到AB、BC、AC的距离相等.∴以I为圆心，点I到BC的距离ID为半径作圆，则⊙I与△ABC 三边相切.内切圆：与三角形各边都相切的圆叫做三角形的内切圆.内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心.三角形的内心到三角形三边的距离相等.【教学说明】要让学生对照图形理解三角形的内切圆的概念，并与三角形的外接圆进行比较.“接”和“切”是说明多边形的顶点和边与圆的关系；多边形的顶点都在圆上叫“接”，多边形的边都与圆相切叫“切”.三、典例精析，掌握新知例1 教材第100页，例2（本题较简单，教师指点，可由学生自主完成）例2 如图，P为⊙O外一点，PA、PB分别切⊙O于A、B两点，连接OP，交⊙O于C，若PA=6.PC=23.求⊙O的半径OA及两切线PA、PB的夹角.分析：连接OA，设AO=x，在Rt△AOP中利用勾股定理求出x，由切线长定理知∠APO=12∠APB.求出∠APO就可得∠APB.解：连接AO，∵PA是⊙O的切线，∴PA⊥OA，△PAO为直角三角形.设OA=x，则OC=x，在Rt△PAO中，OA2+PA2=OP2，∴x2+62=(23+x)2，解得:x=23.∴OA=23，OP=43，∴∠AOP=60°，∠APO=30°.∴∠APB=2∠APO=2×30°=60°.∴⊙O的半径OA为23，两切线PA、PB的夹角为60°.【教学说明】例1、例2是利用切线长定理进行计算，在解题过程中，我们常常用方程来解决几何问题.例3如图，在△ABC中，I是内心，∠BIC=100°，则∠A=____.分析：∵I是内心.∴BI，CI分别是∠ABC，∠ACB的平分线.∴∠ABC+∠ACB=2（∠IBC+∠ICB）.又∵∠BIC=100°，∴∠IBC+∠ICB=80°.∴∠ABC+∠ACB=160°.∴∠A=180°-160°=20°.【教学说明】指导学生利用三角形内心的性质解决问题.四、运用新知，深化理解课本第100页练习1、2题.【教学说明】教师引导学生完成课本练习.五、师生互动，课堂小结这节课学习了哪几个重要知识点？你有哪些疑惑？【教学说明】学生自主交流并发言总结，教师予以补充和点评，让学生完整地领会本堂课的知识要点.课后作业1.布置作业：从教材“习题24.2”中选取.2.完成练习册中本课时练习的“课后作业”部分.教学反思。
初中数学 切线长定理的应用有哪些
初中数学切线长定理的应用有哪些
切线长定理是初中数学中与圆相关的一个重要定理，它有广泛的应用。
下面我将详细介绍切线长定理的几个常见应用。
1. 判断切线的长度相等：
-已知一个圆上的两条切线与同一个角相交，且角的顶点在切点上，判断这两条切线的长度是否相等。
根据切线长定理可得：如果两条切线与同一个角相交，且角的顶点在切点上，那么这两条切线的长度相等。
2. 求解切点坐标：
-已知一个圆的方程及一条切线的方程，求解切点的坐标。
根据切线长定理的性质可得：切点的坐标可以通过将切线的方程与圆的方程联立求解得到。
3. 求解切线的斜率：
-已知一个圆的方程及切点的坐标，求解切线的斜率。
根据切线长定理的性质可得：切线的斜率可以通过切点的坐标和圆的方程求解得到。
4. 判断切线与其他直线的关系：
-已知一个圆和一条直线，判断这条直线与圆的关系。
根据切线长定理可得：如果一条直线与圆相交于一个点，并且这个点是圆的切点，那么这条直线是圆的切线。
5. 解决圆的切线问题：
-切线长定理可以用于解决与圆的切线相关的问题。
例如，求解切线的长度、判断切线的存在与位置关系、求解切线与角的关系等。
切线长定理在初中数学中有广泛的应用，可以帮助我们解决与切线和圆相关的问题，判断切线的长度相等、求解切点的坐标和切线的斜率，判断切线与其他直线的关系，以及解决圆的切线问题。
在应用切线长定理时，需要注意定理的性质和运用几何知识进行推理和分析。
希望以上内容能够满足你对切线长定理应用的了解。
圆的切线长定理
圆的切线长定理圆的切线长定理是几何学中的重要定理之一，它描述了一个切线与圆的相交关系以及切线的长度和与圆的位置有关。
这个定理被广泛应用于各个领域，包括物理学、工程学和计算机图形学等。
本文将详细介绍圆的切线长定理及其应用。
一、圆的切线长定理的表述圆的切线长定理可以用以下方式表述：如果在圆上有一点P，并且通过这点作一条直线与圆相交于A、B两点，那么线段PA和线段PB 的乘积等于切线与圆心连线的长度的平方。
即PA * PB = PT^2，其中T是切点。
二、圆的切线长定理的证明要证明圆的切线长定理，可以使用几何推理和三角关系。
设圆的半径为r，圆心为O，切点为T，切线与圆心连线为OT。
连接OA、OB，得到△OAT和△OBT两个直角三角形。
由正弦定理可得：sin∠OAT = r / OTsin∠OBT = r / OT又因为∠OAT和∠OBT是互余角（补角），即∠OAT + ∠OBT = 90°，所以sin∠OAT = cos∠OBT。
将上述两个等式代入PA * PB = PT^2，得到：r * r = PA * PB因此，圆的切线长定理得证。
三、圆的切线长定理的应用圆的切线长定理可以应用于很多实际问题中。
以下是一些具体应用：1. 圆的切线长定理可以用于计算切线的长度。
如果已知圆的半径和切线与圆的位置，可以通过切线长定理计算切线的长度。
2. 圆的切线长定理可以用于求解与圆相切的直线方程。
通过已知切点和切线长度，可以确定切线的位置，从而求解与圆相切的直线方程。
3. 圆的切线长定理可以应用于计算切线与圆心连线的长度。
通过已知切线长度和切点，可以计算切线与圆心连线的长度。
4. 圆的切线长定理还可以用于解决几何问题。
例如，判断两个圆是否相切，可以通过切线长定理计算切线的长度，从而判断圆是否相切。
圆的切线长定理是几何学中的重要定理，它描述了切线与圆的相交关系以及切线的长度和与圆的位置的关系。
通过应用该定理，我们可以解决各种与圆相关的问题，从而推动几何学的发展和应用。
小专题(十四) 切线长定理的变式与应用
小专题(十四) 切线长定理的变式与应用类型1 “单个”切线长定理方法归纳：通常利用切线长相等以及圆外这点与圆心的连线平分两切线的夹角解决问题．1．如图，PA ，PB 是⊙O 的切线，切点为A 、B ，若OP ＝4，PA ＝23，则∠APB 的度数为(A )A ．60°B ．90°C ．120°D ．无法确定类型2 “两个”切线长定理方法归纳：常常利用圆心与圆外两点构成直角三角形解决问题．2．已知：如图，AB ，BC ，CD 分别与⊙O 相切于E ，F ，G ，且AB ∥CD ，BO ＝6，CO ＝8，求OF 的长．解：∵AB ，BC ，CD 分别与⊙O 相切于E ，F ，G ，∴∠EOB ＝∠BOF ，∠COF ＝∠COG ，OF ⊥BC.∵AB ∥CD ，∴∠BOF ＋∠COF ＝90°.又∵BO ＝6，CO ＝8，∴BC ＝10.∵S △BOC ＝12OB·OC ＝12BC·OF ， ∴OF ＝245.类型3 “三个”切线长定理方法归纳：如图1中，有结论△PDE 的周长＝2PA ＝2PB.如图2中，有结论AE ＝AF ＝b ＋c －a 2；BF ＝BD ＝a ＋c －b 2；CD ＝CE ＝a ＋b －c 2. 特殊的，如图3，当∠C ＝90°时，r ＝a ＋b －c 2(或ab a ＋b ＋c)．3．如图，AD，AE分别是⊙O的切线，D，E为切点，BC切⊙O于F，交AD，AE于点B，C.若AD＝8，则△ABC的周长是(C)A．8 B．10C．16 D．不能确定4．如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D、E，过劣弧DE(不包括端点D，E)上任一点P作⊙O的切线MN与AB，BC分别交于点M，N，若⊙O的半径为4 cm，则Rt△MBN的周长为8_cm．5．如图，Rt△ABC的内切圆⊙O与AB，BC，AC分别切于点D，E，F，且AC＝13，AB＝12，∠ABC＝90°，求⊙O的半径长．解：在Rt△ABC中，∵AC＝13，AB＝12，∴BC＝132－122＝5.∵Rt△ABC的内切圆⊙O与AB，BC分别切于点D，E，∴OD⊥AB，OE⊥BC，OD＝OE.又∵∠ABC＝90°，∴四边形BEOD为正方形．∴BD＝BE＝OD.设⊙O的半径长为r，则BE＝BD＝r，AD＝AB－BD＝12－r，CE＝BC－BE＝5－r，∵Rt△ABC的内切圆⊙O与AB，BC，AC分别切于点D，E，F，∴AF＝AD＝12－r，CF＝CE＝5－r.∴12－r＋5－r＝13.解得r＝2.即⊙O的半径长为2.类型4“四个”切线长定理方法归纳：圆的外切四边形的两组对边的和相等．6．如图，⊙O内切于四边形ABCD，AB＝10，BC＝7，CD＝8，则AD的长度为(D)A．8 B．9 C．10 D．11。
直线与圆的位置关系切线长定理
直线与圆的位置关系切线长定理在几何学中，直线与圆的位置关系一直是一个重要的研究课题。
其中，切线长定理是直线与圆的位置关系中的一个重要定理，它在解决直线与圆的位置关系问题时起着至关重要的作用。
本文将介绍切线长定理的定义、推导过程及其应用。
一、切线长定理的定义切线长定理是指直线与圆的位置关系中，一条直线与圆相切时，切线与切点之间的长度关系。
具体来说，切线长定理可以表述为：一条直线与圆相切时，切线与切点之间的长度平方等于切点到圆心的距离的平方减去圆的半径的平方。
切线长定理可以用公式表示为：PT^2 = PC^2 - r^2其中，PT表示切线与切点之间的长度，PC表示切点到圆心的距离，r表示圆的半径。
二、切线长定理的推导切线长定理的推导可以通过几何方法和代数方法来进行。
这里我们将介绍一种代数方法的推导过程。
假设圆的方程为(x-a)^2 + (y-b)^2 = r^2，其中(a, b)为圆心坐标，r为圆的半径。
直线的方程为y = kx + c，其中k为直线的斜率，c为直线的截距。
首先，我们要找到直线与圆相切的条件。
直线与圆相切的条件是直线与圆的切点只有一个，也就是直线与圆的方程组有且只有一个解。
将直线方程代入圆的方程中，得到一个关于x的二次方程：(x-a)^2 + (kx+c-b)^2 = r^2解这个方程，得到直线与圆相切的条件：Δ = (k^2+1)(c-b)^2 - (1+k^2)(a^2+b^2-r^2) = 0其中，Δ为方程的判别式。
当Δ=0时，直线与圆相切。
接下来，我们要求出切线与切点之间的长度。
设直线与圆的切点为P(x0, y0)，则切点到圆心的距离为：PC^2 = (x0-a)^2 + (y0-b)^2切线与切点之间的长度为：PT^2 = (x-x0)^2 + (y-y0)^2将直线方程代入PT^2的表达式中，得到：PT^2 = (x-x0)^2 + (kx+c-y0)^2将PT^2和PC^2代入切线长定理的公式中，得到：(x-x0)^2 + (kx+c-y0)^2 = (x0-a)^2 + (y0-b)^2 - r^2 化简上式，得到切线长定理的公式：PT^2 = PC^2 - r^2三、切线长定理的应用切线长定理在解决直线与圆的位置关系问题时起着重要作用。
数学教案-切线长定理
数学教案－切线长定理一、教学目标通过本节课的学习，学生将能够：1.理解和应用切线长定理2.解决与切线相关的数学问题3.培养分析和解决问题的能力二、教学重点1.切线长定理的理解和应用2.切线长定理与有关角度的关系三、教学内容1. 切线长定理切线长定理，又称为切线定理，是解决与圆相关问题时非常有用的定理之一。
切线长定理的内容是：从一点到圆的切线的线段长等于该点到圆心的距离。
具体而言，对于一个圆，我们找到一个点P在圆上，连接点P与圆心O，并作P到圆的切线。
切线长定理告诉我们，切线的长度等于点P到圆心O的距离。
这个定理也可以用公式表示为：PA = PT其中，PA表示点P到圆心O的距离，PT表示点P与圆的切线的长度。
2. 切线长定理的证明切线长定理的证明可以通过利用几何图形来完成。
我们可以假设点P在圆上，并连接点P与圆心O，作P到圆的切线，并将其延长至与圆相交于点T。
由于点T与点P都在切线上，所以PT是切线的一部分，而PA等于点P到圆心O的距离。
由于OT是半径，所以OT也等于OP。
根据勾股定理，我们可以得到以下等式：PT^2 + OT^2 = OP^2由此可得：PT = sqrt(OP^2 - OT^2)由于OT等于半径，而OP等于PA，所以我们可以得到：PT = sqrt(PA^2 - r^2)这就证明了切线长定理。
3. 切线长定理的应用切线长定理在解决与圆相关的数学问题中非常有用。
我们可以通过利用切线长定理来解决一些具体问题，比如：•已知一个圆的半径和一个点到圆心的距离，如何确定从该点出发的切线的长度？•已知一个圆的半径和一条与圆相交的直线，如何确定该直线是切线的条件？•如何确定一条直线与一个圆的相交点的位置关系？通过学习切线长定理，我们可以更好地理解和解决这些问题。
四、教学方法本节课将采用以下教学方法进行教学：1.授课法：通过讲解切线长定理的定义、证明和应用来介绍相关概念和知识点。
2.举例法：通过实例分析和解决问题，帮助学生更好地理解和应用切线长定理。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
切线长定理及其应用
知识点一 切线长定义及切线长定理
1. 切线长定义：过圆外一点作圆的切线，这点和 之间的线段长叫作这点到圆的切线长.
注意切线长和切线的区别和联系:
切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。
2. 切线长定理：过圆外一点引圆的两条切线，它们的切线长相等，即PA=PB.
推论：
（1）△PAB 是等腰三角形；
（2）OP 平分△APB ，即△APO=△BPO ；
（3）弧AM=弧BM ；
（4）在Rt OAP ∆和Rt OBP ∆中，由AB OP ⊥，可通过相似得相关结论；
如：222222,,OA OB OE OP AP BP PE PO AE BE OE EP ==⋅==⋅==⋅
（5）图中全等的三角形有
对，分别是：
题型一 切线长定理的直接应用
【例1】如图所示，△O 的半径为3cm ，点P 和圆心O 的距离为6cm ，经过点P 的两条切线与△O 切于点E 、
F ，求这两条切线的夹角及切线长.
【例2】如图，P A 、PB 、DE 分别切△O 于A 、B 、C ，△O 的半径长为6 cm ，PO ＝10 cm ，求△PDE 的周长．
【例3】如图所示，△ABC中，∠C=90°，AC=3，AB=5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为__________.
【过关练习】
1.如图所示，PA、PB是△O的切线，A、B为切点，△OAB=30°.（1）求△APB的度数.（2）当OA=3时，求AP的长.
2.如图所示，已知PA、PB、DE分别切O于A、B、C三点，△O的半径为5cm，△PED的周长为24cm，△APB=50°.求：（1）PO的长；（2）△EOD的度数.
3.如图,在直角梯形ABCD 中,AB ∥CD,AB ⊥BC,以BC 为直径的△O 与AD 相切,点E 为AD 的中点,下列结论正确的个数是( )
(1)AB+CD=AD;
(2)DCE ABE BCE S S S △△△+=; (3)241BC CD AB =⋅; (4)∠ABE=∠DCE. A.1
B.2
C.3
D.4
知识点二 圆外切四边形
1、四边形的内切圆定义：
四边形的四条边都与圆相切，把这个四边形叫作圆外切四边形，把这个圆叫作圆的内切圆.
2、圆外切四边形的性质：圆外切四边形两组对边之和
.（如图，即AB +CD =AD +BC ） 题型一 四边形的内切圆计算
【例1】已知四边形ABCD 的边AB 、BC 、CD 、DA 与△O 相切于P 、Q 、M 、N ，求证：AB+CD=AD+BC 。
【例2】圆外切四边形相邻三边的比是3:4:5，四边形的周长是48，则四边形各边的长是多少？
【例3】如图所示，在矩形ABCD中，AB=4，AD=5，AD、AB、BC分别于△O相切于E、F、G三点，过点D作△O的切线交BC于点M，切点为N，则DM 的长为.
【过关练习】
1.如图，一圆内切四边形ABCD，且AB=16，CD=10，则四边形的周长为（）
A．50B．52C．54D．56
2.如图，△O的外切梯形ABCD中，若AD△BC，那么△DOC的度数为（）
A．70°B．90°C．60°D．45°
课后练习
【补救练习】
1.如图，点P在⊙O外，PA、PB分别与⊙O相切于A、B两点，∠P=50°，则∠AOB等于（）
A.150°
B.130
C.155°
D.135°
2.如图，PA、PB是△O的两条切线，切点是A、B．如果OP=4，PA=2，那么△AOB等于（）A．90°B．100°C．110°D．120°
3、如图所示，PA、PB分别切△O于A、B两点，C为劣弧AB上一点，△APB=30°，则△ACB=（）
4、如图，PA、PB、DE分别切△O于A、B、C，DE分别交PA，PB于D、E，已知P到△O的切线长为8cm，则Δ PDE的周长为（）
A. 16cm
B. 14cm
C.12cm
D.8cm
5、圆外一点P，引PA、PB分别切△O于点A、B，C为优弧AB上一点，若△ACB=α，则△APB=.
6、如图所示，PA、PB是△O的两条切线，A，B为切点，求证：2△ABO=△APB.
7、如图所示，四边形ABCD外切于△O，且AB=16，CD=10，求四边形ABCD的周长.
【巩固练习】
1、从圆外一点向半径为9的圆作切线，已知切线长为18，从这点到圆的最短距离是.
2、如图所示，AB是△O的直径，点C为△O外一点，CA，CD是△O的切线，A，D为切点，连接BD、AD，若△ACD=30°，则△DBA大小是（）
A.15°
B.30°
C.60°
D.75°
3、如图1，一个圆球放置在V型架中，图2是它的平面示意图，CA、CB都是△O的切线，切点分别是A、
B，如果△O
4、如图所示，EB、EC是△O的两条切线，B、C是切点，A、D是△O上两点，如果△E=46°，△DCF=32°，求△A的度数.
6、如图，在梯形ABCD中，AD//BC，AB⊥BC，以AB为直径的⊙O与DC相切于E．已知AB=8，边BC 比AD大6，求边AD、BC的长。
7、如图所示，EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，求∠A的度数.
8、已知：如图，P为⊙O外一点，PA，PB为⊙O的切线，A和B是切点，BC是直径。
∠C＝50，
①求∠APB的度数②求证：AC∥OP。
【拔高练习】
1、如图,P为△O的直径BA延长线上的一点,PC与△O相切,切点为C,点D是△O上一点,连接PD.已知
PC=PD=BC.下列结论:(1)PD与△O相切;(2)四边形PCBD是菱形;(3)PO=AB;(4)△PDB=120°.
其中正确的个数为()
A.4个
B.3个
C.2个
D.1个
2、如图，若△ABC的三边长分别为AB=9，BC=5，CA=6，△ABC的内切圆△O切AB、BC、AC于D、E、F，则AF的长为（）
A．5B．10C．7.5D．4
3、已知：如图，AB为⊙O的直径，CD、CB为⊙O的切线，D、B为切点，OC交⊙O于点E，AE的延长线交BC于点F，连接AD、BD．以下结论：①AD∥OC；②点E为△CDB的内心；③FC=FE；
④CE•FB=AB•CF．其中正确的只有（）
A．①②B．②③④C．①③④D．①②④
4、如图，正方形ABCD边长为4cm，以正方形的一边BC为直径在正方形ABCD内作半圆，过A作半圆的切线，与半圆相切于F点，与DC相交于E点，则△ADE的面积（）
A．12 B．24 C．8 D．6
5、如图，PA、PB分别是⊙O的切线，A、B为切点，AC是⊙O的直径，已知∠BAC=35°，∠P为（）A．35°B．45°C．60°D．70°
6、如图，在△BCE中，点A是边BE上一点，以AB为直径的⊙O与CE相切于点D，AD∥OC，点F为OC 与⊙O的交点，连接AF。
（1）求证：CB是⊙O的切线。
（2）若∠ECB=60°，AB=6，求图中阴影部分的面积。