切线长和切线长定理的应用

合集下载

初中数学第六册切线长定理用途教案

我们先来看看初中数学第六册中介绍的切线长定理是什么？切线长定理是指，如果在圆内任取一点P作一条直线与圆相交，交点分别为A、B，则AP、BP的乘积等于切线BC的平方，即AP × BP = BC^2。

接下来，我们来探讨一下切线长定理在实际生活中有哪些用途。

一、建筑工程
在建筑工程中，切线长定理常被应用于圆柱体的斜侧面上。

以一根圆柱形的管为例子，从管的一侧用尺子量出管径D，再从管的对边上，延长一条与对边平行的线段，用尺子测出该线段的长度L，那么根据切线长定理，我们就可以求出管的斜侧面长度H了。

H=√(L^2 - D^2)
切线长定理的应用，能够非常准确地计算出斜侧面长度，从而更好地指导建筑工程的完成。

二、机械制造
在机械制造中，切线长定理也有着重要的应用。

例如，在汽车发动机的齿轮齿条连接处，就需要应用到切线长定理。

由于齿轮锥与齿条倾角不同，因此需要利用切线长定理来计算出锥齿轮齿高。

通过计算锥齿轮齿高，我们可以精确的控制汽车的齿轮连接处，保证其工作的可靠性和稳定性。

三、科学研究
切线长定理在科学研究中也有着重要的应用。

例如，在医学领域中，我们利用切线长定理，可以计算出人体血液的流速。

当血管壁发生了弯曲，就会形成一个圆弧，我们可以利用切线长定理计算出这个圆弧上的切线长，搭配计时器，就能精确地计算出血液在圆弧上的流速了。

切线长定理在生活和科学研究中的应用是十分广泛的，它不仅解决了生活中的实际问题，还帮助我们更好地认识到圆形和直线的关系，为我们的学习和工作提供了很好的指导。

郭氏数学-圆的切线长定理、弦切角定理、切割线定理、相交弦定理

郭氏数学-圆的切线长定理、弦切角定理、切割线定理、相交弦定理切线长定理、弦切角定理、切割线定理、相交弦定理以及与圆有关的比例线段1.切线长概念切线长是在经过圆外一点的圆的切线上，这点和切点之间的线段的长度，“切线长”是切线上一条线段的长，具有数量的特征，而“切线”是一条直线，它不可以度量长度。

2.切线长定理对于切线长定理，应明确（1）若已知圆的两条切线相交，则切线长相等；（2）若已知两条切线平行，则圆上两个切点的连线为直径；（3）经过圆外一点引圆的两条切线，连结两个切点可得到一个等腰三角形；（4）经过圆外一点引圆的两条切线，切线的夹角与过切点的两个半径的夹角互补；（5）圆外一点与圆心的连线，平分过这点向圆引的两条切线所夹的角。

3.弦切角：顶点在圆上，一边和圆相交，另一边和圆相切的角。

直线AB切⊙O于P，PC、PD为弦，图中几个弦切角呢？（四个）4.弦切角定理：弦切角等于其所夹的弧所对的圆周角。

5.弄清和圆有关的角：圆周角，圆心角，弦切角，圆内角，圆外角。

6.遇到圆的切线，可联想“角”弦切角，“线”切线的性质定理及切线长定理。

7.与圆有关的比例线段定理图形已知结论证法相交弦定理⊙O中，AB、CD为弦，交于P.PA·PB＝PC·PD.连结AC、BD，证：△APC∽△DPB.相交弦定理的推论⊙O中，AB为直径，CD⊥A B于P.PC2＝PA·PB.用相交弦定理.切割线定理⊙O中，PT切⊙O于T，割线PB交⊙O于APT2＝PA·PB连结TA、TB，证：△PTB∽△PAT切割线定理推论PB、PD为⊙O的两条割线，交⊙O于A、CPA·PB＝PC·PD过P作PT切⊙O于T，用两次切割线定理圆幂定理⊙O中，割线PB交⊙O于A，CD为弦P'C·P'D＝r2－OP'2PA·PB＝OP2－r2r为⊙O的半径延长P'O交⊙O于M，延长OP'交⊙O于N，用相交弦定理证；过P作切线用切割线定理勾股定理证8.圆幂定理：过一定点P向⊙O作任一直线，交⊙O 于两点，则自定点P到两交点的两条线段之积为常数||（R为圆半径），因为叫做点对于⊙O的幂，所以将上述定理统称为圆幂定理。

切线长定理课件

练习题1的解答：利用切线长定理， CD=AB^2/2*OA=8^2/2* 5=16cm。
总结与回顾
切线长定理是一个重要的几何定理，可以应用于各种实际问题中。通过本课件的学习，你已经了解了切线长度的定义、切线长定理的表述、应用场景和证明方法。希望你能够运用切线长定理解决更多的问题。
2
基于勾股定理
利用勾股定理和圆的性质，可以得以证明切线长定理。
举例说明切线长定理的应用
建筑设计
通过切线长定理，可以确定建筑中圆形元素的尺寸和位置，使建筑更美观。
光学折射
使用切线长定理可以计算光线在界面上的折射角度，帮助设计光学仪器。
机械工程
切线长定理
切线长定理是关于切线长度的一个重要定理，可以应用于许多实际问题中。本课件将介绍切线长度的定义、表述、应用场景以及证明方法。
切线长度的定义
切线是与圆相切于一点且只与圆有此一点的直线。切线长度是指切线与圆的切点之间的距离。
切线长定理的表述
切线长定理指出，在同一个圆上，相同弧所对的切线长度相等。
在机械设计中，切线长定理可以帮助确定圆形零件的位置和运动轨迹。
练习题及答案解析
1 练习题1
2 练习题2
3 答案解析
如图所示，在圆O中，AB 是切线，CD是弦， AB=8cm，CD=10cm，求弦CD的长度。
已知圆O的半径为5cm，切线AB与弦CD相交于点E，且AB=7cm，求弦CD的长度。
切线长定理的应用场景
几何问题
切线长定理可以帮助我们解决关于圆的几何问题，例如确定切点的位置。
物理应用
在光学中，切线长定理可以用于计算光线在界面上的折射与反射。
工程设计
在建筑和机械设计中，切线长定理可以帮助我们确定圆形零件的尺寸和位置。

切线长定理及应用

切线长定理及应用切线长定理是解决几何问题中常用的定理之一，它在许多实际应用中发挥着重要的作用。

本文将介绍切线长定理的概念、证明以及一些实际应用。

一、切线长定理的概念切线长定理是指在一个圆上，从圆外一点引出的切线与半径的乘积等于切点到圆心的距离的平方。

换句话说，如果从圆外一点引出一条切线，那么切线与半径的乘积等于切点到圆心的距离的平方。

二、切线长定理的证明为了证明切线长定理，我们可以利用几何推理和一些基本的几何定理。

首先，我们可以通过连接圆心、切点和圆上的一个点，构成一个直角三角形。

然后，利用勾股定理和相似三角形的性质，我们可以得出切线长定理的结论。

三、切线长定理的应用切线长定理在实际应用中有着广泛的应用。

以下是一些常见的应用场景：1. 圆的切线问题：切线长定理可以帮助我们解决与圆相关的问题，例如确定切线的长度、判断两条切线是否相等等。

2. 几何建模：在几何建模中，切线长定理可以用于计算和确定物体表面的切线长度，从而帮助我们进行准确的建模和设计。

3. 光学问题：在光学问题中，切线长定理可以用于计算光线的传播路径和角度，从而帮助我们理解光的行为和性质。

4. 工程测量：在工程测量中，切线长定理可以用于计算和确定测量点与目标物之间的距离和位置关系，从而帮助我们进行精确的测量和定位。

5. 数学建模：在数学建模中，切线长定理可以用于建立数学模型，从而帮助我们解决各种实际问题，例如物体运动的轨迹、曲线的切线方程等。

总结：切线长定理是解决几何问题中常用的定理之一，它在圆的切线问题、几何建模、光学问题、工程测量和数学建模等领域都有着广泛的应用。

通过理解和应用切线长定理，我们可以更好地解决实际问题，提高问题求解的准确性和效率。

切线长定理

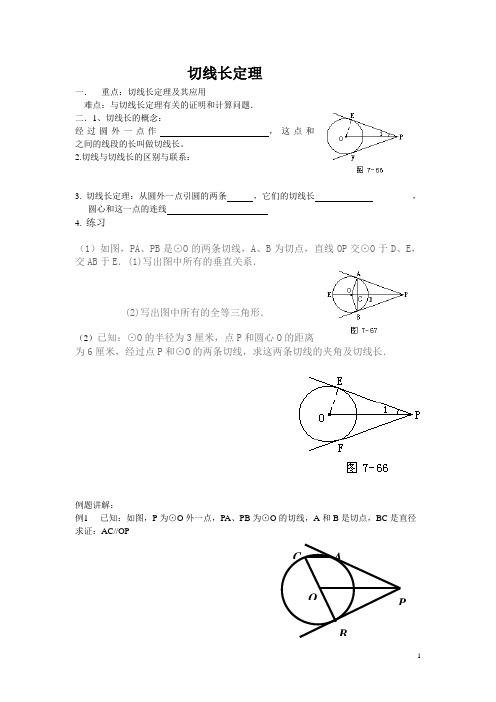
切线长定理一．重点：切线长定理及其应用难点：与切线长定理有关的证明和计算问题．二．1、切线长的概念：经过圆外一点作，这点和之间的线段的长叫做切线长。

2.切线与切线长的区别与联系：3. 切线长定理：从圆外一点引圆的两条，它们的切线长，圆心和这一点的连线 4. 练习（1）如图，PA 、PB 是⊙O 的两条切线，A 、B 为切点，直线OP 交⊙O 于D 、E ，交AB 于E ．(1)写出图中所有的垂直关系．(2)写出图中所有的全等三角形．（2）已知：⊙O 的半径为3厘米，点P 和圆心O 的距离为6厘米，经过点P 和⊙O 的两条切线，求这两条切线的夹角及切线长．例题讲解：例1 已知：如图，P 为⊙O 外一点，PA 、PB 为⊙O 的切线，A 和B 是切点，BC 是直径求证：AC//OPABC OP例2 圆外切四边形的两组对边的和相等．已知：如图，四边形ABCD 的边AB 、BC 、CD 、DA和⊙O 分别相切于L 、M 、N ，P ．求证：AB+CD=AD+BC ．练习：1. 圆内接平行四边形是_____2.圆外切平行四边形是_______ 例题3.如图，某镇在进入镇区的道路交叉口的三角地处建造了一座镇标雕塑，以树立起文明古镇的形象。

已知雕塑中心M 到道路三边AC 、BC 、AB 的距离相等，AC ⊥BC ，BC=30米，AC=40米。

请你帮助计算一下，镇标雕塑中心M 离道路三边的距离有多远？A CB古镇镇商业镇工业区.M弦切角教学重点：弦切角定理及其应用是重点．教学难点：弦切角定理的证明是难点．一．探究1.弦切角的定义：顶点在，一边和圆，另一边和圆的角叫做弦切角。

2. 弦切角定理：弦切角等于 3、推论：如果两个弦切角所夹的弧相等，那么二．例题例1如图，已知AB 是⊙O 的直径，AC 是弦，直线CE 和⊙O 切于点C ,AD ⊥CE ,垂足为D 。

求证： AC 平分∠BAD例2、如图，已知AB 是⊙O 的切线，切点为A ，OB 交⊙O 点C ,AD ⊥OB ,垂足为D 。

切线长定理及应用

切线长定理及应用切线长定理是指在一个圆上，从圆外一点引出两条直线与圆相切，这两条直线的切线长相等。

这是一个非常重要的几何定理，其应用广泛，并被用于解决各种与圆相关的问题。

下面我将详细解释切线长定理及其应用。

首先，我们来证明切线长定理。

考虑一个圆C和直线L1与L2，L1和L2分别与圆C相切于点A和点B。

我们需要证明切线长AP等于切线长BP。

假设圆C的半径为r，圆心为O。

连接OA和OB，与切线AP和BP相交于点C 和点D。

根据切线与半径的性质，我们可以发现∠OAB = ∠OBA = 90度（因为OA和OB分别是切线AP和BP所在直线上的半径）。

因此，三角形OAB是等腰直角三角形，所以OA = OB = r。

另外，我们注意到OC = OD （根据切线与直径的性质），以及O为圆心，所以OC = OD = r。

因此，我们可以得出OC = OD = r，OA = OB = r，根据SSS（边-边-边）准则，三角形OAC和三角形OBD是全等的三角形。

根据全等三角形的定义，对应的角相等，因此∠OCA = ∠ODB。

又因为∠OCA =∠OAB（根据直角三角形性质），所以∠OAB = ∠ODB。

考虑直角三角形AOB和三角形BOC，他们共有角∠OBA和∠OAB。

又根据三角形内角和为180度的性质，我们知道∠OAB + ∠OBA + ∠OBA + ∠OCB = 180度（∠OBA + ∠OBA是两个直角）。

将前面得到的∠OAB = ∠OBA代入，我们可以得到2∠OBA + ∠OCB = 180度。

注意到∠OCB是圆心角，且∠BOA是圆周角，如果我们将∠OCB表示为α，将∠BOA表示为β，根据圆周角和圆心角的关系，我们知道α= 2β。

将α= 2β代入之前的等式，我们得到2∠OBA + 2∠OBA = 180度，化简之后得到4∠OBA = 180度，即∠OBA = 45度。

现在，考虑三角形OAB。

我们可以知道∠OAB = 45度，且OB = OA = r。

切线长和圆与圆的位置关系

切线长和切线长定理及圆与圆的位置关系一、切线长和切线长定理：⑴ 切线长：在经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长．⑵ 切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，圆心和这一点的连线平分两条切线的夹角．二、三角形内切圆1．定义：和三角形各边都相切的圆叫做三角形的内切圆，内切圆的圆心叫做三角形的内心，这个三角形叫做圆的外切三角形．2．多边形内切圆：和多边形的各边都相切的圆叫做多边形的内切圆，这个多边形叫做圆的外切多边形．3．直角三角形的内切圆半径与三边关系OF ED C BACBA CBAcbacba（1）（2）图（1）中，设a b c ，，分别为ABC ∆中A B C ∠∠∠，，的对边，面积为S则内切圆半径（1）s r p =，其中()12p a b c =++；图（2）中，90C ∠=︒，则()12r a b c =+-、abr a b c=++重难点：切线的判定定理；切线的性质定理及其运用它们解决一些具体的题目．1.切线长定理及切线性质的应用例题1（2011·济宁）如图，AB 是⊙O 的直径，AM 和BN 的两条切线，DE 切⊙O 于点E ，交AM 与于点D ，交BN 于点C ，F 是CD 的中点，连接OF 。

（1）求证：OD ∥BE;(2) 猜想：OF 与CD 有何数量关系？并说明理由。

解：（1）证明：连接OE∵AM 、DE 是⊙O 的切线，OA 、OE 是⊙O 的半径 ∴∠ADO=∠EDO,∠DAO=∠DEO=90°…………1分∴∠AOD=∠EOD=21∠AOE …………2分 ∵∠ABE=21∠AOE ∴∠AOD=∠ABE ∴OD ∥BE …………3分 (2) OF =21CD …………4分理由：连接OC∵BE 、CE 是⊙O 的切线∴∠OCB=∠OCE …………5分 ∵AM ∥BN∴∠ADO+∠EDO+∠OCB+∠OCE=180° 由（1）得 ∠ADO=∠EDO∴2∠EDO+2∠OCE=180° 即∠EDO+∠OCE=90° …………6分在Rt △DOC 中， ∵ F 是DC 的中点 ∴OF =21CD ……7分三、圆与圆的位置关系重点：两个圆的五种位置关系中的等价条件及它们的运用．难点：探索两个圆之间的五种关系的等价条件及应用它们解题．易错点：1）圆与圆位置关系中相交时圆心距在两圆半径和与差之间， 2）没有公共点要考虑外离和内含的两种情况 3）有一个公共点要考虑内切与外切两种情况4）两圆相交求的公共弦多对的圆周角，求出圆心距一般都有两种情况圆与圆的位置关系的应用例题2（2011•绍兴）如图，相距2cm 的两个点A 、B 在直线l 上．它们分别以2cm/s 和1cm/s的速度在l 上同时向右平移，当点A ，B 分别平移到点A 1，B 1的位置时，半径为1cm 的⊙A 1，与半径为BB 1的⊙B 相切．则点A 平移到点A 1，所用的时间为为多少秒?考点：圆与圆的位置关系。

切线长定理及其应用

切线长定理及其应用知识点一切线长定义及切线长定理1. 切线长定义：过圆外一点作圆的切线，这点和之间的线段长叫作这点到圆的切线长.注意切线长和切线的区别和联系:切线是直线，不可以度量；切线长是指切线上的一条线段的长，可以度量。

2. 切线长定理：过圆外一点引圆的两条切线，它们的切线长相等，即PA=PB.推论：（1）△PAB 是等腰三角形；（2）OP 平分△APB ，即△APO=△BPO ；（3）弧AM=弧BM ；（4）在Rt OAP ∆和Rt OBP ∆中，由AB OP ⊥，可通过相似得相关结论；如：222222,,OA OB OE OP AP BP PE PO AE BE OE EP ==⋅==⋅==⋅（5）图中全等的三角形有对，分别是：题型一切线长定理的直接应用【例1】如图所示，△O 的半径为3cm ，点P 和圆心O 的距离为6cm ，经过点P 的两条切线与△O 切于点E 、F ，求这两条切线的夹角及切线长.【例2】如图，P A 、PB 、DE 分别切△O 于A 、B 、C ，△O 的半径长为6 cm ，PO ＝10 cm ，求△PDE 的周长．【例3】如图所示，△ABC中，∠C=90°，AC=3，AB=5，D为BC边的中点，以AD上一点O为圆心的⊙O和AB、BC均相切，则⊙O的半径为__________.【过关练习】1.如图所示，PA、PB是△O的切线，A、B为切点，△OAB=30°.（1）求△APB的度数.（2）当OA=3时，求AP的长.2.如图所示，已知PA、PB、DE分别切O于A、B、C三点，△O的半径为5cm，△PED的周长为24cm，△APB=50°.求：（1）PO的长；（2）△EOD的度数.3.如图,在直角梯形ABCD 中,AB ∥CD,AB ⊥BC,以BC 为直径的△O 与AD 相切,点E 为AD 的中点,下列结论正确的个数是( )(1)AB+CD=AD;(2)DCE ABE BCE S S S △△△+=; (3)241BC CD AB =⋅; (4)∠ABE=∠DCE. A.1B.2C.3D.4知识点二圆外切四边形1、四边形的内切圆定义：四边形的四条边都与圆相切，把这个四边形叫作圆外切四边形，把这个圆叫作圆的内切圆.2、圆外切四边形的性质：圆外切四边形两组对边之和.（如图，即AB +CD =AD +BC ）题型一四边形的内切圆计算【例1】已知四边形ABCD 的边AB 、BC 、CD 、DA 与△O 相切于P 、Q 、M 、N ，求证：AB+CD=AD+BC 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

A
第20题 N
C
B D E
F M
O
O 切线长和切线长定理的应用
例（2011·济宁）如图，AB 是⊙O 的直径，AM 和BN 是它的两条切线，DE 切⊙O 于点E ，交AM 与于点D ，交BN
于点C ，F 是CD 的中点，连接OF 。

（1）求证：OD ∥BE;
(2) 猜想：OF 与CD 有何数量关系？并说明理由。

（1）求证：CD 是圆O 的切线；
（2）若2OA =且6AD OC +=，求CD 的长？
C
O D B
A
2、在Rt ABC ∆中，90A ∠=︒，点O 在BC 上，以O 为圆心的圆O 分别与AB 、AC 相切于E 、F ，若A B a =， AC b =，则圆O 的半径为（）
A 、ab
B 、a b ab +
C 、ab a b +
D 、2
a b
+
C E O
F
B
A C
E O
D
B
A P
E
O
F
D
B
A
例1图例2图例3图
3、如图，AB BC ⊥，DC BC ⊥，BC 与以AD 为直径的圆O 相切于点E ，9AB =，4CD =，则四边形ABCD 的面积为。

4、如图，过O 外一点P 作圆O 的两条切线PA 、PB ，切点分别为A 、B ，连结AB ，在AB 、PB 、PA 上分别取一点D 、E 、F ，使AD BE =，BD AF =，连结DE 、DF 、EF ，则EDF ∠=（）
A 、90P ︒∠－
B 、1902P ︒-∠
C 、180P ︒-∠
D 、1
452
P ︒∠-
5、如图，已知ABC ∆中，AC BC =， CAB α∠=（定值），圆O 的圆心O 在AB 上，并分别与AC 、BC 相切于点P 、Q 。

（1）求POQ ∠；
（2）设D 是CA 延长线上的一个动点，DE 与O 相切于点M ，点E 在CB 的延长线上，试判断DOE ∠的大小是否保持不变，并说明理由。

N
Q
P O
D
C
B
A
6、如图，圆O 为Rt ABC ∆的内切圆，点D 、E 、F 为切点，若6AD =，4BD =，则ABC ∆的面积为。

C
E
O F
D
B
A
7、正方形ABCD 中，AE 切以BC 为直径的半圆于E ，交CD 于F ，则:CF FD （）
A 、1∶2
B 、1∶3
C 、1∶4
D 、2∶5
E
O
F
D
C
B
A
8、两个同样大小的肥皂泡黏在一起，其剖面如图1所示（点O ，O′是圆心），分隔两个肥皂泡的肥皂膜PQ 成一条直
线，TP 、NP 分别为两圆的切线，求∠TPN 的大小．
（1） (2)
9．已知：如图，E 是相交两圆⊙M 和⊙O 的一个交点，且ME ⊥NE ，AB 为外公切线，切点分别为A 、B ，连结AE 、BE ．则∠AEB 的度数为（）（A ）145° （B ）140° （C ）135° （D ）130° 10、如图，AB 、AC 是⊙O 的两条切线，切点分别为B 、C ，D 是优弧上的一点，已知∠BAC ＝
80，那么∠BDC ＝__________
度．
11、如图，AB 是⊙O 的直径，四边形ABCD 内接于⊙O ，，，的度数比为3∶2∶4，MN 是⊙O 的切线，C 是切点，
则∠
BCM
的度数为___________．
12、如图，AB ＝8，AC ＝6，以AC 和BC 为直径作半圆，两圆的公切线MN 与AB 的延长线交于D ，则BD 的长为_________．
13、如图，PA 、PB 与⊙O 分别相切于点A 、点B ，AC 是⊙O 的直径，PC 交⊙O 于点D ．已知∠APB ＝
60，AC ＝2，那么
CD 的长为
14、如图，PT 是⊙O 的切线，T 为切点，PB 是⊙O 的割线交⊙O 于A 、B 两点，交弦CD 于点M ，已知：CM ＝10，MD ＝2，
PA ＝MB ＝4，则PT 的长等于__________．
15、木工师傅可以用角尺测量并计算出圆的半径r .用角尺的较短边紧靠O ，并使较长边与O 相切于点C .假设角尺的较长边足够长，角尺的顶点B ，较短边8cm AB .若读得BC 长为cm a ，则用含a 的代数式表示r 为 .。