线量与角量的关系
第3讲 圆周运动的角量描述

第四节圆周运动及其描述上一节学习了一般的平面曲线运动,本节学习一种特殊且常见的曲线运动――圆周运动。
1 圆周运动的线量描述回顾上一节,我们在自然坐标系下使用了位置、速度、加速度等量来描述曲线运动。
这些量称为线量,所以上一节对于曲线运动的描述称为线量描述。
由于圆周运动是一种特殊的曲线运动,因而上一节关于曲线运动的描述完全适用于圆周运动的描述。
所以可以把上一节的结论直接用于圆周运动的线量描述。
位置:s=s(t)速度:dsdt v=τ加速度:22d sdtτ=aτ(1a)2nvR=a n(1b)(1b)式中的R就是圆的半径,而v则是质点做圆周运动的速率。
质点作圆周运动时,如果切向加速度为0,就是所谓的匀速圆周运动......。
2 圆周运动的角量描述极坐标系2.1 角位移除了线量描述形式外,对于圆周运动还有一种常用的描述形式――角量描述。
如图1所示,以圆心为极点,沿着任意方向引出一条线作为极轴,就建立了一个坐标系,称为极坐标系。
在极坐标系中,质点的位置所对应的矢径r与极轴的夹角θ称为质点的角位置,而dθ称为dt时间内的角位移。
注意:1,角位移...d.θ.既有大小,又有方向.........(.但未必是矢量......1)。
其方向由右手定则确定,即:伸出右手,使四指沿着质点旋转的方向弯曲,与四指垂直的拇指所指的方向1矢量的严格定义是:矢量是在空间中有一定的方向和数值,并遵从平行四边形加法法则的量。
即为d θ的正方向。
2,有限大小的角位移不是矢量(因为角位移的合成不符合交换律,比如翻一本书:先x->90,再y ->90,最后z ->90得到的结果,与先x->90,再z ->90,最后y ->90得到的结果不一样),只有..当△..t . .0.时,角位移.....d .θ.才是矢量....。
3,质点作圆周运动时,其角位移只有两种可能的方向,因此可以在标量前...............................加正号或者是负号来指明角位移的方向.................。
大学物理学习知识重点(全)

y第一章 质点运动学主要内容一.描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r r称为位矢位矢r xi yj =+r v v ,大小 r r ==v 运动方程()r r t =r r运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆r rr r r△,r =r△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆r 、r ∆、s ∆的含义(∆≠∆≠∆rr r s ) 2. 速度(描述物体运动快慢和方向的物理量)平均速度 x y r x y i j i j t t tu u u D D ==+=+D D r r r r r V V r 瞬时速度(速度) t 0r dr v lim t dt∆→∆==∆r r r(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x ϖϖϖϖϖϖ+=+==,2222y x v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛==ϖϖ ds dr dt dt=r 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆rr 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆r r r r △ a r方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x ϖϖϖϖρϖ2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x ϖ二.抛体运动运动方程矢量式为 2012r v t gt =+r rr分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
大学物理学C基本内容

《大学物理学C 》课程基本内容第一章 质点的运动1.直角坐标系、极坐标系、自然坐标系※2.质点运动的描述:位置矢量r、位移矢量r ∆=)()(t r t t r -∆+、运动方程)(t r r =。
在直角坐标系中,k t z j t y i t x t r)()()()(++=速度:t r v d d=; 加速度:22d d d d t rt v a ==在直角坐标系中,速度k v j v i v v z y x ++=,加速度k a j a i a a z y x++=自然坐标系中,速度 τ v v ==τ t s d d ,加速度t n a a a +==n rv t v2d d +τ 在极坐标系中,角量的描述:角速度t d d θω=,角加速度22d d d d tt θωα==3.运动学的两类基本问题:第一类问题:已知运动方程求速度、加速度等。
此类问题的基本解法是根据各量定义求导数。
第二类问题:已知速度函数(或加速度函数)及初始条件求运动方程。
此类问题的基本解法是根据各量之间的关系求积分。
例如据txv d d =,可写出积分式⎰x d =⎰t v d .由此求出运动方程)(t x x =。
4.相对运动:位移:t u r r ∆+'∆=∆ ,速度:u v v +'=,加速度:0a a a+'=第七章 气体动理论1.对“物质的微观模型”的认识;对“理想气体”的理解。
※2.理想气体的压强公式23132v n p k ρε==,其中221v m k =ε※理想气体物态方程:RT MmpV = 或 nkT p =理解压强与微观什么有关,即压强的物理含义是什么.※3.理想气体分子的平均平动动能与温度的关系:kT k 23=ε 理解温度与微观什么有关,即温度的物理含义。
※4.能量均分定理:气体处于平衡态时,分子每个自由度上的平均能量均为2kT概念:自由度※理想气体内能公式:RT iM m E 2=5.麦克斯韦气体分子速率分布律 ※麦克斯韦气体分子速率分布函数:定义:v NN v f d d 1)(=函数:22232π2π4)(v v v kTm e kT m f -⎪⎭⎫⎝⎛=以及v v f NNd )(d =;v v Nf N d )(d =;⎰21d )(v v v v Nf ;⎰21d )(v v v v f 等表示的物理含义。
三角测量和导线测量的比较

三角测量在地面上布设一系列连续三角形,采用测角方式测定各三角形顶点水平位置的方法。
是建立国家大地网和工程测量控制网的基本方法。
1617年由荷兰W.斯涅耳首创。
三角测量有两种扩展形式:①向各方向扩展,构成网状,称为三角网,它点位分布均匀,点间互相制约,对低等测量控制作用较强,但推进较慢。
②向某一定方向扩展,构成锁状,称为三角锁,它构成控制骨架,中间以次等三角测量填充,推进迅速,比三角网经济,但控制强度不如三角网。
三角测量作业分选定点位、造标埋石、水平角观测、成果计算等。
点位一般应选在展望良好、易于扩展的有利位置,使构成三角形的相邻点间互相通视。
在选定的点位上建造觇标,供观测照准和升高仪器,同时埋设标石作为三角点的永久性标志。
标石中心点是三角点的实际点位。
水平角观测是三角测量的关键性工作,观测选在通视良好、目标清晰稳定的有利时间进行。
三角测量除测水平角外,还要选择一些三角形的边作为起始边,测量其长度和方位角。
起始边的长度过去用基线尺丈量,20世纪50年代后用电磁波测距仪直接测量。
起始边的方位角用天文测量方法测定。
从一起始点和起始边出发,利用观测的角度值,逐一推算各边的长度和方位角,再进一步推算各三角形顶点在大地坐标系中的水平位置。
导线测量在地面上选择一条适宜的路线,在其中的一些点上设置测站,采取测边和测角方式来测定这些点的水平位置的方法。
它是几何大地测量学中建立国家大地控制网的主要方法之一,也是为地形测图、城市测量和各种工程测量建立控制点的常用方法。
为导线测量选择的测量路线称为导线。
它应当尽可能直伸,但由于地形限制,导线一般成一条折线。
导线上设置测站的点称为导线点。
测量每相邻两点间的距离,并在每一点上观测相邻两边之间的夹角,从一起始点坐标和方位角出发,利用测量的距离和角度,便可依次推算各导线点的水平位置。
为建立国家大地网以及某些城市测量和工程测量所实施的导线测量,称为精密导线测量。
其等级和精度要求与三角测量相同。
线段与角的关系

线段与角的关系线段和角是几何学中重要的概念,在几何问题的解决过程中经常会用到它们。
本文将探讨线段与角的定义、性质以及二者之间的关系。
一、线段的定义和性质线段是指两个点之间的有限部分,它可以用两个端点来唯一确定。
线段有以下性质:1. 长度:线段的长度是指两个端点之间的距离,可以通过勾股定理来计算。
2. 中点:线段的中点是指线段上距离两个端点相等的一个点,它把线段分成两个相等的部分。
3. 垂直平分线:线段的垂直平分线是指与线段垂直且通过线段中点的直线,它把线段分成两个相等的部分。
4. 分割线段:线段可以被分割成任意数量的等长部分。
二、角的定义和性质角是由两条射线共享一个公共端点而形成的图形,公共端点被称为角的顶点。
角的性质包括:1. 角的度量:角的度量是指角度的大小,用度来表示,圆周角的度量范围是0到360度。
可以用直角、钝角和锐角来描述角的大小。
2. 角的分类:根据角的度量大小可以将角分为直角、钝角和锐角。
3. 角的补角和余角:两个角互为补角,当它们的度数之和等于90度时;两个角互为余角,当它们的度数之和等于180度时。
4. 角的平分线:角的平分线是指从角的顶点出发,将角分成两个相等的部分的射线。
三、线段与角的关系线段和角有着密切的关系,常见的包括以下几种情况:1. 一个角的两条边可以看作是一个线段,这个线段被称为角的边。
2. 若线段的一边通过角的顶点,则这条线段与该角有交点。
3. 当角的度数为180度时,其两边共线,形成一条直线。
4. 当角的度数为0度时,其两边重合,形成一个点。
总结:线段是由两个点确定的有限部分,角是由两条射线的公共顶点确定的图形。
线段与角之间存在多种关系,通过分析和利用这些关系,可以在解决几何问题中得到更准确的结果。
本文介绍了线段和角的定义、性质以及二者之间的关系。
在几何学中,对线段和角的理解和运用是解决问题的关键。
通过熟练掌握线段与角之间的关系,我们可以更好地应用它们解决各种几何问题,提高数学问题的解题能力。
普通物理学第二版第七章课后习题答案

第七章 刚体力学7.1.1 设地球绕日作圆周运动.求地球自转和公转的角速度为多少rad/s 估算地球赤道上一点因地球自转具有的线速度和向心加速度.估算地心因公转而具有的线速度和向心加速度(自己搜集所需数据).[解 答]7.1.2 汽车发动机的转速在12s 内由1200rev/min 增加到3000rev/min.(1)假设转动是匀加速转动,求角加速度.(2)在此时间内,发动机转了多少转[解 答](1)22(30001200)1/601.57(rad /s )t 12ωπβ⨯-⨯===V V(2)222220()(30001200)302639(rad)2215.7πωωθβ--===⨯所以 转数=2639420()2π=转7.1.3 某发动机飞轮在时间间隔t 内的角位移为球t 时刻的角速度和角加速度.[解 答]7.1.4 半径为0.1m 的圆盘在铅直平面内转动,在圆盘平面内建立O-xy 坐标系,原点在轴上.x 和y 轴沿水平和铅直向上的方向.边缘上一点A 当t=0时恰好在x 轴上,该点的角坐标满足21.2t t (:rad,t :s).θθ=+求(1)t=0时,(2)自t=0开始转45o 时,(3)转过90o时,A 点的速度和加速度在x 和y 轴上的投影.[解 答](1) A ˆˆt 0,1.2,R j 0.12j(m/s).0,0.12(m/s)x y ωνωνν====∴==v(2)45θ=o时,由2A 1.2t t ,t 0.47(s)42.14(rad /s)v R πθωω=+==∴==⨯v v v得(3)当90θ=o时,由7.1.5 钢制炉门由两个各长1.5m 的平行臂AB 和CD 支承,以角速度10rad/s ω=逆时针转动,求臂与铅直45o 时门中心G 的速度和加速度.[解 答]因炉门在铅直面内作平动,门中心G 的速度、加速度与B 或D点相同。
所以:7.1.6 收割机拔禾轮上面通常装4到6个压板.拔禾轮一边旋转,一边随收割机前进.压板转到下方才发挥作用,一方面把农作物压向切割器,另一方面把切割下来的作物铺放在收割台上,因此要求压板运动到下方时相对于作物的速度与收割机前进方向相反. 已知收割机前进速率为1.2m/s ,拔禾轮直径1.5m ,转速22rev/min,求压板运动到最低点挤压作物的速度.[解 答]取地面为基本参考系,收割机为运动参考系。
刚体运动的描述

刚体的定轴转动是指 刚体上各点都绕同一直线 作圆周运动, 作圆周运动,而直线本身 在空间的位置保持不动的 一种转动。 一种转动。 这条直线称为转轴 转轴。 这条直线称为转轴。 刚体定轴转动的特点: 刚体定轴转动的特点: 1.刚体上各个质点都在作圆周运动,但各质点圆周 刚体上各个质点都在作圆周运动, 刚体上各个质点都在作圆周运动 运动的半径不一定相等。 运动的半径不一定相等。 2.各质点圆周运动的平面垂直于转轴线,圆心在轴 各质点圆周运动的平面垂直于转轴线, 各质点圆周运动的平面垂直于转轴线 线上,这个平面我们称为转动平面。 线上,这个平面我们称为转动平面。 3.各质点的位矢在相同的时间内转过的角度是相同的。 各质点的位矢在相同的时间内转过的角度是相同的。 各质点的位矢
10
ω = ω 0 + βt 1) ( )
1 2 ) θ − θ 0 = ω 0t + βt (2) 2
)、(2) 由(1)、( )式消 t得: )、( 得
2 2 0
ω = ω + 2 β (θ − θ 0 ) (3) )
与匀变速直线运动计算公式有对应关系: 与匀变速直线运动计算公式有对应关系:
dθ ∆θ = 角速度 ω = lim ∆t → 0 ∆ t dt
角速度为角坐标对时间的一次导数。 角速度为角坐标对时间的一次导数。 方向:满足右手定则, 方向:满足右手定则,沿刚体 转动方向右旋大拇指指向。 转动方向右旋大拇指指向。 角速度是矢量, 角速度是矢量,但对于刚体定轴转 动角速度的方向只有两个, 动角速度的方向只有两个,在表示角 速度时只用角速度的正负数值就可表 示角速度的方向,不必用矢量表示。 示角速度的方向,不必用矢量表示。
dθ ω= dt
∆t → 0
圆周运动例题及相对运动n2讲解
bt v
at
dv dt
d(v0 bt ) dt
b
20得 a24n/10到 /13 avR的2 大(v小0 及 Rb方 t )2向。
an at Ra O
7
2.
由at
a
,
n
即b (v0 bt )2 求出t。 R
2024/10/13
8
例6,(例题1-4)一曲柄连杆结构,曲柄OA长为r, 连杆AB长为L,AB一端在A处与曲柄相连,另一端以销子 在B处与活塞相连,当曲柄以匀角速绕o旋转时,通过 连杆将带动B处活塞在汽缸内往返运动,求活塞运动方程。
A
L
r
Q
B
x’ o’ P R o
x
活塞t时刻运动分析图10
A
l B
r
= t
x
x
x OR RB
PR
O
起始点
x r cost l2 r2 sin 2 t
2024/10/13
11
写为:
l2
r2
sin 2
t
l 1
r2
sin 2 2l 2
t
;而
sin2 t 1 cos2t ,移项整理得:
26
例2,货车遇到5m/s垂直下落的大雨,木 板及挡板都是1m,问货车以多大的速度 行驶才使木板不被雨淋。
v牵连 5
2024/10/13
v相对
45o l=1 v牵连 = 5
v绝对= 5 h=1
27
例题3,一升降机以加速度1.22m/s2 上升,当上升 速度为2.44m/s时,有一螺帽自升降机的天花板上 松落,天花板与升降机的底面相距2.74m,计算螺 帽从天花板落到底面所需要的时间和螺帽相对于 升降机外固定柱的下降距离。
2第二讲-自然坐标系---圆周运动的角量描述

解:由 d
dt
0, 0
d dt
又 d
dt d (0 t)dt
0
0t
1 2
t2
d dt
ቤተ መጻሕፍቲ ባይዱ
t
d (0 t)dt
0
0
三、角量与线量的关系
线量: S、 v、 a
角量:、 、
由圆周运动有: S R
一,自然坐标系 1,运动方程 2,速度 3,加速度
二,圆周运动的角量描述 1,角位置 2,角速度 3,角加速度
三,角量与线量的关系 四,一般曲线运动
一、自然坐标系中的运动方程,速度及加速度表示:
p
ˆ
o nˆ
规定:切向单位矢量 ˆ , 指向运动方向
法向单位矢量 nˆ 指向轨道的凹侧
用这样一对正交的切向、法向单位矢量构成坐 标系统称为自然坐标系。
2.角位移 :(在 t内) d 方向由右手螺旋法则确定
3.角速度: 大小:
lim
to t
d
dt
y
t t
B
r A t
o
x
方向:与 d 方向一致
d
4.角加速度: 大小: lim d
t0 t
dt
方向:与 d 方向一致
r
v
方向:nˆ
dˆ 大小: dˆ ˆ d d
则
dˆ
dt
d
dt
nˆ
d ( ) dt
nˆ
1
ds dt
nˆ
v
nˆ
ρ为曲率半径。所以
圆周运动的角量描述 角量与线量的关系

A
反映 反映 的方向变化 因素
的大小变化 因素
无限趋近法向
无限趋近切向
法向加速度
切向加速度
要点归纳法向加速度Fra bibliotek切向加速度
线量描述
切向加速度
0, , v 增大 at dv 0, , v 常量 dt 0, , v 减小
一般曲线运动(自然坐标)
y
a
o a x a
et
en
第三节
圆周运动
线量描述
1、自然坐标系:
切向:质点前进的方向 法向:与切向垂直,指向曲线 凹的一面。
et
en
2、圆周运动的切向加速度和法向加速度(自然
坐标系分析) S =S (t )
v v(t ),a a (t ) ds v et vet dt
线量描述
加速度问题
C
D B
截取 AD = AB 作矢量 和
v et
v ds et vet dt 2 d v d v v a et en dt dt
ds 其中 d 为曲率半径 .
en
例
角位置
角位移
角速度
角加速度
匀变速圆周运动
角线量关系
物理量小结
物理量小结2
角线简例
浅谈力学中线量和角量的关系

枣 庄 学 院 学 报
21 0 0年 第 5期
1 角速 度 的 矢量 性
如 图 1所 示 , 有 一 刚 体 通 过 定 点 D 的 某 转 轴 转 过 了 一 微 小 的 角 度 AO, 为 是 一 有 设 因 方 向 的 量 , 在 在 转 轴 上 截 取 一 有 方 向 的 线 段 △元来 代 表 AO的 量 值 和 方 向 , 有 量 值 为 现 则 l l AO, 向 则 可 用 右 手 螺 旋 法 则 判 断 . 以 人 们 经 常 用 △元来 表 示 角 位 移 . △ : 方 所 如 果 r表 示 刚 体 内 任 一 点 P 在 转 动 前 的 位 置 矢 量 ,r +△ 表 示 转 动 后 P 点 (图 中 为 P ’
[ 关键词 ] 线量 ; 角量 ; 质点组 ; 刚体 [ 中圈分类号 ] 3 3 3 O 1 . [ 文献标识 码】 A [ 文章编 号]0 4— o 7 2 1 )2— 0 1 0 10 7 7 (0 2 0 0 0 — 4
0 引言
对于物理专业学 生或老师来说 , 《理 论 力 学 》是 必 须 掌 握 的 一 门 专 业 理 论 课 .n 是 大 - S 家 都 知 道 , 于 一 种 特 殊 的 质 点 组 一刚 体 而 言 , 矢 量 力 学 中 的 重 点 也 是 难 点 , 时 是 最 对 是 同 复 杂 的 一 部 分 内 容 . 其 原 因 , #tl 是 增 加 了 刚 体 的 转 动 运 动 . 就 无 .z x 所 谓 刚 体 ”-1 是 指 在 外 力 作 用 下 , 体 的 形 状 和 大 小 (尺 寸 ) 持 不 变 , 且 内 部 各 7, 物 保 而 部 分 相 对 位 置 保 持 不 变 , 种 理 想 物 理 模 型 称 之 为 刚 体 . 体 是 一 种 特 殊 的 质 点 组 , 构 这 刚 若 成 刚 体 的 各 质 点 之 间 的 距 离 在 外 力 作 用 下 保 持 不 变 . 称 之 为 刚 体 . 果 物 体 的 刚 性 足 也 如 够 大 , 致 其 中 弹 性 波 的 传 播 速 度 比 该 物 体 的 运 动 速 度 大 很 多 ,9 而 可 以 认 为 弹 性 扰 动 以 /, 的传 播 是 瞬 时 的 , 可 以把 该 物 体 当作 刚 体 处 理 . 就
20130722角量和线量的关系_以圆周运动为例

(184408561) 20:28:59今天的内容不多,我打算以圆周运动为例说一说角量和线量的关系(184408561) 20:29:09这部分内容中学应该提到(184408561) 20:29:53圆周运动,就是轨迹为圆周的运动(184408561) 20:30:31描述运动的办法有很多(184408561) 20:31:00不是非要用哪种办法才醒(184408561) 20:31:02才行(184408561) 20:31:29所选用的方法,必然是希望越简单越好,月直观越好,越方便越好(184408561) 20:32:00在这部分内容里,教材上往往会引入角量这个说法(184408561) 20:32:15什么叫角量,简单来说,那就是与角度有关的量(184408561) 20:32:24为什么要与角度有关(184408561) 20:32:30举个例子(184408561) 20:32:41有没有童鞋玩过CS或者CF?(184408561) 20:33:17游戏中,同伙提醒你,小李,你的2点钟方向有狙击手(184408561) 20:33:20什么意思环境—郭蕾(1394204624) 20:33:58三十度角方向(184408561) 20:34:33以你所在的平面为参考平面,以你当前的视线为参考轴,向右模仿时钟那样绕过一定角度,绕到2点钟方向的时候射击,就可以把敌人击毙(184408561) 20:34:47这里面出现了一个参考角度(184408561) 20:35:12也可以说是这个敌人在参考平面内,想对参考轴的角坐标(184408561) 20:35:45子弹是可以打远处,可以打近处的,但是想击中敌人,必须是沿那个角度才行(184408561) 20:35:58这就是这个角度的重要性(184408561) 20:36:03看个图(184408561) 20:36:14(184408561) 20:36:30任意时刻t,P点的位置,都在圆周上,这是必须的环境—郭蕾(1394204624) 20:36:45嗯嗯嗯(184408561) 20:37:00但是在圆周上的什么位置,这个要确定了,那就相当于确定了P的运动方程(184408561) 20:37:06怎么确定P的位置呢(184408561) 20:37:15到O点的距离,总是R(184408561) 20:37:27相对O点的方位就是时间变化(184408561) 20:37:38相对O点的方位是随时间变化的环境—郭蕾(1394204624) 20:39:21恩(184408561) 20:39:24假如在圆周所在平面上选中x轴作为参考轴,当t时刻P点相对参考点O的位置矢量与x轴正方向之间的夹角为θ,则θ(t),这个对应关系就可以看成确定P 点的条件(184408561) 20:40:03这个θ(t)关系就是P点圆周运动的运动方程(184408561) 20:40:27任意时刻t,对应的θ(t)具体取值,都叫做P点的角坐标,也叫角位置(184408561) 20:40:45在这儿对θ不引入矢量描述(184408561) 20:40:51是为了简单(184408561) 20:41:48经历了Δt,到了t+Δt,P点位置从θ变到了θ+Δθ,这段时间内,Δθ叫做P的角位移(184408561) 20:42:05这里对角位移Δθ引入矢量描述,会让问题变得简单(184408561) 20:42:30多数教材上只对角位移Δθ人为规定了正负(184408561) 20:42:43但实际上是引入矢量描述的一种简化(184408561) 20:42:48需要注意了(184408561) 20:42:54怎么引入矢量描述呢(184408561) 20:43:08用右手螺旋(184408561) 20:43:44(184408561) 20:44:54看图,Δθ如果是逆时针形成的,用右手的四个手指做成逆时针环绕,拇指所指的方向就是Δθ的方向,它的大小就是|Δθ|(184408561) 20:46:01Δθ在我们参考的平面内如果是顺时针形成,用右手的四个手指做成顺时针环绕,拇指所指的方向就是Δθ的方向,大小是|Δθ|(184408561) 20:46:15几乎所有的教材都没这么讲,而把矢量描述留给了角速度(184408561) 20:47:20角速度是运动方程θ(t)(角位置)对时间t的一阶导数(184408561) 20:47:44(184408561) 20:47:58用比值的定义,还可以怎么理解?哪位童鞋尝试回答一下?(184408561) 20:48:21谁对谁的比值??(184408561) 20:48:41结合之前讲过的,能准确地说出来么(184408561) 20:48:47锻炼一下(184408561) 20:48:50别不好意思河工大-李明雪(2450317485) 20:49:11θ对t(184408561) 20:49:36用比值的定义,应该是整个分子比整个分母(184408561) 20:49:53所以应该是dθ对dt的比值河工大-李明雪(2450317485) 20:50:04哦(184408561) 20:50:26很多童鞋会把角速度当成角位移对时间的一阶导数,就是因为弄混了微商定义和比值定义(184408561) 20:50:38再强调一下(184408561) 20:51:08速度是位置矢量对时间的一阶导数,也可以说速度是元位移对时间元增量的比值北理-李怡(1090550743) 20:51:32第一次听课,请老师原谅,有点不懂概念(184408561) 20:51:36角速度是角位置对时间的一阶导数,也可以说角速度是元角位移对时间元增量的比值(184408561) 20:51:48没关系环境—郭蕾(1394204624) 20:52:00元角位移?(184408561) 20:52:35角位置的元赠来那个(184408561) 20:52:41角位置的元增量(184408561) 20:52:43dθ(184408561) 20:52:50就是元角位移环境—郭蕾(1394204624) 20:53:00嗯嗯(184408561) 20:53:04因为角位移Δθ=Σdθ(184408561) 20:53:29组元的意思,对吧(184408561) 20:53:44有组成元素或组成单元的意思(184408561) 20:53:50当然这么说可不准确(184408561) 20:54:15θ对t的一阶导数等同于dθ对dt的比值(184408561) 20:54:34ok?环境—郭蕾(1394204624) 20:54:42OK(184408561) 20:54:49角位移对时间的一阶导数怎么写啊?(184408561) 20:55:09应该是dΔθ/dt,这就不是角速度了河工大-李明雪(2450317485) 20:55:30角加速度(184408561) 20:55:34所以物理学里面,不是光拍拍脑袋就可以了,要真正动动手,把想到的东西写下来验证一下北理-古乔砚(987417613) 20:56:08(184408561) 20:56:15(184408561) 20:56:20看定义(184408561) 20:56:26角速度如果也引入矢量描述(184408561) 20:56:31方向由谁决定?(184408561) 20:56:39咱们前面也讨论过速度的这个问题(184408561) 20:56:47由谁决定啊?北理-李怡(1090550743) 20:56:48dθ(184408561) 20:56:52(184408561) 20:57:08对,角速度的方向有角位置增量的方向决定(184408561) 20:57:55所以,如果dθ是逆时针的绕向,ω也应该是逆时针的绕向(184408561) 20:58:10用右手螺旋作为标准,逆时针对应向上还是向下?北理-李怡(1090550743) 20:58:18方向一致~昌大--吴贤英(545710472) 20:58:26上北理-李怡(1090550743) 20:58:29向上?(184408561) 20:58:48也就是说ω的方向与dθ必然一致北理-李怡(1090550743) 20:59:07嗯嗯(184408561) 20:59:12大家听完之后还需要好好体会一下右手螺旋定则,这是一种很好的方法,并不是说只有这一种方法可以北理-李怡(1090550743) 20:59:42右手螺旋定则不是定义磁电的吗?(184408561) 20:59:49而且目前大家比较统一地都在用,所以自创方法可以,但是在数理学领域就不容易沟通了北理-李怡(1090550743) 20:59:54还可以有这么多北理-李怡(1090550743) 21:00:06哦哦(184408561) 21:00:09角加速度呢?(184408561) 21:00:17(184408561) 21:00:31这个也有类似的讨论,为了节省时间,就不多说了北理-李怡(1090550743) 21:00:46也和上述一样?(184408561) 21:00:59如果对角加速度也引入矢量描述,角加速度的方向由谁决定?北理-李怡(1090550743) 21:01:10d北理-李怡(1090550743) 21:01:14w(184408561) 21:01:17由ω决定吗?北理-李怡(1090550743) 21:01:17d w(184408561) 21:01:26对,应该是由dω决定北理-李怡(1090550743) 21:01:40我有点不会写符号北理-李怡(1090550743) 21:01:43北理-古乔砚(987417613) 21:01:49(184408561) 21:01:56比如说,ω向上,但是ω是变小的,那么角加速度应该是顺时针还是逆时针?(184408561) 21:02:13应该怎么分析呢?北理-李怡(1090550743) 21:02:14逆时针北理-李怡(1090550743) 21:02:17(184408561) 21:02:32ω向上,但是减小,说明dω向下(184408561) 21:02:43也就是角加速度向下北理-李怡(1090550743) 21:02:43为什么?(184408561) 21:02:56向下对应的是?(184408561) 21:03:03顺时针(184408561) 21:03:09向上对应的是逆时针北理-古乔砚(987417613) 21:03:10减小dw<0(184408561) 21:03:22还有问题么?北理-李怡(1090550743) 21:03:22嗯嗯(184408561) 21:03:26北理-李怡(1090550743) 21:03:30数学里面是的(184408561) 21:03:49解释清楚这些,为的是在其他地方用,到用的时候,可就没时间去解释了(184408561) 21:03:54今天的重点来了北理-李怡(1090550743) 21:03:57嗯嗯(184408561) 21:04:35刚才咱们介绍的角坐标,角位移,角速度,角加速度,都与θ或dθ有关系(184408561) 21:04:51也就是说都是“角”量,角的意思体现出来了吧北理-李怡(1090550743) 21:05:05嗯‘’(184408561) 21:05:21圆周运动只能这么表示么?北理-李怡(1090550743) 21:05:29不是吧!(184408561) 21:05:34显然不是,前面就说了,什么方法都行,关键是看方便,、北理-李怡(1090550743) 21:05:43恩(184408561) 21:05:53如果我们还用位置,位移,速度,加速度表示,行不行呢,照样行(184408561) 21:05:59可是物理事实只有一个(184408561) 21:06:23那用角量和所谓的“线”量,必然应该有对应关系啊(184408561) 21:06:32这种对应关系怎么找呢?(184408561) 21:06:42很简单(184408561) 21:06:50书上课没有了啊北理-李怡(1090550743) 21:06:56?(184408561) 21:06:58速度描述的是什么?北理-李怡(1090550743) 21:07:05快慢(184408561) 21:07:09单位时间内的位移,你看,又一种定义,没错吧?北理-李怡(1090550743) 21:07:18(184408561) 21:07:30那也就是单位时间内移动的距离,结合方向性(184408561) 21:07:57圆周运动的方向好办啊,就是沿圆周的切线方向向前(184408561) 21:08:12单位时间内移动的距离呢??怎么算(184408561) 21:08:17用弧长公式(184408561) 21:08:46单为时间内,相对圆心转过的角度是谁?(184408561) 21:08:58就是角速度的大小啊北理-李怡(1090550743) 21:08:59角速度(184408561) 21:09:27半径乘以单位时间内的转角,那不就是单位时间内走过的弧长么(184408561) 21:10:01所以速度的大小,即速率,可以表示成Rω(184408561) 21:10:06v=Rω(184408561) 21:10:44从弧长公式可以得到最基本的一个角量线量关系,也可以说,角量和线量之间的联系就是弧长公式(184408561) 21:10:55有了这个之后,一切都好办了(184408561) 21:11:17刚才说的只是大小,既然咱们已经对角量引入了矢量描述,那么完整的矢量对应关系该怎么写呢?(184408561) 21:11:45要遵守的原则是,速率必须满足v=Rω,方向还必须沿切线(184408561) 21:12:03怎么去构造这个关系?(184408561) 21:13:06从矢量的角度来看,ω与任意时刻质点相对圆心的位置矢量R是什么关系?(184408561) 21:13:15ω向上,R沿径向(184408561) 21:13:19两者必然垂直吧北理-古乔砚(987417613) 21:13:39(184408561) 21:14:05ω要向上的话,那么速度必然是沿切线逆时针绕?还是顺时针绕?北理-李怡(1090550743) 21:14:14逆(184408561) 21:14:17必然是逆时针(184408561) 21:14:27(184408561) 21:14:40所以这个关系可以这样搭建北理-李怡(1090550743) 21:14:45R也有方向?(184408561) 21:14:54位置矢量当然有方向了(184408561) 21:15:03(184408561) 21:15:10叉乘的规则我们知道北理-李怡(1090550743) 21:15:10哦哦(184408561) 21:15:26现在这个角度α等于多少?北理-李怡(1090550743) 21:15:3090(184408561) 21:15:50刚才说了ω与质点相对圆心的位置矢量垂直北理-古乔砚(987417613) 21:16:01对!必定是π/2,(184408561) 21:16:52用右手螺旋判断一下,四个手指先指向ω,然后经过小于π的角度绕向此时所对应的位置矢量,那么拇指必然是与v的方向一致了。
(完整版)大学物理知识点(全)
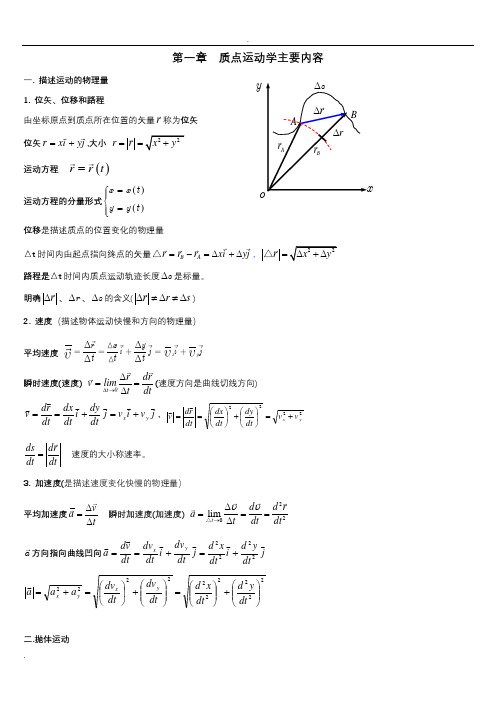
Br ∆ A rB ryr ∆第一章 质点运动学主要内容一. 描述运动的物理量 1. 位矢、位移和路程由坐标原点到质点所在位置的矢量r 称为位矢 位矢r xi yj =+,大小 2r r x y ==+运动方程()r r t =运动方程的分量形式()()x x t y y t =⎧⎪⎨=⎪⎩位移是描述质点的位置变化的物理量△t 时间内由起点指向终点的矢量B A r r r xi yj =-=∆+∆△,2r x =∆+△路程是△t 时间内质点运动轨迹长度s ∆是标量。
明确r ∆、r ∆、s ∆的含义(∆≠∆≠∆r r s ) 2. 速度(描述物体运动快慢和方向的物理量)平均速度xyr x y i j ij t t t瞬时速度(速度) t 0r drv limt dt∆→∆==∆(速度方向是曲线切线方向) j v i v j dt dy i dt dx dt r d v y x +=+==,2222yx v v dt dy dt dx dt r d v +=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛== ds dr dt dt= 速度的大小称速率。
3. 加速度(是描述速度变化快慢的物理量)平均加速度va t ∆=∆ 瞬时加速度(加速度) 220limt d d r a t dt dt υυ→∆===∆△ a 方向指向曲线凹向j dty d i dt x d j dt dv i dt dv dt v d a y x2222+=+== 2222222222⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=+=dt y d dt x d dtdv dt dv a a a y x y x二.抛体运动运动方程矢量式为 2012r v t gt =+分量式为 020cos ()1sin ()2αα==-⎧⎪⎨⎪⎩水平分运动为匀速直线运动竖直分运动为匀变速直线运动x v t y v t gt 三.圆周运动(包括一般曲线运动) 1.线量:线位移s 、线速度dsv dt= 切向加速度t dva dt=(速率随时间变化率) 法向加速度2n v a R=(速度方向随时间变化率)。
角量与线量的关系公式

角量与线量的关系公式在咱们的数学世界里,角量和线量那可是一对非常有趣的“小伙伴”,它们之间存在着一些神奇的关系公式。
先来说说角量吧。
角量通常用角度来表示,比如咱们熟悉的30 度、60 度、90 度等等。
想象一下,你拿着一把扇子,打开的角度不同,扇出来的风的范围也就不同,这就是角量在生活中的一个小小体现。
再讲讲线量。
线量呢,常见的有长度、距离这些。
就像你在操场上跑步,跑过的路程就是线量。
那角量和线量到底有啥关系公式呢?这就好比是两个小伙伴之间的秘密约定。
比如说,在一个圆里,圆心角的度数和它所对应的弧长就有着密切的关系。
假设这个圆的半径是 r,圆心角的度数是 n 度,那么对应的弧长 l 就可以通过一个公式来计算,那就是l = n×π×r÷180 。
我记得有一次给学生们讲这个知识点的时候,有个小家伙特别调皮,一直说:“老师,这也太复杂啦,我记不住!”我就笑着跟他说:“你想想看呀,假如你是个小画家,要画一个大大的扇形蛋糕,这个扇形的角度决定了你能切下来多少蛋糕,而这个角度和蛋糕边缘的长度不就有关系嘛!”这小家伙一听,眼睛一下子亮了,还真就记住了这个公式。
还有一个常见的例子,就是在三角函数中,正弦、余弦这些和线段的长度也有着紧密的联系。
比如在一个直角三角形里,一个锐角的正弦值等于它的对边与斜边的比值。
这就像是一个神秘的密码,通过角度就能解开线段长度的谜题。
咱们再回到生活中,你看那些建筑工人在建造圆形的拱门时,他们就得知道角量和线量的关系,才能确保拱门的形状和尺寸都恰到好处。
还有自行车的车轮,轮辐的长度和车轮转动的角度之间,也隐藏着角量和线量的关系呢。
总之,角量和线量的关系公式就像是一把神奇的钥匙,能帮助我们打开很多数学难题的大门,也能让我们更好地理解这个充满规律和秩序的世界。
所以呀,同学们可一定要好好掌握这些公式,说不定哪天就能派上大用场呢!。
角量与线量的关系公式手写

角量与线量的关系公式手写角的大小可以用弧度或度来测量。
一个角的大小由两条射线构成,这两条射线的端点是一个公共点,也被称为角的顶点。
根据角所在的平面可以分为三种类型:平面角、空间角和超平面角。
平面角是指在同一个平面内的角。
平面角被度量为弧度或度。
角的弧度表示为一个非负实数,它表示弧长与半径之间的比值。
角的度表示为一个非负实数,它表示角所包围的圆的弧长与圆的半径之间的比值。
空间角是指在三维空间中的角。
空间角可以用球面角度量,球面角度量是以角的顶点为球心,以角的两条射线所代表的弦为弧的圆心角。
超平面角是指在高维空间中的角。
超平面角可以用超球面角度量,超球面角度量是以角的顶点为超球面的中心,以角的两条射线所代表的弦对应的超球面上的弧的圆心角。
线量是指线的长度。
线的长度可以用欧几里得距离来度量。
在平面几何中,欧几里得距离是两点之间的直线距离。
在三维空间中,欧几里得距离是两点之间的直线距离的平方根。
在平面几何中,角量与线量之间的关系可以通过三角函数来表示。
三角函数是以角的顶点为原点和两条射线为轴线定义的函数。
三角函数包括正弦函数、余弦函数和正切函数等。
这些函数的值与角量的大小存在一定的关系。
正弦函数是指在一个角的对边与斜边之间的比值。
正弦函数的值范围在-1到1之间。
余弦函数是指在一个角的邻边与斜边之间的比值。
余弦函数的值范围在-1到1之间。
正切函数是指在一个角的对边与邻边之间的比值。
正切函数的值可以是任意实数。
角量与线量之间的关系公式可以通过三角函数来表示。
例如,在一个直角三角形中,正弦函数和余弦函数可以用来表达角量与线量之间的关系。
对于一个直角三角形的角A,角A的正弦函数等于角A的对边与斜边之间的比值,即sin(A) = opposite/hypotenuse。
同样,角A的余弦函数等于角A的邻边与斜边之间的比值,即cos(A) = adjacent/hypotenuse。
通过这些三角函数的关系,我们可以得到角量与线量之间的关系公式。
浅谈力学中线量和角量的关系

浅谈力学中线量和角量的关系惠治鑫【摘要】矢量力学中所涉及到的物理量有矢量也有标量,部分矢量根据质点组的运动状态有线量和角量.如果质点组有转动运动,则在该质点组的运动方程中肯定要涉及到角量,但是角量较线量相对复杂,理解困难.鉴于此,浅谈线量和角量二者关系,提出二者之间的统一表达式,以加深理解和灵活应用.%Vector mechanics involves vectors and scalars. According to the particle group movement state, some vectors in- clude linear vector and angular vector. If the particle group is in rotational motion, then angular vector will certainly be in- volved in the particle group equations of motion. However, angular vector is relatively more complex than linear vector and dif- ficult to understand. In view of this, this paper discusses the relationship between linear vector and angular vector, proposes a unified expression and thus deepens understanding and flexible application.【期刊名称】《枣庄学院学报》【年(卷),期】2012(028)002【总页数】4页(P1-4)【关键词】线量;角量;质点组;刚体【作者】惠治鑫【作者单位】宁夏师范学院物理与信息技术学院,宁夏固原756000【正文语种】中文【中图分类】O313.30 引言对于物理专业学生或老师来说,《理论力学》是必须掌握的一门专业理论课.可是大家都知道,对于一种特殊的质点组-刚体而言,是矢量力学中的重点也是难点,同时是最复杂的一部分内容.就其原因,无外乎是增加了刚体的转动运动.所谓刚体[1~7],是指在外力作用下,物体的形状和大小(尺寸)保持不变,而且内部各部分相对位置保持不变,这种理想物理模型称之为刚体.刚体是一种特殊的质点组,若构成刚体的各质点之间的距离在外力作用下保持不变.也称之为刚体.如果物体的刚性足够大,以致其中弹性波的传播速度比该物体的运动速度大很多,从而可以认为弹性扰动的传播是瞬时的,就可以把该物体当作刚体处理.图1Fig.11 角速度的矢量性如图1所示,设有一刚体通过定点O的某转轴转过了一微小的角度Δθ,因为是一有方向的量,现在在转轴上截取一有方向的线段来代表Δθ的量值和方向,则有量值为方向则可用右手螺旋法则判断.所以人们经常用来表示角位移.如果表示刚体内任一点P在转动前的位置矢量,表示转动后P点(图中为P'点)的位置矢量.因为为无限小量,则必与包含和的平面相互垂直.由几何关系知又因为PM=rsinφ,则即由矢量分析得,从上面讨论可以看出,是一个有大小和方向的量,但是矢量必须遵守矢量加法的对易性,即假设刚体绕O点的转轴作了两次微小振动,转动分别为和点的位置矢量分别: 转动前是转动后是再转动后是忽略高阶微量,所得位移的矢量和为调换上式左边两量顺序,得众所周知,线位移是矢量,遵守矢量的对易性,所以方程左右相等,得所以因为是任意矢量,所以即得是矢量.2 线量和角量的关系由上面的讨论知道是矢量,是刚体绕O点的转轴在Δt时间内转过的角位移.根据角速度的定义[2],(1)(2)又因为(3)将代入(1)式得(4)(4)式是我们提到的第一个线量和角量之间的关系,即线速度和角速度之间的关系.我们现在假设有一个统一的描述线量和角量之间关系的表达式如下:(5)上式中表示线矢量,表示角矢量,表示质点或质点组上某一点的位置矢量.下面将列举几个常见的例子.(6)其中是切向加速度,是一个线量,它只改变质点或质点组质心的速度大小.是法向加速度,它只改变质点组上某点的速度方向.(7)由上式可知(8)对于一些常见的力学公式,我们通常只记住了线量公式,而对角量公式相对模糊.没有关系,只要我们牢记了线量公式,就可以模仿出相应的角量公式.但是我们首先要记住的是线量和角量中的对应量如下表.表1Tab.1物理量位置量速度量加速度惯性量动量力和矩等线量r(m)v(m/s)a(m/s2)m(kg)P(kg·m/s)F(N)等角量θ(rad)ω(rad/s)α(rad/s2)I(kg·m2)J(kgm2rad/s)M(N·m)等我们现在总结常见的线性量计算公式,如表2:表2Tab.2线量角量运动方程vt=v0+ats=s0+v0t+12at2v2r-v20=2asωt=ω0+αtθ=θ0+ω0t+12αt2ω2t-ω20=2αθ动量P=mvJ=Iω动能T=12mv2T=12Iω2动量定理F=dPdtM=dJdt功W=F·rW=M·n运动定理F=maM=Iα等等等由以上两个表中的公式,我们不难看出,只要我们记住线量的力学计算公式,再把相应的力学量符号改变成角量符号,就是我们的角量计算公式.3 结论考虑到刚体转动运动较平动复杂,并且一些角量计算公式比较难以记住.全文围着着线量和角量展开了讨论,从中我们可以得出线量和角量之间有着明显的联系,也给出了线量和角量之间的一种统一表达式.对于表达式的准确与否,还有待大家讨论和深究.另外,由于篇幅有限,在文章中的例子只是个别,未能全部列出,如果读者感兴趣可以参考本文内容.参考文献[1]李得明,陈昌民.经典力学[M].北京:高等教育出版社,2006.[2]周衍柏.理论力学教程(第三版)[M].北京:高等教育出版社,2009.[3]哈尔滨工业大学理论力学教研室.理论力学(第六版)[M].北京:高等教育出版社,2005.[4]尹冠生.理论力学[M].西安:西北工业大学出版社,2000.[5]陈世民.理论力学简明教程[M].北京:高等教育出版社,2007.[6]金尚年,马永利.理论力学[M].北京:高等教育出版社,2009.[7]漆安慎,杜婵英.力学[M].北京:高等教育出版社,2001.。
