成都电子科技大学数字信号处理习题课
∑∫
m =−∞ ∞ −∞
xa (τ )h(t − τ )δ (τ − mT )dτ
π
sin[ (t − mT )] T 内插函数：h(t − mT ) = π (t − mT ) T
π
信号的抽样值xa (mT )经内插函数得到连续信号xa (t )
3.2 采样的恢复
零阶保持器恢复模拟信号 零阶保持器恢复模拟信号
第一章 信号和信号处理
1.信号 1.信号
信号
信息的载体， 信息的载体，携带信息的物理量 携带信息的物理量/ 的物理量/传递信息的函数 传递信息的函数， 的函数， 变量可以是时间 变量可以是时间、 可以是时间、空间、 空间、温度、 温度、距离、 距离、电压等
信号分类
按信号载体的物理特性： 按信号载体的物理特性：点、光声、 光声、磁、机械、 机械、热等 按信号中自变量的数目： 按信号中自变量的数目：
数字信号处理
模拟信号处理： 模拟信号处理：用电阻、 用电阻、电容、 电容、电感等模拟器件处理 数字信号处理： 数字信号处理：实质是数值运算（ 实质是数值运算（加、减、乘、除、延时） 延时）
数字信号处理实现方法
软件、 软件、硬件、 硬件、软硬结合
数字信号处理特点
灵活性好、 灵活性好、高精度、 高精度、高稳定性、 高稳定性、便于开发升级、 便于开发升级、功能强、 功能强、便 于大规模集成
π
解：1）由
f 0 = 50 Hz ，得
采样频率应： f s > 2 f 0 = 100 Hz 采样间隔应为：T < 1 / f s = 0.01s
2）选f s = 200 Hz 则采样间隔为：T = 1/ f s = 0.005s
xa (nT ) = sin(2π f 0 nT + π / 8) = sin(2π f 0 n / f s + π / 8) 50 1 = sin(2π n + π / 8) = sin( π n + π / 8) 200 2 ∞ ˆa (t ) = ∑ xa (nT )δ (t − nT ) ∴x
各种数字信息系统
Enhanced Gaming Webpad Wireless Devices: 802.11, Bluetooth, Others Biometrics Military and Government Cellular, Secure Connectivity Telematics Industry-Specific PDAs Digital Media Processing
2.信号处理 2.信号处理
信号处理 从信号中提取尽可能多的有用信息 增强信号的有用分量 估计信号的特征参数 识别信号的特征 抑制或消除不需要的有害分量 需要对信号： 需要对信号：分析和变换， 分析和变换，扩展、 扩展、压缩、 压缩、滤波参数 估计、 估计、特征识别等加工
2.信号处理 2.信号处理
n =−∞
∞
1 π n = ∑ sin( π n + )δ (t − ) n =−∞ 2 8 200
x(n) = xa (t )
t = nT
1 π = sin( π n + ) 2 8
拓展问题 采样序列为矩形脉冲， 采样序列为矩形脉冲，问采样信号的频谱与原始 模拟信号的频谱关系如何？ 模拟信号的频谱关系如何？ 能否无失真恢复？ 能否无失真恢复？ 条件？ 条件？
−∞
1 h(t ) = 2π
∫
∞
H ( j Ω ) e j Ωt d Ω
= ∫ [ ∑ xa (τ )δ (τ − mT )]h(t − τ )dτ
−∞ ∞
∞
∞
−∞
=
sin[ (t − mT )] T = ∑ xa (mT )h(t − mT ) = ∑ xa (mT ) π m =−∞ m =−∞ (t − mT ) T
课程说明
作业或实验要求
3 次上机实验， 次上机实验，每次4小时， 小时，大作业 作业： 作业：每章内容结束后的下节课交作业
考核方式
理论考试： 理论考试：闭卷考试 2学时 计分方式： 作业、 实验、 计分方式 ：理论考试占70%，作业 、实验 、平时成绩占30%
教材及参考书
教材： 教材： 史林、 史林 、赵树杰 “数字信号处理” 数字信号处理”，科学出版社 参考书： 参考书 ： 1．Oppenheim A.V., Schafer R.W. “Digital Signal Processing”, Prentice Hall Inc. 丁玉美“ 数字信号处理” ２.丁玉美 “数字信号处理 ”，西安电子科技大学出版社 陈怀深等译“ 实现” ３. 陈怀深等译 “数字信号处理及其MATLAB实现 ”，电子工业出版社
k =−∞ ∧ ∧ ∞
∑ 2π a δ ( Ω − kΩ )
k s
fs = 1 T
3.1 采样定理
2π Pδ ( jΩ ) = T ∧ 1 X a ( jΩ ) = 2π 1 = 2π
采样信号的频谱 是原信号频谱的 周期延拓
k =−∞
∑ δ (Ω − kΩ )
s ∞
∞
X a ( jΩ ) ∗ Pδ ( jΩ ) 2π ⋅ T
一维信号( 一维信号(如语言信号) 如语言信号) 二维信号( 二维信号(如图像信号) 如图像信号) 多维信号
按信号是否为确定函数： 按信号是否为确定函数：
确定信号， 确定信号，随机信号
1.信号 1.信号
信号分类
按信号中自变量和幅度的取值特点
时间连续、 时间连续、幅度连续 模拟信号 时间离散、 时间离散、幅度连续 离散时间信号 时间连续、 时间连续、幅度离散 时间离散、 时间离散、幅度离散 数字信号
作业
1.2， 1.2，1.4， 1.4，1.5， 1.5，1.6 自己仿真1.9 自己仿真1.9， 1.9，1.10
Medical Devices
3.模拟信号的数字处理方法 3.模拟信号的数字处理方法
时间连续信号 时间采样 幅度量化 数字信号
离散时间信号
问题1 问题1：采样前后信号频谱的变化？ 采样前后信号频谱的变化？ 问题2 问题2：什么条件下， 什么条件下，可以从采样信号无失真恢复 出原信号？ 出原信号 ？
∧
∞
n =−∞
∑ x ( nT ) δ ( t − nT )
a
∞
3.1 采样定理
采样信号的频谱分析 采样信号的频谱分析
X a ( jΩ ) = FT [ xa ( t )] X a ( jΩ ) = FT [ x a ( t )] Pδ ( jΩ ) = FT [ Pδ ( t )] = Ω s = 2π T
X a(jΩ )
（a ）
Ω
－Ω c
0
Ωc P (jΩ ) δ
采样定理
（b ）
Ω
－Ω s
0
Ωs
＾ X a(jΩ )
Ω
（c ）
－Ω s Ω s 2 0
Ωs 2 Ω s
采样频率 > 信号最高频谱的 2倍
＾ X a(js
Ωs
0
Ω cΩ s
2
3.2 采样的恢复
利用低通滤波器还原满足奈奎斯特采样 利用低通滤波器还原满足奈奎斯特采样定理 奈奎斯特采样定理的 定理的 采样信号。 采样信号。 ˆ ( j Ω) X Ya ( jΩ) a
∫
∞
−∞
X a ( jθ ) ∑ δ ( Ω − k Ω s − θ )dθ
k =−∞
1 ∞ ∞ = ∑ ∫ X a ( jθ ) δ ( Ω − k Ω s − θ )dθ T k =−∞ −∞ 1 ∞ = ∑ X a ( jΩ − jk Ω s ) T k =−∞
3.1 采样定理
采样信号的频谱是模拟信号频谱 采样信号的频谱是模拟信号频谱以采样频率 的频谱是模拟信号频谱以采样频率为 以采样频率为 周期进行周期延拓而成 频谱幅度是原信号频谱幅度的1/T 频谱幅度是原信号频谱幅度的1/T倍 1/T倍 若信号的最高频率 Ωs Ωc > ， 2 Ωs 为折叠频率 2 则延拓分量产生频 谱混叠
3.1 采样定理
采样示意
理想采样
当 τ→0
ˆa (t ) = x a (t )δT (t ) x
3.1 采样定理
采样信号表示 采样信号表示
Pδ ( t ) = ∑ δ ( t − nT ) n =−∞ ⇒ ∞ ∧ x a ( t ) = xa ( t ) ⋅ Pδ ( t ) = ∑ xa ( t ) δ ( t − nT ) n =−∞ xa (t ) =
x (n ) 解码 x a(n T) 零阶保持 ′ (t ) xa 平滑滤波 x a(t )
卷积
H ( jΩ ) = ∫ e − jΩt dt
T
sin ( Ω T 2 ) − j ΩT =T e ΩT 2
0
2
例：模拟信号xa (t ) = sin(2π f0t + )，其中f0 = 50 Hz 8 1 ）求采样频率应为多少？采样间隔应为多少？ 2）若选采样频率f s = 200 Hz，采样间隔为多少？ ˆa (t )的表达式； 写出采样信号x ˆa (t )的时域离散信号x(n)的波形. 3）画出对应x
H[jΩ]
理想低通滤波器:
T H ( jΩ) = 0 Ωs Ω< 2 Ωs Ω≥ 2
H(jΩ) T
-Ωs/2
0
Ωs/2
Ω
ˆ ( jΩ) ⋅ H ( jΩ) = X ( jΩ) Ya ( jΩ) = X a a
讨论
ˆa (t ) → xa (t ) x
Ωs π sin( t ) sin( t ) T Ω s j Ωt 2 = T = e d Ω = Ωs π 2π ∫−Ωs t t 2 T ∞ ˆa (τ )h(t − τ )dτ 输出：ya (t ) = xa (t ) = ∫ x
数字信号处理学习指导与题解 4 khdaw
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
课后答案网，用心为你服务！
最全最多的课后习题参考答案，尽在课后答案网（）！
Khdaw团队一直秉承用心为大家服务的宗旨，以关注学生的学习生活为出发点，
爱校园（） 课后答案网（） 淘答案（）
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
.k h
后 答 案 网
da w. co m
ww
课
电子科技大学DSP上机题目
课件：数字信号处理,第五章,电子科技大学
Example N-point DFT of x[n] cos nRN [n] 6 (N=12) is wanted.
Solution
X [k ] x[n]W
n 0
N 1
kn N
1 [e n 0 2
11
j
2 n 12
e
j
2 n 12
]e
j
2 kn 12
6, k 1, 11 { 0, orthers
Solution 2 Using (B), we get
1 j 12 n j 12 kn 1 j 12 n j 12 kn X [k ] [ e e e e ] 2 n 0 2
~ 11 2 2 2 2
1 11 j 12 ( k 1) n 1 11 j 12 ( k 11) n e e 2 n 0 2 n 0
• Making use of the identity
( k r ) n W N n 0 N 1
N , for k r N , l an integer 0, otherwise
we get
N / 2, G[k ] N / 2, 0, for k r for k N r otherwise
k
Example x[n] cos n 6 has DFS, the coefficients are wanted. Solution 1
1 x[n] e 2
~ 2 j n 12
~
1 e 2
2 j n 12
1 e 2
j
2 n 12
1 e 2
j
2 (11) n 12
电子科大 数字信号处理实验2_FFT的实现
电 子 科 技 大 学实 验 报 告学生姓名：Shrimp 学 号： 指导教师：一、实验室名称：数字信号处理实验室 二、实验项目名称：FFT 的实现 三、实验原理：一．FFT 算法思想：1．DFT 的定义：对于有限长离散数字信号{x[n]}，0 ≤ n ≤ N-1，其离散谱{x[k]}可以由离散付氏变换（DFT ）求得。
DFT 的定义为：21[][]N jnk Nn X k x n eπ--==∑，k=0,1,…N-1通常令2jNN eW π-=，称为旋转因子。
2．直接计算DFT 的问题及FFT 的基本思想：由DFT 的定义可以看出，在x[n]为复数序列的情况下，完全直接运算N 点DFT 需要（N-1）2次复数乘法和N （N-1）次加法。
因此，对于一些相当大的N 值（如1024）来说，直接计算它的DFT 所作的计算量是很大的。
FFT 的基本思想在于，将原有的N 点序列分成两个较短的序列，这些序列的DFT 可以很简单的组合起来得到原序列的DFT 。
例如，若N 为偶数，将原有的N 点序列分成两个（N/2）点序列，那么计算N 点DFT 将只需要约[(N/2)2 ·2]=N 2/2次复数乘法。
即比直接计算少作一半乘法。
因子（N/2）2表示直接计算（N/2）点DFT 所需要的乘法次数，而乘数2代表必须完成两个DFT 。
上述处理方法可以反复使用，即（N/2）点的DFT 计算也可以化成两个（N/4）点的DFT （假定N/2为偶数），从而又少作一半的乘法。
这样一级一级的划分下去一直到最后就划分成两点的FFT 运算的情况。
3．基2按时间抽取（DIT ）的FFT 算法思想：设序列长度为2L N =，L 为整数（如果序列长度不满足此条件，通过在后面补零让其满足）。
将长度为2L N =的序列[](0,1,...,1)x n n N =-，先按n 的奇偶分成两组：12[2][][21][]x r x r x r x r =+=，r=0,1,…,N/2-1DFT 化为：1/21/212(21)0/21/21221200/21/211/22/2[]{[]}[][2][21][][][][]N N N nk rk r kNNNn r r N N rk k rk NNN r r N N rk k rk N NN r r X k DFT x n x n Wx r Wx r W x r W Wx r W x r WWx r W ---+===--==--=====++=+=+∑∑∑∑∑∑∑上式中利用了旋转因子的可约性，即：2/2rkrkNN W W =。
《数字信号处理》自测题3答案——电子科技大学
一．选择与填空：1．若一系统为因果系统，则该系统的单位脉冲响应h(n)应满足0,0)(<≡n n h ，该系统的系统函数应满足 其收敛域为∞≤<-z R x ；若该系统为稳定系统，则该系统的单位脉冲响应h(n)应满足∞<∑∞-∞=n n h )(1=。
2．对下列序列，试求其零极点，Z 变换和收敛域。
a) )()(10n R n x = b) )(5sin )(n u n n x ⎪⎭⎫⎝⎛=π解:a) )1(111)(910110--=--=--z z z z z z X 其收敛域为∞≤<z 0,其零极点分布为: 零点:9个一阶零点9,,1 102 ==k ez k j k π;极点:一个9阶极点;0=zb) ⎪⎪⎭⎫ ⎝⎛-==-∞=--∞=∞=-∑∑∑n n n j n n n j n nz e z e j z nz X 0505021)5sin()(πππ ))(()2.0sin()2.0cos(21)2.0sin(111121552111515πππππππj j j j e z e z z zz z z e z e j ---------=+-=⎪⎪⎪⎭⎫⎝⎛---= 其收敛域为∞≤<z 1,其零极点分布为: 零点:1个一阶零点0=z ;极点:2个一阶极点;2.01πj e z =;2.02πj e z -=3．若对话音信号进行离散时间处理，已知话音信号为实信号，其频率范围为300~3400Hz ，则抽样频率为 >6800Hz 。
4．对连续时间非周期信号的谱分析工具是 傅立叶变换 ，对连续时间周期信号的谱分析工具是 傅立叶级数 ，对周期序列的谱分析工具是 离散傅立叶级数 ，对非周期序列的谱分析工具是 离散傅立叶变换 。
5．若某系统的群延时为常数，则该系统具有的相位特性为 线性相位 。
6．脉冲响应不变法存在频谱混叠的现象，是因为 z s →映射为多对一映射 ；双线性变换法不存在频谱混叠的现象，是因为 z s →映射为一对一映射 ；因此，对于同样指标设计的滤波器，双线性变换法的设计结果 优于 （优于/劣于）脉冲响应不变法的设计结果。
电子科技大学 数字信号处理 第二次编程作业
第二次编程作业加载信号(EEGdata.txt)；分析信号的幅度谱,确定低通FIR数字滤波器的指标；分别利用各种窗函数（Rectangular, Hamming, Kaiser）设计此FIR滤波器；对信号加随机噪声，并用设计的FIR滤波器对含噪声信号进行滤波。
要求：1）给出程序，画出滤波器幅度谱及其增益图(dB)；分析设计的滤波器是否达到指标。
2）利用设计的三种滤波器对加载的信号分别进行滤波，对比分析滤波结果。
程序：data = load('EEGdata.txt');n=1:length(data);xn=0.1*rand(length(data),1)-0.05;x=xn+data;[h0,w0]=freqz(data);[h1,w1]=freqz(x);figure(1)plot(w0/pi,abs(h0),w1/pi,abs(h1),'r');legend('Ô-dataÐźÅƵÆ×ͼ','¼ÓÔëÐźÅƵÆ×ͼ');wp = 0.15*pi;ws = 0.2*pi;DB = ws-wp;N = ceil(2*3.11*pi/DB+1);wc = (wp+ws)/2;wc = wc/pi;win = rectwin(N+1);b = fir1(N, wc, 'low', win);figure(2)freqz(b,1);wp = 0.15*pi;ws = 0.2*pi;DB = ws-wp;N = ceil(2*3.11*pi/DB+1);wc = (wp+ws)/2;wc = wc/pi;win = hamming(N+1);b1 = fir1(N, wc, 'low', win);figure(3)freqz(b1,1);fpts = [0.15, 0.2];mag = [1, 0];dev = [0.01, 0.01];[N, Wn, beta, ftype] = kaiserord(fpts, mag, dev)Kwin = kaiser(N+1, beta);b2 = fir1(N, Wn, Kwin);[h,omega] = freqz(b2,1,512);figure(4)freqz(b2,1);y=filter(b, 1, x);figure(5)subplot(2,1,1);plot(n,data,n,x,'g',n,y,'r');title('¾ØÐδ°Â˲¨·ù¶ÈÆ×Ч¹û¶Ô±Èͼ');lege nd('Ô-ÐźÅdata','¼ÓÔëÐźÅx','Â˲¨ºóÐźÅy');[H,W]=freqz(y);subplot(2,1,2);plot(w0/pi,abs(h0),W/pi,abs(H),'r');title('¾ØÐδ°Â˲¨ÆµÆ×Ч¹û¶Ô±Èͼ') ;legend('Ô-ÐźÅdata','Â˲¨ºóÐźÅy');y1=filter(b1, 1, x);figure(6)subplot(2,1,1);plot(n,data,n,x,'g',n,y1,'r');title('Hamming´°Â˲¨·ù¶ÈÆ×Ч¹û¶Ô±Èͼ'); legend('Ô-ÐźÅdata','¼ÓÔëÐźÅx','Â˲¨ºóÐźÅy1');[H,W]=freqz(y1);subplot(2,1,2);plot(w0/pi,abs(h0),W/pi,abs(H),'r');title('Hamming´°Â˲¨ÆµÆ×Ч¹û¶Ô±Èͼ');legend('Ô-ÐźÅdata','Â˲¨ºóÐźÅy1');y2=filtfilt(b2, 1, x); figure(7) subplot(2,1,1);plot(n,data,n,x,'g',n,y2,'r');title('Kaiser´°Â˲¨·ù¶ÈÆ×Ч¹û¶Ô±Èͼ');l egend('Ô-ÐźÅdata','¼ÓÔëÐźÅx','Â˲¨ºóÐźÅy2'); [H,W]=freqz(y2); subplot(2,1,2);plot(w0/pi,abs(h0),W/pi,abs(H),'r');title('Kaiser´°Â˲¨ÆµÆ×Ч¹û¶Ô±Èͼ');legend('Ô-ÐźÅdata','Â˲¨ºóÐźÅy2');figure(8)plot(n,data,n,y,'c',n,y1,'r',n,y2,'g');title('ÈýÖÖ´°º¯ÊýÂ˲¨Ð§¹û¶Ô±Èͼ');legend('Ô-dataÐźÅ','¾ØÐδ°Â˲¨','Hamming´°Â˲¨','Kaiser´°Â˲¨');0.10.20.30.40.50.60.70.80.9102468101214161800.10.20.30.40.50.60.70.80.91-3000-2000-1000Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )00.10.20.30.40.50.60.70.80.91-100-5050Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )00.10.20.30.40.50.60.70.80.91-3000-2000-1000Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91-150-100-50050Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )0.10.20.30.40.50.60.70.80.91-2000-1500-1000-500Normalized Frequency (⨯π rad/sample)P h a s e (d e g r e e s )0.10.20.30.40.50.60.70.80.91-150-100-50050Normalized Frequency (⨯π rad/sample)M a g n i t u d e (d B )-0.2-0.100.10.2矩形窗滤波幅度谱效果对比图0.10.20.30.40.50.60.70.80.91051015矩形窗滤波频谱效果对比图-0.2-0.100.10.2Hamming 窗滤波幅度谱效果对比图0.10.20.30.40.50.60.70.80.91051015Hamming 窗滤波频谱效果对比图-0.2-0.100.10.2Kaiser 窗滤波幅度谱效果对比图0.10.20.30.40.50.60.70.80.9105101520Kaiser 窗滤波频谱效果对比图结果分析：滤波效果皆不尽如人意，原因是加载的噪声信号是随机信号，各频率皆有，滤波器通带部分的噪声无法滤掉。
电子科技大学《数字信号处理》自测题
１自测题一及答案一．选择与填空：1．数字信号是______(3)___。
（1）时间上和幅度上均连续的理想信号 （2）时间上离散而幅度上连续的信号（3）时间上离散、幅度上量化的非理想信号 （4）时间上连续而幅度上量化的非理想信号2．对于时间上离散的周期信号，可以___(4)___________。
（1）用傅立叶变换（FT ）求其频谱 （2）用离散傅立叶变换（DFT ）求其频谱 （3）可展成傅立叶级数（FS ） （4）可展成离散傅立叶级数（DFS ）3．已知x(n)为16点序列，其DFT 应为___(5)___，IDFT 应为____(6)___。
（1） ∑==15016)(161)(n nK W n x K X （2） nKn W n x K X 1616)()(∑==（3） ∑==1516)()(n nKWn x K X （4） ∑==1515)()(n nKW n x K X（5） ∑==1516)()(K nK WK X n x （6） ∑=-=15016)(161)(K nKW K X n x （7） ∑==15016)(161)(K nK W K X n x （8） ∑=-=15015)(161)(K nKW K X n x 4．数字信号处理中，时域上表征系统的瞬时输出经常用_____(2)_____。
（1）系统的单位脉冲响应 h(n) （2）离散卷积和（3）系统的传递函数H(Z) （4）系统的频响H(e j ω)5．如果对数字滤波器的相频特性不作要求，仅从滤波效率来看，IIR 数字滤波器的效率比FIR 数字滤波 器的效率要___高___，即在相同的通带、阻带滤波性能指标下，__IIR_____数字滤波器结构要简单些， 其滤波器的阶数N 要__低_____。
6．已知某线性相位FIR 数字滤波器的其中一个零点40πjeZ =，根据零点分布规律，其系统函数：H （Z ）=)1)(1(44ππjjeeA ---。
电子科技大学20春《数字信号处理》在线作业1.doc
1.下面关于IIR滤波器设计说法正确的是（）。
A.双线性变换法的优点是数字频率和模拟频率成线性关系B.冲激响应不变法无频率混叠现象C.冲激响应不变法不适合设计高通滤波器D.双线性变换法只适合设计低通、带通滤波器【参考答案】: C2.题目及选项如下图所示A.AB.BC.CD.D【参考答案】: A3.下列关于窗函数设计法的说法中错误的是（）。
A.窗函数的长度增加，则主瓣宽度减小，旁瓣宽度减小B.窗函数的旁瓣相对幅度取决于窗函数的形状，与窗函数的长度无关C.为减小旁瓣相对幅度而改变窗函数的形状，通常主瓣的宽度会增加D.对于长度固定的窗，只要选择合适的窗函数就可以使主瓣宽度足够窄，旁瓣幅度足够小【参考答案】: B4.一个线性移不变系统稳定的充分必要条件是其系统函数的收敛域包括（）。
A.原点B.单位圆C.虚轴D.实轴【参考答案】: B5.题目及选项如下图所示A.AB.BC.CD.D【参考答案】: A6.已知一连续时间信号的最高截止频率是4kHz，则要从该连续时间信号的均匀离散采样值无失真地恢复原信号，则采样频率为（）。
A.2kHzB.4kHzC.6kHzD.8kHz【参考答案】: D7.题目及选项如下图所示A.AB.BC.CD.D【参考答案】: A8.题目及选项如下图所示A.AB.BC.CD.D【参考答案】: A9.对连续时间周期信号的谱分析工具是（）。
A.傅里叶变换B.傅里叶级数C.离散傅里叶变换D.离散傅里叶级数【参考答案】: B10.下面说法中正确的是（）。
A.连续时间非周期信号的频谱为连续周期函数B.连续时间周期信号的频谱为连续周期函数C.离散时间非周期信号的频谱为离散周期函数D.离散时间周期信号的频谱为离散周期函数【参考答案】: D11.题目及选项如下图所示A.AB.BC.CD.D【参考答案】: A12.要处理一个连续时间信号，对其进行采样的频率为6kHz，要无失真的恢复该连续信号，则该连续信号的最高频率可能是（）。
电子科技大学 数字信号处理 上机实验四
电子科技大学生命科学与技术学院标准实验报告（实验）课程名称数字信号处理2012-2013-第2学期电子科技大学教务处制表电子科技大学实验报告学生姓名：张华博学号：2011091010004 指导教师：李永杰实验地点：清水河校区实验时间：2013年月日一、实验室名称：科二 504 机房二、实验名称：FIR滤波器的特性及应用三、实验学时：2学时四、实验原理：五、实验目的：（详细填写）1. 熟悉相位信息的特性2. 测试FIR滤波器的滤波特性六、实验内容：（详细填写）1. 相位信息的作用2. 测试线性相位FIR滤波器的滤波特性七、实验器材（设备、元器件）：八、实验步骤：九、实验数据及结果分析：（详细填写）（包括程序、图、结果等）1、n=0:99;m=2/100:2/100:2;y=sin(0.1*pi*n)+2*cos(0.2*pi*n);XXX = fft(y);plot(m,abs(XXX));title('信号频谱图');figure(2);plot(m,unwrap(angle(XXX))); title('信号相位谱');x1=cos(0.85*pi*n);x2=0.2*n;Pha1=unwrap(angle(XXX))+x1;Pha2=unwrap(angle(XXX))+x2;figure(3)plot(m,Pha1);title('加随机相位的相位谱');figure(4)plot(m,Pha2);title('加线性相位的相位谱');cc1 = abs(XXX).*exp(i*Pha1);dd1 = ifft(cc1, 'symmetric');cc2 = abs(XXX).*exp(i*Pha2);dd2 = ifft(cc2, 'symmetric');figure(5)plot(n,y,'b',n,dd1,'r',n,dd2,': b');title('fft反变换与原信号对比图'); legend('原信号','加随机相位的信号','加线性相位的信号');0.20.40.60.811.21.41.61.820102030405060708090100信号频谱图00.20.40.60.81 1.2 1.4 1.6 1.82510152025信号相位谱00.20.40.60.81 1.2 1.4 1.6 1.82510152025加随机相位后的相位谱00.20.40.60.81 1.2 1.4 1.6 1.8251015202530354045加线性相位后的相位谱102030405060708090100-3-2-1123fft 反变换与原信号对比图2、h=[-1 2 -3 6 -3 2 -1]; %×Ô¼º¹¹Ôìh(n)ÐòÁÐ a=1; %µ±ÎªFIRÂ˲¨Æ÷ʱ£¬È¡a=1; zplane(h,a); M = 100;[H,w] = freqz(h,a,M); figure(2); plot(w,abs(H)); xlabel('\omega'); ylabel('Amplitude'); figure(3);plot(w,unwrap(angle(H))); xlabel('\omega');ylabel('Phase');h1=[-1 2 -3 -3 2 -1]; %×Ô¼º¹¹Ôìh(n)ÐòÁÐ a1=1; %µ±ÎªFIRÂ˲¨Æ÷ʱ£¬È¡a=1; figure(4); zplane(h1,a1); M = 100;[H1,w1] = freqz(h1,a1,M); figure(5); plot(w1,abs(H1));xlabel('\omega');ylabel('Amplitude');figure(6);plot(w1,unwrap(angle(H1)));xlabel('\omega');ylabel('Phase');h2=[-1 2 -3 0 3 -2 1]; %×Ô¼º¹¹Ôìh(n)ÐòÁÐa2=1; %µ±ÎªFIRÂ˲¨Æ÷ʱ£¬È¡a=1;figure(7);zplane(h2,a2);M = 100;[H2,w2] = freqz(h2,a2,M);figure(8);plot(w2,abs(H2));xlabel('\omega');ylabel('Amplitude');figure(9);plot(w2,unwrap(angle(H2)));xlabel('\omega');ylabel('Phase');h3=[-1 2 -3 3 -2 1]; %×Ô¼º¹¹Ôìh(n)ÐòÁÐa3=1; %µ±ÎªFIRÂ˲¨Æ÷ʱ£¬È¡a=1;figure(10);zplane(h3,a3);M = 100;[H3,w3] = freqz(h3,a3,M);figure(11);plot(w3,abs(H3));xlabel('\omega');ylabel('Amplitude');figure(12);plot(w3,unwrap(angle(H3)));xlabel('\omega');ylabel('Phase');-1.5-1-0.50.511.522.5-1.5-1-0.50.511.5Real PartI m a g i n a r y P a r t00.51 1.52 2.53 3.524681012141618A m p l i t u d e0.511.522.533.5-10-9-8-7-6-5-4-3-2-1P h a s e-2-1.5-1-0.500.511.52-1.5-1-0.500.511.5Real PartI m a g i n a r y P a r t00.51 1.52 2.53 3.5123456789ωA m p l i t u d e00.51 1.52 2.53 3.5-5-4-3-2-101234ωP h a s e-2-1.5-1-0.500.511.52-1.5-1-0.50.511.5Real PartI m a g i n a r y P a r t0.511.522.533.5012345678910A m p l i t u d e00.51 1.52 2.53 3.5-12-10-8-6-4-2P h a s e-1-0.500.51-1-0.8-0.6-0.4-0.200.20.40.60.81Real PartI m a g i n a r y P a r t00.51 1.52 2.53 3.524681012ωA m p l i t u d e00.51 1.52 2.53 3.5-5-4-3-2-11ωP h a s eh=[-1 2 -3 6 -3 2 -1]; a=1;coef = sum(abs(h))/sum(a);h = h/coef; zplane(h,a); M = 50;[H,w] = freqz(h,a,M); figure(2); plot(w/pi,abs(H)); figure(3);plot(w/pi,unwrap(angle(H))); n=0:49;xs=sin(0.95*pi*n); xn=sin(0.5*pi*n); x=xs+xn;y = filter(h, a, x); [h2,w2]=freqz(y) figure(4)plot(n,xs,n,y,'r');legend('Ô-ÐźÅ','Â˲¨ºó'); figure(5)plot(w1/pi,abs(h1),w2/pi,abs(h2),'r');title('ƵÆ×ͼ¶Ô±È');legend('Ô-ÐźÅ','Â˲¨ºó');-1.5-1-0.50.511.522.5-1.5-1-0.50.511.5Real PartI m a g i n a r y P a r t00.10.20.30.40.50.60.70.80.910.10.20.30.40.50.60.70.80.910.10.20.30.40.50.60.70.80.91-10-9-8-7-6-5-4-3-2-15101520253035404550-1.5-1-0.50.511.50.10.20.30.40.50.60.70.80.910510152025频谱图对比十、实验结论：（详细填写）1、给一信号相位谱加一线性相位后，做fft 反变换所得图像为原图平移一定相位；若加一随机相位，做反变换后，不仅相位发生平移，而且幅度也发生变化。
电子科大数字信号处理(dsp)matlab作业
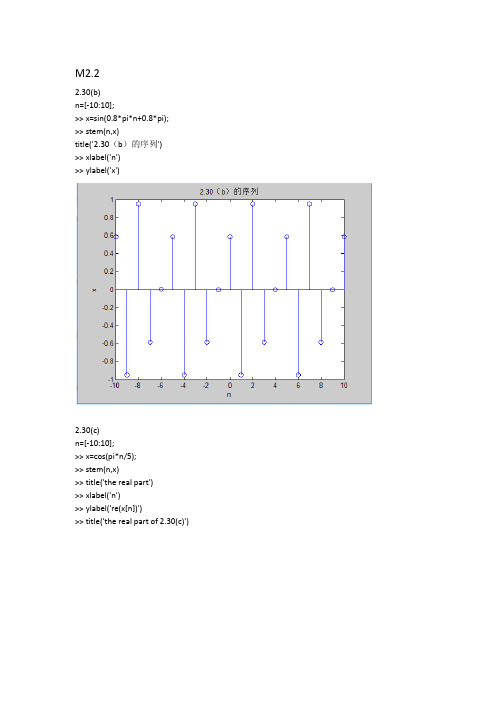
M2.22.30(b)n=[-10:10];>> x=sin(0.8*pi*n+0.8*pi); >> stem(n,x)title('2.30（b）的序列')>> xlabel('n')>> ylabel('x')2.30(c)n=[-10:10];>> x=cos(pi*n/5);>> stem(n,x)>> title('the real part')>> xlabel('n')>> ylabel('re(x[n])')>> title('the real part of 2.30(c)')x=sin(pi*n/10);>> stem(n,x)>> title('the imaginary part of 2.30(c)')>> xlabel('n')>> ylabel('im(x[n])')2.30(d)n=[-20:20];>> x=3*cos(1.3*pi*n)-4*sin(0.5*pi*n+0.5*pi);>> stem(n,x)>> title('2.30(d)的序列')>> xlabel('n')>> ylabel('x[n]')2.30(e)n=[-20:20];>> x=5*cos(1.5*pi*n+0.75*pi)+4*cos(0.6*pi*n)-sin(0.5*pi*n); >> stem(n,x)>> title('2.30(e)的序列')>> xlabel('n')>> ylabel('x[n]')M2.7编写的程序如下% Program M2.7% Computation the discreet time system of exercise 2.40alpha=input('alpha=');y0=1;y1=0.5*(y0+(alpha/y0));while abs(y1-y0)>0.0001y2=0.5*(y1+(alpha/y1));y0=y1;y1=y2;enddisp('y[n]收敛于根号alpha=');y2运行结果如下：alpha=9y[n]收敛于根号alpha=y2 =3.0000alpha=30y[n]收敛于根号alpha=y2 =5.4772经两组数据对比，知已用仿真证明，n趋于无穷时，Y[n]收敛于根号下alpha。