由真值表求逻辑表达式的方法
2009数字[第二课 逻辑函数和逻辑门]
![2009数字[第二课 逻辑函数和逻辑门]](https://img.taocdn.com/s3/m/cb2e2c18f18583d049645926.png)
4 〉 逻辑函数式的常见形式
一个逻辑函数的表达式不是唯一的,可以有多 种形式,并且能互相转换。 例如:
其中,与—或表达式是逻辑函数的最基本表达形式。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
5 〉 表 达 式 → 电 路 图
(1)用与非门实现(Y=AB)
•非:Y=A=AA
•与:Y=AB=AB •或:Y=A+B=A+B=A B
L=A+B
4 、 其 他 常 用 逻 辑 运 算
3〉异或: A
B = AB + AB 相同为0 A A=0 相异为1 A A=1
A 1=? A A 0=? A
4〉同或: A⊙ B = A B=AB + AB 相同为1 相异为0
@ Copyright 杭州电子科技大学 电子信息学院 张珣
二、逻辑函数及其表示方法
* 表 示 方 式
逻辑变量、逻辑函数、真值表、逻辑电路等。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
一、与或非代数系统基本逻辑关系
1、与: Y=X1^X2=X1.X2=X1X2 (逻辑乘) X1 X2 Y
全1为1
有0则0
例: 1^1=? 1^0=? 0^1=? 0^0=?
1 0 0 0
在应用反演规则求反函数时要注意两点: (1)保持运算的优先顺序不变,必要时加括号表明。 (2)变换中,几个变量(一个以上)的公共非号保持不变。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
2 、逻辑规则
4〉展开规则: Y=f(X1,X2,X3,…,Xk) =X1f(0,X2,…,Xk)+X1f(1, X2,…,Xk) =[X1+f(0,X2,…,Xk)][X1 + f(1, X2,…,Xk)]
《数字逻辑基础》-第02章(2)

险象的分类 按险象脉冲的极性分: 若险象脉冲为负极性脉冲,则称为“0”型险象; 若险象脉冲为正极性脉冲,则称为“1”型险象。 按输入变化前后,“正常的输出”是否应该变化分: 若输出本应静止不变,但险象使输出发生了不应有的短暂变化,则 称为静态险象; 在输出应该变化的情况下出现了险象,则称为动态险象。 四种组合险象示意:
静态“0”型险象 输出波形 静态“1”型险象 动态“0”型险象 动态“1”型险象 输入信号变化的时刻
2.5.2
险象的判断与消除
1. 用代数法判断及消除险象 继续考察函数 F AB A C 令B=1、C=1保持不变,令A变化,有:
F A 1 A 1 A A
再看,对F 作变换:
0101 0011 1 1001 „„ X „„ Y „„ C-1 „„ S
S≤ 9
结果 Z = S, W = 0
1 (2) 设 C1 , X 5 Y 9 , ,则 S X Y C1。因S >9,故S不是所求的Z, 15 须对S进行加6修正,而W应为1。
0101 1001 1 1111 „„ X „„ Y „„ C-1 „„ S 1 1 1 1 „„ S 的低4位 0 1 1 0 „„ 6 Z = 0101 结果 W = 1 1 0 1 0 1 „„ Z 丢弃
F A A A A
?
因 A 多经过非门,比 A 的变化有延时,故出现险象。
?
上式中出现
或 形式的项,这样的项会产生险象。
险象判断法: 对于逻辑表达式 F ( xn , xi , x1 ) ,考察 xi (i n 1) 变化、其他量不 变时是否产生险象,则将其他量的固定值代入式中。若得到的表达式 含有形如i xi 或i xi 形式的项,则该逻辑表达式可能产生险象。 x x
组合逻辑电路

输出Y.~Y.为低电平0有效。代码1010~1111
没有使用,称为伪码。由上表可知,当输入伪
码1010~1111时,输出Y9~Y0都为高电平1, 不会出现低电平0。因此译码器不会产生错误译
码。
图13.7 二-十进制译码器逻辑图
1.3 译 码 器
10
1.3 译 码 器
11
1.3.3 BCD-7段显示译码器
二进制码器是用于把二进制 代码转换成相应输出信号的译码 器。常见的有2线-4线译码器、 3线-8线译码器和4线-16线译码 器等。如图13.5所示为集成3线 -8线译码器74LS138的逻辑图 。
图13.5 3线-8线译码器逻辑图
1.3 译 码 器
9
1.3.2 二-十进制译码器
将4位BCD码的10组代码翻译成0~9这10个
图1.11 数据选择器
1. 4选1数据选择器
图1.12所示为4选1数据选择器的逻辑图 ,A1、A0是地址端。D0~D3是4个数据端 ,ST是低电平有效的使能端,具有两个互 补输出端Y和Y。对于不同的二进制地址输 入,可按地址选择D0~D3中一个数据输出 。其功能如表13.8所示。
图1.12 4选1数据选择器逻辑图
1
1.1 组合逻辑电路的分析与设计
2
1.1.1 组合逻辑电路的分析方法
组合逻辑电路的分析是根据给定的逻辑电路图,弄清楚它的逻辑功 能,求出描述电路输出与输入之间的逻辑关系的表达式,列出真值表 。一般方法如下所述。
1)根据给定的逻辑电路的逻辑图,从输入端向输出端逐级写出各 个门对其输入的逻辑表达式,从而写出整个逻辑电路的输出对输入的 逻辑函数表达式。
2)利用逻辑代数运算法则化简逻辑函数表达式。 3)根据化简后的逻辑函数表达式,列出真值表,使逻辑功能更加 清晰。 4)根据化简后的逻辑函数表达式或真值表,分析逻辑功能。 下面通过一个例子说明组合逻辑电路的分析方法。
数字电路与逻辑设计试题与答案

数字电路与逻辑设计(1)班级 学号 姓名 成绩一.单项选择题(每题1分,共10分)1.表示任意两位无符号十进制数需要( )二进制数。
A .6B .7C .8D .9 2.余3码10001000对应的2421码为( )。
A .01010101 B.10000101 C.10111011 D.11101011 3.补码1.1000的真值是( )。
A . +1.0111 B. -1.0111 C. -0.1001 D. -0. 1000 4.标准或-与式是由( )构成的逻辑表达式。
A .与项相或 B. 最小项相或 C. 最大项相与 D.或项相与 5.根据反演规则,()()E DE C C A F ++⋅+=的反函数为( )。
A. E )]E D (C C [A F ⋅++=B. E )E D (C C A F ⋅++=C. E )E D C C A (F ⋅++=D. E )(D A F ⋅++=E C C6.下列四种类型的逻辑门中,可以用( )实现三种基本运算。
A. 与门B. 或门C. 非门D. 与非门7. 将D 触发器改造成T 触发器,图1所示电路中的虚线框内应是( )。
图1A. 或非门B. 与非门C. 异或门D. 同或门8.实现两个四位二进制数相乘的组合电路,应有( )个输出函数。
A . 8 B. 9 C. 10 D. 11 9.要使JK 触发器在时钟作用下的次态与现态相反,JK 端取值应为( )。
A .JK=00 B. JK=01 C. JK=10 D. JK=11 10.设计一个四位二进制码的奇偶位发生器(假定采用偶检验码),需要( )个异或门。
A .2 B. 3 C. 4 D. 5二.判断题(判断各题正误,正确的在括号内记“∨”,错误的在括号内记“×”,并在划线处改正。
每题2分,共10分)1.原码和补码均可实现将减法运算转化为加法运算。
( )2.逻辑函数7),M(1,3,4,6,C)B,F(A,∏=则m(0,2,5)C)B,(A,F ∑=。
第四章:逻辑代数及其化简(2)
包含律:AB AC BC AB AC 证:AB AC BC AB AC A ABC
AB AC ABC ABC
AB1 C AC 1 B
若两个乘积项中分别 包含A和A两个因子, 而这两个乘积项的其 余因子组成第三个乘 积项,则第三个乘积 项是多余的。可消去
定理:任何逻辑函数 F 都可以用最小项之和的形式表示。 而且这种形式是唯一的。 1、 真值表法: 将逻辑函数先用真值表表示,然后再根据真值表写出最 小项之和。 例:将 F ABC BC AC 表示为最小项之和的形式。 解:由最小项特点知:n 个变量都出现,BC 缺变量 A ,
AC缺变量B, BC和AC不是最小项。 所以 F 是一般与-或式,不是最小项之和的标准形式。
例:已知一个奇偶判别函数的真值表(偶 ③ n个输入变量就有2n个 为1,奇为0),试写出它的逻辑函数式。
A 0 0 0
B 0 0 1
C 0 1 0
Y
0
1 1
1
0 0
1
0 1
1
1
0
解: 当ABC=011时, 使乘积项 ABC 1 1 1 1 不同的取值组合。 当ABC=101时, 使乘积项ABC 1 当ABC=110时, 使乘积项ABC 1 因此,Y的逻辑函数应当等于这三个乘积项之和。 Y ABC ABC ABC
二、从逻辑表达式列出真值表 将输入变量的所有状态组合 逐一代入逻辑式,求出函数值, 列成表,即可得到真值表。 例:已知函数 Y A BC ABC 求其对应真值表。 解:将三变量所有取值组合代 入Y式中,将计算结果列表。
A B C 0 0 0 0 0 1
BC
逻辑函数的五种表示方法

逻辑函数的五种表示方法
逻辑函数是计算机科学中的重要概念,它是由逻辑变量和逻辑运算符组成的表达式。
逻辑函数可以用五种不同的方式来表示,分别是真值表、逻辑表达式、卡诺图、逻辑电路和逻辑方程。
1. 真值表
真值表是逻辑函数最基本的表示方法,它列出了所有可能的输入组合和对应的输出值。
真值表可以直观地展示逻辑函数的行为,但是对于复杂的逻辑函数,真值表会变得非常庞大,难以处理。
2. 逻辑表达式
逻辑表达式是逻辑函数的一种代数表示方法,它使用逻辑运算符和逻辑变量来表示逻辑函数。
逻辑表达式可以简化逻辑函数,使得它更易于理解和处理。
逻辑表达式可以使用布尔代数和卡诺图等方法来求解。
3. 卡诺图
卡诺图是一种图形化的逻辑函数表示方法,它使用方格和不同颜色的区域来表示逻辑函数。
卡诺图可以用来简化逻辑函数,减少逻辑门的数量,从而降低电路的成本和功耗。
卡诺图可以用来求解布尔代数和逻辑表达式。
4. 逻辑电路
逻辑电路是逻辑函数的一种物理表示方法,它使用逻辑门和电子元件来实现逻辑函数。
逻辑电路可以用来控制计算机和其他电子设备的行为。
逻辑电路可以使用逻辑表达式和卡诺图等方法来设计和优化。
5. 逻辑方程
逻辑方程是逻辑函数的一种代数表示方法,它使用逻辑变量和逻辑运算符来表示逻辑函数。
逻辑方程可以用来求解逻辑表达式和卡诺图,从而简化逻辑函数。
逻辑方程可以使用布尔代数和其他代数方法来求解。
数字电子技术第4章组合逻辑电路习题解答
、已知8421BCD可用7段译码器,驱动日字LED管,显示出十进制数字。指出下列变换真值表中哪一行是正确的。(注:逻辑“1”表示灯亮)
D
C
B
A
a
b
c
d
e
f
g *
0
0
0
0
0
0
0
0
0
0
0
0
4
0
1
0
0
0
1
1
0
0
1
1
7
0
1
1
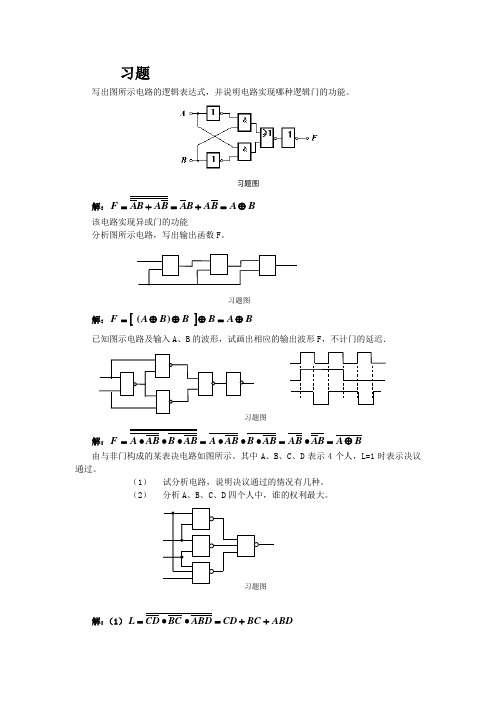
(1)试分析电路,说明决议通过的情况有几种。
(2)分析A、B、C、D四个人中,谁的权利最大。
习题图
解:(1)
(2)
ABCD
L
ABCD
L
0000
0001
0010
0011
0100
0101
0110
0111
0
0
0
1
0
0
1
1
1000
1001
1010
1011
1100
1101
1110
1111
0
0
0
1
0
1
1
1
(3)根据真值表可知,四个人当中C的权利最大。
3) 用与或非门实现。
解:(1)将逻辑函数化成最简与或式并转换成最简与非式。
根据最简与非式画出用与非门实现的最简逻辑电路:电路略。
(2 )由上述卡偌图还可得到最简或与表达式:
即可用或非门实现。
(3)由上步可继续做变换:
逻辑电路

1.1 项目描述数字电路主要研究的是输出信号的状态(0或1)与输入信号的状态(0或1)之间的关系,这是一种因果关系,也就是所谓的逻辑关系,即电路的逻辑功能。
在数字电路中,经常要检测电路的输入与输出是否符合所要求的逻辑关系,但是用万用表测试数字电路电平的高低显得很不方便,可以用逻辑测试笔来测试。
逻辑测试笔也叫做逻辑探针,它是数字电路设计、实验、检查和维修中最简单实用的工具。
1.1.1 项目学习情境:逻辑测试笔的制作与调试图1-1所示为逻辑测试笔的电路原理图,此电路由集成逻辑门构成。
本项目需要完成的主要任务是:①熟悉电路各元器件的作用;②进行电路元器件的安装;③进行电路参数的测试与调整;④撰写电路制作报告。
图1-1 逻辑测试笔电路原理图1.1.2 电路分析与电路元器件参数及功能一、电路分析如图1-1所示电路,当被测点为高电平时,VD1导通,VT1发射极输出高电平,经U1A 反相后,输出低电平,LED1(红色发光二极管)导通而发光。
此时,VD2截止,U2A输出低电平,U3A输出高电平,使LED2(绿色发光二极管)截止而不发光,而U4A输出高电平,使LED3(黄色发光二极管)截止而不发光。
二、电路元器件参数及功能逻辑测试笔电路元器件参数及功能如表1-1所示。
1.2 知识链接1.2.1 数字电路的基本概念电子电路所处理的电信号可以分为两大类:一类是在时间和数值上都是连续变化的信号,称为模拟信号,例如电流信号、电压信号等,如图1-2(a)所示;另一类是在时间和数值上都是离散的信号,称为数字信号,例如计算机中传送的数据信号、IC卡信号等,如图1-2(b)所示。
图1-2 模拟信号与数字信号与模拟电路相比,数字电路具有以下显著的优点:(1) 工作信号是二进制的数字信号,反映在电路上是高低电平两种状态。
(2) 研究的主要问题是电路的逻辑功能。
(3) 电路结构简单,便于集成、系列化生产,成本低廉,使用方便。
(4) 抗干扰性强,可靠性高,精度高。
数字电子技术基础第三版第一章答案

第一章数字逻辑基础第一节重点与难点一、重点:1.数制2.编码(1) 二—十进制码(BCD码)在这种编码中,用四位二进制数表示十进制数中的0~9十个数码。
常用的编码有8421BCD码、5421BCD码和余3码。
8421BCD码是由四位二进制数0000到1111十六种组合中前十种组合,即0000~1001来代表十进制数0~9十个数码,每位二进制码具有固定的权值8、4、2、1,称有权码。
余3码是由8421BCD码加3(0011)得来,是一种无权码。
(2)格雷码格雷码是一种常见的无权码。
这种码的特点是相邻的两个码组之间仅有一位不同,因而其可靠性较高,广泛应用于计数和数字系统的输入、输出等场合。
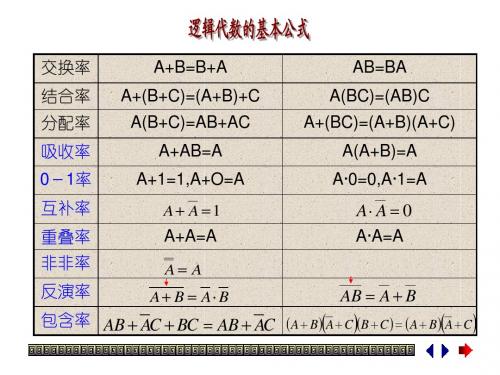
3.逻辑代数基础(1)逻辑代数的基本公式与基本规则逻辑代数的基本公式反映了二值逻辑的基本思想,是逻辑运算的重要工具,也是学习数字电路的必备基础。
逻辑代数有三个基本规则,利用代入规则、反演规则和对偶规则使逻辑函数的公式数目倍增。
(2)逻辑问题的描述逻辑问题的描述可用真值表、函数式、逻辑图、卡诺图和时序图,它们各具特点又相互关联,可按需选用。
(3)图形法化简逻辑函数图形法比较适合于具有三、四变量的逻辑函数的简化。
二、难点:1.给定逻辑函数,将逻辑函数化为最简用代数法化简逻辑函数,要求熟练掌握逻辑代数的基本公式和规则,熟练运用四个基本方法—并项法、消项法、消元法及配项法对逻辑函数进行化简。
用图形法化简逻辑函数时,一定要注意卡诺图的循环邻接的特点,画包围圈时应把每个包围圈尽可能画大。
2.卡诺图的灵活应用卡诺图除用于简化函数外,还可以用来检验化简结果是否最简、判断函数间的关系、求函数的反函数和逻辑运算等。
3.电路的设计在工程实际中,往往给出逻辑命题,如何正确分析命题,设计出逻辑电路呢?通常的步骤如下:1.根据命题,列出反映逻辑命题的真值表; 2.根据真值表,写出逻辑表达式; 3.对逻辑表达式进行变换化简; 4.最后按工程要求画出逻辑图。
第3章 逻辑代数

mmm50 5mm1m7 m72mm8m83mmm994mmm11600mmm111133 m 1mm21155m14 mm((55,,77,,88,,99,,1100,,1133,,1155)) MAMB0 MC0M1DM1M2AM2BM3CM3DM4M4MA6BM6MC11D11MM1A122MBMC1144D ABMCMD((00,,11A,,22B,,33C,,44D,,66,,11A11,B,11C22,,1D144))ABC D ABC D
2 真值表
输入变量 输出 A B C···· Y1 Y2 ···· 输入变量所 输出对应的取值 有可能的取 值
ABC F 000 0 001 0 010 0 011 1 100 0 101 1 110 1 111 1
2. 逻辑函数(表达)式 将逻辑函数中输出变量与输入变量之间的逻辑关系 用与、或、非三种运算符号连接起来的表达式
交换律
7
A·(B·C) = (A·B)·C
16 A+(B+C)=(A+B)+C 结合律
8
A·(B+C)=A·B + A·C 17 A+B·C =(A+B) ·(A+C) 分配律
9
AB A B
18
A B AB
反演律
公式(17)的证明:A+BC=(A+B)(A+C)
证明:
右边 =(A+B)(A+C)
偶式,记作 Y 。
所谓对偶定理是指,若两个逻辑函数式相等,那 么它们的对偶式也相等。
AB AC BC AB AC
( A B)( A C)(B C) ( A B)( A C)
逻辑函数的表示方法及相互转换

自变量 因变量
ABC
F
2)从真值表写标准和之积式A+B+C 0 0 0 0
A+B+C
001
0
找出F = 0的行;
A+B+C
编号
M7 M6 M5 M4 M3 M2 M1 M0
3. 最小项与最大项的性质
全部最小项之和恒为1,全部最大项之积恒
为0。
2n 1
mi 1,
i0
2n 1
Mi 0
i0
任意两个不同的最小项之积恒为0,任意两
个不同的最大项之和恒为1。
mi·mj =0, Mi+Mj=1 相同下标的最小项和最大项互为反函数。
逻辑函数的表示方法 及相互转换
一、逻辑函数的表示方法 真值表描述法 逻辑函数式描述法 逻辑电路图表示法 卡诺图描述法、波形图表示
逻辑函数的描述方法
《数字电子技术基础》第六版
• 真值表 • 逻辑式 • 逻辑图 • 波形图 • 卡诺图 • 计算机软件中的描述方式
各种表示方法之间可以相互转换
《数字电子技术基础》第六版
即:和项都是最大项的或与式。
例:F(A,B,C)
=(A+B+C)(A+B+C)(A+B+C)(A+B+C)
=M1M2M4M6
最大项表达式
=M(1,2,4,6)
5 标准积之和式与标准和之积式的关系
同一函数的两种不同表示形式; 序号间存在一种互补关系,即:
最小项表达式中未出现的最小项的下标必然出现在最 大项表达式中,反之亦然。
相同自变量、相同序号构成的最小项表 达式和最大项表达式互为反函数
数字电路与逻辑设计答案邹红

(5)F A B CD ADB AD AB(C D) A BCD ( AD B) AD ( A B)(C D) A BCD AD B AD AC AD BC BD ( A AD AC) (BCD B BC BD) AD A B AD ( A AD) B ADB
(1)( 378.25 )10=( 101111010.0100 )2=( 572.2 )8=( 17A.4 )16
(2)( 194.5 )10=( 11000010.1000 )2=( 302.4 )8=( C2.8 )16
2 194 2 97 2 48 2 24 2 12 26 23 21 0
1-2 将下列十进制数转换成等值的二进制数、八进制数和十六进制数。要求
二进制数保留小数点后 4 位有效数字。
(1)( 378.25 )10;
(2)( 194.5 )10;
(3)( 56.7 )10;
(4)(27.6) 10;
解法 1:先将十进制数转换成二进制数,再用进制为 2k数之间的特点可以直
接将二进制数转换为等值的八进制数和十六进制数。
码
(9)10→(0111001)ASCII→(57)10→(01110100)格雷 BCD→(11001111)余
3BCD 码
1-8 试总结并说出:
(1)已知真值表写逻辑函数式的方法;
(2)已知逻辑函数式列真值表的方法;
(3)已知逻辑图写逻辑函数式的方法;
(4)已知逻辑函数式画逻辑图的方法;
(5)已知逻辑函数式画波形的方法;
(2)(பைடு நூலகம்6.7)10 =( ?)8421BCD 码=( ?)余 3 BCD 码;
(3)(1000 0101)8421BCD 码=( ?)格雷 BCD 码 ;
第一章 数字逻辑基础

18
例如:开关闭合为 1 断开为 0
二、基本逻辑关系和运算
与逻辑 基本逻辑函数 或逻辑 非逻辑 与运算(逻辑乘) 或运算(逻辑加) 非运算(逻辑非)
1. 与逻辑 决定某一事件的所有条件都具备时,该事件才发生。
A B Y 逻辑表达式 开关 A 开关 B 灯 Y 规定: 0 开关闭合为逻辑 1 0 0 Y = A · 或 Y = AB灭 断B 断 0 断开为逻辑 0 1 0 断 合 灭 灯亮为逻辑 1 1 0 0 合 断 与门 灭 灯灭为逻辑 0 开关 A、B 都闭合时, 1 1 1 合 合 (AND gate) 亮 灯 Y 真值表 才亮。 若有 0 出 0;若全 1 出 1
2、掌握几种常见的复合函数例如:与非、或非、 与或非、异或、同或等。
21
与非逻辑(NAND)
先与后非
或非逻辑 ( NOR ) 先或后非
A B 0 0 0 1 1 0 1 1 A B 0 0 0 1 1 0 1 1
Y 1 1 1 0 Y 1 0 0 0
若有 0 出 1 若全 1 出 0
若有 1 出 0 若全 0 出 1
这种信号可以来自检测元件,如光电传感器。
也可以来自某些特定电路和器件,如模数转换器,
脉冲发生器等。
5
目前广泛使用的计算机,其内部处理的都是这种信 号。各种智能化仪器仪表及电器设备中也越来越多 的采用这种信号。 研究数字电路时注重电路输出、输入间 的逻辑关系,因此不能采用模拟电路的 分析方法。主要的分析工具是逻辑代数, 时序图,逻辑电路图等。 在数字电路中,三极管工作在非线性区, 即工作在饱和状态或截止状态。起电子 开关作用,故又称为开关电路。
(4.79)10 = (0100.01111001)8421
第2讲逻辑函数的表示方法

Z
&
4、由逻辑图求逻辑表达式
由输入到输出,按照每个门的符号写出每个门的逻辑函数, 直到最后得到整个逻辑电路的表达式。
A A
1
AB
&
B B
1
≥1
Y=A B+AB
&
AB
三、逻辑函数表达式的形式 1、基本形式
(1)“与—或”表达式(“积之和”Sum of Products或SP型) 单个逻辑变量进行“与”运算构成的项称为“与项”,由 “与项”进行“或”运算构成的表达式称为“与—或”表达式。 例: F A B BC AB C C D
例:F(A,B,C)= AB C AB (C C ) ( A A )(B B )C
A B C A BC AB C AB C ABC m(1,3,4,5,7)
真值表法:将在真值表中,输出为1所对应的最小项相加, 即为标准“与—或”式
F(A,B,C)=∑m(2,5,6) ABC 000 001 010 011 100 101 110 111 F 0 0 1 0 0 1 1 0
(1)标准“与—或”式 1)由最小项相“或”构成的逻辑表达式,称为标准“与—或”式。
2)一个逻辑函数的标准“与—或”式是唯一的。 3)任何一个逻辑函数都可表示成为标准“与—或”式。其方 法如下: 代数法:① 将函数表示成为一般的“与—或”式; ② 反复利用X=X(Y+ Y ),将表达式中所有非最小项 的“与”项扩展成为最小项。
F 0 0 1 0 0 1 1 0
四、逻辑表达式的变换 1、逻辑函数的“与非”实现
(1)“与非”逻辑的完备性
逻辑非
F A AA
A A
逻辑函数表达式几种常用形式的转换方法

收稿日期: 2011 - 10 - 16. 2009] 141 号) . 基金项目: 辽宁省高等教育教学改革研究 A 类项目( 辽教发[ 作者简介: 马敬敏( 1966 - ) , 女, 高级实验师, 主要从事电子信息工程研究.
330
渤海大学学报( 自然科学版)
第 32 卷
图1
基于最简与或式的变换
Abstract: In logic circuit design, transformation for logic function expression is essential for realizing special logic function with limited logic gates. An exploration is made to gain all kinds of logic function starting from AND - OR expression. The method and process to some usual logic function expressions are derived as well as to changing stander AND - OR expression based on special minterms into XOR expression. It's concluded that the method is simple and convenient,and design efficiency could be promoted. Key words : logic circuit design; logic function; forms of expression; conversion method
数字电路与逻辑设计 第3讲

真值表如下: 真值表如下:
输出 Y2 Y1 Y0 GS
1 × × × × × × × × × × × × × × × 0
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
1 × × × × ×
今后会经常遇到的几种控制信号:(用来增强器件的功能) 今后会经常遇到的几种控制信号: 用来增强器件的功能) EI为使能输入端 低电平有效) 有时也称作片选信号。 为使能输入端( 1 、 EI 为使能输入端 ( 低电平有效 ) , 有时也称作片选信号 。 就 74LS LS148 EI/CS=1 74LS148 来 说 , 当 EI/CS=1 时 , 该 器 件 是 不 工 作 的 , 只 有 在 EI/CS=0时才工作。 EI/CS=0时才工作。 EO为使能输出端 低电平有效) EO只有在 EI=0 为使能输出端( 只有在EI= 2 、 EO 为使能输出端 ( 低电平有效 ) : EO 只有在 EI=0 ( 器件在工 而且所有输入都为1 说明无有效输入) 输出为0 作),而且所有输入都为1(说明无有效输入)时,输出为0。 这时可以将该片的EO接到另一片的EI EO接到另一片的EI上 这时可以将该片的EO接到另一片的EI上(显然这一片的优先权 允许它工作(EI=0 因此实现了扩展。 低),允许它工作(EI=0)。因此实现了扩展。 3 、 GS 为 优 先 编 码 工 作 标 志 ( 低 电 平 有 效 ) : 用 来 区 分 011111111” 此时GS= 编码器处于编码状态) GS=0 I0I1I2…I7=“011111111”(此时GS=0,编码器处于编码状态) I =“011111111 111111111” GS=1 和 I0I1I2…I7=“111111111” 的情况 ( 此时 GS=1 , 编码器处于 I =“111111111 的情况( 此时GS= 非编码状态) 非编码状态)。
数字电子技术基础知识

1 数字电子技术基础知识1.1 学习要求(1)了解数字电路的特点以及数制和编码的概念。
(2)掌握逻辑代数的基本运算法则、基本公式、基本定理和化简方法。
(3)能够熟练地运用真值表、逻辑表达式、波形图和逻辑图表示逻辑函数,并会利用卡诺图化简逻辑函数。
1.2 学习指导本章重点:(1)逻辑函数各种表示方法之间的相互转换。
(2)逻辑函数的化简及变换。
本章难点:(1)逻辑函数各种表示方法之间的相互转换。
(2)逻辑函数的化简及变换。
本章考点:(1)逻辑函数各种表示方法之间的相互转换。
(2)逻辑函数的化简及变换。
1.2.1 数字电路概述1.数字信号与数字电路在数值上和时间上均连续的信号称为模拟信号,对模拟信号进行传输、处理的电子线路称为模拟电路。
在数值上和时间上均不连续的信号称为数字信号,对数字信号进行传输、处理的电子线路称为数字电路。
数字电路的特点:(1)输入和输出信号均为脉冲信号,一般高电平用1表示,低电平用0表示。
(2)电子元件工作在开关状态,即要么饱和,要么截止。
(3)研究的目标是输入与输出之间的逻辑关系,而不是大小和相位关系。
(4)研究的工具是逻辑代数和二进制计数法。
2.数制及其转换(1)数制基数和权:一种数制所具有的数码个数称为该数制的基数,该数制的数中不同位置上数码的单位数值称为该数制的位权或权。
十进制:基数为10,采用的10个数码为0~9,进位规则为“逢十进一”,从个位起各位的权分别为100、101、102、…10n -1。
二进制:基数为2,只有0和1两个数码,进位规则为“逢二进一”,从个位起各位的权分别为20、21、22、…2n -1。
16进制:基数为16,采用的16个数码为0~9、A~F ,进位规则为“逢十六进一”,从个位起各位的权分别为160、161、162、…16n -1。
(2)数制之间的转换其他进制转换为十进制:采用多项式求和法,即将其他进制的数根据基数和权展开为多项式,求出该多项式的和,即得相应的十进制数。
