基于模拟退火算法的TSP算法
1.1通俗解释matlab之模拟退火求TSP问题

1.初识模拟退火算法说起模拟退火算法,不管哪个地方讲反正都有那么一段历史来源,模拟退火据说就是根据物理学上物质分子在温度较高的时候运动剧烈,很容易从一个转台转到另一个状态,而在温度较低的时候运动缓慢,状态也就基本上固定而不宜发生转变。
明不明白这个具体的物理过程无所谓,理解后面算法流程后就明白了什么是退火降温。
说白了,如果和算法结合起来的话,就是高温的时候问题的解很容易发生改变,从一个解很容易变化到另外的一个解,随着温度的降低,解的这种改变性越来越低。
而在每一次降温的过程中,算法都会记录上在本次温度下的所有改变的解中的优秀解,并传递到下一次的降温过程中。
这样,你想一想,开始解的变化范围很大,并一直在寻找优解,慢慢的变化范围变小,就变成了锁定前一次寻找到的最优解。
其实基本上所有的算法都是这样的一个过程,先广度搜索,在集中寻找等等,不同的是不同的算法他们的搜索速度、搜索的准确率不同而已。
2.我要解决的问题既然是优化算法,那就用它来解决一个常见的问题---旅行商问题,也叫TSP问题。
问题是什么样子的呢,就是随机给你不同的地点,要你每个地点走一次的话,怎么走这个地点的顺序才能使得你走的总路程最短呢,像这类问题最好的验证实例就是邮递员了吧,他会想怎么邮递所有的包裹才能使得他要走的总路线最少吧。
好了下面我随便给出30个不同的点代表不同的位置吧,点的左边都在0~1之间,如下:cities1=[0.6606,0.9695,0.5906,0.2124,0.0398,0.1367,0.9536,0.6091,0.8767,0.8148,0.38 76,0.7041,0.0213,0.3429,0.7471,0.4606,0.7695,0.5006,0.3124,0.0098,0.3637,0.5336,0.2 091,0.4767,0.4148,0.5876,0.6041,0.3213,0.6429,0.7471;0.9500,0.6740,0.5029,0.8274,0.9697,0.5979,0.2184,0.7148,0.2395,0.2867,0.8200,0.329 6,0.1649,0.3025,0.8192,0.6500,0.7420,0.0229,0.7274,0.4697,0.0979,0.2684,0.7948,0.43 95,0.8867,0.3200,0.5296,0.3649,0.7025,0.9192];注意了,这就是30对(x,y)的值,在matlab下画出来就如图所示:plot(cities1(1,:),cities1(2,:),'*')现在问题就是怎么首尾相连这些点才能是他们点之间的距离最小。
基于改进模拟退火算法求解TSP问题

基于改进模拟退火算法求解TSP问题姚明海;王娜【期刊名称】《渤海大学学报(自然科学版)》【年(卷),期】2013(034)001【摘要】By analyzing the principles and the shortcomings of traditional simulated annealing algorithm, the improved simulated annealing algorithm is proposed for the characteristic of TSP. The traditional simulated annealing algorithm producing the new solution is random, when the parameter is not accurate. It cant lead to the optimal solution; the traditional simulated annealing algorithm is easy to lose the optimal solution of current. Put forward a new method to select the initial solution and generation the solution, the method of the improved the current solution and adding memory function for optimal solution of current. Experimental test results show that the new algorithm has faster convergence and stability than traditional simulated annealing algorithm.%对传统模拟退火算法的原理和不足进行分析,针对TSP问题的特点提出了改进的模拟退火算法.就传统模拟退火算法生成新解的随机性太强、参数设置不当不能搜索到全局最优解、容易丢失当前最优解等问题提出了新的初始解选择方案、新解生成机制和当前解的改良及增加记忆功能等方法.实验结果表明,新算法传统的模拟退火算法具有更快的收敛速度和更高的稳定性.【总页数】6页(P79-84)【作者】姚明海;王娜【作者单位】渤海大学信息科学与技术学院,辽宁锦州121013;锦州师专计算机系,辽宁锦州121000【正文语种】中文【中图分类】TP31【相关文献】1.基于并行模拟退火算法的TSP问题求解 [J], 郏宣耀2.求解TSP问题的改进模拟退火算法 [J], 杨卫波;赵燕伟3.基于混合遗传模拟退火算法求解TSP问题 [J], 杜宗宗;刘国栋4.求解TSP问题的改进模拟退火算法 [J], 何锦福;符强;王豪东5.一种基于改进模拟退火算法的TSP问题的应用研究 [J], 齐安智因版权原因,仅展示原文概要,查看原文内容请购买。
模拟退火算法(SA)求解TSP问题(C语言实现)

模拟退⽕算法(SA)求解TSP问题(C语⾔实现) 这篇⽂章是之前写的智能算法(遗传算法(GA)、粒⼦群算法(PSO))的补充。
其实代码我⽼早之前就写完了,今天恰好重新翻到了,就拿出来给⼤家分享⼀下,也当是回顾与总结了。
⾸先介绍⼀下模拟退⽕算法(SA)。
模拟退⽕算法(simulated annealing,SA)算法最早是由Metropolis等⼈提出的。
其出发点是基于物理中固体物质的退⽕过程与⼀般组合优化问题之间的相似性。
模拟退⽕算法是⼀种通⽤的优化算法,其物理退⽕过程由以下三部分组成: (1)加温过程 (2)等温过程 (3)冷却过程 其中加温过程对应算法设定的初始温度,等温过程对应算法的Metropolis抽样过程,冷却过程对应控制参数的下降。
这⾥能量的变化就是⽬标函数,要得到的最优解就是能量最低状态。
Metropolis准则是SA算法收敛于全局最优解的关键所在,Metropolis准则以⼀定的概率接受恶化解,这样就使得算法可以跳离局部最优解的陷阱。
模拟退⽕算法为求解传统⽅法难以处理的TSP问题提供了⼀个有效的途径和通⽤的处理框架,并逐渐发展成为⼀种迭代⾃适应启发式概率搜索算法。
模拟退⽕算法可以⽤于求解不同的⾮线性问题,对于不可微甚⾄不连续函数的优化,能以较⼤概率求得全局最优解,该算法还具有较强的鲁棒性、全局收敛性、隐含并⾏性以及⼴泛的适应性,对⽬标函数以及约束函数没有任何要求。
SA 算法实现的步骤如下:(下⾯以最⼩化问题为例) (1)初始化:取温度T0⾜够⼤,令T = T0,取任意解S1,确定每个T时的迭代次数,即 Metropolis链长L。
(2)对当前温度T和k=1,2,3,...,L,重复步骤(3)~(6) (3)对当前解S1随机产⽣⼀个扰动得到⼀个新解 S2. (4)计算S2的增量df = f(S2) - f(S1),其中f(S1)为S1的代价函数。
(5)若df < 0,接受S2作为新的当前解,即S1 = S2;否则S2的接受概率为 exp(-df/T),即随机产⽣(0,1)上的均匀分布的随机数rand,若 exp(-df/T)>rand,则接受S2作为新的当前解,S1 = S2;否则保留当前解。
基于模拟退火算法的TSP问题研究报告附MATLAB程序

minL(T ) dtiti1
i 1
• 解的邻域:随机产生2个位置,让序列T上对应的 两个位置上的城市顺序对换。
max{ dij | j i, j 1, n} min{dij | j i, j 1, n}
i 1 i 1 n n
4.模拟退火算法求TSP问题
岗位职责三工作总结项目运维项目实施银青高速视频监控东毛隧道停车场项目全面实施ip设置贵州独平高速项目全面实施监控室机柜布线四心得体会在这段时间的学习过程中我对部门很多产品从零学起刚到公司的时候感觉压力很大经过这些时间的认真学习和实际操作调整心态现已完全能融入公司的各项岗位职责和管理制度中
TSP问题的模拟退火算法
3. 参数选取
•
t0
优。
tk+1=α*tk maxstep=maxstep+a
t0太大,计算时间增加;t0太小,会过早陷入局部最
4.模拟退火算法求TSP问题
• 解的表示:用一个访问序列T=(t1,t2,t3…,tn,t1)来表示 经过n个城市的顺序。 • 距离矩阵:D=(dij)是由城市i和城市j之间的距离所 组成的距离矩阵。 n • 数学模型:
如需程序,点击上传者,见“我的文档”。
1. 模拟退火简介
1.1 问题讨论
2. 模拟退火算法步骤 3. 参数选取 4. 模拟退火算法求解TSP问题
1模拟退火简介
• 物理解释:材料中的原子原来会停留在使内能 有局部最小值的位置,加热使能量变大,原子 会离开原来位置,而随机在其他位置中移动。 退火冷却时速度较慢,使得原子有较多可能可 以找到内能比原先更低的位置。 • 统计学解释:我们将热力学的理论套用到统计 学上,将搜寻空间内每一点想像成空气内的分 子;搜寻空间内的每一点,也像空气分子一样 带有“动能”,以表示该点对命题的合适程度。 算法先以搜寻空间内一个任意点作起始:每一 步先选择一个“邻居”,然后再计算从现有位 置到达“邻居”的概率。
用模拟退火算法求解TSP

用模拟退火算法求解TSP
TSP问题(旅行商问题)是一个NP难问题。
模拟退火算法是一种解决复杂问题的启发式优化算法,被广泛应用于求解TSP问题。
下面是使用模拟退火算法求解TSP1650的步骤:
1. 初始化:随机生成一个初始解集,即随机生成一个城市序列,并计算其路径长度。
2. 降温:将系统温度下降,即通过调节温度参数来控制搜索范围,随着时间的推移,温度逐渐下降。
3. 移动:通过移动城市序列来扰动当前解集,得到新的解集。
比如,随机选择两个城市交换其顺序,得到新的城市序列。
4. 计算路径长度:计算新的城市序列的路径长度。
5. 判断是否接受新的解集:按照一定概率接受新的解集,比如如果新解集的路径长度更短,则接受新解集,否则以一定概率接受新解集,以避免陷入局部最优解。
6. 重复以上步骤,直到温度降至最低,或者找到满足要求的解。
7. 输出最优解:得到满足要求的解后,输出路径长度和城市序列。
求解TSP1650很困难,需要大量的计算资源和时间,运行时间可能需要数小时或数天。
模拟退火算法解决TSP问题要点

智能优化方法课题报告专业班级:电子信息科学与技术12-3班课题名称:模拟退火算法解决TSP问题指导教师:姚睿学生姓名:蒋文斌学号: 08123453(课题设计时间:2015年3月28日——2015年 4月13日)中国矿业大学计算机学院一、问题描述旅行商问题(Traveling monituihuolesman Problem ,简称TSP )又名货郎担问题,是威廉·哈密尔顿爵士和英国数学家克克曼(T.P.Kirkman)于19世纪初提出的一个数学问题,也是著名的组合优化问题。
问题是这样描述的:一名商人要到若干城市去推销商品,已知城市个数和各城市间的路程(或旅费),要求找到一条从城市1出发,经过所有城市且每个城市只能访问一次,最后回到城市1的路线,使总的路程(或旅费)最小。
TSP 刚提出时,不少人认为这个问题很简单。
后来人们才逐步意识到这个问题只是表述简单,易于为人们所理解,而其计算复杂性却是问题的输入规模的指数函数,属于相当难解的问题。
这个问题数学描述为:假设有n 个城市,并分别编号,给定一个完全无向图G=(V ,E ),V={1,2,…,n},n>1。
其每一边(i,j)∈E 有一非负整数耗费 Ci,j(即上的权记为Ci,j ,i ,j ∈V)。
并设1,i j 0{ij X =边(,)在最优线路上, 其他G 的一条巡回路线是经过V 中的每个顶点恰好一次的回路。
一条巡回路线的耗费是这条路线上所有边的权值之和。
TSP 问题就是要找出G 的最小耗费回路。
人们在考虑解决这个问题时,一般首先想到的最原始的一种方法就是:列出每一条可供选择的路线(即对给定的城市进行排列组合),计算出每条路线的总里程,最后从中选出一条最短的路线。
假设现在给定的4个城市分别为A 、B 、C 和D ,各城市之间的耗费为己知数,如图1-1所示。
我们可以通过一个组合的状态空间图来表示所有的组合,如图1-2所示。
(1-1)图1-1 顶点带权图图1-2 TSP问题的解空间树1.模拟退火是什么?首先,让我们看看模拟退火是如何工作的,以及为什么它是善于解决旅行商问题。
用模拟退火算法解决TSP问题

用模拟退火算法解决TSP问题旅行商问题(Traveling Salesman Problem,TSP)是指一个旅行商要在不重复地经过全部的指定城市之后回到起点,所需要走的最短路径长度是多少。
由于TSP问题具有NP难度,因此传统的精确算法要花费大量的计算资源,得到的结果往往也只能是近似最优解。
而模拟退火算法是一种集合随机性和概率思想的启发式方法,可以快速地在解空间中搜索到一个较优的解。
一、模拟退火算法的原理及过程模拟退火算法是一种以概率为基础的全局优化算法,它的基本思想是利用随机性来逃离局部最优解,让搜索过程在解空间中跳跃,最终逐渐接近全局最优解。
模拟退火算法的过程可以分为三个阶段:初始化阶段、搜索阶段和收敛阶段。
初始化阶段:首先需要对问题进行建模,将问题转化为算法可处理的形式。
在TSP问题中,需要建立一个城市间距离矩阵。
然后随机生成一个初始解,通常是一个随机序列,表示旅行商经过城市的顺序。
搜索阶段:对生成的初始解进行扰动,得到一个新的解,并计算新解的目标函数值。
如果新解比原解更优,则直接接受该解。
如果新解比原解更劣,则有一定的概率接受该解,概率随着时间的推移逐渐降低。
收敛阶段:在搜索过程中,随着温度的不断下降,概率接受劣解的概率越来越小,这时算法逐渐收敛到一个局部最优解,也可能是全局最优解。
二、TSP问题的建模及求解TSP问题可以建立一张城市距离矩阵,然后用随机序列来表示旅行商经过城市的顺序。
目标函数可以定义为旅行商经过所有城市的总路径长度。
假设有n个城市,城市之间的距离矩阵为D,表示第i个城市和第j个城市之间的距离。
而旅行商经过城市的顺序可以用一个长度为n的序列{1,2,...,n}来表示,表示旅行商先经过第1个城市,然后是第2个城市,一直到第n个城市,然后再回到原点。
设目前的解序列为s={s1,s2,...,sn},则其总路径长度为:L(s) = ∑i=1n D(si,si+1) + D(sn,1)其中D(si,si+1)表示城市si和si+1之间的距离,D(sn,1)表示最后回到起点的距离。
模拟退火算法在tsp问题中的应用研究毕业(设计)论文

毕业论文(设计)题目模拟退火算法在TSP问题中的应用研究毕业设计(论文)原创性声明和使用授权说明原创性声明本人郑重承诺:所呈交的毕业设计(论文),是我个人在指导教师的指导下进行的研究工作及取得的成果。
尽我所知,除文中特别加以标注和致谢的地方外,不包含其他人或组织已经发表或公布过的研究成果,也不包含我为获得及其它教育机构的学位或学历而使用过的材料。
对本研究提供过帮助和做出过贡献的个人或集体,均已在文中作了明确的说明并表示了谢意。
作者签名:日期:指导教师签名:日期:使用授权说明本人完全了解大学关于收集、保存、使用毕业设计(论文)的规定,即:按照学校要求提交毕业设计(论文)的印刷本和电子版本;学校有权保存毕业设计(论文)的印刷本和电子版,并提供目录检索与阅览服务;学校可以采用影印、缩印、数字化或其它复制手段保存论文;在不以赢利为目的前提下,学校可以公布论文的部分或全部内容。
作者签名:日期:学位论文原创性声明本人郑重声明:所呈交的论文是本人在导师的指导下独立进行研究所取得的研究成果。
除了文中特别加以标注引用的内容外,本论文不包含任何其他个人或集体已经发表或撰写的成果作品。
对本文的研究做出重要贡献的个人和集体,均已在文中以明确方式标明。
本人完全意识到本声明的法律后果由本人承担。
作者签名:日期:年月日学位论文版权使用授权书本学位论文作者完全了解学校有关保留、使用学位论文的规定,同意学校保留并向国家有关部门或机构送交论文的复印件和电子版,允许论文被查阅和借阅。
本人授权大学可以将本学位论文的全部或部分内容编入有关数据库进行检索,可以采用影印、缩印或扫描等复制手段保存和汇编本学位论文。
涉密论文按学校规定处理。
作者签名:日期:年月日导师签名:日期:年月日目录摘要 (V)ABSTRACT........................................................... V I 第一章前言. (1)1.1 TSP问题的基本概念 (1)1.2 模拟退火算法的背景 (1)1.3 发展趋势 (2)第二章相关知识介绍 (3)2.1模拟退火算法的原理 (3)2.1.1 模拟退火的基本思想 (3)2.1.2 算法对应动态演示步骤 (4)2.2 TSP问题简述 (4)2.3组合优化问题简述 (5)2.4 蚁群算法及其它算法原理 (6)2.4.1蚁群优化算法 (6)2.4.2其它优化算法 (6)第三章问题描述与算法分析研究 (9)3.1应用研究整体规划 (9)3.2应用开发环境 (9)3.2.1开发语言 (9)3.2.2开发平台 (9)3.3 TSP问题的描述和分析 (9)3.4模拟退火算法的分析 (10)3.4.1模拟退火算法模型 (10)3.4.2模拟退火算法与优化问题分析 (11)3.5应用研究方案分析 (11)第四章算法具体设计与编码实现 (12)4.1基于模拟退火算法求解TSP问题详细设计 (12)4.1.1求解TSP问题的模拟退火算法及流程图 (12)4.1.2算法温度的选择和变化 (14)4.1.3定义坐标表的具体参数与具体实现 (15)4.1.4新解的产生方法 (17)4.2求解TSP问题的算法主体模块详细设计 (19)4.3算法的具体编码实现 (20)4.3.1建立城市坐标文本文件 (21)4.3.2 DOS下界面数据输出以及概率统计与分析 (21)第五章算法运行分析 (24)5.1 运行界面图示 (24)5.2 运行结果 (27)第六章结束语 (28)致谢 (29)参考文献 (29)摘要TSP问题是一个典型的NP 完全问题,模拟退火算法是求解此问题的一种理想方法。
模拟退火算法解决TSP问题-代码【范本模板】
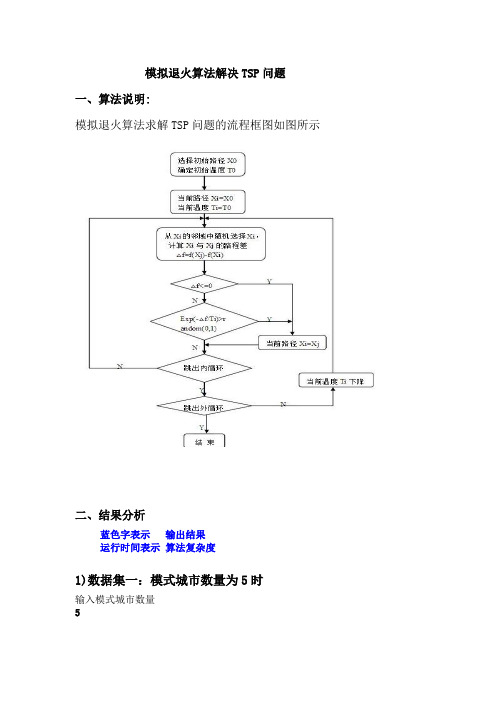
模拟退火算法解决TSP问题一、算法说明:模拟退火算法求解TSP问题的流程框图如图所示二、结果分析蓝色字表示输出结果运行时间表示算法复杂度1)数据集一:模式城市数量为5时输入模式城市数量5为了方便查看,数据和结果保存在文件中〈<<<邻接矩阵保存在文件模拟退火算法—随机产生数据.txt 中〈<<<访问顺序保存在文件模拟退火算法-结果数据.txt 中模拟节点个数 5运行时间: 10 ms邻接矩阵0 1 57 20 811 0 59 49 3657 59 0 90 8220 49 90 0 7581 36 82 75 0访问节点顺序3 5 24 12)数据集二:模式城市数量为10时输入模式城市数量10为了方便查看,数据和结果保存在文件中〈<<<邻接矩阵保存在文件模拟退火算法—随机产生数据.txt 中〈<<〈访问顺序保存在文件模拟退火算法-结果数据。
txt 中模拟节点个数 10运行时间: 15 ms邻接矩阵0 1 57 20 81 59 49 36 90 821 0 75 18 86 71 52 31 2 1057 75 0 37 16 17 99 45 13 120 18 37 0 2 38 54 58 61 6181 86 16 2 0 17 67 46 36 759 71 17 38 17 0 61 79 80 5249 52 99 54 67 61 0 31 88 7336 31 45 58 46 79 31 0 96 9390 2 13 61 36 80 88 96 0 5482 10 1 61 7 52 73 93 54 0访问节点顺序1 7 6 10 82 9 4 5 33)数据集三:模式城市数量为20时输入模式城市数量20为了方便查看,数据和结果保存在文件中〈〈〈〈邻接矩阵保存在文件模拟退火算法-随机产生数据.txt 中<〈〈〈访问顺序保存在文件模拟退火算法-结果数据。
模拟退火算法求解TSP问题 朱健炽
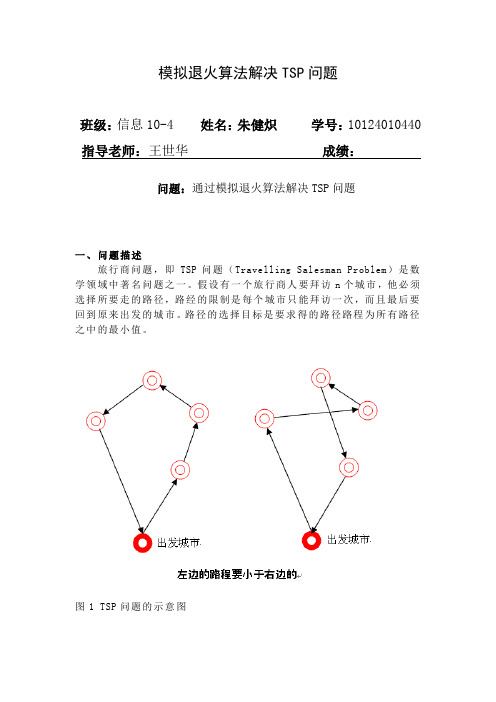
模拟退火算法解决TSP问题班级:信息10-4姓名:朱健炽学号:10124010440指导老师:王世华成绩:问题:通过模拟退火算法解决TSP问题一、问题描述旅行商问题,即TSP问题(Travelling Salesman Problem)是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路经的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
图1 TSP问题的示意图二、遍历算法一个最容易想到的方法是利用排列组合的方法把所有的路径都计算出来,并逐一比较,选出最小的路径。
虽然该方法在理论上是可行的,但路径的个数与城市的个数成指数增长,当城市个数较大时,该方法的求解时间是难以忍受的,甚至是不可能完成的。
以每秒1亿次的计算速度来估算,如果TSP问题包含20个城市时,求解时间长达350年;如果要处理30个城市,则求解时间更长达1+10e16年。
如此长的时间,在实际中完成是难以想象的。
三、模拟退火算法模拟退火算法是解决TSP问题的有效方法之一,其最初的思想由Metropolis在1953年提出,Kirkpatrick在1983年成功地将其应用在组合最优化问题中。
模拟退火算法来源于固体退火原理,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
用固体退火模拟组合优化问题,将内能E模拟为目标函数值f,温度T演化成控制参数t,即得到解组合优化问题的模拟退火算法:由初始解i和控制参数初值t开始,对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代,并逐步衰减t值,算法终止时的当前解即为所得近似最优解,这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程。
求解TSP的模拟退火算法模型可描述如下:解空间:解空间S是遍访每个城市恰好一次的所有路经,解可以表示为{w1,w2 ,……, wn},w1, ……, wn是1,2,……,n的一个排列,表明w1城市出发,依次经过w2, ……, wn城市,再返回w1城市。
基于改进的遗传模拟退火混合算法求解TSP问题

中图分类号 :T 32 P 1
文献标识码 :A
文章编号 :10 — 59 ( 00) 0 — 0 5 0 07 99 21 8 03 — 2
TS Pr blm l i s d o m pr v d G e tc P o e So vng Ba e n I o e ne i Sm ua e i l t d Anne lngAl o ihm a i g rt
,
基于模拟退火算法的TSP研究

本文 是基于模拟 退火算 法的 T P的研 究 ,使 用模拟 退 S 火 算法解 决 T P。了解 T P和模拟 退火算 法 的国内外研 究 S S 现状, 实现模 拟退 火算法 , 并使 该算 法应用 于 T P中 , 终 S 最
个 具有代 表性 的问题 ,它经常被 用来测 试很 多新型算 法 的 性 能, 优化技术 一种成 功的体现 。 是 在优 化算法及 其启发式 搜 索 中, S T P已经成 为 了一种标 准 。研 究 T P 加 深对 T P S, S
算 法的理解 , 我 们继续 学习优化理 论知识有很 大帮助 。 对
解 ; 二 , 针 对 某 些 具 体 问题 , 出 了模 拟 退 火 算 法 的 很 其 是 给
多成功应 用 。事 实上 ,正 是 由于专 家和 学者对 该算 法 的钻 研 ,才使 该算法 从经典 的模拟退火 算法走 到 了今天 的 多样
1 8 ,对 于 3 8座城 市 的 T P问题是 ~个难 题 , 9 0年 1 S 但
是传 统 的动态规 划 、 枝定 界法 、 分 贪婪 法等 方法 , 还是 在 近 些年 的研 究过程 中采用 的各种 智能优 化算法如 : 模拟 退火 、 遗 传算法 、 工神经 网络 、 人 蚁群 算法 等都存在 解 的质量 不 高 或者需要 的时空开销 太大等 问题 圆 。 2 2 模拟 退火算法 的研 究现状 . 在 理论上 ,受到广 大学者 与专家 青睐 的模拟 退火 算法
1 1 意 义 .
pa 3 1 l 8 0的一个次优 解 ,当时使用 了 LnKe g  ̄ 3 i— mih n启 发和 a
路 径 融 合 的变 种 相 结 合 的 方 法 。之 后 , 由 Ke l an在 l Hes u d g
用模拟退火算法或者遗传算法解决TSP问题程序

用模拟退火算法或者遗传算法解决TSP问题程序用模拟退火算法、遗传算法(或蚁群算法)求解10城市的TSP (旅行商)问题,计算旅行封闭的最短旅行距离。
解:用遗传算法解决TSP 问题,首先需要确定城市个数及城市间的距离,随机产生城市序列作为一个个体,确定目标函数,通过遗传算法的复制、交叉、变异求出最优解。
目标函数f x = d i ,i +1 +d (n ,0)n i =0适应度函数F x = ?f x +C max f x <="" p="">遗传算法的步骤为复制+交叉+变异=新一代遗传算法主程序:DG=0.9;MAXDD=100;ZQDX=150;Pc=0.7;Pm=0.01;ZQ=[0 118 1272 2567 1653 2097 1425 1177 3947 1574118 0 1253 2511 1633 2077 1369 1157 3961 15181272 1253 0 1462 380 1490 821 856 3660 3852567 2511 1462 0 922 2335 1562 2165 3995 9331653 1633 380 922 0 1700 1041 1135 3870 4562097 2077 1490 2335 1700 0 2311 920 2170 19201425 1369 821 1562 1041 2311 0 1420 4290 6261177 1157 856 2165 1135 920 1420 0 2870 12903947 3961 3660 3995 3870 2170 4290 2870 0 40901574 1518 385 993 456 1920 626 1290 4090 0];D=size(ZQ,1);EE=CSHZQ(ZQDX,D);disp('初始种群中的一个随机值:')SCXL(EE(1,:));RTH=XLCD(ZQ,EE(1,:));disp('总距离:');disp(num2str(RTH));Q=0;OV=XLCD(ZQ,EE);POV=min(OV);while (Q<maxdd)< p=""> OV=XLCD(ZQ,EE);POV=min(OV);SYD=SHYD(OV);XZ=XUANZE(EE,SYD,DG);XZ=JIAOC(XZ,Pc);XZ=BY(XZ,Pm);XZ=NZ(XZ,ZQ);EE=CCZ(EE,XZ,OV);Q=Q+1;endOV=XLCD(ZQ,EE); [minOV,minInd]=min(OV); disp('最优解:')p=SCXL(EE(minInd(1),:)); disp('总距离:');disp(num2str(OV(minInd(1)))); 初始化全局变量:function EE=CSHZQ(ZQDX,D) EE=zeros(ZQDX,D);for (i=1: ZQDX)EE(i,:)=randperm(D);end适应度函数:function SYD=SHYD(len)SYD=1./len;选择程序:function XZ=XUANZE(EE,SYD,DG)ZQDX =size(EE,1);NSel=max(floor(ZQDX *DG+.5),2);ChrIx=sus(SYD,NSel);XZ=EE(ChrIx,:);function NewChrIx=sus(SYD,Nsel)[Nind,ans]=size(SYD);cumfit=cumsum(SYD);trials=cumfit(Nind)/Nsel*(rand+(0:Nsel-1)');Mf=cumfit(:,ones(1,Nsel));Mt=trials(:,ones(1,Nind))';[NewChrIx,ans]=find(Mt<="Mt);" [ans,shuf]="sort(rand(Nsel,1));</p">NewChrIx=NewChrIx(shuf);交叉:function XZ=JIAOC(XZ,Pc)NSel=size(XZ,1);for (i=1:2:NSel-mod(NSel,2))if (Pc>=rand)[XZ(i,:),XZ(i+1,:)]=ICS(XZ(i,:),XZ(i+1,:));endendICS函数function [a,b]=ICS(a,b)L=length(a);r1=randsrc(1,1,[1:L]);r2=randsrc(1,1,[1:L]);if r1~=r2a0=a;b0=b;s=min([r1,r2]);e=max([r1,r2]);for i=s:ea1=a;b1=b;a(i)=b0(i);b(i)=a0(i);x=find(a==a(i));y=find(b==b(i));i1=x(x~=i);i2=y(y~=i);if ~isempty(i1)a(i1)=a1(i);endif ~isempty(i2)b(i2)=b1(i);endendend变异:function XZ=BY(XZ,Pm) [NSel,L]=size(XZ);for (i=1:NSel)if (Pm>=rand)R=randperm(L);XZ(i,R(1:2))=XZ(i,R(2:-1:1)); endend进化逆转:function XZ=NZ(XZ,ZQ)[row,col]=size(XZ);OV=XLCD(ZQ,XZ);XZ1=XZ;for i=1:rowr1=randsrc(1,1,[1:col]);r2=randsrc(1,1,[1:col]);mininverse=min([r1,r2]);maxinverse=max([r1,r2]);XZ1(1,mininverse:maxinverse)=XZ1(i,maxinverse:-1:mininverse); endOV1=XLCD(ZQ,XZ1);index=OV1<ov;< p="">XZ(index,:)=XZ(index,:);得到新一代:function EE=CCZ(EE,XZ,OV)ZQDX =size(EE,1);NSel=size(XZ,1);[TobjV,index]=sort(OV);EE=[EE(index(1: ZQDX -NSel),:);XZ]; 计算线路长度:function len=XLCD(ZQ,EE)[row,col]=size(ZQ);ZQDX =size(EE,1);len=zeros(ZQDX,1);for (i=1: ZQDX)p=[EE(i,:) EE(i,1)];i1=p(1:end-1);i2=p(2:end);len(i,1)=sum(ZQ ((i1-1)*col+i2)); end输出线路长度:function p=SCXL(R)R=[R,R(1)];N=length(R);p=num2str(R(1));for (i=2:N)p=[p,'->',num2str(R(i))]; enddisp(p)</ov;<></maxdd)<>。
基于并行模拟退火算法的TSP问题求解

郏宣耀:基于并行模拟退火算法的 TSP 问题求解
准则六部分。 从理论上分析,为了使算法最终得到全局最优,应把初始温度设置尽量大,温度下降尽量缓慢。但这导致算法收敛速度 过慢,优化效率降低。实际应用中,通常随机产生一组解,计算其目标函数值的方差作为初始温度。鉴于计算的方便,温度 更新函数一般取指数退温,即 Ti 1 Ti , (0,1) 。为使温度下降不至过快,λ取值一般接近于 1。 状态产生函数的功能是产生一新解,它应尽可能使产生的候选解遍布整个解空间。候选解通常在当前状态的邻域结构内 以一定概率方式产生。其中领域函数与概率方式由问题的性质决定。候选解产生之后若优于当前解则接受其并取代当前解, 若劣于当前解,则由状态接受函数决定是否接受。通常采用 min[1, exp( C / t )] 作为状态接受函数。可见,随着温度的降低, 接受劣解的概率也随之降低以使算法最终收敛到全局最优。 内循环终止准则亦即 Metropolis 抽样稳定准则,它决定当前温度下抽样的次数。理论上每个温度下应使相应的 Markov 链达到平稳概率分布, 但实际应用时显然是无法实现的。 因此, 通常以其它条件代替。 如判断是否达到局部平衡, 控制 Markov 链长等。外循环终止准则即算法终止准则,它决定算法何时结束,理论上要求终止温度趋于 0,但实际上是不实用的。一般 可以设置终止温度的阈值、设置外循环迭代次数、检验系统熵是否稳定等。 基此,模拟退火算法的基本流程可以描述如图 1:
本文首先用一个 20 个城市 TSP 实例进行数值实验, 该 20 个城市的坐标信息如表 1。 文献[8]利用改进遗传算法得到路径 长度为 24.38 的最优解。本文利用多种群并行模拟退火算法运行 20 次,所有 20 次运行中均得到该最优路径,平均 4.218 秒 得到该最优解。 而对该实例使用传统模拟退火算法时平均消耗 6.298 秒才得到最优解, 因此该并行算法显示出了良好的效果。 同时,本文对 35-TSP 实例与 70-TSP 实例分别应用传统模拟退火算法和并行模拟退火算法进行求解,结果如表 2。 表 1 20 个城市的坐标信息 城市序号 表 2 并行 SA 与 SA 算法性能对比
用模拟退火算法求解TSP

经 ,解 可 以表 示 为 f , ., n ,wl .w wl w2, .w } . … , n是 1 , . , ., 2 .n
/ 果 新 路径 长 于 当前 路 径 ,但 ep一 f > / 如 x( r A o r d m(,) ! n a o O1, I J 仍然替换 当前路径
3 .产 生 新 解 S
N C 计算 复杂性 。因此 ,任 何能使该问题的求解得 以简化 P 的方法 ,都将 受到高度 的评价和关注 。 一个最容易想到 的ห้องสมุดไป่ตู้
法是利用排列组合 的方法把所有 的路径都计 算出来 , 并逐一
比较,选 出最小的路径 。虽然该方法在理论上是可行 的,但
路径的个数与城市的个数成指数增长 ,当城 市个数较 大时,
该方法的求解时 间是难 以忍受 的,甚至是不可能完成的 。以
4 .计算增 量 △t C ( ). ( ) = S C S ,其 中 C ( )为 S 评 价函数
每秒 1 亿次 的计算速度来估算 ,如果 T P问题包含 2 S 0个城 市时,求解时间长达 3 0年;如果要处理 3 5 0个城市 ,则求 解 时间更长达 l 1e 6年 。 + 01 如此长 的时间,在实际中完成是
第 3 卷 第 9期 1 21 0 1年 9月
湖 北 广 播 电视 大 掌 掌 报
J u n l f Be Un v ri o r a o Hu i TV i e st y
Vo . 1 No 9 1 , . 3
S pe e. 0 1 1 9 1 0 e t mb r 2 1 , 5  ̄ 6
( 二)模拟退火算法的模型
左 边 的 路 程 l ,、 右 边 的 ・ |J千 -
基于模拟退火算法的TSP问题求解算法研究

基于模拟退火算法的TSP问题求解算法研究旅行商问题(Traveling Salesman Problem,TSP)是运筹学中一个经典的问题,它是一个非常著名的NP难题。
该问题的简化版本就是,给定一些城市和每对城市之间的距离,求解访问每个城市一次且仅一次,并回到起点所需要的最短路径。
这个问题在实际生产和科学研究中具有重要的应用价值,例如供应链物流、电路设计等领域。
由于该问题是NP难问题,传统的精确求解算法在处理较大的实例时会遇到很大的困难。
因此,研究者们通常选择利用启发式算法来求解TSP问题。
其中一种较为经典的启发式算法是模拟退火算法(Simulated Annealing Algorithm,SAA)。
模拟退火算法的基本原理是模拟物质的固化过程,从一个高温状态开始,利用概率方法在状态空间中随机漫步,降低温度,直至固化为止。
在求解TSP问题中,SAA的核心思想是通过迭代寻找更优解,它的求解过程类似于热力学中的退火过程。
SAA解决TSP问题的具体步骤如下:1.建立初始解:随机生成一条回路2.设定初始温度T,以一定的步长降温3.在当前解的邻域内,随机产生一个新解4.计算ΔE = Enew - Eold,其中Enew为新解的目标函数值,Eold为当前解的目标函数值5.当ΔE < 0,接受新解。
当ΔE > 0,计算概率P = exp(-ΔE/T),如果P > rand(0, 1),则接受新解。
6.重复3-5步,直至温度降至指定值在应用SAA求解TSP问题时,邻域搜索空间的大小和搜索速度是需要考虑的两个重要因素。
为了提高算法的效率,改进SAA算法成为了许多研究的重点。
一些常见的SAA改进方法包括:1.使用启发式算子,如2-opt算子和3-opt算子,来生成新解,避免了随机产生新解的盲目性。
2.设置合适的退火迭代次数,可以在短时间内获得较好的解,同时提高搜索速度。
3.采用并行计算的方式,多个线程同时搜索,并将较优解合并,可以进一步提高搜索效率。
模拟退火算法在TSP求解中的应用

模拟退火算法在TSP求解中的应用摘要:模拟退火算法(Simulated Annealing,SA)是一种适合解大规模组合优化问题,特别是解NP完全问题的通用有效近似算法。
它与以往的近似算法相比,具有描述简单、使用灵活、运用广泛、运行效率高等优点,而且特别适合并行计算。
TSP问题即旅行商问题是一个组合优化问题,该问题被证明具有NPC计算复杂性。
因此,研究模拟退化算法的基本原理及其在TSP问题求解中的应用受到高度的关注。
本文首先分析了SA的基本原理,针对TSP问题我们将SA应用到TSP上,并建立了TSP的数学模型,阐述了利用模拟退火算法解TSP 的方法。
最后通过实验证明了模拟退火算法的高效性。
关键词:模拟退火; 组合优化; TSP问题1 引言模拟退火的概念最初是人们为了研究组合优化问题而提出的,用于解决组合优化问题,其原理是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性:通过设定一初始温度和初始状态,伴随温度的不断下降,结合概率突跳特性在解空间中通过邻域函数进行随机搜索,最终得到全局近似最优解。
SA算法在组合优化中取得了很好的效果,能解决传统的优化方法难于解决的许多问题。
SA算法具有较好的全局收敛性和适应性,并隐含着较好的并行性。
SA算法的一些变形方法还表明:利用Metropolis过程并适当地控制温度下降过程的SA算法,在连续变量和混合变量的全局优化问题中具有很强的竞争力。
TSP(Traveling salesman Problem,旅行商问题)是一个组合优化问题。
具有NPC 计算复杂性。
因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
一个最容易想到的方法是利用排列组合的方法把所有的路径都计算出来,并逐一比较,选出最小的路径。
虽然该方法在理论上是可行的,但路径的个数与城市的个数成指数增长,当城市个数较大时,该方法的求解时间是难以忍受的,甚至是不可能完成的。
以每秒 1 亿次的计算速度来估算,如果 TSP 问题包含 20 个城市时,求解时间长达 350 年;如果要处理 30 个城市,则求解时间更长达 1+10e16 年。
模拟退火算法求解TSP问题C++

模拟退火算法求解TSP问题C++预览说明:预览图片所展示的格式为文档的源格式展示,下载源文件没有水印,内容可编辑和复制模拟退火算法的应用—Travelling Salesman Problem 作为模拟退火算法应用,讨论货郎担问题(Travelling Salesman Problem,简记为TSP):设有n个城市,用数码1,…,n代表。
城市i和城市j之间的距离为d(i,j) i, j=1,…,n.TSP问题是要找遍访每个域市恰好一次的一条回路,且其路径总长度为最短.。
将城市编号及其对应的坐标信息放入TSP.txt文件中,由程序读出,进行模拟退火算法的计算,找到最优解并且保存在.txt文本中,涉及到的TSP.txt文本信息格式如下:主要程序变量定义及其功能函数如下://///////////////////////////////////////////////////////////////// ///////////////////#include#include#include#include#include#include/////////////////////////////////////////////////////////////////// /////////////////////// 模板输出函数templatevoid Print(const T *pData, int nsize){for (int i=0; i<="" p="">{cout << *(pData++) << " ";}cout << endl;}/////////////////////////////////////////////////////////////////// /////////////////////#define TSPN 60 // TSP中的城市数目#define T_CONST 10 // 初始化温度时给定的常数温度#define T_INIT 500 // 初始化温度时给定的初始温度#define R_CONST 0.9 // 初始化温度时给定的常数#define R_MIN 0.05 // 初始化温度时的终止条件#define STEPN 400 // 初始化温度时退火的迭代步数#define K_T 0.9 // 降温时的降温参数#define R_ACCEPT 0.3 // 内循环的接受比率指标#define T_ZERO 0.5 // 零度法中的最小温度// 解状态,根据不同问题设定struct ANSWER{int *pAnswer;double *pData;};/************************************************************** ******** * 函数名称:TSPRead()* 输入参数:*pfile -文件名TSPN* 返回值:double* -指向坐标文件的一维数组* 说明:读取TSP坐标文件*************************************************************** ********/ double* TSPRead(char *pfile){double *pBuf, dData, *pData;pBuf = new double[TSPN*2];if (pBuf == NULL){cout << "分配内存出错!" << endl;exit(1);}memset(pBuf, 0, TSPN*2);// 读文件ifstream infile(pfile, ios::in|ios::nocreate);if (!infile){cout << "不能打开文件" << endl;exit(1);}pData = pBuf;for (int i=0; i<="" p="">{infile >> dData; // 读出城市序号for (int j=0; j<2; j++){if (!(infile >> dData)) break;*(pData++) = dData;}}infile.close();return pBuf;}/********************************************************************** * 函数名称:TSPDistance()* 输入参数:x y -城市序号0开始,*pData -城市坐标数组* 返回值:double -两城市间的距离* 说明:计算两个城市间的距离*************************************************************** ********/ double TSPDistance(int x, int y, const double *pData) {double distance;distance = sqrt((*(pData+x*2) - *(pData+y*2)) * (*(pData+x*2) - *(pData+y*2)) + (*(pData+x*2+1) - *(pData+y*2+1)) * (*(pData+x*2+1) - *(pData+y*2+1)));return distance;}/************************************************************** ******** * 函数名称:TSPDeta()* 输入参数:*pfile -文件名* 返回值:double -最大距离与最小距离的估计值* 说明:计算TSP中的最大距离与最小距离的估计值*************************************************************** ********/ double TSPDeta(char *pfile){double *pFile = TSPRead(pfile);Print(pFile, 2*TSPN);double dTmp, dMax, dMin, dSum;dSum = 0.0;for (int i=0; i<="" p="">{dMax = TSPDistance(i, (i+1)%TSPN, pFile);dMin = TSPDistance(i, (i+1)%TSPN, pFile);for (int j=1; j<="" p="">dTmp = TSPDistance(i, (i+1+j)%TSPN, pFile);if (dTmp > dMax) dMax = dTmp;if (dTmp < dMin) dMin = dTmp;}dSum += dMax - dMin;}delete [] pFile;pFile = NULL;return dSum;}/************************************************************** ******** * 函数名称:Equal()* 输入参数:s0 -源目标解s1 -目的解* 返回值:* 说明:两个解之间的复制*************************************************************** ********/ void Equal(ANSWER s1, ANSWER s0){memcpy(s1.pAnswer, s0.pAnswer, TSPN * sizeof(int));memcpy(s1.pData, s0.pData, TSPN * 2 * sizeof(double));}/************************************************************** ******** * 函数名称:Function()* 输入参数:s0 -解* 返回值:double -解的函数值* 说明:求解的函数值*************************************************************** ********/ double Function(ANSWER s0)double dFunc;dFunc = 0.0;for (int i=0; i<="" p="">{// 距离求和dFunc += TSPDistance(*(s0.pAnswer), *(s0.pAnswer + 1), s0.pData);s0.pAnswer++;}return dFunc;}/************************************************************** ******** * 函数名称:InitAnswer()* 输入参数:pfilename -文件名* 返回值:ANSWER -解* 说明:随机产生一个解*************************************************************** ********/ ANSWER InitAnswer(char *pfilename){ANSWER s0;s0.pData = TSPRead(pfilename);s0.pAnswer = new int[TSPN];if (s0.pAnswer == NULL){cout << "分配内存出错!" << endl;exit(1);}memset(s0.pAnswer, 0, TSPN);int *p, *q, num = 0, nflag = 0;p = s0.pAnswer;while (true){int nRand;nRand = rand() % TSPN;q = s0.pAnswer;while (q < p){if (*(q++) == nRand) { nflag = 1; break; }}if (nflag == 1) { nflag = 0; continue; }*(p++) = nRand;num++;if (num >= TSPN) break;}return s0;}/************************************************************** ******** * 函数名称:FindNextAnswer()* 输入参数:s0 -解* 返回值:ANSWER -解* 说明:在解得邻域找到另一个随机的解*************************************************************** ********/ ANSWER FindNextAnswer(ANSWER s0){ANSWER answer;answer.pAnswer = new int[TSPN];memset(answer.pAnswer, 0, sizeof(int)*TSPN);。
基于改进模拟退火算法求解TSP问题

度的不断下降 , 结合概率突跳特性在解空间中随机寻找 目标函数的全局最优解 , 即局部最优解能概率性地
8 0
渤海大学学报( 自然科学版 )
第3 4卷
设 G= ( , ) 为赋权图, ={ l , 2 , …r t } 为顶点集 , E为边集 , 各顶点间距离为 c ( c > O , i , j ∈ ) , 并设 r 1 , 在 最优路 径上
1 0 , 其 它
定性 .
关 键词 : 模拟 退 火算 法 ; T S P; 最优 解
中图分 类号 : T P 3 l 文献标 志码 : A 文章 编号 : 1 6 7 3— 0 5 6 9 ( 2 0 1 3 ) 0 1 — 0 0 7 9— 0 6
0 引 言
旅行 商 问题 ( T r a v e l i n g S a l e s ma n P r o b l e m, 简称 T S P ) ¨ , 也称 为货 郎担 问题 . 目前 T S P问题 已经 被证 明 属于 N P难题 . 由于该 问题 的实 际模 型 在 V L S I 芯片设 计 、 连锁 店 的货 物 配送 、 网络路 由设计 、 物流、 生产 调
跳 出并 最 终趋 于全局 最优 , 进 而达 到搜索 全局 最优 解 的 目的. 但 传 统模 拟 退 火算 法 随机 性 太 强 , 当参 数设 置不适 当时很难 搜索 到全 局最 优解 , 同时在求 解过 程 中经 常会 出现丢 失 当前 最 优解 的问题 . 因此 , 本 文提 出 了一 种 改进 的模拟 退火 算法 , 在 闭合 的解空 间 中采用 边 断裂 的 方式 , 对 当前 解 进行 最 优 组合 , 并 在 新解
基于模拟退火算法的TSP算法

专业综合设计报告课程名称:电子专业综合设计设计名称:基于模拟退火算法的TSP算法姓名:学号:班级:电子0903指导教师:朱正为起止日期:2012.11.1-2012.12.30专业综合设计任务书学生班级:电子0903 学生:学号:20095830 设计名称:基于模拟退火算法的TSP算法起止日期:2012.11.1-2012.12.30 指导教师专业综合设计学生日志专业综合设计考勤表专业综合设计评语表一设计目的和意义 (7)二设计原理 (7)2.1 模拟退火算法的基本原理 (5)2.2 TSP问题介绍 (6)三详细设计步骤 (10)3.1.算法流程 (8)3.2模拟退火算法实现步骤 ......................................................................... 错误!未定义书签。
四设计结果及分析 . (9)4.1 MATLAB程序实现及主函数 (9)4.1.1 计算距离矩阵 (9)4.1.2 初始解 (10)4.1.3 生成新解 (10)4.1.4 Metropolis 准则函数................................................................................................ (10)4.1.5 画路线轨迹图 (11)4.1.6 输出路径函数 (12)4.1.7 可行解路线长度函数 (12)4.1.8 模拟退火算法的主函数 (13)4.2.仿真结果 (15)五体会 (25)六参考文献 (25)基于模拟退火算法的TSP算法一、设计目的和意义旅行商问题是组合优化领域里的一个典型的、易于描述却难以处理的NP难题,其可能的路径数目与城市数目是呈指数型增长的,求解非常困难。
首先介绍了旅行商问题,给出了其数学描述以及实际应用,进而给出解决TSP的一种比较精确的算法——模拟退火算法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专业综合设计报告课程名称:电子专业综合设计设计名称:基于模拟退火算法的TSP算法姓名:学号:班级:电子0903指导教师:朱正为起止日期:2012.11.1-2012.12.30专业综合设计任务书学生班级:电子0903 学生姓名:学号:20095830设计名称:基于模拟退火算法的TSP算法起止日期:2012.11.1-2012.12.30指导教师设计要求:旅行商问题,即TSP问题(Travelling Salesman Problem)又译为旅行推销员问题、货郎担问题,是数学领域中著名问题之一。
假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。
路径的选择目标是要求得的路径路程为所有路径之中的最小值。
此设计是用模拟退火算法来实现TSP问题的寻求最优解。
专业综合设计学生日志时间设计内容2012.11.9初步了解模拟退火算法的TSP算法2012.11.12设计算法流程、确定解题思路2012.11.20讨论算法流程及解题思路的可行性,为仿真做准备2012.12.2运用MATLAB软件进行实验仿真,分析仿真结果2012.12.8整理实验报告2012.12.17 答辩专业综合设计考勤表周星期一星期二星期三星期四星期五专业综合设计评语表指导教师评语:成绩:指导教师:年月日一设计目的和意义 (5)二设计原理 (5)2.1 模拟退火算法的基本原理 (5)2.2 TSP问题介绍 (6)三详细设计步骤 (8)3.1.算法流程 (8)3.2模拟退火算法实现步骤................................................................................. 错误!未定义书签。
四设计结果及分析 (9)4.1 MATLAB程序实现及主函数 (9)4.1.1计算距离矩阵 (9)4.1.2 初始解 (10)4.1.3 生成新解 (10)4.1.4 Metropolis 准则函数................................................................................................ (10)4.1.5 画路线轨迹图 (11)4.1.6 输出路径函数 (12)4.1.7 可行解路线长度函数 (12)4.1.8 模拟退火算法的主函数 (13)4.2.仿真结果 (15)五体会 (18)六参考文献 (18)基于模拟退火算法的TSP算法一、设计目的和意义旅行商问题是组合优化领域里的一个典型的、易于描述却难以处理的NP难题,其可能的路径数目与城市数目是呈指数型增长的,求解非常困难。
首先介绍了旅行商问题,给出了其数学描述以及实际应用,进而给出解决TSP的一种比较精确的算法——模拟退火算法。
然后阐述了模拟退火算法的基本原理,重点说明了其基本思想及关键技术。
最后运用MATLAB语言实现了该算法,并将其运用到解决旅行商问题的优化之中。
数值仿真的结果表明了该方法能够对数据进行全局寻优,有效克服了基于导数的优化算法容易陷入局部最优的问题。
了解模拟退火算法的TSP算法的基本思路及原理,并应用MATLAB实现仿真,熟练掌握MATLAB的操作方式及应用,能正确书写报告。
二、设计原理2.1 模拟退火算法的基本原理模拟退火算法足2O世纪8O年代初提出的一种基于蒙特卡罗(Mente Carlo)迭代求解策略的启发式随机优化算法。
它通过Metropolis接受准则概率接受劣化解并以此跳出局部最优,通过温度更新函数的退温过程进行趋化式搜索并最终进入全局最优解集。
其出发点是基于物理中固体物质的退火过程与一搬的组合优化问题之间的相似性。
模拟退火法是一种通用的优化算法,其物理退火过程由以下三部分组成。
(1)加温过程。
其目的是增强粒子的热运动,使其偏离平衡位置。
当温度足够高时,固体将熔为液体,从而消除系统原先存在的非均匀状态。
(2)等温过程。
对于与周围环境交换热量而温度不变的密封系统,系统状态的自发变化总是朝自由能减少的方向进行的,当自由能达到最小时,系统达到平衡状态。
(3)冷却过程。
使粒子热运动减弱,系统能量下降,得到晶体结构。
其中,加热过程对应算法的设定初温,等温过程对应算法的 Metropolis 抽样过程,冷却过程对应控制参数的下降。
这里能量的变化就是目标函数,要得到的最优解就是能量最低态。
Metropolis 准则是SA算法收敛于全局最优解的关键所在,Metropolis 准则以一定的概率接受恶化解,这样就使算法跳离局部最优的陷阱。
模拟退火算法为求解传统方法难处理的TSP问题提供了一个有效的途径和通用框架,并逐渐发展成一种迭代自适应启发式概率性搜索算法。
模拟退火算法可以用以求解不同的非线性问题,对不可微甚至不连续的函数优化,能以较大的概率求的全局有化解,该算法还具有较强的鲁棒性、全局收敛性、隐含并行性及广泛的适应性,并且能处理不同类型的优化设计变量(离散的、连续的和混合型的),不需要任何的辅助信息,对目标函数和约束函数没有任何要求。
利用 Metropolis 算法并适当的控制温度下降过程,在优化问题中具有很强的竞争力,此设计即为基于模拟退火算法的TSP算法。
SA算法实现过程如下(以最小化问题为例):(1)初始化:取初始温度T0足够大,令T=T,任取初始解S1,确定每个T时的迭代次数,即Metropolis 链长L。
(2)对当前温度T和k=1,2,……,l,重复步骤(3)~(6)。
(3)对当前S1随机扰动产生一个新解S2。
(4)计算S2的增量df=f(S2)-f(S1)其中f为S1的代价函数。
(5)若df<0 ,则接受S2作为新的当前解,即S1=S2;否则计算S2的接受概率exp(-df/T),即随机产生(0,1)区间上均匀分布的随机数 rand,若exp(-df/T)>rand也接受S2作为新的当前解,S1=S2;否则保留当前解S1。
(6)如果满足终止条件Stop,则输出当前解s1为最优解,结束程序。
终止条件Stop 通常为:在连续若干个 Metropolis 链中新解s2都没有被接受时终止算法,或是设定结束温度。
否则按衰减函数衰减 T 后返回步骤(2)。
以上步骤成为 Metropolis 过程。
逐渐降低控制温度,重复 Metropolis 过程,直至满足结束准则 Stop,求出最优解。
2.2 TSP问题介绍旅行商问题(Traveling Salesman Problem,简称TSP)又名货郎担问题,是威廉·哈密尔顿爵士和英国数学家克克曼(T.P.Kirkman)于19世纪初提出的一个数学问题,也是著名的组合优化问题。
问题是这样描述的:一名商人要到若干城市去推销商品,已知城市个数和各城市间的路程(或旅费),要求找到一条从城市1出发,经过所有城市且每个城市只能访问一次,最后回到城市1的路线,使总的路程(或旅费)最小。
TSP刚提出时,不少人认为这个问题很简单。
后来人们才逐步意识到这个问题只是表述简单,易于为人们所理解,而其计算复杂性却是问题的输入规模的指数函数,属于相当难解的问题。
这个问题数学描述为:假设有n个城市,并分别编号,给定一个完全无向图G=(V,E),V={1,2,…,n},n>1。
其每一边(i,j)∈E有一非负整数耗费C i,j(即上的权记为C i,j,i,j∈V)。
G的一条巡回路线是经过V中的每个顶点恰好一次的回路。
一条巡回路线的耗费是这条路线上所有边的权值之和。
TSP问题就是要找出G的最小耗费回路。
人们在考虑解决这个问题时,一般首先想到的最原始的一种方法就是:列出每一条可供选择的路线(即对给定的城市进行排列组合),计算出每条路线的总里程,最后从中选出一条最短的路线。
假设现在给定的4个城市分别为A、B、C和D,各城市之间的耗费为己知数,如图1所示。
我们可以通过一个组合的状态空间图来表示所有的组合,如图(1-1)图 1 顶点带权图图 2 TSP问题的解空间树从图中不难看出,可供选择的路线共有6条,从中很快可以选出一条总耗费最短的路线:顶点序列为(A,C,B,D,A)。
由此推算,若设城市数目为n时,那么组合路径数则为(n-1)!。
很显然,当城市数目不多时要找到最短距离的路线并不难,但随着城市数目的不断增大,组合路线数将呈指数级数规律急剧增长,以至达到无法计算的地步,这就是所谓的“组合爆炸问题”。
假设现在城市的数目增为20个,组合路径数则为(20-1)!≈1.216×1017,如此庞大的组合数目,若计算机以每秒检索1000万条路线的速度计算,也需要花上386年的时间[6]。
三、详细设计步骤3.1算法流程模拟退火算法求解流程框图如图1所示。
图3 模拟退火算法求解流程框图3.2模拟退火算法实现步骤如下:(1)控制参数的设置需要设置的主要控制参数有降温速率q、初始温度T0、结束温度T end以及链长L。
(2)初始解对于n个城市TSP问题,得到的解就是对1~n的一个排序,其中每个数字为对应城市的编号,如对10个城市的TSP问题{1,2,3,4,5,6,7,8,9,10},则|1|10|2|4|5|6|8|7|9|3就是一个合法的解,采用产生随机排列的方法产生一个初始解S。
(3)解变换生成新解通过对当前解S1进行变换,产生新的路径数组即新解,这里采用的变换是产生随机数的方法来产生将要交换的两个城市,用二邻域变换法产生新的路径,即新的可行解S2。
例如n=10时,产生两个[1,10]范围内的随机整数r1和r2,确定两个位置,将其对换位置,如r1=4,r2=79 5 1 6 3 8 7 10 4 2 得到的新解为9 5 1 7 3 8 6 10 4 2(4)Metropolis 准则 若路径长度函数为f (S ),新解的路径为f (S 2),路径差为d f =f (S 2)-f (S 1),则Metropolis 准则为{1,0=exp(),0df P dfdf T <≥如果df<0,则以概率1接受新路线,否则以概率exp (-df/T )接受新路线。
(5)降温利用降温速率q 进行降温,即T=qT,若T 小于结束温度,则停止迭代输出当前状态,否则继续迭代。
四 、设计结果及分析4.1 MATLAB 程序实现及主函数 4.1.1 计算距离矩阵利用给出的N 个城市的坐标,算出N 个城市的两两之间的距离,得到距离矩阵(N ⨯N )。
计算函数为Distance ,得到初始群种。
程序如下4.1.2 初始解function D=Distanse(a) %% 计算两两城市之间的距离 %输入 a 各城市的位置坐标 %输出 D 两两城市之间的距离 row=size(a,1); D=zeros(row,row); for i=1:row for j=i+1:row D(i,j)=((a(i,1)-a(j,1))^2+(a(i,2)-a(j,2))^2)^0.5; D(j,i)=D(i,j); end end初始解的产生直接使用MATLAB自带的函数randperm,如城市格式为N个,则产生初始解:S1=randperm(N);%随机产生一个初始路线4.1.3 生成新解解变换生成新解函数为NewAnswer,程序代码如下:function S2=NewAnswer(S1)%% 输入% S1:当前解%% 输出% S2:新解N=length(S1);S2=S1;a=round(rand(1,2)*(N-1)+1); %产生两个随机位置用来交换W=S2(a(1));S2(a(1))=S2(a(2));S2(a(2))=W; %得到一个新路线4.1.4 Metropolis 准则函数Metropolis 准则函数为Metropolis,程序代码如下:function [S,R]=Metropolis(S1,S2,D,T)%% 输入% S1:当前解% S2: 新解% D: 距离矩阵(两两城市的之间的距离)% T: 当前温度%% 输出% S:下一个当前解% R:下一个当前解的路线距离%%R1=PathLength(D,S1); %计算路线长度N=length(S1); %得到城市的个数R2=PathLength(D,S2); %计算路线长度dC=R2-R1; %计算能力之差if dC<0 %如果能力降低接受新路线S=S2;R=R2;elseif exp(-dC/T)>=rand %以exp(-dC/T)概率接受新路线S=S2;R=R2;else %不接受新路线S=S1;R=R1;end4.1.5 画路线轨迹图画出给的路线的轨迹图函数为DrawPath,程序代码如下:function DrawPath(Chrom,X)%% 画路径函数%输入% Chrom 待画路径% X 各城市坐标位置R=[Chrom(1,:) Chrom(1,1)]; %一个随机解(个体)figure;hold onplot(X(:,1),X(:,2),'o','color',[0.5,0.5,0.5])plot(X(Chrom(1,1),1),X(Chrom(1,1),2),'rv','MarkerSize',20)for i=1:size(X,1)text(X(i,1)+0.05,X(i,2)+0.05,num2str(i),'color',[1,0,0]);endA=X(R,:);row=size(A,1);for i=2:row[arrowx,arrowy] = dsxy2figxy(gca,A(i-1:i,1),A(i-1:i,2));%坐标转换annotation('textarrow',arrowx,arrowy,'HeadWidth',8,'color',[0,0,1]);endhold offxlabel('横坐标')ylabel('纵坐标')title('轨迹图')box on4.1.6 输出路径函数将得到的路径输出显示在Command Window 中,函数名为OutputPath。
