数列的概念经典试题(含答案) 百度文库
数列的概念经典试题(含答案) 百度文库

一、数列的概念选择题1.已知等差数列{}n a 中,13920a a a ++=,则574a a -=( )A .30B .20C .40D .502.在数列{}n a 中,11a =,11n n a a n +=++,设数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和为n S ,若n S m <对一切正整数n 恒成立,则实数m 的取值范围为( ) A .()3,+∞ B .[)3,+∞C .()2,+∞D .[)2,+∞3.已知数列{}n a 的前n 项和223n S n n =-,则10a =( )A .35B .40C .45D .504.设{}n a 是等差数列,且公差不为零,其前n 项和为n S .则“*n N ∀∈,1n n S S +>”是“{}n a 为递增数列”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件5.已知数列,21,n -21是这个数列的( )A .第10项B .第11项C .第12项D .第21项6.已知数列{}n a 的通项公式为23nn a n ⎛⎫= ⎪⎝⎭,则数列{}n a 中的最大项为( ) A .89B .23C .6481D .1252437.数列23451,,,,,3579的一个通项公式n a 是( ) A .21nn + B .23nn + C .23nn - D .21nn - 8.已知数列{}n a 满足11a =,()*11nn n a a n N a +=∈+,则2020a =( ) A .12018B .12019 C .12020D .120219.在数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,则下列结论正确的是( )A .存在正整数0N ,当0n N >时,都有n a n ≤.B .存在正整数0N ,当0n N >时,都有n a n ≥.C .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≤.D .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≥. 10.已知数列{}n a 满足()()*622,6,6n n p n n a n pn -⎧--≤=∈⎨>⎩N ,且对任意的*n ∈N 都有1n n a a +>,则实数p 的取值范围是( )A .71,4⎛⎫ ⎪⎝⎭B .101,7⎛⎫⎪⎝⎭C .()1,2D .10,27⎛⎫⎪⎝⎭11.数列{}n a 满足:12a =,111nn na a a ++=-()*n N ∈其前n 项积为n T ,则2018T =( ) A .6-B .16-C .16D .612.已知数列{}n a 的首项为1,第2项为3,前n 项和为n S ,当整数1n >时,1112()nnn S S S S 恒成立,则15S 等于( )A .210B .211C .224D .22513.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中,提出了一些新的垛积公式,所讨论的高阶等差数列与一般等差数列不同,前后两项之差并不相等,但是逐项差数之差或者高次差成等差数列.对这类高阶等差数列的研究,在杨辉之后一般称为“垛积术”.现有高阶等差数列,其前7项分别为3,4,6,9,13,18,24,则该数列的第19项为( ) A .174B .184C .188D .16014.已知数列{}n a 的首项为2,且数列{}n a 满足111n n n a a a +-=+,数列{}n a 的前n 项的和为n S ,则1008S 等于( ) A .504B .294C .294-D .504-15.已知数列{}n a 满足11a =,122n n a a n n+=++,则10a =( ) A .259B .145 C .3111D .17616.已知数列{}n a 满足111n n n n a a a a ++-=+,且113a =,则{}n a 的前2021项之积为( ) A .23B .13C .2-D .3-17.数列1111,,,57911--,…的通项公式可能是n a =( ) A .1(1)32n n --+B .(1)32n n -+C .1(1)23n n --+D .(1)23nn -+18.设数列{}n a的通项公式为2 nnan+=,要使它的前n项的乘积大于36,则n的最小值为()A.6 B.7 C.8 D.919.公元13世纪意大利数学家斐波那契在自己的著作《算盘书》中记载着这样一个数列:1,1,2,3,5,8,13,21,34,…满足21(1),n n na a a n++=+≥那么24620201a a a a+++++=()A.2021a B.2022a C.2023a D.2024a20.在数列{}n a中,()1111,1(2)nnna a na--==+≥,则5a等于A.32B.53C.85D.23二、多选题21.黄金螺旋线又名等角螺线,是自然界最美的鬼斧神工.在一个黄金矩形(宽长比约等于0.618)里先以宽为边长做正方形,然后在剩下小的矩形里以其宽为边长做正方形,如此循环下去,再在每个正方形里画出一段四分之一圆弧,最后顺次连接,就可得到一条“黄金螺旋线”.达·芬奇的《蒙娜丽莎》,希腊雅典卫城的帕特农神庙等都符合这个曲线.现将每一段黄金螺旋线与其所在的正方形所围成的扇形半径设为a n (n ∈N*),数列{a n}满足a1=a2=1,a n=a n-1+a n-2 (n≥3).再将扇形面积设为b n (n∈N*),则()A.4(b2020-b2019)=πa2018·a2021B.a1+a2+a3+…+a2019=a2021-1C.a12+a22+a32…+(a2020)2=2a2019·a2021D.a2019·a2021-(a2020)2+a2018·a2020-(a2019)2=0 22.著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{}n a称为“斐波那契数列”,记S n为数列{}n a的前n项和,则下列结论正确的是()A.68a=B.733S=C.135********a a a a a++++=D.22212201920202019a a aaa+++=23.(多选题)已知数列{}n a 中,前n 项和为n S ,且23n n n S a +=,则1n n a a -的值不可能为( ) A .2B .5C .3D .424.设等比数列{}n a 的公比为q ,其前n 项和为n S ,前n 项积为n T ,并且满足条件11a >,667711,01a a a a -><-,则下列结论正确的是( ) A .01q <<B .681a a >C .n S 的最大值为7SD .n T 的最大值为6T25.已知数列{}n a 满足112a =-,111n na a +=-,则下列各数是{}n a 的项的有( )A .2-B .23 C .32D .326.等差数列{}n a 的前n 项和为n S ,1385a a S +=,则下列结论一定正确的是( ) A .100a = B .911a a = C .当9n =或10时,n S 取得最大值D .613S S =27.设数列{}n a 的前n 项和为*()n S n N ∈,关于数列{}n a ,下列四个命题中正确的是( )A .若1*()n n a a n N +∈=,则{}n a 既是等差数列又是等比数列B .若2n S An Bn =+(A ,B 为常数,*n N ∈),则{}n a 是等差数列C .若()11nn S =--,则{}n a 是等比数列D .若{}n a 是等差数列,则n S ,2n n S S -,*32()n n S S n N -∈也成等差数列28.已知数列{}2nna n +是首项为1,公差为d 的等差数列,则下列判断正确的是( ) A .a 1=3 B .若d =1,则a n =n 2+2n C .a 2可能为6D .a 1,a 2,a 3可能成等差数列29.无穷等差数列{}n a 的前n 项和为S n ,若a 1>0,d <0,则下列结论正确的是( ) A .数列{}n a 单调递减 B .数列{}n a 有最大值 C .数列{}n S 单调递减D .数列{}n S 有最大值30.{} n a 是等差数列,公差为d ,前项和为n S ,若56S S <,678S S S =>,则下列结论正确的是( ) A .0d <B .70a =C .95S S >D .170S <31.已知数列{}n a 的前n 项和为n S ,前n 项积为n T ,且3201911111a a e e +≤++,则( )A .当数列{}n a 为等差数列时,20210S ≥B .当数列{}n a 为等差数列时,20210S ≤C .当数列{}n a 为等比数列时,20210T >D .当数列{}n a 为等比数列时,20210T <32.在数列{}n a 中,若22*1(2,.n n a a p n n N p --=≥∈为常数),则称{}n a 为“等方差数列”.下列对“等方差数列”的判断正确的是( ) A .若{}n a 是等差数列,则{}n a 是等方差数列 B .{(1)}n -是等方差数列C .若{}n a 是等方差数列,则{}()*,kn a k Nk ∈为常数)也是等方差数列D .若{}n a 既是等方差数列,又是等差数列,则该数列为常数列 33.已知等差数列{}n a 的前n 项和为n S ()*n N ∈,公差0d ≠,690S=,7a 是3a 与9a 的等比中项,则下列选项正确的是( ) A .2d =-B .120a =-C .当且仅当10n =时,n S 取最大值D .当0nS <时,n 的最小值为2234.记n S 为等差数列{}n a 的前n 项和.已知535S =,411a =,则( ) A .45n a n =-B .23n a n =+C .223n S n n =-D .24n S n n =+35.已知{}n a 为等差数列,其前n 项和为n S ,且13623a a S +=,则以下结论正确的是( ). A .10a =0B .10S 最小C .712S S =D .190S =【参考答案】***试卷处理标记,请不要删除一、数列的概念选择题 1.B 解析:B 【分析】利用等差数列{}n a 的通项公式代入可得574a a -的值. 【详解】由13920a a a ++=,得131020a d +=,则有5711144(4)631020a a a d a d a d -=+--=+=. 故选:B. 【点睛】考查等差数列通项公式的运用,知识点较为简单.2.D解析:D 【分析】利用累加法求出数列{}n a 的通项公式,并利用裂项相消法求出n S ,求出n S 的取值范围,进而可得出实数m 的取值范围. 【详解】11n n a a n +=++,11n n a a n +∴-=+且11a =,由累加法可得()()()()12132111232n n n n n a a a a a a a a n -+=+-+-++-=++++=,()122211n a n n n n ∴==-++,22222222222311n S n n n ⎛⎫⎛⎫⎛⎫∴=-+-++-=-< ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭, 由于n S m <对一切正整数n 恒成立,2m ∴≥,因此,实数m 的取值范围是[)2,+∞.故选:D. 【点睛】本题考查数列不等式恒成立问题的求解,同时也考查了累加法求通项以及裂项求和法,考查计算能力,属于中等题.3.A解析:A 【分析】利用()n n n a S S n 12-=-,根据题目已知条件求出数列的通项公式,问题得解.【详解】223n S n n =-,n 2∴≥时,1n n n a S S -=-22(23[2(1)3(1)]n n n n )=-----=45n1n = 时满足11a S = ∴ =45n a n ,∴ 10a =35故选:A. 【点睛】本题考查利用n a 与n S 的关系求通项. 已知n S 求n a 的三个步骤:(1)先利用11a S =求出1a .(2)用1n -替换n S 中的n 得到一个新的关系,利用()n n n a S S n 12-=-便可求出当n 2≥时n a 的表达式.(3)对1n =时的结果进行检验,看是否符合n 2≥时n a 的表达式,如果符合,则可以把数列的通项公式合写;如果不符合,则应该分1n =与n 2≥两段来写. .4.A解析:A 【分析】根据等差数列的前n 项和公式以及充分条件和必要条件的定义进行判断即可. 【详解】{}n a 是等差数列,且公差d 不为零,其前n 项和为n S ,充分性:1n n S S +>,则10n a +>对任意的n *∈N 恒成立,则20a >,0d ≠,若0d <,则数列{}n a 为单调递减数列,则必存在k *∈N ,使得当n k >时,10n a +<,则1n n S S +<,不合乎题意;若0d >,由20a >且数列{}n a 为单调递增数列,则对任意的n *∈N ,10n a +>,合乎题意.所以,“*n N ∀∈,1n n S S +>”⇒“{}n a 为递增数列”;必要性:设10n a n =-,当8n ≤时,190n a n +=-<,此时,1n n S S +<,但数列{}n a 是递增数列.所以,“*n N ∀∈,1n n S S +>”⇐/“{}n a 为递增数列”.因此,“*n N ∀∈,1n n S S +>”是“{}n a 为递增数列”的充分而不必要条件. 故选:A. 【点睛】本题主要考查充分条件和必要条件的判断,结合等差数列的前n 项和公式是解决本题的关键,属于中等题.5.B解析:B 【分析】根据题中所给的通项公式,令2121n -=,求得n =11,得到结果. 【详解】令2121n -=,解得n =11是这个数列的第11项. 故选:B. 【点睛】该题考查的是有关数列的问题,涉及到的知识点有判断数列的项,属于基础题目.6.A解析:A 【分析】由12233nn n n a a +-⎛⎫-=⋅ ⎪⎝⎭,当n <2时,a n +1-a n >0,当n <2时,a n +1-a n >0,从而可得到n =2时,a n 最大. 【详解】解:112222(1)3333n nnn n n a a n n ++-⎛⎫⎛⎫⎛⎫-=+-=⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 当n <2时,a n +1-a n >0,即a n +1>a n ;当n =2时,a n +1-a n =0,即a n +1=a n ; 当n >2时,a n +1-a n <0,即a n +1<a n . 所以a 1<a 2=a 3,a 3>a 4>a 5>…>a n ,所以数列{}n a 中的最大项为a 2或a 3,且2328239a a ⎛⎫==⨯= ⎪⎝⎭.故选:A . 【点睛】此题考查数列的函数性质:最值问题,属于基础题.7.D解析:D 【分析】根据数列分子分母的规律求得通项公式. 【详解】由于数列的分母是奇数列,分子是自然数列,故通项公式为21n na n =-. 故选:D 【点睛】本小题主要考查根据数列的规律求通项公式,属于基础题.8.C解析:C 【分析】根据数列的递推关系,利用取倒数法进行转化,构造等差数列,结合等差数列的性质求出通项公式即可. 【详解】 解:11nn n a a a +=+, ∴两边同时取倒数得11111n n n na a a a ++==+,即1111n na a ,即数列1n a ⎧⎫⎨⎬⎩⎭是公差1d =的等差数列,首项为111a .则11(1)1nn n a =+-⨯=, 得1n a n=, 则202012020a =, 故选:C 【点睛】本题主要考查数列通项公式的求解,结合数列递推关系,利用取倒数法以及构造法构造等差数列是解决本题的关键.考查学生的运算和转化能力,属于基础题.9.A解析:A 【分析】运用数列的单调性和不等式的知识可解决此问题. 【详解】数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,121n n n n a a a a +++∴≥--,设1n n n d a a +=-,则1n n d d +≥,∴数列{}n d 是递减数列.对于A ,由11a =,20192019a =, 则201911220182019a a d d d =+++=,所以1220182018d d d +++=,又1232018d d d d ≥≥≥≥,所以1122018201820182018d d d d d ≥+++≥,故120181d d ≥≥,2018n ∴≥时,1n d ≤,02019N ∃=,2019n >时, 20192019202012019111n n a a d d d n -=+++≤++++=即存在正整数0N ,当0n N >时,都有n a n ≤,故A 正确;结合A ,故B 不正确;对于C ,当n →+∞,且0n d >时,数列{}n a 为递增数列, 则n a 无最大值,故C 不正确;对于D ,由数列{}n d 是递减数列,当存在0n d <时,则n a 无最小值,故D 不正确; 故选:A 【点睛】本题考查了数列的单调性以及不等式,属于基础题.10.D解析:D 【分析】根据题意,得到数列是增数列,结合通项公式,列出不等式组求解,即可得出结果. 【详解】因为对任意的*n ∈N 都有1n n a a +>, 则数列{}n a 单调递增; 又()()*622,6,6n n p n n a n pn -⎧--≤=∈⎨>⎩N ,所以只需67201p p a a ->⎧⎪>⎨⎪<⎩,即21106p p p p<⎧⎪>⎨⎪-<⎩,解得1027p <<. 故选:D. 【点睛】本题主要考查由数列的单调性求参数,属于基础题型.11.A解析:A 【分析】根据递推公式推导出()4n n a a n N *+=∈,且有12341a a a a=,再利用数列的周期性可计算出2018T 的值. 【详解】12a =,()*111++=∈-nn n a a n N a ,212312a +∴==--,3131132a -==-+,411121312a -==+,51132113a +==-,()4n n a a n N *+∴=∈,且()12341123123a a a a ⎛⎫=⨯-⨯-⨯= ⎪⎝⎭,201845042=⨯+,因此,()5042018450421211236T T a a ⨯+==⨯=⨯⨯-=-.故选:A. 【点睛】本题考查数列递推公式的应用,涉及数列周期性的应用,考查计算能力,属于中等题.12.D解析:D 【分析】利用已知条件转化推出1122n n a a a +-==,说明数列是等差数列,然后求解数列的和即可. 【详解】 解:结合1112()nnn S S S S 可知,11122n n n S S S a +-+-=,得到1122n n a a a +-==,故数列{}n a 为首项为1,公差为2的等差数列,则12(1)21n a n n =+-=-,所以1529a =,所以11515()15(291)1522522a a S ++===, 故选:D . 【点睛】本题考查数列的递推关系式的应用,考查数列求和,是基本知识的考查.13.A解析:A 【分析】根据已知条件求得11n n n a a -=--,利用累加法求得19a . 【详解】 依题意:3,4,6,9,13,18,24,1,2,3,4,5,6,所以11n n n a a -=--(2n ≥),且13a =,所以()()()112211n n n n n a a a a a a a a ---=-+-++-+()()12213n n =-+-++++()()()11113322n n n n -+--=+=+.所以19191831742a ⨯=+=. 故选:A 【点睛】本小题主要考查累加法,属于中档题.14.C解析:C 【分析】根据递推公式,算出数列前4项,确定数列周期,即可求出结果. 【详解】∵12a =,111n n n a a a +-=+,∴213a =,311131213a -==-+,41123112a --==--+, 又121111111111n n n n n n n n a a a a a a a a +++---+===--+++,所以421n n n a a a ++=-=, ∴数列{}n a 的周期为4,且123476a a a a +++=-, ∵10084252÷=,∴100872522946S ⎛⎫=⨯-=- ⎪⎝⎭. 故选:C. 【点睛】本题主要考查数列周期性的应用,属于常考题型.15.B解析:B 【分析】 由122n n a a n n +=++转化为11121n n a a n n +⎛⎫-=- ⎪+⎝⎭,利用叠加法,求得23n a n =-,即可求解. 【详解】由122n n a a n n +=++,可得12112(1)1n n a a n n n n +⎛⎫-==- ⎪++⎝⎭,所以()()()()11223211n n n n n n n a a a a a a a a a a -----=-+-+-++-+11111111222*********n n n n n n ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+-++-+ ⎪ ⎪ ⎪ ⎪-----⎝⎭⎝⎭⎝⎭⎝⎭122113n n ⎛⎫=-+=- ⎪⎝⎭,所以102143105a =-=. 故选:B. 【点睛】数列的通项公式的常见求法:1、对于递推关系式可转化为1()n n a a f n +-=的数列,通常采用叠加法(逐差相加法)求其通项公式;2、对于递推关系式可转化为1()n na f n a +=的数列,并且容易求数列{()}f n 前n 项积时,通常采用累乘法求其通项公式; 3、对于递推关系式形如1n n a pa q +=+的数列,可采用构造法求解数列的通项公式.16.B解析:B 【分析】由111n n n n a a a a ++-=+,且113a =,可得:111n n n a a a ++=-,可得其周期性,进而得出结论. 【详解】因为111n n n n a a a a ++-=+,且113a =, 所以111nn na a a ++=-, 21132113a +∴==-,33a =-,412a =-,513a =,⋯⋯, 4n n a a +∴=.123411···2(3)()132a a a a ∴=⨯⨯--⋅⨯=.则{}n a 的前2021项之积50511133=⨯=.故选:B 【点睛】方法点睛:已知递推关系式求通项:(1)用代数的变形技巧整理变形,然后采用累加法、累乘法、迭代法、构造法或转化为基本数列(等差数列或等比数列)等方法求得通项公式.(2)通过具体的前几项找到其规律,如周期性等求解.17.D解析:D 【分析】根据观察法,即可得出数列的通项公式. 【详解】因为数列1111,,,, (57911)--可写成 ()()()()2342322311111,1,1,12,..24.333-⨯-⨯-⨯+⨯+⨯+⨯+-⨯,所以其通项公式为(1)(1)23213nnn a n n -=-=++⨯. 故选:D.18.C解析:C 【分析】先求出数列{}n a 的前n 项的乘积为n D ,令0n D >解不等式,结合*n N ∈,即可求解. 【详解】记数列{}n a 的前n 项的乘积为n D ,则()()12112451232312n n n n n n n D a a a a n n -++++=⋅⋅=⨯⨯⨯⨯⨯=- 依题意有()()12362n n ++>整理得()()23707100n n n n +-=-+> 解得:7n >,因为*n N ∈,所以min 8n =, 故选:C19.A解析:A 【分析】根据数列的递推关系式即可求解. 【详解】由21(1),n n n a a a n ++=+≥ 则2462020246210201a a a a a a a a a +++++++++=+3462020562020201920202021a a a a a a a a a a =+++=+++=+=.故选:A20.D解析:D 【解析】分析:已知1a 逐一求解2345122323a a a a ====,,,. 详解:已知1a 逐一求解2345122323a a a a ====,,,.故选D 点睛:对于含有()1n-的数列,我们看作摆动数列,往往逐一列举出来观察前面有限项的规律.二、多选题21.ABD 【分析】对于A ,由题意得bn =an2,然后化简4(b2020-b2019)可得结果;对于B ,利用累加法求解即可;对于C ,数列{an}满足a1=a2=1,an =an -1+an -2 (n≥3解析:ABD 【分析】对于A ,由题意得b n =4πa n 2,然后化简4(b 2020-b 2019)可得结果;对于B ,利用累加法求解即可;对于C ,数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),即a n -1=a n -2-a n ,两边同乘a n -1 ,可得a n -12=a n -1 a n -2-a n -1 a n ,然后累加求解;对于D ,由题意a n -1=a n -a n -2,则a 2019·a 2021-(a 2020)2+a 2018·a 2020-(a 2019)2,化简可得结果 【详解】由题意得b n =4πa n 2,则4(b 2020-b 2019)=4(4πa 20202-4πa 20192)=π(a 2020+a 2019)(a 2020-a 2019)=πa 2018·a 2021,则选项A 正确; 又数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),所以a n -2=a n -a n -1(n ≥3),a 1+a 2+a 3+…+a 2019=(a 3-a 2)+(a 4-a 3)+(a 5-a 4)+…+(a 2021-a 2020)=a 2021-a 2=a 2021-1,则选项B 正确;数列{a n }满足a 1=a 2=1,a n =a n -1+a n -2 (n ≥3),即a n -1=a n -2-a n ,两边同乘a n -1 ,可得a n-12=a n -1 a n -2-a n -1 a n ,则a 12+a 22+a 32…+(a 2020)2=a 12+(a 2a 1-a 2a 3)+(a 3a 2-a 3a 4)+…+(a 2020a 2019-a 2020a 2021)=a 12-a 2020a 2021=1-a 2020a 2021,则选项C 错误;由题意a n -1=a n -a n -2,则a 2019·a 2021-(a 2020)2+a 2018·a 2020-(a 2019)2=a 2019·(a 2021-a 2019)+a 2020·(a 2018-a 2020)=a 2019·a 2020+a 2020·(-a 2019)=0,则选项D 正确; 故选:ABD. 【点睛】此题考查数列的递推式的应用,考查累加法的应用,考查计算能力,属于中档题22.ABD 【分析】根据,,,计算可知正确;根据,,,,,,累加可知不正确;根据,,,,,,累加可知正确. 【详解】依题意可知,,,, ,,,,故正确; ,所以,故正确; 由,,,,,,可得,故不解析:ABD 【分析】根据11a =,21a =,21n n n a a a ++=+,计算可知,A B 正确;根据12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,累加可知C 不正确;根据2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,累加可知D 正确. 【详解】依题意可知,11a =,21a =,21n n n a a a ++=+,312112a a a =+=+=,423123a a a =+=+=,534235a a a =+=+=,645358a a a =+=+=,故A 正确; 7565813a a a =+=+=,所以712345671123581333S a a a a a a a =++++++=++++++=,故B 正确;由12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,可得13572019a a a a a +++++=242648620202018a a a a a a a a a +-+-+-++-2020a =,故C 不正确;2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,所以2222212342019a a a a a +++++122312342345342019202020182019a a a a a a a a a a a a a a a a a a =+-+-+-+- 20192020a a =,所以22212201920202019a a a a a +++=,故D 正确. 故选:ABD. 【点睛】本题考查了数列的递推公式,考查了累加法,属于中档题.23.BD 【分析】利用递推关系可得,再利用数列的单调性即可得出答案. 【详解】 解:∵,∴时,, 化为:,由于数列单调递减, 可得:时,取得最大值2. ∴的最大值为3. 故选:BD . 【点睛】 本解析:BD 【分析】利用递推关系可得1211n n a a n -=+-,再利用数列的单调性即可得出答案. 【详解】 解:∵23n n n S a +=, ∴2n ≥时,112133n n n n n n n a S S a a --++=-=-, 化为:112111n n a n a n n -+==+--, 由于数列21n ⎧⎫⎨⎬-⎩⎭单调递减, 可得:2n =时,21n -取得最大值2. ∴1n n a a -的最大值为3. 故选:BD . 【点睛】本题考查了数列递推关系、数列的单调性,考查了推理能力与计算能力,属于中档题.24.AD 【分析】分类讨论大于1的情况,得出符合题意的一项. 【详解】 ①, 与题设矛盾. ②符合题意. ③与题设矛盾. ④ 与题设矛盾. 得,则的最大值为.B ,C ,错误. 故选:AD. 【点睛】解析:AD 【分析】分类讨论67,a a 大于1的情况,得出符合题意的一项. 【详解】①671,1a a >>, 与题设67101a a -<-矛盾. ②671,1,a a ><符合题意. ③671,1,a a <<与题设67101a a -<-矛盾. ④ 671,1,a a <>与题设11a >矛盾.得671,1,01a a q ><<<,则n T 的最大值为6T .∴B ,C ,错误.故选:AD. 【点睛】考查等比数列的性质及概念. 补充:等比数列的通项公式:()1*1n n a a qn N -=∈.25.BD 【分析】根据递推关系式找出规律,可得数列是周期为3的周期数列,从而可求解结论. 【详解】 因为数列满足,, ; ; ;数列是周期为3的数列,且前3项为,,3; 故选:. 【点睛】 本题主要解析:BD 【分析】根据递推关系式找出规律,可得数列是周期为3的周期数列,从而可求解结论. 【详解】因为数列{}n a 满足112a =-,111n na a +=-,212131()2a ∴==--;32131a a ==-; 4131112a a a ==-=-; ∴数列{}n a 是周期为3的数列,且前3项为12-,23,3; 故选:BD . 【点睛】本题主要考查数列递推关系式的应用,考查数列的周期性,解题的关键在于求出数列的规律,属于基础题.26.ABD 【分析】由题意利用等差数列的通项公式、求和公式可得,结合等差数列的性质,逐一判断即可得出结论. 【详解】∵等差数列的前项和为,, ∴,解得, 故,故A 正确;∵,,故有,故B 正确; 该数解析:ABD 【分析】由题意利用等差数列的通项公式、求和公式可得19a d =-,结合等差数列的性质,逐一判断即可得出结论. 【详解】∵等差数列{}n a 的前n 项和为n S ,1385a a S +=, ∴()111875282a a d a d ⨯++=+,解得19a d =-, 故10190a a d =+=,故A 正确;∵918a a d d d =+=-=,11110a a d d =+=,故有911a a =,故B 正确; 该数列的前n 项和()21119222n n n n S na d d d n -=+=-⋅ ,它的最值,还跟d 的值有关,故C 错误;由于61656392S a d d ⨯=+=-,131131213392S a d d ⨯=+=-,故613S S =,故D 正确, 故选:ABD. 【点睛】思路点睛:利用等差数列的通项公式以及前n 项和公式进行化简,直接根据性质判断结果.27.BCD 【分析】利用等差等比数列的定义及性质对选项判断得解. 【详解】选项A: ,得是等差数列,当时不是等比数列,故错; 选项B: ,,得是等差数列,故对; 选项C: ,,当时也成立,是等比数列解析:BCD 【分析】利用等差等比数列的定义及性质对选项判断得解. 【详解】选项A: 1*()n n a a n N +∈=,10n n a a +∴-=得{}n a 是等差数列,当0n a =时不是等比数列,故错; 选项B:2n S An Bn =+,12n n a a A -∴-=,得{}n a 是等差数列,故对;选项C: ()11nn S =--,112(1)(2)n n n n S S a n --∴-==⨯-≥,当1n =时也成立,12(1)n n a -∴=⨯-是等比数列,故对;选项D: {}n a 是等差数列,由等差数列性质得n S ,2n n S S -,*32()n n S S n N -∈是等差数列,故对; 故选:BCD 【点睛】熟练运用等差数列的定义、性质、前n 项和公式是解题关键.28.ACD 【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解 【详解】因为,,所以a1=3,an =[1+(n-1)d](n+2n).若d =1,则an =n(n+2n);若d =0,则a2=解析:ACD 【分析】利用等差数列的性质和通项公式,逐个选项进行判断即可求解 【详解】因为1112a =+,1(1)2n n a n d n =+-+,所以a 1=3,a n =[1+(n -1)d ](n +2n ).若d =1,则a n =n (n +2n );若d =0,则a 2=6.因为a 2=6+6d ,a 3=11+22d ,所以若a 1,a 2,a 3成等差数列,则a 1+a 3=a 2,即14+22d =12+12d ,解得15d =-. 故选ACD29.ABD 【分析】由可判断AB ,再由a1>0,d <0,可知等差数列数列先正后负,可判断CD. 【详解】根据等差数列定义可得,所以数列单调递减,A 正确; 由数列单调递减,可知数列有最大值a1,故B 正解析:ABD 【分析】由10n n a a d +-=<可判断AB ,再由a 1>0,d <0,可知等差数列数列{}n a 先正后负,可判断CD. 【详解】根据等差数列定义可得10n n a a d +-=<,所以数列{}n a 单调递减,A 正确; 由数列{}n a 单调递减,可知数列{}n a 有最大值a 1,故B 正确;由a 1>0,d <0,可知等差数列数列{}n a 先正后负,所以数列{}n S 先增再减,有最大值,C 不正确,D 正确. 故选:ABD.30.ABD 【分析】结合等差数列的性质、前项和公式,及题中的条件,可选出答案. 【详解】由,可得,故B 正确; 由,可得, 由,可得,所以,故等差数列是递减数列,即,故A 正确; 又,所以,故C 不正确解析:ABD 【分析】结合等差数列的性质、前n 项和公式,及题中的条件,可选出答案. 【详解】由67S S =,可得7670S S a -==,故B 正确;由56S S <,可得6560S S a -=>, 由78S S >,可得8780S S a -=<,所以876a a a <<,故等差数列{}n a 是递减数列,即0d <,故A 正确; 又()9567897820S S a a a a a a -=+++=+<,所以95S S <,故C 不正确; 又因为等差数列{}n a 是单调递减数列,且80a <,所以90a <, 所以()117179171702a a S a +==<,故D 正确.故选:ABD. 【点睛】关键点点睛:本题考查等差数列性质的应用,解题的关键是熟练掌握等差数列的增减性及前n 项和的性质,本题要从题中条件入手,结合公式()12n n n a S S n --≥=,及()12n n n a a S +=,对选项逐个分析,可判断选项是否正确.考查学生的运算求解能力与逻辑推理能力,属于中档题.31.AC 【分析】将变形为,构造函数,利用函数单调性可得,再结合等差数列与等比数列性质即可判断正确选项 【详解】 由,可得,令, ,所以是奇函数,且在上单调递减,所以, 所以当数列为等差数列时,;解析:AC 【分析】 将3201911111a a e e +≤++变形为32019111101212a a e e -+-≤++,构造函数()1112xf x e =-+,利用函数单调性可得320190a a +≥,再结合等差数列与等比数列性质即可判断正确选项 【详解】 由3201911111a a e e +≤++,可得32019111101212a a e e -+-≤++,令()1112x f x e =-+, ()()1111101111x x x x x e f x f x e e e e --+=+-=+-=++++,所以()1112xf x e =-+是奇函数,且在R 上单调递减,所以320190a a +≥, 所以当数列{}n a 为等差数列时,()320192*********a a S +=≥;当数列{}n a 为等比数列时,且3a ,1011a ,2019a 同号,所以3a ,1011a ,2019a 均大于零, 故()2021202110110T a =>.故选:AC 【点睛】本题考查等差数列与等比数列,考查逻辑推理能力,转化与化归的数学思想,属于中档题32.BCD 【分析】根据等差数列和等方差数列定义,结合特殊反例对选项逐一判断即可. 【详解】对于A ,若是等差数列,如,则不是常数,故不是等方差数列,故A 错误; 对于B ,数列中,是常数, 是等方差数解析:BCD 【分析】根据等差数列和等方差数列定义,结合特殊反例对选项逐一判断即可. 【详解】对于A ,若{}n a 是等差数列,如n a n =,则12222(1)21n n a a n n n --=--=-不是常数,故{}n a 不是等方差数列,故A 错误;对于B ,数列(){}1n-中,222121[(1)][(1)]0n n n n aa ---=---=是常数, {(1)}n ∴-是等方差数列,故B 正确;对于C ,数列{}n a 中的项列举出来是,1a ,2a ,,k a ,,2k a ,数列{}kn a 中的项列举出来是,k a ,2k a ,3k a ,,()()()()2222222212132221k k k k k k k k aa a a a a a a p +++++--=-=-==-=,将这k 个式子累加得()()()()2222222212132221k kk k k k k k aa a a a a a a kp +++++--+-+-++-=,222k k a a kp ∴-=,()221kn k n a a kp +∴-=,{}*(,kn a k N ∴∈k 为常数)是等方差数列,故C 正确; 对于D ,{}n a 是等差数列,1n n a a d -∴-=,则设n a dn m =+{}n a 是等方差数列,()()222112(2)n n n n dn m a a a a d a d d n m d d dn d m --∴-=++++=+=++是常数,故220d =,故0d =,所以(2)0m d d +=,2210n n a a --=是常数,故D 正确.故选:BCD. 【点睛】本题考查了数列的新定义问题和等差数列的定义,属于中档题.33.AD 【分析】运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由二次函数的配方法,结合n 为正整数,可判断C ;由解不等式可判断D . 【详解】等差数列的前n 项和为,公差,由,可解析:AD 【分析】运用等差数列的通项公式和求和公式,解方程可得首项和公差,可判断A ,B ;由二次函数的配方法,结合n 为正整数,可判断C ;由0n S <解不等式可判断D .【详解】等差数列{}n a 的前n 项和为n S ,公差0d ≠,由690S =,可得161590a d +=,即12530a d +=,①由7a 是3a 与9a 的等比中项,得2739a a a =,即()()()2111628a d a d a d +=++,化为1100a d +=,②由①②解得120a =,2d =-,则202(1)222n a n n =--=-,21(20222)212n S n n n n =+-=-,由22144124n S n ⎛⎫=--+ ⎪⎝⎭,可得10n =或11时,n S 取得最大值110; 由2102n S n n -<=,解得21n >,则n 的最小值为22.故选:AD 【点睛】本题考查等差数列的通项公式和求和公式,以及等比中项的性质,二次函数的最值求法,考查方程思想和运算能力,属于中档题.34.AC 【分析】由求出,再由可得公差为,从而可求得其通项公式和前项和公式 【详解】由题可知,,即,所以等差数列的公差,故选:AC. 【点睛】本题考查等差数列,考查运算求解能力.解析:AC 【分析】由535S =求出37a =,再由411a =可得公差为434d a a =-=,从而可求得其通项公式和前n 项和公式 【详解】由题可知,53535S a ==,即37a =,所以等差数列{}n a 的公差434d a a =-=, 所以()4445n a a n d n =+-=-,()2451232n n n S n n --==-.故选:AC. 【点睛】本题考查等差数列,考查运算求解能力.35.ACD 【分析】由得,故正确;当时,根据二次函数知识可知无最小值,故错误;根据等差数列的性质计算可知,故正确;根据等差数列前项和公式以及等差数列的性质可得,故正确. 【详解】因为,所以,所以,即解析:ACD 【分析】由13623a a S +=得100a =,故A 正确;当0d <时,根据二次函数知识可知n S 无最小值,故B 错误;根据等差数列的性质计算可知127S S =,故C 正确;根据等差数列前n 项和公式以及等差数列的性质可得190S =,故D 正确. 【详解】因为13623a a S +=,所以111236615a a d a d ++=+,所以190a d +=,即100a =,故A 正确;当0d <时,1(1)(1)922n n n n n S na d dn d --=+=-+2(19)2dn n =-无最小值,故B 错误;因为127891*********S S a a a a a a -=++++==,所以127S S =,故C 正确; 因为()1191910191902a a S a+⨯===,故D 正确.【点睛】本题考查了等差数列的通项公式、前n项和公式,考查了等差数列的性质,属于中档题.。
高一数学数列的概念试题答案及解析

高一数学数列的概念试题答案及解析1.已知数列{an }满足an= nk n(n∈N*,0 < k < 1),下面说法正确的是( )①当时,数列{an}为递减数列;②当时,数列{an}不一定有最大项;③当时,数列{an}为递减数列;④当为正整数时,数列{an}必有两项相等的最大项.A.①②B.②④C.③④D.②③【答案】C【解析】选项①:当时,,有,,则,即数列不是递减数列,故①错误;选项②:当时,,因为,所以数列可有最大项,故②错误;选项③:当时,,所以,即数列是递减数列,故③正确;选项④:,当为正整数时,;当时,;当时,令,解得,,数列必有两项相等的最大项,故④正确.所以正确的选项为③④.【考点】数列的函数特征.2.在数列中,,,则=()A.B.C.D.【答案】D【解析】由已知可得:由此可猜想数列是以3为周期的周期数列,所以,故选D.另此题也可:设,则有从而可知数列是以0为首项,为公差的等差数列,从而可求得进而求得的值.【考点】数列的概念.3.数列{}中,,则为___________.【答案】19【解析】由已知可得,所以,,。
【考点】数列的递推关系式。
4.数列的一个通项公式是()A.B.C.D.【答案】B【解析】.【考点】数列的通项公式.5.数列1,1,2,3,5,8,x,21,34,55中,x等于()A.11B.12C.13D.14【答案】C【解析】观察数列特点,从第三项起每一项等于它的前两项的和,因此【考点】数列点评:由数列前几项的特点归纳出通项,进而求得任意一项6.在数列{}中,若,则()A.1B.C.2D.1.5【答案】D【解析】根据题意,由于体现了数列的递推式的运用,故选D.【考点】数列的递推式点评:解决的关键是根据首项,结合递推式得到数列的其余的各项,同时能结合周期性得到结论,属于基础题。
7.已知数列的前项和,则 .【答案】=1,当n时,则=,综合上述可知【解析】解:因为,那么当n=1,得到a1结论为8.已知数列中,,若,则()A.B.C.D.【答案】C【解析】解:因为,说明是公差为4的等差数列,,选C9.数列的一个通项公式是A.B.C.D.【答案】D【解析】解:因为数列的前几项为摆动数列,因此一个通项公式是,也可以特殊值验证法得到,选D10.在2与32中间插入7个实数,使这9个实数成等比数列,该数列的第7项是 .【答案】16【解析】记此数列为{an},则设公比为q,则11.若数列的通项公式为,则()A.为递增数列B.为递减数列C.从某项后为递减数列D.从某项后为递增数列【答案】D【解析】解:∵an ="n!" /10n ,∴当n!<10n时,数列{an}为递减数列,当n!>10n时,数列{an}为递递数列,故选D12.已知数列、都是公差为1的等差数列,其首项分别为,且设,则数列的前10项和等于()A.55B.70C.85D.100【答案】C【解析】解:∵a1+b1=5,a1,b1∈N*,a1>b1,a1,b1∈N*(n∈N*),∴a1,b1有3和2,4和1两种可能,当a1,b1为4和1的时,ab1=4,前10项和为4+5+…+12+13=85;当a1,b1为3和2的时,ab1=4,前10项和为4+5+…+12+13=85;故数列{abn}的前10项和等于85,故选C.13.已知数列是首项为1,公比为的等比数列,则.【答案】【解析】解:因为数列是首项为1,公比为的等比数列14.定义一种新的运算“”对任意正整数n满足下列两个条件:(1)则____________【答案】 4023【解析】令是以1为首项,2为公差的等差数列,=402315.,则此数列的通项公式_____;【答案】【解析】解:因为,根据分母的与分子与项数的关系可知16.数列的通项公式为,则此数列的前项的和等于 ( ) A.B.C.D.【答案】B【解析】验证法:17.数列的前n项的和,则= ___ .【答案】【解析】解:因为,当n=1时,则当n2时,则验证当n=1不适合上式,因此得到=18.已知数列1,,,,…的一个通项公式是an=_________.【答案】【解析】分子为2n-1,分母为n2,所以通项公式为19.已知数列{an }的通项公式为an=23-4n,Sn是其前n项之和,则使数列的前n项和最大的正整数n的值为 .【答案】10.【解析】,所以,由得,所以数列的前n项和最大的正整数n的值为1020.在数列中,等于()A.B.C.D.【答案】C【解析】21.在数列中,,,则( )A.B.C.D.【答案】A【解析】解:因为数列中,,22.已知数列的前几项和为.那么这个数列的通项公式= .【答案】.【解析】,当时,,.23.在数列中,,求:⑴数列的最大项⑵数列的前n项和【答案】(1)当;(2)【解析】数列的单调性的运用,求解数列的最大项;运用错位相减法。
高中数学选择性必修二 4 1 数列的概念(精练)(含答案)

4.1 数列的概念1.(2020·宜宾市南溪区第二中学校高一月考)已知数列28n na n =+,则数列{}n a 的第4项为( ) A .110B .16C .14 D .13【答案】B【解析】依题意4244148246a ===+.故选:B. 2.(2020·浙江鄞州·宁波诺丁汉附中高一期中)已知数列的通项公式是()()31{22n n n a n n +=-是奇数是偶数,则23⋅a a 等于( ) A .70 B .28C .20D .8【答案】C【解析】因为()()31{22n n n a n n +=-是奇数是偶数,所以,所以23⋅a a =20.故选C.3.(2020·广西田阳高中高一月考)已知数列的一个通项公式为()11312n n n n a +-+=-,则5a = ( ) A .12B .12-C .932D .932-【答案】A 【解析】()11312n n n n a +-+=-,则()51551531122a +-+=-=.故选:A. 4.(2020·广西田阳高中高一月考)已知数列2,5,22,11…,则25是这个数列的( ) A .第六项 B .第七项C .第八项D .第九项【答案】B题组一 根据通项求项【解析】由数列前几项归纳可知通项公式为n a =,=时,7n =,为数列第七项,故选B.5.(2020·浙江鄞州·宁波咸祥中学高一期中)已知数列{}n a 的通项公式为22n a n n =+,则10(a = )A .100B .110C .120D .130【答案】C【解析】数列{}n a 的通项公式为22n a n n =+,则21010210120a =+⨯=.故选:C.6.(2020·四川高一期中)已知数列{}n a 的通项公式是1(2)2n a n n =+,则220是这个数列的( ) A .第19项 B .第20项 C .第21项D .第22项【答案】B【解析】由题意,令1(2)2202n n +=,则(2)440n n +=,解得20n =或22n =-; 因为*n N ∈,所以20n =,即220是这个数列的第20项.故选:B.7.(2020·四川省苍溪实验中学校高一期中)已知数列2,4,……,则8是该数列的第________项 【答案】118=,解得11n =,所以8是该数列的第11项,故答案为:11.8.(2020·上海高二课时练习)在数列{}n a 中,已知()*cos2n n a n N π=∈,则{}n a 的前6项分别为______. 【答案】0,1,0,1,0,1--【解析】易得1cos02a π==,2cos 1a π==-,33cos02a π==,4cos 21a π==,55cos 02a π==,66cos12a π==-.故答案为:0,1,0,1,0,1-- 9.(2020·上海高二课时练习)已知数列{}n a 的通项公式为1(2)n a n n =+,那么199是这数列的第_____项.【答案】9【解析】令11(2)99n n =+,即22990n n +-=,解得9n =或11-(舍去),则199是这数列的第9项,故答案为: 9. 10.(2020·上海高二课时练习)数列{}n a 中,1003n a n =-(*n N ∈),该数列从第_____项开始每项均为负值. 【答案】34【解析】令10030n a n =-<,解不等式得:1003n >,由于*n N ∈,故34n =.故答案为:34.1.(2020·江西高一月考)数列3579,,,24816--,…的一个通项公式为( ) A .()n n n n21a 12+=-⋅ B .()nn n 2n 1a 12+=-⋅C .()n n 1n n 21a 12++=-⋅ D .()n 1n n2n 1a 12++=-⋅【答案】D【解析】根据分子、分母还有正负号的变化,可知,()12112n n nn a ++=-⋅.故选D. 题组二 根据项写通项2.(2020·四川双流·艺体中学)数列2,43,85,167,329…的一个通项公式a n 等于( ) A .221nn -B .2n nC .221nn -D .221nn +【答案】C【解析】数列2,43,85,167,329… 可写成:12211⨯-,22221⨯-,32231⨯-,42241⨯-,52251⨯-… 所以通项公式a n 2=21nn -.故选C. 3.(2020·上海市杨浦高级中学)已知数列1、0、1、0、,可猜想此数列的通项公式是( ).A .()()1*11n n a n N -⎡⎤=+-∈⎣⎦B .()()*1112nn a n N ⎡⎤=+-∈⎣⎦C .()()()()1*111122n n a n n n N +⎡⎤=+-+--∈⎣⎦ D .()()*11cos 2n a n n N π=-∈【答案】D【解析】对于A 选项,()011121a =+-=≠,不合乎题意; 对于B 选项,()1111012a =⨯-=≠,不合乎题意; 对于C 选项,()4311121312a ⎡⎤=⨯+-+⨯=≠⎣⎦,不合乎题意;对于D 选项,当n 为奇数时,cos 1n π=-,此时()11112n a =⨯+=, 当n 为偶数时,cos 1n π=,此时()11102n a =⨯-=,合乎题意. 故选:D.4.(2018·吉林宽城·长春市养正高中高一期中)根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式n a =__________.【答案】54n -【解析】第一图点数是1;第二图点数6=1+5 ;第三图是11=1+25 ;第四图是16=1+35 则第n 个图点数=1+(n-1)554n a n 故答案为:54n -5.(2019·山东东营·)已知数列{}n a 的前4项依次为23,45-,67,89-,试写出数列{}n a 的一个通项公式n a =______.【答案】12(1)21n nn +-+ 【解析】2,4,6,8,的通项公式为2n ,3,5,7,9,的通项公式为21n , 正负交替的通项公式为1(1)n +-,所以数列{}n a 的通项公式12(1)21n n n a n +=-+.故答案为:12(1)21n n n +-+ 6.(2020·全国高一课时练习)写出下列各数列的一个通项公式,使它的前几项分别是下列各数: (1)5784,,2,,,245--⋯(2)246810,,,,,315356399(3)5,55,555,5555,(4)2,0,2,0,2,0,【答案】(1)()131n n n a n ++=-;(2)()2221n n a n =-;(3)()51019n na =-;(4)()111n n a -=+- 【解析】解(1)考虑到第2,4项的分母恰好是所在项的序号, 于是这个数列的前4项可以改写成4567,,,1234--, 这4项的分母都与项的序号相同,分子都恰好是序号加3,且奇数项为正,偶数项为负, 所以它的一个通项公式为()131n n n a n++=-. (2)考虑到分子2,4,6,8,10恰好是序号的2倍,所以分子应为2n .分母22222321,1541,3561,6381,99101=-=-=-=-=-都为分子的平方数减去1,因此它的一个通项公式为()2221n na n =-.(3)这个数列的第n 项可以是n 个5组成的n 位数555n n a ↑=,用代数式替代省略号,可考虑前4项改写成55559,99,999,99999999⨯⨯⨯⨯,其中9999999999,,,又可表示成1234101,101,101,101----, 这里的10的正整数次幂的指数恰好与数列中项的序号相等, 所以它的一个通项公式为()51019n n a =-. (4)211,011=+=-,考虑到其每一项与序号的关系将前几项分别写成:()()()()012311,11,11,11+-+-+-+-, 因此它的一个通项公式为()111n n a -=+-.1.(2020·眉山市东坡区多悦高级中学校高一期中)在数列{}n a 中,已知11a =,25a =,()*21n n n a a a n N ++=-∈,则5a 等于( )A .4-B .5-C .4D .5【答案】B【解析】由()*21n n n a a a n N++=-∈知:3214a a a 4321a a a 5435a a a故选:B2.(2020·自贡市第十四中学校高一期中)数列3,7,11,15,的一个通项公式是( )A .41n a n =+B .21n a n =+C .41n a n =-D .21n a n =-【答案】C【解析】因为数列3,7,11,15⋯的一个通项公式为41n -,故数列3,7,11,15,⋯的一个通项公式是41n a n =-,故选:C . 3.(2019·河北廊坊·高一期末)数列{}n a 的前几项为11121,3,,8,222,则此数列的通项可能是( )A .542n n a -=B .322n n a -=C .652n n a -=D .1092n n a -=【答案】A题组三 根据递推公式求项【解析】数列为16111621,,,,22222其分母为2,分子是首项为1,公差为5的等比数列,故通项公式为542n n a -=. 4.(2020·安徽黄山·高一期末)数列1111,,,,...24816--的一个通项公式是( ) A .1(1)2+-n nB .(1)2-n nC .sin 2nn πD .cos(1)2nn π+【答案】B 【解析】()111122-=-⨯,()2211142=-⨯,()3311182-=-⨯,()44111162=-⨯ 所以其通项公式是:(1)2-nn 故选:B5.(2020·武汉外国语学校高一月考)数列4,6,10,18,34,……的通项公式n a 等于( ) A .12n + B .21n + C .22n + D .22n +【答案】C【解析】234521134522,22,22,22,22a a a a a =+=+=+=+=+22n n a ∴=+故选:C6.(2020·浙江越城·绍兴一中期中)在数列{}n a 中,()1111,1(2)nnn a a n a --==+≥,则5a 等于A .32B .53C .85D .23【答案】D【解析】已知1a 逐一求解2345122323a a a a ====,,,.故选D7.(2020·吉林前郭尔罗斯县第五中学高一期中)数列12-,2,92-,8,252-,…它的一个通项公式可以是( )A .()212nn n a =-B .()2112n n n a +=- C .22n n a =D .1n n a n =-+ 【答案】A【解析】将1n =代入四个选项可得A 为12-,B 为12,C 为12,D 为12-.所以排除B 、C 选项. 将2n =代入A 、D,得A 为2,D 为23-,所以排除D 综上可知,A 可以是一个通项公式故选:A 8.(2019·息县第一高级中学高二月考(文))数列1-,3,7-,15,…的一个通项公式可以是( ) A .()(1)21nnn a =-⋅- B .(1)(21)nn a n =-⋅- C .()1(1)21n n n a +=-⋅-D .1(1)(21)n n a n +=-⋅-【答案】A【解析】将1n =代入四个选项,可知C 中11,a =D 中11,a =所以排除C 、D.当3n =,代入B 可得35,a =-所以排除B ,即A 正确,故选:A.9.(2018·安徽六安一中高一期末(文))已知*n N ∈,给出4个表达式:①0,1,n n a n ⎧=⎨⎩为奇数为偶数,②1(1)2n n a +-=,③1cos 2n n a π+=,④sin 2n n a π=.其中能作为数列:0,1,0,1,0,1,0,1,…的通项公式的是( ) A .①②③ B .①②④C .②③④D .①③④【答案】A【解析】①②③逐一写出为010101,,,,,可以,④逐一写出为1010101,,,,,,不满足,故选A .10.(2020·湖北十堰·高一期末)数列1111,,,57911--,…的通项公式可能是n a =( ) A .1(1)23n n --+B .(1)32nn -+C .1(1)32n n --+D .(1)23nn -+【答案】D【解析】由115a =-,排除A ,C ,由217a =,排除B.故选:D.11.(2020·金华市曙光学校高一开学考试)数列1-,3,5-,7,9-,,的一个通项公式为( )A .21n a n =-B .(1)(12)nn a n =-- C .(1)(21)nn a n =--D .1(1)(21)n n a n +=--【答案】C【解析】∵数列{a n }各项值为1-,3,5-,7,9-,,∴各项绝对值构成一个以1为首项,以2为公差的等差数列,∴|a n |=2n ﹣1 又∵数列的奇数项为负,偶数项为正,∴a n =(﹣1)n (2n ﹣1).故选C .1.(2019·云南东川明月中学高一期中)数列{}n a 的前n 项和21n S n n =++,则{}n a 的通项公式n a = _____.【答案】()()3122n nn ⎧=⎪⎨≥⎪⎩ 【解析】当1n =时,113a S ==;题组四 公式法求通项当2n ≥时,()()()22111112n n n a S S n n n n n -⎡⎤=-=++--+-+=⎣⎦; ∴()()3122n n a n n ⎧=⎪=⎨≥⎪⎩故答案为()()3122n n n ⎧=⎪⎨≥⎪⎩2.(2019·湖南岳阳)已知数列{}n a ,若1222n a a na n +++=,则数列{}1n n a a +的前n 项和为__________. 【答案】41n n + 【解析】因为122++2n a a na n +⋯=所以1212++12n 1n a a n a ()()-+⋯-=- 两式相减得2n na =所以2n a n=设数列{}1n n a a +的前n 项和为S n 则1223342111n n n n n n n S a a a a a a a a a a a a ---+=+++⋅⋅⋅++2222222222221223342111n n n n n n =⨯+⨯+⨯+⋅⋅⋅⨯+⨯+⨯---+ 1111111111141223342111n n n n n n ⎛⎫=-+-+-+⋅⋅⋅-+-+- ⎪---+⎝⎭ 144111n n n ⎛⎫=-= ⎪++⎝⎭3.(2020·上海市金山中学期中)已知数列{}n a 的前n 项和2231n S n n =-+,则n a =__________.【答案】0,145,2n n a n n =⎧=⎨-≥⎩【解析】当1n =时,110a S ==当2n ≥时,由2231n S n n =-+,得212(1)3(1)1n S n n -=---+,两式相减,145n n n a S S n -=-=-,将1n =代入上式,110a =-≠,∴通项公式为0,145,2n n a n n =⎧=⎨-≥⎩故答案为0,145,2n n a n n =⎧=⎨-≥⎩. 4.(2019·黑龙江哈尔滨市第六中学校期中)已知数列{}n a 前n 项和为n S ,且2n S n =,则n a =_______【答案】21n -.【解析】当1n =时,111a S ==当2n ≥且*n N ∈时,()221121n n n a S S n n n -=-=--=-综上所述:21n a n =-,*n N ∈本题正确结果:21n -5.(2020·河北石家庄·辛集中学)在数列{}n a 中,已知其前n 项和为23n n S =+,则n a =__________. 【答案】15,12,2n n n a n -=⎧=⎨≥⎩【解析】当2n ≥时,111(23)(23)2n n n n n n a S S ---=-=+-+=;当1n =时,11235a S ==+=,不满足上式。
高中数学试题含答案-课时规范练28 数列的概念

课时规范练28数列的概念基础巩固组1.已知数列√5,√11,√17,√23,√29,…,则5√5是它的()A.第19项B.第20项C.第21项D.第22项2.记S n为数列{a n}的前n项和.“任意正整数n,均有a n>0”是“数列{S n}是递增数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.(多选)已知数列{a n}满足a n+1=1-1a n(n∈N*),且a1=2,则()A.a3=-1B.a2 019=12C.S6=3D.2S2 019=2 0194.(2020河北保定高三期末)在数列{a n}中,若a1=1,a2=3,a n+2=a n+1-a n(n∈N*),则该数列的前100项之和是() A.18 B.8 C.5 D.25.(多选)已知数列{a n}:12,13+23,14+24+34,…,110+210+310+…+910,…,若b n=1a n·a n+1,设数列{b n}的前n项和为S n,则()A.a n=n2B.a n=nC.S n=4nn+1D.S n=5nn+16.(2020湖南益阳高三期末)已知{a n}是等差数列,且满足:对∀n∈N*,a n+a n+1=2n,则数列{a n}的通项公式a n=() A.n B.n-1C.n-12D.n+127.已知数列{a n}的首项a1=21,且满足(2n-5)a n+1=(2n-3)a n+4n2-16n+15,则数列{a n}的最小的一项是()A.a5B.a6C.a7D.a88.已知每项均大于零的数列{a n},首项a1=1且前n项和S n满足S n√S n-1-S n-1√S n=2√S n S n-1(n∈N*且n≥2),则a81=()A.638B.639C.640D.6419.设S n为数列{a n}的前n项和,且a1=4,a n+1=S n,n∈N*,则S4=.10.在数列{a n}中,a1=2,a n+1n+1=a nn+ln1+1n,则a n=.11.已知数列{a n}的通项公式为a n=n+13n-16(n∈N*),则数列{a n}的最小项是第项.12.已知数列{a n}满足a1=3,a n+1=4a n+3.(1)写出该数列的前4项,并归纳出数列{a n}的通项公式;公众号:一枚试卷君(2)证明:a n+1+1a n+1=4.综合提升组13.(2020广东中山期末)设数列{a n}的前n项和为S n,且a1=1,{S n+na n}为常数列,则a n=()A.13n-1B.2 n(n+1)C.1(n+1)(n+2)D.5-2n314.(2020安徽江淮十校第三次联考)已知数列{a n}满足a n+1-a nn =2,a1=20,则a nn的最小值为()A.4√5B.4√5-1C.8D.915.(多选)(2020江西赣州教育发展联盟2月联考)已知数列{a n}的前n项和为S n(S n≠0),且满足a n+4S n-1S n=0(n≥2),a1=14,则下列说法正确的是()A.数列{a n}的前n项和为S n=14nB.数列{a n}的通项公式为a n=14n(n+1)C.数列{a n}为递增数列D.数列1S n为递增数列创新应用组16.已知数列{a n}的前n项和为S n,a1=a,a n+1=S n+3n,若a n+1≥a n对∀n∈N*成立,则实数a的取值范围是.17.已知二次函数f(x)=x2-ax+a(a>0,x∈R)有且只有一个零点,数列{a n}的前n项和S n=f(n)(n∈N*).(1)求数列{a n}的通项公式;(2)设c n=1-4a n (n∈N*),定义所有满足c m·c m+1<0的正整数m的个数,称为这个数列{c n}的变号数,求数列{c n}的变号数.参考答案课时规范练28 数列的概念1.C 数列√5,√11,√17,√23,√29,…,中的各项可变形为√5,√5+6,√5+2×6,√5+3×6,√5+4×6,…,所以通项公式为a n =√5+6(n -1)=√6n -1,令√6n -1=5√5,得n=21.2.A ∵a n >0,∴数列{S n }是递增数列,∴“a n >0”是“数列{S n }是递增数列”的充分条件.如数列{a n }为-1,1,3,5,7,9,…,显然数列{S n }是递增数列,但是a n 不一定大于零,还有可能小于零, ∴数列{S n }是递增数列不能推出a n >0.∴“a n >0”是“数列{S n }是递增数列”的不必要条件. ∴“任意正整数n ,均有a n >0”是“数列{S n }是递增数列”的充分不必要条件.3.ACD 数列{a n }满足a 1=2,a n +1=1-1a n(n ∈N *),可得a 2=12,a 3=-1,a 4=2,a 5=12,…,所以a n+3=a n ,数列的周期为3,a 2 019=a 672×3+3=a 3=-1,S 6=3,S 2 019=2 0192. 4.C ∵a 1=1,a 2=3,a n +2=a n +1-a n (n ∈N *),∴a 3=3-1=2, a 4=2-3=-1, a 5=-1-2=-3, a 6=-3+1=-2, a 7=-2+3=1, a 8=1+2=3, a 9=3-1=2, …∴{a n }是周期为6的周期数列,∴S 100=S 16×6+4=16×(1+3+2-1-3-2)+(1+3+2-1)=5.故选C. 5.AC 由题意得a n =1n+1+2n+1+…+nn+1=1+2+3+…+nn+1=n2,∴b n =1n 2·n+12=4n (n+1)=41n −1n+1,∴数列{b n }的前n 项和S n =b 1+b 2+b 3+…+b n =41-12+12−13+13−14+…+1n −1n+1=41-1n+1=4nn+1.故选AC.6.C 由a n +a n+1=2n ,得a n+1+a n+2=2n+2,两式相减得a n+2-a n =2=2d ,∴d=1,又a n +a n +d=2n ,∴a n =n-12.故选C .7.A ∵4n 2-16n+15=(2n-3)(2n-5),∴(2n-5)a n+1=(2n-3)a n +(2n-3)(2n-5), 等式两边同时除以(2n-3)(2n-5),可得a n+12n -3=a n2n -5+1, 可设b n =a n 2n -5,则b n+1=an+12n -3, ∴b n+1=b n +1,即b n+1-b n =1.∵b 1=a 12×1-5=21-3=-7, ∴数列{b n }是以-7为首项,1为公差的等差数列. ∴b n =-7+(n-1)×1=n-8,n ∈N *.∴a n =(n-8)(2n-5)=2n 2-21n+40.可把a n 看成关于n 的二次函数,则根据二次函数的性质,可知其对称轴n=10.52=5.25. ∴当n=5时,a n 取得最小值.故选A .8.C 已知S n √S n -1-S n-1√S n =2√S n S n -1,数列{a n }的每项均大于零,故等号两边同时除以√S n S n -1,可得√S n −√S n -1=2,∴{√S n }是以1为首项,2为公差的等差数列,故√S n =2n-1,S n =(2n-1)2,∴a 81=S 81-S 80=1612-1592=640.故选C .9.32 因为S n 为数列{a n }的前n 项和,且a 1=4,a n+1=S n ,n ∈N *, ① 则当n ≥2时,a n =S n-1, ②由①-②得a n+1-a n =a n ,∴an+1a n=2,则数列{a n }是从第二项起,公比为2的等比数列,又a 2=S 1=4,∴a n =4·2n-2=2n (n ≥2),故a n ={4(n =1),2n (n ≥2).所以S 4=a 5=25=32.10.2n+n ln n 由题意得a n+1n+1−a n n =ln(n+1)-ln n ,a n n −an -1n -1=ln n-ln(n-1)(n ≥2). ∴a 22−a 11=ln 2-ln 1,a 33−a22=ln 3-ln 2,…,a n n−an -1n -1=ln n-ln(n-1)(n ≥2). 累加得a n n −a 11=ln n ,又a 1=2,∴a nn =2+ln n (n ≥2),当n=1时,a 1=2,上式成立,故a n =2n+n ln n. 11.5 a n =n+13n -16=131+193n -16.当n>5时,a n >0,且单调递减, 当n ≤5时,a n <0,且单调递减. ∴当n=5时,a n 最小.12.(1)解 a 1=3,a 2=15,a 3=63,a 4=255.因为a 1=41-1,a 2=42-1,a 3=43-1,a 4=44-1,…, 所以归纳得a n =4n -1. (2)证明 因为a n +1=4a n +3,所以a n+1+1a n +1=4a n +3+1a n +1=4(a n +1)a n +1=4. 13.B ∵数列{a n }的前n 项和为S n ,且a 1=1,∴S 1+1×a 1=1+1=2.∵{S n +na n }为常数列,∴S n +na n =2.当n ≥2时,S n-1+(n-1)a n-1=2,∴(n+1)a n =(n-1)a n-1,从而a 2a 1·a 3a 2·a 4a 3·…·a n a n -1=13·24·35·…·n -1n+1,∴a n =2n (n+1)(n ≥2),当n=1时上式成立,∴a n =2n (n+1).故选B . 14.C 由a n +1-a n =2n ,知a 2-a 1=2×1,a 3-a 2=2×2,…,a n -a n -1=2(n-1),n ≥2.以上各式相加得a n -a 1=n 2-n ,n ≥2,所以a n =n 2-n+20,n ≥2, 当n=1时,a 1=20符合上式,所以a n n =n+20n-1,n ∈N *, 所以当n ≤4时,a n n单调递减,当n ≥5时,a n n单调递增.因为a 44=a55=8,所以ann 的最小值为8.故选C .15.AD 由题意,可知数列{a n }的前n 项和为S n (S n ≠0),且满足a n +4S n-1S n =0(n ≥2),则S n -S n-1=-4S n-1S n (n ≥2),即1S n−1S n -1=4(n ≥2).又因为a 1=14,所以1S 1=4,所以数列1S n是以4为首项,4为公差的等差数列,所以数列1S n为递增数列,且1S n=4+(n-1)×4=4n ,则S n =14n .又因为当n ≥2时,a n =S n -S n-1=14n −14(n -1)=-14n (n -1),a 1=14,所以数列{a n }的通项公式为a n ={14,n =1,-14n (n -1),n ≥2.故选AD. 16.[-9,+∞) 据题意,得a n+1=S n+1-S n =S n +3n ,∴S n+1=2S n +3n ,∴S n+1-3n+1=2(S n -3n ).又S 1-31=a-3,∴数列{S n -3n }是以a-3为首项,2为公比的等比数列,∴S n -3n =(a-3)·2n-1即S n =3n +(a-3)·2n-1.当n=1时,a 1=a ;当n ≥2时,a n =S n -S n-1=3n +(a-3)×2n-1-3n-1-(a-3)×2n-2=2×3n-1+(a-3)×2n-2,∴a n+1-a n =4×3n-1+(a-3)×2n-2.又当n ≥2时,a n+1≥a n 恒成立,∴a ≥3-12×(32)n -2对∀n ∈N *,且n ≥2成立,∴a ≥-9.又a 2=a 1+3,∴a 2≥a 1成立.综上,所求实数a 的取值范围是[-9,+∞).17.解 (1)依题意,得Δ=a 2-4a=0,所以a=0或a=4.又由a>0得a=4,所以f (x )=x 2-4x+4. 所以S n =n 2-4n+4. 当n=1时,a 1=S 1=1-4+4=1; 当n ≥2时,a n =S n -S n -1=2n-5.所以数列{a n }的通项公式为a n ={1,n =1,2n -5,n ≥2.(2)由题意得c n ={-3,n =1,1-42n -5,n ≥2.由c n =1-42n -5可知,当n ≥5时,恒有c n >0. 又因为c 1=-3,c 2=5,c 3=-3, c 4=-13,c 5=15,即c 1·c 2<0,c 2·c 3<0,c 4·c 5<0, 所以数列{c n }的变号数为3.。
高考数学---数列的概念与简单表示法课后作业练习(含答案解析)

高考数学---数列的概念与简单表示法课后作业练习(含答案解析)建议用时:45分钟一、选择题1.数列0,1,0,-1,0,1,0,-1,…的一个通项公式a n等于()A.(-1)n+12B.cosnπ2C.cos n+12πD.cosn+22πD[令n=1,2,3,…,逐一验证四个选项,易得D正确.]2.若S n为数列{a n}的前n项和,且S n=nn+1,则1a5等于()A.56 B.65C.130D.30D[当n≥2时,a n=S n-S n-1=nn+1-n-1n=1n(n+1),所以1a5=5×6=30.]3.记S n为数列{a n}的前n项和.“任意正整数n,均有a n>0”是“{S n}是递增数列”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件A[∵“a n>0”⇒“数列{S n}是递增数列”,∴“a n>0”是“数列{S n}是递增数列”的充分条件.如数列{a n}为-1,1,3,5,7,9,…,显然数列{S n}是递增数列,但是a n 不一定大于零,还有可能小于零,∴“数列{S n}是递增数列”不能推出“a n>0”,∴“a n>0”是“数列{S n}是递增数列”的不必要条件.∴“a n>0”是“数列{S n}是递增数列”的充分不必要条件.] 4.(2019·武汉5月模拟)数列{a n}中,a n+1=2a n+1,a1=1,则a6=() A.32 B.62C.63 D.64C[数列{a n}中,a n+1=2a n+1,故a n+1+1=2(a n+1),因为a1=1,故a1+1=2≠0,故a n+1≠0,所以a n+1+1a n+1=2,所以{a n+1}为等比数列,首项为2,公比为2.所以a n+1=2n即a n=2n-1,故a6=63,故选C.]5.若数列{a n}的前n项和S n=n2-10n(n∈N*),则数列{na n}中数值最小的项是()A.第2项B.第3项C.第4项D.第5项B[∵S n=n2-10n,∴当n≥2时,a n=S n-S n-1=2n-11;当n=1时,a1=S1=-9也适合上式.∴a n=2n-11(n∈N+).记f(n)=na n=n(2n-11)=2n2-11n,此函数图像的对称轴为直线n=114,但n∈N+,∴当n=3时,f(n)取最小值.∴数列{na n}中数值最小的项是第3项.]二、填空题6.已知数列5,11,17,23,29,…,则55是它的第________项.21[数列5,11,17,23,29,…中的各项可变形为5,5+6,5+2×6,5+3×6,5+4×6,…,所以通项公式为a n=5+6(n-1)=6n-1,令6n-1=55,得n=21.]7.若数列{a n}满足a1=1,a2=3,a n+1=(2n-λ)a n(n=1,2,…),则a3等于________.15[令n=1,则3=2-λ,即λ=-1,由a n+1=(2n+1)a n,得a3=5a2=5×3=15.]8.在一个数列中,如果∀n∈N*,都有a n a n+1a n+2=k(k为常数),那么这个数列叫做等积数列,k叫做这个数列的公积.已知数列{a n}是等积数列,且a1=1,a2=2,公积为8,则a1+a2+a3+…+a12=________.28[∵a1a2a3=8,且a1=1,a2=2.∴a3=4,同理可求a4=1,a5=2.a6=4,∴{a n}是以3为周期的数列,∴a1+a2+a3+…+a12=(1+2+4)×4=28.]三、解答题9.(2019·洛阳模拟)已知数列{a n}满足a1=50,a n+1=a n+2n(n∈N*),(1)求{a n}的通项公式;(2)已知数列{b n}的前n项和为a n,若b m=50,求正整数m的值.[解](1)当n≥2时,a n=(a n-a n-1)+(a n-1-a n-2)+…+(a3-a2)+(a2-a1)+a1=2(n-1)+2(n-2)+…+2×2+2×1+50=2×(n-1)n2+50=n 2-n +50.又a 1=50=12-1+50,∴{a n }的通项公式为a n =n 2-n +50,n ∈N *. (2)b 1=a 1=50, 当n ≥2时,b n =a n -a n -1=n 2-n +50-[(n -1)2-(n -1)+50]=2n -2, 即b n =⎩⎪⎨⎪⎧50,n =12n -2,n ≥2.当m ≥2时,令b m =50,得2m -2=50,解得m =26. 又b 1=50,∴正整数m 的值为1或26.10.设数列{a n }的前n 项和为S n .已知a 1=a (a ≠3),a n +1=S n +3n ,n ∈N *,设b n =S n -3n ,(1)求数列{b n }的通项公式;(2)若a n +1≥a n ,n ∈N *,求a 的取值范围. [解] (1)依题意,S n +1-S n =a n +1=S n +3n , 即S n +1=2S n +3n ,由此得S n +1-3n +1=2(S n -3n ), 即b n +1=2b n , 又b 1=S 1-3=a -3,所以数列{b n }的通项公式为b n =(a -3)2n -1,n ∈N *. (2)由(1)知S n =3n +(a -3)2n -1,n ∈N *,于是,当n ≥2时,a n =S n -S n -1=3n +(a -3)2n -1-3n -1-(a -3)2n -2=2×3n-1+(a -3)2n -2,a n +1-a n =4×3n -1+(a -3)2n -2 =2n -2⎣⎢⎡⎦⎥⎤12×⎝ ⎛⎭⎪⎫32n -2+a -3,当n ≥2时,a n +1≥a n ⇒12×⎝ ⎛⎭⎪⎫32n -2+a -3≥0⇒a ≥-9,又a 2=a 1+3>a 1(a ≠3).综上,a 的取值范围是[-9,3)∪(3,+∞).1.已知数列{a n }满足:a 1=1,a n +1=a n a n +2(n ∈N *),若b n +1=(n -λ)⎝ ⎛⎭⎪⎫1a n +1,b 1=-λ,且数列{b n }是递增数列,则实数λ的取值范围是( )A .(2,+∞)B .(3,+∞)C .(-∞,2)D .(-∞,3)C [由a n +1=a n a n +2,知1a n +1=2a n +1,即1a n +1+1=2⎝ ⎛⎭⎪⎫1a n +1,所以数列⎩⎨⎧⎭⎬⎫1a n +1是首项为1a 1+1=2,公比为2的等比数列,所以1a n +1=2n ,所以b n +1=(n -λ)·2n ,因为数列{b n }是递增数列,所以b n +1-b n =(n -λ)2n -(n -1-λ)2n -1=(n +1-λ)2n-1>0对一切正整数n 恒成立,所以λ<n +1,因为n ∈N *,所以λ<2,故选C.]2.(2019·临沂三模)意大利数学家列昂那多·斐波那契以兔子繁殖为例,引入“兔子数列”: 1,1,2,3,5,8,13,21,34,55,…即F (1)=F (2)=1,F (n )=F (n -1)+F (n -2)(n ≥3,n ∈N *),此数列在现代物理“准晶体结构”、化学等都有着广泛的应用.若此数列被2整除后的余数构成一个新数列{a n },则数列{a n }的前2 019项的和为( )A .672B .673C .1 346D .2 019C [由数列1,1,2,3,5,8,13,21,34,55,…各项除以2的余数,可得{a n }为1,1,0,1,1,0,1,1,0,1,1,0,…,所以{a n }是周期为3的周期数列,一个周期中三项和为1+1+0=2, 因为2 019=673×3,所以数列{a n }的前2 019项的和为673×2=1 346,故选C.]3.(2019·晋城三模)记数列{a n }的前n 项和为S n ,若S n =3a n +2n -3,则数列{a n }的通项公式为a n =________.a n =2-⎝ ⎛⎭⎪⎫32n[当n =1时,S 1=a 1=3a 1-1,解得a 1=12;当n ≥2时,S n =3a n +2n -3,S n -1=3a n -1+2n -5,两式相减可得,a n =3a n -3a n -1+2,故a n =32a n -1-1,设a n +λ=32(a n -1+λ),故λ=-2,即a n -2=32(a n -1-2),故a n -2a n -1-2=32.故数列{a n -2}是以-32为首项,32为公比的等比数列,故a n -2=-32·⎝ ⎛⎭⎪⎫32n -1,故a n =2-⎝ ⎛⎭⎪⎫32n .] 4.已知数列{a n }中,a 1=1,其前n 项和为S n ,且满足2S n =(n +1)a n (n ∈N *). (1)求数列{a n }的通项公式;(2)记b n =3n -λa 2n ,若数列{b n }为递增数列,求λ的取值范围. [解] (1)∵2S n =(n +1)a n , ∴2S n +1=(n +2)a n +1,∴2a n +1=(n +2)a n +1-(n +1)a n , 即na n +1=(n +1)a n ,∴a n +1n +1=a nn ,∴a n n =a n -1n -1=…=a 11=1,∴a n =n (n ∈N +). (2)由(1)知b n =3n -λn 2.b n +1-b n =3n +1-λ(n +1)2-(3n -λn 2) =2·3n -λ(2n +1). ∵数列{b n }为递增数列, ∴2·3n -λ(2n +1)>0, 即λ<2·3n2n +1.令c n =2·3n2n +1,即c n +1c n =2·3n +12n +3·2n +12·3n =6n +32n +3>1. ∴{c n }为递增数列, ∴λ<c 1=2,即λ的取值范围为(-∞,2).1.(2019·烟台、菏泽高考适应性练习一)已知数列:1k ,2k -1,…,k 1(k ∈N *),按照k 从小到大的顺序排列在一起,构成一个新的数列{a n }:1,12,21,13,22,31,…,则89首次出现时为数列{a n }的( )A .第44项B .第76项C .第128项D .第144项C [观察分子分母的和出现的规律:2,3,4,5,…,把数列重新分组:⎝ ⎛⎭⎪⎫11,⎝ ⎛⎭⎪⎫12,21,⎝ ⎛⎭⎪⎫13,22,31,…,⎝ ⎛⎭⎪⎫1k ,2k -1,…,k 1,可看出89第一次出现在第16组,因为1+2+3+…+15=120,所以前15组一共有120项;第16组的项为⎝ ⎛⎭⎪⎫116,215,…,710,89…,所以89是这一组中的第8项,故89第一次出现在数列的第128项,故选C.]2.已知二次函数f (x )=x 2-ax +a (a >0,x ∈R )有且只有一个零点,数列{a n }的前n 项和S n =f (n )(n ∈N *).(1)求数列{a n }的通项公式;(2)设c n =1-4a n(n ∈N *),定义所有满足c m ·c m +1<0的正整数m 的个数,称为这个数列{c n }的变号数,求数列{c n }的变号数.[解] (1)依题意,Δ=a 2-4a =0, 所以a =0或a =4. 又由a >0得a =4, 所以f (x )=x 2-4x +4. 所以S n =n 2-4n +4.当n =1时,a 1=S 1=1-4+4=1; 当n ≥2时,a n =S n -S n -1=2n -5. 所以a n =⎩⎪⎨⎪⎧1,n =1,2n -5,n ≥2.(2)由题意得c n =⎩⎪⎨⎪⎧-3,n =1,1-42n -5,n ≥2. 由c n =1-42n -5可知,当n ≥5时,恒有c n >0.又c 1=-3,c 2=5,c 3=-3,c 4=-13,c 5=15,c 6=37, 即c 1·c 2<0,c 2·c 3<0,c 4·c 5<0,所以数列{c n}的变号数为3.。
【精品含答案】高考一轮复习3.1数列的概念基础训练题(理科)

2009届高考一轮复习3.1数列的概念基础训练题(理科)注意:本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分,考试时间45分钟。
第Ⅰ卷(选择题部分 共36分)一、选择题(本大题共6小题,每小题6分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1. 设11n 10n a 2n ++-=,则数列{}n a 从首项到第几项的和最大( ) (A )10 (B )11 (C )10或11 (D )122. 若数列{}n a 的前n 项和公式为)1n (log S 3n +=,则5a 等于( ) (A )6log 5(B )56log 3(C )35log 6(D )5log 33.(2008·衡水模拟)已知数列{}n a 中,*)N n (2n 3n 1a a ,21a 2n 1n 1∈+++==+,则数列{}n a 的通项公式为( )(A )1n 1a n +=(B )1n na n += (C )2n n 1n 21a 2n ++-+= (D )2n 1n a n ++=4. 下面有四个命题:①如果已知一个数列的递推公式及其首项,那么可以写出这个数列的任何一项;②数列 ,65,54,43,32通项公式是1n na n +=;③数列的图象是一群孤立的点;④数列 ,1,1,1,1--与数列 ,1,1,1,1--是同一数列。
其中正确命题的个数是( ) (A )1 (B )2(C )3(D )45.(2007·广东高考)已知数列{}n a 的前n 项和n 9n S 2n -=,第k 项满足8a 5k <<,则k = ( )(A )9(B )8(C )7(D )66. 数列{}n a 中,若1a ,1a 2a a 1n n1n =+=+,则6a 等于( )(A )13 (B )131(C )11(D )111第Ⅱ卷(非选择题部分共64分)二、填空题(本大题共3小题,每小题6分,共18分。
高考数学经典例题集锦:数列(含答案)

数列题目精选精编【典型例题】(一)研究等差等比数列的有关性质 1. 研究通项的性质例题1. 已知数列}{n a 满足1111,3(2)n n n a a a n --==+≥. (1)求32,a a ;(2)证明:312n n a -=. 解:(1)21231,314,3413a a a =∴=+==+=.(2)证明:由已知113--=-n n n a a ,故)()()(12211a a a a a a a n n n n n -++-+-=---1213133312n n n a ---+=++++=, 所以证得312n n a -=.例题2. 数列{}n a 的前n 项和记为11,1,21(1)n n n S a a S n +==+≥(Ⅰ)求{}n a 的通项公式;(Ⅱ)等差数列{}n b 的各项为正,其前n 项和为n T ,且315T =,又112233,,a b a b a b +++成等比数列,求n T .解:(Ⅰ)由121n n a S +=+可得121(2)n n a S n -=+≥,两式相减得:112,3(2)n n n n n a a a a a n ++-==≥,又21213a S =+=∴213a a = 故{}n a 是首项为1,公比为3的等比数列∴13n n a -=(Ⅱ)设{}n b 的公差为d ,由315T =得,可得12315b b b ++=,可得25b = 故可设135,5b d b d =-=+,又1231,3,9a a a ===,由题意可得2(51)(59)(53)d d -+++=+,解得122,10d d ==∵等差数列{}n b 的各项为正,∴0d > ∴2d =∴2(1)3222n n n T n n n -=+⨯=+例题3. 已知数列{}n a 的前三项与数列{}n b 的前三项对应相同,且212322...a a a +++128n n a n -+=对任意的*N n ∈都成立,数列{}n n b b -+1是等差数列.⑴求数列{}n a 与{}n b 的通项公式;⑵是否存在N k *∈,使得(0,1)k k b a -∈,请说明理由.点拨:(1)2112322...28n n a a a a n -++++=左边相当于是数列{}12n n a -前n 项和的形式,可以联想到已知n S 求na 的方法,当2n ≥时,1n n n S S a --=.(2)把k k a b -看作一个函数,利用函数的思想方法来研究k k a b -的取值情况.解:(1)已知212322a a a +++ (1)2n n a -+8n =(n ∈*N )①2n ≥时,212322a a a +++ (2)128(1)n n a n --+=-(n ∈*N )②①-②得,128n n a -=,求得42n n a -=,在①中令1n =,可得得41182a -==,所以42nn a -=(n ∈N*). 由题意18b =,24b =,32b =,所以214b b -=-,322b b -=-,∴数列}{1n n b b -+的公差为2)4(2=---, ∴1n nb b +-=2)1(4⨯-+-n 26n =-,121321()()()n n n b b b b b b b b -=+-+-++-(4)(2)(28)n =-+-++-2714n n =-+(n ∈*N ).(2)k k b a -=2714k k -+-42k-,当4k ≥时,277()()24f k k =-+-42k-单调递增,且(4)1f =, 所以4k ≥时,2()714f k k k =-+-421k-≥, 又(1)(2)(3)0f f f ===,所以,不存在k ∈*N ,使得(0,1)k k b a -∈.例题4. 设各项均为正数的数列{a n }和{b n }满足:a n 、b n 、a n+1成等差数列,b n 、a n+1、b n+1成等比数列,且a 1 = 1, b 1 = 2 , a 2 = 3 ,求通项a n ,b n 解: 依题意得:2b n+1 = a n+1 + a n+2 ① a 2n+1 = b n b n+1 ②∵ a n 、b n 为正数, 由②得21211,+++++==n n n n n n b b a b b a , 代入①并同除以1+n b 得:212+++=n n n b b b , ∴}{n b 为等差数列∵ b 1 = 2 , a 2 = 3 ,29,22122==b b b a 则 ,∴ 2)1(),1(22)229)(1(22+=∴+=--+=n b n n b n n ,∴当n ≥2时,2)1(1+==-n n b b a n n n , 又a 1 = 1,当n = 1时成立, ∴2)1(+=n n a n2. 研究前n 项和的性质例题5. 已知等比数列}{n a 的前n 项和为2nn S a b =⋅+,且13a =. (1)求a 、b 的值及数列}{n a 的通项公式;(2)设n n nb a =,求数列}{n b 的前n 项和n T .解:(1)2≥n 时,a S S a n n n n ⋅=-=--112.而}{n a 为等比数列,得a a a =⋅=-1112,又31=a ,得3=a ,从而123-⋅=n n a .又123,3a a b b =+=∴=-.(2)132n n n n n b a -==⋅, 21123(1)3222n n nT -=++++231111231(2322222n n n n n T --=+++++) ,得2111111(1)232222nn n n T -=++++-,111(1)2412[](1)13232212n n n n n n n T +⋅-=-=---.例题6. 数列{}n a 是首项为1000,公比为110的等比数列,数列{b }n 满足121(lg lg lg )k k b a a a k=+++*()N k ∈, (1)求数列{b }n 的前n 项和的最大值;(2)求数列{|b |}n 的前n 项和n S '. 解:(1)由题意:410nn a -=,∴lg 4n a n =-,∴数列{lg }n a 是首项为3,公差为1-的等差数列,∴12(1)lg lg lg 32k k k a a a k -+++=-,∴1(1)7[3]22n n n nb n n --=-=由100n n b b +≥⎧⎨≤⎩,得67n ≤≤,∴数列{b }n 的前n 项和的最大值为67212S S ==.(2)由(1)当7n ≤时,0n b ≥,当7n >时,0n b <,∴当7n ≤时,212731132()244n n n S b b b n n n -+'=+++==-+当7n >时,12789n n S b b b b b b '=+++----27121132()2144n S b b b n n =-+++=-+∴22113(7)4411321(7)44n n n n S n n n ⎧-+≤⎪⎪'=⎨⎪-+>⎪⎩.例题7. 已知递增的等比数列{n a }满足23428a a a ++=,且32a +是2a ,4a 的等差中项. (1)求{n a }的通项公式n a ;(2)若12log n n nb a a =,12n n S b b b =+++求使1230n n S n ++⋅>成立的n 的最小值.解:(1)设等比数列的公比为q (q >1),由a 1q +a 1q 2+a 1q 3=28,a 1q +a 1q 3=2(a 1q 2+2),得:a 1=2,q =2或a 1=32,q =12(舍)∴a n =2·2(n -1)=2n(2) ∵12log 2nn n n b a a n ==-⋅,∴S n =-(1·2+2·22+3·23+…+n ·2n ) ∴2S n =-(1·22+2·23+…+n ·2n +1),∴S n =2+22+23+…+2n -n ·2n +1=-(n -1)·2n +1-2, 若S n +n ·2n +1>30成立,则2n +1>32,故n >4,∴n 的最小值为5.例题8. 已知数列}{n a 的前n 项和为S n ,且11,,n n S a +-成等差数列,*1,1N n a ∈=. 函数3()log f x x =.(I )求数列}{n a 的通项公式; (II )设数列{}n b 满足1(3)[()2]n n b n f a =++,记数列{}n b 的前n 项和为T n ,试比较52512312n n T +-与的大小. 解:(I )11,,n n S a +-成等差数列,121n n S a +∴=-① 当2n ≥时,121n n S a -=-②. ①-②得:112()n n n n S S a a -+-=-,13+=∴n n a a ,13.n na a +∴=当n =1时,由①得112221S a a ∴==-, 又11,a =2213,3,a a a ∴=∴={}n a ∴是以1为首项3为公比的等比数列,13.n n a -∴=(II )∵()x log x f 3=,133()log log 31n n n f a a n -∴===-,11111()(3)[()2](1)(3)213n n b n f a n n n n ===-++++++,1111111111111()224354657213n T n n n n ∴=-+-+-+-++-+-+++11111()22323n n =+--++525,122(2)(3)n n n +=-++比较52512312n n T +-与的大小,只需比较2(2)(3)n n ++与312 的大小即可. 222(2)(3)3122(56156)2(5150)n n n n n n ++-=++-=+-又2(15)(10)n n =+-∵*,N n ∈∴当*19N n n ≤≤∈且时,5252(2)(3)312,;12312n n n n T +++<<-即 当10n =时,5252(2)(3)312,;12312n n n n T +++==-即 当*10N n n >∈且时,5252(2)(3)312,12312n n n n T +++>>-即.3. 研究生成数列的性质例题9. (I ) 已知数列{}n c ,其中nn n c 32+=,且数列{}n n pc c -+1为等比数列,求常数p ;(II ) 设{}n a 、{}n b 是公比不相等的两个等比数列,n n n b a c +=,证明数列{}n c 不是等比数列.解:(Ⅰ)因为{c n +1-pc n }是等比数列,故有 (c n +1-pc n )2=( c n +2-pc n+1)(c n -pc n -1), 将c n =2n +3n 代入上式,得 [2n +1+3n +1-p (2n +3n )]2=[2n +2+3n +2-p (2n +1+3n +1)]·[2n +3n -p (2n -1+3n -1)], 即[(2-p )2n +(3-p )3n ]2=[(2-p )2n+1+(3-p )3n+1][ (2-p )2n -1+(3-p )3n -1],整理得61(2-p )(3-p )·2n ·3n =0,解得p =2或p =3. (Ⅱ)设{a n }、{b n }的公比分别为p 、q ,p ≠q ,c n =a n +b n .为证{c n }不是等比数列只需证22c ≠c 1·c 3.事实上,22c =(a 1p +b 1q )2=21a p 2+21b q 2+2a 1b 1pq ,c 1·c 3=(a 1+b 1)(a 1 p 2+b 1q 2)= 21a p 2+21b q 2+a 1b 1(p 2+q 2).由于p ≠q ,p 2+q 2>2pq ,又a 1、b 1不为零,因此≠22c c 1·c 3,故{c n }不是等比数列.例题10. n 2( n ≥4)个正数排成n 行n 列:其中每一行的数成等差数列,每一列的数成等比数列,并且所有公比相等已知a 24=1,163,814342==a a 求S=a 11 + a 22 + a 33 + … + a nn解: 设数列{1k a }的公差为d , 数列{ik a }(i=1,2,3,…,n )的公比为q则1k a = a 11 + (k -1)d , a kk = [a 11 + (k -1)d]q k -1依题意得:⎪⎪⎪⎩⎪⎪⎪⎨⎧=+==+==+=163)2(81)(1)3(31143311421124q d a a q d a a q d a a ,解得:a 11 = d = q = ±21 又n 2个数都是正数,∴a 11 = d = q = 21 , ∴a kk = kk2n n S 212132122132⨯++⨯+⨯+=,1432212132122121+⨯++⨯+⨯+=n n S ,两式相减得:n n nS 22121--=-例题11. 已知函数3()log ()f x ax b =+的图象经过点)1,2(A 和)2,5(B ,记()*3,.f n n a n N =∈ (1)求数列}{n a 的通项公式;(2)设n n n nn b b b T a b +++==21,2,若)(Z m m T n ∈<,求m 的最小值;(3)求使不等式12)11()11)(11(21+≥+++n p a a a n对一切*N n ∈均成立的最大实数p .解:(1)由题意得⎩⎨⎧=+=+2)5(log 1)2(log 33b a b a ,解得⎩⎨⎧-==12b a ,)12(log )(3-=∴x x f *)12(log ,1233N n n a n n ∈-==-(2)由(1)得n n n b 212-=, n n n n n T 2122322523211321-+-++++=∴- ① 1132212232252232121+--+-+-+++=n n n n n n n T ② ①-②得)21212121(2121n 22222222221T 211n 2n 2111n n 1n 321n --+-+++++=--+++++= 1n 1n 1n 21n 2212321n 2+-+---=--.n n 2n n 23n 2321n 2213T +-=---=∴-, 设*,232)(N n n n f n ∈+=,则由 1512132121)32(252232252)()1(1<+≤++=++=++=++n n n n n n f n f n n 得*,232)(Nn n n f n ∈+=随n 的增大而减小+∞→∴n 当时,3→n T 又)(Z m m T n ∈<恒成立,3min =∴m(3)由题意得*21)11()11)(11(121N n a a a n p n ∈++++≤对 恒成立记)11()11)(11(121)(21n a a a n n F ++++=,则 ()()11n 21n 2)1n ()1n (4)1n (2)3n 2)(1n 2(2n 2)a 11()a 11)(a 11(1n 21)a 11)(a 11()a 11)(a 11(3n 21)n (F )1n (F 2n 211n n 21=++>+-++=+++=+++++++++=++)(),()1(,0)(n F n F n F n F 即>+∴> 是随n 的增大而增大)(n F 的最小值为332)1(=F ,332≤∴p ,即332max =p .(二)证明等差与等比数列 1. 转化为等差等比数列.例题12. 数列{}n a 中,2,841==a a 且满足n n n a a a -=++122,*N n ∈.⑴求数列{}n a 的通项公式;⑵设||||||21n n a a a S +++= ,求n S ;⑶设n b =1(12)n n a -**12(),()N N n n n T b b b n ∈=+++∈,是否存在最大的整数m ,使得对任意*N n ∈,均有>n T 32m成立?若存在,求出m 的值;若不存在,请说明理由.解:(1)由题意,n n n n a a a a -=-+++112,}{n a ∴为等差数列,设公差为d , 由题意得2832d d =+⇒=-,82(1)102n a n n ∴=--=-.(2)若50210≤≥-n n 则,||||||,521n n a a a S n +++=≤ 时21281029,2n na a a n n n +-=+++=⨯=-6n ≥时,n n a a a a a a S ---+++= 765212555()2940n n S S S S S n n =--=-=-+故⎪⎩⎪⎨⎧+--=40n 9n n n 9S 22n 56n n ≤≥ (3)11111()(12)2(1)21n n b n a n n n n ===--++, ∴n T 1111111111[(1)()()()()]22233411n n n n =-+-+-++-+--+.2(1)n n =+ 若32n m T >对任意*N n ∈成立,即116n m n >+对任意*N n ∈成立, *()1N n n n ∈+的最小值是21,1,162m ∴<m ∴的最大整数值是7.即存在最大整数,7=m 使对任意*N n ∈,均有.32n m T >例题13. 已知等比数列{}n b 与数列{}n a 满足3,n an b n =∈N *. (1)判断{}n a 是何种数列,并给出证明;(2)若8131220,a a m b b b +=求.解:(1)设{}n b 的公比为q ,∵3n an b =,∴()q log 1n a a 3q 331n a 1n a n 1-+=⇒=⋅-。
完整版)数列典型例题(含答案)

完整版)数列典型例题(含答案)等差数列的前n项和公式为代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得代入已知条件,得到解得。
因此,前项和为。
⑵由已知条件可得代入等差数列的前n项和公式,得到化简得因此,前项和为。
8.(2010山东理) 已知等差数列 $a_1,a_2,\ldots,a_n,\ldots$,其中 $a_1=1$,公差为 $d$。
1) 求 $a_5$ 和 $a_{10}$。
2) 满足 $a_1+a_2+\ldots+a_k=100$,$a_1+a_2+\ldots+a_{k+1}>100$,$k\in\mathbb{N}$,求该等差数列的前 $k$ XXX。
考查目的:考查等差数列的通项公式和前项和公式等基础知识,考查数列求和的基本方法以及运算求解能力。
答案:(1) $a_5=5d+1$,$a_{10}=10d+1$;(2) $k=13$,前$k$ 项和为 $819$。
解析:(1) 根据等差数列的通项公式 $a_n=a_1+(n-1)d$,可得 $a_5=1+4d$,$a_{10}=1+9d$。
2) 设该等差数列的前 $k$ 项和为 $S_k$,则由等差数列的前项和公式可得 $S_k=\dfrac{k}{2}[2a_1+(k-1)d]$。
根据已知条件可列出不等式组:begin{cases}S_k=100\\S_{k+1}>100end{cases}将 $S_k$ 代入得:frac{k}{2}[2+(k-1)d]=100整理得:$k^2+kd-400=0$。
数列测试题及答案解析

数列测试题及答案解析一、选择题1. 已知数列{an}满足a1=2,an+1 = 2an,判断数列{an}是否为等比数列。
A. 是B. 不是C. 无法判断答案:A2. 若数列{bn}是等差数列,且b3=5,b5=9,求b7。
A. 11B. 13C. 无法确定答案:B二、填空题1. 给定数列{cn},其中c1=1,cn+1 = cn + n,求c5的值。
答案:152. 已知等差数列{dn}的首项d1=3,公差d=2,求d20的值。
答案:43三、解答题1. 求等比数列{en}的前n项和Sn,若e1=1,公比q=3。
解:根据等比数列前n项和公式Sn = e1 * (1 - q^n) / (1 - q),代入e1=1和q=3,得到Sn = (1 - 3^n) / (1 - 3)。
2. 已知等差数列{fn}的前n项和为Tn,若f1=2,d=3,求T10。
解:根据等差数列前n项和公式Tn = n/2 * (2a1 + (n - 1)d),代入f1=2和d=3,得到T10 = 10/2 * (2*2 + (10 - 1)*3) = 5 * (4 + 27) = 5 * 31 = 155。
四、证明题1. 证明数列{gn},其中gn = n^2,是一个单调递增数列。
证明:设n≥2,我们需要证明对于任意的n,有gn ≥ gn-1。
即证明n^2 ≥ (n-1)^2。
展开得n^2 - (n-1)^2 = 2n - 1 > 0,所以数列{gn}是单调递增的。
2. 证明等差数列{hn}的任意两项hn和hm(m > n)之和等于它们中间项的两倍。
证明:设等差数列{hn}的首项为h1,公差为d。
根据等差数列的定义,hn = h1 + (n - 1)d,hm = h1 + (m - 1)d。
将两项相加得hn + hm = 2h1 + (m + n - 2)d。
由于m > n,所以m + n - 2 = m - 1 + n - 1,即hn + hm = h1 + (m - 1)d + h1 + (n - 1)d = 2h1 + (m + n - 2)d = 2h((m + n - 1)/2),这正是它们中间项的两倍。
高一数列的概念及简单表示方法知识点+例题+练习 含答案
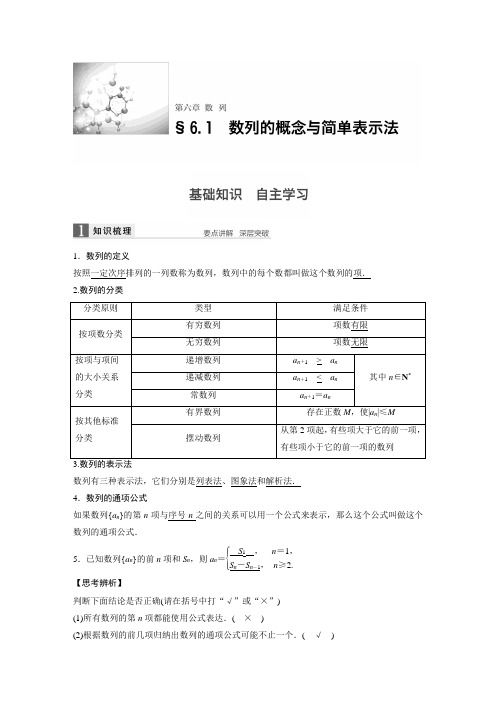
1.数列的定义按照一定次序排列的一列数称为数列,数列中的每个数都叫做这个数列的项. 2.数列的分类 分类原则 类型 满足条件 按项数分类 有穷数列 项数有限 无穷数列 项数无限按项与项间的大小关系分类 递增数列 a n +1__>__a n 其中n ∈N *递减数列 a n +1__<__a n 常数列 a n +1=a n按其他标准分类有界数列 存在正数M ,使|a n |≤M 摆动数列从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列数列有三种表示法,它们分别是列表法、图象法和解析法. 4.数列的通项公式如果数列{a n }的第n 项与序号n 之间的关系可以用一个公式来表示,那么这个公式叫做这个数列的通项公式.5.已知数列{a n }的前n 项和S n ,则a n =⎩⎪⎨⎪⎧S 1 , n =1,S n -S n -1, n ≥2.【思考辨析】判断下面结论是否正确(请在括号中打“√”或“×”) (1)所有数列的第n 项都能使用公式表达.( × )(2)根据数列的前几项归纳出数列的通项公式可能不止一个.( √ )(3)1,1,1,1,…,不能构成一个数列.( × )(4)任何一个数列不是递增数列,就是递减数列.( × )(5)如果数列{a n }的前n 项和为S n ,则对∀n ∈N *,都有a n +1=S n +1-S n .( √ ) (6)在数列{a n }中,对于任意正整数m ,n ,a m +n =a mn +1,若a 1=1,则a 2=2.( √ )1.已知数列{a n }中,a 1=1,1a n +1=1a n +3 (n ∈N *),则a 10=________. 答案128解析 由题意得1a n +1-1a n=3.∴1a 2-1a 1=3,1a 3-1a 2=3,1a 4-1a 3=3,1a 5-1a 4=3,…,1a 10-1a 9=3,对递推式叠加得1a 10-1a 1=27,故a 10=128.2.把1,3,6,10,15,21,…这些数叫做三角形数,这是因为用这些数目的点可以排成一个正三角形(如图).则第7个三角形数是________. 答案 28解析 根据三角形数的增长规律可知第七个三角形数是1+2+3+4+5+6+7=28. 3.数列{a n }的前n 项和记为S n ,a 1=1,a n +1=2S n +1 (n ≥1,n ∈N *),则数列{a n }的通项公式是__________. 答案 a n =3n -1解析 由a n +1=2S n +1可得a n =2S n -1+1 (n ≥2),两式相减得a n +1-a n =2a n ,即a n +1=3a n (n ≥2).又a 2=2S 1+1=3,a 3=3·a 2=32·a 1=32, a 4=3a 3=33… a n =3a n -1=3n -1.4.(教材改编)根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式a n =________.答案 5n -45.已知数列{a n }的前n 项和S n =n 2+1,则a n =________.答案 ⎩⎪⎨⎪⎧2,n =1,2n -1,n ≥2解析 当n =1时,a 1=S 1=2,当n ≥2时, a n =S n -S n -1=n 2+1-[(n -1)2+1]=2n -1,故a n =⎩⎪⎨⎪⎧2,n =1,2n -1,n ≥2.题型一 由数列的前几项求数列的通项公式例1 (1)数列0,23,45,67,…的一个通项公式为________.①a n =n -1n +1(n ∈N *) ②a n =n -12n +1(n ∈N *)③a n =2(n -1)2n -1(n ∈N *) ④a n =2n 2n +1(n ∈N *)(2)数列{a n }的前4项是32,1,710,917,则这个数列的一个通项公式是a n =________.答案 (1)③ (2)2n +1n 2+1解析 (1)注意到分母0,2,4,6都是偶数,对照所给项排除即可.(2)数列{a n }的前4项可变形为2×1+112+1,2×2+122+1,2×3+132+1,2×4+142+1,故a n =2n +1n 2+1.思维升华 根据所给数列的前几项求其通项时,需仔细观察分析,抓住其几方面的特征:分式中分子、分母的各自特征;相邻项的联系特征;拆项后的各部分特征;符号特征.应多进行对比、分析,从整体到局部多角度观察、归纳、联想.根据数列的前几项,写出下列各数列的一个通项公式.(1)-1,7,-13,19,…; (2)0.8,0.88,0.888,…;(3)12,14,-58,1316,-2932,6164,…. 解 (1)数列中各项的符号可通过(-1)n 表示,从第2项起,每一项的绝对值总比它的前一项的绝对值大6,故通项公式为a n =(-1)n (6n -5). (2)数列变为89⎝⎛⎭⎫1-110,89⎝⎛⎭⎫1-1102,89⎝⎛⎭⎫1-1103,…, 故a n =89⎝⎛⎭⎫1-110n . (3)各项的分母分别为21,22,23,24,…,易看出第2,3,4项的分子分别比分母小3. 因此把第1项变为-2-32,原数列化为-21-321,22-322,-23-323,24-324,…,故a n =(-1)n 2n -32n .题型二 由数列的前n 项和求数列的通项公式例2 设数列{a n }的前n 项和为S n ,数列{S n }的前n 项和为T n ,满足T n =2S n -n 2,n ∈N *. (1)求a 1的值;(2)求数列{a n }的通项公式. 解 (1)令n =1时,T 1=2S 1-1,因为T 1=S 1=a 1,所以a 1=2a 1-1,所以a 1=1. (2)n ≥2时,T n -1=2S n -1-(n -1)2, 则S n =T n -T n -1=2S n -n 2-[2S n -1-(n -1)2] =2(S n -S n -1)-2n +1=2a n -2n +1. 因为当n =1时,a 1=S 1=1也满足上式, 所以S n =2a n -2n +1(n ≥1),当n ≥2时,S n -1=2a n -1-2(n -1)+1, 两式相减得a n =2a n -2a n -1-2,所以a n =2a n -1+2(n ≥2),所以a n +2=2(a n -1+2), 因为a 1+2=3≠0,所以数列{a n +2}是以3为首项,公比为2的等比数列. 所以a n +2=3×2n -1,所以a n =3×2n -1-2, 当n =1时也成立, 所以a n =3×2n -1-2.思维升华 数列的通项a n 与前n 项和S n 的关系是a n =⎩⎪⎨⎪⎧S 1,n =1,S n -S n -1,n ≥2.当n =1时,a 1若适合S n -S n -1,则n =1的情况可并入n ≥2时的通项a n ;当n =1时,a 1若不适合S n -S n -1,则用分段函数的形式表示.(1)已知数列{a n }的前n 项和S n =n +1n +2,则a 4=________.(2)已知数列{a n }的前n 项和S n =3n 2-2n +1,则其通项公式为________________.答案 (1)130 (2)a n =⎩⎪⎨⎪⎧2,n =1,6n -5,n ≥2解析 (1)a 4=S 4-S 3 =56-45=130. (2)当n =1时,a 1=S 1=3×12-2×1+1=2; 当n ≥2时,a n =S n -S n -1=3n 2-2n +1-[3(n -1)2-2(n -1)+1] =6n -5,显然当n =1时,不满足上式.故数列的通项公式为a n =⎩⎪⎨⎪⎧2,n =1,6n -5,n ≥2.题型三 由数列的递推关系求通项公式例3 (1)设数列{a n }中,a 1=2,a n +1=a n +n +1,则通项a n =________. (2)数列{a n }中,a 1=1,a n +1=3a n +2,则它的一个通项公式为a n =________. 答案 (1)n (n +1)2+1 (2)2×3n -1-1解析 (1)由题意得,当n ≥2时, a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1) =2+(2+3+…+n )=2+(n -1)(2+n )2=n (n +1)2+1.又a 1=2=1×(1+1)2+1,符合上式,因此a n =n (n +1)2+1.(2)方法一 (累乘法)a n +1=3a n +2,即a n +1+1=3(a n +1), 即a n +1+1a n +1=3, 所以a 2+1a 1+1=3,a 3+1a 2+1=3,a 4+1a 3+1=3,…,a n +1+1a n +1=3.将这些等式两边分别相乘得a n +1+1a 1+1=3n .因为a 1=1,所以a n +1+11+1=3n ,即a n +1=2×3n -1(n ≥1), 所以a n =2×3n -1-1(n ≥2), 又a 1=1也满足上式,故数列{a n }的一个通项公式为a n =2×3n -1-1. 方法二 (迭代法) a n +1=3a n +2,即a n +1+1=3(a n +1)=32(a n -1+1)=33(a n -2+1) =…=3n (a 1+1)=2×3n (n ≥1), 所以a n =2×3n -1-1(n ≥2), 又a 1=1也满足上式,故数列{a n }的一个通项公式为a n =2×3n -1-1.思维升华 已知数列的递推关系,求数列的通项时,通常用累加、累乘、构造法求解. 当出现a n =a n -1+m 时,构造等差数列;当出现a n =xa n -1+y 时,构造等比数列;当出现a n =a n -1+f (n )时,用累加法求解;当出现a na n -1=f (n )时,用累乘法求解.(1)已知数列{a n }满足a 1=1,a n =n -1n·a n -1(n ≥2),则a n =________.(2)已知数列{a n }的前n 项和为S n ,且S n =2a n -1(n ∈N *),则a 5=________. 答案 (1)1n(2)16解析 (1)∵a n =n -1n a n -1 (n ≥2),∴a n -1=n -2n -1a n -2,…,a 2=12a 1.以上(n -1)个式子相乘得 a n =a 1·12·23·…·n -1n =a 1n =1n .当n =1时也满足此等式,∴a n =1n .(2)当n =1时,S 1=2a 1-1,∴a 1=1. 当n ≥2时,S n -1=2a n -1-1, ∴a n =2a n -2a n -1,∴a n =2a n -1. ∴{a n }是等比数列且a 1=1,q =2, 故a 5=a 1×q 4=24=16.题型四 数列的性质命题点1 数列的单调性例4 已知数列{a n }的前n 项和S n =n 2+1,数列{b n }满足b n =2a n +1,且前n 项和为T n ,设c n =T 2n +1-T n .(1)求数列{b n }的通项公式; (2)判断数列{c n }的增减性.解 (1)a 1=2,a n =S n -S n -1=2n -1(n ≥2).∵b n =2a n +1,∴b n =⎩⎨⎧23,n =1,1n , n ≥2,n ∈N *.(2)∵c n =b n +1+b n +2+…+b 2n +1 =1n +1+1n +2+…+12n +1, ∴c n +1-c n =12n +2+12n +3-1n +1=12n +3-12n +2=-1(2n +3)(2n +2)<0, ∴c n +1<c n .∴数列{c n }为递减数列. 命题点2 数列的周期性例5 数列{a n }满足a n +1=11-a n ,a 8=2,则a 1=_____________________________________.答案 12解析 ∵a n +1=11-a n,∴a n +1=11-a n =11-11-a n -1=1-a n -11-a n -1-1=1-a n -1-a n -1=1-1a n -1=1-111-a n -2=1-(1-a n -2)=a n -2, ∴周期T =(n +1)-(n -2)=3. ∴a 8=a 3×2+2=a 2=2. 而a 2=11-a 1,∴a 1=12.命题点3 数列的最值例6 数列{a n }的通项a n =nn 2+90,则数列{a n }中的最大项的值是________.答案119解析 令f (x )=x +90x (x >0),运用基本不等式得,f (x )≥290当且仅当x =310时等号成立.因为a n =1n +90n ,所以1n +90n ≤1290,由于n ∈N *,不难发现当n =9或10时,a n =119最大.思维升华 1.解决数列的单调性问题可用以下三种方法(1)用作差比较法,根据a n +1-a n 的符号判断数列{a n }是递增数列、递减数列或是常数列. (2)用作商比较法,根据a n +1a n (a n >0或a n <0)与1的大小关系进行判断.(3)结合相应函数的图象直观判断. 2.解决数列周期性问题的方法先根据已知条件求出数列的前几项,确定数列的周期,再根据周期性求值. 3.数列的最值可以利用数列的单调性或求函数最值的思想求解.(1)数列{a n }满足a n +1=⎩⎨⎧2a n ,0≤a n ≤12,2a n-1,12<a n<1,a 1=35,则数列的第2 015项为________.(2)设a n =-3n 2+15n -18,则数列{a n }中的最大项的值是________. 答案 (1)25(2)0解析 (1)由已知可得,a 2=2×35-1=15,a 3=2×15=25,a 4=2×25=45,a 5=2×45-1=35,∴{a n }为周期数列且T =4, ∴a 2 015=a 3=25.(2)∵a n =-3⎝⎛⎭⎫n -522+34,由二次函数性质,得当n =2或3时,a n 最大,最大值为0.5.数列中的新定义问题典例 (1)将石子摆成如图所示的梯形形状,称数列5,9,14,20,…为“梯形数”.根据图形的构成,此数列的第2 014项与5的差,即a 2 014-5=__________.(用式子表示)(2)对于数列{x n },若对任意n ∈N *,都有x n +x n +22<x n +1成立,则称数列{x n }为“减差数列”.设b n =2t -tn -12n -1,若数列b 3,b 4,b 5,…是“减差数列”,则实数t 的取值范围是____________.思维点拨 (1)观察图形,易得a n -a n -1=n +2(n ≥2)可利用累加法求解.(2)由“减差数列”的定义,可得关于b n 的不等式,把b n 的通项公式代入,化归为不等式恒成立问题求解.解析 (1)因为a n -a n -1=n +2(n ≥2),a 1=5,所以a 2 014=(a 2 014-a 2 013)+(a 2 013-a 2 012)+…+(a 2-a 1)+a 1=2 016+2 015+…+4+5 =(2 016+4)×2 0132+5=1 010×2 013+5,所以a 2 014-5=1 010×2 013.(2)由数列b 3,b 4,b 5,…是“减差数列”, 得b n +b n +22<b n +1(n ≥3), 即t -tn -12n +t -t (n +2)-12n +2<2t -t (n +1)-12n ,即tn -12n +t (n +2)-12n +2>t (n +1)-12n ,化简得t (n -2)>1. 当n ≥3时,若t (n -2)>1恒成立,则t >1n -2恒成立,又当n ≥3时,1n -2的最大值为1,则t 的取值范围是(1,+∞).答案 (1)1 010×2 013 (2)(1,+∞)温馨提醒 解决数列的新定义问题要做到:(1)准确转化:解决数列新定义问题时,一定要读懂新定义的本质含义,将题目所给定义转化成题目要求的形式,切忌同已有概念或定义相混淆.(2)方法选取:对于数列新定义问题,搞清定义是关键,仔细认真地从前几项(特殊处、简单处)体会题意,从而找到恰当的解决方法.[方法与技巧]1.求数列通项或指定项.通常用观察法(对于交错数列一般用(-1)n 或(-1)n +1来区分奇偶项的符号);已知数列中的递推关系,一般只要求写出数列的前几项,若求通项可用归纳、猜想和转化的方法.2.强调a n 与S n 的关系:a n =⎩⎪⎨⎪⎧S 1, n =1,S n -S n -1, n ≥2. 3.已知递推关系求通项:对这类问题的要求不高,但试题难度较难把握.一般有两种常见思路:(1)算出前几项,再归纳、猜想;(2)利用累加法或累乘法可求数列的通项公式.4.数列的性质可利用函数思想进行研究.[失误与防范]1.数列a n =f (n )和函数y =f (x )定义域不同,其单调性也有区别:y =f (x )是增函数是a n =f (n )是递增数列的充分不必要条件.2.数列的通项公式可能不存在,也可能有多个.3.由a n =S n -S n -1求得的a n 是从n =2开始的,要对n =1时的情况进行验证.A 组 专项基础训练(时间:40分钟)1.数列23,-45,67,-89,…的第10项是________. 答案 -2021解析 所给数列呈现分数形式,且正负相间,求通项公式时,我们可以把每一部分进行分解:符号、分母、分子.很容易归纳出数列{a n }的通项公式a n =(-1)n +1·2n 2n +1,故a 10=-2021. 2.数列{a n }的前n 项积为n 2,那么当n ≥2时,a n =__________.答案 n 2(n -1)2解析 设数列{a n }的前n 项积为T n ,则T n =n 2,当n ≥2时,a n =T n T n -1=n 2(n -1)2. 3.若S n 为数列{a n }的前n 项和,且S n =n n +1,则1a 5=________. 答案 30解析 当n ≥2时,a n =S n -S n -1=n n +1-n -1n =1n (n +1),所以1a 5=5×6=30. 4.若数列{a n }满足:a 1=19,a n +1=a n -3(n ∈N *),则数列{a n }的前n 项和数值最大时,n 的值为________.答案 7解析 ∵a n +1-a n =-3,∴数列{a n }是以19为首项,-3为公差的等差数列,∴a n =19+(n -1)×(-3)=22-3n .∵a 7=22-21=1>0,a 8=22-24=-2<0,∴n =7时,数列{a n }的前n 项和最大.5.已知数列{a n }的通项公式为a n =n 2-2λn (n ∈N *),则“λ<1”是“数列{a n }为递增数列”的______________条件.答案 充分不必要解析 若数列{a n }为递增数列,则有a n +1-a n >0,即2n +1>2λ对任意的n ∈N *都成立,于是有3>2λ,λ<32.由λ<1可推得λ<32,但反过来,由λ<32不能得到λ<1,因此“λ<1”是“数列{a n }为递增数列”的充分不必要条件.6.(2015·大连双基测试)已知数列{a n }的前n 项和S n =n 2+2n +1(n ∈N *),则a n =________.答案 ⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥2 解析 当n ≥2时,a n =S n -S n -1=2n +1,当n =1时,a 1=S 1=4≠2×1+1,因此a n =⎩⎪⎨⎪⎧4,n =1,2n +1,n ≥2. 7.数列{a n }中,已知a 1=1,a 2=2,a n +1=a n +a n +2(n ∈N *),则a 7=________. 答案 1解析 由已知a n +1=a n +a n +2,a 1=1,a 2=2,能够计算出a 3=1,a 4=-1,a 5=-2,a 6=-1,a 7=1.8.已知数列{a n }的前n 项和为S n ,S n =2a n -n ,则a n =________. 答案 2n -1解析 当n =1时,S 1=a 1=2a 1-1,得a 1=1,当n ≥2时,a n =S n -S n -1=2a n -n -2a n -1+(n -1),即a n =2a n -1+1,∴a n +1=2(a n -1+1),∴数列{a n +1}是首项为a 1+1=2,公比为2的等比数列,∴a n +1=2·2n -1=2n ,∴a n =2n -1.9.数列{a n }的通项公式是a n =n 2-7n +6.(1)这个数列的第4项是多少?(2)150是不是这个数列的项?若是这个数列的项,它是第几项?(3)该数列从第几项开始各项都是正数?解 (1)当n =4时,a 4=42-4×7+6=-6.(2)令a n =150,即n 2-7n +6=150,解得n =16或n =-9(舍去),即150是这个数列的第16项.(3)令a n =n 2-7n +6>0,解得n >6或n <1(舍去).所以从第7项起各项都是正数.10.已知数列{a n }中,a 1=1,前n 项和S n =n +23a n. (1)求a 2,a 3;(2)求{a n }的通项公式.解 (1)由S 2=43a 2得3(a 1+a 2)=4a 2, 解得a 2=3a 1=3.由S 3=53a 3得3(a 1+a 2+a 3)=5a 3, 解得a 3=32(a 1+a 2)=6. (2)由题设知a 1=1.当n ≥2时,有a n =S n -S n -1=n +23a n -n +13a n -1, 整理得a n =n +1n -1a n -1. 于是a 1=1,a 2=31a 1, a 3=42a 2, ……a n -1=n n -2a n -2, a n =n +1n -1a n -1. 将以上n 个等式两端分别相乘,整理得a n =n (n +1)2. 显然,当n =1时也满足上式.综上可知,{a n }的通项公式a n =n (n +1)2. B 组 专项能力提升(时间:20分钟)11.已知数列{a n }满足a 1=33,a n +1-a n n =2,则a n n的最小值为________. 答案 10.5解析 由题意可知a n +1=a n +2n ,由迭代法可得a n =a 1+2[1+2+3+4+…+(n -1)]=n 2-n+33,从而a n n =n +33n -1.当n =6时,a n n取得最小值10.5. 12.数列{a n }满足a n +a n +1=12(n ∈N *),a 2=2,S n 是数列{a n }的前n 项和,则S 21=________. 答案 72解析 ∵a n +a n +1=12,a 2=2, ∴a n =⎩⎪⎨⎪⎧-32,n 为奇数,2,n 为偶数.∴S 21=11×⎝⎛⎭⎫-32+10×2=72. 13.定义:称n P 1+P 2+…+P n为n 个正数P 1,P 2,…,P n 的“均倒数”.若数列{a n }的前n 项的“均倒数”为12n -1,则数列{a n }的通项公式为____________. 答案 a n =4n -3解析 ∵n a 1+a 2+…+a n =12n -1, ∴a 1+a 2+…+a n n =2n -1, ∴a 1+a 2+…+a n =(2n -1)n ,a 1+a 2+…+a n -1=(2n -3)(n -1)(n ≥2),当n ≥2时,a n =(2n -1)n -(2n -3)(n -1)=4n -3;a 1=1也适合此等式,∴a n =4n -3.14.若数列{n (n +4)(23)n }中的最大项是第k 项,则k =________. 答案 4解析 由题意得⎩⎨⎧ k (k +4)(23)k ≥(k +1)(k +5)(23)k +1,k (k +4)(23)k ≥(k -1)(k +3)(23)k -1,所以⎩⎪⎨⎪⎧k 2≥10,k 2-2k -9≤0,由k ∈N *可得k =4. 15.(2015·开封模拟)已知数列{a n }中,a n =1+1a +2(n -1)(n ∈N *,a ∈R 且a ≠0). (1)若a =-7,求数列{a n }中的最大项和最小项的值;(2)若对任意的n ∈N *,都有a n ≤a 6成立,求a 的取值范围.解 (1)∵a n =1+1a +2(n -1)(n ∈N *,a ∈R ,且a ≠0), 又a =-7,∴a n =1+12n -9(n ∈N *).结合函数f (x )=1+12x -9的单调性,可知1>a 1>a 2>a 3>a 4,a 5>a 6>a 7>…>a n >1(n ∈N *).∴数列{a n }中的最大项为a 5=2,最小项为a 4=0.(2)a n =1+1a +2(n -1)=1+12n -2-a 2, 已知对任意的n ∈N *,都有a n ≤a 6成立,结合函数f (x )=1+12x -2-a 2的单调性, 可知5<2-a 2<6,即-10<a <-8.。
数列基础测试题及答案

数列基础测试题及答案一、选择题(每题2分,共10分)1. 等差数列{a_n}的首项为1,公差为2,那么a_5的值为:A. 9B. 10C. 11D. 122. 等比数列{b_n}的首项为2,公比为3,那么b_4的值为:A. 24B. 54C. 72D. 1083. 数列{c_n}满足c_1=1,且c_{n+1}=2c_n+1,那么c_3的值为:A. 5B. 9C. 17D. 334. 已知数列{d_n}是等差数列,且d_1=3,d_3=9,那么d_5的值为:A. 15B. 18C. 21D. 245. 数列{e_n}是等比数列,且e_1=8,e_3=64,那么e_5的值为:A. 512C. 128D. 64二、填空题(每题3分,共15分)6. 等差数列{f_n}的首项为5,公差为-1,那么f_7=________。
7. 等比数列{g_n}的首项为3,公比为-2,那么g_5=________。
8. 数列{h_n}满足h_1=2,且h_{n+1}=3h_n-2,那么h_4=________。
9. 已知数列{i_n}是等差数列,且i_2=7,i_5=16,那么i_8=________。
10. 数列{j_n}是等比数列,且j_2=6,j_4=36,那么j_6=________。
三、解答题(每题10分,共20分)11. 已知数列{k_n}是等差数列,且k_1=2,k_3=10,求k_5的值。
12. 已知数列{l_n}是等比数列,且l_1=4,l_3=36,求l_5的值。
答案:一、选择题1. B2. D3. C4. C5. A二、填空题6. 28. 339. 3110. 576三、解答题11. 等差数列的公差d=k_3-k_1=10-2=8,所以k_5=k_3+2d=10+2*8=26。
12. 等比数列的公比q=l_3/l_1=36/4=9,所以l_5=l_3*q^2=36*9^2=2916。
高考数学复习专题九考点23《数列的概念与简单表示法》练习题(含答案)

高考数学复习专题九考点23《数列的概念与简单表示法》练习题(含答案)1.已知数列{}n a 的通项公式为2n a n kn =-,且{}n a 单调递增,则实数k 的取值范围是( ) A.(,2]-∞B.(,2)-∞C.(,3]-∞D.(,3)-∞2.22,24,…,则162( ) A.第8项B.第9项C.第10项D.第11项3.已知在数列{}n a 中,11a =,123n n a a +=+,则n a 等于( ) A.123n -+B.123n ++C.123n --D.123n +-4.数列{}n a 中,12a =,m n m n a a a +=.若155121022k k k a a a ++++++=-,则k =( )A.2B.3C.4D.55.已知数列{}n a 满足32111232n n a a a a n ++++=-,则n a =( ) A.112n-B.312n - C.12nD.2nn 6.已知数列{}n a 的前n 项和为()*n S n ∈N ,且2n S n λ=+.若数列{}n a 为递增数列,则实数λ的取值范围为( ) A.(,1)-∞B.(,2)-∞C.(,3)-∞D.(,4)-∞7.《周髀算经》是中国古代重要的数学著作,其记载的“日月历法”曰:“阴阳之数,日月之法,十九岁为一章,四章为一部,部七十六岁,二十部为一遂,遂千百五二十岁,…,生数皆终,万物复苏,天以更远作纪历”,某老年公寓住有20位老人,他们的年龄(都为正整数)之和恰好为一遂,其中年长者已是奔百之龄(年龄介于90~100),其余19人的年龄依次相差一岁,则年龄最小者的年龄为( ) A.65B.66C.67D.688.已知数列{}n a 的前n 项和为112321 ,,0,3,2,1(3)22n n n n n n a aS a a a a n a a +--∈===⋅=++N .若100m a =,则m =( )A.50B.51C.100D.1019.若数列{}n a 满足12211,1,n n n a a a a a ++===+,则称数列{}n a 为斐波那契数列.1680年卡西尼发现了斐波那契数列的一个重要性质:211(1)(2)n n n na a a n -+-=-≥.在斐波那契数列{}n a 中,若k 满足22111(21)(21)999kki i i i i i a a i a ++==--≤-∑∑,给出下列结论:①k 可以是任意奇数;②k 可以是任意正偶数:③若k 是奇数,则k 的最大值是999;④若k 是偶数,则k 的最大值是500.其中正确结论的序号是( )A.①④B.②③C.①②D.③④10.已知集合{}{}1*21*3,,1333,n n A x x n B x x n --==∈==++++∈N N ∣∣.将A B ⋃的所有元素从小到大排列构成数列{}n c ,其前n 项和为n T ,则下列命题中真命题的个数为( ) ①202320222021c c c =+; ②{}2212n n c c --是等比数列;③使503n T >成立的n 的最小值为100; ④112ni ic =<∑恒成立. A.4B.3C.2D.111.在斐波那契数列{}n a 中,11a =,21a =,()122n n n a a a n --=+>.已知n S 为该数列的前n 项和,若2020S m =,则2022a =_____________.12.已知数列{}n a 中,11a =,()*12n n a a n +=∈N ,则数列{}n a 的通项公式为n a =___________.13.数列{}n a 满足2(1)31n n n a a n ++-=-,前16项和为540,则1=a ___________. 14.已知数列{}n a 满足12a =,且31122(2)234n n a a a a a n n-++++=-≥,则{}n a 的通项公式为_______________.15.已知正项数列{}n a 的前n 项和为n S ,11a =,2211n n n S a S λ++=-,其中λ为常数.(1)证明:12n n S S λ+=+.(2)是否存在实数λ,使得数列{}n a 为等比数列?若存在,求出λ;若不存在,请说明理由.参考答案1.答案:D解析:∵数列{}n a 中()2*n a n kn n =-∈N ,且{}n a 单调递增,10n n a a +∴->对于*n ∈N 恒成立,即()22(1)(1)210n k n n kn n k +-+--=+->对于*n ∈N 恒成立. 21k n ∴<+对于*n ∈N 恒成立,即3k <.故选D.2.答案:B22(2),3(2),4(2),…,由此可归纳该数列的通项公式为()*(2)n n ∈N .又9162(2),所以1629项.故选B.3.答案:D解析:由123n n a a +=+,得()1323n n a a ++=+,且134a +=,则{}3n a +是以4为首项,2为公比的等比数列,则1342n n a -+=⨯,所以123n n a +=-. 4.答案:C解析:因为数列{}n a 中,m n m n a a a +=,令1m =,则112n n n a a a a +==,所以数列{}n a 是首项为2,公比为2的等比数列,则11122k k k a a ++=⋅=.所以()()1011101111210122212212k k k k k k k a a a a +++++++-+++==-=--,则1111552222k k ++-=-,所以4k =,故选C. 5.答案:D 解析:32111232n n a a a a n ++++=-①,当2n 时,31211112312n n a a a a n --++++=--②,则①-②得,1111222n n n n a n -=-=,故(2)2n n n a n =.当1n =时,112a =,也符合2n n na =,故选D. 6.答案:B解析:当1n =时,111a S λ==+;当2n 时,221(1)21n n n a S S n n n λλ-==+---=--.则120n n a a --=>,所以当2n 时,数列{}n a 为递增数列.若数列{}n a 为递增数列,只需21a a >,即31λ>+,所以2λ<.故选B.7.答案:B解析:设年龄最小者的年龄为n ,年龄最大者的年龄为([90,100])m m ∈,所以(1)(18)1520n n n m ++++++=,所以191349n m +=,所以134919m n =-,所以90134919100n -,所以14565661919n ,因为年龄为正整数,所以66n =,故选B.8.答案:D 解析:因为3412122a a a a ⋅=++,所以45a =,同理可得564,7a a ==.令2(3)2nn n a b n a -=+,则11n n b b +=,因为31b =,所以3452 1,2n n n b b b b a a -======+,则有21202(1)2 2 , 32(1)21k k a k k a k k -=+-=-=+-=+,故(1)n n a n =+-.若(1)100m m a m =+-=,则101m =.故选D. 9.答案:B解析:由211(1)(2)n n n na a a n -+-=-≥可得212111(21)(21)1357(1)(21)kkk i i i i i i a ai a k +++==-⋅--=-+-++--∑∑.若k 为偶数,则22111(21)(21)1357(21)kki i i i i i a a i a k k ++==---=-+-+--=-∑∑,此时22111(21)(21)999kki i i i i i a a i a ++==--≤-∑∑,即999k -≤,k 无最大值,所以②正确,④错误;若k 为奇数,则22111(21)(21)1357(21)kki i i i i i a a i a k k ++==---=-+-++-=∑∑,此时22111(21)(21)999k ki i i i i i a a i a ++==--≤-∑∑,即999k ≤,此时k 的最大值为999,所以①错误,③正确.故选B. 10.答案:B解析:设1*3,n n a n -=∈N ,则数列{}n a 是首项为1、公比为3的等比数列,其前n 项和213113332n n n B --=++++=.因为111a B ==,且当2n ≥时,131332n n n --<<, 所以把A B ⋃的所有元素从小到大排列为122334455,,,,,,,,,B a B a B a B a B ,所以212131,32n n n n n n c B c a -+-====.对于①,1221213131322n n nn n n c c c +-+--+=+==,取1011n =,有202320222021c c c =+,故①正确.对于②,因为2213123212n nn n c c ---=-⨯=是常数,所以{}2212n n c c -- 是以1为首项、1为公比的等比数列,故②正确.对于③,易知49503a =,则数列{}n c 的前98项和()()98235012349T a a a B B B B =++++++++()234912350234950B B B B a a a B B B B =++++++++=++++()5123505014931073333224-=⨯+++-=<,前99项和515050509998999850310731531093424T T c T B --⨯-=+=+=+=>,故使得503n T >成立的n 的最小值为99,故③错误.对于④,因为当2n ≥时,0n n B a >>,所以11113n n n B a -<=, 所以2121122311111111111112122333333nn nn i i n n c B B B a a a -=+⎛⎫⎫⎛⎛⎫⎛⎫=+++++++<+++++++=-< ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎝⎭⎭∑,又因为21211112n n i i i i c c -==<<∑∑,所以112ni ic =<∑恒成立,故④正确.11.答案:1m +解析:由已知,得123a a a +=,234a a a +=,…,202020212022a a a +=,以上各式相加,得1234202020222a a a a a a +++++=,即220202022a S a +=.又21a =,2020S m =,所以20221a m =+.12.答案:12n -解析:易知0n a ≠,由()*12n n a a n +=∈N ,可得12n na a +=, 所以当2n ≥时,12nn a a -=, 所以()113211221122222n n n n n n n a a a a a a a a a a -----=⨯⨯⨯⨯=⨯⨯⨯⨯=个, 所以()122n n a n -=≥. 因为当1n =时也满足上式,所以数列{}n a 的通项公式为()1*2n n a n -=∈N . 13.答案:7解析:令()2n k k *=∈N ,则有()22261k k a a k k *++=-∈N , 2468101214165,171,942=,a a a a a a a a ∴+=+=+=+,∴前16项的所有偶数项和 517294192S =+++=偶,∴前16项的所有奇数项和 54092448S =-=奇,令()21n k k *=-∈N ,则有()212164k k a a k k *+--=-∈N .()()()211315375k a a a a a a a a +∴-=-+-+-+ ()2121281464k k a a k +-+-=++++-=()(264)(31)2k k k k k *+-=-∈N ,()211(31)k a k k a k *+∴=-+∈N ,31517192,10,24,44a a a a a a a ∴=+=+=+=+ 1111131151,70,102,140a a a a a a a =+=+=+,∴前16项的所有奇数项和13 S a a =+++奇151182102444701021408a a a =+++++++=+392448=. 17a ∴=.14.答案:1n a n =+解析:依题意数列{}n a 满足12a =,且31122234n n a a a a a n-++++=-①. 当2n =时,1222a a =-,23a =, 3112122341n n n a a aa a a n n -++++++=-+②, ②-①得11n n n a a a n +=-+,121n n a n a ++=+ 则()112n n a n n a n-+=≥, 所以13211221132112n n n n n a a a a n n a a n a a a a n n ---+=⋅⋅⋅⋅⋅=⋅⋅⋅⋅=+-, 1a ,2a 都符合上式.所以{}n a 的通项公式为1n a n =+. 故答案为:1n a n =+. 15.答案:(1)见解析 (2)存在,1λ=.解析:(1)11n n n a S S ++=-,2211n n n S a S λ++=-,()2211n n n n S S S S λ++∴=--,()1120n n n S S S λ++∴--=.0n a >,10n S +∴>,120n n S S λ+∴--=,12n n S S λ+∴=+.(2)12n n S S λ+=+, 122n n S S n λ-∴=+≥(), 两式相减,得1(22)n n a a n +≥=. 212S S λ=+,即2112a a a λ+=+, 21a λ∴=+,由20a >,得1λ>-.若{}n a 是等比数列,则2132a a a =,即22(1)(1)λλ+=+,得1λ=. 经检验,1λ=符合题意.故存在1λ=,使得数列{}n a 为等比数列.。
高中数学选择性必修二 4 1 数列的概念与简单表示法(含答案)

课时同步练4.1 数列的概念与简单表示法(1)一、单选题1.已知数列{}n a 中,2n+5,则3a =( ) A .13 B .12 C .11 D .10【答案】C【解析】由已知得2×3+5=11. 故选C .2.有下面四个结论:①数列的通项公式是唯一的;②每个数列都有通项公式;③数列可以看作一个定义在正整数集上的函数;④数列的图象是坐标平面上有限或无限个离散的点.其中真命题的个数为( ) A .0个B .1个C .2个D .3个 【答案】B【解析】对①,数列1,1,1,1,--其通项公式1(1)n n a +=-,也可以是3(1)n n a +=-,故①错误; 对②,数列的项与n 具备一定的规律性,才可求出数列的通项公式,所以有的数列是无通项公式的,故②错误;对③,数列可以看作一个定义在正整数集上或正整数集的子集上的函数,故③错误; 对④,由数列的定义知命题正确.故选B.3.已知数列-1,0,19,18,…,22n n -,…中,则572是其( ) A .第14项 B .第12项 C .第10项 D .第8项【答案】B 【解析】令22n n-=572,化为:5n 2﹣72n +144=0, 解得n =12,或n =125(舍去). 故选B .4.数列{}n a 的通项公式()*2n a n n =∈N不满足下列递推公式的是( ) A .()122n n a a n -=+ B .()1223n n n a a a n --=-C .()()()11222n n n n a a a a n ---=-D .()122n n a a n -= 【答案】D【解析】将2n a n =代入四个选项得:A. 22(1)2n n =-+ 成立;B. 222(1)2(2)n n n =⨯--- 成立;C. ()2222(1)2(1)][2n n n n -=--- 成立;D. 222n n =⨯ 不恒成立。
高中数学选择性必修二 4 1数列的概念 -B提高练(含答案)

4.1数列的概念(1) -B 提高练一、选择题1.(2020·全国高二课时练习)数列2,0,2,0…的通项公式可以是( )A .()()221,02,n n k k N a n k k N**⎧=+∈⎪=⎨=∈⎪⎩B .()2sin2n n a n N π*=∈ C .()()11nn a n N *=-+∈D .()cos 1n a n n Nπ*=+∈【答案】B【详解】选项A 中,n 取不到1,其通项公式中不含1a ,A 错误;选项B 中,当n 是奇数时,212n a =⨯=,当n 是偶数时,200n a =⨯=,B 正确; 选项C 中,102a =≠,C 错误;选项D 中,1cos 102a π=+=≠,D 错误.故选:B .2.(2020·河南高二月考(理))已知数列{}n a 的通项公式为21nn a =+,则257是这个数列的( )A .第6项B .第7项C .第8项D .第9项【答案】C【详解】令25721n =+,解得8n =.故选:C3.(2020·海伦市第一中学高二期中)大衍数列,来源于《乾坤普》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两翼数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,……则此数列的第40项为( ). A .648 B .722 C .800 D .882【答案】C【详解】由0,2,4,8,12,18,24,32,40,50…,可得偶数项的通项公式:222n a n =.则此数列第40项为2220800⨯=.故选:C4.(2020·全国高二课时练习)已知数列{}n a 的通项公式为2130n na n =+(n *∈N ),且数列{}n a 从第n 项起单调递减,则n 的最小值为( ) A .11 B .12C .13D .不存在【答案】A【详解】2130n n a n =+,()1211130n n a n ++∴=++, ()()212222113021311302131130n n n n n n a a n n n n n n ++-+∴-=-=++++-++,由数列{}n a 从第n 项起单调递减可得10n n a a +-<,即21300n n --+<,n *∈N ,解得n>或n <去),2252123<<,110.5112∴<<, 11n ∴≥,111213a a a ∴>>>,即从第11项起,{}n a 单调递减,n ∴的最小值为11.故选:A .5.(多选题)(2020·沭阳如东中学高二月考)已知数列{}n a 的前4项为2,0,2,0,则该数列的通项公式可能为( )A .0,2,n n a n ⎧=⎨⎩为奇数为偶数B .1(1)1n n a -=-+C .2sin 2n n a π= D .cos(1)1n a n π=-+【答案】BD【详解】因为数列{}n a 的前4项为2,0,2,0,选项A :不符合题设;选项B :01(1)12,a =-+=12(1)10,a =-+=23(1)12,a =-+=34(1)10a =-+=,符合题设;选项C :,12sin2,2a π==22sin 0,a π==332sin22a π==-不符合题设;选项D :1cos 012,a =+=2cos 10,a π=+=3cos 212,a π=+=4cos310a π=+=,符合题设.故选:BD.6. (多选题)(2020·全国高二课时练)若数列{}n a 满足:对任意正整数n ,{}1n n a a +-为递减数列,则称数列{}n a 为“差递减数列”.给出下列数列{}()*n a n N ∈,其中是“差递减数列”的有( )A .3n a n =B .21n a n =+C .n a n =D .ln1n n a n =+ 【答案】CD【详解】对A ,若3n a n =,则13(1)33n n a a n n +-=+-=,所以{}1n n a a +-不为递减数列,故A 错误;对B ,若21n a n =+,则221(1)21n n a a n n n +-=+-=+,所以{}1n n a a +-为递增数列,故B 错误;对C ,若n a n =,则1111n n a a n n n n+-=+-=++,所以{}1n n a a +-为递减数列,故C 正确;对D ,若ln 1n n a n =+,则121111lnln ln ln(1)2122n n n n n n a a n n n n n n++++-=-=⋅=+++++,由函数21ln(1)2y x x=++在(0,)+∞递减,所以数{}1n n a a +-为递减数列,故D 正确.故选:CD . 二、填空题7.(2020·西藏拉萨市二中学高二期中)21211,,,,,,3253n a ---=__________.【答案】()211nn -+ 【详解】数列21211,,,,,,3253---的各项可以顺次整理为:22222,,,,,,23456---分母是项数加1,分子都是2,前面的正负号可用()1n-调节, 得到()211nn a n =-+,8.(2020·安徽宣城市高二期末)已知()2*2020,n a n tn n N t R =-+∈∈,若数列{}n a 中最小项为第3项,则t ∈________. 【答案】(5,7)【详解】因为()22020f x x tx =-+开口向上,对称轴为2t x =,则由题意知57222t <<, 所以(5,7)t ∈.9.(2020·秭归县第一中学高二期中)若数列{a n }为单调递增数列,且212n na n λ=-+,则a 3的取值范围为__________. 【答案】(-∞,6)【详解】当n ≥2时,1121(23)2222n n nn n a a n n λλλ---=-+--+=-,因为数列{a n }为单调递增数列,所以202nλ->对n ≥2(n ∈N )恒成立,即λ<2n +1对n ≥2(n ∈N )恒成立,所以λ<8, 所以3568a λ=+<,故a 3的取值范围为(-∞,6).10.(2020·全国高二课时练习)分形几何学是一门以不规则几何形态为研究对象的几何学,它的创立,为解决传统科学众多领域的难题提供了全新的思路.如图是按照一定的分形规律生长成的一个树形图,则第13行中实心圆点的个数是__________.【答案】144【详解】由题意及图形知,不妨构造数列{}n a 表示第n 行实心圆点的个数的变换规律,其中每一个实心圆点的下一行均分为一个实心圆点与一个空心圆点,每个空心圆点下一行均为实心圆点.故从第三行开始,每行的实心圆点数均为前两行实心圆点数之和.即120,1a a ==,且3n ≥时,12n n n a a a --=+,故第1行到第13行中实心圆点的个数分别为: 0,1,1,2,3,5,8,13,21,34,55,89,144. 三、解答题11.(2020·全国高二课时练)在数列{}n a 中,2293n a n n =-++.(1)-107是不是该数列中的某一项?若是,其为第几项? (2)求数列中的最大项.【详解】(1)令22107,293107,291100n a n n n n =--++=---=,解得10n =或112n =-(舍去).所以10107a =- (2)229105293248n a n n n ⎛⎫=-++=--+ ⎪⎝⎭, 由于*n ∈N ,所以最大项为213a =12.(2021·全国高二课时练)在数列{}n a 中,已知1n an a bn =+,且2369,57a a ==. (1)求通项公式n a ; (2)求证:{}n a 是递增数列;(3)求证:312n a <. 【详解】(1)∵2369,57a a ==, ∴2621539317ab a b ⎧=⎪⎪+⎨⎪=⎪+⎩解得32a b =⎧⎨=⎩ 因此321n na n =+.证明(2)∵13(1)3302(1)121(23)(21)n n n n a a n n n n ++-=-=>+++++,∴1n n a a +>,故{}n a 是递增数列.(3)∵33(21)333222121242n n n a n n n +-===-+++,而*,1n n ∈N , ∴33333,12242242n n a a n <=--=++. 故312n a <.。
【高中数学】新人教A版高二第 1 课时 数列的概念与表示(练习题)

新人教A版高二第 1 课时数列的概念与表示(1212)1.数列−1,3,−5,7,−9,…的一个通项公式为()A.a n=2n−1B.a n=(−1)n(2n−1)C.a n=(−1)n(1−2n)D.a n=(−1)n+1(2n−1)2.数列13,14,15,…,1n,…的第11项是()A.110B.111C.112D.1133.数列2,6,12,20,…的第6项是()A.42B.56C.90D.724.已知n∈N∗,给出4个表达式:①a n={0,n为奇数,1,n为偶数;②a n=1+(−1)n2;③a n=1+cosnπ2;④a n=|sin nπ2|.其中能作为数列:0,1,0,1,0,1,0,1,⋯的通项公式的是()A.①②③B.①②④C.②③④D.①③④5.数列{a n}的通项公式为a n=−58+16n−n2,则()A.{a n}是递增数列B.{a n}是递减数列C.{a n}先增后减,有最大值D.{a n}先减后增,有最小值6.已知a n=n2+n,那么()A.0是数列中的项B.20是数列中的项C.3是数列中的项D.930不是数列中的项7.已知数列{a n}的通项公式为a n=n2−kn,且{a n}为递增数列,则k的取值范围是()A.(−∞,2]B.(−∞,3)C.(−∞,2)D.(−∞,3]8.已知数列{a n}的前4项分别为−12,34,−58,716,则数列{a n}的通项公式是()A.a n=2n−12n B.a n=(−1)n·(2n−1)2nC.a n=2n+12n D.a n=(−1)n·(2n+1)2n9.已知数列{a n}的通项公式为a n=(−1)n(2n−1),则a5=.10.若数列{a n}的通项满足a nn=n−2,那么15是这个数列的第项. 11.已知数列{a n}的通项公式为a n=19−2n,则使a n>0成立的正整数n的最大值为.12.已知对任意的正整数n,都有a n=n2+λn成立.若数列{a n}是递增数列,则实数λ的取值范围是.13.写出下列数列的一个通项公式.(1)0.9,0.99,0.999,0.9999,…;(2)112,245,3910,41617,…;(3)12,34,78,1516,…;(4)3,5,9,17,….14.根据数列{a n}的通项公式,写出数列的前5项,并用图象表示出来.(1)a n=3+(−1)n2;(2)a n=sin(n+1)π2+1.15.已知f(x)={(2a−1)x+4(x⩽1),a x(x>1),数列{a n}(n∈N∗)满足a n=f(n),且{a n}是递增数列,则a的取值范围是()A.(1,+∞)B.(12,+∞) C.(1,3) D.(3,+∞)16.如图所示,有一个n(n⩾2)行n+1列的士兵方阵.(1)写出一个数列,用它表示当n分别为2,3,4,5,6,…时方阵中的士兵人数;(2)说出(1)中数列的第5项与第6项表示的意义,并求a5,a6;(3)若把(1)中的数列记为{a n},求该数列的通项公式;(4)在(3)的数列{a n}中,求a10,并说明a10所表示的实际意义.参考答案1.【答案】:B【解析】:因为数列1,3,5,7,9,…的通项公式为a n=2n−1,由题中数列的奇数项为负,得所求数列的通项公式为a n=(−1)n(2n−1).故选B.2.【答案】:D【解析】:由题意可归纳出所给数列的通项公式为a n=1n+2,所以a11=113.故选 D.3.【答案】:A【解析】:因为2=1×2,6=2×3,12=3×4,20=4×5,…,所以所给数列的第6项为6×7=42.故选A.4.【答案】:A【解析】:①②③逐一写出均为0,1,0,1,0,1,⋯,满足题意,④逐一写出为1,0,1,0,1,0,1,⋯,不满足题意,故选A.5.【答案】:C【解析】:a n=−(n−8)2+6是关于n的二次函数,其图象开口向下.则当n⩽8时,{a n}是递增数列,当n>8时,{a n}是递减数列,当n=8时,a n取得最大值.故选 C.6.【答案】:B【解析】:令n2+n=0,解得n=0或n=−1,因为n∈N∗,所以0不是数列中的项,故选项A错误;令n2+n=20,解得n=4或n=−5(舍),则a4=20,故选项B正确;令n2+n=3,易知该方程无有理数根,则3不是数列中的项,故选项C错误;令n2+n=930,解得n=30或n=−31(舍),则a30=930,即930是数列中的项,故选项D错误.故选 B.7.【答案】:B【解析】:a n+1−a n=(n+1)2−k(n+1)−n2+kn=2n+1−k,因为{a n}为递增数列,所以应满足a n+1−a n>0恒成立,即2n+1−k>0恒成立,即k<2n+1恒成立,又n∈N∗,所以(2n+1)min=3,所以k<3.故选B.8.【答案】:B【解析】:观察数列{a n}的前4项,可知分母为2n,分子是奇数,为2n−1,同时符号正负相间,可用(−1)n表示,所以a n=(−1)n·(2n−1)2n.故选 B.9.【答案】:−9【解析】:令n=5,可得a5=−9.10.【答案】:5【解析】:由a nn =n−2可知an=n2−2n,令n2−2n=15,解得n=5(负值舍去),则15是这个数列的第5项.11.【答案】:9【解析】:由a n=19−2n>0,得n<192,因为n∈N∗,所以n⩽9,则满足题意的正整数n的最大值为9.12.【答案】:λ>−3【解析】:∵数列{a n}是递增数列,∴a n+1−a n=(n+1)2+λ(n+1)−n2−λn=2n+1+λ>0对任意的正整数n恒成立,即λ>−2n−1对任意的正整数n恒成立,∴λ>−3.13(1)【答案】0.9=1−0.1=1−10−1,0.99=1−10−2,0.999=1−10−3,0.9999=1−10−4,故a n=1−10−n(n∈N∗).(2)【答案】112=1+112+1,245=2+2222+1,3910=3+3232+1,41617=4+4242+1,故a n=n+n2n2+1(n∈N∗).(3)【答案】12=21−121=1−121,3 4=22−122=1−122,7 8=23−123=1−123,15 16=24−124=1−124,故a n=2n−12n =1−12n(n∈N∗).(4)【答案】3=1+2,5=1+22,9=1+23,17=1+24,故a n=1+2n(n∈N∗).14(1)【答案】a1=3+(−1)12=1,a2=3+(−1)22=2,a3=1,a4=2,a5=1.图象如图①所示.(2)【答案】a1=sin(1+1)π2+1=sinπ+1=1,a2=sin (2+1)π2+1=0,a3=sin (3+1)π2+1=1,a4=sin (4+1)π2+1=2,a5=sin(5+1)π2+1=1. 图像如图②所示.15.【答案】:D【解析】:因为{a n}是递增数列,所以{a>1,a2>2a−1+4,解得a>3,则a的取值范围是(3,+∞).故选 D.16(1)【答案】当n=2时,表示士兵方阵为2行3列,人数为6;当n=3时,表示士兵方阵为3行4列,人数为12.依此类推.故所求数列为6,12,20,30,42,….(2)【答案】方阵的行数比数列的序号大1,因此第5项表示6行7列方阵中的士兵人数,第6项表示7行8列方阵中的士兵人数,故a5=42,a6=56.(3)【答案】由(1)知该数列的前4项分别为6=2×3,12=3×4,20=4×5,30=5×6,因此a n=(n+1)(n+2).(4)【答案】由(3)知a10=11×12=132,a10表示11行12列方阵中的士兵的人数.。
数列试题及答案

数列试题及答案数列是数学中的一种重要概念,通过研究和分析数列可以揭示出其中的规律和特点。
下面将介绍几道常见的数列试题,并给出详细的解答。
1. 试题一已知数列{an}满足an = 3n - 1,求前10项的和Sn。
解答:首先我们可以算出数列的前10项:a1 = 3(1) - 1 = 2a2 = 3(2) - 1 = 5a3 = 3(3) - 1 = 8...a10 = 3(10) - 1 = 29然后求和:Sn = a1 + a2 + a3 + ... + a10= 2 + 5 + 8 + ... + 29观察可知,每一项等于前一项加上3,因此可以利用等差数列的求和公式求解:Sn = (a1 + a10) * 10 / 2= (2 + 29) * 10 / 2= 31 * 5= 155所以,前10项的和Sn = 155。
2. 试题二给定数列{bn}的前4项为1,3,9,27,请写出该数列的通项公式。
解答:观察可知,每一项等于前一项乘以3,因此可以得出该数列的通项公式为:bn = 3^(n-1)其中,n为项数。
根据该公式可求得后续项。
3. 试题三已知数列{cn}满足c1 = 1,c2 = 2,c3 = 4,且每一项等于前两项之和。
求该数列的第10项。
解答:根据题意,数列的第4项开始每一项等于前两项之和:c4 = c3 + c2 = 4 + 2 = 6c5 = c4 + c3 = 6 + 4 = 10c6 = c5 + c4 = 10 + 6 = 16...通过计算可以得出数列的前10项如下:c1 = 1c2 = 2c3 = 4c4 = 6c5 = 10c6 = 16c7 = 26c8 = 42c9 = 68c10 = 110所以,该数列的第10项为c10 = 110。
4. 试题四已知等差数列{dn}的前4项为2,5,8,11,请写出该数列的通项公式,并求第n项。
解答:观察可知,公差为3,首项为2,因此该等差数列的通项公式为:dn = 2 + 3(n-1)其中,n为项数。
高中数学选择性必修二 4 1 数列的概念尖子生同步培优题典(含答案)

2020-2021年高二数学选择性必修二尖子生同步培优题典4.1数列的概念 解析版学校:___________姓名:___________班级:___________考号:___________注意事项:本卷共16小题,6道单选题,3道多选题,3道填空题,4道解答题。
一、单选题1.已知数列{}n a 中,13=4a ,111n n a a -=-(,2n N n +∈≥),那么2020a 等于( )A .13- B .34C .2D .4【答案】B 【解析】 【分析】根据13=4a ,111n n a a -=-,计算数列的前几项,得到数列{}n a 是以3为周期的数列求解.【详解】因为13=4a ,111n n a a -=-,所以211113a a =-=-, 32114a a =-=, 431314a a =-=, …所以数列{}n a 是以3为周期的数列, 所以202067331134a a a ⨯+===, 故选:B 【点睛】本题主要考查数列的周期性的应用,还考查了运算求解的能力,属于基础题. 2.数列1、1、2、3、5、8、13、21、34、称为斐波那契数列,是意大利著名数学家斐波那契于1202年在他撰写的《算盘全书》中提出的,该数列的特点是:从第三项起,每一项都等于它前面两项的和.在该数列的前2020项中,偶数的个数为( ) A .505 B .673C .674D .1010【答案】B 【解析】 【分析】由斐波那契数列的特点可知,该数列只有第()3k k *∈N 项为偶数,再由202036731=⨯+可求得结果. 【详解】由斐波那契数列的特点,可得此数列只有第()3k k *∈N项为偶数,由于202036731=⨯+,所以前2020项中偶数的个数为673. 故选:B. 【点睛】本题考查斐波那契数列的应用,考查推理能力,属于基础题.3.“干支纪法”是我国记年、月、日、时的序号的传统方法,天干地支简称“干支”,天干指:甲、乙、丙、丁、戊、己、庚、辛、壬、癸.“地支”指:子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥.如,农历1861年为辛酉年,农历1862年为壬戌年,农历1863年为癸亥年,则农历2068年为( ) A .丁亥年 B .丁丑年C .戊寅年D .戊子年【答案】D 【解析】 【分析】由题意得天干是以10为周期的数列,地支是以12为周期的数列,以1861为首项,即可得答案. 【详解】记1a =辛,1b =酉(1861);2a =壬,2b =戌(1862);3a =癸,3b =亥(1863), 所以记天干为数列{}n a ,且最小正周期为10,记地支为数列{}n b ,且最小正周期为12, 故20688a a ==戊,20684b b ==子(2068), 故选:D . 【点睛】本题考查数列的周期性,难点在于需将题目信息转化为所学数列的知识,考查逻辑推理,归纳分析的能力,属中档题.4.原始的蚊香出现在宋代.根据宋代冒苏轼之名编写的《格物粗谈》记载:“端午时,贮浮萍,阴干,加雄黄,作纸缠香,烧之,能祛蚊虫.”如图,为某校数学兴趣小组用数学软件制作的“螺旋蚊香”,画法如下:在水平直线l上取长度为1的线段AB,做一个等边三角形ABC,然后以点B为圆心,AB 为半径逆时针画圆弧,交线段BC的延长线于点D,再以点C为圆心,CD为半径逆时针画圆弧,交线段AC的延长线于点E,以此类推,当得到的“螺旋蚊香”与直线l恰有21个交点时,“螺旋蚊香”的总长度的最小值为()A.310πB.340πC.930πD.1020π【答案】A【解析】【分析】根据画圆弧的规律:分别以B,C,A 为圆心,抽象半径长度的数列,明确圆弧与直线的交点情况,再根据当“螺旋蚊香”与直线l恰有21个交点时,若使“螺旋蚊香”的总长度最小,确定数列的项数,求得最后圆弧的半径即可.【详解】如图所示:当以B为圆心,半径为:1,4,7,10,…除起点外,与直线无交点,①当以C为圆心,半径为:2,5,8,11,…与直线有一个点,②当以A为圆心,半径为:3,6,9,12,…除终点(即①的起点,点A 除外)外,与直线无交点,③所以当“螺旋蚊香”与直线l恰有21个交点时,若使“螺旋蚊香”的总长度最小,则完成整数个循环,所以以B 为圆心的弧与直线只有交点A ,以C 为圆心的弧与直线10个交点,以A 为圆心的弧与直线有10 个交点,即数列②有10项,数列③有10项,所以最后一个圆弧的半径为33(101)30r =+-= ,所以“螺旋蚊香”的总长度的最小值为()()30130112123 (302310332)l πππ+=⨯⨯++++=⨯= . 故选:A 【点睛】本题主要考查数列的抽象与等差数列的通项公式和前n 项和的应用,还考查了分析求解问题的能力,属于中档题.5.衍数列来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和,它是中华传统文化中隐藏着的世界数学史上第一道数列题,该数列从第一项起依次是0,2,4,8,12,18,24,32,40,50…,则该数列第16项为( ) A .152 B .134 C .128 D .102【答案】C 【解析】 【分析】根据数据找出规律,依次写出来即可. 【详解】前10项依次是0,2,4,8,12,18,24,32,40,50,偶数项分别为2,8,18,32,50,…,可得偶数项的通项公式: 222n a n =.所以该数列第16项为21628=128a =⨯. 故选:C. 【点睛】本题考查了数列递推关系、通项公式、归纳法,考查了推理能力与计算能力,属于中档题.6.公元前四世纪,毕达哥拉斯学派对数和形的关系进行了研究.他们借助几何图形(或格点)来表示数,称为形数.形数是联系算术和几何的纽带.如图所示,数列1,6,15,28,45,…,从第二项起每一项都可以用六边形表示出来,故称它们为六边形数,那么该数列的第11项对应的六边形数为( )A .153B .190C .231D .276【答案】C 【解析】 【分析】根据题中所给图与对应的六边形数,记第n 个六边形数为n a ,找出规律,相邻两项差构成等差数列,累加求得22n a n n =-,将11n =代入求得结果.【详解】记第n 个六边形数为n a ,由题意知:11a =,215141a a -==+⨯,32142a a -=+⨯,43143a a -=+⨯,,114(1)n n a a n --=+-,累加得21(1)[543]59[14(1)]212n n n a a n n n -+--=++++-==--,即22n a n n =-,所以21121111231a =⨯-=,故选:C. 【点睛】该题考查的是有关数列的问题,涉及到的知识点有利用累加法求数列的通项公式,属于中档题目.二、多选题7.意大利著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,….,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”,记n S 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68a =B .733S =C .135********a a a a a +++⋅⋅⋅+=D .22212201920202019a a a a a ++⋅⋅⋅⋅⋅⋅+=【分析】由题意可得数列{}n a 满足递推关系12211,1,(3)n n n a a a a a n --===+≥,对照四个选项可得正确答案. 【详解】对A ,写出数列的前6项为1,1,2,3,5,8,故A 正确; 对B ,71123581333S =++++++=,故B 正确;对C ,由12a a =,342a a a =-,564a a a =-,……,201920202018a a a =-,可得:135********a a a a a +++⋅⋅⋅+=.故1352019a a a a +++⋅⋅⋅+是斐波那契数列中的第2020项.对D ,斐波那契数列总有21n n n a a a ++=+,则2121a a a =,()222312321a a a a a a a a =-=-,()233423423a a a a a a a a =-=-,……,()220182018201920172018201920172018a a a a a a a a =-=-,220192019202020192018a a a a a =-2222123201920192020a a a a a a +++⋅⋅⋅⋅⋅⋅+=,故D 正确;故选:ABCD. 【点睛】本题以“斐波那契数列”为背景,考查数列的递推关系及性质,考查方程思想、转化与化归思想,考查逻辑推理能力和运算求解能力,求解时注意递推关系的灵活转换.8.斐波那契数列,又称黄金分割数列、兔子数列,是数学家列昂多·斐波那契于1202年提出的数列.斐波那契数列为1,1,2,3,5,8,13,21,……,此数列从第3项开始,每一项都等于前两项之和,记该数列为(){}F n ,则(){}F n 的通项公式为( )A .(1)1()2n n F n -+=B .()()()11,2F n F n F n n +=+-≥且()()11,21F F ==C .()n nF n ⎡⎤⎥=-⎥⎝⎭⎝⎭⎦D .()n nF n ⎡⎤⎥=+⎥⎝⎭⎝⎭⎦【分析】根据数列的前几项归纳出数列的通项公式,再验证即可; 【详解】解:斐波那契数列为1,1,2,3,5,8,13,21,……,显然()()11,21F F ==,()()()3122F F F =+=,()()()4233F F F =+=,,()()()11,2F n F n F n n +=+-≥,所以()()()11,2F n F n F n n +=+-≥且()()11,21F F ==,即B 满足条件;由()()()11,2F n F n F n n +=+-≥, 所以()()()()11F n n F n n ⎤+-=-⎥⎣⎦所以数列()()1F n n ⎧⎫⎪⎪+⎨⎬⎪⎪⎩⎭为公比的等比数列, 所以()()1nF n n +=⎝⎭()11515()n F F n n -+=+, 令1nn n Fb -=⎝⎭,则11n n b +=+,所以1n n b b +-=, 所以n b⎧⎪⎨⎪⎪⎩⎭32为公比的等比数列,所以1n n b -=+,所以()11152n n n nF n --⎤⎤⎛⎫+⎥⎥=+=- ⎪ ⎪⎥⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦; 即C 满足条件; 故选:BC 【点睛】考查等比数列的性质和通项公式,数列递推公式的应用,本题运算量较大,难度较大,要求由较高的逻辑思维能力,属于中档题.9.对于数列{}n a ,若存在正整数k ()2k ≥,使得1k k a a -<,1k k a a +<,则称k a 是数列{}n a 的“谷值,k 是数列{}n a 的“谷值点”,在数列{}n a 中,若98n a n n=+-,则数列{}n a 的“谷值点”为( ) A .2 B .3C .5D .7【答案】AD 【解析】 【分析】由数列的通项公式求出前七项各项的值,然后根据题意进行求解即可, 【详解】 因为98n a n n =+-,所以123456783761292,,2,,,,,245278a a a a a a a a ========, 当7,n n N ≥∈,9998088n n a n n n n n+->∴=+-=+-,此时数列单调递增, 21a a <,23a a <,76a a <,78a a <,所以数列{}n a 的“谷值点”为2,7. 故选:AD 【点睛】本题考查了数学阅读能力,考查了数学运算能力,考查了数列的单调性,属于中档题.三、填空题10.在数列{}n a 中,11a =,()32122223n n a a a a a n n*++++=∈N ,则n a =______. 【答案】21nn + 【解析】 【分析】由已知得:当2n ≥时,()31211222231n n a a a a a n --++++=-,与原式相减得12n n n a a a n -=-,即11+1n n nn n a a n --=,递推可得答案. 【详解】由题意得:当2n ≥时,()31211222231n n a a a a a n --++++=-,所以12n n n a a a n -=-,即()2211n n na n a --=,也即是11+1n n n n n a a n --=,所以121+1221211n n n n n a n n n a a a n ---===-=-=, 所以21n na n =+,故答案为:21nn +. 【点睛】本题考查由数列的递推式求数列的通项,属于中档题. 11.已知数列{}n a 满足1133,2,n n a a a n +=-=则na n的最小值为__________. 【答案】212【解析】 【分析】先利用累加法求出a n =33+n 2﹣n ,所以331n a n n n =+-,设f (n )331n n=+-,由此能导出n =5或6时f (n )有最小值.借此能得到na n的最小值. 【详解】解:∵a n +1﹣a n =2n ,∴当n ≥2时,a n =(a n ﹣a n ﹣1)+(a n ﹣1﹣a n ﹣2)+…+(a 2﹣a 1)+a 1=2[1+2+…+(n ﹣1)]+33=n 2﹣n +33且对n =1也适合,所以a n =n 2﹣n +33.从而331n a n n n=+- 设f (n )331n n =+-,令f ′(n )23310n-=+>,则f (n )在)+∞上是单调递增,在(0上是递减的,因为n ∈N +,所以当n =5或6时f (n )有最小值.又因为55355a =,66321662a ==, 所以n a n 的最小值为62162a =故答案为 212【点睛】本题考查了利用递推公式求数列的通项公式,考查了累加法.还考查函数的思想,构造函数利用导数判断函数单调性.12.已知数列{}n a 满足:12020a =,()2*11n n n a a a n N +=+-∈,若正整数k 使得2221212 (2) (2021)k k a a a a a a ++++=成立,则k =___________. 【答案】2019 【解析】 【分析】根据()2*11n n n a a a n N +=+-∈可得211n n n a a a +=-+且111n n n a a a ++=+,结合已知条件的等式成立,即可求k 的值; 【详解】()2*11n n n a a a n N +=+-∈知:211n n n a a a +=-+且111n n n a a a ++=+,则:22212213211...11...12020k k k k a a a a a a a a a a k +++++=-++-+++-+=-+, 311212121111......1112021k k k k a a a a a a a a a a ++++++=⋅⋅⋅=+++,而2221212...2 (2021)k k a a a a a a ++++=,∴112018120212021k k a k a +++-+=,即得2019k =.故答案为:2019 【点睛】本题考查了利用数列递推式,结合等式成立求数列的项数,注意结合已知等式中乘积形式、平方形式转化递推式求参数;四、解答题13.数列{}n a 中,254n a n n =-+.(1)18是数列中的第几项?(2)n 为何值时,n a 有最小值?并求最小值.【答案】(1)第7项;(2)2n =或3n =时,最小值为2- 【解析】【分析】(1)令25418n a n n =-+=且n *∈N ,解方程可得n 的值.(2)利用二次函数的单调性和最值可得n a 有最小值以及对应的n 的值.【详解】令25418n a n n =-+=,即25140n n --=,解得:7n =或2n =-(舍)(2)由254n a n n =-+,因为254y x x =-+,开口向上,对称轴52x =所以2n =或3n =时,n a 有最小值为2225242a =-⨯+=- . 【点睛】本题主要考查了判断数列中的项,以及求数列的最小项,属于基础题.14.下面图形都是由小正三角形构成的,设第n 个图形中的黑点总数为()f n .(1)求()()()()2,3,4,5f f f f 的值;(2)找出()f n 与()1f n +的关系,并求出()f n 的表达式.① ② ③ ④【答案】(1)见解析;(2)()23,*.f n n n N =∈ 【解析】【分析】(1)根据题意可直接写出结果;(2)分别计算出()()21f f -,()()32f f -,()()43f f -,()()54f f -,归纳出()()1f n f n +-,再由累加法即可求出()f n 的表达式.【详解】(1)由题意可得:()212f =,()327f =,()448f =,()575f =;(2)因为()()219f f -=; ()()3215f f -=; ()()4321f f -=; ()()5427f f -=; 观察猜想:()()1f n f n +-是一个首项为9公差为6的等差数列,即()()()191663f n f n n n +-=+-⨯=+.因为()()219f f -=;()()3215f f -=;()()4321f f -=;()()5427f f -=;()()163f n f n n --=-;把上述式子累加可得到:()()()()296311332n n f n f n +---==-; 又因为()13f =,所以()23f n n =. 【点睛】本题主要考查归纳推理以及累加法求数列的通项公式,属于常考题型.15.已知数列{}n a 中,11a =,214a =,且1(1))(2,3,4,n n n n a a n n a +-==-. (1)求3a 、4a 的值,(2)设*111()n n b n N a +=-∈试用n b 表示1n b +,并求{}n b 的通项公式; (3)设*1sin 3()cos cos n n n c n N b b +=∈⋅,求数列{}n c 的前n 项和n S . 【答案】(1)317a =,4110a =;(2)11n n n b b n++=,*n N ∈,3n b n =,*n N ∈;(3)()tan 33tan3n +-.【解析】【分析】(1)由数列{}n a 中,11a =,214a =,且1(1)(2,3,4,...)n n n n a n n a a +-==-,分别令2n =和3n =,求出3a 、4a 的值.(2)当2n ≥时,1(1)11111(1)(1)1n n n n n n n a n a n a n a n a n a +⎛⎫---=-==- ⎪---⎝⎭,即11n n n b b n -=-,则11n n n b b n++=,然后用累乘法求解.(3)由1sin 3tan(33)tan 3cos cos n n n c n n b b +==+-⋅,然后利用裂项相消法求解. 【详解】 (1)∵数列{}n a 中,11a =,214a =, 且1(1)(2,3,4,...)n n nn a n n a a +-==- ∴2321(21)1412724a a a -===--, 34312(31)17131037a a a ⨯-===--, ∴317a =,4110a =· (2)当2n ≥时,1(1)11111(1)(1)1n n n n n n n a n a n a n a n a n a +⎛⎫---=-==- ⎪---⎝⎭, ∴当2n ≥时,11n n n b b n -=-, 故11n n n b b n++=,*n N ∈, 累乘得111232...12341n n n n n b b nb n n n n ---=⨯⨯⨯⨯=----, ∵13b =,∴3n b n =,*n N ∈.(3)∵1sin 3cos cos n n n c b b +=⋅ sin(333)tan(33)tan 3cos(33)cos3n n n n n n+-==+-+⋅, ∴12n n S c c c =++⋯+()(tan6tan3)(tan9tan6)tan(33)tan3n n =-+-+++-()tan 33tan3n =+-·【点睛】本题主要考查数列的通项公式和前n 项和的求法以及累乘法和裂项求和法、两角差的正弦公式的应用,还考查了运算求解的能力,属于中档题..16.已知数列{}n a 满足1a t =,111n na a +=+,数列{}n a 可以是无穷数列,也可以是有穷数列,如取1t =时,可得无穷数列:1,2,32,53,...;取12t =-时,可得有穷数列:12-,1-,0. (1)若50a =,求t 的值; (2)若12n a <<对任意2n ≥,*n N ∈恒成立.求实数t 的取值范围;(3)设数列{}n b 满足11b =-,()*111n n b n N b +=-∈,求证:t 取数列{}n b 中的任何一个数,都可以得到一个有穷数列{}n a .【答案】(1)35t =-;(2)1t >;(3)证明见解析. 【解析】【分析】(1)根据题意,得到111n n a a +=-,逐项计算,求出1a ,即可得出结果; (2)根据()*122,n a n n N <<≥∈,得出131122n na a +<=+<,因此只需212a <<即可,由题中条件,求出2a ,得出不等式求解,即可得出结果;(3)由题意,得到111n n b b +=+,设1k a t b ==,()*k N ∈,逐项计算,得出10k a +=,即可证明结论成立.【详解】(1)由111n n a a +=+得111n n a a +=-, ∴41101a ==--,311112a ==---,2121312a ==---,1132513t a ===---; (2)若()*122,n a n n N <<≥∈,则1112n a <<,131122n n a a +<=+<,即112n a +<<,故只要212a <<即可,因为1a t =,所以21t a t +=,∴112t t+<<,解得1t >; (3)由111n n b b +=-得111n n b b +=+, 设1k a t b ==,()*k N ∈,则2111k ka b b -=+= 32111k k a b b --=+=,12111k a b b =+==-,11101k a +=+=-, 故{}n a 有1k +项,为有穷数列.即t 取数列{}n b 中的任何一个数,都可以得到一个有穷数列{}n a .【点睛】本题主要考查由递推公式求数列中的项,考查由数列不等式恒成立求参数的问题,考查有穷数列的证明,属于常考题型.。
高中数学选择性必修二 4 1 1数列的概念(知识梳理+例题+变式+练习)(含答案)

4.1.1数列的概念要点一数列的有关概念1.定义:按照确定的顺序排列的一列数.2.项:数列中的每一个数叫做这个数列的项;排在第一位的数称为这个数列的第1项(也叫首项).3.一般形式:a1,a2,a3,…,a n,…,简记为{}n a.【重点总结】(1)数列的项是指这个数列中的某一个确定的数,是一个函数值,也就是相当于f(n),而项数是指这个数在数列中的位置序号,它是自变量的值,相当于f(n)中的n.(2)数列1,2,3,4,5和数列5,3,2,4,1为两个不同的数列,因为二者的元素顺序不同,而集合{1,2,3,4,5}与这两个数列也不相同,一方面形式上不一致,另一方面,集合中的元素具有无序性.如果数列{a n}的第n项a n与序号n之间的关系可以用一个式子来表示,那么这个公式叫做这个数列的通项公式.要点四数列与函数的关系从函数的观点看,数列可以看作是特殊的函数,关系如下表:【基础自测】1.判断正误(正确的画“√”,错误的画“×”)(1){0,1,2,3,4}是有穷数列.()(2)数列1,2,3,4和数列1,2,4,3是同一数列.()(3)所有自然数能构成数列.()(4)数列1,3,5,7,…,2n +1,…的通项公式是a n =2n +1.( ) 2.若数列{a n }满足a n =2n ,则数列{a n }是( ) A .递增数列 B .递减数列 C .常数列 D .摆动数列【答案】A【解析】a n +1-a n =2n +1-2n =2n >0,∴a n +1>a n ,即{a n }是递增数列.故选A. 3.(多选题)数列-1,1,-1,1,…的通项公式可以为( ) A .a n =(-1)n -1 B .a n =(-1)n C .a n =cos n π D .a n =sin n π 【答案】BC4.数列1,2,7,10,13,…中的第26项为________. 【答案】219【解析】因为a 1=1=1,a 2=2=4,a 3=7,a 4=10,a 5=13,所以a n =3n -2, 所以a 26=3×26-2=76=219.题型一 数列的概念和分类1.数列-11,-20,-27,…,n 2-12n ,…是( ) A .递增数列 B .递减数列 C .常数列 D .摆动数列 【答案】D【解析】该数列从第2项起,第n 项与第n -1项的差为(n 2-12n )-[(n -1)2-12(n -1)]=2n -13,所以该数列的前6项单调递减,从第6项往后单调递增,故选D. 2.已知下列数列:①1,2,22,23,…,260;②1,0.5,0.52,0.53,…; ③-2,2,-2,2,…;④3,3,3,3,…;⑤0,12,23,34,…,n -1n ,…;⑥1,0,-1,…,sin n π2,….其中有穷数列是______;无穷数列是________; 递增数列是________;递减数列是________; 摆动数列是________;常数列是________.(填序号) 【答案】○1 ○2○3○4○5○6 ○1○5 ○2 ○3○6 ○4 【方法归纳】判断数列是哪一种类型的数列时要紧扣概念及数列的特点.对于递增、递减、摆动还是常数列要从项的变化趋势来分析;而有穷还是无穷数列则看项的个数有限还是无限. 题型二 由数列的前n 项求通项公式【例1】写出数列的一个通项公式,使它的前4项是下列各数: (1)-1,12,-13,14;(2)3,3,15,21; (3)0.9,0.99,0.999,0.999 9; (4)3,5,3,5.【解析】(1)任何一个整数都可以看成一个分数,所以此数列可以看做是自然数列的倒数,正负相间用(-1)的多少次幂进行调整,其一个通项公式为a n =(-1)n ·1n.(2)数列可化为3,9,15,21,即3×1,3×3,3×5,3×7,…,每个根号里面可分解成两数之积,前一个因数为常数3,后一个因数为2n -1,故原数列的一个通项公式为a n =3(2n -1)=6n -3. (3)原数列可变形为⎝⎛⎭⎫1-110,⎝⎛⎭⎫1-1102,⎝⎛⎭⎫1-1103,⎝⎛⎭⎫1-1104,…,故数列的一个通项公式为a n =1-110n . (4)数列给出前4项,其中奇数项为3,偶数项为5,所以通项公式的一种表示方法为a n =⎩⎪⎨⎪⎧3 (n 为奇数)5 (n 为偶数).此数列还可以这样考虑,3与5的算术平均数为3+52=4,4+1=5,4-1=3,因此数列的一个通项公式又可以写为a n =4+(-1)n . 【方法归纳】(1)据所给数列的前几项求其通项公式时,需仔细观察分析,抓住以下几方面的特征: ①分式中分子、分母的特征; ②相邻项的变化特征; ③拆项后的特征;④各项符号特征等,并对此进行归纳、联想.(2)观察、分析数列中各项的特点是最重要的,观察出项与序号之间的关系、规律,利用我们熟知的一些基本数列(如自然数列、奇偶数列等)转换而使问题得到解决,对于正负符号变化,可用(-1)n 或(-1)n +1来调整. 【跟踪训练】写出下列数列的一个通项公式:(1)0,3,8,15,24,…; (2)1,-3,5,-7,9,…; (3)112,223,334,445,…;(4)1,11,111,1 111,….【解析】(1)观察数列中的数,可以看到0=1-1,3=4-1,8=9-1,15=16-1,24=25-1,…,所以它的一个通项公式是a n =n 2-1(n ∈N *).(2)数列各项的绝对值为1,3,5,7,9,…,是连续的正奇数,并且数列的奇数项为正,偶数项为负,所以它的一个通项公式为a n =(-1)n +1(2n -1)(n ∈N *).(3)此数列的整数部分1,2,3,4,…恰好是序号n ,分数部分与序号n 的关系为nn +1,故所求的数列的一个通项公式为a n =n +nn +1=n 2+2n n +1(n ∈N *).(4)原数列的各项可变为19×9,19×99,19×999,19×9 999,…,易知数列9,99,999,9 999,…的一个通项公式为a n =10n -1,所以原数列的一个通项公式为a n =19(10n -1)(n ∈N *).题型三 数列的单调性【例2】已知函数f (x )=1-2xx +1(x ≥1),构造数列a n =f (n )(n ∈N *).(1)求证:a n >-2;(2)数列{a n }是递增数列还是递减数列?为什么?【解析】(1)因为f (x )=1-2x x +1=3-2(x +1)x +1=-2+3x +1,所以a n =-2+3n +1.因为n ∈N *,所以a n >-2.(2)数列{a n }为递减数列.理由如下:因为a n =-2+3n +1,所以a n +1-a n =⎝⎛⎭⎫-2+3n +2-⎝⎛⎭⎫-2+3n +1=3n +2-3n +1=-3(n +2)(n +1)<0 即a n +1<a n ,所以数列{a n }为递减数列.先化简f (x )的解析式,再构造{a n },然后判断a n +1-a n 的符号. 【方法归纳】用作差法判断数列的单调性关键是判断符号,为此,一般要对差式进行通分,因式分解等变形;若用作商法则要特别注意分母的符号.【跟踪训练2】已知数列{a n }的第n 项可以表示为2n3n +1,n ∈N *,试判断数列的增减性.【解析】因为{a n }的第n 项为2n 3n +1,所以{a n }的第n +1项为2(n +1)3(n +1)+1.因为2(n +1)3(n +1)+1-2n3n +1=2n +23n +4-2n3n +1=(2n +2)(3n +1)-2n (3n +4)(3n +4)(3n +1)=6n 2+8n +2-6n 2-8n (3n +4)(3n +1)=2(3n +4)(3n +1)>0,所以2(n +1)3(n +1)+1>2n 3n +1,所以数列{a n }的第n +1项大于第n 项,故数列{a n }是递增数列.【易错辨析】忽视数列中n ∈N *致错例3 已知数列{a n }的通项公式为a n =n 2-5n +4,则a n 的最小值为________. 【答案】-2【解析】∵a n =n 2-5n +4=⎝⎛⎭⎫n -522-94, 可知对称轴方程为n =52,又n ∈N *,故n =2或3时, a n 有最小值,且a 2=a 3=-2. 【易错警示】1. 出错原因在求出a n =⎝⎛⎭⎫n -522-94时,忘记n ∈N *了,导致得出错误答案:-94. 2.纠错心得数列的定义域是正整数集合,是特殊的函数,所以解题时一定不要忘记n ∈N *这一条件.一、单选题1.某新冠疫苗接种点统计了一周(星期一至星期日)每天接种加强针的人数(单位:百人)如下:2,4,6,10,16,( ),42,因不慎丢失星期六的数据,根据数据的规律,则星期六的数据为( ) A .18 B .24 C .26 D .28【答案】C 【分析】通过观察数列的规律,可得到从第三个数据起,每个数据等于它前面两个数据之和,根据这一结论可推得结果. 【解析】从第三个数据起,每个数据等于它前面两个数据之和,所以星期六的数据为101626,+=故选:C.2.数列1,2, )A .8项B .7项C .6项D .5项【答案】A 【分析】【解析】,故通项公式为n a 8项.故选:A.3.若数列{}n a 满足12a =,11n n n a a a +=-,则2022a =( ) A .2 B .12C .-1D .-2【答案】C 【分析】由题意得数列{}n a 是周期为3的数列,即可得解. 【解析】由12a =,代入11n n n a a a +=-可得21=2a ,同理可得31=a -.由11n n n a a a +=-,得1=1n n na a a +-,从而有+12+1==1111=11n n n n n n n na a a a a a a a +------, 即2=11n na a +--,从而有3+1===11111n nn n na a a a a +-----, 所以数列{}n a 的周期为3, 所以2022a =36743=1a a ⨯=-. 故选:C.4.已知数列{}n a 满足1124n n n a a a ++=+且31a =,则2022a 的值为( ) A .1 B .2 C .4 D .-4【答案】A 【分析】根据数列的递推公式,可知数列{}n a 是周期为3的周期数列,由此即可求出结果. 【解析】因为数列{}n a 满足1124n n n a a a ++=+且31a =, 所以32324a a a =+,34424a a a =+, 所以2424a a =-=,, 又21224a a a =+,54524a a a =+ 所以1542a a ==-,, 又65624a a a =+,所以61a =所以1234564,2,1,4,2,1a a a a a a ==-===-=,……所以数列{}n a 是周期为3的周期数列,所以2022674331a a a ⨯===. 故选:A.5.已知数列{}n a 满足12a =,111n n n a a a +-=+,则2021a =( )A .2B .13C .12-D .3-【答案】A 【分析】写出数列的前5项,即可得出数列{}n a 是以4为周期的数列,202112a a ==. 【解析】解:因为12a =,所以由已知可得2211213a -==+,311131213a -==-+,41123112a --==--+, 531231a --==-+.可以判断出数列{}n a 是以4为周期的数列, 所以202112a a ==. 故选:A6.大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生原理,数列中的每一项都代表太极衍生过程,是中华传统文化中隐藏着的世界数学史上第一道数列题,其中一列数如下:0,2,4,8,12,18,24,32,40,50,……,按此规律得到的数列记为{}n a ,则15a =( ) A .98 B .112 C .128 D .132【答案】B 【分析】根据题意可得奇数项的通项公式,即可求出. 【解析】奇数项为0,4,12,24,40,…,即222221131517191,,,,,22222-----可得当n 为奇数时,212n n a -=,2151511122a -∴==. 故选:B.7.数列{}n a 满足11a =,21a =,且12n n n a a a --=-,()3n ≥,记数列{}n a 的前n 项和为n S ,则20S =( ) A .0 B .1C .2D .14【答案】C 【分析】利用递推公式求出数列{}n a 的前20项,直接求和. 【解析】因为11a =,21a =,且12n n n a a a --=-,()3n ≥,所以321110a a a -=-==;432011a a a ==--=-;543101a a a =-=--=-; 654110a a a =---==;()765011a a a =--=-=;876101a a a -=-==;同理递推可得:90a =;101a =-;111a =-;120a =;131a =;141a =;150a =;161a =-;171a =-;180a =;191a =;201a =.所以()()()()()()2011001111001111001111S =++++-+-+++++-+-+++++-+-++=2. 故选:C8.在数列{}n a 中,11a =,23a =,35a =,31n n a a +=,则515252021log log log a a a ++⋅⋅⋅+=( ) A .0 B .1 C .5log 3 D .5log 15【答案】B 【分析】计算得到数列周期为6,化简得到原式()2515log a a a =⋅⋅⋅⋅,计算得到答案. 【解析】31n n a a +=,故361n n a a ++=,故6n n a a +=,数列的周期为6.11a =,23a =,35a =,41a =,513a =,615a =,1234561a a a a a a =,()()515252021521212502155log log log lo l l g og o 5g 1a a a a a a a a a ⋅++⋅⋅⋅+=⋅⋅⋅=⋅⋅⋅⋅==.故选:B.二、多选题9.已知数列{a n }中,a 1=3,a n +1=-11n a +,能使a n =3的n 可以为( ) A .22 B .24 C .26 D .28【答案】AD 【分析】通过计算找到数列的周期,即得解. 【解析】解:由a 1=3,a n +1=-11n a +,得a 2=-14,a 3=-43,a 4=3. 所以数列{a n }是周期为3的数列,故a 22=a 28=3. 故选:AD10.下列四个选项中,正确的是( ) A .数列的图象是一群孤立的点B .数列1,1-,1,1-,…与数列1-,1,1-,1,…是同一数列C .数列23,34,45,56,…的一个通项公式是()*1n n a n N n =∈+ D .数列12,14,…,12n是递减数列 【答案】AD 【分析】利用数列通项公式、数列的图象、数列的定义以及数列的单调性依次判断四个选项即可. 【解析】解:对于A ,由数列的通项公式以及*n N ∈可知,数列的图象是一群孤立的点,故选项A 正确; 对于B ,由于两个数列中的数排列的次序不同,因此不是同一数列,故选项B 错误; 对于C ,当通项公式为1n n a n =+时,11223a =≠,不符合题意,故选项C 错误;对于D ,数列11,24,⋯,12n是递减数列,故选项D 正确.故选:AD.第II 卷(非选择题)请点击修改第II 卷的文字说明三、填空题11.在数学课堂上、教师引导学生构造新数列:在数列的每相邻两项之间插入此两项的和,形成新的数列,再把所得数列按照同样的方法不断构造出新的数列,例如将数列1,2进行构造,第一次得到数列1,3,2;第二次得到数列1,4,3,5,2;第()*n n ∈N 次得到数列1,1x ,2x ,3x ,…,k x ,2(共2k +项),则k =______. 【答案】21n -【分析】根据第一次得到数列1,3,2,共1321=+项,第二次得到数列1,4,3,5,2,共2521=+项,第三次得到数列1,5,4,7,3,8,5,7,2,共3921=+项,得到规律求解. 【解析】第一次得到数列1,3,2,共1321=+项; 第二次得到数列1,4,3,5,2,共2521=+项;第三次得到数列1,5,4,7,3,8,5,7,2,共3921=+项;依此第n 次得到数列1,1x ,2x ,3x ,…,k x ,2,共221n k +=+项; 解得21n k =-, 故答案为:21n -12.数列{a n }的通项公式为a n =2,3,n n n n +⎧⎨-⎩是奇数是偶数,则a 3+a 6=________.【答案】8 【解析】a 3+a 6=(3+2)+(6-3)=5+3=8.13.已知数列{}n a 满足12211,2,()n na a a n N a ++==-=-∈,则该数列前26项的和为____.【答案】10- 【分析】根据递推公式可以求出数列的周期,利用周期进行求解即可. 【解析】因为12211,2,()n na a a n N a ++==-=-∈,所以3111a a =-=-,42112a a =-=,5311a a =-=,6412a a =-=-,因此该数列的周期为4,且1234131(2)(1)22a a a a +++=+-+-+=-, 所以该数列前26项的和为:361(2)102-⨯++-=-,故答案为:10-四、解答题14.若数列{}n a 满足12a =,111n n na a a ++=-,n *∈N ,求2021a . 【答案】2【分析】 计算出数列{}n a 的前5项的值,可知数列{}n a 为周期数列,结合数列的周期性可得结果.【解析】解:因为12a =,111n n n a a a ++=-,则1211123112a a a ++===---,23211311132a a a , 3431111211312a a a ,454111321113a a a ,所以,数列{}n a 是周期为4的数列,因此,20214505112a a a ⨯+===.15.根据下面的图形及相应的点数,写出点数构成的数列的一个通项公式,并在横线上和括号中分别填上第5项的图形和点数.(1)(2)(3)【答案】(1)第5项图形见解析,通项公式为54n a n =-,第5项的点数为521a =(2)第5项图形见解析,通项公式为32n b n =-,第5项的点数为513b =(3)第5项图形见解析,通项公式为()2n c n n =+,第5项的点数为535c =【分析】(1)根据图形中点数的规律可作出第5项的图形,并根据各项的点数可归纳出数列的通项公式;(2)根据图形中点数的规律可作出第5项的图形,并根据各项的点数可归纳出数列的通项公式; (3)根据图形中点数的规律可作出第5项的图形,并根据各项的点数可归纳出数列的通项公式. (1)解:设第n 项的点数为()n a n *∈N , 11a =,215a =+,3125a =+⨯,4135a =+⨯,该数列的第5项为514521a =+⨯=,数列{}n a 的一个通项公式为()15154n a n n =+-=-,第5项的图形如下图所示:(2)解:设第n 项的点数为()n b n N *∈, 11b =,213b =+,3123b =+⨯,4133b =+⨯,该数列的第5项为514313b =+⨯=,数列{}n b 的一个通项公式为()13132n b n n =+-=-,第5项的图形如下图所示:(3)解:设第n 项的点数为()n c n N *∈, 113c =⨯,224c =⨯,335c =⨯,446c =⨯,该数列的第5项为55735c =⨯=,数列{}n c 的一个通项公式为()2n c n n =+,第5项的图形如下图所示:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、数列的概念选择题1.若数列的前4项分别是1111,,,2345--,则此数列的一个通项公式为( ) A .1(1)n n --B .(1)n n -C .1(1)1n n +-+D .(1)1n n -+2.已知数列{}n a 满足: 12a =,111n na a +=-,设数列{}n a 的前n 项和为n S ,则2017S =( ) A .1007B .1008C .1009.5D .10103.已知数列{}n a 满足12a =,111n na a +=-,则2018a =( ). A .2B .12 C .1-D .12-4.在数列{}n a 中,10a =,1n a +,则2020a =( ) A .0B .1C.D5.已知数列22333311313571351,,,,,,,...,,,,...2222222222n n n,则该数列第2019项是( ) A .1019892 B .1020192 C .1119892 D .1120192 6.已知数列{}n a 的前n 项和为n S ,且21n S n n =++,则{}n a 的通项公式是( )A .2n a n =B .3,12,2n n a n n =⎧=⎨≥⎩C .21n a n =+D .3n a n =7.在数列{}n a 中,11a =,对于任意自然数n ,都有12nn n a a n +=+⋅,则15a =( )A .151422⋅+B .141322⋅+C .151423⋅+D .151323⋅+8.数列23451,,,,,3579的一个通项公式n a 是( ) A .21nn + B .23nn + C .23nn - D .21nn - 9.在数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,则下列结论正确的是( )A .存在正整数0N ,当0n N >时,都有n a n ≤.B .存在正整数0N ,当0n N >时,都有n a n ≥.C .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≤.D .对常数M ,一定存在正整数0N ,当0n N >时,都有n a M ≥. 10.在数列{}n a 中,()1111,1(2)nn n a a n a --==+≥,则5a 等于A .32B .53 C .85D .2311.下列命题中错误的是( ) A .()()21f n n n N+=-∈是数列的一个通项公式B .数列通项公式是一个函数关系式C .任何一个数列中的项都可以用通项公式来表示D .数列中有无穷多项的数列叫作无穷数列12.在数列{}n a 中,114a =-,111(1)n n a n a -=->,则2019a 的值为( ) A .45B .14-C .5D .以上都不对13.已知数列{}n a 的前n 项和为n S ,若*1n S n N n =∈,,则2a =( ) A .12-B .16-C .16D .1214.已知lg3≈0.477,[x ]表示不大于x 的最大整数.设S n 为数列{a n }的前n 项和,a 1=2且S n +1=3S n -2n +2,则[lg(a 100-1)]=( ) A .45B .46C .47D .4815.在数列{}n a 中,21n n a n +=+,则{}n a ( ) A .是常数列B .不是单调数列C .是递增数列D .是递减数列16.大衍数列,来源于《乾坤普》中对易传“大衍之数五十”的推论,主要用于解释中国传统文化中太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两翼数量总和,是中国传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0,2,4,8,12,18,24,32,40,50,……则此数列的第40项为( ). A .648B .722C .800D .88217.已知数列{}n a 满足2122111,16,2n n n a a a a a ++===则数列{}n a 的最大项为( ) A .92B .102C .8182D .11218.历史上数列的发展,折射出很多有价值的数学思想方法,对时代的进步起了重要的作用,比如意大利数学家列昂纳多·斐波那契以兔子繁殖为例,引入“兔子数列”:即1,1,2,3,5,8,13,21,34,55,89,144,233……即F (1)=F (2)=1,F (n )=F (n -1)+F (n -2),()*3n n N≥∈,,此数列在现代物理及化学等领域有着广泛的应用,若此数列被4整除后的余数构成一个新数列{}n b ,则b 2020=( )A .3B .2C .1D .019.在数列{}n a 中,11(1)1,2(2)nn n a a n a --==+≥,则3a =( ) A .0B .53C .73D .320.数列{}n a 满足111n na a +=-,12a =,则2a 的值为( ) A .1B .-1C .13D .13-二、多选题21.已知数列{}n a :1,1,2,3,5,…其中从第三项起,每个数等于它前面两个数的和,记n S 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68S a = B .733S =C .135********a a a a a ++++= D .2222123202020202021a a a a a a ++++=22.意大利人斐波那契于1202年从兔子繁殖问题中发现了这样的一列数:1,1,2,3,5,8,13,….即从第三项开始,每一项都是它前两项的和.后人为了纪念他,就把这列数称为斐波那契数列.下面关于斐波那契数列{}n a 说法正确的是( ) A .1055a = B .2020a 是偶数C .2020201820223a a a =+D .123a a a +++…20202022a a +=23.已知数列{}n a 满足()*111n na n N a +=-∈,且12a =,则( ) A .31a =- B .201912a =C .332S =D . 2 01920192S =24.已知数列{}n a 中,11a =,1111n n a a n n +⎛⎫-=+ ⎪⎝⎭,*n N ∈.若对于任意的[]1,2t ∈,不等式()22212na t a t a a n<--++-+恒成立,则实数a 可能为( ) A .-4 B .-2C .0D .225.若不等式1(1)(1)2n na n+--<+对于任意正整数n 恒成立,则实数a 的可能取值为( ) A .2- B .1- C .1 D .226.著名数学家斐波那契在研究兔子繁殖问题时,发现有这样一列数:1,1,2,3,5,…,其中从第三项起,每个数等于它前面两个数的和,后来人们把这样的一列数组成的数列{}n a 称为“斐波那契数列”,记S n 为数列{}n a 的前n 项和,则下列结论正确的是( ) A .68a = B .733S =C .135********a a a a a ++++=D .22212201920202019a a a a a +++= 27.已知S n 是等差数列{}n a (n ∈N *)的前n 项和,且S 5>S 6>S 4,以下有四个命题,其中正确的有( )A .数列{}n a 的公差d <0B .数列{}n a 中S n 的最大项为S 10C .S 10>0D .S 11>028.(多选)在数列{}n a 中,若221(2,,n n a a p n n N p *--=≥∈为常数),则称{}n a 为“等方差数列”.下列对“等方差数列”的判断正确的是( ) A .若{}n a 是等差数列,则{}n a 是等方差数列 B .(){}1n- 是等方差数列C .{}2n是等方差数列.D .若{}n a 既是等方差数列,又是等差数列,则该数列为常数列 29.等差数列{}n a 中,n S 为其前n 项和,151115,a S S ==,则以下正确的是( )A .1d =-B .413a a =C .n S 的最大值为8SD .使得0n S >的最大整数15n = 30.定义11222n nn a a a H n-+++=为数列{}n a 的“优值”.已知某数列{}n a 的“优值”2nn H =,前n 项和为n S ,则( )A .数列{}n a 为等差数列B .数列{}n a 为等比数列C .2020202320202S = D .2S ,4S ,6S 成等差数列31.等差数列{}n a 的首项10a >,设其前n 项和为{}n S ,且611S S =,则( ) A .0d > B .0d <C .80a =D .n S 的最大值是8S 或者9S32.数列{}n a 满足11,121nn n a a a a +==+,则下列说法正确的是( )A .数列1n a ⎧⎫⎨⎬⎩⎭是等差数列 B .数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和2n S n = C .数列{}n a 的通项公式为21n a n =- D .数列{}n a 为递减数列33.设等差数列{}n a 的前n 项和为n S ,公差为d .已知312a =,120S >,70a <则( ) A .60a >B .数列1n a ⎧⎫⎨⎬⎩⎭是递增数列C .0n S <时,n 的最小值为13D .数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项34.下面是关于公差0d >的等差数列{}n a 的四个命题,其中的真命题为( ). A .数列{}n a 是递增数列 B .数列{}n na 是递增数列 C .数列{}na n是递增数列 D .数列{}3n a nd +是递增数列35.等差数列{}n a 的前n 项和为n S ,1385a a S +=,则下列结论一定正确的是( ) A .100a = B .当9n =或10时,n S 取最大值 C .911a a <D .613S S =【参考答案】***试卷处理标记,请不要删除一、数列的概念选择题 1.C 解析:C 【分析】根据数列的前几项的规律,可推出一个通项公式. 【详解】设所求数列为{}n a ,可得出()111111a+-=+,()212121a+-=+,()313131a+-=+,()414141a+-=+,因此,该数列的一个通项公式为()111n na n +-=+.故选:C. 【点睛】本题考查利用数列的前几项归纳数列的通项公式,考查推理能力,属于基础题.2.D解析:D 【分析】根据题设条件,可得数列{}n a 是以3为周期的数列,且3132122S =+-=,从而求得2017S 的值,得到答案. 【详解】由题意,数列{}n a 满足: 12a =,111n na a +=-, 可得234111,121,1(1)2,22a a a =-==-=-=--=,可得数列{}n a 是以3为周期的数列,且3132122S =+-= 所以20173672210102S =⨯+=. 故选:D. 【点睛】本题主要考查了数列的递推公式的应用,其中解答中得出数列{}n a 是以3为周期的数列,是解答的关键,着重考查了推理与运算能力,属于中档试题.3.B解析:B 【分析】利用递推关系可得数列{}n a 是以3为周期的周期数列,从而可得2018a . 【详解】 在数列{}n a 中,111n na a +=-,且12a =, 211112a a ∴=-=, 3211121a a =-=-=- , ()41311112a a a =-=--== ∴数列{}n a 是以3为周期的周期数列,201867232=⨯+,2018212a a ∴==.故选:B 【点睛】本题考查了由数列的递推关系式研究数列的性质,考查了数列的周期性,属于基础题.4.A解析:A 【分析】写出数列的前几项,找寻规律,求出数列的周期,问题即可解. 【详解】10a =,1n a +1n =时,2a 2n =时,3a 3n =时,4a ; ∴ 数列{}n a 的周期是320206733110a a a ⨯+∴===故选:A. 【点睛】本题考查周期数列. 求解数列的周期问题时,周期数列的解题方法:根据给出的关系式求出数列的若干项,通过观察归纳出数列的周期,进而求有关项的值或者前n 项的和.5.C解析:C 【分析】 由观察可得()22333311313571351,,,,,,,...,,,,...2222222222n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭项数为21,1,2,4,8,...,2,...k -,注意到101110242201922048=<<=,第2019项是第12个括号里的第995项. 【详解】 由数列()22333311313571351,,,,,,,...,,,,...2222222222n n n ⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,可发现其项数为 21,1,2,4,8,...,2,...k -,则前11个括号里共有1024项,前12个括号里共有2048项,故原数列第2019项是第12个括号里的第995项,第12个括号里的数列通项为11212m -,所以第12个括号里的第995项是1119892. 故选:C. 【点睛】本题考查数列的定义,考查学生观察找出已知数列的特征归纳出其项数、通项,是一道中档题.6.B解析:B 【分析】根据11,1,2n nS n a S S n -=⎧=⎨-≥⎩计算可得;【详解】解:因为21n S n n =++①,当1n =时,211113S =++=,即13a =当2n ≥时,()()21111n S n n -=-+-+②,①减②得,()()2211112n n n n n n a ⎡⎤++--+-+=⎦=⎣所以3,12,2n n a n n =⎧=⎨≥⎩故选:B 【点睛】本题考查利用定义法求数列的通项公式,属于基础题.7.D解析:D 【分析】在数列的递推公式中依次取1,2,3,1n n =- ,得1n -个等式,累加后再利用错位相减法求15a . 【详解】12n n n a a n +=+⋅, 12n n n a a n +-=⋅,12112a a ∴-=⋅, 23222a a -=⋅,34332a a -=⋅11(1)2n n n a a n ---=-⋅,以上1n -个等式,累加得12311122232(1)2n n a a n --=⋅+⋅+⋅++-⋅①又2341122122232(2)2(1)2n n n a a n n --=⋅+⋅+⋅++-⋅+-⋅②①- ②得23112222(1)2n n n a a n --=++++--⋅12(12)(1)2(2)2212n n n n n --=--⋅=-⋅--,(2)23n n a n ∴=-⋅+ ,151515(152)231323a ∴=-⋅+=⋅+,故选:D 【点睛】本题主要考查了累加法求数列通项,乘公比错位相减法求数列的和,由通项公式求数列中的项,属于中档题.8.D解析:D 【分析】根据数列分子分母的规律求得通项公式. 【详解】由于数列的分母是奇数列,分子是自然数列,故通项公式为21n na n =-. 故选:D 【点睛】本小题主要考查根据数列的规律求通项公式,属于基础题.9.A解析:A 【分析】运用数列的单调性和不等式的知识可解决此问题. 【详解】数列{}n a 中,11a =,20192019a =,且*n N ∈都有122n n n a a a ++≥+,121n n n n a a a a +++∴≥--,设1n n n d a a +=-,则1n n d d +≥,∴数列{}n d 是递减数列.对于A ,由11a =,20192019a =, 则201911220182019a a d d d =+++=,所以1220182018d d d +++=,又1232018d d d d ≥≥≥≥,所以1122018201820182018d d d d d ≥+++≥,故120181d d ≥≥,2018n ∴≥时,1n d ≤,02019N ∃=,2019n >时, 20192019202012019111n n a a d d d n -=+++≤++++=即存在正整数0N ,当0n N >时,都有n a n ≤,故A 正确;结合A ,故B 不正确;对于C ,当n →+∞,且0n d >时,数列{}n a 为递增数列, 则n a 无最大值,故C 不正确;对于D ,由数列{}n d 是递减数列,当存在0n d <时,则n a 无最小值,故D 不正确; 故选:A 【点睛】本题考查了数列的单调性以及不等式,属于基础题.10.D解析:D 【解析】分析:已知1a 逐一求解2345122323a a a a ====,,,. 详解:已知1a 逐一求解2345122323a a a a ====,,,.故选D 点睛:对于含有()1n-的数列,我们看作摆动数列,往往逐一列举出来观察前面有限项的规律.11.C解析:C 【分析】根据通项公式的概念可以判定AB 正确;不难找到一些规律性不强的数列,找不到通项公式,由此判定C 错误,根据无穷数列的概念可以判定D 正确. 【详解】数列的通项公式的概念:将数列{} n a 的第n 项用一个具体式子(含有参数n )表示出来,称作该数列的通项公式,故任意一个定义域为正整数集合的或者是其从1开始的一个子集的函数都可以是数列的通项公式,它是一个函数关系,即对于任意给定的数列,各项的值是由n 唯一确定的,故AB 正确; 并不是所有的数列中的项都可以用一个通项公式来表示,比如所有的质数从小到大排在一起构成的数列,至今没有发现统一可行的公式表示,圆周率的各位数字构成的数列也没有一个通项公式可以表达,还有很多规律性不强的数列也找不到通项公式,故C 是错误的; 根据无穷数列的概念,可知D 是正确的. 故选:C.本题考查数列的通项公式的概念和无穷数列的概念,属基础题,数列的通项公式是一种定义在正整数集上的函数,有穷数列与无穷数列是根据数列的项数来分类的.12.A解析:A 【分析】根据递推式可得{}n a 为一个周期为3的数列,求{}n a 中一个周期内的项,利用周期性即可求2019a 的值 【详解】由114a =-,111(1)n n a n a -=->知 21115a a =-= 321415a a =-= 4131114a a a =-=-= 故数列{}n a 是周期为3的数列,而2019可被3整除 ∴2019345a a == 故选:A 【点睛】本题主要考查递推数列,考查数列的周期性,考查合情推理,属于基础题13.A解析:A 【分析】令1n =得11a =,令2n =得21212S a a =+=可解得2a . 【详解】 因为1n S n =,所以11111a S ===, 因为21212S a a =+=,所以211122a =-=-. 故选:A14.C解析:C 【分析】利用数列的递推式,得到a n +1=3a n -2,进而得到a n =3n -1+1,然后代入[lg(a 100-1)]可求解当n ≥2时,S n =3S n -1-2n +4,则a n +1=3a n -2,于是a n +1-1=3(a n -1),当n =1时,S 2=3S 1-2+2=6,所以a 2=S 2-S 1=4.此时a 2-1=3(a 1-1),则数列{a n -1}是首项为1,公比为3的等比数列.所以a n -1=3n -1,即a n =3n -1+1,则a 100=399+1,则lg(a 100-1)=99lg3≈99×0.477=47.223,故[lg(a 100-1)]=47. 故选C15.D解析:D 【分析】由21111n n a n n +==+++,利用反比例函数的性质判断即可. 【详解】在数列{}n a 中,21111n n a n n +==+++, 由反比例函数的性质得:{}n a 是*n N ∈时单调递减数列, 故选:D16.C解析:C 【分析】由0、2、4、8、12、18、24、32、40、50…,可得偶数项的通项公式:222n a n =,即可得出. 【详解】由0,2,4,8,12,18,24,32,40,50…,可得偶数项的通项公式:222n a n =.则此数列第40项为2220800⨯=. 故选:C17.B解析:B 【分析】本题先根据递推公式进行转化得到21112n n n n a a a a +++=.然后令1n n na b a +=,可得出数列{}n b 是等比数列.即11322nn n a a +⎛⎫= ⎪⎝⎭.然后用累乘法可求出数列{}n a 的通项公式,根据通项公式及二次函数的知识可得数列{}n a 的最大项. 【详解】解:由题意,可知: 21112n n n na a a a +++=.令1n n n a b a +=,则112n n b b +=. 21116a b a ==, ∴数列{}n b 是以16为首项,12为公比的等比数列. 111163222n nn b -⎛⎫⎛⎫∴== ⎪⎪⎝⎭⎝⎭.∴11322nn n a a +⎛⎫= ⎪⎝⎭. ∴1211322aa ⎛⎫= ⎪⎝⎭, 2321322a a ⎛⎫= ⎪⎝⎭,111322n n n a a --⎛⎫= ⎪⎝⎭.各项相乘,可得: 12111111(32)222n n na a --⎛⎫⎛⎫⎛⎫=⋯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(1)2511()22n n n --⎛⎫= ⎪⎝⎭ 2115(1)221122n n n ---⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭211552212n n n --+⎛⎫= ⎪⎝⎭21(1110)212n n -+⎛⎫= ⎪⎝⎭.令2()1110f n n n =-+,则,根据二次函数的知识,可知:当5n =或6n =时,()f n 取得最小值. ()2551151020f =-⨯+=-,()2661161020f =-⨯+=-,()f n ∴的最小值为20-. ∴211(1110)(20)1022101112222n n -+⨯--⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.∴数列{}n a 的最大项为102.故选:B . 【点睛】本题主要考查根据递推公式得出通项公式,构造新数列的方法,累乘法通项公式的应用,以及利用二次函数思想求最值;18.A解析:A 【分析】根据条件得出数列{}n b 的周期即可. 【详解】由题意可知“兔子数列”被4整除后的余数构成一个新数列为:1,1,2,3,1,0,1,1,2,3,1,0,……则可得到周期为6,所以b 2020=b 4=3, 故选:A19.B解析:B 【分析】由数列的递推关系式以及11a =求出2a ,进而得出3a . 【详解】11a =,21123a a ∴=+=,321523a a -=+= 故选:B20.B解析:B 【分析】根据数列的递推公式,代入计算可得选项. 【详解】 因为111n n a a +=-,12a =,所以21111112a a ===---, 故选:B. 【点睛】本题考查由数列递推式求数列中的项,属于基础题.二、多选题 21.BCD 【分析】根据题意写出,,,从而判断A ,B 的正误;写出递推关系,对递推关系进行适当的变形,利用累加法即可判断C ,D 的正误. 【详解】对A ,,,故A 不正确; 对B ,,故B 正确; 对C ,由,,解析:BCD 【分析】根据题意写出8a ,6S ,7S ,从而判断A ,B 的正误;写出递推关系,对递推关系进行适当的变形,利用累加法即可判断C ,D 的正误. 【详解】对A ,821a =,620S =,故A 不正确; 对B ,761333S S =+=,故B 正确;对C ,由12a a =,342a a a =-,564a a a =-,…,202120222020a a a =-,可得135********a a a a a +++⋅⋅⋅+=,故C 正确;对D ,该数列总有21n n n a a a ++=+,2121a a a =,则()222312321a a a a a a a a =-=-, ()233423423a a a a a a a a =-=-,…,()220182018201920172018201920172018a a a a a a a a =-=-, 22019a =2019202020192018a a a a -,220202020202120202019a a a a a =-, 故2222123202*********a a a a a a +++⋅⋅⋅+=,故D 正确.故选:BCD 【点睛】关键点睛:解答本题的关键是对CD 的判断,即要善于利用21n n n a a a ++=+对所给式子进行变形.22.AC 【分析】由该数列的性质,逐项判断即可得解. 【详解】对于A ,,,,故A 正确;对于B ,由该数列的性质可得只有3的倍数项是偶数,故B 错误; 对于C ,,故C 正确; 对于D ,,,, , 各式相加解析:AC 【分析】由该数列的性质,逐项判断即可得解.【详解】对于A ,821a =,9211334a =+=,10213455a =+=,故A 正确; 对于B ,由该数列的性质可得只有3的倍数项是偶数,故B 错误;对于C ,20182022201820212020201820192020202020203a a a a a a a a a a +=++=+++=,故C 正确; 对于D ,202220212020a a a =+,202120202019a a a =+,202020192018a a a =+,32121,a a a a a ⋅⋅⋅=+=,各式相加得()2022202120202021202020192012182a a a a a a a a a ++⋅⋅⋅+=+++⋅⋅⋅++, 所以202220202019201811a a a a a a =++⋅⋅⋅+++,故D 错误. 故选:AC. 【点睛】关键点点睛:解决本题的关键是合理利用该数列的性质去证明选项.23.ACD 【分析】先计算出数列的前几项,判断AC ,然后再寻找规律判断BD . 【详解】由题意,,A 正确,,C 正确; ,∴数列是周期数列,周期为3. ,B 错; ,D 正确. 故选:ACD . 【点睛】 本解析:ACD 【分析】先计算出数列的前几项,判断AC ,然后再寻找规律判断BD . 【详解】由题意211122a =-=,311112a =-=-,A 正确,3132122S =+-=,C 正确;41121a =-=-,∴数列{}n a 是周期数列,周期为3. 2019367331a a a ⨯===-,B 错;20193201967322S =⨯=,D 正确.故选:ACD . 【点睛】本题考查由数列的递推式求数列的项与和,解题关键是求出数列的前几项后归纳出数列的性质:周期性,然后利用周期函数的定义求解.24.AB 【分析】由题意可得,利用裂项相相消法求和求出,只需对于任意的恒成立,转化为对于任意的恒成立,然后将选项逐一验证即可求解. 【详解】 ,, 则,,,,上述式子累加可得:,, 对于任意的恒成立解析:AB 【分析】 由题意可得11111n n a a n n n n +-=-++,利用裂项相相消法求和求出122n a n n=-<,只需()222122t a t a a --++-+≥对于任意的[]1,2t ∈恒成立,转化为()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,然后将选项逐一验证即可求解.【详解】111n n n a a n n++-=,11111(1)1n n a a n n n n n n +∴-==-+++,则11111n n a a n n n n --=---,12111221n n a a n n n n ---=-----,,2111122a a -=-, 上述式子累加可得:111n a a n n -=-,122n a n n∴=-<,()222122t a t a a ∴--++-+≥对于任意的[]1,2t ∈恒成立,整理得()()210t a t a --+≤⎡⎤⎣⎦对于任意的[]1,2t ∈恒成立,对A ,当4a =-时,不等式()()2540t t +-≤,解集5,42⎡⎤-⎢⎥⎣⎦,包含[]1,2,故A 正确;对B ,当2a =-时,不等式()()2320t t +-≤,解集3,22⎡⎤-⎢⎥⎣⎦,包含[]1,2,故B 正确;对C ,当0a =时,不等式()210t t +≤,解集1,02⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故C 错误;对D ,当2a =时,不等式()()2120t t -+≤,解集12,2⎡⎤-⎢⎥⎣⎦,不包含[]1,2,故D 错误,故选:AB. 【点睛】本题考查了裂项相消法、由递推关系式求通项公式、一元二次不等式在某区间上恒成立,考查了转化与划归的思想,属于中档题.25.ABC 【分析】根据不等式对于任意正整数n 恒成立,即当n 为奇数时有恒成立,当n 为偶数时有恒成立,分别计算,即可得解. 【详解】根据不等式对于任意正整数n 恒成立, 当n 为奇数时有:恒成立, 由递减解析:ABC 【分析】根据不等式1(1)(1)2n na n +--<+对于任意正整数n 恒成立,即当n 为奇数时有12+a n-<恒成立,当n 为偶数时有12a n<-恒成立,分别计算,即可得解. 【详解】根据不等式1(1)(1)2n na n +--<+对于任意正整数n 恒成立, 当n 为奇数时有:12+a n-<恒成立,由12+n 递减,且1223n<+≤, 所以2a -≤,即2a ≥-, 当n 为偶数时有:12a n<-恒成立, 由12n -第增,且31222n ≤-<, 所以32a <, 综上可得:322a -≤<, 故选:ABC . 【点睛】本题考查了不等式的恒成立问题,考查了分类讨论思想,有一定的计算量,属于中当题.26.ABD 【分析】根据,,,计算可知正确;根据,,,,,,累加可知不正确;根据,,,,,,累加可知正确.【详解】依题意可知,,,, ,,,,故正确; ,所以,故正确; 由,,,,,, 可得,故不解析:ABD 【分析】根据11a =,21a =,21n n n a a a ++=+,计算可知,A B 正确;根据12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,累加可知C 不正确;根据2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,累加可知D 正确. 【详解】依题意可知,11a =,21a =,21n n n a a a ++=+,312112a a a =+=+=,423123a a a =+=+=,534235a a a =+=+=,645358a a a =+=+=,故A 正确; 7565813a a a =+=+=,所以712345671123581333S a a a a a a a =++++++=++++++=,故B 正确;由12a a =,342a a a =-,564a a a =-,786a a a =-,,201920202018a a a =-,可得13572019a a a a a +++++=242648620202018a a a a a a a a a +-+-+-++-2020a =,故C 不正确;2121a a a =,222312312()a a a a a a a a =-=-,233423423()a a a a a a a a =-=-,244534534()a a a a a a a a =-=-,,220192019202020182019202020182019()a a a a a a a a =-=-,所以2222212342019a a a a a +++++122312342345342019202020182019a a a a a a a a a a a a a a a a a a =+-+-+-+- 20192020a a =,所以22212201920202019a a a a a +++=,故D 正确. 故选:ABD. 【点睛】本题考查了数列的递推公式,考查了累加法,属于中档题.27.AC 【分析】由,可得,且,然后逐个分析判断即可得答案 【详解】解:因为,所以,且,所以数列的公差,且数列中Sn 的最大项为S5,所以A 正确,B 错误, 所以,,所以C 正确,D 错误, 故选:AC解析:AC 【分析】由564S S S >>,可得650,0a a ,且650a a +>,然后逐个分析判断即可得答案 【详解】解:因为564S S S >>,所以650,0a a ,且650a a +>,所以数列的公差0d <,且数列{}n a 中S n 的最大项为S 5,所以A 正确,B 错误, 所以110105610()5()02a a S a a +==+>,11111611()1102a a S a +==<, 所以C 正确,D 错误, 故选:AC28.BD 【分析】根据等差数列和等方差数列定义,结合特殊反例对选项逐一判断即可. 【详解】对于A ,若是等差数列,如,则不是常数,故不是等方差数列,故A 错误; 对于B ,数列中,是常数,是等方差数列,故解析:BD 【分析】根据等差数列和等方差数列定义,结合特殊反例对选项逐一判断即可. 【详解】对于A ,若{}n a 是等差数列,如n a n =,则12222(1)21n n a a n n n --=--=-不是常数,故{}na 不是等方差数列,故A 错误;对于B ,数列(){}1n-中,222121[(1)][(1)]0n n n n aa ---=---=是常数,{(1)}n ∴-是等方差数列,故B 正确;对于C ,数列{}2n 中,()()22221112234n n n n n a a ----=-=⨯不是常数,{}2n ∴不是等方差数列,故C 错误;对于D ,{}n a 是等差数列,1n n a a d -∴-=,则设n a dn m =+,{}n a 是等方差数列,()()222112(2)n n n n dn m a a a a d a d d n m d d dn d m --∴-=++++=+=++是常数,故220d =,故0d =,所以(2)0m d d +=,2210n n a a --=是常数,故D 正确.故选:BD. 【点睛】关键点睛:本题考查了数列的新定义问题和等差数列的定义,解题的关键是正确理解等差数列和等方差数列定义,利用定义进行判断.29.BCD 【分析】设等差数列的公差为,由等差数列的通项公式及前n 项和公式可得,再逐项判断即可得解. 【详解】设等差数列的公差为, 由题意,,所以,故A 错误; 所以,所以,故B 正确; 因为, 所以当解析:BCD 【分析】设等差数列{}n a 的公差为d ,由等差数列的通项公式及前n 项和公式可得1215d a =-⎧⎨=⎩,再逐项判断即可得解. 【详解】设等差数列{}n a 的公差为d ,由题意,1115411105112215a d a d a ⨯⨯⎧+=+⎪⎨⎪=⎩,所以1215d a =-⎧⎨=⎩,故A 错误; 所以1131439,129a a d a d a =+==+=-,所以413a a =,故B 正确; 因为()()2211168642n n n a n d n n n S -=+=-+=--+,所以当且仅当8n =时,n S 取最大值,故C 正确; 要使()28640n S n =--+>,则16n <且n N +∈, 所以使得0n S >的最大整数15n =,故D 正确. 故选:BCD.30.AC 【分析】由题意可知,即,则时,,可求解出,易知是等差数列,则A 正确,然后利用等差数列的前n 项和公式求出,判断C ,D 的正误. 【详解】 解:由, 得, 所以时,, 得时,, 即时,, 当时,由解析:AC 【分析】 由题意可知112222n n nn a a a H n-+++==,即112222n n n a a a n -+++=⋅,则2n ≥时,()()111221212n n n n n a n n n ---=⋅--⋅=+⋅,可求解出1n a n =+,易知{}n a 是等差数列,则A 正确,然后利用等差数列的前n 项和公式求出n S ,判断C ,D 的正误. 【详解】 解:由112222n n nn a a a H n-+++==,得112222n n n a a a n -+++=⋅,①所以2n ≥时,()211212212n n n a a a n ---+++=-⋅,②得2n ≥时,()()111221212n n n n n a n n n ---=⋅--⋅=+⋅,即2n ≥时,1n a n =+,当1n =时,由①知12a =,满足1n a n =+.所以数列{}n a 是首项为2,公差为1的等差数列,故A 正确,B 错, 所以()32n n n S +=,所以2020202320202S =,故C 正确.25S =,414S =,627S =,故D 错,故选:AC . 【点睛】本题考查数列的新定义问题,考查数列通项公式的求解及前n 项和的求解,难度一般.31.BD 【分析】由,即,进而可得答案.【详解】 解:, 因为所以,,最大, 故选:. 【点睛】本题考查等差数列的性质,解题关键是等差数列性质的应用,属于中档题.解析:BD 【分析】由6111160S S S S =⇒-=,即950a =,进而可得答案. 【详解】解:1167891011950S S a a a a a a -=++++==, 因为10a >所以90a =,0d <,89S S =最大, 故选:BD . 【点睛】本题考查等差数列的性质,解题关键是等差数列性质的应用,属于中档题.32.ABD 【分析】首项根据得到,从而得到是以首项为,公差为的等差数列,再依次判断选项即可. 【详解】对选项A ,因为,, 所以,即所以是以首项为,公差为的等差数列,故A 正确. 对选项B ,由A 知:解析:ABD 【分析】 首项根据11,121n n n a a a a +==+得到1112n n a a +-=,从而得到1n a ⎧⎫⎨⎬⎩⎭是以首项为1,公差为2的等差数列,再依次判断选项即可.【详解】对选项A ,因为121nn n a a a +=+,11a =, 所以121112n n n n a a a a ++==+,即1112n na a +-=所以1n a ⎧⎫⎨⎬⎩⎭是以首项为1,公差为2的等差数列,故A 正确. 对选项B ,由A 知:112121nn n a数列1n a ⎧⎫⎨⎬⎩⎭的前n 项和()21212nn n S n +-==,故B 正确. 对选项C ,因为121n n a =-,所以121n a n =-,故C 错误. 对选项D ,因为121n a n =-,所以数列{}n a 为递减数列,故D 正确. 故选:ABD 【点睛】本题主要考查等差数列的通项公式和前n 项和前n 项和,同时考查了递推公式,属于中档题.33.ACD 【分析】由已知得,又,所以,可判断A ;由已知得出,且,得出时,,时,,又,可得出在上单调递增,在上单调递增,可判断B ;由,可判断C ;判断 ,的符号, 的单调性可判断D ; 【详解】 由已知解析:ACD 【分析】 由已知得()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,可判断A ;由已知得出2437d -<<-,且()12+3n a n d =-,得出[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d =-,可得出1na 在1,6n n N上单调递增,1na 在7n nN ,上单调递增,可判断B ;由()313117713+12203213a a a S a ⨯==<=,可判断C ;判断 n a ,n S 的符号, n a 的单调性可判断D ; 【详解】由已知得311+212,122d a a a d ===-,()()612112712+12+220a a a a S ==>,又70a <,所以6>0a ,故A 正确;由7161671+612+40+512+3>0+2+1124+7>0a a d d a a d d a a a d d ==<⎧⎪==⎨⎪==⎩,解得2437d -<<-,又()()3+312+3n a n d n d a =-=-,当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,又()1112+3n a n d=-,所以[]1,6n ∈时,1>0na ,7n ≥时,10n a <,所以1na 在1,6n n N上单调递增,1na 在7n n N ,上单调递增,所以数列1n a ⎧⎫⎨⎬⎩⎭不是递增数列,故B 不正确; 由于()313117713+12203213a a a S a ⨯==<=,而120S >,所以0n S <时,n 的最小值为13,故C 选项正确 ;当[]1,6n ∈时,>0n a ,7n ≥时,0n a <,当[]1,12n ∈时,>0n S ,13n ≥时,0nS <,所以当[]7,12n ∈时,0n a <,>0n S ,0nnS a <,[]712n ∈,时,n a 为递增数列,n S 为正数且为递减数列,所以数列n n S a ⎧⎫⎨⎬⎩⎭中最小项为第7项,故D 正确;【点睛】本题考查等差数列的公差,项的符号,数列的单调性,数列的最值项,属于较难题.34.AD 【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项. 【详解】, ,所以是递增数列,故①正确, ,当时,数列不是递增数列,故②不正确, ,当时,不是递增数列,故③不正确, ,因解析:AD 【分析】根据等差数列的性质,对四个选项逐一判断,即可得正确选项. 【详解】0d >,10n n a a d +-=> ,所以{}n a 是递增数列,故①正确,()()2111n na n a n d dn a d n =+-=+-⎡⎤⎣⎦,当12d a n d -<时,数列{}n na 不是递增数列,故②不正确, 1n a a d d n n -=+,当10a d -<时,{}n a n 不是递增数列,故③不正确, 134n a nd nd a d +=+-,因为0d >,所以{}3n a nd +是递增数列,故④正确,故选:AD 【点睛】本题主要考查了等差数列的性质,属于基础题.35.AD 【分析】由求出,即,由此表示出、、、,可判断C 、D 两选项;当时,,有最小值,故B 错误. 【详解】解:,,故正确A.由,当时,,有最小值,故B 错误. ,所以,故C 错误. ,,故D 正确.解析:AD 【分析】由1385a a S +=求出100a =,即19a d =-,由此表示出9a 、11a 、6S 、13S ,可判断C 、D 两选项;当0d >时,10a <,n S 有最小值,故B 错误. 【详解】解:1385a a S +=,111110875108,90,02da a d a a d a ⨯++=++==,故正确A. 由190a d +=,当0d >时,10a <,n S 有最小值,故B 错误.9101110,a a d d a a d d =-==+=,所以911a a =,故C 错误.61656+5415392dS a d d d ⨯==-+=-, 131131213+11778392dS a d d d ⨯==-+=-,故D 正确. 故选:AD 【点睛】考查等差数列的有关量的计算以及性质,基础题.。
