专题学习:锐角三角函数与圆优秀课件
合集下载
《锐角三角函数》PPT教学课件(第1课时)

BC AC
= 12 =
AC
34,所以AC=9.故填9.
随堂训练
AB 6.如图,在Rt△ABC中,∠C=90°,BC
17 15
,则tan
15 A=_8__.
由正切定义可知tan A=BACC , 因为 AB 17 , 可设BC=15a,AB=17a,从而可
BC 15
用勾股定理表示出第三边AC=8a,再用正切的定义求解得 tan A= BC 15 .
由勾股定理可得 AB= BC2 AC2 122 162 =20.
∴AB的长为20.
课堂小结
1.正切的定义: 如图,在Rt△ABC中,如果锐角A确定,那么∠A的对边与邻
边的比便随之确定,这个比叫做 ∠A的正切,记作tan A, 即tan A= A的对边
A的邻边
2.tanA的值越大,梯子(坡)越陡
图①
图②
新课导入
问题引入
如图所示,轮船在A处时,灯塔B位于它 的北偏东35°的方向上.轮船向东航行5 km 到达C处时,轮船位于灯塔的正南方,此时轮 船距灯塔多少千米?(结果保留两位小数)
该实际问题中的已知和所求为图中的哪些角和线段?
(事实上,求轮船距灯塔的距离,就是在Rt△ABC中,已知 ∠C=90°,∠BAC=55°,AC=5 km,求BC长度的问题)
C,C'.
BC AC
与BACC
具有怎样的关系?
在两个直角三角形中,当一对锐角相等
时,这两个直角三角形相似,从而两条对应直
角边的比相等,即当∠A(小于90°)确定时,以 ∠A为锐角的Rt△ABC的两条直角边的比 BC
AC
是确定的.
知识讲解
1.正切的定义
如图所示,在Rt△ABC中,∠C=90°,我们把∠A的对边与邻边的比叫
专题学习:锐角三角函数与圆优秀课件

若若若cocsco∠oss∠C∠=CC==4 5
54,54,D,FD=DF3F=,=33,求,求⊙求⊙O⊙O的O的半的半径半径.径..
★换+构
类型二:利用锐角三角函数值计算
类型二:利用锐角三角函数值计算
知识小结 本节课你有什么收获?
锐角三角函数与圆的两种类型题型 (1)利用定义求三角函数值 (2)利用三角函数值进行计算 直接法、换、构
求sin∠BAC和tan∠ADC的值.
解:连接BC
★构+换
C
A
O·
B
D
类型二:利用锐角三角函数值计算
★直接法
★换+构
类型二:利用锐角三角函数值计算
如如图如图,图,A,BAAB为B为⊙为⊙O⊙O的O的直的直径直径,径,且,且弦且弦弦CDC⊥CDD⊥A⊥BAAB于B于于E,EE,过,过点过点点B B的B的切的切线切线与线与与ADAAD的D的延的延长延长线长线交线交于交于点于点点F.FF..
(1)同圆中,同弧所对的圆周角都相等,等于它所对 的圆心角的(2)半圆或直径所对的圆周角都相等,都等于900(直角). 反之成立.
A
O
B
知识准备
★切线性质 圆的切线 垂直 于经过 切点 的 半径 .
★弦切角定理:
1.弦切角等于它所夹的弧对的 圆周角 .
2.弦切角等于它所夹的弧对圆心角的 一半
(2)两锐角之间的关系 ∠A+∠B=90° b
(3)边角之间的关系
sin
A
A的对边 斜边
a c
C
cos
A
A的邻边 斜边
b c
tan
A
A的对边 A的邻边
a b
c
a
人教版《锐角三角函数》优秀课件初中数学ppt

(C) 0<cosA< 3 2
(D) 3<cosA<1 2
3.特殊角300,450,600角的三角函数值.
锐角a 三角 函数
sin a
cos a
tan a
30° 45° 60°
1
2
3
2
2
2
3
2
1
2
2
2
3
3
1
3
练一练
求下列各式的值: (1) sin230°+ cos230°-tan45°.
(2)3tan 30 tan 45 2sin 60;
求sin∠ABC的值。
构建直角三角形求三角函数值
求sin∠ABC的值。
解:过点A作AD⊥BC于D.
等腰三角形常作底边上的高线。
归纳:已知值,求角 求cosB 及tanB 的值.
(C) 0<cosA<
(D) <cosA<1
求锐角三角函数值的四种常用方法
方法
1
直接用锐角三角函数的定义求 三角函数值
1.如图所示,在 Rt△ABC 中,∠C=90°,BC=3,AC=4,
那么 cosA 的值等于 ( D )
A. 3 4
B. 4 3
C. 3 5
D. 4 5
方法 2 巧设参数求三角函数值
2.在Rt△ABC中,∠C=90°,且sinB=
12 13
,
5
则tanA= 12 .
方法
3 利用等角转化法求三角函数值
3.如图,已知在Rt△ABC中,∠ACB=90°,CD是 斜边AB的中线,过点A作AE⊥CD,AE分别与CD, CB相交于点H,E且AH=2CH,求sin B的值.
17
E
锐角三角函数的基本概念优秀课件

随堂练习 18
相信自己 9. 在 Rt△ABC 中,∠C=90°.
(1)AC=25,AB=27,求 tan A 和 tan B; (2)BC=3,tan A=0.6,求 AC 和 AB; (3)AC=4,tan A=0.8,求 BC.
第二十一页,共二十六页。
10. 如图,在梯形 ABCD 中,AD//BC,AB=DC= 13,AD=8,BC=18. 求 tan B.
第二十六页,共二十六页。
第十二页,共二十六页。
B1 B2
C2
C1
例题欣赏 12
行家看“门道”
例1 下图表示两个自动扶梯,哪一个自动扶梯比较陡?
13 m α
甲
5m ┌
6m ┐β 8m 乙
第十三页,共二十六页。
解:甲梯中, tan 5 5 . 乙梯中, tan 6 3 . 132 52 12 ∵tan β >tan α, 8 4
A. 扩大 100 倍
B. 缩小 100 倍
C. 不变
D. 不能确定
4. 已知∠A,∠B为锐角.
(1)若∠A=∠B,则 tan A
tan B;
(2)若 tan A=tan B,则∠A
∠B.
第十八页,共二十六页。
随堂练习 16
八仙过海,尽显才能
5. 如图,分别根据图(1)和图(2)求 tan A 的值. 6. 在 Rt△ABC 中,∠C=90°. (1)AC=3,AB=6,求 tan A 和 tan B; (2)BC=3,tan A= ,5求 AC 和 AB.
12
第十九页,共二十六页。
随堂练习 17
八仙过海,尽显才能
7. 在 Rt△ABC 中,∠C=90°,AB=15,tan A= , 3
《锐角三角函数》课件

锐角三角函数图像与性质
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
正弦函数图像及性质
周期性
振幅
相位
图像特点
正弦函数具有周期性,周期为2π。
正弦函数的相位表示函数在水平方向上的移动,通过调整相位可以得到不同位置的正弦波。
正弦函数的振幅为1,表示函数在垂直方向上的波动范围。
正弦函数的图像是一条连续的、平滑的曲线,呈现周期性的波动。
余弦函数图像及性质
202X
单击此处添加副标题内容
《锐角三角函数》ppt课件
汇报日期
汇报人姓名
目录
锐角三角函数基本概念
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数图像与性质
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数运算规则
单击此处添加文本具体内容,简明扼要的阐述您的观点。
锐角三角函数在实际问题中应用
乘法运算规则
两个锐角三角函数的除法运算,通常转化为同角三角函数的除法运算,再利用同角三角函数的基本关系式进行化简。
除法运算规则
按照先乘除后加减的运算顺序进行乘除混合运算,注意运算过程中的化简和约分。
乘除混合运算规则
复合运算规则
复合函数的定义域
复合函数的值域
复合函数的单调性
复合函数的周期性
01
02
03
钝角三角函数定义
探讨了钝角三角函数的性质,如取值范围、增减性等,以及与锐角三角函数的异同点。
钝角三角函数的性质
介绍了在直角情况下,一些特殊角的三角函数值,如0°、30°、45°、60°、90°等,以及如何利用这些特殊值进行计算和证明。
直角情况下的特殊值
感谢观看
THANKS
渐近线与间断点
02
锐角三角函数复习课课件

90度角
总结词
正弦值和余弦值不存在,正切值为无穷大
详细描述
在90度角时,正弦函数值和余弦函数值都不存在,因为无法定义与x轴的角度;正切函数值为无穷大 ,因为在直角三角形中,对边长度可以无限小而保持与斜边的比值不变。
03
锐角三角函数的图像与性质
正弦函数图像
总结词
正弦函数图像是一个周期函数,其图像在直角坐标系中呈波 浪形。
用三角函数来处理角度和旋转。
05
常见题型解析与解题技巧
选择题
• 题型特点:选择题通常考察学生对锐角三角函数基础知识的理 解和应用,题目会给出一些具体的数值或图形,要求选择正确 的答案。
选择题
排除法
根据题目给出的选项,逐一排除明显 错误的答案,缩小选择范围。
代入法
对于涉及数值计算的题目,可以将选 项中的数值代入题目中,通过计算验 证答案的正确性。
在研究磁场和电场时,我们经常需要使用锐 角三角函数来描述场的方向和强度。
日常生活中的问题
建筑和设计
在建筑设计、工程规划和土木工程中,锐角 三角函数用于计算角度、高度和距离等参数 ,以确保结构的稳定性和安全性。
游戏和娱乐
在许多游戏和娱乐活动中,锐角三角函数也 起着重要作用。例如,在制作动画、设计游 戏关卡或创建虚拟现实环境时,我们需要使
总结词
正弦值为0,余弦值和正切值不存在
详细描述
在0度角时,正弦函数值为0,表示射线与x轴重合;余弦函数值不存在,因为无 法定义与x轴的角度;正切函数值也不存在,因为没有对边形成直角三角形。
30度角
总结词
正弦值为0.5,余弦值为0.866,正切值为1/3
详细描述
在30度角时,正弦函数值为0.5,表示对边长度为斜边长度的一半;余弦函数值 为0.866,表示邻边长度为斜边长度的一半的平方根;正切函数值为1/3,表示对 边长度与邻边长度的比值。
锐角三角函数课件

余弦函数
1
定义和公式
余弦函数描述直角三角形中的比例关系,其定义和公式为cos(x) = 邻边/斜边。
2
图像和性质
余弦函数的图像呈现波浪形状,具有周期性、振幅和相位差等性质。
3
应用举例
余弦函数在几何、物理、工程等领域有广泛的应用,如研究周期性现象和计算机 图形学。
正切函数
定义和公式 图像和性质 应用举例
和差化积公式
三角函数的和差化积公式可 以将两个三角函数的和、差 表达为一个三角函数的乘积。
倍角公式
三角函数的倍角公式用于计 算两倍角的三角函数值。
总结
特点和应用
锐角三角函数具有周期性、对称性和广泛的 应用,为解决实际问题提供了重要的数学工 具。
实际生活中的应用举例
锐角三角函数在摄影、测量、物理仿真等实 际生活中有广泛的应用。
ห้องสมุดไป่ตู้
扩展和推广
锐角三角函数的研究和应用正在不断扩展和 推广,涉及到更多领域和复杂情况。
未来发展和研究方向
锐角三角函数的未来发展将涉及到更多领域 的交叉研究和深入探索。
正切函数用来描述直角三角形中的比例关系, 其定义和公式为tan(x) = 对边/邻边。
正切函数的图像呈现周期性、无界和渐近线等 特点,其图像在某些范围内会无限逼近无穷。
正切函数在物理、工程、电子等领域中常用于 信号处理和电路分析等方面。
三角函数的关系式
基本关系式
正弦、余弦和正切函数之间 有一系列关系式,如sin²θ + cos²θ = 1等。
特点
锐角三角函数的值域在特 定区间内,具有周期性和 对称性等特点。
正弦函数
定义和公式
正弦函数用来描述直角三角形 中的比例关系,其定义和公式 为sin(x) = 对边/斜边。
初三数学《锐角三角函数》优秀教学ppt课件

14
回归情景,解决问题
15
归纳小结,反思提高
数
锐角三角函数
16
A
归纳小结,反思提高
bc
Ca B
英文 名字 中文名字
三角形中的比 例
取值 范围
sinA ∠A的正弦
a c
0<sinA<1
cosA ∠A的余弦
b c
0<cosA<1
tanA ∠A的正切
a b
tanA>0
17
归纳小结,反思提高
我来说
18
B
锐角α的正弦、余弦、正切 统称为∠α的三角函数
α
AC
8
新知探究,明确定义
• 如图,在Rt⊿ABC中,∠C=Rt∠
sinA= BC AB
cosA= AC AB
tanA=BABCC
sinA=
∠A的对边 斜边
边
斜边
∠AB 的
对邻
边
∠AB的邻对边
11
变变
•
在Rt⊿ABC中,∠C=Rt∠,sinA=
3 5
B 求锐角∠A的余弦
C
A
12
变变变
•
在Rt⊿ABC中,∠C=Rt∠,sinA=
3 5
B CD⊥AB,求锐角∠DCB的余弦
D
C
A
13
• 已知一辆汽车从高架桥引桥的入口到高架
桥路从面数总共学行到驶实了大际约,30回m的归距情离,景若已
知该段引桥的坡角约为15°,请问高架桥 的路面离地大约多少米?
数学九年级下第一章第一 节《锐角三角函数》优秀
教学课件
§1.1.1 锐角三角函数 §1.1 锐角三角函数
回归情景,解决问题
15
归纳小结,反思提高
数
锐角三角函数
16
A
归纳小结,反思提高
bc
Ca B
英文 名字 中文名字
三角形中的比 例
取值 范围
sinA ∠A的正弦
a c
0<sinA<1
cosA ∠A的余弦
b c
0<cosA<1
tanA ∠A的正切
a b
tanA>0
17
归纳小结,反思提高
我来说
18
B
锐角α的正弦、余弦、正切 统称为∠α的三角函数
α
AC
8
新知探究,明确定义
• 如图,在Rt⊿ABC中,∠C=Rt∠
sinA= BC AB
cosA= AC AB
tanA=BABCC
sinA=
∠A的对边 斜边
边
斜边
∠AB 的
对邻
边
∠AB的邻对边
11
变变
•
在Rt⊿ABC中,∠C=Rt∠,sinA=
3 5
B 求锐角∠A的余弦
C
A
12
变变变
•
在Rt⊿ABC中,∠C=Rt∠,sinA=
3 5
B CD⊥AB,求锐角∠DCB的余弦
D
C
A
13
• 已知一辆汽车从高架桥引桥的入口到高架
桥路从面数总共学行到驶实了大际约,30回m的归距情离,景若已
知该段引桥的坡角约为15°,请问高架桥 的路面离地大约多少米?
数学九年级下第一章第一 节《锐角三角函数》优秀
教学课件
§1.1.1 锐角三角函数 §1.1 锐角三角函数
《圆和锐角三角函数》课件

信号处理
圆形三角函数应用于信号处 理和调频调相等领域。
用圆形三角函数解题实例
角度求解
通过已知条件与圆形三角函数求 解角度。
边长计算
通过已知条件与圆形三角函数计 算三角形的边长。
导航应用
利用圆形三角函数在导航中确定 方向与距离。
圆形三角函数扩展应用
波的传播
圆形三角函数应用于描述波 的传播性质,如声波和电磁 波。
周期性现象
通过圆形三角函数可以描述 周期性现象,如天文学中的 行星运动。
《圆和锐角三角函数》 PPT课件
三角函数是数学中重要的概念,涉及到圆、锐角以及它们的相互关系。本课 件将带您深入了解圆和锐角三角函数的相关知识。
三角函数简介Leabharlann 什么是三角函数?它们描述了圆中锐角的特性,通过角度与圆上点的坐标之间的关系,提供了对角度的度量和 计算方法。
正弦、余弦、正切函数
1 正弦函数
描述锐角对应的圆上点的纵坐标与半径之比。
2 余弦函数
描述锐角对应的圆上点的横坐标与半径之比。
3 正切函数
描述正弦和余弦函数值的商,即纵坐标与横坐标之比。
常用三角函数值表
角度
0°
正弦值
0
余弦值
1
正切值
0
30° 1/2 √3/2 √3/3
45° √2/2 √2/2 1
60° √3/2 1/2 √3
90° 1 0 undefined
平面直角坐标系与三角函数关系
坐标系
二维平面上的点由横纵坐标表 示。
正弦
纵坐标与半径之比,描述角的 正弦值。
余弦
横坐标与半径之比,描述角的 余弦值。
圆形三角函数定义
1
《锐角三角函数》_优秀课件

tan A=____,tan B=____.
3.锐角三角函数:∠A的正弦、余弦、正切都是∠A的锐角三角__函数__.
4.常用的三角函数关系:(1)同角的三角函数关系:tan α=
,sin2α+
cos2α=1;
(2)互余角的三角函数关系:如果∠A+∠B=90°,则有sin A=cos B,tan A·tan
.求BC的长.
【获奖课件ppt】《锐角三角函数》_ 优秀课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 优秀课 件1-课 件分析 下载
14.如图,在平面直角坐标系中,已知点B(4,2),BA⊥x轴于A. (1)求∠AOB的三角函数;
(2)设△OAB绕原点逆时针方向旋转90°后得到△ODE,且点A,B的对应点分别为点D, E,请你画出△ODE; (3)求∠E的正切值.
【获奖课件ppt】《锐角三角函数》_ 优秀课 件1-课 件分析 下载
【获奖课件ppt】《锐角三角函数》_ 优秀课 件1-课 件分析 下载
15.已知:如图,在Rt△ABC中,∠C=90°,sin
A=
3 5
,AB=10,点O在AB上,以O
为圆心,OA长为半径的圆与AC,AB分别交于点D,E,连接BD.
算式中不正确的是( C )
A.sin A= BD
BC
C.tan A= CD
BD
B.cos A= AD
AC
D.tan A= BD
CD
8.(巴中)如图,将∠AOB放在边长为1的小正方形组成的网格中,则tan ∠AOB= ____.
第8题图
第10题图
9.在直角三角形中,斜边与一直角边的比是13∶12,最小角为α,则sin α=____, cos α= ____,tan α=____. 10.在等腰三角形ABC中,AC=BC,AB=8,△ABC的面积为40,则tan A =____,tan B=____.
《锐角三角函数》PPT教学课件(第2课时)

1
∠ 的对边 =
= .
2
斜边
A
可得 AB=2BC=70m,即需要准备70m长的水管.
C
知识讲解
1.正弦
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计
算∠A的对边与斜边的比
A
BC
AB
,你能得出什么结论?
即在直角三角形中,当一个锐角等于45°
时,不管这个直角三角形的大小如何,这
数形结合,构造直角三角形).
2.sinA,cosA,tanA各是一个完整的符号,分别表示∠A的正弦
、余弦和正切,记号中习惯省去“∠”;
3.sinA,cosA,tanA分别是一个比值.注意比的顺序,且在直角
三角形中sinA,cosA,tanA均大于0,无单位.
4.sinA,cosA,tanA的大小只与∠A的大小有关,而与直角三角
切比3,分子根号别忘添.
30°,45°,60°角的正切值可以看成是 3, 9 , 27.
当A、B为锐角时,
若A≠B,则
sinA≠sinB,
cosA≠cosB,
tanA≠tanB.
知识讲解
注意
1.从函数角度理解∠A的锐角三角函数:把∠A看成自
变量,其取值范围是0°<∠A<90°,sinA,cosA,
在Rt△ABC中,如果锐角A确定,
那么∠ A 的对边与斜边的比、邻
边与斜边的比都是一个定值.
B
斜
边
A
∠A的邻边
∠A的对边
┌
C
知识讲解
归纳:
在有一个锐角相等的所有直角三角形中,这个锐角的邻边与斜
边的比值是一个常数,与直角三角形的大小无关.
锐角三角函数PPT示范课市公开课一等奖省优质课获奖课件.pptx
第9页
解:(1)在图1中 sin A BC AB
A 45 (2)在图2中,
3 2 62
tan a AO 3OB 3 OB OB
a 60
第10页
本节课你学习了什么知识?
第11页
1?
sin 2 30 +tan 2 45 cos 2 45 +tan 30
+sin 2 60 cos30
解:原式=
1 2
2
3 2
2
1
(2)
cos45 sin45
-tan45
解: 2 2 -1 22
0
第8页
例4、(1)如图,在Rt△ABC中, ∠C=90°,AB= 6 ,BC= 3 。求∠A度数。
(2)如图,已知圆锥高AO等于圆锥底面半径
OB 倍,3 求α. A
B
(2)
63
AC
(1)
O B
B
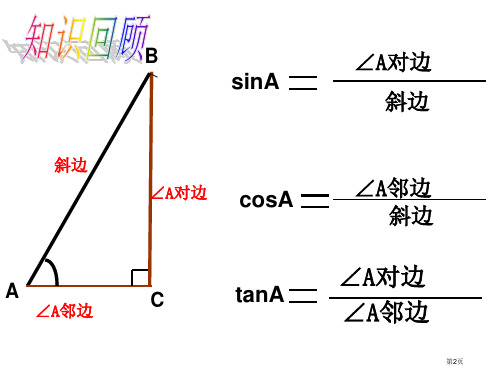
∠A对边
sinA
斜边
斜边
A
∠A邻边
∠A对边 cosA
∠A邻边 斜边
∠A对边
C
tanA
∠A邻边
第2页
1、在Rt △ABC中,∠C=90°,求∠A三角函数值。
① a=9 b=12
② a=9 b=12
2、已知∠A为锐角,sinA= 15 ,求cosA、tanA值。 17
第3页
第4页
Hale Waihona Puke 第5页特殊角三角函数值
2、已知:α为锐角,且满 足 3tan2-4ta+ n3 =0,求α度数。
第12页
3、在Rt△ABC中,∠C=90°,化简
1-2s i
第13页
4、操场里有一个旗杆,老师让小明去测量旗杆高 度,小明站在离旗杆底部10米远处,目测旗杆顶部, 视线与水平线夹角为30度,并已知目高为1.65米.然
人教版数学《锐角三角函数》优质课件3

5
A.3
B.6
C.9
D.12
人教版数学《锐角三角函数》优质课 件3
人教版数学《锐角三角函数》优质课 件3
达标检测 反思目标
3.下列各式中不正确的是( B). A.sin 2 600 cos2 600 1
B.sin30°+cos30°=1
C.sin35°=cos55°
D.tan45°>sin45°
2a 2
tan 60 3a 3
60°
a
设两条直角边长为a,则斜边长= a2 a2 2a
sin 45 a 2 2a 2
cos 45 a 2
45°
2a 2
tan 45 a 1 a
人教版数学《锐角三角函数》优质课 件3
人教版数学《锐角三角函数》优质课 件3
合作探究 达成目标
仔细观察,说说你发现 这张表有哪些规律?
合作探究 达成目标
小组讨论1:在例3中的两个式子中包含几种运算? 运算顺序是怎样的?
【反思小结】含特殊角三角函数值的计算中,一 要注意运算顺序和法则;二要注意特殊角三角函 数值的准确代入.
人教版数学《锐角三角函数》优质课 件3
人教版数学《锐角三角函数》优质课 件3
【针对练一】
1.计算:
(1)2 cos45°; (2)1-2sin30°cos30°.
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a 三角函数
sin a cos a tan a
人教版数学《锐角三角函数》优质课 件3
30°
1 2 3 2
3 3
45°
2 2
2 2
1
60°
3 2
1 2
锐角三角函数PPT比赛课市公开课一等奖省优质课获奖课件.pptx

第10页
【针对练一】
1.计算: (1)2 cos45°;
解: 2 2 2
2
(2)1-2sin30°cos30°. 解: 1 2 1 3 22 1 3 2 2 3 2
第11页
合作探究 达成目标
例4:如图(1),在RtABC中,C 900 ,
AB 6, BC 3, 求A的度数。
(2)如图(2),已知圆锥的高AO等于
第13页
总结梳理 内化目标
熟记特殊三角函数表:
30°
45°
60°
sinα
1
2
3
2
2
2
cosα
3
2
1
2
2
2
tanα
3
3
1
3
要熟记上表,灵活利用
第14页
达标检测 反思目标
1、已知α为锐角,且 1 <cosα< 2 ,则α取
2
2
值范围是( )C
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
展示点评:问题(1)中,有两个变量t与v,当一个量t 改变时,另一个量v伴随它改变而改变,而且对于t每个 确定值,v都有唯一确定值与其对应.问题(2)(3) 也一样.所以这些变量间含有函数关系,它们
解析式分别为 v 1463 ,y 1000 ,S 1.68104 .
t
x
n
第5页
合作探究 达成目标
第3,4,7题 .
• 课后作业:“学生用书”课 后作业部分.
第18页
∠A邻边
第3页
• 1.了解特殊角三角函数值由来 . • 2.熟记30°,45°,60°三角函数值. • 3.依据一个特殊角三角函数值说出这个角.
【针对练一】
1.计算: (1)2 cos45°;
解: 2 2 2
2
(2)1-2sin30°cos30°. 解: 1 2 1 3 22 1 3 2 2 3 2
第11页
合作探究 达成目标
例4:如图(1),在RtABC中,C 900 ,
AB 6, BC 3, 求A的度数。
(2)如图(2),已知圆锥的高AO等于
第13页
总结梳理 内化目标
熟记特殊三角函数表:
30°
45°
60°
sinα
1
2
3
2
2
2
cosα
3
2
1
2
2
2
tanα
3
3
1
3
要熟记上表,灵活利用
第14页
达标检测 反思目标
1、已知α为锐角,且 1 <cosα< 2 ,则α取
2
2
值范围是( )C
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
展示点评:问题(1)中,有两个变量t与v,当一个量t 改变时,另一个量v伴随它改变而改变,而且对于t每个 确定值,v都有唯一确定值与其对应.问题(2)(3) 也一样.所以这些变量间含有函数关系,它们
解析式分别为 v 1463 ,y 1000 ,S 1.68104 .
t
x
n
第5页
合作探究 达成目标
第3,4,7题 .
• 课后作业:“学生用书”课 后作业部分.
第18页
∠A邻边
第3页
• 1.了解特殊角三角函数值由来 . • 2.熟记30°,45°,60°三角函数值. • 3.依据一个特殊角三角函数值说出这个角.
人教新课标九年级数学下册《锐角三角函数》专题PPT课件

第 21 讲 锐角三角函数
义务教育教科书人教版 九年级数学 下册
知识梳理
考点一 锐角三角函数的定义
知识梳理
考点二 特殊锐角的三角函数值
α
sinα
cosα
tanα
30°
45°
60°
知识梳理
考点三 解直角三角形
解直角三角形的定义
在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由这些元素中的一些已知元素,求出所有未知元素的过程叫做解直角三角形.
锐角三角函数
1.锐角三角函数的定义
⑴正弦 ⑵特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系 ②锐角间关系 ③边角间关系
⑶解直角三角形在实际问题中的应用
小结
知识自测
大中考p77“基础知识自测” (时间:5分钟)
作业
大中考p80“优化训练” 1.必做题:1-10题 2.选做题:11、12题
方向(位) 角
定义
指北或指南方向线与目标方向线所成的小于90°的角叫做方向(位)角
h∶l
l
h
α
视线
铅垂线
水平线
视线
仰角
俯角
(2)坡度
tan α =
h
l
α为坡角
知识梳理
探究一 三角函数的概念
B
考点精讲
考点精讲
B
【类题通法】 解答这类问题,常画出草图,结合已知条件构造直角三角形,再根据锐角三角函数的定义求解。
考点精讲
探究四 解直角三角形的实际应用
考点精讲
c
考点精讲
c
考点精讲
2.如图所示,某地下车库的入口处有斜坡AB,其坡度i=1∶1.5,且AB= m.
义务教育教科书人教版 九年级数学 下册
知识梳理
考点一 锐角三角函数的定义
知识梳理
考点二 特殊锐角的三角函数值
α
sinα
cosα
tanα
30°
45°
60°
知识梳理
考点三 解直角三角形
解直角三角形的定义
在直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由这些元素中的一些已知元素,求出所有未知元素的过程叫做解直角三角形.
锐角三角函数
1.锐角三角函数的定义
⑴正弦 ⑵特殊角的三角函数值
3.解直角三角形
⑴定义
⑵解直角三角形的依据
①三边间关系 ②锐角间关系 ③边角间关系
⑶解直角三角形在实际问题中的应用
小结
知识自测
大中考p77“基础知识自测” (时间:5分钟)
作业
大中考p80“优化训练” 1.必做题:1-10题 2.选做题:11、12题
方向(位) 角
定义
指北或指南方向线与目标方向线所成的小于90°的角叫做方向(位)角
h∶l
l
h
α
视线
铅垂线
水平线
视线
仰角
俯角
(2)坡度
tan α =
h
l
α为坡角
知识梳理
探究一 三角函数的概念
B
考点精讲
考点精讲
B
【类题通法】 解答这类问题,常画出草图,结合已知条件构造直角三角形,再根据锐角三角函数的定义求解。
考点精讲
探究四 解直角三角形的实际应用
考点精讲
c
考点精讲
c
考点精讲
2.如图所示,某地下车库的入口处有斜坡AB,其坡度i=1∶1.5,且AB= m.
圆与锐角三角函数

圆与锐角三角函数
圆与锐角三角函数是两种不同的三角函数系统,它们的定义、应用和概念都具有差异。
圆三角函数是用一个单位圆及其上的点构成,包括正弦、余弦、正切、余切、正割、余割六个函数。
在一个单位圆上,以圆心为原点,向右为x轴正向,向上为y轴正向,则对于任意一点(x,y),我们可以定义出对应的三角函数,如下:
正弦函数:sinθ=y
余弦函数:cosθ=x
正切函数:tanθ=y/x
余切函数:cotθ=x/y
正割函数:secθ=1/x
余割函数:cscθ=1/y
圆三角函数广泛用于物理、工程、数学等方面,以描述角度的变化对应于一些量的变化,比如某个物体移动的轨迹、振动的周期等。
锐角三角函数是另一种三角函数系统,由正弦、余弦、正切、余切、正割、余割六个函数构成,但是它们的定义范围不同于圆三角函数。
锐角指的是0到90度之间的角度,因此锐角三角函数只针对这个范围内的角度定义。
它们的值域也在这个范围内,不同于圆三角函数在整个实数范围内的取值。
锐角三角函数的常见定义如下:
正弦函数:sinθ=对边/斜边
余弦函数:cosθ=邻边/斜边
正切函数:tanθ=对边/邻边
余切函数:cotθ=邻边/对边
正割函数:secθ=斜边/邻边
余割函数:cscθ=斜边/对边
锐角三角函数可以用于计算直角三角形的各种参数,例如某个角度的正弦、余弦、正切、余切等,也可以通过已知的角度和其中的一些参数反推出另外的参数,提
供了方便和快捷的计算方式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1)同圆中,同弧所对的圆周角都相等,等于它所对 的圆心角的一半.
D
E
C
O A
B C
(2)半圆或直径所对的圆周角都相等,都等于900(直角). 反之成立.
O
B
知识准备
★切线性质 圆的切线 垂直 于经过 切点 的 半径 .
★弦切角定理:
1.弦切角等于它所夹的弧对的 圆周角 .
2.弦切角等于它所夹的弧对圆心角的 一半
.
★切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,
圆心和这一点的连线平分两条切线的夹角.
O
AB B
O
C
AD A
O
P
B
类型一:利用定义求锐角三角函数值
★直接法
★换
类型一:利用定义求锐角三角函数值 ★构
类型一:利用定义求锐角三角函数值
如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,AC=4.
人教版数学九年级下册
第二十八章 锐角三函数
第8课时 专题学习 锐角三角函数与圆
学习目标
学习目标: 1.会运用解直角三角形的知识解决与圆有关的问题. 2.能选择合适的方法解决锐角三角函数与圆的问题.
知识准备
★在解直角三角形的过程中,一般要用到下面一些关系:
(1)三边之间的关系 a2 b2 c2 (勾股定理) A
求sin∠BAC和tan∠ADC的值.
解:连接BC
★构+换
C
A
O·
B
D
类型二:利用锐角三角函数值计算
★直接法
★换+构
类型二:利用锐角三角函数值计算
如如图如图,图,A,BAAB为B为⊙为⊙O⊙O的O的直的直径直径,径,且,且弦且弦弦CDC⊥CDD⊥A⊥BAAB于B于于E,EE,过,过点过点点B B的B的切的切线切线与线与与ADAAD的D的延的延长延长线长线交线交于交于点于点点F.FF..
若若若cocsco∠oss∠C∠=CC==4 5
54,54,D,FD=DF3F=,=33,求,求⊙求⊙O⊙O的O的半的半径半径.径..
★换+构
类型二:利用锐角三角函数值计算
类型二:利用锐角三角函数值计算
知识小结 本节课你有什么收获?
锐角三角函数与圆的两种类型题型 (1)利用定义求三角函数值 (2)利用三角函数值进行计算 直接法、换、构
数形结合思想、转化思想
已知:⊙O 中,OC⊥AB 于 C 点,AB=16cm, sin AOC 3 5
(1)求⊙O 的半径 OA 的长及弦心距 OC; (2)求 cos∠AOC 及 tan∠AOC.
谢谢聆听
泸州十二中 何琴
(2)两锐角之间的关系 ∠A+∠B=90° b
(3)边角之间的关系
sin
A
A的对边 斜边
a c
C
cos
A
A的邻边 斜边
b c
tan
A
A的对边 A的邻边
a b
c
a
B
知识准备
★垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
★等对等定理
同圆或等圆中,弦、弧、圆心角、圆周角,一组等组组等
★圆周角定理
D
E
C
O A
B C
(2)半圆或直径所对的圆周角都相等,都等于900(直角). 反之成立.
O
B
知识准备
★切线性质 圆的切线 垂直 于经过 切点 的 半径 .
★弦切角定理:
1.弦切角等于它所夹的弧对的 圆周角 .
2.弦切角等于它所夹的弧对圆心角的 一半
.
★切线长定理: 从圆外一点引圆的两条切线,它们的切线长相等,
圆心和这一点的连线平分两条切线的夹角.
O
AB B
O
C
AD A
O
P
B
类型一:利用定义求锐角三角函数值
★直接法
★换
类型一:利用定义求锐角三角函数值 ★构
类型一:利用定义求锐角三角函数值
如图,已知AB是⊙O的直径,点C、D在⊙O上,且AB=5,AC=4.
人教版数学九年级下册
第二十八章 锐角三函数
第8课时 专题学习 锐角三角函数与圆
学习目标
学习目标: 1.会运用解直角三角形的知识解决与圆有关的问题. 2.能选择合适的方法解决锐角三角函数与圆的问题.
知识准备
★在解直角三角形的过程中,一般要用到下面一些关系:
(1)三边之间的关系 a2 b2 c2 (勾股定理) A
求sin∠BAC和tan∠ADC的值.
解:连接BC
★构+换
C
A
O·
B
D
类型二:利用锐角三角函数值计算
★直接法
★换+构
类型二:利用锐角三角函数值计算
如如图如图,图,A,BAAB为B为⊙为⊙O⊙O的O的直的直径直径,径,且,且弦且弦弦CDC⊥CDD⊥A⊥BAAB于B于于E,EE,过,过点过点点B B的B的切的切线切线与线与与ADAAD的D的延的延长延长线长线交线交于交于点于点点F.FF..
若若若cocsco∠oss∠C∠=CC==4 5
54,54,D,FD=DF3F=,=33,求,求⊙求⊙O⊙O的O的半的半径半径.径..
★换+构
类型二:利用锐角三角函数值计算
类型二:利用锐角三角函数值计算
知识小结 本节课你有什么收获?
锐角三角函数与圆的两种类型题型 (1)利用定义求三角函数值 (2)利用三角函数值进行计算 直接法、换、构
数形结合思想、转化思想
已知:⊙O 中,OC⊥AB 于 C 点,AB=16cm, sin AOC 3 5
(1)求⊙O 的半径 OA 的长及弦心距 OC; (2)求 cos∠AOC 及 tan∠AOC.
谢谢聆听
泸州十二中 何琴
(2)两锐角之间的关系 ∠A+∠B=90° b
(3)边角之间的关系
sin
A
A的对边 斜边
a c
C
cos
A
A的邻边 斜边
b c
tan
A
A的对边 A的邻边
a b
c
a
B
知识准备
★垂径定理 垂直于弦的直径平分弦,并且平分弦所对的两条弧.
★等对等定理
同圆或等圆中,弦、弧、圆心角、圆周角,一组等组组等
★圆周角定理
