九年级数学何时获得最大利润
6.何时获得最大利润

第二章 二次函数
2.6
何时获得最大利润
授课人: 王秀莲
义安一中
九年级 数学
第二章 二次函数
2.6 何时获得最大利润 某大型商场的杨总到 T恤衫部 去视察,了解的情况如下:已知 成批购进时单价是20元.根据市 场调查,销售量与销售单价满足 如下关系:在一段时间内,单价 是35元时,销售量是600件,而单 价每降低1元,就可以多销售200 件.于是杨总给该部门王经理下 达一个任务,马上制定出获利最 多的销售方案,这可把王经理给 难住了?你能帮他解决这个问题 吗?
60500 60400 60300 60200
60100
60000
O
5
x1
10
x2
15
20
x/棵
九年级 数学
第二章 二次函数
感悟和反思 通过这节课的学习你有哪些 收获?
九年级 数学
第二章 二次函数
作业
1.单价是20元.根据 市场调查,销售量与销售单价满足如下关系:在一 段时间内,单价是35元时,销售量是600件,而单 价每降低1元,就可以多销售200件,问销售单价是 多少时获利最多 ?
• • • • •
如果设销售单价为x元,(20≤x≤35的整数) 35- x 每件降价____________ 元 600+200( 35- x ) 销售量可以表示_________________件 x -20 每件利润__________元 ( x -20 )[600+200( 35- x ) ] 获得的总利润y =_________________________
九年级 数学
第二章 二次函数
y (600 - 5 x)(100 x) -5 x 100 x 60000
2.7 何时获得最大利润7

【学习目标】掌握如何求最大利润。
【学习重点】求最大利润;【学习难点】如何求出二次函数的表达式,求它的最大值。
【学习过程】一、课前准备1、下列函数中是二次函数的是 ( )A 、y=2+5x 2B 、22xy = C 、2x y -= D 、122++=x x y 2、函数y = 2x 2的图象对称轴是 ,顶点坐标是3、若点P (6,m )是抛物线221x y =上的一点,则m = 4、二次函数的 图像是 线,它的开口向 ,对称轴是 ,顶点 标是 ,最值是5、抛物线122--=x x y 的顶点坐标是( )A 、(1,-2)B 、(-1,0)C 、(-2,1)D 、(2,-1)二、自主学习活动一:问题情景某商店经营T 恤衫,已知成批购进时单价是5元。
根据市场调查,销售量与单价满足如下关系:在一时间内,单价是15元时,销售量是400件,而单价每降低1元,就可以多售出100件。
设销售单价降低x 元,则销售价为(15-x )元,所获得的利润为y ,那么(1)单件利润可表示为: 件;(2)销售量可表示为: 元;(3)所获利润y 可表示为:y= 元;(4)请你计算一下,当销售单价为多少元时,可以获得最大利润?最大利润是多少?25x y -=活动二:课堂练习1、某旅行社组团去外地旅游,30人起组团,每人单价800元。
旅行社对超过30人的团给予优惠,即旅行团每增加一人,每人的单价就降低10元。
你能帮助算一下,当一个旅行团的人数是多少时,旅行社可以获得最大营业额?【课堂小测】1、已知12-=bx y 是二次函数,那么b 的取值范围是______________2、将函数的图象向_____平移_______个单位得到的图象是函数32-=x y 的图象。
3、抛物线4)3(22+-=x y 的开口 ,对称轴是 ,顶点坐标是4、抛物线1)5(32+--=x y 的顶点坐标是( )A 、(-5,1)B 、(5,1)C 、(5,-1)D 、(-5,-1)5、将进货为40元的某种商品按50元一个售出时,能卖出500个。
2.4.2何时获得最大利润上课课件

解:
假设销售单价为x(x≥30)元,销售利润为y元,则 y= -20(x-35)2+4500
y 4500 4420
若规定销售单价不得高于 33元,则如何提高售价,可 在半月内获得最大利润?
0
33
35
X
拓展
某商品现在的售价为每件60元,每星期可卖出300件.市场调查反映:如 果调整价格,每涨价1元,每星期要少卖出10件;每降价1元,每星期可 多卖出18件,已知商品的进价为每件40元,如何定价才能使利润最大? 分析:调整价格包括涨价和降价两种情况,我们先来看涨价的情况. (1)设每件涨价x元,则每星期卖出(300-10x)件,单件商品的利 润为(60+x - 40)元 y = (60+x)(300-10x) -40 (300-10x) 怎样确定x的 取值范围? 即
议一议
某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙 子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接 受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结 5个橙子.问增种多少棵橙子树,可以使橙子的总产量最多? 等量关系:橙子的总产量=每棵橙子树的产量×橙子树的数量
3. 二次函数y=-3(x+4)2-1的对称轴是 直线x=-4 ,顶点 坐标是 (-4 ,-1) 。当x= -4 时,函数有最 大 值,是 -1 。 4.二次函数y=2x2-8x+9的对称轴是 直线x=2 ,顶点 坐标是 (2 ,1) .当x= 2 时,函数有最 小 值,是 1 。
探究
服装厂生产某种品牌的T恤成本是每件10元。根据市场调 查,以单价13元批发给经销商,经销商愿意经销5000件, 并且表示单价每降低0.1元,愿意多经销500件。请你帮助 分析,厂家批发单价是多少时可以获利最多?
何时获得最大利润1

O
27
28
29
30
31
x /元
总结 :
运用函数来决策定价的问题: 运用函数来决策定价的问题:
构建二次函数模型:将问题转化为二次函数的一个具体的表达式. 构建二次函数模型:将问题转化为二次函数的一个具体的表达式. 求二次函数的最大(或最小值) 求二次函数的最大(或最小值)
销售量
600 600+200 + 600+200×2 + × 600+200×3 + × 600+200×4 + ×
总利润
7500 11200 13000 14400 15400
0元 元 1元 元 2元 元 3元 元 4元 元
令王经理非常开心的结论: 令王经理非常开心的结论: Yes! 价格下降,销量增加,总利润不断增加!!! 价格下降,销量增加,总利润不断增加!!!
y=(100+x)(600-5x) = - 5x2+100x+60000 =-5(x-10)2+60500
∵a<0 ∴ y有最大值
b 4ac − b 2 4 × (−5) × 60000 − 100 2 ∴当 x = − = 10时,y = = = 60500 最大值 2a 4a 4 × (−5)
挑战新高
检查求得的最大值或最小值对应的自变量的值必 检查求得的最大值或最小值对应的自变量的值必 须在自变量的取值范围内 。
某商店购进一批单价为20元的日用品,如果以单价30元销售, 某商店购进一批单价为20元的日用品,如果以单价30元销售, 20元的日用品 30元销售 那么半个月内可以售出400 400件 根据销售经验, 那么半个月内可以售出400件.根据销售经验,提高单价会导 致销售量的减少,即销售单价每提高1 销售量相应减少20 致销售量的减少,即销售单价每提高1元,销售量相应减少20 如何提高售价,才能在半个月内获得最大利润? 件.如何提高售价,才能在半个月内获得最大利润?
《百分闯关》2016届九年级数学北师大版下册课件+教案:第二章 二次函数2.4 二次函数的应用(2)

( C)
A.30人 B.40人 C.50人 D.55人
3.教练对小明推铅球的录像进行技术分析,发现铅球行进高度 y(m) 与水平距离 x(m)之间的关系为 y=-112(x-4)2+3,由此可知铅球推出的
距离是( C )
A.2 m B.8 m C.10 m D.12 m 4.将进货单价为 70 元的某种商品按零售价 100 元售出时,每天能 卖出 20 个,若这种商品零售价在一定范围内每降价 1 元,其日销售量就
10.某种商品每天的销售利润y(元)与销售单价x(元)之间满足关系:y= ax2+bx-75,其图象如图所示. (1)销售单价为多少元时,该种商品每天的销售利润最大?最大利润为多 少元? (2)销售单价在什么范围时,该种商品每天的销售利润不低于16元?
解 : (1) ∵ y = ax2 + bx - 75 的 图 象 经 过 点 (5 , 0) , (7 , 16) , ∴ 2459aa++57bb--7755==016,,解得ab==2-01,,∴y=-x2+20x-75=-(x-10)2+25, ∴当销售价为 10 元时,最大利润为 25 元
增加 1 个,为获得最大利润,应降价( A )
A.5 元 B.10 元 C.15 元 D.20 元
5.科技园电脑销售部经市场调查发现,销售某型号电脑所获利润y(元) 与销售台数x(台)满足y=-x2+40x+15600,则当他卖出___2_0___台时, 所获利润最大.
6.有x人结伴去旅游共需支出y元,若x,y之间满足关系式y=2x2- 20x+1050,则当人数x为___5___时,总支出最少.
北师大初中九年级数学下册何时获得最大利润

☺若该批发商平均每天的销售利润不低于1008元,
则每箱苹果的销售价在什么范围内?
52≤x≤68
第5页/共14页
y/元 1200
O
55 60
x /元
(3) ∵a=-3<0,开口向下,对称轴为直线x=60
当x<60时,w随x的增大而增大
又∵x≤55,
∴当x=55时,w最大= -3× (55-60)2+1200=1125
一 复习诊断
1. y 2(x 1)2 7
向下(-1,7), -1,大,7,<-1,>-1,
2.
(x 10), 10(x 10), y 100 10(x 10),即y 10x 200. P (x 8)(10x 200),即P 10x2 280x 1600.
知者加速: 14, 360.
解得: x≥76
∵a= -1<0,开口向下
∴ x>75时, W 随x增大而减小,
∴x=76时, W最大
∴销售价应定为76元。 第9页/共14页
四 效果检测 y/元
45 40
OБайду номын сангаас
x(元/件) y(件)
55 60
…… 55 60 …… 45 40
x /元
70 …… 30 ……
第10页/共14页
五 交流分享
第2页/共14页
二 知识建网 1.求二次函数顶点坐标的方法有哪些? 2.二次函数的增减性. 3.单利润如何表示?总利润呢?
☺对于复习诊断第2题,如果我们设涨价x元,
你能表示销售利润吗?
第3页/共14页
三 典型例题
(1)W (x 40)[90 3(x 50)] 3x2 360x 9600
沪科版数学九年级上册21.6综合与实践-获取最大利润 课件(共23张PPT)

w=[2000-5(x-100)](x-80)
2.某商店将每件进价8元的某种商品按每件10元出售,一天可销出约100件,该店想通过降低售价,增加销售量的办法来提高利润,经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加约10件.将这种商品的售价降低多少时,能使销售利润最大?
由公式可得:当 x=- 时,即x=175,P最大= .∴t=-20x+6000=2500,∴ P=311500 元.
随堂练习
1.进价为80元的某件定价100元时,每月可卖出2000件,价格每上涨1元,销售量便减少5件,那么每月售出衬衣的总件数y(件)与衬衣售价x(元)之间的函数关系为________________.每月利润w(元)与衬衣售价x(元)之间的函数关系式为 . (以上关系式只列式不化简).
解:设每件商品降价x元(0≤x≤2),该商品每天的利润为y元,商品每天的利润y与x的函数关系式是y=(10-x-8)(100+100x),即 y=-100x2+100x+200,配方得 y=-100(x-0.5)2+225,∵x=0.5时,满足0≤x≤2,∴当x=0.5时,函数取得最大值,最大值y=225.∴将这种商品的售价降低0.5元时,能使销售利润最大.
归纳小结
同学们再见!
授课老师:
时间:2024年9月1日
第21章 二次函数与反比例函数
21.6 综合与实践 获取最大利润
学习目标
学习重难点
重点
难点
1.根据已知数据求出二次函数的具体表达式.2.依据二次函数模型解决最大利润问题.
二次函数在最优化问题中的应用.
从现实问题中建立二次函数模型.
回顾复习
二次函数的一般形式:y=ax²+bx+c(a≠0) =当x= 时,y取得最值
二次函数最大利润
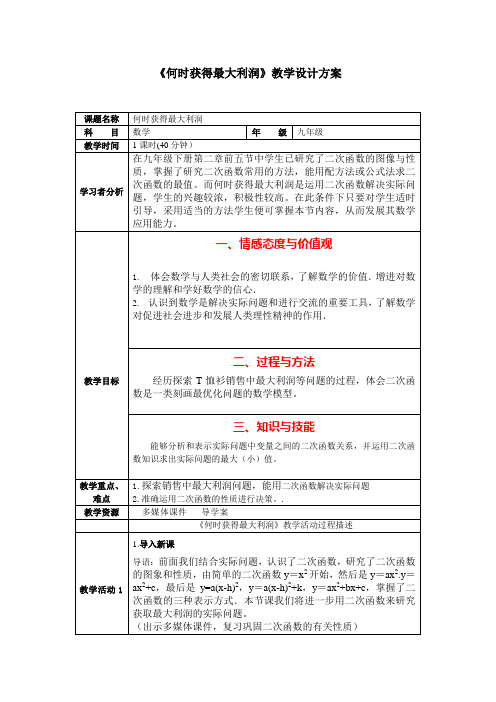
17 2 ) 9112 .5 4
b 100 10 ∵ 2a 2 (5) 4ac b 2 4 (5) 60000 1002 60500 4a 4 (5)
∴当 x=10 时,y 最大=60500. [师]回忆一下我们前面的猜测正确吗? [生]正确. (2) 、议一议 (1)利用函数图象描述橙子的总产量与增种橙子树的棵数之间的 关系. (2)增种多少棵橙子树,可以使橙子的总产量在 60400 个以上? (学生思考后多媒体课件显示) 3、实践应用 某商店购进一批单价为 20 元的日用品,如果以单价 30 元销 售,那么半个月内可以售出 400 件。根据销售经验,提高销售单 价会导致销售量的减少,即销售单价每提高 1 元,销售量相应减 少 20 件。如何提高售价,才能在半个月内获得最大利润? 解:设销售单价提高 x 元,销售利润为 y 元,则 y=(x+30-20)(400-20x) =-20x2+200x+4000 =-20(x-5)2+4500 ∴当 x=5 时,y 最大 =4500 答:当售价提高 5 元时,半月内可获最大利润 4500 元
《何时获得最大利润》教学设计方案
课题名称 科 目 教学时间
何时获得最大利润 数学 1 课时(40 分钟) 年 级 九年级
在九年级下册第二章前五节中学生已研究了二次函数的图像与性 质,掌握了研究二次函数常用的方法,能用配方法或公式法求二 次函数的最值。而何时获得最大利润是运用二次函数解决实际问 学习者分析 题,学生的兴趣较浓,积极性较高。在此条件下只要对学生适时 引导,采用适当的方法学生便可掌握本节内容,从而发展其数学 应用能力。
九年级数学二次函数应用之最大利润问题

变式训练1.为了扩大内需,让惠于农民,丰富农民的业余生活,鼓励送彩电下乡,国家决定对购买彩电的农户实行政府补贴,规定每购买一台彩电,政府补贴若干元,经调查某商场销售彩电台数y(台)与补贴款额x(元)之间大致满足如图①所示的一次函数关系,随着补贴款额x的不断增大,销售量也不断增加,但每台彩电的收益z(元)会相应降低且z与x之间也大致满足如图②所示的一次函数关系。
(1)在政府未出补贴措施前,该商场销售彩电的总收益额为多少元?,(2)在政府补贴政策实施后,分别求出该商场销售彩电台数y和每台家电的收益z与政府补贴款额x之间的函数关系式;(3)要使该商场销售彩电的总收益W(元)最大,政府应将每台补贴款额x定为多少?并求出总收益w的最大值。
题型三:实际问题中的方案决策例3 某小区有一长100 m ,宽80m 的空地,现将其建成花园广场,设计图案如图所示。
阴影区域为绿化区域(四块绿化区域是全等矩形),空白区域为活动区域,且四周出口一样宽,宽度不小于50 m ,不大于60 m 。
预计活动区域每平方米造价60元,绿化区域每平方米造价50元。
(1)设其中一块绿化区域的长边长为xm ,写出工程总造价y (元)与x ( m )的函数式系式(写出x 的取值范围); (2)如果小区投资46.9万元,问能否完成工程任务?若能,请写出x 为整数的所有工程方案;若不能,请说明理由。
(参考数据:732.13 )一、能力培养某公司计划从甲、乙两种产品中选择一种生产并销售,每年产销x件。
已知产销两种产品的有关信息如下表:产品每件售价(万元)每件成本(万元)每年其他费用(万元)每年最大产销量(件)甲 6 a20 200乙20 10 40+0.05x280其中a为常数,且3≤a≤5。
(1)若产销甲乙两种产品的年利润分别为y1万元、y2万元,直接写出y1、y2与x的函数关系式;(2)分别求出产销两种产品的最大年利润;(3)为获得最大年利润,该公司应该选择产销哪种产品?请说明理由。
2.6何时获得最大利润 课件5(数学北师大版九年级下册)

何时获得最大利润 设销售价为x元(x≤13.5元),那么 销售量可表示为 : 500 20013.5 x 销售额可表示为:x500 20013.5 x
果园共有(100+x)棵树,平均每棵树结 (600-5x)个橙子,因此果园橙子的总产量
Y=(100+x)(600-5x)=-5x² +100x+60000 在上述问题中,种多少棵橙子树,可 以使果园橙子的总产量最多?
11 1 121 4 5 x/ 棵 4 6 5 7 6 8 7 9 810 9 1 X/ 棵 11 2 23 3 6 6 6 6 6 6 6 6 6 6 0 6 1 62 y/个 0 0 0 0 0 0 0 0 0 0 0 0 Y/个 0 1 2 3 3 4 4 4 4 5 4 4 13 1 6 3 0 4 5 5
独立 作业
知识的升华
P61 习题2.6 1,2题.
祝你成功!
下课了!
结束寄语
•
生活是数学的源泉.
跳水运动与抛物线
某跳水运动员进行10米跳台跳水训 练时,身体(看成一点)在空中的运动 路线是经过原点O的一条抛物线.在 跳某规定动作时,正常情况下,该运 动员在空中的最高处距水面32/3米, 入水处距池边的距离为4米,同时,运 动员在距水面高度为5米以前,必须 完成规定的翻腾动作,并调整好入 水姿势,否则就会出现失误. (1)求这条抛物线的解析式; (2)在某次试跳中,测得运动员在空 中运动路线是(1)中的抛物线,且运 动员在空中调整好入水姿势时,距 池边的水平距离为18/5米,问此次跳 水会不会失误?并通过计算说明理 由.
(整理)初中数学九年级下册《26何时获得最大利润》

量就相应减少20件。
若销售单价提高x元时,半个月内获得的利润为y元,请写出y与x之间的函数关系式。
销售单价提高多少时,才能在半个月内获得最大利润?最大利润是多少?(三)巩固新知某商店经营T恤衫,已知成批购进时单价是2.5元。
根据市场调查,销售量与销售单价满足如下关系:在一段时间内,单价是13.5元时,销售量是500件,而单价每降低1元,就可以多售出200件。
销售单价是多少时,可以获得最大利润?最大利润是多少?(四)新知应用某果园有100棵橙子树,每一棵树平均结600个橙子.现准备多种一些橙子树以提高产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,且增加的橙子树最多不得超过20棵。
假设果园增种x棵橙子树,果园橙子的总产量为y个,请写出y与x之间的关系式,并回答下列问题. (1)我们曾经利用列表的方法得到一个猜测,增种多少棵橙子树时,总产量最大?x 1 … 8 9 10 11 12y …猜测的结论:当增种______棵橙子树时,橙子的总产量最大,最大产量为______个。
(2)现在请你用所学知识验证一下你的猜测是否正确。
(3)请画出函数的图象。
(4)利用函数图象描述橙子的总产量与增种橙子树的棵数之间通过这个实际问题,让学生感受到二次函数是一类最优化问题的数学模型,并感受数学的应用价值。
经历了探索T恤衫销售中最大利润等问题的过程,提高了学生的运算能力和运算技巧思考并独立完成,并交流结论提高学生运用函数图象解决实际问题的能力学会了分析和表示实际问题中变量之间的二次函数关系,并运用二次函数的知识求出实际问题中的最大(小)值,提高解决问题的能力。
教师指导纠正。
中考数学复习:专题3-16 最大利润问题在中考数学中的体现

最大利润问题在中考数学中的体现【专题综述】利润问题是中考中的热点问题,在今年的中考试题中,出现了很多和利润有关的函数型试题.解决此类试题,需要从已知条件中捕捉函数信息,通过函数关系,进一步解决实际问题.本文最大利润问题在中考数学中的体现举例说明.【方法解读】一、图象型例1. 随着绿城南宁近几年城市建设的快速发展,对花木的需求量逐年提高。
某园林专业户计划投资种植花卉及树木,根据市场调查与预测,种植树木的利润1y 与投资量x 成正比例关系,如图1所示;种植花卉的利润2y 与投资量x 成二次函数关系,如图2所示(注:利润与投资量的单位:万元).(1)分别求出利润1y 与2y 关于投资量x 的函数关系式;(2)如果这位专业户以8万元资金投入种植花卉和树木,他至少获得多少利润?他能获取的最大利润是多少?分析:本题第(1)个问题是已知一次函数和二次函数的图像,求函数的解析式,观察两个函数的图像可知,前者是正比例函数,后者是二次函数,顶点是(0,0),利用待定系数法,先设两个函数的解析式,再将P (1,2),Q (2,2)代入相应的解析式求出参数即可;第(2)个问题是已知自变量的取值范围求二次函数的最值,属于二次函数的条件最值问题.解:(1)设1y =kx ,由图1所示,函数1y =kx 的图像过(1,2),所以2=1⋅k ,2=k故利润1y 关于投资量x 的函数关系式是1y =x 2;因为该抛物线的顶点是原点,所以设2y =2ax ,由图2所示,函数2y =2ax 的图像过(2,2),所以222⋅=a ,21=a 故利润2y 关于投资量x 的函数关系式是221x y =;(2)设这位专业户投入种植花卉x 万元(80≤≤x ),则投入种植树木(x -8)万元,他获得的利润是z 万元,根据题意,得:z =)8(2x -+221x =162212+-x x =14)2(212+-x 当2=x 时,z 的最小值是14;因为80≤≤x ,所以622≤-≤-x ,所以36)2(2≤-x ,所以18)2(212≤-x ,所以32141814)2(212=+≤+-x ,即32≤z ,此时8=x , 当8=x 时,z 的最大值是32.评注:这类试题一般先将函数解析式配方,将函数解析式变成顶点形式,找出顶点坐标和对称轴方程,结合自变量的取值范围,画出函数图像(抛物线的一部分),根据抛物线的对称性、开口方向,确定函数的最大(或最小)值,不宜直接用最值公式,这种解题方法体现了数学中的数形结合的思想,它的优点是直观形象,避免死记公式.二、表格型例2. 红星公司生产的某种时令商品每件成本为20元,经过市场调研发现,这种商品在未来40天内的日销售量m (件)与时间t (天)的关系如下表:时间t (天) 1 36 10 36 … 日销售量m (件) 9490 84 76 24 … 未来40天内,前20天每天的价格y 1(元/件)与时间t (天)的函数关系式为25t 41y 1+=(20t 1≤≤且t 为整数),后20天每天的价格y 2(元/件)与时间t (天)的函数关系式为40t 21y 2+-=(40t 21≤≤且t 为整数)。
北师大版数学九年级下册二次函数的应用第2课时何时获得最大利润课件

知识迁移,活学活用
小结:解题的关键是要理清楚材料中的数量 关系,将实际问题转化为数学模型,利用已学的 数学知识解决实际问题.
具体步骤如下: (1)根据题意,列出二次函数表达式,注意 实际问题中自变量x的取值范围. (2)将二次函数表达式配方为顶点式的情势. (3)根据二次函数图象及其性质,在自变量 的取值范围内求出函数的最值.
请你帮助分析,厂家批发单价是多少时可 以获利最多?
视察学生,合理指点
解:批发价为x元时,获利y元.
则单件利润为(x-10)元,
降价后的销售量为
5
000
+
13 - x 0.1
×
500
件.
则
y
=
(
x
-
10)
5
000
+
13 - x 0.1
×
500
= 5 000( 000(- x2 + 24x - 140)
= -5 000[( x - 12)2 - 4].
所以,当批发价是12元时,获利最多.
知识迁移,活学活用
某旅社有客房120间,每间房的日租金为 160元时,每天都客满,经市场调查发现,如 果每间客房的日租金增加10元,那么客房每天 出租数会减少6间.不考虑其他因素,旅社将每 间客房的日租金提高到多少元时,客房日租金 的总收入最高?最高总收入是多少?
分析:客房日租金的总收入=客房的日租金 ×客房出租的间数.
知识迁移,活学活用
解:设客房的日租金增加x个10元,则客房每天的 出租数减少6x间,设客房日租金的总收入为y元, 则y=(160+10x)(120-6x)=-60(x-2)2+19 440. ∵x ≥0,且120-6x>0,∴0 ≤ x<20. 当x=2时, y有最大值19 440. 这时每间客房的日租金为160+10×2=180(元). 即旅社将每间客房的日租金提高到180元时,客房 日租金的总收入最高,最高总收入为19 440元.
第二章 二次函数

果园共有(100+x)棵树,平均每棵树结 (600-5x)个橙子,因此果园橙子的总产量
Y=(100+x)(600-5x)=-5x² +100x+60000
在上述问题中,种多少棵橙子树,可以使 果园橙子的总产量最多?
x/ 棵 X/ 棵 Y/ 个 Y/ 个
11 2 6 6 0 0 0 1 9 8 5 0 4 4 23 3 5 6 5 7 6 8 79 810 1 1 121 9 11 6 6 6 6 6 6 6 6 0 162 6 0 2 5 5 0 3 2 0 0 3 7 5 0 4 2 0 0 4 5 5 0 4 8 0 0 4 9 5 0 5 0 0 0 4 9 5 0 4 8 0 13 1 6 3 0 4 5 5
• 例2.(08武汉23)(本题10分)某商品 的进价为每件30元,现在的售价为每件4 40元,每星期可卖出150件.市场调查反映: 如果每件的售价每涨1元(售价每件不能高 于45元),那么每星期少卖10件.设每件 涨价x元(x为非负整数),每星期的销量 为y件.(1)求y与x的函数关系式及自变量 x的取值范围;(2)如何定价才能使每星 期的利润最大且每星期销量较大?每星期 的最大利润是多少?
七、教法学法
• 教法:对于函数关系式的列法是重点也是难点, 这要求学生尽量的采用小组合作形式,教师要适 当的参与学生的交流,发现问题,及时的处理问 题,将学习中的问题消灭在萌芽状态,在这部分 内容上,学生要高度的重视,因为这是中考的一 个热点。 • 学法:将实际问题转化为二次函数,在小组中充 分发表自己的见解,敢于说出困惑,请求帮助。 • 学习方式:小组合作交流探究的学习方式。
=-200x2+3700x-8000
( x -2.5 )[500+200(13.5- x )] (4)获得的总利润y=________________________
