必修一到五综合测试卷
高中 综合测试题5 必修1 试题(共15页)

武清区杨村第四中学(zhōngxué)2021高中语文综合测试题5 新人教版必修1本套试卷总分为150分,考试时间是是为120分钟。
Ⅰ阅读鉴赏〔77分〕1-14选择题每一小题3分,其余题按题号后赋分给分。
2.以下各组熟语运用正确的一项是哪一项:( )A.他有一个异常令人羡慕的幸福家庭,大人喜欢小孩,小孩也喜欢大人,一家三口和和美美,互敬互爱,相濡以沫。
B.曾经惊异于长城的蜿蜒,赞叹过大漠的孤烟,但当婀娜的雪松骤然出如今眼前时,他还是不禁为这大自然的巧夺天工所折服。
C.一份HY初级教育考察报告写道:学生无论品德优劣、才能上下,无不趾高气扬、踌躇满志,大有“我因我之为我而不同凡响〞的意味。
D.这些血气方刚的老人们自觉地组成宣传小组,在青少年中广泛宣传“黑网吧〞的危害,继续发挥他们的余热。
3.选出以下句子没有语病的一项。
〔〕A.是否有坚强的意志,是一个合格HY员的关键参考要素。
B.通过这次测验,使我们明白了学习要精益求精的道理。
C.我们全校的学生将来都希望考上理想的大学。
D.“熟读唐诗三百诗,不会写诗也会吟〞这句话,写诗的适用,为文的也适用。
4.以下文学常识有误的一项是哪一项〔〕A.?诗经?是我国最早的一部诗歌总集,按内容(nèiróng)分为“风〞、“雅〞、“颂〞三局部,经常运用“赋〞、“比〞、“兴〞的艺术技巧,“风〞、“雅〞、“颂〞、“赋〞、“比〞、“兴〞合称?诗经?六义。
B.?荷塘月色?作者朱自清原名自华,号实秋,后改名自清,字佩弦。
是我国当代文学史上著名的诗人、散文家、学者,著有?背影?、?春?、?匆匆?、?欧游杂记?等。
C.?孔雀东南飞?是我国古代保存下来的最早的一首长篇叙事诗,与?木兰辞?合称“乐府双璧〞D.冰心,原名谢婉莹,作品有?春水?、?繁星?、?小橘灯?等。
一、古诗文阅读鉴赏〔44分〕5.以下句子中,加点字解释全错的一项是哪一项( )A.槌床便大怒(卧具) 自可断来信(信件)B.渐车帏裳(浸湿) 可怜体无比(得意)C.否泰如天地(坏) 唯夫HY人之偷乐兮〔苟且〕D.叶叶相交通(往来通达) 谢家来贵门(感谢)6.对以下句子的翻译,正确的一项是哪一项( )A.便可白公姥。
高中数学必修1-5综合测试题及答案详解(优秀经典测试卷)

高中数学必修1-5测试卷 总分共150分,考试时间为2个小时一、选择题:本大题共10小题,每小题5分,共50分.1. 已知集合11{2,1,0,1,2}{|28R}2x M N x x +=--=<<∈,,,则M N =A .{0,1}B .{10}-,C .{1,0,1}-D .{2,1,0,1,2}-- 2. 圆2240x y x +-=的圆心坐标和半径分别为A.(2 , 0) , 4B. (2 , 0) , 2C.( 2 , 0) , 4-D. ( 2 , 0) , 2-3. 已知实数列1,a ,b ,c ,2成等比数列,则abc 等于( )A .4 B .±4 C .22 D .±224. 函数()442-+-=x x x f 在区间[]3,1上( )A.没有零点B.只有一个零点C.有两个零点D.以上选项都错误5.右图所示的程序框图,若输入的, , a b c 分别为21, 32,75,则输出的, , a b c 分别是A .75,21, 32B .21, 32, 75C .32,21,75D .75, 32, 216.已知a ,b 满足:||3a =,||2b =,||4a b +=,则||a b -=( )A .3B .5C .3D .107. 如右图为长方体木块堆成的几何体的三视图,则组成此几何体的长方体木块块数共有A .3块B .4块C .5块D .6块8. 圆2220x y y +-=与圆222360x y x +--=的位置关系是A. 相交B. 内切C. 外切D. 相离9. 从编号为1~50的50枚最新研制的某种型号的导弹中随机抽取5枚进行发射试验,若采取每部分选取的号码间隔一样的系统抽样方法,则所选取的5枚导弹的编号可能是A. 1, 2, 3, 4, 5B. 2, 4, 6, 16, 32C. 3, 13, 23, 33, 43D. 5, 10, 15, 20, 2510. 某校1 000名学生的高中数学学业水平考试成绩的频率分布直方图如图所示. 规定不低于90分为优秀等级,则该校学生优秀等级的人数是A. 300B. 150C. 30D. 15二、填空题:本大题共4小题,每小题5分,共20分.11. 若圆C 的半径为1,圆心在第一象限,且与直线430x y -=和x 轴相切,则该圆的标准方程是 12. 假设要考察某企业生产的袋装牛奶质量是否达标,现以500袋牛奶中抽取60袋进行检验,利用随机数表抽样本时,先将500袋牛奶按000,01,…,499进行编号,如果从随机数表第八行第四列的数开始按三位数连续向右读取,请你依次写出最先检测的5袋牛奶的编号: .(下面摘取了随机数表第七行至第九行)84421 75331 57245 50688 77047 44767 21763 35025 83921 2067663016 37859 16955 56719 98105 07175 12867 35807 44395 2387933211 23429 78645 60782 52420 74438 15510 01342 99660 2795413. 经过圆2220x x y ++=的圆心C ,且与直线0x y += 垂直的直线方程是 .14.关于函数()4sin(2),()3f x x x R π=+∈有下列命题: ①()y f x =是以2π为最小正周期的周期函数;②()y f x =可改写为4cos(2)6y x π=-; ③()y f x =的图象关于(,0)6π-对称;④()y f x =的图象关于直线6x π=-对称;其中正确的序号为 。
必修一-必修五综合练习题

必修一~必修五综合练习题一、选择题1.已知{2,1,0,1,2}A =--,{|lg(21)}B x y x ==+,则AB =( )A.∅ B.{1,0,1}- C.{0,1,2} D.{1,0,1,2}-2.已知向量()(),2,1,1m a n a ==-,且m n ⊥,则实数a 的值为( ) A.0 B .2 C.2-或1 D.2-3.执行如图所示的程序框图,如果输入n=3,则输出的S=( )(第3题图) (第4题图) A. B. C. D.4.某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为( ) A.588 B.480 C.450 D.1205.连续地掷一枚质地均匀的骰子2次,则出现向上的点数之和小于4的概率为( ) A .118 B.112 C .19 D .166.已知ABC ∆中,6,30,120AB A B ===,则ABC ∆的面积为( )A.9 B.18 C. D.7.如图所示,一个几何体的主视图和左视图都是边长为4的正方形,中间线段平分正方形,俯视图中有一内切圆,则该几何体的全面积是( )A .648π+B .5612π+C .328π+D .488π+(第7题图) (第8题图) 8.一空间几何体的三视图如图所示,则该几何体的体积为( )A.12 B.6 C.4 D.29.在等差数列{}n a 中,已知51012a a +=,则793a a +=( ) A .12 B.18 C.24 D.3010.若,x y 满足约束条件1010220x y x y x y +-≥⎧⎪-+≥⎨⎪--≤⎩,则目标函数23z x y =+的最大值为( )A.2B.3C.11D.1811.体积为8的正方体的顶点都在同一球面上,则该球的表面积为( )(A)12π (B )323π(C)8π (D)4π12.已知函数()221,1,1x x f x x ax x ⎧+<=⎨+≥⎩,若()()04f f a =,则实数a 等于( )A.12 B .45C.2 D.9 13.同时具有性质:“①最小正周期是π;②图像关于直线3x π=对称;③在区间5,6ππ⎡⎤⎢⎥⎣⎦上是单调递增函数”的一个函数可以是( ) A.cos 23y x π⎛⎫=-⎪⎝⎭B.sin 26y x π⎛⎫=-⎪⎝⎭C.5sin 26y x π⎛⎫=+⎪⎝⎭ D .sin 26x y π⎛⎫=+ ⎪⎝⎭14.已知函数()()g x f x x =-是偶函数,且()34f =,则()3f -=()A .-4B .-2 C.0 D .4 15.下列函数中,既是偶函数又在区间()0,+∞上单调递减的是( )A.ln y x = B .cos y x = C.2y x =-D .12xy ⎛⎫= ⎪⎝⎭16.已知函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭,为了得到()sin 2g x x =的图象,则只需将()f x 的图象( )A .向右平移3π个长度单位 B .向右平移6π个长度单位 C .向左平移6π个长度单位 D.向左平移3π个长度单位17.已知()f x 是定义在R 上的奇函数,当0x ≥时,2()2f x x x =-,则函数()()1g x f x =+的零点的个数是( )A .1B .2C .3 D.4 二、填空题18.某单位要在4名员工(含甲、乙两人)中随机选2名到某地出差,则甲、乙两人中,至少有一人被选中的概率是 .19.已知角α的终边经过点(,6)P x -,且3tan 5α=-,则x 的值为 . 20.若54)sin(=-θπ,)2,0(πθ∈,则2cos 2sin 2θθ-的值等于 . 21.若等比数列{a n }满足a 2+a 4=20,a 3+a 5=40,则a 5+a 7=________. 22.已知函数()2sin()(0,||)2f x x πωϕωϕ=+><的图象如图所示,则(0)f = .(第22题图) (第24题图)23.已知向量()(),1,4,2a m b n ==-,0,0m n >>,若a ∥b ,则18m n+的最小值为 .24.如图,在直三棱柱111ABC A B C -中,0190,2,1ACB AA AC BC ∠====,则异面直线1A B 与AC 所成角的余弦值是____________.三、解答题25.在中,角所对的三边分别为, ,且 (Ⅰ)求; (Ⅱ)求的面积. 26.总体(,)x y 的一组样本数据为:(1)若,x y 线性相关,求回归直线方程; (2)当6x =时,估计y 的值.附:回归直线方程ˆˆˆybx a =+,其中1221ˆˆˆ,ni ii nii x y nx ya y bxb xnx ==-⋅=-=-∑∑27.20名同学参加某次数学考试成绩(单位:分)的频率分布直方图如下:(Ⅰ)求频率分布直方图中a 的值;(Ⅱ)分别求出成绩落在[50,60),[60,70)中的学生人数;(Ⅲ)从成绩在[50,70)的学生中任选2人,求此2人的成绩都在[60,70)中的概率.28.已知(,)2παπ∈,且sincos22αα+=. ABC ∆C B A ,,c b a ,,3B π= 2.b a ==sin 2A ABC∆(1)求cos α的值; (2)若3sin()5αβ-=-,(,)2πβπ∈,求cos β的值.29.在等差数列{}n a 中,2723a a +=-,3829a a +=-. (Ⅰ)求数列{}n a 的通项公式;(Ⅱ)设数列{}n n a b +是首项为1,公比为c 的等比数列,求数列{}n b 的前n 项和n S .30.已知等比数列{}n a 的前n 项和为n S ,4322,6a a S ==. (1)求数列{}n a 的通项公式;(2)若数列{}n b 满足:2log n n n b a a =+,求数列{}n b 的前n 项和n T .31.若二次函数2()f x ax bx c =++(a ,b ,c R ∈)满足(1)()41f x f x x +-=+,且(0)3f =.(1)求()f x 的解析式;(2)设()g x (2)xf =,求()g x 在[]3,0-的最大值与最小值.一、选择题答案18.65 19. 10 20.254 21. 160 22.2 23.29 24. 66。
(word完整版)高中数学必修1到必修5综合试题

11 >????B. 2a >2bC. I a I > I b I数学综合试卷一、选择题(共10题,每题3分,总计30 分)1、执行如图1所示的程序框图,A. [ 6, 2]B.[3 时,停机的概率是 一,加工零件 10停机的概率为A . 01B .1,1 C • 01,2 D .1,01,24、 函数f (x ) x 的图像关于(C)xA y 轴对称B . 直线y x 对称C. 坐标原点对称D .直线y x 对称y 》x,5、设变量x, y 满足约束条件:x 2y < 2,,则z x 3y 的最小值( D )x > 2.A . -10B .C .6D .86、已知过A (-1, a )、 B (a , 8)两点的直线 2x+y-仁0平行,则a 的值为( A )A . -10B . 17C . 5D . 2 7、已知sin ( ??厂a)=3 5,则 cos ( n - 2 a):=(A )7247 24 A .—B.—C .D.--252525 25 8、已知向量(2, -3), b = (3, Y 若 a //b , 则Y 等于(C )292A .-B . -2C .D.--3233 sin 70°9、2 ,J=(C )2 cos 11血3A.—B.C. 2D.22210、若a<b<0,则下列不等式不成立的是( B )C. [ 4,5]D.[3,6]1台机床有3的时间加工零件A ,其余时间加工零件B ,加工A 否是一 t 0?A. 11 30B.7 307C.—10D.1 10■:结束设集合 {m2},N {nZ| K n < 3},则 Ml N如果输入的t [ 2,2],则输出的S 属于(D )5, 1] B 时,停机的概率为2-,则这台机床5■'输入t、填空题(共10题,每题3分,总计30 分)11、某社区对居民进行上海世博会知晓情况的分层调查,已知该社区的青年人、中年人、老年人分别有800人、1600人、1400人,若在老年人中的抽样人数是70人,则在中年人中的抽样人数应该为8012、函数y Asin( X )(人>0,0< v )在一个周期内的图象如右图,此函数的解析式为_y = 2 cos(2x +石)13、圆心为(1 , 1 )且与直线x+y=4相切的圆的方程是(x-1)2+(y-1)2=2.14、ABCD为长方形,AB=2 , BC=1 , O为AB的中点,在长方形ABCD内随机取一点,取到的点到0的距离大于1的概率为1-n /415、在厶ABC中,角A, B, C所对的边分别为a, b, c ,若a=v216、图2为长方体积木块堆成的几何体的三视图,此几何体共由4 块木块堆成。
高中数学必修1-必修5综合测试题(附答案)

高二数学必修1-必修5考试题一、选择题(每小题5分,共40分,在每小题的四个选项中有且只有一个是正确的,请把正确选项填涂在答题卡上。
)1. 对于下列命题:①,1sin 1x R x ,②22,sin cos 1x R xx,下列判断正确的是A. ①假②真B. ①真②假C. ①②都假D. ①②都真2. 条件语句的一般格式是3. 某校为了了解学生的课外阅读情况,随即调查了50名学生,得到他们在某一天各自课外阅读所用时间的数据,结果用右侧的条形图表示。
根据条形图可得这50名学生这一天平均每人的课外阅读时间为A. 0.6 小时B. 0.9 小时C. 1.0 小时D. 1.5 小时4. 有一圆柱形容器,底面半径为10cm ,里面装有足够的水,水面高为12cm ,有一块金属五棱锥掉进水里全被淹没,结果水面高为15cm ,若五棱锥的高为3cm ,则五棱锥的底面积是A. 100cm2B. 100 cm2C. 30cm2D. 300 cm2IF 条件THEN 语句 1 ELSE 语句 2 END IF人数(人) 0 0.5 1.0 1.5 2.0时间(小时)20 15 105A.是满足条件语句 1语句 2否B.是否满足条件语句 2语句 1D.是否满足条件满足条件语句 2语句 1语句 1语句 2 否满足条件是C.5.已知数列1{}nn a pa 为等比数列,且23nnna ,则p 的值为A.2B.3C.2或3D.2或3的倍数6.若α、β表示平面,a 、b 表示直线,则a ∥α的一个充分条件是A. α⊥β且a ⊥βB. αI β=b 且a ∥b C. a ∥b 且b ∥αD. α∥β且aβ7.已知奇函数f(x)和偶函数g(x)满足f(x)+g(x)=2xxaa,若g(a)=a, 则f(a)的值为A.1B.2C.154D.1748. 已知()f x 是以2为周期的偶函数,当[0,1]x时,()f x x ,那么在区间[1,3]内,关于x 的方程()1f x kxk (其中k 走为不等于l 的实数)有四个不同的实根,则k 的取值范围是A .(1,0)B .1(,0)2C .1(,0)3D .1(,0)4题号 12345678答案二、填空题(每小题5分,共30分。
完整word版,高中数学必修1~必修5综合测试(11中)

高中数学必修1~必修5综合测试(11中)(完成时间2小时,满分150分)班级 姓名 学号 一、 选择题:本大题共10小题;第每小题5分,共50分。
在每小题所给出的四个选项中,只有一项是符合题目要求的。
1. 设A=B A x x x B x x x 则},0|{},0|{22 等于 (A )0 (B ){0}(C )(D ){-1,0,1}2. 一个容量为100的样本分成若干组,已知某组的频率为0.3,则该组的频数是 ( ) A. 3 B. 30 C. 10 D. 3003. 若S n 是数列{a n }的前n 项和,且,2n S n 则}{n a 是(A )等比数列,但不是等差数列 (B )等差数列,但不是等比数列 (C )等差数列,而且也是等比数列 (D )既非等比数列又非等差数列 4. 过点A (1,-1)、B (-1,1)且圆心在直线x+y-2=0上的圆的方程是(A )4)1()3(22 y x (B )4)1()3(22 y x (C )4)1()1(22 y x (D )4)1()1(22 y x 5. 若定义在区间(-1,0)内的函数ax f x x f a 则满足,0)()1(log )(2 的取值范围是(A ))21,0((B )]21,0((C )),21((D )),0(6. 若向量a=(3,2),b=(0,-1),c=(-1,2),则向量2b -a 的坐标是(A )(3,-4)(B )(-3,4)(C )(3,4)(D )(-3,-4)7. 设A 、B 是x 轴上的两点,点P 的横坐标为2且|PA|=|PB|.若直线PA 的方程为01 y x ,则直线PB 的方程是(A )05 y x(B )012 y x(C )042 x y (D )072 y x 8. 若则,cos sin ,cos sin ,40b a(A )b a (B )b a (C )1 ab (D )2 ab9. 《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,超过(A ) 800~900元 (B )900~1200元 (C )1200~1500元 (D )1500~2800元10. 若1 b a ,P=b a lg lg ,Q= b a lg lg 21 ,R=2lg b a ,则 (A )R P Q (B )P Q R(C )Q P R (D )P R Q二. 填空题:本大题共4小题,每小题4分,共16分,把答案填在题中横线上。
必修一至必修五理科综合测试1-(1)

高二理科数学一、选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合M ={-1,0,1},N ={x|x 2≤x},则M ∩N =( )A .{0,1}B .{0,-1}C .{-1,1}D .{-1,0,1} 2.函数)34(log 15.0-=x y 的定义域为( )A 、 )1,43(B 、),43(+∞C 、 ),1(+∞D 、),1()1,43(+∞⋃量,则a 在b 方向上的投影为( )3.已知向A. 5B. -5C. -2D. 24.在等差数列{a n }中,已知a 4+a 8=16,则a 2+a 10=( )A.12B.16C.20D.24 5. 要得到函数)33sin(2)(π-=x x f 的图像,只需将函数x x f 3sin 2)(=的图像( )A .向左平移3π 个单位 B .向右平移3π个单位 C .向左平移9π 个单位 D .向右平移9π个单位6.如下图,该程序运行后输出的结果为 ( )A .15B .21C .28D .36 7.在△ABC 中,若3,1===c a b ,则∠C 等于( )A .030 B .060 C .0120 D .01508.已知函数f(x)=x 3-2x 2+2有唯一零点,则下列区间必存在零点的是( )A .)23,2(--B .)1,23(--C .)21,1(--D .)0,21(-9. 与直线04=--y x 和圆02222=-++y x y x 都相切的半径最小的圆的方程是( )A.(x+1)2+(y+1)2=2B. (x+1)2+(y+1)2=4C. (x-1)2+(y+1)2=2 C. (x-1)2+(y+1)2=4 10. 已知3log 3log 22+=a ,3log 9log 22-=b ,2log 3=c 则a,b,c 的大小关系是( )A . a b c =>B . a b c =<C .a b c << D.a b c >>11.下表是降耗技术改造后生产甲产品过程中记录的产量x (吨)与相应的生产能耗y(吨标准煤)的几组对应数据,根据表中提供的数据,求出y 关于x 的线性回归方程ˆy =0.7x+0.35,那么表中m 的值为 ( ))0,3(),1,2(-=-=b aA .4B .3.15C .4.5D .3 12.设()f x 是定义在R 上的减函数,且2222(1015)(1224),f n n f m m m n --≥-++则的取值 范围是( )A .[0,27]B .[0,729]C .[169,196]D .[169,729]二、填空题(本大题共4小题,每小题5分,共20分,将答案填在答题卡相应的位置上.) 13. 2000= 弧度14.一个正方体的展开图如图所示,A 、B 、C 、D 为原正方体的顶点,则在原来的正方体中AB 与CD 的夹角为___________度。
必修第一册全册综合训练卷(解析版)

1必修第一册全册综合训练卷本试卷分第Ⅰ卷(选择题)和第Ⅰ卷(非选择题)两部分.满分150分.考试时间120分钟.第Ⅰ卷(选择题 共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)1.集合A ={x |-1≤x ≤2},B ={x |x <1},则A ∪(∁R B )=( ) A .{x |x >1} B .{x |x ≥-1} C .{x |1<x ≤2}D .{x |1≤x ≤2}【解析】由A ={x |-1≤x ≤2},B ={x |x <1}可知∁R B ={x |x ≥1},∴A ∪(∁R B )={x |x ≥-1}. 故选B.2.函数f (x )=x 2x 2-1+lg(10-x )的定义域为( )A .RB .[1,10]C .(-∞,-1)Ⅰ(1,10)D .(1,10)【解析】要使函数f (x )有意义,需使⎩⎪⎨⎪⎧x 2-1>0,10-x >0,解得x <-1或1<x <10.故选C3.已知f (x )=x 2-ax 在[0,1]上是单调函数,则实数a 的取值范围是( ) A .(-∞,0] B .[1,+∞)C .[2,+∞)D .(-∞,0]Ⅰ[2,+∞)【解析】函数f (x )=x 2-ax 图象的对称轴为直线x =a 2,根据二次函数的性质可知a 2≤0或a2≥1,解得a ≤02或a ≥2.故选D.4.下列函数是偶函数且值域为[0,+∞)的是( ) Ⅰy =|x |;Ⅰy =x 3;Ⅰy =2|x |;Ⅰy =x 2+|x |. A .ⅠⅠ B .ⅠⅠ C .ⅠⅠ D .ⅠⅠ【解析】对于Ⅰ,y =|x |是偶函数,且值域为[0,+∞);对于Ⅰ,y =x 3是奇函数;对于Ⅰ,y =2|x |是偶函数,但值域为[1,+∞);对于Ⅰ,y =x 2+|x |是偶函数,且值域为[0,+∞),所以符合题意的有ⅠⅠ故选C.5.已知a =log 20.2,b =20.2,c =0.20.3,则( ) A .a <b <c B .a <c <b C .c <a <bD .b <c <a【解析】a =log 20.2<log 21=0,b =20.2>20=1,0<c =0.20.3<0.20=1,即0<c <1,则a <c <b . 故选B.6.若sin α>0且tan α<0,则α2的终边在( )A .第一象限B .第二象限C .第一象限或第三象限D .第三象限或第四象限 【解析】 因为sin α>0且tan α<0, 所以α位于第二象限. 所以π2+2k π<α<2k π+π,k ⅠZ ,则π4+k π<α2<k π+π2,k ⅠZ . 当k 为奇数时α2是第三象限的角,当k 为偶数时α2是第一象限的角,3所以角α2的终边在第一象限或第三象限.故选 C.7.函数y =sin(ωx +φ)(x ⅠR ,且ω>0,0≤φ<2π)的部分图象如右图所示,则( ) A .ω=π2,φ=π4B .ω=π3,φ=π6C .ω=π4,φ=π4D .ω=π4,φ=5π4【解析】 ⅠT =4×2=8,Ⅰω=π4.又Ⅰπ4×1+φ=π2,Ⅰφ=π4.故选C8.函数f (x )=2sin x -sin2x 在[0,2π]的零点个数为( ) A .2 B .3 C .4 D .5【解析】 由f (x )=2sin x -sin2x =2sin x -2sin x cos x =2sin x (1-cos x )=0,得sin x =0或cos x =1,Ⅰx Ⅰ[0,2π],Ⅰx =0、π或2π,Ⅰf (x )在[0,2π]的零点个数是3.故选B9.已知lg a +lg b =0,函数f (x )=a x 与函数g (x )=-log b x 的图象可能是( )4【解析】 Ⅰlg a +lg b =0,Ⅰab =1,则b =1a ,从而g (x )=-logb x =log a x ,故g (x )与f (x )=a x 互为反函数,图象关于直线y =x 对称.故选B.10.若αⅠ⎪⎭⎫⎝⎛ππ,2,且sin α=45,则sin ⎪⎭⎫ ⎝⎛+4πa -22cos(π-α)等于( )A.225 B .-25 C.25 D .-225【解析】 sin ⎪⎭⎫⎝⎛+4πa -22cos(π-α) =22sin α+22cos α+22cos α=22sin α+2cos α. Ⅰsin α=45,αⅠ⎪⎭⎫⎝⎛ππ,2,Ⅰcos α=-35.Ⅰ22sin α+2cos α=22×45-2×35=-25. 故选 B11.设函数f (x )=sin(ωx +φ)+cos(ωx +φ)⎪⎭⎫⎝⎛<>2,0πωω的最小正周期为π,且f (-x )=f (x ),则( ) A .f (x )在⎪⎭⎫ ⎝⎛20π,单调递减 B .f (x )在⎪⎭⎫⎝⎛434ππ,单调递减 C .f (x )在⎪⎭⎫ ⎝⎛20π,单调递增 D .f (x )在⎪⎭⎫⎝⎛434ππ,单调递增 【解析】 y =sin(ωx +φ)+cos(ωx +φ)=2sin ⎝⎛⎭⎫ωx +φ+π4,由最小正周期为π得ω=2,又由f (-x )=f (x )可知f (x )为偶函数,由|φ|<π2可得φ=π4,所以y =2cos2x 在⎝⎛⎭⎫0,π2单调递减. 故选 A12.将函数f (x )=23cos 2x -2sin x cos x -3的图象向左平移t (t >0)个单位,所得图象对应的函数为奇函5数,则t 的最小值为( )A.2π3B.π3C.π2D.π6【解析】 将函数f (x )=23cos 2x -2sin x cos x -3=3cos2x -sin2x =2cos ⎝⎛⎭⎫2x +π6的图象向左平移t (t >0)个单位,可得y =2cos ⎝⎛⎭⎫2x +2t +π6的图象.由于所得图象对应的函数为奇函数,则2t +π6=k π+π2,k ⅠZ ,则t 的最小值为π6.故选D.第Ⅰ卷(非选择题 共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.函数f (x )=a x -1+3的图象一定过定点P ,则P 点的坐标是________.【解析】由于函数y =a x 恒过(0,1),而y =a x -1+3的图象可看作由y =a x 的图象向右平移1个单位,再向上平移3个单位得到的,则P 点坐标为(1,4).14.函数f (x )=⎩⎪⎨⎪⎧x 2-1,x ≤0,x -2+ln x ,x >0的零点个数为________.【解析】 令f (x )=0,得到⎩⎪⎨⎪⎧x 2-1=0,x ≤0,解得x =-1;6或⎩⎪⎨⎪⎧x -2+ln x =0,x >0,在同一个直角坐标系中画出y =2-x 和y =ln x 的图象,观察交点个数,如图所示.函数y =2-x 和y =ln x ,x >0在同一个直角坐标系中交点个数是1,所以函数f (x )在x <0时的零点有一个,在x >0时零点有一个,所以f (x )的零点个数为2.15.若函数f (x )=⎩⎪⎨⎪⎧3x ,x ≤0,-2-x ,x >0,则函数y =f [f (x )]的值域是________.【解析】 当x ≤0时,f (x )=3x Ⅰ(0,1],Ⅰy =f [f (x )]=f (3x )=-2-3x Ⅰ⎝⎛⎦⎤-1,-12; 当x >0时,f (x )=-2-x Ⅰ(-1,0),y =f [f (x )] =f (-2-x )=3-2-x Ⅰ⎝⎛⎭⎫13,1. 综上所述,y =f [f (x )]的值域是⎝⎛⎦⎤-1,-12Ⅰ⎝⎛⎭⎫13,1.16.关于函数f (x )=cos ⎪⎭⎫⎝⎛-32πx +cos ⎪⎭⎫ ⎝⎛+62πx ,给出下列命题: Ⅰf (x )的最大值为2;Ⅰf (x )的最小正周期是π;Ⅰf (x )在区间⎥⎦⎤⎢⎣⎡241324ππ,上是减函数;7Ⅰ将函数y =2cos2x 的图象向右平移π24个单位长度后,与函数y =f (x)的图象重合.其中正确命题的序号是________.【解析】 f (x )=cos ⎪⎭⎫⎝⎛-32πx +cos ⎪⎭⎫⎝⎛+62πx =cos ⎪⎭⎫⎝⎛-32πx +sin ⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+-622ππx =cos ⎪⎭⎫ ⎝⎛-32πx -sin ⎪⎭⎫⎝⎛-32πx =2⎣⎡⎦⎤22cos ⎝⎛⎭⎫2x -π3-22sin ⎝⎛⎭⎫2x -π3=2cos ⎝⎛⎭⎫2x -π3+π4=2cos ⎝⎛⎭⎫2x -π12, Ⅰ函数f (x )的最大值为2,最小正周期为π,故ⅠⅠ正确;又当x Ⅰ⎥⎦⎤⎢⎣⎡241324ππ,时,2x -π12Ⅰ[0,π],Ⅰ函数f (x )在⎥⎦⎤⎢⎣⎡241324ππ,上是减函数,故Ⅰ正确;由Ⅰ得y =2cos ⎣⎡⎦⎤2⎝⎛⎭⎫x -π24=2cos ⎝⎛⎭⎫2x -π12,故Ⅰ正确.三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.(本小题满分10分)计算(1)21412⎪⎭⎫ ⎝⎛-(-9.6)0-32-833⎪⎭⎫ ⎝⎛+(1.5)-2; (2)log 2512·log 45-log 133-log 24+5log 52.【解析】 (1)21412⎪⎭⎫ ⎝⎛-(-9.6)0-32-833⎪⎭⎫ ⎝⎛+(1.5)-2 =2149⎪⎭⎫ ⎝⎛-1-32-827⎪⎭⎫ ⎝⎛+2-23⎪⎭⎫ ⎝⎛ =32-1-2-23⎪⎭⎫⎝⎛+=32-1-49+49=12. (2)log 2512·log 45-log 133-log 24+5log 52=-14+1-2+2=34.818.(本小题满分12分)已知函数f (x )=2cos x ·sin ⎪⎭⎫⎝⎛+3πx -3sin 2x +sin x cos x . (1)当x Ⅰ⎥⎦⎤⎢⎣⎡2,0π时,求f (x )的值域; (2)用“五点法”在下图中作出y =f (x )在闭区间⎥⎦⎤⎢⎣⎡-65,6ππ上的简图.【解析】 f (x )=2cos x ·sin ⎪⎭⎫⎝⎛+3πx -3sin 2x +sin x cos x =2cos x ⎝⎛⎭⎫sin x cos π3+cos x sin π3-3sin 2x +sin x cos x =sin2x +3cos2x =2sin ⎪⎭⎫ ⎝⎛+32πx . (1)Ⅰx Ⅰ⎥⎦⎤⎢⎣⎡2,0π,Ⅰπ3≤2x +π3≤4π3, Ⅰ-32≤sin ⎪⎭⎫ ⎝⎛+32πx ≤1, Ⅰ当x Ⅰ⎥⎦⎤⎢⎣⎡2,0π时,f (x )的值域为[-3,2]. (2)由T =2π2,得最小正周期T =π,列表:x-π6π12π37π125π692x +π3π2π3π22π2sin ⎪⎭⎫⎝⎛+32πx 0 2 0 -2 019.(本小题满分12分) 已知A (cos α,sin α),B (cos β,sin β),其中α,β为锐角,且|AB |=105. (1)求cos(α-β)的值; (2)若cos α=35,求cos β的值.【解析】 (1)由|AB |=105, 得(cos α-cos β)2+(sin α-sin β)2=105, Ⅰ2-2(cos αcos β+sin αsin β)=25,Ⅰcos(α-β)=45.(2)Ⅰcos α=35,cos(α-β)=45,α,β为锐角,10Ⅰsin α=45,sin(α-β)=±35.当sin(α-β)=35时,cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=2425. 当sin(α-β)=-35时,cos β=cos[α-(α-β)]=cos αcos(α-β)+sin αsin(α-β)=0. Ⅰβ为锐角,Ⅰcos β=2425.20.(本小题满分12分)已知函数f (x )是定义在区间[-1,1]上的奇函数,对于任意的m ,n Ⅰ[-1,1]有f (m )+f (n )m +n>0(m +n ≠0).(1)判断函数f (x )的单调性;(2)解不等式f ⎪⎭⎫⎝⎛+21x <f (1-x ). 【解析】 (1)设x 1=m ,x 2=-n ,由已知可得f (x 1)-f (x 2)x 1-x 2>0,不妨设x 1<x 2,则f (x 1)<f (x 2),由函数单调性的定义可得函数f (x )在区间[-1,1]上是增函数.(2)由(1)知函数在区间[-1,1]上是增函数.又由f ⎝⎛⎭⎫x +12<f (1-x ),得⎩⎪⎨⎪⎧-1≤x +12≤1,-1≤1-x ≤1,x +12<1-x ,解得0≤x <14.所以不等式f ⎝⎛⎭⎫x +12<f (1-x )的解集为⎩⎨⎧⎭⎬⎫x |0≤x <14.11 21.(本小题满分12分)某村电费收取有以下两种方案供用户选择:方案一:每户每月收管理费2元,月用电不超过30度时,每度0.5元,超过30度时,超过部分按每度0.6元收取.方案二:不收管理费,每度0.58元.(1)求方案一收费L (x )(单位:元)与用电量x (单位:度)间的函数关系;(2)老王家九月份按方案一交费35元,问老王家该月用电多少度?(3)老王家月用电量在什么范围时,选择方案一比选择方案二更好?【解析】 (1)当0≤x ≤30时,L (x )=2+0.5x ;当x >30时,L (x )=2+30×0.5+(x -30)×0.6=0.6x -1,ⅠL (x )=⎩⎪⎨⎪⎧ 2+0.5x ,0≤x ≤30,0.6x -1,x >30.(注:x 也可不取0)(2)当0≤x ≤30时,令L (x )=2+0.5x =35得x =66,舍去;当x >30时,由L (x )=0.6x -1=35得x =60,Ⅰ老王家该月用电60度.(3)设按方案二收费为F (x )元,则F (x )=0.58x .当0≤x ≤30时,由L (x )<F (x ),得2+0.5x <0.58x ,解得x >25,Ⅰ25<x ≤30;当x >30时,由L (x )<F (x ),得0.6x -1<0.58x ,解得x <50,Ⅰ30<x <50.综上,25<x <50.故老王家月用电量在25度到50度范围内(不含25度、50度)时,选择方案一比方案二更好.22.(本小题满分12分)已知函数f (x )=A sin(ωx +φ)+B (A >0,ω>0)的一系列对应值如表: x -π6 π3 5π6 4π3 11π6 7π3 17π612 f (x ) -1 1 3 1 -1 1 3(1(2)根据(1)的结果,若函数y =f (kx )(k >0)的周期为2π3,当x Ⅰ⎥⎦⎤⎢⎣⎡30π,时,方程f (kx )=m 恰有两个不同的解,求实数m 的取值范围.【解析】 (1)设f (x )的最小正周期为T ,则T =11π6-⎝⎛⎭⎫-π6=2π,由T =2πω,得ω=1, 又⎩⎪⎨⎪⎧ B +A =3,B -A =-1,解得⎩⎪⎨⎪⎧A =2,B =1, 令ω·5π6+φ=π2+2k π,k ⅠZ , 即5π6+φ=π2+2k π,k ⅠZ ,取φ=-π3, 所以f (x )=2sin ⎝⎛⎭⎫x -π3+1. (2)因为函数y =f (kx )=2sin ⎝⎛⎭⎫kx -π3+1的周期为2π3,又k >0,所以k =3.令t =3x -π3, 因为x Ⅰ⎥⎦⎤⎢⎣⎡30π,,所以t Ⅰ⎣⎡⎦⎤-π3,2π3, 如图,sin t =s 在⎣⎡⎦⎤-π3,2π3上有两个不同的解,则s Ⅰ⎣⎡⎭⎫32,1,所以方程f (kx )=m 在x Ⅰ⎣⎡⎦⎤0,π3时恰好有两个不同的解,则m Ⅰ[3+1,3),即实数m 的取值范围是[3+1,3).13。
高三第一复习必修1三四五单元综合测试卷
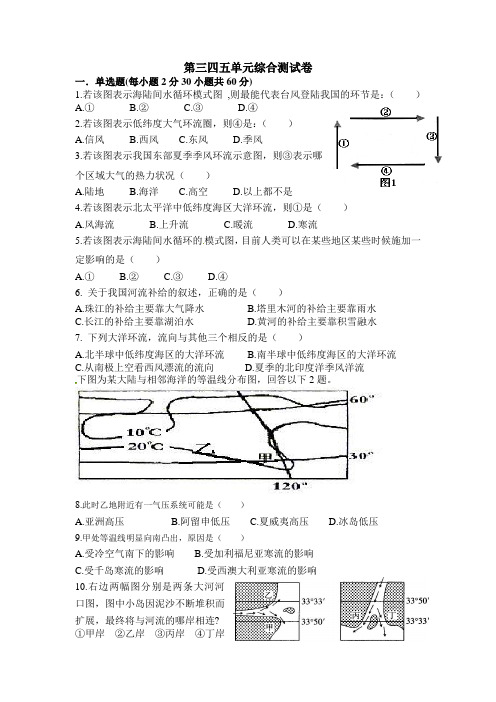
第三四五单元综合测试卷一.单选题(每小题2分30小题共60分)1.若该图表示海陆间水循环模式图,则最能代表台风登陆我国的环节是:()A.①B.②C.③D.④2.若该图表示低纬度大气环流圈,则④是:()A.信风B.西风C.东风D.季风3.若该图表示我国东部夏季季风环流示意图,则③表示哪个区域大气的热力状况()A.陆地B.海洋C.高空D.以上都不是4.若该图表示北太平洋中低纬度海区大洋环流,则①是()A.风海流B.上升流C.暖流D.寒流5.若该图表示海陆间水循环的模式图,目前人类可以在某些地区某些时候施加一定影响的是()A.①B.②C.③D.④6. 关于我国河流补给的叙述,正确的是()A.珠江的补给主要靠大气降水B.塔里木河的补给主要靠雨水C.长江的补给主要靠湖泊水D.黄河的补给主要靠积雪融水7. 下列大洋环流,流向与其他三个相反的是()A.北半球中低纬度海区的大洋环流B.南半球中低纬度海区的大洋环流C.从南极上空看西风漂流的流向D.夏季的北印度洋季风洋流下图为某大陆与相邻海洋的等温线分布图,回答以下2题。
8.此时乙地附近有一气压系统可能是()A.亚洲高压B.阿留申低压C.夏威夷高压D.冰岛低压9.甲处等温线明显向南凸出,原因是()A.受冷空气南下的影响B.受加利福尼亚寒流的影响C.受千岛寒流的影响D.受西澳大利亚寒流的影响10.右边两幅图分别是两条大河河口图,图中小岛因泥沙不断堆积而扩展,最终将与河流的哪岸相连?①甲岸②乙岸③丙岸④丁岸A .①②B .②③C .③④D .①④ 地下水是一种宝贵的水资源。
回答2题11.下图为某地两条河流两测的潜水位等值线示意图,可反映河流与潜水补给关系的一般情况。
图中数字表示潜水位(单位:米)。
读图判断(1)a 图河流和b 图河流均自北向南流 (2)a 图河流自北向南流.b 图河流自南向北流(3)a 图潜水补给河流,b 图河流补给潜水 (4)a 图河流补给潜水,b 图潜水补给河流( )A.(1)(2)B.(3)(4)C.(1)(4)D.(2)(4)12.今年来,我国部分地区封闭了大量的机井,其原因主要是( )(1)减缓地面沉降(2)保护地下水资源(3)地下水开采成本高 (4)这些地区地表水丰富,不需要开采地下水( )A.(1)(2)B.(3)(4)C.(1)(3)D.(2)(4)右图是我国海拔3800 米某内陆湖的水位变化情况。
高中语文 第一学期综合复习检测题 新人教版必修1-5(高二)

人教课标版必修1—5综合复习检测题第Ⅰ卷(选择题共30分)一、(12分,每小题3分)⒈下列词语中,注音和字形均完全正确的一组是()A.颓圮(pǐ)火钵(bó)跫(qíong)音流殇(shāng)曲水B.团箕(qí)癸(guǐ)丑愀(qiǎo)然陨(yǔn)身不衅C.汶(wèn)川戮(lù)力冠冕(miǎn)横槊(shuò)赋诗D.肄(yì)业干(gān)禄解剖(pōu)夙(shù)兴夜寐⒉下列各句中画线成语运用不正确的一项是()A.穿越一个世纪生命历程的巴金先生,不仅为我们留下了《家》和《随想录》,还为我们留下了讲真话的勇气和对人生、对文学的执着的爱,成为现代文坛的泰山北斗,至今尚无人望其项背。
B. 临危受命的烛之武对秦晋两国面和心不和的关系洞若观火,他采取以退为进的策略,终于说退秦师,使郑国化险为夷。
C.2008年5月12日四川汶川县发生8.0级地震后,全球华人以身作则,积极捐款捐物支援灾区,谱写了一曲曲血浓于水的人间赞歌。
D.蔡元培先生在就任北京大学校长的演讲中,鼓励学子砥砺德行,力戒焦躁,振兴中华,责无旁贷。
⒊下列各句,没有语病、用语得体的一句是()A. 5月22至24日,“好运北京2008中国田径公开赛”之所以吸引人们的目光,不光因为它是北京奥运会前人们最后一次进入“鸟巢”观看比赛的机会,更是因为110米栏世界纪录保持者刘翔将在赛事中三度亮相。
B.婴儿在出生后一段时间内,只有需要温暖和食物的要求,却不会区别温暖、食物同给予温暖和食物的母亲。
C.青少年的教育问题,是一个十分复杂而耐心的过程,它决不是一两句话就能奏效的。
D.写此序,是受朋友之托,感谢朋友们对我的信任和尊敬,同时感谢江苏省陶行知研究会和教育厅领导的鼓励。
⒋下列各句中,标点符号运用完全正确、规范的一句是()A.谁也不能突出,如果你想比别人多想、多干、多拥有,那就甭指望有好日子过。
必修第一册-综合检测卷(培优解析版)

必修第一册本卷满分150分,考试时间120分钟。
一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是符合题目要求的.1.设全集U =R ,集合()2log 41{|}A x x =-≤,()()35{|}0B x x x =-->,则()U B A =I ð()A .[2]5,B .[2]3,C .[)24,D .[)34,【答案】D【解析】由于2log (4)124x x -≤∴≤<故集合[)24A =,()()350x x -->3x ∴<或5x >故集合()()35B =-∞⋃+∞,,∴()[)|34UB A ⋂=,ð故选:D 2.已知“x k >”是“311x <+”的充分不必要条件,则k 的取值范围为()A .(],1-∞-B .[)1,+∞C .[)2,+∞D .()2,+∞【答案】C 【解析】因为311x <+,所以13x +>或10x +<,所以解集为()(),12,-∞-+∞,又因为“x k >”是“311x <+”的充分不必要条件,所以(),k +∞是()(),12,-∞-+∞的真子集,所以[)2,k ∈+∞,故选:C.3.若不等式()()222240a x a x -+--<对任意实数x 均成立,则实数a 的取值范围是()A .()2,2-B .[]22-,C .()2,+∞D .(]2,2-【答案】D【解析】当20a -=时,即2a =,此时40-<恒成立,满足条件;当20a -≠时,因为()()222240a x a x -+--<对任意实数x 都成立,所以()()220421620a a a -<⎧⎪⎨∆=-+-<⎪⎩,解得()2,2a ∈-,综上可知,(]2,2a ∈-,故选:D.4.已知奇函数()y f x =在()0,∞+上单调递减,且()30f -=,则不等式(x 3)0xf -<的解集为()A .()()(),00,36,-∞⋃⋃+∞B .()()(),33,03,-∞-⋃-⋃+∞C .()()(),00,33,-∞⋃⋃+∞D .()()(),33,06,-∞-⋃-⋃+∞【答案】A【解析】因为奇函数()y f x =在()0,∞+上单调递减,且()30f -=,所以()f x 在(,0)-∞单调递减,且(3)(3)0f f -=-=,所以当3x <-或03x <<时,()0f x >,当30x -<<或3x >时,()0f x <,当0x <时,不等式(x 3)0xf -<等价于(3)0f x ->,所以33x -<-或033x <-<,解得0x <,当0x >时,不等式(x 3)0xf -<等价于(3)0f x -<,所以330x -<-<或33x ->,解得03x <<或6x >,综上,不等式的解集为()()(),00,36,-∞⋃⋃+∞,故选:A5.已知函数()f x 是定义在R 上的偶函数,且在()0,∞+单调递减,设233231log ,2,24a f b f c f --⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,则,,a b c 的大小关系为()A .a c b <<B .b c a<<C .c b a<<D .b a c<<【答案】A【解析】函数()f x 是定义在R 上的偶函数,且在()0,∞+上单调递减则:()()3331log log 4log 44a f f f ⎛⎫==-= ⎪⎝⎭33log 4log 3=1>,2303202221--<<<=,∴23323log 422-->>,()23323log 422f f f --⎛⎫⎛⎫∴<< ⎪ ⎪⎝⎭⎝⎭即:a c b <<故选:A.6.已知定义在R 上的奇函数f (x )满足()()3f x f x +=-,当(]0,1x ∈时,()2ln xf x x =+,则()2023f =()A .2B .12C .-2D .-12【答案】A【解析】:依题意,()()3f x f x +=-,()()()63f x f x f x +=-+=,函数()f x 的周期为6,故()(2023)(33761)1f f f =⨯+=,又()12ln12f =+=,则(2023)2f =.故选:A .7.若10,0,cos ,cos 2243423ππππβαβα⎛⎫⎛⎫<<-<<+=-= ⎪ ⎪⎝⎭⎝⎭,则cos 2βα⎛⎫+= ⎪⎝⎭()A3B.CD.【答案】Ccos cos cos cos sin sin 2442442442βππβππβππβαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+=+--=+-++- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦,因为0,022ππαβ<<-<<所以3,444πππα⎛⎫+∈ ⎪⎝⎭,,4242πβππ⎛⎫-∈ ⎪⎝⎭,因为1cos 43πα⎛⎫+= ⎪⎝⎭,3cos 423πβ⎛⎫-= ⎪⎝⎭所以sin 43πα⎛⎫+= ⎪⎝⎭,sin 423πβ⎛⎫-= ⎪⎝⎭,则1cos 23βα⎛⎫+= ⎪⎝⎭C 8.已知函数()222sin cos sin (0)24x f x x x ωπωωω⎛⎫=--> ⎪⎝⎭在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数,且在区间[]0,π上恰好取得一次最大值,则ω的取值范围是()A .30,5⎛⎤⎥⎝⎦B .13,25⎡⎤⎢⎥⎣⎦C .15,22⎡⎤⎢⎥⎣⎦D .50,2⎛⎫ ⎪⎝⎭【答案】B【解析】222ππ()2sin cos sin sin 2cos sin 2424x x f x x x x x ωωωωωω⎡⎤⎛⎫⎛⎫=--=-- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦πsin cos 1sin sin (sin 1sin )sin 2x x x x x x xωωωωωωω⎡⎤⎛⎫=-+-=+-= ⎪⎢⎥⎝⎭⎣⎦由π2π2x k ω=+,可得π2π,Z 2k x k ωω=+∈由()f x 在区间[]0,π上恰好取得一次最大值,可得π0π2π2ππ2ωωω⎧≤≤⎪⎪⎨⎪+>⎪⎩,解之得1522ω≤<又()f x 在区间2π5π,36⎡⎤-⎢⎥⎣⎦上是增函数,则5ππ622ππ32ωω⎧≤⎪⎪⎨⎪-≥-⎪⎩,解之得35ω≤综上,ω的取值范围是1325ω≤≤故选:B 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知0a >,0b >,且21a b +=,则下列说法正确的是()A .22a b +的最小值为15B .ab 的最大值为18C .1a b +的最大值为43D .11a b+的最小值为【答案】AB【解析】:对于A :由0a >,0b >,21a b +=,则12a b =-,所以1200b b ->⎧⎨>⎩,解得102b <<,所以22222221(12)541555a b b b b b b ⎛⎫+=-+=-+=-+ ⎪⎝⎭,所以当25b =时,22a b +有最小值15,故A 正确.对于B :由0a >,0b >,12a b =+≥18ab ≤,当且仅当2a b =,即12a =,14b =时等号成立,所以ab 的最大值是18,故B 正确;对于C :由0a >,0b >,21a b +=,则12a b =-,所以1200b b ->⎧⎨>⎩,解得102b <<,所以111121a b b b b -==+-+-,因为102b <<,所以1112b -<-<-,所以1211b -<<--,所以1121b -<<-,即112a b <<+,故C 错误;对于D:112221233a b a b b a a b a b a b +++=+=+++≥+=+,当且仅当2b a a b =,即b =1a -时取等号,故D 错误;故选:AB10.已知定义域为R 的函数()f x 在(,1)-∞-上为增函数,且()1f x -为偶函数,则()A .()f x 的图象关于直线x =-1对称B .()f x 在(1,)-+∞上为增函数C .()()12f f =-D .()()1302f f f ⎛⎫-<<- ⎪⎝⎭【答案】AD【解析】因为()1f x -为偶函数,且函数()f x 在(,1)-∞-上为增函数,所以()f x 的图象关于直线x =-1对称,且()f x 在(1,)-+∞上为减函数,所以A 正确,B不正确;因为()f x 的图象关于直线x =-1对称,()()()132f f f =-≠-,所以C 不正确;因为()f x 的图象关于直线x =-1对称,所以()()02f f =-,1322f f ⎛⎫⎛⎫-=- ⎪ ⎪⎝⎭⎝⎭,又()f x 在(,1)-∞-上为增函数,所以()()3322f f f ⎛⎫-<-<- ⎪⎝⎭,即()()1302f f f ⎛⎫-<<- ⎪⎝⎭,所以D 正确.故选:AD.11.已知()f x ,()g x 都是定义在R 上的函数,其中()f x 是奇函数,()g x 是偶函数,且()()2x f x g x +=,则下列说法正确的是()A .()()f g x 为偶函数B .()00g =C .()()22gx f x -为定值D .()()2,02,0x xx f x g x x -⎧≥+=⎨<⎩【答案】ACD【解析】因为()()2x f x g x +=,所以()()2xf xg x --+-=,又()f x 是奇函数,()g x 是偶函数,所以()()2xf xg x --+=,解得22()2x x g x -+=,22()2x xf x --=.对于A ,()()()()fg g x x f -=,故()()f g x 为偶函数,A 正确;对于B ,()01g =,故B 错误;对于C ,22222222()()122x x x x g x f x --⎛⎫⎛⎫+--=-= ⎪ ⎪⎝⎭⎝⎭,故C 正确;对于D ,当0x ≥时,()222x x f x --=,()()2222222x x x xx f x g x ---++=+;当0x <时,()222x x f x --=,()()2222222x x x xx f x g x ----++=,所以()()2,02,0x x x f x g x x -⎧≥+=⎨<⎩,故D 正确.故选:ACD.12.已知函数()()sin f x A x =+ωϕ(其中0A >,0>ω,ϕπ<)的部分图象如图所示,则下列结论正确的是()A .函数f (x )的图象的周期为T π=B .函数f (x )的图象关于点(12π,0)对称C .函数f (x )在区间[-3π,6π]上的最大值为2D .直线1y =与()11(1212y f x x ππ=-≤≤)图像所有交点的横坐标之和为6π【答案】AC 【解析】依题意,4T =253124πππ-=,得T π=,故A 正确;22πωπ==,2A =,则()()2sin 2f x x ϕ=+,当23x π=时,()f x 取最小值,则23232ππϕ⨯+=,得6π=ϕ,即()2sin 26f x x π⎛⎫=+ ⎪⎝⎭,当12x π=时,2sin 22sin 0121263f ππππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭,故B 错误;当x ∈[-3π,6π],则2,622x πππ⎡⎤+∈-⎢⎥⎣⎦,则()22f x -≤≤,故C 正确;111212x ππ-≤≤,则[]20,26x ππ+∈,设直线1y =与()11(1212y f x x ππ=-≤≤)图像所有交点的横坐标为12,x x ,则122266x x πππ+++=,解得123x x π+=,故D 错误;故选:AC三填空题:本题共4小题,每小题5分,共20分.13.已知命题p :“[]1,2x ∀∈,1a x ≥+”,命题q :“R x ∃∈,2250x x a ++=”,p 的否定是假命题,q 是真命题,则实数a 的取值范围是___________.【答案】253,8⎡⎤⎢⎥⎣⎦【解析】由[]1,2x ∀∈,1a x ≥+得,3a ≥,因p 的否定是假命题,则p 是真命题,于是得3a ≥,因R x ∃∈,2250x x a ++=,即方程2250x x a ++=有实根,则2580a ∆=-≥,解得258a ≤,又q 是真命题,则258a ≤,因此,由p 是真命题,q 也是真命题,可得2538a ≤≤,所以实数a 的取值范围是253,8⎡⎤⎢⎥⎣⎦.故答案为:253,8⎡⎤⎢⎥⎣⎦14.方程()2110mx m x --+=在区间()0,1内有两个不同的根,m 则的取值范围为__.【答案】3m >+【解析】:令()()211f x mx m x =--+,图象恒过点()0,1,方程()211mx m x --+=0在区间()0,1内有两个不同的根,()()2010********Δ0m m m m m f m m >⎧⎧⎪>-⎪⎪<<⎪⎪∴⇒>⎨⎨⎪⎪>-->⎪⎪⎩>⎪⎩,解得3m >+.故答案为:3m >+15.已知()f x 是定义在R 上的奇函数,当0x >时,()f x 为增函数,且()30f =,那么不等式()0xf x <的解集是_______.【答案】()()3,00,3-【解析】因()f x 为奇函数,且在()0,∞+上是增函数,()30f =,则()f x 在(),0∞-上是增函数,且()3(3)0f f -=-=,不等式()0xf x <化为:()()003x f x f >⎧⎨<=⎩或()()003x f x f <⎧⎨>=-⎩,解得03x <<或30x -<<,所以不等式()0xf x <的解集是()()3,00,3-.故答案为:()()3,00,3-16.已知函数2(1)e 01,()21,x x x f x x x x ⎧+≤<=⎨-≥⎩则函数()f x 的值域为___________.若函数()()g x f x k =-有2个零点,则k 的范围是___________.【答案】[)1,-+∞;[1,2e).【解析】因为2(1)e 01()21x x x f x x x x ⎧+≤<=⎨-≥⎩,当01x ≤<时,由10,e 0x y x y =+=>>单调递增,∴()()1e xf x x =+在[0,1)上单调递增,∴当01x ≤<时,()()[,2e)1e 1xf x x ∈=+,当1≥x 时,所以()()22211[1,)f x x x x --==-∈-+∞,综上,函数()f x 的值域为[)1,-+∞,作出函数()f x 的图象与直线y k =如图所示:函数()()g x f x k =-有2个零点,即()y f x =与y k =有2个交点,所以12e k ≤<,即[1,2e)k ∈.故答案为:[)1,-+∞;[1,2e).四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知集合{}114A x x =≤-<,{}23B x x =-<≤,{}2121C x a x a =-<<+.(1)若x C ∈是“x A ∈”的充分条件,求实数a 的取值范围;(2)若()A B C ⊆,求实数a 的取值范围.【答案】(1)3,22⎡⎤⎢⎥⎣⎦;(2)31,2⎛⎫ ⎪⎝⎭.【解析】(1)因为{}114A x x =≤-<,所以{}25A x x =≤<.因为x C ∈是x A ∈的充分条件,所以221532122a a a a ⎧≤⎧+≤⎪⎪⇒⎨⎨-≥≥⎪⎪⎩⎩,解得322a ≤≤,∴3,22a ⎡⎤∈⎢⎥⎣⎦;(2)因为{}23A B x x ⋂=≤≤,()A B C ⊆,所以212213a a -<⎧⎨+>⎩,解得312a <<.故a 的取值范围为31,2⎛⎫ ⎪⎝⎭.18.(12分)已知二次函数()f x 同时满足以下条件:①()()22f x f x +=-,②()01f =,③()23f =-.(1)求函数()f x 的解析式;(2)若()()()4h x f x m x =++,[]1,2x ∈-,求:①()h x 的最小值()m ϕ;②讨论关于m 的方程()m k ϕ=的解的个数.【答案】(1)()241f x x x =-+(2)①()252,4,1,42,42, 2.m m m m m m m ϕ+≤-⎧⎪⎪=--<<⎨⎪-≥⎪⎩;②答案见解析【解析】(1)由()()22f x f x +=-得,对称轴为2x =,设()()22f x a x b =-+,∴()()04123f a b f b ⎧=+=⎪⎨==-⎪⎩,得13a b =⎧⎨=-⎩,∴()()222341f x x x x =--=-+.(2)①()()()241h x f x m x x mx =++=++,[]1,2x ∈-,对称轴2m x =-,ⅰ当12m-≤-即2m ≥时,()h x 在[]1,2-单调递增,()()min 12h x h m =-=-,ⅱ122m -<-<即42m -<<时,()h x 在1,2m ⎡⎤--⎢⎥⎣⎦单调递减,在,22m ⎡⎤-⎢⎥⎣⎦单调递增,∴()2min 124m m h x h ⎛⎫=-=- ⎪⎝⎭,ⅲ当22m-≥即4m ≤-时,()h x 在[]1,2-单调递减,()()min 252h x h m ==+,综上:()()2min52,4,1,42,42, 2.m m m h x m m m m ϕ+≤-⎧⎪⎪==--<<⎨⎪-≥⎪⎩②画出函数()y m ϕ=的图象图下图所示:利用图象的翻转变换得到函数()y m ϕ=的图象如图所示:方程()m k ϕ=的根的个数为函数()y m ϕ=的图象与直线y k =的交点个数,由图象可知:当0k <时,方程()m k ϕ=无解;当01k <<时,方程()m k ϕ=有4个解;当0k =或1k >时,方程()m k ϕ=有2个解;当1k =时,方程()m k ϕ=有3个解.19.(12分)已知函数21()21x x a f x ⋅-=+,且()f x 为奇函数.(1)求a 的值;(2)判断函数()f x 的单调性并证明;(3)解不等式:(21)(2)0f x f x -+->.【答案】(1)1(2)函数()f x 在定义域上单调递增,证明见解析(3)(1,)+∞【解析】(1)由函数为奇函数且定义为R()()f x f x -=-当0x =时,可得的(0)(0)f f -=-故(0)0f =则0021(0)021a f ⋅-==+,得1a =(2)由(1)知21()21x x f x -=+设12x x<()()12221221212121x x x x f x f x ---=-++()()()121212222221121212121x x x x x x -=--+=++++由2x y =在定义域内是单调增函数∵12x x <∴1222x x <即12220x x -<∴()()12f x f x <即函数()f x 在定义域上单调递增.(3)(21)(2)0f x f x -+->,且()f x 为奇函数,∴(21)(2)f x f x ->-+∵函数()f x 单调递增∴212x x ->-+∴1x >∴不等式的解集为(1,)+∞.20.(12分)已知函数()2sin 2cos 232f x x x ππ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭.(1)求函数()f x 在5,66ππ⎡⎤-⎢⎥⎣⎦上的单调区间;(2)若0,2πβ⎛⎫∈ ⎪⎝⎭,1213f βπ⎛⎫-= ⎪⎝⎭,求6cos 2βπ⎛⎫+ ⎪⎝⎭的值.【答案】(1)递增区间为,612ππ⎡⎤-⎢⎥⎣⎦,75,126ππ⎡⎤⎢⎥⎣⎦,递减区间为7,1212ππ⎡⎤⎢⎥⎣⎦;(2)3-.【解析】(1)由题意得()2ππsin 2cos 232f x x x ⎛⎫⎛⎫=++- ⎪ ⎪⎝⎭⎝⎭1cos 2sin 2sin 222x x x =-+1π2sin 2sin 2223x x x ⎛⎫=+=+ ⎪⎝⎭,因为π5π,66x ⎡⎤∈-⎢⎥⎣⎦,所以[]π20,2π3x +∈,令ππ0232x ≤+≤,解得ππ,612x ⎡⎤∈-⎢⎥⎣⎦;令ππ3π2232x ≤+≤,解得π7π,1212x ⎡⎤∈⎢⎥⎣⎦,令3ππ22π23x ≤+≤,得7π5π,126x ⎡⎤∈⎢⎥⎣⎦.所以函数()f x 在π5π,66⎡⎤-⎢⎥⎣⎦上的单调递增区间为ππ,612⎡⎤-⎢⎥⎣⎦,7π5π,126⎡⎤⎢⎥⎣⎦,单调递减区间为π7π,1212⎡⎤⎢⎥⎣⎦.(2)由(1)知ππ1sin 21263f ββ⎛⎫⎛⎫-=+= ⎪ ⎪⎝⎭⎝⎭.因为π0,2β⎛⎫∈ ⎪⎝⎭,所以ππ7π2,666β⎛⎫+∈ ⎪⎝⎭,又因为π11sin 2632β⎛⎫+=< ⎪⎝⎭,所以ππ2,π62β⎛⎫+∈ ⎪⎝⎭,所以π22cos 263β⎛⎫+=- ⎪⎝⎭.21.(12分)已知函数()()2π2cos 10,02f x x ωϕωϕ⎛⎫=+-><< ⎪⎝⎭,且()2f x 的最小正周期为π,将()f x 的图像沿x 轴向左平移π6个单位,得到函数()g x ,其中π3x =为()g x 的一条对称轴.(1)求函数()f x 与()g x 的解析式;(2)若方程()()ππ21033g x f x g x f x t ⎛⎫⎛⎫--+-⋅+-= ⎪ ⎪⎝⎭⎝⎭在区间π5,π126⎡⎤⎢⎥⎣⎦有解,求实数t 的取值范围.【答案】(1)()sin f x x =-;()πsin 6g x x ⎛⎫=-+ ⎪⎝⎭(2)30,8t ⎡+∈⎢⎣⎦【解析】(1)由条件则()()cos 22f x x ωϕ=+且()()2cos 42f x x ωϕ=+的最小正周期为π,则12ω=即()()cos 2f x x ϕ=+,将()f x 的图像沿x 轴方向向左平移π6个单位,得到函数()πcos 26g x x ϕ⎛⎫=++ ⎪⎝⎭且π3x =为()g x 的一条对称轴,即()πππ22π362k k ϕϕ++=+=∈Z 由π0,2ϕ⎛⎫∈ ⎪⎝⎭可得π4ϕ=从而可得()πcos sin 2f x x x ⎛⎫=+=- ⎪⎝⎭()ππ2ππcos cos sin 2636g x x x x ⎛⎫⎛⎫⎛⎫=++=+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.(2)由(1)可知ππsin cos 32g x x x ⎛⎫⎛⎫-=--=- ⎪ ⎪⎝⎭⎝⎭记()()()5,33126H x g x f x g x f x x ππππ⎛⎫⎛⎫⎛⎫⎡⎤=--+-⋅∈ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦⎝⎭即()sin cos sin cos H x x x x x =-+⋅,5,126x ππ⎡⎤∈⎢⎥⎣⎦再记sin cos 4x x x πλ⎛⎫=-=- ⎪⎝⎭,5,126x ππ⎡⎤∈⎢⎥⎣⎦21sin cos 2x x λ-⇒⋅=,2λ⎡∈-⎢⎣代入()H x 中,则()H x 的值域求解问题等价于()()22112122h λλλλλ-=+=---,λ⎡∈⎢⎣的值域,当2λ=-时,()min 1242h λ=-;当1λ=时,()max 1h λ=因此()λh 的值域为1,124⎡⎤-+⎢⎥⎣⎦,也即()H x 为1,124⎡⎤-+⎢⎥⎣⎦原命题“若方程()()21033g x f x g x f x t ππ⎛⎫⎛⎫--+-⋅+-= ⎪ ⎪⎝⎭⎝⎭在区间5,126ππ⎡⎤⎢⎥⎣⎦有解”即等价于()12h t λ=-在λ⎡∈⎢⎣内有解只需()112,124t ⎡⎤-∈-+⎢⎥⎣⎦即可,解得30,8t ⎡+∈⎢⎣⎦即为所求.22.(12分)已知函数()22x x g x a -=-⋅是奇函数.(1)求实数a 的值;并说明函数()g x 的单调性(不证明);(2)若对任意的实数[)0t ∞∈+,,不等式()()22220g t t g t k -+->恒成立,求实数k 的取值范围.【答案】(1)详见解析;(2)1,3⎛⎫-∞- ⎪⎝⎭【解析】(1)解:因为函数()22x x g x a -=-⋅是奇函数,所以()010g a =-=,解得1a =,经检验符合题意;此时()22x x g x -=-,因为2x y =在R 上是增函数,2x y -=在R 上是减函数,所以()g x 在R 上是增函数.(2)因为对任意的实数[)0t ∞∈+,,不等式()()22220g t t g t k -+->恒成立,所以对任意的实数[)0t ∞∈+,,不等式()()2222g t t g k t ->-恒成立,所以对任意的实数[)0t ∞∈+,,2222t t k t ->-恒成立,所以对任意的实数[)0t ∞∈+,,232k t t <-恒成立,令22111323333⎛⎫=-=--≥- ⎪⎝⎭y t t t ,所以13k <-,实数k 的取值范围1,3⎛⎫-∞- ⎪⎝⎭.。
高中数学必修1、2、3、4、5综合试卷及答案详解(优秀经典测试卷)

XXX 中学数学必修1-5测试卷一、选择题(共12个,每个5分,共60分)1.若集合A={1,3,x},B={1,2x },A ∪B={1,3,x}则满足条件的实数x 的个数有( ) (A ) 1个 (B ) 2个 (C )3个 (D ) 4个2.若函数y=f (x )的定义域是[2,4],则y=f (12log x )的定义域是( )(A ) [12,1] (B ) [4,16] (C )[116,14] (D )[2,4 ] 3.设偶函数f (x )的定义域为R ,当[0,)x ∈+∞时f (x )是增函数,则(2),(),(3)f f f π--的大小关系是( )(A )()f π>(3)f ->(2)f - (B )()f π>(2)f ->(3)f - (C )()f π<(3)f -<(2)f - (D )()f π<(2)f -<(3)f - 4.0.7log 0.8a =, 1.1log 0.9b =,0.91.1c =,那么( )(A )a <b <c (B )a <c <b (C )b <a <c (D )c <a <b 5、已知点(1,2),(3,1)A B ,则线段AB 的垂直平分线的方程是( ) A .524=+y x B .524=-y x C .52=+y x D .52=-y x6、 两直线330x y +-=与610x my ++=平行,则它们之间的距离为( ) A .4 B .21313 C .51326 D .710207.直线3x-4y-4=0被圆(x-3)2+y 2=9截得的弦长为( )(A)22(B)4 (C)24(D)28、a ,b ,c 表示直线,M 表示平面,给出下列四个命题:①若a ∥M ,b ∥M ,则a ∥b ;②若b ⊂M ,a ∥b ,则a ∥M ;③若a ⊥c ,b ⊥c ,则a ∥b ;④若a ⊥M ,b ⊥M ,则a ∥b .其中正确命题的个数有( )A 、0个B 、1个C 、2个D 、3个 9.如图是计算12+14+16+…+120的值的一个程序框图,其中在判断框中应填入的条件是( )A .i <10B .i>10C .i <20D .i >20 10.若P (A ∪B )=1,则事件A 与B 的关系是( )A .A 、B 是互斥事件 B .A 、B 是对立事件C .A 、B 不是互斥事件D .以上都不对11.、在等比数列{}n a 中,117a a ⋅=6,144a a +=5,则1020a a 等于( ) A .32B .23 C .23或32 D .﹣32或﹣2312、△ABC 中,已知()()a b c b c a bc +++-=,则A 的度数等于( )A .120B .60C .150D .30 二.填空题(共4个,每个5分,共20分)13.数列{}n a 的前n 项和*23()n n s a n N =-∈,则5a =14、设变量x 、y 满足约束条件⎪⎩⎪⎨⎧≥+-≥-≤-1122y x y x y x ,则y x z 32+=的最大值为15.已知函数()sin()cos()f x x x =+θ++θ是偶函数,且[0,]2πθ∈,则θ的值为 .16.下面有五个命题:①函数y =sin 4x -cos 4x 的最小正周期是π. ②终边在y 轴上的角的集合是{a |a =,2k k Z π∈}. ③在同一坐标系中,函数y =sin x 的图象和函数y =x 的图象有三个公共点. ④把函数3sin(2)3y x π=+的图像向右平移6π得到3sin 2y x =的图像.⑤函数sin()2y x π=-在[0]π,上是单调递减的.其中真命题的序号是 . 三、解答题(共6题,总分70分 17.已知函数213()cos sin cos 1,22f x x x x x R =++∈.(1)求函数()f x 的最小正周期;(2)求函数()f x 在[,]124ππ上的最大值和最小值,并求函数取得最大值和最小值时的自变量x 的值.18.数列{}n a 的前n 项和为n S ,23n n S a n =-(*n N ∈).(Ⅰ)证明数列{3}n a +是等比数列,求出数列{}n a 的通项公式; (Ⅱ)设3n n nb a =,求数列{}n b 的前n 项和n T ;19、△ABC 中,c b a ,,是A ,B ,C 所对的边,S 是该三角形的面积,且cos cos 2B bC a c=-+ (1)求∠B 的大小; (2)若a =4,35=S ,求b 的值。
高中数学必修1、4、5、2、综合测试题附答案

数学必修1一、选择题1.设集合{}012345U =,,,,,,{}035M =,,,{}145N =,,,则()U M C N ⋂=( ) A .{}5 B .{}0,3 C .{}0,2,3,5 D .{}0,1,3,4,52、设集合2{650}M x x x =-+=,2{50}N x x x =-=,则M N 等于 ( ) A.{0}B.{0,5}C.{0,1,5}D.{0,-1,-5} 3、计算:9823log log ⋅= ( )A 12B 10C 8D 64、函数2(01)xy a a a =+>≠且图象一定过点 ( )A (0,1)B (0,3)C (1,0)D (3,0)5、“龟兔赛跑”讲述了这样的故事:领先的兔子看着慢慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点…用S 1、S 2分别表示乌龟和兔子所行的路程,t 为时间,则与故事情节相吻合是 ( )6、函数12log y x = 的定义域是( )A {x |x >0}B {x |x ≥1}C {x |x ≤1}D {x |0<x ≤1}7、把函数x 1y -=的图象向左平移1个单位,再向上平移2个单位后,所得函数的解析式应为 ( ) A 1x 3x 2y --= B 1x 1x 2y ---= C 1x 1x 2y ++= D 1x 3x 2y ++-= 8、设x x e1e )x (g 1x 1x lg )x (f +=-+=,,则 ( ) A f(x)与g(x)都是奇函数 B f(x)是奇函数,g(x)是偶函数C f(x)与g(x)都是偶函数D f(x)是偶函数,g(x)是奇函数9、使得函数2x 21x ln )x (f -+=有零点的一个区间是 ( ) A (0,1) B (1,2) C (2,3) D (3,4)10、若0.52a =,πlog 3b =,2log 0.5c =,则( )A a b c >>B b a c >>C c a b >>D b c a >>二、填空题11、函数5()2log (3)f x x =++在区间[-2,2]上的值域是______12、计算:2391- ⎪⎭⎫ ⎝⎛+3264=______13、函数212log (45)y x x =--的递减区间为______14、函数122x )x (f x -+=的定义域是______ 15.若一次函数b ax x f +=)(有一个零点2,那么函数ax bx x g -=2)(的零点是 .三、解答题16. 计算 5log 3333322log 2log log 859-+-18、已知函数⎪⎩⎪⎨⎧≥<<--≤+=)2(2)21()1(2)(2x x x x x x x f 。
高中数学必修1-5综合测验

8、从3台甲型彩电和2台乙型彩电中任数2台,其中两种品牌的彩电齐全的概率为( )
(A) (B) (C) (D)
9、已知关于 的不等式 的解集为 ,则 的值是( )
(A)10(B)-10 (C)14 (D)-14
10、已知函数 是定义在R上周期函数为 的偶函数,当 时, ,则 , , 的大小关系是( )
=
=
20.解:(1)
又 是奇函数
(2) 、 且
由
即 在R上单调递增
又
(3) 恒成立
恒成立
恒成立 其中
设 ,有
设 对称轴
且 或 且 或 且
得 或 或
综合以上 知:
.
一 选择题
1
2
3
4
5
6
7
8
9
10
D
B
A
C
D
C
C
C
D
A
二 填空题
11 . ; 12. ; 13. : 14. (2).(4)
三 解答题15.
(1)
的单调递增区间是 (
(2)
16 (1)直三菱柱 — 中,
面 面
又 BC=2, ,D是中点,
又
从而 面
(2) 取 的中点 ,在 中,
又 四边形 是平行四边形 面
③设数列 满足 ,求 的前 项和为
20、设函数 对任意的 ,都有 ,当 >0时, >0,且
①判断函数 的奇偶性,且证明;
②判断函数 的单调性,且 在 上的最值;
③问是否存在这样的实数 ,使得 >0对所有的 均成立?若存在,则求出实数 的范围;若不存在,试说明理由。
广州市第八十九中学 必修(1.2.4.5)参考答案
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学必修1-5综合测试卷
姓名: 得分: 编写人:王老师
注意事项:
本试卷分为选择题、填空题和简答题三部分,共计150分,时间120分钟。
一、选择题:本大题10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、设集合2{650}M x x x =-+=,2{50}N x x x =-=,则M
N 等于 ( ) A.{0}
B.{0,5}
C.{0,1,5}
D.{0,-1,-5}
2、已知(,3)a x =,
(3,1)b =, 且a b ⊥, 则x 等于 ( ) A -1 B -9 C 9 D 1
3.函数2(01)x
y a a a =+>≠且图象一定过点 ( )
A (0,1)
B (0,3)
C (1,0)
D (3,0) 4、.函数)2
5
2sin(π+=x y 的一条对称轴方程是 ( )
A .2π-
=x
B .4π-
=x
C .8π
=
x
D .4
5π=
x
1438131
_____{_}{__.
}an a a bn bn log an bnbn n Sn 5.已知等比数列中,=,=,若数列满足=,则数列+的前项和=A .n/n-1 B .1/+n n C .1/n+1 D .1/n-1 6、.已知各顶点都在一个球面上的正四棱柱(其底面是正方形,且侧棱垂直于底面)高为4,体积为16,则这个球的表面积是( ) A.16π B.20π
C.24π D.32π 7、.ABC ∆中,若︒===60,2,1B c a ,则ABC ∆的面积为 ( )
A .
2
1
B .23 C.1
D.3
8、.已知1(2,1)P -, 2(0,5)P 且点P 在12P P 的延长线上, 12||2||PP PP =, 则点P 的坐标为
( ) A. (2,7)-
B. 4(,3)3
C. 2(,3)3
D . (2,11)-
9、把函数y =sin x 的图象上所有点的横坐标都缩小到原来的一半,纵坐标保持不变,再把 图象向左平移4
π
个单位,这时对应于这个图象的解析式 ( )
A .y =cos2x
B .y =-sin2x
C .y =sin(2x -
4
π
) D .y =sin(2x +
4
π)
10.在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,若b a +a b =6cos C ,则
tan C
tan A +tan C tan B 的值是 ( )A. 14 B.1
2
C.4
D. 2 二、填空题:本大题共5小题,每小题5分,满分25分
11.已知,4)4
tan()4tan(
=++-θπθπ且,2π
θπ-<<-则θsin = .
12.在ABC ∆中,0
45,3
B c b ===,那么A =_____________;
13.数列{}n a 的前n 项和*
23()n n s a n N =-∈,则5a =
14.已知函数f(x )=22
3+-+-bx ax mx 且0<f(-1)=f(2)=f(-3)<3则m 的取值范围
15、设,m n 是两条不同的直线,γβα,,是三个不同的平面,给出下列四个命题:
①若m ⊥α,n //α,则n m ⊥ ②若αβ//,βγ//,m ⊥α,则m ⊥γ ③若m //α,n //α,则m n // ④若αγ⊥,βγ⊥,则//αβ
其中正确命题的序号是
三、解答题 :本大题共5小题,满分75分。
解答须写出文字说明、证明过程或演算步骤。
16、已知).1,2(),0,1(==b a
(12分)
(I )求|3|b a
+;
(II )当k 为何实数时,k -a b 与b a
3+平行, 平行时它们是同向还是反向?
17、在ABC ∆中,,,a b c 分别是角,,A B C 的对边,且
cos cos B C b
a c
=-+2.(12分) (1)求角B 的大小;
(2)若b a c =+=134,,求ABC ∆的面积
18、已知等差数列{}n a 的前四项和为10,且237,,a a a 成等比数列(12分)
(1)求通项公式n a
(2)设2n a
n b =,求数列n b 的前n 项和n s
19、如图,在棱长为2的正方体1111ABCD A B C D -中,E 、F 分别是棱1111,A D A B 的
中点.(13分)
(Ⅰ)求异面直线1DE FC 与所成的角 (II )求1BC 和面EFBD 所成的角; (III )求1B 到面EFBD 的距离
20、设函数b a x f ⋅=)(,其中向量a =(2cos x ,1),b =(cos x ,3sin2x ),x ∈R.(13分) (Ⅰ)若f (x )=1-3且x ∈[-
3π,3
π
],求x ; (Ⅱ)若函数y =2sin2x 的图象按向量c =(m ,n )(|m |<
2
π
)平移后得到函数y=f (x )的图象, 求实数m 、n 的值.
21、.若{}n a 的前n 项和为n S ,点),(n S n 均在函数y =
x x 2
1
232-的图像上。
(16分)
(Ⅰ)求数列{}n a 的通项公式 (Ⅱ)设13+=
n n n a a b ,n T 是数列{}n b 的前n 项和,求使得20
n m
T <对所有n N *∈都成立的最小正整数m 。
21如图所示,甲船由A 岛出发向北偏东45°的方向作匀速直线航行,速度为15 2
n mile/h ,在甲船从A 岛出发的同时,乙船从A 岛正南40 n mile 处的B 岛出发,
朝北偏东θ⎝
⎛
⎭⎪⎫tan θ=12的方向作匀速直线航行,速度为m n mile/h.
(1)若两船能相遇,求m .
(2)当m =105时,求两船出发后多长时间距离最近,最近距离为多少
n mile?。
