模糊第1章
高中地理必修一(第一章)知识点总结

第一章第1节宇宙中的地球一、地球在宇宙中的位置1、宇宙的概念:时间和空间的统一,天地万物的总称。
宇宙在空间上无边无际,在时间上无始无终,是运动、发展和变化的物质世界。
2、宇宙中的天体以及它们各自的特点•恒星——明亮发光,发热;相对静止。
例如,太阳是距地球最近的恒星。
•星云——轮廓模糊,云雾状外貌。
由气体和尘埃组成,其主要成分是氢。
•行星——在椭圆轨道上环绕恒星运行的、近似球状的天体。
质量比恒星小,本身不发光,靠反射恒星的光而发亮。
例如地球是目前人们发现唯一存在生命的行星。
•卫星——围绕行星运动的天体,例如月球(卫星)是离地球最近的自然天体。
•流星体——尘粒和固体小块•彗星——扁长轨道,拖着长尾的彗星。
围绕太阳公转的哈雷彗星(周期76年)•星际物质——气体和尘埃3、天体的类型:自然天体——主要为恒星和星云等人造天体——人造卫星,航天飞机,天空实验室等。
宇宙中的距离相近的天体因相互吸引而相互绕转,构成不同级别的天体系统。
4、天体系统的层次二、太阳系中的一颗普通行星太阳系模型图1、按离太阳由近及远的顺序依次是:A水星,B金星,C地球,D火星,E木星,F土星,G天王星,H海王星。
小行星带位于木星和火星之间;木星是体积和质量最大的行星;地球是密度最大的行星。
2、运动特征:同向性、共面性、近圆性。
3、太阳系行星的分类:类地行星:水星,金星,地球,火星巨行星:木星,土星远日行星:天王星,海王星。
4、表现:地球是太阳系中一颗普通的行星。
三,存在生命的行星1、地球的特殊性:地球是太阳系唯一存在生命的行星。
2、地球存在生命的条件:(1)地球所处的宇宙环境条件是:a光照条件稳定,生命从低级各高级的演化没有中断。
b安全的宇宙环境:大小行星互不干扰。
(2)地球的物质条件是:a日地距离适中:适宜的温度。
b体积、质量适中:适合生物呼吸的大气。
c地球上有液体水:海洋、液态水的形成。
第一章第2节太阳对地球的影响一、太阳辐射与地球:太阳的概况:太阳与其他恒星一样能发光发热,是一个巨大炽热的气体星球,主要成分是氢(71%)和氦(27%). 表面温度约为6000K。
智能控制理论及其应用-第一章概述

1.2 智能控制的产生及其发展
(3)智能控制的发展
国际智能自动化学会(International Society Of Intelligent Automation,简称ISIA) 筹委会主席是模糊数学与模糊系统 的创始人L.A.Zadeh教授。筹委会第一次会议已于1995 年10月在加拿大温哥华召开。她的成立将在世界范围内对于 推动智能自动化的研究起到促进作用。 我国也十分重视智能控制理论和应用的研究。1993年在 北京召开了“全球华人智能控制与智能自动化大会”,1994年 在北京和沈阳召开了智能控制两个学术会议,1995年中国智 能自动化学术会议暨智能自动化专业委员会成立大会在天津 召开。
1.2 智能控制的产生及其发展
(1)智能控制的孕育
1966年,Mendel进一步在空间飞行器的学习控制系统 中应用了人工智能技术,并提出了“人工智能控制”的概 念。 1967年,Leondes和Mendel首先正式使用“智能控制” 一词,并把记忆、目标分解等一些简单的人工智能技术用 于学习控制系统,提高了系统处理不确定性问题的能力。 这就标志着智能控制的思想已经萌芽。
1.3 传统控制与智能控制
智能控制的产生来源于被控系统的高度复杂性、高度不 确定性及人们要求越来越高的控制性能,可以概括为,智能 控制是“三高三性”的产物,它的创立和发展需要对当代多种 前沿学科、多种先进技术和多种科学方法,加以高度综合和 利用。 因此,智能控制无疑是控制理论发展的高级阶段。
1.4 智能控制理论的主要特征
1.2 智能控制的产生及其发展
(3)智能控制的发展
美国《IEEE控制系统》杂志1991、1993~1995年多次发 表《智能控制专辑》,英国《国际控制》杂志1992年也发表了 《智能控制专辑》,日文《计测与控制》杂志1994年发表了 《智能系统特集》,德文《电子学》杂志自1991年以来连续发 表多篇模糊逻辑控制和神经网络方面的论文;俄文《自动化与 遥控技术》杂志1994年也发表了自适应控制的人工智能基础及 神经网络方面的研究论文。 如果说智能控制在80年代的应用和研究主要是面向工业过 程控制,那么90年代,智能控制的应用已经扩大到面向军事、 高技术领域和日用家电产品等领域。今天,“智能性”已经成为 衡量“产品”和“技术”高低的标准。
第3章 模糊理论

3 A(1.60)= =0.3 10
……
1 A(1.77)= =0.1 10 10 0.1 0.3 0.6 1 0.5 0.1 FA = + + + + + 1.56 1.60 1.64 1.69 1.73 1.77
A(1.64)=
6 =0.6 10
模糊统计法的特点: ①随着n的增大,隶属频率会趋向稳定,这个 稳定值就是v0对A的隶属度。 ②计算量大。 2、例证法 :从有限个隶属度值,来估计U上的模糊 集A 的隶属度函数。 3、专家经验法:根据专家的经验对每一现象产生 的各种结果的可能性程度,来决定其隶属度函数。 4、二元对比排序法:通过对多个事物之间的两两 对比,来确定某种特征下的顺序,由此来决定这些 事物对该特征的隶属函数的大体形状。
二、模糊控制的特点 1、无需知道被控对象的数学模型 2、是一种反映人类智慧思维的智能控制 模糊控制采用人类思维中的模糊量,如“高”、 “中”、“低”等,且控制量由模糊推理导出 3、易于被人们所接受(核心:控制规则) 4、构造容易 5、鲁棒性好
第二节 模糊集合论基础
一、模糊集的概念
集合:具有某种特定属性的对象全体。 集合中的个体通常用小写英文字母如:u表 示; 集合的全体又称为论域。通常用大写英文字 母如:U表示。 uU表示元素(个体)u在集合论域(全体) U内。
附近隶属函数的范围
重叠鲁棒性=
U
L
( A1 A2 )dx 2(U L)
重叠指数的定义
(0.3~0.7为宜)
求重叠率和重叠鲁棒性
例:
A1
A2
重叠率= 10 / 30 0.333
0 .5 10 重叠鲁棒性= 0.5 2(40 30) 20
第四章计算智能(2)-模糊推理1

经典二值(布尔)逻辑
在经典二值(布尔)逻辑体系中,所有的分类 都被假定为有明确的边界;(突变) 任一被讨论的对象,要么属于这一类,要么不 属于这一类; 一个命题不是真即是假,不存在亦真亦假或非 真非伪的情况。(确定)
1
天气冷热
雨的大小
风的强弱
人的胖瘦
年龄大小
个子高低
2
模糊数学
•模糊概念 模糊概念:从属于该概念到不属于该概念之间 无明显分界线 年轻、重、热、美、厚、薄、快、慢、大、小、 高、低、长、短、贵、贱、强、弱、软、硬、 阴天、多云、暴雨、清晨。 模糊数学就是用数学方法研究模糊现象。
3
模糊数学的产生与基本思想
•产生 1965年,L.A. Zadeh(扎德) 发表了文章《模糊集 》
5
IEEE 系列杂志 主要杂志25种,涉及模糊内容20,000余种 • 国际会议 IFSA (Int. Fuzzy Systems Association) EUFIT、NAFIP、Fuzzy-IEEE、IPMU • 涉及学科 模糊代数,模糊拓扑,模糊逻辑,模糊分析, 模糊概率,模糊图论,模糊优化等模糊数学分支 分类、识别、评判、预测、控制、排序、选择;
并以此数作为 R1°R2 第i行第j列的元素。
R2=
0.2 0.4 0.6
0.8 0.6 0.4
求 R1°R2
42
模糊推理
模糊命题 模糊概念 1 张三是一个年轻人。 2 李四的身高为1.75m左右。模糊数据 3 他考上大学的可能性在60%左右。 对相应事件发生 的可能性或确信 4 明天八成是个好天气。 程度作出判断。 5 今年冬天不会太冷的可能性很大。
33
模糊二元关 系R是以 U×V为论域 的一个模糊 子集,序偶 (u,v)的隶属 度为uR(u,v)
智能控制基础-第1章 绪论

在实际应用方面,智能控制在现代工业体系的39个 工业大类中都有广泛应用,尤其是在一些高精端行 业中,智能控制应用极为广泛。
5
智能控制 基础
怎样才能学好智能控制?
智能控制作为一门新兴学科,发展极快,分支极多, 需要关注学科最新的发展动态;
对于某些复杂的和饱含不确定性的控制过程,根本无法 用传统数学模型来表示,即无法解决建模问题。
第一章 智能控制概述
28
智能控制 基础
5、智能控制的研究对象
应用传统控制理论进行控制必须提出并遵循一些比较苛 刻的线性化假设,而这些假设在应用中往往与实际情况不 相吻合。
为了提高控制性能,传统控制系统可能变得很复杂,从 而增加了设备的投资,减低了系统的可靠性。
控制问题;
领域是控制界当前的研究热
点和今后的发展方向。
第一章 智能控制概述
24
智能控制 基础
4、智能控制与传统控制的关系
然而,智能控制和传统控制又是密不可分的,而不是互 相排斥的。
传统控制是智能控制的一个组成部分,在这个意义下, 两者可以统一在智能控制的框架下;
传统控制在某种程度上可以认为是智能控制发展中的低 级阶段,智能控制是对传统控制理论的发展。
第1章 智能控制概述
智能控制 基础
课程涵盖的内容
智能控制的基本概念、特点、类型、对象特点; 模糊控制器、模糊辨识、自适应模糊控制器; 神经网络控制; 专家系统; 遗传算法、蚁群算法、粒子群算法。
2
智能控制 基础
课程总目标
掌握智能控制的基本概念、特点、主要类型、对象特点; 掌握智能控制的基本理论框架,了解智能控制技术的主要
模糊系统

3. 修正型最大平均法 (modified mean of maxima defuzzifier)
y* = 其中 µC ( y j ) = height (C )
max{ y j } + min{ y j }
j j
2
4. 中心平均法 (modified center average defuzzifier)
■
■
将经过模糊推理之后产生的结论,转换为一明确数值的过程,我们称之 为 “去模糊化 。 去模糊化” 去模糊化 由于不同的模糊规则所采用的后件会有所不同,因此,经过模糊推理后 所得到的结论,有的是以模糊集合 模糊集合来表示(如语言式模糊规则),而有的是 模糊集合 以明确数值 明确数值来表示。 明确数值
3.1.3 模糊推理引擎
■
模糊推理引擎是模糊系统的核心,它可以藉由近似推理 模糊推理 近似推理或模糊推理 模糊推理引擎 近似推理 模糊推理的进行,来仿真 人类的思考决策模式,以达到解决问题的目地。 前提一(premise) 1:x is A´ 前提二(premise) 2:If x is A, Then y is B -----------------------------------------------------------结论:y is B´
■
■ ■
■
推理引擎将藉由这些模糊规则来进行推理,以决定下一步骤所要 推理引擎 采取的决定。 三种规则的主要差别只在于模糊规则的后件有所不同而已 后件有所不同而已。 后件有所不同而已 至于模糊规则从何而来呢?一般说来,有两种取得模糊规则的方 式:第一种方式也是最直接的方式,就是由专家来提供所须的模 专家来提供所须的模 糊规则;第二种方式是先收集一些量测数据后,再经由特定的训 糊规则 练算法则来从量测数据中抽取出模糊规则 量测数据中抽取出模糊规则。 量测数据中抽取出模糊规则 模糊规则中前件与后件的模糊集合,其隶属函数的设定 隶属函数的设定从何而来 隶属函数的设定 呢?假若模糊规则是由人类专家所给定的,则隶属函数就必须由 人类专家一起给定。若模糊规则是由特定的训练算法则从量测数 据中抽取出来的,选定合适的隶属函数型式之后,则以收集之量 测数据来细调隶属函数的参数,以便提高系统的有效性。
第一章模糊集的基本概念

6.集合的运算规律
幂等律: A∪A = A, A∩A = A; 交换律: A∪B = B∪A, A∩B = B∩A; 结合律:( A∪B )∪C = A∪( B∪C ), ( A∩B )∩C = A∩( B∩C ); 吸收律: A∪( A∩B ) = A,A∩( A∪B ) = A; 分配律:( A∪B )∩C = ( A∩C )∪( B∩C ); ( A∩B )∪C = ( A∪C )∩( B∪C ); 0-1律:A∪U = U , A∩U = A ; A∪ = A , A∩ = ; 还原律: (Ac)c = A ; 对偶律: (A∪B)c = Ac∩Bc,(A∩B)c = Ac∪Bc; 排中律: A∪Ac = U, A∩Ac = .
§1.2 模糊理论的数学基础
一 经典集合
1.经典集合具有两条基本属性:
元素彼此相异,即无重复性;范围边界分明, 即一个元素x要么属于集合A(记作xA),要么不属 于集合(记作xA),二者必居其一. 2.集合的表示法 (1)枚举法,A={x1 , x2 ,…, xn}; (2)描述法,A={x | P(x)}.
记R=(rij)n×n, R2 =(rij(2))n×n.
先设R具有传递性.
若rij(2) =0,则有rij(2) ≤ rij .
若rij(2) =1,则由于
rij(2) = ∨{(rik∧rkj) | 1≤k≤n} = 1,
故存在1≤s≤n,使得
(ris∧rsj) = 1,
即ris= 1, rsj= 1.
由于R具有传递性,ris= 1, rsj= 1, 则rij =1. 综上所述 R2≤R. 再设R2≤R,则对任意的 i , j , k,若有 rij =1, rjk = 1,
2.关系的三大特性 定义9 设R为 X 上的关系 (1) 自反性:若 X 上的任何元素都与自己有关 系R,即R (x , x) =1,则称关系 R 具有自反性; (2) 对称性:对于X 上的任意两个元素 x , y, 若 x 与y 有关系R 时,则 y 与 x 也有关系R,即 若R (x , y ) =1,则R ( y , x ) = 1,那么称关系R具 有对称性; (3) 传递性:对于X上的任意三个元素x, y, z, 若x 与y 有关系R,y 与z 也有关系R 时,则x与z 也 有关系R,即若R (x , y ) = 1,R ( y , z ) =1,则R ( x , z ) = 1,那么称关系R具有传递性.
模糊数学方法及其应用(第3版)第四章答案

0.46 ,同理,得到其他两两对比的优先选择比。 0.32 + 0.46
0.41 0.54 ⎞ ⎛ 1 ⎜ ⎟ 1 0.38 ⎟ 模糊优先关系矩阵 R = 0.59 ⎜ ⎜ 0.46 0.62 1 ⎟ ⎝ ⎠
找出每行最小值 0.41, 0.38, 0.46 ,其中最大值 0.46 位于第三行,因此 c 为第一优越对象。 将第三行和第三列划去得到 a 与 b 的模糊优先关系矩阵:
用矩阵作业法解模糊关系方程第一步求最大解040507050405070105040608060104060307040504040504050505040405来代替得到ij04050705040504050405070504040504040505050405070405因为每一列都有非零的元素所以原模糊关系方程有解第三步求极小解种取法选取第一列的第一个元素第二列的第一个元素第三列的第一个元素和第四列的第四个元因此选中了第一行的和第四行的05元素在行中选中的元素中选取最大值第二行和第三行中没有选取元素得到一个解1110405070705同理选取时得到解211070405选取时得到解3110405选取时得到解41105选取时得到解05选取时得到解070405选取时得到解0405选取时得到解05拟极小解为第四步构造解集方程的解集为07100400405020505040404080706010202解
⎛1 0 1 0⎞ ⎜ ⎟ TR ( B) = B o R = (0.7, 0.2, 0) o ⎜ 0 1 0 0 ⎟ = (0.7, 0.2, 0.7, 0) % % % ⎜0 0 1 1⎟ ⎝ ⎠ ⎛1 0 1 0⎞ ⎜ ⎟ 解法 2,由模糊关系矩阵 R = 0 1 0 0 知存在模糊映射 f ( x ) ,使得 ⎜ ⎟ ⎜0 0 1 1⎟ ⎝ ⎠
05-第一章和 1.1、图1-1 共存(隐藏一级标题编号法)(1)

第一章 绪论
1.1 研究背景及意义
图 1-1 AHP-模糊综合评价方法技术路线图
1.2 文献综述
1.3 研究主要内容
1.4 技术路线
第二章 低碳港口相关理论分析
2.1 低碳经济相关理论研究
2.2 低碳港口相关理论研究
2.3 低碳港口相关评定指标
2.4 本章小结
第三章 低碳港口建设方案优化
3.1 问题描述
3.2 优化指标分析
3.3优化模型构建
3.4模型优化与实现
第四章低碳港口规划效用评价体系建立4.1低碳港口规划效用评价指标选取
4.2低碳港口规划效用评价指标分析及量化
4.3评价方法的比较与选择
4.4AHP-模糊分析集成模型构建流程
第五章连云港港低碳港口规划评价实证研究5.1连云港港节能减排现状
5.2连云港港低碳港口规划方案优化
5.3连云港港低碳港口规划方案效用评价
5.4连云港港低碳港口规划建议措施
5.5本章小结
第六章结论与展望
6.1本文的主要结论与创新点
6.2研究展望。
模糊模式识别法

X
Y
~
(
x)
x
0,
μ
o ~
x
1
x
50 5
2
1
,
0 x 50 50 x 200
1,
Y ~
x
1
x
25 5
2
1
,
0 x 25 25 x 200
③ 年轻与年老的隶属函数曲线
年轻 1
年老
0.5
0
25
50 55
年龄 100
7.2.2 隶属函数的确定
隶属函数是模糊集合赖以存在的基石。正确地确定隶属函 数是利用模糊集合恰当地定量表示模糊概念的基础。
头发为n根者为秃头, 头发为n+1根者为秃头, 头发为n+2根者为秃头,
…… 头发为n+k根者为秃头。
其中,k是一个有限整数,显然k完全可以取得很大。
结论:头发很多者为秃头。
类似地:没有头发者不是秃头
2.模糊数学的诞生 模糊数学:有关描述和处理模糊性问题的理论和方法的学科。 模糊数学的基本概念:模糊性。
根据具体研究的需要而定。
2)子集
对于任意两个集合A、B,若A的每一个元素都是B的元素,
则称A是B的“子集”,记为
A B或;B若B中A存在不属于
A的元素,则称A是B的“真子集”,记为
A 。B或B A
3)幂集
对于一个集合A,由其所有子集作为元素构成的集合称
为A的“幂集”。
例:论域X={ 1, 2 },其幂集为
~A
的核为
x0
;
x0
的两边分别有点
x1
和
x2
,使得
A ~
(
x1
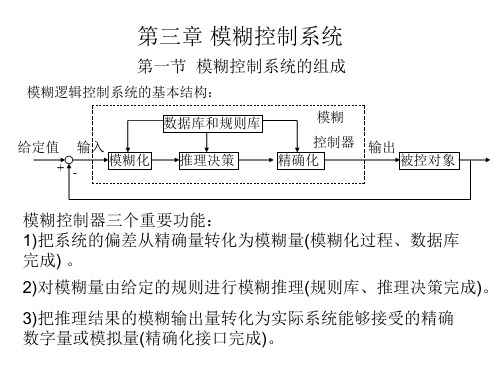
第三章、模糊控制系统
精确量(V0)
∴V0 = 5
当论域V中,其最大隶属度函数对应的输出值多于一个时, 简单取最大隶属度输出的平均即可:
即:当有(v1) µ 2)= L =µc (vJ ) 最大时 µ = (v
1 J 取v0 = ∑ v j J j =1
U 1 , U 2 , L ,U n :输出论域上模糊子集
总的模糊关系: R( 其中:
e , de , u ) = U Ri
n
当ki 取µv (vi )时
重心法
模糊化计算的其它方法:左取大、右取大等。
第二节:模糊控制系统的设计 一、模糊控制器的结构设计 模糊控制器的结构设计包括:输入输出变量选择、模糊化 算法、模糊推理规则和精确化计算方法。 一维模糊控制器 被控对象 输入输出 (按模糊控制器输入变量个数) 变量 多输入多输出 单输入单输出 二维模糊控制器 多维模糊控制器
例:x分成三档(NB、ZE、PB); y y分成两档(NB、PB); 模糊分区形式:
PB NB 0 NB ZE
R1
R2 R4
R3
PB 24
问:在此分档情况下,最大规则数为多少?
x
2 规则库 用一系列模糊条件描述的模糊控制规则就构成模糊控制规则库。 建立 规则库 选择输入变量和输出变量 建立规则(完备性、交叉性、一致性)
完备性:对于任意给定的输入均有相应的控制规则起作用。 交叉性:控制器的输出值总由数条规则来决定。 一致性:规则中不存在相互矛盾的规则。
模糊控制规则建立方法 1)专家经验法: 通过对专家控制经验的咨询形成控制规则库。 实质:通过语言条件语句来模拟人类的控制行为。
模糊数学方法及其应用第版答案

A%
o
R
=
(1,
0.5,
0.8,
0,
0.4,
0.7)
o
⎜ ⎜ ⎜
1 0
0 1
0 0
0⎟ ⎟ = (1, 0.4, 0.7, 0)
0⎟
⎜0 1 0 0⎟ ⎜⎜⎝ 0 0 1 0⎟⎟⎠
⎛1 1 1 0 0 0⎞
f
−1 ( B) %
=
T%R'
(B) %
=
B %
o
R'
=
(1,
0.4,
0.7, 0)
o
⎜ ⎜ ⎜
解:利用波达数的计算方法可知:
a 的波达数为 4 + 2 +1+ 0 + 0 + 2 + 3 + 2 = 14 b 的波达数为 5 + 5 + 0 +1+1+1+1+ 0 = 14 c 的波达数为 2 + 0 + 2 + 3 + 3 + 5 + 2 + 4 = 17 d 的波达数为 3 +1+ 4 + 4 + 5 + 4 + 4 + 5 = 30 e 的波达数为1+ 4 + 5 + 5 + 4 + 0 + 0 +1 = 20
%
x1 x2 x3 x4 x5 x6
⎛1 0 0 0⎞
⎜ ⎜
1
0
0
0 ⎟⎟
⎜1 0 0 0⎟
解法 2,根据模糊映射 f (x) ,可以得到模糊关系矩阵 R = ⎜
⎟
模糊数学 第四章---模糊关系

2.模糊自反关系(fuzzy reflexive relations)
定义 R F ( X X ), 若x X , R( x, x) 1,
则称R为模糊自反关系.
X有限时,R (rij )nn , rii R( xi , xi ) 1 根据主对角线元素是否为1判定R 是否自反
2. 运算
设R, S F ( X Y )
R S ( x, y ) X Y , R( x, y ) S ( x, y ); R S ( x, y ) X Y , R( x, y ) S ( x, y );
( R S )( x, y ) R( x, y ) S ( x, y ) ( R S )( x, y ) R( x, y ) S ( x, y )
设R (rij )nm , S ( sij )nm ,
即R( xi , y j ) rij , S ( xi , y j ) sij
则(R S )( xi , y j ) R( xi , y j ) S ( xi , y j ) rij sij 所以,R S (rij sij )nm .
1
X 有限时,
根据矩阵是否为对称阵判定R 是否对称关系
0.3 0.1 为对称关系. 0.1 0.3
命题3.3 R对称 [0, 1], R 是普通对称关系.
证明: 设R对称,且( x, y) R , 则R( x, y)
故R( y, x) R( x, y) ( y, x) R
类似可得: R S (rij sij ) nm . R c (1 rij )nm .
R 1 ( yi , x j ) R( x j , yi ) rji R S i, j, rij sij
Python数学实验与建模课件第14章模糊数学

第14章
14.1模糊数学基本概念
第7页
定义 14.2 论域U 到[ 0 , 1闭]区间上的任意映射 M : U [0,1], u M (u),
都确定了U 上的一个模糊集合, M (u)叫做 M 的隶属函数,或称为u对 M 的 隶属度。记作 M {(u, M(u)) | u U },使得 M(u) 0.5的点称为模糊集 M 的 过渡点,此点最具有模糊性。
(0.3 0.2) (0.35 0.4) (0.1 0.2)]
[0.3 0.2 0.1, 0.3 0.2 0.1, 0.2 0.35 0.1]
[0.3, 0.3, 0.35].
第14章
14.1模糊数学基本概念
#程序文件 Pex14_6.py import numpy as np a=np.array([0.3,0.35,0.1]); aa=np.tile(a,(len(a),1)) b=np.array([[0.3,0.5,0.2],[0.2,0.2,0.4],[0.3,0.4,0.2]]) c=np.minimum(aa.T,b) # 两个矩阵的元素对应取最小值 T=c.max(axis=0) # 矩阵逐列取最大值 print("T=",T)
x
A。描述这一事实的是特征函数
A(
x
)
1, 0,
唯一确定。
x A, 即集合 A由特征函数 x A,
第14章
14.1模糊数学基本概念
第6页
在模糊数学中,称没有明确边界(没有清晰外延)的集合为模糊集合。 常用大写字母来表示。元素属于模糊集合的程度用隶属度来表示。用于计算 隶属度的函数称为隶属函数。它们的数学定义如下。
的模糊集 M 和 N 可表示为
M
模糊控制—第1章

模糊控制的发展主要分为以下三个阶段: 1、形成期(1974年以前) 1965年,美国加州大学自动控制系L. A. Zedeh教 授提出模糊集合理论,开创了模糊控制数学基础的研 究。 2、发展期(1974-1979年) 1974年,伦敦大学教授E. H. Mamdani 博士利用 模糊逻辑开发了世界上第一台模糊控制的蒸汽机,开 创了模糊控制的历史。 3、高性能控制阶段(1979年——现在)
图1-4 模糊逻辑系统结构
第2章
模糊控制的数学基础
模糊集合论的诞生,解决了数值和模糊概
念间的相互映射问题。以模糊集合论为基础的
模糊数学,在经典数学和充满模糊性的现实世
界之间,架起了一座桥梁,使得模糊性事物有
了定量表述的方法,从而可以用数学方法揭示 模糊性问题的本质和规律。
2. .1 清晰向模糊的转换 三类数学模型 第一类:确定性数学模型 确定性数学模型往往用于描述具有清晰的确定 性、归属界线分明、相互间关系明确的事物。对这类事物 可以用精确的数学函数予以描述,典型的代表学科就是 “数学分析”、“微分方程”、“矩阵分析”等常用的重 要数学分支。 第二类:随机性数学模型 随机性数学模型常用于描述具有或然性或者随 机性的事物,这类事物本身是确定的,但是它的发生与否 却不是确定的。 第三类:模糊性数学模型 模糊性数学模型适用于描述含义不清晰、概念 界线不分明的事物,它的外延不分明,在概念的归属上不 明确。
提出模糊集合定义:
在模糊集合涉及的数值范围——论域U 上,给定了一个映射: A : U [0, 1], x
A ( x)
则称集合A为论域U上的模糊集合或模糊子集;用 A ( x)表示 U中各个元素x属于集合A的程度,称为元素x属于模糊集合A 的隶属函数。当x是一个确定的元素x0时,称 A ( x0 )为元素x0 对模糊集合A的隶属度。 这一定义使得任何一个确定的元素x0,属于一个边界不 清晰的模糊集合A的程度,有了确定的数学方法,个不同的事物处于中间过渡状态时,就会出现 “亦此亦彼”的特性,也就是模糊性。 模糊性起源于事物的发生、发展和变化性,处于过渡 阶段的事物,其最大特征就是性态的不确定性和类属的不明 确性,即模糊性。
photoshop cs6 基础与案例教程第一章

蓝色区域是浮动调板,用来 安放制作需要的各种常用的 调板。
每个调板的右上角(红色区域),都有一个圆形 三角按钮,点击这个按钮后会出现调板功能的选 项。不同的调板点击后出现的菜单也不一样。
每个调板的右下角(绿色区域),都有一个 缩放标志,可以用鼠标拖动此处即可拉伸调 板。一般可伸缩调板都有一个最小尺寸,不 能无限缩小。
“后台存储”复选项
1.2 新增的修饰和变换功能
– 内容识别工具的作用就是选取 图像中的一部分移动或复制到 另外一个位置,经过Photoshop CS6的计算,完成极其真实的 合成效果。 – 内容识别修补工具在更新的 “修补工具”包含“内容识别” 选项,可通过合成邻近内容无 缝替换不需要的图像元素。 – 重新设计的“裁剪工具”提供 交互式的预览,使用户可以获 得更好的视觉效果。一组简化 的工具栏选项包含拉直工具和 长宽比控件(可在图像窗口中 裁剪处于活动状态时调整该控 件)。
1.4.2 常用的图像文件格式
PSD格式 TIF格式 TGA格式 BMP格式 GIF格式 JPEG格式 EPS格式 选择合适的图像文件存储格式
1.
TIF格式
TIF 格式是标签图像格式。可以用于 PC 、 Macintosh以及UNIX工作站3大平台,是这3大平 台上使用最广泛的绘图格式。用TIF格式存储时 应考虑到文件的大小,因为TIF格式的结构要比 其他格式更复杂。但TIF格式支持24个通道,能 存储多于 4个通道的文件格式。TIF格式还允许 使用Photoshop CS6中的复杂工具和滤镜特效。 TIF格式非常适合于印刷和输出。
•
• • •
1.5 视频与3D功能
1、视频功能 重新设计的基于剪辑的“时间轴”面板可为完美视屏的 专业效果提供过渡和特效,可轻松更改剪辑持续时间 和速度,并将动态效果应用到文字、静态图像和只能 对象。 2、3D功能 简化的界面提供画布上的场景编辑,可直观的创建3D 图稿。用户可轻松将阴影拖动到所需位置、将 3D 对象 制作成动画、为 3D 对象提供素描或卡通外观,以及其 他更多功能。
第二章模糊集合(1)

3)向量表示法
F { (u1 ), (u2 ),..., (un )}
此时,元素u应该按次序排列,隶属度值为零的项不能省略。 上例可写为 F={1,0.9,0.75,0.5,0.2,0.1} 上页
具有数学运算、符号运算的逻辑推理 边缘交叉学科 上页
小结
下页
茂名学院计算机与电子信息学院自动化系
—智能控制技术—
第二章 模糊控制的理论基础
第一节 引言
第二节 模糊集合论基础
一、普通集合 二、模糊集合的概念 三、模糊集合的运算 四、隶属函数(MF)的确定 五、模糊关系 上页
小结
下页
茂名学院计算机与电子信息学院自动化系
1 A 0
如果 X A 如果 X A
模糊集合:论域U中的模糊集F用一个在区间[0,1]上
取值的隶属函数
F (u) 来表示,即
F {(u, F (u)) | u U}
上页
小结
下页
茂名学院计算机与电子信息学院自动化系
—智能控制技术—
普通集合
X 6
1
X 6ቤተ መጻሕፍቲ ባይዱ
A 0
3)交换律 A∩B=B∩A, A∪B= B∪A
上页
小结
下页
茂名学院计算机与电子信息学院自动化系
—智能控制技术—
4)分配律 5)同一律 6)零一律 7)吸收律 8)德.摩根律
A∩(B∪C) =(A ∩ B)∪(A ∩ C) ; A∪(B∩C)=(A∪B)∩ (A∪C); A∩U=A, A∪Φ=A; A∩Φ=Φ, A∪U=U; A∩(A∪B)=A, A∪(A ∩ B)=A;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章模糊理论概述1.1. 研究历史回顾1.1.1.模糊数学的背景●经典数学——“科学皇后”●1904年,法国物理学家杜恩(P.Duhem)在其《物理理论的目的和结构》一书中说“同一般常识的模糊陈述,正因其比较精确,反而比较不确定。
”●1923年,大哲学家罗素(B.russel)在其著名论文《论模糊性》中提出“整个语言或多或少是模糊的。
”他特别强调:“当运用于精确符号时,排中律是有效的,但是当符号是模糊的时候,排中律就无效了。
”1.1.2.模糊数学的诞生●1965年,著名控制论专家,美国加州大学伯克莱分校计算机系教授L.A.Zadeh首次提出了模糊集合(Fuzzy set)的概念,发表了题为《模糊集合论》的第一篇有关模糊数学的论文,从而宣告了模糊数学的诞生。
他引入“隶属度”这个概念来描述处于中介过渡事物对差异一方所具有的倾向性程度,这是精确性对模糊性的一种逼近,首次成功地运用数学方法刻划模糊性的现象。
1.1.3.模糊数学的早期发展●在查德教授刚提出模糊集的几年中,研究速度相当慢。
1965年仅查德一篇论文,1966年才两篇,大多数数学家,特别是理论数学家是持怀疑甚至否定态度的。
●苏联著名数学家M.盖尔芳德院士却敏锐地看出扎德的工作的意义,并建议查德应用模糊集论研究人的自然语言。
显示了深刻的洞察力和卓越的预见性,到了1970年,“模糊”观念逐渐为人所知。
●1974年,英国玛丽皇后大学(Queen Marry College)的E.H.Mamdani教授首先将模糊逻辑应用到蒸汽发动机的压力和速度控制中,取得了比常规的PID控制更好的效果。
●1980年(随后不久),丹麦的F.L.Smith公司成功地将模糊控制应用到水泥窑的自动控制中,为模糊理论的应用开辟了崭新的前景。
●自1965到1986年这21年中,已发表论文超过5000篇。
●自1973年到1979年的六年期间,国际会议讨论模糊数学竟达25次,●1983年7月,在马塞召开了“模糊信息,知识模型和判决分析”国际会议,●1984年7月,在夏威夷召开“第一届模糊信息处理”国际会议;●1984年成立了国际性组织“国际模糊系统协会(IFSA)”创办了“Fuzzy sets andsystems”国际杂志;●1985年在西班牙召开”国际模糊系统协会第一届会议“。
●1989年,在日本诞生了国际模糊工程研究所(LIFE)。
●日本是模糊理论在工业控制中应用推广较好的国家◆日立制作的地铁自动操作的模糊控制系统——仙台市的地铁运行。
◆富士电机公司的净水工厂药剂投量的自动控制系统。
◆立石电机公司向市场投放了最早的模糊控制器硬件。
◆松下电器推出了全自动的模糊洗衣机,电饭锅等。
◆三洋电机研究所开发了高质量的彩色复印机的颜色再现控制技术。
日本在92年生产的与模糊技术有关的产品约20亿美元。
1.1.4.模糊数学的研究方向模糊数学的创始人查德教授和齐默曼教授(曾任IFSA主席,西德人)1981年的意见:●一方面是研究模糊性内在规律,也就是探讨模糊语言和模糊逻辑。
在这个方向上,模糊数学与人工智能,知识工程,专家系统等分支有机结合,以增进电脑活性,更好的模拟人思维,对客观事物进行识别,聚类,论证,决策,评价,控制,优化等等,这些都是研究中心课题,。
●另一方面是把模糊集当作一个能概括更加多样化数学概念的框架。
建立处理模糊现象的确切性的数学理论,以拓广数学基础,产生模糊拓扑,模糊拓扑空间,模糊测度和积分,模糊代数,模糊群论,模糊图论,模糊规划,模糊概率……等新的方向。
使经典数学的若干方面在更广阔更深刻意义下向前推进。
同时谈谈模糊数学与传统数学在理论方面关系,从而深化人类对数学中若干基本概念的认识。
1.1.5.我国模糊数学的发展●1976年我国开始注意模糊数学的研究,世界著名模糊学家考夫曼(A.kaufman,法国)山泽(E.SanchZ.法国)。
营野(日本)和美籍华人P.P.Z等先后来华讲学,推动了我国模糊数学的高速发展,很快就拥有一支较强的研究队伍。
●1980年成立了中国模糊集与系统协会。
●1981年,创办《模糊数学》杂志,1987年,创办了《模糊系统与数学》杂志。
●还出版过大量的颇有价值的论著。
例如:汪培庄教授所著《模糊集与随机集落影》,《模糊集合论及其应用》,张文修教授编著的《模糊数学基础》等。
●1988年我国汪培庄教授指导几位博士生研制成功了一台模糊推理机-----分立元件样机。
它的推理速度为1500万次/秒,这表明我国在突破模糊信息处理难关方面迈出重要一步。
最近,我国科研人员在Fuzzy领域中取得了卓越成就。
何新贵院士将Fuzzy方面的论文在国内外权威杂志上发表。
这标志着我国研究已经达到国内外先进水平。
至此,我国已成为全球四大模糊数学研究中心之一。
(美国,西欧,中国,日本)●2005年有两件值得庆祝的大事。
⏹经国际模糊系统协会(IFSA)专家评审,最终确定授予我国四川大学副校长刘应明院士“Fuzzy Fellow奖”。
“Fuzzy Fellow奖”是模糊数学领域的最高奖项,专门授予得到国际公认的,在模糊数学领域做出杰出贡献的科学家。
⏹2005年8月20日,中国运筹会Fuzzy信息与工程分会正式成立。
Fuzzy信息与工程分会成立,是隶属于全国两大数学方向的一级学会之一------中国运筹会,表明Fuzzy数学在我国已取得了应有的地位,尤其是Fuzzy数学的创始人查德教授的出席会议,中国运筹学会理事长,中国科学院数学与系统科学研究院副院长袁亚湘教授和广州大学校长廖建设教授为学会揭牌,这给成立大会增添的极大的光彩。
也极大的鼓舞了全国Fuzzy研究工作者。
Fuzzy信息与工程分会的宗旨:在完善和加强Fuzzy集理论研究的同时,更侧重于Fuzzy技术的应用和Fuzzy产品的开发研究。
1.2. 模糊现象与模糊性模糊数学是研究和处理模糊性现象的数学模糊——Fuzzy:not clear in shape 模糊的,绒毛状的,边界不清的,不分明自然现象客观事物人类现象(思维)性质确定性现象清晰性事物清晰认识(思维)精确性不确定现象模糊性事物模糊认识(思维)模糊性1.2.1.模糊现象自然界现象确定性现象不确定性现象随机现象模糊现象⏹确定性现象◆定义:在一定条件下,必然发生的现象。
◆例:三角形a+b>c我的哥哥是男人数学的定理等◆特点:哲学上:符合一因一果论逻辑上:非此即彼的二值逻辑的规律即一个命题非真即假,一个对象属于或不属于一个集合,二者必居其一,只居其一。
如:命题:猴子是动物。
真狗是植物。
假集合:猴子属于{动物}狗不属于{植物}◆数学工具:经典数学基础是普通集合论——基础是二值逻辑⏹随机现象◆定义:在基本条件一定下,发生各种可能结果的现象。
◆例:掷骰子6种结果抽彩票6种奖(一,二,三,四,鼓励,不中)发射3发导弹4种结果(全中,一,二,不中)◆特点:哲学上:具有一因多果论的性质(对象确定,结果不确定)事物因果关系的不确定性。
逻辑上:仍符合非此即彼的二值逻辑的规律如:命题:掷骰子4点。
真掷骰子8点。
假集合:掷骰子4点属于{骰子可能出现的点数}掷骰子8点不属于{骰子可能出现的点数}◆数学工具:统计数学基础是普通集合论⏹模糊现象◆定义:被研究的对象本身具有不确定性的现象◆例:事物的多少、大小、高低、长短、宽窄等人的老、中、青,胖子、瘦子,健康人、病人,美、丑等天气阴、晴等◆特点:哲学上:每一个概念都有内涵(性质、属性)和外延(范围、边界),而模糊现象的内涵不确定,外延不明晰逻辑上:符合亦此亦彼的多值逻辑的规律如:那个女孩漂亮、不漂亮、一般◆数学工具:模糊数学基础是模糊集合论⏹随机现象与模糊现象的比较◆都属于不确定现象◆随机现象所研究的对象是确定的模糊现象所研究的对象是不确定的◆随机性对应的概念是必然性模糊性对应的概念是精确性◆人类认识本质上是模糊的,此模糊性能更恰当地反映人类的思维方法1.2.2.模糊性客观世界中存在清晰性事物(相对的、有条件的),也存在模糊事物(绝对的)。
所谓清晰事物只是模糊程度比较小,不影响人们对它的精确认识而已,模糊事物比比皆是。
所以说模糊性是事物的客观属性。
⏹人类◆活人和死人◆年龄◆体型◆相貌◆关系◆身体⏹自然界◆天气◆地震◆风⏹食物◆蔬菜和水果◆粮食和蔬菜⏹时间◆季节⏹自然科学◆土质◆产品◆材料⏹社会科学◆价格股市◆社会◆职业共同特点:没有明确的界限,即自身模糊。
亦此亦彼性(模糊性),客观事务的差异在中介过渡中呈现出。
清晰事物是相对的,模糊事物是绝对的。
精确性那个是相对的有条件的,模糊性是绝对的。
●“当系统的复杂性增加时,我们使它精确化的能力将减小。
直到达到一个阈值,一旦超越它,复杂性和精确性将互相排斥。
”⏹模糊控制模模模模模模模模模模模◆对于简单的控制对象或已知模型的控制对象,古典的PID控制、自适应控制、最优控制。
但必须有严格的数学模型。
◆对于模型未知的复杂系统或动态特性常变的控制对象,模糊控制就能发挥其作用。
◆1980年,丹麦工科大学的Ostergaard等人对水泥窑的模糊控制进行了研究,F.L.Smith公司随后制造了专用的模糊控制器。
采用模糊控制器控制水泥窑并正式投入运行,取得了成功。
⏹汽车的控制路面窄,不平,道路纵横交错,运动体总类繁多,方向多变,公路拥挤不堪。
1.3. 人脑与电脑1.3.1.人类的认识与模糊性清晰认识(思维):形式化思维,具有逻辑循序的特点。
模糊认识(思维):可同时进行综合的整体的思考在人类的认识和行为中,本质地存在着模糊性,在人类的生产活动和社交活动中,模糊思维形式和语言表达方式比精确的、清晰的思维形式和表达方式更贴切实际情况,具有更广泛、完美和高效的特征。
●例⏹《红楼梦》第98回,宝玉和宝钗成婚之时,也是黛玉一命归西之时,死前黛玉最后一句话是:“宝玉,你好。
”这句话的下半句之意,多年来红学家们众说纷纭。
“宝玉,你好狠心!”恨“宝玉,你好糊涂!”怨“宝玉,你好怯懦!”悲“宝玉,你好好保重!”爱⏹到车站接人精确信息模糊性信息年龄48岁男性中年男子身高1.76米中等偏高腰围95cm 胖子鼻梁高7.2cm 高鼻梁耳朵长7.2cm 大耳朵戴一副825度近视镜瓶子底深度近视镜模糊不清不得要领形象突出印象深刻1.3.2.人脑与电脑电脑是精确性的化身人脑具有模糊思维能力⏹比较记忆称为记忆仓库——存储器有时间、容量限制外形体积大,重重约1.5kg,体积约1000cm3记忆单元几百万个记忆单元几十万个电子元件含100-150亿神经细胞和9000万个辅助细胞复杂性电脑元件分工专一,不可一物多用每个细胞与大约1000个其他神经细胞联系具有自动补偿功能,且可互相顶替,损伤十分之一时仍可以正常运转⏹计算机模拟人脑的思维:形式化思维(具有逻辑循序的特点)模糊化思维(可进行综合、整体的思考)◆计算机模拟第一种思维取得许多可喜的成就,如computer play chess,有限的语言对话,数学定理的证明,编制计算机程序等。
