精选湖南省高一上学期期末考试数学试题(含答案)
湖南省长沙市教育集团2023-2024学年高一上学期期末考试数学试题含答案

教育集团2023年下学期期末考试试卷高一数学(答案在最后)时量:120分钟分值:150分命题人:一、单选题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有项是符合题目要求的.)1.已知集合{20}A xx =-≤≤∣,{2,1,0,1,2}B =--,则A B = ()A.{2,1,0,1,2}--B.{22}x x -≤≤∣C.{2,1,0}-- D.{20}x -≤≤【答案】C 【解析】【分析】根据交集的定义运算即可.【详解】因为{20}A xx =-≤≤∣,{2,1,0,1,2}B =--,所以{}2,1,0A B =-- ,故选:C. 2.函数()2x f x x=的定义域为()A.(],2-∞ B.(),2-∞C.()(],00,2-∞⋃ D.[)2,+∞【答案】C 【解析】【分析】根据分式和偶次根式有意义的基本要求可构造不等式组求得结果.【详解】由题意得:20x x -≥⎧⎨≠⎩得:2x ≤且0x ≠,()f x \定义域为()(],00,2-∞⋃.故选:C.3.将885- 化为)()360Z,0,360k k αα⎡+⋅∈∈⎣的形式是()A .()1652360︒︒-+-⨯ B.()1953360︒︒+-⨯C.()1952360︒︒+-⨯ D.()1653360︒︒+-⨯【答案】B 【解析】【分析】直接由终边相同的角的概念求解即可.【详解】由600,3α︒︒⎡⎤∈⎣⎦知()88519533195108060︒︒-+-⨯=-= .故选:B.4.十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“=”作为等号使用,后来英国数学家哈利奥特首次使用“<”和“>”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若,,a b c R ∈,则下列命题正确的是()A.若0ab ≠且a b <,则11a b> B.若01a <<,则3a a<C.若0a b >>,则11b ba a+<+ D.若c b a <<且0ac <,则22cb ab <【答案】B 【解析】【分析】利用不等式性质,结合特殊值法,即可判断选项的正误.【详解】A 中,0a b <<有11a b<,错误;B 中,01a <<时,3a a <成立,正确;C 中,2,1a b ==时,2132>,错误;D 中,由题设,当0b =时,220cb ab ==,错误;故选:B5.函数①x y a =;②x y b =;③x y c =;④x y d =的图象如图所示,a ,b ,c ,d 分别是下列四个数:54,13,12中的一个,则a ,b ,c ,d 的值分别是()A.54313,12B.354,13,12C.12,13354,D.13,12,543【答案】C 【解析】【分析】根据指数函数的性质,结合函数图象判断底数的大小关系.【详解】由题图,直线1x =与函数图象的交点的纵坐标从上到下依次为c ,d ,a ,b 5113423>>>.故选:C .6.若角α,β均为锐角,25cos 5α=,3cos()5αβ+=,则sin β=()A.255B.55C.55-D.255【答案】B 【解析】【分析】根据给定条件,利用同角公式及差角的正弦公式计算作答.【详解】角α,β均为锐角,即0αβ<+<π,而3cos()5αβ+=,则4sin()5αβ+=,又5cos 5α=,则5sin 5α=,所以,4535sin sin[()]sin()cos cos()sin 5555βαβααβααβα=+-=+-+=⨯-⨯55=.故选:B7.将函数()4cos 2f x x ⎛π=⎫⎪⎝⎭和直线()1g x x =-的所有交点从左到右依次记为A 1,A 2,A 3,…,A n ,若P 点坐标为(0,1),则12n PA PA PA +++=()A.B.C.D.0【答案】A 【解析】【分析】在同一坐标系中作出()42f x cos x π⎛⎫= ⎪⎝⎭和g (x )=x ﹣1的图象,所有交点从左到右依次记为A 1,A 2,A 3,A 4,A 5根据()31,0A 为()42f x cos x π⎛⎫=⎪⎝⎭的一个对称点,得到15,A A 关于()31,0A 对称,24,A A 关于()31,0A 对称,再用中点坐标公式得到1234535+=+++PA PA PA PA PA PA 求解.【详解】由题意作出图象如图,共得5个交点,根据余弦函数的中心对称性可知,1A 和5A ,2A 和4A 关于3A 对称,()31,1PA =-,152432PA PA PA PA PA +=+= ,∴12+++=n PA PA PA 故选:A.8.定义在()0,∞+上的函数()f x 满足:对()12,0,x x ∀∈+∞,且12x x ≠,都有()()2112120x f x x f x x x ->-成立,且()24f =,则不等式()2f x x>的解集为()A.()4,+∞ B.()0,4 C.()0,2 D.()2,+∞【答案】D 【解析】【分析】构造函数()()f x g x x=,由单调性的定义可判断得()g x 在()0,∞+上单调递增,再将题设不等式转化为()()2g x g >,利用()g x 的单调性即可求解.【详解】令()()f x g x x=,因为对()120,x x ∀∈+∞、,且12x x ≠,都有()()2112120x f x x f x x x ->-成立,不妨设120x x <<,则120x x -<,故()()21120x f x x f x -<,则()()1212f x f x x x <,即()()12g x g x <,所以()g x 在()0,∞+上单调递增,又因为()24f =,所以()()2222f g ==,故()2f x x>可化为()()2g x g >,所以由()g x 的单调性可得2x >,即不等式()2f x x>的解集为()2,+∞.故选:D.二、多选题(本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.)9.若-1<x <4是-3<x <a 的充分不必要条件,则实数a 的值可能是()A.3B.4C.5D.6【答案】BCD 【解析】【分析】由必要条件、充分条件的定义即可得出结果.【详解】∵-1<x <4是-3<x <a 的充分不必要条件,∴{x |-1<x <4}{x |-3<x <a },∴a ≥4,∴实数a 的值可以是4,5,6.故选:BCD .10.若0x >,0y >,0n ≠,R m ∈,则下列各式中,恒等的是()A.()lg lg lg x y x y +=+ B.lglg lg xx y y=-C.log log mnx x my yn= D.1lg lg nx x n=【答案】BD 【解析】【分析】根据对数的运算法则、换底公式逐一判断得解.【详解】因为0x >,0y >,0n ≠,m ∈R ,对于A ,lg lg lg()x y xy +=,A 错误;对于B ,lglg lg xx y y=-,B 正确;对于C ,当1,0x m ≠≠时,lg lg log log lg lg mn nx m x y n y n y y x m x m===,C 错误;对于D ,1lg lg nxx n=,D 正确.故选:BD11.下列说法正确的是()A.向量AB 与CD共线是A ,B ,C ,D 四点共线的必要不充分条件B.若//a b ,则存在唯一实数λ使得b aλ=C.已知()()=1,3,1,1= a b ,则a 与a b l + 的夹角为锐角的充要条件是()5,00,2λ⎛⎫∈-⋃+∞ ⎪⎝⎭D.在△ABC 中,D 为BC 的中点,若AB AC AD AB ACλ+=,则BD 是BA 在BC 上的投影向量【答案】ACD 【解析】【分析】根据向量共线和必要不充分条件定义可判断A ;根据向量共线的充要条件可判断B ;根据向量夹角的坐标运算可判断C ;由平面向量加法和BAC ∠的平分线表示的向量平行的向量可得AD 为BAC ∠的平分线,又因为AD 为BC 的中线可判断 D.【详解】对于A 选项:A ,B ,C ,D 四点共线⇒向量AB 与CD共线,反之不成立,所以A 正确;对于B 选项:当0a = ,0b ≠时,不存在实数λ使得b a λ= ,当0a = ,0b =时,存在无数个实数λ使得b a =,故B 错误;对于C 选项:因为()1,3a = ,()1,1b =r ,所以()1,3a b λλλ+=++ ,则a 与a b l +的夹角为锐角的充要条件是()·0a a b λ+>且a 与a b l + 不同向共线,即()()1,3·1,31931040λλλλλ++=+++=+>1≠,解得()5,00,2λ⎛⎫∈-⋃+∞ ⎪⎝⎭,则实数λ的取值范围是()5,00,2⎛⎫-⋃+∞ ⎪⎝⎭,故C 正确;对于D 选项:由平面向量加法可知:AB ACAB AC+ 为“与BAC ∠的平分线表示的向量平行的向量”因为AB AC AD AB ACλ+=,所以AD 为BAC ∠的平分线,又因为AD 为BC 的中线,所以AD BC ⊥,所以BD是BA 在BC的投影向量,故选项D 正确.故选:ACD.12.函数()()sin f x A x ωϕ=+的图象如图所示,将函数()f x 的图象向右平移π12个单位长度,得到()y g x =的图象,则下列说法正确的是()A.函数()g x 的最大值为3B.函数()g x 关于点π,012⎛⎫⎪⎝⎭对称C.函数()g x 在π0,2⎛⎫⎪⎝⎭上单调递减 D.函数()g x 的最小正周期为π【答案】AD 【解析】【分析】根据给定的函数图象求出函数()f x ,进而求出()g x ,再借助余弦函数的图象和性质,逐项判断即可.【详解】观察图象知,3A =,函数()f x 的周期T 有,35ππ3π()41234T =--=,即πT =,则2ω=,显然5(312f π=,则5ππ22π,Z 122k k ϕ⨯+=+∈,即π2π,Z 3k k ϕ=-+∈,因此π()3sin(2)3f x x =-,πππ()3sin[2(]3sin(2)3cos21232g x x x x =--=-=-,函数()g x 的最大值为3,A 正确;ππ(3cos 0126g =-≠,B 错误;π(0,)2x ∈,()20,πx ∈,函数()g x 在π(0,2上单调递增,C 错误;函数()g x 的最小正周期为2ππ2=,D 正确.故选:AD三、填空题:(本题共4小题,每小题5分,共20分13.命题“,π[]0x ∀∈,sin 0x ≥”否定是_________.【答案】[0,π]x ∃∈,sin 0x <.【解析】【分析】根据给定条件,利用全称量词命题的否定写出结论即得.【详解】命题“,π[]0x ∀∈,sin 0x ≥”是全称量词命题,其否定是存在量词命题,所以命题“,π[]0x ∀∈,sin 0x ≥”否定是:[0,π]x ∃∈,sin 0x <.故答案为:[0,π]x ∃∈,sin 0x <.14.若()2,1,1x x f x a x x-+<⎧⎪=⎨≥⎪⎩是R 上的减函数,则实数a 的取值范围为___________.【答案】(]0,1.【解析】【分析】分段函数单调递减,则每一段均为递减函数,且在分段处,左边的函数值大于等于右边的函数值,从而得到不等式组,求出实数a 的取值范围.【详解】由题意得:012a a >⎧⎨-+≥⎩,解得:01a <≤,故实数a 的取值范围为(]0,1.故答案为:(]0,1.15.把函数cos y x =的图象上的所有点的横坐标缩小到原来的一半(纵坐标不变),然后把图象向左平移4π个单位,则所得图形对应的函数解析式为__________.【答案】sin 2y x =-【解析】【分析】利用三角函数图象的平移变换和伸缩变换求解.【详解】将函数cos y x =的图象上的所有点的横坐标缩小到原来的一半,可得cos 2y x =的图象,再向左平移4π个单位,所得图象的解析式为cos 24y x π⎡⎤⎛⎫=+⎪⎢⎥⎝⎭⎣⎦,即cos 2sin 22y x x π⎛⎫=+=- ⎪⎝⎭.故答案为:sin 2y x =-16.若2sin cos 5αα=-,则tan α=__________.【答案】2-或12-【解析】【分析】利用齐次式法列式,求解方程即得.【详解】由2sin cos 5αα=-,得22sin cos 2sin cos 5αααα=-+,即2tan 2tan 15αα=-+,整理得22tan 5tan 20αα++=,所以tan 2α=-或1tan 2α=-.故答案为:2-或12-四、解答题(本题共6小题,共70分,其中第17题10分,其它每题12分解答应写出文字说明、证明过程或演算步骤.)17.已知集合{}1,2,3A =,{}10B x ax =-≥.(1)当2a =时,求A B ⋂与A B ⋃;(2)若A B A = ,求实数a 的取值范围.【答案】(1){1,2,3}A B ⋂=,1{|}2A B x x =≥ ;(2)1a ≥.【解析】【分析】(1)把2a =代入求出集合B ,再利用交集、并集的定义求解即得.(2)利用给定交集的结果,结合集合的包含关系列式求解即得.【小问1详解】当2a =时,1{|210}{|}2B x x x x =-≥=≥,而{}1,2,3A =,所以{1,2,3}A B ⋂=,1{|}2A B x x =≥ .【小问2详解】由A B A = ,得A B ⊆,则10210310a a a -≥⎧⎪-≥⎨⎪-≥⎩,解得1a ≥,所以实数a 的取值范围是1a ≥.18.已知函数()sin cos (R)f x x x x =-∈.(1)求函数()f x 的单调递增区间;(2)求函数2()1,0,2y f x x x π⎡⎤=+-∈⎢⎥⎣⎦的最大值与最小值.【答案】(1)π3π2π2π44k k 轾-++犏犏臌,,Z k ∈(2,最小值-2,【解析】【分析】(1)根据辅助角公式化简()f x ,利用整体换元法即可求解增区间,(2)由二倍角公式和辅助角公式化简,由整体法即可求解最值.【小问1详解】由于π()sin cos sin 4f x x x x ⎛⎫=-- ⎪⎝⎭,故πππ2π2π242k x k -+≤-≤+,解得π3π2π2π44k x k -+≤≤+,Z k ∈,故函数()f x 的单调递增区间为π3π2π2π44k k 轾-++犏犏臌,,Z k ∈【小问2详解】22ππ()212sin 22cos 22sin 242y f x x x x x x x x⎛⎫⎛⎫=-=----=- ⎪ ⎪⎝⎭⎝⎭π2cos 2,6x ⎛⎫=+ ⎪⎝⎭当π0,2x ⎡⎤∈⎢⎥⎣⎦时,ππ7π2,666x ⎡⎤+∈⎢⎥⎣⎦,故当π5π2π,612x x +==时,取最小值-2,当ππ2,066x x +==19.已知函数()211x b f x x +-=+([]1,1x ∈-)是奇函数,()()221g x x a x =+-+是偶函数.(1)求a b +;(2)判断函数()f x 在[]1,1-上的单调性并说明理由;(3)若函数()f x 满足不等式()()120f t f t -+<,求出t 的范围.【答案】(1)3;(2)单调递增,理由见解析;(3)10,3⎡⎫⎪⎢⎣⎭.【解析】【分析】(1)根据奇偶性的定义将点代入求出a b +即可;(2)先判断()f x 单调性,再用单调性定义证明,注意变形时需要变到几个因式乘积;(3)根据()f x 的奇偶性,将不等式化为()()12f t f t -<-,再根据()f x 的单调性及定义域写出范围解出即可.【小问1详解】解:由题知()211x b f x x +-=+([]1,1x ∈-)是奇函数,()100,11b f b -∴==∴=,()()221g x x a x =+-+ 是偶函数,()()11g g ∴=-,2222a a ∴+-=-+,2a ∴=,故3a b +=;【小问2详解】()f x 在[]1,1-上的单调递增,理由如下:由(1)知()21x f x x =+,任取[]1212,,1,1x x x x <∈-,()()1212221211x x f x f x x x -=-++()()()()22122122121111x x x x x x +-+=++()()22121212221211x x x x x x x x +--=++()()()()12122212111x x x x x x --=++,[]1212,1,1,10x x x x ∈-∴-> ,12120x x x x <∴-< ,()()120,f x f x ∴-<()()12,f x f x <∴故()f x 在[]1,1-上的单调递增;【小问3详解】由(1)(2)知()21x f x x =+是奇函数且在[]1,1-上的单调递增,()()120,f t f t -+<()()()()12,12f t f t f t f t \-<-\-<-,11112112t t t t -≤-≤⎧⎪∴-≤-≤⎨⎪-<-⎩,103t ∴≤<,故10,3t ⎡⎫∈⎪⎢⎣⎭.20.某科技企业决定开发生产一款大型电子设备,生产这种设备的年固定成本为500万元,每生产x 台需要另投入成本()C x (万元),当年产量不足80台时,()21402C x x x =+,当年产量不小于80台时,()101C x x =+81002180x -,若每台设备售价为100万元,通过市场分析,该企业生产的电子设备能全部售完.(1)求年利润y (万元)关于年产量x (台)的函数关系式;(2)年产量为多少台时,该企业在这一电子设备的生产中所获利润最大?并求出这个最大利润.【答案】20.2160500,080,N 281001680,80,N x x x x y x x x x ⎧-+-≤<∈⎪⎪=⎨⎪--≥∈⎪⎩;21.90台,1500万元.【解析】【分析】(1)考虑080x ≤<和80x ≥两种情况,根据()100500y x C x =--计算得到答案.(2)利用二次函数性质和均值不等式依次计算分段函数的最值,比较得到答案.【小问1详解】当080x ≤<,N x ∈时,()2211100500100405006050022y x C x x x x x x =--=---=-+-;当80x ≥,N x ∈时,()8100810010050010010121805001680y x C x x x x x x =--=--+-=--,所以年利润y (万元)关于年产量x (台)的函数关系式是2160500,080,N 281001680,80,N x x x x y x x x x ⎧-+-≤<∈⎪⎪=⎨⎪--≥∈⎪⎩.【小问2详解】当080x ≤<,N x ∈时,()22116050060130022y x x x =-+-=--+,当60x =时,y 最大值为1300;当80x ≥,N x ∈时,8100168016801500y x x =--≤-=,当且仅当8100x x=,即90x =时取等号,而15001300>,所以当90x =时,y 有最大值为1500.21.已知向量33cos ,sin 22x x a ⎛⎫= ⎪⎝⎭ ,cos ,sin 22x x b ⎛⎫=- ⎪⎝⎭ ,函数()1f x a b m a b =⋅-++ ,,,34x m R ππ⎡⎤∈-∈⎢⎥⎣⎦.(1)若()f x 的最小值为-1,求实数m 的值;(2)是否存在实数m ,使函数()()22449g x f x m =+,,34x ππ⎡⎤∈-⎢⎥⎣⎦有四个不同的零点?若存在,求出m 的取值范围;若不存在,请说明理由.【答案】(1)m =(2)764m ≤<.【解析】【详解】试题分析:(1)利用向量数量积的公式化简函数()f x 即可.(2)求出函数()f x 的表达式,利用换元法结合一元二次函数的最值性质进行讨论求解即可.(3)由()g x =0得到方程的根,利用三角函数的性质进行求解即可.试题解析:(1)∵33cos cos sin sin cos22222x x x x a b x ⎛⎫⋅=⋅+⋅-= ⎪⎝⎭,33cos cos ,sin sin 2222x x x x a b ⎛⎫+=+- ⎪⎝⎭ ,∴a b +===∵,34x ππ⎡⎤∈-⎢⎥⎣⎦∴2cos a b x +== ,()cos22cos 1f x x m x =-+22cos 2cos x m x =-,令1cos ,12t x ⎡⎤=∈⎢⎥⎣⎦,∴222y t mt =-∵min 1y =-,对称轴为2m t =,①当122m <即1m <时,当12t =时,min 112y m =-=-∴32m =舍,②当112m ≤≤即12m ≤≤时,当2m t =时,2min 12m y =-=-∴m =,③当12m >即2m >是,当1t =时,min 221y m =-=-∴32m =舍,综上,m =.(2)令()()224049m g x f x =+=,即22242cos 2cos 049m x m x -+=,∴3cos 7m x =或47m ,∵()y g x =,,34x ππ⎡⎤∈-⎢⎥⎣⎦有四个不同的零点,∴方程3cos 7m x =和4cos 7m x =在,34x ππ⎡⎤∈-⎢⎥⎣⎦上共有四个不同的实根,∴312741273477m m m m ≤<≤<≠∴727637{840m m m ≤<≤<≠∴764m ≤<.22.已知函数()ln()()f x x a a R =+∈的图象过点()1,0,2()()2f x g x x e =-.(1)求函数()f x 的解析式;(2)若函数()ln(2)y f x x k =+-在区间()1,2上有零点,求整数k 的值;(3)设0m >,若对于任意1,x m m ⎡⎤∈⎢⎥⎣⎦,都有()ln(1)g x m <--,求m 的取值范围.【答案】(1)()ln f x x =;(2)k 的取值为2或3;(3)()1,2.【解析】【分析】(1)根据题意,得到ln(1)0a +=,求得a 的值,即可求解;(2)由(1)可得()2ln 2y x kx =-,得到2210x kx --=,设2()21h x x kx =--,根据题意转化为函数()y h x =在()1,2上有零点,列出不等式组,即可求解;(3)求得()g x 的最大值()g m ,得出max ()ln(1)g x m <--,得到22ln(1)m m m -<--,设2()2ln(1)(1)h m m m m m =-+->,结合()h m 单调性和最值,即可求解.【详解】(1)函数()ln()()f x x a a R =+∈的图像过点()1,0,所以ln(1)0a +=,解得0a =,所以函数()f x 的解析式为()ln f x x =.(2)由(1)可知()2ln ln(2)ln 2y x x k x kx =+-=-,(1,2)x ∈,令()2ln 20x kx -=,得2210x kx --=,设2()21h x x kx =--,则函数()ln(2)y f x x k =+-在区间()1,2上有零点,等价于函数()y h x =在()1,2上有零点,所以(1)10(2)720h k h k =-<⎧⎨=->⎩,解得712k <<,因为Z k ∈,所以k 的取值为2或3.(3)因为0m >且1m m>,所以1m >且101m <<,因为2()22()22(1)1f x g x x e x x x =-=-=--,所以()g x 的最大值可能是()g m 或1g m ⎛⎫ ⎪⎝⎭,因为22112()2g m g m m m m m ⎛⎫⎛⎫-=--- ⎪ ⎪⎝⎭⎝⎭22122m m m m ⎛⎫=--- ⎪⎝⎭112m m m m ⎛⎫⎛⎫=-+- ⎪⎪⎝⎭⎝⎭21(1)0m m m m -⎛⎫=-⋅> ⎪⎝⎭所以2max ()()2g x g m m m ==-,只需max ()ln(1)g x m <--,即22ln(1)m m m -<--,设2()2ln(1)(1)h m m m m m =-+->,()h m 在(1,)+∞上单调递增,又(2)0h =,∴22ln(1)0m m m -+-<,即()(2)h m h <,所以12m <<,所以m 的取值范围是()1,2.【点睛】已知函数的零点个数求解参数的取值范围问题的常用方法:1、分离参数法:一般命题的情境为给出区间,求满足函数零点个数的参数范围,通常解法为从()f x 中分离出参数,构造新的函数,求得新函数的最值,根据题设条件构建关于参数的不等式,从而确定参数的取值范围;。
2022-2023学年湖南省永州市双牌县第二中学高一数学第一学期期末经典试题含解析

在 中,令 可得 ,则
令 可得 ,可得
任取 且 ,则 ,所以
则
即 ,所以 是R上的增函数
【小问2详解】
(i)由 在 上是单减单减函数,又 单调递增
由复合函数的单调性规律可得 在 上是单减单减函数.
(ii)由 ,
所以 的解为
从而不等式 的解为
,即
即 ,整理可得
即 ,解得 或 ,所以 或
所以原不等式的解集为
C.充要条件D.既不充分也不必要条件
8.已知点 , , ,且满足 ,若点 在 轴上,则 等于
A. B.
C. D.
9.如图是某班 名学生身高的频率分布直方图,那么该班身高在 区间内的学生人数为
A. B.
C. D.
10.函数 零点所在的区间是()
A. B.
C. D.
二、填空题:本大题共6小题,每小题5分,共30分。
(当且仅当 时等号成立)
则 的最小值为9
故答案为:9
12、
【解析】先求出半径,再用扇形 面积公式求解即可.
【详解】由已知半径为 ,
则这条弧所在的扇形面积为 .
故答案为: .
13、
【解析】函数 定义域为
故答案为 .
14、
【解析】根据分段函数的单调性,列出式子 ,进行求解即可.
【详解】由题可知:函数 在 上是减函数
【详解】解:函数 的周期为 ,值域为 , ,
则 的值域为 , ,
故答案为:
三、解答题:本大题共5小题,共70分。解答时应写出文字说明、证明过程或演算步骤。
17、(1) ;
(2) .
【解析】(1)根据给定条件可得 ,再利用诱导公式化简计算作答.
湖南省益阳市2022-2023学年高一上学期期末数学试题含答案

益阳市2022年下学期期末质量检测高一数学(答案在最后)注意事项:1.本试卷包括试题卷和答题卡两部分;试题卷包括单项选择题、多项选择题、填空题和解答题四部分,共4页,时量120分钟,满分150分.2.答题前,考生务必将自己的姓名、考号等填写在本试题卷和答题卡指定位置.请按答题卡的要求在答题上上卡作答,在本试题卷和草稿纸上作答无效.3.考试结束后,将本试题卷和答题卡一并交回.试题卷一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}0,1,2,1,2,3A B ==,则A B ⋃=( )A.∅B.{}1,2C.{}0,1,2D.{}0,1,2,32.已知:sin sin ,:p x y q x y ==,则p 是q 的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件3.函数()()e ln 21xf x x =++的定义域为( ) A.(),∞∞-+ B.()0,∞+ C.1,2∞⎛⎫-+ ⎪⎝⎭ D.1,2∞⎛⎫+ ⎪⎝⎭4.化简:1cos2cos 2x x π-=⎛⎫- ⎪⎝⎭( ) A.sin x B.cos x C.2sin x D.2cos x5.已知函数()2,0,1,0,x x x f x x x ⎧->⎪=⎨+≤⎪⎩,则()2f -=( ) A.6 B.3 C.2 D.1-6.下列函数中是奇函数,且在区间()0,∞+上是增函数的是( )A.3y x =B.ln y x =C.e e x x y -=+D.tan y x =7.为了得到函数2sin 6y x π⎛⎫=-⎪⎝⎭的图象,只要把2sin y x =的图象上的所有的点( ) A.向左平移6π个单位长度 B.向右平移6π个单位长度 C.向左平移3π个单位长度 D.向右平移3π个单位长度 8.已知函数()y f x =的部分图象大致如图所示,则其解析式可以是( )A.()()2ln 12x f x x =+-B.()()2ln 14x f x x =+- C.()2e e x x f x x -=+- D.()3e e 2x x f x x -=--二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.已知函数()2sin f x x =,则( )A.()f x 是R 上的奇函数B.()f x 的最小正周期为2πC.()f x 有最大值1D.()f x 在[]0,π上为增函数10.下列命题正确的是( )A.若a b >,则22a b >B.若33a b >,则a b >C.若0,0a b >>,且6a b +=,则3ab ≤D.若1a >-,则111a a +≥+11.已知231log ,log 23a b c ===,则( ) A.a b > B.b c >C.a c >D.1ac <12.已知函数()()cos32lg 1f x x x x +-+的所有非负零点从小到大依次记为12,,,n x x x ,则( )A.8n =B.9n =C.1211049n x x x π-+++>D.121319n x x x π+++> 三、填空题:本题共4小题,每小题5分,共20分. 13.计算:32916⎛⎫= ⎪⎝⎭__________. 14.若点()3,4P -在角α的终边上,则sin α=__________.15.科学家研究发现,地震时释放出的能量E (单位:焦耳)与地震里氏震级M 之间的关系为lg 4.8 1.5E M =+,记里氏9.0级地震、7.0级地震所释放出来的能量分别为12E E 、,则12E E =__________. 16.已知定义在R 上的奇函数()y f x =满足()1y f x =+是R 上的偶函数,且()112f =,则()()()122022f f f +++=__________.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)(1)已知5,cos 13ABC A =,求tan A 的值. (2)求证:1sin2cos sin cos sin x x x x x+=++. 18.(本小题满分12分)设集合{}251,{1}A xx B x x a =-≤=>-∣∣. (1)当2a =时,求A B ⋂;(2)若A B ⋂≠∅,求a 的取值范围.19.(本小题满分12分)已知函数()222,f x x mx x =-+∈R (1)若()0f x >对一切实数x 都成立,求m 的取值范围;(2)已知2m =,请根据函数单调性的定义证明()f x 在(),2∞-上单调递减.20.(本小题满分12分) 已知函数()()0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的图象与y 轴交于P 点()0,1,若123,,x x x 是方程()10f x -=的三个连续的实根,且122315,88x x x x +=+=. (1)求()f x 的解析式;(2)求()f x 的单调递增区间.21.(本小题满分12分)生物爱好者甲对某一水域的某种生物在自然生长环境下的总量w 进行监测.第一次监测时的总量为0w (单位:吨),此时开始计时,时间用t (单位:月)表示.甲经过一段时间的监测得到一组如下表的数据:为了研究该生物总量与时间的关系,甲通过研究发现可以用以下的两种函数模型来表达w 与t 的变化关系:①0w dw =;①()0log 1(0a w b t w a =++>且1)a ≠.(1)请根据表中提供的前2列数据确定两个函数模型的解析式;(2)根据第3,4列数据,选出其中一个与监测数据差距较小的函数模型;甲发现总量w 由0w 翻一番时经过了2个月,根据你选择的函数模型,若总量w 再翻一番时还需要经过多少个月?(参考数据:lg30.48,lg17 1.23≈≈)22.(本小题满分12分)已知函数()e ex x a f x =-. (1)若函数()f x 是R 上的奇函数,求a 的值;(2)若函数()f x 的在R 上的最小值是,确定a 的值;(3)在(2)的条件下,设()()22e 4e (0x x mf x g x mm -+-=>且1)m ≠,若()g x 在[]0,4上的最小值为1,请确定m 的值. 益阳市2022年下学期普通高中期末考试高一数学参考答案及评分标准一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.D2.B3.C4.C5.B6.A7.B8.A二、多选题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.AB 10.BD 11.ACD 12.BC三、填空题:本题共4小题,每小题5分,共20分.13.2764 14.45 15.310 16.12四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分10分)解:(1)A 是ABC 的内角,()0,A π∴∈,又5cos 13A =,12sin 13A ∴==, sin 12tan cos 5A A A ∴== (2)证明:221sin2sin cos 2sin cos cos sin cos sin x x x x x x x x x+++=++ 2(sin cos )cos sin x x x x+=+ cos sin x x =+18.(本小题满分12分)解:{}{}2513A xx x x =-≤=≤∣∣ (1)当2a =时,{1}B x x =>-∣, {}3{1}{13}A B x x x x x x ∴⋂=≤⋂>-=-<≤∣∣∣(2),13A B a ⋂≠∅∴-<,解得:2a >-,所以,a 的取值范围是()2,∞-+.19.(本小题满分12分)解:(1)x R ∀∈,有()0f x >,即2220x mx -+>恒成立, 2Δ480,m ∴=-<解得m <<m 的取值范围是( (2)由已知有()242f x x x =-+,任取()12,,2x x ∞∈-,设12x x <,()()()()22121122121242424,f x f x x x x x x x x x -=-+-+-=-+-则()12121212,,2,0,40x x x x x x x x ∞∈-<∴-<+-<,所以()()120f x f x ->,即()()12f x f x >,()f x ∴在(),2∞-上单调递减.20.(本小题满分12分)解:(1)123,,x x x 是方程()10f x -=的三个连续的实根,且122315,88x x x x +=+=,记45,x x x x ==是三根之间从左到右的两条相邻对称轴, 则4515,1616x x ==, ()54122T x x ∴=-=,即24Tπωπ==, 再将点P代入得:1ϕ=,且2πϕ<得4πϕ=,()44f x x ππ⎛⎫∴=+ ⎪⎝⎭. (2)由()242242k x k k Z ππππππ-+≤+≤+∈ 解之得:31162162k k x -+≤≤+ ()f x ∴的单调递增区间为()31,162162k k k Z ⎡⎤-++∈⎢⎥⎣⎦. 21.(本小题满分12分)解:(1)由已知将前2列数据代入解析式①得:0024dw dw =⎧⎪⎨=⎪⎩.解之得:02,dw c =⎧⎪⎨=⎪⎩∴①2w =; 将前2列数据代入解析式①得:0024log 3a w b w =⎧⎨=+⎩,解之得:0322log w b a =⎧⎨=⎩, ①()()332log log 122log 12a w a t t =++=++.(2)当8t =时,模型①426w =+=,模型①32log 926w =+=; 当16t =时,模型①27.66w =+≈,模型①32lg172log 17227.13lg3w =+=+≈; ∴选模型①;当总量w 再翻一番时有:()382log 12t =++,解之得26t =,即再经过26-2=24个月时,总量w 能再翻一番.22.(本小题满分12分)解:(1)()f x 是R 上奇函数,()()0f x f x ∴-+=即0,1x x x x e ae e ae a ---+-=∴=;(2)当0a <时,()e e x x a f x =-≥()ln 2a x -=时取等,即2a =∴=-;当0a ≥时,()e ex x a f x =-在R 上单调递增,没有最小值;综上所述,函数()f x 在R 上的最小值是2a =-.(3)由(2)以及()f x 的单调性可知:当[]0,4x ∈时,()442f x e e -⎡⎤∈+⎣⎦, ()()()()()2224422244,x x ee mf x f x mf x x x f x e eg x m m -+----=++∴==, 记()()()24u x f x mf x =--,则()()u x g x m =在[]0,4上的最小值为1, ∴当01m <<时,()u g u m =单调递减,有()[]()max 00,4u x x =∈,当1m >时,()u g u m =单调递增,有()[]()min 00,4u x x =∈,记()t f x =,则()2444,2u t t mt t e e -⎡⎤=--∈+⎣⎦; ①当01m <<时,()22424m m u t t ⎛⎫=--- ⎪⎝⎭,其中12m <, ()u t ∴在442t e e -⎡⎤∈+⎣⎦上单调递增, ()()()24444max 2240u t e e m e e --∴=+-+-=, 解之得44444212m e ee e --=+->+(舍); ①当1m >时,122m >,(a )当m ≤2m ≤()u t 在442t e e -⎡⎤∈+⎣⎦上单调递增, ()(min 840u t u ∴==--=,解之得m =;(b )当()4422m e e -≥+时,4422m e e -≥+,此时()u t 在442t e e -⎡⎤∈+⎣⎦上单调递减,()()()24444min 2240u t e e m e e --∴=+-+-=, 解之得()44444442222m e e e e e e---=+-<++(舍);(c )当()4422m e e -<+时,4422m e e -⎡⎤∈+⎣⎦,此时()u t 在2m t ⎡⎤∈⎢⎥⎣⎦上单调递减,44,22m t e e -⎡⎤∈+⎢⎥⎣⎦上单调递增, ()22min 40242m m m u t u ⎛⎫∴==--< ⎪⎝⎭(舍);综上所述,m =.。
湖南省龙山县皇仓中学2013-2014学年高一上学期期末考试数学试题(尖子班) 含答案

高一上学期期末考试数学试题(含答案)一、选择题:(每小题5分,共40分).1.已知集合N M x x N x M x 则},1|{},12log |{<=<==( ) A .}20|{<<x x B . }10|{<<x x C .}1|{<x xD .φ 2.已知直线ax+y+a-1=0不经过第一象限,则与该直线垂直的直线的倾斜角的取值范围( ) A 3,24ππ⎡⎤⎢⎥⎣⎦ B 3,24ππ⎛⎤ ⎥⎝⎦ C 0,4π⎡⎤⎢⎥⎣⎦ D 0,4π⎛⎤ ⎥⎝⎦3.一个直角梯形的两底长分别为2和5,高为4,绕其较长的底旋转一周,所得的几何体的体积为( ) A .π48 B .π34 C .π45 D .π374.当1>a 时,在同一坐标系中函数x a y -=与x y a log =的图像是 ( )5.正三棱锥内有一个内切球,经过棱锥的一条侧棱和高作截面,正确的图是 ( )A B C D6.已知m 、l 是直线, αβ、是平面, 给出下列命题:①若l 垂直于α内的两条相交直线, 则l ⊥α;②若l 平行于α, 则l 平行α内所有直线;③若m l l m ⊂⊂⊥⊥αβαβ,,,且则; ④若l l ⊂⊥⊥βααβ,且,则;⑤若m l m ⊂⊂αβαβ,,,且∥则∥l . 其中不正确的命题的序号是( )A ①②③B ①②④C ②③④D ②③⑤7.设],[)()(b a x g x f 是定义在同一个区间和上的两个函数,若对任意的],[b a x ∈,都有],[)()(,1|)()(|b a x g x f x g x f 在与则称≤-上是“密切函数”,[a ,b ]称为“密切区间”,设],[32)(43)(2b a x x g x x x f 在与-=+-=上是“密切函数”,则它的“密切区间”可以是 A .[1,4] B .[2,3] C .[3,4] D .[2,4]8.已知函数()f x 满足:①定义域为R ;②x ∀∈R ,有(2)2()f x f x +=;③当[1,1]x ∈-时,()||1f x x =-+.则方程4()log ||f x x =在区间[10,10]-内的解个数是( )A .20B .12C .11D .10二、填空题:请把答案填在题中横线上(每小题5分,共35分).9.已知平面α内有无数条直线都与平面β平行,那么它们的位置关系式10.已知集合26()41{|()1},{|log 1},2x x x a A x B x A B φ--+=<=<⋂=若,则实数a ∈11.求过点P (6,-4)且被圆2220x y +=截得长为62的弦所在的直线方程12. 已知两定点A (-3,5),B (2,15),动点P 在直线3x +4y +9=0上,当PA +PB 取最小值时,这个最小值为13. 如图所示,四边形BCDE 是一个正方形,AB ⊥平面BCDE,则图中互相垂直的平面有 对。
湖南省衡阳市耒阳市第二中学2022-2023学年高一上学期期末数学试题(含答案解析)

湖南省衡阳市耒阳市第二中学2022-2023学年高一上学期期末数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}{}1,0,1,2,13M N x x =-=≤≤,则M N ⋂=A .{}1,0,1,2,3-B .{}1,0,1-C .{}1,2D .{}1,2,32.已知命题:,21x p x x ∃∈≤+N ,则命题p 的否定为()A .,21x x x ∃∈>+N B .,21x x x ∃∈≥+N C .,21x x x ∀∈≤+N D .,21x x x ∀∈>+N 3.若sin 0α>且tan 0α<,则2α的终边在A .第一象限B .第二象限C .第一象限或第三象限D .第三象限或第四象限4.设()35f x ax bx =+-,且()77f -=,则()7f =()A .7-B .7C .17D .17-5.设0.21()a e-=,lg 2b =,6cos π5c =,则()A .a c b <<B .c<a<b C .b<c<aD .c b a<<6.已知函数(12)1(1)()(1)xa x x f x a x -+<⎧=⎨≥⎩在(,)-∞+∞上单调递减,则实数a 的取值范围是()A .12[,]23B .12()23,C .12(]23,D .12[,237.鱼塘中的鱼出现了某种因寄生虫引起的疾病,养殖户向鱼塘中投放一种灭杀寄生虫的药剂,已知该药剂融于水后每立方的含药量y (毫克)与时间t (小时)之间的关系用如图所示的曲线表示.据进一步测定,每立方的水中含药量不少于0.25毫克时,才能起到灭杀寄生虫的效果,则投放该杀虫剂的有效时间为()A .4小时B .7116小时C .7916小时D .5小时8.已知函数y =f (x )的表达式为f (x )=|log 2x |,若0<m <n 且f (m )=f (n ),则2m +n 的取值范围为()A .()1,+∞B .[)1,+∞C .()+∞D .)∞⎡+⎣二、多选题9.设a 、b 、c 为实数且a b >,则下列不等式一定成立的是()A .11a b>B .ln ln a b>C .()20221a b ->D .()()2211a c b c +>+10.已知函数()tan 3f x x π⎛⎫=+ ⎪⎝⎭,则下列关于()f x 的判断正确的是()A .在区间,6ππ⎛⎫⎪⎝⎭上单调递增B .最小正周期是πC .图象关于直线6x π=成轴对称D .图象关于点,06π⎛⎫⎪⎝⎭成中心对称11.下列结论中正确的有()A .若命题“x ∃∈R ,240x x m ++=”为假命题,则实数m 的取值范围是()4,+∞B .若,,a b c ∈R ,则“22ab cb >”的充要条件是“a c >”C .“1a >”是“11a<”的充分不必要条件D .当0x >时,2xx+的最小值为12.已知函数()223,2211,2x x x f x x x ⎧--+≥-=⎨--<-⎩若互不相等的实数123,,x x x 满足()()()123f x f x f x ==,则123x x x ++的值可以是()A .8-B .7-C .6-D .5-三、填空题13.已知71cos 85πα⎛⎫-=⎪⎝⎭,则cos 8πα⎛⎫+= ⎪⎝⎭________.14.函数()2lg 243y kx kx =--+的定义域为R ,则实数k 的取值范围是_______________.15.已知x >0,y >0,且x +2y =xy ,若不等式x +2y >m 2+2m 恒成立,则实数m 的取值范围为________.16.已知函数())22log 31xf x e =+++,[]6,6x ∈-,若()f x 的最大值为M ,最小值为m ,则M m +=______.四、解答题17.已知全集U =R ,集合{}2|120A x x x =--≤,{}|132B x a x a =-≤≤-.(1)当3a =时,求A B ⋂;(2)若A B A ⋃=,求实数a 的取值范围.18.已知函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭.(1)求()f x 的最小正周期和单调递减区间.(2)若0,2x π⎡⎤∈⎢⎣⎦,求()f x 的值域.19.已知函数()221x f x a =-+为奇函数,R a ∈.(1)求a 的值;(2)若()()2240f x x f x k -++--<恒成立,求实数k 的取值范围.20.漳州市某研学基地,因地制宜划出一片区域,打造成“生态水果特色区”.经调研发现:某水果树的单株产量W (单位:千克)与施用肥料x (单位:千克)满足如下关系:()2217,02()850251x x W x x x ⎧+≤≤⎪=⎨-<≤⎪-⎩,且单株施用肥料及其它成本总投入为2010x +元.已知这种水果的市场售价大约为10元/千克,且销路畅通供不应求.记该水果树的单株利润为()f x (单位:元).(1)求函数()f x 的解析式;(2)当施用肥料为多少千克时,该水果树的单株利润最大?最大利润是多少?21.已知函数()()()2110x g x a a -=++>的图象恒过定点A ,且点A 又在函数()()f x x a =+的图象上.(1)求实数a 的值并解不等式()f x a <;(2)函数()()22h x g x =+-的图象与直线2y b =有两个不同的交点时,求b 的取值范围.22.已知函数2()21f x ax x =-+.(Ⅰ)当34a =时,求()f x 在区间[1,2]上的值域;(Ⅱ)当12a ≤时,是否存在这样的实数a ,使方程2()log 04x f x -=在区间[1,2]内有且只有一个根?若存在,求出a 的取值范围;若不存在,请说明理由.参考答案:1.C【解析】根据交集的定义,找出集合M,N 的公共元素即可.【详解】因为集合{}{}1,0,1,2,13M N x x =-=≤≤,所以{}1,2M N = ,故选C.【点睛】本题考查集合的表示方法,交集的定义与运算,属于基础题.2.D【分析】由特称(存在)量词命题的否定是全称量词命题直接可得.【详解】由特称(存在)量词命题的否定是全称量词命题直接可得:命题:,21x p x x ∃∈≤+N 的否定为:,21x x x ∀∈>+N .故选:D 3.C【详解】由sin 0α>且tan 0α<,知α为二象限角,即2,2,2k k k Z παπππ⎛⎫∈++∈ ⎪⎝⎭.则,,242k k k Z αππππ⎛⎫∈++∈ ⎪⎝⎭,当k 为偶数时,2α的终边在第一象限;当k 为奇数时,2α的终边在第三象限.故选C.4.D【分析】根据f (x )=ax 3+bx -5,可得g (x )=f (x )+5=ax 3+bx 为奇函数,根据f (-7)=7,求出g (-7)的值,再根据奇函数的性质,求出g (7)的值,进而得到f (7)的值.【详解】令g (x )=f (x )+5=ax 3+bx ,∵g (-x )=a (-x )3+b (-x )=-ax 3-bx =-g (x ),∴g (x )为奇函数,∵f (-7)=7,∴g (-7)=f (-7)+5=12,又∵g (-7)=-g (7),∴g (7)=-12,又∵g (7)=f (7)+5,∴f (7)=-17,故选:D .5.D【分析】由指数函数的性质求得1a >,由对数函数的性质求得(0,1)b ∈,由三角函数的诱导公式,可得0c <,即可得到答案.【详解】由题意,根据指数函数的性质,可得0.20111((e ea ->==,由对数函数的性质,可得lg 2lg101b =<=且0b >,即(0,1)b ∈,由三角函数的诱导公式,可得6cos cos()cos 0555c ππππ==+=-<,所以c b a <<.故选:D.6.C【分析】分段函数在R 上单调递减,即:各段上都单调递减且分界点在左边解析式的函数值大于等于分界点在右边解析式的函数值.【详解】由题意,120120123121a a a a a-<⎧⎪<<⇒<≤⎨⎪-+≥⎩故选:C.7.C【分析】分01t <≤和1t >两种情况令14y ³,解不等式得到t 的范围即可得到杀虫剂的有效时间.【详解】由题图可知34,011,12t t t y t -<≤⎧⎪=⎨⎛⎫> ⎪⎪⎝⎭⎩,当01t <≤时,令14y ³,即144t ≥,解得1116t ≤≤;当1t >时,令14y ³,即31124t -⎛⎫⎪≥⎝⎭,解得15t <≤,所以投放该杀虫剂的有效时间为17951616-=小时.故选:C.8.D【分析】根据函数的解析式和,m n 的取值范围可求出mn =1,从而利用基本不等式即可求出2m +n 的取值范围.【详解】因为f (x )=|log 2x |,0<m <n 且f (m )=f (n ),所以22log log m n =,即22log log m n -=,所以mn =1.∴2m +n ≥2m =n ,即2m n =故2m +n 的取值范围为)⎡+∞⎣.故选:D .9.CD【分析】取0a b >>,可判断A 选项;利用对数函数的基本性质可判断B 选项;利用指数函数的单调性可判断C 选项;利用不等式的基本性质可判断D 选项.【详解】对于A ,若0a b >>,则11a b<,所以A 错误;对于B ,函数ln y x =的定义域为()0,∞+,而a 、b 不一定是正数,所以B 错误;对于C ,因为0a b ->,所以()20221a b ->,所以C 正确;对于D ,因为210c +>,所以()()2211a c b c +>+,所以D 正确.故选:CD 10.ABD【分析】逐个选项进行验证,结合正切型函数的性质进行判断可得.【详解】对于选项A ,,6x ππ⎛⎫∈ ⎪⎝⎭时,4,323x πππ⎛⎫+∈ ⎪⎝⎭,此时()tan 3f x x π⎛⎫=+ ⎪⎝⎭为增函数;对于选项B ,()tan 3f x x π⎛⎫=+ ⎪⎝⎭的最小正周期为T ωπ==π;对于选项C ,因为(0)()3f f π==,(0)(3f f π≠,所以图象不是关于直线6x π=成轴对称;对于选项D ,令32k x ππ+=,Z k ∈,得23k x ππ=-,令1k =得6x π=,所以图象关于点,06π⎛⎫⎪⎝⎭成中心对称.故选:ABD.【点睛】本题主要考查正切型函数的性质,熟记性质的求解方法是解决本题的关键.侧重考查逻辑推理的核心素养.11.ACD【分析】转化为x ∀∈R ,240x x m ++≠,计算2440m ∆=-<,可得出m 的范围,即可判断A 项;根据不等式的性质,可判断B 项;求出11a<的等价条件为1a >或a<0,即可判断C 项;根据基本不等式,即可判断D 项.【详解】对于A 项,等价于x ∀∈R ,240x x m ++≠,则2440m ∆=-<,解得4m >,故A 项正确;对于B 项,因为22ab cb >,显然20b >,210b>,所以a c >;因为a c >,若0b =,则22ab cb =,故B 项不正确;对于C 项,111a a a--=,所以11a <等价于10a a -<,即()10a a ->,所以1a >或a<0.显然“1a >”是“1a >或a<0”的充分不必要条件,故C 项正确;对于D 项,当0x >时,2xx+≥2x x=,即x D 项正确.故选:ACD.12.CD【分析】首先根据题意画出函数的图象,得到230x x +=,1(7,3]x ∈--,即可得到答案.【详解】函数()223,2211,2x x x f x x x ⎧--+≥-=⎨--<-⎩的图象图所示:设123x x x <<,因为()()()123f x f x f x ==,所以230x x +=,当2113x --=时,7x =-,2115x --=-时,3x =-,所以1(7,3]x ∈--,即1231(7,3]x x x x ++=∈--.故选:CD13.15-【分析】观察出788ππααπ⎛⎫⎛⎫++-= ⎪⎪⎝⎭⎝⎭,然后利用诱导公式求解即可.【详解】因为71cos 85πα⎛⎫-=⎪⎝⎭,所以771cos cos cos 8885πππαπαα⎡⎤⎛⎫⎛⎫⎛⎫+=--=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦.故答案为:15-【点睛】本题考查的是三角函数的诱导公式,较简单.14.3,02⎛⎤- ⎥⎝⎦【分析】根据题意,将问题转化为22430kx kx --+>恒成立问题,结合二次函数的性质即可得解.【详解】由题意可知,22430kx kx --+>恒成立,当0k =时,30>恒成立,当0k ≠时,20Δ16240k k k <⎧⎨=+<⎩,解得302k -<<,综上:302k -<≤,故k 的取值范围为3,02⎛⎤- ⎥⎝⎦.故答案为:3,02⎛⎤- ⎥⎝⎦.15.()4,2-.【分析】利用基本不等式求出x +2y 的最小值,进而得出m 的范围.【详解】∵x >0,y >0,x +2y =xy ,∴21x y+=1,∴2142(2)()4428x y x y x y x y y x +=++=++≥+,当且仅当4x yy x=,即4,2x y ==时等号成立,∴2x y +的最小值为8,由228m m +<解得42m -<<,∴实数m 的取值范围是()4,2-故答案为:()4,2-.16.8【分析】先对()f x 变形得())21log 41xxe f x e -=+++,再构造函数)21()log 1xxe g x x e -=++,判断()g x 为奇函数,从而由奇函数的性质可得答案【详解】由题意可得()))2221log 3log 411xx xe f x e e -=++=++++,令)21()log 1xxe g x e-=++,则()()4f x g x =+,[]6,6x ∈-因为)21()log 1xxe g x e ----=++21log +1x xe e -=121log )1xxe e --=-+21[log )]()1xxe g x e -=-+=-+所以)21()log 1xxe g x e ----=++为奇函数,所以()g x 在[6,6]-最大值与最小值之和为0,所以8M m +=.故答案为:8【点睛】关键点点睛:此题考查函数奇偶性的应用,解决本题的关键是将函数()f x 变形,得到())21log 41xxe f x e -=+++后,判断函数)21()log 1xxe g x x e -=++为奇函数,考查计算能力,属于中档题17.(1){}|24A B x x =≤≤ (2)(],2-∞【分析】(1)先解二次不等式化简集合A ,再根据集合的交集运算即可求得答案;(2)根据题意得到B A ⊆,分类讨论B =∅和B ≠∅两种情况,列出关于a 的不等式组,解之即可.【详解】(1)由2120x x --≤可得34x -≤≤,所以{|34}A x x =-≤≤,又当3a =时,{|27}B x x =≤≤,所以{|24}A B x x ⋂=≤≤.(2)因为A B A ⋃=,所以B A ⊆,当B =∅时,321a a -<-,可得12a <;当B ≠∅时,32113324a a a a -≥-⎧⎪-≥-⎨⎪-≤⎩,可得122a ≤≤;综上:2a ≤,即a 的取值范围为(],2-∞.18.(1)T π=;37,88k k ππππ⎡⎤++⎢⎥⎣⎦,k ∈Z .(2)⎡⎤⎣⎦【解析】(1)由2T πω=得到最小正周期,由3222242k x k πππππ+≤-≤+,k ∈Z ,得到()f x 的单调递减区间;(2)由0,2x π⎡⎤∈⎢⎣⎦得到32444x πππ-≤-≤,从而得到()f x 的值域.【详解】(1)函数()2sin 24f x x π⎛⎫=- ⎪⎝⎭,最小正周期为22T ππ==,由3222242k x k πππππ+≤-≤+,k ∈Z ,得37()88k x k k Z ππππ+≤≤+∈,k ∈Z ,所以()f x 的单调递减区间为37,88k k ππππ⎡⎤++⎢⎥⎣⎦,k ∈Z .(2)因为0,2x π⎡⎤∈⎢⎣⎦,所以32444x πππ-≤-≤,所以sin 214x π⎛⎫-≤ ⎪⎝⎭,()2sin 24f x x π⎛⎫⎡⎤=-∈ ⎪⎣⎦⎝⎭,即()f x的值域为⎡⎤⎣⎦.【点睛】本题考查求正弦型函数的周期,单调区间和值域,属于简单题.19.(1)1a =(2)()2,+∞【分析】(1)根据()00f =得1a =,再检验即可;(2)先证明函数()f x 在R 上是增函数,再根据奇偶性得224x x k -+<恒成立,再结合二次函数性质求解即可.【详解】(1)解:∵函数()f x 是定义在R 上的奇函数,∴()00f =,即02021a -=+,解得1a =;∴()22112121x x x f x -=-=++,∴()()21221112x xx x f x f x ----===-++-,满足奇函数定义,∴1a =(2)解:设12,x x 是R 上的任意两个值,且12x x <,∴()()121222112121⎛⎫⎛⎫-=--- ⎪ ⎪++⎝⎭⎝⎭x x f x f x ()()()1221122222221212121x x x x x x -=-=++++,∵12x x <,∴1222x x <,1211x +>,2211x +>,12220x x -<,∴()()120f x f x -<,即()()12f x f x <,∴()f x 在R 上是增函数;∵()()2240f x x f x k -++--<∴()()224f x x f x k -+<---,∵()f x 为奇函数,∴()()224f x x f x k -+<+,∵()f x 为R 上单调递增函数,∴224x x x k -+<+,即224x x k -+<恒成立,∴()2max 24x x k -+<,∵()2224212x x x -+=--+,∴当1x =时,224x x -+取得最大值为2,∴2k >,即实数k 的取值范围为()2,+∞.20.(1)22020330,02()8049020,251x x x f x x x x ⎧-+≤≤⎪=⎨--<≤⎪-⎩;(2)3千克,最大利润是390元.【解析】(1)根据题意可以直接得到利润表达式;(2)根据定义域求每段函数的利润最大值比较后可得答案.【详解】(1)由已知()()10()2010f x W x x =-+,∴()22017(2010),02()80500(2010),251x x x f x x x x ⎧+-+≤≤⎪=⎨--+<≤⎪-⎩,∴22020330,02()8049020,251x x x f x x x x ⎧-+≤≤⎪=⎨--<≤⎪-⎩.(2)由(1)得当02x ≤≤时,221()2020330203252f x x x x ⎛⎫=-+=-+ ⎪⎝⎭,∴当02x ≤≤时,()()2370f x f ≤=;当25x <≤时,8080()4902049020(1)2011f x x x x x ⎡⎤=--=-+-+⎢⎥--⎣⎦8047020(1)1x x ⎡⎤=-+-⎢⎥-⎣⎦470390≤-=,当且仅当()802011x x =--时,即3x =时等号成立,∵370390<,∴当3x =时,max ()390f x =,即当施用肥料为3千克时,该水果树的单株利润最大,最大利润是390元.【点睛】易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件:(1)“一正二定三相等”“一正”就是各项必须为正数;(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.21.(1)1a =,不等式的解集为()1,0-(2)10,2⎛⎫ ⎪⎝⎭【分析】(1)由指数函数的性质可求得定点,再将定点代入())f x x a =+即可求得a ,再解不等式()f x a <即可求得结果.(2)由(1)求得()g x ,再求得()h x 的解析式,画出图像,由图像可得b 的取值范围.【详解】(1)函数()g x 的图象恒过定点A ,当20x -=时,即2,2x y ==,∴A 点的坐标为()2,2,又A 点在()f x 上,∴()()222f a =+=,解得1a =,()f x a <,∴()10x +<=,∴011x <+<,∴10x -<<,∴不等式的解集为()1,0-;(2)由(1)知()()221x g x g x -==+,∴()()22212x h x g x b =+-=-=,分别画出()y h x =与2y b =的图象,如图所示:由图象可知:021b <<,故b 的取值范围为10,2⎛⎫ ⎪⎝⎭.22.(Ⅰ)1,03⎡⎤-⎢⎥⎣⎦;(Ⅱ)存在,102a <≤.【解析】(Ⅰ)先把34a =代入解析式,再求对称轴,进而得到函数的单调性,即可求出值域;(Ⅱ)函数2()log 4x y f x =-在区间[]1,2内有且只有一个零点,转化为函数2()log h x x =和2()23g x ax x =-+的图象在[]1,2内有唯一交点,根据()g x 中a 是否为零,分类讨论,结合函数的性质,即可求解.【详解】(Ⅰ)当34a =时,23()214f x x x =-+,对称轴为:43x =,所以函数()f x 在区间41,3⎡⎤⎢⎥⎣⎦单调递减,在区间4,23⎛⎤ ⎥⎝⎦单调递增;则()()()min max 41,2033f x f f x f ⎛⎫==-== ⎪⎝⎭,所以()f x 在区间[1,2]上的值域为1,03⎡⎤-⎢⎥⎣⎦;(Ⅱ)由222()log 23log 4x y f x ax x x =-=-+-,令0y =,可得2223log 0ax x x -+-=,即2223log ax x x -+=,令2()23g x ax x =-+,2()log h x x =,[]1,2x ∈,函数2()log 4x y f x =-在区间[]1,2内有且只有一个零点,等价于两个函数()g x 与()h x 的图象在[]1,2内有唯一交点;①当0a =时,()23g x x =-+在[]1,2上递减,2()log h x x =在[]1,2上递增,而()()()()1101,2112g h g h =>==-<=,所以函数()g x 与()h x 的图象在[]1,2内有唯一交点.②当a<0时,()g x 图象开口向下,对称轴为10x a=<,()g x 在[]1,2上递减,2()log h x x =在[]1,2上递增,()g x 与()h x 的图象在[]1,2内有唯一交点,当且仅当(1)(1)(2)(2)g h g h ≥⎧⎨≤⎩,即10411a a +≥⎧⎨-≤⎩,解得112a -≤≤,所以10a -≤<.③当102a <≤时,()g x 图象开口向上,对称轴为12x a =≥,()g x 在[]1,2上递减,2()log h x x =在[]1,2上递增,()g x 与()h x 的图象在[]1,2内有唯一交点,(1)(1)(2)(2)g h g h ≥⎧⎨≤⎩,即10411a a +≥⎧⎨-≤⎩,解得112a -≤≤,所以102a <≤.综上,存在实数11,2a ⎡⎤∈-⎢⎥⎣⎦,使函数2()log 4x y f x =-于在区间[]1,2内有且只有一个点.【点睛】关键点睛:本题主要考查了求一元二次函数的值域问题,以及函数与方程的综合应用,其中解答中把函数的零点问题转化为两个函数图象的交点个数问题,结合函数的性质求解是解答的关键,着重考查转化思想,以及推理与运算能力.。
2022-2023学年湖南省株洲二中高一数学第一学期期末考试试题含解析

当 时, , 或 ,
∴ 或 ;
【小问2详解】
由 是 的充分条件,知: ,
∴ ,解得 ,
∴ 的取值范围为 .
21、(1) , ;
(2)
【解析】(1)解一元一次不等式求集合A,再应用集合的交并补运算求 及 .
(2)由集合的包含关系可得 ,结合已知即可得 的取值范围
【小问1详解】
由 得: ,所以 ,则 ,
参考答案
一、选择题(本大题共12 小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将正确答案涂在答题卡上.)
1、A
【解析】解绝对值不等式求解集,根据充分、必要性的定义判断题设条件间的充分、必要关系.
【详解】由 ,可得 ,
∴“ ”是“ ”的充分而不必要条件.
故选:A.
13.已知集合 ,则 的元素个数为___________.
14.已知 则 _______.
15.函数 函数的定义域为________________
16.已知平面 和直线 ,给出条件:
① ;② ;③ ;④ ;⑤
(1)当满足条件_________时,有 ;
(2)当满足条件________时,有 .(填所选条件的序号)
同理方程 的两个解 也要关于直线 对称,同理
从而可得若关于 的方程 有一个正根,则方程 有两个不同的实数根;
若关于 的方程 有两个正根,则方程 有四个不同的实数根
综合以上情况可得,关于 的方程的解集不可能是 .选D
非选择题
二、选择题(本大题共4小题,每小题5分,共20分,将答案写在答题卡上.)
13、5
,则 ,
,所以 .
19、(1)1(2)
(3)答案见解析
湖南省双峰县第一中学、湘潭县一中2022-2023学年高一数学第一学期期末统考模拟试题含解析
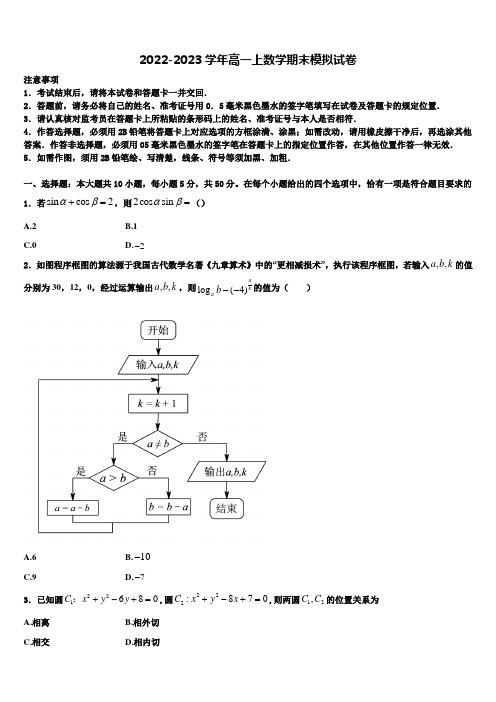
16.若函数
f
x
log 1 2
x, x
0
,则
f
f
2
______
2x , x 0
三、解答题:本大题共 5 小题,共 70 分。解答时应写出文字说明、证明过程或演算步骤。 17.素有“天府之国”美称的四川省成都市,属于亚热带季风性湿润气候.据成都市气象局多年的统计资料显示,成都市
从 1 月份到 12 月份的平均温 (℃)与月份数 (月)近似满足函数
19. (1)试证明差角的余弦公式 C( ) : cos( ) cos cos sin sin ;
(2)利用公式 C( ) 推导:
①和角的余弦公式 C( ) ,正弦公式 S( ) ,正切公式 T( ) ;
②倍角公式 S(2 ) , C(2 ) , T(2 ) .
20.在①两个相邻对称中心的距离为 π ,②两条相邻对称轴的距离为 ,③两个相邻最高点的距离为 ,这三个条件
考点:平面向量的几何运算
5、B
【解析】因为函数
f
x
sin
x 2
6
的最小正周期是
T
2 1 2
4
,故先排除选项 D;又对于选项 C:
f
3
sin
2
3
6
1,对于选项
A:
f
3
sin
2
3
3
1 ,故
A、C
均被排除,应选
B.
6、C
【解析】判断 a, b, c 与 0,1 大小关系,即可得到答案.
【解析】 详解】 f f 10 f lg10 f 1 lg1 0
故选 B 10、B 【解析】根据集合交集定义求解. 【详解】 P Q (1, 4) (2,3) (2,3) 故选:B 【点睛】本题考查交集概念,考查基本分析求解能力,属基础题.
湖南省湘西州2021-2022学年高一上学期期末数学试题含解析

所以 的定义域为 ,关于原点对称.
又因为 ,
所以函数 是奇函数.
因为 在 上单调递增, 在 上单调递减,
所以函数 在 上单调递增.
(2)对任意 ,存在 ,使得不等式 成立,
等价于 ,
由(1)知 在 上单调递增,则 在 上单调递增,
,
函数 的对称轴为 ,
当 时, ,则 ,
(2)利用平移变换,得到 ,再令 求解;
【小问1详解】
解:数据补充完整如下表:
0
0
5
0
-5
0
函数f(x)的解析式为; .
【小问2详解】
将 图象上所有点向左平移 个单位长度,
得到
由 ,可解得:
当 时,可得:
从而可得离原点O最近的对称中心为:
18.已知函数 .
(1)当 时,求关于 的不等式 的解集;
(2)求关于 的不等式 的解集;
对于选项D,指数式 化为对数式为 ,故D正确.
故选:ACD.
9.已知实数 , 满足等式 ,下列式子可以成立的是()
A. B. C. D.
【答案】ABD
【解析】
【分析】分别画出 , 的图象,结合图象即可判断
【详解】分别画出 , 的图象,如示意图:
实数 , 满足等式 ,
可得: ,或 ,或 .
故选:ABD.
17.某同学将“五点法”画函数 在某一个时期内的图象时,列表并填入部分数据,如下表:
(1)请将上述数据补充完整,填写在答题卡上相应位置,并直接写出函数 的解析式;
(2)将 图象上所有点向左平移 个单位长度,得到 图象,求 的图象离原点O最近的对称中心.
【答案】(1)表格见解析,
2022-2023学年湖南省湘潭市高一上学期期末数学试题(解析版)

2022-2023学年湖南省湘潭市高一上学期期末数学试题一、单选题1.已知命题:N,e e x p x x ∃∈≤,则命题p 的否定为( ) A .N,e >e x x x ∃∈ B .N,e e x x x ∃∈≥ C .N,e e x x x ∀∈≤ D .N,e e x x x ∀∈>【答案】D【分析】根据全称命题与特称命题之间的关系即可得出结果.【详解】因为特称命题的否定是全称命题,所以命题p 的否定为N,e e x x x ∀∈>. 故选:D.2.若集合{1,4,7}A =-,{1,3,7,9}B =-,则A B =( ) A .{1,7}- B .{1,3}- C .{1,3,7}- D .{1,3,4,7,9}-【答案】A【分析】利用集合交集的定义求解即可.【详解】因为集合{1,4,7}A =-,{1,3,7,9}B =-, 所以{1,7}A B ⋂=-, 故选:A3.下列函数为增函数的是( ) A .()31log f x x= B .()3f x x =C .()sin f x x =D .()23xf x ⎛⎫= ⎪⎝⎭【答案】B【分析】根据函数的单调性逐项判断即可.【详解】函数()31log f x x =与()23xf x ⎛⎫= ⎪⎝⎭在定义域内为减函数,不符合题意;函数()sin f x x =在π3π22⎛⎫⎪⎝⎭,上为减函数,不符合题意;根据幂函数的性质知()3f x x =为增函数.故选:B.4.若角α是第一象限角,则2α是( ) A .第一象限角 B .第二象限角 C .第一或第三象限角 D .第二或第四象限角【答案】C【分析】根据题意得18018045,2k k k Z α︒⋅<<⋅+∈,分k 为偶数和奇数求解即可.【详解】因为α是第三象限角,所以36036090,k k k Z α⋅<<⋅+∈, 所以18018045,2k k k Z α︒⋅<<⋅+∈,当k 为偶数时,2α是第一象限角, 当k 为奇数时,2α是第三象限角.故选:C . 5.函数()22111x f x x +=-+的部分图像大致为( )A .B .C .D .【答案】A【分析】利用奇偶性和特殊点排除不符合的选项. 【详解】函数()22111x f x x +=-+的定义域为R ,()()()2221211111x x f x f x x x -+-+-=-=-=+-+,因此()f x 是R 上的偶函数,其图象关于y 轴对称,选项C ,D 不满足; 又()1102f =>,所以选项B 不满足,选项A 符合题意. 故选:A6.设0.2.3203,0.3,log 2a b c ===,则( ) A .b a c >> B .a b c >> C .a c b >> D .b c a >>【答案】B【分析】根据指数和对数函数的单调性即可求解. 【详解】因为0.20200.30.3331,00.30.31,log 2log 10a b c =>=<=<==<=,所以a b c >>.故选:B7.从盛有1L 纯酒精的容器中倒出2L 3,然后用水填满;再倒出2L 3,又用水填满;…;连续进行n 次,容器中的纯酒精少于0.01L ,则n 的最小值为( ) A .5 B .6C .7D .8【答案】A【分析】利用指数的运算性质求解即可.【详解】由题意可得21110.0133100n n⎛⎫⎛⎫-=<= ⎪ ⎪⎝⎭⎝⎭,*Z n ∈,因为45111111,3811003213100⎛⎫⎛⎫=>=< ⎪ ⎪⎝⎭⎝⎭,所以5n ≥,故选:A8.已知π3sin 54α⎛⎫-= ⎪⎝⎭,则πsin 210α⎛⎫+= ⎪⎝⎭( )A .716-B .716C .18-D .18【答案】C【分析】利用换元法和二倍角公式求解即可.【详解】令π5t α=-,所以3sin 4t =,π5t α=+,所以2ππ1sin(2)sin(2)cos 212sin 1028t t t α+=+==-=-. 故选:C .二、多选题9.下列等式正确的是( )A .1sin15cos154︒︒=B.22sin 22.51︒-=C.sin 26cos34cos26sin 34︒︒+︒︒= D .tan 71tan 2611tan 71tan 26︒-=+︒︒︒【答案】ACD【分析】利用二倍角公式和两角和差公式求解即可. 【详解】11sin15cos15sin 3024︒︒=︒=,A 正确;22sin 22.51cos 452︒-=-︒=-,B 错误; ()sin 26cos34cos 26sin 34sin 2634sin 60︒︒+︒︒=︒+︒=︒=,C 正确; ()tan 71tan 26tan 7126tan 4511tan 71tan 26︒-︒=︒-︒=︒=+︒︒,D 正确;故选:ACD10.下列命题正确的是( ) A .若0a b >>,0m >,则a b m m> B .若1a b <<,则33a b >C .若0x >且1x ≠,则1ln 2ln x x +≥ D .若正数a ,b 满足2a b +=,则112a b+≥【答案】AD【分析】由不等式的性质和基本不等式的运用,逐个判断选项. 【详解】由不等式的性质可知,A 正确,B 错误; 当()0,1x ∈时,1ln 0ln x x+<,C 错误; 正数a ,b 满足2a b +=,则()1111222221121b a a b a b a b a b ⎛⎫⎛⎫⎛⎫+=++=++≥= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭, 当且仅当1a b ==时,等号成立,D 正确. 故选:AD.11.已知α是第三象限角,且2tan211tan2aα=-,则( )A .tan 1α= B.sin α= C .4sin 25α=D .π1tan 43α⎛⎫-=- ⎪⎝⎭【答案】BC【分析】利用正切的二倍角公式判断A ,利用同角三角函数关系判断B ,利用正弦的二倍角公式判断C ,利用正切的两角差公式判断D.【详解】由题意得22tan2tan 21tan 2ααα==-,A 错误;又α是第三象限角,sin 0α<,所以由22sin cos 1sin tan 2cos ααααα⎧+=⎪⎨==⎪⎩解得sin α=,cos α=,B 正确;4sin 22sin cos 5ααα==,C 正确;πtan 11tan 41tan 3ααα-⎛⎫-== ⎪+⎝⎭,D 错误;故选:BC12.高斯是德国的天才数学家,享有“数学王子”的美誉,以“高斯”命名的概念、定理、公式很多,如高斯函数[]y x =,其中不超过实数x 的最大整数称为x 的整数部分,记作[]x .如[]20222022=,[]1.71=,[]1.52-=-,记函数()[]f x x x =-,则( )A .()2.90.9f -=B .()f x 的值域为[)0,1C .()f x 在[]0,5上有5个零点D .a ∀∈R ,方程()f x x a +=有两个实根【答案】BD【分析】根据高斯函数的定义,结合特殊点的函数值、值域、零点、方程的根、函数图象等知识对选项进行分析,从而确定正确答案.【详解】()[]()2.9 2.9 2.9 2.930.1f -=---=---=,选项A 错误; 当10x -≤<时,[]1x =-,()[]1f x x x x =-=+ 当01x ≤<时,[]0x =,()[]f x x x x =-=; 当12x ≤<时,[]1x =,()[]1f x x x x =-=-……以此类推,可得()[]f x x x =-的图象如下图所示,由图可知,()f x 的值域为[)0,1,选项B 正确; 由图可知,()f x 在[]0,5上有6个零点,选项C 错误;a ∀∈R ,函数()y f x =与y a x =-的图象有两个交点,如下图所示, 即方程()f x x a +=有两个根,选项D 正确.故选:BD三、填空题13.“数摺聚清风,一捻生秋意”是宋代朱翌描写折扇的诗句,折扇出入怀袖,扇面书画,扇骨雕琢,是文人雅士的宠物,所以又有“怀袖雅物”的别号.如图,这是折扇的示意图,已知D 为OA 的中点,4OA =,3π4AOB ∠=,则此扇面(扇环ABCD )部分的面积是__________.【答案】9π2【分析】利用扇形的面积公式可求得扇环的面积.【详解】()2213π9π42242ABCD AOB DOC S S S =-=⨯⨯-=扇环扇形扇形. 故答案为:9π2. 14.若函数()()cos 2f x x ϕ=+的图象关于点π,04⎛⎫⎪⎝⎭对称,请写出一个ϕ的值:ϕ=______.【答案】π8(答案不唯一,符合ππ82k +,Z k ∈即可) 【分析】将2x ϕ+看作一个整体,利用余弦函数的图象和性质求解即可. 【详解】由题意可知ππ2π42k ϕ+=+,Z k ∈, 解得ππ82k ϕ=+,Z k ∈, 故答案为:π8(答案不唯一,符合ππ82k +,Z k ∈即可) 15.已知()sin cos 2sin cos f αααα+=,则πcos 4f ⎛⎫= ⎪⎝⎭__________.【答案】12-##0.5-【分析】利用同角三角函数的关系,求出函数解析式,再代入求值. 【详解】已知()sin cos 2sin cos f αααα+=, 因为()2sin cos 12sin cos αααα+=+,所以令sin cos t αα=+,则()21f t t =-,则π11cos 1422f f ⎛⎫==-=- ⎪⎝⎭⎝⎭. 故答案为:12-16.已知0a >,函数2,0()πsin ,02π5ax a x f x ax x -+-<⎧⎪=⎨⎛⎫+≤≤ ⎪⎪⎝⎭⎩,已知()f x 有且仅有5个零点,则a 的取值范围为__________.【答案】191229,2,10510⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【分析】当2a ≥时,()f x 在(,0)-∞上无零点,所以()f x 在[0,2π]上有且仅有5个零点;当2a <时,()f x 在(,0)-∞上恰有一个零点,所以()f x 在[0,2π]上有且仅有4个零点,利用正弦函数的图象列式可求出结果.【详解】当0x <时,()2f x ax a =-+-,令()0f x =,得21x a=-, 若210a-≥,即2a ≥时,()f x 在(,0)-∞上无零点,所以()f x 在[0,2π]上有且仅有5个零点, 当[0,2π]x ∈时,πππ,2π555ax a ⎡⎤+∈+⎢⎥⎣⎦,所以π5π2π6π5a ≤+<,即1229510a ≤<. 若210a-<,即2a <时,()f x 在(,0)-∞上恰有一个零点,所以()f x 在[0,2π]上有且仅有4个零点,所以π4π2π5π5a ≤+<,即191255a ≤<, 又2a <,所以1925a ≤<. 综上所述:a 的取值范围为191229,2,10510⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭.故答案为:191229,2,10510⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭.四、解答题17.若角α终边上一点P 的坐标为()3,4m m ,其中0m ≠. (1)求tan α的值;(2)若π0,2α⎛⎫∈ ⎪⎝⎭,求πsin 3α⎛⎫+ ⎪⎝⎭的值.【答案】(1)4tan 3α=【分析】(1)利用三角函数的定义求解即可;(2)利用三角函数的定义和正弦的两角和公式求解即可.【详解】(1)因为角α终边上一点P 的坐标为()3,4m m ,且0m ≠, 所以由三角函数的定义可得44tan 33m m α==. (2)因为π0,2α⎛⎫∈ ⎪⎝⎭,所以40,sin 5m α>==,3cos 5α==,所以πππsin sin cos cos sin 333ααα⎛⎫-=+=⎪⎝⎭.18.设全集U =R ,集合{}212200,{ln 2ln3},{25}M x x x N x x P x a x a =-+≤=<=<<+∣∣∣. (1)求(),UMN MN ;(2)若P N ⊆,求a 的取值范围. 【答案】(1){010}MN x x =<≤∣,(){}910UMN x x =≤≤∣(2)][)0,45,∞⎡⋃+⎣【分析】(1)由对数函数的单调性、一元二次不等式的解法化简集合,M N ,再由集合的运算求解即可;(2)讨论P =∅、P ≠∅两种情况,根据包含关系求得a 的取值范围.【详解】(1)由{}212200M xx x =-+≤∣,得{}210M x x =≤≤∣, 由{ln 2ln3}N xx =<∣,得{09}N x x =<<∣,所以{010}M N x x =<≤∣.由{09}N xx =<<∣得{0UN x x =≤∣或9}x ≥,所以(){}910UMN x x =≤≤∣.(2)当P =∅时,25a a ≥+,即5a ≥,符合题意,当P ≠∅时,255920a a a a <+⎧⎪+≤⎨⎪≥⎩,解得04a ≤≤,符合题意.综上,a 的取值范围为][)0,45,∞⎡⋃+⎣.19.已知幂函数()()2211m f x m x -=-⋅在()0,∞+上单调递增.(1)求m 的值; (2)若()20,22f x ax x x∀>≥-,求a 的取值范围. 【答案】(1)2m = (2)[)2,+∞【分析】(1)根据幂函数的性质和概念求解即可;(2)不等式可转化为224a x x ≥-+对0x >恒成立,利用一元二次函数的图象和性质求224x x -+的最大值即可.【详解】(1)因为()()2211m f x m x -=-⋅是幂函数,且在()0,∞+上单调递增,所以()211210m m ⎧-=⎪⎨->⎪⎩,解得2m =.(2)由(1)得()3f x x =,所以0,22a x x x∀>>-, 即224a x x ≥-+对0x >恒成立, 由一元二次函数的图象和性质可得当4122x 时,224x x -+有最大值2,所以2a ≥,即a 的取值范围为[)2,+∞. 20.已知函数()()()22log 4log 2f x x x =---. (1)求()f x 的定义域; (2)求()f x 的值域. 【答案】(1)()4,+∞ (2)(),0∞-【分析】(1)根据对数函数的定义域,列出不等式,解出即可.(2)运用对数运算性质将()f x 化简为22log 12x ⎛⎫- ⎪-⎝⎭,根据(1)中的定义域求得212x --的范围,再根据2log y x =的单调性即可求得()f x 值域.【详解】(1)因为()()()22log 4log 2f x x x =---,所以4020x x ->⎧⎨->⎩,解得4x >, 所以()f x 的定义域为()4,+∞.(2)因为()()()22log 4log 2f x x x =--- 2224222log log log 1222x x x x x ---⎛⎫===- ⎪---⎝⎭, 由(1)知()f x 的定义域为()4,+∞, 所以22x ->,2012x <<-,20112x <-<-, 因为2log y x =是增函数,所以()2log 10f x <=,故()f x 的值域为(),0∞-.21.已知函数2()2ln (1)2n f x x x =+-+. (1)证明:当1n =时,()f x 在(1,e)上有零点.(2)当2n =时,关于x 的方程()f x m =在[1,2]上没有实数解,求m 的取值范围. 【答案】(1)证明见解析 (2)(,3)(62ln2,)-∞++∞【分析】(1)根据零点存在性定理即可计算端点处的函数值进行求证,(2)根据函数的单调性求解()f x 在[1,2]x ∈上的值域,进而根据()min,m f x <⎡⎤⎣⎦ 或()max,m f x >⎡⎤⎣⎦即可求解.【详解】(1)当1n =时,2()2ln 2f x x x =-+, 因为2(1)10,(e)4e 0f f =>=-<,所以(1)(e)0f f <, 因此()f x 在(1,e)上有零点.(2)当2n =时,2()2ln 2f x x x =++,由于2ln ,y x y x ==均为[1,2]x ∈上的单调递增函数,故()f x 在[1,2]x ∈上单调递增.又(1)3,(2)62ln2f f ==+,故()f x 在[1,2]x ∈上的值域为[]3,62ln 2+,且关于x 的方程()f x m =在[1,2]上没有实数解,故()min m f x <⎡⎤⎣⎦ 或()max m f x >⎡⎤⎣⎦,即3m <或62ln 2m >+所以m 的取值范围为(,3)(62ln2,)-∞++∞.22.已知函数()()πsin 0,0,2f x A x A ωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示.(1)求函数()y f x =的解析式;(2)将()y f x =的图像上所有点的横坐标缩短到原来的12,纵坐标不变,再向右平移π6个单位长度得到()y g x =的图像,求函数()g x 的单调递增区间;(3)在第(2)问的前提下,对于任意1ππ,33x ⎡⎤∈-⎢⎥⎣⎦,是否总存在实数2ππ,66x ⎡⎤∈-⎢⎥⎣⎦,使得()()12f x g x m+=成立若存在,求出实数m 的值或取值范围;若不存在,说明理由. 【答案】(1)()πsin 23f x x ⎛⎫=+ ⎪⎝⎭(2)()ππ5ππ,242242k k k ⎡⎤-++∈⎢⎥⎣⎦Z (3)存在,0m =【分析】(1)由题知1A =,7ππ4123T =-,求出T 从而得ω的值,将特殊点代入函数中求出ϕ,即可解决问题;(2)根据函数伸缩变换与平移变换后的到新函数的解析式,根据函数解析式求解单调区间即可; (3)假设存在实数m 的值或取值范围满足题意,根据所给条件先由()()12f x g x m +=,得()()21g x m f x =-,再根据所给的角把()()21,g x m f x -范围求出来,根据范围的包含关系列出不等式解出即可.【详解】(1)由图可知1A =,7πππ41234T =-=,则2ππT ω==,2ω=, 所以()()sin 2f x x ϕ=+,77sin 126ππ1f ϕ⎛⎫⎛⎫=+=- ⎪⎪⎝⎭⎝⎭. 所以7π2π(Z)π62k k ϕ+=-+∈,即5π2π(Z)3k k ϕ=-+∈ 又π2ϕ<,所以当1k =时,π3ϕ=,所以()πsin 23f x x ⎛⎫=+ ⎪⎝⎭.(2)将()y f x =的图像上所有点的横坐标缩短到原来的12,纵坐标不变, 得:πsin 43y x ⎛⎫=+ ⎪⎝⎭,再向右平移π6个单位长度得到:()πππsin 4sin 4633g x x x ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,由πππ2π42π232k x k -+≤-≤+,k ∈Z ,解得ππ5ππ242242k k x -+≤≤+,k ∈Z ,所以函数()g x 的单调递增区间为()ππ5ππ,242242k k k ⎡⎤-++∈⎢⎥⎣⎦Z(3)由()()12f x g x m +=,得()()21g x m f x =-, 由1ππ33x -≤≤,得1ππ2π33x -≤+≤,所以1sin 213x π⎛⎫≤+≤ ⎪⎝⎭, 所以()11,m f x m m ⎡-∈-⎢⎣⎦. 又2ππ66x -≤≤,得2πππ433x -≤-≤,所以2π1sin 43x ⎛⎫-≤-≤⎪⎝⎭.由题可知1,m m ⎡⎡-⊆-⎢⎢⎣⎦⎣⎦,得11m m -≥-⎧⎪⎨≤⎪⎩解得0m =, 所以存在0m =,使得()()12f x g x m +=成立.。
2022-2023学年湖南省衡阳市雁峰区名校高一年级上册学期期末考试数学试卷【含答案】

衡阳市雁峰区名校2022-2023学年高一上学期期末考试数 学考试时间:120分钟 试卷满分:150分一、单选题(本大题共8小题,每小题5分,共40分. 在每小题给出的四个选项中,只有一项是符合题目要求的)1.与角终边相同的角是()20-︒A .B .C .D .300-︒280-︒320︒340︒2.不等式的解集是()2320x x --≥A .B .C .D .213x x ⎧⎫-≤≤⎨⎬⎩⎭213x x ⎧⎫-≤≤⎨⎬⎩⎭213x x x ⎧⎫≤-≥⎨⎬⎩⎭或213x x x ⎧⎫≤-≥⎨⎬⎩⎭或3.“”是“”的()1x >11x <A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件4.函数的零点所在的一个区间是()()152xf x x ⎛⎫=-- ⎪⎝⎭A .B .C .D .()3,2--()2,1--()1,0-()0,15.已知指数函数,将函数的图象上的每个点的横坐标不变,纵坐标扩大()xf x a =()f x 为原来的倍,得到函数的图象,再将的图象向右平移个单位长度,所得图象()g x ()g x 2恰好与函数的图象重合,则a 的值是()()f xA .B .CD .32236.函数(,)的部分图象如图所示,则 ()()()2sin f x x ωϕ=+0ω>2πϕ<()f π=A .B .CD 7.已知函数在上单调递减,则实数的取值范围1()ax f x x a -=-(2,)+∞a 是()A .,,B .(-∞1)(1-⋃)∞+(1,1)-C .,,D .,,(-∞1)(1-⋃2](-∞1)(1-⋃2)8.已知,,,则a ,b ,c 的大小关系为()2022a=2223b =c a b =A .B .C .D .c a b >>b a c >>a c b >>a b c>>二、多选题(本大题共4小题,每小题5分,共20分.全部选对的得5分,部分选对的得2分,有选错的得0分)9.下列说法中正确的是( )A .若a >b ,则B .若-2<a <3,1<b <2,则-3<a -b <12211a bc c >++C .若a >b >0,m >0,则D .若a >b ,c >d ,则ac >bd m m a b <10.下列各式中,值为的是( )12A .B .C .D5πsin62sin 45122-21011.已知函数,,则( )()1212xxf x -=+())lg g x x =-A .函数为偶函数B .函数为奇函数()f x ()g x C .函数在区间上的最大值与最小值之和为0()()()F x f x g x =+[]1,1-D .设,则的解集为()()()F x f x g x =+()()210F a F a +--<()1,+∞12.已知函数,则( )()sin 24f x x π⎛⎫=+ ⎪⎝⎭A .函数的最小正周期为|()|y f x =πB .直线是图象的一条对称轴58x π=()y f x =C.是图象的一个对称中心3(,0)8π()y f x =D .若时,在区间上单调,则的取值范围是或0ω>()f x ω,2ππ⎡⎤⎢⎥⎣⎦ω10,8⎛⎤⎥⎝⎦15,48⎡⎤⎢⎥⎣⎦3、填空题(本大题共4小题,每小题5分,共20分. 把答案填在答题卡中的横线上)13.若函数的最小正周期是,则的取值可以是______.(写()()tan()03f x x πωω=+≠2πω出一个即可).14.已知函数,若,则_____________.()sin 1f x a x bx =++()12f -=()1f =15. 已知:{} ,max , .a ab a b b a b ≥⎧=⎨<⎩设函数,若关于的方程有三个不相等的实数解,(){}1max 2,42x f x x -=--x ()f x t=则实数的取值范围是.16.设函数,若对于任意实数,在区间上()()()2sin 10f x x ωϕω=+->ϕ()f x 3,44ππ⎡⎤⎢⎥⎣⎦至少有2个零点,至多有3个零点,则的取值范围是ω四、解答题(本大题共6小题,共70分. 解答应写出文字说明,证明过程或演算步骤)17.(本小题满分10分)已知f (α)=.2sin ()cos(2)tan()sin()tan(3)παπαπαπααπ-⋅-⋅-+-+⋅-+(1)化简f (α);(2)若α=,求f (α)的值.313π-18.(本小题满分12分)已知集合A ={x ∈R |≥},集合B ={x ∈R |(x ﹣1)(x ﹣a )<0}.a ∈R 22log x 2log 2x ()(1)求集合A ;(2)若B ⊆∁R A ,求a 的取值范围.19.(本小题满分12分)已知函数,,且该函数的图象经过点,.()bf x ax x =+,a b R ∈()1,0-32,2⎛⎫ ⎪⎝⎭(1)求a ,b 的值;(2)已知直线与x 轴交于点T ,且与函数的图像只有一个公共点.求()1y kx m k =+≠()f x 的最大值.(其中O 为坐标原点)OT20.(本小题满分12分)比亚迪是我国乃至全世界新能源电动车的排头兵,新能源电动车汽车主要采用电能作为动力来源,目前比较常见的主要有两种:混合动力汽车、纯电动汽车.有关部门在国道上对比亚迪某型号纯电动汽车进行测试,国道限速.经数次测试,得到该纯电动汽车60km/h 每小时耗电量(单位:)与速度(单位:)的数据如下表所示:Q wh x km/hx0104060Q142044806720为了描述该纯电动汽车国道上行驶时每小时耗电量与速度的关系,现有以下三种函数Q x 模型供选择:①;②;.3211()250Q x x x cx =-+22()13xQ x ⎛⎫=- ⎪⎝⎭3()300log aQ x x b =+(1)当时,请选出你认为最符合表格中所列数据的函数模型(不需要说明理由),060x ≤≤并求出相应的函数表达式;(2)现有一辆同型号纯电动汽车从衡阳行驶到长沙,其中,国道上行驶,高速上行驶50km .假设该电动汽车在国道和高速上均做匀速运动,国道上每小时的耗电量与速度300km Q 的关系满足(1)中的函数表达式;高速路上车速(单位:)满足,x x km/h [80,120]x ∈且每小时耗电量(单位:)与速度(单位:)的关系满足N wh x km/h ).则当国道和高速上的车速分别为多少时,该车辆的2()210200(80120)N x x x x =-+≤≤总耗电量最少,最少总耗电量为多少?21.(本小题满分12分)已知,.sin cos x x t +=t ⎡∈⎣(1)当且是第四象限角时,求的值;12t =x 33sin cos x x -(2)若关于的方程有实数根,求的取值范围.(x ()sin cos sin cos 1x x a x x -++=a )()3322()a b a b a ab b -=-++22.(本小题满分12分)已知函数的定义域为,若存在实数,使得对于任意都存在满足()f x D a 1x D ∈2x D ∈,则称函数为“自均值函数”,其中称为的“自均值数”.()122x f x a +=()f x a ()f x (1)判断函数是否为“自均值函数”,并说明理由:()2x f x =(2)若函数,为“自均值函数”,求的取值范围;()sin()(0)6g x x πωω=+>[0,1]x ∈ω(3)若函数,有且仅有1个“自均值数”,求实数的值.2()23h x tx x =++[0,2]x ∈衡阳市雁峰区名校2022-2023学年高一上学期期末考试数 学参考答案:1.D【分析】由终边相同的角的性质即可求解.【详解】因为与角终边相同的角是,,20-︒20360k -︒+︒Z k ∈当时,这个角为,1k =340︒只有选项D 满足,其他选项不满足.Z k ∈故选:D.2.C【分析】利用一元二次不等式的解法求解即可.【详解】解:232(32)(1)0x x x x --=+-≥解得:.213x x ≤-≥或故选:C.3.A【分析】首先解分式不等式,再根据充分条件、必要条件的定义判断即可.【详解】解:因为,所以,,,11x <10xx -<(1)0x x ∴-<(1)0x x ∴->或,0x ∴<1x >当时,或一定成立,所以“”是“”的充分条件;1x >0x <1x >1x >11x <当或时,不一定成立,所以“”是“”的不必要条件.0x <1x >1x >1x >11x <所以“”是“”的充分不必要条件.1x >11x <故选:A 4.B【分析】由零点的存在性定理求解即可【详解】∵,,()360f -=>()210f -=>,,()120f -=-<()040f =-<根据零点的存在性定理知,函数的零点所在区间为.()f x ()2,1--故选:B 5.D【分析】根据函数图象变换求出变换后的函数解析式,结合已知条件可得出关于实数的a 等式,进而可求得实数的值.a 【详解】由题意可得,再将的图象向右平移个单位长度,得到函数()3xg x a =()g x 2,()23x f x a -=又因为,所以,,整理可得,()xf x a =23x x a a -=23a =因为且,解得0a >1a ≠a =故选:D.6.A【解析】由函数的部分图像得到函数的最小正周期,求出,代入求出()f x ()f x ω5,212π⎛⎫⎪⎝⎭值,则函数的解析式可求,取可得的值.ϕ()f x x π=()f π【详解】由图像可得函数的最小正周期为,则.()f x 521212T πππ⎡⎤⎛⎫=⨯--= ⎪⎢⎥⎝⎭⎣⎦22T πω==又,则,5552sin 22sin 212126f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭5sin 16⎛⎫+= ⎪⎝⎭πϕ则,,则,,5262k ϕπ=π+π+Z k ∈23k πϕπ=-Z k ∈,则,,则,22ππϕ-<<0k =3πϕ=-()2sin 23f x x π⎛⎫=- ⎪⎝⎭()2sin 22sin 33f ππππ⎛⎫∴=-=-= ⎪⎝⎭故选:A.【点睛】方法点睛:根据三角函数的部分图像()()sin 0,0,2f x A x b A πωϕωϕ⎛⎫=++>>< ⎪⎝⎭求函数解析式的方法:(1)求、,;A ()()max min:2f x f x b A -=()()max min2f x f x b +=(2)求出函数的最小正周期,进而得出;T 2T πω=(3)取特殊点代入函数可求得的值.ϕ7.C【分析】先用分离常数法得到,由单调性列不等式组,求出实数的取值范21()a f x a x a -=+-a 围.【详解】解:根据题意,函数,221()11()ax a x a a a f x ax a x a x a --+--===+---若在区间上单调递减,必有,()f x (2,)+∞2102a a ⎧->⎨⎩ 解可得:或,即的取值范围为,,,1a <-12a < a (-∞1)(1-⋃2]故选:C .8.D【详解】分别对,,两边取对数,得,,2022a =2223b =c a b =20log 22a =22log 23b =.log a c b =.()22022lg 22lg 20lg 23lg 22lg 23log 22log 23lg 20lg 22lg 20lg 22a b -⋅-=-=-=⋅由基本不等式,得:,()222222lg 20lg 23lg 460lg 484lg 22lg 20lg 23lg 222222⎛⎫+⎛⎫⎛⎫⎛⎫⋅<=<==⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭所以,()2lg 22lg 20lg 230-⋅>即,所以.0a b ->1a b >>又,所以.log log 1a a c b a =<=a b c >>故选:D .9.AC【分析】利用不等式的性质对各选项逐一分析并判断作答.【详解】对于A ,因c 2+1>0,于是有>0,而a >b ,由不等式性质得,A 211c +2211a bc c >++正确;对于B ,因为1<b <2,所以-2<-b <-1,同向不等式相加得-4<a -b <2,B 错误;对于C ,因为a >b >0,所以,又因为m >0,所以,C 正确;11a b <m m a b <对于D ,且,而,即ac >bd 不一定成立,D 错误.12->-23->-(1)(2)(2)(3)-⋅-<--故选:AC10.ABD【分析】利用诱导公式、指数幂的运算以及特殊角的三角函数值计算各选项中代数式的值,可得出合适的选项.【详解】对于A 选项,;5πππ1sinsin πsin 6662⎛⎫=-==⎪⎝⎭对于B 选项,;221sin 452==对于C 选项,122-==对于D.()121018030302=+=== 故选:ABD.11.BCD【分析】根据题意,利用奇偶性,单调性,依次分析选项是否正确,即可得到答案【详解】对于A :,定义域为,,()1212x x f x -=+R ()()12121212x xx xf x f x -----==-=-++则为奇函数,故A 错误;()f x 对于B :,定义域为,())lgg x x=R ,()()))()lglgg x x x g x -=-=-=-则为奇函数,故B 正确;()g x 对于C :,,都为奇函数,()()()F x f x g x =+()f x ()g x 则为奇函数,()()()F x f x g x =+在区间上的最大值与最小值互为相反数,()()()F x f x g x =+[]1,1-必有在区间上的最大值与最小值之和为0,故C 正确;()F x []1,1-对于D :,则在上为减函数,()1221221122121x x x x xf x ⎛⎫-+-==-=- ⎪+++⎝⎭()f x R在上为减函数,())lg g x x ==()g x R 则在上为减函数,()()()F x f x g x =+R 若即,()()210F a F a +--<()()21F a F a <+则必有,解得,21a a >+1a >即的解集为,故D 正确;()()210F a F a +--<()1,+∞故选:BCD 12.BCD【详解】因为函数的最小正周期为,()sin 24f x x π⎛⎫=+ ⎪⎝⎭22T ππ==而函数周期为,故A 错误;|()|y f x =2π当时,,58x π=553()sin 2sin(18842f ππππ⎛⎫=⨯+==- ⎪⎝⎭所以直线是图象的一条对称轴,故B 正确;58x π=()y f x =故C 正确38x π=33()sin 2sin()0884f ππππ⎛⎫=⨯+== ⎪⎝⎭时,在区间上单调,0ω>()sin(24f x x πωω=+,2ππ⎡⎤⎢⎥⎣⎦即,2,2444x πππωωπωπ⎡⎤+∈++⎢⎥⎣⎦所以或04242πωπππωπ⎧+>⎪⎪⎨⎪+≤⎪⎩423242ππωπππωπ⎧+≥⎪⎪⎨⎪+≤⎪⎩解得或,故D 正确.108ω<≤1548ω≤≤故选:BCD.【点睛】(1)应用公式时注意方程思想的应用,对于sinα+cosα,sinα-cosα,sinαcosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα可以知一求二.(2)关于sinα,cosα的齐次式,往往化为关于tanα的式子.13.2或-2 (写一个即可)14. 015.24t <<【分析】根据函数新定义求出函数解析式,画出函数的图象,利用转化的思想将()f x ()f x 方程的根转化为函数图象的交点,根据数形结合的思想即可得出t 的范围.【详解】由题意知,令,解得,1242x x -=--20x x x ==,根据,得,{}max a a ba b b a b ≥⎧=⎨<⎩,,,121220()4202x x x f x x x x x x--⎧≤⎪=--<<⎨⎪≥⎩,,,作出函数的图象如图所示,()f x 由方程有3个不等的根,()0f x t -=得函数图象与直线有3个不同的交点,()y f x =y t =由图象可得,当时函数图象与直线有3个不同的交点,24t <<()y f x =y t =所以t 的取值范围为.24t <<故答案为:24t <<16.:.1643ω≤<【分析】,只需要研究的根的情况,借助于和的图像,根t x ωϕ=+1sin 2t =sin y t =12y =据交点情况,列不等式组,解出的取值范围.ω【详解】令,则()0f x =()1sin 2x ωϕ+=令,则t x ωϕ=+1sin 2t =则问题转化为在区间上至少有两个,至少有三个t ,使得,sin y t =3,44ππωϕωϕ⎡⎤++⎢⎥⎣⎦1sin 2t =求的取值范围.ω作出和的图像,观察交点个数,sin y t =12y =可知使得的最短区间长度为2π,最长长度为,1sin 2t =223ππ+由题意列不等式的:3222443πππωϕωϕππ⎛⎫⎛⎫≤+-+<+ ⎪ ⎪⎝⎭⎝⎭解得:.1643ω≤<【点睛】研究y =Asin (ωx +φ)+B 的性质通常用换元法(令),转化为研究t x ωϕ=+的图像和性质较为方便.sin y t =17、解:(1)f (a )===sin α•cos α…5分(2)∵α=﹣=﹣6×,∴f (﹣)=cos (﹣)sin (﹣)=cos (﹣6×)sin (﹣6×)=cossin==﹣…10分18、解:(1)根据题意,集合A ={x ∈R |2log 2x ≥log 2(2x )},即,则,得x ≥2,则集合A ={x ∈R |x ≥2},(2)∁R A ={x ∈R |x <2},又集合B ={x ∈R |(x ﹣1)(x ﹣a )<0},①当a =1时,(x ﹣1)2<0,则无解,故B =∅,满足B ⊆∁R A ,②当a >1时,由(x ﹣1)(x ﹣a )<0,得1<x <a ,若B ⊆∁R A ,则a ≤2,得1<a ≤2,③当a <1时,由(x ﹣1)(x ﹣a )<0,得a <x <1,显然满足B ⊆∁R A ,综上所述,a 的取值范围是(﹣∞,2].19.(Ⅰ); (Ⅱ)1.11a b =⎧⎨=-⎩【分析】(Ⅰ)根据已知点的坐标,利用函数的解析式,得到关于的方程组,求解即得;,a b (Ⅱ)设,则直线方程可以写成, 与函数(),0T t ()1y kx m k =+≠()y k x t =-联立,消去,利用判别式求得,利用二次函数的性质求得()1y f x x x ==-y 22114t k k ⎛⎫=- ⎪⎝⎭取得最大值1,进而得到的最大值.2t OT 【详解】(Ⅰ)由已知得,解得;03222a b b a --=⎧⎪⎨+=⎪⎩11a b =⎧⎨=-⎩(Ⅱ)设,则直线方程可以写成,与函数(),0T t ()1y kx m k =+≠()y k x t =-联立,消去,并整理得()1y f x x x ==-y ()2110k x ktx --+=由已知得判别式,()22410k t k --=22114,t k k ⎛⎫=- ⎪⎝⎭当时,取得最大值1,所以.112k =2t maxmax 1OT t ==20.【分析】(1)利用表格中数据进行排除即可得解;(2)在分段函数中分别利用均值不等式和二次函数求出最值即可得解.【详解】(1)解:对于③,当时,它无意义,故不符合题意,3()300log a Q x x b =+0x =对于②,当时,,又,22()13xQ x ⎛⎫=- ⎪⎝⎭10x =1022(10)13Q ⎛⎫=- ⎪⎝⎭100122033<⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝=⎭所以,故不符合题意,故选①,1022(10)113Q ⎛⎫=-< ⎪⎝⎭3211()250Q x x x cx=-+由表中的数据可得,,解得3211021010142050c ⨯-⨯+⨯=160c =∴.(不需要说明理由,写对解析式即可)321()216050Q x x x x =-+(2)解:高速上行驶,所用时间为,300km 300hx 则所耗电量为,()2300300100()()2102006003000f x N x x x x x x x ⎛⎫=⋅=⋅-+=+- ⎪⎝⎭由对勾函数的性质可知,在上单调递增,()f x [80,120]∴,min 100()(80)60080300045750wh80f x f ⎛⎫==⨯+-= ⎪⎝⎭国道上行驶,所用时间为,50km 50hx 则所耗电量为,32250501()()2160100800050g x Q x x x x x x x x ⎛⎫=⋅=⋅-+=-+ ⎪⎝⎭∵,∴当时,,060x ≤≤50x =min ()(50)5500wh g x g ==∴当这辆车在高速上的行驶速度为,在国道上的行驶速度为时,80km/h 50km/h 该车从衡阳行驶到长沙的总耗电量最少,最少为.45750550051250wh +=21.(1)(2)[)1,+∞【分析】(1)由同角三角函数的平方关系求出、的值,再结合立方差sin cos x x sin cos x x -公式可求得所求代数式的值;(2)由已知可得出,,分、211022t at -+-=t ⎡∈⎣0=t 0t <≤时直接验证即可,在时,由参变量分离法可得出,结合基本不0=t 0t <≤112a t t ⎛⎫=+ ⎪⎝⎭等式可求得实数的取值范围,综合可得结果.a 【详解】(1)解:因为,即,则,12t =1sin cos 2x x +=()21sin cos 12sin cos 4x x x x +=+=即,3sin cos 8x x =-所以.()27sin cos 12sin cos 4x x x x -=-=因为是第四象限角,则,,所以,所以x sin 0x <cos 0x >sin cos 0x x -<sin cos x x -=所以()()33223sin cos sin cos sin sin cos cos 18x x x x x x x x ⎛⎫-=-++=-= ⎪⎝⎭(2)解:由,可得,()2sin cos 12sin cos x x x x+=+()21sin cos 12x x t =-则方程可化为,.()sin cos sin cos 1x x a x x -++=211022t at -+-=t ⎡∈⎣①当时,,显然方程无解;0=t 12-≠②当时,方程等价于.0t ≠211022t at -+-=112at t ⎛⎫=+ ⎪⎝⎭当,当且仅当时,等号成立,0t <≤111122t t ⎛⎫+≥⨯= ⎪⎝⎭1t =又,10,t t t →+→+∞故,1112a t t ⎛⎫=+≥ ⎪⎝⎭所以要使得关于的方程有实数根,则.x sin cos (sin cos )1x x a x x -++=1a ≥故的取值范围是.a [)1,+∞22.(1)不是,理由见解析;(2);5[,)6π+∞(3).12-【分析】(1)假定函数是 “自均值函数”,由函数的值域与函数的值()2xf x =2()f x 12y a x =-域关系判断作答.(2)根据给定定义可得函数在上的值域包含函数在上的值域,由此2()g x [0,1]12y a x =-[0,1]推理计算作答.(3)根据给定定义可得函数在上的值域包含函数在上的值域,再借2()h x [0,2]12y a x =-[0,2]助a 值的唯一性即可推理计算作答.(1)假定函数是 “自均值函数”,显然定义域为R ,则存在,对于,()2x f x =()2xf x =R a ∈1x ∀∈R 存在,有,2R x ∈2122x x a+=即,依题意,函数在R 上的值域应包含函数在R 上的值2122x a x =-22()2x f x =12y a x =-域,而当时,值域是,当时,的值域是R ,显然不2R x ∈2()f x (0,)+∞1R x ∈12y a x =-(0,)+∞包含R ,所以函数不是 “自均值函数”.()2xf x =(2)依题意,存在,对于,存在,有,即R a ∈1[0,1]x ∀∈2[0,1]x ∈12()2x g x a +=,21sin()26x a x πω+=-当时,的值域是,因此在的值域1[0,1]x ∈12y a x =-[21,2]a a -22()sin(6g x x πω=+2[0,1]x ∈包含,[21,2]a a -当时,而,则,2[0,1]x ∈0ω>2666x πππωω≤+≤+若,则,,此时值域的区间长度不超过,而区间62ππω+≤2min 1()2g x =2()1g x ≤2()g x 12长度为1,不符合题意,[21,2]a a -于是得,,要在的值域包含,62ππω+>2max()1g x =22()sin()6g x x πω=+2[0,1]x ∈[21,2]a a -则在的最小值小于等于0,又时,递减,22()sin()6g x x πω=+2[0,1]x ∈23[,]622x πππω+∈2()g x 且,()0π=g 从而有,解得,此时,取,的值域是包含于在6πωπ+≥56πω≥12a =12y a x =-[0,1]2()g x 的值域,2[0,1]x ∈所以的取值范围是.ω5[,)6π+∞(3)依题意,存在,对于,存在,有,即R a ∈1[0,2]x ∀∈2[0,2]x ∈12()2x h x a +=,2221232tx x a x ++=-当时,的值域是,因此在的值域1[0,2]x ∈12y a x =-[22,2]a a -2222()23h x tx x =++2[0,2]x ∈包含,并且有唯一的a 值,[22,2]a a -当时,在单调递增,在的值域是,0t ≥2()h x [0,2]2()h x 2[0,2]x ∈[3,47]t +由得,解得,此时a 的值不唯一,不符合[22,2][3,47]a a t -⊆+223247a a t -≥⎧⎨≤+⎩57222a t ≤≤+要求,当时,函数的对称轴为,0t <2222()23h x tx x =++21x t =-当,即时,在单调递增,在的值域是,12t -≥102t -≤<2()h x [0,2]2()h x 2[0,2]x ∈[3,47]t +由得,解得,要a 的值唯一,当且仅当[22,2][3,47]a a t -⊆+223247a a t -≥⎧⎨≤+⎩57222a t ≤≤+,即,则,57222t =+15,22t a =-=12t =-当,即时,,,,102t <-<21t <-2max 11()()3h x h t t =-=-2min ()min{(0),(2)}h x h h =(0)3h =,(2)47h t =+由且得:,此时a 的值不唯一,不符合要求,1[22,2][3,3]a a t -⊆-112t -≤<-531222a t ≤≤-由且得,,要a 的值唯一,当且仅当1[22,2][47,3a a t t -⊆+-1t <-9312222t a t +≤≤-,此时;9312222t t +=-t =a =综上得:或,12t =-t =所以函数,有且仅有1个“自均值数”,实数的值是2()23h x tx x =++[0,2]x ∈12-【点睛】结论点睛:若,,有,则的值域是[]1,x a b ∀∈[]2,x c d ∃∈()()12f x g x =()f x 值域的子集.()g x。
湖南省永州市2020-2021学年高一上学期期末考试数学试题 (解析版)

2020-2021学年湖南省永州市高一(上)期末数学试卷一、选择题(共8小题).1.设全集U={1,2,3},A={1,2},则∁U A=()A.{1}B.{2}C.{3}D.{1,3} 2.365°是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角3.命题“∃x∈R,x﹣1>2”的否定是()A.∃x∈R,x﹣1<2B.∃x∈R,x﹣1≤2C.∀x∈R,x﹣1<2D.∀x∈R,x﹣1≤2 4.扇形的半径为1,圆心角为2,则扇形的面积为()A.1B.2C.3D.45.已知a=log2,b=()﹣2,c=2,则a,b,c的大小关系是()A.b<c<a B.b<a<c C.a<c<b D.a<b<c6.王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其《从军行》传诵至今,内容为:“青海长云暗雪山,孤城遥望玉门关.黄沙百战穿金甲,不破楼兰终不还.”由此推断,“返回家乡”是“攻破楼兰”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件7.函数f(x)=x+cos x的零点所在的区间为()A.(﹣1,﹣)B.(﹣)C.(0,)D.()8.设函数f(x)的定义域为R,f(x+1)=f(x),当x∈(0,1]时,f(x)=x(1﹣x).若存在x∈[m,+∞),使得f(x)=有解,则实数m的取值范围为()A.(﹣∞,]B.(﹣∞,]C.(﹣∞,]D.(﹣∞,]二、多项选择题(共4小题).9.我国著名的数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微;数形结合百般好,隔裂分家万事休.在数学学习和研究中,常用函数的图象来研究函数的性质.下列函数中,在(0,+∞)上单调递增且图象关于y轴对称的是()A.f(x)=x3B.f(x)=x2C.y=x﹣2D.f(x)=|x| 10.设a,b,c∈R,a<b,则下列不等式一定成立的是()A.a+c<b+c B.e﹣a>e﹣b C.ac2<bc2D.<11.将函数f(x)=sin(2x﹣φ)(0<φ<)的图象上所有的点向左平行移动个单位长度,得到偶函数h(x)的图象,则下列结论中正确的有()A.h(x)的图象关于点(,0)对称B.h(x)的图象关于x=对称C.h(x)在[,]上的值域为[,]D.h(x)在[]上单调递减12.若函数f(x)对∀x1,x2∈(1,+∞),(x1≠x2),不等式<1成立,则称f(x)在(1,+∞)上为“平方差减函数”,则下列函数中是“平方差减函数”的有()A.f(x)=﹣2x+1B.f(x)=x2+2x+1C.f(x)=x2﹣log2x D.f(x)=x2﹣x+三、填空题(共4小题).13.已知幂函数y=f(x)的图象过点(2,),则f(4)=.14.已知sinα=,则cos()=.15.若f(x)=,则不等式f(x)>4的解集为.16.十六、十七世纪之交,随着天文、航海、工程、贸易及军事的发展,改进数字计算方法成了当务之急,数学家约翰•纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数,后来数学家欧拉发现了对数与指数的关系,即a b=N⇔b=log a N,现已知a=log36,2b=36,则()×3=.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知集合A={x|x≥2},B={x|3<x≤5}.(1)求A∪B;(2)定义M﹣N={x|x∈M且x∉N},求A﹣B.18.(12分)给定两个条件:①充分不必要,②必要不充分,从上述两个条件中,任选一个补充在下面问题中,并加以解答.问题:已知p:实数x满足x2﹣3ax+2a2<0,a>0.(1)若a=1,求实数x的取值范围;(2)已知q:实数x满足2<x≤3.若存在实数a,使得p是q的_____条件,则求出a 的取值范围;若不存在,请说明理由.19.(12分)如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于P,Q两点,P,Q的纵坐标分别为,.(1)求sinα的值;(2)求α+β.20.(12分)已知函数f(x)=cos4x﹣2sin x cos x﹣sin4x+m(x∈[0,])的最大值为1.(1)求函数f(x)的最小正周期;(2)求使f(x)≥0成立时自变量x的集合.21.(12分)某市为发展农业经济,鼓励农产品加工,助推美丽乡村建设,成立了生产一种饮料的食品加工企业,每瓶饮料的售价为14元,月销售量为9万瓶.(1)根据市场调查,若每瓶饮料的售价每提高1元,则月销售量将减少5000瓶.要使月销售收入不低于原来的月销售收入,该饮料每瓶售价最多为多少元?(2)为了提高月销售量,该企业对此饮料进行技术和销售策略改革,提高每瓶饮料的售价到x元,并投入x2万元作为技术革新费用,投入2万元作为固定宣传费用.试问:技术革新后,要使革新后的月销售收入不低于原来的月销售收入与总投入之和,求月销售量t(万瓶)的最小值,以及t取最小值时的每瓶饮料的售价.22.(12分)已知函数f(x)=e x,g(x)=ln(e x+e﹣x)+2021.(1)判断函数g(x)的奇偶性并证明;(2)若∀x1∈(0,+∞),∃x2∈R,使得f(2x1)+mf(x1)﹣g(x2)>0成立,求实数m 的取值范围.参考答案一、选择题(共8小题).1.设全集U={1,2,3},A={1,2},则∁U A=()A.{1}B.{2}C.{3}D.{1,3}解:∵U={1,2,3},A={1,2},∴∁U A={3}.故选:C.2.365°是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角解:因为365°=360°+5°,5°是第一象限角,所以365°是第一象限角.故选:A.3.命题“∃x∈R,x﹣1>2”的否定是()A.∃x∈R,x﹣1<2B.∃x∈R,x﹣1≤2C.∀x∈R,x﹣1<2D.∀x∈R,x﹣1≤2解:命题“∃x∈R,x﹣1>2”的否定是∀x∈R,x﹣1≤2,故选:D.4.扇形的半径为1,圆心角为2,则扇形的面积为()A.1B.2C.3D.4解:扇形的半径为1,圆心角为2,扇形的弧长为2,所以扇形的面积为:故选:A.5.已知a=log2,b=()﹣2,c=2,则a,b,c的大小关系是()A.b<c<a B.b<a<c C.a<c<b D.a<b<c解:∵,∴a=﹣1,∵=4,∴b=4,∵,∴c=,∴a<c<b,故选:C.6.王昌龄是盛唐著名的边塞诗人,被誉为“七绝圣手”,其《从军行》传诵至今,内容为:“青海长云暗雪山,孤城遥望玉门关.黄沙百战穿金甲,不破楼兰终不还.”由此推断,“返回家乡”是“攻破楼兰”的()A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件解:由题意可知:“返回家乡”则可推出“攻破楼兰”,故“攻破楼兰”是“返回家乡”的必要条件,故选:A.7.函数f(x)=x+cos x的零点所在的区间为()A.(﹣1,﹣)B.(﹣)C.(0,)D.()解:根据题意,f(x)=x+cos x,则f(﹣1)=﹣1+cos1<0,f(﹣)=﹣+cos>﹣+cos>0,则函数f(x)=x+cos x的零点所在的区间为(﹣1,﹣),故选:A.8.设函数f(x)的定义域为R,f(x+1)=f(x),当x∈(0,1]时,f(x)=x(1﹣x).若存在x∈[m,+∞),使得f(x)=有解,则实数m的取值范围为()A.(﹣∞,]B.(﹣∞,]C.(﹣∞,]D.(﹣∞,]解:f(x+1)=f(x),当x∈(0,1]时,f(x)=x(1﹣x).当x∈(1,2]时,f(x)=﹣(x﹣1)(x﹣2).当x∈(2,3]时,f(x)=﹣(x﹣2)(x﹣3).当x∈(3,4]时,f(x)=﹣(x﹣3)(x﹣4).根据f(x)=,结合图象可得,=﹣(x﹣2)(x﹣3),所以x=,所以m,所以m的取值范围为.故选:C.二、多项选择题(共4小题).9.我国著名的数学家华罗庚先生曾说:数缺形时少直观,形缺数时难入微;数形结合百般好,隔裂分家万事休.在数学学习和研究中,常用函数的图象来研究函数的性质.下列函数中,在(0,+∞)上单调递增且图象关于y轴对称的是()A.f(x)=x3B.f(x)=x2C.y=x﹣2D.f(x)=|x|解:对于A,f(x)=x3为奇函数,图象关于原点对称,不符合题意;对于B,f(x)=x2为偶函数,图象关于y轴对称,且在(0,+∞)上单调递增,符合题意;对于C,y=x﹣2=为偶函数,在(0,+∞)上单调递减,不符合题意;对于D,f(x)=|x|为偶函数,图象关于y轴对称,且在(0,+∞)上单调递增,符合题意.故选:BD.10.设a,b,c∈R,a<b,则下列不等式一定成立的是()A.a+c<b+c B.e﹣a>e﹣b C.ac2<bc2D.<解:对于A,因为a<b,所以a+c<b+c,故A正确;对于B,因为a<b,所以﹣a>﹣b,所以e﹣a>e﹣b,故B正确;对于C,若c=0,则ac2=bc2,故C错误;对于D,取a=﹣2,b=﹣1,则=2,=,则>,故D错误.故选:AB.11.将函数f(x)=sin(2x﹣φ)(0<φ<)的图象上所有的点向左平行移动个单位长度,得到偶函数h(x)的图象,则下列结论中正确的有()A.h(x)的图象关于点(,0)对称B.h(x)的图象关于x=对称C.h(x)在[,]上的值域为[,]D.h(x)在[]上单调递减解:将函数f(x)=sin(2x﹣φ)(0<φ<)的图象上所有的点向左平行移动个单位长度,得到函数h(x)=sin(2x+﹣φ)的图象,由于函数h(x)为偶函数,故﹣φ=kπ,所以φ=kπ+,由于0<φ<,所以当k=0时,φ=.所以h(x)=sin(2x+)=sin(2x+)=cos2x,对于A:当x=﹣时,h(﹣)=0,故A正确;对于B:当x=时h()=cos(﹣π)=﹣1,故B正确;当x时,,所以,故C错误;对于D:,所以,根据函数的性质,函数在该区间上单调递减,故D正确.故选:AD.12.若函数f(x)对∀x1,x2∈(1,+∞),(x1≠x2),不等式<1成立,则称f(x)在(1,+∞)上为“平方差减函数”,则下列函数中是“平方差减函数”的有()A.f(x)=﹣2x+1B.f(x)=x2+2x+1C.f(x)=x2﹣log2x D.f(x)=x2﹣x+解:根据题意,设g(x)=f(x)﹣x2,若f(x)在(1,+∞)上为“平方差减函数”,则对∀x1,x2∈(1,+∞),(x1≠x2),不等式<1成立,则有﹣1==×=<0,则有<0,则函数g(x)=f(x)﹣x2在[1,+∞)为减函数,反之,若函数g(x)=f(x)﹣x2在[1,+∞)为减函数,则有=(x1+x2)<0,即f(x)在(1,+∞)上为“平方差减函数”,分析选项:对于A,f(x)=﹣2x﹣1,g(x)=f(x)﹣x2=﹣x2﹣2x﹣1,为开口向下,对称轴为x =﹣1的二次函数,g(x)在区间[1,+∞)为减函数,则f(x)在(1,+∞)上为“平方差减函数”;对于B,f(x)=x2+2x+1,g(x)=f(x)﹣x2=2x+1,g(x)在区间[1,+∞)为增函数,则f(x)在(1,+∞)上不是“平方差减函数”;对于C,f(x)=x2﹣log2x,g(x)=f(x)﹣x2=﹣log2x,g(x)在区间[1,+∞)为减函数,则f(x)在(1,+∞)上为“平方差减函数”;对于D,f(x)=x2﹣x+,g(x)=f(x)﹣x2=﹣x+,g(x)在区间[1,+∞)为减函数,则f(x)在(1,+∞)上为“平方差减函数”;故选:ACD.三、填空题(共4小题).13.已知幂函数y=f(x)的图象过点(2,),则f(4)=2.解:设幂函数y=f(x)=xα,α∈R,其图象过点(2,),∴2α=,解得α=,∴f(x)=,∴f(4)==2.故答案为:2.14.已知sinα=,则cos()=.解:∵sinα=,∴cos()=sinα=,故答案为:.15.若f(x)=,则不等式f(x)>4的解集为(﹣∞,﹣)∪(2,+∞).解:x≥0时,由2x>4,解得x>2,x<0时,由﹣2x+1>4,解得x<﹣,故不等式的解集是(﹣∞,﹣)∪(2,+∞),故答案为:(﹣∞,﹣)∪(2,+∞).16.十六、十七世纪之交,随着天文、航海、工程、贸易及军事的发展,改进数字计算方法成了当务之急,数学家约翰•纳皮尔正是在研究天文学的过程中,为了简化其中的计算而发明了对数,后来数学家欧拉发现了对数与指数的关系,即a b=N⇔b=log a N,现已知a=log36,2b=36,则()×3=.解:因为a=log36,2b=36,所以b=log236,故,,所以,故()×3=.故答案为:.四、解答题:本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)已知集合A={x|x≥2},B={x|3<x≤5}.(1)求A∪B;(2)定义M﹣N={x|x∈M且x∉N},求A﹣B.解:(1)∵A={x|x≥2},B={x|3<x≤5},∴A∪B={x|x≥2};(2)∵M﹣N={x|x∈M且x∉N},A={x|x≥2},B={x|3<x≤5},∴A﹣B={x|2≤x≤3或x>5}.18.(12分)给定两个条件:①充分不必要,②必要不充分,从上述两个条件中,任选一个补充在下面问题中,并加以解答.问题:已知p:实数x满足x2﹣3ax+2a2<0,a>0.(1)若a=1,求实数x的取值范围;(2)已知q:实数x满足2<x≤3.若存在实数a,使得p是q的_____条件,则求出a 的取值范围;若不存在,请说明理由.解:(1)因为a=1,解不等式x2﹣3x+2<0,可得1<x<2,所以实数x的取值范围为(1,2);(2)由x2﹣3ax+2a2<0,a>0,可得a<x<2a,若选①:因为p是q的充分不必要条件,则有a≥2且2a≤3,不等式组无解,所以实数a的值不存在;若选②:因为p是q的必要不充分条件,则有a≤2且2a>3,解得,所以实数a的取值范围为.19.(12分)如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于P,Q两点,P,Q的纵坐标分别为,.(1)求sinα的值;(2)求α+β.解:(1)以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于P,Q两点,P,Q的纵坐标分别为,.∴sinα=,sinβ=.(2)由题意可得cosα==,cosβ==.∵α+β∈(0,π),cos(α+β)=cosαcosβ﹣sinαsinβ=﹣=0,∴α+β=.20.(12分)已知函数f(x)=cos4x﹣2sin x cos x﹣sin4x+m(x∈[0,])的最大值为1.(1)求函数f(x)的最小正周期;(2)求使f(x)≥0成立时自变量x的集合.解:(1)函数f(x)=cos4x﹣2sin x cos x﹣sin4x+m=(cos2x+sin2x)(cos2x﹣sin2x)﹣sin2x+m =cos2x﹣sin2x+m=sim(﹣2x)+m,(x∈[0,]).∴函数f(x)的最小正周期T==π;(2)∵x∈[0,],∴(﹣2x)∈[﹣,],∴sim(﹣2x)∈[﹣,],∴sim(﹣2x)+m∈[m﹣1,m+1],∵f(x)的最大值为1,∴m+1=1,解得m=0.使f(x)≥0成立,即sim(﹣2x)≥0,化为:sim(2x﹣)≤0,∴﹣≤2x﹣≤0,解得:0≤x≤,∴使f(x)≥0成立时自变量x的集合为[0,].21.(12分)某市为发展农业经济,鼓励农产品加工,助推美丽乡村建设,成立了生产一种饮料的食品加工企业,每瓶饮料的售价为14元,月销售量为9万瓶.(1)根据市场调查,若每瓶饮料的售价每提高1元,则月销售量将减少5000瓶.要使月销售收入不低于原来的月销售收入,该饮料每瓶售价最多为多少元?(2)为了提高月销售量,该企业对此饮料进行技术和销售策略改革,提高每瓶饮料的售价到x元,并投入x2万元作为技术革新费用,投入2万元作为固定宣传费用.试问:技术革新后,要使革新后的月销售收入不低于原来的月销售收入与总投入之和,求月销售量t(万瓶)的最小值,以及t取最小值时的每瓶饮料的售价.解:(1)设饮料每瓶售价最多为x元,则[9﹣0.5(x﹣14)]x≥14×9,即x2﹣32x+252≤0,解得:14≤x≤18,所以要使月销售收入不低于原来的月销售收入,该饮料每瓶售价最多为18元.(2)当x>14时,由题意可得,tx≥14×9++2,即当x>14时,t,∵=16,当且仅当即x=16时,等号成立,∴t≥16,所以技术革新后,该饮料月销售量t至少达到16万个时,可使月销售收入不低于原来的月销售收入与总投入之和,此时每瓶饮料的售价为16元.22.(12分)已知函数f(x)=e x,g(x)=ln(e x+e﹣x)+2021.(1)判断函数g(x)的奇偶性并证明;(2)若∀x1∈(0,+∞),∃x2∈R,使得f(2x1)+mf(x1)﹣g(x2)>0成立,求实数m 的取值范围.解:(1)g(x)=ln(e x+e﹣x)+2021为偶函数.理由:g(x)的定义域为R,且g(﹣x)=ln(e﹣x+e x)+2021=g(x),所以g(x)为偶函数;(2)由e﹣x+e x≥2=2,当且仅当x=0时,取得等号,可得g(x)≥ln2+2021,由∀x1∈(0,+∞),∃x2∈R,使得f(2x1)+mf(x1)﹣g(x2)>0成立,可得f(2x)+mf(x)>ln2+2021对x∈(0,+∞)恒成立,即为e2x+me x>ln2+2021对x∈(0,+∞)恒成立,可令t=e x(t>1),则t2+mt>ln2+2021对t∈(1,+∞)恒成立,可得m>=﹣t对t∈(1,+∞)恒成立,设h(t)=﹣t,可得h(t)在t∈(1,+∞)递减,则h(t)<h(1)=ln2+2020,则m≥ln2+2020.即m的取值范围是[ln2+2020,+∞).。
湖南省长沙市2023-2024学年高一上学期期末考试数学试题含答案

长沙市2023-2024学年高一第一学期期末考试数学(答案在最后)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}2430,21x A x x x B y y =-+≤==+,则A B ⋃=()A.()1,+∞ B.[)1,+∞ C.()1,3 D.[)1,3【答案】B 【解析】【分析】解不等式化简集合A ,求出函数的值域化简集合B ,再利用并集的定义求解即得.【详解】解不等式2430x x -+≤,得13x ≤≤,即[1,3]A =,而211x y =+>,则(1,)B =+∞,所以[)1,A B ⋃=+∞.故选:B2.已知空间向量,a b 且2AB a b =+ ,56BC a b =-+ ,72CD a b =-,则一定共线的三点是()A.A ,B ,DB.A ,B ,CC.B ,C ,DD.A ,C ,D【答案】A 【解析】【分析】A 选项,计算出242B a b D AB =+=,A 正确;B 选项,设AB BC μ= ,得到方程组,无解;C选项,设BC mCD = ,得到方程组,无解;D 选项,计算出48AC a b =-+ ,设AC nCD =,得到方程组,无解.【详解】A 选项,5672242BD BC CD a b a b a b AB =+=-++-=+=,所以A ,B ,D 三点共线,A 正确;B 选项,设AB BC μ= ,则()256a b a b μ-+=+ ,即5162μμ-=⎧⎨=⎩,无解,B 错误;C 选项,设BC mCD = ,则()7625a b m a b -= ,即7526m m =-⎧⎨-=⎩,无解,C 错误;D 选项,25648a b a AC AB b a BC b +-+==+-=+ ,设AC nCD =,即()4827a b n a b -+=- ,即7428n n =-⎧⎨-=⎩,无解,D 错误.故选:A3.要得到函数πsin 23y x ⎛⎫=- ⎪⎝⎭的图象,只需将函数sin 2y x =的图象()A.向左平移π6个单位长度 B.向右平移π6个单位长度C.向左平移π3个单位长度D.向右平移π3个单位长度【答案】B 【解析】【分析】根据三角函数平移变换原则直接判断即可.【详解】ππsin 2sin 236y x x ⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,∴只需将sin 2y x =的图象向右平移π6个单位长度即可.故选:B.4.如图,在矩形ABCD 中,2AB AD =,,E F 分别为,BC CD 的中点,G 为EF 中点,则=AG ()A.2133+ AB AD B.1233+AB AD C.3344+AB AD D.2233+AB AD 【答案】C 【解析】【分析】根据向量加法的三角形法则和四边形法则,可得结果.【详解】根据题意:()12AG AE AF =+又12=+=+ AE AB BE AB AD12AF AD DF AD AB=+=+ 所以3344AG AB AD =+ 故选:C【点睛】本题主要考查利用向量的加法法则,熟练掌握向量加法的三角形法则和平行四边形法则,对向量用其它向量表示有很大的作用,属基础题.5.已知下列四组陈述句:①α:集合A B A C ⋂=⋂;β:集合B C =;②α:集合A B C A ⊆⊆⊆;β:集合A B C ==;③:{|21,}x x x n n α∈=+∈Z ;:{|61,}x x x n n β∈=-∈N ;④α:1a b +>;β:2()1a b +>.其中α是β的必要非充分条件的有()A.①②B.③④C.②④D.①③【答案】D 【解析】【分析】根据集合间的关系以及不等式的性质判断求解即可.【详解】①若A B A C ⋂=⋂,则,B C 不一定相等,不是充分条件,若B C =,则A B A C ⋂=⋂一定成立,是必要条件,所以α是β的必要非充分条件,故①符合题意;②若集合A B C A ⊆⊆⊆,则集合A B C ==,反之也成立,所以α是β的充要条件,故②不符合题意;③由{|21,}x x x n n ∈=+∈Z 得不到{|61,}x x x n n ∈=-∈N ,由{|61,}x x x n n ∈=-∈N 能得到{|21,}x x x n n ∈=+∈Z ,所以α是β的必要非充分条件,故③符合题意;④根据不等式的性质由1a b +>可得2()1a b +>,但由2()1a b +>得1a b +>或1a b +<-,即由2()1a b +>得不到1a b +>,所以α是β的充分不必要条件,故④不符合题意;故选:D.6.向量()1,2a = ,()2,1b =-- ,那么向量a b - 在a 上的投影向量为()A.918,55⎛⎫⎪⎝⎭B.12,55⎛⎫ ⎪⎝⎭C.612,55⎛⎫⎪⎝⎭ D.36,55⎛⎫--⎪⎝⎭【答案】A 【解析】【分析】由平面向量的坐标运算、投影向量的计算公式即可求解.【详解】因为()1,2a = ,()2,1b =-- ,所以()3,3a b -=,则a b -在a上的投影向量的模为()cos ,5a b a a b a a b a -⋅-⋅-==,则a b - 在a 上的投影向量为95918,555a a ⎛⎫⋅= ⎪⎝⎭.故选:A .7.浏阳市在全国先行探索高质量发展建设共同富裕示范区,若全市年平均增长率以8%来计算,全市生产总值翻一番需要经过()(四舍五入,lg20.3010,lg30.4771≈≈)A.7年 B.8年C.9年D.10年【答案】C 【解析】【分析】由题意可得()0.0812t+=,结合对数运算法则计算即可得.【详解】若某年生产总值为x ,则t 年后生产总值为()0.081tx +,若市生产总值翻一番,则有()()0.0810.0812ttx x+=+=,即 1.08lg 2lg 2lg 2log 2lg1.08lg108lg1002lg 23lg 32t ====-+-0.3010920.301030.47712≈≈⨯+⨯-,故全市生产总值翻一番需要经过大约9年.故选:C .8.函数()f x 的定义域为D ,若对于任意的12,x x D ∈,当12x x <时,都有()()12f x f x ≤,则称函数()f x 在D 上为非减函数.设函数()f x 在[]0,1上为非减函数,且满足以下三个条件:①()00f =;②()132x f f x ⎛⎫= ⎪⎝⎭;③()()11f x f x -=-,则1500f ⎛⎫⎪⎝⎭等于()A.164 B.132 C.116D.18【答案】A 【解析】【分析】结合题意,结合赋值法得到1233f f ⎛⎫⎛⎫= ⎪⎪⎝⎭⎝⎭、1299f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭、L 直到得到915020127297<<,结合函数()f x 在[]0,1上为非减函数,即可得112500729729f f f ⎛⎫⎛⎫⎛⎫==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.【详解】令1x =,由()()11f x f x -=-,可得()()011f f =-,又()00f =,故()11f =,由()132x f f x ⎛⎫=⎪⎝⎭,故()1111322f f ⎛⎫== ⎪⎝⎭,令13x =,则11111113322f f ⎛⎫⎛⎫-=-=-= ⎪ ⎪⎝⎭⎝⎭,即2132f ⎛⎫= ⎪⎝⎭,令13x =,有11119234f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令23x =,有21219234f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令19x =,有111127298f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令29x =,有212127298f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令127=x ,有11118122716f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令227x =,有21212722716f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令181x =,有111124328132f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令281x =,有212124328132f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令1243x =,有1111729224364f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,令2243x =,有2121729224364f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,由915020127297<<,且12172972964f f ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,又函数()f x 在[]0,1上为非减函数,故112150072972964f f f ⎛⎫⎛⎫⎛⎫===⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:A.【点睛】关键点睛:本题关键在于结合非减函数的性质,通过赋值法逐步得到915020127297<<,从而得到112500729729f f f ⎛⎫⎛⎫⎛⎫==⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.二、多选题:本大题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求,全部选对的得5分,部分选对的得2分,有选错的得0分.9.下列各组向量中,不能作为基底的是()A.()10,0e = ,()21,1e =B.()11,2e = ,()22,1e =-C.()13,4e =- ,234,55e ⎛⎫=-⎪⎝⎭D.()12,6e = ,()21,3e =--【答案】ACD 【解析】【分析】分别判断四个选项中的两个向量是否共线得到答案.【详解】对于A ,()10,0e = ,()21,1e =,由零向量与任意向量共线,可知两个向量不能作为基底;对于B ,因为()11,2e = ,()22,1e =-,所以112(2)50⨯-⨯-=≠,所以两个向量不共线,可以作为基底;对于C ,因为()13,4e =- ,234,55e ⎛⎫=- ⎪⎝⎭,所以433()4055-⨯--⨯=,可知两个向量共线,故不可以作为基底;对于D ,由()12,6e = ,()21,3e =--,得:2(3)6(1)0⨯--⨯-=,可知两个向量共线,故不能作为基底;故选:ACD10.衢州市柯城区沟溪乡余东村是中国十大美丽乡村,也是重要的研学基地,村口的大水车,是一道独特的风景.假设水轮半径为4米(如图所示),水轮中心O 距离水面2米,水轮每60秒按逆时针转动一圈,如果水轮上点P 从水中浮现时(图中0P )开始计时,则()A.点P 第一次达到最高点,需要20秒B.当水轮转动155秒时,点P 距离水面2米C.在水轮转动的一圈内,有15秒的时间,点P 距水面超过2米D.点P 距离水面的高度h (米)与t (秒)的函数解析式为ππ4sin 2306h t ⎛⎫=-+ ⎪⎝⎭【答案】ABD 【解析】【分析】先根据题意求出点P 距离水面的高度h (米)与t (秒)的函数解析式,再从解析式出发求解ABC 选项.【详解】如图所示,过点O 作OC ⊥水面于点C ,作OA 平行于水面交圆于点A ,过点P 作PB ⊥OA 于点B ,则因为水轮每60秒按逆时针转动一圈,故转动的角速度为2ππ6030=(rad /s ),且点P 从水中浮现时(图中0P )开始计时,t (秒)后,可知0π30POP t ∠=,又水轮半径为4米,水轮中心O 距离水面2米,即2OC =m ,04OP =m ,所以00π6OP C AOP ∠=∠=,所以ππ306POA t ∠=-,因为4OP =m ,所以ππ4sin 306t PB ⎛⎫- ⎪⎝⎭=,故ππ4sin 2306h t ⎛⎫=-+ ⎪⎝⎭,D 选项正确;点P 第一次达到最高点,此时ππsin 1306t ⎛⎫-=⎪⎝⎭,令ππ02π36t -=,解得:20t =(s ),A 正确;令ππ4sin 22306t ⎛⎫-+=⎪⎝⎭,解得:530t k =+,Z k ∈,当5k =时,155t =(s ),B 选项正确;ππ4sin 22306t ⎛⎫-+> ⎪⎝⎭,令ππ0π306t <-<,解得:535t <<,故有30s 的时间点P 距水面超过2米,C 选项错误;故答案为:ABD11.若a ,()0,b ∈+∞,1a b +=,则下列说法正确的有()A.11a b a b ⎛⎫⎛⎫++ ⎪⎪⎝⎭⎝⎭的最小值为4B.11a b +++6C.12a b+的最小值为322+D.222a b a b a b +++的最大值是3233+【答案】BCD 【解析】【分析】利用基本不等式依次判断即得.【详解】由a ,()0,b ∈+∞,1a b +=,可得(),0,1a b ∈,对于A ,12a a +≥,当且仅当1a a =,即()10,1a =∉取等号,所以12a a+>,同理12b b +>,故114a b a b ⎛⎫⎛⎫++> ⎪⎪⎝⎭⎝⎭,故A 错误;对于B ,∵()()2112113116a ba b a b a b +++=+++++++++=,当且仅当11a b +=+,即12a b ==时取等号,116a b +++≤11a b +++6,故B 正确;对于C ,()12122332b a a b a b a b a b ⎛⎫+=++=++≥+ ⎪⎝⎭,当且仅当2b a a b=,即21,22a b =-=-时取等号,故12a b+的最小值为32+,故C 正确;对于D ,由题可得1b a =-,()0,1a ∈,∴()222222211111a b a a a a b a b a a a a a a -++=+=+++--++-,而()21133311a a a a a -+=++-≥++,当且仅当131a a +=+,即1a =-时取等号,∴22221313a b a a b a b a a ++=≤++-+,即222a b a b a b +++的最大值是33+,故D 正确.故选:BCD.12.设函数()2πcos (0)3f x x ωω⎛⎫=-> ⎪⎝⎭,已知()f x 在[]0,π上有且仅有4个零点,则()A.ω的取值范围是1925,66⎡⎫⎪⎢⎣⎭B.()y f x =的图象与直线1y =在()0,π上的交点恰有2个C.()y f x =的图象与直线1y =-在()0,π上的交点恰有2个D.()f x 在ππ,42⎛⎫⎪⎝⎭上单调递减【答案】AB 【解析】【分析】对于A,确定2π2π2ππ[,]333πx ω-∈--,根据零点个数确定5π2π7ππ232ω≤-<,求得参数范围;对于B ,C ,采用整体代换思想,结合余弦函数的图象和性质即可判断;对于D ,当,42x ππ⎛⎫∈⎪⎝⎭时,确定2ππ2ππ2π,34323x ωωω⎛⎫-∈-- ⎪⎝⎭,计算π2ππ2π,4323ωω--的范围,从而确定()f x 在ππ,42⎛⎫ ⎪⎝⎭上单调性.【详解】当[]0,πx ∈时,2π2π2ππ[,333πx ω-∈--,因为()f x 在[]0,π上有且仅有4个零点,所以5π2π7ππ232ω≤-<,解得192566ω≤<,故A 正确;又由以上分析可知,函数cos y x =在2π2π[,π33ω--上有且仅有4个零点,且5π2π7ππ232ω≤-<,则在2π7π[,32-上,cos y x =出现两次最大值,此时函数cos y x =的大致图象如图示:即()y f x =在()0,π上两次出现最大值1,即2ππ3x -取0,2π时,()y f x =取最大值,故()y f x =的图象与直线1y =在()0,π上的交点恰有2个,故B 正确;由于当(0,π)x ∈时,2π2π2ππ(,)333πx ω-∈--,5π2π7ππ232ω≤-<,当2πππ3x -=-时,()y f x =取最小值1-,由于2ππ3x -是否取到3π不确定,故()y f x =的图象与直线1y =-在()0,π上的交点可能是1个或2个,故C 错误;当,42x ππ⎛⎫∈ ⎪⎝⎭时,2ππ2ππ2π,34323x ωωω⎛⎫-∈-- ⎪⎝⎭,因为192566ω≤<,所以π2π043ω->,11ππ2π17π122312ω≤-<,故π2π23ω-的值不一定小于π,所以()f x 在ππ,42⎛⎫⎪⎝⎭上不一定单调递减.故选:AB.【点睛】本题考查了复合型余弦函数的解析式中参数的确定以及零点以及最值和单调性问题,综合性强,计算量大,解答时要能综合应用三角函数的相关知识灵活解答,关键是整体代换思想的应用.三、填空题:本大题共4小题,每小题5分,共20分.13.已知函数()y f x =满足()()2f x f x +=,又当()0,1x ∈时,()21x f x =-,则21log 3f ⎛⎫= ⎪⎝⎭__________.【答案】13【解析】【分析】由()()2f x f x +=可得函数()f x 的周期为2,可得2214log log 33f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭,即可得解.【详解】由()()2f x f x +=,故函数()f x 的周期为2,()()222214log log 32log 3log 33f f f f ⎛⎫⎛⎫=-=-= ⎪ ⎪⎝⎭⎝⎭,有222log 2log 3log 4<<,即21log 32<<,故202log 31<-<,即()24log 0,13∈,故24log 32241231141log l 33og 3f f ⎝⎛⎫=-⎛⎫= ⎪=-= ⎪⎝⎭⎭.故答案为:13.14.函数()ππtan 24f x x ⎛⎫=+⎪⎝⎭的单调递增区间为___________【答案】()312,222k k k ⎛⎫-+∈ ⎪⎝⎭Z 【解析】【分析】利用正切型函数的单调性可求得函数()f x 的单调递增区间.【详解】对于函数()ππtan 24f x x ⎛⎫=+ ⎪⎝⎭,由()ππππππ2242k x k k -<+<+∈Z ,可得()312222k x k k -<<+∈Z ,所以,函数()f x 的单调递增区间为()312,222k k k ⎛⎫-+∈ ⎪⎝⎭Z .故答案为:()312,222k k k ⎛⎫-+∈ ⎪⎝⎭Z .15.若1sin 63πα⎛⎫+= ⎪⎝⎭,则5sin 26πα⎛⎫+= ⎪⎝⎭___________.【答案】79【解析】【分析】由5 sin 2sin 2626πππαα⎡⎤⎛⎫⎛⎫+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,结合诱导公式,倍角公式求解即可.【详解】2517sin 2sin 2cos 212sin 126266 699πππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=++=+=-+=-⨯ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故答案为:79【点睛】本题主要考查了诱导公式和倍角公式化简求值,属于中档题.16.借助信息技术计算()*11nn n ⎛⎫+∈ ⎪⎝⎭N 的值,我们发现当1,2,3,10,100,1000,10000,100000,n = 时11n n ⎛⎫+ ⎪⎝⎭的底数越来越小,而指数越来越大,随着n 越来越大,11nn ⎛⎫+ ⎪⎝⎭会无限趋近于e (e 2.71828= 是自然对数的底数).根据以上知识判断,当n 越来越大时,2121n n +⎛⎫+ ⎪⎝⎭会趋近于__________.【答案】4e 【解析】【分析】由422121111122n n n n n +⎡⎤⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎛⎫⎢⎥++⨯+ ⎪ ⎪ ⎪⎢⎥⎝⎭ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣=⎦,结合题意可得,当n 越来越大时,2112n n ⎛⎫ ⎪+ ⎪ ⎪⎝⎭会无限趋近于e ,12n 会无限趋近于0,即可得解.【详解】441222121111111222nnn n n n n ⨯++⎡⎤⎛⎫⎛⎫⎛⎫⎢⎥ ⎪ ⎪ ⎪⎛⎫⎢⎥+++⨯+ ⎪⎪ ⎪ ⎪⎢⎥⎝⎭⎪⎪ ⎪⎢⎥⎝⎭⎝⎭=⎝⎭⎢⎣⎦=⎥,由n 越来越大时,11nn ⎛⎫+ ⎪⎝⎭会无限趋近于e ,故n 越来越大时,2112nn ⎛⎫ ⎪+ ⎪ ⎪⎝⎭会无限趋近于e ,则42112n n ⎡⎤⎛⎫⎢⎥ ⎪⎢⎥+ ⎪⎢⎥ ⎪⎢⎥⎝⎭⎢⎥⎣⎦会无限趋近4e ,又n 越来越大时12n 会无限趋近于0,故112n +会无限趋近于1,故2121n n +⎛⎫+ ⎪⎝⎭会无限趋近于44e 1e ⨯=.故答案为:4e .【点睛】关键点睛:本题关键在于将2121n n +⎛⎫+ ⎪⎝⎭转化为42111122nn n ⎡⎤⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥+⨯+ ⎪ ⎢⎥⎪ ⎪⎢⎥⎝⎭⎝⎭⎢⎥⎣⎦,通过n 越来越大,11n n ⎛⎫+ ⎪⎝⎭会无限趋近于e ,可得n 越来越大,2112nn ⎛⎫ ⎪+ ⎪ ⎪⎝⎭亦会无限趋近于e .四、解答题:本大题共6小题,共70分.解答应写出文字说明、证明或演算步骤.17.函数()2202y sin x πϕϕ⎛⎫=+<< ⎪⎝⎭(的一条对称轴为直线12x π=).(Ⅰ)求ϕ;(Ⅱ)用五点法画出函数()22y sin x ϕ=+在5,66ππ⎡⎤-⎢⎥⎣⎦上的简图.【答案】(Ⅰ)3πϕ=;(Ⅱ)图象见解析.【解析】【分析】(Ⅰ)根据函数()22y sin x ϕ=+的一条对称轴为直线12x π=,可得2122k ⨯+=+ππϕπ,再由02πϕ<<,即可求出结果.(Ⅱ)用描点连线的方法可直接作出函数图象.【详解】(Ⅰ)因为函数()2202y sin x πϕϕ⎛⎫=+<< ⎪⎝⎭的一条对称轴为直线12x π=,所以2122k ⨯+=+ππϕπ,因此()3k k Z πϕπ=+∈,又02πϕ<<,所以3πϕ=(Ⅱ)函数223y sin x π⎛⎫=+⎪⎝⎭在5,66ππ⎡⎤-⎢⎥⎣⎦上的简图如下:【点睛】本题主要考查三角函数的图象和性质,熟记三角函数的性质即可,属于基础题型.18.已知||2a = ,||1b = ,(23)(2)17a b a b -⋅+=.(1)求a 与b的夹角和a b + 的值;(2)设2c ma b =+,2d a b =-,若c与d共线,求实数m 的值.【答案】(1)a 与b 的夹角为23π,a b += ;(2)4m =-.【解析】【分析】(1)根据(23)(2)17a b a b -⋅+=求出1a b ⋅=-,根据数量积关系求出夹角,a b += (2)根据共线定理必存在λ使得:()2,2c ma d b b a λλ=+-=,求解参数.【详解】(1)||2a =,||1b =,(23)(2)17a b a b -⋅+=,2243417a b a b --⋅=,163417a b --⋅=1a b ⋅=-,所以1cos ,2a b a b a b⋅==-⋅,所以a 与b 的夹角为23π,a b +== ;(2)由(1)可得:a 与b不共线,2c ma b =+ ,2d a b =-,若c 与d 共线,则必存在λ使得:()2,2c ma d b b a λλ=+-=,所以2,2m λλ==-,得4m =-.【点睛】此题考查向量的数量积运算,根据数量积关系求向量夹角和模长,利用平面向量基本定理结合向量共线求参数的值.19.已知函数2()2cos cos()sin cos 16f x x x x x x π=--++.(1)求()f x 的最小正周期和最大值;(2)将()f x 的函数图像向左平移ϕ(0)ϕ>个单位后得到的函数()g x 是偶函数,求ϕ的最小值.【答案】(1)T π=,()max 3f x =(2)12π【解析】【分析】(1)首先化简()2sin 213f x x π⎛⎫=++ ⎪⎝⎭,再求函数的周期和最大值;(2)平移后的函数()sin(22)13g x x πϕ=+++,若函数是偶函数,则0x =是函数的对称轴,求参数的取值范围。
2022-2023学年湖南省株洲市高一年级上册学期期末数学试题【含答案】

2022-2023学年湖南省株洲市第二中学高一上学期期末数学试题一、单选题1.已知集合,则的子集的个数是( )51,N M x x x +⎧⎫=>∈⎨⎬⎩⎭M A .15B .8C .7D .16【答案】D【分析】根据不等式的性质,结合子集个数公式进行求解即可.【详解】因为,所以由,N x +∈{}51551,2,3,4x x M x >⇒>⇒<⇒=所以的子集的个数是,M 4216=故选:D2.已知,,则“”是“”的( )a b ∈R 1>a b a b >A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】D【分析】由条件结合充分条件和必要条件的定义判断.【详解】当时,若,则,故充分性不成立.1>a b 0b <a b <当时,若,则 ,故必要性不成立,a b >0b <1a b <所以“”是“”的既不充分又不必要条件.1>a b a b >故选:D3.中国传统文化中很多内容体现了数学的“对称美”.如图所示的太极图是由黑白两个鱼形纹组成的圆形图案,充分体现了相互变化、对称统一的形式美、和谐美.给出定义:能够将以坐标原点O 为圆心的圆的周长和面积同时平分的函数称为此圆的“优美函数”,则下列函数中一定是“优美函数”的为( )A .B .22y x x =-cos y x=C .D .sin y x =1y x x=-【答案】C【分析】根据题意可知优美函数的图像过坐标原点,图像关于坐标原点对称,是奇函数,再分别检验四个选项即可得出正确选项.【详解】根据优美函数的定义可知,优美函数的图像过坐标原点,图像关于坐标原点对称,是奇函数,对于A ,不是奇函数,A 选项错误;22y x x =-对于B ,不是奇函数,B 选项错误;cos y x =对于C ,的定义域为,且是奇函数,C 项正确;sin y x =R 对于D ,的定义域为,所以图像不经过坐标原点,D 选项错误;1y x x =-{}0x x ≠故选:C .4.已知函数的定义域为( )()f x =()()2f x f x -+A .B .C .D .[)0,∞+[]4,0-[]0,2[]0,4【答案】C【分析】根据二次根式的性质,结合复合函数的定义域性质进行求解即可.【详解】由,()24022f x x x =⇒-≥⇒-≤≤于是有,2202222x x x -≤≤⎧⇒≤≤⎨-≤-≤⎩故选:C5.下列函数中,以为最小正周期且在区间上单调递减的是( )ππ0,2⎛⎫⎪⎝⎭A .B .C .D .sin 2y x =cos y x=tan y x=cos2x y =【答案】B【分析】根据三角函数的最小正周期、单调性对选项进行分析,从而确定正确选项.【详解】A 选项,对于函数,由得,sin 2y x =π02x <<02πx <<所以不满足“区间上单调递减”,A 选项错误.sin 2y x =π0,2⎛⎫ ⎪⎝⎭B 选项,对于函数,根据函数的图象可知,函数的最小正周期为,cos y x=cos y x=π且函数在区间上单调递减,符合题意,B 选项正确.π0,2⎛⎫⎪⎝⎭C 选项,对于函数,其在区间上单调递增,不符合题意,C 选项错误.tan y x =π0,2⎛⎫ ⎪⎝⎭D 选项,对于函数,最小正周期,不符合题意,D 选项错误.cos2xy =2π4π12T ==故选:B6.函数的部分图象大致为( )2sin ()||2xfx x =+A.B .C .D .【答案】B【分析】根据奇偶性及函数值的正负判断即可.【详解】因为,定义域为R2sin ()2x f x x =+所以2sin()2sin ()()22x xf x f x x x --==-=--++所以为奇函数,且,排除CD ()f x (0)0f =当时,,即,排除A()0,x π∈sin 0x >()0f x >故选:B.7.若,,,则、、的大小关系为( )0.7e a =πlog 3b =22πlog sin3c =a b c A .B .C .D .b c a >>b a c >>c a b>>a b c>>【答案】D【分析】借助中间量比较大小即可.0,1【详解】解:由题知,,0.70e e 1a =>=ππ0log 3log π1b b <=<==,2222πlog sinlog log 103c c ===<=所以,即.01c b a <<<<a b c >>故选:D8.函数 ,若互不相等,且,则的取值2sin π(01)()lg (1)x x f x x x ≤≤⎧=⎨>⎩a b c 、、()()()f a f b f c ==a b c ++范围是( )A .B .C .D .()1,100()1,11()2,101[]2,11【答案】C【分析】先利用三角函数、对数函数的图像和性质,画出函数的图像,再利用图像数形结合即()f x 可发现、、间的关系和范围,最后求得所求范围.a b c 【详解】函数的图像如图所示:()fx 设,由函数图像数形结合可知:,a b c <<1212a b +=⨯=,0lg 2c <<1100c ∴<<.2101a b c ∴<++<故选:C .二、多选题9.已知,则下列不等式一定成立的是( )33log log a b >A .B .110b a<<()3log 0a b ->C .D .31a b->1132a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭【答案】CD【分析】先求得的关系式,然后对选项逐一分析,从而确定正确答案.,a b 【详解】由于,所以,33log log a b >0a b >>A 选项,由于,所以,所以A 选项错误.0a b >>110a b <<B 选项,当时,,所以B 选项错误.2,1a b ==()33log log 10a b -==C 选项,由于,所以,所以C 选项正确.,0a b a b >->0331a b->=D 选项,在上递减,,所以,所以D 选项正确.13xy ⎛⎫= ⎪⎝⎭R 0a b >>1132ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭故选:CD10)A .B .7πtan3πππ3π2sin cos cos sin 124124⎛⎫+ ⎪⎝⎭C .D .1tan151tan15+︒-︒cos15︒︒【答案】ABC【分析】根据诱导公式,结合两角和的正弦公式、正切公式逐一判断即可.【详解】对于A ,A 正确;7πππtantan 2πtan 333⎛⎫=+== ⎪⎝⎭对于B ,,故B正确:πππ3ππππππ2sin cos cos sin 2sin cos cos sin 2sin 1241241241243⎛⎫⎛⎫+=+== ⎪ ⎪⎝⎭⎝⎭对于C ,,故C 正确;()1tan15tan45tan15tan 4515tan601tan151tan45tan15+︒︒+︒==︒+︒=︒=-︒-︒︒对于D,1cos152cos152⎛⎫︒︒=︒︒ ⎪ ⎪⎝⎭,故D 错误;()()2sin30cos15cos30sin152sin 30152sin15=︒︒-︒︒=︒-︒=︒≠故选:ABC 11.设函数())()()2sin 2x x f ϕ=+π2ϕ≤()0f =A .的最小正周期为B .的图象关于直线对称()f x π()f x 5π12x =C .在上的最小值为D .的图象关于点对称()f x π,π2⎡⎤⎢⎥⎣⎦1-()f x 2π,03⎛⎫⎪⎝⎭【答案】ABD【分析】根据正弦型函数的周期公式、对称性、最值逐一判断即可.【详解】∵∴,又,∴,∴;()02sin f ϕ==sin ϕ=π2ϕ≤π3ϕ=-()π2sin 23f x x ⎛⎫=- ⎪⎝⎭对于A ,的最小正周期,A 正确;()f x 2ππ2T ==对于B ,因为,所以的图象关于直线对称,B 正确;5π5ππ2sin 2212123f ⎛⎫⎛⎫=⨯-= ⎪ ⎪⎝⎭⎝⎭()f x 5π12x =对于C ,当时,,则当,即时,,C 错π,π2x ⎡⎤∈⎢⎥⎣⎦π2π5π2,333x ⎡⎤-∈⎢⎥⎣⎦π3π232x -=11π12x =()min 2f x =-误;对于D ,当时,,此时,∴的图象关于点对称,D 正确.2π3x =π2π3x -=()0f x =()f x 2π,03⎛⎫ ⎪⎝⎭故选:ABD12.已知函数对都有,且函数的图像关于点对称,()f x x ∀∈R ()()2f x f x +=-()1y f x =-()1,0当时,,则下列结论正确的是( )(]0,1x ∈()21x f x =-A .B .在区间上单调递减()20220f =()f x ()7,9C .是上的奇函数D .函数有6个零点()f x R ()log y f x x=-【答案】ACD【分析】先分析清楚函数的单调性,对称性和周期性,再逐项分析.()f x 【详解】对都有,则,x ∀∈R ()()2f x f x +=-()()()42f x f x f x +=-+=即函数是周期函数,周期为4;()f x 令,依题意有,即,()()1g x f x =-()()2g x g x -=-()()()2111f x f x f x --=-=--令 ,则有 ,所以是奇函数,,C 正确;1t x =-()()f t f t =--()f x ()00f =又,令 ,则有,()()()2f x f x f x +=-=-t x =-()()2f t f t -=关于直线 对称;()f x 1x =当时,,当时,,(]0,1x ∈()21x f x =-[)1,0x ∈-()()2112x xf x --=--=-对于A ,,A 正确;()()()()202250542200f f f f =⨯+==-=对于B ,因函数在上递增,函数的周期为4,则在上递增,B 错误;()f x []1,1-()f x ()f x ()7,9对于D ,函数的零点,即函数与图像交点的横坐标,()lg y f x x =-()y f x =lg y x=在同一坐标系内作出函数与的部分图像,如图,()y f x =lg y x=因函数的最大值为1,而当时,,因此函数与图像的交点在()y f x =10x >lg 1x >()y f x =lg y x=内,()0,10观察图像知,函数与图像在内只有6个交点,所以函数有6()y f x =lg y x=()0,10()lg y f x x =-个零点,D 正确;故选:ACD.三、填空题13.函数的图象恒过定点P ,P 在幂函数的图象上,则___________.()log 238a y x =-+()f x ()4f =【答案】64【分析】由题意可求得点,求出幂函数的解析式,从而求得.()2,8P ()f x ()4f 【详解】令,则,故点;2x =8y =()2,8P 设幂函数,()bf x x =则,28b=则;3b =故;()464f =故答案为:64.14.若正实数、,满足,则的最小值为______.a b lg lg 1a b +=52a b +【答案】2【分析】求得的关系式,然后结合基本不等式求得正确答案.,a b 【详解】正数满足,,a b lg lg lg 1,10a b ab ab +===所以,当且仅当时等号成立.522a b +≥=52,,5,2a b a b ===故答案为:215.已知______.πcos 3α⎛⎫-= ⎪⎝⎭2πsin c 63πos αα⎛⎫⎛⎫+++= ⎪ ⎪⎝⎭⎝⎭【答案】0【分析】根据诱导公式进行求解即可.【详解】2πππππsin cos sin cos πcos cos 0,63233π3π3αααααα⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++=-++-+=---= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭故答案为:0四、双空题16.已知函数(,)在区间上单调,且满足()()sin f x x ωϕ=+0ω>Rϕ∈75,126ππ⎛⎫ ⎪⎝⎭.74π12π3f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭(1)若,则函数的最小正周期为______.()56πf x f x ⎛⎫-= ⎪⎝⎭()f x (2)若函数在区间上恰有5个零点,则的取值范围为______.()f x 213,36ππ⎡⎫⎪⎢⎣⎭ω【答案】 π833ω<≤【分析】(1)由题可得对称中心,根据三角函数的性质结合条件判断的大概取值范围,再()f x ω结合条件可得函数的对称轴即可得到的值从而得出最小正周期;ω(2)根据函数的对称中心及的大概取值范围,结合三角函数的图象可得ω,从而解出.2π13π2π523632T T +<≤+【详解】因为函数在区间上单调,且满足,()()sin f x x ωϕ=+75,126ππ⎛⎫⎪⎝⎭74π12π3f f ⎛⎫⎛⎫=- ⎪ ⎪⎝⎭⎝⎭∴对称中心为,()f x 2π,03⎛⎫⎪⎝⎭代入可得,,①12ππ3k ωϕ+=1k Z ∈∵在区间上单调,且对称中心为,()f x 75,126ππ⎛⎫⎪⎝⎭()f x 2π,03⎛⎫ ⎪⎝⎭又∵,,5π2ππ636-=2πππ7π36212-=<∴在区间上单调,()f x π5π,26⎛⎫⎪⎝⎭∴, ,即,5πππ2623T ≥-=23T π≥2π2π3ω≥∴.03ω<≤(1)∵,()56πf x f x ⎛⎫-= ⎪⎝⎭∴关于对称,代入可得,,②()f x 5π12x =2π5ππ122k ωϕ+=+2k Z∈①-②可得,,即,,又,πππ42k ω=-+Z k ∈24k ω=-+Z k ∈03ω<≤∴,;2ω=2ππT ω==(2)∵对称中心为,∴,()f x 2π,03⎛⎫⎪⎝⎭20π3f ⎛⎫= ⎪⎝⎭∵在区间上恰有5个零点,()f x 213,36ππ⎡⎫⎪⎢⎣⎭∵相邻两个零点之间的距离为,五个零点之间即,六个零点之间即,()f x 2T2T 52T ∴只需即可,2π13π2π523632T T +<≤+所以,又∵,81033ω<≤03ω<≤∴.833ω<≤故答案为:;.π833ω<≤五、解答题17.计算:(1);2323272e log 3log 88⎛⎫+-⨯ ⎪⎝⎭(2)()()sin 120cos210cos 300sin150-︒⋅+-︒⋅︒︒【答案】(1);54(2)1.【分析】(1)根据指数幂的运算性质,结合对数换底公式进行求解即可;(2)根据诱导公式,结合两角和正弦公式进行求解即可.【详解】(1);2323279lg3lg8952e log 3log 822384lg2lg344⎛⎫+-⨯=+-⨯=+-= ⎪⎝⎭(2).()()()()sin 120cos210cos 300sin150sin60cos30cos60sin30sin 6030sin901-︒⋅︒+-︒⋅︒=-︒⋅-︒+︒⋅︒=︒+︒=︒=18.已知全集,集合,.U =R 11282x A x +⎧⎫=<<⎨⎬⎩⎭{}3221B x a x a =-<<+(1)当时,求;1a =()U A B ⋃ (2)若,求的取值范围.A B B = a 【答案】(1)或{2x x <}3x ≥(2)[)10,3,2⎡⎤⋃+∞⎢⎥⎣⎦【分析】(1)先求出集合、,进而求出,再根据集合间的并集运算即可;A B U B (2)由可得,分和两种情况讨论即可求解.A B B = B A ⊆B =∅B ≠∅【详解】(1)由,所以,即,113222x -+<<113x -<+<22x -<<所以,{}22A x x =-<<当时,,全集,1a ={}13B x x =<<U =R 所以或,{1U B x x =≤ }3x ≥所以或.(){2U A B x x ⋃=< }3x ≥(2)因为,所以,A B B = B A ⊆当时,满足,所以,解得;B =∅B A ⊆3221a a -≥+3a ≥当时,则,解得.B ≠∅3221322212a a a a -<+⎧⎪-≥-⎨⎪+≤⎩102a ≤≤综上所述,的取值范围是.a [)10,3,2⎡⎤⋃+∞⎢⎥⎣⎦19.已知,.()()ππ6cos sin 2282cos π3sin παααα⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭=---+π0,4α⎛⎫∈ ⎪⎝⎭(1)求的值;tan α(2)若,且的值.π0,2β⎛⎫∈ ⎪⎝⎭πcos 4β⎛⎫+= ⎪⎝⎭αβ+【答案】(1)1tan 2α=(2)π4αβ+=【分析】(1)根据诱导公式化简整理,上下同除,计算即可得答案.cos α(2)根据题意及的范围,可求得的值,根据两角差的余弦公式,βsin 4πβ⎛⎫+ ⎪⎝⎭可得的值,进而可得的值,根据两角和的正切公式,可得的值,即可得答案.cos βtan βtan()αβ+【详解】(1)∵,()()ππ6cos sin 2282cos π3sin παααα⎛⎫⎛⎫-++ ⎪ ⎪⎝⎭⎝⎭=---+∴,解得.6sin cos 6tan 182cos 3sin 23tan αααααα++==--+-+1tan 2α=(2)∵,∴,且π0,2β⎛⎫∈ ⎪⎝⎭ππ3π444β<+<πcos 4β⎛⎫+= ⎪⎝⎭∴,πsin 4β⎛⎫+= ⎪⎝⎭∴ππcos cos 44ββ⎡⎤⎛⎫=+-== ⎪⎢⎥⎝⎭⎣⎦∴,sin β=1tan 3β=∴,()11tan tan 23tan 1111tan tan 123αβαβαβ+++===--⨯又∵,∴.3π0,4αβ⎛⎫+∈ ⎪⎝⎭π4αβ+=20.已知函数.()πcos2cos 213f x x x ⎛⎫=-++ ⎪⎝⎭(1)求函数的最小正周期、单调增区间及对称中心;()f x (2)求函数在上的值域.()f x π02⎛⎫ ⎪⎝⎭,【答案】(1);,;,ππππ,π36k k ⎡⎤-+⎢⎥⎣⎦Z k ∈ππ,1212k ⎛⎫- ⎪⎝⎭Z k ∈(2)1,22⎛⎤ ⎥⎝⎦【分析】(1)先化简函数,可得,再结合正弦函数的性质求解即可;()f x ()πsin 216f x x ⎛⎫=++ ⎪⎝⎭(2)根据正弦函数的性质求解即可.【详解】(1),()πππ1cos2cos 2cos2cos2cos sin2sin cos 213332f x x x x x x x x ⎛⎫=-+=-+=+ ⎪⎝⎭即.()πsin 216f x x ⎛⎫=++ ⎪⎝⎭所以函数的最小正周期.()f x 2ππ2T ==令,,即,πππ2π22π262k x k -≤+≤+Z k ∈ππππ36k x k -≤≤+Zk ∈所以的单调递增区间,.()f x πππ,π36k k ⎡⎤-+⎢⎥⎣⎦Z k ∈令,,解得,π2π6x k +=Z k ∈ππ212k x =-所以对称中心为,.ππ,1212k ⎛⎫- ⎪⎝⎭Z k ∈(2)由(1)知:,()πsin 216f x x ⎛⎫=++ ⎪⎝⎭当,,即,π0,2x ⎛⎫∈ ⎪⎝⎭ππ7π2,666x ⎛⎫+∈ ⎪⎝⎭π1sin 2,162x ⎛⎫⎛⎤+∈- ⎪ ⎥⎝⎭⎝⎦所以在上的值域为.()f x π0,2⎛⎫ ⎪⎝⎭1,22⎛⎤ ⎥⎝⎦21.已知函数为奇函数,.()221x f x a =++R a ∈(1)求的值;a (2)判断函数的单调性,并用单调性的定义证明;()f x (3)若存在,不等式有解,求实数的取值范围.[]2,1x ∈--()()210f x f x t -++<t 【答案】(1);1a =-(2)在上单调递减,证明见解析;()f x R (3).()1,-+∞【分析】(1)根据奇函数的性质,求出参数的值,再代入检验即可;()00f =a (2)根据指数函数的单调性结合条件可得函数的单调性,再利用定义法证明即得;(3)根据函数的奇偶性与单调性得到在有解,然后根据二次函数的性质即21t x x >--+[]2,1x ∈--得.【详解】(1)因为的定义域为R ,又为奇函数,()221x f x a =++()f x 所以,即,解得,()00f =02021a +=+1a =-所以,()21212121xx x f x -=-+=++则,()()12212121x x x x f x f x -----===-++所以为奇函数,()2121x f x =-++故;1a =-(2)在R 上单调递减,()f x 证明:设任意的,且,1x 2R x ∈12x x <所以,()()()()()2112212112222222211212121212121x x x x x x x x f x f x -⎛⎫-=---=-= ⎪++++++⎝⎭又因为,在上单调递增,12x x <2x y =R 所以,即,且,1222x x <21220x x ->()()1221210x x ++>所以,即,()()120f x f x ->()()12f x f x >所以在上单调递减;()f x R (3)因为是定义在上的奇函数,()f x R 所以,()()()()22101f x f x t f x t f x -++<⇒+<-因为函数在上单调递减,()f x R 所以,21x t x +>-因为存在,不等式有解,[]2,1x ∈--()()210f x f x t -++<即在有解,21t x x >--+[]2,1x ∈--因为,[]221511,124x x x ⎛⎫--+=-++∈- ⎪⎝⎭所以,1t >-即实数的取值范围为.t ()1,-+∞22.函数,,记,且为偶函数.()()4log 41x f x =+()()1g x k x =-()()()F x f x g x =-()F x (1)求常数的值;k (2)若对一切,不等式恒成立,求实数的取值范围;a ∈R ()12F a m >-m (3)设,若函数与的图象有且只有一个公共点,求实数的取值()44log 23x M x a a ⎛⎫=⋅- ⎪⎝⎭()F x ()M x a 范围.【答案】(1)32k =(2)1m >-(3){}()31,-⋃+∞【分析】(1)根据偶函数的定义,即可求出常数的值;k (2)将不等式恒成立,转化为恒成立,利用换元法和基本不等式求()12F a m >-()424log 41a a m >+出的最大值,即可得实数的取值范围;()424log 41a a +m (3)将函数与的图象有且只有一个公共点,转化为()F x ()M x 仅有一解,设,依题意只有()444log 41log 223x x x a a ⎛⎫+-=⋅- ⎪⎝⎭20x t =>()()241103h t a t at =---=一个正实根,分类讨论a 的不同情况,即可求出实数的取值范围.m 【详解】(1)由题意可知,,,()()()4log 411x F x k x =+--x ∈R 为偶函数,,()F x ()()F x F x ∴-=即,()()()()44log 411log 411x x k x k x -++-=+--,()()()()44log 411log 411x x x k x k x +-+-=+--,,()230k x ∴-=x ∈R .32k ∴=(2)由(1)得,()()4log 412x x F x =+-条件,即:,()12F a m >-()41log 4122a a m +->-,()()24424log 41log 41a a a m a >-+=+设,()4a t a =∈R 0t ∴>令,444211log log log 112142t U t t t t ==≤=-++++当且仅当,即时等式成立,1t t =1t =,max 1U ∴=-即;1m >-(3)依题意:,即仅有一解,()()M x F x =()444log 41log 223x x x a a ⎛⎫+-=⋅- ⎪⎝⎭则44414log log 223x x x a a +⎛⎫=⋅- ⎪⎝⎭即,故4142234203x x x x a a a a ⎧+=⋅-⎪⎪⎨⎪⋅->⎪⎩()()24122103x x a a --⋅-=设,依题意只有一个正实根.20x t =>()()241103h t a t at =---=当时,,1 1a =()4103h t t =--=(舍)34t ∴=-当时,方程有一正根,一负根,2 1a >()()241103h t a t at =---=由,得.10(0)10a h ->⎧⎨=-<⎩1a >当时,方程有两个相等的正根.3 1a <()()241103h t a t at =---=由,得,21016Δ4(1)09a a a -<⎧⎪⎨=+-=⎪⎩214990a a a <⎧⎨+-=⎩即,()()4330a a -+=其中,当时,符合题意;当时,不符合题意.3a =-12t =34a =2t =-综上所述,实数的取值范围是a {}()31,-⋃+∞【点睛】分类讨论思想是高中数学一项重要的考查内容.分类讨论思想要求在不能用统一的方法解决问题的时候,将问题划分成不同的模块,通过分块来实现问题的求解,体现了对数学问题的分析处理能力和解决能力.。
湖南省长沙市2021-2022学年度高一数学第一学期期末考试【含答案】

;
对于B:原式= ;
对于C:原式= ;
对于D:原式= .
故选:ABD
【点睛】本题考查了两角和的正弦公式,知函数 ,则下列说法中正确的是()
A. 的最小正周期为 B. 在 上单调递增
C.曲线 关于 对称D.曲线 关于 对称
【答案】ABC
∴ ,∴ ,
∴ .
故选:B.
7.若 ,则 ()
A. B. C. D.
【答案】C
【解析】
【分析】将式子先利用二倍角公式和平方关系配方化简,然后增添分母( ),进行齐次化处理,化为正切的表达式,代入 即可得到结果.
【详解】解:因为 ,所以将式子进行齐次化处理得:
.
故选:C.
8.已知 ( ), ( ),则p,q的大小关系为()
因此 .
故答案为:
18.酒驾是严重危害交通安全的违法行为.为了保障交通安全,根据国家有关规定∶100mL血液中酒精含量达到20~79mg的驾驶员即为酒后驾车,80mg及以上认定为醉酒驾车.假设某驾驶员喝了一定量的酒后,其血液中的酒精含量上升到1mg/mL.如果在停止喝酒以后,他血液中酒精含量会以每小时30%的速度减少,那么他至少经过_____小时才能驾驶.(注∶不足1小时,按1小时计算,如计算结果为7.3,就答8小时)
故函数 的图象过定,点 ,故A正确;
根据方程 有两个实数根,可得 ,即 ,
故 是方程 有两个实数根的必要不充分条件,故B错误;
∵ 的反函数是 ,∴ ,故C错误;
若 在区间 上为减函数,
则 在区间 上大于零,且 ,
即 且 ,求得 ,故D正确,
故选:AD.
三、填空题(共5道小题,每小题3分,共15分)
16.命题“ , ”的否定是___________.
湖南省怀化市2022-2023学年高一上学期期末数学试题(1)

怀化市中小学课程改革教育质量监测试题2023年下期期末考试高一数学一,单选题:本大题共8小题,每小题5分,共计40分,在每小题给出地四个选项中,只有一项符合题目要求,请把正确结果地代号填涂在答题卡上.1. 已知集合{}{}1,2,3,4,5,2,4,6,8A B ==,则A B = ( )A. {}2 B. {}4 C. {}2,4 D. {}2,4,6【结果】C 【思路】【思路】依据集合地交集运算法则计算即可.【详解】因为集合{}{}1,2,3,4,5,2,4,6,8A B ==,所以{}2,4A B = .故选:C2. 命题“sin 1x R x ∀∈<,”地否定是( )A. 00,sin 1x R x ∃∈≥ B. 00,sin 1x R x ∃∈<C. 0,sin 1x R x ∀∈≥ D. 0,sin 1x R x ∀∈<【结果】A 【思路】【思路】依据全称命题地否定地写法可得结果.【详解】命题“sin 1x R x ∀∈<,”地否定是00,sin 1x R x ∃∈≥,故结果为:A.3. 函数()()ln 2f x x =+-地定义域是( )A. [)1,2B. []1,2 C. (),2-∞ D. [)1,+∞【结果】A 【思路】【思路】依据被开方数不小于零,对数真数大于零列不等式组得解.【详解】由题可知:1020x x -≥⎧⎨->⎩,解得12x ≤<,所以函数()()ln 2f x x =+-地定义域是[)1,2.故选:A.4. “12x -<”是“03x <<”成立地( )A. 充分不必要款件 B. 必要不充分款件C. 充分必要款件 D. 既不充分也不必要款件【结果】B 【思路】【思路】解出不等式,进而依据不等式所对应集合间地关系即可得到结果.【详解】由1213x x -<⇒-<<,而{}|03x x <<是{}|13x x -<<地真子集,所以“12x -<”是“03x <<”成立地必要不充分款件.故选:B.5. 若一个扇形地半径为2,圆心角为45 ,则该扇形地弧长等于( )A.4πB.2πC. 45πD. 90π【结果】B 【思路】【思路】求圆心角地弧度数,再由弧长公式求弧长.【详解】∵圆心角为45 ,∴ 圆心角地弧度数为4π,又扇形地半径为2,∴ 该扇形地弧长242l ππ=⨯=,故选:B .6. 要得到函数()sin 2(R)f x x x =∈地图像,只需将函数()sin 2()6g x x x R π⎛⎫=-∈ ⎪⎝⎭图地图像A. 向右平移6π个单位 B. 向右平移12π个单位C. 向左平移6π个单位 D. 向左平移12π个单位【结果】D依据三角函数图像变换地知识,直接选出正确选项.【详解】依题意()πsin 212g x x ⎛⎫⎛⎫=-⎪ ⎪⎝⎭⎝⎭,故向左平移12π个单位得到ππsin 2sin 21212x x ⎡⎤⎛⎫+-= ⎪⎢⎥⎝⎭⎣⎦,故选D.【点睛】本小题主要考查三角函数图像变换地知识,属于基础题.7. 缪天荣()19142005-,浙江人,著名眼科专家,我国眼视光学地开拓者.上世纪50年代,我国使用“国际标准视力表”检测视力,采用“小数记录法”记录视力数据,缪天荣发现其中存在不少缺陷.经过3年苦心研究,1958年,他成功研制出“对数视力表”及“5分记录法”.这是一种既符合视力生理又便于统计和计算地视力检测系统,使中国地眼视光学研究站在了世界地巅峰.“5分记录法”将视力L 和视角α(单位:')设定为对数关系:5lg L α=-.如图,标准对数视力表中最大视标E 地视角为10',则对应地视力为5lg10 4.0L =-=.若小明能看清地某行视标E 地大小是最大视标E 地14(相应地视角为2.5′),取lg 20.3=,则其视力用“5分记录法”记录( )A. 3.6B. 4.3C. 4.6D. 4.7【结果】C 【思路】【思路】将 2.5α=代入5lg L α=-,求出L 地值,即可得解.【详解】将 2.5α=代入函数思路式可得105lg 2.55lg 5lg10lg 442lg 2 4.64L =-=-=-+=+≈.故选:C.8. 定义在R 上地奇函数()f x ,满足()()()422f x f x f ++=,则()20221f +=( )A. 2- B. 1- C. 0D. 1【思路】由2x =-得出()20f =,再结合周期性得出函数值.【详解】()()()2222f f f +-=Q ,()()22f f -=-,∴()20f =即(4)()f x f x +=-,(4)(8)f x f x -+=+,则()(8)f x f x =+(2022)1(82526)1(6)1(2)11f f f f ∴+=⨯++=+=-+=故选:D二,多项选择题:本大题共4小题,每小题5分,共20分.在每小题给出地四个选项中,有多项是符合题目要求地,全部选对地得5分,部分选对地得2分,有选错地得0分.9. 下面函数中,在()0,∞+上单调递增地有( )A. 1y x -= B. x y e =C. 2log y x = D. 2y x x=-【结果】BC 【思路】【思路】依据初等函数地性质逐项判断可得正确选项.【详解】函数1y x -=在()0,∞+上单调递减,A 错,函数xy e =在()0,∞+上单调递增,B 对,函数2log y x =()0,∞+上单调递增,C 对,函数2y x x =-在10,2⎛⎫ ⎪⎝⎭上单调递减,D 错,故选:BC.10. 集合201x A xx ⎧⎫-=<⎨⎬+⎩⎭也可以写成( )A. ()(){}210x x x -+< B. 102x xx ⎧⎫+<⎨⎬-⎩⎭C. {1x x <-或}2x > D. ()1,2-【结果】ABD在【思路】先将题中集合A 化为最简形式,再将选项中各集合化简并与题中集合A 比较即可.【详解】对于集合A ,解不等式201x x -<+,即()()21010x x x ⎧-+<⎨+≠⎩,解得12x -<<,所以{}12A x x =-<<.对于A 选项,()(){}{}21012x x x x x -+<=-<<,故A 正确。
2022-2023学年湖南省永州市高一上学期期末数学试题(解析版)

故选:C.
6.玉雕在我国历史悠久,玉雕是采用传统的手工雕刻工艺加工生产成的玉雕工艺.某扇环形玉雕(扇环是一个圆环被扇形截得的一部分)尺寸(单位:cm)如图所示,则该玉雕的面积为()
A. B. C. D.
【答案】A
【解析】
【分析】利用扇形的面积公式,利用大扇形面积减去小扇形面积即可得解.
【详解】如图,设 , ,
13.已知幂函数 的图象过点 ,则 _________.
【答案】
【解析】
【分析】设幂函数 ,根据题意,幂函数 的图象过点 ,代入计算即可求解.
【详解】设函数 ,又因为幂函数 的图象过点 ,
所以 ,解得: ,所以函数 ,
故答案为: .
14.已知 且 ,则 的最小值为________.
【答案】4
【解析】
【分析】
将 代入 中,结合基本不等式即可得解.
【详解】
当且仅当 ,即 时取等
的最小值为4
故答案为:4.
【点睛】本题考查基本不等式的应用,注意“1”的灵活应用和不等式成立的条件.
【详解】全称命题的否定为存在命题,命题 : , ,
则 为 , .
故选:A.
5.已知 , , ,则()
A. B.
C. D.
【答案】C
【解析】
【分析】根据指数函数、对数函数的单调性以及中间值确定 的范围,进行比较即可.
【详解】根据指数函数、对数函数的性质,
由 单调递减可知:
由 单调递减可知:
由 单调递减可知:
1.设集合 , ,则 ()
A. B. C. D.
【答案】D
【解析】
【分析】根据并集概念计算即可.
【详解】 .
故选:D
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南师大附中度高一第一学期期末考试数 学时量:120分钟 满分:150分得分:____________第Ⅰ卷(满分100分)一、选择题:本大题共11小题,每小题5分,共55分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知两点A(a ,3),B(1,-2),若直线AB 的倾斜角为135°,则a 的值为A .6B .-6C .4D .-42.对于给定的直线l 和平面a ,在平面a 内总存在直线m 与直线lA .平行B .相交C .垂直D .异面3.已知直线l 1:2x +3my -m +2=0和l 2:mx +6y -4=0,若l 1∥l 2,则l 1与l 2之间的距离为 A .55B .105C .255D .21054.已知三棱锥P -ABC 的三条侧棱PA 、PB 、PC 两两互相垂直,且PA =2,PB =3,PC =3,则这个三棱锥的外接球的表面积为A .16πB .32πC .36πD .64π5.圆C 1:x 2+y 2-4x -6y +12=0与圆C 2:x 2+y 2-8x -6y +16=0的位置关系是A .内含B .相交C .内切D .外切6.设α,β是两个不同的平面,m ,n 是两条不同的直线,则下列命题中正确的是A .若m∥n,m ⊂β,则n∥βB .若m∥α,α∩β=n ,则m∥nC .若m⊥β,α⊥β,则m∥αD .若m⊥α,m ⊥β,则α∥β7.在空间直角坐标系O -xyz 中,一个四面体的四个顶点坐标分别为A(0,0,2),B(2,2,0),C(0,2,0),D(2,2,2),画该四面体三视图中的正视图时,以xOz 平面为投影面,则四面体ABCD 的正视图为8.若点P(3,1)为圆(x -2)2+y 2=16的弦AB 的中点,则直线AB 的方程为A .x -3y =0B .2x -y -5=0C .x +y -4=0D .x -2y -1=09.已知四棱锥P -ABCD 的底面为菱形,∠BAD =60°,侧面PAD 为正三角形,且平面PAD⊥平面ABCD ,则下列说法中错误的是A .异面直线PA 与BC 的夹角为60°B .若M 为AD 的中点,则AD⊥平面PMBC .二面角P -BC -A 的大小为45°D .BD ⊥平面PAC10.已知直线l 过点P(2,4),且与圆O :x 2+y 2=4相切,则直线l 的方程为A .x =2或3x -4y +10=0B .x =2或x +2y -10=0C .y =4或3x -4y +10=0D .y =4或x +2y -10=011.在直角梯形BCEF 中,∠CBF =∠BCE=90°,A 、D 分别是BF 、CE 上的,AD ∥BC ,且AB =DE =2BC =2AF ,如图1.将四边形ADEF 沿AD 折起,连结BE 、BF 、CE ,如图2.则在折起的过程中,下列说法中错误的是A .AC ∥平面BEFB .直线BC 与EF 是异面直线C .若EF⊥CF,则平面ADEF⊥平面ABCD D .平面BCE 与平面BEF 可能垂直答题卡12.若直线l :x -y +1=0与圆C :(x -a)2+y 2=2有公共点,则实数a 的取值范围是____________. 13.已知一个圆柱的底面直径和母线长都等于球的直径,记圆柱的体积为V 1,球的体积为V 2,则V 1V 2=________.14.已知三棱锥P -ABC 的体积为10,其三视图如图所示,则这个三棱锥最长的一条侧棱长等于________.三、解答题:本大题共3个小题,共30分.解答应写出文字说明,证明过程或演算步骤.15.(本小题满分8分)已知△ABC的三个顶点的坐标分别为A(3,0),B(4,6),C(0,8).(1)求BC边上的高所在直线l的方程;(2)求△ABC的面积.16.(本小题满分10分)已知圆C经过A(-2,1),B(5,0)两点,且圆心C在直线y=2x上.(1)求圆C的标准方程;(2)设动直线l:(m+2)x+(2m+1)y-7m-8=0与圆C相交于P,Q两点,求|PQ|的最小值.17.(本小题满分12分)如图,在三棱柱ABC -A 1B 1C 1中,A 1A ⊥平面ABC ,AB ⊥AC ,AB =AC =AA 1,D 为BC 的中点. (1)证明:A 1B ⊥平面AB 1C;(2)求直线A 1D 与平面AB 1C 所成的角的大小.第Ⅱ卷(满分50分)一、本大题共2个小题,每小题6分,共12分.18.已知集合M =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x|2x <1,N ={y|y =lg (x 2+1)},则N∩∁R M =______.19.已知函数f (x )在定义域R 上单调递减,且函数y =f (x -1)的图象关于点A (1,0)对称.若实数t 满足f (t 2-2t )+f (-3)>0,则t -1t -3的取值范围是( ) A.⎝ ⎛⎭⎪⎫12,+∞ B.⎝ ⎛⎭⎪⎫-∞,12 C.⎝ ⎛⎭⎪⎫0,23 D.⎝ ⎛⎭⎪⎫12,1∪(1,+∞) 二、本大题共3个大题,共38分.20.(本小题满分12分)如图,四棱锥S -ABCD 的底面是正方形,每条侧棱的长都是底面边长的2倍,P 为侧棱SD 上的点. (1)求证:AC⊥SD;(2)若SD⊥平面PAC ,侧棱SC 上是否存在一点E ,使得BE∥平面PAC ?若存在,求SE∶EC 的值;若不存在,试说明理由.设函数f(x)=mx2-mx-1,g(x)=f(x)x-1.(1)若对任意x∈[1,3],不等式f(x)<5-m恒成立,求实数m的取值范围;(2)当m=-14时,确定函数g(x)在区间(3,+∞)上的单调性.已知圆C:(x-a)2+(y-a-2)2=9,其中a为实常数.(1)若直线l:x+y-4=0被圆C截得的弦长为2,求a的值;(2)设点A(3,0),O为坐标原点,若圆C上存在点M,使|MA|=2|MO|,求a的取值范围.湖南师大附中高一第一学期期末考试数学参考答案 第Ⅰ卷(满分100分)一、选择题:本大题共11小题,每小题5分,共55分.12.[-3,1] 13.3214.34三、解答题:本大题共3个小题,共30分.解答应写出文字说明,证明过程或演算步骤. 15.【解析】(1)因为点B(4,6),C(0,8),则k BC =8-60-4=-12.(1分) 因为l⊥BC,则l 的斜率为2.(2分)又直线l 过点A ,所以直线l 的方程为y =2(x -3),即2x -y -6=0.(4分) (2)因为点A(3,0),C(0,8),则|AC|=9+64=73.(5分) 又直线AC 的方程为x 3+y8=1,即8x +3y -24=0,(6分)则点B 到直线AC 的距离d =32+18-2464+9=2673.(7分)所以△ABC 的面积S =12|AC|×d=13. (8分)16.【解析】(1)方法一:因为线段AB 的中点为⎝ ⎛⎭⎪⎫32,12,k AB =-17,则线段AB 的垂直平分线方程为y -12=7⎝ ⎛⎭⎪⎫x -32,即y =7x -10. (2分)联立y =2x ,得x =2,y =4.所以圆心C(2,4), 半径r =|AC|=16+9=5.(4分)所以圆C 的标准方程是(x -2)2+(y -4)2=25.(5分) 方法二:设圆C 的方程为x 2+y 2+Dx +Ey +F =0,则⎩⎨⎧-2D +E +F +5=0,5D +F +25=0,E =2D ,解得D =-4,E =-8,F =-5.(3分) 所以圆C 的方程是x 2+y 2-4x -8y -5=0, 即(x -2)2+(y -4)2=25.(5分)(2)直线l 的方程化为(2x +y -8)+m(x +2y -7)=0.令⎩⎨⎧2x +y -8=0,x +2y -7=0,得⎩⎨⎧x =3,y =2,所以直线l 过定点M(3,2).(7分)由圆的几何性质可知,当l⊥CM 时,弦长|PQ|最短. 因为|CM|=(3-2)2+(2-4)2=5, 则|PQ|min =2r 2-||CM 2=225-5=4 5.(10分)17.【解析】(1)因为A 1A ⊥平面ABC ,则A 1A ⊥AC. 又AC⊥AB,则AC⊥平面AA 1B 1B ,所以AC⊥A 1B.(3分) 由已知,侧面AA 1B 1B 是正方形,则AB 1⊥A 1B. 因为AB 1∩AC =A ,所以A 1B ⊥平面AB 1C.(5分)(2)方法一:连结A 1C ,设AB 1∩A 1B =O ,连CO ,交A 1D 于G. 因为O 为A 1B 的中点,D 为BC 的中点,则G 为△A 1BC 的重心. 因为A 1O ⊥平面AB 1C ,则∠A 1GO 是A 1D 与平面AB 1C 所成的角.(8分) 设AB =AC =AA 1=1,则A 1B =BC =A 1C = 2. 得A 1O =22,A 1G =23A 1D =23×2sin 60°=63. 在Rt △A 1OG 中,sin ∠A 1GO =A 1O A 1G =32,则∠A 1GO =60°. 所以直线A 1D 与平面AB 1C 所成的角为60°.(12分)方法二:分别取AB ,B 1B 的中点E ,F ,连DE ,EF ,DF , 则ED∥AC,EF ∥AB 1, 所以平面DEF∥平面AB 1C.因为A 1B ⊥平面AB 1C ,则A 1B ⊥平面DEF. 设A 1B 与EF 的交点为G ,连DG ,则∠A 1DG 是直线A 1D 与平面DEF 所成的角. (8分) 设AB =AC =AA 1=1,则A 1B =BC =A 1C = 2.得A 1G =34A 1B =324,A 1D =2sin 60°=62. 在Rt △A 1GD 中,sin ∠A 1DG =A 1G A 1D =32,则∠A 1DG =60°. 所以直线A 1D 与平面AB 1C 所成的角为60°. (12分)第Ⅱ卷(满分50分)一、本大题共2个小题,每小题6分,共12分.18.[0,2]【解析】M =(-∞,0)∪(2,+∞),N =[0,+∞),所以N∩∁R M =[0,2].19.B 【解析】因为y =f (x -1)的图象关于点A (1,0)对称,则y =f (x )的图象关于原点对称,即f (x )为奇函数. 由f (t 2-2t )+f (-3)>0,得f (t 2-2t )>-f (-3)=f (3),因为f (x )在R 上是减函数,则t 2-2t <3,即t 2-2t -3<0,得-1<t <3.因为y =t -1t -3=1+2t -3在区间(-1,3)上是减函数,则t -1t -3<12,选B. 二、本大题共3个大题,共38分.20.【解析】(1)连接BD ,设AC 交BD 于点O ,连接SO ,由题意得SO⊥AC,又因为正方形ABCD 中,AC ⊥BD ,所以AC⊥平面SBD,∵SD ⊂平面SBD ,所以AC⊥SD. (6分)(2)在棱SC 上存在一点E ,使得BE∥平面PAC. 设正方形边长为a ,则SD =2a.由SD⊥平面PAC 得PD =2a 4, 故可在SP 上取一点N ,使PN =PD.过点N 作PC 的平行线与SC 的交点为E ,连接BN ,在△BDN 中,易得BN∥PO,又因为NE∥PC,所以平面BEN∥平面PAC ,所以BE∥平面PAC.因为SN∶NP=2∶1,所以SE∶EC=2∶1. (12分)21.【解析】(1)由f(x)<5-m ,得mx 2-mx -1<5-m ,即m(x 2-x +1)<6.因为x 2-x +1=⎝ ⎛⎭⎪⎫x -122+34>0,则m<6x 2-x +1.(3分) 设h(x)=6x 2-x +1,则当x∈[1,3]时,m <h(x)恒成立. 因为y =x 2-x +1在区间[1,3]上是增函数,则h(x)在区间[1,3]上是减函数,h(x)min =h(3)=67. 所以m 的取值范围是⎝⎛⎭⎪⎫-∞,67. (6分) (2)因为f(x)=mx(x -1)-1,则g(x)=mx -1x -1. 当m =-14时,g(x)=-⎝ ⎛⎭⎪⎫x 4+1x -1.(7分) 设x 1>x 2>3,则g(x 1)-g(x 2)=⎝ ⎛⎭⎪⎫x 24+1x 2-1-⎝ ⎛⎭⎪⎫x 14+1x 1-1= x 24-x 14+1x 2-1-1x 1-1=x 2-x 14+x 1-x 2(x 1-1)(x 2-1)= (x 1-x 2)⎣⎢⎡⎦⎥⎤1(x 1-1)(x 2-1)-14.(10分) 因为x 1-1>x 2-1>2,则(x 1-1)(x 2-1)>4,得1(x 1-1)(x 2-1)<14,又x 1-x 2>0,则g(x 1)-g(x 2)<0, 即g(x 1)<g(x 2),所以g(x)在区间(3,+∞)上是减函数.(13分)22.【解析】(1)由圆方程知,圆C 的圆心为C(a ,a +2),半径为3.(2分)设圆心C 到直线l 的距离为d ,因为直线l 被圆C 截得的弦长为2,则d 2+1=9,即d =2 2.(4分) 所以|a +(a +2)-4|2=22,即|a -1|=2,所以a =-1或a =3.(6分) (2)设点M(x ,y),由|MA|=2|MO|,得(x -3)2+y 2=2x 2+y 2,即x 2+y 2+2x -3=0. 所以点M 在圆D :(x +1)2+y 2=4上.其圆心为D(-1,0),半径为2.(8分)因为点M 在圆C 上,则圆C 与圆D 有公共点,即1≤|CD|≤5.(9分)所以1≤(a +1)2+(a +2)2≤5,即⎩⎨⎧a 2+3a +2≥0,a 2+3a -10≤0, 即⎩⎨⎧(a +2)(a +1)≥0,(a -2)(a +5)≤0,(11分) 解得⎩⎨⎧a≤-2或a≥-1,-5≤a≤2,即-5≤a≤-2或-1≤a≤2.故a的取值范围是[-5,-2]∪[-1,2].(13分)。
